100以内素数和
100以内素数和的平均值

100以内素数和的平均值100以内的素数和是指小于或等于100的所有素数(质数)的和。
素数是指只能被1和自身整除的正整数,如2、3、5、7、11等。
本文将探讨100以内素数和的平均值,即将100以内的素数相加后除以素数的个数,以求得平均值。
我们需要找到100以内的素数。
为了方便起见,我们可以使用筛选法来找出这些素数。
筛选法的基本思想是从2开始,将每个素数的倍数标记为非素数,然后继续找到下一个未被标记的数,直到所有数都被标记。
那么,我们先从2开始筛选。
2是一个素数,我们将它保留下来,并将2的倍数(4、6、8、10等)标记为非素数。
接下来,我们找到下一个未被标记的数,即3。
同样地,我们将3保留下来,并将3的倍数(6、9、12等)标记为非素数。
继续这个过程,我们可以找到5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89和97等素数。
现在,我们已经找到了所有的100以内的素数。
接下来,我们将计算这些素数的和,并求出平均值。
为了方便计算,我们可以使用编程语言来实现。
以下是使用Python语言计算100以内素数和平均值的代码:```python# 定义一个函数,用于判断一个数是否为素数def is_prime(n):if n < 2:return Falsefor i in range(2, int(n ** 0.5) + 1):if n % i == 0:return Falsereturn Trueprime_sum = 0 # 素数和的初始值为0prime_count = 0 # 素数个数的初始值为0for i in range(2, 101):if is_prime(i):prime_sum += iprime_count += 1prime_average = prime_sum / prime_countprint("100以内素数和的平均值为:", prime_average)```运行以上代码,我们可以得到100以内素数和的平均值为:41.34(保留两位小数)。
2021背诵100以内质数表小窍门语文

2021背诵100以内质数表小窍门语文
背诵100以内质数表小窍门
在100:1范围内背诵素数表的技巧。
编打油诗,2和3,5和7;11、十三和十七;
十九,二三;二九,三十一;三十七和四十一;
四三,四七,五三,五九,六十一;六十七和七十一;
七三,七九,八三,八九,九十七。
二、规律记忆法
首先记住2和3,2和3的乘积是6。
100以内的素数通常位于6的倍数之前和之后。
例如,5,7,11,13,19,23,29,31,37,41,43。
只有25、35、49、55、65、77、85、91和95的倍数不是素数,这些数字是5或7的倍数。
可以看出,只要不是5或7的
倍数,100内6的倍数的前后两个数字必须是素数。
根据这个特征,你可以记住100以内
的素数。
3、分类记忆
我们可以把100以内的质数分为五类记忆。
第一类:10以内的质数,共4个:2、3、5、7。
第二类:个位数字是1,共5个:11、31、41、61、71。
第1页
第三类:个位数字是3,共6个:13、23、43、53、73、83。
第四类:数字为7,共5位:17、37、47、67和97。
第五类:个位数字是
第9页,共5页:第2页
19、29、59、79、89。
C 使用筛选法求100以内的素数

C 使用筛选法求100以内的素数C++使用筛选法求100以内的素数,具体问题分析及其代码如下:【问题分析】我们可以把100个数看作是沙子和石子,素数是石子,非素数的是沙子,弄个筛子,将沙子筛掉,剩下的就是素数。
1至100这些自然数可以分为三类:(1) 单位数:仅有一个数1.(2) 素数:这个数大于1,且只有它本身和1这样两个正因数。
(3) 合数:除了1和他自身以外,还有其他的正因数。
【代码如下】/********************************************************/* 程序名:素数筛选/* 编程时间:2009年7月27日/* 主要功能:求素数*********************************************************/#include<iostream>using namespace std;//编译命令#include<math.h>const int MAX=100;//定义常量MAXint main()//主函数{int prime[MAX+100]={0};//定义变量并初始化int i,j,k=sqrt(MAX);for(i=2; i<=k; i++)//枚举筛数{if(prime[i]==0)//如果这个数没被筛,就看看{j=i*2;//将原数扩大二倍初始化给jdo{prime[j]=1;//将j筛掉j+=i; //再扩大一倍}while(j<=MAX);//直到最大}}for(i=2; i<=MAX; i++){if(prime[i]==0)//循环输出cout<<i<<" ";}cout<<endl;return 0;//主函数结束}【运行结果】。
100以内的素数表
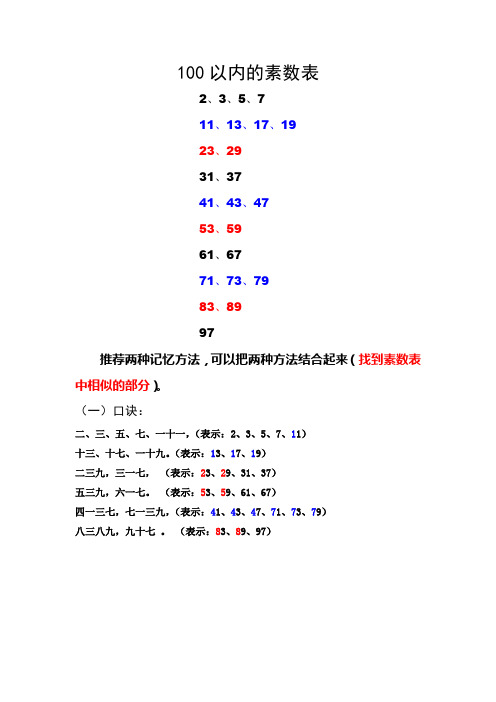
100以内的素数表
2、3、5、7
11、13、17、19
23、29
31、37
41、43、47
53、59
61、67
71、73、79
83、89
97
推荐两种记忆方法,可以把两种方法结合起来(找到素数表中相似的部分)。
(一)口诀:
二、三、五、七、一十一,(表示:2、3、5、7、11)
十三、十七、一十九。
(表示:13、17、19)
二三九,三一七,(表示:23、29、31、37)
五三九,六一七。
(表示:53、59、61、67)
四一三七,七一三九,(表示:41、43、47、71、73、79)
八三八九,九十七。
(表示:83、89、97)
(二)按“3的倍数”的相似特点。
在“3的倍数”中,如5□可以填1、4、7;
1□可以填2、5、8;
3□可以填0、3、6、9。
也就是把数分成了三部分来记忆:
(1) 11、13、17、19(一十几)
41、43、47(四十几)
71、73、79(七十几)
(2) 23、29(二十几)
53、59(五十几)
83、89(八十几)
(3) 31、37(三十几)
61、67(六十几)
97(九十几)
(三)素数的个数:
20以内素数有8个,50以内素数有15个,100以内素数有25个。
[奇数偶数质数合数]100以内质数合数奇数偶数
![[奇数偶数质数合数]100以内质数合数奇数偶数](https://img.taocdn.com/s3/m/8aa27d7049d7c1c708a1284ac850ad02de80078c.png)
[奇数偶数质数合数]100以内质数合数奇数偶数篇一: 100以内质数合数奇数偶数100以内质数合数奇数偶数100以内的质数表2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97100以内的合数表4 6 8 9 10 12 14 15 16 18 20 21 22 24 25 26 27 28 30 32 33 34 35 36 38 39 40 42 44 45 46 48 49 50 51 52 54 55 56 57 58 60 62 63 64 65 66 68 69 70 72 74 75 76 77 78 80 81 82 84 85 86 88 90 92 94 95 96 98 99100以内的奇数表1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 81 83 85 87 89 91 93 95 97 99100以内的偶数表2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,32,34,36,38,40,42,44,46,48,50, 52,54,56,58,60,62,64,66,68,70,72,74,76,78,80,82,84,86,88,90,92,94,96,98,100篇二: 100以内质数合数奇数偶数100以内质数合数奇数偶数100以内的质数表2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97100以内的合数表4 6 8 9 10 12 14 15 16 18 20 21 22 24 25 26 27 28 30 32 33 34 35 36 38 39 40 42 44 45 46 48 49 50 51 52 54 55 56 57 58 60 62 63 64 65 66 68 69 70 72 74 75 76 77 78 80 81 82 84 85 86 88 90 92 94 95 96 98 99100以内的奇数表1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 81 83 85 87 89 91 93 95 97 99100以内的偶数表2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,32,34,36,38,40,42,44,46,48,50, 52,54,56,58,60,62,64,66,68,70,72,74,76,78,80,82,84,86,88,90,92,94,96,9 8,100篇三: 奇数:奇数-概念,奇数-性质奇数数学术语,整数中,能被2整除的数是偶数,不能被2整除的数是奇数,奇数个位为1,3,5,7,9。
素数组合规则解答

基础数论就是要厘清这些奥秘真相,是自然数数论天机谜底。
这是复合“积”范畴与“和”范畴不相同区别。
其它理论,如奇数分解有二种:
“和”的分解与“积”的分解可用逆向思维方法进行。
“和”先分解任意一个奇数,再把剩下偶数按偶数方法进行分解,这样把叠加堆垒形态倒过来进行而已。
3, 具体数字:
1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,33,35,37,39,41,43,45,47,49,51,53,55,57,59,61,63,65,67,69,71,73,75,77,79,81,83,85,87,89,91,93,95,97,99……
称之为偶组合:
偶数个数素数1+1=偶数。
以及(奇数个数数量)叠加组合【三重奇数6N+3和双轨数阳奇(6N+1),阴奇(6N-1)之三列中】奇组合数,
称之为奇组合:
奇数个数素数1+1+1=奇数。
②,“积”是在铁路双轨数中(任意阴阳两种)素数6N±1,经过2^2=4次变換
=6(N1+N2+N3)+1-1+1
=6N+1
这就是阳奇数 6N+1 数理模式
(略)
⑥ 奇数w
=阳+阴+阴
=1+1+1
=P1+P2+P3
=(6N1+1)+(6N2-1)+(6N3-1)
=6(N1+N2+N3)+1-1-1
=6N-1
这就是阴奇数 6N-1 数理模式
乐平林登发
职称经济师
用筛选法求100之内的素数

⽤筛选法求100之内的素数1. ⽤筛选法求100之内的素数【答案解析】素数:约数为1和该数本⾝的数字称为素数,即质数筛选法:⼜称为筛法。
先把N个⾃然数按次序排列起来。
1不是质数,也不是合数,要划去。
第⼆个数2是质数留下来,⽽把2后⾯所有能被2整除的数都划去。
2后⾯第⼀个没划去的数是3,把3留下,再把3后⾯所有能被3整除的数都划去。
3后⾯第⼀个没划去的数是5,把5留下,再把5后⾯所有能被5整除的数都划去。
这样⼀直做下去,就会把不超过N的全部合数都筛掉,留下的就是不超过N的全部质数。
因为希腊⼈是把数写在涂腊的板上,每要划去⼀个数,就在上⾯记以⼩点,寻求质数的⼯作完毕后,这许多⼩点就像⼀个筛⼦,所以就把埃拉托斯特尼的⽅法叫做“埃拉托斯特尼筛”,简称“筛法”。
(另⼀种解释是当时的数写在纸草上,每要划去⼀个数,就把这个数挖去,寻求质数的⼯作完毕后,这许多⼩洞就像⼀个筛⼦。
)【代码实现】//⽤筛选法求100以内的素数#include<stdio.h>int main(){int i, j, k = 0;// 将数组汇总每个元素设置为:1~100int a[100];for (i = 0; i < 100; i++)a[i] = i+1;// 因为1不是素数,把a[0]⽤0标记// 最后⼀个位置数字是100,100不是素数,因此循环可以少循环⼀次a[0] = 0;for (i = 0; i < 99; i++){// ⽤a[i]位置的数字去模i位置之后的所有数据// 如果能够整除则⼀定不是素数,该位置数据⽤0填充for (j = i + 1; j < 100; j++){if (a[i] != 0 && a[j] != 0){//把不是素数的都赋值为0if (a[j] % a[i] == 0)a[j] = 0;}}}printf(" 筛选法求出100以内的素数为:\n");for (i = 0; i < 100; i++){//数组中不为0的数即为素数if (a[i] != 0)printf("%3d", a[i]);}printf("\n");return 0;}【运⾏结果】。
100以内 互质数 最小公倍数 最简分数 偶数 奇数 质数合数

互质数最小公倍数最简分数偶数奇数质数合数约数因数公因数最大公约数和最小公倍数100以内的奇数、偶数、质数、合数表奇数是: 1,3,5,7,9,11……99。
偶数是:0,2,4,6,8,10……100。
质数:2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,7379,83,89,97。
(100以内的质数共有25个)合数是:4,6.8,9,12,14,15,18,20……98,99,100 但是,0和1既不是质数也不是合数。
最小的奇数是1,最小的偶数是0,最小的质数是2,最小的合数是4。
自然数中分为奇数和偶数;但是自然数中除了质数和合数外还有0和1。
两个奇数的和(或差)是偶数,两个偶数的和(或差)是偶数,一个奇数与一个偶数的和(或差)是奇数。
几个质数的积一定是合数。
1、自然数:0、1、2、3、4…一个自然数不是奇数就是偶数。
2、整数:自然数,负数3、小数(1)概念:把整数1平均分成10份,100份,1000份…得到的十分之几、百分之几、千分之几…可以用小数表示(2)小数的性质:在小数的末尾添上零或去掉零小数的大小不变(3)若将小数扩大,是将小数点右移;若将小数缩小,是将小数点左移4、分数(1)分数:把单位“1”平均分成若干份,表示其中一份或几份的数(2)分数单位:表示其中一份的数(3)分数的性质:分数的分子分母同时乘以或除以同一个数(0除外),分数的大小不变(4)分数的分类:①真分数:分子小于分母的分数②假分数:分子等于或大于分母的分数③带分数:假分数可以写成整数与真分数合成数(5)最简分数:分子分母是互质数的分数(6)百分数:一个数是另一个数的百分之几的数5、比的基本性质:比的前项和后项同时乘以或除以同一个数(0除外),分数的大小不变6、偶数:能被2整除的数奇数:不能被2整除的数7、素数(质数又称素数):一个数,只有1和它本身两个因数(或约数),最小的素数是2合数:一个数,如果除了1和本身外还有其他的因数,最小的合数是41既不是合数,也不是素数8、互质数:最大公因数是1的两个数因数(又称约数)定义:两个整数相乘,其中这两个数都叫做积的因数。
用筛选法求100之内的素数

⽤筛选法求100之内的素数⽤筛选法求100之内的素数【答案解析】素数:约数为1和该数本⾝的数字称为素数,即质数筛选法:⼜称为筛法。
先把N个⾃然数按次序排列起来。
1不是质数,也不是合数,要划去。
第⼆个数2是质数留下来,⽽把2后⾯所有能被2整除的数都划去。
2后⾯第⼀个没划去的数是3,把3留下,再把3后⾯所有能被3整除的数都划去。
3后⾯第⼀个没划去的数是5,把5留下,再把5后⾯所有能被5整除的数都划去。
这样⼀直做下去,就会把不超过N的全部合数都筛掉,留下的就是不超过N的全部质数。
因为希腊⼈是把数写在涂腊的板上,每要划去⼀个数,就在上⾯记以⼩点,寻求质数的⼯作完毕后,这许多⼩点就像⼀个筛⼦,所以就把埃拉托斯特尼的⽅法叫做“埃拉托斯特尼筛”,简称“筛法”。
(另⼀种解释是当时的数写在纸草上,每要划去⼀个数,就把这个数挖去,寻求质数的⼯作完毕后,这许多⼩洞就像⼀个筛⼦。
)【代码实现】//⽤筛选法求100以内的素数#include<stdio.h>int main(){int i, j, k = 0;// 将数组汇总每个元素设置为:1~100int a[100];for (i = 0; i < 100; i++)a[i] = i+1;// 因为1不是素数,把a[0]⽤0标记// 最后⼀个位置数字是100,100不是素数,因此循环可以少循环⼀次a[0] = 0;for (i = 0; i < 99; i++){// ⽤a[i]位置的数字去模i位置之后的所有数据// 如果能够整除则⼀定不是素数,该位置数据⽤0填充for (j = i + 1; j < 100; j++){if (a[i] != 0 && a[j] != 0){//把不是素数的都赋值为0if (a[j] % a[i] == 0)a[j] = 0;}}}printf(" 筛选法求出100以内的素数为:\n");for (i = 0; i < 100; i++){//数组中不为0的数即为素数if (a[i] != 0)printf("%3d", a[i]);}printf("\n");return 0;}【运⾏结果】。
