几何组成分析习题及答案.
02结构的几何组成分析--习题

静定结构 无多余约束几何不变体系
二、无多余约束几何不变体系的组成规则有三个: 无多余约束几何不变体系的组成规则有三个:
①三刚片规则 三刚片用不在一直线上的三个铰两两相连。 三刚片用不在一直线上的三个铰两两相连。 ②两刚片规则 两刚片用一个铰和一根不通过此铰的链杆或 不全平行也不交于一点的三根链杆连接。 不全平行也不交于一点的三根链杆连接。 一刚片和一个点用不共线的两根链杆连接。 ③二元体规则 一刚片和一个点用不共线的两根链杆连接。
无法显示图像。计算机可能没有足够的内存以打开该图像,也可能是该图像已 损坏。请重新启动计算机,然后重新打开该文件。如果仍然显示红色 “x”,则 可能需要删除该图像,然后重新将其插入。
结构力学电子教程
2 结构的几何组成分析 (c)
2.5 分析所示体系的几何构造。 分析所示体系的几何构造。 (a) (b)
结构力学电子教程
2 结构的几何组成分析 2.5
2.4
【解】
【解】
结论: 结论:无多余约束的几何 不变体系。 不变体系。 2.6 【解】 I
结论: 结论:有1个多余约束的几 个多余约束的几 何不变体系。 何不变体系。
III
II 结论:无多余约 结论: 束的几何不变体 系。
无法显示图像。计算机可能没有足够的内存以打开该图像,也可能是该图像已 损坏。请重新启动计算机,然后重新打开该文件。如果仍然显示红色 “x”,则 可能需要删除该图像,然后重新将其插入。
无法显示图像。计算机可能没有足够的内存以打开该图像,也可能是该图像已 损坏。请重新启动计算机,然后重新打开该文件。如果仍然显示红色 “x”,则 可能需要删除该图像,然后重新将其插入。
结构力学电子教程
2 结构的几何组成分析
福大结构力学课后习题详细答案..-副本

结构力学(祁皑)课后习题详细答案答案仅供参考第1章1-1分析图示体系的几何组成。
1-1(a)解原体系依次去掉二元体后,得到一个两铰拱(图(a-1))。
因此,原体系为几何不变体系,且有一个多余约束。
1-1 (b)解 原体系依次去掉二元体后,得到一个三角形。
因此,原体系为几何不变体系,且无多余约束。
1-1 (c)(c-2) (c-3)解 原体系依次去掉二元体后,得到一个三角形。
因此,原体系为几何不变体系,且无多余约束。
1-1 (d)(d-1)(d-2)(d-3)解原体系依次去掉二元体后,得到一个悬臂杆,如图(d-1)-(d-3)所示。
因此,原体系为几何不变体系,且无多余约束。
注意:这个题的二元体中有的是变了形的,分析要注意确认。
1-1 (e)解原体系去掉最右边一个二元体后,得到(e-1)所示体系。
在该体系中,阴影所示的刚片与支链杆C组成了一个以C为顶点的二元体,也可以去掉,得到(e-2)所示体系。
在图(e-2)中阴影所示的刚片与基础只用两个链杆连接,很明显,这是一个几何可变体系,缺少一个必要约束。
因此,原体系为几何可变体系,缺少一个必要约束。
1-1 (f)解原体系中阴影所示的刚片与体系的其它部分用一个链杆和一个定向支座相连,符合几何不变体系的组成规律。
因此,可以将该刚片和相应的约束去掉只分析其余部分。
很明显,余下的部分(图(f-1))是一个几何不变体系,且无多余约束。
因此,原体系为几何不变体系,且无多余约束。
1-1 (g)解原体系中阴影所示的刚片与体系的其它部分用三个链杆相连,符合几何不变体系的组成规律。
因此,可以将该刚片和相应的约束去掉,只分析其余部分。
余下的部分(图(g-1))在去掉一个二元体后,只剩下一个悬臂杆(图(g-2))。
因此,原体系为几何不变体系,且无多余约束。
1-1 (h)解原体系与基础用一个铰和一个支链杆相连,符合几何不变体系的组成规律。
因此,可以只分析余下部分的内部可变性。
这部分(图(h-1))可视为阴影所示的两个刚片用一个杆和一个铰相连,是一个无多余约束几何不变体系。
福大结构力学课后习题详细答案(祁皑).. - 副本

结构力学(祁皑)课后习题详细答案答案仅供参考第1章1-1分析图示体系的几何组成。
1-1(a)(解原体系依次去掉二元体后,得到一个两铰拱(图(a-1))。
因此,原体系为几何不变体系,且有一个多余约束。
1-1 (b)解原体系依次去掉二元体后,得到一个三角形。
因此,原体系为几何不变体系,且无多余约束。
1-1 (c)[(c-1)(a)(a-1)(b)(b-1)*(c-2) (c-3)解 原体系依次去掉二元体后,得到一个三角形。
因此,原体系为几何不变体系,且无多余约束。
1-1 (d)!(d-1) (d-2) (d-3)解 原体系依次去掉二元体后,得到一个悬臂杆,如图(d-1)-(d-3)所示。
因此,原体系为几何不变体系,且无多余约束。
注意:这个题的二元体中有的是变了形的,分析要注意确认。
1-1 (e)~解 原体系去掉最右边一个二元体后,得到(e-1)所示体系。
在该体系中,阴影所示的刚片与支链杆C 组成了一个以C 为顶点的二元体,也可以去掉,得到(e-2)所示体系。
在图(e-2)中阴影所示的刚片与基础只用两个链杆连接,很明显,这是一个几何可变体系,缺少一个必要约束。
因此,原体系为几何可变体系,缺少一个必要约束。
1-1 (f)[解 原体系中阴影所示的刚片与体系的其它部分用一个链杆和一个定向支座相(d )(e )(e-1)AB}AB (e-2)(f )(f-1)连,符合几何不变体系的组成规律。
因此,可以将该刚片和相应的约束去掉只分析其余部分。
很明显,余下的部分(图(f-1))是一个几何不变体系,且无多余约束。
因此,原体系为几何不变体系,且无多余约束。
1-1 (g)解 原体系中阴影所示的刚片与体系的其它部分用三个链杆相连,符合几何不变体系的组成规律。
因此,可以将该刚片和相应的约束去掉,只分析其余部分。
余下的部分(图(g-1))在去掉一个二元体后,只剩下一个悬臂杆(图(g-2))。
因此,原体系为几何不变体系,且无多余约束。
东南大学结构力学练习题(附答案)详解

第一部分 平面体系的几何组成分析一、判断题:1、在任意荷载下,仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。
2、图中链杆1和2的交点O 可视为虚铰。
O二、分析题:对下列平面体系进行几何组成分析。
3、 4、ACDBAC DB5、 6、A CDBEABCDE7、 8、ABCD GE FA BCDEFGHK9、 10、11、 12、1234513、 14、15、 16、17、 18、19、 20、1245321、 22、124567831234523、 24、12345625、 26、27、 28、29、 30、31、 32、33、ACBDEF三、在下列体系中添加支承链杆,使之成为无多余约束的几何不变体系。
34、35、第二部分 静定结构内力计算一、判断题:1、静定结构的全部内力及反力,只根据平衡条件求得,且解答是唯一的。
2、静定结构受外界因素影响均产生内力,内力大小与杆件截面尺寸无关。
3、静定结构的几何特征是几何不变且无多余约束。
4、图(a)所示结构||M C =0。
(a)BCa aA ϕ2a2 (b)5、图(b)所示结构支座A 转动ϕ角,M AB = 0,R C = 0。
6、荷载作用在静定多跨梁的附属部分时,基本部分一般内力不为零。
7、图(c)所示静定结构,在竖向荷载作用下,AB 是基本部分,BC 是附属部分。
ABC(c)8、图(d)所示结构B 支座反力等于P /2(。
)↑9、图(e)所示结构中,当改变B 点链杆的方向(不通过A 铰)时,对该梁的影响是轴力有变化。
AB(e)10、在相同跨度及竖向荷载下,拱脚等高的三铰拱,水平推力随矢高减小而减小。
—— 1 ——11、图(f)所示桁架有9根零杆。
(f)a a a a(g)12、图(g)所示桁架有:=== 0。
N 1N 2N 313、图(h)所示桁架DE 杆的内力为零。
a a(h)14、图(i)所示对称桁架在对称荷载作用下,其零杆共有三根。
对图示体系进行几何组成分析(10分)

一、对图示体系进行几何组成分析。
(10分)解:折杆ABC 、CDE 与BD 形成刚片I ,为几何不变体系且无多余约束。
(5分)刚片I 与地面由4链杆相连,整个结构为几何不变且有1个多余约束。
(5分)二、计算图示静定桁架的支座反力及1、2杆的轴力。
(14分)解:求支座反力)(2),(6),(2↑=↑=←=kN R kN Y kN X B A A (6分)求1、2杆的轴力截面法: )(52025111拉kN N N Y ==+⨯-=∑ (4分) 取E 结点: )(240214022压kN N N Y -==⨯--=∑(4分)三、P = 1在图示静定多跨梁ABCD 上移动。
(1)作截面E 的剪力影响线;(2)画出使Q E 达最大值和最小值时可动均布荷载的最不利布置;(3)当可动均布荷载q = 20 kN/m 时,求Q Emax 值。
(16分)(1) Q E 影响线见图(5分)(2)Q Emax 的最不利位置 (3分)Q Emin 的最不利位置 (3分)(3)kN q Q E 38)5332152521(20max =⨯⨯+⨯⨯⨯=∑=+ω(5分) 四、用力法计算图示刚架,画M 图。
EI 为常数(20分)解:1、一次超静定结构,基本体系和基本未知量,如图 (2分)A B C D E0.40.6 +-+0.4 C C D2、列力法方程 01111=∆+P X δ (1分)3、作图和P M M ___1 (6分)4、计算系数、自由项 EI 14411=δ (3分) EIP 8101-=∆ (3分) 5、解方程 kN X 625.51= (1分)6、作M 图 (4分)五、用位移法计算图示刚架,并作M 图。
各杆EI 为常数。
(20分)解:1、以刚结点角位移为基本未知量,得基本体系 (2分);2、绘1M P M 图(图略) (6分)3、列位移法典型方程: 01111=+P F z k (2分)(4分)图(kNm )33.75六、用力矩分配法绘制图示连续梁的弯矩图。
结构力学习题及答案

构造力学习题第2章平面体系的几何组成分析2-1~2-6 试确定图示体系的计算自由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7~2-15 试对图示体系进展几何组成分析。
假设是具有多余约束的几何不变体系,那么需指明多余约束的数目。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-11=W2-1 9-W=2-3 3-W=2-4 2-W=2-5 1-W=2-6 4-W=2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系2-9、2-10、2-15具有一个多余约束的几何不变体系2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。
〔a〕〔b〕(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。
〔a〕〔b〕(c)习题3-2图3-3~3-9 试作图示静定刚架的内力图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定构造的弯矩图是否正确。
(a)(b)(c)(d)局部习题答案3-1〔a 〕m kN M B ⋅=80〔上侧受拉〕,kN F RQB 60=,kN F L QB 60-=〔b 〕m kN M A ⋅=20〔上侧受拉〕,m kN M B ⋅=40〔上侧受拉〕,kN F RQA 5.32=,kN F L QA 20-=,kN F LQB 5.47-=,kN F R QB 20=(c)4Fl M C =〔下侧受拉〕,θcos 2F F L QC =3-2 (a)0=E M ,m kN M F ⋅-=40〔上侧受拉〕,m kN M B ⋅-=120〔上侧受拉〕〔b 〕m kN M RH ⋅-=15(上侧受拉),m kN M E ⋅=25.11〔下侧受拉〕〔c 〕m kN M G ⋅=29(下侧受拉),m kN M D ⋅-=5.8(上侧受拉),m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10〔左侧受拉〕,m kN M DF ⋅=8〔上侧受拉〕,m kN M DE ⋅=20〔右侧受拉〕 3-4 m kN M BA ⋅=120〔左侧受拉〕3-5 m kN M F ⋅=40〔左侧受拉〕,m kN M DC ⋅=160〔上侧受拉〕,m kN M EB ⋅=80(右侧受拉) 3-6 m kN M BA ⋅=60〔右侧受拉〕,m kN M BD ⋅=45〔上侧受拉〕,kN F QBD 46.28=3-7 m kN M C ⋅=70下〔左侧受拉〕,m kN M DE ⋅=150〔上侧受拉〕,m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0〔上侧受拉〕,m kN M BA ⋅=36.0〔右侧受拉〕 3-9 m kN M AB ⋅=10〔左侧受拉〕,m kN M BC ⋅=10〔上侧受拉〕 3-10 〔a 〕错误 〔b 〕错误 〔c 〕错误 〔d 〕正确第4章 静定平面桁架和组合构造的内力分析4-1 试判别习题4-1图所示桁架中的零杆。
平面体系的几何组成分析

平面体系的几何组成分析(总分:100.00,做题时间:90分钟)一、{{B}}判断题{{/B}}(总题数:6,分数:12.00)1.下图所示体系为有一个多余约束的几何不变体系。
(分数:2.00)A.正确B.错误√解析:利用三刚片规则。
可选择AB、CD、EF作为刚片进行分析。
正确答案是无多余约束的几何不变体系。
2.下图所示体系中链杆1和2的交点O可称为虚铰。
(分数:2.00)A.正确B.错误√解析:3.自由度W≤0是体系保持几何不变的充分条件。
(分数:2.00)A.正确B.错误√解析:4.静定结构是无多余约束的几何不变体系,超静定结构是有多余约束的几何不变体系。
(分数:2.00)A.正确√B.错误解析:5.下图所示体系是几何不变体系,且无多余约束。
(分数:2.00)A.正确B.错误√解析:原体系为有一个多余约束的几何不变体系。
6.下图所示对称体系是几何瞬变体系。
(分数:2.00)A.正确√B.错误解析:如下图所示选取刚片,用三刚片规则分析,刚片Ⅰ与Ⅱ交于A点,刚片Ⅰ与Ⅲ交于B点,刚片Ⅱ与Ⅲ交于无穷远处C点,由于A、B的连线与连系刚片Ⅱ、Ⅲ的两杆平行。
根据无穷远点规则判断可知,该体系为几何瞬变体系。
[*]二、{{B}}填空题{{/B}}(总题数:6,分数:12.00)7.下图所示体系的几何组成为______体系。
(分数:2.00)填空项1:__________________ (正确答案:无多余约束的几何不变体系)解析:利用三刚片规则分析。
8.下图所示体系的几何组成为______,______。
(分数:2.00)填空项1:__________________ (正确答案:几何不变体系,无多余约束)解析:先选择基础为一个刚片,然后按“双藤摸瓜”方法找到另外两个刚片。
9.下图所示体系为几何______体系,多余约束数为______个。
(分数:2.00)填空项1:__________________ (正确答案:不变,1)解析:利用三刚片规则分析。
福大结构力学课后习题详细问题详解(祁皑).. - 副本
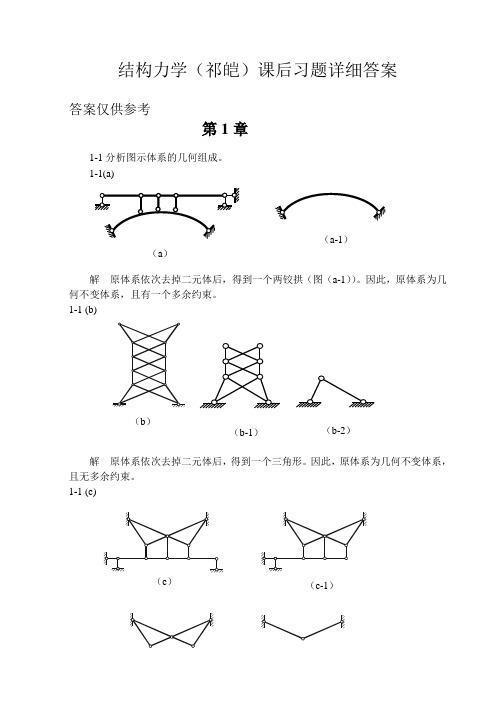
结构力学(祁皑)课后习题详细答案答案仅供参考第1章1-1分析图示体系的几何组成。
1-1(a)解 原体系依次去掉二元体后,得到一个两铰拱(图(a-1))。
因此,原体系为几何不变体系,且有一个多余约束。
1-1 (b)解 原体系依次去掉二元体后,得到一个三角形。
因此,原体系为几何不变体系,且无多余约束。
1-1 (c)(c-1)(a )(a-1)(b )(b-1)(b-2)(c-2) (c-3)解 原体系依次去掉二元体后,得到一个三角形。
因此,原体系为几何不变体系,且无多余约束。
1-1 (d)(d-1) (d-2) (d-3)解 原体系依次去掉二元体后,得到一个悬臂杆,如图(d-1)-(d-3)所示。
因此,原体系为几何不变体系,且无多余约束。
注意:这个题的二元体中有的是变了形的,分析要注意确认。
1-1 (e)解 原体系去掉最右边一个二元体后,得到(e-1)所示体系。
在该体系中,阴影所示的刚片与支链杆C 组成了一个以C 为顶点的二元体,也可以去掉,得到(e-2)所示体系。
在图(e-2)中阴影所示的刚片与基础只用两个链杆连接,很明显,这是一个几何可变体系,缺少一个必要约束。
因此,原体系为几何可变体系,缺少一个必要约束。
1-1 (f)解原体系中阴影所示的刚片与体系的其它部分用一个链杆和一个定向支座相连,符合几何不变体系的组成规律。
因此,可以将该刚片和相应的约束去掉只分析其余部分。
很明显,余下的部分(图(f-1))是一个几何不变体系,且无多余约束。
因此,原体系为几何不变体系,且无多余约束。
1-1 (g)(d ) (e )(e-1)A(e-2)(f )(f-1) (g ) (g-1) (g-2)解 原体系中阴影所示的刚片与体系的其它部分用三个链杆相连,符合几何不变体系的组成规律。
因此,可以将该刚片和相应的约束去掉,只分析其余部分。
余下的部分(图(g-1))在去掉一个二元体后,只剩下一个悬臂杆(图(g-2))。
02-2结构力学第二章 平面体系的几何组成分析-作业答案汇总

38 3 2 29 3 3
3个单铰结点, 3个折算为2个单铰结点的复铰结点
支杆
b3
11/73
(II III) 刚片II
(I II)
刚片III
几何不变且无多余约束
j9 单链杆:12根 复链杆:2根 折算为6根单链杆
W 2 j b 29 12 6 0
5/73
【作业1】分析图示体系的几何构造
图3
【作业1】分析图示体系的几何构造
图4
先考察如图所示结构
∞(II III)
9/73
【作业2】求图示系统的计算自由度
刚片 m 1 单刚结点 g 4 铰结点 h 0 支杆 b 3
内部无多余约束刚片
W 3m 3g 2h b
31 3 4 3 12
10/73
【作业2】求图示系统的计算自由度
刚片 m 8
单刚结点 g 2
W 3m 3g 2h b
铰结点 h 9
刚片 m 14 单铰链结点 h 18
刚片II
刚片III
(I II)
(I III) 刚片I
瞬变体系
其中折算为2个单铰结点的 复铰结点有6个
∞(II III)
其中折算为3个单铰结点的 复铰结点有2个 单刚结点 2个 g 2 和基础相连的支杆 0个 b 0
W 3m 3g 2h b
314 3 2 218 0
∞(II III)
刚片II (I II) (I III) 刚片III
刚片I
几何不变且无多余约束
(I II) 刚片II (I III) 刚片III
刚片I
几何不变且无多余约束
7/73
【作业2】求图示系统的计算自由度
图1 并进行几何构造分析
7月12日第一章几何构造分析随堂练习

7⽉12⽇第⼀章⼏何构造分析随堂练习第1章⼏何构造分析3⼤规则最常⽤的基本刚⽚有以下四种:单链杆、铰结三⾓形、刚结点构件、⼤地刚⽚。
三刚⽚规则三个刚⽚⽤不在同⼀直线上的三个单铰两两铰结,组成的体系是⼏何不变的。
【练习题1-1】试对图⽰平⾯体系进⾏⼏何组成分析。
a.(东南⼤学2011)b.(天津⼤学2016)c.(哈尔滨⼯业⼤学2015)d.(哈尔滨⼯业⼤学2015)提⽰:从前述最常⽤的四种基本刚⽚(单链杆、铰结三⾓形、刚结点构件、⼤地刚⽚)找到规则所需的三个刚⽚,尤其是隐蔽的⼤地刚⽚。
两刚⽚规则两个刚⽚⽤⼀个铰和⼀根不通过此铰的链杆相连,组成的体系是⼏何不变的;或者两个刚⽚⽤三根不全平⾏也不交于同⼀点的链杆相连,为⼏何不变体系。
【练习题1-2】试对图⽰平⾯体系进⾏⼏何组成分析。
⼆元体规则⼆元体:两个刚⽚与⼀个体系间只⽤三个不在⼀直线上的铰两两相连,则两个刚⽚称为⼆元体。
最简单常见的⼆元体是指由两根不在同⼀直线上的链杆连接⼀个新结点的装置。
⼆元体本质上还是在原⼏何体系上构造出⼀个新的铰结三⾓形,因此本质上就是铰结三⾓形。
在⼀个体系上增加或拆除⼆元体,不会改变原有体系的⼏何构造性质。
值得注意的是:构成⼆元体的两根链杆不⼀定是直杆,只要是刚⽚就⾏。
【练习题1-3】试对图⽰平⾯体系进⾏⼏何组成分析。
a.(中南⼤学2012)b.(东南2010)c.(东南2010)d.(北京⼯业⼤学2011)e.(东南⼤学2011)提⽰:找出⼆元体并依次去掉⼆元体,最后分析体系剩余部分的⼏何构造特性。
记住,⼆元体不⼀定得是直杆组成。
2⼤可变体系1. 瞬变与常变的区分瞬变体系与常变体系的两个判定规则:微⼩变形规则让体系发⽣微⼩变形,若三铰依然在同⼀直线上,则是常变体系,不在同⼀直线上,则是瞬变体系。
平⾏等长规则(特别注意平⾏等长的对象是谁)组成⽆穷远铰的两根平⾏链杆与另外两铰的连线等长且始终平⾏(即发⽣微⼩位移后依然平⾏),则为常变体系,否则为瞬变体系。
西北工业大学航空学院结构力学课后题答案第二章结构的几何组成分析
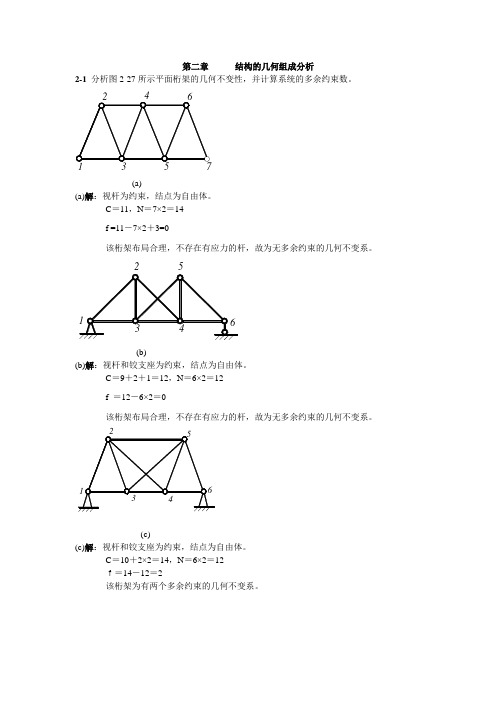
第二章 结构的几何组成分析2-1 分析图2-27所示平面桁架的几何不变性,并计算系统的多余约束数。
3571(a)(a)解:视杆为约束,结点为自由体。
C =11,N =7×2=14f =11-7×2+3=0该桁架布局合理,不存在有应力的杆,故为无多余约束的几何不变系。
(b)(b)解:视杆和铰支座为约束,结点为自由体。
C =9+2+1=12,N =6×2=12f =12-6×2=0该桁架布局合理,不存在有应力的杆,故为无多余约束的几何不变系。
(c)(c)解:视杆和铰支座为约束,结点为自由体。
C =10+2×2=14,N =6×2=12f=14-12=2该桁架为有两个多余约束的几何不变系。
1217(d)(d)解:视杆和铰支座为约束,结点为自由体。
C =30+3=33,N =17×2=34f=33-34=-1故该桁架为几何可变系。
8(e)(e)解:视杆为约束,结点为自由体。
C =13,N =8×2=16f=13-16+3=0将1-2-3-4、5-6-7-8看作两刚片,杆3-6、杆2-7、杆4-5相互平行,由两刚片原则知,为瞬时可变系统。
6(f)(f)解:视杆和固定铰支座为约束,结点为自由体。
C =22+3×2=28,N =14×2=28f=28-28=0将12-13-14、7-11-12、1-2-3-4-5-6-7-8-9-10看作三刚片,三刚片由铰7、铰12、铰14连结,三铰共线,故该桁架为瞬时可变系统。
(g)(g)解:视杆和固定铰支座为约束,结点为自由体。
C=24+4×2=32,N=16×2=32f=32-32=0由于杆15-14-3、杆12-11-4、杆9-5相交于一点,故该桁架为瞬时可变系。
(h)(h)解:视杆和固定铰支座为约束,结点为自由体。
C=12+2×2=16,N=8×2=16f=16-16=0该桁架布局合理,加减二元体之后,无有应力的杆,故该桁架为无多余约束的几何不变系。
《结构力学习题集》平面体系的几何组成分析附答案
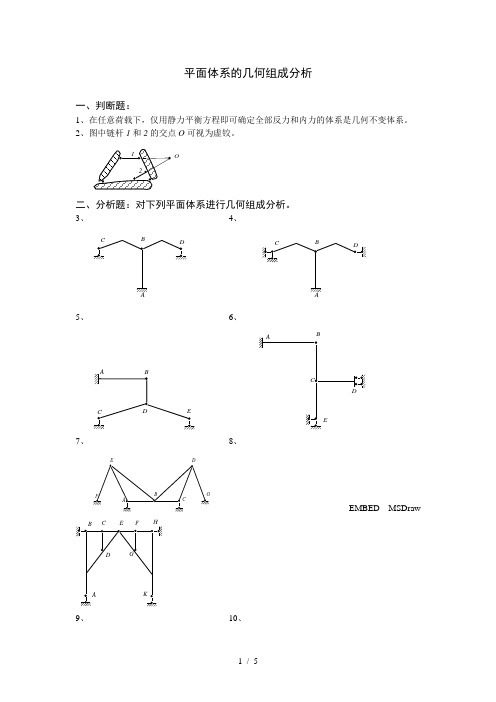
平面体系的几何组成分析一、判断题:1、在任意荷载下,仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。
2、图中链杆1和2的交点O 可视为虚铰。
O二、分析题:对下列平面体系进行几何组成分析。
3、 4、ACDBACDB5、 6、A CD BEABCDE7、 8、ABCDGEFEMBED MSDrawA BCDEFGHK9、 10、EMBED MSDraw EMBEDMSDraw11、 12、1234513、 14、15、 16、17、 18、19、 20、1245321、 22、123456781234523、 24、12345625、 26、27、 28、29、 30、31、32、33、BA CFDE三、在下列体系中添加支承链杆,使之成为无多余约束的几何不变体系。
34、35、平面体系的几何组成分析(参考答案)1、(O)2、(X)3、7、9、10、11、13、14、17、18、19、20、22、23、25、27、28、30、31、32、33、均是无多余约束的几何不变体系。
4、8、12、29、均是几何瞬变体系。
5、15、均是几何可变体系。
6、21、24、26、均是有一个多余约束的几何不变体系。
16、是有两个多余约束的几何不变体系。
友情提示:部分文档来自网络整理,供您参考!文档可复制、编辑,期待您的好评与关注!。
(完整版)几何组成分析习题及答案

题15.7试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 2j -6-r=2×8-9-7=0(2)几何组成分析。
首先把三角形ACD和BCE分别看做刚片I和刚片Ⅱ,把基础看做刚片I,则三个刚片用不共线的三个铰A、B、C分别两两相联,组成一个大的刚片。
在这个大的刚片上依次增加二元体12、DGF、CHG、EIH、IJ3。
最后得知整个体系为几何不变,且无多余约束。
题15.8试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 3m - 2h -r=3×6-2×7—4=0(2)几何组成分析。
刚片AF和AB由不共线的单铰A以及链杆DH相联,构成刚片I,同理可把BICEG部分看做刚片Ⅱ,把基础以及二元体12、34看作刚片I,则刚片I、Ⅱ、Ⅲ由不共线的三个铰F、B、G两两相联,构成几何不变体系,且无多余约束。
题15.9试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 3m - 2h -r=3×14 -2×19 -4一O(2)几何组成分析。
在刚片HD上依次增加二元体DCJ、CBI、BAH构成刚片I,同理可把DMG部分看做刚片Ⅱ,把基础看做刚片I,则刚片I、Ⅱ、Ⅲ由不共线的单铰D,虚铰N、O 相联,构成几何不变体系,且无多余约束。
题15.10试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W-2j—b-r=2×7—11-3一O(2)几何组成分析。
由于AFG部分由基础简支,所以可只分析AFG部分。
可去掉二元体BAC只分析BFGC部分。
把三角形BDF、CEG分别看做附片I和I,刚片I和I由三根平行的链杆相联,因而整个体系为瞬变。
题15.11试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 2j -6-r=2×9-13—5一O(2)几何组成分析。
首先在基础上依次增加二元体12、AE3、AFE、ABF、FI4,成一个大的刚片I。
《建筑力学》习题
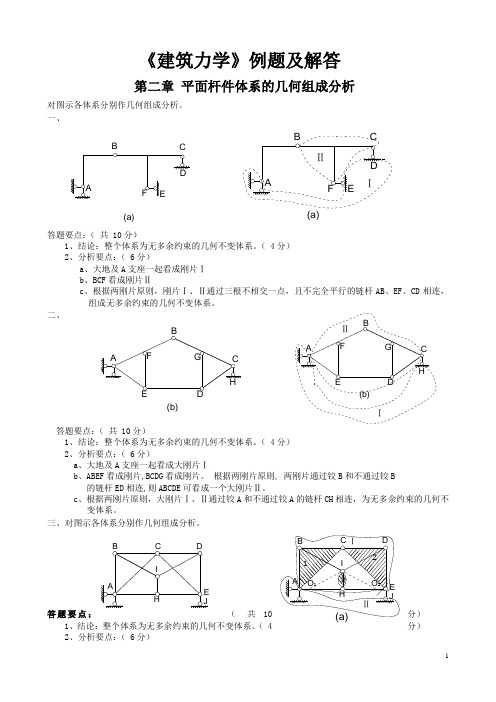
《建筑力学》例题及解答第二章 平面杆件体系的几何组成分析对图示各体系分别作几何组成分析。
一、答题要点:( 共 10分)1、结论:整个体系为无多余约束的几何不变体系。
( 4分)2、分析要点:( 6分)a 、大地及A 支座一起看成刚片Ⅰb 、BCF 看成刚片Ⅱc 、根据两刚片原则,刚片Ⅰ、Ⅱ通过三根不相交一点,且不完全平行的链杆AB 、EF 、CD 相连,组成无多余约束的几何不变体系。
二、答题要点:( 共 10分)1、结论:整个体系为无多余约束的几何不变体系。
( 4分)2、分析要点:( 6分)a 、大地及A 支座一起看成大刚片Ⅰb 、ABEF 看成刚片,BCDG 看成刚片。
根据两刚片原则, 两刚片通过铰B 和不通过铰B 的链杆ED 相连,则ABCDE 可看成一个大刚片Ⅱ。
c 、根据两刚片原则,大刚片Ⅰ、Ⅱ通过铰A 和不通过铰A 的链杆CH 相连,为无多余约束的几何不变体系。
三、对图示各体系分别作几何组成分析。
答题要点:( 共10分)1、结论:整个体系为无多余约束的几何不变体系。
( 4分)2、分析要点:( 6分)A B C DE F A B C DE F G H (a)(b)(a)F E D CB A ⅠⅡBC D EF A B C EF G H (a)(b)(b)H G F E D CBA ⅠⅡA B C D E H I J (a)F A B C D E G H I J K (b)123ⅡⅠO 2O 1(a)J I H E D C B Aa 、将ABC 、CDE 、IH 分别看成钢片1、2、3b 、1、2刚片-用铰C 相连;1、3刚片用虚铰O 2相连(AF 、AH 延长线的交点);2、3刚片用虚铰O 1相连(DI 、EH 延长线的交点)。
三铰不共线,根据三刚片原则,ABCDEH 为无多余约束的內部几何不变体系,可看成大钢片Ⅰ。
c 、大地及A 支座一起看成刚片Ⅱ,刚片Ⅰ、Ⅱ通过铰A 和不通过铰A 的链杆EJ 相连,,根据两刚片原则,可判断整个体系为无多余约束的几何不变体系。
几何构造分析练习题

) )
4、在工程中,瞬变体系不能作为结构的原因是( A.会发生微小位移 B.约束的数量不足 C.正常荷载作用下,可能产生很大的内力 D.会产生较大的位移 5、下图中链杆 1 和链杆 2 的交点可视为虚铰。 (
1
) 。 (福州大学 2012)
) (河北工业大学 2012)
2
6、下图所示体系虽有 3 个多余约束,但未保证其几何不变,哪两根链杆是不能同时去掉的。 ( (中国矿业大学 2012) A.a 和 e B. a 和 b
B 1 A 2 C
瞬变体系与常变体系的两个判定规则: 1) 微小变形规则 让体系发生微小变形,如果三个铰还在同一直线上,则是常变体系,不在同一直线上,则是瞬 变体系。 2) 平行等长规则(特别注意平行等长的对象是谁) 组成无穷远铰的两根平行链杆与另外两铰的连线平行且等长,则为常变体系,否则为瞬变体系。 【例题】图示体系的计算自由度 W 1 ,是几何_________变体系;若在 A 点加一竖向链杆支座,则 称为几何_____________变体系;若在 A 点加一固定铰支座,则称为______变体系。 (哈尔滨工业大 学 2010 年)
J
C
D
E
F
A
B
【练习题】试对图示体系作几何组成分析。 (东南大学 2015,湖南大学 2
J
E A B C
F D
【练习题】试对图示体系作几何组成分析。(东南大学 2013)
D E G H
F
A
B
C
9 / 19
§1-4 计算自由度
所有体系都是由部件加约束组成的。但约束可分为必要约束和多余约束。 体系所有的部件自由度之和减去所有的约束,就是体系的计算自由度。之所以叫计算自由度,是为 了与体系的真实自由度区分开来。体系的真实自由度等于所有部件自由度之和减去必要约束。 1. 单约束与复约束 约束可以分为单约束和复约束,两个刚片间的结合为单结合,三个刚片间的结合相当于两个单 结合。一般说来,n 个刚片间的复结合相当于(n-1)个单结合。 举例说明:用 1 个铰连接 5 个链杆,相当于(5-1)个单铰约束。因为 5 个独立的链杆共有(5×3) 个自由度,用一个铰连接起来后,整体有 2 个平动自由度,外加每根杆有 1 个转动自由度,共有 7 个自由度,因此体系获得了(15-7)=8 个约束,即(5-1)=4 个单铰约束。满足 n 个刚片间的复结 合相当于(n-1)个单结合这一结论。
大学结构力学知识考试练习题及答案131
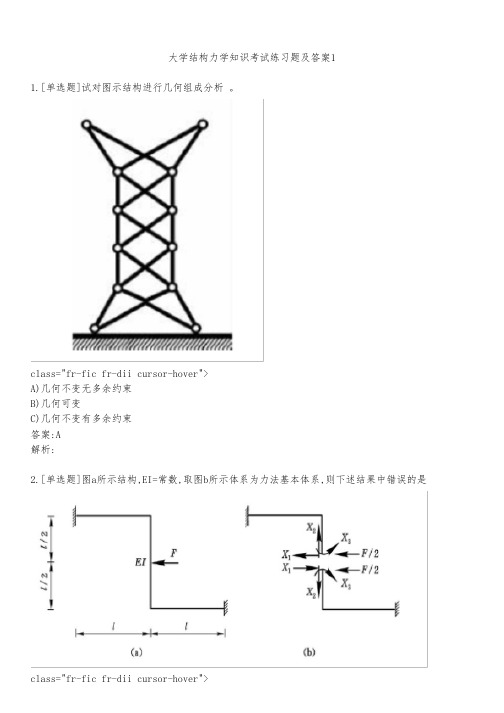
大学结构力学知识考试练习题及答案11.[单选题]试对图示结构进行几何组成分析 。
class="fr-fic fr-dii cursor-hover">A)几何不变无多余约束B)几何可变C)几何不变有多余约束答案:A解析:2.[单选题]图a所示结构,EI=常数,取图b所示体系为力法基本体系,则下述结果中错误的是class="fr-fic fr-dii cursor-hover">A)B)class="fr-fic fr-dii">C)class="fr-fic fr-dii">答案:C解析:3.[单选题]对比图(a)和图(b)两个刚架的关系是A)内力相同, 变形也相同B)内力相同, 变形不同C)内力不同, 变形相同D)内力不同, 变形也不同答案:B解析:4.[单选题]欲使图示体系成为无多余约束的几何不变体系,则需在A端加入 。
class="fr-fic fr-dii cursor-hover">A)定向支座B)固定铰支座C)固定支座D)滑动铰支座答案:C解析:5.[单选题]图示结构:class="fr-fic fr-dii cursor-hover">A)ABC段有内力;B)ABC段无内力;C)CDE段无内力;D)全梁无内力。
答案:B解析:6.[单选题]图示对称结构C截面不为零的是A)剪力B)轴力C)水平位移D)弯矩答案:B解析:7.[单选题]静定结构的内力与刚度A)有关B)比值有关C)绝对大小有关D)无关8.[单选题]图示体系的计算自由度为:class="fr-fic fr-dii cursor-hover">A)-1B)0C)1D)3答案:A解析:9.[单选题]力法基本方程的使用条件是( )构成的超静定结构。
A)弹塑性材料B)微小变形且线性弹性材料C)任意变形的任何材料D)任意变形的线性弹性材料答案:B解析:10.[单选题]联结三个刚片的铰结点,相当于约束数目是 个。
(完整版)西北工业大学航空学院结构力学课后题答案第二章结构的几何组成分析
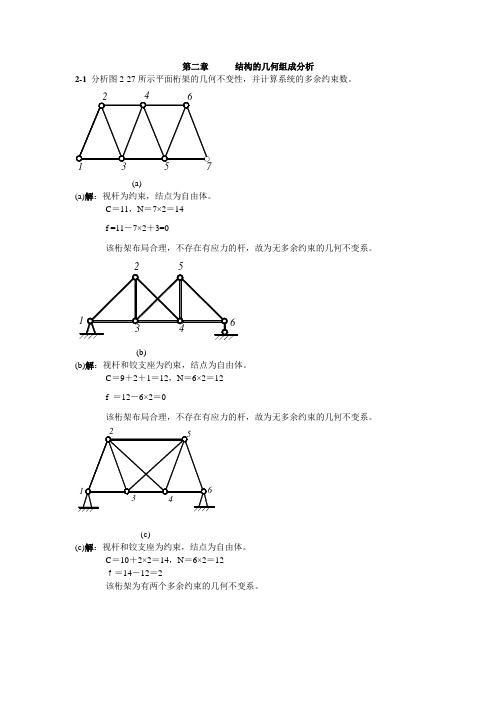
第二章结构的几何组成分析2-1分析图2-27所示平面桁架的几何不变性,并计算系统的多余约束数。
(a)(a)解:视杆为约束,结点为自由体。
C=11,N=7×2=14f =11-7×2+3=0该桁架布局合理,不存在有应力的杆,故为无多余约束的几何不变系。
(b)(b)解:视杆和铰支座为约束,结点为自由体。
C=9+2+1=12,N=6×2=12f =12-6×2=0该桁架布局合理,不存在有应力的杆,故为无多余约束的几何不变系。
(c)(c)解:视杆和铰支座为约束,结点为自由体。
C=10+2×2=14,N=6×2=12f=14-12=2该桁架为有两个多余约束的几何不变系。
1217(d)(d)解:视杆和铰支座为约束,结点为自由体。
C =30+3=33,N =17×2=34f=33-34=-1故该桁架为几何可变系。
(e)(e)解:视杆为约束,结点为自由体。
C =13,N =8×2=16f=13-16+3=0将1-2-3-4、5-6-7-8看作两刚片,杆3-6、杆2-7、杆4-5相互平行,由两刚片原则知,为瞬时可变系统。
6 (f)(f)解:视杆和固定铰支座为约束,结点为自由体。
C =22+3×2=28,N =14×2=28f=28-28=0将12-13-14、7-11-12、1-2-3-4-5-6-7-8-9-10看作三刚片,三刚片由铰7、铰12、铰14连结,三铰共线,故该桁架为瞬时可变系统。
(g)(g)解:视杆和固定铰支座为约束,结点为自由体。
C=24+4×2=32,N=16×2=32f=32-32=0由于杆15-14-3、杆12-11-4、杆9-5相交于一点,故该桁架为瞬时可变系。
(h)(h)解:视杆和固定铰支座为约束,结点为自由体。
C=12+2×2=16,N=8×2=16f=16-16=0该桁架布局合理,加减二元体之后,无有应力的杆,故该桁架为无多余约束的几何不变系。
福大结构力学课后习题详细答案(祁皑)..---副本
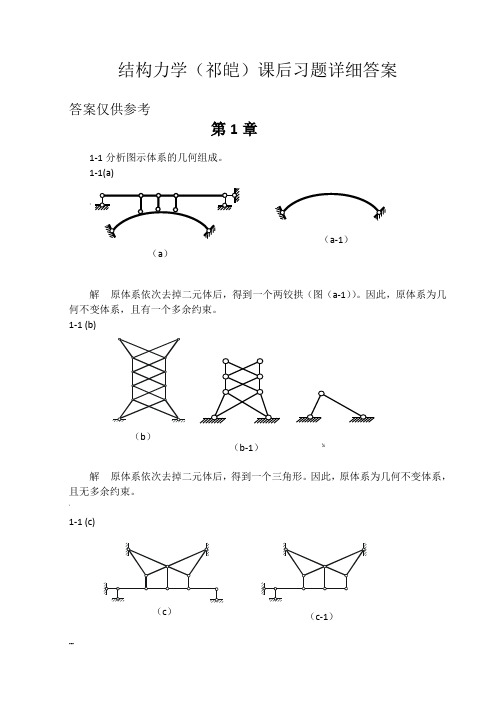
结构力学(祁皑)课后习题详细答案答案仅供参考第1章1-1分析图示体系的几何组成。
1-1(a)解 原体系依次去掉二元体后,得到一个两铰拱(图(a-1))。
因此,原体系为几何不变体系,且有一个多余约束。
1-1 (b)解 原体系依次去掉二元体后,得到一个三角形。
因此,原体系为几何不变体系,且无多余约束。
'1-1 (c)…(c-1)(a )(a-1)(b )(b-1)%(c-2) (c-3)解 原体系依次去掉二元体后,得到一个三角形。
因此,原体系为几何不变体系,且无多余约束。
1-1 (d)((d-1) (d-2) (d-3)解 原体系依次去掉二元体后,得到一个悬臂杆,如图(d-1)-(d-3)所示。
因此,原体系为几何不变体系,且无多余约束。
注意:这个题的二元体中有的是变了形的,分析要注意确认。
1-1 (e);解 原体系去掉最右边一个二元体后,得到(e-1)所示体系。
在该体系中,阴影所示的刚片与支链杆C 组成了一个以C 为顶点的二元体,也可以去掉,得到(e-2)所示体系。
在图(e-2)中阴影所示的刚片与基础只用两个链杆连接,很明显,这是一个几何可变体系,缺少一个必要约束。
因此,原体系为几何可变体系,缺少一个必要约束。
1-1 (f).解 原体系中阴影所示的刚片与体系的其它部分用一个链杆和一个定向支座相(d )(e )(e-1)AB"AB (e-2)(f )(f-1)连,符合几何不变体系的组成规律。
因此,可以将该刚片和相应的约束去掉只分析其余部分。
很明显,余下的部分(图(f-1))是一个几何不变体系,且无多余约束。
因此,原体系为几何不变体系,且无多余约束。
1-1 (g)解 原体系中阴影所示的刚片与体系的其它部分用三个链杆相连,符合几何不变体系的组成规律。
因此,可以将该刚片和相应的约束去掉,只分析其余部分。
余下的部分(图(g-1))在去掉一个二元体后,只剩下一个悬臂杆(图(g-2))。
因此,原体系为几何不变体系,且无多余约束。
几何组成分析举例
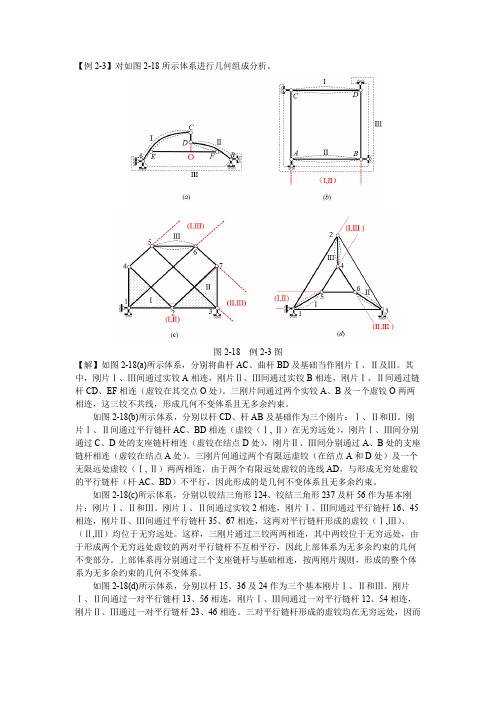
【例2-3】对如图2-18所示体系进行几何组成分析。
图2-18 例2-3图【解】如图2-18(a)所示体系,分别将曲杆AC、曲杆BD及基础当作刚片Ⅰ、Ⅱ及Ⅲ。
其中,刚片Ⅰ、Ⅲ间通过实铰A相连,刚片Ⅱ、Ⅲ间通过实铰B相连,刚片Ⅰ、Ⅱ间通过链杆CD、EF相连(虚铰在其交点O处)。
三刚片间通过两个实铰A、B及一个虚铰O两两相连,这三铰不共线,形成几何不变体系且无多余约束。
如图2-18(b)所示体系,分别以杆CD、杆AB及基础作为三个刚片:Ⅰ、Ⅱ和Ⅲ。
刚片Ⅰ、Ⅱ间通过平行链杆AC、BD相连(虚铰(Ⅰ, Ⅱ)在无穷远处),刚片Ⅰ、Ⅲ间分别通过C、D处的支座链杆相连(虚铰在结点D处),刚片Ⅱ、Ⅲ间分别通过A、B处的支座链杆相连(虚铰在结点A处)。
三刚片间通过两个有限远虚铰(在结点A和D处)及一个无限远处虚铰(Ⅰ, Ⅱ)两两相连,由于两个有限远处虚铰的连线AD,与形成无穷处虚铰的平行链杆(杆AC、BD)不平行,因此形成的是几何不变体系且无多余约束。
如图2-18(c)所示体系,分别以铰结三角形124、铰结三角形237及杆56作为基本刚片:刚片Ⅰ、Ⅱ和Ⅲ。
刚片Ⅰ、Ⅱ间通过实铰2相连,刚片Ⅰ、Ⅲ间通过平行链杆16、45相连,刚片Ⅱ、Ⅲ间通过平行链杆35、67相连,这两对平行链杆形成的虚铰(Ⅰ,Ⅲ)、(Ⅱ,Ⅲ)均位于无穷远处。
这样,三刚片通过三铰两两相连,其中两铰位于无穷远处,由于形成两个无穷远处虚铰的两对平行链杆不互相平行,因此上部体系为无多余约束的几何不变部分。
上部体系再分别通过三个支座链杆与基础相连,按两刚片规则,形成的整个体系为无多余约束的几何不变体系。
如图2-18(d)所示体系,分别以杆15、36及24作为三个基本刚片Ⅰ、Ⅱ和Ⅲ。
刚片Ⅰ、Ⅱ间通过一对平行链杆13、56相连,刚片Ⅰ、Ⅲ间通过一对平行链杆12、54相连,刚片Ⅱ、Ⅲ通过一对平行链杆23、46相连。
三对平行链杆形成的虚铰均在无穷远处,因而形成的上部体系是几何瞬变体系。
几何组成分析思考题1.链杆能否作为刚片刚片能否作为链杆二者
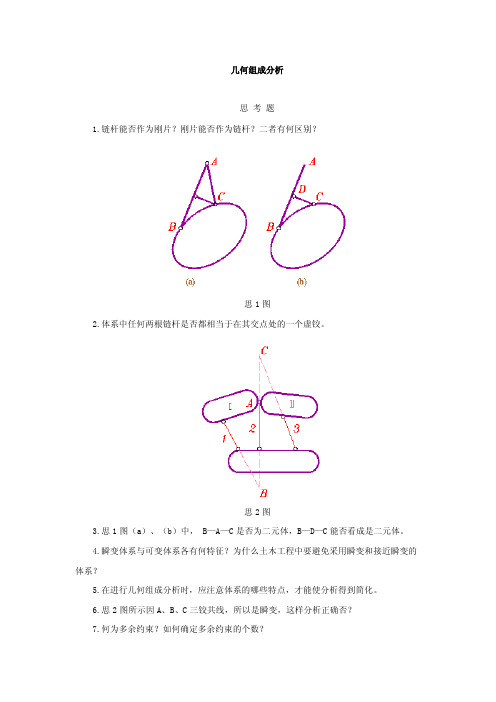
几何组成分析
思考题
1.链杆能否作为刚片?刚片能否作为链杆?二者有何区别?
思1图
2.体系中任何两根链杆是否都相当于在其交点处的一个虚铰。
思2图
3.思1图(a)、(b)中, B—A—C是否为二元体,B—D—C能否看成是二元体。
4.瞬变体系与可变体系各有何特征?为什么土木工程中要避免采用瞬变和接近瞬变的体系?
5.在进行几何组成分析时,应注意体系的哪些特点,才能使分析得到简化。
6.思2图所示因A、B、C三铰共线,所以是瞬变,这样分析正确否?
7.何为多余约束?如何确定多余约束的个数?
习题
1~15 试对图示体系作几何组成分析。
若为多余约束的几何不变体系,则指出其多余约束的数目。
题1图
题2图题3图
题4图题5图题6图
题7图题8图
题9图 10图题11图
题12图题13图
题14图题15图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题15.7试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 2j -6-r=2×8-9-7=0(2)几何组成分析。
首先把三角形ACD和BCE分别看做刚片I和刚片Ⅱ,把基础看做刚片I,则三个刚片用不共线的三个铰A、B、C分别两两相联,组成一个大的刚片。
在这个大的刚片上依次增加二元体12、DGF、CHG、EIH、IJ3。
最后得知整个体系为几何不变,且无多余约束。
题15.8试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 3m - 2h -r=3×6-2×7—4=0(2)几何组成分析。
刚片AF和AB由不共线的单铰A以及链杆DH相联,构成刚片I,同理可把BICEG部分看做刚片Ⅱ,把基础以及二元体12、34看作刚片I,则刚片I、Ⅱ、Ⅲ由不共线的三个铰F、B、G两两相联,构成几何不变体系,且无多余约束。
题15.9试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 3m - 2h -r=3×14 -2×19 -4一O(2)几何组成分析。
在刚片HD上依次增加二元体DCJ、CBI、BAH构成刚片I,同理可把DMG部分看做刚片Ⅱ,把基础看做刚片I,则刚片I、Ⅱ、Ⅲ由不共线的单铰D,虚铰N、O 相联,构成几何不变体系,且无多余约束。
题15.10试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W-2j—b-r=2×7—11-3一O(2)几何组成分析。
由于AFG部分由基础简支,所以可只分析AFG部分。
可去掉二元体BAC只分析BFGC部分。
把三角形BDF、CEG分别看做附片I和I,刚片I和I由三根平行的链杆相联,因而整个体系为瞬变。
题15.11试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 2j -6-r=2×9-13—5一O(2)几何组成分析。
首先在基础上依次增加二元体12、AE3、AFE、ABF、FI4,成一个大的刚片I。
其次,把CDHG部分看做刚片Ⅱ,刚片I、Ⅱ由三根共点的链杆BC、IG、5相联,因而整个体系为瞬变。
题15.12试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W一2j -6-r=2×7- 11-3一O(2)几何组成分析。
由于ABCDEF部分由基础简支,所以可只分析ABCDEF部分。
把三角形ABD看做刚片I,BCF看做刚片I,杆件GE看做刚片Ⅲ,则三个刚片由不共线的单铰B,虚铰Ol、02分别两两相联,构成几何不变体系,且无多余约束。
题15.13试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W= 2j -6-r’=2×6—8-4=0(2)几何组成分析。
把三角形CDF看做刚片I,杆件AB看做刚片Ⅱ,基础和二元体23看做刚片Ⅲ。
刚片I和刚片Ⅱ由链杆BC、AD相联,相当于虚铰D;刚片I和刚片Ⅲ由链杆CE、4相联,相当于虚铰Ol;刚片Ⅱ和Ⅲ由链杆EB、1相联,相当于一个虚铰,三个虚铰不共线,因此构成几何不变体系,且无多余约束。
题15.14试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 2j-b-r=2×12 - 21-3—0(2)几何组成分析。
由于ABCGLKD部分由基础简支,所以可只分析ABCGLKD部分。
在三角形ADE上依次增加二元体ABE、BFE、BCF、CGF、FHE组成刚片I。
将三角形HJI 看做刚片Ⅱ,杆件KL看做刚片Ⅲ。
刚片I和刚片Ⅱ由单铰H相联;刚片Ⅱ和Ⅲ由链杆KI 和JL相联,即在H点由虚铰相联;刚片I和刚片Ⅲ由链杆EK、 FL相联,即在无穷远处由虚铰相联显然,这三个铰共线,因而整个体系为瞬变。
;B题15.15试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W= 3m - 2h -r=3×7-2×9-3=O(2)几何组成分析。
由于ACEFG部分由基础简支,所以可只分析ACEFG部分。
在杆件ABC 上增加二元体BGA构成刚片I,同理可把CDEF部分看做刚片Ⅱ,刚片I和刚片I由不共线的单铰C及链杆GF相联,因而整个体系为几何不变,且无多余约束。
题15.16试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W= 3m一2h -r=3×9—2×13 -3=-2(2)几何组成分析。
由于ADEFG部分由基础简支,所以可只分析ADEFG部分。
把三角形AED看做刚片I,杆BE看做多余约束;把三角形AFG看做刚片I,杆CF看做多余约束。
刚片I和刚片Ⅱ由不共线的铰A及链杆EF相联,因而整个体系为几何不变,且有两个多余约束。
题15.17试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W= 2j -b-r=2×9-15-3=0(2)几何组成分析。
由于ADIHGFEB部分由基础简支,所以可只分析ADIHGFEB部分。
在三角形BEF上依次增加二元体BCE、CGF组成刚片I,同理可把CDIH部分看做刚片Ⅱ。
刚片I和刚片I由不共线的铰C及链杆GH相联,构成一个更大的刚片,然后再增加二元体BAD。
最后得知整个体系为几何不变,且无多余约束。
题15.18试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W= 3m - 2h -r=3×6-2×8-3=-1(2)几何组成分析。
由于ABCDFE部分由基础简支,所以可只分析ABCDFE部分。
在杆件ABCD上依次增加二元体AEB、CFD构成几何不变体系,链杆EF可看做多余约束。
因而整个体系为几何不变,且有一个多余约束。
.题15.19试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W= 2j -b-r=2×6-8—4=O(2)几何组成分析。
把三角形BCE看做刚片I,杆件DF看做刚片Ⅱ,基础上增加二元体12看做刚片I。
刚片Ⅱ和刚片Ⅲ由链杆AD、3相联,即由虚铰F相联;I刚片I和刚片I由链杆BD、EF相联,交点在无穷远处;刚片I和刚片I由链杆AB、4相联,即由虚铰C相联;显然三铰在一条直线上,因而整个体系为瞬变。
题15.20试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W= 2j -b-r=2×8-13 -3=O(2)几何组成分析。
首先在三角形AEF上依次增加二元体ABF、BCF、CGF组成刚片I,而杆件BG可看做一个多余约束。
其次,去掉二元体CDH、GH3。
把基础上增加二元体12看做刚片Ⅱ,则刚片I和刚片1只用铰E相连,因而整个体系为几何可变,但在BCGF部分有一个多余约束。
题15- 21试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W= 2j -6-r=2×9-14-4=O(2)几何组成分析。
首先在体系上依次去掉二元体DAB、BCF、DBF不改变原体系的几何组成性质,所以下面只分析DEF以下部分即可。
把三角形EFI看做刚片I;把杆件DH看做刚片Ⅱ;把基础上增加二元体12看做刚片I。
刚片I和刚片Ⅱ由虚铰F相联;刚片I和刚片Ⅲ由链杆GE及链杆4相连,交点在CI直线上;刚片I和刚片Ⅲ由平行链杆DG及链杆3相联,由于链杆DG、3和直线CI平行,且三直线将在无穷远处相交,所以三个虚铰在同一直线上,因而整个体系为瞬变。
题15.22试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W= 3m一2h一r=3×10 -2×14=2(2)几何组成分析。
该体系没有和基础相联,只需要分析其内部几何性质。
杆件AH和杆件HJ由不共线单铰H和链杆相联构成刚片I;同理可把DMJ部分看做刚片Ⅱ;再把折杆ABCD 和二元体BFC看做刚片Ⅲ。
刚片I、Ⅱ、I由三个不共线的单铰A、J、D两两相联,构成几何不变体系,链杆FJ可看做多余约束。
因而整个体系内部为几何不变,且有一个多余约束。
题15.23试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W= 3m - 2h -r=3×4—2×4-4=0(2)几何组成分析。
把曲杆ACF看做刚片I;曲杆BDE看做刚片Ⅱ,基础和二元体12、34看做刚片Ⅲ。
刚片I、Ⅱ、Ⅲ由不共线的三铰A、B、G两两相联,因而‘整个体系为几何不变,且无多余约束。
题15.24试对图示体系进行几何组成分析。
解体系的自由度为W= 3m-2h-r=3×4-2×3-5=1体系缺少足够的约束,为几何可变体系。
题15.25试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W= 3m - 2h-r=3×2-2×1-4=0(2)几何组成分析。
把ABD部分看做刚片I,BCE部分看做刚片Ⅱ,基础看做刚片I。
刚片I、Ⅱ由单铰B相联,刚片Ⅱ和Ⅲ由链杆3、4相联(即在两杆轴线的点处用一虚铰相联),刚片I和刚片Ⅲ由链杆1、2相联(即在两杆轴线的交点处用一虚铰相联),显然,这三个铰不在一条直线上,因而整个体系为几何不变,且无多余约束。
题15.26试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W= 3m - 2h-r=3×9-2×10 -7=O(2)几何组成分析。
首先在体系上依次去掉二元体EAB、CDH、IEF、GHL、112、6L7,不改变原体系的几何组成性质,所以下面只分析JBCK和基础部分即可。
把折杆JBCK看做刚片I;把基础看做刚片Ⅱ。
刚片I和刚片Ⅱ由不共点的三根链杆3、4、5相联,因而整个体系为几何不变,且无多余约束。
题15.27试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W= 2j - b-r=2×9-14 -4=O(2)几何组成分析。
首先在三角形GHE上依次增加二元体GKH、KLH,把EGKLH部分看做刚片I,同理把LMJFI部分看做刚片Ⅱ,把基础看做刚片Ⅲ,则三个刚片用不共线的三个铰G、L、J分别两两相联,因而整个体系为几何不变,且无多余约束。
题15.28试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W= 2j -b-r=2×13-20-6=0.(2)几何组成分析。
首先在体系上依次去掉二元体JAB、BCD、DEM、FBG、KFG、KGH、HDI、LHI不改变原体系的几何组成性质,所以下面只分析余下部分即可。
杆件JK由三个不共点的链杆1、2、3与基础相连,组成刚片I;杆件LM由三个不共点的链杆4、5和KL与刚片I相联,组成更大的刚片,但链杆6为一多余约束。
杆件IL与更大的刚片只由一个单铰相连,缺少足够的约束,因而整个体系为几何可变。
