安徽省合肥市第八中学2021届高三上学期第二次月考 数学(理)试题
2021年高三上学期第二次月考数学(理)试题 含答案

2021年高三上学期第二次月考数学(理)试题含答案一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1、设为虚数单位,则()A. B. C. D.2、若集合P=,,则集合Q不可能...是()>3、命题“若,则”的逆否命题是()A.“若,则”B.“若,则”C.“若x,则”D.“若,则”4、若函数的定义域是,则函数的定义域是()A.B.C. D.5、定义在R上的偶函数的部分图像如右图所示,则在区间上,下列函数中与的单调性不同的是()A.B.C.D.6. 甲、乙两队进行排球决赛,现在的情形是甲队只要在赢一次就获冠军,乙队需要再赢两局才能得冠军,若两队胜每局的概率相同,则甲队获得冠军的概率为()A. B.C. D.7.在等比数列中,已知,那么()A.4 B.6 C.12 D.168.若△ABC的内角满足sin A+cos A>0,tan A-sin A<0,则角A的取值范围是()A.(0,)B.(,)C.(,)D.(,π)二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分。
(一)必做题(9-13题)9. 不等式的解集是 .10. 的展开式中,的系数是(用数字作答)11. 点是抛物线上一动点,则点到点的距离与到直线的距离和的最小值是___________12. 已知函数是奇函数,则13. 点是圆外一点,则直线与该圆的位置关系是(二)选做题(14 - 15题,考生只能从中选做一题)14.(坐标系与参数方程选做题)已知两面线参数方程分别为和,它们的交点坐标为________.15.(几何证明选讲选做题)如图4,过圆外一点分别作圆的切线和割线交圆于,,且=7,是圆上一点使得=5,∠=∠, 则= 。
三.解答题。
本大题共6小题,满分80分。
解答需写出文字说明、证明过程和演算步骤。
16(本小题满分12分)已知函数(1)求的值;(2)设106,0,,(3),(32),22135f a fππαββπ⎡⎤∈+=+=⎢⎥⎣⎦求的值.17. (本小题满分12分)为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽出取14件和5件,测量产品中的微量元素x,y 的含量(单位:毫克).下表是乙厂的5件产品的测量数据:编号 1 2 3 4 5x 169 178 166 175 180y 75 80 77 70 81 (1)已知甲厂生产的产品共有98件,求乙厂生产的产品数量;(2)当产品中的微量元素x,y满足x≥175,且y≥75时,该产品为优等品。
2021年高三上学期第二次月考数学试题含答案

2021年高三上学期第二次月考数学试题含答案一、选择题:1.复数()A.4﹣2i B.﹣4+2i C.2+4i D.2﹣4i2.若集合A={1,m2},B={3,4},则“m=2”是“A∩B={4}”的()A.充分不必要条件B.必要不充分条件 C.充要条件D.既不充分也不必要条件3.已知平面向量,满足•(+)=3,且||=2,||=1,则向量与的夹角为()A.B.C.D.4.设等差数列{a n}的前n项和为S n,若a2=﹣11,a5+a9=﹣2,则当S n取最小值时,n等于()A.9 B.8 C.7 D.65.已知抛物线y2=8x与双曲线﹣y2=1的一个交点为M,F为抛物线的焦点,若|MF|=5,则该双曲线的渐近线方程为()A.5x±3y=0 B.3x±5y=0 C.4x±5y=0 D.5x±4y=06.定义=a1a4﹣a2a3,若f(x)=,则f(x)的图象向右平移个单位得到的函数解析式为()A.y=2sin(x﹣)B.y=2sin(x+)C.y=2cosx D.y=2sinx7.关于两条不同的直线m、n与两个不同的平面α、β,下列命题正确的是()A.m∥α,n∥β且α∥β,则m∥n B.m⊥α,n⊥β且α⊥β,则m∥nC.m⊥α,n∥β且α∥β,则m⊥n D.m∥α,n⊥β且α⊥β,则m∥n8.函数f(x)是定义在R上的偶函数,且对任意的x∈R,都有f(x+2)=f(x).当0≤x≤1时,f(x)=x2.若直线y=x+a与函数y=f(x)的图象有两个不同的公共点,则实数a的值为()A.n(n∈Z)B.2n(n∈Z)C.2n或(n∈Z)D.n或(n∈Z)9.已知O是坐标原点,点A(﹣2,1),若点M(x,y)为平面区域上的一个动点,则的取值范围是()A.[0,1]B.[0,2]C.[﹣1,0] D.[﹣1,2]10.若函数f(x)满足f(x)+1=,当x∈[0,1]时,f(x)=x,若在区间(﹣1,1]上,方程f(x)﹣mx﹣2m=0有两个实数解,则实数m的取值范围是()A.0<m≤B.0<m<C.<m≤l D.<m<1二、填空题:11.已知f(x)=,定义f1(x)=f′(x),f2(x)=[f1(x)]′,…,f n+1(x)=[f n(x)]′,n∈N*.经计算f1(x)=,f2(x)=,f3(x)=,…,照此规律,则f n(x)=.12.如图是一个算法的流程图.若输入x的值为2,则输出y的值是.13.某圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为的扇形,则该几何体的体积为.14.已知P是直线3x+4y﹣10=0上的动点,PA,PB是圆x2+y2﹣2x+4y+4=0的两条切线,A,B是切点,C是圆心,那么四边形PACB面积的最小值为.15.设全集U={1,2,3,4,5,6},用U的子集可表示由0,1组成的6位字符串,如:{2,4}表示的是第2个字符是1,第4个字符为1,其它均为0的6位字符串010100,并规定空集表示为000000.若A={1,3},集合A∪B表示的字符串为101001,则满足条件的集合B的个数为.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.16.汽车是碳排放量比较大的行业之一,某地规定,从xx年开始,将对二氧化碳排放量超过130g/km的轻型汽车进行惩罚性征税.检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如表(单位:g/km).甲80 110 120 140 150乙100 120 x 100 160经测算得乙品牌轻型汽车二氧化碳排放量的平均值为=120g/km.2016-12-27 高三数学(复读全) 1双考(1)求表中x的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性;(2)从被检测的5辆甲品牌轻型汽车中任取2辆,则至少有一辆二氧化碳排放量超过130g/km 的概率是多少?17.已知函数f(x)=2sinxcosx+2cos2x﹣,x∈R.(Ⅰ)求函数y=f(﹣3x)+1的最小正周期和单调递减区间;(Ⅱ)已知△ABC中的三个内角A,B,C所对的边分别为a,b,c,若锐角A满足f(﹣)=,且a=7,sinB+sinC=,求△ABC的面积.18.已知四棱锥A﹣BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥面ABC,BE∥CD,F 为AD的中点.(Ⅰ)求证:EF∥面ABC;(Ⅱ)求证:平面ADE⊥平面ACD;(Ⅲ)求四棱锥A﹣BCDE的体积.19.已知数列{a n}前n项和S n满足:2S n+a n=1(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设b n=,数列{b n}的前n项和为T n,求证:T n<.20.已知函数f(x)=2(a+1)lnx﹣ax,g(x)=﹣x(1)若函数f(x)在定义域内为单调函数,求实数a的取值范围;(2)证明:若﹣1<a<7,则对于任意x1,x2∈(1,+∞),x1≠x2,有>﹣1.21.在平面直角坐标系中,椭圆:的离心率为,右焦点. (1)求椭圆的方程;(2)点在椭圆上,且在第一象限内,直线与圆:相切于点,且,求点的纵坐标的值.立人中学第二次月考试题数学试题参考答案一、选择题:1~5 B A C C A 6~10 D C C D A二、填空题:11.;12.﹣2;13.2π;14.2;15.4.15【解答】解:若A={1,3},集合A∪B表示的字符串为101001,∴集合B可能是{6},{1,6},{3,6},{1,3,6},故答案为:4.三、解答题:16.【解答】解:(1)由==120得,x=120;==120;S2甲= [(80﹣120)2+(110-120)2+(120-120)2+(140-120)2+(150-120)2]=600;S2乙= [(100﹣120)2+(120-120)2+(120-120)2+(100-120)2+(160-120)2]=480;因为S2甲>S2乙;故乙品牌轻型汽车二氧化碳排放量的稳定性更好;(2)从被检测的5辆甲品牌轻型汽车中任取2辆,共有=10种情况,至少有一辆二氧化碳排放量超过130g/km的情况有×+1=7种,故至少有一辆二氧化碳排放量超过130g/km的概率是.17.【解答】(本小题满分12分)解:(Ⅰ)∵=…∴,∴y=f(﹣3x)+1的最小正周期为…由得:,k∈Z,∴y=f(﹣3x)+1的单调递减区间是,k∈Z…(Ⅱ)∵,∴,∴…∵,∴.由正弦定理得:,即,∴b+c=13…由余弦定理a2=b2+c2﹣2bccosA得:a2=(b+c)2﹣2bc﹣2bccosA,即49=169﹣3bc,∴bc=40 (1)∴…18.【解答】证明:(Ⅰ)取AC中点G,连接FG、BG,∵F,G分别是AD,AC的中点∴FG∥CD,且FG=DC=1.∵BE∥CD∴FG与BE平行且相等∴EF∥BG.EF⊄面ABC,BG⊂面ABC∴EF∥面ABC…(Ⅱ)∵△ABC 为等边三角形∴BG ⊥AC又∵DC ⊥面ABC ,BG ⊂面ABC ∴DC ⊥BG∴BG 垂直于面ADC 的两条相交直线AC ,DC ,∴BG ⊥面ADC . …∵EF ∥BG∴EF ⊥面ADC∵EF ⊂面ADE ,∴面ADE ⊥面ADC . …解:(Ⅲ)方法一:连接EC ,该四棱锥分为两个三棱锥E ﹣ABC 和E ﹣ADC ..…方法二:取BC 的中点为O ,连接AO ,则AO ⊥BC ,又CD ⊥平面ABC , ∴CD ⊥AO ,BC ∩CD=C ,∴AO ⊥平面BCDE ,∴AO 为V A ﹣BCDE 的高,,∴.19.【解答】(I )解:∵2S n +a n =1,∴当n ≥2时,2S n ﹣1+a n ﹣1=1,∴2a n +a n ﹣a n ﹣1=0,化为.当n=1时,2a 1+a 1=1,∴a 1=.∴数列{a n }是等比数列,首项与公比都为.∴.(II )证明:b n ====,∴数列{b n }的前n 项和为T n =++…+=. ∴T n <.20.【解答】解:(1)函数f (x )=2(a +1)lnx ﹣ax 的定义域是(0,+∞), ∴=,∵函数f (x )在定义域内为单调函数,∴f ′(x )≥0或f ′(x )≤0在(0,+∞)上恒成立,则﹣ax +2(a +1)≥0或﹣ax +2(a +1)≤0在(0,+∞)上恒成立, ①当a=0时,则有2≥0恒成立,函数f (x )在(0,+∞)上为增函数; ②当a >0时,函数y=﹣ax +2(a +1)在(0,+∞)上为减函数,∴只要2(a +1)≤0,即a ≤﹣1时满足f ′(x )≤0成立,此时a 无解; ③当a <0时,函数y=﹣ax +2(a +1)在(0,+∞)上为增函数,∴只要2(a +1)≥0,即a ≥﹣1时满足f ′(x )≥0成立,此时﹣1≤a <0; 综上可得,实数a 的取值范围是[﹣1,0];证明:(2)g (x )=﹣x=在(1,+∞)单调递增,∵x 1,x 2∈(1,+∞),不妨设x 1>x 2,∴g (x 1)>g (x 2),∴等价于f (x 1)﹣f (x 2)>﹣g (x 1)+g (x 2),则f (x 1)+g (x 1)>f (x 2)+g (x 2),设h (x )=f (x )+g (x )=2(a +1)lnx ﹣(a +1)x +,则h ′(x )==,2016-12-27 高三数学(复读全) 2双 考∵﹣1<a <7,∴a +1>0,∴2=2,当且仅当时取等号,∴h ′(x )≥2﹣(a +1)=,∵﹣1<a <7,∴>0,即h ′(x )>0,∴h (x )在(1,+∞)上单调递增,满足f (x 1)+g (x 1)>f (x 2)+g (x 2), 即若﹣1<a <7,则对于任意x 1,x 2∈(1,+∞),x 1≠x 2,有>﹣1成立.21.解:(1)∴,,∴,∴椭圆方程为.(2)①当轴时,,,由,解得.②当不垂直于轴时,设,方程为,即, ∵与圆相切,∴,∴,∴,又,所以由,得,∴2202222200(33)123(1)(1)(3)334x k k x k x k +==+++---, ∴.综上:.%Sg31436 7ACC 竌40450 9E02 鸂23930 5D7A 嵺31351 7A77 穷 @ hG36878 900E 逎H22228 56D4 囔。
安徽省合肥八中上学期高三第二次月考

20XX年中学测试中学试题试卷科目:年级:考点:监考老师:日期:2021-2021学年度安徽省合肥八中上学期高三第二次月考物理试卷一、选择题:本题共20小题;每小题3分,共计60分,每小题至少有一个选项符合题意,对的得3分,选对但不全的得1分,错选或不答的得0分。
1.关于速度、速度改变量、加速度,正确的说法是()A.物体运动的速度改变量越大,它的加速度一定越大B.速度很大的物体,其加速度可以很小,可以为零C.某时刻物体的速度为零,其加速度不可能很大D.加速度数值很大时,运动物体的速度一定很快变大2.某同学身高1.6m,在运动会上他参加跳高比赛,起跳后身体横越过了1.6m高度的横杆,据此可估算出他起跳时竖直向上的速度大约为(g取10m/s2)()A.1:6m/sB.2m/sC.4m/sD.7.2m/s3.如图所示为A、B两质点作直线运动的v – t图像,已知两质点在同一直线上运动,由图可知()A.两个质点一定从同一位置出发B.两个质点一定同时由静止开始运动C.t2秒末两质点相遇D.0~t2秒时间内B质点可能领先A4.如图所示,C是水平地面,A、B是两个长方形物块,F是作用在物块B上沿水平方向的力,物体A和B以相同的速度作匀速直线运动,由此可知,A、B间的动摩擦因数μ1和B、C 间的滑动摩擦系数μ2有可能是 ( )A .μ1=0,μ2=0B .μ1=0,μ2≠0C .μ1≠0,μ2=0D .μ1≠0,μ2≠05.如图所示,在水平桌面上放一木块,用从零开始逐渐增大的水平拉力F 拉着木块沿桌面运动,则木块所受到的摩擦力f 随拉力F 变化的图象正确的是( )6.一物体作匀变速直线运动,某时刻速度大小为2m/s ,1s 后速度的大小变为6m/s ,在这1s 内该物体的①位移大小可能等于2m 。
②位移大小可能大于6m 。
③加速度大小可能等于4m/s 2。
④加速度大小可能大于6m/s 2。
则下列说法中正确的是 ( )A .①②B .②③④C .①③④D .①②③④7.从塔顶释放一个小球A ,1s 后从同一地点再释放一个小球B ,设两球都作自由落体运动,则落地前,A 、B 两球之间的距离( )A .保持不变B .不断增大C .不断减小D .有时增大,有时减小8.汽车做匀减速直线运动,在5s 内先后经过路旁相距50m 的电线杆,经过第一根电线杆的速度是15m/s ,则经过第二根电线杆的速度是( )A .3m/sB .5m/sC .8m/sD .10m/s9.作直线运动的物体,经过A 、B 两点的速度分别为V A 和V B ,经过A 和B 的中点的速度为V C ,且V C =21(V A +V B );在AC 段为匀加速直线运动,加速度为a 1,CB 段为匀加速直线运动,加整度为a 2,则( )A .a 1=a 2B .a 1>a 2C .a 1<a 2D .不能确定10.甲、乙两辆汽车沿平直公路从某地同时同向驶向同一目的地,甲车在前一半时间内以速度V 1做匀速运动,后一半时间内以速度V 2做匀速运动;乙车在前一半路程中以速度V 1做匀速运动,在后一半路程中以速度V 2做匀速运动,且V 1≠V 2,则 ( )A .甲先到达B .乙先到达C .甲、乙同时到达D .无法比较11.一球由空中自由下落,碰到桌面立刻反弹,则V – t 图象为图中的(取向上为正)( )12.甲、乙两车以相同的速率V 0在水平地面上相向做匀速直线运动,某时刻乙车先以大小为a 的加速度做匀减速运动,当速率减小到0时,甲车也以大小为a 的加速度做匀减运动。
2021年高三上学期8月月考数学(理)试题 含答案
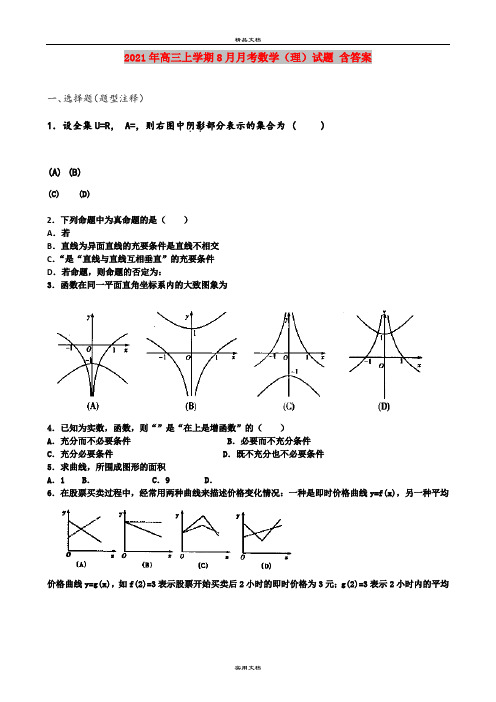
2021年高三上学期8月月考数学(理)试题含答案一、选择题(题型注释)1.设全集U=R, A=,则右图中阴影..部分表示的集合为 ( )(A) (B)(C) (D)2.下列命题中为真命题的是()A.若B.直线为异面直线的充要条件是直线不相交C.“是“直线与直线互相垂直”的充要条件D.若命题,则命题的否定为:3.函数在同一平面直角坐标系内的大致图象为4.已知为实数,函数,则“”是“在上是增函数”的()A.充分而不必要条件 B.必要而不充分条件C.充分必要条件 D.既不充分也不必要条件5.求曲线,所围成图形的面积A.1 B.C.9 D.6.在股票买卖过程中,经常用两种曲线来描述价格变化情况:一种是即时价格曲线y=f(x),另一种平均价格曲线y=g(x),如f(2)=3表示股票开始买卖后2小时的即时价格为3元;g(2)=3表示2小时内的平均价格为3元.下面给出了四个图象,实线表示y=f(x),虚线表示y=g(x),其中可能正确的是7.已知函数的反函数为,则=A.1 B.2 C.3 D.48.函数的最小正周期是,且其图像向右平移个单位后得到的函数是奇函数,则函数的图像()A.关于直线对称 B. 关于直线对称C. 关于点对称D.关于点对称9..右图是计算函数值的程序框图,在①、②、③处应分别填入的是( )A.B.C.D.10.数列满足:,且为递增数列,则实数的取值范围是( )A.B.C.D.11.设定义在上的函数,若关于的方程有3个不同实数解、、,且,则下列说法中错误的是()A. B. C. D.12.定义域为[]的函数图像的两个端点为A、B,M(x,y)是图象上任意一点,其中.已知向量,若不等式恒成立,则称函数f (x)在[a,b]上“k阶线性近似”.若函数在[1,2]上“k阶线性近似”,则实数k 的取值范围为( )A.[0,+∞)B.C.D.第II卷(非选择题)二、填空题(题型注释)13.若不等式对恒成立,则实数的取值范围是.14.从集合中选出由5个数组成的子集,使得这5个数中的任何两个数的和不等于11,则这样的子集共有个.15.对于三次函数,给出定义:设是函数的导数,是的导数,若方程有实数解,则称点为函数的“拐点”。
安徽省合肥市2020-2021学年高三上学期期初调研性检测理科数学试题

合肥市2021届高三调研性检测数学试(理科)(考试时间:120分钟 满分:150分)第Ⅰ卷(60分)一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若复数z满足1zi -=,其中i 是虚数单位,则复数z 的模为( )A.B.C.D. 3B首先根据题意得到z i =,再计算模长即可.因为1zi -=,所以221++===iz i ii.所以==z 故选:B2. 若集合{}1A xx =>∣,{}2230B x x x =--≤∣,则A B =( ) A. (1,3] B. [1,3] C. [1,1)- D. [1,)-+∞A化简集合B ,根据交集的定义,即可求解.{}2230[1,3]B x x x =--≤=-∣, {}1(1,)A x x =>=+∞∣,(1,3]A B ∴=。
故选:A.3. 若变量x ,y 满足约束条件1133x y x y x y -≤⎧⎪+≥-⎨⎪-≥⎩,则目标函数3z x y =+的最小值为( )A. 92- B. 4- C. 3- D. 1D根据变量x ,y 满足1133x y x y x y -≤⎧⎪+≥-⎨⎪-≥⎩,画出可行域,然后平移直线30x y +=,当直线在y 轴上截距最小时,目标函数取得最小值.由变量x ,y 满足1133x y x y x y -≤⎧⎪+≥-⎨⎪-≥⎩,画出可行域如图所示:平移直线30x y +=,当直线在y 轴上截距最小时,经过点1,0A ,此时目标函数取得最小值,最小值是1,故选:D4. 为了保障广大人民群众的身体健康,在新冠肺炎疫情防控期间,有关部门对辖区内15家药店所销售的A 、B 两种型号的口罩进行了抽检,每家药店抽检10包口罩(每包10只),15家药店中抽检的A 、B 型号口罩不合格数(Ⅰ、Ⅱ)的茎叶图如图所示,则下列描述不正确...的是( )A. 估计A 型号口罩的合格率小于B 型号口罩的合格率B. Ⅰ组数据的众数大于Ⅱ组数据的众数C. Ⅰ组数据的中位数大于Ⅱ组数据的中位数D. Ⅰ组数据的方差大于Ⅱ组数据的方差 D根据茎叶图中的数据计算出两种型号口罩的合格率,可判断A 选项的正误;求出两组数据的众数,可判断B 选项的正误;求出两组数据的中位数,可判断C 选项的正误;利用排除法可判断D 选项的正误. 对于A选项,由茎叶图可知,A 型号口罩的不合格数为658210124131416202130199++⨯++⨯++++++=,B 型口罩的不合格数为245682101131416212528180++++⨯++⨯+++++=,A 型号口罩的合格率为1991301115001500-=,B 型口罩的合格率为1801320115001500-=, 所以,A 型口罩的合格率小于B 型口罩的合格率,A 选项正确; 对于B 选项,Ⅰ组数据的众数为12,Ⅱ组数据的众数11,B 选项正确; 对于C 选项,Ⅰ组数据的中位数为12,Ⅱ组数据的11,C 选项正确; 由排除法可知D 选项不正确.故选:D.5. 设数列{}n a 的前n 项和为n S ,若3122n n S a =-,则5S =( )A. 81B. 121C. 243D. 364B利用递推式与等比数列求和的通项公式即可得出.31,22n n S a =-∴当2n ≥时,113122n n S a --=-,∴111313133222222n n n n n n n a S S a a a a ---⎛⎫=-=---=- ⎪⎝⎭, 化简可得:13n n a a -=, 当1n =时,1113122a S a ==-,解得:11a =. ∴数列{}n a 是等比数列,首项为1,公比为3,()()55151113121113a q S q-⨯-∴===--.故选:B.6. 函数cos ()x xx xf x e e -=+在[],ππ-上的图象大致是( )A. B.C .D.A先由函数的奇偶性定义,判断()f x 为奇函数,排除B ,D ,再由()f x 在(0,),(,)22πππ函数值的正负值判断,即可得出结论.cos (),[,]x xx xf x x e eππ-=∈-+定义域关于原点对称, cos ()(),()x xx xf x f x f x e e ---==-∴+是奇函数,图象关于原点对称,排除选项B ,D ,(0,),()0,,()022x f x x f x ππ∈>==,(,),()02x f x ππ∈<,所以选项C 不满足,选项A 满足.故选:A. 7. 周六晚上,小红和爸爸、妈妈、弟弟一起去看电影,订购的4张电影票恰好在同一排且连在一起,为安全起见,每个孩子至少有一侧有家长陪坐,则不同的坐法种数为( ) A. 8 B. 12 C. 16 D. 20C先计算出4个人的全排列,再减去不符合情况的种数即可.4个人坐四个座位,共有4424A =种坐法,当孩子坐在一起并且坐在最边上时,有一个孩子没有大人陪伴,共有222228A A =种,所以每个孩子旁边必须有大人陪着共有24-8=16种坐法. 故选:C .8. 已知函数()2)0,||2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的部分图象如图所示,则函数()f x 的单调递减区间为( )A. 32,2()88k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦B. 3,()88k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦C. 372,2()88k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦D. 37,()88k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦D由图可知,20,218822f f ππππωϕωϕ⎛⎫⎛⎫⎛⎫⎛⎫=+==+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,338288T πππ=-=,从而可求出2,4πωϕ==-,()2)4f x x π=-,进而由3222,242k x k k Z πππππ+≤-≤+∈可求得答案解:由图可知,20,218822f f ππππωϕωϕ⎛⎫⎛⎫⎛⎫⎛⎫=+==+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 所以18k πωϕπ+=,1k Z ∈,2224k ππωϕπ+=+或2232,24k k Z ππωϕπ+=+∈,因为338288T πππ=-=,所以T π=,所以2ππω=, 因为0>ω,所以2ω=, 所以14k πϕπ=-,1k Z ∈,2324k πϕπ=-+或222,4k k Z πϕπ=-+∈ 因为||2ϕπ<,所以4πϕ=-, 所以()2)4f x x π=-,由3222,242k x k k Z πππππ+≤-≤+∈, 解得37,88k x k k Z ππππ+≤≤+∈,所以()f x 的单调递减区间为37,()88k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦,故选:D 由三视图可知,几何体为一个三棱锥A BCD -, 如下图所示:根据三视图可知,4DB =,2DC =,高为2,1182323A BCD V DC DB -∴=⨯⨯⨯⨯=,∴所求几何体体积:83,故选:C .10. 在ABC 中,D 、E 、F 分别是边BC 、CA 、AB 的中点,AD 、BE 、CF 交于点G ,则:①1122EF CA BC =-;②1122BE AB BC =-+;③AD BE FC +=; ④0GA GB GC ++=. 上述结论中,正确的是( ) A. ①② B. ②③C. ②③④D. ①③④C 分析】作出图形,利用平面向量的加法法则可判断①②③④的正误. 如下图所示:对于①,F 、E 分别为AB 、AC 的中点,111222FE BC CA BC ∴=≠-,①错误; 对于②,以BA 、BC 为邻边作平行四边形ABCO ,由平面向量加法的平行四边形法则可得2BE BO BA BC AB BC ==+=-+,1122BE AB BC ∴=-+,②正确;对于③,由②同理可得2AD AB AC =+,1122AD AB AC ∴=+,同理可得1122CF CA CB =+,()102AD BE CF AB AC BA BC CA CB ∴++=+++++=, AD BE CF FC ∴+=-=,③正确;对于④,易知点G 为ABC 的重心,所以,23GA AD =-,23GB BE =-,23GC CF =-,因此,()203GA GB GC AD BE CF ++=-++=,④正确.故选:C. 11. 双曲线()2222:10,0x y C a b a b-=>>的左、右焦点分别为1F 、2F ,M 为C 的渐近线上一点,直线2F M 交C 于点N ,且20F M OM ⋅=,2232F M F N =(O 为坐标原点),则双曲线C 的离心率为( ) A. 5 B. 2 C. 3 D. 2 A设点M 为第一象限内的点,求出直线2F M 的方程,可求得点M 的坐标,由2232F M F N =可求得点N 的坐标,再将点N 的坐标代入双曲线C 的方程,进而可求得双曲线C 的离心率.设点M 为第一象限内的点,可知直线OM 的方程为by x a=,()2,0F c ,2F M OM ⊥,所以,直线2F M 的方程为()ay x c b=--, 联立()b y x a a y x c b ⎧=⎪⎪⎨⎪=--⎪⎩,解得2a x c ab y c ⎧=⎪⎪⎨⎪=⎪⎩,即点2,a ab M c c ⎛⎫ ⎪⎝⎭,设点(),N x y ,()222,,0,a ab b ab F M c c c c c ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭,()2,F N x c y =-,2232F M F N =,()23232b x c c ab y c ⎧-=-⎪⎪∴⎨⎪=⎪⎩,解得222323a c x c ab y c ⎧+=⎪⎪⎨⎪=⎪⎩,即点2222,33a c ab N c c ⎛⎫+ ⎪⎝⎭,将点N 的坐标代入双曲线C 的方程得22222222331a c ab c c a b ⎛⎫+⎛⎫ ⎪ ⎪⎝⎭⎝⎭-=, 可得22249e e e⎛⎫+-= ⎪⎝⎭,整理得25e =,1e >,解得5e =故选:A.12. 已知a 、b R ∈,函数()()3210f x ax bx x a =+++<恰有两个零点,则+a b 的取值范围( )A. (),0-∞B. (),1-∞-C. 1,4⎛⎫-∞- ⎪⎝⎭D. 1,4⎛⎫-∞ ⎪⎝⎭D利用导数分析函数()y f x =的单调性,可得出该函数的极小值()10f x =,由题意得出()()2111321111321010f x ax bx f x ax bx x ⎧=++=⎪⎨=+++='⎪⎩,进而可得23112111223a x xb x x ⎧=+⎪⎪⎨⎪=--⎪⎩,可得出32111222a b x x x +=--,令110t x =<,由0a <可得出12t <-,构造函数()32222g t t t t =--,求得函数()y g t =在区间1,2⎛⎫-∞- ⎪⎝⎭上的值域,由此可求得+a b 的取值范围.()321f x ax bx x =+++且0a <,()2321f x ax bx '=++,24120b a ∆=->, 则方程()0f x '=必有两个不等的实根1x 、2x ,设12x x <, 由韦达定理得1223bx x a+=-,12103x x a=<,则必有120x x <<,且()21113210f x ax bx '=++=,① 当1x x <或2x x >时,()0f x '<;当12x x x <<时,()0f x '>.所以,函数()y f x =的单调递增区间为()12,x x ,单调递减区间为()1,x -∞和()2,x +∞.由于()010f =>,若函数()y f x =有两个零点,则()32111110f x ax bx x =+++=,②联立①②得21132111321010ax bx ax bx x ⎧++=⎨+++=⎩,可得23112111223a x xb x x ⎧=+⎪⎪⎨⎪=--⎪⎩,所以,32111222a b x x x +=--, 令110t x =<,令()32222g t t t t =--,则()a b g t +=, ()3222210a t t t t =+=+<,解得12t <-,()()()()2264223212311g t t t t t t t '=--=--=+-.当12t <-时,()0g t '>,此时,函数()y g t =单调递增,则()321111122222224a b g t g ⎛⎫⎛⎫⎛⎫⎛⎫+=<-=⨯--⨯--⨯-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.故选:D.第Ⅱ卷(90分)二、填空题:本大题共4小题,每小题5分,满分20分.把答案填写在答题卡上的相应位置. 13. 若命题:p 若直线l 与平面α内的所有直线都不平行,则直线l 与平面α不平行;则命题p ⌝是________命题(填“真”或“假”).假先写出p ⌝,再判断真假即可.命题:p 若直线l 与平面α内的所有直线都不平行,则直线l 与平面α不平行; 命题p ⌝:若直线l 与平面α内的所有直线都不平行,则直线l 与平面α平行,假命题. 故答案为:假命题.14. 若直线l 经过抛物线24x y =-的焦点且与圆22(1)(2)1x y -+-=相切,则直线l 的方程为________.0x =或4330x y --=先根据抛物线方程24x y =-,求得焦点坐标()0,1F -,再分直线的斜率不存在和直线的斜率存在时,两种情况设直线方程,然后利用圆心到直线的距离等于半径求解. 因为抛物线方程为24x y =-, 所以焦点坐标为:()0,1F -,当直线的斜率不存在时,设直线方程为:0x =, 圆心到直线的距离为1d r ,符合题意,当直线的斜率存在时,设直线方程为:1y kx =-,即10kx y --=, 圆心到直线的距离为2311k d r k -===+,解得43k =, 所以直线方程为4330x y --=, 故答案为:0x =或4330x y --=15. 已知函数()cos ()f x x x x R =-∈,α,β是钝角三角形的两个锐角,则(cos )f α________(sin )f β (填写:“>”或“<”或“=”).>对函数()f x 求导判断其单调性,再由钝角三角形内角判断cos ,sin αβ的大小. 由()1sin 0f x x '=+≥,可得()f x 在R 上单调递增, 因为α,β是钝角三角形两个锐角,所以2παβ+<,022ππβα<<-<,sin y x =在0,2π⎛⎫ ⎪⎝⎭上单调增,sin sin 2πβα⎛⎫∴<- ⎪⎝⎭,sin cos βα<,所以()(cos )sin f f αβ> 故答案为:>16. 已知三棱锥P ABC -的顶点P 在底面的射影O 为ABC 的垂心,若2ABC OBC PBC S S S ⋅=△△△,且三棱锥P ABC -的外接球半径为3,则PAB PBC PAC S S S ++△△△的最大值为________. 18连AO 交BC 于D ,由顶点P 在底面的射影O 为ABC 的垂心,得AD BC ⊥,进而证明,,BC PA PC AB PD BC ⊥⊥⊥,由2ABC OBC PBC S S S ⋅=△△△。
安徽省合肥八中上学期高三第二次月考 (2)

20XX年中学测试中学试题试卷科目:年级:考点:监考老师:日期:2021-2021学年度安徽省合肥八中上学期高三第二次月考化学试卷可能用到的相对原子质量:H 1 C 12 N 14 O 16 Ca 40 Fe 56 Cu 64第Ⅰ卷(选择题,共48分)一、选择题(本题包括16小题,每小题3分,共48分。
每小题只有一个选项符合题意。
将正确答案转涂到答题卡相应的位置)1.设N A代表阿伏加德罗常数,下列说法正确的是()A.5.6g铁与足量盐酸反应转移的电子数为0.3N AB.100mL2.0mol/L的盐酸与醋酸溶液中氢离子均为0.2N AC.标准状况下,22.4L氦气与22.4L氟气所含原子数均为2N AD.常温常压下,20g重水(D2O)中含有的电子数为10N A2.关于胶体和溶液的叙述中正确的是()A.胶体带电荷,而溶液呈电中性B.胶体是一种较稳定的分散系,而溶液是一种非常稳定的分散系C.胶体加入某些盐可产生沉淀,而溶液不能D.胶体能够发生丁达尔现象,溶液也能发生丁达尔现象3.下列叙述正确的是()A.在氧气还原反应中,肯定有一种元素被氧化,另一种元素被还原B.有单质参加的反应一定是氧化还原反应C.有单质参加的化合反应一定是氧化还原反应D.失电子难的原子,容易获得的电子4.在配制一定物质的量浓度的盐酸溶液时,下列错误操作可使所配制溶液浓度偏高的是()A.用量筒量取浓盐酸时俯视读数B.溶解搅拌时有液体飞溅C.摇匀后见液面下降,再加上至刻度线D.定容时俯视容量瓶瓶颈刻度线5.一化学兴趣小组在家中进行化学实验,按照图1连接好线路发现灯泡不亮,按照图2连接好线路发现灯泡亮,由此得出的结论正确的是()A.NaCl是非电解质B.NaCl溶液是电解质C.NaCl在水溶液中电离出了可以自由移动的离子D.NaCl溶液中水电离出大量的离子6.下列条件下,两瓶气体所含原子数一定相等的是()A.同质量、不同密度的N2和COB.同温度、同体积的H2和N2C.同体积、不同密度的C3H4和C3H6D.同压强、同体积的N2O和CO27.下列离子方程式中正确的是()A.硫酸镁溶液和氢氧化钡溶液反应SO42-+Ba2+ == BaSO4↓B.铜片加入稀硝酸中:Cu + 2NO3-+ 4H+ == Cu2+ + 2NO2↑+2H2OC.FeBr2溶液中加入过量的氯水:2Fe2++2Br-+2Cl2 == Br2+4Cl-+2Fe2+D.等体积等物质的量浓度的NaHCO3和Ba(OH)2两溶液混合:HCO3-+ Ba2+ + OH-== BaCO3↓+H2O8.氢化钙可以作为生氢剂(其中CaH2中氢元素为-1价),反应方程式如下:CaH2+2H2O == Ca(OH)2+2H2↑,其中水的作用是()A.既不是氧化剂也不是还原剂B.是氧化剂C.是还原剂D.既是氧化剂又是还原剂9.离子反应、复分解反应、置换反应和氧化还原反应之间可用集合关系表示,其正确的是()10.有BaCl2T NaCl的混合溶液aL,将它均分成两份。
安徽省合肥市2021届高三一模数学试题及答案(理科)

合肥市2021年高三第一次教学质量检测数学试题(理科)(解析版) (考试时间:120 分钟满分:150分)一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知复数2i1iz -=+(i 为虚数单位),则z 的共轭复数为( ) A.33i 22+ B.33i 22-C.13i 22+ D.13i 22- 【答案】C 【详解】()()()()=-+--=+-=i i i i i i z 111212i 2321-,所以i z 2321+=, 故选:C.2.已知集合{}2xA y y ==,{B x y ==,则A B ⋂=( )A.∅B.[]0,1C.()0,1D.(]0,1【答案】D 【详解】{}x y y A 2==()∞+=,0,{}(]1,1∞-=-==x y x B ,所以(]1,0=B A , 故选;D.3.某商场2020年部分月份销售金额如下表:若用最小二乘法求得回归直线方程为6.171.38ˆ-=x y,则a =( ) A.198.2 B.205 C.211 D.213.5 【答案】B 【详解】 由题意知,5108642++++=x 6=,5850536828613264aa y +=++++=, 因为样本中心点()y x ,在回归直线方程6.171.38ˆ-=x y上, 所以6.1761.385850-⨯=+a,解得205=a , 故选:B.4.若数列{}n a 的前n 项和n S 满足321n n S a =-,则5a =( )A.32B.321C.116- D.16- 【答案】D 【详解】当1=n 时,12311-=a a ,11-=a ,当2≥n 时,12311--=-n n a S ,又123-=n n a S ,两式相减,得1-223n n n a a a -=, 即1-2n n a a -=()2≥n ,所以数列{}n a 为以1-为首项,以2-为公比的等比数列, 所以()()162145-=-⨯-=a ,故选:D.5.已知F 是椭圆E :()222210x y a b a b+=>>的左焦点,椭圆E 上一点()2,1P 关于原点的对称点为Q ,若PQF △的周长为则a b -=( )B.2【答案】A 【详解】取椭圆E 的右焦点F ',连接F P ',F Q ',则四边形F QFP '为平行四边形,则QF F P =',因为PQF ∆的周长为5224+,所以5224+=++PQ QF PF ,所以52242+=+'+PO F P PF ,由椭圆定义知,a F P PF 2='+,因为()1,2P ,所以51222=+=PO ,所以5224522+=+a ,解得22=a , 又点()1,2P 在椭圆E 上,所以11422=+ba , 解得2=b ,所以2222=-=-b a ,故选:A.6.自2019年1月1日起,我国个人所得税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为:个人所得税税额=应纳税所得额⨯税率-速算扣除数.应纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除.其中,“基本减除费用”(免征额)为每年60000元.部分税率与速算扣除数见下表:若某人全年综合所得收入额为249600元,专项扣除占综合所得收入额的20%,专项附加扣除是52800元,依法确定其他扣除是4560元,则他全年应缴纳的个人所得税应该是()A.5712元B.8232元 C.11712元 D.33000元【答案】A 【详解】由题意知,应纳税所得额为()-%20-12496008232060000456052800=--, (]144000,3600082320∈,所以税率为%10,则此人全年应缴纳个人所得税应该为57122520%1082320=-⨯, 故选:A.7.在ABC △中,2AB =,3AC =,2BD DC =,AE EB =,则AD CE ⋅=( )A.76-B.76C.163- D.163【答案】C 【详解】+=+=AB BD AB AD ()AC AB AB AC AB BC 32313232+=-+=+,AC AB AC AE CE -=-=21, 所以=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+=⋅AC AB AC AB CE AD 21323131633226132612222-=⨯-⨯=-AC AB ,故选:C. 【点睛】关键点睛:⑴用向量AB ,AC 作基底表示向量AD ,CE ;⑵用平面向量的数量积运算公式计算CE AD ⋅的值.8.设函数()21log 20,0x x f x x ⎧⎛⎫+>⎪ ⎪=⎝⎭⎨⎪≤⎩.若14,2x ⎛⎫∈- ⎪⎝⎭时,方程()1f x k +=有唯一解,则实数k 的取值范围为( )A.(B.⎡⎣C.()0,2D.[)1,2【答案】B 【详解】因为⎪⎩⎪⎨⎧≤->⎪⎭⎫ ⎝⎛+=0,0,21log )(2x x x x x f ,所以()⎪⎩⎪⎨⎧-≤+-->⎪⎭⎫ ⎝⎛+=+1,11,23log )1(2x x x x x f , 方程k x f =+)1(在⎪⎭⎫ ⎝⎛-21,4上有唯一解,即函数)1(+=x f y 与函数k y =的图象在⎪⎭⎫ ⎝⎛-21,4上有唯一交点,画出)1(+=x f y 在⎪⎭⎫ ⎝⎛-21,4的图象,如图所示,由图象可知31<≤k ,故选:B.【点睛】关键点睛:⑴准确画出函数)1(+=x f y 在⎪⎭⎫ ⎝⎛-21,4的图象;⑵方程k x f =+)1(在⎪⎭⎫ ⎝⎛-21,4上有唯一解,即函数)1(+=x f y 与函数k y =的图象在⎪⎭⎫ ⎝⎛-21,4上有唯一交点.9.我国古代数学名著《九章算术》第五卷“商功”中,把底面为矩形且有一条侧棱与底面垂直的四棱锥称为“阳马”.今有“阳马”P ABCD -,PA AB AD ==,E ,F 分别为棱PB ,PD 的中点.以下四个结论:①PB ⊥平面AEF ;②EF ⊥平面PAC ;③平面PBD ⊥平面AEF :④平面AEF ⊥平面PCD .其中正确的是( ) A.①③ B.①④ C.②③ D.②④【答案】D 【详解】因为AD AB =,四边形ABCD 为矩形,所以四边形ABCD 为正方形, 因为四棱锥ABCD P -有一条侧棱与底面垂直,且AB PA =AD =, 所以⊥PA 平面ABCD ,所以AP AD AB ,,两两互相垂直,如图建立空间直角坐标系xyz A -,则()0,0,0A ,()0,0,2B ,()0,2,2C ,()0,2,0D ,()2,0,0P ,()1,0,1E ,()1,1,0F ,对①:因为()2,0,2-=PB ,()1,1,0=AF ,()0212-1002≠-=⨯+⨯+⨯=⋅AF PB , 所以PB 和AF 不垂直,所以PB 与平面AEF 不垂直,故①错误; 对②:()0,1,1-=EF ,()2,0,0=AP ,()0,2,2=AC ,因为()200101⨯+⨯+⨯-=⋅AP EF 0=,()0002121=⨯+⨯+⨯-=⋅AC EF , 所以AP EF ⊥,AC EF ⊥,A AC AP = ,所以⊥EF 平面PAC ,故②正确; 对③:()2,0,2-=PB ,()0,2,2-=BD ,()1,1,0=AF ,()0,1,1-=EF ,设平面PBD 的法向量为()z y x m ,,= ,由⎪⎩⎪⎨⎧=⋅=⋅0BD m PB m ,得⎩⎨⎧=+-=-022022y x z x ,令1=x ,则()1,1,1=m,设平面AEF 的法向量为()z y x n ,,= ,由⎪⎩⎪⎨⎧=⋅=⋅0EF n AF n ,得⎩⎨⎧=+-=+00y x z y ,令1=x ,则()1,1,1-=n,因为01≠=⋅n m,所以平面PBD 与平面AEF 不垂直,故③错误;对④:()2,2,0-=PD ,()0,0,2-=CD ,设平面PCD 的法向量为()z y x a ,,=,由⎪⎩⎪⎨⎧=⋅=⋅0CD a PD a ,得⎩⎨⎧=-=-02022x z y ,令1=y ,则()1,1,0=a , 又平面AEF 的法向量为()1,1,1-=n,且()0111110=-⨯+⨯+⨯=⋅n a,所以平面⊥AEF 平面PCD ,故④正确; 故②④正确, 故选:D.10.在ABC △中,角A ,B ,C 的对边分别为a ,b ,c .若sin 2sin 2sin cos a A c C b C A +=,则角A 的最大值为( )A.6π B.4π C.3πD.23π 【答案】A【详解】由正弦定理和余弦定理得R a A 2sin =,R b B 2sin =,RcC 2sin =,bc a c b A 2cos 222-+=,由A C b C c A a cos sin 2sin 2sin =+,得⋅⋅=⋅+⋅R c b R c c R a a 22222bc a c b 2222-+, 化简得2222b c a =+,即2222c b a -=,代入bca cb A 2cos 222-+=,得bcc b c b A 22cos 2222--+=234324322=⋅⋅≥+=bc c b bc c b ,当且仅当c b 3=时等号成立,所以⎥⎦⎤⎝⎛∈30π,A ,所以A 的最大值为3π, 故选:A.11.设双曲线C :()222210,0x y a b a b-=>>的左、右焦点分别为1F ,2F ,曲线C 上一点P到x 轴的距离为2a ,12120F PF ∠=︒,则双曲线C 的离心率为( )B.1+C.2+D.4【答案】C 【详解】因为双曲线C 上一点P 到x 轴的距离为a 2, 由等面积法得,212121sin 21221PF F PF PF a F F ∠⋅⋅⋅=⋅⋅, 即︒⋅⋅⋅=⋅⋅120sin 21222121PF PF a c ,所以ac PF PF 3821=, 由余弦定理得,+=21221PF F F ︒-120cos 22122PF PF PF ,即()()22122PF PF c -=213PF PF +,即()2122122212PF PF PF PF PF PF +-=+,即()()2222a c =ac 383⨯+,整理得-+ac c 232032=a , 两边同时除以2a ,得03232=-+e e ,解得23+=e 或23-=e (舍),故选:C.12.若两个正四面体的顶点都是一个棱长为1的正方体的顶点,则这两个正四面体公共部分的体积为( ) A.516 B.14 C.524D.16【答案】D 【详解】如图,在正方体中作出两个四面体,结合立体图形可知,两个四面体的公共部分是以正方体六个面的中心为顶点的正八面体, 将该正八面体分为上、下两个完全相同的正四棱锥,且每个正四棱锥的棱长均为22,高为21,所以该正八面体的体积21223122⨯⎪⎪⎭⎫⎝⎛⨯⨯=V61=,故选:D.【点睛】关键点睛:本题考查空间几何体的特征、多面体体积的求解.解题关键是:⑴在正方体中作出两个正四面体;⑵结合立体图形知,两个四面体的公共部分是以正方体六个面的中心为顶点的正八面体.第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题5分,满分20分.把答案填在答题卡上的相应位置.13.若实数x,y满足条件10,10,220,x yx yx y+-≥⎧⎪-+≥⎨⎪+-≤⎩则32x y-的最小值为 .【答案】2-【详解】由线性约束条件画出可行域,如图中阴影部分,设yxz23-=,则223zxy-=,画出直线23xy=,平移直线,当直线经过()1,0A时,直线的纵截距最大,则yxz23-=取得最小值,所以()2120323min -=⨯-⨯=-y x . 故答案为:2-. 14.若函数()ln a xf x x=的图象在点()()1,1f 处的切线与直线410x y +-=垂直,则a 的值等于 . 【答案】 4 【详解】2ln )(x x a a x f -=',因为直线014=-+y x 的斜率为41-, 所以4)1(='f ,即4=a . 故答案为:4.15.在521x x ⎛⎫- ⎪⎝⎭的展开式中,x 的偶次项系数之和是 .【答案】16- 【详解】521⎪⎭⎫ ⎝⎛-x x 的展开式的第1+r 项为()rr r rr r r x C x x C T 355255111--+-=⎪⎭⎫ ⎝⎛-=,所以当5,3,1=r 时,对应的项为偶次项,所以x 的偶次项系数之和为16553515-=---C C C .故答案为:16-.16. 百善孝为先,孝敬父母是中华民族的传统美德.因父母年事渐高,大张与小张兄弟俩约定:如果两人在同一天休息就一起回家陪伴父母,并把这一天记为“家庭日”.由于工作的特殊性,大张每工作三天休息一天,小张每周星期一与星期五休息,除此之外,他们没有其它休息日.已知2021年1月1日(星期五)是他们约定的“家庭日”,则2021年全年他们约定的“家庭日”共有 个. 【答案】27【详解】 2021年共有365天,记2021年1月1日为第一天,大张三天休息一天,小张每周一或周五休息,他俩同时在2021年1月1日休息, 记集合{}3651,,14≤≤∈+==x Z k k x x A ,{}3651,4717≤≤∈+=+==y Z k k y k y y B ,或,则集合B A 中的元素的个数即为他们约定的“家庭日”的个数.①当171421+=+k k ,则2174k k =()Z k k ∈21,,所以()Z k k k ∈=3317, 因为3651411≤+≤k ,所以9101≤≤k ,则91703≤≤k ,即()Z k k ∈≤≤33130, 所以符合条件的3k 有14个;②当471421+=+k k ,则37421+=k k ()Z k k ∈21,,所以()()134221+=-k k k , 所以()132+k 是4的倍数,所以()Z k k k ∈=+33241,所以()Z k k k ∈-=33214,因为3654712≤+≤k ,所以7361732≤≤-k ,则736114733≤-≤-k ,即()Z k k ∈≤≤3379271,所以符合条件的3k 有13个. 综上,2021年“家庭日”的个数为271314=+. 故答案为:27【点睛】本题考查等差数列的通项、集合的运算.关键点睛:⑴将大张和小张的休息日用等差数列的通项公式表示并用集合的形式表示;⑵集合B A 中的元素的个数即为他们约定的“家庭日”的个数;⑶利用3651411≤+≤k 和3654712≤+≤k ,得到3k 的范围.三、解答题:本大题共6小题,满分70分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)某厂将一种坯件加工成工艺品需依次经过A 、B 、C 三道工序,三道工序相互独立.工序A 的加工成本为70元/件,合格率为78,合格品进入工序B ;工序B 的加工成本为60元/件,合格率为67,合格品进入工序C :工序C 的加工成本为30元/件,合格率为56.每道工序后产生的不合格品均为废品.(1)求一个坯件在加工过程中成为废品的概率;(2)已知坯件加工成本为A 、B 、C 三道工序加工成本之和,求每个坯件加工成本的期望.【答案】(1)83;(2)答案见解析 【详解】⑴ 每道工序生产的都是合格品的概率为85657687=⨯⨯, 则一个坯件在加工过程中成为废品的概率83851=-=P ; ⑵设每个坯件的加工成本为ξ元,则ξ的可能取值为70,130,160()8187170=-==ξP ;()8176187130=⎪⎭⎫ ⎝⎛-⨯==ξP ;()437687160=⨯==ξPξ∴的分布列为14543160811308170=⨯+⨯+⨯=∴ξE ,所以每个坯件加工成本的期望为145. 18.(本小题满分12分)如图,在平面直角坐标系xOy 中,角ϕ的终边与单位圆的交点为A ,圆C :223x y +=与x 轴正半轴的交点是0P .若圆C 上一动点从0P 开始,以rad /s π的角速度逆时针做圆周运动,t 秒后到达点P .设()2f t AP =.(1)若3πϕ=且()0,2t ∈,求函数()f t 的单调递增区间;(2)若123f ⎛⎫= ⎪⎝⎭,536ππϕ<<,求56f ⎛⎫ ⎪⎝⎭. 【答案】(1)⎥⎦⎤⎢⎣⎡34,31;(2)22-4【详解】由已知条件和三角函数的定义得,()ϕϕsin ,cos A ,()t t Pππsin 3,cos 3,则()()222sin 3sin cos 3cos )(t tAP t f πϕπϕ-+-==t t πϕπϕsin sin 32cos cos 324--=()ϕπ--=t cos 324⑴若3πϕ=,则⎪⎭⎫⎝⎛--=3cos 324)(ππt t f 令()Z k k t k ∈+≤-≤πππππ232,解得()Z k k t k ∈+≤≤+234231 又()2,0∈t ,)(t f ∴的单调递增区间为⎥⎦⎤⎢⎣⎡34,31. ⑵由2)31(=f ,653πϕπ<<,得23cos 324=⎪⎭⎫ ⎝⎛--ϕπ 即333cos =⎪⎭⎫⎝⎛-ϕπ, 032<-<-ϕππ , 所以 363sin -=⎪⎭⎫⎝⎛-ϕπ 2243sin 32465cos 324)65(-=⎪⎭⎫⎝⎛-+=⎪⎭⎫ ⎝⎛--=ϕπϕπf . 19.(本小题满分12分)如图,四边形ABCD 中,//AD BC ,90BAD ∠=︒,AB BC ==AD =E ,F 分别是线段AD ,CD 的中点.以EF 为折痕把DEF △折起,使点D 到达点P 的位置,G 为线段PB 的中点.(I )证明:平面//GAC 平面PEF ;(2)若平面PEF ⊥平面ABCFE ,求直线AG 与平面PAC 所成角的正弦值.【答案】(I )答案见解析;(2)105【详解】⑴连接BE 交AC 于点M ,连接GM ,CE由已知可得,四边形ABCE 是正方形,M ∴是线段BE 的中点,G 为线段PB 的中点,GM PE ∥∴⊂GM 平面GAC ,⊄PE 平面GAC ,∥PE ∴平面GAC ,F E , 分别为线段CD AD ,的中点,AC EF ∥∴,⊂AC 平面GAC ,⊄EF 平面GAC ,∥EF ∴平面GAC ,又E EF PE = ,⊂EF PE ,平面PEF ,∴平面∥GAC 平面PEF .⑵ 平面⊥PEF 平面ABCFE ,平面 PEF 平面EF ABCFE =,EF PF ⊥,⊥∴PF 平面ABCFE ,FP FC FE ,,∴两两垂直.以点F 为原点,FP FC FE ,,分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,则()1,0,0P ,()0,1,0C ,()0,2,1B ,()0,1,2A ,⎪⎭⎫⎝⎛21,1,21G , ⎪⎭⎫⎝⎛-=∴21,0,23AG ,()1,1,0-=CP ,()0,0,2=CA设平面PAC 的法向量()z y x n ,,=由⎪⎩⎪⎨⎧=⋅=⋅00CA n CP n ,得⎩⎨⎧==+-020x z y ,令1=y , 则()1,1,0=n, 设直线AG 与平面PAC 所成角为θ,则10522521cos sin =⨯===nθ 所以直线AG 与平面PAC 所成角的正弦值为105. 20.(本小题满分12分)已知F 是抛物线E :()220y px p =>的焦点,直线l :()()0y k x m m =->与抛物线E 交于A ,B 两点,与抛物线E 的准线交于点N .(1)若1k =时,AB =求抛物线E 的方程;(2)是否存在常数k ,对于任意的正数m ,都有2FA FB FN =⋅?若存在,求出k 的值:若不存在,说明理由.【答案】(1)x y 42=;(2)1±=k 【详解】⑴设()11,y x A ,()22,y x B由()⎩⎨⎧-==m x k y px y 22,消去y 得,()0222222=++-m k x p m k x k , l 与抛物线E 交于两点,0≠∴k ,又0,0>>p m ,04822>+=∆∴p mp k 恒成立,⎪⎩⎪⎨⎧=+=+∴22122122m x x k p m x x ,当1=k 时,22122421p mp x x k AB +=-+=, 因为224+=m AB ,所以2242422+=+m p mp , 整理得,()()0222=-++p m p ,0,0>>p m ,2=∴p ,所以抛物线E 的方程为x y 42=; ⑵假设存在常数k 满足题意.抛物线E 的方程为px y 22=,其焦点为⎪⎭⎫⎝⎛0,2p F ,准线方程为2p x -=,⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+--∴2,2p m k p N ,从而22222⎪⎭⎫ ⎝⎛++=p m k p FN 由抛物线的定义得,21p x FA +=,22px FB += , ()222221212124222k p p m p x x p x x p x p x FB FA +⎪⎭⎫ ⎝⎛+=+++=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=∴由2FN FB FA =得,22222222⎪⎭⎫ ⎝⎛++=+⎪⎭⎫ ⎝⎛+p m k p k p p m ,即()0212222=⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛+-k p p m k因为022>⎪⎭⎫ ⎝⎛+p m ,022>k p ,012=-∴k ,即1±=k .所以存在1±=k ,使得2FN FB FA =对于任意的正数m 都成立. 21.(本小题满分12分) 已知函数()ln 1af x x x=++有两个零点. (1)求实数a 的取值范围;(2)记()f x 的两个零点分别为1x ,2x ,求证:1241e x x <(e为自然对数的底数). 【答案】(1)20-<<e a ;(2)答案见解析 【详解】⑴)(x f 的定义域为()∞+,0,2)(xax x f -=' ①当0≤a 时,0)(>'x f 恒成立,)(x f 在()∞+,0上单调递增,)(x f 至多有一个零点,不符合题意;②当0>a 时,0)(='a f ,且当()a x ,0∈时,0)(<'x f ;当()+∞∈,a x 时,0)(>'x f ,)(x f ∴在()a ,0上单调递减,在()+∞,a 上单调递增,从而)(x f 的最小值为2ln )(+=a a f .(i )若0)(≥a f ,即2-≥e a ,此时)(x f 至多有一个零点,不符合题意;(ii )(ii )若0)(<a f ,即20-<<e a ,)(x f 在()+∞,a 上单调递增,0)(<a f ,01)1(>+=a f ,根据零点存在性定理得,)(x f 在()+∞,a 内有且只有一个零点.又 )(x f 在()a ,0上单调递减,且0)(<a f ,考虑11ln 2)(2++=a a a f 的正负. 令11ln 2)(++=xx x g ,()2,0-∈e x , 则012)(2<-='xx x g ,)(x g ∴在()2,0-e 上单调递减, 03)()(22>-=>∴-e e g x g ,即011ln 2)(2>++=aa a f , a a <<20 ,0)(2>∴a f ,0)(<a f ,根据零点存在性定理得,)(x f 在()a ,0内有且只有一个零点.所以,当20-<<e a 时,)(x f 恰有两个零点,符合题意.综上得,20-<<e a .⑵由条件得,⎪⎪⎩⎪⎪⎨⎧=++=++01ln 01ln 2211x a x x a x ,⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎫ ⎝⎛-=--⎪⎪⎭⎫ ⎝⎛+-=+∴2121212111ln ln 211ln ln x x a x x x x a x x()2ln 112ln ln 21111ln ln ln ln 12121212212121121221-⎪⎪⎭⎫ ⎝⎛⋅-+=---+=-⎪⎪⎭⎫ ⎝⎛+--=+x x x x x x x x x x x x x x x x x x x x 要证421-<e x x ,即证4ln ln 21-<+x x ,即证42ln 11121212-<-⎪⎪⎭⎫ ⎝⎛⋅-+x x x x x x , 即证2ln 11121212-<⎪⎪⎭⎫ ⎝⎛⋅-+x x x x x x ,即证2ln 11121212>⎪⎪⎭⎫ ⎝⎛⋅-+x x x x x x ①,设12x x t =,不妨设21x x <,由2210x e x <<<-知,1>t 证①式,即转化为证明:当1>t 时,2ln 11>-+t t t , 设112ln )(+-⋅-=t t t t h ,则()()()22211141)(+-=+-='t t t t t t h , ∴当1>t 时,0)(>'t h 恒成立,即)(t h 在()+∞,1上单调递增, ∴当1>t 时,0)1()(=>h t h ,所以4211e x x <成立. 解法二:不妨设21x x <,由⑴可知,()2,0-∈ea ,()a x ,01∈,()+∞∈,2a x ,)(x f 在()+∞,a 上单调递增,要证4211e x x <,即证4121e x x <,即证()⎪⎪⎭⎫⎝⎛<4121e x f x f , 即证03ln 141>+--x ae x ,即证0-3ln 141<+x ae x由01ln )(111=++=x ax x f ,得()1ln 11+-=x x a , ∴只需证()01ln 3ln 12141<+++x x e x ①,令()1ln 3ln )(24+++=x x e x x h ,则()3ln 21)(4++='x x e xx h , 令()3ln 21)(4++=x x e x x ϕ,则()()5ln 215ln 21)(42442++-=++-='x e xe x e x x ϕ, 由20-<<e x ,得2ln -<x ,241xe <,0)(<'∴x ϕ,)(x ϕ∴在(]2,0-e 上单调递减,且0)(2=-e ϕ, (]2,0-∈∴e x ,0)(>x ϕ,即0)(>'x h ,)(x h ∴在(]2,0-e 上单调递增,且0)(2=-e h ,而21-<<e a x , 0)()(2=<∴-e h x h ,即①式得证,所以4211ex x <成立. 【点睛】方法点睛:⑴研究函数)(x f 零点问题,方法一:令0)(=x f ,参变分离,得到)(x g a =的形式,借助数形结合(几何法)求解;方法二:整体含参通过求导讨论)(x f 的单调性、极值的符号,由数形结合可知函数)(x f 的图象与x 轴的交点情况即函数)(x f 的零点情况. ⑵处理极值点偏移问题的基本策略是利用极值点满足的等式构建不等式,再利用导数讨论不等式对应的函数的单调性即可.22.(本小题满分10分)选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,曲线C 的参数方程为2cos 2tan 1tan x y βββ=⎧⎪⎨=⎪+⎩(β为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系. (1)求曲线C 的极坐标方程:(2)若点M ,N 为曲线C 上两点,且满足3MON π∠=,求2211OMON-的最大值.【答案】(1)()Z k k ∈+≠+=,2sin 31122ππθθρ;(2)233 【详解】⑴化简曲线C 的参数方程得,⎪⎩⎪⎨⎧==ββ2sin 212cos y x (β为参数,且ππβk +≠2,Z k ∈) 消去参数β得曲线C 的普通方程()11422-≠=+x y x .化成极坐标方程为()()()Z k k p ∈+≠=+,21sin 4cos 22ππθθθρ,θρ22sin 311+=∴()Z k k ∈+≠,2ππθ.⑵ 不妨设()θρ,1M ,⎪⎭⎫⎝⎛+32πθρ,N ,则1ρ=OM ,2ρ=ON , - ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++-+=+∴3sin 31sin 31112222πθθON OM⎪⎭⎫⎝⎛+-=--=32sin 2332cos 492sin 433πθθθ 当且仅当()Z k k ∈+=ππθ127时,2211ONOM +取得最大值为233. 23.(本小题满分10分)选修4-5:不等式选讲 已知函数()22f x x a x a =--+. (1)若()11f ≥,求实数a 的取值范围;(2)若对任意x R ∈,()20f x ≤恒成立,求a 的最小值.【答案】⑴⎥⎦⎤ ⎝⎛-∞-21,;(2)0【详解】⑴由1)1(≥f ,得11212≥+--a a ,()⎩⎨⎧≥++--≤∴112211a a a 或()⎪⎩⎪⎨⎧≥+--≤<-11221211a a a 或()⎪⎩⎪⎨⎧≥+-->1121221a a a 解得1-≤a 或211-≤<-a , a ∴的取值范围为⎥⎦⎤ ⎝⎛-∞-21,.⑵ 设t x =2()0≥t ,由已知得,对任意0≥t ,使得0)(≤t f 成立,0)(≤t f ,则a t a t +≤-22,即()()2242a t a t +≤-,即01232≥+at t ,当0=t ,R a ∈;当0>t ,04≥+a t 恒成立,即0≥a ,0≥∴a ,即a 的最小值为0.。
安徽省合肥八中—度上学期高三第二次月考数学试题(理科)全国通用

安徽省合肥八中2007—2008学年度上学期高三第二次月考数学试题(理科)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合I={1,2,3,4},A={1},B={2,4},则=⋃B C A I ( ) A .{1} B .{1,3} C .{3} D .{1,2,3} 2.若集合A={1,m 2},B={2,4},则“m=2”是“A ∩B={4}”的 ( ) A .充要条件 B .充分不必要条件 C .必要不充分条件 D .既不充分也不必要条件 3.曲线),2(2e e y x 在点=处的切线与坐标轴所围三角形的面积为 ( )A .249eB .22eC .22eD .2e4.设)(x f 为可导函数,且12)1()1(lim-=--→xx f f x ,则曲线)(x f y =在点))1(,1(f 处的切线的斜率是( )A .-2B .-1C .21 D .25.设函数⎩⎨⎧≤>+-=-)4(2)4( )1(log )(43x x x x f x 的反函数为=+=--)7()81()(11a f a f x f ,则,且( )A .-2B .-1C .1D .26.函数))((R x x f y ∈=的图象如图所示,则当0<a<1时,函数)(log )(x f x g a =的单调区间是( )A .]21,0[B .),21[)0,(+∞⋃-∞C .]1,[+a aD .)1,21[)0,(⋃-∞7.函数)65(log 221+-=x x y 的单调减区间为( )A .),25(+∞B .)2,(-∞C .)25,(-∞D .(3,+ ∞)8.设函数)(x f 定义在实数集上,它的图象关于直线x=1对称,且当1≥x 时,13)(-=xx f ,则有 ( )A .)32()23()31(f f f <<B .)23()31()32(f f f <<1321239.设)()()(|,13|)(b f a f c f a b c x f x >><<-=且,则下列关系式中一定成立的是( )A .bc33>B .ab 33>C .233<+acD .233>+ac10.若]),[(3||b a x y x ∈=的值域为[1,9],则a b a 222-+的取值范围是 ( )A .[2,4]B .[4,12]C .[2,23]D .[4,16]二、填空题:本大题共5小题,每小题5分,把答案填在题中横线上。
合肥八中高三第二次月考

20XX年高中测试高中试题试卷科目:年级:考点:监考老师:日期:20XX-2021学年度合肥八中高三第二次月考化学试卷可能用到的相对原子质量:H-1 C-12 N-14 O-16 Mg-24 Al-27 S-32 Cl-35.5 Fe-56 Cu-64第I 卷(选择题,共50分)一、选择题:本题包括10小题,每小题2分。
每小题只有一个....选项符合题意。
1.化学用语是学习化学重要工具,下列用来表示物质变化的化学用语中,正确..的是( ) A .电解饱和食盐水时,阳极的电极反应式为:2Cl --2e -=Cl 2↑B .氢氧燃料电池的负极反应式:O 2 + 2H 2O+ 4e - == 4OH -C .粗铜精炼时,与电源正极相连的是纯铜,电极反应式为:Cu -2e - == Cu 2+D .钢铁发生电化腐蚀的正极反应式:Fe -2e - == Fe 2+2.已知(1))g (O 21)g (H 22+ =H 2O (g ) △H 1=a kJ ·1mol -(2))g (O )g (H 222+ =2H 2O (g ) △H 2=b kJ ·1mol -(3))g (O 21)g (H 22+=H 2O (l ) △H 3=c kJ ·1mol -(4))g (O )g (H 222+ =2H 2O (l ) △H 4=d kJ ·1mol -下列关系式中正确的是( ) A . a <c <0B .b >d >0C .2a =b <0D .2c =d >0 3.设C +CO 22CO ;(正反应为吸热反应;反应速率为v 1),N 2+3H 22NH 3;(正反应为放热反应;反应速率为v 2),对于上述反应,当温度升高时,v 1和v 2的变化情况为( )A .同时增大B .同时减小C .增大,减小D .减小,增大 4.下列生产、生活等实际应用,不能..用勒夏特列原理解释的是 ( ) A .实验室中配制FeCl 3溶液时,应向其中加入少量浓盐酸B .合成氨工业中使用铁触媒做催化剂C.饱和FeCl3溶液滴入沸水中可制得氢氧化铁胶体D.热的纯碱溶液去油污效果好5.将0.1mol·L-1的醋酸加水稀释,下列说法正确的是()A.溶液中c(H+)和c(OH-)都减小B.溶液中c(H+)增大C.醋酸的电离平衡向左移动D.溶液的c(OH-)增大6.某化学反应其△H== —122 kJ·mol-1,∆S== 231 J·mol-1·K-1,则此反应在下列哪种情况下可自发进行()A.在任何温度下都能自发进行B.在任何温度下都不能自发进行C.仅在高温下自发进行D.仅在低温下自发进行7.对室温下pH相同、体积相同的醋酸和盐酸两种溶液分别采取下列措施,有关叙述正确的是()A.加适量的醋酸钠晶体后,两溶液的pH均增大B.使温度都升高20℃后,两溶液的pH均不变C.加水稀释2倍后,两溶液的pH均减小D.加足量的锌充分反应后,两溶液中产生的氢气一样多8.下图中A为电源,B为浸透饱和食盐水和酚酞试液的滤纸,C为盛有稀硫酸的电解槽,e、f为Pt电极。
2022学年度上学期高三第二次月考

安徽省合肥八中2022—2022学年度上学期高三第二次月考数学试题〔理科〕一、选择题:本大题共10小题,每题5分,共50分,在每题给出的四个选项中,只有一项为哪一项符合题目要求的.1.集合I={1,2,3,4},A={1},B={2,4},那么=⋃B C A I 〔 〕 A .{1} B .{1,3} C .{3} D .{1,2,3} 2.假设集合A={1,m 2},B={2,4},那么“m=2〞是“A ∩B={4}〞的 〔 〕 A .充要条件 B .充分不必要条件 C .必要不充分条件 D .既不充分也不必要条件 3.曲线),2(2e e y x 在点=处的切线与坐标轴所围三角形的面积为 〔 〕A .249eB .22eC .22eD .2e4.设)(x f 为可导函数,且12)1()1(lim-=--→xx f f x ,那么曲线)(x f y =在点))1(,1(f 处的切线的斜率是〔 〕A .-2B .-1C .21D .25.设函数⎩⎨⎧≤>+-=-)4( 2)4( )1(log )(43x x x x f x 的反函数为=+=--)7()81()(11a f a f x f ,则,且〔 〕A .-2B .-1C .1D .26.函数))((R x x f y ∈=的图象如下图,那么当0<a<1时,函数)(log )(x f x g a =的单调区间是〔 〕A .]21,0[ B .),21[)0,(+∞⋃-∞C .]1,[+a aD .)1,21[)0,(⋃-∞7.函数)65(log 221+-=x x y 的单调减区间为〔 〕A .),25(+∞B .)2,(-∞C .)25,(-∞D .〔3,+ ∞〕8.设函数)(x f 定义在实数集上,它的图象关于直线x=1对称,且当1≥x 时,13)(-=xx f , 那么有〔 〕A .)32()23()31(f f f <<B .)23()31()32(f f f <<C .)31()23()32(f f f <<D .)31()32()23(f f f <<9.设)()()(|,13|)(b f a f c f a b c x f x>><<-=且,那么以下关系式中一定成立的是〔 〕A .bc 33>B .ab 33>C .233<+acD .233>+ac10.假设]),[(3||b a x y x ∈=的值域为[1,9],那么a b a 222-+的取值范围是〔 〕A .[2,4]B .[4,12]C .[2,23]D .[4,16]二、填空题:本大题共5小题,每题5分,把答案填在题中横线上.11.设函数)]}2008([{)(,)(,)(3212312211f f f x x f x x f x x f ,则===-= 12.不等式1|1|+>+x xx x 的解集是 13.函数)2(5)2(1sin )(3--=++=f f bx x a x f ,则,且= 14.当]1,(-∞∈x 时,不等式0631≥++a xx恒成立,那么a 的取值范围是 15.对于函数)(x f 定义域中任意的)(,2121x x x x ≠,有如下结论:①)()()(2121x f x f x x f ⋅=+ ②)()()(2121x f x f x x f +=⋅ ③0)()(2121>--x x x f x f④2)()()2(2121x f x f x x f +<+ 当x x f log )(=时,上述结论中正确结论的序号是三、解做题:本大题共5小题,共75分,解做题应写出文字说明,证实过程或演算步骤.16.〔本小题总分值12分〕函数21)(-+=x x x f 的定义域是集合A,函数])12(lg[)(22a a x a x x g +++-=的定义域是集合B.〔1〕求集合A,B ;〔2〕假设B B A =⋃,求实数a 的取值范围. 17.〔本小题总分值12分〕如图正四棱柱ABCD —A 1B 1C 1D 1的底面边长为1,侧棱长长为2,E,F,G 分别为CC 1,DD 1,AA 1中点.〔1〕求证:A 1F ⊥面BEF ; 〔2〕求证GC 1//面BEF ;〔3〕求直线A 1B 与平面BEF 所成的角.18.〔本小题总分值12分〕对于函数,)(x f 假设存在R x ∈0,使00)(x x f =成立,那么称0x 为)(x f 的不动点,函数.1)1()(2-+++=b x b ax x f 〔1〕当a =1,b=3时,求函数)(x f 的不动点;〔2〕假设对于任意实数b,函数)(x f 恒有两个相异的不动点,求a 的取值范围. 19.〔本小题总分值12分〕设)(211log 2)(log 2)(222x f x b x a x x f 时,,已知=++=有最小值-8. 〔1〕求a,b ;〔2〕求满足x x f 的0)(>的集合A ;〔3〕假设非空集合φ=⋂<-=B A m x x B ,且}|1||{,求实数m 的取值范围. 20.〔本小题总分值13分〕函数)1,0()(≠>=+a a ax f k x 的图象过〔-1,1〕点,其反函数)(1x f-的图象过〔8,2〕点.〔1〕求a,k 的值; 〔2〕假设将)(1x f-的图象向在平移两个单位,再向上平移1个单位,就得到函数)(x g y =的图象,写出)(x g y =的解析式;〔3〕假设函数)()()()(12x F x f x g x F ,求--=的最小值及取最小值时x 的值.21.〔本小题总分值14分〕设函数)1ln(2)1()(2x x x f +-+= 〔1〕求)(x f 的单调增区间和单调减区间;〔2〕假设当]1,11[--∈e ex 时〔其中e =2.71828…〕,不等式m x f <)(恒成立,求实数m的取值范围;〔3〕假设关于x 的方程]2,0[)(2在区间a x x x f ++=上恰有两个相异的实根,求实数a的取值范围.参考答案一、选择题1—5 BBCAA 6—10 DDCCB 二、填空题 11.20081 12.〔-1,0〕 13.7 14.32-≥a 15.②③ 三、解做题:16.〔本小题总分值12分〕解:〔1〕由021≥-+x x 得 }12|{-≤>=x x x A 或 由 0)12(22>+++-a a x a x 得0)]1()[(>+--a x a x∴}1|{a x a x x B <+>=或〔2〕∵B A BB A ⊆∴=⋃ ∴11211≤<-⇒⎩⎨⎧≤+->a a a17.〔本小题总分值12分〕证实:〔1〕略 〔2〕略〔3〕在Rt △A 1FB 中, A 1F=5,21=B A∴510sin 111==∠B A F A BF A ,所以直线A 1B 与平面BEF 所成的角为arcsin 510 18.〔本小题总分值12分〕解:〔2〕a=1,b=3时,由2124 )(0002000--=⇒=++=或得x x x x x x f∴)(x f 不动点为-1和-2〔2〕由题意知,01)(2=-++=b bx ax x x f 即有两不等实根 ∴0)1(42>--=∆b a b 恒成立〔对任意实数b 〕 ∴10016)4(2<<⇒<-=∆'a a a 19.〔本小题总分值12分〕解:〔1〕2)2(log 2log 2)(log 2)(222222a b a x b x a x x f -+-=+-=∵8)(21min -==x f x 时, ∴⎩⎨⎧-=-=⇒⎪⎪⎩⎪⎪⎨⎧-=-=6282221log 22b a a b a 〔2〕0)1)(log 3(log 06log 4)(log 2)(22222>-+⇔>-+=x x x x x f81023log 1log 22<<>⇒-<>⇒x x x x 或或 ∴}8102|{<<>=x x x A 或〔3〕∵φ≠B ∴m>0 }11|{m x m x B +<<-=∵φ=⋂B A 又1+m>1>0 ∴8721811≤⇒⎪⎩⎪⎨⎧≤+≥-m m m∴870≤<m 20.〔本小总分值13分〕解:〔1〕由题意知 ⎩⎨⎧==⇒⎪⎩⎪⎨⎧==⇒⎩⎨⎧==-++-21818)2(1)1(21a k a af f k k〔2〕由〔1〕知12)(+=x x f ∴1log )(21-=-x x f∴)2(log )(2+=x x g 〔x>-2〕〔3〕1)2(log )1(log )2(log )(2222++=--+=xx x x x F ∵0>x ∴222≥+x x ∴25122log )(2=+≥x F 当且仅当 .25)(22min ===x F x x x 时,,即21.〔本小题总分值14分〕解:〔1〕函数定义域为),1(+∞- ∵1)2(2]11)1[(2)(++=+-+='x x x x x x f 由010)( 00)(<<-<'>>'x x f x x f 得由得 ∴增区间:〔0,+∞〕,减区间:〔-1,0〕 〔2〕由00)(=='x x f 得↑↓'+-'-- )( )()1,0()0,11(x f x f e e x∵2122)1(,21)11(2222+>--=-+=-e e e e f e e f ,且 ∴2)1()(]1,11[2max -=-=--∈e e f x f e ex 时, ∴22->e m 时,m x f <)(恒成立.〔3〕0)1ln(21)(2=+-+-⇔++=x a x a x x x f)1ln(21)(x a x x g +-+-=令∵11121)(+-=+-='x x x x g 由110)(10)(<<-<'>>'x x g x x g 得,得 ↑↓]2,1[]1,0[)(,在在x g ,故]2,0[)(2在a x x x f ++=上恰有两相异实根3ln 232ln 220)2(0)1(0)0(-≤<-⇒⎪⎩⎪⎨⎧≥<≥⇔a g g g。
2021年高三上学期8月月考数学试卷(理科)含解析

2021年高三上学期8月月考数学试卷(理科)含解析一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设函数f(x)(x∈R)满足f(x+π)=f(x)+sinx.当0≤x<π时,f(x)=0,则f()=()A.B.C.0 D.﹣2.已知函数f(x)=,则下列结论正确的是()A.f(x)是偶函数B.f(x)是增函数C.f(x)是周期函数D.f(x)的值域为[﹣1,+∞)3.函数f(x)=ln(x2﹣x)的定义域为()A.(0,1)B.[0,1] C.(﹣∞,0)∪(1,+∞)D.(﹣∞,0]∪[1,+∞)4.下列函数中,在区间(0,+∞)上为增函数的是()(x+1)A.y= B.y=(x﹣1)2C.y=2﹣x D.y=log0.55.已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)﹣g(x)=x3+x2+1,则f(1)+g(1)=()A.﹣3 B.﹣1 C.1 D.36.已知函数f(x)=5|x|,g(x)=ax2﹣x(a∈R),若f[g(1)]=1,则a=()A.1 B.2 C.3 D.﹣17.已知实数x,y满足a x<a y(0<a<1),则下列关系式恒成立的是()A.>B.ln(x2+1)>ln(y2+1)C.sinx>siny D.x3>y38.若函数y=log a x(a>0,且a≠1)的图象如图所示,则下列函数图象正确的是()A.B.C.D.9.若函数f(x)=x2+e x﹣(x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,则a的取值范围是()A.(﹣)B.() C.() D.()10.某市生产总值连续两年持续增加,第一年的增长率为p,第二年的增长率为q,则该市这两年生产总值的年平均增长率为()A. B. C.pq D.二、填空题(本大题共5小题,每小题5分,共25分.)11.已知函数f(x)=|x2+3x|,x∈R,若方程f(x)﹣a|x﹣1|=0恰有4个互异的实数根,则实数a的取值范围为.12.函数f(x)=log2x•log2(2x)的最小值为.13.“λ<0”是“数列{a n}(a n=n2﹣2λn,n∈N+)为递增数列”的条件.14.设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)若f(x)在区间[,]上具有单调性,且f()=f()=﹣f(),则f(x)的最小正周期为.15.若将函数f(x)=sin(2x+)的图象向右平移φ个单位,所得图象关于y轴对称,则φ的最小正值是.三、解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.)16.已知二次函数f(x)=ax2+x,若对任意x1、x2∈R,恒有2f()≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.(1)求集合A;(2)设集合B={x||x+4|<α},若集合B是集合A的子集,求a的取值范围.17.已知集合A={x|x2﹣2x﹣8≤0},B={x|x2﹣(2m﹣3)x+m(m﹣3)≤0,m∈R}.(1)若A∩B={2,4},求实数m的值;(2)设全集为R,若A⊆(∁R B),求实数m的取值范围.18.设函数(1)求函数f(x)的单调减区间;(2)若,求函数f(x)的值域.19.已知函数f(x)=alnx﹣ax﹣3(a∈R).(1)若a=﹣1,求函数f(x)的单调区间;(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数g(x)=x3+x2[f′(x)+](f′(x)是f(x)的导数)在区间(t,3)上总不是单调函数,求m的取值范围;(3)求证:×××…×<(n≥2,n∈N*).20.已知函数f(x)=ln(x﹣1)﹣k(x﹣1)+1(1)求函数f(x)的单调区间;(2)若f(x)≤0恒成立,式确定实数k的取值范围.21.已知P(x,y)为函数y=1+lnx图象上一点,O为坐标原点,记直线OP的斜率k=f(x).(Ⅰ)若函数f(x)在区间(m>0)上存在极值,求实数m的取值范围;(Ⅱ)当x≥1时,不等式恒成立,求实数t的取值范围.xx学年山东省临沂十九中高三(上)8月月考数学试卷(理科)参考答案与试题解析一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设函数f(x)(x∈R)满足f(x+π)=f(x)+sinx.当0≤x<π时,f(x)=0,则f()=()A. B. C.0 D.﹣【考点】抽象函数及其应用;函数的值.【专题】函数的性质及应用.【分析】利用已知条件,逐步求解表达式的值即可.【解答】解:∵函数f(x)(x∈R)满足f(x+π)=f(x)+sinx.当0≤x<π时,f(x)=0,∴f()=f()=f()+sin=f()+sin+sin=f()+sin+sin+sin=sin+sin+sin==.故选:A.【点评】本题考查抽象函数的应用,函数值的求法,考查计算能力.2.已知函数f(x)=,则下列结论正确的是()A.f(x)是偶函数B.f(x)是增函数C.f(x)是周期函数D.f(x)的值域为[﹣1,+∞)【考点】余弦函数的单调性.【专题】函数的性质及应用.【分析】由三角函数和二次函数的性质,分别对各个选项判断即可.【解答】解:由解析式可知当x≤0时,f(x)=cosx为周期函数,当x>0时,f(x)=x2+1,为二次函数的一部分,故f(x)不是单调函数,不是周期函数,也不具备奇偶性,故可排除A、B、C,对于D,当x≤0时,函数的值域为[﹣1,1],当x>0时,函数的值域为(1,+∞),故函数f(x)的值域为[﹣1,+∞),故正确.故选:D【点评】本题考查分段函数的性质,涉及三角函数的性质,属基础题.3.函数f(x)=ln(x2﹣x)的定义域为()A.(0,1) B.[0,1]C.(﹣∞,0)∪(1,+∞)D.(﹣∞,0]∪[1,+∞)【考点】函数的定义域及其求法.【专题】函数的性质及应用.【分析】根据函数成立的条件,即可求出函数的定义域.【解答】解:要使函数有意义,则x2﹣x>0,即x>1或x<0,故函数的定义域为(﹣∞,0)∪(1,+∞),故选:C【点评】本题主要考查函数定义域的求法,比较基础.4.下列函数中,在区间(0,+∞)上为增函数的是()A.y= B.y=(x﹣1)2C.y=2﹣x D.y=log0.5(x+1)【考点】对数函数的单调性与特殊点.【专题】函数的性质及应用.【分析】根据基本初等函数的单调性,判断各个选项中函数的单调性,从而得出结论.【解答】解:由于函数y=在(﹣1,+∞)上是增函数,故满足条件,由于函数y=(x﹣1)2在(0,1)上是减函数,故不满足条件,由于函数y=2﹣x在(0,+∞)上是减函数,故不满足条件,由于函数y=log0.5(x+1)在(﹣1,+∞)上是减函数,故不满足条件,故选:A.【点评】本题主要考查函数的单调性的定义和判断,基本初等函数的单调性,属于基础题.5.已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)﹣g(x)=x3+x2+1,则f(1)+g(1)=()A.﹣3 B.﹣1 C.1 D.3【考点】函数解析式的求解及常用方法;函数的值.【专题】函数的性质及应用.【分析】将原代数式中的x替换成﹣x,再结合着f(x)和g(x)的奇偶性可得f(x)+g(x),再令x=1即可.【解答】解:由f(x)﹣g(x)=x3+x2+1,将所有x替换成﹣x,得f(﹣x)﹣g(﹣x)=﹣x3+x2+1,根据f(x)=f(﹣x),g(﹣x)=﹣g(x),得f(x)+g(x)=﹣x3+x2+1,再令x=1,计算得,f(1)+g(1)=1.故选:C.【点评】本题属于容易题,是对函数奇偶性的考查,在高考中,函数奇偶性的考查一般相对比较基础,学生在掌握好基础知识的前提下,做题应该没有什么障碍.本题中也可以将原代数式中的x直接令其等于﹣1也可以得到计算结果.6.已知函数f(x)=5|x|,g(x)=ax2﹣x(a∈R),若f[g(1)]=1,则a=()A.1 B.2 C.3 D.﹣1【考点】函数的值.【专题】函数的性质及应用.【分析】根据函数的表达式,直接代入即可得到结论.【解答】解:∵g(x)=ax2﹣x(a∈R),∴g(1)=a﹣1,若f[g(1)]=1,则f(a﹣1)=1,即5|a﹣1|=1,则|a﹣1|=0,解得a=1,故选:A.【点评】本题主要考查函数值的计算,利用条件直接代入解方程即可,比较基础.7.已知实数x,y满足a x<a y(0<a<1),则下列关系式恒成立的是()A.>B.ln(x2+1)>ln(y2+1)C.sinx>siny D.x3>y3【考点】指数函数的图像与性质;对数函数的图像与性质.【专题】函数的性质及应用.【分析】本题主要考查不等式的大小比较,利用函数的单调性的性质是解决本题的关键.【解答】解:∵实数x,y满足a x<a y(0<a<1),∴x>y,A.若x=1,y=﹣1时,满足x>y,但==,故>不成立.B.若x=1,y=﹣1时,满足x>y,但ln(x2+1)=ln(y2+1)=ln2,故ln(x2+1)>ln(y2+1)不成立.C.当x=π,y=0时,满足x>y,此时sinx=sinπ=0,siny=sin0=0,有sinx>siny,但sinx>siny 不成立.D.∵函数y=x3为增函数,故当x>y时,x3>y3,恒成立,故选:D.【点评】本题主要考查函数值的大小比较,利用不等式的性质以及函数的单调性是解决本题的关键.8.若函数y=log a x(a>0,且a≠1)的图象如图所示,则下列函数图象正确的是()A.B.C.D.【考点】对数函数的图像与性质.【专题】函数的性质及应用.【分析】由题意可得a=3,由基本初等函数的图象和性质逐个选项验证即可.【解答】解:由题意可知图象过(3,1),故有1=log a3,解得a=3,选项A,y=a﹣x=3﹣x=单调递减,故错误;选项B,y=x3,由幂函数的知识可知正确;选项C,y=(﹣x)3=﹣x3,其图象应与B关于x轴对称,故错误;选项D,y=log a(﹣x)=log3(﹣x),当x=﹣3时,y=1,但图象明显当x=﹣3时,y=﹣1,故错误.故选:B.【点评】本题考查对数函数的图象和性质,涉及幂函数的图象,属基础题.9.若函数f(x)=x2+e x﹣(x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,则a的取值范围是()A.(﹣)B.() C.() D.()【考点】函数的图象.【专题】函数的性质及应用.【分析】由题意可得e x0﹣﹣ln(﹣x0+a)=0有负根,函数h(x)=e x﹣﹣ln(﹣x+a)为增函数,由此能求出a的取值范围.【解答】解:由题意可得:存在x0∈(﹣∞,0),满足x02+e x0﹣=(﹣x0)2+ln(﹣x0+a),即e x0﹣﹣ln(﹣x0+a)=0有负根,∵当x趋近于负无穷大时,e x0﹣﹣ln(﹣x0+a)也趋近于负无穷大,且函数h(x)=e x﹣﹣ln(﹣x+a)为增函数,∴h(0)=e0﹣﹣lna>0,∴lna<ln,∴a<,∴a的取值范围是(﹣∞,),故选:A【点评】本题考查的知识点是函数的图象和性质,函数的零点,函数单调性的性质,函数的极限,是函数图象和性质较为综合的应用.10.某市生产总值连续两年持续增加,第一年的增长率为p,第二年的增长率为q,则该市这两年生产总值的年平均增长率为()A. B. C.pq D.【考点】有理数指数幂的化简求值.【专题】函数的性质及应用.【分析】设该市这两年生产总值的年平均增长率为x,可得(1+p)(1+q)=(1+x)2,解出即可.【解答】解:设该市这两年生产总值的年平均增长率为x,则(1+p)(1+q)=(1+x)2,解得x=﹣1,故选:D.【点评】本题考查了指数的运算性质、乘法公式,考查了推理能力与计算能力,属于中档题.二、填空题(本大题共5小题,每小题5分,共25分.)11.已知函数f(x)=|x2+3x|,x∈R,若方程f(x)﹣a|x﹣1|=0恰有4个互异的实数根,则实数a的取值范围为(0,1)∪(9,+∞).【考点】根的存在性及根的个数判断.【专题】函数的性质及应用.【分析】由y=f(x)﹣a|x﹣1|=0得f(x)=a|x﹣1|,作出函数y=f(x),y=a|x﹣1|的图象利用数形结合即可得到结论.【解答】解:由y=f(x)﹣a|x﹣1|=0得f(x)=a|x﹣1|,作出函数y=f(x),y=g(x)=a|x﹣1|的图象,当a≤0,两个函数的图象不可能有4个交点,不满足条件,则a>0,此时g(x)=a|x﹣1|=,当﹣3<x<0时,f(x)=﹣x2﹣3x,g(x)=﹣a(x﹣1),当直线和抛物线相切时,有三个零点,此时﹣x2﹣3x=﹣a(x﹣1),即x2+(3﹣a)x+a=0,则由△=(3﹣a)2﹣4a=0,即a2﹣10a+9=0,解得a=1或a=9,当a=9时,g(x)=﹣9(x﹣1),g(0)=9,此时不成立,∴此时a=1,要使两个函数有四个零点,则此时0<a<1,若a>1,此时g(x)=﹣a(x﹣1)与f(x),有两个交点,此时只需要当x>1时,f(x)=g(x)有两个不同的零点即可,即x2+3x=a(x﹣1),整理得x2+(3﹣a)x+a=0,则由△=(3﹣a)2﹣4a>0,即a2﹣10a+9>0,解得a<1(舍去)或a>9,综上a的取值范围是(0,1)∪(9,+∞),方法2:由f(x)﹣a|x﹣1|=0得f(x)=a|x﹣1|,若x=1,则4=0不成立,故x≠1,则方程等价为a===||=|x﹣1++5|,设g(x)=x﹣1++5,当x>1时,g(x)=x﹣1++5≥,当且仅当x﹣1=,即x=3时取等号,当x<1时,g(x)=x﹣1++5=5﹣4=1,当且仅当﹣(x﹣1)=﹣,即x=﹣1时取等号,则|g(x)|的图象如图:若方程f(x)﹣a|x﹣1|=0恰有4个互异的实数根,则满足a>9或0<a<1,故答案为:(0,1)∪(9,+∞)【点评】本题主要考查函数零点个数的应用,利用数形结合是解决本题的关键,综合性较强,难度较大.12.函数f(x)=log2x•log2(2x)的最小值为﹣.【考点】对数的运算性质.【专题】函数的性质及应用.【分析】设log2x=t∈R,则f(x)=t(1+t)=,利用二次函数的单调性即可得出.【解答】解:设log2x=t∈R,则f(x)=t(1+t)=t2+t=≥﹣,当t=﹣,即,x=时取等号.∴函数f(x)的最小值为﹣.故答案为:﹣.【点评】本题考查了对数的运算性质、二次函数的单调性,考查了推理能力与计算能力,属于中档题.13.“λ<0”是“数列{a n}(a n=n2﹣2λn,n∈N+)为递增数列”的充分不必要条件.【考点】必要条件、充分条件与充要条件的判断.【专题】简易逻辑.【分析】根据递增数列的条件,结合充分条件和必要条件的对应进行判断.【解答】解:∵a n=n2﹣2λn的对称轴为n=λ,∴当λ<0时,a n=n2﹣2λn在n>0时,单调递增,∴数列a n=n2﹣2λn(n∈N*)为递增数列成立.要使数列a n=n2﹣2λn(n∈N*)为递增数列,则对称轴n=λ≤1,∴“λ<0”是“数列a n=n2﹣2λn(n∈N*)为递增数列”的充分不必要条件.故答案为:充分不必要.【点评】本题主要考查充分条件和必要条件的判断,利用递增数列的性质结合二次函数的性质是解决本题的关键.14.设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)若f(x)在区间[,]上具有单调性,且f()=f()=﹣f(),则f(x)的最小正周期为π.【考点】由y=Asin(ωx+φ)的部分图象确定其解析式;三角函数的周期性及其求法.【专题】三角函数的图像与性质.【分析】由f()=f()求出函数的一条对称轴,结合f(x)在区间[,]上具有单调性,且f ()=﹣f()可得函数的半周期,则周期可求.【解答】解:由f()=f(),可知函数f(x)的一条对称轴为x=,则x=离最近对称轴距离为.又f()=﹣f(),则f(x)有对称中心(,0),由于f(x)在区间[,]上具有单调性,则≤T⇒T≥,从而=⇒T=π.故答案为:π.【点评】本题考查f(x)=Asin(ωx+φ)型图象的形状,考查了学生灵活处理问题和解决问题的能力,是中档题.15.若将函数f(x)=sin(2x+)的图象向右平移φ个单位,所得图象关于y轴对称,则φ的最小正值是.【考点】函数y=Asin(ωx+φ)的图象变换.【专题】三角函数的图像与性质.【分析】根据函数y=Asin(ωx+φ)的图象变换规律,可得所得图象对应的函数解析式为y=sin (2x+﹣2φ),再根据所得图象关于y轴对称可得﹣2φ=kπ+,k∈z,由此求得φ的最小正值.【解答】解:将函数f(x)=sin(2x+)的图象向右平移φ个单位,所得图象对应的函数解析式为y=sin[2(x﹣φ)+]=sin(2x+﹣2φ)关于y轴对称,则﹣2φ=kπ+,k∈z,即φ=﹣﹣,故φ的最小正值为,故答案为:.【点评】本题主要考查函数y=Asin(ωx+φ)的图象变换规律,余弦函数的图象的对称性,属于中档题.三、解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.)16.已知二次函数f(x)=ax2+x,若对任意x1、x2∈R,恒有2f()≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.(1)求集合A;(2)设集合B={x||x+4|<α},若集合B是集合A的子集,求a的取值范围.【考点】二次函数的性质.【分析】(1)由对任意x1、x2∈R,恒有2f()≤f(x1)+f(x2)成立,得出a≥0,进一步可知a>0,从而可解不等式.(2)通过集合A,B的关系得到两个集合端点的大小,列出不等式,求出a的范围【解答】解:(1)对任意x1、x2∈R,由f(x1)+f(x2)﹣2f()=成立.要使上式恒成立,所以a≥0.…由f(x)=ax2+x是二次函数知a≠0,故a>0.…,解得.…(2)解得B=(﹣a﹣4,a﹣4),…因为集合B是集合A的子集,所以a﹣4≤0…且,…化简a2+4a﹣1≤0,解得…【点评】本题是先给出新定义﹣﹣凹函数,然后根据这个定义证明.这里主要考查学生接受新内容快慢的能力,将集合间的关系转化为端点的大小的思想方法.17.已知集合A={x|x2﹣2x﹣8≤0},B={x|x2﹣(2m﹣3)x+m(m﹣3)≤0,m∈R}.(1)若A∩B={2,4},求实数m的值;(2)设全集为R,若A⊆(∁R B),求实数m的取值范围.【考点】集合的包含关系判断及应用.【专题】计算题;集合.【分析】(1)根据所给的两个集合的不等式,写出两个集合对应的最简形式,根据两个集合的交集,看出两个集合的端点之间的关系,求出结果.(2)根据所求的集合B,写出集合B的补集,根据集合A是B的补集的子集,求出两个集合的端点之间的关系,求出m的值.【解答】解:(1)由已知得A={x|x2﹣2x﹣8≤0,x∈R}=[﹣2,4],B={x|x2﹣(2m﹣3)x+m2﹣3m≤0,x∈R,m∈R }=[m﹣3,m].∵A∩B=[2,4],∴,∴m=5.(2)∵B=[m﹣3,m],∴∁R B=(﹣∞,m﹣3)∪(m,+∞).∵A⊆∁R B,∴m﹣3>4或m<﹣2.∴m>7或m<﹣2.∴m∈(﹣∞,﹣2)∪(7,+∞)【点评】本题考查集合之间的关系与参数的取值,本题解题的关键是利用集合之间的关系,得到不等式之间的关系,本题是一个基础题.18.设函数(1)求函数f(x)的单调减区间;(2)若,求函数f(x)的值域.【考点】平面向量数量积的运算;两角和与差的正弦函数;正弦函数的定义域和值域.【专题】计算题;三角函数的图像与性质.【分析】(1)根据平面向量数量积的坐标运算公式,结合二倍角的三角公式化简整理,得f (x)═2sin(2x+)+1.再根据正弦函数的单调区间的公式,解不等式可得函数f(x)的单调减区间;(2)根据易得2x+∈[﹣,].结合正弦函数的图象与性质,得2sin(2x+)∈[﹣,],由此不难得到函数f(x)在区间的值域.【解答】解:(1)=2cos2x+sin2x=sin2x+cos2x+1=2sin(2x+)+1令+2kπ≤2x+≤+2kπ,得kπ+≤x≤kπ+,k∈Z,因此,函数f(x)的单调减区间是[kπ+,kπ+],k∈Z,(2)当时,2x+∈[﹣,].∴2sin(2x+)∈[﹣,],得y=2sin(2x+)+1∈[﹣+1,2]即函数f(x)在区间的值域是[﹣+1,2].【点评】本题以平面向量的坐标运算为载体,着重考查了二倍角的三角函数公式、辅助角公式和三角函数的图象与性质等知识,属于基础题.19.已知函数f(x)=alnx﹣ax﹣3(a∈R).(1)若a=﹣1,求函数f(x)的单调区间;(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数g(x)=x3+x2[f′(x)+](f′(x)是f(x)的导数)在区间(t,3)上总不是单调函数,求m的取值范围;(3)求证:×××…×<(n≥2,n∈N*).【考点】利用导数求闭区间上函数的最值;利用导数研究函数的单调性;利用导数研究曲线上某点切线方程.【专题】导数的综合应用.【分析】(1)a=﹣1时,,由此能求出f(x)的单调增区间和单调减区间.(2)由,(2,f(2))点切线倾斜角为45°,求出f'(x)=﹣+2,由此能求出m的取值范(3)构造函数f(x)=x﹣ln(x+1),x>1,由导数性质求出当n≥2,n>ln(n+1),由此能证明×××…×<(n≥2,n∈N*).【解答】(1)解:a=﹣1时,f(x)=﹣lnx+x﹣3,∴x>0,,由,得x=1.x>1时,f′(x)>0;0<x<1时,f′(x)<0.∴f(x)的单调增区间为(1,+∞),单调减区间为(0,1).(2)解:∵f(x)=alnx﹣ax﹣3,∴,∵(2,f(2))点切线倾斜角为45°,∴f'(2)=1,即﹣a=1,则a=﹣2,f'(x)=﹣+2,则g(x)=x3+x2(﹣+2+)=x3+(2+)x2﹣2x,g'(x)=3x2+(4+m)x﹣2,∵函数不单调,也就是说在(t,3)范围内,g'(x)=0有解,∵g'(0)=﹣2<0,∴当且仅当g'(t)<0且g'(3)>0时方程有解,∴3t2+(4+m)t﹣2<0且3×32+3(4+m)﹣2>0,解得﹣<m<﹣3t﹣4,又∵t∈[1,2],∴﹣<m<﹣9,∴m的取值范围(﹣,﹣9).(3)证明:先证明当n≥2,n∈Z时,n>lnn构造函数f(x)=x﹣ln(x+1),x>1则f′(x)=1﹣=,∵x>1,∴f′(x)>0,∴f(x)>f(1)=1﹣ln(1+1)>0∴当n≥2,n∈N*时,n>ln(n+1),∴,,…,,,∴<=.【点评】本题考查函数的单调区间的求法,考查实数的取值范围的求法,考查不等式的证明,解题时要认真审题,注意导数性质和构造法的合理运用.20.已知函数f(x)=ln(x﹣1)﹣k(x﹣1)+1(1)求函数f(x)的单调区间;(2)若f(x)≤0恒成立,式确定实数k的取值范围.【考点】利用导数求闭区间上函数的最值.【专题】导数的概念及应用.【分析】本题(1)先求出函数的导函数,利用导函数值的正负,研究函数的单调性,注意要分类研究;(2)要使f(x)≤0恒成立,就要求函数的最大值小于0,利用(1)的结论,得到求出函数最大值,得到相应的不等关系,解不等式,得到本题结论.【解答】解:(1)∵函数f(x)=ln(x﹣1)﹣k(x﹣1)+1,∴f′(x)=﹣k,(x>1),∴当k≤0时,f′(x)>0,∴函数f(x)在区间(1,+∞)上单调递增;当k>0时,令﹣k>0,则1<x<1+,∴函数f(x)在区间(1,1+)上单调递增;令﹣k<0,则x>1+,∴函数f(x)在区间(1+,+∞)上单调递减.综上,当k≤0时,函数f(x)单调递增区间为(1,+∞);当k>0时,函数f(x)单调递增区间为(1,1+),单调递减区间为(1+,+∞).(2)由(1)知:当k>0时,函数f(x)的最大值为:f(1+)=ln=﹣lnk.∵f(x)≤0恒成立,∴﹣lnk<0,∴k>1.【点评】本题考查了导数与函数的单调性、最值和恒成立问题,本题难度不大,属于基础题.21.已知P(x,y)为函数y=1+lnx图象上一点,O为坐标原点,记直线OP的斜率k=f(x).(Ⅰ)若函数f(x)在区间(m>0)上存在极值,求实数m的取值范围;(Ⅱ)当x≥1时,不等式恒成立,求实数t的取值范围.【考点】函数在某点取得极值的条件;导数在最大值、最小值问题中的应用.【专题】综合题;转化思想;导数的综合应用.【分析】(Ⅰ)由斜率公式求出k=f(x),求出导数f′(x),根据导数符号可判断f(x)的极值情况,要使函数f(x)在区间(其中m>0)上存在极值,须有极值点在该区间内,从而得不等式组,解出即可;(Ⅱ)由得,令,则问题转化为求函数g(x)的最小值问题,利用导数研究函数g(x)的单调性,由单调性即可求得其最小值;【解答】解:(Ⅰ)由题意,x>0,所以,当0<x<1时,f'(x)>0;当x>1时,f'(x)<0.所以f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.故f(x)在x=1处取得极大值.因为函数f(x)在区间(其中m>0)上存在极值,所以,解得.故实数m的取值范围是.(Ⅱ)由得,令,则.令h(x)=x﹣lnx,则,因为x≥1,所以h'(x)≥0,故h(x)在[1,+∞)上单调递增.所以h(x)≥h(1)=1>0,从而g'(x)>0,g(x)在[1,+∞)上单调递增,g(x)≥g(1)=2,所以实数t的取值范围是(﹣∞,2].【点评】本题考查利用导数研究函数的单调性、极值、最值,考查恒成立问题,恒成立问题往往转化为求函数最值解决,体现转化思想.35530 8ACA 諊29195 720B 爋28024 6D78 浸35446 8A76 詶w21858 5562 啢32851 8053 聓Z39633 9AD1 髑20072 4E68 乨37678 932E 錮31874 7C82 粂)39187 9913 餓36954 905A 遚。
安徽省合肥市2024届高三下学期二模数学试卷含答案

2024年合肥市高三第二次教学质量检测数学(答案在最后)(考试时间:120分钟满分:150分)注意事项:1.答卷前,务必将自己的姓名和座位号填写在答题卡和试卷上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,务必擦净后再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集U =R ,集合{}{}220,1A x x x B x x =-->=≥,则()UB A ⋂=ð()A.{}12x x ≤≤ B.{}12x x <≤ C.{}2x x > D.{}12x x ≤<【答案】A 【解析】【分析】解不等式得到A ,进而根据补集和交集求出答案.【详解】{}{2202A x x x x x =-->=>或}1x <-,{}12U A x x =-≤≤ð,故(){}{}{}12112U A B x x x x x x ⋂=-≤≤⋂≥=≤≤ð.故选:A 2.已知i2i z z-=+,则z =()A.12B.2C.1D.2【答案】B 【解析】【分析】由复数的运算和模长计算求出即可.【详解】i i i12i =1iz z z z -=-=+⇒--,所以()()()i 1i i 111i 1i 1i 222z ----===--+-,所以2z ==,故选:B.3.设,αβ是两个平面,,a b 是两条直线,则αβ∥的一个充分条件是()A.,,a b a b αβ∥∥∥B.,,a b a b αβ⊥⊥⊥C.,,a b a b αβ⊥⊥∥D.,,a b a αβ∥∥与b 相交【答案】C 【解析】【分析】通过举反例可判定ABD ,利用线面垂直的判定定理及面面平行的判定定理可判定C.【详解】选项A :当满足,,a b a b αβ∥∥∥时,,αβ可能相交,如图:用四边形ABCD 代表平面α,用四边形AEFD 代表平面β,故A 错误;选项B :当满足,,a b a b αβ⊥⊥⊥时,,αβ可能相交,如图:用四边形ABCD 代表平面α,用四边形AEFD 代表平面β,故B 错误;选项C :因为,a a b b αα⊥⇒⊥∥,又b β⊥,所以αβ∥,故,,a b a b αβ⊥⊥∥是αβ∥的一个充分条件,故C 正确;当满足,,a b a αβ∥∥与b 相交时,,αβ可能相交,如图:用四边形ABCD 代表平面α,用四边形AEFD 代表平面β,故D 错误;故选:C.4.甲、乙两名乒乓球运动员进行一场比赛,采用7局4胜制(先胜4局者胜,比赛结束).已知每局比赛甲获胜的概率均为12,则甲以4比2获胜的概率为()A.164B.332 C.532D.1564【答案】C 【解析】【分析】根据题意只需前5场甲赢3场,再利用独立事件的乘法公式求解.【详解】根据题意,甲运动员前5场内需要赢3场,第6场甲胜,则甲以4比2获胜的概率为33251115C ()()22232⋅⋅⨯=.故选:C .5.常用放射性物质质量衰减一半所用的时间来描述其衰减情况,这个时间被称做半衰期,记为T (单位:天).铅制容器中有甲、乙两种放射性物质,其半衰期分别为12,T T .开始记录时,这两种物质的质量相等,512天后测量发现乙的质量为甲的质量的14,则12,T T 满足的关系式为()A.125125122T T -+= B.125125122T T +=C.22125125122log log T T -+= D.22125125122log log T T +=【答案】B 【解析】【分析】设开始记录时,甲乙两种物质的质量均为1,可得512天后甲,乙的质量,根据题意列出等式即可得答案.【详解】设开始记录时,甲乙两种物质的质量均为1,则512天后,甲的质量为:15121()2T ,乙的质量为:25121()2T ,由题意可得21151251251221111()()()2422T T T +=⋅=,所以125125122T T +=.故选:B .6.已知函数()22,113,1x x x f x x x ⎧-≤⎪=⎨-->⎪⎩,若关于x 的方程()()10f x f a --=至少有两个不同的实数根,则a 的取值范围是()A.(]),4-∞-+∞B.[]1,1-C.(-D.⎡-⎣【答案】D 【解析】【分析】作出函数的图象,由题意可得()y f x =的图象与(1)y f a =-至少有两个不同的交点,从而得1(1)1f a -≤-≤,结合图象可得115a ≤-≤,求解即可.【详解】因为222,12,1()2,131|3,14,3x x x x x x f x x x x x x x ⎧-≤⎧-≤⎪⎪==-<<⎨⎨--⎪⎩⎪-+≥⎩,作出函数的图象,如图所示:由此可知函数()y f x =在(,1)-∞和(3,)+∞上单调递减,在(1,3)上单调递增,且()1f 1=-,()3f 1=,又因为关于x 的方程()(1)0f x f a --=至少有两个不同的实数根,所以()(1)f x f a =-至少有两个不同的实数根,即()y f x =的图象与(1)y f a =-至少有两个不同的交点,所以1(1)1f a -≤-≤,又因为当1x ≤时,2()2f x x x =-,令221x x -=,可得1x =-;当3x ≥时,()4f x x =-,令41x -=-,解得5x =,又因为1(1)1f a -≤-≤,所以115a -≤-≤,解得4a -≤≤.故选:D .7.记ABC 的内角,,A B C 的对边分别为,,a b c ,已知1112,1tan tan tan tan c A B A B=++=.则ABC 面积的最大值为()A.1B.1C.D.【答案】A 【解析】【分析】由题意及正切与正弦与余弦的关系,两角和的正弦公式及余弦公式可得角C 的大小,再由余弦定理及基本不等式可得ab 的最大值,进而求出该三角形的面积的最大值.【详解】因为1111tan tan tan tan A B A B++=,可得tan tan 1tan tan A B A B ++=,即sin sin sin sin 1cos cos cos cos A B A BA B A B++=,整理可得sin cos cos sin cos cos sin sin A B A B A B A B ++=,即sin()cos()A B A B +=-+,在三角形中sin()sin A B C +=,cos()cos A B C +=-,即sin cos C C =,()0,πC ∈,可得π4C =;由余弦定理可得222π2cos 24c b a ab ab =+-≥,当且仅当a b =时取等号,而2c =,所以2(2ab ≤=+,所以11sin 2(21222ABC S ab C =≤⨯+⨯= .即该三角形的面积的最大值为1.故选:A .8.已知双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点分别为12,F F ,点P 在双曲线左支上,线段2PF 交y 轴于点E ,且23PF PE = .设O 为坐标原点,点G 满足:213,0PO GO GF PF =⋅=,则双曲线C 的离心率为()A.12B.1C.1+D.2+【答案】D 【解析】【分析】设000(,)(0)P x y x <,根据题设条件得到02c x =-,22074c y =,再利用00(,)P x y 在椭圆上,得到42241240c a c a -+=,即可求出结果.【详解】如图,设000(,)(0)P x y x <,12(,0),(,0)F c F c -,则直线2PF 的方程为00()y y x c x c=--,令0x =,得到00cy y x c -=-,所以0(0,)cy E x c--,0200000(,),(,)cy PF c x y PE x y x c-=--=--- ,因为23PF PE = ,所以003c x x -=-,得到02cx =-,故0(,)2c P y -,又3PO GO = ,所以0(,)63y c G -,得到02107(,))263cG y c F PF y ==--- ,又210GF PF ⋅= ,所以22070123y c -+=,得到22074c y =①,又因为0(,)2c P y -在双曲线上,所以2202241c y a b -=②,又222b c a =-③,由①②③得到42241240c a c a -+=,所以421240e e -+=,解得26e =+或26e =-,又1e >,所以226(2e =+=+,得到2e =+,故选:D.二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知圆22:1O x y +=,圆22:()(1)4,R C x a y a -+-=∈,则()A.两圆的圆心距OC 的最小值为1B.若圆O 与圆C 相切,则a =±C.若圆O 与圆C 恰有两条公切线,则a -<<D.若圆O 与圆C 相交,则公共弦长的最大值为2【答案】AD 【解析】【分析】根据两点的距离公式,算出两圆的圆心距1d ≥,从而判断出A 项的正误;根据两圆相切、相交的性质,列式算出a 的取值范围,判断出B,C 两项的正误;当圆O 的圆心在两圆的公共弦上时,公共弦长有最大值,从而判断出D 项的正误.【详解】根据题意,可得圆22:1O x y +=的圆心为(0,0)O ,半径1r =,圆22:()(1)4C x a y -+-=的圆心为(,1)C a ,半径2R =.对于A ,因为两圆的圆心距1d OC ==≥,所以A 项正确;对于B ,两圆内切时,圆心距||1d OC R r ==-=1=,解得0a =.两圆外切时,圆心距||3d OC R r ==+=3=,解得a =±.综上所述,若两圆相切,则0a =或a =±,故B 项不正确;对于C ,若圆O 与圆C 恰有两条公切线,则两圆相交,||(,)d OC R r R r =∈-+,(1,3),可得13<<,解得a -<<0a ≠,故C 项不正确;对于D ,若圆O 与圆C 相交,则当圆22:1O x y +=的圆心O 在公共弦上时,公共弦长等于22r =,达到最大值,因此,两圆相交时,公共弦长的最大值为2,故D 项正确.故选:AD .10.已知等比数列{}n a 的公比为q ,前n 项和为n S ,则()A.11n nS S qS +=+B.对任意*232,,,n n n n n n S S S S S ∈--N 成等比数列C.对任意*n ∈N ,都存在q ,使得23,2,3n n n S S S 成等差数列D.若10a <,则数列{}21n S -递增的充要条件是10q -<<【答案】ACD 【解析】【分析】对于A :分1q =,1q ≠两种情况计算可判断A ;对于B :1q =-可说明不成立判断B ;,分1q =,1q ≠两种情况计算可判断C ;根据2121211(1)n n n S S a q q -+--=+,若21{}n S -是递增数列,可求q 判断D.【详解】对于A :当1q =时,11(1)n S n a +=+,1111(1)n S qS a na n a +=+=+,故成立,当1q ≠时,1111)1n n a q S q ++-=-(,11111(1)(1)11n n n a q a q S qS a q q q+--+=+⨯=--,所以11+=+n n S a qS 成立,故A 正确;对于B :当1q =-时,20S =,所以232,,n n n n n S S S S S --不成等比数列,故B 错误;对于C :当1q =时,12131,24,39n n n S na S na S na ===,故23,2,3n n n S S S 不成等差数列,当1q ≠时,若存在q ,使23,2,3n n n S S S 成等差数列,则23223n n n S S S ⨯=+,则23111(1)(1)(1)43111n n n a q a q a q q q q---⨯=+⨯---,整理得24(1)13(1)n n n q q q +=+++,所以230n n q q -=,所以13nq =,所以对任意*N n ∈,都存在q ,使得23,2,3n n n S S S 成等差数列,故C 正确;对于D :2121212211(1)n n n n n S S a a a q q -+-+-=+=+,若21{}n S -是递增数列,则可得211(1)0n a q q-+>,因为10a <,所以21(1)0n q q -+<,可解得10q -<<,所以若10a <,则数列21{}n S -递增的充要条件是10q -<<,故D 正确.故选:ACD.11.已知函数()ππsin sin sin 66f x x x ⎛⎫=+-- ⎪⎝⎭,则()A.函数()f x 在π,π2⎡⎤⎢⎥⎣⎦上单调递减B.函数5π1122y f x ⎛⎫=++ ⎪⎝⎭为奇函数C.当ππ,22x ⎡⎤∈-⎢⎥⎣⎦时,函数()41y f x =+恰有两个零点D.设数列{}n a 是首项为π6,公差为π6的等差数列,则()2024120272i i f a ===-∑【答案】BCD 【解析】【分析】利用三角恒等变换化简()f x ,再利用正弦函数单调性奇偶性判断ABC ,利用裂项相消及累加求和判断D.【详解】易知7πππ1sinsin 123422224⎛⎫=+=+⋅= ⎪⎝⎭,同理π7πsincos 12124==,()ππsin sin sin66f x x x ⎛⎫=+-- ⎪⎝⎭211sin cos 222x x -=+-7π1sin 2122x ⎛⎫=+-⎪⎝⎭对A,π7π13π19π,π,,,2121212x x ⎡⎤⎡⎤∈+∈⎢⎥⎢⎥⎣⎦⎣⎦()f x 先减后增,故A 错误;对B,5π1122y f x ⎛⎫=++ ⎪⎝⎭sin 2x =-为奇函数,故B 正确;对C,ππ,22x ⎡⎤∈-⎢⎥⎣⎦,7ππ13π,,121212t x ⎡⎤=+∈⎢⎥⎣⎦则sin t 在ππ,122⎛⎫ ⎪⎝⎭单调递增,在π13π,212⎛⎫⎪⎝⎭单调递减,即()f x 在ππ,212⎛⎫-- ⎪⎝⎭单调递增,在ππ,122⎛⎫- ⎪⎝⎭单调递减,又π12f ⎛⎫-= ⎪⎝⎭)12144-->-,ππ111sin 2412244244f -⎛⎫-=-==-- ⎪⎝⎭,故函数()41y f x =+恰有两个零点,故C 正确;对D ,易知π6n n a =,令()πsin sin 6g x x x ⎛⎫=+- ⎪⎝⎭,则()()12f x g x =-,()1ππsinsin 36g a =-,()2ππsin sin 23g a =-,……………………..()20242024ππ2023ππsin sin 6666g a ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭,则()120242024ππππ13sin sin sin 337π666222i i g a =⎛⎫⎛⎫∑=+-=+-=-⎪ ⎪⎝⎭⎝⎭,故()()112024202412027202422i i i i f a g a ==∑==∑-⨯=-,故D 正确.故选:BCD.【点睛】关键点点睛:本题考查三角函数的性质及数列求和应用,关键是利用利用裂项相消及累加求和判断D.三、填空题:本题共3小题,每小题5分,共15分.12.在6x ⎛- ⎝的展开式中,3x 的系数为_________.【答案】15【解析】【分析】利用6x ⎛- ⎝的通项公式36216(1)C (06,N)r r r r T x r r -+=-≤≤∈,即可求出结果.【详解】因为6x ⎛- ⎝的展开式的通项公为3662166C ((1)C (06,N)rr r r r rr T x x r r --+==-≤≤∈,由3632r -=,得到2r =,所以3x 的系数为226(1)C 15-=,故答案为:15.13.抛物线2:4C y x =的焦点为F ,准线为,l A 为C 上一点,以点F 为圆心,以AF 为半径的圆与l 交于点,B D ,与x 轴交于点,M N ,若AB FM =,则AM = _________.【答案】【解析】【分析】首先得到抛物线的焦点坐标与准线方程,设准线与x 轴交于点E ,根据圆的性质及抛物线的定义可得ABF △为等边三角形,即可求出BF ,再在AFM △中利用余弦定理计算可得.【详解】抛物线2:4C y x =的焦点为()1,0F ,准线l :=1x -,设准线与x 轴交于点E ,则()1,0E -,依题意B 、D 均在y 轴的左侧,又AB FM =,所以M 也在y 轴的左侧且B 点在x 轴上方,又AD 为圆F 的直径,所以π2ABD ∠=,即AB BD ⊥,由抛物线的定义可知AB AF =,又BF AF =,所以ABF △为等边三角形,所以π3BAF AFB ∠=∠=,则π3BFM AFN ∠=∠=,所以4cos EF BF BFM==∠,所以4BF AF MF ===,2π3AFM ∠=,在AFM △中AM ===故答案为:14.已知实数,,x y z ,满足20y z +-=,则+++_________.【答案】+【解析】【分析】建立空间直角坐标系,将所求转化为距离和的最小值,利用几何关系求得最值.【详解】如图,设正方体的边长为2,建立如图所示的空间直角坐标系,设(),,P x y z 为空间任意一点,因为20y z +-=,则P 在平面11ABC D 所在的平面内运动,表示P 与点()10,0,0A 和点()12,0,0B 的距离之和,因为1A 关于平面11ABC D 的对称点为D ,故111PA PB DB +≥=,当且仅当P 为1DB 中点即P 为正方体中心时等号成立;表示P 与点()1,0,2M 和点()1,2,0N 的距离之和,则PM PN MN +≥=,当且仅当P 在MN 所在直线上时等号成立,++的最小值为+,当且仅当P 为正方体中心时等号成立故答案为:+【点睛】关键点点睛:本题考查空间中距离最值问题,关键是利用空间坐标系将所求转化为距离和,并注意等号成立条件.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.如图,在四棱锥P ABCD -中,底面ABCD 是边长为2的菱形,60,BAD M ∠=︒是侧棱PC 的中点,侧面PAD 为正三角形,侧面PAD ⊥底面ABCD .(1)求三棱锥M ABC -的体积;(2)求AM 与平面PBC 所成角的正弦值.【答案】(1)12(2)11.【解析】【分析】(1)作出辅助线,得到线线垂直,进而得到线面垂直,由中位线得到M 到平面ABCD 的距离为2,进而由锥体体积公式求出答案;(2)证明出BO AD ⊥,建立空间直角坐标系,求出平面的法向量,进而由法向量的夹角余弦值的绝对值求出线面角的正弦值.【小问1详解】如图所示,取AD 的中点O ,连接PO .因为PAD 是正三角形,所以PO AD ⊥.又因为平面PAD ⊥底面,ABCD PO ⊂平面PAD ,平面PAD ⋂平面ABCD AD =,所以PO ⊥平面ABCD ,且PO =.又因为M 是PC 的中点,M 到平面ABCD 的距离为2,12π22sin 23ABC S =⨯⨯⨯=△所以三棱锥M ABC -的体积为131322=.【小问2详解】连接,BO BD ,因为π3BAD ∠=,所以ABD △为等边三角形,所以BO AD ⊥,以O 为原点,,,OA OB OP 所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,则(()()(),1,0,0,0,,2,P A B C -,所以(()1,,,2,,,,2,0,02222M AM PB BC ⎛⎫⎛⎫-=-==- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭.设平面PBC 的法向量为(),,n x y z =,则00PB n BC n ⎧⋅=⎪⎨⋅=⎪⎩,即020x =-=⎪⎩,解得0x =,取1z =,则1y =,所以()0,1,1n =.设AM 与平面PBC 所成角为θ,则sin cos ,11AM n AM n AM nθ⋅===⋅.即AM 与平面PBC 所成角的正弦值为11.16.已知椭圆2222:1(0)x y Ca b a b+=>>的右焦点为F ,左顶点为A ,短轴长为,且经过点31,2⎛⎫ ⎪⎝⎭.(1)求椭圆C 的方程;(2)过点F 的直线l (不与x 轴重合)与C 交于,P Q 两点,直线,AP AQ 与直线4x =的交点分别为,M N ,记直线,MF NF 的斜率分别为12,k k ,证明:12k k ⋅为定值.【答案】(1)22143x y+=;(2)证明见解析.【解析】【分析】(1)由题意得b =,将点3(1,)2代入椭圆的方程可求得2a 的值,进而可得椭圆的方程;(2)设:1l x ty =+,1(P x ,1)y ,2(Q x ,2)y ,联立直线l 和椭圆的方程,可得122634ty y t +=-+,122934y y t =-+,直线PA 的方程为11(2)2y y x x =++,令4x =,得116(4,)2y M x +,同理226(4,2y N x +,由斜率公式计算即可.【小问1详解】因为2b =,所以b =,再将点31,2⎛⎫ ⎪⎝⎭代入22213x y a +=得21314a +=,解得24a =,故椭圆C 的方程为22143x y +=;【小问2详解】由题意可设()()1122:1,,,,l x ty P x y Q x y =+,由221143x ty x y =+⎧⎪⎨+=⎪⎩可得()2234690t y ty ++-=,易知0∆>恒成立,所以12122269,3434t y y y y t t +=-=-++,又因为()2,0A -,所以直线PA 的方程为()1122y y x x =++,令4x =,则1162=+y y x ,故1164,2y M x ⎛⎫ ⎪+⎝⎭,同理2264,2y N x ⎛⎫⎪+⎝⎭,从而()()111212126266,413333y x y y k k ty ty +===-++,故()()()212121222212121222363643419189333993434y y y y t k k t t ty ty t y y t y y t t -+====-+++++--+++为定值.17.树人中学高三(1)班某次数学质量检测(满分150分)的统计数据如下表:性别参加考试人数平均成绩标准差男3010016女209019在按比例分配分层随机抽样中,已知总体划分为2层,把第一层样本记为123,,,,n x x x x ,其平均数记为x ,方差记为21s ;把第二层样本记为123,,,,m y y y y ,其平均数记为y ,方差记为22s ;把总样本数据的平均数记为z ,方差记为2s .(1)证明:()(){}22222121x s n s z m y m n z s ⎡⎤⎡⎤=+-++-⎢⎥⎢⎥⎣⎦⎣⎦+;(2)求该班参加考试学生成绩的平均数和标准差(精确到1);(3)假设全年级学生的考试成绩服从正态分布()2,N μσ,以该班参加考试学生成绩的平均数和标准差分别作为μ和σ的估计值.如果按照16%,34%,34%,16%的比例将考试成绩从高分到低分依次划分为,,,A B C D 四个等级,试确定各等级的分数线(精确到1).附:()18,19P X μσμσ-≤≤+≈.【答案】(1)证明见解析;(2)平均数为96分,标准差为18分;(3)将114X ≥定为A 等级,96114X ≤<定为B 等级,7896X ≤<定为C 等级,78X <定为D 等级.【解析】【分析】(1)利用平均数及方差公式即可求解;(2)利用平均数及方差公式,结合标准差公式即可求解;(3)根据(2)的结论及正态分布的特点即可求解.【小问1详解】()()222111n mi i i i s x z y z m n ==⎡⎤=-+-⎢⎥+⎣⎦∑∑()()22111n mi i i i x x x z y y y z m n ==⎡⎤=-+-+-+-⎢⎥+⎣⎦∑∑()()()()2222111()2()()2()n mi i i i i i x x x z x x x z y y y z y y y z m n ==⎧⎫⎡⎤⎡⎤=-+-+--+-+-+--⎨⎬⎣⎦⎣⎦+⎩⎭∑∑()()()123112(2(2()0nni i n i i x x x z x z x x x z x x x x nx ==--=--=-++++-=⎡⎤⎣⎦∑∑ ,同理()12()0nii yy y z =--=⎡⎤⎣⎦∑.所以{}222221()(x y s n s x z m s y z m n ⎡⎤⎡⎤=+-++-⎣⎦⎣⎦+.【小问2详解】将该班参加考试学生成绩的平均数记为z ,方差记为2s ,则()13010020909650z =⨯+⨯=,所以{}222130256(10096)20361(9096)32250s ⎡⎤⎡⎤=+-++-=⎣⎦⎣⎦18≈,所以18s ≈.即该班参加考试学生成绩的平均数为96分,标准差约为18分.【小问3详解】由(2)知96,18μσ==,所以全年级学生的考试成绩X 服从正态分布()296,18N ,所以()()961896180.68,960.5P X P X -≤≤+≈≥=.()(7896)(96114)0.34,114(78)0.16P X P X P X P X ≤<=≤<≈≥=<≈.故可将114X ≥定为A 等级,96114X ≤<定为B 等级,7896X ≤<定为C 等级,78X <定为D 等级.18.已知曲线():e e xxC f x x =-在点()()1,1A f 处的切线为l .(1)求直线l 的方程;(2)证明:除点A 外,曲线C 在直线l 的下方;(3)设()()1212,f x f x t x x ==≠,求证:1221etx x t +<--.【答案】(1)e e y x =-+;(2)证明见解析;(3)证明见解析.【解析】【分析】(1)求导,得到()()10,1e f f '==-,利用导数的几何意义写出切线方程;(2)令()e e e e xxg x x x =-+-+,二次求导得到函数单调性,结合特殊点函数值,得到所以()()10g x g ≥=,当且仅当1x =等号成立,得到证明;(3)求导得到()f x 的单调性,结合函数图象得到01t <<,不妨令120,01x x <<<,结合曲线C 在()1,0点的切线方程为()e e x x ϕ=-+,得到231etx x <=-+,转化为证明122x t <-,又111e e x x t x =-,只要证11112e 2e 2x xx x <--,令()2e 2e 2,0xxF x x x x =---<,求导得到函数单调性,结合特殊点函数值得到答案.【小问1详解】因为()e e xxf x x =-,所以()()()10,e ,1e xf f x x f =-''==-,所以直线l 的方程为:()e 1y x =--,即e ey x =-+【小问2详解】令()e e e e xxg x x x =-+-+,则()e e e e e e xxxxg x x x =--++=-+',令()()h x g x =',则()()1e xh x x +'=,由()0h x '>,解得1x >-,由()0h x '<,解得1x <-,所以()h x 在(),1∞--上单调递减,在()1,∞-+上单调递增,当x →-∞时,()()e,10h x h →-=,所以()g x 在(),1∞-上单调递减,在()1,∞+上单调递增,所以()()10g x g ≥=,当且仅当1x =等号成立,所以除切点()1,0之外,曲线C 在直线l 的下方.【小问3详解】由()e 0xf x x '=->,解得()0,e 0xx f x x <=-<',解得0x >,所以()f x 在(),0∞-上单调递增,在()0,∞+上单调递减,()()max ()01,10f x f f ===,当x →-∞时,()0f x →.因为()()1212,f x f x t x x ==≠,则01t <<,不妨令120,01x x <<<.因为曲线C 在()1,0点的切线方程为()e e x x ϕ=-+,设点()3,x t 在切线上,有()3e 1t x =--,故31etx =-+,由(1)知()0,1x ∈时,()()x f x ϕ>,则()()()223x f x t x ϕϕ>==,即231etx x <=-+,要证:1221etx x t +<--,只要证:121121e et tx x x t +<+-<--,只要证:122x t <-,又111e e xxt x =-,只要证:11112e 2e 2x xx x <--,令()2e 2e 2,0xxF x x x x =---<,则()2e 1xF x x '=--,易证()F x '在(),1∞--上单调递增,在()1,0-上单调递减,所以()()2110eF x F ≤-=-'<',所以()F x 在(),0∞-上单调递减,所以()()00F x F >=成立,所以原命题成立.【点睛】关键点点睛:本题关键是利用函数在零点处的切线方程,得到31e t x =-+,且231etx x <=-+,从而只需证明122x t <-,再勾股函数进行求解.19.在数学中,广义距离是泛函分析中最基本的概念之一.对平面直角坐标系中两个点()111,P x y 和()222,P x y ,记1212121212max ,11tx x y y PP x x y y ⎧⎫--⎪⎪=⎨⎬+-+-⎪⎪⎩⎭,称12t PP 为点1P 与点2P 之间的“t -距离”,其中{}max ,p q 表示,p q 中较大者.(1)计算点()1,2P 和点()2,4Q 之间的“t -距离”;(2)设()000,P x y 是平面中一定点,0r >.我们把平面上到点0P 的“t -距离”为r 的所有点构成的集合叫做以点0P 为圆心,以r 为半径的“t -圆”.求以原点O 为圆心,以12为半径的“t -圆”的面积;(3)证明:对任意点()()()111222333131223,,,,,,t t t P x y P x y P x y PP PP P P ≤+.【答案】(1)23;(2)4;(3)证明见解析.【解析】【分析】(1)根据所给定义直接计算即可;(2)依题意可得1max ,112xy x y⎧⎫⎪⎪=⎨++⎪⎪⎩⎭,再分类讨论,从而确定“t -圆”的图形,即可求出其面积;(3)首先利用导数说明函数()()01tf t t t=≥+的单调性,结合绝对值三角不等式证明即可.【小问1详解】由定义知,1224122||max ,max ,112124233t PQ ⎧⎫--⎪⎪⎧⎫===⎨⎬⎨⎬+-+-⎩⎭⎪⎪⎩⎭;【小问2详解】设(),P x y 是以原点O 为圆心,以12为半径的t -圆上任一点,则1max ,112xy x y ⎧⎫⎪⎪=⎨⎬++⎪⎪⎩⎭.第21页/共21页若1112y x yx ≤=++,则11x y ⎧=⎪⎨≤⎪⎩;若1112xy x y ≤=++,则有11y x ⎧=⎪⎨≤⎪⎩.由此可知,以原点O 为圆心,以12为半径的“t -圆”的图形如下所示:则“t -圆”的面积为224⨯=.【小问3详解】考虑函数()()01t f t t t =≥+.因为()210(1)f t t ='>+,所以()f t 在[)0,∞+上单调递增.又131223x x x x x x -≤-+-,于是1312231223131223122312231111x x x x x x x x x x x x x x x x x x x x x x x x --+---≤=++-+-+-+-+-+-+-1223122311x x x x x x x x --≤++-+-,同理,131223131223111y y y y y y y y y y y y ---≤++-+-+-.不妨设1313131311y y x x y y x x --≤+-+-,则13122313131223111t x x x x x x PP x x x x x x ---=≤++-+-+-1212232312122323max ,max ,1111x x y y x x y y x x y y x x y y ⎧⎫⎧⎫----⎪⎪⎪⎪≤+⎨⎬⎨⎬+-+-+-+-⎪⎪⎪⎪⎩⎭⎩⎭1223t t PP P P =+.【点睛】关键点点睛:本题关键是理解“t -距离”的定义,再结合不等式及导数的知识解答.。
2021年高三上学期8月月考数学理试题

2021年高三上学期8月月考数学理试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至6页.共150分.考试时间120分钟.第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分,在每一小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,集合,则()A. B. C. D.2.函数的图像()A.关于原点对称B.关于直线对称C.关于轴对称D.关于直线对称3.命题命题,则是成立的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4()A.B.C.D.5.若,其中,则()A.B.C.D.6.在4次独立重复试验中,随机事件恰好发生一次的概率不大于其恰好发生两次的概率,则事件在一次试验中发生的概率的取值范围是()A.B.C.D.7.已知是函数的零点,若,则的值满足()A.B.C.D.的符号不确定8.函数,若,则的所有可能值为()A.B.C.D.9.将两名男生、五名女生的照片排成一排贴在光荣榜上,恰有三名女生的照片贴在两名男生的照片之间的概率为()A .B .C .D . 10.对于函数(其中,),选取的一组值计算和,所得出的正确结果一定不可能...是( )A .和B .和C .和D .和第Ⅱ卷(非选择题,共100分)二、填空题:本大题共5小题,每小题5分,共25分.请把答案填在答题卡上中的横线上. 11.函数对于任意实数满足条件,若,则 .12.甲、乙两人独立解同一个问题,甲解出这个问题的概率是,乙解出这个问题的概率是,那么恰好有一人解出这个问题的概率是 .13.设曲线在点处的切线与轴的交点的横坐标为,令,则 . 14.曲线在点处的切线与两坐标轴的交点为、,向圆 内随机投一点,则该点落在内的概率是 . 15.设有两个命题、,其中命题对于任意的,不等式恒成立;命题在上为减函数.如果两个命题中有且只有一个是真命题,那么实数的取值范围是 .三、解答题:本大题共6小题,满分75分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)学校推荐学生参加某著名高校的自主招生考试,经过申请、资格认定后初选,已确定甲班有4名同学入围,还有包括乙班在内的三个班各有2名同学入围,若要从这些入围的同学中随机选 出4名同学参加该校的自主招生考试.(1)求在已知甲班恰有2名同学入选的条件下乙班有同学入选的概率; (2)求甲班入选人数的期望. 17.(本小题满分12分) 已知221:12,:210(0)3x p q x x m m --≤-+-≤>,且是的必要不充分条件,求实数的取值范围.18.(本小题满分12分) 已知函数的图像与函数的图像关于点对称.(1)求函数的解析式;(2)若,且在区间上的值不小于,求实数的取值范围.19.(本小题满分12分) 已知函数.(1)若在点处的切线斜率为,求实数的值; (2)若在处取得极值,求函数的单调区间.20.(本小题满分13分) 已知函数(、均为正常数).(1)证明函数在内至少有一个零点;(2)设函数在处有极值,对于一切,不等式总成立,求的取值范围;21. (本小题满分14分)已知函数.(1)若函数在区间上不是单调函数,试求的取值范围;(2)设函数(]118()()(2)1(1,(1))333h x f x a x a x b b '=++-+∈->-,如果存在 ,对任意都有成立,试求的最大值.参考答案一、选择题 BABAB ;ACCDD 二、填空题11.;12.;13.;14.;15..三、解答题 16.解:(1)已知甲班恰有2名同学入围的情况,下另2名从其余班内选出,此时乙班有同学入选的概率:……………………………4分(2)可取值:……………………………………………………………6分 ……………………………………………………………7分 ……………………………………………………………8分 ……………………………………………………………9分 ……………………………………………………………10分 ……………………………………………………………11分………………………………………………………………………………12分 17.解:∵是的必要不充分条件,∴是的充分不必要条件……………………………………………………………2分 由,得……………………………6分 ∴,由,得………………………………………………………9分 ∵是的充分不必要条件∴是的真子集………………………………………………………………………10分 即…………………………………………………………………12分 18.解:(1)设函数图像上任意一点坐标为…………………………………1分 则点关于点对称点为在图像上……………………4分∴…………………………………………………………………5分 即…………………………………………………………………6分 (2)∵(]1()()6(0,2)a a g x f x x x x x+=+=+≥∈……………………………………8分 ∴,即……………………………10分∵,∴…………………………………………………………………12分 19.解:(1)……………………………………2分 ∵在点处的切线斜率为∴,∴…………………………………………………………………4分 (2)∵在处取得极值,∴………………………………………5分即…………………………………………………………………………………6分……………………………………………………………7分10分∴的单调增区间是和;单调减区间是和……………………………………………………12分 20.解:(1)∵…………………………………………………………………2分[]()sin()()sin()10f a b a a b a b b a a b +=+-++=+-≤…………………………4分∴函数在内至少有一个零点……………………………………………6分 (2)∵,∴…………………………………7分由题意得,即……………………………………8分 问题等价于对一切恒成立…………………………9分 记,则()1sin cos 1)4g x x x x π'=--=+……………………………………10分 ∵………………………………………………………11分 ∴ 即∴,即在上是减函数……………………………………………12分 ∴,于是,故的取值范围是………………………13分21.解:(1)由题意知,在区间内有不重复的零点…………1分 由,得………………………………………………2分∵,∴…………………………………………………………3分 令,…………………………………………………4分故在区间上是增函数………………………………………………5分 其值域为,∴的取值范围是……………………………………6分 (2)∵,由已知得:在区间上恒成立,即…①…………………………………………7分当时,不等式①成立………………………………………………………………8分 当时,不等式①化为:…②………………9分 令,由于二次函数的图像是开口向下的抛物线,故它在闭区间上的最小值必在区间端点处取得,又………………10分 ∴不等式②恒成立的充要条件是,即, ,∵这个关于的不等式在区间上有解, ∴,即,………………………11分 ,又,故……………………12分从而,此时唯有符合条件……………………………………14分H36999 9087 邇 27900 6CFC 泼40486 9E26 鸦35213 898D 覍25305 62D9 拙33789 83FD 菽32087 7D57 絗D30132 75B4 疴a29239 7237 爷31641 7B99 箙29408 72E0 狠。
合肥八中高三数学上期第二次月考试题(理科)

合肥八中2021年高三数学上期第二次月考试题〔理科〕合肥八中2021年高三数学上期第二次月考试题〔理科〕一、选择题:本大题共10小题,每题5分,共50分,在每题给出的四个选项中,只有一项为哪一项符合题目要求的.1.角是第( )象限A.一B.二C.三D.撕2.集合 ,假设且 ,那么A. B. C. D.3.以下四个选项错误的选项是A.命题假设 ,那么的逆否命题是假设 ,那么B.假设为真命题,那么均为真命题C.假设命题 ,那么D. 是成立的充分而不必要条件4.角的终边上有一点的坐标为 ,那么角的最小正值为A. B. C. D.5.设实数满足 ,且 ,那么的值为A. B.10 C.20 D.1006.函数的最大值为4,最小值为0,且该函数图象的相邻两个对称轴之间的最短间隔为 ,直线是该函数图象的一条对称轴,那么该函数的解析式是A. B. C. D.7. 的值是A. B.2 C. D.8.设函数是二次函数, ,假设函数的值域是 ,那么函数的值域是A. B. C. D.9.设函数 ,假设为函数的一个极值点,那么以下图象不可能为的图象的是A B C D10.设函数 ,假设实数满足 ,那么A. B. C. D.二、填空题:本大题共5小题,每题5分,共25分,请将答案写在答题卷的相应位置上.11.函数的单调递减区间为12.设扇形的周长为8cm,面积为4cm ,那么该扇形的圆心角的弧度数为13. ,那么14.利民厂某产品的年产量在100吨至300吨之间,年消费的总本钱 (万元)与年消费量 (吨)之间的关系可近似第表示为 ,那么每吨的本钱最低时的年产量为吨15.设函数的定义域为 ,假设存在非零实数使得对于任意实数 ,有且 ,那么称函数为上的高调函数。
给出以下三个命题: (1)函数是上的1高调函数 (2)函数是上的高调函数 (3)假设定义域为的函数为上的高调函数,那么实数的取值范围是 .其中正确的命题是 (写出你认为正确的所有命题的序号)三、解答题:本大题共6小题,共75分,解容许写出必要的文字说明,证明过程或演算步骤.16(本小题总分值12分)集合 ,命题 ;命题 .(Ⅰ)假设命题为假命题,务实数的取值范围;(Ⅱ)假设命题为真命题,务实数的取值范围.17(本小题总分值12分)函数(Ⅰ)当时,求函数的值域;(Ⅱ)假如对任意的 ,不等式恒成立,务实数的取值范围. 18(本小题总分值12分)设的内角所对的边长分别为,且 .(Ⅰ)求角的大小;(Ⅱ)假设角 , 边上的中线的长为,求的面积.19(本小题总分值13分)函数为实常数)(Ⅰ)当时,求曲线在处的切线方程;(Ⅱ)当时,讨论函数在区间(0,1)上的单调性,并求出相应的单调区间.20(本小题总分值13分)函数 .(Ⅰ)将写成的形式,并求出该函数图象的对称中心; (Ⅱ)在中,角所对的边分别为 ,且满足 ,求的取值范围. 21(本小题总分值13分)函数 .(Ⅰ)当时,求函数的单调区间;(Ⅱ)假设 ,求证: ;(Ⅲ)假设为函数的图象上的两点,记为直线的斜率,假设 ,为的导函数,求证: .参考答案一、CDBDABDBDA二、11、12. 2 13.3 14. 200 15. ②③三、17.【答案】:(1)h(x)=(4-2log2x)log2x=-2(log2x-1)2+2,因为x[1,4],所以log2x[0,2].故函数h(x)的值域为[0,2].4分(2)由f(x2)f(x)g(x)得 (3-4log2x)(3-log2x)log2x,令t=log2x,因为x[1,4],所以t=log2x[0,2],所以(3-4t)(3-t)t对一切t[0,2]恒成立,①当t=0时,k②当t(0,2]时,k3-4t3-tt恒成立,即k4t+9t-15恒成立,因为4t+9t12,当且仅当4t=9t,即t=32时取等号,所以4t+9t-15的最小值为-3,即k的取值范围为(-,-3).8分18. 【答案】(1)∵(2b-3c)cos A=3acos C,(2sin B-3sin C)cos A=3sin Acos C.即2sin Bcos A=3sin Acos C+3sin Ccos A.2sin Bcos A=3sin B.∵sin B0,cos A=32,∵0(2)由(1)知A=B=6,所以AC=BC,C=23,设AC=x,那么MC=12x.又AM=7,在△AMC中,由余弦定理得AC2+MC2-2ACMCcos C=AM2,即x2+x22-2xx2cos 120=(7)2,解得x=2,故S△ABC=12x2sin 23=3.12分19.【答案】(1)当a=-1时,f(x)=x2+x-ln x,那么f(x)=2x+1-1x,(2分)所以f(1)=2,且f(1)=2.所以曲线y=f(x)在x=1处的切线的方程为:y-2=2(x-1),即:y=2x.(4分)(2)由题意得f(x)=2x-(1+2a)+ax= (10),由f(x)=0,得x1=12,x2=a,(5分)①当0由f(x)0,又知x0,得a所以函数f(x)的单调增区间是(0,a)和12,1,单调减区间是a,12,②当a=12时,f(x)0,且仅当x=12时,f(x)=0,所以函数f(x)在区间(0,1)上是单调增函数.③当12由f(x)0,又知x0,得12所以函数f(x)的单调增区间是0,12和(a,1),单调减区间是12,a,④当a1时,由f(x)0,又知x0得0由f(x)0,又知x0,得12所以函数f(x)的单调增区间是0,12,单调减区间是12,1.(12分)20.【答案】由 =0即即对称中心的横坐标为 6分(Ⅱ)由b2=ac即的值域为 .综上所述,,值域为 . 13分2021年高三数学上期第二次月考试题就分享到这里了,更多相关信息请继续关注高考数学试题栏目!。
安徽省合肥八中等2021届高三物理上学期联考试题(二)新人教版

安徽省合肥八中等最新届高三上学期联考(二)物理试题本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
全卷满分100分,考试时间90分钟。
所有答案均在答题卷上,否则无效。
考试结束后只交答题卷。
一、选择题(本大题共10小题,每小题4分,计40分。
每小题的四个选项中,只有一个选项符合要求)1.如图所示为一个质点直线运动的v-t图像,已知质点的质量为2kg,则由图象作出如下判断中正确的是A.在18s-22s时间内,质点的位移为24mB.在整个过程中,BC段加速度最大C.在整个过程中,E点所表示的状态是离出发点最远D.在5s-22s时间内合外力所做的功为119J2.如图所示,a、b、c是在地球大气层外圆形轨道上绕地球运行的三颗不同人造卫星。
下列说法中正确的是A.b、c的线速度大小相等,且大于a的线速度B.b、c运行周期相同,且小于a的运行周期C.b、c向心加速度大小相等,且小于a的向心加速度D.b、c的向心力大小相等,且小于a的向心力3.如图所示,一光滑大圆环固定在竖直平面内,环上套着两上小球A和B(中央有孔),A、B间由细绳连接着,它们处于图中所示位置时恰好能保持静止状态。
此情况下,B球与环中心O处于同一水平面上,A、B间的细绳呈伸直状态,与水平线成30°夹角。
则关于A、B小球的质量关系及绳中拉力的说法中正确的是A.m A=m B B.m A=2m BC.T=m a g D.T=2m A g4.如图所示,两根长度不同的细线,一端固定于同一点O点,另一端各系一个质量不同的小铁球A和B,两小球恰好在同一水平面绕C做匀速圆周运动,则A.它们做圆周运动的周期相等B.它们所需的向心力跟轨道半径成反比C.它们做圆周运动的线速度大小相等D.它们受到绳的拉力一定相等5.如图甲所示,在升降机的顶部它装了一个能够显示拉力大小的传感器,传感器下方挂上一轻质弹簧,弹簧下端挂一个质量为m的小球,若升降机在匀速运行过程中突然停止,并以此时为零时刻,在后面一段时间内传感器显示弹簧弹力F随时间t的变化关系如图乙所示,g为重力加速度,则A.升降机停止前在向下运动B.0-t1时间内小球处于失重状态,速率不断增大C.t2-t3时间内小球处于超重状态,速率不断减小D.t2-t4时间内小球处于超重状态,速率先减小后增大6.如图所示,水平桌面光滑,物块和小车在水平外力F作用下向左加速运动,物块M相对车厢静止于竖直车厢壁上,当水平外力F适当减小时,以下说法中正确的是A.M受到静摩擦力减小B.M受到的合外力可能向左下方C.M受到车厢壁的压力不主烃D.M受到车厢壁的压力增大7.如图所示,水平桌面光滑,A、B先体间的动摩擦因数为μ(可认为最大静摩擦力),A、B、C物体的质量均为m,滑轮光滑,砝码盘中可以任意加减砝码,在保持A、B、C三个物体相对静止共同向左运动的情况下,B与C间绳子所能达到的最大拉力为A.13μmg B.23μmgC.12μmg D.μmg8.如图所示,质量为m的物体放在粗糙的水平面上,两次都是从静止开始以相同的加速度移动同样的距离。
安徽省合肥八中等2021届高三数学上学期联考试题(二)理 新人教A版

安徽省合肥八中等最新届高三上学期联考(二)数学理试题本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分。
本卷满分150分,考试时间:1 20分钟。
所有答案均在答题卷上,否则无效。
考试结束后只交答题卷。
第Ⅰ卷 选择题(共50分)一、选择题(本题包括10小题,每小题5分,共50分。
每小题只有一个选项符合题意。
请把正确答案填涂在答题卷的相应位置) 1. 已知i 是虚数单位,则11i ii i +++= ( )A .3122i - B .3122i +C .1322i - D .1322i + 2. 设集合{}2|60,Q x x x x N =--<∈,且P Q ⊆,则满足条件的集合P 的个数是( ) A .4 B . 8C . 16D . 无数个3.设p 、q 是两个命题,21251:1(||3)0,:066p og x q x x ->-+>,则p 是q 的 ( )A . 充分而不必要条件B .必要而不充分条件C . 充分不必要条件D .既不充分也不必要条件4. 函数()sin()f x A x ωϕ=+(其中0,||2A πϕ><)的图象如图所示,为了得到()sin 2g x x =的图像,则只要将()f x 的图像( )A .向右平移6π个单位长度 B .向右平移12π个单位长度C .向左平移6π个单位长度D .向左平移12π个单位长度5.在△ABC 中,内角A ,B ,C 的对边分别是a ,b ,c ,若1sin cos ,2,4sin CB A==S △ABC=4( )A .4B .3C . 2D . 16.将4个颜色互不相同的球全部收入编号为1和2的两个盒子里,使得放入每个盒子里的球的个数不小于该盒子的编号,则不同的放球方法有 ( ) A . 10种 B .20种 C . 36种 D .52种7.在△ABC 中,tanA 是以-4为第三项,4为第七项的等差数列的公差,tanB 是以13为第三项,9为第六项的等比数列的公比,则这个三角形是( )三角形A .等腰直角B . 钝角C . 锐角D . 非等腰的直角8.已知各项都为正数的等比数列{a n }中,a 2a 4=4,a 1+a 2+a 3=14,则满足121..9n n n a a a ++>的最大正整数n 的值为 ( )A . 3B . 4C . 5D . 69. 已知函数()f x 是(,)-∞+∞上的偶函数,若对于0x ≥,都有(2)()f x f x +=-,且当[0,2)x ∈ 时,2()1(1)f x og x =+ ,则(2013)(2014)f f +-的值为( ) A .-2 B . -1 C .1 D . 210.在平面直角坐标系中,O 是坐标原点,两定点A ,B 满足{}.3|,21,,OA OB OAOB P OP OA OB R λμλμλμ+====++≤∈所表示的区域的面积是( )A .2 B .2 C .2D .2第Ⅱ卷 非选择题(共100分)二、填空题(本大题包括5小题,每小题5分,共25分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
15.已知定义在R上的偶函数 满足 ,当 ,则 __________.
16.给出以下四个命题,其中所有真命题的序号为___________.
①函数 在区间 上存在一个零点,则 的取值范围是 ;
②“ ”是“ 成等比数列”的必要不充分条件;
一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设全集 ,集合 ,则
A. B.
C. D.
2.设 : 在 内单调递增, : ,则 是 的
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
3.已知定义在 上的函数 ( 为实数)为偶函数,记 , ,,则 、 、 的大小关系为
所以当 米且 米时,可使得活动中心的截面面积最大. .............12分
方法二:欲使活动中心内部空间尽可能大,则影长EG恰为 米,则此时点 为 ,
设过点G的上述太阳光线为 ,则 所在直线方程为y- =- (x-30),
即 .........10分
由直线 与半圆H相切,得 .
而点H(r,h)在直线 的下方,则3r+4h-100<0,
∴AB,故
.
18.(1)3或 ;(2) 或 .
【解析】
(1)由 的面积 得 ,
,于是在 中,由余弦定理:
或 .
(2)法一: 中,由余弦定理, 或 ,
再由正弦定理, 或 .
法二:由 的面积 ,得 或 .
19.(1) (2)
解析:
(1)
由题意可得周期 ,所以
所以
故函数 的对称轴方程为
即
(2)由条件知 ,且
A. B. C. D.
11.已知函数 ,若函数 有三个不同的零点,则实数 的取值范围是
A. B.
C. D.
12.设函数 ,若函数 恰有三个零点x1, x2, x3(x1<x2<x3),则x1+ x2+ x3的取值范围是
A. B. C. D.
二、填空题:本大题共4小题,每小题5分,共20分.
13.已知集合 , , ,若集合 的子集的个数为8,则 的取值范围为__________.
易知 与 关于 对称,则
所以
.
20.(1) ;(2) 的取值范围为 .
【解析】(Ⅰ)因为 ,
所以 ,由正弦定理,得 ,
所以 ,又因为 ,所以 .
(Ⅱ)由(Ⅰ)知, ,所以 ,
所以
,
,因为 ,所以 ,
所以当 时, 取得最大值 ;
当 时, .
所以 的取值范围为
21.(1)既不是奇函数也不是偶函数(Βιβλιοθήκη )见解析解析:(2)
22.(Ⅰ)能(Ⅱ) 米且 米
解析:如图所示,以点A为坐标原点,AB所在直线为x轴,建立平面直角坐标系.
(1)因为 , ,所以半圆的圆心为 ,
半径 .设太阳光线所在直线方程为 ,
即 ,...............2分
则由 ,
解得 或 (舍).
故太阳光线所在直线方程为 ,...............4分
A. B. C. D.
9.在 中, 分别为 所对的边,若函数 有极值点,则 的最小值是
A. 0 B. C. D. -1
10.我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径.“开立圆术”相当于给出了已知球的体积V,求其直径d的一个近似公式 ,人们还用过一些类似的近似公式.根据π=3.14159…判断,下列近似公式中最精确的一个是
令 ,得 米 米.
所以此时能保证上述采光要求. ...............5分
(2)设 米, 米,则半圆的圆心为 ,半径为 .
方法一:设太阳光线所在直线方程为 ,
即 ,由 ,
解得 或 (舍). ...7分
故太阳光线所在直线方程为 ,
令 ,得 ,由 ,得 . .....9分
所以
.
当且仅当 时取等号.
A. B. C. D.
4.已知 ,则函数 的图象大致为
A. B.
C. D.
5.设函数 ,则不等式 的解集是
A. B. C. D.
6.若 ,则 的值为
A. B. C. D.
7.在 中,角A,B,C所对的边分别为a,b,c,已知 , ,则 =
A. B. C. 或 D.
8.已知 的外接圆半径为 ,角 所对的边分别为 ,若 ,则 面积的最大值为
(1)求函数 的对称轴方程;
(2)若函数 在 上的零点为 ,求 的值.
20.(12分)在 中, .
(Ⅰ)求 的大小;
(Ⅱ)求 的取值范围.
21.(12分)已知函数
(1)判断函数 的奇偶性,并说明理由
(2)讨论函数 的零点个数
22.(12分)如图所示,某街道居委会拟在 地段的居民楼正南方向的空白地段 上建一个活动中心,其中 米.活动中心东西走向,与居民楼平行.从东向西看活动中心的截面图的下部分是长方形 ,上部分是以 为直径的半圆.为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长 不超过 米,其中该太阳光线与水平线的夹角 满足 .
即 ,从而 ................10分
又 .
当且仅当 时取等号.
③ , ;
④若 ,则 .
三、解答题:共70分,解答时应写出必要的文字说明、演算步骤.
17.(10分)已知命题 :实数 满足 ;命题 :实数 满足 ,若 是 的必要不充分条件,求实数 的取值范围.
18.(12分)在 中, , , 的面积为 .
设 为 的中点,求 的长度.
求 的值.
19.(12分)已知函数 图像的两条相邻对称轴为 .
2021届高三年级第一学期第二次考试
理科数学
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
(1)若设计 米, 米,问能否保证上述采光要求?
(2)在保证上述采光要求的前提下,如何设计 与 的长度,可使得活动中心的截面面积最大?(注:计算中 取3)
理科数学
参考答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
B
D
A
C
C
B
C
D
D
A
A
13. 14. 15. 16.②③④
17. .
解析:令
∵“若 则 ”的逆否命题为“若 则 ”,又 是 的必要不充分条件,∴ 是 的必要不充分条件,
