混凝土结构设计原理05偏压构件正截面
混凝土结构设计原理ch6.2偏压

第7章 钢筋混凝土偏心受压构件正截面承载力计算 (Strength of Reinforced Concrete Eccentric Members)
本章要点
偏心受压构件正截面的承载力计算,包括: 破坏特征、基本假定、附加偏心距、偏心距 调节、系数弯矩增大系数、大、小偏心受压 的判别、计算公式; 偏心受压构件正截面的设计、计算,包括 “非对称配筋”与“对称配筋”柱的设计; 偏心受压构件斜截面的承载力计算; 偏心受压构件的配筋构造。
o 钢筋混凝土受压柱按 长细比不同可分为短 柱、长柱和细长柱
昆明理工大学建工学院
第6章 混凝土受压构件正截面承载力计算edited 2013 混凝土结构设计原理
N
A
短柱
o ei N0 N N1ei N1
B 长柱 C N1 f1
长细比l0/h =5~30的长柱。 ◆ f 与ei相比已不能忽略。 ◆ f 随轴力增大而增大,柱 跨中弯矩M = N ( ei + f ) 的增长速度大于轴力N的 增长速度。 ◆ 即M随N 的增加呈明显的 非线性增长。
h0 e0 N
偏心受压构件的破坏形态与 偏心距e0和纵向钢筋配筋率 有关
昆明理工大学建工学院
e0较大 As适中
第6章 混凝土受压构件正截面承载力计算edited 2013 混凝土结构设计原理
1 大偏心破坏(受拉破坏)的特征
N M
N
fyAs
f'yA's
fyAs
f'yA's
M较大,N较小 As配筋合适
N
昆明理工大学建工学院
第6章 混凝土受压构件正截面承载力计算edited 2013 混凝土结构设计原理
混凝土结构设计原理偏压构件正截面教授级别PPT课件

0.006 5
0.05bh
bh
16 对称配筋计算方案的初步确定
ei 0.3h0 且 N Nb
ei 0.3h0 或
ei 0.3h0 但 N Nb
大偏 小偏
界限破坏(大偏): b
Nb 1 fcbh0b
M e0 N
ea max20mm
ei e0 ea
1.0
07 非对称配筋截面设计计算方案
ei 0.3h0
先按大偏压计算
ei 0.3h0
按小偏压计算
08 同时求拉筋和压筋 [大偏]
N 1 Ne
fcbx f 1 fcbx h0
' y
As'
0.5
f x
y
As
f
' y
As'
h0
as'
11 小偏 [同时求拉筋和压筋 ]
远筋一般不屈服,过多无用
N
1 fcbx
f
' y
As'
b
1 1
fy As
Ne
1
fcbx
h0 0.5x
f
' y
As'
h0 as'
0.002bh
As
max
20 偏压构件箍筋形式(二)
内折角
正确
内折角 错误
关键: (b 总用筋量最少)
As'
Ne 1 fcbh02 b 0.5b2
混凝土结构设计原理05偏压构件正截面

M 2x
N
x
Cm 0.7 0.3
M1 0.7 0.3 0.939 0.982 0.7 M2
M Cmns M2 0.982 1.038 165 168kNm M2 165kNm
M 168 106 e0 542mm 3 N 310 10
' ' ' Ne f A h a y s 0 s x 1 1 2 2 1 f c bh0
b h0 h 0 ' 2 a s
As
1 f c bx f y' As' N
fy
0.002 bh
大偏压两侧钢筋均未知
关键: x
远筋一般不屈服,过多无用
2 1 b
ξ h / h0
s
As' As'
h / h0
ξ h / h0 ξ h / h0
h / h0
s
2 1 b
s fy'
s f y' h / h0
As' As'
M s M 0
1
排架结构的柱:
框架结构柱
s
N 1 Dh
j
剪力墙结构、框-剪结构及筒体结构
s
1 H 2 G 1 0.14 Ec J d
2
排架结构柱:
1 l0 s 1 M 0 / N e0 / h0 h c 1500
偏压构件不需考虑自身挠曲影响条件
第5讲 钢筋混凝土单向偏压构件正截面承载力设计
混凝土结构设计原理PPT课件第7章 偏心受压构件正截面承载力计算

钢筋的应力
si cu E s ( hoi
x 1)
ci
为了保证构件破坏时,大偏心 受压构件截面上的受压钢筋能达 到抗压强度设计值,必须满足
0 Nd
es
e 0
x 2a s
若x 2a x 2a s,近似取 s,则:
e s
0 N d e s M u f sd As (h0 as )
7.3.4矩形截面偏心受压构件对称配筋的计算方法 对称配筋: 截面设计 大、小偏心受压构件的判别: 假设为大偏心受压,则:
N f cd bx x N f cd b
As = A's,
fsd = f'sd , as = a's
若ξ ≤ ξ b,为大偏心受压构件,则:
若2a s x b h0 若x 2a s
A´s已知,As未知。 根据基本公式:
x As (h0 a Ne s f cd bx (h0 ) f sd s) 2
求得受压区高度:
As (h0 a 2Nes f sd s ) x h0 h0 f cd b
2
若满足:
2a s x b h0 取 s f sd
f cd bf x( e s h0 x As e ) f sd As e s f sd s 2
As f sd As
es
e 0
N
e s
ys
f cd bf x
hf
As f sd As
适用条件: x b h0
b
bf
a s
2a s x hf
短柱
柱:在压力作用下产 生纵向弯曲 ––– 材料破坏 ––– 失稳破坏
结构设计原理偏心受压构件

本章主题
• 偏心受压构件的破坏形态及其特征 • 大偏心受压破坏(受拉破坏) • 小偏心受压破坏(受压破坏) • 界限破坏
• 偏心弯曲的影响 • 当长细比较大时,破坏时会产生较大的纵向弯曲,使构件偏心距增大,变形增大,承载力下降,还可
能出现失稳破坏。
• 矩形截面偏心受压构件正截面承载力计算 • 基本公式的引出及其应用条件 • 配筋设计 • 承载力验算
2、大、小偏心受压正截面承载力计算图式
esη e0 e's
γ0Nd
a's
x
fcd
A's
fs'dA's
x
fcdbx
h/ 2
ho
h0
h
as
σAs
As b
as
esη e0 e's
3、计算公式 纵轴方向力的平衡 :
A s 合力点取矩:
A
' s
合力点取矩:
N 0 d 作用点取矩 :
γ0Nd
h/ 2
a's
★两个基本方程中有三个未知数,
取补充条件
b ,即 x bh0
As、A's和 x,故无唯一解。 与双筋梁类似,为使总配筋面积 (As+As')最小?可取x=ξbh0
令 N0Nd、 Mu Nes
As' Nes
fcdbh02b(10.5b)
fs'd(h0as' )
≥
m' inbh
取 s fsd
As
4 10
应变图
160 剖面 A-A
P=97KN 195KN
265KN
应力图
混凝土结构设计原理~习题+答案-第六章受压构件正截面承截力

两种偏心受压破坏形态的界限与受弯构件两种破坏的界限相同,即 在破坏进纵向钢筋应力达到屈服强度,同时受压区混凝土亦达到极限压 应变εcu值,此时其相对受压区高度称为界限相对受压区高度ξb。 当:时,属于大偏心受压破坏;
η-lo法 原规范在偏心受压构件的截面设计计算中,采用由标准偏心受压柱 (两端铰支,作用有等偏心距轴压力的压杆)求得的偏心距增大系数η 与柱段计算长度lo相结合的方法,来估算附加弯矩。这种方法也称为η-lo 法,属于近似方法之一。GB50010—2002仍保留了此种方法。
考虑二阶效应的弹性分析法 假定材料性质是弹性的,各构件的刚度则采用折减后的弹性刚度。 但它考虑了结构变形的非线性,也就是考虑了二阶效应的影响。由它算 得的各构件控制截面的最不利内力可以直接用于截面的承载力设计,而 不再需要像原规范那样通过偏心距增大系数η来增大相应截面的初始偏 心距。考虑二阶效应的弹性分析法的关键是如何对构件的弹性刚度加以 折减, 新规范规定:当按考虑二阶效应的弹性分析方法时,可在结构分析 中对构件的弹性抗弯刚度EсI(I为不计钢筋的混凝土毛截面的惯性矩)
设该构件为大偏心构件,则令
求得: 故该构件属于大偏心受压构件 则: ,则 因: 则:
3. 某方形截面柱,截面尺寸为600×600mm。柱子的计算长度为3m。轴 向压力设计值为N=3500kN,弯矩设计值为。混凝土强度等级为 C30(fc=14.3N/mm2),纵向受力钢筋采用HRB335级钢 (=300N/mm2),若设计成对称配筋,求所需的钢筋面积。 3、解:设,则
计算温度系数,因 查表得,=0.875。 则:
,因此, 因此符合配筋率要求。
5.钢筋混凝土偏心受压构件

5.2 轴心受压柱正截面受压承载能力
二、轴心受压螺旋箍筋柱的正截面受压承截力计算
螺旋箍筋和焊接环筋柱
螺旋箍筋柱和焊接环筋柱 的配箍率高,而且不会像普通 箍筋那样容易“崩出”,因而 能约束核心混凝土在纵向受压 时产生的横向变形,从而提高 了混凝土抗压强度和变形能力, 这种受到约束的混凝土称为 “约束混凝土”。
1 杆端弯矩同号时的二阶效应 (1)控制截面的转移
杆端弯矩同号时的二阶效应(P-δ效应)
5.4 偏心受压构件二阶效应
(2)考虑二阶效应的条件
杆端弯矩同号时,发生控制截面转移的情况是不 普遍的,为了减少计算工作量,《混凝土结构设计 规范》规定,当只要满足下述三个条件中的一个条 件时,就要考虑二阶效应:
此外,在长期荷载作用下,由于混 凝土的徐变,侧向挠度将增大更多,从 而使长柱的承载力降低的更多,长期荷 载在全部荷载中所占的比例越多,其承 载力降低的越多。
5.2 轴心受压柱正截面受压承载能力
《混凝土结构设计规范》采用稳定系数φ来表示长柱承载力的降低 程度
5.2 轴心受压柱正截面受压承载能力
2 承载力计算公式
方形、矩形截面箍筋形式 I形、L形截面箍筋形式
5.2 轴心受压柱正截面受压承载能力
在实际工程结构中,由于混凝土材料的非匀质性,纵 向钢筋的不对称布置,荷载作用位置的不准确及施工时不 可避免的尺寸误差等原因,使得真正的轴心受压构件几乎 不存在。但在设计以承受恒荷载为主的多层房屋的内柱及 桁架的受压腹杆等构件时,可近似地按轴心受压构件计算。 另外,轴心受压构件正截面承载力计算还用于偏心受压构 件垂直弯矩平面的承载力验算。
Ass 0
dcor
s
Ass1
Nu ( fc r ) Acor f yAs
混凝土结构设计原理第五版思考题参考答案

问答题参考答案绪 论1. 什么是混凝土结构?根据混凝土中添加材料的不同通常分哪些类型?答:混凝土结构是以混凝土材料为主,并根据需要配置和添加钢筋、钢骨、钢管、预应力钢筋和各种纤维,形成的结构,有素混凝土结构、钢筋混凝土结构、钢骨混凝土结构、钢管混凝土结构、预应力混凝土结构及纤维混凝土结构。
混凝土结构充分利用了混凝土抗压强度高和钢筋抗拉强度高的优点。
2.钢筋与混凝土共同工作的基础条件是什么?答:混凝土和钢筋协同工作的条件是:(1)钢筋与混凝土之间产生良好的粘结力,使两者结合为整体;(2)钢筋与混凝土两者之间线膨胀系数几乎相同,两者之间不会发生相对的温度变形使粘结力遭到破坏;(3)设置一定厚度混凝土保护层;(4)钢筋在混凝土中有可靠的锚固。
3.混凝土结构有哪些优缺点?答:优点:(1)可模性好;(2)强价比合理;(3)耐火性能好;(4)耐久性能好;(5)适应灾害环境能力强,整体浇筑的钢筋混凝土结构整体性好,对抵抗地震、风载和爆炸冲击作用有良好性能;(6)可以就地取材。
钢筋混凝土结构的缺点:如自重大,不利于建造大跨结构;抗裂性差,过早开裂虽不影响承载力,但对要求防渗漏的结构,如容器、管道等,使用受到一定限制;现场浇筑施工工序多,需养护,工期长,并受施工环境和气候条件限制等。
4.简述混凝土结构设计方法的主要阶段。
答:混凝土结构设计方法大体可分为四个阶段:(1)在20世纪初以前,钢筋混凝土本身计算理论尚未形成,设计沿用材料力学的容许应力方法。
(2)1938年左右已开始采用按破损阶段计算构件破坏承载力,50年代,出现了按极限状态设计方法,奠定了现代钢筋混凝土结构的设计计算理论。
(3)二战以后,设计计算理论已过渡到以概率论为基础的极限状态设计方法。
(4)20世纪90年代以后,开始采用或积极发展性能化设计方法和理论。
第2章 钢筋和混凝土的力学性能1.软钢和硬钢的区别是什么?设计时分别采用什么值作为依据?答:有物理屈服点的钢筋,称为软钢,如热轧钢筋和冷拉钢筋;无物理屈服点的钢筋,称为硬钢,如钢丝、钢绞线及热处理钢筋。
混凝土结构设计原理试题库及其参考答案

混凝土结构设计原理试题库及其参考答案混凝土结构设计原理试题库及其参考答案混凝土结构设计原理试题库及其参考答案一、判断题第1章钢筋和混凝土的力学性能1.混凝土立方体试块的尺寸越大,强度越高。
()2.混凝土在三向压力作用下的强度可以提高。
()3.普通热轧钢筋受压时的屈服强度与受拉时基本相同。
()4.钢筋经冷拉后,强度和塑性均可提高。
()5.冷拉钢筋不宜用作受压钢筋。
()6.C20表示fcu=20N/mm。
()7.混凝土受压破坏是由于内部微裂缝扩展的结果。
()8.混凝土抗拉强度随着混凝土强度等级提高而增大。
()9.混凝土在剪应力和法向应力双向作用下,抗剪强度随拉应力的增大而增大。
()10.混凝土受拉时的弹性模量与受压时相同。
()11.线性徐变是指压应力较小时,徐变与应力成正比,而非线性徐变是指混凝土应力较大时,徐变增长与应力不成正比。
()12.混凝土强度等级愈高,胶结力也愈大()13.混凝土收缩、徐变与时间有关,且互相影响。
()第3章轴心受力构件承载力1.轴心受压构件纵向受压钢筋配置越多越好。
()2.轴心受压构件中的箍筋应作成封闭式的。
()3.实际工程中没有真正的轴心受压构件。
()4.轴心受压构件的长细比越大,稳定系数值越高。
()5.轴心受压构件计算中,考虑受压时纵筋容易压曲,所以钢筋的抗压强度设计值最大取为400N/mm。
()6.螺旋箍筋柱既能提高轴心受压构件的承载力,又能提高柱的稳定性。
()第4章受弯构件正截面承载力1.混凝土保护层厚度越大越好。
()2.对于x hf的T形截面梁,因为其正截面受弯承载力相当于宽度为bf的矩形截面梁,所以其配筋率应按''2As来计算。
()b'fh03.板中的分布钢筋布置在受力钢筋的下面。
()4.在截面的受压区配置一定数量的钢筋对于改善梁截面的延性是有作用的。
()5.双筋截面比单筋截面更经济适用。
()6.截面复核中,如果b,说明梁发生破坏,承载力为0。
混凝土结构设计原理第五章 钢筋混凝土受压构件的正截面受力原理及承载能力

第五章 钢筋混凝土受压构件的正截面 受力原理及承载能力
§5-2 轴心受压构件的正截面受力原理及承载能力 2)配有间接钢筋的轴心受压柱的正截面承载力计算
f fc 4 r
当间接钢筋达到屈服时
r
2 fy Ass1 dcors
f
fc
8 fy Ass1 dcors
1 N
ea
h0
lc h
2
c
c
0.5 fc A N
e0 M 2 N
式中: ζc-截面曲率修正系数,当ζc >1.0时,取1.0 。
第五章 钢筋混凝土受压构件的正截面 受力原理及承载能力
§5-4 矩形截面偏心受压构件的正截面承载能力分析 5.4.1 基本公式及适用条件 受弯构件正截面计算的基本假定适用于偏心受压构件 从实验分析,远离轴向力一侧钢筋是否屈服是判别大 小偏心的界限。 在应变符合平截面假定的情况下,上述原则,可转化为:
ns -弯距增大系数
当 Cmns 1.0 时,取 Cmns 1.0
对剪力墙肢类及核心筒墙肢类构件,可取 Cmns 1.0
第五章 钢筋混凝土受压构件的正截面 受力原理及承载能力
§5-3 偏心受压构件的正截面受力原理
我国《规范》给出的弯矩增大系数的计算公式为:
ns
1 1300M2
第五章 钢筋混凝土受压构件的正截面 受力原理及承载能力
§5-1 受压构件的基本构造要求 5.1.3 受压构件的材料要求 混凝土和钢筋分别有什么要求? 5.1.4 基本配筋构造要求 1)纵筋 直径:不宜小于12mm,一般16mm~32mm 根数:不少于四根;布置;偏心受压 h 600mm 时设构造筋直径10mm~16mm ,间距不超 过300mm。
第五章受压构件的截面承载力(小偏压三种情况说明)
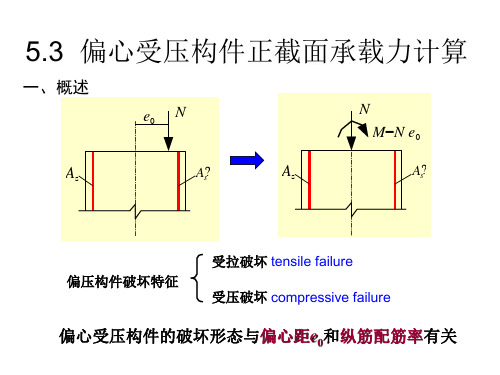
h ¢ ¢ N u e 1 f c bh0 (h0 ) f y¢ As (h0 a¢ s) 2
e¢ h a¢ s (e0 ea ) 2
f ¢yAs
a1f cbx h0 – a¢ s h¢ 0
ssA¢s
a¢ s
as
大偏心受压不对称配筋
不对称配筋
小偏心受压不对称配筋 实际工程中,受压构件常承受变号弯矩作用,所以采用对称配筋
对称配筋不会在施工中产生差错,为方便施工通常采用对称配筋
大偏心受压对称配筋 对称配筋 小偏心受压对称配筋
5.6 非对称配筋截面的承载力计算
大小偏心分界限
当 < b 属于大偏心破坏形态 > b 属于小偏心破坏形态
e0b
Nb
界限破坏时: =b,由平衡条件得 f y As 1 fcbh0b
界限破坏
当受拉钢筋屈服的同时,受压边缘混凝土应变 达到极限压应变。
大小偏心受压的分界:
As h0
A¢s
x h0
xb b h0
s y
g h 0.002
当 < b ––– 大偏心受压 ab
b c d e f
x0
a¢¢ a¢ a xcb
= b ––– 界限破坏状态 ad
cu
(1)偏心距小,构件全截面受压,靠近纵向力一侧压应力 大,最后该区混凝土被压碎,同时压筋达到屈服强度,另一 侧钢筋受压,但未屈服。 (2)偏心距小 ,截面大部分受压,小部分受拉,破坏时压区 混凝土压碎,受压钢筋屈服,另一侧钢筋受拉,但由于离中 和轴近,未屈服。 (3)偏心距大,但受拉钢筋配置较多。由于受拉钢筋配置较多, 钢筋应力小,破坏时达不到屈服强度,破坏是由于受压区混 凝土压碎而引起,类似超筋梁。 特征:破坏是由于混凝土被压碎而引起的,破坏时靠近纵向力 一侧钢筋达到屈服强度,另一侧钢筋可能受拉也可能受压, 但都未屈服。
《混凝土结构设计原理》第六章-课堂笔记

《混凝土结构设计原理》第六章受压构件正截面承载力计算课堂笔记♦主要内容受压构件的构造要求轴心受压构件承载力的计算偏心受压构件正截面的两种破坏形态及英判别偏心受压构件的N厂血关系曲线偏心受压构件正截面受压承载力的计算偏心受压构件斜截面受剪承载力的汁算♦学习要求1.深入理解轴心受压短柱在受力过程中,截而应力重分布的概念以及螺旋箍筋柱间接配筋的概念。
2.深入理解偏心受压构件正截而的两种破坏形式并熟练掌握其判别方法。
3.深入理解偏心受压构件的Nu-Mu关系曲线。
4.熟练掌握对称配筋和不对称配筋矩形截而偏心受压构件受压承载力的计算方法。
5.掌握受压构件的主要构造要求和规定。
♦重点难点偏心受压构件正截而的破坏形态及其判别;偏心受压构件正截面承载力的计算理论:对称配筋和不对称配筋矩形截面偏心受压构件受压承载力的计算方法:偏心受压构件的Nu-Mu关系曲线;偏心受压构件斜截面抗剪承载力的计算。
6.1受压构件的一般构造要求结构中常用的柱子是典型的受压构件。
6.1.1材料强度混凝上:受压构件的承载力主要取决于混凝丄强度,一般应采用强度等级较髙的混凝上,目前我国一般结构中柱的混凝土强度等级常用C30-C40,在髙层建筑中,C50-C60级混凝上也经常使用。
6.1.2截面形状和尺寸柱常见截面形式有圆形、环形和方形和矩形。
单层工业厂房的预制柱常采用工字形截面。
圆形截面主要用于桥墩、桩和公共建筑中的柱。
柱的截面尺寸不宜过小,一般应控制在lo/b^30及l°/hW25°当柱截面的边长在800mm以下时,一般以50mm为模数,边长在800mm以上时,以100mm为模数。
6.1.3纵向钢筋构造纵向钢筋配筋率过小时,纵筋对柱的承载力影响很小,接近于素混凝土柱,纵筋不能起到防止混凝上受压脆性破坏的缓冲作用。
同时考虑到实际结构中存在偶然附加弯矩的作用(垂直于弯矩作用平面),以及收缩和温度变化产生的拉应力,规定了受压钢筋的最小配筋率。
混凝土设计原理第5章作业题解答

混凝土结构设计原理作业题第5章 受压构件正截面的性能与设计5-1(基本题目) 已知某四层四跨现浇框架结构的底层内柱,截面尺寸为mm mm 400400⨯,轴心压力设计值m H kN N 9.3,3090==,混凝土强度等级为C40,钢筋用HRB400级。
求纵向钢筋截面面积/s A ,并绘制截面配筋图(含构造配筋)。
解答:按《混凝土结构设计规范》规定,按式,查表5-1,得按式(5-1)求A ’s223//1213)4001.19983.09.0103090(3601)9.0(1mm A f N f A c y s=⨯-⨯⨯=-=ϕ如果采用4根直径20mm 纵筋,A ’s =1256,故上述A 的计算中没有减去是正确的,且由附表18知,%55.0min =ρ,min /ρρ ,可以。
截面每一侧配筋率,可以。
故满足受压纵筋最小配筋率(全部纵向钢筋的%55.0min =ρ;一侧纵向钢筋的)的要求。
选用4根直径20mm 纵筋,A ’s =1256。
5-2(基本题目)根据建筑要求,某现浇柱截面尺寸定为mm mm 250250⨯,由两端支承情况决定其计算高度m l 8.20=;柱内配有4根直径为22的HRB400级钢筋作为纵筋;构件混凝土强度等级为C40,柱的轴向力设计值kN N 1500=。
试问截面是否安全。
解答:由, 查表5-1,得按式(5-1),得116.1)101500/()152********.19(962.09.0/)(9.032// =⨯⨯+⨯⨯⨯=+N A f A f s y c ϕ故截面是安全的。
5-3(基本题目)已知:某旅馆底层门厅内现浇钢筋混凝土柱,一类环境,承受轴心压力设计值kN N 6000=,从基础顶面至二层楼面高度为m H 2.5=。
混凝土强度等级为C40,由于建筑要求柱截面为圆形,直径为mm d 470=。
柱中纵筋用HRB400级钢筋,箍筋用HPB300级钢筋。
求柱中配筋。
解答:先按配有普通纵筋和箍筋柱计算。
结构设计原理(21-2)--偏压构件正截面的受力特点和破坏形态
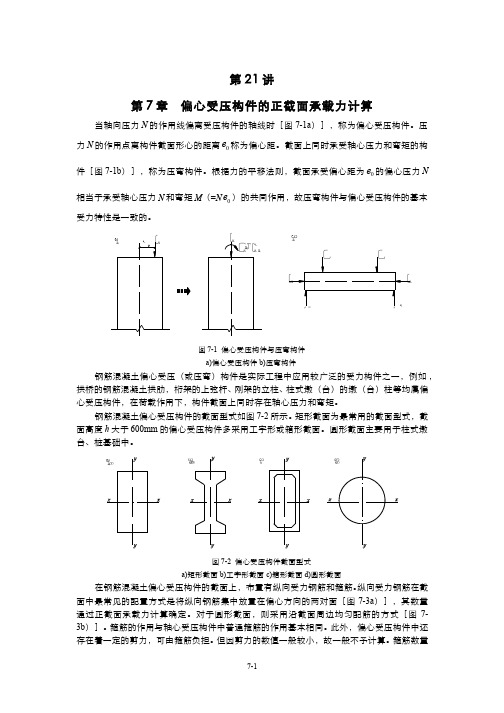
及间距按普通箍筋柱的构造要求确定。
纵向钢筋
纵向钢筋 箍筋
箍筋
纵向钢筋
箍筋
箍筋
纵向钢筋
图 7-3 偏心受压构件截面钢筋布置形式 a)纵筋集中配筋布置 b)纵筋沿截面周边均匀布置
§7.1 偏心受压构件正截面受力特点和破坏形态
钢筋混凝土偏心受压构件也有短柱和长柱之分。本节以矩形截面的偏心受压短柱的试验 结果,介绍截面集中配筋情况下偏心受压构件的受力特点和破坏形态。
7-3
剖面 应变图 应力图
偏心压力
柱半高度侧向变位
图 7-6 小偏心受压短柱试验
沿柱高的侧向变位
图 7-7 小偏心受压短柱破坏形态 a)破坏形态 b)局部放大
(1)当纵向偏心压力偏心距很小时,构件截面将全部受压,中和轴位于截面以外[图
第 21 讲
第 7 章 偏心受压构件的正截面承载力计算
当轴向压力 N 的作用线偏离受压构件的轴线时[图 7-1a)],称为偏心受压构件。压
力 N 的作用点离构件截面形心的距离 e0 称为偏心距。截面上同时承受轴心压力和弯矩的构
件[图 7-1b)],称为压弯构件。根据力的平移法则,截面承受偏心距为 e0 的偏心压力 N
筋配筋量进一步增大,则截面破坏时将形成斜线 ae 所示的受拉钢筋达不到屈服的小偏心受 压状态。
当进入全截面受压状态后,混凝土受压较大一侧的边缘极限压应变将随着纵向压力 N
偏心距的减小而逐步有所下降,其截面应变分布如斜线 af、a' g 和垂直线 a''h 所示顺序变化
在变化的过程中,受压边缘的极限压应变将由 cu 逐步下降到接近轴心受压时的 0.002。
7-4
而小部分受拉[图 7-8b)]。中和轴距受拉钢筋 As 很近,钢筋 As 中的拉应力很小,达不到
混凝土结构设计原理第八章1-受压构件(偏压理论)
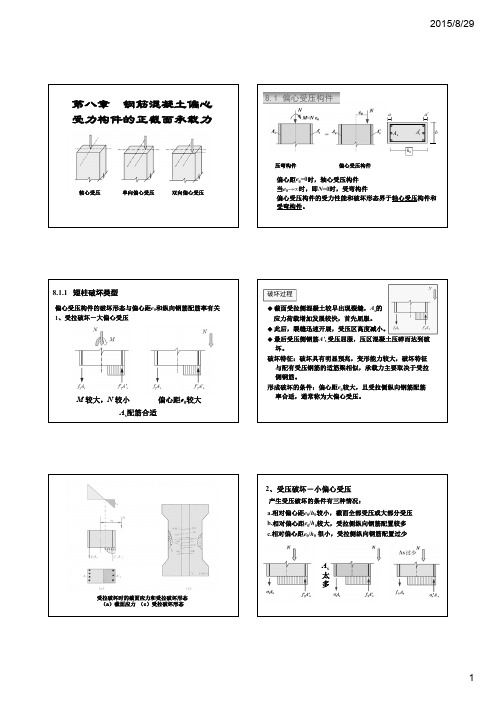
轴心受压单向偏心受压双向偏心受压压弯构件偏心受压构件偏心距e=0时,轴心受压构件当e→∞时,即N=0时,受弯构件偏心受压构件的受力性能和破坏形态界于轴心受压构件和受弯构件。
8.1偏心受压构件aM 较大,N 较小偏心距e0较大A s配筋合适◆截面受拉侧混凝土较早出现裂缝,应力荷载增加发展较快,首先屈服。
◆此后,裂缝迅速开展,受压区高度减小。
受压屈服,压区混凝土压碎而达到破破坏特征:破坏具有明显预兆,变形能力较大,破坏特征与配有受压钢筋的适筋梁相似,承载力主要取决于受拉较大,且受拉侧纵向钢筋配筋破坏过程受拉破坏时的截面应力和受拉破坏形态(a)截面应力(c)受拉破坏形态A s 太多A s太多破坏过程◆“a、b”:靠近N侧混凝土和纵筋的压应力较大,远离N侧纵筋应力较小。
◆“c”:远离N侧可能出现“反向破坏”:远离N侧混凝土和纵筋的压应力较大,靠近N侧纵筋应力较小。
◆截面最后是由于压应力较大处的混凝土首先压碎而达到破坏,该位置的纵筋压屈。
破坏特征:承载力主要取决于压坏区混凝土和此位置纵筋,破坏时受压区受压破坏时的截面应力和受压破坏形态(a)、(b)截面应力(c)受压破坏形态界限破坏:与适筋梁和超筋梁的界限情况类似小偏心受压破坏:基本计算假定与附加偏心矩考虑施工误差、荷载作用位置的不确定性及材料的不均匀等原因的不利影响,引入附加偏心距标准柱的挠曲变形框架的侧向变形(侧移)近似做法(《混规》):将未考虑P—Δ效应的一阶弹性分析所得的结构杆端弯矩乘以适当的增大系数ηs精确方法:按考虑实际变形特性的非线性有限单元方法,或按考虑结构的几何非线性的弹性分析方法直接计算出考虑P—Δ效应的内力一、由侧移产生的P —Δ二阶效应当需考虑δ的影响,用M代替M0杆端弯矩同号杆端弯矩异号令偏心矩增大系数平截面假定考虑徐变影响,界限破坏时非界限破坏时ζ杆端弯矩相同时f'基本计算公式适用条件ξ或x ≤ξh或ξ若取'取矩)f'◆《规范》规定,受压构件全部纵向钢筋的配筋率当混凝土强度等级大于C60时,应按规定增加侧钢筋取矩Ne e'Ne e'对轴向力N x =β1x nσs=E sεse适用条件ξb< ξ≤ h / h0配筋率条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 b 1
fy
fy
as
h0
a
' s
h
非对称配筋截面设计计算方案
ei 0.3h0
先按大偏压计算
ei 0.3h0
应按小偏压计算
大偏压已知压筋求拉筋
As' 0.002bh
N 1 fcbx f Ne 1 fcbx h0
' y
As'
0.5
f x
y
As
f
' y
As'
h0
as'
s
1 H2 G
1 0.14
EcJd
排架结构柱:
s
1
1500M0
1 /N
e0 /
h0
l0 h
2
c
偏压构件不需考虑自身挠曲影响条件
1、构件端部弯矩绝对值(同一主轴方向)比值:MM
1 2
0.9
2、轴压比:
N 0.9
fc A
3、构件长细比:
lc i
34 12 M1 M2
M1 —— 绝对值较小者(考虑侧移影响后的端部弯矩) M 2 —— 绝对值较大者(考虑侧移影响后的端部弯矩)
a
' s
h/ 2
ei e'
a
' s
h/ 2
e'
ei
h 2
as'
e'
h 2
ei
as'
矩形截面小偏纵筋面积计算
远筋一般不屈服,过多无用
N
1 fcbh0
f
' y
As'
s As
0.002bh
Ne
1
fcbh02 1 0.5
f
' y
As'
h0
as'
As
max
ቤተ መጻሕፍቲ ባይዱ
Ne
'
fcbh
f
as'
As'
Ne 1 fcbxh0 0.5x
fy' h0 as'
0.002bh
As
1 fcbx
f
' y
As'
fy
N
0.002bh
大偏压构件纵筋面积计算技术处理
① 如果 x bh0:压筋过弱,按压筋未知重算
②
如果
x 2as' :压筋过强,
As
fy
Ne' h0 as'
ei e'
构件按单曲率弯曲时M1 / M2 取正号,否则取负号
考虑自身挠曲影响偏压构件弯矩设计值
M Cmns M2 M2
Cm
0.7 0.3
M1 M2
0.7
ns
1
1300
1 M2 N
ea
lc h
c
h0
c
0.5 fc A N
1.0
ea max h / 30 20mm
当无需考虑自身挠曲影响时,取 ns 1.0 对剪力墙结构,取 C m ns 1.0
险向 端
截 面 偏 离 柱
压 力 引 起 了 附
弯 矩 作 用 产
端加 生
,弯 了
控矩 挠
制曲
弯变
矩形
增
大
1. 一阶弯矩最大处与二阶弯矩最大处处相接近时,弯矩增加得最多 2. 两端弯矩值不相等但单曲率弯曲时,弯矩增加得较多 3. 两端弯矩值不相等且双曲率弯曲时,弯矩增加得较少甚至很少
有侧移时偏压长柱二阶效应
偏心距较 小或偏心 距较大但 远筋较多
偏心距很小
偏心距特小
大偏 小偏
b b
大小偏压判别
界限破坏
s y
y s y
远侧钢筋受拉屈服 同时
近侧混凝土被压碎
大偏
小偏
cu
b b b
无侧移时偏压长柱挠曲变形二阶效应
一阶变形 最终变形 一阶弯矩 最终弯矩
结原条
果因件
:::
危轴 两
As b
as
单向偏心受压构件
e
N
e'
x As'
h0
a
' s
h
近远 侧侧 :: 距距 离离 轴轴 向向 力力 较较 近远 一一 侧侧
偏压短柱破坏形态
偏心距较大、远筋不多
大偏压 (受拉破坏)
远筋受拉屈服→→近侧混凝土压碎
小偏压 (受压破坏)
近侧混凝土压碎;远筋受拉不屈服 近侧混凝土压碎;远筋受压不屈服 远侧混凝土压碎(反向破坏)
h0
a
' s
h
矩形截面小偏压构件正截面承载力
N
1 fcbx
f
' y
As'
s As
Ne 1 fcbx
h0 0.5x
f
' y
As'
h0 as'
eN
ei e'
h e ei 2 as
ei e0 ea
M e0 N
s As
As b
1 fc
f
' y
As'
x As'
f
' y
s
2.768
1.0
ns
1
1300
h0 M2 N
ea
lc h
2
c
1
360
3500 2 1.0
1300
165 106 310 103
20
400
1.038
M2x N x
Cm
0.7 0.3 M1 M2
0.7 0.3 0.939
0.982
0.7
M Cmns M2 0.9821.038165 168kNm M2 165kNm
+
=
或
由在 竖因 向水 荷平 载荷 引载 起产 了生 附了 加侧 弯移 矩的
框 架 柱 中
☆ 端部或端部附近的弯矩相对加大 ☆
偏压构件考虑侧移二阶效应后端部弯矩
框架结构、剪力墙结构、框-剪结构及筒体结构中的柱、墙:
M Mns s M0
排架结构的柱:
M sM0
框架结构柱
s
1
1
Nj
Dh
剪力墙结构、框-剪结构及筒体结构
' y
h0'
h0' as
0.5h
(轴压比大于1.0)
s
1 b 1
fy
ξ h / h0
s
21 b
h / h0
h / h0
s
21 b
ξ h / h0 ξ h / h0
s fy'
s h/
f
' y
h0
As'
As'
As'
As'
As
例501 300400 lcx 3.5 lcy 4.375 C30 HRB400
x
1
1
2
Ne
f
' y
As'
h0
1 fcbh02
as'
h0
b h0
2as'
As
1
fcbx
f
' y
As'
fy
N
0.002bh
大偏压两侧钢筋均未知
关键: x
hb
0
(总用筋量最少)
N 1 Ne
fcbx f
1 fcbx h0
' y
As'
0.5
fy
x
As
f
' y
As'
h0
M2x 165 M1x 155
h0 h as 400 40 360mm
ea
20mm
h 30
400 30
13mm
N 310 as' as 40 As' ? As ?
z
N M1x
M1 155 0.939 0.9 M2 165
c
0.5 fc A N
0.514.3 300 400 310 103
矩形截面大偏压构件正截面承载力
N
1 fcbx
f
' y
As'
fy As
Ne 1 fcbx
h0 0.5x
f
' y
As'
h0 as'
e
N
ei e'
2as' x bh0
fy As
1 fc fy' As'
h e ei 2 as
x
As
As'
ei e0 ea M
e0 N
b as
M 168106 e0 N 310103 542mm
ei e0 ea 542 20 562mm 0.3h0 0.3 360 108mm
