模糊控制算法c程序
模糊PID的c语言算法

#include <cvirte.h>#include <userint.h>#include "succus.h"#include <rs232.h>#include <ansi_c.h>#include <formatio.h>#include <math.h>#include <string.h>#define parameterPID 0.1 //PID常数#define maxcontroldata 10 //最大控制量#define parameterfuzzy 12 //模糊控制常数#define Pe1 4 //隶属度范围#define Pe2 8#define Psess1 2#define Psess2 4#define parainput 100 //输入常数static int panelHandle;static int L_PIDstart; //运行标签static int L_fuzzystart;static float P_control; //获得参数static float I_control;static float D_control;static int whatmode;static float model_K; //模型参数static float model_T;static float model_t;static float cycle; //设定周期static float savedata[3]; //储存偏差量static float savecontrol[20]; //存储控制量static float result[2]; //存储仿真结果static float getsum;static char senddata[22]; //通信协议static char recievedata[18];static char nak[6];static char ack[6];int main (int argc, char *argv[]){if (InitCVIRTE (0, argv, 0) == 0)return -1; /* out of memory */if ((panelHandle = LoadPanel (0, "succus.uir", PANEL)) < 0)return -1;OpenComConfig (2, "", 9600, 0, 8, 1, 512, 512); //打开串口senddata[0] = 5; //构造协议senddata[1] = '0';senddata[2] = 'A';senddata[3] = 'F';senddata[4] = 'F';senddata[5] = 'W';senddata[6] = 'W';senddata[7] = '0';senddata[8] = 'D';senddata[9] = '5';senddata[10] = '0';senddata[11] = '6';senddata[12] = '4';senddata[13] = '0';senddata[14] = '1';senddata[21] = 0;recievedata[0] = 5;recievedata[1] = '0';recievedata[2] = 'A';recievedata[3] = 'F';recievedata[4] = 'F';recievedata[5] = 'W';recievedata[6] = 'R';recievedata[7] = '0';recievedata[8] = 'D';recievedata[9] = '5';recievedata[10] = '0';recievedata[11] = '0';recievedata[12] = '0';recievedata[13] = '0';recievedata[14] = '1';recievedata[15] = '4';recievedata[16] = '0';recievedata[17] = 0;nak[0] = 21;nak[1] = '0';nak[2] = 'A';nak[3] = 'F';nak[4] = 'F';nak[5] = 0;ack[0] = 6;ack[1] = '0';ack[2] = 'A';ack[3] = 'F';ack[4] = 'F';ack[5] = 0;FlushInQ (2);FlushOutQ (2);DisplayPanel (panelHandle);RunUserInterface ();CloseCom (2);DiscardPanel (panelHandle);return 0;}int CVICALLBACK autosetPIDCallback (int panel, int control, int event,void *callbackData, int eventData1, int eventData2){switch (event){case EVENT_COMMIT:SetCtrlVal (panelHandle, PANEL_PARAMETER_P, 20.0);SetCtrlVal (panelHandle, PANEL_PARAMETER_I, 0.0);SetCtrlVal (panelHandle, PANEL_PARAMETER_D, 0.0);break;}return 0;}int CVICALLBACK fuzzycontrolCallback (int panel, int control, int event,void *callbackData, int eventData1, int eventData2){switch (event){case EVENT_COMMIT:L_fuzzystart = 1;GetCtrlVal (panelHandle, PANEL_WORKMODE, &whatmode); //获得工作状态if(whatmode == 0){GetCtrlVal (panelHandle, PANEL_EMLUATOR_K, &model_K); //模型GetCtrlVal (panelHandle, PANEL_EMLUATOR_T, &model_T);GetCtrlVal (panelHandle, PANEL_EMLUATOR_t, &model_t);}GetCtrlVal (panelHandle, PANEL_SAMPLINGTIME, &cycle);SetCtrlAttribute (panelHandle, PANEL_TIMER, ATTR_INTERVAL, cycle);SetCtrlAttribute (panelHandle, PANEL_TIMER, ATTR_ENABLED, 1); //获得抽样时间。
模糊PID控制温控系统设计C语言程序代码

模糊PID控制温控系统设计C语言程序代码介绍本文介绍了使用模糊PID控制方法来设计温控系统的C语言程序代码。
本温控系统使用传感器读取室内温度,然后根据读取的数值对应调整冷风机的风速和加热器的加热时间,从而控制室内温度达到一个设定值。
系统设计本温控系统采用模糊PID控制方法,具体实现流程如下:1.根据设定温度和当前室内温度计算出误差值2.使用模糊控制方法将误差值转化为温度调节量3.根据模糊控制输出的温度调节量计算出PID控制器的输出4.根据PID控制器的输出调节冷风机的风速和加热器的加热时间系统设计中需要使用的传感器,冷风机和加热器的具体型号及参数需要根据实际情况进行选择。
此处不做详细说明。
程序代码实现以下代码实现了上述系统设计,包括模糊控制和PID控制。
// 温控系统C语言程序代码#include<stdio.h>#include<stdlib.h>// 模糊控制double GetTemperatureByFuzzy(double error){double delta = 0.5; // 设定的温度调节步长double result = 0;if (error <= -5){result = 1;}else if (error > -5 && error < 0){result = (error + 5) / 5.0;}else if (error >= 0 && error < 5){result = (5 - error) / 5.0;}else{result = 0;}return result * delta;}// PID控制double GetTemperatureByPID(double error, double lastError, double integ ral){double Kp = 0.5; // 比例系数double Ki = 0.01; // 积分系数double Kd = 0.1; // 微分系数double deltaT = 0.1; // 采样时间double derivate = (error - lastError) / deltaT;double result = Kp * error + Ki * integral + Kd * derivate;return result;}// 主函数int main(){double setTemp = 25; // 设定温度double curTemp = 24; // 当前温度,需要从传感器读取double lastError = 0; // 上一次的误差值double integral = 0; // 积分项while (1){double error = setTemp - curTemp; // 计算当前误差值double fuzzyTemp = GetTemperatureByFuzzy(error); // 模糊控制integral += error; // 更新积分项double pidTemp = GetTemperatureByPID(error, lastError, integra l); // PID控制lastError = error; // 更新上一次误差值// 根据pidTemp和fuzzyTemp调节冷风机的风速和加热器的加热时间,省略// 读取传感器更新当前温度,省略// curTemp = GetCurTemp();// 采样时间,省略// sleep(1);}}本文介绍了使用模糊PID控制方法来设计温控系统的C语言程序代码。
基于模糊控制的速度跟踪控制问题(C语言以及MATLAB仿真实现)

基于模糊控制的速度控制——地面智能移动车辆速度控制系统问题描述利用模糊控制的方法解决速度跟踪问题,即已知期望速度(desire speed),控制油门(throttle output)和刹车(brake output)来跟踪该速度。
已知输入:车速和发动机转速(值可观测)。
欲控制刹车和油门电压(同一时刻只有一个量起作用)。
算法思想模糊控制器是一语言控制器,使得操作人员易于使用自然语言进行人机对话。
模糊控制器是一种容易控制、掌握的较理想的非线性控制器,具有较佳的适应性及强健性(Robustness)、较佳的容错性(Fault Tolerance)。
利用控制法则来描述系统变量间的关系。
不用数值而用语言式的模糊变量来描述系统,模糊控制器不必对被控制对象建立完整的数学模式。
Figure 1模糊控制器的结构图模糊控制的优点:(1)模糊控制是一种基于规则的控制,它直接采用语言型控制规则,出发点是现场操作人员的控制经验或相关专家的知识,在设计中不需要建立被控对象的精确的数学模型,因而使得控制机理和策略易于接受与理解,设计简单,便于应用。
(2)由工业过程的定性认识出发,比较容易建立语言控制规则,因而模糊控制对那些数学模型难以获取,动态特性不易掌握或变化非常显著的对象非常适用。
(3)基于模型的控制算法及系统设计方法,由于出发点和性能指标的不同,容易导致较大差异;但一个系统语言控制规则却具有相对的独立性,利用这些控制规律间的模糊连接,容易找到折中的选择,使控制效果优于常规控制器。
(4)模糊控制是基于启发性的知识及语言决策规则设计的,这有利于模拟人工控制的过程和方法,增强控制系统的适应能力,使之具有一定的智能水平。
简化系统设计的复杂性,特别适用于非线性、时变、模型不完全的系统上。
模糊控制的缺点1.模糊控制的设计尚缺乏系统性,这对复杂系统的控制是难以奏效的。
所以如何建立一套系统的模糊控制理论,以解决模糊控制的机理、稳定性分析、系统化设计方法等一系列问题;2.如何获得模糊规则及隶属函数即系统的设计办法,这在目前完全凭经验进行;3.信息简单的模糊处理将导致系统的控制精度降低和动态品质变差。
simulink模糊pid控制模型转c语言代码 -回复

simulink模糊pid控制模型转c语言代码-回复Simulink模糊PID控制模型转C语言代码Simulink是MATLAB软件中一款用于进行动态系统建模和仿真的工具。
它通过图形化界面提供了易于使用的建模环境,使得用户能够快速构建和测试各种控制系统。
然而,有时我们可能需要将Simulink模型转换为C语言代码,以便在嵌入式系统或其他平台上实现实时控制。
在本篇文章中,我们将介绍如何将Simulink模糊PID控制模型转换为C语言代码。
第一步:理解模糊PID控制器原理在进行代码转换之前,我们先来了解一下模糊PID控制器的原理。
PID 控制器是一种经典的控制器,由比例项、积分项和微分项组成。
它通过对系统实际输出与期望输出的差异进行反馈控制,从而调整系统输入,使得输出接近期望值。
模糊PID控制器与传统PID控制器的主要区别在于它使用了模糊逻辑来处理不确定性和模糊性。
模糊逻辑是一种基于模糊集合理论的控制方法,它可以模拟人的思维方式,通过模糊化的输入和输出变量进行推理和决策。
第二步:在Simulink中设计模糊PID控制模型在Simulink中设计模糊PID控制模型是实现模糊PID控制器代码转换的前提。
我们可以使用Fuzzy Logic Toolbox提供的工具来创建和调整模糊逻辑系统。
首先,我们需要创建输入和输出变量。
输入变量通常是系统的误差(Current Error)和误差的变化率(Error Rate),输出变量一般为控制量(Control Signal)。
然后,我们可以根据实际情况定义模糊集合和模糊规则,以及选择适当的模糊控制器类型(如模糊反向推理控制器或模糊自适应控制器)。
完成模糊PID控制模型设计后,我们可以在Simulink中进行仿真和调试,确保模型能够正确地实现期望的控制效果。
第三步:使用MATLAB Coder将Simulink模型转换为C语言代码实现模糊PID控制模型的C语言代码转换,我们可以使用MATLAB Coder。
PID控制算法的c语言实现十二模糊PID的参数整定

PID控制算法的c语⾔实现⼗⼆模糊PID的参数整定这⼏天⼀直在考虑如何能够把这⼀节的内容说清楚,对于PID⽽⾔应⽤并没有多⼤难度,按照基本的算法设计思路和成熟的参数整定⽅法,就算是没有经过特殊训练和培训的⼈,也能够在较短的时间内容学会使⽤PID算法。
可问题是,如何能够透彻的理解PID算法,从⽽能够根据实际的情况设计出优秀的算法呢。
通过讲述公式和基本原理肯定是最能说明问题的,可是这样的话怕是犯了“专家”的错误了。
对于门槛⽐较低的技术⼈员来讲,依然不能透彻理解。
可是说的⼊⽿了,能不能透彻说明也是⼀个问题,所以斟酌了⼏天,整理了⼀下思路才开始完成PID系列⽂章的最后⼀篇。
我所说的最后⼀篇不代表PID的功能和发展就⽌步与此,仅仅是说明,透过这⼀些列的⽂章,基本上已经可以涵盖PID设计的要点,⾄于更深⼊的研究,就交给有需要的读者去做。
上⼀节中⼤致讲述了⼀下模糊算法。
实际上模糊算法的很多概念在上⼀节中并没有深⼊的解释。
举的例⼦也只是为了说明模糊算法的基本含义,真正的模糊算法是不能这么设计的,当然也不会这么简单。
模糊算法的核⼼是模糊规则,如果模糊规则制定的出⾊,那么模糊算法的控制效率就⾼。
其实这是智能算法的⼀般特性,规则是系统判断和处理的前提。
那么就说说PID的规则该怎么制定。
我们知道,模糊算法的本质是对PID的三个参数进⾏智能调节。
那么⾸先要提出的问题是如何对PID的参数进⾏调节?这个问题其实是参数整定的问题,现实当中有很多整定⽅法。
可是我们需要从根本上了解为什么这么整定,才能知道该如何建⽴数学模型进⾏分析。
那么要回答如何整定参数的问题,就需要先明⽩PID参数的作⽤都是什么?对系统有什么影响?我们从作⽤和副作⽤两个⽅⾯说明参数对系统的影响。
1.⽐例环节Kp,作⽤是加快系统的响应速度,提⾼系统的调节精度,副作⽤是会导致超调;2.积分环节Ki,作⽤是消除稳态误差,副作⽤是导致积分饱和现象;3.微分环节Kd,作⽤是改善系统的动态性能,副作⽤是延长系统的调节时间。
基于模糊控制的速度跟踪控制问题(C语言以及MATLAB仿真实现)

基于模糊控制的速度控制——地面智能移动车辆速度控制系统问题描述利用模糊控制的方法解决速度跟踪问题,即已知期望速度(desire speed),控制油门(throttle output)和刹车(brake output)来跟踪该速度。
已知输入:车速和发动机转速(值可观测)。
欲控制刹车和油门电压(同一时刻只有一个量起作用)。
算法思想模糊控制器是一语言控制器,使得操作人员易于使用自然语言进行人机对话。
模糊控制器是一种容易控制、掌握的较理想的非线性控制器,具有较佳的适应性及强健性(Robustness)、较佳的容错性(Fault Tolerance)。
利用控制法则来描述系统变量间的关系。
不用数值而用语言式的模糊变量来描述系统,模糊控制器不必对被控制对象建立完整的数学模式。
Figure 1模糊控制器的结构图模糊控制的优点:(1)模糊控制是一种基于规则的控制,它直接采用语言型控制规则,出发点是现场操作人员的控制经验或相关专家的知识,在设计中不需要建立被控对象的精确的数学模型,因而使得控制机理和策略易于接受与理解,设计简单,便于应用。
(2)由工业过程的定性认识出发,比较容易建立语言控制规则,因而模糊控制对那些数学模型难以获取,动态特性不易掌握或变化非常显著的对象非常适用。
(3)基于模型的控制算法及系统设计方法,由于出发点和性能指标的不同,容易导致较大差异;但一个系统语言控制规则却具有相对的独立性,利用这些控制规律间的模糊连接,容易找到折中的选择,使控制效果优于常规控制器。
(4)模糊控制是基于启发性的知识及语言决策规则设计的,这有利于模拟人工控制的过程和方法,增强控制系统的适应能力,使之具有一定的智能水平。
简化系统设计的复杂性,特别适用于非线性、时变、模型不完全的系统上。
模糊控制的缺点1.模糊控制的设计尚缺乏系统性,这对复杂系统的控制是难以奏效的。
所以如何建立一套系统的模糊控制理论,以解决模糊控制的机理、稳定性分析、系统化设计方法等一系列问题;2.如何获得模糊规则及隶属函数即系统的设计办法,这在目前完全凭经验进行;3.信息简单的模糊处理将导致系统的控制精度降低和动态品质变差。
模糊逻辑系统的C 语言实现方法

模糊逻辑系统的C语言实现方法贺维,江汉红,王海峰,张朝亮(武汉海军工程大学湖北武汉 430033)摘要:本文首先介绍了三种专门用于模糊逻辑控制系统设计的软件系统。
详细地介绍了利用软件进行模糊逻辑控制系统设计的基本原理以及模糊控制器的软件程序设计方法。
实验表明,模糊逻辑系统的C语言实现方法是完全可行的,并且能够大大减少工作量。
关键词:模糊逻辑C语言C Language Realize Method of Fuzzy Logic SystemHE-wei JIANG Han-hong WANG Hai-feng ZHANG Chao-liang(Naval University of Engineering, Wuhan 430033, China)Abstract: This paper presents three special software systems for the the design of hardware circuit of Fuzzy Logic control system. The paper introduced the composing and working principle in detail . The way of designing and programming of Fuzzy Logic control system is also presented in detail in the paper. In the end the results of experiment shows that C Language realize method is completely viable,and can reduce lots of workload.Key words: Fuzzy Control C Language1.引言对于模糊控制的实现是模糊控制在实际应用中的一个重要环节。
模糊PID控制算法的C#实现

模糊PID控制算法的C#实现跑起来的效果看每个类的test⽅法,⾃⼰调⽤来测试⽬的是看看哪个算法好⽤,移植的时候⽐较单纯没有研究懂算法,代码结构也没改动,只是移植到C#⽅便查看代码和测试,⼤家要拷贝也很⽅便,把整个类拷贝到.cs⽂件即可第⼀段算法来⾃模糊PID控制算法的C++实现:blog。
csdn。
net/shuoyueqishilove/article/details/78236541这段算法在实际值低于⽬标值是⼯作正常,超过后会有问题,不知道如何调教using System;using System.Collections.Generic;using System.Diagnostics;using System.Linq;using System.Text;using System.Threading.Tasks;namespace FuzzyPID{class FuzzyPID{public const int N = 7;double target; //系统的控制⽬标double actual; //采样获得的实际值double e; //误差double e_pre_1; //上⼀次的误差double e_pre_2; //上上次的误差double de; //误差的变化率double emax; //误差基本论域上限double demax; //误差辩化率基本论域的上限double delta_Kp_max; //delta_kp输出的上限double delta_Ki_max; //delta_ki输出上限double delta_Kd_max; //delta_kd输出上限double Ke; //Ke=n/emax,量化论域为[-3,-2,-1,0,1,2,3]double Kde; //Kde=n/demax,量化论域为[-3,-2,-1,0,1,2,3]double Ku_p; //Ku_p=Kpmax/n,量化论域为[-3,-2,-1,0,1,2,3]double Ku_i; //Ku_i=Kimax/n,量化论域为[-3,-2,-1,0,1,2,3]double Ku_d; //Ku_d=Kdmax/n,量化论域为[-3,-2,-1,0,1,2,3]int[,] Kp_rule_matrix = new int[N, N];//Kp模糊规则矩阵int[,] Ki_rule_matrix = new int[N, N];//Ki模糊规则矩阵int[,] Kd_rule_matrix = new int[N, N];//Kd模糊规则矩阵string mf_t_e; //e的⾪属度函数类型string mf_t_de; //de的⾪属度函数类型string mf_t_Kp; //kp的⾪属度函数类型string mf_t_Ki; //ki的⾪属度函数类型string mf_t_Kd; //kd的⾪属度函数类型double[] e_mf_paras; //误差的⾪属度函数的参数double[] de_mf_paras;//误差的偏差⾪属度函数的参数double[] Kp_mf_paras; //kp的⾪属度函数的参数double[] Ki_mf_paras; //ki的⾪属度函数的参数double[] Kd_mf_paras; //kd的⾪属度函数的参数double Kp;double Ki;double Kd;double A;double B;double C;public FuzzyPID(double e_max, double de_max, double kp_max, double ki_max, double kd_max, double Kp0, double Ki0, double Kd0){emax = e_max;demax = de_max;delta_Kp_max = kp_max;delta_Ki_max = ki_max;delta_Kd_max = kd_max;e = target - actual;de = e - e_pre_1;Ke = (N / 2) / emax;Kde = (N / 2) / demax;Ku_p = delta_Kp_max / (N / 2);Ku_i = delta_Ki_max / (N / 2);Ku_d = delta_Kd_max / (N / 2);Kp = Kp0;Ki = Ki0;A = Kp + Ki + Kd;B = -2 * Kd - Kp;C = Kd;}//三⾓⾪属度函数double trimf(double x, double a, double b, double c){double u;if (x >= a && x <= b)u = (x - a) / (b - a);else if (x > b && x <= c)u = (c - x) / (c - b);elseu = 0;return u;}//正态⾪属度函数double gaussmf(double x, double ave, double sigma){double u;if (sigma < 0){throw new Exception("In gaussmf, sigma must larger than 0");}u = Math.Exp(-Math.Pow(((x - ave) / sigma), 2));return u;}//梯形⾪属度函数double trapmf(double x, double a, double b, double c, double d){double u;if (x >= a && x < b)u = (x - a) / (b - a);else if (x >= b && x < c)u = 1;else if (x >= c && x <= d)u = (d - x) / (d - c);elseu = 0;return u;}//设置模糊规则Matrixpublic void setRuleMatrix(int[,] kp_m, int[,] ki_m, int[,] kd_m){for (int i = 0; i < N; i++)for (int j = 0; j < N; j++){Kp_rule_matrix[i, j] = kp_m[i, j];Ki_rule_matrix[i, j] = ki_m[i, j];Kd_rule_matrix[i, j] = kd_m[i, j];}}//设置模糊⾪属度函数的⼦函数void setMf_sub(string type, double[] paras, int n){int N_mf_e = 0, N_mf_de = 0, N_mf_Kp = 0, N_mf_Ki = 0, N_mf_Kd = 0;switch (n){case0:if (type == "trimf" || type == "gaussmf" || type == "trapmf")mf_t_e = type;elsethrow new Exception("Type of membership function must be \"trimf\" or \"gaussmf\" or \"trapmf\"");if (mf_t_e == "trimf")N_mf_e = 3;else if (mf_t_e == "gaussmf")N_mf_e = 2;else if (mf_t_e == "trapmf")N_mf_e = 4;e_mf_paras = new double[N * N_mf_e];for (int i = 0; i < N * N_mf_e; i++)e_mf_paras[i] = paras[i];break;if (type == "trimf" || type == "gaussmf" || type == "trapmf")mf_t_de = type;elsethrow new Exception("Type of membership function must be \"trimf\" or \"gaussmf\" or \"trapmf\"");if (mf_t_de == "trimf")N_mf_de = 3;else if (mf_t_de == "gaussmf")N_mf_de = 2;else if (mf_t_de == "trapmf")N_mf_de = 4;de_mf_paras = new double[N * N_mf_de];for (int i = 0; i < N * N_mf_de; i++)de_mf_paras[i] = paras[i];break;case2:if (type == "trimf" || type == "gaussmf" || type == "trapmf")mf_t_Kp = type;elsethrow new Exception("Type of membership function must be \"trimf\" or \"gaussmf\" or \"trapmf\"");if (mf_t_Kp == "trimf")N_mf_Kp = 3;else if (mf_t_Kp == "gaussmf")N_mf_Kp = 2;else if (mf_t_Kp == "trapmf")N_mf_Kp = 4;Kp_mf_paras = new double[N * N_mf_Kp];for (int i = 0; i < N * N_mf_Kp; i++)Kp_mf_paras[i] = paras[i];break;case3:if (type == "trimf" || type == "gaussmf" || type == "trapmf")mf_t_Ki = type;elsethrow new Exception("Type of membership function must be \"trimf\" or \"gaussmf\" or \"trapmf\"");if (mf_t_Ki == "trimf")N_mf_Ki = 3;else if (mf_t_Ki == "gaussmf")N_mf_Ki = 2;else if (mf_t_Ki == "trapmf")N_mf_Ki = 4;Ki_mf_paras = new double[N * N_mf_Ki];for (int i = 0; i < N * N_mf_Ki; i++)Ki_mf_paras[i] = paras[i];break;case4:if (type == "trimf" || type == "gaussmf" || type == "trapmf")mf_t_Kd = type;elsethrow new Exception("Type of membership function must be \"trimf\" or \"gaussmf\" or \"trapmf\"");if (mf_t_Kd == "trimf")N_mf_Kd = 3;else if (mf_t_Kd == "gaussmf")N_mf_Kd = 2;else if (mf_t_Kd == "trapmf")N_mf_Kd = 4;Kd_mf_paras = new double[N * N_mf_Kd];for (int i = 0; i < N * N_mf_Kd; i++)Kd_mf_paras[i] = paras[i];break;default: break;}}//设置模糊⾪属度函数的类型和参数public void setMf(string mf_type_e, double[] e_mf,string mf_type_de, double[] de_mf,string mf_type_Kp, double[] Kp_mf,string mf_type_Ki, double[] Ki_mf,string mf_type_Kd, double[] Kd_mf){setMf_sub(mf_type_e, e_mf, 0);setMf_sub(mf_type_de, de_mf, 1);setMf_sub(mf_type_Kp, Kp_mf, 2);setMf_sub(mf_type_Ki, Ki_mf, 3);setMf_sub(mf_type_Kd, Kd_mf, 4);}//实现模糊控制{double[] u_e = new double[N],u_de = new double[N],u_u = new double[N];int[] u_e_index = new int[3], u_de_index = new int[3];//假设⼀个输⼊最多激活3个模糊⼦集double delta_Kp, delta_Ki, delta_Kd;double delta_u;target = t;actual = a;e = target - actual;de = e - e_pre_1;e = Ke * e;de = Kde * de;/* 将误差e模糊化*/int j = 0;for (int i = 0; i < N; i++){if (mf_t_e == "trimf")u_e[i] = trimf(e, e_mf_paras[i * 3], e_mf_paras[i * 3 + 1], e_mf_paras[i * 3 + 2]);//e模糊化,计算它的⾪属度else if (mf_t_e == "gaussmf")u_e[i] = gaussmf(e, e_mf_paras[i * 2], e_mf_paras[i * 2 + 1]);//e模糊化,计算它的⾪属度else if (mf_t_e == "trapmf")u_e[i] = trapmf(e, e_mf_paras[i * 4], e_mf_paras[i * 4 + 1], e_mf_paras[i * 4 + 2], e_mf_paras[i * 4 + 3]);//e模糊化,计算它的⾪属度if (u_e[i] != 0)u_e_index[j++] = i; //存储被激活的模糊⼦集的下标,可以减⼩计算量}for (; j < 3; j++) u_e_index[j] = 0; //富余的空间填0/*将误差变化率de模糊化*/j = 0;for (int i = 0; i < N; i++){if (mf_t_de == "trimf")u_de[i] = trimf(de, de_mf_paras[i * 3], de_mf_paras[i * 3 + 1], de_mf_paras[i * 3 + 2]);//de模糊化,计算它的⾪属度else if (mf_t_de == "gaussmf")u_de[i] = gaussmf(de, de_mf_paras[i * 2], de_mf_paras[i * 2 + 1]);//de模糊化,计算它的⾪属度else if (mf_t_de == "trapmf")u_de[i] = trapmf(de, de_mf_paras[i * 4], de_mf_paras[i * 4 + 1], de_mf_paras[i * 4 + 2], de_mf_paras[i * 4 + 3]);//de模糊化,计算它的⾪属度if (u_de[i] != 0)u_de_index[j++] = i; //存储被激活的模糊⼦集的下标,可以减⼩计算量}for (; j < 3; j++) u_de_index[j] = 0; //富余的空间填0double den = 0, num = 0;/*计算delta_Kp和Kp*/for (int m = 0; m < 3; m++)for (int n = 0; n < 3; n++){num += u_e[u_e_index[m]] * u_de[u_de_index[n]] * Kp_rule_matrix[u_e_index[m], u_de_index[n]];den += u_e[u_e_index[m]] * u_de[u_de_index[n]];}delta_Kp = num / den;delta_Kp = Ku_p * delta_Kp;if (delta_Kp >= delta_Kp_max) delta_Kp = delta_Kp_max;else if (delta_Kp <= -delta_Kp_max) delta_Kp = -delta_Kp_max;Kp += delta_Kp;if (Kp < 0) Kp = 0;/*计算delta_Ki和Ki*/den = 0; num = 0;for (int m = 0; m < 3; m++)for (int n = 0; n < 3; n++){num += u_e[u_e_index[m]] * u_de[u_de_index[n]] * Ki_rule_matrix[u_e_index[m], u_de_index[n]];den += u_e[u_e_index[m]] * u_de[u_de_index[n]];}delta_Ki = num / den;delta_Ki = Ku_i * delta_Ki;if (delta_Ki >= delta_Ki_max) delta_Ki = delta_Ki_max;else if (delta_Ki <= -delta_Ki_max) delta_Ki = -delta_Ki_max;Ki += delta_Ki;if (Ki < 0) Ki = 0;/*计算delta_Kd和Kd*/den = 0; num = 0;for (int m = 0; m < 3; m++)for (int n = 0; n < 3; n++){num += u_e[u_e_index[m]] * u_de[u_de_index[n]] * Kd_rule_matrix[u_e_index[m], u_de_index[n]];den += u_e[u_e_index[m]] * u_de[u_de_index[n]];}delta_Kd = num / den;if (delta_Kd >= delta_Kd_max) delta_Kd = delta_Kd_max;else if (delta_Kd <= -delta_Kd_max) delta_Kd = -delta_Kd_max;Kd += delta_Kd;if (Kd < 0) Kd = 0;A = Kp + Ki + Kd;B = -2 * Kd - Kp;C = Kd;delta_u = A * e + B * e_pre_1 + C * e_pre_2;delta_u = delta_u / Ke;if (delta_u >= 0.95 * target) delta_u = 0.95 * target;else if (delta_u <= -0.95 * target) delta_u = -0.95 * target;e_pre_2 = e_pre_1;e_pre_1 = e;return delta_u;}void showMf(string type, double[] mf_paras){int tab = 0;if (type == "trimf")tab = 2;else if (type == "gaussmf")tab = 1;else if (type == "trapmf")tab = 3;this.WriteLine($"函数类型:{mf_t_e}");this.WriteLine("函数参数列表:");double[] p = mf_paras;for (int i = 0; i < N * (tab + 1); i++){this.Write(p[i] + "");if (i % (tab + 1) == tab)this.Write("\r\n");}}public void showInfo(){this.WriteLine("Info of this fuzzy controller is as following:");this.WriteLine($"基本论域e:[{-emax},{emax}]");this.WriteLine($"基本论域de:[{-demax},{demax}]");this.WriteLine($"基本论域delta_Kp:[{-delta_Kp_max},{delta_Kp_max}]");this.WriteLine($"基本论域delta_Ki:[{-delta_Ki_max},{delta_Ki_max}]");this.WriteLine($"基本论域delta_Kd:[{-delta_Kd_max},{delta_Kd_max}]");this.WriteLine("误差e的模糊⾪属度函数参数:");showMf(mf_t_e, e_mf_paras);this.WriteLine("误差变化率de的模糊⾪属度函数参数:");showMf(mf_t_de, de_mf_paras);this.WriteLine("delta_Kp的模糊⾪属度函数参数:");showMf(mf_t_Kp, Kp_mf_paras);this.WriteLine("delta_Ki的模糊⾪属度函数参数:");showMf(mf_t_Ki, Ki_mf_paras);this.WriteLine("delta_Kd的模糊⾪属度函数参数:");showMf(mf_t_Kd, Kd_mf_paras);this.WriteLine("模糊规则表:");this.WriteLine("delta_Kp的模糊规则矩阵");for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){this.Write(Kp_rule_matrix[i, j]);}this.Write("\r\n");}this.WriteLine("delta_Ki的模糊规则矩阵"); ;for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){this.WriteLine(Ki_rule_matrix[i, j]);}WriteEnd();}this.WriteLine("delta_Kd的模糊规则矩阵"); ;for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){WriteEnd();}this.WriteLine($"误差的量化⽐例因⼦Ke={Ke}");this.WriteLine($"误差变化率的量化⽐例因⼦Kde={Kde}");this.WriteLine($"输出的量化⽐例因⼦Ku_p={Ku_p}");this.WriteLine($"输出的量化⽐例因⼦Ku_i={Ku_i}");this.WriteLine($"输出的量化⽐例因⼦Ku_d={Ku_d}");this.WriteLine($"设定⽬标target={target}");this.WriteLine($"误差e={e}");this.WriteLine($"Kp={Kp}");this.WriteLine($"Ki={Ki}");this.WriteLine($"Kd={Kd}");WriteEnd();}public void Write(object str){Console.Write(str);}public void WriteLine(object str){Console.WriteLine(str);}public void WriteEnd(){Console.Write("\r\n");}public static void test(){int NB = -3;int NM = -2;int NS = -1;int ZO = 0;int PS = 1;int PM = 2;int PB = 3;double target = 300;double actual = 400;double u = 0;int[,] deltaKpMatrix = new int[7, 7] {{PB,PB,PM,PM,PS,ZO,ZO},{PB,PB,PM,PS,PS,ZO,NS},{PM,PM,PM,PS,ZO,NS,NS},{PM,PM,PS,ZO,NS,NM,NM},{PS,PS,ZO,NS,NS,NM,NM},{PS,ZO,NS,NM,NM,NM,NB},{ZO,ZO,NM,NM,NM,NB,NB}};int[,] deltaKiMatrix = new int[7, 7]{{NB,NB,NM,NM,NS,ZO,ZO},{NB,NB,NM,NS,NS,ZO,ZO},{NB,NM,NS,NS,ZO,PS,PS},{NM,NM,NS,ZO,PS,PM,PM},{NM,NS,ZO,PS,PS,PM,PB},{ZO,ZO,PS,PS,PM,PB,PB},{ZO,ZO,PS,PM,PM,PB,PB}};int[,] deltaKdMatrix = new int[7, 7]{{PS,NS,NB,NB,NB,NM,PS},{PS,NS,NB,NM,NM,NS,ZO},{ZO,NS,NM,NM,NS,NS,ZO},{ZO,NS,NS,NS,NS,NS,ZO},{ZO,ZO,ZO,ZO,ZO,ZO,ZO},{PB,NS,PS,PS,PS,PS,PB},{PB,PM,PM,PM,PS,PS,PB}};double[] e_mf_paras = { -3, -3, -2, -3, -2, -1, -2, -1, 0, -1, 0, 1, 0, 1, 2, 1, 2, 3, 2, 3, 3 };double[] de_mf_paras = { -3, -3, -2, -3, -2, -1, -2, -1, 0, -1, 0, 1, 0, 1, 2, 1, 2, 3, 2, 3, 3 };double[] Kp_mf_paras = { -3, -3, -2, -3, -2, -1, -2, -1, 0, -1, 0, 1, 0, 1, 2, 1, 2, 3, 2, 3, 3 };double[] Ki_mf_paras = { -3, -3, -2, -3, -2, -1, -2, -1, 0, -1, 0, 1, 0, 1, 2, 1, 2, 3, 2, 3, 3 };double[] Kd_mf_paras = { -3, -3, -2, -3, -2, -1, -2, -1, 0, -1, 0, 1, 0, 1, 2, 1, 2, 3, 2, 3, 3 };var fuzzypid = new FuzzyPID(1500, 1000, 0.3, 0.9, 0.6, 0.01, 0.04, 0.01);fuzzypid.setMf("trimf", e_mf_paras, "trimf", de_mf_paras, "trimf", Kp_mf_paras, "trimf", Ki_mf_paras, "trimf", Kd_mf_paras); fuzzypid.setRuleMatrix(deltaKpMatrix, deltaKiMatrix, deltaKdMatrix);for (int i = 0; i < 50; i++){u = fuzzypid.realize(target, actual);actual += u;Console.WriteLine($"{i} {target} {u} {actual}");// target = 300;//}}//fuzzypid.showInfo();}}}第⼆段来⾃模糊PID控制温控系统设计⽅案C语⾔程序代码: wenku。
步进电机模糊pid算法基本原理,c语言实现

步进电机模糊pid算法基本原理,c语言实现模糊PID(Proportional-Integral-Derivative)控制算法结合了模糊逻辑和传统PID控制算法,旨在提高系统的鲁棒性和稳定性。
步进电机作为一种常见的执行器,可以通过模糊PID算法实现精确的位置控制。
以下是模糊PID算法的基本原理以及C语言实现的简要步骤:模糊PID算法基本原理:1.模糊化输入和输出:将系统的输入(误差)和输出(控制量)进行模糊化,将其转换为模糊集合。
2.模糊规则库:建立模糊规则库,其中包含了一系列模糊规则,用于描述输入与输出之间的关系。
这些规则可以根据经验知识或系统模型来确定。
3.模糊推理:通过模糊规则库对模糊化的输入进行推理,得到模糊输出。
通常采用最大最小原则或加权平均等方法进行推理。
4.去模糊化:将模糊输出转换为确定性的控制量,即进行去模糊化操作。
常用的方法包括最大隶属度法、加权平均法等。
5.PID调节器:利用模糊输出和经典PID控制算法相结合,调节系统的控制量,使系统达到期望的运行状态。
C语言实现步骤:1.模糊化输入和输出:定义输入误差和输出控制量的模糊集合,并实现模糊化函数。
2.模糊规则库:定义一系列模糊规则,描述输入和输出之间的关系。
3.模糊推理:根据输入误差和模糊规则库进行推理,得到模糊输出。
4.去模糊化:实现去模糊化函数,将模糊输出转换为确定性的控制量。
5.PID调节器:结合经典PID控制算法,根据模糊输出和去模糊化后的控制量进行调节。
以下是一个简单的C语言实现示例:// 模糊化函数float fuzzyfication(float error) {// 省略具体实现,根据误差值计算归属度return fuzzy_value;}// 模糊规则库float fuzzy_rule(float error) {// 省略具体实现,定义模糊规则return fuzzy_output;}// 去模糊化函数float defuzzyfication(float fuzzy_output) {// 省略具体实现,根据模糊输出计算确定性的控制量return control_output;}int main() {float error = 0.0; // 输入误差float fuzzy_input = fuzzyfication(error); // 模糊化输入float fuzzy_output = fuzzy_rule(fuzzy_input); // 模糊推理float control_output = defuzzyfication(fuzzy_output); // 去模糊化输出// 利用确定性的控制量进行PID调节// 省略PID控制算法的实现// 控制步进电机运动return 0;}在实际应用中,模糊PID算法需要根据具体的系统和需求进行调试和优化,以实现良好的控制效果。
模糊控制算法c程序

由于项目需要,需要模糊控制算法,之前此类知识为0,经过半个多月的研究,终于有的小进展。
开始想从强大的互联网上搜点c代码来研究下,结果搜遍所有搜索引擎都搜不到,以下本人从修改的模糊控制代码,经过自己修改后可在vc6.0,运行!输入e表示输出误差,ec表示误差变化率,经过测试具有很好的控制效果,对于非线性系统和数学模型难以建立的系统来说有更好的控制效果!现将其公开供大家学习研究!#include <stdio.h>#include"math.h"#define PMAX 100#define PMIN -100#define DMAX 100#define DMIN -100#define FMAX 100 /*语言值的满幅值*/int PFF[4]={0,12,24,48};/*输入量D语言值特征点*/int DFF[4]={0,16,32,64};/*输出量U语言值特征点*/int UFF[7]={0,15,30,45,60,75,90};/*采用了调整因子的规则表,大误差时偏重误差,小误差时偏重误差变化*//*a0=0.3,a1=0.55,a2=0.74,a3=0.89 */int rule[7][7]={//误差变化率-3,-2,-1, 0, 1, 2, 3 // 误差{-6,-6,-6,-5,-5,-5,-4,}, // -3{-5,-4,-4,-3,-2,-2,-1,}, // -2{-4,-3,-2,-1, 0, 1, 2,}, // -1{-4,-3,-1, 0, 1, 3, 4,}, // 0{-2,-1, 0, 1, 2, 3, 4,}, // 1{ 1, 2, 2, 3, 4, 4, 5,}, // 2{ 4, 5, 5, 5, 6, 6, 6}}; // 3/**********************************************************/int Fuzzy(int P,int D) /*模糊运算引擎*/{int U; /*偏差,偏差微分以及输出值的精确量*/unsigned int PF[2],DF[2],UF[4]; /*偏差,偏差微分以及输出值的隶属度*/ int Pn,Dn,Un[4];long temp1,temp2;/*隶属度的确定*//*根据PD的指定语言值获得有效隶属度*/if(P>-PFF[3] && P<PFF[3]){if(P<=-PFF[2]){Pn=-2;PF[0]=FMAX*((float)(-PFF[2]-P)/(PFF[3]-PFF[2]));}else if(P<=-PFF[1]){Pn=-1;PF[0]=FMAX*((float)(-PFF[1]-P)/(PFF[2]-PFF[1]));}else if(P<=PFF[0]){Pn=0;PF[0]=FMAX*((float)(-PFF[0]-P)/(PFF[1]-PFF[0]));}else if(P<=PFF[1]){Pn=1; PF[0]=FMAX*((float)(PFF[1]-P)/(PFF[1]-PFF[0]));}else if(P<=PFF[2]){Pn=2; PF[0]=FMAX*((float)(PFF[2]-P)/(PFF[2]-PFF[1]));}else if(P<=PFF[3]){Pn=3; PF[0]=FMAX*((float)(PFF[3]-P)/(PFF[3]-PFF[2]));}}else if(P<=-PFF[3]){Pn=-2; PF[0]=FMAX;}else if(P>=PFF[3]){Pn=3; PF[0]=0;}PF[1]=FMAX-PF[0];if(D>-DFF[3] && D<DFF[3]){if(D<=-DFF[2]){Dn=-2;DF[0]=FMAX*((float)(-DFF[2]-D)/(DFF[3]-DFF[2])); }else if(D<=-DFF[1]){Dn=-1;DF[0]=FMAX*((float)(-DFF[1]-D)/(DFF[2]-DFF[1]));}else if(D<=DFF[0]){Dn=0;DF[0]=FMAX*((float)(-DFF[0]-D)/(DFF[1]-DFF[0]));}else if(D<=DFF[1]){Dn=1;DF[0]=FMAX*((float)(DFF[1]-D)/(DFF[1]-DFF[0]));}else if(D<=DFF[2]){Dn=2; DF[0]=FMAX*((float)(DFF[2]-D)/(DFF[2]-DFF[1])); }else if(D<=DFF[3]){Dn=3; DF[0]=FMAX*((float)(DFF[3]-D)/(DFF[3]-DFF[2])); }}else if(D<=-DFF[3]){Dn=-2;DF[0]=FMAX;else if(D>=DFF[3]){Dn=3;DF[0]=0;}DF[1]=FMAX-DF[0];/*使用误差围优化后的规则表rule[7][7]*//*输出值使用13个隶属函数,中心值由UFF[7]指定*/ /*一般都是四个规则有效*/Un[0]=rule[Pn-1+3][Dn-1+3];Un[1]=rule[Pn+3][Dn-1+3];Un[2]=rule[Pn-1+3][Dn+3];Un[3]=rule[Pn+3][Dn+3];if(PF[0]<=DF[0])UF[0]=PF[0];elseUF[0]=DF[0];if(PF[1]<=DF[0])UF[1]=PF[1];elseUF[1]=DF[0];if(PF[0]<=DF[1])UF[2]=PF[0];elseUF[2]=DF[1];if(PF[1]<=DF[1])UF[3]=PF[1];elseUF[3]=DF[1];/*同隶属函数输出语言值求大*/if(Un[0]==Un[1]){if(UF[0]>UF[1])UF[1]=0;elseUF[0]=0;if(Un[0]==Un[2]){if(UF[0]>UF[2])UF[2]=0;elseUF[0]=0;}if(Un[0]==Un[3]){if(UF[0]>UF[3])UF[3]=0;elseUF[0]=0;}if(Un[1]==Un[2]){if(UF[1]>UF[2])UF[2]=0;elseUF[1]=0;}if(Un[1]==Un[3]){if(UF[1]>UF[3])UF[3]=0;elseUF[1]=0;}if(Un[2]==Un[3]){if(UF[2]>UF[3])UF[3]=0;elseUF[2]=0;}/*重心法反模糊*//*Un[]原值为输出隶属函数标号,转换为隶属函数值*/ if(Un[0]>=0)Un[0]=UFF[Un[0]];elseUn[0]=-UFF[-Un[0]];if(Un[1]>=0)Un[1]=UFF[Un[1]];elseUn[1]=-UFF[-Un[1]];if(Un[2]>=0)Un[2]=UFF[Un[2]];elseUn[2]=-UFF[-Un[2]];if(Un[3]>=0)Un[3]=UFF[Un[3]];elseUn[3]=-UFF[-Un[3]];temp1=UF[0]*Un[0]+UF[1]*Un[1]+UF[2]*Un[2]+UF[3]*Un[3]; temp2=UF[0]+UF[1]+UF[2]+UF[3];U=temp1/temp2;return U;}void main(){int a=0,e,ec;/*int nowpoint,p1,p2=1;FILE *in,*out;in=fopen("in.txt","r");out=fopen("out.txt","w");*///while(!feof(in))while(1){//fscanf(in,"%d",&nowpoint);//p1=nowpoint;//e=0-nowpoint;//ec= p1-p2;printf("请输入e:");scanf("%d",&e);printf("请输入ec:");scanf("%d",&ec);a=Fuzzy(e,ec);//fprintf(out,"%d ",a);//printf("%d: ",p1);printf("e: %d ec: %d ",e,ec);printf("a: %d \n",a); //p2=p1;}//fclose(in);//fclose(out);}。
控制系统中的模糊控制算法设计与实现

控制系统中的模糊控制算法设计与实现现代控制系统在实际应用中,往往面临着多变、复杂、非线性的控制问题。
传统的多变量控制方法往往无法有效应对这些问题,因此,模糊控制算法作为一种强大的控制手段逐渐受到广泛关注和应用。
本文将从控制系统中的模糊控制算法的设计和实现两个方面进行介绍,以帮助读者更好地了解和掌握这一领域的知识。
一、模糊控制算法的设计1. 模糊控制系统的基本原理模糊控制系统是一种基于模糊逻辑的控制系统,其基本思想是通过将输入和输出变量模糊化,利用一系列模糊规则来实现对系统的控制。
模糊控制系统主要由模糊化、规则库、模糊推理和解模糊四个基本部分组成,其中规则库是模糊控制系统的核心部分,包含了一系列的模糊规则,用于描述输入和输出变量之间的关系。
2. 模糊控制算法的设计步骤(1)确定输入和输出变量:首先需要明确系统中的输入和输出变量,例如温度、压力等。
(2)模糊化:将确定的输入和输出变量进行模糊化,即将其转换为模糊集合。
(3)建立模糊规则库:根据实际问题和经验知识,建立一系列模糊规则。
模糊规则关联了输入和输出变量的模糊集合之间的关系。
(4)模糊推理:根据当前的输入变量和模糊规则库,利用模糊推理方法求解输出变量的模糊集合。
(5)解模糊:将求解得到的模糊集合转换为实际的输出值,常用的方法包括最大值法、加权平均法等。
3. 模糊控制算法的设计技巧(1)合理选择输入和输出变量的模糊集合:根据系统的实际需求和属性,选择合适的隶属函数,以便更好地描述系统的特性。
(2)精心设计模糊规则库:模糊规则库的设计是模糊控制算法的关键,应根据实际问题与经验知识进行合理的规则构建。
可以利用专家经验、试验数据或者模拟仿真等方法进行规则的获取和优化。
(3)选用合适的解模糊方法:解模糊是模糊控制算法中的一项重要步骤,选择合适的解模糊方法可以提高控制系统的性能。
常用的解模糊方法有最大值法、加权平均法、中心平均法等,应根据系统的需求进行选择。
PLC实现模糊控制算法的关键技术研究与应用

果 采用 常规 P I D控制算 法 , 不 仅参 数调整 困难 , 而
且 得不 到理想 效果 。而模 糊控 制具有 不依 赖被 控
过 程数 学模 型 、 对参 数 变 化 不敏 感 及鲁 棒 性 强 等 特点 , 因此 , 采 用 模 糊控 制 算 法 , 特别 是 采 用 模 糊
自适应 P I D控 制算 法 来设 计 过程 控 制 系统 , 能 更 好 地适 应 控 制 系 统 的参 数 变 化 和工 作 条 件 的 变
收 稿 日期 : 2 0 1 3 - 0 8 — 1 3 ( 修改稿) 基金项目: 吉 林 省 教 育 厅 科 学 技 术 研 究 项 目( 吉 教 科 合 字 [ 2 0 0 8 ] 第 2 1 3号 )
由于 P L C是按 照 巡 回扫描 方 式工 作 的 , 它 在
第 l 0期
1 模 糊控 制算 法主程序 P L C模 糊控 制系统 结构 如 图 1所示 。传感 器
即停 止 当前 程序 , 转去 执行 中断处 理子程 序 ; 计数 中断是 一种 高速 计数 中断模 式 , 即对 P L C指 定输 入端 输入 的脉 冲 信 号进 行 高 速计 数 , 当达 到设 定 次数 ( 即计 数器 设 定值 为零 ) 时, P L C就 中断 当前 程序 , 转 去执行 中断处 理子 程序 。 因此 , 利用 P L C
化
工
自 动 化
及 仪
表
第4 0卷
P I G 实现模 糊 控 制算 法 的关 键 技术 研 究 与应 用
郑 文 张 运 波
( 长 春工 程 学 院 电 气 与 信息 工 程 学 院 , 长春 1 3 0 0 1 2 )
摘
要
模糊PID控制温控系统设计C语言程序代码

模糊PID控制温控系统设计C语言程序代码请注意,由于1200字的限制,下面的代码只是模糊PID控制温控系统的一个简单示例。
如果您需要更详细和完整的代码,请提供更多的细节和规格要求。
```c#include <stdio.h>//PID参数float kp = 0.5; // 比例系数float ki = 0.2; // 积分系数float kd = 0.1; // 微分系数//PID变量float integral = 0; // 积分累计float previous_error = 0; // 上一次的误差//温度传感器读取函数,返回当前温度float read_temperatur//实现温度传感器读取的代码逻辑//返回当前温度值//控制器输出函数,将控制信号发送给执行机构void control_output(float control_signal)//实现将控制信号发送给执行机构的代码逻辑int mai//设置设定温度float setpoint = 25.0;//主循环while (1)//获取当前温度float current_temperature = read_temperature(;//计算误差float error = setpoint - current_temperature;//计算PID控制信号float p_term = kp * error;integral += ki * error;float d_term = kd * (error - previous_error);float control_signal = p_term + integral + d_term; //更新上一次的误差previous_error = error;//输出控制信号control_output(control_signal);}return 0;```上述代码中,我们首先定义了PID参数和变量,以及温度传感器读取函数和控制器输出函数。
plc 模糊pid控制算法 -回复

plc 模糊pid控制算法-回复PLC 模糊PID 控制算法近年来,随着工业自动化技术的发展,PLC(可编程逻辑控制器)在工业生产中扮演着愈加重要的角色。
其中,PID(比例-积分-微分)控制算法作为一种经典的控制算法,在工业自动化领域被广泛应用。
然而,PID 算法在实际应用中往往表现出灵敏度低、容易受到干扰等问题。
为了克服这些问题,研究人员提出了模糊PID 控制算法,本文将对该算法进行详细的介绍和解析。
1. 算法原理模糊PID 控制算法是一种基于模糊逻辑的PID 控制算法。
它利用模糊控制的特点将PID 算法的参数进行动态调整,以适应不同的控制对象和环境。
该算法的主要思想是对于每个输入变量,通过模糊化和模糊推理得到相应的输出变量,再通过去模糊化得到最终的控制量。
具体而言,模糊PID 控制算法由以下几个步骤组成:a. 模糊化:将输入变量进行模糊化处理,将其转化为模糊集合。
b. 模糊推理:利用模糊规则库对模糊集合进行推理,得到相应的输出变量。
c. 去模糊化:将输出变量进行去模糊化处理,得到最终的控制量。
2. 参数调整模糊PID 控制算法相比于传统的PID 控制算法在参数调整方面更为复杂。
传统的PID 控制算法通过手动调整比例系数、积分时间和微分时间来实现控制效果的优化,而模糊PID 控制算法需要对模糊化、模糊规则库以及去模糊化等多个参数进行调整。
a. 模糊化参数:模糊化参数决定了输入变量在模糊集合中的划分方式,通过增加或减少模糊集合的数量和范围,可以改变模糊化的精度和灵敏度。
b. 模糊规则库:模糊规则库是模糊PID 控制算法的核心部分,它由一系列模糊规则组成,每条规则都描述了输入变量和输出变量之间的关系。
通过调整规则库的大小和规则的权重,可以改变控制算法的响应速度和稳定性。
c. 去模糊化参数:去模糊化参数决定了输出变量从模糊集合到实际控制量的映射方式。
通过调整去模糊化参数,可以改变控制算法的输出范围和分辨率。
模糊控制原理简介
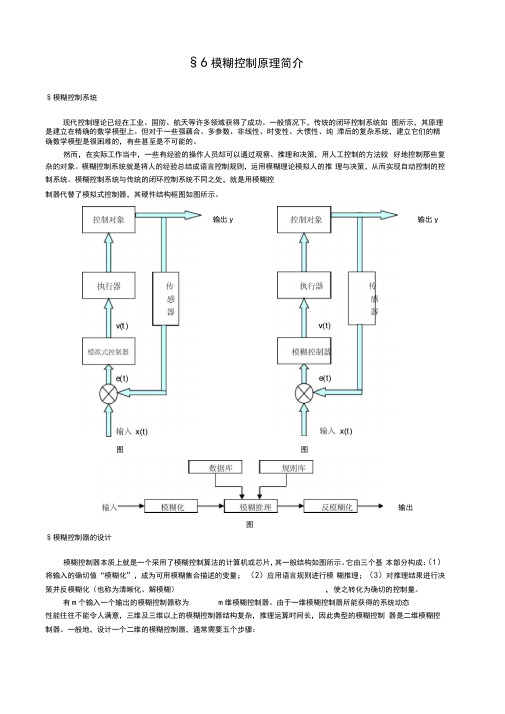
§6模糊控制原理简介§模糊控制系统现代控制理论已经在工业、国防、航天等许多领域获得了成功。
一般情况下,传统的闭环控制系统如 图所示,其原理是建立在精确的数学模型上。
但对于一些强藕合、多参数、非线性、时变性、大惯性、纯 滞后的复杂系统,建立它们的精确数学模型是很困难的,有些甚至是不可能的。
然而,在实际工作当中,一些有经验的操作人员却可以通过观察、推理和决策,用人工控制的方法较 好地控制那些复杂的对象。
模糊控制系统就是将人的经验总结成语言控制规则,运用模糊理论模拟人的推 理与决策,从而实现自动控制的控制系统。
模糊控制系统与传统的闭环控制系统不同之处,就是用模糊控 制器代替了模拟式控制器,其硬件结构框图如图所示。
§模糊控制器的设计模糊控制器本质上就是一个采用了模糊控制算法的计算机或芯片,其一般结构如图所示。
它由三个基 本部分构成:(1)将输入的确切值“模糊化”,成为可用模糊集合描述的变量; (2)应用语言规则进行模 糊推理;(3)对推理结果进行决策并反模糊化(也称为清晰化、解模糊),使之转化为确切的控制量。
有m 个输入一个输出的模糊控制器称为m 维模糊控制器。
由于一维模糊控制器所能获得的系统动态性能往往不能令人满意,三维及三维以上的模糊控制器结构复杂,推理运算时间长,因此典型的模糊控制 器是二维模糊控制器。
一般地,设计一个二维的模糊控制器,通常需要五个步骤:输出y(t ) 输出y(t )图 图输出图确定输入变量与输出变量及其模糊状态; 输入变量的模糊化; 建立模糊控制规则;进行模糊推理; 输出变量的反模糊化。
确定输入变量与输出变量及其模糊状态 根据问题的背景,确定出输入变量E I 、E 2和输出变量u 。
输入、输出变量的模糊状态按照控制品质的要求可分为三类:控制品质要求较高的场合,变量的模糊状态取为负大(NB )、负中(NM )、负小(NS )、零(ZO )、正小(PS )、正中(PM )、正大(PB )负大(NB )、负中(NM )、负小(NS )、负零(NZ )、正零(PZ )、正小(PS )、正中(PM )、正大(PB ); 控制品质要求一般的场合,变量的模糊状态取为负大(NB )、负小(NS )、零(ZO )、正小(PS )、正大(PB )负大(NB )、负小(NS )、负零(NZ )、正零(PZ )、正小(PS 、正大(PB );控制品质要求较低的场合,变量的模糊状态取为负大(NB )、零(ZO )、正大(PB )负大(NB )、负零(NZ )、正零(PZ )、正大(PB )。
模糊逻辑系统的C语言实现方法

模糊逻辑系统的C语言实现方法贺维,江汉红,王海峰,张朝亮(武汉海军工程大学湖北武汉 430033)摘要:本文首先介绍了三种专门用于模糊逻辑控制系统设计的软件系统。
详细地介绍了利用软件进行模糊逻辑控制系统设计的基本原理以及模糊控制器的软件程序设计方法。
实验表明,模糊逻辑系统的C语言实现方法是完全可行的,并且能够大大减少工作量。
关键词:模糊逻辑C语言C Language Realize Method of Fuzzy Logic SystemHE-wei JIANG Han-hong WANG Hai-feng ZHANG Chao-liang(Naval University of Engineering, Wuhan 430033, China)Abstract: This paper presents three special software systems for the the design of hardware circuit of Fuzzy Logic control system. The paper introduced the composing and working principle in detail . The way of designing and programming of Fuzzy Logic control system is also presented in detail in the paper. In the end the results of experiment shows that C Language realize method is completely viable,and can reduce lots of workload.Key words: Fuzzy Control C Language1.引言对于模糊控制的实现是模糊控制在实际应用中的一个重要环节。
C语言实现模糊控制算法

if(XU[0]<=YU[0])//规则前提的可信度取小运算
ZU[0]=XU[0]; else
标题文本预设
ZU[0]=YU[0];
if(XU[1]<=YU[0])//规则前提的可信度取小运算
ZU[1]=XU[1];
else
ZU[1]=YU[0];
if(XU[0]<=YU[1])//规则前提的可信度取小运算
C语言实现模糊控制算法
C语言实现模糊控制算法--以洗衣机的模糊控制为例
模糊控制器结构
选用两输入单输出模糊控制器。控制器的输入为衣物的泥污和油污,输出
为洗涤时间。
标题文本预设
此部分内容作为文字排版占位显示
定义输入、输出模糊集
(建议使用主题字体)
泥污的模糊集表示为:SD(泥污少)、MD(泥污中)、LD(泥污多); 油污的模糊集表示为:NG(油污少)、MG(油污中)、LG(油污多); 洗涤时间的模糊集为: VS(很短)、S(短)、M(中)、L(长)、VL(很长)。
此部分内容作为文字排版占位显示 (建议使用主题字体)
C语言实现模糊控制算法--以洗衣机的模糊控制为例
重心法反模糊
for(i=0;i<4;i++) ZUmax[i]=ZU[i];
for(j=0;j<3;j++)//冒泡法排序 从小到大排 for(i=0;i<3-j;i++) if(ZUmax[i]>=ZUmax[i+1]) { Zij=ZUmax[i]; ZUmax[i]=ZUmax[i+1]; ZUmax[i+1]=Zij; }
油污Y
MG
0
min(3/5,μM(z)) min(1/5,μL(z))
simulink模糊pid控制模型转c语言代码 -回复

simulink模糊pid控制模型转c语言代码-回复"Simulink模糊PID控制模型转C语言代码"在控制系统中,PID(比例-积分-微分)控制器被广泛应用于实现对系统的稳定和精确控制。
然而,当面对非线性、不确定性或者复杂度较高的系统时,传统的PID控制往往无法满足需求。
这时,模糊控制成为一种有效的替代方法。
模糊PID控制结合了传统的PID控制和模糊控制的优点,是在复杂系统控制中常用的一种方法。
本文将介绍如何将Simulink模糊PID控制模型转化为C语言代码的步骤。
第一步:设计模糊PID控制模型在Simulink环境下,设计一个模糊PID控制模型。
首先,根据系统特性选择合适的输入和输出变量,如温度和控制信号。
然后,选择适当的模糊集合和隶属函数。
根据系统的动态响应,确定合适的模糊规则,并使用模糊推理机制进行系统的控制。
最后,评估和调整模型以满足系统的需求。
第二步:构建模糊PID控制器的C语言数据结构根据设计的模糊PID控制模型,构建对应的C语言数据结构。
首先,定义输入和输出变量的数据类型和范围。
然后,定义模糊控制器的数据结构,包括模糊集合、隶属函数和模糊规则等。
最后,定义需要使用的参数,如模糊PID控制器的增益和偏差。
第三步:实现模糊控制算法在C语言中,实现模糊控制算法。
首先,读取输入变量的传感器数据,如温度值。
然后,将传感器数据映射到相应的模糊集合上,并计算隶属度。
接下来,使用模糊推理机制基于模糊规则来确定输出变量的控制信号。
最后,使用PID控制算法对控制信号进行修正,以实现系统的稳定和精确控制。
第四步:测试和优化C语言代码在C语言环境下,对已实现的模糊PID控制算法进行测试和优化。
首先,使用模拟数据或者仿真实验验证C语言代码的正确性和准确性。
然后,根据需要对代码进行调整和优化,以满足系统的性能要求。
最后,使用实际系统进行验证和性能测试,对模糊PID控制算法进行进一步改进和优化。
模糊PID控制温控系统设计方案C语言程序代码

/********************************************************************模糊 PID 控制温控系统仿真设计 C 程序代码********************************************************************/#include<reg52.h>#define uchar unsigned char#define uint unsigned int#define PULSE 200#define number 0.035sbit SDO = P2^0。
sbit SDI = P2^1。
sbit CS = P2^2。
sbit CLK = P2^3 。
sbit EOC = P2^4。
sbit RS = P2^5。
sbit RW = P2^6。
sbit EN = P2^7。
sbit KEY1= P3^0 。
sbit KEY2= P3^1 。
sbit KEY3= P3^2 。
sbit KEY4= P3^3 。
sbit KEY5= P3^4 。
sbit IN1 = P3^5。
sbit IN2 = P3^6。
sbit ENA = P3^7。
uchar flag。
uchar flag_start。
float S_temp=60.0。
float P_temp=20.0。
float Kp 。
float Ki 。
float Kd 。
float Err=0.0。
float Last_Err=0.0。
float D_Err=0.0 。
float Sum_Err=0.0。
float U=0.0。
/******************************函数功能:延时******************************/void delay_ms(uchar z){uchar i。
uchar j。
模糊逻辑控制的C语言实现

合 。隶属度函数可以是任何函数,只要其值域在0 到 1
之间即可。常用的隶
表1 隶属度函数数值表
属度函数有:高 斯 型 、下标 论域值 大 中 小 零
梯 形 、三 角 形 、钟 形等, 0 -6 1 0 0
0
本文采用了高斯型隶 1 -5.933 33 1 0 0
关键词:模糊逻辑控制;VC+ + ;实现
中图分类号:TP273
文献标识码:A
doi:10.3969/j.issn.1665-2272.2017.11.056
0 引言 模 糊 逻 辑 控 制 是 智 能 控 制 的 一 种 ,以 模 糊 集 合 论 、
模 糊 语 言 变 量 和 模 糊 逻 辑 推 理 为 基 础 。其 算 法 的 基 本 运 算 单 元 是 模 糊 集 合 ,模 糊 集 合 与 普 通 集 合 定 义 基 本 相 同 ,但是其不具备普通集合的确定性,也 就 是 说 ,一 个元素是否属于模糊集合不是用要么是该集合元素, 要 么 不 是 该 集 合 元 素 表 示 ,而 是 用 属 于 该 集 合 的 程 度 表 示 ,最大值为1袁表示完全属于该集合,最小值为0袁 表示不属于该集合,在 0 到 1 之间可以任意取值,表示 在多大程度上属于该模糊集合。 1 模糊推理原理
后 得 到 的 隶 属 度 值 ,其 输 出 是 整 个 前 件 的 隶 属 度 ,模糊
逻辑算子可取模糊算子中的任意一个,常 用的“与”算
子有:m in(最小)和 Prod(代数积)。常用的“或”算子有院
max(最大)和 probor(概率或)。本论文米用了最大和最
小算子。
1.猿蕴含运算(规则库)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由于项目需要,需要模糊控制算法,之前此类知识为0,经过半个多月的研究,终于有的小进展。
开始想从强大的互联网上搜点c代码来研究下,结果搜遍所有搜索引擎都搜不到,以下本人从修改的模糊控制代码,经过自己修改后可在,运行!输入e表示输出误差,ec表示误差变化率,经过测试具有很好的控制效果,对于非线性系统和数学模型难以建立的系统来说有更好的控制效果!现将其公开供大家学习研究!#include <>#include""#define PMAX 100#define PMIN -100#define DMAX 100#define DMIN -100#define FMAX 100 /*语言值的满幅值*/int PFF[4]={0,12,24,48};/*输入量D语言值特征点*/int DFF[4]={0,16,32,64};/*输出量U语言值特征点*/int UFF[7]={0,15,30,45,60,75,90};/*采用了调整因子的规则表,大误差时偏重误差,小误差时偏重误差变化*//*a0=,a1=,a2=,a3= */int rule[7][7]={//误差变化率 -3,-2,-1, 0, 1, 2, 3 // 误差{-6,-6,-6,-5,-5,-5,-4,}, // -3{-5,-4,-4,-3,-2,-2,-1,}, // -2{-4,-3,-2,-1, 0, 1, 2,}, // -1{-4,-3,-1, 0, 1, 3, 4,}, // 0{-2,-1, 0, 1, 2, 3, 4,}, // 1{ 1, 2, 2, 3, 4, 4, 5,}, // 2{ 4, 5, 5, 5, 6, 6, 6}}; // 3/**********************************************************/int Fuzzy(int P,int D) /*模糊运算引擎*/{int U; /*偏差,偏差微分以及输出值的精确量*/ unsigned int PF[2],DF[2],UF[4]; /*偏差,偏差微分以及输出值的隶属度*/int Pn,Dn,Un[4];long temp1,temp2;/*隶属度的确定*//*根据PD的指定语言值获得有效隶属度*/if(P>-PFF[3] && P<PFF[3]){if(P<=-PFF[2]){Pn=-2;PF[0]=FMAX*((float)(-PFF[2]-P)/(PFF[3]-PFF[2]));}else if(P<=-PFF[1]){Pn=-1;PF[0]=FMAX*((float)(-PFF[1]-P)/(PFF[2]-PFF[1]));}else if(P<=PFF[0]){Pn=0;PF[0]=FMAX*((float)(-PFF[0]-P)/(PFF[1]-PFF[0]));}else if(P<=PFF[1]){Pn=1; PF[0]=FMAX*((float)(PFF[1]-P)/(PFF[1]-PFF[0]));}else if(P<=PFF[2]){Pn=2; PF[0]=FMAX*((float)(PFF[2]-P)/(PFF[2]-PFF[1]));}else if(P<=PFF[3]){Pn=3; PF[0]=FMAX*((float)(PFF[3]-P)/(PFF[3]-PFF[2]));}}else if(P<=-PFF[3]){Pn=-2; PF[0]=FMAX;}else if(P>=PFF[3]){Pn=3; PF[0]=0;}PF[1]=FMAX-PF[0];if(D>-DFF[3] && D<DFF[3]){if(D<=-DFF[2]){Dn=-2;DF[0]=FMAX*((float)(-DFF[2]-D)/(DFF[3]-DFF[2])); }else if(D<=-DFF[1]){Dn=-1;DF[0]=FMAX*((float)(-DFF[1]-D)/(DFF[2]-DFF[1]));}else if(D<=DFF[0]){Dn=0;DF[0]=FMAX*((float)(-DFF[0]-D)/(DFF[1]-DFF[0]));}else if(D<=DFF[1]){Dn=1;DF[0]=FMAX*((float)(DFF[1]-D)/(DFF[1]-DFF[0]));}else if(D<=DFF[2]){Dn=2; DF[0]=FMAX*((float)(DFF[2]-D)/(DFF[2]-DFF[1]));}else if(D<=DFF[3]){Dn=3; DF[0]=FMAX*((float)(DFF[3]-D)/(DFF[3]-DFF[2]));}}else if(D<=-DFF[3]){Dn=-2;DF[0]=FMAX;}else if(D>=DFF[3]){Dn=3;DF[0]=0;}DF[1]=FMAX-DF[0];/*使用误差范围优化后的规则表rule[7][7]*//*输出值使用13个隶属函数,中心值由UFF[7]指定*//*一般都是四个规则有效*/Un[0]=rule[Pn-1+3][Dn-1+3];Un[1]=rule[Pn+3][Dn-1+3];Un[2]=rule[Pn-1+3][Dn+3];Un[3]=rule[Pn+3][Dn+3];if(PF[0]<=DF[0])UF[0]=PF[0];elseUF[0]=DF[0];if(PF[1]<=DF[0])UF[1]=PF[1];elseUF[1]=DF[0];if(PF[0]<=DF[1])UF[2]=PF[0];elseUF[2]=DF[1];if(PF[1]<=DF[1])UF[3]=PF[1];elseUF[3]=DF[1];/*同隶属函数输出语言值求大*/if(Un[0]==Un[1]){if(UF[0]>UF[1])UF[1]=0;elseUF[0]=0;}if(Un[0]==Un[2]){if(UF[0]>UF[2])UF[2]=0;elseUF[0]=0;}if(Un[0]==Un[3]){if(UF[0]>UF[3])UF[3]=0;elseUF[0]=0;}if(Un[1]==Un[2]){if(UF[1]>UF[2])UF[2]=0;elseUF[1]=0;}if(Un[1]==Un[3]){if(UF[1]>UF[3])UF[3]=0;elseUF[1]=0;}if(Un[2]==Un[3]){if(UF[2]>UF[3])UF[3]=0;elseUF[2]=0;}/*重心法反模糊*//*Un[]原值为输出隶属函数标号,转换为隶属函数值*/if(Un[0]>=0)Un[0]=UFF[Un[0]];elseUn[0]=-UFF[-Un[0]];if(Un[1]>=0)Un[1]=UFF[Un[1]];elseUn[1]=-UFF[-Un[1]];if(Un[2]>=0)Un[2]=UFF[Un[2]];elseUn[2]=-UFF[-Un[2]];if(Un[3]>=0)Un[3]=UFF[Un[3]];elseUn[3]=-UFF[-Un[3]];temp1=UF[0]*Un[0]+UF[1]*Un[1]+UF[2]*Un[2]+UF[3]*Un[3]; temp2=UF[0]+UF[1]+UF[2]+UF[3];U=temp1/temp2;return U;}void main(){int a=0,e,ec;/*int nowpoint,p1,p2=1;FILE *in,*out;in=fopen("","r");out=fopen("","w");*///while(!feof(in))while(1){//fscanf(in,"%d",&nowpoint);//p1=nowpoint;//e=0-nowpoint;//ec= p1-p2;printf("请输入e:");scanf("%d",&e);printf("请输入ec:");scanf("%d",&ec);a=Fuzzy(e,ec);//fprintf(out,"%d ",a);//printf("%d: ",p1);printf("e: %d ec: %d ",e,ec);printf("a: %d \n",a);//p2=p1;}//fclose(in);//fclose(out);}。
