教科版物理必修一课件第一章第3讲运动图像追及相遇问题

分析:x-t图像反映物体做直线运动的位移随时间变化的规律， 不是物体运动的轨迹，(1)错；x-t图像若是一条平行于t轴的直 线，表示物体处于静止状态，若是倾斜直线，表示物体做匀速 直线运动，v-t图像是一条平行于t轴的直线，说明物体做匀速 直线运动，(2)错、(3)对；x-t图像与时间轴围成的面积无任何 意义，(4)错；v-t图像的交点表示两个物体的速度相等，x-t图 像的交点表示两个物体相遇，(5)错、(6)对；物体相向运动相 遇时，各自发生的位移大小之和等于开始时二者之距，(7)对。
高中物理课件
（金戈铁骑 整理制作）
第3讲运动图像追及相遇问题
知识点1匀变速直线运动的图像Ⅱ 1.直线运动的x-t图像 (1)物理意义：反映了物体做直线运动的_位__移__随_时__间__变化的 规律。 (2)斜率的意义：图线上某点切线斜率的大小表示物体_速__度__ 的大小，斜率正负表示物体_速__度__的方向。
v-t图像
轴
横轴为时间t,纵轴为 位移x
横轴为时间t,纵轴为速度v
线
倾斜直线表示匀速直线 倾斜直线表示匀变速直线
运动
运动
斜率
表示速度
表示加速度
面积
无实际意义
图线和时间轴围成的面积 表示位移
纵截距
表示初位置
表示初速度
拐点表示从一种运动变 拐点表示从一种运动变为另
特殊点 为另一种运动,交点表 一种运动,交点表示速度相
2.常见类型 (1)两个做匀减速直线运动物体的追及相遇问题。 (2)两个做匀加速直线运动物体的追及相遇问题。 (3)求追及相遇过程中距离的极值问题。
3.解题思路 用图像法解决追及相遇问题时应把握的三个环节:
环节
基本要求
定量画图时需根据物体在不同阶段的运动情况,通 画 图 过定量计算分阶段、分区间逐一描图
【解析】(1)当甲车速度减至等于乙车速度时两车的距离最大，
设该减速过程经过的时间为t，则
v乙=v甲-at 解得：t=12s
此时甲、乙间的距离为
x

v甲t

1 2
at 2

v乙t
1012 m 1 0.5122 m 412 m 36 m
2
(2)设甲车减速到零所需时间为t1，则有：
【规范解答】(1)设汽车的质量为m,轮胎与路面间的动摩擦因
数为μ,根据牛顿第二定律,汽车刹车时有
μmg=ma
对汽车的刹车过程由运动学公式得:
-2ax=-v2 由以上两式得 x v2
2g
即刹车痕迹与刹车前车速的平方成正比。
(2)汽车相撞时的速度为40km/h,根据图像可知从这个速度减 到零,汽车还要向前滑行10m,撞前汽车已经滑行20m,所以,如 果汽车不相撞滑行30m后停下。滑行30m对应的初速度即图 中的A点对应速度。故汽车刹车前的速度为68km/h。
示相遇
来自百度文库
等
【典例透析1】(多选)一物体自t=0时开始做直线运动，其速 度—时间图像如图所示。下列选项正确的是()
A.在0～6s内，物体离出发点最远为30m B.在0～6s内，物体经过的路程为40m C.在0～4s内，物体的平均速度为7.5m/s D.在5～6s内，物体做匀减速直线运动
【解题探究】请分析物体运动的速度—时间图像，回答下列 问题： (1)0～6s内，物体的运动方向是否发生变化？什么时刻离出 发点最远？ 提示:由图像可得，0～5s内物体沿正方向运动，5～6s物体 沿负方向运动，即第5s末物体离出发点最远。 (2)v-t图像中“面积”的含义是什么？如何根据v-t图像求平 均速度？ 提示:图线与时间轴所围的“面积”表示位移的大小，求得位 移可用公式求v 平x均速度。
答案：见规范解答
图像法在解决追及相遇问题中的应用 1.方法概述 (1)图像可以直观地叙述物理过程,并鲜明地表示物理量间的各 种关系。利用图像解决物理问题,是学好物理的一种重要方法。 (2)追及相遇问题涉及的过程比较复杂，如果用公式法求解， 有时不仅计算量大，而且难以将过程叙述清楚，而使用图像法 求解，往往会比较直观。
考点1运动图像的应用(三年6考) 深化理解
【考点解读】 1.应用运动图像的三点注意 (1)无论是x-t图像还是v-t图像都只能描述直线运动。 (2)x-t图像和v-t图像都不表示物体运动的轨迹。 (3)x-t图像和v-t图像的形状由x与t、v与t的函数关系决定。
2.应用运动图像解题“六看”
x-t图像
度加速运动，甲车匀速行驶，乙车追上甲车前，两车有最大距
离18m,求乙车的加速度大小。
【解析】当甲、乙两车速度相等时有最大距离，则
v甲=v乙+a′t
对甲车：x甲=v甲t
对乙车： x乙

v甲
2
v乙
t
又有：Δxm=x甲-x乙
代入数值，解以上各式得：a′=1m/s2
答案：1m/s2
【总结提升】追及相遇问题的求解方法 1.解题思路
知识点2追及和相遇问题 1.追及问题的两类情况 (1)若后者能追上前者，追上时，两者处于_同__一__位置，且后者 速度一定不小于前者速度。 (2)若后者追不上前者，则当后者速度与前者速度_相__等__时，两 者相距最近。 2.相遇问题 相向运动的物体，当各自发生的位移大小之和_等__于__开始时两 物体间的距离时即相遇。
2.解题技巧 (1)紧抓“一图三式”,即：过程示意图,时间关系式、速度关系 式和位移关系式。 (2)审题应抓住题目中的关键字眼,充分挖掘题目中的隐含条件, 如“刚好”“恰好”“最多”“至少”等,往往对应一个临界状 态,满足相应的临界条件。 (3)若被追赶的物体做匀减速运动，一定要注意追上前该物体 是否已经停止运动，另外还要注意最后对解的讨论分析。
2.直线运动的v-t图像 (1)物理意义：反映了做直线运动的物体的_速__度__随_时__间__变化 的规律。 (2)斜率的意义：图线上某点切线斜率的大小表示物体_加__速__度__ 的大小，斜率正负表示物体_加__速__度__的方向。 (3)“面积”的意义： ①图线与时间轴围成的面积表示相应时间内的_位__移__大__小__。 ②若面积在时间轴的上方,表示位移方向为_正__方__向__；若面积在 时间轴的下方,表示位移方向为_负__方__向__。
【变式备选】(多选)如图所示是某质点做直线运动的v-t图像， 由图可知这个质点的运动情况是()
A.前5s做的是匀速运动 B.5～15s内做匀加速运动，加速度为1m/s2 C.15～20s内做匀减速运动，加速度为-3.2m/s2 D.质点15s末离出发点最远，20秒末回到出发点
【解析】选A、C。由图像可知前5s做的是匀速运动，A正确；
5～15s内做匀加速运动，加速度为0.8m/s2，B错误；15～ 20s内做匀减速运动，其加速度为m/1s62=-3.2m/s2，C正
5
确；质点在20s末离出发点最远，质点一直做方向不变的直线
运动，D错误。
考点2追及和相遇问题(三年3考) 解题技巧
【考点解读】讨论追及、相遇的问题,其实质就是分析讨论两 物体在同一时刻能否到达相同的空间位置问题。 1.追及相遇问题中的两个关系和一个条件 (1)两个关系： 即时间关系和位移关系，这两个关系可通过画运动示意图得到。 (2)一个条件： 即两者速度相等，它往往是物体间能否追上、追不上或(两者) 距离最大、最小的临界条件，也是分析判断的切入点。
mx =320m42，1平0 均速度m/s=7.5m/vs， xt故
30 4
C正确；在5～6s内，物体沿负方向做匀加速直线运动，故D
错误。
【总结提升】用速度—时间图像巧得四个运动量 (1)运动速度：从速度轴上直接读出。 (2)运动时间：从时间轴上直接读出时刻，取差得到运动时间。 (3)运动加速度：从图线的斜率得到加速度，斜率的大小表示 加速度的大小，斜率的正负反映了加速度的方向。 (4)运动的位移：从图线与时间轴围成的面积得到位移，图线 与时间轴围成的面积表示位移的大小，第一象限的面积表示与 规定的正方向相同，第四象限的面积表示与规定的正方向相反。
【解题探究】(1)分析甲、乙两车的运动情况，明确两个 问题： ①两车相距最大距离时速度满足的条件：_甲__、__乙__两__车__速__度__ _相__等__。 ②求乙车追上甲车所用时间的方法：_先__判__断__甲__车__何__时__停__下__，__ _再__计__算__乙__车__追__上__甲__车__的__时__间__。 (2)请画出甲、乙两车的运动过程简图： 提示:
【变式训练】(多选)如图所示是A、B两个物体做直线运动的速 度图像，下列说法正确的是() A.物体A做加速直线运动 B.物体B做减速直线运动 C.物体A的加速度为正值，B的 加速度为负值，所以A的加速度 大于B的加速度 D.物体B的速度变化比物体A的速度变化快
【解析】选A、D。由两物体的速度图像可知，两物体速度的 绝对值都在增大，则都在做加速运动，物体A的速度为正，图 线的斜率为正，说明A沿正方向做匀加速运动；物体B的速度 为负，图线的斜率为负，说明B沿负方向做匀加速运动，A正 确、B错误；物体A的加速度的绝对值为1m/s2，物体B的加速 度的绝对值为2m/s2，所以物体B的加速度大于物体A的加速 度，从而物体B的速度变化比物体A的速度变化快，C错、D对。 故选A、D。
=t120sva甲
t1时间内：
x甲

v甲 2
t1

10 2
20
m
100
m
x乙=v乙t1=4×20m=80m
此后乙车运动时间：
t2

x甲 x乙 v乙

20 4
s5 s
故乙车追上甲车需t1+t2=25s
答案：(1)36m(2)25s
【互动探究】若甲车经过乙车旁边时，乙车开始以恒定的加速
【备选例题】
考查内容
利用图像信息解决实际问题
【典例透析】如图所示为汽车刹车痕迹长度x(即刹车距离)
与刹车前车速v(汽车刹车前匀速行驶)的关系图像。例如,
当刹车痕迹长度为40m时,刹车前车速为80km/h。
(1)假设刹车时,车轮立即停止转动,尝试用你学过的知识定量 推导并说明刹车痕迹与刹车前车速的关系。 (2)在处理一次交通事故时,交警根据汽车损坏程度估计出碰撞 时的车速为40km/h,并且已测出刹车痕迹长度为20m,请你根据 图像帮助交警确定出该汽车刹车前的车速,并在图像中的纵轴 上用字母A标出这一速度。由图像知,汽车刹车前的速度为多少？
2.追及相遇问题常见的情况 假设物体A追物体B,开始时，两个物体相距x0,有两种常见情况: (1)A追上B时，必有xA-xB=x0，且vA≥vB。 (2)要使两物体恰好不相撞，两物体同时到达同一位置时速度 相同，必有xA-xB=x0，vA=vB。若使两物体保证不相撞，此时应 有vA<vB。
【典例透析2】(2013·泸州模拟)甲车以10m/s的速度在平直的 公路上匀速行驶，乙车以4m/s的速度与甲车平行同向做匀速直 线运动，甲车经过乙车旁边开始以0.5m/s2的加速度刹车，从 甲车刹车开始计时，求： (1)乙车在追上甲车前，两车相距的最大距离； (2)乙车追上甲车所用的时间。
t
【解析】选B、C。根据图像可知，前5s物体沿正方向运动，
第6s物体沿负方向运动，所以物体离出发点最远的时刻是第
5大s小末m，x2=前551ms21的，0 位所移以m离=出x31发5m点2，最 52第远6为1s0内35的m位，移故A错误；
6s内的路程s=x1+x2=40m，故B正确；前4s内的位移是
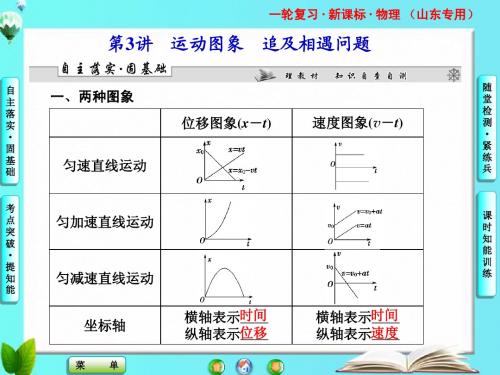
从不同的角度描绘同一物理过程所进行的变换,如 转换图 将x-t图像转换成v-t图像等
利用图像中斜率、面积、截距、交点等的含义进 用 图 行定性分析或定量计算,进而解决相关问题
【典例】两辆完全相同的汽车,沿水平路面一前一后均以20m/s的 速度前进。若前车突然以恒定的加速度刹车,在它刚停止时,后车 以前车刹车时的加速度的2倍开始刹车。已知前车刹车的过程中 所行驶的距离为100m,若要保证两车在上述情况下不相撞,则两车 在匀速行驶时保持的最小距离是多少?
【思考辨析】 (1)x-t图像是物体的运动轨迹。() (2)x-t图像是一条直线，说明物体一定做匀速直线运动。() (3)v-t图像是一条平行于t轴的直线，说明物体做匀速直线运 动。() (4)x-t图像与时间轴围成的面积表示物体运动的路程。() (5)两条v-t图像的交点表示两个物体相遇。() (6)两条x-t图像的交点表示两个物体相遇。() (7)相向运动的物体各自发生的位移大小之和等于开始时二者 之距时即相遇。()