小学二年级奥数题:三角形图案
小学二年级奥数题图形及复习资料

一、计算题。
( 共101题)1. 图2-26是由四个扁而长的圆圈组成的,在交点处有8个小圆圈.请你把1、2、3、4、5、6、7、8这八个数分别填在8个小圆圈中。
要求每个扁长圆圈上的四个数字的和都等于18。
答案:2. 在图2-24中,三个圆圈两两相交形成七块小区域,分别填上1~7七个自然数,在一些小区域中,自然数3、5、7三个数已填好,请你把其余的数填到空着的小区域中,要求每个圆圈中四个数的和都是15。
答案:15=1+2+5+7,15=1+3+4+7,15=1+3+5+6,15=2+3+4+6 其中1和3用的次数最多,图中最中间的局部被三个圆包围,所以1和3应当填在里面。
但题目总3已填好,所以只能填1。
1填好后其他的也就好确定了。
答案见下图3. 图2-23中有三个大圆,在大圆的交点上有六个小圆圈。
请你把1、2、3、4、5、6六个数分别填在六个小圆圈里,要求每个大圆上的四个小圆圈中的数之和都是14。
答案:案把14拆成4个自然数的和,如下14=1+2+5+6;14=1+3+4+6;14=2+3+4+5。
先把一个数填入,然后试一下确定其他数的位置。
答案如下图4. 将2、4、6、8、10、12、14、16、18填在下面图表,使每一横行、竖行、斜行的三个数相加的和都相等。
答案:案九宫格填九数的方法,确定中间是10最关键了,然后我们对这些数加和除以3,就有了相等的和应当是30,图形如下(有许多种,但是中间那个确定是10)5. 细致视察下面的图形,找出改变规律,猜猜在第3组的右框空白格内填一个什么样的图答案:6. 请看下图,共有多少个正方形答案:30 个正方形。
小结小方格16 个,4 个小方格为一个正方形共 9 个,9 个小方格为一个正方形共 4 个,最大的(16 个小方格)是 1 个。
16+9+4+1=30(个)共计30 个正方形。
7. 细致视察这些图案可以发觉,他们是依据下面这5个图案为一组,循环往复排列的,请问第52个图形是什么答案:8. 把上面一排的立体图形剪开,可以剪成下面哪种图形的样子动手试一试。
小学二年级奥数题图形(DOC)

小学二年级奥数题图形(DOC)一、计算题。
(共101题)1.图2-26是由四个扁而长的圆圈组成的,在交点处有8个小圆圈.请你把1、2、3、4、5、6、7、8这八个数分别填在8个小圆圈中。
要求每个扁长圆圈上的四个数字的和都等于18。
2.在图2-24中,三个圆圈两两相交形成七块小区域,分别填上1~7七个自然数,在一些小区域中,自然数3、5、7三个数已填好,请你把其余的数填到空着的小区域中,要求每个圆圈中四个数的和都是15。
3.图2-23中有三个大圆,在大圆的交点上有六个小圆圈。
请你把1、2、3、4、5、6六个数分别填在六个小圆圈里,要求每个大圆上的四个小圆圈中的数之和都是14。
4.将2、4、6、8、10、12、14、16、18填在下面图表,使每一横行、竖行、斜行的三个数相加的和都相等。
5.仔细观察下面的图形,找出变化规律,猜猜在第3组的右框空白格内填一个什么样的图6.请看下图,共有多少个正方形7.仔细观察这些图案可以发现,他们是按照下面这5个图案为一组,循环往复排列的,请问第52个图形是什么8.把上面一排的立体图形剪开,可以剪成下面哪种图形的样子动手试一试。
9.请把下图中长方形分成形状相同、大小相等的两块,然后再拼成一个正方形.10.在空格中填入合适的数11.下图表示\宝塔\,它们的层数不同,但都是由一样大的小三角形摆成的。
仔细观察后,请你回答:(1)五层的\宝塔\的最下层包含多少个小三角形(2)整个五层\宝塔\一共包含多少个小三角形(3)从第(1)到第(10)的十个\宝塔\,共包含多少个小三角形12.数一数,有()个长方形。
13.请你将下面图形分成形状大小相同的四部分,你能行吗14.请你将下面的图形拼成一个大长方形的宣传板,上面从左到右写着\快乐学习\几个字。
请你在大长方形图中将这几个字表示出来。
15.你能将下面的图形分成形状大小相同的四部分吗其中AB=AD=EF=BC,DE=FC16.如图有5个点,在两个点之间可以画出一条线段,画出的图形中一共可以得到()条线段.17.将14个大小一样的小正方体摆成下面的图形,然后将表面涂成红色再分开,有()个小正方形的面没有被涂色。
新版小学二年级数学上册三角形的初步认识练习题

新版小学二年级数学上册三角形的初步认识练习题1. 这些图形中哪些是三角形?请将所有三角形用线段连接出来。
图1:[A] [B] [C] [D]图2:[E] [F] [G] [H]图3:[I] [J] [K] [L]图4:[M] [N] [O] [P]2. 请写出下面图形中的三角形的名字。
图1:__、__、__图2:__、__、__图3:__、__、__图4:__、__、__3. 在下面的图中,用一条线把每组三角形的相同边连接起来。
图1:[A] [B] [C]图2:[D] [E] [F]图3:[G] [H] [I]图4:[J] [K] [L]4. 请数一数下面图形中的三角形有多少个?图1:__个图2:__个图3:__个图4:__个5. 请在下面图形中找出相同的三角形,并用相同的颜色标记出来。
图1:图2:6. 请在下面的图形中找出三角形的相同部分,并用相同的符号标记出来。
图1:图2:7. 请将下面图形中的三角形按大小排列,从最大到最小。
图1:[A] [B] [C]图2:[D] [E] [F]图3:[G] [H] [I]图4:[J] [K] [L]8. 下面的图形中是否有等边三角形?如果有,请画出来。
图1:[是/否]图2:[是/否]图3:[是/否]图4:[是/否]9. 请观察下面图形,填写它们的边长。
图1:边长AB:__边长BC:__边长CA:__图2:边长DE:__边长EF:__边长FD:__图3:边长GH:__边长HI:__边长IG:__图4:边长JK:__边长KL:__边长LJ:__10. 请写出一个你见过或想象过的特别的三角形,并描述它的特点。
三角形奥数题

相似三角形奥数题121.如图,等腰△ABC中,AB=AC,D为BC中点,DE⊥AC于E,F 为DE的中点,AF、BE交于H,求证:AF⊥BE。
2.如图,△ABC中,∠C=90°,D、E是BC边上的点,且∠ABC=1 2∠ADC=13∠AEC。
若BD=11,DE=5,求AC。
3.如图,等腰Rt△ABC中,B=90,AD是BC边的中线,BE⊥AD交AC于E,EF⊥BC。
若AB=BC=a,求EF。
4.如图,在锐角三角形ABC中,AD、CE分别为BC、AB边上的高,△ABC和△BDE的面积分别等于18和2,DE=22,求点B到AC的距离。
5.如图,△ABC中,DE∥BC,已知S△OBC=n2,S△BOD=mn(n>m),其中O为BE和CD的交点,求S BCED和S ADE 。
6.如图,D 为等边△ABC 的边BC 上一点。
已知BD=1,CD=2,CH ⊥AD 于点H ,连结BH 。
试证:∠BHD=60°。
7.如图,平行四边形ABCD 的面积是60,E 、F 分别是AB 、BC 的中点,AF 与DE 、DB 分别交于G 、H ,求四边形EBHG 的面积。
8.如图,在等边△ABC 的BC 边上有一点D ,BD : DC=1 : 2,作CH ⊥AD ,H 为垂足,连结BH ,求证:△ADB ∽△BDH 。
9.如图,△ABC 中,BC=2AC ,D 、E 分别是BC 、AB 上的点,且∠1=∠2=∠3。
如果△ABC 、△EBD 、△ADC 的周长为m 、m 1、m 2,求12m m m的值。
10.如图,在直线l 的同侧有三个相邻的等边三角形△ABC 、△ADE 、△AFG ,且G 、A 、B 都在直线l 上,设这三个三角形边长分别为a 、b 、c ,连结GD 交AE 于N ,连BN 交AC 于L ,求AL 的长。
11.如图,△PQR 与△P'Q'R'是两个全等的等边三角形,六边形ABCDEF 的边长分别记为AB=a 1,BC=b 1,CD=a 2,DE=b 2,EF=a 3,FA=b 3,求证:a 12+a 12+a 12= b 12+b 12+b 1212.如图,设P 、Q 是线段BC 上的两定点,且BP=CQ ,A 为BC 外一动点,当A 运动到使∠BAP=∠CAQ 时,△ABC 是什么三角形?证明你的结论。
小学奥数《三角形的认识》教学课件

本讲主要内容: 三角形的定义; 三角形的分类; 三角形的三边关系; 三角形的内角和; 三角形的外角和。
新知探究
mathematics
知识梳理
数学知识点
mathematics
总一关:认识三角形 按边分类; 按角分类
新知探究
mathematics
第三关:多边形内(外)角和 每增加一条边,内角增加180度; 任意多边形外角和都是360度
1
2
3
1
3
2
其它多边形的内角和都 是通过三角形得到的
数学例题
mathematics
例题1: (1)三角形是由___________条边,___________个角,___________个顶点构成的; 下图 是一个三角形,如果用字母 A、B、C 分别表示三角形的三个顶点,那么这个三角形可以表 示为___________。 (2)三角形可以按照角来分: 三个角都是锐角的三角形叫做____________________; 有一个角是直角的三角形叫做____________________; 有一个角是钝角的三角形叫做____________________。 (3)三角形也可以按照边来分: 有两条边相等的三角形叫做____________________; 三条边都相等的三角形叫做____________________。
多边形内角和: 设边数为n,内角和为180°×(n-2)。 多边形外角和: 任意多边形外角和是360°。
2 1
1
3
2
4
1
3
2
数学例题
mathematics
例题3: (1)三角形三个内角的角度之和是多少度?你是怎么得到的呢? (2)如图 1,∠1+∠2+∠3+∠4=___________. (3)如图 2,∠1+∠2+∠3+∠4+∠5=____________. (4)如图 3,∠1+∠2+∠3+∠4+∠5+∠6=______________. (5)通过以上题目,总结: n边形的内角和=______________.
小学二年级奥数题图形及答案

一、计算题。
( 共101题)1.图2-26是由四个扁而长的圆圈组成的,在交点处有8个小圆圈.请你把1、2、3、4、5、6、7、8这八个数分别填在8个小圆圈中。
要求每个扁长圆圈上的四个数字的和都等于18。
答案:2.在图2-24中,三个圆圈两两相交形成七块小区域,分别填上1~7七个自然数,在一些小区域中,自然数3、5、7三个数已填好,请你把其余的数填到空着的小区域中,要求每个圆圈中四个数的和都是15。
答案:15=1+2+5+7,15=1+3+4+7,15=1+3+5+6,15=2+3+4+6 其中1和3用的次数最多,图中最中间的部分被三个圆包围,所以1和3应该填在里面。
但题目总3已填好,所以只能填1。
1填好后其他的也就好确定了。
答案见下图3.图2-23中有三个大圆,在大圆的交点上有六个小圆圈。
请你把1、2、3、4、5、6六个数分别填在六个小圆圈里,要求每个大圆上的四个小圆圈中的数之和都是14。
答案:案把14拆成4个自然数的和,如下14=1+2+5+6;14=1+3+4+6;14=2+3+4+5。
先把一个数填入,然后试一下确定其他数的位置。
答案如下图4.将2、4、6、8、10、12、14、16、18填在下面图表,使每一横行、竖行、斜行的三个数相加的和都相等。
答案:案九宫格填九数的方法,确定中间是10最关键了,然后我们对这些数加和除以3,就有了相等的和应该是30,图形如下(有很多种,但是中间那个肯定是10)5.仔细观察下面的图形,找出变化规律,猜猜在第3组的右框空白格内填一个什么样的图?答案:6.请看下图,共有多少个正方形?答案:30 个正方形。
小结小方格16 个,4 个小方格为一个正方形共 9 个,9 个小方格为一个正方形共 4 个,最大的(16 个小方格)是 1 个。
16+9+4+1=30(个)共计 30 个正方形。
7.仔细观察这些图案可以发现,他们是按照下面这5个图案为一组,循环往复排列的,请问第52个图形是什么?答案:8.把上面一排的立体图形剪开,可以剪成下面哪种图形的样子?动手试一试。
三角形奥数题

相似三角形奥数题121.如图,等腰△ABC中,AB=AC,D为BC中点,DE⊥AC于E,F 为DE的中点,AF、BE交于H,求证:AF⊥BE。
2.如图,△ABC中,∠C=90°,D、E是BC边上的点,且∠ABC=1 2∠ADC=13∠AEC。
若BD=11,DE=5,求AC。
3.如图,等腰Rt△ABC中,B=90,AD是BC边的中线,BE⊥AD交AC于E,EF⊥BC。
若AB=BC=a,求EF。
4.如图,在锐角三角形ABC中,AD、CE分别为BC、AB边上的高,△ABC和△BDE的面积分别等于18和2,DE=22,求点B到AC的距离。
5.如图,△ABC中,DE∥BC,已知S△OBC=n2,S△BOD=mn(n>m),其中O为BE和CD的交点,求S BCED和S ADE 。
6.如图,D为等边△ABC的边BC上一点。
已知BD=1,CD=2,CH⊥AD于点H,连结BH。
试证:∠BHD=60°。
7.如图,平行四边形ABCD的面积是60,E、F分别是AB、BC的中点,AF与DE、DB分别交于G、H,求四边形EBHG的面积。
8.如图,在等边△ABC 的BC 边上有一点D ,BD : DC=1 : 2,作CH ⊥AD ,H 为垂足,连结BH ,求证:△ADB ∽△BDH 。
9.如图,△ABC 中,BC=2AC ,D 、E 分别是BC 、AB 上的点,且∠1=∠2=∠3。
如果△ABC 、△EBD 、△ADC 的周长为m 、m 1、m 2,求12m m m的值。
10.如图,在直线l 的同侧有三个相邻的等边三角形△ABC 、△ADE 、△AFG ,且G 、A 、B 都在直线l 上,设这三个三角形边长分别为a 、b 、c ,连结GD 交AE 于N ,连BN 交AC 于L ,求AL 的长。
11.如图,△PQR 与△P'Q'R'是两个全等的等边三角形,六边形ABCDEF 的边长分别记为AB=a 1,BC=b 1,CD=a 2,DE=b 2,EF=a 3,FA=b 3,求证:a 12+a 12+a 12= b 12+b 12+b 12为BC 外一动点,当A 运动到使∠BAP=∠CAQ 时,△ABC 是什么三角形?证明你的结论。
小学二年级奥数题图形及答案

⼩学⼆年级奥数题图形及答案⼀、计算题。
( 共101题)1.图2-26是由四个扁⽽长的圆圈组成的,在交点处有8个⼩圆圈.请你把1、2、3、4、5、6、7、8这⼋个数分别填在8个⼩圆圈中。
要求每个扁长圆圈上的四个数字的和都等于18。
答案:2.在图2-24中,三个圆圈两两相交形成七块⼩区域,分别填上1~7七个⾃然数,在⼀些⼩区域中,⾃然数3、5、7三个数已填好,请你把其余的数填到空着的⼩区域中,要求每个圆圈中四个数的和都是15。
答案:15=1+2+5+7,15=1+3+4+7,15=1+3+5+6,15=2+3+4+6 其中1和3⽤的次数最多,图中最中间的部分被三个圆包围,所以1和3应该填在⾥⾯。
但题⽬总3已填好,所以只能填1。
1填好后其他的也就好确定了。
答案见下图3.图2-23中有三个⼤圆,在⼤圆的交点上有六个⼩圆圈。
请你把1、2、3、4、5、6六个数分别填在六个⼩圆圈⾥,要求每个⼤圆上的四个⼩圆圈中的数之和都是14。
答案:案把14拆成4个⾃然数的和,如下14=1+2+5+6;14=1+3+4+6;14=2+3+4+5。
先把⼀个数填⼊,然后试⼀下确定其他数的位置。
答案如下图4.将2、4、6、8、10、12、14、16、18填在下⾯图表,使每⼀横⾏、竖⾏、斜⾏的三个数相加的和都相等。
答案:案九宫格填九数的⽅法,确定中间是10最关键了,然后我们对这些数加和除以3,就有了相等的和应该是30,图形如下(有很多种,但是中间那个肯定是10)5.仔细观察下⾯的图形,找出变化规律,猜猜在第3组的右框空⽩格内填⼀个什么样的图?答案:6.请看下图,共有多少个正⽅形?答案:30 个正⽅形。
⼩结⼩⽅格16 个,4 个⼩⽅格为⼀个正⽅形共 9 个,9 个⼩⽅格为⼀个正⽅形共 4 个,最⼤的(16 个⼩⽅格)是 1 个。
16+9+4+1=30(个)共计 30 个正⽅形。
7.仔细观察这些图案可以发现,他们是按照下⾯这5个图案为⼀组,循环往复排列的,请问第52个图形是什么?答案:8.把上⾯⼀排的⽴体图形剪开,可以剪成下⾯哪种图形的样⼦?动⼿试⼀试。
小学二年级奥数题图形及答案(DOC)

⼩学⼆年级奥数题图形及答案(DOC)⼀、计算题。
( 共101题)1.图2-26是由四个扁⽽长的圆圈组成的,在交点处有8个⼩圆圈.请你把1、2、3、4、5、6、7、8这⼋个数分别填在8个⼩圆圈中。
要求每个扁长圆圈上的四个数字的和都等于18。
答案:2.在图2-24中,三个圆圈两两相交形成七块⼩区域,分别填上1~7七个⾃然数,在⼀些⼩区域中,⾃然数3、5、7三个数已填好,请你把其余的数填到空着的⼩区域中,要求每个圆圈中四个数的和都是15。
答案:15=1+2+5+7,15=1+3+4+7,15=1+3+5+6,15=2+3+4+6 其中1和3⽤的次数最多,图中最中间的部分被三个圆包围,所以1和3应该填在⾥⾯。
但题⽬总3已填好,所以只能填1。
1填好后其他的也就好确定了。
答案见下图3.图2-23中有三个⼤圆,在⼤圆的交点上有六个⼩圆圈。
请你把1、2、3、4、5、6六个数分别填在六个⼩圆圈⾥,要求每个⼤圆上的四个⼩圆圈中的数之和都是14。
答案:案把14拆成4个⾃然数的和,如下14=1+2+5+6;14=1+3+4+6;14=2+3+4+5。
先把⼀个数填⼊,然后试⼀下确定其他数的位置。
答案如下图4.将2、4、6、8、10、12、14、16、18填在下⾯图表,使每⼀横⾏、竖⾏、斜⾏的三个数相加的和都相等。
答案:案九宫格填九数的⽅法,确定中间是10最关键了,然后我们对这些数加和除以3,就有了相等的和应该是30,图形如下(有很多种,但是中间那个肯定是10)5.仔细观察下⾯的图形,找出变化规律,猜猜在第3组的右框空⽩格内填⼀个什么样的图?答案:6.请看下图,共有多少个正⽅形?答案:30 个正⽅形。
⼩结⼩⽅格16 个,4 个⼩⽅格为⼀个正⽅形共 9 个,9 个⼩⽅格为⼀个正⽅形共 4 个,最⼤的(16 个⼩⽅格)是 1 个。
16+9+4+1=30(个)共计 30 个正⽅形。
7.仔细观察这些图案可以发现,他们是按照下⾯这5个图案为⼀组,循环往复排列的,请问第52个图形是什么?8.把上⾯⼀排的⽴体图形剪开,可以剪成下⾯哪种图形的样⼦?动⼿试⼀试。
小学二年级奥数题图形及答案之令狐文艳创作
一、计算题。
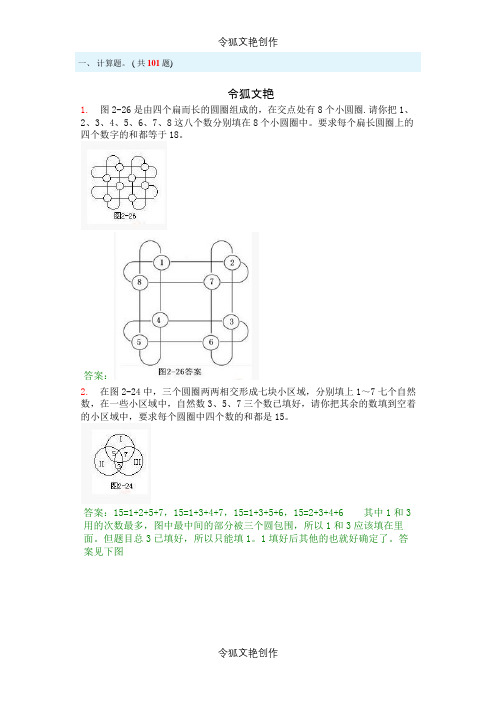
( 共101题)令狐文艳1.图2-26是由四个扁而长的圆圈组成的,在交点处有8个小圆圈.请你把1、2、3、4、5、6、7、8这八个数分别填在8个小圆圈中。
要求每个扁长圆圈上的四个数字的和都等于18。
答案:2.在图2-24中,三个圆圈两两相交形成七块小区域,分别填上1~7七个自然数,在一些小区域中,自然数3、5、7三个数已填好,请你把其余的数填到空着的小区域中,要求每个圆圈中四个数的和都是15。
答案:15=1+2+5+7,15=1+3+4+7,15=1+3+5+6,15=2+3+4+6 其中1和3用的次数最多,图中最中间的部分被三个圆包围,所以1和3应该填在里面。
但题目总3已填好,所以只能填1。
1填好后其他的也就好确定了。
答案见下图3.图2-23中有三个大圆,在大圆的交点上有六个小圆圈。
请你把1、2、3、4、5、6六个数分别填在六个小圆圈里,要求每个大圆上的四个小圆圈中的数之和都是14。
答案:案把14拆成4个自然数的和,如下14=1+2+5+6;14=1+3+4+6;14=2+3+4+5。
先把一个数填入,然后试一下确定其他数的位置。
答案如下图4.将2、4、6、8、10、12、14、16、18填在下面图表,使每一横行、竖行、斜行的三个数相加的和都相等。
答案:案九宫格填九数的方法,确定中间是10最关键了,然后我们对这些数加和除以3,就有了相等的和应该是30,图形如下(有很多种,但是中间那个肯定是10)5.仔细观察下面的图形,找出变化规律,猜猜在第3组的右框空白格内填一个什么样的图?答案:6.请看下图,共有多少个正方形?答案:30 个正方形。
小结小方格16 个,4 个小方格为一个正方形共 9 个,9 个小方格为一个正方形共 4 个,最大的(16 个小方格)是 1 个。
16+9+4+1=30(个)共计 30 个正方形。
7.仔细观察这些图案可以发现,他们是按照下面这5个图案为一组,循环往复排列的,请问第52个图形是什么?答案:8.把上面一排的立体图形剪开,可以剪成下面哪种图形的样子?动手试一试。
小学二年级奥数题图形及答案
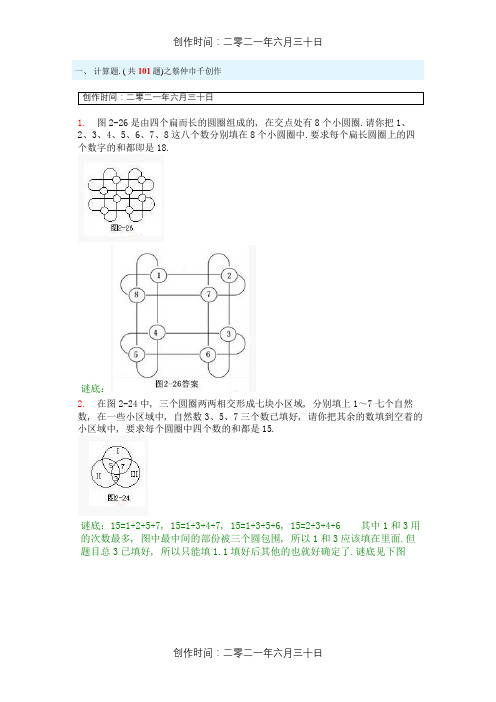
一、计算题. ( 共101题)之蔡仲巾千创作创作时间:二零二一年六月三十日1.图2-26是由四个扁而长的圆圈组成的, 在交点处有8个小圆圈.请你把1、2、3、4、5、6、7、8这八个数分别填在8个小圆圈中.要求每个扁长圆圈上的四个数字的和都即是18.谜底:2.在图2-24中, 三个圆圈两两相交形成七块小区域, 分别填上1~7七个自然数, 在一些小区域中, 自然数3、5、7三个数已填好, 请你把其余的数填到空着的小区域中, 要求每个圆圈中四个数的和都是15.谜底:15=1+2+5+7, 15=1+3+4+7, 15=1+3+5+6, 15=2+3+4+6 其中1和3用的次数最多, 图中最中间的部份被三个圆包围, 所以1和3应该填在里面.但题目总3已填好, 所以只能填1.1填好后其他的也就好确定了.谜底见下图3.图2-23中有三个年夜圆, 在年夜圆的交点上有六个小圆圈.请你把1、2、3、4、5、6六个数分别填在六个小圆圈里, 要求每个年夜圆上的四个小圆圈中的数之和都是14.谜底:案把14拆成4个自然数的和, 如下14=1+2+5+6;14=1+3+4+6;14=2+3+4+5.先把一个数填入, 然后试一下确定其他数的位置.谜底如下图4.将2、4、6、8、10、12、14、16、18填在下面图表, 使每一横行、竖行、斜行的三个数相加的和都相等.谜底:案九宫格填九数的方法, 确定中间是10最关键了, 然后我们对这些数加和除以3, 就有了相等的和应该是30, 图形如下(有很多种, 可是中间那个肯定是10)5.仔细观察下面的图形, 找出变动规律, 猜猜在第3组的右框空白格内填一个什么样的图?谜底:6.请看下图, 共有几多个正方形?谜底:30 个正方形.小结小方格16 个, 4 个小方格为一个正方形共 9 个, 9 个小方格为一个正方形共 4 个, 最年夜的(16 个小方格)是 1 个. 16+9+4+1=30(个)共计 30 个正方形.7.仔细观察这些图案可以发现, 他们是依照下面这5个图案为一组, 循环往复排列的, 请问第52个图形是什么?谜底:8.把上面一排的立体图形剪开, 可以剪成下面哪种图形的样子?入手试一试.谜底:9.请把下图中长方形分成形状相同、年夜小相等的两块, 然后再拼成一个正方形.谜底:10.在空格中填入合适的数谜底:方法一九个数分成三组, 第一组中有8+18=2×13, 即第一个数与第三个数的和是中间那个数的二倍.同样第三组中16+30=2×23, 所以中间一组2×=12+24=36.故应填18.方法二将这九个数横的作一排, 第一排中有8+4=12, 12+4=16, 即后面的数比前面的数年夜4, 第三排中有18+6=24, 24+6=30, 后面的数比前面的数年夜6, 再看第二排应是13+5=18, 18+5=23, 所以空格中应填18.11.下图暗示"浮图", 它们的层数分歧, 但都是由一样年夜的小三角形摆成的.仔细观察后, 请你回答:(1)五层的"浮图"的最下层包括几多个小三角形?(2)整个五层"浮图"一共包括几多个小三角形?(3) 从第(1)到第(10)的十个"浮图", 共包括几多个小三角形?谜底:(1)数一数"浮图"每层包括的小三角形数:第几层1 2 3 4 ……小三角形数1 3 5 7 ……可见1, 3, 5, 7是个奇数列, 所以由这个规律猜出第五层应包括的小三角形是9个.(2)整个五层塔共包括的小三角形个数是:1+3+5+7+9=25(个).(3)每个"浮图"所包括的小三角形数可列表如下:几层塔一二三四五六七八九十小三角形数 1 4 9 16 25 36 49 64 81 100凑十法求和:12.数一数, 有( )个长方形.谜底:分类计数由一个小长方形组成4个;由两个小长方形组成2个;由四个小长方形组成1个.所以共有4+2+1=7(个)13.请你将下面图形分成形状年夜小相同的四部份, 你能行吗?谜底:14.请你将下面的图形拼成一个年夜长方形的宣传板, 上面从左到右写着"快乐学习"几个字.请你在年夜长方形图中将这几个字暗示出来.谜底:15.你能将下面的图形分成形状年夜小相同的四部份吗?其中AB=AD=EF=BC, DE=FC谜底:16.如图有5个点, 在两个点之间可以画出一条线段, 画出的图形中一共可以获得( )条线段.谜底:横排方向有2+1+1=4(条)线段, 竖列方向有2条线段, 斜向有4条线段, 所以共有4+2+4=10(条)线段17.将14个年夜小一样的小正方体摆成下面的图形, 然后将概况涂成红色再分开, 有( )个小正方形的面没有被涂色.谜底:14个小正方形共有14*6=84(个)面, 其中被涂色的有6*4+9*2=42(个)面, 那么没有被涂色的应该有84-42=42(个)面18.有十一根火柴棍, 摆成如图所示的算式.这个算式显然是分歧毛病的, 你能只移动其中一根, 使等式成立吗?谜底:19.在图中, 一共有_____个四边形, _______条线段谜底:20.找出下面图形变动的规律, 并在横线上画出第四幅图.谜底:四个图都是在顺时针方向移动, 每次移动一格, 所以横线上的图应该是如图所示.21.桌上有7个正放着的酒杯.每次翻3个, 最少翻几次, 正放着的7个杯子都底朝上.谜底:最少翻转3次, 可将正放着的7只杯子都翻成底朝上.翻法如下第一次翻从左数起的第1、2、3三只杯子, 翻后成为第二次翻从左数起的第3、4、5三只杯子, 翻后成为第三次翻动从左数起3、6、7三只杯子, 翻后成为22.下面是由10个小圆片摆成的三角形图案, 请你移动3个小圆片, 使三角形图案倒过来.谜底:23.下面是由6个小圆片摆成的三角形图案, 请你只移动2个小圆片, 使三角形图案倒过来.入手摆一摆.谜底:24.兔妈妈把10个萝卜分成4份, 然后从左往右按1个、2个、3个、4个的顺序排列好, 然后对小兔子们说:"你们只能移动一个萝卜的位置, 然后使这些萝卜的顺序倒过来按4、3、2、1的顺序排列, 谁对了, 这些萝卜就都送给他吃."小朋友, 你来试一试!谜底:25.把20个棋子放到下图中的空白方格里, 每个格子都要放, 问怎样放才华使每边的棋子加起来都是6个?谜底:案四个角各放1个, 其余四格各放4个, 这样数来每边都是6个.26.请你移动二枚棋子, 使横行、竖行上的几个数和相等.谜底:横行五个数之和为 , 竖行四个数之和为 , 两个和数相差 .要使横、竖行几个数的和相等, 方法一使和小的一行(横行)增加4;方法二使和年夜的一行(竖行)减少4;方法三使和小的一行增加2, 而和年夜的一行减少2.于是我们不难找出问题的谜底, 谜底不惟一7和5可以换, 5和3可以换, 3和1可以换.27.把15枚硬币放在桌子上, 摆成"T"字形(如下图), 从右数到下, 或从左数到下, 都是11枚, 现在小明拿走了1枚, 请你把剩下的重摆一下, 使从左数到上, 或从右数到上, 仍然是11枚.谜底:28.桌子上顺次放着3个白棋子和3个黑棋子(见图1).请你将棋子移动三次, 每次移动2个, 而且2个棋子的前后顺序不能变动, 把棋子的排列顺序酿成黑白相间的(见图2).请入手做一做.谜底:29.看下面的图形, 说出图中一共有几多个长方形?有几多个三角形?有几多条线段?谜底:30.如果在陆地上可以随便走, 而对每座桥只许通过一次, 那么一个人要连续地走完这七座桥怎么个走法?谜底:很容易看出图中共有4个奇点, 它不能一笔画成, 因而人们根本不能一次连续不竭地走过七座桥.31.如下图所示, 一个长方形由28个小正方形组成.请把它划分成形状相同、年夜小相等的四块, 你能做出几多种划分方法?谜底:32.如下图所示, 一只蚂蚁从一个正方体的A点沿着棱爬向B点, 如不故意绕远, 一共有几种分歧的走法?33.找规律:第五排有几颗珠子( )谜底:第二排比第一排多一个, 第三排比第二排多两个, 第四排比第三排多三个, 第五排比第四排多四个, 所以第五排有7+4=11个珠子.34.如下图所示, 若每个圆圈里都有五只蚂蚁, 问右图中一共应有几多只蚂蚁?谜底:一共只有5只蚂蚁.如右图所示, 每一个圆圈里都有五只蚂蚁.35.在下面各式中移动1根火柴棍, 使各式酿成正确的算式.谜底:① 把11的一个1挪到1上, 酿成7, 7+7=14② 把21的1挪到减号上, 2+2=436.请把1~9九个数字填入下图中, 要求每行、每列和每条对角线上三个数的和都要即是15.谜底:案从1~9这九个数字中, 5是处于中间的一个数, 而4与6, 3与7, 2与8, 1与9之和都正好是10.所以5应当填在中心的空格中, 而其他八个数字应当填到周边的方格中.把5填在中心空格后, 检验考试几次, 最终获得正确的谜底, 下图就是一个符合要求的解答.37.如下图所示, 一个年夜长方体的概况上都涂上红色, 然后切成18个小立方体(切线如图中虚线所示).在这些切成的小立方体中, 问:(1)1面涂成红色的有几个?(2)2面涂成红色的有几个?(3)3面涂成红色的有几个?谜底:仔细观察图形, 并发挥想像力, 可知(1)上下两层中间的2块只有一面涂色; (2)每层四边中间的1块有两面涂色, 上下两层共8块; (3)每层四角的4块有三面涂色, 上下两层共有8块.最后检验一下小立体总块数2+8+8=18(个).这道题主要考察的就是学生的观察能力和空间想象能力.38.请看下图, 共有几多个三角形?谜底:自力的三角形有7个, 由4个三角形组成的三角形有1个, 加上最年夜的三角形, 因此共有7+1+1=9个三角形.39.下图中标出的数暗示每边长, 单元是厘米.它的周长是几多厘米?谜底:平移转化为求长方形的周长, 长方形的长5+6=11(厘米), 宽1+3=4(厘米), 周长(11+4)×2=30(厘米), [(5+6)+(1+3)]×2=30(厘米), 它的周长是30厘米.40.求下图的周长?谜底:将原图通过平移转化为右上图, 即有周长为500×4=2000(米).41.算一算, 猜一猜谜底:两个正方形的和即是8, 那一个正方形就是4, 那三角形加正方形即是6, 那么三角形即是2, 同理圆即是5,谜底 4+2+5=1142.如图有( )个三角形谜底:先数由一部份组成的三角形.共有6个.再数由4部份组成的三角形有2个.6+2=8.总共的三角形共有8个43.根据图, 想一想, 一颗五角星即是几个圆?谜底:由图知道, 1个三角=2个圆, 1颗五角星=3个三角, 那么3个三角=6个圆, 所以, 1颗五角星=3个三角=6个圆, 即1颗五角星=6个圆.44.看图回答, ( )杯水可以注满一壶.谜底:谜底2×4=8(杯)45.仔细观察, “?”处填什么图形?谜底:第一排箭头分别向左、向上、向右, 第二排与第一排规律相同, 所以第三排问号处箭头应向右.46.1个苹果和几个草莓一样重?谜底:由第二幅图知道, 1个苹果和2个梨一样重, 1个梨和2个草莓一样重, 那么2个梨和4个草莓一样重, 所以1个苹果=2个梨=4个草莓.47.1只小狗与3只小兔子一样重;1只小兔子和3只小鸡一样重.问: 1只小狗和几只小鸡一样重?谜底:由第二幅图知道, 1只小兔子和3只小鸡一样重, 那么3只小兔子和9只小鸡一样重, 又知道1只小狗与3只小兔子一样重.从而知道1只小狗和9只小鸡一样重.48.下面是用火柴棒摆成的算式, 但这个算式是不成立的.只要移动1根火柴棒, 算式就成立了.你会移动吗?谜底:我们可以这样想:用4根火柴棒可以组成2个“+”号、4个“-”号, 或者1个“+”号、或者1个“+”和2个“-”号;再看结果100, 它可能是和或者是差.经推理, 只能用4个火柴棒组成1个“+”和2个“-”号, 才华使结果即是100.49.数一数、图中有几多长方形?谜底:分层数, 每层有3+2+1=6个, 共6层(看左侧的线段数), 6×6=36个.50.数一数、图中有几多条线段.谜底:用公式法, 数出基本线段有四条4+3+2+1=10条.51.下面是由几何图形组成的帆船图形,请依照一定的规律,在标序号处画出符合规律的小帆船.谜底:52.观察下图的变换, 在(4)中画出怎样的图形?谜底:通过观察, 发现此图是逆时针旋转53.将3、4、5、6、7、8、9、10这八个数, 分别填在下面的方格处(每个数只能用一次), 并符合下面的要求, 你应该怎样填呢?谜底:3+10-4=96-5+7=854.下图是用18根火柴棒摆成的图形.请你拿失落4根火柴棒, 酿成5个三角形.谜底:55.如下面图(1)中所示.请你只移动3根火柴把3个三角形酿成5个三角形.谜底:56.数一数, 图中有几多个长方形?谜底:单个长方形有 4个, 两个长方形组成的有 2个, 四个长方形组成的有1个.共有 4+2+1=7个.57.将第二排的哪一个图形填入第一排的空格, 才华使第一排的图形有一定的规律性?谜底:根据观察发现第一排的第一幅图到第二幅图少了圆中间的横, 所以谜底是第二排的第 3个.58.下图中, 加一条线或去一条线后, 一笔画出每个图形.谜底:图中奇点个数为4个(多于2个), 在加线或去线时注意在两个奇点间进行即可.59.下面的数列是有一定例律的, 其中有一个数与其他规律是不符的, 把它找出来.用圆圈圈上.谜底:(1) 48, 此题规律是 9 的倍数.(2) 13, 规律是两个数一组, 前面一个数字比后面年夜1.(3) 30, 从第三个数开始, 每个数都是前两个数的和.60.在下列各式数字之间加上相应的符号+、-、×、÷、( ), 使等式成立.谜底:(4+4)÷4-4÷4=1 (4+4)÷4-4+4=261.请把 1、2、3、4、5、6、7、8、9 这九个数填写在下面的方格里, 使每个算式的和都即是 15.(数字不能重复使用)谜底:1+5+9=152+6+7=153+4+8=1562.下面是用15根火柴棒摆成的4个正方形.请你移动2根火柴棒, 酿成6个正方形.谜底:案谜底不惟一63.下面是用16根火柴棒摆成的 5个正方形.请你移动2根火柴棒, 酿成4个正方形.谜底:案谜底不惟一64.按数字规律填出下图中空缺的数:谜底:本题的规律为上面两个数的和即是下面两个数的乘积, 因此应该填7.65.下面的图形一共有几多个圆点?谜底:方法一分层数1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1=100(个)方法二10+10+10+10+10+10+10+10+10+10=100(个)66.三种图形, 有分歧的摆法.请摆一摆, 画一画.谜底:共有6种分歧的摆法.67.下面的符号各代表几?谜底:(1)(2)68.把1, 2, 3, 4, 5, 6六个数, 分别填入○内, 使每条线上3个数的和相等.谜底:比力三个已知数1, 2, 3, 和1比2年夜1, 3年夜2.还剩下三个数4, 5, 6要我们来填, 5+6=11, 6+4=10, 5+4=9, 要使每边和相等,5+6+1=6+4+2=5+4+3=12, 谜底如下69.在下面的圆圈里填上合适的数, 使每条线上的三个数之和都得15.谜底:知道每边的和是15, 而且知道了其中的两个数, 要求另一个数是几多, 一般我们用减法可以直接计算出结果.圆圈里这三个数分别是15-6-8=1、15-8-3=4、15-6-3=6.谜底如下70.下面的方框各应该填几?谜底:案在这个题目中, 我们要从低位开始考虑, 而且一定要注意进位和退位的问题, 除方法更考察学生的口算能力.71.用图中已有的三个数填满其余的空格, 每个数字必需使用三次.使得每行、每列和两条对角线上的三个数之和相等.谜底:根据每行、每列、每对角线上缺少的数字进行推理, 谜底图下72.贪吃的小熊口袋里只有25元钱, 他跑到“味多美”餐厅年夜吃年夜喝了一顿, 把钱全都花光了.下面是快餐厅出售的食品, 你知道小熊可能吃了些什么吗?(每种食物只能要一份)谜底:因为小熊把钱全都花光了, 所以小熊吃到的几种食品的钱数和应是25元.看一看哪几样食品的钱数相加和是25, 小熊就吃到了哪几样食品.因为10+6+5=25 (元)所以小熊可能吃的是因为10+8+2+5=25 (元)所以小熊可能吃的是因为8+2+6+4+5=25 (元)所以小熊可能只有炸鸡块没吃, 其余都各吃了一份.73.下图是按一定例律排列的.找出它的变动规律后, 试填出所缺少的图形.谜底:通过观察、比力可以发现, 第一行和第二行的三个小图形是相同的, 所分歧的只是它们的排列顺序.还可以发现, 从第一行变到第二行, 每个小图形都往右移动了一个图形的位置, 而且第一行最左边的图形占了第二行最右边的位置.所以第三行"?"处应填74.找规律, 在空格里填上合适的数75.请你把1、2、3这三个数填在图中的方格中, 使每行、每列和每条对角线上的三个数字之和都相等.谜底:这样想, 如果每行的三个数分别是1、2、3, 每列的三个数也分别是1、2、3, 那么自然满足每行、每列的三个数之和相等这个条件的要求.试着填填看.有三种分歧的填法, 检查一下, 只有图9—4的填法, 满足对角线上的三个数之和与每行、每列三数之和相等这个条件的要求.76.如图所示, 白色和黑色的三角形按顺序排列.当两种三角形的数量相差个12时, 白色三角形有_____个.谜底:根据题意可知, 每个图形两种三角形的个数相差依次成数列1,2,3,4…… 排列, 所以第12 个图形的两种三角形的个数相差为12 , 这个图形的白色三角形的个数是1+2+3+……+11=66 (个).77.把一块地(如下图)分给5个种植小组, 每组分得的土地的形状和年夜小要相同, 怎样分?谜底:78.下面两个图形能拼成一个长方体吗?谜底:左边图形第一层有6个小正方体, 第二层有3个小正方体, 要想拼生长方体, 第二层差了3个小正方体, 我们可以用右图中右边的三个小正方体补上, 这样只剩下了右图中左边的4个小正方体, 可现在需要在左图的第三层放6个小正方体才可以拼成一个长方体, 所以这两个图形不能拼成一个长方体.79.如下图所示是一个由小立方体构成的塔, 请你数一数并计算出共有几多块?谜底:从上往下数, 第一层1块;第二层4块;第三层9块;第四层16块;总数1+4+9+16=30(块).80.下面的图形一共有几多个圆点?谜底:方法一分层数1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1=100(个)方法二 10+10+10+10+10+10+10+10+10+10=100(个)81.把2, 3, 4, 5, 6, 7, 8这七个数分别填入圆圈中, 使两个正方形中四个数之和相等19.谜底:先考虑求两个正方形公共的中间数.2+3+4+5+6+7+8+重叠数=19+19.重叠数=3, 那么中间圆圈里面应该填3.剩下的数中2+6+8=4+5+7=19-3=16, 所以每个正方形中, 剩下的三个数应该填2, 6, 8或4, 5, 782.把1~8八个数字分别填入图中八个空格中, 使图上四边正好组成加、减、乘、除四个等式.谜底:观察这幅图, 用8个数组成四个等式.从左上角开始先作减法和除法, 得出结果之后再分别作加法和乘法获得右下角的数字.所以问题的关键是左上角的数字与右下角的数字.它们应该是较年夜的且能够作乘法与除法的数.即8和6, 无妨取左上角是8, 右下角是6, 再试填其他数字.也可取左上角是6, 右下角是8, 再试填其他数字.83.如下图所示砖墙是由正六边形的特型砖砌成, 中间有个“雪花”状的墙洞, 问需要几块正六边形的砖才华把它补好?谜底:仔细观察, 并发挥想象力可得出谜底, 如下图, 用七块正六边形的砖可把这个墙洞补好.如果入手画一画, 就会看得更清楚了.84.你能把下边的图形分成2块, 使它们的年夜小、形状都一样吗?试试看.谜底:85.观察下面的图形, 并在空白处填上适当的图形谜底:86.观察下列各组图的变动规律, 并在方框里画出相关的图形?谜底:87.数一数有几多个三角形?谜底:左边是一个规则图形, 有 4+3+2+1=10个, 右边同时是一个规则图形, 有 4+3+2+1=10个, 合起来的三角形有 4个, 共有 10+10+4=24个.88.在下面的图中, 包括苹果的正方形一共有( )个.谜底:包括1个基本正方形的带苹果正方形有1个, 包括4个基本正方形的带苹果正方形有4个, 包括9个基本正方形的带苹果正方形有6个, 包括16个基本正方形的带苹果正方形有2个, 所以共有1+4+6+2=13 (个).89.顺序观察下面图形, 并按其变动规律在“?”处填上合适的图形.谜底:每个图逐个加三个圆点, 而且是依照加实心三个、空心三个的顺序递减的.90.把下图分割成 4 块形状年夜小相同的图形, 使每个图形中都含有一只小猴, 你能做到吗?谜底:切成 L 状即可, 谜底不惟一91.下面是用15根火柴棒摆成的4个正方形.请你移动2根火柴棒, 酿成6个正方形.谜底:案谜底不惟一92.根据图中数字的规律, 在最上边的空格中填上合适的数.谜底:64, 每个数字是下面的两个数字之和93.把写着1到100这100个号码的牌子, 像下面这样一次分给四个人, 你知道第73号牌子会落在谁的手里吗?谜底:案观察会发现分给小明的牌子号码是1, 5, 9, 13···号码除以4余1;分给小英的牌子号码是2, 6, 10, 14···除以4余2;分给小芳的牌子号码是3, 7, 11···除以4余3;分给小军的牌子号码是4, 8, 12···除以4余0;(整除)因此, 试用4除73看看余几?73÷4=18···余1.可见73号牌子会落到小明手里.94.认真观察,找规律填数谜底:规律是每个图形里的3个数相加的和都是12.95.下图中有几多个三角形?谜底:6+5+4+3+2+1=21(个)96.找规律, 在空格里填上合适的数谜底:案第一个三角形的周边的三个小三角形中, 2.3.5三个数相加的和, 与中间小三角形中的数相等, 都是10, 可知, 每个三角形周边三个小三角形里的数相加的和, 就是中间小三角形里的数, 就是10, 也就是说, 中间小三角形里的数连续减去周边两个三角形里的数的差, 就是第三个小三角形里的数, 根据这一规律, 第三个三角形里的数是10-1-4=5, 第四个三角形里, 上边的小三角形里的数是10-7-3=097.在六面体的极点B和E处各有一只蚂蚁(见下图), 它们角逐看谁能爬过所有的棱线, 最终达到终点D.已知它们的爬速相同, 哪只蚂蚁能获胜?谜底:这道题只要求爬过所有的棱, 没要求不能重复.可是两只蚂蚁爬速相同, 如果一只不重复地爬遍所有的棱, 而另一只必需重复爬某些棱, 那么前一只蚂蚁爬的路程短, 自然先达到D点, 因而获胜.问题酿成从B到D与从E到D哪个是一笔画问题.图中只有E, D两个奇点, 所以从E到D可以一笔画出, 而从B到D却不能, 因此E点的蚂蚁获胜.98.数一数图中共有几个三角形?谜底:一共有35个三角形99.图是五个年夜小相同的铁环连在一起的图形.它的长度是几多?谜底:如上图所示.关键是求出重叠的"环扣"数(每个长6毫米).因为五个连在一起的"环扣"数为 5-1=4(个), 所以重叠部份的长为12×(5-1)=48(毫米),又4厘米=40毫米, 所以五个铁环连在一起长40×5-12×(5-1)=152(毫米).100.小兵和小军用玩具枪做打靶游戏, 见下图所示.他们每人打了两发子弹.小兵共打中6环, 小军共打中5环.又知没有哪两发子弹打到同一环带内, 而且百发百中.你知道他俩打中的都是哪几环吗?谜底:小兵打中的是1环和5环, 小军打中的是2环和3环.101.看下图, 彤彤做语文作业用几分钟?做数学作业用几分钟?一共用几小时?谜底:从4点10分到4点40分, 钟表走30分钟;从4点40分到5点10分, 钟表走30分钟.钟表一共走 30分+30分=60分 60分=1小时彤彤做语文作业和数学作业各用30分钟.一共用1小时.二、简答题. ( 共1题)1.数一数, 图2-1和图2-2中各有几多黑方块和白方块?谜底:仔细观察图2-1, 可发现黑方块和白方块同样多.因为每一行中有4个黑方块和4个白方块, 共有8行, 所以黑方块是4×8=32(个) 白方块是4×8=32(个) 再仔细观察图2-2, 从上往下看第一行白方块5个, 黑方块4个; 第二行白方块4个, 黑方块5个; 第三、五、七行同第一行, 第四、六、八行同第二行; 但最后的第九行是白方块5个, 黑方块4个.可见白方块总数比黑方块总数多1个. 白方块总数5+4+5+4+5+4+5+4+5=41(个) 黑方块总数4+5+4+5+4+5+4+5+4=40(个) 再一种方法是每一行的白方块和黑方块共9个. 共有9行, 所以, 白、黑方块的总数是9×9=81(个). 由于白方块比黑方块多1个, 所以白方块是41个, 黑方块是40个.创作时间:二零二一年六月三十日。
奥数之图形问题及答案

奥数之图形问题及答案 Company Document number:WTUT-WT88Y-W8BBGB-BWYTT-19998图形问题(一)1.如图,在三角形ABC中,D是AB的中点,E是DB的中点,F是BC的中点,如果三角形ABC的面积是96cm2,那么三角形AEF的面积是多少平方厘米CFA D E B解:三角形ABF与三角形ABC有公用的顶点A,并且它们的底BC和BF在同一条直线上,所以它们的高相等,而三角形ABF的底BF只有三角形ABC的底BC的一半,所以三角形ABF的面积等于三角形ABC的一半,是96÷2=48(cm2)。
同理,三角形AFD的面积是48÷2=24(cm2),三角形DEF的面积是24÷2=12(cm2),因此,三角形AEF的面积是24+12=36(cm2)。
答:三角形AEF的面积是36 cm2。
2.如图所示,大正方形的边长为12 cm,小正方形的边长为10 cm,求阴影部分的面积。
解:阴影三角形的面积无法直接求出,可以用两个正方形面积的和,减去阴影部分周围三个三角形的面积。
所以,阴影部分的面积是122+102-12×(12+10)÷2-102÷2-12×(12-10)÷2=144+100-132-50-12=50(cm2)。
答:阴影部分的面积是50 cm2。
3.把三角形ABC的边AB三等分,AC四等分,如图。
已知三角形ADE的面积是1 cm2,求三角形ABC的面积是多少平方厘米AE DB C解:三角形AEC的面积是三角形AED的4倍,三角形ABC的面积是三角形AEC的3倍,所以三角形ABC的面积是三角形AED的4×3=12倍,是12(cm2)。
4.一个任意四边形ABCD,将各边延长一倍,得到四边形EFGH如图。
已知四边形ABCD的面积是5 cm2,那么四边形EFGH的面积是多少平方厘米HEA DB C GF解:连接BD、BE,三角形ABD、ABE、BEF的面积相等,所以三角形AEF的面积是三角形ABD的2倍,同理,三角形CHG的面积是三角形BCD的2倍,所以三角形AEF与CGH面积的和是四边形ABCD的2倍;同理,三角形EDH与BFG面积的和也是四边形ABCD的2倍。
三角形奥数题

三角形奥数题5.如图,△ABC中,DE∥BC,已知S△OBC=n2,S△=mn(n>m),其中O为BE和CD的交点,求S BCED BOD和S ADE 。
6.如图,D为等边△ABC的边BC上一点。
已知BD=1,CD=2,CH⊥AD于点H,连结BH。
试证:∠BHD=60°。
7.如图,平行四边形ABCD的面积是60,E、F分别是AB、BC的中点,AF与DE、DB分别交于G、H,求四边形EBHG的面积。
8.如图,在等边△ABC的BC边上有一点D,BD : DC=1 : 2,作CH⊥AD,H为垂足,连结BH,求证:△ADB∽△BDH。
9.如图,△ABC中,BC=2AC,D、E分别是BC、AB上的点,且∠1=∠2=∠3。
如果△ABC、△EBD、△ADC的周长为m、m1、m2,求12m mm的值。
10.如图,在直线l的同侧有三个相邻的等边三角形△ABC、△ADE、△AFG,且G、A、B都在直线l上,设这三个三角形边长分别为a 、b 、c ,连结GD 交AE 于N ,连BN 交AC 于L ,求AL 的长。
11.如图,△PQR 与△P'Q'R'是两个全等的等边三角形,六边形ABCDEF 的边长分别记为AB=a 1,BC=b 1,CD=a 2,DE=b 2,EF=a 3,FA=b 3,求证:a 12+a 12+a 12=b 12+b 12+b 1212.如图,设P 、Q 是线段BC上的两定点,且BP=CQ ,A 为BC 外一动点,当A 运动到使∠BAP=∠CAQ 时,△ABC是什么三角形?证明你的结论。
13.如图,△ABC的面积是其内接矩形△QRS面积的三倍,并且边BC与高AD的值是有理数,问矩形PQRS周长的值在什么情况下是有理数?在什么情况下是无理数?14.如图,在△ABC 中,∠BAC=60°,∠ACB=45°⑴求这个三角形三边之比AB : BC :AC ;⑵设P 为△ABC 内一点,且PA=62+,PB=326,PC=3226,求∠APB 、∠BPC 、∠CPA 。
小学奥数教程:三角形(一)全国通用(含答案)

小学奥数教程:三角形(一)全国通用(含答案)一、三角形的定义三角形是由三条线段组成的图形,每两条线段之间都有一个角。
二、三角形的分类根据边长关系,三角形可以分为以下几类:1. 等边三角形:三条边的长度都相等。
等边三角形:三条边的长度都相等。
2. 等腰三角形:两条边的长度相等,另一条边的长度不等。
等腰三角形:两条边的长度相等,另一条边的长度不等。
3. 直角三角形:其中一个角为直角,即90度。
直角三角形:其中一个角为直角,即90度。
4. 锐角三角形:三个角都是锐角,即小于90度的角。
锐角三角形:三个角都是锐角,即小于90度的角。
5. 钝角三角形:其中一个角是钝角,即大于90度的角。
钝角三角形:其中一个角是钝角,即大于90度的角。
三、三角形的性质三角形有一些特点和性质:1. 内角和:三角形的内角和等于180度。
内角和:三角形的内角和等于180度。
2. 外角和:三角形的外角和等于360度。
外角和:三角形的外角和等于360度。
3. 角平分线:三角形的内角的平分线相交于三角形的内心。
角平分线:三角形的内角的平分线相交于三角形的内心。
4. 中线:三角形的三条中线相交于三角形的重心。
中线:三角形的三条中线相交于三角形的重心。
5. 高线:三角形的三条高线相交于三角形的垂心。
高线:三角形的三条高线相交于三角形的垂心。
四、三角形的计算计算三角形的面积和周长时,可以根据不同类型的三角形采用不同的方法:1. 等边三角形:面积和周长可以直接计算。
等边三角形:面积和周长可以直接计算。
2. 等腰三角形:根据底边和腰的长度计算面积和周长。
等腰三角形:根据底边和腰的长度计算面积和周长。
3. 直角三角形:使用勾股定理和正弦、余弦、正切等三角函数计算面积和周长。
直角三角形:使用勾股定理和正弦、余弦、正切等三角函数计算面积和周长。
4. 一般三角形:使用海伦公式计算面积,根据边长计算周长。
一般三角形:使用海伦公式计算面积,根据边长计算周长。
二年级找规律填△图形

1.按照下面所绘图形的排列规律,第25个图形是________.(画出草图)□△○△□△○△□△○△……2.仔细观察下面的图,想一想,第3幅图问号处应填什么图形?3.仔细观察下面的图形,想一想,第4幅图应画怎样的图形?4.根据下面前三幅图的变化规律,在第4幅图中画出阴影部分.5.想一想,方框内应有多少个小圆点?6.按照图形的变化规律,在“?”处画出相符的图形.7.观察图的排列规律,在“?”处填上恰当的图形.8.下面哪个图形和其他几个图形不一样,找出来,并打上“√”.9.观察下列黑白小球的排列规律,然后回答方框内有几个白球,几个黑球?10.四个小动物排座位,如下图:一开始,小老鼠坐在第1号,小猴子坐第2号,小兔坐第3号,小猫坐第4号.以后它们多次地交换位子:第一次上下两排交换,第二次(在第一次交换之后)左右两列交换,第三次上下两排交换,第四次左右两列交换,……这样换下去,问:第十次交换后,小兔子坐在第几号位子上?1.□提示:在这列图形中出现的图形有:正方形、三角形、圆,且三种图形出现的规律是:按照正方形→三角形→圆→三角形的顺序4个一组循环出现.因25÷4=6……1,所以横线上应填第一个图形,即正方形.2.☆△提示:观察前两组图形可知,第一、二组都是由□○☆△组成,但顺序不同.第一组中的左边两个,在第二组中变为右边两个,而另外三个按原来的顺序移到了最左边.按此规律,“?”处应分别填上“☆”“△”.3.提示:观察前三幅图,大圆内都是■○△◇组成的,第一幅图中的图形按逆时针方向旋转可得到第二幅图形,第二幅图形按逆时针方向旋转可得到第三幅图形,同理可推得第四幅图形.4.提示:第一幅图的阴影部分均按顺时针方向旋转一格便可得到第二幅图,第二幅图中的阴影部分均按顺时针方向旋转一格便可得到第三幅图,由此,第三幅图中的阴影部分均按顺时针方向旋转一格便可得到第四幅图.5.方框内应填25个圆点.6.提示:观察前三幅图可知,前一幅图按逆时针方向旋转一格便可得到下一幅图.提示:通过观察可知,从上到下每一横行圆的个数逐次减少1,三角的个数逐次增加1,由此推得“?”处的图形.8.(1)提示:图中的几何图形的共同特点是在图形内部都有一个同一类型的图形.但1、3、4、5内部的图形都较小,只有2内部图形较大,且位置和其它几个图形不同.(2)提示:这五幅图形都是由相同的两个图形重叠而成的,但不同的是前四个图形都是下面的图形盖住了上面的图形,只有5不同,是上面的图形盖住了下面的图形.9.9个白球,3个黑球.提示:观察图形可知,黑、白小球按照2个黑球,1个白球,2个黑球,3个白球,2个黑球,5个白球……的规律排列,即每组都是先有2个黑球,白球的个数每次增加2.10.小兔坐在第2号位置上.提示:小兔子开始在第3号位置上,第四次交换后,小兔子又回到原位,因10÷4=2……2,所以小兔第十次交换后应与第二次交换后的位置相同.。
小学二年级奥数题图形及答案
一、计算题。
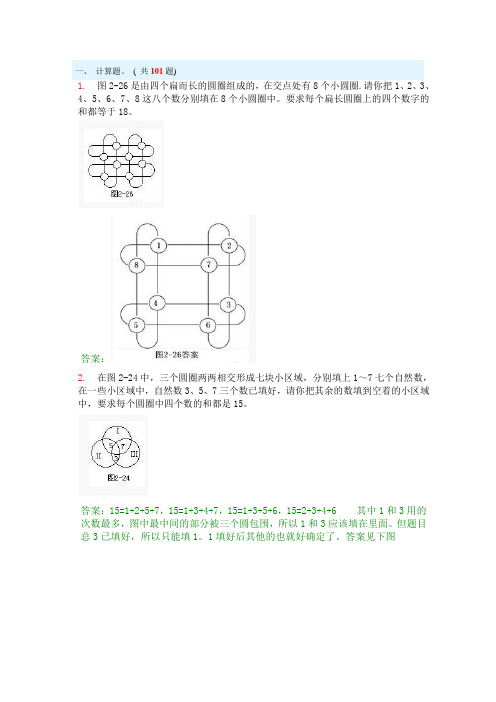
( 共101题)1.图2-26是由四个扁而长的圆圈组成的,在交点处有8个小圆圈.请你把1、2、3、4、5、6、7、8这八个数分别填在8个小圆圈中。
要求每个扁长圆圈上的四个数字的和都等于18。
答案:2.在图2-24中,三个圆圈两两相交形成七块小区域,分别填上1~7七个自然数,在一些小区域中,自然数3、5、7三个数已填好,请你把其余的数填到空着的小区域中,要求每个圆圈中四个数的和都是15。
答案:15=1+2+5+7,15=1+3+4+7,15=1+3+5+6,15=2+3+4+6 其中1和3用的次数最多,图中最中间的部分被三个圆包围,所以1和3应该填在里面。
但题目总3已填好,所以只能填1。
1填好后其他的也就好确定了。
答案见下图3.图2-23中有三个大圆,在大圆的交点上有六个小圆圈。
请你把1、2、3、4、5、6六个数分别填在六个小圆圈里,要求每个大圆上的四个小圆圈中的数之和都是14。
答案:案把14拆成4个自然数的和,如下14=1+2+5+6;14=1+3+4+6;14=2+3+4+5。
先把一个数填入,然后试一下确定其他数的位置。
答案如下图4.将2、4、6、8、10、12、14、16、18填在下面图表,使每一横行、竖行、斜行的三个数相加的和都相等。
答案:案九宫格填九数的方法,确定中间是10最关键了,然后我们对这些数加和除以3,就有了相等的和应该是30,图形如下(有很多种,但是中间那个肯定是10)5.仔细观察下面的图形,找出变化规律,猜猜在第3组的右框空白格内填一个什么样的图?答案:6.请看下图,共有多少个正方形?答案:30 个正方形。
小结小方格16 个,4 个小方格为一个正方形共 9 个,9 个小方格为一个正方形共 4 个,最大的(16 个小方格)是 1 个。
16+9+4+1=30(个)共计 30 个正方形。
7.仔细观察这些图案可以发现,他们是按照下面这5个图案为一组,循环往复排列的,请问第52个图形是什么?答案:8.把上面一排的立体图形剪开,可以剪成下面哪种图形的样子?动手试一试。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小编导语:同学们在课上学习气氛比较紧张,巨人数学网根据二年级同学课上学习的知识点,为二年级同学们精心准备了一些可以放松一下的试题,让我们在轻松的环境下完成学习任务,本道二年级奥数题是关于如何放置三角形图案的试题,这是一道很有代表性的试题,请同学们认真做题,并总结同类型试题应该注意的事项,避免以后再犯同类错误。
下面是由10个小圆片摆成的三角形图案,请你移动3个小圆片,使三角形图案倒过来.答案:。
