圆锥曲线技巧之圆锥曲线第二定义 习题
高考数学 圆锥曲线的概念,解题方法、题型、易误点总结 试题

卜人入州八九几市潮王学校数学概念、方法、题型、易误点技巧总结——圆锥曲线1.圆锥曲线的两个定义:〔1〕第一定义中要重视“括号〞内的限制条件:椭圆中,与两个定点F,F的间隔的和等于常数,且此常数一定要大于,当常数等于时,轨迹是线段F F,当常数小于时,无轨迹;双曲线中,与两定点F,F的间隔的差的绝对值等于常数,且此常数一定要小于|F F|,定义中的“绝对值〞与<|F F|不可无视。
假设=|F F|,那么轨迹是以F,F为端点的两条射线,假设﹥|F F|,那么轨迹不存在。
假设去掉定义中的绝对值那么轨迹仅表示双曲线的一支。
比方:①定点,在满足以下条件的平面上动点P的轨迹中是椭圆的是A.B.C.D.〔答:C〕;②方程表示的曲线是_____〔答:双曲线的左支〕〔2〕第二定义中要注意定点和定直线是相应的焦点和准线,且“点点距为分子、点线距为分母〞,其商即是离心率。
圆锥曲线的第二定义,给出了圆锥曲线上的点到焦点间隔与此点到相应准线间隔间的关系,要擅长运用第二定义对它们进展互相转化。
如点及抛物线上一动点P〔x,y〕,那么y+|PQ|的最小值是_____〔答:2〕2.圆锥曲线的HY方程〔HY方程是指中心〔顶点〕在原点,坐标轴为对称轴时的HY位置的方程〕:〔1〕椭圆:焦点在轴上时〔〕〔参数方程,其中为参数〕,焦点在轴上时=1〔〕。
方程表示椭圆的充要条件是什么?〔ABC≠0,且A,B,C同号,A≠B〕。
比方:①方程表示椭圆,那么的取值范围为____〔答:〕;②假设,且,那么的最大值是____,的最小值是___〔答:〕〔2〕双曲线:焦点在轴上:=1,焦点在轴上:=1〔〕。
方程表示双曲线的充要条件是什么?〔ABC≠0,且A,B异号〕。
比方:①双曲线的离心率等于,且与椭圆有公一共焦点,那么该双曲线的方程_______〔答:〕;②设中心在坐标原点,焦点、在坐标轴上,离心率的双曲线C过点,那么C的方程为_______〔答:〕〔3〕抛物线:开口向右时,开口向左时,开口向上时,开口向下时。
圆锥曲线知识点+例题+练习含答案(整理)(20201128025357)
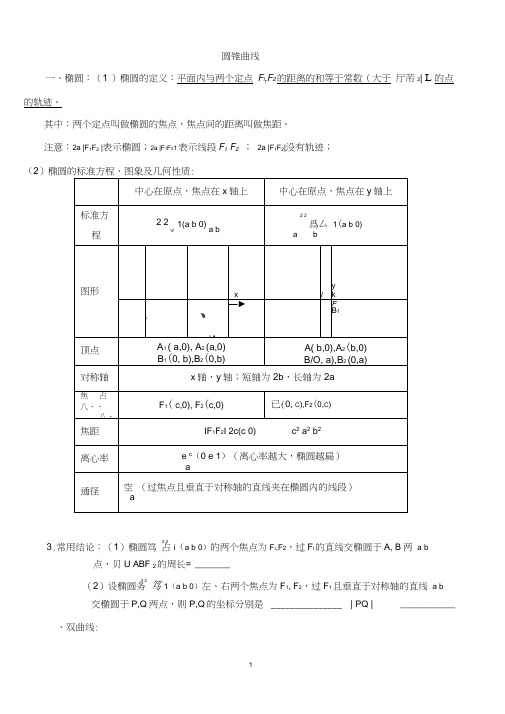
圆锥曲线一、椭圆:(1 )椭圆的定义:平面内与两个定点F I,F2的距离的和等于常数(大于厅芾2| L 的点的轨迹。
其中:两个定点叫做椭圆的焦点,焦点间的距离叫做焦距。
注意:2a |F1F2 |表示椭圆;2a |F1F21表示线段F1 F2;2a |F1F2|没有轨迹;(2)椭圆的标准方程、图象及几何性质:2 23.常用结论:(1)椭圆笃占i(a b 0)的两个焦点为F I,F2,过F i的直线交椭圆于A, B两 a b点,贝U ABF 2的周长= _______2 2(2)设椭圆务笃1(a b 0)左、右两个焦点为F1, F2,过F1且垂直于对称轴的直线 a b交椭圆于P,Q两点,则P,Q的坐标分别是_______________ | PQ | ___________ 、双曲线:(1)双曲线的定义:平面内与两个定点 F i , F 2的距离的差的绝对值等于常数(小于 | F 1F 2 |) 的点的轨迹。
其中:两个定点叫做双曲线的焦点,焦点间的距离叫做焦距。
注意:|PFj IPF 2I 2a 与 | PF 2 | | PF i | 2a ( 2a | F 1F 2 |)表示双曲线的一支。
2a | F 1F 2 |表示两条射线;2a | F 1F 2 |没有轨迹;(2)双曲线的标准方程、图象及几何性质:顶点 A 1( a,0), A 2(a,0)B 1(0, a),B 2(0,a)对称轴x 轴,y 轴;虚轴为 2b,实轴为2a 焦 占 八、、 八、、F 1( C ,0),F 2(C ,0)F 1 (0, C ), F 2(0,C )焦距El2C (C 0) 2 C2.2a b离心率e C (e 1) a(离心率越大,开口越大)渐近线b y —xaa y— xb通径2 b 2a(4)等轴双曲线为x 2 y 2 t 2,其离心率为 2中心在原点,焦点在x 轴上中心在原点,焦点在y 轴上标准 方程2x~2 a2y1( a 0,b0)b2y~2a2(3)双曲线的渐近线:①求双曲线匚〔的渐近线,可令其右边的1为0,即得乂 .2 ' 2a 2b 22yb 2,因式分解得到A y 0。
圆锥曲线解题十招全归纳

《圆锥曲线解题十招全归纳》招式一:弦的垂直平分线问题 (2)招式二:动弦过定点的问题 (4)招式四:共线向量问题 (6)招式五:面积问题 (13)招式六:弦或弦长为定值、最值问题 (16)招式七:直线问题 (20)招式八:轨迹问题 (24)招式九:对称问题 (30)招式十、存在性问题 (33)招式一:弦的垂直平分线问题例题1、过点T(-1,0)作直线l 与曲线N :2y x =交于A 、B 两点,在x 轴上是否存在一点E(0x ,0),使得ABE ∆是等边三角形,若存在,求出0x ;若不存在,请说明理由。
解:依题意知,直线的斜率存在,且不等于0。
设直线:(1)l y k x =+,0k ≠,11(,)A x y ,22(,)B x y 。
由2(1)y k x y x=+⎧⎨=⎩消y 整理,得2222(21)0k x k x k +-+= ① 由直线和抛物线交于两点,得2242(21)4410k k k ∆=--=-+> 即2104k <<② 由韦达定理,得:212221,k x x k -+=-121x x =。
则线段AB 的中点为22211(,)22k k k--。
线段的垂直平分线方程为:221112()22k y x k k k --=--令y=0,得021122x k =-,则211(,0)22E k -ABE ∆为正三角形,∴211(,0)22E k -到直线AB 的距离d 。
AB =21k =+2d k=21k +=k =053x =。
【涉及到弦的垂直平分线问题】这种问题主要是需要用到弦AB 的垂直平分线L 的方程,往往是利用点差或者韦达定理........产生弦AB 的中点坐标M ,结合弦AB 与它的垂直平分线L 的斜率互为负倒数,写出弦的垂直平分线L 的方程,然后解决相关问题,比如:求L 在x 轴y 轴上的截距的取值范围,求L 过某定点等等。
有时候题目的条件比较隐蔽,要分析后才能判定是有关弦AB 的中点问题,比如:弦与某定点D 构成以D 为顶点的等腰三角形(即D 在AB 的垂直平分线上)、曲线上存在两点AB 关于直线m 对称等等。
圆锥曲线中第二定义的三类用法(共10张PPT)

第二定义
第二定义:椭圆或双曲线中的一点P,满足条件
PF2 PD
e
(式右x 准线a2对应右焦点),其中PF2 称作焦半径,准线公
c
第二定义
例:在平面直角坐标系
xoy
中双曲线
x2 3
y2
1
的右准线与它的两条渐近线分别交于点P,Q,
其中 焦点是 ,F1, F2 ,则四边形 的面积是_______.
x2 a2
y2 b2
1 的左焦点 ,交椭圆于A,B 两点,且有 | AF | 3 | B F | ,求椭圆的离心率.
解析:AF, B F 为左焦点上的焦半径,所以过A,B 两点
分别作垂直于准线的直线且和准线交于D,E 两点,
从B 点作 BH AD .
因为| AF | 3 | B F | ,设 BF m ,则 AF 3m
是右 ,根
据第二定义
PF2 PD
e
,解得
PF2
5 4
PD
5
所以
|
PM
|
4 5
|
PF2
|
PM
PD
因此当P,M,D三点共线时 PM PD 取得最小值,最小
值为从 M到右准线的距离 MH, MH 6 16 14 55
第二定义
本次课重点需要注意三点 :
(1)是第二定义的用法; (2)是注意例2这个题目的常规做法,此外下次课会给出这种例题的常用结论; (3)需要注意焦半径的取值范围,这个范围是求离心率取值范围题目中常用的
在 RT PF1F2 中,满足 PF12 所以在 RT PF1F2 中,SPF1F
1
解析几何 第二讲 圆锥曲线的概念与性质,与弦有关的计算问题——2023届高考数学二轮复习含解析

专题七 解析几何 第二讲 圆锥曲线的概念与性质,与弦有关的计算问题1.若椭圆2222:1(0)x y C a b a b+=>>的短轴长等于焦距,则椭圆的离心率为( )A.122.已知O 是坐标原点,椭圆221259x y +=上的一点M 到左焦点1F 的距离为2,N 是MF 的中点,则ON 的长为( ) A.8B.6C.5D.43.若π0,2α⎛⎫∈ ⎪⎝⎭,方程22sin cos 1x y αα+=表示焦点在y 轴上的椭圆,则α的取值范围是( )A.π0,4⎛⎫ ⎪⎝⎭B.π0,3⎛⎫⎪⎝⎭C.ππ,42⎛⎫⎪⎝⎭ D.ππ,32⎛⎫⎪⎝⎭ 4.已知双曲线2222:1(0,0)x y T a b a b-=>>,直线y b =-与T 交于A ,B 两点,直线7y b =与T交于C ,D 两点,四边形ABCD 的两条对角线交于点E ,60AEB ∠=︒,则双曲线T 的离心率为( )C.2D.45.已知双曲线22122:1(0,0)x y C a b a b-=>>1C 同渐近线的双曲线2C 过点A ,直线:40l x y +-=与x 轴、y 轴分别交于B ,C 两点,且与双曲线2C 交于D ,若CD CB λ=,则λ=( ) A.2B.58C.38D.36.双曲线E 与椭圆22:162x y C +=焦点相同且离心率是椭圆C E的标准方程为( )A.2213y x -=B.2221y x -=C.22122x y -= D.2213x y -= 7.已知F 为抛物线2:4C y x =的焦点,,过F 作两条互相垂直的直线1l ,2l ,直线1l 与C 交于A ,B 两点,直线2l 与C 交于D ,E 两点,则||||AB DE +的最小值为( )A.16B.14C.12D.108.(多选)已知点P 为双曲线2222:1(0,0)x y C a b a b-=>>所在平面内一点,12(,0),(,0)F c F c -分别为C 的左、右焦点,2121,4PF F F PF c ⊥=,线段12,PF PF 分别交双曲线于,M N 两点,11PF MF λ=,22PF NF μ=.设双曲线的离心率为e ,则下列说法正确的有( )A.若1PF 平行渐近线,则2e =B.若4λ=,则2e = C.若3μ=,则eD.λμ9. (多选)已知椭圆C 的中心在原点,焦点1F ,2F 在y 轴上,且短轴长为2,离心率1F 作y 轴的垂线,交椭圆C 于P ,Q 两点,则下列说法正确的是( ) A.椭圆方程为2213y x +=B.椭圆方程为2213x y +=C.3PQ =D.2PF Q △的周长为10. (多选)已知抛物线2:2(0)C y px p =>的焦点为F ,若()01,M y 为抛物线C 上一点,直线MF的斜率为M 为圆心的圆与C 的准线相切于点Q ,则下列说法正确的是( )A.抛物线C 的准线方程为3x =-B.直线MF 与抛物线C 相交所得的弦长为15C.MFQ △外接圆的半径为4D.若抛物线C 上两点之间的距离为8,则该线段的中点到y 轴距离的最小值为111.双曲线222:1(0)4x y C b b-=>的一条渐近线方程为320x y +=,则双曲线C 的焦距为__________.12.已知1F ,2F 是椭圆2222:1(0)x y C a b a b +=>>的两个焦点,P 为C 上一点,且1260F PF ∠=︒,12||5||PF PF =,则C 的离心率为______.13.已知抛物线22(0)y px p =>的准线为l ,点P 在抛物线上,PQ l ⊥于点Q ,(2,0)M 与抛物线的焦点不重合,且||||PQ PM =,120MPQ ∠=︒,则p =______________.14.已知抛物线2:2(0)C x py p =>的焦点为,F O 为坐标原点,的点P 在抛物线C 上,满足||||PF PO =. (1)求抛物线C 的方程.(2)过抛物线C 上的点A 作抛物线C 的切线,l A 与O 不重合,过O 作l 的垂线,垂足为B ,直线BO 与抛物线C 交于点D .当原点到直线AD 的距离最大时,求点A 的坐标.15.如图,已知椭圆22112x y +=.设A ,B 是椭圆上异于(0,1)P 的两点,且点10,2Q ⎛⎫⎪⎝⎭在线段AB 上,直线PA ,PB 分别交直线132y x =-+于C ,D 两点.(Ⅰ)求点P 到椭圆上点的距离的最大值; (Ⅱ)求||CD 的最小值.答案以及解析1.答案:C解析:由题意,得b c =,则2222b a c c =-=,a =,则椭圆的离心率c e a==. 2.答案:D解析:椭圆221259x y +=上的一点M 到左焦点1F 的距离为2,则点M 到右焦点2F 的距离为8.又N 是1MF 的中点,所以2142ON MF ==. 3.答案:C解析:方程22sin cos 1x y αα+=,即22111sin cos x y αα+=表示焦点在y 轴上的椭圆,则11cos sin αα>.又π0,2α⎛⎫∈ ⎪⎝⎭,所以cos sin αα<,所以ππ,42α⎛⎫∈ ⎪⎝⎭. 4.答案:A解析:在22221x y a b-=中,令y b =-,得x =,不妨设,),(,)A b B b --,同理可得(,7),,7)C b D b -, 由对称性可知,四边形ABCD 的两条对角线的交点E 在y 轴上. 易知直线AC的方程为)y x b =-,令0x =,得3b y =,即0,3b E ⎛⎫⎪⎝⎭. 因为60AEB ∠=︒,所以ABE △是等边三角形,|E A y y AB -=,所以22483b a b ==,因为222c a b =+,所以22358a c =,所以e =. 5.答案:C解析:由题意,双曲线1C的离心率c e a ==1ba=,∴设222:(0)C x y αα-=≠,将点A 代入得48α-=,解得4α=-,222:144y x C ∴-=,与直线l 联立得52D y =.易得0,4B C y y ==,CD CB λ=,()5,4,042D C B C x x x x λ⎛⎫∴--=-- ⎪⎝⎭,解得38λ=,故选C. 6.答案:C解析:由题知,椭圆22162x y +=的焦点坐标为(2,0)和(2,0)-设双曲线E的标准方程为22221(0,0)x y a b a b -=>>,则224a b +=且2a =,解得222a b ==,所以双曲线E 的标准方程为22122x y -=,故选C.7.答案:A解析:如图所示,设直线AB 的倾斜角为θ,过A ,B 分别作准线的垂线,垂足为1A ,1B ,则1||AF AA =,1||BF BB =,过点F 向1AA 引垂线FG ,得||||cos ||||AG AF pAF AF θ-==, 则||1cos p AF θ=-,同理,||1cos pBF θ=+,则22||||||sin p AB AF BF θ=+=,即24|si |n AB θ=, 因为1l 与2l 垂直,所以直线DE 的倾斜角为π2θ+或π2θ-, 则24||cos DE θ=,则2244||||sin cos AB DE θθ+=+22224416sin cos sin 21sin 22θθθθ===⎛⎫⎪⎝⎭, 则易知||||AB DE +的最小值为16. 故选A. 8.答案:ACD解析:本题考查双曲线的定义、离心率问题、焦半径问题.由题意12PF F △为直角三角形,点P坐标为(,)c ±,直线1PF斜率1260k PF F =∠=.不妨设点P 在第一象限,如图.选项A,若1PF 平行渐近线,则ba,得2e =,故A 正确.选项B,若4λ=,则1MF c =.连接2MF (图略),由1260PF F ∠=︒,解得221,21)MF a MF MF c =∴=-=,得1e ,故B 错误.选项C,若3μ=,则2NF =.连接1NF (图略),由2190PF F ∠=︒,解得112,2NF a NF NF ∴=-=,得e 故C 正确. 选项D,114PF c MF λ==,14cMF λ∴=,点M 的坐标为2,M M cx c y λ=-=,代入双曲线方程得()2222ac c b λ+=,22b NF a =,则22PF NF λμμ==∴==故D 正确.故选ACD.9.答案:ACD解析:由已知,得22b =,3c a =,则1b =.又222a b c =+,所以23a =,所以椭圆的方程为2213y x+=.由题意,得223b PQ a ===,2PF Q △的周长为4a =.故选ACD. 10.答案:ACD解析:过点M 作MB 垂直于x 轴,垂足为B ,MF k =-,∴直线MF 的倾斜角为120°,60MFB ∴∠=︒,在Rt MBF △中,30BMF ∠=︒,||2||212pMF BF ⎛⎫∴==- ⎪⎝⎭,又由抛物线的定义可得||12pMF =+,21122p p ⎛⎫∴-=+ ⎪⎝⎭,解得6p =,∴抛物线C 的方程为212y x =,抛物线C 的准线方程为3x =-,故A 正确;易知直线MF的方程为3)y x =-,代入抛物线C 的方程,得21090x x -+=,解得1x =或9x =,∴直线MF 与抛物线C 相交所得弦长为19616++=,选项B 不正确;易得M ,(3,0)F,(3,Q -,||QF ==120QMF ∠=︒,设MFQ △外接圆的半径为r,根据正弦定理可得||28sin QF r QMF ====∠,4r ∴=,选项C正确;设抛物线C 上的两点分别为()11,G x y ,()22,H x y ,则||||||8GF HF GH +≥=,当且仅当G ,H ,F 三点共线时,等号成立,由抛物线的定义可知,1212||||6GF FH x x p x x +=++=++,所以1268x x ++≥,即122x x +≥,所以线段GH 的中点到y 轴的距离122122x x +≥=,选项D 正确.故选ACD. 11.答案:解析:根据题意,双曲线222:1(0)4x y C b b -=>C:x 24-y 2b 2=1(b >0)的焦点在x 轴上,则其渐近线方程为2by x =±,又由该双曲线的一条渐近线方程为320x y +=,即32y =-=3=;所以2c ==15PF =122PF +=153a =,2PF =12PF F 中,由余弦定理可得:22212121212||||||2||||cos F F PF PF PF PF F PF =+-⋅∠,而1260F PF ∠=︒,即222255429933a a a c a =+-⨯⨯712=,可得离心率c e a ==13.答案:45解析:如图,设抛物线的焦点为F ,连接PF ,由拖物线的定义知||||PQ PF =,又||||PQ PM =,所以||||PF PM =,由PQ l ⊥及120MPQ ∠=︒,得60PMF ∠=︒,于是PFM △为正三角形,||22pMF =-,所以点P 的坐标为1242p p ⎛⎫⎫+- ⎪⎪ ⎪⎝⎭⎝⎭, 将其代入22(0)y px p =>,得23221424p p p ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭,即2556480p p +-=,即(12)(54)0p p +⋅-=,所以45p =. 14.答案:(1)24x y =(2)(2)-或( 解析:本题考查抛物线的标准方程,直线与抛物线的位置关系.(1)依题意设点1),(0,0),(0,)2p P O F p ,由||||PF PO =,又0p >,解得2p =,所以抛物线C 的方程为24x y =.(2)设()22,(0)A t t t ≠,由214y x =求导,得12y x '=, 所以过点A 的切线l 斜率为122k t t =⨯=, 所以切线l 的方程为2(2)y t t x t -=-, 即2y tx t =-.因为直线OB 与切线l 垂直,所以1OB k t=-, 直线OB 方程为1y x t=-,即0x ty +=,由20,4,x ty x y +=⎧⎨=⎩解得24,4,x ty t ⎧=-⎪⎪⎨⎪=⎪⎩或0,0x y =⎧⎨=⎩(舍).即点244(,)D t t-.因为()22442,,(,)A t t D t t-,所以22242422ADt t t k t t t --==+, 则直线AD 的方程为222(2)2t y t x t t--=-,即()22240t x ty t --+=. 原点到直线AD 的距离d ===2≤=,当且仅当224t t=,即t =,等号成立. 所以原点到直线AD 的距离最大为2,此时点A 坐标为(2)-或(.15.解析:(Ⅰ)设,sin )([0,2))M θθθ∈π是椭圆上任意一点,由(0,1)P ,知222221441144||12cos (1sin )1311sin 2sin 11sin 111111PM θθθθθ⎛⎫=+-=--=-+≤ ⎪⎝⎭, 故||PM即点P(Ⅱ)易知直线AB 的斜率存在,设直线AB :12y kx =+,联立直线AB 与椭圆的方程,整理得22130124k x kx ⎛⎫++-= ⎪⎝⎭, 设()11,A x y ,()22,B x y ,则122112k x x k +=-+,12231412x x k =-⎛⎫+ ⎪⎝⎭.直线PA 的方程为1111y y x x -=+,代入132y x =-+, 整理得111114422(21)1C x x x x y k x ==+-+-. 同理可得,222224422(21)1D x x x x y k x ==+-+-,则||C D CD x =-224(21)1x k x =-+-=====341431kk⨯+≥+=,当且仅当3|4|4k=,即3||16k=时等号成立,所以当3||16k=时,||CD.11。
第2讲 圆锥曲线第二定义与焦半径公式(解析版)

第2讲圆锥曲线第二定义与焦半径公式参考答案与试题解析一.选择题(共5小题)1.已知点P 是双曲线22184x y -=上的动点,1F ,2F 为该双曲线的左右焦点,O 为坐标原点,则12||||||PF PF OP +的最大值为()A.B .2CD【解答】解:由题意,分子最大且分母最小时,即P 在顶点处取得最大值,不妨取顶点,0),则12||||||PF PF OP +=,故选:D .2.已知双曲线222:1(0)4x y C a α-=>的右支上的点0(P x ,0)y 满足121||3||(PF PF F =,2F 分别是双曲线的左右焦点),则00(cy c x +为双曲线C 的半焦距)的取值范围是()A.)+∞B .[2,25)2C.252D .[2,【解答】解:由双曲线的第二定义可知10||PF ex a =+,20||PF ex a =-, 右支上的点0(P x ,0)y 满足12||3||PF PF =,0003()2ex a ex a ex a ∴+=-⇒=,由c e a=,解得202a x c=,P 在右支上,可得202a x a c= ,可得12ca< ,即12e < ,则22220022201164(1)422x c c y e x a a e+=+-=+-,令2e t =,14t < ,可得2202011611613244()4222c y e t t x e t t+=+-=+-=+-而132()()2f t t t=+在(1,4]递减,132()[62t t +∈,332,2002522c y x ∴+<,故选:B .3.已知点P 是双曲线22221(0,0)x y a b a b-=>>上的动点,1F ,2F 分别是其左、右焦点,O 为坐标原点,若12||||||PF PF OP +的最大值是,则此双曲线的离心率是()AB.2C .32D .2【解答】解:不妨设P 为右支上的一点,(,)P x y 其中x a ,1||PF ex a =+,2||PF ex a =-,||OP ==∴12||||)||PF PF x a OP +==∴当x a =时,取得最大值,∴=,∴e =故选:B .4.已知F 为抛物线2:4C y x =的焦点,过F 作两条互相垂直的直线1l ,2l ,直线1l 与C 交于A ,B 两点,直线2l 与C 交于D ,E 两点,则当||||AB DE +取得最小值时,四边形ADBE 的面积为()A .32B .16C .24D .8【解答】解:因为AB DE ⊥,要使||||AB DE +最小,而||||AB DE + 由抛物线的对称性可得A 与D ,B 与E 关于x 轴对称,所以可得直线DE 的斜率为1,又过抛物线的焦点(1,0),所以直线DE 的方程为:1y x =-,214y x y x=-⎧⎨=⎩,整理可得2440y y --=,124y y +=,124y y =-,所以可得||8DE ===,所以11883222ABCD S DE AB =⋅=⨯⨯=四边形.故选:A .5.过椭圆22143x y +=的右焦点F 作两条相互垂直的直线分别交椭圆于A ,B ,C ,D 四点,则11||||AB CD +的值为()A .18B .16C .1D .712【解答】解:由椭圆22143x y +=,得椭圆的右焦点为(1,0)F ,当直线AB 的斜率不存在时,:1AB x =,则:0CD y =.此时||3AB =,||4CD =,则11117||||3412AB CD +=+=;当直线AB 的斜率存在时,设:(1)(0)AB y k x k =-≠,则1:(1)CD y x k=--.又设点1(A x ,1)y ,2(B x ,2)y .联立方程组22(1)3412y k x x y =-⎧⎨+=⎩,消去y 并化简得2222(43)84120k x k x k +-+-=,∴221212228412,3434k k x x x x k k -+==++,2212(1)||34k AB k +∴=+,由题知,直线CD 的斜率为1k-,同理可得2212(1)||43k CD k +=+.∴22117(1)7||||12(1)12k AB CD k ++==+为定值.故选:D .二.填空题(共3小题)6.已知P 是椭圆22:184x y C +=上的动点,1F ,2F 分别是其左右焦点,O 是坐标原点,则12||||||PF PF PO - 的取值范围是[.【解答】解:设P 的坐标为(,)m n 椭圆22:184x y C +=中,28a =,24b =,2c ∴==,得椭圆的准线方程为2a x c=±,即4x =±作出椭圆的右准线,设P 在右准线上的射影为Q ,连结PQ ,根据圆锥曲线的统一定义,得2||||PF e PQ =,2||||)22PF e PQ m ∴==-=,同理可得1||2PF=,||PO =,∴12))||||22||m PF PF PO +--= 点(,)P m n 在椭圆22184x y +=上,得22184m n +=,∴2224(1482m m n =-=-,由此可得12||||||PF PF PO -= ,得22122||||4()8||PF PF m m PO -=+ ,2[0m ∈ ,2]a 即2[0m ∈,8],得224[08m m ∈+,2],∴12||||[||PF PF PO -∈,.故答案为:[7.已知F 为抛物线2:4C y x =的焦点,过F 作两条互相垂直的直线1l ,2l ,直线1l 与C 交于A 、B 两点,直线2l 与C 交于D 、E 两点,则11||||AB DE +的值为14.【解答】解:根据题意可得,抛物线24y x =的焦点坐标为(1,0)F ,准线方程为1x =-,设直线1:(1)(0)l y k x k =-≠, 直线1l ,2l 互相垂直,∴直线2l 的斜率为1k -,即得21:(1)l y x k=--,设1(A x ,1)y ,2(B x ,2)y ,3(C x ,3)y ,4(E x ,4)y ,则分别将直线1l ,2l 的方程与抛物线方程联立组成方程组可得,22222(1)(24)04y k x k x k x k y x=-⎧⇒-++=⎨=⎩;21(1)4y x k y x⎧=--⎪⎨⎪=⎩⇒2222121(4)0x x k k k -++=由韦达定理可得,212224k x x k ++=,2342241k x x k ++=,由抛物线性质可知,抛物线上的点到焦点的距离等于到准线的距离,∴2212222444||112k k AB x x k k ++=+++=+=,2234224||112441k DE x x k k +=+++=+=+,∴2221111||||44444k AB DE k k +=+=++.故答案为:14.8.已知F 为抛物线2:4C y x =的焦点,过F 作两条互相垂直的直线1l ,2l ,直线1l 与C 交于A 、B 两点,直线2l 与C 交于D 、E 两点,则||4||AB DE +的最小值为36.【解答】解:抛物线2:4C y x =的焦点(1,0)F ,准线方程为1x =-,设直线1l 的方程为(1)y k x =-,0k ≠,联立方程组24(1)y xy k x ⎧=⎨=-⎩,则2222(42)0k x k x k -++=,设1(A x ,1)y ,2(B x ,2)y ,可得12242x x k+=+,由抛物线的定义可得1224||24AB x x k=++=+,由12l l ⊥,可将上式中的k 换为1k-,可得2||44DE k =+,则221||4||204(4)2036AB DE k k +=+++= .当且仅当2k =±时,上式取得等号,则||4||AB DE +的最小值为36.故答案为:36.三.解答题(共6小题)9.已知斜率为k 的直线l 与椭圆22:143x y C +=交于A ,B 两点,线段AB 的中点为(1M ,)(0)m m >.(1)证明:12k <-;(2)设F 为C 的右焦点,P 为C 上一点,且0FP FA FB ++=.证明:||FA ,||FP ,||FB 成等差数列,并求该数列的公差.【解答】解:(1)设1(A x ,1)y ,2(B x ,2)y , 线段AB 的中点为(1,)M m ,122x x ∴+=,122y y m+=将A ,B 代入椭圆22:143x y C +=中,可得2211222234123412x y x y ⎧+=⎪⎨+=⎪⎩,两式相减可得,121212123()()4()()0x x x x y y y y +-++-=,即12126()8()0x x m y y -+-=,12126384y y k x x m m-∴==-=--点(1,)M m 在椭圆内,即211,(0)43m m +<>,解得302m <<∴3142k m =-<-.①(2)由题意得(1,0)F ,设3(P x ,3)y ,则1231110x x x -+-+-=,1230y y y ++=,由(1)及题设得3123()1x x x =-+=,312()20y y y m =-+=-<.又点P 在C 上,所以34m =,从而3(1,)2P -,3||2FP = .于是1||22x FA =- .同理2||22xFB =- .所以121||||4()32FA FB x x +=-+= ,故||||2||FA FB FP += ,即||FA ,||FP ,||FB成等差数列.设改数列的公差为d ,则1212||||||||||2d FB FA x x =-=-= ②将34m =代入①得1k =-.所以l 的方程为74y x =-+,代入C 的方程,并整理得2171404x x -+=.故122x x +=,12128x x =,代入②解得||28d =.所以该数列的公差为28或28-.10.已知斜率为k 的直线l 与椭圆22:198x y C +=交于A 、B 两点,线段AB 的中点为(1M ,)(0)t t >.(Ⅰ)证明:13k <-;(Ⅱ)设F 为C 的右焦点,Q 为C 上的一点,且0FQ FA FB ++= ,证明:||FA ,||FQ,||FB成等差数列.【解答】(本小题满分12分)证明:(Ⅰ)设1(A x ,1)y ,2(B x ,2)y ,则有221122221(1)981(2)98x y x y ⎧+=⋯⋯⎪⎪⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⎨⎪+=⋯⋯⎪⎩(2分)(1)-(2)得12121212()()()()098x x x x y y y y +-+-+=.122x x += ,122y y t +=.∴12122()2()098x x t y y --+=.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(3分)∴121289y y k x x t-==--.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(4分)由题设可知点(1,)M t 在椭圆内,∴21198t +<,解得803t <<,∴818319983k t =-<-=- .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(5分)(Ⅱ) 0FQ FA FB ++=,M 为AB 的中点,∴2FQ FM =-,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(6分)(1,)M t ,(1,2)Q t ∴-.点(1,2)Q t -在椭圆上,∴214198t +=.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(7分)又403t t >∴=.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(8分)由(Ⅰ)知89k t =-,所以23k =-.∴直线l 的方程为42(1)33y x -=--,即223y x =-+.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(9分)由直线l 的方程与椭圆方程联立,得22223198y x x y ⎧=-+⎪⎪⎨⎪+=⎪⎩消y 化简得2230x x --=,解得11x =-,23x =.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(10分)从而得8(1,)3A -,(3,0)B ,又8(1,0),(1,)3F Q -,∴10||3FA ==,8||3FQ = ,||2FB = .⋯⋯⋯⋯⋯⋯⋯(11分)∴||FA ,||FQ ,||FB成等差数列.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(12分)11.已知1F 、2F 是椭圆22221(0)x y a b a b+=>>的左、右焦点,且离心率12e =,点P 为椭圆上的一个动点,△12PF F 的内切圆面积的最大值为43π.(1)求椭圆的方程;(2)若A ,B ,C ,D 是椭圆上不重合的四个点,满足向量1F A 与1F C 共线,1F B 与1F D共线,且0AC BD =,求||||AC BD + 的取值范围.【解答】解:(1)由几何性质可知,当,△12PF F 的内切圆面积的最大值时,即,12PF F S 取最大值,且121()22PF F max S c b bc == ,由243r ππ=,解得3r =,又由△12PF F 的周长为22a c +定值,∴223bc a c =+,又12c e a ==,可得2a c =,即b =,2c ∴=,b =4a =,故椭圆方程为2211612x y +=,(2)①当直线AC 和BD 中有一条垂直x 轴时,||||6814AC BD +=+=,②当直线AC 的斜率存在但不为0时,设AC 的方程为:(2)y k x =+,由22(2)11612y k x x y =+⎧⎪⎨+=⎪⎩得2222(34)1616480k x k x k +++-=,代入弦长公式得,2224(1)||34k AC k +=+ ,同理由221(2)11612y x kx y ⎧=-+⎪⎪⎨⎪+=⎪⎩,消去y ,代入弦长公式得2224(1)||34k BD k +=+ ,2222222168(1)168||||11(34)(43)121(1)k AC BD k k k k +∴+==+++-++,令21(0,1)1t k =∈+,则212(12t t -++∈,49]4,由①②可知||||AC BD + 的取值范围是96[7,14].12.已知椭圆22221(0)x y a b a b +=>>经过点)2-,且椭圆的离心率12e =,过椭圆的右焦点F 作两条互相垂直的直线,分别交椭圆于点A 、B 及C 、D .(Ⅰ)求椭圆的方程;(Ⅱ)求证:11||||AB CD +为定值;(Ⅲ)求9||||16AB CD +的最小值.【解答】解:()I 由12c e a ==,得2214c a =,222244()a c a b ∴==-,2234a b ∴=.(1),⋯(1分)由椭圆过点知,223314a b+=.(2)⋯(2分)联立(1)、(2)式解得24a =,23b =.⋯(3分)故椭圆的方程是22143x y +=.⋯(4分)11()||||II AB CD +为定值712⋯(5分)证明:椭圆的右焦点为(1,0)F ',分两种情况.1︒当直线AB 的斜率不存在时,:1AB x =,则:0CD y =.此时||3AB =,||4CD =,117||||12AB CD +=;⋯(6分)2︒当直线AB 的斜率存在时,设:(1)(0)AB y k x k =-≠,则1:(1)CD y x k=--.又设点1(A x ,1)y ,2(B x ,2)y .联立方程组22(1)3412y k x x y =-⎧⎨+=⎩,消去y 并化简得2222(43)84120k x k x k +-+-=,∴2122843k x x k +=+,212241243k x x k -=⋯+ (7分)∴12|||AB x x ==-==2212(1)43k k +=+,⋯(8分)由题知,直线CD 的斜率为1k-,同理可得2212(1)||43k CD k +=⋯+(9分)所以2211777||||12(1)12k AB CD k ++==+为定值.⋯(10分)(Ⅲ)解:由()II 知117||||12AB CD +=,∴912911||||(||||)()16716||||AB CD AB CD AB CD +=++⋯(11分)9||1225||16()716||||CD AB AB CD =++122521(7164+= ,⋯(12分)当且仅当9||||16||||CD AB AB CD =,即3||||4AB CD =,即||3AB =,||4CD =时取等号⋯(13分)∴9||||16AB CD +的最小值为214.⋯(14分)13.已知椭圆22122:1(0)x y C a b a b +=>>的长轴长为4,离心率为12,一动圆2C 过椭圆1C 右焦点F ,且与直线1x =-相切.(1)求椭圆1C 的方程及动圆圆心轨迹2C 的方程;(2)过F 作两条互相垂直的直线,分别交椭圆1C 于P ,Q 两点,交曲线2C 于M ,N 两点,求四边形PMQN 面积的最小值.【解答】解:(1)由已知可得2222423112a a b a c c c e a =⎧=⎧⎪⇒⇒=-=⎨⎨===⎩⎪⎩,则所求椭圆方程221:143x y C +=.由已知可得动圆圆心轨迹为抛物线,且抛物线C 的焦点为(1,0),准线方程为1x =-,则动圆圆心轨迹方程为22:4C y x =.(2)当直线MN 的斜率不存在时,||4MN =,此时PQ 的长即为椭圆长轴长,||4PQ =,从而11||||44822PMQN S MN PQ =⋅=⨯⨯=.设直线MN 的斜率为k ,则0k ≠,直线MN 的方程为:(1)y k x =-,直线PQ 的方程为1(1)y x k=--,设1(M x ,1)y ,2(N x ,2)y ,3(P x ,3)y ,4(Q x ,4)y ,由2(1)4y k x y x=-⎧⎨=⎩,消去y 可得2222(24)0k x k x k -++=,由抛物线定义可知:2221222244||||||1124k MN MF NF x x k k +=+=+++=+=+,由221(1)143y x k x y ⎧=--⎪⎪⎨⎪+=⎪⎩,消去y 得222(34)84120k x x k +-+-=,从而234212(1)|||34k PQ x x k +=-=+,∴222224211412(1)(1)||||(4)24223434PMQN k k S MN PQ k k k k ++=⋅=+=++,令21k t +=,0k > ,则1t >,则22222221242424211||||34(1)(0,3)2123(1)4(1)3213PMQN t t S MN PQ t t t t t t t t t =⋅===--+∈-+-----,所以2248213PMQN S t t =>--,所以四边形PMQN 面积的最小值为8.14.平面直角坐标系xOy 中,已知F 为椭圆22221x y a b+=的右焦点,且24a b +=,过F 作两条互相垂直的直线交椭圆分别于A 、B 与C 、D .以F 为极点,x 轴正半轴为极轴建立极坐标系.(Ⅰ)求椭圆的极坐标方程与1||AB 的代数表达式;(Ⅱ)求11||||AB CD +的取值范围.【解答】解:由已知24b a =-,(Ⅰ)设(,0)F c,2222a a c b p c c c c -=-===c e a a==,以右焦点F 为极点,x 轴正半轴为极轴,建立极坐标系,则椭圆的极坐标方程为1cos ep e ρθ=+,即22cos ab ac c ρθ=+,其中c =设(A A ρ,)θ,则(B B ρ,)θπ+,222||1cos 1cos()1cos 1cos 1A B ep ep ep ep ep AB e e e e e cos ρρθπθθθθ∴=+=+=+=++++--,2211||2e cos AB ep θ-=,即22221||2a c cos AB ab θ-=;(Ⅱ)由(Ⅰ)得,22222222(112||||22a c cos a c cos AB CD ab ab πθθ-+-+=+2222222222222222422222(4)a c cos a c sin a c a b a a ab ab ab ab a a θθ---+-+=+===-.24a b += ,222240c a b a a ∴=-=+->,且4a <,4a <<.记f (a )242(4)a a a a -+=-,则f '(a )22(4)(34)2(4)a a a a +-=-,当142a -<<时,f '(a )0>,f (a )为增函数,则f (a)1(8+∈,)+∞,即11||||AB CD +∈,)+∞.。
圆锥曲线的最值定值范围经典题型

圆锥曲线最值/范围/定值/定点问题一、圆锥曲线的最值问题方法1:定义转化法①根据圆锥曲线的定义列方程;②将最值问题转化为距离问题求解.例1、已知点F是双曲线x24-y212=1的左焦点,定点A的坐标为(1,4),P是双曲线右支上的动点,则|PF|+|P A|的最小值为________.方法2:数形结合(切线法)当所求的最值是圆锥曲线上的点到某条直线的距离的最值时:①求与直线平行的圆锥曲线的切线;②求出两平行线的距离即为所求的最值.例2、求椭圆x22+y2=1上的点到直线y=x+23的距离的最大值和最小值,并求取得最值时椭圆上点的坐标.方法3:参数法(函数法)①选取合适的参数表示曲线上点的坐标;②求解关于这个参数的函数最值例3、在平面直角坐标系xOy中,点P(x,y)是椭圆x23+y2=1上的一个动点,则S=x+y的最大值为________.方法4:基本不等式法①将最值用变量表示.②利用基本不等式求得表达式的最值.例4、求椭圆x23+y2=1内接矩形ABCD面积的最大值.二、圆锥曲线的范围问题方法1:曲线几何性质法①由几何性质建立关系式;②化简关系式求解.例1、已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左,右焦点分别为F 1,F 2,点P 在双曲线的右支上,且|PF 1|=4|PF 2|,则此双曲线中ac的取值范围是________.方法2:判别式法当直线和圆锥曲线相交、相切和相离时,分别对应着直线和圆锥曲线方程联立消元后得到的一元二次方程的判别式大于零、等于零、小于零 ① 联立曲线方程,消元后求判别式;②根据判别式大于零、小于零或等于零结合曲线性质求解.例2、在平面直角坐标系xOy 中,经过点(0,2)且斜率为k 的直线l 与椭圆x 22+y 2=1有两个不同的交点P 和Q . (1)求k 的取值范围;(2)设椭圆与x 轴正半轴、y 轴正半轴的交点分别为A ,B ,是否存在常数m ,使得向量OP →+OQ →与AB →共线?如果存在,求m 值;如果不存在,请说明理由.三、圆锥曲线的定值、定点问题 方法1:特殊到一般法根据特殊情况能找到定值(或定点)的问题① 根据特殊情况确定出定值或定点;②对确定出来的定值或定点进行一般情况的证明.例1、已知双曲线C :x 2-y 22=1,过圆O :x 2+y 2=2上任意一点作圆的切线l ,若l 交双曲线于A ,B 两点,证明:∠AOB 的大小为定值.方法2:引进参数法定值、定点是变化中的不变量,引入参数找出与变量与参数没有关系的点(或值)即是定点(或定值).① 引进参数表示变化量;②研究变化的量与参数何时没有关系,找到定值或定点例2、如图所示,曲线C 1:x 29+y 28=1,曲线C 2:y 2=4x ,过曲线C 1的右焦点F 2作一条与x 轴不垂直的直线,分别与曲线C 1,C 2依次交于B ,C ,D ,E 四点.若G 为CD 的中点、H 为BE 的中点,证明|BE |·|GF 2||CD |·|HF 2|为定值.一、圆锥曲线的最值问题答案:例1解析 如图所示,根据双曲线定义|PF |-|PF ′|=4, 即|PF |-4=|PF ′|.又|P A |+|PF ′|≥|AF ′|=5, 将|PF |-4=|PF ′|代入,得|P A |+|PF |-4≥5,即|P A |+|PF |≥9,等号当且仅当A ,P ,F ′三点共线, 即P 为图中的点P 0时成立,故|PF |+|P A |的最小值为9.故填9. 例2.解 设椭圆的切线方程为y =x +b , 代入椭圆方程,得3x 2+4bx +2b 2-2=0. 由Δ=(4b )2-4×3×(2b 2-2)=0,得b =±3.当b =3时,直线y =x +3与y =x +23的距离d 1=62,将b =3代入方程3x 2+4bx +2b 2-2=0,解得x =-233,此时y =33,即椭圆上的点⎝ ⎛⎭⎪⎫-233,33到直线y =x +23的距离最小,最小值是62; 当b =-3时,直线y =x -3到直线y =x +23的距离d 2=362,将b =-3代入方程3x 2+4bx +2b 2-2=0,解得x =233,此时y =-33,即椭圆上的点⎝ ⎛⎭⎪⎫233,-33到直线y =x +23的距离最大,最大值是362. 例3 解析 因为椭圆x 23+y 2=1的参数方程为⎩⎨⎧x =3cos φy =sin φ,(φ为参数).故可设动点P 的坐标为(3cos φ,sin φ),其中0≤φ<2π.因此S =x +y =3cos φ+sin φ=2⎝ ⎛⎭⎪⎫32cos φ+12sin φ=2sin ⎝ ⎛⎭⎪⎫φ+π3,所以,当φ=π6时,S 取最大值2.故填2. 二、圆锥曲线的范围问题答案:例1.解析 根据双曲线定义|PF 1|-|PF 2|=2a ,设|PF 2|=r , 则|PF 1|=4r ,故3r =2a ,即r =2a 3,|PF 2|=2a3.根据双曲线的几何性质,|PF 2|≥c -a ,即2a 3≥c -a ,即c a ≤53,即e ≤53.又e >1, 故双曲线的离心率e 的取值范围是⎝ ⎛⎦⎥⎤1,53.故填⎝ ⎛⎦⎥⎤1,53.例2.解 (1)由已知条件,知直线l 的方程为y =kx +2,代入椭圆方程,得x 22+(kx +2)2=1,整理得⎝ ⎛⎭⎪⎫12+k 2x 2+22kx +1=0.①由直线l 与椭圆有两个不同的交点P 和Q ,得Δ=8k 2-4⎝ ⎛⎭⎪⎫12+k 2=4k 2-2>0,解得k <-22或k >22,即k 的取值范围为⎝ ⎛⎭⎪⎫-∞,-22∪⎝ ⎛⎭⎪⎫22,+∞.(2)设P (x 1,y 1),Q (x 2,y 2),则OP →+OQ →=(x 1+x 2,y 1+y 2).由方程①,知x 1+x 2=-42k 1+2k 2.②又y 1+y 2=k (x 1+x 2)+22=221+2k 2.③由A (2,0),B (0,1),得AB→=(-2,1).所以OP →+OQ →与AB →共线等价于x 1+x 2=-2(y 1+y 2), 将②③代入,解得k =22.由(1)知k <-22或k >22, 故不存在符合题意的常数k .三、圆锥曲线的定值、定点问题答案:例1.证明 当切线的斜率不存在时,切线方程为x =±2. 当x =2时,代入双曲线方程,得y =±2, 即A (2,2),B (2,-2),此时∠AOB =90°, 同理,当x =-2时,∠AOB =90°.当切线的斜率存在时,设切线方程为y =kx +b , 则|b |1+k2=2,即b 2=2(1+k 2). 由直线方程和双曲线方程消掉y , 得(2-k 2)x 2-2kbx -(b 2+2)=0, 由直线l 与双曲线交于A ,B 两点. 故2-k 2≠0.设A (x 1,y 1),B (x 2,y 2). 则x 1+x 2=2kb2-k 2,x 1x 2=-(b 2+2)2-k 2,y 1y 2=(kx 1+b )(kx 2+b )=k 2x 1x 2+kb (x 1+x 2)+b 2 =-k 2b 2-2k 22-k 2+2k 2b 22-k 2+2b 2-k 2b 22-k 2=2b 2-2k 22-k 2,故x 1x 2+y 1y 2=-b 2-22-k 2+2b 2-2k 22-k 2=b 2-2(1+k 2)2-k 2,由于b 2=2(1+k 2),故x 1x 2+y 1y 2=0,即OA →·OB →=0,∠AOB =90°.综上可知,若l 交双曲线于A ,B 两点,则∠AOB 的大小为定值90°. 例2.证明 由题意,知F 1(-1,0),F 2(1,0), 设B (x 1,y 1),E (x 2,y 2),C (x 3,y 3),D (x 4,y 4), 直线y =k (x -1),代入x 29+y 28=1,得8⎝ ⎛⎭⎪⎫y k +12+9y 2-72=0,即(8+9k 2)y 2+16ky -64k 2=0,则y 1+y 2=-16k 8+9k 2,y 1y 2=-64k 28+9k 2.同理,将y =k (x -1)代入y 2=4x ,得ky 2-4y -4k =0, 则y 3+y 4=4k ,y 3y 4=-4, 所以|BE |·|GF 2||CD |·|HF 2|=|y 1-y 2||y 3-y 4|·12|y 3+y 4|12|y 1+y 2|=(y 1-y 2)2(y 1+y 2)2·(y 3+y 4)2(y 3-y 4)2=(y 1+y 2)2-4y 1y 2(y 1+y 2)2·(y 3+y 4)2(y 3+y 4)2-4y 3y 4=(-16k )2(8+9k 2)2+4×64k 28+9k 2(-16k )2(8+9k 2)2·⎝ ⎛⎭⎪⎫4k 2⎝ ⎛⎭⎪⎫4k 2+16=3为定值.。
新高考 核心考点与题型 圆锥曲线 第2讲 双曲线及其性质 - 解析

第2讲 双曲线的标准方程和几何性质1.双曲线的定义平面内到两个定点F 1,F 2的距离的差的绝对值等于常数2a (2a <|F 1F 2|)的点P 的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.2.双曲线的标准方程(1)中心在坐标原点,焦点在x 轴上的双曲线的标准方程为x 2a 2-y 2b 2=1(a >0,b >0).(2)中心在坐标原点,焦点在y 轴上的双曲线的标准方程为y 2a 2-x 2b 2=1(a >0,b >0).3.双曲线的几何性质标准方程 x 2a 2-y 2b 2=1(a >0,b >0) y 2a 2-x 2b 2=1(a >0,b >0) 范围 |x |≥a ,y ∈R|y |≥a ,x ∈R对称性 对称轴:x 轴,y 轴;对称中心:原点 焦点 F 1(-c,0),F 2(c,0) F 1(0,-c ),F 2(0,c ) 顶点 A 1(-a,0),A 2(a,0)A 1(0,-a ),A 2(0,a )轴 线段A 1A 2,B 1B 2分别是双曲线的实轴和虚轴;实轴长为2a ,虚轴长为2b 焦距|F 1F 2|=2c离心率e =c a= 1+b 2a2∈(1,+∞) e 是表示双曲线开口大小的一个量,e 越大开口越大.渐近线 y =±b axy =±a bxa ,b ,c 的关系a 2=c 2-b 2考点一 双曲线的定义及应用【例1-1】 已知圆C 1:(x +3)2+y 2=1和圆C 2:(x -3)2+y 2=9,动圆M 同时与圆C 1及圆C 2相外切,则动圆圆心M 的轨迹方程为____________.如图所示,设动圆M 与圆C 1及圆C 2分别外切于A 和B .根据两圆外切的条件,得|MC 1|-|AC 1|=|MA |,|MC 2|-|BC 2|=|MB |,因为|MA |=|MB |,所以|MC 1|-|AC 1|=|MC 2|-|BC 2|,即|MC 2|-|MC 1|=|BC 2|-|AC 1|=2, 所以点M 到两定点C 1,C 2的距离的差是常数且小于|C 1C 2|=6.又根据双曲线的定义,得动点M 的轨迹为双曲线的左支(点M 与C 2的距离大,与C 1的距离小), 其中a =1,c =3,则b 2=8.故点M 的轨迹方程为x 2-y 28=1(x ≤-1).【例1-2】已知F 1,F 2为双曲线C :x 2-y 2=2的左、右焦点,点P 在C 上,|PF 1|=2|PF 2|, 则cos ∠F 1PF 2=( ) A.14B.35C.34D.45解析由x 2-y 2=2,知a =b =2,c =2.由双曲线定义知,|PF 1|-|PF 2|=2a =22,又|PF 1|=2|PF 2|, ∴|PF 1|=42,|PF 2|=22,在△PF 1F 2中,|F 1F 2|=2c =4,由余弦定理,得 cos ∠F 1PF 2=|PF 1|2+|PF 2|2-|F 1F 2|22|PF 1|·|PF 2|=34.规律方法1.利用双曲线的定义判定平面内动点的轨迹是否为双曲线,进而根据要求可求出曲线方程;2.在“焦点三角形”中,常利用正弦定理、余弦定理,经常结合||PF 1|-|PF 2||=2a ,运用平方的方法,建立与|PF 1|,|PF 2|的联系,一般地,双曲线的焦点三角形有以下性质: (1)(2c)2=|PF 1|2+ |PF 2|2−2|PF 1||PF 2|cos∠F 1PF 2,得到:|PF 1||PF 2|= 2b 21− cos∠F 1PF 2;(2)S ∆F1PF 2= 12|PF 1||PF 2|sin∠F 1PF 2=b 2sin∠F 1PF 21− cos∠F 1PF 2=b 2tan(∠F 1PF22)【变式1】 已知△ABC 的顶点A (-5,0),B (5,0),△ABC 内切圆的圆心在直线x =2上,则顶点C 的轨迹方程是( )A.x 24-y 221=1(x >2)B.y 24-x 221=1(y >2)C.x 221-y 24=1D.y 24-x 22=1 【解析】选A 如图,△ABC 与内切圆的切点分别为G ,E ,F . |AG |=|AE |=7,|BF |=|BG |=3,|CE |=|CF |,所以|CA |-|CB |=7-3=4.根据双曲线定义,所求轨迹是以A ,B 为焦点,实轴长为4的双曲线的右支,方程为x 24-y 221=1(x >2).【变式2】已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2,左、右焦点分别为F 1,F 2,点A 在双曲线C上,若△AF 1F 2的周长为10a ,则△AF 1F 2的面积为( ) A.215a 2 B.15a 2 C.30a 2D.15a 2解析 由双曲线的对称性不妨设A 在双曲线的右支上,由e =ca=2,得c =2a ,∴△AF 1F 2的周长为|AF 1|+|AF 2|+|F 1F 2|=|AF 1|+|AF 2|+4a ,又△AF 1F 2的周长为10a ,∴|AF 1|+|AF 2|=6a ,又∵|AF 1|-|AF 2|=2a ,∴|AF 1|=4a ,|AF 2|=2a ,在△AF 1F 2中,|F 1F 2|=4a , ∴cos ∠F 1AF 2=|AF 1|2+|AF 2|2-|F 1F 2|22|AF 1|·|AF 2|=(4a )2+(2a )2-(4a )22×4a ×2a =14.又0<∠F 1AF <π,∴sin ∠F 1AF 2=154,∴S △AF 1F 2=12|AF 1|·|AF 2|·sin ∠F 1AF 2=12×4a ×2a ×154=15a 2. 【变式3】双曲线C 的渐近线方程为y =±233x ,一个焦点为F (0,-7),点A (2,0),点P 为双曲线第一象限内的点,则当点P 的位置变化时,△P AF 周长的最小值为( ) A.8B.10C.4+37D.3+317由已知得双曲线方程为y 24-x 23=1,设双曲线的另一个焦点为F ′,则|PF |=|PF ′|+4,△P AF 的周长为|PF |+|P A |+|AF |=|PF ′|+4+|P A |+3,当F ′,P ,A 三点共线时,|PF ′|+|P A |有最小值,为|AF ′|=3,故△P AF 的周长的最小值为10. 考点二 双曲线的标准方程【例2-1】已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A ,B两点.设A ,B 到双曲线的同一条渐近线的距离分别为d 1和d 2,且d 1+d 2=6,则双曲线的方程为( ) A.x 24-y 212=1 B.x 212-y 24=1 C.x 23-y 29=1 D.x 29-y 23=1 由d 1+d 2=6,得双曲线的右焦点到渐近线的距离为3,所以b =3.因为双曲线x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2,所以c a =2,所以a 2+b 2a 2=4,所以a 2+9a 2=4,解得a 2=3,所以双曲线的方程为x 23-y 29=1.【例2- 2】已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的一条渐近线方程为y =52x ,且与椭圆x 212+y 23=1有公共焦点,则C 的方程为( )A.x 28-y 210=1B.x 24-y 25=1C.x 25-y 24=1D.x 24-y 23=1 解析 由题设知b a =52①,又由椭圆x 212+y 23=1与双曲线有公共焦点, 易知a 2+b 2=c 2=9②,由①②解得a =2,b =5,则双曲线C 的方程为x 24-y 25=1.规律方法1.利用待定系数法求双曲线标准方程的关键是:设出双曲线方程的标准形式,根据已知条件,列出关于参数a ,b ,c 的方程并求出a ,b ,c 的值.2.不知道焦点在横纵坐标的曲线,可设为为mx 2+ny 2=1(当m >0,n >0,m ≠n ,为椭圆方程,当mn <0,m≠n ,为双曲线,当m=n ≠0,为圆)3. 与x 2a 2+y 2b 2=1(a >b >0)有共同焦点的曲线可设为12222=-+-kb y k a x (2b k <,为共焦点椭圆;22a k b <<为共焦点双曲线)4. 与x 2a 2±y 2b 2=1(a >b >0)有相同离心率的曲线可设为12222=±mb y ma x 5. 与双曲线x 2a 2-y 2b 2=1(a >0,b >0)共渐近线bx ±ay =0的双曲线方程为x 2a 2-y 2b2=λ(λ≠0).【变式1】 已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)过点(2,3),且实轴的两个端点与虚轴的一个端点组成一个等边三角形,则双曲线C 的标准方程是( ) A.x 212-y 2=1 B.x 29-y 23=1 C.x 2-y 23=1 D.x 223-y 232=1 解析 (1)由双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)过点(2,3),且实轴的两个端点与虚轴的一个端点组成一个等边三角形,可得⎩⎨⎧2a 2-3b 2=1,b a=3,解得⎩⎨⎧a =1,b =3,∴双曲线C 的标准方程是x 2-y 23=1. 【变式2】已知双曲线的渐近线方程为2x ±3y =0,且双曲线经过点P (6,2),则双曲线的方程为________________.由双曲线的渐近线方程为y =±23x ,可设双曲线方程为x 29-y 24=λ(λ≠0).因为双曲线过点P (6,2),所以69-44=λ,λ=-13,故所求双曲线方程为y 243-x 23=1.【变式3】经过点P (3,27),Q (-62,7)的双曲线的标准方程为____________.【解析】设双曲线方程为mx 2+ny 2=1(mn <0),因为所求双曲线经过点P (3,27),Q (-62,7),所以 ⎩⎪⎨⎪⎧9m +28n =1,72m +49n =1,解得⎩⎨⎧m =-175,n =125.故所求双曲线标准方程为y 225-x 275=1.考点三 双曲线的性质 多维探究角度1 求双曲线的渐近线【例3-1】 双曲线x 2a 2-y 2b 2=1(a >0,b >0)的离心率为3,则其渐近线方程为( )A.y =±2xB.y =±3xC.y =±22x D.y =±32x 解析 法一 由题意知,e =c a =3,所以c =3a ,所以b =c 2-a 2=2a ,即ba =2,所以该双曲线的渐近线方程为y =±ba x =±2x .法二 由e =ca =1+⎝⎛⎭⎫b a 2=3,得b a =2,所以该双曲线的渐近线方程为y =±b ax =±2x . 规律方法【变式1】已知双曲线C :x m 2-y n 2=1(m >0,n >0)的离心率与椭圆x 25+y 16=1的离心率互为倒数,则双曲线C 的渐近线方程为( )A .4x ±3y =0B .3x ±4y =0C .4x ±3y =0或3x ±4y =0D .4x ±5y =0或5x ±4y =0 【解析】 由题意知,椭圆中a =5,b =4,∴椭圆的离心率e = 1-b 2a 2=35, ∴双曲线的离心率为1+n 2m 2=53,∴n m =43,∴双曲线的渐近线方程为y =±n m x =±43x ,即4x ±3y =0. 【变式2】已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的一个焦点为F ,点A ,B 是C 的一条渐近线上关于原点对称的两点,以AB 为直径的圆过F 且交C 的左支于M ,N 两点,若|MN |=2,△ABF 的面积为8,则C 的渐近线方程为( )A .y =±3xB .y =±33x C .y =±2x D .y =±12x 【解析】设双曲线的另一个焦点为F ′,由双曲线的对称性,可得四边形AFBF ′是矩形, ∴S △ABF =S △ABF ′,即bc =8,由⎩⎪⎨⎪⎧x 2+y 2=c 2,x 2a 2-y 2b 2=1可得y =±b 2c ,则|MN |=2b 2c =2,即b 2=c ,∴b =2,c =4,∴a =c 2-b 2=2 3,∴C 的渐近线方程为y =±33x , 角度2 求双曲线的离心率【例3-2】 (1)(2018·全国Ⅲ卷)设F 1,F 2是双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点,O 是坐标原点.过F 2作C 的一条渐近线的垂线,垂足为P .若|PF 1|=6|OP |,则C 的离心率为( ) A. 5B.2C. 3D.2解析 不妨设一条渐近线的方程为y =b a x ,则F 2到y =b a x 的距离d =|bc |a 2+b 2=b ,在Rt △F 2PO 中,|F 2O |=c ,所以|PO |=a ,所以|PF 1|=6a ,又|F 1O |=c ,所以在△F 1PO 与Rt △F 2PO 中,根据余弦定理得cos ∠POF 1=a 2+c 2-(6a )22ac =-cos ∠POF 2=-a c ,则3a 2+c 2-(6a )2=0,得3a 2=c 2,所以e =ca= 3.【例3-3】已知双曲线C 1:x 2a 2-y 2b 2=1(a >0,b >0),圆C 2:x 2+y 2-2ax +34a 2=0,若双曲线C 1的一条渐近线与圆C 2有两个不同的交点,则双曲线C 1的离心率的取值范围是( ) A.⎝⎛⎭⎫1,233B.⎝⎛⎭⎫233,+∞ C.(1,2)D.(2,+∞)由双曲线方程可得其渐近线方程为y =±b a x ,即bx ±ay =0,圆C 2:x 2+y 2-2ax +34a 2=0可化为(x -a )2+y 2=14a 2,圆心C 2的坐标为(a ,0),半径r =12a ,由双曲线C 1的一条渐近线与圆C 2有两个不同的交点,得|ab |a 2+b 2<12a ,即c >2b ,即c 2>4b 2,又知b 2=c 2-a 2,所以c 2>4(c 2-a 2),即c 2<43a 2,所以e =c a <233,又知e >1,所以双曲线C 1的离心率的取值范围为⎝⎛⎭⎫1,233.规律方法 求双曲线离心率或其取值范围的方法1.求a ,b ,c 的值,由c 2a 2=a 2+b 2a 2=1+b 2a 2直接求e ;或者结合双曲线性质e =c a = 2c 2a = |F 1F 2||PF 1−PF 2| = sinF 1PF 2sinPF 2F 1− sinPF 1F 2 2.列出含有a ,b ,c 的齐次方程(或不等式),借助于b 2=c 2-a 2消去b ,然后转化成关于e 的方程(或不等式) 【变式1】在平面直角坐标系xOy 中,双曲线C :y 2a 2-x 2b 2=1(a >0,b >0)的一条渐近线与圆(x -2)2+(y -1)2=1相切,则C 的离心率为( ) A.43B.54C.169D.2516双曲线C 的渐近线方程为by ±ax =0,结合图形易知与圆相切的只可能是by -ax =0,又圆心坐标为(2,1), 则|b -2a |a 2+b 2=1,得3a =4b ,所以9a 2=16b 2=16(c 2-a 2),则e 2=2516,又e >1,故e =54.【变式2】 已知抛物线y 2=4x的焦点为F ,准线为l .若l 与双曲线x 2a 2-y 2b2=1(a >0,b >0)的两条渐近线分别交于点A 和点B ,且|AB |=4|OF |(O 为原点),则双曲线的离心率为( )A.2B.3 C .2 D.5【解析】由已知易得,抛物线y 2=4x 的焦点为F (1,0),准线l :x =-1,所以|OF |=1.又双曲线的两条渐近线的方程为y =±b a x ,不妨设点A ⎝⎛⎭⎫-1,b a ,B ⎝⎛⎭⎫-1,- b a ,所以|AB |=2b a =4|OF |=4,所以ba =2,即b =2a ,所以b 2=4a 2.又双曲线方程中c 2=a 2+b 2,所以c 2=5a 2,所以e =ca = 5.故选D.角度3 与双曲线有关的范围(最值)问题【例3-4】 已知M (x 0,y 0)是双曲线C :x 22-y 2=1上的一点,F 1,F 2是C 的两个焦点,若MF 1→·MF 2→<0,则y 0的取值范围是( ) A.⎝⎛⎭⎫-33,33 B.⎝⎛⎭⎫-36,36 C.⎝⎛⎭⎫-223,223 D.⎝⎛⎭⎫-233,233 解析 因为F 1(-3,0),F 2(3,0),x 202-y 20=1,所以MF 1→·MF 2→=(-3-x 0,-y 0)·(3-x 0,-y 0)=x 20+y 2-3<0,即3y 20-1<0,解得-33<y 0<33. 规律方法 与双曲线有关的取值范围问题的解题思路 (1)若条件中存在不等关系,则借助此关系直接变换转化求解.(2)若条件中没有不等关系,要善于发现隐含的不等关系或借助曲线中不等关系来解决.【变式】已知焦点在x 轴上的双曲线x 28-m +y 24-m =1,它的焦点到渐近线的距离的取值范围是________.对于焦点在x 轴上的双曲线x 2a 2-y 2b 2=1(a >0,b >0),它的一个焦点(c ,0)到渐近线bx -ay =0的距离为|bc |b 2+a2=b .本题中,双曲线x 28-m +y 24-m =1即x 28-m -y 2m -4=1,其焦点在x 轴上,则⎩⎪⎨⎪⎧8-m >0,m -4>0,解得4<m <8,则焦点到渐近线的距离d =m -4∈(0,2).基础巩固题组 (建议用时:40分钟)一、选择题1.设双曲线x 2a 2-y 2b 2=1(a >0,b >0)的虚轴长为2,焦距为23,则双曲线的渐近线方程为( )A.y =±12xB.y =±22x C.y =±2xD.y =±2x解析 因为2b =2,所以b =1,因为2c =23,所以c =3,所以a =c 2-b 2=2,所以双曲线的渐近线方程为y =±b a x =±22x .答案 B2.双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的一个焦点为F ,过点F 作双曲线C 的一条渐近线的垂线,垂足为A ,且交y 轴于B ,若A 为BF 的中点,则双曲线的离心率为( ) A. 2B. 3C.2D.62解析 由题易知双曲线C 的一条渐近线与x 轴的夹角为π4,故双曲线C 的离心率e =⎝⎛⎭⎫cos π4-1= 2. 答案 A3.已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2,则点(4,0)到C 的渐近线的距离为( )A. 2B.2C.322D.22解析 法一 由离心率e =ca =2,得c =2a ,又b 2=c 2-a 2,得b =a ,所以双曲线C 的渐近线方程为y =±x .由点到直线的距离公式,得点(4,0)到C 的渐近线的距离为41+1=2 2. 法二 离心率e =2的双曲线是等轴双曲线,其渐近线方程是y =±x ,∴点(4,0)到C 的渐近线的距离为41+1=2 2. 答案 D4.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的离心率为32,过右焦点F 作渐近线的垂线,垂足为M .若△FOM 的面积为5,其中O 为坐标原点,则双曲线的方程为( ) A.x 2-4y 25=1B.x 22-2y 25=1C.x 24-y 25=1D.x 216-y 220=1 解析 由题意可知e =c a =32,可得b a =52,取一条渐近线为y =ba x ,可得F 到渐近线y =b a x 的距离d =bca 2+b2=b ,在Rt △FOM 中,由勾股定理可得|OM |=|OF |2-|MF |2=c 2-b 2=a ,由题意可得12ab =5,联立⎩⎨⎧b a =52,12ab =5,解得⎩⎨⎧a =2,b =5,所以双曲线的方程为x 24-y25=1.答案 C5.已知F 2,F 1是双曲线y 2a 2-x 2b 2=1(a >0,b >0)的上、下两个焦点,过F 1的直线与双曲线的上下两支分别交于点B ,A ,若△ABF 2为等边三角形,则双曲线的渐近线方程为( ) A.y =±2x B.y =±22x C.y =±6xD.y =±66x 解析 根据双曲线的定义,可得|BF 1|-|BF 2|=2a ,∵△ABF 2为等边三角形,∴|BF 2|=|AB |,∴|BF 1|-|AB |=|AF 1|=2a ,又∵|AF 2|-|AF 1|=2a ,∴|AF 2|=|AF 1|+2a =4a ,∵在△AF 1F 2中,|AF 1|=2a ,|AF 2|=4a ,∠F 1AF 2=120°,∴|F 1F 2|2=|AF 1|2+|AF 2|2-2|AF 1|·|AF 2|cos 120°,即4c 2=4a 2+16a 2-2×2a ×4a ×⎝⎛⎭⎫-12=28a 2,亦即c 2=7a 2,则b =c 2-a 2=6a 2=6a ,由此可得双曲线C 的渐近线方程为y =±66x . 答案 D 二、填空题6.直线l :y =2x +10过双曲线x 2a 2-y 2b 2=1(a >0,b >0)一个焦点且与其一条渐近线平行,则双曲线方程为________________.解析 由题意得一个焦点为F (-5,0),c =5,ba =2,又a 2+b 2=c 2,所以a 2=5,b 2=20,所以双曲线方程为x 25-y 220=1.7.设双曲线x 29-y 216=1的右顶点为A ,右焦点为F .过点F 且平行于双曲线的一条渐近线的直线与双曲线交于点B ,则△AFB 的面积为________.解析 a 2=9,b 2=16,故c =5.∴A (3,0),F (5,0),不妨设直线BF 的方程为y =43(x -5),代入双曲线方程解得B ⎝⎛⎭⎫175,-3215.∴S △AFB =12|AF |·|y B |=12·2·3215=3215. 8.已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,O 为坐标原点.P 是双曲线在第一象限上的点,直线PO ,PF 2分别交双曲线C 左、右支于M ,N .若|PF 1|=2|PF 2|,且∠MF 2N =60°,则双曲线C 的离心率为________.解析 由题意,|PF 1|=2|PF 2|,由双曲线的定义可得,|PF 1|-|PF 2|=2a ,可得|PF 1|=4a ,|PF 2|=2a , 又|F 1O |=|F 2O |,|PO |=|MO |,得四边形PF 1MF 2为平行四边形,又∠MF 2N =60°,可得∠F 1PF 2=60°, 在△PF 1F 2中,由余弦定理可得,4c 2=16a 2+4a 2-2·4a ·2a ·cos 60°,即4c 2=20a 2-8a 2,c 2=3a 2, 可得c =3a ,所以e =ca = 3.三、解答题9.已知双曲线的中心在原点,焦点F 1,F 2在坐标轴上,离心率为2,且过点P (4,-10). (1)求双曲线的方程;(2)若点M (3,m )在双曲线上,求证:MF 1→·MF 2→=0. (1)解 ∵e =2,∴可设双曲线的方程为x 2-y 2=λ(λ≠0).∵双曲线过点(4,-10),∴16-10=λ,即λ=6.∴双曲线的方程为x 2-y 2=6,即x 26-y 26=1. (2)证明 法一 由(1)可知,a =b =6,∴c =23,∴F 1(-23,0),F 2(23,0), ∴k MF 1=m 3+23,k MF 2=m 3-23,k MF 1·k MF 2=m 29-12=-m 23.∵点M (3,m )在双曲线上,∴9-m 2=6,m 2=3,故k MF 1·k MF 2=-1,∴MF 1⊥MF 2.∴MF 1→·MF 2→=0. 法二 由(1)可知,a =b =6,∴c =23,∴F 1(-23,0),F 2(23,0),MF 1→=(-23-3,-m ),MF 2→=(23-3,-m ),∴MF 1→·MF 2→=(3+23)×(3-23)+m 2=-3+m 2, ∵点M (3,m )在双曲线上,∴9-m 2=6,即m 2-3=0,∴MF 1→·MF 2→=0.10.设A ,B 分别为双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右顶点,双曲线的实轴长为43,焦点到渐近线的距离为 3.(1)求双曲线的方程; (2)已知直线y =33x -2与双曲线的右支交于M ,N 两点,且在双曲线的右支上存在点D ,使OM →+ON →=tOD →,求t 的值及点D 的坐标.解 (1)由题意知a =23,∵一条渐近线为y =b a x ,即bx -ay =0.∴由焦点到渐近线的距离为3,得|bc |b 2+a2= 3. 又∵c 2=a 2+b 2,∴b 2=3,∴双曲线的方程为x 212-y 23=1. (2)设M (x 1,y 1),N (x 2,y 2),D (x 0,y 0),其中x 0≥2 3.又OM →+ON →=tOD →,即(x 1,y 1)+(x 2,y 2)=t (x 0,y 0),则x 1+x 2=tx 0,y 1+y 2=ty 0.将直线方程y =33x -2代入双曲线方程x 212-y 23=1得x 2-163x +84=0,其中Δ=(163)2-4×84>0, 则x 1+x 2=163,y 1+y 2=33(x 1+x 2)-4=12.∴⎩⎨⎧x 0y 0=433,x 2012-y 203=1.解得⎩⎨⎧x 0=43,y 0=3. ∴t =4,点D 的坐标为(43,3).能力提升题组(建议用时:20分钟)11.已知F 1,F 2分别是双曲线x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点,P 是双曲线上一点,若|PF 1|+|PF 2|=6a ,且△PF 1F 2的最小内角为π6,则双曲线的渐近线方程为( ) A.y =±2xB.y =±12xC.y =±22xD.y =±2x解析 不妨设P 为双曲线右支上一点,则|PF 1|>|PF 2|,由双曲线的定义得|PF 1|-|PF 2|=2a ,又|PF 1|+|PF 2|=6a ,所以|PF 1|=4a ,|PF 2|=2a .又因为⎩⎪⎨⎪⎧2c >2a ,4a >2a ,所以∠PF 1F 2为最小内角,故∠PF 1F 2=π6. 由余弦定理,可得(4a )2+(2c )2-(2a )22·4a ·2c =32,即(3a -c )2=0,所以c =3a ,则b =2a , 所以双曲线的渐近线方程为y =±2x .答案 D12.已知点F 为双曲线E :x 2a 2-y 2b2=1(a >0,b >0)的右焦点,直线y =kx (k >0)与E 交于不同象限内的M ,N 两点,若MF ⊥NF ,设∠MNF =β,且β∈⎣⎡⎦⎤π12,π6,则该双曲线的离心率的取值范围是( )A.[2,2+6]B.[2,3+1]C.[2,2+6]D.[2,3+1]解析 如图,设左焦点为F ′,连接MF ′,NF ′,令|MF |=r 1,|MF ′|=r 2,则|NF |=|MF ′|=r 2,由双曲线定义可知r 2-r 1=2a ①,∵点M 与点N 关于原点对称,且MF ⊥NF ,∴|OM |=|ON |=|OF |=c ,∴r 21+r 22=4c 2②,由①②得r 1r 2=2(c 2-a 2),又知S △MNF =2S △MOF ,∴12r 1r 2=2·12c 2·sin 2β,∴c 2-a 2=c 2·sin 2β, ∴e 2=11-sin 2β,又∵β∈⎣⎡⎦⎤π12,π6,∴sin 2β∈⎣⎡⎦⎤12,32,∴e 2=11-sin 2β∈[2,(3+1)2]. 又e >1,∴e ∈[2,3+1].答案 D13.已知椭圆M :x 2a 2+y 2b 2=1(a >b >0),双曲线N :x 2m 2-y 2n2=1.若双曲线N 的两条渐近线与椭圆M 的四个交点及椭圆M 的两个焦点恰为一个正六边形的顶点,则椭圆M 的离心率为________;双曲线N 的离心率为________. 解析 设椭圆的右焦点为F (c ,0),双曲线N 的渐近线与椭圆M 在第一象限内的交点为A ,由题意可知A ⎝⎛⎭⎫c 2,3c 2,由点A 在椭圆M 上得,c 24a 2+3c 24b 2=1,∴b 2c 2+3a 2c 2=4a 2b 2, ∵b 2=a 2-c 2,∴(a 2-c 2)c 2+3a 2c 2=4a 2(a 2-c 2),∴4a 4-8a 2c 2+c 4=0,∴e 4椭-8e 2椭+4=0, ∴e 2椭=4±23,∴e 椭=3+1(舍去)或 e 椭=3-1,∴椭圆M 的离心率为3-1. ∵双曲线的渐近线过点A ⎝⎛⎭⎫c 2,3c 2,∴渐近线方程为y =3x ,∴n m =3, 故双曲线的离心率e 双=m 2+n 2m 2=2. 14.已知椭圆C 1的方程为x 24+y 2=1,双曲线C 2的左、右焦点分别是C 1的左、右顶点,而C 2的左、右顶点分别是C 1的左、右焦点.(1)求双曲线C 2的方程;(2)若直线l :y =kx +2与双曲线C 2恒有两个不同的交点A 和B ,且OA →·OB →>2(其中O 为原点),求k 的取值范围.解 (1)设双曲线C 2的方程为x 2a 2-y 2b 2=1(a >0,b >0),则a 2=3,c 2=4,再由a 2+b 2=c 2,得b 2=1. 故C 2的方程为x 23-y 2=1. (2)将y =kx +2代入x 23-y 2=1,得(1-3k 2)x 2-62kx -9=0. 由直线l 与双曲线C 2交于不同的两点,得⎩⎨⎧1-3k 2≠0,Δ=(-62k )2+36(1-3k 2)=36(1-k 2)>0,∴k 2≠13且k 2<1.① 设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=62k 1-3k 2,x 1x 2=-91-3k 2. ∴x 1x 2+y 1y 2=x 1x 2+(kx 1+2)(kx 2+2)=(k 2+1)x 1x 2+2k (x 1+x 2)+2=3k 2+73k 2-1. 又∵OA →·OB →>2,得x 1x 2+y 1y 2>2,∴3k 2+73k 2-1>2,即-3k 2+93k 2-1>0,解得13<k 2<3.② 由①②得13<k 2<1,故k 的取值范围为⎝⎛⎭⎫-1,-33∪⎝⎛⎭⎫33,1.。
高中数学选修2-1圆锥曲线基本知识点与典型题举例(后附答案)汇总
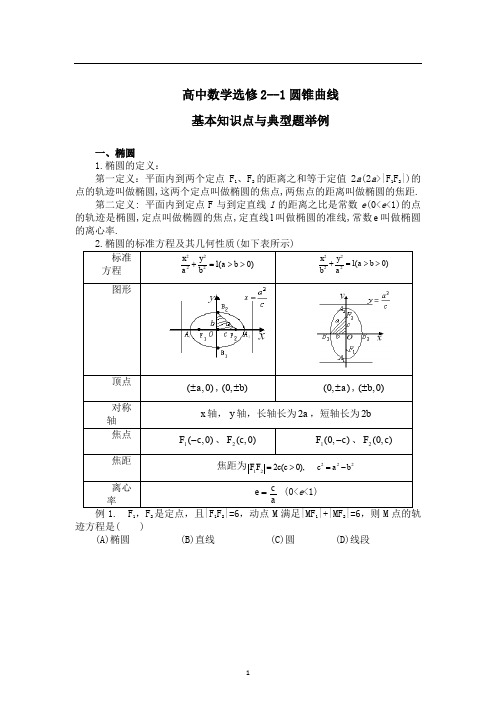
高中数学选修2--1圆锥曲线基本知识点与典型题举例一、椭圆1.椭圆的定义:第一定义:平面内到两个定点F1、F2的距离之和等于定值2a(2a>|F1F2|)的点的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距.第二定义: 平面内到定点F与到定直线l的距离之比是常数e(0<e<1)的点的轨迹是椭圆,定点叫做椭圆的焦点,定直线l叫做椭圆的准线,常数e叫做椭圆的离心率.121212迹方程是( )(A)椭圆 (B)直线 (C)圆 (D)线段例 2. 已知ABC ∆的周长是16,)0,3(-A ,B )0,3(, 则动点的轨迹方程是( )(A)1162522=+y x (B))0(1162522≠=+y y x (C)1251622=+y x (D))0(1251622≠=+y y x例3. 若F (c ,0)是椭圆22221x y a b+=的右焦点,F 与椭圆上点的距离的最大值为M ,最小值为m ,则椭圆上与F 点的距离等于2M m+的点的坐标是( ) (A)(c ,2b a±) 2()(,)b B c a -± (C)(0,±b ) (D)不存在例4 设F 1(-c ,0)、F 2(c ,0)是椭圆22x a +22y b=1(a >b >0)的两个焦点,P 是以F 1F 2为直径的圆与椭圆的一个交点,若∠PF 1F 2=5∠PF 2F 1,则椭圆的离心率为( )(A)2 (B)32 (D)3例5. P 点在椭圆1204522=+y x 上,F 1、F 2是两个焦点,若21PF PF ⊥,则P 点的坐标是 .例6. 写出满足下列条件的椭圆的标准方程:(1)长轴与短轴的和为18,焦距为6; . (2)焦点坐标为)0,3(-,)0,3(,并且经过点(2,1); . (3)椭圆的两个顶点坐标分别为)0,3(-,)0,3(,且短轴是长轴的31; ____.(4)离心率为23,经过点(2,0); .例7. 12F F 、是椭圆2214x y +=的左、右焦点,点P 在椭圆上运动,则12||||PF PF ⋅的最大值是 .二、双曲线1.双曲线的定义:第一定义:平面内到两个定点F 1、F 2的距离之差的绝对值等于定值2a (0<2a <|F 1F 2|)的点的轨迹叫做双曲线,这两个定点叫做双曲线的焦点,两焦点的距离叫做双曲线的焦距.第二定义: 平面内到定点F 与到定直线l 的距离之比是常数e (e >1)的点的轨迹是双曲线,定点叫做双曲线的焦点,定直线l 叫做双曲线的准线,常数e 叫做双曲线的离心率例8 .命题甲:动点P 到两定点A 、B 的距离之差的绝对值等于2a (a >0);命题乙: 点P 的轨迹是双曲线。
圆锥曲线的第二定义双曲线的第二定义

圆锥曲线的第二定义-双曲线的第二定义巧用圆锥曲线第二定义解题整警巧用圆锥曲线第二定义解题黔西南民族职业技术学院姚忠安【摘要】圆锥曲线第二定义,揭示了圆锥曲线的内在联系。
应用圆锥曲线第二定义求解圆锥曲线的轨迹方程、离心率、与圆锥曲线有关的最值等非常简单,它能使问题化繁为简,提高准确率,达到事半功倍的效果。
【关键词】圆锥曲线第二定义轨迹离心率最值条件中的三个,用圆锥曲线定义来解决比较简单。
求圆锥曲线的离心率二例4过椭圆的左焦点F作直线与椭圆交于A、B.两点,l:B:lIFIAF=53,且直线与长轴的夹角为6。
,求椭圆的离心率。
0解:如图,作椭圆的左准线l过A、B两点分别作左准线的垂线,垂足分别为c、D,由圆锥曲线的定II君Il圆锥曲线第二定义:平面内动点M定XY到点F的距离与它到定直线1距离的比是常数e的点的轨迹,当0e1是椭圆;当e1是抛<<时=时物线;当e1是双曲线。
e离心率,F焦点。
>时是是求圆锥曲线的轨迹方程一例1经过点M轴率e专的点Pxy的轨迹方程。
:解:依题意,所求的点P的轨迹方程是以y轴为右准线的椭圆方程,设椭圆的右焦点F因x,。
为P在椭圆上且过椭圆的右顶点,由第二定义知点即X4工,。
yo_-XI=XOY=,所以椭圆右焦点,8CX6lO0。
f一2,・为F,又’M在椭圆上,由一、F\~定,止喜即/4+。
{,j)一x化简得P的轨迹方程为:即,椭圆的离心率为e=1+9))右焦点,X为右准线,离.50为=2心率e的圆锥曲线的轨迹方程。
=2解:依题意,所求曲线的轨迹方程为双曲线,设M曲线上任一点,由圆锥曲线第二定xY为例5已知一抛物线以椭圆三+。
1的左焦点.;F为顶点,以椭圆的右焦点F为焦点,P抛物线与椭圆的一个交点,如果椭圆的离为一l,心率满足=,求e的值。
解:如图,设椭圆的左准线与抛物线的准线分别为l。
,过点P作1垂线,垂足分别为A、、l.的、l义,有=,与2即喜,简2化得所线的为:;一善:求曲方程堕l例3已知圆锥曲线过点A.一4一8,它的一个焦点为F=B,由圆锥曲线第二定义可知,一e即l,l=eIpI①又。
圆锥曲线常用的二次结论专题练习

圆锥曲线常用的二次结论专题练习圆锥曲线常用结论专题练一、椭圆的标准方程椭圆的标准方程为x^2/a^2+y^2/b^2=1,其中a>b>0.1.通径:过椭圆的一个焦点且与长轴垂直的弦的长为a,称为通径。
2.离心率:椭圆离心率e=a/sqrt(a^2-b^2)。
3.焦点弦:设过焦点F的直线的倾斜角为α,则焦点弦AB=2b^2/(a-cosα)。
4.垂径定理:对于弦AB的中点M,过M作弦的垂线,垂足为K,则MK^2=b^2-a^2cos^2θ。
5.焦三角形:设椭圆的焦点为F1和F2,点P为椭圆上一点,则焦三角形面积S=b^2tanθ/2,其中θ为角F1PF2的大小。
二、双曲线的标准方程双曲线的标准方程为x^2/a^2-y^2/b^2=1,其中a>0,b>0.1.离心率:双曲线离心率e=c/a,其中c=sqrt(a^2+b^2)。
2.焦点到渐近线的距离:焦点到渐近线的距离为b/sqrt(c^2-a^2)。
3.垂径定理:对于弦AB的中点M,过M作弦的垂线,垂足为K,则MK^2=b^2+a^2cos^2θ。
三、抛物线的标准方程抛物线的标准方程为y^2=2px,其中p>0.1.焦点坐标:抛物线的焦点为F(p,0)。
2.弦长公式:设抛物线上两点为P1(x1,y1)和P2(x2,y2),则弦P1P2的长度为|P1P2|=sqrt[(x1-x2)^2+(y1-y2)^2]。
3.垂足坐标公式:设抛物线上一点为P(x,y),则过点P作抛物线的准线垂线的垂足坐标为(x,y/2)。
四、点F是圆锥曲线一个焦点设焦点为F,离心率为e,焦点在x轴上,过F的弦AB与x轴夹角为θ,F分AB所成的比为λ,则有ecosθ=λ-1/λ+1,或者e^2=1+k^2/λ^2,其中k=AF。
练题:1.设直线l过双曲线C的一个焦点,且与C的一条对称轴垂直,l与C交于A,B两点,|AB|为C的实轴长的2倍,则C的离心率为3.2.已知椭圆E的中心在坐标原点,离心率为2,E的右焦点与抛物线C:y^2=8x的焦点重合,A,B是C的准线与E的两个交点,则|AB|=9.3.已知椭圆x^2/4+y^2/3=1的左、右焦点分别为F1,F2,过F1的直线l交椭圆于A,B两点,若|BF2|+|AF1|的最大值为5,则椭圆的长半轴为3.4.已知椭圆E:x^2/45+y^2/36=1,过点F的直线交E于A,B两点。
三个圆锥曲线第二定义

三个圆锥曲线第二定义
三个圆锥曲线的第二定义是指它们可以通过在空间中移动一个直角圆锥来得到。
这三个圆锥曲线分别为椭圆、抛物线和双曲线。
椭圆是一个闭合的曲线,其定义为离心率小于1的圆锥截面。
在几何上,可以将椭圆看作是一个圆沿着一条直线的轨迹。
椭圆具有两个焦点和一个长轴和短轴,它们之间的距离是固定的。
抛物线是一个开口向上或向下的曲线,其定义为离心率等于1
的圆锥截面。
在几何上,可以将抛物线看作是一个点沿着一条直线的轨迹。
抛物线有一个焦点和一个直线称为准线,它们之间的距离是相等的。
双曲线是一个开口向左和向右的曲线,其定义为离心率大于1
的圆锥截面。
在几何上,可以将双曲线看作是一对不相交的直线沿着一条直线的轨迹。
双曲线有两个焦点和两条渐近线,它们之间的距离是固定的。
这三个圆锥曲线是数学中的常见曲线,它们在几何学、物理学和工程学等领域中具有广泛的应用。
圆锥曲线-基本定义-第二定义

学术正刊 圆锥曲线 基本定义
高中 2 LeO 著 第二定义
定义3.0(圆锥曲线第二定义):平面内到定点与定直线的距离的比为常数e(e >0)的点的轨迹,称之为圆锥曲线。
定义3.1(圆锥曲线焦点):称这个定点为圆锥曲线的焦点。
定义3.2(圆锥曲线准线):称这条定直线为圆锥曲线的准线。
定义3.3(圆锥曲线离心率):称这个常数e 为圆锥曲线的离心率。
定义3.4(圆锥曲线焦准距):焦点到其对应准线的距离称之为圆锥曲线的焦准距。
图1 图2
解:如图1,给定离心率e 和焦准距p ,建立直角坐标系,将焦点定于坐标原点,准线垂直横轴。
设P 点坐标P (x,y ),根据“圆锥曲线第二定义”有:
|PF |PD =e ⋯〈1〉 代入坐标,解得:
√x 2+y 2
x +p =e ⋯〈2〉 〈2〉式化简得:
(1−e 2)∙x 2−2e 2px +y 2−e 2p 2=0⋯〈3〉
〈3〉式即为圆锥曲线的统一方程。
如图2,当离心率取不同值时,得到对应三种不同的圆锥曲线:
{e ∈(0,1), 1−e 2>0,表示椭圆;
e =1, 1−e 2=0,表示抛物线;e ∈(1,∞),1−e 2<0,表示双曲线。
三种圆锥曲线分别对坐标系进行适当平移后,可得三种圆锥曲线的标准方程。
证毕。
圆锥曲线第二定义与焦半径公式知识点练习含答案(高考数学提升复习)

第2讲 圆锥曲线第二定义与焦半径公式一.选择题(共5小题)1.已知点P 是双曲线22184x y -=上的动点,1F ,2F 为该双曲线的左右焦点,O 为坐标原点,则12||||||PF PF OP +的最大值为( )A .B .2C D2.已知双曲线222:1(0)4x y C a α-=>的右支上的点0(P x ,0)y 满足121||3||(PF PF F =,2F 分别是双曲线的左右焦点),则00(cy c x +为双曲线C 的半焦距)的取值范围是( )A .)+∞B .[2,25)2C .25)2D .[2,3.已知点P 是双曲线22221(0,0)x y a b a b -=>>上的动点,1F ,2F 分别是其左、右焦点,O 为坐标原点,若12||||||PF PF OP +( )A B C .32D .24.已知F 为抛物线2:4C y x =的焦点,过F 作两条互相垂直的直线1l ,2l ,直线1l 与C 交于A ,B 两点,直线2l 与C 交于D ,E 两点,则当||||AB DE +取得最小值时,四边形ADBE的面积为( ) A .32B .16C .24D .85.过椭圆22143x y +=的右焦点F 作两条相互垂直的直线分别交椭圆于A ,B ,C ,D 四点,则11||||AB CD +的值为( ) A .18B .16C .1D .712二.填空题(共3小题)6.已知P 是椭圆22:184x y C +=上的动点,1F ,2F 分别是其左右焦点,O 是坐标原点,则12||||||PF PF PO -的取值范围是 .7.已知F 为抛物线2:4C y x =的焦点,过F 作两条互相垂直的直线1l ,2l ,直线1l 与C 交于A 、B 两点,直线2l 与C 交于D 、E 两点,则11||||AB DE +的值为 . 8.已知F 为抛物线2:4C y x =的焦点,过F 作两条互相垂直的直线1l ,2l ,直线1l 与C 交于A 、B 两点,直线2l 与C 交于D 、E 两点,则||4||AB DE +的最小值为 .三.解答题(共6小题)9.已知斜率为k 的直线l 与椭圆22:143x y C +=交于A ,B 两点,线段AB 的中点为(1M ,)(0)m m >. (1)证明:12k <-;(2)设F 为C 的右焦点,P 为C 上一点,且0FP FA FB ++=.证明:||FA ,||FP ,||FB 成等差数列,并求该数列的公差.10.已知斜率为k 的直线l 与椭圆22:198x y C +=交于A 、B 两点,线段AB 的中点为(1M ,)(0)t t >.(Ⅰ)证明:13k <-;(Ⅱ)设F 为C 的右焦点,Q 为C 上的一点,且0FQ FA FB ++=,证明:||FA ,||FQ ,||FB 成等差数列.11.已知1F 、2F 是椭圆22221(0)x y a b a b +=>>的左、右焦点,且离心率12e =,点P 为椭圆上的一个动点,△12PF F 的内切圆面积的最大值为43π.(1)求椭圆的方程;(2)若A ,B ,C ,D 是椭圆上不重合的四个点,满足向量1F A 与1F C 共线,1F B 与1F D 共线,且0AC BD =,求||||AC BD +的取值范围.12.已知椭圆22221(0)x y a b a b +=>>经过点,且椭圆的离心率12e =,过椭圆的右焦点F 作两条互相垂直的直线,分别交椭圆于点A 、B 及C 、D . (Ⅰ)求椭圆的方程; (Ⅱ)求证:11||||AB CD +为定值; (Ⅲ)求9||||16AB CD +的最小值.13.已知椭圆22122:1(0)x y C a b a b +=>>的长轴长为4,离心率为12,一动圆2C 过椭圆1C 右焦点F ,且与直线1x =-相切.(1)求椭圆1C 的方程及动圆圆心轨迹2C 的方程;(2)过F 作两条互相垂直的直线,分别交椭圆1C 于P ,Q 两点,交曲线2C 于M ,N 两点,求四边形PMQN 面积的最小值.14.平面直角坐标系xOy 中,已知F 为椭圆22221x y a b+=的右焦点,且24a b +=,过F 作两条互相垂直的直线交椭圆分别于A 、B 与C 、D .以F 为极点,x 轴正半轴为极轴建立极坐标系.(Ⅰ)求椭圆的极坐标方程与1||AB 的代数表达式; (Ⅱ)求11||||AB CD +的取值范围.第2讲 圆锥曲线第二定义与焦半径公式参考答案与试题解析一.选择题(共5小题)1.已知点P 是双曲线22184x y -=上的动点,1F ,2F 为该双曲线的左右焦点,O 为坐标原点,则12||||||PF PF OP +的最大值为( )A .B .2C D【解答】解:由题意,分子最大且分母最小时,即P 在顶点处取得最大值,不妨取顶点,0),则12||||||PF PF OP +=,故选:D .2.已知双曲线222:1(0)4x y C a α-=>的右支上的点0(P x ,0)y 满足121||3||(PF PF F =,2F 分别是双曲线的左右焦点),则00(cy c x +为双曲线C 的半焦距)的取值范围是( )A .)+∞B .[2,25)2C .25)2D .[2,【解答】解:由双曲线的第二定义可知10||PF ex a =+,20||PF ex a =-, 右支上的点0(P x ,0)y 满足12||3||PF PF =, 0003()2ex a ex a ex a ∴+=-⇒=,由c e a=, 解得202a x c=,P 在右支上,可得202a x a c=, 可得12ca<,即12e <,则22220022201164(1)422x c c y e x a a e+=+-=+-, 令2e t =,14t <, 可得2202011611613244()4222c y e t t x e t t+=+-=+-=+- 而132()()2f t t t =+在(1,4]递减,132()[62t t +∈,33)2, 2002522c y x ∴+<, 故选:B .3.已知点P 是双曲线22221(0,0)x y a b a b -=>>上的动点,1F ,2F 分别是其左、右焦点,O 为坐标原点,若12||||||PF PF OP+( )AB C .32D .2【解答】解:不妨设P 为右支上的一点,(,)P x y 其中x a , 1||PF ex a =+,2||PF ex a =-,||OP =∴12||||)||PF PF x a OP +=∴当x a =时,取得最大值,∴=∴e =故选:B .4.已知F 为抛物线2:4C y x =的焦点,过F 作两条互相垂直的直线1l ,2l ,直线1l 与C 交于A ,B 两点,直线2l 与C 交于D ,E 两点,则当||||AB DE +取得最小值时,四边形ADBE的面积为( ) A .32B .16C .24D .8【解答】解:因为AB DE ⊥,要使||||AB DE +最小,而||||2|||AB DE AB + 由抛物线的对称性可得A 与D ,B 与E 关于x 轴对称, 所以可得直线DE 的斜率为1,又过抛物线的焦点(1,0), 所以直线DE 的方程为:1y x =-,214y x y x=-⎧⎨=⎩,整理可得2440y y --=,124y y +=,124y y =-,所以可得||8DE =, 所以11883222ABCD S DE AB =⋅=⨯⨯=四边形. 故选:A .5.过椭圆22143x y +=的右焦点F 作两条相互垂直的直线分别交椭圆于A ,B ,C ,D 四点,则11||||AB CD +的值为( ) A .18B .16C .1D .712【解答】解:由椭圆22143x y +=,得椭圆的右焦点为(1,0)F , 当直线AB 的斜率不存在时,:1AB x =, 则:0CD y =.此时||3AB =,||4CD =,则11117||||3412AB CD +=+=; 当直线AB 的斜率存在时,设:(1)(0)AB y k x k =-≠,则1:(1)CD y x k =--.又设点1(A x ,1)y ,2(B x ,2)y . 联立方程组22(1)3412y k x x y =-⎧⎨+=⎩, 消去y 并化简得2222(43)84120k x k x k +-+-=,∴221212228412,3434k k x x x x k k -+==++, 22222221212222841212(1)||()41()4343434k k k AB x x x x kk k k -+∴=+-=+-=+++, 由题知,直线CD 的斜率为1k-,同理可得2212(1)||43k CD k +=+.∴22117(1)7||||12(1)12k AB CD k ++==+为定值. 故选:D .二.填空题(共3小题)6.已知P 是椭圆22:184x y C +=上的动点,1F ,2F 分别是其左右焦点,O 是坐标原点,则12||||||PF PF PO -的取值范围是 [ .【解答】解:设P 的坐标为(,)m n椭圆22:184x y C +=中,28a =,24b =,2c ∴=,得椭圆的准线方程为2a x c=±,即4x =±作出椭圆的右准线,设P 在右准线上的射影为Q ,连结PQ , 根据圆锥曲线的统一定义,得2||||PF e PQ =,2||||)PF e PQ m ∴=-=,同理可得1||PF =, ||PO m =∴12))||||||PF PF PO --=点(,)P m n 在椭圆22184x y+=上,得22184m n +=,∴2224(1)482m m n =-=-, 由此可得12||||||PF PF PO -=,得22122||||4()8||PF PF m m PO -=+,2[0m ∈,2]a 即2[0m ∈,8],得224[08m m ∈+,2],∴12||||[||PF PF PO -∈.故答案为:[7.已知F 为抛物线2:4C y x =的焦点,过F 作两条互相垂直的直线1l ,2l ,直线1l 与C 交于A 、B 两点,直线2l 与C 交于D 、E 两点,则11||||AB DE +的值为 14.【解答】解:根据题意可得,抛物线24y x =的焦点坐标为(1,0)F ,准线方程为1x =-, 设直线1:(1)(0)l y k x k =-≠, 直线1l ,2l 互相垂直,∴直线2l 的斜率为1k -,即得21:(1)l y x k=--, 设1(A x ,1)y ,2(B x ,2)y ,3(C x ,3)y ,4(E x ,4)y ,则分别将直线1l ,2l 的方程与抛物线方程联立组成方程组可得,22222(1)(24)04y k x k x k x k y x=-⎧⇒-++=⎨=⎩; 21(1)4y x k y x⎧=--⎪⎨⎪=⎩⇒2222121(4)0x x k k k -++= 由韦达定理可得,212224k x x k++=,2342241k x x k ++=, 由抛物线性质可知,抛物线上的点到焦点的距离等于到准线的距离,∴2212222444||112k k AB x x k k ++=+++=+=, 2234224||112441k DE x x k k +=+++=+=+, ∴2221111||||44444k AB DE k k +=+=++. 故答案为:14. 8.已知F 为抛物线2:4C y x =的焦点,过F 作两条互相垂直的直线1l ,2l ,直线1l 与C 交于A 、B 两点,直线2l 与C 交于D 、E 两点,则||4||AB DE +的最小值为 36 .【解答】解:抛物线2:4C y x =的焦点(1,0)F ,准线方程为1x =-, 设直线1l 的方程为(1)y k x =-,0k ≠,联立方程组24(1)y xy k x ⎧=⎨=-⎩,则2222(42)0k x k x k -++=,设1(A x ,1)y ,2(B x ,2)y , 可得12242x x k +=+, 由抛物线的定义可得1224||24AB x x k =++=+,由12l l ⊥,可将上式中的k 换为1k -,可得2||44DE k =+, 则222211||4||204(4)208436AB DE k k k+=+++=.当且仅当2k =±时,上式取得等号, 则||4||AB DE +的最小值为36. 故答案为:36.三.解答题(共6小题)9.已知斜率为k 的直线l 与椭圆22:143x y C +=交于A ,B 两点,线段AB 的中点为(1M ,)(0)m m >.(1)证明:12k <-;(2)设F 为C 的右焦点,P 为C 上一点,且0FP FA FB ++=.证明:||FA ,||FP ,||FB 成等差数列,并求该数列的公差.【解答】解:(1)设1(A x ,1)y ,2(B x ,2)y , 线段AB 的中点为(1,)M m ,122x x ∴+=,122y y m +=将A ,B 代入椭圆22:143x y C +=中,可得2211222234123412x y x y ⎧+=⎪⎨+=⎪⎩, 两式相减可得,121212123()()4()()0x x x x y y y y +-++-=,即12126()8()0x x m y y -+-=,12126384y y k x x m m-∴==-=-- 点(1,)M m 在椭圆内,即211,(0)43m m +<>, 解得302m <<∴3142k m =-<-.① (2)由题意得(1,0)F ,设3(P x ,3)y ,则1231110x x x -+-+-=,1230y y y ++=,由(1)及题设得3123()1x x x =-+=,312()20y y y m =-+=-<.又点P 在C 上,所以34m =,从而3(1,)2P -,3||2FP =.于是1||(22xFA x =-.同理2||22x FB =-. 所以121||||4()32FA FB x x +=-+=,故||||2||FA FB FP+=,即||FA ,||FP ,||FB 成等差数列.设改数列的公差为d ,则1212||||||||||2d FB FA x x =-=-=②将34m =代入①得1k =-. 所以l 的方程为74y x =-+,代入C 的方程,并整理得2171404x x -+=. 故122x x +=,12128x x =,代入②解得||d =.所以该数列的公差为28或28-. 10.已知斜率为k 的直线l 与椭圆22:198x y C +=交于A 、B 两点,线段AB 的中点为(1M ,)(0)t t >.(Ⅰ)证明:13k <-;(Ⅱ)设F 为C 的右焦点,Q 为C 上的一点,且0FQ FA FB ++=,证明:||FA ,||FQ ,||FB 成等差数列.【解答】(本小题满分12分)证明:(Ⅰ)设1(A x ,1)y ,2(B x ,2)y , 则有221122221(1)981(2)98x y x y ⎧+=⋯⋯⎪⎪⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⎨⎪+=⋯⋯⎪⎩(2分)(1)-(2)得12121212()()()()098x x x x y y y y +-+-+=.122x x +=,122y y t +=.∴12122()2()098x x t y y --+=.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(3分) ∴121289y y k x x t -==--.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(4分)由题设可知点(1,)M t 在椭圆内,∴21198t +<,解得803t <<, ∴818319983k t =-<-=-.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(5分) (Ⅱ)0FQ FA FB ++=,M 为AB 的中点,∴2FQ FM =-,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(6分)(1,)M t ,(1,2)Q t ∴-.点(1,2)Q t -在椭圆上,∴214198t +=.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(7分)又403t t >∴=.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(8分)由(Ⅰ)知89k t =-,所以23k =-.∴直线l 的方程为42(1)33y x -=--,即223y x =-+.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(9分)由直线l 的方程与椭圆方程联立,得22223198y x x y ⎧=-+⎪⎪⎨⎪+=⎪⎩消y 化简得2230x x --=,解得11x =-,23x =.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(10分) 从而得8(1,)3A -,(3,0)B , 又8(1,0),(1,)3F Q -,∴10||(3FA =-=,8||3FQ =,||2FB =.⋯⋯⋯⋯⋯⋯⋯(11分)∴||FA ,||FQ ,||FB 成等差数列.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(12分)11.已知1F 、2F 是椭圆22221(0)x y a b a b +=>>的左、右焦点,且离心率12e =,点P 为椭圆上的一个动点,△12PF F 的内切圆面积的最大值为43π.(1)求椭圆的方程;(2)若A ,B ,C ,D 是椭圆上不重合的四个点,满足向量1F A 与1F C 共线,1F B 与1F D 共线,且0AC BD =,求||||AC BD +的取值范围.【解答】解:(1)由几何性质可知,当,△12PF F 的内切圆面积的最大值时, 即,12PF F S取最大值,且121()22PF F maxSc b bc ==,由243r ππ=,解得r =,又由△12PF F 的周长为22a c +定值,∴22bc a c =+, 又12c e a ==,可得2a c =,即b =2c ∴=,b =4a =,故椭圆方程为2211612x y +=,(2)①当直线AC 和BD 中有一条垂直x 轴时,||||6814AC BD +=+=, ②当直线AC 的斜率存在但不为0时,设AC 的方程为:(2)y k x =+,由22(2)11612y k x x y =+⎧⎪⎨+=⎪⎩得2222(34)1616480k x k x k +++-=,代入弦长公式得,2224(1)||34k AC k +=+,同理由221(2)11612y x kx y ⎧=-+⎪⎪⎨⎪+=⎪⎩,消去y ,代入弦长公式得2224(1)||34k BD k +=+, 2222222168(1)168||||11(34)(43)121(1)k AC BD k k k k +∴+==+++-++,令21(0,1)1t k =∈+, 则212(12t t -++∈,49]4, 由①②可知||||AC BD +的取值范围是96[7,14]. 12.已知椭圆22221(0)x y a b a b +=>>经过点,且椭圆的离心率12e =,过椭圆的右焦点F 作两条互相垂直的直线,分别交椭圆于点A 、B 及C 、D . (Ⅰ)求椭圆的方程; (Ⅱ)求证:11||||AB CD +为定值; (Ⅲ)求9||||16AB CD +的最小值. 【解答】解:()I 由12c e a ==,得2214c a =,222244()a c a b ∴==-,2234a b ∴=.(1),⋯(1分)由椭圆过点知,223314a b+=.(2)⋯(2分) 联立(1)、(2)式解得24a =,23b =.⋯(3分)故椭圆的方程是22143x y +=.⋯(4分)11()||||II AB CD +为定值712⋯(5分) 证明:椭圆的右焦点为(1,0)F ',分两种情况.1︒当直线AB 的斜率不存在时,:1AB x =,则:0CD y =.此时||3AB =,||4CD =,117||||12AB CD +=;⋯(6分) 2︒当直线AB 的斜率存在时,设:(1)(0)AB y k x k =-≠,则1:(1)CD y x k =--.又设点1(A x ,1)y ,2(B x ,2)y . 联立方程组22(1)3412y k x x y =-⎧⎨+=⎩, 消去y 并化简得2222(43)84120k x k x k +-+-=,∴2122843k x x k +=+,212241243k x x k -=⋯+(7分)∴12|||AB x x =-12()x x +426416((4k -=2212(1)43k k +=+,⋯(8分) 由题知,直线CD 的斜率为1k-,同理可得2212(1)||43k CD k +=⋯+(9分) 所以2211777||||12(1)12k AB CD k ++==+为定值.⋯(10分)(Ⅲ)解:由()II 知117||||12AB CD +=, ∴912911||||(||||)()16716||||AB CD AB CD AB CD +=++⋯(11分) 9||1225||16()716||||CD AB AB CD =++122521(7164+=,⋯(12分) 当且仅当9||||16||||CD AB AB CD =,即3||||4AB CD =,即||3AB =,||4CD =时取等号⋯(13分) ∴9||||16AB CD +的最小值为214.⋯(14分)13.已知椭圆22122:1(0)x y C a b a b +=>>的长轴长为4,离心率为12,一动圆2C 过椭圆1C 右焦点F ,且与直线1x =-相切.(1)求椭圆1C 的方程及动圆圆心轨迹2C 的方程;(2)过F 作两条互相垂直的直线,分别交椭圆1C 于P ,Q 两点,交曲线2C 于M ,N 两点,求四边形PMQN 面积的最小值.【解答】解:(1)由已知可得2222423112a a b a c c c e a =⎧=⎧⎪⇒⇒=-=⎨⎨===⎩⎪⎩, 则所求椭圆方程221:143xy C +=.由已知可得动圆圆心轨迹为抛物线,且抛物线C 的焦点为(1,0),准线方程为1x =-,则动圆圆心轨迹方程为22:4C y x =.(2)当直线MN 的斜率不存在时,||4MN =, 此时PQ 的长即为椭圆长轴长,||4PQ =, 从而11||||44822PMQN S MN PQ =⋅=⨯⨯=. 设直线MN 的斜率为k ,则0k ≠,直线MN 的方程为:(1)y k x =-,直线PQ 的方程为1(1)y x k=--,设1(M x ,1)y ,2(N x ,2)y ,3(P x ,3)y ,4(Q x ,4)y , 由2(1)4y k x y x=-⎧⎨=⎩,消去y 可得2222(24)0k x k x k -++=, 由抛物线定义可知:2221222244||||||1124k MN MF NF x x k k +=+=+++=+=+, 由221(1)143y x k x y ⎧=--⎪⎪⎨⎪+=⎪⎩,消去y 得222(34)84120k x x k +-+-=,从而234212(1)|||34k PQ x x k +=-=+,∴222224211412(1)(1)||||(4)24223434PMQNk k S MN PQ k k k k ++=⋅=+=++, 令21k t +=,0k >,则1t >,则22222221242424211||||34(1)(0,3)2123(1)4(1)3213PMQNt t S MN PQ t t t t t t tt t =⋅===--=-+∈-+-----,所以2248213PMQN S t t=>--, 所以四边形PMQN 面积的最小值为8.14.平面直角坐标系xOy 中,已知F 为椭圆22221x y a b+=的右焦点,且24a b +=,过F作两条互相垂直的直线交椭圆分别于A 、B 与C 、D .以F 为极点,x 轴正半轴为极轴建立极坐标系.(Ⅰ)求椭圆的极坐标方程与1||AB 的代数表达式;(Ⅱ)求11||||AB CD +的取值范围. 【解答】解:由已知24b a =-,(Ⅰ)设(,0)F c,2222a a c b p c c c c -=-==,c e a =,以右焦点F 为极点,x 轴正半轴为极轴,建立极坐标系,则椭圆的极坐标方程为1cos epe ρθ=+,即22cos ab ac c ρθ=+,其中c == 设(A A ρ,)θ,则(B B ρ,)θπ+,222||1cos 1cos()1cos 1cos 1A B ep ep ep ep epAB e e e e e cos ρρθπθθθθ∴=+=+=+=++++--, 2211||2e cos AB ep θ-=,即22221||2a c cos AB abθ-=; (Ⅱ)由(Ⅰ)得,22222222()112||||22a c cos a c cos AB CD ab ab πθθ-+-+=+2222222222222222422222(4)a c cos a c sin a c ab a a ab ab ab ab a a θθ---+-+=+===-. 24a b +=,222240c a b a a ∴=-=+->,且4a <,4a <<. 记f (a )242(4)a a a a -+=-,则f '(a )22(4)(34)2(4)a a a a +-=-4a <<时,f '(a )0>,f (a )为增函数,则f (a)∈)+∞,即11||||AB CD +∈)+∞.。
2020年高考数学圆锥曲线中第二定义的三类用法(共10张PPT)

1
2
PF22
PF1
F1F22 ,即
PF2
1 2
(e2 x02
e2 4)
x02 1
6
注意:此题有更简单的做法, 上述方法只是为了巩固焦半
径的知识
第二定义
(2)离心率问题
例2:倾斜角为
6
的直线过椭圆
x2 y2 a2 b2
1 的左焦点 ,交椭圆于A,B 两点,且有 | AF | 3 | B F | ,求椭圆的离心率.
,解得
PF2
5 4
PD
5
所以
|
PM
|
4 5
|
PF2
|
PM
PD
因此当P,M,D三点共线时 PM PD 取得最小值,最小
值为从 M到右准线的距离 MH, MH 6 16 14 55
第二定义
本次课重点需要注意三点 :
(1)是第二定义的用法; (2)是注意例2这个题目的常规做法,此外下次课会给出这种例题的常用结论; (3)需要注意焦半径的取值范围,这个范围是求离心率取值范围题目中常用的
解析:AF, B F 为左焦点上的焦半径,所以过A,B 两点
分别作垂直于准线的直线且和准线交于D,E 两点,
从B 点作 BH AD .
因为| AF | 3| B F | ,设 BF m ,则 AF 3m
又因为 AF
AD
所以 AH
BF BE
2m
e
,则
BE
BF e
m e
,
AD
AF ,
e
3m e
为双曲线的左右焦点,
求
|
PM
|
4 5
|
PF2
第50讲 圆锥曲线热点问题 第2课时 定点、定值、探索性问题

解:(1)依题意,当点A与上顶点重合时,A(0,b),因为==(1,-b),所以B(4,-b),又点B在椭圆E上,所以+=1,解得a2=18,则b2=a2-32=9,所以椭圆E的标准方程为+=1.
课堂考点探究
(2)证明:当直线l不垂直于y轴时,设其方程为x=my+3,设A(x1,y1),B(x2,y2).由消去x并整理得,(m2+2)y2+6my-9=0,易知Δ>0,则y1+y2=-,y1y2=-.因为k1=,k2=,所以k1+k2=+===0.当直线l垂直于y轴时,k1=k2=0,所以k1+k2=0.综上,k1+k2为定值0.
练习3 已知椭圆+=1(a>b>0)的离心率e=,过点A(0,-b)和B(a,0)的直线与原点的距离为.(1)求椭圆的标准方程.(2)已知定点E(-1,0),直线y=kx+2(k≠0)与椭圆交于C,D两点,则是否存在实数k,使以CD为直径的圆过点E?若存在,求出k的值;若不存在,请说明理由.
课堂考点探究
课堂考点探究
方法二:当直线MN的斜率存在时,设其方程为y=kx+m,由得(3+4k2)x2+8kmx+4m2-12=0,由Δ>0,得m2<3+4k2.设M(x1,y1),N(x2,y2),则x1+x2=-,x1·x2=.由题意可知A1(-2,0),A2(2,0),则直线A1M:y=(x+2),令x=4,得y=.直线A2N:y=(x-2),令x=4,得y=,所以=.由+=1,得=-,即=-,所以(x1+2)·(x2+2)+4(kx1+m)·(kx2+m)=0,即(4k2+1)x1x2+(2+4km)(x1+x2)+4m2+4=0,化简得(m-2k)(m+k)=0,解得m=2k或m=-k.
圆锥曲线第二定义的应用 ppt课件

点M在左支上
y
x
F1
F2
抛物线的焦半径公式:
点 P ( x 0 , y 0 )在对应抛物线上
,
y 2 2 px ( p 0 ) :| PF
|
x0
p; 2
y 2 2 px ( p 0 ) :| PF
| x 0
p; 2
x 2 2 py ( p 0 ) :| PF
|
y0
直线m与椭圆的交点到直线l的距离最近。
且d 4025 15 41
y
4252 41
dm maixn
4025 42 52
65 41
41
x o
思考:最大的距离是多少?
例 变 形3: 已 知 椭 圆 2 x5 2y921, 直 线 l: 4x-5y400.椭 圆 上
是 否 存 在 一 点 , 它 到 直 线 l的 距 离 最 小 大? y 最 小 大距 离 是 多 少 ?
例 3: 已 知 椭 圆 x2y21, 直 线 l: 4x-5y400.椭 圆 上 25 9
是 否 存 在 一 点 , 它 到 直 线 l的 距 离 最 小 ? y 最 小 距 离 是 多 少 ?
解 : 设 直 线 m 平 行 于 l,
则 l可 写 成 : 4 x 5 y k 0
x o
4x5y k 0
M
A
F1
O
F2
X
(1) 求 MA MF2的范围
解:椭圆的方程为
x2 y2 1
a3,b 5,c2
95
e 2 3
F1(2,0)
F2 (2, 0)
l1
:
x
p 2
l2 : x
p 2
专题40:圆锥曲线的二级结论6页

过定点
M
a a
2 2
b2 b2
x0
,
a2 a2
b2 b2
y0 .
16. P 为双曲线
x2 a2
y2 b2
1(a 0,b 0) 上一点,若 F
是一个焦点,以 PF
为直径的圆与圆
x 2 y 2 a 2 的位置关系是外切或内切.
17.过双曲线焦点的弦被焦点分得两个焦半径倒数和是定值
2a b2
为
AB 的中点,则 kOM
kAB
b2 a2
.
7.以焦点弦为直径的圆必与对应准线相交.
第3页共6页
8.以焦半径 PF 为直径的圆必与以实轴为直径的圆外切.
9.设 P 为双曲线上一点,则 F1PF2 的内切圆必切于与 P 在同侧的顶点.
10.双曲线
x a
2 2
y2 b2
1(a 0,b 0) 的两个顶点为 A1(a, 0) , A2 (a, 0) ,与 y 轴平行的直线交双曲
为
Q
a2 m
,
0
.
24.从双曲线
x2 a2
y2 b2
1( a
0, b
0 )的右焦点向双曲线的动切线引垂线,则垂足的轨迹为
圆: x2 y2 a2 .
25.双曲线上任一点 P 处的切线交准线于 M ,P 与相应的焦点 F 的连线交双曲线于 Q ,则 MQ
必与该双曲线相切,且 MF PQ .
28.
若
A,
B
是椭圆
x2 a2
y2 b2
1( a b 0 )的左右顶点,点 P 是直线 x t ( t
a,t 0 )上的
一个动点( P 不在椭圆上),直线 PA 及 PB 分别与椭圆相交于 M , N ,则直线 MN 必与 x 轴相
