圆的基本图形1
圆的基本概念与性质

圆的基本概念与性质圆是几何中的一种基本图形,具有独特的性质和特点。
本文将介绍圆的基本概念和性质,探讨其在数学和日常生活中的应用。
一、圆的基本概念圆是由一个平面内距离中心固定点相等的所有点构成的集合。
其中,固定点称为圆心,距离圆心的长度称为半径。
圆由圆心和半径唯一确定。
二、圆的性质1. 圆的直径圆的直径是连接圆上任意两点,并通过圆心的线段。
直径的长度等于圆半径的2倍。
2. 圆的周长圆的周长是指圆上任意两点之间的距离,也可以理解为圆的边界长度。
周长的计算公式为C=2πr,其中C表示周长,r表示半径。
3. 圆的面积圆的面积是指圆内部所有点组成的区域。
面积的计算公式为A=πr^2,其中A表示面积,r表示半径。
4. 弧圆上两点之间的部分称为圆弧。
弧对应的圆心角等于弧所夹的圆心角。
5. 弦圆上连接两点的线段称为弦。
如果弦通过圆心,则称为直径。
否则,称为弦。
6. 切线与圆相切且仅有一个切点的直线称为圆的切线。
切线与半径垂直。
7. 弦切角圆的内部一点与两条相交弦之间的角称为弦切角。
同弧切角相等。
三、圆的应用圆的概念和性质在数学中有广泛应用,也在日常生活中有所体现。
以下为几个常见的应用场景:1. 几何图形圆是许多其他几何图形的基础,例如圆柱体、圆锥体和圆环等。
了解圆的概念和性质,有助于我们更好地理解和应用这些几何图形。
2. 建筑设计在建筑设计中,圆形结构常常被运用。
圆形的建筑物可以提供良好的结构稳定性和美观性。
例如,圆形拱门和圆顶常常用于教堂和宫殿等建筑中。
3. 工程测量圆的性质在工程测量中有重要的应用。
通过测量圆的半径或直径,可以计算出工程中需要的其他参数,如周长、面积和体积。
4. 自然现象许多自然现象中都存在圆形,例如太阳、月亮、风旋涡等。
理解圆的概念和性质,有助于我们更好地解释和研究这些自然现象。
结语圆是几何学中的基本概念之一,具有独特的性质和广泛的应用。
通过了解圆的基本概念和性质,我们能够更好地理解几何学知识,并将其应用于实际生活中。
圆的定义确定基本要素

圆的定义确定基本要素
圆是平面几何中的基本图形,其定义确定了它所具有的基本要素。
圆
是由位于同一平面上且与一个给定点的距离相等的所有点组成的集合。
在
这个定义中,可以确定圆的三个基本要素:圆心、半径和圆周。
首先,圆心是圆的一个重要特征。
圆心是圆的几何中心点,可以看作
所有点距离圆周最远的点。
圆心通常用大写字母O来表示。
圆心的位置决
定了圆的整体位置和方向。
其次,半径是圆的另一个重要要素。
半径是从圆心到圆周上的任意一
点之间的距离,通常用小写字母r表示。
半径的长度决定了圆的大小,不
同的半径长度可以得到不同大小的圆。
半径之间的比较也可用于表示两个
圆的大小关系。
由以上定义可以看出,圆的基本要素之间存在一定的关系。
圆心是圆
形状的中心点,半径是从圆心到圆周上的任意一点的距离,圆周是由圆心
到圆周上的所有点组成的曲线。
这些要素的定义确定了圆的特征和性质。
除了上述基本要素之外,圆还具有一些其他的重要性质。
例如,所有
半径长度相等的圆都具有相等的面积和周长。
两个直径相等的圆,其半径
和面积也相等。
圆与直线的关系也是研究圆的重要内容之一,例如,切线
是与圆周相切且只有一个交点的直线。
总之,圆的定义确定了它所具有的基本要素,包括圆心、半径和圆周。
这些要素之间相互关联,共同决定了圆的形状、大小和位置。
圆的性质和
关系是研究平面几何的重要课题,对于理解和应用圆的概念具有重要意义。
《圆的认识(一)》圆PPT

自主学习反馈
1、指出下面各圆的半径和直径。
直径d
半径r
自主学习反馈
填一填
1 2
3
(1)( )2 号线段表示直径。
(2)( )3 号线段表示半径。
(3)两端都在圆上的线段中, ( 直)径最长。
探究新知
探究一:
哪种方式更公平?
不公平
不公平
公平
圆上的任意一点到圆的中心点的距离都相等。
探究新知
探究二:
想一想,画一画,圆的大小与什么有关系?圆的位置与什么有关系?
圆的大小与半径的长短有关系。 圆的位置与圆心有关系。
知识运用
为什么车轮都要做成圆的? 车轴装在哪里?
知识运用
为什么车轮都要做成圆的? 车轴装在哪里?
知识运用
分别用硬纸板做成下面的图形。
A
A
A
知识运用
描出滚动过程中A点留下的痕迹。
A
知识运用
互动新授
想一想,画一画,圆的大小与什么有关系?圆的 位置与什么有关系?
互动新授
合作做一做,想一想
车轮为什图形,代替车轮。
互动新授
互动新授
你发现了什么?
行驶起来平稳 圆在滚动时,圆心在一条直线上,正方 形和椭圆形的中心到图形边上各点的距离不 相等,运动的轨迹是波浪形。
课堂小结
在 同 圆 或 等 圆
圆的认识(一)
圆心(O):决定圆的位置
直径(D):无数条、相等 d=2r
半径(r):决定圆的大小、 无数条、相等
六年级上册
圆的认识(一)
情境导入 你从中读出哪些数学信息?
本节目标
1.结合生活实际和丰富多彩的活动,在观察和操作中体会圆的结构特征。 2.在画圆的过程中,理解同圆中半径、直径以及直径和半径之间的关系,体会圆心和半 径的作用,会用圆规画圆。 3.能用圆的知识解释生活中的简单现象,感受数学与生活密切相关。
圆的基本性质

圆的基本性质圆是几何学中最基本的图形之一,具有许多独特的性质和特征。
在本文中,我将介绍圆的基本性质,包括圆的定义、圆的半径和直径、圆心和弧、圆的面积和周长等。
通过了解这些基本性质,我们可以更好地理解和运用圆形。
1. 圆的定义圆是由一条与一个固定点距离相等的点构成的集合。
这个固定点被称为圆心,圆心到圆上的任意一点的距离被称为半径。
圆内部的点到圆心的距离都小于半径,而圆外部的点到圆心的距离都大于半径。
2. 圆的半径和直径圆的半径是从圆心到圆上任意一点的距离。
圆的直径是通过圆心,并且两个端点都在圆上的线段。
圆的直径是半径的两倍,也是圆的最长线段。
3. 圆心和弧圆心是圆的中心点。
圆上的弧是由圆上的两个点以及它们之间的弧长所确定的。
圆的弧可以被度量为角度,弧度或弧长。
4. 圆的面积圆的面积是圆内部所包围的空间。
圆的面积公式为:面积= π * r²,其中π(pi)是一个无理数,约等于3.14159,r是圆的半径。
这个公式表明,圆的面积正比于半径的平方。
5. 圆的周长圆的周长是圆上所有点之间的距离总和。
圆的周长也被称为圆周长或圆的周长。
圆的周长公式为:周长= 2 * π * r,其中2πr是一个圆的直径。
6. 圆的切线在圆上的每个点上都有一个与切线相切的方向。
切线是与圆只有一个交点的直线,且与圆的切点处于圆上的切线角度为90度。
7. 圆的弦圆上的任意两个点之间的线段被称为弦。
最长的弦是圆的直径。
8. 圆的弧度弧度是一种用于度量圆上弧长的单位。
一个圆的弧长等于半径的弧度数乘以圆心角的弧度。
总结:在几何学中,圆拥有许多独特的性质和特征。
通过了解圆的定义、圆的半径和直径、圆心和弧、圆的面积和周长等基本性质,我们可以更好地理解和应用圆形。
圆在许多领域中都有广泛的应用,如工程、建筑、数学等。
掌握圆的基本性质对于解决与圆相关的问题非常重要。
通过学习和应用这些性质,我们可以更好地理解圆,并在实际生活和学习中运用它们。
圆的基本认识和性质

圆的基本认识和性质圆是几何中最基本的图形之一,它在我们的日常生活中无处不在。
本文将围绕圆的基本认识和性质展开讨论,帮助读者更好地理解和应用圆的知识。
一、圆的定义圆是由与一个点距离相等的所有点构成的集合。
这个点被称为圆心,与圆心距离相等的线段被称为半径,而通过圆心且连接两个不同点的线段被称为直径。
二、圆的性质1. 圆的特征每一个圆都具有以下几个特征:A. 圆的周长:圆的周长是圆上所有点到圆心的距离之和,由于所有这些距离相等,因此圆的周长等于圆周率π乘以直径。
用公式表示为:C = πd,其中C为圆的周长,d为直径。
B. 圆的面积:圆的面积是圆内部所有点与圆心的距离之和。
用公式表示为:S = πr²,其中S为圆的面积,r为半径。
C. 圆的弧长:圆上的弧是两个点之间的连续线段。
圆的弧长是指圆上弧的长度,其计算方法与周长类似。
2. 圆的内角性质在圆上的任意一条弦所对的圆心角都是相等的,且都等于该弦所对的弧所对的圆心角。
此外,圆上任意一点到圆心的连线,与该点处的切线所构成的角是直角。
3. 圆的切线性质圆上任意一点处的切线与半径的夹角是直角。
此外,切线与半径的夹角是切线切到点的圆弧所对的圆心角的一半。
三、圆的应用1. 圆的测量通过测量圆的直径、半径或弧长,我们可以计算出圆的周长和面积。
这在实际应用中非常重要,例如在建筑、制造和工程等领域。
2. 圆形物体的运动和旋转许多物体在运动或旋转时可近似认为是圆形的,比如车轮、盘子、风车等。
研究这些圆形物体的运动规律对于工程师和物理学家而言是至关重要的。
3. 圆的几何定理运用圆的几何定理,我们可以解决一些复杂的几何问题。
比如,利用圆的内角性质可以证明三角形的内角和等于180度;利用圆的切线性质可以解决与切线相关的问题等。
四、总结通过对圆的基本认识和性质的讨论,我们可以看到圆在几何学中的重要性和广泛应用。
准确理解圆的定义、特征和性质,对于我们解决实际问题和学习更高级的数学概念都具有重要意义。
圆的基本概念与性质

圆的基本概念与性质圆是几何学中最基本的图形之一,它具有独特的形状和性质。
本文将对圆的基本概念和一些重要性质进行详细介绍。
一、圆的定义圆是由平面上距离一个固定点一定距离的所有点组成的集合。
这个固定点被称为圆心,而这个距离被称为半径。
二、圆的常用符号在几何学中,圆常用符号“O”表示圆心,用字母“r”表示半径。
因此,一个圆可以用符号“O(r)”表示。
三、圆的性质1. 圆的对称性由于圆的定义是以一个固定点为中心,所有距离这个点相等的点的集合,因此圆具有天然的对称性。
任意一条直径将圆分成两个等边的半圆,半圆上的所有点与圆心的距离相等。
2. 圆的直径、半径和弦在圆中,直径是通过圆心并且两端点都在圆上的线段;半径是从圆心到圆上的任意一点的线段,它等于圆的半径;弦是圆上连接两个点的线段,不经过圆心。
3. 圆的周长和面积圆的周长定义为圆上的一条完整弧所对应的长度,可以用公式C =2πr来计算,其中C表示周长,r表示半径。
圆的面积定义为圆内所有点所组成的区域的大小,可以用公式A = πr²来计算,其中A表示面积,r表示半径。
4. 圆的切线和法线圆上的切线是与圆相切的直线,它只与圆在切点相交。
切线与半径构成的夹角为90度。
法线是与切线垂直的直线,它通过切点并与切线垂直相交。
5. 圆的弧度制和度数制圆的弧度制是一种用弧长比半径的面度来度量角度的方式。
一个圆的弧长等于半径的弧度数。
度数制是人们常见的度量角度的方式,一个圆被等分为360度,1度等于圆的1/360。
四、圆的相关定理和应用1. 圆上的三角形圆上的三角形是指三个顶点都在圆上的三角形。
它有很多特殊性质,如圆上的两条弧所对应的角相等,半径与割线所包围的弧所对应的角相等等。
2. 切线定理和切割定理切线定理指的是切线与半径的关系,即切线的平方等于切点处外切圆的半径与切点到圆心的距离之积。
切割定理指的是弦分割定理和切线分割定理,它们描述了切线和弦所分割的弧长和线段之间的关系。
圆的基本知识

圆的基本知识圆是几何学中的一种基本图形,也是我们日常生活中经常接触到的形状。
圆由无数个点构成,这些点到圆心的距离都相等。
下面我将介绍一些关于圆的基本知识。
首先,圆由圆心和半径构成。
圆心是圆的中心点,通常用字母O表示。
半径是从圆心到圆上任意一点的距离,通常用字母r表示。
圆的半径是圆的重要属性之一,决定了圆的大小。
其次,圆与直径相关。
直径是从圆的一边到另一边通过圆心的线段,直径的长度等于圆的半径的两倍,即直径d=2r。
直径是圆的最长的线段,可以切割圆成两个相等的半圆。
第三,圆与周长相关。
周长是圆上所有点到圆心的距离之和,通常用字母C表示。
圆的周长与其半径之间有一定的关系,可以用公式C=2πr来表示,其中π是一个无理数,约等于3.14。
根据这个公式,我们可以计算出任意圆的周长。
第四,圆与面积相关。
面积是圆所占据的平方单位的总量,通常用字母A表示。
圆的面积与其半径之间也有一定的关系,可以用公式A=πr²来表示。
根据这个公式,我们可以计算出任意圆的面积。
最后,圆还有一些其他的特点。
圆是对称的,即圆上的任意两点与圆心的距离相等。
在直径上的两点与圆心的距离等于半径的距离。
圆还可以与直线相交,相交的点称为切点,切点位于圆的周边。
圆还可以在平面上移动,旋转和缩放,但不会改变其形状。
总的来说,圆是一种具有特定属性的几何图形,包括圆心、半径、直径、周长和面积等。
了解圆的基本知识对于学习几何学和解决实际问题都具有重要意义。
圆的认识和画圆的方法

圆的认识和画圆的方法圆是几何中最基本的图形之一,是一个平面上所有离一个固定点的距离都相等的点的轨迹。
在数学和几何学中,圆常被用于描述的许多问题和形式,如几何图形、方程式、轨迹等等。
了解圆的认识和画圆的方法对于学习和应用数学和几何学具有重要的意义。
圆的性质1.圆内所有的点到圆心的距离都相等,这个距离叫做圆的半径。
2.圆内孤立点到圆心的距离是最短的,这个距离等于圆的半径。
3.圆的直径是通过圆心的两个点,它是圆的最长直径。
4.根据直径的定义,圆的半径是直径的一半。
5.圆的周长等于半径乘以2π,表示为C=2πr。
6.圆的面积等于半径的平方乘以π,表示为A=πr²。
画圆有多种方法,其中常见的方法有以下几种:1.以半径画圆:在纸上画一条直线作为半径,选择一个点作为圆心,用指南针或其他工具,在圆心为中心,以半径的长度在纸上画弧,然后用直尺连接弧上的点,即可画出圆来。
2.以直径画圆:首先在纸上画一条直线,确定为直径,然后用直尺找到直径的中点,作为圆心,在圆心处画弧,然后用直尺连接弧上的点,即可画出圆来。
3.使用圆规画圆:圆规的作用是保持一定的距离,为画弧提供便利。
使用圆规时,先锁定一定的距离,然后固定一个脚在纸上,用另一个脚沿着一个点画弧,然后移动圆规,再次以相同的距离固定一个脚在弧上,然后从刚画的弧上的一个点开始画另一个弧,然后再次移动圆规,以此类推,直到画出一个完整的圆。
4.使用曲线工具画圆:在现代绘图软件和计算机辅助设计(CAD)软件中,通常有专门的工具或命令用于创建圆形。
用户只需输入圆的半径或直径,选择一个起始点和一个终点,软件就会自动绘制一个完美的圆。
无论是哪种画圆的方法,都需要注意以下细节:1.圆心的位置应该明确,并且在画圆的过程中不要改变。
2.半径或直径的长度要准确,否则画出的图形会出现偏差。
3.使用曲线工具或软件绘图时,应该选择适当的设置,以获得预期的圆形。
总结通过学习圆的性质和画圆的方法,我们能更好地理解和应用数学和几何学中的圆相关知识。
圆的知识点总结

圆的知识点总结一、圆的基本概念1、圆的定义平面上到定点的距离等于定长的所有点组成的图形叫做圆。
定点称为圆心,定长称为半径。
以点 O 为圆心的圆记作“⊙O”,读作“圆O”。
2、圆的要素圆心:确定圆的位置。
半径:决定圆的大小。
直径:通过圆心并且两端都在圆上的线段叫做直径。
直径是圆内最长的弦。
二、圆的性质1、圆的对称性圆是轴对称图形,其对称轴是任意一条通过圆心的直线。
圆是中心对称图形,其对称中心是圆心。
2、垂径定理垂直于弦的直径平分弦且平分弦所对的两条弧。
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
3、弧、弦、圆心角的关系在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等。
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧相等。
4、圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半。
同弧或等弧所对的圆周角相等。
半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径。
三、圆的周长和面积1、圆的周长圆的周长 C =2πr 或 C =πd,其中 r 是半径,d 是直径,π 是圆周率,约等于 314。
2、圆的面积圆的面积 S =πr²四、圆与直线的位置关系1、相离直线和圆没有公共点。
2、相切直线和圆只有一个公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个公共点叫做切点。
3、相交直线和圆有两个公共点,这时我们说这条直线和圆相交,这条直线叫做圆的割线。
五、切线的性质和判定1、切线的性质圆的切线垂直于经过切点的半径。
2、切线的判定经过半径的外端并且垂直于这条半径的直线是圆的切线。
六、圆与圆的位置关系1、外离两个圆没有公共点,并且每个圆上的点都在另一个圆的外部。
2、外切两个圆有唯一的公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的外部。
3、相交两个圆有两个公共点。
圆基本图形和结论
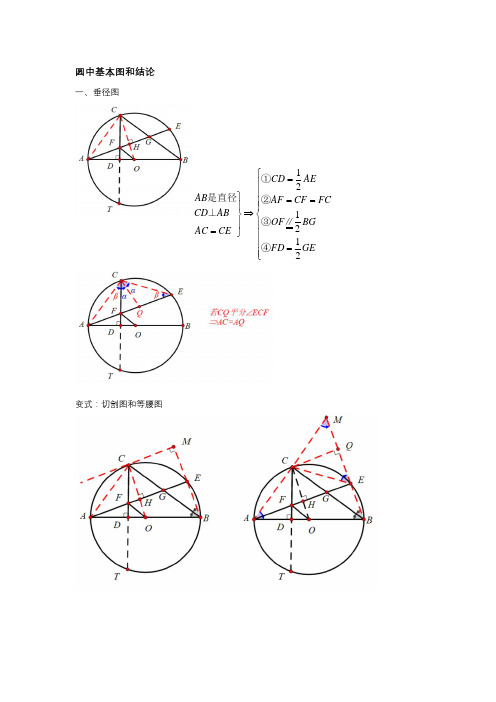
圆中基本图和结论一、 垂径图121212CD AE AB AF CF FCCD AB OF BGAC CE FD GE ⎧=⎪⎪⎫==⎪⎪⎪⇒⎬⎨⎪⎪=⎭⎪⎪=⎪⎩①是直径②⊥③∥④变式:切割图和等腰图条件:AB⊥CD(圆的内接四边形,对角线互相垂直:垂美四边形)五、等腰图——圆心在腰上七、弧中点、角平分线、等腰、垂径八、角平分线图——对角互补邻边相等——旋转九、折弦内外角平分线条件:直径AD⊥BC结论:①角平分线:PA平分∠BPF,PD平分∠BPC;②旋转全等:△ABE≌△ACF,△BDM≌△DCN③PB-PC=2PE,PB+PC=2PN十、切割图十一、双切图十二、三切图,12PA PB APO BPO BAC DBC OP AB EA EB AM BM AC PA PB BCM PAB N PAB =∠=∠=∠=∠⎧⎪==⎪⎫⎪⇒⎬⎨⎭⎪⎪⎪⎩①,②⊥,为直径、为切线③AB ⊥BC ,OE=④为△的内心,为△的外心十三、内外心图 (1)内心鸡爪型(2)内外心连线垂直角平分线()122121222AF AB AC BC AB BC BC OI AD BDE AIF AF BC MD MIOI AD AI DI CD DC DM CM AC CM DCM DAC DA DC AC AB BM ⎫=+-⎪⎪⇒+=⎬⎪⇒⇒=⎪⎭=⎧⇒==⎫⎪⇒===⇒=⎬⎨⎭⎪=⎩⊥≌⊥∽(3)内外心距离推导22422ABC ABC ABC abc R S S r C OI R Rr ⎧=⎪⎪⎪=⎨⎪⎪=-⎪⎩十四、折叠圆。
圆的知识梳理

圆的知识梳理
圆是一个平面上的几何图形,由所有到一个定点距离相等的点组成。
以下是关于圆的一些基本知识梳理:
1. 圆的要素:一个圆由圆心、半径和圆周组成。
圆心是圆的中心点,通常用字母O表示。
半径是圆心到圆周上任意一点的
距离,通常用字母r表示。
而圆周是由无数个半径相等的点组
成的曲线。
2. 直径:直径是通过圆心的一条线段,它的两个端点都在圆周上。
直径的长度等于半径的两倍。
3. 弧长:弧是圆周上的一段曲线,两端点分别与圆上的两个点相连。
弧长是弧所对应的圆心角所度过的圆周弧度数,通常用字母s表示。
弧长与圆心角之间有以下关系:s = rθ,其中θ
为圆心角的弧度数。
4. 弧度制:弧度制是一种用于测量角度的单位制。
一个圆的圆周长度被定义为2π弧度,在弧度制下,一个完整的圆周对应
角度为360°。
5. 圆的面积:圆的面积是指圆内部的所有点所围成的平面区域,通常用字母A表示。
圆的面积公式为A = πr²,其中π是一个
无理数,约等于3.14159。
6. 圆的周长:圆的周长是指圆周的长度,通常用字母C表示。
圆的周长公式为C = 2πr,即周长等于圆周的长度。
7. 圆与其他图形的关系:圆与其他图形之间存在许多关系,例如,正方形的对角线长度等于边长的√2倍;平行于圆的直线在圆上的截弦相等;半径垂直于切线;等等。
这些知识点可以帮助我们理解和计算圆的相关特性和性质,并且在数学和几何学中有广泛的应用。
圆的第一二三定义

圆的第一二三定义圆(circle)是一种最简单的形状,所有的点到中心的距离都相等,与其他图形形状的的性质有所不同。
圆的研究可追溯到古希腊,一般而言,圆有三种不同的定义。
第一定义是极限定义。
极限定义是指,当圆内部的所有点距离中心点的距离均不超过指定的距离时,这个图形就称为圆。
极限定义是圆的最基本定义,它被认为是欧几里德提出的圆的一种定义。
第二定义是切线定义。
切线定义是指,给定一个圆,任意一个点都可以从这个圆上出发,当点以恒定速度移动时,从圆心经过点,所经过的最短距离就是称为这个点到圆心的距离。
也就是说,任何一个圆上的点,其到圆心的距离总是等于这个圆的半径。
最后一个定义是圆面积定义。
这个定义也是由欧几里得提出的,它指出,一个圆的面积等于其半径乘以π的平方。
这个定义使得我们可以使用图形的面积来衡量一个圆的大小,这也是我们常用的方法。
以上三个定义,可以简单统称为圆的定义。
它们是圆的基本性质,是我们用来定义圆的最基本的方法。
其中极限定义和切线定义都是基于条件的定义,而圆面积定义则是基于数学表达式的定义。
而这三个定义,就是构成圆的基本性质,我们可以借助它们来研究圆,把它们当作圆的第一、二、三定义。
圆的性质是由这三个定义产生的,它们也就是圆学的基础,为我们提供了理解圆的原理和特征,也是圆学发展的重要基础。
圆学研究的结果也为人类创造出了许多形状美丽的图形,让我们的生活更加美好精彩。
圆的第一、二、三定义是圆的基本性质,它们给我们提供了一个很直观的理解圆的方法:极限定义是指当所有点距离中心点的距离不超过指定距离时,就称为圆;切线定义是指任意一个点以定速度移动时,所经过的最短距离就是其到圆心的距离;圆面积定义是指圆的面积等于其半径乘以π的平方。
以上三个定义是圆学的根基,是我们理解和研究圆的基本原理,也是人类创造出美丽的图形的基础。
数学有哪些关于圆的知识点

圆的知识:一、圆的定义。
1、以定点为圆心,定长为半径的点组成的图形。
2、在同一平面内,到一个定点的距离都相等的点组成的图形。
二、圆的各元素。
1、半径:圆上一点与圆心的连线段。
2、直径:连接圆上两点有经过圆心的线段。
3、弦:连接圆上两点线段(直径也是弦)。
4、弧:圆上两点之间的曲线部分。
半圆周也是弧。
(1)劣弧:小于半圆周的弧。
(2)优弧:大于半圆周的弧。
5、圆心角:以圆心为顶点,半径为角的边。
6、圆周角:顶点在圆周上,圆周角的两边是弦。
7、弦心距:圆心到弦的垂线段的长。
补充内容:三、圆的基本性质。
1、圆的对称性。
(1)圆是轴对称图形,它的`对称轴是直径所在的直线。
(2)圆是中心对称图形,它的对称中心是圆心。
(3)圆是旋转对称图形。
2、垂径定理。
(1)垂直于弦的直径平分这条弦,且平分这条弦所对的两条弧。
(2)推论:平分弦(非直径)的直径,垂直于弦且平分弦所对的两条弧。
平分弧的直径,垂直平分弧所对的弦。
3、圆心角的度数等于它所对弧的度数。
圆周角的度数等于它所对弧度数的一半。
(1)同弧所对的圆周角相等。
(2)直径所对的圆周角是直角;圆周角为直角,它所对的弦是直径。
4、在同圆或等圆中,两条弦、两条弧、两个圆周角、两个圆心角、两条弦心距五对量中只要有一对量相等,其余四对量也分别相等。
5、夹在平行线间的两条弧相等。
6、设⊙O的半径为r,OP=d。
7、(1)过两点的圆的圆心一定在两点间连线段的中垂线上。
(2)不在同一直线上的三点确定一个圆,圆心是三边中垂线的交点,它到三个点的距离相等。
(直角三角形的外心就是斜边的中点。
圆中基本图形及结论

《圆的证明与计算》专题研究圆的证明与计算是中考中的一类重要的问题,此题完成情况的好坏对解决后面问题的发挥有重要的影响,所以解决好此题比较关键。
一、考点分析:1.圆中的重要定理:(1)圆的定义:主要是用来证明四点共圆.(2)垂径定理:主要是用来证明——弧相等、线段相等、垂直关系等等.(3)三者之间的关系定理: 主要是用来证明——弧相等、线段相等、圆心角相等.(4)圆周角性质定理及其推轮: 主要是用来证明——直角、角相等、弧相等.(5)切线的性质定理:主要是用来证明——垂直关系.(6)切线的判定定理: 主要是用来证明直线是圆的切线.(7)切线长定理: 线段相等、垂直关系、角相等.2.圆中几个关键元素之间的相互转化:弧、弦、圆心角、圆周角等都可以通过相等来互相转化.这在圆中的证明和计算中经常用到.二、考题形式分析:主要以解答题的形式出现,第1问主要是判定切线;第2问主要是与圆有关的计算:①求线段长(或面积);②求线段比;③求角度的三角函数值(实质还是求线段比)。
三、解题秘笈:1、判定切线的方法:(1)若切点明确,则“连半径,证垂直”。
常见手法有:全等转化;平行转化;直径转化;中线转化等;有时可通过计算结合相似、勾股定理证垂直;(2)若切点不明确,则“作垂直,证半径”。
常见手法:角平分线定理;等腰三角形三线合一,隐藏角平分线;总而言之,要完成两个层次的证明:①直线所垂直的是圆的半径(过圆上一点);②直线与半径的关系是互相垂直。
在证明中的关键是要处理好弧、弦、角之间的相互转化,要善于进行由此及彼的联想、要总结常添加的辅助线.例:(1)如图,AB是⊙O的直径,BC⊥AB,AD∥OC交⊙O于D点,求证:CD为⊙O 的切线;(2)如图,以Rt △ABC 的直角边AB 为直径作⊙O ,交斜边AC 于D ,点E 为BC 的中点,连结DE ,求证:DE 是⊙O 的切线.(3)如图,以等腰△ABC 的一腰为直径作⊙O ,交底边BC 于D ,交另一腰于F ,若DE ⊥AC 于E (或E 为CF 中点),求证:DE 是⊙O 的切线.(4)如图,AB 是⊙O 的直径,AE 平分∠BAF ,交⊙O 于点E ,过点E 作直线ED ⊥AF ,交AF 的延长线于点D ,交AB 的延长线于点C ,求证:CD 是⊙O 的切线.2、与圆有关的计算:计算圆中的线段长或线段比,通常与勾股定理、垂径定理与三角形的全等、相似等知识的结合,形式复杂,无规律性。
六年级上册数学圆

六年级上册数学圆一、圆的认识1、日常生活中的圆2、画图、感知圆的基本特征(1)实物画图(2)系绳画图3、对比,感知圆的特征:我们以前学过的长方形、正方形、平行四边形、梯形、三角形等,都是曲线段围成的平面图形,而圆是由曲线围成的一种平面图形。
【归纳】:圆是由一条曲线围成的封闭图形二、圆的各部分名称1、圆心:用圆规画出圆以后,针尖固定的一点就是圆心,通常用字母O 表示,圆心决定圆的位置2、半径:连接圆心到圆上任意一点的线段叫做半径。
一般用字母r表示。
把圆规两脚分开,两脚之间的距离就是圆的半径。
3、直径:通过圆心并且两端都在圆上的线段叫做直径。
一般用字母d 表示。
直径是一个圆内最长的线段三、圆的主要特征1、在同圆或等圆内,有无数条半径,有无数条直径。
所有的半径都相等,所有的直径都相等。
2、在同圆或等圆内,直径的长度是半径的2倍,半径的长度是直径的1/2。
用字母表示为:d=2r或r=d/23、如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形是轴对称图形。
圆是轴对称图形且有无数条对称轴四、圆的周长的认识1、围成圆的曲线的长叫做圆的周长2、周长与圆的直径有关,圆的直径越长,圆的周长就越大五、圆周率的意义及圆的周长公式1、圆周率实验:在圆形纸片上做个记号,与直尺0刻度对齐,在直尺上滚动一周,求出圆的周长。
发现一般规律,就是圆周长与它直径的比值是一个固定数(π)。
3、圆周率:任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率。
用字母π(pai) 表示。
4、一个圆的周长总是它直径的3倍多一些,这个比值是一个固定的数。
圆周率π是一个无限不循环小数。
在计算时,一般取π≈3.14。
5、在判断时,圆周长与它直径的比值是π倍,而不是3.14倍。
世界上第一个把圆周率算出来的人是我国的数学家祖冲之。
6、圆的周长公式:C= πd —→d = C ÷π或C=2πr —→r = C ÷2π7、区分周长的一半和半圆的周长:(1)周长的一半:等于圆的周长÷2 计算方法:2πr ÷2 即πr (2)半圆的周长:等于圆的周长的一半加直径。
与圆有关的定义

与圆有关的定义
与圆有关的定义有很多,以下是其中的一部分:
1.圆的基本定义:圆是由曲线围成的一种平面图形。
在几何学中,圆可以定义为平面
上所有与给定点(称为圆心)距离相等的点的集合。
这个距离被称为半径。
在代数学中,圆可以定义为满足特定方程的点的集合。
2.圆心:是圆内的一个特定点,所有到圆上任意一点的距离都相等。
圆心确定圆的位
置。
3.半径:是从圆心到圆上任意一点的线段。
半径确定圆的大小。
在同圆或等圆内,有
无数条半径,且所有的半径都相等。
4.直径:是通过圆心并且两端都在圆上的线段。
它是圆内最长的线段。
在同圆或等圆
内,直径的长度是半径的2倍,半径的长度是直径的1/2。
5.弦:是连接圆上任意两点的线段。
6.弧:是圆上任意两点间的部分。
其中大于半圆的弧称为优弧,小于半圆的弧称为劣
弧。
此外,圆还具有对称性,即如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。
圆就是这样一个轴对称图形,任何经过圆心的直线都是其对称轴。
圆的十种表示方法

圆的十种表示方法1.引言概述部分的内容可以如下所示:1.1 概述圆是几何学中最基本的图形之一。
它具有无限个点,这些点到一个固定点的距离都相等。
圆的独特性质使它在各个学科和领域都有广泛的应用,如数学、物理、工程、艺术等。
而圆的表示方法则是研究和描述圆形特性的关键。
本文将介绍圆的十种表示方法,通过详细分析每一种方法的特点和使用场景,旨在帮助读者更好地理解和运用圆的概念。
每一种表示方法都有其独特的优劣势,因此在实际应用中需要根据具体情况选择最适合的方法。
在正文部分,我们将依次介绍每一种表示方法,并深入探讨其原理和应用。
其中,有些方法是传统的几何学表示方式,如欧几里德几何中的坐标表示法、半径表示法等;而另一些方法则是现代数学和计算机科学的成果,如参数方程表示法、向量表示法等。
通过本文的阅读,您将会了解到圆的不同表示方法在实际问题中的特点和用途。
这些方法既可以帮助我们更深入地研究圆的性质,又可以为解决实际问题提供有效的数学工具和计算方法。
总之,本文将从多个角度全面介绍圆的表示方法,希望能够为读者提供全面、准确、深入的圆形知识,激发读者对几何学的兴趣,并为相关学科领域的研究和应用提供有益的指导。
接下来的章节将详细介绍每一种表示方法及其相关内容。
1.2文章结构文章结构部分的内容可以按照以下方式编写:1.2 文章结构本文将以如下结构来展开探讨圆的十种表示方法:2.1 第一种表示方法* 描述:介绍第一种表示方法,并说明其原理和应用场景。
* 举例:给出一个具体的例子,以便读者更好地理解。
2.2 第二种表示方法* 描述:介绍第二种表示方法,并说明其原理和应用场景。
* 举例:给出一个具体的例子,以便读者更好地理解。
2.3 第三种表示方法* 描述:介绍第三种表示方法,并说明其原理和应用场景。
* 举例:给出一个具体的例子,以便读者更好地理解。
2.4 第四种表示方法* 描述:介绍第四种表示方法,并说明其原理和应用场景。
* 举例:给出一个具体的例子,以便读者更好地理解。
圆的证明与计算 (基本图形)

圆的证明与计算(基本图形)圆的证明与计算是中考中的一类重要的问题,此题完成情况的好坏对解决后面问题的发挥有重要的影响,所以解决好此题比较关键。
一、考点分析:1.圆中的重要定理:(1)圆的定义:主要是用来证明四点共圆.(2)垂径定理:主要是用来证明——弧相等、线段相等、垂直关系,以及中点等等.(3)三者之间的关系定理: 主要是用来证明——弧相等、线段相等、圆心角相等.(4)圆周角性质定理及其推论: 主要是用来证明——直角、角相等、弧相等.(5)切线的性质定理:主要是用来证明——垂直关系.(6)切线的判定定理: 主要是用来证明直线是圆的切线.(7)切线长定理: 线段相等、垂直关系、角相等.2.圆中几个关键元素之间的相互转化:弧、弦、圆心角、圆周角等都可以通过相等来互相转化.这在圆中的证明和计算中经常用到.二、考题形式分析:主要以解答题的形式出现,近几年武汉市中考题的22题的第1问主要是判定切线;第2问主要是与圆有关的计算:①求线段长(或面积);②求线段比;③求角度的三角函数值(实质还是求线段比)。
三、解题方法:1、判定切线的方法:(1)若切点明确,则“连半径,证垂直”。
常见手法有:全等转化;平行转化;直径转化;中线转化等;有时可通过计算结合相似、勾股定理证垂直;(2)若切点不明确,则“作垂直,证半径”。
常见手法:角平分线定理;等腰三角形三线合一,隐藏角平分线;(07武汉)22.(本题8分)如图,等腰三角形ABC中,AC=BC=10,AB=12。
以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E。
(1)求证:直线EF是⊙O的切线;(2)求sin∠E的值。
(第22题图)(10武汉)22.(本题满分8分) 如图,点O 在∠APB 的平分线上,⊙O 与PA 相切于点C . (1) 求证:直线PB 与⊙O 相切;(2) PO 的延长线与⊙O 交于点E .若⊙O 的半径为3,PC=4.求弦CE 的长.2、与圆有关的计算:计算圆中的线段长或线段比,通常与勾股定理、垂径定理与三角形的全等、相似等知识的结合,形式复杂,无规律性。
关于圆的知识点

关于圆的知识点圆是平面几何中的一种基本图形,具有很多独特的性质和特征。
本文将介绍圆的定义、性质和应用,帮助读者更全面地了解圆的知识。
一、圆的定义圆是指平面上到一个定点距离相等的所有点所构成的图形。
这个定点叫做圆心,距离叫做半径。
圆的符号常用字母"O"来表示圆心,半径常用字母"r"来表示。
二、圆的性质1. 圆的周长和面积圆的周长是指圆的边界的长度,我们可以利用周长公式来计算圆的周长:周长 = 2πr,其中π近似取值为3.14或22/7。
圆的面积是指圆所覆盖的平面区域的大小,我们可以用面积公式来计算圆的面积:面积 = πr²。
2. 圆的直径圆的直径是指圆的两个边界点之间的直线段的长度,直径是圆的最长的线段,其长度等于圆的半径的两倍,即直径 = 2r。
3. 圆的弧圆的边界上的一段称为圆弧,圆弧的长度叫做弧长。
如果圆弧的长度正好是圆的周长的一部分,我们称它为圆周角度,它的弧长等于圆周长的1/360,即弧长= 2πr/360。
4. 圆的切线圆上的一条直线,与圆只有一个公共点,这个点叫做切点,这条直线叫做切线。
切线与半径垂直。
三、圆的应用1. 圆的几何应用圆的几何应用非常广泛,可以应用在建筑设计、道路规划、地球表面分割等方面。
例如,建筑设计中常使用圆柱体、圆锥体、圆形拱门等结构,这些结构具有稳定性和美观性。
2. 圆的数学应用圆的数学应用涉及到数学运算和数据处理。
例如,在计算机图形学中,圆经常用于绘制和处理图形,通过计算机的算法可以准确地绘制出圆的形状。
另外,圆的数学模型还广泛应用于物理学和工程学的研究和实践中。
3. 圆的日常应用圆在日常生活中也有很多应用。
例如,轮胎、圆形饼干、碗、杯子等都是圆形的,圆形的物品在制造和使用上更加方便和美观。
总之,圆是平面几何中的重要图形,具有独特的性质和广泛的应用。
通过深入了解圆的定义、性质和应用,我们能够更好地理解圆的概念,提高对几何学的理解和运用能力。
