数学《同角三角比的关系与诱导公式》教案(沪教版高一)
高一数学辅导教案:同角三角函数与诱导公式

1.同角关系及诱导公式要注意象限角对三角函数符号的影响,尤其是利用平方关系在求三角函数
3
值时,进行开方时要根据角的象限或范围,判断符号后,正确取舍.
2.三角求值、化简是三角函数的基础,在求值与化简时,常用方法有:(1)弦切互化法:主要利用
公式 tan x=csoins xx化成正弦、余弦函数;(2)和积转换法:如利用(sin θ±cos θ)2=1±2sin θcos θ 的关系 进行变形、转化;(3)巧用“1”的变换:1=sin2 θ+cos2θ=cos2θ(1+tan2 θ)=tan 4π=…. 七、课堂小测
一、作业检查
作业完成情况:优□ 良□ 中□ 差□
二、内容回顾
1.sin 585°的值为( )
A.-
2 2
2 B. 2
C.-
3 2
3 D. 2
2.已知 sin(π+θ)=- 3cos(2π-θ),|θ|<2π,则 θ 等于( )
A.-6π
B.-π3
π
π
C.6
D.3
3.已知 tan θ=2,则ssiinnπ2π2+-θθ--csoinsππ--θθ=(
【例
1】
(1)已知
tan
α=2,则24ssiinn
α-3cos α-9cos
αα=___________,
沪教版数学高一下册-5.3同角三角比的关系和诱导公式-同角三角比的关系 教案设计

同角三角比的关系【教学目标】1、知识目标:知道同角三角比的八个恒等式;知道某一角的三角比,会求出其它三角比。
2、情感目标:学生通过自己对公式的推理证明,体会数学推理的乐趣。
3、技能目标:观察能力,合理分析能力,综合应用能力。
【教学重点与难点】重点:同角三角比恒等式的识记和应用。
难点:应用同角三角比恒等式求解各个三角比。
【教学过程】一、复习旧知识、引入课题:例、已知31tg =α,求αctg 。
同学们回答“3”。
那么,如果告诉你αcos 的值,让你求αsin 或者其它三角比,你们会求吗?比如已知54cos =α,让你求其它三角比的问题?答:“不会”。
那么通过本节课的学习后,相信你们肯定会求这类问题的。
前面几节课我们学习了诱导公式,也就是不同角的同一三角比之间的关系。
那么相同角的不同三角比之间有没有关系呢?答案:是有的。
我们这节课的主要内容就是研究相同角的不同三角比之间的关系,我们到时会发现很多有趣的关系。
为了研究问题方便,我们先回忆一下各个三角比的定义:r y sin =α,r x cos =α,x y tg =α,y x ctg =α,x y tg =α,y r csc =α,xrsec =α(222y x r +=)大家一起来观察六个三角比,寻找一下里面两个三角比之间的关系:1. 1csc sin =⋅αα 利用倒数关系,我们可以分别用αsin 、αcos 、αtg 表示2. 1sec cos=⋅αα αααctg ,sec ,csc ,所以,我们以后主要研究正弦、余弦、 3. 1=⋅ααctg tg 和正切三种三角比。
4. αααcos sin =tg 利用商数关系,我们可以用正弦和余弦的比来表示正切 5. αααsin cos =ctg 和余切。
6. 1cos sin 22=+αα7. αα22sec 1=+tg8. αα22csc 1=+ctg以上这些恒等式揭示了同一个角的各个三角比之间的关系。
数学《同角三角比的关系与诱导公式》教案(沪教版高一)
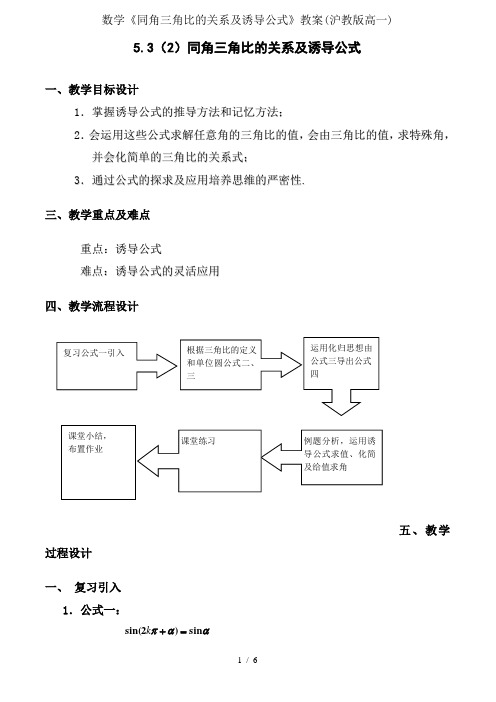
5.3(2)同角三角比的关系及诱导公式一、教学目标设计1.掌握诱导公式的推导方法和记忆方法;2.会运用这些公式求解任意角的三角比的值,会由三角比的值,求特殊角,并会化简单的三角比的关系式;3.通过公式的探求及应用培养思维的严密性.三、教学重点及难点重点:诱导公式难点:诱导公式的灵活应用四、教学流程设计五、教学过程设计一、 复习引入1.公式一:ααπsin )2sin(=+kααπcos )2cos(=+kααπtan )2tan(=+kααπcot )2cot(=+k (其中α∈k )用角度可写成:ααsin )360sin(=+︒⋅kααcos )360cos(=+︒⋅kααtan )360tan(=+︒⋅kααcot )360cot(=+⋅ k (其中Z ∈k )2 .讨论公式一的作用:把任意角的正弦、余弦、正切化为0º―360º之间角的正弦、余弦、正切,其方法是先在0º―360º内找出及角α终边相同的角,再把它写成诱导公式一的形式,然后得出结果.这组公式可以统一概括为)Z )(()2(∈=+k f f απαk 的形式,上述一组公式叫做任意角三角比的第一组诱导公式,其特征是:等号两边是同名三角比,且符号都为正.说明]运用公式时,注意“弧度”及“角度”两种度量制不要混用,如写成︒=+︒80sin )280sin(πk ,3cos )3603cos(ππ=︒⋅+k 是不对的.二、学习新课 1.公式推导公式二:αα-sin sin(=-)ααcos cos(=-) 它说明角-α及角α的正弦值互为相反数,而它们的余弦值相等.这是因为,若角α的终边及单位圆交于点P(x ,y),则角-α的终边及单位圆的交点必为P ´P(x ,-y)(如图1).由正弦、余弦三角比的定义,即可得sin α=y , cos α=x,sin(-α)=-y, cos(-α)=x,所以:sin(-α)= -sin α, cos(-α)= cos α 由三角比的商数关系,得:ααααααtan cos sin )cos()sin()tan(-=-=--=- 即 ααtan tan(-=-)类似可得ααcot )cot(-=-这组公式叫任意角三角比的第二组诱导公式练习:求3π-的正弦、余弦、正切和余切的值.[说明]公式二也可以由特殊到一般,既从特殊三角比的计算,猜测出公式,再证明.公式三:ααπ-sin sin(=+) α-sin 180sin(=+︒) ααπ-cos cos(=+) α180cos(=+︒) ααπtan tan(=+) α180tan(=+︒) ααπcot )cot(=+ αsin )180cot(=+ 它刻画了角180º+α及角α的正弦值(或余弦值)之间的关系,这个关系是:以角α终边的反向延长线为终边的角的正弦值(或余弦值)及角α的正弦值(或余弦值)是一对相反数.这是因为若设α的终边及单位圆交于点P( x ,y),则角α终边的反向延长线,即180º+α角的终边及单位圆的交点必为P ´(-x ,-y)(如图2).由正弦、余弦三角比的定义,即可得sin α=y , cos α=x,-y)sin(180º+α)=-y, cos(180º+α)=-x,所以 :sin(180º+α)=-sin α,cos(180º+α)=-cos α.[说明]公式二、三的获得主要借助于单位圆及正弦、余弦比的定义.根据点P 的坐标准确地确定点P ´的坐标是关键,这里充分利用了对称的性质.直观的对称形象为我们准确写出P ´的坐标铺平了道路,体现了数形结合这一数学思想的优越性.练习:求下列三角比的值: (1) 210cos ; (2)分析:本题是诱导公式二的巩固性练习题.求解时,只须设法将所给角分解成180º+α或(π+α),α为锐角即可.解:(1)cos210º=cos(180º+30º)=-cos30º=-23; (2)sin45π=sin()=-sin 4π=-22. 公式四:把第三组公式中的α换成α-,得第四组诱导公式:ααπsin sin(=-) ααsin 180sin(=-︒)ααπ-cos cos(=-) αα-cos 180cos(=-︒)ααπtan tan(-=-) ααtan 180tan(-=-︒)ααπcot )cot(-=- ααcot )180cot(-=-[说明]这组公式均可由前面学过的诱导公式直接推出,体现了把未知问题化为已知问题处理这一化归的数学思想.公式的推导并不难,然而推导中的化归意识和策略是值得我们关注的.四组诱导公式可概括为:k ·360º+α(k ∈Z ),-α,180º±α,360º-α的三角比值,等于α的同名三角比的值,前面加上一个把α看成锐角时原三角比的符号.[说明]这里的“同名三角比值”是指等号两边的三角比名称相同;“把α看成锐角”是指α原本是任意角,这里只是把它视为锐角处理;“前面加上一个……符号”是指α的同名三角比值未必就是最后结果,前面还应添上一个符号(正号或负号,主要是负号,正号可省略),而这个符号是把任意角α视为锐角情况下的原三角比的符号.应注意讲清这句话中每一词语的含义,特别要讲清为什么要把任意角α看成锐角.建议通过实例分析说明.练习:求下列各式的值:(1)sin(-34π);(2)cos(-60º)-sin(-210º) 分析:本题是诱导公式二、三的巩固性练习题.求解时一般先用诱导公式三把负角的正弦、余弦化为正角的正弦、余弦,然后再用诱导公式二把它们化为锐角的正弦、余弦来求.解:(1)sin(-34π)=-sin()=sin 3π=23; (2)原式=cos60º+sin(180º+30º)=cos60º-sin30º=21-21=02.例题分析例1:利用诱导公式,求下列各三角比:(1); (2)例2化简:)3cot()sin()tan()cot()2cos(απαππααπαπ----+- 例3根据条件,求角x :(1) 已知;(2)已知),[,33tan ππ-∈=x x .[说明]由三角比求特殊角的问题,是个“反”问题,对学生是个难点问题,教师可先缩小范围,如考虑在[0,2π]上,求角,再考虑[0,2)π等. 三、巩固练习P49 练习 5.3(2)四、课堂小结通过本节课的教学,我们获得了诱导公式.值得注意的是公式右端符号的确定.在运用诱导公式进行三角比的求值或化简中,我们又一次使用了转化的数学思想.通过进行角的适当配凑,使之符合诱导公式中角的结构特征,培养了我们思维的灵活性.五、作业布置习题5.3 A 组:1;4(1)(2);5B 组:1;4。
沪教版数学高一下册- 5.2任意角的三角比-同角三角比的关系 教案设计

同角三角比的关系【教学目标】1、感悟同角三角比关系的获得过程;理解并掌握同角三角比关系,并能够通过它们解决三 角比的求值、化简、证明等问题;2、在三角恒等式的变形过程中感受数学方法的灵活性;获得解决问题带来的愉悦。
【教学重点与难点】用同角三角比的关系式进行恒等变形和解决求值、化简、证明等问题。
【教学过程】一、【知识要点】1、任意角三角比的定义:角α的终边上任取一点(,)P x y,r =sin y r α=,cos x r α=,tan y x α=, cot xy α=,sec rx α=,csc ry α=。
2、同角三角比的关系:倒数关系:1csc sin =⋅αα,1sec cos =⋅αα,1cot tan =⋅αα。
商数关系:αααcos sin tan =(cos 0)α≠,αααsin cos cot =(sin 0)α≠。
平方关系:1cos sin 22=+αα,αα22sec tan 1=+,αα22csc cot 1=+。
二、【热身练习】1、已知α为第二象限角,化简1sin 1cot 2tan 1cos 122-++xx x x = 2、已知53sin +-=m m θ,)2(524cos πθπθ<<+-=m m ,则θtan = 3、化简:22sin 62tan54cot 45tan36sin 28+⋅⋅+o o o o o =三、【例题解析】1、已知54cos =α,且α是第四象限角,求角α的其他三角比的值。
【变式】:已知5tan 12α=,求sin α、cos α和cot α。
2、已知3tan =α,求:(1)ααααsin 4cos 3sin 3cos 2+-; (2)ααcos sin 3;【变式】:若αααcos sin 3sin 12⋅=+,求αtan 的值。
3、已知51cos sin =+αα,)π,0(∈α,求: (1)ααcos sin ; (2)ααcot tan +; (3)ααcos sin -。
高一数学必修4《同角三角函数的基本关系与诱导公式》教学设计
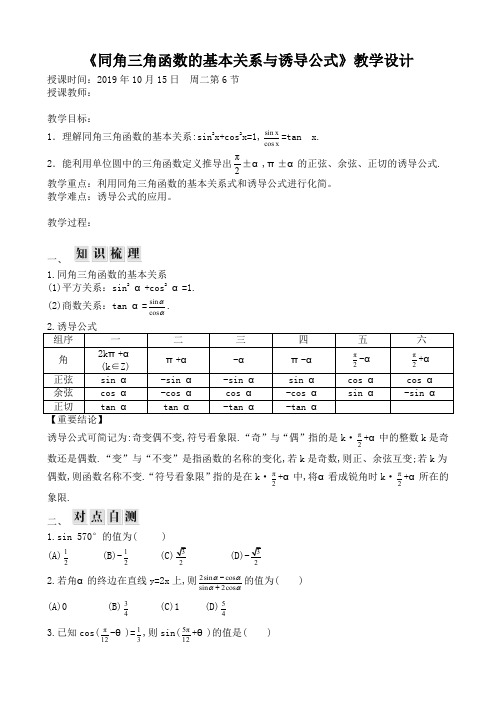
《同角三角函数的基本关系与诱导公式》教学设计授课时间:2019年10月15日 周二第6节 授课教师:教学目标:1.理解同角三角函数的基本关系:sin 2x+cos 2x=1,sin cos x x=tan x.2.能利用单位圆中的三角函数定义推导出π2±α,π±α的正弦、余弦、正切的诱导公式. 教学重点:利用同角三角函数的基本关系式和诱导公式进行化简。
教学难点:诱导公式的应用。
教学过程:一、1.同角三角函数的基本关系(1)平方关系:sin 2 α+cos 2 α=1. (2)商数关系:tan α=sin cos αα.诱导公式可简记为:奇变偶不变,符号看象限.“奇”与“偶”指的是k ·π2+α中的整数k 是奇数还是偶数.“变”与“不变”是指函数的名称的变化,若k 是奇数,则正、余弦互变;若k 为偶数,则函数名称不变.“符号看象限”指的是在k ·π2+α中,将α看成锐角时k ·π2+α所在的象限.二、1.sin 570°的值为( )(A)12(B)-122.若角α的终边在直线y=2x 上,则2sin cos sin 2cos αααα-+的值为( ) (A)0(B)34(C)1 (D)543.已知cos(π12-θ)=13,则sin(5π12+θ)的值是( )(A)13(B) (C)-134.tan 750°= .5.下面结论正确的是 .①若α,β为任意角,则sin 2α+cos 2β=1. ②若α∈R,则tan α=sin cos αα恒成立.③sin(π+α)=-sin α成立的条件是α为锐角.④诱导公式的记忆口诀中“奇变偶不变,符号看象限”,其中的奇、偶是指π2的奇数倍和偶数倍,变与不变指函数名称的变化. 三、考点一 同角三角函数的基本关系【例1】 (1)化简;(2)已知π2<α<π且sin αcos α=k(k 为常数),则 cos α-sin α= ;(3)已知角α满足tan α=3,求下列各式的值: ①sin 4cos 5sin 2cos αααα-+; ②sin 2α+2sin αcos α-3cos 2α. (2)sin θ+cos θsin θcos θsin θ-cos θ,上述转化过程中,开方要根据θ的范围确定正负.(3)关于sin α,cos α的齐次式,或含有sin 2α,cos 2α及sin αcos α的式子求值时,可将【跟踪训练1】 (1)化简.(2)已知tan tan 6αα-=-1,求下列各式的值.①2cos 3sin 3cos 4sin αααα-+;②1-3sin αcos α+3cos 2α.考点二 三角函数的诱导公式 【例2】 化简下列各式:(1)π11πsin(2π-)cos(π)cos()cos()229πcos(π)sin(3π)sin(π)sin()2αααααααα++-----+ ;(2) sin(π)sin(π)sin(π)cos(π)n n n n αααα++-+- (n ∈Z).【例3】 已知cos(π6-α,求cos(5π6+α)-sin 2(α-π6)的值.(1)诱导公式用法的一般思路: ①sin(-1 200°)·cos 1 290°+cos(-1 020°)·sin(-1 050°)+tan 855°;②cos 2(π4-α)+cos 2(π4+α).(2)求证:cos(2π)π3cos(π)sin()sin(π)22θθθθ-++-++cos(π)3cos sin(π)12θθθ-⎡⎤--⎢⎥⎣⎦=22sin θ.考点三 三角函数求值中的隐含条件(易混易错)【例4】 设θ为第二象限角,若tan(θ+π4)=12,则sin θ+cos θ= .易错分析:本题解答时易出现以下错误: (1)不能提炼隐含信息tan(θ+π4)>0.(2)利用同角三角函数平方关系,开方运算时忽视三角函数符号的判定.(3)开方后由角的范围不能确定三角函数符号时,要结合函数值的符号进一步缩角. 四、课时小结五、作业:课时集训对应章节。
沪教版数学高一下册-5.3 同角三角比的关系和诱导公式-同角三角比的关系——证明与化简 课件(共18张PPT)

只 要 证 c o s s e c s i n t a n .
即 c o s c o 1 s s c io n s 2 ,利 用 平 方 关 系 即 可 。
例2. 证明: 1 1 sseecc ttaan n 1 cossin .
同角三角比的关系——证明与化简
复习:同角三角比的8个关系式
1. 倒数关系
sin csc 1 cos sec 1 tan cot 1
2. 商数关系
tan sin cos 0
cos
cot cos sin 0
sin
3. 平方关系
sin 2 cos2 1 tan 2 1 sec2 cot2 1 csc2
再代入计算即可。
例1. 化简:
1sin6 x cos6 x 1sin4 xcos4 x.
解:(将1代换成 、 ) sin2xcos2x3 sin2xcos2x2
1 s in 6 x c o s 6 x s in 2 x c o s 2 x 3 s in 6 x c o s 6 x 3 s in 4 x c o s 2 x 3 s in 2 x c o s 4 x 3 s in 2 x c o s 2 x s in 2 x c o s 2 x 3 s in 2 x c o s 2 x ,
证:(利用三角比的定义)
sin y,c o sx,ta n y,se cr
r
r
x
x
其中 r x2 y2,代入化简。
课堂练习
1. 证明: tan1 1 c so in s cot1 1 c so in s .
沪教版高一数学(下)5.3 同角三角比的关系和诱导公式教案

同角三角比的关系和诱导公式【教学目标】1.复习巩固三角比的定义;2.由三角比的定义,找出同角三角比的基本关系式;3.理解同角公式都是特定意义的恒等式;4.会简单应用同角公式。
【教学重难点】重点:同角公式的推导与应用;难点:三角比符号的确定及公式的变形应用。
【教学过程】一、情景引入1.背景:如果53sin =α,α为第一象限的角,如何求角α的其它三角比值; 2.思考。
问题1:已知角α终边上一点),(y x P ,22y x r +=,则角α的六个三角比分别是什么? yr x r x y y x r x r y ======ααααααcsc ;sec ;cot ;tan ;cos ;sin 。
问题2:当角α分别在不同的象限时,ααααcot tan cos sin 、、、的符号分别是怎样的? 3.讨论:由于α的三角比都是由r y x 、、表示的,则角α的六个三角比之间有什么关系?二、学习新课1.探求公式。
(板书课题:同角的三角比的基本关系。
)2.由三角比的定义,我们可以得到以下关系:1cos sin 22=+αα。
理论证明:(采用定义)。
αααππαααααtan cos sin )(221cos sin cos ,sin 122222==⨯=÷=∈+≠=+∴===+x y x r r y r x r y Z k k r x r y r y x 时,当且οοΘ; (1)倒数关系:⎪⎩⎪⎨⎧=⋅=⋅=⋅1cot tan 1sec cos 1csc sin αααααα;(2)商数关系:⎪⎩⎪⎨⎧==ααααααsin cos cot cos sin tan ; (3)平方关系:⎪⎩⎪⎨⎧=+=+=+αααααα222222csc cot 1sec tan 11cos sin 。
说明:①注意“同角”,至于角的形式无关重要,如14cos 4sin 22=+αα,2tan 2cos 2sin ααα=等; ②注意这些关系式都是对于使它们有意义的角而言的,如),2(1cot tan Z k k ∈≠=⋅πααα; ③对这些关系式不仅要牢固掌握,还要能灵活运用(正用、反用、变形用),如:αα2sin 1cos -±=,αα22cos 1sin -=,αααtan sin cos =等。
同角三角比的关系和诱导公式教案

同角三角比的关系和诱导公式教案一、同角三角比的关系1. 正弦值:在一个直角三角形中,取一个锐角θ,将其对边的边长记作a,斜边的边长记作c,则其正弦值sinθ等于对边与斜边的比值,即sinθ = a / c。
2. 余弦值:在同一个直角三角形中,其余弦值cosθ等于邻边与斜边的比值,即cosθ = b / c,其中邻边的边长记作b。
3. 正切值:在同一个直角三角形中,其正切值tanθ等于对边与邻边的比值,即tanθ = a / b。
通过这些关系,我们可以得到以下结论:- sin(90° - θ) = cosθ:角度θ的补角的正弦值等于角度θ的余弦值。
- cos(90° - θ) = sinθ:角度θ的补角的余弦值等于角度θ的正弦值。
- tanθ = sinθ / cosθ:正切值等于正弦值与余弦值的比值。
二、诱导公式诱导公式是通过已知的三角比的关系,推导出其他角度的三角比的公式。
1. 诱导公式1:sin(-θ) = -sinθ这个公式表明,一个角度的正弦值与它的相反角的正弦值相等,但符号相反。
2. 诱导公式2:cos(-θ) = cosθ这个公式表明,一个角度的余弦值与它的相反角(或补角)的余弦值相等。
3. 诱导公式3:tan(-θ) = -tanθ这个公式是通过正切值等于正弦值除以余弦值推导得出的。
4. 诱导公式4:sin(180° - θ) = sinθ这个公式表明,一个角度与它的补角非常相似,仅仅正弦值的符号改变。
5. 诱导公式5:cos(180° - θ) = -cosθ这个公式说明,一个角度与它的补角非常相似,仅仅余弦值的符号改变。
以上是常见的诱导公式,它们是基于已知的三角比关系而推导得出的。
三、诱导公式的应用诱导公式的应用十分广泛,可以简化计算和证明过程,提高效率。
以下是一些使用诱导公式的具体例子:2. 计算cos75°:根据诱导公式5,cos75° = -cos(180° - 75°) = -cos105°。
高一数学同角三角比的关系与诱导公式2.doc
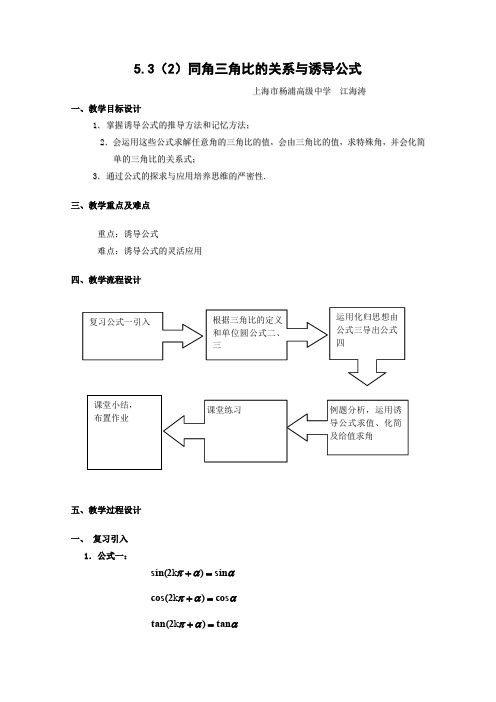
5.3(2)同角三角比的关系与诱导公式上海市杨浦高级中学 江海涛一、教学目标设计1.掌握诱导公式的推导方法和记忆方法;2.会运用这些公式求解任意角的三角比的值,会由三角比的值,求特殊角,并会化简单的三角比的关系式;3.通过公式的探求与应用培养思维的严密性. 三、教学重点及难点 重点:诱导公式难点:诱导公式的灵活应用 四、教学流程设计五、教学过程设计 一、 复习引入 1.公式一:ααπsin )2sin(=+k ααπcos )2cos(=+kααπtan )2tan(=+kααπcot )2cot(=+k (其中α∈k )用角度可写成:ααsin )360sin(=+︒⋅kααcos )360cos(=+︒⋅k ααtan )360tan(=+︒⋅kααcot )360cot(=+⋅k (其中Z ∈k ) 2 .讨论公式一的作用:把任意角的正弦、余弦、正切化为0º―360º之间角的正弦、余弦、正切,其方法是先在0º―360º内找出与角α终边相同的角,再把它写成诱导公式一的形式,然后得出结果.这组公式可以统一概括为)Z )(()2(∈=+k f f απαk 的形式,上述一组公式叫做任意角三角比的第一组诱导公式,其特征是:等号两边是同名三角比,且符号都为正.说明]运用公式时,注意“弧度”与“角度”两种度量制不要混用,如写成︒=+︒80sin )280sin(πk ,3cos)3603cos(ππ=︒⋅+k 是不对的.二、学习新课 1.公式推导公式二:αα-sin sin(=-) ααcos cos(=-)它说明角-α与角αα的终边与单位圆交于点P(x ,y),则角-α的终边与单位圆的交点必为P ´(x ,-y)(如图1).由正弦、余弦三角比的定义,即可得 sin α=y , cos α=x, sin(-α)=-y, cos(-α)=x,所以:sin(-α)= -sin α, cos(-α)= cos α 由三角比的商数关系,得:ααααααtan cos sin )cos()sin()tan(-=-=--=-P即 ααtan tan(-=-)类似可得ααcot )cot(-=-这组公式叫任意角三角比的第二组诱导公式 练习:求3π-的正弦、余弦、正切和余切的值.[说明]公式二也可以由特殊到一般,既从特殊三角比的计算,猜测出公式,再证明.公式三:用角度可表示如下:ααπ-sin sin(=+)αα-sin 180sin(=+︒) ααπ-cos cos(=+)αα-cos 180cos(=+︒) ααπtan tan(=+)ααtan 180tan(=+︒) ααπcot )cot(=+ ααsin )180cot(=+它刻画了角180º+α与角α的正弦值(或余弦值)之间的关系,这个关系是:以角α终边的反向延长线为终边的角的正弦值(或余弦值)与角α的正弦值(或余弦值)是一对相反数.这是因为若设α的终边与单位圆交于点P( x ,y),则角α终边的反向延长线,即180º+α角的终边与单位圆的交点必为P ´(-x ,-y)(如图2).由正弦、余弦三角比的定义,即可得sin α=y , cos α=x, sin(180º+α)=-y,cos(180º+α)=-x,所以 :sin(180º+α)=-sin α,cos(180º+α)=-cos α.[说明]公式二、三的获得主要借助于单位圆及正弦、余弦比的定义.根据点P 的坐标准确地确定点P ´的坐标是关键,这里充分利用了对称的性质.直观的对称形象为我们准确写出P ´的坐标铺平了道路,体现了数形结合这一数学思想的优越性.练习:求下列三角比的值: (1)210cos ;(2)45sinπ 分析:本题是诱导公式二的巩固性练习题.求解时,只须设法将所给角分解成180º+α或(π+α),α为锐角即可.解:(1)cos210º=cos(180º+30º)=-cos30º=-23;-y)(2)sin 45π=sin(4ππ+)=-sin 4π=-22.公式四:把第三组公式中的α换成α-,得第四组诱导公式: ααπsin sin(=-) ααsin 180sin(=-︒)ααπ-cos cos(=-)αα-cos 180cos(=-︒) ααπtan tan(-=-)ααtan 180tan(-=-︒) ααπcot )cot(-=- ααcot )180cot(-=-[说明]这组公式均可由前面学过的诱导公式直接推出,体现了把未知问题化为已知问题处理这一化归的数学思想.公式的推导并不难,然而推导中的化归意识和策略是值得我们关注的.四组诱导公式可概括为:k ·360º+α(k ∈Z ),-α,180º±α,360º-α的三角比值,等于α的同名三角比的值,前面加上一个把α看成锐角时原三角比的符号.[说明]这里的“同名三角比值”是指等号两边的三角比名称相同;“把α看成锐角”是指α原本是任意角,这里只是把它视为锐角处理;“前面加上一个……符号”是指α的同名三角比值未必就是最后结果,前面还应添上一个符号(正号或负号,主要是负号,正号可省略),而这个符号是把任意角α视为锐角情况下的原三角比的符号.应注意讲清这句话中每一词语的含义,特别要讲清为什么要把任意角α看成锐角.建议通过实例分析说明.练习:求下列各式的值:(1)sin(-34π);(2)cos(-60º)-sin(-210º) 分析:本题是诱导公式二、三的巩固性练习题.求解时一般先用诱导公式三把负角的正弦、余弦化为正角的正弦、余弦,然后再用诱导公式二把它们化为锐角的正弦、余弦来求.解:(1)sin(-34π)=-sin(3ππ+)=sin 3π=23; (2)原式=cos60º+sin(180º+30º)=cos60º-sin30º=21-21=0 2.例题分析例1:利用诱导公式,求下列各三角比:(1)326sinπ; (2))413tan(π- 例2化简:)3cot()sin()tan()cot()2cos(απαππααπαπ----+-例3根据条件,求角x : (1) 已知)2,0[,21sin π∈=x x ; (2)已知),[,33tan ππ-∈=x x . [说明]由三角比求特殊角的问题,是个“反”问题,对学生是个难点问题,教师可先缩小范围,如考虑在[0,2π]上,求角,再考虑[0,2)π等. 三、巩固练习 P49 练习 5.3(2) 四、课堂小结通过本节课的教学,我们获得了诱导公式.值得注意的是公式右端符号的确定.在运用诱导公式进行三角比的求值或化简中,我们又一次使用了转化的数学思想.通过进行角的适当配凑,使之符合诱导公式中角的结构特征,培养了我们思维的灵活性.五、作业布置习题5.3 A 组:1;4(1)(2);5 B 组:1;4。
高三数学一轮复习:诱导公式及同角三角比的关系(教案)

第二课时 诱导公式及同角三角比的关系(教案)【复习目标】1.掌握同角三角比的关系和诱导公式;2.能利用同角三角比的关系及诱导公式进行三角比的化简、求值、证明. 【知识梳理】1.同角三角比的基本关系式 : (1)平方关系:22sin cos 1αα+=,222222111tan sec ,1cot csc cos sin αααααα+==+==; (2)商数关系:sin cos tan ,cot cos sin αααααα==; (3)倒数关系:tan 1,sin csc 1,cos sec 1cot αααααα⋅=⋅=⋅=. 2.正弦、余弦、正切的诱导公式:一般用“奇变偶不变,符号看象限”的口诀 记住α-,απ+k 2,απ±2,απ±,απ±23的正弦、余弦、正切的三角函数,应用诱导公式重点是“函数名称”与“正负号”的判断.3.基本关系式和诱导公式是同角三角函数和异角三角函数的桥梁,有了它们,我们可以将任意角的三角函数转化为易求的]2,0[π范围内来研究,其思路是:负角化正角,大角化小角,保留特殊角. 【基础练习】 1.若1tan 3θ=,32πθπ<<,则sin cos θθ⋅的值为( B ) A.310±B.310C.103D.±2.已知x 为锐角,且2tan 3sin 7x y +=,tan 6sin 1x y -=,则sin x 的值为 ( C )ABCD .133.已知1sin 1cos 2x x +=-,则cos sin 1xx -的值是( B )A .12-B .12C .2D .2-4.已知1tan 2α=-,则2212sin cos sin cos αααα+-的值是( C ) A .13 B .3 C .13- D .3-5.若1sin()2πθ+=-,则3cos()2πθ-=______12-_______. 6.若34x π=,则3sin()2sin()4cos 23cos()444x x x x πππ++--++=_____2_______.【典型例题】【例1】 已知3sin 5m m θ-=+,42cos 5m m θ-=+,2πθπ<<,求θ的六个三角比. 解:1cos sin 22=+x x ,1)524()53(22=+-++-∴m m m m ,解得:8=m ,0=m ,又0cos ,0sin ],,2[<>∴∈x x x ππ,故 0=m (舍去)所以8=m ,此时512512sin ,cos ,tan ,cot ,1313125θθθθ==-=-=- 1313sec ,csc 125θθ=-=.【例2】已知sin 2cos 0x x +=,求下列各式的值:(1)sin cos cos 3sin x x x x+-; (2)2sin sin cos 3x x x ++.解:(1)原式2cos cos cos 1cos 3(2cos )7cos 7x x x x x x -+-===---;(2)原式2222222sin sin cos 3(sin cos )4tan tan 3sin cos tan 1x x x x x x x x x x +++++==++, 又sin 2cos x x =-,∴tan 2x =-,∴原式175=.【例3】已知51cos sin =+x x (π<<x 0),求x tan 的值. 解:51cos sin =+x x ,251)cos (sin 2=+x x ,即251cos sin 21=+x x ,2512cos sin -=∴x x ,πππ<<∴<<x x 2,0 ,则2549)cos (sin 2=-x x ,得57cos sin =-x x ,故53cos ,54sin -==x x ,所以34tan -=x .说明:因为1cos sin 22=+x x ,所以x x cos sin +,x x cos sin -,x x cos sin 这三个式子,已知其中一个式子的值,其余两式的值可以求出,即“知一求二”.一般方法是:令t x x =+cos sin ,]2,2[-∈t ,那么21cos sin 2-=t x x ,222)cos (sin t x x -=-,从而利用方程的思想将问题得以解决.【例4】已知方程01)c o t (t a n 2=++-x x θθ有一根是32+,求:θθc o s l o g s i n l o g 221-的值. 解:设方程另一根为α,由根与系数的关系得:⎩⎨⎧=++=++1)32(cot tan 32αθθα,则4cot tan =+θθ,4sin cos cos sin =+θθθθ,41cos sin =θθ, 而12112221log sin log cos log (sin cos )log 24θθθθ-===.【例5】 已知α解:)sin 1)(sin 1()sin 1)(sin 1()sin 1)(sin 1()sin 1)(sin 1(αααααααα-+----+++=原式 |cos |sin 1|cos |sin 1sin 1)sin 1(sin 1)sin 1(2222αααααααα--+=----+=cos 0αα∴< 是第二象限角,αααααt a n 2c o s s i n 1c o s s i n 1-=----+=∴原式 (注意象限、符号)【例6】csc cot αα=-成立,求角α终边所在的位置.解:由1cos sin αα-===且1cos csc cot sin αααα--=,1cos 1cos sin sin αααα--=1cos 0sin 0sin ααα-⇒>⇒>,故角α终边在第一象限或第二象限或y 轴正半轴上.【例7】 已知()()()()()()sin cos cot cos 1n x n x f x x n n Z n x ππππ--⋅+=-∈+-⎡⎤⎣⎦求:76f π⎛⎫⎪⎝⎭的值. 解:(1)当2()n k k Z =∈时,()()()()()sin 2cos 2cot 2cos cos 21k x k x f x x k x k x ππππ--⋅+=-=+-⎡⎤⎣⎦;762f π⎛⎫∴=-⎪⎝⎭(2)当21()n k k Z =+∈时,()()()()()sin 21cos 2cot 21cos cos 211k x k x f x x k x k x πππππ-+-⋅++⎡⎤⎣⎦=-+=-⎡⎤⎣⎦++-⎡⎤⎣⎦76f π⎛⎫∴=⎪⎝⎭【例8】 已知)32tan()0()3cos(326αππαπαπ-≠=+<<,求,m m 的值. 解:因为)(332παπαπ+-=-, 所以:)]3(cos[)32cos(παπαπ+-=-=)3cos(πα+-=-m 由于,326παπ<<所以,2320παπ<-<于是:)32(cos 1)32sin(2απαπ--=-=21m -, 所以:tan )32cos()32sin()32(απαπαπ--=-=m m 21--. 说明:通过观察,获得角3πα+与角απ-32之间的关系式απ-32=π()3πα-+,为顺利利用诱导公式求2cos()3πα-的值奠定了基础,这是求解本题的关键.【例9】 已知角α终边上的一点是P 43(,)55m m-,且5sin()cot(7)02παπα++<,求33sin cos αα+的值.解:25cos sin()cot(7)cos cot 02sin πααπαααα++==<,且45m -与35m 异号,∴α是第四象限的角,∴0m <,故1||PO m ==-, ∴3sin ||5y PO α==-,4cos ||5x PO α==, ∴33sin cos αα+12537=.【例10】设α是第三象限角,是否存在这样的实数m ,使得sin α、cos α是关于x 的方程286210x mx m +++=的两根?若存在,求出实数m ;若不存在,说明理由.解:()236322103sin cos 04211sin cos 082m m m m m m m αααα⎧∆=-+≥⇒≥≤⎪⎪⎪+=-<⎨⎪+⎪⋅=>⇒>-⎪⎩ 又22sin cos 1αα+=()2sin cos 2sin cos 1αααα∴+-=29421168m m +-= 298200m m ∴--=1029m m ==-或均不满足条件,所以实数m 不存在.【巩固练习】1.化简11()(1cos )sin tan x x x+-的结果是( A ) A .sin x B .cos x C .1sin x + D .1cos x +2.已知(0,1)a ∈,x 是三角形的一个内角,22tan 1a x a =-,则cos x 的值是( C )A .221a a +B .2211a a -+ C .2211a a -+ D .2211a a -±+ 3.371115799sin sin sin sin sin44444πππππ⋅⋅ 的值为( C )A .10012-B .20012- C .10012 D .200124.已知α=2tan α-.5.6622sin cos 3sin cos x x x x ++的化简结果是___1_______. 6.已知cot csc 5x x +=,则sin x =___513_________. 7.化简:sin[(1)]cos[(1)]()sin()cos()k k k Z k k πθπθπθπθ++⋅+-∈-⋅+答案:分k 为偶数、奇数讨论.原式=1- 8.如果锐角θ满足(tan cot )3log sin 4θθθ+=-,求tan log cos θθ的值. 解:已知即1sin cos 3logsin 4θθθ=-,由换底公式得sin sin log sin 314log sin cos θθθθθ=-, 即sin 13(1log cos )4θθ=--+,解得sin 1log cos 3θθ=,∴原式sin sin sin sin 1log cos log cos 13sin 11log cos 2log 1cos 3θθθθθθθθθ====--.9.已知()(,),(cos )(cos )2f x f f παπαα∈+-若化简. 答案:2csc α10.(1)证明:22sec tan 1αα-=; (2)若22sec tan ,csc cot ,,7m mm n n nαααα+=+=+其中为既约分数求的值. 答案:(1)略;(2)44m n +=.。
同角三角比的关系和诱导公式教案

同角三角比的关系和诱导公式1.公式: 1cos sin22=+αααααtan cos sin = 1cot tan =⋅αα 2.推广:1cos sin 22=+αα这种关系称为平方关系,类似的平方关系还有:1tan sec 22=-αα 1cot csc 22=-αα3.αααtan cos sin =这种关系称为商数关系,类似的商数关系还有:αααcot sin cos = 4.1cot tan =α⋅α这种关系称为倒数关系。
类似的倒数关系还有:1sin csc =α⋅α1cos sec =α⋅α第二组诱导公式的推导由负角的定义,可知角α与角-α的终边关于x 轴对称(如图)。
在角α的终边上取一点P ,使OP的长为1,此时点P 的坐标为(cos α,sin α)。
点P 关于x 轴的对称点P '(cos α,-sin α)一定在角-α的终边上,且O P '的长为1,因此点P '的坐标又可表示为(cos (-α),sin (-α))所以有sin (-α)=-sin αcos (-α)=cos α由三角比的商数关系得:tan (-α)=-tan αcot (-α)=-cot α第三组诱导公式的推导将角α的终边绕着原点O 按逆时针方向旋转π弧度,得到角π+α的终边,可知角α和角π+α的终边关于原点O 对称得: sin (π+α)=-sin α cos (π+α)=-cos αtan (π+α)=tan α cot (π+α)=cot α第四组诱导公式的推导sin (π-α)=sin α cos (π-α)=-cos αtan (π-α)=-tan α cot (π-α)=-cot α例1.已知sin 2cos αα=,求下列各式的值:(1)sin 4cos 5sin 2cos αααα-+ (2)2sin 2sin cos ααα+例2.已知tan 1tan 6αα=--,求下列各式的值:(1)213sin cos 3cos ααα-+ (2)2cos 3cos 3cos 4sin αααα-+例3.已知sin()cos(2)tan(2)()3tan()cos()2f παπαπααπαπα+--=----(1) 若1860α=-,求()f α (2) 若33cos()25πα-=,求()f α的值。
沪教版数学高一下册-5.3同角三角比的关系和诱导公式-诱导公式 教案设计

课题:5.3诱导公式(1)【教学目标】1、理解并掌握诱导公式的基本内容,应用诱导公式解决三角式的求值、化简问题;2、经历诱导公式的推导过程,体验数形结合、化归与转化等数学思想方法;3、通过诱导公式学习,领悟不同角的三角比的内在联系,感受三角的个性美。
【教学重点】诱导公式的推导。
【教学难点】寻找诱导公式的推导方法。
【教材内容分析】诱导公式是教材在研究了同角的三角比关系的基础之上安排的,对比同角三角比的关系,诱导公式则是研究不同角的但关系又非常密切的三角比的关系,其内容在三角比中占有非常重要的地位,无论是计算、化简还是证明都运用灵活,公式繁多,又不容易死记硬背,很容易给学习留下隐患;因此教学中要引起学生的高度重视,要准确把握学生的学习基础和学习情况,充分展示知识的发生过程,揭示知识之间的内在联系,关注学生对知识的理解,切实为后续的学习和灵活运用打好基础。
【教学过程】一【复习引入】问题1:任意角的三角比的定义。
引入:上节课中我们学习了同一个角的三角比之间的关系,能够由角所在的象限和它的一个三角比求出其余的三角比。
其实,不同角但关系非常密切的两个角的三角比之间也有一定的联系。
问题2:与角α终边相同的所有角(包含α)的集合。
由这两个问题总结出任意角三角比的第一组诱导公式:ααπsin )2sin(=+k ,ααπcos )2cos(=+k ,ααπtan )2tan(=+k ,ααπcot )2cot(=+k 。
作用:这组公式可以把任意角的三角比转化为)2,0[π区间上的角的三角比。
(设计目的:复习回顾第一组诱导公式的形成过程及其应用,加深学生对公式和作用的理解) 引入:过渡:接下来我们继续研究角α与α-的终边对称关系及三角比之间的关系。
二【新知探究】问题3:角α与α-呢?探究过程:1、角α与α-(1)如右图1,在直角坐标系中,已知角α的终边OP ,请在图1中作出角α-的终边:(2)角α与角α-的终边关于 x 轴 对称。
5.3同角三角比的关系与诱导公式(1)教案和作业

同角三角比的关系与诱导公式(1)2012年 月 日 班级 姓名教学目标 由三角比的定义,找出同角三角比的基本关系式;会简单应用同角公式. 教学重点 同角三角比公式的推导与应用教学难点 三角比符号的确定及公式的变形应用教学过程一、 同角三角比的关系式:1.已知角α终边上一点),(y x P ,22y x r +=,则角α的六个三角比分别是. αsin = ;αcos = ; αtan = ; αcot = ;αsec = ; αcsc = .2.讨论角α的六个三角比之间有什幺关系?(师生共同研究总结)(1)倒数关系: .(2)商数关系: .(3)平方关系: . 注意①“同角”与角的形式无关:如14cos 4sin 22=+αα,2tan 2cos 2sin ααα=等; ②关系式都是对于它们有意义的角而言的,如),2(1cot tan Z k k ∈≠=⋅πααα;③对这些关系式不仅要牢固掌握,还要能灵活运用(顺用、逆用、变形用),如:αα2sin 1cos -±=,αα22cos 1sin -=, αααtan sin cos =等。
二.公式的应用例题1:已知,54cos =α且α为第四象限的角,求α的其他三角比的值;练习:已知54sin -=α,且α为第三象限的角,求α的其他三角比的值;例题2:已知 125tan =α,求ααcos sin 、和αcot ;练习:已知2cot -=α,求ααcos sin 、的值;例3.化简)cos 1)(tan 1sin 1(ααα-+. (总结: 切化弦 )练习:(1)化简2sin 12- (2))(cos sin 21是第四象限角θθθ-小结:(1)同角三角比基本关系式及成立的条件;(2)求三角比的值时,首先确定角的终边位置,再根据关系式求值同角三角比的关系与诱导公式(1)(作业)2012年 月 日 班级 姓名1.角α的六个三角比之间有的关系是:(1)倒数关系: .(2)商数关系: .(3)平方关系: .2.若α是第二象限角,化简1sec cot 2-αα= ; αα2tan 1cos +=3.化简0400cos 1-= 4.已知54sin =α,并且α是第二象限角,求α的其他三角函数值.5.已知178cos -=α,求sin α、tan α的值.6.已知2tan -=α,Z k k k ∈++∈),2,22(ππππα,求ααcos ,sin 的值.7.若α是第三象限角,且2sec -=α,求αααtan ,cos ,sin 的值.8.)sin (tan cot 222ααα-。
5.3同角三角比关系和诱导公式(1)教案

5.3课题:同角三角比关系和诱导公式(1)(教案)教学目的:1、理解同角三角比的关系式的导出,知道这些关系式成立的条件2、掌握已知角的一个三角比,求它的其它三角比的方法 教学重点:理解同角三角比关系式的导出,知道这些关系式成立的条件 教学过程: (一)、引入我们已学习了任意角三角比的定义, 如图所示:在α的终边上任取一点()y x P ,, 点P 与原点的距离()022>+=r y x r ,则角α的六个三角比的值是:r y =αsin xy =αtan xr =αsec rx =αcos yx =αcot yr =αcsc (二)、新课 一、观察x y =αtan 及yx =αcot ,由 1cot tan =⋅=⋅y xx y αα,可知它们互为倒数,思考:(1)α应满足什么条件?α应使αtan 、αcot 有意义,∴()Z k k k ∈≠+≠παππα且2(即Z k k ∈≠,2πα)(2)是否还有其他倒数关系?α应满足什么条件?(3)同角的六个三角比之间除了倒数关系是否还有其他关系?α应满足什么条件? 二、概念或定理或公式教学(推导)由r y =αsin ,yr=αcsc ,可知αsin ,αcsc 互为倒数,()Z k k ∈≠πα 由r x =αcos ,x r =αsec ,可知αcos ,αsec 互为倒数,()Z k k ∈+≠2ππα 由r y =αsin ,r x =αcos ,x y =αtan ,可知当0cos ≠α时,αααcos sin tan =,所以αsin 、αcos 、αtan 之间存在商数关系,α应满足()Z k k ∈+≠2ππα而αsin 、αcos 、αcot 之间也存在商数关系,αααsin cos cot =,α应满足0sin ≠α即()Z k k ∈≠πα 由r y =αsin ,r x=αcos ,122=+y x ,可知αsin ,αcos 有如下的平方关系:1cos sin 222222222==+=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=+r r r x y r x r y αα,即1c o ss i n 22=+αα,R ∈α 同理 αα22sec 1tan =+ ,()Z k k ∈+≠2ππααα22csc 1cot =+ ,()Z k k ∈≠πα同角三角比关系有三种,分别是:倒数关系、商数关系、平方关系倒数关系:1csc sin =⋅αα 1s e c c o s=⋅αα 1c o t t a n =⋅αα 商数关系:αααcos sin tan =αααs i n c o s c o t =平方关系:1cos sin 22=+αα αα22s e c 1t a n =+ αα22c s c 1c o t =+ 注:上面这些关系式都是恒等式,即当α取关系式的两边都有意义的任意值时,关系式两边的值都相等 三、(概念辨析或变式问题) 填空:(1)⋅αcsc1=;=αcos 1; =⋅ααcot tan(2)=⋅ααcos tan ;=ααc o t c o s(3)=-α2cos 1; =-α2s e c 1; =-1c s c 2α(4)下列四个命题中错误的是 ① ② ③ ④①21tan =α且31cot =α ②31sin =α且32cos =α ③21sin =α且2csc -=α ④34sec =α且31tan =α四、典型例题 例1、已知54cos =α,且α是第四象限角,求角α的其他三角比。
沪教版高一数学(下)5.3 同角三角比的关系和诱导公式学案

同角三角比的关系和诱导公式【学习目标】1.运用同角三角比关系解决一些三角恒等式的化简和证明。
2.运用诱导公式进行简单三角式的求值、化简与恒等式的证明。
【学习重难点】同角三角比关系的灵活应用。
【学习过程】一、自主学习(一)知识点罗列1.同角三角比中的关系:平方关系:1cos sin 22=+αα⇒αα22cos 1sin -=、αα22sin 1cos -=;αα22sec tan 1=+⇒αα22tan 1sec =-、1tan sec 22=-αα;αα22csc cot 1=+⇒αα22cot 1csc =-、1cot csc 22=-αα。
商数关系:αααcos sin tan =; αααsin cos cot =。
倒数关系:ααcos 1sec =; ααsin 1csc =; ααtan 1cot =。
2.根据第一组诱导公式写出任意角三角比的其他三个诱导公式:(1)___________________________(2)___________________________(3)___________________________(二)小试牛刀 已知31tan =α,试计算αααααcot cos cos sin sin 2224++的值。
先化简再求值可使运算简便。
=++αααααcot cos cos sin sin 2224___________________________=αcot 131。
二、典型例题例1.证明下列恒等式。
(1))cot (csc sin )1)(sec sin 1(22222A A A A A -=--。
证明:左边___________________________________;右边A A 22sin 1sin =⋅= 左边=右边;所以)cot (csc sin )1)(sec sin 1(22222A A A A A -=--成立。
数学高一(下)沪教版(同角三角比的关系式和诱导公式(一))教师版

7、已知tanα=2,则 =__________.
解析: = = + =tanα+ =2+ = .
答案:
8、已知tanα+ = ,则tan2α+ + =__________.
解析:tanα+ = ,
∴ + = = .
∴tan2α+ +
=(tanα+ )2-2+
=( )2-2+ = .
答案:
三、解答题
例3、已知 ,求下列各式的值。
(1)
(2)
【解】方法一:由 ,得
(1)原式
(2)原式
方法二:
(1)
(2)
变式练习:已知 ,求下列各式的值:
(1) ;(2) ;
(3)
答案:(1) (2) (3) (4) (5) (6) (7) (8)
例4、求下列各三角比的值。
(1) ;(2) ;(3) ;(4) (5)sin210°
(1)平方关系: , , ;
(2)倒数关系: , , ;
(3)商数关系: ,( ) ( )
2、诱导公式:诱导公式可用十个字概括为:奇变偶不变,符号看象限
:,,;
:,,;
:,,;
:,,;
:,,;
:,,;
:,,;
:,,;
:,,;
【典型例题分析】
例1、已知 ,求 值。
答案:
当 是第一象限角时,
当 是第三象限角时,
精锐教育学科教师辅导讲义
年级:高一辅导科目:数学课时数:3
课题
同角三角比的关系式和诱导公式(一)
教学目的
1、理解和掌握同角三角比的八个关系式,并能用这些关系式解决一些三角恒等变换的化简与证明问题;
2、掌握诱导公式并能够运用诱导公式进行化简、求值、与恒等证明。
同角三角函数的基本关系与诱导公式 教案

第二节同角三角函数的基本关系与诱导公式[最新考纲] 1.理解同角三角函数的基本关系式:sin2α+cos2α=1,sin αcos α=tan α;2.能利用单位圆中的三角函数线推导出π2±α,π±α的正弦、余弦、正切的诱导公式.1.同角三角函数的基本关系式(1)平方关系:sin2α+cos2α=1;(2)商数关系:tan α=sin αcos α.2.诱导公式组序一二三四五六角2kπ+α(k∈Z)π+α-απ-απ2-απ2+α正弦sin α-sin α-sin αsin αcos αcos α余弦cos α-cos αcos α-cos αsin α-sin α正切tan αtan α-tan α-tan α口诀函数名不变,符号看象限函数名改变符号看象限[常用结论]1.同角三角函数关系式的常用变形(sin α±cos α)2=1±2sin αcos α;sin α=tan α·cos α. 2.诱导公式的记忆口诀“奇变偶不变,符号看象限”,其中的奇、偶是指π2的奇数倍和偶数倍,变与不变指函数名称的变化.一、思考辨析(正确的打“√”,错误的打“×”) (1)若α,β为锐角,则sin 2α+cos 2β=1. ( ) (2)若α∈R ,则tan α=sin αcos α恒成立. ( ) (3)sin(π+α)=-sin α成立的条件是α为锐角. ( ) (4)若sin(k π-α)=23(k ∈Z ),则sin α=23. ( ) [答案] (1)× (2)× (3)× (4)× 二、教材改编1.化简sin 690°的值是( )A.12 B .-12 C.32 D .-32 B [sin 690°=sin(720°-30°)=-sin 30°=-12.选B.]2.若sin α=55,π2<α<π,则tan α= . -12 [∵π2<α<π, ∴cos α=-1-sin 2α=-255,∴tan α=sin αcos α=-12.] 3.已知tan α=2,则sin α+cos αsin α-cos α的值为 .3 [原式=tan α+1tan α-1=2+12-1=3.]4.化简cos ⎝ ⎛⎭⎪⎫α-π2sin ⎝ ⎛⎭⎪⎫52π+α·sin(α-π)·cos(2π-α)的结果为 .-sin 2α [原式=sin αcos α·(-sin α)·cos α=-sin 2α.]考点1 同角三角函数基本关系式 同角三角函数基本关系的应用技巧(1)弦切互化:利用公式tan α=sin αcos α实现角α的弦切互化.(2)和(差)积转换:利用(sin α±cos α)2=1±2sin αcos α进行变形、转化. (3)“1”的变换:1=sin 2α+cos 2α=cos 2α(tan 2α+1)=sin 2α⎝ ⎛⎭⎪⎫1+1tan 2α.“知一求二”问题(1)[一题多解]已知cos α=k ,k ∈R ,α∈⎝ ⎛⎭⎪⎫π2,π,则sin(π+α)=( ) A .-1-k 2 B.1-k 2 C .±1-k 2D .-k(2)(2019·福州模拟)若α∈⎝ ⎛⎭⎪⎫π2,π,sin(π-α)=35,则tan α=( )A .-43 B.43 C .-34D.34(1)A (2)C [(1)法一:(直接法)由cos α=k ,α∈⎝ ⎛⎭⎪⎫π2,π得sin α=1-k 2,所以sin(π+α)=-sin α=-1-k 2.故选A.法二:(排除法)易知k <0,从而sin(π+α)=-sin α<0,排除选项BCD ,故选A.(2)因为α∈⎝ ⎛⎭⎪⎫π2,π,sin α=35,所以cos α=-45,所以tan α=-34.]利用同角三角函数的基本关系求解问题的关键是熟练掌握同角三角函数的基本关系的正用、逆用、变形.同角三角函数的基本关系本身是恒等式,也可以看作是方程,对于一些题,可利用已知条件,结合同角三角函数的基本关系列方程组,通过解方程组达到解决问题的目的,此时应注意在利用sin2α+cos2α=1求sin α或cos α时,符号的选取.弦切互化(1)(2019·郑州模拟)已知sin α+3cos α3cos α-sin α=5,则cos2α+12sin 2α的值是()A.35B.-35C.-3 D.3(2)已知θ为第四象限角,sin θ+3cos θ=1,则tan θ=.(1)A(2)-43[(1)由sin α+3cos α3cos α-sin α=5得tan α+33-tan α=5,可得tan α=2,则cos2α+12sin 2α=cos 2α+sin αcos α=cos2α+sin αcos αcos2α+sin2α=1+tan α1+tan2α=35.故选A.(2)由(sin θ+3cos θ)2=1=sin2θ+cos2θ,得6sin θcos θ=-8cos2θ,又因为θ为第四象限角,所以cos θ≠0,所以6sin θ=-8cos θ,所以tan θ=-43.]若已知正切值,求一个关于正弦和余弦的齐次分式的值,则可以通过分子、分母同时除以一个余弦的齐次幂将其转化为一个关于正切的分式,代入正切值就可以求出这个分式的值,这是同角三角函数关系中的一类基本题型.sin α±cos α与sin αcos α关系的应用(1)若|sin θ|+|cos θ|=233,则sin4θ+cos4θ=()A.56 B.1718C.89 D.23(2)已知θ为第二象限角,sin θ,cos θ是关于x的方程2x2+(3-1)x+m=0(m∈R)的两根,则sin θ-cos θ=()A.1-32 B.1+32C. 3 D.- 3(1)B(2)B[(1)因为|sin θ|+|cos θ|=233,两边平方,得1+|sin 2θ|=43.所以|sin 2θ|=13.所以sin4θ+cos4θ=1-2sin2θcos2θ=1-12sin22θ=1718.故选B.(2)因为sin θ,cos θ是方程2x2+(3-1)x+m=0(m∈R)的两根,所以sin θ+cos θ=1-32,sin θ·cos θ=m2,可得(sin θ+cos θ)2=1+2sin θ·cos θ=1+m=2-32,解得m=-32.因为θ为第二象限角,所以sin θ>0,cos θ<0,即sin θ-cos θ>0,因为(sin θ-cos θ)2=1-2sin θ·cos θ=1-m=1+32,所以sin θ-cosθ=1+32=1+32.故选B.]对于sin α+cos α,sin α-cos α,sin αcos α这三个式子,知一可求二,若令sin α+cos α=t(t∈[-2,2]),则sin αcos α=t2-12,sin α-cos α=±2-t2(注意根据α的范围选取正、负号),体现了方程思想的应用.1.已知sin(π+α)=-13,则tan⎝⎛⎭⎪⎫π2-α值为()A.2 2 B.-2 2C.24D.±2 2D[因为sin(π+α)=-13,所以sin α=13,cos α=±223,tan⎝⎛⎭⎪⎫π2-α=cos αsin α=±2 2.故选D.]2.已知tan θ=2,则sin θ+cos θsin θ+sin2θ的值为()A.195 B.165C.2310 D.1710C[原式=sin θ+cos θsin θ+sin 2θ=sin θ+cos θsin θ+sin2θsin2θ+cos2θ=tan θ+1tan θ+tan2θtan2θ+1,将tan θ=2代入,得原式=2310.故选C.]3.已知sin x+cos x=3-12,x∈(0,π),则tan x=()A.-33 B.33C. 3 D.- 3D[因为sin x+cos x=3-12,且x∈(0,π),所以1+2sin x cos x=1-32,所以2sin x cos x=-32<0,所以x为钝角,所以sin x-cos x=(sin x-cos x)2=1+32,结合已知解得sin x=32,cos x=-12,则tan x=sin xcos x=- 3.]4.若3sin α+cos α=0,则1cos2α+2sin αcos α的值为.103[3sin α+cos α=0⇒cos α≠0⇒tan α=-1 3,1cos2α+2sin αcos α=cos2α+sin2αcos2α+2sin αcos α=1+tan2α1+2tan α=1+⎝⎛⎭⎪⎫-1321-23=103.]考点2诱导公式的应用应用诱导公式的一般思路(1)化大角为小角,化负角为正角;(2)角中含有加减π2的整数倍时,用公式去掉π2的整数倍.(1)设f (α)=2sin (π+α)cos (π-α)-cos (π+α)1+sin 2α+cos ⎝ ⎛⎭⎪⎫3π2+α-sin 2⎝ ⎛⎭⎪⎫π2+α(1+2sin α≠0),则f ⎝ ⎛⎭⎪⎫-23π6= .(2)已知cos ⎝ ⎛⎭⎪⎫π6-θ=a ,则cos ⎝ ⎛⎭⎪⎫5π6+θ+sin ⎝ ⎛⎭⎪⎫2π3-θ的值是 .(1)3 (2)0 [(1)因为f (α)=(-2sin α)(-cos α)+cos α1+sin 2α+sin α-cos 2α=2sin αcos α+cos α2sin 2α+sin α=cos α(1+2sin α)sin α(1+2sin α)=1tan α,所以f ⎝ ⎛⎭⎪⎫-23π6=1tan ⎝ ⎛⎭⎪⎫-23π6=1tan ⎝ ⎛⎭⎪⎫-4π+π6=1tan π6= 3.(2)因为cos ⎝ ⎛⎭⎪⎫5π6+θ=cosπ-⎝ ⎛⎭⎪⎫π6-θ=-cos ⎝ ⎛⎭⎪⎫π6-θ=-a ,sin ⎝ ⎛⎭⎪⎫2π3-θ=sin π2+⎝ ⎛⎭⎪⎫π6-θ=cos ⎝ ⎛⎭⎪⎫π6-θ=a ,所以cos ⎝ ⎛⎭⎪⎫5π6+θ+sin ⎝ ⎛⎭⎪⎫2π3-θ=0.] (1)已知角求值问题,关键是利用诱导公式把任意角的三角函数值转化为锐角的三角函数值求解.转化过程中注意口诀“奇变偶不变,符号看象限”的应用.(2)对给定的式子进行化简或求值时,要注意给定的角之间存在的特定关系,充分利用给定的关系结合诱导公式将角进行转化.特别要注意每一个角所在的象限,防止符号及三角函数名出错.1.化简:tan (π+α)cos (2π+α)sin ⎝ ⎛⎭⎪⎫α-3π2cos (-α-3π)sin (-3π-α)= .-1 [原式==tan αcos αsin ⎝ ⎛⎭⎪⎫π2+α(-cos α)sin α=tan αcos αcos α(-cos α)sin α=-tan αcos αsin α=-sin αcos α·cos αsin α=-1.]2.已知角α终边上一点P (-4,3),则cos ⎝ ⎛⎭⎪⎫π2+α·sin (-π-α)cos ⎝ ⎛⎭⎪⎫11π2-α·sin ⎝ ⎛⎭⎪⎫9π2+α的值为 .-34 [原式=(-sin α)sin α(-sin α)cos α=tan α,根据三角函数的定义得tan α=-34.]考点3 同角三角函数基本关系式和诱导公式的综合应用 求解诱导公式与同角关系综合问题的基本思路和化简要求 基本思路①分析结构特点,选择恰当公式;②利用公式化成单角三角函数;③整理得最简形式 化简要求①化简过程是恒等变换;②结果要求项数尽可能少,次数尽可能低,结构尽可能简单,能求值的要求出值已知f (x )=(+)(-)cos 2[(2n +1)π-x ](n ∈Z ).(1)化简f (x )的表达式; (2)求f ⎝ ⎛⎭⎪⎫π2 018+f ⎝ ⎛⎭⎪⎫504π1 009的值.[解] (1)当n 为偶数,即n =2k (k ∈Z )时, f (x )=cos 2(2k π+x )·sin 2(2k π-x )cos 2[(2×2k +1)π-x ]=cos 2x ·sin 2(-x )cos 2(π-x )=cos 2x ·(-sin x )2(-cos x )2=sin 2x ;当n 为奇数,即n =2k +1(k ∈Z )时,f (x )=cos 2[(2k +1)π+x ]·sin 2[(2k +1)π-x ]cos 2{[2×(2k +1)+1]π-x }=cos 2[2k π+(π+x )]·sin 2[2k π+(π-x )]cos 2[2×(2k +1)π+(π-x )]=cos 2(π+x )·sin 2(π-x )cos 2(π-x )=(-cos x )2sin 2x (-cos x )2=sin 2x , 综上得f (x )=sin 2x .(2)由(1)得f ⎝ ⎛⎭⎪⎫π2 018+f ⎝ ⎛⎭⎪⎫504π1 009=sin 2π2 018+sin 21 008π2 018 =sin 2π2 018+sin 2⎝ ⎛⎭⎪⎫π2-π2 018=sin 2π2 018+cos 2π2 018=1.(1)利用同角三角函数关系式和诱导公式求值或化简时,关键是寻求条件、结论间的联系,灵活使用公式进行变形.(2)注意角的范围对三角函数符号的影响.1.已知α为锐角,且2tan(π-α)-3cos ⎝ ⎛⎭⎪⎫π2+β+5=0,tan(π+α)+6sin(π+β)-1=0,则sin α的值是( )A.355 B.377 C.31010D.13C [由已知可得-2tan α+3sin β+5=0.tan α-6sin β-1=0,解得tan α=3,又α为锐角,故sin α=31010.]2.已知tan(π-α)=-23,且α∈⎝⎛⎭⎪⎫-π,-π2,则cos(-α)+3sin(π+α)cos(π-α)+9sin α=.-15[由tan(π-α)=-23,得tan α=23,则cos(-α)+3sin(π+α)cos(π-α)+9sin α=cos α-3sin α-cos α+9sin α=1-3tan α-1+9tan α=1-2-1+6=-15.]3.已知sin α+cos α=-15,且π2<α<π,则1sin(π-α)+1cos(π-α)的值为.3512[由sin α+cos α=-15平方得sin αcos α=-1225,∵π2<α<π,∴sin α-cos α=(sin α+cos α)2-4sin αcos α=7 5,∴1sin(π-α)+1cos(π-α)=1sin α-1cos α=cos α-sin αsin αcos α=-75-1225=3512.][教师备选例题]已知-π<x<0,sin(π+x)-cos x=-1 5.(1)求sin x-cos x的值;(2)求sin 2x+2sin2x1-tan x的值.[解](1)由已知,得sin x+cos x=1 5,两边平方得sin2x+2sin x cos x+cos2x=125,整理得2sin x cos x=-2425.∵(sin x-cos x)2=1-2sin x cos x=49 25,由-π<x<0知,sin x<0,又sin x cos x=-1225<0,∴cos x>0,∴sin x-cos x<0,故sin x-cos x=-75.(2)sin 2x+2sin2x1-tan x=2sin x(cos x+sin x)1-sin xcos x=2sin x cos x(cos x+sin x)cos x-sin x=-2425×1575=-24175.7。
5.3同角三角比的关系和诱导公式(4)教案

课题:5.3(4)同角三角比关系和诱导公式(教案)教学目的:1、熟练掌握同角三角比关系,并应用其进行求值、化简和证明2、熟练掌握四组诱导公式,并应用其进行求值、化简和证明教学重点:同角三角比的关系和诱导公式的应用 教学过程: (一)引入一、(设置情境)已知ABC ∆中,53sin =A ,求A cos ,A tan 的值 已知角的一个三角比的值,可以求它的其它三角比的值,当角的象限不确定时应讨论二、(双基回顾) 1、同角三角比的关系:(1)平方关系:1cos sin 22=+αα,αα22sec tan 1=+,αα22csc cot 1=+;(2)商数关系:αααcos sin tan =,αααsin cos cot =;(3)倒数关系:1csc sin =αα,1sec cos =αα,1cot tan =αα; 2、诱导公式:四组诱导公式,把任意角的三角比化为锐角三角比3、“1”的代换:ααcsc sin 1=、ααsec cos 1=、ααcot tan 1=、αα22cos sin 1+=、αα22tan sec 1-=、αα22cot csc 1-=、4tan1π=、4cot1π=;(二)新课 一、典型例题例1、已知ABC ∆中,53sin =A ,求A cos ,A tan 的值 解:因为053sin >=A ,所以A 在第一象限或A 在第二象限 A 在第一象限时,54cos =A ,43tan =AA 在第二象限时,54cos -=A ,43tan -=A例2、化简:()()()()()()αππααππααπαπ+-⋅--⋅+-sin 5cos 3cos 2tan tan sin解:原式=1sin cos cos tan tan sin =--⋅-⋅-αααααα例3、化简ααcos 1cos 1+-ααcos 1cos 1-+-(παπ2<<) 解:原式=αα22cos 1)cos 1(--αα22cos 1)cos 1(-+-|sin ||cos 1|αα-=|sin ||cos 1|αα+- 因为παπ2<<,所以0sin <α,1cos 1<<-α,所以0cos 1>±α原式ααsin cos 1--==-+-ααsin cos 1αααcot 2sin cos 2=--=例4、已知θ是第四象限角,51cos sin =+θθ,求:(1)θθcos sin -;(2)θθ33cos sin +;(3)θθcot tan +;(4)θtan解:(1)()()2549cos sin cos sin 21cos sin 2512cos sin 51cos sin 22=-⇒⎪⎭⎪⎬⎫-=--=⇒=+θθθθθθθθθθ 又 θ是第四象限角,则57cos sin -=-θθ (2)θθ33cos sin +=+-+=)cos cos sin )(sin cos (sin 22θθθθθθ12537 (3)1225cos sin cos sin sin cos cos sin cot tan 22-=+=+=+θθθθθθθθθθ (4)⎪⎩⎪⎨⎧-=⇒=-=⇒⎪⎭⎪⎬⎫-=-=+43tan 54cos 53sin 57cos sin 51cos sin θθθθθθθ 二、课堂练习 1、已知⎪⎭⎫ ⎝⎛∈23,ππα,求αααα22tan 1sec 1sec tan +⋅+-⋅的值 (1-)2、已知0cos 3sin =-αα,求αααα22sin 3cos sin 8cos 3-+的值 ( 0 )三、拓展探究 1、已知416sin =⎪⎭⎫⎝⎛+πx ,求⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+x x 611cos 67sin 2ππ的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.3(2)同角三角比的关系与诱导公式
上海市杨浦高级中学 江海涛
一、教学目标设计
1.掌握诱导公式的推导方法和记忆方法;
2.会运用这些公式求解任意角的三角比的值,会由三角比的值,求特殊角,并会化简单的三角比的关系式;
3.通过公式的探求与应用培养思维的严密性. 三、教学重点及难点 重点:诱导公式
难点:诱导公式的灵活应用 四、教学流程设计
五、教学过程
设计
一、 复习引入 1.公式一:
ααπsin )2sin(=+k ααπcos )2cos(=+k
ααπtan )2tan(=+k
复习公式一引入
运用化归思想由公式三导出公式 四
根据三角比的定义 和单位圆公式二、三
例题分析,运用诱导公式求值、化简及给值求角
课堂练习
课堂小结, 布置作业
ααπcot )2cot(=+k (其中α∈k )
用角度可写成:ααsin )360sin(=+︒⋅k
ααcos )360cos(=+︒⋅k ααtan )360tan(=+︒⋅k
ααcot )360cot(=+⋅
k (其中Z ∈k ) 2 .讨论
公式一的作用:把任意角的正弦、余弦、正切化为0º―360º之间角的正弦、余弦、正切,其方法是先在0º―360º内找出与角α终边相同的角,再把它写成诱导公式一的形式,然后得出结果.
这组公式可以统一概括为)Z )(()2(∈=+k f f απαk 的形式,上述一组公式叫做任意角三角比的第一组诱导公式,其特征是:等号两边是同名三角比,且符号都为正.
说明]运用公式时,注意“弧度”与“角度”两种度量制不要混用,如写成︒=+︒80sin )280sin(πk ,
3
cos
)3603
cos(
π
π
=︒⋅+k 是不对的.
二、学习新课 1.公式推导
公式二:
αα-sin sin(=-) ααcos cos(=-)
它说明角-α与角α的正弦值互为相反数,而它们的余弦值相等.这是因为,若角α的终边与单位圆交于点P(x ,y),则角-α的终边与单位圆的交点必为P ´(x ,-y)(如图1).由正弦、余弦三角比的定义,即可得
sin α=y , cos α=x, sin(-α)=-y, cos(-α)=x,
所以:sin(-α)= -sin α, cos(-α)= cos α 由三角比的商数关系,得:αα
α
αααtan cos sin )cos()sin()tan(-=-=--=
-
即 ααtan tan(-=-)
类似可得ααcot )cot(-=-
α
α
- x
y
P(x,y)
P ’(x ,-y)
O
M
这组公式叫任意角三角比的第二组诱导公式 练习:求3
π
-
的正弦、余弦、正切和余切的值.
[说明]公式二也可以由特殊到一般,既从特殊三角比的计算,猜测出公式,再证明.
公式三:
用角度可表示如下:
ααπ-sin sin(=+) αα-sin 180sin(=+︒) ααπ-cos cos(=+)
αα-cos 180cos(=+︒) ααπtan tan(=+)
ααtan 180tan(=+︒) ααπcot )cot(=+ ααsin )180cot(=+
它刻画了角180º+α与角α的正弦值(或余弦值)之间的关系,这个关系是:以角α终边的反向延长线为终边的角的正弦值(或余弦值)与角α的正弦值(或余弦值)是一对相反数.这是因为若设α的终边与单位圆交于点P( x ,y),则角α终边的反向延长线,即180º+α角的终边与单位圆的交点必为P ´(-x ,-y)(如图2).由正弦、余弦三角比的定义,即可得sin α=y , cos α=x,
sin(180º+α)=-y,
cos(180º+α)=-x,
所以 :sin(180º+α)=-sin α,cos(180º+α)=-cos α.
[说明]公式二、三的获得主要借助于单位圆及正弦、余弦比的定义.根据点P 的坐标准确地确定点P ´的坐标是关键,这里充分利用了对称的性质.直观的对称形象为我们准确写出P ´的坐标铺平了道路,体现了数形结合这一数学思想的优越性.
练习:求下列三角比的值: (1)
210cos ;
(2)4
5sin
π
分析:本题是诱导公式二的巩固性练习题.求解时,只须设法将所给角分解成180º+α或(π+α),
α为锐角即可.
解:(1)cos210º=cos(180º+30º)=-cos30º=-
2
3; (2)sin 45π=sin(4ππ+)=-sin 4
π
=-22.
公式四:
把第三组公式中的α换成α-,得第四组诱导公式:
M
P(x,y)
y
M’
α + 180
α
x P’(-x ,-y)
O
ααπsin sin(=-) ααsin 180sin(=-︒)
ααπ-cos cos(=-)
αα-cos 180cos(=-︒) ααπtan tan(-=-)
ααtan 180tan(-=-︒) ααπcot )cot(-=- ααcot )180cot(-=-
[说明]这组公式均可由前面学过的诱导公式直接推出,体现了把未知问题化为已知问题处理这一化归的数学思想.公式的推导并不难,然而推导中的化归意识和策略是值得我们关注的.
四组诱导公式可概括为:
k ·360º+α(k ∈Z ),-α,180º±α,360º-α的三角比值,等于α的同名三角比的值,前面加
上一个把α看成锐角时原三角比的符号.
[说明]这里的“同名三角比值”是指等号两边的三角比名称相同;“把α看成锐角”是指α原本是任意角,这里只是把它视为锐角处理;“前面加上一个……符号”是指α的同名三角比值未必就是最后结果,前面还应添上一个符号(正号或负号,主要是负号,正号可省略),而这个符号是把任意角α视为锐角情况下的原三角比的符号.应注意讲清这句话中每一词语的含义,特别要讲清为什么要把任意角α看成锐角.建议通过实例分析说明.
练习:求下列各式的值:(1)sin(-
3
4π
);(2)cos(-60º)-sin(-210º) 分析:本题是诱导公式二、三的巩固性练习题.求解时一般先用诱导公式三把负角的正弦、余弦化为正角的正弦、余弦,然后再用诱导公式二把它们化为锐角的正弦、余弦来求.
解:(1)sin(-
34π)=-sin(3ππ+)=sin 3π
=2
3; (2)原式=cos60º+sin(180º+30º)=cos60º-sin30º=21-2
1
=0 2.例题分析
例1:利用诱导公式,求下列各三角比: (1)326sin
π; (2))4
13tan(π
-
例2化简:
)
3cot()sin()
tan()cot()2cos(απαππααπαπ----+-
例3根据条件,求角x :
(1) 已知)2,0[,2
1
sin π∈=
x x ; (2)已知),[,3
3
tan ππ-∈=
x x . [说明]由三角比求特殊角的问题,是个“反”问题,对学生是个难点问题,教师可先缩小范围,如考虑在[0,
2
π
]上,求角,再考虑[0,2)π等. 三、巩固练习 P49 练习 5.3(2) 四、课堂小结
通过本节课的教学,我们获得了诱导公式.值得注意的是公式右端符号的确定.在运用诱导公式进行三角比的求值或化简中,我们又一次使用了转化的数学思想.通过进行角的适当配凑,使之符合诱导公式中角的结构特征,培养了我们思维的灵活性.
五、作业布置
习题5.3 A 组:1;4(1)(2);5 B 组:1;4。
