高中物理 1.3简谐运动的图像和公式同步练习(含解析)教科版选修34
物理(教科版选修34)练习活页作业(三)简谐运动的图像和公式

活页作业(三)简谐运动的图像和公式知识点一简谐运动的图像1.弹簧振子做简谐运动,其位移x与时间t的关系如图所示,则()A.在t=1 s时,速度的值最大,方向为负,加速度为零B.在t=2 s时,速度的值最大,方向为负,加速度为零C.在t=3 s时,速度的值最大,方向为正,加速度最大D.在t=4 s时,速度的值最大,方向为正,加速度最大解析:当t=1 s时,位移最大,加速度最大,速度为零,选项A错误;当t=2 s时,位移为零,加速度为零,而速度最大.速度方向要看该点切线斜率的正负,t=2 s时,速度为负值,选项B正确;当t=3 s时,位移最大,加速度最大,速度为零,选项C错误;当t =4 s时,位移为零,加速度为零,速度最大,方向为正,选项D错误.答案:B2.(多选)弹簧振子做简谐运动,振动图像如图所示,则下列说法正确的是()A.t1、t2时刻振子的速度大小相等,方向相反B.t1、t2时刻振子的位移大小相等,方向相反C.t2、t3时刻振子的速度大小相等,方向相反D.t2、t4时刻振子的位移大小相等,方向相反解析:从图像可以看出,t1、t2时刻振子位于同一位置,位移大小相同,方向相同,速度大小相等,方向相反,故选项A正确,选项B错误;t2、t3时刻振子位移大小相等,方向相反,速度大小相等,方向相同,故选项C错误;t2、t4时刻,振子分别位于平衡位置两侧且对称,位移大小相等,方向相反,故选项D正确.答案:AD3.(多选)如图所示是一弹簧振子在水平面内做简谐运动的振动图像,则振子在() A.t1和t4时刻具有相同的动能和速度B.t3和t5时刻具有相同的动能和不同的速度C.t3和t4时刻具有相同的加速度D.t2和t5时刻振子所受回复力大小之比为2∶1解析:由简谐运动的对称性及运动规律分析可知选项B、D正确.答案:BD4. 一单摆做小角度摆动,其振动图像如图所示,以下说法正确的是()A.t1时刻摆球速度最大,悬线对它的拉力最小B.t2时刻摆球速度为零,悬线对它的拉力最小C.t3时刻摆球速度为零,悬线对它的拉力最大D.t4时刻摆球速度最大,悬线对它的拉力最大解析:由振动图像可看出,t1和t3时刻,小球偏离平衡位置的位移最大,此时其速度为零,悬线对它的拉力最小,故选项A,C错误;t2时刻和t4时刻,小球位于平衡位置,其速度最大,悬线的拉力最大,故选项B错误,选项D正确.答案:D5.(多选)如图所示为甲、乙两单摆的振动图像,则()A.若甲、乙两单摆在同一地点摆动,则甲、乙两单摆的摆长之比l甲∶l乙=2∶1B.若甲、乙两单摆在同一地点摆动,则甲、乙两单摆的摆长之比l甲∶l乙=4∶1C.若甲、乙两摆摆长相同,且在不同的星球上摆动,则甲、乙两摆所在星球的重力加速度之比g甲∶g乙=4∶1D.若甲、乙两摆摆长相同,且在不同的星球上摆动,则甲、乙两摆所在星球的重力加速度之比g甲∶g乙=1∶4解析:由图像可知T甲∶T乙=2∶1,若两单摆在同一地点,g相等,由周期公式T=2πlg得l甲∶l乙=4∶1;若两摆长相等,则所在星球的重力加速度之比为g甲∶g乙=1∶4,故选项B、D正确.答案:BD6.如图所示是某弹簧振子的振动图像,由图可知()A.振子的振幅为10 cmB .振子的周期为16 sC .第12 s 末振子的速度为负值,加速度为零D .第16 s 末振子的加速度最大,速度为零解析:振幅是位移的最大值的大小,故振幅为5 cm ,故A 错误;周期是完成一次全振动的时间,故周期为16 s ,故B 正确;第12 s 末振子的位移为负的最大,故速度为零,没有方向,加速度最大,故C 错误;第16 s 末振子的位移为零,振子经过平衡位置,故速度最大,加速度最小,故D 错误.答案:B知识点二 简谐运动的表达式7.一质点做简谐运动,从平衡位置运动到最远点需要14周期,则从平衡位置走过该距离的一半所需要的时间为( )A .18周期 B .16周期 C .110周期 D .112周期 解析:根据简谐运动的图像及表达式,x =A sin 2πT t ,将t =T 4代入,x =A ,再将x =A 2代入,知t =T 12,故D 项正确. 答案:D8.(多选)如图是一做简谐运动的物体的振动图像,下列说法中正确的是( )A .1.5 s 末和2.5 s 末速度与加速度方向均相同B .3 s 末振动质点的加速度最大C .物体的振动方程为x =10sin 4πt cmD .物体的振动方程为x =10sin 50πt cm解析:由振动图像知1.5 s 末物体正处于从正向最大位移处向平衡位置运动的过程,而2.5 s 末物体正处于从平衡位置向负向最大位移处运动的过程,故物体在这两个时刻速度大小、方向均相同,但加速度方向相反,选项A 错误;3 s 末物体处于负向最大位移处,加速度最大,选项B 正确;由图像可知A =10 cm ,T =4×10-2 s ,初相φ=0,故表达式x =A sin ⎝⎛⎭⎫2πT t +φ=10sin 50πt cm ,选项C 错误,选项D 正确. 答案:BD9.(多选)一简谐振子沿x 轴振动,平衡位置在坐标原点t =0时刻振子的位移x =-0.1 m ;t =43 s 时刻x =0.1 m ;t =4 s 时刻x =0.1 m .该振子的振幅和周期可能为( ) A .0.1 m ,83s B .0.1 m,8 s C .0.2 m ,83 s D .0.2 m,8 s 解析:若振幅A =0.1 m 时,T =83 s ,则43s 为半周期,从-0.1 m 处运动到0.1 m 处,符合运动实际,4 s -43 s =83s 为一个周期,正好返回0. 1 m 处,所以A 项正确.若A =0.1 m ,T =8 s ,43 s 只是T 的16,不可能由负的最大位移处运动到正的最大位移处,所以B 项错误.若A =0.2 m ,T =83 s ,43 s =T 2,振子可以由-0.1 m 运动到对称位置,4 s -43s =83s =T ,振子可以由0.1 m 返回0.1 m ,所以C 项正确.若A =0.2 m ,T =8 s ,43 s =2×T 12,而sin ⎝⎛⎭⎫2πT ×T 12=12,即T 12时间内,振子可以从平衡位置运动到0.1 m 处;再经83s 又恰好能由0.1 m 处运动到0.2 m 处后,再返回0.1 m 处,故D 项正确.答案:ACD10.如图所示是弹簧振子的振动图像,请回答下列问题.(1)振子的振幅、周期、频率分别为多少?(2)根据振动图像写出该简谐运动的表达式.解析:(1)由振动图像可知,振子的振幅A =2 cm.周期T =0.8 s ,频率f =1T=1.25 Hz. (2)由图像可知振子的角速度ω=2πT=2.5π,简谐运动的初相φ=0. 将A =2 cm ,ω=2.5π,φ=0代入x =A sin(ωt +φ)得x =2sin 2.5πt (cm).答案:(1)2 cm 0.8 s 1.25 Hz(2)x =2sin 2.5πt (cm)。
【学案导学 备课精选】2015年高中物理 1.3简谐运动的图像和公式同步练习(含解析)教科版选修3-4

第3节 简谐运动的图像和公式1.以横坐标表示________,纵坐标表示________________________________________,描绘出简谐运动的质点的________随________变化的图像,称为简谐运动的图像(或振动图像).简谐运动的图像是一条________(或________)曲线.2.由简谐运动的图像,可以直接读出物体振动的________和________.用图像记录振动的方法在实际生活中有很多应用,如医院里的________________、监测地震的____________等.3.简谐运动的表达式:x =________________或x =________________.其中A 表示简谐运动的________,T 和f 分别表示简谐运动的周期和频率,________或________表示简谐运动的相位,Φ表示t =0时的相位,叫做初相位,简称初相.频率相同、初相不同的两个振动物体的相位差是________.4.如图1所示是一做简谐运动的物体的振动图像,下列说法正确的是( )图1A .振动周期是2×10-2sB .第2个10-2s 内物体的位移是-10 cm C .物体的振动频率为25 Hz D .物体的振幅是10 cm5.摆长为l 的单摆做简谐运动,若从某时刻开始计时(即取t =0),当振动至t =3π2l g时,摆球恰具有负向最大速度,则单摆的振动图像是下图中的( )6.物体A 做简谐运动的振动位移x A =3sin (100t +π2) m ,物体B 做简谐运动的振动位移x B =5sin (100t +π6) m .比较A 、B 的运动( )A .振幅是矢量,A 的振幅是6 m ,B 的振幅是10 m B .周期是标量,A 、B 周期相等为100 sC .A 振动的频率f A 等于B 振动的频率f BD .A 的相位始终超前B 的相位π3概念规律练知识点一 简谐运动的图像1.如图2所示是表示一质点做简谐运动的图像,下列说法正确的是( )图2A.t1时刻振子正通过平衡位置向上正方向运动B.t2时刻振子的位移最大C.t3时刻振子正通过平衡位置向上正方向运动D.该图像是从平衡位置计时画出的2.如图3所示是某质点做简谐运动的振动图像,根据图像中的信息,回答下列问题:图3(1)质点离开平衡位置的最大距离是多少?(2)在1.5 s和2.5 s两个时刻,质点向哪个方向运动?(3)质点在第2秒末的位移是多少?在前4秒内的路程是多少?知识点二简谐运动的表达式3.一物体沿x轴做简谐运动,振幅为8 cm,频率为0.5 Hz,在t=0时,位移是4 cm,且向x轴负方向运动,试写出用正弦函数表示的振动方程.知识点三简谐运动的相位、相位差4.如图4所示,A、B为两弹簧振子的振动图像,求它们的相位差.图45.有两个振动的振动方程分别是:x 1=3sin (100πt +π3) cm ,x 2=5sin (100πt +π4)cm ,下列说法正确的是( )A .它们的振幅相同B .它们的周期相同C .它们的相位差恒定D .它们的振动步调一致 方法技巧练根据图像判断物体运动情况的技巧6.如图5所示为质点P 在0~4 s 内的振动图像,下列叙述正确的是( )图5A .再过1 s ,该质点的位移是正向最大B .再过1 s ,该质点的速度方向向上C .再过1 s ,该质点运动到平衡位置D .再过1 s ,该质点的速度为零7.如图6所示为一弹簧振子的振动图像,如果振子的质量为0.2 kg ,求:图6(1)从计时开始经过多少时间位移第一次达到最大;(2)从第2 s 末到第3 s 末这段时间内弹簧振子的加速度、速度、位移各是怎样变化的.1.关于简谐运动的图像,下列说法中正确的是( ) A .表示质点振动的轨迹是正弦或余弦曲线B .由图像可判断任一时刻质点相对平衡位置的位移方向C.表示质点的位移随时间变化的规律D.由图像可判断任一时刻质点的速度方向2.如图7所示是某振子做简谐运动的图像,以下说法中正确的是( )图7A.因为振动图像可由实验直接得到,所以图像就是振子实际运动的轨迹B.振动图像反映的是振子位移随时间变化的规律,并不是振子运动的实际轨迹C.振子在B位置的位移就是曲线BC的长度D.振子运动到B点时的速度方向即为该点的切线方向3.如图8是用频闪照相的方法获得的弹簧振子的位移—时间图像,下列有关该图像的说法正确的是( )图8A.该图像的坐标原点建立在弹簧振子的平衡位置B.从图像可以看出小球在振动过程中是沿t轴方向移动的C.为了显示小球在不同时刻偏离平衡位置的位移,可让底片沿垂直x轴方向匀速运动D.图像中小球的疏密显示出相同时间内小球位置变化的快慢不同4.如图9所示为弹簧振子的振动图像,关于振子的振动,下列描述正确的是( )图9A.振子沿如图所示的曲线运动B.图像描述的是振子的位移随时间变化的规律C.从0.5 s到1.5 s内振子先加速运动后减速运动D.从1 s到2 s内振子先减速运动后加速运动5.如图10所示为某质点在0~4 s内的振动图像,则( )图10A.质点在3 s末的位移为2 mB.质点在4 s末的位移为8 mC.质点在4 s内的路程为8 mD.质点在4 s内的路程为零6.在水平方向上做简谐运动的质点,其振动图像如图11所示.假设向右的方向为正方向,则物体的位移向左且速度向右的时间段是( )图11A.0 s到1 s内B .1 s 到2 s 内C .2 s 到3 s 内D .3 s 到4 s 内7.一个质点做简谐运动,它的振动图像如图12所示,则( )图12A .图中的曲线部分是质点的运动轨迹B .有向线段OA 是质点在t 1时间内的位移C .有向线段OA 在x 轴的投影是质点在t 1时刻的位移D .有向线段OA 的斜率是质点在t 1时刻的瞬时速率8.如图13所示,是质点做简谐运动的图像.由此可知( )图13A .t =0时,质点位移、速度均为零B .t =1 s 时,质点位移最大,速度为零C .t =2 s 时,质点位移为零,速度沿负向最大D .t =4 s 时,质点停止运动9.有一个弹簧振子,振幅为0.8 cm ,周期为0.5 s ,初始时具有负方向的最大加速度,则它的振动方程是( )A .x =8×10-3sin ⎝⎛⎭⎪⎫4πt +π2 mB .x =8×10-3sin ⎝⎛⎭⎪⎫4πt -π2 mC .x =8×10-1sin ⎝⎛⎭⎪⎫πt +32π mD .x =8×10-1sin ⎝ ⎛⎭⎪⎫4πt +π2 m10.某质点做简谐运动,其位移随时间变化的关系式为x =A sin π4t ,则质点( )A .第1 s 末与第3 s 末的位移相同B .第1 s 末与第3s 末的速度相同C .3 s 末至5 s 末的位移方向都相同D .3 s 末至5 s 末的速度方向都相同 11.一弹簧振子沿x 轴振动,振幅为4 cm ,振子的平衡位置位于x 轴上的O 点.图14甲中的a 、b 、c 、d 为四个不同的振动状态:黑点表示振子的位置,黑点上的箭头表示运动的方向.图乙给出的①②③④四条振动图线,可用于表示振子的振动图像的是( )甲乙 图14A .若规定状态a 时t =0,则图像为①B .若规定状态b 时t =0,则图像为②C .若规定状态c 时t =0,则图像为③D .若规定状态d 时t =0,则图像为④12.如图15所示为A 、B 两个简谐运动的位移—时间图像.试根据图像写出:图15(1)A 的振幅是______cm ,周期是________s ;B 的振幅是________cm ,周期是________s. (2)这两个简谐运动的位移随时间变化的关系式. (3)在时间t =0.05 s 时两质点的位移分别是多少?13.两个简谐运动的表达式分别为x 1=4a sin(4πbt +π2),x 2=2a sin(4πbt +3π2).求它们的振幅之比,各自的频率,以及它们的相位差.14.某质点的振动方程为x =5sin(2.5πt +π2)cm ,画出该质点的振动图像.第3节 简谐运动的图像和公式答案课前预习练1.时间 摆球相对于平衡位置的位移 位移x 时间t 正弦 余弦 2.周期 振幅 心电图仪 地震仪3.Asin(2πT t +Φ) Asin(2πft +Φ) 振幅 2πT t +Φ 2πft +Φ Φ2-Φ14.BCD5.D 6.CD 课堂探究练 1.BC点评 质点做简谐运动的情况要和振动图像结合起来,利用简谐运动的图像来分析简谐运动的运动过程会更直观、方便.2.见解析解析 由图像上的信息,结合质点的振动过程可知(1)质点离开平衡位置的最大距离就是x 的最大值为10 cm ;(2)在1.5 s 后质点位移减小,因此是向平衡位置运动,在2.5 s 后质点位移增大,因此是背离平衡位置运动;(3)质点第2秒末在平衡位置,因此位移为零.质点在前4秒内完成一个周期性运动,其路程为10 cm×4=40 cm.点评 对于振动图像,不要错误地理解为振子的振动轨迹,振子位移的起始位置为平衡位置,应该与运动学中物体的位移区分开.3.x =0.08sin (πt +56π) m解析 简谐运动振动方程的一般表达式为x =Asin(ωt +Φ).根据题给条件有A =0.08 m ,ω=2πf =π,所以x =0.08sin (πt +Φ) m .将t =0时x =0.04 m 代入振动方程得0.04=0.08sin Φ,解得初相Φ=π6或Φ=56π.因为t =0时,速度方向沿x 轴负方向,即位移在减小,所以取Φ=56π,所求的振动方程为x =0.08sin (πt +56π) m.点评 对于给定的位移,可能解得两个初相值,这要根据题意做出判断,舍去不合题意的值.4.12π 解析 该题考查相位差的求法,由图像可知这两个振动的周期相同,均为0.4 s ,因此有确定的相位差.而相位差为初相之差.t =0时,x A =Asin ΦA ,x A =0,ΦA =0,x B =Asin ΦB ,x B =-A ,ΦB =-12πΦA -ΦB =12π点评 在给定振动图像的条件下,可由图像直接读出振幅A 及初相Φ、周期T ,从而写出位移与时间的关系式x =Asin 2πT t +Φ,初相即取t =0时,由sin Φ的取值判定的ΦA 值.5.BC点评 要理解x =Asin(2πft +Φ)中各字母所对应的物理量及各物理量的意义. 6.AD方法总结 简谐运动的图像反映了质点在不同时刻的位移情况,另外根据图像的形式还可以推断出下一时刻的运动趋势,因此解此类问题应先画出再过1 s 的振动图像.画图像时只要将振动图像随时间延伸即可,而图像形状不变,然后再根据图像寻找规律.7.见解析解析 (1)由图知,在计时开始的时刻振子恰好以沿x 轴正方向的速度通过平衡位置,此时弹簧振子具有最大速度,随着时间的延续,速度不断减小,而位移逐渐加大,经t =1 s ,其位移达到最大.(2)由图知,在t =2 s 时,振子恰好通过平衡位置,此时加速度为零,随着时间的延续,位移不断变大,加速度也变大,速度不断变小,当t =3 s 时,位移达到负向最大值,加速度达到正向最大值,速度等于零.方法总结 充分利用图像的直观性,把图像与振动过程联系起来,图像上的一个点表示振动过程中的一个状态(位置、振动方向等),图线上的一段对应振动的一个过程,解题关键是判断好平衡位置、最大位移及振动方向.课后巩固练 1.BCD 2.B 3.ACD 4.B 5.C 6.D 7.C 8.BC9.A [2πT =4π,当t =0时,具有负方向的最大加速度,则x =A ,所以初相Φ=π2,表达式为x =8×10-3sin ⎝⎛⎭⎪⎫4πt +π2 m ,A 正确.]10.AD11.AD12.(1)0.5 0.4 0.2 0.8(2)x A =0.5sin (5πt +π) cm ,x B =0.2sin cm(2.5πt +π2) cm(3)x A =-24 cm ,x B =0.2sin 58π cm 解析 (1)由图像知:A 的振幅是0.5 cm ,周期是0.4 s ;B 的振幅是0.2 cm ,周期是0.8 s.(2)由图像知:A 中振动的质点已振动了12周期,φ=π,由T =0.4 s ,得ω=2πT =5π,则简谐运动的表达式为x A =0.5sin (5πt +π) cm.B 中振动的质点从平衡位置沿正方向已振动了14周期,φ=π2,由T =0.8 s 得ω=2πT =2.5π,则简谐运动的表达式为x B =0.2sin(2.5πt +π2) cm.(3)将t =0.05 s 分别代入两个表达式中得:x A =0.5sin(5π×0.05+π)cm =-0.5×22cm =-24cm ,x B =0.2sin(2.5π×0.05+π2)cm =0.2sin 58π cm.13.A 1∶A 2=2∶1 f 1=f 2=2b ΔΦ=π 解析 它们的振幅之比A 1A 2=4a 2a =21;它们的频率相同,都是f =ω2π=4πb2π=2b ;它们的相位差ΔΦ=Φ2-Φ1=3π2-π2=π,可见它们反相.14.质点的振动图像见下图解析 该题考查的是根据振动方程画质点的振动图像.由题意知,振幅A =5 cm.周期T =2πω=2π2.5π=0.8 s .当t =0时,x =5 cm ,由此可作出图像,见答案中图.习题课 对简谐运动的理解提升基础练1.如图1所示,下列振动系统不可看做弹簧振子的是( )图1A.如图甲所示,竖直悬挂的轻弹簧及小铅球组成的系统B.如图乙所示,放在光滑斜面上的铁块及轻弹簧组成的系统C.如图丙所示,光滑水平面上,两根轻弹簧系住一个小球组成的系统D.蹦极运动中的人与弹性绳组成的系统2.质点沿x轴做简谐运动,平衡位置为坐标原点O,质点经过a点和b点时速度相同,所花时间t ab=0.2 s;质点由b点再次回到a点花的最短时间t ba=0.4 s;则该质点做简谐运动的频率为( )A.1 Hz B.1.25 HzC.2 Hz D.2.5 Hz3.如图2所示为某物体做简谐运动的图像,下列说法中正确的是( )图2A.由P→Q,位移在增大B.由P→Q,速度在增大C.由M→N,位移先减小后增大D.由M→N,位移始终减小4.一弹簧振子在一条直线上做简谐运动,第一次先后经过M、N两点时速度v(v≠0)相同,那么,下列说法正确的是( )A.振子在M、N两点受回复力相同B.振子在M、N两点对平衡位置的位移相同C.振子在M、N两点加速度大小相等D.从M点到N点,振子先做匀加速运动,后做匀减速运动5.图3为甲、乙两单摆的振动图像,则( )图3A.若甲、乙两单摆在同一地点摆动,则甲、乙两单摆的摆长之比l甲∶l乙=2∶1B.若甲、乙两单摆在同一地点摆动,则甲、乙两单摆的摆长之比l甲∶l乙=4∶1C.若甲、乙两摆摆长相同,且在不同的星球上摆动,则甲、乙两摆所在星球的重力加速度之比g甲∶g乙=4∶1D.若甲、乙两摆摆长相同,且在不同的星球上摆动,则甲、乙两摆所在星球的重力加速度之比g甲∶g乙=1∶4提升练6.一个质点a做简谐运动的图像如图4所示,下列结论正确的是( )图4A.质点的振幅为4 cmB.质点的振动频率为0.25 HzC.质点在10 s内通过的路程是20 cmD.质点从t=1.5 s到t=4.5 s的过程中经过的路程为6 cm7.如图5甲所示是演示简谐运动图像的装置,当漏斗下面的薄木板N被匀速地拉出时,振动着的漏斗中漏出的沙在板上形成的曲线显示出摆的位移随时间变化的关系.板上的直线OO 1代表时间轴,图乙中是两个摆中的沙在各自板上形成的曲线,若板N 1和板N 2拉动的速度v 1和v 2的关系为v 2=2v 1,则板N 1、N 2上曲线所代表的周期T 1和T 2的关系为( )图5A .T 2=T 1B .T 2=2T 1C .T 2=4T 1D .T 2=14T 18.如图6所示为某一质点的振动图像,由图像可知在t 1和t 2两时刻,质点的速度v 1、v 2,加速度a 1、a 2的大小关系为( )图6A .v 1<v 2,方向相同B .v 1>v 2,方向相反C .a 1>a 2,方向相同D .a 1>a 2,方向相反9.如图7所示是一简谐运动的振动图像,则下列说法正确的是( )图7A .该简谐运动的振幅为6 cm ,周期为8 sB .6~8 s 时间内,振子由负向最大位移处向平衡位置运动C .图中的正弦曲线表示振子的运动轨迹D .该振动图像对应的表达式为x =3sin (πt4) cm10.如图8所示,一升降机在箱底装有若干弹簧,设在某次事故中,升降机吊索在空中断裂,忽略摩擦力,则升降机在从弹簧下端触地后直到最低点的一段运动过程中( )图8A .升降机的速度不断减小B .升降机的加速度不断变大C .升降机的加速度最大值等于重力加速度值D .升降机的加速度最大值大于重力加速度值11.一个质点在平衡位置O 点的附近做简谐运动,它离开O 点后经过3 s 时间第一次经过M 点,再经过2 s 第二次经过M 点,该质点再经过________ s 第三次经过M 点.若该质点由O 点出发在20 s 内经过的路程是20 cm ,则质点做简谐振动的振幅为________ cm.12.跳板跳水运动员在起跳前都要随跳板上下振动几次,若想获得最好的起跳高度,你认为应在何处起跳?________(填“最高点”“最低点”或“平衡位置”).13. 如图9所示,将质量m A =100 g 的平台A 连接在劲度系数k =200 N/m 的弹簧上端,形成竖直方向的弹簧振子,在A 的上方放置m B =m A 的物块B ,使A 、B 一起上下振动.若弹簧原长为5 cm ,求:图9(1)当系统进行小振幅振动时,平衡位置离地面C 的高度; (2)当振幅为0.5 cm 时,B 对A 的最大压力;(3)为使B 在振动中始终与A 接触,振幅不得超过多少?习题课 对简谐运动的理解提升答案1.D 2.B 3.AC 4.C 5.BD 6.BC 7.D 8.AD 9.BD10.D 11.14或103 4或43解析 根据简谐运动的周期性和对称性分析解决问题.作出该质点振动的图像如下图所示,则M 点的位置可能有两个,即如下图所示的M 1或M 2.(1)第一种情况若是位置M 1,由图可知T 14=3 s +1 s =4 s ,T 1=16 s ,根据简谐运动的周期性,质点第三次经过M 1时所需时间为一个周期减第二次经过M 点的时间,故Δt 1=16 s -2 s =14 s.质点在20 s 内(即n =2016=54个周期内)的路程为20 cm ,故由5A 1=20 cm ,得振幅A 1=4 cm.(2)第二种情况若是位置M 2,由图可知3T 24=3 s +1 s =4 s ,T 2=163s.根据对称性,质点第三次经过M 2时所需时间为一个周期减第二次经过M 点的时间, 故Δt 2=163 s -2 s =103s.质点在20 s 内(即n =20163=154个周期内)的路程为20 cm.故由15A 2=20 cm ,得振幅A 2=43cm.12.最低点解析 在最低点,人和板的作用力最大,板对人做功最多,人获得的动能最大,跳的最高.13.(1)4 cm (2)1.5 N (3)1 cm解析 (1)将A 与B 整体作为振子,当A 、B 处于平衡位置时,根据平衡条件得 kx 0=(m A +m B )g 解得弹簧形变量x 0=(m A +m B )g k =(0.1+0.1)×10200m=0.01 m =1 cm平衡位置距地面高度h =l 0-x 0=5 cm -1 cm =4 cm(2)已知A 、B 一起振动的振幅A =0.5 cm ,当A 、B 振动到最低点位置时,加速度最大,其值为am =kA m A +m B =200×0.0050.1+0.1m/s 2=5 m/s 2方向竖直向上.取B 物块为研究对象,B 受重力m B g 、A 对B 的支持力N ,其合外力为F =N -m B g , 根据牛顿第二定律得N -m B g =m B am 解得N =m B g +m B am =m B (g +am) =0.1×(10+5) N =1.5 N根据牛顿第三定律,B 对A 的最大压力大小为 N′=N =1.5 N.(3)取B 为研究对象,当B 振动到最高点时受重力m B g 和A 对B 的支持力N 1,其合力为B 的回复力即F 回=m B g -N 1.根据牛顿第二定律得m B g -N 1=m B a当N 1=0时,B 振动的加速度达到最大值,其最大值为am′=g =10 m/s 2取A 与B 整体为研究对象,受到的最大回复力为 F 回m =kA′=(m A +m B )am′则振动系统的振幅为A′=(m A +m B )am′k=(0.1+0.1)×10200m=0.01 m =1 cm 当振幅A′>1 cm 时,B 与A 将分离,为使B 在振动中始终与A 接触,振动系统的振幅A′≤1 cm.。
教科版选修3-4 1.3简谐运动的图像和公式 课时检测(解析版)

2021-2022学年教科版选修3-41.3简谐运动的图像和公式课时检测〔解析版〕一、选择题(此题共6小题,每题6分,共36分)1.(2021·内江高二检测)一竖直弹簧振子做简谐运动,其振动图像如下图,那么在(-Δt)和(+Δt)(Δt是微小的时间)两时刻,弹簧振子的( )A.相对平衡位置的位移相同B.速度相同C.加速度相同D.弹性势能相同【解析】选B。
在两时刻振子的位移大小相等、方向相反,加速度大小相等方向相反,速度相同,弹性势能不同,应选B。
2.装有砂粒的试管竖直静立于水面,如下图,将管竖直提起少许,然后由静止释放并开始计时,在一定时间内试管在竖直方向近似做简谐运动。
假设取竖直向上为正方向,那么如下图描述试管振动的图像中可能正确的选项是( )【解析】选D。
试管在竖直方向上做简谐运动,平衡位置是在重力与浮力相等的位置,开始时向上提起的距离,就是其偏离平衡位置的位移,为正向最大位移,故正确答案为D。
3.(多项选择)一质点做简谐运动,其位移x与时间t的关系图像如下图,由图可知( )A.质点振动的频率是4HzB.质点振动的振幅是2 cmC.t=3s时,质点的速度最大D.在t=3s时,质点的振幅为零【解析】选B、C。
由题图可以直接看出振幅为2 cm,周期为4s,所以频率为 Hz,所以选项A 错误,B正确;t=3s时,质点经过平衡位置,速度最大,所以选项C正确;振幅等于质点偏离平衡位置的最大位移,与质点的位移有着本质的区别,t=3s时,质点的位移为零,但振幅仍为2 cm,所以选项D错误。
4.(多项选择)一质点做简谐运动的振动图像如下图,质点的速度与加速度方向相同的时间段是( )s sss【解析】选B、D。
质点做简谐运动时加速度方向与回复力方向相同,与位移方向相反,总是指向平衡位置;位移增加时速度与位移方向相同,位移减小时速度与位移方向相反。
综上可知B、D正确,A、C错误。
5.(多项选择)如图为某质点的振动图像,由图像可知( )A.质点的振动方程为x=-2sin50πt(cm)B.在 s时质点的速度为负向最大时刻质点的振动方向向下D.从 s至 s质点的位移增大,速度减小【解析】选A、D。
2019-2020学年高中物理 第一章 3 简谐运动的图像和公式练习(含解析)教科版选修3-4

3.简谐运动的图像和公式课时过关·能力提升1.关于一质点做简谐运动的图像,下列说法中正确的是 ()A.表示质点振动的轨迹是正弦或余弦曲线B.由图像可判断任一时刻质点相对平衡位置的位移方向C.表示质点的位移随时间变化的规律D.由图像可判断任一时刻质点的速度方向解析:振动图像表示位移随时间的变化规律,不是运动轨迹,选项A错误,选项C正确;由图像可以判断某时刻质点的位移和速度方向,选项B、D正确.答案:BCD2.一个质点做简谐运动的图像如图所示,从图中可以知道()A.在t=0时,质点位移为零,速度和加速度也为零B.在t=4 s时,质点的速度最大,方向沿y轴的负方向C.在t=3 s时,质点振幅为-5 cm,周期为4 sD.无论何时,质点的振幅都是5 cm,周期都是4 s解析:t=0、t=4s时,质点位于平衡位置,x=0,a=0,速度最大,方向沿y轴正方向;质点振动周期T=4s,振幅A=5cm,选项D正确.答案:D3.一单摆做简谐运动,其位移随时间变化的关系式为x=A siA.此单摆的周期为2 sB.2 s末回复力沿正方向C.3 s末速度方向沿正方向D.4 s末摆球受到的回复力为零解析:由位移随时间变化的关系式x=A si,ωrad/s,则T s=8s,故A错误;2s 末位移大小为x=A si,故2s末回复力沿负方向,故B错误;周期为8s,故3s,故C错误;4s末位移大小为x=A si,回复力为零,故D正确.答案:D4.有两个振动,其表达式分别是x1=3siA.它们的振幅相同B.它们的周期相同C.它们的相位差恒定D.它们的振动步调一致解析:由简谐运动的公式可看出,两振动的振幅分别为3cm 和6cm,选项A错误;角速度ω=100πrad/s相同,周期T,选项B正确;相位差Δφ,故相位差恒定,选项C正确,选项D错误.答案:BC5.一弹簧振子做简谐运动,其振动图像如图所示,那么A.①②B.②③C.③④D.①④解析:对,由已知可知两时刻振子的位置关于平衡位置对称,所以速度、加速度、位移大小相等,由图像可知速度方向也相同,但位移、加速度方向不同,所以①④正确,②③错误,选项D正确.答案:D6.(2018·天津理综)一振子沿x轴做简谐运动,平衡位置在坐标原点.t=0时振子的位移为-0.1 m,t=1 s时位移为0.1 m,则()A.若振幅为0.1 m,振子的周期可能B.若振幅为0.1 m,振子的周期可能C.若振幅为0.2 m,振子的周期可能为4 sD.若振幅为0.2 m,振子的周期可能为6 s解析:由题意可知振子在1s内由-0.1m的位置运动到0.1m的位置,若其振幅为0.1m,则Δt=n s(n=0,1,2,3,…),则n=1时T s,但T不可能等s,选项A正确、B错误.若简谐运动的振幅为0.2m,需分几种情况进行讨论,若t=0和t=1s时质点沿x轴正向振动,满足n s(n=0,1,2,…),当n=0时,T=6s;若t=0时质点沿x轴正向振动,t=1s时质点沿x轴负向振动,或t=0时质点沿x轴负向振动,t=1s时质点沿x轴正向振动,满足n s(n=0,1,2,…);若t=0和t=1s时质点沿x轴负向振动,满足(n s(n=0,1,2,…),可得C错误,D正确.答案:AD7.A、B两人先后观察同一弹簧振子在竖直方向上下振动的情况.(1)A开始观察时,振子正好在平衡位置并向下运动,试在图甲中画出A观察到的弹簧振子的振动图像.已知经过1 s后,振子第一次回到平衡位置,振子振幅为5 cm(设平衡位置上方为正方向,时间轴上每格代表0.5 s).(2)B在A观察3.5 s后,开始观察并记录时间,试在图乙上画出B观察到的弹簧振子的振动图像.解析:(1)由题意知,振子的振动周期T=2s,振幅A=5cm.根据正方向的规定,A观察时,振子从平衡位置向-x方向运动,经t=0.5s,达到负向最大位移.画出的A观察到的振子的振动图像如图甲所示.(2)因为t=3.5s,这时振子的状态跟经过时间t',所以B 开始观察时,振子正好处于正向最大位移处.画出的B观察到的振子的振动图像如图乙所示.答案:见解析8.根据如图所示的振动图像,(1)算出下列时刻振子对平衡位置的位移.①t1=0.5 s;②t2=1.5 s.(2)将位移随时间的变化规律写成x=A sin(ωt+φ)的形式并指出振动的初相位是多少.解析:(1)由题图知,x=A cosωt=10co t1=0.5s 时,x=cm;t2=1.5s时,x=-cm.(2)x=10si cm,初相位φ答案:(1)9.如图所示,某质点做简谐运动的振动图像,根据图像中的信息,回答下列问题:(1)质点在第2 s末的位移;(2)质点振动过程中位移的最大值;(3)在前4 s内,质点经过的路程.解析:(1)由x-t图像可以读出2s末质点的位移为零.(2)质点的最大位移在前4s发生在1s末和3s末,位移大小为10cm.(3)前4s质点正好完成一个往复的全振动.先朝正方向运动了距离为10cm的一个来回,又在负方向上进行了一个10cm距离的来回,故总路程为40cm.答案:(1)0(2)10 cm(3)40 cm。
2015年高二物理同步精练1.3《简谐运动的图像和公式》(Word版含解析)(教科版选修3-4)

题组一对简谐运动图像的理解1.如图1所示是某振子做简谐运动的图像,以下说法中正确的是()图1A.因为振动图像可由实验直接得到,所以图像就是振子实际运动的轨迹B.振动图像反映的是振子位移随时间变化的规律,并不是振子运动的实际轨迹C.振子在B位置的位移就是曲线BC的长度D.振子运动到B点时的速度方向即为该点的切线方向答案 B解析振动图像表示振子位移随时间变化的规律,并不是振子运动的实际轨迹,B对,A、C错.由于图像不是质点的运动轨迹,因此切线的方向并不表示速度的方向,D错.2.一质点做简谐运动,其位移x与时间t的关系图像如图2所示,由图可知()图2A.质点振动的频率是4 HzB.质点振动的振幅是2 cmC.t=3 s时,质点的速度最大D.在t=3 s时,质点的振幅为零答案BC解析由题图可以直接看出振幅为2 cm,周期为4 s,所以频率为0.25 Hz,所以选项A错误,B正确.t=3 s时,质点经过平衡位置,速度最大,所以选项C正确.振幅等于质点偏离平衡位置的最大位移,与质点的位移有着本质的区别,t=3 s时,质点的位移为零,但振幅仍为2 cm,所以选项D错误.3.如图3所示为某物体做简谐运动的图像,下列说法中正确的是()图3A.由P→Q,位移在增大B.由P→Q,速度在增大C.由M→N,位移先减小后增大D.由M→N,位移始终减小答案AC解析由P→Q,质点远离平衡位置运动,位移增大而速度减小,选项A正确,B错误;由M→N,质点先向着平衡位置运动,经过平衡位置后又远离平衡位置运动,因而位移先减小后增大,选项C正确,D错误.4.如图4所示为某质点做简谐运动的图像,则下列说法正确的是()图4A.质点在0.7 s时,正在远离平衡位置B.质点在1.5 s时的位移最大C.1.2 s到1.4 s,质点的位移在增大D.1.6 s到1.8 s,质点的位移在增大答案BC解析由于位移是指由平衡位置指向质点所在位置的有向线段,故质点在0.7 s时正在向平衡位置运动,所以A项错误;质点在1.5 s时的位移到达最大,故B正确;质点在1.2 s到1.4 s时间内,正在远离平衡位置,所以其位移在增大,故C正确;1.6 s到1.8 s时间内,质点正向平衡位置运动,所以其位移在减小,故D项错误.5.一质点做简谐运动的振动图像如图5所示,则该质点()图5A.在0~0.01 s内,速度与加速度同向B.在0.01 s~0.02 s内,速度与回复力同向C.在0.025 s时,速度为正,加速度为正D.在0.04 s时,速度最大,回复力为零答案AC解析F、a与x始终反向,所以由x的正负就能确定a的正负.在x-t图像上,图线各点切线的斜率表示该点的速度,由斜率的正负又可确定v的正负,由此判断A、C正确.6.一个弹簧振子沿x轴做简谐运动,取平衡位置O为x轴坐标原点.从某时刻开始计时,经过四分之一周期,振子具有沿x轴正方向的最大加速度.能正确反映振子位移x与时间t 关系的图像是()答案 A解析根据F=-kx及牛顿第二定律得a=Fm=-km x,当振子具有沿x轴正方向的最大加速度时,其具有沿x轴负方向的最大位移,故选项A正确,选项B、C、D错误.7.图6甲所示为以O点为平衡位置,在A、B两点间做简谐运动的弹簧振子,图乙为这个弹簧振子的振动图像,由图可知下列说法中正确的是()图6A .在t =0.2 s 时,弹簧振子可能运动到B 位置B .在t =0.1 s 与t =0.3 s 两个时刻,弹簧振子的速度相同C .从t =0到t =0.2 s 的时间内,弹簧振子的动能持续地增加D .在t =0.2 s 与t =0.6 s 两个时刻,弹簧振子的加速度相同答案 A8.如图7甲所示是一个弹簧振子的示意图,O 是它的平衡位置,振子在B 、C 之间做简谐运动,规定向右为正方向.图乙是它的速度v 随时间t 变化的图像.下列说法中正确的是( )甲 乙图7A .t =2 s 时刻,它的位置在O 点左侧4 cm 处B .t =3 s 时刻,它的速度方向向左,大小为2 m/sC .t =4 s 时刻,它的加速度为方向向右的最大值D .振子在一个周期内通过的路程是16 cm答案 C题组二 简谐运动表达式的应用9.有一个弹簧振子,振幅为0.8 cm ,周期为0.5 s ,初始时具有负方向的最大加速度,则它的振动方程是( )A .x =8×10-3sin ⎝⎛⎭⎫4πt +π2 m B .x =8×10-3sin ⎝⎛⎭⎫4πt -π2 m C .x =8×10-1sin ⎝⎛⎭⎫πt +32π m D .x =8×10-1sin ⎝⎛⎭⎫4πt +π2 m答案 A解析 ω=2πT =4π rad/s ,当t =0时,具有负方向的最大加速度,则x =A ,所以初相φ=π2,表达式为x =8×10-3sin ⎝⎛⎭⎫4πt +π2 m ,A 正确. 10.某质点做简谐运动,其位移随时间变化的关系式为x =A sin π4t ,则质点( ) A .第1 s 末与第3 s 末的位移相同B .第1 s 末与第3s 末的速度相同C .3 s 末至5 s 末的位移方向都相同D .3 s 末至5 s 末的速度方向都相同答案 AD解析 由表达式x =A sin π4t 知,ω=π4,简谐运动的周期T =2πω=8 s .表达式对应的振动图像如图所示.质点在1 s 末的位移x 1=A sin(π4×1)=22A 质点在3 s 末的位移x 3=A sin(π4×3)=22A ,故A 正确.由前面的计算可知t =1 s 和t =3 s 质点连续通过同一位置,故两时刻质点速度大小相等,但方向相反,B 错误;由x -t 图像可知,3 s ~4 s 内质点的位移为正值,4 s ~5 s 内质点的位移为负值,C 错误;同样由x -t 图像可知,在时间3 s ~5 s 内,质点一直向负方向运动,D 正确.11.做简谐运动的小球按x =0.05cos (2πt +π/4) m 的规律振动.(1)求振动的圆频率、周期、频率、振幅和初相位;(2)当t 1=0.5 s 、t 2=1 s 时小球的位移分别是多少?答案 (1)振幅A =0.05 m ,初相位φ0=π/4,圆频率ω=2π rad/s ,周期T =1 s ,频率f =1Hz(2)-0.025 2 m 0.025 2 m解析 (1)根据表达式可以直接判断振幅A =0.05 m ,初相位φ0=π4,圆频率ω=2π rad/s ,根据公式T =2πω=1 s ,频率f =1T=1 Hz. (2)将t 1=0.5 s 、t 2=1 s 代入x =0.05cos (2πt +π/4) m 得x 1=0.05cos (5π/4) m =-0.025 2 m ,x 2=0.05cos (9π/4) m =0.025 2 m.题组三 综合应用12.如图8甲所示是演示简谐运动图像的装置,当漏斗下面的薄木板N 被匀速地拉出时,振动着的漏斗中漏出的沙在板上形成的曲线显示出摆的位移随时间变化的关系.板上的直线OO 1代表时间轴,图乙中是两个摆中的沙在各自板上形成的曲线,若板N 1和板N 2拉动的速度v 1和v 2的关系为v 2=2v 1,则板N 1、N 2上曲线所代表的周期T 1和T 2的关系为( )图8A .T 2=T 1B .T 2=2T 1C .T 2=4T 1D .T 2=14T 1 答案 D解析 在木板上由摆动着的漏斗中漏出的沙形成的曲线显示出摆的位移随时间变化的规律,即沙摆的振动图像.由于拉动木板的速度不同,所以N 1、N 2上两条曲线的时间轴(横轴)的单位长度代表的时间不等.如果确定了N 1、N 2上两条曲线的时间轴的单位长度与时间的对应关系后,就可以确定各条曲线代表的沙摆完成一次全振动所需的时间,即振动周期,从而可以确定T 1、T 2的关系.由题图可知,薄木板被匀速拉出的距离相同,且v 2=2v 1,则木板N 1上时间轴单位长度代表的时间t 1是木板N 2上时间轴单位长度代表的时间t 2的两倍,即t 1=2t 2.由题图乙可知,T 1=t 1,T 2=12t 2,从而得出T 1=4T 2.正确选项为D. 13.(2014·浙江·17)一位游客在千岛湖边欲乘坐游船,当日风浪较大,游船上下浮动.可把游船浮动简化成竖直方向的简谐运动,振幅为20 cm ,周期为3.0 s .当船上升到最高点时,甲板刚好与码头地面平齐.地面与甲板的高度差不超过10 cm 时,游客能舒服地登船.在一个周期内,游客能舒服登船的时间是( )A .0.5 sB .0.75 sC .1.0 sD .1.5 s答案 C解析 由振动周期T =3.0 s 、ω=2πT、A =20 cm 知,游船做简谐运动的振动方程x =A sin ωt =20sin 2π3t (cm).在一个周期内,当x =10 cm 时,解得t 1=0.25 s ,t 2=1.25 s .游客能舒服登船的时间Δt =t 2-t 1=1.0 s ,选项C 正确,选项A 、B 、D 错误.14.如图9所示为A 、B 两个简谐运动的位移—时间图像.试根据图像写出:图9(1)A 的振幅是____cm ,周期是________s ;B 的振幅是________cm ,周期是________s.(2)这两个简谐运动的位移随时间变化的关系式.(3)在时间t =0.05 s 时两质点的位移分别是多少?答案 (1)0.5 0.4 0.2 0.8(2)x A =0.5sin (5πt +π) cm ,x B =0.2sin (2.5πt +π2) cm (3)x A =-24 cm ,x B =0.2sin 58π cm 解析 (1)由图像知:A 的振幅是0.5 cm ,周期是0.4 s ;B 的振幅是0.2 cm ,周期是0.8 s.(2)由图像知:A 中振动的质点从平衡位置沿正方向已振动了12周期,φ=π,由T =0.4 s ,得ω=2πT=5π,则简谐运动的表达式为x A =0.5sin (5πt +π) cm.B 中振动的质点从平衡位置沿正方向已振动了14周期,φ=π2,由T =0.8 s 得ω=2πT=2.5π,则简谐运动的表达式为x B =0.2sin (2.5πt +π2) cm. (3)将t =0.05 s 分别代入两个表达式中得:x A =0.5sin (5π×0.05+π)cm =-0.5×22cm =-24cm ,x B =0.2sin(2.5π×0.05+π2)cm =0.2sin 58π cm.15.一物体沿x 轴做简谐运动,振幅为8 cm ,频率为0.5 Hz ,在t =0时,位移是4 cm ,且向x 轴负方向运动.(1)试写出用正弦函数表示的振动方程.(2)10 s 内通过的路程是多少?答案 (1)x =0.08sin (πt +56π) m (2)160 cm 解析 (1)简谐运动振动方程的一般表达式为x =A sin (ωt +φ).根据题给条件,有:A =0.08 m ,ω=2πf =π rad/s.所以x =0.08sin (πt +φ) m .将t =0,x =0.04 m 代入得0.04=0.08sin φ,解得初相位φ=π6或φ=56π,因为t =0时,速度方向沿x 轴负方向,即位移在减小,所以取φ=56π.故所求的振动方程为x =0.08sin (πt +56π) m. (2)周期T =1f=2 s ,所以t =5T ,因一个周期内通过的路程是4A ,则10 s 内通过的路程s =5×4A =20×8 cm =160 cm.。
教科版选修3-4 1.3简谐运动的图像和公式 课后训练(解析版)

2021-2022学年教科版选修3-4 1.3简谐运动的图像和公式 课后训练〔解析版〕1.一质点做简谐运动,其位移x 与时间t 关系曲线如图1-3-4所示,由图可知( )图1-3-4A .质点振动的频率是4 HzB .质点振动的振幅是2 cmC .在t =3 s 时,质点的速度最大D .在t =4 s 时,质点所受的合外力为零解析:选BC 从振动图像可知振幅A =2 cm ,周期T =4 s ,那么频率为f =1T=0.25 Hz 。
t =3 s 时,质点位于平衡位置,速度最大,而t =4 s 时,质点位于最大位移处,所以回复力最大。
2.如图1-3-6所示是一做简谐运动的物体的振动图像,以下说法中正确的选项是( )图1-3-6A .振动周期是2×10-2 sB .第2×10-2 s 内物体的位移是-10 cmC .物体的振动频率为25 HzD .物体的振幅是10 cm解析:选BCD 周期是完成一次全振动所用的时间,在图像上是两相邻极大值间的距离,所以周期是4×10-2 s ,故A 错误。
又f =1T,所以f =25 Hz ,故C 正确。
正、负极大值表示物体的振幅,所以振幅A =10 cm ,故D 正确。
第2×10-2s 内初位置是10 cm ,末位置是0,根据位移的概念有x =-10 cm ,故B 正确。
3.有一个弹簧振子,振幅为0.8 cm ,周期为0.5 s ,初始时具有负方向的最大加速度,那么它的运动表达式是( )A .x =8×10-3sin(4πt +π2) m B .x =8×10-3sin(4πt -π2) m C .x =8×10-1sin(πt +32π) m D .x =8×10-1sin(4πt +π2) m解析:选A ω=2πT=4π,当t =0时,具有负方向的最大加速度,那么x =A ,所以初相φ=π2,表达式为x =8×10-3×sin(4πt +π2) m ,A 正确。
(1)简 谐 运 动 同步练习 物理选修3-4同步练习Word版含解析

课时跟踪检测(一)简谐运动1.关于机械振动的位移和平衡位置,以下说法正确的是()A.平衡位置就是物体振动范围的中心位置B.机械振动的位移是指以平衡位置为起点的位移C.机械振动的物体运动的路程越大发生的位移也越大D.机械振动的位移是指振动物体偏离平衡位置最远时的位移2.如图1所示,对做简谐运动的弹簧振子m的受力分析正确的是()图1A.重力、支持力、弹簧的弹力B.重力、支持力、弹簧的弹力、回复力C.重力、支持力、回复力、摩擦力D.重力、支持力、摩擦力3.做简谐运动的弹簧振子在某段时间内速度越来越大,则这段时间内()A.振子的位移越来越大B.振子正向平衡位置运动C.振子速度与位移同向D.振子速度与位移方向相反4.如图2所示,在光滑水平面上振动的弹簧振子的平衡位置为O,把振子拉到A点,OA=1 cm,然后释放振子,经过0.2 s振子第1次到达O点,如果把振子拉到A′点,OA′=2 cm,则释放振子后,振子第1次到达O点所需的时间为()图2A.0.2 s B.0.4 sC.0.1 s D. 0.3 s5.如图3所示,弹簧振子在BC间振动,O为平衡位置,BO=OC=5 cm,若振子从B 到C的运动时间是1 s,则下列说法中正确的是()图3A.振子从B经O到C完成一次全振动B.振动周期是1 s,振幅是10 cmC.经过两次全振动,振子通过的路程是20 cmD.从B开始经过3 s,振子通过的路程是30 cm6.当一弹簧振子在竖直方向上做简谐运动时,下列说法中正确的是()A.振子在振动过程中,速度相同时,弹簧的长度一定相等,弹性势能相等B.振子从最低点向平衡位置运动的过程中,弹簧弹力始终做负功C.振子在运动过程中的回复力由弹簧弹力和振子重力的合力提供D.振子在运动过程中,系统的机械能守恒7.如图4所示,试证明光滑斜面上的小球连在弹簧上,把原来静止的小球沿斜面拉下一段距离后释放,小球的运动是简谐运动。
图48.如图5所示,弹簧振子以O点为平衡位置在B、C两点之间做简谐运动,B、C相距20 cm,当振子经过B点时开始计时,经过0.5 s,振子首次到达C点。
高二物理:1.3《简谐运动的图象和公式》同步练习(教科版选修3-4)

第3节 简谐运动的图像和公式 测试题1.关于简谐运动的周期,频率,振幅,下列说法中哪些是正确的( ) A .振幅是矢量,方向从平衡位置指向最大位移处 B .周期和频率的乘积是一个常数C .振幅增加,周期也必然增加,而频率减小D .频率与振幅有关2.如图所示的是某质点做简谐运动的振动图象,从图中可以知道( )A .t 1和t 3时刻,质点的速度相同B .t 1到t 2时间内,速度与加速度方向相同C .t 2到t 3时间内,速度变大,而加速度变小D .t 1和t 3时刻, 质点的加速度相同3.如图的是一个质点做简谐运动的振动图象,从图中可以知道( )A .在t=0时,质点位移为零,速度和加速度也零B .在t=4s 时,质点的速度最大,方向沿y 轴的负方向C .在t=3s 时,质点振幅为-5cm,周期为4sD .无论何时,质点的振幅都是5cm, 周期都是4s4.如图所示是一弹簧振子在水平面内做简谐运动 的振动图象,则振动系统在( ) A .t 3和t 4时刻,振子具有不同的动能和速度B .t 3和t 5时刻,振子具有相同的动能和不同的速度C .t 1和t 4时刻,振子具有相同的加速度D .t 2和t 5时刻,振子所受的回复力大小之比为2:15.有两 个简谐运动的振动方程:则下列说法中正确的是( )A .它们的振幅相同B .它们的周期相同C .它们的相差恒定D .它们的振动步调一致 6.一个弹簧振子做简谐运动的周期是0.025S,当振子从平衡位置开始向右运动,经过0.17s 时,振子的运动情况是( )A .正在向右做减速运动B .正在向右做加速运动C .正在向左做减速运动D .正在向左做加速运动7.甲,乙两 物体做简谐运动,甲振动20次时,乙振动了40次,则甲,乙振动周期之比是 ,若甲的振幅减小了2倍而乙的振幅不变,则甲,乙周期之比是5 -53),3100sin(66100sin(621ππππ+=+=t x t x8.如图所示的是一简谐运动图象,由图可知,振动质点的频率是 H Z , 质点需经过 s 通过的路程是为0.84m, 在图中画出B,D 时刻质点的运动方向.9.一个质点经过平衡位置O ,在A 、B,它的振动图象如图(2),则OB ,第0.2s 末质点的速度方向,加速度大小为 ,第0.4s 末质点的加速度方向 ,质点从O 运动到B 再到A 需时间t= ,在第4s 内完成 次全振动.※10.某一弹簧振子做简谐运动,若从振子经过某一位置A .当振子再次与零时刻的速度相同时,经过的时间一定是半周期 B .当振子再次经过A 时,经过的时间一定是半周期C .当振子的加速度再次与零时刻的加速度相同时,一定又到达位置AD .一定还有另一个位置跟位置A 有相同的位移※11.一弹簧 振子做简谐运动,周期为T,则下列说法中正确的是( ) A .若t 时刻和(t +t ∆)时刻振子运动位移的大小相等,方向相同,则t ∆一定等于T 的整数倍 B .若t 时刻和(t +t ∆)时刻振子运动速度的大小相等,方向相反, 则t ∆一定等于T 的整数倍C .若t ∆=T,则在t 时刻和(t +t ∆)时刻振子运动的加速度一定相等D .若t ∆=T/2,则在t 时刻和(t +t ∆)时刻弹簧的长度一定相等※12.如图所示,一个质点在平衡位置O 点附近做简谐运动,B,C 两点分别为质点振动过程中的最大位移处,若从O 点开始计时,经过3s 质点第一次 经过M 点,再继续运动,又经过0.3s 它第二次经过M 点,则再经过 s 该质点第三次经过M 点13.一弹簧振子在一条直线上做简谐运动,第一次先后经过M,N 两点时速度V(V ≠0)相同,那么下列说法正确的是( )A .振子在M,N 两点所受回复力相同B .振子在M,N 两点对平衡位置的位移相同C .振子在M,N 两点加速度大小相等D .从M 点到N 点,振子先做匀加速运动,后做匀减速运动t/s -2 t/s -2 · · · O C B M · · · · O CB M · N ·参考答案:。
高中物理教科版选修3-4配套课件1.3 简谐运动的图像和公式 课件(教科版选修3-4)

(6)从图像可看出质点在不同时刻之间的相位差.
【变式1】
弹簧振子做简谐运动的振动图像如图1-3-5所示,则 ( A.t=0时,质点位移为零,速度为零,加速度为零 B.t=1 s时,质点位移最大,速度为零,加速度最大 C.t1和t2时刻振子具有相同的速度 ).
D.t3和t4时刻振子具有相同的加速度
图1-3-5
2π x=Asin T t+φ或x=Asin(2πft+φ)
A表示简谐运动的 振幅 . T、f是简谐运动的 周期 和 频率 . ft+φ叫简谐运动的 相位 . t=0时的相位φ叫做 初相位 ,简称初相. 频率相同,初相不同的两个振动物体的相位差:φ2-φ1.
一、由简谐运动的图像还可获得的信息 任意时刻质点的位移的大小和方向.
如图1-3-2所示,质点在t1、t2时刻的位移分别为x1和-x2.
图1-3-2
任意时刻质点的振动方向:看下一时刻质点的位置,如图 1-3-3
中a点,下一时刻离平衡位置更远,故a此刻向上振动.
图1-3-3
任意时刻质点的速度、加速度、位移的变化情况及大小比较
看 下一时刻质点的位置,判断是远离还是靠近平衡位置:若远 离平衡位置,则速度越来越小,加速度、位移越来越大;若靠 近平衡位置,则速度越来越大,加速度、位移越来越大,如图 中b,从正位移向着平衡位置运动,则速度为负且增大,位移、
3 简谐运动的图像和公式
1.会简谐运动的图像是一条正弦或
余弦曲线. 3.了解初相和相位差的概念,理解相位的物理意义. 4.了解简谐运动位移方程中各量的物理意义,能依据振动方程描 绘振动图像.
一、简谐运动的图像 图像的绘制及应用 (1)绘制方法:在弹簧振子的 小球 上安装一绘图笔,让一条纸
物理(教科版选修34)练习周末培优练(二)单摆简谐运动的图像和公式

周末培优练(二) 单摆 简谐运动的图像和公式1.如图所示,一摆长为l 的单摆,在悬点的正下方的P 处有一钉子,P 与悬点相距l -l ′,则这个摆做小幅度摆动时的周期为( )A .2πlg B .2πl ′g C .π⎝⎛⎭⎪⎫l g+l ′g D .2πl +l ′2g解析:碰钉子前摆长为l ,故周期T 1=2πlg ,碰钉子后摆长变为l ′,则周期T 2=2πl ′g ,所以此摆的周期T =T 12+T 22=π⎝ ⎛⎭⎪⎫lg+l ′g . 答案:C2.如图所示为两个单摆的振动图像,从图像中可以知道它们的( )A .摆球质量相等B .振幅相等C .摆球同时改变速度方向D .摆长相等解析:由振动图像可知T 1=4 s ,T 2=4 s .故摆长相同,振幅不同.B 错误,D 正确;由T =2πlg知,T 与质量无关,质量大小无法确定.A 错误;由于计时起点不同,速度方向改变的时刻不同,C 错误.答案:D3.(多选)如图所示是甲、乙两个单摆做简谐运动的图像,则下列说法中正确的是( )A .甲、乙两摆的振幅之比为2∶1B .t =2 s 时,甲摆的重力势能最小,乙摆的动能为零C .甲、乙两摆的摆长之比为4∶1D .甲、乙两摆摆球在最低点时向心加速度大小相等解析:由振动图像可知甲、乙两单摆振幅之比为2∶1,A 正确.t =2 s 时;甲处在平衡位置,重力势能最小,乙在最大位移处,动能为零,B 正确,因T 甲=4 s ,T 乙=8 s .故T 甲T 乙=L 甲L 乙,L 甲L 乙=14,C 错误;由a =v 2L ,因v 无法比较,故D 错误.答案:AB4.如图甲所示是利用砂摆演示简谐运动图像的装置.当盛砂的漏斗下面的薄木板被水平匀速拉出时,做简谐运动的漏斗漏出的砂在板上形成的曲线显示出砂摆的振动位移随时间变化的关系.第一次以速度v 1匀速拉动木板,图乙给出了砂摆振动的图线;第二次使砂摆的振幅减半,再以速度v 2匀速拉动木板,图丙给出了砂摆振动的图线.由此可知,砂摆两次振动的周期T 1和T 2以及拉动木板的速度v 1和v 2的关系是( )A .T 1∶T 2=2∶1B .T 1∶T 2=1∶2C .v 1∶v 2=2∶1D .v 1∶v 2=1∶2解析:本题考查单摆做简谐运动的特征,其周期与振幅无关.根据单摆做简谐运动的条件知,T 1∶T 2=1∶1,再结合图示分析,设图示板的位移为x ,x =v 12T 1,x =v 24T 2,故v 1∶v 2=2∶1,C 正确.答案:C5.如图所示是甲、乙两个单摆做简谐运动的图像,以向右的方向作为摆球偏离平衡位置位移的正方向,从t =0时刻起,当甲第一次到达右方最大位移处时( )A .乙在平衡位置的左方,正向右运动B .乙在平衡位置的左方,正向左运动C .乙在平衡位置的右方,正向右运动D .乙在平衡位置的右方,正向左运动解析:本题考查单摆运动规律,要求学生利用图像进行分析.从图中可看出,当甲第一次到达右方最大位移处时为t=1.5 s时刻,此时乙处在正向位移处,即偏离平衡位置向右的某个位置,并且正向平衡位置运动,故乙处在平衡位置右方,正向左运动,D对.答案:D6.一质点沿直线做简谐运动的图像如图所示,以下说法中正确的是()A.该质点振动频率为0.25 HzB.在0.01 s<t<0.02 s内,质点的速度与加速度方向相同C.在0.025 s时,质点的速度与加速度方向相同D.在0.04 s时,质点的动能最大解析:由振动图像知T=0.04 s,f=1T=25 Hz,A错误;在0.01 s~0.02 s内,质点远离平衡位置做减速运动,速度与加速度方向相反,B错误;在0.025 s时,质点从最大位移处向平衡位置运动,速度与加速度方向相同,C正确;在0.04 s时,质点处于最大位置处,速度最小,动能最小,D错误.答案:C7.(多选)如图所示是弹簧振子做简谐运动的振动图像,可以判定()A.从t1到t2时间内系统的动能不断增大,势能不断减小B.从t2到t3时间内振幅不断增大C.t3时刻振子处于平衡位置处,动能最大D.t1、t4时刻振子的动能、速度都相同解析:选项内容分析结论A 从t1到t2时间内,x减小,弹力做正功,系统的动能不断增大,势能不断减小正确B 振幅是离开平衡位置的最大距离,从t2到t3时间内,变化的是位移而不是振幅错误C t3时刻振子的位移为零,速度最大,动能最大正确D t1、t4时刻位移相同,即振子处于同一位置,速度等大反向,动能相同错误答案:AC8. (多选)如图所示是质点做简谐运动的振动图像,由此可知()A .t =0时,质点的位移、速度均为零B .t =1 s 时,质点的位移为正向最大,速度为零,加速度为负向最大C .t =2 s 时,质点的位移为零,速度为负向最大值,加速度为零D .质点的振幅为5 cm ,周期为2 s解析:t =0时,质点的位移为零,但是速度不为零,选项A 错误;t =1 s 时,质点的位移为正向最大,速度为零,由a =-km x 可知加速度为负向最大,选项B 正确;t =2 s 时,质点的位移为零,速度为负向最大值,由a =-km x 可知加速度为零,选项C 正确;由图像可知质点的振幅为5 cm ,周期为4 s ,选项D 错误.答案:BC9.甲、乙两弹簧振子,振动图像如图所示,则可知( )A .两弹簧振子完全相同B .两弹簧振子所受回复力最大值之比F 甲∶F 乙=2∶1C .振子甲速度为零时,振子乙速度最大D .振子的振动频率之比f 甲∶f 乙=2∶1解析:由图可知f 甲∶f 乙=1∶2,因此振子不相同,选项A 、D 错误.由图可知选项C 正确.因F 甲=k 甲A 甲,F 乙=k 乙A 乙,由于k 甲和k 乙关系未知,因此无法判断F 甲∶F 乙=2∶1,所以选项B 错误.答案:C10.某质点做简谐运动,其位移随时间变化的关系式为x =8sin π2t (cm),则( )A .质点的振幅为16 cmB .质点的振动周期为2 sC .在0~1 s 内,质点的速度逐渐减小D .在1~2 s 内,质点的动能逐渐减小解析:根据简谐运动的表达式x =A sin 2πT t 可知振幅A =8 cm ,周期T =2πω=4 s ,选项A 、B 错误;根据简谐运动的表达式可画出质点的振动图像,如图所示,由图可知,在0~1 s内,质点由平衡位置向正的最大位移处运动,速度逐渐减小,在1~2 s 内,质点由正的最大位移向平衡位置运动,速度逐渐增大,动能逐渐增大,选项C 正确,D 错误.答案:C11.某质点做简谐运动,其位移随时间变化的关系式为x =10sin ⎝⎛⎭⎫π4t cm ,则下列关于质点运动的说法中正确的是( )A .质点做简谐运动的振幅为5 cmB .质点做简谐运动的周期为4 sC .在t =4 s 时质点的速度最大D .在t =4 s 时质点的位移最大解析:由x =10sin ⎝⎛⎭⎫π4t cm 可知,A =10 cm ,ω=2πT =π4 rad/s ,得T =8 s .t =4 s 时,x =0,说明质点在平衡位置,此时质点的速度最大、位移为0,所以只有选项C 正确.答案:C12.一物体沿x 轴做简谐运动,振幅为8 cm ,频率为0.5 Hz ,在t =0时,位移是4 cm ,且向x 轴负方向运动.(1)试写出用正弦函数表示的振动方程. (2)10 s 内通过的路程是多少.解析:(1)简谐运动振动方程的一般表达式为x =A sin(ωt +φ).根据题给条件,有:A =0.08 m ,ω=2πf =π.所以x =0.08sin(πt +φ)m.将t =0,x =0.04 m ,代入得0.04=0.08 sin φ,解得初相位φ=π6或φ=56π,因为t =0时,速度方向沿x 轴负方向,即位移在减小,所以取φ=56π.故所求的振动方程为x =0.08 sin ⎝⎛⎭⎫πt +56πm . (2)周期T =1f =2 s ,所以t =5T ,则通过的路程s =5×4A =20×8 cm =160 cm.答案:(1)x =0.08 sin ⎝⎛⎭⎫πt +56πm (2)160 cm。
2019-2020学年高中物理 第一章 1 简谐运动练习(含解析)教科版选修3-4

1.简谐运动课时过关·能力提升1.简谐运动属于()A.匀变速运动B.匀速直线运动C.变加速运动D.匀加速直线运动解析:根据简谐运动的特征a=,物体的加速度大小和方向随位移的变化而变化,位移作周期性变化,加速度也作周期性变化,所以简谐运动是变加速运动.答案:C2.如图所示,能正确反映做简谐运动的物体所受回复力与位移关系的图像是()解析:做简谐运动的物体所受回复力与位移关系的表达式为F=-kx,可见选项B正确.答案:B3.一质点在A、B间做简谐运动,P、Q是其振动过程中关于平衡位置O对称的两点.当质点由A 向B运动,先后经过P、Q两点时,质点的()A.受力相同B.速度相同C.位移相同D.加速度相同解析:物体经过关于平衡位置对称的位置时,位移大小相等,方向相反,所以位移不同,故C错误.由F=-kx知,位移大小相等、方向相反,则回复力也大小相等、方向相反,所以回复力不同,故A错误.物体经过关于平衡位置对称的位置时,根据对称性可知,若运动方向相同,则速度是相同的,故B正确.由a=,位移大小相等、方向相反,则加速度也大小相等、方向相反,所以加速度不同,故D错误.答案:B4.弹簧振子在光滑水平面上做简谐运动,在振子向平衡位置运动的过程中()A.振子所受的弹力逐渐增大B.振子的位移逐渐增大C.振子的速度逐渐减小D.振子的加速度逐渐减小解析:弹簧振子在光滑水平面上做简谐运动,在振子向平衡位置运动的过程中,位移减小,由F=kx知,振子所受的弹力减小,加速度减小,弹力做正功,振子动能增加,选项D正确.答案:D5.如图所示,质量为m的小球放在劲度系数为k的轻弹簧上,使小球上下振动而又始终未脱离弹簧,则()A.最大振幅AB.最大振幅AC.最大振幅AD.最大振幅A解析:最大振幅满足kA=mg解得A小球在最高点和最低点所受回复力大小相同,故有F m-mg=mg解得F m=2mg.答案:A6.做简谐运动的弹簧振子质量为0.2 kg,当它运动到平衡位置左侧20 cm时受到的回复力是4 N;当它运动到平衡位置右侧40 cm时,它的加速度为()A.20 m/s2,向右B.20 m/s2,向左C.40 m/s2,向右D.40 m/s2,向左解析:加速度方向指向平衡位置,因此方向向左.由力和位移的大小关系F=kx可知,当x=40cm时,F=8N,a m/s2.答案:D7.下列运动中是简谐运动的是()A.打乒乓球时乒乓球的运动B.思考中的人来回走动C.上端固定的轻质弹簧的下端悬挂一个钢球,钢球上下来回运动D.从高处下落到光滑水泥地面上的小钢球的运动解析:打乒乓球时乒乓球的运动和思考中的人的来回走动没有规律,不是简谐运动,故A、B错误;轻质弹簧的下端悬挂一个钢球,上端固定,组成振动系统,钢球以受力平衡处为平衡位置上下做简谐运动,C正确;从高处下落到光滑水泥地面上的小钢球的运动过程为自由落体,不是简谐运动,故D错误. 答案:C8.质点做简谐运动的周期为0.4 s,振幅为0.1 m,从质点通过平衡位置开始计时,则经5 s,质点通过的路程等于m,位移为m.解析:质点通过的路程s·4A m=5m,5s 的时间为12.5个周期,质点回到平衡位置,位移为零.答案:509.质点以O为平衡位置做简谐运动,它离开平衡位置向最大位移处运动的过程中,经0.15 s第一次通过A点,再经0.1 s第二次通过A点,再经多少时间第三次通过A点?此质点振动的周期是多少?解析:质点振动情况如图所示.O点为平衡位置,B点为最大位移处,质点的振动周期设为T,那T=4×(0.15+0.05)s=0.8s,由振动的对称性可知,再经过Δt=T-t2=0.7s质点第三次通过A点.答案:0.7 s0.8 s10.一质量为m、侧面积为S的正方体木块,放在水面上静止(平衡),如图所示.现用力向下将其压入水中一定深度后(未全部浸入)撤掉外力,木块在水面上下振动,试判断木块的振动是否为简谐运动.解析:以木块为研究对象,设静止时木块浸入水中Δx深,当木块被压入水中x撤掉外力后受力情况如图所示.规定向下为正方向,则mg=ρ水gSΔx①F=mg-F浮②F浮=ρ水gS(Δx+x)③联立①②③解得F=mg-ρ水gS(Δx+x)=-ρ水gSx 令k=ρ水gS,可得F=-kx所以木块的振动是简谐运动.答案:是。
教科版高中物理选修3-4第一章简谐运动的图像和公式练习

3.简谐运动的图像和公式课时过关·能力提升1.关于一质点做简谐运动的图像,下列说法中正确的是 ()A.表示质点振动的轨迹是正弦或余弦曲线B.由图像可判断任一时刻质点相对平衡位置的位移方向C.表示质点的位移随时间变化的规律D.由图像可判断任一时刻质点的速度方向解析:振动图像表示位移随时间的变化规律,不是运动轨迹,选项A错误,选项C正确;由图像可以判断某时刻质点的位移和速度方向,选项B、D正确.答案:BCD2.一个质点做简谐运动的图像如图所示,从图中可以知道()A.在t=0时,质点位移为零,速度和加速度也为零B.在t=4 s时,质点的速度最大,方向沿y轴的负方向C.在t=3 s时,质点振幅为-5 cm,周期为4 sD.无论何时,质点的振幅都是5 cm,周期都是4 s解析:t=0、t=4s时,质点位于平衡位置,x=0,a=0,速度最大,方向沿y轴正方向;质点振动周期T=4s,振幅A=5cm,选项D正确.答案:Dt,以下说法正确的是()3.一单摆做简谐运动,其位移随时间变化的关系式为x=A si nπ4A.此单摆的周期为2 sB.2 s末回复力沿正方向C.3 s末速度方向沿正方向D.4 s末摆球受到的回复力为零解析:由位移随时间变化的关系式x=A si nπ4t可得,ω=π4rad/s,则T=2πt=2ππ4s=8s,故A错误;2s末位移大小为x=A si nπ4t=t sin(π4×2)=t,力的方向与位移方向相反,故2s末回复力沿负方向,故B错误;周期为8s,故3s末(38t)的速度方向为负方向,故C错误;4s末位移大小为x=A si nπ4t=t sin(π4×4)=0,质点位于平衡位置,回复力为零,故D正确.答案:D4.有两个振动,其表达式分别是x1=3si n(100πt+π3)cm,t2=6sin(100πt+π4)cm,下列说法正确的是()A.它们的振幅相同B.它们的周期相同C.它们的相位差恒定D.它们的振动步调一致解析:由简谐运动的公式可看出,两振动的振幅分别为3cm 和6cm,选项A错误;角速度ω=100πrad/s相同,周期T=2πt 也相同,选项B正确;相位差Δφ=π3−π4=π12,为定值,故相位差恒定,选项C正确,选项D错误.答案:BC5.一弹簧振子做简谐运动,其振动图像如图所示,那么在(t2-Δt)和(t2+Δt)(Δt是微小的时间)两时刻,振子的:①速度相同;②加速度相同;③相对平衡位置的位移相同;④振动的能量相同.以上选项中正确的是()A.①②B.②③C.③④D.①④解析:对于(t2-Δt)和(t2+Δt)两时刻,由已知可知两时刻振子的位置关于平衡位置对称,所以速度、加速度、位移大小相等,由图像可知速度方向也相同,但位移、加速度方向不同,所以①④正确,②③错误,选项D正确.答案:D6.(2018·天津理综)一振子沿x轴做简谐运动,平衡位置在坐标原点.t=0时振子的位移为-0.1 m,t=1 s时位移为0.1 m,则()A.若振幅为0.1 m,振子的周期可能为23sB.若振幅为0.1 m,振子的周期可能为45sC.若振幅为0.2 m,振子的周期可能为4 sD.若振幅为0.2 m,振子的周期可能为6 s解析:由题意可知振子在1s内由-0.1m的位置运动到0.1m的位置,若其振幅为0.1m,则Δt=n+12t=1s(n=0,1,2,3,…),则n=1时T=23s,但T不可能等于45s,选项A正确、B错误.若简谐运动的振幅为0.2m,需分几种情况进行讨论,若t=0和t=1s时质点沿x轴正向振动,满足n+16t=1s(n=0,1,2,…),当n=0时,T=6s;若t=0时质点沿x轴正向振动,t=1s时质点沿x轴负向振动,或t=0时质点沿x轴负向振动,t=1s时质点沿x轴正向振动,满足n+12t=1s(n=0,1,2,…);若t=0和t=1s时质点沿x轴负向振动,满足(n+56)t=1s(n=0,1,2,…),可得C错误,D正确.答案:AD7.A、B两人先后观察同一弹簧振子在竖直方向上下振动的情况.(1)A开始观察时,振子正好在平衡位置并向下运动,试在图甲中画出A观察到的弹簧振子的振动图像.已知经过1 s后,振子第一次回到平衡位置,振子振幅为5 cm(设平衡位置上方为正方向,时间轴上每格代表0.5 s).(2)B在A观察3.5 s后,开始观察并记录时间,试在图乙上画出B观察到的弹簧振子的振动图像.解析:(1)由题意知,振子的振动周期T=2s,振幅A=5cm.根据正方向的规定,A观察时,振子从平衡位置向-x方向运动,经t=0.5s,达到负向最大位移.画出的A观察到的振子的振动图像如图甲所示.(2)因为t=3.5s=74t,根据振动的重复性,这时振子的状态跟经过时间t'=34t的状态相同,所以B开始观察时,振子正好处于正向最大位移处.画出的B观察到的振子的振动图像如图乙所示.答案:见解析8.根据如图所示的振动图像,(1)算出下列时刻振子对平衡位置的位移.①t1=0.5 s;②t2=1.5 s.(2)将位移随时间的变化规律写成x=A sin(ωt+φ)的形式并指出振动的初相位是多少.解析:(1)由题图知,x=A cosωt=10co sπ2t,则t1=0.5s 时,x=5√2cm;t2=1.5s时,x=-5√2cm.(2)x=10si n(π2t+π2)cm,初相位φ=π2.答案:(1)5√2cm,−5√2cm(2)t=10sin(π2t+π2)cmπ29.如图所示,某质点做简谐运动的振动图像,根据图像中的信息,回答下列问题:(1)质点在第2 s末的位移;(2)质点振动过程中位移的最大值;(3)在前4 s内,质点经过的路程.解析:(1)由x-t图像可以读出2s末质点的位移为零.(2)质点的最大位移在前4s发生在1s末和3s末,位移大小为10cm.(3)前4s质点正好完成一个往复的全振动.先朝正方向运动了距离为10cm的一个来回,又在负方向上进行了一个10cm距离的来回,故总路程为40cm.答案:(1)0(2)10 cm(3)40 cm。
高三物理简谐运动的图象试题答案及解析

高三物理简谐运动的图象试题答案及解析1.一简谐横波在某一时刻的波形图如图甲所示,图乙为介质中x =2m处的质点P以此时刻为计时起点的振动图象。
则该波沿x轴_________ (填“正方向”、“负方向”)传播,该波的波速为__________m/s。
【答案】正方向 20【解析】由图乙可知,时的切线斜率为负,表示质点P沿y轴负方向振动,由质点的振动方向和波的传播方向间的关系“逆着传播方向看上则上,下则下”知:这列波沿x轴正方向传播;由波形图甲知此列简谐横波的波长为,由图乙可知,周期为,由得:此波的波速是。
【考点】本题考查质点的振动方向和波的传播方向间的关系;简谐波的波长、频率和波速的关系;波动图象和振动图象,意在考查考生的理解能力、推理能力和分析综合能力。
2.在均匀介质中,一列沿x轴正向传播的横波,其波源O在第一个周期内的振动图象,如右图所示,则该波在第一个周期末的波形图是()【答案】D【解析】因为介质中所以质点起振的方向都与振源起振的方向相同,由振动图象知波源开始振动的方向为负y方向,故第一个周期末开始振动的质点,其振动方向也是负y方向,根据上下波法可判断,A、C错误;由振动图象知,后半个周期振幅较大,根据波的传播特点知,B错误;D正确。
【考点】本题考查机械振动、机械波3.如图甲是一列简谐横波在t=0.01s时刻的波形图,图乙是质点P的振动图象,则下列说法正确的是()A.t=0.005s时,1m<x<2m范围内的质点正在向y轴的负方向运动B.从t=0.01s到t=0.025s,该波沿x轴负方向传播了1.5mC.从t=0.01s到t=0.015s,质点Q的动能逐渐减小D.从t=0.01s到t=0.025s,在1s内质点R通过的路程为30cm【答案】AC【解析】由图像可知,该机械波的波长为2m,周期为0.02s,故波速为,结合乙图可以看出,机械波沿x轴正方向传播,故可知在0.005s时刻,P点位于波谷,故1m<x<2m范围内的质点向y轴负方向运动,所以选项A正确;从t=0.01s到t=0.025s,机械波传播的距离,但向x正方向传播,所以选项A错误;在0.01s时刻,Q点位于平衡位置,接下来的四分之一个周期内,该点远离平衡位置,动能减小,所以选项C正确;由图像可知,波的振幅为10cm,R点从计时开始向y轴正方向运动,二分之一周期后,位于关于x轴的对称点位置,此后的四分之一个周期,该点向y轴负方向运动,路程小于一个振幅,所以该点在此段时间内通过的路程小于30cm,所以选项D正确;【考点】机械振动、机械波4.如图甲所示,为一列沿x轴传播的简谐横波在t=0时刻的波形图。
教科版选修3-4 1.3简谐运动的图像和公式 课时训练(解析版)

2021-2022学年教科版选修3-41.3简谐运动的图像和公式 课时训练〔解析版〕1.一质点做简谐运动,其位移x 与时间t 的关系图像如图9所示,由图可知()图9A.质点振动的频率是4Hz ,振幅是2cmB.质点经过1s 通过的路程总是2cm~3s 内,质点通过的路程为6cmD.t =2s 时,质点的振幅为零答案 C解析 由题图可以直接看出振幅为2cm ,周期为4s ,所以频率为,所以A 错误;质点在1s 即14个周期内通过的路程不一定等于一个振幅,所以B 错误;因为t =0时质点在平衡位置处,0~3s 为34T ,质点通过的路程为3A =6cm ,所以C 正确;振幅等于质点偏离平衡位置的最大距离,与质点的位移有着本质的区别,t =2s 时,质点的位移为零,但振幅仍为2cm ,所以D 错误.2.(多项选择)甲、乙两弹簧振子的振动图像如图10所示,那么可知()图10A.两弹簧振子完全相同B.振子的振动频率之比f 甲∶f 乙=1∶2C.振子甲速度为零时,振子乙速度最大D.两弹簧振子所受回复力最大值之比F 甲∶F 乙=2∶1答案 BC解析 由振动图像读出两弹簧振子的振幅和周期不同,那么两弹簧振子一定不完全相同,故A 错误;两弹簧振子振动周期之比T 甲∶T 乙=2∶1,频率之比是f 甲∶f 乙=1∶2,故B 正确;由题图看出,甲在最大位移处时,乙在平衡位置,即振子甲速度为零时,振子乙速度最大,故C 正确;由振动图像读出两振子位移最大值之比x 甲∶x 乙=2∶1,根据简谐运动的特征F =-kx ,由于弹簧的劲度系数k 可能不等,回复力最大值之比F 甲∶F 乙不一定等于2∶1,故D 错误.3.(多项选择)如图6所示为甲、乙两单摆的振动图像,那么()图6A.假设甲、乙两单摆在同一地点摆动,那么甲、乙两单摆的摆长之比为l 甲∶l 乙=2∶1B.假设甲、乙两单摆在同一地点摆动,那么甲、乙两单摆的摆长之比为l 甲∶l 乙=4∶1C.假设甲、乙两单摆摆长相同,且在不同的星球上摆动,那么甲、乙两单摆所在星球的重力加速度之比为g 甲∶g 乙=4∶1D.假设甲、乙两单摆摆长相同,且在不同的星球上摆动,那么甲、乙两单摆所在星球的重力加速度之比为g 甲∶g 乙=1∶4答案 BD解析 由题图可知T 甲∶T 乙=2∶1,由公式T =2πl g可知:假设两单摆在同一地点,那么两单摆摆长之比为l 甲∶l 乙=4∶1,故A 错误,B 正确;假设两单摆摆长相等,那么所在星球的重力加速度之比为g 甲∶g 乙=1∶4,故C 错误,D 正确.4.(多项选择)某质点做简谐运动,其位移随时间变化的关系式为x =A sin π4t ,那么质点() A.第1s 末与第3s 末的位移相同B.第1s 末与第3s 末的速度相同C.第3s 末与第5s 末的位移方向相同D.第3s 末与第5s 末的速度方向相同答案 AD解析 根据x =A sin π4t 可求得该质点振动周期为T =8s ,那么该质点振动图像如下图,图像的斜率为正表示速度为正,反之为负,由图可以看出第1s 末和第3s 末的位移相同,但斜率一正一负,故速度方向相反,选项A 正确,B 错误;第3s 末和第5s 末的位移方向相反,但两点的斜率均为负,故速度方向相同,选项C 错误,D 正确.5.(多项选择)物体A 做简谐运动的振动方程是x A =3sin ⎝⎛⎭⎪⎫100t +π2m ,物体B 做简谐运动的振动方程是x B =5sin ⎝⎛⎭⎪⎫100t +π6m.比拟A 、B 的运动() A.振幅是矢量,A 的振幅是6m ,B 的振幅是10mB.周期是标量,A 、B 周期相等,都为100sC.A 振动的频率f A 等于B 振动的频率f BD.A 的相位始终超前B 的相位π3答案 CD解析 振幅是标量,A 、B 的振动范围分别是6m 、10m ,但振幅分别为3m 、5m ,A 错;A 、B的周期均为T =2πω=2π100s =×10-2s ,B 错;因为T A =T B ,故f A =f B ,C 对;Δφ=φA -φB =π3,为定值,D 对. 6.一个小球和轻质弹簧组成的系统,按x 1=5sin (8πt +14π) cm 的规律振动. (1)求该振动的周期、频率、振幅和初相;(2)另一简谐运动表达式为x 2=5sin (8πt +54π) cm,求它们的相位差. 答案 (1)14s4Hz5cm π4(2)π 解析 (1)ω=8π rad/s,由ω=2πT 得T =14s , f =1T =4 Hz.由x 1=5sin (8πt +14π) cm 知A =5 cm , φ1=π4(2)由Δφ=(ωt +φ2)-(ωt +φ1)=φ2-φ1得Δφ=54π-π4=π. 7.如图11所示为A 、B 两个简谐运动的位移—时间图像.请根据图像答复:图11(1)A 的振幅是cm ,周期是s ;B 的振幅是cm ,周期是s.(2)写出这两个简谐运动的位移随时间变化的关系式;(3)在t =时两质点的位移分别是多少?答案(2)x A =0.5sin (5πt +π) cm,x B =cm(3)x A ′=-24cm ,x B ′=58πcm 解析 (1)由题图知:A 的振幅是,周期是;B 的振幅是,周期是0.8s.(2)t =0时刻A 中振动的质点从平衡位置开始沿负方向振动,φA =π,由T A =,得ωA =2πT A=5πrad/s.那么A 简谐运动的表达式为x A =0.5sin (5πt +π) cm.t =0时刻B 中振动的质点从平衡位置沿正方向已振动了14周期,φB =π2,由T B =得ωB =2πT B=,那么B 简谐运动的表达式为x B =cm.(3)将t =分别代入两个表达式中得:x A ′=0.5sin (5π×+π) cm=-×22cm =-24cm ,x B ′=cm =58πcm.。
2016-2017学年物理高二教科版选修3-4自我小测:第1章3

自我小测1.一简谐运动的图像如图所示,在0.1~0.15 s这段时间内().A.加速度增大,速度变小,加速度和速度的方向相同B.加速度增大,速度变小,加速度和速度方向相反C.加速度减小,速度变大,加速度和速度方向相同D.加速度减小,速度变大,加速度和速度方向相反2.如图所示为质点P在0~4 s内的振动图像,下列叙述正确的是().A.再过1 s,该质点的位移是正向最大B.再过1 s,该质点的速度方向向上C.再过1 s,该质点的加速度方向向上D.再过1 s,该质点的加速度最大3.劲度系数为20 N/m的弹簧振子,它的振动图像如图所示,在图中A点对应的时刻().A.振子所受弹力大小为0.5 N,方向指向x轴负方向B.振子的速度方向指向x轴正方向C.在0~4 s内振子做了1.75次全振动D.在0~4 s内振子通过的路程为0.35 m,位移为零4.一个质点做简谐运动的图像如图所示,下列说法正确的是().A .质点振动频率为4 HzB .在10 s 内质点经过的路程为20 cmC .在5 s 末,质点做简谐运动的相位为3π2D .t =1.5 s 和t ′=4.5 s 5.物体A 做简谐运动的位移x A =3sin (100t +π2)m ,物体B 做简谐运动的位移x B =5sin (100t +π6)m .比较A 、B 的运动( ). A .振幅是矢量,A 的振幅是6 m ,B 的振幅是10 mB .周期是标量,A 、B 的周期相等,为100 sC .A 振动的频率f A 等于B 振动的频率f BD .A 的相位始终超前B 的相位π36.如图a 所示为一弹簧振子的振动图像,规定向右的方向为正方向,试根据图像分析以下问题:(1)如图b 所示的振子振动的起始位置是____,从初始位置开始,振子向________(填“右”或“左”)运动.(2)在图b 中,找出图像中的O 、A 、B 、C 、D 各对应振动过程中的哪个位置?即O 对应________,A 对应________,B 对应________,C 对应________,D 对应________.(3)在t =2 s 时,振子的速度方向与t =0时速度的方向________.(4)质点在前4 s 内的位移等于________.7.已知某人心电图记录仪的出纸速度(纸带移动的速度)为2.5 cm/s ,如图所示是用此仪器记录下的某人的心电图(图中每个大格的边长为0.5 cm ).(1)由图可知此人的心率是________次/分,它的心脏每跳一次所需的时间是________ s.(2)如果某人的心率是75次/分,他的心脏每跳一次大约输送8×10-5 m3的血液,他的血压(可看做他的心脏跳动时压送血液的压强)的平均值是1.5×104Pa,据此估算此人的心脏跳动时做功的平均功率约为多大?8.(2011·山东济宁模拟)一质点做简谐运动,其位移和时间关系如图所示.(1)求t=0.25×10-2 s时的位移;(2)在t=1.5×10-2 s到2×10-2 s的振动过程中,质点的位移、回复力、速度、动能、势能如何变化?(3)在t=0到8.5×10-2 s时间内,质点的路程、位移各多大?参考答案1答案:B 解析:由图像可知,在0.1~0.15 s 这段时间内,位移为负且增大,表明物体远离平衡位置,则加速度增大,速度减小,二者反向.2答案:AD 解析:依题意,再经过1 s ,振动图像将延伸到正向位移最大处,这时质点的位移为正向最大,弹力的方向与位移方向相反,大小与位移成正比,所以弹力为负向最大,故加速度也为负向最大,此时振动物体的速度为零,无方向.3答案:AB 解析:由图像可知A 在t 轴上方,位移x =0.025 m ,所以弹力F =kx =20×0.025 N =0.5 N ,即弹力大小为0.5 N ,方向指向x 轴负方向,选项A 正确;由图可知,若在A 点作图像的切线,该切线与x 轴正方向的夹角小于90°,切线的斜率为正值,即振子的速度方向指向x 轴正方向,选项B 正确;由图像可看出,t =0时刻振子的位移最大,在t 轴上方;t =4 s 时刻振子的位移也最大,也在t 轴上方;在0~4 s 内振子完成了两次全振动,选项C 错误;由于t =0时刻和t =4 s 时刻振子都在最大位移处,故在0~4 s 内振子完成了两次全振动,所以这段时间内振子通过的路程为2×4×0.05 m =0.4 m ,选项D 错误.4答案:BD 解析:由振动图像可直接得到周期为4 s ,频率1f T==0.25 Hz ,故选项A 是错误的;一个周期内简谐运动的质点经过的路程是4A =8 cm,10 s 为2.5个周期,故质点经过的路程为20 cm ,选项B 是正确的;由图像知,位移与时间的关系x =A sin (ωt +φ0)=0.02sin (π2t )m .当t =5 s 时,其相位ωt +φ0=π2×5=5π2,故C 不正确;在1.5 s 和4.5 s 两时刻,质点的位移相同,与振幅的关系是x ′=A sin 135°A ,故D 正确. 5答案:CD 解析:振幅是标量,A 、B 的振动范围分别是6 m 、10 m ,但振幅分别为3 m 、5 m ,故A 错.A 、B 的周期22π2πs 6.2810s 100T ω==⨯-=,故B 错.因T a =T b ,故f a =f b ,故C 对.△φ=φA -φB =πππ263-=,故D 对. 6答案:(1)E 右 (2)E G E F E (3)相反 (4)0解析:(1)由x -t 图像知,在t =0时,物体在平衡位置,故起始位置为E ;从t =0时刻开始,振子向正的位置处运动,即向右运动.(2)由x -t 图像知:O 点、B 点、D 点对应平衡位置的E 点,A 点在正的最大位移处,对应G 点;C 点在负的最大位移处,对应F 点.(3)t =2 s 时,图像斜率为负,即速度方向为负方向;t =0时,斜率为正,速度方向为正方向.故两时刻速度方向相反.(4)4 s 末振子回到平衡位置,故位移为零.7答案:(1)75 0.8 (2)1.5 W解析:(1)由题图知两次心跳间隔为4小格,每小格边长为0.5 cm ,所以心脏每跳一次的时间40.5s 0.8s 2.5t ⨯==.此时人的心率11600.8f t ==⨯次/分=75次/分. (2)每心跳一次心脏压送血液做功: W =P △V =1.5×104×8×10-5 J =1.2 J 故心脏跳动做功的平均功率 1.2W=1.5W 0.8W P t ==.8答案:(1) (2)变大 变大 变小 变小 变大 (3)34 cm 2 cm解析:(1)由题图可知A =2 cm ,T =2×10-2 s ,振动方程为x =A sin (ωt -π2)=-A cos ωt =-2cos (22π210t -⨯)cm =-2cos (102πt )cm当t =0.25×10-2 s 时x =-2cosπ4cm =. (2)由题图可知在1.5×10-2~2×10-2 s 时间内,质点的位移变大,回复力变大,速度变小,动能变小,势能变大.(3)在0至8.5×10-2 s 的时间内质点的路程为s =17A =34 cm ,位移大小为2 cm.。
高中物理课时训练(三)简谐运动的图像和公式教科版选修3-4(new)
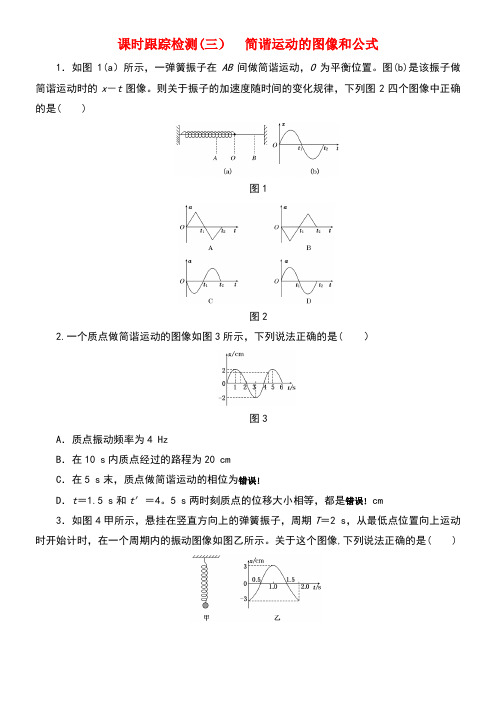
课时跟踪检测(三)简谐运动的图像和公式1.如图1(a)所示,一弹簧振子在AB间做简谐运动,O为平衡位置。
图(b)是该振子做简谐运动时的x-t图像。
则关于振子的加速度随时间的变化规律,下列图2四个图像中正确的是( )图1图22.一个质点做简谐运动的图像如图3所示,下列说法正确的是( )图3A.质点振动频率为4 HzB.在10 s内质点经过的路程为20 cmC.在5 s末,质点做简谐运动的相位为错误!D.t=1.5 s和t′=4。
5 s两时刻质点的位移大小相等,都是错误! cm3.如图4甲所示,悬挂在竖直方向上的弹簧振子,周期T=2 s,从最低点位置向上运动时开始计时,在一个周期内的振动图像如图乙所示。
关于这个图像,下列说法正确的是( )图4A.t=1.25 s时,振子的加速度为正,速度也为正B.t=1。
7 s时,振子的加速度为负,速度也为负C.t=1。
0 s时,振子的速度为零,加速度为负向最大值D.t=1。
5 s时,振子的速度为零,加速度为负向最大值4.如图5为某一质点的振动图像,由图可知,在t1和t2两时刻|x1|〉|x2|,质点速度v、v2与加速度a1、a2的关系为()1图5A.v1〈v2,方向相同B.v1<v2,方向相反C.a1>a2,方向相同D.a1〉a2,方向相反5.(北京高考)一个弹簧振子沿x轴做简谐运动,取平衡位置O为x轴坐标原点。
从某时刻开始计时,经过四分之一周期,振子具有沿x轴正方向的最大加速度。
能正确反映振子位移x与时间t关系的图像是( )图66.劲度系数为20 N/cm的弹簧振子,它的振动图像如图7所示,在图中A点对应的时刻()图7A.振子所受的弹力大小为0.5 N,方向指向x轴的负方向B.振子的速度方向指向x轴的正方向C.在0~4 s内振子作了1.75次全振动D.在0~4 s内振子通过的路程为0.35 cm,位移为07.如图8所示是某质点做简谐运动的振动图像,根据图像中的信息,回答下列问题:图8(1)振幅、周期各是多大?(2)写出这个简谐运动的位移随时间变化的关系式。
四川省天全中学高中物理 1.3 简谐运动的图像和公式练习题 教科版选修34
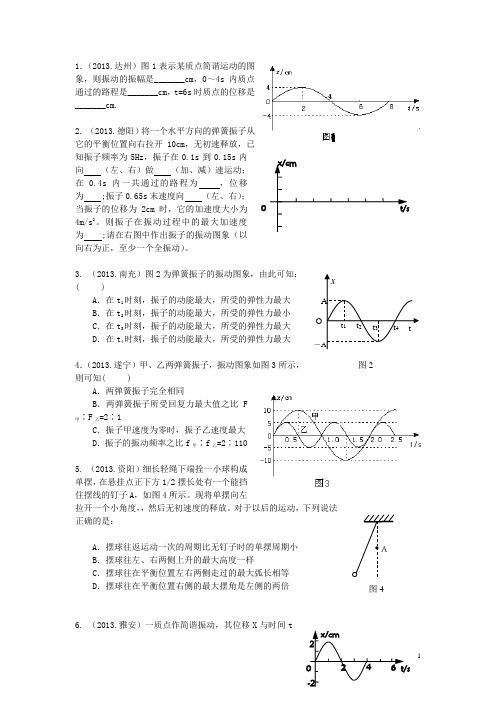
11.(2013.达州)图1表示某质点简谐运动的图象,则振动的振幅是_______cm ,0~4s 内质点通过的路程是_______cm ,t=6s 时质点的位移是_______cm.2. (2013.德阳)将一个水平方向的弹簧振子从它的平衡位置向右拉开10cm ,无初速释放,已知振子频率为5Hz ,振子在0.1s 到0.15s 内向 (左、右)做 (加、减)速运动;在0.4s 内一共通过的路程为 ,位移为 ;振子0.65s 末速度向 (左、右);当振子的位移为2cm 时,它的加速度大小为4m/s 2。
则振子在振动过程中的最大加速度为 ;请在右图中作出振子的振动图象(以向右为正,至少一个全振动)。
3. (2013.南充)图2为弹簧振子的振动图象,由此可知:( )A .在t 1时刻,振子的动能最大,所受的弹性力最大B .在t 2时刻,振子的动能最大,所受的弹性力最小C .在t 3时刻,振子的动能最大,所受的弹性力最大D .在t 4时刻,振子的动能最大,所受的弹性力最大4.(2013.遂宁)甲、乙两弹簧振子,振动图象如图3所示,则可知( )A .两弹簧振子完全相同B .两弹簧振子所受回复力最大值之比F甲∶F 乙=2∶1C .振子甲速度为零时,振子乙速度最大D .振子的振动频率之比f 甲∶f 乙=2∶1105. (2013.资阳)细长轻绳下端拴一小球构成单摆,在悬挂点正下方1/2摆长处有一个能挡住摆线的钉子A ,如图4所示。
现将单摆向左拉开一个小角度,,然后无初速度的释放。
对于以后的运动,下列说法正确的是:A .摆球往返运动一次的周期比无钉子时的单摆周期小B .摆球往左、右两侧上升的最大高度一样C .摆球往在平衡位置左右两侧走过的最大弧长相等D .摆球往在平衡位置右侧的最大摆角是左侧的两倍6. (2013.雅安)一质点作简谐振动,其位移X 与时间tt 2 t 4 x t 3 A-A O t 1 t图2 t/sx/cm2 4 6 2-2 t/s x/cm 0 A图42 的关系曲线图,由图可知( )A.由0时刻开始计时,质点的轨迹是一条正弦曲线B.质点振动的频率为2HzC.在t=3秒末,质点的加速度负向最大D.在t=4秒末,质点的速度负向最大7. (2013.乐山)右图为甲、乙两个物体的振动图象,则( )A.甲、乙两振动的振幅分别是2m ,1mB.甲、乙的振动频率之比为1:2C.前四秒内甲,乙两物体的加速度均为负值D.第二秒末甲的速度最大,乙的加速度最大8.(2013.眉山)图5所示为质点P 在0~4s 内的运动图象,下列叙述正确的是( )A .再过1s ,该质点的位移是负的最大B .再过1s ,该质点的速度沿正方向C .再过1s ,该质点的加速度沿正方向D .再过1s ,该质点加速度最大9.(2013.内江)甲乙两人先后观察同一弹簧振子在竖直方向上的振动情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3节 简谐运动的图像和公式1.以横坐标表示________,纵坐标表示________________________________________,描绘出简谐运动的质点的________随________变化的图像,称为简谐运动的图像(或振动图像).简谐运动的图像是一条________(或________)曲线.2.由简谐运动的图像,可以直接读出物体振动的________和________.用图像记录振动的方法在实际生活中有很多应用,如医院里的________________、监测地震的____________等.3.简谐运动的表达式:x =________________或x =________________.其中A 表示简谐运动的________,T 和f 分别表示简谐运动的周期和频率,________或________表示简谐运动的相位,Φ表示t =0时的相位,叫做初相位,简称初相.频率相同、初相不同的两个振动物体的相位差是________.4.如图1所示是一做简谐运动的物体的振动图像,下列说法正确的是( )图1A .振动周期是2×10-2sB .第2个10-2s 内物体的位移是-10 cm C .物体的振动频率为25 Hz D .物体的振幅是10 cm5.摆长为l 的单摆做简谐运动,若从某时刻开始计时(即取t =0),当振动至t =3π2l g时,摆球恰具有负向最大速度,则单摆的振动图像是下图中的( )6.物体A 做简谐运动的振动位移x A =3sin (100t +π2) m ,物体B 做简谐运动的振动位移x B =5sin (100t +π6) m .比较A 、B 的运动( )A .振幅是矢量,A 的振幅是6 m ,B 的振幅是10 m B .周期是标量,A 、B 周期相等为100 sC .A 振动的频率f A 等于B 振动的频率f BD .A 的相位始终超前B 的相位π3概念规律练知识点一 简谐运动的图像1.如图2所示是表示一质点做简谐运动的图像,下列说法正确的是( )图2A.t1时刻振子正通过平衡位置向上正方向运动B.t2时刻振子的位移最大C.t3时刻振子正通过平衡位置向上正方向运动D.该图像是从平衡位置计时画出的2.如图3所示是某质点做简谐运动的振动图像,根据图像中的信息,回答下列问题:图3(1)质点离开平衡位置的最大距离是多少?(2)在1.5 s和2.5 s两个时刻,质点向哪个方向运动?(3)质点在第2秒末的位移是多少?在前4秒内的路程是多少?知识点二简谐运动的表达式3.一物体沿x轴做简谐运动,振幅为8 cm,频率为0.5 Hz,在t=0时,位移是4 cm,且向x轴负方向运动,试写出用正弦函数表示的振动方程.知识点三简谐运动的相位、相位差4.如图4所示,A、B为两弹簧振子的振动图像,求它们的相位差.图45.有两个振动的振动方程分别是:x 1=3sin (100πt +π3) cm ,x 2=5sin (100πt +π4)cm ,下列说法正确的是( )A .它们的振幅相同B .它们的周期相同C .它们的相位差恒定D .它们的振动步调一致 方法技巧练根据图像判断物体运动情况的技巧6.如图5所示为质点P 在0~4 s 内的振动图像,下列叙述正确的是( )图5A .再过1 s ,该质点的位移是正向最大B .再过1 s ,该质点的速度方向向上C .再过1 s ,该质点运动到平衡位置D .再过1 s ,该质点的速度为零7.如图6所示为一弹簧振子的振动图像,如果振子的质量为0.2 kg ,求:图6(1)从计时开始经过多少时间位移第一次达到最大;(2)从第2 s 末到第3 s 末这段时间内弹簧振子的加速度、速度、位移各是怎样变化的.1.关于简谐运动的图像,下列说法中正确的是( ) A .表示质点振动的轨迹是正弦或余弦曲线B .由图像可判断任一时刻质点相对平衡位置的位移方向C.表示质点的位移随时间变化的规律D.由图像可判断任一时刻质点的速度方向2.如图7所示是某振子做简谐运动的图像,以下说法中正确的是( )图7A.因为振动图像可由实验直接得到,所以图像就是振子实际运动的轨迹B.振动图像反映的是振子位移随时间变化的规律,并不是振子运动的实际轨迹C.振子在B位置的位移就是曲线BC的长度D.振子运动到B点时的速度方向即为该点的切线方向3.如图8是用频闪照相的方法获得的弹簧振子的位移—时间图像,下列有关该图像的说法正确的是( )图8A.该图像的坐标原点建立在弹簧振子的平衡位置B.从图像可以看出小球在振动过程中是沿t轴方向移动的C.为了显示小球在不同时刻偏离平衡位置的位移,可让底片沿垂直x轴方向匀速运动D.图像中小球的疏密显示出相同时间内小球位置变化的快慢不同4.如图9所示为弹簧振子的振动图像,关于振子的振动,下列描述正确的是( )图9A.振子沿如图所示的曲线运动B.图像描述的是振子的位移随时间变化的规律C.从0.5 s到1.5 s内振子先加速运动后减速运动D.从1 s到2 s内振子先减速运动后加速运动5.如图10所示为某质点在0~4 s内的振动图像,则( )图10A.质点在3 s末的位移为2 mB.质点在4 s末的位移为8 mC.质点在4 s内的路程为8 mD.质点在4 s内的路程为零6.在水平方向上做简谐运动的质点,其振动图像如图11所示.假设向右的方向为正方向,则物体的位移向左且速度向右的时间段是( )图11A.0 s到1 s内B .1 s 到2 s 内C .2 s 到3 s 内D .3 s 到4 s 内7.一个质点做简谐运动,它的振动图像如图12所示,则( )图12A .图中的曲线部分是质点的运动轨迹B .有向线段OA 是质点在t 1时间内的位移C .有向线段OA 在x 轴的投影是质点在t 1时刻的位移D .有向线段OA 的斜率是质点在t 1时刻的瞬时速率8.如图13所示,是质点做简谐运动的图像.由此可知( )图13A .t =0时,质点位移、速度均为零B .t =1 s 时,质点位移最大,速度为零C .t =2 s 时,质点位移为零,速度沿负向最大D .t =4 s 时,质点停止运动9.有一个弹簧振子,振幅为0.8 cm ,周期为0.5 s ,初始时具有负方向的最大加速度,则它的振动方程是( )A .x =8×10-3sin ⎝⎛⎭⎪⎫4πt +π2 mB .x =8×10-3sin ⎝⎛⎭⎪⎫4πt -π2 mC .x =8×10-1sin ⎝⎛⎭⎪⎫πt +32π mD .x =8×10-1sin ⎝ ⎛⎭⎪⎫4πt +π2 m10.某质点做简谐运动,其位移随时间变化的关系式为x =A sin π4t ,则质点( )A .第1 s 末与第3 s 末的位移相同B .第1 s 末与第3s 末的速度相同C .3 s 末至5 s 末的位移方向都相同D .3 s 末至5 s 末的速度方向都相同 11.一弹簧振子沿x 轴振动,振幅为4 cm ,振子的平衡位置位于x 轴上的O 点.图14甲中的a 、b 、c 、d 为四个不同的振动状态:黑点表示振子的位置,黑点上的箭头表示运动的方向.图乙给出的①②③④四条振动图线,可用于表示振子的振动图像的是( )甲乙 图14A .若规定状态a 时t =0,则图像为①B .若规定状态b 时t =0,则图像为②C .若规定状态c 时t =0,则图像为③D .若规定状态d 时t =0,则图像为④12.如图15所示为A 、B 两个简谐运动的位移—时间图像.试根据图像写出:图15(1)A 的振幅是______cm ,周期是________s ;B 的振幅是________cm ,周期是________s. (2)这两个简谐运动的位移随时间变化的关系式. (3)在时间t =0.05 s 时两质点的位移分别是多少?13.两个简谐运动的表达式分别为x 1=4a sin(4πbt +π2),x 2=2a sin(4πbt +3π2).求它们的振幅之比,各自的频率,以及它们的相位差.14.某质点的振动方程为x =5sin(2.5πt +π2)cm ,画出该质点的振动图像.第3节 简谐运动的图像和公式答案课前预习练1.时间 摆球相对于平衡位置的位移 位移x 时间t 正弦 余弦 2.周期 振幅 心电图仪 地震仪3.Asin(2πT t +Φ) Asin(2πft+Φ) 振幅 2πT t +Φ 2πft+Φ Φ2-Φ14.BCD5.D 6.CD 课堂探究练 1.BC点评 质点做简谐运动的情况要和振动图像结合起来,利用简谐运动的图像来分析简谐运动的运动过程会更直观、方便.2.见解析解析 由图像上的信息,结合质点的振动过程可知(1)质点离开平衡位置的最大距离就是x 的最大值为10 cm ;(2)在1.5 s 后质点位移减小,因此是向平衡位置运动,在2.5 s 后质点位移增大,因此是背离平衡位置运动;(3)质点第2秒末在平衡位置,因此位移为零.质点在前4秒内完成一个周期性运动,其路程为10 cm×4=40 cm.点评 对于振动图像,不要错误地理解为振子的振动轨迹,振子位移的起始位置为平衡位置,应该与运动学中物体的位移区分开.3.x =0.08sin (πt+56π) m解析 简谐运动振动方程的一般表达式为x =Asin(ωt+Φ).根据题给条件有A =0.08 m ,ω=2πf=π,所以x =0.08sin (πt+Φ) m.将t =0时x =0.04 m 代入振动方程得0.04=0.08sin Φ,解得初相Φ=π6或Φ=56π.因为t =0时,速度方向沿x 轴负方向,即位移在减小,所以取Φ=56π,所求的振动方程为x =0.08sin (πt+56π) m.点评 对于给定的位移,可能解得两个初相值,这要根据题意做出判断,舍去不合题意的值.4.12π 解析 该题考查相位差的求法,由图像可知这两个振动的周期相同,均为0.4 s ,因此有确定的相位差.而相位差为初相之差.t =0时,x A =Asin ΦA ,x A =0,ΦA =0,x B =AsinΦB ,x B =-A ,ΦB =-12πΦA -ΦB =12π点评 在给定振动图像的条件下,可由图像直接读出振幅A 及初相Φ、周期T ,从而写出位移与时间的关系式x =Asin 2πT t +Φ,初相即取t =0时,由sinΦ的取值判定的ΦA 值.5.BC点评 要理解x =Asin(2πft+Φ)中各字母所对应的物理量及各物理量的意义. 6.AD方法总结 简谐运动的图像反映了质点在不同时刻的位移情况,另外根据图像的形式还可以推断出下一时刻的运动趋势,因此解此类问题应先画出再过1 s 的振动图像.画图像时只要将振动图像随时间延伸即可,而图像形状不变,然后再根据图像寻找规律.7.见解析解析 (1)由图知,在计时开始的时刻振子恰好以沿x 轴正方向的速度通过平衡位置,此时弹簧振子具有最大速度,随着时间的延续,速度不断减小,而位移逐渐加大,经t =1 s ,其位移达到最大.(2)由图知,在t =2 s 时,振子恰好通过平衡位置,此时加速度为零,随着时间的延续,位移不断变大,加速度也变大,速度不断变小,当t =3 s 时,位移达到负向最大值,加速度达到正向最大值,速度等于零.方法总结 充分利用图像的直观性,把图像与振动过程联系起来,图像上的一个点表示振动过程中的一个状态(位置、振动方向等),图线上的一段对应振动的一个过程,解题关键是判断好平衡位置、最大位移及振动方向.课后巩固练 1.BCD 2.B 3.ACD 4.B 5.C 6.D 7.C 8.BC9.A [2πT =4π,当t =0时,具有负方向的最大加速度,则x =A ,所以初相Φ=π2,表达式为x =8×10-3sin ⎝⎛⎭⎪⎫4πt+π2 m ,A 正确.]10.AD11.AD12.(1)0.5 0.4 0.2 0.8(2)x A =0.5sin (5πt+π) cm,x B =0.2sin cm(2.5πt+π2) cm(3)x A =-24 cm ,x B =0.2sin 58π cm 解析 (1)由图像知:A 的振幅是0.5 cm ,周期是0.4 s ;B 的振幅是0.2 cm ,周期是0.8 s.(2)由图像知:A 中振动的质点已振动了12周期,φ=π,由T =0.4 s ,得ω=2πT =5π,则简谐运动的表达式为x A =0.5sin (5πt+π) cm.B 中振动的质点从平衡位置沿正方向已振动了14周期,φ=π2,由T =0.8 s 得ω=2πT =2.5π,则简谐运动的表达式为x B =0.2sin(2.5πt+π2) cm.(3)将t =0.05 s 分别代入两个表达式中得:x A =0.5sin(5π×0.05+π)cm=-0.5×22cm =-24cm ,x B =0.2sin(2.5π×0.05+π2)cm =0.2sin 58π cm.13.A 1∶A 2=2∶1 f 1=f 2=2b ΔΦ=π 解析 它们的振幅之比A 1A 2=4a 2a =21;它们的频率相同,都是f =ω2π=4πb2π=2b ;它们的相位差ΔΦ=Φ2-Φ1=3π2-π2=π,可见它们反相.14.质点的振动图像见下图解析 该题考查的是根据振动方程画质点的振动图像.由题意知,振幅A =5 cm.周期T =2πω=2π2.5π=0.8 s .当t =0时,x =5 cm ,由此可作出图像,见答案中图.习题课 对简谐运动的理解提升基础练1.如图1所示,下列振动系统不可看做弹簧振子的是( )图1A.如图甲所示,竖直悬挂的轻弹簧及小铅球组成的系统B.如图乙所示,放在光滑斜面上的铁块及轻弹簧组成的系统C.如图丙所示,光滑水平面上,两根轻弹簧系住一个小球组成的系统D.蹦极运动中的人与弹性绳组成的系统2.质点沿x轴做简谐运动,平衡位置为坐标原点O,质点经过a点和b点时速度相同,所花时间t ab=0.2 s;质点由b点再次回到a点花的最短时间t ba=0.4 s;则该质点做简谐运动的频率为( )A.1 Hz B.1.25 HzC.2 Hz D.2.5 Hz3.如图2所示为某物体做简谐运动的图像,下列说法中正确的是( )图2A.由P→Q,位移在增大B.由P→Q,速度在增大C.由M→N,位移先减小后增大D.由M→N,位移始终减小4.一弹簧振子在一条直线上做简谐运动,第一次先后经过M、N两点时速度v(v≠0)相同,那么,下列说法正确的是( )A.振子在M、N两点受回复力相同B.振子在M、N两点对平衡位置的位移相同C.振子在M、N两点加速度大小相等D.从M点到N点,振子先做匀加速运动,后做匀减速运动5.图3为甲、乙两单摆的振动图像,则( )图3A.若甲、乙两单摆在同一地点摆动,则甲、乙两单摆的摆长之比l甲∶l乙=2∶1B.若甲、乙两单摆在同一地点摆动,则甲、乙两单摆的摆长之比l甲∶l乙=4∶1C.若甲、乙两摆摆长相同,且在不同的星球上摆动,则甲、乙两摆所在星球的重力加速度之比g甲∶g乙=4∶1D.若甲、乙两摆摆长相同,且在不同的星球上摆动,则甲、乙两摆所在星球的重力加速度之比g甲∶g乙=1∶4提升练6.一个质点a做简谐运动的图像如图4所示,下列结论正确的是( )图4A.质点的振幅为4 cmB.质点的振动频率为0.25 HzC.质点在10 s内通过的路程是20 cmD.质点从t=1.5 s到t=4.5 s的过程中经过的路程为6 cm7.如图5甲所示是演示简谐运动图像的装置,当漏斗下面的薄木板N被匀速地拉出时,振动着的漏斗中漏出的沙在板上形成的曲线显示出摆的位移随时间变化的关系.板上的直线OO 1代表时间轴,图乙中是两个摆中的沙在各自板上形成的曲线,若板N 1和板N 2拉动的速度v 1和v 2的关系为v 2=2v 1,则板N 1、N 2上曲线所代表的周期T 1和T 2的关系为( )图5A .T 2=T 1B .T 2=2T 1C .T 2=4T 1D .T 2=14T 18.如图6所示为某一质点的振动图像,由图像可知在t 1和t 2两时刻,质点的速度v 1、v 2,加速度a 1、a 2的大小关系为( )图6A .v 1<v 2,方向相同B .v 1>v 2,方向相反C .a 1>a 2,方向相同D .a 1>a 2,方向相反9.如图7所示是一简谐运动的振动图像,则下列说法正确的是( )图7A .该简谐运动的振幅为6 cm ,周期为8 sB .6~8 s 时间内,振子由负向最大位移处向平衡位置运动C .图中的正弦曲线表示振子的运动轨迹D .该振动图像对应的表达式为x =3sin (πt4) cm10.如图8所示,一升降机在箱底装有若干弹簧,设在某次事故中,升降机吊索在空中断裂,忽略摩擦力,则升降机在从弹簧下端触地后直到最低点的一段运动过程中( )图8A .升降机的速度不断减小B .升降机的加速度不断变大C .升降机的加速度最大值等于重力加速度值D .升降机的加速度最大值大于重力加速度值11.一个质点在平衡位置O 点的附近做简谐运动,它离开O 点后经过3 s 时间第一次经过M 点,再经过2 s 第二次经过M 点,该质点再经过________ s 第三次经过M 点.若该质点由O 点出发在20 s 内经过的路程是20 cm ,则质点做简谐振动的振幅为________ cm.12.跳板跳水运动员在起跳前都要随跳板上下振动几次,若想获得最好的起跳高度,你认为应在何处起跳?________(填“最高点”“最低点”或“平衡位置”).13. 如图9所示,将质量m A =100 g 的平台A 连接在劲度系数k =200 N/m 的弹簧上端,形成竖直方向的弹簧振子,在A 的上方放置m B =m A 的物块B ,使A 、B 一起上下振动.若弹簧原长为5 cm ,求:图9(1)当系统进行小振幅振动时,平衡位置离地面C 的高度; (2)当振幅为0.5 cm 时,B 对A 的最大压力;(3)为使B 在振动中始终与A 接触,振幅不得超过多少?习题课 对简谐运动的理解提升答案1.D 2.B 3.AC 4.C 5.BD 6.BC 7.D 8.AD 9.BD10.D 11.14或103 4或43解析 根据简谐运动的周期性和对称性分析解决问题.作出该质点振动的图像如下图所示,则M 点的位置可能有两个,即如下图所示的M 1或M 2.(1)第一种情况若是位置M 1,由图可知T 14=3 s +1 s =4 s ,T 1=16 s ,根据简谐运动的周期性,质点第三次经过M 1时所需时间为一个周期减第二次经过M 点的时间,故Δt 1=16 s -2 s =14 s.质点在20 s 内(即n =2016=54个周期内)的路程为20 cm ,故由5A 1=20 cm ,得振幅A 1=4 cm.(2)第二种情况若是位置M 2,由图可知3T 24=3 s +1 s =4 s ,T 2=163s.根据对称性,质点第三次经过M 2时所需时间为一个周期减第二次经过M 点的时间, 故Δt 2=163 s -2 s =103s.质点在20 s 内(即n =20163=154个周期内)的路程为20 cm.故由15A 2=20 cm ,得振幅A 2=43cm.12.最低点解析 在最低点,人和板的作用力最大,板对人做功最多,人获得的动能最大,跳的最高.13.(1)4 cm (2)1.5 N (3)1 cm解析 (1)将A 与B 整体作为振子,当A 、B 处于平衡位置时,根据平衡条件得 kx 0=(m A +m B )g 解得弹簧形变量x 0=(m A +m B )g k =(0.1+0.1)×10200m=0.01 m =1 cm平衡位置距地面高度h =l 0-x 0=5 cm -1 cm =4 cm(2)已知A 、B 一起振动的振幅A =0.5 cm ,当A 、B 振动到最低点位置时,加速度最大,其值为am =kA m A +m B =200×0.0050.1+0.1m/s 2=5 m/s 2方向竖直向上.取B 物块为研究对象,B 受重力m B g 、A 对B 的支持力N ,其合外力为F =N -m B g , 根据牛顿第二定律得N -m B g =m B am 解得N =m B g +m B am =m B (g +am) =0.1×(10+5) N =1.5 N根据牛顿第三定律,B 对A 的最大压力大小为 N′=N =1.5 N.(3)取B 为研究对象,当B 振动到最高点时受重力m B g 和A 对B 的支持力N 1,其合力为B 的回复力即F 回=m B g -N 1.根据牛顿第二定律得m B g -N 1=m B a当N 1=0时,B 振动的加速度达到最大值,其最大值为am′=g =10 m/s 2取A 与B 整体为研究对象,受到的最大回复力为 F 回m =kA′=(m A +m B )am′则振动系统的振幅为A′=(m A +m B )am′k=(0.1+0.1)×10200m=0.01 m =1 cm 当振幅A′>1 cm 时,B 与A 将分离,为使B 在振动中始终与A 接触,振动系统的振幅A′≤1 cm.。
