[课件]电磁学习题课答案PPT
合集下载
大物电磁学课后答案3经典.ppt
(1)电流强度在10秒内均匀的有零增加到3安培; (2)电流强度从18安培起,每过0.01秒减少一半,直到零。
解:(1)I 3 t 10
q
I dt
010
t 10
dt
15(库 仑)
(2)q I0k
1 2
I
0k
1 4
I0k
I0k(1 1 / 2 1 / 4 ) 180.011/(11/ 2)0.36(库 仑)
安培起,每过0.01秒减少一半,直到零。求导线产生的热量。
解:
3
2
(1) I 10 t dQ I rdt
| Q
t
(
3
t)2 Rdt
3
Rt3
10
180(焦)
0 10
10 0
2
2
2
(2) Q Q1 Q 2 Q 3 I1 Rt I 2Rt I 3Rt
Rt[I02
(
I0
/
2)2
电势差为4.25伏特,当该电池放电时,通过的电流为4安培两极
间的电势差为3.90伏特,求该电池的电动势和电阻。
解:
I1r 4.25 I 2r 3.90
精品文档
r
0.05(欧 4.10(伏
姆) 特)
6
3-10 设在图中所示的电路中,三个电容开始时均不带电,求将 它们与A、B、C点联结后,各极板上的电量。
7
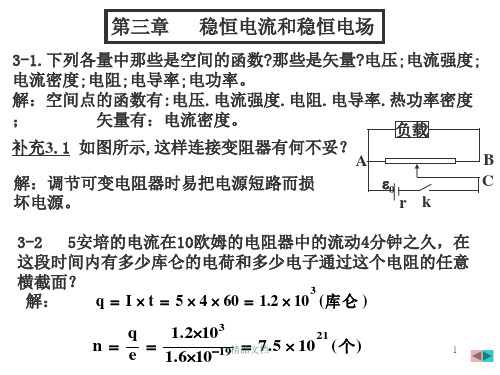
补 Rr;3(2==充330)..3a06.,欧欧4d一姆姆两电,,点R路4求电=如1:势.(图01差欧),通其;姆(过中4,)每bb1点,=个c6接.电两0地伏阻点,,的电rR1电1势==01流差.04.;(00(5欧欧2))a姆姆每,b,,个,c2R电=,28d=源.各20.的伏点5欧端特电姆电势,压。
大学物理电磁学习题的总结PPT课件

由对称性,各处受力向外, 在同一平面内,M=0, 使小线圈扩大。
第28页/共159页
例题. 均匀带电细杆AB,电荷线密度为λ,绕垂直于
直线的轴O以角速度ω匀速转动
求:1. O点的磁感应强度Bo 2. 磁矩m
3. 若a>>b,求Bo及 m
电流强度: dI
dq
dq
dr
T 2
2
1.
dB0
0
2r
dI
0
2r
(设导线本身不带电,且对电场无影响)
A
B
第9页/共159页
例8.在一不带电的金属球旁,有一点电荷+q,金属 球半径为R, 求:(1)金属球上感应电荷在球心处产生的电场强度
及此时球心处的电势U; (2)若将金属球接地,球上的净电荷为何?
已知+q与金属球心间距离为r。
r
o
q
第10页/共159页
例9 :三个“无限长”的同轴导体圆柱面A、B、C,
流
I=20A,求通过斜线面积的磁通量。
x处的(磁感r1强=r度3=1为0:cm,l=25cm )
B
μ0I
2x
2π
μ0I
d
x
I1
dΦm B dS
r1
Φm
d r1
r3
(
μ0I
2x
作业17-5.
1
I
a
O
2I be c
第23页/共159页
作业17-8.无限长同轴电缆由一导体圆柱和一与它同轴的导体圆筒所构成.使用时, 电流I从一导体流入,从另一导体流出,设导体中的电流均匀分布在横截面上.圆柱 的半径为r1,圆筒的内外半径分别为r2和r3,试求空间各处的磁感应强度.
第28页/共159页
例题. 均匀带电细杆AB,电荷线密度为λ,绕垂直于
直线的轴O以角速度ω匀速转动
求:1. O点的磁感应强度Bo 2. 磁矩m
3. 若a>>b,求Bo及 m
电流强度: dI
dq
dq
dr
T 2
2
1.
dB0
0
2r
dI
0
2r
(设导线本身不带电,且对电场无影响)
A
B
第9页/共159页
例8.在一不带电的金属球旁,有一点电荷+q,金属 球半径为R, 求:(1)金属球上感应电荷在球心处产生的电场强度
及此时球心处的电势U; (2)若将金属球接地,球上的净电荷为何?
已知+q与金属球心间距离为r。
r
o
q
第10页/共159页
例9 :三个“无限长”的同轴导体圆柱面A、B、C,
流
I=20A,求通过斜线面积的磁通量。
x处的(磁感r1强=r度3=1为0:cm,l=25cm )
B
μ0I
2x
2π
μ0I
d
x
I1
dΦm B dS
r1
Φm
d r1
r3
(
μ0I
2x
作业17-5.
1
I
a
O
2I be c
第23页/共159页
作业17-8.无限长同轴电缆由一导体圆柱和一与它同轴的导体圆筒所构成.使用时, 电流I从一导体流入,从另一导体流出,设导体中的电流均匀分布在横截面上.圆柱 的半径为r1,圆筒的内外半径分别为r2和r3,试求空间各处的磁感应强度.
电磁学 习题与讨论课ppt课件

电磁学 习题与 讨论课
有一外半径R1、内半径R2的金属球壳, 其 中放一半径为R3的金属球,球壳和球均 解: (1) 电荷分布如图所示球面q, 壳内表 -8C 带有电量10 的正电荷。问:(1) 两球电 (2) 面-q,壳外表面2q 荷分布。(2) 球心的电势。(3) 球壳电势。 由高斯定律可得:
0 R
0 r R Q E r R 2 4 0r
求均匀带电球体(Q、R)的电场分 布。
S
q
R
o
r P
E
1 n 2 q i内 r S E4 sE d i 1 0 q内 E 4 0 r 2
r R : q q 内
q E外 4π0r2
//
qi x E 2 2 32 4 π ( x R ) 0
讨论:1、环心处 E 0 E 0 2、 x dE 3、令 0 dx R x 处E有极大值 2
qx
2
4π0(x R )
2
3 2
均匀带电圆平面的电场(电荷面密度)。
dr
r O P x
x [ 1 ] 2 2 2 0 x R
+ + R2 + +
+ ++
-
-
+
+
+
R3 +
+
E 0 ( r R ) 3 3 q E ( R r R ) 2 3 2 2 4 π r 0 E 0 ( R r R ) 1 2 1
+
R1
+
+
+
+
-
+
有一外半径R1、内半径R2的金属球壳, 其 中放一半径为R3的金属球,球壳和球均 解: (1) 电荷分布如图所示球面q, 壳内表 -8C 带有电量10 的正电荷。问:(1) 两球电 (2) 面-q,壳外表面2q 荷分布。(2) 球心的电势。(3) 球壳电势。 由高斯定律可得:
0 R
0 r R Q E r R 2 4 0r
求均匀带电球体(Q、R)的电场分 布。
S
q
R
o
r P
E
1 n 2 q i内 r S E4 sE d i 1 0 q内 E 4 0 r 2
r R : q q 内
q E外 4π0r2
//
qi x E 2 2 32 4 π ( x R ) 0
讨论:1、环心处 E 0 E 0 2、 x dE 3、令 0 dx R x 处E有极大值 2
qx
2
4π0(x R )
2
3 2
均匀带电圆平面的电场(电荷面密度)。
dr
r O P x
x [ 1 ] 2 2 2 0 x R
+ + R2 + +
+ ++
-
-
+
+
+
R3 +
+
E 0 ( r R ) 3 3 q E ( R r R ) 2 3 2 2 4 π r 0 E 0 ( R r R ) 1 2 1
+
R1
+
+
+
+
-
+
电磁学静电场习题课.ppt

●
+Q
+
O
2R
E2
Q
4 0 (3R)2
r0
Eb
E1
E2
5Q
18 0 R2
r0
2019/12/1
17
17(P102)A、B为真空中两个平行的“ 无限大”均匀
带电平面,已知两平面间的电场强度大小为E 0 ,两平面
外密侧度电分场别强为度σA大=-小2ε都0 E为0/ E3 0/
E 0 (r a)
σ
E
a 0r
(r a)
E
2 0r
(r a)
2019/12/1
λ
a ●P E
aλ
r PE
●
7
习题集
1(P98)一点电荷,放在球形高斯面的中心处。下列 哪一种情况,通过高斯面的电通量发生变化。 [ B ]
(A)将另一点电荷放在高斯面外。 (B)将另一点电荷放进高斯面内。 (C)将球心处的点电荷移开,但仍在高斯面内。 (D)将高斯面半径缩小。
当 r << L 时,E=
E=
λL / 4πε0 r。2
λ/ 2πε0 r ;当 r > > L 时,
R
分析: 当 r << L 时,带电圆柱面 可视为无限长,其场强大小为:
E
2 0r
当 r >> L 时,带电圆柱面可视为
λ
L
r ●P ●
r >>L P
点电荷,其场强大小为:
E
Q
4 0r 2
de
E
ds
+Q
+
O
2R
E2
Q
4 0 (3R)2
r0
Eb
E1
E2
5Q
18 0 R2
r0
2019/12/1
17
17(P102)A、B为真空中两个平行的“ 无限大”均匀
带电平面,已知两平面间的电场强度大小为E 0 ,两平面
外密侧度电分场别强为度σA大=-小2ε都0 E为0/ E3 0/
E 0 (r a)
σ
E
a 0r
(r a)
E
2 0r
(r a)
2019/12/1
λ
a ●P E
aλ
r PE
●
7
习题集
1(P98)一点电荷,放在球形高斯面的中心处。下列 哪一种情况,通过高斯面的电通量发生变化。 [ B ]
(A)将另一点电荷放在高斯面外。 (B)将另一点电荷放进高斯面内。 (C)将球心处的点电荷移开,但仍在高斯面内。 (D)将高斯面半径缩小。
当 r << L 时,E=
E=
λL / 4πε0 r。2
λ/ 2πε0 r ;当 r > > L 时,
R
分析: 当 r << L 时,带电圆柱面 可视为无限长,其场强大小为:
E
2 0r
当 r >> L 时,带电圆柱面可视为
λ
L
r ●P ●
r >>L P
点电荷,其场强大小为:
E
Q
4 0r 2
de
E
ds
电磁第一章(习题和解答).ppt

q
2 0 R2
1-9一半径为R的半球面,均匀地带有电荷,电
荷面密度为 ,求球面中心处的场强。
解:1)如图在半球面上用
z r Rsin
极坐标取任意面元
rd
dS rdRd R2 sindd
Rd
它在球心产生的场强
dE
dq
dE 4 0 R2
dS 4 0 R2
sindd
4 0
由对称性分析可知
d
4 0
方向沿z 轴负向
1-10半径为R的带电细园环,线电荷密度 0 cos ,
0 为常数, 为半径R与x轴夹角,如图所示,求
圆环中心处的电场强度。
Y
解: 0 cos ,即分 布
关于x轴 对 称 E的 方 向 必 在x轴 上
dq Rd R0 cos d
dE
dq
4 0 R
2
0 cos d 4 0 R
解: (补偿法)由于对称性,均匀带电圆环在圆心处
场强为零。 q d
+ E=
E
均匀带电圆环 d L 所以q可视为点电荷
E
q
4 0 R2
d 4 0 R2
Q Q
2R d 2R
E
9 109
3.12 109 2 102
2 (50 102 )3
0.715v / m
1-8 如图所示,一细玻璃棒被弯成半径为R的半圆周,
F13
1
4 0
q1q3 r123
F23
1
4 0
q2q3 r223
r12
q1
q3
q2
r13
r23
F12 F13
F23 F13
解得:
q3 (
大物电磁学课后答案4ppt课件

解: (1) eE evB v E/B 3.75103 (米/秒)
(2)E,V,B 两两垂直
4-10 已知一电量为q的粒子垂直入射到磁感应强度为B的均匀磁
场以前,经过电压为V的电场加速,粒子的初速度可以忽略不计
,进入磁场后经过半圆到达照像底片上的P点,已知粒子入口至
P点的距离为x,求该粒子质量。
4-6在下列两种情况下能否用安培环路定理求磁感应强度B,为什 么?(1)有限长载流直 导线产生的场;(2)圆电流产生的场。
答(2)(圆1)安电培流环产路生定的理场不lB是 d高l 度0对n 称Ii 中的的场B,故是也闭不合能电用流。产生,故不能用!
4-7一个质子,一个氘核和一个 粒子,通过相同的电位差加速 后,进入一均匀磁场中,此时它们的运动方向与B正交。试比较 这些粒子的动能;(2)如果质子在磁场中运动的圆形轨道半径为 10厘米,则氘核和 粒子的轨道半径为多少?
的方向与线圈平面平行,求此时该线圈绕OO’ 轴的磁力矩。
解:
0
B
求线圈的磁矩P
P IS I R 2 ,方向垂直纸面
磁力矩
M P B PB R2IB
L oR I B
O
补充4.3一根载流长直导线被折成如图所示的形状,已知电流强 度为20安, =120o,L=2厘米,求A点的磁感应强度B。
2
2
0I 2 2 R
d
0I 2R
dI
x
dB
柱面横截面图
(沿x正向)
12
4-15 载流长直导线弯成图中三种形状,求O点的磁感应强度B。
解:(a)分成4段
B1 B3 0
B2
(2)E,V,B 两两垂直
4-10 已知一电量为q的粒子垂直入射到磁感应强度为B的均匀磁
场以前,经过电压为V的电场加速,粒子的初速度可以忽略不计
,进入磁场后经过半圆到达照像底片上的P点,已知粒子入口至
P点的距离为x,求该粒子质量。
4-6在下列两种情况下能否用安培环路定理求磁感应强度B,为什 么?(1)有限长载流直 导线产生的场;(2)圆电流产生的场。
答(2)(圆1)安电培流环产路生定的理场不lB是 d高l 度0对n 称Ii 中的的场B,故是也闭不合能电用流。产生,故不能用!
4-7一个质子,一个氘核和一个 粒子,通过相同的电位差加速 后,进入一均匀磁场中,此时它们的运动方向与B正交。试比较 这些粒子的动能;(2)如果质子在磁场中运动的圆形轨道半径为 10厘米,则氘核和 粒子的轨道半径为多少?
的方向与线圈平面平行,求此时该线圈绕OO’ 轴的磁力矩。
解:
0
B
求线圈的磁矩P
P IS I R 2 ,方向垂直纸面
磁力矩
M P B PB R2IB
L oR I B
O
补充4.3一根载流长直导线被折成如图所示的形状,已知电流强 度为20安, =120o,L=2厘米,求A点的磁感应强度B。
2
2
0I 2 2 R
d
0I 2R
dI
x
dB
柱面横截面图
(沿x正向)
12
4-15 载流长直导线弯成图中三种形状,求O点的磁感应强度B。
解:(a)分成4段
B1 B3 0
B2
电磁学习题课答案..

作业1分析
作业二: 1、如图所示,两个同心的均匀带电球面,内球面半径为 R1,带电量
Q1,外球面半径为 R2,带电量为 Q2。设无穷远处为电势零点。
求: (1) 空间各处电场强度的分布;
(2)在内球面内,距中心为r处的P点的电势。 解:(1)依据高斯定律,有
O
Q1
R1
Q2
r
R2
P
r<R1
Q=0
E1=0
R1<r< R2
r> R2
Q= Q1
Q= Q1 +Q2
E2= Q1/(40r2)
E3= (Q1+Q2 )/(40r2) 方向均沿径向向外。
(2)由电势定义式:
此结论也可由电 =0+ [-Q /(4 R )+ Q /(4 R )]+ [(Q +Q )/(4 R )] 1 0 2 1 0 1 1 2 0 2 势叠加分析得到 = Q1/(40R1)+Q2 /(40R2 )
(a)为抗磁质,因为它在磁场中产生的 附加磁场与外磁场方向相反。 (b)为顺磁质,因为它在外磁场中产生 的附加磁场与外磁场方向相同。
11
作业六:
1、一根铜棒长
,水平放置,可绕距离a端为
处和棒垂直的轴在水平面以 的角速度旋转。铜棒置于竖直向上的磁感应强度 的匀强磁场中,如图所示, 求: (1) 铜棒的电动势 (2) a,b两端哪端的电势高? 解: (1)将棒ab分成无穷多小段,取一小段dr, 棒转动时dr产生的动生电动势:
1
2、电量分别为q1,q2,q3的三个点电荷分别位于同
一圆周的三个点上,如图所示.设无穷远处为电势
零点,圆半径为R,则b点处的电势U= ( )
作业二: 1、如图所示,两个同心的均匀带电球面,内球面半径为 R1,带电量
Q1,外球面半径为 R2,带电量为 Q2。设无穷远处为电势零点。
求: (1) 空间各处电场强度的分布;
(2)在内球面内,距中心为r处的P点的电势。 解:(1)依据高斯定律,有
O
Q1
R1
Q2
r
R2
P
r<R1
Q=0
E1=0
R1<r< R2
r> R2
Q= Q1
Q= Q1 +Q2
E2= Q1/(40r2)
E3= (Q1+Q2 )/(40r2) 方向均沿径向向外。
(2)由电势定义式:
此结论也可由电 =0+ [-Q /(4 R )+ Q /(4 R )]+ [(Q +Q )/(4 R )] 1 0 2 1 0 1 1 2 0 2 势叠加分析得到 = Q1/(40R1)+Q2 /(40R2 )
(a)为抗磁质,因为它在磁场中产生的 附加磁场与外磁场方向相反。 (b)为顺磁质,因为它在外磁场中产生 的附加磁场与外磁场方向相同。
11
作业六:
1、一根铜棒长
,水平放置,可绕距离a端为
处和棒垂直的轴在水平面以 的角速度旋转。铜棒置于竖直向上的磁感应强度 的匀强磁场中,如图所示, 求: (1) 铜棒的电动势 (2) a,b两端哪端的电势高? 解: (1)将棒ab分成无穷多小段,取一小段dr, 棒转动时dr产生的动生电动势:
1
2、电量分别为q1,q2,q3的三个点电荷分别位于同
一圆周的三个点上,如图所示.设无穷远处为电势
零点,圆半径为R,则b点处的电势U= ( )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电磁学习题 课答案
2、电量分别为q1,q2,q3的三个点电荷分别位于同
一圆周的三个点上,如图所示.设无穷远处为电势
零点,圆半径为R,则b点处的电势U= (
U1b q1 40 2R
电势叠加原理
)
q2 U2b 4 0 2R
U3b q3 40 2R
q q q 3 1 2 U b 2 R4 4 R4 R 0 0 2 0 2
E ' 0
q q d1 d2 0S 0S
UUE d E d A B 1 1 22
[ q /( S )]( d d ) [ q /( S )]( d t ) 0 1 2 0
由此得:
C q /( U U ) S /( d t ) A B 0
因C值仅与 d、t 有关,与 d1、d2 无关,故金属片的安放位置对电容无影响。
B=
0
I
2 R
x
0
I
a b = ln 2 a
0
l
dx x x
7
dm=
I
2 x
0
dxl =
Il
2
ab 1 dx a
Il
作业三:
1、一个带电粒子垂直射入均匀磁场中,如果粒子的质量增加为原来的2 倍,入射速度也增加为原来的2倍,而磁场的磁感应强度增大为原来的4 倍,则通过粒子运动轨道所围面积的磁通量增大为原来的( (A) 2倍 (B) 4倍 (C) 0.5倍 (D) 1倍
2
作业三:
1、有两个彼此远离的金属球,一大一小,所带电荷同号等量,问
这两个球的电势是否相等?为什么?用一根细导线将两球相连,是
否会出现电荷流动?说明原因。 答:这两球的电势不相等,因为球面电荷的电势与球的半径及所 带电荷量有关,公式为 q /4oR ,两球的半径不同,故电势不同。 用一根细线相连,会出现电荷的流动,因为它们形成了一个导体, 静电平衡时,电势处处相等,所以电荷要重新分布。 2、以下说法正确的是( A )
如何变化(D
)
(B) 不变,B不变 (D) 不变,B增大
(A) 增大,B也增大 (C) 增大,B也不变
3、如图所示,在垂直和水平的两个金属圆中 (半径为R)通以相等的电流 I ,问圆心 O
点处的磁感应强度大小及方向如何?
根据圆电流中心处磁感应强度公式,水平金属圆在O 点的磁感应强度大小为:
(1)场强 内部场强为零,外部场强与导体表面垂直, ; E 0
孤立导体达到静电平衡表面场强大小为 (2)电势
表面是等势面,导体是等势体 。
2、将一个电中性的导体放在静电场中,在导体上感应出相等
的正负电荷量,导体是否为等势体?如果把导体一分为二,使
它们分别带上等量异号电荷,则这两部分 v v = B S = B R = B 1 B q Bq
22 2
2
22 2 m2 v m v = 4 4 2 1 4 B q Bq 2 2
8
2、如图所示,在无限长载流直导线附近作一个球形闭合曲面S,当面S 向长直导线靠近时,穿过面S的磁通量 和面上各点的磁感应强度B将
两段载流导线所受的合力的大小为 多大?
d FI d l B
0 F B I a s i n 6 0
a b 120° I
B
3 F B Ia 2
2、若一平面载流线圈在磁场中既不受力,也不受力矩作用,这说明:( (A)该磁场一定均匀,且线圈的磁矩方向一定与磁场方向平行.
A
)
(B)该磁场一定不均匀,且线圈的磁矩方向一定与磁场方向平行.
3 1 0 0 BI 1 BI U H RH 2 8 1 9 3 8 . 4 1 0 1 . 6 1 0 1 1 0 d nq d
(l)电容C等于多少?
(2)金属片放在两极板间的位置对电容值有无影响? 解:设极板上分别带电量+q和-q;金属片与A板距离
为d1,与B板距离为d2;金属片与A板间场强为:
5
E q /( S ) 1 0
金属板与B板间场强为: 金属片内部场强为: 则两极板间的电势差为:
E q /( S ) 2 0
(C)该磁场一定均匀,且线圈的磁矩方向一定与磁场方向垂直. (D)该磁场一定不均匀,且线圈的磁矩方向一定与磁场方向垂直.
10
3、一宽b=2.0cm,厚d=1.0mm的铜片,放在B=3.0T的磁场中,磁场垂 直通过铜片,如果铜片载有电流100A,已知铜片中自由电子的密度
2 8 3 是n 求此时产生的霍耳电势差的大小是多少? = 8 . 41 0m
(A) 在电势不变的区域内,电场强度一定为零
(B) 在电势为零处,场强一定为零
(C) 场强为零处,电势一定为零 (D) 在均匀电场中,各点电势相等
3
3、在均匀电场中,各点的( (A) 电势相等
B ) (B) 电势梯度相等
(C) 电势和电势梯度都不相等
作业四:
(D) 电势梯度为零
1、导体处于静电平衡状态时,具有如下特点:
6
作业二:
、载有电流为 I 的无限长导线,弯成如图所示形状,其中有一部分为半 1
,
。
径为 R 半圆弧,则其圆心 O 点的磁感应强度的大小为
方向为
半无限长加半圆,注意方向正好相反 垂直纸面向里
I
0
1 (1 ) 4R
试求通过矩 , 、 如图载流长直导线的电流为 I2 形面积的磁通量。
a
b
答:是等势体 如果把导体一分为二,两部分的电势不相等
4
3、当一个带电导体达到静电平衡时,表面曲率较大处电荷密度较大, 故其表面附近的场强较大。
孤立导体达到静电平衡表面场强大小为
( ×
E 0
)
作业2分析
作业一:
3、如图:一空气平行板电容器,两极板面积均为 S,板间距离为 d( d远 小于极板线度),在两极板间平行地插入一面积也是S、厚度为 t(< d) 的金属片。 试求:
0I 竖直金属圆在O点的磁感应强度大小为 2 R
故O点叠加后的磁感应强度大小为
0I 2 R
方向垂直向下;
方向垂直指向纸面内。 方向为斜下450指向纸面内
9
2 0I 2R
作业四:
1、如图,一根通电流 I 的导线,被折成长度分别为a、b,夹角为 120°的
两段,并置于均匀磁场 B 中,若导线的长度为 b 的一段与 B 平行,则a,b
2、电量分别为q1,q2,q3的三个点电荷分别位于同
一圆周的三个点上,如图所示.设无穷远处为电势
零点,圆半径为R,则b点处的电势U= (
U1b q1 40 2R
电势叠加原理
)
q2 U2b 4 0 2R
U3b q3 40 2R
q q q 3 1 2 U b 2 R4 4 R4 R 0 0 2 0 2
E ' 0
q q d1 d2 0S 0S
UUE d E d A B 1 1 22
[ q /( S )]( d d ) [ q /( S )]( d t ) 0 1 2 0
由此得:
C q /( U U ) S /( d t ) A B 0
因C值仅与 d、t 有关,与 d1、d2 无关,故金属片的安放位置对电容无影响。
B=
0
I
2 R
x
0
I
a b = ln 2 a
0
l
dx x x
7
dm=
I
2 x
0
dxl =
Il
2
ab 1 dx a
Il
作业三:
1、一个带电粒子垂直射入均匀磁场中,如果粒子的质量增加为原来的2 倍,入射速度也增加为原来的2倍,而磁场的磁感应强度增大为原来的4 倍,则通过粒子运动轨道所围面积的磁通量增大为原来的( (A) 2倍 (B) 4倍 (C) 0.5倍 (D) 1倍
2
作业三:
1、有两个彼此远离的金属球,一大一小,所带电荷同号等量,问
这两个球的电势是否相等?为什么?用一根细导线将两球相连,是
否会出现电荷流动?说明原因。 答:这两球的电势不相等,因为球面电荷的电势与球的半径及所 带电荷量有关,公式为 q /4oR ,两球的半径不同,故电势不同。 用一根细线相连,会出现电荷的流动,因为它们形成了一个导体, 静电平衡时,电势处处相等,所以电荷要重新分布。 2、以下说法正确的是( A )
如何变化(D
)
(B) 不变,B不变 (D) 不变,B增大
(A) 增大,B也增大 (C) 增大,B也不变
3、如图所示,在垂直和水平的两个金属圆中 (半径为R)通以相等的电流 I ,问圆心 O
点处的磁感应强度大小及方向如何?
根据圆电流中心处磁感应强度公式,水平金属圆在O 点的磁感应强度大小为:
(1)场强 内部场强为零,外部场强与导体表面垂直, ; E 0
孤立导体达到静电平衡表面场强大小为 (2)电势
表面是等势面,导体是等势体 。
2、将一个电中性的导体放在静电场中,在导体上感应出相等
的正负电荷量,导体是否为等势体?如果把导体一分为二,使
它们分别带上等量异号电荷,则这两部分 v v = B S = B R = B 1 B q Bq
22 2
2
22 2 m2 v m v = 4 4 2 1 4 B q Bq 2 2
8
2、如图所示,在无限长载流直导线附近作一个球形闭合曲面S,当面S 向长直导线靠近时,穿过面S的磁通量 和面上各点的磁感应强度B将
两段载流导线所受的合力的大小为 多大?
d FI d l B
0 F B I a s i n 6 0
a b 120° I
B
3 F B Ia 2
2、若一平面载流线圈在磁场中既不受力,也不受力矩作用,这说明:( (A)该磁场一定均匀,且线圈的磁矩方向一定与磁场方向平行.
A
)
(B)该磁场一定不均匀,且线圈的磁矩方向一定与磁场方向平行.
3 1 0 0 BI 1 BI U H RH 2 8 1 9 3 8 . 4 1 0 1 . 6 1 0 1 1 0 d nq d
(l)电容C等于多少?
(2)金属片放在两极板间的位置对电容值有无影响? 解:设极板上分别带电量+q和-q;金属片与A板距离
为d1,与B板距离为d2;金属片与A板间场强为:
5
E q /( S ) 1 0
金属板与B板间场强为: 金属片内部场强为: 则两极板间的电势差为:
E q /( S ) 2 0
(C)该磁场一定均匀,且线圈的磁矩方向一定与磁场方向垂直. (D)该磁场一定不均匀,且线圈的磁矩方向一定与磁场方向垂直.
10
3、一宽b=2.0cm,厚d=1.0mm的铜片,放在B=3.0T的磁场中,磁场垂 直通过铜片,如果铜片载有电流100A,已知铜片中自由电子的密度
2 8 3 是n 求此时产生的霍耳电势差的大小是多少? = 8 . 41 0m
(A) 在电势不变的区域内,电场强度一定为零
(B) 在电势为零处,场强一定为零
(C) 场强为零处,电势一定为零 (D) 在均匀电场中,各点电势相等
3
3、在均匀电场中,各点的( (A) 电势相等
B ) (B) 电势梯度相等
(C) 电势和电势梯度都不相等
作业四:
(D) 电势梯度为零
1、导体处于静电平衡状态时,具有如下特点:
6
作业二:
、载有电流为 I 的无限长导线,弯成如图所示形状,其中有一部分为半 1
,
。
径为 R 半圆弧,则其圆心 O 点的磁感应强度的大小为
方向为
半无限长加半圆,注意方向正好相反 垂直纸面向里
I
0
1 (1 ) 4R
试求通过矩 , 、 如图载流长直导线的电流为 I2 形面积的磁通量。
a
b
答:是等势体 如果把导体一分为二,两部分的电势不相等
4
3、当一个带电导体达到静电平衡时,表面曲率较大处电荷密度较大, 故其表面附近的场强较大。
孤立导体达到静电平衡表面场强大小为
( ×
E 0
)
作业2分析
作业一:
3、如图:一空气平行板电容器,两极板面积均为 S,板间距离为 d( d远 小于极板线度),在两极板间平行地插入一面积也是S、厚度为 t(< d) 的金属片。 试求:
0I 竖直金属圆在O点的磁感应强度大小为 2 R
故O点叠加后的磁感应强度大小为
0I 2 R
方向垂直向下;
方向垂直指向纸面内。 方向为斜下450指向纸面内
9
2 0I 2R
作业四:
1、如图,一根通电流 I 的导线,被折成长度分别为a、b,夹角为 120°的
两段,并置于均匀磁场 B 中,若导线的长度为 b 的一段与 B 平行,则a,b
