第三讲、序列相关性的检验
《序列相关性》课件

序列相关性的类型
01
02
03
正相关
当一个观测值增加时,另 一个观测值也增加,反之 亦然。
负相关
当一个观测值增加时,另 一个观测值减少,反之亦 然。
无相关性
两个观测值之间不存在明 显的依赖关系。
序列相关性产生的原因
01
02
03
04
季节性影响
某些时间序列数据会受到季节 性因素的影响,导致观测值之
间存在周期性依赖关系。
偏相关系数检验
总结词
偏相关系数检验是一种用于检验时间序列数据之间是否存在长期均衡关系的统计方法。
详细描述
偏相关系数检验基于时间序列数据的偏相关图,通过计算偏相关系数,判断时间序列数 据之间是否存在长期均衡关系。如果存在长期均衡关系,则说明时间序列数据之间存在
某种稳定的关联性,可能存在协整关系。
04 序列相关性对模型的影响
个体差异性和时间趋势性。
02 03
序列相关性分析
面板数据的序列相关性分析是对不同个体或区域上的时间序列数据进行 相关性检验和建模的过程,主要考察不同个体或区域在同一时间点上的 数据是否具有相关性。
总结
面板数据的序列相关性分析是研究面板数据的重要手段,有助于揭示不 同个体或区域在同一时间点上的数据关联和动态变化。
经济因素
经济活动中的各种因素可能导 ຫໍສະໝຸດ 时间序列数据之间存在相关性。
政策因素
政策变动或干预可能对时间序 列数据产生影响,导致观测值
之间存在相关性。
其他因素
如气候变化、人口增长等也可 能对时间序列数据产生影响, 导致观测值之间存在相关性。
02 序列相关性在统计学中的 应用
线性回归模型中的序列相关性
什么是序列相关性如何进行序列相关性的检验与处理

什么是序列相关性如何进行序列相关性的检验与处理序列相关性是指一系列数据中存在的相关性或依赖关系。
它可以帮助我们了解数据的趋势、周期性以及对未来数据的预测。
在统计学中,序列相关性的检验和处理是非常重要的,可以帮助我们提取有用的信息和建立可靠的模型。
本文将介绍序列相关性的定义、如何进行序列相关性的检验以及处理方法。
一、序列相关性的定义序列相关性是指时间序列数据中的观察值之间的相关性或依赖关系。
当一个时间序列的观察值和它之前或之后的观察值之间存在关联时,就可以说这个时间序列是相关的。
序列相关性表明序列中的数据点之间存在某种模式或趋势,这对于分析和预测时间序列数据具有重要意义。
二、序列相关性的检验为了检验时间序列数据是否存在相关性,我们可以使用常用的统计方法,例如自相关函数(ACF)和偏自相关函数(PACF)。
自相关函数是衡量一个时间序列和其滞后版本之间相关性的统计指标。
它可以帮助我们确定序列中的周期性模式。
在自相关函数图中,横轴表示滞后阶数,纵轴表示相关系数。
如果自相关函数在某个滞后阶数上超过了置信区间,那么可以认为有相关性存在。
偏自相关函数是衡量一个时间序列和其滞后版本之间相关性的统计指标,消除了其他滞后版本的影响。
在偏自相关函数图中,横轴表示滞后阶数,纵轴表示相关系数。
如果偏自相关函数在某个滞后阶数上超过了置信区间,那么可以认为有相关性存在。
另外,我们还可以使用单位根检验(ADF检验)来检验序列是否平稳。
平稳序列的相关性更容易进行建模和预测。
如果序列通过了单位根检验,那么就可以认为序列是平稳的。
三、序列相关性的处理如果时间序列数据存在相关性,那么我们可以采取一些方法进行处理,以消除或减小相关性的影响。
首先,可以进行差分操作。
差分是指将时间序列的每个观察值与其滞后版本之间的差异进行计算。
差分后的序列通常更容易建模,因为它们消除了相关性。
如果还存在差分后的序列中的相关性,可以继续进行更高阶的差分操作。
序列相关性

如果(1) ρ >0,即随机项存在自相关; 且
xt x s / ∑ xt2 >0,即 X 存在序列正相关,则有 (2) ∑
t ≺s
var( β 1 ) >
~
∑x
σ2
2 t
ˆ = var( β 1 )
(2.5.4)
在实际经济问题中的自相关,大多是 正自相关,且一般经济变量X的时间序列 也大多为正自相关,因此(2.5.4)在多 数经济问题中成立。 这说明,当随机项存在自相关时,参 数的OLS估计量的方差较无自相关时大。
(2)设定偏误:模型中未含应包括的变量 设定偏误:
例如:
如果对牛肉需求的正确模型应为: 如果对牛肉需求的正确模型应为:
Yt=β0+β1X1t+β2X2t+β3X3t+µt
其中:Y=牛肉需求量,X1=牛肉价格, X2=消费者收入,X3=猪肉价格
但如果模型设定为: 但如果模型设定为:
Yt= β0+β1X1t+β2X2t+vt 则该式中,vt= β3X3t+µt, 于是在猪肉价格影响牛肉消费量的情况下,这种 这种 模型设定的偏误往往导致随机项中有一个重要的系 统性影响因素,使其呈序列相关性。 统性影响因素,使其呈序列相关性。
~
E(β1 ) = E(∑kt Yt ) = E(β1 + ∑kt µt ) = β1
~
但,可以证明
n −1 ∑ xt xt +1 2 2 2 σ 2σ ~ ρ t =1n + +ρ var(β1 ) = 2 2 ∑ xt ∑ xt ∑ xt2 t =1
∑x x
t =1 t n t =1
(1)序列相关性检验 序列相关性检验 (2)自相关性检验 自相关性检验 (3)多重共线性检验 多重共线性检验 (4)随机解释变量检验 随机解释变量检验
序列相关性

(四)拉格朗日乘数检验(Lagrange Multiplier)
• LM检验是由布劳殊(Breusch)与戈弗雷(Godfrey) 于1978年提出的,也被称为GB检验。 • 拉格朗日乘数检验克服了DW检验的缺陷,适合于高阶序 列相关以及模型中存在滞后被解释变量的情形。
对于模型
Yt 0 1 X1t 2 X 2t k X kt t
§4.2
序列相关性
一、序列相关性的概念
二、实际经济问题中的序列相关性
三、序列相关性的后果
四、序列相关性的检验
五、序列相关性的补救
四、序列相关性的检验
基本思路 :
首先, 采用 OLS 法估计模型, 以得随机误差项的
~ e i 表示: “近似估计量” ,用
~ Y (Y ˆ) e i i i 0 ls
t 2 n t
n
t 1
其中:ρ为一阶自相关系数
) 2(1 )
et 2 ~
t 1
一阶自回归模型:i=i-1+i 的参数估计。
由于自相关系数的值介于-1和+1之间,因此:
0≤DW≈2(1-ρ)≤4 如果存在完全一阶正相关,即=1,则 D.W. 0 完全一阶负相关,即= -1, 则 D.W. 4 完全不相关,即=0,则 D.W.2
检验时需要事先确定准备检验的阶数P,实际检验中,可从1阶、2
阶、…逐次向更高阶检验。
检验结果显著时,可以说明存在序列相关,但是并不一定代表序列 相关的阶数一定能够达到所检验的阶数。
◦ 低阶序列相关的存在往往会导致高阶序列相关检验的显著性 ◦ 具体阶数的判断,需要结合辅助回归中自相关系数的显著性
4-dL
# D.W.检验统计量的说明
4.2 序列相关性

Yt= 0+1Xt+vt
因此,由于vt= 2Xt2+t, ,包含了产出的平方对随 机项的系统性影响,随机项也呈现序列相关性。
3、数据的“编造”
在实际经济问题中,有些数据是通过已知数据 生成的。 因此,新生成的数据与原数据间就有了内在的 联系,表现出序列相关性。 例如:季度数据来自月度数据的简单平均,这 种平均的计算减弱了每月数据的波动性,从而使 随机干扰项出现序列相关。 还有就是两个时间点之间的“内插”技术往往 导致随机项的序列相关性。
Yi=0+1X1i+kXki+Yi-1+i
(4)回归含有截距项
D.W. 统计量:
杜宾和瓦森针对原假设:H0: =0, 即不存在一 阶自回归,构如下造统计量:
D.W . ~ ~ (e e
t 2 t n t 1
)2
~ e
t 1
n
2
t
该统计量的分布与出现在给定样本中的X值有复杂 的关系,因此其精确的分布很难得到。
其 中 : 被 称 为 自 协 方 差 系 数 ( coefficient of autocovariance)或一阶自相关系数(first-order coefficient of autocorrelation)
除此之外统称为高阶序列相关。如: μi=ρ1μi-1+ρ2μi-2+εi ,称为二阶序列相关。
二、实际经济问题中的序列相关性
•
• • • •
没有包含在解释变量中的经济变量固有的 惯性。 模型设定偏误(Specification error)。主 要表现在模型中丢掉了重要的解释变量或 模型函数形式有偏误。 数据的“编造”。 时间序列数据作为样本时,一般都存在序 列相关性。 截面数据作为样本时,一般不考虑序列相 关性。
面板数据模型中的序列相关性假设是什么如何进行假设检验

面板数据模型中的序列相关性假设是什么如何进行假设检验面板数据模型中的序列相关性假设是指面板数据中不同个体之间的观察值在时间上彼此独立,即序列相关性为零。
这个假设对于面板数据模型的正确性和统计推断的有效性至关重要。
接下来,我们将对序列相关性假设进行详细探讨,并介绍如何进行假设检验。
一、面板数据模型中的序列相关性假设面板数据模型是一种同时考虑跨个体和跨时间的数据结构。
在该模型中,每个个体在不同时间点上都有多个观察值,这些观察值之间可能存在相关性。
面板数据模型的序列相关性假设为每个个体的观察值之间在时间上是相互独立的,即不存在序列相关性。
序列相关性假设的满足意味着面板数据模型可以通过经典线性回归模型进行估计和推断,同时可以有效控制个体效应和时间效应的固定效应。
如果序列相关性假设不成立,即存在序列相关性,那么经典线性回归模型将产生无偏性和有效性上的问题。
二、检验序列相关性假设的方法为了检验面板数据模型中的序列相关性假设,常用的方法是计算序列相关系数,并进行显著性检验。
以下介绍两种常见的序列相关性检验方法:Lagrange Multiplier检验和Wooldridge检验。
1. Lagrange Multiplier检验Lagrange Multiplier检验是一种广义矩估计方法,用于测试序列相关性是否存在。
该检验的原假设为面板数据中的序列相关性不存在。
检验步骤如下:首先,估计一个序列相关的面板数据模型,例如固定效应模型或随机效应模型。
然后,计算模型的残差,并将残差平方与时间序列上的滞后差异进行回归。
最后,使用卡方分布检验残差回归的显著性,若p值小于显著性水平,则拒绝原假设,表示存在序列相关性。
2. Wooldridge检验Wooldridge检验是另一种常用的序列相关性检验方法,特别适用于面板数据模型。
该检验的原假设为序列相关性不存在。
检验步骤如下:首先,估计一个面板数据模型,并计算模型中的残差。
接下来,将残差序列进行平方,得到平方残差序列。
列举序列相关性的检验方法

列举序列相关性的检验方法序列相关性是指一个序列中两个以上元素的关联性。
序列相关性的检验方法主要有独立性检验、协方差分析、操作码分析、最大似然推定、极大似然推定、回归分析、相关系数等。
独立性检验是在分类数据中检验定性变量两两之间是否独立的一种方法,它实质上是针对每对类别进行比较,以确定它们相关性的概率,从而来看传统的概率论和统计学的独立性是否满足的。
例如,在一个试验中,如果测试变量x和y是独立的,则将按照此原则检查服从正态分布的观测值的概率分布,以检验观测的频率是否与理论值一致。
协方差分析是一种利用协方差检验解释变量之间的相关性的方法。
协方差分析过程中,可以推断一个变量是否受另一个变量影响,从而把变量之间的相关性准确衡量出来。
可以采用多个统计指标,如处理值协方差、数组协方差和管理技术方差等。
操作码分析是一种操作码技术,主要用于分析序列在紧密连接的散列表中的结构特征,以寻求解决数据集中的相关问题的有效方法。
操作码分析的主要思想是将散列表中的每一个数据项当成一个操作码,根据数据项间的排列情况分析有关表示的问题。
最大似然估计是一种根据观测数据和一定的概率分布模型确定参数值的统计技术。
这种技术主要是通过极大似然估计法对参数进行估计,从而得到最佳参数和其他统计量。
序列相关性检验中也可以采用最大似然估计来检验序列中不同字段之间是否存在联系。
极大似然推定也是一种基于极大似然值的技术,它的思想是找出一个最适合的(概率模型)参数向量,使其能够最大程度地拟合观测数据。
极大似然推定方法在序列相关性检验中也有着广泛的应用,是检验序列元素间相关性的有力工具。
回归分析方法是根据一组观测值,确定其两个变量之间存在相关性的技术。
回归分析也被广泛用于序列相关性检验。
计量经济学-序列相关性

PART 03
序列相关性检验方法
杜宾-瓦特森检验
检验原理
通过计算残差序列的一阶自相关系数来检验序列相关性。
检验步骤
首先估计回归模型,计算残差;然后计算残差的自相关系数;最后 根据自相关系数和样本量确定临界值,判断序列相关性。
优缺点
简单易行,但仅适用于一阶自相关的情况,对于高阶自相关检验效 果较差。
将检验结果以表格或图形形式展示出 来,包括检验统计量、P值等。若存 在序列相关性,可采用差分法、 ARIMA模型等方法进行处理,并重新 进行参数估计和检验。
根据检验结果和处理结果,对模型的 适用性和可靠性进行评估。若模型存 在严重序列相关性问题,则需要重新 考虑模型设定和估计方法。
PART 06
总结与展望
检验步骤
在原始回归模型中添加滞后项作为解释变量;然后估计辅 助回归模型,得到回归系数的估计值;最后根据回归系数 的估计值构造统计量,进行假设检验。
优缺点
可以检验任意阶数的自相关,但需要注意滞后项的选择和 模型的设定。
PART 04
序列相关性处理方法
差分法
一阶差分法
通过计算相邻两个时期的数据差值来消除序列相 关性。
运用最小二乘法(OLS)或其他估计方法,对模型参数进行估计。在 EViews中,可通过"Quick"菜单选择"Estimate Equation"选项进行参数估 计。
序列相关性检验及处理结果展示
01
序列相关性检验
02
处理结果展示
03
结果解读
采用Durbin-Wu-Hausman检验、 Breusch-Godfrey检验等方法,检验 模型是否存在序列相关性。在EViews 中,可通过"View"菜单选择 "Residual Diagnostics"选项进行检 验。
第六章序列相关性

或共同下降,ut-1和ut的正负符 号相同的可能性较大。
的运动模式,ut-1和ut的正负 符号相反的可能性较大。
第一节 序列相关性概念
ut
o
t
=0
• =0,无自相关。 • 即ut-1对ut的影响很小。
第一节 序列相关性概念
第一节 序列相关性概念
四、一阶线性自回归形式的期望、方差和协方差
Yt* Yt Yt1
自相关往往可写成如下形式:
i=i-1+i
-1<<1
第一节 序列相关性概念
其中: 被称为自协方差系数(coefficient of autocovariance)
或一阶自相关系数(first-order coefficient of autocorrelation)
t 是满足以下标准的OLS假定的随机干扰项:
存在正自相关 不能确定 无自相关 不能确定
4-dL <D.W.<4
存在负自相关
不
正能 相确 关定
无自相关
不
能负 确相 定关
0 dL dU
2
4-dU 4-dL 4
第三节 序列相关性的检验
当D.W.值在2左右时,模型不存在一阶自相关。
证明: 展开D.W.统计量:
n
e~t2
n
e~t
2 1
2
n
e~t e~t1
D.W . t2
t2
t2
n e~t2
(*)
t 1
n ~et ~et1
D.W . 2(1 t2
) 2(1 )
n ~et2
t 1
第三节 序列相关性的检验
这里,
序列相关性

序列相关性
序列相关性(SequenceCorrelation)是一种重要的统计学技术,它用来衡量和分析两个或多个相关序列之间的关系,以检测和预测未来的变化。
它最早出现在电信行业,用于诊断信号传输出现的问题。
随着数字信号处理技术在各个领域的普及,序列相关性也被用于科学、工程、金融和经济等许多领域,以检测和预测未来的变化。
序列相关性通常是指两个或多个相关时间序列之间的相关性,即两个序列中时间上相邻元素之间的空间关系。
它以线性方式来衡量数据集之间的相关性,反映出其内在的结构和未来的变化趋势。
序列相关性的测量可以使用线性回归的方法,也可以使用非线性方法,例如波动率,均值行走和自相关函数。
这些方法用于通过检测输入序列中存在的规律性,预测时间序列中未来的变化。
例如,均值行走可以用于分析具有相同或类似序列趋势的时间序列,从而预测未来的变化。
序列相关性也可以用于比较数据集之间的关系,例如销售数据、价格数据和交易数据等。
这种研究可以揭示不同因素对销售情况的影响,从而帮助管理者做出有效的营销决策。
此外,序列相关性可以帮助投资者识别投资组合,以便减少投资风险和收益率波动。
它也可以用于评估金融市场中风险和投资回报的关系。
序列相关性有助于揭示数据间隐藏的关系,并预测未来的变化
趋势。
它也可以用于比较数据集之间的关系,可以帮助投资者识别投资组合,以及评估金融市场中风险和投资回报的关系。
因此,序列相关性在许多行业的应用非常普遍,帮助企业在投资和运营方面取得更好的成绩。
序列相关性
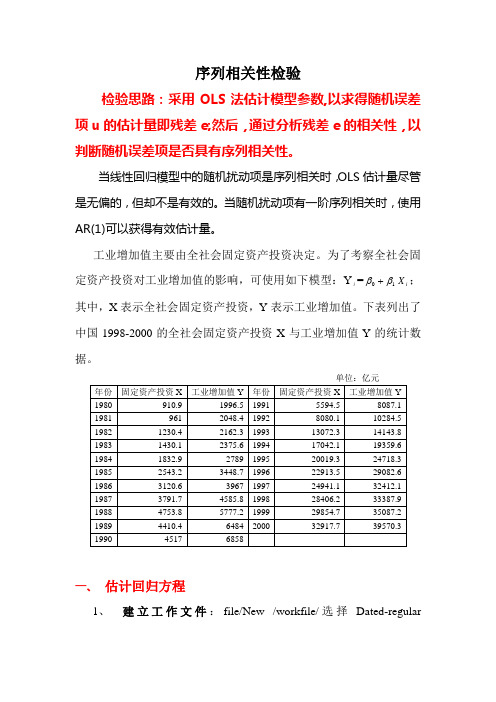
序列相关性检验检验思路:采用OLS法估计模型参数,以求得随机误差项u的估计量即残差e;然后,通过分析残差e的相关性,以判断随机误差项是否具有序列相关性。
当线性回归模型中的随机扰动项是序列相关时,OLS估计量尽管是无偏的,但却不是有效的。
当随机扰动项有一阶序列相关时,使用AR(1)可以获得有效估计量。
工业增加值主要由全社会固定资产投资决定。
为了考察全社会固定资产投资对工业增加值的影响,可使用如下模型:Yi =1ββ+iX;其中,X表示全社会固定资产投资,Y表示工业增加值。
下表列出了中国1998-2000的全社会固定资产投资X与工业增加值Y的统计数据。
一、估计回归方程1、建立工作文件:file/New /workfile/选择Dated-regularfrequency, Annual,OK.2、插入数据:quick/Empty group/粘贴,并分别将Obs的名字修改为X和Y变量。
3、回归分析:quick/estimate equation/y c x二、序列相关性检验方法1:图示法(1)得残差图:在回归方程界面点击View/Actual, Fitted, residual/ residual Graph,出现(2)判断:随机干扰项存在正序列相关性。
方法2:杜宾-瓦森(D.W)检验法由OLS法的估计结果知:D.W.=1.282353。
本例中,在5%的显=1.22,著性水平下,解释变量个数为2,样本容量为21,查表得dld u=1.42,而D.W.=1.282353,位于下限与上限之间,不能确定相关性。
方法3:拉格朗日乘数(LM)检验法首先,在方程窗口中点击View\Residual Test\Serial Correlation LM Test,选择滞后期为p=2,屏幕将显示信息图中给出nR^2=9.227442,Prob.Chi-Square(2)=0.0099,表示临界概率,故显著性水平去1%。
计量经济学之序列相关性

H0 : 1 2 p 0
备择假设H为 1 ( H1:i i 1,2,, p) 中至少有一个不为零 若为真,则LM统计量在大样本下渐进 2 服从自由度为p的 分布:
LM nR ~
2
其中,n, (p)
2
R
2
分别是辅助回归方程(6)的样本容量和可决系 数
e e e e e e e e e e
t t t 1 t 1 t t 1 2 t 2 t 1 2 t
2 t 1
(3)
当n充分大时, et2 et21 有 et et 1 ˆ et2 所以
ˆ ˆ ˆ
(19)
三 自相关系数ρ的估计
广义差分法得以实施的关键是计算出自相关系数ρ的值,因此,必 须采用一些适当的方法对自回归系数ρ进行估计,通常适用的方法主 要有:经验法、利用 D.W.估计、科克伦-奥科特迭代法等。
下面我们着重介绍一下科克伦-奥科特迭代法: 科克伦-奥科特迭代法其实就是进行一系列的迭代,每一次迭代 都能得到比前一次更好的ρ的估计值。为了叙述方便,我们采用一元 回归模型来阐明这种方法, 多元回归模型下的迭代法与一元回归的原 理相同。 假设给定模型 Yt = β0 + β1 X t + μt 其中, μt = ρ1 μt−1 + ρ2 μt−2 + ⋯ + ρp μt−p + εt t=1+p,2+p,…,n (22) (21)
如果含有 k 个解释变量的多元回归模型(2)存在 p 阶序列相关 性,也可作类似变换,变换结果为
∗ Yt∗ = β0 1 − ρ1 − ⋯ − ρp + β1 X1t + β2 X∗ + ⋯ + βk X∗ + εt 2t kt ∗ 其中,Xit = Xit − ρ1 Xi(t−1) − ⋯ − ρp Xi(t−p)(i=1,2,…,p)。
序列相关性

拉格朗日乘数(Lagrange multiplier)检验
序列相关性的处理
最常用的方法是广义最小二乘法(GLS: Generalized least squares)和广义差分法 (Generalized Difference)。
处理序列相关性的实例
经济理论指出,商品进口主要由进口国的 经济发展水平,以及商品进口价格指数与 国内价格指数对比因素决定的。 由于无法取得中国商品进口价格指数, 我们主要研究中国商品进口与国内生产总 值的关系。(下表)。
五、科克伦-奥科特(CochraneOrcutt)法估计模型
1、在Eviews主画面顶部按钮中点击 quick/estimate equation,在弹出Equation Specification的窗口中键入M C GDP AR(1), 然后点击OK,得到模型的估计结果输出
五、科克伦-奥科特(CochraneOrcutt)法估计模型
若 0<D.W.<dL 存在正自相关 dL<D.W.<dU 不能确定 dU <D.W.<4-dU 无自相关 4-dU <D.W.<4- dL 不能确定 4-dL <D.W.<4 存在负自相关
完全一阶正相关, 即=1, 则 D.W. 0 完全一阶负相关, 即= -1, 则 D.W. 4 完全不相关, 即=0, 则 D.W.2
三、在Eviews输出窗口中阅读 Durbing-Watson统计量
双击窗口中eq01,打开模型估计结果。在 输出结果左下角(阴影部分)显示有统计 量值。根据模型中解释变量个数及样本容 量查临界值表,从而可以判断模型中的随 机误差项是否存在自相关性。本例中解释 变量个数为2(包括常数项),样本容量为 24,查表得dl= ,du= ,而DW dl , 故:
序列相关性

序列相关性
序列相关性是统计学中的一个基本概念,它是指在一个序列中,前后两个元素之间可能存在的相互关系。
换句话说,如果前一个元素的变化对后一个元素的变化有影响,则可以说两个元素之间存在序列相关性。
序列相关性通常用来模拟某种可能的趋势,或者在数据集中确定某种特定的规律。
序列相关性可以在两个不同的元素之间用来检测潜在的相关性。
例如,如果两个实验组中,两个不同的元素在同一组中表现出相同的变化趋势,这就表明它们之间存在序列相关性。
从统计学的角度来看,可以通过确定序列相关性来判断实验结果是否具有可靠性。
序列相关性可以用来研究特定型号的趋势,以及判断某件事物在未来的特定时间段内的发展趋势。
考虑到每一次的变化 with the在实际的世界中都可能带来影响,序列相关性就可以作为研究趋势的基础,从而对未来可能发生的几率和变化描绘出一幅更清晰的图景。
此外,序列相关性还可以用来定义某种特定的模式。
例如,由于序列元素之间可能存在非常多的相互关系,因此可以判断某种特定的发展趋势。
同样的,序列相关性也可以用来检验数据集中的连续性,以便对因变量更有效的测量及预测。
序列相关性在统计学的很多方面都有重要的应用,它主要用来分析数据的相关性和预测趋势,以及判断某件事物在未来的特定时间段内的发展趋势。
考虑到序列元素之间可能存在许多复杂的关系,因此序列相关性可以用来模拟任何实际情况,从而提供有效的分析和预测。
第三讲、序列相关性的检验

1992
1993 1994
7539
8395 9281
1504.637
1605.813 1644.222
8711.156
10326.95 13760.55
9748.009
13143.88 15471.3
二、序列相关性的检验
• 1、散点图法: • 2、D—W检验法: • 3、B.G检验:
1、散点图法:
• 原理:若数据不存在序列相关性,则et和et-1成随
机关系,两者的差较为适中,此时DW值则会取一个 适中值。而若存在序列相关性的话,则DW的分子会 过大或过小,进而影响DW的值。具体的数学证明见 李子奈书P62。
(e
DW
t2
n
t n
et 1 )
2 t
2
e
t 1
Durbin-Watson检验用于随机误差项之间是否存在一 阶自相关的情况。 DW∈(0,4) DW值在每次的ols估计中都会由EViews系统自动算 出,因此这种方法比较简便易行。
• 第二步、在命令栏键入Scat resid resid(-1) 得到
残差的散点图(见下页图):
判断标准:
1、若散点在四个 象限呈无规律的散 布状态,则模型不 存在自相关。
2、若散点多散布在一三象限,则模型存在着严重的正自相关。
3、若散点多散布在二四象限,则模型存在着严重的负自相关。
2、D—W检验法:
1、广义最小二乘法:
由于WLS步骤和异方差基本相同,另外经常 出现进行一次或多次广义最小二乘法后, 仍不能良好地消除序列相关性的情况。因 此我们不再讲述WLS的具体操作步骤。
2、差分法
• 原理:采用普通最小二乘法估计原模型,得到随
序列相关性的拉格朗日乘数检验原理

序列相关性的拉格朗日乘数检验原理拉格朗日乘数检验原理是一种统计方法,用于检验序列相关性。
该方法基于拉格朗日乘数,通过构建模型来评估序列之间的相关性。
假设我们有两个序列X和Y,我们想要确定它们之间是否存在相关性。
为了进行拉格朗日乘数检验,我们首先需要建立一个线性回归模型。
假设我们的模型是:
Y=βX+ε
其中,β是回归系数,ε是误差项。
我们的目标是检验β是否为零,即X和Y之间是否存在相关性。
为了实施拉格朗日乘数检验,我们需要构建一个约束模型。
我们引入一个拉格朗日乘数λ,将约束条件加入到模型中,得到新的模型:Y=βX+λ(X-Y)
我们的目标是最小化模型的误差平方和。
通过对模型进行最小二乘估计,我们可以得到回归系数β和拉格朗日乘数λ的估计值。
然后,我们可以使用拉格朗日乘数检验统计量来评估序列之间的相关性。
该统计量定义为:
LM=nR²
其中,n是样本容量,R²是回归方程的决定系数。
该统计量的分布近似于卡方分布。
我们使用卡方分布表来确定临界值,以判断序列之间的相关性是否显著。
如果检验统计量LM大于临界值,则可以拒绝零假设,即X 和Y之间存在相关性。
相反,如果检验统计量LM小于临界值,则接
受零假设,即X和Y之间不存在相关性。
拉格朗日乘数检验原理是一种用于检验序列相关性的统计方法。
通过构建约束模型和使用拉格朗日乘数检验统计量,我们可以评估序列之间的相关性,并判断其是否显著。
序列相关的LM检验

与
D.W.统计量仅检验扰动项是否存在一阶自相关不同,Breush-Godfrey LM检验(Lagrange multiplier,即拉格朗日乘数检验)也可应用于检验回归方程的残差序列是否存在高阶自相关,而且在方程中存在滞后因变量的情况下,LM检验仍然有效。
LM检验原假设为:
直到p阶滞后不存在序列相关,p为预先定义好的整数;备选假设是:
存在p阶自相关。
检验统计量由如下辅助回归计算。
LM检验通常给出两个统计量:
F统计量和T×R2统计量。
在EView软件中的操作方法:
选择View/Residual Tests/Serial correlation LM Test,一般地对高阶的,含有ARMA误差项的情况执行Breush-Godfrey LM。
在滞后定义对话框,输入要检验序列的最高阶数。
LM统计量显示,在5%的显著性水平拒绝原假设,回归方程的残差序列存在序列相关性。
因此,回归方程的估计结果不再有效,必须采取相应的方式修正残差的自相关性。
1/ 1。
序列相关性的检验与修正

序列相关性的检验与修正案例:书本P115进口与国内生产总值的关系。
一检验准备工作:建立工作文件,导入数据。
采用OLS方法建立进口方程。
在命令框输入:equation Eq01.ls m c gdp建立残差序列在命令框输入:series e=resid建立残差序列的滞后一期序列在命令框输入:series e_lag1=resid(-1)方法1:利用两个残差序列画图、观察。
方法2:查看回归方程的DW值=0.628,存在序列相关。
方法3:LM检验在命令框输入:equation Eq02.ls e c gdp e(-1) e(-2)可得LM1=15.006在命令框输入:scalar chi1=@qchisq(0.95,2)可得chi1=5.99可以判定模型存在2阶序列相关。
简便方法:在方程eq01窗口中点击View/Residual Test/Series Correlation LM Test,并选择滞后期为2,则会得到如下图所示的信息。
注:LM计算结果与上面有差异,因为这里的辅助回归所采用的resid(-1)、resid(-2)的缺失值用0补齐。
检验是否存在更高阶的序列相关。
继续在命令框输入:equation Eq03.ls e c gdp e(-1) e(-2) e(-3)可得LM2=14.58在命令框输入:scalar chi2=@qchisq(0.95,3)可得chi2=7.185仍然存在序列相关性,但由于e(-3)的参数不显著,可认为不存在3阶序列相关。
在方程eq01窗口中点击View/Residual Test/Series Correlation LM Test ,并选择滞后期为3,则会得到如下图所示的信息。
显然,LM 检验的结果拒绝原假设(无序列相关),表明存在序列相关性。
二 序列相关性的修正与补救广义差分法就是广义最小二乘法(GLS ),但损失了部分样本观测值,损失的数量依赖于序列相关性的阶数(如一阶序列相关,至少损失1个样本值)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2485.255
2567.282 2730.836 3047.297 3772.504 4226.804 5034.796 5895.601 5951.881 6246.959 7084.703
2340.483
2543.536 2897.213 3385.98 4178.396 4650.277 5413.767 6070.256 6225.664 6404.548 7416.325
3093
3277 3514 3770 4107 4495 4973 5452 5848 6212 6775
724.1036
806.6926 855.8979 961.6996 997.2444 1039.368 1081.406 1102.651 1068.334 1286.002 1396.986
1992
1993 1994
7539
8395 9281
1504.637
1605.813 1644.222
8711.156
10326.95 13760.55
9748.009
13143.88 15471.3
二、序列相关性的检验
• 1、散点图法: • 2、D—W检验法: • 3、B.G检验:
1、散点图法:
• 第二步、在命令栏键入Scat resid resid(-1) 得到
残差的散点图(见下页图):
判断标准:
1、若散点在四个 象限呈无规律的散 布状态,则模型不 存在自相关。
2、若散点多散布在一三象限,则模型存在着严重的正自相关。
3、若散点多散布在二四象限,则模型存在着严重的负自相关。
2、D—W检验法:
具体步骤:
• 对数据进行ols估计,在所得的对话框中:
判断标准:
• (1)DW<dL,存在正自相关 • (2)DW>4-dL,存在负自相关 • (3)dU<DW<4-dU,不存在自相关性 • dL与dU的值是根据不同样本的容量N和解释变量的个数P, 在给定的不同显著性水平下查得的。 • 直观上理解,DW值越靠近2,则越不具备自相关性。
第三步、将变量都取对数:
• 依次输入命令:
genr ly=log(y) genr lx1=log(x1) genr lx4=log(x4) genr lx5=log(x5)
• 依次输入命令:
第四步、构造滞后变量:
genr lly=ly-0.653829*ly(-1) genr llx1=lx1-0.653829*lx1(-1) genr llx4=lx4-0.653829*lx4(-1) genr llx5=lx5-0.653829*lx5(-1)
我们将拿李子奈书P86的模型作例子:
具体的参数选择和变换这里就不赘述了,大 家看书即可,书上一目了然。 数据见下页:
年份(年)
1971 1972 1973 1974 1975 1976 1977 1978 1979 1980
发电量(亿 千瓦时) Y
1384 1524 1668 1688 1958 2031 2234 2566 2820 3006
四、修正结果的再检验:
• 下面我们再利用第一部分的三种检验方法 进行检验:
1、散点图法: 2、D—W检验法: 3、B.G检验:
• 具体检验过程从略,结果我们可以看到修 正方法良好的消除了序列相关性。
五、说明
• 正如上一章最后说的一样,序列相关性同 异方差一样,是回归过程的一种情况,很 多情况下并不能完全消除,这要看我们关 注的参数指标谁更重要来进行选择。
• 原理:此方法即为计算当前残差与滞后一期残差的散点
图。如果大部分点落在一、三象限,则表明随机项存在正 自相关。如果大部分点落在二、四象限则表明随机项存在 负相关。
具体操作方法: • 第一步、建立工作文档,输入数据并作OLS估计。
目的是得到残差resid。(具体的数据选择和修正步 骤见书,此处从略)
傻瓜EViews系列
第三讲、序列相关性的检验 与消除: By Jimmy
jimmy_young2005@
一、序列相关性产生的原因与后果 二、序列相关性的检验 三、序列相关性的修正
四、修正结果的再检验
五、说明
一、序列相关性产生的原因与后果:
• 原因:数据违背了OLS估计的五条基本前提假设 之一: co v( x i , x j ) 0 ( i j ) • 在这种情况下数据具有了多重共线性,对于某两 个或多个解释变量而言,它们之间存在着相关性。 • 具体的经济问题中,一般经验告诉我们,时间序 列为基础的数据所建立的模型,往往存在着多重 共线性。
• 后果: 由于多重共线性的存在已经使数据违背了OLS估
计的五大基本原则,若不对数据进行处理就进行OLS估计, 则会出现以下后果:
• (1)参数的估计量非有效(方差不再是估计值中最小的)。 • (2)变量的显著性检验失去意义。 • (3)模型的预测失效。
• 这些后果的详细解释和其它后果的产生请参阅李子奈版《计量经济学》 P70
判断标准:
观察表中Probability: 若值非常小,我们就 拒绝原假设(原数据 不存在序列相关性), 接受备择假设(原数 据存在序列相关性), 即认为模型具有自相 关性。
若值非常大,我们就接受原假设(原数据不存在序列相关性),拒绝备 择假设(原数据存在序列相关性),即认为模型不具有自相关性。
三、序列相关性的修正:
3、Breusch-Godfrey检验(简称B.G检
验、二阶段迭代法): 具体操作方法:
• 第一步、在OLS估
计结果对话框中选择
view——Residual test——serial correlation LM test 。
第二步、设定用以检验的序列相关的阶数。
键入1表示检验一阶序列相关。
第三步、点击确定后,出现估计的对话框:
1、广义最小二乘法:
由于WLS步骤和异方差基本相同,另外经常 出现进行一次或多次广义最小二乘法后, 仍不能良好地消除序列相关性的情况。因 此我们不再讲述WLS的具体操作步骤。
2、差分法
• 原理:采用普通最小二乘法估计原模型,得到随
机误差项的“近似估计值”,然后利用该“近似 估计值”求得随机误差项相关系数的估计量。语 言可能不太好表达,大家可以随着差分法的步骤 一步步地体会。
至此,我们建立的workfile中便多了许多数据,
如图:
第五步、对新构造的这组数据(lly llx1 llx4 llx5)进行
ols估计:键入命令: Ls lly c llx1 llx4 llx5 ,得到 OLS估计结果:
结果分析:
• 估计结果为:
lly 0.826012 0.173875 llX 1 0.728069 llX 4 0.422714 llX 5
• 原理:若数据不存在序列相关性,则et和et-1成随
机关系,两者的差较为适中,此时DW值则会取一个 适中值。而若存在序列相关性的话,则DW的分子会 过大或过小,进而影响DW的值。具体的数学证明见 李子奈书P62。
(e
DW
t2
n
t n
et 1 )
2 t
2
e
t 1
Durbin-Watson检验用于随机误差项之间是否存在一 阶自相关的情况。 DW∈(0,4) DW值在每次的ols估计中都会由EViews系统自动算 出,因此这种方法比较简便易行。
• 序列相关性的修正主要有两种方法:
1、广义最小二乘法 2、差分法
说明:可能会出现进行一次或多次广义最小二乘法后,仍
不能良好地消除序列相关性的情况,这时可以进行差分法对 数据进行修正。 但差分法对数据的影响较大,这会造成修正后的估计值有比 较大的误差。两种方法各有利弊。 一般进行差分法后,不但能将序列相关性消除,而且能将异 方差性的影响一并消除。
• (5.123767) (1.307397) (3.211654) (1.914285)
^
• R-squared=0.976516 Durbin-Watson stat=1.015270 F-statistic = 263.3549
• 若常数项的显著性不显著,则可以舍去常 数项再进行估计。具体过程从略。
郑重声明
此课件只能用于同学学习参考,未经 书面授权不得做其他用途,尤其是不得做 商业用途。 课件作者
调整后的农 业总产值(亿元) X1
538.5779 534.5599 578.4023 594.132 603.7374 599.9047 598.9484 642.5943 639.548 676.8635
调整后轻工业总产 值(亿元) X2
941.0164 1003.65 1105.839 1132.299 1289.234 1319.964 1491.803 1663.024 1860.783 2193.141
具体步骤:
• 第一步、首先对原始数据进行ols估计,得到残
差序列(为了下面好表示,我们命残差为e,命令 为genr e=resid)
• 第二步、对残差及其滞后变量进行ols估计,目
的是找到其系数。输入命令ls e e(-1) c得到:
将这个系数记录下来: Coefficient=0.653829
调整后重工业 总产值(亿元) X3
1249.546 1336.679 1443.431 1415.146 1636.861 1668.186 1900.729 2195.811 2398.544 2458.484
1981
1982 1983 1984 1985 1986 1987 1988 1989 1990 1991
