第10章 微观经济学博弈论初步
第10章 微观经济学博弈论初步

不存在纯策略纳什均衡的混合策略模型
和纯策略组合不同,混合策略组合 是一个概率向量组合,每一个概率向量 是相应参与人的一个混合策略。
利用期望支付的公式可得甲厂商条
件混合策略为:
1q1 0.7
p1 0,1q1 0.7
0q1
乙厂商条件混合策略为:
1 p1 0.5
q1 0,1 p1 0.5
一、博弈树(例子:竞争者—垄断 者博弈)
描述序贯博弈的工具是“博弈树” ,由“点”(包括“起点”、“中间点 ”、“终点”)、连接点的“线段”以 及标在这些点和线段旁边的文字和数字 组成。
以博弈树来描述的完全信息的动态 博弈称为扩展型博弈。
竞争者—垄断者博弈
二、纳什均衡Biblioteka 竞争者—垄断者博弈中,纳什均衡 为(进入,容忍)。下面的博弈中,两 个纳什均衡:(足球,足球)、(芭蕾 、芭蕾) 。
上 甲厂商 下
乙厂商
左
右
5,6
2,4
4,1
2,3
4.最优性
在完全信息的静态博弈中,如果纳
什均衡存在,既可能是最优的,也可能
不是最优的。
上 甲厂商 下
乙厂商
左
右
5,6
1,4
4,1
2,3
纳什均衡(下,右)不是最优的。
六、纳什均衡和社会福利
1.囚徒困境和寡头合作的不稳定性
李四
坦白 不坦白
张三
坦白 不坦白
0, p 0.5
由两家粥店的条件混合策略可得混 合策略的纳什均衡为:
p,1 p,q,1 q 0.5,0.5,0.5,0.5 即当粥店1选择混合策略(0.5,0.5 )、粥店2选择混合策略(0.5,0.5)时 ,博弈达到了均衡。
S315大学高数第10章 博弈论初步

20
第十章 博弈论初步 第二节 同时博弈:纯策略均衡
条件策略下划线法: 用下划线分别来表示甲厂商和乙厂商的条件策略。 在甲厂商的支付矩阵中,找出每一列的最大者;在乙
厂商的支付矩阵中,找出每一行的最大者。 都有划线的支付组合为条件均衡策略。
甲厂商的策略
的个体,至少有两个,有时可以引入一个虚拟的参与 人如“自然” 。 策略(Strategies/actions) :是一项规则,一组可选择 的行动集合。 参与人应该在什么条件下选择什么样的 行动,以保证自身利益最大化。 支付(Payoffs) :参与人得到的报酬,所得到的支付 都是所有策略共同作用的结果——支付组合。
8
第十章 博弈论初步 第一节 博弈论和策略行为
博弈论重要性 20世纪70 年代以后,博弈论形成了一个完整的体系;从80 年代
开始,博弈论逐渐成为主流经济学的一部分,甚至成为微观经济学的 基础。
1994年:纳什(Nash)、泽尔腾(Selten)和海萨尼(Harsanyi) 3位数学家因在非合作博弈的均衡分析理论方面作出了开创性的贡献, 对博弈论和经济学产生了重要影响而获得了诺贝尔经济学奖。
1950年,22岁的纳什获得博士学位。博士论文为“非 合作的赛局”(后被称为“纳什均衡”) ,该论文仅28 页。
18
第十章 博弈论初步 第二节 同时博弈:纯策略均衡
1958年,纳什得了严重的精神分裂症。他的妻子艾莉 西亚,一直守护在纳什身边,并走过了唯一的儿子同 样罹患精神分裂症的震惊与哀伤……漫长的岁月证明, 与艾莉西亚结婚,也许是纳什一生中比获得诺贝尔奖 更重要的事情。
12
第十章 博弈论初步
第二节 同时博弈:纯策略均衡
第十章博弈论(微观经济学-南开大学刘骏民)

⒋寻求纳什平衡 首先思索A的战略,关于B的每一个给定战略,找出A
的最优战略,在其对应的支付下划一横线,再用相似的方 法找出B的最优战略。完成这个进程后,假设某个支付组 合的两个数字下都有线,这个支付组合所对应的战略组合 就是一个纳什平衡。
表10-7 寻求纳什均衡Βιβλιοθήκη 参与人BLC
R
参与人A
U
0,2 1,4
三、博弈的要素
博弈的要素包括参与人、举动、信息、战略、支付、 结果战争衡,其中,参与人、战略和支付是描画一个博 弈所需求的最基本的要素,参与人、举动和结果统称为 博弈规那么。
①参与人:指一个博弈中的决策主体在囚徒困境模 型中,有两个参与人,即〝囚徒A〞和〝囚徒B〞。
②举动:是参与人在博弈的某个时点的决策变量。 在囚徒困境模型中,囚徒A、B都只要两种举动可供选择, 即〝坦率〞和〝供认〞。
一切参与人占优战略的组合称为占优战略平衡。
⒉重复剔除的占优平衡
思索〝智猪博弈〞例子。猪圈里围着中间猪,一头大 猪,一头小猪。猪圈的一头有一个猪槽,另一头装置了一 个按钮,控制着猪食的供应。按下一按钮会有8个单位的 猪食进槽,但按下按钮的猪需求付出2个单位的本钱。假 定大猪先到,大猪吃到7个单位,小猪只能吃1个单位;假 定同时到,大猪吃5个单位,小猪吃3个单位;假定小猪先 到,大猪和小猪各吃4个单位。表10-5的Ⅰ表列出对应不同 战略组合的支付水平,如第一格表示中间猪同时按下按钮, 就会同时走到猪食槽,大猪吃5个单位,小猪吃3个,扣除 2个单位的本钱,支付水平区分为3和1。
20世纪70年代以后,经济学家末尾强调团体理性。
⒉博弈论与主流经济学 博弈论进入主流经济学,反映了经济学开展的以下几
个趋向:①经济学研讨的对象越来越转向集体,坚持了一 些没有微观基础的假定;②经济学越来越转向人与人之间 竞争与协作的研讨,特别是经济学留意到理性人的团体理 性行为能够招致的团体非理性;③经济学越来越注重对信 息的研讨。
第十章博弈论初步-PPT精品

▪ 1、纳什均衡的定义:
▪ 设 s(s1, .., .sn)是n人博弈G={ ; S1, .., . Sn u1,.., . un } 的一个策略组合。如果对于每个局中人 i , ui(s1 , ., .s .i 1 , si , si 1 , ., .s .n )≥ ui(s1 , ., .s .i 1 , si, si 1 , ., .s .n )
第十章 博弈论初步 Game Theory
博弈论概述 纳什均衡 序贯博弈与重复博弈 进入威慑
第一节 博弈论概述
▪ 什么是博弈? ▪ 拍卖金钱 ▪ 海盗博弈 ▪ 田忌赛马 ▪ 围棋和象棋
齐王
田忌
上
中
下
上 赢,输 赢,输 赢,输
中 输,赢 赢,输 赢,输
下 输,赢 输,赢 赢,输
一、博弈的基本要素
ui(si,si) ≥ ui(si,si) 对于所有si Si 都成立,则我们称策略组合
s(s1, .., .sn)
是该博弈的一个纳什均衡。
▪ 纳什简介: ▪ 约翰·纳什生于1928年6月13日。父亲是电子工程师
与教师,第一次世界大战的老兵。纳什小时孤独内 向。纳什的数学天分大约在14岁开始展现。他在普 林斯顿大学读博士时刚刚二十出头,但他的一篇关 于非合作博弈的博士论文和其他相关文章,确立了 他博弈论大师的地位。在20世纪50年代末,他已是 闻名世界的科学家了。 ▪ 然而,30岁的时候,纳什和他惟一儿子都罹患精神 分裂症。半个世纪之后,在他妻子(艾利西亚—— —麻省理工学院物理系毕业生)的精心照料下,和 她的儿子一样,纳什教授渐渐康复,并在1994年获 得诺贝尔经济学奖。 ▪ 影片《美丽心灵》是一部以纳什的生平经历为基础 而创作的人物传记片。该片荣获2019年奥斯卡金像 奖。
微观经济学PPT课件:第十章 博弈论

卖
卖
不卖 3A 不卖 4B 不卖 5A
卖
卖
卖
不卖 (0,0)
(1,0)
(0,2)
(3,0)
(0,4)
(5,0)
1A 不卖 2B
卖
卖
不卖 3A 不卖 4B 不卖 5A
卖
卖
卖
不卖 (0,0)
(1,0)
(0,2)
(3,0)
(0,4)
(5,0)
简化的蜈蚣博弈1
1A 不卖 2B 不卖 3A 不卖 4B 不卖 5A
-纳什均衡:e点 ((0.5,0.5),(0.7,0.3))
0.5
1
p1
第四节 完全信息动态博弈
参与人的决策有先有后,且后行动的参与人可以观察到先 行动的参与人已经采取的策略
一、博弈树与纳什均衡
• 博弈树模型又称扩展式博弈模型 • 以博弈树来描述的序贯博弈又叫做扩展型博弈
行业外 企业A
不进入 进入
因为动态博弈有决策秩序,所以在出现多重纳什均衡时 • 静态博弈常常无法确定最终实现的是哪一个均衡 • 动态博弈往往能够确定一个最终的均衡
第十章 博弈论
概念界定 静态博弈 动态博弈
第一节 概念界定
一、博弈论
• 研究在策略性环境中,进行策略性决策和采取策略性行动的
科学。
二、博弈论的基本要素
➢参与人/局中人( Player) ➢策略(Strategies)
• 策略空间:参与者可以选择的策略的全体。 ➢支付(Payoff)
• 支付矩阵(Payoff Matrix,收益矩阵/报酬矩阵)
p2=1-p1 q2=1-q1
乙
q1 q2 左右
混合策略组合:
《西方经济学》讲义 第十章 博弈论初步

第十章博弈论初步一、教学目的使学生具备博弈论的思维,会使用博弈的方法来分析经济问题,掌握博弈论的基本概念和应用。
二、教学重点博弈论的基本概念、参与人、行动、信息,纯策略均衡,混合策略均衡。
三、教学难点纳什均衡的概念、策略选择。
四、教学方法讲授和讨论五、教学安排本章计划安排6学时六、教学步骤(一)课程导入传统博弈论纳什均衡解的概念是以博弈规则、参与者的理性以及参与者的收益函数都是共同知识为前提的。
现实生活中的人们并不是理性的,行为主体很难在短时间内准确地寻找到自己的最优决策,同时对其他主体的行为预测也同样不可能准确无误。
列举“囚徒困境”、“智猪博弈”的例子,引发学生对博弈的思考,理解策略的意义和应用性。
(二)课堂教学设计以寡头市场为例引入教学内容:我们知道,在寡头市场上(寡头市场又成为垄断市场。
它是指几家厂商控制整个市场的产品的生产和销售的这样一种市场组织),厂商们之间的行为是相互影响的,每个厂商都需要首先推测或者了解其他厂商对自己所要采取的某一行动的反应,然后在考虑到其他厂商这些反应方式的前提下,再采取对自己最有利的行动。
在寡头市场上的每一个厂商都是这样思考和行动的,因此,厂商之间行为的相互影响和相互作用的关系如同博弈。
(三)教案内容第一节博弈论和策略行为一、博弈论的含义博弈论是研究在策略性环境中如何进行策略性决策和采取策略性行动的科学。
策略性环境是指,每一个人进行的决策和采取的行动都会对其他人产生影响;策略性决策和策略性行动是指,每个人要根据其他人的可能反应来决定自己的决策和行动。
二、博弈的三个基本要素三个基本要素,即参与人、参与人的策略和参与人的支付。
所谓参与人(或称局中人),就是在博弈中进行决策的个体;所谓参与人的策略,指的是一项规则,根据该规则,参与人在博弈的每一时点上选择如何行动;所谓参与人的支付则是指,在所有参与人都选择了各自的策略且博弈已经完成之后,参与人获得的效用(或期望效用)。
微观经济学 寡头市场与博弈理论

B
不进入
进入 进入 不进入
(1,2)
(5,0) (-2,-2)
(2,0)
均衡结果:(竞争性定价,不进入)。
说明对垄断厂商的规制,可以在无需直接管制下,也可能 会出竞争性价格。只要放开市场准入性。
余向华
版权所有
五、斯威齐模型与寡头市场价格刚性问题
目的:解释为什么有时寡头的产量和价格不会对一定范 围内的成本变动做出反应,即成本变了价格不变。
1、寡头垄断市场的基本特征 2、寡头间策略互动的现代分析工具—博弈论初步
3、寡头间的竞争分析
4、寡头间的合谋问题
第一节 寡头垄断市场的基本特征
1、少数几家大厂商(寡头)控制了大部分甚至全
部的市场份额。
2、存在较强的进入壁垒 3、寡头之间在决策上存在明显的相互依存 4、寡头间既可能合谋,又可能在多个维度展开竞 争,充满了不确定性 这也是现实的市场中一种非常常见的市场结构。
基本假设——每个寡头都认为对手会“跟跌不跟涨”
如果自己提高价格,其他寡头将不会跟随涨价
因此涨价时需求更富有弹性
如果自己试图通过降价来提高市场份额,也达不 到预定的目标,因为其他企业也将随着降价
因此,降价时缺乏弹性
这个假设产生了折弯的需求曲线。
P
C A
MC1 MC0
P0
B E
D1 F
G
坦白
张三
不坦白
先讯问张三,再讯问
李四,则博弈结构变 为动态博弈:
坦白
李四
不坦白 坦白
李四
不坦白
此时行动时间的先后 使双方的最优策略会 是什么呢?
西方经济学微观部分第十章博弈论初步

策略1 策略2
b p 1 ( b 1 1 b 1 ) 2 ( 1 p 1 )b 2 ( 1 b 2 )2
b11
策
参 p1 略
A的p1 条件010,1混 合aaa策 000略为与人A p:2 策略12
a11 b21
a21
b12 a12
b22 a22
[习题] 博弈论初步
[习题] 博弈论 初步
p1
单击添加副标题
第十章 博弈论初 步
西方经济学 (微观部分)
*自嘲* 一介学究,惶惶似狗。 东拼西凑,闲来插柳。 或存疏漏,等着挨揍。 钱财无有,知识半斗。 交流携手,相逢美酒。 余望何求?潮起云收。
第十章 博弈论初步 目录
目 录 /CONTENTS
1
第一节 ○
博弈论和
○
策略行为
2
第二节
3
0 q10.7 1 p10.5 7
1
9– 8–
2
第三节 混合策略均衡 二、混合策略的纳什均衡
第三节 混合策 略均衡
二 混合策略的纳什均衡
❖ 即使纯策略的纳什均衡不存在,相应的混合策
略纳什均衡总会存在。
❖ 纯策略纳什均衡作为 ·q1 1 特例被包括在混合策 略纳什均衡之中。 0.7·
❖ 混合策略博弈的均衡
[案例] “华容 道”里的纳什
均衡(1)
小 道
孔 明
大 路
[案例]“华容道”里的纳什均衡(1)
[案例] “华容道”里的纳什均衡(1)
曹操 小道 大路
被擒
逃脱
擒住 逃脱
空等 被擒
空等
擒住
❖ 孔明曰:“亮夜观乾象,操贼未合身亡。 留这人情, 教云长做了,亦是美事。” 玄德曰:“先生神算,世所罕及!”
微观经济学第十章博弈论

博弈论的基本概念
策略
参与者为达到最优目标而采取的 行动方案。
信息
参与者对其他参与者的行动或策 略的了解程度。
01
02
参与者
参与博弈的决策主体,可以是个 人、组织或国家。
03
04
收益
参与者在博弈中获得的利益或损 失。
博弈论的应用场景
01
02
03
04
商业竞争
企业间竞争策略、市场份额争 夺等。
政治外交
05
博弈论的实际应用
商业竞争中的博弈策略
竞争策略
企业可以利用博弈论来制定竞争 策略,例如通过分析竞争对手的
可能行动来制定最优反应。
合作博弈
企业也可以通过合作博弈来寻求共 赢,例如通过建立战略联盟或进行 合作研发来共同开拓市场或降低成 本。
市场进入与退出
博弈论可以帮助企业分析市场进入 和退出的可能性,以及制定相应的 策略。
感谢您的观看
THANKS
政策制定中的博弈论应用
政策制定
政府可以利用博弈论来制定政策, 例如通过分析利益相关方的博弈
行为来制定最优政策。
政策执行
政府也可以利用博弈论来分析政 策的执行效果,例如通过分析利 益相关方的反应来评估政策的可
行性。
政策调整
博弈论可以帮助政府根据利益相 关方的反应来调整政策,以实现
更好的政策效果。
国际关系中的博弈策略
纳什均衡的应用实例
囚徒困境
两个囚犯选择坦白或沉默,在给定对 方选择的情况下,自己选择坦白是最 优策略,最终导致两个囚犯都坦白, 实现了纳什均衡。
寡头竞争
公共资源过度使用
在公共资源的使用中,每个个体都追 求自身利益最大化,最终导致公共资 源过度使用,这也是一种纳什均衡的 现象。
西方经济学 10 博弈论初步1

开 战
800
900
1200
1300 900
军演 开 战 不 开 战 800 700 600 1200
不军演 1300 900 1300 900
河南理工大工大学xhq
河南理工大学xhq
河南理工大学xhq
河南理工大学xhq
河南理工大学xhq
河南理工大学xhq
河南理工大学xhq
• 案例:关于中国核心利益问题的威胁 • • • 南海 台湾 等 中国怎么办? 美国怎么办?
•
大国博弈:美韩黄海军演
河南理工大学xhq
河南理工大学xhq
河南理工大学xhq
美国 军演 中 国不 开 战 不军演 600 1300 900
第十章 博弈论初步
河南理工大学xhq
• 博弈论是一种分析问题的有效方法 • ——分析人的行为
•
——自己的策略选择
河南理工大学xhq
• 田忌赛马的故事
河南理工大学xhq
一、博弈的内涵
• 博——对抗;弈——下棋
•
• •
每一个决策和行为(每一步棋)
都针对对方并考虑对方的策略和举措 策略上,“虚虚实实,真假难辩”
-5 -7 -5 -1 -1 0 -7 0
这种情况是: 对方策略变化,自己策略也跟着变化 现实中的博弈很多是如此。
河南理工大学xhq
• 博弈均衡:双方都不想单方面改变自己策略的稳定 状态。 有以下两种情况: • 占优博弈均衡: • • 博弈均衡时的策略双方都是占优策略的均衡 如(-8,-8)均衡 也不想改变自己策略的状态
河南理工大学xhq
• 其他博弈基本概念: • 报酬矩阵(支付矩阵):参与者在各种情况下采取各 种策略所获得的不同结果关系
微观经济学第10章 博弈论

第一节 博弈论概述
一、经济学与博弈论
博弈论又称为对策论或游戏论,是研究决策主体的行 为发生直接相互作用时的决策以及这种决策的均衡问题。 博弈论被应用于政治、外交、军事、经济等领域。近20年 来,博弈论在经济学中得到了广泛的应用,它对寡头理论、 信息经济学等方面的发展做出了重要贡献。
在现实生活中,经济人在经济活动中要与他人 相互合作,但同时还存在着冲突。现实生活中信息 并不总是完备的,这使得价格机制并不总是实现合 作和解决冲突的最有效安排 。
在非合作博弈中,主要代表人物是纳什、泽尔腾、海萨尼等。到20 世纪70年代,博弈论开始被纳入到主流经济学的教科书和研究著作之中。 特别是最近十几年来,博弈论在经济学中得到了广泛的运用,尤其是在 揭示经济行为相互制约的性质方面。1994年诺贝尔经济学奖授予给三位 博弈论专家约翰·纳什(JOHN F.NASH)、约翰·海萨尼(JOHN C. HARSANYI)莱因哈德·泽尔腾。三人在非合作博弈的均衡分析理论方面做 出了开创性德贡献对博弈论和经济学产生了重大影响。2005年诺贝尔经 济学奖再度授予两位博弈论专家罗伯特·奥曼(Robert J. Aumann)和 托马斯·谢林(Thomas C. Schelling),就是对博弈论在经济学中的应 用成就所给予的高度评价与广泛认可。
当研究领域由价格制度转向非价格制度时,博 弈论逐渐成为经济学的基石。
博弈论研究的是具有相互影响作用的行为主体 的决策行为及其均衡的理论。
在一个博弈中,很多个体都希望通过选择 一定的行为使自己的效用达到最大化。并且, 每个个体的最终效用都依赖于所有的个体所做 出的选择。这种相互影响的环境,每个个体可 能选择的行为,以及一系列的所有可能的效用 组合被称为是博弈。
第十章博弈论与竞争策略微观经济学叶德磊编著

乙
左右
甲 上 13, 3 9, 4 下 17, 2 7, 8
4、对于右下图表示的博弈,其上策均衡或纳什均衡由哪 一个格子代表的策略组合来表示? A. 左上角 B. 右上角 C. 左下角 D. 右下角
5、乒乓球团体赛中双方出场阵营的选择和确定属于 A. 静态博弈 B. 动态博弈 C. 零和博弈 D. 合作博弈
第四节 不完全信息博弈: 静态与动态分析
一.不完全信息静态博弈:贝叶斯均衡
贝叶斯均衡通常被描述为:在给定自己的类型和对手类
型的概率分布的情况下,每个参与者的期望效用达到了最大
化从而没有参与者愿意改变自己的行为或策略。
在下图的博弈中假定在位企业属于高成本类型的企业的
概率大于0.2,潜在企业选择进入才是最优的。
下图博弈中,厂商A和B的上策都是做广告。上策均衡就是 两家厂商都选择做广告的策略。
厂 商B 做广告 不做广告
做广告 厂商A 不做广告
10,5 6,8
15,0 10,2
广告博弈的得益矩阵
2.纳什均衡指的是在给定竞争对手的选择行为后,博弈方
选择了它所能选择的最好的策略(或采取了它所能采取的最
好的行动)。
(一)合作博弈和非合作博弈 1.合作博弈:如果各博弈方能达成某种有约束力的契约
或协议(包括默契)以使他们选择共同的或联合的策略。 2.非合作博弈:反之,就属于非合作博弈。
(二)单人博弈、双人博弈和多人博弈 (三)有限策略博弈和无限策略博弈 (四)零和博弈、常和博弈与变和博弈
1.零和博弈:是指在博弈中,一方的得益就是另一方的损 失,所有博弈方的得益总和为零。
2、下列正确的表述是 A、任何市场竞争都可由市场博弈来概括 B、剔除不可置信的威胁后的纳什均衡属于精炼贝 叶斯纳 什均衡 C、股票投资者之间的博弈属于零和博弈 D、“摸着石子过河”属于完全信息动态博弈
经济学课件博弈论初步
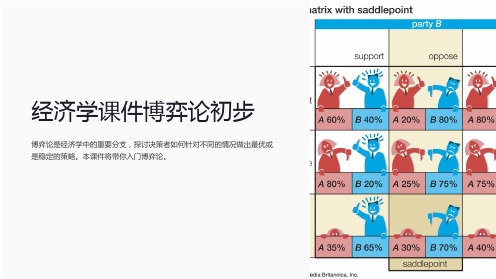
博弈论是经济学中的重要分支,探讨决策者如何针对不同的情况做出最优或 是稳定的策略。本课件将带你入门博弈论。
博弈基础
玩家、策略、收益
博弈论的基础概念包括玩家(两 个或多个决策者)、策略(决策 者可选的不同行动)、收益(每 个玩家的利益)。
零和博弈和非零和博弈
纳什均衡
零和博弈是指通过一方赢得另外 一方的损失来实现收益。相反, 非零和博争中的博弈论应 用
通过博弈论模型,企业可以 优化价格、销售策略、广告 推广等方面来获得利益。
政治决策中的博弈论应 用
政治决策中的博弈论应用广 泛,例如国际贸易、军备竞 赛、公共压试验等。
社会博弈中的博弈论应 用
社会博弈包括合作、交叉、 竞争等情形。了解博弈论可 以让我们更好地了解社会行 为。
纳什均衡指的是玩家做出的最优 决策,即使其他玩家对此决策做 出的反应已知,其决策仍然是最 好的。
重要概念解析
1
支配策略
在某种情况下,一种选择比其他所有选
调和纳什均衡
2
择都要好,无论其他玩家选择什么。
指对于每个玩家而言,都不再存在更好
的策略。
3
子博弈完美均衡
针对某个博弈中的某个子博弈,所有玩 家都采取的策略构成了一个完美均衡。
2 博弈论的局限性
博弈论研究过程中需要进行简化和假设,从而忽略部分现实中的因素,需要结合其他学 科进行研究。
3 博弈论的未来趋势
随着经济、政治、社会等领域的日益发展,博弈论在有限理性、混合策略和进化博弈等 方面仍有很多研究空间。
博弈论的拓展
两人博弈论
多人博弈论
博弈树
常用的两人博弈论包括囚徒困境、 鸽子与鹰、石头剪子布等。
微观经济学 第十章

17
寡头厂商的共谋及其特征
寡头市场上只有少数厂商,对市场的影响举足轻重。 每个厂商为了获得更大市场份额,往往降价竞争。但是,其他厂
4
博弈的划分(博弈论的理论体系)
行动顺序 信息
静态
完全信息
完全信息静态博弈 纳什均衡
纳什(1950,1951)
不完全信 息
不完全信息静态博弈 贝叶斯纳什均衡
海萨尼(1967-1968)
动态
完全信息动态博弈 子博弈精练纳什均衡
泽尔腾(1965)
不完全信息动态博弈 精练贝叶斯纳什均衡
泽尔腾(1965) Kreps 和Wilson(1982) Fudenberg 和Tirole(1991)
人的选择,就是同时行动 • 博弈分析的目的是预测均衡结果
8
(一)占优战略及其均衡
参与人选择的最佳战略不依赖于其他参与人的战略选 择,这样的最佳战略称为占优战略。
囚徒 B
坦白 抵赖
囚徒A
坦白
-8,-8 -10,0
抵赖
0,-10 -1,-1
四种行动选择组合 中,(抵赖、抵赖) 是帕累托最优的
-8大于-10 0大于-1
15
通俗地说,纳什均衡的含义就是:给定你的策略,我 的策略是最好的策略;给定我的策略,你的策略也是 你的最好的策略。即双方在给定的策略下不愿意调整 自己的策略。
囚徒A
坦白
囚徒 B
抵赖
坦白
-8,-8 -10,0
抵赖
0,-10 -1,-1
(坦白,坦白)是纳什均衡,而(不坦白,坦白)、 (坦白,不坦白)和(不坦白,不坦白)都不是纳什 均衡。
微观经济学
第十章 博弈论与信息不对称
第十章---博弈论初步精选全文完整版

甲 (式乙)
p.61
p.42
A B
混合策略组合及其支付也就有无限多的可能。
q.31 C 4,6 7,3
乙
.q72 D 9,1 2,8 9
不存在纯策略均衡时的混合策略均衡3
• 条件混合策略:参与人在假定其他参与人按某一概率选择某一策略
的条件下设计的对自己而言具有相对优势的(即期望支付最大的)混合 策略,称为“条件混合策略”。
• 对乙而言,如果假定甲合作,那么乙合作的支付为6,比不合作的支付 多1,因此合作是甲合作条件下乙的条件策略;假定甲不合作,那么乙的 条件策略是也不合作,乙若合作支付只有1,不合作则可得到3。
• 条件策略组合:参与人以其他参与人选择某一策略为条件的条件策略与
作为它的条件的对方策略之间的组合,称为“条件优势策略组合”或
• 假q2=定1-(q1p代1,入p甲2)与、乙(各q自1,的q2期)望的支取付值表从达0到式1有无,限经多整可理能可,得把:p2=1-p1和 E甲= p1(7-10q1)+5q1+2(式1); E乙= 5q1(2p1-1)-7p1+8(式2)
• 每个参与人需要确定,在另一参与人为其混合策略选择某个概率值时, 己方混合策略的概率向量应怎样取值,才能使自己的期望支付最大。
e点的坐标是p1=0.5,q1=0.7,则纳什均衡 时p2=0.5,q2=0.3 。
q1 1
本题中混合策略的纳什均衡还可表示为:
((p1 , p2),(q1 ,q2) )= ((0.5 , 0.5),(0.7 , 0.3) )。 0.7 本题中,只有唯一的这个纳什均衡点。
1
q1<0.7
p1= [0,1] q1 = 0.7
《微观经济学》第十章博弈论与信息不对称.

2.博弈的扩展式
脆 -3,-3 8,10 10,8 -3,-3
脆
厂商1 (1) 甜
厂商2 (2)
厂商2 (3)
甜 脆 甜
图10-1: 产品选择的博弈扩展形式
第四节 威胁、承诺与可信性
一、空头威胁
表10-9:承诺后的市场进入博弈 垄断者 商战 默许 潜在 进入 进入 不进入 者 —5,10 5,9 0,24 0,24 垄断者 商战 默许
厂商B 厂商B
做广告不做广告 做广告不做广告
厂 做广告 商 不做广告 A
10,8 18, 3 2,17 15,12
厂 做广告 商 不做广告 A
10,8 18, 3 2,17 20,12
三、纳什均衡
表10-4:性 别 之 战 女
足球赛 音乐会 男 足球赛 2,1 0,0 音乐会 0,0 1,2 厂商 1 脆 甜 脆 甜
本章复习思考题
1.说明上策均衡与纳什均衡之间的联系? 2.假定企业A和B都是服装制造商,它们都可以选择生产高档或 中档产品,其支付矩阵如下(利润单位:万元): 企业B 中档 企业A 中档 高档 高档 100,80
(1)这两个企业有没有上策? (2)该博弈中有几个纳什均衡?有几个?请指出。 (3)若企业A可以先决定生产其产品,试用博弈的扩展形式来分 析该博弈中的纳什均衡。
表10-8:市场进入博弈
潜在 进入 者
进入 不进 入
—5,10 5,15 0,30 0,30
二、承诺与可信的威胁
第五节 信息不对称
一、信息不完全与信息不对称 二、逆向选择与市场信号 1.逆向选择 2.市场信号 三、道德风险与激励机制 1.道德风险 2.委托代理问题 3.激励机制的设计
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
根据参与人的数量,可分为二人博 弈和多人博弈;
根据参与人拥有的策略的数量,可 分为有限博弈和无限博弈;
根据参与人的支付情况,可分为零 和博弈和非零和博弈;
根据参与人是否能够达成有效的协 议,可分为合作博弈和非合作博弈;
根据参与人是否了解有关博弈的所 有信息,可分为完全信息博弈和不完全 信息博弈;
0, p 0.5
由两家粥店的条件混合策略可得混 合策略的纳什均衡为:
p,1 p,q,1 q 0.5,0.5,0.5,0.5 即当粥店1选择混合策略(0.5,0.5 )、粥店2选择混合策略(0.5,0.5)时 ,博弈达到了均衡。
简化的情侣博弈(1)
第二步,再对简化博弈重复步骤一 ,直到最后,得到原博弈的一个最简博 弈。这个最简博弈,就是原博弈的解; 而在存在多重纳什均衡时,它就是对纳 什均衡的精炼。
简化的情侣博弈(2)
四、精炼的纳什均衡与效率
对参与人来说,由逆向归纳法“精 炼”出来的完全信息动态博弈的纳什均 衡也不一定是有效率的。
1,5 2,3
利用下划线法得出,纳什均衡是(不
合作,不合作)。
五、纳什均衡的存在性、唯一性和 最优性
1.存在性 完全信息的静态博弈中,(纯策略 的)纳什均衡可能存在也可能不存在。
没有纳什均衡的完全信息静态博弈
甲厂商
上 下
乙厂商
左
右
4,6
9,1
7,3
2,8
2.唯一性 在完全信息的静态博弈中,如果纳 什均衡存在,既可能是唯一的,也可能 是不唯一的。
解:(1)该博弈的纯策略纳什均衡 为(咸粥,甜粥)和(甜粥,咸粥)。
先考虑粥店1的策略,假定粥店2选 择生产甜粥,则粥店1的最优策略为生产 咸粥,此时得到支付为2;若粥店2选择 生产咸粥,则粥店1的最优策略为生产甜 粥,此时双方都得到支付2。
同理,考虑粥店1的策略选择,若粥 店1选择生产甜粥,则粥店2的最优策略 为生产咸粥;若粥店1选择生产咸粥,则 粥店2的最优策略为生产甜粥。
蜈蚣博弈
简化的蜈蚣博弈(1)
简化的蜈蚣博弈(2)
10.3 名校考研真题详解
【例10.1】假定某地有两家粥店,它 们同时决定是生产甜粥还是生产咸粥。 各种可能的情况如下面支付矩阵所示:
粥店1
甜粥 咸粥
粥店2 甜粥 咸粥 -1,-1 2,2 2,2 -1,-1
求解此博弈的全部纳什均衡(包括
纯策略和混合策略纳什均衡)。
借用条件混合策略可确定混个混合策略纳什均衡
借用条件混合策略可确定混合策略 的纳什均衡。
无穷多个混合策略纳什均衡
第四节 完全信息动态博弈
在完全信息动态博弈中,参与人的 决策有先有后,特别是,后行动的参与 人可以观察到先行动的参与人已经采取 了的策略。
一、博弈树(例子:竞争者—垄断 者博弈)
描述序贯博弈的工具是“博弈树” ,由“点”(包括“起点”、“中间点 ”、“终点”)、连接点的“线段”以 及标在这些点和线段旁边的文字和数字 组成。
以博弈树来描述的完全信息的动态 博弈称为扩展型博弈。
竞争者—垄断者博弈
二、纳什均衡
竞争者—垄断者博弈中,纳什均衡 为(进入,容忍)。下面的博弈中,两 个纳什均衡:(足球,足球)、(芭蕾 、芭蕾) 。
5,6
1,4
4,1
2,3
纳什均衡(下,右)不是最优的。
六、纳什均衡和社会福利
1.囚徒困境和寡头合作的不稳定性
李四
坦白 不坦白
张三
坦白 不坦白
-8,-8 -20,0
0,-20 -1,-1
博弈中,存在唯一一个稳定的非最
优纳什均衡(坦白,坦白)。对参与人
来说,结果不是最优,却有利于社会。
“囚徒困境”的例子可以用来很好 地解释寡头市场的一个重要特征,即寡 头厂商之间合作的不稳定性。寡头之间 这种合作(如共谋垄断)的不稳定性尽 管对参与人不利,但却有利于促进竞争 ,从而提高整个社会的福利。
根据参与人在策略的实施上是否具 有“同时性”,可分为静态博弈(或同 时博弈)和动态博弈(或序贯博弈)。
第二节 完全信息静态博弈:纯
策略均衡
一、支付矩阵(例子:寡头博弈)
寡头博弈:合作与不合作
合作 甲厂商 不合作
乙厂商
合作 不合作
5,6
1,5
7,1
2,3
二、条件策略和条件策略组合
把甲厂商在乙厂商选择策略条件下 的最优策略称为甲厂商的条件策略; 把与甲厂商的条件策略相联系的策略 组合称为甲厂商的条件策略组合。
因此,该博弈的纯策略纳什均衡为 (咸粥,甜粥)和(甜粥,咸粥)。
(2)假定粥店1以概率p选择生产甜 粥,以概率 1 p选择生产咸粥,粥店2以 概率q选择生产甜粥,以概率 1 q选择生 产咸粥。
粥店1的期望支付为:
E1 pq 2 p 1 q 21 p q 1 p1 q p 3 6q 3q 1
三、纳什均衡
纳什均衡,指的是参与人的这样一 种策略组合。在该策略组合上,任何参 与人单独改变策略都不会得到好处。如 果在一个策略组合中,当所有其他人都 不改变策略时,没有人会改变自己的策 略,则该策略组合就是一个纳什均衡。
在纳什均衡的定义中,有两个问题 需要注意:
第一,“单独改变策略”是指任何 一个参与人在所有其他人都不改变策略 的情况下改变自己的策略。
三、纳什均衡的精炼:逆向归纳法
在存在多重纳什均衡的场合,有一 些纳什均衡似乎不合理。所谓对纳什均 衡的“精炼”,就是要从众多的纳什均 衡中进一步确定“更好”的纳什均衡。
纳什均衡的精炼方法通常使用 “逆 向归纳法”,具体包括以下两个步骤:
第一步,先从博弈最后阶段的每一 个决策点开始,确定相应参与人此时所 选择的策略,并把参与人所放弃的其他 策略删除,从而得到原博弈的一个简化 博弈。
0 p1
借用条件混合策略可确定混合策略 的纳什均衡。
二、只有一个纯策略均衡时的混合 策略均衡
存在唯一一个纯策略纳什均衡的混合策略模型
借用条件混合策略可确定混合策略 的纳什均衡。
纯策略纳什均衡往往作为特例被包 括在混合策略纳什均衡之中。
三、具有多个纯策略均衡时的混合 策略均衡
存在两个纯策略纳什均衡的混合策略模型
2.广告大战
A厂商
做广告 不做广告
B厂商
做广告 不做广告
7,7
12,5
5,12 10,10
纳什均衡(做广告,做广告)不仅对参与 人不是最优的,且对整个社会也不是最优的。
第三节 完全信息静态博弈: 混合策略均衡
一、不存在纯策略均衡时的混合策 略均衡
在每一个参与人都只有有限多个纯 策略的博弈中,至少存在一个混合策略 纳什均衡。
甲厂商
上 下
乙厂商
左
右
5,6
1,4
4,1
2,3
3.稳定性 在完全信息的静态博弈中,如果纳 什均衡存在,既可能是稳定的,也可能 是不稳定的。
上 甲厂商 下
乙厂商
左
右
5,6
2,4
4,1
2,3
4.最优性
在完全信息的静态博弈中,如果纳
什均衡存在,既可能是最优的,也可能
不是最优的。
上 甲厂商 下
乙厂商
左
右
国内外经典教材名师讲堂
高鸿业《西方经济学》 (微观部分)(第6版)
第10章 博弈论初步
10.1 主要内容
第一节 博弈论和策略行为 第二节 完全信息静态博弈:纯策略 均衡 第三节 完全信息静态博弈:混合策 略均衡 第四节 完全信息动态博弈
10.2 本章内容要点解析 第一节 博弈论和策略行为
博弈论是研究在策略性环境中如何 进行策略性决策和采取策略性行动的科 学。
不存在纯策略纳什均衡的混合策略模型
和纯策略组合不同,混合策略组合 是一个概率向量组合,每一个概率向量 是相应参与人的一个混合策略。
利用期望支付的公式可得甲厂商条
件混合策略为:
1q1 0.7
p1 0,1q1 0.7
0q1
乙厂商条件混合策略为:
1 p1 0.5
q1 0,1 p1 0.5
粥店1的条件混合策略可以表示为:
1, q 0.5
p 0,1, q 0.5
0, q 0.5
粥店2的期望支付为:
E2 pq 21 p q 2 p 1 q 1 p1 q q 3 6 p 3p 1
粥店2的条件混合策略可以表示为:
1, p 0.5
q 0,1, p 0.5
第二,“不会得到好处”是指任何 一个参与人在单独改变策略之后自己的 支付不会增加。
四、寻找纳什均衡的方法——条件 策略下划线法
第一,用下划线来表示甲厂商的条 件策略。
第二,用下划线来表示乙厂商的条 件策略。
第三,确定博弈的均衡。
寡头博弈:合作与不合作
乙厂商
合作 不合作
甲厂商
合作 不合作
5,6 7,1
