第八章 气体与蒸汽的流动
工程热力学(王修彦)

.
Ma2 1 dcf dA cf A
b )M a 1 c f c d c f 与 d A 同 号 ,c f A
当Ma > 1时, dcf>0 →dA>0 ,采用渐扩喷管;
.
c )M a 1 c f c c f d A 0
截面上Ma=1,cf=c,称临界截面(minimum cross-sectional area)[也称喉部(throat)截面],临界截面上速度达当地音速 (velocity of sound)
4) cf cr 21p0v01(cr)1
21p0v012111
21p0v0
21RgT0
ccr RgTcr
. 与上式是否矛盾?
3.背压pb对流速的影响
a)收缩喷管:
p b p c r p 2 p bc f 2 c 2M a 2 1
p b p c r p 2 p c rc f 2 c 2M a 2 1
工程热力学课件
华北电力大学
工程热物理教研室制作 2015年1月
.
第八章 气体和蒸汽的流动 (Gas and Steam Flow)
.
工程中有许多流动问题需考虑宏观动能和位能,特别 是喷管(nozzle; jet)、扩压管(diffuser)及节流阀(throttle valve)内流动过程的能量转换情况。
c c r R g T c r 1 .4 2 8 4.2 7 1 4 9 2 .0 0 m s 1 7
o r 2 h 0 h cr 2 c p T 0 T cr
2 1 0 4.8 0 9 4 2 4 4 .2 1 4 9 2 .0 0 m /s 8 7
A cf
.
2
p2 T2 qm2 cf2 2
8-气体蒸汽的流动和压缩

c ─称为当地声速。
, 表达式 Ma
流体的流动速度 当地声速
cf c
当 cf<c, Ma<1,是亚声速气流;当 cf>c,Ma>1,超声速气流;
当 cf=c,Ma=1,是声速气流。
第九章
第8章 气体、蒸汽的流动和压缩 气体与蒸汽的流动
8.1.2 气体在喷管与扩压管中的定熵流动
1)气体流速的变化与其状态参数之间的关系 (1)流速与压力之间的关系
1)临界压力比
临界压力比是指喷管内气体的临界压力pcr与滞止压力的比值。即
cr
pcr =定值 p0
pcr 2 1 vcr 0 ( ) p k 1
临界压力比vcr与气体的性质有关,是绝热指数的单值函数。针对不同 性质的气体,vcr是一个确定的常数。且 单原子气体: 1.67, cr 0.487 双原子气体: 1.4, cr 0.528 多原子气体: 1.3, cr 0.546
(1)
(2) 流速与比体积之间的关系 过程方程的微分形式可写成 将其代入(1)式,有
dc f cf
1 dv 1 dv 2 Ma v Ma 2 v
(2)
第8章
气体、蒸汽的流动和压缩
8.1.2 气体在喷管与扩压管中的定熵流动
dc f cf
dc f 1 dp dp 2 Ma 2 Ma p p cf
(1) (2)
dc f cf
dc f 1 dv dv 2 Ma 2 Ma v v cf
(3) 流速与声速之间的关系 适用于任何气体的声速方程为 c pv 也可写成 c2 pv 其微分为 2cdc pdv vdp 等式两边同时除以pv,整理得 dc 1 dv dp
工程热力学第三版电子教案教学计划6
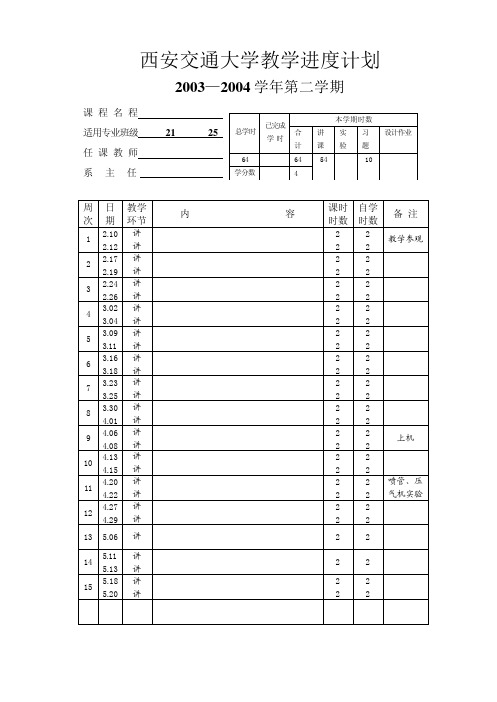
工程热力学 能动 26、2 7、28 赵小明 傅秦生
李国君
总学 已完
本学期学时
课外学时
合计 讲课 实验 机时 讨论 实验
64
64 54
10
学分 4
数
周日
教 学
次期
环 节
1 2.10 讲 2.12 讲
2 2.17 讲 2.19 讲
3 2.24 讲 2.26 讲
4 3.2 讲 3.4 讲
5 3.9 讲 3.11 讲
课课
内外
备
学学
注
时时
2 2 电教片 2 2 参观
22
23
24
22
22
22
22
23
24
22
22
22
22
22
22
14 5. 11 讲
气体与蒸气的流动
2 4 喷管实
5. 14 讲
第九章 压气机的热力过程
22 验
15 5. 18 讲
压气机的热力过程
22
5. 21 讲
第十章 气体动力循环
22
16 5. 25 讲
6 3.16 讲 3.18 讲
7 3.23 讲 3.25 讲
8 3.30 讲 4.1 讲
9
4. 6 4. 8
讲 讲
10
4. 13 4. 15
讲 讲
11 4. 20 讲 4. 22 讲
12 4. 27 讲 4. 29 讲
13 5. 6 讲
14 5. 11 讲 5. 13 讲
内
容
绪论 第一章 基本概念 第二章 热力学第一定律
15 5.18 5.20
讲 讲
第十三章 湿空气 复习 机动 考试
蒸汽流量计算

解 首先判断背压是大于还是小于临界压力:
P2' 0.50.5Pcr 0.528
P1 1
P1
背压小于临界压力,故 P2 Pcr 。
2k wg2 wg,cr k1RT1 571ms
2
qm qm,maxA2
2k
2
k1
P1
0.39kgs
k1k1 v1
第三节 气体和蒸汽的绝热节流
绝热节流:1、h1 = h2 2、p2 < p1 3、sg > 0 ,s2 > s1 , sf=0 4、v2 > v1
dAA(Ma2
1)
dwg wg
气体和蒸汽的可逆绝热流动
二、喷管截面的变化规律
1、当喷管的进口流速为亚 音速, Ma2-1为负值,喷管 是渐缩型的。
dwg 0
Ma<1
dAA(Ma2
1)
dwg wg
Ma≤1
2、当喷管的进口流速为超 音速,Ma2-1为正值,喷管是 渐放型的。
3、当气流由亚音速增加到 超音速喷管应是缩放型的。 该喷管又称为拉伐尔喷管, 最小截面处的流动为临界流 动。
当 p2 / p1 = 0,即出口处为真空时,出口流速达到最大
k
k
wgma x 2k1p1v1 2k1R1T
当 p2 / p1 = 1时,即进出口没有压差时,流速为零。
二、临界速度和临界压力比
沿喷管的可逆绝热流动中,气流速度等于当地音速的截 面称为“临界截面”。临界截面上的温度、压力、速度分别 称为临界温度、临界压力、临界速度。
qm
Aw g v
1、对于渐缩喷管:出口截面为最小截面
qm
A2 wg 2 v2
理想气体 v2 v1(pp12)1k v1(pp12)1k
工程热力学课程内容

824:《工程热力学》课程考试大纲1、本考试科目简介工程热力学是能源工程、机械工程、航空航天工程、材料工程、化学工程、生物工程等领域专业的重要技术基础课,在许多工程领域中有广泛应用。
本课程研究能源转换、利用,特别是热能转换成机械能的原理、途径、规律及提高转换效率的方法。
主要内容有:热力学能、功和热;热力学第一定律;能量的可用性、熵和热力学第二定律;理想气体和水蒸气的性质;热力过程和热力循环的分析。
2、考试内容要求第一章基本概念基本概念,如系统、外界、开口系统、闭口系统、绝热系统、孤立系统、平衡状态、状态参数、可逆过程、循环、功和热等等。
熟练掌握基本概念。
第二章热力学第一定律热力学第一定律:热力学第一定律的实质—能量守衡与转换定律在热现象中的应用、总能、热力学能、焓、膨胀功、技术功、热力学第一定律的第一解析式和稳定流动能量方程式及其应用。
熟练掌握本章基本概念、基本理论及基本计算。
第三章理想气体的性质理想气体的性质:理想气体和实际气体的概念、理想气体状态方程、理想气体的比热容和热力学能、焓、熵的定义、计算;理想气体混合气体的性质:理想气体混合物、理想气体的各种成分表示法、理想气体的分压力定律、分体积定律、折合气体常数和折合摩尔质量、混合气体的热力学能和焓、混合气体的熵。
熟练掌握本章基本概念、基本理论及基本计算。
第四章理想气体基本的热力过程理想气体的基本热力过程:定温过程、定压过程、定容过程、可逆绝热(定熵)过程和多变过程的过程方程、参数变化和过程中功及热量的计算及过程的p-v图和T-s图。
熟练掌握本章基本概念、基本理论及基本计算。
第五章热力学第二定律热过程的方向性、热力学第二定律的表述;卡诺循环和卡诺定理、克劳修斯积分不等式、熵流和熵产、熵方程、孤立系统的熵增原理;作功能力、作功能力损失与熵产和用平衡方程。
熟练掌握本章基本概念、基本理论及基本计算。
第六章水蒸气饱和状态、饱和温度、饱和压力、饱和湿蒸汽、干度、三相点、水蒸气状态的确定、水的定压加热汽化过程及其在p-v图和T-s上的表示、水蒸气定压过程的热量、水蒸气绝热过程的功;熟练掌握本章基本概念、基本理论。
工程热力学和传热学08气体蒸汽流动

临界截面上的温度、压力、速度分别称为临界温度、临 界压力、临界速度。 Tcr 、 Pcr 、 Wg,cr 临界压力与进口压力之比称为“临界压力比”
wg ,cr c
pcr 1 2 即: RT1 1 ( ) RTcr 1 p1
pcr cr p1
Ma
பைடு நூலகம்
wg c
马赫数是研究气体流动特性的一个很重要的数值。 Ma>1,超音速流动 Ma=1,临界流动 Ma<1,亚音速流动
气流的马赫数对气流截面的变化规律有很大的影响。
水蒸汽、可逆绝热过程
k
cp cv
κ=1.3 取经验数据
过热蒸汽
κ=1.135 饱和蒸汽
比体积变化率与 流速变化率之比
dwg dA dv v 分析: ( 1) A dwg wg wg
如为理想气体 可逆绝热流动:
T2 p2 ( ) T1 p1
1
p2 1 wg 2 2 p1v1 1 ( ) 1 p1
适用于理想气体的可逆绝热过程 当 p2 / p1 = 0,即出口处为真空时,出口流速达到最大
wg ,max 2
1
截面上Ma=1,cf,cr=c,称临界截面[也称喉 部截面],临界截面上速度达当地音速 。
第二节
一、流速
气体和蒸汽在喷管中的流速和质量流量
将开口系统稳定流动能量方程应用于喷管: 1 2 2 q h2 h1 ( wg 2 wg1 ) ws 2
q 0,ws 0
2 2
wg 2 wg1 2(h1 h2 )
qm,max
0
β 1/ 2
cr
8流体力学-第八章 气体一维定常流动

M数很小,说明单位质量气体的动能相对于内能而言很小, 速度的变化不会引起气体温度的显著变化 ,对不可压流体来 说,不仅可以认为密度是常值而且温度T也是常值。
流动参数增加为四个:p、ρ、T、和u,
已经有了三个基本方程,它们是:状态方程、连续方程和理想 流的动量方程(即欧拉方程)。
2021/3/31
19
规
律
26
总结
临界流速达到当地声速cf ,cr kpcr / cr
喷管 dcf>0
Ma<1 dA<0 渐缩
Ma=1 dA=0 临界截面
Ma>1 dA>0 渐扩
Ma<1→Ma>1 dA<0→dA>0 缩放(拉伐尔)
dc f d cf
Ma<1
dc f d cf
dc f d cf
dc f d cf
(c)
在的垂直平面的下游半空间(成为扰动
B
2 3
区)内传播,永远不可能传播到上游半
4
空间(成为寂静区)。
u+c0=2c0 →
3c
2021/3/31
22
2
4
二、亚、超声速流场中小扰动的传播特性
气流A超马声赫锥速流动 Ma>1
vc
vc
由的图扰可动o 见波,不2由 仅c 于 不3c能u>向c0上,游相传对播气,流反传而播被
2)对于气体等可压流,流速的变化取决于截面和密度的综合 变化。超音速时比体积的增加要大于流速的增大,因此,只 有增大通流面积才能保证通过一定不变的质量流量。
一、声速和马赫数
小扰动在弹性介质中的传播速度为声速,气体经历小扰动而压 缩及恢复过程并无能量损耗,作定熵过程处理,对理想气体:
油气储运工程专业课程.doc

油气储运工程专业课程油气储运工程专业油气储运工程专业是研究油气和城市燃气储存、运输及管理的一门穿插性高新技术学科。
业务培养目标:本专业培养具备工程流体力学、物理化学、油气储运工程等方面知识,能在国家与省、市的开展方案部门、交通运输规划与设计部门、油气储运管理部门等从事油气储运工程的规划、勘查设计、施工工程管理和研究、开发等工作的高级工程技术人才。
业务培养要求:本专业学生主要学习油气储运工艺、设备设施方面的根本理论和根本知识,受到识图制图、上机操作、工程测量、工程概预算的根本训练,具有进行油气储运系统的规划、设计与运行管理的根本能力。
主干学科:工程流体力学、油气储运工程学主要课程:工程力学、工程流体力学、工程热力学、传热学、物理化学、泵与压缩机、电工与电子技术、油气管道设计与管理、油气集输、油库设计与管理、油气储运工程最优化、技术经济学等主要实践性教学环节:包括工程制图、测量实习、金工实习、施工实习等一般安排18周。
主要专业实验:油气质量检测、物理化学等修业年限:四年授予学位:学士学位相近专业:采矿工程石油工程矿物加工工程勘察技术与工程资源勘察工程地质工程矿物资源工程油气储运工程煤及煤层气工程资源勘查工程开设学校:中国石油大学重庆科技学院石油大学长江大学武汉理工大学浙江海洋学院中国地质大学榆林学院(省A专业) 四川大学华南农业大学西南石油大学西安石油大学大庆石油学院课程编号:05040120工程热力学Engineering Thermodynamics总学时:48学时总学分:3学分课程性质:技术根底课开设学期及周学时分配:第5学期,周时数3适用专业及层次:过程装备及控制专业、油气储运专业相关课程:大学物理,物理化学、化工原理教材:(《工程热力学》,沈维道等编,高等教育出版社推荐参考书:(1、《工程热力学》,严家禄编,高等教育出版社,1989第二版2、《工程热力学》,曾丹苓、敖越、朱克雄等编,高等教育出版社,1986第二版 3、《热力学》,王竹溪编,高等教育出版社,1955)一、课程目的及要求工程热力学是一门专业技术根底课,其任务是培养学生运用热力学的定律、定理及有关的理论知识,对热力过程进行热力学分析的能力;初步掌握工程设计与研究中获取物性数据,对热力过程进行有关计算的方法。
工程热力学第四版课后思考题答案

第一章基本概念与定义1.答:不一定。
稳定流动开口系统内质量也可以保持恒定2.答:这种说法是不对的。
工质在越过边界时,其热力学能也越过了边界。
但热力学能不是热量,只要系统和外界没有热量地交换就是绝热系。
3.答:只有在没有外界影响的条件下,工质的状态不随时间变化,这种状态称之为平衡状态。
稳定状态只要其工质的状态不随时间变化,就称之为稳定状态,不考虑是否在外界的影响下,这是他们的本质区别。
平衡状态并非稳定状态之必要条件。
物系内部各处的性质均匀一致的状态为均匀状态。
平衡状态不一定为均匀状态,均匀并非系统处于平衡状态之必要条件。
4.答:压力表的读数可能会改变,根据压力仪表所处的环境压力的改变而改变。
当地大气压不一定是环境大气压。
环境大气压是指压力仪表所处的环境的压力。
5.答:温度计随物体的冷热程度不同有显著的变化。
6.答:任何一种经验温标不能作为度量温度的标准。
由于经验温标依赖于测温物质的性质,当选用不同测温物质的温度计、采用不同的物理量作为温度的标志来测量温度时,除选定为基准点的温度,其他温度的测定值可能有微小的差异。
7.答:系统内部各部分之间的传热和位移或系统与外界之间的热量的交换与功的交换都是促使系统状态变化的原因。
8.答:(1)第一种情况如图1-1(a ),不作功(2)第二种情况如图1-1(b ),作功(3)第一种情况为不可逆过程不可以在p-v 图上表示出来,第二种情况为可逆过程可以在p-v 图上表示出来。
9.答:经历一个不可逆过程后系统可以恢复为原来状态。
系统和外界整个系统不能恢复原来状态。
10.答:系统经历一可逆正向循环及其逆向可逆循环后,系统恢复到原来状态,外界没有变化;若存在不可逆因素,系统恢复到原状态,外界产生变化。
11.答:不一定。
主要看输出功的主要作用是什么,排斥大气功是否有用。
第二章 热力学第一定理1.答:将隔板抽去,根据热力学第一定律w u q +∆=其中0,0==w q 所以容器中空 气的热力学能不变。
第八章稳定流动基本方程

速度变化与管道截面积变化之间的关系
dA dc 2 Ma 1 A c
马赫数与喷管选型
当Ma<1时 dc>0 ,则 dA<0 渐缩型喷管 当Ma>1时 dc>0, 则 dA>0 渐扩型喷管 当Ma<1 →Ma>1时,则dA<0→dA>0 缩放型喷管(拉伐尔喷管) 缩放型喷管喉部Ma=1,c=a处于临界状态 当气体在喷管中充分膨胀时,声速沿着气流 方向逐渐降低.
rc
cr
喷管中气体流量的计算
适用于任何性质的气体
可逆, 不可逆过程
A2c2 qm v2
rc nim
c A
rc
v
xam m
q
气体在喷管中有摩擦流动
气体在喷管中有摩擦流动是不可逆过程,有 能量损耗,工程上用以描述这种情况的有速 度系数,喷管效率和能量损失系数三种方式. 喷管的速度系数φ:喷管出口气体实际流 速与出口气体理想流速之比.
q m v 2 4 0.0896 A 4.67 10 4 m 2 467 mm 2 c2 767 .46
例题2
利用节流测量管道中湿蒸汽的干度.
h
p1
p2
1
2
t2
x1
s
作业
思考题:200页8,9,10,11,12,13.
作业题:8-2,8-4,8-7,8-9,8-11,8-13,8-14,815.
滞止焓 滞止温度 滞止压力 滞止比体积
1 2 h c pT c 2
0
c T 0T p c2
T p 0 p T RrT 0 0 v 0 p
0 k k 1
2
或
T v 0 v 0 T
工程热力学第八章(气体与蒸汽的流动)09(理工)(沈维道第四版)

扩压管( ) ◆四、扩压管(2)
当M入>1, , M出<1时 时
dA dc 2 = M −1 dp 与 dc 异号 A c
应先收缩 应先收缩, 收缩
(
)
超音速流入 亚音速流出 流入, 即超音速流入,亚音速流出 显然,为使得dp>0 显然,为使得 后再扩张 当M =1后再扩张,从而使 出口 <1,即采用 后再扩张,从而使M , 缩放型扩压管 缩放型扩压管
c 定义式: 定义式: M = a
◆3、气体流动速度分类 气体流动速度 速度分类
M <1时, c <a 时 M =1时, c =a 时 M >1时, c >a 时 音速
8314.5 J/(kg.K) = 343m/s a = kRgT = M a = 1.4 × 287 × 293
只能在有介质 亚音速流动 声音只能在 亚音速流动 声音只能在有介质 的场中传播 传播, 的场中传播,不能 音 速流动 真空中传播 在真空中传播 超音速流动 超音速流动 如:在20℃的空气中 ℃
dA dc dv dA dc dρ + − =0 + + =0 或 A c v ρ A c
(7-2) )
3、动量方程 、 由 δq = dh + δwt = dh − vdp 得 − dh = − vdp 由
2 c2 (c2 − c12 ) 得 − dh = d ( ) h1 − h2 = 2 2
a= ∂p ( ) ∂ρ s
过程式: 过程式: dp + k dv = 0 p v 定熵过程 压力波的传播过程 可作定熵过程 定熵过程处理 可作定熵过程处理
a = kpv
理想气体
a = kRgT
2021年注册公用设备工程师(暖通空调)基础考试题库

2021年注册公用设备工程师(暖通空调)《基础考试》题库【历年真题(部分视频讲解)+章节题库+模拟试题】目录•第一部分历年真题[部分视频讲解]o【公共基础(上午)】▪2020年注册公用设备工程师(暖通空调)《公共基础考试》真题及详解▪2019年注册公用设备工程师(暖通空调)《公共基础考试》真题及详解▪2018年注册公用设备工程师(暖通空调)《公共基础考试》真题及详解[部分视频讲解]▪2017年注册公用设备工程师(暖通空调)《公共基础考试》真题及详解[部分视频讲解]▪2016年注册公用设备工程师(暖通空调)《公共基础考试》真题及详解[部分视频讲解]▪2014年注册公用设备工程师(暖通空调)《公共基础考试》真题及详解[部分视频讲解]详解[部分视频讲解]▪2012年注册公用设备工程师(暖通空调)《公共基础考试》真题及详解[部分视频讲解]▪2011年注册公用设备工程师(暖通空调)《公共基础考试》真题及详解[部分视频讲解]▪2010年注册公用设备工程师(暖通空调)《公共基础考试》真题及详解[部分视频讲解]▪2009年注册公用设备工程师(暖通空调)《公共基础考试》真题及详解▪2008年注册公用设备工程师(暖通空调)《公共基础考试》真题及详解o【专业基础(下午)】▪2020年注册公用设备工程师(暖通空调)《专业基础考试》真题及详解▪2019年注册公用设备工程师(暖通空调)《专业基础考试》真题及详解▪2018年注册公用设备工程师(暖通空调)《专业基础考试》真题及详解▪2017年注册公用设备工程师(暖通空调)《专业基础考试》真题及详解详解▪2014年注册公用设备工程师(暖通空调)《专业基础考试》真题及详解▪2013年注册公用设备工程师(暖通空调)《专业基础考试》真题及详解[部分视频讲解]▪2012年注册公用设备工程师(暖通空调)《专业基础考试》真题及详解[部分视频讲解]▪2011年注册公用设备工程师(暖通空调)《专业基础考试》真题及详解[部分视频讲解]▪2010年注册公用设备工程师(暖通空调)《专业基础考试》真题及详解▪2009年注册公用设备工程师(暖通空调)《专业基础考试》真题及详解▪2008年注册公用设备工程师(暖通空调)《专业基础考试》真题及详解▪2007年注册公用设备工程师(暖通空调)《专业基础考试》真题及详解▪2006年注册公用设备工程师(暖通空调)《专业基础考试》真题及详解详解•第二部分章节题库o【公共基础(上午)】▪第一章高等数学▪第一节空间解析几何▪第二节微分学▪第三节积分学▪第四节无穷级数▪第五节常微分方程▪第六节线性代数▪第七节概率与数理统计▪第二章普通物理▪第一节热学▪第二节波动学▪第三节光学▪第三章普通化学▪第一节物质的结构与物质状态▪第二节溶液▪第三节化学反应速率及化学平衡▪第四节氧化还原反应与电化学▪第五节有机化学▪第四章理论力学▪第一节静力学▪第二节运动学▪第三节动力学▪第五章材料力学▪第一节拉伸与压缩▪第二节剪切与挤压▪第三节扭转▪第四节截面的几何性质▪第五节弯曲▪第六节应力状态与强度理论▪第七节组合变形▪第八节压杆稳定▪第六章流体力学▪第一节流体的主要物性与流体静力学▪第二节流体动力学基础▪第三节流动阻力与能量损失▪第四节孔口、管嘴和有压管道恒定流▪第五节明渠恒定流▪第六节渗流、井和集水廊道▪第七节相似原理与量纲分析▪第七章电气与信息▪第一节电磁学概念▪第二节电路知识▪第三节电动机与变压器▪第四节信号与信息▪第五节模拟电子技术▪第六节数字电子技术▪第八章计算机应用基础▪第一节计算机系统▪第二节信息表示▪第三节常用操作系统▪第四节计算机网络▪第九章工程经济▪第一节资金的时间价值▪第二节财务效益与费用估算▪第三节资金来源与融资方案▪第四节财务分析▪第五节经济费用效益分析▪第六节不确定性分析▪第七节方案经济比选▪第八节改扩建项目经济评价特点▪第九节价值工程▪第十章法律法规▪第一节中华人民共和国建筑法▪第二节中华人民共和国安全生产法▪第三节中华人民共和国招标投标法▪第四节中华人民共和国合同法▪第五节中华人民共和国行政许可法▪第六节中华人民共和国节约能源法▪第七节中华人民共和国环境保护法▪第八节建设工程勘察设计管理条例▪第九节建设工程质量管理条例▪第十节建设工程安全生产管理条例o【专业基础(下午)】▪第1章工程热力学▪ 1.1 基本概念▪ 1.2 准静态过程、可逆过程与不可逆过程▪ 1.3 热力学第一定律▪ 1.4 气体性质▪ 1.5 理想气体基本热力过程及气体压缩▪ 1.6 热力学第二定律▪ 1.7 水蒸气和湿空气▪ 1.8 气体和蒸汽的流动▪ 1.9 动力循环▪ 1.10 制冷循环▪第2章传热学▪ 2.1 导热理论基础▪ 2.2 稳态导热▪ 2.3 非稳态导热▪ 2.4 导热问题数值解▪ 2.5 对流换热分析▪ 2.6 单相流体对流换热及准则关联式▪ 2.7 凝结与沸腾换热▪ 2.8 热辐射的基本定律▪ 2.9 辐射换热计算▪ 2.10 传热与换热器▪第3章工程流体力学及泵与风机▪ 3.1 流体动力学基础▪ 3.2 相似原理和模型实验方法▪ 3.3 流动阻力和能量损失▪ 3.4 管路计算▪ 3.5 特定流动分析▪ 3.6 气体射流▪ 3.7 气体动力学基础▪ 3.8 泵与风机与网络系统的匹配▪第4章自动控制▪ 4.1 自动控制与自动控制系统的一般概念▪ 4.2 控制系统数学模型▪ 4.3 线性系统的分析与设计▪ 4.4 控制系统的稳定性与对象的调节性能▪ 4.5 控制系统的误差分析▪ 4.6 控制系统的综合和校正▪第5章热工测试技术▪ 5.1 测量技术的基本知识▪ 5.2 温度的测量▪ 5.3 湿度的测量▪ 5.4 压力的测量▪ 5.5 流速的测量▪ 5.6 流量的测量▪ 5.7 液位的测量▪ 5.8 热流量的测量▪ 5.9 误差与数据处理▪第6章机械基础▪ 6.1 机械设计的基本知识▪ 6.2 平面机构的自由度▪ 6.3 平面连杆机构▪ 6.4 凸轮机构▪ 6.5 螺纹连接▪ 6.6 带传动▪ 6.7 齿轮机构▪ 6.8 轮系▪ 6.9 轴▪ 6.10 滚动轴承▪第7章职业法规▪7.1 中华人民共和国建筑法▪7.2 中华人民共和国节约能源法▪7.3 中华人民共和国环境保护法▪7.4 中华人民共和国水污染防治法▪7.5 中华人民共和国固体废物污染环境防治法▪7.6 中华人民共和国招投标法▪7.7 中华人民共和国合同法▪7.8 民用建筑节能管理规定▪7.9 建设工程安全生产管理条例▪7.10 建设工程质量管理条例▪7.11 工程建设监理规定▪7.12 蒙特利尔议定书▪7.13 绿色建筑评价标准▪7.14 城镇燃气设计规范▪7.15 锅炉房设计规范▪7.16 特种设备安全监察条例▪7.17 通风与空调工程施工质量验收规范▪7.18 氢气站设计规范▪7.19 大气污染物综合排放标准▪7.20 氧气站设计规范▪7.21 地源热泵系统工程技术规范▪7.22 建设工程勘察设计管理条例▪7.23 建筑设计防火规范▪7.24 大气污染区综合排放标准▪7.25 压缩空气站设计规范▪7.26 安全防范工程技术标准▪7.27 工业金属管道工程施工规范•第三部分模拟试题o【公共基础(上午)】▪注册公用设备工程师(暖通空调)《公共基础考试》模拟试题及详解(一)▪注册公用设备工程师(暖通空调)《公共基础考试》模拟试题及详解(二)o【专业基础(下午)】▪注册公用设备工程师(暖通空调)《专业基础考试》模拟试题及详解(一)▪注册公用设备工程师(暖通空调)《专业基础考试》模拟试题及详解(二)内容简介本题库是2021年注册公用设备工程师(暖通空调)《基础考试》的题库,包括历年真题(部分视频讲解)、章节题库和模拟试题三大部分:(1)第一部分为历年真题(部分视频讲解):本部分包含:①公共基础考试(上午)2008~2014、2016~2020年的考试真题,其中共有264道真题配有视频讲解;②专业基础考试(下午)2008~2011年、2013年、2016~2020年的考试真题,并给出了详尽的答案和解析,其中共有166道真题(2011~2013年)配有视频讲解。
沈维道《工程热力学》考研考点精讲

考点精讲工程热力学考试指导及课程说明主讲:程老师沈维道《工程热力学》考研辅导课程1、沈维道《工程热力学》考点精讲及复习思路2、沈维道《工程热力学》名校真题解析及典型题精讲精练3、沈维道《工程热力学》冲刺串讲及模拟四套卷精讲本课程使用教材《工程热力学》第三版作者:沈维道,蒋智敏,童钧耕主编出版社:高等教育出版社出版时间:2001-6-1《工程热力学》第4版作者:沈维道,童钧耕主编出版社:高等教育出版社出版时间:2007-6-1《工程热力学》第4版作者:曾丹岺主编出版社:高等教育出版社出版时间:2002-12-1《工程热力学》作者:朱明善等编著出版社:清华大学出版社出版时间:2011-6-1《工程热力学》作者:冯青,李世武,张丽编著出版社:西北工业大学出版社出版时间:2006-9-1《工程热力学》(第三版)作者:华自强,张忠进编出版社:高等教育出版社出版时间:2000-7-1《工程热力学》第二版作者:毕明树、冯殿义、马连湘编出版社:化学工业出版社出版时间:2008-1-1《工程热力学》作者:朱明善等编著出版社:清华大学出版社出版时间:1995-7-1《工程热力学》第四版作者:华自强等编出版社:高等教育出版社出版时间:2009-11-1《工程热力学》(第五版)作者:廉乐明等编出版社:中国建筑工业出版社出版时间:2007-1-1《工程热力学》作者:王修彦主编出版社:机械工业出版社出版时间:2008-1-1《工程热力学》作者:严家騄,王永青编著出版社:中国电力出版社出版时间:2007-9-1考试分值分布一般来说,在硕士研究生入学考试中,工程热力学专业课满分为150分。
大家首先要认真仔细地阅读自己打算报考院校的招生简章,确定考试教材,然后阅读考试大纲,确认考试范围。
尤其是,要根据近年(一般三年内)的真题,了解分值的分布、题型,以及该院校出题的倾向和偏好。
考试分值分布考研的工程热力学试题,一般来说题型分为两大类:概念题和计算题。
武汉理工大学轮机工程工程热力学与传热学气体和蒸气的流动作业答案

qm
A2 wg2 v2
10 104 343.9 kg/m3 0.064
5.373kg/m3
综上,有出口流速为343.9m/s,出口流量5.373kg/m3,出口温度21.1℃ 出口比体积0.064m3 /kg 注:该题也可利用教材中公式8-10c来计算流速,式8-13计算流量,殊途同归。
7. 在燃气轮机装置中,燃烧室产生的燃气的压力为 0.8MPa,温度为 700℃。燃气通过 喷管获得高速气流,以带动燃气轮机对外做功。若已知喷管背压 pb=0.2MPa,燃气的气体常 数为 289.4J/(kg·K),绝热指数 κ=1.3,试分别求出采用渐缩喷管和缩放喷管时的出口流速。
解:先求出临界压力比c
(
2
) 1
1
(
2
1.3
)1.31
1.3 1
0.5457
当pb
0.2MPa时,pb p1
0.2 0.8
0.25
Pcr P1
c
0.5457
说明对于渐缩喷管,出口达到了临界状态,出口压力等于临界压力;
对于渐缩渐扩喷管,出口压力等于背压pb 0.2MPa。
对于渐缩喷管,
出口流速wg2 wg,cr
5、答: 当流道内的流速等于当地音速时,对应的截面为临界截面,该截面上的压力称为临界压
力 pcr,临界压力与滞止压力的比值称为临界压力比。当入口速度相对较小时,也可用进口 压力代替滞止压力,此时临界压力比即为临界压力与进口压力的比值。
临界压力比只与气体的物性有关,具体地,与绝热指数 κ 的大小有关。对于理想气体, κ 等于定压比热容与定容比热容的比值;而对于水蒸气,κ 只是一个经验数据,随水蒸气所 处的状态不同而变化,并不等于定压比热容与定容比热容之比。
工程热力学气体与蒸汽的流动

第八章 气体与蒸汽的流动工程中,常要处理气体与蒸汽在管路设备,如喷管、扩压管、节流阀内的流动过程。
例如蒸汽轮机、燃气轮机等动力设备中,使高压的气体通过喷管,产生高述度流动,然后利用高述气流冲击叶轮旋转而输出机械功。
火箭尾喷管,喷射式抽气器及扩压管等是工程上常见的另一些实例。
此外,热力工程上还常遇到 气体或蒸汽流经 门、孔板等狭窄通道时产生的节流现象。
本章主要讨论气体在流经喷管等设备时气流参数变话与流道截面积的关系及流动过程中气体能量传递和转化等问题。
此外还将简要地讨论绝热节流过程。
流体在流经空间任何一点时,其全部参数都不随时间而变化的流动过程。
称为稳定流动。
工程中,最常见的工则的流动都是稳定的或接近稳定的流动。
严格地说。
运动流体在流道的同截面上的不同点,由于受摩插力及传热等影响,流述、压力、温度等参数也有所不同,但为研就问题简变起见,常取同一 截面上某参数的平均植作为该面上各点该参数的植,这眼样问题就可简化为沿流动方向上的一维问题。
实际流动问题都是不可逆的,而且流动过程中工质可能与外界有热量交换。
但是。
一般热力管道外都包有隔热保温材料,而且流体流过如喷管这样的设备的时简很短,与外界的换热也很小,为简便起见,把问题看成可逆绝热过程,由此而造程,由此而造成的误差利用实验系数修正。
因此,本章主要讨论可逆绝热过程,由此而造成的误差利用实验系数修正。
因此,本章主要讨论可逆绝热的一维稳定流动。
第一节 稳定流动的基本方程式一、连续性方程定流动中,任一截面的一切参数均不随时简而变,故流经一定截面的质量流量应为定植,不随时简而变。
设图8—1中流经截面1—1和2—2的质量分别为q m 1q m 2,流速为cfl 和cf2,比体积为v1和v2,流道截面面积为A1、A2。
若在此两截面间没有引进或排出流体,则据质量守恒原理有将上式微分,并整理得图8—1一维稳定流动常数=Α==Α=Α===vc v c v c q q q f 22f 211f 1m 2m 1m L (8—1) 0=−+Αvdv c dc A d f f (8—la ) 式(8—1)称做稳定流动的连续性方程式。
同济大学暖通考研传热学大纲

科目 815 传热学命题单位:机械工程学院考试大纲基本要求1.掌握热量传递的三种基本方式及传热过程所遵循的基本规律,学会对传热过程进行分析和计算的基本方法。
2.掌握导热的基本规律。
能对无内热源的简单几何形状物体,在常物性条件下的稳态导热和传热过程进行熟练的分析计算。
较深刻地了解物体在被持续加热或冷却时的温度场及热流随时间而变化的规律。
能应用集总参数法和诺模图来计算在对流边界条件下的非稳态导热问题。
3.较深刻地了解各种因素对对流换热的影响。
对受迫对流换热、自然对流换热现象的物理特征及有关准则有正确的理解。
对相变换热现象特征有所了解,并能运用准则方程进行计算。
4.掌握热辐射的基本定律。
熟悉由透明介质所隔开的物体表面辐射换热的基本计算方法。
对气体辐射换热的特性和特征有所了解。
5.掌握换热器的两种基本计算方法:对数平均温度差法和传热效率-单元数法。
基本内容绪论1.传热学的研究对象及其应用介绍。
2.热量传递的三种基本方式:导热、对流和辐射。
3.传热过程与传热系数。
第一章导热理论基础1.导热基本概念。
温度场。
温度梯度。
傅里叶定律。
2.导热系数。
3.导热微分方程。
4.导热过程的单值性条件。
第二章稳态导热1.通过单平壁和复合平壁的导热。
2.通过单圆筒壁和复合圆筒壁的导热。
临界热绝缘直径。
3.通过肋壁的导热,肋片效率。
4.通过接触面的导热。
5.二维稳态导热问题。
第三章非稳态导热1.非稳态导热过程的特点。
2.对流换热边界条件下非稳态导热,诺模图,集总参数法。
3.常热流通量边界条件下非稳态导热。
第四章导热问题数值解1.泰勒级数法和热平衡法。
2.导热问题的数值计算,节点方程的建立及求解。
3.非稳态导热问题的数值计算,显式差分格式及其稳定性,隐式差分格式。
第五章对流换热分析1.对流换热过程和影响对流换热的因素。
对流换热过程微分方程式。
2.对流换热微分方程组。
3.流动边界层,热边界层,边界层换热微分方程组及其求解。
4.边界层换热积分方程组及其求解。
工程热力学第八章

二、流量计算 根据连续方程,喷管各截面的质量流量 相等。但各种形式喷管的流量大小都受最小 截面控制,因而通常按最小截面(收缩喷管 的出口截面、缩放喷管的喉部截面)来计算 流量,即: A2 c f 2 收缩喷管: qm v2 缩放喷管:
qm Acr c fcr vcr
代入速度公式可得:
qv A2
8-3 喷管的计算
喷管的计算:
喷管的设计计算:
据给定条件(气流初参数、流量及背 压),选择喷管的外形及确定几何尺寸。
喷管的校核计算:
已知喷管的形ห้องสมุดไป่ตู้和尺寸及不同的工作条 件,确定出口流速和通过喷管的流量。
一、流速计算及其分析
1、计算流速的公式:
h0 h2
出口流速:
c2 f2 2
h1
缩放喷管(拉伐尔喷管):
缩放喷管可实现气流从亚声速变为超声速,在 喷管最小截面(喉部截面或临界截面)处Ma=1,在 临界截面处的参数称为临界参数(以下标cr表示), 如:
c f ,cr c kP cr vcr
喷管内参数变化示意图
对于扩压管管(dcf < 0) : Ma>1,超声速流动,dA<0,截面收缩; Ma=1, 声速流动,dA=0,截面缩至最小; Ma<1, 亚声速流动,dA>0,截面扩张;
临界速度:
cf 2
k 1 k kp0 v0 p2 2 1 k 1 p0
k
c f 2,cr
k 2 p0 v0 k 1 k 2 Rg T0 k 1
pcr 2 k 1 cr ( ) p0 k 1
二、渐缩渐放喷管
在设计工况下:喉道处为临界状态,收缩段为 亚音速,扩张段为超音速;图中ABC。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
avg 微分:
dp k dv 0
pv
k?? Const, avg., empirical
热能工程教研室
四、声速方程
理想气体
c kpv kRgT
当地声速
是一个状态参数
定义
马赫数 Ma c f c
Ma<1: Ma=1: Ma>1:
亚声速; 当地声速; 超声速。
q
h
c
2 f
2
gz wi
简化
h2
c
2 f
2
2
h1
c
2 f
1
2
h
c
2 f
2
常数
对于微元过程
dh
d
(
c
2 f
)
0
2
绝热不作功的稳定流动中,任一截面上工质的焓与 其动能之和保持定值:气体动能的增加等于焓降
热能工程教研室
二、稳定流动能量方程式
任一截面上气体的焓和气体流动动能的和恒为常数
当气体绝热滞止时速度为零
问题:
气体流速与压力及流道截面面积之间到底有 什么样的关系?促使流速改变的条件是什么 (力学条件和几何条件)?
热能工程教研室
一、力学条件
dp kMa 2 dcf
p
cf
力学条件
dcf和dp的符号总是相反
加速,压力降低;减速,压力升高
应用:
如果要获得高速气流,必须应用某种设 计,使气流膨胀,降低压力:喷管
热能工程教研室
p0
p(T0 T
k
) k 1
二、稳定流动能量方程式
对于水蒸气
绝热过程无法用方程表示
计算出滞止焓
h h0
后其它滞止参
h1
数可从h-s图
上读得。
0
0 p1 1 t1
x=1 s
热能工程教研室
三、过程方程式
过程物理描述: 绝热,无摩擦,无扰动
可逆绝热过程
可以用理想气体定比热容定熵过程 来描述气体稳定流动过程
2
m·2
cf2
v2 2
热能工程教研室
一、连续性方程
考虑稳定流动,流经任何截面的流量为定值
根据质量守恒原理
•
•
•
m1 m2 m
A1c f 1
A2c f 2
Acf
常数
v1
v2
v
将上式微分,并整理得
稳定流动的连 续性方程式
热能工程教研室
dA dcf dv 0 A cf v
一、连续性方程
热能工程教研室
Nozzles and Diffusers
热能工程教研室
A nozzle is a device that increases the velocity of a fluid at the expense of pressure
A diffuser is a device that slows a fluid down
第八章
气体与蒸汽的流动
背景
动力工程中经常遇到气体和蒸汽在管路设备内 的流动过程:
喷管(nozzle) 扩压管(diffuser)
节流(throttle valve)
气体和蒸气在流经这些设备时气流 运动参数和状态参数如何变化?
这些变化与流道截面积有何关系?
气体不同形式能量之间传递和转化 遵循何种规律等?
Assumptions for analysis
Steady state (稳定流动) Adiabatic boundaries(边界绝热) Equilibrium states at inlet and outlet(进出口质量一定) Mass average velocities adequate for calculations
热能工程教研室
二、几何条件
dA (Ma2 1) dcf
A
cf
喷管(dcf > 0)
Ma<1,亚声速流动,dA<0,气流截面收缩
Ma=1,声速流动,dA=0,气流截面缩至最小
Ma>1,超声速流动,dA>0,气流截面扩张
喷管的要求:亚音速流必须是渐缩喷管;超音速流必 须是渐扩喷管;从亚音速到超音速必须是渐缩渐扩喷 管(拉伐尔喷管),在喉部达到音速。
热能工程教研室
二、几何条件
各种喷管的形状
dcf dv cf v
dcf dv cf v
dcf dv dcf dv dcf dv cf v cf v cf v
Ma<1
dA<0 渐缩
热能工程教研室
Ma>1
Ma<1 Ma=1
Ma>1
dA>0 渐扩
dA<0 dA=0 dA>0 缩放
dA dcf dv 0 A cf v
适用条件:稳定流动 与可逆性无关
描述了流道内流体的流速、比体积和截面面积之间的关系
流道的截面面积增加率,等于 比体积增加率与流速增加率之差
不可压缩流体:
dA dc f 0 A cf
界面面积与流速成反比
热能工程教研室
二、稳定流动能量方程式
对控制体应用稳定流动能量方程式
热能工程教研室
一维稳定非功绝热流动的基本方程组
dA dcf dv 0 A cf v
dh
d
(
c
2 f
)
0
2
dp k dv 0 pv
理想气体
c kpv kRgT
热能工程教研室
§8-2促使流速改变的条件
从物质守恒、动量守恒、和能量守恒的角度来 分析稳定一元流动,管内流速的变化取决于压力和 截面面积的变化。
热能工程教研室
Nozzles and diffusers are shaped so that they cause large changes in fluid velocities and thus kinetic energies.
“passive”----no work component
h0
h2
c
2 f
2
2
h1
c
2 f
1
2
h
c
2 f
2
总焓或滞止焓
热能工程教研室
二、稳定流动能量方程式
对于理想气体 若把比热容近似当作定值
c pT0
cpT1
c
2 f
1
2
cpT2
c
2 f
2
2
cpT
c
2 f
2
T0
T
c
2 f
2c p
滞止温度
据绝热过程方程式,理想气体比热容近似
当作定值时的滞止压力为
如果要获得高压气流,必须应用某种设 计,使气流减速:扩压管
热能工程教研室
二、几何条件
dA dcf dv 0
A cf v
dv Ma2 dc f
v
cf
dA (Ma2 1) dcf
A
cf
几何条件
当流速变化时,气流截面面积的变化规律不 但与流速是高于当地声速还是低于当地声速 有关,还与流速是增加还是降低,即是喷管 还是扩压管有关。
(平均质量流速可计算)
No shaft work(无轴功) Change in potential energy is negligible(势能可忽略)
热能工程教研室
§8-1稳定流动的基本方程式
一、连续性方程
考虑右图所示的一 维流动(截面平均 参数而言)
绝热稳定流动
m·1
1Cf1v11 Nhomakorabea取图示的控制体(开口系统)
