人教A版高中数学选修《导数综合练习题》
(完整word)人教A版高中数学选修2-2《导数综合练习题》

导数练习题1.(本题满分12分)已知函数d x b a c bx ax x f +--++=)23()(23的图象如图所示.(I )求d c ,的值;(II )若函数)(x f 在2=x 处的切线方程为0113=-+y x ,求函数)(x f 的解析式;(III )在(II )的条件下,函数)(x f y =与mx x f y ++'=5)(31的图象有三个不同的交点,求m 的取值范围. 2.(本小题满分12分)已知函数)(3ln )(R a ax x a x f ∈--=. (I )求函数)(x f 的单调区间;(II )函数)(x f 的图象的在4=x 处切线的斜率为,23若函数]2)('[31)(23mx f x x x g ++=在区间(1,3)上不是单调函数,求m 的取值范围.3.(本小题满分14分)已知函数c bx ax x x f +++=23)(的图象经过坐标原点,且在1=x 处取得极大值. (I )求实数a 的取值范围;(II )若方程9)32()(2+-=a x f 恰好有两个不同的根,求)(x f 的解析式;(III )对于(II )中的函数)(x f ,对任意R ∈βα、,求证:81|)sin 2()sin 2(|≤-βαf f .4.(本小题满分12分)已知常数0>a ,e 为自然对数的底数,函数x e x f x -=)(,x a x x g ln )(2-=. (I )写出)(x f 的单调递增区间,并证明a e a >; (II )讨论函数)(x g y =在区间),1(a e 上零点的个数. 5.(本小题满分14分)已知函数()ln(1)(1)1f x x k x =---+.(I )当1k =时,求函数()f x 的最大值;(II )若函数()f x 没有零点,求实数k 的取值范围;6.(本小题满分12分)已知2x =是函数2()(23)x f x x ax a e =+--的一个极值点(⋅⋅⋅=718.2e ). (I )求实数a 的值;(II )求函数()f x 在]3,23[∈x 的最大值和最小值.7.(本小题满分14分)已知函数)0,(,ln )2(4)(2≠∈-+-=a R a x a x x x f (I )当a=18时,求函数)(x f 的单调区间; (II )求函数)(x f 在区间],[2e e 上的最小值. 8.(本小题满分12分)已知函数()(6)ln f x x x a x =-+在(2,)x ∈+∞上不具有...单调性. (I )求实数a 的取值范围;(II )若()f x '是()f x 的导函数,设22()()6g x f x x '=+-,试证明:对任意两个不相等正数12x x 、,不等式121238|()()|||27g x g x x x ->-恒成立. 9.(本小题满分12分)已知函数.1,ln )1(21)(2>-+-=a x a ax x x f(I )讨论函数)(x f 的单调性;(II )证明:若.1)()(,),,0(,,521212121->--≠+∞∈<x x x f x f x x x x a 有则对任意10.(本小题满分14分)已知函数21()ln ,()(1),12f x x a xg x a x a =+=+≠-.(I )若函数(),()f x g x 在区间[1,3]上都是单调函数且它们的单调性相同,求实数a 的取值范围;(II )若(1,]( 2.71828)a e e ∈=L ,设()()()F x f x g x =-,求证:当12,[1,]x x a ∈时,不等式12|()()|1F x F x -<成立.11.(本小题满分12分)设曲线C :()ln f x x ex =-( 2.71828e =⋅⋅⋅),()f x '表示()f x 导函数. (I )求函数()f x 的极值;(II )对于曲线C 上的不同两点11(,)A x y ,22(,)B x y ,12x x <,求证:存在唯一的0x 12(,)x x ∈,使直线AB 的斜率等于0()f x '. 12.(本小题满分14分)定义),0(,,)1(),(+∞∈+=y x x y x F y ,(I )令函数22()(3,log (24))f x F x x =-+,写出函数()f x 的定义域;(II )令函数322()(1,log (1))g x F x ax bx =+++的图象为曲线C ,若存在实数b 使得曲线C 在)14(00-<<-x x 处有斜率为-8的切线,求实数a 的取值范围;(III )当,*x y ∈N 且x y <时,求证(,)(,)F x y F y x >.导数练习题答案1.(本题满分12分)已知函数d x b a c bx ax x f +--++=)23()(23的图象如图所示.(I )求d c ,的值;(II )若函数)(x f 在2=x 处的切线方程为0113=-+y x ,求函数)(x f 的解析式;(III )在(II )的条件下,函数)(x f y =与mx x f y ++'=5)(31的图象有三个不同的交点,求m 的取值范围.解:函数)(x f 的导函数为 b a c bx ax x f 2323)(2'--++= …………(2分) (I )由图可知 函数)(x f 的图象过点(0,3),且0)1('=f 得⎩⎨⎧==⇒⎩⎨⎧=--++=03023233c d b a c b a d …………(4分)(II )依题意3)2('-=f 且5)2(=f⎩⎨⎧=+--+-=--+534648323412b a b a b a b a解得 6,1-==b a 所以396)(23++-=x x x x f …………(8分) (III )9123)(2+-='x x x f .可转化为:()m x x x x x x +++-=++-534396223有三个不等实根,即:()m x x x x g -+-=8723与x 轴有三个交点; ()()()42381432--=+-='x x x x x g ,()m g m g --=-=⎪⎭⎫ ⎝⎛164,273. …………(10分) 当且仅当()01640276832<--=>-=⎪⎭⎫ ⎝⎛m g m g 且时,有三个交点, 故而,276816<<-m 为所求. …………(12分)2.(本小题满分12分)已知函数)(3ln )(R a ax x a x f ∈--=. (I )求函数)(x f 的单调区间;(II )函数)(x f 的图象的在4=x 处切线的斜率为,23若函数]2)('[31)(23mx f x x x g ++=在区间(1,3)上不是单调函数,求m 的取值范围.解:(I ))0()1()('>-=x xx a x f(2分)当(][)+∞>,1,1,0)(,0减区间为的单调增区间为时x f a当[)(];1,0,,1)(,0减区间为的单调增区间为时+∞<x f a 当a=1时,)(x f 不是单调函数 (5分)(II )32ln 2)(,22343)4('-+-=-==-=x x x f a a f 得 2)4()(',2)22(31)(223-++=∴-++=∴x m x x g x x mx x g (6分)2)0(',)3,1()(-=g x g 且上不是单调函数在区间Θ⎩⎨⎧><∴.0)3(',0)1('g g (8分)⎪⎩⎪⎨⎧>-<∴,319,3m m (10分))3,319(--∈m (12分)3.(本小题满分14分)已知函数c bx ax x x f +++=23)(的图象经过坐标原点,且在1=x 处取得极大值. (I )求实数a 的取值范围;(II )若方程9)32()(2+-=a x f 恰好有两个不同的根,求)(x f 的解析式;(III )对于(II )中的函数)(x f ,对任意R ∈βα、,求证:81|)sin 2()sin 2(|≤-βαf f .解:(I ),23)(,00)0(2b ax x x f c f ++='=⇒=320)1(--=⇒='a b f),323)(1()32(23)(2++-=+-+='∴a x x a ax x x f由33210)(+-==⇒='a x x x f 或,因为当1=x 时取得极大值,所以31332-<⇒>+-a a ,所以)3,(:--∞的取值范围是a ;…………(4分) (依题意得:9)32(272-=+a ,解得:9-=a所以函数)(x f 的解析式是:x x x x f 159)(23+-=…………(10分)(III )对任意的实数βα,都有,2sin 22,2sin 22≤≤-≤≤-βα在区间[-2,2]有: 230368)2(,7)1(,7430368)2(=+-==-=---=-f f f ,7)1()(=f x f 的最大值是7430368)2()(-=---=-f x f 的最小值是 函数]2,2[)(-在区间x f 上的最大值与最小值的差等于81, 所以81|)sin 2()sin 2(|≤-βαf f .…………(14分) 4.(本小题满分12分)已知常数0>a ,e 为自然对数的底数,函数x e x f x -=)(,x a x x g ln )(2-=. (I )写出)(x f 的单调递增区间,并证明a e a >; (II )讨论函数)(x g y =在区间),1(a e 上零点的个数. 解:(I )01)(≥-='x e x f ,得)(x f 的单调递增区间是),0(+∞, …………(2分) ∵0>a ,∴1)0()(=>f a f ,∴a a e a >+>1,即a e a >. …………(4分)(II )a x a x a x x g )22)(22(22)(-+=-=',由0)(='x g ,得22ax =,列表当2x )222(a,无极大值. …………(6分)由(I )a e a >,∵⎪⎩⎪⎨⎧>>22a a e e aa ,∴22a e a>,∴22ae a >01)1(>=g ,0))(()(22>-+=-=a e a e a e e g a a a a …………(8分)(i )当122≤a,即20≤<a 时,函数)(x g y =在区间),1(a e 不存在零点 (ii )当122>a ,即2>a 时若0)2ln 1(2>-a a ,即e a 22<<时,函数)(x g y =在区间),1(a e 不存在零点若0)2ln 1(2=-a a ,即e a 2=时,函数)(x g y =在区间),1(a e 存在一个零点e x =;若0)2ln 1(2<-a a ,即e a 2>时,函数)(x g y =在区间),1(a e 存在两个零点;综上所述,)(x g y =在(1,)a e 上,我们有结论:当02a e <<时,函数()f x 无零点; 当2a e = 时,函数()f x 有一个零点; 当2a e >时,函数()f x 有两个零点.…………(12分) 5.(本小题满分14分)已知函数()ln(1)(1)1f x x k x =---+.(I )当1k =时,求函数()f x 的最大值;(II )若函数()f x 没有零点,求实数k 的取值范围; 解:(I )当1k =时,2()1x f x x -'=-)(x f 定义域为(1,+∞),令()0,2f x x '==得, ………………(2分)∵当(1,2),x ∈时()0f x '>,当(2,),x ∈+∞时()0f x '<, ∴()(1,2)f x 在内是增函数,(2,)+∞在上是减函数∴当2x =时,()f x 取最大值(2)0f = ………………(4分)(II )①当0k ≤时,函数ln(1)y x =-图象与函数(1)1y k x =--图象有公共点, ∴函数()f x 有零点,不合要求; ………………(8分) ②当0k >时,1()11()111kk x k kx k f x k x x x +-+-'=-==---- ………………(6分)令1()0,k f x x k +'==得,∵1(1,),()0,k x f x k +'∈>时1(1,),()0x f x k'∈++∞<时,∴1()(1,1)f x k+在内是增函数,1[1,)k++∞在上是减函数,∴()f x 的最大值是1(1)ln f k k+=-,∵函数()f x 没有零点,∴ln 0k -<,1k >,因此,若函数()f x 没有零点,则实数k 的取值范围(1,)k ∈+∞.………………(10分) 6.(本小题满分12分)已知2x =是函数2()(23)x f x x ax a e =+--的一个极值点(⋅⋅⋅=718.2e ). (I )求实数a 的值;(II )求函数()f x 在]3,23[∈x 的最大值和最小值.解:(I )由2()(23)x f x x ax a e =+--可得22()(2)(23)[(2)3]x x x f x x a e x ax a e x a x a e '=+++--=++--……(4分)∵2x =是函数()f x 的一个极值点,∴(2)0f '=∴2(5)0a e +=,解得5a =- ……………(6分) (II )由0)1)(2()(>--='x e x x x f ,得)(x f 在)1,(-∞递增,在),2(+∞递增,由0)(<'x f ,得)(x f 在在)2,1(递减∴2)2(e f =是()f x 在]3,23[∈x 的最小值; ……………(8分)2347)23(e f =,3)3(e f = ∵)23()3(,0)74(4147)23()3(23233f f e e e e e f f >>-=-=-∴()f x 在]3,23[∈x 的最大值是3)3(e f =. ……………(12分)7.(本小题满分14分)已知函数)0,(,ln )2(4)(2≠∈-+-=a R a x a x x x f (I )当a=18时,求函数)(x f 的单调区间; (II )求函数)(x f 在区间],[2e e 上的最小值. 解:(Ⅰ)x x x x f ln 164)(2--=,xx x x x x f )4)(2(21642)('-+=--= 2分由0)('>x f 得0)4)(2(>-+x x ,解得4>x 或2-<x 注意到0>x ,所以函数)(x f 的单调递增区间是(4,+∞) 由0)('<x f 得0)4)(2(<-+x x ,解得-2<x <4,注意到0>x ,所以函数)(x f 的单调递减区间是]4,0(. 综上所述,函数)(x f 的单调增区间是(4,+∞),单调减区间是]4,0( 6分 (Ⅱ)在],[2e e x ∈时,x a x x x f ln )2(4)(2-+-= 所以xax x x a x x f -+-=-+-=242242)('2,设a x x x g -+-=242)(2当0<a 时,有△=16+4×208)2(<=-a a ,此时0)(>x g ,所以0)('>x f ,)(x f 在],[2e e 上单调递增, 所以a e e e f x f -+-==24)()(2min 8分当0>a 时,△=08)2(2416>=-⨯-a a , 令0)('>x f ,即02422>-+-a x x ,解得221a x +>或221a x -<; 令0)('<x f ,即02422<-+-a x x , 解得221a -221ax +<<. ①若221a+≥2e ,即a ≥22)1(2-e 时, )(x f 在区间],[2e e 单调递减,所以a e e e f x f 244)()(242min -+-==.②若2221e ae <+<,即222)1(2)1(2-<<-e a e 时间, )(x f 在区间]221,[a e +上单调递减,在区间],221[2e a +上单调递增, 所以min )(xf )221(a f +=)221ln()2(322a a a a +-+--=. ③若221a+≤e ,即a <0≤22)1(-e 时,)(x f 在区间],[2e e 单调递增,所以a e e e f x f -+-==24)()(2min综上所述,当a ≥222)1(-e 时,a e a x f 244)(24min -+-=;当222)1(2)1(2-<<-e a e 时,)221ln()2(322)(min aa a a x f +-+--=; 当a ≤2)1(2-e 时,a e e x f -+-=24)(2min14分 8.(本小题满分12分)已知函数()(6)ln f x x x a x =-+在(2,)x ∈+∞上不具有...单调性. (I )求实数a 的取值范围;(II )若()f x '是()f x 的导函数,设22()()6g x f x x '=+-,试证明:对任意两个不相等正数12x x 、,不等式121238|()()|||27g x g x x x ->-恒成立. 解:(I )226()26a xx af x x xx-+'=-+=, ………………(2分)∵()f x 在(2,)x ∈+∞上不具有...单调性,∴在(2,)x ∈+∞上()f x '有正也有负也有0, 即二次函数226y x x a =-+在(2,)x ∈+∞上有零点 ………………(4分) ∵226y x x a =-+是对称轴是32x =,开口向上的抛物线,∴222620y a =⋅-⋅+<的实数a 的取值范围(,4)-∞ ………………(6分)(II )由(I )22()2a g x x x x =+-,方法1:2222()()62(0)a g x f x x x x x x '=-+=+->, ∵4a <,∴323233444244()22a x x g x x x x x x-+'=-+>-+=,…………(8分) 设2344()2h x x x =-+,3448124(23)()x h x x x x-'=-= ()h x 在3(0,)2是减函数,在3(,)2+∞增函数,当32x =时,()h x 取最小值3827∴从而()g x '3827>,∴38(())027g x x '->,函数38()27y g x x =-是增函数,12x x 、是两个不相等正数,不妨设12x x <,则22113838()()2727g x x g x x ->-∴212138()()()27g x g x x x ->-,∵210x x ->,∴1212()()3827g x g x x x ->- ∴1212()()g x g x x x --3827>,即121238|()()|||27g x g x x x ->- ………………(12分)方法2:11(,())M x g x 、22(,())N x g x 是曲线()y g x =上任意两相异点,121222121212()()2()2g x g x x x ax x x x x x -+=+--,12x x +>Q 4a <12221212122()22x x a a x x x x x x +∴+->+-1242x x >- ………(8分)设0t t =>,令32()244MN k u t t t ==+-,()4(32)u t t t '=-, 由()0u t '>,得2,3t >由()0u t '<得20,3t <<()u t ∴在)32,0(上是减函数,在),32(+∞上是增函数,)(t u ∴在32=t 处取极小值2738,38()27u t ∴≥,∴所以1212()()g x g x x x --3827>即121238|()()|||27g x g x x x ->- ………………(12分)9.(本小题满分12分)已知函数.1,ln )1(21)(2>-+-=a x a ax x x f(I )讨论函数)(x f 的单调性;(II )证明:若.1)()(,),,0(,,521212121->--≠+∞∈<x x x f x f x x x x a 有则对任意(1))(x f 的定义域为),0(+∞,xa x x x a ax x x a a x x f )1)(1(11)('2-+-=-+-=-+-= 2分(i )若2,11==-a a 即,则 .)1()('2xx x f -=故)(x f 在),0(+∞单调增加. (ii )若.0)(',)1,1(,21,1,11<-∈<<><-x f a x a a a 时则当故而)1,1()(,0)(',),1()1,0(->+∞∈-∈a x f x f x a x 在故时及当单调减少,在(0,a-1), ),1(+∞单调增加.(iii )若),1(),1,0(,)1,1()(,2,11+∞-->>-a a x f a a 在单调减少在同理可得即 单调增加.(II )考虑函数x x f x g +=)()( .ln )1(212x x a ax x +-+-= 由 .)11(1)1(121)1()('2---=---⋅≥-+--=a a xa x x a a x x g 由于单调增加在即故),0()(,0)(',5+∞><x g x g a a ,从而当021>>x x 时有 ,0)()(,0)()(212121>-+->-x x x f x f x g x g 即 故1)()(2121->--x x x f x f ,当210x x <<时,有1)()()()(12122121->--=--x x x f x f x x x f x f10.(本小题满分14分)已知函数21()ln ,()(1),12f x x a xg x a x a =+=+≠-.(I )若函数(),()f x g x 在区间[1,3]上都是单调函数且它们的单调性相同,求实数a 的取值范围;(II )若(1,]( 2.71828)a e e ∈=L ,设()()()F x f x g x =-,求证:当12,[1,]x x a ∈时,不等式12|()()|1F x F x -<成立.解:(I )(),()1a f x x g x a x''=+=+, ……………(2分)∵函数(),()f x g x 在区间[1,3]上都是单调函数且它们的单调性相同,∴当[1,3]x ∈时,2(1)()()()0a x a f x g x x++''⋅=≥恒成立, ……………(4分) 即2(1)()0a x a ++≥恒成立, ∴21a a x >-⎧⎨≥-⎩在[1,3]x ∈时恒成立,或21a a x<-⎧⎨≤-⎩在[1,3]x ∈时恒成立, ∵91x -≤≤-,∴1a >-或9a ≤- ………………(6分)(II )21()ln ,(1)2F x x a x a x =+-+,()(1)()(1)a x a x F x x a xx--'=+-+=∵()F x 定义域是(0,)+∞,(1,]a e ∈,即1a >∴()F x 在(0,1)是增函数,在(1,)a 实际减函数,在(,)a +∞是增函数 ∴当1x =时,()F x 取极大值1(1)2M F a ==--,当x a =时,()F x 取极小值21()ln 2m F a a a a a ==--, ………………(8分)∵12,[1,]x x a ∈,∴12|()()|||F x F x M m M m -≤-=- ………………(10分)设211()ln 22G a M m a a a =-=--,则()ln 1G a a a '=--,∴1[()]1G a a''=-,∵(1,]a e ∈,∴[()]0G a ''>∴()ln 1G a a a '=--在(1,]a e ∈是增函数,∴()(1)0G a G ''>=∴211()ln 22G a a a a =--在(1,]a e ∈也是增函数 ………………(12分)∴()()G a G e ≤,即2211(1)()1222e G a e e -≤--=-, 而22211(1)(31)1112222e e e ----=-<-=,∴()1G a M m =-< ∴当12,[1,]x x a ∈时,不等式12|()()|1F x F x -<成立. ………………(14分) 11.(本小题满分12分)设曲线C :()ln f x x ex =-( 2.71828e =⋅⋅⋅),()f x '表示()f x 导函数. (I )求函数()f x 的极值;(II )对于曲线C 上的不同两点11(,)A x y ,22(,)B x y ,12x x <,求证:存在唯一的0x 12(,)x x ∈,使直线AB 的斜率等于0()f x '. 解:(I )11()0ex f x e xx -'=-==,得1x e= 当x 变化时,()f x '与()f x 变化情况如下表:∴当1x e=时,()f x 取得极大值()2f e=-,没有极小值; …………(4分)(II )(方法1)∵0()AB f x k '=,∴2121021ln ln ()1x x e x x e x x x ----=-,∴21201ln 0x x xx x --= 即20211ln ()0x x x x x --=,设2211()ln ()xg x x x x x =--211211()ln ()x g x x x x x =--,1/211()ln 10x x g x x =->,1()g x 是1x 的增函数,∵12x x <,∴2122222()()ln()0x g x g x x x x x <=--=; 222211()ln ()x g x x x x x =--,2/221()ln 10x x g x x =->,2()g x 是2x 的增函数, ∵12x x <,∴1211111()()ln ()0xg x g x x x x x >=--=,∴函数2211()ln ()xg x x x x x =--在12(,)x x 内有零点0x , …………(10分)又∵22111,ln 0x x x x >∴>,函数2211()ln ()xg x x x x x =--在12(,)x x 是增函数, ∴函数2121()ln x x xg x x x -=-在12(,)x x 内有唯一零点0x ,命题成立…………(12分)(方法2)∵0()AB f x k '=,∴2121021ln ln ()1x x e x x e x x x ----=-, 即020112ln ln 0x x x x x x -+-=,012(,)x x x ∈,且0x 唯一设2112()ln ln g x x x x x x x =-+-,则1121112()ln ln g x x x x x x x =-+-, 再设22()ln ln h x x x x x x x =-+-,20x x <<,∴2()ln ln 0h x x x '=-> ∴22()ln ln h x x x x x x x =-+-在20x x <<是增函数 ∴112()()()0g x h x h x =<=,同理2()0g x >∴方程2112ln ln 0x x x x x x -+-=在012(,)x x x ∈有解 …………(10分)∵一次函数在12(,)x x 2112()(ln ln )g x x x x x x =-+-是增函数 ∴方程2112ln ln 0x x x x x x -+-=在012(,)x x x ∈有唯一解,命题成立………(12分) 注:仅用函数单调性说明,没有去证明曲线C 不存在拐点,不给分. 12.(本小题满分14分)定义),0(,,)1(),(+∞∈+=y x x y x F y ,(I )令函数22()(3,log (24))f x F x x =-+,写出函数()f x 的定义域;(II )令函数322()(1,log (1))g x F x ax bx =+++的图象为曲线C ,若存在实数b 使得曲线C 在)14(00-<<-x x 处有斜率为-8的切线,求实数a 的取值范围;(III )当,*x y ∈N 且x y <时,求证(,)(,)F x y F y x >. 解:(I )22log (24)0x x -+>,即2241x x -+> ……………………(2分)得函数()f x 的定义域是(1,3)-, ……………………(4分) (II )22322()(1,log (1))1,g x F x ax bx x ax bx =+++=+++设曲线00(41)C x x -<<-在处有斜率为-8的切线, 又由题设,23)(,0)1(log 2232b ax x x g bx ax x ++='>+++∴存在实数b 使得⎪⎩⎪⎨⎧>+++-<<--=++1114823020300020bx ax x x b ax x 有解, ……………………(6分)由①得,238020ax x b ---=代入③得082020<---ax x ,200028041x ax x ⎧++>⎪∴⎨-<<-⎪⎩由有解, ……………………(8分) 方法1:0082()()a x x <-+-,因为041x -<<-,所以0082()[8,10)()x x -+∈-, 当10a <时,存在实数b ,使得曲线C 在)14(00-<<-x x 处有斜率为-8的切线………………(10分)方法2:得08)1()1(208)4()4(222>+-⨯+-⨯>+-⨯+-⨯a a 或,1010,10.a a a ∴<<∴<或 ………………(10分) 方法3:是222(4)(4)802(1)(1)80a a ⎧⨯-+⨯-+≤⎪⎨⨯-+⨯-+≤⎪⎩的补集,即10a < ………………(10分)(III )令2)1ln(1)(,1,)1ln()(xx x xx h x x x x h +-+='≥+=由 又令,0),1ln(1)(>+-+=x x xxx p 0)1(11)1(1)(22<+-=+-+='∴x x x x x p , ),0[)(+∞∴在x p 单调递减. ……………………(12)分0()(0)0,1()0,x p x p x h x '∴><=∴≥<当时有当时有 ),1[)(+∞∴在x h 单调递减,x y y x y x x y yy x x y x )1()1(),1ln()1ln(,)1ln()1ln(,1+>+∴+>+∴+>+<≤∴有时, ).,(),(,x y F y x F y x N y x ><∈∴*时且当 ………………(14分)①②③。
高中数学第一章导数及其应用模块综合检测新人教A选修22

【优化方案】2021-2021学年高中数学 第一章 导数及其应用模块综合检测 新人教A 版选修2-2(时间:120分钟,满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合标题问题要求的)1.在△ABC 中,E ,F 分别为AB ,AC 的中点,则有EF ∥BC .这个命题的大前提为( )A .三角形的中位线平行于第三边B .三角形的中位线等于第三边的一半C .EF 为中位线D .EF ∥CB答案:A2.⎠⎛01(ex +2x)dx =( ) A .1 B .e -1C .eD .e +1解析:选C .⎠⎛01(ex +2x)dx =(ex +x2)10=e ,故选C . 3.复数(1-i 2)2=a +bi(a ,b ∈R ,i 是虚数单位),则a2-b2的值为( ) A .0 B .1C .2D .-1解析:选D .(1-i 2)2=1-2i +i22=-i =a +bi.所以a =0,b =-1,所以a2-b2=0-1=-1. 4.下列求导运算正确的是( )A .(x +3x )′=1+3x2B .(log2x)′=1xln 2C .(3x)′=3xlog3eD .(x2cos x)′=-2xsin x解析:选B.(x +3x )′=1-3x2,所以A 不正确;(3x)′=3xln 3,所以C 不正确;(x2cos x)′=2xcos x +x2·(-sin x),所以D 不正确;(log2x)′=1xln 2,所以B 正确.故选B.5.用反证法证明命题:“若(a -1)(b -1)(c -1)>0,则a ,b ,c 中至少有一个大于1”时,下列假设中正确的是( )A .假设a ,b ,c 都大于1B .假设a ,b ,c 都不大于1C .假设a ,b ,c 中至多有一个大于1D .假设a ,b ,c 中至多有两个大于1解析:选B.a ,b ,c 中至少有一个大于1的否认为a ,b ,c 都不大于1.6.已知函数f(x)=2x +1x +2,则函数y =f(x)的单调增区间是( )A .(-∞,+∞)B .(-∞,-2)C .(-2,+∞)D .(-∞,-2)和(-2,+∞)解析:选D .据解析式可知函数f(x)的定义域为{x|x ∈R ,x≠-2},由于f′(x)=3x +22>0,故函数f(x)在(-∞,-2)和(-2,+∞)上分别为增函数.7.已知集合A ={x|x2+y2=4},集合B ={x||x +i|<2,i 为虚数单位,x ∈R},则集合A 与B 的关系是( )A .AB B .B AC .A∩B =AD .A∩B =∅解析:选B.|x +i|=x2+1<2,即x2+1<4,解得-3<x <3,∴B =(-3,3),而A =[-2,2],∴B A ,故选B.8.用数学归纳法证明12+22+…+(n -1)2+n2+(n -1)2+…+22+12=n 2n2+13时,从n =k 到n =k +1,等式左边应添加的式子是( )A .(k -1)2+2k2B .(k +1)2+k2C .(k +1)2D .13(k +1)[2(k +1)2+1]解析:选B.n =k 时,左边=12+22+…+(k -1)2+k2+(k -1)2+…+22+12,n =k +1时,左边=12+22+…+(k -1)2+k2+(k +1)2+k2+(k -1)2+…+22+12,∴从n =k 到n =k +1,左边应添加的式子为(k +1)2+k2.9.若P =a +a +7,Q =a +3+a +4(a≥0),则P ,Q 的大小关系为( )A .P >QB .P =QC .P <QD .由a 的取值确定解析:选C .要比力P 与Q 的大小,只需比力P2与Q2的大小,只需比力2a +7+2a a +7与2a +7+2a +3a +4的大小,只需比力a2+7a 与a2+7a +12的大小,即比力0与12的大小,而0<12,故P <Q.10.如图,暗影部分的面积为( )A .⎠⎛ab [f(x)-g(x)]dx B .⎠⎛ac [g(x)-f(x)]dx +⎠⎛cb [f(x)-g(x)]dx C .⎠⎛ac [f(x)-g(x)]dx +⎠⎛cb [g(x)-f(x)]dx D .⎠⎛ab [g(x)-f(x)]dx 解析:选B.∵在区间(a ,c)上g(x)>f(x),而在区间(c ,b)上g(x)<f(x).∴S =⎠⎛a c [g(x)-f(x)]dx +⎠⎛cb [f(x)-g(x)]dx ,故选B.11.设函数f(x)在R 上可导,其导函数为f′(x),且函数y =(1-x)f′(x)的图象如图所示,则下列结论中必然成立的是( )A .函数f(x)有极大值f(2)和极小值f(1)B .函数f(x)有极大值f(-2)和极小值f(1)C .函数f(x)有极大值f(2)和极小值f(-2)D .函数f(x)有极大值f(-2)和极小值f(2)解析:选D .由题图可知,当x <-2时,f′(x)>0;当x =-2时,f′(x)=0;当-2<x <1时,f′(x)<0;当1<x <2时,f′(x)<0;当x =2时,f′(x)=0;当x >2时,f′(x)>0.由此可以获得函数f(x)在x =-2处取得极大值,在x =2处取得极小值.12.观察数表:1 2 3 4 … 第一行2 3 4 5 … 第二行3 4 5 6 … 第三行4 5 6 7 … 第四行… … … …第一列 第二列 第三列 第四列按照数表中所反映的规律,第n 行与第n -1列的交叉点上的数应该是( )A .2n -1B .2n +1C .n2-1D .2n -2解析:选D .按照数表可知,第1行第1列上的数为1,第2行第2列上的数为3,第3行第3列上的数为5,第4行第4列上的数为7,那么,由此可以推导出第n 行与第n 列交叉点上的数应该是2n -1,故第n 行与第n -1列的交叉点上的数应为2n -2.二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中的横线上)13.设复数i 满足i(z +1)=-3+2i(i 为虚数单位),则z 的实部是________.解析:由i(z +1)=-3+2i ,获得z =-3+2i i -1=2+3i -1=1+3i.答案:114.已知某商品生产成本C 与产量q 的函数关系式为C =100+4q ,价格p 与产量q 的函数关系式为p =25-18q ,则产量q =________时,利润L 最大.解析:收入R =q·p =q(25-18q)=25q -18q2.利润L =R -C =(25q -18q2)-(100+4q)=-18q2+21q -100(0<q <200),L′=-14q +21,令L′=0,即-14q +21=0,求得独一的极值点q =84.∴产量q 为84时,利润L 最大.答案:8415.已知圆的方程是x2+y2=r2,则经过圆上一点M(x0,y0)的切线方程为x0x +y0y =r2.类比上述性质,可以获得椭圆x2a2+y2b2=1类似的性质为________. 解析:圆的性质中,经过圆上一点M(x0,y0)的切线方程就是将圆的方程中的一个x 与y 分别用M(x0,y0)的横坐标与纵坐标替换.故可得椭圆x2a2+y2b2=1类似的性质为:过椭圆x2a2+y2b2=1上一点P(x0,y0)的切线方程为x0x a2+y0y b2=1.答案:经过椭圆x2a2+y2b2=1上一点P(x0,y0)的切线方程为x0x a2+y0y b2=116.(2021·山东省实验中学月考)给出下列四个命题:①若f′(x 0)=0,则x0是f(x)的极值点;②“可导函数f(x)在区间(a ,b)上不单调”等价于“f(x)在区间(a ,b)上有极值”;③若f(x)>g(x),则f′(x)>g′(x);④如果在区间[a ,b]上函数y =f(x)的图象是一条连续不断的曲线,则该函数在[a ,b]上必然能取得最大值和最小值.其中真命题的序号是________(把所有真命题的序号都填上).解析:②④显然正确;对f(x)=x3,有f′(0)=0,但x =0不是极值点,故①错;f(x)=x +1>g(x)=x ,但f′(x)=g′(x)=1,故③错.答案:②④三、解答题(本大题共6小题,共74分.解答应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分12分)已知复数z1=2-3i ,z2=15-5i 2+i 2. 求:(1)z1+z 2;(2)z1·z2;(3)z1z2.解:z2=15-5i 2+i 2=15-5i 3+4i =53-i 3-4i 3+4i 3-4i =5-15i 5 =1-3i.(1)z1+z 2=(2-3i)+(1+3i)=3.(2)z1·z2=(2-3i)(1-3i)=2-9-9i =-7-9i.(3)z1z2=2-3i 1-3i =2-3i 1+3i 1-3i 1+3i =2+9+3i 10=1110+310i. 18.(本小题满分12分)求函数f(x)=ex x -2的单调区间. 解:函数f(x)的定义域为(-∞,2)∪(2,+∞).f′(x)=ex x -2-ex x -22=ex x -3x -22. 因为x ∈(-∞,2)∪(2,+∞),所以ex >0,(x -2)2>0.由f′(x)>0,得x >3,所以函数f(x)的单调递增区间为(3,+∞);由f′(x)<0,得x <3,又定义域为(-∞,2)∪(2,+∞),所以函数f(x)的单调递减区间为(-∞,2)和(2,3).19.(本小题满分12分)已知a ,b ,c >0,且a +b +c =1,求证:(1)a2+b2+c2≥13; (2)a +b +c ≤ 3.证明:(1)∵a2+19≥23a ,b2+19≥23b ,c2+19≥23c ,∴(a2+19)+(b2+19)+(c2+19)≥23a +23b +23c =23.∴a2+b2+c2≥13.(2)∵a·13≤a +132,b·13≤b +132,c·13≤c +132, 三式相加得a 3+b 3+c 3≤12(a +b +c)+12=1, ∴a +b +c ≤ 3.20.(本小题满分12分)已知数列{an}满足Sn +an =2n +1.(1)写出a1,a2,a3,并推测an 的表达式;(2)用数学归纳法证明所得的结论.解:(1)由Sn +an =2n +1,当n =1时,S1=a1,∴a1+a1=2×1+1,得a1=32.当n =2时,S2=a1+a2,则a1+a2+a2=5,将a1=32代入得a2=74. 同理可得a3=158.∴an =2n +1-12n =2-12n .(2)证明:当n =1时,结论成立.假设n =k 时,命题成立,即ak =2-12k ;当n =k +1时,Sn +an =2n +1,则a1+a2+…+ak +2ak +1=2(k +1)+1.∵a1+a2+…+ak =2k +1-ak ,∴2ak +1=4-12k ,ak +1=2-12k +1成立. ∴当n =k +1时,结论也成立.∴按照上述知对于任意自然数n ∈N*,结论成立.21.(本小题满分13分)设函数f(x)=x3+ax2+x +1,a ∈R.(1)若x =1时,函数f(x)取得极值,求函数f(x)在x =-1处的切线方程;(2)若函数f(x)在区间(12,1)内不单调,求实数a 的取值范围.解:(1)由已知得f′(x)=3x2+2ax +1,f′(1)=0,故a =-2,∴f(x)=x3-2x2+x +1,当x =-1时,f(-1)=-3,即切点坐标为(-1,-3). 又f′(-1)=8,∴切线方程为8x -y +5=0.(2)f(x)在区间(12,1)内不单调,即f′(x)=0在(12,1)内有解,令f′(x)=3x2+2ax +1=0,则2ax =-3x2-1.由x ∈(12,1),得2a =-3x -1x .令h(x)=-3x -1x ,由h′(x)=-3+1x2=0,知h(x)在(33,1)上单调递减,在(12,33]上单调递增,∴h(1)<h(x)≤h(33),即h(x)∈(-4,-23].∴-4<2a≤-23,即-2<a≤- 3.而当a =-3时,f′(x)=3x2-23x +1=(3x -1)2≥0,不满足题意. 综上,实数a 的取值范围为(-2,-3).22.(本小题满分13分)已知函数f(x)=38x2-2x +2+ln x.(1)求函数y =f(x)的单调区间;(2)若函数y =f(x)在[em ,+∞)(m ∈Z)上有零点,求m 的最大值.解:(1)函数f(x)的定义域为(0,+∞).f′(x)=34x -2+1x =3x -2x -24x , 当f′(x)>0时,x ∈(0,23)∪(2,+∞);当f′(x)<0时,x ∈(23,2),所以函数f(x)的单调递增区间为(0,23)和(2,+∞),单调递减区间为[23,2].(2)由(1)知y 极大值=f(23)=56+ln 23>0,y 极小值=f(2)=ln 2-12>0.当x >0且x→0时f(x)<0,故f(x)在定义域上存在独一零点x0,且x0∈(0,23).若m≥0,则em≥1,[em ,+∞)⊂(23,+∞),此区间不存在零点,舍去,故m <0.当m =-1时,x ∈[1e ,+∞),f(1e )=1+38e2-2e >0,又(1e ,23)为增区间,此区间不存在零点,舍去.当m =-2时,x ∈[1e2,+∞),f(1e2)=1e2(38e2-2)<0,又(1e2,23)为增区间,且y =f(23)>0,故x0∈(1e2,23).综上,m 的最大值为-2.。
人教A版选修2-2章末综合测评(一) 导数及其应用.docx

高中数学学习材料马鸣风萧萧*整理制作章末综合测评(一) 导数及其应用(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若函数y =f (x )在区间(a ,b )内可导,且x 0∈(a ,b ),则lim h →0f (x 0+h )-f (x 0-h )h 的值为( )A .f ′(x 0)B .2f ′(x 0)C .-2f ′(x 0)D .0【解析】 lim h →0f (x 0+h )-f (x 0-h )h=2lim h →0f (x 0+h )-f (x 0-h )2h=2f ′(x 0),故选B .【答案】 B2.设曲线y =ax 2在点(1,a )处的切线与直线2x -y -6=0平行,则a =( ) A .1 B.12 C .-12 D .-1【解析】 y ′=2ax ,于是切线斜率k =y ′|x =1=2a ,由题意知2a =2,∴a =1. 【答案】 A3.下列各式正确的是( ) A .(sin a )′=cos a (a 为常数) B .(cos x )′=sin x C .(sin x )′=cos xD .(x -5)′=-15x -6【解析】 由导数公式知选项A 中(sin a )′=0;选项B 中(cos x )′=-sin x ;选项D 中(x -5)′=-5x -6.【答案】 C4.函数f (x )=(x -3)e x 的单调递增区间是( ) A .(-∞,2) B .(0,3) C .(1,4)D .(2,+∞)【解析】 f ′(x )=(x -2)e x ,由f ′(x )>0,得x >2,所以函数f (x )的单调递增区间是(2,+∞).【答案】 D5.若函数f (x )=13x 3-f ′(1)·x 2-x ,则f ′(1)的值为( ) A .0 B .2 C .1 D .-1【解析】 f ′(x )=x 2-2f ′(1)·x -1,则f ′(1)=12-2f ′(1)·1-1,解得f ′(1)=0. 【答案】 A6.如图1所示,图中曲线方程为y =x 2-1,用定积分表示围成封闭图形(阴影部分)的面积是( )图1A.⎪⎪⎪⎪⎠⎛02(x 2-1)d x B.⎠⎛02(x 2-1)d x C.⎠⎛02|x 2-1|d x D.⎠⎛01(x 2-1)d x -⎠⎛12(x 2-1)d x 【解析】 S =⎠⎛01[-(x 2-1)]d x +⎠⎛12(x 2-1)d x =⎠⎛02|x 2-1|d x .【答案】 C7.函数f(x)=x3+3x2+3x-a的极值点的个数是()A.2 B.1C.0 D.由a确定【解析】f′(x)=3x2+6x+3=3(x2+2x+1)=3(x+1)2≥0,∴函数f(x)在R 上单调递增,无极值.故选C.【答案】C8.若函数f(x)=-x3+3x2+9x+a在区间[-2,-1]上的最大值为2,则它在该区间上的最小值为()A.-5 B.7C.10 D.-19【解析】∵f(x)′=-3x2+6x+9=-3(x+1)(x-3),所以函数在[-2,-1]内单调递减,所以最大值为f(-2)=2+a=2.∴a=0,最小值f(-1)=a-5=-5.【答案】 A9.已知y=f(x)是定义在R上的函数,且f(1)=1,f′(x)>1,则f(x)>x的解集是()A.(0,1) B.(-1,0)∪(0,1)C.(1,+∞) D.(-∞,-1)∪(1,+∞)【解析】不等式f(x)>x可化为f(x)-x>0,设g(x)=f(x)-x,则g′(x)=f′(x)-1,由题意g′(x)=f′(x)-1>0,∴函数g(x)在R上单调递增,又g(1)=f(1)-1=0,∴原不等式⇔g(x)>0⇔g(x)>g(1).∴x>1,故选C.【答案】 C10.已知函数f(x)=x2+2x+a ln x,若函数f(x)在(0,1)上单调,则实数a的取值范围是()A.a≥0 B.a<-4C.a≥0或a≤-4 D.a>0或a<-4【解析】 f ′(x )=2x +2+ax ,x ∈(0,1), ∵f (x )在(0,1)上单调,∴f ′(x )≥0或f ′(x )≤0在(0,1)上恒成立,∴2x +2+a x ≥0或2x +2+ax ≤0在(0,1)上恒成立, 即a ≥-2x 2-2x 或a ≤-2x 2-2x 在(0,1)上恒成立.设g (x )=-2x 2-2x =-2⎝ ⎛⎭⎪⎫x +122+12,则g (x )在(0,1)上单调递减,∴g (x )max =g (0)=0,g (x )min =g (1)=-4. ∴a ≥g (x )max =0或a ≤g (x )min =-4. 【答案】 C11.曲线y =ln(2x -1)上的点到直线2x -y +3=0的最短距离为( ) A. 5 B .2 5 C .3 5D .2【解析】 设曲线上的点A (x 0,ln(2x 0-1))到直线2x -y +3=0的距离最短, 则曲线上过点A 的切线与直线2x -y +3=0平行. 因为y ′=12x -1·(2x -1)′=22x -1, 所以y ′|x =x 0=22x 0-1=2,解得x 0=1. 所以点A 的坐标为(1,0).所以点A 到直线2x -y +3=0的距离为d =|2×1-0+3|22+(-1)2=55= 5. 【答案】 A12.已知二次函数f (x )=ax 2+bx +c 的导数为f ′(x ),f ′(0)>0,且对于任意实数x ,有f (x )≥0,则f (1)f ′(0)的最小值为( ) 【导学号:62952063】A .3 B.52 C .2D.32【解析】 由题意,得f ′(x )=2ax +b .由对任意实数x ,有f (x )≥0,知图象开口向上,所以a >0,且Δ=b 2-4ac ≤0,所以ac ≥b 24.因为f ′(0)>0,所以b >0,且在x =0处函数递增. 由此知f (0)=c >0.所以f (1)f ′(0)=a +b +c b ≥b +2ac b ≥b +2b 24b=2.【答案】 C二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)13.⎠⎜⎛π2 (3x +sin x )d x =__________. 【解析】 ⎠⎜⎛0π2 (3x +sin x )d x =⎝ ⎛⎭⎪⎫3x 22-cos x ⎪⎪⎪π20=⎣⎢⎡⎦⎥⎤32×⎝ ⎛⎭⎪⎫π22-cos π2-(0-cos 0)=3π28+1.【答案】 3π28+114.若曲线y =e -x 上点P 处的切线平行于直线2x +y +1=0,则点P 的坐标是________.【解析】 设P (x 0,y 0),∵y =e -x ,∴y ′=-e -x , ∴点P 处的切线斜率为k =-e -x 0=-2, ∴-x 0=ln 2,∴x 0=-ln 2, ∴y 0=e ln 2=2,∴点P 的坐标为(-ln 2,2). 【答案】 (-ln 2,2)15.直线y =a 与函数f (x )=x 3-3x 的图象有三个相异的公共点,则a 的取值范围是__________.【导学号:62952064】【解析】 令f ′(x )=3x 2-3=0,得x =±1,可求得f (x )的极大值为f (-1)=2, 极小值为f (1)=-2,如图所示,-2<a <2时,恰有三个不同公共点.【答案】 (-2,2)16.周长为20 cm 的矩形,绕一条边旋转成一个圆柱,则圆柱体积的最大值为________cm 3.【解析】 设矩形的长为x ,则宽为10-x (0<x <10),由题意可知所求圆柱的体积V =πx 2(10-x )=10πx 2-πx 3,∴V ′(x )=20πx -3πx 2.由V ′(x )=0,得x =0(舍去),x =203, 且当x ∈⎝ ⎛⎭⎪⎫0,203时,V ′(x )>0,当x ∈⎝ ⎛⎭⎪⎫203,10时,V ′(x )<0,∴当x =203时,V (x )取得最大值为4 00027π cm 3. 【答案】 4 00027π三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分)已知曲线y =x 3+x -2在点P 0处的切线l 1平行于直线4x -y -1=0,且点P 0在第三象限,(1)求P 0的坐标;(2)若直线l ⊥l 1,且l 也过切点P 0,求直线l 的方程. 【解】 (1)由y =x 3+x -2,得y ′=3x 2+1, 由已知得3x 2+1=4,解得x =±1. 当x =1时,y =0;当x =-1时,y =-4.又因为点P0在第三象限,所以切点P0的坐标为(-1,-4).(2)因为直线l⊥l1,l1的斜率为4,所以直线l的斜率为-1 4,因为l过切点P0,点P0的坐标为(-1,-4),所以直线l的方程为y+4=-14(x+1),即x+4y+17=0.18.(本小题满分12分)已知函数f(x)=a ln(x+1)+12x2-ax+1(a>0).(1)求函数y=f(x)在点(0,f(0))处的切线方程;(2)当a>1时,求函数y=f(x)的单调区间和极值.【解】(1)f(0)=1,f′(x)=ax+1+x-a=x(x-a+1)x+1,f′(0)=0,所以函数y=f(x)在点(0,f(0))处的切线方程为y=1.(2)函数的定义域为(-1,+∞),令f′(x)=0,即x(x-a+1)x+1=0.解得x=0或x=a-1.当a>1时,f(x),f′(x)随x变化的变化情况为x(-1,0) 0 (0,a-1) a-1 (a-1,+∞) f′(x) +0 -0 +f(x) 单调递增↗极大值单调递减↘极小值单调递增↗可知f(x)的单调减区间是(0,a-1),单调增区间是(-1,0)和(a-1,+∞),极大值为f(0)=1,极小值为f(a-1)=a ln a-12a2+32.19.(本小题满分12分)已知函数f(x)=x2-m ln x,h(x)=x2-x+a,(1)当a=0时,f(x)≥h(x)在(1,+∞)上恒成立,求实数m的取值范围;(2)当m=2时,若函数k(x)=f(x)-h(x)在区间[1,3]上恰有两个不同零点,求实数a的取值范围.【解】(1)由f(x)≥h(x)在(1,+∞)上恒成立,得m≤xln x在(1,+∞)上恒成立,令g(x)=xln x,则g′(x)=ln x-1(ln x)2,故g′(e)=0,当x∈(1,e)时,g′(x)<0;x∈(e,+∞)时,g′(x)>0.故g(x)在(1,e)上单调递减,在(e,+∞)上单调递增,故当x=e时,g(x)的最小值为g(e)=e.所以m≤e.(2)由已知可知k(x)=x-2ln x-a,函数k(x)在[1,3]上恰有两个不同零点,相当于函数φ(x)=x-2ln x与直线y=a有两个不同的交点,φ′(x)=1-2x=x-2x,故φ′(2)=0,所以当x∈[1,2)时,φ′(x)<0,所以φ(x)单调递减,当x∈(2,3]时,φ′(x)>0,所以φ(x)单调递增.所以φ(1)=1,φ(3)=3-2ln 3,φ(2)=2-2ln 2,且φ(1)>φ(3)>φ(2)>0,所以2-2ln 2<a≤3-2ln 3.所以实数a的取值范围为(2-2ln 2,3-2ln 3].20.(本小题满分12分)某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V m3.假设建造成本仅与表面积有关,侧面的建造成本为100元/m2,底面的建造成本为160元/m2,该蓄水池的总建造成本为12 000π元(π为圆周率).(1)将V表示成r的函数V(r),并求该函数的定义域;(2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.【解】(1)因为蓄水池侧面的总成本为100·2πrh=200πrh(元),底面的总成本为160πr2元,所以蓄水池的总成本为(200πrh+160πr2)元.又根据题意200πrh+160πr2=12 000π,所以h=15r(300-4r2),从而V(r)=πr2h=π5(300r-4r3).因为r >0,又由h >0可得r <53, 故函数V (r )的定义域为(0,53). (2)因为V (r )=π5(300r -4r 3), 所以V ′(r )=π5(300-12r 2).令V ′(r )=0,解得r 1=5,r 2=-5(因为r 2=-5不在定义域内,舍去). 当r ∈(0,5)时,V ′(r )>0,故V (r )在(0,5)上为增函数; 当r ∈(5,53)时,V ′(r )<0,故V (r )在(5,53)上为减函数. 由此可知,V (r )在r =5处取得最大值,此时h =8. 即当r =5,h =8时,该蓄水池的体积最大.21.(本小题满分12分)抛物线y =ax 2+bx 在第一象限内与直线x +y =4相切.此抛物线与x 轴所围成的图形的面积记为S .求使S 达到最大值的a ,b 值,并求S 的最大值.【解】 由题设可知抛物线为凸形,它与x 轴交点的横坐标分别为x 1=0,x 2=-b a ,所以S =⎠⎛0-ba (ax 2+bx )d x =16a 2b 3, ①又直线x +y =4与抛物线y =ax 2+bx 相切,即它们有唯一的公共点, 由方程组⎩⎨⎧x +y =4,y =ax 2+bx ,得 ax 2+(b +1)x -4=0,其判别式Δ=0, 即(b +1)2+16a =0.于是a =-116(b +1)2,代入①式得: S (b )=128b 33(b +1)4(b >0),S ′(b )=128b 2(3-b )3(b +1)5;令S ′(b )=0,得b =3,且当0<b <3时,S ′(b )>0; 当b >3时,S ′(b )<0.故在b =3时,S (b )取得极大值,也是最大值,即a =-1,b =3时,S 取得最大值,且S max =92. 22.(本小题满分12分)已知函数f (x )=a ln x x +1+bx,曲线y =f (x )在点(1,f (1))处的切线方程为x +2y -3=0.(1)求a ,b 的值;(2)求证:当x >0,且x ≠1时,f (x )>ln xx -1. 【导学号:62952065】【解】 (1)f ′(x )=a ⎝ ⎛⎭⎪⎫x +1x -ln x(x +1)2-bx 2,由于直线x +2y -3=0的斜率为-12,且过点(1,1),故⎩⎪⎨⎪⎧f (1)=1,f ′(1)=-12,即⎩⎪⎨⎪⎧b =1,a 2-b =-12,解得⎩⎨⎧a =1,b =1,(2)证明:由(1)知,f (x )=ln x x +1+1x, 所以f (x )-ln x x -1=11-x 2⎝ ⎛⎭⎪⎫2ln x -x 2-1x . 设函数h (x )=2ln x -x 2-1x (x >0),则h ′(x )=2x -2x 2-(x 2-1)x 2=-(x -1)2x 2.所以当x ≠1时,h ′(x )<0,而h (1)=0, 所以当x ∈(0,1)时,h (x )>0,得f (x )>ln xx -1; 当x ∈(1,+∞)时,h (x )<0,得f (x )>ln xx -1. 故当x >0,且x ≠1时,f (x )>ln xx -1.。
导数综合练习题(详细解答)

导数练习题(B )1.(本题满分12分)已知函数d x b a c bx ax x f +--++=)23()(23的图象如图所示. (I )求d c ,的值;(II )若函数)(x f 在2=x 处的切线方程为0113=-+y x ,求函数)(x f 的解析式;(III )在(II )的条件下,函数)(x f y =与m x x f y ++'=5)(31的图象有三个不同的交点,求m 的取值范围. 2.(本小题满分12分)已知函数)(3ln )(R a ax x a x f ∈--=.(I )求函数)(x f 的单调区间;(II )函数)(x f 的图象的在4=x 处切线的斜率为,23若函数]2)('[31)(23mx f x x x g ++=在区间(1,3)上不是单调函数,求m 的取值范围.3.(本小题满分14分)已知函数c bx ax x x f +++=23)(的图象经过坐标原点,且在1=x 处取得极大值. (I )求实数a 的取值范围;(II )若方程9)32()(2+-=a x f 恰好有两个不同的根,求)(x f 的解析式;(III )对于(II )中的函数)(x f ,对任意R ∈βα、,求证:81|)sin 2()sin 2(|≤-βαf f . 4.(本小题满分12分)已知常数0>a ,e 为自然对数的底数,函数x e x f x -=)(,x a x x g ln )(2-=.(I )写出)(x f 的单调递增区间,并证明a e a >; (II )讨论函数)(x g y =在区间),1(a e 上零点的个数. 5.(本小题满分14分)已知函数()ln(1)(1)1f x x k x =---+. (I )当1k =时,求函数()f x 的最大值;(II )若函数()f x 没有零点,求实数k 的取值范围; 6.(本小题满分12分)已知2x =是函数2()(23)xf x x ax a e =+--的一个极值点(⋅⋅⋅=718.2e ).(I )求实数a 的值;(II )求函数()f x 在]3,23[∈x 的最大值和最小值. 7.(本小题满分14分)已知函数)0,(,ln )2(4)(2≠∈-+-=a R a x a x x x f (I )当a=18时,求函数)(x f 的单调区间;(II )求函数)(x f 在区间],[2e e 上的最小值. 8.(本小题满分12分)已知函数()(6)ln f x x x a x =-+在(2,)x ∈+∞上不具有...单调性. (I )求实数a 的取值范围;(II )若()f x '是()f x 的导函数,设22()()6g x f x x '=+-,试证明:对任意两个不相等正数12x x 、,不等式121238|()()|||27g x g x x x ->-恒成立. 9.(本小题满分12分) 已知函数.1,ln )1(21)(2>-+-=a x a ax x x f (I )讨论函数)(x f 的单调性;(II )证明:若.1)()(,),,0(,,521212121->--≠+∞∈<x x x f x f x x x x a 有则对任意10.(本小题满分14分)已知函数21()ln ,()(1),12f x x a xg x a x a =+=+≠-. (I )若函数(),()f x g x 在区间[1,3]上都是单调函数且它们的单调性相同,求实数a 的取值范围; (II )若(1,](2.71828a e e ∈=,设()()()F x f x g x =-,求证:当12,[1,]x x a ∈时,不等式12|()()|1F x F x -<成立.11.(本小题满分12分)设曲线C :()ln f x x ex =-( 2.71828e =⋅⋅⋅),()f x '表示()f x 导函数.(I )求函数()f x 的极值;(II )对于曲线C 上的不同两点11(,)A x y ,22(,)B x y ,12x x <,求证:存在唯一的0x 12(,)x x ∈,使直线AB 的斜率等于0()f x '. 12.(本小题满分14分)定义),0(,,)1(),(+∞∈+=y x x y x F y,(I )令函数22()(3,log (24))f x F x x =-+,写出函数()f x 的定义域;(II )令函数322()(1,log (1))g x F x ax bx =+++的图象为曲线C ,若存在实数b 使得曲线C 在)14(00-<<-x x 处有斜率为-8的切线,求实数a 的取值范围;(III )当,*x y ∈N 且x y <时,求证(,)(,)F x y F y x >.导数练习题(B )答案1.(本题满分12分)已知函数d x b a c bx ax x f +--++=)23()(23的图象如图所示. (I )求d c ,的值;(II )若函数)(x f 在2=x 处的切线方程为0113=-+y x ,求函数)(x f 的解析式;(III )在(II )的条件下,函数)(x f y =与m x x f y ++'=5)(31的图象有三个不同的交点,求m 的取值范围.解:函数)(x f 的导函数为 b a c bx ax x f 2323)(2'--++= …………(2分) (I )由图可知 函数)(x f 的图象过点(0,3),且0)1('=f得 ⎩⎨⎧==⇒⎩⎨⎧=--++=03023233c d b a c b a d …………(4分)(II )依题意 3)2('-=f 且5)2(=f解得 6,1-==b a所以396)(23++-=x x x x f …………(8分)(III )9123)(2+-='x x x f .可转化为:()m x x x x x x +++-=++-534396223有三个不等实根,即:()m x x x x g -+-=8723与x 轴有三个交点; 42381432--=+-='x x x x x g ,()m g m g --=-=⎪⎭⎫ ⎝⎛164,273. …………(10分)当且仅当()01640276832<--=>-=⎪⎭⎫ ⎝⎛m g m g 且时,有三个交点,故而,276816<<-m 为所求. …………(12分)2.(本小题满分12分)已知函数)(3ln )(R a ax x a x f ∈--=.(I )求函数)(x f 的单调区间;(II )函数)(x f 的图象的在4=x 处切线的斜率为,23若函数]2)('[31)(23mx f x x x g ++=在区间(1,3)上不是单调函数,求m 的取值范围.解:(I ))0()1()('>-=x xx a x f(2分) 当(][)+∞>,1,1,0)(,0减区间为的单调增区间为时x f a 当[)(];1,0,,1)(,0减区间为的单调增区间为时+∞<x f a 当a=1时,)(x f 不是单调函数 (5分)(II )32ln 2)(,22343)4('-+-=-==-=x x x f a a f 得2)4()(',2)22(31)(223-++=∴-++=∴x m x x g x x mx x g (6分)⎩⎨⎧><∴.0)3(',0)1('g g (8分)⎪⎩⎪⎨⎧>-<∴,319,3m m (10分))3,319(--∈m(12分)3.(本小题满分14分)已知函数c bx ax x x f +++=23)(的图象经过坐标原点,且在1=x 处取得极大值. (I )求实数a 的取值范围;(II )若方程9)32()(2+-=a x f 恰好有两个不同的根,求)(x f 的解析式;(III )对于(II )中的函数)(x f ,对任意R ∈βα、,求证:81|)sin 2()sin 2(|≤-βαf f . 解:(I ),23)(,00)0(2b ax x x f c f ++='=⇒=320)1(--=⇒='a b f由33210)(+-==⇒='a x x x f 或,因为当1=x 时取得极大值, 所以31332-<⇒>+-a a ,所以)3,(:--∞的取值范围是a ; …………(4分)(II依题意得:9)32(272-=+a ,解得:9-=a 所以函数)(x f 的解析式是:x x x x f 159)(23+-=…………(10分)(III )对任意的实数βα,都有,2sin 22,2sin 22≤≤-≤≤-βα在区间[-2,2]有:230368)2(,7)1(,7430368)2(=+-==-=---=-f f f函数]2,2[)(-在区间x f 上的最大值与最小值的差等于81, 所以81|)sin 2()sin 2(|≤-βαf f .…………(14分)4.(本小题满分12分)已知常数0>a ,e 为自然对数的底数,函数x e x f x -=)(,x a x x g ln )(2-=. (I )写出)(x f 的单调递增区间,并证明a e a >; (II )讨论函数)(x g y =在区间),1(a e 上零点的个数.解:(I )01)(≥-='x e x f ,得)(x f 的单调递增区间是),0(+∞, …………(2分)∵0>a ,∴1)0()(=>f a f ,∴a a e a >+>1,即a e a >. …………(4分)(II )ax a x a x x g )22)(22(22)(-+=-=',由0)(='x g ,得2a x =,列表当2x )222( …………(6分)由(I )a e a >,∵⎪⎩⎪⎨⎧>>22a a e e aa ,∴22a e a>,∴22a e a >01)1(>=g ,0))(()(22>-+=-=a e a e a e e g a a a a …………(8分)(i )当122≤a,即20≤<a 时,函数)(x g y =在区间),1(a e 不存在零点 (ii )当122>a,即2>a 时若0)2ln 1(2>-aa ,即e a 22<<时,函数)(x g y =在区间),1(a e 不存在零点若0)2ln 1(2=-aa ,即e a 2=时,函数)(x g y =在区间),1(a e 存在一个零点e x =;若0)2ln 1(2<-aa ,即e a 2>时,函数)(x g y =在区间),1(a e 存在两个零点;综上所述,)(x g y =在(1,)ae 上,我们有结论: 当02a e <<时,函数()f x 无零点; 当2a e = 时,函数()f x 有一个零点; 当2a e >时,函数()f x 有两个零点.…………(12分) 5.(本小题满分14分)已知函数()ln(1)(1)1f x x k x =---+. (I )当1k =时,求函数()f x 的最大值;(II )若函数()f x 没有零点,求实数k 的取值范围;解:(I )当1k =时,2()1xf x x -'=-)(x f 定义域为(1,+∞),令()0,2f x x '==得, ………………(2分) ∵当(1,2),x ∈时()0f x '>,当(2,),x ∈+∞时()0f x '<, ∴()(1,2)f x 在内是增函数,(2,)+∞在上是减函数∴当2x =时,()f x 取最大值(2)0f = ………………(4分) (II )①当0k ≤时,函数ln(1)y x =-图象与函数(1)1y k x =--图象有公共点,∴函数()f x 有零点,不合要求; ………………(8分)②当0k >时,1()11()111k k x k kx k f x k x x x +-+-'=-==---- ………………(6分)令1()0,k f x x k +'==得,∵1(1,),()0,k x f x k +'∈>时1(1,),()0x f x k '∈++∞<时, ∴1()(1,1)f x k +在内是增函数,1[1,)k++∞在上是减函数,∴()f x 的最大值是1(1)ln f k k+=-,∵函数()f x 没有零点,∴ln 0k -<,1k >,因此,若函数()f x 没有零点,则实数k 的取值范围(1,)k ∈+∞.………………(10分) 6.(本小题满分12分)已知2x =是函数2()(23)xf x x ax a e =+--的一个极值点(⋅⋅⋅=718.2e ). (I )求实数a 的值;(II )求函数()f x 在]3,23[∈x 的最大值和最小值.解:(I )由2()(23)xf x x ax a e =+--可得22()(2)(23)[(2)3]x x x f x x a e x ax a e x a x a e '=+++--=++--……(4分)∵2x =是函数()f x 的一个极值点,∴(2)0f '=∴2(5)0a e +=,解得5a =- ……………(6分) (II )由0)1)(2()(>--='x e x x x f ,得)(x f 在)1,(-∞递增,在),2(+∞递增,由0)(<'x f ,得)(x f 在在)2,1(递减∴2)2(e f =是()f x 在]3,23[∈x 的最小值; ……………(8分)2347)23(e f =,3)3(e f = ∵)23()3(,0)74(4147)23()3(23233f f e e e e e f f >>-=-=- ∴()f x 在]3,23[∈x 的最大值是3)3(e f =. ……………(12分)7.(本小题满分14分)已知函数)0,(,ln )2(4)(2≠∈-+-=a R a x a x x x f (I )当a=18时,求函数)(x f 的单调区间;(II )求函数)(x f 在区间],[2e e 上的最小值. 解:(Ⅰ)x x x xf ln 164)(2--=,xx x x x x f )4)(2(21642)('-+=--= 2分由0)('>x f 得0)4)(2(>-+x x ,解得4>x 或2-<x 注意到0>x ,所以函数)(x f 的单调递增区间是(4,+∞) 由0)('<x f 得0)4)(2(<-+x x ,解得-2<x <4, 注意到0>x ,所以函数)(x f 的单调递减区间是]4,0(. 综上所述,函数)(x f 的单调增区间是(4,+∞),单调减区间是]4,0(6分(Ⅱ)在],[2e e x ∈时,x a x x x f ln )2(4)(2-+-=所以xax x x a x x f -+-=-+-=242242)('2, 设a x x x g -+-=242)(2当0<a 时,有△=16+4×208)2(<=-a a ,此时0)(>x g ,所以0)('>x f ,)(x f 在],[2e e 上单调递增,所以a e e e f x f -+-==24)()(2min 8分当0>a 时,△=08)2(2416>=-⨯-a a ,令0)('>x f ,即02422>-+-a x x ,解得221a x +>或221a x -<;令0)('<x f ,即02422<-+-a x x , 解得221a -221ax +<<. ①若221a +≥2e ,即a ≥22)1(2-e 时, )(x f 在区间],[2e e 单调递减,所以a e e e f x f 244)()(242min -+-==.②若2221e ae <+<,即222)1(2)1(2-<<-e a e 时间, )(x f 在区间]221,[a e +上单调递减,在区间],221[2e a +上单调递增, 所以min )(xf )221(a f +=)221ln()2(322a a a a +-+--=. ③若221a +≤e ,即a <0≤22)1(-e 时,)(x f 在区间],[2e e 单调递增,所以a e e e f x f -+-==24)()(2min综上所述,当a ≥222)1(-e 时,a e a x f 244)(24min -+-=;当222)1(2)1(2-<<-e a e 时,)221ln()2(322)(min aa a a x f +-+--=; 当a ≤2)1(2-e 时,a e e x f -+-=24)(2min 14分8.(本小题满分12分)已知函数()(6)ln f x x x a x =-+在(2,)x ∈+∞上不具有...单调性. (I )求实数a 的取值范围;(II )若()f x '是()f x 的导函数,设22()()6g x f x x'=+-,试证明:对任意两个不相等正数12x x 、,不等式121238|()()|||27g x g x x x ->-恒成立. 解:(I )226()26a x x af x x x x-+'=-+=, ………………(2分)∵()f x 在(2,)x ∈+∞上不具有...单调性,∴在(2,)x ∈+∞上()f x '有正也有负也有0, 即二次函数226y x x a =-+在(2,)x ∈+∞上有零点 ………………(4分)∵226y x x a =-+是对称轴是32x =,开口向上的抛物线,∴222620y a =⋅-⋅+< 的实数a 的取值范围(,4)-∞ ………………(6分)(II )由(I )22()2a g x x x x =+-,方法1:2222()()62(0)a g x f x x x x x x'=-+=+->,∵4a <,∴323233444244()22a x x g x x x x x x -+'=-+>-+=,…………(8分)设2344()2h x x x =-+,3448124(23)()x h x x x x -'=-=()h x 在3(0,)2是减函数,在3(,)2+∞增函数,当32x =时,()h x 取最小值3827 ∴从而()g x '3827>,∴38(())027g x x '->,函数38()27y g x x =-是增函数,12x x 、是两个不相等正数,不妨设12x x <,则22113838()()2727g x x g x x ->-∴212138()()()27g x g x x x ->-,∵210x x ->,∴1212()()3827g x g x x x ->- ∴1212()()g x g x x x --3827>,即121238|()()|||27g x g x x x ->- ………………(12分) 方法2: 11(,())M x g x 、22(,())N x g x 是曲线()y g x =上任意两相异点,121222121212()()2()2g x g x x x ax x x x x x -+=+--,12x x +>4a <12221212122()22x x a a x x x x x x +∴+->1242x x >+ ………(8分)设0t t =>,令32()244MN k u t t t ==+-,()4(32)u t t t '=-, 由()0u t '>,得2,3t >由()0u t '<得20,3t << ()u t ∴在)32,0(上是减函数,在),32(+∞上是增函数,)(t u ∴在32=t 处取极小值2738,38()27u t ∴≥,∴所以1212()()g x g x x x --3827>即121238|()()|||27g x g x x x ->- ………………(12分) 9.(本小题满分12分)已知函数.1,ln )1(21)(2>-+-=a x a ax x x f (I )讨论函数)(x f 的单调性;(II )证明:若.1)()(,),,0(,,521212121->--≠+∞∈<x x x f x f x x x x a 有则对任意(1))(x f 的定义域为),0(+∞,xa x x x a ax x x a a x x f )1)(1(11)('2-+-=-+-=-+-= 2分(i )若2,11==-a a 即,则 .)1()('2xx x f -=故)(x f 在),0(+∞单调增加. (ii )若.0)(',)1,1(,21,1,11<-∈<<><-x f a x a a a 时则当故而)1,1()(,0)(',),1()1,0(->+∞∈-∈a x f x f x a x 在故时及当单调减少,在(0,a-1), ),1(+∞单调增加.(iii )若),1(),1,0(,)1,1()(,2,11+∞-->>-a a x f a a 在单调减少在同理可得即单调增加.(II )考虑函数x x f x g +=)()( .ln )1(212x x a ax x +-+-=由 .)11(1)1(121)1()('2---=---⋅≥-+--=a a xa x x a a x x g 由于单调增加在即故),0()(,0)(',5+∞><x g x g a a ,从而当021>>x x 时有故1)()(2121->--x x x f x f ,当210x x <<时,有1)()()()(12122121->--=--x x x f x f x x x f x f 10.(本小题满分14分)已知函数21()ln ,()(1),12f x x a xg x a x a =+=+≠-. (I )若函数(),()f x g x 在区间[1,3]上都是单调函数且它们的单调性相同,求实数a 的取值范围;(II )若(1,](2.71828a e e ∈=,设()()()F x f x g x =-,求证:当12,[1,]x x a ∈时,不等式12|()()|1F x F x -<成立.解:(I )(),()1af x xg x a x''=+=+, ……………(2分)∵函数(),()f x g x 在区间[1,3]上都是单调函数且它们的单调性相同,∴当[1,3]x ∈时,2(1)()()()0a x a f x g x x++''⋅=≥恒成立, ……………(4分) 即2(1)()0a x a ++≥恒成立, ∴21a a x >-⎧⎨≥-⎩在[1,3]x ∈时恒成立,或21a a x<-⎧⎨≤-⎩在[1,3]x ∈时恒成立, ∵91x -≤≤-,∴1a >-或9a ≤- ………………(6分)(II )21()ln ,(1)2F x x a x a x =+-+,()(1)()(1)a x a x F x x a x x--'=+-+=∵()F x 定义域是(0,)+∞,(1,]a e ∈,即1a >∴()F x 在(0,1)是增函数,在(1,)a 实际减函数,在(,)a +∞是增函数∴当1x =时,()F x 取极大值1(1)2M F a ==--,当x a =时,()F x 取极小值21()ln 2m F a a a a a ==--, ………………(8分)∵12,[1,]x x a ∈,∴12|()()|||F x F x M m M m -≤-=- ………………(10分)设211()ln 22G a M m a a a =-=--,则()ln 1G a a a '=--, ∴1[()]1G a a''=-,∵(1,]a e ∈,∴[()]0G a ''> ∴()ln 1G a a a '=--在(1,]a e ∈是增函数,∴()(1)0G a G ''>=∴211()ln 22G a a a a =--在(1,]a e ∈也是增函数 ………………(12分)∴()()G a G e ≤,即2211(1)()1222e G a e e -≤--=-, 而22211(1)(31)1112222e e e ----=-<-=,∴()1G a M m =-< ∴当12,[1,]x x a ∈时,不等式12|()()|1F x F x -<成立. ………………(14分)11.(本小题满分12分)设曲线C :()ln f x x ex =-( 2.71828e =⋅⋅⋅),()f x '表示()f x 导函数.(I )求函数()f x 的极值;(II )对于曲线C 上的不同两点11(,)A x y ,22(,)B x y ,12x x <,求证:存在唯一的0x 12(,)x x ∈,使直线AB 的斜率等于0()f x '. 解:(I )11()0ex f x e x x -'=-==,得1x e= 当x 变化时,()f x '与()f x 变化情况如下表:∴当1x e=时,()f x 取得极大值()2f e =-,没有极小值; …………(4分)(II )(方法1)∵0()AB f x k '=,∴2121021ln ln ()1x x e x x e x x x ----=-,∴21201ln 0x x x x x --=即20211ln()0x x x x x --=,设2211()ln ()xg x x x x x =-- 211211()ln ()x g x x x x x =--,1/211()ln 10x x g x x =->,1()g x 是1x 的增函数,∵12x x <,∴2122222()()ln ()0xg x g x x x x x <=--=;222211()ln ()x g x x x x x =--,2/221()ln 10x x g x x =->,2()g x 是2x 的增函数,∵12x x <,∴1211111()()ln ()0xg x g x x x x x >=--=,∴函数2211()ln ()xg x x x x x =--在12(,)x x 内有零点0x , …………(10分)又∵22111,ln 0x x x x >∴>,函数2211()ln ()xg x x x x x =--在12(,)x x 是增函数,∴函数2121()ln x x xg x x x -=-在12(,)x x 内有唯一零点0x ,命题成立…………(12分) (方法2)∵0()AB f x k '=,∴2121021ln ln ()1x x e x x e x x x ----=-, 即020112ln ln 0x x x x x x -+-=,012(,)x x x ∈,且0x 唯一设2112()ln ln g x x x x x x x =-+-,则1121112()ln ln g x x x x x x x =-+-, 再设22()ln ln h x x x x x x x =-+-,20x x <<,∴2()ln ln 0h x x x '=-> ∴22()ln ln h x x x x x x x =-+-在20x x <<是增函数 ∴112()()()0g x h x h x =<=,同理2()0g x >∴方程2112ln ln 0x x x x x x -+-=在012(,)x x x ∈有解 …………(10分) ∵一次函数在12(,)x x 2112()(ln ln )g x x x x x x =-+-是增函数∴方程2112ln ln 0x x x x x x -+-=在012(,)x x x ∈有唯一解,命题成立………(12分) 注:仅用函数单调性说明,没有去证明曲线C 不存在拐点,不给分. 12.(本小题满分14分)定义),0(,,)1(),(+∞∈+=y x x y x F y,(I )令函数22()(3,log (24))f x F x x =-+,写出函数()f x 的定义域;(II )令函数322()(1,log (1))g x F x ax bx =+++的图象为曲线C ,若存在实数b 使得曲线C 在)14(00-<<-x x 处有斜率为-8的切线,求实数a 的取值范围;(III )当,*x y ∈N 且x y <时,求证(,)(,)F x y F y x >.解:(I )22log (24)0x x -+>,即2241x x -+> ……………………(2分)得函数()f x 的定义域是(1,3)-, ……………………(4分) (II )22322()(1,log (1))1,g x F x ax bx x ax bx =+++=+++设曲线00(41)C x x -<<-在处有斜率为-8的切线,又由题设,23)(,0)1(log 2232b ax x x g bx ax x ++='>+++∴存在实数b 使得⎪⎩⎪⎨⎧>+++-<<--=++1114823020300020bx ax x x b ax x 有解, ……………………(6分)由①得,238020ax x b ---=代入③得082020<---ax x ,①②③200028041x ax x ⎧++>⎪∴⎨-<<-⎪⎩由有解, ……………………(8分) 方法1:0082()()a x x <-+-,因为041x -<<-,所以0082()[8,10)()x x -+∈-,当10a <时,存在实数b ,使得曲线C 在)14(00-<<-x x 处有斜率为-8的切线………………(10分)方法2:得08)1()1(208)4()4(222>+-⨯+-⨯>+-⨯+-⨯a a 或,1010,10.a a a ∴<<∴<或 ………………(10分)方法3:是222(4)(4)802(1)(1)80a a ⎧⨯-+⨯-+≤⎪⎨⨯-+⨯-+≤⎪⎩的补集,即10a < ………………(10分) (III )令2)1ln(1)(,1,)1ln()(xx x xx h x x x x h +-+='≥+=由 又令,0),1ln(1)(>+-+=x x xxx p 0)1(11)1(1)(22<+-=+-+='∴x x x x x p , ),0[)(+∞∴在x p 单调递减. ……………………(12)分 ),1[)(+∞∴在x h 单调递减,x y y x y x x y yy x x y x )1()1(),1ln()1ln(,)1ln()1ln(,1+>+∴+>+∴+>+<≤∴有时,).,(),(,x y F y x F y x N y x ><∈∴*时且当 ………………(14分)。
人教A版高中数学选修一导数单元练习卷.docx

高二文科班选修1-1——导数及其应用单元练习卷班级 姓名 号数 成绩一、选择题(本大题共10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知32()32f x ax x =++且(1)4f '-=,则实数a 的值等于( )A .193B .163C .133D .1032.已知曲线122+=x y 在点M 处的瞬时变化率为-4,则点M 的坐标是( ) A (1,3) B (-4,33) C (-1,3) D 不确定 3. 函数y =x 2cos x 的导数为( )A .y ′=x 2cos x -2x sin xB .y ′=2x cos x +x 2sin xC .y ′=2x cos x -x 2sin xD .y ′=x cos x -x 2sin x 4. 若曲线y =f (x )在点(x 0,f (x 0))处的切线方程为2x -y -1=0,则( )A .f ′(x 0)>0B .f ′(x 0)<0C .f ′(x 0)=0D .f ′(x 0)不存在 5.函数5224+-=x x y 的单调减区间为( )A.(]]1,0[,1,-∞-B.[)+∞-,1],0,1[C.[-1,1]D.[)+∞--∞,1),1,( 6.函数5123223+--=x x x y 在[0,3]上的最大值和最小值依次是( ) A.12, -15 B.5, -15 C.5, -4 D.-4, -15 7.若)0()(23>+++=a d cx bx ax x f 为增函数,则( )A.032>-ac bB.0,0>>c bC.0,0>=c bD. 032≤-ac b8.已知函数32()39f x x ax x =++-在3x =-时取得极值,则实数a 的值是( ) A .2 B .3 C .4 D .59.设函数f (x)在定义域内可导,y = f (x)的图象如图所示,则导函数y =f ′(x)的图象可能是( )A. B. C. D.10.函数)(x f 的定义域为开区间),(b a ,导函数)(x f '在),(b a 内的图象如图所示,则函数)(x f 在开区间),(b a 内有极小值点( )A .1个B .2个C .3个D .4个二、填空题:(本大题共6小题,每小题4分,共24分,答案写在横线上) 11.与直线2x -6y +1=0垂直,且与曲线y =x 3+3x 2-1相切的直线方程是____________ 12.函数32y x x x =--的单调区间为___________________ 13、已知函数()f x 在1x =处可导,且0(13)(1)lim12t f t f t→+-=,则(1)f '=14、设函数12)(23+++=bx ax x x f 在3-=x 处有极大值,在2=x 处有极小值,则a =____,=b ______15、已知函数 n m mx x f -=)( 的导数为 38)('x x f =, 则 =n m .16、设函数1()22(0),f x x x x=+-< 则()f x 的最大值为 .三、解答题:(本大题共4小题,共36分。
人教A版高二数学选修1-1第三章导数综合练习(1) .docx

高中数学学习材料马鸣风萧萧*整理制作高二数学选修1-1第三章导数综合练习(1)一、选择题1. 已知函数f(x)在x=1处的导数为1,则 xf x f x 2)1()1(lim 0-+→=( ) A .2 B .1 C . 21 D .41 2. 已知函数f (x )=ax 2+c ,且f ′(1)=2,则a 的值为A.1B.2C.-1D.03. 已知函数f(x)在x=1处的导数为3,则f(x)的解析式可能为( )A .(x-1)3+3(x-1)B .2(x-1)2C .2(x-1)D .x-14. 曲线3x 2-y +6=0在x =-61处的切线的倾斜角是 A.4π B.-4π C.43π D.-43π 5. 函数y =(2x +1)3在x =0处的导数是A.0B.1C.3D.66. 若函数y=x ·2x 且y ’=0,则x 的值为 ( ) A .-2ln 1 B .2ln 1 C .-ln 2 D .ln 2 7.设曲线2x y =在点P 处的切线斜率为3,则点P 的坐标为A .(3,9)B .(-3,9)C .(49,23)D .(49,23-) 8.函数)0,4(2cos π在点x y =处的切线方程是A .024=++πy xB .024=+-πy xC .024=--πy xD .024=-+πy x9.曲线y=x 3+x-2在点P 0处的切线平行于直线y=4x-1,则P 0的坐标是A.(0,1)B.(1,0)C.(-1,0)D.(1,4)10.一质点做直线运动,由始点起经过ts 后的距离为s=41t 4-4t 3+16t 2,则速度为零的时刻是 A.4s 末 B.8s 末 C.0s 与8s 末 D.0s,4s,8s 末 x y 12-=11.函数 的导数是A .B .C .D .12.函数A .4x +3B .4x -1C .4x -5D .4x -313.曲线y =x 3的切线中斜率等于1的直线A .不存在B .存在,有且仅有一条C .存在,有且恰有两条D .存在,但条数不确定14.下列命题正确的是( )(A )(lgx )’=1x (B )(lgx )’=ln10x(C )(3x )’=3x (D )(3x )’=3x ·ln3 15.设f (x )为可导函数,且满足0(1)(1)lim 2x f f x x→--=-1,则曲线y =f (x )在点(1, f (1))处的切线的斜率是 (A )2 (B )-1 (C )21 (D )-2 16.若曲线y =f (x )在点(x 0, f (x 0))处的切线方程为2x -y +1=0,则( )(A )f ’(x 0)>0 (B )f ’(x 0)<0 (C )f ’(x 0)=0 (D )f ’(x 0)不存在二、填空题17.函数y =sin x cos x 的导数为 .18曲线13++=x x y 在点(1,3)处的切线方程是_____________________。
人教A版高中数学选修导数及其应用同步练习(1)
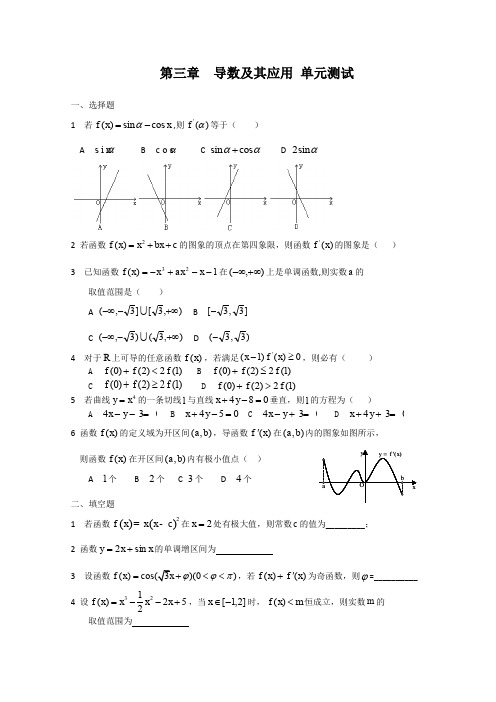
第三章 导数及其应用 单元测试一、选择题1 若()sin cos f x x α=-,则'()f α等于( )A s i n αB c o s αC sin cos αα+D 2sin α2 若函数2()f x x bx c =++的图象的顶点在第四象限,则函数'()f x 的图象是( ) 3 已知函数1)(23--+-=x ax x x f 在),(+∞-∞上是单调函数,则实数a 的取值范围是( )A ),3[]3,(+∞--∞B ]3,3[-C ),3()3,(+∞--∞D )3,3(-4 对于R 上可导的任意函数()f x ,若满足'(1)()0x f x -≥,则必有( )A (0)(2)2(1)f f f +<B (0)(2)2(1)f f f +≤ C(0)(2)2(1)f f f +≥ D (0)(2)2(1)f f f +>5 若曲线4y x =的一条切线l 与直线480x y +-=垂直,则l 的方程为( )A 430x y --=B 450x y +-=C 430x y -+=D 430x y ++= 6 函数)(x f 的定义域为开区间),(b a ,导函数)(x f '在),(b a 内的图象如图所示, 则函数)(x f 在开区间),(b a 内有极小值点( ) A 1个 B 2个 C 3个 D 4个二、填空题1 若函数()()2f x x x c =-在2x =处有极大值,则常数c 的值为_________; 2 函数x x y sin 2+=的单调增区间为3设函数())(0)f x ϕϕπ=+<<,若()()f x f x '+为奇函数,则ϕ=__________ 4 设321()252f x x x x =--+,当]2,1[-∈x 时,()f x m <恒成立,则实数m 的 取值范围为5 对正整数n ,设曲线)1(x x y n -=在2x =处的切线与y 轴交点的纵坐标为n a ,则 数列1n a n ⎧⎫⎨⎬+⎩⎭的前n 项和的公式是 三、解答题1 求函数3(1cos 2)y x =+的导数2 求函数y =3 已知函数32()f x x ax bx c =+++在23x =-与1x =时都取得极值 (1)求,a b 的值与函数()f x 的单调区间(2)若对[1,2]x ∈-,不等式2()f x c <恒成立,求c 的取值范围4 已知23()log x ax bf x x++=,(0,)x ∈+∞,是否存在实数a b 、,使)(x f 同时满足下列两个条件:(1))(x f 在(0,1)上是减函数,在[)1,+∞上是增函数;(2))(x f 的最小值是1,若存在,求出a b 、,若不存在,说明理由参考答案一、选择题1 A ''()sin ,()sin f x x f αα== 2 A 对称轴'0,0,()22bb f x x b -><=+,直线过第一、三、四象限 3 B '2()3210f x x ax =-+-≤在),(+∞-∞恒成立,24120a a ∆=-≤⇒≤≤4 C 当1x ≥时,'()0f x ≥,函数()f x 在(1,)+∞上是增函数;当1x <时,'()0f x ≤,()f x 在(,1)-∞上是减函数,故()f x 当1x =时取得最小值,即有(0)(1),(2)(1),f f f f ≥≥得(0)(2)2(1)f f f +≥5 A 与直线480x y +-=垂直的直线l 为40x y m -+=,即4y x =在某一点的导数为4,而34y x '=,所以4y x =在(1,1)处导数为4,此点的切线为430x y --=6 A 极小值点应有先减后增的特点,即'''()0()0()0f x f x f x <→=→> 二、填空题1 6 '22'2()34,(2)8120,2,6f x x c xc f c c c =-+=-+==或,2c =时取极小值2 (,)-∞+∞ '2c o s 0y x =+>对于任何实数都成立 36π''()))f x ϕϕϕ=-++=+()())3f x f x πϕ'+=++要使()()f x f x '+为奇函数,需且仅需,32k k Z ππϕπ+=+∈,即:,6k k Z πϕπ=+∈ 又0ϕπ<<,所以k 只能取0,从而6πϕ=4 (7,)+∞ ]2,1[-∈x 时,max ()7f x =5 122n +- ()()/11222,:222(2)n nn x y n y nx --==-++=-+-切线方程为, 令0x =,求出切线与y 轴交点的纵坐标为()012ny n =+,所以21n na n =+,则数列1n a n ⎧⎫⎨⎬+⎩⎭的前n 项和()12122212n n n S +-==-- 三、解答题1 解:3236(1cos 2)(2cos )8cos y x x x =+=='5'548cos (cos )48cos (sin )y x x x x =⋅=⋅-548sin cos x x =-2 解:函数的定义域为[2,)-+∞,'y ==当2x ≥-时,'0y >,即[2,)-+∞是函数的递增区间,当2x =-时,min 1y =- 所以值域为[1,)-+∞3 解:(1)32'2(),()32f x x ax bx c f x x ax b =+++=++由'2124()0393f a b -=-+=,'(1)320f a b =++=得1,22a b =-=-'2()32(32)(1)f x x x x x =--=+-,函数()f x 的单调区间如下表:所以函数()f x 的递增区间是(,)3-∞-与(1,)+∞,递减区间是2(,1)3-; (2)321()2,[1,2]2f x x x x c x =--+∈-,当23x =-时,222()327f c -=+为极大值,而(2)2f c =+,则(2)2f c =+为最大值,要使2(),[1,2]f x c x <∈- 恒成立,则只需要2(2)2c f c >=+,得1,2c c <->或4 解:设2()x ax bg x x++=∵()f x 在(0,1)上是减函数,在[1,)+∞上是增函数 ∴()g x 在(0,1)上是减函数,在[1,)+∞上是增函数∴⎩⎨⎧==3)1(0)1('g g ∴⎩⎨⎧=++=-3101b a b 解得⎩⎨⎧==11b a经检验,1,1a b ==时,()f x 满足题设的两个条件。
高中数学新人教A版选修1-1练习导数及其应用

回扣验收特训(三) 导数及其应用1.下面求导运算正确的是()A. (2x)'= 2x log2eB. (x3sin x)'= 3x2cosx1贝U △= 1—4c>0,解得cv 1.43.已知函数f(x)= 2x3+ ax2+ 36x—24在x = 2处有极值,则该函数的一个递增区间是( )A. (2,3)B. (3,+s )C. (2 ,+^ )D.(―汽3)解析:选B 因为函数f(x) = 2x3+ ax2+ 36x—24在x = 2处有极值,又f' (x)= 6x2+ 2ax+ 36,所以f' (2) = 0 解得a=—15.令f' (x)> 0,解得x> 3 或x v 2,所以函数的一个递增区间是(3, + s).4.已知f(x) = 3x2+ ln x,贝V li A xm>0 f " 2&&f 1- & =( )A. 7時C . 21D . —21解析:选 C T f' (x) = 6x +1,f 1 + 2 A x —f 1 — A x/■ li mA x f0 A xf(1 + 2 A x fd —Z\ ,=3li m = 3f' (1) = 21.3 Ac ^0 3 A x1sin x, 1D. (x+ 1。
眇)=1+ 而解析:选 D (2x)' = 2x ln 2, (x3sin x)' 2 3=3x sin x+ x cosx,osx cosx+ xsin x离,(x+ log3x)' = 1+ xln 32.已知函数1 if(x)= 3x3—2x2+ cx+ d有极值,则c的取值范围为()3 2iA. c v 4 B.C< 11 C. c>41 c> 4解析:选A 由题意得f' (x)= x2—x + c,若函数f(x)有极值,C.5. 函数y= In x—x在x€ (0, e]上的最大值为()A. eB. 1C. —1D. —e解析:选C 函数y= ln x —x的定义域为(0 ,+^),1 1 一x又y' = -—1 = ------ ,令y' = 0 得x= 1,x x当x € (0,1)时,y' >0,函数单调递增;当x€ (1, e)时,y' <0,函数单调递减.当x = 1时,函数取得最大值一1,故选C.1 e c 一一6. 已知函数f(x)=—;x3+ 2x2+ 2x,若存在满足0W x°w 3的实数x°,使得曲线y= f(x)3在点(X0, f(X0))处的切线与直线x+ my—10 = 0垂直,则实数m的取值范围是()A. [6,+^ )B. ( — 8, 2]C . [2,6]D . [5,6]解析:选 C f' (x)=—x2+ 4x+ 2 =—(x —2)2+ 6,因为x°€ [0,3],所以f' (x°)€[2,6],又因为切线与直线x + my—10= 0垂直,所以切线的斜率为m,所以m的取值范围是[2,6].7. _______________________________________________ 曲线y= C OS x在点M n, 0 '处的切线方程为_______________________________________________ .“ ,iCosx、—xsin x—cosx解析:y'=亍'= --------------- x2 --------- ,•••切线的斜率k= y' x=n =—2.2 n•所求切线的方程为y—0=—ni x—n即y= —2x +1.n答案:y= —2x+1n8. _________________________________________________ 函数f(x) = 12x —x3在区间[—3,3]上的最小值是__________________________________________ .解析:f' (x)= 12—3x2.令f' (x)= 0,得x= 2 或x =—2.因为f(—3) =—9, f( —2) =—16, f(2) = 16, f(3) = 9,所以函数f(x)在区间[—3,3]上的最小值是一16.答案:—169.设X i, X2是函数f(x) = x3—2ax2+ a2x的两个极值点,若x i< 2v x?,则实数a的取值范围是_________ .解析:由题意得f' (x)= 3x2—4ax+ a2的两个零点X i, X2满足X i< 2< X2, 所以f' (2) = 12—8a+ a2< 0,解得2< a< 6.答案:(2,6)10. 已知函数f(x) = e x(ax+ b) —x2+ 4x,曲线y= f(x)在点(0, f(0))处的切线方程为y= 2x—3.(1) 求a, b的值;⑵讨论f(x)的单调性,并求f(x)的极小值.解:(1)f' (x)= e x(ax+ a+ b)—2x + 4.•••曲线在点(0, f(0))处的切线方程为y= 2x —3.••• f(0) = —3, f' (0) = 2,b= —3, b=—3,•解得a + b+ 4= 2, |a= 1.x 2(2) 由(1)知f(x) = e(x—3) —x + 4x,f' (x)= e x(x—2)—2x+ 4 = (x—2)(e x—2).令f' (x)= 0,得x= In 2 或x = 2.•••当x € (—a, In 2) U (2 ,+s)时,f' (x)> 0;当x € (In 2,2)时,f' (x)< 0,故f(x)在(—a, in 2), (2, + a)上单调递增,在(In 2,2)上单调递减.•••当x = 2时,函数f(x)取得极小值,且极小值为f(2) = 4—e2.11. 某工厂某种产品的年产量为 1 000x 吨,其中x € [20,100],需要投入的成本为C(x)(单位:万元),当x€ [20,80]时,C(x)= 土2—30x + 500;当x€ (80,100]时,C(x)=四輕.若每吨商品售价为血万元,通过市场分析,该厂生产的商品能全部售完.(1)写出年利润L(x)(单位:万元)关于x的函数关系式;(2)年产量为多少吨时,该厂所获利润最大?解:(1)由题意,知L(x)= 1 000ln x—C(x) =9.设X i, X2是函数f(x) = x3—2ax2+ a2x的两个极值点,若x i< 2v x?,则实数a的取000ln x —x —30x + 500 , x€ [20, 80],1 000ln x —, x € 80, 100].⑵当x€•••L(x)在[20,50)上单调递增,在[50,80)上单调递减, •••当 x = 50 时,L(x)max = 1 000ln 50 - 250; 当 x € (80,100]时,L(x)= 1 000ln x - 20 000单调递增, px• L(x)max = 1 000ln 100 - 2 000.•/ 1 000ln 50 - 250 - (1 000ln 100 - 2 000) =1 750 -1 000ln 2 > 1 750 - 1 000 > 0,•••当x = 50,即年产量为 50 000吨时,利润最大,最大利润为(1 000ln 50 - 250)万元.12.已知函数f(x)= ax 3 + bx 1 2 + cx的导函数为h(x), f(x)的图象在点(一2, f( - 2))处的切 0,又直线y = x 是函数g(x)= kxe x 的图象的一条切线.(1)求函数f(x)的解析式及k 的值;⑵若f(x)w g(x)- m + 1对于任意x € [0,+^ )恒成立,求 m 的取值范围. 解:(1)由 f(x)= ax 3 + bx 2 + cx , 可知 h(x)= f ' (x)= 3ax 2+ 2bx + c.由f(x)在(-2, f(-2))处的切线方程为 3x -y + 4= 0可知, f( - 2)=- 8a + 4b - 2c =- 2, f ' (- 2)= 12a -4b + c = 3, 又由 h ' (x)= 6ax + 2b 可知,4a + 2b = 0,1由①②③,解得 a =云,b = 1, c = 1,xp (x) = e — x — 1,再令 0(x)= e x — x — 1, / (x)= e x — 1 = 0,解得 x = 0.1所以f(x)的解析式为f(x) = ?x 3+ x 2+ x.由题意,g(x)= kxe x 与y = x 相切可知函数在原点或 (—In k ,- In k)处切线斜率为1.因为 g ' (x)= k(e x + xe x ),所以 g ' (0) = k = 1 或 g ' (- ln k)= 1,得 k = 1. 综上可得k 的值为1.⑵若f(x)w g(x)- m + 1对任意x € [0, + g )恒成立, 即 £X 3+ x 2+ x < xe x - m + 1 恒成立, 2则 m - 1 w xe x - ^x 3 — x 2- x 恒成立. 设 q(x)= xe x -^x 3- x 2- x = x e x -护-x - 1 , x :2线方程为3x - y + 4 = 0,且h '2 =所以当x€ [0,+ g)时,(x)>0,所以g x)在[0, + g)上单调递增,所以g x)》机0) = 0,即卩p' (x) > 0,所以p(x)在[0,+ g)上单调递增,所以p(x)> p(0) = 0, 所以当x€ [0,+g)时,q(x)>0恒成立,且q(0) = 0, 因此,m— 1 < 0即可,贝U m W 1.故m 的取值范围为(—g, 1].。
人教A版数学高二选修2-2 第一章《导数及其应用》金牌综合能力检测题

消去y ,得ax 2+154x -9=0,其判别式Δ=0⇒a =-2564;若k =274,切线方程为y =274(x -1),由⎩⎨⎧y =274(x -1),y =ax 2+154x -9消去y ,得ax 2-3x -94=0,其判别式Δ=0⇒a =-1. 答案:A8.若f (x )=-12x 2+b ln(x +2)在(-1,+∞)上是减函数,则b 的取值范围是( )A .[-1,+∞)B .(-1,+∞)C .(-∞,-1]D .(-∞,-1)解析:∵f ′(x )=-x +b x +2,由题知,f ′(x )<0在(-1,+∞)上恒成立,即-x +bx +2<0,∴b <x (x +2)=(x +1)2-1. ∴b <-1.又当b =-1时,f ′(x )=-x -1x +2=-x (x +2)+1x +2=-(x +1)2x +2<0,∴b ≤-1. 答案:C9.由y =sin x ,y =cos x ,x =0,x =π所围成图形的面积可表示为( ) A.⎠⎛0π(sin x -cos x )dxC.⎠⎛0π(cos x -sin x )dx解析:由y =sin x ,y =cos x ,x =0,x =π所围成的图形,如下图的阴影部分.答案:B10.已知f (a )=⎠⎛01(2ax 2-a 2x )dx ,则f (a )的最大值为( )A .-12B.19C.29D .不存在解析:⎠⎛01(2ax 2-a 2x )dx=(23ax 3-12a 2x 2)|10=23a -12a 2, 即f (a )=23a -12a 2=-12(a 2-43a +49)+29=-12(a -23)2+29,∴当a =23时,f (a )有最大值29.答案:C11.(2009·青岛模拟)如右图,在一个长为π,宽为2的矩形OABC 内,由曲线y =sin x (0≤x ≤π)与x 轴围成如图所示的阴影部分,向矩形OABC 内随机投一点(该点落在矩形OABC 内任何一点是等可能的),则所投的点落在阴影部分的概率是( )A.1π B.2π C.3πD.π4解析:根据几何概型的意义,所投的点落在阴影部分的概率是S 阴影S 矩形,由S 阴影=⎠⎛0πsin xdx=(-cos x )|π0=2,所求概率为S 阴影S 矩形=22π=1π.12.f (x )是定义在(0,+∞)上的非负可导函数,且满足xf ′(x )+f (x )≤0,对任意正数a ,b ,若a <b ,则必有( )A .af (b )≤bf (a )B .bf (a )≤af (b )C .af (a )≤f (b )D .bf (b )≤f (a )解析:设函数F (x )=xf (x ),∴F ′(x )=[xf (x )]′=f (x )+xf ′(x )≤0,∴F (x )=xf (x )在(0,+∞)上单调递减.∵a <b ,∴F (a )≥F (b ),即af (a )≥bf (b ).又∵0<a <b ,f (b )≥0,∴af (a )≤bf (a ),bf (b )≥af (b ).∴bf (a )≥af (b ).答案:A二、填空题:本大题共4小题,每小题5分,共20分. 13.⎠⎛02(2x -e x )dx =________.解析:⎠⎛02(2x -e x )dx =(x 2-e x )|20=4-e 2+1=5-e 2. 答案:5-e 214.(2009·海淀区模拟)已知函数f (x )=sin(ωx +φ)(ω>0,|φ|<π2)的导函数y =f ′(x )的部分图象如右图所示,且导函数f ′(x )有最小值-2,则ω=________,φ=________.解析:f ′(x )=ωcos(ωx +φ),依题意,得ω=2,2cos(π3+φ)=-1,解得φ=π3.答案:2 π315.若函数y =a (x 3-x )的单调递减区间为(-33,33),则a 的取值范围是________. 解析:∵y ′=a (3x 2-1),令y ′<0,当a >0时,不等式的解集为(-33,33); 当a <0时,不等式的解集为(-∞,-33)∪(33,+∞). ∵已知函数y =a (x 3-x )在(-33,33)上单调递减,答案:a >016.物体A 以速度v =3t 2+1在一直线上运动,在此直线上物体A 出发的同时,物体B 在物体A 的正前方5 m 处以v =10t 的速度与A 同向运动,当t =________ s 时,两物体相遇,相遇时物体A 走过________m.解析:设A 追上B 时,所用的时间为t 0,依题意有s A =s B +5,即10tdt +5,t 30+t 0=5t 20+5,即t 0(t 20+1)=5(t 20+1),解得t 0=5 s .所以s A =5t 20+5=130(m).答案:130三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分)(2009·浙江高考)已知函数f (x )=x 3+(1-a )x 2-a (a +2)x +b (a ,b ∈R ).(1)若函数f (x )的图象过原点,且在原点处的切线斜率是-3,求a ,b 的值; (2)若函数f (x )在区间(-1,1)上不单调...,求a 的取值范围. 解:(1)由函数f (x )的图象过原点,得b =0, 又f ′(x )=3x 2+2(1-a )x -a (a +2), f (x )在原点处的切线斜率是-3, 则-a (a +2)=-3, 所以a =-3,或a =1.(2)由f ′(x )=0,得x 1=a ,x 2=-a +23.又f (x )在(-1,1)上不单调,即⎩⎨⎧-1<a <1,a ≠-a +23,或⎩⎪⎨⎪⎧-1<-a +23<1,a ≠-a +23.解得⎩⎪⎨⎪⎧ -1<a <1,a ≠-12,或⎩⎪⎨⎪⎧-5<a <1,a ≠-12,x (-∞,-a ) -a (-a ,a ) a (a ,+∞) f ′(x ) +0 -0 +f (x )极大值极小值由此可得,函数x =-a 处取得极大值2+2a 32;在x =a 处取得极小值2-2a 32.根据列表讨论,可作出函数的草图(如右图所示),因为极大值f (-a )=2+2a 32>0,故当极小值f (a )=2-2a 32<0,即a >1时,方程x 3-3ax+2=0有三个不同的实根;当极小值f (a )=2-2a 32>0,即0<a <1时,方程x 3-3ax +2=0有唯一的实根.21.(本小题满分12分)已知函数f (x )=13ax 3-bx 2+(2-b )x +1,在x =x 1处取得极大值,在x =x 2处取得极小值,且0<x 1<1<x 2<2.(1)证明a >0;(2)求z =a +2b 的取值范围. 解:求函数f (x )的导数得 f ′(x )=ax 2-2bx +2-b .(1)证明:由函数f (x )在x =x 1处取得极大值,在x =x 2处取得极小值,知x 1,x 2是f ′(x )=0的两个根.所以f ′(x )=a (x -x 1)(x -x 2). 当x <x 1时,f ′(x )>0,函数为增函数, 由x -x 1<0,x -x 2<0得a >0. (2)在题设下,0<x 1<1<x 2<2等价于⎩⎨⎧f ′(0)>0,f ′(1)<0,f ′(2)>0.即。
导数的运算——综合练习(解析版)

导数的运算——综合练习一.选择题(共40小题)1.若f′(x)是函数f(x)=x3+2x+1的导函数,则f′(﹣1)的值为()A.1 B.3 C.1或3 D.42.若f(x)=x5,f′(x0)=20,则x0的值为()A.B.±C.﹣2 D.±23.下列求导运算正确的是()A.(cosx)'=sinx B.(3x)'=3x log3eC.D.(x2cosx)′=﹣2xsinx4.已知函数f(x)=sinx﹣cosx,且f′(x)=2f(x),则tan2x的值是()A.﹣B.C.﹣D.5.已知函数f(x)=,若f′(1)=,则实数a的值为()A.2 B.4 C.6 D.86.已知函数f(x)=6﹣x3,g(x)=e x﹣1,则这两个函数的导函数分别为()A.f′(x)=6﹣3x2,g′(x)=e x B.f′(x)=﹣3x2,g′(x)=e x﹣1C.f′(x)=﹣3x2,g′(x)=e x D.f′(x)=6﹣3x2,g′(x)=e x﹣17.已知f(x)=lnx,则f′(e)的值为()A.1 B.﹣1 C.e D.8.已知函数f(x)的导函数为f′(x),且满足f(x)=2xf′(1)+lnx,则f′(2)=()A.B.1 C.﹣1 D.﹣9.已知,则f'(2)=()A.B.C.2 D.﹣210.下列求导运算正确的是()A.(log2x)′=B.(x+)′=1+C.(cosx)′=sinx D.()′=11.若f(x)=,f'(x)为f(x)的导函数,则f'(x)=()A.f'(x)= B.f'(x)=C.f'(x)= D.f'(x)=12.已知函数f(x)=x2+2xf′(2017)﹣2017lnx,则f′(2017)=()A.2016 B.﹣2016 C.2017 D.﹣201713.已知f'(x)是f(x)=sinx+acosx的导函数,且f'()=,则实数a的值为()A.B.C.D.114.已知函数f(x)的导函数f'(x),且满足f(x)=2xf'(1)+lnx,则f′(1)=()A.﹣1 B.﹣e C.1 D.e15.下列函数在点x=0处没有切线的是()A.y=3x2+cosx B.y=xsinx C.D.16.f'(x)是函数f(x)的导函数,且f(x)=﹣x2+2x f'(2017)+2017㏑x,则f'(1)=()A.2016 B.6045 C.2017 D.604817.已知函数f(x)=f´()cosx+sinx,则f()=()A.B.﹣1 C.1 D.018.函数y=sin(lnx)的导数y′=()A.ln(cosx)B.cos(lnx)C.﹣cos(lnx)D.cos(lnx)19.已知函数f(x)=ln(ax﹣1)的导函数是f'(x),且f'(2)=2,则实数a的值为()A.B.C.D.120.设f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,f n+1(x)=f n′(x),n∈N,则f2017(x)=()A.sinx B.﹣sinx C.cosx D.﹣cosx21.已知f1(x)=cosx,f2(x)=f1′(x),f3(x)=f2′(x),f4(x)=f3′(x),…,f n(x)=f n﹣1′(x),则f2015(x)等于()A.sinx B.﹣sinx C.cosx D.﹣cosx22.函数(x>0),若x0满足f'(x0)=0,设m∈(0,x0),n∈(x0,+∞),则()A.f'(m)<0,f'(n)<0 B.f'(m)>0,f'(n)>0 C.f'(m)<0,f'(n)>0 D.f'(m)>0,f'(n)<023.若函数f(x)在其定义域的一个子集[a,b]上存在实数m(a<m<b),使f(x)在m处的导数f'(m)满足f(b)﹣f(a)=f'(m)(b﹣a),则称m是函数f(x)在[a,b]上的一个“中值点”,函数在[0,b]上恰有两个“中值点”,则实数b的取值范围是()A.,B.(3,+∞)C.,D.,24.设函数f(x)=x3﹣ax2+2bx+1的导函数为f′(x),若函数f′(x)的图象关于直线x=对称,且当x∈[1,π]时,恒有f(x)≥1,则实数b的取值范围为()A.(,+∞)B.[,1]C.(﹣∞,]D.[,+∞)25.已知定义在(0,+∞)上的单调函数f(x),对∀x∈(0,+∞),都有f[f(x)﹣log2x]=3,则方程f(x)﹣f′(x)=2的解所在的区间是()A.(0,) B.(1,2) C.(,1) D.(2,3)26.已知二次函数f(x)=ax2+bx+c的导数为f′(x),f′(0)>0,对于任意实数x,有,则的最小值为()A.2 B.C.3 D.27.已知函数f(x)及其导数f'(x),若存在x0使得f(x0)=f'(x0),则称x0是f(x)的一个“巧值点”.给出下列五个函数:①f(x)=x2,②f(x)=e﹣x,③f(x)=lnx,④f(x)=tanx,其中有“巧值点”的函数的个数是()A.1 B.2 C.3 D.428.已知函数,其导函数记为f'(x),则f(2017511)+f'(2017511)+f(﹣2017511)﹣f'(﹣2017511)=()A.0 B.1 C.2 D.201751129.[x]表示不超过x的最大整数,若f′(x)是函数f(x)=ln|x|导函数,设g(x)=f(x)f′(x),则函数f=[g(x)]+[g(﹣x)]的值域是()A.{﹣1,0}B.{0,1}C.{0}D.{偶数}30.定义:如果函数f(x)在[m,n]上存在x1,x2(m<x1<x2<n)满足f′(x1)=,f′(x2)=,则称函数f(x)是[m,n]上的“双中值函数”.已知函数f(x)=x3﹣x2+a是[0,a]上“双中值函数”,则实数a的取值范围是()A.(,)B.(,3) C.(,1) D.(,1)31.已知函数f(x)=asinx+bx3+1(a,b∈R),f′(x)为f(x)的导函数,则f(2016)+f(﹣2016)+f′(2017)﹣f′(﹣2017)=()A.2017 B.2016 C.2 D.032.已知f(x)=1+(1+x)+(1+x)2+(1+x)3+…+(1+x)n,则f'(0)=()A.n B.n﹣1 C.D.n(n+1)33.设函数f(x)=x3+x2+,其中θ∈(﹣,),则导数f′(1)的取值范围是()A.(﹣,1]B.(﹣,1)C.(﹣,)D.(﹣,]34.已知函数f0(x)=sinx+cosx,f1(x)=f′0(x),f2(x)=f′1(x),…f n+1(x)=f′n(x),n∈N,那么f2017=()A.cosx﹣sinx B.sinx﹣cosx C.sinx+cosx D.﹣sinx﹣cosx35.定义方程f(x)=f′(x)的实数根x0叫做函数f(x)的“新驻点”,若函数g(x)=x3﹣1,h(x)=2x,φ(x)=ln(x+1)的“新驻点”分别为α,β,γ,则α,β,γ的大小关系为()A.α>β>γ B.β>α>γ C.γ>α>β D.β>γ>α36.设f1(x)=sinx,定义f n+1(x)为f n(x)的导数,即f(x)=f n′(x),n∈N*,若△ABC的内角A满足f1(A)+f2(A)+…+f2018(A)=0,则cosA的值为()A.1 B.﹣1 C.D.﹣37.已知函数f(x)及其导数f′(x),若存在x0,使得f(x0)=f′(x0),则x0称为f(x)的一个“巧值点”,则下列函数中有“巧值点”的是()①f(x)=x2;②f(x)=e﹣x;③f(x)=lnx;④f(x)=tanx;⑤f(x)=.A.①③⑤B.①③④C.②③④D.②⑤38.设函数f n′(x)是f n(x)的导函数,f0(x)=e x(cosx+sinx),f1(x)=,f2(x)=,…,(n∈N),则f2016(x)=()A.e x(cosx+sinx)B.e x(cosx﹣sinx)C.﹣e x(cosx+sinx)D.e x(sinx﹣cosx)39.已知函数f(x)=e x﹣2ax,函数g(x)=﹣x3﹣ax2.若不存在x1,x2∈R,使得f′(x1)=g′(x2),则实数a的取值范围为()A.(﹣2,3)B.(﹣6,0)C.[﹣2,3]D.[﹣6,0]40.已知函数f(x)=lnx+tanα(α∈(0,))的导函数为f′(x),若使得f′(x0)=f(x0)成立的x0<1,则实数α的取值范围为()A.(,)B.(0,)C.(,)D.(0,)二.填空题(共6小题)41.已知在R上可导,F(x)=f(x3﹣1)+f(1﹣x3),则F′(1)=.42.已知f(x)=f(4﹣x),当x≤2时,f(x)=e x,f′(3)+f(3)=.43.设定义域为(0,+∞)的单调函数f(x),对任意的x∈(0,+∞),都有f[f(x)﹣log2x]=6,若x0是方程f(x)﹣f′(x)=4的一个解,且x0∈(a,a+1)(a∈N*),则实数a=.44.已知函数y=f(x)的导函数为f'(x)=cosx﹣5,且f(0)=0,如果f(1﹣ax)+f(1﹣ax2)<0恒成立,则实数a的取值范围是.45.已知函数f(x)满足f(0)=﹣1,其导函数f′(x)满足f′(x)>k>1,则下列结论中正确的是.(1)f()>﹣1;(2)f()>;(3)f()<;(4)f()<f()46.若函数f(x)的导数f′(x)存在导数,记f′(x)的导数为f n(x).如果f(x)对任意x∈(a,b),都有f n(x)<0成立,则f(x)有如下性质:f()≥.其中n∈N*,x1,x2,…,x n∈(a,b).若f(x)=sinx,则f n(x)=;根据上述性质推断:当x1+x2+x3=π且x1,x2,x3∈(0,π)时,根据上述性质推断:sinx1+sinx2+sinx3的最大值为.导数的运算——综合练习参考答案与试题解析一.选择题(共40小题)1.若f′(x)是函数f(x)=x3+2x+1的导函数,则f′(﹣1)的值为()A.1 B.3 C.1或3 D.4【分析】先求函数f(x)的导函数,然后在导函数解析式中把x代﹣1求值.【解答】解:因为函数f(x)=x3+2x+1,所以其导函数f′(x)=x2+2,所以f′(﹣1)=(﹣1)2+2=3.故选B.2.若f(x)=x5,f′(x0)=20,则x0的值为()A.B.±C.﹣2 D.±2【分析】根据函数的导数公式解方程即可.【解答】解:函数的导数f′(x)=5x4,∵f′(x0)=20,∴5x04=20,得x04=4,则x0=±,故选:B.3.下列求导运算正确的是()A.(cosx)'=sinx B.(3x)'=3x log3eC.D.(x2cosx)′=﹣2xsinx【分析】根据函数的导数公式进行判断即可.【解答】解:(cosx)'=﹣sinx,A不正确;(3x)'=3x ln3,B不正确(lgx)′=,C正确;(x2cosx)′=2xcosx﹣x2sinx,D不正确故选:C.4.已知函数f(x)=sinx﹣cosx,且f′(x)=2f(x),则tan2x的值是()A.﹣B.C.﹣D.【分析】求出f(x)的导函数,根据f′(x)=2f(x)列出关系式,计算即可求出tan2x的值.【解答】解:求导得:f′(x)=cosx+sinx,∵f′(x)=2f(x),∴cosx+sinx=2(sinx﹣cosx),即3cosx=sinx,∴tanx=3,则tan2x===﹣.故选C5.已知函数f(x)=,若f′(1)=,则实数a的值为()A.2 B.4 C.6 D.8【分析】根据导数的公式即可得到结论【解答】解:函数f(x)=,则f′(x)=∵f′(1)=,即f′(1)==,∴a=4.故选:B6.已知函数f(x)=6﹣x3,g(x)=e x﹣1,则这两个函数的导函数分别为()A.f′(x)=6﹣3x2,g′(x)=e x B.f′(x)=﹣3x2,g′(x)=e x﹣1C.f′(x)=﹣3x2,g′(x)=e x D.f′(x)=6﹣3x2,g′(x)=e x﹣1【分析】根据导数的运算法则求导即可.【解答】解:f′(x)=﹣3x2,g′(x)=e x,故选:C7.已知f(x)=lnx,则f′(e)的值为()A.1 B.﹣1 C.e D.【分析】利用导数的运算法则即可得出.【解答】解:∵,∴.故选D.8.已知函数f(x)的导函数为f′(x),且满足f(x)=2xf′(1)+lnx,则f′(2)=()A.B.1 C.﹣1 D.﹣【分析】已知函数f(x)的导函数为f′(x),利用求导公式对f(x)进行求导,再把x=1代入,x=2代入求解即可.【解答】解:∵函数f(x)的导函数为f′(x),且满足f(x)=2xf′(1)+ln x,(x>0)∴f′(x)=2f′(1)+,把x=1代入f′(x)可得f′(1)=2f′(1)+1,解得f′(1)=﹣1,∴f′(2)=2f′(1)+=﹣2+=﹣.故选D.9.已知,则f'(2)=()A.B.C.2 D.﹣2【分析】把给出的函数求导,在其导函数中取x=2,则f′(2)可求.【解答】解:∵f′(x)=﹣+3f′(2),∴f′(2)=﹣+3f′(2),解得:f′(2)=,故选:A.10.下列求导运算正确的是()A.(log2x)′=B.(x+)′=1+C.(cosx)′=sinx D.()′=【分析】利用导数的运算法则即可得出.【解答】解:=,=1﹣,(cosx)′=﹣sinx,=,可知:只有A正确.故选:A.11.若f(x)=,f'(x)为f(x)的导函数,则f'(x)=()A.f'(x)= B.f'(x)=C.f'(x)= D.f'(x)=【分析】根据导数的运算法则计算即可.【解答】解:∵f(x)=,∴f'(x)=,故选:B12.已知函数f(x)=x2+2xf′(2017)﹣2017lnx,则f′(2017)=()A.2016 B.﹣2016 C.2017 D.﹣2017【分析】对函数f(x)的解析式求导,得到其导函数,把x=2017代入导函数中,列出关于f'(2017)的方程,进而得到f'(2017)的值【解答】解:求导得:f′(x)=x+2f′(2017)﹣令x=2017,得到f′(2017)=2017+2f′(2017)﹣1,解得:f′(2017)=﹣2016,故选:B13.已知f'(x)是f(x)=sinx+acosx的导函数,且f'()=,则实数a的值为()A.B.C.D.1【分析】求出f(x)的导数,由条件解方程,即可得到所求a的值.【解答】解:由题意可得f'(x)=cosx﹣asinx,由可得,解之得.故选:B.14.已知函数f(x)的导函数f'(x),且满足f(x)=2xf'(1)+lnx,则f′(1)=()A.﹣1 B.﹣e C.1 D.e【分析】已知函数f(x)的导函数为f′(x),利用求导公式对f(x)进行求导,再把x=1代入,即可求解;【解答】解:∵函数f(x)的导函数为f′(x),且满足f(x)=2xf′(1)+ln x,(x>0),∴f′(x)=2f′(1)+,把x=1代入f′(x)可得f′(1)=2f′(1)+1,解得f′(1)=﹣1,故选A15.下列函数在点x=0处没有切线的是()A.y=3x2+cosx B.y=xsinx C.D.【分析】根据导数的定义可得答案.【解答】解:∵在x=0处不可导.故选D.16.f'(x)是函数f(x)的导函数,且f(x)=﹣x2+2x f'(2017)+2017㏑x,则f'(1)=()A.2016 B.6045 C.2017 D.6048【分析】根据导数的运算法则求导,代值计算即可.【解答】解:∵f′(x)=﹣x+2f'(2017)+,∴f′(2017)=﹣2017+2f'(2017)+1,解得f′(2017)=2016,∴f′(1)=﹣1+2×2016+2017=6048,故选:D.17.已知函数f(x)=f´()cosx+sinx,则f()=()A.B.﹣1 C.1 D.0【分析】先求导,再代值计算即可.【解答】解:∵f(x)=f´()cosx+sinx,∴f′(x)=﹣f´()sinx+cosx,∴f′()=﹣f´()×+,∴f′()=﹣1,∴f(π)=(﹣1)×(﹣)+=﹣1,故选:B18.函数y=sin(lnx)的导数y′=()A.ln(cosx)B.cos(lnx)C.﹣cos(lnx)D.cos(lnx)【分析】根据题意,令t=lnx,则y=sint,根据复合函数的导数公式进行求导即可答案.【解答】解:根据题意,令t=lnx,则y=sint,则其导数y′=cos(t)•(lnx)′=cos(lnx)•(lnx)′=cos(lnx),故选:D.19.已知函数f(x)=ln(ax﹣1)的导函数是f'(x),且f'(2)=2,则实数a的值为()A.B.C.D.1【分析】利用导数的运算法则即可得出.【解答】解:由f(x)=ln(ax﹣1)可得,由f'(2)=2,可得,解之得.故选:B.20.设f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,f n+1(x)=f n′(x),n∈N,则f2017(x)=()A.sinx B.﹣sinx C.cosx D.﹣cosx【分析】由题意对函数的变化规律进行探究,发现呈周期性的变化,且其周期是4,故只须研究清楚f2010(x)是一个周期中的第几个函数即可得出其解析式.【解答】解:由题意f0(x)=sinx,f1(x)=f0′(x)=cosx,f2(x)=f1′(x)=﹣sinx,f3(x)=f2′(x)=﹣cosx,f4(x)=f3′(x)=sinx,由此可知,在逐次求导的过程中,所得的函数呈周期性变化,从0开始计,周期是4,∵2017=4×504+1,f2010(x)是一周中的第三个函数,故f2017(x)=cosx.故选:C.21.已知f1(x)=cosx,f2(x)=f1′(x),f3(x)=f2′(x),f4(x)=f3′(x),…,f n(x)=f n﹣1′(x),则f2015(x)等于()A.sinx B.﹣sinx C.cosx D.﹣cosx【分析】对函数连续求导研究其变化规律,可以看到函数解析式呈周期性出现,以此规律判断求出f2015(x)【解答】解:由题意f1(x)=cosx,f2(x)=f1′(x)=﹣sinx,f3(x)=f2′(x)=﹣cosx,f4(x)=f3′(x)=sinx,f5(x)=f4′(x)=cosx,…由此可知,在逐次求导的过程中,所得的函数呈周期性变化,从0开始计,周期是4,∵2015=4×503+3,故f2015(x)=f3(x)=﹣cosx故选:D22.函数(x>0),若x0满足f'(x0)=0,设m∈(0,x0),n∈(x0,+∞),则()A.f'(m)<0,f'(n)<0 B.f'(m)>0,f'(n)>0 C.f'(m)<0,f'(n)>0 D.f'(m)>0,f'(n)<0【分析】根据题意,对f(x)求导可得f′(x),若f'(x0)=0,则有=1,将m、n的值代入计算可得答案.【解答】解:根据题意,函数(x>0),其导数f′(x)=e x﹣=,若f'(x0)=0,则有=1,当m∈(0,x0),即m<x0,f'(m)=<0,n∈(x0,+∞),即n>x0,f'(n)=>0,故选:C.23.若函数f(x)在其定义域的一个子集[a,b]上存在实数m(a<m<b),使f(x)在m处的导数f'(m)满足f(b)﹣f(a)=f'(m)(b﹣a),则称m是函数f(x)在[a,b]上的一个“中值点”,函数在[0,b]上恰有两个“中值点”,则实数b的取值范围是()A.,B.(3,+∞)C.,D.,【分析】根据新定义得到x1,x2为方程x2﹣2x﹣b2+b=0在(0,b)上有两个不同根,构造函数g(x)=x2﹣2x﹣b2+b,列出不等式组,解得即可【解答】解:f′(x)=x2﹣2x,设=b2﹣b,由已知可得x1,x2为方程x2﹣2x﹣b2+b=0在(0,b)上有两个不同根,令g(x)=x2﹣2x﹣b2+b,则>>>>,解得<b<3,故选:C24.设函数f(x)=x3﹣ax2+2bx+1的导函数为f′(x),若函数f′(x)的图象关于直线x=对称,且当x∈[1,π]时,恒有f(x)≥1,则实数b的取值范围为()A.(,+∞)B.[,1]C.(﹣∞,]D.[,+∞)【分析】根据f′(x)的图象判断f(x)在[1,π]上的单调性,列出不等式解出.【解答】解:f′(x)=3x2﹣2ax+2b,∵函数f′(x)的图象关于直线x=对称,∴=,即a=2.∴f(x)=x3﹣2x2+2bx+1,f′(x)=3x2﹣4x+2b,△=16﹣24b,(1)若△=16﹣24b≤0,即b时,f′(x)≥0,∴f(x)在[1,π]上是增函数,∴f min(x)=f(1)=2b≥1,解得b≥,∴b≥.排除B,C.(2)若△=16﹣24b>0,即b<时,令f′(x)=0,解得x=.①若1≥,即b<时,f′(x)在[1,π]上恒大于或等于0,∴f(x)在[1,π]上是增函数,∴f min(x)=f(1)=2b≥1,解得b≥,∴≤b<.排除A.故选:D.25.已知定义在(0,+∞)上的单调函数f(x),对∀x∈(0,+∞),都有f[f(x)﹣log2x]=3,则方程f(x)﹣f′(x)=2的解所在的区间是()A.(0,) B.(1,2) C.(,1) D.(2,3)【分析】设t=f(x)﹣log2x,则f(x)=log2x+t,又由f(t)=3,即log2t+t=3,解可得t的值,可得f (x)的解析式,由二分法分析可得h(x)的零点所在的区间为(1,2),结合函数的零点与方程的根的关系,即可得答案.【解答】解:根据题意,对任意的x∈(0,+∞),都有f[f(x)﹣log2x]=3,又由f(x)是定义在(0,+∞)上的单调函数,则f(x)﹣log2x为定值,设t=f(x)﹣log2x,则f(x)=log2x+t,又由f(t)=3,即log2t+t=3,解可得,t=2;则f(x)=log2x+2,f′(x)=,将f(x)=log2x+2,f′(x)=代入f(x)﹣f′(x)=2,可得log2x+2﹣=2,即log2x﹣=0,令h(x)=log2x﹣,分析易得h(1)=﹣<0,h(2)=1﹣>0,则h(x)=log2x﹣的零点在(1,2)之间,则方程log2x﹣=0,即f(x)﹣f′(x)=2的根在(1,2)上,故选:B.26.已知二次函数f(x)=ax2+bx+c的导数为f′(x),f′(0)>0,对于任意实数x,有,则的最小值为()A.2 B.C.3 D.【分析】由对于任意实数x,f(x)≥0成立求出a的范围及a,b c的关系,求出f(1)及f′(0),作比后放缩去掉c,通分后利用基本不等式求最值.【解答】解:∵f(x)≥0,知>,∴c.又f′(x)=2ax+b,∴f′(0)=b>0,f(1)=a+b+c.∴≥1+=≥1+=2.当且仅当4a2=b2时,“=”成立.故选A.27.已知函数f(x)及其导数f'(x),若存在x0使得f(x0)=f'(x0),则称x0是f(x)的一个“巧值点”.给出下列五个函数:①f(x)=x2,②f(x)=e﹣x,③f(x)=lnx,④f(x)=tanx,其中有“巧值点”的函数的个数是()A.1 B.2 C.3 D.4【分析】根据题意,依次分析四个函数,分别求函数的导数,根据条件f(x0)=f′(x0),确实是否有解即可.【解答】解:根据题意,依次分析所给的函数:①、若f(x)=x2;则f′(x)=2x,由x2=2x,得x=0或x=2,这个方程显然有解,故①符合要求;②、若f(x)=e﹣x;则f′(x)=﹣e﹣x,即e﹣x=﹣e﹣x,此方程无解,②不符合要求;③、f(x)=lnx,则f′(x)=,若lnx=,利用数形结合可知该方程存在实数解,③符合要求;④、f(x)=tanx,则f′(x)=()′=,即sinxcosx=1,变形可sin2x=2,无解,④不符合要求;故选:B.28.已知函数,其导函数记为f'(x),则f(2017511)+f'(2017511)+f(﹣2017511)﹣f'(﹣2017511)=()A.0 B.1 C.2 D.2017511【分析】先求导,再判断导函数f'(x)的奇偶性,f(x)=1+,设g(x)=,判断其奇偶性,即可求出答案.【解答】解:f(x)=1+,∴f′(x)=,∴f′(﹣x)==f′(x),∴f′(x)为偶函数,∴f'(2017511)﹣f'(﹣2017511)=0,设g(x)=,则g(﹣x)=﹣=﹣g(x),∴g(x)为奇函数,∴f(2017511)+f(﹣2017511)=1+g(2017511)+1+g(﹣2017511)=2,∴f(2017511)+f'(2017511)+f(﹣2017511)﹣f'(﹣2017511)=2,故选:C29.[x]表示不超过x的最大整数,若f′(x)是函数f(x)=ln|x|导函数,设g(x)=f(x)f′(x),则函数f=[g(x)]+[g(﹣x)]的值域是()A.{﹣1,0}B.{0,1}C.{0}D.{偶数}【分析】先对函数g(x)进行化简,根据[x]表示不超过x的最大整数,针对x进行分类讨论,发现规律,问题得以解决.【解答】解:由题意可知g(x)=f(x)•f′(x)=,>,<,不妨设x>0,则y=[g(x)]+[g(﹣x)]=[]+[]当∈(0,1),则∈(﹣1,0),[]=0,[]=﹣1,y=[g(x)]+[g(﹣x)]=﹣1当=0,则=0,[]=0,[]=0,y=[g(x)]+[g(﹣x)]=0依此类推可得y=[g(x)]+[g(﹣x)]的值域是{﹣1,0},故选A.30.定义:如果函数f(x)在[m,n]上存在x1,x2(m<x1<x2<n)满足f′(x1)=,f′(x2)=,则称函数f(x)是[m,n]上的“双中值函数”.已知函数f(x)=x3﹣x2+a是[0,a]上“双中值函数”,则实数a的取值范围是()A.(,)B.(,3) C.(,1) D.(,1)【分析】令f′(x)=3x2﹣2x==a2﹣a,a2﹣a=3x2﹣2x,x∈[0,a].令g(x)=3x2﹣2x﹣a2+a,根据函数f(x)=x3﹣x2+a是[0,a]上“双中值函数”,可得方程3x2﹣2x﹣a2+a=0在x∈(0,a)有两个不等实数根.必须满足:g(0)>0,<0,g(a)>0.解出即可得出.【解答】解:令f′(x)=3x2﹣2x==a2﹣a,∴a2﹣a=3x2﹣2x,x∈[0,a].令g(x)=3x2﹣2x﹣a2+a,∵函数f(x)=x3﹣x2+a是[0,a]上“双中值函数”,∴方程3x2﹣2x﹣a2+a=0在x∈(0,a)有两个不等实数根.∴g(0)>0,<0,g(a)>0.解得<<1.∴实数a的取值范围是,.故选:C.31.已知函数f(x)=asinx+bx3+1(a,b∈R),f′(x)为f(x)的导函数,则f(2016)+f(﹣2016)+f′(2017)﹣f′(﹣2017)=()A.2017 B.2016 C.2 D.0【分析】根据函数的解析式求出函数的导数,结合函数的奇偶性建立方程关系进行求解即可.【解答】解:函数的导数f′(x)=acosx+3bx2,则f′(x)为偶函数,则f′(2017)﹣f′(﹣2017)=f′(2017)﹣f′(2017)=0,由f(x)=asinx+bx3+1得f(2016)=asin2016+b•20163+1,f(2016)=asin2016+b•20163+1,f(﹣2016)=﹣asin2016﹣b•20163+1,则f(2016)+f(﹣2016)=2,则f(2016)+f(﹣2016)+f′(2017)﹣f′(﹣2017)=2+0=2,故选:C32.已知f(x)=1+(1+x)+(1+x)2+(1+x)3+…+(1+x)n,则f'(0)=()A.n B.n﹣1 C.D.n(n+1)【分析】根据题意,对函数f(x)求导,计算可得f′(x),将x=0代入计算可得答案.【解答】解:根据题意,f(x)=1+(1+x)+(1+x)2+(1+x)3+…+(1+x)n,则其导数f′(x)=1+2(1+x)+3(1+x)2+4(1+x)3+…+n(1+x)n﹣1,则f'(0)=1+2+3+4+…+n=;故选:D.33.设函数f(x)=x3+x2+,其中θ∈(﹣,),则导数f′(1)的取值范围是()A.(﹣,1]B.(﹣,1)C.(﹣,)D.(﹣,]【分析】求导,当x=1时,f′(1)=+=sin(θ+),由θ∈(﹣,),即可求得θ+∈(﹣,),根据正弦函数的性质,即可求得导数f′(1)的取值范围.【解答】解:f(x)=x3+x2+,f′(x)=x2+x,f′(1)=+=sin(θ+),由θ∈(﹣,),则θ+∈(﹣,),则sin(θ+)∈(﹣,1],∴导数f′(1)的取值范围(﹣,1],故选A.34.已知函数f0(x)=sinx+cosx,f1(x)=f′0(x),f2(x)=f′1(x),…f n+1(x)=f′n(x),n∈N,那么f2017=()A.cosx﹣sinx B.sinx﹣cosx C.sinx+cosx D.﹣sinx﹣cosx【分析】根据题意,利用导数的运算法则依次计算f1(x)、f2(x)、f2(x)…的值,分析可得f n(x)+4=f n(x),即可得f2017(x)=f504×4+1(x)=f1(x),即可得答案.【解答】解:根据题意,∵f0(x)=sinx+cosx,∴f1(x)=f0′(x)=cosx﹣sinx,f2(x)=f1′(x)=﹣sinx﹣cosx,f3(x)=﹣cosx+sinx,f4(x)=sinx+cosx,以此类推,可得出f n(x)=f n(x)+4(x)=f1(x)=cosx﹣sinx;∴f2017(x)=f504×4+1故选:A35.定义方程f(x)=f′(x)的实数根x0叫做函数f(x)的“新驻点”,若函数g(x)=x3﹣1,h(x)=2x,φ(x)=ln(x+1)的“新驻点”分别为α,β,γ,则α,β,γ的大小关系为()A.α>β>γ B.β>α>γ C.γ>α>β D.β>γ>α【分析】由题设中所给的定义,对三个函数所对应的方程进行研究,分别计算求出α,β,γ的值或存在的大致范围,再比较出它们的大小即可选出正确选项【解答】解:①∵g(x)=x3﹣1,∴g′(x)=3x2,由g(x)=g′(x),得x3﹣1=2x2,∵2x2>0,(x=0时不成立),∴x3﹣1>0,∴x>1,∴α>1.②∵h(x)=2x,∴h′(x)=2,由h(x)=h′(x),解得x=1,∴β=1.③∵φ(x)=ln(x+1),∴φ′(x)=,由φ(x)=φ′(x),得到ln(x+1)=,令m(x)=ln(x+1)﹣,则m′(x)=+,因此函数m(x)在(﹣1,+∞)单调递增.∵m(0)=﹣1<0,m(1)=ln2﹣>0,∴0<γ<1.综上可知:α>β>γ.故选:A.36.设f1(x)=sinx,定义f n+1(x)为f n(x)的导数,即f(x)=f n′(x),n∈N*,若△ABC的内角A满足f1(A)+f2(A)+…+f2018(A)=0,则cosA的值为()A.1 B.﹣1 C.D.﹣【分析】根据导数公式直接进行求导,得到函数f n(x)具备周期性,然后根据周期性将条件进行化简,即可得到结论.(x)=f′n(x),【解答】解:∵f1(x)=sinx,f n+1∴f2(x)=f′1(x)=cosx,f3(x)=f′2(x)=﹣sinx,f4(x)=f'3(x)=﹣cosx,f5(x)=f′4(x)=sinx,f6(x)=f′5(x)=cosx,(x)=f′n(x),具备周期性,周期性为4.∴f n+1且f1(x)+f2(x)+f3(x)+f4(x)=cosx﹣sinx+sinx﹣cosx=0,∵f1(A)+f2(A)+…+f2018(A)=0,∴f1(A)+f2(A)=sinA+cosA=0,∴A=135°,故cosA=﹣,故选:D.37.已知函数f(x)及其导数f′(x),若存在x0,使得f(x0)=f′(x0),则x0称为f(x)的一个“巧值点”,则下列函数中有“巧值点”的是()①f(x)=x2;②f(x)=e﹣x;③f(x)=lnx;④f(x)=tanx;⑤f(x)=.A.①③⑤B.①③④C.②③④D.②⑤【分析】求出函数的导数,使f(x)=f′(x),如果有解,则存在存在“巧值点”.【解答】解:①中的函数f(x)=x2,f′(x)=2x.要使f(x)=f′(x),则x2=2x,解得x=0或2,可见函数有巧值点;对于②中的函数,要使f(x)=f′(x),则e﹣x=﹣e﹣x,由对任意的x,有e﹣x>0,可知方程无解,原函数没有巧值点;对于③中的函数,要使f(x)=f′(x),则lnx=,由函数f(x)=lnx与y=的图象知,它们有交点,因此方程有解,原函数有巧值点;对于④中的函数,f (x)=tanx,f′(x)=,要使f(x)=f′(x),则tanx=,即sinxcosx=1,即sin2x=2,无解,∴原函数没有巧值点,故④错误;对于⑤中的函数,要使f(x)=f′(x),则=﹣,解得x=﹣1,原函数有巧值点;故有“巧值点”的函数为①③⑤.故选:A.38.设函数f n′(x)是f n(x)的导函数,f0(x)=e x(cosx+sinx),f1(x)=,f2(x)=,…,(n∈N),则f2016(x)=()A.e x(cosx+sinx)B.e x(cosx﹣sinx)C.﹣e x(cosx+sinx)D.e x(sinx﹣cosx)【分析】我们易得到f n(x)表达式以8为周期,呈周期性变化,由于2016÷8余0,故f2008(x)=f0(x),进而得到答案【解答】解:∵f0(x)=e x(cosx+sinx),∴f0′(x)=e x(cosx+sinx)+e x(﹣sinx+cosx)=2e x cosx,∴f1(x)==e x cosx,∴f1′(x)=e x(cosx﹣sinx),∴f2(x)==e x(cosx﹣sinx),∴f2′(x)=e x(cosx﹣sinx)+e x(﹣sinx﹣cosx)=﹣2e x sinx,∴f3(x)=﹣e x sinx,∴f3′(x)=﹣e x(sinx+cosx),∴f4(x)=﹣e x(cosx+sinx),∴f4′(x)=﹣2e x cosx,∴f5(x)=﹣e x cosx,∴f6(x)=﹣e x(cosx﹣sinx),∴f7(x)=e x sinx,∴f8(x)=e x(cosx+sinx),…,∴f2016(x)=f(0)=e x(cosx+sinx),故选:A.39.已知函数f(x)=e x﹣2ax,函数g(x)=﹣x3﹣ax2.若不存在x1,x2∈R,使得f′(x1)=g′(x2),则实数a的取值范围为()A.(﹣2,3)B.(﹣6,0)C.[﹣2,3]D.[﹣6,0]【分析】先求导,分别求出导函数的最值,再根据不存在x1,x2∈R,使得f′(x1)=g′(x2),得到关于a的不等式解得即可.【解答】解:∵函数f(x)=e x﹣2ax,函数g(x)=﹣x3﹣ax2,∴f′(x)=e x﹣2a>﹣2a,g′(x)=﹣3x2﹣2ax=﹣3(x+)2+≤,∵不存在x1,x2∈R,使得f′(x1)=g′(x2),∴﹣2a≥,解得﹣6≤a≤0,故选:D.40.已知函数f(x)=lnx+tanα(α∈(0,))的导函数为f′(x),若使得f′(x0)=f(x0)成立的x0<1,则实数α的取值范围为()A.(,)B.(0,)C.(,)D.(0,)【分析】由于f′(x)=,f′(x0)=,f′(x0)=f(x0),可得=ln x0+tan α,即tan α=﹣ln x0,由0<x0<1,可得﹣ln x0>1,即tan α>1,即可得出.【解答】解:∵f′(x)=,f′(x0)=,f′(x0)=f(x0),∴=ln x0+tan α,∴tan α=﹣ln x0,又∵0<x0<1,∴可得﹣ln x0>1,即tan α>1,∴α∈(,).故选:A.二.填空题(共6小题)41.已知在R上可导,F(x)=f(x3﹣1)+f(1﹣x3),则F′(1)=0.【分析】根据题意,由F(x)的解析式对其求导可得F'(x),将x=0代入,化简变形即可得答案.【解答】解:根据题意,F(x)=f(x3﹣1)+f(1﹣x3),则F'(x)=3x2f'(x3﹣1)﹣3x2f'(1﹣x3),则F'(1)=3f'(0)﹣3f'(0)=0.故答案为:0.42.已知f(x)=f(4﹣x),当x≤2时,f(x)=e x,f′(3)+f(3)=0.【分析】由f(x)=f(4﹣x)可得,函数f(x)的图象关于直线x=2对称,则f(3)=f(1),f′(3)=﹣f′(1),进而得到答案.【解答】解:由f(x)=f(4﹣x)可得,函数f(x)的图象关于直线x=2对称,当x≤2时,f(x)=e x,f′(x)=e x,∴f(3)=f(1)=e,f′(3)=﹣f′(1)=﹣e,故f′(3)+f(3)=0,故答案为:0.43.设定义域为(0,+∞)的单调函数f(x),对任意的x∈(0,+∞),都有f[f(x)﹣log2x]=6,若x0是方程f(x)﹣f′(x)=4的一个解,且x0∈(a,a+1)(a∈N*),则实数a=1.【分析】由题意可得f(x)﹣log2x为定值,设为t,代入可得t=4,进而可得函数的解析式,化方程有解为函数F(x)=f(x)﹣f′(x)﹣4=log2x﹣有零点,易得F(1)<0,F(2)>0,由零点的判定可得答案.【解答】解:根据题意,对任意的x∈(0,+∞),都有f[f(x)﹣log2x]=6,又由f(x)是定义在(0,+∞)上的单调函数,则f(x)﹣log2x为定值,设t=f(x)﹣log2x,则f(x)=t+log2x,又由f(t)=6,可得t+log2t=6,可解得t=4,故f(x)=4+log2x,f′(x)=,又x0是方程f(x)﹣f′(x)=4的一个解,所以x0是函数F(x)=f(x)﹣f′(x)﹣4=log2x﹣的零点,分析易得F(1)=﹣<0,F(2)=1﹣=1﹣>0,故函数F(x)的零点介于(1,2)之间,故a=1,故答案为:144.已知函数y=f(x)的导函数为f'(x)=cosx﹣5,且f(0)=0,如果f(1﹣ax)+f(1﹣ax2)<0恒成立,则实数a的取值范围是(﹣8,0] .【分析】由题意函数的导函数f'(x)=cosx﹣5<0恒成立,故函数是减函数,再由函数是奇函数将不等式f(1﹣ax)+f(1﹣ax2)<0转化为f(1﹣ax)<f(ax2﹣1),由单调性及定义转化为不等式,再分类讨论即可求出a的取值范围【解答】解:∵﹣1≤cosx≤1,∴f'(x)=cosx﹣5<0,∴函数f(x)在R上单调递减,∵f′(x)=cosx﹣5为偶函数及f(0)=0可得f(x)为奇函数由f(1﹣ax)+f(1﹣ax2)<0可得,f(1﹣ax)<﹣f(1﹣ax2)=f(ax2﹣1)即1﹣ax>ax2﹣1∴a(x2+x)<2,当x<﹣1或x>0时,x2+x>0,则a<=∵>0,∴a≤0,当﹣1<x<0时,x2+x<0,则a>=当x=﹣时,(x+)2﹣有最小值,则有最大值﹣8,∴a>﹣8,当x2+x=0时,恒成立,综上所述a的取值范围为(﹣8,0],故答案为(﹣8,0].45.已知函数f(x)满足f(0)=﹣1,其导函数f′(x)满足f′(x)>k>1,则下列结论中正确的是(1),(2),(4).(1)f()>﹣1;(2)f()>;(3)f()<;(4)f()<f()【分析】根据导数的概念得出>k>1,(1),(2)分别取x=,x=判断即可,(4)根据函数的单调性判断即可.【解答】解:∵f′(x)=,且f′(x)>k>1,∴>k>1,即>k>1,对于(1),令x=,即有f()+1>•k=1,即为f()>0,故(1)正确;对于(2),当x=时,f()+1>•k=,即f()>﹣1=,故f()>,故(2)正确;对于(3),由(2)可得f()>>﹣1=,故(3)不正确,对于(4),函数递增,故(4)正确.故正确个数为3,故选;(1)(2)(4)46.若函数f(x)的导数f′(x)存在导数,记f′(x)的导数为f n(x).如果f(x)对任意x∈(a,b),都有f n(x)<0成立,则f(x)有如下性质:f()≥.其中n∈N*,x1,x2,…,x n∈(a,b).若f(x)=sinx,则f n(x)=﹣sinx;根据上述性质推断:当x1+x2+x3=π且x1,x2,x3∈(0,π)时,根据上述性质推断:sinx1+sinx2+sinx3的最大值为.【分析】构造函数f(x)=sinx,x∈(0,π),求导,则f″(x)=﹣sinx,由正弦函数的图象可知f″(x)<0成立,根据函数的性质sinx1+sinx2+sinx3≤3sin(),即可求得sinx1+sinx2+sinx3的最大值.【解答】解:设f(x)=sinx,x∈(0,π),则f′(x)=cosx,则f″(x)=﹣sinx,x∈(0,π),f(x)有如下性质:f()≥.则sinx1+sinx2+sinx3≤3sin()=3×sin=,∴sinA+sinB+sinC的最大值为,故答案为:﹣sinx,。
高中数学 第一章导数及其应用综合测试 新人教A版选修22

高中数学 第一章导数及其应用综合测试 新人教A 版选修22第Ⅰ卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是最符合题目要求的.)1、已知函数21y x =+的图象上一点(1,2)及邻近一点()12x,y +∆+∆,则yx∆∆等于( )A.2B.2xC.22()x +∆ D.2x +∆ 2、设1(),f x x =则()()limx a f x f a x a→--等于( ) 221211. . . .A B C D a a a a--3、曲线221y x =-+在点()0,1处的切线的斜率是( ) A.4- B.0 C.4 D.不存在4、如果曲线()y f x =在点00(,())x f x 处的切线方程为230x y +-=,那么( ) A.0()0f x '> B.0()0f x '< C.0()0f x '= D.不存在5、下列函数在点0x =处没有切线的是( ) A.23cos y x x =+ B.sin y x x = C.1cos y x =D.12y x x=+ 6、函数222y x ln x =-的的单调递增区间是 ( )A.1(0,)2 B.2(0,)4 C.1(,)2+∞ D.1(,0)2-和1(0,)27、若函数()y f x =是定义在R 上的可导函数,则0()0f x '=是0x 为函数()y f x =的极值点的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 8、下列各式中值为1的是 ( )A.10xdx ⎰ B.()101x dx +⎰ C.101dx ⎰ D.1012dx ⎰9、若函数2()f x x bx c =++的图象的顶点在第四象限,则函数()f x '的图象是( )10、曲线()by f x ax x==-在点(2,(2))f 处的切线方程为74120x y --=,则,a b 的值分别为 ( )A.13a b =⎧⎨=⎩ B.13a b =-⎧⎨=⎩ C.13a b =⎧⎨=-⎩ D.13a b =-⎧⎨=-⎩11、设函数()y f x =在(,)a b 上的导函数为'()f x ,'()f x 在(,)a b 上的导函数为''()f x ,若在(,)a b 上,''()0f x <恒成立,则称函数函数()f x 在(,)a b 上为“凸函数”.已知当2m ≤时,3211()62f x x mx x =-+在(1,2)-上是“凸函数”.则()f x 在(1,2)-上 ( )A.既有极大值,也有极小值B.既有极大值,也有最小值C.有极大值,没有极小值D.没有极大值,也没有极小值12、如图,曲线()y f x =上任一点P 的切线PQ 交x 轴于Q ,过P 作PT 垂直于x 轴于T ,若PTQ ∆的面积为12,则y 与'y 的关系满足 ( )A.'y y =B.'y y =-C.2'y y =D.2'y y =第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中的横线上.)13、函数xe x xf )3()(-=的单调递增区间是_____________ 14、曲线1y x=和2y x =在它们交点处的两条切线与x 轴所围成的三角形面积是 . 15、已知函数b ax x ax x f +-+=63)(23在x =2处取得极值9,则2a b +=16、已知函数32()(,)f x x ax bx a b =++∈R 的图象如图 所示,它与直线0y =在原点处相切,此切线与函数图象所围 区域(图中阴影部分)的面积为274,则a 的值为 . 三、解答题(本大题共6小题,共74分,解答应写出必要的文字说明、证明过程及演算步骤.)17、(12分)Oyx求由曲线2,,y x y x ==及2y x =围成的平面图形面积.18、(12分)已知函数32()(1)48(2)f x ax a x a x b =+-+-+的图象关于原点成中心对称. (1)求,a b 的值;(2)求()f x 的单调区间及极值.19、(12分)某厂生产产品x 件的总成本32()120075c x x =+(万元),已知产品单价P(万元)与产品件数x 满足:2kP x=,生产100件这样的产品单价为50万元. (1)设产量为x 件时,总利润为()L x (万元),求()L x 的解析式;(2)产量x 定为多少件时总利润()L x (万元)最大?并求最大值(精确到1万元).20、(12分) 设函数329()62f x x x x a =-+-. (1)对于任意实数x ,()f x m '≥恒成立,求m 的最大值;(2)若方程()0f x =有且仅有一个实根,求a 的取值范围.21、(12分)已知函数1()ln(1),01xf x ax x x-=++≥+,其中0a > (1)若()f x 在x =1处取得极值,求a 的值; (2)求()f x 的单调区间;(3)若()f x 的最小值为1,求a 的取值范围。
人教A版选修一高二数学测试题:导数与定积分.docx

1.已知32()967,f x ax x x =++-若(1)4f '-=,则a 的值等于( ) A.193 B.163 C.103 D.1332.下列求导运算正确的是 ( )A . 2212)1(xx x x +='+ B . x a x a ln )(log =' C . 2(cos )'2sin x x x x =- D . 3211)1(x x x -='+3.曲线13-=x y 在1=x 处的切线方程为 ( )A.22-=x yB. 33-=x yC.1=yD.1=x4.已知曲线23ln 4x y x =-的一条切线的斜率为12,则切点的横坐标为( ) A 12B 1C 2D 3 5、x x x x f --=23)(的单调减区间是( ) A.()31,-∞- B.),1(∞ C.()31,-∞-,),1(∞ D.)1,31(- 6.函数a x x y +-=2332的极大值是6,则a 的值为( )A .6B . 5C .7D .1 7.32()32f x x x =-+在区间[]1,1-上的最大值是( )(A)-2 (B)0 (C)2 (D)48.曲线x y e =在点(2,2e )处的切线与坐标轴所围成三角形的面积为( ) A 294e B 22e C 2e D 22e 9.、在独立性检验中,统计量2χ有两个临界值:3.841和6.635;当2χ>3.841时,有95%的把握说明两个事件有关,当2χ>6.635时,有99%的把握说明两个事件有关,当2χ≤3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的2χ=20.87,根据这一数据分析,认为打鼾与患心脏病之间A .有95%的把握认为两者有关B .约有95%的打鼾者患心脏病C .有99%的把握认为两者有关D .约有99%的打鼾者患心脏病 10.设a <b,函数2()()y x a x b =--的图像可能是11.复数iz -=11的共轭复数是 12.函数()x ax x f -=3在R 上为减函数,则a 的取值范围是_______13.(理)函数()2sin(3)4f x x π=+,则=)('x f ; (理)定积分dx x ⎰+102)1(的值是 ;(文)函数sin x y x=的导数为______ ; (文)已知函数4532)(23+-+=x x x x f ,则=-')3(f ____ ;14、已知函数1)(23+++=bx ax x x f 在x=-3和x=1时取得极值.(2)求函数()f x 在[-4,2]上的最大值和最小值.15、已知函数f (x )=x 3-3x 2-9x +11.(1)写出函数f (x )的递减区间;(2)讨论函数f(x)的极大值或极小值,如有写出极值.16、(本小题满分10分)已知与曲线32y x x=+-相切的直线与直线261035-+=互相垂直x y(Ⅰ)求切点坐标;(Ⅱ)求切线方程。
高中数学导数及其应用测试卷新人教A版选修

导数应用测试题一、选择题:(本大题共12小题,每小题5分, 共60分) 1.设函数f(x)在0x 处可导,则xx f x x f x ∆-∆-→∆)()(lim000等于 ( )A .)('0x fB .)('0x f -C .)('0x f --D .)(0x f -- 2.若13)()2(lim000=∆-∆+→∆xx f x x f x ,则)('0x f 等于 ( ) A .32 B .23C .3D .2 3.曲线x x y 33-=上切线平行于x轴的点的坐标是( )A .(-1,2)B .(1,-2)C .(1,2)D .(-1,2)或(1,-2)4.若函数f(x)的导数为f ′(x)=-sinx ,则函数图像在点(4,f (4))处的切 线的倾斜角为( )A .90°B .0°C .锐角D .钝角5.函数5123223+--=x x x y 在[0,3]上的最大值、最小值分别是 ( )A .5,-15B .5,-4C .-4,-1D .5,-166.一直线运动的物体,从时间t 到t+△t 时,物体的位移为△s ,那么ts t ∆∆→∆0lim 为( )A .从时间t 到t+△t 时,物体的平均速度B .时间t 时该物体的瞬时速度C .当时间为△t 时该物体的速度D .从时间t 到t+△t 时位移的平均变化率7.关于函数762)(23+-=x x x f ,下列说法不正确的是 ( )A .在区间(∞-,0)内,)(x f 为增函数B .在区间(0,2)内,)(x f 为减函数C .在区间(2,∞+)内,)(x f 为增函数D .在区间(∞-,0)),2(+∞⋃内,)(x f 为增函数8.对任意x ,有34)('x x f =,f(1)=-1,则此函数为 ( ) A .4)(x x f = B .2)(4-=x x f C .1)(4+=x x f D .2)(4+=x x f9.函数y=2x 3-3x 2-12x+5在[0,3]上的最大值与最小值分别是 ( )A.5 , -15B.5 , 4C.-4 , -15D.5 , -1610.抛物线y=x 2到直线x-y-2=0的最短距离为 ( )A .2B 。
人教A版高中数学选修一 选修1-1第三章导数综合练习(2).docx

高二数学选修1-1第三章导数综合练习(2)一、选择题1.设M 和m 分别是函数f (x )在[a ,b ]上的最大值和最小值,若m =M ,则f ′(x )A.等于0B.小于0C.等于1D.不确定2.设f (x )=ax 3+bx 2+cx +d (a >0),则f (x )为增函数的充要条件是A.b 2-4ac >0B.b >0,c >0C.b =0,c >0D.b 2-3ac <03. 函数y =1+3x -x 3有A.极小值-1,极大值1B.极小值-2,极大值3C.极小值-2,极大值2D.极小值-1,极大值34、已知f(x)=2x 3-6x 2+m ( m 为常数),在[ -2,2]上有最大值3,那么函数在[ -2,2]上的最小值为( )A .-37B .-29C .-5D .-115、下列函数存在极值的是( ) A .y= x1 B .y= x2 C .y=x3 D .y=2 6、若f(x)=mx 3+12mx 2+36mx-13(m<0)有极大值33m ,则极小值为( )A .0B .33C .-13D -267. 函数,93)(23-++=x ax x x f 已知3)(-=x x f 在时取得极值,则a =A .2B .3C .4D .58.已知二次函数y =ax 2+(a 2+1)x 在x =1处的导数值为1,则该函数的最大值是 ( )A .B .C .D .9.设函数f (x)在定义域内可导,y = f (x)的图象如图所示,则导函数y =f ′(x)的图象可能是A. B. C. D.1625825425225o x y o x y o x y o x y y o x10.下列说法:000000000000000()()(1)lim ,()()lim ,()()(3)lim ,tan ()()(4)lim ()x x x x x x x x f x f x A A x x x x f x f x A A x x x x f x f x A art A x x f x f x y f x x x x x →→→→-=--==--=--==-若则是物体在到内的平均速度(2)若则是物体在时的瞬时速度若则的倾斜角为若不存在,则曲线在处无切线 其中错误的说法的个数是 A .1 B 、2 C 、3 D 、411.函数f (x) =x 3 +ax 2 +bx +c,其中a,b,c 为实数,当a 2 – 3b<0时,f (x)是A .增函数;B 、减函数C .常数;D 、不是单调函数,也不是常数12.(2005年高考·湖南卷·理6)设f 0(x ) = sinx ,f 1(x )=f 0′(x ),f 2(x )=f 1′(x ),…,f n +1(x ) = f n ′(x ),n ∈N ,则f 2005(x )= A .sinx B .-sinx C .cos x D .-cosx13.设f (x )在点x =x 0处可导,且0(7)()limx f x x f x x∆→+∆-∆=1,则f ’(x 0)=( ) (A )1 (B )0 (C )7 (D )71 14.函数y =x 3-3x 2-8x +5在区间[-4, 4]上的最大值是( )(A )-22 (B )-71 (C )-15 (D )1015.函数f (x )=x 2+x 在闭区间[-1, 0]上的最小值为( ) (A )0 (B )-41 (C )21 (D )-2 16.给出下面四个命题:① 函数y =x 2-5x +4(-1≤x ≤1)的最大值为10,最小值为-49;② 函数y =2x 2-4x +1 (2<x <4)的最大值为17,最小值为1;③ 函数y =x 3-12x (-3<x <2)的最大值为16,最小值为-16;④ 函数y =x 3-12x (-2<x <2)无最大值,也无最小值,其中正确的命题有( )(A )1个 (B )2个 (C )3个 (D )4个二、填空题17.设函数f (x )在区间[a ,b ]上满 足f ′(x )<0,则f (x )在[a ,b ]上的最小值为______, 最大值为18.设 。
最新人教A版高中数学选修2-2 第一章 导数及其应用 综合检测习题(含答案解析)

第一章导数及其应用综合检测时间120分钟,满分150分。
一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2010·全国Ⅱ文,7)若曲线y=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,则( ) A.a=1,b=1B.a=-1,b=1C.a=1,b=-1D.a=-1,b=-1[答案] A[解析] y′=2x+a,∴y′|x=0=(2x+a)|x=0=a=1,将(0,b)代入切线方程得b=1.2.一物体的运动方程为s=2t sin t+t,则它的速度方程为( )A.v=2sin t+2t cos t+1B.v=2sin t+2t cos tC.v=2sin tD.v=2sin t+2cos t+1[答案] A[解析] 因为变速运动在t0的瞬时速度就是路程函数y=s(t)在t0的导数,S′=2sin t+2t cos t+1,故选A.3.曲线y=x2+3x在点A(2,10)处的切线的斜率是( )A.4B.5C.6D.7[答案] D[解析] 由导数的几何意义知,曲线y=x2+3x在点A(2,10)处的切线的斜率就是函数y=x2+3x在x =2时的导数,y′|x=2=7,故选D.4.函数y=x|x(x-3)|+1( )A.极大值为f(2)=5,极小值为f(0)=1B.极大值为f(2)=5,极小值为f(3)=1C.极大值为f(2)=5,极小值为f(0)=f(3)=1D.极大值为f(2)=5,极小值为f(3)=1,f(-1)=-3[答案] B[解析] y =x |x (x -3)|+1=⎩⎪⎨⎪⎧x 3-3x 2+1 (x <0或x >3)-x 3+3x 2+1 (0≤x ≤3) ∴y ′=⎩⎪⎨⎪⎧3x 2-6x (x <0或x >3)-3x 2+6x (0≤x ≤3)x 变化时,f ′(x ),f (x )变化情况如下表:x (-∞,0)0 (0,2) 2 (2,3) 3 (3,+∞)f ′(x ) ++-+f (x )无极值极大值5极小值1极大极小故应选B.5.(2009·安徽理,9)已知函数f (x )在R 上满足f (x )=2f (2-x )-x 2+8x -8,则曲线y =f (x )在点(1,f (1))处的切线方程是( )A .y =2x -1B .y =xC .y =3x -2D .y =-2x +3 [答案] A[解析] 本题考查函数解析式的求法、导数的几何意义及直线方程的点斜式. ∵f (x )=2f (2-x )-x 2+8x -8, ∴f (2-x )=2f (x )-x 2-4x +4, ∴f (x )=x 2,∴f ′(x )=2x ,∴曲线y =f (x )在点(1,f (1))处的切线斜率为2,切线方程为y -1=2(x -1),∴y =2x -1. 6.函数f (x )=x 3+ax 2+3x -9,已知f (x )在x =-3时取得极值,则a 等于( ) A .2 B .3 C .4 D .5 [答案] D[解析] f ′(x )=3x 2+2ax +3, ∵f (x )在x =-3时取得极值, ∴x =-3是方程3x 2+2ax +3=0的根, ∴a =5,故选D.7.设f (x ),g (x )分别是定义在R 上的奇函数和偶函数.当x <0时,f ′(x )g (x )+f (x )g ′(x )>0,且g (-3)=0,则不等式f (x )g (x )<0的解集是( )A.(-3,0)∪(3,+∞)B.(-3,0)∪(0,3)C.(-∞,-3)∪(3,+∞)D.(-∞,-3)∪(0,3)[答案] D[解析] 令F(x)=f(x)·g(x),易知F(x)为奇函数,又当x<0时,f′(x)g(x)+f(x)g′(x)>0,即F′(x)>0,知F(x)在(-∞,0)内单调递增,又F(x)为奇函数,所以F(x)在(0,+∞)内也单调递增,且由奇函数知f(0)=0,∴F(0)=0.又由g(-3)=0,知g(3)=0∴F(-3)=0,进而F(3)=0于是F(x)=f(x)g(x)的大致图象如图所示∴F(x)=f(x)·g(x)<0的解集为(-∞,-3)∪(0,3),故应选D.8.下面四图都是同一坐标系中某三次函数及其导函数的图象,其中一定不正确的序号是( )A.①②B.③④C.①③D.①④[答案] B[解析] ③不正确;导函数过原点,但三次函数在x=0不存在极值;④不正确;三次函数先增后减再增,而导函数先负后正再负.故应选B.9.(2010·湖南理,5)⎠⎛241xd x 等于( )A .-2ln2B .2ln2C .-ln2D .ln2 [答案] D[解析] 因为(ln x )′=1x,所以 ⎠⎛241xdx =ln x |42=ln4-ln2=ln2.10.已知三次函数f (x )=13x 3-(4m -1)x 2+(15m 2-2m -7)x +2在x ∈(-∞,+∞)是增函数,则m 的取值范围是( )A .m <2或m >4B .-4<m <-2C .2<m <4D .以上皆不正确 [答案] D[解析] f ′(x )=x 2-2(4m -1)x +15m 2-2m -7,由题意得x 2-2(4m -1)x +15m 2-2m -7≥0恒成立,∴Δ=4(4m -1)2-4(15m 2-2m -7) =64m 2-32m +4-60m 2+8m +28 =4(m 2-6m +8)≤0, ∴2≤m ≤4,故选D.11.已知f (x )=x 3+bx 2+cx +d 在区间[-1,2]上是减函数,那么b +c ( ) A .有最大值152B .有最大值-152C .有最小值152D .有最小值-152[答案] B[解析] 由题意f ′(x )=3x 2+2bx +c 在[-1,2]上,f ′(x )≤0恒成立.所以⎩⎪⎨⎪⎧f ′(-1)≤0f ′(2)≤0即⎩⎪⎨⎪⎧2b -c -3≥04b +c +12≤0令b +c =z ,b =-c +z ,如图 过A ⎝⎛⎭⎪⎫-6,-32得z 最大, 最大值为b +c =-6-32=-152.故应选B.12.设f (x )、g (x )是定义域为R 的恒大于0的可导函数,且f ′(x )g (x )-f (x )g ′(x )<0,则当a <x <b 时有( )A .f (x )g (x )>f (b )g (b )B .f (x )g (a )>f (a )g (x )C .f (x )g (b )>f (b )g (x )D .f (x )g (x )>f (a )g (x ) [答案] C [解析] 令F (x )=f (x )g (x )则F ′(x )=f ′(x )g (x )-f (x )g ′(x )g 2(x )<0f (x )、g (x )是定义域为R 恒大于零的实数∴F (x )在R 上为递减函数, 当x ∈(a ,b )时,f (x )g (x )>f (b )g (b )∴f (x )g (b )>f (b )g (x ).故应选C.二、填空题(本大题共4个小题,每小题4分,共16分.将正确答案填在题中横线上) 13.⎠⎛-2-1d x(11+5x )3=________.[答案]772[解析] 取F (x )=-110(5x +11)2,从而F ′(x )=1(11+5x )3则⎠⎛-2-1d x(11+5x )3=F (-1)-F (-2) =-110×62+110×12=110-1360=772.14.若函数f (x )=ax 2-1x的单调增区间为(0,+∞),则实数a 的取值范围是________.[答案] a ≥0[解析] f ′(x )=⎝ ⎛⎭⎪⎫ax -1x ′=a +1x2,由题意得,a +1x2≥0,对x ∈(0,+∞)恒成立,∴a ≥-1x2,x ∈(0,+∞)恒成立,∴a ≥0.15.(2009·陕西理,16)设曲线y =xn +1(n ∈N *)在点(1,1)处的切线与x 轴的交点的横坐标为x n ,令a n=lg x n ,则a 1+a 2+…+a 99的值为________.[答案] -2[解析] 本小题主要考查导数的几何意义和对数函数的有关性质.k =y ′|x =1=n +1,∴切线l :y -1=(n +1)(x -1), 令y =0,x =n n +1,∴a n =lg nn +1, ∴原式=lg 12+lg 23+…+lg 99100=lg 12×23×…×99100=lg 1100=-2.16.如图阴影部分是由曲线y =1x,y 2=x 与直线x =2,y =0围成,则其面积为________.[答案] 23+ln2[解析] 由⎩⎪⎨⎪⎧y 2=x ,y =1x,得交点A (1,1)由⎩⎪⎨⎪⎧x =2y =1x得交点B ⎝ ⎛⎭⎪⎫2,12.故所求面积S =⎠⎛01x d x +⎠⎛121xd x=23x 32| 10+ln x | 21=23+ln2. 三、解答题(本大题共6个小题,共74分.解答应写出文字说明、证明过程或演算步骤) 17.(本题满分12分)(2010·江西理,19)设函数f (x )=ln x +ln(2-x )+ax (a >0). (1)当a =1时,求f (x )的单调区间;(2)若f (x )在(0,1]上 的最大值为12,求a 的值.[解析] 函数f (x )的定义域为(0,2),f ′(x )=1x -12-x+a ,(1)当a =1时,f ′(x )=-x 2+2x (2-x ),所以f (x )的单调递增区间为(0,2),单调递减区间为(2,2);(2)当x ∈(0,1]时,f ′(x )=2-2xx (2-x )+a >0,即f (x )在(0,1]上单调递增,故f (x )在(0,1]上的最大值为f (1)=a ,因此a =12.18.(本题满分12分)求曲线y =2x -x 2,y =2x 2-4x 所围成图形的面积.[解析] 由⎩⎪⎨⎪⎧y =2x -x 2,y =2x 2-4x 得x 1=0,x 2=2.由图可知,所求图形的面积为S =⎠⎛02(2x -x 2)d x +|⎠⎛02(2x 2-4x )d x |=⎠⎛02(2x -x 2)d x -⎠⎛02(2x 2-4x )d x .因为⎝⎛⎭⎪⎫x 2-13x 3′=2x -x 2,⎝ ⎛⎭⎪⎫23x 3-2x 2′=2x 2-4x ,所以S =⎝⎛⎭⎪⎫x 2-13x 3⎪⎪⎪20-⎝ ⎛⎭⎪⎫23x 3-2x 2⎪⎪⎪2=4.19.(本题满分12分)设函数f (x )=x 3-3ax +b (a ≠0).(1)若曲线y =f (x )在点(2,f (2))处与直线y =8相切,求a ,b 的值; (2)求函数f (x )的单调区间与极值点.[分析] 考查利用导数研究函数的单调性,极值点的性质,以及分类讨论思想. [解析] (1)f ′(x )=3x 2-3a .因为曲线y =f (x )在点(2,f (2))处与直线y =8相切, 所以⎩⎪⎨⎪⎧f ′(2)=0,f (2)=8.即⎩⎪⎨⎪⎧3(4-a )=0,8-6a +b =8.解得a =4,b =24.(2)f ′(x )=3(x 2-a )(a ≠0).当a <0时,f ′(x )>0,函数f (x )在(-∞,+∞)上单调递增,此时函数f (x )没有极值点. 当a >0时,由f ′(x )=0得x =±a .当x ∈(-∞,-a )时,f ′(x )>0,函数f (x )单调递增; 当x ∈(-a ,a )时,f ′(x )<0,函数f (x )单调递减; 当x ∈(a ,+∞)时,f ′(x )>0,函数f (x )单调递增. 此时x =-a 是f (x )的极大值点,x =a 是f (x )的极小值点. 20.(本题满分12分)已知函数f (x )=12x 2+ln x .(1)求函数f (x )的单调区间; (2)求证:当x >1时,12x 2+ln x <23x 3.[解析] (1)依题意知函数的定义域为{x |x >0}, ∵f ′(x )=x +1x,故f ′(x )>0,∴f (x )的单调增区间为(0,+∞). (2)设g (x )=23x 3-12x 2-ln x ,∴g ′(x )=2x 2-x -1x,∵当x >1时,g ′(x )=(x -1)(2x 2+x +1)x>0,∴g (x )在(1,+∞)上为增函数, ∴g (x )>g (1)=16>0,∴当x >1时,12x 2+ln x <23x 3.21.(本题满分12分)设函数f (x )=x 3-92x 2+6x -a .(1)对于任意实数x, f ′(x )≥m 恒成立,求m 的最大值;(2)若方程f (x )=0有且仅有一个实根,求a 的取值范围.[分析] 本题主要考查导数的应用及转化思想,以及求参数的范围问题. [解析] (1)f ′(x )=3x 2-9x +6=3(x -1)(x -2).因为x ∈(-∞,+∞).f ′(x )≥m ,即3x 2-9x +(6-m )≥0恒成立. 所以Δ=81-12(6-m )≤0,得m ≤-34,即m 的最大值为-34.(2)因为当x <1时,f ′(x )>0;当1<x <2时,f ′(x )<0;当x >2时f ′(x )>0. 所以当x =1时,f (x )取极大值f (1)=52-a ,当x =2时,f (x )取极小值f (2)=2-a .故当f (2)>0或f (1)<0时,方程f (x )=0仅有一个实根,解得a <2或a >52.22.(本题满分14分)已知函数f (x )=-x 3+ax 2+1(a ∈R ).(1)若函数y =f (x )在区间⎝ ⎛⎭⎪⎫0,23上递增,在区间⎣⎢⎡⎭⎪⎫23,+∞上递减,求a 的值; (2)当x ∈[0,1]时,设函数y =f (x )图象上任意一点处的切线的倾斜角为θ,若给定常数a ∈⎝ ⎛⎭⎪⎫32,+∞,求θ的取值范围;(3)在(1)的条件下,是否存在实数m ,使得函数g (x )=x 4-5x 3+(2-m )x 2+1(m ∈R )的图象与函数y =f (x )的图象恰有三个交点.若存在,请求出实数m 的值;若不存在,试说明理由.[解析] (1)依题意f ′⎝ ⎛⎭⎪⎫23=0,由f ′(x )=-3x 2+2ax ,得-3⎝ ⎛⎭⎪⎫232+2a ·23=0,即a =1.(2)当x ∈[0,1]时,tan θ=f ′(x )=-3x 2+2ax =-3⎝ ⎛⎭⎪⎫x -a 32+a23.由a ∈⎝ ⎛⎭⎪⎫32,+∞,得a 3∈⎝ ⎛⎭⎪⎫12,+∞. ①当a 3∈⎝ ⎛⎦⎥⎤12,1,即a ∈⎝ ⎛⎦⎥⎤32,3时,f ′(x )max =a 23,f (x )min =f ′(0)=0.此时0≤tan θ≤a 23. ②当a3∈(1,+∞),即a ∈(3,+∞)时,f ′(x )max =f ′(1)=2a -3,f ′(x )min =f ′(0)=0,此时,0≤tan θ≤2a -3.又∵θ∈[0,π),∴当32<a ≤3时,θ∈⎣⎢⎡⎦⎥⎤0,arctan a 23, 当a >3时,θ∈[0,arctan(2a -3)].(3)函数y =f (x )与g (x )=x 4-5x 3+(2-m )x 2+1(m ∈R )的图象恰有3个交点,等价于方程-x 3+x 2+1=x 4-5x 3+(2-m )x 2+1恰有3个不等实根,∴x 4-4x 3+(1-m )x 2=0,显然x =0是其中一个根(二重根),方程x 2-4x +(1-m )=0有两个非零不等实根,则⎩⎪⎨⎪⎧Δ=16-4(1-m )>01-m ≠0∴m >-3且m ≠1故当m >-3且m ≠1时,函数y =f (x )与y =g (x )的图象恰有3个交点.。
人教A版高中数学选修一高二(文)导数综合测试

1.函数 f ( x) x eln x 的单调递增区间为()
A. ( 0, ) B. ( ,0) C. ( 0, ) 和 ( ,0) D. R
2. 若曲线 y x4 的一条切线 l 与直线 x 4 y 8 0 垂直,则切线 l 的方程为 ()
A. 4 x y 3 0 B. x 4 y 5 0 C. 4 x y 3 0 D. x 4 y 3 0
所以 f (x) 在 ( 1,1) 上单调递减,在 ( , 1], 1, 上单调递增 . …………… 5 分
所以 f (x) 的极小值为 f (1) 2 . …………………………………… 7 分
(Ⅱ)因为 f ( x) 3x2 3a ≥ 3a ,…………………………………… 9 分
所以,要使直线 x y m 0 对任意的 m R 总不是曲线 y f ( x) 的切线,当且仅当
AB的斜率恒大于 1,求实数
------------------------------------------------------------------- 奋斗没有终点任何时候都是一个起点
-----------------------------------------------------
------------------------------------------------------------------- 奋斗没有终点任何时候都是一个起点
-----------------------------------------------------
高二数学(文)导数综合测试
1. A 2. A 3. B 4. B 5. A 6.- 4
7. (0,3) .
高三导数练习题 高三数学选修单元测试题五套 人教版 高三数学选修单元测试题五套 人教版

(高三)导数--对数函数与指数函数的导数练习题A.(x +x 1)′=1+21x; B.(log 2x )′=2ln 1x ; C.(3x )′=3x log 3e ; D.(x 2cos x )′=-2x sin x y =ln(3-2x -x 2)的导数为 A.32+x B.2231x x -- C.32222-++x x x D.32222-+-x x x y =lncos2x 的导数为A.-tan2x B.-2tan2xx x y =xx a22-(a >0且a ≠1),那么y ′为 A.xx a22-ln a ; B.2(ln a )xx a22-; C.2(x -1)xx a22-·ln a ; D.(x -1)xx a 22-ln ay =x ln 的导数为x x ln ; B.xx ln 2 ; C.xx ln 1 ;D.xx ln 21y =sin32x 的导数为A.2(cos32x )·32x ·ln3 ;B.(ln3)·32x ·cos32x ; 2x ;2x ·cos32xy =xx e e 2)12(+,则y ′=___________.y =59++x x 的切线中,经过原点的切线为 9.(1)函数y =x22的导数为y ′=__________;(2)函数y =log 3cos x 的导数为__________. y =e x -e ln x 在点(e ,1)处的切线方程为___________. y =ln(21x +-x )的导数.y =x x (x >0)的导数.f (x )满足:af (x )+bf (x 1)=xc(其中a 、b 、c 均为常数,且|a |≠|b |),试求f ′(x ).高三第三章导数--复合函数的导数练习题y =2)13(1-x 的导数是A.3)13(6-x ;B.2)13(6-x ;C.-3)13(6-x ;D.-2)13(6-x y =21sin2x +sin x ,那么y ′是 ; B.既有最大值,又有最小值的偶函数 ; y =sin 3(3x +4π)的导数为 2(3x +4π)cos(3x +4π2(3x +4π)cos(3x +4π) 2(3x +4π) D.-9sin 2(3x +4π)cos(3x +4π) y =cos(sin x )的导数为A.-[sin(sin x )]cos x ;B.-sin(sin x );C.[sin(sin x )]cos x ;D.sin(cos x ) y =cos2x +sin x 的导数为A.-2sin2x ;x +x x 2cos ;C.-2sin2x +x x 2sin ;x -xx2cos y =11+x 上点P (1,21)且与过P 点的切线夹角最大的直线的方程为 y -8x +7=0y +8x +7=0 C.2y +8x -9=0y -8x +9=0 y =(1+sin3x )3是由___________两个函数复合而成.y =sin3x 在点P (3π,0)处切线的斜率为___________. y =x sin(2x -2π)cos(2x +2π)的导数是.10.(1)y =)32cos(π-x 的导数为;(2)y =cos 3x 1的导数是___________.11.若可导函数f (x )是奇函数,求证:其导函数f ′(x )是偶函数.12.用求导方法证明:21C 2C n n + +…+n nn C =n ·2n -1.高三第三章导数--函数的单调性练习题f (x )在[a ,b ]上连续,在(a ,b )内可导,且x ∈(a ,b )时,f ′(x )>0,又f (a )<0,则 A.f (x )在[a ,b ]上单调递增,且f (b )>0;B.f (x )在[a ,b ]上单调递增,且f (b )<0C.f (x )在[a ,b ]上单调递减,且f (b )<0;D.f (x )在[a ,b ]上单调递增,但f (b )的符号无法判断 y =3x -x 3的单调增区间是A.(0,+∞);B.(-∞,-1) ;C.(-1,1);D.(1,+∞) y =f (x )=ax 3+x 在x ∈(-∞,+∞)内是增函数,则A.a >0;B.a <0 ;C.a =1;D.a =31 4.f (x )=x +x2(x >0)的单调减区间是A.(2,+∞);B.(0,2) ;C.(2,+∞);D.(0,2) y =sin x cos 2x 在(0,2π)上的减区间为A.(0,arctan22); B.(arctan2,22π) ; C.(0,2π) ;D.(arctan 2,21π) y =x ln x 在区间(0,1)上是A.单调增函数B. 在(0,e 1)上是减函数,在(e 1,1)上是增函数 C.单调减函数 D.在(0,e 1)上是增函数,在(e1,1)上是减函数7.(1)函数f (x )=cos 2x 的单调减区间是__________; (2)函数y =2x +sin x 的增区间为_________. 8.(1)函数y =232+-x x x 的增区间是_________; (2)函数y =x x ln 的减区间是___________.9.已知0<x <2π,则tan x 与x +33x 的大小关系是tan x ___________x +33x .10.已知函数f (x )=kx 3-3(k +1)x 2-k 2+1(k >0).若f (x )的单调递减区间是(0,4), (1)求k 的值;(2)当k <x 时,求证:2x >3-x1.11.试证方程sin x =x 只有一个实根.12.三次函数f (x )=x 3-3bx +3b 在[1,2]内恒为正值,求b 的取值X 围.(高三)§3.3 函数的和、差、积、商的导数练习题f (x )=sin α-cos x ,则f ′(α)等于α;α ;α+cos α;α 2.f (x )=ax 3+3x 2+2,若f ′(-1)=4,则a 的值等于A.319;B.316 ;C.313; D.310 y =22xax + (a >0)的导数为0,那么x 等于A.a ;B.±a ;C.-a ;D.a 2y =x sin x 的导数为A.y ′=2x sin x +x cos xB.y ′=xx 2sin +x cos xC.y ′=xx sin +x cos x; D.y ′=xx sin -x cos xy =xxsin 的导数为 A.y ′=2sin cos x x x x + B.y ′=2sin cos x x x x - C.y ′=2cos sin x x x x - D.y ′=2cos sin x x x x +y =x 2cos x 的导数为A.y ′=2x cos x -x 2sin x;B.y ′=2x cos x +x 2sin x ;C.y ′=x 2cos x -2x sin x;D.y ′=x cos x -x 2sin x x -6y +1=0垂直,且与曲线y =x 3+3x 2-1相切的直线方程是____ s =t 2(1+sin t ),则当t =2π时,瞬时速度为_______ 9.(1)f (x )=354337xx x x ++,则f ′(x )=______; (2)f (x )=xx++-1111,则f ′(x )=_______.10.已知f (x )=xx2cos 12sin +,则f ′(x )=_______.11.求过点(2,0)且与曲线y =x1相切的直线的方程.12.水以20米3/分的速度流入一圆锥形容器,设容器深30米,上底直径12米,试求当水深10米时,水面上升的速度.高三第三章导数--函数的极值练习题f ′(x 0)=0时,则f (x 0)为f (x )的极大值 ; f ′(x 0)=0时,则f (x 0)为f (x )的极小值 f ′(x 0)=0时,则f (x 0)为f (x )的极值; f (x 0)为函数f (x )的极值且f ′(x 0)存在时,则f ′(x 0)=0 2.下列四个函数,在x =0处取得极值的函数是①y =x 3②y =x 2+1 ③y =|x | ④y =2x A.①②B.②③ C.③④D.①③ y =216x x+的极大值为 ; ; ; y =x 3-3x 的极大值为m ,极小值为n ,则m +n 为 ; ; ; 5.y =ln 2x +2ln x +2的极小值为A.e -1B.0 C.-1 6.y =2x 3-3x 2+a 的极大值为6,那么a 等于B.0C.5 f (x )=x 3-3x 2+7的极大值为___________. y =3x 5-5x 3共有___________个极值.y =-x 3+48x -3的极大值为___________;极小值为___________.f (x )=x -3223x 的极大值是___________,极小值是___________.y =x 3+ax 2+bx +27在x =-1时有极大值,在x =3时有极小值,则a =______,b =______.f (x )=x 3+ax 2+bx +c ,当x =-1时,取得极大值7;当xa 、b 、c 的值.f (x )=x +xa+b 有极小值2,求a 、b 应满足的条件.y =f (x )为三次函数,且图象关于原点对称,当x =21时,f (x )的极小值为-1,求函数的解析式.(高三)§《函数的最值》练习题( )y =f (x )在区间[a ,b ]上的最大值是M ,最小值是m ,若M =m ,则f ′(x )( ) 0 C.小于0 y =234213141x x x ++,在[-1,1]上的最小值为( ) ;B.-2 ;C.-1;D.1213 212xx y +=在( ) A .()()间内是减函数;内是增函数,在其余区,内是增函数;11.,.-+∞∞-B A ()()间内是增函数内是减函数,在其余区,内是减函数;11.,.-+∞∞-D C5.函数y =122+-x x x 的最大值为( ) A.33; C.21; D.236函数x x x f cos 3sin )(3+=的值域为( ) [][][)()3,3.;4,4.;3,3.;4,4.----D C B Ay x ,为正实数,且满足,3,3,2=+≤≤y x y x ,则334y x +的最大值是( )A.24 ;B. 27 ;C. 33 ;D. 458.设f (x )=ax 3-6ax 2+b 在区间[-1,2]上的最大值为3,最小值为-29,且a >b ,则( ) A.a =2,b =29 B.a =2,b =3 C.a =3,b =2D.a =-2,b =-3 9.函数f (x )=sin2x -x 在[-2π,2π]上的最大值为_____;最小值为____ 10.函数x x x y 9623+-=在[]2,1-上当=x 时,=max y ;当=x 时,=min y11.函数4431)(3+-=x x x f 的极大值是,极小值是. 12.函数21x x y -+=的最大值是,最小值是13.函数x ax x f +=3)(恰有三个单调区间,则a 的取值X 围是.14.将正数a 分成两部分,使其立方和为最小,这两部分应分成____和____.15.在半径为R 的圆内,作内接等腰三角形,当底边上高为______时,它的面积最大.16.有一边长分别为8与5的长方形,在各角剪去相同的小正方形,把四边折起作成一个无盖小盒,要使纸盒的容积最大,问剪去的小正方形的边长应为多少?17.函数b ax ax x f ++=233)(在区间[]2,1-的最大值为10,最小值为8-,求b a ,的值18.设曲线()0≥=-x ey x在点()t e t M -,处的切线l 与x 轴y 轴所围成的三角形面积为().t S 求:(1)切线l 的方程;(2)().t S 的最大值(高三)§几种常见函数的导数练习题s =41t 4-3,则t =5时的瞬时速率为A.5 m/s ;B.25 m/s ;C.125 m/s ;D.625 m/s y =x n(n ∈N )在点P (2,)22n 处切线斜率为20,那么n 为 ; B.6 ;; f (x )=x x x 的导数是A.81x(x >0)B.-887x(x >0);C.8781x(x >0);D.881x- (x >0)4.f (x )与g(x )是定义在R 上的两个可导函数,若f (x ),g(x )满足f ′(x )=g ′(x ),则f (x )与g (x )满足A.f (x )=g (x ) ;B.f (x )-g (x )为常数函数 ;C.f (x )=g (x )=0 ;D.f (x )+g (x )为常数函数 5.两车在十字路口相遇后,又沿不同方向继续前进,已知A 车向北行驶,速率为30 km/h,B 车向东行驶,速率为40 km/h,那么A 、B 两车间直线距离的增加速率为 A.50 km/hB.60 km/h C.80 km/hD.65 km/hAB 长为20 cm,AM 段的质量与A 到M 的距离平方成正比,当AM =2 cm 时,AM 段质量为8 g,那么,当AM =x 时,M 处的细杆线密度ρ(x )为x; B .4x ; x; x y =x 4的斜率等于4的切线的方程是___________.l 1为曲线y 1=sin x 在点(0,0)处的切线,l 2为曲线y 2=cos x 在点(2π,0)处的切线,则l 1与l 2的夹角为___________. y =cos x 上的点(21,6π)且与过这点的切线垂直的直线方程为. y =sin x (0<x <π)上取一点M ,使过M 点的切线与直线y =x 23平行,则M 点的坐标为___________.11.路灯距地平面为8 m,一个身高为1.6 m 的人以84 m/min 的速率在地面上行走,从路灯在地平面上射影点C ,沿某直线离开路灯,求人影长度的变化速率v .12.已知直线x +2y -4=0与抛物线y 2=4x 相交于A 、B 两点,O 是坐标原点,试在抛物线的弧上求一点P ,使△P AB 面积最大.。
人教A版高中数学选修导数及其应用高考试题

导数的概念与运算第1题. ()f x '是31()213f x x x =++的导函数,则(1)f '-的值是 . 答案:3第2题.已知二次函数2()f x ax bx c =++的导数为()f x ',(0)0f '>,对于任意实数x ,有()0f x ≥,则(1)(0)f f '的最小值为( ) A.3 B.52 C.2 D.32答案:C第3题.设函数()f x 是R 上以5为周期的可导偶函数,则曲线()y f x =在5x =处的切线的斜率为( ) A.15-B.0 C.15 D.5答案:B第4题.已知曲线23ln 4x y x =-的一条切线的斜率为12,则切点的横坐标为( ) A .3B .2C .1D .12 答案:A第5题.曲线32242y x x x =--+在点(13)-,处的切线方程是 .答案:520x y +-=第6题.已知对任意实数x ,有()()f x f x -=-,()()g x g x -=,且0x >时,()0f x '>,()0g x '>,则0x <时( )A.()0f x '>,()0g x '>B.()0f x '>,()0g x '< C.()0f x '<,()0g x '> D.()0f x '<,()0g x '<答案:B导数的概念和性质第1题.设函数()f x 是R 上以5为周期的可导偶函数,则曲线()y f x =在5x =处的切线的斜率为( ) A.15-B.0 C.15 D.5 答案:B第2题. ()f x 是定义在(0)+∞,上的非负可导函数,且满足()()0xf x f x '+≤.对任意正数a b ,,若a b <,则必有( )A . ()()af b bf a ≤B .()()bf a af b ≤C .()()af a f b ≤D .()()bf b f a ≤ 答案:A第3题. 设()f x '是函数()f x 的导函数,将()y f x =和()y f x '=的图象画在同一个直角坐标系中,不可能正确的是( )答案:D 第4题.已知对任意实数x ,有()()()(f x f x g x g x -=--=,,且0x >时,()0()0f x g x ''>>,,则0x <时( )A .()0()0f x g x ''>>,B .()0()0f x g x ''><,C .()0()0f x g x ''<>,D .()0()0f x g x ''<<, 答案:B A . B . C . D .。
人教A版高中数学选修导数及其应用综合测试—

数学选修2-2第一章试卷一、选择题(本大题共16小题,每小题5分,共80分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
) 1. 已知函数f (x ) = a x 2 +c ,且(1)f '=2 , 则a 的值为 ( ) A.1B.2C.-1D. 02. 已知函数()f x 在1x =处的导数为3,则()f x 的解析式可能为 ( ) A .(x - 1)3+3(x - 1) B .2(x - 1)2C .2(x - 1)D .x - 1 3. 已知函数()f x 在1x =处的导数为1,则 0(1)(1)3limx f x f x x→--+=( )A .3B .23-C . 13D .32-4. 函数y = (2x +1) 3在x = 0处的导数是 ( )A.0B.1C.3D.6 5.函数)0,4(2cos π在点x y =处的切线方程是 ( )A .024=++πy xB .024=+-πy xC .024=--πy xD .024=-+πy x 6.曲线3cos (0)2y x x π=≤≤与坐标轴围成的面积是 ( ) A. 4 B.52C. 3D. 2 7.一质点做直线运动,由始点起经过t s 后的距离为s =41t 4- 4t 3 + 16t 2,则速度为零的时刻是 ( ) A.4s 末 B.8s 末 C.0s 与8s 末 D.0s,4s,8s 末 8.函数313y x x =+- 有 ( )A.极小值-1,极大值1B. 极小值-2,极大值3C.极小值-1,极大值3D. 极小值-2,极大值29. 已知自由下落物体的速度为V = g t ,则物体从t = 0到t 0所走过的路程为( ) A .2012gt B .20gt C . 2013gt D .2014gt 10.如果10N 的力能使弹簧压缩10cm ,为在弹性限度内将弹簧拉长6cm ,则力所做的功为( )A .0.28JB .0.12JC .0.26JD .0.18J 11、一物体在力()41F x x =-(单位:N)的的作用下,沿着与力F 相同的方向,从x=1m 处运动到x=3m 处, 则力()F x 所作的功为( )A. 10JB. 12JC. 14JD. 16J12、若函数3()33f x x bx b =-+在(0,1)内有极小值 , 则( )()A 01b << ()B 1b < ()C 0b > ()D 12b <13、函数32()23125f x x x x =--+在[]0,3上最大值和最小值分别是( )(A )5 , -15 (B )5,-4 (C)-4,-15 (D)5,-1614、若函数()f x 的导数为221x -+,则()f x 可以等于( ) A. 、321x -+ B 、1x + C.、4x - D 、323x x -+15、函数2sin(2)y x x =+导数是( ) A..2cos(2)x x +B.22sin(2)x x x +C.2(41)cos(2)x x x ++D.24cos(2)x x +16、函数2()2ln f x x x =-的递增区间是 ( )A.1(0,)2 B.11(,0)(,)22-+∞及 C.1(,)2+∞ D.11(,)(0,)22-∞-及 二、填空题:(每题4分共24分)11.函数32y x x x =--的单调增区间为___________________________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
导数练习题1.(本题满分12分)已知函数d x b a c bx ax x f +--++=)23()(23的图象如图所示.(I )求d c ,的值;(II )若函数)(x f 在2=x 处的切线方程为0113=-+y x ,求函数)(x f 的解析式;(III )在(II )的条件下,函数)(x f y =与mx x f y ++'=5)(31的图象有三个不同的交点,求m 的取值范围. 2.(本小题满分12分)已知函数)(3ln )(R a ax x a x f ∈--=. (I )求函数)(x f 的单调区间;(II )函数)(x f 的图象的在4=x 处切线的斜率为,23若函数]2)('[31)(23mx f x x x g ++=在区间(1,3)上不是单调函数,求m 的取值范围.3.(本小题满分14分)已知函数c bx ax x x f +++=23)(的图象经过坐标原点,且在1=x 处取得极大值. (I )求实数a 的取值范围;(II )若方程9)32()(2+-=a x f 恰好有两个不同的根,求)(x f 的解析式;(III )对于(II )中的函数)(x f ,对任意R ∈βα、,求证:81|)sin 2()sin 2(|≤-βαf f .4.(本小题满分12分)已知常数0>a ,e 为自然对数的底数,函数x e x f x -=)(,x a x x g ln )(2-=. (I )写出)(x f 的单调递增区间,并证明a e a >; (II )讨论函数)(x g y =在区间),1(a e 上零点的个数. 5.(本小题满分14分)已知函数()ln(1)(1)1f x x k x =---+.(I )当1k =时,求函数()f x 的最大值;(II )若函数()f x 没有零点,求实数k 的取值范围; 6.(本小题满分12分)已知2x =是函数2()(23)x f x x ax a e =+--的一个极值点(⋅⋅⋅=718.2e ). (I )求实数a 的值;(II )求函数()f x 在]3,23[∈x 的最大值和最小值.7.(本小题满分14分)已知函数)0,(,ln )2(4)(2≠∈-+-=a R a x a x x x f(I )当a=18时,求函数)(x f 的单调区间; (II )求函数)(x f 在区间],[2e e 上的最小值. 8.(本小题满分12分)已知函数()(6)ln f x x x a x =-+在(2,)x ∈+∞上不具有...单调性. (I )求实数a 的取值范围;(II )若()f x '是()f x 的导函数,设22()()6g x f x x '=+-,试证明:对任意两个不相等正数12x x 、,不等式121238|()()|||27g x g x x x ->-恒成立. 9.(本小题满分12分)已知函数.1,ln )1(21)(2>-+-=a x a ax x x f(I )讨论函数)(x f 的单调性;(II )证明:若.1)()(,),,0(,,521212121->--≠+∞∈<x x x f x f x x x x a 有则对任意10.(本小题满分14分)已知函数21()ln ,()(1),12f x x a xg x a x a =+=+≠-.(I )若函数(),()f x g x 在区间[1,3]上都是单调函数且它们的单调性相同,求实数a 的取值范围;(II )若(1,]( 2.71828)a e e ∈=L ,设()()()F x f x g x =-,求证:当12,[1,]x x a ∈时,不等式12|()()|1F x F x -<成立. 11.(本小题满分12分)设曲线C :()ln f x x ex =-( 2.71828e =⋅⋅⋅),()f x '表示()f x 导函数. (I )求函数()f x 的极值;(II )对于曲线C 上的不同两点11(,)A x y ,22(,)B x y ,12x x <,求证:存在唯一的0x 12(,)x x ∈,使直线AB 的斜率等于0()f x '. 12.(本小题满分14分)定义),0(,,)1(),(+∞∈+=y x x y x F y ,(I )令函数22()(3,log (24))f x F x x =-+,写出函数()f x 的定义域;(II )令函数322()(1,log (1))g x F x ax bx =+++的图象为曲线C ,若存在实数b 使得曲线C 在)14(00-<<-x x 处有斜率为-8的切线,求实数a 的取值范围;(III )当,*x y ∈N 且x y <时,求证(,)(,)F x y F y x >.导数练习题答案1.(本题满分12分)已知函数d x b a c bx ax x f +--++=)23()(23的图象如图所示.(I )求d c ,的值;(II )若函数)(x f 在2=x 处的切线方程为0113=-+y x ,求函数)(x f 的解析式; (III )在(II )的条件下,函数)(x f y =与m x x f y ++'=5)(31的图象有三个不同的交点,求m 的取值范围.解:函数)(x f 的导函数为 b a c bx ax x f 2323)(2'--++= …………(2分) (I )由图可知 函数)(x f 的图象过点(0,3),且0)1('=f 得⎩⎨⎧==⇒⎩⎨⎧=--++=0323233c d b a c b a d …………(4分)(II )依题意 3)2('-=f 且5)2(=f解得 6,1-==b a 所以396)(23++-=x x x x f …………(8分) (III )9123)(2+-='x x x f .可转化为:()m x x x x x x +++-=++-534396223有三个不等实根,即:()m x x x x g -+-=8723与x 轴有三个交点; 42381432--=+-='x x x x x g()m g m g --=-=⎪⎭⎫ ⎝⎛164,273. …………(10分) 当且仅当()01640276832<--=>-=⎪⎭⎫ ⎝⎛m g m g 且时,有三个交点, 故而,276816<<-m 为所求. …………(12分)2.(本小题满分12分)已知函数)(3ln )(R a ax x a x f ∈--=. (I )求函数)(x f 的单调区间;(II )函数)(x f 的图象的在4=x 处切线的斜率为,23若函数]2)('[31)(23mx f x x x g ++=在区间(1,3)上不是单调函数,求m 的取值范围.解:(I ))0()1()('>-=x xx a x f (2分)当(][)+∞>,1,1,0)(,0减区间为的单调增区间为时x f a当[)(];1,0,,1)(,0减区间为的单调增区间为时+∞<x f a 当a=1时,)(x f 不是单调函数 (5分)(II )32ln 2)(,22343)4('-+-=-==-=x x x f a a f 得 2)4()(',2)22(31)(223-++=∴-++=∴x m x x g x x mx x g (6分)⎩⎨⎧><∴.0)3(',0)1('g g (8分)⎪⎩⎪⎨⎧>-<∴,319,3m m (10分))3,319(--∈m (12分)3.(本小题满分14分)已知函数c bx ax x x f +++=23)(的图象经过坐标原点,且在1=x 处取得极大值. (I )求实数a 的取值范围;(II )若方程9)32()(2+-=a x f 恰好有两个不同的根,求)(x f 的解析式;(III )对于(II )中的函数)(x f ,对任意R ∈βα、,求证:81|)sin 2()sin 2(|≤-βαf f .解:(I ),23)(,00)0(2b ax x x f c f ++='=⇒=320)1(--=⇒='a b f由33210)(+-==⇒='a x x x f 或,因为当1=x 时取得极大值, 所以31332-<⇒>+-a a ,所以)3,(:--∞的取值范围是a ;…………(4分) (依题意得:9)32()32(2762+-=++a a a ,解得:9-=a所以函数)(x f 的解析式是:x x x x f 159)(23+-=…………(10分)(III )对任意的实数βα,都有,2sin 22,2sin 22≤≤-≤≤-βα在区间[-2,2]有: 230368)2(,7)1(,7430368)2(=+-==-=---=-f f f 函数]2,2[)(-在区间x f 上的最大值与最小值的差等于81, 所以81|)sin 2()sin 2(|≤-βαf f .…………(14分) 4.(本小题满分12分)已知常数0>a ,e 为自然对数的底数,函数x e x f x -=)(,x a x x g ln )(2-=. (I )写出)(x f 的单调递增区间,并证明a e a >; (II )讨论函数)(x g y =在区间),1(a e 上零点的个数. 解:(I )01)(≥-='x e x f ,得)(x f 的单调递增区间是),0(+∞, …………(2分) ∵0>a ,∴1)0()(=>f a f ,∴a a e a >+>1,即a e a >. …………(4分)(II )a x a x a x x g )22)(22(22)(-+=-=',由0)(='x g ,得22a x =,列表当2x )222(a,无极大值. …………(6分)由(I )a e a >,∵⎪⎩⎪⎨⎧>>22a a e e aa ,∴22a e a>,∴22ae a >01)1(>=g ,0))(()(22>-+=-=a e a e a e e g a a a a …………(8分)(i )当122≤a,即20≤<a 时,函数)(x g y =在区间),1(a e 不存在零点 (ii )当122>a ,即2>a 时若0)2ln 1(2>-a a ,即e a 22<<时,函数)(x g y =在区间),1(a e 不存在零点若0)2ln 1(2=-a a ,即e a 2=时,函数)(x g y =在区间),1(a e 存在一个零点e x =;若0)2ln 1(2<-a a ,即e a 2>时,函数)(x g y =在区间),1(a e 存在两个零点;综上所述,)(x g y =在(1,)a e 上,我们有结论:当02a e <<时,函数()f x 无零点; 当2a e = 时,函数()f x 有一个零点; 当2a e >时,函数()f x 有两个零点.…………(12分) 5.(本小题满分14分)已知函数()ln(1)(1)1f x x k x =---+.(I )当1k =时,求函数()f x 的最大值;(II )若函数()f x 没有零点,求实数k 的取值范围; 解:(I )当1k =时,2()1x f x x -'=-)(x f 定义域为(1,+∞),令()0,2f x x '==得, ………………(2分)∵当(1,2),x ∈时()0f x '>,当(2,),x ∈+∞时()0f x '<, ∴()(1,2)f x 在内是增函数,(2,)+∞在上是减函数∴当2x =时,()f x 取最大值(2)0f = ………………(4分)(II )①当0k ≤时,函数ln(1)y x =-图象与函数(1)1y k x =--图象有公共点, ∴函数()f x 有零点,不合要求; ………………(8分)②当0k >时,1()11()111kk x k kx k f x k x x x +-+-'=-==---- ………………(6分)令1()0,k f x x k +'==得,∵1(1,),()0,k x f x k +'∈>时1(1,),()0x f x k'∈++∞<时,∴1()(1,1)f x k +在内是增函数,1[1,)k++∞在上是减函数,∴()f x 的最大值是1(1)ln f k k+=-,∵函数()f x 没有零点,∴ln 0k -<,1k >,因此,若函数()f x 没有零点,则实数k 的取值范围(1,)k ∈+∞.………………(10分) 6.(本小题满分12分)已知2x =是函数2()(23)x f x x ax a e =+--的一个极值点(⋅⋅⋅=718.2e ). (I )求实数a 的值;(II )求函数()f x 在]3,23[∈x 的最大值和最小值.解:(I )由2()(23)x f x x ax a e =+--可得22()(2)(23)[(2)3]x x x f x x a e x ax a e x a x a e '=+++--=++--……(4分)∵2x =是函数()f x 的一个极值点,∴(2)0f '=∴2(5)0a e +=,解得5a =- ……………(6分) (II )由0)1)(2()(>--='x e x x x f ,得)(x f 在)1,(-∞递增,在),2(+∞递增,由0)(<'x f ,得)(x f 在在)2,1(递减∴2)2(e f =是()f x 在]3,23[∈x 的最小值; ……………(8分)2347)23(e f =,3)3(e f = ∵)23()3(,0)74(4147)23()3(23233f f e e e e e f f >>-=-=-∴()f x 在]3,23[∈x 的最大值是3)3(e f =. ……………(12分)7.(本小题满分14分)已知函数)0,(,ln )2(4)(2≠∈-+-=a R a x a x x x f (I )当a=18时,求函数)(x f 的单调区间; (II )求函数)(x f 在区间],[2e e 上的最小值. 解:(Ⅰ)x x x x f ln 164)(2--=, xx x x x x f )4)(2(21642)('-+=--= 2分由0)('>x f 得0)4)(2(>-+x x ,解得4>x 或2-<x注意到0>x ,所以函数)(x f 的单调递增区间是(4,+∞) 由0)('<x f 得0)4)(2(<-+x x ,解得-2<x <4,注意到0>x ,所以函数)(x f 的单调递减区间是]4,0(. 综上所述,函数)(x f 的单调增区间是(4,+∞),单调减区间是]4,0( 6分 (Ⅱ)在],[2e e x ∈时,x a x x x f ln )2(4)(2-+-= 所以xax x x a x x f -+-=-+-=242242)('2, 设a x x x g -+-=242)(2当0<a 时,有△=16+4×208)2(<=-a a ,此时0)(>x g ,所以0)('>x f ,)(x f 在],[2e e 上单调递增, 所以a e e e f x f -+-==24)()(2min 8分当0>a 时,△=08)2(2416>=-⨯-a a , 令0)('>x f ,即02422>-+-a x x ,解得221a x +>或221a x -<; 令0)('<x f ,即02422<-+-a x x , 解得221a -221ax +<<. ①若221a+≥2e ,即a ≥22)1(2-e 时, )(x f 在区间],[2e e 单调递减,所以a e e e f x f 244)()(242min -+-==.②若2221e ae <+<,即222)1(2)1(2-<<-e a e 时间, )(x f 在区间]221,[a e +上单调递减,在区间],221[2e a +上单调递增, 所以min )(xf )221(a f +=)221ln()2(322a a a a +-+--=. ③若221a+≤e ,即a <0≤22)1(-e 时,)(x f 在区间],[2e e 单调递增,所以a e e e f x f -+-==24)()(2min综上所述,当a ≥222)1(-e 时,a e a x f 244)(24min -+-=;当222)1(2)1(2-<<-e a e 时,)221ln()2(322)(min aa a a x f +-+--=; 当a ≤2)1(2-e 时,a e e x f -+-=24)(2min14分 8.(本小题满分12分)已知函数()(6)ln f x x x a x =-+在(2,)x ∈+∞上不具有...单调性. (I )求实数a 的取值范围;(II )若()f x '是()f x 的导函数,设22()()6g x f x x '=+-,试证明:对任意两个不相等正数12x x 、,不等式121238|()()|||27g x g x x x ->-恒成立.解:(I )226()26a x x af x x x x-+'=-+=, ………………(2分)∵()f x 在(2,)x ∈+∞上不具有...单调性,∴在(2,)x ∈+∞上()f x '有正也有负也有0, 即二次函数226y x x a =-+在(2,)x ∈+∞上有零点 ………………(4分) ∵226y x x a =-+是对称轴是32x =,开口向上的抛物线,∴222620y a =⋅-⋅+<的实数a 的取值范围(,4)-∞ ………………(6分)(II )由(I )22()2a g x x xx =+-,方法1:2222()()62(0)a g x f x x x x x x'=-+=+->, ∵4a <,∴323233444244()22a x x g x x x x x x -+'=-+>-+=,…………(8分)设2344()2h x x x =-+,3448124(23)()x h x x x x-'=-= ()h x 在3(0,)2是减函数,在3(,)2+∞增函数,当32x =时,()h x 取最小值3827∴从而()g x '3827>,∴38(())027g x x '->,函数38()27y g x x =-是增函数,12x x 、是两个不相等正数,不妨设12x x <,则22113838()()2727g x x g x x ->-∴212138()()()27g x g x x x ->-,∵210x x ->,∴1212()()3827g x g x x x ->- ∴1212()()g x g x x x --3827>,即121238|()()|||27g x g x x x ->- ………………(12分)方法2:11(,())M x g x 、22(,())N x g x 是曲线()y g x =上任意两相异点,121222121212()()2()2g x g x x x ax x x x x x -+=+--,12x x +>Q 4a <12221212122()22x x a a x x x x x x +∴+->+-1242x x >- ………(8分)设0t t =>,令32()244MN k u t t t ==+-,()4(32)u t t t '=-, 由()0u t '>,得2,3t >由()0u t '<得20,3t <<()u t ∴在)32,0(上是减函数,在),32(+∞上是增函数,)(t u ∴在32=t 处取极小值2738,38()27u t ∴≥,∴所以1212()()g x g x x x --3827>即121238|()()|||27g x g x x x ->- ………………(12分)9.(本小题满分12分)已知函数.1,ln )1(21)(2>-+-=a x a ax x x f(I )讨论函数)(x f 的单调性;(II )证明:若.1)()(,),,0(,,521212121->--≠+∞∈<x x x f x f x x x x a 有则对任意(1))(x f 的定义域为),0(+∞,xa x x x a ax x x a a x x f )1)(1(11)('2-+-=-+-=-+-= 2分(i )若2,11==-a a 即,则 .)1()('2xx x f -=故)(x f 在),0(+∞单调增加. (ii )若.0)(',)1,1(,21,1,11<-∈<<><-x f a x a a a 时则当故而)1,1()(,0)(',),1()1,0(->+∞∈-∈a x f x f x a x 在故时及当单调减少,在(0,a-1), ),1(+∞单调增加.(iii )若),1(),1,0(,)1,1()(,2,11+∞-->>-a a x f a a 在单调减少在同理可得即 单调增加.(II )考虑函数x x f x g +=)()( .ln )1(212x x a ax x +-+-= 由 .)11(1)1(121)1()('2---=---⋅≥-+--=a a xa x x a a x x g 由于单调增加在即故),0()(,0)(',5+∞><x g x g a a ,从而当021>>x x 时有 故1)()(2121->--x x x f x f ,当210x x <<时,有1)()()()(12122121->--=--x x x f x f x x x f x f10.(本小题满分14分)已知函数21()ln ,()(1),12f x x a xg x a x a =+=+≠-.(I )若函数(),()f x g x 在区间[1,3]上都是单调函数且它们的单调性相同,求实数a 的取值范围;(II )若(1,]( 2.71828)a e e ∈=L ,设()()()F x f x g x =-,求证:当12,[1,]x x a ∈时,不等式12|()()|1F x F x -<成立.解:(I )(),()1a f x x g x a x''=+=+, ……………(2分)∵函数(),()f x g x 在区间[1,3]上都是单调函数且它们的单调性相同,∴当[1,3]x ∈时,2(1)()()()0a x a f x g x x++''⋅=≥恒成立, ……………(4分) 即2(1)()0a x a ++≥恒成立, ∴21a a x >-⎧⎨≥-⎩在[1,3]x ∈时恒成立,或21a a x<-⎧⎨≤-⎩在[1,3]x ∈时恒成立, ∵91x -≤≤-,∴1a >-或9a ≤- ………………(6分)(II )21()ln ,(1)2F x x a x a x =+-+,()(1)()(1)a x a x F x x a xx--'=+-+=∵()F x 定义域是(0,)+∞,(1,]a e ∈,即1a >∴()F x 在(0,1)是增函数,在(1,)a 实际减函数,在(,)a +∞是增函数 ∴当1x =时,()F x 取极大值1(1)2M F a ==--,当x a =时,()F x 取极小值21()ln 2m F a a a a a ==--, ………………(8分)∵12,[1,]x x a ∈,∴12|()()|||F x F x M m M m -≤-=- ………………(10分)设211()ln 22G a M m a a a =-=--,则()ln 1G a a a '=--,∴1[()]1G a a''=-,∵(1,]a e ∈,∴[()]0G a ''>∴()ln 1G a a a '=--在(1,]a e ∈是增函数,∴()(1)0G a G ''>=∴211()ln 22G a a a a =--在(1,]a e ∈也是增函数 ………………(12分)∴()()G a G e ≤,即2211(1)()1222e G a e e -≤--=-, 而22211(1)(31)1112222e e e ----=-<-=,∴()1G a M m =-< ∴当12,[1,]x x a ∈时,不等式12|()()|1F x F x -<成立. ………………(14分) 11.(本小题满分12分)设曲线C :()ln f x x ex =-( 2.71828e =⋅⋅⋅),()f x '表示()f x 导函数. (I )求函数()f x 的极值;(II )对于曲线C 上的不同两点11(,)A x y ,22(,)B x y ,12x x <,求证:存在唯一的0x 12(,)x x ∈,使直线AB 的斜率等于0()f x '. 解:(I )11()0ex f x e x x -'=-==,得1x e= 当x 变化时,()f x '与()f x 变化情况如下表:∴当1x e=时,()f x 取得极大值()2f e=-,没有极小值; …………(4分)(II )(方法1)∵0()AB f x k '=,∴2121021ln ln ()1x x e x x e x x x ----=-,∴21201ln 0x x xx x --=即20211ln()0x x x x x --=,设2211()ln ()xg x x x x x =-- 211211()ln ()x g x x x x x =--,1/211()ln 10x x g x x =->,1()g x 是1x 的增函数, ∵12x x <,∴2122222()()ln ()0xg x g x x x x x <=--=;222211()ln ()x g x x x x x =--,2/221()ln 10x x g x x =->,2()g x 是2x 的增函数, ∵12x x <,∴1211111()()ln ()0xg x g x x x x x >=--=,∴函数2211()ln ()xg x x x x x =--在12(,)x x 内有零点0x , …………(10分)又∵22111,ln 0x x x x >∴>,函数2211()ln ()xg x x x x x =--在12(,)x x 是增函数, ∴函数2121()ln x x xg x x x -=-在12(,)x x 内有唯一零点0x ,命题成立…………(12分)(方法2)∵0()AB f x k '=,∴2121021ln ln ()1x x e x x e x x x ----=-, 即020112ln ln 0x x x x x x -+-=,012(,)x x x ∈,且0x 唯一设2112()ln ln g x x x x x x x =-+-,则1121112()ln ln g x x x x x x x =-+-, 再设22()ln ln h x x x x x x x =-+-,20x x <<,∴2()ln ln 0h x x x '=-> ∴22()ln ln h x x x x x x x =-+-在20x x <<是增函数 ∴112()()()0g x h x h x =<=,同理2()0g x >∴方程2112ln ln 0x x x x x x -+-=在012(,)x x x ∈有解 …………(10分)∵一次函数在12(,)x x 2112()(ln ln )g x x x x x x =-+-是增函数 ∴方程2112ln ln 0x x x x x x -+-=在012(,)x x x ∈有唯一解,命题成立………(12分) 注:仅用函数单调性说明,没有去证明曲线C 不存在拐点,不给分. 12.(本小题满分14分)定义),0(,,)1(),(+∞∈+=y x x y x F y ,(I )令函数22()(3,log (24))f x F x x =-+,写出函数()f x 的定义域;(II )令函数322()(1,log (1))g x F x ax bx =+++的图象为曲线C ,若存在实数b 使得曲线C 在)14(00-<<-x x 处有斜率为-8的切线,求实数a 的取值范围;(III )当,*x y ∈N 且x y <时,求证(,)(,)F x y F y x >. 解:(I )22log (24)0x x -+>,即2241x x -+> ……………………(2分)得函数()f x 的定义域是(1,3)-, ……………………(4分) (II )22322()(1,log (1))1,g x F x ax bx x ax bx =+++=+++设曲线00(41)C x x -<<-在处有斜率为-8的切线, 又由题设,23)(,0)1(log 2232b ax x x g bx ax x ++='>+++∴存在实数b 使得⎪⎩⎪⎨⎧>+++-<<--=++1114823020300020bx ax x x b ax x 有解, ……………………(6分)由①得,238020ax x b ---=代入③得082020<---ax x ,200028041x ax x ⎧++>⎪∴⎨-<<-⎪⎩由有解, ……………………(8分) 方法1:0082()()a x x <-+-,因为041x -<<-,所以0082()[8,10)()x x -+∈-, 当10a <时,存在实数b ,使得曲线C 在)14(00-<<-x x 处有斜率为-8的切线………………(10分)方法2:得08)1()1(208)4()4(222>+-⨯+-⨯>+-⨯+-⨯a a 或,1010,10.a a a ∴<<∴<或 ………………(10分) 方法3:是222(4)(4)802(1)(1)80a a ⎧⨯-+⨯-+≤⎪⎨⨯-+⨯-+≤⎪⎩的补集,即10a < ………………(10分)(III )令2)1ln(1)(,1,)1ln()(xx x xx h x x x x h +-+='≥+=由 又令,0),1ln(1)(>+-+=x x xxx p 0)1(11)1(1)(22<+-=+-+='∴x x x x x p , ),0[)(+∞∴在x p 单调递减. ……………………(12)分),1[)(+∞∴在x h 单调递减,x y y x y x x y yy x x y x )1()1(),1ln()1ln(,)1ln()1ln(,1+>+∴+>+∴+>+<≤∴有时, ).,(),(,x y F y x F y x N y x ><∈∴*时且当 ………………(14分)①②③。
