第三章高等数学基础知识-空间解析几何题库1-2-10
高等数学(解析几何)图形

y2
z
L
投影柱面
x2 y2 1
得交线L:
1
所求投影曲线为
x2 y2 1 z 1
x2 y2 1
x2 y2 1 .
.
z 0
.
o
.
.
x
y
z =0
2
25. 空间曲线作为投影柱面的交线(1)
2 y2 z2 4x 4z
L:
y
2
3z 2
关于xoy面:
(x,y,z) (x,y,-z)
关于x轴:
(x,y,z) (x,-y,-z)
M(x,y,z)
y
P
(x,y,-z)
关于原点:
(x,y,z) (-x,-y,-z)
.
2. 两矢量和在轴上的投影 两矢量的和在轴上的投影等于投影的和
c
B A
A´
B´
c´
u
2. 两矢量和在轴上的投影 两矢量的和在轴上的投影等于投影的和
.
1. 空间直角坐标系
八个卦限
z
0 y
x
1. 空间直角坐标系
八个卦限
z
0 y
.
x
1. 空间直角坐标系
八个卦限
点的坐标
Ⅳ
Ⅲ
z z
Ⅱ
Ⅰ
M (x,y,z)
M (x,y,z)
0
y
y
.
x
N
x
Ⅵ
Ⅷ
Ⅴ
1. 空间直角坐标系
z
坐标和点
z
(x,y,z) M
M (x,y,z)
00
y
解析几何-吕林根-课后习题解答一到五
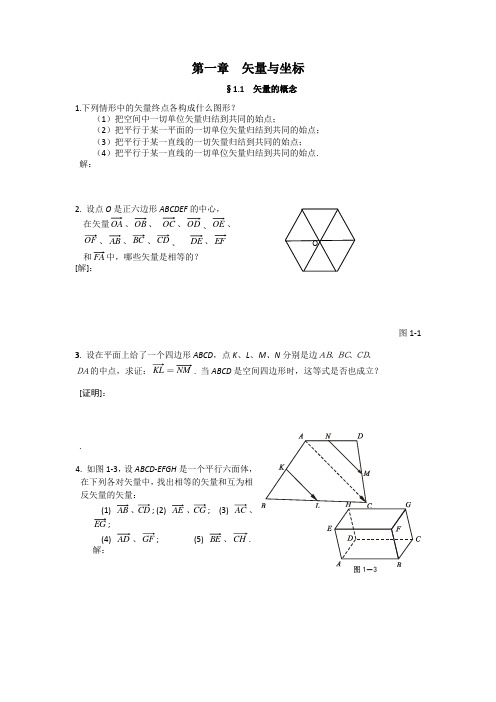
第一章矢量与坐标§1.1 矢量的概念1.下列情形中的矢量终点各构成什么图形?(1)把空间中一切单位矢量归结到共同的始点;(2)把平行于某一平面的一切单位矢量归结到共同的始点;(3)把平行于某一直线的一切矢量归结到共同的始点;(4)把平行于某一直线的一切单位矢量归结到共同的始点.解:2. 设点O是正六边形ABCDEF的中心,在矢量OA、OB、OC、OD、OE、OF、AB、BC、CD、DE、EF和FA中,哪些矢量是相等的?[解]:图1-13. 设在平面上给了一个四边形ABCD,点K、L、M、N分别是边AB、BC、CD、DA的中点,求证:KL=NM. 当ABCD是空间四边形时,这等式是否也成立?[证明]:.4. 如图1-3,设ABCD-EFGH是一个平行六面体,在下列各对矢量中,找出相等的矢量和互为相反矢量的矢量:(1) AB、CD; (2) AE、CG; (3) AC、EG;(4) AD、GF; (5) BE、CH.解:§1.2 矢量的加法1.要使下列各式成立,矢量b a ,应满足什么条件? (1=+ (2+=+ (3-=+ (4+=- (5= 解:§1.3 数量乘矢量1 试解下列各题.⑴ 化简)()()()(→→→→-⋅+--⋅-b a y x b a y x .⑵ 已知→→→→-+=3212e e e a ,→→→→+-=321223e e e b ,求→→+b a ,→→-b a 和→→+b a 23.⑶ 从矢量方程组⎪⎩⎪⎨⎧=-=+→→→→→→by x ay x 3243,解出矢量→x ,→y .解:2 已知四边形ABCD 中,→→→-=c a AB 2,→→→→-+=c b a CD 865,对角线→AC 、→BD 的中点分别为E 、F ,求→EF . 解:3 设→→→+=b a AB 5,→→→+-=b a BC 82,)(3→→→-=b a CD ,证明:A 、B 、D 三点共线. 解:4 在四边形ABCD中,→→→+=baAB2,→→→--=baBC4,→→→--=baCD35,证明ABCD为梯形.解:6. 设L、M、N分别是ΔABC的三边BC、CA、AB的中点,证明:三中线矢量AL, BM, CN可以构成一个三角形.7. 设L、M、N是△ABC的三边的中点,O是任意一点,证明OBOA++OC=OL+OM+ON.解:8. 如图1-5,设M是平行四边形ABCD的中心,O是任意一点,证明OA+OB+OC+OD=4OM.解:9在平行六面体ABCDEFGH(参看第一节第4题图)中,证明→→→→=++AGAHAFAC2.证明:.10.用矢量法证明梯形两腰中点连续平行于上、下两底边且等于它们长度和的一半.解11. 用矢量法证明,平行四边行的对角线互相平分.解12. 设点O 是平面上正多边形A 1A 2…A n 的中心,证明: 1OA +2OA +…+n OA =0.解,13.在12题的条件下,设P 是任意点,证明 证明:§1.4 矢量的线性关系与矢量的分解1.在平行四边形ABCD 中,(1)设对角线,,b BD a AZ ==求.,,,DA CD BC AB 解(2)设边BC 和CD 的中点M 和N ,且q AN P AM ==,求CD BC ,。
高等数学 空间解析几何与向量代数练习题与答案(优选.)

最新文件---------------- 仅供参考--------------------已改成-----------word 文本 --------------------- 方便更改空间解析几何与矢量代数小练习一 填空题 5’x9=45分1、 平行于向量)6,7,6(-=a 的单位向量为______________.2、 设已知两点)2,0,3()1,2,4(21M M 和,计算向量21M M 的模_________________, 方向余弦_________________和方向角_________________3、以点(1,3,-2)为球心,且通过坐标原点的球面方程为__________________.4、方程0242222=++-++z y x z y x 表示______________曲面.5、方程22x y z +=表示______________曲面.6、222x y z +=表示______________曲面.7、 在空间解析几何中2x y =表示______________图形.二 计算题 11’x5=55分1、求过点(3,0,-1)且与平面3x-7y+5z-12=0平行的平面方程.2、求平行于x 轴且过两点(4,0,-2)和(5,1,7)的平面方程.3、求过点(1,2,3)且平行于直线51132-=-=z y x 的直线方程.4、求过点(2,0,-3)且与直线⎩⎨⎧=+-+=-+-012530742z y x z y x 垂直的平面方5、已知:k i OA 3+=,k j OB 3+=,求OAB ∆的面积。
参考答案一 填空题1、⎩⎨⎧⎭⎬⎫-±116,117,1162、21M M =2,21cos ,22cos ,21cos ==-=γβα,3,43,32πγπβπα=== 3、14)2()3()1(222=++-+-z y x4、以(1,-2,-1)为球心,半径为6的球面5、旋转抛物面6、 圆锥面7、 抛物柱面二 计算题1、04573=-+-z y x2、029=--z y3、531221-=-=-z y x 4、065111416=---z y x5 219==∆S最新文件---------------- 仅供参考--------------------已改成-----------word 文本 --------------------- 方便更改赠人玫瑰,手留余香。
空间解析几何与向量代数三

高等数学( B )—向量代数与空间解析几何练习题及解答1、 已知 M 11,2,3 , M 2 0,1, 2 ,M 1M 2 的坐标式? M 1M 2 ?与 M 1M 2 平行的单位向量?方向余弦?[解]:1) M 1M 20 1,1 2, 2 31,1,5M 1M 2 21 222)1 5 273) cosx 2 x 1 1,cosy 2 y 1 1,cosz 2 z 1 5M 1M 227 M 1M 227M 1M 2274)与 M 1M 2 平行的单位向量为:cos ,cos ,cos1 , 1 , 5 。
272727x 1y z 1 x y 1z 2 2、 设直线n4与直线1平行,求 n,m 。
2m3[解 ] : s 12,n,4 , s 2 m,1,3 ,因为两直线平行,r m 1 n 1 p 1 2 n 4 4 3 所以 l 1 / /l 2s 1 / / s 2s 1s 2。
m 2n 2 p 2n, m2m 1 333Ax y 2z 1 与平面: 3x y z3垂直,求 A 。
、 已知平面:[解 ] : n 1A,1, 2 , n 2 3, 1,1 ,因为两平面垂直,所以12n 1 n 2 n 1 n 2 0 A 1 A 2 B 1B 2 C 1C 2 0 A 3 1 1 210 A14、 已知平面x 1 y z 1 : x By 3z 1 0 与直线4垂直,求 B , m 。
m6[ 解 ]: n 1,B, 3 , s m,4,6 ,因为垂直,所以有n/ / s n s 0m4 6 。
1BB2, m 235、 求由 a 1,2,3 , b 1,2,4 为邻边组成的平行四边形的面积。
[ 解] :由两向量叉积的几何意义知:以a ,b 为邻边组成的平行四边行的面积S a bi j k86, 43,222,7,4a b 123,因为124故 S a b22269 。
7426、求以A x1, y1, z1, B x2, y2, z2, C x3 , y3, z3为顶点的三角形面积。
大学高数空间解析几何

学习空间解析几何有助于培养人的逻辑思维和抽象 思维能力,提高解决问题的能力。
空间解析几何的历史与发展
早期发展
空间解析几何起源于17世纪,随着笛卡尔坐标系的建立和 解析几何方法的完善,开始形成独立的数学分支。
近代发展
随着计算机科学和数学的不断发展,空间解析几何在理论 和应用方面都取得了重要进展,如微分几何、线性代数和 微分方程等与空间解析几何的交叉融合。
详细描述
如果两个平面的法向量 $mathbf{a}$ 和 $mathbf{b}$ 是共线的,即存在一个非零实数 $lambda$ 使得 $mathbf{a} = lambda mathbf{b}$,那么这两个平面就是平行的。如果两个平面的法向量不共线,那么 这两个平面就是相交的。
04
空间几何的应用
空间几何在计算机图形学中的应用
01
02
03
三维建模
空间几何用于创建三维模 型,包括曲面建模、实体 建模和参数化建模等。
光照计算
空间几何用于计算物体表 面的光照效果,以实现逼 真的渲染效果。
动画制作
空间几何用于动画制作中 的骨骼绑定、运动轨迹规 划和角色动画等,以创建 动态的视觉效果。
05
空间几何的习题与解答
平面与平面的交线
总结词求平面与平面Fra bibliotek交线,需要消元法或参数方程法。
详细描述
平面与平面的交线可以通过消元法或参数方程法来求解。消元法是通过联立两个平面的方程组,然后消元得到一 个一元一次方程,这个一元一次方程就是两平面的交线。参数方程法则是设定一个参数,将两个平面的方程都表 示成参数的函数,然后令参数相等,解出交线的参数方程。
未来展望
随着科技的不断进步和应用领域的拓展,空间解析几何将 继续发挥重要作用,并有望在人工智能、机器学习等领域 取得新的突破和应用。
解析几何第三章习题及解答

第三章 常见曲面习题3.11.证明:如果2220a b c d ++->,那么由方程2222220x y z ax by cz d ++++++=给出的曲面是一球面,求出它的球心坐标和半径。
证明:将方程配方得222222()()()x a y b z c a b c d +++++=++-,由2220a b c d ++->,得到方程表示球心是(,,)a b c ---2.求过三点(3,0,0),(0,2,0),(0,0,1)的圆的方程。
解:空间中的圆可由过三点(3,0,0),(0,2,0),(0,0,1)的一个球面和一个平面的交线表示,设过该三点的球面方程为2220x y z ax by cz d ++++++=,得到930,420,10a d b d c d ++=⎧⎪++=⎨⎪++=⎩球面方程为22294(1)032d dx y z x y d z d ++++---++=,其中d 任意。
过该三点的平面方程是132x yz ++=,所以所求圆的方程可以为 2226()2(9)3(4)6(1)60,23660x y z d x d y d z d x y z ⎧++-+-+-++=⎨++-=⎩ 其中d 任意。
3.证明曲线24224324,1,(,)1,1t x t t t y t t t t z t t ⎧=⎪++⎪⎪=∈-∞+∞⎨++⎪⎪=⎪++⎩在一球面上,并此球面方程。
证明:因为曲线满足2322222224242422242424()()()111()(1)11tt t x y z t t t t t t t t t t y t t t t++=++++++++=++==++++即22211()24x y z +-+=,所以曲线在一个球面上。
4.适当选取坐标系,求下列轨迹的方程(1)到两定点距离之比等于常数的点的轨迹; (2)到两定点距离之和等于常数的点的轨迹; (3)到定平面和定点等距离的点的轨迹。
空间解析几何及多元微分学练习题参考答案

空间解析几何和多元微分学练习题参考答案1.若®®®®++=k j i a 863,2=®b ,则与®a ,x 轴均垂直的向量=®b þýüîíì-±56,58,0。
2.以点A )0,0,2(,B )0,3,0(,C )6,0,0(,D )8,3,2(为顶点的四面体的体积V=14。
3.曲线ïîïíì=+-=-+4)2(4)2(2222y x z x 在yoz 面上的投影曲线方程为:ïîïíì=+-±=+±044422x y z ,投影柱面方程为:44422+-±=+±y z 。
4.xoz 面上的曲线19422=-z x 分别绕x 轴和z 轴旋转所成旋转曲面方程为:1994222=--z y x ,1944222=-+z y x 。
5.求两平面0622:1=+-+z y x p ,884:2=-+-z y x p 所成二面角的角平分面方程。
解:法一,设),,(z y x P 为所求平面上任意一点,则由题意有:2222228)1(4884)2(21622+-+-+-=-+++-+z y x z y x消去绝对值得 )884()6222(3-+-±=+-+z y x z y 即026147010257=-+-=+++z y x z y x 和法二,所求平面过两平面1p 与2p 的交线,故可设其方程为:0)622(884=+-++-+-z y x z y x l在该平面上任取一点, 如令4430--===l lz y x 可得,然后由点)443,0,0(--l l 到两平面的距离相等可解得3±=l ,从而得到所求平面方程。
高等数学试题库

第一章 函数、极限与连续一、 判断题:1.极限)(lim 0x f x x →存在的充要条件是)0(0-x f 与)0(0+x f 都存在。
( )2.如果)0(0-x f 与)0(0+x f 都存在且相等,则)(lim 0x f x x →存在。
( )3.如果函数)(x f 在0x 处既左连续且右连续,则)(x f 在0x 连续。
( ) 4.如果)(lim 0x f x x →存在,则)(x f 在0x 连续。
( )5.如果函数)(x f 在0x 连续,则)(lim 0x f x x →存在。
( )6.极限 2200limy x xyy x +→→存在 。
( )7.如果)(x f 在()b a ,内连续,则)(x f 在()b a ,内必有最大值和最小值。
( ) 8.如果)(x f 在[]b a ,内连续,则)(x f 在[]b a ,内必有最大值和最小值。
( ) 9.极限 ()e x xx -=-→1lim 0。
( )10.极限21946853lim 2323=-++-∞→x x x x x 。
( ) 二、 填空题:1.函数1)3ln(2222-++--=y x y x y 的定义域是 。
2. 函数4192222-++--=y x y x y 的定义域是 。
3.若⎪⎩⎪⎨⎧<=>+=0,00,,1)(x x x x x f π,则=-)]}1([{f f f 。
4. 函数 x y 2sin ln =的复合过程是 。
5. 一切初等函数在其 内都是连续的。
6. 设arctgx x y 2-=,则)(lim x y x --∞→= 。
7. 如果322sin 3lim0=→x mx x ,则m = 。
8. 设⎪⎩⎪⎨⎧≥-<<≤-+=2,2221,1,32)(2x x x x x x x x f ,则)(lim 1x f x →= 。
9. 函数11)(2+-=x x x f 的间断点是 。
高等数学空间解析几何练习

向量代数与空间解析几何第一部分 向量代数___线性运算[内容要点]:1. 向量的概念.2. 向量的线性运算.3. 向量的坐标,利用坐标作向量的线性运算.[本部分习题]1. 指出下列各点所在的坐标轴、坐标面或哪个卦限.2. 求点(1,3,2)--关于点(1,2,1)-的对称点坐标.3. 求点(4,3,5)M --到各坐标轴的距离.4. 一向量的起点为(1,4,2)A -,终点为(1,5,0)B -,求AB →在x 轴、y 轴、z 轴上的投影,并求||AB →。
5. 已知两点1M 和2(3,0,2)M ,计算向量12M M −−→的模、方向余弦和方向角.6. 已知{3,5,4},{6,1,2},{0,3,4},a b c →→→==-=--求234a b c →→→-+及其单位向量.7.设358,247,54,a i j k b i j k c i j k →→→→→→→→→→→→=++=--=--求向量43l a b c →→→→=+-在x 轴上的投影以及在y 轴上的分向量. 第二部分 向量代数___向量的“积”[内容要点]:1.向量的数量积、向量积的概念、坐标表示式及其运算规律。
2.向量的混合积的概念、坐标表示式及其几何意义。
3.向量垂直、平行、共面的条件.[本部分习题]1. 设{3,1,2},{1,2,1},a b →→=--=-求:(1);(2);(3)cos(,);(4)Pr ;(5)Pr .a b a b a b a b j b j a →→→→→→→→⋅⨯2. 设{2,3,1},{1,1,3},{1,2,0},a b c →→→=-=-=-求:3. 112233a b a b a b ≥++ 其中,(1,2,3)i i a b i =均为实数,并指出等号成立的条件.4.设{3,5,2},{2,1,9},a b →→=-=试求λ的值,使得:(1)a b λ→→+与z 轴垂直;(2)a b λ→→+与a →垂直,并证明此时||a b λ→→+取最大值。
专升本空间解析几何-3

椭球面
抛物面
圆锥面
高等数学 一、曲面及其方程
1.曲面方程及其图形 一般地,如果曲面S与三元方程存在如下关系: (1)曲面S上任一点的坐标都满足方程F(x,y,z)=0. (2)不在曲面S上的点不满足方程. 那么F(x,y,z)=0称为曲面S的方程,而曲面S称为方程的图形.
高等数学
例 1 求与两定点 M1 (1,1,0), M( )等距离的点的轨迹方 程。 2 2,2,1
若改为:求圆心在M0(x0,y0,z0)球面方程。
高等数学 曲面方程
高等数学
方程也可以写成
2 2 2 x 2 y 2 z 2 2 x0 x 2 y0 y 2 z0 z x0 y0 z0 R 2 0,
若记A 2 x0 , B 2 y0 , C 2 z0 , 则有x 2 y 2 z 2 Ax By Cz D 0, 称为球面的一般方程. 1 1 1 1 ( x A) 2 ( y B) 2 ( z C ) 2 ( A2 B 2 C 2 4 D) 2 2 2 4 1.当A2 B 2 C 2 4 D 0时, 上式为一般方程.
x2 y2 z2 2 2 1的形状 : 2 a b c
用xOy坐标面( z 0)截此平面, 所得截痕为中心在 原点, 两个半轴分别为a, b的椭圆 : x2 y2 2 2 1 b a z 0
高等数学
用平行于坐标面 xoy的平面z z1截此曲面, 所得截痕是中心在 z轴上的椭圆:
高等数学 曲面方程
例2 求与原点距离为定长 r的点的轨迹。
解 设动点 P 的坐标为 ( x, y, z ) ,则与原点的距离为
op r ,
第三章高等数学基础知识-空间解析几何题库1-1-8

第三章高等数学基础知识-空间解析几何题
库1-1-8
问题:
[单选]方程表示()。
A.锥面
B.单叶双曲面
C.双叶双曲面
D.椭圆抛物线
问题:
[单选]曲面x2-y2=z在xOz平面上的截痕是()。
A.A
B.B
C.C
D.D
xOz平面y=0。
问题:
[单选]方程表示()。
A.椭球面
B.平面上椭圆
C.椭圆柱面
D.椭圆柱面在平面上的投影曲线
题干中的方程表示平面y=1上的椭圆. (安徽11选5 https://)
问题:
[单选]设空间直线的对称式方程为,则该直线必()。
A.过原点且垂直于x轴
B.过原点且垂直于y轴
C.过原点且垂直于z轴
D.过原点且平行于x轴
问题:
[单选]在空间直角坐标系中表示()。
A.一个点
B.两条直线
C.两个平面的交线,即直线
D.两个点
问题:
[问答题]设,且a≠b,记|a-b|=m,求a-b与x轴正方向的夹角的余弦值。
问题:
[问答题]已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5)。
(1)求以向量为一组邻边的平行四边形的面积S;
(2)若向量a分别与向量垂直,且,求向量a的坐标。
高数---第1讲 空间解析几何题型

常考题型及解法与技巧题型一 向量的运算1 [2012大纲](1)设 22,5,(,)3a b a b π=== ,则λ= 时,向量17m a b λ=+ 与3n a b =- 相互垂直;(2)设23m a b =+ ,3n a b =- , 12,1,(,)3a b a b π=== ,则m n ⨯= ; (3)设()2a b c ⨯⋅= ,则[()()]()a b b c c a +⨯+⋅+=2 [2012常考题型]设32,1,2,3A a b c a b c =+-=== ,a 与b 的夹角为3π,b 与c 的夹角为3π,c 与a 的夹角为2π,则A = 题型二 求平面、直线的方程(一)平面方程1、[2012大纲P96] 求过点(1,2,1)且与直线1210:10x y z L x y z +-+=⎧⎨-+-=⎩和220:0x y z L x y z -+=⎧⎨-+=⎩平行的平面方程.2、[2012大纲P96] 一个平面过两个平面1:50x y z ∏++=和2:40x z ∏-+=的交线,且与平面3:48120x y z ∏--+=成45 角,求此平面方程.3、[2012精解P58] 设平面∏过原点和点(6,3,2)M -,且与平面1:428x y z ∏-+=垂直,求此平面方程.4、[北航P357] 求以下平面方程.(1)过点(1,2,3)且与直线112211x y z +-+==-垂直的平面方程. (2)过点(2,5,1)-且平行于直线1123:1031x y z L ---==和2132:245x y z L ++-==的平面方程. (3)过平面1:2310x y z ∏--+=与平面2:0x y z ∏++=的交线且与平面2∏垂直的平面方程.5、[北航P357] 求椭球面2222321x y z ++=上点0000(,,)P x y z 处的切平面∏的方程,使平面过已知直线6321:212x y z L ---==-. 6、[2010P117] 求过点(1,2,1)M -且与直线2,34,1x t y t z t =-+=-=-垂直的平面方程7、[第四届(2013)全国预赛] 求通过直线2320:55430x y z L x y z +-+=⎧⎨+-+=⎩的两两相互垂直的平面1∏和2∏,使其中一个平面过点(4,3,1)-.(二)直线方程1、[2012大纲P96] 设直线l 过点(1,2,1)A 且与直线111:321x y z l -+==垂直,与直线2:2x l y z ==相交,求直线l 的方程.2、[北航P355] 求过点(1,2,3)A --且平行于平面:62310x y z ∏--+=又与直线113:325x y z L -+-==-相交的直线方程. 3、[2012精解P59] 求过点(1,2,3M -,垂直于直线:456x y z l ==且平行于平面:789100x y z ∏+++=的直线方程.练习:[北航P354] 求过点(1,0,2)P -且与平面:3460x y z ∏+-+=平行,又同直线32:141x y z L -+==垂直的直线方程. 4、[2012精解P59] 求经过点(2,3,1)P -且与直线12:345x y z L -+==垂直相交的直线方程. 练习:[北航P354] 求过点(2,1,3)P 且与直线11:321x y z L +-==-垂直相交的直线方程. 5、[北航P356] 在平面:10x y z ∏+++=内求垂直于直线10:20y z L x z -+=⎧⎨+=⎩的直线方程. 题型三 点、线、面的关系1 [2012大纲P97] (1)已知平面29x ky z +-=与平面230x y z -+=的夹角为4π,求k . (2)求点(1,2,3)P 到平面:23410x y z ∏-+-=的距离. (3)求直线3230:3230x y L y z --=⎧⎨-+=⎩与平面:1021130x y z ∏+--=的夹角.(4)求点(1,0,1)P -到直线3:3270x y L x y z -=⎧⎨+++=⎩的垂直距离. 练习:[BHP358]求点(1,1,0)P -到直线2330:0y z L x y --=⎧⎨-=⎩的距离. 2、[2012大纲P98] (1)直线13:234x y z l +==与直线2122:112x y z l -+-==的关系是( ) A.相互垂直 B.斜交 C.互相平行 D.异面直线(2)设直线3210:21030x y z L x y z +++=⎧⎨--+=⎩,平面:4220x y z ∏-+-=,则A.L 平行于∏ B.L 在∏上 C.L 垂直于∏ D.L 与∏斜交3、[北航P358]求直线11:011 x y zL -==与22:210x y zL+==-之间的距离.练习:(1)[2010P119]求异面直线131 :210 x y zL --==与212:101x y zL+-==之间的最短距离.(2)[第二届全国数学竞赛(2010)预赛]求直线10 :x yLz -=⎧⎨=⎩与直线2213:421x y zL---==--的距离.题型四求曲面的方程1、[2012大纲P98]求直线2:203x y zL-==绕z轴旋转一周所得旋转曲面的方程.2、[2012大纲P99]求以曲线2224:1x y zx y z⎧++=Γ⎨++=⎩为准线,母线平行于z轴的柱面方程.3、[北航P359]求准线是2225:x yz⎧+=Γ⎨=⎩,母线平行于向量(5,3,2)l=的柱面方程.4、[北航P359]设柱面的准线方程为2222221:222x y zx y z⎧++=⎪Γ⎨++=⎪⎩,而母线的方向矢量为{}0,0,1,求此柱面方程.5、[北航P359]设曲线222:x yz⎧-=Γ⎨=⎩,(1)求绕x轴旋所形成的旋转面方程;(2)求绕y轴旋转所形成的旋转面方程.题型五投影曲线1、[2012大纲P99]设曲线2222244:8312x y z zx y z z⎧++=⎪Γ⎨-+=⎪⎩,求它在xoy坐标面上的投影方程.2、[BHP359]求22:20y z xx y z⎧+=Γ⎨+-=⎩在三个坐标面上的投影方程.3、[2012精解P60]求直线11:111x y zL--==-在平面:210x y z∏-+-=上的投影直线l的方程,并求l绕y轴旋转一周所成曲面的方程.4、[2012大纲P97]求直线10:10x y zLx y z+--=⎧⎨-++=⎩在平面:0x y z∏++=上的投影直线的方程.。
空间解析几何复习题答案

2 2 2 ⎧ ⎪x + y = a (3) ⎨ 。 2 2 2 ⎪ x + z = a ⎩ 8.4.2 分别求母线平行于 x 轴及 y 轴而且通过曲线 2 2 2 ⎧ ⎪ 2 x + y + z = 16 ⎨ 2 2 2 ⎪ ⎩x + z − y = 0
的柱面方程。 答案:母线平行于 x 轴的柱面方程: 3 y 2 − z 2 = 16 ;母线平行于 y 轴的柱面方程: 3x 2 + 2x 2 = 16 。 8.4.3 求在 yOz 平面内以坐标原点为圆心的单位圆的方程(任写出三种不同形式的方程) 。 ⎧x 2 + y 2 + z 2 = 1 ⎧ y 2 + z 2 =1 ⎧x 2 + y 2 + z 2 = 1 答案: ⎨ ;⎨ ; ⎪ 。 ⎨ 2 2 ⎪ ⎩x = 0 ⎩x = 0 ⎩y + z =1 8.4.4 指出下列方程所表示的曲线 ⎧ x 2 + y 2 + z 2 + 25 (1) ⎨ ⎩x = 3 ⎧ x 2 − 4 y 2 + z 2 = 25 (3) ⎨ ; ⎩ x = −3 ⎧ x 2 + 4 y 2 + 9 z 2 = 30 (2) ⎨ ; ⎩z = 1 ⎧ y 2 + z 2 − 4x + 8 = 0 (4) ⎨ ; ⎩y = 4
4 3⎞ ⎛ 4 3⎞ 答案: ⎛ ⎜ 0, , − ⎟ , ⎜ 0, − , ⎟ 5⎠ ⎝ 5 5⎠ ⎝ 5 8.2.7 已知 | a |= 3, | b |= 26, | a × b |= 72 ,计算 a ⋅ b 。 答案: ±30 8.2.8 已知 | a |= 3, | b |= 5 ,问 λ 为何值时 a + λb 与 a − λb 互相垂直? 3 5 8.2.9 已知向量 a = 2i − 3 j + k , b = i − j + 3k 和 c = i − 3 j ,计算 (1) (a ⋅ b)c − (a ⋅ c )b ; (2) (a + b) × (b + c ) ; 答案: ± 答案: (1) (-3,-13,-33) ; (2) (4,-1,-4) ; (3)7
空间解析几何(练习题参考答案)

1. 过点M o (1,1-,1)且垂直于平面01201=+++=+--z y x z y x 及的平面方程.39.02=+-z y3. 在平面02=--z y x 上找一点p ,使它与点),5,1,2()1,3,4(-)3,1,2(--及之间的距离相等.7.)51,1,57(.5.已知:→→-AB prj D C B A CD,则)2,3,3(),1,1,1(),7,1,5(),3,2,1(= ( )A .4B .1C .21D .2 7.设平面方程为0=-y x ,则其位置( )A .平行于x 轴B .平行于y 轴C .平行于z 轴D .过z 轴. 8.平面0372=++-z y x 与平面0153=-++z y x 的位置关系( ) A .平行 B .垂直 C .相交 D .重合 9.直线37423zy x =-+=-+与平面03224=---z y x 的位置关系( ) A .平行 B .垂直 C .斜交 D .直线在平面内 10.设点)0,1,0(-A 到直线⎩⎨⎧=-+=+-07201z x y 的距离为( )A .5B .61 C .51 D .81 5.D 7.D 8.B 9.A 10.A .3.当m=_____________时,532+-与m 23-+互相垂直.4.设++=2,22+-=,243+-=,则)(b a p r j c += .4. 过点),,(382-且垂直平面0232=--+z y x 直线方程为______________. 10.曲面方程为:44222=++z y x ,它是由曲线________绕_____________旋转而成的.3.34-=m ; 4.2919 9.332212--=+=-x y x ; 10.曲线1422=+z y 绕z 轴旋转而成.1.设{}{}{}0,2,1,3,1,1,1,3,2-=-=-=,则=⨯⨯)(( ) A .8 B .10 C .{}1,1,0-- D .{}21,1,23.若==-+=,则14//236( ) A .)4612(-+± B .)612(+± C .)412(-± D .)46(-± 4.若ϕ与,则3121321)2,1,2(),1,2,2(),1,1,1(M M M M M M M ( ) A .6π B .2π C .3π D .4π6.求平面062=-+-z y x 与平面052=-++z y x 的夹角( ) A .2π B .6π C .3π D .4π 8.设点⎩⎨⎧=-+-=+-+-04201)2,1,3(z y x z y x l M o ,直线,则M O 到l 的距离为( )A .223 B .553 C .453 D .229.直线夹角为与平面62241312=++-=-=-z y x z y x ( ) A .30o B .60o C .90oD .65arcsin1.D 3.A 4.C 6.C 8.A 9.D7.求与平面4362=+-z y x 平行平面,使点)8,2,3(为这两个平面公垂线中点. 3.确定k 值,使三个平面:328,1423,23=--=++=+-z y x z y x z y kx 通过同一条直线.5.求以向量i k k j j i +++,,为棱的平行六面体的体积.7.与平面0522=+++z y x ,且与三个坐标面所构成的四面体体积为1的平面方程_____________________.8.动点到点(0,0,5)的距离等于它到x 轴的距离的曲面方程为________________. 9.曲面方程:259916222=--z y x 则曲面名称为________________.10.曲线⎪⎩⎪⎨⎧-+-=--=2222)1()1(2y x z yx z 在y z 面上的投影方程______________.1.设32+-=,+=2,++-=,则与+是否平行__________.1.不平行7.33222±=++z y x ; 8.25102-=-z x ;9.双叶双曲面; 10.⎩⎨⎧==+--++02342222x z y z yz y练习题选参考答案1.两非零向量→a 、→b 垂直,则有0=⋅→→b a 或0Pr =→→a j b;平行则有0=⨯→→b a 或→→=b a λ或两向量对应坐标成比例。
高数空间解析几何

这些双曲线都以 z0=0所对应的直线
yb a
x 为共同渐近线
对 x = x0 是形状相同开口朝下的抛物线
对 y = y0 则是形状相同开口朝上的抛物线
L
z
双曲抛物面是抛物 线 l 当其顶点沿抛 物线L平行移动所 产生的曲面
o
l
x
y
双曲抛物面是直纹面
x2 y2
a2
b2
z
双曲抛物面(马鞍面)
圆锥面的顶点 , 圆锥面的半顶角a ( 0< a <p / 2)
建立以顶点为原点,旋转轴为 z 轴, 半顶角 为 a 的圆锥面方程
yoz 坐标面上直线L的方程 z = y cota
故 L 绕 z 轴旋转的方程 z = yx2 y2 cota
)
L
a
.
令 cota = a ,则所求圆锥面方程为 z2 a2 ( x2 y2 ),
设时刻 t 时动点 M 位于 (x, y, z)
z 设 M 在 xoy 平面上的投影M′(x, y, 0)
螺距
t
o
M
x A M y
x a cost y a sint
z vt
螺旋线的参数方程
y M
a
t A
x
逃逸实验: 0-0试验
逃逸塔
塔高8米,位于飞 船顶部,它装有 10台发动机
z2
c2
1
在平面上,双曲线有渐近线。
相仿,单叶双曲面和双叶双曲面
有渐近锥面。
用z=h去截它们,当|h|无限增大时,
双曲面的截口椭圆与它的渐近锥面 的
截口椭圆任意接近,即:
x
双曲面和锥面任意接近。
高等数学:空间解析几何

a和向量b的数量积(内 积),这种运算也称为点乘,记作a·
b,即
由数量积的定义7-2以及向量夹角的定义7-1可以得到:
(1)a·
a=|a|2;
(2)向量a 和向量b 互相垂直的充分必要条件是a·
b=0.
空间解析几何
两个向量的数量积满足下列运算规律:
当向量a和b至少有一个是零向量时,规定其夹角<a,b>可
以在0到π之间任意取值.
空间解析几何
在物理中,我们已经知道,若力F 作用在物体上,使其产生
位移s,则该力所作的功为
即F 所作的功W 是向量F 和s的模相乘再乘以它们夹角的余
弦.这种运算在其他问题中也 会遇到,因此我们引入向量的结
构性运算.
空间解析几何
例7-13 设一平面与x 轴、y 轴和z 轴的交点分别为
P(a,0,0)、Q(0,b,0)和 R(0,0,c),求这个平面的方程,其中a ≠0,b
≠0,c ≠0.
解 设所求平面的一般方程为
空间解析几何
由 题意可知P(a,0,0)、Q(0,b,0)和R(0,0,c)三点都在该平
面上,所以这三点的 坐标都满足一般方程,即有
空间解析几何
.
例7-16 求点(1,-2,-1)到平面2x +y-2z+4=0的距离.
解 由式(7-13)可得
空间解析几何
7.4 空间直线方程
一、 直线方程
如图7-10所示,在空间直角坐标系中给定一条直线L,任一
个与这条直线平行的非零向量s={a,b,c}称为该直线的方向向
量.在直线L 上取一个定点M0(x0,y0,z0),设M(x,y,z)是直线L上任
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章高等数学基础知识-空间解析几何题
库1-2-10
问题:
[单选]曲面x2-y2=z在xOz平面上的截痕是()。
A.A
B.B
C.C
D.D
xOz平面y=0。
问题:
[单选]方程表示()。
A.椭球面
B.平面上椭圆
C.椭圆柱面
D.椭圆柱面在平面上的投影曲线
题干中的方程表示平面y=1上的椭圆.
问题:
[单选]设空间直线的对称式方程为,则该直线必()。
A.过原点且垂直于x轴
B.过原点且垂直于y轴
C.过原点且垂直于z轴
D.过原点且平行于x轴
(江西11选5 https://)
问题:
[单选]在空间直角坐标系中表示()。
A.一个点
B.两条直线
C.两个平面的交线,即直线
D.两个点
问题:
[问答题]设,且a≠b,记|a-b|=m,求a-b与x轴正方向的夹角的余弦值。
问题:
[问答题]已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5)。
(1)求以向量为一组邻边的平行四边形的面积S;
(2)若向量a分别与向量垂直,且,求向量a的坐标。
问题:
[问答题]求两个平行平面之间的距离。
问题:
[问答题]求与直线及直线都平行且经过坐标原点的平面方程。
