上海市2016年普陀区初三数学二模试卷
2016届上海普陀区初三数学一模试卷+答案(word版)

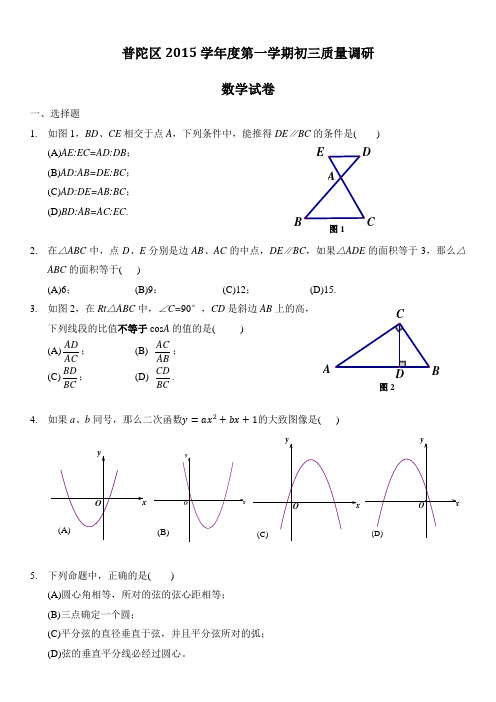
普陀区2015学年度第一学期初三质量调研数 学 试 卷 2016.1(时间:100分钟,满分:150分)考生注意:1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)[下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上]1. 如图1,BD 、CE 相交于点A ,下列条件中,能推得DE ∥BC 的条件是( ▲ ) (A )AE ∶EC =AD ∶DB ; (B )AD ∶AB =DE ∶BC ; (C )AD ∶DE =AB ∶BC ; (D )BD ∶AB =AC ∶EC .2.在△ABC 中,点D 、E 分别是边AB 、AC 的中点,DE ∥BC ,如果△ADE 的面积等于3,那么△ABC 的面积等于( ▲ )(A )6; (B )9; (C )12; (D )15.3.如图2,在Rt △ABC 中,∠C =90°,CD 是斜边AB 上的高,下列线段的比值不等于...cos A 的值的是( ▲ ) (A )AD AC; (B )AC AB; (C )BD BC; (D )CD BC.4.如果a 、b 同号,那么二次函数21y ax bx =++的大致图像是( ▲ )DCBA图2E DCBA图15.下列命题中,正确的是( ▲ )(A )圆心角相等,所对的弦的弦心距相等; (B )三点确定一个圆;(C )平分弦的直径垂直于弦,并且平分弦所对的弧; (D )弦的垂直平分线必经过圆心.6.已知在平行四边形ABCD 中,点M 、N 分别是边BC 、CD 的中点,如果a AB =,b AD =,那么向量MN 关于a 、b 的分解式是( ▲ ) (A )1122a b -; (B )1122a b -+; (C )1122a b +; (D )1122a b --.二、填空题:(本大题共12题,每题4分,满分48分) 7.如果:2:5x y =,那么yx xy +-= ▲ . 8.计算:2()()a b a b ++-= ▲ .9.计算: 2sin 45cot 30tan 60+= ▲ .10.已知点P 把线段AB 分割成AP 和PB (AP >PB ) 两段,如果AP 是AB 和PB 的比例中项,那么:AP AB 的值等于 ▲ .11.在函数①c bx ax y ++=2,②22)1(x x y --=,③2255xx y -=,④22+-=x y 中,y 关于x 的二次函数是 ▲ .(填写序号) 12.二次函数223y x x =+-的图像有最 ▲ 点.13.如果抛物线n mx x y ++=22的顶点坐标为(1,3),那么n m +的值等于 ▲ .14.如图3,点G 为△ABC 的重心,DE 经过点G ,DE ∥AC , EF ∥AB ,如果DE 的长是4,那么CF 的长是 ▲ .15.如图4,半圆形纸片的半径长是1cm ,用如图所示的方法将纸片对折,使对折后半圆的中点M 与圆心O 重合,那么折痕CD 的长是 ▲ cm .图316.已知在Rt △ABC 中,∠C =90°,点P 、Q 分别在边AB 、AC 上,4AC =,3BC AQ ==,如果△APQ 与△ABC 相似,那么AP 的长等于 ▲ .17.某货站用传送带传送货物.为了提高传送过程的安全性,工人师傅将原坡角为45°的传送带AB ,调整为坡度31:=i 的新传送带AC (如图5所示).已知原传送带AB 的长是24米.那么新传送带AC 的长是 ▲ 米.18.已知A (3,2)是平面直角坐标系中的一点,点B 是x 轴负半轴上一动点,联结AB ,并以AB 为边在x 轴上方作矩形ABCD ,且满足:1:2BC AB =,设点C 的横坐标是a ,如果用含a 的代数式表示点D 的坐标,那么点D 的坐标是 ▲ .三、解答题:(本大题共7题,满分78分)19.(本题满分10分)已知:如图6,在梯形ABCD 中,AD ∥BC ,13AD BC =,点M 是边BC 的中点,AD a =,AB b =.(1)填空:BM = ▲ ,MA = ▲ .(结果用a 、b 表示).(2)直接在图中画出向量2a b +.(不要求写作法,但要指出图中表示结论的向量)O图4图5图6M B20.(本题满分10分)将抛物线212y x =先向上平移2个单位,再向左平移m (m >0)个单位,所得新抛物线经过点(-1,4),求新抛物线的表达式及新抛物线与y 轴交点的坐标.21.(本题满分10分)如图7,已知AD 是⊙O 的直径,AB 、BC 是⊙O 的弦,AD ⊥BC ,垂足是点E ,8BC =,2DE =.求⊙O 的半径长和sin ∠BAD 的值.22.(本题满分10分)如图8,已知有一块面积等于12002cm 的三角形铁片ABC ,已知底边BC 与底边上的高的和为100cm (底边BC 大于底边上的高),要把它加工成一个正方形铁片,使正方形的一边EF 在边BC 上,顶点D 、G 分别在边AB 、 AC 上,求加工成的正方形铁片DEFG 的边长.图7DA图8F GE D CB A23.(本题满分12分)已知:如图9,在四边形ABCD 中,ADB ACB ∠=∠,延长AD 、BC 相交于点E ,求证:(1)△ACE ∽△BDE ; (2)BE DC AB DE =.24.(本题满分12分)如图10,已知在平面直角坐标系xOy 中, 二次函数273y ax x c =-+的图像经过 点A (0, 8)、B (6, 2),C (9, m ),延长AC 交x 轴于点D . (1)求这个二次函数的解析式及m 的值; (2)求ADO ∠的余切值;(3)过点B 的直线分别与y 轴的正半轴、x 轴、线段AD 交于点P (点A 的上方)、M 、Q ,使以点P 、A 、Q 为顶点的三角形与△MDQ 相似,求此时点P 的坐标.图10图9EDC B A25.(本题满分14分)如图11,已知锐角∠MBN 的正切值等于3,△PBD 中,∠BDP =90°,点D 在∠MBN 的边BN 上,点P 在∠MBN 内,PD =3,BD =9.直线l 经过点P ,并绕点P 旋转,交射线BM 于点A ,交射线DN 于点C .设CACP=x , (1)求x =2时,点A 到BN 的距离;(2)设△ABC 的面积为y ,求y 关于x 的函数解析式,并写出函数的定义域; (3)当△ABC 因l 的旋转成为等腰三角形时,求x 的值.l PNMDCBA图11 PNMDB 备用图普陀区2015学年度第一学期九年级数学期终考试试卷参考答案及评分说明一、选择题:(本大题共6题,每题4分,满分24分)1.(A); 2.(C); 3.(C); 4.(D); 5.(D); 6. (B).二、填空题:(本大题共12题,每题4分,满分48分)7.73; 8. b a +3; 9. 213 ; 10.215-; 11.④; 12. 低; 13.1; 14.2; 15.3;16 17.8; 18.三、解答题(本大题共7题,其中第19---22题每题10分,第23、24题每题12分,第25题14分,满分78分)19.解:(1;32MA a b =--. ··········································· (3分+3分) (2)答案略. ·············································································· (4分)20.解:由题意可设新抛物线的表达式是2)(212++=m x y . ··························· (2分) 该图像经过点(-1,4),∴把1-=x ,4=y 代入2)(212++=m x y ,得 2)1(2142++-=m . 解得31=m , 21m =-(不合题意,舍去). ································· (4分) ∴此时新抛物线的表达式是2)3(212++=x y . ·································· (1分)令0=x ,得213=y . ···································································· (2分) ∴新抛物线2)3(212++=x y 与y 轴的交点坐标为(0,213). ··········· (1分)21、解:联结OB . ··················································································· (1分) AD 是⊙O 的直径,BC 是⊙O 的弦,AD ⊥BC ,垂足为点E ,∴∠090=OEB ,BC EC BE 21==. ·········································· (2分) 又 8BC =,∴4BE =. ························································· (1分) 设⊙O 的半径长是x ,则2OE x =-.在Rt △OEB 中,∠090=OEB ,∴222BO OE BE =+,即2224(2)x x +-=,解得5x =. ··············· (2分)∴⊙O 的半径长是5. ·································································· (1分) ∴1028AE AD DE =-=-=. ················································· (1分)由勾股定理得:AB = ························································ (1分) 在Rt △AEB 中,∠090=AEB , ∴sin∠5BE BAD AB ===················································ (1分)22.解法一:过点A 作AH ⊥BC ,垂足为H ,交DG 于P . ······························· (1分)由题意得:11200,2100.BC AH BC AH ⎧=⎪⎨⎪+=⎩ ·············································· (1分)解得:60,40.BC AH =⎧⎨=⎩································································ (1分)设正方形DEFG 的边长为x cm .∵四边形DEFG 是正方形,EF 在边BC 上,∴DG ∥BC .得△ADG ∽△ABC . ····························································· (1分)由AH ⊥BC .得AP ⊥DG ,即AP 是△ADG 的高. ······················ (1分) ∴AP DGAH BC=. ································································· (1分) ∵PH ⊥BC ,GF ⊥BC , ∴PH =GF ,AP=AH-PH=AH-GF . ··········· (1分) ∴AH GF DGAH BC-=. ························································· (1分)得404060x x-=, 解得24x =. ············································ (1分) 答:加工成的正方形铁片DEFG 的边长等于24cm . ··················· (1分)解法二:过点A 作AH ⊥BC ,垂足为H ,交DG 于P . ···························· (1分)设正方形DEFG 的边长是x cm ,AH =h cm ,BC =a cm .由题意得:2400a h =,100a h +=. ·································· (1分)∵四边形DEFG 是正方形,EF 在边BC 上,∴DG ∥BC .得△ADG ∽△ABC . ····························································· (1分) 由AH ⊥BC .得AP ⊥DG ,即AP 是△ADG 的高. ······················ (1分) ∴AP DGAH BC=. ································································· (1分) ∵PH ⊥BC ,GF ⊥BC , ∴PH =GF ,AP=AH-PH=AH-GF . ··········· (1分)∴h x xh a-=. ··································································· (1分) 得ah x a h =+=2400100=24. ····················································· (2分)答:加工成的正方形铁片DEFG 的边长等于24cm . ··················· (1分)23. 证明:(1)∵+180ADB BDE ∠∠=,+180ACB ACE ∠∠=, ··············· (2分)又∵ADB ACB ∠=∠, ························································· (1分) ∴BDE ACE ∠=∠. ·························································· (1分) ∵AEC BED ∠=∠, ·························································· (1分) ∴△AEC ∽△BED . ························································ (1分) (2)∵△AEC ∽△BED ,∴DE BECE AE =. ·································································· (1分) ∴DE CEBE AE=. ································································· (1分) ∵DEC BEA ∠=∠, ·························································· (1分) ∴△DEC ∽△BEA . ························································· (1分) ∴DC DEAB BE=. ·································································· (1分) ∴BE DC AB DE =. ························································ (1分)24.解:(1)由题意得8,72366.3c a c =⎧⎪⎨=-⨯+⎪⎩解得2,98.a c ⎧=⎪⎨⎪=⎩ ································· (2分) ∴这个二次函数的解析式是227893y x x =-+. ···························· (1分) ∵点C (9, m )在这个二次函数的图像上,∴把9x =,y m =代入解析式,得5m =. ································· (1分) 所以m 的值为5.(2)解一:由(1)得C (9, 5).设直线AC 的表达式是()0y kx b k =+≠, 由题意得8,59.b k b =⎧⎨=+⎩解得1,38.k b ⎧=-⎪⎨⎪=⎩ ∴直线AC 表达式是183y x =-+. ················································· (2分) ∴点D 的坐标是(24, 0). ···························································· (1分) 在Rt △ADO 中,cot 3ODADO AO∠==. ······································· (1分) 解二:由(1)得C (9, 5).过点C 作CE ⊥x 轴,由CE ∥y 轴,可得CE DEAO DO=. ······················· (1分) 得598DO DO-=. ·········································································· (1分) 解得24DO =. ·········································································· (1分) 在Rt △ADO 中,cot 3ODADO AO∠==. ······································· (1分) (3)∵AQP MQD ∠=∠, QMD ∠>APQ ∠,∴△APQ 与△MDQ 相似只能APQ MDQ ∠=∠. ···························· (1分) 可得cot cot APQ MDQ ∠=∠.过点B 作BF ⊥y 轴,在Rt △FBP 中,cot 3PF APQ BF∠==, 解得18PF =. ··········································································· (2分)∴点P 的坐标是(0, 20). ··························································· (1分)25、解:(1)过点A 作AH ⊥BN ,垂足为点H . ············································· (1分)由∠BDP =90°,可得PD ∥AH . ·········································· (1分)∴AH CA PD CP=. ····································································· (1分) ∵CA CP =x , x =2,PD =3, 得:=6AH . ······································································· (1分)(2) 同理得:=3AH x . ································································ (1分)在Rt △ABH 中,由tan 3MBN ∠=,可得BH x =, ·················· (1分)从而9DH x =-.∵ PD ∥AH ,∴CH CA CD CP =. 得:9=1x CD x --. ·································································· (1分) ∵12ABC S BC AH =, ∴193921x y x x -⎛⎫=+ ⎪-⎝⎭. 化简得:2121x y x =-.(1<x ≤9)······································· (1分+1分) H l P NMD C B A(3)过点P 作PQ ∥AB ,交BN 于点Q .则△PQC ∽△ABC .由△ABC 是等腰三角形,可得△PQC 是等腰三角形.由PQ ∥AB ,可得tan 3PQD ∠=.∴=1DQ,PQ .① 如果AB AC =,得PQ PC =.∴1CD DQ ==.∴1052CB x CQ ===. ······························································ (1分) ②如果AB BC =,得PQ QC =.∴QC =1DC =. ················································ (1分)∴55CB x CQ ===. ..................................................... (1分) ③如果AC BC =,得PC QC =.在Rt △PDC 中,由勾股定理得:4CD =. ································· (1分) ∴9413145CB x CQ +===+. ························································· (1分) 综上所述,当△ABC 因l 的旋转成为等腰三角形时,x 的值等于5和135.Q lPNMD C B A。
2017年上海普陀区中考数学二模--2017.04.20

普陀区2016学年度第二学期初三质量调研数 学 试 卷(时间:100分钟,满分:150分)一、选择题(本大题共6题,满分24分)[下列各题的四个选项中,有且只有一个选项是正确的, 选择正确项的代号并填涂在答题纸的相应位置上]1.下列计算正确的是( )A. 236a a a ⋅=B. 33a a a ÷=C. 333a b ab +=D. ()236a a =2.是同类二次根式,那么这个根式是( )A. B. C. D. 3.在学校举办的“中华诗词大赛”中,有11名选手进入决赛,他们的决赛成绩各不相同,其中一名参赛选手想知道自己是否能进入前6名,他需要了解这11名学生成绩的( )A. 中位数B. 平均数C. 众数D. 方差4.如图1,在△ABC 中,点D 、E 分别在边AB 、AC 上,如果50A ∠=°,那么12∠+∠的大小为( )A. 130°B. 180°C. 230°D. 260°5.如图2,在△ABC 中,中线AD 、CE 交于点O ,设AB a = ,BC b = ,那么向量AO 用向量a 、b 表示为( ) A. 12a b + B. 2133a b + C. 2233a b + D, 1124a b +6.在△ABC 中,6AB AC ==,2cos 3B ∠=,以点B 为圆心,AB 为半径作圆B ,以点C 为圆心,半径长为13作圆C ,圆B 与圆C 的位置关系是( )A. 外切B. 相交C. 内切D. 内含二、填空题(本大题共12题,每题4分,满分48分)7.分解因式:34a a −=____________8.方程x =____________9.不等式组23030x x −< ≥的解集是____________ 10.函数y =的定义域是____________ 11.如果关于x 的方程230x x c −+=没有实数根,那么c 的取值范围是____________12.已知反比例函数k y x=(k 是常数,0k ≠)的图像在第二、四象限,点()11,A x y 和点()22,B x y 在函数的图像上,当120x x <<时,可得1y ______2y (填“>”、“=”、“<”)13.一次抽奖活动设置了翻奖牌(图3展示的分别是翻奖牌的正反两面),抽奖时,你只能看到正面,你可以在9个数字中任意选中一个数字,可见抽中一副球拍的概率是19,那么请你根据题意写出一个事件,使这个事件发生的概率是13,这个事件是____________14.正八边形的中心角等于____________度15.如图4,在△ABC 中,D 、E 分别是边AB 、AC 上的点,如果12ADAE DB EC ==,那么△ADE 与△ABC 周长的比是____________16某班学生参加环保知识竞赛,已知竞赛得分都是整数,把参赛学生的成绩整理后分为6个小组,画出竞赛成绩的频数分布直方图(如图5所示),根据图中的信息,可得成绩高于60分的学生占全班参赛人数的百分率是____________17.一个滑轮起重装置如图6所示,滑轮的半径是10cm ,当滑轮的一条半径OA 绕轴心O 按逆时针方向旋转的角度为120°时,重物上升____________cm (结果保留π)18.如图7,将△ABC 绕点B 按逆时针方向旋转得到△ EBD ,点E 、点D 分别与点A 、点C 对应,且点D 在边AC 上,边DE 交边AB 于点F ,△BDC ∽△ABC ,已知BC =,5AC =,那么△DBF的面积等于____________三、解答题(本大题共7题,满分78分)19.(本题满分10分) 计算:()32017113sin 602− +−+−°20.(本题满分10分)解方程组:22320449x y x xy y −+= ++=21.(本题满分10分)在平面直角坐标系xOy 中,已知正比例函数的图像与反比例函数8y x=的图像交于点(),4A m . (1)求正比例函数的解析式;(2)将正比例函数的图像向下平移6个单位得到直线l ,设直线l 与x 轴的交点为B ,求∠ABO 的正弦值.22.(本题满分10分)上海首条中运量公交线路71路已正式开通,这线路西起沪青平公路申昆路,东至延安东路中山东一路,全长17.5千米,71路车行驶于专设的公交车道,又配以专用的公交信号灯,经测试,早晚高峰时段71路车在专用车道内行驶的平均速度比在非专用车道每小时快6千米,因此单程可节省时间22.5分钟,求早晚高峰时段71路车在专用车道内行驶的平均车速.23.(本题满分12分)已知:如图8,在平行四边形ABCD 中,AC 为对角线,E 是边AD 上一点,BE ⊥AC 交AC 于点F ,BE 、CD 的延长线交于点G ,且∠ABE =∠CAD .(1)求证:四边形ABCD 是矩形;(2)如果AE EG =,求证:2AC BC BG =⋅.24.(本题满分12分)如图9,在平面直角坐标系xOy 中,二次函数()220y x x m m =−+>的对称轴与比例系数为5的反比例函数图像交于点A ,与x 轴交于点B ,抛物线的图像与y 轴交于点C ,且3OC OB =.(1)求点A 的坐标;(2)求直线AC 的表达式;(3)点E 是直线AC 上一动点,点F 在x 轴上方的平面内,且使以A 、B 、E 、F 为顶点的四边形是菱形,直接写出点F 的坐标.25.(本题满分14分)如图10,半圆O 的直径10AB =,有一条定长为6的动弦CD 在弧AB 上滑动(点C 、点D 分别不与点A 、点B 重合),点E 、F 在AB 上,EC CD ⊥,FD CD ⊥.(1)求证:EO OF =;(2)联络OC ,如果△ECO 中有一个内角等于45°,求线段EF 的长;(3)当动弦CD 在弧AB 上滑动时,设变量CE x =,四边形CDFE 面积为S ,周长为l ,问:S 与l 是否分别随着x 的变化而变化?试用所学的函数知识直接写出它们的函数解析式及函数定义域,以说明你的结论.参考答案1-6:DCACBB7、()()22a a a +−8、1x =9、302x ≤< 10、5x ≠11、94c > 12、<13、抽中一张唱片14、4515、1:316、80%17、203π 18、451619、9−20、11x y = = 或13515x y =− =−21、(1)2y x =,(222、20千米/小时 23、(1)证明略;(2)证明略.24、(1)(1,5)A ;(2)23y x =+;(3)(1或95,42 25、(1)证明略;(2;(3)面积为定值,24S =;14l =+定义域:08x <<。
初中数学上海市普陀区中考模拟数学二模考试题考试卷及答案.docx

xx学校xx学年xx 学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题(每空xx 分,共xx分)试题1:如图11-1,已知梯形ABCD中,AD∥BC,∠D=90°,BC=5,CD=3,cotB=1,P是边BC上的一个动点(不与点B、点C重合),过点P作射线PE,使射线PE交射线BA于点E,∠BPE=∠CPD。
(1)如图11-2,当点E与点A重合时,求∠DPC的正切值;(2)当点E落在线段AB上时,设BP=,BE=,试求与之间的函数解析式,并写出的取值范围;(3)设以BE长为半径的和以AD长为直径的相切,求BP的长。
试题2:如图10,在平面直角坐标系中,二次函数的图像经过点,,,点D是点C关于原点的对称点,联结BD,点E是轴上的一个动点,设点E的坐标为,过点E作轴的垂线交抛物线于点P。
(1)求这个二次函数解析式;(2)当点E在线段OB上运动时,直线交BD于点Q,当四边形CDQP是平行四边形时,求的值;评卷人得分(3)是否存在点P,使△BDP是不以BD为斜边的直角三角形,如果存在,请直接写出点P的坐标;如果不存在,请说明理由。
试题3:如图9,在△ABC中,点D、E分别在边BC、AC上,BE、AD相交于点G,EF∥AD交BC于点F,且,联结FG。
(1)求证:FG∥CE;(2)设∠BAD=∠C,求证:四边形AGFE是菱形。
试题4:本市为了给市容营造温馨和谐的夜间景观,准备在一条宽7.4米的道路上空利用轻轨桥墩,安装呈大中小三个同心圆的景观灯带,如图8,已知EF表示路面宽度,轻轨桥墩上设有两处限高标志,分别表示等腰梯形的下底边到路面的距离为2.9米和等腰梯形的上底边到路面的距离为3.8米,大圆直径等于AD,三圆半径的比等于1:2:3.试求这三个圆形灯带的总长为多少米?(结果保留π)(参考数据:)试题5:已知,如图7,在平面直角坐标系中,直线与轴交于点A,在第一象限内与反比例函数图像交于点B,BC垂直于轴,垂足为点C,且OC=2OA。
上海市普陀区2018-2019学年初三下学期二模考数学试卷(解析版)

【答案】
【解析】
【分析】
直接利用坡比的定义得出 BC 的长,进而利用勾股定理得出答案.
【详解】解:由题意可得:AC=2, BC=3×2=6;
故
中,
的解集是______.
【答案】 【解析】 【分析】 首先解每个不等式,然后确定两个不等式的解集的公共部分,即是不等式组的解集. 【详解】解:
解不等式
,得: ,
解不等式
,得:x≥-1,
则不等式组的解集为
,
故答案为:
.
【点睛】本题考查的是解一元一次不等式组,熟知解一元一次不等式的基本步骤是解答此题的关键.
【详解】解:(A)π≈3.14,故 A 错误;
故选:A.
【点睛】本题考查无理数,解题的关键是正确理解 π,本题属于基础题型.
4.下列函数中,如果 , 的值随 的值增大而增大,那么这个函数是()
A.
;
B.
;
C.
;
【答案】D
【解析】
【分析】
D.
.
2
直接利用一次函数以及反比例函数和二次函数的增减性进而分析得出答案.
故答案为: .
【点睛】此题主要考查了解直角三角形的应用,正确应用勾股定理是解题关键.
在 16.如图, 、 是△ 的中线,交于点 ,设
,
,那么向量 用向量 、 表示是______.
【答案】 【解析】 【分析】 求出 ,再根据
,求解即可.
【详解】解:∵AD、BE 是△ ABC 的中线,交于点 O,
8
2016年普陀初三一模数学试题以及答案
BCDBAC普陀区2015学年度第一学期初三质量调研数学试卷一、选择题1. 如图1,BD 、CE 相交于点A ,下列条件中,能推得DE ∥BC 的条件是( ) (A)AE:EC=AD:DB ;(B)AD:AB=DE:BC ; (C)AD:DE=AB:BC ; (D)BD:AB=AC:EC .2. 在△ABC 中,点D 、E 分别是边AB 、AC 的中点,DE ∥BC ,如果△ADE 的面积等于3,那么△ABC 的面积等于( ) (A)6;(B)9;(C)12;(D)15.3. 如图2,在Rt △ABC 中,∠C=90°,CD 是斜边AB 上的高,下列线段的比值不等于cos A 的值的是( )(A)ADAC ; (B)ACAB ; (C)BD BC;(D) CD BC.4. 如果a 、b 同号,那么二次函数y =ax 2+bx +1的大致图像是( )5. 下列命题中,正确的是( )(A)圆心角相等,所对的弦的弦心距相等; (B)三点确定一个圆;(C)平分弦的直径垂直于弦,并且平分弦所对的弧; (D)弦的垂直平分线必经过圆心。
图1图2BOB6. 已知在平行四边形ABCD 中,点M 、N 分别是边BC 、CD 的中点,如果AB ⃗⃗⃗⃗⃗ =a ,AD ⃗⃗⃗⃗⃗ =b⃗ ,那么向量MN ⃗⃗⃗⃗⃗⃗⃗ 关于a 、 b ⃗ 的分解式是( ) (A) 12a −12b ⃗ ;(B)− 12a +12b⃗ ;(C) 12a +12b⃗ ;(D) (B)− 12a −12b⃗ . 二、填空题7. 如果x:y=2:5,那么y xx y-+=__________; 8. 计算:2(a +b ⃗ )+( a −b⃗ )=_________; 9. 计算:2sin 45cot 30tan 60︒+︒⋅︒=____________;10. 已知点P 把线段分割成AP 和PB (AP>PB )两段,如果AP 是AB 和PB 的比例中项,那么AP:AB的值等于________;11. 在函数①y =ax 2+bx +c ,②y =(x −1)2−x 2,③y =5x 2−5x 2,④y =−x 2+2中,y 关于x的二次函数是___________(填写序号);12. 二次函数y =x 2+2x −3的图像有最_______点;(填“高”或“低”)13. 如果抛物线y =2x 2+mx +n 的顶点坐标为(1,3),那么m+n 的值等于_______;14. 如图3,点G 为△ABC 的重心,DE 经过点G ,DE ∥AC ,EF ∥AB ,如果DE 长是4,那么CF 的长是_________;15. 如图4,半圆形纸片的半径长是1cm ,用如图所示的方法将纸片对折,使对折后半圆的中点M 与圆心O 重合,那么折痕CD 的长是________cm ;16. 已知在Rt △ABC 中,∠C=90°,点P 、Q 分别在边AB 、AC 上,AC=4,BC=AQ=3,如果△APQ与△ABC 相似,那么AP 的长等于________;17. 某货站用传送带传送货物,为了提高传送过程的安全性,工人师傅将原坡角为45°的传送带AB ,调整为坡度i=1:√3的新传送带AC (如图5所示),已知原传送带AB 的长是4√2米。
2016上海中考数学二模试卷含闵行,普陀,杨浦,虹口,黄浦,松江,浦东,长宁8个区包括答案

闵行区2015-2016学年第二学期九年级质量调研考试2016.4数学试卷(考试时间100分钟,满分150分)考生注意:1.本试卷含三个大题,共25题.2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确选项的代号并填涂在答题纸的相应位置上】1.如果单项式22n a b c是六次单项式,那么n的值取(A)6;(B)5;(C)4;(D)3.2(A;(B(C1;(D1.3.下列函数中,y随着x的增大而减小的是(A)3y x=;(B)3y x=-;(C)3yx=;(D)3yx=-.4.一鞋店销售一种新鞋,试销期间卖出情况如下表,对于鞋店经理来说最关心哪种尺码的鞋畅销,那么下列统计量对该经理来说最有意义的是(A)平均数;(B)中位数;(C)众数;(D)方差.5.下列图形中,既是轴对称又是中心对称图形的是(A)正五边形;(B)等腰梯形;(C)平行四边形;(D)圆.6.下列四个命题,其中真命题有(1)有理数乘以无理数一定是无理数;(2)顺次联结等腰梯形各边中点所得的四边形是菱形;(3)在同圆中,相等的弦所对的弧也相等;(4)如果正九边形的半径为a,那么边心距为sin20a⋅o.(A)1个;(B)2个;(C)3个;(D)4个.二、填空题:(本大题共12题,每题4分,满分48分) 7.计算:22-= ▲ .8.在实数范围内分解因式:32a a -= ▲ . 92=的解是 ▲ . 10.不等式组30,43x x x -≥⎧⎨+>-⎩的解集是 ▲ .11.已知关于x 的方程20x x m --=没有实数根,那么m 的取值范围是 ▲ .12.将直线213y x =-+向下平移3个单位,那么所得到的直线在y 轴上的截距为 ▲ .13.如果一个四边形的两条对角线相等,那么称这个四边 形为“等对角线四边形”.写出一个你所学过的特殊 的等对角线四边形的名称 ▲ .14.如图,已知在梯形ABCD 中,AD // BC ,且BC = 3AD ,点E 是边DC 的中点.设AB a =uu u r r ,AD b =uuu r r ,那么 AE =uu u r ▲ (用a r 、b r的式子表示).15.布袋中有大小、质地完全相同的4个小球,每个小球上分别标有数字1、2、3、4,如果从布袋中随机抽取两个小球,那么这两个小球上的数字之和为偶数的概率是 ▲ .16.9月22日世界无车日,某校开展了“倡导绿色出行”为主题的调查,随机抽查了部分师生,将收集的数据绘制成下列不完整的两种统计图.已知随机抽查的教师人数为学生人数的一半,根据图中信息,乘私家车出行的教师人数是 ▲ .17.点P 为⊙O 内一点,过点P 的最长的弦长为10cm ,最短的弦长为8cm ,那么OP的长等于 ▲ cm .18.如图,已知在△ABC 中,AB = AC ,1tan 3B ∠=,将△ABC 翻折,使点C 与点A 重合,折痕DE 交边BC 于点D ,交边AC 于点E ,那么BDDC的值为 ▲ . ABD C(第14题图)EABC(第18题图)(第16题图) 乘公车 y % 步行 x %骑车 25%私家车 15%学生出行方式扇形统计图师生出行方式条形统计图三、解答题:(本大题共7题,满分78分)19.(本题满分10分)110212(cos60)32--++-o.20.(本题满分10分)解方程:222421242xx x x x x-+=+--.21.(本题满分10分,其中每小题各5分)如图,已知在△ABC中,∠ABC = 30º,BC = 8,sin A∠=,BD是AC边上的中线.求:(1)△ABC的面积;(2)∠ABD的余切值.22.(本题满分10分,其中每小题各5分)如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i =1∶512,且AB = 26米.为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过53º时,可确保山体不滑坡.(1)求改造前坡顶与地面的距离BE的长.(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)(参考数据:sin530.8≈o,cos530.6≈o,tan53 1.33≈o,cot530.75≈o).BCD(第21题图)BDC(第22题图)F23.(本题满分12分,其中每小题各6分)如图,已知在矩形ABCD 中,过对角线AC 的中点O 作 AC 的垂线,分别交射线AD 和CB 于点E 、F ,交边DC 于 点G ,交边AB 于点H .联结AF ,CE . (1)求证:四边形AFCE 是菱形; (2)如果OF = 2GO ,求证:2GO DG GC =⋅. 24.(本题满分12分,其中每小题各4分)如图,已知在平面直角坐标系xOy 中,抛物线22y ax x c =++与x 轴交于 点A (-1,0)和点B ,与y 轴相交于点C (0,3),抛物线的对称轴为直线l . (1)求这条抛物线的关系式,并写出其对称轴和顶点M 的坐标;(2)如果直线y kx b =+经过C 、M 两点,且与x 轴交于点D ,点C 关于直 线l 的对称点为N ,试证明四边形CDAN(3)点P 在直线l 上,且以点P 为圆心的圆经过A 、B 两点,并且与直线CD 相切, 求点P 的坐标.(第24题图)(第23题图)AB CDE FGOH25.(本题满分14分,其中第(1)小题各4分,第(2)、(3)小题各5分)如图,已知在△ABC中,AB = AC = 6,AH⊥BC,垂足为点H.点D在边AB上,且AD = 2,联结CD交AH于点E.(1)如图1,如果AE = AD,求AH的长;(2)如图2,⊙A是以点A为圆心,AD为半径的圆,交AH于点F.设点P为边BC上一点,如果以点P为圆心,BP为半径的圆与⊙A外切,以点P为圆心,CP为半径的圆与⊙A内切,求边BC的长;(3)如图3,联结DF.设DF = x,△ABC的面积为y,求y关于x的函数解析式,并写出自变量x的取值范围.(第25题图3)普陀区2015-2016学年度第二学期初三质量调研数学试卷 2016年4月13日(时间:100分钟,满分析150分)一、选择题:(本大题共6题,每题4分,满分24分)1、据统计,2015年上海市全年接待国际旅游入境者共80016000人次,80016000用科学记数法表示是( )(A )8.0016⨯610; (B )8.0016710⨯; (C )8100016.8⨯; (D )9100016.8⨯2、下列计算结果正确的是( )(A )824a a a =⋅; (B )()624a a =; (C )()222b a ab =; (D )()222b a b a -=-.3、下列统计图中,可以直观地反映出数据变化的趋势的统计图是( )(A )折线图; (B )扇形图; (C )统形图; (D )频数分布直方图。
上海市普陀区2016届九年级12月质量调研(一模)数学试题

普陀区2015-2016学年度第一学期初三质量调研数学2015.12.29一、选择题:(本大题共6题,每题4分,满分24分)1. 如图1,BD、CE相交于点A,下列条件中,能推得DE∥BC的条件是()2. 在△ABC中,点D、E分别是边AB、AC的中点,DE∥BC,如果△ADE的面积等于3,那么△ABC的面积等于()(A)6 (B) 9 (C)12 (D)153. 如图2,在Rt△ABC中,∠C=90°,CD是斜边AB上的高,下列线段的比值不等于cosA的值的是()4. 如果a、b同号,那么二次函数的大致图像是()5. 下列命题中,正确的是()(A) 圆心角相等,所对的弦的弦心距相等 (B) 三点确定一个圆(C) 平分弦的直径垂直于弦,并且平分弦所对的弧 (D) 弦的垂直平分线必经过圆心6. 已知在平行四边形ABCD中,点M、N分别是边BC、CD的中点,如果,,那么向量关于的分解式是()二、填空题:(本大题共12题,每题4分,满分48分)7. 如果,那么=_____8. 计算:=9.计算:=_______10. 已知点P把线段分割成AP和PB两段(AP>PB),如果AP是AB和PB的比例中项,那么的值等于________11. 在函数中,y关于x的二次函数是.(填写序号)12. 二次函数的图像有最点.(填:“高”或“低”)13. 如果抛物线的顶点坐标为(1,3),那么m+n的值等于________14. 如图3,点G为△ABC的重心,DE经过点G,,如果DE的长是4,那么CF的长是_______15. 如图4,半圆形纸片的半径长是1cm,用如图所示的方法将纸片对折,使对折后半圆的中点M与圆心O重合,那么折痕CD的长是________cm16. 已知在Rt△ABC中,∠C=90°,点P、Q分别在边AB、AC上,AC=4,BC=AQ=3,如果△APQ与△ABC 相似,那么AP的长等于17. 某货站用传送带传送货物,为了提高传送过程的安全性,工人师傅将原坡角为45°的传送带AB,调整为坡度的新传送带AC(如图所示).已知原传送带AB的长是AC的长是米.18. 已知A(3,2)是平面直角坐标中的一点,点B 是x轴负半轴上一动点,联结AB,并以AB为边在x轴上方作矩形ABCD,且满足BC:AB=1:2,设点C的横坐标是a,如果用含a的代数式表示D点的坐标,那么D点的坐标是.三、解答题:(本大题共7题,满分78分)19. (本题满分10分)已知:如图6,在梯形ABCD中,AD∥BC,,点M是边BC的中点(1)填空:(结果用表示)⑵直接在图中画出向量.(不要求写作法,但要指出图中表示结论的向量)20. (本题满分10分)将抛物线先向上平移2个单位,再向左平移个单位,所得新抛物线经过点(-1,4),求新抛物线的表达式及新抛物线与y轴交点的坐标.21. (本题满分10分)如图,已知AD是的直径,AB、BC是的弦,AD⊥BC,垂足是点E,BC=8,DE=2,求的半径长和的值.22. (本题满分10分)已知:如图8,有一块面积等于的三角形纸片ABC,已知底边与底边BC上的高的和为100cm(底边BC大于底边上的高),要把它加工成一个正方形纸片,使正方形的一边EF在边BC上,顶点D、G分别在边AB、AC上,求加工成的正方形铁片DEFG的边长.23. (本题满分10分)已知,如图9,在四边形ABCD中,,延长AD、BC相交于点E求证:⑴△ACE∽△BDE;⑵24. (本题满分12分)已知,如图10,在平面直角坐标系xoy中,二次函数的图像经过点、,延长AC交x轴于点D.⑴求这个二次函数的解析式及的m值;⑵求∠ADO的余切值;⑶过点B的直线分别与y轴的正半轴、x轴、线段AD交于点P(点A的上方)、M、Q,使以点P、A、Q 为顶点的三角形与相似,求此时点P的坐标.25. (本题满分14分)如图,已知锐角的∠MBN正切值等于3,△PBD中,,点D在∠MBN的边BN上,点P在∠MBN 内,PD=3,BD=9.直线l经过点P,并绕点P旋转,交射线BM于点A,交射线DN于点C.设⑴求x=2时,点A到BN的距离;⑵设△ABC的面积为y,求y关于x的函数解析式,并写出函数的定义域;ABC△yy x⑶当△ABC因l的旋转成为等腰三角形时,求x的值.。
2016年上海静安、青浦区初三中考二模数学、语文、英语试卷及答案

(一)默写 (15 分)
1、浮云游子意,__________________。
(《送友人》)
2、______________,无言谁会凭阑意。
(《蝶恋花》)
3、山河破碎风飘絮,______________。
(《过零丁洋》)
4、______________________,故克之。
(《曹刿论战》)
5、 谈笑有鸿儒,__________________。
绩(环)为:7,8,10,6,9,那么这两位运动员中 ▲ 的成绩较稳定. 14.某班进行一次班级活动,要在 2 名男同学和 3 名女同学中,随机选出 2 名学生担任主持人,那
么选出的 2 名学生恰好是 1 男 1 女的概率是 ▲ .
15. 在 Rt△ABC 中,∠C=90°,∠A、∠B 的平分线相交于点 E,那么∠AEB 的度数是 ▲ .
(《陋室铭》)
(二)阅读下面这首作品,完成 6-7 题(4 分)
观沧海
东临碣石,以观沧海。
水何澹澹,山岛竦峙。
树木丛生,百草丰茂。
秋风萧瑟,洪波涌起。
日月之行,若出其中;
星汉灿烂,若出其里。
幸甚至哉,歌以咏志。
6、本篇作者曾出现在以下哪篇课文中?(
)(2 分)
A.《武松打虎》 B.《煮酒论英雄》 C.《明湖居听书》 D.《劳山道士》
节水量( m3 ) 0.2 0.3 0.4 0.5 0.6
家庭数(个)
1
2
2
4
1
那么这 10 个家庭的节水量( m3 )的平均数和中位数分别是
(A)0.42 和 0.4 (B)0.4 和 0.4 (C)0.42 和 0.45 (D)0.4 和 0.45
5.如图,已知点 D、E 分别在△ABC 边 AB、AC 上,DE//BC,
2016上海各区初中数学二模试题及解答

十分遗憾最低的同学仍然只得了 56 了。这说明本次考试分数的众数是(
)
A、82;
B、91;
C、11;
D、56;
5、如果点 K、L、M、N 分别是四边形 ABCD 的四条边 AB、BC、CD、DA 的中点,且四边形 KLMN
是菱形,那么下列选项正确的是(
)
A、AB⊥BC;
B、AC⊥BD;
C、AB=BC;
6、如图 1,梯形 ABCD 中,AD∥BC,AB=DC,∠DBC=45°,
D、AC=BD;
AD
点 E 在 BC 上,点 F 在 AB 上,将梯形 ABCD 沿直线 EF 翻折,
F
使得点 B 与点 D 重合。如果 AD 1 ,那么 AF 的值是(
)
BC 4
BF
A、 1 ; 2
B、 3 ; 5
C、 2 ; 3
三、解答题(本大题共 7 题,满分 78 分)
19.(本题满分 10 分)
1
计算: 273 (
3
1)2
1 2
1
2 3 1
M C
N
B
A
(第 18 题图)
20.(本题满分 10 分)
解方程组:
x 2y 1
x2
3xy
2y2
0
21.(本题满分 10 分,其中每小题各 5 分)
如图,在平面直角坐标系 xOy 中,一次函数 y kx b (k 0) 的图像经过 A(0, 2) , B(1, 0)
BF 相交于 H,BF 与 AD 的延长线相交于 G.求证:
(1)CD=BH; (2)AB 是 AG 和 HE 的比例中项.
A
D
G
HF
B
上海市普陀区中考模拟数学试卷及答案

2008学年度第二学期普陀区初三质量调研数学试卷2009.4(时间:100分钟,满分:150分)考生注意:所有答案务必按照规定在答题纸上完成,写在试卷上不给分一、单项选择题:(本大题共6题,每题4分,满分24分)[下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上] 1.下列运算正确的是……………………………………………………………………( ).(A) 221-=-;(B) 632)(mn mn = ; (C) 39±= ; (D) 426m m m =÷ .2. 在49,a 9,25xy ,92+a ,23+x ,1.0中,是最简二次根式的个数是( ). (A) 1; (B) 2; (C) 3; (D) 4. 3.下列语句错误的是……………………………………………………………………( ).(A )如果m 、n 为实数,那么m (n a )=(mn )a;(B )如果m 、n 为实数,那么(m +n )a =m a +n a;(C )如果m 、n 为实数,那么m (a +b )=m a+ m b ;(D )如果k =0或0 =a ,那么k a=0.4.顺次连结菱形的各边中点所得到的四边形是………………………………………( ).(A) 平行四边形; (B)菱形; (C) 矩形; (D)正方形. 5.下列说法中正确的是…………………………………………………………………( ).(A) 每个命题都有逆命题; (B) 每个定理都有逆定理; (C) 真命题的逆命题是真命题; (D) 真命题的逆命题是假命题.6. 给出下列关于三角形的条件:①已知三边;②已知两边及其夹角;③已知两角及其夹边;④已知两边及其中一边的对角. 利用尺规作图,能作出唯一的三角形的条件是…( ). (A) ①②③; (B) ①②④; (C) ②③④; (D) ①③④.二、填空题:(本大题共12题,每题4分,满分48分)[请将结果直接填入答题纸的相应位置] 7.分解因式:652--x x = . 8.如果3=a ,那么a2= . 9.请你根据如图写出一个乘法公式:.a a bb(第9题)10.用科学计数法表示-0.00000628= . 11.已知方程3124-=+-x ax 的解为1=x ,那么a 2的值为 .12.不等式组⎪⎩⎪⎨⎧-≥-<-3132,31x x 的解集是 .13.从数字1、2、3中任取两个不同的数字组成一个两位数,那么这个两位数小于23的概率是 .14. 某市2008年的人均GDP 约为2006年的人均GDP 的1.21倍,如果该市每年的人均GDP 增长率相同,均为x ,那么可列出方程: __.15.已知点G 是△ABC 的重心,△ABC 的面积为182cm ,那么△AGC 的面积为 2cm . 16. 某人在斜坡上走了13米,上升了5米,那么这个斜坡的坡比i = . 17.在Rt △ABC 中,∠C =90°,AC =5,BC =8,如果以点C 为圆心作圆,使点A 在圆C 内,点B 在圆C 外,那么圆C 半径r 的取值范围为 .18.已知圆1O 与圆2O 相切,圆1O 的半径长为3cm ,21O O =7cm ,那么圆2O 的半径长是 cm .三、解答题(本大题共7题,其中第19---22题每题10分,第23、24题每题12分,第25题14分, 满分78分)19.计算:1)41(45cos 2)1(18-+︒---π.20.解方程:2)2(-x x +2-x x -6=0.21.如图,在梯形ABCD 中,AD ∥BC ,AB=DC=AD ,∠C =60°,AE ⊥BD 于点E .(1) 求∠ABD 的度数; (2) 求证:BC=2CD ; (3) 如AE =1,求梯形ABCD 的面积.22. 2008年5月,某中学开展了向四川地震灾区某小学捐赠图书活动,全校共有1200名学生,每人都捐赠了一定数量的图书.已知各年级人数比例分布扇形统计图如图1所示,学校为了了解各年级捐赠情况,从各年级中随机抽查了部分学生,进行了捐赠情况的统计调查,绘制成如图2的频数分布直方图,根据以上信息解答下列问题: (1)学校人数最少的是 年级; (2)人均捐赠图书最多的是 年级; (3)估计九年级共捐图书 册; (4)全校大约共捐图书 册.A B C D E第21题23.如图,双曲线xy 5=在第一象限的一支上有一 点C (1,5),过点C 的直线0(>+-=k b kx y 与x 轴交于点A (a ,0)、与y 轴交于点B . (1)求点A 的横坐标a 与k 之间的函数关系式; (2)当该直线与双曲线在第一象限的另一交点D 的横坐标是9时,求△COD 的面积.24. 已知:如图所示,点P 是⊙O 外的一点,PB 与⊙O 相交于点A 、B ,PD 与⊙O 相 交于C 、D ,AB=CD . 求证:(1)PO 平分∠BPD ;(2)P A=PC ;(3)AE EC =.25.如图,在平面直角坐标系xOy 中,O 点A 、C 的坐标分别为(2,0)、(1,33将△AOC 绕AC 的中点旋转180°,点O 落到点B 的位置,抛物线x ax y 322-=点A ,点D 是该抛物线的顶点.(1)求证:四边形ABCO 是平行四边形; (2)求a 的值并说明点B 在抛物线上;(3)若点P 是线段OA 上一点,且∠APD=∠求点P 的坐标;(4) 若点P 是x 轴上一点,以P 、A 、D 为顶点作平行四边形,该平行四边形的另一顶点在y 轴 上,写出点P 的坐标.O DC PA B第24题E 第25题2008学年度第二学期普陀区九年级质量调研数学试卷参考答案及评分说明一、单项选择题:(本大题共6题,每题4分,满分24分)1.(D) ; 2.(B) ; 3.(D); 4.(C) ; 5.(A) ; 6.(A) .二、填空题:(本大题共12题,每题4分,满分48分)7. )1)(6(+-x x ; 8. 6; 9. 2222)(b ab a b a ++=+; 10. 61028.6-⨯-; 11. -1; 12.12≤<-x ;13.21; 14.21.1)1(2=+x ; 15.6; 16.1∶2.4; 17.85<<r ; 18.4或10.三、解答题(本大题共7题,其中第19---22题每题10分,第23、24题每题12分,第25题14分,满分78分)19.解: 原式=4222123+⨯--…………………………………………………………8′(各2分)=322+. …………………………………………………………………………………2′ 20.解:设y x x=-2,………………………………………………………………………………………1′ 方程转化为:062=-+y y . …………………………………………………………………2′解得:21=y ,32-=y .…………………………………………………………………………2′当21=y 时,22=-x x,解得:4=x .…………………………………………………………1′ 经检验:4=x 是此方程的解. ……………………………………1′当32-=y 时,32-=-x x,解得:23=x .…………………………………………………1′ 经检验:23=x 是此方程的解. …………………………………1′ 所以原方程的解是:41=x ,232=x . ………………………………………………………1′21.解:∵AD ∥BC ,………………………………………………………………………………………1′ ∴∠2=∠3.………………………………………………………………………………………1′ 又∵AB=AD , ∴∠1=∠3. ……………………………………………………………………………………1′ ∴∠1=∠2.………………………………………………………………………………………1′ ∵四边形ABCD 是梯形, AB=DC ,∠C =60°, ∴∠1=∠2=30°. ………………………………………………………………………………1′ 即∠ABD =30°. ∴∠BDC=90°.…………………………………………………………………………………1′ ∴BC=2CD .………………………………………………………………………………………1′ 又∵AE ⊥BD ,AE =1,………………………………………………………………………………1′ ∴AB=2,3=BE . …………………………………………………………………………1′ ∴CD =2,32=BD .∴3222113221⨯⨯+⨯⨯=ABCDS 梯形=33.…………………………………………1′AB CD E第21题 1 2 322.六,八,1080,5430. (2′,2′,2′,4′)23.解:(1)∵点C (1,5)在直线)0(>+-=k b kx y∴b k +⋅-=15,∴5+=k b ,………………………………1′ ∴5++-=k kx y .…………………………1′ ∵点A (a ,0)在直线5++-=k kx y 上, ∴50++-=k ka .…………………………1′ ∴15+=ka .…………………………………1′ (2)∵直线与双曲线在第一象限的另一交点D 的横坐标是9,设点D (9,y ),…………………………………………………………………………1′∴95=y . ∴点D(9,95). ……………………………………………………………………………1′ 代入5++-=k kx y , 可解得:95=k ,……………………………………………………………………………1′ 95095+-=x y . ………………………………………………………………1′可得:点A(10,),点B(,950). …………………………………………………………2′ ∴BOC AOD AOB COD S S S S ∆∆∆∆--==1950219510219501021⨯⨯-⨯⨯-⨯⨯ ………………………………………1′=)1110(95021--⨯ =)1110(95021--⨯=9200……………………………………………………………………………1′=9222.24.证明:(1)分别取弧AB 、CD 的中点M 、N ,联接OM 、ON 交PB 于点F 、交PD 于点G ,………………………………………………1′ ∴OM ⊥PB ,ON ⊥PD .……………………………………………………………………1′∵AB=CD ,∴OF=OG .……………………………………1′∴PO 平分∠BPD .……………………………1′ (2)∵PO 平分∠BPD ,∴∠1=∠2.∵OF ⊥PB ,OG ⊥PD ,∴∠3=∠4. ∴PF= P G .…………………………………1′∵AB=CD ,∴2ABAF =,2CDCG =.……………………………………………………………1′ ∴AF=CG .………………………………………………………………………………1′∴P A=PC . ………………………………………………………………………………1′(3) ∵AB=CD ,∴AB CD =.…………………………………………………………………………1′∵OF ⊥PB ,OG ⊥PD , ∴12AM AB =,12CN CD =. ∴AM CN =.…………………………………………………………………………1′∵∠3=∠4,∴ME NE =.…………………………………………………………………………1′∴AE CE =.…………………………………………………………………………1′21 O DC PA B 第24题 F G E 3 4 MN25.(1)证明:∵△AOC 绕AC 的中点旋转180°,点O 落到点B 的位置, ∴△ACO ≌△CAB . ………………………………………………………………………1′∴AO=CB,CO=AB ,……………………………………………………………………1′∴四边形ABCO 是平行四边形. …………………………………………………………1′(2)解:∵抛物线x ax y 322-=经过点A ,点A 的坐标为(2,0),……………………………………………………………………1′∴344=-a ,解得:3=a . …………………………………………………………1′∴x x y 3232-=.∵四边形ABCO 是平行四边形,∴OA ∥CB .∵点C 的坐标为(1,33),………………………………………………………………1′∴点B的坐标为(3,33). ………………………………………………………………1′把3=x 代入此函数解析式,得: 333639332332=-=⨯-⨯=y .∴点B 的坐标满足此函数解析式,点B 在此抛物线上. …………………………………1′∴顶点D 的坐标为(1,-3). ……………………………………………………………1′(3)联接BO ,过点B 作BE ⊥x 轴于点E , 过点D 作DF ⊥x 轴于点F .tan ∠BOE =3,tan ∠DAF=3,∴tan ∠BOE=tan ∠DAF .∴∠BOE=∠DAF . ………………1′ ∵∠APD=∠OAB ,∴△APD ∽△OAB . ………………1′设点P 的坐标为(x ,0), ∴OBADOA AP =,第25题∴6222=-x ,解得:34=x .………………1′ ∴点P 的坐标为(34,0).(4))0,1(1P ,)0,1(2-P ,3(3,0)P ……………………………………………………………2′。
最新上海市普陀区中考数学模拟试题参考答案优秀名师资料

2010学年第二学期普陀区质量调研考试数学卷答案要点与评分标准一.选择题:(本大题共6题,满分24分)1.C ; 2.A ; 3.D ; 4.C ; 5.B ; 6.A二.填空题:(本大题共12题,满分48分)7.8; 8.()()22a a b a b +-; 9.3x =; 10.64.2510⨯;11.2+ 12.二、四; 13.0.6a ; 14.35; 15.DC BC =或DAC BAC ∠=∠或∠D =∠B ; 16.2133a b +; 17.14+ 18.ππ2三.解答题:(本大题共7题,满分78分)19.解:245(2),21.3x x x x ⎧++⎪⎨-<⎪⎩≤①②由①得x ≥-2.……………………………………………………………………(3分)由②得x <3.……………………………………………………………………(3分)不等式组的解集在数轴上表示如下:………………………………(2分)所以原不等式组的解集为-2≤x <3.………………………………………(1分) 所以原不等式组的整数解为-2,-1,0,1,2.………………………(1分)20.解:设123-=x xy ,则原方程变形为0322=--y y .……………………………(2分) 解这个方程,得 .3,121=-=y y ………………………………………………(2分)∴1123-=-x x 或3123=-x x. 解得 51=x 或1=x .………………………………………………………………(4分)经检验:51=x 或1=x 都是原方程的解.………………………………………(1分)∴原方程的解是51=x 或1=x .………………………………………………(1分)21.解:(1) 作图正确…………………………………………………………………(2分)∵矩形ABCD ,∴90B ∠=,BC AD =. ∵在Rt △ABC 中,AB =4,AD =2∴由勾股定理得:AC =……………………………………………(1分) 设EF 与AC 相交与点O ,由翻折可得AO CO ==……………………………………………(1分) 90AOE ∠=.∵在Rt △ABC 中, tan 1BCAB ∠=, 在Rt △AOE 中,tan 1EOAO∠=.∴EO BCAO AB=, ……………………………(1分)∴2EO =. ……………………………(1分)同理:FO =.∴EF =. ……………………………………………………………(1分)(2)过点E 作EH CD ⊥垂足为点H ,……………………………………………(1分)2EH BC ==……………………………………………………………………(1分)∴sin 5EH EFC EF ∠===.…………………………………………(1分)22.(1)60; …………………………………………………………………………(3分) (2)90; …………………………………………………………………………(3分) (3)0.7. …………………………………………………………………………(4分) 23.(1) 证明:∵AB AC =,AH CB ⊥,∴BH HC =.……………………………………………………(2分) ∵FH EH =,∴四边形EBFC 是平行四边形.………………………………(2分) 又∵AH CB ⊥,∴四边形EBFC 是菱形.…………………………………………(2分)(2)证明:∵四边形EBFC 是菱形.∴1232ECF ∠=∠=∠.…………………………………………(2分) H 1OFE DCBA∵AB AC =,AH CB ⊥,∴142BAC ∠=∠.………(1分) ∵BAC ∠=ECF ∠∴43∠=∠.……………(1分) ∵AH CB ⊥∴41290∠+∠+∠=.…(1分) ∴31290∠+∠+∠=.即:AC CF ⊥.…………………(1分)24.解:(1) 联结AC ,过点C 作CH AB ⊥,垂直为H ,由垂径定理得:AH =12AB =2,…………………………………(1分) 则OH =1.…………………………………………………………(1分) 由勾股定理得:CH =4.…………………………………………(1分) 又点C 在x 轴的上方,∴点C 的坐标为()1,4.………………(1分) (2)设二次函数的解析式为()20y ax bx c a =++≠由题意,得0,093,4.a b c a b c a b c =-+⎧⎪=++⎨⎪=++⎩解这个方程组,得1,2,3.a b c =-⎧⎪=⎨⎪=⎩………………………………………(3分)∴ 这二次函数的解析式为y =-x 2+2x +3.………………………………(1分)(3)点M 的坐标为()2,3…………………………………………………(2分) 或(45),-或(421)-,-……………………………(2分)25.解:(1)在Rt △ABC 中,∵∠A =30°,∴60ABC ∠=.………………………………………………………(1分) 由旋转可知:'B C BC =,'60B ABC ∠=∠=,'B CB α∠=∠ ∴△'B BC 为等边三角形.……………(2分)∴'B CB α∠=∠=60.……………(1分) (2)① 当090α︒<<︒时,点D 在AB 边上(如图).∵ DE ∥''A B ,4321H FECBA EDB'A'CBA∴CD CECA CB=''..…………………………………………………(1分) 由旋转性质可知,CA ='CA ,CB ='CB , ∠ACD=∠BCE .∴ CD CECA CB =,.…………………………………………………(1分) ∴CD CACE CB=. ∴ △CAD ∽△CBE . .………………………………………(1分) ∴BE BCAD AC=. ∵∠A =30° ∴y x=BC AC =.……………………………………………(1分)∴3y x =(0﹤x ﹤2)…………………………………………(2分)②当090α︒<<︒时,点D 在AB 边上AD =x ,2BD AB AD x =-=-,∠DBE=90°.此时,11(2)22BDES SBD BE x ==⨯=-=. 当S =13ABC S ∆=.整理,得 2210x x -+=.解得 121x x ==,即AD =1. …………………………………(2分)当90120α︒<<︒时,点D 在AB 的延长线上(如图).仍设AD =x ,则2BD x =-,∠DBE=90°..11(2)22BDES SBD BE x ==⨯=-=. 当S =13ABC S ∆时,=. EDB'A'CBA整理,得 2210x x --=.解得 11x =,21x =.即AD =…………………………………………………(2分)综上所述:AD =1或AD =。
上海市普陀区中考数学第二次模拟试题

上海市普陀区中考数学第二次模拟试题考生注意:1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:〔本大题共6题,每题4分,总分值24分〕[以下各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上]1. 以下计算中,错误的选项是 ······················· 〔▲〕 〔A 〕120180=; 〔B 〕422=-;〔C 〕2421=; 〔D 〕3131=-.2.以下二次根式中,最简二次根式是 ···················· 〔▲〕 〔A 〕a 9; 〔B 〕35a ; 〔C 〕22b a +; 〔D 〕21+a . 3.如果关于x 的方程022=++c x x 没有实数根,那么c 在2、1、0、3-中取值是 · 〔▲〕 〔A 〕2; 〔B 〕; 〔C 〕0; 〔D 〕3-.4.如图1,直线CD AB //,点E 、F 分别在AB 、CD 上,CFE ∠:EFB ∠3=:4,如果40B ∠=,那么BEF ∠= ······························ 〔▲〕 〔A 〕20; 〔B 〕40; 〔C 〕60; 〔D 〕80.5. 自1993年起,联合国将每年的3月22日定为“世界水日〞,宗旨是唤起公众的节水意识,加强水资源保护.某校在开展“节约每一滴水〞的活动中,从初三年级随机选出20名学生统计出各自家庭一个月的节约用水量,有关数据整理如下表. 节约用水量〔单位:吨〕 1 2 家庭数46532ABCDF E图1这组数据的中位数和众数分别是······················〔▲〕〔A 〕,; 〔B 〕,; 〔C 〕,; 〔D 〕,.6. 如图2,两个全等的直角三角形纸片的直角边分别为a 、b )(b a ≠,将这两个三角形的一组等边重合,拼合成一个无重叠的几何图形,其中轴对称图形有 ··········· 〔▲〕 〔A 〕3个; 〔B 〕4个; 〔C 〕5个; 〔D 〕6个.二、填空题:〔本大题共12题,每题4分,总分值48分〕 7.计算:xy x 3122⋅= ▲ . 8.方程32x x =+的根是 ▲ .9.大型纪录片?厉害了,我的国?上映25天,累计票房约为402700000元,成为中国纪录电影票房冠军.402700000用科学记数法表示是 ▲ .10.用换元法解方程312122=+-+x x x x 时,如果设y xx =+21,那么原方程化成以y 为“元〞的方程是 ▲ .11.正比例函数的图像经过点M (2-)、),(11y x A 、),(22y x B ,如果21x x <,那么1y ▲ 2y .〔填“>〞、“=〞、“<〞〕12.二次函数的图像开口向上,且经过原点,试写出一个符合上述条件的二次函数的解析式: ▲ .〔只需写出一个〕13.如果一个多边形的内角和是720,那么这个多边形的边有 ▲ 条.14.如果将“概率〞的英文单词 probability 中的11个字母分别写在11张一样的卡片上,字面朝下随意放在桌子上,任取一张,那么取到字母b 的概率是 ▲ .15.xx 年春节期间,反季游成为出境游的热门,中国游客青睐的目的地仍主要集中在温暖的东南亚地区.据调查发现xx 年春节期间出境游约有700万人,游客目的地分布情况的扇形图如图3所示,从中可知出境游东南亚 地区的游客约有 ▲ 万人.16. 如图4,在梯形ABCD 中,BC AD //,AD BC 3=,点E 、F 分别是边AB 、CD 的中点.设a AD =,b DC =,那么向量EC 用向量a 、b 表示是 ▲ .图2A东南亚欧美澳新16%港澳台 15%韩日11%其他13%图317. 如图5,矩形ABCD 中,如果以AB 为直径的⊙O 沿着BC 滚动一周,点B 恰好与点C 重合,那么y xO ABC图6ABBC的值等于 ▲ .〔结果保存两位小数〕18. 如图6,在平面直角坐标系xOy 中,△ABC 的顶点A 、C 在坐标轴上,点B 的坐标是(22).将△ABC 沿x 轴向左平移得到△111A B C ,点1B 落在函数6y x=-的图像上.如果此时四边形11AA C C 的面积等于552,那么点1C 的坐标是 ▲ .三、解答题:〔本大题共7题,总分值78分〕19.〔此题总分值10分〕先化简,再求值:42442222---++÷+x x x x x x x ,其中22x =-.20.〔此题总分值10分〕求不等式组()7153,31>34x x x x ⎧++⎪⎨--⎪⎩≥的整数解.21.〔此题总分值10分〕如图7,在Rt △ABC 中,90C ∠=,点D 在边BC 上,DE ⊥AB ,点E 为垂足,7AB =,45DAB ∠=,3tan 4B =. (1)求DE 的长; (2)求CDA ∠的余弦值.22.〔此题总分值10分〕小张同学尝试运用课堂上学到的方法,自主研究函数21y x =的图像与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:ABCDE 图7ABCDE F图4BC DO A 图5〔1〕函数21y x =的定义域是 ▲ ; 〔2〕下表列出了y 与x 的几组对应值:x … 2-32- m34- 12- 12341 32 2… y…14491694416914914…表中m 的值是 ▲ ;〔3〕如图8,在平面直角坐标系xOy 中,描出以表中各组对应值为坐标的点,试由描出的点画出该函数的图像; 〔4〕结合函数21y x =的图像,写出这个 函数的性质: ▲ .〔只需写一个〕23.〔此题总分值12分〕:如图9,梯形ABCD 中,AD ∥BC ,DE ∥AB ,DE 与对角线AC 交于点F ,FG ∥AD ,且FG EF =.〔1〕求证:四边形ABED 是菱形; 〔2〕联结AE ,又知AC ⊥ED ,求证:212AE EF ED =.24.〔此题总分值12分〕如图10,在平面直角坐标系xOy 中,直线3y kx =+与x 轴、y 轴分别相交于点A 、B ,并与图8ABC DE F G图9抛物线21742y x bx =-++的对称轴交于点()2,2C ,抛物线的顶点是点D .〔1〕求k 和b 的值;〔2〕点G 是y 轴上一点,且以点B 、C 、G 为顶点的三角形与△BCD 相似,求点G 的坐标; 〔3〕在抛物线上是否存在点E :它关于直线AB 的对称点F 恰好在y 轴上.如果存在,直接写出点E 的坐标,如果不存在,试说明理由.25.〔此题总分值14分〕P 是O ⊙的直径BA 延长线上的一个动点,P ∠的另一边交O ⊙于点C 、D ,两点位于AB 的上方,AB =6,OP m =,1sin 3P =,如图11所示.另一个半径为6的1O ⊙经过点C 、D ,圆心距1OO n =.〔1〕当6m =时,求线段CD 的长;〔2〕设圆心1O 在直线AB 上方,试用n 的代数式表示m ;〔3〕△1POO 在点P 的运动过程中,是否能成为以1OO 为腰的等腰三角形,如果能,试求出此时n 的值;如果不能,请说明理由.参考答案及评分说明一、选择题:〔本大题共6题,每题4分,总分值24分〕图10xy1 1OOAB备用图PDOABC 图111.(B); 2.(C); 3.(A); 4.(C); 5.(D); 6.(B). 二、填空题:〔本大题共12题,每题4分,总分值48分〕 三、解答题〔本大题共7题,其中第19---22题每题10分,第23、24题每题12分,第25题14分,总分值78分〕19.解:原式()()22+22(2)22x x x x x x x -=-+-+ ··············· 〔3分〕122x x x =-++······················ 〔2分〕 12x x -=+.························· 〔1分〕 当2x =-时,原式=················· 〔1分〕··················· 〔1分〕=·················· 〔2分〕 20.解:由①得,2x ≥-. ························ 〔3分〕由②得,x <3. ························ 〔3分〕 ∴原不等式组的解集是2<3x -≤. ··············· 〔2分〕 所以,原不等式组的整数解是2-、1-、0、、2. ········· 〔2分〕21.解:〔1〕∵DE ⊥AB ,∴︒=∠90DEA又∵45DAB ∠=,∴AE DE =. ················· 〔1分〕7.323x y ; 8. 3x =;9. 810027.4⨯ ; 10. 32=-yy ; 11.>;12. 2y x =等;13.6; 14.112; 15.315; 16.b a212+; 17.;18.(5-211).在Rt △DEB 中,︒=∠90DEB ,43tan =B ,∴43=BE DE . ······· 〔1分〕 设x DE 3=,那么x AE 3=,x BE 4=.∵7AB =,∴743=+x x ,解得1=x . ·············· 〔2分〕 ∴3=DE . ·························· 〔1分〕 (2) 在Rt △ADE 中,由勾股定理,得23=AD . ··········· 〔1分〕同理得5=BD . ························ 〔1分〕 在Rt △ABC 中,由43tan =B ,可得54cos =B .∴528=BC . ···· 〔1分〕 ∴53=CD . ·························· 〔1分〕∴102cos ==∠AD CD CDA . ··················· 〔1分〕即CDA ∠ 22.解:〔1〕0x ≠的实数; ·························· 〔2分〕 〔2〕1-; ······························ 〔2分〕 〔3〕图(略); ····························· 〔4分〕 〔4〕图像关于y 轴对称; 图像在x 轴的上方;在对称轴的左侧函数值y 随着x 的增大而增大,在对称轴的右侧函数值y 随着x 的增大而减小; 函数图像无限接近于两坐标轴,但永远不会和坐标轴相交等. ····· 〔2分〕 23.证明:〔1〕∵ AD ∥BC ,DE ∥AB ,∴四边形ABED 是平行四边形. ······ 〔2分〕∵FG ∥AD ,∴FG CFAD CA=. ···················· 〔1分〕 同理EF CFAB CA = . ························ 〔1分〕 得FG AD =EF AB∵FG EF =,∴AD AB =. ···················· 〔1分〕 ∴四边形ABED 是菱形. ····················· 〔1分〕〔2〕联结BD ,与AE 交于点H .∵四边形ABED 是菱形,∴12EH AE =,BD ⊥AE . ········ 〔2分〕 得90DHE ∠= .同理90AFE ∠=.∴DHE AFE ∠∠=. ······················· 〔1分〕 又∵AED ∠是公共角,∴△DHE ∽△AFE . ············ 〔1分〕∴EH DEEF AE =. ························· 〔1分〕 ∴212AE EF ED =.······················· 〔1分〕 24.解:〔1〕 由直线3y kx =+经过点()2,2C ,可得12k =-. ············ 〔1分〕由抛物线21742y x bx =-++的对称轴是直线2x =,可得1b =. ····· 〔1分〕 (2) ∵直线132y x =-+与x 轴、y 轴分别相交于点A 、B ,∴点A 的坐标是()6,0,点B 的坐标是()0,3. ············ 〔2分〕 ∵抛物线的顶点是点D ,∴点D 的坐标是92,2⎛⎫ ⎪⎝⎭. ··········· 〔1分〕 ∵点G 是y 轴上一点,∴设点G 的坐标是()0,m .∵△BCG 与△BCD 相似,又由题意知,GBC BCD ∠=∠,∴△BCG 与△BCD 相似有两种可能情况: ············· 〔1分〕 ①如果BG BC CB CD =,解得1m =,∴点G 的坐标是()0,1.〔1分〕②如果BG BC CD CB =,那么352m -=,解得12m =,∴点G 的坐标是10,2⎛⎫ ⎪⎝⎭. 〔1分〕综上所述,符合要求的点G 有两个,其坐标分别是()0,1和10,2⎛⎫ ⎪⎝⎭.〔3〕点E 的坐标是91,4⎛⎫- ⎪⎝⎭或92,2⎛⎫ ⎪⎝⎭. ················· 〔2分+2分〕 25.解:〔1〕过点O 作OH ⊥CD ,垂足为点H ,联结OC .在Rt △POH 中,∵1sin 3P =,6PO =,∴2OH =. ········· 〔1分〕 ∵AB =6,∴3OC =. ······················ 〔1分〕由勾股定理得 CH = ····················· 〔1分〕∵OH ⊥DC ,∴2CD CH ==. ··············· 〔1分〕 〔2〕在Rt △POH 中,∵1sin 3P =, PO m =,∴3mOH =. ········ 〔1分〕 在Rt △OCH 中,2293m CH ⎛⎫- ⎪⎝⎭=. ················ 〔1分〕在Rt △1O CH 中,22363m CH n ⎛⎫-- ⎪⎝⎭=. ·············· 〔1分〕可得 2236933m m n ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭=,解得23812n m n -=. ········· 〔2分〕〔3〕△1POO 成为等腰三角形可分以下几种情况:● 当圆心1O 、O 在弦CD 异侧时①1OP OO =,即m n =,由23812n n n-=解得9n =. ········· 〔1分〕即圆心距等于O ⊙、1O ⊙的半径的和,就有O ⊙、1O ⊙外切不合题意舍去.〔1分〕②11O P OO =n =,解得23m n =,即23n 23812n n-=,解得n ········· 〔1分〕 ● 当圆心1O 、O 在弦CD 同侧时,同理可得 28132n m n-=.∵1POO ∠是钝角,∴只能是m n =,即28132n n n-=,解得n . ·· 〔2分〕综上所述,n .如有侵权请联系告知删除,感谢你们的配合!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
普陀区2015-2016学年度第二学期初三质量调研
数学试卷 2016年4月13日 (时间:100分钟,满分析150分)
一、选择题:(本大题共6题,每题4分,满分24分)
1、据统计,2015年上海市全年接待国际旅游入境者共80016000人次,80016000用科学记数法表示是( )
(A )8.0016⨯610;
(B )8.0016710⨯; (C )8100016.8⨯; (D )9
100016.8⨯ 2、下列计算结果正确的是( ) (A )824a a a =⋅; (B )()624a a =; (C )()222b a ab =; (D )()222
b a b a -=-. 3、下列统计图中,可以直观地反映出数据变化的趋势的统计图是( )
(A )折线图; (B )扇形图; (C )统形图; (D )频数分布直方图。
4、下列问题中,两个变量成正比例关系的是( )
(A )等腰三角形的面积一定,它的底边和底边上的高;
(B )等边三角形的面积与它的边长;
(C )长方形的长确定,它的周长与宽;
(D )长方形的长确定,它的面积与宽。
5、如图1,已知321////l l l ,64==DF DE ,,那么下列结论正确的是( )
(A )1:1:=EF BC ; (B )2:1:=AB BC ;
(C )3:2:=CF AD ; (D )3:2:=CF BE
6、如果圆形纸片的直径是8cm ,用它完全覆盖正六边形,那么正六边形的边长最大不能超过( )
(A )2cm ; (B )23cm ; (C )4cm ; (D )43Cm 。
二、填空题:(本大题共12题,每题4分,满分48分)
7、分解因式:=-2
2mb ma ___________;
8、方程x x =+2的根是________; 9、不等式组⎩
⎨⎧>+>1320-2x x 的解集是_____________; 10、如果关于x 的方程04
72=-++a x x 有两个相等的实数根,那么a 的值等于________;
11、函数x
x y 41-=的定义域是__________; 12、某飞机如果在1200米的上空测得地面控制点的俯角为30°,那么此时飞机离控制点之间的距离是____米;
13、一个口袋中装有3个完全相同的小球,它们分别标有数字0,1,3,从口袋中随机摸出一个小球记下数字后不放回,摇匀后再随机摸出一个小球,那么两次摸出小球的数字的和为素数的概率是________;
14、如图2,在四边形ABCD 中,点P N M 、、分别是BD BC AD 、、的中点,如果b
a ==,那么
=MN ________________;(用b a 和表示)
15、如果某市6月份日平均气温统计如图3所示,那么在日平均气温这组数据中,中位数是________;
16、已知点()11y x A ,和点()22y x B ,在反比例函数x
k y =的图像上,如果当210x x <<,可得21y y <,那么k ______________;(填“>”、“=”、“”<)
17、如图4,点F E 、分别在正方形ABCD 的边BC AB 、上,EF 与对角线BD 交于点G ,如果35==BF BE ,,那么EF FG :的比值是_______;
18、如图5①,在矩形ABCD 中,将矩形折叠,使点B 落在边AD 上,这时折痕与边BC AD 和分别交于点E 、点F 。
然后再展开铺平,以F E B 、、为顶点的BEF ∆称为矩形ABCD 的“折痕三角形”。
如图5②,在矩形ABCD 中,42==BC AB ,,当“折痕BEF ∆”面积最大时,点E 的坐标为_________。
二、解答题:(本大题共7题,满分78)
19、(本题满分10分) 计算:160tan 2312332
2-︒-⎪⎭
⎫ ⎝⎛+-+--。
20、(本题满分10分) 解方程组:⎩⎨⎧=+-=+0
23522y xy x y x
21、(本题满分10分)
已知:如图6,在ABC ∆中,,,2413===BC AC AB 点D P 、分别在边AC BC 、上,AB AD AP ⋅=2,求APD ∠的正弦值。
22、(本题满分10分)
自20004年5月1日起施行的《中华人民共和国道路交通安全法实施条例》中规定:超速行驶属违法行为。
为确保行车安全,某一段全程为200千米的高速公路限速120千米/时(即任意一时刻的车速都不能超过120千米/时)。
以下是王师傅和李师傅全程行驶完这线段高速公路时的对话片断。
王:“你的车速太快了,平均每小时比我快20千米,比我少用30分钟就行驶完了全程。
”李:“虽然我的车速快,但是最快速度比我的平均速度只快15%,并没有超速违法啊。
”李师傅超速违法吗?为什么?
如图7,已知在四边形ABCD 中,BC AD //,对角线BD AC 、相交于点BD O ,平分ABC ∠,过点D 作AB DF //分别交BC AC 、于点F E 、。
(1)求证:四边形ABCD 是菱形;(2)设AB AC ⊥,求证:EF AB OE AC ⋅=⋅。
24、(本题满分12分)
如图8,在平面直角坐标系xoy 中,二次函数c bx x y ++=
231的图像与y 轴交于点A ,与双曲线x
y 8=有一个公共点B ,它的横坐标为4,过点B 作直线x l //轴,与该二次函数图像交于另一个点C ,直线AC 的截距是-6。
(1)求二次函数的解析式;(2)求直线AC 的表达式;(3)平面内是否存在点D ,使D C B A 、、、为顶点的四边形是等腰梯形,如果存在,求出点D 坐标,如果不存在,说明理由。
如图9,在ABC Rt ∆中,4
3tan 1490==︒=∠A AC C ,,,点D 是边AC 上一点,8=AD ,点E 是边AB 上一点,以点E 为圆心,EA 为半径作圆,经过点D ,点F 是边AC 上一动点(点F 不与
C A 、重合),作EF FG ⊥,交射线BC 于点G 。
(1)用直尺圆规作出圆心E ,并求圆E 的半径长(保留作图痕迹);(2)当点G 的边BC 上时,设y CG x AF ==,,求y 关于x 的函数解
析式,并写出它的定义域;(3)联结EG ,当F C G EFG ∆∆与相似时,推理判断以点G 为圆心、CG
为半径的圆G 与圆E 可能产生的各种位置关系。
参考答案。
