六年级奥数-等积变形(教师版)
小学六年级上学期数学《等积变形》教学设计

“等积变形”教学设计
教学内容:
小学数学几何初步知识教学中,关于等体积的物体之间相互转化的规律解决有关的实际问题。
教学目标:
1、使学生明白在物体的形状的转变中,体积不变的规律。
2、运用等积变形的思想正确寻找题目中的等量关系。
3、正确运用等积变形的思想解决生活中的实际问题。
教学重点:
明白等积变形的数学思想,会运用等积变形的思想正确寻找题目中的等量关系运用规律解决实际问题。
教学过程:
一、知识回顾
1.三角形面积公式S▲= 1
底×高
2
2.同底等高的三角形面积相等。
二、例1:求三角形面积。
动画制作讲解
发现规律:
1.找两个正方形平行的对角线,且有一条是三角形的底边。
2.平行线上移动三角形顶点,至已知边长正方形顶点重合。
变式1:求三角形面积。
变式2:求三角形面积。
三、例2:求三角形面积。
动画制作讲解
发现规律:
1.找3个正方形平行的对角线,且有一条是三角形的底边。
2.平行线上移动三角形顶点,至已知边长正方形顶点重合。
变式:求三角形面积。
四、小结
五、例3
推导
变式:
六、本课总结
1. 用同底等高的三角形面积相等来解决问题
2. 用等高且底成比例的三角形面积也成比例来解决问题
3. 转化思想。
等积变形解题技巧

等积变形解题技巧
等积变形是解题过程中常用的一种技巧,主要涉及在物体形状变化过程中,体积保持不变的一种理想状态。
解题时,需要遵循以下步骤:
1. 确定物体形状变化前后的体积。
2. 理解等积变形的含义,即物体形状变化前后体积相等。
3. 根据等积变形原则,判断物体形状变化前后体积相等的条件。
4. 运用等积变形技巧,将问题转化为容易解决的形式。
5. 解答问题时,要细心分析每个步骤,确保思路清晰、计算准确。
以一个例子说明:有一个长方体容器,长30厘米、宽20厘米、高10厘米,里面的水深6厘米。
问如何通过等积变形将水全部导出?
首先,我们需要理解等积变形的含义,即物体的形状变化前后体积不变。
对于这个例子,我们可以考虑将长方体容器中的水倒入另一个容器,使水的高度与容器的底面相平。
然后,我们需要确定水在两个容器中的体积。
由于水的体积不变,所以我们可以计算出长方体容器中水的体积,即为倒入另一个容器的水的体积。
最后,我们可以通过计算来验证是否能够通过等积变形将水全部导出。
根据题目给出的数据,我们可以计算出长方体容器中水的体积为
30×20×6=3600立方厘米。
由于另一个容器的底面面积大于长方体容器的底面面积,所以水的高度会低于10厘米。
因此,我们可以将水全部导出。
以上是等积变形解题技巧的简单介绍和示例,希望能对您有所帮助。
等积变形(课件)六年级上册数学苏教版

一个装满水的长方体的水槽,长30厘米,宽25 厘米,高30厘米。现在竖直放入一个长12厘米, 宽12厘米,高40厘米的长方体铁块,那么水溢 出多少毫升?
现有空的长方体容器A和水深24厘米的长方体容器B(如 图),要将容器B的水倒一部分给A,使两容器水的高度相 同,这时水深是几厘米?倒入B中的水是多少立方厘米?
一个A长方体铁皮盒容器,长40cm、宽30cm、高35cm, 此时水深12cm。倒入另一个空的B长方体铁皮盒容器, 长40cm、宽30cm、高25厘米,要使水深相同,那么A要 向B倒入多少立方厘米的水才能使水深相同?
有两个水池,长8分米、宽6分米、水深3分米的甲水池, 和空着的长6分米、宽和高都是4分米的乙水池。从甲水 池往乙水池中抽水,使两个水池中水面同样高,此时水 面高多少分米?
在一个正方体水箱内测量,棱长3米,水深2米, 投入一个长方体石块后,水面上升0.2米,这个石 块的长和宽都是1米,高是多少米?
在一个长25厘米、宽为20厘米、高14厘米无盖的玻 璃缸中装满水,此时把一块棱长为10厘米的正方体 铁块放入玻璃缸中,然后再把这块铁块从缸中取出, 那么此时玻璃缸里的水有多高?
等积变形
把一个棱长为4厘米的正方体橡皮泥捏成一个长6厘米, 宽2厘米的长方体,这个长方体的高是多少?
捏的过程中,体积不变
熔铸时,体积不变
锻造时,体积不变
一个棱长8厘米的正方体框架,如果改做成一个长为16 厘米,宽为4厘米的长方体框架,高是多少厘米?
对比
一个棱长8厘米的正方体框架,如果改做成一个长为16 厘米,宽为4厘米的长方体框架,高是多少厘米?
一个棱长8厘米的正方体钢坯,锻造成 一个长为16厘米,宽为4厘米的长方体 钢锭,高是多少厘米?
六年级等积变换刘军辉

教育学科教师辅导讲义学员编号:年级:课时数:学员姓名:辅导科目:学科教师:授课类型T (等积变换) C (专题方法主题)T (学法与能力主题)授课日期时段教学内容一、同步知识梳理知识点1:等积变换模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比;baS2S1DCBA如左图12::S S a b=③夹在一组平行线之间的等积变形,如右上图ACD BCDS S=△△;反之,如果ACD BCDS S=△△,则可知直线AB平行于CD.④正方形的面积等于对角线长度平方的一半;⑤三角形面积等于与它等底等高的平行四边形面积的一半;二、同步题型分析题型1:等积变换的基本应用。
例1:如图,三角形ABC中,AB是AD的5倍,AC是AE的3倍,如果三角形ADE的面积等于1,那么三角形ABC的面积是多少?EDCBA AB CD E【解析】连接BE.∵3EC AE=∴3ABC ABES S=又∵5AB AD=∴515ADE ABE ABCS S S=÷=÷,∴1515ABC ADES S==.例2:如图,在三角形ABC中,,D为BC的中点,E为AB上的一点,且BE=13AB,已知四边形EDCA 的面积是35,求三角形ABC的面积.【解】根据定理:ABCBED∆∆=3211⨯⨯=61,所以四边形ACDE的面积就是6-1=5份,这样三角形35÷5×6=42。
题型2:等积变换的能力提升。
例1:如图,正方形ABCD的边长为6,AE=1.5,CF=2.长方形EFGH的面积为.【解析】连接DE,DF,则长方形EFGH的面积是三角形DEF面积的二倍.三角形DEF的面积等于正方形的面积减去三个三角形的面积,66 1.562262 4.54216.5DEFS=⨯-⨯÷-⨯÷-⨯÷=△,所以长方形EFGH面积为33.例2:长方形ABCD的面积为362cm,E、F、G为各边中点,H为AD边上任意一点,问阴影_H_G_F_E_D_C_B_A_A_B_C_D_E_F_G_H12EFGB S =边三等分,分别与P 点连接,求阴影部分面积. P DCBAA B C D(P )PDC BA【解析】 (法1)特殊点法.由于P 是正方形内部任意一点,可采用特殊点法,假设P 点与A 点重合,则阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的14和16,所以阴影部分的面积为2116()1546⨯+=平方厘米. (法2)连接PA 、PC .由于PAD ∆与PBC ∆的面积之和等于正方形ABCD 面积的一半,所以上、下两个阴影三角形的面积之和等于正方形ABCD 面积的14,同理可知左、右两个阴影三角形的面积之和等于正方形ABCD 面积的16,所以阴影部分的面积为2116()1546⨯+=平方厘米.检测题3:如右图所示,已知三角形ABC 面积为1,延长AB 至D ,使BD=AB ;延长BC 至E ,使CE=2BC ;延长CA 至F ,使AF=3AC ,求三角形DEF 的面积。
六年级奥数第3讲等积变形

六年级奥数第3讲等积变形
引言
本文档将介绍六年级奥数第3讲的等积变形。
通过本讲的研究,学生将能够更深入地理解等积变形的概念和方法,并能够应用于相
关问题的解决。
等积变形的定义
等积变形是指在保持图形面积不变的前提下,通过改变形状、
角度或尺寸等方式进行变换的过程。
在等积变形中,图形的比例关
系和形状特征保持不变。
例题解析
以下是一些关于等积变形的例题解析,以帮助学生更好地理解
和掌握相关知识。
例题1
已知一个长方形的长为12cm,宽为8cm,将其等比例缩小为
原来的一半,请计算缩小后长方形的长和宽分别是多少?
解析:由于题目要求等比例缩小为原来的一半,可以将长和宽都除以2来计算。
因此,缩小后的长方形的长为6cm,宽为4cm。
例题2
一个三角形的底边长为10cm,高为8cm。
将该三角形的底边长保持不变,将高等比例放大为原来的2倍,请计算放大后三角形的高和面积分别是多少?
解析:根据等积变形的性质,底边长不变,高放大为原来的2倍意味着面积放大为原来的2倍。
因此,放大后三角形的高为
16cm,面积为80平方厘米。
总结
通过学习本讲的等积变形概念和例题解析,我们了解到等积变形是指在保持图形面积不变的前提下进行变换的过程。
在计算等积变形时,可以利用比例关系和形状特征来解决相关问题。
希望同学们通过本讲的学习,能够更熟练地运用等积变形的方法解决各类数学问题。
六年级奥数 第34讲 等积变形

30×20×24÷(40×30+30×20)=8(厘米)。
7. 175.84米
把圆筒展开后,横截面(圆环)变成一个长方形(长是纸的长度,宽是纸的厚度),圆筒横截面(圆环)的面积就是长方形的面积,所以长方形的长(纸的长度)等于圆环的面积除以纸的厚度。3.14×[(38÷2)2-(18÷2)2]÷(0.5÷10)÷100=175.84(米)。
6. 7.25厘米
×π×( )2×3÷[π×( )2]+7=7.25(厘米)
【池中戏水】
1.答案不唯一
2. 6.4厘米
(第2题)
连接AG,在正方形ABCD中,△ABG的底和高分别为正方形边AB与BC,所以,它的面积是正方形ABCD面积的一半。同样,在长方形EBGF中,三角形ABG的底为长方形的长BG,高为长方形的宽EB,所以它的面积也是长方形EBGF面积的一半。由此得出长方形EBGF的面积与正方形的面积相等,即长方形EBGF的面积也为64平方厘米。所以,长方形EBGF的宽为64÷10=6.4(厘米)。
8. 5倍
设正方体的棱长为 ,切开后两个长方体的表面积之和是 ×8.长方体 的表面积是 ×8× ,底面积是 ;长方体 的表面积是 ×8× ,底面积是 ,所以长方体 的体积是长方体 的5倍。
9.
【海上冲浪】
(第1题)
1. 3平方厘米
连结CF。S△BDF=1,则S△CDF=2,S△CBF=3。由于S△ABE= S△CBE,S△AFE= S△CFE,可得S△ABF= S△CBF=3,设S△AFE=S△CFE=a,则有S△ABD:S△ADC=1:2,即(1+2):(2+a+a)=1:2,求得a=2,所以S△CDFE=1+2=3(平方厘米)。
2022-2023学年小学六年级奥数典型题测评卷14《等积变形》(解析版)

【六年级奥数举一反三—全国通用】测评卷14《等积变形》试卷满分:100分考试时间:100分钟姓名:_________班级:_________得分:_________一.选择题(共5小题,满分15分,每小题3分)1.(2014•迎春杯)如图,大正六边形内部有7个完全一样的小正六边形,已知阴影部分的面积是180平方厘米.那么大正六边形的面积是()平方厘米.A.240 B.270 C.300 D.360【分析】按题意,显然可以将图进行分割,分割后阴影部分有六个面积相等的小正六边形,而空白部分是3个面积相等的小正六边形,利用面积之比不难求得大正六边形的面积.【解答】解:如图所示,将图分割成面积相等的小正三角形,显然,图中的空白部分的面积和等于3个小正六边形.而阴影部分由6个小正六边形组成,所以,大正六边形是由9个小正六边形组成的.一个小正六边形的面积为:180÷6=30(平方厘米),大正六边形的面积为:30×9=270(平方厘米),故选:B.2.(2014•迎春杯)如图,大正方形的边长为14,小正方形的边长为10,阴影部分的面积之和是()A.25 B.40 C.49 D.50【分析】按题意,将图①逆时针旋转90°,阴影部分可拼成一等腰直角三角形,不难求得阴影部分的面积.【解答】解:根据分析,如下图所示,图①逆时针旋转90°,阴影部分可拼成一等腰直角三角形,S=142÷4=49故选:C.3.(2006•创新杯)图中,将两个正方形放在一起,大、小正方形的边长分别为10,6,则图中阴影部分面积为()A.42 B.40 C.38 D.36【分析】由图意可知:阴影部分的面积就等于两个正方形的面积和减去两个空白三角形的面积,利用正方形和三角形的面积公式即可求解.【解答】解:10×10+6×6﹣6×(10+6)÷2﹣10×10÷2=100+36﹣48﹣50=38答:阴影部分的面积是38.故选:C。
等积变形教案

等积变形教案教案标题:等积变形教案教案目标:1. 理解等积变形的概念和特征;2. 掌握等积变形的基本性质和相关公式;3. 能够应用等积变形解决实际问题。
教学重点:1. 理解等积变形的概念;2. 掌握等积变形的基本性质和相关公式。
教学难点:1. 能够应用等积变形解决实际问题。
教学准备:1. 教学课件;2. 板书工具;3. 实物模型或图片。
教学过程:Step 1: 引入(5分钟)1. 利用实物模型或图片展示不同形状的物体,引导学生思考:当形状发生变化时,它们的面积或体积是否会改变?2. 引导学生讨论并总结等积变形的概念:当形状发生变化时,保持面积或体积不变的变形称为等积变形。
Step 2: 理解等积变形(10分钟)1. 利用教学课件或板书,展示不同形状的图形,并要求学生观察并比较它们的面积变化情况。
2. 引导学生发现等积变形的特点:无论形状如何变化,面积保持不变。
3. 通过实例让学生进一步理解等积变形的概念和特点。
Step 3: 掌握等积变形的基本性质和相关公式(15分钟)1. 引导学生观察等积变形的图形,并总结等积变形的基本性质:对于任意等积变形,相应边长的比例、面积的比例和周长的比例都保持不变。
2. 利用教学课件或板书,展示等积变形的相关公式,并解释其含义。
3. 通过实例让学生掌握等积变形的公式运用方法。
Step 4: 应用等积变形解决实际问题(20分钟)1. 提供一些实际问题,要求学生运用等积变形的概念和公式解决问题。
2. 引导学生分析问题,确定解决思路,并进行计算。
3. 鼓励学生在小组内合作讨论,互相交流解题思路和方法。
Step 5: 总结与拓展(5分钟)1. 对本节课所学内容进行总结,强调等积变形的概念、特点和基本性质。
2. 鼓励学生拓展思维,思考其他与等积变形相关的问题。
教学延伸:1. 学生可以通过使用几何软件或实际测量等方式,验证等积变形的基本性质。
2. 学生可以进一步研究等积变形在实际生活中的应用,如建筑设计、地图缩放等。
小学六年级奥数-等积变形
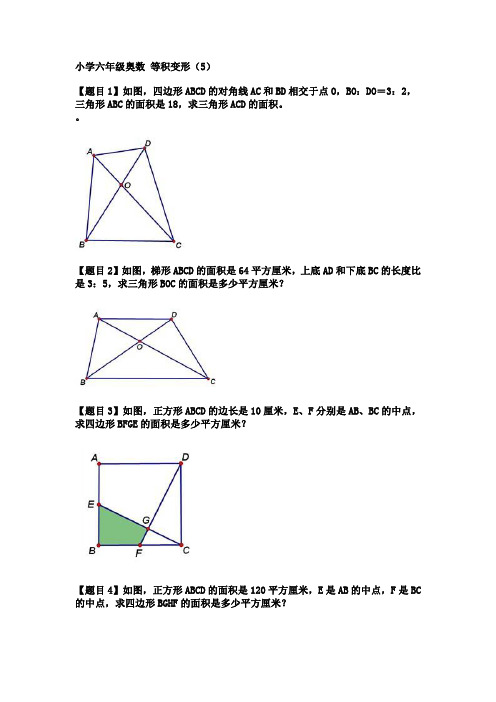
小学六年级奥数等积变形(5)
【题目1】如图,四边形ABCD的对角线AC和BD相交于点O,BO:DO=3:2,三角形ABC的面积是18,求三角形ACD的面积。
【题目2】如图,梯形ABCD的面积是64平方厘米,上底AD和下底BC的长度比是3:5,求三角形BOC的面积是多少平方厘米?
【题目3】如图,正方形ABCD的边长是10厘米,E、F分别是AB、BC的中点,求四边形BFGE的面积是多少平方厘米?
【题目4】如图,正方形ABCD的面积是120平方厘米,E是AB的中点,F是BC 的中点,求四边形BGHF的面积是多少平方厘米?
【题目5】如图,平行四边形ABCD的面积是60平方厘米,BE=2AE,BF:FC=5:3,四边形ADGE的面积是多少平方厘米?
【题目6】如图,在三角形ABC中,G是AC的中点,D、E、F是BC的四等分点,且三角形ABD的面积比四边形CFNG的面积大6平方厘米,求三角形ABC的面积。
【题目7】如图,如图,在三角形ABC中,G是AC的中点,D、E、F是BC的四等分点,且三角形ABM的面积比四边形CFNG的面积大6平方厘米,求三角形ABC 的面积。
小学奥数几何五大模型短期班第一讲教师版讲义

7 / 14
【解析】 A
4 2
B
C
将正六角星等分为 12 个相同的等边三角形,其中三角形 ABC 由 9 个组成,占总体 的 9 3.
12 4 A
4 D
11
B
13
E 2C
根据鸟头模型,
SBDE
1113 15 15
SABC
143 225
3 4
S总
=
143 300
S总
,
S阴影
SABC
C
G Q
F
P
O
H
K
G Q
F
P
O
H
K
A
B
E
A
B
E
【解析】 对于这种几个正方形并排放在一起的图形,一般可以连接正方形同方向的对角线, 连得的这些对角线互相都是平行的,从而可以利用面积比例模型进行面积的转化. 如右图所示,连接 FK 、GE 、 BD ,则 BD / /GE / /FK ,根据几何五大模型中的面 积比例模型,可得 SDGE SBGE , SKGE SFGE ,所以阴影部分的面积就等于正方 形 GFEB 的面积,即为102 100 平方厘米.
1.已知正方形 ABCD 边长为10,正方形 BEFG 边长为6,求阴影部分的面积.
A
D
A
D
F G
F G
J
I
J
I
B
ECH
B
E
C
H
【解析】如果注意到 DF 为一个正方形的对角线(或者说一个等腰直角三角形的斜边),那么 容易想到 DF 与 CI 是平行的.所以可以连接 CI 、 CF ,如上图. 由于 DF 与 CI 平行,所以 DFI 的面积与 DFC 的面积相等.而 DFC 的面积为 10 4 1 20 ,所以 DFI 的面积也为 20. 2
六年级数学等积变形

六年级数学等积变形1,一个盛水的圆柱形水桶,内底面周长为6028分米,当一个长方形的物体投入水中时,水面上升1分米,量得这个长方体的长为3;14分米,宽为1分米,他的高是多少?2,在长为15厘米,宽为12厘米的长方体水箱中,有10厘米深的水,现沉入一个高为10厘米的圆锥形铁块《全部浸入水中》,水面上升了2厘米,求圆锥的底面积?3,甲,乙两个圆柱体容器,底面积比为4:3,甲容器水深7厘米,以容器水深3厘米,再往两容器中各注入同样多的水,直到水深相等,这时水深多少厘米?4,一个棱长为1分米的正方体木块,从这个木块中各出一个最大的圆锥,求这个圆锥的表面积和体积?5,用一张长3米宽1米的长方形铁皮可以做成无底的圆柱形管子,此圆柱形管子的最大面积是多少?6,一个胶水瓶,它的瓶身呈圆柱形《不包括瓶颈》,容积是32;4立方厘米,当瓶子正放时,瓶内胶水深为8厘米,瓶子倒放时,空余部分为2厘米,则瓶内所装水的体积是多少?7;有A;B两个圆柱形容器,最初在容器A里装有2升水,容器B是空的。
现在往两个容器中以每分钟0;4升的流量注入水,4分钟后,两个容器的水面高度相等。
设B的底面半径为5厘米,那么A的底面直径是多少厘米?8;将一个圆柱体木块沿上下底面圆心切成四块,表面积增加48平方厘米;若将这个圆柱体切成三块小圆柱体,表面积增加50;24平方厘米。
现在把这个圆柱体木块削成一个最大的圆锥体,体积减少多少立方厘米?9;圆钢切削成一个最大的圆锥体,切削掉的部分部分重8千克,这段圆钢重多少㎏?10;棱长是4分米的立方体钢坯切削成一个最大的圆柱,这个圆柱的体积是多少立方分米?11;一个体积为60立方厘米的圆柱,削成一个最大的圆锥,这个圆锥的体积是多少立方厘米?12;一车箱是长方体,长4米,宽1;5米,高4分米,装满沙,堆成一个高5分米的圆锥,底面积多少㎡13;一个底面周长15;7m高10m的圆柱铁块,熔成一个底面积是25㎡的圆锥,圆锥的高是多少m?14;把一个体积是18㎝³的圆柱削成一个最大的圆锥,削成的圆锥体积是多少㎝³?15;正方体钢材,棱长6分米,把它削成一个最大的圆锥体零件,零件的体积是多少?。
六年级奥数优胜教育第3讲:等积变形含答案

第三讲等积变形例1:如图,正方形ABCD的边长为6,AE=1.5,CF=2.长方形EFGH的面积为.例2:长方形ABCD的面积为36cm2,E、F、G为各边中点,H为AD边上任意一点,问阴影部分面积是多少?A H DE GB F C例3:如图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD=15,四边形EFGO的面积为.A DE OGB F C例4:已知ABC为等边三角形,面积为400,D、E、F分别为三边的中点,已知甲、乙、丙面积和为143,求阴影五边形的面积.(丙是三角形HBC)例5:如图,已知CD=5,DE=7,EF=15,FG=6,线段AB将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG的面积是.A AC D E F G C D E FGB B例6:如图在△ABC中,D,E分别是AB,AC上的点,且AD:AB=2:5,AE:AC=4:7,△S ADE=16平方厘米,求△ABC的面积.AAD DE EB C B C例7:如图在△ABC中,D在BA的延长线上,E在AC上,且AB:AD=5:2,AE:EC=3:2,△S ADE=12平方厘米,求△ABC的面积.DAEB CDAEB C例8:如图,平行四边形ABCD,BE=AB,C F=2CB,G D=3DC,HA=4A D,平行四边形ABCD的面积是2,求平行四边形ABCD与四边形EFGH的面积比.H HA B E A B EG D C G D CF例9:如图所示的四边形的面积等于多少?FC O131213D1312131212AB例10:如图所示,∆ABC中,∠ABC=90︒,AB=3,BC=5,以AC为一边向∆ABC外作正方形ACDE,中心为O,求∆OBC的面积.EEO DODA3B5CA3B5C F A1.如图所示,正方形ABCD的边长为8厘米,长方形EBGF的长BG为10厘米,那么长方形的宽为几厘米?_E_E_A_B_A_B_F_F_D_G_C_D_G_C2.在边长为6厘米的正方形ABCD内任取一点P,将正方形的一组对边二等分,另一组对边三等分,分别与P点连接,求阴影部分面积.A D A(P)D A DP PB C B C B CC C甲乙3.如图,长方形ABCD的面积是36,E是AD的三等分点,AE=2ED,则阴影部分的面积为.A E DA E DMNO OB B4.如图,三角形ABC中,AB是AD的5倍,AC是AE的3倍,如果三角形ADE的面积等于1,那么三角形ABC的面积是多少?A AD E DEB C B C5.如图,三角形ABC被分成了甲(阴影部分)、乙两部分,BD=DC=4,B E=3,AE=6,乙部分面积是甲部分面积的几倍?A AE B甲乙D C BED CB6.如图,以正方形的边AB为斜边在正方形内作直角三角形ABE,∠AEB=90︒,AC、B D 交于O.已知AE、BE的长分别为3cm、5cm,求三角形OBE的面积.C B C BO E OEFD A D A7.如下图,六边形ABCDEF中,AB=ED,AF=CD,BC=EF,且有AB平行于ED,AF 平行于CD,BC平行于EF,对角线FD垂直于BD,已知F D=24厘米,BD=18厘米,请问六边形ABCDEF的面积是多少平方厘米?B G BAC ACF D F DE E角形 BCD 的面积的 ,且 AO = 2 ,DO = 3 ,那么 CO 的长度是 DO 的长度的_________倍.EBE8.如图,三角形 ABC 的面积是 1 , E 是 AC 的中点,点 D 在 BC 上,且 BD : DC = 1: 2 , AD 与 BE 交于点 F .则四边形 DFEC 的面积等于 .AEBDFC9.如图,长方形 ABCD 的面积是 2 平方厘米, EC = 2DE , F 是 DG 的中点.阴影部分的面积是多少平方厘米?AD ADBGFECBxF x y Gy EC10.四边形 ABCD 的对角线 AC 与 BD 交于点 O (如图所示).如果三角形 ABD 的面积等于三13ADOBCC11.如图,平行四边形 ABCD 的对角线交于 O 点,△CEF 、△OEF 、△ODF 、△BOE 的面 积依次是 2、4、4 和 6.求:⑴求 △OCF 的面积;⑵求 △GCE 的面积.ADOF GBEC12.如图,长方形 ABCD 中, BE : EC = 2:3 , DF : FC = 1: 2 ,三角形 DFG 的面积为 2 平方 厘米,求长方形 ABCD 的面积.AGDFAGDFBCC13.如图,正方形ABCD面积为3平方厘米,M是AD边上的中点.求图中阴影部分的面积.B CGA M D14.在下图的正方形ABCD中,E是BC边的中点,AE与BD相交于F点,三角形BEF的面积为1平方厘米,那么正方形ABCD面积是平方厘米.A DFB E C15.已知ABCD是平行四边形,BC:CE3:2,三角形ODE的面积为6平方厘米.则阴影部分的面积是平方厘米.A DA DO OB C E B C E1.右图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是平方厘米.A D A D992121O44B E B E CCDA 的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数 ,那么,2.右图中 ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米), 阴影部分的面积是 平方厘米.AD AD881616O 2 2BEC BEC3.如图,长方形 ABCD 被 CE 、 DF 分成四块,已知其中 3 块的面积分别为 2、5、8 平方厘 米,那么余下的四边形 OFBC 的面积为___________平方厘米.A EFB A EFB225O ?5O ?88DC D C4.如图, ∆ABC 是等腰直角三角形, DEFG 是正方形,线段 AB 与 CD 相交于 K 点.已知正 方形 DEFG 的面积 48, AK : KB = 1:3 ,则 ∆BKD 的面积是多少?DA G DA GKKBEF C B E M F C5.下图中,四边形 ABCD 都是边长为 1 的正方形,E 、F 、G 、H 分别是 AB ,BC ,CD ,mn(m + n ) 的值等于.AH D A H DEG E GBFC BFC1.用三种不同的方法,把任意一个三角形分成四个面积相等的三角形.2.用三种不同的方法将任意一个三角形分成三个小三角形,使它们的面积比为及 1∶3∶4.3.如右图,在梯形 ABCD 中,AC 与 BD 是对角线,其交点 △O ,求证:AOB 与△COD 面积相等.4.如右图,把四边形 ABCD 改成一个等积的三角形.5.如右图,已知在△ABC 中,BE=3AE ,CD=2AD .若△ADE 的面积为 1 平方厘米.求三角形 ABC的面积.6.如下页图,在△ABC 中,BD=2AD ,AG=2CG ,BE=EF=FC=面积的几分之几?1 3BC ,求阴影部分面积占三角形 A BC7.如右图,ABCD 为平行四边形,EF 平行 △A C ,如果 ADE 的面积为 4 平方厘米.求三角形 CDF的面积.8.如右图,四边形ABCD面积为1,且AB=AE,BC=BF,DC=CG,AD=DH.求四边形EFGH的面积.9.如右图,在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若△S ADE=1,求△BEF的面积.△S ACD = △S BCD ,则可知直线 AB 平行于 CD .E第三讲 等积变形1.等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如图 S : S = a : b12③夹在一组平行线之间的等积变形,如图 △S ACD = △S BCD ;反之,如果④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于 它们的高之比. 2.鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在 △ABC 中,D , E 分别是 AB, AC 上的点如图 ⑴(或 D 在 BA 的延长线上, 在 AC 上),则S△ABC :S△ADE=(AB⨯AC):(AD⨯AE)3.蝶形定理任意四边形中的比例关系(“蝶形定理”):①S:S=S:S或者S⨯S=S⨯S②AO:OC=(S+S):(S+S)124313241243蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.DAS2S1OS4S3B C梯形中比例关系(“梯形蝶形定理”):①S:S=a2:b213②S:S:S:S=a2:b2:ab:ab;1324③S的对应份数为(a+b)2.4.相似模型(一)金字塔模型(二)沙漏模型A E F DAD F EB GC B G C①AD AE DE AF===AB AC BC AG;②:=AF2:AG2.△S ADE△S ABC所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具.在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.5.共边定理(燕尾模型和风筝模型)共边定理:若直线AO和BC相交于D(有四种情形),则有S∆ABO :S∆ACO=BD:DC在三角形ABC中,AD,BE,CF相交于同一点O,那么S:S=BD:DC.∆ABO∆ACO上述定理给出了一个新的转化面积比与线段比的手段,因为∆ABO和∆ACO的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径.AFEBOD C1.了解三角形的底、高与面积的关系,会通过分析以上关系解题。
六年级数学奥数培优教案(下册)三角形之等积变形

我们已经知道三角形的面积公式为: S ∆ =21⨯ 底⨯高 。
这个公式告诉我们:三角形面积的大小,取决于三角形底和高的乘积.如果三角形的底不变,高越大(小),三角形面积也就越大(小).同样若三角形的高不变,底越大(小),三角形面积也就越大(小).这说明;当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.为便于实际问题的研究,我们还会常常用到以下结论:【结论 1】等底等高------若两个三角形等底等高,则这两个三角形的面积相同(图①);【结论 2】同底看高------若两个三角形等底,但高不等,则这两个三角形面积比等于高之比(图②);【结论 3】同高看底------若两个三角形等高,但底不等,则这两个三角形面积比等于底之比(图③);=∆∆DBC ABC s s : ;=∆∆DBC ABC s s : ;=∆∆ADC ABD s s :【例1】用三种不同的方法,把任意一个三角形分成四个面积相等的三角形.【例2】如图,在△ABC 中, FC : DF : BD = 4 : 3 : 2 ,已知△AFC 的面积为 48cm 2,E 为 AF 的中点。
求阴影部分的面积。
专题:三角形之等积变形【例 3】如右图,长方形 ADEF 的面积是 16 平方厘米,三角形 ADB 的面积是 3 平方厘米,三角形 ACF 的面积是 4 平方厘米,则三角形 ABC 的面积是多少?AFC DBE1、如图,△ABC 的每边长都是 96cm ,用折线把这个三角形分割成面积相等的 4 个三角形,求线段 CE 和 CF 的长度和为 。
2、用三种不同的方法将任意一个三角形分成三个小三角形,使它们的面积比为及 1∶3∶4。
3、如图,△ABC 的面积为 1,且 BD =21DC , AF = 21FD , CE = EF ,则△DEF 的面积是多少?4、如图,已知在△ABC 中,BE=3AE ,CD=2AD .若△ADE 的面积为 1 平方厘米.求三角形 ABC 的面积.1、如图,怎样把四边形 ABCD 改成一个等积的三角形?(作图说明)2、如图,在△ABC 中,BD = 2AD ,AG = 2CG ,BE = EF = FC = 31BC ,求阴影部分面积占△ABC面积的几分之几?3、如图,在平行四边形 ABCD 中,直线 CF 交 AB 于 E ,交 DA 延长线于 F ,若 S △ADE =1,求△BEF 的面积.4。
小学六年级数学第3讲:等积变形(教师版).docx

第三讲普积变形知识械理1.等积模型①等底等高的两个三角形而积相等;②两个三角形高相等,而积比等于它们的底Z比; 两个三角形底相等,血积比等于它们的高之比;如图: S2 = a: b③夹在一组平行线之间的等积变形,如图氐①反之,如果s△心=S△灿,则可知直线AB平行于CD.④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面枳的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.2.鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在△ ABC屮,分别是A3, AC上的点如图(1)(或D在脑的延长线上,E在AC上),图(i)3.蝶形定理任意四边形中的比例关系(“蝶形定理”):(DS1:S2=S4:S3或者S,X S3=S2X54 (2)AO:OC = (S1+52):(S4 + 53)蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方而可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.①S|沾3 =亍:b2②S] : S、: S2: S4 = a2: b2: ab: ab ;③S的对应份数为(a + b)2.4.相似模型(一)金字塔模型(-)沙漏模型T AD _ AE _ _ AF~ AB~~AC~~BC~~^G'②S&BC= AF? : AG2•所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的屮位线.三角形中位线定理:三角形的屮位线长等于它所对应的底边氏的一半.相似三角形模型,给我们提供了三角形Z间的边与血积关系相互转化的工具.在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.5•共边定理(燕尾模型和风筝模型)共边定理:若直线A0和BC相交于D (有四种情形),则有S E・S MCO =BD:DC在三角形ABC中,AD, BE , CF相交于同一点0,那么: S^co = BD: DC .上述定理给出了一个新的转化面积比与线段比的手段,因为AAB0和AACO的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形Z屮,为三角形屮的三角形面积对应底边Z间提供互相联系的途径.AE教学重•难&1 •了解三角形的底、高与面积的关系,会通过分析以上关系解题。
小学数学几何五大模型教师版

小学数学几何五大模型教师版五大几何模型简介等积变换模型:等积变换模型有四个基本特点,分别是:等底等高的两个三角形面积相等;两个三角形高相等,面积之比等于底之比;两个三角形底相等,面积在之比等于高之比;在一组平行线之间的等积变形。
例如,对于一个三角形ABC,如果D、E、F 分别是BC、AC、AD的中点,那么三角形DEF的面积可以通过等积变换模型求得。
鸟头(共角)定理模型:鸟头(共角)定理模型有两个基本特点,分别是:两个三角形中有一个角相等或互补,这两个三角形叫共角三角形;共角三角形的面积之比等于对应角两夹边的乘积之比。
例如,在一个三角形ABC中,如果D、E分别是AB、AC上或AB、AC延长线上的点,那么可以通过共角定理求得S△ADE:S△ABC=(AD:AB)×(AE:AC)。
蝴蝶模型:蝴蝶模型有两个基本特点,分别是:梯形中比例关系(“梯形蝴蝶定理”);任意四边形中的比例关系(“蝴蝶定理”)。
例如,在一个梯形ABCD中,如果对角线AC、BD交于点O,已知△AOB、△BOC的面积分别为25平方厘米、35平方厘米,那么可以通过梯形蝴蝶定理求得梯形ABCD的面积。
另外,在一个四边形ABCD中,如果对角线AC、BD交于点O,且三角形ABD的面积等于三角形BCD面积的1/3,且AO=2、DO=3,那么可以通过蝴蝶定理求得CO的长度是DO长度的几倍。
相似模型:相似模型有两个基本特点,分别是:两个相似三角形的面积之比等于它们的边长之比的平方;两个相似四边形的面积之比等于它们的边长之比的平方。
例如,在一个相似三角形ABC和DEF中,如果AB:DE=2:3,BC:EF=3:4,那么可以通过相似模型求得S△ABC:S△DEF=4:9.相似三角形是指形状相同但大小不相等的两个三角形,要找到相似模型的前提是平行线。
平行于三角形一边的直线和其他两边或两边延长线相交,所构成的三角形与原三角形相似。
相似三角形的一切对应线段(对应高、对应边)的比等于相似比,周长的比等于相似比,面积的比等于相似比的平方。
最新小学奥数 三角形的等积变形教师版

A
乙 E
甲
B
D
C
连接 AD.因为 BE=3,AE=6,所以 BE:AE=3:6=1:2,设甲部分的面积为 1 个单位,那么三角形
AED 的面积为 2 个单位,这样 ABD 的面积为 3 个单位,因为 BD:CD=1:1,所以三角形 ADC
的面积也为 3 个单位,这样乙部分的面积为 3+3-1=5 个单位,所以乙部分是甲部分面积的 5
,它们 所对的顶点同为 A 点,(也就是它们的高相等)那么这两个三角形的面积相
等. 同时也可以知道△ABC 的面积是△ABD 或△AEC 面积的 3 倍.
例如在右图中,△ABC 与△DBC 的底相同(它们的底都是 BC),它所对的两个顶 点 A、D 在与底 BC 平行的直线上,(也就是它们的高相等),那么这两个三角形 的面积相等.
-1-
例如右图中,△ABC 与△DBC 的底相同(它们的底都是 BC),△ABC 的高是△DBC 高的 2 倍(D 是 AB 中点,AB=2BD,有 AH=2DE),则△ABC 的面积是△DBC 面积的 2 倍.
上述结论,是我们研究三角形等积变形的重要依据. 例 1 用三种不同的方法,把任意一个三角形分成四个面积相等的三角形.
方法 2:如右图,先将 BC 二等分,分点 D、连结 AD,得到两个等积 三角形,即△ABD 与△ADC 等积.然后取 AC、AB 中点 E、F,并连结 DE、 DF.以而得到四个等积三角形,即△ADF、△BDF、△DCE、△ADE 等积.
-2-
例 2 用三种不同的方法将任意一个三角形分成三个小三角形,使它们的面积比 为及 1∶3∶4.
A
B
E
C
D
如图,连接 AD,因为 BC:CE=1:1,所以三角形 ACD 的面积:三角形 ABC 的面积=1:1, 所以三角形 ACD 的面积=1,三角形 ABD 的面积=2,因为 AB:BE=1:2,所以三角形 ADE 的 面积为 4. 5、三角形 ABC 被分成了甲、乙两部分,BD=DC=4,BE=3,AE=6,乙部分面积是甲部分面积的 几倍?
六年级数学教案 等积变形-优秀

等积变形的教学设计学习目标:1. 通过“转化”的思想,会解决等积变形问题。
2.会灵活运用所学知识,解决生活中的实际问题。
教学过程:一、回顾旧知。
1、圆柱、圆锥、长方体和正方体的体积公式。
2、计算:(1) 圆柱:d=4dm h=10dm V=?(2) 圆锥: V=15立方分米 s底=3平方分米 h=?(3)长方体:V=150立方米 b=10米 h=3米 a=?二、探究新知。
1、一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。
这个瓶子的容积是多少?2、有一种饮料瓶的瓶身呈圆柱形(不包括瓶颈),容积是30立方厘米.现在瓶中装有一些饮料,正放时饮料的高度是20厘米,倒放时空余部分的高度为5厘米,瓶内现有饮料多少立方厘米?3、如图,两个正方形并排放在-起,则阴影部分的面积为cm².(结果保留π)。
思考:1.题中的变和不变分别是什么?2.可得到怎样的等量关系?3.怎样求圆柱钢筋的长度呢?做一做:1.一个圆锥形沙堆,底面积是25.12平方米,高是1.8米。
用这堆沙在10米宽的公路上铺3厘米厚的路面,能铺多少米?2.一个圆柱形铁块,底面半径10厘米,高5厘米,把它熔铸成一个底面积是157平方厘米的圆锥形铁块,圆锥的高是多少?三、课堂小结。
解决等积变形问题:1.物体的形状改变,体积不变。
2.长方体、正方体、圆柱体,求体积时,通用公式V=sh。
3.利用圆锥体积公式求底面积或高时,体积的3倍除以高或底面积。
四、拓展延伸。
一个圆柱形容器与一个圆锥形容器的底面积都是15平方厘米,用圆锥形容器盛水倒入圆柱形容器中,4次正好装满。
已知圆锥形容器的高是9厘米,圆柱形容器的高是多少?五、课堂检测。
1.一个棱长是3分米的正方体容器装满水后,倒入一个底面积是9平方分米的圆锥形容器里正好装满,这个圆锥的高是()分米。
2.把一个棱长是6厘米的正方体铁块熔铸成一个底面积是10平方厘米的圆柱形铁块,这个圆柱形铁块的高是多少厘米?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三讲 等积变形1.等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如图12::S S a b =③夹在一组平行线之间的等积变形,如图ACDBCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比. 2.鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△3.蝶形定理任意四边形中的比例关系(“蝶形定理”):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.梯形中比例关系(“梯形蝶形定理”): ①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.4.相似模型(一)金字塔模型 (二) 沙漏模型S 4S 3S 2S 1O DCBA①AD AE DE AFAB AC BC AG===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形. 5.共边定理(燕尾模型和风筝模型)共边定理:若直线AO 和BC 相交于D (有四种情形),则有::ABO ACO S S BD DC ∆∆=在三角形ABC 中,AD ,BE ,CF 相交于同一点O ,那么::ABO ACO S S BD DC ∆∆=. 上述定理给出了一个新的转化面积比与线段比的手段,因为ABO ∆和ACO ∆的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径.GF E ABCD AB CDEFG OFE DCBA1.了解三角形的底、高与面积的关系,会通过分析以上关系解题。
2.能在解题中发现题目中所涉及的几何模型。
例1:如图,正方形ABCD 的边长为6,AE =1.5,CF =2.长方形EFGH 的面积为 .分析:连接DE ,DF ,则长方形EFGH 的面积是三角形DEF 面积的二倍.三角形DEF 的面积等于正方形的面积减去三个三角形的面积,66 1.562262 4.54216.5DEF S =⨯-⨯÷-⨯÷-⨯÷=△,所以长方形EFGH 面积为33.例2:长方形ABCD 的面积为362cm ,E 、F 、G 为各边中点,H 为AD 边上任意一点,问阴影部分面积是多少?分析:解法一:寻找可利用的条件,连接BH 、HC ,如下图:E可得:12EHB AHB S S ∆∆=、12FHB CHB S S ∆∆=、12DHG DHC S S ∆∆=,而36ABCD AHB CHB CHD S S S S ∆∆∆=++= 即11()361822EHB BHF DHG AHB CHB CHD S S S S S S ∆∆∆∆∆∆++=++=⨯=;而EHB BHF DHG EBF S S S S S ∆∆∆∆++=+阴影,11111()()36 4.522228EBF S BE BF AB BC ∆=⨯⨯=⨯⨯⨯⨯=⨯=. 所以阴影部分的面积是:1818 4.513.5EBF S S ∆=-=-=阴影解法二:特殊点法.找H 的特殊点,把H 点与D 点重合,那么图形就可变成右图:这样阴影部分的面积就是DEF ∆的面积,根据鸟头定理,则有:5.133621213621212136212136=⨯⨯-⨯⨯⨯-⨯⨯-=--=∆∆CFDAED ABCD S S S S 阴影例3:如图所示,长方形ABCD 内的阴影部分的面积之和为70,8AB =,15AD =,四边形EFGO 的面积为 .分析:利用图形中的包含关系可以先求出三角形AOE 、DOG 和四边形EFGO 的面积之和,以及三角形AOE 和DOG 的面积之和,进而求出四边形EFGO 的面积.由于长方形ABCD 的面积为158120⨯=,所以三角形BOC 的面积为1120304⨯=,所以三角形AOE 和DOG 的面积之和为312070204⨯-=;EG(H)B又三角形AOE 、DOG 和四边形EFGO 的面积之和为111203024⎛⎫⨯-= ⎪⎝⎭,所以四边形EFGO的面积为302010-=.另解:从整体上来看,四边形EFGO 的面积=三角形AFC 面积+三角形BFD 面积-白色部分的面积,而三角形AFC 面积+三角形BFD 面积为长方形面积的一半,即60,白色部分的面积等于长方形面积减去阴影部分的面积,即1207050-=,所以四边形的面积为605010-=.例4:已知ABC 为等边三角形,面积为400,D 、E 、F 分别为三边的中点,已知甲、乙、丙面积和为143,求阴影五边形的面积.(丙是三角形HBC )分析:因为D 、E 、F 分别为三边的中点,所以DE 、DF 、EF 是三角形ABC 的中位线,也就与对应的边平行,根据面积比例模型,三角形ABN 和三角形AMC 的面积都等于三角形ABC 的一半,即为200. 根据图形的容斥关系,有ABCABN AMC AMHN S S S S S ∆∆∆-=+-丙,即400 200200AMHN S S -=+-丙,所以AMHN S S =丙.又ADF AMHN S S S S S ∆+=++乙甲阴影,所以1143400434ADF S S S S S ∆=++-=-⨯=乙甲丙阴影.例5:如图,已知5CD =,7DE =,15EF =,6FG =,线段AB 将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG 的面积是 .分析:连接AF ,BD .根据题意可知,571527CF =++=;715628DG =++=;所以,1527BE CBF FS S ∆∆=,1227BE CBF C S S ∆∆=,2128AEG ADG S S ∆∆=,728AED ADG S S ∆∆=, 于是:2115652827ADG CBFS S ∆∆+=;712382827ADG CBF S S ∆∆+=; 可得40ADG S ∆=.故三角形ADG 的面积是40.例6:如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.BGFE DC BAABC DE FG分析:连接BE ,::2:5(24):(54)ADE ABES S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 .例7:如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.分析:连接BE ,::2:5(23):(53)ADE ABES S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△,所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比例8:如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.分析:连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补, ∴111133ABC FBE S AB BC S BE BF ⋅⨯===⋅⨯△△. 又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.EDCBAEDCBAEDCBAEDCB AHGAB CD EFHGAB CD EF所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△.所以213618ABCD EFGH S S ==.例9:如图所示的四边形的面积等于多少?分析:题目中要求的四边形既不是正方形也不是长方形,难以运用公式直接求面积. 我们可以利用旋转的方法对图形实施变换:把三角形OAB 绕顶点O 逆时针旋转,使长为13的两条边重合,此时三角形OAB 将旋转到三角形OCD 的位置.这样,通过旋转后所得到的新图形是一个边长为12的正方形,且这个正方形的面积就是原来四边形的面积.因此,原来四边形的面积为1212144⨯=.(也可以用勾股定理)例10:如图所示,ABC ∆中,90ABC ∠=︒,3AB =,5BC =,以AC 为一边向ABC ∆外作正方形ACDE ,中心为O ,求OBC ∆的面积.分析:如图,将OAB ∆沿着O 点顺时针旋转90︒,到达OCF ∆的位置.由于90ABC ∠=︒,90AOC ∠=︒,所以180OAB OCB ∠+∠=︒.而OCF OAB ∠=∠, 所以180OCF OCB ∠+∠=︒,那么B 、C 、F 三点在一条直线上. 由于OB OF =,90BOF AOC ∠=∠=︒,所以BOF ∆是等腰直角三角形,且斜边BF 为538+=,所以它的面积为218164⨯=.根据面积比例模型,OBC ∆的面积为516108⨯=.A1.如图所示,正方形ABCD 的边长为8厘米,长方形EBGF 的长BG 为10厘米,那么长方形的宽为几厘米?DB13131212答案;本题主要是让学生会运用等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形).三角形面积等于与它等底等高的平行四边形面积的一半. 证明:连接AG .(我们通过ABG △把这两个长方形和正方形联系在一起).∵在正方形ABCD 中,G 12AB S AB AB =⨯⨯△边上的高, ∴12ABG ABCD S S =W △(三角形面积等于与它等底等高的平行四边形面积的一半) 同理,12ABG EFGB S S =△. ∴正方形ABCD 与长方形EFGB 面积相等. 长方形的宽8810 6.4=⨯÷=(厘米).2.在边长为6厘米的正方形ABCD 内任取一点P ,将正方形的一组对边二等分,另一组对边三等分,分别与P 点连接,求阴影部分面积.答案;(法1)特殊点法.由于P 是正方形内部任意一点,可采用特殊点法,假设P 点与A 点重合,则阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的14和16,所以阴影部分的面积为2116()1546⨯+=平方厘米. (法2)连接PA 、PC .由于PAD ∆与PBC ∆的面积之和等于正方形ABCD 面积的一半,所以上、下两个阴影三角形的面积之和等于正方形ABCD 面积的14,同理可知左、右两个阴影三角形的面积之和等于正方形ABCD 面积的16,所以阴影部分的面积为2116()1546⨯+=平方厘米.3.如图,长方形ABCD 的面积是36,E 是AD 的三等分点,2AE ED =,则阴影部分的面积为 .答案;如图,连接OE .P DCBAA B C D(P )PDC BAOABC DENMOABCDE _ A _ B_ G_ C _E _F_ D_ A_ B_ G_ C _E_F_ D根据蝶形定理,1:::1:12COE CDE CAE CDE ON ND S S S S ∆∆∆∆===,所以12OEN OED S S ∆∆=;1:::1:42BOE BAE BDE BAE OM MA S S S S ∆∆∆∆===,所以15OEM OEA S S ∆∆=.又11334OED ABCD S S ∆=⨯=矩形,26OEA OED S S ∆∆==,所以阴影部分面积为:1136 2.725⨯+⨯=.4.如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?答案;连接BE . ∵3EC AE = ∴3ABC ABE S S =V V 又∵5AB AD =∴515ADE ABE ABC S S S =÷=÷V V V ,∴1515ABC ADE S S ==V V .5.如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?答案;连接AD .∵3BE =,6AE =∴3AB BE =,3ABD BDE S S =V V 又∵4BD DC ==,∴2ABC ABD S S =V V ,∴6ABC BDE S S =V V ,5S S =乙甲.B6.如图,以正方形的边AB 为斜边在正方形内作直角三角形ABE ,90AEB ∠=︒,AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形OBE 的面积.答案;如图,连接DE ,以A 点为中心,将ADE ∆顺时针旋转90︒到ABF ∆的位置.那么90EAF EAB BAF EAB DAE ∠=∠+∠=∠+∠=︒,而AEB ∠也是90︒,所以四边形AFBEE D C B A A B C D E乙甲E DCBA ABCDE甲乙F是直角梯形,且3AF AE ==, 所以梯形AFBE 的面积为:()1353122+⨯⨯=(2cm ).又因为ABE ∆是直角三角形,根据勾股定理,222223534AB AE BE =+=+=,所以21172ABD S AB ∆==(2cm ). 那么()17125BDE ABD ABE ADE ABD AFBE S S S S S S ∆∆∆∆∆=-+=-=-=(2cm ),所以12.52OBEBDE S S ∆∆==(2cm ). 7.如下图,六边形ABCDEF 中,AB ED =,AF CD =,BC EF =,且有AB 平行于ED ,AF 平行于CD ,BC 平行于EF ,对角线FD 垂直于BD ,已知24FD =厘米,18BD =厘米,请问六边形ABCDEF 的面积是多少平方厘米?答案;如图,我们将BCD ∆平移使得CD 与AF 重合,将DEF ∆平移使得ED 与AB 重合,这样EF 、BC 都重合到图中的AG 了.这样就组成了一个长方形BGFD ,它的面积与原六边形的面积相等,显然长方形BGFD 的面积为2418432⨯=平方厘米,所以六边形ABCDEF 的面积为432平方厘米.8.如图,三角形ABC 的面积是1,E 是AC 的中点,点D 在BC 上,且:1:2BD DC =,AD 与BE 交于点F .则四边形DFEC 的面积等于 .答案;方法一:连接CF ,根据燕尾定理,12ABF ACF S BD S DC ==△△,1ABF CBF S AES EC==△△, 设1BDFS =△份,则2DCF S =△份,3ABF S =△份,3AEF EFC S S ==△△份,如图所标FEABDCGFEABDCFED CBA33321F E DC BAABCDEF所以551212DCEF ABC S S ==△ 方法二:连接DE ,由题目条件可得到1133ABD ABC S S ==△△, 11212233ADE ADC ABC S S S ==⨯=△△△,所以11ABD ADE S BF FE S ==△△, 111111122323212DEF DEB BEC ABC S S S S =⨯=⨯⨯=⨯⨯⨯=△△△△,而211323CDE ABC S S =⨯⨯=△△.所以则四边形DFEC 的面积等于512.9.如图,长方形ABCD 的面积是2平方厘米,2EC DE =,F 是DG 的中点.阴影部分的面积是多少平方厘米?答案;设1DEFS =△份,则根据燕尾定理其他面积如图所示551212BCD S S ==△阴影平方厘米.10.四边形ABCD 的对角线AC 与BD 交于点O (如图所示).如果三角形ABD 的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍.答案;在本题中,四边形ABCD 为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形.看到题目中给出条件:1:3ABD BCD S S =V V ,这可以向模型一蝶形定理靠拢,于是得出一种解法.又观察题目中给出的已知条件是面积的关系,转化为边的关系,可以得到第二种解法,但是第二种解法需要一个中介来改造这个”不良四边形”,于是可以作AH 垂直BD 于H ,CG 垂直BD 于G ,面积比转化为高之比.再应用结论:三角形高相同,则面积之比等于底边之比,得出结果.请老师注意比较两种解法,使学生体会到蝶形定理的优势,从而主观上愿意掌握并使用蝶形定理解决问题.解法一:∵::1:3ABD BDC AO OC S S ∆∆==,∴236OC =⨯=,∴:6:32:1OC OD ==. 解法二:作AH BD ⊥于H ,CG BD ⊥于G .∵13ABD BCD S S ∆∆=,∴13AH CG =,∴13AODDOC S S ∆∆=, ∴13AO CO =,∴236OC =⨯=,∴:6:32:1OC OD ==.y B CD EGE D CBAEDB A AB C DOH GA BC D OC11.如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.答案;⑴根据题意可知,BCD △的面积为244616+++=,那么BCO △和CDO ∆的面积都是1628÷=,所以OCF △的面积为844-=;⑵由于BCO △的面积为8,BOE △的面积为6,所以OCE △的面积为862-=,根据蝶形定理,::2:41:2COE COF EG FG S S ∆∆===,所以::1:2GCE GCF S S EG FG ∆∆==,那么11221233GCE CEF S S ∆∆==⨯=+. 12.如图,长方形ABCD 中,:2:3BE EC =,:1:2DF FC =,三角形DFG 的面积为2平方厘米,求长方形ABCD 的面积.答案;连接AE ,FE .因为:2:3BE EC =,:1:2DF FC =,所以3111()53210DEF ABCD ABCD S S S =⨯⨯=V 长方形长方形.因为12AED ABCD S S =V 长方形,11::5:1210AG GF ==,所以510AGD GDF S S ==V V 平方厘米,所以12AFD S =V 平方厘米.因为16AFD ABCD S S =V 长方形,所以长方形ABCD 的面积是72平方厘米.13.如图,正方形ABCD 面积为3平方厘米,M 是AD 边上的中点.求图中阴影部分的面积.答案;因为M 是AD 边上的中点,OGF EDCBAABCD EF GABCD EFGBA所以:1:2AM BC =,根据梯形蝶形定理可以知道 22:::1:12:12:21:2:2:4AMG ABG MCG BCG S S S S =⨯⨯=△△△△()(), 设1AGM S =△份,则123MCD S =+=△ 份, 所以正方形的面积为1224312++++=份,224S =+=阴影份,所以:1:3S S =阴影正方形, 所以1S =阴影平方厘米.14.在下图的正方形ABCD 中,E 是BC 边的中点,AE 与BD 相交于F 点,三角形BEF 的面积为1平方厘米,那么正方形ABCD 面积是 平方厘米.答案;连接DE ,根据题意可知:1:2BE AD =,根据蝶形定理得2129S =+=梯形()(平方厘米),3ECD S =△(平方厘米),那么12ABCD S =W (平方厘米).15.已知ABCD 是平行四边形,:3:2BC CE =,三角形ODE 的面积为6平方厘米.则阴影部分的面积是 平方厘米.答案;连接AC .由于ABCD 是平行四边形,:3:2BC CE =,所以:2:3CE AD =, 根据梯形蝶形定理,22:::2:23:23:34:6:6:9COE AOC DOE AOD S S S S =⨯⨯=V V V V所以6AOC S =V (平方厘米),9AODS =V (平方厘米),6915ABC ACD S S ==+=V V (平方厘米), 阴影部分面积为61521+=(平方厘米).1.右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),A BCDEF BB阴影部分的面积是 平方厘米.答案:连接AE .由于AD 与BC 是平行的,所以AECD 也是梯形,那么OCD OAE S S ∆∆=.根据蝶形定理,4936OCD OAE OCE OAD S S S S ∆∆∆∆⨯=⨯=⨯=,故236OCDS ∆=,所以6OCD S ∆=(平方厘米).2.右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是 平方厘米.答案:连接AE .由于AD 与BC 是平行的,所以AECD 也是梯形,那么OCD OAE S S ∆∆=. 根据蝶形定理,2816OCDOAE OCE OAD S S S S ∆∆∆∆⨯=⨯=⨯=,故216OCD S ∆=,所以4OCD S ∆=(平方厘米).另解:在平行四边形ABED 中,()111681222ADE ABED S S ∆==⨯+=Y (平方厘米), 所以1284AOE ADE AOD S S S ∆∆∆=-=-=(平方厘米),根据蝶形定理,阴影部分的面积为8244⨯÷=(平方厘米).3.如图,长方形ABCD 被CE 、DF 分成四块,已知其中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC 的面积为___________平方厘米.答案:连接DE 、CF .四边形EDCF 为梯形,所以EOD FOC S S ∆=V ,又根据蝶形定理,EOD FOC EOF COD S S S S ∆∆∆∆⋅=⋅,所以2816EOD FOC EOF COD S S S S ∆∆∆∆⋅=⋅=⨯=,所以4EOD S ∆=(平方厘米),4812ECD S ∆=+=(平方厘米).那么长方形ABCD 的面积为12224⨯=平方厘米,四边形OFBC 的面积为245289---=(平方厘米).4.如图,ABC ∆是等腰直角三角形,DEFG 是正方形,线段AB 与CD 相交于K 点.已知正方形DEFG 的面积48,:1:3AK KB =,则BKD ∆的面积是多少?BBBB?852O A B CDEF?852O A BC DEF答案:由于DEFG 是正方形,所以DA 与BC 平行,那么四边形ADBC 是梯形.在梯形ADBC 中,BDK ∆和ACK ∆的面积是相等的.而:1:3AK KB =,所以ACK ∆的面积是ABC ∆面积的11134=+,那么BDK ∆的面积也是ABC ∆面积的14.由于ABC ∆是等腰直角三角形,如果过A 作BC 的垂线,M 为垂足,那么M 是BC 的中点,而且AM DE =,可见ABM ∆和ACM ∆的面积都等于正方形DEFG 面积的一半,所以ABC ∆的面积与正方形DEFG 的面积相等,为48.那么BDK ∆的面积为148124⨯=.5.下图中,四边形ABCD 都是边长为1的正方形,E 、F 、G 、H 分别是AB ,BC ,CD ,DA 的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数mn,那么,()m n +的值等于 .答案:左、右两个图中的阴影部分都是不规则图形,不方便直接求面积,观察发现两个图中的空白部分面积都比较好求,所以可以先求出空白部分的面积,再求阴影部分的面积. 如下图所示,在左图中连接EG .设AG 与DE 的交点为M .左图中AEGD 为长方形,可知AMD ∆的面积为长方形AEGD 面积的14,所以三角形AMD 的面积为21111248⨯⨯=.又左图中四个空白三角形的面积是相等的,所以左图中阴影部分的面积为111482-⨯=.如上图所示,在右图中连接AC 、EF .设AF 、EC 的交点为N .BBEEBEE可知EF ∥AC 且2AC EF =.那么三角形BEF 的面积为三角形ABC 面积的14,所以三角形BEF 的面积为21111248⨯⨯=,梯形AEFC 的面积为113288-=.在梯形AEFC 中,由于:1:2EF AC =,根据梯形蝶形定理,其四部分的面积比为:221:12:12:21:2:2:4⨯⨯=,所以三角形EFN 的面积为3118122424⨯=+++,那么四边形BENF 的面积为1118246+=.而右图中四个空白四边形的面积是相等的,所以右图中阴影部分的面积为111463-⨯=.那么左图中阴影部分面积与右图中阴影部分面积之比为11:3:223=,即32m n =,那么325m n +=+=.1.用三种不同的方法,把任意一个三角形分成四个面积相等的三角形. 答案:方法1:如图,将BC 边四等分(BD=DE=EF=FC=14BC ),连结AD 、AE 、AF ,则△ABD 、△ADE 、△AEF 、△AFC 等积。
