施工图设计时非常实用的坐标方位角计算程序
测量学坐标方位角怎么计算

测量学坐标方位角怎么计算引言在测量学中,测量坐标方位角是一个常见且重要的问题。
方位角是指一个点相对于某个参考点的方向,通常用于导航、位置定位和地图绘制等应用中。
本文将介绍如何计算测量学中的坐标方位角。
坐标系与方位角概念在进行坐标方位角的计算之前,需要先了解一些基本概念。
在测量学中,我们常用的坐标系是笛卡尔坐标系,它由水平方向的x轴和垂直方向的y轴构成。
而方位角则以正北方向为参考,顺时针计算。
方位角的表示通常采用度数制,以360度为一圈。
0度表示正北方向,90度表示正东方向,180度表示正南方向,270度表示正西方向。
方位角计算方法要计算一个点相对于参考点的方位角,需要知道两点在笛卡尔坐标系中的坐标。
设参考点的坐标为(x1, y1),目标点的坐标为(x2, y2),则方位角的计算公式如下:方位角 = atan2(y2 - y1, x2 - x1) * (180 / pi)其中,atan2是一个数学函数,用于计算给定点的反正切值。
需要注意的是,由于计算结果是弧度制,所以要将其转换为度数制。
实例演示为了更好地理解方位角的计算方法,我们来进行一个实例演示。
假设参考点的坐标为(3, 4),目标点的坐标为(8, 6)。
我们希望计算目标点相对于参考点的方位角。
首先,我们需要代入上述计算公式:方位角 = atan2(6 - 4, 8 - 3) * (180 / pi)接下来,我们可以用计算器或者编程语言中的数学库来计算,得到方位角为45.96 度。
结论测量学中坐标方位角的计算是通过参考点和目标点的笛卡尔坐标来进行的。
通过代入方位角的计算公式,我们可以得到一个点相对于参考点的方向。
这在导航、位置定位和地图绘制等应用中具有重要的作用。
希望本文对于测量学中坐标方位角的计算有所帮助,能够帮助读者更好地理解和应用这一概念。
参考文献•Wikipedia.。
测量坐标方位角计算汇总

测量坐标方位角计算汇总在现代测量仪器和技术的支持下,测量坐标方位角变得更加准确和方便。
本文将介绍一些常用的测量坐标方位角的方法和技术,以及相关的计算方法和公式。
一、方位角的定义和表示方式方位角是指从参考方向(通常是北方向)开始,按照顺时针方向旋转到目标物体的方向所需要的角度。
在地理坐标系统中,通常使用度数来表示方位角。
例如,0度表示正北方向,90度表示正东方向,180度表示正南方向,270度表示正西方向。
方位角通常用数字表示,也可以用度分秒来表示。
度分秒是一种用时分秒来度量角度的表示方法。
例如,45度可以表示为45°,也可以表示为45°00’00’’。
二、测量坐标方位角的方法1.罗盘法:罗盘法是一种使用磁罗盘测量方位角的方法。
该方法利用地球的磁场方向作为参考,通过测量磁罗盘的指针指向来确定目标物体的方位角。
罗盘法的精度通常受到地球磁场的影响,需要进行磁偏角的校正。
2.GPS测量法:全球定位系统(GPS)是一种使用卫星信号测量位置和方向的技术。
通过接收多个卫星信号并计算其相对位置,可以确定接收器的位置和方位角。
GPS测量法具有高精度和实时性的优势,广泛应用于地理测量和导航领域。
3.光电测量法:光电测量法利用光线来测量目标物体的方位角。
该方法通过测量光线从光源到目标物体的传播方向和角度来确定方位角。
光电测量法通常需要专用的测量仪器和设备,如光电传感器和激光测距仪。
三、测量坐标方位角的计算方法和公式1.方位角的计算可以根据物体在地理坐标系统中的坐标值进行计算。
假设目标物体的坐标为(X1,Y1),参考点的坐标为(X0,Y0)。
方位角的计算公式如下:方位角 = atan2(Y1 - Y0, X1 - X0)其中,atan2函数是反正切函数,可以通过计算两点之间的纬度差和经度差得到方位角。
2.方位角的计算还可以根据目标物体在地图上的距离和方向进行计算。
假设目标物体与参考点的距离为D,目标物体相对于参考点的方向为A。
坐标方位角的推算公式

坐标方位角的推算公式好嘞,以下是为您生成的关于“坐标方位角的推算公式”的文章:在咱们学习测量和地理相关知识的时候,坐标方位角的推算公式那可是相当重要的家伙。
就好像是一把神奇的钥匙,能帮咱们打开准确确定位置和方向的大门。
先来说说啥是坐标方位角。
想象一下,你站在一个大地图前面,地图上有好多点,从一个点指向另一个点的那个角度,就是坐标方位角啦。
坐标方位角的推算公式就像是一个解题的小窍门。
比如说,在一个测量工作中,咱们知道了 A 点到 B 点的方位角,然后又知道了 B 点到C 点的方位角,那怎么算出 A 点到 C 点的方位角呢?这时候推算公式就派上用场啦!我记得有一次,我们在学校组织的实地测量活动中,就遇到了这样的问题。
那是一个阳光明媚的上午,我们分成小组,拿着测量仪器,在校园里的一片空地上进行测量。
我和我的小伙伴们负责测量几个特定点之间的距离和方位角。
当时,我们好不容易测好了 A 点到 B 点的方位角,又接着测了 B 点到 C 点的。
可等到要算 A 点到 C 点的方位角时,大家都有点懵了。
“哎呀,这可咋办呀?”一个小伙伴着急地挠挠头。
我静下心来,想起了老师讲过的坐标方位角推算公式。
“别慌,咱们按照公式来!”我说道。
然后,我带着大家一步一步地套用公式。
先把之前测量得到的数据整理好,再按照公式的步骤进行计算。
这过程中,有小伙伴不小心把数据写错了,又得重新再来。
但大家都没有放弃,一直在互相鼓励。
终于,我们算出了 A 点到 C 点的坐标方位角,那一刻,大家都开心得跳了起来。
那种通过自己的努力和知识解决问题的成就感,真的是太棒了!说回坐标方位角的推算公式,它其实并不复杂,只要记住几个关键的步骤就行。
首先,要明确前后两个方位角的关系,是左角还是右角。
然后,根据不同的情况,选择对应的公式进行计算。
比如说,如果是左角,那公式就是:后一坐标方位角 = 前一坐标方位角 + 180° - 左角。
要是右角呢,公式就是:后一坐标方位角 = 前一坐标方位角 + 右角 - 180°。
测量坐标方位角计算

测量坐标方位角计算坐标方位角是指一个点相对于原点的方向角度。
测量坐标方位角是非常重要的,特别是在地理测量、导航以及机器人控制等领域。
在这篇文章中,我将解释测量坐标方位角的原理和方法,并提供一些实际应用的示例。
首先,坐标方位角是以正北方向为参考的,顺时针方向测量。
通常用一个角度值表示,范围从0度到360度。
0度表示正北方向,90度表示正东方向,180度表示正南方向,270度表示正西方向。
方位角 = arctan(y / x)其中,y是点相对于原点在y轴上的坐标值,x是点相对于原点在x轴上的坐标值,arctan是反正切函数。
这个公式的推导过程比较简单。
假设原点为O,目标点为A,OA的长度为r,目标点的坐标为(x, y)。
那么,根据三角函数的定义,tan(方位角)等于直角三角形的对边长度y除以临边长度x,即tan(方位角) = y / x。
而反正切函数就是这个比值的反函数,即arctan(y / x)。
在实际应用中,可以使用计算机程序来计算坐标方位角。
许多编程语言和软件包都提供了计算三角函数的函数或方法。
比如,在Python中,可以使用math库中的atan2函数来计算坐标方位角。
这个函数接受两个参数,y和x,然后返回坐标方位角的弧度值。
要转换为角度值,可以再将弧度值乘以180并除以π,即angle = atan2(y, x) * 180 / π。
除了使用三角函数,还可以使用向量运算来计算坐标方位角。
假设有两个向量,一个是原点指向目标点的向量A,一个是x轴的单位向量B。
那么,两个向量的夹角就是坐标方位角。
具体而言,可以使用以下公式来计算坐标方位角:方位角= arccos(A · B / (,A,× ,B,))其中,A · B表示向量A和向量B的内积,A,和,B,分别表示向量A和向量B的长度,arccos是反余弦函数。
当然,以上只是理论上的计算方法,实际上还需考虑一些附加因素。
坐标方位角怎么计算例题

坐标方位角怎么计算例题坐标方位角是测量工程学中描述两个点间方位关系的重要参数。
它是以仪器支撑点为原点,令仪器视线向右方向作为正方向,用仪器所观测视线与参考方向夹角的度数值来描述工程中两个点的关系。
因此,坐标方位角的测量非常重要,它可以用来测量地面物体和天体之间的角度。
根据不同的计算公式,坐标方位角的计算可以分为两类:一类是极坐标方位角,另一类是直角坐标方位角。
极坐标方位角是指从极点出发,从极点到待测地点的方向角,一般采用角度表示,范围为0°~360°。
计算极坐标方位角的公式为: =arctan(Y/X),其中θ为极坐标方位角,X和Y为待测点的二维坐标。
直角坐标方位角,也称为笛卡尔坐标方位角,是指从参考原点出发,从原点到待测点的方向角,一般采用弧度表示,范围为-π~+π。
计算直角坐标方位角的公式为:=atan2(Y,X),其中θ为直角坐标方位角,X和Y为待测点的二维坐标。
对于坐标方位角的测量,首先要把参考点和测量点的二维坐标值给出,然后根据上述计算公式,通过程序或者直接算式求出两点之间的坐标方位角。
此外,坐标方位角的测量还可以通过采用仪器的方式来进行。
常见的测量仪器有建筑学仪器、经纬仪、罗盘等,它们可以帮助我们准确测量两个点之间的坐标方位角。
如果采用仪器的方式进行,我们需要先确定参考点和待测点的位置,然后从参考点出发,仪器顺次测量待测点,最后利用仪器显示出的坐标方位角即可求得测量结果。
总结起来,坐标方位角的测量十分重要,也是测量工程学中的重要技术之一。
坐标方位角的计算可以结合实际情况,采取经典公式计算或者搭配仪器来进行测量。
以上是坐标方位角怎么计算的基本概要,希望能够帮助到你!。
角度、坐标测量计算公式细则

计算细则1、坐标计算:X1=X+Dcosα,Y1=Y+Dsinα。
式中 Y、X为已知坐标,D为两点之间的距离,Α为方位角。
2、方位角计算:1)、方位角=tan=两坐标增量的比值,然后用计算器按出他们的反三角函数(±号判断象限)。
2)、方位角:arctan(y2-y1)/(x2-x1)。
加减180(大于180就减去180(还大于360就在减去360)、小于180就加180 如果x轴坐标增量为负数,则结果加180°。
如果为正数,则看y轴的坐标增量,如果Y轴上的结果为正,则算出来的结果就是两点间的方位角,如果为负值,加360°。
S=√(y2-y1)+(x2-x1),1)、当y2-y1>0,x2-x1>0时;α=arctan(y2-y1)/(x2-x1)。
2)、当y2-y1<0,x2-x1>0时;α=360°+arctan(y2-y1)/(x2-x1)。
3)、当x2-x1<0时;α=180°+arctan(y2-y1)/(x2-x1)。
再用两点之间的距离公式可算距离(根号下两个坐标距离差的平方相加)。
拨角:arctan(y2-y1)/(x2-x1)1、例如:两条巷道要互相平行掘进的话,求它们的拨角:方法(前视边方位角减后视边方位)在此后视边方位要加减180°,若拨角结果为负值为左偏“逆时针”(+360°就可化为右偏,正值为右偏“顺时针”。
2、在图上标识方位的方法:就是导线边与Y轴的夹角。
3、高程计算:目标高程=测点高程+?h+仪器高—占标高。
4、直角坐标与极坐标的换算:(直角坐标用坐标增量表示;极坐标用方位角和边长表示) 1)、坐标正算(极坐标化为直角坐标)已知一个点的坐标及该点至未知点的距离和方位角,计算未知点坐标方位角,知A(Xa,Ya)、Sab、αab,求B(Xa,Ya)解:?Xab=Sab×COSαab 则有Xb=Xa+?Xab?Yab=Sab×SINαab Yb=Ya+?Yab2)、坐标反算,已知两点的坐标,求两点的距离(称反算边长)和方位角(称反算方位角)的方法已知A(Xa,Ya)、B(Xb,Yb),求αab、Sab。
XY-SQ坐标、方位角、距离标准通用计算程序

XY-SQ坐标、方位角、距离标准通用计算程序⑵XY—SQ程序设计AC MODE 5 1 XY ALPHA — ALPHA SQ EXE 1A″X0″ B″Y0″ C″X1″ D″Y1″∶Lbl 3∶Pol ((C-A ), (D-B ∶″1.XY=>SQ〞∶″2.SQ=>XY〞∶{K}∶K =1 => Goto 0∶≠> Goto 1∶Lbl 0 ∶{X Y }∶Pol (X-A , Y-B ∶S= I ▲ J<0 => Q= 360+ J ▲≠> Q= J ▲Goto 3 ∶Lbl 1∶{ S W }∶X〝XP〞= A+ Rec (S , W+J ) ▲Y〝YP〞=B+J ▲Goto 3 EXE⑶说明①功能:计算测点到控制点的距离及方位角;由观察水平角、平距计算测点的坐标。
②计算器输入及显示X0? 输入控制点或测站坐标,米Y0?X1? 输入后視点坐标,米Y1?X? 输入所求点坐标,米Y?S= 显示两点的距离,米Q= 显示测点到控制点的方位角,度。
S? 输入平距(米),W? 输入水平角(度),XP= 显示点P的坐标。
YP=③当K=1时,计算测点到控制点的距离及方位角,当K≠1时,由观察水平角、平距计算测点的坐标。
⑷计算例、控制点DA29 (229540.940,477984.580 )、后視点A30(229081.728,477624.140),拟放中桩P(229500.384,477900.260),计算两点的距离及方位角,支点B1观察角E=75°30′29″,平距716.304m。
计算支点B1的坐标。
选择程序:AC FILE △选取XY—SQ程序EXE 输入数据顺序:X0? 229540.940 EXE 输入控制点坐标,米Y0? 477984.580 EXEX1? 229081.728 EXE 输入后视点坐标,米,只计算距离及方位角可以不输。
Y1? 477624.140 EXE1. XY=>SQ2. 2.SQ=>XYK? 1 EXE 输入计算方式,输入1,选择计算测点到控制点的距离及方位角,X? 229500.384 EXE 输入中桩坐标,米Y? 477900.260 EXES= 93.566 EXE 显示距离,米Q= 244.31351 EXE 显示方位角,度。
坐标计算程序及坐标计算公式

坐标计算程序及坐标计算公式一、坐标计算公式直线段:中桩公式:x=x1+(z-c)*cosay=y1+(z-c)*sina边桩公式:x=x1+(z-c)*cosa±d*cos(a-90)y=y1+(z-c)*sina±d*sin(a-90)说明: x1——起点x坐标,y1——起点y坐标,z——计算点桩号, c——起点桩号,a——方位角,d——距中桩距离。
“±”左边桩为“+”,右边桩为“-”。
二、方位角计算公式1、直线段方位角图纸提供。
2、若为单一圆曲线时,起点用直线段方位角图纸提供。
3、若为缓和曲线时:第一段缓和曲线方位角为直线段方位角图纸提供;第二段圆曲线起点方位角a1=a0±Ls*180/2∏r。
第三段缓和曲线方位角a2=a1±L*360/2∏r。
(a0为直线段方位角,Ls为缓和曲线长度,L为圆曲线长度,r为圆曲线半径,“±”右偏角为“+”、左偏角为“-”。
)三、5800计算器坐标程序坐标程序由1个主程序、5个子程序和1个数据库组成进入计算器编程模式(5:PROG—1:NEW新建程序名—3:EDIT),输写程序。
1、主程序adminFix 3(回车换行)Lb1 0:150→DimZ:“ZX→0,A→1,B1→2,B2→3,C→4,D→5,CR→6”?N:N→Z[149]:Prog “DAT2”:“ZS=>1,FS=>2”?N:If N=1:Then Goto 1:Else N=2=>Goto 2:IfEnd:Goto 0:Lb1 1:?S:“ANG=”?M:?Z:S=0=>Goto 0:0→N(回车换行)Lb1 5:Isz N:If S≤Z[8N+2]+Z[8N+4]:Then N→J:Prog“DAT1”:Else Goto5:IfEnd(回车换行)Abs(S-0)→W:Prog“SUB1”:“XS=”:X◢“YS=” :Y◢“FWI=”:F-M→F:If F≤360:Then F→F:Else F-360→F:IfEnd:F►DMS◢Goto4(回车换行)Lb1 2:?X:?Y:“ANG=”?M:M→Z[148]:If M<90:Then 180-M→M:IfEnd(回车换行)X-Z[4]:Y-Z[5]:X=0=>Goto 0:0→N(回车换行)Lb1 A:Isz N:N→Z[150]:Z[8N+3]-M→A:Z[8(N+1)+3]-M→B:Prog “ZX1”:If Z[6]×Z[7]≤0:Then N→J:Prog “DAT1”:Goto B:IfEnd(回车换行)Z[8N+3]+M→A:Z[8(N+1)+3]+M→B:Prog “ZX1”:If Z[6]×Z[7] ≤0:Then N→J:Prog “DAT1”:Goto B:Else Goto A: IfEnd(回车换行)Lb1 B:Prog “SUB2” (回车换行)Z[150]→N:0+W→S:If S>Z[8N+2]+Z[8N+4]+.001:Then Goto A: IfEnd(回车换行)If N>13:Then 0→N: Goto A: IfEnd(回车换行)If Z[148]>90: Then S+2Zsin(M-90) →S: IfEnd:“S=”:S◢“Z=”: Z◢“OK→2,NO→1”?N:If N=1: Then Z[150]→N: Goto A:Else Goto 2: IfEnd(回车换行)Lb1 4 :0→J:“DIST=”:Pol (X-Z[1],Y-Z[2])→I◢ J-F:If F<0:Then F+360→F:IfEnd:“FW=”: F►DMS◢ Goto 12、子程序DAT1Z[8J]→U:Z[8J+1]→V:Z[8J+2]→O:Z[8J+3]→G:Z[8J+4]→G:Z[8J+4]→H:Z[8J+5]→P:Z[8J+6]→R:Z[8J+7]→Q:1÷P→C:(P-R)÷(2HPR)→D:(180÷∏)→E:Return3、子程序ss“A”?→A:If A<0:Then 10A◢Else 9A◢IfEnd:Ans×1.05(回车)4、子程序SUB1.1184634425→A:.2393143352→B:.28444444444→N:.046910077→K:.2307653449→L:.5→Z[3]:U+W(Acos(G+QEKW(C+KWD))+Bcos(G+QELW(C+LWD))+Ncos(G+QEZ[3]W(C +Z[3]WD))+Bcos(G+QE(1-L)W(C+(1-L)WD))+Acos(G+QE(1-K)W(C+(1-K)WD)))→X:V+W(Asin(G+QEKW(C+KWD))+Bsin(G+QELW(C+LWD))+Nsin(G+QEZ[3]W(C+Z[3 ]WD))+Bsin(G+QE(1-L)W(C+(1-L)WD))+Asin(G+QE(1-K)W(C+(1-K)WD))) →Y:G+QEW(C+WD)+M→F:X+Zcos(F)→X:Y+Zsin(F)→Y: Return5、子程序SUB2G-M→T:Abs((Y-V)cos(T)-(X-U)sin(T))→W:0→Z:Lb1 0:Pros “SUB1” (回车换行)T+QEW(C+WD)→L:(Z[5]-Y)cos(L)-(Z[4]-X)sin(L)→Z:If Abs(Z)<1×10∧(-4):Then Goto 1:Else W+Z→W: Goto 0: IfEnd(回车换行)Lb1 1:0→Z:Prog“SUB1”:(Z[5]-Y)÷sin(F-2M+180)→Z:Return6、子程序ZX1(Z[5]-Z[8N+1])cos(A)-(Z[4]-z[8N])sin(A)→Z[6]:(Z[5]-Z[8(N+1)+1])C5]-Z[8(N+1)+1])cos(B)-(Z[4]-Z[8(N+1)]sin(B)→Z[7]:Return7、数据库DAT2If N=0:Then起点X坐标→Z[8]:起点Y坐标→Z[9]:起点桩号→Z[10]:起点坐标方位角→Z[11]:曲线长度→Z[12]:起点半径→Z[13]:终点半径→Z[14]:曲线转向(左转为“-1”右转为“+1”直线为“0”)→Z[15]:Return IfEnd(依次把所有平曲线要素输完)If N=1:Then起点X坐标→Z[8]:起点Y坐标→Z[9]:起点桩号→Z[10]:起点坐标方位角→Z[11]:曲线长度→Z[12]:起点半径→Z[13]:终点半径→Z[14]:曲线转向(左转为“-1”右转为“+1”直线为“0”)→Z[15]:Return IfEnd(依次把所有平曲线要素输完)说明:1、所有路线都是从Z[8]开始。
建筑工程测量:坐标方位角推算

建筑工程测量坐标方位角推算为了计算导线点的坐标,首先应推算出导线各边的坐标方位角(以下简称方位角)。
如果导线和国家控制点或测区的高级点进行了连接,则导线各边的方位角是由已知边的方位角来推算;如果测区附近没有高级控制点可以连接,称为独立测区,则须测量起始边的方位角,再以此观测方位角来推算导线各边的方位角。
如图7-1所示,设A 、B 、C 为导线点,AB 边的方位角αAB 为已知,导线点B 的左角为 β左 现在来推算BC 边的方位角αBC 。
由正反方位角的关系,可知:αBC = αAB - 180︒则从图中可以看出:αBC = αAB + β左 = αAB - 180︒ + β左 (7-1)根据方位角不大于360︒ 的定义,当用上式算出的方位角大于360︒,则减去360︒ 即可。
当用右角推算方位角时,如图7-2所示: αBA = αAB + 180︒则从图中可以看出αBC = αBA + 180︒ - β右 (7-2)用(7-2)式计算 αBC 时,如果 αAB + 180︒ 后仍小于 β右 时,则应加360︒ 后再减 β右。
根据上述推导,得到导线边坐标方位角的一般推算公式为:⎩⎨⎧-+︒±=右左后前ββαα180 (7-3) 式中:α前、α后 ——是导线点的前边方位角和后边方位角。
如图7-3所示,以导线的前进方向为参考,导线点B 的后边是AB 边,其方位角为 α前;前边是BC 边,其方位角为α前。
图7-2 坐标方位角推算示意图图7-1 坐标方位角推算示意图图7-3坐标方位角推算标准图180︒ 前的正负号取用,是当α后<180︒ 时,用“+”号;当α后>180︒ 时,用“-”号。
导线的转折角是左角(β左)就加上;右角(β右)就减去。
方位角的计算方法

方位角的计算方法(原创版2篇)目录(篇1)1.方位角的定义2.计算方位角的基本公式3.方位角的应用实例正文(篇1)方位角是一种用来描述物体位置和方向的度量方式,通常用于地图、导航和测量等领域。
在我们生活中,方位角是一个非常实用的工具,它能帮助我们更准确地找到目标位置。
那么,如何计算方位角呢?接下来,我将为大家详细介绍方位角的计算方法。
首先,我们来了解一下方位角的定义。
方位角是指从正北方向开始,逆时针旋转到目标方向的角度。
换句话说,就是从北往东、南、西旋转到目标方向的角度。
这个角度的范围是0°到360°,其中0°表示正北方向,90°表示正东方向,180°表示正南方向,270°表示正西方向,360°又回到了正北方向。
接下来,我们来介绍一下计算方位角的基本公式。
假设我们现在要计算从正北方向逆时针旋转到目标方向的角度,那么我们可以使用以下公式:方位角 = 目标方向角度 - 180°其中,目标方向角度是指从正北方向开始,逆时针旋转到目标方向的角度。
如果目标方向在正北方向的左侧,那么目标方向角度是正值;如果目标方向在正北方向的右侧,那么目标方向角度是负值。
举个例子,假设我们要计算从正北方向逆时针旋转到西南方向的方位角。
首先,我们需要确定西南方向相对于正北方向的角度。
在地图上,我们可以看到西南方向与正北方向的夹角大约是45°。
因此,目标方向角度为45°。
将这个值代入公式,我们可以得到:方位角= 45° - 180° = -135°这意味着,从正北方向逆时针旋转135°就可以到达西南方向。
方位角在实际应用中具有重要意义。
例如,在导航系统中,我们可以通过输入目标位置的经纬度和当前位置的经纬度,计算出目标相对于当前位置的方位角,从而为出行提供准确的方向指引。
此外,方位角还在地图制作、航空航天、地质勘探等领域发挥着重要作用。
方位角计算方法

坐标方位角:以坐标纵轴的北端顺时针旋转到某直线的夹角γ>0边线点坐标计算曲率变化点坐标的计算道路设计中,一般只给出了中线交点的坐标,如图1所示的i,j,k点的坐标及曲线参数,它们包括偏角γ,切线长T,缓和曲线长l0,曲线总长L,外距E及曲率半径R。
测设前需根据上述设计参数求出ZH,HY,YH,HZ等曲率变化点的平面坐标,其中ZH和HZ点的坐标计算公式为xZH=xj+Tcosαji (1a)yZH=yj+Tsinαji (1b)xHZ=xj+Tcosαjk (2a)yHZ=yj+Tsinαjk (2b)式中αji,αjk分别为j点至i点及j点至k点的坐标方位角。
在图1所示的ZH-x′-y′假定坐标系中,HY点的坐标为〔1〕(3a) (3b) 则(4a) 4b)HY点的大地坐标为xHY=xZH+SZH-HYcos(αij+R′ΖΗ-ΗY) (5a)yHY=yZH+SZH-HYsin(αij+R′ΖΗ-ΗY) (5b)需注意的是,式(4b)仅要求为象限角,且R′ZH-HY是有符号的。
如以i→j→k为前进方向,本文定义偏角γ的符号为,相对于i→j方向,j→k右偏角时γ>0,左偏角时γ<0。
由图1不难看出,当γ>0时,式(3b)中的y′HY取“+”号,故R′ZH-HY>0;而r<0时,式(3b)中y′HY取“-”号,故R′ZH-HY<0。
可见,编程时可以通过γ的正负自动对y′HY取号。
因缓和曲线ZH-HY与缓和曲线HZ-YH是对称的,所以YH点的大地坐标为xYH=xHZ+SZH-HYcos(αkj-R′ΖΗ-ΗY) (6a)yYH=yHZ+SZH-HYsin(αkj-R′ΖΗ-ΗY) (6b)缓和曲线中线点与边线点的坐标计算当曲线弧长l在区间(0,l0)取值时,中线点位于缓和曲线ZH-HY内。
令C=Rl0,当γ>0时,距ZH点曲线长为l,缓和曲线中线上对应P点在ZH-x′-y′直角坐标系中的坐标为〔1〕(7a) (7b)与P点相对应的缓和曲线边线点的坐标为〔2〕(8a) (8b)式中:ρ=57.29577951,为弧度转换为度的系数;D为道路的半宽。
角度坐标测量计算公式细则

角度坐标测量计算公式细则文件编码(008-TTIG-UTITD-GKBTT-PUUTI-WYTUI-8256)计算细则1、坐标计算:X1=X+Dcosα,Y1=Y+Dsinα。
式中 Y、X为已知坐标,D为两点之间的距离,Α为方位角。
2、方位角计算:1)、方位角=tan=两坐标增量的比值,然后用计算器按出他们的反三角函数(±号判断象限)。
2)、方位角:arctan(y2-y1)/(x2-x1)。
加减180(大于180就减去180(还大于360就在减去360)、小于180就加180如果x轴坐标增量为负数,则结果加180°。
如果为正数,则看y轴的坐标增量,如果Y轴上的结果为正,则算出来的结果就是两点间的方位角,如果为负值,加360°。
S=√(y2-y1)+(x2-x1),1)、当y2-y1>0,x2-x1>0时;α=arctan(y2-y1)/(x2-x1)。
2)、当y2-y1<0,x2-x1>0时;α=360°+arctan(y2-y1)/(x2-x1)。
3)、当x2-x1<0时;α=180°+arctan(y2-y1)/(x2-x1)。
再用两点之间的距离公式可算距离(根号下两个坐标距离差的平方相加)。
拨角:arctan(y2-y1)/(x2-x1)1、例如:两条巷道要互相平行掘进的话,求它们的拨角:方法(前视边方位角减后视边方位)在此后视边方位要加减180°,若拨角结果为负值为左偏“逆时针”(+360°就可化为右偏,正值为右偏“顺时针”。
2、在图上标识方位的方法:就是导线边与Y轴的夹角。
3、高程计算:目标高程=测点高程+h+仪器高—占标高。
4、直角坐标与极坐标的换算:(直角坐标用坐标增量表示;极坐标用方位角和边长表示)1)、坐标正算(极坐标化为直角坐标)已知一个点的坐标及该点至未知点的距离和方位角,计算未知点坐标方位角,知A(Xa,Ya)、Sab、αab,求B(Xa,Ya)解:Xab=Sab×COSαab 则有Xb=Xa+XabYab=Sab×SINαab Yb=Ya+Yab2)、坐标反算,已知两点的坐标,求两点的距离(称反算边长)和方位角(称反算方位角)的方法已知A(Xa,Ya)、B(Xb,Yb),求αab、Sab。
方位角计算坐标公式

方位角计算坐标公式方位角是指从某点的指北方向线起,依顺时针方向到目标方向线之间的水平夹角。
在数学、地理、工程等领域中,方位角的计算坐标公式可是相当重要的工具。
咱先来说说方位角的基本概念。
想象一下,你站在一个空旷的地方,面前有一个目标点,你要知道从你所在的位置看向那个目标点的方向角度,这就是方位角。
比如说,你正对着北方,然后顺时针转动到目标点的角度就是方位角啦。
那方位角计算坐标公式到底是啥呢?其实就是通过已知点的坐标和目标点的坐标来算出方位角。
具体的公式是:$tan\alpha = \frac{y_2 - y_1}{x_2 - x_1}$然后通过反正切函数就能得到方位角$\alpha$啦。
这里的$(x_1,y_1)$是已知点的坐标,$(x_2, y_2)$是目标点的坐标。
给大家举个例子哈。
比如说有两个点,A 点的坐标是(3, 4),B 点的坐标是(7, 8)。
咱们来算算从 A 点看向 B 点的方位角。
首先,按照公式,$x_1 = 3$,$y_1 = 4$,$x_2 = 7$,$y_2 = 8$。
那么,$tan\alpha = \frac{8 - 4}{7 - 3} = \frac{4}{4} = 1$。
然后通过反正切函数,就知道$\alpha = 45°$。
这就意味着从 A 点看向 B 点的方位角是 45°。
在实际生活中,方位角的计算坐标公式用处可大了。
就拿建筑施工来说吧,工程师们要确定建筑物的朝向、道路的走向,就得靠这个公式来准确计算方位角。
我之前就碰到过这么个事儿,有一次去一个建筑工地,当时工人们正在打地基,但是因为方位角没算对,导致一开始的基础部分就有点偏差。
后来发现问题后,赶紧重新计算方位角,调整施工方案,这才避免了更大的错误。
你瞧,就这么一个小小的方位角计算,如果出错了,那带来的麻烦可不小。
在地理测量中,方位角也很关键。
比如测量山峰的位置、河流的走向等等。
还有导航系统,也是依靠方位角来为我们指引方向的。
方位角及坐标计算

方位角及坐标计算公路工程各点方位角及坐标计算公式(一)各点方位角计算:1、第一直线段(k0~zh):f=arctgδy/δx备注:直线方位角必须考量象限角就可以厘定恰当线路迈向2、第一缓解曲线段(kzh~khy):δ1=(k0-kzh)2/(2rlh)×180/π3、圆曲线段(khy~kyh):δ2=[2(k0-kzh)-lh]/2r×180/πδ2=(khy-kzh)/2r×180/π+(k0-khy)/r×180/π无缓和曲线时:δ2=(k0-khy)/r×180/π(即圆曲线圆心角)4、第二缓和曲线段(kyh~khz):δ3=(khz-k0)2/(2rlh)×180/π5、第二直线段(khz~kzh):f±α(左偏时f-α,右偏时f+α)备注:k0――排序点的程α――曲线交点偏角lh――缓和曲线长(注意有时第一和第二缓和曲线长不一样)(二)各点坐标计算xzh=xjd-t?cosfxhz=xjd+t?cos(f±α)yzh=yjd-t?sinfyhz=yjd+t?sin(f±α)1、第一直线段:x=xzh+(k0-kzh)?cosf中桩y=yzh+(k0-kzh)?sinfx边=x中±b?cos(f-δ)边桩y边=y中±b?sin(f-δ)备注:b――中桩至所求点的距离(左幅时为+b,右幅时为-b,当设计轴线与线路不横向时b取斜短,即b/sinδ)设计轴线线路方向。
bδ图s-12、第一缓和曲线段:xx=xzh-y′?sinθ+x′?cosθxx′x′中桩′y=yzh+y′?cosθ+x′?sinθyzhyθhzx边=x中±b?cos(f+μδ1-δ)hyyh边桩y边=y中±b?sin(f+μδ1-δ)jdy′注:(本公式只适用与图s-2线形)图s-2μ――曲线左转为-1,右转为+1θ――线路方位角与y轴所缠的锐角,见到图s-2y′=l-l5/(40r2lh2);x′=l3/(6rlh)-l7/(336r3lh3);(r―圆曲线半径,l―缓解曲线就任一点至曲线起点长度)3、圆曲线段:x=xhy+2r?sinφ?cos(f+μ(ξ+φ))中桩y=yhy+2r?sinφ?s in(f+μ(ξ+φ))x边=x中±b?cos(f+μδ2-δ)边桩y边=y中±b?sin(f+μδ2-δ)备注:φ=(k0-khy)/2r×180/π;ξ=(khy-kzh)/2r×180/π4、第二缓解曲线段:x=xhz-y′?sinθ+x′?cosθ中桩y=yhz-y′?cosθ-x′?sinθx边=x中±b?cos(f+μδ1-δ)边桩y边=y中±b?sin(f+μδ1-δ)注:1、本公式只适用于与图s-2线形,其他线形可以根据本线形公式转换2、式中符号与第一缓解曲线意义相同3、注意有时第一缓和曲线长和第二缓和曲线长不一样4、第二直线段:x=xhz+(k0-khz)?cos(f±α)中桩y=yhz+(k0-khz)?sin(f±α)x边=x中±b?cos(f±α-δ)边桩y边=y中±b?sin(f±α-δ)备注:f――第一直线段的方位角(三)用casiofx-4500p计算已知坐标点在线路上的里程和距中线距离1、直线段(已知坐标x、y)pol(x-xhz,y-yhz):k=v?cos(f-w)+khzb=v?sin(f-w)备注:1、在fx-4500p中计算结果取走变量储存区v和w,必须表明储存区内容时按rclv、w键。
测量坐标方位角的计算

测量坐标方位角的计算1. 引言在测量与导航领域中,坐标方位角是一项关键的计算任务。
它用于确定一个目标点与参考点之间的方向关系。
在地理测量、天文导航、航空导航等领域都有广泛的应用。
本文将介绍测量坐标方位角的计算方法和应用。
2. 坐标系统和角度表示测量坐标方位角需要基于一个坐标系统,并使用适当的角度表示方法。
下面是常用的坐标系统和角度表示方法:2.1 坐标系统常用的坐标系统包括直角坐标系、极坐标系和球坐标系。
在测量坐标方位角时,通常使用的是直角坐标系。
直角坐标系中,一个点的位置由X、Y和Z三个坐标值表示。
2.2 角度表示角度可以用度数表示,也可以用弧度表示。
度数表示是我们常见的表示方法,如0度代表正北方向。
弧度表示则基于单位圆中的弧长与半径的比值。
在测量坐标方位角时,常用的是度数表示。
3. 坐标方位角的计算方法测量坐标方位角的计算方法通常基于三角函数。
下面介绍两种常见的计算方法:3.1 方法一:基于线段的方向向量假设参考点的坐标为P1(X1, Y1)和目标点的坐标为P2(X2, Y2)。
首先计算两点之间的距离D,即:D = sqrt((X2 - X1)^2 + (Y2 - Y1)^2)接下来计算目标点相对于参考点的X轴和Y轴位移,分别为X和Y:X = X2 - X1Y = Y2 - Y1然后计算方位角A,即目标点相对于参考点的方向与X轴正方向之间的夹角。
可以使用反正切函数计算:A = atan2(Y, X)最后将A转换为度数表示即可。
3.2 方法二:基于坐标系转换这种方法首先将直角坐标系转换为极坐标系。
计算方法为:R = sqrt(X^2 + Y^2)A = atan2(Y, X)其中R为目标点相对于参考点的距离(极径),A为目标点相对于参考点的方向(极角)。
最后将A转换为度数表示即可。
4. 应用举例测量坐标方位角的计算方法在实际应用中具有广泛的应用。
以下是一些实际应用举例:4.1 地图导航在地图导航中,我们经常需要计算目标位置相对于当前位置的方位角。
测量坐标方位角怎么算

测量坐标方位角怎么算在测量领域中,坐标方位角是一种用来表示物体相对于某一基准方向的角度。
它在地理测量、天文测量以及其他许多领域中都有重要的应用。
测量坐标方位角可以帮助我们准确定位物体在空间中的位置。
本文将简要介绍测量坐标方位角的计算方法。
1. 坐标方位角的定义坐标方位角是从基准方向逆时针旋转的角度,以度(°)为单位。
在测量中,我们通常使用北方作为基准方向,将其定义为0°或360°。
其他方向相对于北方的角度从0°到360°之间进行测量。
2. 坐标系的选择在计算坐标方位角之前,我们需要选择适当的坐标系。
常用的坐标系包括直角坐标系和极坐标系。
直角坐标系使用直角坐标轴(x、y、z轴)来表示物体的位置,而极坐标系则使用径向和角度来表示。
3. 测量坐标方位角的步骤和公式测量坐标方位角的步骤如下:步骤1:确定基准方向,通常选择北方作为基准方向,定义为0°或360°。
步骤2:将物体的位置表示为坐标(x,y)或(r,θ),根据所选择的坐标系。
步骤3:使用以下公式计算坐标方位角:•在直角坐标系中,可以使用反正切函数(atan2)来计算坐标方位角。
公式如下:方位角(θ) = atan2(y, x)•在极坐标系中,坐标方位角直接等于角度(θ)。
4. 示例为了更好地理解坐标方位角的计算过程,我们可以通过一个示例来说明。
假设我们有一个物体的位置坐标为(3,4),我们想计算该物体相对于北方的坐标方位角。
在直角坐标系中,我们有:方位角(θ) = atan2(4, 3)根据计算得到的结果,θ的值约为53.13°。
5. 总结测量坐标方位角是一种常见的测量技术,可以帮助我们准确描述物体在空间中的位置。
通过选择适当的坐标系,并运用相应的公式,我们可以计算出物体相对于基准方向的角度。
这种技术在地理测量、天文测量等领域有着广泛的应用。
希望本文对于理解测量坐标方位角的计算方法有所帮助,并能在相关测量工作中起到指导作用。
测量学坐标方位角怎么算

测量学坐标方位角怎么算引言测量学中,坐标方位角是用来描述一个点相对于参考系的位置的一个参数。
它以参考系的参照点为原点,测量从参照点开始的角度,以顺时针方向为正方向表示。
测量学中的方位角通常使用度数或弧度作为单位。
本文将详细介绍如何计算测量学中的坐标方位角。
坐标系在测量学中,常用的坐标系有直角坐标系和极坐标系。
直角坐标系以两条互相垂直的直线为坐标轴,通过给定的点的横坐标和纵坐标来确定点的位置。
而极坐标系则以一个原点和一个角度来确定点的位置。
在计算坐标方位角时,我们一般使用极坐标系。
坐标方位角的计算测量学中的坐标方位角的计算一般遵循以下步骤:1.确定参照点和目标点的坐标。
通常使用直角坐标系表示。
2.将坐标转换为极坐标。
通过计算目标点与参照点之间的距离和目标点相对于参照点的角度。
3.确定角度的正负方向。
通常以顺时针方向为正方向。
4.将角度转换为度数或弧度。
下面将具体介绍每个步骤的计算方法。
步骤 1:确定参照点和目标点的坐标首先,我们需要确定参照点和目标点在直角坐标系中的坐标。
假设参照点的坐标为(x1, y1),目标点的坐标为(x2, y2)。
步骤 2:将坐标转换为极坐标接下来,我们需要将直角坐标转换为极坐标。
使用以下公式计算目标点与参照点之间的距离(d)和目标点相对于参照点的极坐标角度(θ):d = sqrt((x2 - x1)^2 + (y2 - y1)^2)θ = atan2(y2 - y1, x2 - x1)步骤 3:确定角度的正负方向在测量学中,通常以顺时针方向为正方向。
如果需要将正方向设置为逆时针方向,可以在计算时对角度进行取反操作。
步骤 4:将角度转换为度数或弧度最后,根据需求将角度转换为度数或弧度。
如果需要将角度转换为度数,可以通过以下公式计算:角度(度数) = θ * (180 / π)如果需要将角度转换为弧度,可以直接使用极坐标角度(θ)。
结论通过以上步骤,我们可以计算测量学中的坐标方位角。
坐标方位角计算程序设计
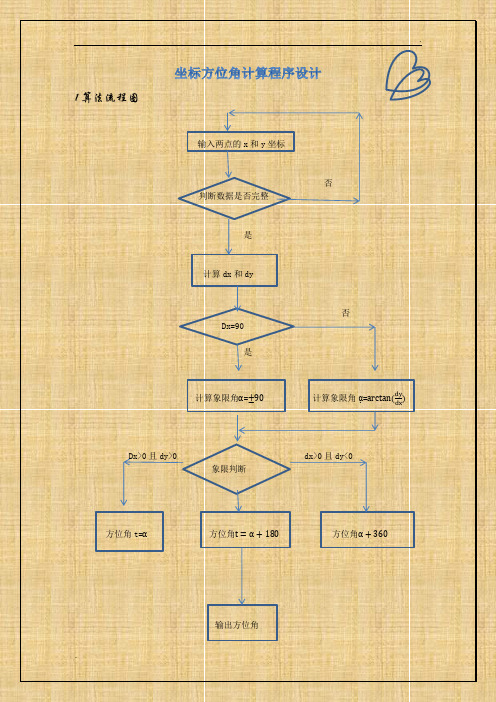
1算法流程图
输入两点的x和y坐标
否
判断数据是否完整
是
计算dx和dy
否
Dx=90
是
)
计算象限角α=±90计算象限角ᾳ=arctan(dy
dx
Dx>0且dy>0 dx>0且dy<0
象限判断
方位角t=α方位角t=α+180方位角α+360
输出方位角
2窗体及控件属性
对象属性值对象属性值
文本框1
名称Text1
文本框3
名称Text3 caption
将属性置为
空
caption
将属性置为
空
标签1caption a点x坐标标签3caption b点x坐标
文本框2
名称Text2
文本框4
名称Text4 caption
将属性置为
空
caption
将属性置为
空
标签2caption a点y坐标标签4caption b点y坐标文本框5
名称Text5框架1caption请输入坐标
caption 将属性置为
空
框架2caption
方位角(度分
秒)
标签5caption A到b的方位
角为
命令按钮1
名称Command1
窗体caption 计算坐标方
位角
caption计算方位角
3程序界面设计
4代码编写。
施工坐标 测量坐标怎么计算

施工坐标测量坐标怎么计算引言在建筑工程和土木工程中,施工坐标的测量是一个重要的环节。
施工坐标的准确计算对于工程的质量和进度都有着至关重要的影响。
本文将介绍施工坐标的测量方法和计算过程,帮助读者了解如何正确计算测量坐标。
施工坐标和测量坐标施工坐标是建筑工程中用于标定和定位各个构件和设备的坐标系统。
通过精确的施工坐标,施工人员可以准确地确定各种建筑构件的位置和相对关系。
测量坐标是施工现场对于施工坐标的实际测量数据。
测量坐标的准确性直接决定了施工坐标的准确性。
测量坐标的计算方法1. 坐标系的建立在开始计算测量坐标之前,需要先建立合适的坐标系。
常用的坐标系有直角坐标系和极坐标系。
在直角坐标系中,通过两个垂直的坐标轴来确定一个点的位置;在极坐标系中,通过一个点到原点的距离和点与正半轴的夹角来确定一个点的位置。
根据实际情况选择合适的坐标系。
2. 选取控制点在进行测量时,需要选取一些已知坐标的控制点作为参考。
这些控制点可以是已建立的基准点或者人工设置的控制点。
控制点的选取要尽可能覆盖整个工程区域,以提高计算的准确性。
3. 测量控制点的坐标使用合适的测量工具,例如全站仪或者测距仪,对选取的控制点进行测量。
测量时要注意使用合适的测量方法,避免误差的产生。
根据测量结果,记录下每个控制点的坐标。
4. 计算测量坐标通过已知的控制点坐标,可以计算其他未知点的测量坐标。
计算的方法根据选取的坐标系而定。
在直角坐标系中,可以使用数学几何中的相关公式进行计算;在极坐标系中,可以使用三角函数等方法进行计算。
5. 验证计算结果计算完成后,需要对计算结果进行验证。
可以使用已知的控制点进行验证,比较计算结果与测量结果的差异。
如果差异较大,则需要重新检查测量数据和计算过程,找出可能存在的错误。
总结施工坐标的测量是建筑工程中不可或缺的一环。
本文介绍了测量坐标的计算方法,包括建立坐标系、选取控制点、测量控制点的坐标、计算测量坐标和验证计算结果等步骤。
