初中数学三角形证明题经典题型训练
全等三角形经典题型50题(含答案)
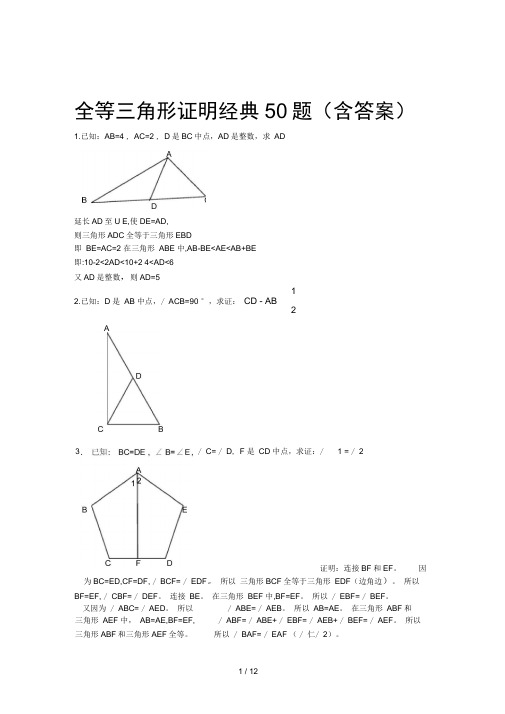
全等三角形证明经典50题(含答案)1.已知:AB=4 , AC=2 , D 是BC 中点,AD 是整数,求 AD延长AD 至U E,使DE=AD, 则三角形ADC 全等于三角形EBD即 BE=AC=2 在三角形 ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=512.已知:D 是 AB 中点,/ ACB=90 °,求证: CD - AB2为BC=ED,CF=DF, / BCF= / EDF 。
所以 三角形BCF 全等于三角形 EDF (边角边)。
所以BF=EF, / CBF= / DEF 。
连接 BE 。
在三角形 BEF 中,BF=EF 。
所以 / EBF= / BEF 。
/ ABE= / AEB 。
所以 AB=AE 。
在三角形 ABF 和 / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF 。
所以/ C= / D , F 是 CD 中点,求证:/ 1 = / 2证明:连接BF 和EF 。
因又因为 / ABC= / AED 。
所以 三角形 AEF 中, AB=AE,BF=EF, 三角形ABF 和三角形AEF 全等。
所以 / BAF= / EAF ( / 仁/ 2)。
A3因为 EB = EF ,CE = CE , 所以△ CEBCEF 所以/ B = / CFE 因为/ B +/ D = 180° / CFE + / CFA = 180° 所以/ D = / CFA 因为 AC 平分/ BAD 所以/ DAC = / FAC 又因为 AC = AC 所以△ ADC 也厶AFC ( SAS ) 所以AD = AF 所以AE = AF + FE = AD + BE12.如图,四边形 ABCD 中,AB // DC ,BE 、CE 分别平分/ ABC 、/ BCD ,且点 E 在AD 上。
初中数学 全等三角形经典题型50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形证明经典30题

全等三角形证明经典30题1. 两角和相等定理证明:设△ABC 和△DEF 是两个三角形,如果∠A = ∠D 且∠B = ∠E,则可以通过以下步骤证明△ABC ≌△DEF:步骤一:通过顶角顶点 C 、 F、和共边 CF 作直线段 CF,延长直线段 CF 至点 X,使得 CX = CE。
步骤二:连接线段 AX。
步骤三:证明∠AXB = ∠EXF:由于∠A = ∠D,所以∠AXB = ∠DXE(共同的角度)。
又由于∠B = ∠E,所以∠DXE = ∠EXF。
因此,∠AXB = ∠EXF。
步骤四:证明∠ABX = ∠EFX:由于∠B = ∠E,所以∠ABX = ∠EXF(共同的角度)。
因此,∠ABX = ∠EFX。
步骤五:证明 AB = EF:由于 CX = CE,且∠ABX = ∠EFX,根据 SSS(边-边-边)全等三角形定理,则可得∆ABX ≌ ∆EFX。
因此,AB = EF。
综上所述,根据两角和相等定理,已经证明了△ABC ≌△DEF。
2. SAS全等三角形定理证明:设△ABC 和△DEF 是两个三角形,如果 AB = DE,∠A = ∠D,且 AC = DF,则可以通过以下步骤证明△ABC ≌△DEF:步骤一:连接线段 BC 和 EF。
步骤二:证明∠ABC = ∠DEF:由于 AB = DE,且∠A = ∠D,根据线段角度定理,可得∠ABC = ∠DEF。
步骤三:证明 BC = EF:由于 AC = DF,且∠ABC = ∠DEF,根据 SAS(边-角-边)全等三角形定理,可得△ABC ≌△DEF。
综上所述,根据SAS全等三角形定理,已经证明了△ABC ≌△DEF。
3. SSS全等三角形定理证明:设△ABC 和△DEF 是两个三角形,如果 AB = DE,BC = EF,且AC = DF,则可以通过以下步骤证明△ABC ≌△DEF:步骤一:连接线段 AC 和 DF。
步骤二:连接线段 BC 和 EF。
人教版初中数学全等三角形证明题(经典50题)

人教版初中数学全等三角形证明题(经典50题)(含答案)1.已知:A B=4,A C=2,D 是B C 中点,A D 是整数,求A D?AB CD解析:延长A D 到E,使DE=A D,则三角形A D C 全等于三角形E B D即BE=A C=2 在三角形A B E 中,AB-BE<A E<A B+B E即:10-2<2A D<10+2 4<A D<6又A D 是整数,则A D=512.已知:D 是A B 中点,∠AC B=90°,求证:C D AB2ADC B3.已知:BC=D E,∠B=∠E,∠C=∠D,F 是C D 中点,求证:∠1=∠2A 12BEC F D证明:连接 BF 和 EF 。
因为 BC=E D,CF=D F,∠BCF=∠ED F 。
所以 三角形 B CF 全等于三角形 E DF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接 BE 。
在三角形 BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠A B C=∠A E D 。
所以 ∠A BE=∠AE B 。
所以 A B=A E 。
在三角形 A BF 和三角形 AEF 中, A B =A E,BF=EF, ∠ABF=∠A B E+∠EBF=∠A E B+∠BEF=∠A EF 。
所以 三角 形 A BF 和三角形 AEF 全等。
所以 ∠B AF=∠E AF (∠1=∠2)。
A 4. 已知:∠1=∠2,C D=D E ,EF//AB ,求证:EF=A C证明: 过 E 点,作 E G//AC ,交 A D 延长线于 G 则2 1 FCD∠DE G=∠D C A ∵C D=D E ∴⊿A D C ≌⊿G D E , ∠D G E=∠2A A S又 E( ) B∴E G=A C ∵EF//AB ∴∠DFE=∠1 ∵∠1=∠2 ∴∠DFE=∠D G E ∴EF=E G ∴EF=A C5. 已知:A D 平分∠B A C ,A C=A B+B D ,求证:∠B=2∠CACB D证明: 在 A C 上截取 AE=A B ,连接 E D ∵AD 平分∠B A C ∴∠E A D=∠BA D 又 ∵AE=A B , A D=A D ∴⊿AE D ≌⊿A B D ( S AS ) ∴∠AE D=∠B , D E=D B ∵A C =A B+B DA C =A E+CE ∴CE=D E ∴∠C=∠E D C ∵∠AE D=∠C+∠E D C=2∠C ∴∠B= 2∠C6. 已知:A C 平分∠B A D ,C E ⊥A B ,∠B+∠D=180°,求证:AE=A D +B E证明:在B C上截取BF=B A,连接EF.∠A BE=∠FBE,BE=BE,则⊿A BE≌ΔFBE(SAS),∠EFB=∠A;A B平行于C D,则:∠A+∠D=180°;又∠EFB+∠EFC=180°,则∠EFC=∠D;又∠FCE=∠D C E,CE=CE,故⊿FCE≌ΔDCE(AAS),FC=CD. 所以,BC=BF+FC=A B+C D.13.已知:A B//E D,∠E A B=∠B D E,E DA F=CCFA B证明:A B//ED,A E//BD推出AE=B D,又有AF=C D,EF=B CA D则:△AE D 是等腰三角形。
三角形相似证明基础50题

33、如图,已知△ABC中,∠ACB=90°,AC=BC,点E、F在AB 上,∠ECF=45°.(1)求证:△ACF∽BEC;(2)设△ABC的面积为S,求 证:AF·BE=2S.
45° A E F B C
34、如图,在ABCD中,过点B作BE⊥CD,垂足为E,连结AE,F为AE上一点,且 ∠BFE=∠C.(1)求证:△ABF∽△EAD;(2)若AB=4,∠BAE=30°,求AE 的长;(3)在(1)(2)的条件下,若AD=3,求BF的长.
CD的中点,△ADQ与△QCP是否相似?为什么?
5、如图,CD是Rt△ABC的斜边AB上的高,∠BAC的平分线分别交 BC、CD于点E、F,AC·AE=AF·AB吗?说明理由。
6、如图,AD是Rt△ABC斜边BC上的高,DE⊥DF,且DE和DF分别交 AB、
7、已知:如图,D是△ABC的边AC上一点,且CD=2AD,AE⊥BC于E, 若BC=13, △BDC的面积是39, 求AE的长。
8、已知:如图,在△ABC中,AB=AC,AD⊥AB,AD交BC于点E, DC⊥BC,与AD交于点D. 求证:AC2=AE·AD.
B C D A E
9、已知:如图,在△ABC中,∠CAB=90°,AD⊥BC于点D,点E是 AC边的中点,ED的延长线与AB的延长线交于点F. 求证:△AFD ∽△DFB.
B C D M N E A
40、如图,等腰三角形ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上 点,且满足AB2=DB·CE. (1)求证:△ADB∽△EAC;(2)若∠BAC=40°,求∠DAE的度数
A B C E D
45、如图ΔABC中,∠C=900, BC = 8cm, AC = 6cm,点P从B出发,沿BC方 向以2cm/s的速度移动,点Q从C出发,沿CA方向以1cm/s的速度移动.若P、 Q分别同时从B、C出发,经过多少时间以C、P、Q为顶点的三角形与以C、 B、A为顶点的三角形相似? 9分
全等三角形经典题型50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为BC=ED,CF=DF,∠BCF=∠EDF。
所BC DF ADBCBC以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF。
又因为 ∠ABC=∠AED。
所以 ∠ABE=∠AEB。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA,∠DGE=∠2又∵CD=DE∴⊿ADC≌⊿GDE(AAS)∴EG=AC∵EF//AB∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED≌⊿ABD(SAS)∴∠AED=∠B,DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BECDB ABA CDF2 1 E证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE⊥AB 所以∠CEB=∠CEF=90° 因为EB =EF ,CE =CE , 所以△CEB≌△CEF 所以∠B=∠CFE 因为∠B+∠D=180°,∠CFE+∠CFA =180° 所以∠D=∠CFA 因为AC 平分∠BAD 所以∠DAC=∠FAC 又因为AC =AC 所以△ADC≌△AFC(SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
八年级三角形的证明题

八年级三角形的证明题一、等腰三角形性质相关证明题(8题)1. 已知:在△ABC中,AB = AC,AD是BC边上的中线。
求证:AD⊥BC。
- 证明:- 因为AB = AC,AD是BC边上的中线,所以BD = DC(中线的定义)。
- 在△ABD和△ACD中,AB = AC(已知),BD = CD(已证),AD = AD(公共边)。
- 所以△ABD≌△ACD(SSS)。
- 则∠ADB=∠ADC(全等三角形对应角相等)。
- 又因为∠ADB + ∠ADC = 180°(平角的定义),所以∠ADB = ∠ADC = 90°,即AD⊥BC。
2. 已知:在等腰△ABC中,AB = AC,∠A = 36°,求证:∠B = 72°。
- 证明:- 因为AB = AC,所以∠B = ∠C(等腰三角形两底角相等)。
- 又因为∠A+∠B + ∠C = 180°(三角形内角和定理),∠A = 36°。
- 设∠B = x,则∠C = x,可得方程36°+x + x = 180°。
- 2x=180° - 36°,2x = 144°,解得x = 72°,即∠B = 72°。
3. 已知:在△ABC中,AB = AC,D是AC上一点,且AD = BD = BC。
求∠A的度数。
- 证明:- 设∠A=x,因为AD = BD,所以∠ABD = ∠A=x(等边对等角)。
- 则∠BDC=∠A + ∠ABD = 2x(三角形外角性质)。
- 因为BD = BC,所以∠C = ∠BDC = 2x。
- 又因为AB = AC,所以∠ABC = ∠C = 2x。
- 根据三角形内角和定理,∠A+∠ABC+∠C = 180°,即x + 2x+2x = 180°。
- 5x = 180°,解得x = 36°,所以∠A = 36°。
初中专项训练全等三角形证明经典50题(含答案)
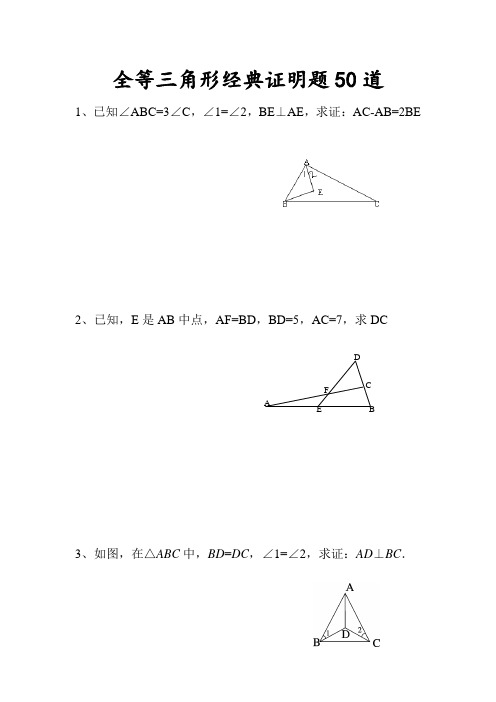
全等三角形经典证明题50道1、已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE2、已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC3、如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .FAEDC B4.如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.求证:∠OAB=∠OBA5.(5分)如图,已知AD∥BC,∠P AB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.PCEDBA6.(6分)如图①,E、F分别为线段AC上的两个动点,且DE ⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC 于点M.(1)求证:MB=MD,ME=MF(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.7.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点,(1)求证:△AED ≌△EBC .(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):8.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .OEDCB AFE D CB A25、如图:DF=CE ,AD=BC ,∠D=∠C 。
求证:△AED ≌△BFC 。
FEDCBA证明:∵DF=CE , ∴DF-EF=CE-EF , 即DE=CF ,在△AED 和△BFC 中,∵ AD=BC , ∠D=∠C ,DE=CF ∴△AED ≌△BFC (SAS )26、(10分)如图:AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
八年级全等三角形简单证明题及答案(15道)

∴BC=ED.
全等三角形的判定与性 质.
01
如图,在△ABC中, ∠C=90°,点D是AB边上的 一点,DM⊥AB,且 DM=AC,过点M作 ME∥BC交AB于点E.求证: △ABC≌△MED。
02
证明:∵MD⊥AB,
∴∠MDE=∠C=90°,
∵ME∥BC,
∴∠B=∠MED,
在△ABC与△MED中, ∠B=∠MED ∠C=∠EDM DM=AC ,
∠D=∠B , ∴△ADF≌△CBE(ASA), ∴AF=CE, ∴AF+EF=CE+EF,即
AE=CF.
全等三角形的判定与性 质.
11.在△ABC中,AB=CB,∠ABC=90°,F为AB延 长线上一点,点E在BC上,且AE=CF.求证: Rt△ABE≌Rt△CBF;
证明:∵∠ABC=90°,
角平分线的性质;全等三角形的判定与性质.
全等三角形的判定.
如图,在△ABC中, AB=AC,AD平分 ∠BAC.求证: ∠DBC=∠DCB.
解:∵AD平分∠BAC, ∴∠BAD=∠CAD. ∴在△ACD和△ABD中 AB=AC ∠BAD=∠CAD
AD=AD , ∴△ACD≌△ABD, ∴BD=CD, ∴∠DBC=∠DCB.
:∵AC平分∠BAD,
∴∠BAC=∠DAC,
在△ABC和△ADC中, AB=AD ∠BAC=∠DAC AC=AC ,
∴△ABC≌△ADC.
全等三角形的判定.
9.如图,已知 点E,C在线段
BF上, BE=CF, AB∥DE, ∠ACB=∠F.
求证: △ABC≌△DEF
.
证明:∵AB∥DE,
∴∠B=∠DEF.
全等三角形的判定与性质.
初二数学-全等三角形证明经典50题
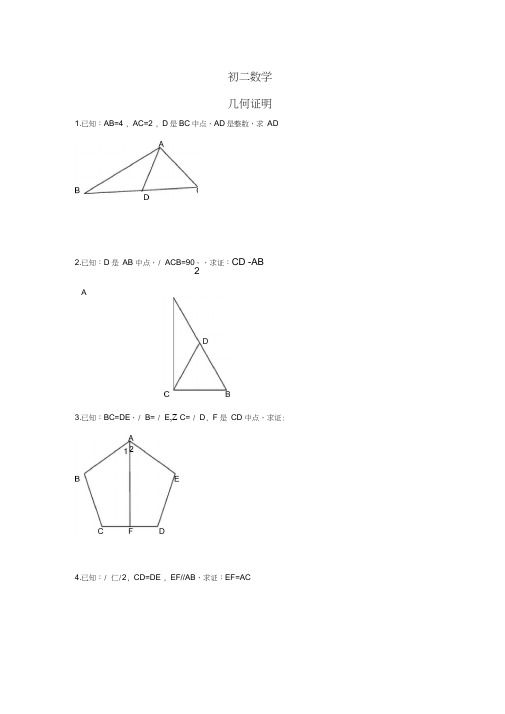
初二数学几何证明1.已知:AB=4 , AC=2 , D是BC中点,AD是整数,求AD2.已知:D 是AB 中点,/ ACB=90。
,求证:CD -AB2A3.已知:BC=DE,/ B= / E,Z C= / D, F 是CD 中点,求证:4.已知:/ 仁/2, CD=DE , EF//AB,求证:EF=AC已知:AD 平分/ BAC , AC=AB+BD ,求证:/ B=2 / C7.已知:AB=4 , AC=2 , D 是BC 中点,AD 是整数,求 ADD5. AE=AD+BE,求证: O6.8.已知:D 是AB 中点,/ ACB=90 °,求证:CD 1 AB29.已知:BC=DE,/ B= / E,/ C= / D, F 是CD 中点,求证:12.已知:AC 平分/ BAD , CE丄AB , / B+ / D=180 °,求证:AE=AD+BECD=DE , EF//AB,求证:EF=AC10.已知:/ 1 = / 2,c12.如图,四边形ABCD中,AB // DC, BE、CE分别平分/ ABC、/ BCD,且点E在AD 上。
求证:BC=AB+DC。
D14.已知:AB=CD,/ A= / D,求证:/ B= / CB15. P 是/ BAC 平分线 AD 上一点,AC>AB ,求证:PC-PB<AC-AB17.已知,E 是 AB 中点,AF=BD , BD=5 , AC=7,求 DC18. ( 5 分)如图,在△ ABC 中,BD=DC ,/ 仁/2,求证:AD 丄 BC .19. ( 5分)如图,0M 平分/ POQ , MA 丄OP,MB 丄OQ , A 、B 为垂足,AB 交0M 于点N . 求证:/ OAB= /OBA16.已知/ ABC=3 / C ,Z 1 = / 2, BE 丄 AE ,求证:AC-AB=2BE20. ( 5分)如图,已知 AD // BC ,/ PAB 的平分线与/ CBA 的平分线相交于 E , CE 的连线 交 AP 于D .求证:AD+BC=AB .(6分)如图,△ ABC 中,AD 是/ CAB 的平分线,且 AB=AC+CD ,求证:/ C=2/ B22. (6分)如图①,E 、F 分别为线段 AC 上的两个动点,且 DE 丄AC 于E , BF 丄AC 于F , 若AB=CD , AF=CE , BD 交 AC 于点 M .(1) 求证:MB = MD , ME=MF(2) 当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立 请给予证明;若不成立请说明理由.23. ( 7分)已知:如图, DC // AB ,且DC =AE , E 为AB 的中点,(1)求证:△ AEDEBC.21.(2)观看图前,在不添辅助线的情况下,除△EBC夕卜,请再写出两个与△ AED的面积相等的三角形.(直接写出结果,不要求证明):24. (7分)如图,△ ABC中,/ BAC=90度,AB=AC, BD是/ ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F .求证:BD=2CE.25、(10分)如图: DF=CE AD=BC/ D=Z G 求证:△26、(10分)如图:AE、BC交于点M F点在AM上,求证:AM>^ ABC的中线。
全等三角形经典题型50题(含答案解析)
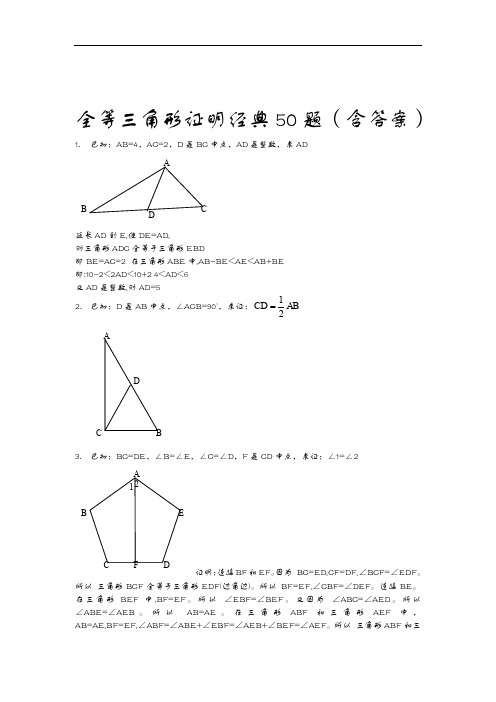
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF和三ADBC角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DG E ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠E DC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形经典题型50题(含答案)
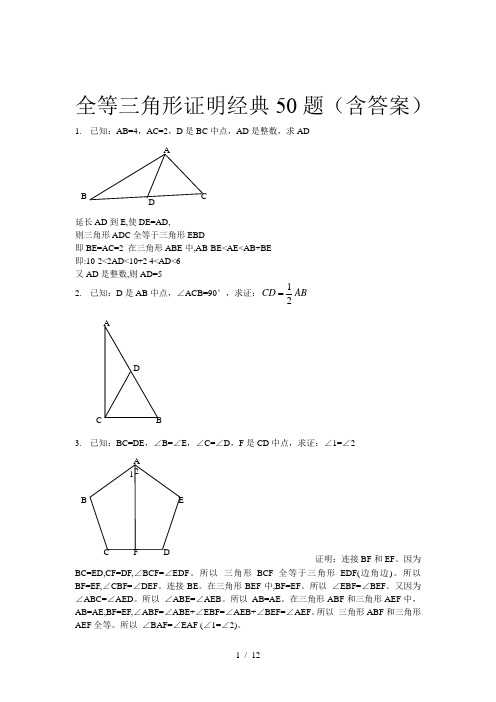
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠ED C ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB=∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形经典题型50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
【强烈推荐、吐血推荐】全等三角形、等腰三角形典型证明题62道(含答案)

全等三角形证明经典62题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2ABAD BC3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGB ACDF21 E∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2AD B C∵在△ABE中AB-BE<AE<AB+BE ∵AB=4即4-2<2AD<4+21<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:12 CD AB9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF 和EF 。
全等三角形经典题型50题(含答案)
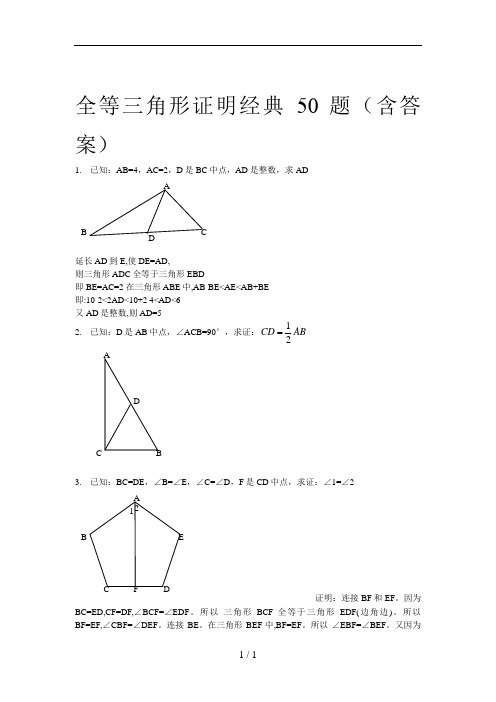
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为ADBC∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE(AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
人教版初中数学全等三角形证明题(经典50题)
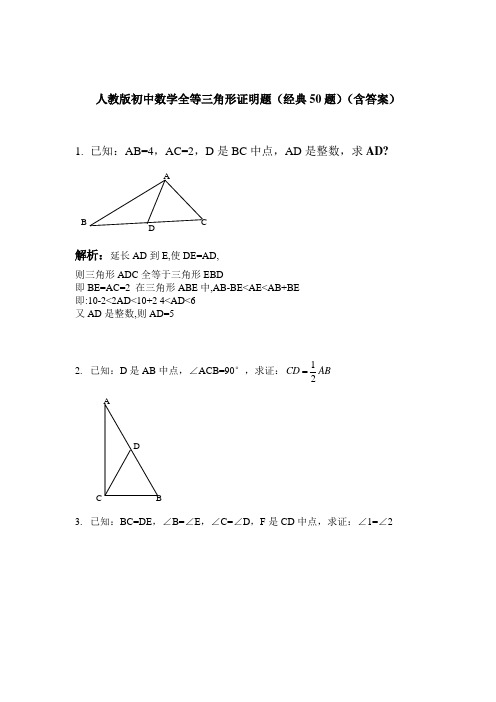
∴三角形FAB为等腰三角形,AB=AF,BE=EF在三角形DEF与三角形BEC中,∠EBC=∠DFE,且BE=EF,∠DEF=∠CEB,∴三角形DEF与三角形BEC为全等三角形,∴DF=BC∴AB=AF=AD+DF=AD+BC
证明:∵AB平行CD(已知)∴∠B=∠C(两直线平行,内错角相等)∵M在BC的中点(已知)∴EM=FM(中点定义)在△BME和△CMF中BE=CF(已知)∠B=∠C(已证)EM=FM(已证)∴△BME全等与△CMF(SAS)∴∠EMB=∠FMC(全等三角形的对应角相等)
∴∠EMF=∠EMB+∠BMF=∠FMC+∠BMF=∠BMC=180°(等式的性质)
25、如图:DF=CE,AD=BC,∠D=∠C。求证:△AED≌△BFC。
26、如图:AE、BC交于点M,F点在AM上,BE∥CF,BE=CF。
求证:AM是△ABC的中线。
证明:∵BE‖CF∴∠E=∠CFM,∠EBM=∠FCM∵BE=CF
∴△BEM≌△CFM
∴BM=CM∴AM是△ABC的中线.
27、如图:在△ABC中,BA=BC,D是AC的中点。求证:BD⊥AC。
22.如图①,E、F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M.
(1)求证:MB=MD,ME=MF
(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.
分析:通过证明两个直角三角形全等,即Rt△DEC≌Rt△BFA以及垂线的性质得出四边形BEDF是平行四边形.再根据平行四边形的性质得出结论.
全等三角形经典题型50题(含答案)
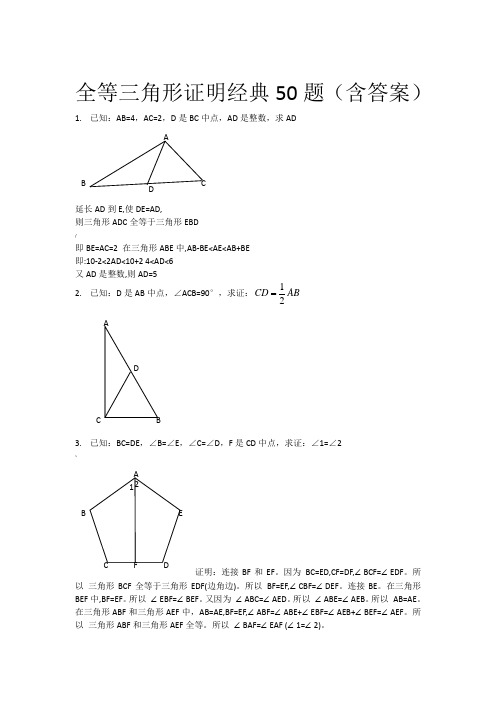
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD /即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2 ~证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
BADBCC(4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
初中数学三角形证明题经典题型训练

三角形证明中经典题11.如图,在△ABC中,∠ C=90°, AB的垂直平分线交AB与 D,交 BC于 E,连接 AE,若 CE=5, AC=12,则 BE 的长是()A. 13B. 10C. 12D. 52 .如图,在△ ABC中,AB=AC,∠ A=36°, BD、CE分别是∠ ABC、∠ BCD的角平分线,则图中的等腰三角形有()A. 5 个B. 4 个C. 3 个D. 2 个3.如图,在△ABC中, AD是它的角平分线,AB=8cm, AC=6cm,则 S △ABD: S△ACD=()A. 4: 3B. 3: 4C. 16: 9D. 9: 164.如图,在△ABC中, AB=AC,∠ A=40°, AB的垂直平分线交A B于点 D,交 AC于点 E,连接 BE,则∠ CBE的度数为()A. 70°B. 80°C. 40°D. 30°5.如图,在△ ABC中, AB=AC,且 D为 BC上一点, CD=AD, AB=BD,则∠ B 的度数为()A. 30°B. 36°C. 40°D. 45°6.如图,点O在直线 AB上,射线OC平分∠ AOD,若∠ AOC=35°,则∠ BOD等于()A. 145°B. 110°C. 70°D. 35°7 .如图,在△ ABC中,∠ ACB=90°, BA的垂直平分线交BC边于 D,若 AB=10,AC=5,则图中等于60°的角的个数是()A. 2B. 3C. 4D. 58.如图,已知BD是△ ABC的中线, AB=5, BC=3,△ ABD和△ BCD的周长的差是()A. 2B. 3C. 6D.不能确定9.在 Rt△ ABC中,如图所示,∠C=90°,∠ CAB=60°,AD平分∠ CAB,点 D 到 AB的距离 DE=3.8cm,则 BC等于()A. 3.8cm B. 7.6cm C. 11.4cm D. 11.2cm10 .△ ABC中,点 O是△ ABC内一点,且点 O到△ ABC三边的距离相等;∠A=40°,则∠ BOC=()A. 110°B. 120°C. 130°D. 140°11 .如图,已知点P 在∠ AOB的平分线OC上, PF⊥ OA,PE⊥ OB,若PE=6,则PF 的长为()A. 2B. 4C. 6D. 812 .如图,△ ABC中, DE是 AB的垂直平分线,交则△ ABC的周长是()BC于点D,交AB于点E,已知AE=1cm,△ ACD的周长为12cm,A. 13cm B. 14cm C. 15cm D. 16cm13.如图,∠ BAC=130°,若 MP和 QN分别垂直平分AB 和 AC,则∠ PAQ等于()A. 50°B. 75°C. 80°D. 105°14.如图,要用“ HL”判定 Rt △ ABC和 Rt△ A′ B′ C′全等的条件是()A.AC=A′ C′, BC=B′ C′ B.∠A=∠ A′, AB=A′ B′C.AC=A′ C′, AB=A′ B′ D.∠B=∠ B′, BC=B′ C′15.如图, MN是线段 AB 的垂直平分线, C 在 MN外,且与 A 点在 MN的同一侧, BC交 MN于 P 点,则()A. BC>PC+AP B. BC< PC+AP C. BC=PC+AP D. BC≥ PC+AP16.如图,已知在△ABC中, AB=AC, D为 BC上一点, BF=CD, CE=BD,那么∠ EDF等于()A. 90°﹣∠ A B.90°﹣∠ A C. 180°﹣∠ A D.45°﹣∠ A17.如图,在△ ABC中, AB=AC, AD平分∠ BAC,那么下列结论不一定成立的是()A.C.△ ABD≌△ ACDAD是△ ABC的角平分线B.D.AD是△ ABC的高线△ABC是等边三角形三角形证明中经典题21. 如图,已知: E 是∠ AOB的平分线上一点,EC⊥ OB, ED⊥OA, C、D 是垂足,连接CD,且交 OE于点 F.(1)求证: OE是 CD的垂直平分线.(2)若∠ AOB=60°,请你探究 OE, EF 之间有什么数量关系?并证明你的结论.2. 如图,点 D 是△ ABC中 BC边上的一点,且AB=AC=CD,AD=BD,求∠ BAC的度数.3.如图,在△ ABC中, AD平分∠ BAC,点 D 是 BC的中点, DE⊥ AB 于点 E, DF⊥AC于点F.求证:( 1)∠ B=∠ C.( 2)△ ABC是等腰三角形.4 如图, AB=AC,∠ C=67°, AB 的垂直平分线EF交 AC于点 D,求∠ DBC的度数.5. 如图,△ ABC中, AB=AD=AE, DE=EC,∠ DAB=30°,求∠ C 的度数.6.阅读理解:“在一个三角形中,如果角相等,那么它们所对的边也相等.”简称“等角对等边” ,如图,在△ ABCAB、 AC于点 D、 E,请你用“等角对等中,已知∠ ABC和∠ ACB的平分线上交于点 F,过点 F 作 BC的平行线分别交边”的知识说明 DE=BD+CE.7. 如图, AD是△ ABC的平分线, DE, DF分别垂直AB、 AC于 E、 F,连接 EF,求证:△ AEF是等腰三角形.2015 年 05 月 03 日初中数学三角形证明组卷参考答案与试题解析一.选择题(共20 小题)1.( 2015?涉县模拟)如图,在△AC=12,则 BE的长是()ABC中,∠ C=90°, AB的垂直平分线交AB与D,交BC于E,连接AE,若CE=5,A13 B 10 C 12 D 5....考线段垂直平分线的性质.菁优网版权所有点:分先根据勾股定理求出AE=13,再由 DE是线段 AB的垂直平分线,得出BE=AE=13.析:解解:∵∠ C=90°,答:∴AE=,∵DE是线段 AB的垂直平分线,∴BE=AE=13;故选: A.点本题考查了勾股定理和线段垂直平分线的性质;利用勾股定理求出AE是解题的关评:键.2.(2015?淄博模拟)如图,在△ABC中, AB=AC,∠ A=36°, BD、CE分别是∠ ABC、∠ BCD的角平分线,则图中的等腰三角形有()A 5 个B 4 个C 3 个D 2 个考等腰三角形的判定;三角形内角和定理.菁优网版权所有点:专证明题.题:分根据已知条件和等腰三角形的判定定理,对图中的三角形进行分析,即可得出答案.析:解解:共有 5 个.答:( 1)∵ AB=AC∴△ ABC是等腰三角形;(2)∵ BD、 CE分别是∠ ABC、∠ BCD的角平分线∴∠ EBC= ∠ ABC,∠ ECB= ∠BCD,∵△ ABC是等腰三角形,∴∠ EBC=∠ ECB,∴△ BCE是等腰三角形;(3)∵∠ A=36°, AB=AC,∴∠ ABC=∠ ACB= ( 180°﹣ 36°) =72°,又BD是∠ ABC的角平分线,∴∠ ABD= ∠ ABC=36° =∠ A,∴△ ABD是等腰三角形;同理可证△ CDE和△ BCD是等腰三角形.故选: A.点此题主要考查学生对等腰三角形判定和三角形内角和定理的理解和掌握,属于中档评:题.3.( 2014 秋?西城区校级期中)如图,在△ABC中, AD是它的角平分线,AB=8cm,AC=6cm,则 S △ABD:S△ACD=()A 4: 3B 3: 4C 16: 9D 9: 16....考角平分线的性质;三角形的面积.菁优网版权所有点:专计算题.题:分首先过点 D 作 DE⊥ AB, DF⊥ AC,由 AD是它的角平分线,根据角平分线的性质,析:即可求得 DE=DF,由△ ABD的面积为 12,可求得 DE与 DF的长,又由 AC=6,则可求得△ ACD的面积.解解:过点 D 作 DE⊥ AB, DF⊥ AC,垂足分别为E、 F, ( 1 分)答:∵ AD是∠ BAC的平分线, DE⊥ AB,DF⊥AC,∴ DE=DF,, ( 3 分)∴ S△ ABD= ?DE?AB=12,∴ DE=DF=3, ( 5 分)∴ S△ ADC= ?DF?AC= × 3× 6=9, (6分)∴S△ABD: S△ACD=12: 9=4:3.故选 A.点此题考查了角平分线的性质.此题难度不大,解题的关键是熟记角平分线的性评:质定理的应用,注意数形结合思想的应用,注意辅助线的作法.4.( 2014?丹东)如图,在△ABC中, AB=AC,∠ A=40°, AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠ CBE的度数为()A 70°B 80°C 40°D 30°....考点:线段垂直平分线的性质;等腰三角形的性质.菁优网版权所有专题:几何图形问题.分析:由等腰△ ABC中, AB=AC,∠ A=40°,即可求得∠ ABC的度数,又由线段 AB的垂直平分线交 AB于 D,交 AC于 E,可得 AE=BE,继而求得∠ ABE的度数,则可求得答案.解答:解:∵等腰△ ABC中, AB=AC,∠ A=40°,∴∠ ABC=∠C==70°,∵线段 AB的垂直平分线交AB于 D,交 AC于 E,∴A E=BE,∴∠ ABE=∠A=40°,∴∠ CBE=∠ABC﹣∠ ABE=30°.故选: D.点评:此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度不大,注意掌握数形结合思想的应用.5.( 2014?南充)如图,在△ ABC中, AB=AC,且 D 为 BC上一点, CD=AD, AB=BD,则∠ B 的度数为()A 30°B 36°C 40°D 45°....考等腰三角形的性质.菁优网版权所有点:分求出∠ BAD=2∠CAD=2∠B=2∠ C 的关系,利用三角形的内角和是180°,求∠ B,析:解解:∵ AB=AC,答:∴∠ B=∠ C,∵ AB=BD,∴∠ BAD=∠ BDA,∵ CD=AD,∴∠ C=∠ CAD,∵∠ BAD+∠ CAD+∠ B+∠C=180°,∴ 5∠ B=180°,∴∠ B=36°故选: B.点本题主要考查等腰三角形的性质,解题的关键是运用等腰三角形的性质得出∠BAD=2评:∠ CAD=2∠ B=2∠ C 关系.6.( 2014?山西模拟)如图,点O在直线 AB上,射线OC平分∠ AOD,若∠ AOC=35°,则∠ BOD等于()A145°B110° C 70° D 35°....考角平分线的定义.菁优网版权所有点:分首先根据角平分线定义可得∠ AOD=2∠ AOC=70°,再根据邻补角的性质可得∠BOD析:的度数.解解:∵射线 OC平分∠ DOA.答:∴∠ AOD=2∠ AOC,∵∠ COA=35°,∴∠ DOA=70°,∴∠ BOD=180°﹣ 70° =110°,故选: B.点此题主要考查了角平分线定义,关键是掌握角平分线把角分成相等的两部分.评:7.( 2014?雁塔区校级模拟)如图,在△ABC中,∠ ACB=90°, BA的垂直平分线交BC边于 D,若 AB=10, AC=5,则图中等于60°的角的个数是()A 2B 3C 4D5....考点:线段垂直平分线的性质.菁优网版权所有分析:根据已知条件易得∠B=30°,∠ BAC=60°.根据线段垂直平分线的性质进一步求解.解答:解:∵∠ ACB=90°,AB=10,AC=5,∴∠ B=30°.∴∠ BAC=90°﹣ 30° =60°∵ DE垂直平分BC,∴∠ BAC=∠ ADE=∠BDE=∠ CDA=90°﹣ 30° =60°.∴∠ BDE对顶角 =60°,∴图中等于60°的角的个数是4.故选 C.点评:此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.由易到难逐个寻找,做到不重不漏.8.( 2014 秋?腾冲县校级期末)如图,已知BD是△ ABC的中线, AB=5,BC=3,△ ABD和△ BCD的周长的差是()A 2B 3C 6D 不能确定....考点:三角形的角平分线、中线和高.菁优网版权所有专题:计算题.分析:根据三角形的中线得出AD=CD,根据三角形的周长求出即可.解答:解:∵ BD是△ ABC的中线,∴AD=CD,∴△ ABD和△ BCD的周长的差是:(AB+BD+AD)﹣( BC+BD+CD)=AB﹣ BC=5﹣ 3=2.故选 A.点评:本题主要考查对三角形的中线的理解和掌握,能正确地进行计算是解此题的关键.9.( 2014 春?栖霞市期末)在 Rt △ ABC中,如图所示,∠ C=90°,∠ CAB=60°,AD平分∠ CAB,点 D到 AB的距离 DE=3.8cm,则 BC等于()A 3.8cmB 7.6cm C11.4cm D11.2cm....考点:角平分线的性质.菁优网版权所有分析:由∠ C=90°,∠ CAB=60°,可得∠ B 的度数,故 BD=2DE=7.6,又 AD平分∠ CAB,故DC=DE=3.8,由 BC=BD+DC求解.解答:解:∵∠ C=90°,∠ CAB=60°,∴∠ B=30°,在 Rt △BDE中, BD=2DE=7.6,又∵ AD平分∠ CAB,∴DC=DE=3.8,∴BC=BD+DC=7.6+3.8=11.4.故选 C.点评:本题主要考查平分线的性质,由已知能够注意到D到 AB 的距离 DE即为 CD长,是解题的关键.10.( 2014 秋?博野县期末)△ ABC中,点 O是△ ABC内一点,且点 O到△ ABC三边的距离相等;∠ A=40°,则∠BOC=()A110° B 120°C130°D140°....考角平分线的性质;三角形内角和定理;三角形的外角性质.菁优网版权所有点:专计算题.题:分由已知, O到三角形三边距离相等,得O是内心,再利用三角形内角和定理即可求析:出∠ BOC的度数.解解:由已知, O到三角形三边距离相等,所以O是内心,答:即三条角平分线交点, AO, BO, CO都是角平分线,所以有∠ CBO=∠ABO= ∠ ABC,∠ BCO=∠ ACO= ∠ ACB,∠ABC+∠ ACB=180﹣ 40=140∠OBC+∠ OCB=70∠BOC=180﹣ 70=110°故选 A.点此题主要考查学生对角平分线性质,三角形内角和定理,三角形的外角性质等知识评:点的理解和掌握,难度不大,是一道基础题.11.( 2013 秋?潮阳区期末)如图,已知点 P 在∠ AOB的平分线OC上,PF⊥ OA,PE⊥ OB,若 PE=6,则 PF 的长为()A 2B 4C6D8....考点:角平分线的性质;全等三角形的判定与性质.菁优网版权所有专题:计算题.分析:利用角平分线性质得出∠POF=∠ POE,然后利用AAS定理求证△ POE≌△ POF,即可求出 PF 的长.解答:解:∵ OC平分∠ AOB,∴∠ POF=∠ POE,∵PF⊥ OA,PE⊥ OB,∴∠ PFO=∠ PEO,PO为公共边,∴△POE≌△ POF,∴PF=PE=6.故选 C.点评:此题考查学生对角平分线性质和全等三角形的判定与性质的理解和掌握,解答此题的关键是求证△ POE≌△ POF.12.(2013 秋?马尾区校级期末)如图,△ ABC中,DE是AB的垂直平分线,交BC于点D,交AB于点E,已知AE=1cm,△ ACD的周长为 12cm,则△ ABC的周长是()A13cm B 14cm C 15cm D 16cm....考线段垂直平分线的性质.菁优网版权所有点:分要求△ ABC的周长,先有AE 可求出 AB,只要求出 AC+BC即可,根据线段垂直平分线析:的性质可知, AD=BD,于是 AC+BC=AC+CD+AD等于△ ACD的周长,答案可得.解解:∵ DE是 AB的垂直平分线,答:∴ AD=BD, AB=2AE=2又∵△ ACD的周长 =AC+AD+CD=AC+BD+CD=AC+BC=12∴△ ABC的周长是 12+2=14cm.故选 B点此题主要考查线段的垂直平分线的性质:线段的垂直平分线上的点到线段的两个端评:点的距离相等;进行线段的等效转移,把已知与未知联系起来是正确解答本题的关键.13.( 2013 秋?西城区期末)如图,∠ BAC=130°,若 MP和 QN分别垂直平分 AB 和 AC,则∠ PAQ等于()A50° B 75° C 80° D 105°....考线段垂直平分线的性质.菁优网版权所有点:分根据线段垂直平分线性质得出BP=AP, CQ=AQ,推出∠ B=∠ BAP,∠ C=∠QAC,求出析:∠ B+∠C,即可求出∠ BAP+∠ QAC,即可求出答案.解解:∵ MP和 QN分别垂直平分AB和 AC,答:∴ BP=AP, CQ=AQ,∴∠ B=∠ PAB,∠ C=∠ QAC,∵∠ BAC=130°,∴∠ B+∠ C=180°﹣∠ BAC=50°,∴∠ BAP+∠ CAQ=50°,∴∠ PAQ=∠ BAC﹣(∠ PAB+∠ QAC) =130°﹣ 50° =80°,故选: C.点本题考查了等腰三角形的性质,线段垂直平分线性质,三角形的内角和定理,注评:意:线段垂直平分线上的点到线段两个端点的距离相等,等边对等角.14.( 2014 秋?东莞市校级期中)如图,要用“HL”判定 Rt△ ABC和 Rt △ A′B′ C′全等的条件是()A AC=A′C′,B∠ A=∠ A′,.BC=B′C′.AB=A′ B′C AC=A′C′,D∠ B=∠ B′,.AB=A′B′.BC=B′ C′考直角三角形全等的判定.菁优网版权所有点:分根据直角三角形全等的判定方法(HL)即可直接得出答案.析:解解:∵在 Rt △ABC和 Rt△ A′ B′C′中,答:如果 AC=A′ C′, AB=A′ B′,那么 BC一定等于 B′ C′,Rt △ABC和 Rt△ A′ B′C′一定全等,故选 C.点此题主要考查学生对直角三角形全等的判定的理解和掌握,难度不大,是一道基评:础题.15.( 2014 秋?淄川区校级期中)如图,MN是线段AB的垂直平分线,C在MN外,且与A 点在MN的同一侧,BC交MN于 P 点,则()A BC> PC+APB BC<PC+APC BC=PC+APD BC≥ PC+AP....分析:从已知条件进行思考,根据垂直平分线的性质可得通过等量代换得到答案.解答:解:∵点P 在线段 AB的垂直平分线上,PA=PB,结合图形知BC=PB+PC,∴PA=PB.∵ BC=PC+BP,∴BC=PC+AP.故选 C.点评:本题考查了垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等;结合图形,进行线段的等量代换是正确解答本题的关键.16.( 2014 秋?万州区校级期中)如图,已知在△ABC中, AB=AC, D为 BC上一点, BF=CD, CE=BD,那么∠ EDF等于()A 90°﹣∠ A B90°﹣∠ A C 180°﹣∠ A D45°﹣∠ A....考点:等腰三角形的性质.菁优网版权所有分析:由 AB=AC,利用等边对等角得到一对角相等,再由BF=CD, BD=CE,利用 SAS得到三角形FBD与三角形 DEC全等,利用全等三角形对应角相等得到一对角相等,即可表示出∠ EDF.解答:解:∵ AB=AC,∴∠ B=∠ C°,在△ BDF和△ CED中,,∴△ BDF≌△ CED( SAS),∴∠ BFD=∠CDE,∴∠ FDB+∠EDC=∠ FDB+∠ BFD=180°﹣∠ B=180°﹣=90° + ∠ A,则∠ EDF=180°﹣(∠ FDB+∠EDC) =90°﹣∠ A.故选 B.点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.17.( 2014 秋?泰山区校级期中)如图,在△ABC中, AB=AC, AD平分∠ BAC,那么下列结论不一定成立的是()A△ ABD≌△B AD是△ ABC 的.ACD.高线C AD是△ ABC的D△ ABC是等边.角平分线.三角形考点:等腰三角形的性质.菁优网版权所有分析:利用等腰三角形的性质逐项判断即可.解答:解:A、在△ ABD和△ ACD中,,所以△ ABD≌△ ACD,所以A正确;B、因为 AB=AC, AD平分∠ BAC,所以 AD是 BC边上的高,所以 B 正确;C、由条件可知 AD为△ ABC的角平分线;D、由条件无法得出 AB=AC=BC,所以△ ABC不一定是等边三角形,所以 D不正确;故选 D.点评:本题主要考查等腰三角形的性质,掌握等腰三角形“三线合一”的性质是解题的关键.18.( 2014 秋?晋江市校级月考)如图,点P 是△ ABC内的一点,若PB=PC,则()A 点 P 在∠ABC .的平分线上C点 P 在边 AB .的垂直平分线上B 点 P 在∠ ACB .的平分线上D点 P 在边 BC .的垂直平分线上考点:线段垂直平分线的性质.菁优网版权所有分析:根据到线段两端点的距离相等的点在这条线段的垂直平分线上由PC=PB即可得出P 在线段 BC的垂直平分线上.解答:解:∵ PB=PC,∴P 在线段 BC的垂直平分线上,故选 D.点评:本题考查了角平分线的性质和线段垂直平分线定理,注意:到线段两端点的距离相等的点在这条线段的垂直平分线上,角平分线上的点到角的两边的距离相等.19.( 2013?河西区二模)如图,在∠ ECF的两边上有点B,A,D,BC=BD=DA,且∠ ADF=75°,则∠ ECF的度数为()A 15°B 20°C 25°D 30°....考等腰三角形的性质.菁优网版权所有点:分根据等腰三角形的性质以及三角形外角和内角的关系,逐步推出∠ECF的度数.析:解解:∵ BC=BD=DA,答:∴∠ C=∠BDC,∠ ABD=∠ BAD,∵∠ ABD=∠ C+∠ BDC,∠ ADF=75°,∴3∠ ECF=75°,∴∠ECF=25°.故选:C.点考查了等腰三角形的性质:等腰三角形的两个底角相等,三角形外角和内角的运评:用.20.( 2013 秋?盱眙县校级期中)如图,P 为∠ AOB的平分线OC上任意一点, PM⊥ OA于 M, PN⊥OB于 N,连接 MN交OP于点 D.则① PM=PN,② MO=NO,③ OP⊥ MN,④ MD=ND.其中正确的有()A 1 个B 2 个C 3 个D 4 个....考角平分线的性质.菁优网版权所有点:分由已知很易得到△OPM≌△ OPN,从而得角相等,边相等,进而得△OMP≌△ ONP,△析:PMD≌△ PND,可得 MD=ND,∠ ODN=∠ ODM=9O°,答案可得.解解: P 为∠ AOB的平分线 OC上任意一点, PM⊥ OA于 M, PN⊥OB于 N答:连接 MN交 OP于点 D,∴∠ MOP=∠ NOP,∠ OMP=∠ ONP, OP=OP,∴△ OPM≌△ OPN,∴MP=NP,OM=ON,又 OD=OD点评:∴△ OMD≌△ OND,∴ MD=ND,∠ ODN=∠ ODM=9O°,∴ OP⊥MN∴① PM=PN,② MO=NO,③ OP⊥ MN,④ MD=ND都正确.故选 D.本题主要考查了角平分线的性质,即角平分线上的一点到两边的距离相等;发现并利用△ OMD≌△ OND是解决本题的关键,证明两线垂直时常常通过证两角相等且互补来解决.二.解答题(共10 小题)21.( 2014 秋?黄浦区期末)如图,已知ON是∠ AOB的平分线, OM、OC是∠ AOB外的射线.(1)如果∠ AOC=α,∠ BOC=β,请用含有α,β的式子表示∠ NOC.(2)如果∠ BOC=90°, OM平分∠ AOC,那么∠ MON的度数是多少?考点:角平分线的定义.菁优网版权所有分析:( 1)先求出∠ AOB=α﹣β,再利用角平分线求出∠AON,即可得出∠NOC;( 2)先利用角平分线求出∠AOM= ∠ AOC,∠ AON= ∠ AOB,即可得出∠ MON= ∠BOC.解答:解:( 1)∵∠ AOC=α,∠ BOC=β,∴∠ AOB=α﹣β,∵ON是∠ AOB的平分线,∴∠ AON= (α﹣β),∠ NOC=α﹣(α﹣β)=(α+β);(2)∵OM平分∠AOC,ON平分∠AOB,∴∠ AOM= ∠ AOC,∠ AON= ∠AOB,∴∠ MON=∠ AOM﹣∠ AON= (∠ AOC﹣∠ AOB) =∠BOC=× 90°=45°.点评:本题考查了角平分线的定义和角的计算;弄清各个角之间的数量关系是解决问题的关键.22.(2014 秋?阿坝州期末)如图,已知: E 是∠ AOB的平分线上一点,EC⊥OB,ED⊥ OA, C、D是垂足,连接CD,且交OE于点 F.(1)求证: OE是 CD的垂直平分线.(2)若∠ AOB=60°,请你探究 OE, EF 之间有什么数量关系?并证明你的结论.考点:线段垂直平分线的性质.菁优网版权所有专题:探究型.分析:( 1)先根据 E 是∠ AOB的平分线上一点, EC⊥ OB, ED⊥ OA得出△ ODE≌△OCE,可得出 OD=OC,DE=CE, OE=OE,可得出△ DOC是等腰三角形,由等腰三角形的性质即可得出 OE是 CD的垂直平分线;(2)先根据 E 是∠ AOB的平分线,∠ AOB=60°可得出∠ AOE=∠BOE=30°,由直角三角形的性质可得出 OE=2DE,同理可得出 DE=2EF即可得出结论.解答:解:( 1)∵ E 是∠ AOB的平分线上一点,EC⊥OB, ED⊥OA,∴DE=CE, OE=OE,∴Rt △ODE≌ Rt △OCE,∴OD=OC,∴△ DOC是等腰三角形,∵OE是∠ AOB的平分线,∴OE是CD的垂直平分线;(2)∵OE是∠AOB的平分线,∠AOB=60°,∴∠ AOE=∠ BOE=30°,∵ EC⊥OB, ED⊥ OA,∴ OE=2DE,∠ ODF=∠OED=60°,∴∠ EDF=30°,∴DE=2EF,∴OE=4EF.点评:本题考查的是角平分线的性质及直角三角形的性质、等腰三角形的判定与性质,熟知以上知识是解答此题的关键.23.( 2014 秋?花垣县期末)如图,在△ABC中,∠ ABC=2∠ C, BD平分∠ ABC, DE⊥ AB( E 在 AB之间),DF⊥ BC,已知BD=5, DE=3, CF=4,试求△ DFC的周长.考点:角平分线的性质.菁优网版权所有分析:根据角平分线的性质可证∠ABD=∠CBD,即可求得∠ CBD=∠ C,即 BD=CD,再根据角平分线上的点到角两边距离相等即可求得DE=DF,即可解题.解答:解:∵∠ ABC=2∠ C, BD平分∠ ABC,∴∠ CBD=∠ C,∴BD=CD,∵BD平分∠ABC,∴ DE=DF,∴△ DFC的周长 =DF+CD+CF=DE+BD+CF=3+5+4=12.点评:本题考查了角平分线上点到角两边距离相等的性质,考查了角平分线平分角的性质,考查了三角形周长的计算,本题中求证DE=DF是解题的关键.24.( 2014 秋?大石桥市期末)如图,点 D 是△ ABC中 BC边上的一点,且AB=AC=CD, AD=BD,求∠ BAC的度数.考点:等腰三角形的性质.菁优网版权所有分析:由AD=BD得∠ BAD=∠ DBA,由AB=AC=CD得∠ CAD=∠ CDA=2∠ DBA,∠ DBA=∠ C,从而可推出∠ BAC=3∠ DBA,根据三角形的内角和定理即可求得∠DBA的度数,从而不难求得∠ BAC的度数.解答:解:∵ AD=BD∴设∠ BAD=∠ DBA=x°,∵AB=AC=CD∴∠ CAD=∠ CDA=∠BAD+∠ DBA=2x°,∠ DBA=∠C=x°,∴∠ BAC=3∠ DBA=3x°,∵∠ ABC+∠ BAC+∠C=180°∴5x=180°,∴∠ DBA=36°∴∠ BAC=3∠ DBA=108°.点评:此题主要考查学生对等腰三角形的性质及三角形内角和定理的综合运用能力;求得角之间的关系利用内角和求解是正确解答本题的关键.25.( 2014 秋?安溪县期末)如图,在△ABC中, AB=AC,∠ A=α.( 1)直接写出∠ABC的大小(用含α的式子表示);( 2)以点 B 为圆心、BC长为半径画弧,分别交AC、 AB于D、 E 两点,并连接BD、 DE.若=30°,求∠BDE的度数.考点:等腰三角形的性质.菁优网版权所有分析:(1)根据三角形内角和定理和等腰三角形两底角相等的性质即可求得∠ABC的大小;( 2)根据等腰三角形两底角相等求出∠BCD=∠ BDC,再求出∠ CBD,然后根据∠ABD=∠ ABC﹣∠ CBD,求得∠ ABD,再根据三角形内角和定理和等腰三角形两底角相等的性质计算即可得解.解答:解:( 1)∠ ABC的大小为×( 180°﹣α) =90°﹣α;(2)∵ AB=AC,∴∠ ABC=∠ C=90°﹣α=90°﹣× 30°=75°,由题意得: BC=BD=BE,由BC=BD得∠ BDC=∠ C=75°,∴∠ CBD=180°﹣ 75°﹣ 75° =30°,∴∠ ABD=∠ ABC﹣∠ CBD=75°﹣ 30° =45°,由 BD=BE得.点评:故∠ BDE的度数是67.5 °.本题考查了三角形内角和定理、等腰三角形的性质,主要利用了等腰三角形两底角相等,熟记性质是解题的关键.26.( 2014 秋?静宁县校级期中)如图,在△ABC中, AD平分∠ BAC,点 D 是 BC的中点, DE⊥ AB于点 E,DF⊥ AC 于点F.求证:( 1)∠ B=∠ C.( 2)△ ABC是等腰三角形.考等腰三角形的判定.菁优网版权所有点:分由条件可得出DE=DF,可证明△BDE≌△CDF,可得出∠B=∠C,再由等腰三角形的析:判定可得出结论.解证明:( 1)∵ AD平分∠ BAC, DE⊥ AB 于点 E, DF⊥ AC于点 F,答:∴ DE=DF,在Rt△ BDE和 Rt △ CDF中,,∴Rt△ BDE≌ Rt△ CDF(HF),∴∠ B=∠ C;( 2)由( 1)可得∠ B=∠ C,∴△ ABC为等腰三角形.点本题主要考查等腰三角形的判定及全等三角形的判定和性质,利用角平分线的性质评:得出 DE=DF是解题的关键.27.( 2012 秋?天津期末)如图,AB=AC,∠ C=67°, AB 的垂直平分线EF 交 AC于点 D,求∠ DBC的度数.考点:分析:解答:线段垂直平分线的性质;等腰三角形的性质.求出∠ ABC,根据三角形内角和定理求出∠求出∠ ABD,即可求出答案.解:∵ AB=AC,∠ C=67°,∴∠ ABC=∠ C=67°,∴∠ A=180°﹣ 67°﹣ 67°=46°,菁优网版权所有A,根据线段垂直平分线得出AD=BD,∵EF 是AB的垂直平分线,∴ AD=BD,∴∠ A=∠ABD=46°,∴∠ DBC=67°﹣ 46° =21°.点评:本题考查了线段垂直平分线,三角形的能或定理,等腰三角形的性质和判定等知识点,关键是求出∠ ABC和∠ ABD的度数,题目比较好.28.( 2013 秋?高坪区校级期中)如图,△ABC中, AB=AD=AE, DE=EC,∠ DAB=30°,求∠ C的度数.考点:等腰三角形的性质.菁优网版权所有分析:首先根据 AB=AD=AE,DE=EC,得到∠ B=∠ ADB,∠ ADE=∠ AED,∠ C=∠EDC,从而得到∠ ADE=∠ AED=∠ C+∠ EDC=2∠ C,根据∠ DAB=30°,求得∠ B=∠ ADB=75°,利用∠ADC=∠ ADE+∠EDC=3∠C=105°,求得∠ C 即可.解答:解:∵ AB=AD=AE, DE=EC,∴∠ B=∠ ADB,∠ ADE=∠AED,∠ C=∠ EDC,∴∠ ADE=∠ AED=∠ C+∠ EDC=2∠ C,∵∠ DAB=30°,∴∠ B=∠ ADB=75°,∴∠ ADC=∠ ADE+∠ EDC=3∠ C=105°,∴∠ C=35°.点评:本题考查了等腰三角形的性质,解题的关键是利用等腰三角形的性质求得有关角的度数.29.( 2012 春?扶沟县校级期中)阅读理解:“在一个三角形中,如果角相等,那么它们所对的边也相等.角对等边”,如图,在△ ABC中,已知∠ ABC和∠ ACB的平分线上交于点F,过点 F 作 BC的平行线分别交点 D、 E,请你用“等角对等边”的知识说明DE=BD+CE.”简称“等AB、AC于考等腰三角形的性质.菁优网版权所有点:专证明题.题:分由 DE∥ BC, BF平分∠ ABC, CF 平分∠ ACB可知, DB=DF, CE=EF.便可得出结论.析:解证明:∵ BF 平分∠ ABC(已知), CF平分∠ ACB(已知),答:∴∠ ABF=∠ CBF,∠ ACF=∠ FCB;又∵ DE平行 BC(已知)∴∠ DFB=∠ FBC(两直线平行,内错角相等),∠ EFC=∠ FCB(两直线平行,内错角相等),∴∠ DBF=∠ DFB,∠ EFC=∠ ECF(等量代换)∴DF=DB, EF=EC(等角对等边)∴DE=BD+CE.点此题考查学生对等腰三角形的判定与性质和平行线的性质的理解和掌握,主要利评:用等腰三角形两边相等.稍微有点难度是一道中档题.30.( 2011?龙岩质检)如图, AD是△ ABC的平分线, DE,DF分别垂直 AB、 AC于 E、 F,连接 EF,求证:△ AEF是等腰三角形.考等腰三角形的判定;全等三角形的判定与性质.菁优网版权所有点:专证明题.题:分根据角平分线的性质知∠ BAD=∠ CAD;然后根据已知条件“ DE,DF 分别垂直 AB、析:AC于 E、 F”得到∠ DEA=∠ DFA=90°;再加上公共边 AD=AD,从而证明,△ ADE≌△ ADF;最后根据全等三角形的对应边相等证明△AEF的两边相等,所以△ AEF 是等腰三角形.解证明:∵ AD是△ ABC的平分线,答:∴∠ BAD=∠ CAD,( 3 分)又∵ DE, DF分别垂直 AB、 AC于 E, F∴∠ DEA=∠ DFA=90°( 6 分)又∵ AD=AD,∴△ ADE≌△ ADF.( 8 分)∴ AE=AF,即△ AEF是等腰三角形(10 分)点本题综合考查了等腰三角形的判定、全等三角形的判定与性质.解答此题时,根评:据全等三角形的判定定理 ASA判定△ ADE≌△ ADF.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.选择题(共20小题)1.(涉县模拟)如图,在△ABC中,∠C=90°,AB的垂直平分线交AB与D,交BC于E,连接AE,若CE=5,AC=12,则BE的长是()A .13B.10C.12D.52.(淄博模拟)如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD 的角平分线,则图中的等腰三角形有()A .5个B.4个C.3个D.2个3.(西城区校级期中)如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=()A .4:3B.3:4C.16:9D.9:164.(丹东)如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE的度数为()A70°B80°C40°D30°....5.(南充)如图,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B 的度数为()A .30°B.36°C.40°D.45°6.(山西模拟)如图,点O在直线AB上,射线OC平分∠AOD,若∠AOC=35°,则∠BOD 等于()A .145°B.110°C.70°D.35°7.(雁塔区校级模拟)如图,在△ABC中,∠ACB=90°,BA的垂直平分线交BC边于D,若AB=10,AC=5,则图中等于60°的角的个数是()A .2B.3C.4D.58.(腾冲县校级期末)如图,已知BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD 的周长的差是()A .2B.3C.6D.不能确定9.(栖霞市期末)在Rt△ABC中,如图所示,∠C=90°,∠CAB=60°,AD平分∠CAB,点D到AB的距离DE=3.8cm,则BC等于()A .3.8cm B.7.6cm C.11.4cm D.11.2cm10.(博野县期末)△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等;∠A=40°,则∠BOC=()A .110°B.120°C.130°D.140°11.(潮阳区期末)如图,已知点P在∠AOB的平分线OC上,PF⊥OA,PE⊥OB,若PE=6,则PF的长为()A .2B.4C.6D.812.(马尾区校级期末)如图,△ABC中,DE是AB的垂直平分线,交BC于点D,交AB于点E,已知AE=1cm,△ACD的周长为12cm,则△ABC的周长是()A .13cm B.14cm C.15cm D.16cm13.(西城区期末)如图,∠BAC=130°,若MP和QN分别垂直平分AB和AC,则∠PAQ 等于()2020初中数学几何——三角形证明专项练习A .50°B.75°C.80°D.105°14.(东莞市校级期中)如图,要用“HL”判定Rt△ABC和Rt△A′B′C′全等的条件是()A.AC=A′C′,BC=B′C′B.∠A=∠A′,AB=A′B′C.AC=A′C′,AB=A′B′D.∠B=∠B′,BC=B′C′15.(淄川区校级期中)如图,MN是线段AB的垂直平分线,C在MN外,且与A点在MN的同一侧,BC交MN于P点,则()A .BC>PC+AP B.BC<PC+AP C.BC=PC+AP D.BC≥PC+AP16.(万州区校级期中)如图,已知在△ABC中,AB=AC,D为BC上一点,BF=CD,CE=BD,那么∠EDF等于()A .90°﹣∠A B.90°﹣∠A C.180°﹣∠A D.45°﹣∠A17.(泰山区校级期中)如图,在△ABC中,AB=AC,AD平分∠BAC,那么下列结论不一定成立的是()2020A.△ABD≌△ACD B.AD是△ABC的高线C.AD是△ABC的角平分线D.△ABC是等边三角形18.(晋江市校级月考)如图,点P是△ABC内的一点,若PB=PC,则()A.点P在∠ABC的平分线上B.点P在∠ACB的平分线上C.点P在边AB的垂直平分线上D.点P在边BC的垂直平分线上19.(河西区二模)如图,在∠ECF的两边上有点B,A,D,BC=BD=DA,且∠ADF=75°,则∠ECF的度数为()A .15°B.20°C.25°D.30°20.(盱眙县校级期中)如图,P为∠AOB的平分线OC上任意一点,PM⊥OA于M,PN⊥OB 于N,连接MN交OP于点D.则①PM=PN,②MO=NO,③OP⊥MN,④MD=ND.其中正确的有()A1个B2个C3个4个二.解答题(共10小题)21.(黄浦区期末)如图,已知ON是∠AOB的平分线,OM、OC是∠AOB外的射线.(1)如果∠AOC=α,∠BOC=β,请用含有α,β的式子表示∠NOC.(2)如果∠BOC=90°,OM平分∠AOC,那么∠MON的度数是多少?22.(阿坝州期末)如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.(1)求证:OE是CD的垂直平分线.(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.23.(花垣县期末)如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,DE⊥AB(E在AB之间),DF⊥BC,已知BD=5,DE=3,CF=4,试求△DFC的周长.24.(大石桥市期末)如图,点D是△ABC中BC边上的一点,且AB=AC=CD,AD=BD,求∠BAC的度数.25.(安溪县期末)如图,在△ABC中,AB=AC,∠A=α.(1)直接写出∠ABC的大小(用含α的式子表示);(2)以点B为圆心、BC长为半径画弧,分别交AC、AB于D、E两点,并连接BD、DE.若=30°,求∠BDE的度数.26.(静宁县校级期中)如图,在△ABC中,AD平分∠BAC,点D是BC的中点,DE⊥AB 于点E,DF⊥AC于点F.求证:(1)∠B=∠C.2020(2)△ABC是等腰三角形.27.(天津期末)如图,AB=AC,∠C=67°,AB的垂直平分线EF交AC于点D,求∠DBC 的度数.28.(高坪区校级期中)如图,△ABC中,AB=AD=AE,DE=EC,∠DAB=30°,求∠C 的度数.29.(扶沟县校级期中)阅读理解:“在一个三角形中,如果角相等,那么它们所对的边也相等.”简称“等角对等边”,如图,在△ABC中,已知∠ABC和∠ACB的平分线上交于点F,过点F作BC的平行线分别交AB、AC于点D、E,请你用“等角对等边”的知识说明DE=BD+CE.2020初中数学几何——三角形证明专项练习30.(龙岩质检)如图,AD是△ABC的平分线,DE,DF分别垂直AB、AC于E、F,连接EF,求证:△AEF是等腰三角形.2020参考答案与试题解析一.选择题(共20小题)1.(涉县模拟)如图,在△ABC中,∠C=90°,AB的垂直平分线交AB与D,交BC于E,连接AE,若CE=5,AC=12,则BE的长是()A .13B.10C.12D.5考点:线段垂直平分线的性质.分析:先根据勾股定理求出AE=13,再由DE是线段AB的垂直平分线,得出BE=AE=13.解答:解:∵∠C=90°,∴AE=,∵DE是线段AB的垂直平分线,∴BE=AE=13;故选:A.点评:本题考查了勾股定理和线段垂直平分线的性质;利用勾股定理求出AE是解题的关键.2.(淄博模拟)如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD 的角平分线,则图中的等腰三角形有()A .5个B.4个C.3个D.2个考点:等腰三角形的判定;三角形内角和定理.专证明题.题:分析:根据已知条件和等腰三角形的判定定理,对图中的三角形进行分析,即可得出答案.解答:解:共有5个.(1)∵AB=AC∴△ABC是等腰三角形;(2)∵BD、CE分别是∠ABC、∠BCD的角平分线∴∠EBC=∠ABC,∠ECB=∠BCD,∵△ABC是等腰三角形,∴∠EBC=∠ECB,∴△BCE是等腰三角形;(3)∵∠A=36°,AB=AC,∴∠ABC=∠ACB=(180°﹣36°)=72°,又BD是∠ABC的角平分线,∴∠ABD=∠ABC=36°=∠A,∴△ABD是等腰三角形;同理可证△CDE和△BCD是等腰三角形.故选:A.点评:此题主要考查学生对等腰三角形判定和三角形内角和定理的理解和掌握,属于中档题.3.(西城区校级期中)如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=()A .4:3B.3:4C.16:9D.9:16考点:角平分线的性质;三角形的面积.专题:计算题.分析:首先过点D作DE⊥AB,DF⊥AC,由AD是它的角平分线,根据角平分线的性质,即可求得DE=DF,由△ABD的面积为12,可求得DE与DF的长,又由AC=6,则可求得△ACD的面积.解答:解:过点D作DE⊥AB,DF⊥AC,垂足分别为E、F…(1分)∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,∴DE=DF,…(3分)∴S△ABD=•DE•AB=12,∴DE=DF=3…(5分)∴S△ADC=•DF•AC=×3×6=9…(6分)∴S△ABD:S△ACD=12:9=4:3.故选A.点评:此题考查了角平分线的性质.此题难度不大,解题的关键是熟记角平分线的性质定理的应用,注意数形结合思想的应用,注意辅助线的作法.4.(丹东)如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE的度数为()A .70°B.80°C.40°D.30°考点:线段垂直平分线的性质;等腰三角形的性质.专题:几何图形问题.分析:由等腰△ABC中,AB=AC,∠A=40°,即可求得∠ABC的度数,又由线段AB的垂直平分线交AB于D,交AC于E,可得AE=BE,继而求得∠ABE的度数,则可求得答案.解答:解:∵等腰△ABC中,AB=AC,∠A=40°,∴∠ABC=∠C==70°,∵线段AB的垂直平分线交AB于D,交AC于E,∴AE=BE,∴∠ABE=∠A=40°,∴∠CBE=∠ABC﹣∠ABE=30°.故选:D.点评:此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度不大,注意掌握数形结合思想的应用.5.(南充)如图,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B 的度数为()A .30°B.36°C.40°D.45°考点:等腰三角形的性质.分析:求出∠BAD=2∠CAD=2∠B=2∠C的关系,利用三角形的内角和是180°,求∠B,解答:解:∵AB=AC,∴∠B=∠C,∵AB=BD,∴∠BAD=∠BDA,∵CD=AD,∴∠C=∠CAD,∵∠BAD+∠CAD+∠B+∠C=180°,∴5∠B=180°,∴∠B=36°故选:B.点评:本题主要考查等腰三角形的性质,解题的关键是运用等腰三角形的性质得出∠BAD=2∠CAD=2∠B=2∠C关系.6.(山西模拟)如图,点O在直线AB上,射线OC平分∠AOD,若∠AOC=35°,则∠BOD 等于()A .145°B.110°C.70°D.35°考角平分线的定义.点:分析:首先根据角平分线定义可得∠AOD=2∠AOC=70°,再根据邻补角的性质可得∠BOD的度数.解答:解:∵射线OC平分∠DOA.∴∠AOD=2∠AOC,∵∠COA=35°,∴∠DOA=70°,∴∠BOD=180°﹣70°=110°,故选:B.点评:此题主要考查了角平分线定义,关键是掌握角平分线把角分成相等的两部分.7.(雁塔区校级模拟)如图,在△ABC中,∠ACB=90°,BA的垂直平分线交BC边于D,若AB=10,AC=5,则图中等于60°的角的个数是()A .2B.3C.4D.5考点:线段垂直平分线的性质.分析:根据已知条件易得∠B=30°,∠BAC=60°.根据线段垂直平分线的性质进一步求解.解答:解:∵∠ACB=90°,AB=10,AC=5,∴∠B=30°.∴∠BAC=90°﹣30°=60°∵DE垂直平分BC,∴∠BAC=∠ADE=∠BDE=∠CDA=90°﹣30°=60°.∴∠BDE对顶角=60°,∴图中等于60°的角的个数是4.故选C.点评:此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.由易到难逐个寻找,做到不重不漏.8.(腾冲县校级期末)如图,已知BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD 的周长的差是()2020初中数学几何——三角形证明专项练习A .2B.3C.6D.不能确定考点:三角形的角平分线、中线和高.专题:计算题.分析:根据三角形的中线得出AD=CD,根据三角形的周长求出即可.解答:解:∵BD是△ABC的中线,∴AD=CD,∴△ABD和△BCD的周长的差是:(AB+BD+AD)﹣(BC+BD+CD)=AB﹣BC=5﹣3=2.故选A.点评:本题主要考查对三角形的中线的理解和掌握,能正确地进行计算是解此题的关键.9.(栖霞市期末)在Rt△ABC中,如图所示,∠C=90°,∠CAB=60°,AD平分∠CAB,点D到AB的距离DE=3.8cm,则BC等于()A .3.8cm B.7.6cm C.11.4cm D.11.2cm考点:角平分线的性质.分析:由∠C=90°,∠CAB=60°,可得∠B的度数,故BD=2DE=7.6,又AD平分∠CAB,故DC=DE=3.8,由BC=BD+DC求解.解答:解:∵∠C=90°,∠CAB=60°,∴∠B=30°,在Rt△BDE中,BD=2DE=7.6,又∵AD平分∠CAB,∴DC=DE=3.8,∴BC=BD+DC=7.6+3.8=11.4.故选C.点评:本题主要考查平分线的性质,由已知能够注意到D到AB的距离DE即为CD长,是解题的关键.10.(博野县期末)△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等;∠A=40°,则∠BOC=()A .110°B.120°C.130°D.140°考点:角平分线的性质;三角形内角和定理;三角形的外角性质.专题:计算题.分析:由已知,O到三角形三边距离相等,得O是内心,再利用三角形内角和定理即可求出∠BOC的度数.解答:解:由已知,O到三角形三边距离相等,所以O是内心,即三条角平分线交点,AO,BO,CO都是角平分线,所以有∠CBO=∠ABO=∠ABC,∠BCO=∠ACO=∠ACB,∠ABC+∠ACB=180﹣40=140∠OBC+∠OCB=70∠BOC=180﹣70=110°故选A.点评:此题主要考查学生对角平分线性质,三角形内角和定理,三角形的外角性质等知识点的理解和掌握,难度不大,是一道基础题.11.(潮阳区期末)如图,已知点P在∠AOB的平分线OC上,PF⊥OA,PE⊥OB,若PE=6,则PF的长为()A .2B.4C.6D.8考点:角平分线的性质;全等三角形的判定与性质.专题:计算题.分析:利用角平分线性质得出∠POF=∠POE,然后利用AAS定理求证△POE≌△POF,即可求出PF的长.解答:解:∵OC平分∠AOB,∴∠POF=∠POE,∵PF⊥OA,PE⊥OB,∴∠PFO=∠PEO,PO为公共边,∴△POE≌△POF,∴PF=PE=6.故选C.点评:此题考查学生对角平分线性质和全等三角形的判定与性质的理解和掌握,解答此题的关键是求证△POE≌△POF.12.(马尾区校级期末)如图,△ABC中,DE是AB的垂直平分线,交BC于点D,交AB于点E,已知AE=1cm,△ACD的周长为12cm,则△ABC的周长是()A .13cm B.14cm C.15cm D.16cm考点:线段垂直平分线的性质.分析:要求△ABC的周长,先有AE可求出AB,只要求出AC+BC即可,根据线段垂直平分线的性质可知,AD=BD,于是AC+BC=AC+CD+AD等于△ACD的周长,答案可得.解答:解:∵DE是AB的垂直平分线,∴AD=BD,AB=2AE=2又∵△ACD的周长=AC+AD+CD=AC+BD+CD=AC+BC=12∴△ABC的周长是12+2=14cm.故选B点评:此题主要考查线段的垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等;进行线段的等效转移,把已知与未知联系起来是正确解答本题的关键.13.(西城区期末)如图,∠BAC=130°,若MP和QN分别垂直平分AB和AC,则∠PAQ 等于()A .50°B.75°C.80°D.105°考点:线段垂直平分线的性质.分根据线段垂直平分线性质得出BP=AP,CQ=AQ,推出∠B=∠BAP,∠C=∠QAC,析:求出∠B+∠C,即可求出∠BAP+∠QAC,即可求出答案.解答:解:∵MP和QN分别垂直平分AB和AC,∴BP=AP,CQ=AQ,∴∠B=∠PAB,∠C=∠QAC,∵∠BAC=130°,∴∠B+∠C=180°﹣∠BAC=50°,∴∠BAP+∠CAQ=50°,∴∠PAQ=∠BAC﹣(∠PAB+∠QAC)=130°﹣50°=80°,故选:C.点评:本题考查了等腰三角形的性质,线段垂直平分线性质,三角形的内角和定理,注意:线段垂直平分线上的点到线段两个端点的距离相等,等边对等角.14.(东莞市校级期中)如图,要用“HL”判定Rt△ABC和Rt△A′B′C′全等的条件是()A .AC=A′C′,BC=B′C′B.∠A=∠A′,AB=A′B′C .AC=A′C′,AB=A′B′D.∠B=∠B′,BC=B′C′考点:直角三角形全等的判定.分析:根据直角三角形全等的判定方法(HL)即可直接得出答案.解答:解:∵在Rt△ABC和Rt△A′B′C′中,如果AC=A′C′,AB=A′B′,那么BC一定等于B′C′,Rt△ABC和Rt△A′B′C′一定全等,故选C.点评:此题主要考查学生对直角三角形全等的判定的理解和掌握,难度不大,是一道基础题.15.(淄川区校级期中)如图,MN是线段AB的垂直平分线,C在MN外,且与A点在MN的同一侧,BC交MN于P点,则()A .BC>PC+AP B.BC<PC+AP C.BC=PC+AP D.BC≥PC+AP考点:线段垂直平分线的性质.分析:从已知条件进行思考,根据垂直平分线的性质可得PA=PB,结合图形知BC=PB+PC,通过等量代换得到答案.解答:解:∵点P在线段AB的垂直平分线上,∴PA=PB.∵BC=PC+BP,∴BC=PC+AP.故选C.点评:本题考查了垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等;结合图形,进行线段的等量代换是正确解答本题的关键.16.(万州区校级期中)如图,已知在△ABC中,AB=AC,D为BC上一点,BF=CD,CE=BD,那么∠EDF等于()A .90°﹣∠A B.90°﹣∠A C.180°﹣∠A D.45°﹣∠A考点:等腰三角形的性质.分析:由AB=AC,利用等边对等角得到一对角相等,再由BF=CD,BD=CE,利用SAS得到三角形FBD与三角形DEC全等,利用全等三角形对应角相等得到一对角相等,即可表示出∠EDF.解答:解:∵AB=AC,∴∠B=∠C°,在△BDF和△CED中,,∴△BDF≌△CED(SAS),∴∠BFD=∠CDE,∴∠FDB+∠EDC=∠FDB+∠BFD=180°﹣∠B=180°﹣=90°+∠A,则∠EDF=180°﹣(∠FDB+∠EDC)=90°﹣∠A.故选B.点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.17.(泰山区校级期中)如图,在△ABC 中,AB=AC ,AD 平分∠BAC ,那么下列结论不一定成立的是()A .△ABD ≌△ACD B .AD 是△ABC 的高线C .AD 是△ABC 的角平分线D .△ABC 是等边三角形考点:等腰三角形的性质.分析:利用等腰三角形的性质逐项判断即可.解答:解:A 、在△ABD 和△ACD 中,,所以△ABD ≌△ACD ,所以A 正确;B 、因为AB=AC ,AD 平分∠BAC ,所以AD 是BC 边上的高,所以B 正确;C 、由条件可知AD 为△ABC 的角平分线;D 、由条件无法得出AB=AC=BC ,所以△ABC 不一定是等边三角形,所以D 不正确;故选D .点评:本题主要考查等腰三角形的性质,掌握等腰三角形“三线合一”的性质是解题的关键.18.(晋江市校级月考)如图,点P 是△ABC 内的一点,若PB=PC ,则()A .点P 在∠ABC 的平分线上B .点P 在∠ACB 的平分线上C .点P 在边AB 的垂直平分线上D .点P 在边BC 的垂直平分线上考点:线段垂直平分线的性质.分析:根据到线段两端点的距离相等的点在这条线段的垂直平分线上由PC=PB即可得出P 在线段BC的垂直平分线上.解答:解:∵PB=PC,∴P在线段BC的垂直平分线上,故选D.点评:本题考查了角平分线的性质和线段垂直平分线定理,注意:到线段两端点的距离相等的点在这条线段的垂直平分线上,角平分线上的点到角的两边的距离相等.19.(河西区二模)如图,在∠ECF的两边上有点B,A,D,BC=BD=DA,且∠ADF=75°,则∠ECF的度数为()A .15°B.20°C.25°D.30°考点:等腰三角形的性质.分析:根据等腰三角形的性质以及三角形外角和内角的关系,逐步推出∠ECF的度数.解答:解:∵BC=BD=DA,∴∠C=∠BDC,∠ABD=∠BAD,∵∠ABD=∠C+∠BDC,∠ADF=75°,∴3∠ECF=75°,∴∠ECF=25°.故选:C.点评:考查了等腰三角形的性质:等腰三角形的两个底角相等,三角形外角和内角的运用.20.(盱眙县校级期中)如图,P为∠AOB的平分线OC上任意一点,PM⊥OA于M,PN⊥OB 于N,连接MN交OP于点D.则①PM=PN,②MO=NO,③OP⊥MN,④MD=ND.其中正确的有()A .1个B.2个C.3个D.4个考点:角平分线的性质.分析:由已知很易得到△OPM≌△OPN,从而得角相等,边相等,进而得△OMP≌△ONP,△PMD≌△PND,可得MD=ND,∠ODN=∠ODM=9O°,答案可得.解答:解:P为∠AOB的平分线OC上任意一点,PM⊥OA于M,PN⊥OB于N 连接MN交OP于点D,∴∠MOP=∠NOP,∠OMP=∠ONP,OP=OP,∴△OPM≌△OPN,∴MP=NP,OM=ON,又OD=OD∴△OMD≌△OND,∴MD=ND,∠ODN=∠ODM=9O°,∴OP⊥MN∴①PM=PN,②MO=NO,③OP⊥MN,④MD=ND都正确.故选D.点评:本题主要考查了角平分线的性质,即角平分线上的一点到两边的距离相等;发现并利用△OMD≌△OND是解决本题的关键,证明两线垂直时常常通过证两角相等且互补来解决.二.解答题(共10小题)21.(黄浦区期末)如图,已知ON是∠AOB的平分线,OM、OC是∠AOB外的射线.(1)如果∠AOC=α,∠BOC=β,请用含有α,β的式子表示∠NOC.(2)如果∠BOC=90°,OM平分∠AOC,那么∠MON的度数是多少?考点:角平分线的定义.分析:(1)先求出∠AOB=α﹣β,再利用角平分线求出∠AON,即可得出∠NOC;(2)先利用角平分线求出∠AOM=∠AOC,∠AON=∠AOB,即可得出∠MON=∠BOC.解答:解:(1)∵∠AOC=α,∠BOC=β,∴∠AOB=α﹣β,∵ON是∠AOB的平分线,∴∠AON=(α﹣β),∠NOC=α﹣(α﹣β)=(α+β);(2)∵OM平分∠AOC,ON平分∠AOB,∴∠AOM=∠AOC,∠AON=∠AOB,∴∠MON=∠AOM﹣∠AON=(∠AOC﹣∠AOB)=∠BOC=×90°=45°.点评:本题考查了角平分线的定义和角的计算;弄清各个角之间的数量关系是解决问题的关键.22.(阿坝州期末)如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.(1)求证:OE是CD的垂直平分线.(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.考点:线段垂直平分线的性质.专题:探究型.分析:(1)先根据E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA得出△ODE≌△OCE,可得出OD=OC,DE=CE,OE=OE,可得出△DOC是等腰三角形,由等腰三角形的性质即可得出OE是CD的垂直平分线;(2)先根据E是∠AOB的平分线,∠AOB=60°可得出∠AOE=∠BOE=30°,由直角三角形的性质可得出OE=2DE,同理可得出DE=2EF即可得出结论.解答:解:(1)∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,∴DE=CE,OE=OE,∴Rt△ODE≌Rt△OCE,∴OD=OC,∴△DOC是等腰三角形,∵OE是∠AOB的平分线,∴OE是CD的垂直平分线;(2)∵OE是∠AOB的平分线,∠AOB=60°,∴∠AOE=∠BOE=30°,∵EC⊥OB,ED⊥OA,∴OE=2DE,∠ODF=∠OED=60°,∴∠EDF=30°,∴DE=2EF,∴OE=4EF.点评:本题考查的是角平分线的性质及直角三角形的性质、等腰三角形的判定与性质,熟知以上知识是解答此题的关键.23.(花垣县期末)如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,DE⊥AB(E在AB之间),DF⊥BC,已知BD=5,DE=3,CF=4,试求△DFC的周长.考点:角平分线的性质.分析:根据角平分线的性质可证∠ABD=∠CBD,即可求得∠CBD=∠C,即BD=CD,再根据角平分线上的点到角两边距离相等即可求得DE=DF,即可解题.解答:解:∵∠ABC=2∠C,BD平分∠ABC,∴∠CBD=∠C,∴BD=CD,∵BD平分∠ABC,∴DE=DF,∴△DFC的周长=DF+CD+CF=DE+BD+CF=3+5+4=12.点评:本题考查了角平分线上点到角两边距离相等的性质,考查了角平分线平分角的性质,考查了三角形周长的计算,本题中求证DE=DF是解题的关键.24.(大石桥市期末)如图,点D是△ABC中BC边上的一点,且AB=AC=CD,AD=BD,求∠BAC的度数.考点:等腰三角形的性质.分析:由AD=BD得∠BAD=∠DBA,由AB=AC=CD得∠CAD=∠CDA=2∠DBA,∠DBA=∠C,从而可推出∠BAC=3∠DBA,根据三角形的内角和定理即可求得∠DBA的度数,从而不难求得∠BAC的度数.解答:解:∵AD=BD∴设∠BAD=∠DBA=x°,∵AB=AC=CD∴∠CAD=∠CDA=∠BAD+∠DBA=2x°,∠DBA=∠C=x°,∴∠BAC=3∠DBA=3x°,∵∠ABC+∠BAC+∠C=180°∴5x=180°,∴∠DBA=36°∴∠BAC=3∠DBA=108°.点评:此题主要考查学生对等腰三角形的性质及三角形内角和定理的综合运用能力;求得角之间的关系利用内角和求解是正确解答本题的关键.25.(安溪县期末)如图,在△ABC中,AB=AC,∠A=α.(1)直接写出∠ABC的大小(用含α的式子表示);(2)以点B为圆心、BC长为半径画弧,分别交AC、AB于D、E两点,并连接BD、DE.若=30°,求∠BDE的度数.考点:等腰三角形的性质.分析:(1)根据三角形内角和定理和等腰三角形两底角相等的性质即可求得∠ABC的大小;(2)根据等腰三角形两底角相等求出∠BCD=∠BDC,再求出∠CBD,然后根据∠ABD=∠ABC﹣∠CBD,求得∠ABD,再根据三角形内角和定理和等腰三角形两底角相等的性质计算即可得解.解答:解:(1)∠ABC的大小为×(180°﹣α)=90°﹣α;(2)∵AB=AC,∴∠ABC=∠C=90°﹣α=90°﹣×30°=75°,由题意得:BC=BD=BE,由BC=BD得∠BDC=∠C=75°,∴∠CBD=180°﹣75°﹣75°=30°,∴∠ABD=∠ABC﹣∠CBD=75°﹣30°=45°,由BD=BE得.故∠BDE的度数是67.5°.点评:本题考查了三角形内角和定理、等腰三角形的性质,主要利用了等腰三角形两底角相等,熟记性质是解题的关键.26.(静宁县校级期中)如图,在△ABC中,AD平分∠BAC,点D是BC的中点,DE⊥AB 于点E,DF⊥AC于点F.求证:(1)∠B=∠C.(2)△ABC是等腰三角形.考点:等腰三角形的判定.分析:由条件可得出DE=DF,可证明△BDE≌△CDF,可得出∠B=∠C,再由等腰三角形的判定可得出结论.解答:证明:(1)∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,∴DE=DF,在Rt△BDE和Rt△CDF中,,∴Rt△BDE≌Rt△CDF(HF),∴∠B=∠C;(2)由(1)可得∠B=∠C,∴△ABC为等腰三角形.点评:本题主要考查等腰三角形的判定及全等三角形的判定和性质,利用角平分线的性质得出DE=DF是解题的关键.27.(天津期末)如图,AB=AC,∠C=67°,AB的垂直平分线EF交AC于点D,求∠DBC 的度数.考点:线段垂直平分线的性质;等腰三角形的性质.分析:求出∠ABC,根据三角形内角和定理求出∠A,根据线段垂直平分线得出AD=BD,求出∠ABD,即可求出答案.解答:解:∵AB=AC,∠C=67°,∴∠ABC=∠C=67°,∴∠A=180°﹣67°﹣67°=46°,∵EF是AB的垂直平分线,∴AD=BD,∴∠A=∠ABD=46°,∴∠DBC=67°﹣46°=21°.点评:本题考查了线段垂直平分线,三角形的能或定理,等腰三角形的性质和判定等知识点,关键是求出∠ABC和∠ABD的度数,题目比较好.28.(高坪区校级期中)如图,△ABC中,AB=AD=AE,DE=EC,∠DAB=30°,求∠C的度数.考点:等腰三角形的性质.分析:首先根据AB=AD=AE,DE=EC,得到∠B=∠ADB,∠ADE=∠AED,∠C=∠EDC,从而得到∠ADE=∠AED=∠C+∠EDC=2∠C,根据∠DAB=30°,求得∠B=∠ADB=75°,利用∠ADC=∠ADE+∠EDC=3∠C=105°,求得∠C即可.解答:解:∵AB=AD=AE,DE=EC,∴∠B=∠ADB,∠ADE=∠AED,∠C=∠EDC,∴∠ADE=∠AED=∠C+∠EDC=2∠C,∵∠DAB=30°,∴∠B=∠ADB=75°,∴∠ADC=∠ADE+∠EDC=3∠C=105°,∴∠C=35°.点评:本题考查了等腰三角形的性质,解题的关键是利用等腰三角形的性质求得有关角的度数.29.(扶沟县校级期中)阅读理解:“在一个三角形中,如果角相等,那么它们所对的边也相等.”简称“等角对等边”,如图,在△ABC中,已知∠ABC和∠ACB的平分线上交于点F,过点F作BC的平行线分别交AB、AC于点D、E,请你用“等角对等边”的知识说明DE=BD+CE.2020初中数学几何——三角形证明专项练习考点:等腰三角形的性质.专题:证明题.分析:由DE∥BC,BF平分∠ABC,CF平分∠ACB可知,DB=DF,CE=EF.便可得出结论.解答:证明:∵BF平分∠ABC(已知),CF平分∠ACB(已知),∴∠ABF=∠CBF,∠ACF=∠FCB;又∵DE平行BC(已知)∴∠DFB=∠FBC(两直线平行,内错角相等),∠EFC=∠FCB(两直线平行,内错角相等),∴∠DBF=∠DFB,∠EFC=∠ECF(等量代换)∴DF=DB,EF=EC(等角对等边)∴DE=BD+CE.点评:此题考查学生对等腰三角形的判定与性质和平行线的性质的理解和掌握,主要利用等腰三角形两边相等.稍微有点难度是一道中档题.30.(龙岩质检)如图,AD是△ABC的平分线,DE,DF分别垂直AB、AC于E、F,连接EF,求证:△AEF是等腰三角形.考点:等腰三角形的判定;全等三角形的判定与性质.专题:证明题.分析:根据角平分线的性质知∠BAD=∠CAD;然后根据已知条件“DE,DF分别垂直AB、AC于E、F”得到∠DEA=∠DFA=90°;再加上公共边AD=AD,从而证明,△ADE≌△ADF;最后根据全等三角形的对应边相等证明△AEF的两边相等,所以△AEF是等腰三角形.2020解答:证明:∵AD是△ABC的平分线,∴∠BAD=∠CAD,(3分)又∵DE,DF分别垂直AB、AC于E,F∴∠DEA=∠DFA=90°(6分)又∵AD=AD,∴△ADE≌△ADF.(8分)∴AE=AF,即△AEF是等腰三角形(10分)点评:本题综合考查了等腰三角形的判定、全等三角形的判定与性质.解答此题时,根据全等三角形的判定定理ASA判定△ADE≌△ADF.。
