中考几何证明题集锦(主要是与圆有关的)

合集下载

初三经典几何证明练习题(含问题详解)

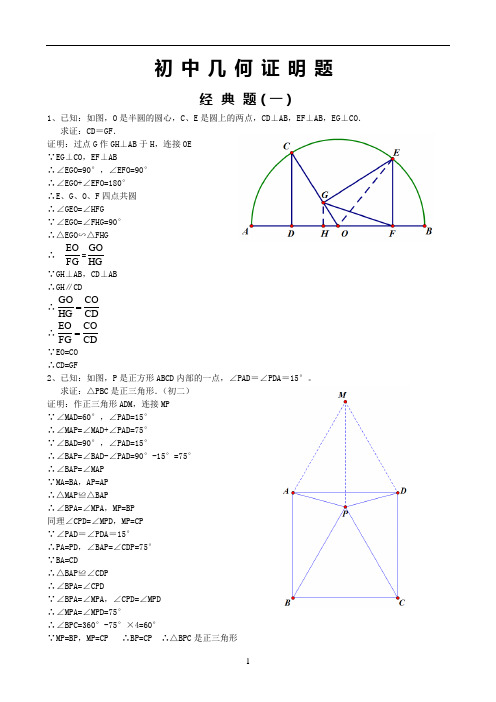
初三几何证明题经典题（一）1、已知：如图，O是半圆的圆心，C、E是圆上的两点，CD⊥AB，EF⊥AB，EG⊥CO．求证：CD＝GF．2、已知：如图，P是正方形ABCD部的一点，∠PAD＝∠PDA＝15°。

求证：△PBC是正三角形．（初二）3、已知：如图，在四边形ABCD中，AD＝BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN于E、F．求证：∠DEN＝∠F．经典题（二）1、已知：△ABC中，H为垂心（各边高线的交点），O为外心，且OM⊥BC于M．（1）求证：AH＝2OM；（2）若∠BAC＝600，求证：AH＝AO．2、设MN是圆O外一条直线，过O作OA⊥MN于A，自A引圆的两条割线交圆O于B、C及D、E，连接CD并延长交MN于Q，连接EB并延长交MN于P.求证：AP＝AQ．3、如图,分别以△ABC的AB和AC为一边,在△ABC的外侧作正方形ABFG和正方形ACDE，点O是DF的中点，OP⊥BC求证：BC=2OP证明：分别过F、A、D作直线BC的垂线，垂足分别是L、M、N∵OF=OD，DN∥OP∥FL∴PN=PL∴OP是梯形DFLN的中位线∴DN+FL=2OP∵ABFG是正方形∴∠ABM+∠FBL=90°又∠BFL+∠FBL=90°∴∠ABM=∠BFL又∠FLB=∠BMA=90°，BF=AB∴△BFL≌△ABM∴FL=BM同理△AMC≌△CND∴CM=DN∴BM+CN=FL+DN∴BC=FL+DN=2OP经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．证明：连接BD 交AC 于O 。

过点E 作EG ⊥AC 于G ∵ABCD 是正方形 ∴BD ⊥AC 又EG ⊥AC ∴BD ∥EG 又DE ∥AC ∴ODEG 是平行四边形又∠COD=90° ∴ODEG 是矩形 ∴EG=OD=21BD=21AC=21AE ∴∠EAG=30° ∵AC=AE∴∠ACE=∠AEC=75° 又∠AFD=90°-15°=75° ∴∠CFE=∠AFD=75°=∠AEC ∴CE=CF2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．证明：连接BD ，过点E 作EG ⊥AC 于G ∵ABCD 是正方形 ∴BD ⊥AC ，又EG ⊥AC∴BD ∥EG 又DE ∥AC ∴ODEG 是平行四边形又∠COD=90° ∴ODEG 是矩形 ∴EG =OD =21BD=21AC=21CE ∴∠GCE=30° ∵AC=EC3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）证明：过点F 作FG ⊥CE 于G ，FH ⊥CD 于H ∵CD ⊥CG ∴HCGF 是矩形 ∵∠HCF=∠GCF ∴FH=FG ∴HCGF 是正方形 ∴CG=GF∵AP ⊥FP∴∠APB+∠FPG=90°∵∠APB+∠BAP=90°∴∠FPG=∠BAP又∠FGP=∠PBA∴△FGP ∽△PBA∴FG ：PB=PG ：AB4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）证明：过点E 作EK ∥BD ，分别交AC 、AF 于M 、K ，取EF 的中点H ，连接OH 、MH 、EC设AB=x ，BP=y ，CG=zz ：y=（x-y+z ）：x化简得（x-y ）·y =（x-y ）·z∵x-y ≠0∴y=z即BP=FG∴△ABP ≌△PGF∴∠CAE=∠CEA=21∠GCE=15° 在△AFC 中∠F =180°-∠FAC-∠ACF =180°-∠FAC-∠GCE=180°-135°-30°=15°∵EH=FH∴OH ⊥EF ，∴∠PHO=90° 又PC ⊥OC ，∴∠POC=90° ∴P 、C 、H 、O 四点共圆 ∴∠HCO=∠HPO又EK ∥BD ，∴∠HPO=∠HEK∴∠HCM=∠HEM∴H 、C 、E 、M 四点共圆 ∴∠ECM=∠EHM 又∠ECM=∠EFA ∴∠EHM=∠EFA ∴HM ∥AC ∵EH=FH经典题(四)1、已知：△ABC 是正三角形，P 是三角形一点，PA ＝3，PB ＝4求∠APB 的度数．（初二）解：将△ABP 绕点B 顺时针方向旋转60°得△BCQ ，连接PQ 则△BPQ 是正三角形 ∴∠BQP=60°，PQ=PB=3在△PQC 中，PQ=4，CQ=AP=3，PC=5 ∴△PQC 是直角三角形 ∴∠PQC=90°∴∠BQC=∠BQP+∠PQC=60°+90°=150° ∴∠APB=∠BQC=150°2、设P 是平行四边形ABCD 部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）∴EM=KM ∵EK ∥BD ∴KMODAM AO EM OB == ∴OB=OD又AO=CO∴四边形ABCD 的对角证明：过点P 作AD 的平行线，过点A 作PD 的平行线，两平行线相交于点E ，连接BE ∵PE ∥AD ，AE ∥PD ∴ADPE 是平行四边形 ∴PE=AD ，又ABCD 是平行四边形 ∴AD=BC ∴PE=BC又PE ∥AD ，AD ∥BC ∴PE ∥BC∴BCPE 是平行四边形 ∴∠BEP=∠PCB ∵ADPE 是平行四边形 ∴∠ADP=∠AEP3、设ABCD 为圆接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）证明：在BD 上去一点E ，使∠BCE=∠ACD ∵CD⌒ =CD ⌒ ∴∠CAD=∠CBD ∴△BEC ∽△ADC ∴ACBCAD BE∴AD ·BC=BE ·AC ……………………① ∵∠BCE=∠ACD∴∠BCE+∠ACE=∠ACD+∠ACE 即∠BCA=∠ECD∵BC⌒=BC ⌒,∴∠BAC=∠BDC △BAC ∽△EDC又∠ADP=∠ABP ∴∠AEP=∠ABP ∴A 、E 、B 、P 四点共圆 ∴∠BEP=∠PAB ∴∠PAB=∠PCB∴CDACDE AB∴AB ·CD=DE ·AC ……………………②4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）证明：过点D 作DG ⊥AE 于G ，作DH ⊥FC 于H ，连接DF 、DE ∴S △ADE =12AE ·DG ，S △FDC =12FC ·DH又S △ADE =S △FDC =12S □ABCD∴AE ·DG=FC ·DH 又AE=CF ∴DG=DH∴点D 在∠APC 的角平分线上 ∴∠DPA ＝∠DPC经典题（五）1、设P 是边长为1的正△ABC 任一点，L ＝PA ＋PB ＋PC ，求证：3≤L ＜2．证明：（1）将△BPC 绕B 点顺时针旋转60°的△BEF ，连接PE ，∵BP=BE ，∠PBE=60° ∴△PBE 是正三角形。

专题25 圆的有关计算与证明(共50题)(原卷版)-2023年中考数学真题分项汇编(全国通用)

专题25圆的有关计算与证明（50题）一、单选题1．（2023·新疆·统考中考真题）如图，在O 中，若30ACB ∠=︒，6OA =，则扇形OAB (阴影部分)的面积是()A ．12πB ．6πC ．4πD ．2π2．（2023·江苏连云港·统考中考真题）如图，矩形ABCD 内接于O ，分别以AB BC CD AD 、、、为直径向外作半圆．若4,5==AB BC ，则阴影部分的面积是（）A ．41204π-B ．41202π-C ．20πD ．203．（2023·湖北荆州·统考中考真题）如图，一条公路的转弯处是一段圆弧（ AC ），点O 是这段弧所在圆的圆心，B 为 AC 上一点，OB AC ⊥于D ．若3003m AC =，150m BD =，则 AC 的长为（）A ．300m πB ．200m πC ．150m πD ．1003mπA ．21cm 4πB 5．（2023·四川达州·统考中考真题）如图，四边形段90︒的圆心角的圆心为为A BCD 、、、循环，则A ．40452πB ．20236．（2023·四川广安·统考中考真题）如图，在等腰直角心，AC 为半径画弧，交AB 于点积是（）A ．π2-B ．2π2-7．（2023·江苏苏州·统考中考真题）如图，AB 是半圆O 的直径，点,C D 在半圆上， CDDB =，连接,,OC CA OD ，过点B 作EB AB ⊥，交OD 的延长线于点E ．设OAC 的面积为1,S OBE △的面积为2S ，若1223S S =，则tan ACO ∠的值为（）A ．2B ．223C ．75D ．32二、填空题8．（2023·重庆·统考中考真题）如图，在矩形ABCD 中，2AB =，4BC =，E 为BC 的中点，连接AE DE ，，以E 为圆心，EB 长为半径画弧，分别与AE DE ，交于点M ，N ，则图中阴影部分的面积为________．（结果保留π）9．（2023·黑龙江绥化·统考中考真题）如图，O 的半径为2cm ，AB 为O 的弦，点C 为 AB 上的一点，将 AB 沿弦AB 翻折，使点C 与圆心O 重合，则阴影部分的面积为_______．（结果保留π与根号）10．（2023·重庆·统考中考真题）如图，O 是矩形ABCD 的外接圆，若4,3AB AD ==，则图中阴影部分的面积为___________．（结果保留π）14．（2023·天津·统考中考真题）如图，在每个小正方形的边长为且顶点A，B均在格点上．（1）线段AB的长为________（2）若点D在圆上，AB与CD为等边三角形，并简要说明点15．（2023·江苏苏州·统考中考真题）如图，在H AH=．以点A为圆心，,3一个圆锥的侧面，记这个圆锥底面圆的半径为r r-=________________的半径为2r，则1216．（2023·四川自贡·统考中考真题）如图，小珍同学用半径为8cm ，圆心角为100︒的扇形纸片，制作一个底面半径为2cm 的圆锥侧面，则圆锥上粘贴部分的面积是________2cm ．三、解答题17．（2023·四川南充·统考中考真题）如图，AB 与O 相切于点A ，半径OC AB ∥，BC 与O 相交于点D ，连接AD ．(1)求证：OCA ADC ∠∠=；(2)若12,tan 3AD B ==，求OC 的长．18．（2023·四川成都·统考中考真题）如图，以ABC 的边AC 为直径作O ，交BC 边于点D ，过点C 作CE AB ∥交O 于点E ，连接AD DE ，，B ADE ∠=∠．(1)求证：AC BC =；(2)若tan 23B CD ==，，求AB 和DE 的长．(1)求证：90ADC BAC ∠-∠=︒；（请用两种证法解答）(2)若ACP ADC ∠=∠，O 的半径为3，4CP =，求AP 的长．(1)求BED ∠的度数；(2)如图2，过点A 作O 的切线交BC 延长线于点F ，过点D 作DG 235,4AD DE ==，求DG 的长．21．（2023·浙江杭州·统考中考真题）在边长为1的正方形ABCD 中，点射线BE 与射线CD 交于点F ．(1)若13ED =，求DF 的长．(2)求证：1AE CF ⋅=．(3)以点B 为圆心，BC 长为半径画弧，交线段BE 于点G ．若EG ED =，求ED 的长．22．（2023·河北·统考中考真题）装有水的水槽放置在水平台面上，其横截面是以AB 为直径的半圆O ，50cm AB =，如图1和图2所示，MN 为水面截线，GH 为台面截线，MN GH ∥．计算：在图1中，已知48cm MN =，作OC MN ⊥于点C ．（1）求OC 的长．操作：将图1中的水面沿GH 向右作无滑动的滚动，使水流出一部分，当30ANM ∠=︒时停止滚动，如图2．其中，半圆的中点为Q ，GH 与半圆的切点为E ，连接OE 交MN 于点D ．探究：在图2中(1)求证：2AOB ∠=∠(2)若4,5AB BC ==径，45ABD ∠=︒，直线l 与三条线段CD 、CA 、DA 的延长线分别交于点E 、F 、G ．且满足45CFE ∠=︒．(1)求证：直线l ⊥直线CE ；(2)若AB DG =；①求证：ABC GDE △≌△；②若312R CE ==，，求四边形ABCD 的周长．25．（2023·天津·统考中考真题）在O 中，半径OC 垂直于弦AB ，垂足为D ，60AOC ∠=︒，E 为弦AB 所对的优弧上一点．(1)如图①，求AOB ∠和CEB ∠的大小；(2)如图②，CE 与AB 相交于点F ，EF EB =，过点E 作O 的切线，与CO 的延长线相交于点G ，若3OA =，求EG 的长．26．（2023·江苏苏州·统考中考真题）如图，ABC 是O 的内接三角形，AB 是O 的直径，5,25AC BC ==，点F 在AB 上，连接CF 并延长，交O 于点D ，连接BD ，作BE CD ⊥，垂足为E ．(1)求证：DBE ABC △∽△；(2)若2AF =，求ED 的长．27．（2023·四川达州·统考中考真题）如图，ABC ABD 、内接于O AB BC P = ，，是OB 延长线上的一点，PAB ACB ∠=∠，AC BD 、相交于点E ．(1)求证：AP 是O 的切线；(2)若24BE DE ==，，30P ∠=︒，求AP 的长．28．（2023·湖南·统考中考真题）如图，AB 是O 的直径，AC 是一条弦，D 是 AC 的中点，DE AB ⊥于点E ，交AC 于点F ，交O 于点H ，DB 交AC 于点G ．(1)求证：AF DF =．(2)若55,sin 25AF ABD =∠=，求O 的半径．29．（2023·湖南怀化·统考中考真题）如图，AB 是O 的直径，点P 是O 外一点，PA 与O 相切于点A ，点C 为O 上的一点．连接PC 、AC 、OC ，且PC PA =．(1)求证：PC 为O 的切线；(2)延长PC 与AB 的延长线交于点D ，求证：PD OC PA OD ⋅=⋅；(3)若308CAB OD ∠=︒=，，求阴影部分的面积．30．（2023·四川眉山·统考中考真题）如图，ABC 中，以AB 为直径的O 交BC 于点E ．AE 平分BAC ∠，过点E 作ED AC ⊥于点D ，延长DE 交AB 的延长线于点P ．(1)求证：PE 是O 的切线；(2)若1sin ,43P BP ∠==，求CD 的长．31．（2023·安徽·统考中考真题）已知四边形(1)如图1，连接,OA CA ，若OA BD ⊥，求证；CA 平分BCD ∠；(2)如图2，E 为O 内一点，满足,AE BC CE AB ⊥⊥，若BD =32．（2023·吉林长春·统考中考真题）【感知】如图①，点A 、B 、的大小为__________度．【探究】小明遇到这样一个问题：如图②，O 是等边三角形ABC 的外接圆，点P 在 AC 上（点P 不与点A 、C 重合），连结PA 、PB 、PC ．求证：PB PA PC =+．小明发现，延长PA 至点E ，使AE PC =，连结BE ，通过证明PBC EBA ≌△△，可推得PBE 是等边三角形，进而得证．下面是小明的部分证明过程：证明：延长PA 至点E ，使AE PC =，连结BE ，四边形ABCP 是O 的内接四边形，180BAP BCP ∴∠+∠=︒．180BAP BAE ∠+∠=︒ ，BCP BAE ∴∠=∠．ABC 是等边三角形．BA BC ∴=，(SAS)PBC EBA ∴ ≌请你补全余下的证明过程．【应用】如图③，O 是ABC 的外接圆，90ABC AB BC ∠=︒=，，点P 在O 上，且点P 与点B 在AC 的两侧，连结PA 、PB 、PC ．若22PB PA =，则PB PC的值为__________．33．（2023·四川泸州·统考中考真题）如图，AB 是O 的直径，210AB =，O 的弦CD AB ⊥于点E ，6CD =．过点C 作O 的切线交AB 的延长线于点F ，连接BC ．∠；(1)求证：BC平分DCF(2)G为 AD上一点，连接CG交AB于点H，若34．（2023·黑龙江绥化·统考中考真题）如图，行弦，弦AB交MC于点H．点A在¼MC上，点⋅=⋅．(1)求证：MH CH AH BH(2)求证：AC BC=．(3)在⊙O中，沿弦ND所在的直线作劣弧ND NG的长．35．（2023·广东·统考中考真题）综合探究如图1，在矩形ABCD中(AB>BD于点E，连接CA'．(1)求证：AA CA '⊥'；(2)以点O 为圆心，OE 为半径作圆．①如图2，O 与CD 相切，求证：3AA CA '='；②如图3，O 与CA '相切，1AD =，求O 的面积．36．（2023·山东·统考中考真题）如图，AB 为O 的直径，C 是圆上一点，D 是 BC 的中点，弦DE AB ⊥，垂足为点F ．(1)求证：BC DE =；(2)P 是»AE 上一点，6,2AC BF ==，求tan BPC ∠；(3)在（2）的条件下，当CP 是ACB ∠的平分线时，求CP 的长．37．（2023·山东·统考中考真题）如图，已知AB 是O 的直径，CD CB =，BE 切O 于点B ，过点C 作CF OE ⊥交BE 于点F ，若2EF BF =．(1)如图1，连接BD ，求证：ADB OBE △≌△；(2)如图2，N 是AD 上一点，在AB 上取一点M ，使60MCN ∠=︒，连接MN ．请问：三条线段MN BM DN ，，有怎样的数量关系？并证明你的结论．38．（2023·浙江杭州·统考中考真题）如图，在O 中，直径AB 垂直弦CD 于点E ，连接,,AC AD BC ，作CF AD ⊥于点F ，交线段OB 于点G （不与点,O B 重合），连接OF ．(1)若1BE =，求GE 的长．(2)求证：2BC BG BO =⋅．(3)若FO FG =，猜想CAD ∠的度数，并证明你的结论．39．（2023·湖北宜昌·统考中考真题）如图1，已知AB 是O 的直径，PB 是O 的切线，PA 交O 于点C ，43AB PB ==，．(1)填空：PBA ∠的度数是_________，PA 的长为_________；(2)求ABC 的面积；(3)如图2，CD AB ⊥，垂足为D ．E 是 AC 上一点，5AE EC =．延长AE ，与DC ，BP 的延长线分别交于点,F G ，求EF FG的值．40．（2023·山东滨州·统考中考真题）如图，点E 是ABC 的内心，AE 的延长线与边BC 相交于点F ，与ABC 的外接圆相交于点D ．(1)求证：::ABF ACF S S AB AC =△△；(2)求证：::AB AC BF CF =；(3)求证：2AF AB AC BF CF =⋅-⋅；(4)猜想：线段,,DF DE DA 三者之间存在的等量关系．（直接写出，不需证明．）41．（2023·浙江台州·统考中考真题）我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系，用直线上点的位置刻画圆上点的位置，如图，AB 是O 的直径，直线l 是O 的切线，B 为切点．P ，Q 是圆上两点（不与点A 重合，且在直径AB 的同侧），分别作射线AP ，AQ 交直线l 于点C ，点D ．(1)如图1，当6AB =，BP的长为π时，求BC 的长．(2)如图2，当34AQ AB =， BP PQ =时，求BC CD的值．(3)如图3，当6sin 4BAQ ∠=，BC CD =时，连接BP ，PQ ，直接写出(1)求CE 的长和y 关于x 的函数表达式．(2)当PH PN <，且长度分别等于PH ，PN ，a 的三条线段组成的三角形与(3)延长PN 交半圆O 于点Q ，当1534NQ x =-时，求43．（2023·新疆·统考中考真题）如图，AB 是O 的直径，点接AF ，过点C 作AF 的垂线，交AF 的延长线于点D 交AC 于点H ．(1)求证：CE 是O 的切线；(2)若tan 34E =，4BE =，求FH 的长．44．（2023·云南·统考中考真题）如图，BC 是O 的直径，A 是O 上异于B C 、的点．O 外的点E 在射线CB 上，直线EA 与CD 垂直，垂足为D ，且DA AC DC AB ⋅=⋅．设ABE 的面积为1,S ACD 的面积为2S ．(1)判断直线EA 与O 的位置关系，并证明你的结论；(2)若21,BC BE S mS ==，求常数m 的值．45．（2023·浙江宁波·统考中考真题）如图1，锐角ABC 内接于O ，D 为BC 的中点，连接AD 并延长交O 于点E ，连接,BE CE ，过C 作AC 的垂线交AE 于点F ，点G 在AD 上，连接,BG CG ，若BC 平分EBG ∠且BCG AFC ∠=∠．(1)求BGC ∠的度数．(2)①求证：AF BC =．②若AG DF =，求tan GBC ∠的值，(3)如图2，当点O 恰好在BG 上且1OG =时，求AC 46．（2023·四川遂宁·统考中考真题）如图，四边形D 的直线l 交BA 的延长线于点M ，交BC 的延长线于点(1)求证：MN 是O 的切线；(2)求证：2AD AB CN =⋅；(3)当6AB =，3sin 3DCA ∠=时，求AM 的长．47．（2023·四川广安·统考中考真题）如图，以Rt ABC △E 是BC 的中点，连接OE DE 、．(1)求证：DE 是O 的切线．(2)若4sin ,55C DE ==，求AD 的长．(3)求证：22DE CD OE =⋅．48．（2023·浙江嘉兴·统考中考真题）已知，AB 是半径为1的O 的弦，O 的另一条弦CD 满足CD AB =，且CD AB ⊥于点H （其中点H 在圆内，且AH BH CH DH >>，）．(1)在图1中用尺规作出弦CD 与点H （不写作法，保留作图痕迹）．(2)连结AD ，猜想，当弦AB 的长度发生变化时，线段AD 的长度是否变化？若发生变化，说明理由：若不变，求出AD 的长度；(3)如图2，延长AH 至点F ，使得HF AH =，连结CF ，HCF ∠的平分线CP 交AD 的延长线于点P ，点M 为AP 的中点，连结HM ，若12PD AD =．求证：MH CP ⊥．49．（2023·浙江·统考中考真题）如图，在O 中，AB 是一条不过圆心O 的弦，点,C D 是 AB 的三等分点，直径CE 交AB 于点F ，连结AD 交CF 于点G ，连结AC ，过点C 的切线交BA 的延长线于点H ．(1)求证：AD HC ∥；(2)若2OG GC=，求tan FAG ∠的值；(3)连结BC 交AD 于点N ，若O ①若52OF =，求BC 的长；②若10AH =，求ANB 的周长；③若88HF AB ⋅=，求BHC △的面积．50．（2023·四川宜宾·统考中考真题）如图，以CD AF ⊥交AF 的延长线于点D ，交点N ．(1)求证：CD 是O 的切线；(2)求证：EM EN =；(3)如果N 是CM 的中点，且AB =。

初中数学几何证明经典试题（含答案）

初中数学几何证明经典试题（含答案）初中几何证明题经典题（一）1、已知：如图，O是半圆的圆心，C、E是圆上的两点，CD⊥AB，EF⊥AB，EG⊥CO．求证：CD＝GF．（初二）.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH ＝∠OEG,即△GHF∽△OGE,可得EOG F=G OG H=C OC D,又CO=EO，所以CD=GF得证。

2、已知：如图，P是正方形ABCD内点，∠PAD＝∠PDA＝150．求证：△PBC是正三角形．（初二）.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH ＝∠OEG,即△GHF∽△OGE,可得EOG FG OG H=C OC D,又CO=EO，所以CD=GF得证。

.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH ＝∠OEG,即△GHF∽△OGE,可得EOG F=G OG H=C OC D,又CO=EO，所以CD=GF得证。

APCDBAFGCEBO3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）D 2C 2 B 2A 2D 1C 1B 1C B DAA 1BF2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEFB 、D ．求证：AB ＝DC ，BC ＝AD．（初三）经典1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC 上的点，∠DCA＝300，∠EBA＝200，求∠BED的度数．经典题（一）1.如下图做GH⊥AB,连接EO。

初中数学几何证明经典试题(含答案)

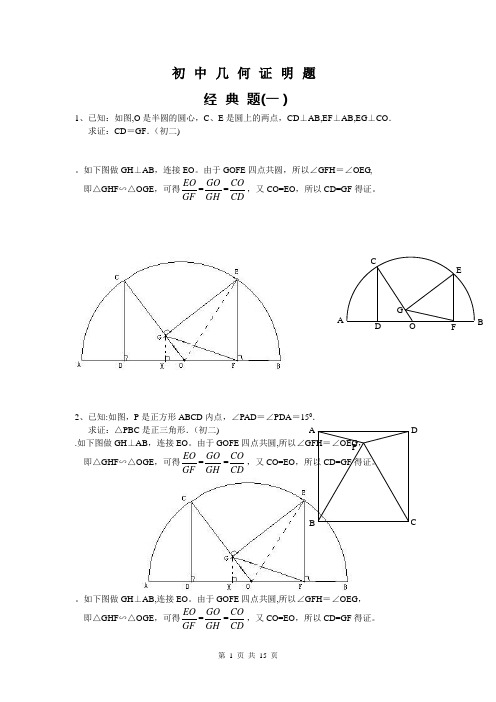
初中几何证明题经典题(一）1、已知：如图,O是半圆的圆心，C、E是圆上的两点，CD⊥AB,EF⊥AB,EG⊥CO．求证：CD＝GF．（初二)。

如下图做GH⊥AB，连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE ，可得EOGF=GOGH=COCD，又CO=EO，所以CD=GF得证。

2、已知:如图，P是正方形ABCD内点，∠PAD＝∠PDA＝150．求证：△PBC是正三角形．（初二).如下图做GH⊥AB，连接EO。

由于GOFE四点共圆,所以∠GFH＝∠OEG，即△GHF∽△OGE，可得EOGF=GOGH=COCD，又CO=EO，所以CD=GF得证。

如下图做GH⊥AB,连接EO。

由于GOFE四点共圆,所以∠GFH＝∠OEG，即△GHF∽△OGE，可得EOGF=GOGH=COCD，又CO=EO，所以CD=GF得证。

APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二)4、已知：如图，在四边形ABCD 中，AD ＝BC,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典题(二）1、已知：△ABC 中，H 为垂心(各边高线的交点），O 为外心，且OM ⊥BC 于M ．（1）求证:AH ＝2OM; （2）若∠BAC ＝600，求证：AH ＝AO ．（初二）D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HEOF2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A,自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．(初二）3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证:AP ＝AQ ．(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG,点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．（初二经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC,AE ＝AC,AE 与CD 相交于F ．求证：CE ＝CF ．(初二）2、如图，四边形ABCD 为正方形，DE ∥AC,且CE ＝CA,直线EC 交DA 延长线于F ．求证：AE ＝AF ．(初二）3、设P 是正方形ABCD 一边求证：PA ＝PF ．（初二)4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线D ．求证：AB ＝DC ，BC ＝AD．（初三)经典1、已知：△ABC 是正三角形,P 是三角形内一点，PA ＝3，PB ＝4,PC 求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二)3、设ABCD 为圆内接凸四边形,求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三)4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题(五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点,求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a,PB ＝2a ，PC ＝3a,求正方形的边长．C BD A F PD E CB A APCBACPDA CBPD4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC上的点，∠DCA＝300，∠EBA＝200，求∠BED的度数．经典题（一)1.如下图做GH⊥AB,连接EO。

初三圆的证明题

1、已知圆O的半径为5cm，点P到圆心O的距离为3cm，则点P与圆O的位置关系是A. 点P在圆O内B. 点P在圆O上C. 点P在圆O外D. 无法确定（答案）A2、圆O中，弦AB与弦CD相交于点E，若∠AEC = 60°，且AE = CE，则∠ADC等于A. 30°B. 60°C. 90°D. 120°（答案）B3、在圆O中，直径AB垂直于弦CD于点E，若AB = 10，CD = 6，则OE的长度为A. 8B. 5C. 4D. 3（答案）C4、圆O的内接四边形ABCD中，∠A : ∠B : ∠C = 2 : 3 : 4，则∠D的度数为A. 60°B. 90°C. 120°D. 150°（答案）B5、已知圆O的两条弦AB和CD相交于点P，若AP = PB，且∠APD = 60°，则∠CPD的度数为A. 30°B. 60°C. 90°D. 120°（答案）D6、圆O的半径为r，点A、B、C在圆上，且AB = BC，若∠AOB = 120°，则△ABC的面积为A. (√3/4)r2B. (√3/2)r2C. (3/4)r2D. r2（答案）A7、圆O的切线l与半径OA垂直于点A，点B在切线l上，且OB = 2OA，则∠OBA的度数为A. 30°B. 45°C. 60°D. 90°（答案）C8、在圆O中，弦AB与弦AC的夹角为60°，若AB = AC，且圆的半径为R，则△ABC的面积为A. (√3/2)R2B. (√3/4)R2C. (1/2)R2D. (1/4)R2（答案）B。

初中经典几何证明练习题集(含答案解析)

初中经典几何证明练习题集(含答案解析)本页仅作为文档页封面，使用时可以删除This document is for reference only-rar21year.March初中几何证明题经典题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．证明：过点G 作GH ⊥AB 于H ，连接OE∵EG ⊥CO ，EF ⊥AB∴∠EGO=90°，∠EFO=90°∴∠EGO+∠EFO=180°∴E 、G 、O 、F 四点共圆∴∠GEO=∠HFG∵∠EGO=∠FHG=90°∴△EGO ∽△FHG ∴FG EO =HGGO ∵GH ⊥AB ，CD ⊥AB∴GH ∥CD ∴CDCO HG GO = ∴CD CO FG EO = ∵EO=CO∴CD=GF2、已知：如图，P 是正方形ABCD 内部的一点，∠PAD ＝∠PDA ＝15°。

求证：△PBC 是正三角形．（初二）证明：作正三角形ADM ，连接MP∵∠MAD=60°，∠PAD=15°∴∠MAP=∠MAD+∠PAD=75°∵∠BAD=90°，∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75°∴∠BAP=∠MAP∵MA=BA，AP=AP∴△MAP≌△BAP∴∠BPA=∠MPA，MP=BP同理∠CPD=∠MPD，MP=CP∵∠PAD＝∠PDA＝15°∴PA=PD，∠BAP=∠CDP=75°∵BA=CD∴△BAP≌∠CDP∴∠BPA=∠CPD∵∠BPA=∠MPA，∠CPD=∠MPD∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP，MP=CP ∴BP=CP ∴△BPC是正三角形3、已知：如图，在四边形ABCD中，AD＝BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN于E、F．求证：∠DEN＝∠F．证明:连接AC，取AC的中点G,连接NG、MG∵CN=DN，CG=DG1AD∴GN∥AD，GN=2∴∠DEN=∠GNM∵AM=BM，AG=CG1BC∴GM∥BC，GM=2∴∠F=∠GMN∵AD=BC∴GN=GM∴∠GMN=∠GNM∴∠DEN=∠F经典题（二）1、已知：△ABC中，H为垂心（各边高线的交点），O为外心，且OM⊥BC于M．（1）求证：AH＝2OM；（2）若∠BAC＝600，求证：AH＝AO．（初二）证明：（1）延长AD交圆于F，连接BF，过点O作OG⊥AD于G∵OG⊥AF∴AG=FG∵AB⌒ =AB⌒∴∠F=∠ACB又AD⊥BC，BE⊥AC∴∠BHD+∠DBH=90°∠ACB+∠DBH=90°∴∠ACB=∠BHD∴∠F=∠BHD∴BH=BF又AD⊥BC∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2（GH+DH）=2GD 又AD⊥BC，OM⊥BC，OG⊥AD∴四边形OMDG是矩形∴OM=GD ∴AH=2OM（2）连接OB、OC∵∠BAC=60∴∠BOC=120°∵OB=OC，OM⊥BC1∠BOC=60°∴∠OBM=30°∴∠BOM=2∴BO=2OM由（1）知AH=2OM∴AH=BO=AO2、设MN是圆O外一条直线，过O作OA⊥MN于A，自A引圆的两条割线交圆O于B、C及D、E，连接CD并延长交MN于Q，连接EB并延长交MN于P.求证：AP＝AQ．证明：作点E关于AG的对称点F，连接AF、CF、QF∵AG⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF即∠PAE=∠QAF∵E、F、C、D四点共圆∴∠AEF+∠FCQ=180°∵EF⊥AG，PQ⊥AG∴EF∥PQ∴∠PAF=∠AFE∵AF=AE∴∠AFE=∠AEF∴∠AEF=∠PAF∵∠PAF+∠QAF=180°∴∠FCQ=∠QAF∴F、C、A、Q四点共圆∴∠AFQ=∠ACQ又∠AEP=∠ACQ∴∠AFQ=∠AEP 在△AEP和△AFQ中∠AFQ=∠AEPAF=AE∠QAF=∠PAE∴△AEP≌△AFQ ∴AP=AQ3、设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）证明：作OF ⊥CD 于F ，OG ⊥BE 于G ，连接OP 、OQ 、OA 、AF 、AG∵C 、D 、B 、E 四点共圆∴∠B=∠D ，∠E=∠C∴△ABE ∽△ADC ∴DF BGFD 2BG 2DC BEAD AB ===∴△ABG ∽△ADF∴∠AGB=∠AFD∴∠AGE=∠AFC∵AM=AN ，∴OA ⊥MN又OG ⊥BE ，∴∠OAQ+∠OGQ=180°∴O 、A 、Q 、E 四点共圆∴∠AOQ=∠AGE同理∠AOP=∠AFC∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°，OA=OA∴△OAQ ≌△OAP∴AP=AQ4、如图,分别以△ABC的AB和AC为一边,在△ABC的外侧作正方形ABFG和正方形ACDE，点O是DF的中点，OP⊥BC求证：BC=2OP（初二）证明：分别过F、A、D作直线BC的垂线，垂足分别是L、M、N∵OF=OD，DN∥OP∥FL∴PN=PL∴OP是梯形DFLN的中位线∴DN+FL=2OP∵ABFG是正方形∴∠ABM+∠FBL=90°又∠BFL+∠FBL=90°∴∠ABM=∠BFL又∠FLB=∠BMA=90°，BF=AB∴△BFL≌△ABM∴FL=BM同理△AMC≌△CND∴CM=DN∴BM+CN=FL+DN∴BC=FL+DN=2OP经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）证明：连接BD 交AC 于O 。

初三经典几何证明练习题(含问题详解)

求证：△PBC是正三角形．（初二）3、已知：如图，在四边形ABCD中，AD＝BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN于E、F．求证：∠DEN＝∠F．经典题（二）1、已知：△ABC中，H为垂心（各边高线的交点），O为外心，且OM⊥BC于M．（1）求证：AH＝2OM；（2）若∠BAC＝600，求证：AH＝AO．2、设MN是圆O外一条直线，过O作OA⊥MN于A，自A引圆的两条割线交圆O于B、C及D、E，连接CD并延长交MN于Q，连接EB并延长交MN于P.求证：AP＝AQ．3、如图,分别以△ABC的AB和AC为一边,在△ABC的外侧作正方形ABFG和正方形ACDE，点O是DF的中点，OP⊥BC求证：BC=2OP证明：分别过F、A、D作直线BC的垂线，垂足分别是L、M、N∵OF=OD，DN∥OP∥FL∴PN=PL∴OP是梯形DFLN的中位线∴DN+FL=2OP∵ABFG是正方形∴∠ABM+∠FBL=90°又∠BFL+∠FBL=90°∴∠ABM=∠BFL又∠FLB=∠BMA=90°，BF=AB∴△BFL≌△ABM∴FL=BM同理△AMC≌△CND∴CM=DN∴BM+CN=FL+DN∴BC=FL+DN=2OP经典题（三）1、如图，四边形ABCD为正方形，DE∥AC，AE＝AC，AE与CD相交于F．求证：CE＝CF．证明：连接BD 交AC 于O 。

过点E 作EG ⊥AC 于G ∵ABCD 是正方形 ∴BD ⊥AC 又EG ⊥AC ∴BD ∥EG 又DE ∥AC ∴ODEG 是平行四边形又∠COD=90° ∴ODEG 是矩形 ∴EG=OD=21BD=21AC=21AE ∴∠EAG=30°∵AC=AE∴∠ACE=∠AEC=75° 又∠AFD=90°-15°=75° ∴∠CFE=∠AFD=75°=∠AEC ∴CE=CF2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．证明：连接BD ，过点E 作EG ⊥AC 于G ∵ABCD 是正方形 ∴BD ⊥AC ，又EG ⊥AC ∴BD ∥EG 又DE ∥AC∴ODEG 是平行四边形又∠COD=90° ∴ODEG 是矩形∴EG =OD =21BD=21AC=21CE∴∠GCE=30°∵AC=EC3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）证明：过点F 作FG ⊥CE 于G ，FH ⊥CD 于H ∵CD ⊥CG ∴HCGF 是矩形 ∵∠HCF=∠GCF ∴FH=FG ∴HCGF 是正方形 ∴CG=GF ∵AP ⊥FP ∴∠APB+∠FPG=90° ∵∠APB+∠BAP=90° ∴∠FPG=∠BAP 又∠FGP=∠PBA ∴△FGP ∽△PBA 设AB=x ，BP=y ，CG=z z ：y=（x-y+z ）：x 化简得（x-y ）·y =（x-y ）·z ∵x-y ≠0 ∴y=z 即BP=FG∴△ABP ≌△PGF∴∠CAE=∠CEA=21∠GCE=15°在△AFC 中∠F =180°-∠FAC-∠ACF =180°-∠FAC-∠GCE =180°-135°-30°=15° ∴∠F=∠CEA ∴AE=AFPE PB A∴FG ：PB=PG ：AB4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）证明：过点E 作EK ∥BD ，分别交AC 、AF 于M 、K ，取EF 的中点H ，连接OH 、MH 、EC ∵EH=FH∴OH ⊥EF ，∴∠PHO=90° 又PC ⊥OC ，∴∠POC=90° ∴P 、C 、H 、O 四点共圆 ∴∠HCO=∠HPO 又EK ∥BD ，∴∠HPO=∠HEK ∴∠HCM=∠HEM ∴H 、C 、E 、M 四点共圆 ∴∠ECM=∠EHM 又∠ECM=∠EFA ∴∠EHM=∠EFA ∴HM ∥AC ∵EH=FH经典题(四)1、已知：△ABC 是正三角形，P 是三角形一点，PA ＝3，PB ＝4，PC ＝5．求∠APB 的度数．（初二）解：将△ABP 绕点B 顺时针方向旋转60°得△BCQ ，连接PQ 则△BPQ 是正三角形 ∴∠BQP=60°，PQ=PB=3在△PQC 中，PQ=4，CQ=AP=3，PC=5 ∴△PQC 是直角三角形 ∴∠PQC=90°∴∠BQC=∠BQP+∠PQC=60°+90°=150° ∴∠APB=∠BQC=150°2、设P 是平行四边形ABCD 部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）证明：过点P 作AD 的平行线，过点A 作PD 的平行线，两平行线相交于点E ，连接BE ∵PE ∥AD ，AE ∥PD∴ADPE 是平行四边形∴PE=AD ，又ABCD 是平行四边形∴AD=BC∴PE=BC又PE ∥AD ，AD ∥BC ∴PE ∥BC ∴BCPE 是平行四边形 ∴∠BEP=∠PCB ∵ADPE 是平行四边形 ∴∠ADP=∠AEP∴EM=KM ∵EK ∥BD ∴KMODAM AO EM OB == ∴OB=OD 又AO=CO ∴四边形ABCD 的对角线互相平分 ∴ABCD 是平行四边形 ∴AB=DC ，BC=AD 又∠ADP=∠ABP ∴∠AEP=∠ABP ∴A 、E 、B 、P 四点共圆 ∴∠BEP=∠PAB ∴∠PAB=∠PCB3、设ABCD 为圆接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）证明：在BD 上去一点E ，使∠BCE=∠ACD ∵CD⌒ =CD ⌒ ∴∠CAD=∠CBD ∴△BEC ∽△ADC∴ACBC AD BE = ∴AD ·BC=BE ·AC ……………………① ∵∠BCE=∠ACD∴∠BCE+∠ACE=∠ACD+∠ACE 即∠BCA=∠ECD ∵BC⌒=BC ⌒,∴∠BAC=∠BDC △BAC ∽△EDC ∴CDACDE AB =∴AB ·CD=DE ·AC ……………………②4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）证明：过点D 作DG ⊥AE 于G ，作DH ⊥FC 于H ，连接DF 、∴S △ADE =12AE ·DG ，S △FDC =12FC ·DH又S △ADE =S △FDC =12S □ABCD∴AE ·DG=FC ·DH 又AE=CF ∴DG=DH∴点D 在∠APC 的角平分线上 ∴∠DPA ＝∠DPC经典题（五）1、设P 是边长为1的正△ABC 任一点，L ＝PA ＋PB ＋PC ，求证：3≤L ＜2．证明：（1）将△BPC 绕B 点顺时针旋转60°的△BEF ，连接PE ， ∵BP=BE ，∠PBE=60° ∴△PBE 是正三角形。

(完整版)初中数学圆的证明题专项练习大全(精华)

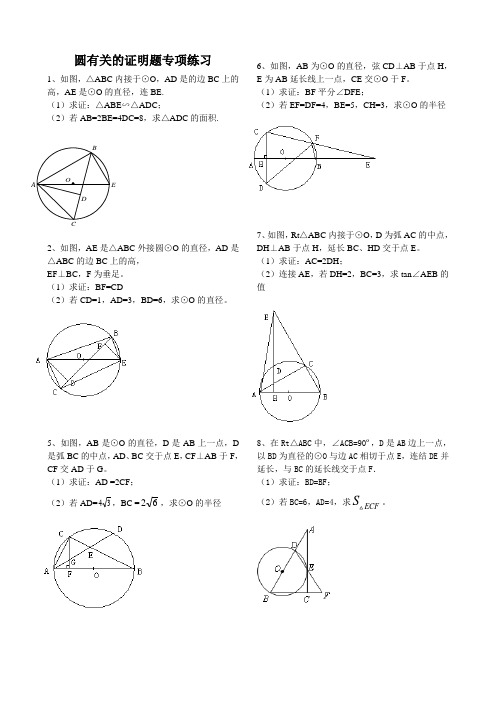
OABCDE圆有关的证明题专项练习1、如图，△ABC 内接于⊙O ，AD 是的边BC 上的高，AE 是⊙O 的直径，连BE. （1）求证：△ABE ∽△ADC ；（2）若AB=2BE=4DC=8，求△ADC 的面积.2、如图，AE 是△ABC 外接圆⊙O 的直径，AD 是△ABC 的边BC 上的高， EF ⊥BC ，F 为垂足。

（1）求证：BF=CD（2）若CD=1，AD=3，BD=6，求⊙O 的直径。

5、如图，AB 是⊙O 的直径，D 是AB 上一点，D 是弧BC 的中点，AD 、BC 交于点E ，CF ⊥AB 于F ，CF 交AD 于G 。

（1）求证：AD =2CF ；（2）若AD=34，BC =62，求⊙O 的半径6、如图，AB 为⊙O 的直径，弦CD ⊥AB 于点H ，E 为AB 延长线上一点，CE 交⊙O 于F 。

（1）求证：BF 平分∠DFE ；（2）若EF=DF=4，BE=5，CH=3，求⊙O 的半径7、如图，Rt △ABC 内接于⊙O ，D 为弧AC 的中点，DH ⊥AB 于点H ，延长BC 、HD 交于点E 。

（1）求证：AC=2DH ；（2）连接AE ，若DH=2，BC=3，求tan ∠AEB 的值8、在Rt △ABC 中，∠ACB=90º，D 是AB 边上一点，以BD 为直径的⊙O 与边AC 相切于点E ，连结DE 并延长，与BC 的延长线交于点F ．（1）求证：BD=BF ；（2）若BC=6，AD=4，求ECF S 。

9、如图，⊙O 中，直径DE ⊥弦AB 于H 点，C 为圆上一动点，AC 与DE 相交于点F 。

(1)求证△AOG ∽△FAO 。

(2)若OA=4，OF=8，H 点为OD 的中点，求CGF S 。

10、如图，在⊙O 中，弦AB 、CD 相交于AB 的中点E ，连接AD 并延长至F 点，使DF=AD,连接BC 、BF 。

（1）、求证：△CBE ∽△AFB 。

中考专题复习——圆的相关证明(附答案)

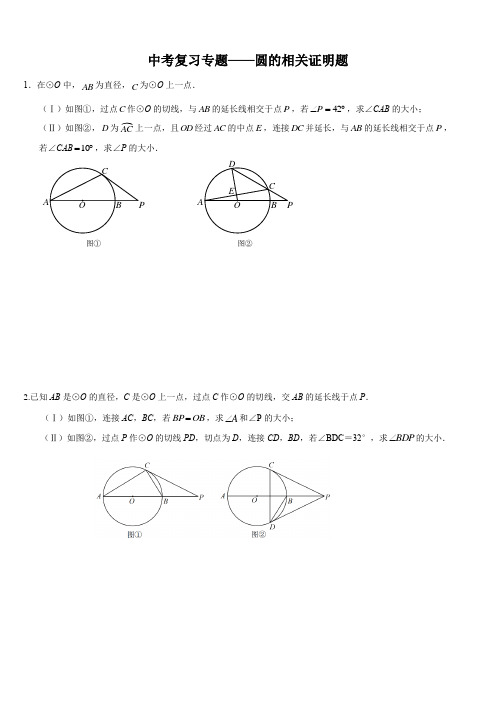
中考复习专题——圆的相关证明题1．在⊙O 中，AB 为直径，C 为⊙O 上一点．（Ⅰ）如图①，过点C 作⊙O 的切线，与AB 的延长线相交于点P ，若P ∠︒=42，求∠CAB 的大小；（Ⅱ）如图②，D 为上一点，且OD 经过AC 的中点E ，连接DC 并延长，与AB 的延长线相交于点P ，若∠CAB ︒=10，求∠P 的大小．2.已知AB 是⊙O 的直径，C 是⊙O 上一点，过点C 作⊙O 的切线，交AB 的延长线于点P ．（Ⅰ）如图①，连接AC ，BC ，若OB BP =，求A ∠和∠P 的大小；（Ⅱ）如图②，过点P 作⊙O 的切线PD ，切点为D ，连接CD ，BD ，若∠BDC ＝32°，求BDP ∠的大小．图①图②O B COB D CPE AC3.已知点A ，B ，C 是⊙O 上的三个点，︒=∠120AOB . （Ⅰ）如图①，若AC =BC ，求C ∠和CAO ∠的大小；（Ⅱ）如图②，过点C 作⊙O 的切线，交BA 的延长线于点D ，若AC =AD ，求CAO ∠的大小.4.已知AB 为⊙O 的直径，C 为⊙O 上一点，AD 和过点C 的切线互相垂直，垂足为D ，AD 交⊙O 于点E ．（Ⅰ）如图①，求证：AC 平分DAB ∠；（Ⅱ）如图②，过B 作BF AD ∥交⊙O 于点F ，连接CF ，若45AC =4DC =，求CF 和⊙O 半径的长． ABCDEO图①ABCDEO图②F5.已知，△DBC内接于⊙O，DB＝DC．（Ⅰ）如图①，过点B作射线BE交⊙O于点A，若∠EAD＝75°，求∠BDC的度数．（Ⅱ）如图②，分别过点B、点D作⊙O的切线相交于点E，若∠E=30°，求∠BDC的度数.①②6.已知P A，PB分别与⊙O相切于点A,B，PO交⊙O于点F，且其延长线交⊙O于点C，∠BCP=28°，E为CF上一点，延长BE交⊙O于点D.（Ⅰ）如图1，求∠CDB与∠APB的大小；（Ⅱ）如图2，当BC=CE时，求∠PBE的大小.7.在ABC △中90B ∠=︒D 为AC 上一点，以CD 为直径的⊙O 与AB 相切于点E ，与BC 相交于点F ，连接CE ．（Ⅰ）如图①，若27ACE ∠=︒，求A ∠和ECB ∠的大小；（Ⅱ）如图②，连接EF ，若//EF AC ，求A ∠的大小．8. 已知：在⊙O 中OA BC ⊥垂足为E ，点D 在⊙O 上．（Ⅰ）如图①若50AOB ∠=︒，求ADC ∠和∠CAO 的大小；（Ⅱ）如图②CD ∥AO ，过点D 作⊙O 的切线，与BC 的延长线相交于点P ，若26∠=︒ABC 求∠P 的大小．图①图②ABCF OED ABCOED F 图①O EDCBA图②POE DCBA9.如图，在⊙O 中，直径AB 与弦CD 相交于点E ，58ABC ∠=︒. （Ⅰ）如图①若85AEC ∠=︒，求BAD ∠和CDB ∠的大小；（Ⅱ）如图②若CD AB ⊥过点D 作⊙O 的切线DF ，与AB 的延长线相交于点F ，求F ∠的大小．10. 已知AB 是⊙O 的直径，CD 、CB 是⊙O 的弦，且AB CD ∥.（Ⅰ）如图①若25ABC ∠=︒，求BAC ∠和ODC ∠的大小；（Ⅱ）如图②过点C 作⊙O 的切线，与BA 的延长线交于点F 若OD CF ∥求ABC ∠的大小．图①图②EABO DCFE ABO DC图②图①11. 如图，⊙O 是△ABC 的外接圆，AE 切⊙O 于点A ，AE 与直径BD 的延长线相交于点E ．（Ⅰ）如图①，若∠C =71°，求∠E 的大小；（Ⅱ）如图②，当AE =AB ，DE =2时，求∠E 的大小和⊙O 的半径．12. 已知DA 、DC 分别与⊙O 相切于点A 点C ，延长DC 交直径AE 的延长线于点P ．（Ⅰ）如图①若DC =PC ，求∠P 的度数；（Ⅱ）如图②在⊙O 上取一点B ，连接AB 、BC 、BE ，当四边形ABCD 是平行四边形时，求∠P 及∠AEB 的大小． OEEDCBAD O C BA图①图②DECAPOB图① 图②ECAPOD13.如图①，AB 是⊙O 的弦，OE ⊥AB ，垂足为P ，交AB 于点E ，且OP =3PE ，AB =74．（Ⅰ）求⊙O 的半径；（Ⅱ）如图②过点E 作⊙O 的切线CD ，连接OB 并延长与该切线交于点D ，延长OA 交CD 于C ，求OC 的长．图②图①EP A BCODP EOBA参考答案1.解：（Ⅰ）如图，连接OC∵ ⊙O 与PC 相切于点C ∴ OC PC ⊥，即90OCP ∠=︒ ∵ 42P ∠=︒∴ 9048COB P ∠=︒-∠=︒ 在Rt OPC △中，48CAB ACO COP ∠+∠=∠=︒ ∵OA =OC ∴∠CAB =∠ACO ∴ 24CAB ∠=︒（Ⅱ）∵ E 为AC 的中点∴ OD AC ⊥，即90AEO ∠=︒在Rt AOE △中，由10EAO ∠=︒得9080AOE EAO ∠=︒-∠=︒ ∴ 1402ACD AOD ∠=∠=︒∵ ACD ∠是ACP △的一个外角∴ 30P ACD CAP ∠=∠-∠=︒2. 解：（Ⅰ）如图①连接OC ∵PC 是⊙O 的切线∴︒=∠90OCP ∵OB BP =∴OB BC =∵OC OB =∴BOC ∆为等边三角形， ∴∠BOC=60° ∴︒=∠=∠3021BOC A ∠P=90°－∠COB ＝30°（Ⅱ）如图② 连接OC 、OD 设CD 交OP 于点E∵PC ，PD 是⊙O 的切线∴PD PC = ︒=∠=∠90ODP OCP ∵OD OC =∴OP 为CD 的垂直平分线 ∴︒=∠=∠90DEP CEP∵∠BDC ＝32°∴∠OBD ＝90°－∠BDC ＝58° ∵OB OD =∴∠ODB ＝∠OBD ＝58° ∴∠BDP ＝90°－58°＝32°3.解：（Ⅰ）∵︒=∠120AOB ∴∠ACB= 12 ∠AOB=60°如图① 连接OC∵AC =BC ∴∠AOC=∠BOC∵∠AOC+∠BOC +∠AOB=360° ∴∠AOC =12 （360°-120°）=120° ∵OA OC ∴∠CAO=∠ACO=12（180°-120°）=30°O AB PCOAB D CPE（Ⅱ）如图② 连接OC设∠ACD= x ∵ACAD ∴∠ACD =∠ADC= x∴∠CAB=2x ∵∠AOB=120°OAOB ∴∠OAB =∠OBA= 12（180°-120°）=30°∵CD 是⊙O 的切线∴∠OCD=90° ∵OAOC ∴∠OCA =∠OAC∴90°－x=2x －30° 解得x=40° ∴∠CAB=80°∴∠CAO=∠CAB －∠OAB =50°4.（Ⅰ）证明：连接OC ∵CD 为⊙的切线∴OC CD ⊥即90OCM OCD ∠=∠=︒ ∵AD CD ⊥垂足为D ∴90ADC ∠=︒ ∵90ADC OCM ∠=∠=︒∴OC AD ∥ ∴DAC ACO ∠=∠∵OC OA =∴CAO ACO ∠=∠∴DAC CAO ∠=∠∴AC 平分DAB ∠ （Ⅱ）解：连接AF 延长CO 交AF 于G ∵AB 为⊙的直径 ∴=90AFB ∠︒ ∵OC AD BF AD ∥，∥ ∴CO BF ∥∴90AFB AGC ∠=∠=︒ ∴OC AF ⊥由垂径定理可得AC=CF∴45AC CF == ∵90ADC ∠=︒22O O ABC DEOF GABCDEOM∴90ADC DCO AGC ∠=∠=∠=︒ ∴四边形ADCG 是矩形∴8AD CG == 4CD AG == 在Rt AGO 中，得222AG OG AO += 设OC x =则,8OA x OG x ==- 可得方程()22248x x +-=解得5x =． ∴⊙半径的长为545CF =．5.（Ⅰ）解：∵四边形ABCD 是⊙O 的内接四边形∴∠DAB +∠C ＝180° ∵∠EAD +∠DAB ＝180° ∴∠C ＝∠EAD ∵∠EAD ＝75° ∴∠C ＝75° ∵DB ＝DC∴∠DBC ＝∠C ＝75°∴∠BDC ＝180°﹣∠C ﹣∠DBC ＝30°（Ⅱ）解：连结OB OD∵EB ED 与⊙O 相切于点B 点D∴ED OD ⊥⊥，EB OB ∴ ︒=∠︒=∠90ODE 90，OBE∵︒=∠+∠+∠+∠360BOD ODE E OBE ︒=∠30E ∴︒=∠150BOD∴︒=∠=∠7521BOD C ∵DB ＝DC ，∴∠DBC ＝∠C ＝75°，∴∠BDC ＝180°﹣∠C ﹣∠DBC ＝30° O6. （I ）解：连接OB∵P A 、PB 与圆O 相切于点A 点,B∴PO 平分∠APB 且∠PBO ＝90° ∵∠BCP ＝28°∴∠BOP ＝2∠BCP ＝28°×2＝56° ∴∠BPO ＝90°－∠BOP ＝90°－56°＝34° ∴∠APB ＝2∠BPO ＝2×34°＝68°又∠BDC ＝BOC ∠21＝)180(21BOP ∠- ∴∠BDC = 62)56180(21=-∴∠APB =68°∠BDC= 62 （II ）连接OB∵BC ＝CE ∴∠CBE ＝∠CEB∵∠BCP ＝28° ∴∠CBE ＝76228180=-∵OB ＝OC ∴∠OBC ＝∠OCB ＝28° ∴∠EBO ＝∠CBE －∠OBC ＝76°－28°＝48° ∵P A 与圆O 相切于点A∴OB ⊥PB ∴∠PBO ＝90°∴∠PBE ＝90°－ ∠EBO ＝90°－48°＝42°7.解：（Ⅰ）如图连接OE ．∵ AB 与⊙O 相切∴ OE AB ⊥，即90AEO ∠=︒ ∵ 27ACE ∠=︒∴ 254AOE ACE ∠=∠=︒ ∴ 9036A AOE ∠=︒-∠=︒ ∵ OE OC =∴ OEC OCE ∠=∠∵ 90B ∠=︒∴ //OE BC ∴ ECB OEC ∠=∠ ∴ 27ECB ∠=︒ （Ⅱ）如图，连接OE OF∵ //OE BC //EF AC ∴ 四边形OEFC 为平行四边形 ∴ OE CF = ∴ OC OF CF == ∴ 60ACB ∠=︒∴ 9030A ACB ∠=︒-∠=︒ABCOED F ABCF OED8. 解：（Ⅰ）∵OA BC ⊥ ∴AB AC = 90∠=︒AEC∴∠=∠ACB ADC ∵1252∠=∠=︒ACB AOB∴25∠=∠=︒ADC ACB9065∠=︒-∠=︒CAO ACB（Ⅱ）连接BD . 由OA BC ⊥知，90∠=∠=︒AEB BEO∴ 9064∠=︒-∠=︒OAB ABC ∵AO ∥CD ∴90∠=∠=︒BCD BEO ∴BD 是⊙O 的直径又PD 与⊙O 相切∴⊥BD PD . 即90∠=︒BDP∵=OA OB ∴64∠=∠=︒OBA OAB∴642636∠=∠-∠=︒-︒=︒CBD ABO ABC ∴9052∠=︒-∠=︒P CBD9. （Ⅰ）∵∠AEC 是ΔBEC 的一个外角 58ABC ∠=︒85AEC ∠=︒27C AEC ABC ∴∠=∠-∠=︒∵在⊙O 中BAD C ∠=∠27BAD ∴∠=︒ AB 为⊙O 的直径90ADB ∴∠=︒ ∵在⊙O 中58ADC ABC ∠=∠=︒ 又CDB ADB ADC ∠=∠-∠32CDB ∴∠=︒（Ⅱ）连接OD∵CD ⊥AB 90CEB ∴∠=︒．9032E E CB BC =-∴∠=∠︒︒∴264DOB DCB ∠=∠=︒ ∵DF 是⊙O 的切线∴90ODF ∠=︒90906426F DOB ∴∠=︒-∠=︒-︒=︒图②POE DCBA图①O E DCBA10. 解：（Ⅰ）如图连接OC ∵ AB 是⊙O 的直径 ∴ 90ACB ∠=︒∴ 90BAC ABC ∠+∠=︒由25ABC ∠=︒得65BAC ∠=︒又AB CD ∥得25ABC BCD ∠=∠=︒ ∵ OB OC = ∴ 25OCB ABC ∠==∠=︒ 则50OCD OCB BCD ∠=∠+∠=︒ 由OC OD =得50ODC OCD ∠=∠=︒（Ⅱ）如图，连接OC∵CF 切⊙O 于点C ∴OC FC ⊥则90OCF ∠=︒∵ OD CF ∥ ∴ 90DOC OCF ∠=∠=︒ 又OC OD =则45ODC OCD ∠==∠=︒ 由AB CD ∥得45BOD ODC ∠=∠=︒∴135BOC DOC BOD ∠=∠+∠=︒ ∵ OC OB = ∴22.5ABC OCB ∠=∠=︒11. 解：（Ⅰ）连接OA .∵AE 切⊙O 于点A ∴OA ⊥AE ，∴∠OAE =90° ∵∠C =71° ∴∠AOB =2∠C =2×71°=142° 又∵∠AOB +∠AOE =180° ∴∠AOE =38° ∵∠AOE +∠E =90° ∴∠E =90°﹣38°=52° （Ⅱ）连接OA 设∠E = x .∵AB =AE ∴∠ABE =∠E = x ∵OA =OB ∴∠OAB =∠ABO = x ∴∠AOE =∠ABO +∠BAO =2x∵AE 是⊙O 的切线∴OA ⊥AE ，即∠OAE =90°在△OAE 中∠AOE +∠E =90°即2x +x =90°解得30x =︒∴∠E =30° 在Rt △OAE 中OA =21OE∵OA =OD ∴OA =OD =DE∵DE =2∴OA =2即⊙O 的半径为212.解：（Ⅰ）∵DA 、DC 是⊙O 的切线 ∴DA ＝DC OA ⊥DA ∴∠DAO ＝90°∵DC =PC ∴DA ＝DC =PC ∵∠DAP ＝90° ∴sin P=DP AD =21∴∠P=30° （Ⅱ）连接OC 、AC∵DA ，DC 是⊙O 的切线 ∴DA ＝DC∵四边形ABCD 是平行四边形∴□ABCD 是菱形 ∴DA =DC =CB =AB ∠ABC =∠ADC ∵∠AOC =2∠ABC ∴∠AOC =2∠ADC∵DA 、DC 是⊙O 的切线∴OA ⊥AD OC ⊥DC ∴∠DAO ＝∠DCO ＝90°∵∠ADC +∠DCO+∠AOC +∠DAO =360° ∴∠ADC +∠AOC =180°∴3∠ADC ＝180°∴∠ADC ＝60°∴∠P ＝90°－∠ADC ＝30°，∠ABC =60°又AB =BC ∴△ABC 是等边三角形 ∴∠ACB ＝60° ∴∠AEB ＝∠ACB=60°13. 解：（Ⅰ）∵OE ⊥AB∴1272APAB 设PE =x 则OP =3x OA =OE =4x在Rt OAP △中222OA OP AP =+即2216928x x =+ 解得x =2（负舍）∴4x =8 ∴半径OA 为8 （Ⅱ）∵ CD 为⊙O 的切线 ∴OE ⊥CD又∵OE ⊥AB ∴AB //CD ∴34OA OP OCOE∴323OCECAPODB。

初中数学几何证明经典题含答案

初中几何证明题经典题〔一〕1、：如图，O是半圆的圆心，C、E是圆上的两点，CD⊥AB，EF⊥AB，EG⊥CO．求证：CD＝GF．〔初二〕.如下列图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

2、：如图，P是正方形ABCD内点，∠PAD＝∠PDA＝150．求证：△PBC是正三角形．〔初二〕.如下列图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

.如下列图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

APCDBAFGCEBOD3、如图，四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．〔初二〕4、：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典题〔二〕1、：△ABC 中，H 为垂心〔各边高线的交点〕，O 为外心，且OM ⊥BC 于M ．〔1〕求证：AH ＝2OM ；〔2〕假设∠BAC ＝600，求证：AH ＝AO ．〔初二〕D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 AN FE CDMB· A DHEM CBOF2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．〔初二〕3、如果上题把直线MN 由圆外平移至圆内，那么由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．〔初二〕4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典题〔三〕1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．〔初二〕2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．〔初二〕3、设P 是正方形ABCD 一边求证：PA ＝PF ．〔初二〕4、如图，PC 切圆O 于C ，AC 为圆的直径，PEFB 、D ．求证：AB ＝DC ，BC ＝AD．〔初三〕经典 1、：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5求：∠APB 的度数．〔初二〕2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．〔初二〕3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．〔初三〕4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．〔初二〕经典难题〔五〕1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．C BD A F PD E CB A APCBACBPDA CBPD4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC上的点，∠DCA＝300，∠EBA＝200，求∠BED的度数．经典题〔一〕⊥AB,连接EO。

中考难点突破圆的证明题50道(含详细解析)

中考难点突破——圆的证明题练习50道（含详细解析）一．解答题（共50小题）1．如图，在△ABC中，AB=AC，以AB为直径的圆交AC于点D，交BC于点E，延长AE至点F，使EF=AE，连接FB，FC．（1）求证：四边形ABFC是菱形；（2）若AD=7，BE=2，求半圆和菱形ABFC的面积．2．如图，已知△ABC内接于⊙O，AB是直径，OD∥AC，AD=OC．（1）求证：四边形OCAD是平行四边形；（2）填空：①当∠B=时，四边形OCAD是菱形；②当∠B=时，AD与⊙O相切．3．如图，AC是⊙O的直径，OB是⊙O的半径，PA切⊙O于点A，PB与AC的延长线交于点M，∠COB=∠APB．（1）求证：PB是⊙O的切线；（2）当OB=3，PA=6时，求MB、MC的长．4．如图，△ABC内接于⊙O，∠B=60°，CD是⊙O的直径，点P是CD延长线上的一点，且AP=AC．（1）求证：PA是⊙O的切线；（2）若PD=√3，求⊙O的直径．5．如图，点B、C、D都在⊙O上，过点C作CA∥BD交OD的延长线于点A，连接BC，且∠B=∠A=30°，BD=2√3．（1）求证：AC是⊙O的切线；（2）求由线段AC、AD与弧CD所围成的阴影部分的面积．6．如图，已知AB是⊙O的直径，点C、D在⊙O上，点E在⊙O外，∠EAC=∠D=60°．（1）求∠ABC的度数；（2）求证：AE是⊙O的切线；（3）当BC=4时，求劣弧AC的长．7．已知：如图，△ABC中，AC=BC，以BC为直径的⊙O交AB于点D，过点D 作DE⊥AC于点E，交BC的延长线于点F．求证：（1）AD=BD；（2）DF是⊙O的切线．8．如图，AB是⊙O的直径，C、D两点在⊙O上，若∠C=45°，（1）求∠ABD的度数；（2）若∠CDB=30°，BC=3，求⊙O的半径．9．如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，且AC=CD，∠ACD=120°．（1）求证：CD是⊙O的切线；（2）若⊙O的半径为2，求图中阴影部分的面积．10．如图，已知⊙O中，AB为直径，AB=10cm，弦AC=6cm，∠ACB的平分线交⊙O于D，求线段BC，AD，BD的长．11．如图，AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC交于点E．（1）若∠B=70°，求∠CAD的度数；（2）若AB=4，AC=3，求DE的长．12．如图，△ABC中，∠C=90°，AC=3，AB=5，点O在BC边的中线AD上，⊙O 与BC相切于点E，且∠OBA=∠OBC．（1）求证：AB为⊙O的切线；（2）求⊙O的半径；（3）求tan∠BAD．13．如图，⊙O的直径AD长为6，AB是弦，∠A=30°，CD∥AB，且CD=√3．（1）求∠C的度数；（2）求证：BC是⊙O的切线；（3）求阴影部分面积．14．如图，在△ABC中，AB=AC，AE是∠BAC的平分线，∠ABC的平分线BM交AE于点M，点O在AB上，以点O为圆心，OB的长为半径的圆经过点M，交BC于点G，交AB于点F．（1）求证：AE为⊙O的切线；（2）当BC=4，AC=6时，求⊙O的半径；（3）在（2）的条件下，求线段BG的长．15．如图，四边形ABCD 内接于⊙O，BD是⊙O的直径，过点A作⊙O的切线AE交CD的延长线于点E，DA平分∠BDE．（1）求证：AE⊥CD；（2）已知AE=4cm，CD=6cm，求⊙O的半径．16．如图，在Rt△ABC中，∠C=90°，AD是∠BAC的平分线，经过A、D两点的圆的圆心O恰好落在AB上，⊙O分别与AB、AC相交于点E、F．（1）判断直线BC与⊙O的位置关系并证明；（2）若⊙O的半径为2，AC=3，求BD的长度．17．如图，在△ABC中，AB=BC，D是AC中点，BE平分∠ABD交AC于点E，点O是AB上一点，⊙O过B、E两点，交BD于点G，交AB于点F．（1）判断直线AC与⊙O的位置关系，并说明理由；（2）当BD=6，AB=10时，求⊙O的半径．18．如图，△ABC 内接于⊙O ，∠B=60°，CD 是⊙O 的直径，点P 是CD 延长线上的一点，且AP=AC ．（1）求证：PA 是⊙O 的切线；（2）若AB=4+√3，BC=2√3，求⊙O 的半径．19．如图，已知⊙O 是以AB 为直径的△ABC 的外接圆，过点A 作⊙O 的切线交OC 的延长线于点D ，交BC 的延长线于点E ．（1）求证：∠DAC=∠DCE ；（2）若AB=2，sin ∠D=13，求AE 的长．20．如图，△ABC 内接于⊙O ，AB 是直径，⊙O 的切线PC 交BA 的延长线于点P ，OF ∥BC 交AC 于点E ，交PC 于点F ，连接AF ；（1）判断AF 与⊙O 的位置关系并说明理由．（2）若⊙O 的半径为4，AF=3，求AC 的长．21．已知四边形ABCD 是平行四边形，以AB 为直径的⊙O 经过点D ，∠DAB=45°．（Ⅰ）如图①，判断CD 与⊙O 的位置关系，并说明理由；（Ⅱ）如图②，E 是⊙O 上一点，且点E 在AB 的下方，若⊙O 的半径为3cm ，AE=5cm ，求点E 到AB 的距离．22．如图，⊙O 为△ABC 的外接圆，BC 为⊙O 的直径，AE 为⊙O 的切线，过点B作BD ⊥AE 于D ．（1）求证：∠DBA=∠ABC ；（2）如果BD=1，tan ∠BAD=12，求⊙O 的半径．23．如图，△ABC 中，AB=AC ，点D 为BC 上一点，且AD=DC ，过A ，B ，D 三点作⊙O ，AE 是⊙O 的直径，连结DE ．（1）求证：AC 是⊙O 的切线；（2）若sinC=45，AC=6，求⊙O 的直径．24．如图，已知三角形ABC的边AB是⊙O的切线，切点为B．AC经过圆心O并与圆相交于点D、C，过C作直线CE丄AB，交AB的延长线于点E．（1）求证：CB平分∠ACE；（2）若BE=3，CE=4，求⊙O的半径．25．如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P，弦CE平分∠ACB，交AB点F，连接BE．（1）求证：AC平分∠DAB；（2）求证：PC=PF；（3）若tan∠ABC=43，AB=14，求线段PC的长．26．如图，AB是⊙O的直径，C是AB延长线上一点，CD与⊙O相切于点E，AD ⊥CD于点D．（1）求证：AE平分∠DAC；（2）若AB=4，∠ABE=60°．①求AD的长；②求出图中阴影部分的面积．27．如图，AB是⊙O的直径，点C是⊙O上一点，AD和过点C的切线互相垂直，垂足为D，直线DC与AB的延长线相交于P．弦CE平分∠ACB，交直径AB于点F，连结BE．（1）求证：AC平分∠DAB；（2）探究线段PC，PF之间的大小关系，并加以证明；（3）若tan∠PCB=34，BE=5√2，求PF的长．28．在△ABC中，∠ACB=90°，经过点C的⊙O与斜边AB相切于点P．（1）如图①，当点O在AC上时，试说明2∠ACP=∠B；（2）如图②，AC=8，BC=6，当点O在△ABC外部时，求CP长的取值范围．29．如图，⊙O是△ABC的外接圆，∠ABC=45°，AD是⊙O的切线交BC的延长线于D，AB交OC于E．（1）求证：AD∥OC；（2）若AE=2√5，CE=2．求⊙O的半径和线段BE的长．30．如图，以△ABC的一边AB为直径作⊙O，⊙O与BC边的交点D恰好为BC 的中点，过点D作⊙O的切线交AC边于点E．（1）求证：DE⊥AC；（2）连接OC交DE于点F，若sin∠ABC=34，求OFFC的值．31．如图，△ABC内接于⊙O，AD是⊙O直径，过点A的切线与CB的延长线交于点E．（1）求证：EA2=EB•EC；（2）若EA=AC，cos∠EAB=45，AE=12，求⊙O的半径．32．如图，已知AB是⊙O的直径，点C、D在⊙O上，∠D=60°且AB=6，过O 点作OE⊥AC，垂足为E．（1）求OE的长；（2）若OE的延长线交⊙O于点F，求弦AF、AC和弧CF围成的图形（阴影部分）的面积S．33．如图，AB是⊙O的直径，点C在⊙O上，∠ABC的平分线与AC相交于点D，与⊙O过点A的切线相交于点E．（1）∠ACB=°，理由是：；（2）猜想△EAD的形状，并证明你的猜想；（3）若AB=8，AD=6，求BD．34．如图，在△ABC中，AB=AC，AE是角平分线，BM平分∠ABC交AE于点M，经过B、M两点的⊙O交BC于点G，交AB于点F，FB恰为⊙O的直径．（1）判断AE与⊙O的位置关系，并说明理由；（2）当BC=4，AC=3CE时，求⊙O的半径．35．如图，AB是⊙O的直径，点C在⊙O上，CE⊥AB于E，CD平分∠ECB，交过点B的射线于D，交AB于F，且BC=BD．（1）求证：BD是⊙O的切线；（2）若AE=9，CE=12，求BF的长．36．在Rt△ABC中，∠ACB=90°，BE平分∠ABC，D是边AB上一点，以BD为直径的⊙O经过点E，且交BC于点F．（1）求证：AC是⊙O的切线；（2）若BF=6，⊙O的半径为5，求CE的长．37．如图，在平面直角坐标系中，以点M（0，√3）为圆心，以2√3长为半径作⊙M交x轴于A、B两点，交y轴于C、D两点，连接AM并延长交⊙M于P 点，连接PC交x轴于E．（1）求点C、P的坐标；（2）求证：BE=2OE．38．如图，AB是圆O的直径，O为圆心，AD、BD是半圆的弦，且∠PDA=∠PBD．延长PD交圆的切线BE于点E（1）判断直线PD是否为⊙O的切线，并说明理由；（2）如果∠BED=60°，PD=√3，求PA的长．（3）将线段PD以直线AD为对称轴作对称线段DF，点F正好在圆O上，如图2，求证：四边形DFBE为菱形．39．如图，AB是⊙O的直径，弦CD⊥AB于点E，点P在⊙O上，且PD∥CB，弦PB与CD交于点F（1）求证：FC=FB；（2）若CD=24，BE=8，求⊙O的直径．40．如图，AC是⊙O的直径，PA切⊙O于点A，点B是⊙O上的一点，且∠BAC=30°，∠APB=60°．（1）求证：PB是⊙O的切线；（2）若⊙O的半径为2，求弦AB及PA，PB的长．41．如图所示，以Rt△ABC的直角边AB为直径作圆O，与斜边交于点D，E为BC边上的中点，连接DE．（1）求证：DE是⊙O的切线；（2）连接OE，AE，当∠CAB为何值时，四边形AOED是平行四边形？并在此条件下求sin∠CAE的值．42．如图，已知AB为⊙O的弦，C为⊙O上一点，∠C=∠BAD，且BD⊥AB于B．（1）求证：AD是⊙O的切线；（2）若⊙O的半径为3，AB=4，求AD的长．43．如图，在Rt△ABC中，∠C=90°，∠BAC的平分线AD交BC边于点D．以AB 上一点O为圆心作⊙O，使⊙O经过点A和点D．（1）判断直线BC与⊙O的位置关系，并说明理由；（2）若AC=3，∠B=30°，且⊙O与AB边的另一个交点为E，求线段BD、BE与劣弧DE所围成的阴影部分的图形面积．（结果保留根号和π）44．如图，已知AB为⊙O的直径，CD是弦，且AB⊥CD于点E．连接AC、OC、BC．（1）求证：∠ACO=∠BCD．（2）若BE=3，CD=8，求BC 的长．45．如图，AB 是⊙O 的直径，点D ，E 在⊙O 上，∠A=2∠BDE ，点C 在AB 的延长线上，∠C=∠ABD ．（1）求证：CE 是⊙O 的切线；（2）若BF=2，EF=√13，求⊙O 的半径长．46．如图，AB 是⊙O 的直径，点F ，C 是⊙O 上两点，且AF̂=FC ̂=CB ̂，连接AC ，AF ，过点C 作CD ⊥AF 交AF 延长线于点D ，垂足为D ．（1）求证：CD 是⊙O 的切线；（2）若CD=2√3，∠CAB=30°，求⊙O 的半径．47．如图，在等腰△ABC 中，AB=BC ，以BC 为直径的⊙O 与AC 相交于点D ，过点D 作DE ⊥AB 交CB 延长线于点E ，垂足为点F ．（1）判断DE 与⊙O 的位置关系，并说明理由；（2）若⊙O 的半径R=5，tanC=12，求EF 的长．48．如图，AB为⊙O的直径，D为AĈ的中点，连接OD交弦AC于点F，过点D 作DE∥AC，交BA的延长线于点E．（1）求证：DE是⊙O的切线；（2）连接CD，若OA=AE=4，求四边形ACDE的面积．49．如图，已知⊙O的直径CD=6，A，B为圆周上两点，且四边形OABC是平行四边形，过A点作直线EF∥BD，分别交CD，CB的延长线于点E，F，AO与BD交于G点．（1）求证：EF是⊙O的切线；（2）求AE的长．50．如图，已知⊙O的半径为5，PA是⊙O的一条切线，切点为A，连接PO并延长，交⊙O于点B，过点A作AC⊥PB交⊙O于点C、交PB于点D，连接BC，当∠P=30°时，（1）求弦AC的长；（2）求证：BC∥PA．圆的证明题练习50道参考答案与试题解析一．解答题（共50小题）1．如图，在△ABC中，AB=AC，以AB为直径的圆交AC于点D，交BC于点E，延长AE至点F，使EF=AE，连接FB，FC．（1）求证：四边形ABFC是菱形；（2）若AD=7，BE=2，求半圆和菱形ABFC的面积．【解答】（1）证明：∵AB是直径，∴∠AEB=90°，∴AE⊥BC，∵AB=AC，∴BE=CE，∵AE=EF，∴四边形ABFC是平行四边形，∵AC=AB，∴四边形ABFC是菱形．（2）设CD=x．连接BD．∵AB是直径，∴∠ADB=∠BDC=90°，∴AB2﹣AD2=CB2﹣CD2，∴（7+x）2﹣72=42﹣x2，解得x=1或﹣8（舍弃）∴AC=8，BD=√82−72=√15，∴S=8√15．菱形ABFC∴S半圆=12•π•42=8π．2．如图，已知△ABC内接于⊙O，AB是直径，OD∥AC，AD=OC．（1）求证：四边形OCAD是平行四边形；（2）填空：①当∠B=30°时，四边形OCAD是菱形；②当∠B=45°时，AD与⊙O相切．【解答】解：（1）∵OA=OC，AD=OC，∴OA=AD，∴∠OAC=∠OCA，∠AOD=∠ADO，∵OD∥AC，∴∠OAC=∠AOD，∴∠OAC=∠OCA=∠AOD=∠ADO，∴∠AOC=∠OAD，∴OC∥AD，∴四边形OCAD是平行四边形；（2）①∵四边形OCAD是菱形，∴OC=AC，又∵OC=OA，∴OC=OA=AC，∴∠AOC=60°，∴∠B=12∠AOC=30°；故答案为30．②∵AD 与⊙O 相切，∴∠OAD=90°，∵AD ∥OC ，∴∠AOC=90°，∴∠B=12∠AOC=45°；故答案为：45°3．如图，AC 是⊙O 的直径，OB 是⊙O 的半径，PA 切⊙O 于点A ，PB 与AC 的延长线交于点M ，∠COB=∠APB ．（1）求证：PB 是⊙O 的切线；（2）当OB=3，PA=6时，求MB 、MC 的长．【解答】证明：（1）∵AC 是⊙O 的直径，PA 切⊙O 于点A ，∴PA ⊥OA∴在Rt △MAP 中，∠M +∠P=90°，而∠COB=∠APB ，∴∠M +∠COB=90°，∴∠OBM=90°，即OB ⊥BP ，∴PB 是⊙O 的切线；（2）∵∠COB=∠APB ，∠OBM=∠PAM ，∴△OBM ∽△APM ，∴MB AM =OB AP =OM PB =12，设MB=x ，则MA=2x ，MO=2x ﹣3，∴MP=4x ﹣6，在Rt △AMP 中，（4x ﹣6）2﹣（2x ）2=62，解得x=4或0（舍去）∴MB=4，MC=2．4．如图，△ABC 内接于⊙O ，∠B=60°，CD 是⊙O 的直径，点P 是CD 延长线上的一点，且AP=AC ．（1）求证：PA是⊙O的切线；（2）若PD=√3，求⊙O的直径．【解答】解：（1）证明：连接OA，∵∠B=60°，∴∠AOC=2∠B=120°，又∵OA=OC，∴∠OAC=∠OCA=30°，又∵AP=AC，∴∠P=∠ACP=30°，∴∠OAP=∠AOC﹣∠P=90°，∴OA⊥PA，∴PA是⊙O的切线．（2）在Rt△OAP中，∵∠P=30°，∴PO=2OA=OD+PD，又∵OA=OD，∴PD=OA，∵PD=√3，∴2OA=2PD=2√3．∴⊙O的直径为2√3．5．如图，点B 、C 、D 都在⊙O 上，过点C 作CA ∥BD 交OD 的延长线于点A ，连接BC ，且∠B=∠A=30°，BD=2√3．（1）求证：AC 是⊙O 的切线；（2）求由线段AC 、AD 与弧CD 所围成的阴影部分的面积．【解答】（1）证明：连接OC ，交BD 于E ，∵∠B=30°，∠B=12∠COD ， ∴∠COD=60°，∵∠A=30°，∴∠OCA=90°，即OC ⊥AC ，∴AC 是⊙O 的切线；（2）解：∵AC ∥BD ，∠OCA=90°，∴∠OED=∠OCA=90°，∴DE=12BD=√3， ∵sin ∠COD=DE OD， ∴OD=2，在Rt △ACO 中，tan ∠COA=AC OC ，∴AC=2√3，∴S 阴影=12×2×2√3﹣60π×22360=2√3﹣2π3． 6．如图，已知AB 是⊙O 的直径，点C 、D 在⊙O 上，点E 在⊙O 外，∠EAC=∠D=60°．（1）求∠ABC 的度数；（2）求证：AE是⊙O的切线；（3）当BC=4时，求劣弧AC的长．【解答】解：（1）∵∠ABC与∠D都是弧AC所对的圆周角，∴∠ABC=∠D=60°；（2）∵AB是⊙O的直径，∴∠ACB=90°．∴∠BAC=30°，∴∠BAE=∠BAC+∠EAC=30°+60°=90°，即BA⊥AE，∴AE是⊙O的切线；（3）如图，连接OC，∵∠ABC=60°，∴∠AOC=120°，∴劣弧AC的长为120⋅π×4180=8π3．7．已知：如图，△ABC中，AC=BC，以BC为直径的⊙O交AB于点D，过点D 作DE⊥AC于点E，交BC的延长线于点F．求证：（1）AD=BD；（2）DF是⊙O的切线．【解答】证明：（1）连接CD，∵BC为⊙O的直径，∴CD⊥AB．∵AC=BC，∴AD=BD．（2）连接OD；∵AD=BD，OB=OC，∴OD是△BCA的中位线，∴OD∥AC．∵DE⊥AC，∴DF⊥OD．∵OD为半径，∴DF是⊙O的切线．8．如图，AB是⊙O的直径，C、D两点在⊙O上，若∠C=45°，（1）求∠ABD的度数；（2）若∠CDB=30°，BC=3，求⊙O的半径．【解答】解：（1）∵∠C=45°，∴∠A=∠C=45°，∵AB是⊙O的直径，∴∠ADB=90°，∴∠ABD=45°；（2）连接AC，∵AB是⊙O的直径，∴∠ACB=90°，∵∠CAB=∠CDB=30°，BC=3，∴AB=6，∴⊙O的半径为3．9．如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，且AC=CD，∠ACD=120°．（1）求证：CD是⊙O的切线；（2）若⊙O的半径为2，求图中阴影部分的面积．【解答】证明：（1）连接OC，∵CD=AC，∴∠CAD=∠D，又∵∠ACD=120°，∴∠CAD=12（180°﹣∠ACD）=30°，∵OC=OA，∴∠A=∠1=30°，∴∠COD=60°，又∵∠D=30°，∴∠OCD=180°﹣∠COD﹣∠D=90°，∴CD是⊙O的切线；（2）∵∠A=30°，∴∴∠1=2∠A=60°∠1=2∠A=60°．∴∴S扇形OBC =60π×22360=23π，在Rt△OCD中，CD=OC⋅tan60°=2√3．∴S Rt△OCD=12OC×CD=12×2×2√3=2√3．∴图中阴影部分的面积为2√3﹣23π．10．如图，已知⊙O中，AB为直径，AB=10cm，弦AC=6cm，∠ACB的平分线交⊙O于D，求线段BC，AD，BD的长．【解答】解：∵AB是⊙O的直径，∴∠ACB=∠ADB=90°，∵AB=10cm，AC=6cm，∴BC=√AB2−AC2=8（cm），∵∠ACB 的平分线CD 交⊙O 于点D ，∴AD̂=BD ̂， ∴AD=BD ，∴∠BAD=∠ABD=45°，∴AD=BD=AB•cos45°=10×√22=5√2（cm ）． 11．如图，AB 是半圆O 的直径，C 、D 是半圆O 上的两点，且OD ∥BC ，OD 与AC 交于点E ．（1）若∠B=70°，求∠CAD 的度数；（2）若AB=4，AC=3，求DE 的长．【解答】解：（1）∵AB 是半圆O 的直径，∴∠ACB=90°，又∵OD ∥BC ，∴∠AEO=90°，即OE ⊥AC ，∠CAB=90°﹣∠B=90°﹣70°=20°，∠AOD=∠B=70°．∵OA=OD ，∴∠DAO=∠ADO=12（180°﹣∠AOD ）=12（180°﹣70°）=55°， ∴∠CAD=∠DAO ﹣∠CAB=55°﹣20°=35°；（2）在直角△ABC 中，BC=√AB 2−AC 2=√42−32=√7．∵OE ⊥AC ，∴AE=EC ，又∵OA=OB ，∴OE=12BC=√72．又∵OD=12AB=2，∴DE=OD ﹣OE=2﹣√72． 12．如图，△ABC 中，∠C=90°，AC=3，AB=5，点O 在BC 边的中线AD 上，⊙O与BC 相切于点E ，且∠OBA=∠OBC ．（1）求证：AB 为⊙O 的切线；（2）求⊙O 的半径；（3）求tan ∠BAD ．【解答】（1）证明：如图，作OF 垂直AB 于点F ，∵⊙O 与BC 相切于点E ，∴OE ⊥BC又∠OBA=∠OBC ，∴OE=OF ，∴AB 为⊙O 的切线（2）解：∵∠C=90°，AC=3，AB=5，∴BC=√AB 2−AC 2=4，又D 为BC 的中点，∴CD=DB=2，∵S △ACD +S △COB +S △AOB =S △ABC设⊙O 的半径为r ，即12AC•CD +12BD•r +12AC ⋅BC ∴6+2r +5r=12∴r=67∴⊙O 的半径为67（3）解：∵∠C=90°，OE ⊥BC ，∴OE ∥AC ，∴Rt △ODE ∽Rt △ADC ，∴OE AC =DE DC， ∴DE=47， ∴BF=BE=187， ∴AF=AB ﹣BF=177， ∴tan ∠BAD=OF AF =617．13．如图，⊙O 的直径AD 长为6，AB 是弦，∠A=30°，CD ∥AB ，且CD=√3．（1）求∠C 的度数；（2）求证：BC 是⊙O 的切线；（3）求阴影部分面积．【解答】（1）解：如图，连接BD ，∵AD 为圆O 的直径，∴∠ABD=90°，∴BD=12AD=3， ∵CD ∥AB ，∠ABD=90°，∴∠CDB=∠ABD=90°，在Rt △CDB 中，tanC=BD CD =√3=√3， ∴∠C=60°；（2）证明：连接OB ，∵OA=OB ，∴∠OBA=∠A=30°，∵CD ∥AB ，∠C=60°，∴∠ABC=180°﹣∠C=120°，∴∠OBC=∠ABC ﹣∠ABO=120°﹣30°=90°，∴OB ⊥BC ，∴BC 为圆O 的切线；（3）解：过点O 作OE ⊥AB ，则有OE=12OA=32， ∵AB=√AD 2−BD 2=√62−32=3√3，∴S △OAB =12AB•OE=12×3√3×32=9√34， ∵∠AOB=180°﹣2∠A=120°，∴S 扇形OAB =120×32π360=3π，则S 阴影=S 扇形OAB ﹣S △AOB =3π﹣9√34．14．如图，在△ABC 中，AB=AC ，AE 是∠BAC 的平分线，∠ABC 的平分线BM 交AE 于点M ，点O 在AB 上，以点O 为圆心，OB 的长为半径的圆经过点M ，交BC 于点G ，交AB 于点F ．（1）求证：AE 为⊙O 的切线；（2）当BC=4，AC=6时，求⊙O 的半径；（3）在（2）的条件下，求线段BG 的长．【解答】（1）证明：连接OM ，如图1，∵BM 是∠ABC 的平分线，∴∠OBM=∠CBM ，∵OB=OM ，∴∠OBM=∠OMB ，∴∠CBM=∠OMB ，∴OM ∥BC ，∵AB=AC ，AE 是∠BAC 的平分线，∴AE ⊥BC ，∴OM ⊥AE ，∴AE 为⊙O 的切线；（2）解：设⊙O 的半径为r ，∵AB=AC=6，AE 是∠BAC 的平分线，∴BE=CE=12BC=2， ∵OM ∥BE ，∴△AOM ∽△ABE ，∴OM BE =AO AB ，即r 2=6−r 6，解得r=32，即设⊙O 的半径为32；（3）解：作OH ⊥BE 于H ，如图，∵OM ⊥EM ，ME ⊥BE ，∴四边形OHEM 为矩形，∴HE=OM=32， ∴BH=BE ﹣HE=2﹣32=12，∵OH⊥BG，∴BH=HG=1 2，∴BG=2BH=1．15．如图，四边形ABCD 内接于⊙O，BD是⊙O的直径，过点A作⊙O的切线AE交CD的延长线于点E，DA平分∠BDE．（1）求证：AE⊥CD；（2）已知AE=4cm，CD=6cm，求⊙O的半径．【解答】（1）证明：连接OA．∵AE是⊙O切线，∴OA⊥AE，∴∠OAE=90°，∴∠EAD+∠OAD=90°，∵∠ADO=∠ADE，OA=OD，∴∠OAD=∠ODA=∠ADE，∴∠EAD+∠ADE=90°，∴∠AED=90°，∴AE⊥CD；（2）解：过点O作OF⊥CD，垂足为点F．∵∠OAE=∠AED=∠OFD=90°，∴四边形AOFE 是矩形．∴OF=AE=4cm ．又∵OF ⊥CD ，∴DF=12CD=3cm ．在Rt △ODF 中，OD=√OF 2+DF 2=5cm ，即⊙O 的半径为5cm ．16．如图，在Rt △ABC 中，∠C=90°，AD 是∠BAC 的平分线，经过A 、D 两点的圆的圆心O 恰好落在AB 上，⊙O 分别与AB 、AC 相交于点E 、F ．（1）判断直线BC 与⊙O 的位置关系并证明；（2）若⊙O 的半径为2，AC=3，求BD 的长度．【解答】解：（1）BC 与⊙O 相切．证明：连接OD ．∵AD 是∠BAC 的平分线，∴∠BAD=∠CAD ．又∵OD=OA ，∴∠OAD=∠ODA ．∴∠CAD=∠ODA ．∴OD ∥AC ．∴∠ODB=∠C=90°，即OD ⊥BC ．又∵BC 过半径OD 的外端点D ，∴BC 与⊙O 相切．（2）由（1）知OD ∥AC ．∴△BDO ∽△BCA ．∴BO BA =DO CA． ∵⊙O 的半径为2，∴DO=OE=2，AE=4．∴BE+2BE+4=23． ∴BE=2．∴BO=4，∴在Rt △BDO 中，BD=√BO 2−OD 2=2√3．17．如图，在△ABC 中，AB=BC ，D 是AC 中点，BE 平分∠ABD 交AC 于点E ，点O 是AB 上一点，⊙O 过B 、E 两点，交BD 于点G ，交AB 于点F ．（1）判断直线AC 与⊙O 的位置关系，并说明理由；（2）当BD=6，AB=10时，求⊙O 的半径．【解答】解：（1）AC 与⊙O 相切．理由如下：连结OE ，如图，∵BE 平分∠ABD ，∴∠OBE=∠DBO ，∵OE=OB ，∴∠OBE=∠OEB ，∴∠OBE=∠DBO ，∴OE ∥BD ，∵AB=BC ，D 是AC 中点，∴BD ⊥AC ，∴OE ⊥AC ，∴AC 与⊙O 相切；（2）设⊙O 半径为r ，则AO=10﹣r ，由（1）知，OE ∥BD ，∴△AOE ∽△ABD ，∴AO AB =OE BD ，即10−r 10=r 6， ∴r=154，即⊙O 半径是154．18．如图，△ABC 内接于⊙O ，∠B=60°，CD 是⊙O 的直径，点P 是CD 延长线上的一点，且AP=AC ．（1）求证：PA 是⊙O 的切线；（2）若AB=4+√3，BC=2√3，求⊙O 的半径．【解答】（1）证明：连接OA ，∵∠B=60°，∴∠AOC=2∠B=120°，又∵OA=OC ，∴∠OAC=∠OCA=30°，又∵AP=AC ，∴∠P=∠ACP=30°，∴∠OAP=∠AOC ﹣∠P=90°，∴OA ⊥PA ，∴PA 是⊙O 的切线；（2）解：过点C 作CE ⊥AB 于点E ．在Rt △BCE 中，∠B=60°，BC=2√3，∴BE=12BC=√3，CE=3， ∵AB=4+√3，∴AE=AB ﹣BE=4，∴在Rt △ACE 中，AC=√AE 2+CE 2=5，∴AP=AC=5．∴在Rt △PAO 中，OA=5√33， ∴⊙O 的半径为5√33．19．如图，已知⊙O 是以AB 为直径的△ABC 的外接圆，过点A 作⊙O 的切线交OC 的延长线于点D ，交BC 的延长线于点E ．（1）求证：∠DAC=∠DCE ；（2）若AB=2，sin ∠D=13，求AE 的长．【解答】解：（1）∵AD 是圆O 的切线，∴∠DAB=90°．∵AB 是圆O 的直径，∴∠ACB=90°．∵∠DAC +∠CAB=90°，∠CAB +∠ABC=90°，∴∠DAC=∠B ．∵OC=OB ，∴∠B=∠OCB ．又∵∠DCE=∠OCB ．∴∠DAC=∠DCE ．（2）∵AB=2，∴AO=1．∵sin ∠D=13， ∴OD=3，DC=2．在Rt △DAO 中，由勾股定理得AD=√OD 2−OA 2=2√2．∵∠DAC=∠DCE ，∠D=∠D ，∴△DEC ∽△DCA ．∴DC AD =DE DC ，即2√2=ED 2．解得：DE=√2．∴AE=AD﹣DE=√2．20．如图，△ABC内接于⊙O，AB是直径，⊙O的切线PC交BA的延长线于点P，OF∥BC交AC于点E，交PC于点F，连接AF；（1）判断AF与⊙O的位置关系并说明理由．（2）若⊙O的半径为4，AF=3，求AC的长．【解答】（1）证明：连接OC，如图所示：∵AB是⊙O直径，∴∠BCA=90°，∵OF∥BC，∴∠AEO=90°，∠1=∠2，∠B=∠3，∴OF⊥AC，∵OC=OA，∴∠B=∠1，∴∠3=∠2，在△OAF和△OCF中，{OA=OC ∠3=∠2 OF=OF，∴△OAF≌△OCF（SAS），∴∠OAF=∠OCF，∵PC是⊙O的切线，∴∠OCF=90°，∴∠OAF=90°，∴FA⊥OA，∴AF是⊙O的切线；（2）∵⊙O的半径为4，AF=3，∠OAF=90°，∴OF=√AF 2+OA 2=√32+42=5∵FA ⊥OA ，OF ⊥AC ，∴AC=2AE ，△OAF 的面积=12AF•OA=12OF•AE ， ∴3×4=5×AE ，解得：AE=125， ∴AC=2AE=245．21．已知四边形ABCD 是平行四边形，以AB 为直径的⊙O 经过点D ，∠DAB=45°．（Ⅰ）如图①，判断CD 与⊙O 的位置关系，并说明理由；（Ⅱ）如图②，E 是⊙O 上一点，且点E 在AB 的下方，若⊙O 的半径为3cm ，AE=5cm ，求点E 到AB 的距离．【解答】解：（1）CD 与圆O 相切．证明：如图①，连接OD ，则∠AOD=2∠DAB=2×45°=90°，∵四边形ABCD 是平行四边形，∴AB ∥DC ．∴∠CDO=∠AOD=90°．∴OD ⊥CD ．∴CD 与圆O 相切．（2）如图②，作EF ⊥AB 于F ，连接BE ，∵AB 是圆O 的直径，∴∠AEB=90°，AB=2×3=6．∵AE=5，∴BE=√AB 2−AE 2=√11，∵sin ∠BAE=BE AB =EF AE． ∴√116=EF 5∴EF=5√116．22．如图，⊙O 为△ABC 的外接圆，BC 为⊙O 的直径，AE 为⊙O 的切线，过点B作BD ⊥AE 于D ．（1）求证：∠DBA=∠ABC ；（2）如果BD=1，tan ∠BAD=12，求⊙O 的半径．【解答】（1）证明：如图，连接OA ，∵AE 为⊙O 的切线，BD ⊥AE ，∴∠DAO=∠EDB=90°，∴∠DBA=∠BAO ，又∵OA=OB ，∴∠ABC=∠BAO ，∴∠DBA=∠ABC ；（2）解：∵BD=1，tan ∠BAD=12， ∴AD=2，∴AB=√22+12=√5，∴cos ∠DBA=√55； ∵∠DBA=∠CBA ，∴BC=AB cos∠CBA =√5√55=5．∴⊙O 的半径为2.5．23．如图，△ABC 中，AB=AC ，点D 为BC 上一点，且AD=DC ，过A ，B ，D 三点作⊙O ，AE 是⊙O 的直径，连结DE ．（1）求证：AC 是⊙O 的切线；（2）若sinC=45，AC=6，求⊙O 的直径．【解答】（1）证明：∵AB=AC ，AD=DC ，∴∠C=∠B ，∠1=∠C ，又∵∠E=∠B ，∴∠1=∠E ，∵AE 是⊙O 的直径，∴∠ADE=90°，∴∠E +∠EAD=90°，∴∠1+∠EAD=90°，即∠EAC=90°，∴AE ⊥AC ，∴AC 是⊙O 的切线；（2）解：过点D 作DF ⊥AC 于点F ，如图，∵DA=DC ，∴CF=12AC=3，在Rt △CDF 中，∵sinC=DF DC =45，设DF=4x ，DC=5x ，∴CF=√CD 2−DF 2=3x ，∴3x=3，解得x=1，∴DC=5，∴AD=5，∵∠ADE=∠DFC=90°，∠E=∠C ，∴△ADE ∽△DFC ，∴AE DC =AD DF ，即AE 5=54，解得AE=254，即⊙O 的直径为254．24．如图，已知三角形ABC 的边AB 是⊙O 的切线，切点为B ．AC 经过圆心O 并与圆相交于点D 、C ，过C 作直线CE 丄AB ，交AB 的延长线于点E ．（1）求证：CB 平分∠ACE ；（2）若BE=3，CE=4，求⊙O 的半径．【解答】（1）证明：如图1，连接OB ，∵AB 是⊙0的切线，∴OB ⊥AB ，∵CE 丄AB ，∴OB ∥CE ，∴∠1=∠3，∵OB=OC ，∴∠1=∠2∴∠2=∠3，∴CB 平分∠ACE ；（2）如图2，连接BD ，∵CE 丄AB ，∴∠E=90°，∴BC=√BE 2+CE 2=√32+42=5，∵CD 是⊙O 的直径，∴∠DBC=90°，∴∠E=∠DBC ，∴△DBC ∽△CBE ，∴CD BC =BC CE， ∴BC 2=CD•CE ，∴CD=524=254，∴OC=12CD=258，∴⊙O的半径=25 8．25．如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P，弦CE平分∠ACB，交AB点F，连接BE．（1）求证：AC平分∠DAB；（2）求证：PC=PF；（3）若tan∠ABC=43，AB=14，求线段PC的长．【解答】（1）证明：∵PD切⊙O于点C，∴OC⊥PD，又∵AD⊥PD，∴OC∥AD，∴∠ACO=∠DAC ．∵OC=OA ，∴∠ACO=∠CAO ，∴∠DAC=∠CAO ，即AC 平分∠DAB ；（2）证明：∵AD ⊥PD ，∴∠DAC +∠ACD=90°．又∵AB 为⊙O 的直径，∴∠ACB=90°．∴∠PCB +∠ACD=90°，∴∠DAC=∠PCB ．又∵∠DAC=∠CAO ，∴∠CAO=∠PCB ．∵CE 平分∠ACB ，∴∠ACF=∠BCF ，∴∠CAO +∠ACF=∠PCB +∠BCF ，∴∠PFC=∠PCF ，∴PC=PF ；（3）解：∵∠PAC=∠PCB ，∠P=∠P ，∴△PAC ∽△PCB ，∴PC PB =AP PC．又∵tan ∠ABC=43， ∴AC BC =43， ∴PC PB =43，设PC=4k ，PB=3k ，则在Rt △POC 中，PO=3k +7，OC=7，∵PC 2+OC 2=OP 2，∴（4k ）2+72=（3k +7）2，∴k=6 （k=0不合题意，舍去）．∴PC=4k=4×6=24．26．如图，AB是⊙O的直径，C是AB延长线上一点，CD与⊙O相切于点E，AD ⊥CD于点D．（1）求证：AE平分∠DAC；（2）若AB=4，∠ABE=60°．①求AD的长；②求出图中阴影部分的面积．【解答】（1）证明：连接OE，如图，∵CD与⊙O相切于点E，∴OE⊥CD，∵AD⊥CD，∴OE∥AD，∴∠DAE=∠AEO，∵AO=OE，∴∠AEO=∠OAE，∴∠OAE=∠DAE，∴AE平分∠DAC；（2）解：①∵AB是直径，∴∠AEB=90°，∠ABE=60°．∴∠EAB=30°，在Rt △ABE 中，BE=12AB=12×4=2， AE=√3BE=2√3，在Rt △ADE 中，∠DAE=∠BAE=30°，∴DE=12AE=√3， ∴AD=√3DE=√3×√3=3；②∵OA=OB ，∴∠AEO=∠OAE=30°，∴∠AOE=120°，∴阴影部分的面积=S 扇形AOE ﹣S △AOE=S 扇形AOE ﹣12S △ABE =120⋅π⋅22360﹣12•12•2√3•2 =43π﹣√3．27．如图，AB 是⊙O 的直径，点C 是⊙O 上一点，AD 和过点C 的切线互相垂直，垂足为D ，直线DC 与AB 的延长线相交于P ．弦CE 平分∠ACB ，交直径AB 于点F ，连结BE ．（1）求证：AC 平分∠DAB ；（2）探究线段PC ，PF 之间的大小关系，并加以证明；（3）若tan ∠PCB=34，BE=5√2，求PF 的长．【解答】解：（1）连接OC．∵OA=OC，∴∠OAC=∠OCA．∵PC是⊙O的切线，AD⊥CD，∴∠OCP=∠D=90°，∴OC∥AD．∴∠CAD=∠OCA=∠OAC．即AC平分∠DAB．（2）PC=PF．证明：∵AB是直径，∴∠ACB=90°，∴∠PCB+∠ACD=90°又∵∠CAD+∠ACD=90°，∴∠CAB=∠CAD=∠PCB．又∵∠ACE=∠BCE，∠PFC=∠CAB+∠ACE，∠PCF=∠PCB+∠BCE．∴∠PFC=∠PCF．∴PC=PF．（3）连接AE．∵∠ACE=∠BCE，̂=BÊ，∴AE∴AE=BE．又∵AB是直径，∴∠AEB=90°．AB=√2BE=10，∴OB=OC=5．∵∠PCB=∠PAC ，∠P=∠P ，∴△PCB ∽△PAC ．∴PB PC =BC CA． ∵tan ∠PCB=tan ∠CAB=34． ∴PB PC =BC CA =34．设PB=3x ，则PC=4x ，在Rt △POC 中，（3x +5）2=（4x ）2+52，解得x 1=0，x 2=307．∵x ＞0，∴x =307，∴PF=PC=1207．28．在△ABC 中，∠ACB=90°，经过点C 的⊙O 与斜边AB 相切于点P ．（1）如图①，当点O 在AC 上时，试说明2∠ACP=∠B ；（2）如图②，AC=8，BC=6，当点O 在△ABC 外部时，求CP 长的取值范围．【解答】解：（1）当点O 在AC 上时，OC 为⊙O 的半径，∵BC ⊥OC ，且点C 在⊙O 上，∴BC 与⊙O 相切．∵⊙O 与AB 边相切于点P ，∴BC=BP，∴∠BCP=∠BPC=180°−∠B2，∵∠ACP+∠BCP=90°，∴∠ACP=90°﹣∠BCP=90°﹣180°−∠B2=12∠B．′即2∠ACP=∠B；（2）在△ABC中，∠ACB=90°，AB=√AC2+BC2=10，如图，当点O在CB上时，OC为⊙O的半径，∵AC⊥OC，且点C在⊙O上，∴AC与⊙O相切，连接OP、AO，∵⊙O与AB边相切于点P，∴OP⊥AB，设OC=x，则OP=x，OB=BC﹣OC=6﹣x，∵AC=AP，∴BP=AB﹣AP=10﹣8=2，在△OPA中，∠OPA=90°，根据勾股定理得：OP2+BP2=OB2，即x2+22=（6﹣x）2，解得：x=8 3，在△ACO中，∠ACO=90°，AC2+OC2=AO2，∴AO=√AC2+OC2=83√10．∵AC=AP，OC=OP，∴AO垂直平分CP，∴根据面积法得：CP=2×AC⋅OCAO=85√10，则符合条件的CP长大于85√10．由题意可知，当点P与点A重合时，CP最长，综上，当点O在△ABC外时，8√105＜CP≤8．。

2024年中考数学复习重难点题型训练—圆的相关证明与计算(含答案解析)

2024年中考数学复习重难点题型训练—圆的相关证明与计算（含答案解析）类型一基本性质有关的1.(2022·湖南省郴州市)如图，在△ABC中，AB=AC.以AB为直径的⊙O与线段BC交于点D，过点D作DE⊥AC，垂足为E，ED的延长线与AB的延长线交于点P．(1)求证：直线PE是⊙O的切线；(2)若⊙O的半径为6，∠P=30°，求CE的长．【答案】(1)连接OD，根据AB=AC，OB=OD，得∠ACB=∠ODB，从而OD//AC，由DE⊥AC，即可得PE⊥OD，故PE是⊙O的切线；(2)连接AD，连接OD，由DE⊥AC，∠P=30°，得∠PAE=60°，又AB=AC，可得△ABC 是等边三角形，即可得BC=AB=12，∠C=60°，而AB是⊙O的直径，得∠ADB=90°，可得BD=CD=12BC=6，在Rt△CDE中，即得CE的长是3．本题考查圆的综合应用，涉及圆的切线，等腰三角形性质及应用，含特殊角的直角三角形三边关系等，解题的关键是判定△ABC是等边三角形．2.(2022·辽宁省盘锦市)如图，△ABC内接于⊙O，∠ABC=45°，连接AO并延长交⊙O于点D，连接BD，过点C作CE//AD与BA的延长线交于点E．(1)求证：CE与⊙O相切；(2)若AD=4，∠D=60°，求线段AB，BC的长．【答案】(1)连接OC，根据圆周角定理得∠AOC=90°，再根据AD//EC，可得∠OCE=90°，从而证明结论；(2)过点A作AF⊥EC交EC于F，由AD是圆O的直径，得∠ABD=90°，又AD=4，60°，即得AB=3BD=23，根据∠ABC=45°，知△ABF是等腰直角三角形，AF=BF=2AB= 6，又△AOC是等腰直角三角形，OA=OC=2，得AC=22，故CF=AC2−AF2=2，从而BC=BF+CF=6+2．本题主要考查了圆周角定理，切线的判定与性质，含30°角的直角三角形的性质等知识，作辅助线构造特殊的直角三角形是解题的关键．3.（2021·山东临沂市·中考真题）如图，已知在⊙O中，＝＝，OC与AD相交于点AB BC CDE．求证：（1）AD∥BC（2）四边形BCDE为菱形．【答案】（1）见解析；（2）见解析【分析】（1）连接BD ，根据圆周角定理可得∠ADB=∠CBD ，根据平行线的判定可得结论；（2）证明△DEF ≌△BCF ，得到DE=BC ，证明四边形BCDE 为平行四边形，再根据 BCCD =得到BC=CD ，从而证明菱形．【详解】解：（1）连接BD ，∵ AB BCCD ==，∴∠ADB=∠CBD ，∴AD ∥BC ；（2）连接CD ，∵AD ∥BC ，∴∠EDF=∠CBF ，∵ BCCD =，∴BC=CD ，∴BF=DF ，又∠DFE=∠BFC ，∴△DEF ≌△BCF （ASA ），∴DE=BC ，∴四边形BCDE 是平行四边形，又BC=CD ，∴四边形BCDE 是菱形．【点睛】本题考查了垂径定理，圆周角定理，弧、弦、圆心角的关系，全等三角形的判定和性质，菱形的判定，解题的关键是合理运用垂径定理得到BF=DF ．4.（2021·四川南充市·中考真题）如图，A ，B 是O 上两点，且AB OA =，连接OB 并延长到点C ，使BC OB =，连接AC ．（1）求证：AC 是O 的切线．（2）点D ，E 分别是AC ，OA 的中点，DE 所在直线交O 于点F ，G ，4OA =，求GF 的长．【答案】（1）见解析；（2）【分析】（1）先证得△AOB 为等边三角形，从而得出∠OAB=60°，利用三角形外角的性质得出∠C=∠CAB=30°，由此可得∠OAC=90°即可得出结论；（2）过O 作OM ⊥DF 于M ，DN ⊥OC 于N ，利用勾股定理得出AC=30°的直角三角形的性质得出DN ，再根据垂径定理和勾股定理即可求出GF 的长．【详解】（1）证明：∵AB=OA ，OA=OB∴AB=OA=OB∴△AOB 为等边三角形∴∠OAB=60°，∠OBA=60°∵BC=OB∴BC=AB∴∠C=∠CAB又∵∠OBA=60°=∠C+∠CAB∴∠C=∠CAB=30°∴∠OAC=∠OAB+∠CAB=90°∴AC 是⊙O 的切线；（2）∵OA=4∴OB=AB=BC=4∴OC=8∴AC=∵D 、E 分别为AC 、OA 的中点，∴OE//BC ，DC=过O 作OM ⊥DF 于M ，DN ⊥OC 于N则四边形OMDN 为矩形∴DN=OM在Rt △CDN 中，∠C=30°，∴DN=12DC=∴OM=3连接OG ，∵OM ⊥GF∴GF=2MG=222OG OM -=()22243-=213【点睛】本题考查了切线的判定、垂径定理、等边三角形的性质和判定，熟练掌握相关的知识是解题的关键．5.（2021·安徽中考真题）如图，圆O 中两条互相垂直的弦AB ，CD 交于点E ．（1）M 是CD 的中点，OM ＝3，CD ＝12，求圆O 的半径长；（2）点F 在CD 上，且CE ＝EF ，求证：AF BD ⊥．【答案】（1）35；（2）见解析．【分析】（1）根据M 是CD 的中点，OM 与圆O 直径共线可得OM CD ⊥，OM 平分CD ，则有6MC =，利用勾股定理可求得半径的长；（2）连接AC ，延长AF 交BD 于G ，根据CE EF =，AE FC ⊥，可得AF AC =，12∠=∠，利用圆周角定理可得2D ∠=∠，可得1D ∠=∠，利用直角三角形的两锐角互余，可证得90AGB ∠=︒，即有AF BD ⊥．【详解】（1）解：连接OC ，∵M 是CD 的中点，OM 与圆O 直径共线∴OM CD ⊥，OM 平分CD ，90OMC ∴∠=︒12CD = 6MC ∴=．在Rt OMC △中．OC ===∴圆O 的半径为（2）证明：连接AC ，延长AF 交BD 于G ．CE EF = ，AE FC⊥AF AC∴=又CE EF= 12∠∠∴= BCBC = 2D∴∠=∠1D∴∠=∠中在Rt BED∠+∠=︒90D B∴∠+∠=︒B190AGB∴∠=︒90∴⊥AF BD【点睛】本题考查了垂径定理，圆周角定理，直角三角形的两锐角互余，勾股定理等知识点，熟练应用相关知识点是解题的关键．∠是 AD所对的圆周角，6.（2021·浙江中考真题）如图，已知AB是⊙O的直径，ACD∠=︒．30ACD∠的度数；（1）求DABAB=，求DF的（2）过点D作DE AB⊥，垂足为E，DE的延长线交⊙O于点F．若4长．【答案】（1）60︒；（2）23【分析】（1）连结BD ，根据圆周角性质，得B ACD ∠=∠；根据直径所对圆周角为直角、直角三角形两锐角互余的性质计算，即可得到答案；（2）根据含30°角的直角三角形性质，得12AD AB =；根据垂径定理、特殊角度三角函数的性质计算，即可得到答案．【详解】（1）连结BD ，30ACD ∠=︒30B ACD \Ð=Ð=°AB Q 是O 的直径，90ADB ∴∠=︒，9060DAB B ∴∠=︒-∠=︒（2）90ADB ∠=︒ ，30B ∠=︒，4AB =∴122AD AB ==60DAB ∠=︒ ，DE AB ⊥，且AB 是直径sin 60EF DE AD︒∴===2DF DE =∴=．【点睛】本题考查了圆、含30°角的直角三角形、三角函数的知识；解题的关键是熟练掌握圆周角、垂径定理、含30°角的直角三角形、三角函数、直角三角形两锐角互余的性质，从而完成求解．7.（2021·湖南中考真题）如图，ABC 是O 的内接三角形，AC 是O 的直径，点D 是 BC的中点，//DE BC 交AC 的延长线于点E ．（1）求证：直线DE 与O 相切；（2）若O 的直径是10，45A ∠=︒，求CE 的长．【答案】（1）见解析；（2）5CE =．【分析】（1）连接OD ，由点D 是 BC的中点得OD ⊥BC ，由DE//BC 得OD ⊥DE ，由OD 是半径可得DE 是切线；（2）证明△ODE 是等腰直角三角形，可求出OE 的长，从而可求得结论．【详解】解：（1）连接OD 交BC 于点F ，如图，∵点D 是 BC的中点，∴OD ⊥BC ，∵DE//BC∴OD ⊥DE∵OD 是O 的半径∴直线DE 与O 相切；（2）∵AC 是O 的直径，且AB=10,∴∠ABC=90°，152OC OA AB ===∵OD ⊥BC∴∠OFC=90°∴OD//AB 45BAC ∠=︒∴45DOE ∠=︒∵90ODE ∠=︒∴45OED ∠=∴5DE OD OC ===由勾股定理得，OE =∴5CE OE OC =-=．【点睛】此题主要考查了切线的判定与性质的综合运用，熟练掌握切线的判定与性质是解答此题的关键．8.（2021·湖南张家界市·中考真题）如图，在Rt AOB 中，90∠=︒ABO ，30OAB ∠=︒，以点O 为圆心，OB 为半径的圆交BO 的延长线于点C ，过点C 作OA 的平行线，交O 于点D ，连接AD ．（1）求证：AD 为O 的切线；（2）若2OB =，求弧CD 的长．【答案】（1）见解析；（2）23π【分析】（1）连接OB ，先根据直角三角形的性质得到∠AOB=60°，再运用平行线的性质结合已知条件可得60AOD ∠=︒，再证明AOB AOD △≌△可得90ADO ABO ∠=∠=︒即可；（2）先求出∠COD ，然后再运用弧长公式计算即可．【详解】（1）证明：连接OD∵30OAB ∠=︒，90B ∠=︒∴60AOB ∠=︒又∵//CD AO∴60C AOB ∠=∠=︒∴2120BOD C ∠=∠=︒∴60AOD ∠=︒又∵,OB OD AO AO==∴()AOB AOD SAS ≌∴90ADO ABO ∠=∠=︒又∵点D 在O 上∴AD 是O 的切线；（2）∵120BOD ∠=︒∴60COD ∠=︒∴602223603l ππ=⨯⨯=．【点睛】本题主要考查了圆的切线的证明、弧长公式等知识点，掌握圆的切线的证明方法成为解答本题的关键．9.（2020•齐齐哈尔）如图，AB 为⊙O 的直径，C 、D 为⊙O 上的两个点，AC=CD =DB ，连接AD ，过点D 作DE ⊥AC 交AC 的延长线于点E ．（1）求证：DE 是⊙O 的切线．（2）若直径AB ＝6，求AD 的长．【分析】（1）连接OD ，根据已知条件得到∠BOD =13×180°＝60°，根据等腰三角形的性质得到∠ADO＝∠DAB＝30°，得到∠EDA＝60°，求得OD⊥DE，于是得到结论；（2）连接BD，根据圆周角定理得到∠ADB＝90°，解直角三角形即可得到结论．【解析】（1）证明：连接OD，=CD =DB ，∵AC∴∠BOD=13×180°＝60°，=DB ，∵CD∴∠EAD＝∠DAB=12∠BOD＝30°，∵OA＝OD，∴∠ADO＝∠DAB＝30°，∵DE⊥AC，∴∠E＝90°，∴∠EAD+∠EDA＝90°，∴∠EDA＝60°，∴∠EDO＝∠EDA+∠ADO＝90°，∴OD⊥DE，∴DE是⊙O的切线；（2）解：连接BD，∵AB为⊙O的直径，∴∠ADB＝90°，∵∠DAB＝30°，AB＝6，∴BD=12AB＝3，∴AD=62−32=33．10.（2020•深圳）如图，AB为⊙O的直径，点C在⊙O上，AD与过点C的切线互相垂直，垂足为D．连接BC并延长，交AD的延长线于点E．（1）求证：AE＝AB；（2）若AB＝10，BC＝6，求CD的长．【分析】（1）证明：连接AC、OC，如图，根据切线的性质得到OC⊥CD，则可判断OC∥AD，所以∠OCB＝∠E，然后证明∠B＝∠E，从而得到结论；（2）利用圆周角定理得到∠ACB＝90°，则利用勾股定理可计算出AC＝8，再根据等腰三角形的性质得到CE＝BC＝6，然后利用面积法求出CD的长．【解析】（1）证明：连接AC、OC，如图，∵CD为切线，∴OC⊥CD，∴CD⊥AD，∴OC∥AD，∴∠OCB＝∠E，∵OB＝OC，∴∠OCB＝∠B，∴∠B＝∠E，∴AE＝AB；（2）解：∵AB为直径，∴∠ACB＝90°，∴AC=102−62=8，∵AB＝AE＝10，AC⊥BE，∴CE＝BC＝6，∵12CD•AE=12AC•CE，∴CD=6×810=245．11.（2020•陕西）如图，△ABC是⊙O的内接三角形，∠BAC＝75°，∠ABC＝45°．连接AO并延长，交⊙O于点D，连接BD．过点C作⊙O的切线，与BA的延长线相交于点E．（1）求证：AD∥EC；（2）若AB＝12，求线段EC的长．【分析】（1）连接OC，由切线的性质可得∠OCE＝90°，由圆周角定理可得∠AOC＝90°，可得结论；（2）过点A作AF⊥EC交EC于F，由锐角三角函数可求AD＝83，可证四边形OAFC是正方形，可得CF＝AF＝43，由锐角三角函数可求EF＝12，即可求解．【解析】证明：（1）连接OC，∵CE与⊙O相切于点C，∴∠OCE＝90°，∵∠ABC＝45°，∴∠AOC＝90°，∵∠AOC+∠OCE＝180°，∴∴AD∥EC（2）如图，过点A作AF⊥EC交EC于F，∵∠BAC＝75°，∠ABC＝45°，∴∠ACB＝60°，∴∠D＝∠ACB＝60°，∴sin∠ADB=AB AD==83，∴AD=∴OA＝OC＝43，∵AF⊥EC，∠OCE＝90°，∠AOC＝90°，∴四边形OAFC是矩形，又∵OA＝OC，∴四边形OAFC是正方形，∴CF＝AF＝43，∵∠BAD＝90°﹣∠D＝30°，∴∠EAF＝180°﹣90°﹣30°＝60°，∵tan∠EAF=EF AF=3，∴EF=3AF＝12，∴CE＝CF+EF＝12+43．类型二与三角形全等、相似有关的12.(2022·辽宁省营口市)如图，在△ABC中，AB=AC，以AB为直径作⊙O与AC交于点E，过点A作⊙O的切线交BC的延长线于点D．(1)求证：∠D=∠EBC；(2)若CD=2BC，AE=3，求⊙O的半径．【答案】(1)根据切线的性质可得∠DAO=90°，从而可得∠D+∠ABD=90°，根据直径所对的圆周角是直角可得∠BEC=90°，从而可得∠ACB+∠EBC=90°，然后利用等腰三角形的性质可得∠ACB=∠ABC，从而利用等角的余角相等即可解答；(2)根据已知可得BD=3BC，然后利用(1)的结论可得△DAB∽△BEC，从而利用相似三角形的性质可得AB=3EC，然后根据AB=AC，进行计算即可解答．本题考查了圆周角定理，等腰三角形的性质，切线的性质，相似三角形的判定与性质，熟练掌握切线的性质，以及相似三角形的判定与性质是解题的关键．13.（2022·北部湾）如图，在△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作DE⊥AB，垂足为E，延长BA交⊙O于点F.（1）求证：DE是⊙O的切线（2）若AE DE=23，AF=10，求⊙O的半径.【答案】（1）证明：连接OD；∵OD=OC，∴∠C=∠ODC，∵AB=AC，∴∠B=∠C，∴∠B=∠ODC，∴OD∥AB，∴∠ODE=∠DEB；∵DE⊥AB，∴∠DEB=90°，∴∠ODE=90°，即DE⊥OD，∴DE是⊙O的切线（2）解：连接CF，由（1）知OD⊥DE，∵DE⊥AB，∴OD∥AB，∵OA=OC，∴BD=CD，即OD是△ABC的中位线，∵AC是⊙O的直径，∴∠CFA=90°，∵DE⊥AB，∴∠BED=90°，∴∠CFA=∠BED=90°，∴DE∥CF，∴BE=EF，即DE是△FBC的中位线，∴CF=2DE，∵AE DE=23，∴设AE=2x，DE=3k，CF=6k，∵AF=10，∴BE=EF=AE+AF=2k+10，∴AC=BA=EF+AE=4k+10，在Rt△ACF中，由勾股定理，得AC2=AF2+CF2，即(4k+10)2=102+(6k)2，解得：k=4，∴AC=4k+10=4×4+10=26，∴OA=13，即⊙O的半径为13.【知识点】平行线的判定与性质；等腰三角形的性质；圆周角定理；切线的判定；三角形的中位线定理【解析】【分析】（1）连接OD ，根据等腰三角形的性质可得∠C=∠ODC ，∠B=∠C ，则∠B=∠ODC ，推出OD ∥AB ，由平行线的性质可得∠ODE=∠DEB=90°，即DE ⊥OD ，据此证明；（2）连接CF ，由（1）知OD ⊥DE ，则OD ∥AB ，易得OD 是△ABC 的中位线，根据圆周角定理可得∠CFA=90°，根据垂直的概念可得∠BED=90°，则DE ∥CF ，推出DE 是△FBC的中位线，得CF=2DE ，设AE=2x ，DE=3k ，CF=6k ，则BE=EF=2k+10，AC=BA=4k+10，根据勾股定理可得k 的值，然后求出AC 、OA ，据此可得半径.14.（2021·江苏无锡市·中考真题）如图，四边形ABCD 内接于O ，AC 是O 的直径，AC 与BD 交于点E ，PB 切O 于点B ．（1）求证：PBA OBC ∠=∠；（2）若20PBA Ð=°，40ACD ∠=︒，求证：OAB CDE V V ∽．【答案】（1）见详解；（2）见详解【分析】（1）由圆周角定理的推论，可知∠ABC=90°，由切线的性质可知∠OBP=90°，进而即可得到结论；（2）先推出20OCB OBC ∠=∠=︒，从而得∠AOB=40°，继而得∠OAB=70°，再推出∠CDE=70°，进而即可得到结论．【详解】证明：（1）∵AC 是O 的直径，∴∠ABC=90°，∵PB 切O 于点B ，∴∠OBP=90°，∴90PBA ABO OBC ABO ∠+∠=∠+∠=︒，∴PBA OBC ∠=∠；（2）∵20PBA Ð=°，PBA OBC ∠=∠，∴20OBC ∠=︒，∵OB=OC ，∴20OCB OBC ∠=∠=︒，∴∠AOB=20°+20°=40°，∵OB=OA ，∴∠OAB=∠OBA=(180°-40°)÷2=70°，∴∠ADB=12∠AOB=20°，∵AC 是O 的直径，∴∠ADC=90°，∴∠CDE=90°-20°=70°，∴∠CDE=∠OAB ，∵40ACD ∠=︒，∴40ACD AOB ∠=∠=︒，∴OAB CDE V V ∽．【点睛】本题主要考查圆的性质以及相似三角形的判定定理，掌握圆周角定理的推论，相似三角形的判定定理，切线的性质定理，是解题的关键．15.（2020•衢州）如图，△ABC 内接于⊙O ，AB 为⊙O 的直径，AB ＝10，AC ＝6，连结OC ，弦AD分别交OC，BC于点E，F，其中点E是AD的中点．（1）求证：∠CAD＝∠CBA．（2）求OE的长．【分析】（1）利用垂径定理以及圆周角定理解决问题即可．（2）证明△AEC∽△BCA，推出CE AC=AC AB，求出EC即可解决问题．【解析】（1）证明：∵AE＝DE，OC是半径，=CD ，∴AC∴∠CAD＝∠CBA．（2）解：∵AB是直径，∴∠ACB＝90°，∵AE＝DE，∴OC⊥AD，∴∠AEC＝90°，∴∠AEC＝∠ACB，∴△AEC∽△BCA，∴CE AC=AC AB，∴CE6=610，∴CE＝3.6，∵OC=12AB＝5，∴OE＝OC﹣EC＝5﹣3.6＝1.4．16.（2020•铜仁市）如图，AB是⊙O的直径，C为⊙O上一点，连接AC，CE⊥AB于点E，D 是直径AB延长线上一点，且∠BCE＝∠BCD．（1）求证：CD是⊙O的切线；（2）若AD＝8，BE CE=12，求CD的长．【分析】（1）连接OC，根据圆周角定理得到∠ACB＝90°，根据余角的性质得到∠A＝∠ECB，求得∠A＝∠BCD，根据等腰三角形的性质得到∠A＝∠ACO，等量代换得到∠ACO＝∠BCD，求得∠DCO＝90°，于是得到结论；（2）设BC＝k，AC＝2k，根据相似三角形的性质即可得到结论．【解析】（1）证明：连接OC，∵AB是⊙O的直径，∴∠ACB＝90°，∵CE⊥AB，∴∠CEB＝90°，∴∠ECB+∠ABC＝∠ABC+∠CAB＝90°，∴∠A＝∠ECB，∵∠BCE＝∠BCD，∴∠A＝∠BCD，∵OC＝OA，∴∠A＝∠ACO，∴∠ACO＝∠BCD，∴∠ACO+∠BCO＝∠BCO+∠BCD＝90°，∴∠DCO＝90°，∴CD是⊙O的切线；（2）解：∵∠A＝∠BCE，∴tanA=BC AC=tan∠BCE=BE CE=12，设BC＝k，AC＝2k，∵∠D＝∠D，∠A＝∠BCD，∴△ACD∽△CBD，∴BC AC=CD AD=12，∵AD＝8，∴CD＝4．17.（2020•衡阳）如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，过点A和点D的圆，圆心O在线段AB上，⊙O交AB于点E，交AC于点F．（1）判断BC与⊙O的位置关系，并说明理由；（2）若AD＝8，AE＝10，求BD的长．【分析】（1）连接OD，根据平行线判定推出OD∥AC，推出OD⊥BC，根据切线的判定推出即可；（2）连接DE，根据圆周角定理得到∠ADE＝90°，根据相似三角形的性质得到AC=325，根据勾股定理得到CD=AD2−AC2==根据相似三角形的性质即可得到结论．【解析】（1）BC与⊙O相切，理由：连接OD，∵OA＝OD，∴∠OAD＝∠ODA，∵AD平分∠BAC，∴∠BAD＝∠CAD，∴∠ODA＝∠CAD，∴OD∥AC，∵∠C＝90°，∴∠ODC＝90°，∴OD⊥BC，∵OD为半径，∴BC是⊙O切线；（2）连接DE，∵AE是⊙O的直径，∴∠ADE＝90°，∵∠C＝90°，∴∠ADE＝∠C，∵∠EAD＝∠DAC，∴△ADE∽△ACD，∴AE AD=AD AC，108=8AC，∴AC=325，∴CD=AD2−AC2==245，∵OD⊥BC，AC⊥BC，∴△OBD∽△ABC，∴OD AC=BD BC，∴5325=BD BD+245，∴BD=1207．18.（2020•遵义）如图，AB是⊙O的直径，点C是⊙O上一点，∠CAB的平分线AD交BC 于点D，过点D作DE∥BC交AC的延长线于点E．（1）求证：DE是⊙O的切线；（2）过点D作DF⊥AB于点F，连接BD．若OF＝1，BF＝2，求BD的长度．【分析】（1）连接OD，由等腰三角形的性质及角平分线的性质得出∠ADO＝∠DAE，从而OD∥AE，由DE∥BC得∠E＝90°，由两直线平行，同旁内角互补得出∠ODE＝90°，由切线的判定定理得出答案；（2）先由直径所对的圆周角是直角得出∠ADB＝90°，再由OF＝1，BF＝2得出OB的值，进而得出AF和BA的值，然后证明△DBF∽△ABD，由相似三角形的性质得比例式，从而求得BD2的值，求算术平方根即可得出BD的值．【解析】（1）连接OD，如图：∵OA＝OD，∴∠OAD＝∠ADO，∵AD平分∠CAB，∴∠DAE＝∠OAD，∴∠ADO＝∠DAE，∴OD∥AE，∵DE∥BC，∴∠E＝90°，∴∠ODE＝180°﹣∠E＝90°，∴DE是⊙O的切线；（2）∵AB是⊙O的直径，∴∠ADB＝90°，∵OF＝1，BF＝2，∴OB＝3，∴AF＝4，BA＝6．∵DF⊥AB，∴∠DFB＝90°，∴∠ADB＝∠DFB，又∵∠DBF＝∠ABD，∴△DBF∽△ABD，∴BD BA=BF BD，∴BD2＝BF•BA＝2×6＝12．∴BD＝23．19.（2019•陕西）如图，⊙O的半径OA＝6，过点A作⊙O的切线AP，且AP＝8，连接PO 并延长，与⊙O交于点B、D，过点B作BC∥OA，并与⊙O交于点C，连接AC、CD．（1）求证：DC∥AP；（2）求AC的长．【分析】（1）根据切线的性质得到∠OAP＝90°，根据圆周角定理得到∠BCD＝90°，根据平行线的性质和判定定理即可得到结论；（2）根据勾股定理和相似三角形的判定和性质定理即可得到结论．【解析】（1）证明：∵AP是⊙O的切线，∴∠OAP＝90°，∵BD是⊙O的直径，∴∠BCD＝90°，∵OA∥CB，∴∠AOP＝∠DBC，∴∠BDC＝∠APO，∴DC∥AP；（2）解：∵AO∥BC，OD＝OB，∴延长AO交DC于点E，则AE⊥DC，OE=12BC，CE=12CD，在Rt△AOP中，OP=62+82=10，由（1）知，△AOP∽△CBD，∴DB OP=BC OA=DC AP，即1210=BC6=DC8，∴BC=365，DC=485，∴OE=185，CE=245，在Rt△AEC中，AC=AE2+CE2==20（2021·云南中考真题）如图，AB 是O 的直径，点C 是O 上异于A 、B 的点，连接AC 、BC ，点D 在BA 的延长线上，且DCA ABC ∠=∠，点E 在DC 的延长线上，且BE DC ⊥．（1）求证：DC 是O 的切线：（2）若2,33OA BE OD ==，求DA 的长．【答案】（1）见解析；（2）910【分析】（1）连接OC ，根据圆周角定理得到∠ACB=90°，根据等量代换得到∠DCO=90°，即可证明DC 是圆O 的切线；（2）根据已知得到OA=2DA ，证明△DCO ∽△DEB ，得到DO CO DB EB =，可得DA=310EB ，即可求出DA 的长．【详解】解：（1）如图，连接OC ，由题意可知：∠ACB 是直径AB 所对的圆周角，∴∠ACB=90°，∵OC ，OB 是圆O 的半径，∴OC=OB ，∴∠OCB=∠ABC ，又∵∠DCA=∠ABC ，∴∠DCA=∠OCB ，∴∠DCO=∠DCA+∠ACO=∠OCB+∠ACO=∠ACB=90°，∴OC ⊥DC ，又∵OC 是圆O 的半径，∴DC 是圆O 的切线；（2）∵23OA OD =，∴23OA OA DA =+，化简得OA=2DA ，由（1）知，∠DCO=90°，∵BE ⊥DC ，即∠DEB=90°，∴∠DCO=∠DEB ，∴OC ∥BE ，∴△DCO ∽△DEB ，∴DO CO DB EB =，即33255DA OA DA DA DA OA OB DA EB+===++，∴DA=310EB ，∵BE=3，∴DA=310EB=3931010⨯=，经检验：DA=910是分式方程的解，∴DA=910．【点睛】本题考查了圆周角定理，相似三角形的判定和性质，切线的判定，正确的作出辅助线，证明切线，得到相似三角形是解题的关键．21.（2021·江苏扬州市·中考真题）如图，四边形ABCD 中，//AD BC ，90BAD ∠=︒，CB CD =，连接BD ，以点B 为圆心，BA 长为半径作B ，交BD 于点E ．（1）试判断CD 与B 的位置关系，并说明理由；（2）若AB =，60BCD ∠=︒，求图中阴影部分的面积．【答案】（1）相切，理由见解析；（2）π-【分析】（1）过点B 作BF ⊥CD ，证明△ABD ≌△FBD ，得到BF=BA ，即可证明CD 与圆B 相切；（2）先证明△BCD 是等边三角形，根据三线合一得到∠ABD=30°，求出AD ，再利用S △ABD -S 扇形ABE 求出阴影部分面积．【详解】解：（1）过点B 作BF ⊥CD ，∵AD ∥BC ，∴∠ADB=∠CBD ，∵CB=CD ，∴∠CBD=∠CDB ，∴∠ADB=∠CDB ，又BD=BD ，∠BAD=∠BFD=90°，∴△ABD ≌△FBD （AAS ），∴BF=BA ，则点F 在圆B 上，∴CD 与圆B 相切；（2）∵∠BCD=60°，CB=CD ，∴△BCD 是等边三角形，∴∠CBD=60°∵BF ⊥CD ，∴∠ABD=∠DBF=∠CBF=30°，∴∠ABF=60°，∵AB=BF=，∴AD=DF=tan30AB ⋅︒=2，∴阴影部分的面积=S △ABD -S 扇形ABE=(230122360π⨯⨯⨯-=π-．【点睛】本题考查了切线的判定，全等三角形的判定和性质，等边三角形的判定和性质，扇形面积，三角函数的定义，题目的综合性较强，难度不小，解题的关键是正确做出辅助线．22.（2020•上海）如图，△ABC中，AB＝AC，⊙O是△ABC的外接圆，BO的延长线交边AC 于点D．（1）求证：∠BAC＝2∠ABD；（2）当△BCD是等腰三角形时，求∠BCD的大小；（3）当AD＝2，CD＝3时，求边BC的长．【分析】（1）连接OA．利用垂径定理以及等腰三角形的性质解决问题即可．（2）分三种情形：①若BD＝CB，则∠C＝∠BDC＝∠ABD+∠BAC＝3∠ABD．②若CD＝CB，则∠CBD＝∠CDB＝3∠ABD．③若DB＝DC，则D与A重合，这种情形不存在．分别利用三角形内角和定理构建方程求解即可．（3）如图3中，作AE∥BC交BD的延长线于E．则AE BC=AD DC=23，推出AO OH=AE BH=43，设OB＝OA＝4a，OH＝3a，根据BH2＝AB2﹣AH2＝OB2﹣OH2，构建方程求出a即可解决问题．【解析】（1）证明：连接OA．A∵AB＝AC，=AC ，∴AB∴OA⊥BC，∴∠BAO＝∠CAO，∵OA＝OB，∴∠ABD＝∠BAO，∴∠BAC＝2∠BAD．（2）解：如图2中，延长AO交BC于H．①若BD＝CB，则∠C＝∠BDC＝∠ABD+∠BAC＝3∠ABD，∵AB＝AC，∴∠ABC＝∠C，∴∠DBC＝2∠ABD，∵∠DBC+∠C+∠BDC＝180°，∴8∠ABD＝180°，∴∠C＝3∠ABD＝67.5°．②若CD＝CB，则∠CBD＝∠CDB＝3∠ABD，∴∠C ＝4∠ABD ，∵∠DBC+∠C+∠CDB ＝180°，∴10∠ABD ＝180°，∴∠BCD ＝4∠ABD ＝72°．③若DB ＝DC ，则D 与A 重合，这种情形不存在．综上所述，∠C 的值为67.5°或72°．（3）如图3中，作AE ∥BC 交BD 的延长线于E ．则AE BC =AD DC =23，∴AO OH =AE BH =43，设OB ＝OA ＝4a ，OH ＝3a ，∵BH 2＝AB 2﹣AH 2＝OB 2﹣OH 2，∴25﹣49a 2＝16a 2﹣9a 2，∴a 2=2556，∴BH =∴BC ＝2BH =23.（2021·云南中考真题）如图，AB 是O 的直径，点C 是O 上异于A 、B 的点，连接AC 、BC ，点D 在BA 的延长线上，且DCA ABC ∠=∠，点E 在DC 的延长线上，且BE DC ⊥．（1）求证：DC是O的切线：（2）若2,33OA BEOD==，求DA的长．【答案】（1）见解析；（2）9 10【分析】（1）连接OC，根据圆周角定理得到∠ACB=90°，根据等量代换得到∠DCO=90°，即可证明DC是圆O的切线；（2）根据已知得到OA=2DA，证明△DCO∽△DEB，得到DO CODB EB=，可得DA=310EB，即可求出DA的长．【详解】解：（1）如图，连接OC，由题意可知：∠ACB是直径AB所对的圆周角，∴∠ACB=90°，∵OC，OB是圆O的半径，∴OC=OB，∴∠OCB=∠ABC，又∵∠DCA=∠ABC，∴∠DCA=∠OCB，∴∠DCO=∠DCA+∠ACO=∠OCB+∠ACO=∠ACB=90°，∴OC⊥DC，又∵OC 是圆O 的半径，∴DC 是圆O 的切线；（2）∵23OA OD =，∴23OA OA DA =+，化简得OA=2DA ，由（1）知，∠DCO=90°，∵BE ⊥DC ，即∠DEB=90°，∴∠DCO=∠DEB ，∴OC ∥BE ，∴△DCO ∽△DEB ，∴DO CO DB EB =，即33255DA OA DA DA DA OA OB DA EB +===++，∴DA=310EB ，∵BE=3，∴DA=310EB=3931010⨯=，经检验：DA=910是分式方程的解，∴DA=910．【点睛】本题考查了圆周角定理，相似三角形的判定和性质，切线的判定，正确的作出辅助线，证明切线，得到相似三角形是解题的关键．类型三与锐角三角函数有关24.(2022·辽宁省铁岭市)如图，△ABC内接于⊙O，AC是⊙O的直径，过OA上的点P作PD⊥AC，交CB的延长线于点D，交AB于点E，点F为DE的中点，连接BF．(1)求证：BF与⊙O相切；(2)若AP=OP，cosA=45，AP=4，求BF的长．【答案】(1)连接OB，根据直径所对的圆周角是直角可得∠ABC=90°，从而可得∠ABD=90°，进而利用直角三角形三角形斜边上的中线可得BF=EF=12AD，然后利用等腰三角形的性质可得∠FEB=∠FBE，从而可得∠FBE=∠AEP，最后根据垂直定义可得∠EPA=90°，从而可得∠A+∠AEP=90°，再利用等腰三角形的性质可得∠A=∠OBA，从而可得∠OBA+∠FBE= 90°，进而可得∠OBF=90°，即可解答；(2)在Rt△AEP中，利用锐角三角函数的定义求出AE的长，从而利用勾股定理求出PE的长，然后利用同角的余角相等可得∠AEP=∠C，从而可证△APE∽△DPC，进而利用相似三角形的性质可求出DP的长，最后求出DE的长，即可解答．本题考查了解直角三角形，切线的判定与性质，圆周角定理，三角形的外接圆与外心，直线与圆的位置关系，熟练掌握解直角三角形，以及切线的判定与性质是解题的关键．25.(2022·四川省广安市)如图，AB为⊙O的直径，D、E是⊙O上的两点，延长AB至点C，连接CD ，∠BDC =∠BAD ．(1)求证：CD 是⊙O 的切线．(2)若tan∠BED =23，AC =9，求⊙O 的半径．【答案】（1）连接OD ，由圆周角定理得出∠ADB =90°，证出OD ⊥CD ，由切线的判定可得出结论；(2)证明△BDC∽△DAC ，由相似三角形的性质得出CD AC =BC CD =BD DA =23，由比例线段求出CD 和BC 的长，可求出AB 的长，则可得出答案．本题考查了切线的判定，相似三角形的判定与性质，锐角三角函数的定义，圆周角定理，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．26.（2021·山东菏泽市·中考真题）如图，在O 中，AB 是直径，弦CD AB ⊥，垂足为H ，E 为 BC上一点，F 为弦DC 延长线上一点，连接FE 并延长交直径AB 的延长线于点G ，连接AE 交CD 于点P ，若FE FP =．（1）求证：FE 是O 的切线；（2）若O 的半径为8，3sin 5F =，求BG 的长．【答案】（1）见解析；（2）=2BG 【分析】（1）连接OE ，证明OE ⊥EF 即可；（2）由3sin 5F =证得4sin 5G =，运用正弦的概念可得结论．【详解】解：（1）证明：连接OE ，如图，∵OA=OE∴∠OAE=∠OEA ．∵EF=PF ，∴∠EPF=∠PEF∵∠APH=∠EPF ，∴∠APH=∠EPF ，∴∠AEF=∠APH ．∵CD ⊥AB ，∴∠AHC=90°．∴∠OAE+∠APH=90°．∴∠OEA+∠AEF=90°∴∠OEF=90°∴OE ⊥EF ．∵OE 是O 的半径∴EF 是圆的切线，（2）∵CD ⊥AB∴FHG ∆是直角三角形∵3sin 5F =∴35GH FG =设3GH x =，则5FG x=由勾股定理得，4FH x=由（1）得，OEG ∆是直角三角形∴4sin 5OE FH x G OG FG x===∴45OE OG =，即45OE OE BG =+∵8OE =∴8485BG =+解得，2BG =【点睛】此题主要考查了圆的切线的判定，勾股定理和解直角三角形等知识，熟练掌握切线的判定是解答此题的关键．27.（2022·黔东南）（1）请在图中作出△ABC 的外接圆⊙O （尺规作图，保留作图痕迹，不写作法）；的中点，过点B的（2）如图，⊙O是△ABC的外接圆，AE是⊙O的直径，点B是CE切线与AC的延长线交于点D.①求证：BD⊥AD；②若AC=6，tan∠ABC=34，求⊙O的半径.【答案】（1）解：如下图所示（2）解：①如下图所示，连接OC、OB∵BD是⊙O的切线∴OB⊥BD对应的圆周角，∠COE是CE 对应的圆心角∵∠CAE是CE∴∠COE=2∠CAE的中点∵点B是CE∴∠COE=2∠BOE∴∠CAE=∠BOE∴∠CAE=∠BOE∴AD//OB∴BD⊥AD②如下图所示，连接CE对应的圆周角∵∠ABC与∠AEC是AC∴∠ABC=∠AEC∵AE是⊙O的直径∴∠ACE=90°∴tan∠AEC=AC CE=34∴CE=8∵AE2=CE2+AC2∴AE=10∴⊙O的半径为5.【知识点】圆周角定理；三角形的外接圆与外心；切线的性质；解直角三角形；作图-线段垂直平分线【解析】【解答】（1）∵△ABC的外接圆⊙O的圆心为任意两边的垂直平分线的交点，半径为交点到任意顶点的距离，∴做AB、AC的垂直平分线交于点O，以OB为半径，以O为圆心做圆即可得到△ABC 的外接圆；【分析】（1）利用尺规作图分别作出AC，AB的垂直平分线，两垂直平分线交于点O，然后以点O为圆心，OB的长为半径画圆即可.（2）①连接OC，OB，利用切线的性质可证得OB⊥BD，利用圆周角定理可证得∠COE=2∠CAE，由点B是弧CE的中点，可推出∠CAE=∠BOE，利用平行线的判定定理可证得AD∥OB，由此可证得结论；②连接CE，利用同弧所对的圆周角相等，可证得∠ABC=∠AEC，利用直径所对的圆周角是直角，可推出∠ACE=90°；再利用解直角三角形求出CE的长，利用勾股定理求出AE的长.28.（2022·鄂州）如图，△ABC内接于⊙O，P是⊙O的直径AB延长线上一点，∠PCB=∠OAC，过点O作BC的平行线交PC的延长线于点D.（1）试判断PC与⊙O的位置关系，并说明理由；（2）若PC＝4，tanA＝12，求△OCD的面积.【答案】（1）解：PC与⊙O相切，理由如下：∵AB是圆O的直径，∴∠ACB=90°，∴∠OCB+∠OCA=90°，∵OA=OC，∴∠OCA=∠OAC，∵∠PCB=∠OAC，∴∠PCB=∠OCA，∴∠PCB+∠OCB=∠OCA+∠OCB=90°，即∠PCO=90°，∴PC与⊙O相切（2）解：∵∠ACB=90°，tanA=12，∴BC AC=12，∵∠PCB=∠OAC，∠P=∠P，∴△PBC∽△PCA，∴PC PA=PB PC=BC CA=12，∴PA=8，PB=2，∴AB=6，∴OC=OB=3，∴OP=5，∵BC∥OD，∴△PBC∽△POD，∴PB OP=PC PD，即25=4PD，∴PD=10，∴CD=6，∴S△OCD=12OC⋅CD=9【知识点】等腰三角形的性质；圆周角定理；切线的判定；相似三角形的判定与性质；锐角三角函数的定义【解析】【分析】（1）由圆周角定理得∠ACB=90°，根据等腰三角形的性质可得∠OCA=∠OAC，结合∠PCB=∠OAC得PCB=∠OCA，结合∠OCB+∠OCA=90°可得∠PCO=90°，据此证明；（2）根据三角函数的概念可得BC AC=12，易证△PBC∽△PCA，根据相似三角形的性质可得PA、PB，然后求出AB、OP，证明△PBC∽△POD，根据相似三角形的性质可得PD，由PD-PC=CD可得CD，然后根据三角形的面积公式进行计算.29.（2022·毕节）如图，在△ABC中，∠ACB=90∘，D是AB边上一点，以BD为直径的⊙O与AC相切于点E，连接DE并延长交BC的延长线于点F.（1）求证：BF=BD；（2）若CF=1，tan∠EDB=2，求⊙O直径.【答案】（1）证明：连接OE，如下图所示：∵AC为圆O的切线，∴∠AEO=90°，∵AC⊥BC，∴∠ACB=90°，∴OE∥BC，∴∠F=∠DEO，又∵OD=OE，∴∠ODE=∠DEO，∴∠F=∠ODE，∴BD=BF.（2）解：连接BE，如下图所示：由(1)中证明过程可知：∠EDB=∠F，。

初中数学几何证明经典试题(含答案)

初中几何证明题经典题（一）1、已知：如图，O是半圆的圆心，C、E是圆上的两点，CD⊥AB，EF⊥AB，EG⊥CO．求证：CD＝GF．(初二).如下图做GH⊥AB，连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE ，可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证.2、已知：如图，P是正方形ABCD内点,∠PAD＝∠PDA＝150．求证:△PBC是正三角形．（初二）。

如下图做GH⊥AB，连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE，可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证.。

如下图做GH⊥AB，连接EO.由于GOFE四点共圆,所以∠GFH＝∠OEG，即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

APCDBAFGCEBOD3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中,AD ＝BC,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典题（二）1、已知：△ABC 中,H 为垂心（各边高线的交点)，O 为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM; （2)若∠BAC ＝600，求证：AH ＝AO ．(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HEOF2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E,直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证:CE ＝CF ．（初二）2、如图,四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证:AE ＝AF ．（初二）3、设P 是正方形ABCD 一边求证：PA ＝PF ．（初二)4、如图,PC 切圆O 于C,AC 为圆的直径，PEF 为圆的割线，D ．求证：AB ＝DC ，BC ＝AD ．（初三）经典1、已知：△ABC是正三角形，P 是三角形内一点，PA ＝3，PB ＝4,PC 求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．(初二）3、设ABCD 为圆内接凸四边形,求证:AB ·CD ＋AD ·BC ＝AC ·BD ．（初三)4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．(初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证:≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点,求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a,PB ＝2a ，PC ＝3a ，求正方形的边长．C BD A F PD E CB A APCBACPDA CBPD4、如图,△ABC中，∠ABC＝∠ACB＝800,D、E分别是AB、AC上的点,∠DCA＝300，∠EBA＝200，求∠BED的度数．经典题（一)1.如下图做GH⊥AB，连接EO.由于GOFE四点共圆,所以∠GFH＝∠OEG，即△GHF∽△OGE ，可得EOGF=GOGH=COCD，又CO=EO，所以CD=GF得证。

《圆》的计算及证明题之中考真题精选汇编(1)

《圆》的计算及证明题之中考真题精选汇编（1）1．如图1，在⊙O中，AB为⊙O的直径，点C为⊙O上一点，AD为∠CAB的平分线交⊙O 于点D，连接OD交BC于点E．（1）求∠BED的度数；（2）如图2，过点A作⊙O的切线交BC延长线于点F，过点D作DG∥AF交AB于点G．若AD＝2√35，DE＝4，求DG的长．2．如图，在平面直角坐标系中，点P在第一象限内，⊙P与x轴相切于点C，与y轴相交于点A（0，8），B（0，2）．连接AC，BC．（1）求点P的坐标；（2）求cos∠ACB的值．3．如图，圆内接四边形ABCD的对角线AC，BD交于点E，BD平分∠ABC，∠BAC＝∠ADB．（1）求证DB平分∠ADC，并求∠BAD的大小；（2）过点C作CF∥AD交AB的延长线于点F，若AC＝AD，BF＝2，求此圆半径的长．4．如图，已知⊙O是等边三角形ABC的外接圆，连接CO并延长交AB于点D，交⊙O于点E，连接EA，EB．（1）写出图中一个度数为30°的角：，图中与△ACD全等的三角形是；（2）求证：△AED∽△CEB；（3）连接OA，OB，判断四边形OAEB的形状，并说明理由．5．如图，AB是⊙O的直径，FD为⊙O的切线，CD与AB相交于点E．过点D的线DF∥AB，交CA的延长线于点F，CF＝CD．（1）求∠F的度数；（2）若DE•DC＝8，求⊙O的半径．6．如图，AB是⊙O的直径，C是⊙O上一点，过点C作CD⊥AB于点E，交⊙O于点D，点F是AB延长线上一点，连接CF，AD，∠FCD＝2∠DAF．（1）求证：CF是⊙O切线；（2）若AF＝10，sin F=23，求CD的长．7．如图，AB为⊙O的直径，D，E是⊙O上的两点，延长AB至点C，连接CD，∠BDC＝∠A．（1）求证：△ACD∽△DCB；（2）求证：CD是⊙O的切线；（3）若tanE=35，AC＝10，求⊙O的半径．8．如图，AB是⊙O的直径，点C，E在⊙O上，∠CAB＝2∠EAB，点F在线段AB的延长线上，且∠AFE＝∠ABC．（1）求证：EF与⊙O相切；（2）若BF＝1，sin∠AFE=45，求BC的长．9．如图，四边形ABCD是⊙O的内接四边形，AB是直径，C是BD̂的中点，过点C作CE ⊥AD交AD的延长线于点E．（1）求证：CE是⊙O的切线；（2）若BC＝6，AC＝8，求CE，DE的长．10．如图，AB是⊙O的直径，AC是弦，D是AĈ上一点，P是AB延长线上一点，连接AD，DC，CP．（1）求证：∠ADC﹣∠BAC＝90°；（请用两种证法解答）（2）若∠ACP＝∠ADC，⊙O的半径为3，CP＝4，求AP的长．11．如图，等腰△ABC内接于⊙O，AB＝AC，BD是边AC上的中线，过点C作AB的平行线交BD的延长线于点E，BE交⊙O于点F，连接AE，FC．（1）求证：AE为⊙O的切线；（2）若⊙O的半径为5，BC＝6，求FC的长．̂的中点，过点C作CD⊥AE，交12．如图，AB为⊙O的直径，E为⊙O上一点，点C为EBAE的延长线于点D，延长DC交AB的延长线于点F．（1）求证：CD是⊙O的切线；（2）若DE＝1，DC＝2，求⊙O的半径长．13．如图，⊙O是△ABC的外接圆，AD是⊙O的直径，F是AD延长线上一点，连接CD，CF，且∠DCF＝∠CAD．（1）求证：CF是⊙O的切线；（2）若AD＝10，cos B=35，求FD的长．14．如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，DE⊥AC，垂足为E．（1）求证：DE是⊙O的切线；（2）若∠C＝30°，CD＝2√3．求BD的长．15．综合与实践：数学模型可以用来解决一类问题，是数学应用的基本途径．通过探究图形的变化规律，再结合其他数学知识的内在联系，最终可以获得宝贵的数学经验，并将其运用到更广阔的数学天地．（1）发现问题：如图1，在△ABC和△AEF中，AB＝AC，AE＝AF，∠BAC＝∠EAF＝30°，连接BE，CF，延长BE交CF于点D．则BE与CF的数量关系：，∠BDC＝°；（2）类比探究：如图2，在△ABC和△AEF中，AB＝AC，AE＝AF，∠BAC＝∠EAF＝120°，连接BE，CF，延长BE，FC交于点D．请猜想BE与CF的数量关系及∠BDC 的度数，并说明理由；（3）拓展延伸：如图3，△ABC和△AEF均为等腰直角三角形，∠BAC＝∠EAF＝90°，连接BE，CF，且点B，E，F在一条直线上，过点A作AM⊥BF，垂足为点M．则BF，CF，AM之间的数量关系：；（4）实践应用：正方形ABCD中，AB＝2，若平面内存在点P满足∠BPD＝90°，PD＝1，则S△ABP．16．如图，OA，OB，OC都是⊙O的半径，∠ACB＝2∠BAC．（1）求证：∠AOB＝2∠BOC；（2）若AB＝4，BC=√5．求⊙O的半径．̂的中点，弦DE⊥AB，垂足为点F．17．如图，AB为⊙O的直径，C是圆上一点，D是BC（1）求证：BC＝DE；̂上一点，AC＝6，BF＝2，求tan∠BPC；（2）P是AE（3）在（2）的条件下，当CP是∠ACB的平分线时，求CP的长．̂=BD̂，DE⊥AC于点E，DE交BF 18．如图，△ABC内接于⊙O，AB是⊙O的直径，BC于点F，交AB于点G，∠BOD＝2∠F，连接BD．（1）求证：BF是⊙O的切线；（2）判断△DGB的形状，并说明理由；（3）当BD＝2时，求FG的长．19．如图，在Rt△ABC中，∠B＝90°，AD平分∠BAC交BC于点D，点E是斜边AC上一点，以AE为直径的⊙O经过点D，交AB于点F，连接DF．（1）求证：BC是⊙O的切线；（2）若BD＝5，tan∠ADB=√3．求图中阴影部分的面积．（结果保留π）20．如图，MN为⊙O的直径，且MN＝15，MC与ND为圆内的一组平行弦，弦AB交MC 于点H．点A在MĈ上，点B在NĈ上，∠OND+∠AHM＝90°．（1）求证：MH•CH＝AH•BH；（2）求证：AĈ=BĈ；（3）在⊙O中，沿弦ND所在的直线作劣弧ND̂的轴对称图形，使其交直径MN于点G．若sin∠CMN=35，求NG的长．21．【感知】如图①，点A、B、P均在⊙O上，∠AOB＝90°，则锐角∠APB的大小为度．【探究】小明遇到这样一个问题：如图②，⊙O是等边三角形ABC的外接圆，点P在AC上（点P不与点A、C重合），连接P A、PB、PC．求证：PB＝P A+PC．小明发现，延长P A至点E，使AE＝PC，连接BE，通过证明△PBC≌△EBA．可推得△PBE是等边三角形，进而得证．下面是小明的部分证明过程：证明：延长P A至点E，使AE＝PC，连接BE．∵四边形ABCP是⊙O的内接四边形，∴∠BAP+∠BCP＝180°，∵∠BAP+∠BAE＝180°，∴∠BCP＝∠BAE，∵△ABC是等边三角形，∴BA＝BC，∴△PBC≌△EBA（SAS）．请你补全余下的证明过程．【应用】如图③，⊙O是△ABC的外接圆，∠ABC＝90°，AB＝BC，点P在⊙O上，且点P与点B在AC的两侧，连接P A、PB、PC，若PB=2√2PA，则PBPC的值为．22．如图，作CF⊥OE，交BE于点F，若EF＝2BF．（1）如图1，连接BD，求证：△ADB≌△OBE；（2）如图2，N是AD上一点，在AB上取一点M，使∠MCN＝60°，连接MN．请问：三条线段MN，BM，DN有怎样的数量关系？并证明你的结论．23．如图，已知△ABC内接于⊙O，CO的延长线交AB于点D，交⊙O于点E，交⊙O的切线AF于点F，且AF∥BC．（1）求证：AO∥BE；（2）求证：AO平分∠BAC．24．如图，PO平分∠APD，P A与⊙O相切于点A，延长AO交PD于点C，过点O作OB ⊥PD，垂足为B．（1）求证：PB是⊙O的切线；（2）若⊙O的半径为4，OC＝5，求P A的长．25．如图，在Rt△ABC中，∠ACB＝90°，∠BAC的平分线AD交BC于点D，∠ADC的平分线DE交AC于点E．以AD上的点O为圆心，OD为半径作⊙O，恰好过点E．（1）求证：AC是⊙O的切线；（2）若CD＝12，tan∠ABC=34，求⊙O的半径．26．综合探究如图1，在矩形ABCD中（AB＞AD），对角线AC，BD相交于点O，点A关于BD的对称点为A′．连接AA′交BD于点E，连接CA′．（1）求证：AA'⊥CA'；（2）以点O为圆心，OE为半径作圆．①如图2，⊙O与CD相切，求证：AA′=√3CA′；②如图3，⊙O与CA′相切，AD＝1，求⊙O的面积．27．如图，在⊙O中，AB是直径，点C是圆上一点．在AB的延长线上取一点D，连接CD，使∠BCD＝∠A．（1）求证：直线CD是⊙O的切线；（2）若∠ACD＝120°，CD＝2√3，求图中阴影部分的面积（结果用含π的式子表示）．28．如图，在菱形ABCD中，DH⊥AB于H，以DH为直径的⊙O分别交AD，BD于点E，F，连接EF．（1）求证：①CD是⊙O的切线；②△DEF∽△DBA；（2）若AB＝5，DB＝6，求sin∠DFE．29．装有水的水槽放置在水平台面上，其横截面是以AB为直径的半圆O，AB＝50cm，如图1和图2所示，MN为水面截线，GH为台面截线，MN∥GH．计算：在图1中，已知MN＝48cm，作OC⊥MN于点C.（1）求OC的长．操作：将图1中的水槽沿GH向右作无滑动的滚动，使水流出一部分，当∠ANM＝30°时停止滚动．如图2．其中，半圆的中点为Q，GH与半圆的切点为E，连接OE交MN 于点D．探究：在图2中．（2）操作后水面高度下降了多少？̂的长度，并比较大小．（3）连接OQ并延长交GH于点F，求线段EF与EQ30．（1）如图①，在△OAB中，OA＝OB，∠AOB＝120°，AB＝24．若⊙O的半径为4，点P在⊙O上，点M在AB上，连接PM，求线段PM的最小值；（2）如图②所示，五边形ABCDE是某市工业新区的外环路，新区管委会在点B处，点E处是该市的一个交通枢纽．已知：∠A＝∠ABC＝∠AED＝90°，AB＝AE＝10000m，BC＝DE＝6000m．根据新区的自然环境及实际需求，现要在矩形AFDE区域内（含边界）修一个半径为30m的圆型环道⊙O；过圆心O，作OM⊥AB，垂足为M，与⊙O交于点N．连接BN，点P在⊙O上，连接EP．其中，线段BN、EP及MN是要修的三条道路，要在所修道路BN、EP之和最短的情况下，使所修道路MN最短，试求此时环道⊙O的圆心O到AB的距离OM的长．。

九年级数学圆证明题专题

圆证明专题1．如图，已知在⊙O 中，AB =43，AC 是⊙O 的直径，AC ⊥BD 于F ，∠A =30°．（1）求图中阴影部分的面积；（2）若用阴影扇形OBD 围成一个圆锥侧面，请求出这个圆锥的底面圆的半径．2．AB 是⊙O 的直径，BC 是弦，OD ⊥BC 于E ，交弧BC 于D 。

(1)请写出四个正确的结论；(2)若BC=6，ED=2，求⊙O 的半径。

3.已知：如图，ABC △中，AB AC =，以AB 为直径的⊙O 交BC 于点P ，PD AC ⊥于点D ．（1）求证：PD 是⊙O 的切线；（2）若1202CAB AB ∠==，，求BC 的值4．如图，在Rt △ABC 中，∠B=90°，∠A 的平分线交BC 于D ，E 为AB 上一点，DE=DC ，以D 为圆心，以DB 的长为半径画圆。

求证：（1）AC 是⊙D 的切线；（2）AB+EB=AC 。

AB C D OF EOBAC DCPBOAD5．已知：⊙O 的直径AB 和弦CD ，且AB ⊥CD 于E ，F 为DC 延长线上一点，连结AF 交⊙O 于M 。

求证：∠AMD ＝∠FMC 。

6．已知AB 是☉O 的直径，AC 是弦，CD 切☉O 于点C ，交AB 的延长线于点D ，120ACD ∠=，10BD =．（1）求证：CA CD =；（2）求☉O 的半径．7．ABC △内接于⊙O ，点D 在半径OB 的延长线上，30BCD A ∠=∠=°．（1）试判断直线CD 与⊙O 的位置关系，并说明理由；（2）若⊙O 的半径长为1，求由弧BC 、线段CD 和BD 所围成的阴影部分面积（结果保留π和根号）．8. 如图，PA ，PB 是⊙O 的切线，点A ，B 为切点，AC 是⊙O 的直径，∠ACB =70°．求∠P 的度数．BCOAOC BDOP C BA9. 如图，已知点C 、D 在以O 为圆心，AB 为直径的半圆上，且BD OC ⊥于点M 、AB CF ⊥于点F 交BD 于点E ，8=BD ，2=CM 。

往年中考关于圆的证明汇总(有答案)

①求出点 C 的坐标； ②直线 BC 是否为⊙O 的切线？请作出判断，并说明理由．
23 图
24 图
24、如图，⊙M 与 x 轴相切于点 C，与 y 轴的一个交点为 A。
（1）求证：AC 平分∠OAM；（2）如果⊙M 的半径等于 4，∠ACO=300，求 AM 所在直线的解析式．
25、如图，在直角三角形 ABC 中，∠ABC=90°．
1、如图，在⊙O 中，AB，CD 是直径，BE 是切线，B 为切点，连接 AD，BC，BD．
（1）求证：△ABD≌△CDB；
（2）若∠DBE=37°，求∠ADC 的度数．
1图
2图
2、如图，△ABC 中，∠ACB=90°，D 是边 AB 上的一点，E 是 BC 上的一点，以 EC 为直径的⊙O 经过点 D，OA⊥CD 于点
连接 AF． (1)证明：∠F＝∠CAD；(2)试判断直线 AF 与⊙O 的位置关系，并给出证明．
11 图
12 图
12、如图，AB 是半圆 O 的直径，点 C 是⊙O 上一点（不与 A，B 重合），连接 AC，BC，过点 O 作 OD∥AC 交 BC 于点 D，
在 OD 的延长线上取一点 E，连接 EB，使∠OEB=∠ABC．
那么图中两个扇形（即阴影部分）的面积之和
两等圆⊙A，⊙B外切，为．
35 图
36 图
36、如图所示，AB 是⊙O 的直径，AE 是弦，C 是劣弧 AE 的中点，过 C 作 CD⊥AB 于点 D，CD 交 AE 于点 F，过 C 作 CG
∥AE 交 BA 的延长线于点 G．
（1）求证：CG 是⊙O 的切线．（2）求证：AF=CF．（3）若∠EAB=30°，CF=2，求 GA 的长．
33 图

初中经典几何证明练习题集(含答案解析)

初中几何证明题经典题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．证明：过点G 作GH ⊥AB 于H ，连接OE ∵EG ⊥CO ，EF ⊥AB∴∠EGO=90°，∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ，CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知：如图，P 是正方形ABCD 内部的一点，∠PAD ＝∠PDA ＝15°。

求证：△PBC 是正三角形．（初二）证明：作正三角形ADM ，连接MP ∵∠MAD=60°，∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°，∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ，AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ，MP=BP 同理∠CPD=∠MPD ，MP=CP ∵∠PAD ＝∠PDA ＝15°∴PA=PD ，∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ，∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ，MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．证明:连接AC ，取AC 的中点G,连接NG 、MG ∵CN=DN ，CG=DG ∴GN ∥AD ，GN=21AD ∴∠DEN=∠GNM ∵AM=BM ，AG=CG ∴GM ∥BC ，GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）证明：（1）延长AD 交圆于F ，连接BF ，过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ，BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2（GH+DH ）=2GD 又AD ⊥BC ，OM ⊥BC ，OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM （2）连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ，OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由（1）知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线，过O 作OA ⊥MN 于A ，自A 引圆的两条割线交圆O 于B 、C 及D 、E ，连接CD 并延长交MN 于Q ，连接EB 并延长交MN 于P. 求证：AP ＝AQ ．证明：作点E 关于AG 的对称点F ，连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ，PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）证明：作OF ⊥CD 于F ，OG ⊥BE 于G ，连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ，∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN ， ∴OA ⊥MN 又OG ⊥BE ，∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°，OA=OA ∴△OAQ ≌△OAP在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ，点O 是DF 的中点，OP ⊥BC求证：BC=2OP （初二）证明：分别过F 、A 、D 作直线BC 的垂线，垂足分别是L 、M 、N ∵OF=OD ，DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形 ∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°，BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）证明：连接BD 交AC 于O 。