人教版七年级数学试题:5.1.1相交线练习题
(整理)新人教版初中数学七年级下册单元同步练习试题全册

5.1.1-2相交线、垂线检测题一、填空1.如图,直线AB,CD 相交于O,OE 平分∠AOD,FO ⊥OD 于O,∠1=40°,则∠2=•___ __,∠4=______.421D CAB (5)OFE D C A B NM(6)O FE(第1题图) (第2题图)2.如图,AB ⊥CD 于O,EF 为过点O 的直线,MN 平分∠AOC,若∠EON=100•°,•那么 ∠EOB=________,∠BOM=________.3.如图,AB 是一直线,OM 为∠AOC 的角平分线,ON 为∠BOC 的角平分线,则OM,ON 的位置关系是_______.4.直线外一点与直线上各点连结的线段中,以_________为最短.5.从直线外一点到这条直线的________叫做这点到直线的距离.C AB NM(7)DCA B(8)O(第3题图) (第7题图) (第8题图)6.经过直线外或直线上一点,有且只有______直线与已知直线垂直.7.如图,要证BO ⊥OD,请完善证明过程,并在括号内填上相应依据:∵AO ⊥CO,∴∠AOC=__________(___________).又∵∠COD=40°(已知),∴∠AOD=_______.•∵∠BOC=∠AOD=50°(已知),∴∠BOD=_______, ∴_______⊥_______(__________).8. 如图,点B 到AC 的距离是线段_________的长度,_________是线段BC 到A 的距离二、选择9.下列语句正确的是( )A.相等的角为对顶角B.不相等的角一定不是对顶角C.不是对顶角的角都不相等D.有公共顶点且和为180°的两个角为邻补角10.两条相交直线与另外一条直线在同一平面内,它们的交点个数是( ) A.1 B.2 C.3或2 D.1或2或311.如图10,PO ⊥OR,OQ ⊥PR,能表示点到直线(或线段)的距离的线段有( ) A.1条 B.2条 C.3条 D.5条(10)PQDCAB(11)O D C AB(12)FE (第11题图) (第12题图) (第14题图)12.如图,OA ⊥OB,OC ⊥OD,则( )A.∠AOC=∠AODB.∠AOD=∠DOBC.∠AOC=∠BODD.以上结论都不对 13.下列说法正确的是( )A.在同一平面内,过已知直线外一点作这条直线的垂线有且只有一条B.连结直线外一点和直线上任一点,使这条线段垂直于已知直线C.作出点P 到直线的距离D.连结直线外一点和直线上任一点的线段长是点到直线的距离 14.如图,与∠C 是同旁内角的有( ). A.2 B.3 C.4 D.5 15.下列说法正确的是( ).A.两条直线相交成四个角,如果有三个角相等,那么这两条直线垂直.B.两条直线相交成四个角,如果有两个角相等,那么这两条直线垂直.C.两条直线相交成四个角,如果有一对对顶角互余,那么这两条直线垂直.D.两条直线相交成四个角,如果有两个角互补,那么这两条直线垂直. 16.如果∠1与∠2互为补角,且∠1>∠2,那么∠2的余角是( )A. 12(∠1+∠2)B. 12∠1C. 12(∠1-∠2)D.12∠2三、作图题17、如图,按要求作出:(1)AE ⊥BC 于E; (2)AF ⊥CD 于F;(3)连结BD,作AG ⊥BD 于G.18、如下左图,一辆汽车在直线形的公路AB 上由A 向B 行驶,M 、N 分别是位于公路AB 两侧的村庄,(1)现在公路AB 上修建一个超市C ,使得到M 、N 两村庄距离最短,请在图中画出点C (2)设汽车行驶到点P 位置时离村庄M 最近;行驶到点Q 位置时,距离村庄N 最近,请在图中公路AB 上分别画出P 、Q 两点的位置。
人教版七年级下学期数学-5.1相交线(练习题)

人教版七年级下学期数学-5.1相交线练习题一、单选题1.如图,河道的同侧有、两地,现要铺设一条引水管道,从地把河水引向、两地.下列四种方案中,最节省材料的是()A.B.C.D.2.如图,直线AB、CD相交于O,且∠AOC=2∠BOC,则∠AOD的度数为()A.30°B.45°C.60°D.75°3.如图,直线AB,CD相交于点O,,OF平分,则的大小为()A.40°B.50°C.65°D.70°4.如图,在中,,,垂足为点D,那么点A到直线的距离是线段()的长.A.B.C.D.5.如图,直线AB,CD,EO相交于点O,已知OA平分∠EOC,若∠EOC:∠EOD=2:3,则∠BOD 的度数为()A.40°B.37°C.36°D.35°6.如图所示,与∠α构成同位角的角的个数为()A.1B.2C.3D.47.在下列语句中,正确的是().A.在平面上,一条直线只有一条垂线;B.过直线上一点的直线只有一条;C.过直线上一点且垂直于这条直线的直线有且只有一条;D.垂线段的长度就是点到直线的距离8.平面上三条直线两两相交最多能构成对顶角的对数是().A.7B.6C.5D.49.如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是()①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD =∠BOC.A.①②③B.①②④C.①③④D.②③④10.如图,下列6种说法:①∠1与∠4是内错角;②∠1与∠2是同位角;③∠2与∠4是内错角;④∠4与∠5是同旁内角;⑤∠2与∠4是同位角;⑥∠2与∠5是内错角.其中正确的有()A.1个B.2个C.3个D.4个二、填空题11.已知直线AB与直线CD相交于点O,∠AOC:∠BOC=2:1,射线OE⊥CD,则∠AOE的度数为.12.如图,直线AB、CD、EF相交于点O,若∠1+∠2=150°,则∠3=°.13.如图,直线AB、CD相交于点O,OE平分,OF平分.若,则的度数为°.14.若与是对顶角,与互余,且,则的度数为°.15.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOM=35°,则∠CON的度数为.三、计算题16.如图,O为直线AB上一点,OC⊥AB,并且∠AOD=130°.求∠COD的度数.17.如图所示,直线AB、CD、EF相交于点O,CD⊥AB,∠AOE:∠AOD=3:5,求∠BOF与∠DOF的度数.四、综合题18.如图,在所标注的角中.(1)对顶角有对,邻补角有对;(2)若,,求与的度数.19.如图,点在直线外,点在直线上,连接.选择适当的工具作图.(1)在直线上作点,使,连接;(2)在的延长线上任取一点,连接;(3)在,,中,最短的线段是,依据是.20.如图,直线、相交于点,且平分,平分.(1)求证:平分;(2)求的度数.答案解析部分1.【答案】D【解析】【解答】解:依据垂线段最短,以及两点之间,线段最短,可得最节省材料的是:故答案为:D.【分析】利用垂线段最短,以及两点之间线段最短求解即可。
人教版最全七年级数学下册全册同步练习及单元测验卷及答案

第五章相交线与平行线5.1.1 相交线复习检测(5分钟):1、如图所示,/1和/2是对顶角的图形有()A.1个B.2 个C.3 个D.4 个2、如图,若/ 1=60° ,那么/ 2=3、如图是一把剪刀,其中 1 40,则24、如图三条直线AB,CD,EF相交于一点O, /AOD勺对顶角是,/AOC勺邻补角是,若/ A0C=50 ,贝U/ BOD= ./ COB= J AOE+ DOB + COF=5、如图,直线AB,CD相交于0,0评分/ AOC若/ AOD/DOB=50 ,?求/EOB勺度数.6、如图,直线a,b,c两两相交,/1=2/ 3, / 2=68° ,求/4的度数5.1.2 垂线复习检测(5分钟):1、两条直线互相垂直,则所有的邻补角都相等.()2、一条直线不可能与两条相交直线都垂直.()3、两条直线相交所成的四个角中,如果有三个角相等,那么这两条直线互相垂直.()4、两条直线相交有一组对顶角互补,那么这两条直线互相垂直.().5、如图1,OAL OB,OCL OC,O为垂足,若/AOC=3 5,则/BOD=.6、如图2,A0± BO,O为垂足,直线CDi点O,且/ BOD=2AOC则/ BOD=.7、如图3,直线AB CD相交于点0,若/E0D=40 , /B0C=130,那么射线0E与直线AB的位置关系是C8、已知:如图,直线AB,射线0位于点的位置关系.9、如图,AC± BC,C为垂足,CD± AB,D为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC= 6 ,那么点C 到AB 的距离是,点A 到BC 的距离是,点B 到CD 的距离是 ,A 、B 两点间的距离是.10、如图,在线段AB AG AD AE AF 中AD 最短.小明说垂线段最短,因此线段AD 的 长是点A 到BF 的距离,对小明的说法,你认为对吗?11、用三角尺画一个是30的/AOB 在边OA±任取一点P,过P 作POL OB,垂足为Q, 量一量OP 的长,你发现点P 到OB 的距离与OP 长的关系吗?5.1.3同位角、内错角、同旁内角3、如图(6),直线DE 截AB, AC,构成八个角: ①、指出图中所有的同位角、内错角、同旁内角复习检测(5分钟):1、如图(4),卜列说法不正确的是( )人./1与/2是同位角 B. / 2与/ 3是同位角C. / 1与/ 3是同位角D. / 1与/ 4不是同位角2、如图(5),直线AB CDM 直线EF 所g, / A 和一 错角,/A 班是同旁内角.^ /\ \ /--- ---------- 4 届 -------------------- R图⑷ 图⑸—是同位角,/ A 和 ________ 是内A40(3) c'②、/人与/5, /A 与/6, /A 与/8,分别是哪一条直线截哪两条直线而成的什么 角?4、如图(7),在直角 ABCt\ / C= 90 , DU AC 于 E,交 A.一 L①、指出当BG DE 被AB 所截时,/ 3的同位角、内错角和礴内他(门②、若/ 3+/ 4=180试说明/ 1 = /2=/3的理由.5.2.1平行线复习检测(5分钟):1、在同一平面内,两条直线的位置关系有2、两条直线L 1与L 2相交点A,如果L 1//L ,那么12与L ()3、在同一平面内,一条直线和两条平行线中一条直线相交,那么这条直线与平行线中的另一边必.D ./3=/4 D. /BACW ACD4、两条直线相交,交点的个数是 ,两条直线平行,交点的个数是 _____________ 个.判断题5、6、7、85、不相交的两条直线叫做平行线.()6、如果一条直线与两条平行线中的一条直线平行,那么它与另一条直线也互相平行.()7、过一点有且只有一条直线平行于已知直线.()8、读下列语句,并画出图形后判断.(1)直线a 、b 互相垂直,点P 是直线a 、b 外一点,过P 点的直线c 垂直于直线b. (2)判断直线a 、c 的位置关系,并借助于三角尺、直尺验证.9、试说明三条直线的交点情况,进而判定在同一平面内三条直线的位置情况5.2.2平行线的判定复习检测(10分钟):1、如图1所示,下列条件中,能判断AB// CD 的是()DAFCA./BADh BCDB. /1 = /2;C.AD C B如图5,直线a,b 被直线c 所截,现给出下列四个条件: ?①/ 1 = /5;②/ 1=/7;③/ 2+/ 3=180 ;@Z4=Z 7.其中能说明 a // b 的条件序号为() A.①② B.①③ C.①④ D. ③④如果/ 9=,那么AD// BC;如果/ 9=,那么AB// CD.7、在同一平面内,若直线a,b,c 满足a±b,a ±c,则b 与c 的位置户系是8、如图所示,BE 是AB 的延长线,量得/ CBEh A=/ C. //.... AB E(1) 由/ CBEh A 可以判断//,根据是.⑵ 由/ CBEh C 可以判断//,根据是2、 如图2所示,如果/ D=/ EFC 那么()A.AD // BCB.EF // BC 3、 F 列说法错误的是()A.同位角不一定相等B. 内错角都相等C. 同旁内角可能相等D.同旁内角互补,两直线平行4、 5、如图5,如果/ 3=/7,那么,理由是 如果/ 5=/ 3,那么 ,理由是 如果/ 2+ /5=那么a // b,理由是6、如图4,若/ 2=/6,则,如果/3+/4+/ 5+/ 6=180 ,那么(4)C.AB // DCD.AD9、已知直线a、b被直线c所截,且/1+/ 2= 试判断直线a、b的位置关系,并说明理由.10、如图,已知AEM DG , 1 2 ,试问EF是否平行GH并说明理由.11、如图所示,已知/ 1=/ 2,AC平分/ DAB试说明DCI AB.12、如图所示,已知直线EF和AB,CM别相交于K,H,且EGL AB,/CHF=60 / E=30°试说明AB// CD.13、提高训练:如图所示,已知直线a,b,c,d,e,且/ 1=/ 2, / 3+/4=180° ,则a与c平行吗?劝什么?5.3.1平行线的性质复习检测(10分钟):1、如图1所示,AB//CD则与/ 1相等的角(/1除外)共有()A.5 个B.4 个C.3 个D.2 个 B AA B —(4) (5) (6)5、如图5,在甲、乙两地之间要修一条笔直的公路,从甲地测得公路的走向是南偏西(3)2、如图 2 所示,CD// AB,O 评分/ AOD,OFOE,/D=50,则/BOF 为(A.35B.30C.253、如图 3 所示,AB II CD,Z D=80CAD=, /ACD=?.4、如图 4,若 AD// BC,则/=/ D.20/ABC 廿=180 ;若 DC/ZAB,则/=/A,/ CAD:/ BAC=3:2则/56° ,甲、乙两地同时开工,若干天后公路准确接通,则乙地所修公路的走向是,因为.6、河南)如图6所示,已知AB// CD直线EF分别交AB,CD于E,F,EG?平分/ B-EF,若/ 1=72 ,贝U/2=.7、如图,AB/ZCQ / 1 = 102° ,求/ 2、/3、/4、/ 5的度数,并说明根据?8、如图,ERiz\ABC勺一个顶点A,且EF// BC 如果/ B= 40° , / 2= 75° ,那么/1、/3、/G / BAO /B+ 是多少度,并说明依据?9、如图,已知:DE/ZCB,/1 = /2,求证:CD平分/ ECB.10、如图所示,把一张长方形纸片ABCD& EF折叠,若/ EFG=50 ,求/ DEG勺度数.1111、如图所示,已知:AE平分/BAC CE平分/ACD且AB//CD求证:/1+/ 2=90° . 证明:・•. AB//CD (已知)・♦/BAC/ACD180 , ()又.. AE平分/ BAC C评分/ ACD (). 1 1•• 1 - BAC , 2 万ACD,( ___________________ ) __________1 1 0 0. .1 2 -( BAC ACD) —1800 90°.2 2即Z1+Z 2=90 .结论:若两条平行线被第三条直线所截,则一组同旁内角的平分线互相.推广:若两条平行线被第三条直线所截,则一组同位角的平分线互相^5.3.2命题、定理、证明复习检测(5分钟):1、判断下列语句是不是命题(1)延长线段AB( ) (3)画线段AB的中点( (2)两条直线相交,只有一交点((4)若|x|=2 ,则x=2 ( )134、命题:①对顶角相等;②垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等.其中假命题有()A.1 个B.2个C.3个D.4个5、分别指出下列各命题的题设和结论(1)如果a// b, b // c,那么all c ⑵ 同旁内角互补,两直线平行 6、分别把下列命题写成“如果……,那么……”的形式 (1)两点确定一条直线; (2)等角的补角相等;(3)内错角相等.7、如图,已知直线a 、b 被直线c 所截,在括号内为下面各小题的推理填上适当的根据(1) '.'all b,「•/ 1=/ 3( ); (2) ・// 1=/ 3, ..・all b( ); (3) '.'all b,「•/ 1=/ 2( );(4) 「a// b,「./ 1+/ 4=180o ( (5) ・// 1=/ 2, ..・all b( ); (6) •// 1+/ 4=180o,「.a// b( ). 8、已知:如图 ABL BG BCLCD 且/ 1=/ 2, 证明:.「AB!BG BCLCD (已知)= =90(5)角平分线是一条射线( 2、下列语句不是命题的是( A.两点之间,线段最短 C.x 与y 的和等于0吗? 3、下列命题中真命题是( )A.两个锐角之和为钝角)B.不平行的两条直线有一个交点 D.对顶角不相等.B.两个锐角之和为锐角D.锐角小于它的余角・ ・•/ 1 = /2 (已知)(等式性质)/ ACB=90 ()・ ••/ BCD^/ ACD 勺余角・ ・•/BCD^/B 的余角(已知) ・•・ / ACDN B ()5.4平移复习检测(5分钟):1、下列哪个图形是由左图平移得到的( )B.沿射线EC 的方向移动C 冰C.沿射线BD 的方向移动BD 长;D.沿射线BD 的方向移动DC 长3、下列四组图形中,?有一组中的两个图形经过平移其中一个能得到 -另一个,这组图形9、已知: 求证: 证明: BE// CF (/ ACDM B・•. ACL BC (已知)2、如图所示,4FDE 经过怎样的平移可得到4A.沿射线EC 的方向移动DB 长; 如图,ACL BCC 垂足为CABC.()4、如图所示,△ DEF经过平移可以得到△ ABC那的对应角和ED的对应边分-别是()A. / F,ACB. / BOD,BA;C. / F,BAD.5、在平移过程中,对应线段()A.互相平行且相等;B.互相垂直且相等C.互相平行(或在同一条直线上)且相等6、在平移过程中,平移后的图形与原来的图形________ 都相同,?因-此对应线段和对应角7、如图所示,平移△ ABC可得到△ DEF,如果// C=60 ,那么/ E=?-度,/ EDF=/F= ______ 度,/DOB= .........8、将正方形ABCDg对角线AC方向平移,且平移后的图形的一个顶点恰好在AC的中点。
2020-2021学年人教版数学 七年级下册 5.1 相交线 垂线段 同步练习

5.1 相交线垂线段基础训练知识点1 垂线段的定义1.下列说法正确的是()A.垂线段就是垂直于已知直线的线段B.垂线段就是垂直于已知直线并且与已知直线相交的线段C.垂线段是一条竖起来的线段D.过直线外一点向该直线作垂线,这一点到垂足之间的线段叫垂线段2.如图,下列说法不正确的是()A.点B到AC的垂线段是线段ABB.点C到AB的垂线段是线段ACC.线段AC是点A到BC的垂线段D.线段BD是点B到AD的垂线段知识点2 垂线段的性质3.如图,计划在河边建一水厂,过C点作CD⊥AB于D点.在D点建水厂,可使水厂到村庄C的路程最短,这样设计的依据是__________.4.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在()A.A点B. B点C.C点D.D点5.如图,已知AC⊥BC,CD⊥AB,垂足分别是C,D,那么以下线段大小的比较必定成立的是()A.CD>ADB.AC<BCC.BC>BDD.CD<BD6.如图,AD⊥BD,BC⊥CD,AB=6 cm,BC=4 cm,则BD的长度的取值范围是()A.大于4 cmB.小于6 cmC.大于4 cm或小于6 cmD.大于4 cm且小于6 cm7.如图,在三角形ABC中,∠C=90°,AC=3,点P可以在直线BC上自由移动,则AP的长不可能是()A.2.5B.3C.4D.5知识点3 点到直线的距离8.如图所示的是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段的长度.9.下列图形中,线段PQ的长表示点P到直线MN的距离的是()10.如图,其长能表示点到直线(线段)的距离的线段的条数是()A.3B.4C.5D.611.如图,三角形ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是()A.线段CA的长B.线段CD的长C.线段AD的长D.线段AB的长12.点到直线的距离是指()A.直线外一点到这条直线的垂线的长度B.直线外一点到这条直线上的任意一点的距离C.直线外一点到这条直线的垂线段D.直线外一点到这条直线的垂线段的长度13.如图,AB⊥AC,AD⊥BC,如果AB=4 cm,AC=3 cm,AD=2.4 cm,那么点C到直线AB的距离为()A.3 cmB.4 cmC.2.4 cmD.无法确定易错点对垂线段的性质理解不透彻而致错14.点P为直线m外一点,点A,B,C为直线m上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线m的距离()A.等于4 cmB.等于2 cmC.小于2 cmD.不大于2 cm提升训练考查角度1 利用点到直线的距离的定义进行识别15.如图,AB⊥AC,AD⊥BC,垂足分别为A,D,则图中能表示点到直线距离的线段共有()A.2条B.3条C.4条D.5条考查角度2 利用作垂线法作图16.如图,已知钝角三角形ABC中,∠BAC为钝角.(1)画出点C到AB的垂线段;(2)过点A画BC的垂线;(3)画出点B到AC的垂线段,并量出其长度.考查角度3 利用垂线段的性质比较大小17.如图,直线AB,CD相交于点O,P是CD上一点.(1)过点P画AB的垂线段PE;(2)过点P画CD的垂线,与AB相交于F点;(3)说明线段PE,PO,FO三者的大小关系,其依据是什么?考查角度4 利用垂线段的性质解实际应用题18.如图,一辆汽车在直线形的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄,设汽车行驶到点P位置时,离村庄M最近,行驶到点Q位置时,离村庄N最近,请你在AB上分别画出P,Q两点的位置.探究培优拔尖角度1 利用垂线段的性质进行方案设计(建模思想)19.如图,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.(1)不考虑其他因素,请你画图确定蓄水池H的位置,使它到四个村庄的距离之和最小;(2)计划把河水引入蓄水池H中,怎样开渠最短?并说明根据.拔尖角度2 利用垂线段的性质解决绝对值问题(数形结合思想)20.在如图所示的直角三角形ABC中,斜边为BC,两直角边分别为AB,AC,设BC=a,AC=b,AB=c.(1)试用所学知识说明斜边BC是最长的边;(2)试化简|a-b|+|c-a|+|b+c-a|.参考答案1.【答案】D2.【答案】C3.【答案】垂线段最短4.【答案】A5.【答案】C6.【答案】D解:根据“垂线段最短”可知BC<BD<AB,所以BD大于4 cm且小于6 cm.7.【答案】A8.【答案】BN或AM9.【答案】A解:对于选项A,PQ⊥MN,Q是垂足,故线段PQ的长为点P到直线MN 的距离.10.【答案】C解:线段AB的长度可表示点B到AC的距离,线段CA的长度可表示点C到AB的距离,线段AD的长度可表示点A到BC的距离,线段CD 的长度可表示点C到AD的距离,线段BD的长度可表示点B到AD的距离,所以共有5条.11.【答案】B12.【答案】D13.【答案】A解:因为AB⊥AC,所以点C到直线AB的距离是线段AC的长度,即3 cm.14.错解:B诊断:点到直线的距离是指这个点到直线的垂线段的长度.虽然垂线段最短,但是并没有说明PC是垂线段,所以垂线段的长度可能小于2 cm,也可能等于2 cm.正解:D15.【答案】D16.解:如图:(1)CD即为所求;(2)直线AE即为所求;(3)BF即为所求.长度略.17.解:(1)如图所示.(2)如图所示.(3)PE<PO<FO,其依据是垂线段最短.18.解:如图所示.19.解:(1)如图,连接AD,BC,交于点H,则H点为蓄水池的位置,它到四个村庄的距离之和最小.(2)如图,过点H作HG⊥EF,垂足为G,则沿HG开渠最短.根据:连接直线外一点与直线上各点的所有线段中,垂线段最短.分析:本题考查了垂线段的性质在实际生活中的运用.体现了建模思想的运用.20.解:(1)因为点C与直线AB上点A,B的连线中,CA是垂线段,所以AC<BC.因为点B与直线AC上点A,C的连线中,AB是垂线段,所以AB<BC.故AB,AC,BC中,斜边BC最长.(2)因为BC>AC,AB<BC,AC+AB>BC,所以原式=a-b-(c-a)+b+c-a=a.。
新人教版七年级数学下册全册教案附同步练习及单元测试卷(含答案)

新人教版七年级数学下册全册教案附同步练习及单元测试卷(含答案)第五章相交线与平行线5.1.1相交线教学目标:1.理解对顶角和邻补角的概念,能在图形中辨认.2.掌握对顶角相等的性质和它的推证过程.3.通过在图形中辨认对顶角和邻补角,培养学生的识图能力.重点:在较复杂的图形中准确辨认对顶角和邻补角.难点:在较复杂的图形中准确辨认对顶角和邻补角.教学过程一、创设情境,引入课题先请同学观察本章的章前图,然后引导学生观察,并回答问题.学生活动:口答哪些道路是交错的,哪些道路是平行的.教师导入:图中的道路是有宽度的,是有限长的,而且也不是完全直的,当我们把它们看成直线时,这些直线有些是相交线,有些是平行线.相交线、平行线都有许多重要性质,并且在生产和生活中有广泛应用.所以研究这些问题对今后的工作和学习都是有用的,也将为后面的学习做些准备.我们先研究直线相交的问题,引入本节课题.二、探究新知,讲授新课1.对顶角和邻补角的概念学生活动:观察上图,同桌讨论,教师统一学生观点并板书.【板书】∠1与∠3是直线AB、CD相交得到的,它们有一个公共顶点O,没有公共边,像这样的两个角叫做对顶角.学生活动:让学生找一找上图中还有没有对顶角,如果有,是哪两个角?学生口答:∠2和∠4再也是对顶角.紧扣对顶角定义强调以下两点:(1)辨认对顶角的要领:一看是不是两条直线相交所成的角,对顶角与相交线是唇齿相依,哪里有相交直线,哪里就有对顶角,反过来,哪里有对顶角,哪里就有相交线;二看是不是有公共顶点;三看是不是没有公共边.符合这三个条件时,才能确定这两个角是对顶角,只具备一个或两个条件都不行.(2)对顶角是成对存在的,它们互为对顶角,如∠1是∠3的对顶角,同时,∠3是∠1的对顶角,也常说∠1和∠3是对顶角.2.对顶角的性质提出问题:我们在图形中能准确地辨认对顶角,那么对顶角有什么性质呢?学生活动:学生以小组为单位展开讨论,选代表发言,井口答为什么.【板书】∵∠1与∠2互补,∠3与∠2互补(邻补角定义),∴∠l=∠3(同角的补角相等).注意:∠l与∠2互补不是给出的已知条件,而是分析图形得到的;所以括号内不填已知,而填邻补角定义.或写成:∵∠1=180°-∠2,∠3=180°-∠2(邻补角定义),∴∠1=∠3(等量代换).学生活动:例题比较简单,教师不做任何提示,让学生在练习本上独立完成解题过程,请一个学生板演。
5_1_1相交线 (分层作业)【2023春人教版七下数学精品备课】 解析版

5.1 相交线第1课时相交线参考答案与试题解析夯基训练知识点1 邻补角1.识别邻补角应同时满足以下三条:①有公共_____________;②有一条公共边;③两角的另一边_____________.1.【答案】①顶点③分别互为反向延长线2.邻补角是指( )A.和为180°的两个角B.有公共顶点且互补的两个角C.有一条公共边且相等的两个角D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角2.【答案】D3.下列选项中,∠1与∠2互为邻补角的是( )3.【答案】D解:根据邻补角的定义是有公共顶点且有一条公共边,另一边互为反向延长线的两个角,故选项D正确。
4.如图,∠1的邻补角是( )A.∠BOCB.∠BOE和∠AOFC.∠AOFD.∠BOC和∠AOF4.【答案】B解:根据邻补角的定义,与∠1有公共顶点且有一条公共边,另一边互为反向延长线的角为∠BOE和∠AOF,故选项B正确。
5.如图,∠α的度数等于( )A.135°B.125°C.115°D.105°5.【答案】A解:根据邻补角的性质可知。
6.如图所示,直线AB和CD相交所成的四个角中,∠1的邻补角是________.6.【答案】∠2和∠4解析:根据邻补角的概念判断:有一个公共顶点、一条公共边,另一边互为延长线.∠1和∠2、∠1和∠4都满足有一个公共顶点和一条公共边,另一边互为延长线,故为邻补角.故答案为∠2和∠4.方法总结:邻补角的定义包含了两层含义:相邻且互补.但需要注意的是:互为邻补角的两个角一定互补,但互补的角不一定是邻补角.知识点2 对顶角及其性质7识别对顶角应同时满足:①有公共___________;②两个角的两边___________.7.【答案】①顶点②分别互为反向延长线8.如图,小强和小丽一起玩跷跷板,横板AB绕O上下转动,当小强从A到A'的位置时,∠AOA'=45°,则∠BOB'的度数为___________,理由是___________.8.【答案】45°;对顶角相等9.如图,直线AB,CD相交于点O,则∠1 ∠2,根据的是;∠2+∠3= ,根据的是.9.【答案】=;对顶角相等;180°;邻补角的定义10.下列语句正确的是( )A.顶点相对的两个角是对顶角B.有公共顶点并且相等的两个角是对顶角C.两条直线相交,有公共顶点的两个角是对顶角D.两条直线相交,有公共顶点且没有公共边的两个角是对顶角10.【答案】D解:A错误,如图①,∠1与∠2的顶点相对,但∠1与∠2不是对顶角;B错误,如图②,∠1与∠2有公共顶点,且∠1=∠2,但∠1与∠2不是对顶角;C错误,如图③,∠1与∠2是两条直线相交且有公共顶点的角,但∠1与∠2不是对顶角;D正确.11.下列图形中∠1与∠2互为对顶角的是( )11.解析:观察∠1与∠2的位置特征,只有C中∠1和∠2同时满足有公共顶点,且∠1的两边是∠2的两边的反向延长线.故选C.方法总结:判断对顶角只看两点:①有公共顶点;②一个角的两边分别是另一个角的两边的反向延长线.12.如图,直线AB、CD相交于点O,若∠BOD=42°,OA平分∠COE,求∠DOE的度数.12.解析:根据对顶角的性质,可得∠AOC与∠BOD的关系,根据OA平分∠COE,可得∠COE 与∠AOC的关系,根据邻补角的性质,可得答案.解:由对顶角相等得∠AOC=∠BOD=42°.∵OA平分∠COE,∴∠COE=2∠AOC=84°.由邻补角的性质得∠DOE=180°-∠COE=180°-84°=96°.方法总结:解决此类问题的关键是在图中找出对顶角和邻补角,根据两种角的性质找出已知角和未知角之间的数量关系.题型总结题型1 利用对顶角的性质求角13.如图,直线AB,CD,EF相交于点O,如果∠AOC=65°,∠DOF=50°.(1)求∠BOE的度数;(2)通过计算∠AOF的度数,你发现射线OA有什么特殊性吗?13.解:(1)因为∠AOC=65°,所以∠BOD=∠AOC=65°.又因为∠BOE+∠BOD+∠DOF=180°,∠DOF=50°,所以∠BOE=180°-65°-50°=65°.(2)因为∠AOF=∠BOE=65°,且∠AOC=65°,所以∠AOF=∠AOC,所以射线OA是∠COF的平分线.题型2 利用邻补角及对顶角的性质求角(方程思想)14.补全解答过程:如图,已知直线AB,CD相交于点O,OA平分∠EOC,若∠EOC∶∠EOD=2∶3,求∠BOD的度数.解:由∠EOC∶∠EOD=2∶3,设∠EOC=2x°,则∠EOD=3x°.因为∠EOC+∠____________=180°(____________),所以2x+3x=180,解得x=36.所以∠EOC=72°.因为OA平分∠EOC(已知),所以∠AOC=12∠EOC=36°.因为∠BOD=∠AOC(____________),所以∠BOD=____________.14.EOD;平角的定义(邻补角的性质);对顶角相等;36°15.如图,直线AC,EF相交于点O,OD是∠AOB的平分线,OE在∠BOC内,∠BOE=12∠EOC,∠DOE=72°,求∠AOF的度数.15.解析:因为已知量与未知量的关系较复杂,所以想到列方程解答,根据观察可设∠BOE =x,则∠AOF=∠EOC=2x,然后根据对顶角和邻补角找到等量关系,列方程.解:设∠BOE=x,则∠AOF=∠EOC=2x.∵∠AOB与∠BOC互为邻补角,∴∠AOB=180°-3x.∵OD平分∠AOB,∴∠DOB=12∠AOB=90°-32x.∵∠DOE=72°,∴90°-32x+x=72°,解得x=36°.∴∠AOF=2x=72°.方法总结:在相交线中求角的度数时,就要考虑使用对顶角相等或邻补角互补.若已知关系较复杂,比如出现比例或倍分关系时,可列方程解决角度问题.拓展培优拓展角度1 利用邻补角的性质求折叠中的角(折叠法)16.将一张长方形纸片按图中的方式折叠,BC,BD为折痕,求∠CBD的大小.16.解:由折叠的性质可知∠ABC=∠A'BC,∠EBD=∠E'BD,所以∠A'BC=12∠ABE',∠E'BD=12∠EBE'.由∠ABE'与∠EBE'互为邻补角,得∠ABE'+∠EBE'=180°,因此∠CBD=∠A'BC+∠E'BD=12∠ABE'+12∠EBE'=12(∠ABE'+∠EBE')=90°点拨:此题运用了折叠法,解题时关键要弄清折叠前后哪些角对应相等.拓展角度2 利用邻补角及对顶角的定义进行计数(基本图形法)17.下列各图中的直线都相交于一点.(1)(2)若n 17.解:(1)2;6;12;4;12;24(2)对顶角共有n(n-1)对,邻补角共有2n(n-1)对.技巧解:巧数图形中对顶角或邻补角的对数:(1)在复杂图形中数对顶角或邻补角的对数时,我们一般先确定图形中包含有几个两条直线相交的基本图形;(2)在每个基本图形中有2对对顶角、4对邻补角,从而计算出所有对顶角、邻补角的对数. 拓展角度3 与对顶角有关的探究问题18.我们知道:两直线交于一点,对顶角有2对;三条直线交于一点,对顶角有6对;四条直线交于一点,对顶角有12对……(1)10条直线交于一点,对顶角有________对;(2)n(n ≥2)条直线交于一点,对顶角有________对.18.解析:(1)仔细观察计算对顶角对数的式子,发现式子不变的部分及变的部分的规律,得出结论,代入数据求解.如图①,两条直线交于一点,图中共有()4244-⨯=2对对顶角;如图②,三条直线交于一点,图中共有()6264-⨯=6对对顶角;如图③,四条直线交于一点,图中共有()8284-⨯=12对对顶角……按这样的规律,10条直线交于一点,那么对顶角共有()202204-⨯=90(对).故答案为90;(2)利用(1)中规律得出答案即可.由(1)得n(n ≥2)条直线交于一点,对顶角的对数为()2n 224n -=n(n -1).故答案为n(n -1).方法总结:解决探索规律的问题,应全面分析所给的数据,特别要注意观察符号的变化规律,发现数据的变化特征.。
人教版七年级数学下册第五章相交线练习试题(含答案) (20)

人教版七年级数学下册第五章相交线练习试题(含答案) 如图,直线AB,CD,EF相交于点O,且AB⊥CD,∠1=25°,求∠2的度数?【答案】65°【解析】试题分析:直接利用邻补角的定义得出∠BOE=65°,再根据对顶角相等,即可得出答案.试题解析:∵直线AB,CD,EF相交于点O,且AB⊥CD∴∠BOC=90°,∵∠1=25°,∴∠BOE=65°,∴∠2=∠BOE=65°.92.如图,直线AB,CD相交于点O,且∠1=∠2.(1)指出∠1的对顶角;(2)若∠2和∠3的度数比是2:5,求∠4和∠AOC的度数.【答案】(1)∠1的对顶角是∠AOC;(2)∠AOC=40°.【解析】分析:(1)根据对顶角的定义解答;(2)先求出∠1、∠2、∠3的比,再根据平角的定义列式求出这三个角,再根据对顶角相等求解.详解:(1)∠1的对顶角是∠AOC;(2)∵∠1=∠2,∠2和∠3的度数比是2:5,∴∠1:∠2:∠3=2:2:5,设∠2=2x,则∠1=2x,∠3=5x,由题意得,2x+2x+5x=180∘,解得x=20,所以,∠1=40∘,∠2=40∘,∠3=100∘,根据对顶角相等,∠4=∠BOC=40∘,∠AOC=∠1=40∘.点睛:考查对顶角的概念以及平角的概念,熟练掌握对顶角的性质,平角的性质是解题的关键.93.如图:已知直线AB、CD相交于点O,∠COE=90°(1)若∠AOC=36°,求∠BOE的度数;(2)若∠BOD:∠BOC=1:5,求∠AOE的度数.【答案】(1)54°;(2)120°【解析】试题分析:(1)根据平角的定义求解即可;(2)根据平角的定义可求∠BOD,根据对顶角的定义可求∠AOC,根据角的和差关系可求∠AOE的度数.试题解析:解:(1)∠∠AOC=36°,∠COE=90°,∠∠BOE=180°﹣∠AOC﹣∠COE=54°;=30°,∠∠AOC=30°,(2)∠∠BOD:∠BOC=1:5,∠∠BOD=180°×115∠∠AOE=30°+90°=120°.94.如图,△ABC中,∠A+∠B=900.⑴根据要求画图:①过点C画直线MN∥AB②过点C画AB的垂线,交AB于点D.⑵请在⑴的基础上回答下列问题:①已知∠B+∠DCB=900,则∠A与∠DCB的大小关系为__________,理由是__________.②图中线段_________的长度表示点A到直线CD的距离.【答案】(1)作图见解析(2)①;∠A=∠DCB;同角的余角相等;②AD 【解析】【分析】【详解】试题分析:(1)根据题意画出MN∠AB,CD∠AB于D;(2)①根据同角的余角相等可判断∠A=∠DCB;②根据点到直线的距离的定义求解.试题解析:解:(1)①如图,MN为所求;②如图,CD为所求;(2)①∠∠B+∠DCB=90°,∠B+∠A=90°,∠∠A=∠DCB;②线段AD长度表示点A到直线CD的距离.故答案为∠A=∠DCB,同角的余角相等;AD.95.如图所示,射线OM与直线交于点O,OM平分∠AOB,求∠AOM 度数,并用符号表示OM与AB的位置关系.【答案】90°.【解析】试题分析:根据角平分线定义得出∠AOM=12∠AOB,代入求出∠AOM=90°,根据垂直定义得出即可.试题解析:∵∠AOB=180°,OM平分∠AOB,∴∠AOM=12∠AOB=12×180°=90°,∴OM⊥AB.96.如图,是一条河,C是河边AB外一点:(1)过点C要修一条与河平行的绿化带,请作出正确的示意图.(2)现欲用水管从河边AB,将水引到C处,请在图上测量并计算出水管至少要多少?(本图比例尺为1:2000)【答案】详见解析.【解析】试题分析:(1)过点C作AB的平行线.(2)过点C作CD垂直于AB交AB于点D.根据垂线段最短,可得CD长度最小,量出CD的长度,然后按比例尺求出实际的距离.试题解析:如图:(1)过点C画一平行线平行于AB.(2)过点C作CD垂直于AB交AB于点D.然后用尺子量CD的长度,再按1:2000的比例求得实际距离即可.经测量0.9,=CD cm⨯==cm m0.92000180018.97.已知:如图所示,∠1=∠2,∠3=∠4,GF ∠AB 于G 点,那么CD 与AB 是否互相垂直?试判断并说明理由.【答案】相互垂直,证明详见解析.【解析】试题分析:首先由GF AB ⊥可得2490∠+∠=︒, 又因为1234∠=∠∠=∠,, 得到1390∠+∠=︒, 由此即可得到CD 与AB 的位置关系.试题解析:相互垂直.理由:∵GF AB ⊥∴2490∠+∠=︒,而1234∠=∠∠=∠,,∴1390∠+∠=︒,CD AB ∴⊥.98.如图,将一副三角尺的直角顶点重合在一起.()1若DOB ∠与DOA ∠的比是2:11,求BOC ∠的度数.()2若叠合所成的(090)BOC n n ∠=<<,则AOD ∠的补角的度数与BOC ∠的度数之比是多少?【答案】(1)70°;(2)1:1.【解析】试题分析:根据条件可知∠AOB =∠COD =90°,并且∠AOD =∠AOB +∠COD ﹣∠BOC =180°﹣∠BOC ,根据这个关系就可以求解.试题解析:解:(1)设∠DOB =2x °,则∠DOA =11x °.∵∠AOB =∠COD ,∴∠AOC =∠DOB =2x °,∠BOC =7x °.又∵∠AOD =∠AOB +∠COD ﹣∠BOC =180°﹣∠BOC ,则得方程:11x =180﹣7x ,解得:x =10,∴∠BOC =70°.(2)∵∠AOD =∠AOB +∠COD ﹣∠BOC =180°﹣∠BOC ,∴∠AOD 与∠BOC 互补,则∠AOD 的补角等于∠BOC .故∠AOD 的补角的度数与∠BOC 的度数之比是1:1.点睛:正确认识∠AOD =∠AOB +∠COD ﹣∠BOC =180°﹣∠BOC 这一个关系是解题的关键,这是一个常用的关系,需熟记.99.如图,//30100CE AB B AOB ∠=∠=,,,求C ∠和ODE ∠的度数.【答案】30°,130°.【解析】试题分析:由已知能得出∠COD =∠AOB =100°(对顶角相等),再由CE ∥AB ,可求出∠C =∠B =30°,根据三角形外角定理可求出∠ODE 的度数.试题解析:解:∵CE ∥AB ,∴∠C =∠B =30°.∠COD =∠AOB =100°(对顶角相等),∠ODE =∠C +∠COD =30°+100°=130°(三角形外角和定理).点睛:本题考查了的知识点是平行线的性质、对顶角及三角形外角定理,解题的关键是由平行线的性质和对顶角求出∠C 和∠ODE 的度数.100.如图,直线AB 与CD 相交于点O OP ,是BOC ∠的平分线,OF CD ⊥,如果40AOD ∠=.求:()1COP ∠的度数;()2BOF ∠的度数.【答案】(1)20°;(2)50°【解析】试题分析:(1)先由对顶角相等得出∠BOC =∠AOD =40°,再根据角平分线定义即可求解;(2)先由OF ⊥CD 得出∠COF =90°,再根据∠BOF =∠COF ﹣∠BOC 即可求解.试题解析:解:(1)∵直线AB 与CD 相交于点O ,∴∠BOC =∠AOD =40°.∵OP 是∠BOC 的平分线,∴∠COP =12∠BOC =20°; (2)∵OF ⊥CD ,∴∠COF =90°,∴∠BOF =∠COF ﹣∠BOC =90°﹣40°=50°.点睛:本题考查了对顶角的性质,垂直的定义,角平分线的定义,是基础知识,需熟练掌握.。
(完整word版)人教版初中数学七年级下册相交线练习题附参考答案

人教版初中数学七年级下册相交线练习题附参考答案1.在两条直线相交所成的四个角中,( )不能判定这两条直线垂直A.对顶角互补 B.四对邻补角 C.三个角相等 D.邻补角相等答案:B说明:两条直线相交,已有四对邻补角,因此,选项B不足以判定这两条直线垂直;而根据垂直的定义,对顶角、邻补角的性质不难判断其它选项的说法都可以判定这两条直线垂直;所以答案为B.2.如图,在三角形ABC中,AC⊥BC,CD⊥AB于D,则下列关系不成立的是( )A.AB>AC>ADB.AB>BC>CDC.AC+BC>ABD.AC>CD>BC答案:D说明:由垂线段最短的性质,可知AB>AC,AB>BC,AC>AD,BC>CD都成立,即选项A、B中的关系都是正确的;再由两点之间线段最短,可知AB<AC+BC成立,所以选项C也正确;只有选项D中CD>BC不成立,答案为D.3.图中,∠1和∠2是同位角的是( )A B C D答案:D说明:由同位角的概念可知,一条直线与两条直线相交,同位角位置相同且有一边在同一直线上,这样可以判断选项A、B、C中的∠1与∠2都不是同位角,只有选项D中的∠1与∠2是同位角,答案为D.填空题:1.如图,直线a,b,c交于O,∠1 = 30º,∠2 = 50º,则∠3 =________.答案:100º说明:如图,∠3的对顶角为∠4,所以∠3 =∠4;又∠1+∠2+∠4 = 180º,∠1 = 30º,∠2 = 50º,所以∠4 = 180º−30º−50º = 100º,即∠3 = 100º.2.如图,直线AB、CD交于O,OA平分∠EOC,且∠EOD = 120º,则∠BOD =_______.答案:30º说明:因为∠BOD =∠COA,∠EOD+∠EOC = 180º,OA平分∠EOC,所以∠EOD+2∠COA = 180º,再由∠EOD = 120º,可得∠COA = 30º,即∠BOD = 30º.3.已知如图,①∠1与∠2是_______被_______所截成的_______角;②∠2与∠3是_______被_______截成的_______角;③∠3与∠A是_______被_______截成的_______角;④AB、AC被BE截成的同位角_______,内错角_______,同旁内角_______;⑤DE、BC被AB截成的同位角是_______,内错角_______,同旁内角_______.答案:①DE、BC;BE;内错角②AC、BC;BE;同旁内角③AB、BE;AC;同位角④不存在;∠ABE与∠3;∠ABE与∠AEB⑤∠ADE与∠ABC;不存在;∠EDB与∠DBC4.在三角形ABC中,AC⊥BC,CD⊥AB于D,如图,则在图中共有______对互余的角,______对互补的角,______对邻补角,点A到CD的距离是______,到BC的距离是______,到点B的距离是______,点C 到直线AB的距离是______.答案:有4对互余的角:∠ACD与∠A;∠A与∠B;∠B与∠BCD;∠BCD与∠ACD;有3对互补的角:∠CDA与∠CDB;∠ACB与∠CDA;∠ACB与∠CDB;有1对邻补角:∠CDA与∠CDB;点A到CD的距离是AD;点A到BC的距离是AC;点A到点B的距离是AB;点C到直线AB的距离是CD.解答题:1.如图,已知直线AB、CD、EF相交于O,OG⊥AB,且∠FOG = 32º,∠COE = 38º,求∠BOD.答案:因为AB、CD、EF交于O,所以∠FOD =∠COE =38º又因为OG⊥AB,所以∠BOD = 90º−∠FOD−∠FOG = 90º−32º−38º = 20º.2.如图,已知OA⊥OB,OC⊥OD,且∠AOD:∠BOC = 4:5,求∠BOC的度数.答案:因为OA⊥OB,OC⊥OD所以∠AOB =∠DOC =90º即∠AOD+∠BOC = 180º又因为∠AOD:∠BOC = 4:5所以∠BOC = ×180º = 100º.3.如图,直线AB、CD交于O,∠AOE = 30º,∠BOC = 2∠AOC,求∠DOF.解答:∵AB、CD交于O∴∠AOC+∠BOC = 180º又∵∠BOC = 2∠AOC∴3∠AOC = 180º∴∠AOC = 60º又∵∠AOE = 30º∴∠DOF = 30º。
5.1.1相交线

在我们的生活的世界中,蕴涵着大 量的相交线和平行线,
这节课我们就来学习相交线所成的角
注意观察用剪刀剪布时剪把手张 角的变化与剪刀张角是怎样变化的
如果把剪刀的构造看作是两条相交的 直线,以上就关系到两条直线相交所 成的角的问题,
画直线AB、CD相交于点O A
1
2 4
O
D
3
C
B
练习:下列说法对不对 1.邻补角可以看成是平角被过它顶点的一 条射线分成的两个角 2.邻补角是互补的两个角,互补的 两个角是邻补角 3.对顶角相等,相等的两个角是对顶角
[练习]课本P9-1,2
例题:如图,直线a,b相交, 1 求
2 , 3, 4
40
的度数
巩固练习 教科书5页练习 已知,如图 AOC 35 , COF 80 求: AOD 和 DOF 的度数
,
[作业]课本 P 10-7,8
一判断题 1如果两个角有公共顶点和一条公共过,而且 这两个角互为补角,那么它们互为邻补角( )
2两条直线相交,如果它们所成的邻补角相等, 那么一对对顶角就互补( ) 二填空题
如图,直线AB、CD、EF相交于点O, AOE
的对顶角是 若
,
,
COF
的邻补角是
130
AOC
:AOE
=
=2:3, EOD
则 BOC
初中数学同步训练必刷题(人教版七年级下册5

初中数学同步训练必刷题(人教版七年级下册5.1.1 相交线)一、单选题1.(2022七下·承德期末)下列四个图形中,∠1与∠2是对顶角的是()A.B.C.D.2.(2022七上·南海期中)直线AB和直线CD相交于点O,若∠AOC=40°,则∠BOC等于()A.140°B.60°C.40°D.160°3.(2022七下·崇川期末)如图,直线AB与CD相交于点O,∠AOC:∠AOD=2:3,则∠BOD等于()A.36°B.72°C.60°D.75°(4.(2022九上·南宁开学考)如图,直线AB,CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOC 的度数是()A.115°B.125°C.135°D.145°5.(2022七下·承德期末)如图,小明手持手电筒照向地面,手电筒发出的光线CO与地面AB形成了两个角,∠BOC=8∠AOC,则∠BOC的度数是()A.160°B.150°C.120°D.20°6.(2022七下·延庆期末)如图,直线AB,CD相交于点O,如果∠1=35°,那么∠2的度数是()A.35°B.55°C.145°D.165°7.(2022七下·钦州期末)如图,直线AB,CD,EO相交于点O,已知OA平分∠EOC,若∠EOC:∠EOD =2:3,则∠BOD的度数为()A.40°B.37°C.36°D.35°8.(2022七下·东明期末)如图,直线AB、CD相交于点O,且∠AOC+∠BOD=110°,则∠AOD的度数为()A.125°B.120°C.110°D.100°9.(2022七下·青县期末)如图,直线AB、CD相交于点O,下列描述一定正确的是()A.∠1和∠2互为对顶角B.∠1和∠3互为邻补角C.∠1=∠2D.∠1=∠310.(2022七下·江油期中)如图,直线AB、CD相交于O,OA平分∠EOC,若∠EOC=70°,那么∠BOD 的度数是()A.30°B.35°C.45°D.40°二、填空题11.(2022七下·五常期末)若∠1和∠2是对顶角,∠1=36°,则∠2的度数是度.12.(2022七下·大连期末)如图,∠1与∠2是对顶角,∠1=α+10°,∠2=40°,则α=°.13.(2022七下·富川期末)如图,直线AB,CD相交于点O,OE是∠AOD的平分线,若∠BOD=40°,则∠COE的度数为.14.(2022七下·榆林期末)若∠1与∠2是对顶角,∠3与∠2互余,且∠3=37∘,则∠1的度数为°. 15.(2022七下·雨花期末)如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.若∠AOC=76°,则∠BOF的度数为°.16.(2022七下·义乌开学考)如图,点O 在直线AB 上,过点O 作射线OC,若∠AOC=53°17′28″,则∠BOC 的度数是.17.(2021七下·涿鹿期末)在同一平面内的三条直线,它们的交点个数可能是.18.(2021七下·玉林期末)如图,两直线交于点O,若∠3=3∠2,则∠1的度数是.19.(2021七下·孝义期中)如图是某城市一座古塔底部平面图,在不能进入塔内测量的情况下,学习兴趣小组设计了如图所示的一种测量方案,学习兴趣小组认为测得∠COD的度数就是∠AOB的度数.其中的数学原理是.20.(2021七下·滦南期末)小明用一副三角板自制对顶角的“小仪器”,第一步固定直角三角板ABC,并将边AC延长至点P,第二步将另一块三角板CDE的直角顶点与三角板ABC的直角顶点C 重合,摆放成如图所示,延长DC至点F,∠PCD与∠ACF就是一组对顶角,若∠ACF=30∘,则∠PCD=,若重叠所成的∠BCE=n∘(0∘<n<90∘),则∠PCF的度数.三、解答题21.(2022七下·中山期末)如图,直线AB,CD相交于点O,OE平分∠BOC,OF∠CD,若∠BOE=72°,求∠AOF的度数.22.(2022七下·韩城期中)如图,直线AB,CD相交于点O,∠BOC=125°,∠AOE=∠BOD,求∠DOE的度数.23.(2022七下·河源期中)如图,直线a,b相交于点O,已知3∠1−∠2=100°,求∠3的度数.24.(2021七下·南沙期中)如图,直线AB、CD、EF相交于点O,OG平分∠COF,∠1=30°,∠2=45°.求∠3的度数.25.(2022七下·黄州期中)如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=72°,∠DOF=90°.(1)求∠DOE的度数;(2)求∠EOF的度数.26.(2021七下·瑶海期末)如图,直线AB,CD和EF相交于点O,(1)写出∠AOC,∠BOF的对顶角;(2)如果∠AOC=70°,∠BOF=20°,求∠BOC和∠DOE的度数.27.(2021七下·武昌期中)如图,直线MD、CN相交于点O,OA是∠MOC内的一条射线,OB是∠NOD 内的一条射线,∠MON=70°.(1)若∠BOD=12∠COD,求∠BON的度数;(2)若∠AOD=2∠BOD,∠BOC=3∠AOC,求∠BON的度数.28.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分,(1)直接写出图中∠AOC的对顶角为, ∠BOE的邻补角为;(2)若,且=2:3,求的度数.答案解析部分1.【答案】C【知识点】对顶角及其性质【解析】【解答】解:对顶角指的是有一个公共顶点,并且一个角的两边是另一个角两边的反向延长线的两个角,所以:A 、两角没有公共顶点,不符合题意;B 、两角也是只有一条边互为反向延长线,另一条边没有互为反向延长线,不符合题意;C 、两角有一个公共顶点,并且一个角的两边是另一个角两边的反向延长线的两个角,符合题意;D 、两角只有一条边互为反向延长线,另一条边没有互为反向延长线,不符合题意; 故答案为:C .【分析】有一个公共顶点,并且一个角的两边是另一个角两边的反向延长线的两个角是对顶角,据此逐一判断即可.2.【答案】A 【知识点】邻补角【解析】【解答】解:∵∠AOC=40°,∴∠BOC=180°-∠AOC=180°-40°=140°, 故答案为:A .【分析】利用邻补角求出∠BOC 的度数即可。
寒假预习《5.1.1 相交线》课时检测卷精选 2021-2022学年人教版数学七年级下册(含答案)

寒假预习《5.1.1 相交线》同步测试培优卷精选 2021-2022学年人教版数学七年级下册(含答案)一、精心选一选1. 根据语句“直线1l与直线2l相交,点M在直线1l上,直线2l不经过点M.”画出的图形是()A.B.C.D.2. 下列各图中,∠1和∠2是对顶角的是( )A.B.C.D.3. 如图,对顶角量角器中α∠的度数为()A.120°B.60°C.90°D.50°4. 下面各图中∠1和∠2是对顶角的是()A.B.C .D .5. 如图,直线AB ,CD 交于点O ,射线OM 平分∠AOD ,若∠BOD=760,则∠BOM等于( )A .B .C .D .6. 两条直线相交于一点,则共有对顶角的对数为( )A .1对B .2对C .3对D .4对7. 如图所示,直线AB ,CD 交于点O ,射线OM 平分AOC ∠.若38AOM ∠=︒,则BOC∠等于( )A .104︒B .144︒C .106︒D .136︒8. 如图,直线AB ,CD 相交于点O ,OE AB ⊥,垂足为点O ,若50BOD ∠=︒,则COE∠的度数为( )A .40°B .45°C .50°D .55°9. 下列结论中错误的是( )A .连接两点的线段叫两点之间的距离B .两点之间,线段最短C .同角的补角相等D .两点确定一条直线二、细心填一填10. 如图,两条直线AB ,CD 交于点O ,射线OM 是∠AOC 的平分线,若∠BOD =80°,则∠BOM 的度数是__.11. 如图是一把剪刀,若∠AOB+∠COD=60°,则∠BOD=____°.12. 如图,直线AB,CD相交于点O,∠EOC=70°,OA平分∠EOC,则∠BOD=________.13. 若∠α=70°,则它的补角是________.14. 如图,直线AB、CD相交于点O,OE平分∠BOD,若∠AOD-∠DOB=60°,则∠EOB=___.15. 已知,如图,直线AB、CD相交于O,OE平分∠BOD且∠AOE=150°,∠AOC的度数为______.16. 如图,直线AB、CD相交于点O,135∠=︒,则直线AB与直线CD的夹角是BOC______︒.17. 如图,直线AB和OC相交于点O,∠AOC=100°,则∠1=_______度.18. 如图,直线AB CD 、相交于O 点,OE AB ⊥.(1)2∠和3∠互为___角; 1∠和3∠互为_______角;2∠和4∠互为___角. (2)若125∠=︒,那么2∠=_________;3BOE ∠=∠-∠______=_______︒-____︒=___︒;4∠=∠_____1-∠=__︒-____︒=______︒.三、用心做一做19. 如图,直线AB 、CD 相交于点O ,DOE BOD ∠∠=,OF 平分AOE ∠,20BOD ∠︒=.(1)求AOE ∠的度数;(2)求COF ∠的度数.20. 如图所示,已知∠AOC=160°,OC 平分∠BOD ,OE 平分∠AOD ,求∠BOE 的度数.21. 如图,直线BC 与MN 相交于点O ,AO ⊥BC ,OE 平分∠BON ,若∠EON=20°.求∠AOM 和∠NOC 的度数.22. 如图,已知DM 平分ADC ∠,BM 平分ABC ∠,且27A ∠=︒,33M ∠=︒,求C ∠的度数.23. 已知O 为直线AB 上一点,射线OD 、OC 、OE 位于直线AB 上方,OD 在OE 的左侧,120AOC ∠=︒,DOE α∠=.(1)如图1,70α=︒,当OD 平分AOC ∠时,求EOB ∠的度数.(2)如图2,若2DOC AOD ∠=∠,且80α<︒,求EOB ∠(用α表示). (3)若90α=︒,点F 在射线OB 上,若射线OF 绕点O 顺时针旋转n ︒(0180n <<︒),2FOA AOD ∠=∠,OH 平分EOC ∠,当120FOH ∠=︒时,求n 的值.24. 如图,要测得两堵墙形成的∠AOB 的度数,但人不能进入围墙,请你写出两种不同的测量方法,并说明几何道理.参考答案一、精心选一选1. D【分析】利用直线2l 不经过点M 可判断A ,利用点M 在直线1l 上,不在直线2l 上可判断B ,利用点M 在直线1l 外可判断C ,根据直线1l 与直线2l 相交,点M 在直线1l 上,直线2l 不经过点M 可判断D .【详解】解:A .直线2l 不经过点M ,故本选项不合题意;B .点M 在直线1l 上,不在直线2l 上,故本选项不合题意;C .点M 在直线1l 外,故本选项不合题意;D .直线1l 与直线2l 相交,点M 在直线1l 上,直线2l 不经过点M ,故本选项符合题意;答案:D .【点睛】本题考查根据语句画图问题,掌握画图的基本语句是解题关键. 2. B【分析】根据对顶角的定义对各图形判断即可.【详解】解:A 、∠1和∠2不是对顶角,故选项错误;B 、∠1和∠2是对顶角,故选项正确;C 、∠1和∠2不是对顶角,故选项错误;D 、∠1和∠2不是对顶角,故选项错误.故选B .【点睛】本题考查了对顶角的定义,是基础题,熟记概念并准确识图是解题的关键. 3. B【分析】根据量角器的读数以及的对顶角相等即可求得α∠的度数.【详解】由图可知α∠的对顶角为60︒,根据对顶角相等,则α∠的度数为60︒, 故选B .【点睛】本题考查了量角器的使用,对顶角相等,理解对顶角相等是解题的关键. 4. C【解析】【分析】根据对顶角的定义对各选项分析判断后利用排除法求解.【详解】A 、∠1和∠2不是对顶角,故A 错误;B 、∠1和∠2不是对顶角,故B 错误;C 、∠1和∠2是对顶角,故C 正确;D 、∠1和∠2不是对顶角,是邻补角,故D 错误.故选:C .【点睛】本题考查了对顶角、邻补角,熟记概念并准确识图是解题的关键.5. C【解析】角平分线定义,对顶角的性质,补角的定义.由∠BOD=760,根据对顶角相等的性质,得∠AOC=760,根据补角的定义,得∠BOC=1040.由射线OM 平分∠AOD ,根据角平分线定义,∠COM=380.∴∠BOM=∠COM +∠BOC=1420.故选C .6. B如图,直线AB、CD相交于一点O,图中的∠AOD和∠BOC,∠AOC和∠BOD 是对顶角,共计2对.故选B.7. A【分析】根据2∠的度数,利用平角的定义计算即可.∠=∠AOC AOM计算AOC【详解】∵OM平分AOC∠,38∠=︒,AOM∴∠=∠=⨯︒=︒,AOC AOM223876∴∠=︒-∠=︒-︒=︒.BOC AOC180********故选:A.【点睛】本题考查了角的平分线,平角的定义,熟记角的定义,平角的定义是解题的关键.8. A【分析】根据对顶角相等得到AOC∠的度数.∠,再根据作余角定义,求COE【详解】解:∵50⊥∠=∠=,OE ABAOC BOD︒∴90905040∠=︒-∠=︒-︒=︒,COE AOC故选:A.本题考查了对顶角的性质和互为余角的性质,熟悉相关性质并能进行计算是解题的关键.9. A【分析】根据两点之间的距离,同角的余角或补角相等,两点确定一条直线,线段的性质即可判断.【详解】解:A、连接两点的线段的长度叫两点之间的距离,故错误;B、两点之间,线段最短,故正确;C、同角的补角相等,故正确;D、两点确定一条直线,故正确;故选A.【点睛】本题考查了对余角或补角,直线的性质,线段的性质的理解和运用,知识点有:同角的余角或补角相等,两点确定一条直线,两点之间线段最短二、细心填一填10. 140°【分析】先根据对顶角相等得出∠AOC=80°,再根据角平分线的定义得出∠COM,最后解答即可.【详解】解:∵∠BOD=80°,∴∠AOC=80°,∠COB=100°,∵射线OM是∠AOC的平分线,∴∠COM=40°,∴∠BOM=40°+100°=140°,故答案为:140°.【点睛】此题考查对顶角和角平分线的定义,关键是得出对顶角相等.11. 150【分析】根据对顶角相等得到∠AOB的度数,再根据邻补角的定义即可得出结论.【详解】∵∠AOB=∠COD,∠AOB+∠COD=60°,∴∠AOB=∠COD=30°,∴∠BOD=180°-∠AOB=180°-30°=150°.故答案为150°.【点睛】本题考查了对顶角相等和邻补角的定义.求出∠AOB的度数是解题的关键.12. 35°【详解】试题分析:∵∠EOC=70°,OA平分∠EOC,∴∠AOC=12∠EOC=12×70°=35°,∴∠BOD=∠AOC=35°.故答案为35°.点睛:本题考查了角平分线的定义,对顶角相等的性质,熟记定义并准确识图是解题的关键.13. 110°.【详解】试题分析:根据定义∠α的补角度数是180°﹣70°=110°.故答案是110°.考点:余角和补角.14. 30°【详解】∵∠AOD-∠BOD=60°,∴∠AOD=∠BOD+60°,∵AB为直线,∴∠AOD+∠BOD=∠AOB=180°,∴∠BOD+60°+∠BOD=180°,∴∠BOD=60°,∵OE平分∠BOD,∴∠EOB=30°故答案为: 30°.15. 60°【解析】根据两直线相交,对顶角相等,可推出∠AOC=∠DOB,又根据OE平分∠BOD,x,∠AOE=150°,可求∠AOC.设∠AOC=x, ∠AOD=180°-x,∠DOE=12x,解:设∠AOC=x, ∠AOD=1800-x,∠AOC=∠DOB,OE平分∠BOD,∠DOE=12x=150°,x=60°, ∠AOC=60°∵∠AOE=150°,∴180°-x+ 12故答案为60°“点睛”本题主要考查对顶角的性质以及角平分线的定义,邻补角,解决问题的关键是用方程思想解题.16. 45【分析】先根据邻补角的定义求出∠AOC,再根据直线的夹角为锐角解答.【详解】解:∵∠BOC=135°,∴∠AOC=180°-∠BOC=180°-135°=45°,∴直线AB与直线CD的夹角是45°.故答案为:45.【点睛】本题考查了邻补角的定义,要注意直线的夹角是锐角.17. 80.【解析】试题分析:由邻补角互补,得∠1=180°﹣∠AOC=180°﹣100°=80°,故答案为80.考点:对顶角、邻补角.18. 余余邻补25 2 90 25 65 AOB180 25155根据余角、补角、邻补角、平角的定理计算求解即可.【详解】解:∵OE AB ⊥,∴90AOE EOB ==︒∠∠,∴2390=+︒∠∠,1390∠+∠=︒,∴2∠和3∠互为余角; 1∠和3∠互为余角;∵24180∠+∠=︒且有公共边,∴2∠和4∠互为邻补角;∵125∠=︒,1∠和2∠互为对顶角,∴1225∠=∠=︒,32BOE ∠=∠-∠=90︒-25︒=65︒;4∠=∠AOB 1-∠=180︒-25︒=155︒.故答案为:余;余;邻补;25︒;2;90;25;65;AOB ;180;25;155.【点睛】本题考查的是余角和补角、对顶角和邻补角的概念,如果两个角的和等于90°(直角),就说这两个角互为余角,如果两个角的和等于180°(平角),就说这两个角互为补角.三、用心做一做19. (1)140︒;(2)90︒【分析】(1)因为DOE BOD =∠,求出∠BOE ,得出AOE ∠;(2)利用180COF DOE EOF ∠=︒-∠-∠,从而求出COF ∠的度数.【详解】解:(1)20BOD ∠=︒,DOE BOD ∠=∠,202040BOE ∴∠=︒+︒=︒,18040140AOE ∴∠=︒-︒=︒;(2)20DOE ∠=︒,111407022EOF AOE ∠=∠=⨯︒=︒, 180207090COF ∴∠=︒-︒-︒=︒.本题考查了平角的性质、对顶角、角平分线的性质,解题的关键是根据题意得出各角之间的关系.20. 110°【分析】先利用平角的概念求出∠BOC的度数,然后利用角平分线的定义即可求出∠BOD的度数和∠EOD的度数,最后利用∠BOE=∠EOD+∠BOD即可求解.【详解】∵∠AOC=160°,∠AOC+∠BOC=180°,∴∠BOC=180°-160°=20°.∵OC平分∠BOD,∴∠BOD=2∠BOC=40°.又∵∠AOD+∠BOD=180°,∴∠AOD=180°-40°=140°.∵OE平分∠AOD,∴∠EOD=12∠AOD=70°,∴∠BOE=∠EOD+∠BOD=70°+40°=110°.【点睛】本题主要考查角平分线的定义,平角的定义和角的和与差,掌握角平分线的定义是解题的关键.21. 50AOM︒∠=,140NOC︒∠=.【解析】【分析】要求∠AOM的度数,可先求它的余角.由已知∠EON=20°,结合角平分线的概念,即可求得∠BON.再根据对顶角相等即可求得;要求∠NOC的度数,根据邻补角的定义即可.【详解】解:∵OE平分∠BON,∴∠BON=2∠EON=2×20°=40°,∴∠NOC=180°-∠BON=180°-40°=140°,∠MOC=∠BON=40°,∵AO ⊥BC ,∴∠AOC=90°,∴∠AOM=∠AOC-∠MOC=90°-40°=50°,所以∠NOC=140°,∠AOM=50°. 【点睛】结合图形找出各角之间的关系,利用角平分线的概念,邻补角的定义以及对顶角相等的性质进行计算.22. 39C ∠=︒.【分析】根据角平分线的性质及对顶角相等可求得,2C M A ∠=∠-∠,然后再利用已知条件及角的和差计算求解即可.【详解】解:如图所示:设BC 与MD 的交点为E DM 平分ADC ∠,BM 平分ABC ∠21CDQ ∴∠=∠,22ABQ ∠=∠在CDQ ∆与ABQ ∆中,CQD AQB ∠=∠2122C A ∴∠+∠=∠+∠①在CDE ∆与MBE ∆中,CED MEB ∠=∠12C M ∴∠+∠=∠+∠②用2⨯-②①得:2C M A ∠=∠-∠27A ∠=︒,33M ∠=︒2332739C ∴∠=⨯︒-︒=︒故39C∠=︒【点睛】角平分线的性质及对顶角相等、角的和差计算是本题的考点,根据题意求得2C M A∠=∠-∠是解题的关键.23. (1)50°;(2)140EOBα∠=︒-;(3)168或72.【分析】(1)利用角平分线的定义和邻补角的定义求得∠BOC和∠EOC,再利用角的和差即可求得∠BOE;(2)先根据已知数量关系求得∠DOE,再利用角的和差即可得出结论;(3)设BOF n∠=︒,分①若DOE∠在AOC∠的内部,②当DOE∠在射线OC的两侧时两种情况,利用角的和差列出方程求解即可.【详解】解:(1)∵120AOC∠=︒,OD平分AOC∠,∴60AOD DOC∠=∠=︒,60BOC∠=︒,又70DOEα∠==︒,∴706010COE∠=︒-︒=︒,∴6050BOE COE∠=︒-∠=︒;(2)∵120AOC∠=︒,2DOC AOD∠=∠,∴1403AOD AOC∠=∠=︒,80DOC∠=︒,60BOC∠=︒,∴80EOCα∠=︒-,∴6080140 EOB BOC EOCαα∠=∠+∠=︒+︒-=︒-;(3)①如图,若DOE∠在AOC∠的内部设BOF n∠=︒则依题意有:()11118090222AOD FOA n n ∠=∠=︒-︒=︒-︒, ∵120AOC ∠=︒,90DOE α∠==︒,∴1209030AOD EOC AOC DOE ∠+∠=∠-∠=︒-︒=︒,又∵OH 平分EOC ∠,∴()113022EOH EOC AOD ∠=∠=︒-∠111309030224n n ⎛⎫=︒-︒+︒=︒-︒ ⎪⎝⎭, 又120FOH ∠=︒,∴1118090903012024n n n ︒-︒+︒-︒+︒+︒-︒=︒,∴168n =;②当DOE ∠在射线OC 的两侧时如图设BOF n ∠=︒,则依题意有119022AOD AOF n ∠=∠=︒-︒,∵120AOC ∠=︒,90DOE α∠==︒,∴190120602COE AOD n ∠=∠+︒-︒=︒-︒,又OH 平分EOC ∠,∴113024EOH EOC n ∠=∠=︒-︒,又120FOH ∠=︒,∴1130909012042n n n ⎛⎫︒+︒-︒+︒-︒-︒=︒ ⎪⎝⎭, ∴72n =,∴综上所述OF 顺时针旋转的角度为168或72.【点睛】本题考查邻补角的有关计算,角平分线的有关计算,角的和差,一元一次方程的应用.(3)中能分类讨论画出图形,结合图形利用角的和差列出方程是解题关键.24. 见解析【分析】根据邻补角和对顶角的性质进行设计即可.【详解】方法一:如图所示,延长AO至C,测量∠BOC的度数,根据邻补角的性质得:∠AOB=180°-∠BOC,即可求解;方法二:如图所示,分别延长AO,BO,测量∠COD的度数,根据对顶角相等得:∠AOB=∠COD,即可求解.【点睛】本题考查邻补角和对顶角的实际应用,熟记基本定义和性质并灵活运用是解题关键.。
人教版七年级数学下册 第5章 相交线和平行线 综合练习(含答案)

人教版 七年级数学 第5章 相交线与平行线综合练习(含答案)一、单选题(共有11道小题)1.下面各图中∠1与∠2是对顶角是( ).2.如图,直线123,,l l l 交于一点,直线14l l P ,若∠=124°,∠2=88°,则∠3的度数为()A.26°B.36° C.46° D.56°3.下列图形中,与是对顶角的是( )4.如图,直线l ∥m ∥n ,等边△ABC 的顶点B 、C 分别在直线n 和m 上,边BC 与直线n 所夹锐角为25°,则∠ 的度数为( )A .25°B .45°C .35°D .30°5.下列命题中的真命题是( )A .三个角相等的四边形是矩形B .对角线互相垂直且相等的四边形是正方形C .顺次连接矩形四边中点得到的四边形是菱形D .正五边形既是轴对称图形又是中心对称图形CBl 4DCBA6.如图,AB ∥CD,EF 交AB 、CD 于点E 、F ,EG 平分∠BEF ,交CD 于点G. 若∠1=40°,则∠EGF=( )A .20°B .40°C .70°D .110° 7.下列说法中正确的是( )A .两直线被第三条直线所截得的同位角相等B .两直线被第三条直线所截得的同旁内角互补C .两平行线被第三条直线所截得的同位角的平分线互相垂直D .两平行线被第三条直线所截得的同旁内角的平分线互相垂直8.下列四个图中,α∠与β∠成邻补角的是( )A BC D9.下列命题是真命题的有( ) ①对顶角相等;②两直线平行,内错角相等;③两个锐角对应相等的两个直角三角形全等; ④有三个角是直角的四边形是矩形;⑤平分弦的直径垂直于弦,并且平分弦所对的弧。
A .1个 B .2个 C .3个 D.4个10.如图,若AB CD ∥,70BEF ∠=︒,则B F C ∠+∠+∠的度数为( )A.215︒B.250︒C.320︒D.360︒11.如图,已知直线a ∥b ,且a 与b 之间的距离为4,点A 到直线a 的距离为2,点B 到直线b 的距离为3,AB=a 上找一点M ,在直线b 上找一点N ,满足MN ⊥a 且AM+MN+NB 的长度和最短,则此时AM+NB=( )A .6B .8C .10D .12DBβαβαβαβαDC FEBA12.如图,直线a //b ,n 直线l 与a 相交于点P ,与直线b 相交于点Q ,PM ⊥l 于点P ,若∠1=50 °,则∠2= °.命题“相等的角是对顶角”是 命题. (填“真”或“假”) 14.根据图在( )内填注理由:①∵B CEF ∠=∠(已知)∵AB CD ∥( ) ②∵B BED ∠=∠(已知)∴AB CD ∥( ) ③∵180B CEB ∠+∠=°(已知)∴AB CD ∥( )15.若平面上有4条直线两两相交且无三线共点,则共有同旁内角 对.16.如图AB CD EF CG ∥∥,平分140110ACE A E ∠∠=︒∠=︒,,.则______DCG ∠=.三、计算题(共有1道小题)17.已知如图所示,AB DE ∥,116D ∠=︒,93DCB ∠=︒,求B ∠的度数.图2FC EB DA GF EDCB AD C EBADCFEBA18.找出下图中用数字表示的各角中,哪些是同位角,内错角?哪些是同旁内角?19.如图,一条公路修在湖边时,需拐弯绕湖而过,如果第一次拐的角A ∠是120o ,第二次拐的角B ∠是150︒,第三次拐的角是C ∠,这时的道路恰好和第一次拐弯之前的道路平行,求C ∠的大小.20.已知,如图360B BED D ∠+∠+∠=︒.求证:AB CD ∥.21.⑴ 两条平行直线被第三条直线所截,有几对同位角,几对内错角,几对同旁内角.⑵ 三条平行直线呢?四条、五条呢? ⑶ 你发现了什么规律.22.证明:三角形三个内角的和等于180︒.23.平面上有()2n n ≥条直线两两相交,试证明:所得的角中至少有一个角不大于180n︒.1234图1CEB DA NEDCBA24.已知AB CD ∥,点M N ,分别在AB CD ,上.(1)AB CD ,间有一点E ,点E 在直线MN 左侧,如图1,求证AME CNE MEN ∠+∠=∠.(2)当AB CD ,间的点E 在直线MN 右侧时,如图2,AME CNE MEN ∠∠∠,,直线有什么关系?(3)如图3,当点E 在AB CD ,外侧时,探索AME CNE MEN ∠∠∠,,之间有何关系?图1NME DCBA图2NME D CBA图3NMEDCB A答案一、单选题(共有11道小题)1.下面各图中∠1与∠2是对顶角是( ).参考答案:B2.如图,直线123,,l l l 交于一点,直线14l l P ,若∠=124°,∠2=88°,则∠3的度数为( )A.26°B.36°C.46°D.56°参考答案:B3.下列图形中,与是对顶角的是( )参考答案:C4.如图,直线l ∥m ∥n ,等边△ABC 的顶点B 、C 分别在直线n 和m上,边BC 与直线n 所夹锐角为25°,则∠ 的度数为( )CBl 4DCBAA .25°B .45°C .35°D .30°参考答案:C5.下列命题中的真命题是( )A .三个角相等的四边形是矩形B .对角线互相垂直且相等的四边形是正方形C .顺次连接矩形四边中点得到的四边形是菱形D .正五边形既是轴对称图形又是中心对称图形参考答案:C6.如图,AB ∥CD,EF 交AB 、CD 于点E 、F ,EG 平分∠BEF ,交CD 于点G. 若∠1=40°,则∠EGF=( )A .20°B .40°C .70°D .110°参考答案:C7.下列说法中正确的是( )A .两直线被第三条直线所截得的同位角相等B .两直线被第三条直线所截得的同旁内角互补C .两平行线被第三条直线所截得的同位角的平分线互相垂直D .两平行线被第三条直线所截得的同旁内角的平分线互相垂直参考答案:D8.下列四个图中,α∠与β∠成邻补角的是( )A BC D参考答案:C9.下列命题是真命题的有( ) ①对顶角相等;②两直线平行,内错角相等;③两个锐角对应相等的两个直角三角形全等; ④有三个角是直角的四边形是矩形;⑤平分弦的直径垂直于弦,并且平分弦所对的弧。
5.1相交线习题

(D)(C)(B)(A)22211121《5.1相交线》练习题班级 姓名 得分一:填空、选择题(每题5分)1、直线AB 、CD 相交于点O ,若∠AOC=50度,则∠∠BOD= 。
2、如右图,直线AB 与CD 相交于点O ,射线OE 平分∠已知∠AOD=40度,则∠COE= ,∠BOD= 3、若∠1与∠2是对顶角,∠3与∠2互余,且∠3=60那么∠1= 。
4、若∠1与∠2是对顶角,且∠1与∠2互余,则∠1=__ ___5、如图,直线AB 、CD 交于点O ,则 (1)若∠1+∠3=68度,则∠1= 。
(2)若∠2:∠3=4:1,则∠2= 。
(3)若∠2-∠1=100度,则∠3= 。
第5题6、下列各图中,∠1和∠2是对顶角的是( )7、已知直线AB 、CD 相交于点O ,则与∠AOC 互补的角有( )A 、1个B 、2个C 、3个D 、4个 第7题 8、如图,三条直线两两相交,其中对顶角共有( ) A 、3对 B 、4对 C 、5对 D 、6对9、下列说法错误的是 ( ) 第9题A 、对顶角的平分线成一个平角B 、对顶角相等C 、相等的角是对顶角D 、对顶角的余角相等 10、如右图,直线AB 、CD 交于点O ,OE 、OF 是过O 点 的两条射线,其中构成对顶角的是( ) A 、∠AOF 与 ∠DOE B 、∠EOF 与∠BOEC 、∠BOC 与∠AOD D 、∠COF 与∠BOD321O DBCA ODCBAOF EDCB AEDOCBA321OFE D CB A11、下列说法中正确的个数有 ( )(1)直线外一点与直线上各点连接的所有线中垂线段最短。
(2)画一条直线的垂线段可以画无数条。
(3)在同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直。
(4)从直线外一点到这条直线的垂线段叫做点到直线的距离。
A 、1个 B 、2个 C 、3个 D 、4个12、如图2-28,∠1与∠2不能构成同位角的图形是 ( )13、如图2-29,图中共有同旁内角( )A .2B .3C .4D .514、如图2-30,与∠1构成同位角的共有 ( )A .1个B .2个C .3个D .4个三:解答题(每题10分)15、如图,直线AD 和BE 相交于O 点,OC ⊥AD ,∠COE=70度,求∠AOB 的度数。
人教版七年级下册数学5.1.1相交线与平行线练习题(含答案)
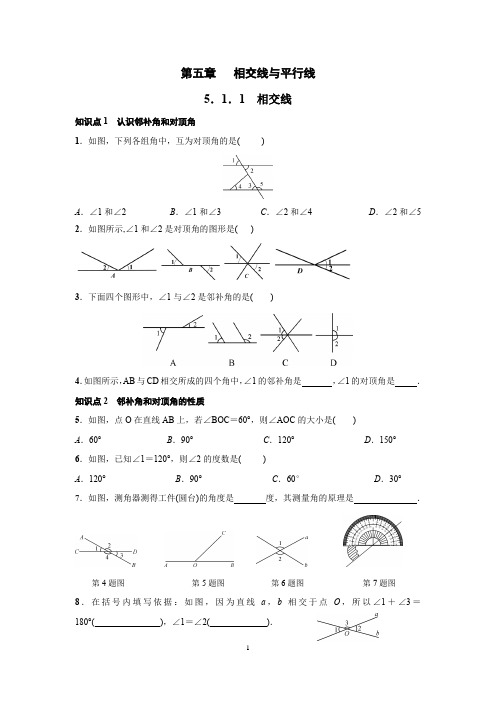
第五章相交线与平行线5.1.1相交线知识点1认识邻补角和对顶角1.如图,下列各组角中,互为对顶角的是( )A.∠1和∠2 B.∠1和∠3 C.∠2和∠4 D.∠2和∠5 2.如图所示,∠1和∠2是对顶角的图形是( )3.下面四个图形中,∠1与∠2是邻补角的是( )4.如图所示,AB与CD相交所成的四个角中,∠1的邻补角是,∠1的对顶角是.知识点2邻补角和对顶角的性质5.如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( )A.60° B.90° C.120° D.150°6.如图,已知∠1=120°,则∠2的度数是( )A.120° B.90° C.60°D.30°7.如图,测角器测得工件(圆台)的角度是度,其测量角的原理是.第4题图第5题图第6题图第7题图8.在括号内填写依据:如图,因为直线a,b相交于点O,所以∠1+∠3=180°( ),∠1=∠2( ).AB9.如右图所示,直线AB,CD,EF 相交于点O ,则①∠AOD 的对顶角是___________,∠EOC 的对顶角是___________②∠AOC 的邻补角是_________________,∠BOE 的邻补角是__________________. ③若∠AOC=50°,求∠BOD ,∠COB 的度数. 解:∵∠AOC=50° ∴∠BOD=__________=________( ); ∵∠BOC+∠AOC=180°∴∠COB=180°-∠________( )=180°-________°=________°10.如图,直线AB ,CD 相交于点O ,∠EOC =70°,OA 平分∠EOC ,求∠BOD 的度数.【综合训练】11.下列说法正确的有( )①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.A .1个B .2个C .3个D .4个 12.如图,三条直线l 1,l 2,l 3相交于一点,则∠1+∠2+∠3=( )A .90°B .120°C .180°D .360°13.如图所示,直线AB 和CD 相交于点O.若∠AOD 与∠BOC 的和为236°,则∠AOC 的度数为( )A .62°B .118°C .72°D .59°第12题图 第13题图14.两条直线相交所成的四个角中,有两个角分别是(2x -10)°和(110-x )°,则x = . 15.若∠1的对顶角是∠2,∠2的邻补角是∠3,且∠3=45°,则∠1的度数为 . 16.如图,直线a ,b ,c 两两相交,∠1=80°,∠2=2∠3,则∠4=.17.如图所示, 直线AB,CD 相交于点O,OE 平分∠AOD,∠AOC=120°,求∠BOD,∠AOE 的度数.解:∵∠AOC=120°∴∠BOD=__________=________( );∵OE 平分∠AOD ∴∠AOE=21___________( ) ∵∠AOD+∠AOC=180°∴∠AOD=180°-∠________( )=_________________________=___________ ∠AOE=____________.18.如图,直线AB ,CD 相交于点O ,∠AOE =∠BOE ,OB 平分∠DOF.若∠DOE =50°,求∠DOF 的度数.19.如图,l 1,l 2,l 3交于点O ,∠1=∠2,∠3∶∠1=8∶1,求∠4的度数.20.探究题:(1)三条直线相交,最少有 个交点,最多有 个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;(2)四条直线相交,最少有 个交点,最多有 个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;(3)依次类推,n 条直线相交,最少有 个交点,最多有 个交点,对顶角有 对,邻补角有 对.OE DC BA第五章相交线与平行线5.1.1相交线答案知识点1认识邻补角和对顶角1.如图,下列各组角中,互为对顶角的是( A )A.∠1和∠2 B.∠1和∠3 C.∠2和∠4 D.∠2和∠5 2.如图所示,∠1和∠2是对顶角的图形是( C )3.下面四个图形中,∠1与∠2是邻补角的是( D )4.如图所示,AB与CD相交所成的四个角中,∠1的邻补角是∠2,∠4,∠1的对顶角是∠3.知识点2邻补角和对顶角的性质5.如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( C )A.60° B.90° C.120° D.150°6.如图,已知∠1=120°,则∠2的度数是( A )A.120° B.90° C.60°D.30°AB 7.如图,测角器测得工件(圆台)的角度是40度,其测量角的原理是对顶角相等.8.在括号内填写依据:如图,因为直线a ,b 相交于点O , 所以∠1+∠3=180°(邻补角互补), ∠1=∠2(对顶角相等).9.如右图所示,直线AB,CD,EF 相交于点O ,则①∠AOD 的对顶角是_∠BOC__,∠EOC 的对顶角是__∠DOF___ ②∠AOC 的邻补角是_∠AOD____,∠BOE 的邻补角是___∠AOE__. ③若∠AOC=50°,求∠BOD ,∠COB 的度数.解:∵∠AOC=50°∴∠BOD=_∠AOC_=_50°(对顶角相等); ∵∠BOC+∠AOC=180°∴∠COB=180°-∠AOC (邻补角互补) =180°- 50° = 130°10.如图,直线AB ,CD 相交于点O ,∠EOC =70°,OA 平分∠EOC ,求∠BOD 的度数.解:因为OA 平分∠EOC ,∠EOC =70°, 所以∠AOC =12∠EOC =35°.所以∠BOD =∠AOC =35°. 【综合训练】11.下列说法正确的有( B )①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.A .1个B .2个C .3个D .4个 12.如图,三条直线l 1,l 2,l 3相交于一点,则∠1+∠2+∠3=( C )A .90°B .120°C .180°D .360°13.如图所示,直线AB 和CD 相交于点O.若∠AOD 与∠BOC 的和为236°,则∠AOC 的度数为( A )A .62°B .118°C .72°D .59° 14.两条直线相交所成的四个角中,有两个角分别是(2x -10)°和(110-x )°,则x=40或80. 15.若∠1的对顶角是∠2,∠2的邻补角是∠3,且∠3=45°,则∠1的度数为135°. 16.如图,直线a ,b ,c 两两相交,∠1=80°,∠2=2∠3,则∠4=140°.17.如图所示, 直线AB,CD 相交于点O,OE 平分∠AOD,∠AOC=120°,求∠BOD,∠AOE 的度数.解:∵∠AOC=120°∴∠BOD= ∠AOC = 120° (对顶角相等); ∵OE 平分∠AOD∴∠AOE=21∠AOD∵∠AOD+∠AOC=180°∴∠AOD=180°-∠AOC (邻补角互补)=180°-120°= 60° ∠AOE= 30°.18.如图,直线AB ,CD 相交于点O ,∠AOE =∠BOE ,OB 平分∠DOF.若∠DOE =50°,求∠DOF 的度数.解:因为∠AOE =∠BOE ,且∠AOE +∠BOE =180°, 所以∠AOE =∠BOE =90°. 因为∠DOE =50°,所以∠DOB =∠BOE -∠DOE =40°.因为OB 平分∠DOF ,所以∠DOF =2∠DOB =80°.OE DCBA19.如图,l 1,l 2,l 3交于点O ,∠1=∠2,∠3∶∠1=8∶1,求∠4的度数. 解:设∠1=∠2=x °,则∠3=8x °. 由∠1+∠2+∠3=180°,得 10x =180.解得x =18. 所以∠1=∠2=18°. 所以∠4=∠1+∠2=36°. 20.探究题:(1)三条直线相交,最少有1个交点,最多有3个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;(2)四条直线相交,最少有1个交点,最多有6个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;(3)依次类推,n 条直线相交,最少有1个交点,最多有n (n -1)2个交点,对顶角有n(n -1)对,邻补角有2n(n -1)对.解:(1)图略,对顶角有6对,邻补角有12对. (2)图略,对顶角有12对,邻补角有24对.。
《5.1相交线》练习题

(D)(C)(B)(A)22211121《5.1相交线》练习题一1、下列各图中,∠1和∠2是对顶角的是( )2、已知直线AB 、CD 相交于点O ,则与∠AOC 互补的角有 ( ) A 、1个 B 、2个 C 、3个 D 、4个3、如图,三条直线两两相交,其中对顶角共有 ( ) A 、3对 B 、4对 C 、5对 D 、6对4、如图,直线AB 、CD 交于点O ,OE 、OF 是过O 点的两条射线,其中构成对顶角的是 ( )A 、∠AOF 与 ∠DOEB 、∠EOF 与∠BOEC 、∠BOC 与∠AOD D 、∠COF 与∠BOD5、下列说法错误的是 ( )A 、对顶角的平分线成一个平角B 、对顶角相等C 、相等的角是对顶角D 、对顶角的余角相等 6、如图,直线AB 与CD 相交于点O ,∠AOD+∠BOC=236度,则∠AOC 的度数为 ( )A 、72度B 、62度C 、124度D 、144度 7、如图,点A 到直线CD 的距离是指哪条线段长 ( )A 、ACB 、CDC 、AD D 、BD 8、在“同一平面内,过一点有且只有一条直线与已知直线垂直”中这一点的位置 ( )A 、在直线的上方B 、在直线的下方C 、在直线上D 、可以任意位置9、下列说法中正确的个数有 ( ) (1)直线外一点与直线上各点连接的所有线中垂线段最短。
(2)画一条直线的垂线段可以画无数条。
(3)在同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直。
(4)从直线外一点到这条直线的垂线段叫做点到直线的距离。
A 、1个 B 、2个 C 、3个 D 、4个10、如图2-27,∠BAC 和∠ACD 是( )A .同位角B .同旁内角C .内错角D .以上结论都不对O F E D CBA ODCBADABC11、如图2-28,∠1与∠2不能构成同位角的图形是 ( )12、如图2-29,图中共有同旁内角 对A .2B .3C .4D .513、如图2-30,与∠1构成同位角的共有 ( )A .1个B .2个C .3个D .4个 14、如图2-31,下列判断正确的是 [ ]A .4对同位角,4对内错角,2对同旁内角B .4对同位角、4对内错角,4对同旁内角C .6对同位角,4对内错角,4对同旁内角D .6对同位角,4对内错角,2对同旁内角15、如图,直线AB 、CD 相交于点O ,若∠AOC=50度,则∠BOC= ,∠AOD= ∠BOD= 。
2020--2021学年人教版七年级数学下册 5.1 ---5.4 期末分节同步检测题 含答案

5.1 相交线-点到直线的距离班级:__________ 姓名:__________分数:__________一、选择题1. 点到直线的距离是指( )A.从直线外一点到这条直线的垂线B.从直线外一点到这条直线的垂线段C.从直线外一点到这条直线的垂线的长D.从直线外一点到这条直线的垂线段的长2. 下列说法正确的是( )A.若线段,则点是线段的中点B.相等的角是对顶角C.过一点有且只有一条直线与已知直线垂直D.从直线外一点到这条直线的垂线段,叫做点到直线的距离3. 为直线外一点,,,为直线上三点,,则点到直线的距离为()A. B. C. D.不大于4. 如图,在三角形中,于点,则下列说法错误的是()A.点到直线的距离为线段的长度B.点到直线的距离为线段的长度C.点到直线的距离为线段的长度D.点到直线的距离为线段的长度5. 如图,为直线外一点,点,,在直线上,且,垂足为,,则下列说法中错误的是()A.线段的长度叫点到直线的距离B.,,三条线段中,最短试卷第2页,总39页C.线段的长度叫点到直线的距离D.线段的长度等于点到直线的距离6. 下列说法正确的是()A.过,两点的直线的长度是,两点之间的距离B.线段就是,两点之间的距离C.在连接,两点的所有线中,最短线的长度是,两点之间的距离D.乘火车从上海到北京要走千米,这就是说上海站与北京站之间的距离是千米7. 如图,点在直线外,在过点的四条线段中表示点到直线距离的是线段()A. B. C. D.8. 如图所示,右,,,则下列说法正确个数为()①到的距离为;②到的距离为;③到的距离为;④到的距离为.A. B. C. D.9. 如图所示,,垂足为,连接,下列说法正确的是()①线段是,两点间的距离②线段的长度是,两点间的距离③线段是点到直线的距离④线段的长度是点到直线的距离.A.①③B.②④C.②③D.①④试卷第4页,总39页10. 如图,于,于,于,下列说法错误的是()A.点到的距离是的长度B.点到的距离是的长度C.点到的距离是的长度D.点到的距离是的长度11. 如图所示,,于,则下列结论中,正确的个数为()①;②与互相垂直;③点到的垂线段是线段;④点到的距离是线段的长度;⑤线段的长度是点到的距离;⑥线段是点到的距离;⑦.A.个B.个C.个D.个12. 如图,直线外一点,点、、、都在直线上,则点到直线的距离是A.线段的长度B.线段的长度C.线段的长度D.线段的长度二、填空题13. 如图,点,,在直线上,,则点到直线的距离是________.14. 如图,,,,,则点到的距试卷第6页,总39页离为________.15. 如图,,,能表示点到直线(或线段)的距离的线段有________条.16. 如图,,为垂足,,为垂足,,,,,,那么点到的距离是________,点到的距离是________,点到的距离是________,,两点间的距离是________.三、解答题17.(10分) 如图,,,,.(1)试说出点到直线的距离;点到直线的距离;(2)点到直线的距离是多少?你是怎样求得的?试卷第8页,总39页参考答案5.1 相交线-点到直线的距离一、选择题1.【答案】D2.【答案】C3.【答案】D4.【答案】C5.【答案】D6.【答案】C7.【答案】D8.【答案】A9.【答案】B10.【答案】C11.【答案】A12.【答案】C二、填空题13.【答案】14.试卷第10页,总39页【答案】15.【答案】16.【答案】,,,三、解答题(本题共计 1 小题,共计10分)17.【答案】解:(1)∵,,,∴点到直线的距离,点到直线的距离分别是:,.(2)设点到直线的距离为,的面积,∴ ,∴ .∴ 点到直线的距离为.5.2 平行线及其判定1.下列表示方法正确的是( )A.a∥A B.AB∥cd C.A∥B D.a∥c2.有下列生活实例:①交通道口斑马线;②天上的彩虹;③体操的纵队;④百米跑道线;⑤火车铁轨线.其中属于平行线的有( )A.1个 B.2个 C.3个 D.4个3. 在同一平面内的两条不重合的直线的位置关系是( ) A.垂直或相交 B.平行、垂直或相交 C.平行或相交D.平行或垂直4. 下列说法:①一条直线的平行线只有一条;②过一点有且只有一条直线与已知直线平行;③同一平面内,若一直线与两平行线中的一条相交,那么它也和另一条相交.其中错误的个数是( )A.0 B.1 C.2 D.35. 下列说法错误的是( )A.过一点有且只有一条直线与已知直线平行B.平行于同一条直线的两条直线平行C.若a∥b,b∥c,c∥d,则a∥dD.同一平面内,若一条直线与两平行线中的一条相交,那么它也和另一条相交6.下列推理正确的是()A.因为a∥b,b∥c,所以c∥d B.因为a∥c,b∥d,所以c ∥dC.因为a∥b,a∥c,所以b∥c D.因为a∥b,c∥d,所以a ∥c试卷第12页,总39页7.a、b、c为同一平面内任意三条直线,交点可能有() A.1个或2个 B.1个或2个或3个C.0个或1个或2个或3个D.都不对8. 在同一个平面内,的两条直线叫做平行线.直线a 平行于b,记作 .9. 经过直线外一点,有且条直线与这条直线平行.如果两条直线都与第三条直线,那么这两条直线也互相.10. 直线l同侧有A、B、C三点,如果A、B两点确定的直线l1与B、C两点确定的直线l2都与l平行,则A、B、C三点的位置关系是,其理论依据是.11. 观察如图所示的长方体后,用符号表示下列两棱的位置关系:A1B1 AB,AA1 AB,A1D1 C1D1,AD BC(⊥;∥).12.如图所示,能相交的是 (填序号),平行的是 (填序号).13. 如图,在下面的方格纸中,找出互相平行的线段,并用符号表示出来: .14. 如图,若AB∥CD,经过点E可画EF∥AB,则EF与CD的关系是,理由是.15. 如图,完成下列各题:(1)用直尺在网格中完成:①画出直线AB的一条平行线,②经过C点画直线垂直于CD;(2)用符号表示上面①、②中的平行、垂直关系.16. 如图,取一张长方形的硬纸片ABCD对折,MN是折痕,把平面ABNM平摊在桌面上,另一个面CDMN可任意改变位置,试判断AB与CD之间的关系,并说明理由.分别是直线EF外两点.17. 如图,P、Q试卷第14页,总39页(1)过P画直线AB∥EF,过Q画直线CD∥EF;(2)AB与CD有怎样的位置关系?为什么?18. [实践]①画∠AOB=60°,在∠AOB内任取一点P,过P作直线CD∥AO,又过点P作直线EF∥OB;②测量:∠CPE、∠EPD、∠DPF、∠CPF的度数.[探究]①这些角的边与∠AOB的边有何关系?②这些角的度数与∠AOB的度数之间存在什么关系?[发现]把你的发现用一句话概括出来.答案;1---7 DDCCA CC8. 不相交a∥b9. 只有一平行平行10. 在同一条直线上过直线外一点,有且只有一条直线与已知直线平行11. ∥ ⊥ ⊥∥12. ③⑤13. CD∥MN,GH∥PN14. 平行如果两条直线都与第三条直线平行,那么这两条直线也互相平行15. 解:(1)如图;(2)EF∥AB,MC⊥CD.16. 解:AB与CD平行.理由:∵AB∥MN,CD∥MN,∴AB∥CD.17. 解:(1)如图:(2)AB∥CD.理由:因为AB∥EF,CD∥EF,所以AB∥CD.试卷第16页,总39页18. 解:实践:①画图②∠CPE=120°,∠EPD=60°,∠DPF=120°,∠CPF=60°;探究:①平行,②相等或互补;发现:如果两个角的两边分别平行,那么这两个角相等或互补.5.3《平行线的性质》1. 如图,在中,,则的度数为()A. B. C. D.2. 如图,已知,,,是某公园内的四个凉亭,图中的连线是甬道,且,,若米,则下列判断中不正确的是()A.甬道可能为米B.甬道可能为米C.甬道可能为米D.甬道可能为米3. 如图,直线,将含有角的三角板的直角顶点放在直线上,若,则的度数为()A. B. C. D.4. 如图,,平分,则等于()A. B. C. D.5. 将一直角三角尺与两边平行的硬纸条如图所示放置,下列结论();();();().其中错误的个数是()试卷第18页,总39页A. B. C. D.6. 如图,下列说法错误的是()A.若,则B.若,则C.若,则D.若,则7. 下列命题中,正确的是()A.和互为相反数B.和互为绝对值C.绝对值为的数是D.的绝对值是8. 下列命题中的真命题是( )A.锐角大于它的余角B.锐角大于它的补角C.钝角大于它的补角D.锐角与钝角之和等于平角9. 甲、乙、丙、丁四个小朋友在院里玩球,忽听“砰”的一声,球击中了李大爷家的窗户.李大爷跑出来查看,发现一块窗户玻璃被打裂了.李大爷问:“是谁闯的祸?”甲说:“是乙不小心闯的祸.”乙说:“是丙闯的祸.”丙说:“乙说的不是实话.”丁说:“反正不是我闯的祸.”如果这四个小朋友中只有一个人说了实话,请你帮李大爷判断一下,究竟是谁闯的祸()A.甲B.乙C.丙D.丁10. 下列句子中,属于命题的是A.直线和垂直吗B.作线段的垂直平分线C.同位角相等,两直线平行D.画11. 如图,,平分,且,则________.12. 如图,已知,平分,平分,则________.试卷第20页,总39页13. 把命题“邻补角互补”改写成“如果…,那么…”的形式________.14. 下列说法:①两条不相交的直线叫平行线;②两条不相交的线段,在同一平面内必平行;③经过直线外一点有且只有一条直线与这条直线平行;④若直线,那么.其中错误的是________.(填序号)15. 如图,是的角平分线,,,问是否是的平分线?为什么?16. 如图,在三角形中,,且是的角平分线,那么与有什么关系?并说明理由.17. 如图,直线,平分.求的度数.18. 如图,已知.试探索:试卷第22页,总39页与之间的关系;与之间的关系.参考答案人教版七年级下册数学同步练习5.3《平行线的性质》一、选择题1.【答案】B【解答】解:因为,,所以.因为,所以.故选.2.【答案】A【解答】解:由,若米,得,,,故不符合题意;故选.3.【答案】A【解答】解:过点作,如图:试卷第24页,总39页则,∵,∴,∵,∴,∴,故选.4.【答案】B【解答】解:∵平分,∴,∵,∴,故选.5.【答案】A【解答】解:∵纸条的两边平行,∴()(同位角);(2)(内错角);(4)(同旁内角)均正确;又∵直角三角板与纸条下线相交的角为,∴(),正确.故选:.6.【答案】C【解答】解:.若,则,利用了平行公理,正确;.若,则,利用了内错角相等,两直线平行,正确;.,不能判断,错误;.若,则,利用同旁内角互补,两直线平行,正确.故选:.7.【答案】D【解答】、∵和互为相反数,∴选项不符合题意;、∵和的绝对值为,∴选项不符合题意;、∵绝对值为的数是和,∴选项不符合题意;、∵的绝对值是,试卷第26页,总39页∴选项符合题意;8.【答案】C【解答】解:,锐角大于它的余角,不一定成立,故本选项错误;,锐角小于它的补角,故本选项错误;,钝角大于它的补角,本选项正确;,锐角与钝角之和等于平角,不一定成立,故本选项错误.故选.9.【答案】D【解答】解:本题可分三种情况进行讨论:①若甲真,则乙假,丙真,丁真;这种情况下,三人说了实话,显然与条件不符;②若甲假,乙真,则丙假,丁真;这种情况下,两人说了实话,显然与条件不符;③若甲假,乙假,则丙真,丁假;这种情况下,只有丙说了实话,符合题目给出的条件.由于丁说了假话,因此闯祸的人一定是丁.故选.10.【答案】C【解答】、直线和垂直吗?这是疑问句,不是命题,所以选项错误;、作线段的垂直平分线,这是描叙性语言,不是命题,所以选项错误;.同位角相等,两直线平行是命题,所以选项正确;、画,这是描叙性语言,不是命题,所以选项错误.故选二、填空题11.【答案】【解答】解:因为,,所以.因为平分,所以.又,所以.故答案为:.【答案】【解答】解:如图,过作,过作,∵,∴,∴,∴,又∵平分,平分,∴,∴,∵,试卷第28页,总39页∴,∴,故答案为:.13.【答案】如果两个角是邻补角,那么它们互补.【解答】解:表示为:如果两个角是邻补角,那么它们互补.14.【答案】①②【解答】解:①在同一平面内,两条不相交的直线叫平行线;故错误;②两条不相交的线段,在同一平面内不一定平行;故错误;③经过直线外一点有且只有一条直线与这条直线平行;故正确;④若直线那么,故正确;其中错误的是①②,故答案为:①②.三、解答题15.【答案】解:是.∵是的角平分线,∴.∵,∴,.∴,∴是的平分线.【解答】解:是.∵是的角平分线,∴.∵,∴,.∴,∴是的平分线.16.【答案】解:,理由如下:∵是的平分线,∴,∵,∴,∴.17.【答案】解:【解答】解:因为,试卷第30页,总39页所以,因为平分,所以,所以,所以.18.【答案】解:解:【解答】解:(1)如图,过点作,则:,,∴,∴,∴,即:∴.(2)过点作,则:,∵ ,∴ ,∴ ,∴ ,即:.5.4《平移》一.选择题1.下列各组图形可以通过平移互相得到的是()A .B .C .D .2.下列情形中,哪个物体的运动是平移运动()A.行驶的汽车B.开启中的推拉窗C.飞翔的大雁D.打地基时的桩子3.在下列图案中,不能用平移得到的图案是()A .B .C .D .4.把△ABC沿BC方向平移,得到△A'B'C',随着平移距离的不断增大,△A'B'C'的面积大小变化情况是()A.增大B.减小C.不变D.不确定5.把长度为10cm的线段向下平移8cm所得的线段长度是()A.10cm B.8cm C.6cm D.18cm 6.下列选项中,平移三角形A能与三角形B重合的选项是()A .B .C .D .7.如图,△DEF经过怎样的平移得到△ABC()A.把△DEF向左平移4个单位,再向下平移2个单位试卷第32页,总39页B.把△DEF向右平移4个单位,再向下平移2个单位C.把△DEF向右平移4个单位,再向上平移2个单位D.把△DEF向左平移4个单位,再向上平移2个单位8.如图,△ABC沿AC方向平移得到△DEF,已知DF=7,DC=3,那么平移的距离为()A.3B.4C.5D.7二.填空题9.下列几种运动中,(1)水平运输带上砖的运动;(2)笔直的高速公路上行使的汽车的运动(忽略车轮的转动);(3)升降机上下做机械运动;(4)足球场上足球的运动.属于平移的有(填上所有你认为正确的序号).10.如图,将直线l1沿着AB的方向平移得到直线l2,若∠1=50°,则∠2的度数是.11.如图,多边形的相邻两边均互相垂直,则这个多边形的周长为.12.如图是一个会场的台阶的截面图,要在上面铺上地毯,则所需地毯的长度是.13.如图,将△ABC沿着某一方向平移一定的距离得到△DEF,则下列结论:①AD∥CF;②AC=DF;③∠ABC=∠DFE;④∠DAE=∠AEB.正确有(填序号即可).14.如图,△DEF是由△ABC沿直线BC向右平移得到,若BC=6,当点E刚好移动到BC的中点时,则CF=.15.如图,在△ABC中,BC=10cm,D是BC的中点,将△ABC沿BC向右平移得△A′DC′,则点A平移的距离AA′=cm.16.如图是用三角尺和直尺画平行线的示意图,将三角尺ABC沿着直尺PQ平移到三角尺A′B′C′的位置,就可以画出AB的平行线A′B′.若AC′=9cm,A′C =2cm,则直线AB平移的距离为cm.三.解答题17.把△ABC向右平移3格,再向上平移2格,画出所得到的△A′B′C,并说出线段AB与A′B′的大小及位置关系.试卷第34页,总39页18.如图所示,平移△ABC,使点A移动到点A',画出平移后的△A'B'C'(保留作图痕迹),并写出作法.19.如图,将△ABC,向右平移4个格子,再向下平移2个格子.(1)请你画出经过两次平移后的△DEF(A与D、B与E、C与F对应);(2)若每个小正方形的边长为1个单位长度,连接BE和CE,请你求出△BCE的面积.20.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.(1)现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.请画出平移后的△A′B′C′;(2)线段BC与B′C′的关系是;(3)△A′B′C′的面积为.参考答案一.选择题1.【解答】解:观察图形可知图案C通过平移后可以得到.故选:C.2.【解答】解:A、行驶的汽车,不属于平移,故本选项不合题意;B、开启中的推拉窗,属于旋转,故本选项不合题意;C、飞翔的大雁,不属于平移,故本选项不合题意;D、打地基时的桩子,属于平移,故本选项符合题意误.故选:D.3.【解答】解:A、两个图形的阴影部分不同,不能用平移得到,符合题意;B、可由一个或2个简单图形平移得到,不符合题意;C、可由一个或2个简单图形平移得到,不符合题意;D、可由上下两个图形向右平移得到,不符合题意;故选:A.4.【解答】解:∵△ABC沿BC方向平移,得到△A'B'C',∴AA′∥BC,∴S△A′B'C'=S△ABC.故选:C.5.【解答】解:平移前后的线段的长度不变,∴平移后的线段的长为10cm,故选:A.6.【解答】解:平移三角形能与三角形重合的选项是B选项.故选:B.7.【解答】解:根据图形,△DEF向左平移4个单位,向下平移2个单位,即可得到△ABC.试卷第36页,总39页故选:A.8.【解答】解:由题意平移的距离为CF=DF﹣DC=4,故选:B.二.填空题9.【解答】解:(1)水平运输带上砖的运动,是平移变换;(2)笔直的高速公路上行使的汽车的运动(忽略车轮的转动),是平移变换;(3)升降机上下做机械运动,是平移变换;(4)足球场上足球的运动,是旋转运动.所以属于平移的有(1)(2)(3)共3种.故答案是:(1)(2)(3).10.【解答】解:∵将直线l1沿着AB的方向平移得到直线l2,∴l1∥l2,∵∠1=50°,∴∠2的度数是50°.故答案为:50°.11.【解答】解:多边形周长为:(5+16)×2=21×2=42,故答案为:42.12.【解答】解:楼梯的长为5m,高为2.5m,则所需地毯的长度是5+2.5=7.5(m).故答案为:7.5m.13.【解答】解:∵△ABC沿着某一方向平移一定的距离得到△DEF,∴①AD∥CF,正确;②AC=DF,正确;③∠ABC=∠DEF,故原命题错误;④∠DAE=∠AEB,正确.所以,正确的有①②④.故答案为:①②④.14.【解答】解:由平移的性质可得:BC=EF,BE=CF,∵BC=6,点E刚好移动到BC的中点,∴BE=EC=CF=3,故答案为:3.15.【解答】解:观察图象可知平移的距离=AA′=BD=BC=5(cm),故答案为5.16.【解答】解:AC+A′C′=AC′﹣A′C=9﹣2=7(cm),A′C′=7÷2=3.5(cm),CC′=A′C+A′C′=2+3.5=5.5(cm).故直线AB平移的距离为5.5cm.故答案为:5.5.三.解答题17.【解答】解:如图,△A′B′C为所作,线段AB与A′B′平行且相等.18.【解答】解:如图,△A′B′C′即为所求.19.【解答】解:(1)如图,△DEF即为所求.(2)S△BCE =×2×2=2.20.【解答】解:(1)如图,△A′B′C′为所作;(2)线段BC与B′C′的关系是平行且相等;试卷第38页,总39页(3)△A′B′C′的面积=3×3﹣×1×2﹣×2×3﹣×3×1=.故答案平行且相等;.。
5.1.1 相交线 人教版七年级数学下册重难点专项练习(含答案)

5.1.1《相交线》重难点题型专项练习考查题型一邻补角的定义典例1.(2022秋·广西南宁·七年级统考期中)下列四个图中,与互为邻补角的是( )A.B.C.D.【答案】D【分析】根据邻补角的定义作出判断即可.【详解】解:根据邻补角的定义可知:只有D图中的是邻补角,其它都不是.故选:D.【点睛】本题考查了邻补角的定义,正确把握定义:只有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.变式1-1.(2022秋·广西柳州·七年级统考期中)下列各图中,∠1与∠2互为邻补角的是()A.B.C.D.【答案】D【分析】根据对顶角的定义:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角,进行判定即可得出答案.【详解】解:根据对顶角的定义即可判断D选项中,∠1与∠2互为邻补角.故选:D.【点睛】本题主要考查了对顶角,熟练掌握对顶角的定义进行求解是解决本题的关键.变式1-2.(2022秋·福建龙岩·七年级校联考期中)下列图形中,∠1与∠2是邻补角的是()A.B.C.D.【答案】A【分析】根据邻补角的概念进行判定即可得出答案.【详解】解:A.因为∠1与∠2是邻补角,故A选项符合题意;B.因为∠1与∠2有公共顶点且两边互为延长线,所以B选项∠1与∠2是对顶角,故B选项不符合题意;C.因为∠1与∠2的和显然不是180°,所以∠1与∠2不是邻补角,故C选项不符合题意;D.因为∠1与∠2不相邻、不互补,所以∠1与∠2不是邻补角,故D选项不符合题意;故选:A.【点睛】本题考查的是邻补角的定义,解题关键是明白定义的本质,一是相邻,二是互补.变式1-3.(2022秋·重庆荣昌·七年级统考期末)下列各图中,∠1与∠2是邻补角的是( )A.B.C.D.【答案】D【分析】根据邻补角的定义进行解答即可.【详解】解:A.不是两条直线相交组成的角,故A不符合题意;B.另一边没有互为反向延长线,不是邻补角,故B不符合题意;C.不是两条直线相交组成的角,故C不符合题意;D.是邻补角,故D符合题意.故选D.【点睛】本题考查邻补角的定义,正确把握定义:只有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.考查题型二准确找出邻补角典例2.(2022春·福建福州·七年级校考期末)如图,直线AB、MN相交于一点O,,则∠COM的邻补角是()A.∠AON B.∠AOC C.∠NOC D.∠MOB【答案】C【分析】相邻且互补的两个角互为邻补角【详解】解:∠COM与∠NOC相邻且互补,所以互为邻补角.故选:C【点睛】熟记邻补角的定义是解题的关键.变式2-1.(2022秋·陕西宝鸡·七年级统考期中)如图,∠1的邻补角是()A.∠BOC B.∠BOC和∠AOF C.∠AOE D.∠BOE和∠AOF【答案】D【分析】根据邻补角的定义:邻补角是指两条直线相交后所得的有一个公共顶点且有一条公共边的两个角,或两个角有一个公共顶点并且一个角的两条边是另一个角两条边的反向延长线,进行判断即可得到答案.【详解】解:∠1的邻补角是∠AOF和∠BOE,故选D.【点睛】本题主要考查了邻补角的定义,解题的关键在于能够熟练掌握邻补角的定义.变式2-2.(2021秋·上海宝山·七年级校考期中)如图,直线AB和CD相交于点O,下列选项中与∠AOC互为邻补角的是( )A.∠BOC B.∠BOD C.∠DOE D.∠AOE【答案】A【详解】解:图中与互为邻补角的是和,故选:A.【点睛】本题考查了邻补角,熟练掌握邻补角的定义(两个角有一条公共边,且它们的另一边互为反向延长线,具有这种关系的两个角互为邻补角)是解题关键.变式2-3.如图所示,三条直线AB,CD,EF相交于点O,则的邻补角有()A.1个B.2个C.3个D.4个【答案】B【分析】根据邻补角的特征:①相加等于180°,②有一条公共边,进行判断选择即可.【详解】因为构成的两边与直线AB和EF有关,从直线AB来看,的邻补角是,从直线EF来看,的邻补角是,所以的邻补角有2个,故选B.【点睛】本题考查的是邻补角的定义,能够深刻理解邻补角的定义是解题的关键.考查题型三对顶角的定义典例3.(2022春·黑龙江哈尔滨·七年级哈尔滨市第四十九中学校校考阶段练习)下列四个图形中,和是对顶角的是().A.B.C.D.【答案】D【分析】根据对顶角的定义,对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角,据此即可判断.【详解】解:A、两角只有一条边互为反向延长线,另一条边没有互为反向延长线,不符合题意;B、两角没有公共顶点,两角也是只有一条边互为反向延长线,另一条边没有互为反向延长线,不符合题意;C、两角只有一条边互为反向延长线,另一条边没有互为反向延长线,不符合题意;D、两角有一个公共顶点,并且一个角的两边是另一个角两边的反向延长线的两个角,符合题意;故选:D.【点睛】本题考查了对顶角的定义,属于基础题,熟练掌握对顶角的概念是解决本题的关键.变式3-1.(2022秋·福建福州·七年级校考期中)下列各图中,和是对顶角的是()A.B.C.D.【分析】根据对顶角的两边互为反向延长线对各图形分析判断后进行解答.【详解】解:根据对顶角的定义:A.和顶点不在同一位置,不是对顶角;B.和角度不同,不是对顶角;C.和顶点不在同一位置,不是对顶角;D.和是对顶角;故选:D.【点睛】本题主要考查了对顶角,正确把握对顶角的定义是解题关键.变式3-2.(2022秋·辽宁大连·七年级校联考期中)下列各图中,∠1与∠2是对顶角的是()A.B.C.D.【答案】C【分析】根据对顶角的定义解决此题.【详解】解:根据对顶角的定义(具有共同顶点,两边互为反向延长线的两个角互为对顶角),观察四个选项,只有选项C符合题意.故选:C.【点睛】本题主要考查对顶角,熟练掌握对顶角的定义是解决本题的关键.对顶角的定义:具有共同顶点,两边互为反向延长线的两个角互为对顶角.变式3-3.(2022秋·河北邯郸·七年级校考阶段练习)如图,直线,,相交于一点,则的对顶角是()A.B.C.D.【分析】根据对顶角的意义解答.【详解】解:根据对顶角的意义可知,∠2 的对顶角是∠4,故选:C.【点睛】本题考查对顶角的意义,熟练掌握对顶角的意义是解题关键.考查题型四对顶角的性质典例4.(2022秋·陕西西安·七年级校考期中)如图,两条直线交于点,若,则的度数为()A.B.C.100D.【答案】D【分析】由对顶角,邻补角的性质,即可计算.【详解】解:,,,,.故选:D.【点睛】本题主要考查了对顶角,邻补角的性质,对顶角相等,邻补角互补是解题的关键.变式4-1.(2022秋·江苏南通·七年级统考阶段练习)如图,直线相交于点O,,则( )A.B.C.D.【答案】A【分析】由对顶角相等求解再利用邻补角互补可得答案.【详解】解:∵∴∵∴故选A.【点睛】本题考查的是对顶角的性质,邻补角的性质,掌握“对顶角相等,邻补角互补”是解本题的关键.变式4-2.如图,直线AB、CD相交于点O.若,则的大小为()A.B.C.D.【答案】C【分析】根据对顶角相等,以及,求得,根据邻补角即可求解.【详解】解:∵,,∴,∴,故选C.【点睛】本题考查了对顶角相等,邻补角,掌握以上知识是解题的关键.变式4-3.(2022秋·云南大理·七年级校考期中)如图,直线AB,CD相交于点O,OE⊥AB,∠COE=68°,则∠BOD的度数为()A.22°B.32°C.68°D.112°【答案】A【分析】由OE⊥AB可得∠AOE=90°,根据∠COE=68°,进而求出∠AOC的度数,再根据对等角相等即可求出∠BOD的度数.【详解】∵OE⊥AB,∴∠AOE=90°,又∵∠COE=68°,∴∠AOC=∠AOE-∠COE=22°,∴∠BOD=∠AOC=22°(对等角相等)故选:A.【点睛】本题主要考查垂直的定义及对等角的性质,熟练掌握垂直的定义和对等角的性质是解决问题的关键.考查题型五利用邻补角的性质求角度典例5.(2022秋·辽宁大连·七年级统考期末)如图,直线a,b相交,若∠3=2∠1,则∠4的度数为______°.【答案】60【分析】先根据邻补角的定义计算得到∠1的度数,然后根据对顶角相等得到∠4的度数.【详解】解:∵∠3=2∠1,∠1+∠3=180°,∴∠1+2∠1=180°,∴3∠1=180°,∴∠1=60°,∴∠4=∠1=60°.故答案为:60.【点睛】本题考查了对顶角、邻补角.解题的关键是掌握对顶角、邻补角的定义:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角;只有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.变式5-1.(2022秋·吉林四平·七年级校考阶段练习)如图,两直线交于点O,若∠1=34°,则∠2=______°;∠3=______°.【答案】 146 34【分析】根据邻补角及对顶角的性质求解.【详解】解:∵∠1,∠2互为邻补角,∴∠1+∠2=180°,∵∠1=34°,∴∠2=180°-∠1=146°,∵∠1与∠3互为对顶角,∴∠3=∠1=34°.故答案为:146,34.【点睛】本题考查对顶角与邻补角的含义,解题关键是掌握邻补角与对顶角的性质.变式5-2.(2022秋·江西九江·七年级统考期中)如图,过直线AB上一点O作射线,,平分,则的度数为__________.【答案】##75度【分析】先根据,求出,再根据平分,即可得出答案.【详解】解:∵,∴,∵平分,∴.故答案为:.【点睛】本题主要考查了角平分线的有关计算,领补角的计算,解题的关键是根据邻补角求出.变式5-3.(2021春·黑龙江哈尔滨·七年级哈尔滨市萧红中学校考阶段练习)如图直线与直线相交于点,平分,,则的度数为___________°.【答案】【分析】利用邻补角求得,再利用角平分线的定义得,再利用对顶角性质得,最后求出即可.【详解】解:∵,∴,∵平分,∴,∵,∴故答案为:【点睛】此题考查了对顶角、邻补角,以及角平分线定义,熟练掌握各自的性质是解本题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.1.1 相交线
班级_________________ 姓名_____________
一、选择题:
1.如图所示,∠1和∠2是对顶角的图形有( )
A.1个
B.2个
C.3个
D.4个 2.如图1所示,三条直线AB,CD,EF 相交于一点O,则∠AOE+∠DOB+∠COF 等于( • )
A.150°
B.180°
C.210°
D.120°
图1 图2 图3 3.下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不
相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个
B.2个
C.3个
D.4个 4. 如图2所示,直线AB 和CD 相交于点O,若∠AOD 与∠BOC 的和为236°,则∠AOC•的度数为( )
1
2
1
2
1
2
2
1
O
F E D C
B
A O D
C
B
A 60︒30︒
34
l 3
l 2
l 1
12
A.62°
B.118°
C.72°
D.59°
5.如图3所示,直线L 1,L 2,L 3相交于一点,则下列答案中,全对的一组是( )
A.∠1=90°,∠2=30°,∠3=∠4=60°;
B.∠1=∠3=90°,∠2=∠4=30
C.∠1=∠3=90°,∠2=∠4=60°;
D.∠1=∠3=90°,∠2=60°,∠4=30° 二、填空题:
6.如图4所示,AB 与CD 相交所成的四个角中,∠1的邻补角是______,∠1的对顶角___.
图4 图5 图6 7.如图4所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.
8.如图5所示,直线AB,CD,EF 相交于点O,则∠AOD 的对顶
角是_____,∠AOC 的邻补角是_______;若∠AOC=50°,则∠BOD=______,∠COB=_______.
9.如图6所示,已知直线AB,CD 相交于O,OA 平分∠EOC,∠
EOC=70°,则∠BOD=•______.
10.对顶角的性质是______________________.
3
4D C
B
A 12O
F
E
D C
B A O
E
D C
B
A
11.如图7所示,直线AB,CD 相交于点O,若∠1-∠2=70, 则∠BOD=_____,∠2=____.
图7 图8 图9 12.如图8所示,直线AB,CD 相交于点O,OE 平分∠AOC,若
∠AOD-∠DOB=50°,•则∠EOB=______________. 13.如图9所示,直线AB,CD 相交于点O,已知∠
AOC=70°,OE 把∠BOD 分成两部分,• 且∠BOE:∠EOD=2:3,则∠EOD=________. 三、解答题:
14.如图所示,AB,CD,EF 交于点O,∠1=20°,∠BOC=80°,求∠2的度数.
15.如图所示,L 1,L 2,L 3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.
O
D
C B
A 1
2
O
E D C
B
A O
E D
C
B
A
O
F E
D
C
B
A 1
2
16. 如图所示,AB,CD 相交于点O,OE 平分∠AOD,∠AOC=120°,
求∠BOD,∠AOE•的 度数.
17.如图所示,直线AB 与CD 相交于点O,∠AOC:∠AOD=2:3,求∠BOD 的度数.
18.如图所示,直线a,b,c 两两相交,∠1=2∠3,∠2=65°,求∠4的度数.
19.若4条不同的直线相交于一点,则图中共有几对对顶角?
34
l 3
l 2l 1
1
2O
E C
B
A O
D
C
B A
c
b
a
3
4
1
2
若n条不同的直线相交于一点呢?。
