第三章静电场中的电介质
静电场中的电介质
在国际单位制中，ε的单位为法拉每米（F·m–1）。
3．电介质的击穿
如果外电场足够大，电介质分子就会摆脱分子的束缚成为 自由电子，电介质的绝缘性被破坏而成为导体，这个过程称为 电介质的击穿，这个外电场的场强称为击穿场强。下表所示为 几种电介质的相对电容率和击穿场强。
1.3 电介质中的高斯定理
1.2 电介质的极化
电介质的极化是指在外电场作用下电介质表面产生极化电 荷的现象。其中，极化电荷又称束缚电荷，是指在外电场中， 均匀介质内部各处仍成电中性，但在介质表面出现的不能离开 电介质到其他带电体，也不能在电介质内部自由移动的电荷。
1．电介质极化的机理
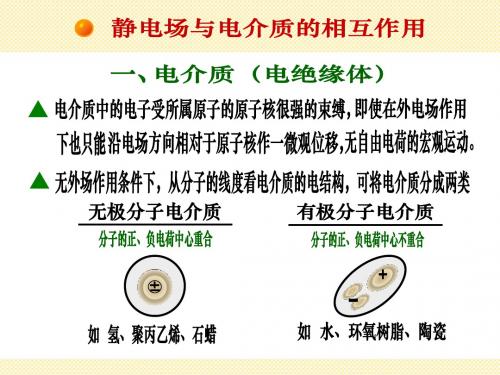
由于组成电介质的分子结构不同，所以在外电场中极化 的微观机理也有所不同。对于无极分子，在外电场E0的作用 下，正、负电荷的中心被电场力拉开，使得正、负电荷中心 产生相对位移（这种极化称为位移极化），形成电偶极子。
由于受到外电场E0的作用，这些电偶极子的电偶极矩P 的方向将转向与外电场E0的方向一致。这样，在垂直E0方向 的介质两端表面就会出现正负电荷，如下图所示。
无外点场时，无极分子 正负电荷中心重合
外电场作用下，正负电荷 中心分离，形成电偶极子
电介质在垂直于外电场的 两端表面出现极化电荷
对于有极分子，无外电场时，虽然每个分子都有一定的电 偶极矩，但由于分子作无规则的热运动，所以各电偶极子的电 偶极矩的取向是杂乱无章的，对外不呈现出电性，如左图所示 但有外电场E0时，每个分子都受到一个力偶矩的作用。在此力 偶矩的作用下，有极分子的电偶极矩方向将转向与外电场基本 一致的方向，这种极化称为转向极化，其结果是电介质的两端 出现等量异号的电荷，如中图和右图所示。
物理学
静电场中的电介质
第 三 章 静电场中的电介质
第 三 章 静电场中的电介质 （6学时）一、目的要求1．掌握电介质极化机制，熟悉极化强度、极化率、介电常数等概念。
2．会求解极化强度和介质中的电场。
3．掌握有介质时的场方程。
4．理解电场能量、能量密度概念，会求电场的能量 。
二、教学内容与学时分配 1．电介质与偶极子（ 1学时） 2．电介质的极化（1学时） 3．极化电荷（ 1学时）4．有电介质时的高斯定理（1学时） 5．有介质的场方程（1学时） 6．电场的能量（1学时） 三、本章思路本章主要研究电介质在静电场中的特性，其基本思路是：电介质与偶极子→电介质的极化→电介质的极化规律 →有介质的静电场方程 →静电场的能量。
四、重点难点重点：有介质的静电场方程 难点：电介质的极化规律。
五、讲授要点§3.1 电介质与偶极子一、教学内容 1．电介质概述 2．电介质与偶极子3．偶极子在外电场中受到的力矩 4．偶极子激发的静电场 二、教学方式、 讲授三、讲课提纲 1.电介质概述电介质是绝缘材料，如橡胶、云母、玻璃、陶瓷等。
特点：分子中正负电荷结合紧密，处于束缚状态，几乎没有自由电荷。
当导体引入静电场中时，导体对静电场有很大的影响，因静电感应而出现的感应电荷产生的静电场在导体内部将原场处处抵消，其体内00='+=E E E ϖϖϖ，且表现出许多特性，如导体是等势体、表面是等分为面、电荷只能分布在表面等；如果将电介质引入电场中情况又如何呢？实验表明，电介质对电场也有影响，但不及导体的影响大。
它不能将介质内部的原场处处抵消，而只能削弱。
介质内的电场00≠'+=E E E ϖϖϖ。
2．电介质与偶极子 (1)电介质的电结构电介质原子的最外层电子不像金属导体外层电子那样自由，而是被束缚在原子分子上，处于事缚状态。
一般中性分子的正负电荷不止一个，且不集中于一点，但它们对远处一点的影响可以等效为一个点电荷的影响，这个等效点电荷的位置叫做电荷“重心”。
静电场中的电介质
C 与 d S 0 有关
S
C ； d C
插入介质
0S q C u A uB d
C
0 r S
d
C
（2）球形电容器 已知
设+q、-q 场强分布： E 电势差：
RB
RA RB
q
r q
B A
RA
q 4 0 r 2
q q
RB
1 1 u A uB dr ( ) 2 4 0 RA RB R A 4 0 r
f
pe
pe
3;
+ E + 外 + + + +
在外电场中有极分子的固有电 矩要受到一个力矩作用，电矩方 向趋于外电场方向。但由于热运 动的存在，不会完全一致。
有极分子的取向极化！
+ E + 外 + + + +
+
两端面出现极化电荷层
电介质被极化的宏观效果
①外电场越强，极化电荷越多； ②电介质不均匀，则不仅在电介质表面会出现极 化电荷，在电介质内部也会出现极化电荷； ③对均匀电介质，在其内部任一小区域内，正负 电荷数量仍然相等，因而仍然表现出电中性。
二、电极化强度和极化电荷
单位体积内分子电偶极矩的矢量和 P
1、电极化强度(矢量)
pi
V
物理意义：描述了电介质极化强弱，反映了电介质 内分子电偶极矩排列的有序或无序程度。
在各向同性的电介质中，P 0 E
称为电介质的电极化率，它取决于电介质的性质。
2、极化电荷和自由电荷 极化电荷
E E0
++++++ r + ------- C
2.静电场中的电介质
自由电荷 束缚电荷
1 E dS
S
0
q
S
0
1
0
P dS
S
( 0 E P) dS q0
S S
电位移矢量定义：
D 0E P
( 0 E P) dS q0
S S
自由电荷
3、极化（束缚）电荷与极化强度的关系： 对于均匀的电介质，极化电荷集中在它的表面。电介质 产生的一切宏观效果都是通过未抵消的束缚电荷来体现。
如图，在平板电容器两极板间的介 质内沿着方向取一长度为dl，横截面为 dS的小圆柱体，在其内部极化可视为 是均匀的。
dl
' dS
' dS
P
点的总场强为：
' 退极化场 是电介质中的总电场强度。 E E E 0 E0 是自由电荷产生的电场。
' E 是极化电荷产生的退极化场
E E0 E'
' '
2.电极化强度矢量
宏观上，电介质极化程度用电极化强度矢量来描述， 其定义式为：
P lim
pi
S S S in
Pn '
P dS dS
'
极化强度力线
在任一曲面内极化电荷的负值等于极化强度的通量。
四、电介质中的高斯定理
根据介质极化和 真空中高斯定律 ' P d S q
S S
S
电位移矢量
0
' ( q q 0 ) S
1 E dS
(2)对各向同性电介质( P e 0 E)
第三章 静电场中的电介质习题及答案
第三章 静电场中的电介质 一、判断题1、当同一电容器内部充满同一种均匀电介质后，介质电容器的电容为真空电容器的r ε1倍。
×2、对有极分子组成的介质，它的介电常数将随温度而改变。
√3、在均匀介质中一定没有体分布的极化电荷。
（内有自由电荷时，有体分布） ×4、均匀介质的极化与均匀极化的介质是等效的。
×5、在无限大电介质中一定有自由电荷存在。
√6、如果一平行板电容器始终连在电源两端，则充满均匀电介质后的介质中的场强与真空中场强相等。
√7、在均匀电介质中，如果没有体分布的自由电荷，就一定没有体分布的极化电荷。
√8、在均匀电介质中，只有P为恒矢量时，才没有体分布的极化电荷。
P =恒矢量 0=∂∂+∂∂+∂∂z P y P x P zy x⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-=zP y P x P z y x p ρ×9、电介质可以带上自由电荷，但导体不能带上极化电荷。
√10、电位移矢量D仅决定于自由电荷。
×11、电位移线仅从正自由电荷发出，终止于负自由电荷。
√12、在无自由电荷的两种介质交界面上，P fE E 线连续，线不连续。
(其中，f E为自由电荷产生的电场，p E 为极化电荷产生的电场)√13、在两种介质的交界面上，当界面上无面分布的自由电荷时，电位移矢量的法向分量是连续的。
√14、在两种介质的交界面上，电场强度的法向分量是连续的。
× 15、介质存在时的静电能等于在没有介质的情况下，把自由电荷和极化电荷从无穷远搬到场中原有位置的过程中外力作的功。
× 16、当均匀电介质充满电场存在的整个空间时，介质中的场强为自由电荷单独产生的场强的r ε分之一。
√二、选择题1. 一平行板真空电容器，充电到一定电压后与电源切断，把相对介质常数为r ε的均匀电介质充满电容器。
则下列说法中不正确的是：（A ） 介质中的场强为真空中场强的r ε1倍。
第三章 电场中的电介质
注意： 是由介质2指向介质1 en
4.电介质外表面极化电荷面密度
ˆ dq P dS P dSn PndS
dq ˆ P n Pn dS
内
dS
P
面外
l
dS
ˆ P n
ˆ n
介质外法线方向
23
讨论：1）介质与真空界面
介质极化强度为 P2 ，真空
n
真空
极化强度为P1 0 ( P1
' P2 n P2n
pi )。 V
+
+
+
介质
n
2）介质金属界面
介质极化强度为 P2 ，金属内
电场为零，故极化强度 P1 0
金属
+
+
+
介质
' P2 n P2n
在极化的介质内任意作一闭合面S。
基本认识：
1）S 把位于S 附近的电介质分子分为两部分，
一部分在 S 内 ， 一部分在 S 外；
2）只有电偶极矩穿过S 的分子对
S内外的极化电荷才有贡献；
S
或被S截为两段的偶极子才对极化电荷有贡献。
17
1. 面元dS附近分子对面S内极化电荷的贡献
在dS附近薄层内认为介质均匀极化 以dS为底、长为l（偶极子正负电 荷的距离）作斜圆柱。 只有中心落在薄层内的偶极子才 对面S内电荷有贡献。所以，
E0
-
E 介质
+ + +
E E0 E
26
例1 平行板电容器 ,自由电荷面密度为0 其间充满相对介电常数为r的均匀的各向 同性的线性电介质。 0 0 求:板内的场强。
大物电磁学第三章习题静电场中的电介质
第三章 练习题一、选择题1、［ C ］关于D r的高斯定理，下列说法中哪一个是正确的？(A) 高斯面内不包围自由电荷，则面上各点电位移矢量D r为零．(B) 高斯面上D r 处处为零，则面内必不存在自由电荷． (C) 高斯面的D r通量仅与面内自由电荷有关．(D) 以上说法都不正确．2、［ D ］静电场中，关系式 0D E P ε=+r r r(A) 只适用于各向同性线性电介质． (B) 只适用于均匀电介质． (C) 适用于线性电介质． (D) 适用于任何电介质．3、［ B ］一导体球外充满相对介电常量为r ε的均匀电介质，若测得导体表面附近场强为E ，则导体球面上的自由电荷面密度0σ为：(A)0E ε. (B) E ε. (C) r E ε . (D) 0()E εε- .4、［ A ］一平行板电容器中充满相对介电常量为r ε的各向同性的线性电介质．已知介质表面极化电荷面密度为σ'±，则极化电荷在电容器中产生的电场强度的大小为：(A)0σε'． (B) 0r σεε'． (C) 02σε'． (D) rσε'． 5、［ B ］一平行板电容器始终与端电压一定的电源相联．当电容器两极板间为真空时，电场强度为0E r ，电位移为0D r，而当两极板间充满相对介电常量为r ε的各向同性的线性电介质时，电场强度为E r ，电位移为D r，则(A) 00,r E E D D ε==r rr r ． (B) 00,r E E D D ε==r r r r．(C) 00,r r E E D D εε==r r r r ． (D) 00,E E D D ==r r r r．6、 [ C ]一空气平行板电容器，两极板间距为d ，充电后板间电压为U 。
然后将电源断开，在两板间平行地插入一厚度为d/3的与极板等面积的金属板，则板间电压变为（A ）3U . (B)13U . (C) 23U . (D U .7、［ B ］一空气平行板电容器充电后与电源断开，然后在两极板间充满某种各向同性、均匀电介质，则电场强度的大小E 、电容C 、电压U 、电场能量W 四个量各自与充入介质前相比较，增大(↑)或减小(↓)的情形为(A) E ↑，C ↑，U ↑，W ↑． (B) E ↓，C ↑，U ↓，W ↓． (C) E ↓，C ↑，U ↑，W ↓． (D) E ↑，C ↓，U ↓，W ↑．8、［ B ］真空中有“孤立的”均匀带电球体和一“孤立的”的均匀带电球面，如果它们的半径和所带的电荷都相等．则它们的静电能之间的关系是 (A) 球体的静电能等于球面的静电能. (B) 球体的静电能大于球面的静电能. (C) 球体的静电能小于球面的静电能.(D) 球体内的静电能大于球面内的静电能，球体外的静电能小于球面外的静电能． 9、［ B ］如图所示, 一球形导体，带有电荷q ，置于一任意形状的空腔导体中．当用导线将两者连接后，则与未连接前相比系统静电场能量将(A) 增大． (B) 减小． (C) 不变． (D) 如何变化无法确定．10、[ D ]图示为一均匀极化的各向同性电介质圆柱体，已知电极化强度为P ϖ，圆柱体表面上束缚电荷面密度0σ'=的地点是图中的(A) a 点． (B) b 点． (C) c 点． (D) d 点．二、填空题1、分子的正负电荷中心重合的电介质叫做无极分子电介质，在外电场作用下，分子的正负电荷中心发生相对位移，电介质的这种极化形式叫：____ __极化。
章静电场中的电介质
（2）偶极子中垂面上的场强
E
E
q
40 (r 2
l2 ) 4
4 0 r 2
q (1
l2 4r 2
)
q • l2
r
•q
A
E
E
E
E
2E
cos
2
q
40 (r2
l2
4)
l 2
r2
l2 4
ql
40 (r2
l2
4
)3 2
略去二阶小量
E
p
4 0 r 3
小结：
偶极子激发的静电场 （1）偶极子在p的延长线上的场
呈现电性。分子正负电荷“重心”不重合。
的
分
_+
类
2.无极分子(nonpolar molecules):在无外场作用下整个
分子无电矩(电偶极矩为零)。例如，CO2 H2 N2 O2 He ，分子正负电荷“重心”重合。
1.无电场时 有极分子
无极分子
分子热运动，各分子电偶极矩的取向杂乱无章， 整个电介质宏观上对外呈电中性 2. 有电场时 有极分子介质-----取向极化 (orientation polarization) 无极分子介质-----位移极化(displacement polarization)
强
（2）偶极子中垂面上的场强
（3）偶极子在空间任一点的 场强，用球坐标系表示
E(r,
)
p
4 0r3
(er
2 Cos
e
Sin
)
E
2p
4 0r 3
p
E 40r3
E
q
4 0r 2
为场点到偶极子的连线与P的夹角
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
越过 dS 的极化的 正电荷总量
d 体积内极化留下的 负电荷总量
d q '正 d q '负 q n d q n ld S c o s
dq ' PdS cos
若要表示通过dS单位面元的极化电量
'
dq '
dS ˆ ' P en
ˆ P c os P en
结合以上关系联立求解。 2 在各向同性的介质中， 与 P 成正比关系， E 是标量常数。
E 在各向异性的介质中， 与 P 不成正比关系，
是矢量或张量。（3个或9个分量）
§3.4
3.4.1
极化电荷
极化电荷
q ', ', '
极化电荷及其密度
自由电荷及其密度
q, ,
4、对包围介质的整个表面S，由电荷守恒定律：极化穿 出表面的束缚电荷总量等于面内净余的极化电荷的负值
P d S q ' ( 3 -2 2 )
S内
例1：求沿轴向均匀极化的电介质圆棒上的极化电荷分 布。已知极化强度为P
n
右端面： 左端面： 侧面：
'e
P
ˆ ' P en P
3.4.2&3 极化强度与极化电荷的关系：
以无极分子的位移极化为例：
n
P
dS
n
P E
l
d d S co s l
体元大小
l 为每个分子在外电场作用下的平均移动距离。 设负电荷不动，正电荷沿外场方向移动距离l， 则原 体积中的分子，其正电荷将越过表面到体积外去。体 积内将留下等量负电荷。
3）感应和极化的结果，都是宏观上出现电荷的重新分 布，出现感应和极化电荷。
不同之处： 1）导体在静电平衡后：
E E 0 E '感 应 0 E E 0 E '极 化 0
介质在极化稳定后：
2）介质在极化稳定后，介质不是等位体；介质表面 不是等位面；介质表面电场不一定与表面垂直 3）导体静电感应，内部自由电荷运动。
e e'
E' E0 E
e' e
P
n
解：右表面 e ' P 左表面 e ' P 上、下表面 e ' 0 e' 退极化场：E '
P
0 0 这里 P 由 E 的大小、方向决定
例4 求均匀极化的电介质在球心产生的退极化 场。已知介质的极化强度为 P0
cos
2
sin d
0
2
d
0
2 P
0
cos
2
d ( cos )
0
P 2 0
cos
2
0
d (cos )
P 2 0
(
P
1 3
cos
3
)
0
3 0
即
E '
P 3 0
( ez )
q
例5 求沿轴均匀极化的电介质细棒中点的退极 化场。已知细棒截面积 S ，长度 l ，极化 强度为 P 解： 两端面极化电荷大小
P E
在国际单位制中，确定比例系数
P 0 E （ 3 -1 7 ）
其中： 0 真空中的介电常数。 介质的极化率，由介质种类决定 说明： 1，实际问题，已知 结合
E0
e
E '
e ' P n P cos
e'
0
P e 0 E E E0 E '
引入极化强度矢量P 1、定义：
外场 E 0 0 p 0, p 0 p 0, p 0 外场 E 0 0 p 0, p 0 p 0, p 0
无极分子
有极分子
定义：单位体积内分子电偶极矩的矢量和。
即： P
S
D 0 E P 电位移矢量
真空中，P = 0, 代入上式：
D 0E
S
D dS q0
S
称此式为有介质时的高斯定理。
说明：
1、计算时不出现极化电荷，使计算简单。
2、电位移矢量与电场强度的关系：
P 0 E 各向同性的介质中 D 0E P 0E 0 E 0 (1 ) E 0 r E
P
q
ez
e' P
q ' e ' S PS
( q ') ez 2 l 2
E'
则： 由场强叠加原理：
q'
0
1 E ' 4 1 4 0
l 2
2q'
2
2
1 4
0
l 2
e z 2 PS e z 2 0 l
E E0 E ' 在介质内部： E 0 与 E ' 反向。 且 E ' E 0 但方向与E 0 相同。 E E0 在介质外部退极化场不能保证与 E 0方向相反。
电场 E 0方向相反，称为退极化场。
例3 求插在平行板电容器中的电介质板内的退 极化场。已知介质的极化强度为 P
n
当 P 与 n 夹角为钝角时，
' 0
4、对介质与金属界面 在静电平衡时，金属极化强度为零。令法线方向 由介质指向金属，则 ' P c o s P e n ˆ 5、两种介质界面 一般令法线方向由介质2指向介质1，则
ˆ ' ( P2 P1 ) e n (3 -2 4 )
E0
极化电荷：均匀介质内部处处保持电中性。介质 表面出现了正、负电荷分布。
2、有极分子的转向极化
- +
有极分子在外场中发生偏转 而产生的极化称为转向极化。
p
Eo
+
F
-
p
V
n p n q l （ 3 -1 6 ）
说明：
1）P 是矢量。大小表示极化程度； 方向为极化方向。 2） P 大小、方向均不变时，为均匀极化。否则为 非均匀极化。
3）P
的单位。
p V ql V 库仑 米 米
3
~
~
~
库仑 米
2
3.3.3 极化强度与场强的关系： 实验发现：在各向同性的介质中，有：
F Eo
有极分子的取向极化： 无外场时，无规则的热运动，使分子电偶极矩取 向杂乱无章，宏观不显电性。
有外场时，分子电偶极矩受到力矩作用，取向转 向外电场方向，产生取向极化。 E
0
极化电荷：均匀介质内 部处处保持电中性。介 质表面出现了正、负电 荷分布。
3.3.2
极化强度
E0
E '
解1： 已知 若知 '
0 '
（1） （2）
0
且
Hale Waihona Puke 其中E E0 E ' ' P n P P 0 E
（3） （4） （5）
联立求解： 3代入1、2，
E 1
0
( ')
1
0
( P )
再代入5
P
1
1 4
0
dq ' R 1
2
dE z ' dE ' cos Ez ' 1 4 P 4 P 4 4
0 0 0
dq '
0
4
R
2
cos
e ' sin cos d d
sin cos
2
dd
第三章 §3.1 概述
静电场中的电介质
一、电介质的极化：
1、电介质——就是绝缘介质，是完全不导电的。
2、电介质极化（以均匀介质，均匀极化为例）： E0
+ + +
q
E'
q
+ + + + + + +
+ + +
+ + + + + + +
外电场
E0
介质极化
极化电荷
E
极化场
E'
S
S
q'
介质极化后，面内的极化电荷与极化强度的关系
S
P dS q '
S
代入上式，消去
S
q' 0 E dS q0
S
S
P dS
S
S
( 0 E P ) d S q 0
定义：辅助量
S
( 0 E P ) d S q 0
说明：
1、对均匀介质，体内无净余的束缚电荷。
2、对极化电荷分布的讨论，适用于位移极化， 也适用于取向极化。 3、对介质、真空表面，面法向由介质指向真空。 介质表面的束缚电荷为： ' P c o s P e ˆ