悬崖跳水水池深度设定问题
6悬崖跳水的水池深度

6悬崖跳⽔的⽔池深度悬崖跳⽔的⽔池深度摘要近年来世界上新兴⼀种跳⽔⽐赛叫红⽜悬崖跳⽔世界杯⽐赛。
是⼀种⾮常危险、挑战⼈类极限的⽐赛,⽐赛规定男⼦跳台⾼度为23⾄28⽶,⼥⼦为18⾄23⽶。
我国福建连城的冠⾘⼭就举⾏过这样的⽐赛,那⾥的跳台⾼度是男⼦28⽶,⼥⼦20⽶。
⼀、问题重述国际⾼空跳⽔是近年来刚兴起的体育运动项⽬,⽐赛规定男⼦跳台⾼度为23⾄28⽶,⼥⼦为18⾄23⽶。
⾼空跳⽔⼗分德惊险刺激,跳⽔员从很⾼的悬崖上或特制的超⾼跳台上起跳并完成空中动作后⼊⽔。
近年来很多⼈为了寻求惊险刺激使悬崖跳⽔备受欢迎,但是,与此同时,悬崖跳⽔危险性较⼤,容易出现伤亡事故,稍有不慎就会头⾻碎裂。
为了减少跳⽔运动员的跳⽔事故和尽量减少⽔池建设的成本避免不必要的浪费,因此,⽔池的深度应满⾜的条件尤为重要。
下落过程中,运动员的⾝体受到重⼒和空⽓阻⼒作⽤,是做加速运动的。
运动员在⽔中受到阻⼒与浮⼒作⽤,抵消⾝体的重⼒作⽤,使运动员在⽔中做减速运动,直到速度减为零。
此时运动员下落的深度即为⽔池的最低深度。
需要完成的任务:1.跳台下⾯的⽔池要多深才能安全,请⼤家给以计算;2.分析两个体重不同的⼈跳⽔时哪个需要更深的⽔。
⼆、问题分析悬崖跳⽔涉及物理⼒学问题,所以对运动员进⾏受⼒分析尤为重要。
同时解决⽔池深度问题还应把运动员的体重、⾝⾼、体积等因素考虑进去,因为这些对⽔池的深度都有影响。
同时⽔池的深度应保证运动员的⼈⾝安全和尽量减少⽔池建设的成本。
为了把运动员的受⼒更清楚地表⽰出来,以便下⼀步的研究,我们把运动员的受⼒分为三部分。
跳台⾄⽔⾯的过程:运动员从跳台起跳到脚接触⽔⾯,排除⽔平风⼒对运动员的影响,也就是只考虑运动员所受竖直⽅向上的⼒。
运动员受到重⼒和空⽓浮⼒等两个⼒作⽤,⽽空⽓阻⼒少于重⼒,所以运动员是做加速运动。
但是由于空⽓阻⼒随着速度的增加⽽增⼤,⽽重⼒是不变的,所以,运动员是做加速度减少的加速运动,速度⼀直增⼤。
悬崖跳水水池深度设定问题

一、问题重述近年来世界上新兴一种跳水比赛叫红牛悬崖跳水世界杯比赛。
是一种非常危险、挑战人类极限的比赛,比赛规定男子跳台高度为23至28米,女子为18至23米。
我国福建连城的冠豸山就举行过这样的比赛,那里的跳台高度是男子28米,女子20米。
请大家做两件事:1.跳台下面的水池要多深才能安全,请大家给以计算;2.分析两个体重不同的人跳水时哪个需要更深的水。
二、问题分析要探讨水深安全的问题,就要考虑各种偶然因素,考虑各种客观因素对运动员的起跳姿势的影响(包括失误)。
运动员下落水中后要有足够小的速度与池底接触(如果能接触),但考虑到各种未知因素,身体应不与池底接触。
故所求的最小深度应是运动员以各种姿势跳水后所到最深处离水面的距离。
运动员的整个运动过程可分为四个阶段:第一阶段:运动员起跳到身体即将接触水面的下落运动;第二阶段:身体与水的碰撞过程,即固体与流体的碰撞问题;第三阶段:身体入水的过程,该过程中身体没有完全入水;第四阶段:身体完全入水后在水(流体)中的运动情况。
三、模型假设假设一:在第一阶段,运动员起跳后不是标准的自由落体运动,而是平动和转动的合成运动。
可28米和20米的下落高度中由重力做的功远大于起跳时由摩擦力矩产生的转动动能,况且在接触水面时人呈舒展姿势,由角动量守恒可得此时运动员的转动动能很小。
转速也小使得摩擦力矩做的功小。
故可以将第一阶段的运动简化为平动,而忽略转动。
假设二:在第一阶段中起跳时,初速度很小,其方向也不确定故可以忽略不计。
假设三:在空中下落过程中,将人体等效看成圆柱体。
假设四:在考虑第二阶段中与在第三阶段时,人与水的碰撞问题及人进入水的过程中,可将人看成一圆台,两个圆柱的模型。
并且假设圆台的的底面与水面碰撞,这是由于水的粘滞系数小于水的压差阻力系数,在该种情况下碰撞损失的动能越少,而且在后面的运动中阻力越小(这会使下落深度越大)。
假设五:在第四阶段中将人的模型重新简化为假设三中的圆柱体模型。
悬崖跳水安全保障问题

悬崖跳水安全保障问题摘要本文研究了悬崖跳水安全保障问题,从理论分析与计算的角度探讨水池深度的设定问题,以及跳水运动员脚先入水、还是头先入水,通过建立物理模型,运用物理学、理论力学知识,结合微分方程学方法进行求解。
对于问题一:在运动员从空中掉下撞击水面时,水给运动员的抨击力就等于运动员给水面的撞击力,运动员刚接触水面的瞬间,受到竖直向下的重力以及竖直向上的水的阻力。
运动员给水的撞击力就是水给运动员的阻力与自身重力之和,即水(撞)f mg F +=,再根据收集的人体头部与脚部所能承受的压力对比,得出脚先着水。
对于问题二:本文将建立物理模型,将跳水运动员看作圆柱形,用物理动力学理论,将跳水运动看做三个物理过程:1、运动员从跳台至水面过程;2、运动员由水面直至完全进入中的过程;3、运动员由水中直至水池底部的过程。
三类过程分别建立动态方程,结合微分方程学求解。
最后应用Matlab 软件绘图展示结果,通过计算得出:男子安全水池深度为17.0558m ,女子水池深度为15.0349m 。
对于问题三:根据物理质量公式,结合运动员悬崖跳水三个具体物理运动的方程进行分析,得出高度、底面积与质量之间的联系,从而判断体重不同者与水池深度大小的关系,得到结果:体重越大的人跳水时需要更深的水。
关键词:物理动力学;微分方程;MATLAB 软件;空气动力学;牛顿第二定律1 问题重述近年来世界上新兴一种跳水比赛叫红牛悬崖跳水世界杯比赛。
在这种比赛中运动员从高空悬崖跳下来,身体在重力的作用下快速自由下落。
比赛规定男子跳台高度为23至28米,女子为18至23米。
我国福建连城的冠豸山就举行过这样的比赛,那里的跳台高度是男子28米,女子20米。
我们把运动员看成圆柱形,在下落过程中,运动员还未落水之前受到重力和空气阻力的作用,作加速度减小的的加速运动;入水后运动员的身体受到水的阻力与浮力作用,而抵消身体的重力作用,使运动员在水中做减速运动,直至速度达到安全速度。
悬崖跳水问题

悬崖跳水问题建模培训作业(一):论文题目:论文成员;赣南师范学院09计本(2)刘琳岚赣南师范学院09数本(1)汪灵枝赣南师范学院09数本(1)钟建忠2011年八月三号内容摘要;本文主要探讨悬崖跳水的安全问题,主要讨论为保证跳水者安全,水深满足的条件,为选址提供合理的依据。
针对问题一“跳台下面的水池要多深才能安全”建立物理模型,将其归纳为四个阶段;运动员空中,碰撞、进入、完全进入。
逐个对其建立运动状态方程,并结合微分方程学简化求解。
其动力学方程为ma=F阻+F浮-mg(规定向下为正方向);阻力方程为F阻=KSV(气体)和F阻=0.5PSCV2(液体) 求得最终结果水池的深度的最小值为;男子组7.6m女子组 5.2m针对问题二;结合运动员悬崖跳水四个具体物理运动的总方程进行分析,得出高度、底面积与质量之间的联系,从而判断体重不同者与水池深度大小的关系,得到结果:体重越大的人跳水时需要更深的水。
关键词动力学方程阻力微分方程学一·问题的重述近年来世界上新兴一种跳水比赛叫红牛悬崖跳水世界杯比赛。
悬崖跳水,即运动员从高空悬崖跳下来,身体在重力的作用下快速自由下落,这是一种非常危险、挑战人类极限的比赛,所以比赛中安全问题显得非常重要。
比赛规定男子跳台高度为23至28米,女子为18至23米。
我国福建连城的冠豸山就举行过这样的比赛,那里的跳台高度是男子28米,女子20米。
下落过程中,在空气重视受空气阻力的影响。
运动员的身体入水后受到水的阻力与浮力作用,抵消身体的重力作用,使运动员在水中做减速运动,直至速度降为零。
为了保证运动员的人身安全,水池建立必须有足够的深度,另一方面,尽量节约水池建设的成本可避免无意义的浪费。
所以水池深度设定必须在满足不造成运动员人身伤害的同时达到最低成本消耗的要求。
需完成任务:1.根据福建连城冠豸山跳台高度,计算跳台下面的水池要多深才能安全;2.分析两个体重不同的人跳水时哪个需要更深的水。
悬崖跳水水池深度的设定

论文题目:悬崖跳水水池深度设定问题姓名:杨凯学号:0912202-27 专业:电子信息姓名:廖建强学号:1003313-34 专业:城市地下工程与隧道姓名:李丽君学号:0909302-44 专业:信息与计算科学2011 年 8月 9 日悬崖跳水水池安全深度的问题摘要悬崖跳水是一项当今颇受媒体关注的一项民间运动。
由于悬崖跳水非常具有挑战性,进几年在国外非常流行。
虽然本国的悬崖跳水项目没有的到发展,但安全问题颇受全世界的关注。
悬崖跳水安全受诸多因素的影响例如:水池深度、天气、跳板、风速、空气压强、水的密度、悬崖高度等等。
但悬崖跳水一般性选择天朗气清、惠风和畅的日子,安全问题主要来自水池的深度。
由于自然条件的限制,改造自然的成本非常大,在保证运动员安全的基础上我们也要考虑社会所需的经济成本。
本文探讨悬崖跳水水池深度设定问题,以实现水池深度设定既保证运动员人身安全且使成本消耗最低为目标进行建模。
对于悬崖跳水运动我们可以近似的看做三个物理过程:1、运动员在空中下落;2、运动员从空中进入水中;3、运动员入水后。
三类过程分别建立动态方程,结合微分方程求解,最后应用MATLAB 软件绘图展示结果:男子安全水池深度为17.04148m ,女子水池深度为15.0348m 。
对于水池的深度影响主要由水的流体阻力、水的浮力和人跳水的高度决定,本模型主要根据第三个过程确定水池的深度,在第二个过程中讨论人的体重和水池的深度的问题。
入水后人体的运动符合牛顿第二定律:mg f F dthd m -+=浮22 水的阻力方程为:212d f C Sv ρ=水 根据人体完全入水后的速度可以得出水池的深度'i i i H H L =+(i H 为人的高度i L 为人完全入水时脚底与水池底部的距离)由于人跳水时在空中下落过程符合牛顿第二定律,根据跳水员得跳水高度我们可以求解出接触水面时的速度。
根据牛顿第二定律求解出人体质量和和速度的关系,再根据模型二、三推导出人体质量和水池深度的关系。
水上极限运动

水上极限运动作者:贺中来源:《青岛画报·新航程》2019年第03期最危险的项目一一悬崖跳水悬崖跳水,是被称为世界上最惊险的体育项目,其最早源于海边渔民业余的娱乐活动,是指运动员从海边或瀑布、河流旁的悬崖上做出各种姿势的跳水动作,然后跳入水中。
比赛规则要求,男子起跳高度为23-28米,女子起跳高度为18-23米,降落的速度将达到每小时78-100公里。
也许我们已经对奥运会上的竞技跳水司空见惯。
但如果站到二三十米高的陡峭悬崖上,抛弃所有的恐惧和顾虑一头扎入深不可测的海水中,那的确十分疯狂。
进行悬崖跳水的运动员必须经过严格训练,以便让自己的身体可以应付和水面撞击时产生的巨大冲击力。
当跳水者接触水面的时候,由于巨大的重力施加到身体,他们经常会遭遇痉挛和抽筋,大量肾上腺素会流进血管。
在落入水中的瞬间,一定要确保双脚朝下,并且保持身体笔直。
如果跳水者的脑袋先落进水中,那么将会引发严重的脑震荡,甚至头骨碎裂。
因为悬崖跳水的危险系数较高,容易出现伤害事故,所以在世界上开展得并不普遍,目前和悬崖跳水相关的赛事只有少数几个。
新手课堂1.在完成动作后,必须脚部先入水,下肢入水可以减轻水面对脑部的冲击力。
2.参赛选手需要具备过硬的身体和心理素质,克服恐惧心理,不要轻易尝试。
3.对水池深度、天气、跳板、风速等有较为清晰的了解。
悬崖跳水好去处丹佛红石公园:丹佛红石公园位于美国佛蒙特州最大的城市柏林顿市,游客可以在这里的湖边进行悬崖跳水。
湖边跳水听起来轻而易举,但是这里的跳台约24米高,游客可以沿着陡峭岩壁爬到狭窄的跳台上,选择不同高度起跳。
毒蛇的巢穴:毒蛇的巢穴在愛尔兰戈尔韦湾中最大的岛屿伊尼什莫尔岛上。
2012年,红牛悬崖跳水世界系列赛比赛就在这里举行。
这里是一个天然形成的岩石空穴,呈完美的长方形结构。
悬崖边的跳台距海面约26米高,光站在上面就已经让人头晕目眩了。
海上捕风者——风筝冲浪风筝冲浪的原理相当简单,就是将充气风筝用两条或四条强韧的绳子连接到手持横杆上,操作横杆来控制风筝上升、下降及转向,并结合脚下踩着的各式滑板,在海面上滑行,甚至将人带离水面做出各种花样的翻腾动作。
勾股定理的实际案例计算水池的深度与倾斜度

勾股定理的实际案例计算水池的深度与倾斜度勾股定理的实际案例:计算水池的深度与倾斜度勾股定理是数学中的重要定理之一,它描述了直角三角形中的关系,具体表达为:直角三角形的两个直角边的平方和等于斜边的平方。
这个定理在实际生活中有广泛的应用,其中之一就是计算水池的深度与倾斜度。
本文将以勾股定理为基础,介绍如何利用该定理来解决水池相关问题。
一、水池深度的计算假设我们有一个矩形水池,已知水池的宽度为3米,长度为4米。
现在我们需要求解水池的深度。
为了方便计算,我们建立如下坐标系:水平方向为x轴,竖直方向为y轴。
水池的一角作为坐标原点,其中一条边与x轴重合。
水面平行于x轴且离原点的距离为d,我们需要计算深度h。
根据勾股定理,我们可以得到如下等式:3² + h² = d²①同时,由于水池的矩形形状,我们还可以得到以下等式:d = 4 - a ②将式②代入式①,我们可以得到:3² + h² = (4 - a)²化简得到:9 + h² = 16 - 8a + a²整理得到二次方程:h² + 8a - 7 = 0通过求解上述二次方程,我们可以得到水池的深度h。
二、水池倾斜度的计算接下来,我们将讨论水池的倾斜度的计算。
假设水池的x轴长度为5米,y轴长度为3米,且水池底部不平坦。
我们需要求解水池的倾斜度,即水平方向单位长度变化对应的竖直方向单位长度变化。
为了解决这个问题,我们可以沿水平方向选取两个点A和B,其中A点的坐标为(x1, y1),B点的坐标为(x2, y2)。
通过计算AB线段的斜率,我们可以得到水池的倾斜度。
根据斜率的定义,我们可以得到以下等式:斜率 k = (y2 - y1) / (x2 - x1)取A点坐标为(0, 0),B点坐标为(5, 3),带入上述公式计算斜率:k = (3 - 0) / (5 - 0) = 3/5因此,水池的倾斜度为3/5。
实验题目3--人工瀑布的设计问题

人工瀑布的设计问题
瀑布是指水从悬崖或陡坡上倾泻下来而形成的水体景观。
瀑布以其由山水有机结合的特点,成为极富吸引力的自然景观。
随着园林事业的蓬勃发展,人工瀑布景观已经成为人们喜闻乐见的水景景观形式。
瀑布一般分为自然瀑布和人工瀑布两种,自然瀑布通常是江河遇到地面断层而形成的,人工瀑布正是基于这一原理而设计的,人工构造自然地质断层的挑水坎,使得水流冲出挑水坎之后,再下落以致形成非常好看的抛物线形状的水流。
如图,某景点一人工瀑布是在离地面10米的高处建造一段水平的横水槽,将地面水池里的水用水泵抽入到了水槽中,该水槽末端设置一个坡度而形成一个挑水坎,当水流达到一定的速度时,水就能沿着水槽冲上挑水坎再下落以致形成瀑布。
现设水泵将水提到10米处时,水流速度为6米/秒,试在这种条件下设计挑水坎,并设计出相应的瀑布下端与水槽基底的水平距离d。
跳水场地标准
FR 5.1 跳板FR 5.1.1跳板至少为4.8m长,0.5m宽。
所有国际游泳联合会赛事中,跳板的型号应由国际泳联决定。
FR 5.1.2 跳板的表面应防滑。
FR 5.1.3跳板应该有可移动支点,方便运动员调节。
FR 5.1.4从安装跳板支撑点的平台到跳板表面的距离应为0.365m。
从支撑点调节装置(0.676m长)前沿到支撑平台前沿的距离不超过0.68m。
如果平台的前沿长于这个距离,超过规定距离的顶端表面应该以垂直:水平为1:3的比例向下倾斜。
FR 5.1.5支点后方到其中心线的最小距离建议符合跳板制造商提供的推荐值。
FR 5.1.6活动支点到位后,跳板应绝对水平地安装在平台的前沿。
FR 5.1.7跳板应安装在平台的一侧或两侧。
双人跳水比赛时,应至少有两块跳板安装在同一高度上,且不应有任何的障碍物妨碍双人跳水运动员互相观察对方的动作。
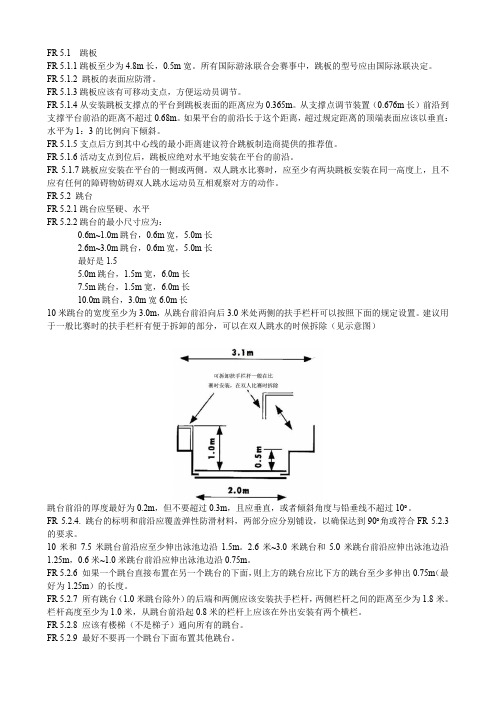
FR 5.2 跳台FR 5.2.1跳台应坚硬、水平FR 5.2.2跳台的最小尺寸应为:0.6m~1.0m跳台,0.6m宽,5.0m长2.6m~3.0m跳台,0.6m宽,5.0m长最好是1.55.0m跳台,1.5m宽,6.0m长7.5m跳台,1.5m宽,6.0m长10.0m跳台,3.0m宽6.0m长10米跳台的宽度至少为3.0m,从跳台前沿向后3.0米处两侧的扶手栏杆可以按照下面的规定设置。
建议用于一般比赛时的扶手栏杆有便于拆卸的部分,可以在双人跳水的时候拆除(见示意图)跳台前沿的厚度最好为0.2m,但不要超过0.3m,且应垂直,或者倾斜角度与铅垂线不超过10︒。
FR 5.2.4. 跳台的标明和前沿应覆盖弹性防滑材料,两部分应分别铺设,以确保达到90︒角或符合FR 5.2.3的要求。
10米和7.5米跳台前沿应至少伸出泳池边沿1.5m。
2.6米~3.0米跳台和5.0米跳台前沿应伸出泳池边沿1.25m,0.6米~1.0米跳台前沿应伸出泳池边沿0.75m。
FR 5.2.6 如果一个跳台直接布置在另一个跳台的下面,则上方的跳台应比下方的跳台至少多伸出0.75m(最好为1.25m)的长度。
悬崖跳水水池深度问题

悬崖跳水水池深度问题摘 要本文探讨悬崖跳水水池深度设定问题,以实现水池深度设定既保证运动员人身安全且使成本消耗最低为目标。
对此问题,将建立物理模型,运用物理学、流体力学知识,结合微分方程进行求解。
对于问题一,本文将建立物理模型,将跳水运动员形体模拟为椭圆锥,用物理动力学解题思路,对悬崖跳水过程细化为三阶段:跳台至水面过程、空气至水中过程与水面至水池底部,并逐个对其建立运动状态方程,结合微分方程求得结果见下表(详见第11页):i)(m H i )(m h i )(kg m i 性别 最大深度)(m 最小深度)(m1 28 1.78 75 男 9.06 5.542 23 1.65 60 女 8.32 4.32 3 23 1.78 75 男 8.58 4.89 4181.6560女7.453.90对于问题二,通过对运动员悬崖跳水过程进行分析,我们得到:ih vK v g dh dv 人气ρρ231-= vg v h gh h v K dh dv i i -+=33223人水人水ρρρρvgv g h v K dh dv i -+=人水人水ρρρρ232由于人体密度保持不变,所以当两人体重不同时,存在三种情况:人的底面积相同,高度不同;人的高度相同,底面积不同;人的底面积与高度都不同。
那么,本文将人的体重不同定义为底面积相同,密度相同,高度不同。
结合运动员悬崖跳水的三个方程进行分析,得出结论:体重越大的人跳水时需要更深的水(详见第11页)。
关键词:物理动力学;流体力学;微分方程;运动状态方程一、问题重述近年来世界上新兴一种跳水比赛叫红牛悬崖跳水世界杯比赛。
是一种非常危险、挑战人类极限的比赛,比赛规定男子跳台高度为23至28米,女子为18至23米。
我国福建连城的冠豸山就举行过这样的比赛,那里的跳台高度是男子28米,女子20米。
现要求我们解决以下两个问题:问题一:跳台下面的水池要多深才能安全,请大家给以计算;问题二:分析两个体重不同的人跳水时哪个需要更深的水。
悬崖跳水安全深度的数学模型

2 1 02
文 章编 号 :0 5 3 4 ( 0 2 0 — 0 5 0 2 9— 06 2 1 )10 9— 5
悬崖跳水 安全 深度 的数学模 型
熊 小峰 , 鄢 化 彪 , 陈 兵
( 江西理工大学理学院 , 江西 赣州 3 10 ) 4 00
摘
要: 针对 悬崖 跳 水的 水池 安全 水 深 问题 , 通过 对人 体在 跳 水运 动过 程 的 受 力分析 , 用 机械 利
e ta td r ssa c o f ce to tr fo t e d t fwa e e t f sa d r i i g p o s a s f t r x r c e e it n e c ef i n fwa e r m h a a o tr d p h o tn a d d vn o l , ae wae i
形 体 的上 部分 为 圆柱 体 , 半 部分 为 锥体 , 下 在实 际
应 用 中可 假 设 圆 柱 体 的 高 与 锥 体 的高 近似 相 等 .
设 P水 为水 的 密 度 , 浮 水对 运 动 员 的浮 力 , 为
f水 水对 运动员 的 阻力 , 水 水 的阻力 系数 , 水 为 C为 s 为 人 体在水 中与运 动方 向垂直 的投影 面积 , 为运动 V排
2 模 型 建 立 与 求 解
在 建 模过 程 中 , 方便 起 见 , 人把 人 形 等效 为 有
成 锥 形 体 , 于 人 体 型 的特 点 , 形 体 的 模 型 存 鉴 锥
在 较 大 的误 差 , 本模 型 把运 动 员 等效 为 楔 形体 , 楔
图 2 楔形 体锥 形部 分入水 过 程示 意图
员 浸没在水 中的体 积. 根 据机械 能守 恒定 律(1 : 得 - 2
悬崖跳水的水池深度设定问题数学建模论文 精品

数学建模论文论文题目:悬崖跳水的水池深度设定问题摘要:在红牛悬崖跳水世界杯比赛的背景下,本文经讨论研究了跳水水池的深度设定问题,以保证运动员的安全及投资建设水池的成本合理为目的。
对此,本文将建立物理模型,运用物理学,微分方程学,理论力学等数学方法,结合MATLAB 编程进行求解。
对于问题一:我们假设将人体设为一个均匀圆柱体,并建立物理模型,用物理动力学解题思路,对悬崖跳水物理过程细化为运动员空中、入水与水中三个运动过程,并逐个对其建立运动状态方程,结合微分方程学简化求解,最后用MATLAB 软件画图展示结果,从图中得到:男子的安全水池深度为12.85米,女子的安全水池深度为8.82米;对于问题二:根据物理质量公式,结合运动员悬崖跳水三个具体物理运动的总方程进行分析,得出高度与质量等之间的联系,从而判断体重不同者与水池深度大小的关系,得到结果:体重越大的人跳水时需要更深的水。
该模型建立亮点一体现在其充分运用了物理知识,同时结合微分法简化了求解难度;亮点二体现在用MATLAB软件画图展示结果,直观准确。
关键字:物理动力学、能量转换、微分方程学、MATLAB1 问题重述近年来世界上新兴一种跳水比赛叫红牛悬崖跳水世界杯比赛。
是一种非常危险、挑战人类极限的比赛,比赛规定男子跳台高度为23至28米,女子为18至23米。
我国福建连城的冠豸山就举行过这样的比赛,那里的跳台高度是男子28米,女子20米。
需要完成的任务:1.跳台下面的水池要多深才能安全,请大家给以计算;2.分析两个体重不同的人跳水时哪个需要更深的水。
2 问题分析要探讨跳水者的安全问题,需要分析在跳水者进入水之后继续下落的深度,从而在速度减为0时而不撞击池底而受伤,以保证跳水者的绝对安全经分析,把跳水过程具体化,形象化后,悬崖跳水可分为三个阶段,在下文并逐个对其建立了运动状态方程:第一阶段:从跳板到水面;运动员从跳板跳下,再空中完成一系列的动作之后在重力的作用下会快速自由下落,在此期间,会受到恒定不变的重力及方向向上的空气阻力,且空气阻力越来越大,使运动员做加速度减小的加速运动,并且在到达水面时速度最大。
数学建模 跳水问题

目录摘要 (1)1、问题重述 (2)1.1问题背景 (2)1.2问题提出 (2)2、问题分析 (2)3、问题假设 (3)4、符号说明 (3)5、模型建立于求解 (3)5.1问题一模型建立与求解 (3)5.1.1跳水运动员入水前下落模型 (4)5.1.2碰撞过程分析 (5)5.1.3完全进入水中直到速度为0的过程 (5)5.2问题二模型建立与求解 (6)6、模型评价与改进 (7)6.1模型评价与检验 (7)6.1.1模型检验: (7)6.1.2模型评价: (7)6.2模型的改进: (7)7、参考文献 (8)附录 (8)悬崖跳水的水池深度摘要本文主要以跳台高度:男子28米,女子20米作为讨论对象,通过建立微分方程模型,将人体看成为一个长方体模型,用matlab 软件求解出了为保证运动运的跳水安全,水池深度需要满足的条件以及对于轻重不同的运动员哪种需要更深的水。
问题一,采用高等物理动力学以及流体力学知识,将跳水问题分为3个过程——空气中运动过程、与水的碰撞过程、完全进入水中的过程。
在空气中运动过程中,通过牛顿第二定律,得出微分方程,从而建立微分方程模型,利用matlab 软件求解微分方程模型可以得出悬崖高度s 关于时间t的函数关系如下所示:s =速度v 关于时间t的函数关系:v =m 表示人体质量,g 表示重力加速度。
由于本文主要根据福建连城的冠豸山举办的悬崖跳水环境考虑, g 这里取9.790,k 表示空气中人体所受阻力的系数:CρS (C 是空气阻力系数,ρ是空气密度,S 为人体迎风面积)。
通过关系式,得出了空中运动过程中速度刚要碰到水的速度v 0。
然后,在与水碰撞过程中,利用流体力学的有关基础知识,从能量角度分析,人水系统总能量守恒,列出方程:222230122111222mv mv Sgv T Sv T ρρ=++水水 2012mv mv Sv T ρ-=水2v TS V =人解出入水时的速度v 1。
悬崖跳水的水池深度研究

悬崖跳水的水池深度摘要一、问题重述近年来世界上新兴一种跳水比赛叫红牛悬崖跳水世界杯比赛。
是一种非常危险、挑战人类极限的比赛,比赛规定男子跳台高度为23至28米,女子为18至23米。
我国福建连城的冠豸山就举行过这样的比赛,那里的跳台高度是男子28米,女子20米。
应用数学建模的方法研究和解决下面的问题。
(1) 为了确保参赛选手的安全,跳台下面的水池要多深才能安全,请大家给以计算;(2) 当有两个不同体重的人跳水,那个需要的水更深。
二、问题分析对于问题一,我们主要分解成两个过程进行分析:1. 人从悬崖上跳下来在空中的受力过程。
2. 人与水接触到进入水中的速度第一次为零的受力过程。
其中过程2又分三个小过程分别为:1. 人刚与水接触时的碰撞过程。
2. 人的一部分进入水中的受力过程。
3. 人完全进入水中的过程。
对于问题二,我们可以根据问题一的分析结果对体重不同的人进行比较,得出结论。
三、符号说明四、模型假设五、模型建立与模型求解5.1 问题(一)5.1.1 人在空气中的运动过程和受力过程人在悬崖上时,把人等效成一个圆柱型。
人的体重为m,人等效成的圆柱l。
体的截面积为s,身高为l,悬崖的高度为h。
当人跳下时有一个上跳距离为1当人在空中运动时,因为水平方向的位移非常小,因此在空中的运动轨迹可以等效成垂直向下的运动轨迹好,合速度也是垂直向下的。
因为有空气,所以考虑空气阻力的影响,各系数假设如下:A 表示人与空气相对运动时的横截面积,Cw 表示空气的阻力系数,v 表示人下坠的速度。
空气阻力的公式如下:空f =A*Cw*v^2。
整个过程如下图所示:人下降过程图人在空中的受力图如下与水接触前的速度为0v ,H 为人下降时距悬崖的距离,且人的下坠方式是头向下则可以列出下面的运动方程:mg -2)(ACw H d =22dt Hm d ;应用matlab 求出H 与t 的函数为:H=((m*log(A))/2 + (m*log(Cw))/2 -(m*log(g))/2-(m*log(m))/2+m*log(c2-c1/(2*exp((2*A^(1/2)*Cw^(1/2)*g^(1/2)*t)/m^(1/2)))) + A^(1/2)*Cw^(1/2)*g^(1/2)*m^(1/2)*t)/(A*Cw);为了求出在接触水面时,人的速度最大,因此把空气阻力忽略后运动方程满足下面: 22dtH md mg =; 所以gh v 20=;5.1.2 人与水的接触到第一次速度为零的过程分析为了考虑人所能进入的最深的距离,因此我们假设人们入水时的姿势是双手合并朝下的,以此来减小刚与水碰撞时的能量损失,因此我们把人体等效成一个上面为圆柱体,下端圆锥体的模型。
悬崖跳水安全深度

悬崖跳水的水池深度摘要:模型讨论分析运动员所需水池深度的问题,即保证跳水运动员的安全,又要使建造水池的成本最低,因此水池需要设定合理的深度。
模型中运用了物理学知识,并用微分方程来解决变量问题。
问题一将运动员下落的具体过程进行分析分为三个阶段:未入水阶段;未完全入水阶段及完全入水阶段。
未入水阶段:运动员受到空气阻力的影响和自身重力的影响,运动员做无初速度的自由落体运动。
未完全入水阶段:运动员从刚开始接触到水面到完全进入水中这段距离,运动员的速度受到水的浮力、自身的重力、水的阻力影响,做减速运动。
完全入水阶段:运动员完全进入水中以后,运动员的速度受到自身重力、水的浮力、水的阻力影响,做减速运动直到速度减小为零。
运用牛顿定律及微分方程对运动员下落进行分析,并对各个阶段进行分析建立方程模型。
运用MATLAB软件进行编程求解得出男女运动员所需的安全深度分为17.3036H=,25.6330H=。
问题二:当跳水运动员的体重不同,假设跳水运动员的密度相同,则跳水运动员的身高、半径至少有一个量不同。
跳水运动员体重不同时有三种情况:跳水运动员的身高相同,半径不同,体重与半径成正相关;跳水运动员的半径相同,身高不同,体重与身高成正相关;跳水运动员的身高和半径都不同,体重至少与其中的一个量成正相关。
对上三种情况进行综合分析,跳水运动员的体重越大所需的水池深度越大。
关键词:微分方程运动阶段安全深度体重影响一、问题重述:近年来世界上新兴一种跳水比赛叫红牛悬崖跳水世界杯比赛。
是一种非常危险、挑战人类极限的比赛,比赛规定男子跳台高度为23至28米,女子为18至23米。
我国福建连城的冠豸山就举行过这样的比赛,那里的跳台高度是男子28米,女子20米。
本文跳台高度男子取28米,女子跳台高度取20米作为研究。
请大家做两件事:1.跳台下面的水池要多深才能安全,请大家给以计算;2.分析两个体重不同的人跳水时哪个需要更深的水。
二、问题假设1.假设跳水人体形状为锥形,最大直径为人的肩宽,高为运动员的身高加臂展2.假设运动员下落时身体紧绷形状规则,下落轨迹是条直线3.假设风速水速为零,不影响运动员下落4.假设运动员从跳板上跳下时为自由落体运动5.假设运动员在整个运动过程中没有动量、能量损失6.假设运动员在水中的速度为零时的深度为水池的安全深度7.假设运动员的体型都符合国际跳水运动体型要求标准8.跳水运动员跳水时脚先入水三、符号说明i:2(1为男运动员,2为女运动员)h:员的高度ir:动员的肩宽im:员的体重iH:崖的深度x:第一阶段运动员下降的高度H:安全深度ih:第二阶段运动员下降的深度3h:第三阶段运动员下降的深度4v:速度V:刚接触水面时的速度1iV:完全进入水面时的速度2iC:空气阻力系数dρ:空气密度3ρ:水的密度4s:受力面积k:空气中阻力与速度平方的比例系数1ik:水中阻力与速度平方的比例系数2ig:重力加速度h':跳水运动员在水中下沉的高度四、问题分析对于问题进行分析建立模型,本题要求解决水池的安全深度及体重对水池安全深度的影响,水池深度既要保证运动员的人身安全又要保证水池建造成本费用最低。
水深要求关于游泳馆及水池的几点说明

精心整理
关于标准游泳馆、跳水馆、室内游泳池、室内跳水池、室外游泳池、室外跳水
池的几点说明
1、根据建筑型式分类,室内带观众座位的称为游泳馆;不带观众座位的称为室内游泳池。
2
34
56(1A : 1.8m 。
B (2寸为(3
(4)花样游泳池:由于池子面积较小,规定动作可在跳水池中进行,自选动作可在游泳池中进行。
平面尺寸为30m×20m 或12m×12m,水深保证≥3m。
其他部位≥2.5m。
(5)练习池:也称非专业成年人水池,平面形状尺寸不限,水深0.9m―1.35m 以上。
(6)儿童练习池:一般为6岁以上儿童学游泳或练习使用,平面形状尺寸不限,水深0.6m―1.1m 以上。
精心整理
(7)幼儿戏水池:主要为6岁以下儿童使用,平面形状尺寸不限,水深0.3m―0.6m 以上。
(8)海浪池:平面尺寸长≥25m,宽≥5m,水深1.5m左右。
各地可根据自己场地的实际情况,对照上述说明按照登记表所列指标选择填报。
物理习题

年级:高一 科目:物理潜水员从高61m 的悬崖上跃入水中,已知压下7.23m 的范围内有礁石,则潜水员跳出时的最小水平速度应多大才能避开礁石?解:由已知h =61m ,设他做平抛运动时最小水平初速为v 0时,才可避开礁石,下落时间为t 那么221gt h =,得gh t 2= 水平位移x =v 0t 得s m s m h g x v /2/6128.923.720≈⨯⨯==轻杆一段固定一质量为m 的小球以另一端O 为圆心,是小球在树枝平面内做半径为R 的圆周运动,则( )A 、小球过最高点时的最小速度是B 、小球过最高点时,杆所受弹力可以为零C 、小球过最高点时,球的速度v >时,球对杆产生向下的压力 D 、小球过最高点时,球的速度v <时,杆对球产生向下的拉力老师,A 不对吗?解:由于是球杆模型,故最高点最小速度可以为0,故A 错误。
当最高点速度gR v =时,即只有重力提供向心力,故杆所受的弹力为0,B 正确。
gR v >,则向心力m g Rv m F >=2,所以小球受杆向下的拉力,球对杆向上的拉力,所以C 错误。
同时可判断D 也错误。
答案:B 。
在电影中经常看到这样的镜头:直升机沿水平方向飞行,某人沿着系在直升机上的绳索向上攀升.如果直升机水平飞行的速度为4m/s ,人沿绳索向上运动的速度为1m/s 。
试在以下两种情况下计算人对地的速度绳索保持在竖直方向时人对地的速度绳索与竖直方向的夹角为30度时人对地的速度解答: 绳索保持在竖直方向时:sm v v v /1722=+=人机 方向斜向上。
绳索与竖直方向的夹角为30度时:sm s m v v v v v /21/41760cos 2022=+=++=人机人机 方向斜向上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数模第二次培训论文论文题目:悬崖跳水水池深度设定问题姓名1:李辉树学号:******** 专业:信计专业姓名1:彭记译学号:******** 专业:信计专业姓名1:游美玲学号:******** 专业:信计专业2011 年7月9 日悬崖跳水水池深度设定问题摘要本文探讨悬崖跳水水池深度设定问题,以实现水池深度设定既保证运动员人身安全且使成本消耗最低为目标。
对此问题,将建立物理模型,运用物理学、理论力学知识,结合微分方程学方法进行求解。
对于问题一,本文将建立物理模型,将跳水运动员形似锲形,用物理动力学解题思路,对悬崖跳水物理过程细化为运动员空中、入水与水中三个运动过程,并逐个对其建立运动状态方程,结合微分方程学简化求解,最后用Mathematic 软件画图展示结果,从图中得到:男子水池深度为9.3米,女子水池深度为7.8米。
其中动力学方程为:mg f F dthd m -+=浮22; 阻力方程为:221Sv C f d ρ=。
对于问题二,根据物理质量公式,结合运动员悬崖跳水三个具体物理运动的总方程进行分析,得出高度、底面积与质量之间的联系,从而判断体重不同者与水池深度大小的关系,得到结果:体重越大的人跳水时需要更深的水。
该模型建立亮点一体现在其充分运用了物理知识,同时结合微分法简化了求解难度;亮点二体现在用Mathematic 软件画图展示结果,直观准确。
关键词:物理动力学;微分方程学;运动状态方程;Mathematic 软件一、问题重述近年来世界上新兴一种跳水比赛叫红牛悬崖跳水世界杯比赛。
悬崖跳水,即运动员从高空悬崖跳下来,身体在重力的作用下快速自由下落,这是一种非常危险、挑战人类极限的比赛,所以比赛中安全问题显得非常重要。
比赛规定男子跳台高度为23至28米,女子为18至23米。
我国福建连城的冠豸山就举行过这样的比赛,那里的跳台高度是男子28米,女子20米。
下落过程中,运动员的身体入水后受到水的阻力与浮力作用,抵消身体的重力作用,使运动员在水中做减速运动,直至速度降为零。
为了保证运动员的人身安全,水池建立必须有足够的深度,另一方面,尽量节约水池建设的成本可避免无意义的浪费。
所以水池深度设定必须在满足不造成运动员人身伤害的同时达到最低成本消耗的要求。
需完成任务:1.根据福建连城冠豸山跳台高度,计算跳台下面的水池要多深才能安全;2.分析两个体重不同的人跳水时哪个需要更深的水。
二、问题分析悬崖跳水运动涉及的为物理动力学问题。
本文需解决水池深度设定问题及考虑运动员不同质量对水池深度设定的影响,水池深度设定需满足不造成运动员人身伤害的同时达到最低成本消耗的要求。
即跳水运动员落入水中速度降为最小时,该时刻运动员所在深度即为最佳水池深度。
将悬崖跳水运动的物理过程具体、细致化,从以下三个过程分析。
跳台至水面过程:运动员从跳台跳下,在空中完成动作后落入水中。
在这个过程中受到竖直向下的重力与竖直向上的空气阻力影响,重力为恒定的,空气阻力逐渐增大,运动员做加速度减小,速度增大的运动,到达水面时速度达到最大。
空气至水中过程:运动员以最大速度,身体笔直、双手紧贴,脚先着水的方式垂直入水。
这个过程中进入水中部分身体受到水的竖直向上的浮力和阻力,整个身体受到竖直向下的重力,运动员做加速度极大的减速运动。
由于入水身体高度为变化的,所以在计算时需考虑动态求浮力与阻力。
水面至水池底部过程:运动员身体全部进入水中,做减速运动直至速度减为零达到水池底部。
运动员受到竖直向上的水的浮力、阻力和竖直向下的重力,重力与浮力恒定,水的阻力逐渐减小,导致做加速度减小的减速运动。
为了保证运动员的人身安全,水池建立必须有足够的深度,避免运动员因撞击池底而受伤;另一方面,尽量节约水池建设的成本可以避免无意义的浪费。
所以最佳水池深度为运动员在水下速度最小时的深度。
根据第一问的求解分析,改变质量的值,同时考虑锲形高度与半径的变化得出结果。
三、模型假设1、假设跳水运动员跳水状态形似锲形下落,质量分布均匀,其中跳水运动员的高度即锲形高度,人的脚部为锲形底部,人体的肩宽即锲形直径(如下图示);2、假设跳水运动员以身体笔直,双手紧贴,脚先着水的方式垂直入水,速度方向垂直向下;3、假设忽略跳水运动员的蹬板过程;4、假设风速水速为零,不影响运动员下落;5、假设人水短暂碰撞过程没有能量损失;6、假设男女跳水运动员身高、质量及肩宽符合20-25岁跳水运动员国际标准。
7、假设运动员落入水中速度降为最小即速度为零,此时的深度为安全深度零界。
四、符号说明符号意义说明H'跳台距水面的高度(i=1或2)iH跳水运动员的高度(锲形高度)ih人的脚部(锲形底部)与水面距离r人体的一半肩宽(锲形半径)im人体质量iρ流体的密度η流体粘滞系数f流体阻力v落体瞬时速度R雷诺系数ed C阻力系数g重力加速度(29.8/g m s =)浮F水中受到的浮力五、模型的建立与求解问题一:5.1.1 建模思路对悬崖跳水运动员跳水三个细分运动过程受力分析: (1)跳台至水面过程:运动员受到竖直向下的恒定重力与竖直向上的空气阻力影响,空气阻力逐渐增大,运动员做加速度减小的加速运动,到达水面时速度达到最大。
(2)空气至水中过程:运动员进入水中部分身体受到水的竖直向上的浮力和阻力,整个身体受到竖直向下的重力,运动员做加速度极大的减速运动。
(3)水面至水池底部过程:运动员受到竖直向上的水的浮力、水的阻力和竖直向下的恒定重力,水的阻力逐渐减小,导致做加速度减小的减速运动,减速运动直至速度减为最小达到水池底部。
当跳水运动员落入水中速度降为零时,该时刻运动员所在深度即为最佳水池深度。
根据三个过程受力表达式,结合微分法简化,应用Mathematic 软件画图展示结果。
其中整个下降过程重力不变为质量与重力加速度之积;水的浮力为水的密度,重力加速度与锲形入水体积之积;空气和水的阻力为需根据雷诺系数确:当雷诺系数大于10-3时,阻力系数为0.4,且与2v 成正比;当雷诺系数e R 小于10-3大于1时,阻力系数为4.01624+++=ee d R R C ,且与2v 成正比;当雷诺系数小于1时,阻力系数为eR 24,且与v 成正比。
5.1.2 模型建立 (1)跳台至水面过程:建立运动状态方程:气f mg dt hd m -=22;即:mf g dt dv气-=; ①其中空气阻力为:221Sv C f d ρ=气;雷诺系数为:ηρvH R e =; ②物体与流速垂直方向的最大横截面积:2r S π=。
图一 运动员由跳台至水面过程(2)空气至水中过程:建立运动状态方程:mg F f dthd m -22浮水+=; 其中水的浮力为:2323H gh r F ρπ=浮;代入水的阻力与浮力公式得:g mH g h r m H v h r dh dv v -+=232222232.0ρπρπ 。
③图二 运动员由空气至水中过程(3)水面至水池底部过程:建立运动状态方程:mg F f dthd m -22浮水+=; ④ 其中水的浮力为:g H r F ρπ231=浮。
图三 运动员由水面至水池底部过程5.1.3 模型求解通过对20-25岁跳水运动员国际标准查询,男女跳水运动员对应跳台高度、身高、质量及肩宽平均为:;,,,;,,,kg m m r m H m H kg m m r m H m H 6038.065.1207545.078.1282222'1111'========水和空气所对应的密度与粘滞系数如下:s Pa m g ⋅⨯=⋅=-5-3101.8193.21气气,ηρ;s Pa m g ⋅⨯=⋅=-5-31005.011水水,ηρ;(1)跳台至水面过程:将H R s Pa m g e ,,,气气35-310101.8193.21--=⋅⨯=⋅=ηρ的值代入②中得到8≈v 为分界点,即:⎪⎩⎪⎨⎧∝≈≥∝+++=<224.084.016248v f C v v f R R C v d e e d 气,,,,; 代入①中得:⎪⎪⎪⎩⎪⎪⎪⎨⎧-=≥+++-=<m v r g dh dv v v m v HvHv r g dh dv v v 22222.08/)4.01624(218ρπηρρηρπ,,; 通过将公式与数据输入Mathematic 软件,得到图像如下:图四 男子由跳台至水面过程时速度与高度关系图五 女子由跳台至水面过程时速度与高度关系从图中可得到,到达水面时的男子速度为23.7m/s ,女子速度为19.7m/s 。
(2)空气至水中过程:通过将公式③与相应数据输入Mathematic 软件,得到图像如下:图六 男子由空气至水中过程时速度与高度关系图六 女子由空气至水中过程时速度与高度关系从图中可得到,全部进入水面时男子速度将为16.8m/s ,女子速度将为8.7m/s 。
(3)水面至水池底部过程: 将H R s Pa m g e ,101005.01135-3--=⋅⨯=⋅=,,水水ηρ的值代入②中得到6≈v 为分界点,即:⎪⎩⎪⎨⎧∝≈≥∝+++=<224.064.016246v f C v v f R R C v d e e d 气,,,,; 代入④中得到:⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=≥-+++=<gm g H r m v r dh dv v v g m g H r m v Hv Hv r dh dv v v 32.063/)1624(216222222ρπρπρπηρρρπ,,; 通过将公式与数据输入Mathematic 软件,得到图像如下:图七 男子由水面至水池底部过程时速度与高度关系图八 女子由水面至水池底部过程时速度与高度关系从图中可得到,到达水面底部时的男子跳水水池深度为9.3m ,女生跳水水池深度为7.8m 。
5.1.4 模型分析与检验模型建立将物理运动根据运动状态分阶段受力分析,求解时充分结合了物理学、理论力学以及微分方程学解决本文问题,使得解题过程简化。
同时应用图形展示结果,形象易理解。
解决了本题问题一。
问题二:5.2.1 建模思路 若两人体重不同,由于人体密度保持不变,则存在三种情况:人的底面积相,高度不同;人的高度相同,底面积不同;人的底面积与高度都不同。
结合运动员悬崖跳水三个具体物理运动的总方程进行分析,得出高度、底面积与质量之间的联系,从而判断体重不同者的水池深度大小。
5.2.2 模型建立锲形质量计算公式:SH m ρ31=;建立运动状态方程:Hv C v g dh dv f mg dt h d m d 人气气ρρ2322-=⇒-=; ⑤ vg v H gh H v C dh dv mg F f dt h d m d -+=⇒+=332223-人水人水浮水ρρρρ; ⑥ vg v g H v C dh dv mg F f dt h d m d -+=⇒+=人水人水浮水ρρρρ23-22。
