习题7及其解答
习题7及其解答7.1 选择题1．在下列运算符中，不能重载的是( b )。
(a) ! (b) sizeof (c) new (d) delete2．下列关于运算符重载的描述中，( d )是正确的。
(a) 可以改变参与运算的操作数个数(b) 可以改变运算符原来的优先级(c) 可以改变运算符原来的结合性(d) 不能改变原运算符的语义3．下列函数中，不能重载运算符的函数是( b )。
(a) 成员函数(b) 构造函数(c) 普通函数 (d) 友员函数4．要求用成员函数重载的运算符是( a )。
(a) = (b) == (c) <= (d) ++5．要求用友员函数重载的运算符是( c )。
(a) = (b) [] (c) << (d) ()6．下面关于类型转换的描述中，错误的是( a )。
(a) 任何形式的构造函数都可以实现数据类型转换。
(b) 带非默认参数的构造函数可以把基本类型数据转换成类类型对象。
(c) 类型转换函数可以把类类型对象转换为其他指定类型对象。
(d) 类型转换函数只能定义为一个类的成员函数，不能定义为类的友员函数。
7.2 阅读下列程序，写出执行结果1．#include <iostream>using namespace std;class T{ public :T() { a = 0; b = 0; c = 0; }T( int i, int j, int k ){ a = i; b =j; c = k; }void get( int &i, int &j, int &k ){ i = a; j = b; k = c; }T operator* ( T obj );private:int a , b , c;};T T::operator* ( T obj ){ T tempobj;tempobj.a = a * obj.a;tempobj.b = b * obj.b;tempobj.c = c * obj.c;return tempobj;}int main(){ T obj1( 1,2,3 ), obj2( 5,5,5 ), obj3;int a , b , c;obj3 = obj1 * obj2;obj3.get( a, b, c );cout<<"( obj1*obj2 ): "<<"a = "<<a<<'\t'<<"b = "<<b<<'\t'<<"c = "<<c<<'\t'<<endl;(obj2*obj3).get( a, b, c );cout<<"( obj2*obj3 ): "<<"a = "<<a<<'\t'<<"b = "<<b<<'\t'<<"c = "<<c<<'\t'<<endl;}【解答】( obj1 * obj2 ): a = 5 b = 10 c = 15( obj2 * obj3 ): a = 25 b = 50 c = 752．#include <iostream>using namespace std;class Vector{ public:Vector(){ }Vector(int i,int j){ x = i ; y = j ;}friend Vector operator+ ( Vector v1, Vector v2 ){ Vector tempVector ;tempVector.x = v1.x + v2.x ;tempVector.y = v1.y + v2.y ;return tempVector ;}void display(){ cout << "( " << x << ", " << y << ") "<< endl ; }private:int x , y ;};int main(){ Vector v1( 1, 2 ), v2( 3, 4 ), v3 ;cout << "v1 = " ;v1.display() ;cout << "v2 = " ;v2.display() ;v3 = v1 + v2 ;cout << "v3 = v1 + v2 = " ;v3.display() ;}【解答】v1 = ( 1, 2 )v2 = ( 3, 4 )v3 = v1 + v2 = ( 4, 6 )7.3 思考题1．一个运算符重载函数被定义为成员函数或友员函数，从定义方式、解释方式和调用方式上有何区别？可能会出现什么问题？请用一个实例说明之。
【解答】以二元运算符为例。
可能会出现的问题：（1）运算符的左右操作数不同，须用友员函数重载；（2）当运算符的操作需要修改类对象状态时，应用成员函数重载。
（3）友员函数不能重载运算符 = () [] ->必须要用友员函数重载的运算符 >> <<程序略。
2．类类型对象之间，类类型和基本类型对象之间用什么函数进行类型转换？归纳进行类型转换的构造函数和类型转换函数的定义形式、调用形式和调用时机。
【解答】构造函数可以把基本类型、类类型数据转换成类类型数据；类类型转换函数可以在类类型和基本数据类型之间做数据转换。
7.4 编程题1．分别使用成员函数和友员函数编写程序重载运算符“+”，使该运算符能实现两个字符串的连接。
【解答】（1）使用成员函数#include <iostream>#include<cstring>using namespace std;class s{ public:s(){ *str = '\0'; }s( char *pstr ){ strcpy( str,pstr );}char *gets(){ return str;}s operator+( s obj );private:char str[10];};s s::operator+( s obj ){ strcat( str,obj.str );return str; //或return *this}int main(){ s obj1( "Visual" ),obj2( " C++" ),obj3;obj3 = obj1 + obj2;cout << obj3.gets() << endl;}（2）使用友员函数#include <iostream>#include<cstring>using namespace std;class s{ public:s(){ *str= '\0'; }s( char *pstr ){ strcpy( str,pstr );}char *gets(){ return str;}friend s operator+( s obj1,s obj2 );private:char str[100];};s operator+( s obj1,s obj2 ){ s tempobj;strcat( tempobj.str,obj1.str );strcat( tempobj.str,obj2.str );return tempobj;}int main(){ s obj1( "Visual" ),obj2( " C++" ),obj3;obj3 = obj1 + obj2;cout << obj3.gets() << endl;}2．定义一个整数计算类Integer，实现短整数 +，-，*，/ 基本算术运算。
要求可以进行数据范围检查（-32768～32767，或自行设定），数据溢出时显示错误信息并中断程序运行。
【解答】#include <iostream>using namespace std;class Integer{ private:short a;public:Integer (short n=0){ a=n;}Integer operator +(Integer);Integer operator -(Integer);Integer operator *(Integer);Integer operator /(Integer);Integer operator =(Integer);void display(){ cout<<a<<endl; }};Integer Integer::operator+(Integer x){ Integer temp;if(a+x.a<-32768||a+x.a>32767){ cout<<"Data overflow!"<<endl; abort(); }temp.a=a+x.a;return temp;}Integer Integer::operator-(Integer x){ Integer temp;if(a-x.a<-32768||a-x.a>32767){ cout<<"Data overflow!"<<endl; abort(); }temp.a=a-x.a;return temp;}Integer Integer::operator*(Integer x){ Integer temp;if(a*x.a<-32768||a*x.a>32767) {cout<<"Data overflow!"<<endl; abort();}temp.a=a*x.a;return temp;}Integer Integer::operator/(Integer x){ Integer temp;if(a/x.a<-32768||a/x.a>32767){ cout<<"Data overflow!"<<endl; abort(); }temp.a=a/x.a;return temp;}Integer Integer::operator=(Integer x){ a=x.a;return *this;}int main(){ Integer A(90),B(30),C;cout<<"A=";A.display();cout<<"B=";B.display();C=A+B;cout<<"C=A+B="; C.display();C=A-B;cout<<"C=A-B="; C.display();C=A*B;cout<<"C=A*B="; C.display();C=A/B;cout<<"C=A/B="; C.display();}3．定义一个实数计算类Real，实现单精度浮点数 +，-，*，/ 基本算术运算。
习题解答
第7章思考题及习题7参考答案一、填空1. AT89S52单片机任何一个端口要想获得较大的驱动能力，要采用电平输出。
答：低2.检测开关处于闭合状态还是打开状态，只需把开关一端接到I/O端口的引脚上，另一端接地，然后通过检测来实现。
答： I/O端口引脚的电平3. “8”字型的LED数码管如果不包括小数点段共计段，每一段对应一个发光二极管，有和两种。
答：7，共阳极，共阴极4. 对于共阴极带有小数点段的数码管，显示字符“6”（a段对应段码的最低位）的段码为，对于共阳极带有小数点段的数码管，显示字符“3”的段码为。
答：7DH，B0H5. 已知8段共阳极LED数码显示器要显示某字符的段码为A1H(a段为最低位)，此时显示器显示的字符为。
答：d6. LED数码管静态显示方式的优点是：显示闪烁，亮度，比较容易，但是占用的线较多。
答：无，较高，软件控制，I/O口7. 当显示的LED数码管位数较多时，一般采用显示方式，这样可以降低，减少的数目。
答：动态，成本，I/O端口8. LCD 1602是型液晶显示模块，在其显示字符时，只需将待显示字符的由单片机写入LCD 1602的显示数据RAM（DDRAM），内部控制电路就可将字符在LCD上显示出来。
答：字符，ASCII码9. LCD 1602显示模块内除有字节的 RAM外，还有字节的自定义，用户可自行定义个5×7点阵字符。
答：80，显示数据，64，字符RAM，810．当按键数目少于8个时，应采用式键盘。
当按键数目为64个时，应采用式键盘。
答：独立，矩阵11．使用并行接口方式连接键盘，对独立式键盘而言，8根I/O口线可以接个按键，而对矩阵式键盘而言，8根I/O口线最多可以接个按键。
答：8，6412．LCD 1602显示一个字符的操作过程为：首先，然后，随后，最后。
答：读忙标志位BF，写命令，写显示字符，自动显示字符13．由于微型打印机TPμP-40A/16A是一种外设，因此单片机与微型打印机的的命令与数据传送，必须采用方式。
程兰征版物理化学习题解答7
第七章 电池电动势及极化现象习题解答1、已知0.100mol/kgBaCl 2溶液中，γ±=0.501，求BaCl 2的活度。
解：m ±=34m B =0.1587mol/kg ，a ±=34γ±·m B =0.07953a B = 4（γ±·m B ）3=5.03×10-42、在25℃，Ag(s)+0.5Hg 2Cl 2(s)=AgCl(s)+Hg(l)的ΔHθ(298K)=7950J/mol ，又知Ag 、AgCl 、Hg 2Cl 2、Hg 的标准摩尔熵分别为：42.7、96.1、196.0、77.4J ·K -1·mol -1。
求下列电池的标准电动势及其温度系数：Ag(s),AgCl(s)|KCl(aq)|Hg 2Cl 2(s),Hg(l)解：ΔSθ(298K)=96.1+77.4-42.7-0.5×196.0=32.8（J ·K -1·mol -1）ΔG θ(298K)=7950-298×32.8=-1824.4（J/mol ） E θ= -1824.4/1×(-96500)=0.01891(V)p )(TE∂∂=32.8/1×(96500)=3.4×10-4(V/K)3、查标准电极电势表（表7-1），计算下列电池的电动势（25℃）。
（1）Ag,AgBr|Br -(a =0.10)||Cl -(a =0.010)|AgCl,Ag （2）Pt,H 2(p θ)|HCl(a ±=0.10)|Cl 2(p =5066Pa),Pt（3）Pt,H 2(p θ)|HCl(a ±=0.10)|Hg 2Cl 2,Hg （4）K-Hg(a =0.010)|KOH(a ±=0.50)|HgO,Hg （5）Pb,PbSO 4|CdSO 4(0.20mol/kg,γ±=0.11)||CdSO 4(0.020mol/kg, γ±=0.32)|PbSO 4,Pb（6）Zn|Zn 2+(a =0.01)||Fe 2+(a =0.001),Fe 3+(a =0.10)|Pt 解：（1）AgCl+Br - =AgBr+Cl -E =0.2223-0.0713-10.0010.0lg 10592.0=0.2102V（2）0.5 H 2+ 0.5Cl 2=HClE =1.3583-0.0-0.5225)(5066/101310.0lg 10592.0=1.4382V(注意：a = a ±2)书上答案不对（3）0.5H 2+ 0.5Hg 2Cl 2=Hg+HClE =0.2799-0.0-110.0lg 10592.02=0.3983V书上答案不对（4）K+0.5HgO+0.5H 2O=Hg+KOH E =0.0986-(-2.924)-010.050.0lg 10592.02=2.9398V[注意：Eθ(HgO/Hg)=0.0986V] 书上答案不对（5）SO 42-(0.20mol/kg, γ±=0.11) =SO 42-(0.020mol/kg, γ±=0.32)近似：a +=a -= a ±=m ±γ±E =-0.1120.00.32020.0lg 20592.0⨯⨯=0.01587V书上答案不对（6）Zn+2Fe 3+=Zn 2++2Fe 2+E =0.770-(-0.7628)-2210.00.01001.0lg 20592.0⨯=1.7104V4、电池Pb,PbCl 2|KCl(aq)|AgCl,Ag 在25℃、p θ下的E θ=0.490V （1）写出电极反应和电池反应；（2）求电池反应的θm r S ∆、θm r G ∆、θm r H ∆，已知p )(TE ∂∂=-1.80×10-4V ·K -1解：正极：2AgCl+2e=2Ag+2Cl - ；负极：Pb-2e+2Cl -=PbCl 2电池反应：Pb+2AgCl=PbCl 2+2Agθm r G ∆=-2×96500×0.490=-94570(J/mol) θm r S ∆=2×96500×(-1.80×10-4)=-34.74(J ·K -1·mol -1)θm r H ∆=-94570+298×(-34.74)=-104922.5(J/mol)5、试验测出具有下列电池反应的可逆电池，其电动势与温度的关系式为：Cd(s)+Hg 22+=Cd 2++2Hg(l)E t =[0.6708+1.02×10-4(t/℃-25)-2.4×10-6(t/℃-25)2]V求该反应在40℃时的θm r H ∆、θm r G ∆、θm r S ∆。
算法与程序实践习题解答7(枚举)
《算法与程序实践》习题解答7——枚举枚举是基于已有的知识进行答案猜测的一种问题求解策略。
在求解一个问题时，通常先建立一个数学模型，包括一组变量，以及这些变量需要满足的条件。
问题求解的目标就是确定这些变量的值。
根据问题的描述和相关的知识，能为这些变量分别确定一个大概的取值范围。
在这个范围内对变量依次取值，判断所取的值是否满足数学模型中的条件，直到找到（全部）符合条件的值为止。
这种解决问题的方法称作“枚举”。
例如“求小于N的最大素数”。
其数学模型是：一个整型变量n，满足：（1）n不能够被[2，n）中的任意一个素数整除；（2）n与N之间没有素数。
利用已有的知识，能确定n 的大概取值范围{2}{2*i+1|1<=i,2*i+1<N}。
在这个范围内从小到大依次取值，如果n不能够被[2，n）中的任意一个素数整除，则满足条件(1)。
在这个范围内找到的最后一个素数也一定满足条件(2)，即为问题的解。
枚举是用计算机求解问题最常用的方法之一，常用来解决那些通过公式推导、规则演绎的方法不能解决的问题。
而且，枚举也是现代科学研究和工程计算的重要手段，因为科学研究是在发现问题的规律之前解决问题，然后再寻找不同问题之间的共同规律。
在采用枚举的方法进行问题求解时，要注意3个方面的问题。
●建立简洁的数学模型。
数学模型中变量的数量要尽量少，它们之间相互独立。
这样问题解的搜索空间的维度就小。
反应到程序代码中，循环嵌套的层次少。
模型中的每个条件要反应问题的本质特征。
“求小于N 的最大素数”中的条件（1）是“n不能够被[2，n）中的任意一个素数整除”，而不是“n不能够被[2，n）中的任意一个整数整除”。
这个条件极大的降低了判断n是否是素数的计算开销。
●减小搜索的空间。
利用已有的知识缩小数学模型中各个变量的取值范围，避免不必要的计算。
反应到程序代码中，循环体被执行的次数就少。
除2 之外的其它素数都是奇数，因此“小于N 的最大素数”一定在集合{2，2*i+1|1<=i，2*i+1<N}中。
模电课后(康华光版)习题答案7
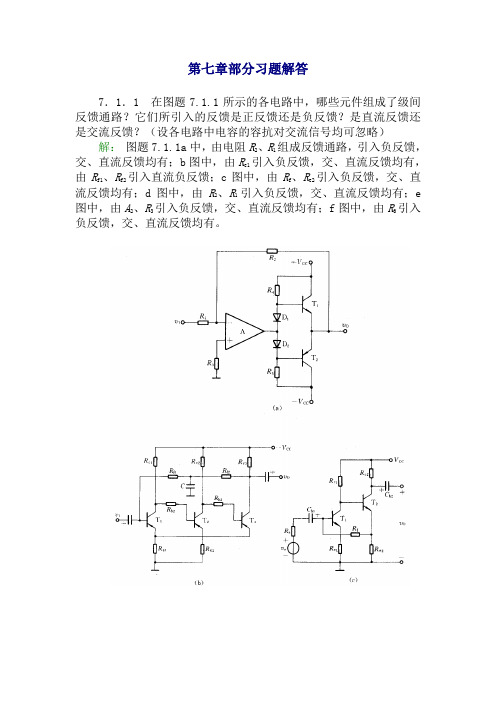
第七章部分习题解答7．1．1在图题7.1.1所示的各电路中，哪些元件组成了级间反馈通路？它们所引入的反馈是正反馈还是负反馈？是直流反馈还是交流反馈？（设各电路中电容的容抗对交流信号均可忽略）解：图题7.1.1a中，由电阻R2、R1组成反馈通路，引入负反馈，交、直流反馈均有；b图中，由R e1引入负反馈，交、直流反馈均有，由R f1、R f2引入直流负反馈；c图中，由R f、R e2引入负反馈，交、直流反馈均有；d图中，由R2、R1引入负反馈，交、直流反馈均有；e 图中，由A2、R3引入负反馈，交、直流反馈均有；f图中，由R6引入负反馈，交、直流反馈均有。
图题7.1.17．2.2 试指出图题7.1.5a、b所示电路能否实现规定的功能，若不能，应如何改正？解：图题7.1.5a电路不能实现规定的功能，因引入了正反馈。
应将运放的同相端和反相端位置互换。
图b电路也不能实现规定的功能。
应将R与R L位置互换。
图题7.1.57．2.4 由集成运放A 及BJT T 1、T 2组成的放大电路如图题7.1.7所示，试分别按下列要求将信号源v s 、电阻R f 正确接入该电路。
（1） 引入电压串联负反馈； （2） 引入电压并联负反馈； （3） 引入电流串联负反馈； （4） 引入电流并联负反馈。
图题7.1.7解： （1）a-c 、b-d 、h-i 、j-f（2）a-d 、b-c 、h-I 、j-f （3）a-d 、b-c 、g-i 、j-e （4）a-c 、b-d 、g-i 、j-e7．4．1 一放大电路的开环电压增益为A VO =104，当它接成负反馈放大电路时，其闭环电压增益为A VF =50，若A VO 变化10%，问A VF 变化多少？解： 因为200501014===+VF VO V VO A A F A所以，当A VO 变化10%时，A VF 变化%05.0%102001=⨯=VF VF A dA7．4．5 电路如图题7.3.10所示。
工程力学习题答案7 廖明成
第七章 杆类构件的应力分析与强度计算习 题7.1 图示阶梯形圆截面杆AC ，承受轴向载荷1200 kNF =与2100 kN F =, AB 段的直径mm 401=d 。
如欲使BC 与AB 段的正应力相同，试求BC 段的直径。
题7.1图解：如图所示：物体仅受轴力的作用，在有两个作用力的情况下经分析受力情况有：AB 段受力：1NAB F F = BC 段受力：12NBC F F F =+AB 段正应力：1221440.04NAB NAB AB AB F F F A d σππ⨯===⨯ BC 段正应力：()12222244NBC NBC BCBC F F F F A d d σππ+⨯===⨯ 而BC 与AB 段的正应力相同 即，BC AB σσ= 解出：249d mm ==7.2 图示轴向受拉等截面杆，横截面面积2500 mm A =，载荷50 kN F =。
试求图示斜截面()o30=α m-m 上的正应力与切应力，以及杆内的最大正应力与最大切应力。
mm题7.2图解：拉杆横截面上的正应力605000010050010N F F Pa MPa A A σ︒-====⨯ 应用斜截面上的正应力和剪应力公式：2300cos σσα︒︒= 030sin 22στα︒︒=有图示斜截面m-m 上的正应力与切应力为：3075MPa σ︒= 3043.3MPa τ︒=当0=α时，正应力达到最大，其值为max 0100MPa σσ︒== 即：拉压杆的最大正应力发生在横截面上，其值为100MPa 。
当45=α时，切应力最大，其值为0max 502MPa στ︒==即拉压杆的最大切应力发生在与杆轴成45的斜截面上，其值为50MPa 。
7.3图示结构中AC 为钢杆，横截面面积21200 mm A =，许用应力[]1160 Mpa σ=;BC 为铜杆，横截面面积22300 mmA =，许用应力[]2100 Mpa σ=。
《微机原理与接口技术》习题解答7
《微机原理与接口技术》习题解答习题77.1 什么是中断？常见的中断源有哪几类？CPU响应中断的条件是什么？【解答】中断是指CPU在正常执行程序时，由于内部/外部时间或程序的预先安排引起CPU暂时终止执行现行程序，转而去执行请求CPU为其服务的服务程序，待该服务程序执行完毕，又能自动返回到被中断的程序继续执行的过程。
常见的中断源有：一般的输入/输出设备请求中断；实时时钟请求中断；故障源；数据通道中断和软件中断。
CPU响应中断的条件：若为非屏蔽中断请求，则CPU执行完现行指令后，就立即响应中断。
CPU若要响应可屏蔽中断请求，必须满足以下三个条件：①无总线请求；②CPU 允许中断；③CPU执行完现行指令。
7.2 简述微机系统的中断处理过程。
【解答】（1）中断请求：外设需要进行中断处理时，向CPU提出中断请求。
（2）中断响应：CPU执行完现行指令后，就立即响应非屏蔽中断请求。
可屏蔽中断请求，CPU若要响应必须满足三个条件。
（3）中断处理：保护现场、开中断、中断服务。
（4）中断返回：CPU执行IRET中断返回指令时，自动把断点地址从堆栈中弹出到CS 和IP中，原来的标志寄存器内容弹回Flags，恢复到原来的断点继续执行程序。
7.3 软件中断和硬件中断有何特点？两者的主要区别是什么？【解答】硬件中断由外部硬件产生，是由CPU外部中断请求信号触发的一种中断，分为非屏蔽中断NMI和可屏蔽中断INTR。
软件中断是CPU根据某条指令或者对标志寄存器的某个标志位的设置而产生的，也称为内部中断。
通常有除法出错中断、INTO溢出中断、INT n中断、断点中断和单步中断等。
两者的主要区别：硬件中断由外部硬件产生，而软件中断与外部电路无关。
7.4 中断优先级的排队有哪些方法？采用软件优先级排队和硬件优先级排队各有什么特点？【解答】软件优先级排队：各中断源的优先权由软件安排。
优点是电路比较简单，可以直接修改软件查询顺序来修改中断优先权，不必更改硬件。
数据库系统概论第五版第七章习题解答和解析
第七章习题解答和解析1. 试述数据库设计过程。
答：这里只概要列出数据库设计过程的六个阶段:(1) 需求分析;(2) 概念结构设计;(3) 逻辑结构设计;(4) 数据库物理设计;(5) 数据库实施;(6) 数据库运行和维护。
这是一个完整的实际数据库及其应用系统的设计过程。
不仅包括设计数据库本身,还包括数据库的实施、运行和维护。
设计一个完善的数据库应用系统往往是上述六个阶段的不断反复。
解析：希望读者能够认真阅读《概论》7.1 的内容,了解并掌握数据库设计过程。
2.试述数据库设计过程中结构设计部分形成的数据库模式。
答：数据库结构设计的不同阶段形成数据库的各级模式,即:(1) 在概念设计阶段形成独立于机器特点,独立于各个 DB MS 产品的概念模式,在本篇中就是 E-R 图;(2) 在逻辑设计阶段将 E-R 图转换成具体的数据库产品支持的数据模型,如关系模型,形成数据库逻辑模式,然后在基本表的基础上再建立必要的视图(View),形成数据的外模式;(3) 在物理设计阶段,根据 DB MS 特点和处理的需要,进行物理存储安排,建立索引,形成数据库内模式。
读者可以参考《概论》上图7.4。
图中概念模式是面向用户和设计人员的,属于概念模型的层次;逻辑模式、外模式、内模式是 DBMS 支持的模式,属于数据模型的层次,可以在 DBMS 中加以描述和存储。
3.需求分析阶段的设计目标是什么 ? 调查的内容是什么 ?答需求分析阶段的设计目标是通过详细调查现实世界要处理的对象(组织、部门、企业等),充分了解原系统(手工系统或计算机系统)工作概况,明确用户的各种需求,然后在此基础上确定新系统的功能。
调查的内容是“数据”和“处理”,即获得用户对数据库的如下要求:(1) 信息要求,指用户需要从数据库中获得信息的内容与性质,由信息要求可以导出数据要求,即在数据库中需要存储哪些数据;(2) 处理要求,指用户要完成什么处理功能,对处理的响应时间有什么要求,处理方式是批处理还是联机处理;(3) 安全性与完整性要求。
单片机原理及接口技术(C51编程)(第2版)-习题答案 - 第7章习题解答
第7章思考题及习题7参考答案一、填空1．如果采用晶振的频率为3MHz，定时器/计数器T x（x=0,1）工作在方式0、1、2下，其方式0的最大定时时间为，方式1的最大定时时间为，方式2的最大定时时间为。
答：32.768ms，262.144ms，1024µs2．定时器/计数器用作计数器模式时，外部输入的计数脉冲的最高频率为系统时钟频率的。
答：1/243．定时器/计数器用作定时器模式时，其计数脉冲由提供，定时时间与有关。
答：系统时钟信号12分频后，定时器初值4．定时器/计数器T1测量某正单脉冲的宽度，采用方式可得到最大量程？若时钟频率为6MHz，求允许测量的最大脉冲宽度为。
答：方式1定时,131.072ms。
5. 定时器T2 有3种工作方式：、和，可通过对寄存器中的相关位进行软件设置来选择。
答：捕捉，重新装载（增计数或减计数），波特率发生器，T2CON6. AT89S52单片机的晶振为6MHz，若利用定时器T1的方式1定时2ms，则（TH1）= ，（TL1）= 。
答：FCH，18H。
二、单选1．定时器T0工作在方式3时，定时器T1有种工作方式。
A.1种B.2种 C．3种D．4种答：C2. 定时器T0、T1工作于方式1时，其计数器为位。
A.8位B.16位C.14位D.13位答：B3. 定时器T0、T1的GATE x=1时，其计数器是否计数的条件。
A. 仅取决于TR x状态B. 仅取决于GATE位状态C. 是由TR x和INT x两个条件来共同控制D. 仅取决于INT x的状态答：C4. 定时器T2工作在自动重装载方式时，其计数器为位。
A.8位B. 13位C.14位D. 16位答：D5. 要想测量INT0引脚上的正单脉冲的宽度，特殊功能寄存器TMOD的内容应为。
A.87HB. 09HC.80HD. 00H答：B三、判断对错1．下列关于T0、T1的哪些说法是正确的。
A.特殊功能寄存器SCON，与定时器/计数器的控制无关。
《固体物理学》房晓勇主编教材-习题参考解答07第七章 能带结构分析
()
()
间的运动轨迹是一条垂直于 B 德平面和等能面所截成的曲线，显然电子从曲线 k1 点运动曲线 k2 点所需 的时间为
J G
t2 − t1 =
∫
t2
dt =
t1
∫
k2
k1
dk dk / dt
其中 dk 是 k 空间曲线的弧元
3
第七章 能带结构分析
G G J G JJ G J G dk 由= = −ev × B = −ev⊥ × B dt JJ G J G v⊥ 为垂直于 B 德速度分量，可得
N = 2×
S2
( 2π )
2
2 × π kF
N ⎞ ⎛ k F = ⎜ 2π 2 ⎟ S ⎠ ⎝
1/ 2
= ( 2nπ )
1/ 2
7.3 试证明，当 n / na = 1.36 时，费米球和面心立方晶格的第一布里渊区相切，其中 na 是原子数密度。 解：参考陈金富 13.6 面心立方晶格原子数密度 nα = 界的最近距离 km = 4
5
第七章 能带结构分析 同理可用 ω =
2π eB =2
dA ( E ) dE
7.7 考虑两个能带
E (k ) = ±
=2k 2Δ + Δ2 ∗ m
式中Δ为一常数。设所有取正号的正能态都是空的，所有取负号的负能态都是填满的。 （1）在 t=0 时刻加上一个电子于正能带上的 ( k0 , 0, 0 ) ，并施加一个电场 E = Ez k ′ ，求 t 时刻的电流 （2）当 t → ∞ 时，上述情况如何？ （3）在相同条件下，如果负能带出现一个空穴，求其电流。 解：参考陈金富 13.16 （1）正能带上只有一个电子，它对电流的贡献，根据《固体物理学》式 7-20
水产生物统计习题7答案
水产生物统计习题7答案水产生物统计习题7答案统计学是一门研究数据收集、分析和解释的学科，它在各个领域中都有广泛的应用。
水产生物统计学是统计学在水产生物学领域的应用，通过对水产生物数据的统计分析，可以帮助我们了解和解释水产生物的特征和变化规律。
在水产生物统计学的学习中，习题是非常重要的一部分。
通过解答习题，我们可以巩固和应用所学的知识，提高解决实际问题的能力。
下面是水产生物统计学习题7的答案，希望对大家的学习有所帮助。
题目1：某渔场对一种鱼类进行了调查，得到了100个样本的体长数据，如下所示：15.2 14.8 17.5 16.3 15.9 16.7 15.6 15.4 16.1 15.8...17.2 16.5 15.7 16.8 15.3 16.0 15.9 15.6 16.2 15.8要求：计算这批鱼类的平均体长和标准差。
解答：首先，计算平均体长。
将100个样本的体长相加，然后除以100，即可得到平均体长。
标准差的计算需要进行多个步骤，首先计算每个样本与平均体长的差值，然后将这些差值平方，再将平方值相加并除以样本数，最后将结果开方，即可得到标准差。
题目2：某湖泊中的鱼类数量随时间的变化情况如下表所示：时间（年）鱼类数量（万尾）2000 102001 122002 152003 182004 222005 25要求：绘制该湖泊中鱼类数量随时间变化的折线图，并根据图形分析鱼类数量的变化趋势。
解答：为了绘制折线图，我们需要将时间和鱼类数量的数据进行配对。
然后，选择一个适当的比例，将时间和鱼类数量的数据转换为坐标点。
最后，通过连接这些坐标点，即可得到折线图。
通过观察折线图，我们可以看到鱼类数量随时间的增加而增加，呈现出逐年递增的趋势。
题目3：某渔场对鱼类的重量进行了调查，得到了100个样本的重量数据，如下所示：0.3 0.5 0.4 0.6 0.2 0.8 0.7 0.4 0.9 0.5...0.6 0.5 0.4 0.7 0.3 0.5 0.6 0.8 0.4 0.5要求：计算这批鱼类的重量的中位数和四分位数。