第七章习题解答
第7章习题解答

z 2 = z 1 + 130
2 z z ) 2 + 100 z ( z ) = 0 1 - ( 1 + 130 1 + 82 1 + 130
2 - 260 z z ´ 130 = 0 1 - 130 + 182 1 + 82
78 z ´ 130 - 130 2 = -48 ´ 130 = -6240 1 = 82 z 1 = -80 z 2 = z 1 + 130 = 130 - 80 = 50 f = 40cm
p 3 . 14 - 8 2 l 2 ´ 6328 ´ 10 - 3 ④ q= = = 2 . 315 ´ 10 rad pw0 3 . 14 ´ 0 . 0174
(5)有一个平凹腔,凹面镜曲率半径 R=5m,腔长 L=1m,光波长l=0.5mm,求①两镜 面上的基模光斑半径②基模高斯光束的远场发散角 解:①
2、双凹腔两反射镜面曲率半径分别为 R1=100cm、R2=82cm,腔长 L=130cm,求等价共焦 腔的焦参数。 解:
z1 +
f 2 = - R 1 z 1
z 1 +
f 2 = -100 z 1
2 2 z 100 z 1 + 1 + f = 0
w 0 =
f l
p
=
0 . 4 R l
p
(2)对称双凹腔长为 L,反射镜曲率半径 R=2.5L,光波长为l,求镜面上的基模光斑半 径。 解:
L L 2 f 2 = ( 2 R - L ) = (2 ´ 2 . 5 L - L ) = L 4 4 f = L
2 z 2
f
2
普通化学第七章课后习题解答

第七章沉淀反应参考答案P 142【综合性思考题】:给定体系0.02mol/LMnCl 2溶液(含杂质Fe 3+),经下列实验操作解答问题。
(已知K θSPMn(OH)2=2.0×10-13,K θSPMnS =2.5×10-13,K θbNH3=1.8×10-5,K θaHAc =1.8×10-5①与0.20mol/L 的NH 3.H 2O 等体积混合,是否产生Mn(OH)2沉淀?解:等体积混合后浓度减半,[Mn 2+]=0.01mol/L ,c b =[NH 3.H 2O]=0.10mol/L∵是一元弱碱体系,且c b /K b θ>500∴10.0108.1][5⨯⨯=⋅=--b b c K OH θ又∵ 622108.101.0][][--+⨯⨯=⋅=OH Mn Q c=1.8×10-8> K θSPMn(OH)2=2.0×10-13∴ 产生Mn(OH)2沉淀。
②与含0.20mol/L 的NH 3.H 2O 和0.2mol/LNH 4Cl 的溶液等体积混合,是否产生Mn(OH)2沉淀? 解:混合后属于NH 3.H 2O~NH 4Cl 的碱型缓冲液体系此时浓度减半:c b =[NH 3.H 2O]=0.2V/2V=0.1(mol.L -1)c S= [NH 4+]=0.2V/2V=0.1(mol.L -1)[Mn 2+]=0.02V/2V=0.01(mol.L -1)A 、求[OH -] 用碱型缓冲液计算式求算:s b b c c K OH ⋅=-θ][ 55108.11.01.0108.1--⨯=⨯⨯= B 、求Qc 22][][-+⋅=OH Mn Q c=0.01×[1.8×10-5]2=3.24×10-12C 、比较θ2)(,OH Mn SP K ∵13)(,100.22-⨯=>θOH Mn SP C K Q故有Mn(OH)2沉淀产生。
最新(完美版)第七章习题答案_数值分析

第七章习题解答2、试确定系数a ,b 的值使220[()cos ]ax b x dx p+-ò达到最小解:设220(,)[()cos ]I a b ax b x dx p=+-ò确定a ,b 使(,)I a b 达到最小,必须满足0,0I Ia b ¶¶==¶¶即3222222000022222000012[cos ]0cos 248212[cos ]0cos 82a b ax b x xdx a x dx b xdx xxdx a b ax b x dx a xdx b dx xdx p p p p p p p pp p p p p ììì+=-+-=+=ïïïïïïÞÞíííïïï+=+-=+=ïïïîîîòòòòòòòò解得:0.6644389, 1.1584689a b »-»5、试用Legendre 多项式构造()f x x =在[-1, 3]上的二次最佳平方逼近多项式 解:作变量代换,将区间[-1, 3]变为[-1, 1],令21x t =+,即12x t -=则()()(21)21(11)F t f x f t t t ==+=+-££对()F t 利用Legendre 多项式求其在}{21,,span t t上的最佳平方逼近多项式20()()j j j S t C P t ==å,其中11(,)21()()(0,1,2)(,)2j j j j j P f j C F t P t dt j P P -+===ò20121()=1,()=t,()=(31)2P t P t P t t - 则有:1121012112111212212121215[(21)(21)]24311[(21)(21)]285(31)(31)45[(21)(21)]22264C t dt t dt C t tdt t tdt t t C t dt t dt ---------=--++==--++=--=--++=òòòòòò 01251145()()()()4864S t P t P t P t \=++则()f x 在[-1, 3]上的最佳二次逼近多项式*01222151111451()()()()()()2428264251114511=()((3()1))4826422135+82243512x x x x S t S t S P P P x x x x ----===++--++-+=7、确定一条经过原点的二次曲线,使之拟合下列数据ix123iy0.2 0.5 1.0 1.2并求平方误差2d解:设2012()1,(),()x x x x x j j j ===由题,拟合函数须过原点 则令001122()()()()f x C x C x C x j j j =++,其中00C =,即212()f x C x C x =+ 12000.2110.5,,24 1.039 1.2Y f f æöæöæöç÷ç÷ç÷ç÷ç÷ç÷===ç÷ç÷ç÷ç÷ç÷ç÷èøèøèø 11122122(,)(,)1436(,)(,)3698G f f f f f f f f æöæö==ç÷ç÷èøèø 12(,) 6.1(,)15.3Y F Y f f æöæö==ç÷ç÷èøèø得法方程GC F = 121436 6.1369815.3C C æöæöæö=ç÷ç÷ç÷èøèøèø解方程得:120.61840.0711C C »»-2()0.61840.0711f x x x \=-误差222121(,) 2.730.6184(,)0.0711(,)0.04559j j j YC Y Y Y df f f ==-=-´+´=å8、已知一组数据ix1 2 3iy3 2 1.5试用拟合函数21()S x a bx =+拟合所给数据解:令2()f x a bx =+ 201()1,()x x x j j ==01()()()f x a x b x j j =+则123113111114,219213y A F y y æöæö÷ç÷çæöç÷ç÷ç÷ç÷===ç÷ç÷ç÷ç÷èøç÷ç÷ç÷ç÷èøèøT T a A A A F b æö\=ç÷èø,即331422514983a b æöç÷æöæö=ç÷ç÷ç÷ç÷èøèøç÷èø解方程组得0.3095,0.0408a b == 即210.30950.0408()x f x y=+=从而有21()0.30950.0408S x x =+补充题:用插值极小化法求()sin f x x =在[0, 1]上的二次插值多项式2()P x ,并估计误差 解:作变量替换1(1)2x t =+,将[0, 1]变换[-1, 1]取插值点11(21)cos 0,1,2222(1)K K x K n p+=+=+ 0120.933001270.50.0669873x x x ===利用这些点做插值商表i xi y一阶插商 二阶插商0.9330127 0.80341740.5 0.479425 0.74863250.0669873 0.0659372 0.9549092 -0.23818779则:20.9330127()0.80)0.2341740.743818779(0.9330127)(0.5)86325(x P x x x ---=+-同时误差213322()()()22(1)!3!24n n M M M R x f x P x n --+=-£==+其中(3)3max ()M f x = 由于1(1)2x t =+,即21t x =- 则(3)(3)3max (21)max sin (21)8max cos(21)8[0,1]M f x x x x =-=-=-=Î281()243R x \£=。
第七章 傅里叶变换习题解答

习题 七1.证明:如果f (t )满足傅里叶变换的条件,当f (t )为奇函数时,则有⎰+∞⋅=0d sin )()(ωωωt b t f其中()⎰+∞⋅=0tdt sin π2)(ωωt f b当f (t )为偶函数时,则有⎰+∞⋅=0cos )()(ωωtd w a t f其中⎰+∞⋅=2tdt c f(t))(ωωπos a证明:因为ωωωd G t f t i ⎰+∞∞-=e )(π21)(其中)(ωG 为f (t )的傅里叶变换 ⎰⎰+∞∞-+∞∞--⋅==dt t i t t f dt e t f G ti )sin (cos )()()(ωωωω⎰⎰+∞∞-+∞∞-⋅-⋅=tdt t f i t t f ωωsin )(cos )(当f (t )为奇函数时,t cos f(t)ω⋅为奇函数,从而⎰+∞∞-=⋅0tdt cos f(t)ωt sin f(t)ω⋅为偶函数,从而⎰⎰+∞∞-+∞⋅=⋅0.sin f(t)2tdt sin f(t)tdt ωω故.sin f(t)2)(0tdt i G ωω⋅-=⎰+∞有)()(ωωG G -=-为奇数。
ωωωωπωωπωd t i t G d e G t f t i )sin (cos )(21)(21)(+⋅=⋅=⎰⎰+∞∞-+∞∞-=1()sin d ()sin d 2ππi G i t G t ωωωωωω+∞+∞-∞⋅=⋅⎰⎰ 所以,当f(t)为奇函数时,有02()b()sin d .b()=()sin dt.πf t t f t t ωωωωω+∞+∞=⋅⋅⎰⎰其中 同理,当f(t)为偶函数时,有()()cos d f t a t ωωω+∞=⋅⎰.其中 02()()cos πa f t tdt ωω+∞=⋅⎰2.在上一题中,设()f t=21,0,1ttt⎧<⎪⎨≥⎪⎩.计算()aω的值.解:120011120012222()()cos d cos d0cos d πππ221cos d d sinππ122sin sin2dππ2sinπ2sinπa f t t t t t t t tt t t tt t t tωωωωωωωωωωωωωωω+∞+∞=⋅=⋅+⋅=⋅=⋅=⋅⋅-⋅=⋅=⎰⎰⎰⎰⎰⎰3.计算函数sin,6π()0,6πt tf tt⎧≤⎪=⎨≥⎪⎩的傅里叶变换.解:6π6π6π6π6π2()()()d sin d sin(cos sin)d2sin sin dsin6ππ(1)i t i tf f u f t e t t e tt t i t ti t t tiωωωωωωω+∞---∞--=⋅=⋅=⋅-=-⋅=-⎰⎰⎰⎰4.求下列函数的傅里叶变换||(1)()tf t e-=解:||(||)0(1)(1)2F()()()d d d2d d1i t t i t t i tt i t if f t e t e e t e te t e tωωωωωωω+∞+∞+∞----+-∞-∞-∞+∞--+-∞-∞==⋅==+=+⎰⎰⎰⎰⎰(2)2()t f t t e -=⋅解:因为2222214F[].()(2)2.t t t t e ee et t e ω-----==⋅-=-⋅而所以根据傅里叶变换的微分性质可得224()F()tG t e e ωω--=⋅=(3)2sin π()1tf t t =- 解:222202200sin π()F()()d 1sin π(cos sin )d 11[cos(π)cos(π)]sin πsin 2d 2d 11cos(π+)cos(π-)d d ()11sin ,||π20,|i tt G f e t t tt i t t tt t t t i t i t t tt t i t i t t t iωωωωωωωωωωωωω+∞--∞+∞-∞+∞+∞-∞+∞+∞==⋅-=⋅---+--⋅=-=---=----≤=⎰⎰⎰⎰⎰⎰利用留数定理当当|π.⎧⎪⎨⎪≥⎩ (4)41()1f t t =+ 解:4444401cos sin ()d d d 111cos cos 2d d 11i tt t G e t t i tt t t t t t tt t ωωωωωω+∞+∞+∞--∞-∞-∞+∞+∞-∞==-+++==++⎰⎰⎰⎰⎰41R(z)=1z +,则R(z)1)i i +-+.R()d 2π[R())]2π[R()1)]i t i z i z t e t i res z e i i res z e i ωωω+∞-∞⋅=⋅⋅++⋅⋅-+⎰故.|44cos ||||d Re[d ]sin )1122i tt e t t t t ωωωωω+∞+∞--∞-∞==+++⎰⎰(5) 4()1t f t t =+ 解:4444()d 1sin cos d d 11sin d 1i tt G e tt tt t t t i t t t t t i tt ωωωωω+∞--∞+∞+∞-∞-∞+∞-∞=⋅+⋅=⋅-++⋅=-+⎰⎰⎰⎰ 同(4).利用留数在积分中的应用,令4R()=1zz z+则44|sin d ()Im(d )11sin22i tt tt e i t i t t t ie ωωωω+∞+∞-∞-∞-⋅⋅-=-++=-⋅⋅⎰⎰.5.设函数F(t )是解析函数,而且在带形区域.|Im()|8t <内有界.定义 函数2()G ω为22222()F()d .i t G t e t ωω--=⋅⎰ 证明当10时.有21P V ()d F()2πi t G e t t ωω+∞-∞⋅⋅→⎰ 对所有实数t 成立. (书上有推理过程)6.求符号函数 1,0sgn 1,0||t t t t t -<⎧==⎨>⎩的傅里叶变换. 解:因为1F(())π().u t i δωω=+⋅把函数sgn()t 与u(t)作比较. 不难看出 sgn()()().t u t u t =--故.[]11F[sgn()]F(())F(())π()[π()]π()22π()()t u t u t i i i i δωδωωδωδωωω=--=+⋅-+⋅--=+--=7.已知函数()f t 的傅里叶变换()00F()=π()(),ωδωωδωω++-求()f t解:[]00000000001()F(F())=π()()d 2πF(cos )=cos d d 2π[()()]()cos i ti t i t i t i tf t e t t e te e e tf t tωωωωωωδωωδωωωωωδωωδωωω+∞-∞+∞--∞-+∞--∞=⋅++-⋅+=⋅=++-=⎰⎰⎰而所有8.设函数()f t 的傅里叶变换F()ω,a 为一常数.证明:1F[()]()=F ||1F[()]()()d ()d i ti t f at a a f at f at et f at e at a ωωωωω+∞+∞---∞-∞⎛⎫⋅ ⎪⎝⎭=⋅=⋅⎰⎰解:当a >0时,令u=at .则1F[()]()()d u i t a f at f u e u aω-+∞-∞=⋅⎰当a <0时,令u=at ,则1F[()]()F()f at aaωω=-.故原命题成立.9.设()[]();F F f ωω=证明()()[]()F f t ωω=--F .证明:()[]()()()()()[]()()[]()()[]()e d e d ed e d e d .i t i u i i u u i t F f t f uf t u t f u f uu u f t F t ωωωωωωω+∞+∞--∞-∞+∞+∞--⋅⋅---∞-∞+∞-⋅--∞=⋅=-⋅--=⋅=⋅=⋅=-⎰⎰⎰⎰⎰10.设()[]()F F f ωω=,证明:()[]()()()0001cos 2F f t F F t ωωωωωω⋅=-++⎡⎤⎣⎦以及()[]()()()0001sin .2F f t F F t ωωωωωω⋅=--+⎡⎤⎣⎦证明:()[]()()()()()0000000e +e cos 21e e 22212i t i ti t i t F f t F t f t F F f f t t F F ωωωωωωωωω--⎡⎤⋅=⋅⎢⎥⎣⎦⎧⎫⎡⎤⎡⎤=+⋅⋅⎨⎬⎢⎥⎢⎥⎣⎦⎣⎦⎩⎭=-++⎡⎤⎣⎦同理:()[]()()(){}()()0000000e e sin 21e e 212i t i t i t i t Ff t F f t t i F F f f t t i F F iωωωωωωωωω--⎡⎤-⋅=⋅⎢⎥⎣⎦=-⎡⎤⎡⎤⋅⋅⎣⎦⎣⎦=--+⎡⎤⎣⎦11.设()()π0,0sin ,0t 200e ,t t t f g t t t -⎧<⎧≤≤⎪==⎨⎨≥⎩⎪⎩,其他计算()*f g t .解:()())*(d f y g y t f g t y +∞-∞-=⎰当t y o -≥时,若0,t <则()0,f y =故()*f g t =0.若0,0,2t y t π<≤<≤则()()()00()d sin d *t ty f y g y e y t f g t y t y -=⋅--=⎰⎰若,0..222t t y t y t πππ>≤-≤⇒-≤≤则()()2sin d *ty t e y t f g y t π--⋅-=⎰故()()()20,01,0sin cos e *221e .1e 22t t t t t t f g t t πππ--<⎧⎪⎪<≤-+=⎨⎪⎪>+⎩12.设()u t 为单位阶跃函数,求下列函数的傅里叶变换.()()()0e sin 1at f t u t t ω-=⋅()()()()()()()00000000002002e sin e e sin e e e e e 211e d d d d e 2d 2at i t at i t i t i t ati ta i t a i t ttG F t u f t t t i i it ta i ωωωωωωωωωωωωωωωω+∞-∞+∞+∞+∞+--------+--++⎡⎤⎡⎤⎣∞⎣⎦⎦=====-=⋅⋅⋅⋅⋅-⋅⋅++⎰⎰⎰⎰⎰解:。
第七章习题解答

计算图示各系统的动能:(1)偏心圆盘的质量为,偏心距OC m e =,对质心的回转半径为C ρ,绕轴O 以角速度0ω转动(图a )。
(2)长为l ,质量为的匀质杆,其端部固结半径为,质量为的匀质圆盘。
杆绕轴O 以角速度m r m 0ω转动(图b )。
(3)滑块A 沿水平面以速度移动,重块B 沿滑块以相对速度下滑,已知滑块A 的质量为,重块B 的质量为(图c )。
1v 2v 1m 2m (4)汽车以速度沿平直道路行驶,已知汽车的总质量为0v M ,轮子的质量为m ,半径为R ,轮子可近似视为匀质圆盘(共有4个轮子)(图d )。
解:(1) 222200111()222C C C T mv J m e 2ωρω=+=+(2) 2222111(83)326O J ml mr ml m l r =++=+2220011(83)212O T J m l r 22ωω==+(3) 22121122A B T m v m v =+2221121212221212221211(2cos150)2211()m v m v v v v m m v m v m v v °=+++=++(4) ()2222000211111(4)422222v T M m v mv mR M m v R ⎛⎞=−+⋅+⋅⋅=+⎜⎟⎝⎠20一常力矩M 作用在绞车的鼓轮上,轮的半径为r ,质量为。
缠在鼓轮上绳索的末端A 系一质量为的重物,沿着与水平倾斜角为1m 2m α的斜面上升,如图所示。
重物与斜面间的滑动摩擦系数为μ。
绳索的质量不计,鼓轮可看成为匀质圆柱体,开始时系统静止。
求鼓轮转过ϕ角时的角速度。
解:为一自由度理想约束系统。
取鼓轮、重物及绳索组成的系统为研究对象,受力图如下图所示。
鼓轮转过ϕ角时系统的动能为2222212111222T m r m r 2ωω=⋅⋅+ 重力、摩擦力和力矩M 在此有限路程上所做的功为122sin W M Fr m gr ϕϕϕ→α=−−根据动能定理,有()222212211sincos 42m r m r M m gr ωωαμ+=−+αϕ⎡⎤⎣⎦ ω=绞车提升一质量为m 的重物,如图所示。
第七章习题答案解析

第七章 不完全竞争的市场1、根据图中线性需求曲线d 和相应的边际收益曲线MR ,试求:(1)A 点所对应的MR 值;(2)B 点所对应的MR 值。
解答:(1)根据需求的价格点弹性的几何意义,可得A 点的需求的价格弹性为:25)515(=-=d e 或者 2)23(2=-=d e 再根据公式)11(d e P MR -=,则A 点的MR 值为:MR=2×(2×1/2)=1 (2)与(1)类似,根据需求的价格点弹性的几何意义,可得B 点的需求的价格弹性为:21101015=-=d e 或者 21131=-=d e 再根据公式d e MR 11-=,则B 点的MR 值为:1)2111(1-=-⨯=MR 2、图7-19是某垄断厂商的长期成本曲线、需求曲线和收益曲线。
试在图中标出:(1)长期均衡点及相应的均衡价格和均衡产量;(2)长期均衡时代表最优生产规模的SAC 曲线和SMC 曲线;(3)长期均衡时的利润量。
解答:本题的作图结果下图所示:(1)长期均衡点为E 点,因为,在E 点有MR=LMC 。
由E 点出发,均衡价格为P 0,均衡数量为Q 0。
(2)长期均衡时代表最优生产规模的SAC 曲线和SMC 曲线如图所示。
在Q 0 的产量上,SAC 曲线和LAC 曲线相切;SMC 曲线和LMC 曲线相交,且同时与MR 曲线相交。
(3)长期均衡时的利润量有图中阴影部分的面积表示,即л=(AR(Q 0)-SAC(Q 0)Q 03、已知某垄断厂商的短期成本函数为30001461.023++-=Q Q Q STC ,反需求函数为P=150-3.25Q求:该垄断厂商的短期均衡产量与均衡价格。
解答:因为140123.02+-==Q Q dQ dSTC SMC且由225.3150)25.3150()(Q Q Q Q Q Q P TR -=-==得出MR=150-6.5Q根据利润最大化的原则MR=SMCQ Q Q 5.6150140123.02-=+-解得Q=20(负值舍去)以Q=20代人反需求函数,得P=150-3.25Q=85所以均衡产量为20 均衡价格为854、已知某垄断厂商的成本函数为236.02++=Q Q TC ,反需求函数为P=8-0.4Q 。
第7章习题详细解答

第7章习题解答7—1判断题(对的打√,不对的打×)1。
数字电路分为门电路和时序逻辑电路两大类。
(× )2。
边沿触发器和基本RS触发器相比,解决了空翻的问题.(×)3. 边沿触发器的状态变化发生在CP上升沿或下降沿到来时刻,其他时间触发器状态均不变。
(√)4. 基本RS 触发器的输入端就是直接置0端和直接置1端。
(√)23 的计数器。
(×)5。
3位二进制计数器可以构成模为16。
十进制计数器最高位输出的周期是输入CP脉冲周期的10倍。
(√)7. 构成一个7进制计数器需要7个触发器。
(×)8.当时序电路存在无效循环时该电路不能自启动.( √)9。
寄存器要存放n位二进制数码时,需要n2个触发器。
(×)10.同步计数器的计数速度比异步计数器快。
(√)11。
在计数器电路中,同步置零与异步置零的区别在于置零信号有效时,同步置零还需要等到时钟信号到达时才能将触发器置零,而异步置零不受时钟的控制。
(√)12。
计数器的异步清零端或异步置数端在计数器正常计数时应置为无效状态。
(√)13。
自启动功能是任何一个时序电路都具有的。
(× )14。
无论是用置零法还是用置数法来构成任意N进制计数器时,只要置零或置数控制端是异步的,则在状态循环过程中一定包含一个过渡状态;只要是同步的,则不需要过渡状态。
(√)15。
用置零法或置位法可以设计任意进制的计数器.(×)7—2 由或非门组成的基本RS触发器如图7—38所示,已知R、S的电压波形,试画出与之对应的Q和Q的波形。
图7—38 题7-2图解:由或非门组成的基本RS触发器的特性表,可得该题的输出端波形如下图所示:或非门RS 触发器特性表 题7—2 波形图7—3由与非门组成的基本RS 触发器如图7-39所示,已知R 、S 的电压波形,试画出与之对应的Q 和Q 的波形。
图7-39 题7-3图解:由与非门组成的基本RS 触发器的特性表,可得该题的输出端波形如下图所示:与非门RS 触发器特性表 题7—3波形图7-4已知如图7-40所示的各触发器的初始状态均为0,试对应画出在时钟信号CP 的连续作用下各触发器输出端Q 的波形。
(完整版)大学物理学(课后答案)第7章

第七章课后习题解答一、选择题7-1 处于平衡状态的一瓶氦气和一瓶氮气的分子数密度相同,分子的平均平动动能也相同,则它们[ ](A) 温度,压强均不相同 (B) 温度相同,但氦气压强大于氮气的压强 (C) 温度,压强都相同 (D) 温度相同,但氦气压强小于氮气的压强分析:理想气体分子的平均平动动能32k kT ε=,仅与温度有关,因此当氦气和氮气的平均平动动能相同时,温度也相同。
又由理想气体的压强公式p nkT =,当两者分子数密度相同时,它们压强也相同。
故选(C )。
7-2 理想气体处于平衡状态,设温度为T ,气体分子的自由度为i ,则每个气体分子所具有的[ ](A) 动能为2i kT (B) 动能为2iRT(C) 平均动能为2i kT (D) 平均平动动能为2iRT分析:由理想气体分子的的平均平动动能32k kT ε=和理想气体分子的的平均动能2ikT ε=,故选择(C )。
7-3 三个容器A 、B 、C 中装有同种理想气体,其分子数密度n 相同,而方均根速率之比为()()()1/21/21/222::2A B Cv v v =1:2:4,则其压强之比为A B C p :p :p[ ](A) 1:2:4 (B) 1:4:8 (C) 1:4:16 (D) 4:2:1=,又由物态方程p nkT =,所以当三容器中得分子数密度相同时,得123123::::1:4:16p p p T T T ==。
故选择(C )。
7-4 图7-4中两条曲线分别表示在相同温度下氧气和氢气分子的速率分布曲线。
如果()2p O v 和()2p H v 分别表示氧气和氢气的最概然速率,则[ ](A) 图中a 表示氧气分子的速率分布曲线且()()22p p O H /4v v =(B) 图中a 表示氧气分子的速率分布曲线且()()22p p O H /1/4v v =(C) 图中b 表示氧气分子的速率分布曲线且()()22p p O H /1/4v v =(D) 图中b 表示氧气分子的速率分布曲线且()()22p p O H /4v v =分析:在温度相同的情况下,由最概然速率公式p ν=质量22H O M M <,可知氢气的最概然速率大于氧气的最概然速率,故曲线a 对应于氧分子的速率分布曲线。
第7章习题解答

第七章习题解答一、填空1.一个操作系统的可扩展性,是指该系统能够跟上先进计算技术发展的能力。
2.在引入线程的操作系统中,线程是进程的一个实体,是进程中实施调度和处理机分派的基本单位。
3.一个线程除了有所属进程的基本优先级外,还有运行时的当前优先级。
4.在Windows 2000中,具有1~15优先级的线程称为可变型线程。
它的优先级随着时间配额的用完,会被强制降低。
5.Windows 2000在创建一个进程时,在内存里分配给它一定数量的页帧,用于存放运行时所需要的页面。
这些页面被称为是该进程的“工作集”。
6.Windows 2000采用的是请求调页法和集群法相结合的取页策略,把页面装入到内存的页帧里的。
7.分区是磁盘的基本组成部分,是一个能够被格式化和单独使用的逻辑单元。
8.MFT是一个数组,是一个以数组元素为记录构成的文件。
9.只要是存于NTFS卷上的文件,在MFT里都会有一个元素与之对应。
10.在Windows 2000的设备管理中,整个I/O处理过程都是通过I/O请求包(IRP)来驱动的。
二、选择1.在引入线程概念之后,一个进程至少要拥有D 个线程。
A. 4 B.3 C.2 D.12.在Windows 2000中,只有A 状态的线程才能成为被切换成运行状态,占用处理器执行。
A.备用B.就绪C.等待D.转换3.Windows 2000是采用C 来实现对线程的调度管理的。
A.线程调度器就绪队列表B.线程调度器就绪队列表、就绪位图C.线程调度器就绪队列表、就绪位图、空闲位图D.线程调度器就绪队列表、空闲位图4.在Windows 2000里,一个线程的优先级,会在A 时被系统降低。
A.时间配额用完B.请求I/O C.等待消息D.线程切换5.在单处理机系统,当要在进程工作集里替换一页时,Windows2000实施的是B 页面淘汰策略。
A. FIFO(先进先出)B.LRU(最近最久未用)C.LFU(最近最少用)D.OPT(最优)6.在页帧数据库里,处于下面所列A 状态下的页帧才可以变为有效状态。
高等数学第七章习题详细解答

第七章习题答案习题7.01.下列各种情形中,P 为E 的什么点?(1)如果存在点P 的某一邻域()U P ,使得()⊂c U P E (c E 为E 的余集); (2)如果对点P 的任意邻域()U P ,都有, ()(),C U P E U P E φφ≠≠; (3)如果对点P 的任意邻域()U P ,都有. 解 (1)P 为E 的外点;(2)P 为E 的边界点;(3)P 为E 的聚点。
2.判定下列平面点集的特征(说明是开集、闭集、区域、还是有界集、无界集等?)并分别求出它们的导集和边界.(1) (){},0≠x y y ;(2) (){}22,620≤+≤x y x y ; (3) (){}2,≤x y y x ;(4) ()(){}()(){}2222,11,24+-≥⋂+-≤x y x y x y x y .解 (1) 是开集,是半开半闭区域,是无界集,导集为2R ,边界集为(){},0=x y y ;(2)既不是开集也不是闭集,是半开半闭区域,是有界集,导集为(){}22,620≤+≤x y x y ,边界集为(){}2222,=6=20++,x y x y x y ;(3) 是闭集,是半开半闭区域,是无界集,导集为集合本身,边界集为(){}2,=x y y x ;是闭集,是闭区域,是有界集,导集为集合本身,边界集为()()(){}2222,11,24+-=+-=x y x y x y习题7.11. 设求1. 解 令,=-=yu x y v x,解得,11==--u uv x y v v,故()22,11⎛⎫⎛⎫=- ⎪ ⎪--⎝⎭⎝⎭u uv f u v v v ,即()()21+,1=-u v f u v v ,所以,()()21+y ,1=-x f x y y φ≠-}){()(P E P U 22,,y f x y x y x ⎛⎫-=- ⎪⎝⎭(,).f x y2.已知函数()22,cot =+-x f x y x y xy y,试求(),f tx ty .2. 解 因为()22,cot =+-y f x y x y xy x,所以,()2222,cot ,=+-t y f tx ty tx ty txty t x即()()222,cot =+-y f tx ty t x y t xy x.3.求下列各函数的定义域 (1) 25)1(=-+z ln y xy ;(2) =z ;(3) =z(4) )0;=>>u R r(5) =u3. 解 (1)(){}2,510-+>x y yxy ;(2)(){},0->x y x y ;(3)(){}2,≥x y x y ;(4)(){}22222,<++≤x y r x y z R ;(5)(){}222,≤+x y z x y4. 求下列各极限:(1) ()()233,0,31lim →-+x y x yx y ;(2)()(,1,1ln lim→+x x y y e(3)()(,0,0lim→x y(4)()(,0,0lim→x y ;(5)()()(),0,2sin lim→x y xy x ;(6)()()()()222222,0,01cos lim→-++x y x y x y xy e.4. 解 (1)()()2333,0,31101lim 0327→--==++x y x y x y ;(2)()(()1,1,1ln ln 11lim2→+++===x x y y e e e (3)()()()(,0,0,0,0limlim→→=x y x y ()(,0,01lim4→==x y (4)()(()()),0,0,0,01limlim→→=x y x y xy xy()()),0,0=lim1=2→+x y(5)()()()()()(),0,2,0,2sin sin limlim 122→→=⋅=⋅=x y x y xy xy y x xy(6)()()()()()()()()()222222222222222,0,0,0,01cos 1cos limlim→→-+-++=⋅++x y x y x y x y x y x y xy xy eex y()()()()()()()2222222022,0,0,0,01cos 10limlim=02→→-++=⋅⋅=+x y x y x y x y xy e exy5.证明下列极限不存在: (1)()(),0,0lim→-+x y x yx y ;(2)()(),0,0lim→+-x y xyxy x y .5. (1) 解 令=y kx ,有()(),0,001limlim 1→→---==+++x y x x y x kx kx y x kx k ,k 取不同值,极限不同,故()(),0,0lim→-+x y x yx y 不存在.(2) 解令=x y()()22,0,00lim lim 1→→==+-x y x xy x xy x yx ;令2=x y()()()()22,0,02,0,0022lim lim lim 0221→→→===+-++x y y y y xy y y xy x y y y y ;01≠,故()(),0,0lim→+-x y xyxy x y不存在.6.函数=y z a 为常数)在何处间断?6. 解 因为=y z 是二元初等函数,且函数只在点集(){,x y y 上无定义,故函数在点集(){,x y y 上间断.7.用 εδ- 语言证明()(,0,0lim0→=x y .7. 证明 对0∀>ε,要使220-=≤=<ε2<ε,取=2δε<δ0-<ε,所以()(,0,0lim 0→=x y习题7.21. 设()(),sin 1arctan ,π==+-xy xz f x y e y x y 试求()1,1x f 及()1,1y f1. 解()221,sin arctan 1=+++xy x x yf x y ye y xx yyπ22=sin arctan+++xy x xy ye y y x y π.()()222,sin cos 11-=++-+xy xyy x y f x y xe y e y x x yπππ 222sin cos -=+++xyxyx x xe y e y x y πππ()()1,1,1,1∴=-=-x y f e f e2.设(),ln 2⎛⎫=+ ⎪⎝⎭y f x y x x ,求()1,0'x f ,()1,0'y f .2. 解()()222122,22--==++x yx y x f x y y x x y x x()2112,22==++y x f x y yx y x x()()11,011,02∴==,x y f f . 3.求下列函数的偏导数(1) 332=++z x y xy ,(2) ()1=+xz xy , (3) ()222ln =+z y x y ,(4) ln tan=y z x, (5) ()222ln =+z x x y ;(6)=z (7) ()sec =z xy ;(8) ()1=+yz xy ;(9) ()arctan =-zy x y ;(10) .⎛⎫=⎪⎝⎭zx u y 3. 解 (1)2232,32z z x y y x x y ∂∂=+=+∂∂(2)因为 ()ln 1,x xy z e+=所以()()()()ln 1ln 11ln 111x x xy z xy xy e xy xy xy x xy xy +⎛⎫⎛⎫∂=++=+++ ⎪ ⎪∂++⎝⎭⎝⎭()()22ln 1111x x xy z x x e xy y xy xy +⎛⎫⎛⎫∂==+ ⎪ ⎪∂++⎝⎭⎝⎭(3)()2322222222,2ln z xy z y y x y x x y y x y ∂∂==++∂+∂+(4)222222sec sec 111sec ,sec tan tan tantan y yy z y y z y x x y y y y x x x y x x x x x x x x∂∂⎛⎫⎛⎫=-=-== ⎪ ⎪∂∂⎝⎭⎝⎭ (5)()32222222222ln ,z x z x y x x y x x y y x y ∂∂=++=∂+∂+(6)z z x y ∂∂====∂∂(7)()()()()sec tan ,sec tan z z y xy xy x xy xy x y ∂∂==∂∂(8)()()22ln 1111y y xy z y y e xy x xy xy +⎛⎫⎛⎫∂==+ ⎪ ⎪∂++⎝⎭⎝⎭()()()()ln 1ln 11ln 111y y xy z xy xy e xy xy xy y xy xy +⎛⎫⎛⎫∂=++=+++ ⎪ ⎪∂++⎝⎭⎝⎭ (9)()()()()()()()11222ln ,,111z z zz z z z x y z x y x y x y u u u x y z x y x y x y ------∂∂∂==-=∂∂∂+-+-+-(10)因为 ln,x z yu e=所以ln ln ln 21,,ln zzx x x z z z y y y u z x z u z x x z u x e e e x x xy y x y y y y z y y y⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫∂∂∂=⋅==⋅-=-= ⎪ ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭4.设ln=z ,求证: 12∂∂+=∂∂z z xy x y . 4.证明 因为ln,z =所以z zx y∂∂====∂∂从而有12 z zx yx y∂∂+=+=+=∂∂5.求下列函数的二阶偏函数:(1)已知33sin sin=+z x y y x,求2∂∂∂zx y;(2)已知ln=xz y,求2∂∂∂zx y;(3)已知(ln=z x,求22∂∂z x和2∂∂∂z x y;(4)arctan=yzx求22222,,∂∂∂∂∂∂∂z z zx y x y和2∂∂∂zy x.5. 解(1)3323sin sin,3sin coszz x y y x x y y xx∂=+∴=+∂从而有223cos3coszx y y xx y∂=+∂∂(2)ln ln1,lnx xzz y y yx x∂⎛⎫=∴= ⎪∂⎝⎭从而有()()()ln1ln1ln11ln ln ln ln1xx xz yxy y y x yx y x y x--⎛⎫∂=+⋅=+⎪∂∂⎝⎭(3)(()1222 ln,zz x x yx-∂=∴===+∂从而有()()3322222222122zx y x x x yx--∂=-+=-+∂()()332222222122z x y y y x y x y --∂=-+=-+∂∂ (4)22221arctan,1y z y y z x xx x y y x ∂⎛⎫=∴=⋅-=- ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭ 222111z x yx x y y x ∂⎛⎫=⋅= ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭从而有()()()()2222222222222222222,x y y z xy z y x x x y x y x y x y -++∂∂-===∂∂∂+++ ()()2222222222222222,z xy z x y xy x y y y x x y x y x y ⎛⎫∂-∂+--=== ⎪∂∂∂+⎝⎭++ 6. 设()ln =z y xy ,求2∂∂∂z x y 及22∂∂zy .6. 解 因为()ln ,z y xy =所以()(),ln ln 1z y y z x y xy y xy x xy x y xy∂∂===+=+∂∂从而有22211,.z z x y x y y∂∂==∂∂∂ 习题7.31. 求下列函数的全微分.(1) 2222+=-s t u s t ;(2) ()2222+=+x y xyz x y e;(3) ()arcsin0=>xz y y;(4) ⎛⎫-+ ⎪⎝⎭=y x x y z e ;1.解 (1)()()222232322222222()()22222∂--+⋅---==∂--u s s t s t s s st s t s s s t s t()()222223232222222()()22222u t s t s t t ts t ts s t s t s t ∂--+---==∂-- ()()2322222244u u st t dz ds dt ds dt s t s t s t ∂∂-∴=+=-∂∂--(2)()()()222222222222++++∂=++⋅∂x y x y xyxyx y x y yzxe x y exxy()2222222244222222+++⎛⎫--=++⋅=+ ⎪⎝⎭x y x y x y xyxyxyx y x y xe x y e x e x y x y()()()22222222222-2+++∂=++⋅∂x y x y xy xyy x x y xzye x y eyxy()()2222222222442222+++-+⎛⎫-=+⋅=+ ⎪⎝⎭x y x y x y xyxyxyy x x y y x yeey e xy xy2244442222x y xyz z x y y x dz dx dy x edx y dy x y x y xy +⎛⎫⎛⎫∂∂--∴=+=+++ ⎪ ⎪∂∂⎝⎭⎝⎭ (3)2222211∂=⋅==∂--⎛⎫yzxyyy x y x x22⎛⎫⎛⎫∂=-=-= ⎪ ⎪∂⎝⎭⎝⎭z x x yy y z zdz dx dy x y∂∂∴=+=∂∂(4)22221y x y x x y x y z y y x e e x x y x y ⎛⎫⎛⎫-+-+ ⎪ ⎪⎝⎭⎝⎭⎛⎫∂-=-= ⎪∂⎝⎭ 22221y x y x x y x y z x x y e e y x y xy ⎛⎫⎛⎫-+-+ ⎪ ⎪⎝⎭⎝⎭⎛⎫∂-=-+= ⎪∂⎝⎭222222y x y x x y x y z z z y x x y dz dx dy e dx e dy x y y x y xy⎛⎫⎛⎫-+-+ ⎪ ⎪⎝⎭⎝⎭∂∂∂--∴=+==+∂∂∂ 2. 求函数2arctan1=+xz y 在1,1==x y 处的全微分.2.解()()()()()()()22222222222222222211111111111++∂++=⋅=⋅=∂++++++++y y z y y x xy y x y y xy()()()()()()22222222222222211222111111+∂-⋅--=⋅=⋅=∂++++++++y z x y xy xyx yy y x y y xy()()21,11125111z x ∂+∴==∂++ , ()()21,12125111∂-⋅==-∂++z y ()1,12255dz dx dy ∴=- 3. 求函数22=-xyz x y 当2,1,0.02,0.01==∆=∆=x y x y 时的全微分和全增量,并求两者之差.3.解 ()()()(),, 2.02,1.011,1z z x x y y z x y z z ∆=+∆+∆-=-()()22222.02 1.0121 2.0420.6670.667021 4.08 1.0232.02 1.01⨯⨯=-=-=-=--- ()()()2223222222222--⋅∂--===-∂---y x y xy x z x y y y x x y x y x y ()()()()22322222222--⋅-∂+==∂--x x y xy y z x xy y x y x y ()2,111413z x ∂∴=-=-∂- ,()()22,182110941z y ∂+⨯==∂- ()2,11100.020.010.070.0110.00439dz ∴=-⨯+⨯=-+=00.0040.004z dz ∴∆-=-=-.*4讨论函数()()()()(),0,0,0,,0,0⎧≠⎪=⎨⎪=⎩xy x y f x y x y 在()0,0点的连续性、可导性、可微性以及其偏导函数在()0,0的连续性.4.解()()()()()(),0,0,0,0lim,lim 00,0x y x y f x y xy f →→===(),f x y ∴在()0,0点连续 又()()()00,00,0000,0limlim 0x x x f x f f x x∆→∆→∆--===∆∆ ()()()000,0,0000,0limlim 0y y y f y f f y y∆→∆→∆--===∆∆ ()()0,00,0,00x y f f ∴==.()(()(,0,0,0,0,0,00limlim limx y x y f x yf z dzρρ→∆∆→∆∆→∆∆--∆-==()()()0,0,0x y<∆∆→∆lim0z dzρρ→∆-∴=故函数(),f x y 在()0,0点可微. 由()(),0,0x y ≠时(),=-x f x yy xy()23222sinx yy xy=-+(),=-y f x y x xy ()23222xy x xy=-+()(),0,0lim 0x y y →= ,()()()()23,0,0222lim→=+x y x yy kx xy()()()33323222=lim11→==+⋅+x kx ky kx k xk ,k 不同值不同()()()23,0,0222lim→∴+x y xy xy 不存在,故()()(),0,0lim ,xx y f x y →不存在.(),x f x y ∴在()0,0点不连续,同理可证(),y f x y 在点()0,0不连续.*5.计算()2.050.99的近似值.5.解 令00,1,2,0.01,0.05yz x x y x y ===∆=∆= 则1,ln y y z z yx x x x y-∂∂==∂∂ ()()1,21,22,0z zx y ∂∂∴==∂∂ ()()()2.0521,21,20.991120.0100.0510.02 1.02∂∂∴≈+∆+∆=+⨯+⨯=+=∂∂z zx y x y*6.设有厚度为,内高为,内半径为的无盖圆柱形容器,求容器外壳体积的近似值(设容器的壁和底的厚度相同).6.解 设容器底面积半径为r ,高为h则容器体积2V r h π=22,V Vrh r r hππ∂∂==∂∂ 22∴=+dV rhdr r dh ππ002,10,0.1,0.1r cm h cm r cm h cm ==∆=∆=()()22,102,1020.10.1400.140.1 4.4∴∆≈=⋅+⋅=⨯+⨯=V dV rh r πππππ*7. 测得直角三角形两直角边的长分别为7±0.1cm 和24±0.1cm ,试求利用上述二值来计算斜边长度时的绝对误差和相对误差.0.1cm 10cm 2cm7.解 设直角三角形的直角边长分别为,x y ,则斜边z =,zz xy∂∂==∂∂由题意007,24,0.1,0.1x y x y δδ====z ∴的绝对误差为()()7,247,247240.10.10.242525∂∂=+=⨯+⨯=∂∂z x y z z x y δδδz 的相对误差()7,240.240.009625=≈zz δ 习题7.41.设,,,求. 1.解 ()3222sin 22cos 23cos 6---∂∂=⋅+⋅=⋅-⋅=-∂∂x y x y t t du z dx z dy e t e t e t t dt x dt y dt2.设,而,,求. 2.解2123∂∂=⋅+⋅=+∂∂dz z dy z dV x dx u dx V dx2341-=x3.设,,,求,. 3.解 ()()222cos 2sin ∂∂∂∂∂=⋅+⋅=-+-∂∂∂∂∂z z u z v uv v y u uv y x u x v x()()2222222cos sin sin cos cos 2cos sin sin x y y x y y x y x y y y =-+-()23sin cos cos sin x y y y y =-()()()222sin 2cos z z u z v uv v x y u uv x y y u y v y∂∂∂∂∂=+=--+-∂∂∂∂∂ ()()()2222222cos sin sin sin cos 2cos sin cos x y y x y x y x y x y y x y =--+-()()3333cos sin 2cos sin sin cos x y y x y y y y =+-+2e x y u -=sin x t =3y t =d d u tarccos()z u v =-34u x =3v x =d d zx22z u v uv =-cos u x y =sin v x y =zx ∂∂z y∂∂4.设,而,,求,. 4.解 222ln 3∂∂∂∂∂⎛⎫=⋅+⋅=⋅+- ⎪∂∂∂∂∂⎝⎭z z u z v u y u v x u x v x v x()()()2322632ln 326ln 3x y y y y x y x y x x x x +⎛⎫=+-=+-- ⎪⎝⎭5.设求5.解 ()()1wf x xy xyz y yz x ∂'=++++∂()()()()1wf x xy xyz x xz x z f x xy xyz y∂''=+++=+++∂ ()()wf x xy xyz xy xyf x xy xyz z ∂''=++=++∂6.求下列函数的一阶偏导数(其中具有一阶连续偏导数):(1);(2);(3);(4).6.解 (1)()()222222∂''=-⋅=-∂z f x y x xf x y x()()()222222∂''=-⋅-=--∂zf x y y yf x y y(2)121110∂'''=+⋅=∂u f f f x y y12122211u x x f f f f y y z y z ⎛⎫∂⎛⎫''''=-+=-+ ⎪ ⎪∂⎝⎭⎝⎭122220∂⎛⎫'''=⋅+-=- ⎪∂⎝⎭u y y f f f z z z (3)1231231∂''''''=⋅+⋅+⋅=++∂uf f y f yz f yf yzf x123230∂'''''=⋅+⋅+⋅=+∂uf f x f xz xf xzf y2ln z u v =32u x y =+y v x =zx ∂∂z y∂∂(),w f x xy xyz =++,,.w w wx y z∂∂∂∂∂∂f 22()z f x y =-,x y u f y z ⎛⎫= ⎪⎝⎭(,,)u f x xy xyz =22(,e ,ln )xy u f x y x =-123300∂''''=⋅+⋅+⋅=∂uf f f xy xyf z (4)1231231122∂''''''=⋅+⋅⋅+⋅=++∂xy xyu f x f e y f xf ye f f x x x()12312202∂'''''=⋅-+⋅+⋅=-+∂xy xy uf y f e x f yf xe f y7.求下列函数的二阶偏导数,,(其中具有二阶连续偏导数):(1),(2). 7.解(1)22121222∂''''=⋅+⋅=+∂zf xy f y xyf y f x22121222∂''''=⋅+⋅=+∂zf x f xy x f xyf y()()222211112212222222∂'''''''''∴=+⋅+⋅+⋅+⋅∂zyf xy f xy f y y f xy f y x233341111221222422yf x y f xy f xy f y f '''''''''=++++ 23341111222244yf x y f xy f y f '''''''=+++()()2222111122212222222∂''''''''''=+⋅+⋅++⋅+⋅∂∂zxf xy f x f xy yf y f x f xy x y322223111122212222422xf x yf x y f yf x y f xy f ''''''''''=+++++ 32231111222222522xf x yf x y f yf xy f ''''''''=++++()2222211122212222222∂'''''''''=+++⋅+⋅∂zx f x x f xy xf xy f x f xy y43221112222424x f x yf xf x y f '''''''=+++(2)()()222222∂''=+⋅=+∂zf x y x xf x y x()()222222∂''=+⋅=+∂zf x y y yf x y y22zx∂∂2z x y ∂∂∂22z y ∂∂f 22(,)z f x y xy =22()z f x y =+()()()()2222222222222224∂''''''∴=+++⋅=+++∂zf x y xf x y x f x y x f x y x()()22222224∂'''=+⋅=+∂∂z xf x y y xyf x y x y()()()()2222222222222224∂''''''=+++⋅=+++∂zf x y yf x y y f x y y f x y y8.设其中F 是可微函数,证明8.解()()()cos sin sin cos cos cos sin sin ux F y x x x xF y x x∂''=+--=--∂ ()sin sin cos uF y x y y∂'=-∂ ()()cos cos cos cos sin sin cos cos sin sin cos u uy x x xF y x y yF y x x x y∂∂''∴+=--+-⎡⎤⎣⎦∂∂ ()()cos cos cos cos sin sin cos cos sin sin cos cos x y x yF y x x yF y x x y ''=--+-=.习题7.51.设,φ⎛⎫= ⎪⎝⎭x y z z 其中为可微函数,求∂∂+∂∂z z x y x y . 1.解 z是,x y函数由方程xx z y φ⎛⎫= ⎪⎝⎭确定。
第七章 刚体力学习题及解答

第七章刚体力学习题及解答7。
1.1 设地球绕日作圆周运动.求地球自转和公转的角速度为多少rad/s?估算地球赤道上一点因地球自转具有的线速度和向心加速度。
估算地心因公转而具有的线速度和向心加速度(自己搜集所需数据)。
解:7.1.2 汽车发动机的转速在12s内由1200rev/min增加到3000rev/min。
(1)假设转动是匀加速转动,求角加速度.(2)在此时间内,发动机转了多少转?解:( 1)( 2)所以转数 =7.1.3 某发动机飞轮在时间间隔t内的角位移为球 t时刻的角速度和角加速度.解:7.1.4 半径为0。
1m的圆盘在铅直平面内转动,在圆盘平面内建立坐标系,原点在轴上。
x和y轴沿水平和铅直向上的方向.边缘上一点A当t=0时恰好在x轴上,该点的角坐标满足求(1)t=0时,(2)自t=0开始转时,(3)转过时,A点的速度和加速度在x和y轴上的投影。
解:( 1)( 2) 时,由( 3)当时,由7。
1。
5 钢制炉门由两个各长1.5m的平行臂AB和CD支承,以角速度逆时针转动,求臂与铅直时门中心G的速度和加速度.解:因炉门在铅直面内作平动,门中心 G的速度、加速度与B或D点相同.所以:7。
1.6 收割机拔禾轮上面通常装4到6个压板。
拔禾轮一边旋转,一边随收割机前进。
压板转到下方才发挥作用,一方面把农作物压向切割器,另一方面把切割下来的作物铺放在收割台上,因此要求压板运动到下方时相对于作物的速度与收割机前进方向相反.已知收割机前进速率为 1。
2m/s,拔禾轮直径1.5m,转速22rev/min,求压板运动到最低点挤压作物的速度.解:取地面为基本参考系,收割机为运动参考系。
取收割机前进的方向为坐标系正方向7。
1.7 飞机沿水平方向飞行,螺旋桨尖端所在半径为150cm,发动机转速2000rev/min。
(1)桨尖相对于飞机的线速率等于多少?(2)若飞机以250km/h的速率飞行,计算桨尖相对于地面速度的大小,并定性说明桨尖的轨迹。
第七章 练习题参考答案

V1 V3 V6
7. 对下图所示的有向图
(1) 画出它的邻接表 (2) 根据邻接表写出其拓扑排序序列
解:(1)邻接表为
0
2
5∧
2
3
4∧
2 3∧
4∧
1
2
3
6∧
1
4∧
(2)由邻接表可得拓朴排序序列:
1 5 2 3 64
8.已知n个顶点的有向图用邻接矩阵表示,编 写函数,计算每对顶点之间的最短路径。
4 18 ∧
2
1 12
32
5 22 ∧
3
1 16
22
44∧
4
1 18
34
5 10 ∧
5
2 22
4 10 ∧
解:(1) V1
12 V2
16 2
18
4 V3 22
V4
10 V5
(2)深度优先遍历的结点序列:v1,v2,v3,v4,v5
广度优先搜索的结点序列:v1,v2,v3,v4,v5
(3)最小生成树
CD CA CAB
CD CA CAB
CD CA CABΒιβλιοθήκη CD3DB
DB
DB DBC
DBCA DB DBC
DBCA DB DBC
10.对于如图所示的AOE网,求出各活动可能 的最早开始时间和允许的最晚开始时间, 哪些是关键活动?
a1=4
v2
v1
a3=2
a2=3
v3
a5=6 v4
a4=4
解:
顶点 Ve Vl V1 0 0 V2 4 4 V3 6 6 v4 10 10
if(length[i][k]+length[k][j]<length[i][j]) { length[i][j]=length[i][k]+length[k][j];
(完整版)大学物理学(课后答案)第7章

第七章课后习题解答一、选择题7-1处于平衡状态的一瓶氦气和一瓶氮气的分子数密度相同,分子的平均平动动能也相同,则它们[ ](A) 温度,压强均不相同 (B) 温度相同,但氦气压强大于氮气的压强(C) 温度,压强都相同 (D) 温度相同,但氦气压强小于氮气的压强分析:理想气体分子的平均平动动能,仅与温度有关,因此当氦气和32k kTε=氮气的平均平动动能相同时,温度也相同。
又由理想气体的压强公式,p nkT =当两者分子数密度相同时,它们压强也相同。
故选(C )。
7-2 理想气体处于平衡状态,设温度为T ,气体分子的自由度为i ,则每个气体分子所具有的[ ](A) 动能为(B) 动能为2ikT 2iRT(C) 平均动能为(D) 平均平动动能为2ikT 2iRT分析:由理想气体分子的的平均平动动能和理想气体分子的的平均动32k kT ε=能,故选择(C )。
2ikT ε=7-3 三个容器A 、B 、C 中装有同种理想气体,其分子数密度n 相同,而方均根速率之比为,则其压强之比为 [ ]()()()1/21/21/222::2A B Cvv v =1:2:4A B C p :p :p (A)(B)(C)(D) 1:2:41:4:81:4:164:2:1,又由物态方程,所以当三=p nkT =容器中得分子数密度相同时,得。
故选择(C )。
123123::::1:4:16p p p T T T ==7-4 图7-4中两条曲线分别表示在相同温度下氧气和氢气分子的速率分布曲线。
如果和分别表示氧气和氢气的最概然速率,则[ ]()2p O v ()2p H vh(A) 图中a 表示氧气分子的速率分布曲线且()()22p p O H /4v v =(B) 图中a 表示氧气分子的速率分布曲线且()()22p p O H /1/4v v =(C) 图中b 表示氧气分子的速率分布曲线且()()22p p O H /1/4v v =(D) 图中b 表示氧气分子的速率分布曲线且()()22p p O H /4v v =分析:在温度相同的情况下,由最概然速率公式p ν=尔质量,可知氢气的最概然速率大于氧气的最概然速率,故曲线对22H O M M <a 应于氧分子的速率分布曲线。
习题解答第7章
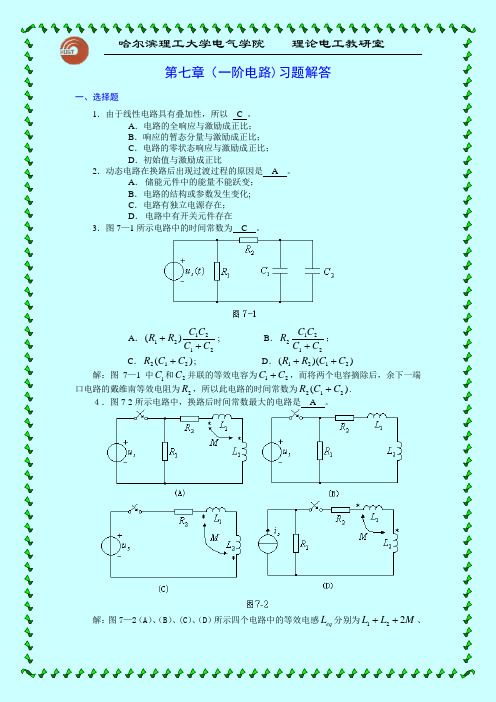
A. ; B. ;
C. ; D.
解:由求解一阶电路的三要素法 可知在原电路中 V, V。当初始状态不变而输入增加一倍时,有
V
二、填空题
1.换路前电路已处于稳态,已知 , , , . 时,开关由 掷向 ,则图7—3所示电路在换路后瞬间的电容电压 V, V。
作用时的响应为
作用时的响应为
总的零状态响应为
8.图7—14所示电路中,激励为单位冲激函数 A,求零状态响应 。
解:设激励为 ,用三要素法求电路的单位阶跃响应。
,
,
电流的单位阶跃响应为
根据单位冲激响应和单位阶跃响应的关系,可得电路中的 :
9.图7—15所示电路中, , ,求 时的响应 。
解:应用叠加原理求解此题.
第七章(一阶电路)习题解答
一、选择题
1.由于线性电路具有叠加性,所以C。
A.电路的全响应与激励成正比;
B.响应的暂态分量与激励成正比;
C.电路的零状态响应与激励成正比;
D.初始值与激励成正比
2.动态电路在换路后出现过渡过程的原因是A。
A.储能元件中的能量不能跃变;
B.电路的结构或参数发生变化;
C.电路有独立电源存在;
解: 由 时刻电路得:
,
换路后,电容 , 构成纯电容的回路(两电容并联),电容电压发生强迫跃变,此时应由电荷守恒原理求解换路后瞬刻的电容电压。由 得:
……①
…… ②
由以上两式解得
2.图7—4所示电路的时间常数 .
解:将储能元件开路,独立电源置 后,可得求戴维南等效电阻的电路如图7—4(a)所示。由于电路中含有受控源,因此需用外加电压法求戴维南等效电阻 .由图7—4(a)得
第七章恒定磁场-习题解答

7-3 如图所示,一无限长载流绝缘直导线弯成如附图所示的
形状。求使o点的磁感应强度为零的半径a和b的比值。
解 该载流系统由三部分组成,o点的磁感
应强度为载有相同电流的无限长直导线
及两个半径分别为a和b的圆环分别在该
处激发的磁感应强度的矢量和。设磁场 方向以垂直纸面向内为正,向外为负。
方向垂直纸面向里。 (2)由磁矩定义
方向垂直纸面向里。
第七章、稳恒磁场
7-20 质谱仪的构造原理如图所示。离子源S提供质量为M、
电荷为q的离子。离子初速很小,可以看作是静止的,然后经
过电压U的加速,进入磁感应强度为B的均匀磁场,沿着半圆
周运动,最后到达记录底片P上。测得离子在P上的位置到入
口处A的距离为x。试证明该离子的质量为:M ? qB 2 x 2 。
或由磁感应线是闭合曲线,也可推知
??
Φaefd
?
? Φabcd
?
0.24Wb
? Φ ? ?B?dS ? 0
第七章、稳恒磁场
7-9 一个非均匀磁场磁感应强度的变化规律为B=ky(k为常 量),方向垂直纸面向外。磁场中有一边长为a的正方形线 框,其位置如图所示。求通过线框的磁通量。
解 在线框内坐标为y处取一长为a宽为 dy的矩形面积元dS,在dS中磁场可认 为是均匀的,则通过dS的磁通量
? I2l
? 0 I1
2πx1
I2l
? ?7.2?
F2 10?4
? B2I2l N
?
? 0 I1
2πx2
I2l
负号表示合力方向水平向左。
第七章、稳恒磁场
习题7-16 一长直导线通有电流I =20A,另一导线ab通 有电流I?=10A,两者互相垂直且共面,如图所示。求导 线ab所受的作用力和对o点的力矩。
第七章 习题及答案

第七章 相关与回归分析一、单项选题题1、当自变量X 减少时,因变量Y 随之增加,则X 和Y 之间存在着( ) A 、线性相关关系 B 、非线性相关关系 C 、正相关关系 D 、负相关关系2、下列属于函数关系的有( )A 、身高与体重之间B 、广告费用支出与商品销售额之间C 、圆面积与半径之间D 、施肥量与粮食产量之间 3、下列相关程度最高的是( )A 、r=0.89B 、r=-0.93C 、r=0.928D 、r=0.8 4、两变量x 与y 的相关系数为0.8,则其回归直线的判定系数为( ) A 、0.80 B 、0.90 C 、0.64 D 、0.50 5、在线性回归模型中,随机误差项被假定服从( )A 、二项分布B 、t 分布C 、指数分布D 、正态分布6、物价上涨,销售量下降,则物价与销售量之间的相关属于( ) A 、无相关 B 、负相关 C 、正相关 D 、无法判断7、相关分析中所涉及的两个变量( )A 、必须确定哪个是自变量、哪个是因变量B 、都不能为随机变量C 、都可以是随机变量D 、不是对等关系 8、单位产品成本y (元)对产量x (千件)的回归方程为:t t x y 2.0100-=∧,其中“—0.2”的含义是( )A 、产量每增加1件,单位成本下降0.2元B 、产量每增加1件,单位成本下降20%C 、产量每增加1000件,单位成本下降20%D 、产量每增加1000件,单位成本平均下降0.2元E 、产量每增加1000件,单位成本平均下降20% 二、多项选择题1、下列说法正确的有( )A 、相关分析和回归分析是研究现象之间相关关系的两种基本方法B 、相关分析不能指出变量间相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化情况 C、回归分析可以不必确定变量中哪个是自变量,哪个是因变量 D、相关分析必须事先研究确定具有相关关系的变量中哪个为自变量,哪个为因变量 E、相关分析中所涉及的变量可以都是随机变量,而回归分析中因变量是随机的,自变量是非随机的2、判定现象之间有无相关关系的方法有()A、计算回归系数B、编制相关表C、绘制相关图D、计算相关系数E、计算中位数3、相关关系按相关的形式可分为()A、正相关B、负相关C、线性相关D、非线性相关E、复相关4、在直线回归方程∧yt=∧β1+∧β2Xt中,回归系数∧β2的数值()A、表明两变量之间的平衡关系B、其正、负号表明两变量之间的相关方向C、表明两变量之间的密切程度D、表明两变量之间的变动比例E、在数学上称为斜率5、下列那些项目属于现象完全相关()A、r=0B、r= —1C、r= +1D、y的数量变化完全由X的数量变化所确定E、r=0.986、在回归分析中,要求所涉及的两个变量x和y()A、必须确定哪个是自变量、哪个是因变量B、不是对等关系C、是对等关系D、一般来说因变量是随机的,自变量是非随机变量E、y对x的回归方程与x对y的回归方程是一回事7、下列有相关关系的是()A、居民家庭的收入与支出B、广告费用与商品销售额C、产量与单位产品成本D、学生学习的时间与学习成绩E、学生的身高与学习成绩8、可决系数2r=86.49%时,意味着()A 、自变量与因变量之间的相关关系密切B 、因变量的总变差中,有80%可通过回归直线来解释 C 、因变量的总变差中,有20%可由回归直线来解释 D 、相关系数绝对值一定是0.93 E 、相关系数绝对值一定是0.8649 三、填空题1、相关系数r 的取值范围为 。
第七章习题解答

习 题 七1. 判断下面所定义的变换,哪些是线性的,哪些不是:(1) 在向量空间V 中,σ (ξ)=ξ+α,α是V 中一固定的向量;(2) 在向量空间R 3中,σ (x 1, x 2, x 3)=),,(233221x x x x +;(3) 在向量空间R 3中,σ (x 1, x 2, x 3)=),,2(13221x x x x x +-; (4) 把复数域看作复数域上的向量空间,σ (ξ)=ξ. 解 (1)当0=α时,σ是线性变换;当0≠α时,σ不是线性变换; (2)σ不是线性变换; (3)σ是线性变换; (4)σ不是线性变换;2. 设V 是数域F 上一维向量空间. 证明,σ是V 的一个线性变换的充要条件是:存在F 中的一个数a ,使得对任意ξ∈V ,都有σ (ξ)=a ξ .证明:充分性显然.必要性:令σ是ν的一个线性变换,设1ξ是ν的一个基.则νξσ∈)(1.那么)(1ξσ可由1ξ线性表示,不妨设11)(ξξσa =.对任意的νξ∈,有1ξξk =,则ξξξξσξσξσa k a a k k k =====)()()()()(1111.3. 设σ是向量空间V 的线性变换,如果σ k -1ξ≠0, 但σ k ξ=0,求证ξ, σξ, …, σk -1ξ (k >0)线性无关.证明: 令++σξξ10l l ┄ +011=--ξσk k l ┈┈┈┈(1)(1)式两端用1-k σ作用得:++-ξσξσkk l l 110+0221=--ξσk k l由已知得: ==+ξσξσ1k k=,022=-ξσk 01≠-ξσk ,所以有00=l .则(1)式变为: +σξ1l +011=--ξσk k l ┈┈┈┈(2)(2)式两端用2-k σ 作用得:ξσξσkk l l 211+-+0321=--ξσk k l同理01=l .重复上述过程有: ==10l l 01=-k l . 4. 在向量空间R [x ]中,σ (f (x ))=f '(x ), τ (f (x ))=xf (x ), 证明,στ -τσ=ι.证明:对任意][)(x R x f ∈,有))(())()((x f x f σττσστ=-=-+=-=-)()()()())((())(('''x xf x xf x f x f x f x x f τστσ)(x f .所以στ -τσ=ι.5. 在向量空间R 3中,线性变换σ, τ如下:σ (x 1, x 2, x 3)=(x 1, x 2, x 1+x 2)τ (x 1, x 2, x 3)=(x 1+x 2-x 3, 0, x 3-x 1-x 2)(1) 求στ, τσ, σ2;(2) 求σ+τ, σ -τ, 2σ.解: (1) =---+=),0,(),,(213321321x x x x x x x x x σστ,(321x x x -+0,),,()321321x x x x x x τ=-+,∴τστ=.)0,0,0(),,(),,(2121321=+=x x x x x x x ττσ,∴0=τσ ),,(),,(21213212x x x x x x x +=σσ=),,(2121x x x x +.∴σσ=2.(2) ),,)((321x x x τσ+=),,(321x x x σ+),,(321x x x τ ),,(2121x x x x +=+),0,(213321x x x x x x ---+),,2(32321x x x x x -+=.),,)((321x x x τσ-=),,(321x x x σ),,(321x x x τ-),,(2121x x x x +=),0,(213321x x x x x x ---+-=)22,,(321232x x x x x x -++-.2),,(2321=x x x σ),,(2121x x x x +=)22,2,2(2121x x x x +.6. 已知向量空间R 3的线性变换σ为σ (x 1, x 2, x 3)=(x 1+x 2+x 3, x 2+x 3,-x 3) 证明,σ是可逆变换,并求σ-1.证明:),0,0,1(),0,0,1(=σ, ),0,1,1(),0,1,0(=σ,),1,1,1(),1,0,0(-=σ.∴ σ关于3R 的一个基),0,0,1(, ),0,1,0(,),1,0,0(的矩阵为:⎪⎪⎪⎭⎫ ⎝⎛-=100110111A . 显然,A 可逆,所以σ是可逆变换,而且⎪⎪⎪⎭⎫ ⎝⎛--=-1001100111A所以-=⎪⎪⎪⎭⎫⎝⎛=--132113211(),,(x x x x A x x x σ,2x ,32x x +)3x -.7. 设σ, τ, ρ都是向量空间V 的线性变换,试证,(1)如果σ, τ都与ρ可交换,则στ, σ2也都与ρ可交换(若对任意α∈V ,都有στ (α)=τσ (α),就说σ与τ可交换);(2)如果σ+τ, σ-τ都与ρ可交换,则σ, τ也都与ρ可交换. 证:(1)由已知ρττρρσσρ==,.那么==)()(τρσρστ)(ρτσ =)()(στρτσρ=.22)()()(ρσσσρρσσσρσρσ====.(2)同理可证.8. 证明,数域F 上的有限维向量空间V 的线性变换σ是可逆变换的充分必要条件是σ把非零向量变为非零向量.证明:不妨设ν是n 维的. ,,21ξξ,n ξ是它的一个基.σ关于这个基的矩阵为A .显然,σ可逆当且仅当A 可逆. σ把非零向量变为非零向量当且仅当{}0=σKer ,而秩σ=秩A ,σ的零度=σker dim .且秩σ+σ的零度=n.所以秩σ=n 当且仅当σ的零度是0,即A 可逆当且仅当0=σKer .故σ可逆当且仅当σ把非零向量变为非零向量.9. 证明,可逆线性变换把线性无关的向量组变为线性无关的向量组. 证明:令σ是向量空间ν的可逆线性变换, ,,21αα,m α是ν的一组线性无关的向量,令++)()(2211ασασk k +0)(=m m k ασ.两端用1-σ作用得: +11αk +0=m m k α.由已知 ,,21αα,m α 线性无关,所以: ==21k k =0=m k .故 ),(),(21ασασ,)(m ασ 线性无关.10. 设{ε1, ε2, ε3}是F 上向量空间V 的一个基. 已知V 的线性变换σ在{ε1,ε2, ε3}下的矩阵为A =⎪⎪⎪⎭⎫⎝⎛333231232221131211a a aa a a a a a (1) 求σ在{ε1, ε3, ε2}下的矩阵;(2) 求σ在{ε1, k ε2, ε3}下的矩阵(k ≠0,k ∈F );(3) 求σ在{ε1, ε1+ε2, ε3}下的矩阵. 解:(1)⎪⎪⎪⎭⎫⎝⎛=222321323331121311231231),,(),,(a a a a a a a a a εεεεεεσ. (2)⎪⎪⎪⎪⎭⎫⎝⎛=33323123222113121132132111),,(),,(a ka a a k a a k a ka a k k εεεεεεσ. (3) =+),,(3211εεεεσ),,(3211εεεε+⎪⎪⎪⎭⎫⎝⎛++---+-⋅33323131232221212313222112112111a a a aa a a a a a a a a a a a11. 在R 3中定义线性变换σ如下σ (x 1, x 2, x 3)=(2x 2+x 3, x 1-4x 2, 3x 1),∀(x 1, x 2, x 3)∈R 3. (1) 求σ在基ε1=(1, 0, 0), ε2=(0, 1, 0), ε3=(0, 0, 1)下的矩阵;(2) 利用(1)中结论,求σ在基α1=(1, 1, 1),α2=(1, 1, 0),α3=(1, 0, 0)下的矩阵.解:(1) ⎪⎪⎪⎭⎫⎝⎛-=003041120),,(),,(321321εεεεεεσ (2)从基{}321,,εεε到基{}321,,ααα的过渡矩阵为⎪⎪⎪⎭⎫⎝⎛=001011111P .σ在{}321,,ααα下的矩阵为:⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛--=⋅⎪⎪⎪⎭⎫ ⎝⎛-⋅-0010111110030411200111101000030411201P P =⎪⎪⎪⎭⎫ ⎝⎛---156266333. 12. 已知M 2(F )的两个线性变换σ,τ如下σ (X )=X ⎪⎪⎭⎫⎝⎛-1111, τ (X )=⎪⎪⎭⎫⎝⎛-0201X , ∀X ∈M 2(F ). 试求σ+τ, στ在基E 11, E 12, E 21, E 22下的矩阵. 又问σ和τ是否可逆?若可逆,求其逆变换在同一基下的矩阵. 证明:⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=+021202011111)(111111E E E τσ =12112E E +222102E E +-.⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=+200102011111)(121212E E E τσ =12110E E +222120E E -+.⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=+110002011111)(212121E E E τσ=121100E E +2221E E ++.⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=+10002011111)(222222E E E τσ =121100E E +2221E E -+.所以τσ+在基22211211,,,E E E E 下的矩阵为⎪⎪⎪⎪⎪⎭⎫⎝⎛---=1120110200010012A . 同理可证στ在基22211211,,,E E E E 下的矩阵.121111)(E E E +=σ,121112)(E E E -=σ,222112112100)(E E E E E +++=σ,=)(22E σ2221121100E E E E -++.所以σ在此基下的矩阵为:⎪⎪⎪⎪⎪⎭⎫⎝⎛--=110110000110011B . 显然,B 可逆.所以σ可逆. σ在同一基下的矩阵为:⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=-21210021*******1210021211B. 同理可讨论τ的可逆性及求τ的矩阵.13. 设σ是数域F 上n 维向量空间V 的一个线性变换. W 1, W 2是V 的子空间,并且V =W 1⊕W 2证明,σ是可逆变换的充要条件是V =σ ( W 1)⊕σ ( W 2)证明:令 ,1α,r α是1W 的一个基. 令 ,1+r α,n α是2W 的一个基. 由已知得: ,1α, n α是ν的一个基.必要性:设σ可逆,则 ),(1ασ,)(r ασ, )(1+r ασ,)(n ασ 也是ν的一个基.但=)(1W σ£( ),(1ασ,)(r ασ). =)(2W σ£( )(1+r ασ,)(n ασ)所以=ν+)(1W σ)(2W σ,⋂)(1W σ}0{)(2=W σ,故V =σ ( W 1)⊕ σ ( W 2).充分性:将必要性的过程倒过去即可.14. 设R 3的线性变换σ定义如下:σ (x 1, x 2, x 3)=(2x 1-x 2, x 2-x 3, x 2+x 3)求σ在基ε1=(1, 0, 0), ε2=(0, 1, 0), ε3=(0, 0, 1) 及基η1=(1, 1, 0), η2=(0, 1, 1),η3=(0, 0, 1)下的矩阵.解: σ在基{ε1, ε3, ε2}下的矩阵为:⎪⎪⎪⎭⎫⎝⎛--=110110012A . σ在基{321,,ηηη}下的矩阵为:⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛=-110110011101100121100110011B =⎪⎪⎪⎭⎫⎝⎛--211110011. 15. 在M 2(F )中定义线性变换σ为σ (X )=⎪⎪⎭⎫⎝⎛-3210X , ∀X ∈M 2(F ). 求σ在基{ E 11, E 12, E 21, E 22}下的矩阵,其中E 11=⎪⎪⎭⎫⎝⎛0001, E 12=⎪⎪⎭⎫ ⎝⎛0010, E 21=⎪⎪⎭⎫ ⎝⎛0100, E 22=⎪⎪⎭⎫⎝⎛1000. 解: σ在基{22211211,,,E E E E }下的矩阵为⎪⎪⎪⎪⎪⎭⎫⎝⎛--=30200302100001A . 16. 证明,与n 维向量空间V的全体线性变换可交换的线性变换是数量变换.证明:由105P 习题二及第10题的结论易得. 17. 给定R 3的两个基α1=(1, 0, 1), α2=(2, 1, 0), α3=(1, 1, 1);和 β1=(1, 2,-1), β2=(2, 2, -1), β3=(2, -1, -1). σ是R 3的线性变换,且σ(αi )=βi ,i =1, 2,3. 求(1) 由基{α1, α2 , α3}到基{β1, β2 , β3}的过渡矩阵; (2) σ关于基{α1, α2 , α3}的矩阵; (3) σ关于基{β1, β2 , β3}的矩阵.解: (1)令)0,0,1(1=ε,)0,1,0(2=ε,)1,0,0(3=ε.则由{α1, α2 , α3}到{ε1,ε3, ε2}的过渡矩阵为:1101110121-⎪⎪⎪⎭⎫⎝⎛. 由基{ε1, ε3, ε2}到基{β1, β2 , β3}的过渡矩阵为:⎪⎪⎪⎭⎫ ⎝⎛101110221. 所以由基{α1, α2 , α3}到基{β1, β2 , β3}的过渡矩阵为:⎪⎪⎪⎭⎫ ⎝⎛----⋅⎪⎪⎪⎭⎫ ⎝⎛---=-1111222211111101211P =⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---252112323123232 (2) σ ==),,(),,(321321βββαααP ),,(321ααα.所以σ在),,(321ααα下的矩阵为:⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---252112323123232. σ关于基{β1, β2 , β3}的矩阵为: ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---252112323123232 18. 设α1=(-1, 0, -2), α2=(0, 1, 2), α3=(1, 2, 5),β1=(-1, 1, 0), β2=(1, 0, 1), β3=(0, 1, 2),ξ=(0, 3, 5)是R 3中的向量,σ是R 3的线性变换,并且σ(α1)=(2, 0, -1), σ(α2)=(0, 0, 1),σ(α3)=(0, 1, 2).(1) 求σ关于基{β1, β2 , β3}的矩阵; (2) 求σ(ξ)关于基{α1, α2 , α3}的坐标; (3) 求σ(ξ)关于基{β1, β2 , β3}的坐标. 解:令⎪⎪⎪⎭⎫⎝⎛--=5222101011T ,⎪⎪⎪⎭⎫⎝⎛-=2101011112T .则从基{α1, α2 , α3}到基{β1, β2 , β3}的过渡矩阵为:⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛----=⋅=-0101210011222341212211T T T T . 又321135310311)1,0,2()(αααασ-+-=-=321203231)1,0,0()(αααασ+-==321300)2,1,0()(αααασ++==所以σ关于),,(321ααα的矩阵为:⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛---03135132310031311.从而σ关于基{β1, β2 , β3}的矩阵为:⋅⎪⎪⎪⎭⎫ ⎝⎛-==-2111000011AT T B ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---03135132310031311⎪⎪⎪⎭⎫ ⎝⎛-⋅010121001= ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----31353103132343132310. (2)==)5,3,0(ξ321353135ααα+-.所以关于)(ξσ),,(321ααα的坐标为:⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-⋅926967956353135A 由(2)可知=)(ξσ⋅),,(321ααα⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--926967956=(β1, β2 , β3)⋅⋅-1T ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--926967956 所以关于)(ξσ{β1, β2 , β3}的坐标为:⋅-1T ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--926967956=⋅⎪⎪⎪⎭⎫ ⎝⎛-211100001⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--926967956=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--971926956. 19. 设R 3有一个线性变换σ定义如下:σ (x 1, x 2, x 3)=(x 1+x 2,x 2+x 3,x 3),∀(x 1, x 2, x 3)∈R 3.下列R 3的子空间哪些在σ之下不变?(1) {(0, 0, c )| c ∈R }; (2) {(0, b , c )| b , c ∈R };(3) {(a , 0, 0)| a ∈R }; (4) {(a , b , 0)| a , b ∈R }; (5) {(a , 0, c )| a , c ∈R }; (6) {(a , -a , 0)| a ∈R }.解:(3)与(4)在σ之下不变.20. 设σ是n 维向量空间V 的一个线性变换,证明下列条件等价: (1) σ (V )=V ; (2) ker σ={0}.证明:因为秩σ+σ的零度=n. 所以秩σ=n 当且仅当σ的零度是0,即n =)(dim νσ当且仅当0ker dim =σ,因此V V =)(σ当且仅当}0{=σK e r .21. 已知R 3的线性变换σ定义如下:σ (x 1, x 2, x 3)=(x 1+2x 2-x 3, x 2+x 3, x 1+x 2-2x 3),∀(x 1, x 2, x 3)∈R 3. 求σ的值域σ (V )与核Ker σ的维数和基.解: σ关于基)0,0,1(1=ε,)0,1,0(2=ε,)1,0,0(3=ε的矩阵为:⎪⎪⎪⎭⎫ ⎝⎛--=211110121A .)1,0,1()(1=εσ,)1,1,2()(2=εσ,)(νσ ))(),((21εσεσL =.),(ker ξσL =其中)1,1,3(-=ξ,1ker dim =σ.22. 设σ是向量空间V 的一个线性变换,W 是σ的一个不变子空间,证明,W 是σ 2的不变子空间.证明:由不变子空间的定义易证. 23. 设σ是数域F 上n (>0)维向量空间V 的一个线性变换,{α1, α2 ,…, αr , αr +1,…, αn }是V 的基. 证明,如果{α1, α2 ,…, αr }是Ker σ的基,那么{σ (αr +1),…,σ (αn )}是Im σ的基.证明:已知{α1, α2 ,…, αr }是Ker σ的基, 则σ (αi )=0, i =1,2, …, r . 令 l r +1σ (αr +1)+ l r +2σ (αr +2)+ …+ l n σ (αn )=0, 则σ ( l r +1αr +1+…+ l n αn )=0, l r +1αr +1+…+ l n αn ∈ Ker σ .所以 l r +1αr +1+…+ l n αn =l 1α 1+…+ l r αr但 α1, α2 ,…, αr , αr +1,…, αn 是V 的一个基, 故 l r +1=…= l n =0. 所以 σ (αr +1),…, σ (αn ) 线性无关.又 Im σ = £(σ (α1), σ (α2)…, σ (αn )) = (σ (αr +1),…, σ (αn )).从而结论成立.24. 对任意α∈R 4,令σ (α)=A α,其中A =⎪⎪⎪⎪⎪⎭⎫⎝⎛---2122552131211201 求线性变换σ的核与象. 解: α1 = ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--02232, α2 =⎪⎪⎪⎪⎪⎭⎫⎝⎛--1021, Ker σ =£(α1,α2). σ (ε1) = ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-2111, σ (ε2) = ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-2220. Im σ =£(σ (ε1), σ (ε2)).25. 设 σ,τ 是向量空间V 的线性变换,且σ+τ=ι,στ=τσ=θ. 这里ι是V 的恒等变换,θ 是V 的零变换. 证明:(1) V =σ(V )⊕τ (V ); (2) σ(V )=Ker τ.证明: (1) ∀ξ∈ V, ξ=ι (ξ)=(σ+τ)(ξ)=σ (ξ)+τ (ξ).所以V =σ (V )+τ (V ).对任意ξ∈σ (V )∩τ (V ). 则ξ=σ (ξ1)+ τ (ξ2).由已知条件可得ξ= ι (σ (ξ1)) = (σ+τ)(σ (ξ1)) = σ·(σ (ξ1) = σ·(τ (ξ2)= στ (ξ2) = 0 . 故结论成立.(2 ) 对任意σ (ξ)∈σ (V ), 则 τ(σ (ξ))= 0, 所以 σ (ξ)∈Ker τ .反之, 对任意ξ∈Ker τ , 则τ(ξ)= 0.由已知条件可得,ξ= (σ+τ)(ξ)=σ (ξ)+τ (ξ)=σ (ξ),所以ξ∈σ (V ).26. 在向量空间F n [x ]中,定义线性变换τ为:对任意f (x )∈F n [x ],τ(f (x )) =x f '(x )-f (x ). 这里f '(x )表示f (x )的导数. (1)求Ker τ及Im τ;(2)证明,V =Ker τ⊕Im τ. 解: (1) 令τ ( f (x )) = x f'(x )-f (x ) = 0其中 f (x ) = a 0 + a 1x + … + a n x n . 则(a 1x +2a 2x 2+ … +n a n x n )- f (x ) = 0(0- a 0) + ( a 1- a 1)x + (2a 2- a 2) x 2+ … + (n a n -a n )x n= 0 有 ⎪⎪⎩⎪⎪⎨⎧===00020na a a, 所以 f (x ) = a 1x ,Ker τ =£(x ), Im τ=£(1,x 2, … ,x n ).(2) 显然 .27. 已知向量空间V 的线性变换σ在基{ε1, ε2, ε3}下的矩阵为A =⎪⎪⎪⎭⎫⎝⎛--121101365 求σ的本征值及相应的本征向量. 问是否存在V 的一个基使得σ 关于这个基的矩阵是对角阵?解: 本征值λ=2 (三重), 属于λ=2的线性无关的本征向量为:ξ1=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛0131 , ξ2=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-1031, 故σ 不能对角化.28. 设σ是向量空间V 的可逆线性变换,证明 (1) σ的本征值一定不为0; (2) 如果λ是σ 的本征值,那么λ1是σ-1的本征值.证明: (1) 反设σ 有一本征值为0,则存在ξ≠0,ξ∈ V , 使得σ (ξ)=0·ξ= 0 . 因为σ 可逆, 所以 σ -1(σ (ξ))=0, 即ξ= 0.矛盾.(2) 设λ是σ 的本征值,由(1)得λ≠0,且有σ (ξ)=λξ,ξ≠0.σ -1(σ (ξ))=λσ -1 (ξ). 即 σ -1 (ξ)=λ1ξ, 所以结论成立.补 充 题1. 设σ是数域F 上n 维向量空间V 的一个线性变换. 证明 (1) Ker σ ⊆Ker σ2⊆ Ker σ3⊆…(2) Im σ ⊇Im σ2 ⊇Im σ3 ⊇…证明: (1)对任意正整数n ,下证Ker σ n ⊆ Ker σ n +1 对任意ξ∈ Ker σ n., σ n(ξ)=0, σ (σ n(ξ))=0 即σn +1(ξ)=0, 所以ξ∈ Ker σn +1.(2) 对任意正整数n ,下证Im σ n ⊇Im σ n +1.对任意ξ∈Im σ n +1, 则存在 η∈ V , 使得ξ=σn +1(η)=σ n (σ (η))∈Im σ n.2. 设A 是数域F 上的n 阶矩阵. 证明,存在F 上的一个非零多项式f (x ), 使得f (A )=0.[不用Cayley-Hamilton 定理证. ]证明: 由于dimM n (F) = n 2, 所以I, A, A 2, …, A 2n线性相关,故存在F 上的不全为零的一组数k 0,, k 1, … ,k 2n ,使得+++2210A k A k I k ┄+022=nn Ak .取=)(x f +++2210x k x k k ┄+ 022=nn xk ,结论得证.3. 设V 是n 维向量空间, σ是V 的一个可逆线性变换, W 是σ的一个不变子空间. 证明, W 也是σ-1的不变子空间.证明:令{α1, α2 ,…, αr }是W 的一个基,因为W 是σ的不变子空间,所以 ,1,)(=∈i i ωασ,r .又σ是可逆的,所以 ),(1ασ,)(r ασ线性无关,故),(1ασ,)(r ασ也是W 的一个基.因为r i i i ,,1,))((1=∈=-ωαασσ.所以W 关于1-σ不变.4. 设σ是数域F 上向量空间V 的一个线性变换, σ2=σ. 证明: (1) Ker σ ={ξ-σ (ξ)|ξ∈V }; (2) V =Ker σ ⊕Im σ ;(3) 若τ是V 的一个线性变换, 那么Ker σ 和Im σ 都在τ之下不变的充要条件是στ=τσ.[提示:证(3)的必要性,利用(2). ]证明:(1)对于任意的,ker σξ∈则.0)(=ξσ那么{}V ∈-∈-=-=ξξσξξσξξξ)()(0.反之,任意的{}V ∈-∈-ξξσξξσξ)()(,有-=-)())((ξσξσξσ0)()()(2=-=ξσξσξσ,故σξσξker )(∈-.(2)由(1)的解果可知:σσIm ker +=V ,对任意的σσξIm ker ⋂∈,则有:)()(211ησησηξ=-=,因此0)()()(121=-=ησησξσ. 同时还有:ξησησξσ===)()()(222所以0=ξ,结论成立.(3)充分性易证.必要性:设Ker σ 和Im σ 都在τ之下不变,由(2)的结论得:1,ξξξ=∈∀V ),(2ξσ+其中σξker 1∈.又因为+-=+-=-))(())(())()(())((1121ξστξτσξσξτσστξτσστ )()))(((222ξτσξστσ-.由已知,,Im ))((,ker )(21σξστσξτ∈∈不妨设)())((32ξσξστ=,所以)()())(())(())((2323=-=-=-ξτσξσξστξσσξτσστ.5. 设σ是数域F 上n 维向量空间V 的一个线性变换, σ2=ι. 证明, V =W 1⊕W 2, 这里W 1={ξ∈V |σ(ξ)=ξ},W 2={η∈V |σ(η)=-η}.[提示:∀α∈V ,α=21(α+σ(α))+21(α-σ(α)). ]证明:首先对2)(2)(,ασαασααα-++=∈∀V ,由于=+)2)((ασασ2)(2)()(2ασαασασ+=+,=-)2)((ασασ=-2)()(2ασασ 2)(ασα--所以12)(W ∈+ασα,22)(W ∈-ασα,故21W W V +=.其次对任意的21W W ⋂∈α,则αασ=)(,αασ-=)(.所以0,02==αα.那么V =W 1⊕W 2,结论成立.6. 设V 是复数域C 上一个n 维向量空间, σ, τ是V 的线性变换, 且στ=τσ . 证明(1) 对σ的每一本征值λ来说,V λ={ξ∈V |σ(ξ)=λξ}是τ的不变子空间; (2) σ与τ有一公共本征向量.[提示:证(2)时,考虑τ在V λ上的限制. ] 证明: (1)易证.(2).由(1)可知λV 是τ的不变子空间.则λτV 是λV 的一个线性变换.因此λτV 在复数域C 上一定有一个本征值,不妨设为μ.即存在λαV ∈≠0,使得μαατλ=))((V .而)())((ατατλ=V ,所以α是τ的属于μ的一个本征向量.由α的取法,结论得证.7. 设A 是秩为r 的n 阶半正定矩阵. 证明,W ={ξ∈R n |ξ T A ξ=0}是R n 的n -r 维子空间.[提示:利用习题三第33题的结论,可得W 是齐次线性方程组BX =0的解空间. ]证明:由习题三第33题的结论得:B B A T =,其中B 是秩为r 的n r ⨯矩阵.则)()(ξξξξξξB B B B A T T T T ==,那么0=ξξA T当且仅当0=ξB .=W{}0=∈ξξB Rn.因为秩r B =,所以齐次线性方程组0=Bx 的解空间是r n -维的.即r n W -=dim .8. 设σ,τ是F 上向量空间V 的线性变换,且σ2=σ,τ2=τ. 证明,(1) Im σ=Im τ 当且仅当 στ=τ, τσ=σ; (2) Ker σ=Ker τ 当且仅当 στ=σ, τσ=τ.证明:(1)必要性:设τσm m I I =,,V ∈∀ξ则σξτIm )(∈.令)()(1ξσξτ=,则)()())(()(11ξτξσξσσξστ===.所以τστ=.同理可证στσ=.充分性:设τστ=,στσ=.对任意的σξσIm )(∈,则τξστξτσξσIm ))(())(()(∈==所以τσIm Im ⊆,同理可证στIm Im ⊆. (2)必要性:设Ker σ=Ker τ.对任意的V ∈ξ,因为0)()())((2=-=-ξτξτξξττ所以τξξτker )(∈-,则0))((=-ξξτσ,即)())((ξσξτσ=,故σστ=.同理可证ττσ=.充分性:设ττσ=,σστ=.对任意的σξker ∈,则0)(=ξσ.且0)0())(())(()(====τξστξτσξτ所以τξker ∈,故τσker ker ⊆.同理可证στker ker ⊆.。
第7章习题解答

第7章思考题及习题7参考答案一、填空1. AT89S52单片机任何一个端口要想获得较大的驱动能力,要采用电平输出。
答:低2.检测开关处于闭合状态还是打开状态,只需把开关一端接到I/O端口的引脚上,另一端接地,然后通过检测来实现。
答:I/O端口引脚的电平3. “8”字型的LED数码管如果不包括小数点段共计段,每一段对应一个发光二极管,有和两种。
答:7,共阳极,共阴极4. 对于共阴极带有小数点段的数码管,显示字符“6”(a段对应段码的最低位)的段码为,对于共阳极带有小数点段的数码管,显示字符“3”的段码为。
!答:7DH,B0H5. 已知8段共阳极LED数码显示器要显示某字符的段码为A1H(a段为最低位),此时显示器显示的字符为。
答:d6. LED数码管静态显示方式的优点是:显示闪烁,亮度,比较容易,但是占用的线较多。
答:无,较高,软件控制,I/O口7. 当显示的LED数码管位数较多时,一般采用显示方式,这样可以降低,减少的数目。
答:动态,成本,I/O端口8. LCD 1602是型液晶显示模块,在其显示字符时,只需将待显示字符的由单片机写入LCD 1602的显示数据RAM(DDRAM),内部控制电路就可将字符在LCD上显示出来。
答:字符,ASCII码-9. LCD 1602显示模块内除有字节的RAM外,还有字节的自定义,用户可自行定义个5×7点阵字符。
答:80,显示数据,64,字符RAM,810.当按键数目少于8个时,应采用式键盘。
当按键数目为64个时,应采用式键盘。
答:独立,矩阵11.使用并行接口方式连接键盘,对独立式键盘而言,8根I/O口线可以接个按键,而对矩阵式键盘而言,8根I/O口线最多可以接个按键。
答:8,6412.LCD 1602显示一个字符的操作过程为:首先,然后,随后,最后。
答:读忙标志位BF,写命令,写显示字符,自动显示字符13.由于微型打印机TPµP-40A/16A是一种外设,因此单片机与微型打印机的的命令与数据传送,必须采用方式。
第7章 习题解答
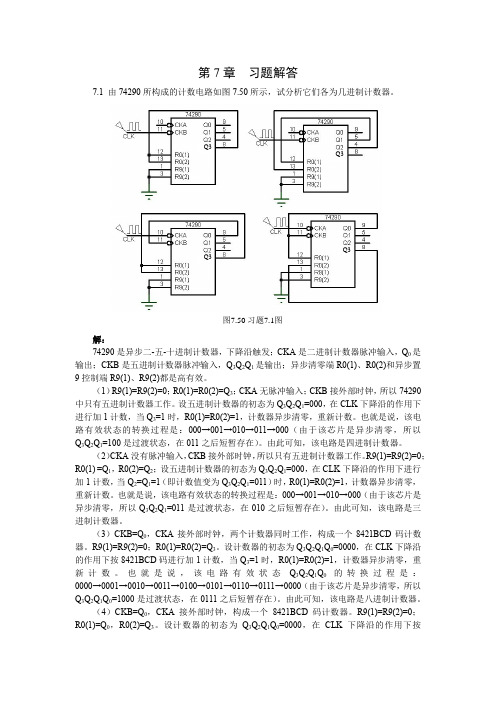
第7章 习题解答7.1 由74290所构成的计数电路如图7.50所示,试分析它们各为几进制计数器。
图7.50 习题7.1图Q3Q3Q3Q3解:74290是异步二-五-十进制计数器,下降沿触发;CKA 是二进制计数器脉冲输入,Q 0是输出;CKB 是五进制计数器脉冲输入,Q 3Q 2Q 1是输出;异步清零端R0(1)、R0(2)和异步置9控制端R9(1)、R9(2)都是高有效。
(1)R9(1)=R9(2)=0;R0(1)=R0(2)=Q 3;CKA 无脉冲输入;CKB 接外部时钟,所以74290中只有五进制计数器工作。
设五进制计数器的初态为Q 3Q 2Q 1=000,在CLK 下降沿的作用下进行加1计数,当Q 3=1时,R0(1)=R0(2)=1,计数器异步清零,重新计数。
也就是说,该电路有效状态的转换过程是:000→001→010→011→000(由于该芯片是异步清零,所以Q 3Q 2Q 1=100是过渡状态,在011之后短暂存在)。
由此可知,该电路是四进制计数器。
(2)CKA 没有脉冲输入,CKB 接外部时钟,所以只有五进制计数器工作。
R9(1)=R9(2)=0;R0(1) =Q 1,R0(2)=Q 2;设五进制计数器的初态为Q 3Q 2Q 1=000,在CLK 下降沿的作用下进行加1计数,当Q 2=Q 1=1(即计数值变为Q 3Q 2Q 1=011)时,R0(1)=R0(2)=1,计数器异步清零,重新计数。
也就是说,该电路有效状态的转换过程是:000→001→010→000(由于该芯片是异步清零,所以Q 3Q 2Q 1=011是过渡状态,在010之后短暂存在)。
由此可知,该电路是三进制计数器。
(3)CKB=Q 0,CKA 接外部时钟,两个计数器同时工作,构成一个8421BCD 码计数器。
R9(1)=R9(2)=0;R0(1)=R0(2)=Q 3。
设计数器的初态为Q 3Q 2Q 1Q 0=0000,在CLK 下降沿的作用下按8421BCD 码进行加1计数,当Q 3=1时,R0(1)=R0(2)=1,计数器异步清零,重新计数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章习题解答填空题1.解 由于100113,55x EX p ++++===,故由35p =解得µ35p =.2.解 似然函数为12(,,;)n L x x x λK 12211()niii nnx x ni i i i x eex λλλλ=--==∑==∏∏,故ln L 112ln ln n ni i i i n x x λλ===-+∑∑,由ln d L d λ12ni i n x λ==-∑0=,得λ的最大似然估计量为ˆλ2X=. 3.解 由222()(1)E X kS E X kES EX kDX np knp p np +=+=+=+-=,得1k =-.4.解 222222112()()()3nniii i xE XE X nE X n x dx θθθ=====∑∑⎰32222532x n dx n θθθθ==⎰. 由22215()2ni i E cX cn θθ===∑,解得25c n=. 5.解 由于123EX EX EX μ===,且由题意有123()E X aX bX μ+-=,2342E bX X aX μ(--)=,得11a b +-=,211b a --=解得2a =,2b =.6.解 由于21σ=,所以μ的置信度为1α-的置信区间为22(,)x x αα+,将40,x =1σ=,0.025216,0.05, 1.96n U U αα====代入其中,即得μ的置信度为0.95的置信区间是(39.51,40.49).7.解 由于μ未知,且10,10.90=-=n α,得220.050.95(9)16.919,(9) 3.325==χχ,2σ的置信水平为0.90的置信区间为222222122(1)(1)935935(,)(,)(651.63,3315.79)(1)(1)16.919 3.325n S n S n n ααχχ---⨯⨯==--. 8.解 由于μ的置信度为0.95的置信区间为0.0250.025(x U x U -+,所以得0.02524l U =≤.又因为0.025 1.96U =,解得2(2 1.96)15.3664n ≥⨯=,所以n 至少取16.选择题1.解 似然函数1111()(;),1,1,2(1)(1)nni i ni i L f x x i n θθθθθ=====≤≤=--∏∏L ;()L θ为θ的单增函数,而θ的取值范围为1min i i nx θ≤≤≤,故当1min i i nx θ≤≤=时,()L θ取最大值,所以θ最大似然估计量$1min ii nX θ≤≤=,选(A ). 2.解 因为ˆˆE a b aE b a b θθθ(+)=+=+,而2222ˆˆˆˆE D E D θθθθθθ()=+()=+>,所以ˆa b θ+是a b θ+的无偏估计,2ˆθ是2θ的有偏估计,选(B).3.解 因为1E X EX λ==,所以X 是1λ的无偏估计. 由于X 为连续型随机变量,故对于任意的常数a ,{}0P X a ==,所以不存在常数a ,使得1P ==或1P ==,利用柯西-许瓦兹不等式得1E X EX>2[E 211E =()=,得11EX E X λ>=,所以1X是λ的有偏估计,选(C ). 4.解 由于,1,2,3i EX i μ==,故得123E E E μμμμ∧∧∧===,而467E μμμ∧=≠,所以123,,μμμ∧∧∧为 μ的无偏估计,而4μ∧为 μ的有偏估计,故舍去4μ∧.又由于123,,X X X 相互独立,且2,1,2,3i DX i σ==,故计算得222124719,,18325D D D μσμσμσ∧∧∧===,其中2D μ∧最小,故选(B ).5.解 222221110E X DX EX σσ()=+()=+=,所以21X 为2σ的无偏估计.2222121212[()]()[()]2E X X D X X E X X σσ-=-+-=≠,所以212()X X -为2σ的有偏估计,舍去.2222111111n n n i i i i i E X E X n n n σσ===()=()==∑∑∑,所以211n i i X n =∑为2σ的无偏估计. 22E S σ()=,所以2S 为2σ的无偏估计.由于2212~X χσ(1),所以2122X Dσ=,得2412D X σ()=.进而2221111n ni ii i D X D X n n==()=()=∑∑4421122ni nn σσ==∑. 由于222~n S n χσ(-1)(-1),所以222n S Dn σ(-1)=(-1),得242D S n σ()=-1.因为n >1,所以211n i i X n =∑为2σ的无偏估计,且方差最小,选(C ).6.解 由题意知,9.76510.235102x +==,所以(A )正确.由于0.0510.235100.235U =-=,且0.05 1.645U =0.23511.6457==, 解得49n =,所以(B )正确.由于0.0251.96U =,故μ的置信度为95%的置信区间为0.025(x U ±=1(10 1.96)7±⋅(100.280)(9.720,10.280)=±=,所以(C )正确.0.050.0250.0251.6450.901.960.952U U U ==≠,所以(D )不正确,选(D ).解答题(A类)1.解 ⑴ 因为总体X 服从参数为p 的几何分布,故1=EX p,由1==X EX p 解得p 的矩估计量为µ1=M p X. ⑵ 似然函数为11121(,,,;)(1)(1)ni i i nx nx nn i L x x x p p p p p =--=∑=(-)=-∏L ,故1ln ln ()ln(1)n i i L n p x n p ==+--∑,令1ln 1()01ni i d L n x n dp p p==--=-∑,解得p 的极大似然估计量为µ11===∑L nii np XX. 2.解 ⑴ 由1λ==X EX ,解得λ的矩估计量为$1λ=M X . ⑵ 似然函数为1121(,,,;)()niii nx x nn i L x x x eeλλλλλ=--=∑==∏L ,故1ln ln λλ==-∑ni i L n X ,1ln ni i d L n x dp λ==-∑,令ln 0=d L dp,解得λ的极大似然估计量为$11L nii nXXλ===∑. 3.解 由题意知X 为连续型随机变量,其密度函数为1,1,(;)0,1.x f x x x βββ+⎧>⎪=⎨⎪≤⎩⑴ 由111+∞+==⋅=-⎰X EX x dx xββββ,解得β的矩估计量为ˆ1=-MXX β. ⑵ 似然函数为11112()()inni n L x x x x βββββ++===∏L ,故1ln ()ln (1)ln ni i L n x βββ==-+∑,1ln ln ni i d L n x d βββ=()=-∑.令ln ()0d L d ββ=,得β的极大似然估计量为1ˆln ==∑Lnii nXβ.4.解 似然函数()(1)N n NL θθθ-=-,ln ()L θ=ln ()ln(1)N n N θθ+--.令ln d Ld θ01Nn N θθ-=-=-,解得θ的极大似然估计值为$N nθ=. 5.解 ⑴(;)EX xf x dx θ+∞-∞=⎰1022(1)x x dx dx θθθθ=+-⎰⎰142θ=+.令X EX =,即142X θ=+,得θ的矩估计量为$122X θ=-. ⑵因为22(4)4[()]E X DX EX =+2114[()]42DX n θ=++22414DX n θθθ=+++>,因此24X 不是2θ的无偏估计量.6.解 此为2k =的情形.由1211,1()(1)m i i mi i X X EX np m X X DX np p m ==⎧===⎪⎪⎨⎪-==-⎪⎩∑∑解得n 和p 的矩估计量为2221111,1()1()====----∑∑))m i mi i i Xn p X X m X X X X m . 7.解 由于22111222[()]()()nnni i i i i i i i i i i i E X X X E X X X E X EX EX ---===⎡⎤-=-=-⎣⎦∑∑∑2222()(1)ni n σμμμσ=⎡⎤=+-⋅=-⎣⎦∑, 所以2(1)EY c n σ=-,令2EY σ=,解得11c n =-. 8.证 由于22212()()E S E S σ==,故µ222222121()1()11()22n E S m E S n m E n m n m σσσσ(-)+(-)(-)+(-)===+-+-,所以µ2σ是2σ的无偏估计. 9.解 ⑴由于X 与Y 均服从正态分布,且相互独立,所以Z X Y =-服从正态分布,又20,3EZ DZ DX DY σ==+=,从而2~(0,3)Z X Y N σ=-,故Z 的密度函数为2226(,)z f z σσ-=,(,)z ∈-∞+∞.⑵似然函数为2222116226221)(6)()ni i i z n n nz i L e σσσπσ=----=∑()==∏,则222211ln ln(6)ln()226nii n n L zσπσσ=()=---∑,令222241ln 110()26nii d L n z d σσσσ=()=-⋅+=∑,解得µ22113n i i Z n σ==∑. ⑶由于µ2211()()3n ii E E Z n σ==∑21()3E Z =21[()]3DZ EZ =+2221(30)3σσ=+=,所以^2σ为2σ的无偏估计量.10.证 由于)E X EY μ==,故111ˆ()()22E E X EY μμμμ=+=+=,211ˆ(2)(2)33E E X EY μμμμ=+=+=, 所以12ˆˆ,μμ均为μ的无偏估计. 又由于11,2DX DY n n==,且X 与Y 相互独立,故 111113ˆ()()4428D DX DY n n n μ=+=+=,211111ˆ(4)(4)9923D DX DY n n nμ=+=+⋅=.因为12ˆˆD D μμ>,所以2ˆμ比1ˆμ更有效. 11.证⑴由于E X EY μ==,所以()EZ aE X bEY a b a b μμμμ=+=+=+=,表明Z 是μ的无偏估计.⑵ 由于22121211,D X DY n n σσ==,且X 和Y 相互独立,故 2222222222121212121111(1)DZ a D X b DY a b a a n n n n σσσσ=+=+=+- 22222122212221121()a a n n n n σσσσ=+-+, 故当222212222*********2112()n n a n n n n σσσσσσ-=-=++,2212221121n b a n n σσσ=-=+时,DZ 最小. 12.证由切比雪夫不等式及概率的性质得$$$$21{}{}1D P P E θθθεθθεε≥-<=-<≥-,且依题意$2lim(1)1n D θε→∞-=,所以由夹逼定理,有$lim {}1n P θθε→∞->=,即$θ是θ的一致估计. 13.解 ⑴由于2σ未知,且10,10.95=-=n α,得0.0252(1)(9) 2.2622-==t n t α,故μ的置信水平为0.95的置信区间为22(((--+-x t n x t n αα(457.5 2.2622457.5 2.2622=-+(432.3047,482.6953)=. ⑵ 由于μ未知,且10,10.90=-=n α,得220.050.95(9)16.919,(9) 3.325==χχ,σ的置信水平为0.90的置信区间为)(25.69,57.94)==. 14.解 设机器A 生产的钢管内径为X ,机器B 生产钢管的内径为Y ,则211~(,)X N μσ,222~(,)Y N μσ,而两总体方差未知但相等,故12μμ-的置信度为1-α的置信区间为121222(()(2)()(2)--+--++-x y t n n s x y t n n s αα,其中s ω由题意知,12120.05218,13,10.90,0.05,(2)(29) 1.69912==-==+-==n n t n n t ααα,2291.73,93.75,0.34,0.29====X Y x y s s ,代入上式后计算得总体均值差12μμ-的置信度为0.90的置信区间为( 2.37, 1.67)--.15.解 设X 表示化验员A 对某种聚合物中的含氯量的测定值,Y 表示化验员B 对某种聚合物中的含氯量的测定值,则总体22~(,),~(,)A A B B X N Y N μσμσ.由于两个样本相互独立,两总体的均值A μ与B μ都未知,且1210,10.90,0.05,10.95,22==-==-=n n ααα查表得120.05120.9510.052211(1,1)(9,9) 3.18,(1,1)(9,9)(9,9) 3.18---==--===F n n F Fn n F F αα0.3145=,又220.5419,0.6065ABs s ==,所以22ABσσ的置信水平为0.90的置信区间为2222121212211(,)(1,1)(1,1)-⋅⋅----A A B B s s s F n n s Fn n αα0.541910.54191(,)(0.2810,2.8413)0.6065 3.180.60650.3145=⋅⋅=.16.解 设汽车轮胎磨坏时所行驶的路程为X ,则2~(,)X N μσ.由于总体X 的方差2σ未知,且0.0516,10.95,(1)(15) 1.7531,41116,6346=-=-====n t n t x s αα,所以μ的0.95置信下限为(41116 1.753138443--=-=x t n α(公里). 17.解 由于均值μ未知,且由题意知2210.955,10.95,(1)(4)0.71-=-=-==n n ααχχ,再由样本值计算得11.9=s ,所以σ的置信度0.95置信上限为28.2==(C o ).解答题(B类)1.解 ⑴设{},0,1,2i p P X i i ===,则221p θ=(-),且201210122121EX p p p p θθ=⋅+⋅+⋅=+(-)=(-),得121p θθ=(-),2201211p θθθθ=-(-)-(-)=,故X 的分布律为22012~2(1)(1)X q q q q 骣÷ç÷ç÷ç÷--桫. ⑵由21EX X θ=(-)=,解得q 的矩估计量为1ˆ12MX θ=-.由于111ˆ11121222ME E X EX θθθ=-=-=-⋅(-)=,所以ˆq是q 的无偏估计. ⑶似然函数为441234{0}{1}{1}{2}41L P X P X P X P X θθθ()======(-),则ln ()ln 44ln 4ln 1L θθθ=++(-),令ln 4401d L d θθθθ()=-=-,解得q 的极大似然估计值为1ˆ=2Lθ. 2.解 ⑴ 由2223X EX x xdx θθθ==⋅=⎰,解得θ的矩估计量为$32M X θ=. ⑵ 似然函数为1222122()()nni n ni L x x x x θθθ===∏L ,0,1,2,,i x i n θ≤≤=L .由于()L θ为θ的单调减少函数,且θ的取值范围为1max i i nx θ≤≤≥,所以当1max i i nx θ≤≤=时,θ的取值最小,从而()L θ的取得最大值,故θ的极大似然估计量为$1max L i i nX θ≤≤=.3.解 ⑴ 由于0=EX ,故根据低阶矩优先原则,采用二阶原点矩建立方程2222201111()22σσσσ+∞+∞---∞=====∑⎰⎰xxn i i X E X x e dx x e dx n , 从中解得σ的矩估计量为µσ=M ⑵ 似然函数为11111()22niii x nx n ni L e e σσσσσ=--=∑==∏,故11ln ln 2ln ni i L n n x σσσ=()=---∑,21ln 1nii d L n xd σσσσ=()=-+∑,令ln 0d L d σσ()=,解得σ的极大似然估计为µ11σ==∑n L i i X n . 4.⑴证 由于221()ET E X S n =-221E X E S n=()-()2222n n σσμμ=(+)-=,所以T 是2μ的无偏估计量.⑵解 当0,1μσ==时,~(0,1)X N .故22~(1)nX χ,22(1)~(1)n S n χ--,且X 与2S 独立,所以221()DT D X S n =-2221D X D S n=()+()22222111()[(1)](1)D nX D n S n n n =+⋅-- 222211121222(1)(1)(1)1(1)n n n n n n n n =⋅+⋅⋅-=⋅+=---.5.证 ⑴ 因为12ˆE EX EY μμμμ=-=-=,所以ˆX Y μ=-是12μμμ=-的无偏估计.⑵由于X与Y 相互独立,故ˆμ的方差为1414ˆ()60D D X Y DX DY n m n nμ=-=+=+=+-. 为求解方便,将正整数n 视为正实数,则有22ˆ1414()60(60)dD dn n n n n μ'=+=-+--,令22140(60)n n -+=-,解得20n =,40m =,可进一步验证此时ˆμ的方差达到最小. 6.解 ⑴设X 为任取一张卡片的号码,则12~111N X NNN ⎛⎫ ⎪⎪ ⎪⎝⎭L L,12(,,,)n X X X L 为来自总体X 的简单随机样本.①由12N X EX +==,解得µ21M N X =-. ②似然函数111nn i L N N N =()==∏,1i x N ≤≤.L 为N 的单减函数,而N 的取值为 111max ,max 1,max 2,i i i i ni ni nx x x ≤≤≤≤≤≤++L .当1max i i nN x ≤≤=时,L 取最大值,故µ1max L ii nN X ≤≤=. ⑵①µ12121212M N ENE X EX N +=-=-=-=,所以µM N为N 的无偏估计量. ②µ1max L ii nN X ≤≤=的分布律为 µ1{}{max }L i i nP N k P X k ≤≤===11{max }{max 1}i ii n i nP X k P X k ≤≤≤≤=≤-≤- 1()()n nk k N N-=-,1,2,,k N =L , 所以µ11[()()]Nn n L k k k E N k N N =-=-∑121[()()()]n n n N N N N N N -=-+++<L ,由于µlim L n E NN →∞=,所以µL N 为N 的有偏估计量,且为渐进无偏估计量. 7.解 ⑴由于11E ()2n E X X μμ∧=+=,211()42n D D X X σμ∧=+=,所以22222E()E 022D σσμμμμμ∧∧∧-=+(-)=+=.⑵由于221n S nσ∧-=,且由第六章例3.2 知42222(),()1E S D S n σσ==-,所以 221n E n σσ∧-()=,24222212(1)n n D D S n n σσ∧(-)-=()=, 因此2222222E()()σσσσσ∧∧∧-=+-D E 44222222(1)1(21)()σσσσ---=+-=n n n n n n. 解答题(C类)1.解 此为2k =的情形.⑴ 由1222211,2()1()12=+⎧==⎪⎪⎨-⎪-==⎪⎩∑n ii X EX X X DX n θθθθ解得12,θθ的矩估计量分别为µµ12,MMX X θθ==+. ⑵ 由于X 的密度函数为()1221121,,;,0,,⎧≤≤⎪-=⎨⎪⎩x f x θθθθθθ其它故似然函数为12121212111(,),,1,2,,()ni ni L x i n θθθθθθθθ===≤≤=--∏L ,由此可得L 关于1θ为单增函数,关于2θ为单减函数.又1θ和2θ的取值范围分别为1211min ,max i i i ni nx x θθ≤≤≤≤≤≥,故当1211min ,max i i i ni nx x θθ≤≤≤≤==时,L 取得最大值,所以12,θθ的极大似然估计量分别为µµ**11211min ,max i i nL L i ni nX X X X θθ≤≤≤≤====. 2.解 ⑴此为2k =的情形.由于1~X E μθ-(),进而计算得2,EX DX θμθ=+=.由方程组221,1()n i i X X X n θμθ=⎧=+⎪⎨-=⎪⎩∑解得,q m 的矩估计量为,MM M X X θμθ∧∧∧===-=-.⑵似然函数为11()()/111(,)ni i i nx x ni L eeμθμθθμθθ=----=∑=()=∏=,,1,2,,i x i n μ≥=L .由于(,)L q m 关于m 为单增函数,且1min i i nx μ≤≤≤,所以1min L i i nX μ∧≤≤=.又11ln (,)ln ()ln ()ni i nL n x n X θμθμθμθθ==---=-+-∑,令ln (,)L θμθ∂=∂2()0nnX μθθ---=,解得1min L L i i nX X X θμ∧∧≤≤=-=-.3.解 ⑴n X 的分布律为1000120012001000{}k k n n nC C P X k C --==, 0,1,2,,1000k =L . ⑵由题意知,现从总体n X 中取了一个容量为1的样本,并得观测值1100k =,因此似然函数为100900120012001000(){100}n n nC C L n P X C -===. 现在的问题是:求n ∧,使得()L n ∧为最大值.由于10090012001200100010090012001120010001()(1200)(1000)(2200)1200000(1)(2100)(2200)100n n n n C C C L n n n n n C C L n n n n n nC -------+===---+. 当1001200000n ≤,即12000n ≤时,()1(1)L n L n ≥-,表明()L n 随着n 增大而不减少.当1001200000n ≥,即12000n ≥时,()1(1)L n L n ≤-,表明()L n 随着n 增大而不增加.因此当12000n =时,()L n 取最大值,所以n 的极大似然估计值为12000n ∧=.4.解 记11p θ=-,22p θθ=-,23p θ=,则~(,),1,2,3i i N B n p i =.于是22112233123[(1)()]ET a EN a EN a EN n a a a θθθθ=++=-+-+.若使T 是θ的无偏估计,则有22123[(1)()]n a a a θθθθθ-+-+=.因此得10a =,21321,0a a a a n -=-=,解得13210,a a a n===.由于123N N N n ++=,故1231()1N T N N n n=+=-,其中1~(,1)N B n -θ,故11221(1)(1)(1)N n DT D DN n n n nθθθθ--=-===.5.解 ⑴2n =,故12S X X ===-. 由于12(,)X X 为来自总体2(0,)X N σ:的一个简单随机样本,故由正态分布的性质知212~(0,2)X X N σ-.S的分布函数为12(){}}S F s P S s P X s =≤=-≤. 当0s <时,()0S F s =; 当0s ≥时,()}}2()1S s sF s P s P σσ=≤=≤=Φ-.从而S的概率密度为2222(),0,,0,()()0,00,0.s S S s s s f s F s s s σϕσσ-⎧⎧≥≥⎪'===⎨⎪<⎩<⎩⑵由于2222220()s s S ES sf s ds s ds e σσσ+∞--+∞+∞-∞====≠⎰⎰,所以S 不是σ的无偏估计.6.证 ⑴ 因为µ111111()22222E E X E X EX θθθθ++=-=-=-=-=,所以µ1θ是θ的无偏估计.⑵ 由于总体X 密度函数和分布函数分别为1,1,(;)0,,x f x θθθ<<+⎧=⎨⎩其它 和0,,(;),1,1, 1.x F x x x x θθθθθθ≤⎧⎪=-<<+⎨⎪≥+⎩故*1max ni i nX X ≤≤=概率密度为*11(),1()[(;)](;)0,nn n X n x x f x n F x f x θθθθθ--⎧-<<+==⎨⎩其它,,所以111(max )()1n i i nnE X x n x dx n θθθθ+-≤≤=⋅-=++⎰,从而有 µ211(max )(max )1111ii i ni n n n n nE E X E X n n n n θθθ≤≤≤≤=-=-=+-=++++,所以µ2θ是θ的无偏估计.。
