齿轮啮合原理-第九章
齿轮啮合原理讲解

齿轮啮合原理讲解齿轮是一种将旋转动力传递给其他轴的机械装置。
它由多个齿轮齿面的啮合组成,通过齿轮的啮合传递力矩和旋转速度。
齿轮的啮合原理关乎到许多机械设备的正常运转和效率,本文将详细讲解齿轮啮合原理的相关内容。
一、齿轮啮合类型齿轮按照齿形的不同可以分为直齿轮、斜齿轮、渐开线齿轮等类型。
其中,直齿轮是最常见的类型,其齿面与轴线平行。
斜齿轮的齿面则与轴线成一定角度,而渐开线齿轮则通过曲线来使齿轮啮合时传递力矩更平稳。
不同类型的齿轮在啮合时会有一些差异,但其核心原理并无本质区别,即齿轮的齿面通过啮合传递力矩和旋转速度。
二、齿轮啮合原理齿轮啮合原理主要通过两个因素来解释,分别是齿形和齿数比。
1. 齿形齿形是指齿轮齿面上的曲线。
不同齿形的齿轮啮合可以传递力矩和旋转速度,同时还能保持动力传递的平稳性和高效性。
直齿轮的齿形是一种简单的曲线,其齿面与轴线平行。
斜齿轮的齿形较为复杂,其齿面与轴线成一定角度。
渐开线齿轮的齿形则通过特殊的曲线来实现更平滑的啮合。
无论是哪种齿形的齿轮,在啮合时都会形成一种特定的啮合曲线,这种曲线能够保证齿轮间的正常啮合并传递力矩。
2. 齿数比齿数比是指两个啮合齿轮的齿数之比。
齿数比决定了齿轮系统的传动比率。
当两个齿轮齿数比为1时,即齿数相等,齿轮系统称为齿轮副。
齿数比大于1时,称为减速器,可以将高速旋转的输入轴的转矩增大,同时降低旋转速度。
齿数比小于1时,称为增速器,可以将输入轴的转矩减小,同时增加旋转速度。
齿数比的大小还会影响到齿轮系统的传动效率。
较小的齿数比能够提高系统的传动效率,但相应地会降低传动比率。
较大的齿数比则能够提高传动比率,但传动效率会受到一定影响。
三、齿轮啮合的优势和应用齿轮啮合原理的应用广泛,主要得益于其独特的优势。
1. 力矩传递和转速调节齿轮能够将动力源的旋转运动转换为其他轴上的旋转运动,并通过传递力矩实现力量的放大或减小。
通过调整齿数比和齿形,齿轮系统可以实现不同的力矩和转速需求。
机械原理齿轮啮合

机械原理齿轮啮合齿轮是一种常见的机械传动元件,通过齿与齿之间的啮合运动来传递动力和扭矩。
在机械原理中,齿轮的啮合原理是一个重要的研究领域。
本文将详细介绍齿轮的啮合原理及其相关的机械原理。
1. 齿轮的类型齿轮可以分为直齿轮、斜齿轮、园柱齿轮、锥齿轮和蜗杆齿轮等几种类型。
不同类型的齿轮具有不同的使用场景和特点。
2. 啮合传动原理齿轮的啮合传动原理是通过齿与齿之间的啮合来传递旋转运动和扭矩。
在啮合过程中,齿轮的齿数、模数、压力角和齿轮啮合面的接触性能等因素会影响传动效果和传动特性。
3. 齿轮啮合的计算齿轮啮合的计算是为了确定齿轮的尺寸和传动特性。
计算包括齿轮的模数、齿宽、齿数比、节圆直径等参数的确定,以及齿轮啮合传动的效率和扭矩的计算等内容。
4. 齿轮的设计齿轮的设计是根据具体的传动需求和工作环境来确定齿轮的型号、材料和加工工艺等。
设计需要考虑齿轮的载荷、传动比、传动效率、噪音和寿命等因素。
5. 齿轮的制造和加工齿轮的制造和加工是将设计好的齿轮图纸转化为实际的零件和组装件的过程。
加工齿轮需要考虑齿轮材料、齿轮加工工艺和齿轮精度等因素。
6. 齿轮的润滑和维护齿轮的润滑和维护是保证齿轮传动正常运行和延长使用寿命的重要手段。
润滑可以采用油润滑和脂润滑两种方式,维护则包括定期检查、清洗和更换润滑剂等工作。
7. 齿轮的故障分析与排除在使用过程中,齿轮可能会出现故障,如齿面磨损、断齿、齿面剥落等。
通过故障分析和排除,可以找出故障原因,并采取相应的修复措施。
总结:机械原理中的齿轮啮合是一门复杂的学科,涉及到齿轮设计、制造、加工、润滑和维护等多个方面。
了解齿轮的啮合原理及相关的机械原理可以帮助我们更好地理解机械传动的原理和工作方式,为机械设计和应用提供基础知识和理论支持。
在实际的工程应用中,合理设计和使用齿轮可以提高机械传动的效率和可靠性,减少故障和损坏的发生。
齿轮的啮合原理是机械工程师必备的基础知识,也是机械原理学习的重点内容之一。
齿轮啮合原理

齿轮啮合原理齿轮是一种常见的机械传动装置,其啮合原理是指两个或多个齿轮之间通过齿与齿之间的啮合来传递动力和运动的原理。
齿轮传动具有传动比稳定、传动效率高、传动平稳等优点,因此在各种机械设备中得到广泛应用。
本文将从齿轮的基本概念、齿轮的分类、齿轮的啮合原理等方面来详细介绍齿轮啮合原理。
首先,我们来了解一下齿轮的基本概念。
齿轮是由圆柱形或锥形的齿轮齿条组成的,它们通过啮合来传递动力和运动。
齿轮一般由齿轮轮毂和齿组成,齿轮轮毂是齿轮的中心部分,齿是齿轮的外部部分,齿轮的啮合就是指两个或多个齿轮的齿之间的啮合。
其次,齿轮按照其外形和结构可以分为直齿轮、斜齿轮、锥齿轮等不同类型。
直齿轮是最常见的一种齿轮,其齿轮齿条与齿轮轴线平行,适用于传递平行轴间的运动和动力。
斜齿轮的齿轮齿条与齿轮轴线呈一定夹角,适用于传递非平行轴间的运动和动力。
锥齿轮的齿轮轮毂呈圆锥形,适用于传递轴线相交的运动和动力。
最后,我们来详细介绍一下齿轮的啮合原理。
齿轮的啮合原理是指两个或多个齿轮之间通过齿与齿之间的啮合来传递动力和运动。
当两个齿轮啮合时,它们之间会产生一定的啮合力,这种啮合力会使齿轮产生转动,从而传递动力和运动。
齿轮的啮合原理是基于齿轮齿条的啮合,通过齿与齿之间的啮合来实现动力和运动的传递。
总之,齿轮啮合原理是一种常见的机械传动原理,它通过齿与齿之间的啮合来传递动力和运动。
齿轮按照其外形和结构可以分为直齿轮、斜齿轮、锥齿轮等不同类型,不同类型的齿轮适用于不同的传动场合。
通过了解齿轮的基本概念、齿轮的分类、齿轮的啮合原理等方面的知识,可以更好地理解和应用齿轮传动装置。
希望本文对大家有所帮助,谢谢阅读。
第九章齿轮传动改

弧齿(曲线齿)
交错轴斜齿轮传动 交错轴 蜗杆传动
准双曲面齿轮传动
1)平行轴间齿轮传动
2) 空间非平行轴传动,如图所示。
2、按照齿轮传动工作情况分:
1)开式
2)闭式
3)半开式
3、按照齿面硬度(350HBS)分: 1)软齿面齿轮
2)硬齿面齿轮
4、按照齿轮圆周速度分:
1)低速 (v<3m/s)
2)中速
分度圆、模数
z 设 d r为任意圆的直径, 为齿轮的齿数,根据齿距的定义可得 d p 或 pr r d r r z mr z z
分度圆 上式中含有无理数“ ”,为了便于设计、制造及互换使用,我 pr 们在齿轮上取一圆,使该圆上的 值等于一些比较简单的数值, 并使该圆上齿廓的压力角等于规定的某一数值,这个圆称为分度 圆。分度圆上的压力角以 表示,我国采用20°为标准值,其他 各国常用的压力角还有15°、14.5°等等。 模数 分度圆上的齿距对 的比值以m 来表示,称为模数。
啮合弧 齿距 p
DC
标准圆柱齿轮的重合度的近似计算
标准圆柱齿轮的重合度可按下式近似计算:
1 1 1.88 3.2 cos z 1 z2
对于直齿圆柱齿轮, 0 。若大、小齿轮的齿数 z 2 z1 17 ,代 入上式得 1.504 。可见,一般情况下 总大于1。齿轮精度高。 允许的 值可小些;反之,精度愈低, 值就要求大些。
*
d f 2 ( z 2 2ha 2c * )m (70 2 1 2 0.25) 2 135mm
*
h (2ha c* )m (2 1 0.25) 2 4.5mm d d2 m 2 a 1 ( z1 z 2 ) (20 70) 90mm 2 2 2
齿轮内啮合原理

齿轮内啮合原理
齿轮内啮合原理是指两个或多个齿轮通过它们的齿来相互传递力和运动的机械原理。
齿轮通常是圆盘形状,上面有一定数量的齿。
当两个齿轮的齿将互相咬合时,它们就能够通过摩擦和力矩的传递来实现一定的运动。
齿轮内啮合原理的关键在于齿轮的齿与齿之间的啮合。
啮合齿轮的齿可以是直齿、斜齿、椭圆齿等形状,但必须满足一定的几何要求,以确保它们能够顺利地互相咬合并传递力和运动。
在齿轮内啮合过程中,两个齿轮之间会形成一对啮合点,它们沿着齿轮的齿廓线上移动。
这时,啮合点的位置会随着齿轮的旋转而改变。
齿轮内啮合的主要作用是改变旋转速度和扭矩。
当两个齿轮的啮合齿数不同时,它们的旋转速度和扭矩之间会产生转换关系。
一般来说,大齿轮的旋转速度较慢,扭矩较大;而小齿轮的旋转速度较快,扭矩较小。
齿轮内啮合原理常被应用于各种机械传动系统中,如汽车变速箱、工业机械、钟表等。
通过合理设计齿轮的齿数和齿廓形状,可以实现不同速度和不同扭矩的输出,以满足各种工作要求。
同时,齿轮传动还具有传动效率高、传动稳定、使用寿命长等优点。
因此,齿轮内啮合原理在机械工程领域中具有重要的应用价值。
第九章 齿轮传动

⌢⌢ BK = AB
2、发生线即是渐开线任意点的法线, 又是基圆的切线。 3、渐开线齿廓接触点的法线与该点速 度方向线所夹的锐角 α 称为该点压 k 力角。
cos α k = OB rb = OK rk
4、基圆内无渐开线。 5、切点B是K点的曲率中心, 线段BK是K点的曲率半径。
2、渐开线的特性 、
§ 9.5.4齿轮传动精度的选择
§ 9.6.1 轮齿的失效形式
• 1 轮齿折断 发生在齿根部分: 齿根弯曲应力最 大、受到脉动循 环或对称循环的 变应力;有应力 集中。 严重过载或大的 冲击载荷。
2 齿面疲劳点蚀
• 对于开式齿轮传动,因其齿 面磨损的速度较快,当齿面 还没有形成疲劳裂纹时,表 层材料已被磨掉,故通常见 不到点蚀现象。因此,齿面 点蚀一般发生在软齿面闭式 齿轮传动中。
3齿面磨损 齿面磨损
• 齿面磨损是开式齿 轮传动的主要失效 形式。 形式。
4 齿面胶合
• 齿面胶合通常出现在齿 面相对滑动速度较大的 齿顶和齿根部位。 齿顶和齿根部位。齿面 发生胶合后,也会使轮 齿失去正确的齿廓形状, 从而引起冲击、振动和 噪声并导致失效。
§ 9.6.2
齿轮材料
1.锻钢 锻钢 锻钢因具有强度高、韧性好、便于制造、便于热处理等 优点,大多数齿轮都用锻钢制造。 (1)软齿面齿轮:齿面硬度<350HBS,常用中碳钢和中碳 合金钢,如45钢.40Cr,35SiMn等材料,进行调质或正火 处理。这种齿轮适用于强度。精度要求不高的场合,轮坯 经过热处理后进行插齿或滚齿加工,生产便利、成本较低。 在确定大.小齿轮硬度时应注意使小齿轮的齿面硬度比 大齿轮的齿面硬度高30一50HBS,这是因为小齿轮受载荷 次敷比大齿轮多,且小齿轮齿根较薄.为使两齿轮的轮齿 接近等强度,小齿轮的齿面要比大齿轮的齿面硬一些。
齿轮齿条啮合原理

齿轮齿条啮合原理
嘿,朋友!今天咱就来好好唠唠齿轮齿条啮合原理!你知道吗,这就好比两个好伙伴,相互配合,共同完成一件大事!
就说咱平时骑的自行车吧,那链条和齿轮的配合,不就是齿轮齿条啮合原理的一个生动例子嘛!当我们用力蹬脚蹬子时,链条带动齿轮转动,而齿轮又推动着自行车前进,这一系列动作,多么神奇!
齿轮就像是一个非常有干劲的小伙伴,而齿条呢,则像是一个特别听话的跟随者。
齿轮转动的时候,一个个齿就像是小拳头,用力地推动着齿条前进。
这不就跟赛场上接力比赛似的,一棒接一棒,传递着力量!
想象一下,如果齿轮和齿条之间不配合好,那会怎么样?肯定乱套啦!就跟两个合作的人总是闹别扭,事情还怎么干得成呢!
再看看那些大型机械,比如起重机。
起重机的起重臂能够灵活地上下移动,这里面可少不了齿轮齿条的完美啮合呀!如果它们不和谐,能把重物稳稳地吊起和放下吗?肯定不行嘛!
齿轮齿条啮合原理真的太重要啦!它们的相互配合就像是一场精彩的舞蹈,谁也离不开谁。
在我们的生活中,到处都能看到它们配合的身影。
我们应该为这样的奇妙原理而感叹,不是吗?
我的观点就是,齿轮齿条啮合原理虽然看似简单,却是我们现代生活中不可或缺的一部分。
我们要好好珍惜和利用它,让它为我们创造更多的美好和便利!。
机械原理第九章 轮系.ppt

定轴轮系的传动比计算
轮系的传动比
i1 k
1 k
✓ 传动比的大小 ✓ 输入、输出轴的转向关系
定轴轮系的传动比计算
一、传动比的大小
i15
1 5
?
i1
2
1 2
z2 z1
i23 32
z3 z2
i34
3 4
z4 z3
i45
4 5
z5 z4
i1 5 1 i1i1 52 i23 i3 4i4 51 2 3 4
2、输入、输出轮的轴线相互平行 画箭头方法确定,可在传动比大小前加正或负号
3、输入、输出齿轮的轴线不平行 画箭头方法确定,且不能在传动比大小前加正或负号
§9.3 周转轮系的传动比计算
定轴轮系传动比计算公式
周转轮系传动比计算
?
反转法原理,将周转 轮系转化为定轴轮系
周转轮系的传动比计算
一、周转轮系传动比计算的基本思路
5
2345
z2z3z4z5 z1z2 z3 z4
所有从动轮齿数的乘积 所有主动轮齿数的乘积
二、传动比转向的确定
定轴轮系的传动比计算
1、平面定轴轮系(各齿轮轴线相互平行)
i15
1 5
(1)3 z2 z3 z4 z5 z1z2 z3 z4
z2z3z4z5 z1z2 z3 z4
惰轮
i1k
1 k
i1H 1i1HK
如果给定另外两个基本构件的角速度1、H中的任意一
个,可以计算出另外一个,从而可以计算周转轮系的传 动比。
周转轮系的传动比计算
三、使用转化轮系传动比公式时的注意事项
1、转化轮系的1轮、k轮和系杆H的轴线需平行
i1H3 1 3 H H(1)2Z Z1 2Z Z23
齿轮啮合仪工作原理
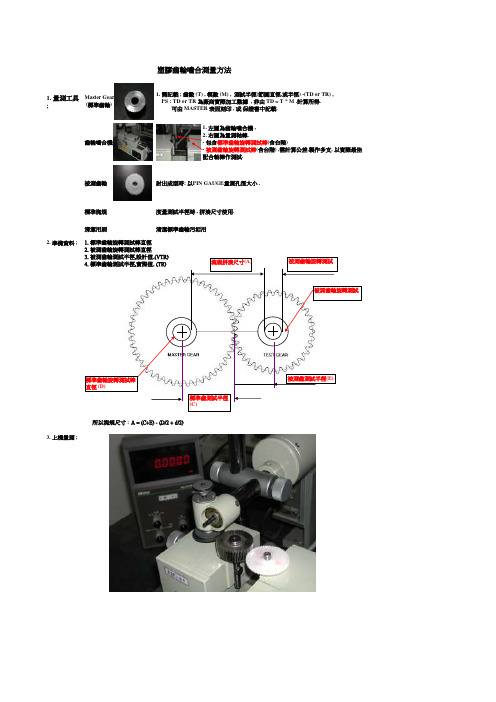
1. 量測工具 ;
2. 準備資料 ;
3. 上機量測 ;標準塊規度量測試半徑時 , 拼湊尺寸使用.
塑膠齒輪嚙合測量方法
齒輪嚙合機
Master Gear
(標準齒輪)
被測齒輪
1. 需記載 ; 齒數 (T) , 模數 (M) , 測試半徑(節圓直徑,或半徑) -(TD or TR) ,
PS : TD or TR 為廠商實際加工數據 , 非由 TD = T * M .計算所得.
可由 MASTER 表面刻印 , 或保證書中記載.
射出成型時: 以PIN GAUGE量測孔徑大小 .
1. 左圖為齒輪嚙合機 ,
2. 右圖為量測軸棒.
- 包含標準齒輪旋轉測試棒(含台階)
- 被測齒輪旋轉測試棒(含台階) ,需計算公差,製作多支, 以實際最
佳配合軸棒作測試.
所以塊規尺寸 :A = (C+E) - (D/2 + d/2)
清潔用刷清潔標準齒輪污垢用
4. 標準齒輪測試半徑,實際值. (TR)
3. 被測齒輪測試半徑,設計值.(VTR)
2. 被測齒輪旋轉測試棒直徑
1. 標準齒輪旋轉測試棒直徑
被測齒輪旋轉測試
標準齒輪旋轉測試棒
直徑(D)
塊規拼湊尺寸(A)被測齒輪旋轉測試
標準齒測試半徑
(C)
被測齒測試半徑(E)。
齿轮啮合原理-第九章

(1
(0) 1
)
1 2
2F 12
(1
(0) 1
)2
m21(1
(0) 1
)
1 2
m2' 1
(1
(0) 1
)2
式中m21(1)在中央接触点处等于N1/N2 ,而m2' 1 是选取的定值。传动函数(1 1(0) )
表示为线性函数和抛物线函数之和。线性函数是没有安装误差的齿轮传
v(1) s
a13
a33 a23tg1
v(1) q
a33tg1 a13 a23tg1
*确定接触椭圆
我们的目标是要建立小齿轮齿 面 1的参数 , (12) K f 和Kh 与瞬时 接触椭圆长轴长度的关系。所 考察的这个椭圆在中央接触点, 并且两接触曲面的弹性逼近量 是从试验数据得出的已知值。 基于六个步骤可以得到接触椭 圆的短轴2b表达式:
(9.3.14)
根据隐函数组存在的定理,如果下列条件正确:
函数 [ f1, f2 , f3, f4 , f5 ] C1 方程(9.3.13)在点 P是0 满足的;
右侧的雅可比行列式不等于零
可以证明函数(9.3.14)在一点的邻域内是存在的,
P0 (10 ,10 ,10 , 20 ,20 ,20 )
利用计算机技术对齿轮啮合过 程中的齿面接触情况及传动误 差进行分析,从而可在实际切齿 前对轮齿的啮合情况进行预控, 以减少试切时间。在进行TCA 的过程中,要表达大、小轮的齿 面方程,需要经过大量的坐标变 换及矩阵运算,同时还要求解相 当复杂的非线性方程组
齿轮和接触痕迹的计算机模拟 是一项能够显著改善齿轮工艺 和质量的重大成就
齿式棘轮机构
无级变速机构的特点:其变速范围和传动 比在使用中均限制在一定范围内,不能随 意扩大,由于摩擦,也不能保证准确的传 动比。
§9-2 换向机构
换向机构——在输入轴转向不变的条件下, 可使输出轴转向改变的机构。
三星轮换向机构 离合器锥齿轮换向机构
三星轮换向机构
1-主动齿轮 2、3-惰轮 4-从动齿轮
4.摩擦式棘轮机构简介
靠偏心楔块(棘爪)和 棘轮间的楔紧所产生的摩擦 力来传递运动。
特点:转角大小的变化 不受轮齿的限制,在一定范 围内可任意调节转角,传动 噪声小,但在传递较大载荷 时易产生滑动。
1-偏心楔块(棘爪) 2-棘轮 3-止回棘爪
二、槽轮机构
1.槽轮机构的组成和工作原理
1-拨盘 2—圆销 3—槽轮
倍增速变速机构
拉键变速机构
1-弹簧键 2-从动套筒轴 3-主动轴 4-手柄轴
有级变速机构的特点:可以实现在一定转 速范围内的分级变速,具有变速可靠、传 动比准确、结构紧凑等优点,但高速回转 时不够平稳,变速时有噪声。
二、无级变速机构
无级变速机构——依靠摩擦来传递转矩,适 当改变主动件和从动件的转动半径,使输出轴的 转速在一定的范围内无级变化。
齿式棘轮机构
2.齿式棘轮机构的常见类型及特点
外啮合式
外啮合式棘轮机构
内啮合式
内啮合式
3.齿式棘轮机构转角的调节
棘轮的转角 θ 大小与棘爪每往复一次推过的齿数 k 有 关:
360 kzk——棘爪每往复一次推的齿数; z——棘轮的齿数 。
(1)改变棘爪的运动范围
(2)利用覆盖罩
2.机械式换向机构的常用类型和工作原理。 3.棘轮机构、槽轮机构、不完全齿轮机构等间歇机构 的常见类型和工作原理。
齿轮齿条啮合的基本原理

齿轮齿条啮合的基本原理
齿轮齿条的啮合原理是通过齿轮上的齿与齿条上的凹槽互相嵌合来传递运动和力量。
首先,齿轮上有一定数量的齿,它们分布在齿轮的外圆上。
齿轮的齿形一般为直齿或斜齿,齿间的间距也是固定的。
齿条上则有一系列的凹槽,凹槽的形状与齿轮的齿形相匹配,使齿轮的齿能够准确地嵌入凹槽中。
当齿轮开始转动时,齿轮的齿会逐个地嵌入齿条的凹槽中。
这个过程使得齿轮和齿条之间建立起紧密的接触。
由于齿轮和齿条的齿形互相匹配,齿轮的旋转运动将会被准确地传递给齿条,使得齿条也开始运动。
通过更换齿轮和齿条的尺寸和齿数,可以实现不同传动比的设置。
传动比指的是齿轮转动一周时,齿条的移动距离。
通过改变齿轮的尺寸和齿数,传动比可以增大或减小,从而实现不同的速度和力量传递要求。
齿轮齿条的啮合原理可用于各种机械装置,如传动系统、起重装置等,具有传递力量稳定、精度高、可靠性好等特点。
齿轮啮合原理

齿轮啮合原理齿轮是一种常见的机械传动装置,它通过齿轮的啮合来传递动力和运动。
齿轮传动具有传递功率大、传动效率高、传动精度高等优点,因此在各种机械设备中得到广泛应用。
了解齿轮啮合原理对于理解齿轮传动的工作原理和性能具有重要意义。
齿轮啮合是指两个或多个齿轮的齿与齿之间相互啮合,从而传递动力和运动的过程。
在齿轮啮合中,齿轮的齿顶、齿谷和齿根都会发生接触和相互作用,这种接触和作用形成了齿轮传动的基础。
齿轮啮合的原理可以简单描述为齿轮的啮合是通过齿轮的齿顶和齿谷之间的相互啮合来传递动力和运动的。
当两个齿轮啮合时,它们的齿顶和齿谷会相互接触,并且在齿轮传动的过程中,齿轮的齿顶和齿谷会不断地相互进入和退出。
这种进入和退出的过程形成了齿轮的啮合运动,从而实现了齿轮的传动功能。
在齿轮啮合的过程中,齿轮的齿顶和齿谷之间的啮合是非常关键的。
齿顶和齿谷的啮合质量直接影响着齿轮传动的工作性能和传动效率。
如果齿轮的齿顶和齿谷啮合不良,就会导致齿轮传动的噪音增加、传动效率降低甚至损坏齿轮。
为了保证齿轮的啮合质量,需要注意以下几点。
首先,齿轮的齿顶和齿谷的啮合面要保持良好的光洁度和精度。
其次,齿轮的啮合面要保持一定的润滑条件,以减小摩擦和磨损。
最后,齿轮的啮合面要保持一定的啮合间隙,以便于齿轮的正常工作和运动。
总的来说,齿轮啮合原理是齿轮传动的基础,了解齿轮啮合原理对于理解齿轮传动的工作原理和性能具有重要意义。
在实际应用中,需要注意保证齿轮的啮合质量,以确保齿轮传动的正常工作和运动。
希望本文对于读者们对齿轮啮合原理有所帮助。
齿轮啮合原理-第九章.

1 传动误差的概念和传动误差抛物线函数的预先设定 * 理想齿轮传动的传动函数是线性的,
并且表示为:
N1 1 N2 i 是齿轮的转角 式中 Ni 是齿轮的齿数,
2
由于有安装误差(相错角改变,在非渐 开线齿轮的情况下最短中心距的改变, 弧齿锥齿轮、准双曲面齿轮和蜗轮蜗杆 的轴向位移),传动函数变为逐段近于 线性的函数,所具有的周期为一对齿啮 合循环的周期。由于循环连接处角速度 的跳动,加速度值趋近于无限大,这样 将引起很大的振动
转换循环和啮合方程
为了恢复齿面的接触,我们假定两齿轮之一,比方说主动齿轮1是静 止的,而从动齿轮2绕其轴线转过一补偿角 d q 。当齿面接触恢复时,称这 个啮合循环为转换循环。在循环起点,∑1和∑2彼此在一条线接触;在循 环终点,∑1和∑2彼此在一个点接触。在转换循环以内,∑1和∑2彼此不 接触。 接触点沿∑1和∑2 的位移和与∑2一起运动的位移之间的关系式如下:
9.2
局部接触综合
局部接触综合的构想是在[Litvin 1968 的专著]中提出的,后来在[Lit vin和Gutman 1980的文章]中用来研究准双曲面齿轮,又在[Litvin和 Zhang1991(b)的专著]中用来研究弧齿圆锥齿轮。
齿轮的局部接触综合必须保证: (i)在中央选取的接触点M具有所需要的传动比 (ii)所希望的齿面上接触迹线切线的方向 (iii)所希望的点M处接触椭圆长轴的长度 (iv)预先设定的最大传动误差控制等级的抛物线函数
啮合和接触的计算机模拟
组员:樊毅啬 李 轩
张永清 彭昌琰
第九章 啮合和接触的计算机模拟
9.1 引言
齿轮啮合原理

螺旋面加工中刀具干涉检查研究1课题背景随着机械制造工业的发展,各种新型螺杆机构不断涌现。
螺杆泵、螺杆马达(钻具)、螺旋挤压机、螺杆式气体压缩机等设备在石油钻采、化工、轻工、军工、造船、橡塑等行业的应用日益广泛。
虽然螺杆机构的设计制造技术具有悠久的历史,但由于新型螺杆机构的螺旋面廓形设计比较复杂,精度要求不断提高[1][2],一些大型螺杆的加工效率和制造成本问题越来越突出,而且国内外尚未制定出系统的设计制造标准。
因此,从客观上促进了螺旋面加工技术的不断发展,使之成为目前机械制造领域中倍受关注的研究课题[3]。
目前,在三坐标数控螺杆铣床上,采用截面包络法加工复杂螺杆是一项新的螺杆加工工艺。
与传统的展成法与成形法加工相比,该工艺方法具有切削用量大、加工效率高、刀具结构简单、对工件型线适应广、调整方便、可控精度高等许多优点。
它是一种使标准刃形刀具相对于工件按一定规律作包络运动,加工出工件螺旋表面的铣削方法。
其编程思想是从端截面出发,采用等精度曲线逼近的方法,使刀具切削刃在工件的接触轨迹在给定的精度范围内逼近工件的理论轮廓。
使用这种编程方法加工出的螺杆能够满足一般精度螺杆的加工要求。
目前,国产及进口专用机床所提供的编程系统均采用平面包络的计算方法,即认为在加工过程中刀具与工件的接触点(简称刀触点)轨迹为平面曲线,而实际上在三坐标专用铣床上进行包络加工时,刀触点轨迹为复杂的空间曲线。
因此,按平面包络计算方法得到的刀具轨迹及数控程序必然存在理论误差,影响加工精度。
如何才能找到一种快速高效的基于空间包络加工原理的编程方法,已经成为螺旋面数控加工研究领域的热点问题[4]。
在众多的研究成果中,基于最小有向距离理论并结合五点寻优方法而得到的最小有向距离算法[5],是一种基于空间包络加工原理的编程方法,它解决了迭代算法中存在的收敛性问题,避免了全局区域内大量的点集计算,具有计算速度快、原理简单等特点,已成为一种非常有效的在复杂螺旋面数控加工中计算刀位轨迹的方法。
齿轮的啮合原理

齿轮的啮合原理
齿轮的啮合原理是指两个齿轮之间的传动关系。
当两个齿轮啮合时,它们的齿轮齿廓相互咬合,从而实现转动的传递。
齿轮的啮合原理主要有以下几点:
1. 齿廓的设计:齿轮的齿廓是根据传动需求和角动量守恒原理进行设计的。
常见的齿面有直齿、斜齿、蜗杆齿等各种类型,每种类型都有其特定的应用领域和传动效果。
2. 正齿轮的啮合:正齿轮的啮合是指齿廓间的啮合角度在单行齿轮传动中为顶隙角,即两齿轮齿廓的齿峰与齿谷之间留有一定的间隙。
这样的啮合方式可以减小齿轮间的压力和摩擦,提高传动效率。
3. 正反齿轮的啮合:正反齿轮的啮合是指一对齿轮中,一个为正齿轮,另一个为反齿轮。
正反齿轮的啮合可以实现轴线的交叉传动,用于改变传动方向或实现不同速度比的传动。
4. 啮合间隙的控制:为了确保齿轮的正常工作,啮合间隙需要适当控制。
间隙过小会导致啮合卡死或齿轮齿面磨损,间隙过大会使啮合不稳定,降低传动效率。
因此,在设计和制造过程中需要对啮合间隙进行精确的控制。
总之,齿轮的啮合原理是通过齿廓的设计和啮合方式的选择来实现转动的传递。
合理的啮合设计能够提高齿轮传动的效率和可靠性。
齿轮啮合原理-第九章

2 轮齿接触分析解决的基本课题
给定齿轮两齿面的方程以及两回转轴线之间的相错角和最短距离; 齿轮的两齿面处于点接触,需要确定: (i)传动误差 (ii)齿轮两齿面上的接触迹线 (iii)如同一组瞬时接触椭圆那样的接迹线 注:在确定接触迹线时,要考虑到由于齿面的弹性变形,它们的接 触将扩展为一椭圆区域,并且接触椭圆的中心是理论接触点
*确定导数 m2' 1
将预先设定的传动函数表示为
2
(0 2
)
F (1
(0 1
)
)
这里, (0 1
)
和
( 2
0
)
是齿轮1和2的初始转角,它们保证两齿面在中央接触点M相
切触。利用到二次项的Taylor展开式,我们可以得到
2
(0) 2
F (1
(0) 1
)
F 1
(2)
vr vr
(12)
vr
量 vr 和 (1) vr (2)位于接触迹线。假定2
上的主曲率和主方向是已知的。
我们可以认为两接触迹线的切线
与单位矢量es 构成夹角为1和 2
通过啮合方程的微分式和矢量关系 可以得到
tg1
a31vq(12) (a33 a31vs(12) )tg2 a33 a3(2 vq(12) vs(12)tg2)
2 局部接触综合的过程通过以下步骤步骤完成
(i)确定导数
m2' 1
1
(m21 )
式中
m21
(1
)
(2) (1)
是瞬时动比函数
(ii)确定接触迹线的切线
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
假定啮合循环内所预期的传动误差的最大值是已知的,由上式可以确定m
' 21
*确定接触迹线的切线
推导接触迹线的切线
矢量 , 和 位于切平面,矢 (1)
(2)
vr vr
v (12 ) r
量 v r 和 (1 ) v r ( 2 )位于接触迹线。假定 2
上的主曲率和主方向是已知的。
我们可以认为两接触迹线的切线
这样的传动误差函数型式能使我们吸收有齿轮安装误差引起的传动 误差的线性函数,以及降低振动的等级
1 传动误差的概念和传动误差抛物线函数的预先设定
* 理想齿轮传动的传动函数是线性的,
并且表示为: 2
N N
1 2
1
式中N i 是齿轮的齿数, i 是齿轮的转角
由于有安装误差(相错角改变,在非渐 开线齿轮的情况下最短中心距的改变, 弧齿锥齿轮、准双曲面齿轮和蜗轮蜗杆 的轴向位移),传动函数变为逐段近于 线性的函数,所具有的周期为一对齿啮 合循环的周期。由于循环连接处角速度 的跳动,加速度值趋近于无限大,这样 将引起很大的振动
2 局部接触综合的过程通过以下步骤步骤完成
(i)确定导数
m2' 1
1
(m21)
式中
m21
(1
)
(2) (1)
是瞬时传动比函数
(ii)确定接触迹线的切线
(iii)确定接触椭圆的长轴
应用于弧齿锥齿轮和准双曲齿轮的局部接触综合是根据这样的假定, 大齿轮的机床刀具安装调整值是已经给定的,并且大齿轮在中央接触 点处的主曲率和主方向也是已知的。局部接触综合方法能使我们确定 出小齿轮的机床刀具的安装调整值,这种安装调整值可以在中央接触 点M及其邻域内给出改善了的啮合和接触状态
*确定导数 mΒιβλιοθήκη ' 21将预先设定的传动函数表示为
(0) 22
F(11(0))
这里,
( 1
0
)
和
( 2
0
)
是齿轮1和2的初始转角,它们保证两齿面在中央接触点M相
切触。利用到二次项的Taylor展开式,我们可以得到
2 2 ( 0 ) F ( 1 1 ( 0 ) ) F 1 ( 1 1 ( 0 ) ) 1 2 2 F 1 2 ( 1 1 ( 0 ) ) 2 m 2 1 ( 1 1 ( 0 ) ) 1 2 m 2 '1 ( 1 1 ( 0 ) ) 2
利用计算机技术对齿轮啮合过 程中的齿面接触情况及传动误 差进行分析,从而可在实际切齿 前对轮齿的啮合情况进行预控, 以减少试切时间。在进行TCA 的过程中,要表达大、小轮的齿 面方程,需要经过大量的坐标变 换及矩阵运算,同时还要求解相 当复杂的非线性方程组
齿轮和接触痕迹的计算机模拟 是一项能够显著改善齿轮工艺 和质量的重大成就
式中m 21 (1 )在中央接触点处等于N1/N2
,而m
' 21
是选取的定值。传动函数(1
(0 1
)
)
表示为线性函数和抛物线函数之和。线性函数是没有安装误差的齿轮传
动的理想函数。抛物线函数是传动误差函数。综合出的齿轮一定传递具
有抛物线型传动误差函数的回转运动,该函数用下式表示
2(1)12m2'1(11(0))2
2 轮齿接触分析解决的基本课题
给定齿轮两齿面的方程以及两回转轴线之间的相错角和最短距离; 齿轮的两齿面处于点接触,需要确定: (i)传动误差 (ii)齿轮两齿面上的接触迹线 (iii)如同一组瞬时接触椭圆那样的接迹线 注:在确定接触迹线时,要考虑到由于齿面的弹性变形,它们的接 触将扩展为一椭圆区域,并且接触椭圆的中心是理论接触点
* 预先设定的抛物线函数( 21)a12和线性函数(22)b1 的
相互影响问题
Litvin等证明了上述两函数之和是一抛物线函数,并且其斜率与初始抛物线 函数的斜率相同。这个新的传动误差抛物线函数相对初始给定的抛物线函 数仅有一些移动。这就是说,预先设定的传动误差抛物线函数能够吸收由 齿轮安装误差引起的传动误差线性函数。
9.2 局部接触综合
局部接触综合的构想是在[Litvin 1968 的专著]中提出的,后来在[Lit vin和Gutman 1980的文章]中用来研究准双曲面齿轮,又在[Litvin和 Zhang1991(b)的专著]中用来研究弧齿圆锥齿轮。
齿轮的局部接触综合必须保证: (i)在中央选取的接触点M具有所需要的传动比 (ii)所希望的齿面上接触迹线切线的方向 (iii)所希望的点M处接触椭圆长轴的长度 (iv)预先设定的最大传动误差控制等级的抛物线函数
3 轮齿接触分析的主要构想和主要目标
•TCA的主要构想基于相啮合的两齿面切触的模拟。确定瞬时接触椭 圆需要有关相切触的两齿面的主曲率和主方向的知识 •TCA的主要目标是分析齿轮的啮合和切触。确定改善啮合和接触状 态的机床刀具安装调整值是齿轮综合的主要课题
4 线接触两齿面接触分析计算
在对于初始为线接触得两齿面进行啮合和接触模拟的情况下,将出 现一些特殊的问题。如直齿外齿轮、平行轴螺旋齿齿轮和蜗轮蜗杆 传动。 齿轮两齿面的瞬时线接触仅仅在理论上对于无安装误差和制造误差 的理想齿轮传动时存在的。实际上,由于齿轮的安装误差,齿面的 线接触被点接触代替。在分析计算中,首先要确定转换点——理论 接触线上的一个点,在该店开始实际的点接触。求出转换点以后, 就可能在转换点邻域内确定出位于点接触迹线上的点,然后开始齿 轮接触分析计算
与单位矢量e s 构成夹角为 1 和 2
通过啮合方程的微分式和矢量关系 可以得到
tg1a a 33 13 vq ( 12a )3 ( 2(v aq (3 1 3 2) av 31 s(1 v2 s()1 t2 g ))t2 g ) 2
v(1) s
a13
a33
a23tg1
v(1) q
a33tg1 a13 a23tg1
*确定接触椭圆
我们的目标是要建立小齿轮齿 面 1 的参数 , (1 2 ) K f 和K h 与瞬时 接触椭圆长轴长度的关系。所 考察的这个椭圆在中央接触点, 并且两接触曲面的弹性逼近量 是从试验数据得出的已知值。 基于六个步骤可以得到接触椭 圆的短轴2b表达式:
啮合和接触的计算机模拟
组员:樊毅啬 张永清 李 轩 彭昌琰
第九章 啮合和接触的计算机模拟
➢9.1 引言 ➢9.2 局部接触综合 ➢9.3 轮齿接触分析 ➢9.4 两包络曲面曲线接触转换为点接触 ➢9.5 边缘接触
9.1 引言
1 轮齿接触分析(Tooth Contact Analysis ,即TCA)
