高等概率论课件
概率论 高等院校概率论课件JXHD2-~1

§2.3 连续型随机变量及其分布一. 连续型随机变量的概率分布二. 三种常用分布一. 连续型随机变量及其分布定义2-4 注1:连续型v r .X 的分布函数)(x F 是连续函数。
注2:概率密度)(x f 具有如下性质:(1)0)(≥x f ;(2)⎰∞+∞-=1)(dx x f ;(3)⎰=-=<≤21)()()(}{1221x x dx x f x F x F x X x P ;若v r .X 的分布函数)(x F 可表示成 ⎰∞-=xdu u f x F )()( (2-7)其中)(x f 为一非负可积函数,则称X 为连续型v r .,)(x f 称为X 的概率密度(或概率分布、分布密度)。
(4)若)(x f 在x 点连续,则)()(x f x F ='。
由(2-8)式知,若不计高阶无穷小,则有 xx f x x X x P ∆=∆+<≤)(}{即X 落在小区间),[x x x ∆+上的概率近似等于x x f ∆)(。
注3:若X 是连续型v r .,则R a ∈∀,0}{==a X P 。
结论:若A 是不可能事件,则0)(=A P ,反之不然。
}{b X a P <≤}{b X a P <<= }{b X a P ≤<=}{b X a P ≤≤=几种常用分布:(1)均匀分布:设随机变量X 在有限区间][b a ,内取值,且其分布密度为⎪⎩⎪⎨⎧≤≤-=其他,,01)(bx a a b x f ,则称X在有限区间][b a ,上服从均匀分布,记为)(~b a U X ,。
其分布函数为(自行验证)⎪⎩⎪⎨⎧>≤<--≤=b x b x a a b ax a x x F ,,,10)(Uniform Distribution⎩⎨⎧≤>-=-0001)(x x e x F x,,λ 一般地,若随机变量X 的概率密度⎩⎨⎧≤>=-000)(x x e x f x,,λλ其中0>λ为常数,则称X 服从参数为 λ的指数分布。
概率论 高等院校概率论课件JXHD53-1

§5.3 假 设 检 验再如糖厂用自动包装机装糖,每箱的标准重量规定为100kg ,某日开工后,抽测了9箱,其重量如下(单位kg ):99.3,98.7,100.5,101.2,98.3,99.7,99.5,102.1,100.5,问此包装机是否正常工作。
例如要检查纺织厂中纱的强力是否达到了标准,我们只能抽出一小部分纱,然后根据这部分纱的质量来推断整批纱的质量是否合格。
上面两例具有一个共同特点,就是从样本出发,对总体的某种假设作出判断——假设是否成立。
如包装机装糖一例中,用μ表示糖箱的平均重量,则问题即为对假设1000=μ:H 作出肯定或否定的回答。
在统计上,对总体所作的种种假设称为统计假设, [引例] 某厂有一批产品共200件,须经检验合格才能出厂,按照国家标准次品率不得超过1%,今在其中任意抽取5件,发现这个5件中有次品,问这批产品能否出厂?解:设这批产品的次品率为μ,则问题化为检验假设01.00≤μ:H 是否成立。
由样本出发来判断统计假设是否成立称为假设检验。
现假定0H 成立,看会出现什么结果,此时200件产品中最多有二件次品,任意抽取5件,那么5件中无次品的概率为⎪⎪⎪⎩⎪⎪⎪⎨⎧=件中没有件次品时。
,当件中有一件次品时;,当件中有两件次品时;,当无次品200200200)(520052005200519952005198C C C C C C P 显然 95.052005198>≥C C P (无次品) 05.0<(有次品)P 上面的分析讨论中,我们基于一个基本原理——实际推断原理,同时用了反证法的思想.假设总体),(2~σμN X ,n X X X ,,,21 为来自总体X 的一个样本,其观察值为n x x x ,,, 21 。
一.2σ已知,检验假设000(μμμ=:H 已知) 构造统计量n X U 20σμ-= (5-49)则当0H 成立时,U 服从标准正态分布,即)10(~,N U ,对于给定的10<<α(α通常比较小),由 αλ=>}{U P (5-50)查标准正态分布表可求得λ。
概率论 高等院校概率论课件JXHD2-1

第二章随机变量及其分布§2.1随机变量及其分布函数§2.2 离散型随机变量及概率分布§2.3 连续型随机变量及概率分布§2.4 多维随机变(向)量及其分布§2.5 随机变量的独立性§2.6随机变量函数的分布基本要求重点与难点JXHD2-7概率篇CH2LX基本要求1.理解随机变量、随机变量的分布函数概念及性质。
2.理解概率分布的概念及其性质。
3.会利用概率分布及分布函数计算有关事件的概率。
4.掌握六种常用分布,会查泊松分布、正态分布表。
5.了解多维随机变量的概念。
了解二维随机变量的联合分布函数及其性质,了解二维随机变量的联合概率分布及其性质,并会用它们计算有关事件的概率。
6.知道二维随机变量的边缘分布以及与联合分布的关系,了解条件分布。
7.理解随机变量独立性的概念及应用独立性进行有关计算。
8.会求简单随机变量函数的概率分布及两个独立随机变量的函数(和、最大值、最小值)的分布。
重点与难点1.随机变量的分布函数概念及性质。
2.概率分布(离散型随机变量的分布律,连续型随机变量的概率密度)的概念及性质。
3.概率分布与分布函数的关系及正态分布的有关计算。
4.二维随机变量的边缘分布以及与联合分布的关系。
5.随机变量独立性及应用。
6.简单随机变量函数的分布。
1.随机变量的分布函数、概率分布及其关系。
2.二维随机变量的边缘分布及计算。
3.随机变量函数的分布及两个独立随机变量的函数的分布。
§2.1 随机变量及其分布函数掷骰子试验}654321{,,,,,=Ω; 掷硬币试验}{T H ,=Ω 一.随机变量 [引例1] 掷骰子试验,}654321{,,,,,=Ω,令 ),,,,,(654321)(==i i i X 则X 是定义在Ω上的单值实函数,称X 为随机变量。
[引例2] 掷硬币试验,样本空间}{T H ,=Ω,令⎩⎨⎧===Te H e e Y ,,01)(则Y 是定义在Ω上的单值实函数,称 Y 为随机变量。
概率论 高等院校概率论课件JXHD3-3

§3.3 相关系数与相关阵一.协方差(Covariance) 与相关系数当Y X ,独立时,0))((=-=--EXEY EXY EY Y EX X E 定义3-5 设X 与Y 是两个随机变量,若))((EY Y EX X E --存在,则称其为随机变量X 与Y 的协方差,记为)(Cov Y X ,,即)(Cov Y X , =))((EY Y EX X E -- (3-17)称 DY DX Y X XY ),(Cov =ρ (3-18) 为X 与Y 的相关系数或标准协方差。
Correlation Coefficient Standard Covariance由前讨论知)(Cov Y X , EXEY EXY -= (3-19)且易证下面的等式DY DX Y X D +=+)(+2)(Cov Y X , (3-20) 由协方差的定义容易得到它有如下性质:(1))(Cov Y X ,=)(Cov X Y ,;(2))(Cov bY aX ,=ab )(Cov Y X ,,其中b a ,为常数;(3))(Cov 21Y X X ,+=)(Cov 1Y X ,+)(Cov 2Y X , 只证(3),其它自证。
(3))(Cov 21Y X X ,+=)(Cov 1Y X ,+)(Cov 2Y X ,事实上,)(Cov 21Y X X ,+))](([2121EY Y X X E X X E -+-+=+--=))([(11EY Y EX X E )])((22EY Y EX X --+--=))((11EY Y EX X E ))((22EY Y EX X E --)(Cov 1Y X ,=)(Cov 2Y X ,+ 定理3-4 设XY ρ是随机变量X 与Y 的相关系数,则有1≤XY ρ;且1=XY ρ的充要条件是X 与Y 依概率1线性相关,即存在常数b a ,使1}{=+=bX a Y P 。
概率论高等院校概率论课件

应用场景
强大数定律在统计学中用于 估计极端事件发生的概率和 风险,在决策理论中用于评 估最优策略和期望收益,在 可靠性工程中用于分析系统 的可靠性和寿命。
注意事项
强大数定律的应用有一定的 限制条件,例如随机序列必 须是独立同分布的。此外, 强大数定律并不能保证每个 随机事件的绝对正确性,而 只是给出了最大值分布的稳 定性。
连续随机过程
如布朗运动,每一步都是连续 的,每一步的状态都是连续的
。
随机游走与布朗运动
随机游走
一个随机过程,其中每一步都是随机的,通 常用来描述粒子的无规则运动。
布朗运动
一种连续随机过程,由大量微小粒子在流体 中无规则运动产生,通常用来描述微观粒子 的运动。
马尔科夫链与马尔科夫过程
马尔科夫链
一个随机过程,其中下一个状态只依赖于当前状态,与过去状态 无关。
注意事项
大数定律的前提是试验次数必须足够多,并且随 机事件之间必须是独立的。此外,大数定律并不 能保证每个随机事件的绝对正确性,而只是给出 了频率趋于概率的稳定性。
强大数定律
总结词
强大数定律是概率论中的重 要定理之一,它描述了随机 序列中最大值的分布性质。
详细描述
强大数定律指出,对于任意 给定的正整数序列$a_n$和 $b_n$,有$lim_{n to infty} frac{a_n}{b_n} = 1$的概率 为1。这个定理说明了随机 序列中最大值的分布具有很 强的稳定性。
随机变量的性质
随机变量具有可测性、可加性和有限 可加性。
离散型随机变量及其分布
离散型随机变量的定义
离散型随机变量是在样本空间中取有 限个或可数个值的随机变量。
离散型随机变量的分布
概率论 高等院校概率论课件JXHD6-1

第六章回归分析回归分析是研究变量间相关关系的一个统计分支,它主要解决以下面几个问题:(1)确定几个特定的变量之间是否存在相关关系,如果存在,找出它们之间合适的数学表达式;(2)根据一个或几个变量的值,预测或控制另一个变量的取值,并且要知道这种预测或控制可达到什么样的精确度;(3)进行因素分析,在共同影响一个变量的许多变量(因素)之间找出哪些因素重要,哪些因素次要,这些因素之间有什么关系等。
回归分析一元线性回归多元线性回归逐步回归非线性回归与回归诊断一元线性回归建立模型参数估计显著性检验预测预报一.建立模型引例1.一个作匀速直线运动的质点,在时刻t 的位置是S ,则S a bt =+,其中 a 为质点在t =0时刻的初始位置,b 为平均速度。
观测到的数据是ε+=s y ,其中ε是随机误差(测量误差)。
于是我们有ε+=s y ε++=bt a (6-1) 其中t 是非随机的,ε是随机的,通常认为E ε=0,显然y 也是随机的。
为了估计a 、b ,现在 n 个不同时刻作观察,得n 组观察值)(i i y t ,n i ,21 ,,=。
即 y i =i i bt a ε++ (i n =12,,, )用向量矩阵形式表示如下:εβ+=X Y 其中,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n y y y Y 21,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n εεεε 21,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n t t t X 21111,⎪⎭⎫ ⎝⎛=b a β。
问题:如何利用Y X 、的观测值来估计参数a 、b ,进一步预测未来时刻t 质点的位置。
引例2.在硝酸钠(3NaNO )的溶解度试验中,测得在不同温度C X 0下溶解于100份水中的硝酸钠份数y 数据见下表:x i 0 4 10 15 21 29 36 51 68y i 66.7 71.0 76.3 80.6 85.7 92.9 99.4 113.6 125试找出X 与Y 之间的关系。
图6-1bx a +εy =+(6-2)20406080100120140020406080 Y X =+βε 问题:如何利用观测值来估计参数a 、b ,从而确定y 与x 的近似线性关系。
概率论 高等院校概率论课件JXHD0-0

00.10.2
0.3
0.4
0.5
-4-3-2-101234
概率论与数理统计
电子教案研制单位:石油大学应用数学系
概率论与数理统计
绪论篇
概率论篇
数理统计篇
概率论篇
第一章随机事件与概率
第二章随机变量及其分布
第三章随机变量的数字特征第四章大数定律与中心极限定理
数理统计篇数理统计初步因素分析回归分析正交试验设计
数理统计是一个应用非常广泛的数学分支,它以概率论作为理论基础。
它的任务是:研究如何用有效地方法去搜集、整理和分析带有随机性影响的数据,并对所关心的问题作出推断和预测,直接为决策行动提供依据和建议。
凡是有大量数据出现的地方都要用到数理统计。
也就是说,数理统计是直接从随机现象的观察值去研究它的客观规律。
高等概率论课件
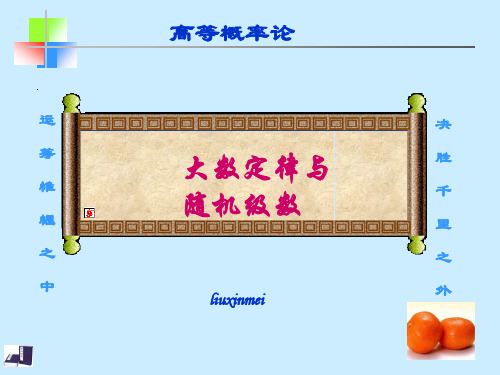
n j
j
n
2 (Yn ) n2
收敛,应用(7)于{{Yn
E(Yn )} },我们得出结论:
1 n
n j1 Y j E(Y j ) 0
a.e.
显然当 n 时,因为{X n }独立同分布,所以 E( X n ) E( X1 ) E(Yn ) E( X1 )
故我们也有
1 n
n
E(Y j )
我们可以得到
{X n Yn}
n
n
x an dFn (x)
(x)
E ( ( x))
n
x an (an )dFn (x) n
(an )
由 5.2 定义知X n 与Yn 是等价序列,所以
n
X n 也几乎处处收敛。 an
对于一个概率为 1 的集中的每一个 w ,将克罗内克引理应用于(3),我们得 到 推论: 在定理 5.4.1 的假设下,我们有
lim _____ Sn
n n
a.e
定理5.4.3
设 {X n } 是一个独立同分布的随机变量序列,且 E( X1 ) . 设 an 是满足条件
an n 的正数列,则我们有
(11) (12)
lim _____ Sn 0 a.e.;或者
n an
a.e.
按
{ X n an}
( X 1 An)
n
因为随机变量独立同分布,故有 ( X n An)
n
根据定理 4.2.4:如果事件{X }是独立的,则 n
( X n ) ( X n , i.o) 1
n
可得
{ X n An,i.o.} 1
而 Sn Sn1
Xn
An蕴含着 Sn
概率论 高等院校概率论课件JXHD4-1

第四章大数定律与中心极限定理大数定律中心极限定理要求:1.理解解切比雪夫(Chebyshev)不等式;理解切比雪夫定理和伯努利定理。
2.理解林德伯格-列维定理(独立同分布的中心极限定理)和棣莫弗拉普拉斯定理(二项分布以正态分布为极限)。
概率篇引理(Chebyshev’s 不等式):若r v .X 具有期望EX =μ,方差DX =σ2,则对于任意的ε>0有 P X {}-≥≤μεσε22 (4-1) 证明:(只证连续型)设X 的概率密度为f x (),则 ⎰≥-=≥-εμεμx dx x f X P )(}{dx x f x x )()(22⎰≥--≤εμεμ2222)()(1εσμε=-≤⎰∞+∞-dx x f x §4.1 大数定律 或 P X {}-<≥-μεσε122 (4-2) 若X N ~(,)μσ2,则P X {}.-<=μσ30997,即事件“X -<μσ3”的发生几乎是可以肯定的。
但对任意的随机变量X (不知其分布),若EX DX ==μσ,2,那么事件“X -<μσ3”的概率又如何来估计呢?law of large numbers上式说明随机变量X 取值于开区间)(εμεμ+-,的概率不小于221εσ-,例如:设X 的分布未知,记EX =μ,DX =σ2,取εσ=3,则 显然方差2σ越小则221εσ-越大,从而随机变量X 取值于开区间)(εμεμ+-,的概率也越大。
即X 的取值越集中在均值μ的附近, 这说明方差是刻画随机变量的概率分布对均值的集中程度。
P X {}.-<≥-=-≈μσσσ3191190888922例如:设X 的分布未知,记EX =μ,DX =σ2,取εσ=3,则 P X {}.-<≥-=-≈μσσσ3191190888922若取σε4=,则P X {}.-<≥-=-≈μσσσ411611160935722这就是说无论X 服从什么分布,它落在σμ4<-x 内的概率不小于0.93,这种估计在实际应用中形成了所谓σ—原则。
概率论 高等院校概率论课件JXHD1-5

§1.5 条件概率条件概率乘法公式全概率公式贝叶斯(Bayes) 公式CH1事件B 已发生的条件下事件A 发生的概率,记为)(B A P [引例] 设10件产品中有5件不合格品,而5件不合格品中有3件次品2件废品,现从10件产品中任取一件,求(1)取得废品的概率;(2)已知取到的是不合格品,它是废品的概率。
解:设事件A 表示“取得废品”;事件B 表示“取得不合格品”,则(1)取得废品的概率5/1)(=A P (2)已知取到的是不合格品,它是废品的概率为52)|(=B A P )()(B n AB n =)()()()(ΩΩ=n B n n AB n )()(B P AB P =条件概率Conditional Probabilitydef 1-3 可以验证)|(B A P 满足公理化定义,即(1)1)|(0≤≤B A P ;(2)1)|(=ΩB P ; (3)若 ,,n A A A ,,21是两两互不相容的事件,则 )|()|((11∑∞=∞==n n n n B A P B A P (1-4)B 为样本空间Ω中的两个事件,))B AB (1-3) 发生的条件下事件A 发生的条件概率。
设BA 、为样本空间Ω中的两个事件,0)(>B P ,则称)()(ˆ)|(B P AB P B A P = (1-3) 为事件B 发生的条件下事件A 发生的条件概率。
思考题:条件概率与无条件概率有何区别与联系?由引例及定义1-3不难总结出求条件概率的一般方法:1B 在缩小的样本空间中计算A 发生的概率)|(B A P ;0)(AB P 、)(B ,再按 既然不用定义1-3也可求条件概率)|(B A P ,因此上述定义式可反过来应用,即先求概率)|(B A P 、)(B P ,由此计算)(AB P 。
即得计算积事件概率的乘法公式:事件发生后,在缩小的样本空间中计算事件 02在样本空间中先计算)(AB P P 定义计算)|(B A P 。
高等数学 概率论与数理统计课件(一)

高等数学概率论与数理统计课件(一)高等数学概率论与数理统计课件1. 课程简介•高等数学概率论与数理统计是大学数学专业的一门重要课程。
•它是数学学科的基础,也是应用数学的重要工具。
•本课程旨在帮助学生掌握概率论与数理统计的基本概念、理论和方法。
2. 概率论部分2.1 概率的基本概念•概率的定义和性质•随机事件的概率计算方法•条件概率与独立事件2.2 随机变量和概率分布•随机变量的定义和性质•离散型随机变量和连续型随机变量•常见概率分布:离散型和连续型2.3 随机变量的数字特征•期望、方差、标准差的定义和计算•切比雪夫不等式•大数定律和中心极限定理3. 数理统计部分3.1 统计基础•总体和样本的统计特征•参数估计和区间估计•假设检验的基本思想3.2 参数估计•点估计和区间估计的概念•常见的参数估计方法:极大似然估计、矩估计等•置信区间的计算和解释3.3 假设检验•假设检验的基本原理•假设检验的步骤和流程•常见的假设检验方法:单样本、两样本和多样本检验4. 课程学习方法•注重理论和实践相结合,理论指导实践、实践检验理论。
•多做习题,通过刷题巩固知识点。
•参考相关教材和参考书,拓宽知识广度和深度。
•加强课后讨论和交流,与同学共同解决问题。
•关注概率论与数理统计的应用领域,扩展应用实践。
5. 课程考核方式•平时成绩:课堂参与、作业完成情况等。
•期中考试:对课程前半部分的知识进行考核。
•期末考试:对整个课程的知识进行考核。
•课程项目:根据实际情况进行论文、实验等形式进行综合评估。
6. 学习资源推荐•《高等数学》教材,北京大学出版社。
•《概率论与数理统计教程》教材,清华大学出版社。
•《概率论与数理统计习题集》辅导书,高等教育出版社。
•在线学习资源:Coursera、edX、网易云课堂等平台提供的相关课程。
7. 小结•高等数学概率论与数理统计课程是数学专业学生不可或缺的重要课程。
•本课程旨在帮助学生掌握概率论与数理统计的基本概念、理论和方法。
概率论 高等院校概率论课件JXHD7-2

§7.2 多因素方差分析Variance analysis of multiple factor 建立模型参数估计统计检验7-1一.建立模型设A 、B 为两个因子,A 有k 个水平1A ,2A ,k A , ,B 有r 个水平r B B B ,,, 21,两个因子共有kr 个水平组合j i B A (k i ,,3,2,1 =;r j ,,3,2,1 =)。
设对每一个水平组合j i B A 做了n 次试验(这里只讨论每个水平所作试验次数相同的情形),试验结果为ijn ij ij y y y ,,,21 (k i ,,3,2,1 =;r j ,,3,2,1 =)。
假定对水平组合j i B A 试验结果的理论值为ij μ,即ijl Ey =ij μ,则ijl y 可分解为modelingijl ij ijl y εμ+= k i ,,3,2,1 =;r j ,,3,2,1 =; n l ,,2,1 = (7-9)其中ijl ε为试验误差,它是一个随机变量。
ijl ε(k i ,,3,2,1 =;r j ,,3,2,1 =;n l ,,2,1 =)独立同分布)0(2σ,N 。
通常假定为了反映因子A 、B 的水平变化对试验结果影响的大小,将ij μ再进行分解,记∑∑===ki rj ijkr 111μμ∑==rj ij i r 11μμ(k i ,,,21=) (7-10) ∑==ki ij j k v 11μ(r j ,,,21=) (7-11) 于是有=ij μ+μ+-)(μμi +-)(μj v )(μμμ+--j i ij v μ=ˆ++i α+j βijγ其中,i α=μμ-i ,j β=μ-j v ,ij γ=μμμ+--j i ij v ,不难验证:∑=ki i 1α=0, ∑==rj j 10β, ∑∑====ki rj ij ij 110γγ,两个因素方差分析的一般数学模型:⎪⎪⎩⎪⎪⎨⎧===⋅⋅==++++=∑∑∑∑====,,1,,1,,1),0( 0= 0= 0,2111r 1j n l r j k i dN i i y ijl k i k i r j ij ij j i ijl ij j i ijl ;;,,,,σεγγβαεγβαμ(7-12)需要解决如下问题:(1)估计未知参数μ,i α,j β,ij γ(n l r j k i ,,1,,1,,1 ===;;);(2)考察因子A 和因子B 的水平变化对试验结果的影响有无显著差异,以及因子A 和因子B 有无交互作用,归结为下述三个假设检验:需要解决如下问题:(1)估计未知参数μ,i α,j β,ij γ(n l r j k i ,,1,,1,,1 ===;;);(2)考察因子A 和因子B 的水平变化对试验结果的影响有无显著差异,以及因子A 和因子B 有无交互作用,归结为下述三个假设检验:02101====k H ααα :; 02110====r H βββ :;:11H ij γ=0,r j k i ,,1,,1 ==;。
高等数学概率论与数理统计课件PPT大全

(AB)C=(AC)(BC) 4、对偶(De Morgan)律:
A B A B, AB A B
可推广 Ak Ak , Ak Ak .
k
k
k
k
例:甲、乙、丙三人各向目标射击一发子弹,以A、 B、C分别表示甲、乙、丙命中目标,试用A、B、C
定义:(p8) 事件A在n次重复试验中出现nA次,则 比值nA/n称为事件A在n次重复试验中 出现的频率,记为fn(A). 即 fn(A)= nA/n.
历史上曾有人做过试验,试图证明抛掷匀质硬币时 ,出现正反面的机会均等。
实验者
De Morgan Buffon
K. Pearson K. Pearson
随机事件
二、样本空间(p2)
1、样本空间:试验的所有可能结果所
组成的集合称为样本空间,记为={e};
2、样本点: 试验的单个结果或样本空间 的单元素称为样本点,记为e. 3.由样本点组成的单点集 称为基本事件, 也记为e.
幻灯片 6
随机事件
1.定义 样本空间的任意一个子集称为随机事件, 简称“ 事件”.记作A、B、C等
P( AB) P( AC) P(BC) P( ABC )
30% 3 10% 0 0 0 80%
例1.3.2.在110这10个自然数中任取一数,求
(1)取到的数能被2或3整除的概率,
(2)取到的数即不能被2也不能被3整除的概率,
(3)取到的数能被2整除而不能被3整除的概率。
解:设A—取到的数能被2整除; P(A) 1 P(B) 3
的概率有多大?
3.分组问题
例3:30名学生中有3名运动员,将这30名学生平均 分成3组,求: (1)每组有一名运动员的概率; (2)3名运动员集中在一个组的概率。 解:设A:每组有一名运动员;B: 3名运动员集中在一组
概率论 高等院校概率论课件JXHD1-6

§1.6 事件的独立性设B A 、为两个事件,0)(>B P ,一般)|()(B A P A P ≠。
[引例] 设试验E 为抛掷甲、乙两枚匀质硬币,观察正(H )、反(T )面出现的情况。
分析:设事件A 表示:“甲币出现正面”;事件B 表示:“乙币出现正面”,则试验E 的样本空间}{TT TH HT HH ,,,=Ω由此21)(=A P ,21)(=B P ,而2/1)(/)()|(==B P AB P B A P ,即2/1)()|(==A P B A P ,于是由乘法公式)|()()(B A P B P AB P =)()(A P B P =Independence of Event定义1-4 设B A 、两个事件,如果 )()()(A P B P AB P =则称B A 、为相互独立事件。
由定义1-4易证,若事件A 与事件B 相互独立,则 (1)B A 与、B A 与、B A 与也相互独立;(2))|()()|()(A B P B P B A P A P ==,。
证明:(1)欲证明B A 、相互独立,只需证)()()(B P A P B A P =即可。
而)()(AB A P B A P -=)()()(B P A P A P -=))(1)((B P A P -=)()(B P A P =所以事件A 与事件B 相互独立。
同理)()(AB B P B A P -=)()()(B P A P B P -= ))(1)((A P B P -=)()(B P A P =所以事件A 与事件B 相互独立。
)()(B A P B A P =)(1B A P -=)()()(1AB P B P A P +--=)()()()(1B P A P B P A P +--=)()()](1)][(1[B P A P B P A P =--=所以事件A 与事件B 相互独立。
对于事件A 与事件B ,由于例1-17 甲、乙两人各自同时向敌机射击,已知甲击中敌机的概率为0.6,乙击中敌机的概率为0.5,求敌机被击中的概率。
概率论 高等院校概率论课件JXHD7-3

§7.3 正交试验设计Orthogonal experimental design 一.正交表二.正交试验的特点三.水平数不同的试验四.有交互作用的试验7-1一.正交表正交表有)2(78L 、)3(49L 、)5(625L 、)23(4112 L 等等,如:表7-9 )3(49L 水 因平 子 A B CD 试验号1 1 1 1 12 1 2 2 23 1 3 3 34 2 1 2 35 2 2 3 16 2 3 1 27 3 1 3 28 3 2 1 39 3 3 2 1Orthogonal layout正交表中L 表示正交表,其余三个数各有几种不同的含义。
现以)3(49L 为例说明如下:(1))3(49L 中的9表示试验次数,4表示因子个数,3表示水平数;(2))3(49L 的用法:该表最多可安排3个水平的因子4个,共做9次试验;(3))3(49L 的结构:该表有9行,4列,表中有3个反应水平的数字1、2、3,见表7-9。
(4))3(49L 的效率:)3(49L 只从43个试验中找出9个来做,经分析仍能找到43个试验中水平组合较好的或最好的。
二.正交试验的特点假定四个因子间没有交互作用,用i i i i d c b a 、、、分别表示因子A 、B 、C 、D 的主效应。
9次试验结果以921y y y ,,, 表示,于是由方差分析模型和)3(49L 正交表可知: ⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧+++++=+++++=+++++=+++++=+++++=+++++=+++++=+++++=+++++=912339831238723137621326513225432124333313222212111111εμεμεμεμεμεμεμεμεμd c b a y d c b a y d c b a y d c b a y d c b a y d c b a y d c b a y d c b a y d c b a y (7-29)由于 ∑=31i i a =∑=31i i b =∑=31i i c =∑=31i i d =0951y y y ++即 )(31)(319511951εεεμ++++=++d y y y 类似地, 762276233εεεμ++++=++d y y y 843384333εεεμ++++=++d y y y )(31)(31ˆ95119511εεεμ++++=++=d y y y k D (7-30))(31)(31ˆ76227622εεεμ++++=++=d y y y k D (7-31))(31)(31ˆ84338433εεεμ++++=++=d y y y k D (7-32)951133εεεμ++++=d ⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧+++++=+++++=+++++=+++++=+++++=+++++=+++++=+++++=+++++=912339831238723137621326513225432124333313222212111111εμεμεμεμεμεμεμεμεμd c b a y d c b a y d c b a y d c b a y d c b a y d c b a y d c b a y d c b a y d c b a y (7-29)因此D 的主效应估计为 ⎪⎩⎪⎨⎧-=-=-=μμμD D D k d k d k d 332211ˆˆˆ (7-33)同理可估计出其他三个因子的主效应。
概率论 高等院校概率论课件JXHD5-1
数理统计初步数理统计的基本概念参数估计假设检验§5.1数理统计的基本概念一.总体、样品、样本二.的联合分布四.统计量n X X X ,,21五.抽样分布返回三.频率分布表与直方图一.总体、样品、样本样品:从总体中随机抽取的一个个体;总体:要研究对象的全体;样本:由若干个样品构成,样本中包含样品的个 数称为样本长度。
(1)总体是一个v r ⋅,记为X ,其分布函数F x ()称为总体分布函数;(2)样品也是一个v r ⋅,它与总体同分布; (3)样本是由若干独立同分布的r v ⋅所构成,样品的个数称为样本长度。
Population SampleSample size设X 为一个总体,n X X X ,,, 21为来自总体的一个长度为n 的样本,它的观察值为n x x x ,,,21 。
由n X X X ,,, 21的独立性知,若X 的分布函数为)(x F ,则n X X X ,,, 21的联合分布函数为二.n X X X ,,, 21的联合分布 *F (n x x x ,,,21 )=∏=n i i x F 1)( (5-1)Allied Distribution若X 的分布密度为)(x f ,则n X X X ,,, 21的联合分布密度为*f (n x x x ,,,21 )=f x i i n()=∏1 (5-2)若X 是离散型随机变量,其概率分布为 ,,2,1),( ===k x X P p k k 则X X X n 12,,, 的联合概率分布为n n i i i i n i i p p p x X x X x X P 2121},,,{21====,2,1,,,21=n i i i三、频率分布表与直方图设x x x n 12,,, 是总体X 的一组样本值,可用频率分布表与直方图粗略地描述总体X 的分布。
设总体X 是离散型随机变量,x x x n 12,,, 是总体X 的一组样本值。
大学概率课件(全)

(a)放回抽样情况 在袋中依次取两只球,每一种取法为一个样本点, 而第一种取法的第一次取球有6只球可供选择,第二 次仍有6只球可供选择,根据组合法的乘法原理,这 种抽球试验的样本空间共有6×6个样本点;若事件A 发生,由第一次有4只球可供抽取,第二次仍有4只 球可供抽取,故A含有4×4个样本点,同理B中含有 2×4个样本点,故
2、几何概型的计算公式
试验可看作是在某一可度量(如长度、面积、 体积等)的区域Ω内任取一点,则此时样本 空间即为区域Ω内的点的全体,而随机事 件A={取到的点落在某子区域SA内}的概率 为
由频率的性质可知概率满足: 1 非负性:AΩ,0P(A)1; 2 规范性:P(Ω)=1; 3 有限可加性:若A1,A2,,An互斥,则
P ( Ai ) P ( Ai )
i 1 i 1
n
n
第二节
古典概型
若试验具有下述两特点:
1、试验的可能结果只有有限个
2、每个可能结果出现的可能性相等
例2.1 设某射手对一目标连续进行三次射击,
记Ai {第i次击中目标},那么,Ai {第i次 1) B j {三次射击中恰好有 j次击中目标}, j 0,1,2,3 2)C k {三次射击中至少有 k次击中目标}, k 0,1,2,3
射击未中目标 },试用Ai,i 1,2,3表示事件:
实验者
蒲丰
投掷次数n
4040
正面出现频数n
2048
频率f(A)
0.50692
摩根
费勒 皮尔逊 皮尔逊 罗曼诺夫斯基
4092
10000 12000 24000 80640
2048
4979 6019 12012 39699
概率论 高等院校概率论课件JXHD0-1

绪论篇随机现象任务与研究方式概率论起源发展简史应用前景学习方法指导必然现象与随机现象在一定条件下,某些事情一定发生或一定不发生的现象。
在一定条件下,可能发生也可能不发生的现象。
必然现象:随机现象:Necessity PhenomenonRandom Phenomenon任务与研究方式概率论与数理统计的任务:研究和揭示随机现象的统计规律性。
从数量的侧面研究随机现象统计规律。
研究方式:The Task of Probability and Statistics Statistics LawStudy manner概率论起源Origin 概率论与数理统计是一门古老的学科,它起源于十七世纪资本主义上升的初期,这时航海商业有了很大的发展,关闭的封建社会经济正在被航海商业经济所取代。
然而航海商业是冒风险的事业,人们自然要关心大量投资是否有利可图?怎样估计出现各种不幸事故与自然灾害的可能性?在桥牌活动中,经常需要判断某种花色在对方手中的分配等等。
从某种意义上讲,概率论与数理统计正是从研究这类问题开始的。
发展简史Simple history 尽管概率论与数理统计发展较早,但形成一门严谨的学科是在上世纪三十年代,由前苏联数学家柯尔莫奇洛夫给出了概率的公理化定义后,才得以迅速发展。
特别是,电子计算机的问世,进一步加速了概率论与数理统计的发展。
六十年代后,形成了许多新的统计分支:时间序列分析、统计推断、稳键统计、投影寻踪等,从事这方面的理论,尤其是应用方面研究的科技工作者也越来越多,目前它几乎遍及所有科学技术领域。
应用前景Prospect 概率论与数理统计应用呈现出极其状观的局面,尤其在质量管理、计量经济学、计量心理学、保险数学方面起着重要的作用。
数理统计已渗透于工业统计、农业统计、水文统计、统计医学、统计力学、统计物理学、统计化学、统计教育学、统计体育学、统计心理学等许多领域。
气象预报、产量预报、地震预报、石油勘探开发、可靠性工程等凡是有数据需要处理的地方,都离不开概率统计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
an
n
xj 0
j 1
a.e.
, 1 p 2; an n ,则
(7)
n
1 np
E
(
X
n
p)
1 n
n j 1
X
j
0
a.e
定理5.4.2
设{xn} 是一个独立同分布的随机变量序列,则我们有
(8)
E( X1 )
Sn n
EX1
(17)
n
an (aN
aN x an
x dF(x))) ()
因为 E( X1)
,如果 an n
保持有界,则(12)中的级数不可能收敛,所以对于固
定的
N,当
n 时,因为 an n
n an
0
n an
aN
0 ,所以(17)中的第
一项趋向于 0. 后面一项被下面式子所界,
(18) n
b1
x1 a1
, b2
x1 a1
x2 a2
bn
n xj j1 a j
于是有
x1 a1
b1 ,
x2 a2
b2 b1 ,
xn an
bn bn1
S 1 an
n
xj
j 1
1 an
n j 1
aj
xj aj
1 an
[a1b1
a2 (b2
b1 ) a3 (b3
b2 ) an (bn
( X 1 An)
n
因为随机变量独立同分布,故有 ( X n An)
n
根据定理 4.2.4:如果事件{X }是独立的,则 n
( X n ) ( X n , i.o) 1
n
可得
{ X n An,i.o.} 1
而 Sn Sn1
Xn
An蕴含着 Sn
An 2
或者
S n1
An 2
{ Sn
An , i.o.} 1 2
故有
这意味着对于每个 A,存在一个零集 Z(A),使得如果 w \ Z ( A) ,则
(a)
____
lim
Sn (w)
A.
n n
2
设 Z Z (m), 则 Z 仍为零集,且如果 w \ Z ,则(a)式对每个 A 成立,因
M 1
而上极限为 ,故有
则对于每个 0 我们有
max
1 jn
Sj
2 (Sn
2
)
.
定理 5.3.2
设 X n 是具有有限平均值的随机变量,设存在一个 A 使得
n : X n E( X n ) A
则对于每个 0 我们有
max
1 jn
Sj
s
(2 A 4 ) 2 2 (Sn )
.
定理 5.3.3
an
n
aj
j N 1
dF(x)
aN x an
n
j
j N 1
dF ( x)
aN x an
因为对于 j n na j j ,我们用 代替(18)式右边的 n;作为(13)中收敛
的余项,当 N 时它趋向于 0.因此当 n 时(16)中的量趋向于 0,由(14)
和(15)式得 1 an
lim _____ Sn
n n
a.e
定理5.4.3
设 {X n } 是一个独立同分布的随机变量序列,且 E( X1 ) . 设 an 是满足条件
an n 的正数列,则我们有
(11) (12)
lim _____ Sn 0 a.e.;或者
n an
a.e.
按
{ X n an}
j 1
E(X1) ,
因而
1
n
n
Yj
j 1
E(X1)
a.e
由{X }与{Y }等价,根据定理 5.2.1 知 1
n
n
n
n
Yj
j 1
可用 1 n
n j 1
X
j
来代替,即
1
n
n
Xj
j 1
Sn n
E(X1)
a.e
证明了(8).
证明(9):由条件 E( X1 ) 蕴含 E( X1 A) 因而由定理 3.2.1 有
所以有
1 an
n
(a j1 a j )
j 1
1 an
n
(a j1 a j )
j0
1 an (an
a0
)
1
且 bn b ,而 b 是一个有界数,不妨设 b M
引理证毕.
1
an
n
xj
j 1
b b M M
0.
现假设 是 R' 上的一个正值连续偶函数,使得当 x 增加时,有
(1)
x
an
x (x) an (an )
由此有 E(Yn )
n an
n
(x) x an (an )dFn (x)
n
E((Xn )) (an )
即 E(Yn ) 几乎处处收敛的,又因为(5)式也是几乎处处收敛的, an
所以 Yn 也几乎处处收敛,最后,由 (x) 1
n an
(an )
n j
j
n
2 (Yn ) n2
收敛,应用(7)于{{Yn
E(Yn )} },我们得出结论:
1 n
n j1 Y j E(Y j ) 0
a.e.
显然当 n 时,因为{X n }独立同分布,所以 E( X n ) E( X1 ) E(Yn ) E( X1 )
故我们也有
1 n
n
E(Y j )
n
1 n2
n j 1
j1 x j x 2 dFn ( x) = j 1
j 1
x
j
x 2 dFn
(x)
n 1
1 n2
j
x dF(x) C
j 1 x j j 1
j
C j
x dF(x)
j 1 x j
j 1
C E( X1 )
在上面我们已经应用了估计式 n 2 C ,其中 C 是某个常数, j 1.于是
bn1 )]
1 an
[(a1
a2 )b1
(a2
a3 )b2
(an1
an )bn1
a nbn
]
1 an
[
n
(a j
j 1
a j1 )b j
anbn ]
1
an
n
(a j a j1 )b j bn
j 1
bn
1 an
n
(a j1 a j )b j
j 1
因为 an 递增 有 a j1 a j 0 ,
设 X n 是独立的随机变量,对于一个固定的常数 A>0,定义
Yn
(w)
X n (w), 如果 X n (w)
0,
如果
X
n
(w)
A.
A:
则级数 X n 几乎处处收敛的充要条件是下面的三级数都收敛;
n
(ⅰ) X n A X n Yn ,
n
n
(ⅱ) E (Yn )
n
(ⅲ)
2 (Yn )
(Yn )几乎处处收敛.
其次我们有
(Yn )
1
n an
n an
x an x d Fn (x)
1
= n an
x an x d Fn ( x)
n
x
an
x an
dFn (x) ,
此处由( E( X n )
xdFn
(x)
0
)由(1)中的第一个假设
对于 x an
有 (x) (an )
我们可以得到
{X n Yn}
n
n
x an dFn (x)
(x)
E ( ( x))
n
x an (an )dFn (x) n
(an )
由 5.2 定义知X n 与Yn 是等价序列,所以
n
X n 也几乎处处收敛。 an
对于一个概率为 1 的集中的每一个 w ,将克罗内克引理应用于(3),我们得 到 推论: 在定理 5.4.1 的假设下,我们有
n
强大数定律的主要内容
❖ 克罗内克引理
设{xk } 是实数的一个序列,{ak }是一个 0 且 的一个数列,则
n
xn an
1 an
n
x j 0.
j 1
证明:
对于1 n ,令
bn
n xj j1 a j
.
如果再记 a0 0 , b0 0 ,则我们有
阿贝尔变换为
xn an (bn bn1 )
(x) , (x)
x
x2
上式为下面定理 5.4.1 的一个条件,在这里我们不必考虑它是怎么来的,只要知
道它们的性质,即 (x) 随着 x 的增加而增加,而 (x) 随 x 的增加而减小.
x
x2
定理5.4.1
设{xn } 是一个独立随机变量序列,且对于每个 n ,E(xn ) 0 ;又 0 an .
dF(x) .
n
an 2
k 1
ak 1 x ak
所以由定理 5.4.1 Yn 几乎处处收敛,因而由 kronecker 引理有 n an
(15)
1
an
n
Yk
k 1
0
a.e.
当 n 时,我们来估计下面这个量
(16)
1
an
n
k
k 1
1 an
n k 1
xdF(x) .
x an
