第一、二、三章习题
高等数学(二)(线性代数)一 第二三章 习题集(部分)

设有矩阵,(m≠n),下列运算结果不是阶矩阵的是().A、BAB、ABC、D、设矩阵A可以左乘矩阵B,则().A、B、C、D、若|A|=0,则A=().A、0矩阵B、数字0C、不一定是0矩阵D、A中有零元素两个n阶初等矩阵的乘积为().A、初等矩阵B、单位矩阵C、可逆阵D、不可逆阵若m×n阶矩阵A中的n个列线性无关,则A的秩().A、大于mB、大于nC、等于nD、等于n矩阵A经有限次初等行变换后变成矩阵B,则().A、A与B相似B、A与B不等价C、A与B相等D、r(A)=r(B)设m×n阶矩阵A,B的秩分别为,则分块矩阵(A,B)的秩r适合关系式(). A、B、C、D、矩阵A经过初等变换后().A、不改变它的秩B、改变它的秩C、改变它的行秩D、改变它的列秩设A为三阶方阵,且|A|=-2,则矩阵|A|A行列式||A|A|=().A、16B、-16C、8D、-8两矩阵A与B既可相加又可相乘的充要条件是().A、A、B是同阶方阵B、A的行数=B的行数C、A的列数=B的列数D、A的行数、列数分别等于B的行数、列数初等矩阵().A、相乘仍为初等阵B、相加仍为初等阵C、都可逆D、以上都不对线性方程组有解的充分必要条件是a=().A、B、-1C、D、1存在有限个初等矩阵,使是A为可逆矩阵的().A、必要条件B、充分条件C、充要条件D、无关条件矩阵A经过有限次初等行变换后变成矩阵B,则().A、r(A)≠r(B)B、A与B相等C、A的行向量组与B的行向量组等价D、A与B不等价设,,,,则向量组共有()个不同的极大无关组.A、1B、2C、3D、4设n阶矩阵A的秩为r,则结论()成立.A、|A|≠0B、|A|=0C、r>nD、已知矩阵则().A、0B、1C、2D、3设A、B均为n阶方阵,则必有().A、|A+B|=|A|+|B|B、AB=BAC、|AB|=|BA|D、若均为n阶可逆矩阵,则(). A、B、C、D、阵的行向量组().A、一定线性无关B、一定线性相关C、不能确定D、以上都不对一个向量组若有两个或两个以上的极大无关组,则各个极大无关组所含向量个数必().A、不相等B、相等C、大于零且小于2D、大于零且小于3设是齐次线性方程组的三个线性无关的解向量,则().A、一定是的基础解系B、不一定是的解C、不一定是的解D、有可能是的基础解系设A,B均为n阶矩阵,如果则必有().A、A=EB、B=0C、A=BD、AB=BA设n阶矩阵A,B,C满足ABC=E,则必有().A、ACB=EB、BAC=EC、CBA=ED、BCA=E设矩阵,则下列结论不正确的是().A、A是上三角矩阵B、A是下三角矩阵C、A是对称矩阵D、A是可逆矩阵设矩阵,则下列结论正确的是().A、A是上三角矩阵B、A是下三角矩阵C、A是对称矩阵D、A是对角矩阵已知,则A=().A、B、C、D、下列矩阵中,不是初等矩阵的是().A、B、C、D、设是齐次线性方程组的二个线性无关的解向量,则().A、一定是的一个基础解系B、有可能是的一个基础解系C、不是的一个解D、不是的一个解设A为n阶方阵,且|A|=8,A*是A的伴随矩阵,则AA*是().A、数量矩阵B、单位矩阵C、三角矩阵若矩阵A中有一个r阶子式D≠0,且A中有一个含有D的r+1阶子式等于零,则一定有(). A、B、设n阶方阵A可逆,数k≠0,则().A、B、C、D、给定矩阵,,,下列()运算可行.A、ACB、CBC、ABCD、AB-BC. =().A、B、C、D、一个n维向量组线性相关的充要条件是其中().A、含有零向量B、有两个向量的对应分量成比例C、有一个向量是其余向量的线性组合D、每一个向量是其余向量的线性组合设A与B都是n阶方阵,则r(A+B)().A、B、C、D、?若A为n阶可逆矩阵,下列各式正确的是().A、B、C、D、C和D都不对若齐次线性方程组(Ⅰ)有非零解,则(Ⅰ)的系数行列式().A、等于1B、等于5C、等于零D、不等于零D不对设A是m×n矩阵,齐次线性方程组是非齐次线性方程组的导出组,则(). A、仅有零解时,有唯一解B、有非零解时,有无穷多解C、有无穷多解时,仅有零解D、有无穷多解时,有非零解C不对设向量可由向量组线性表示,则表示法唯一的充要条件是().A、全为非零向量AB不对选C或DB、全为零向量C、线性相关D、线性无关。
建筑设备基础知识与识图(第2版)课后习题

习题答案及解析第一章习题答案1.简述流体主要物理性质的定义。
在实际工程中如何考虑?1.流体的密度:指各点密度相同的均质流体,单位体积的质量,用ρ表示(kg/ m 3)。
实际工程中计算压力管道、水池、水箱的压强、选择水泵、风机型号时的重要参数;特别应该注意的是水的密度在4℃以下时的变化规律,敷设在室外管道中的水在冰冻时,密度减小,体积增大,致使管道漏水,所以室外的管道应考虑防冻结措施。
2.流体的容重:指各点密度相同的均质流体,单位体积的重量,用γ表示(N/ m 3)。
在计算中,容重的数值等于流体的质量与重力加速度的乘积。
3.流体的压缩性:指流体所受的压力增大时,其体积缩小,密度增大的性质。
压缩性对实际工程的影响很小,可以不予考虑。
4.流体的热膨胀性:流体因温度升高使原有的体积增大,密度减小的性质。
热膨胀性在热水供应系统及热水采暖系统中,充满水的管道,在温度升高而膨胀时,会造成管道爆裂而漏水;而温度降低水的体积减小时,又造成水量不足。
需要设置膨胀水箱应对热膨胀性的影响。
5.流体的黏滞性:流体在运动时,由于内摩擦力的作用,使流体具有抵抗相对变形(运动)的性质。
流体在运动过程中,必须克服黏性力,因此要不断消耗运动流体所具有的能量,所以是研究沿程水头损失的重要参数,而计算水头损失是计算水泵扬程的重要依据。
2.流体静压强的特性如何?流体静压强有哪几种计算形式?各种形式在什么情况下应用?(1)特性:静压强的方向性:流体具有各个方向上的静压强,流体的静压强处处垂直并指向固体壁面;静压强的大小:静止流体中任意一点的静压强大小与其作用方向无关,仅与其高度或深度有关。
气体的静压强沿高度变化小,密闭容器可以认为静压强处处相等。
(2)计算形式及其应用:液下不同深度两个表面的压强关系p 2=p 1+γh当上表面设在水平面,即上表面压强为液体表面压强p 0时, p =p 0+γh当上表面压强为0时 p =γh3.试述绝对压强、相对压强和真空压强的定义,以及三者之间的关系。
第1、2、3、4章练习题

第一章练习题1、物质能以液态形式存在的最高温度为(A)沸腾温度Tb (B)玻义耳温度TB (C)临界温度Tc2、当压缩因子Z<1时,表示该实际气体(A)易压缩(B)不易压缩(C)无法确定3、下列何种条件下真实气体可以液化()(A)Tr>1,Pr>1 (B)Tr>1,Pr<1 (C)Tr=1,Pr<1 (D)Tr<1,Pr=14、对理想气体,压缩因子Z=1。
能否说当气体的Z=1 时,该气体必定是理想气体。
答案:(不能,因为在实际气体的等温线与理想气体的等温线交点处,Z=1)5、当温度足够低时,任何实际气体的Z~P 曲线与理想气体的Z~P 曲线均交于两点。
试解释这种现象。
答案:(这是因为当温度足够低时,气体的玻义耳温度高于体系温度,Z~p 曲线出现极小值。
)6、从范德华方程出发并结合玻义耳温度定义,证明(1)在足够高的温度,实际气体的压缩因子Z>1 。
(2)在低温,低压下,Z<1 。
答案:(当T<=TB,Z>1)(3)当a=0 ,Z 随压力p 的增加而线性增加。
答案:(当a=0,Z=1+bp/RT,恒温时,p 增加,Z 增大。
)7、下列说法何者正确?(1)临界压力是气体可被液化的最低压力。
(2)气体被液化的必要条件是气体温度小于波义耳温度(3)在临界点,饱和液体与饱和蒸气的密度相同。
(4)气体的临界状态与气体的性质无关。
答案:(3)8、气体A、B、C 都服从范德华方程,其范德华常数a和b的大小顺序为a(A)=a(B)>a(C);b(C)>b(B)>b(A)。
问三种气体临界温度的大小顺序。
答案:(T c(A)>T c(B)>T c(C))9、某气体的状态方程为,式中b为常数,n为物质的量。
若该气体经一等温过程,压力自p1变至p2,则下列状态函数的变化,何者为零?(ΔU)第二章练习题1、指出下列说法的错误。
(1)因Qp =ΔH,Qv=ΔU,所以Qp 和Qv 都是状态函数。
新教材 人教A版高中数学选择性必修第一册全册各章节课后练习题 含解析

选择性必修第一册全册课后练习题本文档还有大量公式,在网页中显示可能会出现位置错误的情况,下载后均可正常显示,请放心下载练习!第一章空间向量与立体几何................................................................................................ - 2 -1.1.1空间向量及其线性运算......................................................................................... - 2 -1.1.2空间向量的数量积运算......................................................................................... - 8 -1.2空间向量基本定理.................................................................................................. - 15 -1.3.1空间直角坐标系 .................................................................................................. - 22 -1.3.2空间运算的坐标表示........................................................................................... - 28 -1.4.1.1空间向量与平行关系 ....................................................................................... - 34 -1.4.1.2空间向量与垂直关系 ....................................................................................... - 42 -1.4.2用空量研究距离、夹角问题............................................................................... - 51 -章末测验 ....................................................................................................................... - 64 - 第二章直线和圆的方程...................................................................................................... - 78 -2.1.1倾斜角与斜率 ...................................................................................................... - 78 -2.1.2两条直线平行和垂直的判定............................................................................... - 83 -2.2.1直线的点斜式方程............................................................................................... - 87 -2.2.2直线的两点式方程............................................................................................... - 92 -2.2.3直线的一般式方程............................................................................................... - 97 -2.3.1两条直线的交点坐标......................................................................................... - 102 -2.3.2两点间的距离公式............................................................................................. - 102 -2.3.3点到直线的距离公式......................................................................................... - 107 -2.3.4两条平行直线间的距离..................................................................................... - 107 -2.4.1圆的标准方程 .................................................................................................... - 113 -2.4.2圆的一般方程 .................................................................................................... - 118 -2.5.1直线与圆的位置关系......................................................................................... - 122 -2.5.2圆与圆的位置关系............................................................................................. - 128 -章末测验 ..................................................................................................................... - 135 - 第三章圆锥曲线的方程.................................................................................................... - 144 -3.1.1椭圆及其标准方程............................................................................................. - 144 -3.1.2.1椭圆的简单几何性质 ..................................................................................... - 150 -3.1.2.2椭圆的标准方程及性质的应用...................................................................... - 156 -3.2.1双曲线及其标准方程......................................................................................... - 164 -3.2.2双曲线的简单几何性质..................................................................................... - 171 -3.3.1抛物线及其标准方程......................................................................................... - 178 -3.3.2抛物线的简单几何性质..................................................................................... - 184 -章末测验 ..................................................................................................................... - 191 - 模块综合测验 ..................................................................................................................... - 202 -第一章 空间向量与立体几何1.1.1空间向量及其线性运算一、选择题1.空间任意四个点A ,B ,C ,D ,则DA →+CD →-CB →等于( ) A .DB → B .AC → C .AB → D .BA → D [DA →+CD →-CB →=DA →+BD →=BA →.]2.设有四边形ABCD ,O 为空间任意一点,且AO →+OB →=DO →+OC →,则四边形ABCD 是( )A .平行四边形B .空间四边形C .等腰梯形D .矩形A [∵AO →+OB →=DO →+OC →,∴AB →=DC →. ∴AB →∥DC →且|AB →|=|DC →|. ∴四边形ABCD 为平行四边形.]3.已知A ,B ,C 三点不共线,对平面ABC 外的任一点O ,下列条件中能确定点M 与点A ,B ,C 一定共面的是( )A .OM →=OA →+OB →+OC → B .OM →=2OA →-OB →-OC → C .OM →=OA →+12OB →+13OC →D .OM →=13OA →+13OB →+13OC → D [由OM →=13OA →+13OB →+13OC →,可得3OM →=OA →+OB →+OC →⇒OM →-OA →+OM →-OB →+OM →-OC →=0, 即AM →=-BM →-CM →.所以AM →与BM →,CM →在一个平面上,即点M 与点A ,B ,C 一定共面.] 4.若空间中任意四点O ,A ,B ,P 满足OP →=mOA →+nOB →,其中m +n =1,则( )A .P ∈AB B .P ∉ABC .点P 可能在直线AB 上D .以上都不对A [因为m +n =1,所以m =1-n , 所以OP →=(1-n )OA →+nOB →, 即OP →-OA →=n (OB →-OA →), 即AP →=nAB →,所以AP →与AB →共线. 又AP →,AB →有公共起点A ,所以P ,A ,B 三点在同一直线上, 即P ∈AB .]5.已知在长方体ABCD -A 1B 1C 1D 1中,点E 是A 1C 1的中点, 点F 是AE 的三等分点,且AF =12EF ,则AF →=( )A .AA 1→+12AB →+12AD → B .12AA 1→+12AB →+12AD →C .12AA 1→+16AB →+16AD → D .13AA 1→+16AB →+16AD →D [如图所示,AF →=13AE →,AE →=AA 1→+A 1E →,A 1E →=12A 1C 1→,A 1C 1→=A 1B 1→+A 1D 1→,A 1B 1→=AB →,A 1D 1→=AD →,所以AF →=13⎝ ⎛⎭⎪⎫AA 1→+12A 1C 1→=13AA 1→+16AB →+16AD →,故选D.]二、填空题6.已知A ,B ,C 三点不共线,O 为平面ABC 外一点,若由OM →=-2OA →+OB →+λOC →确定的点M 与A ,B ,C 共面,则λ=________.2 [由M 、A 、B 、C 四点共面知:-2+1+λ=1,即λ=2.]7.在平行六面体ABCD -A 1B 1C 1D 1中,M 为AC 与BD 的交点,若A 1B 1→=a ,A 1D 1→=b ,A 1A →=c ,用a ,b ,c 表示D 1M →,则D 1M →=________.12a -12b +c [D 1M →=D 1D →+DM → =A 1A →+12(DA →+DC →) =c +12(-A 1D 1→+A 1B 1→) =12a -12b +c .]8.在空间四边形ABCD 中,E ,F 分别是AB ,CD 的中点,则EF →和AD →+BC →的关系是________.(填“平行”,“相等”或“相反”)平行 [设G 是AC 的中点,则EF →=EG →+GF →=12BC →+12AD →=12(AD →+BC →) 所以2EF →=AD →+BC →, 从而EF →∥(AD →+BC →).] 三、解答题9.如图,在空间四边形ABCD 中,G 为△BCD 的重心,E ,F 分别为边CD 和AD 的中点,试化简AG →+13BE →-12AC →,并在图中标出化简结果的向量.[解] ∵G 是△BCD 的重心,BE 是CD 边上的中线,∴GE →=13BE →.又12AC →=12(DC →-DA →)=12DC →-12DA →=DE →-DF →=FE →, ∴AG →+13BE →-12AC →=AG →+GE →-FE →=AF →(如图所示).10.在长方体ABCD -A 1B 1C 1D 1中,M 为DD 1的中点,点N 在AC 上,且AN ∶NC =2∶1,求证:A 1N →与A 1B →,A 1M →共面.[证明] ∵A 1B →=AB →-AA 1→, A 1M →=A 1D 1→+D 1M →=AD →-12AA 1→, AN →=23AC →=23(AB →+AD →), ∴A 1N →=AN →-AA 1→ =23(AB →+AD →)-AA 1→=23(AB →-AA 1→)+23(AD →-12AA 1→) =23A 1B →+23A 1M →, ∴A 1N →与A 1B →,A 1M →共面.11.(多选题)若A ,B ,C ,D 为空间不同的四点,则下列各式为零向量的是( ) A .AB →+2BC →+2CD →+DC → B .2AB →+2BC →+3CD →+3DA →+AC →C.AB →+CA →+BD →D.AB →-CB →+CD →-AD →BD [A 中,AB →+2BC →+2CD →+DC →=AB →+2BD →+DC →=AB →+BD →+BD →+DC →=AD →+BC →;B 中,2AB →+2BC →+3CD →+3DA →+AC →=2AC →+3CA →+AC →=0;C 中,AB →+CA →+BD →=AD →+CA →;D 中,AB →-CB →+CD →-AD →=AB →+BC →+CD →+DA →表示A →B →C →D →A 恰好形成一个回路,结果必为0.]12.(多选题)有下列命题,其中真命题的有( ) A .若AB →∥CD →,则A ,B ,C ,D 四点共线 B .若AB →∥AC →,则A ,B ,C 三点共线C .若e 1,e 2为不共线的非零向量,a =4e 1-25e 2,b =-e 1+110e 2,则a ∥b D .若向量e 1,e 2,e 3是三个不共面的向量,且满足等式k 1e 1+k 2e 2+k 3e 3=0,则k 1=k 2=k 3=0BCD [根据共线向量的定义,若AB →∥CD →,则AB ∥CD 或A ,B ,C ,D 四点共线,故A 错;因为AB →∥AC →且AB →,AC →有公共点A ,所以B 正确;由于a =4e 1-25e 2=-4-e 1+110e 2=-4b ,所以a ∥b ,故C 正确;易知D 也正确.]13.(一题两空)已知A ,B ,C 三点共线,则对空间任一点O ,若OA →=2OB →+μOC →,则μ=________;存在三个不为0的实数λ,m ,n ,使λOA →+mOB →+nOC →=0,那么λ+m +n 的值为________.-1 0 [由A 、B 、C 三点共线,∴2+μ=1,∴μ=-1,又由λOA →+mOB →+nOC →=0得OA →=-m λOB →-n λOC →由A ,B ,C 三点共线知-m λ-nλ=1,则λ+m +n =0.]14.设e 1,e 2是平面上不共线的向量,已知AB →=2e 1+k e 2,CB →=e 1+3e 2,CD →=2e 1-e 2,若A ,B ,D 三点共线,则实数k 为________.-8 [因为BD →=CD →-CB →=e 1-4e 2,AB →=2e 1+k e 2,又A ,B ,D 三点共线,由共线向量定理得12=-4k ,所以k =-8.]15.如图所示,已知四边形ABCD 是平行四边形,点P 是ABCD 所在平面外的一点,连接P A ,PB ,PC ,PD .设点E ,F ,G ,H 分别为△P AB ,△PBC ,△PCD ,△PDA 的重心.(1)试用向量方法证明E ,F ,G ,H 四点共面;(2)试判断平面EFGH 与平面ABCD 的位置关系,并用向量方法证明你的判断. [证明] (1)分别连接PE ,PF ,PG ,PH 并延长,交对边于点M ,N ,Q ,R ,连接MN ,NQ ,QR ,RM ,∵E ,F ,G ,H 分别是所在三角形的重心,∴M ,N ,Q ,R 是所在边的中点,且PE →=23PM →,PF →=23PN →,PG →=23PQ →,PH →=23PR →.由题意知四边形MNQR 是平行四边形,∴MQ →=MN →+MR →=(PN →-PM →)+(PR →-PM →)=32(PF →-PE →)+32(PH →-PE →)=32(EF →+EH →).又MQ →=PQ →-PM →=32PG →-32PE →=32EG →.∴EG →=EF →+EH →,由共面向量定理知,E ,F ,G ,H 四点共面.(2)平行.证明如下:由(1)得MQ →=32EG →,∴MQ →∥EG →, ∴EG →∥平面ABCD .又MN →=PN →-PM →=32PF →-32PE → =32EF →,∴MN →∥EF →. 即EF ∥平面ABCD . 又∵EG ∩EF =E ,∴平面EFGH 与平面ABCD 平行1.1.2空间向量的数量积运算一、选择题1.已知a ⊥b ,|a |=2,|b |=3,且(3a +2b )⊥(λa -b ),则λ等于( ) A .32 B .-32 C .±32 D .1A [∵a ⊥b ,∴a ·b =0,∵3a +2b ⊥λa -b ,∴(3a +2b )·(λa -b )=0, 即3λa 2+(2λ-3)a ·b -2b 2=0,∴12λ-18=0,解得λ=32.]2.已知空间四边形ABCD 的每条边和对角线的长都等于a ,点E ,F 分别是BC ,AD 的中点,则AE →·AF →的值为( )A .a 2B .12a 2C .14a 2D .34a 2C [AE →·AF →=12(AB →+AC →)·12AD →=14(AB →·AD →+AC →·AD →)=14⎝ ⎛⎭⎪⎫a ×a ×12+a ×a ×12=14a 2.]3.已知长方体ABCD -A 1B 1C 1D 1,则下列向量的数量积一定不为0的是( ) A .AD 1→·B 1C →B .BD 1→·AC →C .AB →·AD 1→ D .BD 1→·BC →D [对于选项A ,当四边形ADD 1A 1为正方形时,可得AD 1⊥A 1D ,而A 1D ∥B 1C ,可得AD 1⊥B 1C ,此时有AD 1→·B 1C →=0;对于选项B ,当四边形ABCD 为正方形时,AC ⊥BD ,易得AC ⊥平面BB 1D 1D ,故有AC ⊥BD 1,此时有BD 1→·AC →=0;对于选项C ,由长方体的性质,可得AB ⊥平面ADD 1A 1,可得AB ⊥AD 1,此时必有AB →·AD 1→=0;对于选项D ,由长方体的性质,可得BC ⊥平面CDD 1C 1,可得BC ⊥CD 1,△BCD 1为直角三角形,∠BCD 1为直角,故BC 与BD 1不可能垂直,即BD 1→·BC →≠0.故选D.]4.在棱长为a 的正方体ABCD -A 1B 1C 1D 1中,向量BA 1→与向量AC →所成的角为( )A .60°B .150°C .90°D .120°D [BA 1→=BA →+AA 1→,|BA 1→|=2a ,AC →=A B →+AD →,|AC →|=2a .∴BA 1→·AC →=BA →·AB →+BA →·AD →+AA 1→·AB →+AA 1→·AD →=-a 2. ∴cos 〈BA 1→,AC →〉=-a 22a ·2a =-12.∴〈BA 1→,AC →〉=120°.]5.如图所示,在平行六面体ABCD -A ′B ′C ′D ′中,AB =1,AD =2,AA ′=3,∠BAD =90°,∠BAA ′=∠DAA ′=60°,则AC ′的长为( )A .13B .23C .33D .43B [∵AC ′→=AB →+BC →+CC ′→,∴AC ′→2=(AB →+BC →+CC ′→)2=AB →2+BC →2+CC ′→2+2(AB →·BC →+AB →·CC ′→+BC →·CC ′→) =12+22+32+2(0+1×3cos 60°+2×3cos 60°) =14+2×92=23,∴|AC ′→|=23,即AC ′的长为23.] 二、填空题6.已知a ,b 是空间两个向量,若|a |=2,|b |=2,|a -b |=7,则cos 〈a ,b 〉=________.18[将|a -b |=7两边平方,得(a -b )2=7. 因为|a |=2,|b |=2,所以a ·b =12.又a ·b =|a ||b |cos 〈a ,b 〉,故cos 〈a ,b 〉=18.]7.已知a ,b 是异面直线,A ,B ∈a ,C ,D ∈b ,AC ⊥b ,BD ⊥b ,且AB =2,CD =1,则a ,b 所成的角是________.60° [AB →=AC →+CD →+DB →,∴CD →·AB →=CD →·(AC →+CD →+DB →)=|CD →|2=1, ∴cos 〈CD →,AB →〉=CD →·AB →|CD →||AB →|=12,∴异面直线a ,b 所成角是60°.]8.已知|a |=2,|b |=1,〈a ,b 〉=60°,则使向量a +λb 与λa -2b 的夹角为钝角的实数λ的取值范围是________.(-1-3,-1+3) [由题意知 ⎩⎨⎧(a +λb )·(λa -2b )<0,cos 〈a +λb ,λa -2b 〉≠-1. 即⎩⎨⎧(a +λb )·(λa -2b )<0,(a +λb )·(λa -2b )≠-|a +λb ||λa -2b |,得λ2+2λ-2<0.∴-1-3<λ<-1+ 3.] 三、解答题9.如图,在四棱锥P -ABCD 中,底面ABCD 是边长为1的正方形,侧棱P A 的长为2,且P A 与AB 、AD 的夹角都等于60°,M 是PC 的中点,设AB →=a ,AD →=b ,AP →=c .(1)试用a ,b ,c 表示出向量BM →; (2)求BM 的长.[解] (1)∵M 是PC 的中点,∴BM →=12(BC →+BP →)=12[AD →+(AP →-AB →)] =12[b +(c -a )]=-12a +12b +12c .(2)由于AB =AD =1,P A =2,∴|a |=|b |=1,|c |=2,由于AB ⊥AD ,∠P AB =∠P AD =60°,∴a·b =0,a·c =b·c =2·1·cos 60°=1, 由于BM →=12(-a +b +c ),|BM →|2=14(-a +b +c )2=14[a 2+b 2+c 2+2(-a·b -a·c +b·c )]=14[12+12+22+2(0-1+1)]=32.∴|BM →|=62,∴BM 的长为62.10.如图,已知直三棱柱ABC -A ′B ′C ′中,AC =BC =AA ′,∠ACB =90°,D ,E 分别为AB ,BB ′的中点.(1)求证:CE ⊥A ′D ;(2)求异面直线CE 与AC ′所成角的余弦值. [解] (1)证明:设CA →=a ,CB →=b ,CC ′→=c , 根据题意得|a |=|b |=|c |,且a·b =b·c =c·a =0. ∴CE →=b +12c ,A ′D →=-c +12b -12a .∴CE →·A ′D →=⎝ ⎛⎭⎪⎫b +12c ·⎝ ⎛⎭⎪⎫-c +12b -12a =-12c 2+12b 2=0, ∴CE →⊥A ′D →,即CE ⊥A ′D .(2)∵AC ′→=-a +c ,∴|AC ′→|=2|a |,|CE →|=52|a |, ∵AC ′→·CE →=(-a +c )·⎝ ⎛⎭⎪⎫b +12c =12c 2=12|a |2, ∴cos 〈AC ′→,CE →〉=12|a |22×52|a |2=1010.∴异面直线CE 与AC ′所成角的余弦值为1010.11.(多选题)在正方体ABCD -A 1B 1C 1D 1中,下列命题正确的有( ) A .(AA 1→+AD →+AB →)2=3AB →2 B .A 1C →·(A 1B 1→-A 1A →)=0 C .AD 1→与A 1B →的夹角为60° D .正方体的体积为|AB →·AA 1→·AD →|AB [如图,(AA 1→+AD →+AB →)2=(AA 1→+A 1D 1→+D 1C 1→)2=AC 1→2=3AB →2;A 1C →·(A 1B 1→-A 1A →)=A 1C →·AB 1→=0;AD 1→与A 1B →的夹角是D 1C →与D 1A →夹角的补角,而D 1C →与D 1A →的夹角为60°,故AD 1→与A 1B →的夹角为120°;正方体的体积为|AB →||AA 1→||AD →|.故选AB.]12.已知正方体ABCD -A 1B 1C 1D 1的棱长为1,若E 是底面正方形A 1B 1C 1D 1的中心, 则AC 1→与CE →( )A .重合B .平行但不重合C .垂直D .无法确定C [AC 1→=AB →+AD →+AA 1→,CE →=CC 1→+C 1E →=AA 1→-12(AB →+AD →),于是AC 1→·CE →=(AB →+AD →+AA 1→)·⎣⎢⎡⎦⎥⎤AA 1-12(AB →+AD →)=AB →·AA 1→-12AB →2-12AB →·AD →+AD →·AA 1→-12AD →·AB →-12AD →2+AA 1→2-12AA 1→·AB →-12AA 1→·AD →=0-12-0+0-0-12+1-0-0=0,故AC 1→⊥CE →.]13.(一题两空)如图,在长方体ABCD -A 1B 1C 1D 1中,设AD =AA 1=1,AB =2,P 是C 1D 1的中点,则B 1C →·A 1P →=________,B 1C →与A 1P →所成角的大小为________.1 60° [法一:连接A 1D ,则∠P A 1D 就是B 1C →与A 1P →所成角.连接PD ,在△P A 1D 中,易得P A 1=DA 1=PD =2,即△P A 1D 为等边三角形,从而∠P A 1D =60°,即B 1C →与A 1P →所成角的大小为60°.因此B 1C →·A 1P →=2×2×cos 60°=1.法二:根据向量的线性运算可得B 1C →·A 1P →=(A 1A →+AD →)·⎝⎛⎭⎪⎫AD →+12AB →=AD →2=1. 由题意可得P A 1=B 1C =2,则2×2×cos 〈B 1C →,A 1P →〉=1,从而〈B 1C →,A 1P →〉=60°.]14.已知在正四面体D -ABC 中,所有棱长都为1,△ABC 的重心为G ,则DG 的长为________.63 [如图,连接AG 并延长交BC 于点M ,连接DM ,∵G 是△ABC 的重心,∴AG =23AM ,∴AG →=23AM →,DG →=DA →+AG →=DA →+23AM →=DA →+23(DM →-DA →)=DA →+23⎣⎢⎡⎦⎥⎤12(DB →+DC →)-DA →=13(DA →+DB →+DC →),而(DA →+DB →+DC →)2=DA →2+DB →2+DC →2+2DA →·DB →+2DB →·DC →+2DC →·DA →=1+1+1+2(cos 60°+cos 60°+cos 60°)=6,∴|DG →|=63.]15.如图,正四面体V -ABC 的高VD 的中点为O ,VC 的中点为M .(1)求证:AO ,BO ,CO 两两垂直;(2)求〈DM →,AO →〉.[解] (1)证明:设VA →=a ,VB →=b ,VC →=c ,正四面体的棱长为1, 则VD →=13(a +b +c ),AO →=16(b +c -5a ), BO →=16(a +c -5b ),CO →=16(a +b -5c ),所以AO →·BO →=136(b +c -5a )·(a +c -5b )=136(18a ·b -9|a |2)=136(18×1×1×cos 60°-9)=0,所以AO →⊥BO →,即AO ⊥BO .同理,AO ⊥CO ,BO ⊥CO . 所以AO ,BO ,CO 两两垂直.(2)DM →=DV →+VM →=-13(a +b +c )+12c =16(-2a -2b +c ),所以|DM →|=⎣⎢⎡⎦⎥⎤16(-2a -2b +c )2=12. 又|AO →|=⎣⎢⎡⎦⎥⎤16(b +c -5a )2=22,DM →·AO →=16(-2a -2b +c )·16(b +c -5a )=14, 所以cos 〈DM →,AO →〉=1412×22=22. 又〈DM →,AO →〉∈[0,π], 所以〈DM →,AO →〉=π4.1.2空间向量基本定理一、选择题1.若向量{a ,b ,c }是空间的一个基底,则一定可以与向量p =2a +b ,q =2a-b 构成空间的另一个基底的向量是( )A .aB .bC .cD .a +bC [由p =2a +b ,q =2a -b 得a =14p +14q ,所以a 、p 、q 共面,故a 、p 、q 不能构成空间的一个基底,排除A ;因为b =12p -12q ,所以b 、p 、q 共面,故b 、p 、q 不能构成空间的一个基底,排除B ;因为a +b =34p -14q ,所以a +b 、p 、q 共面,故a +b 、p 、q 不能构成空间的一个基底,排除D.]2.在平行六面体ABCD -A 1B 1C 1D 1中,M 是上底面对角线AC 与BD 的交点,若A 1B 1→=a ,A 1D 1→=b ,A 1A →=c ,则B 1M →可表示为( )A .12a +12b +cB .12a -12b +cC .-12a -12b +cD .-12a +12b +cD [由于B 1M →=B 1B →+BM →=B 1B →+12(BA →+BC →) =-12a +12b +c ,故选D.]3.若向量MA →,MB →,MC →的起点M 与终点A ,B ,C 互不重合,且点M ,A ,B ,C 中无三点共线,满足下列关系(O 是空间任一点),则能使向量MA →,MB →,MC →成为空间一个基底的关系是( )A .OM →=13OA →+13OB →+13OC → B .MA →≠MB →+MC → C .OM →=OA →+OB →+OC →D .MA →=2MB →-MC →C [若MA →,MB →,MC →为空间一组基向量,则M ,A ,B ,C 四点不共面.选项A 中,因为13+13+13=1,所以点M ,A ,B ,C 共面;选项B 中,MA →≠MB →+MC →,但可能存在实数λ,μ使得MA →=λMB →+μMC →,所以点M ,A ,B ,C 可能共面;选项D 中,四点M ,A ,B ,C 显然共面.故选C.]4.空间四边形OABC 中,OA →=a ,OB →=b ,OC →=c ,点M 在OA 上,且OM →=2MA →,N 为BC 中点,则MN →为( )A .12a -23b +12cB .-23a +12b +12cC .12a +12b -23cD .23a +23b -12cB [MN →=MA →+AB →+BN →=13OA →+OB →-OA →+12(OC →-OB →)=-23OA →+12OB →+12OC →=-23a +12b +12c .]5.平行六面体ABCD -A 1B 1C 1D 1中,向量AB →,AD →,AA 1→两两的夹角均为60°且|AB →|=1,|AD →|=2,|AA 1→|=3,则|AC 1→|等于( )A .5B .6C .4D .8A [在平行六面体ABCD -A 1B 1C 1D 1中有,AC 1→=AB →+AD →+CC 1→=AB →+AD →+AA 1→所以有|AC 1→|=|AB →+AD →+AA 1→|,于是有|AC 1→|2=|AB →+AD →+AA 1→|2=|AB →|2+|AD →|2+|AA 1→|2+2|AB →|·|AD →|·cos 60°+2|AB →|·|AA 1→|·cos 60°+2|AD →||AA 1→|·cos 60°=25,所以|AC 1→|=5.]二、填空题6.在四面体OABC 中,OA →=a ,OB →=b ,OC →=c ,D 为BC 的中点,E 为AD 的中点,则OE →=________.(用a ,b ,c 表示)12a +14b +14c [因为在四面体OABC 中,OA →=a ,OB →=b ,OC →=c ,D 为BC 的中点,E 为AD 的中点,所以OE →=12(OA →+OD →)=12OA →+12OD →=12a +12×12(OB →+OC →)=12a +14(b +c )=12a +14b +14c .]7.已知{a ,b ,c }是空间的一个单位正交基底,{a +b ,a -b ,c }是空间的另一个基底,若向量m 在基底{a ,b ,c }下表示为m =3a +5b +9c ,则m 在基底{a +b ,a -b,3c }下可表示为________.4(a +b )-(a -b )+3(3c ) [由题意知,m =3a +5b +9c ,设m =x (a +b )+y (a -b )+z (3c )则有⎩⎨⎧ x +y =3x -y =53z =9,解得⎩⎨⎧x =4y =-1z =3.则m 在基底{a +b ,a -b,3c }可表示为m =4(a +b )-(a -b )+3(3c ).] 8.在四棱锥P -ABCD 中,ABCD 为平行四边形,AC 与BD 交于O ,G 为BD 上一点,BG =2GD ,P A →=a ,PB →=b ,PC →=c ,试用基底{a ,b ,c }表示向量PG →=________.23a -13b +23c [因为BG =2GD ,所以BG →=23BD →. 又BD →=BA →+BC →=P A →-PB →+PC →-PB →=a +c -2b , 所以PG →=PB →+BG →=b +23(a +c -2b ) =23a -13b +23c .] 三、解答题9.如图所示,正方体OABC -O ′A ′B ′C ′,且OA →=a ,OC →=b ,OO ′→=c .(1)用a ,b ,c 表示向量OB ′→,AC ′→;(2)设G ,H 分别是侧面BB ′C ′C 和O ′A ′B ′C ′的中心,用a ,b ,c 表示GH →.[解] (1)OB ′→=OB →+BB ′→=OA →+OC →+OO ′→=a +b +c . AC ′→=AC →+CC ′→=AB →+AO →+AA ′→=OC →+OO ′→-OA →=b +c -a . (2)法一:连接OG ,OH (图略), 则GH →=GO →+OH →=-OG →+OH → =-12(OB ′→+OC →)+12(OB ′→+OO ′→) =-12(a +b +c +b )+12(a +b +c +c ) =12(c -b ).法二:连接O ′C (图略),则GH →=12CO ′→=12(OO ′→-OC →) =12(c -b ).10.如图,在平行六面体ABCD -A 1B 1C 1D 1中,MA →=-13AC →,ND →=13A 1D →,设AB →=a ,AD →=b ,AA 1→=c ,试用a ,b ,c 表示MN →.[解] 连接AN ,则MN →=MA →+AN →.由已知可得四边形ABCD 是平行四边形,从而可得 AC →=AB →+AD →=a +b , MA →=-13AC →=-13(a +b ), 又A 1D →=AD →-AA 1→=b -c ,故AN →=AD →+DN →=AD →-ND →=AD →-13A 1D →=b -13(b -c ), 所以MN →=MA →+AN → =-13(a +b )+b -13(b -c ) =13(-a +b +c ).11.(多选题)已知a ,b ,c 是不共面的三个向量,则下列向量组中,不能构成一个基底的一组向量是( )A .2a ,a -b ,a +2bB .2b ,b -a ,b +2aC .a,2b ,b -cD .c ,a +c ,a -cABD [对于A ,因为2a =43(a -b )+23(a +2b ),得2a 、a -b 、a +2b 三个向量共面,故它们不能构成一个基底;对于B ,因为2b =43(b -a )+23(b +2a ),得2b 、b -a 、b +2a 三个向量共面,故它们不能构成一个基底;对于C ,因为找不到实数λ、μ,使a =λ·2b +μ(b -c )成立,故a 、2b 、b -c 三个向量不共面,它们能构成一个基底;对于D ,因为c =12(a +c )-12(a -c ),得c 、a +c 、a -c 三个向量共面,故它们不能构成一个基底,故选ABD.]12.(多选题)给出下列命题,正确命题的有( )A .若{a ,b ,c }可以作为空间的一个基底,d 与c 共线,d ≠0,则{a ,b ,d }也可以作为空间的一个基底B .已知向量a ∥b ,则a ,b 与任何向量都不能构成空间的一个基底C .A ,B ,M ,N 是空间四点,若BA →,BM →,BN →不能构成空间的一个基底,则A ,B ,M ,N 四点共面D .已知{a ,b ,c }是空间的一个基底,若m =a +c ,则{a ,b ,m }也是空间的一个基底ABCD [根据基底的概念,知空间中任何三个不共面的向量都可作为空间的一个基底.显然B 正确.C 中由BA →,BM →,BN →不能构成空间的一个基底,知BA →,BM →,BN →共面.又BA →,BM →,BN →过相同点B ,知A ,B ,M ,N 四点共面.所以C 正确.下面证明AD 正确:A 假设d 与a ,b 共面,则存在实数λ,μ,使得d =λa +μb ,∵d 与c 共线,c ≠0,∴存在实数k ,使得d =k c .∵d ≠0,∴k ≠0,从而c =λk a +μk b ,∴c 与a ,b 共面,与条件矛盾,∴d 与a ,b 不共面.同理可证D 也是正确的.于是ABCD 四个命题都正确,故选ABCD.]13.(一题两空)已知空间的一个基底{a ,b ,c },m =a -b +c ,n =x a +y b +c ,若m 与n 共线,则x =________,y =________.1 -1 [因为m 与n 共线, 所以存在实数λ,使m =λn ,即a -b +c =λx a +λy b +λc ,于是有⎩⎨⎧1=λx ,-1=λy ,1=λ,解得⎩⎨⎧x =1,y =-1.]14.(一题多空)已知e 1,e 2是空间单位向量,e 1·e 2=12.若空间向量b 满足b ·e 1=2,b ·e 2=52,且对于任意x ,y ∈R ,|b -(x e 1+y e 2)|≥|b -(x 0e 1+y 0e 2)|=1(x 0,y 0∈R ),则x 0=________,y 0=________,|b |=________.1 2 22 [由题意可令b =x 0e 1+y 0e 2+e 3,其中|e 3|=1,e 3⊥e i ,i =1,2.由b ·e 1=2得x 0+y 02=2,由b ·e 2=52得x 02+y 0=52,解得x 0=1,y 0=2,∴|b |=(e 1+2e 2+e 3)2=2 2.]15.在平行六面体ABCD -A 1B 1C 1D 1中,设AB →=a ,AD →=b ,AA 1→=c ,E ,F 分别是AD 1,BD 的中点.(1)用向量a ,b ,c 表示D 1B →,EF →;(2)若D 1F →=x a +y b +z c ,求实数x ,y ,z 的值. [解] (1)如图,D 1B →=D 1D →+DB →=-AA 1→+AB →-AD →=a -b -c ,EF →=EA →+AF →=12D 1A →+12AC →=-12(AA 1→+AD →)+12(AB →+AD →)=12(a -c ). (2)D 1F →=12(D 1D →+D 1B →)=12(-AA 1→+AB →-AD 1→) =12(-AA 1→+AB →-AD →-DD 1→) =12(a -c -b -c )=12a -12b -c , ∴x =12,y =-12,z =-1.1.3.1空间直角坐标系一、选择题1.空间两点A ,B 的坐标分别为(x ,-y ,z ),(-x ,-y ,-z ),则A ,B 两点的位置关系是( )A .关于x 轴对称B .关于y 轴对称C .关于z 轴对称D .关于原点对称B [纵坐标相同,横坐标和竖坐标互为相反数,故两点关于y 轴对称.] 2.已知A (1,2,-1),B (5,6,7),则直线AB 与平面xOz 交点的坐标是( ) A .(0,1,1) B .(0,1,-3)C .(-1,0,3)D .(-1,0,-5)D [设直线AB 与平面xoz 交点坐标是M (x ,y ,z ),则AM →=(x -1,-2,z +1),AB →=(4,4,8),又AM →与AB →共线,∴AM →=λAB →,即⎩⎨⎧x -1=4λ,-2=4λ,z +1=8λ,解得x =-1,z =-5,∴点M (-1,0,-5).故选D.]3.设A (3,3,1),B (1,0,5),C (0,1,0),则AB 的中点M 到点C 的距离|CM |=( ) A .534 B .532 C .532D .132 C [M ⎝ ⎛⎭⎪⎫2,32,3 ,|CM |=4+⎝ ⎛⎭⎪⎫32-12+9=532.] 4.如图,在空间直角坐标系中,正方体ABCD -A 1B 1C 1D 1的棱长为1,B 1E =14A 1B 1,则BE →等于( )A .⎝ ⎛⎭⎪⎫0,14,-1B .⎝ ⎛⎭⎪⎫-14,0,1C .⎝ ⎛⎭⎪⎫0,-14,1D .⎝ ⎛⎭⎪⎫14,0,-1C [{DA →,DC →,DD 1→}为单位正交向量,BE →=BB 1→+B 1E →=-14DC →+DD 1→,∴BE →=⎝ ⎛⎭⎪⎫0,-14,1.] 5.设{i ,j ,k }是单位正交基底,已知向量p 在基底{a ,b ,c }下的坐标为(8,6,4),其中a =i +j ,b =j +k ,c =k +i ,则向量p 在基底{i ,j ,k }下的坐标是( )A .(12,14,10)B .(10,12,14)C .(14,12,10)D .(4,3,2)A [依题意,知p =8a +6b +4c =8(i +j )+6(j +k )+4(k +i )=12i +14j +10k ,故向量p 在基底{i ,j ,k }下的坐标是(12,14,10).]二、填空题6.在空间直角坐标系中,已知点P (1,2,3),过点P 作平面yOz 的垂线PQ ,则垂足Q 的坐标为________.(0,2,3) [过P 的垂线PQ ⊥面yOz ,则Q 点横坐标为0,其余不变,故Q (0,2,3).]7.设{e 1,e 2,e 3}是空间向量的一个单位正交基底,a =4e 1-8e 2+3e 3,b =-2e 1-3e 2+7e 3,则a ,b 的坐标分别为________.(4,-8,3),(-2,-3,7) [由题意可知a =(4,-8,3),b =(-2,-3,7).] 8.如图所示,以长方体ABCD -A 1B 1C 1D 1的顶点D 为坐标原点,过D 的三条棱所在的直线为坐标轴,建立空间直角坐标系,若DB 1→的坐标为(4,3,2),则AC 1→的坐标为________.(-4,3,2) [由DB 1→=DA →+DC →+DD 1→,且DB 1→=(4,3,2),∴|DA →|=4,|DC →|=3,|DD 1→|=2,又AC 1→=-DA →+DC →+DD 1→,∴AC 1→=(-4,3,2).]三、解答题9.已知三棱柱ABC -A 1B 1C 1中,侧棱AA 1⊥底面ABC ,所有的棱长都是1,建立适当的坐标系,并写出各点的坐标.[解] 如图所示,取AC 的中点O 和A 1C 1的中点O 1,可得BO ⊥AC ,OO 1⊥AC ,分别以OB ,OC ,OO 1所在直线为x 轴、y 轴、z 轴建立空间直角坐标系.∵三棱柱各棱长均为1,∴OA =OC =O 1C 1=O 1A 1=12,OB =32. ∵A ,B ,C 均在坐标轴上,∴A ⎝ ⎛⎭⎪⎫0,-12,0,B ⎝ ⎛⎭⎪⎫32,0,0,C ⎝ ⎛⎭⎪⎫0,12,0.∵点A 1与C 1在yOz 平面内, ∴A 1⎝ ⎛⎭⎪⎫0,-12,1,C 1⎝ ⎛⎭⎪⎫0,12,1.∵点B 1在xOy 平面内的射影为B ,且BB 1=1,∴B 1⎝ ⎛⎭⎪⎫32,0,1,即各点的坐标为A ⎝ ⎛⎭⎪⎫0,-12,0,B ⎝ ⎛⎭⎪⎫32,0,0,C ⎝ ⎛⎭⎪⎫0,12,0,A 1⎝ ⎛⎭⎪⎫0,-12,1,B 1⎝ ⎛⎭⎪⎫32,0,1,C 1⎝ ⎛⎭⎪⎫0,12,1. 10.棱长为1的正方体ABCD -A 1B 1C 1D 1中,E ,F ,G 分别为棱DD 1,D 1C 1,BC 的中点,以{AB →,AD →,AA 1→}为正交基底,求下列向量的坐标:(1)AE →,AF →,AG →; (2)EF →,EG →,DG →.[解] 在正交基底{AB →,AD →,AA 1→}下,(1)AF →=12AB →+AD →+AA 1→, AE →=AD →+12AA 1→,AG →=AB →+12AD →,∴AE →=⎝ ⎛⎭⎪⎫0,1,12,AF →=⎝ ⎛⎭⎪⎫12,1,1,AG →=⎝ ⎛⎭⎪⎫1,12,0.(2)EF →=AF →-AE →=12AB →+12AA 1→,∴EF →=⎝ ⎛⎭⎪⎫12,0,12;EG →=AG →-AE →=AB →-12AD →-12AA 1→,∴EG →=⎝ ⎛⎭⎪⎫1,-12,-12;DG →=AG →-AD →=AB→-12AD →,∴DG →=⎝ ⎛⎭⎪⎫1,-12,0.11.(多选题)下列各命题正确的是( ) A .点(1,-2,3)关于平面xOz 的对称点为(1,2,3) B .点⎝ ⎛⎭⎪⎫12,1,-3关于y 轴的对称点为⎝ ⎛⎭⎪⎫-12,1,3C .点(2,-1,3)到平面yOz 的距离为1D .设{i ,j ,k }是空间向量的单位正交基底,若m =3i -2j +4k ,则m =(3,-2,4).ABD [“关于谁对称谁不变”,∴A 正确,B 正确,C 中(2,-1,3)到面yOz 的距离为2,∴C 错误.根据空间向量的坐标定义,D 正确.]12.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,P 为正方体内一动点(包括表面),若AP →=xAB →+yAD →+zAA 1→,且0≤x ≤y ≤z ≤1.则点P 所有可能的位置所构成的几何体的体积是( )A .1B .12C .13D .16D [根据向量加法的几何意义和空间向量基本定理,满足0≤x ≤y ≤1的点P 在三棱柱ACD -A 1C 1D 1内;满足0≤y ≤z ≤1的点P 在三棱柱AA 1D 1-BB 1C 1内,故同时满足0≤x ≤y ≤1,0≤y ≤z ≤1的点P 在这两个三棱柱的公共部分(如图),即三棱锥A -A 1C 1D 1,其体积是13×12×1×1×1=16.]13.三棱锥P -ABC 中,∠ABC 为直角,PB ⊥平面ABC ,AB =BC =PB =1,M为PC 的中点,N 为AC 的中点,以{BA →,BC →,BP →}为基底,则MN →的坐标为________.⎝ ⎛⎭⎪⎫12,0,-12 [MN →=BN →-BM → =12(BA →+BC →)-12(BP →+BC →) =12BA →-12BP →, 故MN →=⎝ ⎛⎭⎪⎫12,0,-12.] 14.已知O 是坐标原点,点A (2,0,-2),B (3,1,2),C (2,-1,7). (1)若点P 满足OP →=OA →+OB →+OC →,则点P 的坐标为________; (2)若点P 满足AP →=2AB →-AC →,则点P 的坐标为________.(1)(7,0,7) (2)(4,3,-3) [(1)中OP →=OA →+OB →+OC →=(2i -2k )+(3i +j +2k )+(2i -j +7k )=7i +0j +7k ,∴P (7,0,7).(2)中,AP →=2AB →-AC →得OP →-OA →=2OB →-2OA →-OC →+OA →,∴OP →=2OB →-OC →=2(3i +j +2k )-(2i -j +7k ) =4i +3j -3k ,∴P (4,3,-3).]15.如图,在正四棱锥P -ABCD 中,底面ABCD 是边长为1的正方形,O 是AC 与BD 的交点,PO =1,M 是PC 的中点.设AB →=a ,AD →=b ,AP →=c .(1)用向量a ,b ,c 表示BM →.(2)在如图的空间直角坐标系中,求BM →的坐标.[解] (1)∵BM →=BC →+CM →,BC →=AD →,CM →=12CP →,CP →=AP →-AC →,AC →=AB →+AD →,∴BM →=AD →+12(AP →-AC →)=AD →+12AP →-12(AB →+AD →)=-12AB →+12AD →+12AP →=-12a +12b +12c .(2)a =AB →=(1,0,0),b =AD →=(0,1,0).∵A (0,0,0),O ⎝ ⎛⎭⎪⎫12,12,0,P ⎝ ⎛⎭⎪⎫12,12,1,∴c =AP →=OP →-OA →=⎝ ⎛⎭⎪⎫12,12,1,∴BM →=-12a +12b +12c =-12(1,0,0)+12(0,1,0)+12⎝ ⎛⎭⎪⎫12,12,1=⎝ ⎛⎭⎪⎫-14,34,12.1.3.2空间运算的坐标表示一、选择题1.已知三点A (1,5,-2),B (2,4,1),C (a,3,b +2)在同一条直线上,那么( ) A .a =3,b =-3 B .a =6,b =-1 C .a =3,b =2D .a =-2,b =1C [根据题意AB →=(1,-1,3),AC →=(a -1,-2,b +4), ∵AB →与AC →共线,∴AC →=λAB →, ∴(a -1,-2,b +4)=(λ,-λ,3λ),∴⎩⎨⎧a -1=λ,-2=-λ,b +4=3λ,解得⎩⎨⎧a =3,b =2,λ=2.故选C.]2.已知a =(2,3,-4),b =(-4,-3,-2),b =12x -2a ,则x 等于( ) A .(0,3,-6) B .(0,6,-20) C .(0,6,-6)D .(6,6,-6)B [由题a =(2,3,-4),b =(-4,-3,-2),设x =(w ,y ,z )则由b =12x -2a ,可得(-4,-3,-2)=12(w ,y ,z )-2(2,3,-4)=⎝ ⎛⎭⎪⎫12w ,12y ,12z-(4,6,-8)=⎝ ⎛⎭⎪⎫12w -4,12y -6,12z +8,解得w =0,y =6,z =-20,即x =(0,6,-20).]3.已知向量a =(1,0,-1),则下列向量中与a 成60°夹角的是( ) A .(-1,1,0) B .(1,-1,0) C .(0,-1,1)D .(-1,0,1)B [不妨设向量为b =(x ,y ,z ),A .若b =(-1,1,0),则cos θ=a ·b |a |·|b |=-12×2=-12≠12,不满足条件. B .若b =(1,-1,0),则cos θ=a ·b |a |·|b |=12×2=12,满足条件. C .若b =(0,-1,1),则cos θ=a ·b |a |·|b |=-12×2=-12≠12,不满足条件. D .若b =(-1,0,1),则cos θ=a ·b |a |·|b |=-22×2=-1≠12,不满足条件.故选B.]4.已知向量a =(-2,x,2),b =(2,1,2),c =(4,-2,1),若a ⊥(b -c ),则x 的值为( )A .-2B .2C .3D .-3A [∵b -c =(-2,3,1),a ·(b -c )=4+3x +2=0,∴x =-2.]5.已知A 、B 、C 三点的坐标分别为A (4,1,3),B (2,-5,1),C (3,7,λ),若AB →⊥AC →,则λ等于( )A .28B .-28C .14D .-14D [AB →=(-2,-6,-2),AC →=(-1,6,λ-3),∵AB →⊥AC →,∴AB →·AC →=-2×(-1)-6×6-2(λ-3)=0,解得λ=-14.] 二、填空题6.已知a =(1,1,0),b =(0,1,1),c =(1,0,1),p =a -b ,q =a +2b -c ,则p ·q =________.-1 [∵p =a -b =(1,0,-1),q =a +2b -c =(0,3,1), ∴p ·q =1×0+0×3+(-1)×1=-1.]7.已知空间三点A (1,1,1),B (-1,0,4),C (2,-2,3),则AB →与CA →的夹角θ的大小是________.120° [AB →=(-2,-1,3),CA →=(-1,3,-2),cos 〈AB →,CA →〉=(-2)×(-1)+(-1)×3+3×(-2)14·14=-12,∴θ=〈AB →,CA →〉=120°.]8.如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,E 、F 分别是棱BC 、DD 1上的点,如果B 1E ⊥平面ABF ,则CE 与DF 的和的值为________.1 [以D 1A 1、D 1C 1、D 1D 分别为x ,y ,z 轴建立空间直角坐标系(图略),设CE =x ,DF =y ,则易知E (x,1,1),B 1(1,1,0),∴B 1E →=(x -1,0,1),又F (0,0,1-y ),B (1,1,1),∴FB →=(1,1,y ),由于AB ⊥B 1E ,若B 1E ⊥平面ABF ,只需FB →·B 1E →=(1,1,y )·(x -1,0,1)=0⇒x +y =1.] 三、解答题9.已知空间中三点A (-2,0,2),B (-1,1,2),C (-3,0,4),设a =AB →,b =AC →. (1)求向量a 与向量b 的夹角的余弦值;(2)若k a +b 与k a -2b 互相垂直,求实数k 的值.[解] (1)∵a =(1,1,0),b =(-1,0,2),∴a·b =(1,1,0)·(-1,0,2)=-1, 又|a |=12+12+02=2,|b |=(-1)2+02+22=5,∴cos 〈a ,b 〉=a ·b |a ||b |=-110=-1010,即向量a 与向量b 的夹角的余弦值为-1010.(2)法一:∵k a +b =(k -1,k,2),k a -2b =(k +2,k ,-4),且k a +b 与k a -2b 互相垂直,∴(k -1,k,2)·(k +2,k ,-4)=(k -1)(k +2)+k 2-8=0,∴k =2或k =-52, ∴当k a +b 与k a -2b 互相垂直时,实数k 的值为2或-52. 法二:由(1)知|a |=2,|b |=5,a·b =-1,∴(k a +b )·(k a -2b )=k 2a 2-k a ·b -2b 2=2k 2+k -10=0,得k =2或k =-52. 10.已知正三棱柱ABC -A 1B 1C 1,底面边长AB =2,AB 1⊥BC 1,点O ,O 1分别是边AC ,A 1C 1的中点,建立如图所示的空间直角坐标系.(1)求正三棱柱的侧棱长;(2)求异面直线AB 1与BC 所成角的余弦值. [解] (1)设正三棱柱的侧棱长为h ,由题意得A (0,-1,0),B (3,0,0),C (0,1,0),B 1(3,0,h ),C 1(0,1,h ), 则AB 1→=(3,1,h ),BC 1→=(-3,1,h ), 因为AB 1⊥BC 1,所以AB 1→·BC 1→=-3+1+h 2=0, 所以h = 2.(2)由(1)可知AB 1→=(3,1,2),BC →=(-3,1,0), 所以AB 1→·BC →=-3+1=-2.因为|AB 1→|=6,|BC →|=2,所以cos 〈AB 1→,BC →〉=-226=-66.所以异面直线AB 1与BC 所成角的余弦值为66.11.(多选题)若向量a =(1,2,0),b =(-2,0,1),则下列结论正确的是( )。
概率论与数理统计习题第一章第三章

1.1 写出以下随机试验的样本空间:(1) 某篮球运发动投篮时, 连续5 次都命中, 观察其投篮次数; 解:连续5 次都命中,至少要投5次以上,故}{ ,7,6,51=Ω; (2) 掷一颗匀称的骰子两次, 观察前后两次出现的点数之和; 解:}{12,11,4,3,22 =Ω; (3) 观察某医院一天内前来就诊的人数;解:医院一天内前来就诊的人数理论上可以从0到无穷,所以}{ ,2,1,03=Ω;(4) 从编号为1,2,3,4,5 的5 件产品中任意取出两件, 观察取出哪两件产品; 解:属于不放回抽样,故两件产品不会一样,编号必是一大一小,故:()}{;51,4≤≤=Ωj i j i (5) 检查两件产品是否合格;解:用0 表示合格, 1 表示不合格,那么()()()()}{1,1,0,1,1,0,0,05=Ω;(6) 观察某地一天内的最高气温和最低气温(假设最低气温不低于T1, 最高气温不高于T2); 解:用x 表示最低气温, y 表示最高气温;考虑到这是一个二维的样本空间,故:()}{216,T y x T y x ≤≤=Ω ;(7) 在单位圆内任取两点, 观察这两点的间隔 ; 解:}{207 x x =Ω;(8) 在长为l 的线段上任取一点, 该点将线段分成两段, 观察两线段的长度. 解:()}{l y x y x y x =+=Ω,0,0,8 ;1.3 设样本空间}{20≤≤=Ωx x , 事件A =}{15.0≤≤x x ,}{6.18.0≤=x x B 详细写出以下各事件:(1)AB ; (2) B A - ; (3) B A -; (4) B A ⋃ (1)AB }{18.0≤=x x ; (2) B A -=}{8.05.0≤≤x x ;(3) B A -=}{28.05.00≤⋃≤≤x x x ; (4) B A ⋃=}{26.15.00≤⋃≤≤x x x1.6 按从小到大次序排列)()(),(),(),(B P A P AB P B A P A P +⋃, 并说明理由.解:由于),(,B A A A AB ⋃⊆⊆故)()()(B A P A P AB P ⋃≤≤,而由加法公式,有:)()()(B P A P B A P +≤⋃ 1.7 假设W 表示昆虫出现残翅, E 表示有退化性眼睛, 且P(W) = 0.125; P(E) = 0.075, P(WE) = 0.025, 求以下事件的概率: (1) 昆虫出现残翅或退化性眼睛;(2) 昆虫出现残翅, 但没有退化性眼睛; (3) 昆虫未出现残翅, 也无退化性眼睛.解:(1) 昆虫出现残翅或退化性眼睛对应事件概率为:175.0)()()()(=-+=⋃WE P E P W P E W P(2) 由于事件W 可以分解为互斥事件E W WE ,,昆虫出现残翅, 但没有退化性眼睛对应事件 概率为:1.0)()()(=-=W E P W P E W P(3) 昆虫未出现残翅, 也无退化性眼睛的概率为:825.0)(1)(=⋃-=E W P E W P . 1.8 设A 与B 是两个事件, P(A) = 0.6; P(B) = 0.8。
电磁学习题答案1-3章

第一章 习题一1、电量Q 相同的四个点电荷置于正方形的四个顶点上,0点为正方形中心,欲使每个顶点的电荷所受电场力为零,则应在0点放置一个电量q =-(1+2√2)Q/4 的点电荷。
2、在点电荷系的电场中,任一点的电场强度等于各点电荷单独在该点产生场强的矢量和,这称为电场强度叠加原理。
3、一点电荷电场中某点受到的电场力很大,则该点的电场强度E :( C )(A)一定很大 (B)一定很小 (C)可能大也可能小4、两个电量均为+q 的点电荷相距为2a ,O 为其连线的中点,求在其中垂线上场强具有极大值的点与O 点的距离R 。
解法一:22020214141aR qπεr q πεE E +=== 21E E E+=,θE θE θE E cos 2cos cos 121=+=2222042a R R a R q πε++=()2/32202a R R πεq +=E 有极值的条件是:()0222/522220=+-=a R R a πεq dR dE 即 0222=-R a ,解得极值点的位置为:a R 22=∵ ()2/722220223223a R a R πεqR dR E d +-=,而 0398402/222<-==aπεqdR E d a R ∴ 中垂线上场强具有极大值的点与O 点的距离为a R 22= 且 ()202/3220m a x 332/2/2aπεq a a a πεq E =+=解法二:θaq πεr q πεE E 2202021sin 4141===,21E E E +=+qθE θE θE E cos 2cos cos 121=+=θθaq πεcos sin 21220=)cos (cos 21320θθaq πε-=E 有极值的条件是:0)sin 3sin 2(2320=-=θθaπεq θd dE E 有极值时的θ满足:31cos 32sin 1cos 0sin 2211====θ,θ;θ,θ )cos 7cos 9(2)cos sin 9cos 2(232022022θθa πεq θθθa πεq θd E d -=-= 0)cos 7cos 9(22011320221>=-==a πεq θθa πεq θd E d θθ 032)cos 7cos 9(22022320222<-=-==aπεq θθa πεq θd E d θθ 可见 θ = θ2时,E 有极大值。
会计学一二章习题

5.会计要素是会计报表通常所含有的大类项目, 主要有6个会计要素,分别为( )、 )、 )、 )、 主要有6个会计要素,分别为( )、( )、( )、( )、 ( )和( ) )和 6.资产是指由过去的交易事项形成并由企业拥有 的或者( )的资源,该资源预期会给企业带来( )。 的或者( )的资源,该资源预期会给企业带来( )。 7.会计的基本程序具体包括( )、( .会计的基本程序具体包括( )、 )、 )和 )。 )、( )和( )。 8.所有者权益是企业( )在企业资产中享有的经济 .所有者权益是企业( )在企业资产中享有的经济 利益。其金额等于( )减去( )后的金额。 利益。其金额等于( )减去( )后的金额。 9.2006年新准则出台了( )项具体会计准则。 2006年新准则出台了( )项具体会计准则。 10.会计要素的计量属性包括( )、( )、( )、( ) 10.会计要素的计量属性包括( )、 )、 )、 和( ),新的企业会计准则规定企业在对会计要素 ),新的企业会计准则规定企业在对会计要素 进行计量时,一般应当采用( )计量属性。 进行计量时,一般应当采用( )计量属性。
7.我国企业会计准则规定以( )作为会计年度。 .我国企业会计准则规定以( )作为会计年度。 A.营业年度 B.农历年度 C.日历年度 D.期末 8.下列( )肯定既是会计主体又是法律主体。 .下列( )肯定既是会计主体又是法律主体。 A.甲生产车间 B.乙销售部门 C.丙上市公司 D.丁大学数学系 9.按照权责发生制确认基础,( )应作为本期收 .按照权责发生制确认基础,( )应作为本期收 入。 A.收到上月产品销售收入存人银行 B.预收下月产品销售收入存人银行 C.本月销售产品收入存入银行 D.上月利息收入存入银行
4.下列不属于会计核算基本前提的是( )。 .下列不属于会计核算基本前提的是( )。 A.货币计量 B.会计主体 C.历史成本 D.持续经营 5.在经济生活中存在不确定性和许多风险, 因此在进行会计核算时应遵循的会计一般 原则是( )。 原则是( )。 A.重要性 B.真实性 C.谨慎性 D.相关性 6.下列原则中( )是会计的生命和灵魂。 .下列原则中( )是会计的生命和灵魂。 A.谨慎性原则 B.客观性原则 C.可比性原则 D.明晰性原则
现代测试技术课后习题及答案

复习(重点)一、中期考试题(含第一、二、三章) 重点习题:二、填空选择题:第五、九、十章。
如: 1. ±1误差称为最大量化误差2.直接数字合成(DDS )技术的优缺点。
三、判断题第四、九章。
四、简答题:1.简单电路原理分析,如P155图4-6;锁相环倍频分频2.框图分析(简述) :测频、测周及时间间隔原理;示波器扫描发生器环组各部份的组成及作用;外差式频谱分析仪组成框图原理;逻辑分析仪 五、计算题:1.(含中期考试计算题)及第九章2.累进性系统误差、周期性误差的判别,简述测量数据处理的步骤(要求给出相应的公式及判据),例3-4。
3.计算由±1误差所引起的测周误差。
付加:1.现代自动测试系统特点2. PXI 总线的特点及应用领域?第一章一、填空题1.相对误差定义 与 的比值。
通常用百分数表示。
2.广义测量是指为了获得对被测对象 而进行的实验过程。
3.狭义测量测量是为了确定被测对象的 而进行的实验过程。
4.测量误差主要的来源 、 、 、 和 。
5.仪表的准确度越高,测量结果越 。
6.信息的的获取的过程是由 和 两大环节组成。
二、计算题1、用量程为10V 、1.5级的电压表分别测量3V 和8V 的电压,试问哪一次测量的准确度高?为什么?解:xm=10V,A1=3V ,A2=8V2、某被测电压为3.50V ,仪表的量程为5V ,测量时该表的示值为3.53V ,求:⑴ 绝对误差与修正值各为多少?%5.1%100=⨯∆=XmXm γ%5.110⨯=∆X %5%10011=⨯∆=A XA γ◆⑵实际相对误差及引用误差各为多少?◆⑶该电压表的精度等级属哪一级别?第二章◆一、选择题:◆ 1.从基本的测量对象来看,电子测量是对( ) 的测量。
◆ A.电信号 B. 电路C.电系数D.电参数◆ 2.测量系统的理想静态特性为().◆A.y=Sx+S0 B.y=Sx C.y=S D.y=Sx+S0+x2◆ 3. 电子信息技术应用在电子测量中的优点有()。
单片机第一至第三章练习题答案

一.指出指令中哪些是非法指令?(正确的打√,错的打×)MOV A,R7 (√)ADDC B,R6(×)SETB 30H.0(×)MOV R5,R2 (×)SUBB A,@R1(√)CJNE @R0,#64H,LABEL(√)MOV A,@R0 (√)PUSH R6(×)DJNZ @R0,LABEL(×)MOV SBUF,@R1(√)PUSH B (√)RR B(×)MOV R7,@R1(×)POP @R1 (×)RLC A(√)MOV @R2,#64H (×)ANL R7,A (×)CLR A(√)DEC DPTR (×)ORL A,R7(√)CLR B(×)INC DPTR (√)XRL C,ACC.5(×)MOVX @R0,PSW(×)二.判断正误题(正确的打√,错的打×)(×)1.程序计数器PC和数据指针DPTR均是可寻址的16位专用寄存器。
(√)2.PSW.4=1,PSW.3=0选中2区工作寄存器。
(×)3.指令MOV @R0, A 的源操作数属于寄存器寻址。
(×)4.假设晶振频率fosc=6MHz,则执行指令MOV A,R0 需4us。
(√)5.查表指令MOVC A,@A+PC的查表地址范围是当前指令以下的256字节。
(√)6.单片机是一种微型计算机。
(×)7.MCS-51单片机的I/O口编址和存储器编址是独立的。
(√) 8.MCS-51单片机共有111条指令,7种寻址方式。
(×)9.Intel 8031 单片机内部有4kBROM。
三.阅读程序1.执行MOV A,#12HCLR CSUBB A,#15H后(A)=_FDH______(Cy)= 1 (OV)= 0 (P)= 1 (AC)=__1______2.执行MOV A,#34HADD A,#39H后(A)=_6DH______继续执行DA A后(A)=73H______3.若(30H)=56H ,(40H)=60H ,(50H)=78H ,执行下列指令后PUSH 30HPUSH 40HPUSH 50HPOP 30H (30H)=78H_________POP 40H (40H)=_60H________POP 50H (50H)=_56H________4.MOV A,#10HMOV DPTR,#3100HMOV R0,#30HMOV 31H,#89HMOV @R0,#1FH 整个程序执行后XCHD A,@R0 (A)= 98H_______MOV R0,31H (R0)=_89H________XCH A,31H (30H)=_10H________MOVX @DPTR,A (31H)=__1FH_______SWAP A (3100H)=89H_________END5.3000H SJMP LOOP300AH LOOP: MOV A,#30H已知SJMP LOOP 指令(PC)源=3000H, (PC)目=300AH,求该指令第二个字节rel为__08H_______。
初二物理一二三章练习题

初二物理一二三章练习题第一章:物理学研究的对象和任务物理学是自然科学的一门重要学科,它研究物质和能量的基本规律及其相互关系。
本章主要介绍了物理学的基本概念和研究对象,以及物理学的任务和发展历程。
以下是一些初二物理章练习题,希望能帮助你对于本章的内容有一个更好的理解。
1. 物理学研究的对象是什么?答:物理学研究自然界中的物质和能量。
2. 物理学的任务是什么?答:物理学的任务是揭示自然界的规律、发展科学技术、改善人类生活。
3. 物理学的基本学科包括哪些方面?答:物理学的基本学科包括力学、热学、光学、电学、声学。
4. 力学研究的是什么?答:力学研究物体的运动和受力条件。
5. 热学研究的是什么?答:热学研究物体的热现象及其规律。
6. 光学研究的是什么?答:光学研究光的传播、反射、折射、干涉等现象及其规律。
7. 电学研究的是什么?答:电学研究电荷、电场、电流、电磁感应等电现象及其规律。
8. 声学研究的是什么?答:声学研究声音的产生、传播、反射、衍射等现象及其规律。
第二章:物理量和国际单位制物理学研究的是自然界中的物理现象,对于这些现象的描述和测量需要使用物理量和单位。
本章主要介绍了物理量的概念、物理量的分为基本物理量和导出物理量,以及国际单位制等内容。
以下是一些与物理量和国际单位制相关的练习题:1. 什么是物理量?答:物理量是用于描述物理现象的量,具有数值和单位。
2. 物理量分为哪两类?答:物理量分为基本物理量和导出物理量。
3. 什么是基本物理量?答:基本物理量是国际上约定的具有独立量纲的物理量,如长度、质量、时间等。
4. 什么是导出物理量?答:导出物理量是通过基本物理量及其定义关系导出的物理量,如速度、加速度、力等。
5. 国际单位制是什么?答:国际单位制是国际上统一使用的计量系统,用于规定物理量的单位和其与基本单位的关系。
6. 国际单位制中长度的基本单位是什么?答:国际单位制中长度的基本单位是米。
7. 国际单位制中质量的基本单位是什么?答:国际单位制中质量的基本单位是千克。
推销第一、三章练习

《现代推销实务》练习题〔第一、三章〕一、不定项选择题1、在推销活动中,推销员必须坚持以〔〕为中心A.企业 B.产品 C.市场 D.顾客2、推销就是要〔〕A.将顾客不需要的产品也能卖给他们B.将顾客可用可不用的产品卖给他们C.将肯定能满足顾客某种需要的产品卖给他们3、下列哪个不属于推销活动的三大基本要素〔〕.A.推销对象 B. 推销过程 C. 推销产品 D.推销人员4、推销计划制定前先要确定〔〕.A.推销方案 B. 推销目标 C.推销洽谈要点 D.推销策略和技巧5、推销模式"迪伯达"模式〔DIPADA〕中,"P"代表的是〔〕A.愿望和需求B.接受C.证实D.决定6、在推销过程中淘汰不宜推销产品的推销模式是〔〕A.费比模式B.埃德帕模式C.爱达模式D.迪伯达模式7、"我卖什么,顾客就买什么"属于下列哪项观念〔〕A生产观念 B推销观念 C市场营销观念 D产品观念8、推销的核心职能是〔〕A生产商品 B销售商品 C服务 D满足消费需要9、当顾客有着明确的购买愿望和购买目标时,适合的推销模式是A.费比模式 B.爱德帕模式 C.迪伯达模式 D.爱达模式10、向批发商、厂商和零售商推销各种工业品、无形产品常用〔〕A.爱达模式B.费比模式C.埃德帕模式D.迪伯达模式11、推销人员在推销过程中,首先推销的是〔〕A.商品的本身 B.自己C.商品本身 D.商品生产的企业12、适用于顾客比较被动的情况,也适用于一些易于携带的生活用品和办公用品的推销,新推销人员能及面对的是陌生推销对象的推销模式是〔〕A.AIDA B.DIPADAC.IDEPA D.FABE13、爱达模式的四个阶段依次是〔〕A.行动 B.欲望 C.注意 D.兴趣14、你认为推销员成交失败的原因主要是〔〕A.害怕失败 B.顾客难缠 C.没有主动提出成交D.思想顾虑 E.对推销品缺乏信心15、推销员向顾客分析产品利益的好方法是〔〕A.IDEPA B.DIPADAC.FABE D.AIDI16、"迪伯达"模式中,角色开始发生变化的阶段是〔〕A.证实推销的产品符合顾客需求 B.促使顾客接受所推销的产品C.刺激顾客的购买欲望 D.促使顾客采取购买行动二、判断题1、推销员进门前,如果门是开启的,可以不必按门铃或敲门.〔〕2、爱达模式的推销步骤首先是唤起顾客兴趣.〔〕3、推销渠道越短越好,因为中间环节少了,各种费用也少了.〔〕4、一级渠道的销售方式中,产品从厂家到消费者手中经过的中间环节是零售商环节.〔〕5、部门的推销目标就是为了更多的赢利.〔〕6、推销效益目标是推销活动目标的基本保证.〔〕7、现代推销应重点关注把商品销售给顾客,而不是售后服务.〔〕8、推销计划开始实施,制定推销计划的工作就算完成了.〔〕9、每个推销人员在推销过程中必须自始至终的执行推销计划.〔〕10、直销人员是指那些向批发商、零售商销售产品的推销员.〔〕11、推销员最基本的职责是提供服务.〔〕12、推销对象一定是最终消费者或使用者.三、简答题1、你认为现代推销人员应该具备哪些素质和能力?2、有人说:"顾客首先信任推销员了才可能购买商品."这话对不对?试用实例说明.四、案例分析题1、在吃饭时,几名推销员凑在一起讨论推销方法.其中一名推销员说:"说到推销方法,最重要的还是灵活性.如果每一次业务活动前都做好充分的准备,深思熟虑每一个细节,那就失去了灵活性,何况客户的情况千差万别,也根本没有办法去做充分的准备,推销全靠随机应变,计划是没有用的."你觉得这位推销员的话正确吗?为什么?2、小王是一家软件公司的推销员.最近他拿到了一份50万元的大单.恰好他的一个同学刚新开了一家软件公司,得知道他签了一份大单,就对他说:"你把这单给我,利润有20%,我俩各一半."小王不免有些动心.一来可给同学一个支持,二来公司的报酬每月工资几百元,加上提成也不过几千元,相比之下确实差得很远.但现在公司领导对他又很不错,正准备提拔他做业务经理.这单"跳"还是不"跳"?小王在犹豫.思考:小王该不该"跳单"?.你认为推销人员最重要的素质是什么?3、推销员:"您好.我是喜乐公司的王涛,我带来了一种新型的调料盒,您看,就是这种." 顾客:"调料盒?我家有,不买!"推销员:"那您的调料盒一定有好几件了?"顾客:"那当然,你看,这是花椒盒,这是味精盒,这是......"推销员:"真不少,看来您对烹调很内行啊,光调料盒就排了这么一大溜,挺占地方吧?"顾客:"为了吃得可口,没办法."推销员〔开始示范产品〕:"您看,这种调料盒能分装十种调料,可以挂起来,对,就挂这儿.您看,既卫生又好看,不占地方,用着特别方便,如果用它,您的厨房就更利索了."顾客:"是不错,多少钱?"推销员:"5元钱,一种调料盒仅5元钱挺便宜的."顾客:"确实不贵."推销员:"那就把这套留给您吧."顾客:"好,给你钱."问题:〔1〕推销员使用了哪一种推销模式?〔2〕结合案例分析该推销员运用此模式的好处和特点.4、有位推销人员去访问一个家庭,这家人一向对他热情、客气.但这次却出乎意料,对他置之不理,几乎是把他赶出来,而且在他出来时,还飞过来一只碗,正打在他的脑袋上."这到底是为什么"?他对此实在是不可思议.思前想后,觉得自己从没有什么对不起这家的.于是他发誓再也不去这家了.他的领导知道后,认为不管是什么样的理由,这样客气有礼的家庭是绝不会做出如此粗暴之事的.于是决定和这位推销人员一起去拜访.这位推销人员却想不通.他的领导便开导他说:"如果两家公司,一家给你月薪500元,一家给你月薪600元,你选择哪一家?"这位推销人员肯定地回答说是后者.他的领导反驳说:"不一定.如果月薪500元的公司是在不断涨薪水,而月薪600元的公司,是在逐步降薪水,那么你选择哪个?当然要选择前者.所以凡事不要只看表面,我看这家一定发生了什么事,今天你再拜访一趟,保证不会有碗打到你头上."果然如此,原来那天这家夫妇正在吵架,激动之下,控制不住情绪,便迁怒于推销人员.事情过后夫妇俩非常过意不去,频频道歉,并且答应购买推销品,双方非常愉快地成交了.思考与分析:1、这个案例说明了什么问题?2、推销人员应如何面对突发事件?3 、推销人员的领导为什么要与该推销人员一起到顾客家中去拜访?4 、如果你在推销活动中遇到类似情况时你应如何处理?。
初二物理上第一二章练习题

初二物理上第一二章练习题一、选择题1. 下列选项中,属于自然现象的是:A. 水蒸气凝结成水珠B. 火上飞出一个气球C. 电力为人们提供照明D. 彩虹出现在天空中2. 身体与磁铁之间的作用力是:A. 电力B. 重力C. 磁力D. 力3. 将闪电变成有用的电能的装置是:A. 变压器B. 发电机C. 电视机D. 洗衣机4. 火是由下列哪种物质燃烧产生的:A. 水B. 瓦斯C. 汽油D. 纸5. 在火灾中,最先应该做的事情是:A. 把门窗关上B. 迅速疏散C. 熄灭火源D. 搜救财物6. 下列属于气体的是:A. 橡皮B. 铁C. 氧气D. 木头7. “氢氧化钠”是以下哪种物质的化学式:A. 食盐C. 硫酸D. 纳OH8. 玛丽取下天花板上的瓷砖,发现下面是一层波纹状的铁片。
玛丽通过观察瓷砖的位置和天花板下面的铁片,可以推断出瓷砖被支撑在天花板的哪一面?A. 上面B. 下面C. 左面D. 右面9. 德国科学家欧姆曾经研究了电流的大小和导线电阻之间的关系,他的发现被称为“欧姆定律”。
下列哪个选项正确地表达了欧姆定律?A. 电流与电阻成反比B. 电阻与电流成正比C. 电流与电阻无关D. 电阻与电流成反比10. 下列哪一项属于速度的计量单位?A. 度C. 米/秒D. 瓦特二、填空题1. 表现出物体位置变化的量叫做_________。
2. 对物体施加作用的力与物体的_________成正比。
3. 电流的单位是_________。
4. 可以把水变成蒸气的热量是_________。
5. 藏身处发生了火灾时,应该迅速_________。
6. “H2O”表示的化学物质是_________。
7. 电压的单位是_________。
8. 悬挂在墙上的挂钟,指针在摆动的同时,也发生了_________。
9. 想要增大电流,可以加大_____________。
10. 用于测量速度的仪器是_________。
三、简答题1. 请解释物体的运动状态可以有哪三种。
作业3第一二章习题

经济法作业(第三次)第一、二章习题一单项选择题1 下列法律制度中,属于我国经济体系中经济组织法的是()。
A、外商独资企业B、仲裁法C、会计法D、消费者权益保护法2下列法律行为中属于附期限的法律行为的是()。
A、甲乙两方签订购销合同规定,甲方自合同签订之日起五个月后一次性付清全部款项B、乙双方签订合同规定,只有乙方按时按质供应第一批货物后,双方洽谈签订第二批购销合同事宜C、乙双方约定,任何一方若中奖500万元,均应无偿捐赠对方100万元D、甲乙双方约定,无论哪一方先分到新房,均应先租给丙方,供丙方结婚用3 下列代理行为中,属于视同有权代理的是()。
A、甲代理乙与甲签订协议B、甲同时代理乙、丙双方签订乙丙双方之间的协议C、甲持有乙的合同专用章,代理乙与丙签订协议D、在乙的书面委托期限已超过的情况下,代理乙与丙签订协议4 下列命题中,正确的是()。
A、技术进出口合同争议提起诉讼的期限为2年B、国际货物买卖合同争议申请仲裁的期限为4年C、当事人各方在协议中对诉讼时效另有规定的,从其约定D、经济纠纷案件经法院一审判决后,无论当事人上诉讼与否,第一审判决均无法律效力5 诉讼时效中止,只能发生于时效期间的( )。
A、最后3个月内B、最后4个月内C、最后5个月内D、最后6个月内6 土地出让和转让法律关系的客体是( )。
A、土地B、行为C、土地使用权 D 、土地所有权7作为经济法重要形式之一的司法解释是指( )在总结实践经验的基础上发布的指导文件和法律解释。
A、最高人民法院 B高级人民法院 C中级人民法院 D、基层人民法院8.下列行为中,属于代理行为的是()。
1 / 5A.居间行为 B.行纪行为 C.代保管物品行为D.保险公司业务员的揽保行为9 甲公司业务经理乙长期在丙餐厅签单招待客户,餐费由公司按月结清。
后乙因故辞职,月底餐厅前去结账时,甲公司认为,乙当月的几次用餐都是招待私人朋友,因而拒付乙所签单的餐费。
根据相关法律的规定,下列选项中,正确的是()A、甲公司应当付款B、甲公司应当付款,乙承担连带责任C、甲公司有权拒绝付款D、甲公司应当承担补充责任10 2010年5月5日,甲拒绝向乙支付到期租金,乙忙于事务一直未向甲主张权利。
电路分析基础第四版课后习题第一章第二章第三章第四章答案
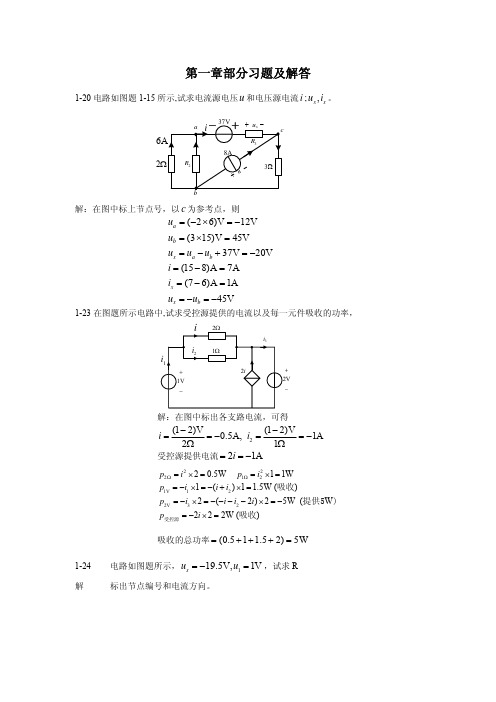
+ 42V
−
i1
18Ω
i2 3Ω
i3
gu
2−5
解
设网孔电流为 i1, i2 , i3 ,则 i3 = −guA = −0.1uA ,所以只要列出两个网孔方程
27i1 −18i2 = 42 −18i1 + 21i2 − 3(−0.1uA ) = 20
因 uA = 9i1 ,代入上式整理得
−15.3i1 + 21i2 = 20
⎪⎩i3 = 4A
第二章部分习题及解答
2-1 试用网孔电流法求图题所示电路中的电流 i 和电压 uab 。
4Ω
1Ω
i2
+
7V
−
i1
2Ω
i3 i
+ 3V
−
解
设网孔电流为 i1, i2 ,i3 ,列网孔方程
⎪⎨⎧3−ii11
− i2 − 2i3 = 7 + 8i2 − 3i3 = 9
⎪⎩−2i1 − 3i2 + 5i3 = −12
解得
i1 = 4.26A uA = (9× 4.26)V = 38.34V i3 = −0.1uA = −3.83A
2-8 含 CCVS 电路如图题 2-6 所示,试求受控源功率。
1Ω i3
5Ω
+
i 4Ω
+
50V i1 −
20Ω i2
15i −
2−6
解
标出网孔电流及方向,
⎧⎪⎨2−52i01i−1 +202i42i−2 −5i43 i=3
50 = −15i
⎪⎩−5i1 − 4i2 +10i3 = 0
又受控源控制量 i 与网孔电流的关系为 i = i1 − i2
软件工程课后习题_第1,2,3章

第一章:一.判断题:1.软件就程序,编软件就是编写程序。
()2.软件危机的主要表现是软件需求增加,软件价格上升。
()3.软件工程科学出现的主要原因是软件危机的出现。
()4.与计算机科学的理论研究不同,软件工程是一门原理性学科()二.选择题1.在下列选项中,()不是软件的特征A系统性与复杂性 B 可靠性与一致性C 抽象性与智能性D 有形性与可控性2.软件危机的主要原因是:A软件工具落后 B 软件生产能力不足C 对软件的认识不够D 软件本身的特点及开发方法3.下列说法正确是的是A 20世纪50年代提出了软件工程的概念B 20世纪60年代提出了软件工程的概念C 20世纪70年代提出了客户机/服务器技术D 20世纪80年代软件工程学达到成熟4.( )是将系统化的规范的可定量的方法应用于软件的开发,运行和维护的过程。
它包括方法、工具和过程三个要素A 软件生命周期B 软件测试C 软件工程D 软件过程5.在下列选项中,()不属于软件工程学科索要研究的基本内容。
A 软件工程材料B 软件工程目标C 软件工程原理D 软件工程过程6.软件工程的三要素是()A技术,方法和工具 B 方法,对象和类 C 方法,工具和过程 D 过程,模型和方法7.用来辅助软件开发,运行,维护,管理,支持等过程中的活动的软件成为软件开发工具,通常也称为()工具A CADB CAIC CAMD CASE三简答题1.与计算机硬件相比,计算机软件有哪些特点?2.软件就是程序吗?如何定义软件?3.什么是软件危机?是什么原因导致了软件危机?4.为什么说软件工程的开发能在一定程度上解决软件危机的各种弊端?5.请简述软件工程的研究内容。
6.请简述软件工程的三要素。
7.请简述软件工程的目标,过程和原则。
8.请简述软件工程的基本原则。
9.请简述现代软件工程与传统软件工程显著的区别与改进。
第二章:一判断题1.瀑布模型的最大优点是将软件开发的各个阶段划分得十分清晰。
《职业道德》一,二,三章课后知识题及答案解析

《职业道德》第一、二、三章课后习题及答案第一章一、单项选择题(共10题)1. 关于职业,准确的说法是(B)A、职业也俗称为工作B、职业是社会发展到一定阶段的产物,是人类社会生产和生活发展变化的必然结果C、职业永恒存在不会消失D、职业可以脱离社会的发展而独立存在2. 关于道德,正确的说法是(C)A、道德就是做好人好事B、做事符合他人利益就是有道德C、道德就是处理人与人、人与社会、人与自然之间关系的特殊行为规范D、道德因人、因时而异,没有确定的目标3. 道德的三大领域分别是(A)A、职业道德、家庭美德和社会公德B、职业道德、家庭美德和集体道德C、家庭美德、个人道德和集体道德D、家庭美德、社会公德和个人道德4. 关于职业道德,正确的说法是(D)A、职业道德有助于增强企业凝聚力,但是无助于促进企业进步B、职业道德有助于提高劳动生产率,但无助于降低生产成本C、职业道德有助于提高产品质量,但无助于提高企业荣誉和形象D、职业有助于提高员工职业技能,增强企业竞争力5. 我国社会主义道德建设的原则是(A)A、集体主义B、人道主义C、功利主义D、利己主义6. 我国社会主义道德建设的核心是(D)A、爱岗敬业B、艰苦奋斗C、诚实守信D、为人民服务7. 《中共中央关于加强社会主义精神文明建设若干问题的决议》规定我国职业道德建设规范是(B)A、求真务实、开拓创新、艰苦奋斗、服务人民、促进发展B、爱岗敬业、诚实守信、办事公道、服务人民、奉献社会C、以人为本、解放思想、实事求是、与时俱进、促进和谐D、文明礼貌、勤俭节约、团结互助、遵纪守法、开拓创新8. 职业道德的“五个要求”既包含基础性的要求也有较高的要求,其中基本要求是(A)A、爱岗敬业B、诚实守信C、奉献社会D、办事公道9. 在社会主义道德建设中,全社会精神文明状况的重要标志是(C)A、职业道德B、家庭美德C、社会公德D、个人道德10. 为了弘扬家庭美德,我们要大力提倡的主要思想道德是(D)A、尊老爱幼、诚实守信、男女平等、夫妻和睦、勤俭持家B、诚实守信、男女平等、夫妻和睦、勤俭持家、爱岗敬业C、男女平等、夫妻和睦、勤俭持家、诚实守信、爱岗敬业D、尊老爱幼、男女平等、夫妻和睦、勤俭持家、邻里团结二、多项选择题(共5题)1. 职业的内涵主要有以下几个方面(ABCDE)A、职业是个人获得经济收入的来源,是赖以生存以及维持家庭生活的手段B、职业是个人所从事的特定工作,是促进个性发展的手段C、职业是社会生产和生活中从事劳动的体现,是个人为社会做出贡献的途径D、职业是个人获得非经济收入(如:名誉、地位、权利)的只要来源E、职业生活使个人进入某种社会情境F、职业只与个人利益有关,与他人利益无关2. 马克思主义关于道德的论述主义包含(ACD)A、一个社会的道德的性质、内容是由社会主义生产方式、经济关系决定的B、道德是人类社会一直存在的,不由社会经济关系决定C、道德是以善与恶、好与坏、偏私与公正等作为标准来调整人们之间的行为的D、道德不是由专门的机构来制定和强制实施的,而是依赖社会舆论和人们的信念、传统、习惯和教育的力量来调节的3. 职业道德的基本特征有(ABCD)A、行业性和公共性B、适当范围有限性和多样性C、一定的强制性和稳定性D、利益相关性4. 职业道德有什么作用(ABDEF)A、调节职业交往中从业人员内部以其与服务对象间的关系B、有助于维护和提高行业的信誉,促进行业发展C、与个人利益没有任何关系,对个人发展没有促进作用D、有助于提高全社会的道德水准E、有助于调节党、政府与群众的关系F、承载着职业所赋予的特殊作用5. 社会主义职业道德的基本特征有(ABCDE)A、社会主义职业道德是社会主义道德体系的组成部分B、社会主义职业道德的内容具有人民性C、社会主义职业道德的形成和发展具有“灌输性”D、社会主义职业道德的核心是树立新的劳动态度E、社会主义职业道德具有相对独立的规范体系第二章一、单项选择题(共10题)1. 关于职业道德的基本原则的描述,正确的是(B)A、职业道德的基本原则不会因为社会的性质不同而不同B、职业道德的基本原则是人们在职业活动中调节职业关系和个人利益与社会利益关系时所必须遵循的根本的职业道德规范C、在相同社会的不同阶段,职业道德的基本原则不会随着社会的发展和实践的演变被赋予不同的内涵和要求D、职业道德的基本原则是长久存在的,不因社会的改变而改变2. 在我国整体社会价值体系中居于核心地位的是(D)A、社会主义集体主义B、全心全意为人民服务原则C、忠于职守的原则D、社会主义核心价值体系3. 关于集体主义的叙述,正确的是(A)A、集体主义作为公民道德建设的原则,是社会主义经济、政治和文化建设的必然要求B、在处理各种不同利益关系中,应该坚持个人利益的原则C、集体主义的实质就是个人在坚持个人利益的前提下携手维护集体的根本利益D、集体主义与平均主义是完全相同的4. 下列不属于职业理想的作用的是(C)A、导向作用B、调节作用C、升职作用D、激励作用5. 下列关于职业态度的描述,不正确的是(B)A、职业态度主要是指从业人员对自己所从事职业的看法以及表现得行为举止B、职业态度就是劳动态度,它与从业人员对社会及对其他社会成员履行职责义务没有关系C、职业态度包括选择方法、工作取向、独立决策能力与选择过程的观念D、职业态度就是个人对职业选择所持的观念和态度6. 关于职业义务的描述,不正确的是(A)A、职业义务与职业环境、职业实践和各个职业在整个社会中的地位没有关系B、职业义务是普遍存在的道德要求C、职业义务是道德关系的客观反映D、职业义务具有利他性和无偿性两个基本特性7. 下列不属于职业义务含义的是(D)A、职业义务是指公民和法人按法律规定应尽的责任B、职业义务是指在道德方面应尽的责任C、职业义务是指不要报酬的奉献D、职业义务是指从业人员一定要履行的责任8. 职业义务的核心是(A)A、职业责任B、无私奉献C、忠于职守D、工作能力9. 下列不属于职业纪律的是(B)A、职业性B、创新性C、安全性D、自律性10. 下列不属于职业良心在职业活动中的重要作用的是(A)A、职业良心具有促进作用B、职业良心具有动机定向的作用C、职业良心能够起到监督作用D、职业良心具有评价作用二、多项选择题(共5题)1. 社会主义核心价值体系包括哪些基本内容(ABCD)A、马克思主义指导思想B、中国特色社会主义共同理想C、以爱国主义为核心的民族精神和以改革创新为核心的时代精神D、以“八荣八耻”为主要内容的社会主义荣辱观E、全心全意为人民服务的思想2. 集体主义的科学含义包含哪些(BCD)A、坚持个人利益高于一切利益,一切言论和行为都要以个人利益为出发点和归宿点B、广大人民群众的根本利益高于一切,人民的一切言论和行动都必须以这个社会的集体利益为出发点和归宿点C、在保证集体利益的前提下,要把国家、集体和个人三者的利益结合起来,尽可能保证和满足成员的个人利益D、当国家利益、集体利益和个人利益三者发生矛盾,甚至发生冲突时,个人利益要服从国家和集体的利益E、在处理各种不同利益关系中,应该坚持个人利益的原则3. 社会主义职业道德体系的主要范畴包含(ABDE)A、职业理想和职业态度B、职业义务和职业纪律C、职业职责和职业态度D、职业良心和职业荣誉E、职业尊严和职业作风4. 如何正确树立职业理想(ABCDE)A、坚持科学的世界观B、树立正确的人生观C、树立正确的职业观D、前面地认识自己D、前面地了解社会5. 下列属于职业纪律的是(BCD)A、时间纪律和合作纪律B、时间纪律和组织纪律C、岗位纪律和协作纪律D、安全卫生纪律和品行纪律E、组织纪律和合作纪律第三章一、单项选择题(共10题)1. 关于职业技能的叙述,不正确的是(A)A、职业技能就是从事某行业所具有的能力B、职业技能是一组动作序列的组合,是指能使人们顺利完成某项职业活动的程序和行为模式的总和C、按照所涉及的技能的类型不同,职业技能可以看作是动作技能与心智技能的复合体D、按照所涉及的宽度和深度不同,职业技能是具有分层结构的2. 下列不属于职业技能层次体系的是(D)A、基础技能层B、专业技能层C、特定技能层D、高级技能层3. 下列不属于教师职业的基本技能层的是(D)A、正常的体力和智力水平B、语言和书面表达能力C、教育学和心理学的基本知识D、创新能力4. 下列不属于教师职业的专业技能层的是(B)A、知识处理能力B、写作能力C、教学组织能力D、多媒体应用能力5. 下列不属于教师职业的特定技能层的是(B)A、相应的专业知识B、教学组织能力C、写作能力D、教育研究和创新能力6. 下列不属于职业能力的层次的是(C)A、职业特定技能B、行业通用技能C、高级技能D、核心技能7. 职业技能培训的重要性不包括的是(C)A、职业技能是构成生产力的重要因素B、职业技能优劣是体现劳动者素质高低的重要条件C、职业技能是从业人员素质高低的评估标准D、搞好技能培训是国家和学生的统一要求8. 下列属于德国职业技能培训的基本形式的是(A)A、双元制B、蓝领工人白领化制度C、脱产研修制度D、技能竞赛9. 关于职业道德和职业技能的关系叙述,错误的是(D)A、职业道德与职业技能相互依存B、职业技能是职业道德的前提和条件C、职业技能是职业道德的最基本要求D、职业道德与职业技能相互独立,互补依存10. 要想立足社会并成就一番事业,从业人员除了要刻苦学习现代专业知识和技能外,还需要(C)A、搞好人际关系B、得到领导的赏识C、加强职业道德修养D、创立自己的小集团二、多项选择题(共5题)1. 关于职业能力内涵的叙述,正确的有(ABCD)A、基于行为主义心理学的职业能力内涵─职业能力即职业技能B、基于认知主义心理学的职业能力内涵─职业能力即职业知识C、基于人本主义心理学的职业能力内涵─职业能力即职业潜能D、基于建构主义心理学的职业能力内涵─职业能力即情境性的综合能力E、传统的科学体系认为,职业能力与生俱来2. 职业技能的特征有(ABCDE)A、技术的先进性B、知识的密集性C、技能的综合性D、信息的开放性E、更新的快速性3. 职业技能培训在社会变革中的作用有(BCDE)A、职业技能的培训重要性在于组织保持和组织发展B、学习者可以通过培训来改变自己,提高自己的职业素质C、学习者通过培训机会来获得必要的知识和技能,从而得以在社会变革中发挥作用D、个人和团体得以学习如何有效道德地发挥集体作用,从而强化组织功能E、个人和团体通过培训改变态度和行为,从而推动社会变革的进程4. 吸取发达国家发展职业教育的经验,我们可以从以下哪些方面来培训职业技能(ABCDE)A、完善技能人才培养法律保障机制B、高度重视职业技能培训C、职业教育要体现终身教育思想D、完善的职业技能鉴定和技能竞赛制度E、注重发展高等职业教育5. 职业学院在教育教学方面有哪些特点(BCE)A、宽基础单一型的教学内容B、优势互补的教学场地C、协调一致的教学文件D、刚性的层次结构E、平等合作的办学方式。
画法几何及机械制图习题集完整答案第一、二、三章

b′ k′
20
a′
Z
a〞
k 〞 b〞
X
20
O a
YW
k b
YH
3—3
求作线段CD的侧面投影,并在该直线上取一点K,使CK=20mm。
Z
d′
k′ 20 k〞
d〞
c′ X c O
c〞
YW
k
d
YH
3—4 求直线AB的水平迹点M及正面迹点N的 两面投影。
( 1) N a′ b′ X n a b′ b b m′ O X b′ b O ( 2) N n′ a′ a
(3)
1—5 标注下列各平面图形的尺寸(按1:1量取整数)
(4)
1-6分析平面图形的尺寸,补齐漏注的尺寸,并注明定位尺寸
定形
?
定位 定位 定位 定位
30 定位
15
f”
f
f
15
15
5
3—2 已知水平线AB在H面上方20mm,求作它的其余投影,并 在该直线上取一点K,使AK=20mm.
(2) b′
a′ c′
a′
△Z
c′
d′ d′
X
b 实长
O
X
b′ 实长
O d
d a c
△Z
a (b) c
3—19 水平线AK是等腰三角形△ABC底边BC的高,点B在V面 前方10mm,点C在H面内,求作△ABC的两面投影。
b′
k′ X
a′
c′
b
八年级物理练习题(第一至第三章第二节)

八年级物理练习题(第一至第三章第二节)一.选择题。
1.初冬的某个夜晚,放在屋外的金属盒内的水结了冰,这说明夜里的气温()A.一定比0 ℃低B.可能是0 ℃,也可能比0 ℃低C.一定是0 ℃D.可能是0 ℃,也可能比0 ℃高2.图4-1-2为意大利物理学家伽利略制造的世界上第一支温度计。
它是由长颈玻璃瓶倒插在液体槽里构成的。
当外界温度改变时,可由玻璃管中的液面高低来标记温度。
那么下列说法中正确的是()图4-1-23.把盛有碎冰块的大试管插入烧杯里的碎冰块中,用酒精灯在烧杯底部慢慢加热,如图4-2-4所示。
当烧杯中的冰块大部分熔化时,试管中的冰()图4-2-44.以下现象中不属于机械运动的是:()A.蜡烛燃烧 B.电梯上升 C.飞机的飞行 D.正在下沉的潜艇5.有两杯水,里面都有没熔化的冰块,一杯在阳光下,一杯在荫凉处,则()A.在阳光下的水的温度高; B.在荫凉处的水的温度高;C.两杯水的温度一样高; D.两杯水温度的高低无法进行比较.6.图①中读数方法正确的是()A.a B.b C.c D.都不正确7.用体温计测得甲的体温为37.50℃,若没有甩过,又用它依次去量乙和丙的体温,已知它们的实际体温为36.90℃和38.60℃,那么两次测温后下列数据正确的是()A.36.90℃和38.60℃B.37.50℃和38.60℃C.36.90℃和37.50℃D.37.50℃和37.50℃8.下列说法正确的是()A.物体放热时,温度不一定降低B.所有的固体都能熔化,而且都有熔点9.下列判断物体运动情況的说法中,以地面为参照物的是:()A.太阳从东方升起 B. 客车里的乘客认为司机是静止C. 月亮躲进云里D. 飞机里的飞行员看到大地在运动10.小明同学乘坐在运动的翻滚车中时,感觉地面上的人和建筑物都在旋转,这时他选取参照物是:()A.翻滚车B.轨道C.地面上的树D.地面上的建筑物11.有一首歌的歌词唱道:“月亮在白莲花般的云朵里穿行”,这里选取的参照物是:()A.地面 B.云朵 C.人 D.月亮二.填空题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
操作系统(1、2章习题)一、单选题1.操作系统是一组()。
A.文件管理程序B.中断处理程序C.资源管理程序D.设备管理程序2.从用户观点看,操作系统是()。
A.用户与计算机之间的接口B.控制和管理计算机资源的软件C.合理的组织计算机工作流程的软件D由若干层次的程序按一定的结构组成的有机体3.()不是操作系统关心的主要问题。
A.管理计算机裸机B.设计、提供用户程序与计算机硬件系统的界面C.管理计算机系统资源D.高级程序设计语言的编译器4.现代OS具有并发性和共享性,是()的引入导致的。
A.单道程序B.磁盘C.对象D.多道程序5.引入多道程序的目的在于()。
A.充分利用CPU,减少CPU等待时间B.提高实时响应速度C.有利于代码共享,减少主、辅存信息交换量D.充分利用存储器6.在单一处理机上执行程序,多道程序的执行是在()进行的。
A.同一时刻B.同一时间间隔内C.某一固定时刻D某一固定时间间隔内7.批处理系统的主要缺点是()。
A.CPU的利用率不高B.失去了交互性C.不具备并行性D以上都不是8.在分时系统中,时间片一定,(),响应时间越长。
A.内存越多B.用户数越多C.后备队列越短D用户数越少9.在下列性质中,哪一个不是分时系统的特征。
()A.交互性B.同时性C.及时性D独占性11 要求在规定的时间内对外界的请求必须给予及时响应的OS是()。
A.多用户分时系统B.实时系统C.批处理系统时间D.网络操作系统12.下面6个系统中,必须是实时操作系统的有()个。
i.航空订票系统ii.过程控制系统iii.机器口语翻译系统iv.计算机辅助系统v.办公自动化系统vi.计算机激光照排系统A.1B.2C.3D.413.()对多道批处理系统最重要。
A.实时性B.交互性C.共享性D.运行效率14.()对多用户分时系统最重要。
A.实时性B.交互性C.共享性D.运行效率15.( )对实时系统最重要。
A.及时性B.交互性C.共享性D.运行效率16.现代操作系统的基本特征是()、资源共享和操作的异步性。
A.多道程序设计B.中断处理C.程序的并发执行D.实现分时与实时处理17.在下面关于并发性的叙述中正确的是()。
A.并发性是指若干事件在同一时刻发生B.并发性是指若干事件在不同时刻发生C.并发性是指若干事件在同一时间间隔内发生D.并发性是指若干事件在不同时间间隔内发生18以下()项功能不是操作系统具备的主要功能。
A.内存管理B.中断处理C.文档编辑D.CPU调度19.分布式系统与网络系统的主要区别是()A.并行性B.透明性C.共享性D.复杂性20( )操作系统允许在一台主机上同时连接多台终端,多个用户可以通过各自的终端同时交互地使用计算机。
A.网络B.分布式C.分时D.实时21.()不是多道程序系统A.单用户单任务B.多道批处理系统C.单用户多任务D.多用户分时系统22.CPU状态分为系统态和用户态,从用户态转换到系统态的唯一途径是()。
A.运行进程修改程序状态字B.中断屏蔽C.系统调用D.进程调度程序23.Windows98是()操作系统。
A.多用户分时B.批处理系统C.单用户多任务D.单用单任务24.用户要在程序一级获得系统帮助,必须通过()。
A.进程调度B.作业调度C.键盘命令D.系统调用25.()操作系统必须提供的功能。
A.GUIB.为进程提供系统调用命令C.处理中断D.编译源程序26. 单操作系统完成了用户请求的“系统功能调用”后,应让中央处理器()工作。
A.维持在管态B.从管态转换到目态C.维持在目态D.从目态转换到管态27.任何两个并发进程之间存在着()的关系。
A.各自完全独立B.拥有共享变量C.必须互斥D.可能相互制约28.并发进程执行的相对速度是()。
A.由进程的程序结构决定的B.由进程自己来控制的C.在进程被创建时确定的D.与进程调度策略有关的29.并发进程中与共享变量有关的程序段称为()。
A.共享子程序B.临界区C.管理区D.公共数据区30.用来实现进程同步与互斥的PV操作实际上是由()过程组成的。
A.一个可被中断的B.一个不可被中断的C.两个可被中断的 D. 两个不可被中断的31.进程从运行态变为等待态可能由于()。
A.执行了V操作B.执行了P操作C.时间片用完D.有高优先级进程就绪32.用PV操作管理互斥使用的资源时,信号量的初值应定义为()。
A.任意整数B.1 C.O D.-133.现有n个具有相关临界区的并发进程,如果某进程调用P操作后变为等待状态,则调用P操作时信号量的值必定为()。
A.≤0 B.1 C.n-1 D.n34.用PV操作管理临界区时把信号量的初值定义为1,现已有一个进程在临界区,但有n个进程在等待进人临界区,这时信号量的值为()。
A.-1 B.1 C.-n D.n35.用V操作唤醒一个等待进程时,被唤醒进程的状态应变成()状态。
A.执行B.就绪C.运行D.收容36.有一共享文件可供n个并发进程使用,但限制最多m个进程(n≥m≥1)可同时读文件,用PV操作进行管理时其信号量的初值应该为()。
A.n B.m C.u-m D.137.当一个任务需要若干进程协同完成时,进程之间需要交换一定数量的信息,把这种信息交换称为()。
A.进程唤醒B.进程通信C.进程互斥D.进程同步38.进程间采用信箱通信方式时,send原语把发送者的信件存放到()中。
A.信箱B.消息缓冲区C.接收者的PCB D.指定的工作区39.采用信箱方式进行通信的系统中,信箱是一种()资源。
A.可共享的硬件B.不可共享的硬件C.可共享的软件D.不可共享的软件40.使用PV操作后,()系统死锁。
A.能检测B.能解除C.仍可能出现D.不会出现41.系统出现死锁时一定同时保持了四个必要条件,对资源采用按序分配算法后可破坏其中的()条件。
A.互斥B.占有且等待C.可抢占资源D.循环等待42.资源的静态分配算法在解决死锁问题中是用于()死锁。
A.防止B.避免C.检测D.解除43.在讨论死锁问题时,采用银行家算法分配资源可以()死锁。
A.防止B.避免C.检测D.解除二、填空题1.操作系统是计算机系统中的一个__________,它管理和控制计算机系统中的__________.2.在多道程序环境下的各道程序,从宏观上来说,它们在__________运行,但从微观上来看,则以__________方式运行。
3.操作系统是计算机系统的核心软件。
按功能特征的不同,可把操作系统分为____________、____________ 、____________ 、个人机系统、网络操作系统和分布式操作系统等基本类型。
其中____________ 的主要目标是提高系统的吞吐率和效率,而____________是一旦有处理请求和要求处理的数据时,CPU就应该立即处理该数据并将结果及时送回。
4.根据服务对象不同,常用的处理机操作系统主要分为如下三种类型:允许多个用户在其终端上同时交互地使用计算机的操作系统称为____________,它通常采用____________策略为用户服务;允许用户把若干个作业提交计算机系统集中处理的操作系统称为____________,衡量这种系统性能的一个主要指标是系统的____________;在____________的控制下,计算机系统能及时处理由过程控制反馈的数据并作出响应。
设计这种系统时,应首先考虑系统的____________。
5.现代操作系统的两个最基本特征是_____________和___________。
6.实时系统应具有两个基本特征____________和___________。
7.用户和操作系统之间的接口主要有____________和____________两类。
8.在主机控制下进行的输入/输出操作称为____________操作。
9.UNIX系统是____________操作系统,DOS系统是____________操作系统。
10.计算机系统是由计算机________和计算机________两大部分组成。
11.不配有任何软件的计算机通常被称为___________。
12.计算机的软件可分成________、________和应用软件三类。
13.操作系统管理的计算机系统中的资源可分成_______资源和_______资源两大类。
14.操作系统的形成与发展与_________技术的发展密切相关。
15._________操作系统能充分利用中央处理器与各种外围设备的并行工作能力。
16._________操作系统使用户能直接操纵计算机系统进行交互式的工作。
17.在用于控制生产流水线的计算机系统中应配置________操作系统。
18.在实时操作系统控制下,计算机系统对接收到的_________信号应及时处理。
19.设计实时操作系统时必须首先考虑系统的_______和________,其次才考虑系统效率。
20.网络操作系统的功能是实现各台计算机之间的________以及网络中________的共享。
21.分布式操作系统能使系统中若干台计算机________完成一个共同的任务。
22.分布式操作系统是把_________分布在几台计算机上并行地运行。
23.把不允许用户程序中直接使用的指令称为_________指令。
24.中央处理器区分两种工作状态,它们是_______和_______。
25.中央处理器处于_______时拒绝执行特权指令。
26.________是用来控制指令执行顺序并且保留和指示与程序有关的系统状态。
27.每个程序都要有一个________来刻画本程序的执行状态。
28.中央处理器设置一个________寄存器用来存放当前运行程序的PSW。
29.由操作系统提供的可供用户程序执行中调用的子程序被称为__________。
30.用户程序中使用_________指令来请求调用操作系统功能。
31.当用户请求调用操作系统功能时应使中央处理器的工作状态从_________转换成________。
32.从资源管理的观点看,操作系统的功能可分成________、________、_______、_______和_______五大部分。
33.一个进程独占处理器顺序执行时具有_______和_______两个特性。
34.把一组可同时执行的进程称为_______进程。
35.有交往的并发进程在竞争共享资源时会出现_______错误。
36.把并发进程中涉及到对共享变量进行访问的程序段称为_______。
37.用PV操作管理相关临界区时,任何一个进程要进人自己的临界区前应调用_______、操作,退出临界区时应调用_______操作。
38.系统中存在多个进程时,这些进程对共享资源的使用存在着不同的相互制约关系,制约关系可归结为两种,一种是_______关系,另一种是_______关系。
