R语言实验报告习题详解

合集下载

R语言实验报告—回归分析在女性身高与体重的应用

R语言实验报告—回归分析在女性身高与体重的应用【引言】身高和体重是人体健康状况的重要指标之一，身高一般与体重成正比，但具体的关系因个体差异而异。

为了探究女性身高与体重之间的关系，并通过回归分析建立二者之间的数学模型，本实验使用R语言进行实验。

【数据获取与处理】从网上收集了100名女性的身高和体重数据作为样本。

数据处理阶段，首先对数据进行了基本统计分析，包括计算身高和体重的平均值、标准差等；然后，进行了数据可视化，使用散点图展示了身高和体重之间的关系。

【回归建模】接下来，使用R语言进行回归分析建模。

假设身高为自变量x，体重为因变量y，建立线性回归模型y=β0+β1x+ε，其中ε为误差项。

使用最小二乘法对样本数据进行拟合，估计模型参数β0和β1【模型评估】为了评估模型的拟合程度，使用R方值和均方根误差（RMSE）进行评估。

R方值越接近1表示模型拟合效果越好，RMSE值越小表示模型预测结果与实际数据越接近。

【结果讨论】根据回归分析得到的模型参数估计值，可以判断女性身高和体重之间存在正相关关系。

同时，R方值为0.8，表明模型拟合效果较好。

但是，RMSE为3.2，表示模型的预测误差较大，可能存在其他影响体重的因素未考虑。

【结论】回归分析可以帮助我们了解女性身高和体重之间的关系，并建立数学模型预测体重。

本实验结果显示女性的身高与体重存在正相关关系。

但是，模型的预测效果可能还可以改进，需要进一步考虑其他可能的影响因素，例如年龄、饮食习惯等。

[2] Guo SS, Chumlea WC. Tracking of body mass index in children in relation to overweight in adulthood. Am J Clin Nutr, 1999, 70(1):145S-148S.【附录】实验中使用的R代码如下：```R#数据处理与可视化data <- read.csv("data.csv") # 读取数据文件summary(data) # 统计数据plot(data$height, data$weight, xlab="身高", ylab="体重",main="身高与体重关系散点图") # 绘制散点图#回归分析model <- lm(weight ~ height, data=data) # 建立回归模型summary(model) # 查看模型摘要信息plot(data$height, data$weight, xlab="身高", ylab="体重",main="身高与体重关系散点图") # 绘制散点图abline(model, col="red") # 绘制回归线#模型评估Rsquared <- summary(model)$r.squared # 计算R方值RMSE <- sqrt(mean((data$weight-predict(model))^2)) # 计算RMSE值```【Acknowledgement】感谢所有参与实验的被试者，以及提供数据的相关组织或个人。

R语言实验报告

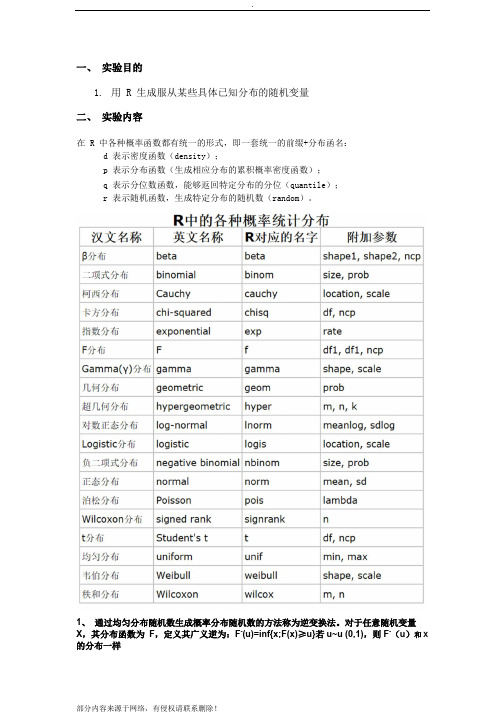
一、实验目的1.用 R 生成服从某些具体已知分布的随机变量二、实验内容在 R 中各种概率函数都有统一的形式，即一套统一的前缀+分布函名：d 表示密度函数（density）；p 表示分布函数（生成相应分布的累积概率密度函数）；q 表示分位数函数，能够返回特定分布的分位（quantile）；r 表示随机函数，生成特定分布的随机数（random）。

1、通过均匀分布随机数生成概率分布随机数的方法称为逆变换法。

对于任意随机变量X，其分布函数为F，定义其广义逆为：F-(u)=inf{x;F(x)≥u}若u~u (0,1)，则F-（u）和X 的分布一样Example 1 如果X~Exp（1）（服从参数为 1 的指数分布），F（x）=1-e-x。

若u=1-e-x并且u~u(0,1)，则X=-logU~Exp(1)则可以解出x=-log(1-u)通过随机数生成产生的分布与本身的指数分布结果相一致R 代码如下：nsim = 10^4U = runif(nsim)X = -log(U)Y = rexp(nsim)X11(h=3.5)Xpar(mfrow=c(1,2),mar=c(2,2,2,2))hist(X,freq=F,main="Exp from Uniform",ylab="",xlab="",ncl=150,col="grey",xlim=c(0,8))curve(dexp(x),add=T,col="sienna",lwd=2)hist(Y,freq=F,main="Exp from R",ylab="",xlab="",ncl=150,col="grey",xlim=c(0,8))curve(dexp(x),add=T,col="sienna",lwd=2)2、某些随机变量可由指数分布生成。

R语言总和性试验

中北大学理学院实验报告实验课程名称：R语言与统计分析实验类别：验证型专业：应用统计学班级： 13080441学号： 1308044142姓名：吴庚雷中北大学理学院R语言与统计分析综合实验【实验类型】验证性【实验目的】（1）掌握利用R语言实现数据处理并进行严格的统计分析；（2）学会运用R语言进行程序的编写；（3）熟练掌握R语言绘图功能；（4）掌握R语言统计分析中的“参数估计”，“假设检验”，“方差分析”，“回归分析”，等基本分析函数。

【实验要求】（1）实验过程要求用R软件完成；（2）实验结果逐个导入Word文档，并按问题作出解释；（3）实验报告按照既定格式书写。

【实验仪器与软件平台】计算机 R软件【实验前的预备知识】1、实验室电脑要求安装有R软件；2、上实验课程的学生要对涉及到的统计概念有所了解；3、要求学生事先查阅并熟悉R的相关命令。

【实验内容】第二章：1、用rep()构造一个向量x，它由3个3,4个2,5个1构成。

x<-rep(c(3,2,1),c(3,4,5))2、由1.2...16构成两个方阵，其中矩阵A按列输入，矩阵B按行输入，并计算以下：A<-matrix(1:16,4,4)B<-matrix(1:16,4,4,byrow=TRUE)1、C=A+B2、> D=A*B3、> E=A%*%B4、F<-A[-3,][,1] [,2] [,3] [,4][1,] 1 5 9 13 [2,] 2 6 10 14 [3,] 4 8 12 16> G<-B[,-3][,1] [,2] [,3][1,] 1 2 4[2,] 5 6 8[3,] 9 10 12[4,] 13 14 16> H=F%*%G3、函数solve()有两个作用；solve（A,b）可用于求解线性方程组Ax=b,solve(A)可用于求解矩阵A的逆，用两种方法编程求解方程组Ax=b的解。

报告R语言实验五..docx

实验五常见分布的相关计算、随机抽样与模拟【实验类型】验证性【实验学时】2 学时【实验目的】1、掌握常见分布的分布函数、密度函数(或分布列)及分位数的计算方法；2、掌握样本统计量的计算方法及所表达的意义；3、了解随机模拟的基本思想及其应用。

【实验内容】1、组合数与组合方案的生成、概率的计算，2、常见分布的分布函数、密度函数(或分布列)以及分位数的计算；3、随机数的生成与随机模拟(蒙特卡洛仿真) 。

【实验方法或步骤】第一部分、课件例题：1.#从1～5 个数中，随机取3个的全部组合combn(1:5,3) # 共10 种组合方案combn(1:5,3,FUN=mean) # 对每种组合方案求均值choose(5,3) # 从5 个数里面选3个的组合数目choose(50,3)factorial(10) # 计算10！3.#3. 从一副完全打乱的52张扑克中任取 4 张，计算下列事件的概率#(1) 抽取 4 张依次为红心A，方块A，黑桃A和梅花A的概率1/prod(49:52) #prod() 表示连乘积#(2) 抽取 4 张为红心A，方块A，黑桃A和梅花A的概率．1/choose(52,4)4.设在15 只同类型的零件中有2只是次品，一次任取3只，以X表示次品的只数，求X的分布律．x<-c(1,1,rep(0,13));x # 样本空间( 用1 表示次品, 0 为正品) X<-combn(x,3,FUN=sum) #从样本空间中任取 3 个元素的方案，并对每个方案求和，共455 个数(取值0,1,2 )p<-numeric(3) # 定义p 为数值型的 3 维向量，且初值为0for (i in 1:3)p[i]<-sum(X==i-1)/length(X) #sum(X==i-1) 表示对X 取值为i-1 的个数求和,X 的长度为455# 例5.3 ：计算3σ 原则对应的概率x <- 1:3; p <- pnorm(x) - pnorm(-x); p# 例5.4 ：令α=0.025 ，计算上α 分位点z α alpha <- 0.025; z <- qnorm(1-alpha); z6.#例5.5 ：计算P{X≤160} ，其中X~U[150,200] 。

r语言实验报告

武夷学院实验报告课程名称：大数据挖掘与统计机器学习项目名称：多元统计分析与R语言建模姓名：__张树捷__专业：数学与应用数学班级：__2班_学号：__20171071203__同组成员：无_时间：______一、实验部分：P37 3m=seq(0,3000,by=300)hist(as.matrix(jie),m,freq=F,col=1:7)m=seq(0,3000,by=300)hist(as.matrix(jie),m,freq=T,col=1:7)m=seq(0,96000,by=3000)t<-as.matrix(jie)cumsum(t)hist(cumsum(t),m,freq=F,col=1:12,las=3) 累计频率图：p55 二、2barplot(apply(dier,1,mean),las=3)#按行作均值条形图barplot(apply(dier,2,mean))#按列作均值图条形图boxplot(dier)#按列作箱尾图boxplot(dier,horizontal = T)#箱尾图中图形按水平放置stars(dier,full=T,key.loc = c(13,1.5))#具有图例的360度星相图stars(dier,full=T,draw.segments = T,key.loc = c(13,1.5))#具有图例的3 60度彩色星相图summary(dier)#数据分析图表faces(dier,ncol.plot = 7)#按每行7个作脸谱图library(MSG)#加载msg包andrews_curve(dier)#绘制调和曲线图P87 4cor(disan)#计算相关系数矩阵plot(disan)#散点图library(psych)#加载psych包corr.test(disan)#y，x1，x2，x3的相关系数fm=lm(y~.,data=disan)#显示多元线性回归模型summary(fm)#多元线性回归系数t检验（拟合优度检验）由于P<0.05,于是在05.0=α水平处拒绝0H ，接受1H ，即x1,x2，x3与y 之间存在回归关系。

R语言实验三

实验三数组的运算、求解方程（组）和函数极值、数值积分【实验类型】验证性【实验学时】2 学时【实验目的】1、掌握向量的四则运算和内积运算、矩阵的行列式和逆等相关运算；2、掌握线性和非线性方程（组）的求解方法，函数极值的求解方法；3、了解 R 中数值积分的求解方法。

【实验内容】1、向量与矩阵的常见运算；2、求解线性和非线性方程（组）；3、求函数的极值，计算函数的积分。

【实验方法或步骤】第一部分、课件例题：1.向量的运算x<-c(-1,0,2)y<-c(3,8,2)v<-2*x+y+1vx*yx/yy^xexp(x)sqrt(y)x1<-c(100,200); x2<-1:6; x1+x22.x<-1:5y<-2*1:5x%*%ycrossprod(x,y)x%o%ytcrossprod(x,y)outer(x,y)3.矩阵的运算A<-matrix(1:9,nrow=3,byrow=T);AA+1 #A的每个元素都加上1B<-matrix(1:9,nrow=3); BC<-matrix(c(1,2,2,3,3,4,4,6,8),nrow=3); C D<-2*C+A/B; D #对应元素进行四则运算x<-1:9A+x #矩阵按列与向量相加E<-A%*%B; E #矩阵的乘法y<-1:3A%*%y #矩阵与向量相乘crossprod(A,B) #A的转置乘以Btcrossprod(A,B) #A乘以B的转置4.矩阵的运算A<-matrix(c(1:8,0),nrow=3);At(A) #转置det(A) #求矩阵行列式的值diag(A) #提取对角线上的元素A[lower.tri(A)==T]<-0;A #构造A对应的上三角矩阵qr.A<-qr(A);qr.A #将矩阵A分解成正交阵Q与上三角阵R的乘积，该结果为一列表Q<-qr.Q(qr.A);Q;R<-qr.R(qr.A);R #显示分解后对应的正交阵Q与上三角阵Rdet(Q);det(R);Q%*%R #A=Q*Rqr.X(qr.A) #显示分解前的矩阵5.解线性方程组A<-matrix(c(1:8,0),nrow=3,byrow=TRUE)b<-c(1,1,1)x<-solve(A,b); x #解线性方程组Ax=bB<-solve(A); B #求矩阵A的逆矩阵BA%*%B #结果为单位阵6.非线性方程求根f<-function(x) x^3-x-1 #建立函数uniroot(f,c(1,2)) #输出列表中f.root为近似解处的函数值，iter为迭代次数，estim.prec为精度的估计值uniroot(f,lower=1,upper=2) #与上述结果相同polyroot(c(-1,-1,0,1)) #专门用来求多项式的根，其中c(-1,-1,0,1)表示对应多项式从零次幂项到高次幂项的系数7.求解非线性方程组（1）自编函数： (Newtons.R)Newtons<-function (funs, x, ep=1e-5, it_max=100){index<-0; k<-1while (k<=it_max){ #it_max 表示最大迭代次数x1 <- x; obj <- funs(x);x <- x - solve(obj$J, obj$f); #Newton 法的迭代公式norm <- sqrt((x-x1) %*% (x-x1))if (norm<ep){ index<-1; break #index=1 表示求解成功}; k<-k+1 }obj <- funs(x);list(root=x, it=k, index=index, FunVal= obj$f)} # 输出列表（2）调用求解非线性方程组的自编函数funs<-function(x){ f<-c(x[1]^2+x[2]^2-5, (x[1]+1)*x[2]-(3*x[1]+1)) # 定义函数组J<-matrix(c(2*x[1], 2*x[2], x[2]-3, x[1]+1), nrow=2,byrow=T) # 函数组的 Jacobi 矩阵list(f=f, J=J)} # 返回值为列表 : 函数值 f 和 Jacobi 矩阵 Jsource("F:/wenjian_daima/Newtons.R") # 调用求解非线性方程组的自编函数Newtons(funs, x=c(0,1))8.一元函数极值f<-function(x) x^3-2*x-5 # 定义函数optimize(f,lower=0,upper=2) # 返回值 : 极小值点和目标函数f<-function(x,a) (x-a)^2 # 定义含有参数的函数optimize(f,interval=c(0,1),a=1/3) # 在函数中输入附加参数9.多元函数极值（1）obj <-function (x){ # 定义函数F<-c(10*(x[2]-x[1]^2),1-x[1]) # 视为向量sum (F^2) } # 向量对应分量平方后求和nlm(obj,c(-1.2,1))（2）fn<-function(x){ # 定义目标函数F<-c(10*(x[2]-x[1]^2), 1-x[1])t(F)%*%F } # 向量的内积gr <- function(x){ # 定义梯度函数F<-c(10*(x[2]-x[1]^2), 1-x[1])J<-matrix(c(-20*x[1],10,-1,0),2,2,byrow=T) #Jacobi 矩阵2*t(J)%*%F } # 梯度optim(c(-1.2,1), fn, gr, method="BFGS")最优点 (par) 、最优函数值 (value)10.梯形求积分公式（1）求积分程序： (trape.R)trape<-function(fun, a, b, tol=1e-6){ # 精度为 10 -6N <- 1; h <- b-a ; T <- h/2 * (fun(a) + fun(b)) # 梯形面积 repeat{h <- h/2; x<-a+(2*1:N-1)*h; I <-T/2 + h*sum(fun(x)) if(abs(I-T) < tol) break; N <- 2 * N; T = I }; I}（2）source("F:/wenjian_daima/trape.R") # 调用函数f<-function(x) exp(-x^2)trape(f,-1,1)（3）常用求积分函数f<-function(x)exp(-x^2) # 定义函数integrate(f,0,1)integrate(f,0,10)integrate(f,0,100)integrate(f,0,10000) # 当积分上限很大时，结果出现问题integrate(f,0,Inf) # 积分上限为无穷大ft<-function(t) exp(-(t/(1-t))^2)/(1-t)^2 # 对上述积分的被积函数 e 2 作变量代换 t=x/(1+x) 后的函数integrate(ft,0,1) # 与上述计算结果相同，且精度较高第二部分、教材例题：1.随机抽样（1）等可能的不放回的随机抽样:> sample(x, n) 其中x为要抽取的向量, n为样本容量（2）等可能的有放回的随机抽样:> sample(x, n, replace=TRUE)其中选项replace=TRUE表示有放回的, 此选项省略或replace=FALSE表示抽样是不放回的sample(c("H", "T"), 10, replace=T)sample(1:6, 10, replace=T)（3）不等可能的随机抽样:> sample(x, n, replace=TRUE, prob=y)其中选项prob=y用于指定x中元素出现的概率, 向量y与x等长度sample(c("成功", "失败"), 10, replace=T, prob=c(0.9,0.1))sample(c(1,0), 10, replace=T, prob=c(0.9,0.1))2.排列组合与概率的计算1/prod(52:49)1/choose(52,4)3.概率分布qnorm(0.025) #显著性水平为5%的正态分布的双侧临界值qnorm(0.975)1 - pchisq(3.84, 1) #计算假设检验的p值2*pt(-2.43, df = 13) #容量为14的双边t检验的p值4.limite.central( )的定义limite.central <- function (r=runif, distpar=c(0,1), m=.5,s=1/sqrt(12),n=c(1,3,10,30), N=1000) {for (i in n) {if (length(distpar)==2){x <- matrix(r(i*N, distpar[1],distpar[2]),nc=i)}else {x <- matrix(r(i*N, distpar), nc=i)}x <- (apply(x, 1, sum) - i*m )/(sqrt(i)*s)hist(x,col="light blue",probability=T,main=paste("n=",i), ylim=c(0,max(.4, density(x)$y)))lines(density(x), col="red", lwd=3)curve(dnorm(x), col="blue", lwd=3, lty=3, add=T)if( N>100 ) {rug(sample(x,100))}else {rug(x)}}}5.直方图x=runif(100,min=0,max=1)hist(x)6.二项分布B（10，0.1）op <- par(mfrow=c(2,2))limite.central(rbinom,distpar=c(10,0.1),m=1,s=0.9)par(op)7.泊松分布: pios（1）op <- par(mfrow=c(2,2))limite.central(rpois, distpar=1, m=1, s=1, n=c(3, 10, 30 ,50)) par(op)8.均匀分布：unif(0,1)op <- par(mfrow=c(2,2))limite.central( )par(op)9.指数分布：exp(1)op <- par(mfrow=c(2,2))limite.central(rexp, distpar=1, m=1, s=1)par(op)10.混合正态分布的渐近正态性mixn <- function (n, a=-1, b=1){rnorm(n, sample(c(a,b),n,replace=T))}limite.central(r=mixn, distpar=c(-3,3),m=0, s=sqrt(10), n=c(1,2,3,10)) par(op)11.混合正态分布的渐近正态性op <- par(mfrow=c(2,2))mixn <- function (n, a=-1, b=1){rnorm(n, sample(c(a,b),n,replace=T))}limite.central(r=mixn, distpar=c(-3,3),m=0,s=sqrt(10),n=c(1,2,3,10)) par(op)第三部分、课后习题：3.1a=sample(1:100,5)asum(a)3.2（1）抽到10、J、Q、K、A的事件记为A，概率为P(A)=1(5220)其中在R中计算得：> 1/choose(52,20)[1] 7.936846e-15（2）抽到的是同花顺P(B)=(41)(91) (525)在R中计算得：> (choose(4,1)*choose(9,1))/choose(52,5) [1] 1.385e-053.3#(1)x<-rnorm(1000,mean=100,sd=100)hist(x)#(2)y<-sample(x,500)hist(y)#(3)mean(x)mean(y)var(x)var(y)3.4x<-rnorm(1000,mean=0,sd=1) y=cumsum(x)plot(y,type = "l")plot(y,type = "p")3.5x<-rnorm(100,mean=0,sd=1) qnorm(.025)qnorm(.975)t.test(x)由R结果知：理论值为[-1.96,1.96]，实际值为：[-0.07929,0.33001]3.6op <- par(mfrow=c(2,2))limite.central(rbeta, distpar=c(0.5 ,0.5),n=c(30,200,500,1000))par(op)3.7N=seq(-4,4,length=1000)f<-function(x){dnorm(x)/sum(dnorm(x))}n=f(N)result=sample(n,replace=T,size = 1000)standdata=rnorm(1000)op<-par(mfrow=c(1,2)) #1行2列数组按列（mfcol）或行（mfrow）各自绘图hist(result,probability = T)lines(density(result),col="red",lwd=3)hist(standdata,probability = T)lines(density(standdata),col="red",lwd=3) par(op)。

R语言实验六

R语言实验六实验六重要的参数检验与功效检验【实验类型】验证性【实验学时】2 学时【实验目的】1、掌握假设检验的基本思想；2、掌握重要的参数检验及功效检验的求解方法；3、了解非参数假设检验的基本思想及求解方法。

【实验内容】1、参数检验（t 检验、F 检验、二项分布检验和泊松检验等）的计算；2、功效检验的计算；3、非参数检验（符号与秩检验、分布的检验、相关性检验等）的求解。

【实验方法或步骤】第一部分、课件例题：#1 例6.2X<-c(159, 280, 101, 212, 224, 379, 179, 264,222, 362, 168, 250, 149, 260, 485, 170)t.test(X, alternative = "greater", mu = 225) #单侧检验由于p值(= 0.257)>0.05，不能拒绝原假设，接受H 0 ，即认为平均寿命不大于225h#2 例6.3X<-c(78.1, 72.4, 76.2, 74.3, 77.4, 78.4, 76.0, 75.5, 76.7, 77.3) Y<-c(79.1, 81.0, 77.3, 79.1, 80.0, 79.1,79.1, 77.3, 80.2, 82.1) t.test(X, Y, al = "l", var.equal = T) #H 1 :μ 1 -μ 2 <0t.test(X, Y, al = "l") #使用总体方差不同模型t.test(X, Y, al = "l", paired = TRUE) #配对数据检验## 公式形式obtain<-data.frame(value = c(78.1, 72.4, 76.2, 74.3, 77.4, 78.4, 76.0,75.5, 76.7, 77.3, 79.1, 81.0, 77.3, 79.1,80.0, 79.1, 79.1, 77.3, 80.2, 82.1),group = gl(2, 10)) #生成2水平、各有10个元素的因子向量t.test(value ~ group, data = obtain,alternative = "less", var.equal = TRUE)由于p值(= 0.000218)<0.05，拒绝原假设，即接受H 1 ，再利用μ 1 -μ 2 的置信区间，可以说明新操作方法能够提高得率。

R语言实验四

R语言编程技术实验报告
题目：数据的导入导出
院系：计算机科学与工程学院
班级：170408
姓名：刘馨雨
学号：20172693
【实验题目】
数据的导入导出。

【实验目的】
1.熟练掌握从一些包中读取数据。

2.熟练掌握csv文件的导入。

3.创建一个数据框，并导出为csv格式。

【实验内容与实现】
1.创建一个csv文件（内容自定），并用readtable函数导入该文件。

图1.1 vim命令，按shift+zz可保存退出。

图1.2 进入R语言环境
图1.3 读取文件
2.查看R语言自带的数据集airquality（纽约1973年5-9月每日空气质量）。

图2 截了前24行
3.列出airquality的前十列，并将这前十列保存到air中。

图3.1 列出前十列
图3.2 保存到air数据框中
图3.3 保存到air.csv中并读取4.任选三个列，查看airquality中列的对象类型。

图4 查看3、4、5行数据类型5.使用names查看airquality数据集中各列的名称
图5
6.将air这个数据框导出为csv格式文件。

（write.table (x, file ="", sep ="", s =TRUE, s =TRUE, quote =TRUE)）
图6 导出为test.csv并查看当前目录文件
【实验心得】
1.第3题出现了三个错误。

2.第4题出现了两个错误。

3.第5题出错name改为names。

4.第6题出现的错误没太明白，准备上课询问老师。

r语言上级实验一

r语言上级实验一理学院实验报告班级：学号：姓名：实验编号：01实验一：初识R软件一、实验目的与要求：１、了解R软件的安装、启动和退出。

２、掌握软件包的安装和载入。

3、掌握R软件帮助功能。

4、会使用R的集成开发环境Tinn-R或Rstudio。

5、掌握用R进行基本的代数运算。

6、掌握用R生成向量、矩阵、数据框和列表的方法。

7、掌握提取数据子集的方法。

二、实验内容：1.按N的不同取值，计算∑=-Nii12)12(1,并求其与log(N)+1.0的距离，其中N=100，500，1000，1500.#计算其值> N<-c(100,500,1000,1500)> for(k in 1:length(N))+ {+ s=0+ for(i in 1:N[k]){+ s=s+1/(2*i-1)^2+ }+ print(s)+ }[1] 1.231201[1] 1.233201[1] 1.233451[1] 1.233534#求距离> y<-abs(s-(log(N)+1.0))> y[1] 4.371636 5.981074 6.674221 7.0796872.联合命令rep()和seq()生成(1,2,3,4,5,2,3,4,5,6,3,4,5,6,7,4,5,6,7,8,5,6,7,8,9). #用rep生成> rep(1:5,5)+rep(0:4,rep(5,5))[1] 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 5 6 7 8 9 #用seq 生成> rep(seq(1,5),5)+rep(seq(0,4),rep(5,5))[1] 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 5 6 7 8 93. 利用命令matrix()将矩阵=4912011411435A 输入变量A ，并求A 的行列式、逆矩阵，T AA (转置命令为t())、A A T .#输入变量A> A<-matrix(c(35,14,1,4,11,0,12,9,4),nrow=3,ncol=3,byrow=T) > A [,1] [,2] [,3][1,] 35 14 1 [2,] 4 11 0 [3,] 12 9 4#计算A 值 > det(A) [1] 1220#计算A 逆> solve (A) %*%A[,1] [,2] [,3] [1,] 1.000000e+00 -5.551115e-17 0.000000e+00 [2,] -1.387779e-17 1.000000e+00 -1.734723e-18 [3,] -4.440892e-16 -4.440892e-16 1.000000e+00#计算AA T > A%*%t(A)[,1] [,2] [,3] [1,] 1422 294 550 [2,] 294 137 147 [3,] 550 147 241#计算A T A> t(A)%*%A[,1] [,2] [,3] [1,] 1385 642 83 [2,] 642 398 50[3,] 83 50 174. (1)利用命令data.frame()将下表数据读入变量sea,Season Salinity(盐度) Temperature winter 29.19 4 winter 27.37 6 spring24.997.3spring 28.79 8.2 spring 33.28 9.1 summer 32.69 18.1 summer31.9 17 summer NA 21 autumn 32.53 15.1 autumn32.53 13.8>Season<-c("winter","winter","spring","spring","spring","summer","summer ","summer","autu mn","autumn")> Salinity<-c(29.19,27.37,24.99,28.79,33.28,32.69,31.9,NA,32.53,32.53) > Temperature<-c(4,6,7.3,8.2,9.1,18.1,17,21,15.1,13.8) > sea<-data.frame(Season,Salinity,Temperature) > seaSeason Salinity Temperature 1 winter 29.19 4.0 2 winter 27.37 6.0 3 spring 24.99 7.3 4 spring 28.79 8.2 5 spring 33.28 9.1 6summer 32.69 18.1 7 summer 31.90 17.0 8 summer NA 21.0 9 autumn 32.53 15.1 10 autumn 32.53 13.8 > class(sea)[1] "data.frame"(2)将盐度的标准化变量加到这个数据框中；(标准化公式：ni s x x ，x 是样本均值，n s 是样本方差)；#将标准化变量加入> sea<-data.frame(Season,Salinity,Temperature,scale(Salinity)) > seaSeason Salinity Temperature scale.Salinity.1 winter 29.19 4.0 -0.40437122 winter 27.37 6.0 -1.03160603 spring 24.99 7.3 -1.85183624 spring 28.79 8.2 -0.54222505 spring 33.28 9.1 1.00518406 summer 32.69 18.1 0.80184977 summer 31.90 17.0 0.52958848 summer NA 21.0 NA9 autumn 32.53 15.1 0.746708110 autumn 32.53 13.8 0.7467081(3)从数据框sea提取包含season和temperature变量的子数据框存入变量sea1，并计算温度的平均值和标准差；> sea1<-data.frame(sea$Season,sea$Temperature)> sea1Season Temperature1 winter 4.02 winter 6.03 spring 7.34 spring 8.25 spring 9.16 summer 18.17 summer 17.08 summer 21.09 autumn 15.110 autumn 13.8> mean(Temperature)[1] 11.96> sd(Temperature)[1] 5.782963(4) 从数据框sea提取包含season和salinity变量的子数据框存入变量sea2，并计算盐度的平均值和标准差(结果不能为NA)；> sea2<-data.frame(sea$Season,sea$Salinity)> sea2sea.Season sea.Salinity1 winter 29.192 winter 27.373 spring 24.994 spring 28.795 spring 33.286 summer 32.697 summer 31.908 summer NA9 autumn 32.5310 autumn 32.53> mean(Salinity,na.rm=T)[1] 30.36333> sd(Salinity,na.rm=T)[1] 2.901625(5)利用命令list() 将上表读入变量sea.list, 再将盐度的标准化变量加入到这个列表中，并比较该方法与数据框方法的区别。

R语言分析（二）——薛毅R语言第二章后面习题解析

做着习题，又不断查着书，这样，书籍也熟悉了，习题也做完了，感觉特别爽的还是。。。
解答：上面题目中第二小问是个错误的，改写成D=A ，才有下面的答案（1）（2）（3）：
（4）：（5）： 2.3题答案： 2.4题答案： 2.5题的答案：完成的答案如下图所示：
1，生成纯文本和csv，并读取
2，使用excel打开生成的csv
博客园用户登录代码改变世界密码登录短信登录忘记登录ቤተ መጻሕፍቲ ባይዱ户名忘记密码记住我登录第三方登录/注册没有账户, 立即注册
R语言分析（二） ——薛毅 R语言第二章后面习题解析
包括2.2—2.6中间的习题，2.2的习题中第三问和第四问，应该有其他的解答方法，但我看他的题目，似乎是在A和B的基础上进行，所以就选择了使用for循环的方法

R语言实验报告4

R语言实验报告4
R语言实验报告4
本次实验的内容是利用R语言在数据分析的过程中，对数据进行可视
化分析，帮助用户更好地理解数据的分布及其特征。

一、实验环境准备
首先，我们需要准备实验环境，包括Rstudio的安装及R语言的安装，以及对R语言相关的统计分析和可视化工具包的安装。

二、实验数据的准备
其次，我们需要准备实验的数据，这里我们选择了一个世界各国GDP
数据集，包含了全球各个国家2000-2024年的GDP数据。

三、数据可视化分析
实验的思路是将数据以不同的图形进行可视化展示，以便更加直观地
查看各个国家的GDP变化和特征。

1.箱线图。

在R语言中，我们可以使用boxplot(函数来绘制箱线图，下面我们来实现：
```
boxplot(GDP ~ Country, data = world_gdp, col = "blue")
```
从箱线图中我们可以看出，在2024年，不同国家的GDP水平有很大的不同，印度和俄罗斯的GDP水平最高，而秘鲁和尼加拉瓜的GDP水平则相对较低。

2.柱状图。

下面我们使用barplot(函数来绘制柱状图，来更加清晰地看出每个国家在2000-2024年GDP的变化情况：
```
barplot(t(GDP), beside=TRUE, col=rainbow(20))
```
从柱状图中可以看出，在2000-2024年，不同国家的GDP变化幅度有很大的不同，主要有三种情况：美国和日本的GDP增长幅度较大。

R语言实验报告

一、试验目的R是用于统计分析、绘图的语言和操作环境。

R是属于GNU系统的一个自由、免费、源代码开放的软件，它是一个用于统计计算和统计制图的优秀工具。

本次试验要求掌握了解R语言的各项功能和函数，能够通过完成试验内容对R语言有一定的了解，会运用软件对数据进行分析。

二、试验环境Windows系统，RGui（32-bit）三、试验内容模拟产生电商专业学生名单(学号区分)，记录高数、英语、网站开发三科成绩，然后进行统计分析。

假设有的100 名学生，起始学号为210222001，各科成绩取整，高数成绩为均匀分布随机数，都在75分以上。

英语成绩为正态分布，平均成绩80，标准差为7。

网站开发成绩为正态分布，平均成绩83，标准差为18。

把正态分布中超过100分的成绩变成100分。

1 把上述信息组合成数据框，并写到文本文件中;2计算各种指标:平均分，每个人的总分，最高分，最低分，（使用apply 函数）3求总分最高的同学的学号4绘各科成绩直方图、散点图、柱状图丶饼图丶箱尾图（要求指定颜色和缺口）5画星相图，解释其含义6画脸谱图，解释其含义，7画茎叶图、qq图四、试验实现（一）按要求随机生成学号，和对于的高数、英语、网站开发三科成绩。

A、生成学号B、生成高数成绩高数成绩要求：高数成绩为均匀分布随机数，都在75分以上均匀分布函数：runif(n,min=0,max=1)其中，n 为产生随机值个数（长度），min为最小值，max为最大值。

C、生成英语成绩英语成绩要求：正态分布，平均成绩80，标准差为7正态分布函数：rnorm(n, mean = 0, sd = 1)其中，n 为产生随机值个数（长度），mean 是平均数，sd 是标准差。

D、生成网站开发成绩网站开发成绩要求：网站开发成绩为正态分布，平均成绩83，标准差为18。

其中大于100的都记为100。

（二）把上述信息组合成数据框，并写到文本文件中; 计算各种指标:平均分，每个人的总分，最高分，最低分，（使用apply 函数）A、生成文本文件B、打开数据框C、在数据框中命名变量D、计算各种指标:平均分，每个人的总分，最高分，最低分平均分（x4）：总分(x5)：最低分(x6)：最高分(x7)：（三）将生成成绩写入文本文件中（四）求总分最高的同学的学号（五）绘各科成绩直方图、散点图、柱状图丶饼图丶箱尾图（要求指定颜色和缺口）直方图散点图柱状图饼图箱尾图（要求指定颜色和缺口）（六）画星相图，解释其含义（七）画脸谱图，解释其含义（八）画茎叶图（九）qq图五、试验总结这次试验是我第一次接触R语言，刚开始遇到了很多困难，对于R语言一窍不通，后来经过老师的悉心指导，以及自己积极的去查找资料，对R语言有了进一步的了解。

R语言实验报告—习题详解

R语言实验报告习题详解学院：班级：学号：姓名：导师：成绩：目录一、实验目的..................................................................二、实验内容..................................................................1.1问题叙述..............................................................1.2问题求解..........................................................................................................................................................................................................1.3结果展示..............................................................2.1问题叙述..............................................................2.2问题求解..........................................................................................................................................................................................................2.3结果展示..............................................................3.1问题叙述..............................................................3.2问题求解......................................................................................................................................................................................................................................................................................................................................................3.3结果展示..............................................................4.1问题叙述..............................................................4.2问题求解..........................................................................................................................................................................................................4.3结果展示..............................................................5.1问题叙述..............................................................5.2问题求解..........................................................................................................................................................................................................5.3结果展示..............................................................6.1问题叙述..............................................................6.2问题求解..........................................................................................................................................................................................................6.3结果展示..............................................................三、实验总结..................................................................一、实验目的R是用于统计分析、绘图的语言和操作环境。

R语言实验报告4

实验目的根据教科书上数据，作图，以及实现关于分布的假设检验，要求选择的数据除了服从正态分布外，还应选择一些其它类型的数据实验内容（一）根据教科书上数据，作图基本图形：直方图、条形图、点图和箱线图（参考书本例题mtcars）、饼图和扇形图（书本例题：国别数据）attach(mtcars)opar <- par(no.readonly=TRUE)par(mfrow=c(3,1))hist(wt)hist(mpg)hist(disp)par(opar)detach(mtcars)attach(mtcars)layout(matrix(c(1,1,2,3), 2, 2, byrow = TRUE))hist(wt)hist(mpg)hist(disp)detach(mtcars)attach(mtcars)plot(wt, mpg)abline(lm(mpg~wt))title("Regression of MPG on Weight")detach(mtcars)pdf("mygraph.pdf")attach(mtcars)plot(wt, mpg)abline(lm(mpg~wt))title("Regression of MPG on Weight")detach(mtcars)attach(mtcars)opar <- par(no.readonly=TRUE)par(mfrow=c(2,2))plot(wt,mpg, main="Scatterplot of wt vs. mpg") plot(wt,disp, main="Scatterplot of wt vs. disp") hist(wt, main="Histogram of wt")boxplot(wt, main="Boxplot of wt")par(opar)detach(mtcars)饼图和扇形图（书本例题：国别数据）par(mfrow=c(2,2))slices <- c(10, 12,4, 16, 8)lbls <- c("US", "UK", "Australia", "Germany", "France")pie(slices, labels = lbls,main="Simple Pie Chart")pct <- round(slices/sum(slices)*100)lbls <- paste(lbls, pct)lbls <- paste(lbls,"%",sep="")pie(slices,labels = lbls, col=rainbow(length(lbls)), main="Pie Chart with Percentages")library(plotrix)slices <- c(10, 12,4, 16, 8)lbls <- c("US", "UK", "Australia", "Germany", "France") fan.plot(slices, labels = lbls, main="Fan Plot")核密度图d <- density(mtcars$mpg) # returns the density dataplot(d) # plots the resultsd <- density(mtcars$mpg)plot(d, main="Kernel Density of Miles Per Gallon")polygon(d, col="red", border="blue")rug(mtcars$mpg, col="brown")（二）关于分布的假设检验（来自书本数据男女老少体重）> fit <- lm(weight ~ height, data=women)> summary(fit)Call:lm(formula = weight ~ height, data = women)Residuals:Min 1Q Median 3Q Max-1.7333 -1.1333 -0.3833 0.7417 3.1167Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) -87.51667 5.93694 -14.74 1.71e-09 ***height 3.45000 0.09114 37.85 1.09e-14 ***---Signif. codes: 0 ‘***’0.001 ‘**’0.01 ‘*’0.05 ‘.’0.1 ‘’1Residual standard error: 1.525 on 13 degrees of freedomMultiple R-squared: 0.991, Adjusted R-squared: 0.9903F-statistic: 1433 on 1 and 13 DF, p-value: 1.091e-14> women$weight[1] 115 117 120 123 126 129 132 135 139 142 146 150 154 159 164> fitted(fit)1 2 3 4 5 6 7 8 112.5833 116.0333 119.4833 122.9333 126.3833 129.8333 133.2833 136.73339 10 11 12 13 14 15140.1833 143.6333 147.0833 150.5333 153.9833 157.4333 160.8833> residuals(fit)1 2 3 4 5 62.41666667 0.96666667 0.51666667 0.06666667 -0.38333333 -0.833333337 8 9 10 11 12 -1.28333333 -1.73333333 -1.18333333 -1.63333333 -1.08333333 -0.5333333313 14 150.01666667 1.56666667 3.11666667> plot(women$height,women$weight,+ main="Women Age 30-39",+ xlab="Height (in inches)",+ ylab="Weight (in pounds)")通过结果可知^y=-87.52+3.45x（^y为体重的估计量，x为身高）fit <- lm(weight ~ height, data=women)> par(mfrow=c(2,2))> plot(fit)> newfit <- lm(weight ~ height + I(height^2), data=women) > par(opar)> par(mfrow=c(2,2))> plot(newfit)线性模型的假设检验：由于global statp=0.0023251，因此不通过假设检验，从而我们考虑多项式线性模型：新的回归模型是^y=261.87818-7.35*x+0.083*x^2,且通过了ols回归模型所有的统计假设。

R语言上机实验三

R语⾔上机实验三理学院实验报告班级：学号：姓名：实验编号：实验三：概率和分布的R实现⼀、实验⽬的与要求：１、会⽤R给出常见分布的概率密度、概率、分位数和随机数。

２、会利⽤sample命令进⾏随机抽样，prod，choose命令计算概率。

3、会利⽤R绘制各类分布的图形。

4、会利⽤choose，prod命令计算古典概率。

⼆、实验内容：1.从⼀副扑克牌(52张)中随机抽5张，求下列概率(1) 抽到的是10，J，Q，K，A；> 4/choose(52,5)[1] 1.539077e-06(2) 抽到的是同花顺。

> 9*choose(4,1)/choose(52,5)[1] 1.385169e-05注：同花顺是指5张同⼀⾊牌能按从⼩到⼤连续排序，如2<3<4<5<6，3<4<5<6<7，…，10 2.模拟随机游动:(1)从两点分布中产⽣1000个随机数;> x<-rbinom(1000,1,0.5)> x(2)⽤函数ifelse( )将上⾯随机数中的0替换成-1;> ifelse(x==0,-1,1 )(3)⽤函数cumsum( )作出累积和; > y<-ifelse(x==0,-1,1 )> cumsum(y)(4)使⽤命令plot( ) 作出随机游动的⽰意图. > plot(cumsum(y))3.在同⼀个图形中画出统计的四⼤分布密度曲线(dnorm, dchisq, dt, df)，注意不同分布有不同的线型、颜⾊和宽度，还有图形都要在同⼀⽅框中，最后⽤图例说明(legend)。

> curve(dnorm(x,0,1),xlim=c(-1,5),ylim=c(0,0.5),col=1,lwd=1,lty=1)> curve(dchisq(x,1),xlim=c(-1,5),ylim=c(0,0.5),lwd=2,lty=2,col=2,add=T)> curve(dt(x,1),xlim=c(0,8),ylim=c(0,0.5),lwd=3,lty=3,col=3,add=T)> curve(dt(x,1,1),xlim=c(0,8),ylim=c(0,0.5),lwd=4,lty=4,col=4,add=T)> legend('topright',c("dnorm","dchisp","dt","df"),lty=c(1,2,3,4),col=c(1,2,3,4),lwd=c(1,2,3,4))> curve(dnorm(x,0,1),xlim=c(-1,5),ylim=c(0,0.5),col=1,lwd=1,lty=1)> curve(dchisq(x,1),xlim=c(-1,5),ylim=c(0,0.5),lwd=2,lty=8,col=2,add=T)> curve(dt(x,1),xlim=c(0,8),ylim=c(0,0.5),lwd=5,lty=3,col=7,add=T)> curve(dt(x,1,1),xlim=c(0,8),ylim=c(0,0.5),lwd=4,lty=4,col=4,add=T)> legend('topright',c("dnorm","dchisp","dt","df"),lty=c(1,8,3,4),col=c(1,2,7,4),lwd=c(1,2,5,4))>4. 除本章给出的标准分布外, ⾮标准的随机变量X的抽样可通过格式点离散化⽅法实现.设p (x )为X 的密度函数, 其抽样步骤如下(1) 在X 的取值范围内等间隔地选取N 个点x 1, x 2,…, x N , 例如取N =1000; (2) 计算p (x i ); i = 1, 2, …, N ;(3) 正则化p (x i ); i =1, 2,…,N , 使其成为离散的分布律, 即每⼀项除以∑=Ni ix p 1)(;(4) 按离散分布抽样⽅法使⽤命令sample( )从x i , i = 1, 2, … ,N 有放回地抽取n 个数, 例如 n =1000.注：前⾯４⼩步是⽤来编⼀个函数，功能是对给定的概率密度产⽣随机数，形式应与ｒｎｏｒｍ差不多。

r语言实操例题

r语言实操例题以下是一个简单的R语言实操例题，通过这个例题可以了解R 语言的基本操作和数据处理方法：题目：使用R语言对一组销售数据进行处理和分析1. 数据导入和清洗首先，我们需要将销售数据导入到R语言中。

假设销售数据存储在一个名为"sales.csv"的CSV文件中，可以使用以下代码将其导入到R 语言中：```r# 导入数据sales <- read.csv("sales.csv")# 查看数据head(sales)```接下来，我们需要对数据进行清洗。

假设销售数据中存在一些缺失值，我们可以使用以下代码对缺失值进行处理：```r# 处理缺失值sales$sales_amount[is.na(sales$sales_amount)] <- 0```2. 数据探索和分析在数据清洗完成后，我们可以开始对数据进行探索和分析。

首先，我们可以使用以下代码绘制销售数据的条形图：```r# 绘制条形图barplot(sales$sales_amount, main="Sales Amount", xlab="Product", ylab="Sales Amount")```接下来，我们可以使用以下代码计算每个产品的销售占比：```r# 计算销售占比sales$sales_percentage <-round((sales$sales_amount / sum(sales$sales_amount)) * 100, 2)```最后，我们可以使用以下代码绘制每个产品的销售占比饼图：```r# 绘制饼图pie(sales$sales_percentage, main="Sales Percentage", labels=sales$product)```通过以上实操例题，我们可以了解到R语言在数据处理和分析方面的强大功能。

R语言实验4

R语言实验4实验4 R绘图（一）一、实验目的：1.掌握描述性统计分析中常用的统计量；2.掌握R语言绘制直方图、密度估计曲线、经验分布图和QQ图的方法；3.掌握R语言绘制茎叶图、箱线图的方法；4.掌握W检验方法和K-S检验方法完成数据的正态分布检验。

二、实验内容：练习：要求：①完成练习并粘贴运行截图到文档相应位置(截图方法见下)，并将所有自己输入文字的字体颜色设为红色（包括后面的思考及小结），②回答思考题，③简要书写实验小结。

④修改本文档名为“本人完整学号姓名1”，其中1表示第1次实验，以后更改为2,3,...。

如文件名为“1305543109张立1”，表示学号为1305543109的张立同学的第1次实验，注意文件名中没有空格及任何其它字符。

最后连同数据文件、源程序文件等（如果有的话，本次实验没有），一起压缩打包发给课代表，压缩包的文件名同上。

截图方法：法1：调整需要截图的窗口至合适的大小，并使该窗口为当前激活窗口（即该窗口在屏幕最前方），按住键盘Alt键（空格键两侧各有一个）不放，再按键盘右上角的截图键（通常印有“印屏幕”或“Pr Scrn”等字符），即完成截图。

再粘贴到word文档的相应位置即可。

法2：利用QQ输入法的截屏工具。

点击QQ输入法工具条最右边的“扳手”图标，选择其中的“截屏”工具。

）1.自行完成教材P107页开始的3.1-3.2节中的例题。

2.以前在做实验1的练习时，我们画过直方图。

当时的题目是这样的：利用hist()函数画直方图。

>X<-c(35,40,40,42,37,45,43,37,44,42,41,39)> hist(X)这次实验先重新运行以上命令后，接着运行以下命令：> windows() #R作图会覆盖前一幅图，此命令是新开一个画图窗口> hist(X, freq=F)把两个图分别截下复制到下面，进行比较，你发现有什么不同？答：纵坐标不同，一个是频数（Frequency），一个是密度(Density)如果想把这两幅图画在同一个画图窗口中，可以输入以下命令：> par(mfrow=c(1,2)) #在一个窗口里放多张图，这里是1行2列共2个图> hist(X)> hist(X,freq=F)运行结果截图：3.（习题3.1）某单位对100名女生测定血清总蛋白含量（g/L），数据如下：74.3 78.8 68.8 78.0 70.4 80.5 80.5 69.7 71.2 73.5 79.5 75.6 75.0 78.8 72.0 72.0 72.0 74.3 71.2 72.0 75.0 73.5 78.8 74.3 75.8 65.0 74.3 71.2 69.7 68.0 73.5 75.0 72.0 64.3 75.8 80.3 69.7 74.3 73.5 73.5 75.8 75.8 68.8 76.5 70.4 71.2 81.2 75.0 70.4 68.0 70.4 72.0 76.5 74.3 76.5 77.6 67.3 72.0 75.0 74.3 73.5 79.5 73.5 74.7 65.0 76.5 81.6 75.4 72.7 72.7 67.2 76.572.7 70.4 77.2 68.8 67.3 67.3 67.3 72.7 75.873.5 75.0 73.5 73.5 73.5 72.7 81.6 70.3 74.3 73.5 79.5 70.4 76.5 72.7 77.2 84.3 75.0 76.570.4计算均值、方差、标准差、极差、标准误、变异系数、偏度、峰度。

正交试验设计的R语言实现

正交试验设计的R语言实现正交设计利用部分处理组合代表全面试验，能够大大减少试验实施的人力物力。

但由此也减少了方差分析时的误差自由度，降低了均值检验的灵敏度。

因此正交设计统计分析的重点不是方差分析，而是选择最优组合。

本文以一个实例，介绍正交设计统计分析的一般方法。

例题：为解决花菜留种问题，提高种子产量，对四个因素各两个水平设计了正交试验，结果列于下表，试进行方差分析并筛选最优组合。

1. 方差分析首先对所有因素效应进行初步方差分析，R语言函数为aov()。

R代码：a=factor(c(1,1,1,1,2,2,2,2))b=factor(c(1,1,2,2,1,1,2,2))ab=factor(c(1,1,2,2,2,2,1,1))c=factor(c(1,2,1,2,1,2,1,2))ac=factor(c(1,2,1,2,2,1,2,1))d=factor(c(1,2,2,1,2,1,1,2))yield=c(350,325,425,425,200,250,275,375)data=data.frame(a,b,c,d,ab,ac,yield)result=aov(yield~a+b+c+d+ab+ac)summary(result)程序运行结果：由上表可知，各项变异来源的F值均不显著，这是由于各因素均为2水平，导致试验误差的自由度过小，仅为1，因此达到显著的临界F值过大。

解决这个问题的根本办法是增加试验的重复数，也可以将小于1的变异项（即D和A×B）合并为误差项，从而提高假设检验的灵敏度。

具体操作如下：result_1=aov(yield~a+b+c+ac)summary(result_1)程序运行结果：以上结果可知，A、B和AC互作达到显著水平，而C因素不显著。

一般只有达到显著时才有必要选择最优组合。

2. 选择最优组合由于产量越大越好，因此选择方差分析显著的因素中产量较大的处理。

虽然C因素不显著，但AC互作表现显著，因此可在选择A处理的基础上进一步选择C。