几何证明题复习题答案
2020年中考数学压轴题-专题28几何证明综合复习(判定四边形形状)(解析版)

专题28 几何证明综合复习(判定四边形形状)教学重难点1.培养学生通过探索和证明,发展推理意识和能力2.通过证明举例的学习和实践,懂得演绎推理的一般规则,并掌握规范表达的格式;了解证明之前进行分析的基本思路;3.体会用“分析综合法”探求解题思路;4.学习添置辅助线的基本方法,会添置常见的辅助线;5.会用文字语言、图形语言、符号语言三种数学语言进行证明说理。
【说明】:本部分为知识点方法总结性梳理,目的在于让学生能从题目条件和所证明结论,去寻找证明思路,用时大概 5-8 分钟左右。
【知识点、方法总结】:中考几何题证明思路总结几何证明题重点考察的是学生的逻辑思维能力,能通过严密的" 因为"、"所以 " 逻辑将条件一步步转化为所要证明的结论。
这类题目出法相当灵活,不像代数计算类题目容易总结出固定题型的固定解法,而更看重的是对重要模型的总结、常见思路的总结。
所以本文对中考中最常出现的若干结论做了一个较为全面的思路总结。
一、证明两线段相等1.两全等三角形中对应边相等。
2.同一三角形中等角对等边。
3.等腰三角形顶角的平分线或底边的高平分底边。
4.平行四边形的对边或对角线被交点分成的两段相等。
5.直角三角形斜边的中点到三顶点距离相等。
6.线段垂直平分线上任意一点到线段两段距离相等。
7.角平分线上任一点到角的两边距离相等。
8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。
9.同圆(或等圆)中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。
10.两前项(或两后项)相等的比例式中的两后项(或两前项)相等。
、证明两角相等1.两全等三角形的对应角相等。
2.同一三角形中等边对等角。
3.等腰三角形中,底边上的中线(或高)平分顶角。
4.两条平行线的同位角、内错角或平行四边形的对角相等。
5.同角(或等角)的余角(或补角)相等。
6.同圆(或圆)中,等弦(或弧)所对的圆心角相等;7.相似三角形的对应角相等;8.等于同一角的两个角相等。
中考复习初中数学几何证明 试题(含答案)
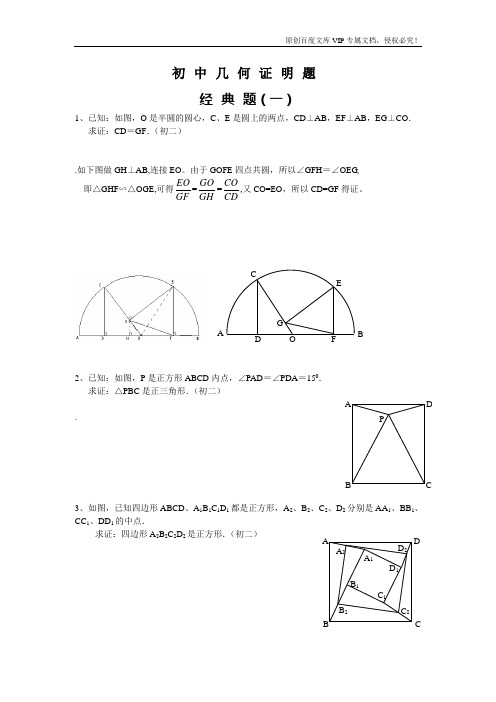
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二).如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG , 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF 得证。
2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二).3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)APCDB D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 AFGCEBOD4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.BF求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5. 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值. A P CB P A D CB C B D A F PD E CB A APCB3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
2023届高考数学总复习:立体几何复习题附答案

a,
在 Rt△FCM 中,tan∠FCM .
,
∴sin∠FCM ,
故直线 CF 与平面 ACDE 所成角的正弦值为 . 2.如图,在三棱柱 ABC﹣A1B1C1 中,BC⊥平面 AA1C1C,D 是 AA1 的中点,△ACD 是边长
为 1 的等边三角形. (1)证明:CD⊥B1D; (2)若 BC ,求二面角 B﹣C1D﹣B1 的大小.
,令
由(1)知,平面 B1C1D 的一个法向量为
,得
,, ,
, ,,
故 th< , >
,
所以二面角 B﹣C1D﹣B1 的大小为 30°.
第3页共3页
在直角梯形 AEFB 中,有 AF EF,BF
쳌
∴AF2+BF2=AB2,即 AF⊥BF.
∵BC∩BF=B,BC、BF⊂平面 BCF,
∴AF⊥平面 BCF.
EF,AB=2EF,
(2)解:∵AE⊥平面 ABC,AE⊂平面 ACDE,∴平面 ACDE⊥平面 ABC,
又平面 ABC∥平面 DEF,∴平面 ACDE⊥平面 DEF.
【解答】解:(1)证明:因为△ACD 是边长为 1 的等边三角形,所以∠ADC=60°,∠ DA1C1=120° 因为 D 是 AA1 的中点,所以 AD=A1D=A1C1=1,即△A1C1D 是等腰三角形, 则∠A1DC1=30°,故∠CDC1=90°,即 CD⊥C1D, 因为 BC⊥平面 AA1C1C,BC∥B1C1,所以 B1C1⊥平面 AA1C1C, 因为 CD⊂平面 AA1C1C,所以 B1C1⊥CD, 因为 B1C1∩C1D=C1,B1C1⊂平面 B1C1D,C1D⊂平面 B1C1D,所以 CD⊥平面 B1C1D, 因为 B1D⊂平面 B1C1D,所以 CD⊥B1D;
立体几何复习专题及答案-高中数学

立体几何复习专题姓名: 班级:考点一、空间中的平行关系1.如图,在三棱锥P ABC -中,02,3,90PA PB AB BC ABC ====∠=,平面PAB ⊥平面ABC ,D 、E 分别为AB 、AC 的中点. (1)求证:DE //平面PBC ; (2)求证:AB PE ⊥;(3)求三棱锥B PEC -的体积.2. 如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,PCD △为等边三角形,平面PAC ⊥平面PCD ,PA CD ⊥,2CD =,3AD =,(Ⅰ)设G H ,分别为PB AC ,的中点,求证:GH ∥平面PAD ; (Ⅱ)求证:PA ⊥平面PCD ;3.如图,七面体ABCDEF 的底面是凸四边形ABCD ,其中2AB AD ==,120BAD ∠=︒,AC ,BD 垂直相交于点O ,2OC OA =,棱AE ,CF 均垂直于底面ABCD .(1)证明:直线DE 与平面BCF 不.平行;4.(2014新课标Ⅱ)如图,四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点.(Ⅰ)证明:PB ∥平面AEC ;(Ⅱ)设二面角D AE C --为60°,AP =1,AD =3,求三棱锥E ACD -的体积.考点二、空间中的垂直关系5.如图,在四面体ABCD 中,E ,F 分别是线段AD ,BD 的中点,90ABD BCD ∠=∠=,2EC =,2AB BD ==,直线EC 与平面ABC 所成的角等于30.(1)证明:平面EFC ⊥平面BCD ;6.已知某几何体的直观图和三视图如下图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.(1)求证:BN ⊥平面11C B N ;(2)设M 为AB 中点,在C B 边上求一点P ,使//MP 平面1C NB ,求CBPP 的值.7.(2016全国I )如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF为正方形,2AF FD =,90AFD ∠=,且二面角D AF E --与二面角C BE F --都是60.(I )证明:平面ABEF⊥平面EFDC ;(II )求二面角E BC A --的余弦值.考点三、折叠问题和探究性问题中的位置关系8.如图 1,在直角梯形ABCD 中, //,AB CD AB AD ⊥,且112AB AD CD ===.现以AD 为一边向外作正方形ADEF ,然后沿边AD 将正方形ADEF 翻折,使ADEF 平面与平面ABCD 垂直, M 为ED 的中点,如图 2.(1)求证: //AM 平面BEC ;(2)求证: BC ⊥平面BDE ; .9.如图,在边长为4的正方形ABCD 中,点E,F 分别是AB,BC 的中点,点M 在AD 上,且14AM AD =,将AED,DCF 分别沿DE,DF 折叠,使A,C 点重合于点P ,如图所示2.()1试判断PB 与平面MEF的位置关系,并给出证明;()2求二面角M EF D --的余弦值.10.如图所示,直角梯形ABCD 中,//AD BC ,AD AB ⊥,22AB BC AD ===,四边形EDCF 为矩形,3CF =,平面EDCF ⊥平面ABCD . (1)求证:DF //平面ABE ;(2)求平面ABE 与平面EFB 所成锐二面角的余弦值. (3)在线段DF 上是否存在点P ,使得直线BP 与平面ABE 所成角的正弦值为34,若存在,求出线段BP 的长,若不存在,请说明理由.11.如图1,在边长为4的正方形ABCD中,E是AD的中点,F是CD的中点,现-.将三角形DEF沿EF翻折成如图2所示的五棱锥P ABCFE(1)求证:AC//平面PEF;(2)若平面PEF⊥平面ABCFE,求直线PB与平面PAE所成角的正弦值.12.(2011•浙江)如图,在三棱锥P﹣ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2(1)证明:AP⊥BC;(2)在线段AP上是否存在点M,使得二面角A﹣MC﹣β为直二面角?若存在,求出AM的长;若不存在,请说明理由.13.如图,在直三棱柱111ABC A B C -中,底面ABC 为等边三角形,122CC AC ==.(Ⅰ)求三棱锥11C CB A -的体积;(Ⅱ)在线段1BB 上寻找一点F ,使得1CF AC ⊥,请说明作法和理由.考点四、知空间角求空间角问题14.(2014天津)如图四棱锥P ABCD -的底面ABCD 是平行四边形,2BA BD ==2AD =,5PA PD ==E ,F 分别是棱AD ,PC 的中点.(Ⅰ)证明: EF ∥平面PAB ; (Ⅱ)若二面角P AD B --为60°, (ⅰ)证明:平面PBC ⊥平面ABCD(ⅱ)求直线EF 与平面PBC 所成角的正弦值. PCDBF15.四棱锥P ABCD -中,底面ABCD 为矩形,PA ABCD ⊥平面,E 为PD 的中点.(1)证明://E PB A C 平面;(2)设13AP AD ==,,三棱锥P ABD -的体积34V =,求二面角D -AE -C 的大小16.如图,四棱锥P ABCD -中, PA ⊥底面ABCD ,底面ABCD 是直角梯形,90ADC ∠=︒, //AD BC , AB AC ⊥, 2AB AC ==,点E 在AD 上,且2AE ED =.(Ⅰ)已知点F 在BC 上,且2=CF FB ,求证:平面PEF ⊥平面PAC ;(Ⅱ)当二面角--A PB E 的余弦值为多少时,直线PC 与平面PAB 所成的角为45︒?立体几何专题参考答案1. (1)证明:∵在△ABC 中,D 、E 分别为AB 、AC 的中点,∴DE ∥BC . ∵DE ⊄平面PBC 且BC ⊂平面PBC ,∴DE ∥平面PBC . (2)证明:连接PD .∵PA =PB ,D 为AB 的中点,∴PD ⊥AB .∵DE ∥BC ,BC ⊥AB ,∴DE ⊥AB .又∵PD 、DE 是平面PDE 内的相交直线, ∴AB ⊥平面PDE .∵PE ⊂平面PDE ,∴AB ⊥PE .(3)解:∵PD ⊥AB ,平面PAB ⊥平面ABC ,平面PAB ∩平面ABC =AB ,∴PD ⊥平面ABC ,可得PD 是三棱锥P -BEC 的高. 又∵33,2BECPD S==,1332B PEC P BEC BEC V V S PD --∆∴==⨯=. 2.(I )见解析;(II )见解析;(III )33. (I )证明:连接BD ,易知AC BD H ⋂=,BH DH =,又由BG PG =,故GHPD ,又因为GH ⊄平面PAD ,PD ⊂平面PAD , 所以GH ∥平面PAD .(II )证明:取棱PC 的中点N ,连接DN ,依题意,得DN PC ⊥, 又因为平面PAC ⊥平面PCD ,平面PAC平面PCD PC =,所以DN ⊥平面PAC ,又PA ⊂平面PAC ,故DN PA ⊥, 又已知PA CD ⊥,CD DN D =,所以PA ⊥平面PCD . 3.(1)见解析;(2)23535本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
2020年数学中考复习:压轴几何证明题的解法(含答案)

2020年数学中考复习:压轴几何证明题的解法1.(2019.葫芦岛)如图,△ABC 是等腰直角三角形,∠ACB =900,D 是射线CB 上一点(点D 不与点B 重合),以AD 为斜边作等腰直角三角形ADE (点E 和点C 在AB 的同侧),连接CE 。
(1)如图①,当点D 与点C 重合时,直接写出CE 与AB 的位置关系;(2)如图②,当点D 与点C 不重合时,(1)的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)当∠EAC =150时,请直接写出AB CE 的值。
解析:(1)由∠ECA =∠CAB =450,可得EC ∥AB 。
(2)由22=AB AC =AD AE ,且∠EAC =∠DAB ,可得△EAC ∽△DAB 进而得出∠ECA =∠DBA =450=∠CAB ,所以CE ∥AB .(3)此问分两种情况点D 在BC 上,点D 在CB 延长线上。
①当点D 在BC 上时,如图(2),此时∠CAB =150能得出∠CAD =300,这样就有33=AC CD ,也就是BC -DB =33AC ,BC =AC ,所以BD =333-AC 。
又由△EAC ∽△DAB 得21=BD CE ,因此有BD =2CE ,所以可得CE =6623-AC ,又AB =2AC ,因此ABCE =63-3.当D 点在CB 延长线上时,∠CDA =300,解三角形得3AC =3CD 。
CD =BC +BD ,由△AEC ∽△ABD ,可得BD =2AC ,就能得到CE =AC2-13,AB =2AC ,所以2-13=AB CE . 2.(2019.沈阳)思维启迪:(1)如图1,A ,B 两点分别位于一个池塘的两端,小亮想用绳子测量A ,B 间的距离,但绳子不够长,聪明的小亮想出一个办法:先在地上取一个可以直接到达B 点的点C ,连接BC ,取BC 的中点P (点P 可以直接到达A 点),利用工具过点C 作CD ∥AB 交AP 的延长线于点D ,此时测得CD =200米,那么A ,B 间的距离是_200_米。
初中几何证明题库:矩形

初中几何证明题库:矩形本页仅作为文档页封面,使用时可以删除This document is for reference only-rar21year.March例8.如图,已知矩形纸片ABCD,AD=2,AB=4.将纸片折叠,使顶点A与边CD 上的点E重合,折痕FG分别与AB,CD交于点G,F,AE与FG交于点O.(1)如图1,求证:A,G,E,F四点围成的四边形是菱形;(2)如图2,当△AED的外接圆与BC相切于点N时,求证:点N是线段BC的中点;(3)如图2,在(2)的条件下,求折痕FG的长.【答案】解:(1)由折叠的性质可得,GA=GE,∠AGF=∠EGF,∵DC∥AB,∴∠EFG=∠AGF。
∴∠EFG=∠EGF。
∴EF=EG=AG。
∴四边形AGEF是平行四边形(EF∥AG,EF=AG)。
又∵AG=GE,∴四边形AGEF是菱形。
(2)连接ON,∵△AED是直角三角形,AE是斜边,点O是AE的中点,△AED的外接圆与BC相切于点N,∴ON⊥BC。
∵点O是AE的中点,∴ON是梯形ABCE的中位线。
∴点N是线段BC的中点。
(3)∵OE、ON均是△AED的外接圆的半径,∴OE=OA=ON=2。
∴AE=AB=4。
在Rt△ADE中,AD=2,AE=4,∴∠AED=30°。
在Rt△OEF中,OE=2,∠AED=30°,∴OF=。
3∴FG=2OF=。
3【考点】翻折变换(折叠问题),折叠对称的性质,菱形的判定,梯形中位线性质,锐角三角函数定义,特殊角的三角函数值。
【分析】(1)根据折叠的性质判断出AG=GE,∠AGF=∠EGF,再由CD∥AB得出∠EFG=∠AGF,从而判断出EF=AG,得出四边形AGEF是平行四边形,从而结合AG=GE,可得出结论。
(2)连接ON,则ON⊥BC,从而判断出ON是梯形ABCE的中位线,从而可得出结论。
(3)根据(1)可得出AE=AB,从而在Rt△ADE中,可判断出∠AED为30°,在Rt△EFO中求出FO,从而可得出FG的长度。
「空间解析几何复习资料含答案」

空间解析几何练习题1. 求点),,(c b a M 分别关于(1)xz 坐标面(2)x 轴(3)原点 对称点的坐标.2. 设 )2,,3(x A -与)4,2,1(-B 两点间的距离为29,试求x .3. 证明 )3,2,1(A )5,1,3(B )3,4,2(C 是一个直角三角形的三个顶点.4. 设ABC ∆的三边a BC =,b CA =,c AB =,三边的中点依次为D ,E,F ,试用向量c b a表示 AD ,BE ,CF ,并证明:0=++CF BE AD .5. 已知:k j i a 2+-=,k j i b -+=3求b a 32+,b a 32-.6. 已知:向量a 与x 轴,y 轴间的夹角分别为060=α,0120=β求该向量a 与z 轴间的夹角γ.7. 设向量a 的模是5,它与x 轴的夹角为4π,求向量a 在x 轴上的投影. 8. 已知:空间中的三点)2,1,0(-A ,)5,3,1(-B ,)2,1,3(--C 计算:AC AB 32-,AC AB 4+.9. 设{}1,0,2-=a ,{}2,2,1--=b 试求b a -,b a 52+,b a +3. 10. 设:{}1,2,2-=a ,试求与a 同方向的单位向量.11. 设:k j i a 253++=,k j i b 742--=,k j i c 45-+=,c b a u -+=34试求(1)u 在y 轴上的投影;(2)u 在x 轴和z 轴上的分向量;. 12. 证明:22)()(b a b a b a -=-⋅+. 13. 设:{}1,0,3-=a ,{}3,1,2--=b 求b a ⋅,∧⋅)(b a .14. 设→→→→-+=k j x i a 2,→→→→+-=k j i b 23且→→⊥b a 求x 15. 设{}2,1,0-=a ,{}1,1,2-=b 求与a 和b 都垂直的单位向量.16. 已知:空间中的三点)0,1,1(A ,)3,1,2(-B ,)2,1,2(-C 求ABC ∆的面积.17. (1)设a ∥b 求b a ⋅ (2)1==求b a ⋅18. 3=5=,试确定常数k 使b k a +,b k a -相互垂直.19. 设向量a 与b 互相垂直,∧⋅)(c a 3π=,∧⋅)(c b 6π=1=2=3=b ++.20. 设:k j i a 53+-=,k j i b 32+--=求b a ⋅21. 设:k j i a --=63,k j i b 54-+=求(1)a a ⋅;(2))3()23(b a b a -⋅+;(3)a 与b 的夹角.22. 设:∧⋅)(b a 6π=1=3=,.23. 设:{}2,1,1-=a ,{}1,2,1--=b ,试求:(1)b a ⋅;(2)b a ⨯;(3)∧⋅)cos(b a .24. 3=26=72=,求b a ⋅.25. 设a 与b 相互垂直,3=4=,试求(1))()(b a b a -⨯+;(2))2()3(b a b a -⨯-. 26. 设:0=++c b a 证明:a c c b b a ⨯=⨯=⨯27. 已知:k j i a -+=23,k j i b 2+-=,求(1)b a ⨯;(2))32()2(b a b a -⨯+;(3)i b a ⨯+)((4)b i a +⨯. 28. 求与{}1,2,2=a {}6,10,8---=b 都垂直的单位向量.29. 已知:{}1,6,3--=a ,{}5,4,1-=b ,{}12,4,3-=c 求c b a b c a )()(⋅+⋅在向量c 上的投影. 30. 设:d c b a ⨯=⨯,d b c a ⨯=⨯且c b ≠,d a ≠证明d a -与c b -必共线. 31. 设:b a 3+与b a 57-垂直,b a 4-与b a 27-垂直,求非零向量a 与b 的夹角.32. 设:{}6,3,2-=a {}2,2,1--=b 向量c 在向量a 与b 423=,求向量c 的坐标.33. 4=3=,∧⋅)(b a 6π=求以b a 2+和b a 3-为边的平行四边形面积.34. 求过点)1,2,7(0-P ,且以{}3,4,2-=n 为法向量的平面方程.ﻩ35. 过点)1,0,1(0-P 且平行于平面53=--z y x 的平面方程. ﻩ36. 过点)2,3,1(-M 且垂直于过点)1,2,2(-A 与)1,2,3(B 的平面方程. 37. 过点)2,1,3(-A ,)1,1,4(--B ,)2,0,2(C 的平面方程.38. 过点)1,1,2(0P 且平行于向量{}1,1,2=a 和{}3,2,3-=b 的平面方程.39. 过点M o (1,1-,1)且垂直于平面01201=+++=+--z y x z y x 及的平面方程. 40. 将平面方程 01832=+-+z y x 化为截距式方程,并指出在各坐标轴上的截距.41. 建立下列平面方程(1)过点(3-,1,2-)及z 轴;(2)过点A(3-,1,2-)和B(3,0,5)且平行于x 轴; (3)平行于x y 面,且过点A(3,1,5-);(4)过点P 1(1,5-,1)和P 2(3,2,2-)且垂直于x z 面. 42. 求下列各对平面间的夹角(1),62=+-z y x 32=++z y x ;(2)09543=--+z y x ,07662=-++z y x . 43. 求下列直线方程(1)过点(2,1-,3-)且平行于向量{}123,,--=s ; (2)过点M o (3,4,2-)且平行z 轴; (3)过点M 1(1,2,3)和M 2(1,0,4); (4)过原点,且与平面0623=-+-z y x 垂直. 44. 将下列直线方程化为标准方程(1)⎩⎨⎧=--+=-+-084230432z y x z y x ; (2)⎩⎨⎧-=+=422z y y x ; (3)⎩⎨⎧=+=-+00123z y z x45. 将下列直线方程化成参数式方程(1)⎩⎨⎧-==-+-250125z y z y x ; (2)⎪⎩⎪⎨⎧=-+=-025126y z x .46. 求过点(1,1,1)且同时平行于平面012=+-+z y x 及012=+-+z y x 的直线方程.47. 求过点(3,1,2-)且通过直线12354zy x =+=-的平面方程. 48. 求通过两直线211111-=-+=-z y x 与 112111-=+=--z y x 的平面方程. 64.求下列各对直线的夹角 (1)74211+=-=-z y x ,131256--=-=+z y x ; (2)⎩⎨⎧=-+-=-+-012309335z y x z y x ,⎩⎨⎧=-++=+-+0188302322z y x z y x .49. 证明直线31141+=-=-z y x 与 ⎩⎨⎧=--+=++0207z y x z y x 相互平行. 50. 设直线 l的方程为:nz y x 42311+=--=- 求n为何值时,直线l 与平面052=+--z y x 平行?51. 作一平面,使它通过z 轴,且与平面0752=--+z y x 的夹角为3π.52. 设直线l在平面01:=+++z y x π 内,通过直线⎩⎨⎧=+=++0201:1z x z y l与平面π的交点,且与直线l1垂直、求直线l 的方程. 53. 求过点(1,2,1)而且与直线⎩⎨⎧=-+-=+-+01012z y x z y x 与 ⎩⎨⎧=+-=+-02z y x z y x 平行的平面方程. 54. 一动点到坐标原点的距离等于它到平面04=-z 的距离,求它的轨迹方程.55. 直线⎩⎨⎧=-+=-+023012:z x y x l 与平面012:=--+z y x π 是否平行?若不平行,求直线l与平面π的交点,若平行,求直线l 与平面π的距离.56. 设直线l经过两直线35811:1--==--z y x l ,⎪⎩⎪⎨⎧--=+=+=tz t y tx l 101152143:2 的交点,而且与直线l 1与l 2都垂直,求直线l 的方程. 57. 已知直线:⎩⎨⎧=-+-=+-+04201:1z y x z y x l 及点 )213(,,-p 过点p作直线l与直线l 1垂直相交,求直线l的方程.58. 方程:019224222=-+--++z y x z y x 是否为球面方程,若是球面方程,求其球心坐标及半径. 59. 判断方程:11462222=-+-++z y x z y x 是否为球面方程,若是球面方程,求其球心坐标及半径.60. 将曲线:⎩⎨⎧==052y xz 绕x 轴旋转一周,求所成的旋转曲面方程.61. 将曲线:⎩⎨⎧==+0369422z y x 绕y 轴旋转一周,求所成的旋转曲面方程.62. 说明下列旋转曲面是怎样形成的(1)10343222=++z y x ; (2)24222=+-z y x ; (3)1222=--z y x ; (4)222)(y x a z +=-. 63. 指出下列方程在空间中表示什么样的几何图形(1)14322=+y x ; (2)13222=-y x ; (3)x z 42=; (4)13422=+z y .自测题 (A )(一) 选择题1.点M)5,1,4(-到 x y 坐标面的距离为( )A.5 B.4 C.1 D.422.点A )3,1,2(-关于y z 坐标面的对称点坐标 ( ) A.)3,1,2(-- B .)3,1,2(-- C.)3,1,2(- D .)3,1,2(-- 3.已知向量{}{}{}3,1,4,2,2,2,1,5,3--==-=c b a ,则=+-c b a 432( )A .{}16,0,20B .{}20,4,5-C .{}20,0,16- D.{}16,0,20- 4.设向量k j i a 424--=,k j i b 236+-=,则)3)(23(b a b a +-=( ) A.20 B .16- C.32 D.32-5.已知:→→-AB prj D C B A CD,则)2,3,3(),1,1,1(),7,1,5(),3,2,1(= ( )A.4 B .1 C.21D.2 6.设=-⨯+-+=+-=)()(22b a b a k j i b k j i a ,则, ( ) A .k j i 53++- B.k j i 1062++- C.k j i 1062-- D .k j i 543++ 7.设平面方程为0=-y x ,则其位置( )A .平行于x 轴 B.平行于y 轴 C.平行于z 轴 D.过z 轴. 8.平面0372=++-z y x 与平面0153=-++z y x 的位置关系( ) A.平行 B.垂直 C.相交 D.重合 9.直线37423zy x =-+=-+与平面03224=---z y x 的位置关系( ) A.平行 B .垂直 C.斜交 D .直线在平面内 10.设点)0,1,0(-A 到直线⎩⎨⎧=-+=+-07201z x y 的距离为( )A.5 B .61 C.51 D.81 (二) 填空题1.设=--x B x A ,则,两点间的距离为,,与29)421()2,,3(_________.2.设c b a u 23-+-=,c b a v +-=2,则=-v u 32_______________. 3.当m=_____________时,k j i 532+-与k j m i 23-+互相垂直.4.设kj i a ++=2,kj i b 22+-=,kj i c 243+-=,则)(b a prj c += .4. 设k j i a +-=2,k j i b 32-+=,则)2()2(b a b a -⨯+=_________. 5. 与)0,3,4()1,2,3(--B A 和等距离的点的轨迹方程为_______________. 6. 过点),,(715,),,(204-且平行于z 轴的平面方程_______________. 7. 设平面:03222,01=--+=+-+z y x z y x 与 平行,则它们之间的距离_________.8. 过点),,(382-且垂直平面0232=--+z y x 直线方程为______________. 10.曲面方程为:44222=++z y x ,它是由曲线________绕_____________旋转而成的.(三) 解答题1.求平行于{}的单位向量2,3,6-=a .2.已知作用于一点的三个力{}{}{}5,4,3,3,2,1,4,3,2321-==--=F F F 求合力的大小与方向.3. 如果{}1,1,2-=a ,{}1,2,1-=b 求a 在b 上的投影.4. 用向量方法,求顶点在)4,4,3(),5,3,1(),1,1,2(-----的三角形的三个内角. 5. 设k i a 2+-=,k j i b -+=2,k j i c 22++=,试将下列各式用k j i ,,表示. (1) c b a ⨯⨯)(; (2))()(c a b a ⨯⨯⨯.6. 求经过点(1,2,0)且通过z 轴的平面方程.7. 在平面02=--z y x 上找一点p,使它与点),5,1,2()1,3,4(-)3,1,2(--及之间的距离相等. 8. 求过 )1,0,0(),0,1,0(),0,0,1( 的圆的方程,并求该圆在坐标平面xoy 上的投影曲线方程. 9.求过点(1,2,1)且同时平行0132=-++z y x 和053=+-+z y x 两平面的直线方程. 10.方程:12222=++z y x 表示什么图形?自测题(B)(一) 选择题1.设{}{}{}0,2,1,3,1,1,1,3,2-=-=-=c b a ,则=⨯⨯c b a )(( ) A .8 B .10 C.{}1,1,0-- D.{}21,1,22.设{}{}2,2,2,2,1,1-=-=b a ,则同时垂直于a 和b 的单位向量( ) A.}0,21,21{± B.}0,21,21{± C.}0,2,2{± D.}0,2,2{±3.若==-+=b a b k j i a ,则,14//236( ) A.)4612(k j i -+± B.)612(j i +± C.)412(k i -± D.)46(k j -± 4.若ϕ的夹角与,则3121321)2,1,2(),1,2,2(),1,1,1(M M M M M M M ( ) A .6π B .2π C.3π D.4π5.过)320()231(),412(321,,和,,,,M M M ---,的平面方程( ) A.015914=--+z y x B.06872=--+z y x C .015914=-+-z y x D.015914=-++z y x 6.求平面062=-+-z y x 与平面052=-++z y x 的夹角( ) A.2π B .6π C.3π D .4π 7.直线⎩⎨⎧=+++=+++0022221111D z C y B x A D z C y B x A 各系数满足( )条件,使它与y 轴相交.A.021==A A B.2121D D B B =C.021==C CD.021==D D 8.设点⎩⎨⎧=-+-=+-+-04201)2,1,3(z y x z y x l M o ,直线,则M O 到l 的距离为( )A .223 B .553 C.453 D.229.直线夹角为与平面62241312=++-=-=-z y x z y x ( ) A.30o B .60o C .90o D .65arcsin10.过点)5,2,1(---且和三个坐标平面都相切的球面方程( )A .22225)1()1()1(=+++++z y x B.22225)5()5()5(=+++++z y x C.22225)2()2()2(=+++++z y x D.22225)5()5()5(=-+-+-z y x (二) 填空题1.设k j i a 32+-=,j i b +=2,k j i c ++-=,则c b a 与+是否平行__________. 2.设}8,5,3{=a ,}7,4,2{--=b ,}4,1,5{-=c ,则c b a -+34在x 轴上的投影_________________.3.化简:=⨯--⨯+++⨯++a c b b c b a c c b a )()()(__________________.4.直线 ⎩⎨⎧=---=-+-01205235:z y x z y x l 和平面 07734:=-+-z y x π的___________位置关系.5.过直线⎩⎨⎧=+-+=-+-025014z y x z y x 且与x 轴平行的平面方程___________________.6.原点==+-k kz y x ,则,的距离为到平面262)0,0,0(_________________. 7.与平面0522=+++z y x ,且与三个坐标面所构成的四面体体积为1的平面方程_____________________.8.动点到点(0,0,5)的距离等于它到x 轴的距离的曲面方程为________________. 9.曲面方程:259916222=--z y x 则曲面名称为________________.10.曲线⎪⎩⎪⎨⎧-+-=--=2222)1()1(2y x z yx z 在y z 面上的投影方程______________. (三) 解答题1.设}0,1,1{},1,1,0{},1,1,1{===c b a 并令c z b y a x d ++=(x ,y ,z 为数量) 求 (1)d ; (2)当z y x d ,,}3,2,1{时,=. 2.求平行于}2,3,6{-=a 的单位向量.3.确定k值,使三个平面:328,1423,23=--=++=+-z y x z y x z y kx 通过同一条直线.4.已知两个不平行的向量a 与b ,2=⋅b a 1=4=,设)(3)(2Xa b b a c -⨯=,求(1))(c b a +⋅; (; (3)的夹角余与c b 弦. 5.求以向量i k k j j i +++,,为棱的平行六面体的体积. 6.垂直平分连接)3,5,2(),1,3,4(B A -的线段的平面方程.7.求与平面4362=+-z y x 平行平面,使点)8,2,3(为这两个平面公垂线中点.8.在平面02=--z y x 上找一点p 使它与点)3,1,2()1,3,4(),5,1,2(---及之间的距离相等. 9.方程:0448422=-+-+y x y x 表示什么曲面?9. 方程组⎩⎨⎧=-++=--++0122046222z y x y x z y x 图形是什么?若是一个圆,求出它的中心与半径.参考答案 参考答案练习题1.(1)),,(c b a -; (2)),,(c b a --; (3)),,(c b a ---.2.51-==x x 或. 3.算出距离后,证明满足勾股定理 4.略5.k j i b a ++=+1132; k j i b a 75732+--=-.6.13545或=γ. 7.225. 8.}13,4,11{4},18,8,11{32-=+-=-AC AB AC AB .9.}5,2,7{3},12,10,9{52},1,2,1{--=+--=+=-b a b a b a . 10.单位向量为}31,32,32{-.11.(1)7; (2)u 在x 轴的分向量i 13,u 在z 轴的分向量k 9-; (3)299=u.12.利用数量积运算法则. 13.9-=⋅b a ; 70359arccos)(-=∧πb a . 14.x =4. 15.单位向量:)24(211k j i ++±. 16.1723=∆ABC S .17.(1)若a 与b 同向,则b a b a ⋅=⋅,若a 与b反向,则b a b a ⋅-=⋅;(2))cos(b a ∧.18.53±=k . 19.3617+=++c b a . 20.16=⋅b a .21.(1)46; (2)2-; (3)4838arccos)(-=∧πb a . 22.23. 23.(1)3; (2)k j i 333--; (3)21.24.30±。
初三数学各区二模专题复习5--几何证明题

初三数学专题复习---几何证明题1.如图,在△ABC 与△ABD 中, BC 与AD 相交于点O ,∠1=∠2,CO = DO .求证:∠C =∠D .2.已知:如图,E ,F 在BC 上,且AE ∥DF ,AB ∥CD ,AB =CD .求证:BF = CE .3. 已知:如图,点E 、F 分别为□ABCD 的BC 、AD 边上的点,且∠1=∠2.求证:AE =FC .4.已知,如图,点D 在边BC 上,点E 在△ABC 外部,DE 交AC 于F ,若AD =AB , ∠1=∠2=∠3.求证:BC=DE . 证明:21DOCBAFEDCBA21FEDCBA321F E A BC D5.已知:如图,菱形ABCD 中,过AD 的中点E 作AC 的垂线EF ,交AB 于点M ,交CB的延长线于点F .如果FB 的长是2,求菱形ABCD 的周长.6.如图,在矩形ABCD 中,E 是边CB 延长线上的点,且EB=AB ,DE 与AB 相交于点F ,AD=2,CD=1,求AE 及DF 的长.7.已知:如图,四边形ABCD 中,BC =CD =DB ,∠ADB =90°,sin ∠ABD =54,S △BCD =39. 求四边形ABCD 的周长.8.如图,梯形纸片ABCD 中,AD //BC ,∠B =30º.折叠纸片使BC 经过点A ,点B 落在点B ’处,EF 是折痕,且BE =EF =4,AF ∥CD . (1)求∠BAF 的度数; (2)当梯形的上底AD 多长时,线段DF 恰为该梯形的高? 解:MFEBCDA FEDCBAD CB A A B D EC B 'FDAB9.如图, △OAB 和△COD 均为等腰直角三角形,90AOB COD ∠=∠=︒, 连接AC 、BD .求证: AC BD =.10.已知:如图,在四边形ABCD 中, 60=∠C ,135=∠DAB ,8=BC ,62=AB求DC 的长.11.如图:已知在等边三角形ABC 中,点D 、E 分别是AB 、BC 延长线上的点,且BD =CE .求证:DC =EA .12.在Rt △ABC 中,∠ACB =90°,BC =4.过点A 作A E ⊥AB 且AB =AE ,过点E 分别作E F ⊥AC ,ED ⊥BC ,分别交AC 和BC 的延长线与点F ,D .若FC =5,求四边形ABDE的周长.13.如图,AB 是∠DAC 的平分线,且AD =AC .求证:BD =BCDC B AD CO B AA DC E B E F DA BC14. 已知:如图, P 是线段AB 的中点,线段MN 经过点P ,MA ⊥AB ,NB ⊥AB . 求证:AM=BN.15. 如图,AC //EG , BC //EF , 直线GE 分别交BC 、BA 于P 、D ,且AC=GE , BC=FE . 求证:∠A =∠G .16. 如图,在四边形ABCD 中,∠ADB =∠CBD =90︒,BE//CD 交AD 于E , 且EA=EB .若AB=54,DB =4, 求四边形ABCD 的面积.17.已知:如图,∠C =∠CAF =90°,点E 在AC 上,且AE =BC ,EF ⊥AB 于点D .求证:AB =FE .18.如图,在四边形ABCD 中,AC 平分∠BAD ,CE AB ⊥于E .设CD =CB =34,AD =9,AB =15. 求B ∠的余弦值及AC 的长.ABPM NGF E D C BA P EDCB AO B E AC DO B EACD 19.如图,在△ABC 中,AD 是中线,分别过点B 、C 作AD 及其延长线的垂线BE 、CF ,垂足分别为点E 、F .求证:BE =CF . 证明:20.如图1,已知平行四边形ABCD 中,对角线AC BD ,交于点O ,E 是BD 延长线上的点,且ACE △是等边三角形. ⑴求证:四边形ABCD 是菱形;⑵如图2,若2AED EAD ∠=∠,AC =6.求DE 的长.图1图221.如图,点F,G分别在△ADE的AD,DE边上,C,B依次为GF延长线上两点,AB=AD,∠BAF=∠CAE,∠B=∠D.(1)求证:BC=DE;(2)若∠B=35°,∠AFB=78°,直接写出∠DGB 的度数.22. 如图,在平行四边形ABCD中,点E,F分别是AB,CD的中点.(1)求证:四边形AEFD是平行四边形;(2)若∠A=60°,AB=2AD=4,求BD的长.初三数学专题复习---几何证明题 答案1.证明: ∠1=∠2, ∴OA=OB .…1分 在△COA 和△DOB 中 , OA=OB , ∠AOC =∠BOD , CO=DO .∴△COA ≌△DOB . ∴∠C =∠D . 2.证明:∵ AE ∥DF ,∴∠1=∠2. ∵ AB ∥CD , ∴ ∠B =∠C .在△ABE 和 △DCF 中,12,,,B C AB DC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ △ABE ≌△DCF . ∴ BE =CF . ∴BE -EF =CF -EF . 即BF =CE .3.证明:∵四边形ABCD 是平行四边形, ∴AB=CD ,∠B=∠D.∵∠1=∠2,△ABE ≌△CDF.AE=CF.4.证明:∵∠1=∠2=∠3∴DAE BAC ∠=∠………………… 又∵AFE DFC ∠=∠∴E C ∠=∠ …………………… 在△ABC 和△ADE 中21FEDCBA⎪⎩⎪⎨⎧=∠=∠∠=∠AD AB E C DAE BAC … ∴△ABC ≌△ADE ∴BC=DE . 5.解:联结BD . ∵在菱形ABCD 中, ∴AD ∥BC ,AC ⊥BD 又∵EF ⊥AC , ∴BD ∥EF .∴四边形EFBD 为平行四边形 ∴FB = ED =2 ∵E 是AD 的中点. ∴AD =2ED =4.∴菱形ABCD 的周长为4416⨯=.6.解:∵四边形ABCD 是矩形,且AD=2,CD=1,∴BC=AD=2,AB=CD=1,∠ABC =∠C= 90°,AB ∥DC .∴EB=AB=1. 在Rt △ABE 中,222AE AB BE =+=.在Rt △DCE 中,22221310D E D C C E =+=+=.∵AB ∥DC , ∴12EF EB DF BC ==.设EF x =,则2DF x =. ∵EF DF DE +=,∴210x x +=.∴103x =.∴22103DF x ==. 7.解:过C 作CE ⊥BD 于E.∵∠ADB=90°,sin ∠ABD= ,∴AD=4x,AB=5x.∴DB=3x ∵BC=CD=DB ,∴DE= ,∠CDB=60°. ∴tan ∠CDB= ∴CE= . ∵S △BCD= ,∴ ∴ x=2. ∴AD=8,AB=10,CD=CB=6.∴四边形ABCD 的周长=AD+AB+CD+CB=30.8. 解:(1)∵BE =EF ∴∠EFB =∠B ,由题意,△EF B '≌△BEF∴∠EFB ’ =∠EFB =∠B=30°∴△BFA 中,︒=︒-︒-︒-︒=∠90303030180BAF (2)联结DF ,∵AD //BC ,AF ∥CD ∴四边形AFCD 是平行四边形 ∴∠C =∠A FB =60° ∴CD =AF =3230cos =︒EF 若BC DF ⊥,则360cos =︒=CD FC 此时3=AD.9. 证明:∵ 90,AOB COD ∠=∠=︒ ∴ .AOC BOD ∠=∠∵ △OAB 与△COD 均为等腰三角形,∴ ,.OA OB OC OD ==在△AOC 和△BOD 中,,,,AO BO AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩∴ △AOC ≌△BOD .∴ AC BD =.10.解:如图,过B 作BE //AD 交CD 于E ,过A 作AF ⊥BE 于F …………1分∴︒=∠=∠90ADC BEC ,︒=∠-︒=∠45180A ABE ,AF =DE ……2分Rt △BEC 中,4218cos =⨯=∠⋅=C BC CE ……………3分 Rt △ABF 中322262sin =⨯=∠⋅=ABF AB AF ∴324+=DC 11.证明:∵ △ABC 是等边三角形,∴ BC =AC ,∠1=∠2=60°. ∴ ∠3=∠4=120°. ∵ BD =CE , ∴ △BDC ≌△CEA .∴DC =EA .12.解:∵ ∠ACB =90°,A E ⊥AB ,∴ ∠1+∠B =∠1+∠2=90°.∴ ∠B =∠2.∵ E F ⊥AC , ∴ ∠4=∠5 =90°.∴ ∠3=∠4. ∵ AB =AE ,∴ △ABC ≌△EAF . ∴ BC =AF ,AC =EF . ∵ BC =4, ∴ AF =4. ∵ FC =5, ∴ AC =EF=9.DCBA EF4321A DCEB7651243EF D A B C在Rt △ABC 中,22AB BC AC =+=2249+=97. ∴ AE =97.∵ ED ⊥BC ,∴ ∠7=∠6 =∠5= 90°. ∴ 四边形EFCD 是矩形.∴ CD =EF =9,ED =FC =5.∴ 四边形ABDE 的周长=AB +BD +DE +EA =97+4+9+5+97=18+297. 13.证明: AB 是∠DAC 的平分线,∴CAB DAB ∠=∠…在ADB ∆和ACB ∆中⎪⎩⎪⎨⎧=∠=∠=AB AB CAB DAB ACAD … ∴ADB ∆≌ACB ∆ ∴BD =BC …14. 证明:∵ P 是线段AB 的中点,∴ AP=BP.∵MA ⊥AB ,NB ⊥AB ,∴ ∠MAP=∠NBP=90°. 在△MAP 和△NBP 中,又∵∠APM=∠BPN , ∴△MAP ≌△NBP. ∴ AM=BN15.证明:∵ AC //EG ,∴ C CPG ∠=∠. ∵ BC //EF ,∴ CPG FEG ∠=∠.∴ C FEG ∠=∠.在△ABC 和△GFE 中,,,,AC GE C FEG BC FE =⎧⎪∠=∠⎨=⎪⎩ D ABC数学试卷 第 11 页 (共 6页)∴ △ABC ≌△GFE .∴A G ∠=∠. 16.解: ∵∠ADB =∠CBD =90︒,∴ DE ∥CB .∵ BE ∥CD ,∴ 四边形BEDC 是平行四边形. ………1分 ∴ BC=DE .在Rt △ABD 中,由勾股定理得 2222(45)48AD AB BD =-=-=.设DE x =,则8EA x =-.∴8EB EA x ==-.在Rt △BDE 中,由勾股定理得 222DE BD EB +=.∴ 22248x x +=-(). ∴ 3x =. ∴ 3BC DE ==. ∴1116622.22ABD BDC ABCD S S S BD AD BD BC ∆∆=+=⋅+⋅=+=四边形17.证明:∵EF ⊥AB 于点D ,∴ ∠ADE =90°.∴ ∠1 +∠2=90°.又∵∠C =90°, ∴ ∠1+∠B =90°. ∴ ∠B =∠2. 在△ABC 和△FEA 中,2,,.B BC AE C FAE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ △ABC ≌△FEA . ∴ AB =FE .18.解:如图,在AB 上截取AF AD =,连结CF .∵ AC 平分∠BAD ,∴12∠=∠. 又AC AC =, ∴△ADC ≌△AFC .∴ AF =AD =9,CF=CD =CB 34=.------------2分数学试卷 第 12 页 (共 6页)∴△CBF 是等腰三角形. 又∵CE AB ⊥于E , ∴ EF =EB =21BF =21(AB -AF )=3. 在Rt △BEC 中,33cos 343434BE B BC ===. 在Rt △BEC (或Rt △FEC )中,由勾股定理得 CE =5.在Rt △AEC 中,由勾股定理 得AC =13.∴ B ∠的余弦值为33434,AC 的长为13. 19.证明: AD 是中线∴BD=CD -分别过点B 、C 作AD 及其延长线的垂线BE 、CFCFD E ∠=∠∴中和在CFD BED ∆∆ ⎪⎩⎪⎨⎧∠=∠=∠=∠CDF BDE CDBD CFD E ()AAS CFD BED ∆≅∆∴ CF BE =∴20.证明:⑴ 平行四边形ABCD ∴OA =OC -ACE △是等边三角形 ∴OE ⊥AC ∴BD ⊥AC平行四边形ABCD ∴四边形ABCD 是菱形⑵ ACE △是等边三角形,OE ⊥AC∴∠AEO =AEC ∠21=30°2AED EAD ∠=∠ ∴∠EAD =15° ∴∠ADB =45°四边形ABCD 是菱形 ∴AD =DC , BD ⊥AC图2OBEACD数学试卷 第 13 页 (共 6页)∴∠CDB =∠ADB =45°∠ADC =90°,∴ADC ∆是等腰直角三角形∴OA =OC =OD =AC 21=3,ACE △是等边三角形, ∠EAO =60°在Rt ∆AOE 中,OE =OAtan 60°=33 ∴DE =OE -OD =333-21.(1)证明:如图1.∵ ∠BAF =∠CAE ,∴ BAF CAF CAE CAF ∠-∠=∠-∠.∴ BAC DAE ∠=∠. ………………… 1分 在△ABC 和△ADE 中,,,,B D AB AD BAC DAE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ △A B C ≌△A D E. ……………………………………………… ∴ BC=DE. ………………………………………………………………… (2)∠DGB 的度数为67︒.22. (1)证明:∵ 四边形ABCD 是平行四边形, ∴ AB ∥CD 且AB=CD . ﹍﹍﹍﹍1分 ∵ 点E ,F 分别是AB ,CD 的中点,∴ CD DF AB AE 21,21==.∴ AE=DF . ∴ 四边形AEFD 是平行四边形.(2)解:过点D 作DG ⊥AB 于点G . ∵ AB =2AD =4,∴ AD =2.在Rt △AGD 中,∵90,60,AGD A ∠=︒∠=︒ AD =2, ∴ .360sin ,160cos =︒⋅==︒⋅=AD DG AD AG ∴ 3BG AB AG =-=.在Rt △DGB 中,∵90,3,3,DGB DG BG ∠=︒== ∴.329322=+=+=BG DG DB图1F GDEA C B图2GFEDCBA。
几何复习题及答案

几何复习题及答案一、选择题1. 一个三角形的内角和是多少度?A. 90度B. 180度C. 360度D. 270度答案:B2. 如果一个圆的半径是5厘米,那么它的周长是多少?A. 10π厘米B. 20π厘米C. 30π厘米D. 40π厘米答案:B3. 一个矩形的长是10厘米,宽是5厘米,它的面积是多少?A. 25平方厘米B. 50平方厘米C. 75平方厘米D. 100平方厘米答案:B4. 一个正方体的棱长是4厘米,它的表面积是多少?A. 64平方厘米B. 96平方厘米C. 128平方厘米D. 192平方厘米答案:A5. 一个直角三角形的两条直角边分别是3厘米和4厘米,斜边是多少?A. 5厘米B. 7厘米C. 8厘米D. 10厘米答案:A二、填空题6. 一个圆的直径是14厘米,它的半径是________厘米。
答案:7厘米7. 如果一个平行四边形的对角线互相平分,那么这个平行四边形是________。
答案:矩形8. 一个正五边形的内角是________度。
答案:108度9. 一个长方体的长、宽、高分别是2米、3米和4米,它的体积是________立方米。
答案:24立方米10. 一个等腰三角形的底角是70度,那么它的顶角是________度。
答案:40度三、简答题11. 描述如何使用勾股定理来解决实际问题。
答案:勾股定理适用于直角三角形,即在一个直角三角形中,直角边的平方和等于斜边的平方。
例如,如果我们知道直角三角形的两条直角边的长度,我们可以使用勾股定理来计算斜边的长度。
12. 解释什么是相似三角形,并给出一个例子。
答案:相似三角形是指两个三角形的对应角相等,对应边的比例相等的三角形。
例如,如果一个三角形的三个角分别是30度、60度和90度,另一个三角形的三个角也是30度、60度和90度,那么这两个三角形就是相似的。
四、计算题13. 一个圆柱的底面半径是3厘米,高是10厘米,求它的体积。
答案:圆柱体积的计算公式是V = πr²h,其中 r 是底面半径,h 是高。
《微分几何》复习题与参考答案

《微分几何》复习题与参考答案一、填空题1.极限232lim[(31)i j k]t t t →+-+=138i j k -+.2.设f ()(sin )i j t t t =+,2g()(1)i j t t t e =++,求0lim(()())t f t g t →⋅= 0 .3.已知{}42r()d =1,2,3t t -⎰, {}64r()d =2,1,2t t -⎰,{}2,1,1a =,{}1,1,0b =-,则4622()()a r t dt+b a r t dt=⨯⋅⋅⎰⎰{}3,9,5-.4.已知()r t a '=(a 为常向量),则()r t =ta c +.5.已知()r t ta '=,(a 为常向量),则()r t = 212t a c +.6. 最“贴近”空间曲线的直线和平面分别是该曲线的___ 切线___和 密切平面____.7. 曲率恒等于零的曲线是_____ 直线____________ .8. 挠率恒等于零的曲线是_____ 平面曲线________ .9. 切线(副法线)和固定方向成固定角的曲线称为 一般螺线 . 10. 曲线()r r t =在t = 2处有3αβ=,则曲线在t = 2处的曲率k = 3 . 11. 若在点00(,)u v 处v 0u r r ⨯≠,则00(,)u v 为曲面的_ 正常______点. 12. 已知()(2)(ln )f t t j t k =++,()(sin )(cos )g t t i t j =-,0t >,则4()df g dt dt ⋅=⎰4cos 62-.13.曲线{}3()2,,t r t t t e =在任意点的切向量为{}22,3,t t e . 14.曲线{}()cosh ,sinh ,r t a t a t at =在0t =点的切向量为{}0,,a a . 15.曲线{}()cos ,sin ,r t a t a t bt =在0t =点的切向量为{}0,,a b .16.设曲线2:,,t t C x e y e z t -===,当1t =时的切线方程为2111-=--=-z ee y e e x . 17.设曲线t t t e z t e y t e x ===,sin ,cos ,当0t =时的切线方程为11-==-z y x . 18. 曲面的曲纹坐标网是曲率线网的充要条件是____F =M =0_ ______________. 19. u -曲线(v -曲线)的正交轨线的微分方程是 _____ E d u +F d v =0(F d u +G d v =0)__. 20. 在欧拉公式2212cos sin n k k k θθ=+中,θ是 方向(d) 与u -曲线 的夹角. 21. 曲面的三个基本形式,,I II III 、高斯曲率K 、平均曲率H 之间的关系是20H K III -II +I = . 22.已知{}r(,),,u v u v u v uv =+-,其中2,sin u t v t ==,则drd t={}2c o s ,2c o s ,2c o s t t t t v t u t +-+.23.已知{}r(,)cos cos ,cos sin ,sin a a a ϕθϕθϕθϕ=,其中t =ϕ,2t =θ,则dr(,)d tϕθ={}sin cos 2cos sin ,sin sin 2cos cos ,cos a at a at a ϕθϕθϕθϕθϕ---+.24.设(,)r r u v =为曲面的参数表示,如果0u v r r ⨯≠,则称参数曲面是正则的;如果:()r G r G → 是 一一对应的 ,则称曲面是简单曲面.25.如果u -曲线族和v -曲线族处处不相切,则称相应的坐标网为 正规坐标网 . 26.平面{}r(,),,0u v u v =的第一基本形式为22d d u v +,面积微元为d d u v .27.悬链面{}r(,)cosh cos ,cosh sin ,u v u v u v u =第一基本量是22cosh 0,cosh E u F G u ===,. 28.曲面z axy =上坐标曲线0x x =,0y y =229.正螺面{}(,)cos ,sin ,r u v u v u v bv =的第一基本形式是2222d ()d u u b v ++. 30.双曲抛物面{}r(,)(),(),2u v a u v b u v uv =+-的第一基本形式是2222222222(4)d 2(4)d d (4)d a b v u a b uv u v a b u v +++-++++.31.正螺面{}(,)cos ,sin ,r u v u v u v bv =的平均曲率为 0 .32.方向(d)d :d u v =是渐近方向的充要条件是22()020n k d Ldu Mdudv Ndv =++=或. 33. 方向(d)d :d u v =和(δ)δ:δu v =共轭的充要条件是(,)0()0dr δr Ldu δu M du δv dv δu Ndv δv =+++=II 或.34.λ是主曲率的充要条件是0E L F MF MG Nλλλλ--=--.35.(d)d :d u v =是主方向的充要条件是22d d d d 00d d d d dv dudv du E u F v L u M vE F G F u G v M u N vL M N-++==++或. 36. 根据罗德里格斯定理,如果方向(d)(d :d )u v =是主方向,则n n dn k dr k =-,其中是沿方向(d)的法曲率.37.旋转曲面中的极小曲面是平面 或悬链面.38.测地曲率的几何意义是曲面S 上的曲线在P 点的测地曲率的绝对值等于(C )在P 点的切平面∏上的正投影曲线(C*)的曲率. 39.,,g n k k k 之间的关系是222g n k k k =+.40.如果曲面上存在直线,则此直线的测地曲率为 0 . 41.正交网时测地线的方程为d ds du dsdv dsθθθ⎧⎪⎪⎪⎨⎪⎪⎪⎩. 42.曲线是曲面的测地线,曲线(C )上任一点在其切平面的正投影曲线是 直线 . 二、单项选择题1.已知{}(),,t t r t e t e -=,则r (0)''为( A ).A. {}1,0,1;B. {}1,0,1-;C. {}0,1,1;D. {}1,0,1-. 2.已知()()r t r t λ'=,λ为常数,则()r t 为( C ).A. ta λ;B. a λ;C. t e a λ;D. e a λ. 其中a 为常向量.3. 曲线(C)是一般螺线,以下命题不正确的是( D ).A .切线与固定方向成固定角;B .副法线与固定方向成固定角;C .主法线与固定方向垂直;D .副法线与固定方向垂直.4. 曲面在每一点处的主方向( A )A .至少有两个;B .只有一个;C .只有两个;D .可能没有. 5.球面上的大圆不可能是球面上的( D )A .测地线;B .曲率线;C .法截线;D .渐近线.. 6. 已知{}r(,),,x y x y xy =,求(1,2)dr 为( D ).A. {}d ,d ,d 2d x y x y +;B. {}d d ,d d ,0x y x y +-;C. {}d -d ,d +d ,0x y x y ;D. {}d ,d ,2d d x y x y +. 7.圆柱螺线{}cos ,sin ,r t t t =的切线与z 轴( C ).A. 平行;B. 垂直;C. 有固定夹角4π; D. 有固定夹角3π. 8.设平面曲线:()C r r s =,s 为自然参数,αβ,是曲线的基本向量.叙述错误的是( C ).A. α为单位向量;B. αα⊥;C. k αβ=-;D. k βατγ=-+. 9.直线的曲率为( B ).A. -1;B. 0;C. 1;D. 2.10.关于平面曲线的曲率:()C r r s =不正确的是( D ).A. ()()k s s α=;B. ()()k s s ϕ=,ϕ为()s α的旋转角;C. ()k s αβ=-⋅;D. ()|()|k s r s =.11.对于曲线,“曲率恒等于0”是“曲线是直线”的( D ).A. 充分不必要条件;B. 必要不充分条件;C. 既不充分也不必要条件;D. 充要条件. 12.下列论述不正确的是( D ).A. ,αβγ,均为单位向量;B. αβ⊥;C. βγ⊥;D. αβ. 13.对于空间曲线C ,“挠率为零”是“曲线是直线”的(B ).A. 充分不必要条件;B. 必要不充分条件;C. 既不充分也不必要条件;D. 充要条件. 14.2sin4),cos 1(),sin (t a z t a y t t a x =-=-=在点2π=t 的切线与z 轴关系为( D ). A. 垂直; B. 平行; C. 成3π的角; D. 成4π的角. 15.椭球面2222221x y z a b c++=的参数表示为( C ).A. {}{},,cos cos ,cos sin ,sin x y z ϕθϕθϕ=;B. {}{},,cos cos ,cos sin ,sin x y z a b ϕθϕθϕ=;C. {}{},,cos cos ,cos sin ,sin x y z a b c ϕθϕθϕ=;D. {}{},,cos cos ,sin cos ,sin 2x y z a b c ϕθϕθθ=.16.曲面{}2233(,)2,,r u v u v u v u v =-+-在点(3,5,7)M 的切平面方程为( B ).A. 2135200x y z +-+=;B. 1834410x y z +--=;C. 756180x y z +--=;D. 1853160x y z +-+=.17.球面{}(,)cos cos ,cos sin ,sin r u v R u v R u v R u =的第一基本形式为( D ).A. 2222(d sin d )R u u v +;B. 2222(d cosh d )R u u v +;C. 2222(d sinh d )R u u v +;D. 2222(d cos d )R u u v +. 18.正圆柱面{}(,)cos ,sin ,r u v R v R v u =的第一基本形式为( C ).A. 22d d u v +;B. 22d d u v -; C 222d d u R v +; D. 222d d u R v -. 19.在第一基本形式为222(d ,d )d sinh d u v u u v =+I 的曲面上,方程为12()u v v v v =≤≤的曲线段的弧长为( B ).A . 21cosh cosh v v -;B . 21sinh sinh v v -;C . 12cosh cosh v v -;D . 12sinh sinh v v -.20.设M 为正则曲面,则M 的参数曲线网为正交曲线网的充要条件是( B ).A . 0E =;B . 0F =;C . 0G =;D . 0M =. 21.高斯曲率为零的的曲面称为( A ).A .极小曲面;B .球面;C .常高斯曲率曲面;D .平面. 22.曲面上直线(如果存在)的测地曲率等于( A ).A . 0;B . 1;C .2;D . 3. 23.当参数曲线构成正交网时,参数曲线u-曲线的测地曲率为( B ).A .B .C .D . 24.如果测地线同时为渐近线,则它必为( A ).A . 直线;B . 平面曲线;C . 抛物线;D . 圆柱螺线. 三、判断题(正确打√,错误打×)1. 向量函数()r r t =具有固定长度,则()()r t r t '⊥. √2. 向量函数()r r t =具有固定方向,则()()r t r t '. √3. 向量函数()r t 关于t 的旋转速度等于其微商的模()r t '. ×4. 曲线Γ的曲率、挠率都为常数,则曲线Γ是圆柱螺线. ×5. 若曲线Γ的曲率、挠率都为非零常数,则曲线Γ是圆柱螺线. √6. 圆柱面{cos ,sin ,},r R R z θθ=z -线是渐近线. √7. 两个曲面间的变换等距的充要条件是它们的第一基本形式成比例. ×8. 两个曲面间的变换等角的充要条件是它们的第一基本形式成比例. √9. 等距变换一定是保角变换. √10. 保角变换一定是等距变换. × 11. 空间曲线的位置和形状由曲率与挠率唯一确定. × 12. 在光滑曲线的正常点处,切线存在但不唯一. × 13. 若曲线的所有切线都经过定点,则该曲线一定是直线.√ 14. 在曲面的非脐点处,有且仅有两个主方向. √ 15. 高斯曲率与第二基本形式有关,不是内蕴量. × 16. 曲面上的直线一定是测地线.√ 17. 微分方程A(,)B(,)0u v du u v dv +=表示曲面上曲线族. ×18. 二阶微分方程22(,)2(,)(,)0A u v du B u v dudv C u v dv ++=总表示曲面上两族曲线. × 19. 坐标曲线网是正交网的充要条件是0F =,这里F 是第一基本量. √ 20. 高斯曲率恒为零的曲面必是可展曲面. √ 21. 连接曲面上两点的所有曲线段中,测地线一定是最短的. × 22. 球面上的圆一定是测地线. × 23. 球面上经线一定是测地线. √24. 测地曲率是曲面的内蕴量. √ 四、计算题1.求旋轮线)cos 1(),sin (t a y t t a x -=-=的π20≤≤t 一段的弧长.解 旋轮线{}()(sin ),(1cos )r t a t t a t =--的切向量为{}()cos ,sin r t a a t a t '=-,则在π20≤≤t 一段的弧长为:220()d 8s r t t t a ππ'===⎰⎰.2.求曲线t te z t t y t t x ===,cos ,sin 在原点的切向量、主法向量、副法向量. 解 由题意知 {}()sin cos ,cos sin ,t t r t t t t t t t e te '=+-+, {}()2cos sin ,2sin cos ,2t t r t t t t t t t e te ''=---+,在原点,有 (0)(0,1,1),(0)(2,0,2)r r '''==, 又 ()(), r r r r r r r r r r r αβ'''''''''⋅-⋅=='''''⋅⨯,r r r r γ'''⨯='''⨯, 所以有22666333(0,,),(,,),(,,)αβγ==-=-. 3.圆柱螺线为{}()cos ,sin ,r t a t a t bt =,①求基本向量,,αβγ; ②求曲率k 和挠率τ.解 ①{}()sin ,cos ,r t a t a t b '=-,{}()cos ,sin ,0r t a t a t ''=--,又由公式()(), ,r rr r r r r r r r rr r r r αβγ''''''''''''⋅-⋅⨯===''''''''⋅⨯⨯ }{}}sin ,cos ,,cos ,sin ,0,sin ,cos ,a t a t b t t b t b t a αβγ∴=-=--=-②由一般参数的曲率公式3()r r k t r '''⨯='及挠率公式2(,,)()r r r t r r τ''''''='''⨯ 有22a k a b =+,22b a b +=τ. 4.求正螺面{}(,)cos ,sin ,r u v u v u v bv =的切平面和法线方程. 解 {}cos ,sin ,0u r v v =,{}sin ,cos ,v r u v u v b =-,切平面方程为cos sin cos sin 00sin cos x u v y u v z bv v v u vu vb---=-,sin cos 0,b v x b u y uz buv ⇒⋅-⋅+-=法线方程为cos sin sin cos x u v y u v z bvb v b v u---==-. 5.求球面{}(,)cos cos ,cos sin ,sin r a a a ϕθϕθϕθϕ=上任一点处的切平面与法线方程. 解 {}sin cos ,sin sin ,cos r a a a ϕϕθϕθϕ=--, {}cos sin ,cos cos ,0r a a θϕθϕθ=-,312sin cos sin sin cos cos sin cos cos 0e e e r r a a a a a ϕθϕθϕθϕϕθϕθ⨯=--- {}2cos cos cos ,cos sin ,sin a ϕϕθϕθϕ=---∴ 球面上任意点的切平面方程为{}{}2cos cos ,cos sin ,sin cos cos cos ,cos sin ,sin 0,x a y a z a a ϕθϕθϕϕϕθϕθϕ---⋅---=即cos cos cos sin sin 0x y z a θϕϕθϕ⋅+⋅+⋅-=, 法线方程为2(cos cos ,cos sin ,sin )cos (cos cos ,cos sin ,sin ),x a y a z a a ϕθϕθϕλϕϕθϕθϕ---=⋅---即cos cos cos sin sin cos cos cos sin sin x a y a z a ϕθϕθϕϕθϕθϕ---==.6.求圆柱螺线cos ,sin ,x a t y a t z t ===在点(,0,0)a 处的密切平面. 解 (){s i n ,c o s ,r t a t a t '=-(){c o s ,s i n ,r t a t a t ''=-- 所以曲线在原点的密切平面的方程为00sin cos 10cos sin 0x a y z a t a t =a ta t------, 即sin )(cos )sin 0t x t y az a t -+-=(.7.求旋转抛物面22()z a x y =+的第一基本形式.解 参数表示为{}22(,),,()r x y x y a x y =+,{}1,0,2x r ax =,{}0,1,2y r ay =,2214x x E r r a x =⋅=+,24x y F r r a xy =⋅=,2214y y G r r a y =⋅=+,2222222(d ,d )(14)d 8d d (14)d x y a x x a xy x y a y y ∴=++++I .8.求正螺面{}(,)cos ,sin ,r u v u v u v bv =的第一基本形式. 解 {}cos ,sin ,0u r v v =,{}sin ,cos ,v r u v u v b =-,1u u E r r =⋅=,0u v F r r =⋅=,22v v G r r u b =⋅=+,2222(d ,d )d ()d u v u u b v ∴=++I .9.计算正螺面{}(,)cos ,sin ,r u v u v u v bv =的第一、第二基本量. 解 {}cos ,sin ,0u r v v =,{}sin ,cos ,v r u v u v b =-,{}0,0,0uu r =,{}sin ,cos ,0uv r v v =-,{}cos ,sin ,0vv r u v u v =--,{}cos sin 0sin ,cos ,sin cos u v i j k r r v v b v b v u u v u v b⨯==--,sin ,cos ,u v u v b v b v u r r n r r -⨯==⨯, 1u u E r r =⋅=,0u vF r r =⋅=,22v vG r r u b =⋅=+, 0uu L r n =⋅=,uv M r n =⋅=,0vv N r n =⋅=.10.计算抛物面22z x y =+的高斯曲率和平均曲率.解 设抛物面的参数表示为{}22(,),,r x y x y x y =+,则{}1,0,2x r x =,{}0,1,2y r y =,{}0,0,2xx r =,{}0,0,0xy yx r r ==,{}002yy r =,,,{}1022,2,1012x y i j kr r x x y y⨯==--,22,2,1||4x y x y r r x y n r r x ⨯--==⨯214x x Er r x =⋅=+, 4x y F r r xy =⋅=, 214y y G r r y =⋅=+,xx L r n =⋅=, 0xy M r n =⋅=, yy N r n =⋅=,2222222222404441(14)(14)(4)(441)LN M x y K EG F x y xy x y --++===-++-++, 2232222124422(441)GL FM EN x y H EG Fx y -+++=⋅=-++. 11. 计算正螺面{}(,)cos,sin ,r u v u v u v av =的高斯曲率. 解 直接计算知1E =,0F =,22G u a =+,0L =,M =,0N =,222222()LN M a K EG F u a -∴==--+.12. 求曲面2z xy =的渐近线.解 2z x y =,则2z p y x∂==∂,2z q xy y ∂==∂,220z r x ∂==∂,22z s y x y ∂==∂∂, 222z t x y ∂==∂ 所以,L =0,M =N =20=,化简得(2)0dy ydx xdy +=, 020d y y d x x d y =+=或渐近线为y=C 1,x 2y =C 213. 求螺旋面{}cos ,sin ,r u v u v bv =上的曲率线. 解 u v r {cos ,sin v,0},r {u sin v,u cos v,b}v ==-2222u u v vE r 1,F r r 0,G r u b ,===⋅===+{}{}u vu v bsin v,bcos v,u bsin v,bcos v,u r r n r r bsin v,bcos v,u--⨯===⨯- {}{}{}uu uvvv r =0,0,0,r =sin v,cos v,0,r ucos v,usin v,0-=--,L 0,M N 0===曲率线的微分方程为:2222dv dudv du 10u b =00-+ 或du bu dv 221+±=积分得两族曲率线方程:12v ln(u c v u)c .=+=+和14. 求马鞍面22{,,}r u v u v =-在原点处沿任意方向的法曲率.解 {1,0,2},{0,1,==-u v r ur v ,22214,4,14==+==-=+u u v E r u F r r uv G v2222(14)8(14)=+-++u du uvdudv v dv Ⅰu v 2u v 2u,2v,1r r n r r 4u -⨯==⨯ uu 2L nr 4u ==uv M n r 0,== vv 2N n r 4u ==22=-Ⅱ, n k =ⅡⅠ. 15. 求抛物面22()z a x y =+在(0,0)点的主曲率. 解 曲面方程即22{,,()},=+r x y a x y{1,0,2},{0,1,2},==x y r ax r ay E(0,0)F(0,0)G(0,0)=1,=0,=1,{0,0,2},{0,0,0},{0,0,2}===xx xy yy r a r r a ,L(0,0)a M(0,0)N(0,0)=2,=0,=2a,代入主曲率公式,NN2a k 0002a k -=-,所以两主曲率分别为 12k k 2a == .16. 求曲面22{,,}r u v u v =+在点(1,1)的主方向.解 {}u r =,u 1,02,{},v r ,v =01,2 2214,4,14E u F uv G v =+==+ (1,)5(1,)4(1,)5;E F G 1=,1=,1= 0,L M N ===2(1,1)(1,1),(1,1)0,3L N M === 代入主方向方程,得()()0du dv du dv +-=,即在点(1,1)主方向:1:1;:1:1du dv u v δδ=-=.17. 求曲面23(,){,,}r u v u v u v =+上的椭圆点,双曲点和抛物点. 解 由23{,,},r u v u v =+ 得{}u r =,u 1,02,{}2,v r ,v =01,3{}{}{}u u u v v v r =,r =,r =,v 0,02,0,00,0,06, 0,L M N ===2241241vLN M .u +9v +-=①v >0时,是椭圆点;②v <0时,是双曲点;③v =0时,是抛物点. 18. 求曲面32(,){,,}r u v v u u v =+上的抛物点的轨迹方程. 解 由32(,){,,},r u v v u u v =+ 得{}u r =u,0,21,{}2,v r v ,=30,1{}{}{}u u u v v v r =,r =,r =v ,0,20,0,00,6,00, 20,L M N ===令320LN M .-=得u =0 或v =0所以抛物点的轨迹方程为 {}r=v ,,v 30或{}0r=,u ,u 2. 19.求圆柱螺线(){cos ,sin ,}r t a t a t bt =自然参数表示.解 由(){cos ,sin ,},r t a t a t bt =得{sin ,cos ,}r a t a t b '=-, 2()r t a '=弧长(),t s t =⎰t =曲线的自然参数表示为(){sinr s a a =20. 求挠曲线的主法线曲面的腰曲线.解 设挠曲线为a a s =(),则主法线曲面为:r=a s v s ,β()+() 则,a =a=α',b ==-k βατγ'+a b =k,''-2,22b =k +τ' 所以腰曲线是222a b kr=a s s =a s s k bββτ'''()-()()+()+ 21.求位于正螺面cos ,sin ,x u v y u v z av ===上的圆柱螺线00cos ,sin ,x u v y u v z av ===(0u =常数)的测地曲率.解 因为正螺面的第一基本形式为2222d ()d u u a v =++Ι,螺旋线是正螺面的v -曲线0u u =,由2πθ=得d 0d s θ=.由正交网的坐标曲线的测地曲率得0220g u k u a==+. 五、证明题1. 设曲线:(s),r r =证明:2()k -;r ,r ,r =k .ταγτ=⋅⑴⑵证明 ⑴由伏雷内公式,得=k =-,αβγτβ,两式作点积,得=-k =-k,αγτββτ⋅⋅k =-.ταγ∴⋅⑵r=r==k ,ααβ, 2()r=k +k =k +k -k +=-k +k +k βββατγαβτγ22()()()r ,r ,r =,k ,-k +k +k =,k ,k =k .αβαβτγαβτγτ∴2. 设曲线:(s),r r = 证明:3()()r ,r ,r =k k -k .ττ证明 由伏雷内公式,得r==k αβ, 2()r=k +k =k +k -k +=-k +k +k βββατγαβτγ323()(2)r =-kk +-k +k-k +k +k ατβττγ232()(())(3()(2))r ,r ,r =k -k +k +k -kk +-k +k-k +k +k βαβτγατβττγ⨯3232()(3()(2))=k +k -kk +-k +k-k +k +k γταατβττγ33432=-k k +k k +k τττ3()=k k -k ττ3. 曲线Γ:()r r s =是一般螺线,证明1:r R ds αβΓ=-⎰也是一般螺线(R 是曲线Γ的曲率半径). 证明 1r R d s αβ=-⎰,两边关于s 微商,得11ds R R ds αααβ=+-1R R R αββ=+-R α=, 1αα∴,由于Γ是一般螺线,所以Γ也是一般螺线.4. 证明曲线(){sin (),s (),}(r t a t dt a co t dt bt a,b ϕϕ=⎰⎰是常数)是一般螺线.证明 (){s i n (),c o s ()r t a t a t b ϕϕ'= (){()cos (),()sin (),0},r t a t t a t t ϕϕϕϕ''''=-2()(){cos (),sin (),0}(){sin ()cos ()0}r t a t t t a t t t ϕϕϕϕϕϕ''''''=-+-,,(r r a t ϕ''''⨯=32()()r r r a b t ϕ'''''''=-,,, 322(),r r a k t a b r ϕ'''⨯'==+'()222(),r r r b t a b r r τϕ'''''''==-+'''⨯,, k a bτ∴=- . 5.曲面S 上一条曲线(C), P 是曲线(C)上的正常点,n g k ,k ,k 分别是曲线(C)在点P 的曲率、法曲率与测地曲率,证明222n g k =k +k .证明 测地曲率()g k k k n βεβα=⋅=⋅⨯(,,)k n k n αβγ==⋅sin k .θ=± (θ是主法向量β与法向量n 的夹角)法曲率cos n k k n k βθ=⋅=,222n g k =k +k .∴6. 证明曲线{}cos ,sin ,0t t r e t e t =的切向量与曲线的位置向量成定角.证明 对曲线上任意一点,曲线的位置向量为{}cos ,sin ,0t t r e t e t =,该点切线的切向量为:{}(cos sin ),(sin cos ),0t t r e t t e t t '=-+,则有:2cos 22t t r r r r e θ'⋅==='4π. 由所取点的任意性可知,该曲线与曲线的切向量成定角.7.证明:若r '和r ''对一切t 线性相关,则曲线是直线.证明 若r '和r ''对一切t 线性相关,则存在不同时为0的(),()f t g t 使()()()()0f t r t g t r t '''+=, 则 ,()()0, t r t r t '''∀⨯= 又3()r r k t r '''⨯=',故t ∀有()0k t =.于是该曲线是直线.8. 证明圆柱螺线bt z t a y t a x ===,sin ,cos 的主法线和z 轴垂直相交.证明 由题意有{}{}()sin ,cos ,,()cos ,sin ,0r t a t a t b r t a t a t '''=-=--,由()()r r r r r r r r r β''''''''⋅-⋅=''''⋅⨯知{}cos ,sin ,0t t β=--. 另一方面z 轴的方向向量为{}0,0,1a =,而0a β⋅=,故a β⊥,即主法线与z 轴垂直.9.证明曲线t a z t t a y t a x cos ,cos sin ,sin 2===的所有法平面皆通过坐标原点.证明 由题意可得{}()sin 2,cos2,sin r t a t a t a t '=-,则任意点的法平面为0)cos (sin )cos sin (2cos )sin (2sin 00000020=---+-t a z t a t t a y t a t a x t a 将点(0,0,0)代入上述方程有左边)cos 0(sin )cos sin 0(2cos )sin 0(2sin 00000020t a t a t t a t a t a t a ---+-===0右边, 故结论成立.10.证明曲线222132225,1x t+t ,y t t z t =+=-+=-为平面曲线,并求出它所在的平面方程. 证明 {}222132225,1r t+t ,t t t =+-+-,{}34210,2r +t,t t '=-+-,{}410,2r ,''=-,{}00,0r ,'''=(,,)0r r r ,''''''=0τ=,所以曲线是平面曲线. 它所在的平面就是密切平面{}(0)32,0r ,'=-, {}(0)410,2r ,''=-密切平面方程为12132004102x y z -=----, 化简得其所在的平面方程是2x +3y +19z –27=0.11. 证明如果曲线的所有切线都经过一个定点,那么它是直线.证明 设曲线方程()r r s =,定点的向径为0R ,则0()()r s R s λα-=两边求微商,得()()()()s s s s k αλαλαλαλβ=+=+(1())()0s s k λαλβ--= 由于,αβ线性无关,∴100k λλ⎧-⎨⎩==∴ k =0曲线是直线.12. 证明如果曲线的所有密切平面都经过一个定点,那么它是平面曲线.证明 取定点为坐标原点,曲线的方程为 ()r r t =,则曲面在任一点的密切平面方程为 ((),(),())0r t r t r t ρ'''-=因任一点的密切平面过定点,所以((),(),())0o r t r t r t '''-=, 即 ((),(),())r t r t r t '''=所以 ()r r t =平行于固定平面, 所以 ()r r t =是平面曲线.13. 若一条曲线的所有法平面包含非零常向量e ,证明曲线是直线或平面曲线.证明 根据已知条件,得0.............e α⋅=①,①两边求导,得 0e α⋅=,由伏雷内公式得 0k e β⋅=,ⅰ)0k =,则曲线是直线;ⅱ)0e β⋅= 又有①可知 γ‖e因e 是常向量,所以γ是常向量,于是 ||||0,τγ== 所以0τ= ,所以曲线为平面曲线. 14. 设在两条挠曲线,ΓΓ的点之间建立了一一对应关系,使它们在对应的点的副法线互相平行,证明它们在对应点的切线和主法线也分别平行.证明 γγ±12= , 21ds ds γγ±12= 由伏雷内公式得211ds ds τβτβ±122=12ββ∴±= 进而12αα=± 15. 证明挠曲线(0τ≠)的主法线曲面是不可展曲面.证明 设挠曲线为()r r s =,则挠率0τ≠,其主法线曲面的方程是:()()r s t s ρβ=+ 取(),()a r s b s β==,则(),()k a s b s αβατγ''===-+所以, (,,)((),(),k )((),(),k )((),(),)0a b b s s s s s s αβατγαβααβτγτ''=-=-≠++=所以挠曲线的主法线曲面不是可展曲面.16. 证明挠曲线(0τ≠)的副法线曲面是不可展曲面.证明 设挠曲线为()r r s =,则挠率0τ≠,其副法线曲面的方程是:()()r s t s ργ=+取(),()a r s b s γ==,则(),()a s b s αγτβ''===-所以, (,,)((),(),)0a b b s s αγτβτ''=-=≠,所以挠曲线的副法线曲面不是可展曲面.17. 证明每一条曲线在它的主法线曲面上是渐近线.证明 设曲线r r(s),=则曲线的主法线曲面为r r s +v s β=()() ,s r v k vk v αατγατγ++=+(-)=(1-) ()v r =s β,s v s v r r n==r r vk ⨯⨯(1-)-(1- 沿曲线(v =0)n=γ, 所以主法向量与曲面的法向量夹角,2πθ=n cos 0,k k θ==所以曲线是它的主法线曲面上的渐近线.18. 证明二次锥面{cos ,sin ,}r au bu cu θθ=沿每一条直母线只有一个切平面.证明 {c o s ,s i n ,}{c o s ,s i n ,}θθθθϕθ===+r a u b u c u u a b c u 为直纹面(0,(),()0ϕθϕθ'=), 所以,曲面可展,即沿每一条直母线只有一个切平面.也可以用高斯曲率K =0证明. 19. 给出曲面上一条曲率线Γ,设Γ上每一处的副法向量和曲面在该点处的法向量成定角,求证Γ是一平面曲线. 证明 设副法向量和曲面在该点处的法向量成定角θ0,则cos γθ0n=两边求微商,得 0γγn+n=由于曲线Γ是曲率线,所以αn,进而0γn=,由伏雷内公式得0τβ-n=⑴0τ=时,Γ是一平面曲线⑵n 0β=,即n β⊥,n kcos =0k θ=,又因为Γ是曲率线,所以0n dn k dr =-=即n 是常向量,所以Γ是平面曲线.20.求证正螺面上的坐标曲线(即u -曲线族v -曲线族)互相垂直.证明 设正螺面的参数表示是{}(,)cos ,sin ,r u v u v u v bv =,则{}cos ,sin ,0u r v v =,{}sin ,cos ,v r u v u v b =-,{}{}cos ,sin ,0sin ,cos ,0u v r r v v u v u v b ⇒⋅=⋅-=,故正螺面上的坐标曲线互相垂直.21. 证明在曲面上的给定点处,沿互相垂直的方向的法曲率之和为常数.证明 由欧拉公式2212cos sin θθ=+n k k k*n 1in ππθθ=±-±-k k 222cos ()+k s ()221in cos k θθ=222s +k 所以*n n 12k k k k +=+=常数.22. 如果曲面上非直线的测地线Γ均为平面曲线,则Γ必是曲率线.证明 因为曲线Γ是非直线的测地线,所以沿此曲线有,β=±n从而(),κατγ=±-+n 又因为曲线是平面曲线,所以0,τ=进一步n κα=±.由罗德里格斯定理可知曲线的切线方向为主方向,故所给曲线为曲率线.23. 证明在曲面()()z f x f y =+上曲线族x =常数,y =常数构成共轭网.证明 曲面的向量表示为 {}(,),,()(),r x y x y f x f y =+x =常数,y =常数是两族坐标曲线.{1,0,}x r f '=,{0,1,}y r g '=.{0,0,},{0,0,0},{0,0,},xx xy yy r f r r g ''''===因为0xy r r M r ⨯==,所以坐标曲线构成共轭网,即曲线族 x =常数, y =常数构成共轭网.24.证明马鞍面z xy =上所有点都是双曲点.证明 参数表示为{}(,),,r x y x y xy =,则{}1,0,x r y =,{}0,1,y r x =,{}0,0,0xx r =,{}0,0,1xy r =,{}0,0,0yy r =,{},,1x y r r y x ⨯=--,2,,1||x yx y rr y x n r r x ⨯--==⨯+ 0xx L r n =⋅=, xy M r n =⋅=0yy N r n =⋅=,222221100011LN M x y x y ∴-=⨯-=-<++++, 故马鞍面z xy =上所有点都是双曲点. 25.如果曲面上某点的第一与第二基本形式成比例,即(d ,d )(d ,d )u v u v II I 与方向无关,则称该点是曲面的脐点;如果曲面上所有点都是脐点,则称曲面是全脐的.试证球面是全脐的. 证明 设球面的参数表示为{}(,)cos cos ,cos sin ,sin r u v R v u R v u R v =,则{}cos sin ,cos cos ,0u r R v u R v u =-,{}sin cos ,sin sin ,cos v r R v u R v u R v =--,{}cos cos ,cos sin ,0uu r R v u R v u =--,{}sin sin ,sin cos ,0uv vu r r R v u R v u ==-, {}cos cos ,cos sin ,sin vv r R v u R v u R v =---,22cos uu E r r R v =⋅=,0u v F r r =⋅=,2v v G r r R =⋅=,2cosL R v==-,0M ==,N R ==-,1(,,)(,,)L M N E F G R∴=-,故球面是全脐的. 26.证明平面是全脐的.证明 设平面的参数表示为{}(,),,0r x y x y =,则{}1,0,0x r =,{}0,1,0y r =,{}0,0,0xx r =,{}0,0,0xy r =,{}0,0,0yy r =, 1x x E r r =⋅=,0x y F r r =⋅=,1y y G r r =⋅=,0xx L r n =⋅=,0xy M r n =⋅=,0yy N r n =⋅=(,,)0(,,)L M N E F G ∴=,故平面是全脐的.27.证明曲面3x y z +=的所有点为抛物点.证明 曲面的参数表示为{}1/3(,),,()r x y x y x y =+,则{}2/3131,0,()x r x y -=+, {}2/3130,1,()y r x y -=+, {}5/3230,0,()xx r x y -=-+,{}5/3290,0,()xy r x y -=-+, {}5/3290,0,()yy r x y -=-+, {}2/32/31133(),(),1x y r r x y x y --⨯=-+-+, ||x y x y r r n r r ⨯=⨯,{}5/3290,0,()xx L r n x y n -=⋅=-+⋅,{}5/3290,0,()xy M r n x y n -=⋅=-+⋅, {}5/3290,0,()yy N r n x y n -=⋅=-+⋅ 20LN M ⇒-=, ∴曲面3x y z +=的所有点为抛物点.28.求证正螺面{}(,)cos ,sin ,r u v u v u v av =是极小曲面. 证明 {}cos ,sin ,0u r v v =,{}sin ,cos ,v r u v u v a =-, {}0,0,0uu r =,{}sin ,cos ,0uv r v v =-,{}cos ,sin ,0vv r u v u v =--,{}cos sin 0sin ,cos ,sin cos u v i j k r r v v a v a v u u v u va⨯==--, sin ,cos ,||u v u v a v a v u r r n r r -⨯==⨯, 1u u E r r =⋅=,0u v F r r =⋅=,22v v G r r a u =⋅=+, 0uu L r n =⋅=,uv M r n =⋅=,0vv N r n =⋅=,21210,22EN FM GL H EG F -+∴=⋅==-故正螺面是极小曲面. 29. 圆柱面{cos ,sin ,}r a u a u v =上的纬线是测地线. 证明 由{cos ,sin ,},r a u a u v ={sin ,cos ,0}ur -a u a u =,{0,0,1}v r =,2,0, 1.E a F G ===g d k ds θθθ=-, 纬线是u -线,此时0θπ=或, 0.g k ∴= 所以,纬线是测地线.30.证明极小曲面上的点都是双曲点或平点.证明 1202k k H +==, 12k k ∴=-, 21220K k k k ∴=⋅=-≤ 当0K =时,120k k ==, ∴极小曲面的点都是平点; 当0K <时,极小曲面的点都是双曲点.31. 证明 (1)如果测地线同时是渐近线,则它是直线;(2)如果测地线同时是曲率线,则它一定是平面曲线. 证明 (1) 因为曲线是测地线,所以0=g k , 曲线又是渐近线,所以,0=n k ,而222=+n g k k k ,所以k=0,故所给曲线是直线. (2) 证法1 因曲线是测地线,所以沿此曲线有βn ,所以βdn , 又曲线是曲率线,所以αdn dr , 所以(k )ατγα-+,所以0τ=,故所给曲线是平面曲线. 证法2 因所给曲线既是测地线又为曲率线,所以沿此曲线有,,n n βα 而γαβ=⨯,所以,n γα=±⨯从而()(0)0n n k n γααβ=±⨯+⨯=±-⨯+=, 又γτβ=-,所以0τ=,故所给曲线是平面曲线.。
微分几何试题库(解答与证明题)

1 求曲线 2(){,,}t r r t t t e ==在t=0点的密切平面和主法线。
(ZN)2 求圆柱螺线cos ,sin ,x a t y a t z t ===在点(,0,0)a 处的密切平面和主法线。
(ZN) 3求圆柱螺线cos ,sin ,x t y t z t ===在点(1,0,0)处的基本向量,,αβγ和密切平面、副法线。
(LTP 34)4 求曲线 {sin ,cos ,}t r t t t t te =在原点的切线和法平面。
(XTP 54)5 求圆柱螺线 {cos ,sin ,}r t t t = 在(0,1,)2π点的切线和法平面。
(ZN)6 设 (S)为曲线(C)的切线曲面,证明(S)沿任意一直母线l 的切平面就是(C)在切线l 的切点处的密切平面。
(KWD193)7 求圆柱螺线 (){cos ,sin ,}()r a a b θθθθθ=-∞<<+∞的曲率与挠率。
(LTP 42) 8 求曲线 (){(1sin ),(1cos ),}r t a t a t bt =--的曲率和挠率。
9 求曲线22(){,,}23t t r t t = 的曲率和挠率。
10 求圆柱螺线{cos ,sin ,}r t t t =的曲率和挠率。
11.证明曲线x=1+3t+22t ,y=2-2t+52t ,z=1-2t 为平面曲线,并求出它所在的平面方程 。
(XTP 54)12已知曲线33{cos ,sin ,cos 2}r t t t =。
求(1)基本向量,,αβγ;(2)曲率和挠率。
(XTP 54)13设曲线Γ的副法向量1{sin ,cos ,1}2t t γ=-,求它的切向量α和主法向量β,并证明它的曲率和挠率之比是常数。
(KWD92)14若曲线(C ):()r r s =的挠率τ 为非零常数,(C )的主法向量与副法向量分别为,βγ。
证明1():()C r s ds βγτ=-⎰的曲率为常数,且||k τ=,并求()C 的挠率τ.(KWD96)15 证明一空间曲线为一般螺线的充分必要条件是向量k ταγ+具有固定方向。
几何证明选讲知识点汇总与练习(内含答案)

⼏何证明选讲知识点汇总与练习(内含答案)《⼏何证明选讲》知识点归纳与练习(含答案)⼀、相似三⾓形的判定及有关性质平⾏线等分线段定理平⾏线等分线段定理:如果⼀组平⾏线在⼀条直线上截得的线段相等,那么在其他直线上截得的线段也相等。
推理1:经过三⾓形⼀边的中点与另⼀边平⾏的直线必平分第三边。
推理2:经过梯形⼀腰的中点,且与底边平⾏的直线平分另⼀腰。
平分线分线段成⽐例定理平分线分线段成⽐例定理:三条平⾏线截两条直线,所得的对应线段成⽐例。
推论:平⾏于三⾓形⼀边的直线截其他两边(或两边的延长线)所得的对应线段成⽐例。
相似三⾓形的判定及性质相似三⾓形的判定:定义:对应⾓相等,对应边成⽐例的两个三⾓形叫做相似三⾓形。
相似三⾓形对应边的⽐值叫做相似⽐(或相似系数)。
由于从定义出发判断两个三⾓形是否相似,需考虑6个元素,即三组对应⾓是否分别相等,三组对应边是否分别成⽐例,显然⽐较⿇烦。
所以我们曾经给出过如下⼏个判定两个三⾓形相似的简单⽅法:(1)两⾓对应相等,两三⾓形相似;(2)两边对应成⽐例且夹⾓相等,两三⾓形相似;(3)三边对应成⽐例,两三⾓形相似。
预备定理:平⾏于三⾓形⼀边的直线和其他两边(或两边的延长线)相交,所构成的三⾓形与三⾓形相似。
判定定理1:对于任意两个三⾓形,如果⼀个三⾓形的两个⾓与另⼀个三⾓形的两个⾓对应相等,那么这两个三⾓形相似。
简述为:两⾓对应相等,两三⾓形相似。
判定定理2:对于任意两个三⾓形,如果⼀个三⾓形的两边和另⼀个三⾓形的两边对应成⽐例,并且夹⾓相等,那么这两个三⾓形相似。
简述为:两边对应成⽐例且夹⾓相等,两三⾓形相似。
判定定理3:对于任意两个三⾓形,如果⼀个三⾓形的三条边和另⼀个三⾓形的三条边对应成⽐例,那么这两个三⾓形相似。
简述为:三边对应成⽐例,两三⾓形相似。
引理:如果⼀条直线截三⾓形的两边(或两边的延长线)所得的对应线段成⽐例,那么这条直线平⾏于三⾓形的第三边。
定理:(1)如果两个直⾓三⾓形有⼀个锐⾓对应相等,那么它们相似;(2)如果两个直⾓三⾓形的两条直⾓边对应成⽐例,那么它们相似。
中考复习初中数学几何证明经典试题(含答案)
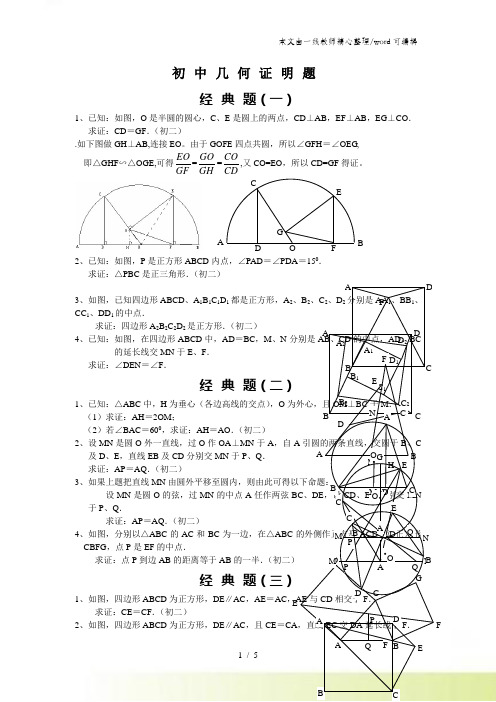
P CG FAD E初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二).如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG , 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF 得证。
2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 的延长线交MN 于E 、F .求证:∠DEN =∠F . 经典1、已知:△ABC 中,H 为垂心(各边高线的交点),O (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 设MN 是圆O 的弦,过MN 的中点A 任作两弦于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二) 经典题(三) 1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .AQ P NM · O B D AF D AFGCEBO D求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二) 4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,=AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5. 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA DPC .(初二) 经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC , 求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数. 经典题(一)1.如下图做GH ⊥AB,连接EO 。
中考数学总复习《圆的切线证明》专题训练(附带答案)

中考数学总复习《圆的切线证明》专题训练(附带答案)学校:___________班级:___________姓名:___________考号:___________⊥于点D,E是AC上一点,以BE为直径的O交1.如图,在ABC中,AB=AC,AD BC∠=︒.BC于点F,连接DE,DO,且90DOB(1)求证:AC是O的切线;(2)若1DF=,DC=3,求BE的长.、2.如图,在O中,BC为非直径弦,点D是BC的中点,CD是ABC的角平分线.∠=∠;(1)求证:ACD ABC(2)求证:AC是O的切线;(3)若1BD=,3BC=时,求弦BD与BD围城的弓形面积.是O的切线;=,且AC BD已知等腰ABC,AB=AC为直径作O交BC于点延长线于点F.是O的切线;CD=2,求O的半径.与O相离,,交O于点A是O上一点,连于点C,且PB(1)求证:PB是O的切线;(2)若25AC=,OP=5,求O的半径.6.如图,点O是ABC的边AC上一点,以点O为圆心,OA为半径作O,与BC相切于点E,连接OB,OE,O交OB于点D,连接AD并延长交CB的延长线于点F,且AOD EOD.∠=∠(1)求证:AB是O的切线;BC=,AC=8,求O的半径.(2)若107.如图,AB 是O 的直径,AC 是O 的弦.(1)尺规作图:过点C 作O 的切线,交AB 的延长线于点D (保留作图痕迹,不写作法);(2)若2BD OB ==,求AC 的长.8.如图,ABCD 的顶点,,A B C 在O 上,AC 为对角线,DC 的延长线交O 于点E ,连接,,OC OE AE .(1)求证:AE BC =;(2)若AD 是O 的切线6,40OC D =∠=︒,求CE 的长.9.如图,Rt ABC △中90C ∠=︒,点E 为AB 上一点,以AE 为直径的O 上一点D 在BC 上,且AD 平分BAC ∠.(1)证明:BC 是O 的切线;(2)若42BD BE ==,,求AB 的长.10.如图,已知O 的弦AB 等于半径,连接OA 、OB ,并延长OB 到点C ,使得BC OB =,连接AC ,过点A 作AE OB ⊥于点E ,延长AE 交O 于点D .(1)求证:AC 是O 的切线;(2)若6BC =,求AD 的长.11.如图,线段AB 经过O 的圆心.O 交O 于A ,C 两点,AD 为O 的弦,连接BD ,30A ABD ∠=∠=︒连接DO 并延长交O 于点E ,连接BE 交O 于点F .(1)求证:BD 是O 的切线;(2)若1BC =,求BF 的长.12.如图,AB 为O 的直径,C 为O 上一点,CD BD ABC CBD ⊥∠=∠.(1)求证:CD 为O 的切线.(2)当1,4BD AB ==时,求CD 的长.13.如图 已知AB 是O 的直径 BC AB ⊥于B E 是OA 上的一点ED BC ∥交O 于D OC AD ∥ 连接AC 交ED 于F .(1)求证:CD 是O 的切线;(2)若8AB = 1AE = 求ED EF 的长.14.如图 AB 是O 的直径 AC BC ,是弦 点D 在AB 的延长线上 且DCB DAC ∠=∠ O 的切线AE 与DC 的延长线交于点E .(1)求证:CD 是O 的切线;(2)若O 的半径为2 30D ∠=︒ 求AE 的长.15.如图 已知AB 是O 的直径 点P 在BA 的延长线上 弦BC 平分PBD ∠且BD PD ⊥于点D .(1)求证:PD 是O 的切线.(2)若8cm 6cm AB BD , 求弧AC 的长.为O的直径在O上连接的延长线交于E.是O的切线;∠tan BDF为O的直径的平分线交O于点E BC的延长线于点(1)求证:DE 为O 切线;(2)若10AB = 6BC = 求DE 的长.18.如图 O 是ABC 的外接圆 点D 在BC 延长线上 且满足CAD B ∠=∠.(1)求证:AD 是O 的切线;(2)若AC 是BAD ∠的平分线 3sin 5B =4BC = 求O 的半径.参考答案:1.【分析】此题重点考查圆周角定理 切线的判定定理 勾股定理 三角形的中位线定理 等腰三角形的“三线合一” 线段的垂直平分线的性质等知识 正确地作出辅助线是解题的关键.是O的切线;+=314是O的直径90︒则22BE=+4(22)⊥AD BC是O的半径是O的切线.)连接EFDC=DF33+=+BD DF∠OE DOBDE=.3是O的直径90︒.中EF=中BE=(3)23312π- 【分析】此题考查了解直角三角形 切线的判定以及扇形的面积.注意掌握辅助线的作法 .(1)点D 是BC 的中点 可以得到BD CD = 即可得到DBC DCB ∠∠= 再根据角平分线的定义得到ACD BCD ∠∠= 进而得到结论;(2)连接OC OD OB 则可得到OD BC ⊥ 然后根据等边对等角可以得到90OCD ACD ∠∠+=︒ 即可得到结论(3)先求出60ODB ∠=︒ 继而利用OBD OBD S S S=-阴影部分扇形求得答案.【详解】(1)解:如图 ∵点D 是BC 的中点∵BD CD =∵DBC DCB ∠∠=又∵CD 是ABC 的角平分线∵ACD BCD ∠∠=∵ACD ABC ∠∠=;(2)证明:如图 连接OC OD OB∵点D 是BC 的中点∵OD BC ⊥∵90ODC BCD ∠∠+=︒∵OD OC =∵ODC OCD ∠∠=又∵ACD BCD ∠∠=∵90OCD ACD ∠∠+=︒即OC AC ⊥∵OC 是O 的半径∵AC 是O 的切线;Rt BDE 中 ODB ∠=60ODB =︒OB OD =∵OBD 是等边三角形BOD ∠=OBD S S==阴影部分.(1)见解析(2)23进而得出BFG 是等边三角形 是O 的切线;)解:如图所示∵OD AC ⊥∵AD CD =∵BD AC =∵BD AC =∵AD BC =∵AD CD BC ==;∵AB 为半圆O 的直径∵90CAB CBA ∠+∠=︒∵30DAC CAB ABD ∠=∠=∠=︒∵60GBF G ∠=∠=︒ 12GB AG =∵BFG 是等边三角形 223AB AG BG BG =-=∵3233BF BG AB ===. 【点睛】本题考查了切线的判定 弧与弦的关系 直径所对的圆周角是直角 勾股定理 等边三角形的性质与判定 垂径定理 熟练掌握以上知识是解题的关键.4.(1)证明(2)233【分析】本题主要考查切线的性质和判定及特殊角的三角函数的应用 掌握切线问题中的辅助线的作法是解题的关键.(1)连接OD 证明ODB C ∠=∠ 推出AC OD ∥ 即可证明结论成立;(2)连接AD 在Rt CED 中 求得利用三角形函数的定义求得30C ∠=︒ 60AOD ∠=︒ 在Rt ADB 中 利用勾股定理列式计算求得圆的半径即可.【详解】(1)证明:连接OD又OB OD=B ODB∴∠=∠ODB∴∠=∠AC OD∥DF AC⊥OD DF∴⊥DF∴是O的切线;(2)连接AD设O半径为Rt CED中3,CE CD=22ED CD∴=-又cosCE CCD ∠=30C∴∠=︒30B∴∠=︒60AOD=∠AB是O的直径.90ADB∴∠=︒12AD AB r ∴== ∵AB AC =∵2CD BD ==又222AD BD AB +=2222(2)r r ∴+=233r ∴=(负值已舍). 5.(1)证明见解析(2)3【分析】本题考查的是勾股定理的应用 等腰三角形的性质 切线的判定 熟练的证明圆的切线是解本题的关键;(1)连接OB 证明PCB PBC ∠=∠ OAB OBA ∠=∠ 再证明90PBC OBA ∠+∠=︒即可;(2)设O 的半径为r 表示()()22222255PC AC AP r =-=-- 222225PB OP OB r =-=- 再利用PB PC =建立方程求解即可.【详解】(1)解:连接OB∵PB PC = OA OB =∵PCB PBC ∠=∠ OAB OBA ∠=∠∵OP l ⊥ OAB PAC ∠=∠∵90BCP CAP BCP OAB ∠+∠=︒=∠+∠∵90PBC OBA ∠+∠=︒∵90OBP ∠=︒∵OB PB ⊥是O 的切线;)设O 的半径为l 2AC =2AC AP =-PB BP 2OP OB =-∵O 的半径为【点睛】.(1)见解析(2)3【分析】本题主要考查切线的判定和性质证AOB EOB ≌ 得出的半径为r 则OE OA =根据AOB EOB ≌得求得4CE = 在Rt OCE 中运用勾股定理列式求出r 的值即可. )证明:在AOB 和EOB 中∵()SAS AOB EOB ≌OAF OEF ∠=∠BC 与O 相切OE BC ⊥90OAB OEB ∠=∠=︒AF是O 的半径是O 的切线;(2)解:在Rt CAB △中 90108CAB BC AC ∠=︒==,,∵22221086AB BC AC =-=-=设圆O 的半径为r 则,OE OA r ==∵8OC r =-∵,AOB EOB ≌∵6BE AB ==∵10,BC =∵1064,CE BC BE =-=-=在Rt OCE 中 222OE CE OC +=∵()22248r r +=-解得3r =.∵O 的半径为3.7.(1)作图见解析(2)4π3【分析】本题考查了作图 复杂作图 切线的性质 等边三角形的判定与性质 弧长的计算 熟练掌握切线的性质 弧长公式是解答本题的关键.(1)根据题意 连接OC 作OC CD ⊥ 交AB 的延长线于点D 由此得到答案. (2)根据题意 得到OBC △是等边三角形 求出120AOC ∠=︒ 再利用弧长公式 得到答案.【详解】(1)解:如图所示 CD 即为所求.(2)如图所示 连接BCBD)证明:在ABCD中AE AD ∴=∵AE BC =.(2)解:连接OA 过点O 作OF CE ⊥于点F 如图所示:AD 是O 的切线OA AD ∴⊥OA BC ∴⊥AB AC ∴=40AEC B D ︒∠=∠=∠=40ACB B ∴∠=∠=︒在ABCD 中 AD BC ∥40DAC ACB ∴∠=∠=︒又180100DAE D AEC ∠=︒-∠-∠=︒60CAE DAE CAD ∴∠=∠-∠=︒2120COE CAE ∴∠=∠=︒OC OE =30OCE ∴∠=︒OF CE ⊥22cos3063CE CF OC ∴==⋅︒=.【点睛】本题主要考查了切线的性质 解直角三角形 圆周角定理 平行四边形的性质垂径定理 等腰三角形的判定 解题的关键是作出辅助线 熟练掌握相关的判定和性质.9.(1)证明详见解析;(2)8.【分析】本题考查了切线的判定 勾股定理等知识 熟练掌握切线的判定定理 勾股定理是解题的关键.(1)连接OD 根据平行线判定推出OD AC ∥ 推出OD BC ⊥ 根据切线的判定推出即可;(2)根据勾股定理求出3OD OA OE === 再根据线段的和差求解即可.【详解】(1)证明:连接OD∵OA OD =∵OAD ODA ∠=∠∵AD 平分BAC ∠∵BAD CAD ∠=∠∵ODA CAD ∠=∠∵OD AC ∥∵180C ODC ∠+∠=︒∵90C ∠=︒∵90ODC ∠=︒∵OD BC ⊥∵OD 为半径∵BC 是O 的切线;(2)解:设OD OE r ==在Rt ODB △中 42BD BE ==,∵2OB r =+由勾股定理 得:()22242r r +=+ 解得:3r =∵3OD OA OE ===∵628AB =+=.10.(1)证明见解析;(2)63.【分析】(1)先证明OAB 是等边三角形 再由性质得出60AOB OAB OBA ∠=∠=∠=︒ 再由BC AB =和角度和差即可求解;(2)先根据等边三角形性质求出132OE OA == 再根据勾股定理求得33AE = 最后由垂径定理即可求解;此题考查了等边三角形的判定与性质 勾股定理和垂径定理 解题的关键是熟练掌握以上知识点的应用.【详解】(1)证明:∵AB OA OB ==∵OAB 是等边三角形∵60AOB OAB OBA ∠=∠=∠=︒∵BC OB =∵BC AB =∵1302BAC BCA OBA ∠=∠=∠=︒ ∵90OAC OAB BAC ∠=∠+∠=︒又∵OA 为O 的半径∵AC 是O 的切线;(2)解:∵6BC =∵6AB OA OB ===∵AD OB ⊥于点E∵30OAE ∠=︒∵132OE OA == ∵2233AE OA OE =-=∵AE OB ⊥∵263AD AE ==.11.(1)见解析∠=)证明:BAD60︒6090︒-︒=OD是O的半径∴直线BD是O的切线;==(2)解:设OD OC△中sin30在Rt BDO解得:1r==+OB OCDE是O的直径∴∠=︒DFE90∠=∠即DFB BDE∠=∠DBF DBE∴△∵BDEBFD△BF BD∴=BD BE337BF ∴= 解得:377BF =. 【点睛】本题考查了切线的判定和性质 相似三角形的性质和判定 圆周角定理 勾股定理等知识点 作出辅助线构造出相似三角形是解题关键.12.(1)见详解(2)3【分析】(1)连接OC 由∠=∠OCB ABC ABC CBD ∠=∠ 得OCB CBD ∠=∠ 则OC BD ∥ 所以18090OCD D ∠=︒-∠=︒ 即可证明CD 为O 的切线;(2)由AB 为的直径 得90ACB ∠=︒ 则ACB D ∠=∠ 而ABC CBD ∠=∠ 所以C ABC BD ∽△△ 则AB CB CB BD = 可求得CB BD AB =⋅ 由勾股定理得22CD CB BD =-.【详解】(1)证明:连接OC 则OC OB =OCB ABC ∴∠=∠ABC CBD ∠=∠OCB CBD ∴∠=∠OC BD ∴∥CD BD ⊥90D ∴∠=︒18090OCD D ∴∠=︒-∠=︒OC 是O 的半径 且CD OC ⊥CD ∴为O 的切线.(2)解:AB 为的直径ABC∠=ABC CBD ∴∽∴AB CBCB BD=1,4BD AB==1 CB BD AB∴=⋅=22CD CB BD∴=-=CD∴的长是【点睛】此题重点考查等腰三角形的性质AD OC∥ADO∴∠OA OD=ADO DAO ∴∠=∠DOC BOC ∴∠=∠OD OB OC OC ==,ODC OBC ∴≌△△∴OBC ODC ∠=∠BC AB ⊥∴90OBC ODC ∠=∠=︒OD 为经过圆心的半径∴CD 是O 的切线;(2)如图所示:作DM BC ⊥交BC 于点M8AB = 1AE =1432OA OB OD AB OE OA AE ∴=====-=, 227DE BM OD OE ==-=令=7CM x CB CD x ==+, 7BE DM ==∴在222Rt DMC CM DM CD +=△,222(7)7x x ∴+=+解得:37x =47BC ∴=DE BC ∥ADE ABC ∴△△∽是O的切线.2)在Rt△是O的切线得出Rt EAD中【详解】(1)证明:连接.是O的直径+∠OCA OCBDCB OCB+∠OCD=︒.90是半径经过O的半径外端∵CD 是O 的切线.(2)解:在Rt OCD △中∵90OCD ∠=︒ 30D ∠=︒ 2OC =∵4OD =.∵6AD AO OD =+=.∵AE 是O 的切线 切点为A∵OA AE ⊥.在Rt EAD 中∵90EAD ∠=︒ 30D ∠=︒ 6AD =∵3tan 306233AE AD =⋅︒=⨯=. 15.(1)见解析(2)4π3【分析】本题考查圆与三角形的综合问题 掌握与圆有关的性质 正确作出辅助线是关键.(1)连接OC 根据条件证明OC BD ∥ 即可证明;(2)根据PCO PDB ∽可得PA 利用余弦值可求出COP ∠ 通过弧长公式求解即可.【详解】(1)证明:连接OC 如图∵OC OB =∵OCB OBC ∠=∠∵弦BC 平分PBD ∠∵DBC OBC ∠=∠∵OCB DBC ∠=∠.∵OC BD ∥∵BD PD ⊥∵OC PD ⊥.为O 的半径是O 的切线;)解:连接OC∵PCO PDB ∽OC PO BD PB= 8cm AB = BD =14cm 2OC AB ==4468PA PA +=+ Rt OCP 中cos COP ∠=60COP =︒AC 的长=(1)证明见解析; 是O 的切线;证明FBD FDA ∽ 得到1tan tan 4BD A BDF AD ∠=∠== 进而得到164DF = 即可求解; 本题考查了切线的判定 相似三角形的判定与性质 等腰三角形的性质 余角性质 根据题意 正确作出辅助线是解题的关键.【详解】(1)证明:连结OD∵CO AB ⊥∵90E C ∠+∠=︒∵FE FD = OD OC =∵E FDE ∠=∠ ∠=∠C ODC∵90FDE ODC ∠+∠=︒∵90ODF ∠=︒∵OD DF ⊥∵FD 是O 的切线;(2)解:连结AD ,OD BD 如图∵AB 为O 的直径∵90ADB ∠=︒∵90∠+∠=︒A ABD∵OB OD =∵OBD ODB ∠=∠∵90A ODB ∠+∠=︒∵FBD FDA ∽DF BD AF AD= 在Rt △ABD 中 tan ∠164DF = 3DF =的平分线交O 于点E∵ED OE ⊥∵DE 为O 切线.(2)过点O 作OM BC ⊥于点M 10AB = 6BC =则132MC MB BC ===,152OB OE AB === 四边形OEDM 时矩形∵DE OM =根据勾股定理 得224DE OM OB BM ==-=.18.(1)见解析(2)103【分析】(1)连接OA OC 与AB 相交于点E 如图 由OA OC = 可得OAC OCA ∠=∠ 根据圆周角定理可得12B AOC ∠=∠ 由已知CAD B ∠=∠ 可得2AOC CAD ∠=∠ 根据三角形内角和定理可得180OCA CAO AOC ∠+∠+∠=︒ 等量代换可得90CAO CAD ∠+∠=︒ 即可得出答案;(2)根据角平分线的定义可得BAC DAC ∠=∠ 由已知可得BAC B =∠∠ 根据垂径定理可得 OC AB ⊥ BE AE = 在Rt BEC △中 根据正弦定理可得3sin 45CE CE B BC === 即可算出CE 的长度 根据勾股定理可算出22BE BC CE =-的长度 设O 的半径为r 则125OE OC CE r =-=- 在Rt AOE △中 222OA OE AE =+ 代入计算即可得出答案. 【详解】(1)证明:连接OA OC 与AB 相交于点E 如图OA OC =OAC ∴∠AC AC =∴12B ∠=CAD ∠=AOC ∴∠=OCA ∠+2CAO ∴∠+CAO ∴∠+OAD ∴∠OA 是O 的半径AD ∴是O 的切线;(2)解:AC 是∠BAC DAC ∴∠=∠CAD B ∠=∠BAC B ∴∠=∠OC AB ∴⊥ BE =在Rt BEC △中4BC =sin CE B BC ∴=125CE ∴=BE BC ∴=设O 的半径为r ,则125OE OC CE r =-=-在Rt AOE △中222OA OE AE =+ 222121655r r ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭ 解得:103r =. 【点睛】本题主要考查了切线的性质与判定,垂径定理,勾股定理及解直角三角形, 熟练掌握切线的性质与判定,垂径定理及解直角三角形的方法进行求解是解决本题的关键.。
空间解析几何例题

第4章 向量代数与空间解析几何习题解答习题4.1一、计算题与证明题1.已知1||=a , 4||=b , 5||=c , 并且0=++c b a . 计算a c c b b a ⨯+⨯+⨯. 解:因为1||=a , 4||=b , 5||=c , 并且0=++c b a 所以a 与b 同向,且b a +与c 反向 因此0=⨯b a ,0=⨯c b ,0=⨯a c 所以0=⨯+⨯+⨯a c c b b a2.已知3||=⋅b a , 4||=⨯b a , 求||||b a ⋅. 解:3cos ||=⋅=⋅θb a b a (1)4sin ||=⋅=⨯θb a b a (2)()222)1(+得()252=⋅b a所以 5=⋅b a3.设力k j i F 532++-=作用在点)1,6,3(A , 求力F 对点)2,7,1(,-B 的力矩的大小. 解:因为()1,6,3A ,()2,7,1-B 所以()31,2--=AB力矩()()k j i k j i F AB M 53232++-⨯-+-=⨯=kj i kj i kj i 41614321252325331532312-+=--+-----=---=所以,力矩的大小为()13641614222=-++=M4.已知向量x 与)2,5,1(,-a 共线, 且满足3=⋅x a ρρ, 求向量x 的坐标. 解:设x 的坐标为()z y x ,,,又()2,5,1-=a则325=-+=⋅z y x x a (1)又x 与a 共线,则0=⨯a x 即()()()05252512125251=-+++--=+---=-k y x j x z i z y ky x j y x i z y z yx kj i所以()()()05252222=-+++--y x x z z y即010*********22=-++++xy xz yz z y x (2) 又x 与a 共线,x 与a 夹角为0或π()30325110cos 222222222⋅++=-++⋅++⋅==z y x z y x ax整理得 103222=++z y x (3) 联立()()()321、、解出向量x 的坐标为⎪⎭⎫⎝⎛-51,21,101 5.用向量方法证明, 若一个四边形的对角线互相平分, 则该四边形为平行四边形.证明:如图所示,因为平行四边形ABCD 的对角线 互相平分,则有MA CN ND BM ==,由矢量合成的三角形法则有MA BM BA +=MA BM BM MA MD CM CD +=+=+=所以CD BA =即BA 平行且等于CD四边形ABCD 是平行四边形6.已知点)7,8,3(A , )3,2,1(--B 求线段AB 的中垂面的方程. 解:因为()7,8,3A ,)3,2,1(--BAB 中垂面上的点到B A 、的距离相等,设动点坐标为()z y x M ,,,则由MB MA =得()()()()()()222222321783++-++=-+-+-z y x z y x化简得027532=-++z y x这就是线段AB 的中垂面的方程。
2019年中考数学二轮复习专题练【几何图形的证明及计算问题】附答案解析

2019年中考数学二轮复习专题练【几何图形的证明及计算问题】附答案解析类型一与全等三角形有关的证明及计算1.如图,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,点M为BC中点,N为线段AM 上的点,且MB=MN.(1)求证:BN平分∠ABE;(2)若BD=1,连接DN,当四边形DNBC为平行四边形时,求线段BC的长;第1题图2.如图①,在等腰三角形ABC中,AB=AC,在底边BC上取一点D,在边AC上取一点E,使AE=AD,连接DE,在∠ABD的内部作∠ABF=2∠EDC,交AD于点F.(1)求证:△ABF是等腰三角形;(2)如图②,BF的延长线交AC于点G.若∠DAC=∠CBG,延长AC至点M,使GM=AB,连接BM,点N是BG的中点,连接AN,试判断线段AN、BM之间的数量关系,并证明你的结论.第2题图3.如图①,在△ABC中,∠ACB=90°,AC=BC,E为AC边上的一点,F为AB边上一点,连接CF,交BE于点D,且∠ACF=∠CBE,CG平分∠ACB交BD于点G.(1)求证:CF=BG;(2)如图②,延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB =CP+CF;(3)在(2)问的条件下,当∠GAC=2∠FCH时,若S△AEG=33,BG=6,求AC的长.图①图②第3题图4.如图①,在Rt△ABC中,AC=BC,∠ACB=90°,点D,E分别在AC,BC上,且CD=CE.(1)求证:∠CAE=∠CBD;(2)如图②,F是BD的中点,连接CF交AE于点M,求证:AE⊥CF;(3)如图③,F,G分别是BD,AE的中点,连接GF,若AC=2 2 ,CE=1,求△CGF的面积.第4题图5.如图①,在正方形ABCD中,O是对角线AC上一点,点E在BC的延长线上,且OE=OB,OE交CD于点F.(1)求证:△OBC≌△ODC;(2)求证:∠DOE=∠ABC;(3)把正方形ABCD改为菱形,其他条件不变(如图②),若∠ABC=52°,求∠DOE的度数.第5题图6.已知:如图①,等腰直角△ABC和△ECD中,∠ACB=∠ECD=90°,AC=BC,EC=DC.(1)求证:BE=AD;(2)如图②,若将△ECD绕点C按逆时针方向旋转一个锐角,①延长BE交AD于点F,交AC于点O.求证:BF⊥AD;②如图③,取BE的中点M,AD的中点N,连接MN,NC,求∠MNC的度数.第6题图类型二与相似三角形有关的证明及计算1.如图①,已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的点,过点Q作AC的垂线交线段AB(如图①)或线段AB的延长线(如图②)于点P.(1)当点P在线段AB上时,求证:△AQP∽△ABC;(2)当△PQB为等腰三角形时,求AP的长.第1题图2. 如图,在四边形ABCD 中,AC 平分∠DAB ,∠ADC =∠ACB =90°,E 为AB 的中点,连接DE 、CE .(1)求证:AC 2=AB ·AD ; (2)求证:CE ∥AD ;(3)若AD =5,AB =7,求ACAF 的值.第2题图3. 如图①,在△ABC 中,AB =AC ,点D 、E 、F 分别在BC 、AB 、AC 上,∠EDF =∠B. (1)求证:DE ·CD =DF ·BE ;(2)如图②,若D 为BC 中点,连接EF ,A D. ①求证:DE 平分∠BEF ;②若四边形AEDF 为菱形,求∠BAC 的度数及AEAB 的值.第3题图4. 如图①,△ABC 中,点D 在线段AB 上,点E 在线段CB 延长线上,且BE =CD ,EP ∥AC 交直线CD 的延长线于点P ,交直线AB 的延长线于点F ,∠ADP =∠AC B.(1)图①中是否存在与AC 相等的线段?若存在,请找出,并加以证明,若不存在,说明理由; (2)若将“点D 在线段AB 上,点E 在线段CB 延长线上”改为“点D 在线段BA 延长线上,点E 在线段BC 延长线上”,其他条件不变(如图②).当∠ABC =90°,∠BAC =60°,AB =2时,求线段PE 的长.第4题图5. 如图①,△ABC 中,BC >AC ,CD 平分∠ACB 交AB 于D ,E ,F 分别是AC ,BC 边上的两点,EF 交CD 于H .(1)若∠EFC =∠A ,求证:CE ·CD =CH ·BC ;(2)如图②,若BH 平分∠ABC ,CE =CF ,BF =3,AE =2,求EF 的长;(3)如图③,若CE ≠CF ,∠CEF =∠B ,∠ACB =60°,CH =5,CE =4 3 ,求 AC BC 的值.第5题图类型三与全等和相似三角形有关的证明及计算1.如图,等边△ABC边长是8,过点C的直线l∥AB,点D为BC上一点(不与点B,C重合),将一个60°角的顶点放在D处,它的边始终过点A,另一边与直线l交于点E,DE交AC于点F.(1)若BD=6,求CF的长;(2)若点D是BC的中点,判定△ADE的形状,并给出证明;(3)若点D不是BC的中点,则(2)中的结论成立吗?如果成立,请给予证明,如果不成立,请说明理由.第1题图2.如图①,在△ABC中,AC=BC,∠ACB=90°,点D、P分别为AC、AB的中点,连接BD、CP,CP交BD于点E,点F在AB上且∠ACF=∠CB D.(1)求证:CF=BE;(2)如图②,过点A 作AG ⊥AB 交BD 的延长线于点G . ①若CF =6,求DG 的长; ②设CF 交BD 于点H ,求HECH 的值.第2题图3. 如图①,已知D 是△ABC 的边BC 上的中点,DE ⊥AB 于点E ,DF ⊥AC 于点F ,且BE =CF ,点M 、N 分别是AE 、DE 上的点,AN ⊥FM 于点G .(1)若∠BAC =90°,求证:△ABC 为等腰直角三角形; (2)如图②,若∠BAC ≠90°,AF =2DF . ①求证:FM AN =EM DN ; ②求AN ∶FM 的值.图① 图②第3题图4. (2018六安市模拟)我们知道,三角形三个内角平分线的交点叫做三角形的内心,已知点I 为△ABC 的内心.(1)如图①,连接AI 并延长交BC 于点D ,若AB =AC =3,BC =2,求ID 的长; (2)如图②,过点I 作直线交AB 于点M ,交AC 于点N . ①若MN ⊥AI ,求证:MI 2=BM ·CN ;②如图③,AI 的延长线交BC 于点D ,若∠BAC =60°,AI =4,求1AM +AN1的值.第4题图5. 如图①,在△ABC 中,∠ACB =90°,AC =BC ,顶点C 恰好在直线l 上,过A 、B 分别作AD ⊥l ,BE ⊥l ,垂足分别为D 、E .(1)求证:DE=AD+BE;(2)如图②,在△ABC中,当AC=kBC,其他条件不变,猜想DE与AD、BE的关系,并证明你的结论;(3)如图③,在Rt△ABC中,AC=4,BC=12,∠ACB=90°,点D是AC的中点,点E在BC上,过点E作EF⊥DE交AB于点F,若恰好EF=2DE,求CE的长.图①图②图③第5题图6.如图①,在等腰Rt△ABC中,∠ACB=90°,AC=BC, D为AB的中点,连接CD,将一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF 与AC交于点M,DE与BC交于点N.(1)若CE=CF,求证:△DCE≌△DCF;(2)如图②,在∠EDF绕点D旋转的过程中:①探究线段AB与CE、CF之间的数量关系,并证明;②若AB=42,CE=2CF,求DN的长.第6题图类型一 与全等三角形有关的证明及计算1. (1)证明:∵AB =AC ,点M 是BC 的中点,∴AM ⊥BC ,∠BAM =∠CAM , ∴∠CAM +∠ACM =90°, ∵AC ⊥BD ,∴∠MBE +∠ACM =90°, ∴∠BAN =∠CAM =∠MBE , ∵MB =MN , ∴∠MNB =∠MBN ,∵∠MNB =∠ABN +∠BAN ,∠MBN =∠MBE +∠NBE , ∴∠ABN +∠BAN =∠MBE +∠NBE , ∴∠ABN =∠NBE , 即BN 平分∠ABE ;(2)解:连接DN ,∵点M 为BC 中点,MB =MN , ∴MB =MN =12BC ,∵四边形DNBC 为平行四边形, ∴BN =CD ,BN ∥CD , ∴∠DBN =∠BDC , 由(1)知∠ABN =∠DBN , ∴∠ABN =∠BDC , ∵AB =BD =1, ∴△ABN ≌△BDC , ∴AN =BC ,∴AM =AN +MN =32BC ,参考答案由(1)中条件可知AM ⊥BC ,即∠AMB =90°, ∴AM 2+MB 2=AB 2,即(32BC )2+(12BC )2=1,解得BC =105.第1题解图2. (1)证明:∵等腰三角形ABC 中,AB =AC ,∴∠ABD =∠ACD , ∵AE =AD , ∴∠ADE =∠AED ,∵∠BAD +∠ABD =∠ADE +∠EDC ,∠EDC +∠ACD =∠AED , ∴∠BAD =2∠EDC , ∵∠ABF =2∠EDC , ∴∠BAD =∠ABF , ∴△ABF 是等腰三角形; (2)解:AN =12BM .证明:如解图,延长CA 至点H ,使AG =AH ,连接BH , ∵点N 是BG 的中点,点A 是HG 的中点, ∴AN =12BH ,∵(1)中已证明∠BAD =∠ABF ,且∠DAC =∠CBG , ∴∠CAB =∠CBA , ∴CA =CB 又∵AB =AC ,∴△ABC 是等边三角形,∠BAC =∠BCA =60°, ∴∠BAH =∠BCM , ∵GM =AB ,AB =AC , ∴AC =GM , ∴CM =AG , ∴AH =CM ,在△BAH 和△BCM 中,⎩⎨⎧AB =BC∠BAH =∠BCM AH =CM, ∴△BAH ≌△BCM (SAS), ∴BH =BM , ∴AN =12BM .第2题解图3. (1)证明:∵∠ACB =90°,AC =BC ,∴∠A =45°, ∵CG 平分∠ACB , ∴∠ACG =∠BCG =45°, ∴∠A =∠BCG , 在△BCG 和△CAF 中,⎩⎨⎧∠A =∠BCGAC =BC∠ACF =∠CBE,∴△BCG ≌△CAF (ASA), ∴CF =BG ;(2)证明:∵PC ∥AG , ∴∠PCA =∠CAG ,∵AC =BC ,∠ACG =∠BCG ,CG =CG , ∴△ACG ≌△BCG (SAS ), ∴∠CAG =∠CBE ,∵∠PCG =∠PCA +∠ACG =∠CAG +45°=∠CBE +45°,∠PGC =∠GCB +∠CBE =∠CBE +45°, ∴∠PCG =∠PGC , ∴PC =PG ,∵PB =BG +PG ,BG =CF , ∴PB =CP +CF ;(3)解:如解图,过E 作EM ⊥AG ,交AG 于M , ∵S △AEG =12AG ·EM =33, 由(2)得:△ACG ≌△BCG , ∴BG =AG =6, ∴ 12×6×EM =33, 解得EM =3,设∠FCH =x °,则∠GAC =2x °, ∴∠ACF =∠EBC =∠GAC =2x °, ∵∠ACH =45°, ∴2x +x =45, 解得x =15,∴∠ACF =∠GAC =30°,在Rt △AEM 中,AE =2EM =23, AM =(23)2-(3)2=3, ∴M 是AG 的中点,第3题解图∴AE =EG =23, ∴BE =BG +EG =6+23, 在Rt △ECB 中,∠EBC =30°, ∴CE =12BE =3+3,∴AC =AE +EC =23+3+3=33+3. 4. (1)证明:在△ACE 和△BCD 中,⎩⎨⎧AC =BC∠ACE =∠BCD CE =CD, ∴△ACE ≌△BCD , ∴∠CAE =∠CBD ;(2)证明:在Rt △BCD 中,点F 是BD 的中点, ∴CF =BF , ∴∠BCF =∠CBF , 由(1)知,∠CAE =∠CBD , ∴∠BCF =∠CAE ,∴∠CAE +∠ACF =∠BCF +∠ACF =∠BCA =90°, ∴∠AMC =90°, ∴AE ⊥CF ;(3)解:∵AC =2 2 , ∴BC =AC =2 2 , ∵CE =1, ∴CD =CE =1,在Rt △BCD 中,根据勾股定理得,BD =CD 2+BC 2=3 , ∵点F 是BD 中点, ∴CF =DF =12BD =32 ,同理:EG =12AE =32 ,如解图,连接EF ,过点F 作FH ⊥BC 于点H , ∵∠ACB =90°,点F 是BD 的中点, ∴FH =12CD =12,∴S △CEF =12CE ·FH =12×1×12=14, 由(2)知,AE ⊥CF ,∴S △CEF =12CF ·ME =12×32ME =34ME , ∴ 34ME =14,∴ME =13 ,∴GM =EG -ME =32-13=76 ,∴S △CFG =12CF ·GM =12×32×76=78. 5. (1)证明:∵AC 是正方形ABCD 的对角线,∴BC =DC ,∠BCA =∠DCA , 在△OBC 和△ODC 中,⎩⎨⎧BC =DC∠BCO =∠DCO CO =CO, ∴△OBC ≌△ODC (SAS);(2)证明:由(1)知,△OBC ≌△ODC , ∴∠CBO =∠CDO , ∵OE =OB , ∴∠CBO =∠E , ∴∠CDO =∠E , ∵∠DFO =∠EFC ,∴180°-∠DFO -∠CDO =180°-∠EFC -∠E ,即∠DOE =∠DCE ,第4题解图∵AB ∥CD , ∴∠DCE =∠ABC , ∴∠DOE =∠ABC ;(3)解:∵AC 是菱形ABCD 的对角线, ∴BC =DC ,∠BCA =∠DCA , 在△BCO 和△DCO 中,⎩⎨⎧BC =DC∠BCO =∠DCO CO =CO, ∴△BCO ≌△DCO (SAS), ∴∠CBO =∠CDO , ∵OE =OB , ∴∠CBO =∠E , ∴∠CDO =∠E , ∵∠DFO =∠EFC ,∴180°-∠DFO -∠CDO =180°-∠EFC -∠E , 即∠DOE =∠DCE , ∵AB ∥CD , ∴∠DCE =∠ABC , ∴∠DOE =∠ABC =52°. 6. (1)证明:在△BEC 和△ACD 中,⎩⎨⎧BC =AC∠ACB =∠ECD EC =DC, ∴△BEC ≌△ADC (SAS), ∴BE =AD ;(2)①证明:∵∠ACB =∠ECD =90°, ∴∠ACB -∠ACE =∠ECD -∠ACE , 即∠BCE =∠ACD ,在△BEC 和△ADC 中,⎩⎨⎧BC =AC∠BCE =∠ACD EC =DC, ∴△BEC ≌△ADC (SAS), ∴∠CBE =∠CAD ,在△BCO 和△AFO 中,∠CBE =∠CAD ,∠BOC =∠AOF , ∴∠AFB =∠ACB =90°, ∴BF ⊥AD ;②解:如解图,连接MC , ∵∠ACB =∠ECD =90°, ∴∠BCE =∠ACD , 又∵AC =BC ,EC =DC , ∴△BEC ≌△ADC ,∴∠CBE =∠CAD ,AD =BE , ∵M 是BE 的中点,N 是AD 的中点, ∴BM =AN ,在△BMC 和△ANC 中,⎩⎨⎧BM =AN∠CBE =∠CAD BC =AC, ∴△BMC ≌△ANC (SAS), ∴CM =CN ,∠BCM =∠ACN , ∴∠ACN +∠MCA =∠BCM +∠MCA , ∴∠MCN =∠ACB =90°, ∴△MCN 是等腰直角三角形, ∴∠MNC =45°.第6题解图类型二 与相似三角形有关的证明及计算1. (1)证明:∵PQ ⊥AQ ,∴∠AQP =90°=∠ABC . 在△AQP 与△ABC 中, ∵∠AQP =∠ABC , ∠QAP =∠BAC , ∴△AQP ∽△ABC ;(2)解:在Rt △ABC 中,AB =3,BC =4,由勾股定理得AC =5. ①当点P 在线段AB 上时,如题图①所示. ∵∠QPB 为钝角,∴当△PQB 为等腰三角形时,只可能是PB =PQ , 由(1)可知,△AQP ∽△ABC , ∴P A AC =PQBC ,即3-PB 5=BP 4, 解得PB =43,∴AP =AB -PB =3-43=53;②当点P 在线段AB 的延长线上时,如题图②所示. ∵∠QBP 为钝角,∴当△PQB 为等腰三角形时,只可能是PB =BQ . ∴∠BQP =∠P ,∵∠BQP +∠AQB =90°,∠A +∠P =90°, ∴∠AQB =∠A ,∴BQ =AB , ∴AB =BP ,∴AP =2AB =2×3=6.综上所述,当△PQB 为等腰三角形时,AP 的长为53或6. 2. (1)证明:∵AC 平分∠DAB ,∴∠DAC =∠CAB .又∵∠ADC =∠ACB =90°, ∴△ADC ∽△ACB , ∴AD AC =AC AB , ∴AC 2=AB ·AD ;(2)证明:∵E 为AB 的中点, ∠ACB =90°, ∴CE =12AB =AE , ∴∠EAC =∠ECA , ∵∠DAC =∠CAB , ∴∠DAC =∠ECA . ∴AD ∥CE ; (3)解:∵CE ∥AD , ∴∠DAF =∠ECF , 又∵∠DF A =∠EFC , ∴△AFD ∽△CFE , ∴AD CE =AF CF , ∵CE =12AB , ∴CE =12×7=72, ∵AD =5,∴572=AFCF,∴CFAF=710,∴AF+CFAF=1+CFAF=1710,即ACAF=1710.3. (1)证明:∵△ABC中,AB=AC,∴∠B=∠C,∵∠B+∠BDE+∠DEB=180°,∠BDE+∠EDF+∠FDC=180°,∠EDF=∠B,∴∠FDC=∠DEB,∴△CFD∽△BDE,∴DEDF=BECD,即DE·CD=DF·BE;(2)①证明:由(1)证得△BDE∽△CFD,∴BECD=DEDF,∵D为BC中点,∴BD=CD,∴BEBD=DEDF,∵∠B=∠EDF,∴△BDE∽△DFE,∴∠BED=∠DEF,∴ED平分∠BEF;②解:∵四边形AEDF为菱形,∴∠AEF=∠DEF,由(2)知,∠BED=∠DEF,∵∠AEF+∠DEF+∠BED=180°,∴∠AEF =60°,∵AE =AF ,∴∠BAC =60°.∵AB =AC ,∴△ABC 是等边三角形,∴∠B =60°,又∵∠BED =∠AEF =60°,∴△BED 是等边三角形,∴BE =DE ,∵AE =DE ,∴AE =BE =12AB ,∴AE AB =12.4. 解:(1)AC =BF .证明如下:∵∠ADP =∠ACD +∠A ,∠ACB =∠ACD +∠BCD ,∠ADP =∠ACB ,∴∠BCD =∠A ,又∵∠CBD =∠ABC ,∴△CBD ∽△ABC ,∴ CD AC =BC BA ,①∵FE ∥AC ,∴∠CAB =∠EFB ,又∵∠ABC =∠FBE ,∴△ABC ∽△FBE ,∴ BC BA =BE BF ,②由①②可得CD AC =BE BF ,∵BE =CD ,∴BF =AC ;(2)∵∠ABC =90°,∠BAC =60°,∴∠ACB =30°=∠ADP ,∴∠BCD =60°,∠ACD =60°-30°=30°,∵PE ∥AC ,∴∠E =∠ACB =30°,∠CPE =∠ACD =30°,∴CP =CE ,∵BE =CD ,∴BE -CE =CD -CP ,∴BC =DP ,∵∠ABC =90°,∠D =30°,∴BC =12CD ,∴DP =12CD ,即P 为CD 的中点,又∵PF ∥AC ,∴F 是AD 的中点,∴FP 是△ADC 的中位线,∴FP =12 AC ,∵∠ABC =90°,∠ACB =30°,∴AB =12AC ,∴FP =AB =2,∵DP =CP =BC ,CP =CE ,∴BC =CE ,即C 为BE 的中点,又∵EF ∥AC ,∴A 为FB 的中点,∴AC 是△BEF 的中位线,∴EF =2AC =4AB =8,∴PE =EF -FP =8-2=6.5. (1)证明:∵∠EFC +∠FEC +∠ECF =180°,∠A +∠B +∠ACB =180°,又∵∠EFC =∠A ,∠ECF =∠ACB ,∴∠CEF =∠B ,∵∠ECH =∠DCB ,∴△ECH ∽△BCD ,∴EC BC =CH CD ,∴CE ·CD =CH ·BC ;(2)解:如解图①,连接AH .∵BH 、CH 分别是∠ABC 和∠ACB 的平分线,∴AH 是∠BAC 的平分线,∴∠BHC =180°-12(∠ABC +∠ACB )=180°-12(180°-∠BAC )=90°+12∠BAC =90°+∠HAE ,∵CE =CF ,∠HCE =∠HCF ,∴CH ⊥EF ,HF =HE ,∴∠CHF =90°,∵∠BHC =∠BHF +∠CHF =∠BHF +90°,∴∠HAE =∠BHF ,∵CE =CF ,∴∠CFE =∠CEF ,∴∠AEH =∠BFH ,∴△AEH ∽△HFB ,∴ AE HF =EH FB ,∴FH ·EH =6,∴HE =HF =6,∴EF =26;第5题解图①(3)解:如解图②,作HM ⊥AC 于M ,HN ⊥BC 于N .设HF =x ,FN =y .∵∠HCM =∠HCN =30°,HC =5,∴HM =HN =52 ,CM =CN =532,∵CE =4 3 ,∴EM =332, ∴EH =EM 2+HM 2=13 ,∵S △HCF ∶S △HCE =FH ∶EH =FC ∶EC ,∴x ∶13=(y + 532)∶43,又∵x 2=y 2+(52)2 ,解得y =5314或332,∵当y =332时,CF =CN +NF =43,又∵CE ≠CF ,∴y ≠332,即FN =5314,∴CF =2037 ,∵∠CEF =∠B ,∠ECF =∠ACB ,∴△ECF ∽△BCA ,∴ EC BC =CFAC ,∴ AC BC =CF EC =203743=57.第5题解图②类型三 与全等和相似三角形有关的证明及计算1. 解:(1)∵△ABC 是等边三角形,∴∠B =∠FCD =60°,∵∠BAD =180°-60°-∠ADB ,∠FDC =180°-∠ADE -∠ADB =180°-60°-∠ADB , ∴∠BAD =∠FDC ,∴△ABD ∽△DCF ,∴AB DC =BD CF ,∴CF =DC ·BD AB =(8-6)×68=32;(2)△ADE 是等边三角形.证明:若D 点是BC 边中点,则AD ⊥BC ,∴∠CDE =∠ADC -∠ADE =90°-60°=30°,又∵l ∥AB ,∴∠DCE =180°-∠ABC =180°-60°=120°,∴∠CED =180°-∠DCE -∠CDE =180°-120°-30°=30°,即∠CDE =∠CED ,∴CE =CD .在△ACD 和△ACE 中,⎩⎨⎧AC =AC∠ACD =∠ACE =60°DC =EC,∴△ACD ≌△ACE (SAS),∴AD =AE ,又∵∠ADE =60°,∴△ADE 是等边三角形;(3)(2)中结论仍然成立.证明:如解图,过点D 作DG ∥l 交AC 于点G ,则△GDC ∽△ABC , ∴△GDC 是等边三角形,∴DG =DC ,∠GDC =∠DGC =60°,∵∠ADE =60°,∴∠ADE =∠GDC ,∴∠ADG =∠EDC ,又∵∠AGD =180°-60°=120°,∠DCE =180°-∠ABC =120°,∴∠AGD =∠DCE ,在△ADG 和△EDC 中,⎩⎨⎧∠ADG =∠EDCDG =DC ∠AGD =∠DCE ,∴△ADG ≌△EDC (ASA),∴AD =DE ,又∵∠ADE =60°,∴△ADE 是等边三角形.2. (1)证明:∵P 为AB 的中点,AC =BC ,∠ACB =90°, ∴∠BCE =12∠ACB =12×90°=45°,∠A =45°,∴∠A =∠BCE ,在△ACF 和△CBE 中第1题解图⎩⎨⎧∠A =∠BCEAC =BC ∠ACF =∠CBD,∴△ACF ≌△CBE (ASA),∴CF =BE ;(2)解:①由(1)得CF =BE ,∴BE =CF =6,∵AC =BC ,CE 平分∠ACB ,P 为AB 的中点,∴CP ⊥AB ,∵AG ⊥AB ,∴CE ∥AG ,∴∠GAD =∠ECD ,又∵∠ADG =∠CDE ,∴△ADG ∽△CDE ,∵点D 是AC 的中点,∴AD =CD ,即相似比k =1,∴△ADG ≌△CDE ,∴DG =DE =12GE ,∵CE ∥AG 且P 为AB 中点,∴GE =BE =6,∴DG =3;②设EP =a ,由(2)① 得EP ∥AG ,∴AG =2a ,又由上题得△ADG ≌△CDE ,∴CE =AG =2a ,∴CP =CE +EP =3a ,∵等腰直角△ABC 中 CP ⊥AB ,∴BP =CP =3a ,由题得∠ACP =∠CBP =45°,∵∠ACF =∠CBD ,∴∠ACP -∠ACF =∠CBP -∠CBD ,即∠HCE =∠PBE , ∵∠CEH =∠PEB ,∴∠CHE =180°-∠CEH -∠HCE ,∠BPE =180°-∠PBE -∠PEB , ∴∠CHE =∠BPE =90°,∴△CHE 是直角三角形,∴△CHE ∽△BPE ,∴HE CH =PE BP =a 3a =13.3. (1)证明:∵DE ⊥AB ,DF ⊥AC ,∴∠BED =∠CFD =90°,∵D 是BC 的中点,∴BD =CD ,在Rt △BED 和Rt △CFD 中,⎩⎨⎧BD =CDBE =CF ,∴Rt △BED ≌Rt △CFD (HL),∴∠B =∠C ,∵∠BAC =90°,∴△ABC 为等腰直角三角形;(2)①证明:如解图,连接AD 、EF ,相交于点O ,∵由(1)可得Rt △BED ≌Rt △CFD ,∴∠B =∠C ,DE =DF ,∴AB =AC ,∵BE =CF ,∴AE =AF ,∴AD ⊥EF ,又∵∠NEM =∠MGN =90°,∴∠GME +∠ENG =∠DNG +∠ENG =180°, ∴∠EMF =∠DNA ,又∵∠AEO +∠EAO =90°,∠EAO +∠NDA =90°, ∴∠AEO =∠NDA ,∴△FME ∽△AND ,∴FM AN =EM DN ;第3题解图②解:设AF =2k ,DF =k ,在Rt △ADF 中,AD =(2k )2+k 2=5k , 由①可得∠B =∠C ,DE =DF ,∴AD 垂直平分EF ,则OF =12EF ,∵DF ⊥AC ,∴S △ADF =12×5k ·OF =12×2k ×k ,∴OF =255k ,EF =455k ,∴ADEF =54,又∵△FME ∽△AND ,∴AN FM =AD EF =54,即AN ∶FM =5∶4.4. (1)解:如解图①中,作IE ⊥AB 于E .设ID =x , ∵AB =AC =3,AI 平分∠BAC ,∴AD ⊥BC ,BD =CD =1,在Rt △ABD 中,AD =AB 2-BD 2=32-12=2 2 ,在△BEI 和△BDI 中,⎩⎨⎧∠EBI =∠DBI ,∠BEI =∠BDI =90°,BI =BI ,∴△BEI ≌△BDI ,∴ID =IE =x ,BD =BE =1,AE =2,在Rt △AEI 中,∵AE 2+EI 2=AI 2,∴22+x 2=(22-x )2 ,∴x =22,∴ID =22;第4题解图(2)①证明:如解图②,连接BI 、CI .∵I 是内心,∴∠MAI =∠NAI ,∵AI ⊥MN ,∴∠AIM =∠AIN =90°,又∵AI =AI ,∴△AMI ≌△ANI (ASA),∴∠AMN =∠ANM ,∴∠BMI =∠CNI ,设∠BAI =∠CAI =α,∠ACI =∠BCI =β,∴∠NIC =90°-α-β,∵∠ABC =180°-2α-2β,∴∠MBI=90°-α-β,∴∠MBI=∠NIC,∴△BMI∽△INC,∴BMNI=MINC,∴NI·MI=BM·CN,∵NI=MI,∴MI2=BM·CN;②解:如解图③,过点N作NG∥AD交MA的延长线于G. ∵NG∥AD,∴∠ANG=∠DAN,∠AGN=∠BAD,∵∠BAC=60°,∴∠BAD=∠DAN=30°,∴∠ANG=∠AGN=30°,∴AN=AG,NG=3AN,∵AI∥NG,∴∠MIA=∠MNG,∠MAI=∠MGN,∴△AMI∽△GMN,∴AMMG=AING,∴AMAM+AN=43AN,∴AM+ANAM=3AN4,∴1AM+1AN=34.第4题解图③5.(1)证明:∵∠ACB =90°,∴∠ACD +∠BCE =90°,∵AD ⊥DE ,BE ⊥DE ,∴∠DAC +∠DCA =90°,∠ADC =∠BEC ,∴∠DAC =∠ECB ,在△ADC 和△CEB 中,⎩⎨⎧∠ADC =∠CEB∠DAC =∠ECBAC =CB,∴△ADC ≌△CEB (AAS),∴AD =CE ,CD =BE ,∴DE =CE +DC =AD +BE ;(2)解:DE =kBE +1k AD .证明:∵∠ACB =90°,∴∠ACD +∠BCE =90°,∵AD ⊥DE ,∴∠DAC +∠DCA =90°,∴∠DAC =∠ECB ,∵AD ⊥DE ,BE ⊥DE ,∴∠ADC =∠CEB =90°,∴△ADC ∽△CEB ,∴AD CE =DC BE =AC BC =k ,∴DC =kBE ,CE =1k AD ,∴DE =DC +CE =kBE +1k AD ;(3)解:如解图,过点F 作FG ⊥BC 于点G ,∵AC =4,D 是AC 的中点,∴CD =2,∵EF =2DE ,易证△DCE ∽△EGF ,FG =2CE ,EG =2DC =4, 设CE =x ,则BG =BC -CG =12-4-x =8-x ,∵FG ⊥BC ,AC ⊥BC ,∴∠ACB =∠FGB =90°,∵∠B =∠B ,∴△FGB ∽△ACB ,∴FG AC =BG BC ,即2x 4=8-x 12,解得x =87,即CE 的长为87.第5题解图6. (1)证明:∵∠ACB =90°,AC =BC ,D 为AB 的中点,∴∠BCD =∠ACD =45°,∠BCE =∠ACF =90°,∴∠DCE =∠DCF =135°,在△DCE 与△DCF 中,⎩⎨⎧CE =CF∠DCE =∠DCFCD =CD,∴△DCE ≌△DCF (SAS);(2) ①解:AB 2=4CE ·CF .证明:∵∠DCF =∠DCE =135°,∴∠CDF +∠F =180°-135°=45°,∵∠CDF +∠CDE =45°,∴∠F =∠CDE ,∴△CDF ∽△CED , ∴CD CE =CF CD ,即CD 2=CE ·CF ,∵∠ACB =90°,AC =BC ,CD 平分∠ACB ,∴CD =AD =BD =12AB ,∴(12AB )2=CE ·CF ,∴AB 2=4CE ·CF ;②解:如解图,过D 作DG ⊥BC 于G ,由①得AB 2=4CE ·CF , ∵AB =42,CE =2CF ,∴CE =4,CF =2,∵DG ⊥BC 于G ,由题得∠B =45°,BD =12AB =2 2∴△DGB 是等腰直角三角形,∴BG =DG =22·sin 45°=2,∵DG ⊥BC ,AC ⊥BC ,∴DG ∥AC 即DG ∥CE ,∴∠ECN =∠DGN 又∵∠ENC =∠DNG ∴△CEN ∽△GDN ,∴CE DG =CN NG =42=2,又∵D 点为AB 中点,DG ∥AC ,∴CG =BG =2, ∴NG =13CG =23,在Rt △DGN 中,DN =DG 2+NG 2=22+(23)2=2103.第6题解图。
初二数学几何计算与勾股定理证明题

初二数学每日复习内容第十七、八章——几何计算与证明1.已知,平行四边形ABCD 中,连接AC,AC=AB,过点B 作BE⊥AC,垂足为E,延长BE 与CD 相交于点F.(1)如图1,若AE=3,CE=2,求线段AD 的长.(2)如图2,若∠BAC=45°,过点F 作FG⊥AD 于点G,连接AF、EG,求证:AC=EG参考答案1.【解答】解:(1)∵BE⊥AC,∴∠AEB=∠BEC=90°,∵AE=3,CE=2,∴AC=AB=5,∴BE==4,∴BC===2 ,∵四边形ABCD 是平行四边形,∴AD=BC=2 ;(2)∵BE⊥AC,∴∠AEB=∠BEC=90°,∵∠BAC=45°,∴△AEB 是等腰直角三角形,∴∠ABE=45°,∵AB∥CD,∴∠ACF=45°,∠ABC+∠DCB=180°,设∠CBE=x,∴∠ABC=45°+x,∵AB=AC,∴∠ABC=∠ACB=45°+x,∵∠EBC+∠ECB=90°,∴x+45°+x=90°,∴x=22.5°,∴∠EBC=22.5°,∠ACB=67.5°,∵∠ABF=∠ACF=45°,∴A,B,C,F 四点共圆,∴∠CAF=∠CBE=22.5°,∵FG⊥AD,∴∠AGF=∠AEF=90°,∴A,E,F,G 四点共圆,∴∠EGF=∠EAF=22.5°,∴∠AGE=67.5°,∵∠CAD=∠ACB=67.5°,∴∠EAG=∠AGE,∴AE=GE,∵AC=AB=AE,∴AC=EG.第十七、八章——几何计算与证明1.已知在平行四边形ABCD 中,AB=BD,BE⊥AD 于点E,CF⊥BD 分别与BD、BE 交于点G、点F,连接GE.(1)若BF=1,CF=,求平行四边形ABCD 的面积.(2)若CF=AB,求证:GE=BG.参考答案【解答】(1)解:∵四边形ABCD 是平行四边形,∴AD∥BC,∵BE⊥AD,∴BE⊥BC,∵CF=,BF=1,∴BC=2,∴AD=BC=2,∵BD=AB,BE⊥AD,∴DE=AD=1=BF,∵∠BCF+∠CBG=∠CBG+∠DBE,∴∠BCF=∠DBE,∵∠DEB=∠FBC=90°,∴△DEB≌△FBC(AAS),∴BE=BC=2,∴S▱ABCD=AD•BE=2×2=4;(2)证明:由(1)知:△DEB∽△FBC,∵CF=AB=BD,∴△DEB≌△FBC,∴BF=DE,BE=BC=2DE,==BF•BC,设DE=x,则BC=AD=2x,CF=x,S△BCFx•BG=x•2x,∴BG=x,∴DG=x﹣x=x,过G 作GH⊥AD 于H,sin∠EDG==,∴GH=x,cos∠EDG==,DH=,∴EH=x﹣=,∴EG===,∴==,∴EG=BG.第十七、八章——几何计算与证明1.如图,正方形ABCD 的边长为2,对角线AC、BD 相交于点O,E 是OC 的中点,连接BE,过点A 作AM⊥BE 于点M,交BD 于点F.(1)求证:AF=BE;(2)求点E 到BC 边的距离.参考答案1.【解答】(1)证明:∵四边形ABCD 为正方形,∴OA=OB,∠AOB=∠BOC=90°,∵AM⊥BE 于点M,∴∠AME=90°,∴∠MAE=∠OBE,在△AOF 和△BOE 中,∴△AOF≌△BOE(ASA),∴AF=BE;(2)解:作EN⊥BC 于N,如图,∵四边形ABCD 为正方形,∴OC=BC=×2 =2,∠OCB=45°,∵E 是OC 的中点,∴CE=1,在Rt△ECN 中,∵∠ECN=45°,∵△CEN 为等腰直角三角形,∴EN=CE=,即点E 到BC 边的距离为.第十七、八章——几何计算与证明1.如图,在平行四边形ABCD 中,点O 是对角线AC 的中点,点E 是BC 上一点,且AB=AE,连接EO 并延长交AD 于点F.过点B 作AE 的垂线,垂足为H,交AC 于点G.(1)若AH=3,HE=1,求△ABE 的面积;(2)若∠ACB=45°,求证:DF=CG.参考答案1.【解答】解:(1)∵AH=3,HE=1,∴AB=AE=4,又∵Rt△ABH 中,BH==,=AE×BH=×4×=;∴S△ABE(2)如图,过A 作AM⊥BC 于M,交BG 于K,过G 作GN⊥BC 于N,则∠AMB=∠AME=∠BNG=90°,∵∠ACB=45°,∴∠MAC=∠NGC=45°,∵AB=AE,∴BM=EM=BE,∠BAM=∠EAM,又∵AE⊥BG,∴∠AHK=90°=∠BMK,而∠AKH=∠BKM,∴∠MAE=∠NBG,设∠BAM=∠MAE=∠NBG=α,则∠BAG=45°+α,∠BGA=∠GCN+∠GBC=45°+α,∴AB=BG,∴AE=BG,在△AME 和△BNG 中,,∴△AME≌△BNG(AAS),∴ME=NG,在等腰Rt△CNG 中,NG=NC,∴GC=NG=ME=BE,∴BE=GC,∵O 是AC 的中点,∴OA=OC,∵四边形ABCD 是平行四边形,∴AD∥BC,AD=BC,∴∠OAF=∠OCE,∠AFO=∠CEO,∴△AFO≌△CEO(AAS),∴AF=CE,∴AD﹣AF=BC﹣EC,即DF=BE,∴DF=BE=CG.第十七、八章——几何计算与证明1.已知四边形ABCD 是矩形,连接AC,点E 是边CB 延长线上一点,CA=CE,连接AE,F 是线段AE 的中点,(1)如图1,当AD=DC 时,连接CF 交AB 于M,求证:BM=BE;(2)如图2,连接BD 交AC 于O,连接DF 分别交AB、AC 于G、H,连接GC,若∠FDB=30°,S 四边形GBOH=,求线段GC 的长.参考答案1.【解答】证明:(1)如图1,∵AC=EC,F是AE的中点,∴CF⊥AE,∴∠AFC=90°,∵四边形ABCD 是矩形,AD=DC,∴矩形ABCD 为正方形,∴AB=BC,∠ABC=90°,∴∠AFC=∠ABC,∵∠AMF=∠BMC,∴∠EAB=∠MCB,∵∠ABE=∠ABC=90°,∴△AEB≌△CMB,∴BE=BM;(2)如图2,连接BF 并延长交直线AD 于M,∵F 是AE 的中点,∴AF=EF,∵四边形ABCD 是矩形,∴AD∥BC,AC=BD,∴∠M=∠FBE,∵∠AFM=∠EFB,∴△AMF≌△EBF,∴FM=BF,AM=BE,∵AD=BC,∴AD+AM=BC+BE,即DM=CE,∵AC=CE,∴EC=DM=AC=BD,∴△DMB 是等腰三角形,∵F 是BM 的中点,∴DF 平分∠BDM,∵∠BDF=30°,∴∠BDM=60°,∴△BDM 是等边三角形,∴∠M=60°,在Rt△BCD 中,∠BDC=90°﹣60°=30°,∴∠DBC=60°,∵OB=OC,∴∠DBC=∠OCB=60°,∴△ACE 为等边三角形,在△OHD 中,∠HOD=∠BOC=60°,∴∠OHD=90°,设OH=x,则OD=2x,BD=4x,BC=2x,∴DH =x,AH=x,DC=AB=2 x,Rt△ABC 中,∠ACE=60°,∴∠BAC=30°,∴cos30°=,AG==,∴BG=AB﹣AG=2 x﹣=••2x﹣•x•,∴S四边形GBOH=S△DGB﹣S△OHD,=BG•AD﹣OH•DH,=x=,解得:x2=9,x=±3,∴BC=2x=6,BG=×3=4 ,由勾股定理得:CG===2 .第十七、八章——几何计算与证明1.如图1,在矩形ABCD 中,AC 为对角线,延长CD 至点E 使CE=CA,连接AE.F 为AB 上的一点,且BF=DE,连接FC.(1)若DE=1,CF=,求CD 的长;(2)如图2,点G 为线段AE 的中点,连接BG 交AC 于H,若∠BHC+∠ABG=60°,求证:AF+CE=AC.参考答案1.【解答】解:(1)设CD=x.∵四边形ABCD是矩形,∴∠ADC=∠B=90°,AD=BC,在Rt△BCF 中,BC==,∵AC=CE=x+1,在Rt△ADC 中,∵AC2=AD2+CD2,∴(x+1)2=x2+()2,∴x=3,∴CD=3.(2)如图2 中,连接CG.作FJ⊥AC 于J.∵CA=CE,AG=EG,∴CG⊥AE,∠ACG=∠ECG,∵∠AGC=∠ABC=90°,∴∠AGC+∠ABC=180°,∴A、G、C、B 四点共圆,∴∠ABG=∠ACG,∴∠ACG=∠ECG=∠ABG,设∠ACG=∠ECG=∠ABG=x,则∠BAH=∠ACD=2x,∠BHC=∠BAH+∠ABG =3x,∵∠BHC+∠ABG=60°,∴4x=60°,∴x=15°,∴∠FAJ=30°,∠DAC=∠ACB=60°,∠CAE=75°,∴∠EAD=15°,∵DE=BF,∠ADE=∠CBF,AD=BC,∴△ADE≌△CBF,∴∠BCF=∠DAE=15°,∴∠FCJ=45°,∴CJ=FJ,设CJ=FJ=a,则AJ=a,AF=2a,AC=a+ a,∴==﹣1,∴AF=(﹣1)AC,∴AF=AC﹣AC,∵AC=CE,∴AF+CE=AC.第十七、八章——几何计算与证明1.如图,在菱形中ABCD 中,∠ABC=60°,点F 为AD 边上一点,连接BF 交对角线AC 于点G.(1)如图1,已知CF⊥AD 于F,菱形的边长为6,求线段FG 的长度;(2)如图2,已知点E 为AB 边上一点,连接CE 交线段BF 于点H,且满足∠FHC=60°,CH=2BH,求证:AH⊥CE.参考答案1.【解答】解:(1)如图1,∵四边形ABCD是菱形,∴AD=CD,∠D=∠ABC=60°,∴△ACD 是等边三角形,∵CF⊥AD,∴AF=DF=3,由勾股定理得:CF==3 ,∵AD∥BC,∴∠BCF=∠CFD=90°,∵BC=6,Rt△BCF 中,BF==3 ,∵AF∥BC,∴=,∴BG=2FG,∴FG=BF=,(2)如图2,∵∠FHC=60°,∴∠BHC=120°,∵AD∥BC,∠ABC=60°,∴∠BAD=120°=∠BHC,∠AFC=∠HBC,∴△BHC∽△FAB,∴,∵CH=2BH,∴AB=2AF,∴F 是AD 的中点,∵△ADC 是等边三角形,∴∠ACF=∠ACD=30°,∵∠CAF=∠FHC=60°,∴A、H、C、F 四点共圆,∴∠AHC+∠AFC=180°,∵∠AFC=90°,∴∠AHC=90°,∴AH⊥CE.第十七、八章——勾股计算与证明1.如图,四边形ACEF 为正方形,以AC 为斜边作Rt△ABC,∠B=90°,AB=4,BC=2,延长BC 至点D,使CD=5,连接DE.(1)求正方形的边长;(2)求DE 的长.2.如图,已知正方形ABCD 的边长为,连接AC、BD 交于点O,CE 平分∠ACD 交BD 于点E,(1)求DE 的长;(2)过点E 作EF⊥CE,交AB 于点F,求BF 的长;(3)过点E 作EG⊥CE,交CD 于点G,求DG 的长.参考答案1.【解答】解:(1)在Rt△ABC中,AB=4,BC=2,AC===2,∴正方形边长为2;(2)∵∠B=90°,∴∠BAC+∠BCA=90°,∵∠ACE=90°,∴∠BCA+∠ECD=90°,∴∠BAC=∠ECD,又∵=,∴△ABC∽△CED,∴=,∴DE=.2.【解答】解:(1)∵四边形ABCD是正方形,∴∠ABC=∠ADC=90°,∠DBC=∠BCA=∠ACD=45°,∵CE 平分∠DCA,∴∠ACE=∠DCE=∠ACD=22.5°,∴∠BCE=∠BCA+∠ACE=45°+22.5°=67.5°,∵∠DBC=45°,∴∠BEC=180°﹣67.5°﹣45°=67.5°=∠BCE,∴BE=BC=,在Rt△ACD 中,由勾股定理得:BD==2,∴DE=BD﹣BE=2﹣;(2)∵FE⊥CE,∴∠CEF=90°,∴∠FEB=∠CEF﹣∠CEB=90°﹣67.5°=22.5°=∠DCE,∵∠FBE=∠CDE=45°,BE=BC=CD,∴△FEB≌△ECD,∴BF=DE=2﹣;(3)延长GE 交AB 于F,由(2)知:DE=BF=2﹣,由(1)知:BE=BC=,∵四边形ABCD 是正方形,∴AB∥DC,∴△DGE∽△BFE,∴=,∴=,解得:DG=3 ﹣4.初二数学每日复习内容第十七、八章——勾股计算与证明1.如图,平行四边形ABCD 中,CG⊥AB 于点G,∠ABF=45°,F 在CD 上,BF 交CD 于点E,连接AE,AE⊥AD.(1)若BG=1,BC=,求EF 的长度;(2)求证:CE+ BE=AB.2.在菱形ABCD 中以B 为顶点作等腰△BEF,已知∠EBF+∠ABC=180°.(1)如图1,当BF 与BD 重合时,点E 在AD 边上已知∠A=30°,AE=6,求BE 的长.(2)如图2,连接AF、CE,BE 与AF 于点G.若G 为AF 中点,求证:CE=2BG.参考答案1.【解答】解:(1)∵CG⊥AB,∴∠AGC=∠CGB=90°,∵BG=1,BC=,∴CG==3,∵∠ABF=45°,∴BG=EG=1,∴CE=2,∵四边形ABCD 是平行四边形,∴AB∥CD,∴∠GCD=∠BGC=90°,∠EFG=∠GBE=45°,∴CF=CE=2,∴EF=CE=2 ;(2)如图,延长AE 交BC 于H,∵四边形ABCD 是平行四边形,∴BC∥AD,∴∠AHB=∠HAD,∵AE⊥AD,∴∠AHB=∠HAD=90°,∴∠BAH+∠ABH=∠BCG+∠CBG=90°,∴∠GAE=∠GCB,在△BCG与△EAG中,,∴△BCG≌△EAG(AAS),∴AG=CG,∴AB=BG+AG=CE+EG+BG,∵BG=EG=BE,∴CE+ BE=AB.2【.解答】解:(1)如图1,过E点作EM⊥AB于M点在Rt△AME中,∠A=30°,所以ME=AE=×6=3.∵四边形ABCD 是菱形,∴AB=AD.∴∠ADB==75°.∵BE=BD,∴∠BED=∠ADB=75°.∴∠ABE=75°﹣30°=45°,∴△MEB 是等腰直角三角形.∴BE=ME=.(2)延长AB 至H 点,使得BH=AB,连接FH.∵G 点为AF 中点,B 点为AH 中点∴FH=2BG.∵∠HBC+∠ABC=180°,∠EBF+∠ABC=180°,∴∠HBC=∠EBF.∴∠HBC+∠CBF=∠EBF+∠CBF,即∠HBF=∠CBE.在△HBF 和△CBE 中∴△HBF≌△CBE(SAS).∴CE=HF.∴CE=2BG.初二数学每日复习内容第十七、八章——勾股计算与证明1.已知:如图,在△ABC 和△ABE 中,∠ACB=∠AEB=90°,D 是AB 中点,联结DC、DE、CE,F 是CE 中点,联结DF.(1)求证:DC=DE;(2)若AB=10,CE=8,求DF 的长.2.如图,在四边形ABCD 中,∠BAD=∠BCD=90°,AC、BD 相交于点E,点G、H 分别是AC、BD 的中点.(1)求证:HG⊥AC;(2)当AC=8cm,BD=10cm 时,求GH 的长.参考答案1.【解答】解:(1)∵∠ACB=90°,D是AB中点,∴CD=AB,同理:ED=AB,∴CD=ED;(2)∵CD=ED,F 是CE 中点,∴DF⊥CE,∵CD=AB,AB=10,∴CD=5,∵F 是CE 中点,CE=8,∴CF=4,∴DF==3.2.【解答】解:(1)如图,连接AH、CH,∵∠BAD=∠BCD=90°,H 为BD 的中点,∴AH=CH=BD,∵G 为AC 的中点,∴GH⊥AC;(2)∵BD=10,∴AH=BD=5,∵AC=8,∴AG=AC=4,∵GH⊥AC,即∠HGA=90°,∴GH===3.第十七、八章——勾股计算与证明1.如图,在平行四边形ABCD 中,∠ABC=45°,E、F 分别在CD 和BC 的延长线上,AE∥BD,∠EFC=30°,AB=2.求CF 的长.2.如图,已知AC⊥BC,AD⊥BD,E 为AB 的中点,(1)如图1,求证:△ECD 是等腰三角形;(2)如图2,CD 与AB 交点为F,若AD=BD,EF=3,DE=4,求CD 的长.参考答案1.【解答】解:∵四边形ABCD 是平行四边形,∴AB∥CD,AB=DC,∵AE∥DB,∴四边形ABDE 是平行四边形,∴AB=DE=CD,即D 为CE 中点,∵AB=2,∴CE=4,∵AB∥CD,∴∠ECF=∠ABC=45°,过E 作EH⊥BF 于点H,∵CE=4,∠ECF=45°,∴EH=CH=2,∵∠EFC=30°,∴FH=2 ,∴CF=2 +2 .2.【解答】(1)证明:∵AC⊥BC,AD⊥BD,∴∠ACB=90°,∠ADB=90°,又∵E 为AB 的中点,∴CE=AB,DE=AB∴CE=DE,即△ECD 是等腰三角形;(2)∵AD=BD,E 为AB 的中点,∴DE⊥AB,已知DE=4,EF=3,∴DF=5,过点E 作EH⊥CD,∵∠FED=90°,EH⊥DF,∴EH==,∴DH==,∵△ECD 是等腰三角形,∴CD=2DH=.第十七、八章——勾股计算与证明1.如图,菱形ABCD 的对角线AC、BD 相交于点O,过点D 作DE∥AC 且DE=AC,连接CE、OE,连接AE交OD 于点F.(1)求证:OE=CD;(2)若菱形ABCD 的边长为2,∠ABC=60°.求AE 的长.2.如图,点G 是正方形ABCD 对角线CA 的延长线一点,对角线BD 与AC 交于点O,以线段AG 为边作一个正方形AEFG,连接EB、GD.(1)求证:EB=GD;(2)若AB=5,AG=2 ,求EB 的长.参考答案1.【解答】(1)证明:在菱形ABCD 中,OC=AC.∴DE=OC.∵DE∥AC,∴四边形OCED 是平行四边形.∵AC⊥BD,∴平行四边形OCED 是矩形.∴OE=CD.(2)在菱形ABCD 中,∠ABC=60°,∴AC=AB=2.∴在矩形OCED 中,CE=OD=.在Rt△ACE 中,AE=.2.【解答】(1)证明:在△GAD 和△EAB 中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,∴∠GAD=∠EAB,在△GAD 和△EAB 中,∴△GAD≌△EAB,∴EB=GD;(2)∵四边形ABCD 是正方形,AB=5,∴BD⊥AC,AC=BD=5,∴∠DOG=90°,OA=OD=BD=,∵AG=2 ,∴OG=OA+AG=,由勾股定理得,GD==,∴EB=.第十七、八章——勾股计算与证明1.如图,已知E 为▱ABCD 的DC 边延长线上的一点,且CE=CD,连接AE 分别交BC,BD 于点F,G.(1)求证:△AFB≌△EFC;(2)若AE=12,求FG 的长.2.如图,在矩形ABCD 中,E 是AD 上一点,PQ 垂直平分BE,分别交AD、BE、BC 于点P、O、Q,连接BP、EQ.(1)求证:△BOQ≌△EOP;(2)求证:四边形BPEQ 是菱形;(3)若AB=6,F 为AB 的中点,OF+OB=9,求PQ 的长.参考答案1.【解答】(1)证明:在平行四边形ABCD 中,∵AB∥CD,∴∠BAF=∠CEF,∠ABF=∠ECF,∵AB=CD,CE=CD,∴AB=CE,在△AFB 和△EFC 中,∴△AFB≌△EFC.(2)∵ED∥AB,∴,∵EC=CD,CD=BA,AE=12,∴EF=AF=6,∵ED∥BA,,∵ED=2BA,∴,解得:FG=2.2.【解答】(1)证明:∵PQ 垂直平分BE,∴PB=PE,OB=OE,∵四边形ABCD 是矩形,∴AD∥BC,∴∠PEO=∠QBO,在△BOQ 与△EOP 中,,∴△BOQ≌△EOP(ASA),(2)∵△BOQ≌△EOP∴PE=QB,又∵AD∥BC,∴四边形BPEQ 是平行四边形,又∵QB=QE,∴四边形BPEQ 是菱形;(3)解:∵O,F 分别为PQ,AB 的中点,∴AE+BE=2OF+2OB=18,设AE=x,则BE=18﹣x,在Rt△ABE 中,62+x2=(18﹣x)2,解得x=8,BE=18﹣x=10,∴OB=BE=5,设PE=y,则AP=8﹣y,BP=PE=y,在Rt△ABP 中,62+(8﹣y)2=y2,解得y=,在Rt△BOP 中,PO==,∴PQ=2PO=.第十七、八章——勾股计算与证明1.如图,在正方形ABCD 中,点P 为AD 延长线上一点,连接AC、CP,F 为AB 边上一点,满足CF⊥CP,过点B 作BM⊥CF,分别交AC、CF 于点M、N(1)若AC=AP,AC=4 ,求△ACP 的面积;(2)若BC=MC,证明:CP﹣BM=2FN.2.如图,在▱ABCD 中,∠ACB=45°,点E 在对角线AC 上,BE=BA,BF⊥AC 于点F,BF 的延长线交AD 于点G.点H 在BC 的延长线上,且CH=AG,连接EH.(1)若BC=12,AB=13,求AF 的长;(2)求证:EB=EH.1.【解答】解:(1)∵AC=AP,AC=4,∴AP=.AD=CD=4∴S△ACP=AP×CD=××4=7 ;(2)在CF 上截取FN=NG,连接BG,∵四边形ABCD 是正方形,∴AB=CB=CD,∠CBF=∠CDP=∠BCF+ ∠FCD=90°,又∵CF⊥CP,∴∠DCP+∠FCD=90°,∴∠BCF=∠BCD,在△BCF 和△DCP 中,,∴△BCF≌△DCP,∴CF=CP,∵BC=MC,BM⊥CF,∴∠BCF=∠ACF=∠BCA=22.5°,∴∠CFB=67.5°,∵FC⊥BM,FN=NG∴BF=BG∴∠FBG=45°,∠FBN=22.5°∴∠CBG=45°,在△BCG 和△BAN 中,,∴△BCG≌△ABM,∴BM=CG,∴CF﹣CG=FG,∵BF=BG,BM⊥CF,∴FN=NG,∴CP﹣BM=2FN.2.【解答】解:(1)如图,∵BF⊥AC,∠ACB=45°,BC=12,∴等腰Rt△BCF 中,BF=sin45°×BC=12,又∵AB=13,∴Rt△ABF 中,AF==5;(2)如图,连接GE,过A 作AP⊥AG,交BG 于P,连接PE,∵BE=BA,BF⊥AC,∴AF=FE,∴BG 是AE 的垂直平分线,∴AG=EG,AP=EP,∵∠GAE=∠ACB=45°,∴△AGE 是等腰直角三角形,即∠AGE=90°,△APE 是等腰直角三角形,即∠APE =90°,∴∠APE=∠PAG=∠AGE=90°,又∵AG=EG,∴四边形APEG 是正方形,∴PF=EF,AP=AG=CH,又∵BF=CF,∴BP=CE,∵∠APG=45°=∠BCF,∴∠APB=∠HCE=135°,∴△APB≌△HCE(SAS),∴AB=EH,又∵AB=BE,∴BE=EH.第十七、八章——勾股计算与证明1.已知:如图,在Rt△ABC 中,∠C=90°,CD 平分∠ACB,AD⊥CD,垂足为点D,M 是边AB 的中点,AB=20,AC=10,求线段DM 的长.2.探究:如图,分别以△ABC 的两边AB 和AC 为边向外作正方形ANMB 和正方形ACDE,NC、BE 交于点P.求证:∠ANC=∠ABE.应用:Q 是线段BC 的中点,若BC=6,则PQ 的长度是多少?参考答案1.【解答】解:延长AD 交BC 于E,∵∠C=90°,∴BC==10 ,∵CD 平分∠ACB,AD⊥CD,∴∠ACD=∠ECD,∠ADC=∠EDC=90°,∴∠CAD=∠CED,∴CA=CE=10,∴AD=DE,∵M 是边AB 的中点,∴DM=BE=×(10 ﹣10)=5 ﹣5.2.【解答】证明:∵四边形ANMB 和ACDE 是正方形,∴AN=AB,AC=AE,∠NAB=∠CAE=90°,∵∠NAC=∠NAB+∠BAC,∠BAE=∠BAC+∠CAE,∴∠NAC=∠BAE,在△ANC 和△ABE 中,ANAN=AB,∠NAC=∠BAE,AC=AE∴△ANC≌△ABE(SAS),∴∠ANC=∠ABE.解:如图所示:∵四边形NABM 是正方形,∴∠NAB=90°,∴∠ANC+∠AON=90°,∵∠BOP=∠AON,∠ANC=∠ABE,∴∠ABP+∠BOP=90°,∴∠BPC=∠ABP+∠BOP=90°,∵Q 为BC 中点,BC=6,∴PQ=BC=3.。
中考《第三讲:几何证明与计算题》专题复习含答案试卷分析解析
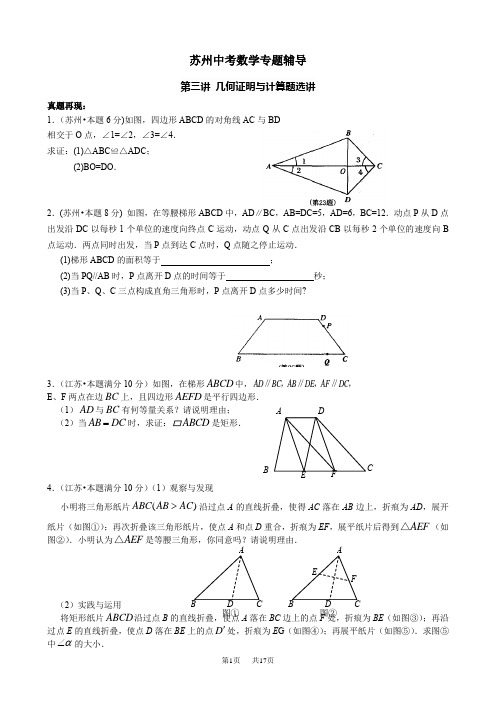
苏州中考数学专题辅导第三讲几何证明与计算题选讲真题再现:1.(苏州•本题6分)如图,四边形ABCD的对角线AC与BD相交于O点,∠1=∠2,∠3=∠4.求证:(1)△ABC≌△ADC;(2)BO=DO.2.(苏州•本题8分) 如图,在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12.动点P从D点出发沿DC以每秒1个单位的速度向终点C运动,动点Q从C点出发沿CB以每秒2个单位的速度向B 点运动.两点同时出发,当P点到达C点时,Q点随之停止运动.(1)梯形ABCD的面积等于;(2)当PQ//AB时,P点离开D点的时间等于秒;(3)当P、Q、C三点构成直角三角形时,P点离开D点多少时间?3.(江苏•本题满分10分)如图,在梯形中,E、F两点在边上,且四边形是平行四边形.(1)与有何等量关系?请说明理由;(2)当时,求证:是矩形.4.(江苏•本题满分10分)(1)观察与发现小明将三角形纸片沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图①);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到(如图②).小明认为是等腰三角形,你同意吗?请说明理由.(2)实践与运用将矩形纸片沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点处,折痕为E G(如图④);再展平纸片(如图⑤).求图⑤中的大小.ABCD AD BC AB DE AF DC∥,∥,∥,BC AEFDAD BCAB DC=ABCD()ABC AB AC>AEF△AEF△ABCDD'α∠A DCFEBACDB图①ACDB图②FE5.(苏州•本题6分) 如图,C 是线段AB 的中点,CD 平分∠ACE ,CE 平分 ∠BCD ,CD=CE .(1)求证:△ACD ≌△BCE ;(2)若∠D=50°,求∠B 的度数.6.(苏州•本题8分) 如图,在△ABC 中,∠C=90°,AC=8,BC=6.P 是AB 边上的一个动点(异于A 、B 两点),过点P 分别作AC 、BC 边的垂线,垂足为M 、N .设AP=x . (1)在△ABC 中,AB= ;(2)当x= 时,矩形PMCN 的周长是14;(3)是否存在x 的值,使得△PAM 的面积、△PBN 的面积与矩形PMCN 的面积同时相等?请说出你的判断,并加以说明.7.(苏州•本题6分)如图,已知四边形ABCD 是梯形,AD ∥BC ,∠A =90°,BC =BD ,CE ⊥BD ,垂足为E .(1)求证:△ABD ≌△ECB ;(2)若∠DBC =50°,求∠DCE 的度数. 8.(苏州•本题8分)如图,小明在大楼30米高(即PH =30米)的窗口P 处进行观测,测得山坡上A 处的俯角为15°,山脚B 处的俯角为60°,已知该山坡的坡度i (即tan ∠ABC )为1:,点P 、H 、B 、C 、A 在同一个平面上.点H 、B 、C 在同一条直线上,且PH ⊥HC . (1)山坡坡角(即∠ABC )的度数等于 ▲ 度;(2)求A 、B 两点间的距离(结果精确到0.1米,参考数据:≈1.732).33E D C F B A 图③ E D C A B F GA D E CB F G图④ 图⑤9. (苏州•本题6分) 如图,在梯形ABCD 中,已知AD ∥BC ,AB =CD ,延长线段CB 到E ,使BE =AD ,连接AE 、AC .(1)求证:△ABE ≌CDA ;(2)若∠DAC =40°,求∠EAC 的度数.10.(苏州•本题8分)如图,已知斜坡AB 长60米,坡角(即∠BAC )为30°,BC ⊥AC .现计划在 斜坡中点D 处挖去部分坡体(用阴影表示)修建一个平行于水平线CA 的平台DE 和一条 新的斜坡BE .(请将下面2小题的结果都精确到0.1米,参考数据:≈1. 732).(1)若修建的斜坡BE 的坡角(即∠BEF )不大于45°,则平台DE 的长最多为 米; (2)—座建筑物GH 距离坡脚A 点27米远(即AG =27米),小明在D 点测得建筑物顶部H 的仰角(即∠HDM )为30°.点B 、C 、A 、G 、H 在同一个平面上,点C 、A 、G 在同一条直线上,且HG 丄CG,问建筑物GH 高为多少米?11.(7分)(•苏州)如图,在一笔直的海岸线l 上有A ,B 两个观测站,A 在B 的正东方向,AB =2(单位:km ).有一艘小船在点P 处,从A 测得小船在北偏西60°的方向,从B 测得小船在北偏东45°的方向.(1)求点P 到海岸线l 的距离;(2)小船从点P 处沿射线AP 的方向航行一段时间后,到达点C 处.此时,从B 测得小船在北偏西15°的方向.求点C 与点B 之间的距离.(上述2小题的结果都保留根号)12.(8分)(•苏州)如图,点P 是菱形ABCD 对角线AC 上的一点,连接DP 并延长DP 交边AB 于点E ,连接BP 并延长BP 交边AD 于点F ,交CD 的延长线于点G .(1)求证:△APB ≌△APD ;(2)已知DF :FA =1:2,设线段DP 的长为x ,线段PF 的长为y . ①求y 与x 的函数关系式;②当x =6时,求线段FG 的长.13.(6分)(•苏州)如图,在Rt △ABC 中,∠ACB =90°,点D 、F 分别在AB ,AC 上,CF =CB .连接CD ,将线段CD 绕点C 按顺时针方向旋转90°后得CE ,连接EF . (1)求证:△BCD ≌△FCE ;(2)若EF ∥CD .求∠BDC 的度数.14.(8分)(•苏州)如图,在△ABC 中,AB =AC .分别以B 、C 为圆心,BC 长为半径在BC 下方画弧,设两弧交于点D ,与AB 、AC 的延长线分别交于点E 、F ,连接AD 、BD 、CD . (1)求证:AD 平分∠BAC ;(2)若BC =6,∠BAC =50︒,求、的长度之和(结果保留). 15.(苏州•8分)如图,在菱形ABCD 中,对角线AC 、BD 相交于点O,过点D 作对角线BD 的垂线交BA 的延长线于点E .(1)证明:四边形ACDE 是平行四边形; (2)若AC=8,BD=6,求△ADE 的周长.16. (苏州•本题8分)如图,,,点在边上,,和相交于点.(1)求证:≌;DE DFπ∠A =∠B AE =BE D C A 12∠=∠AE D B O C ∆AE D ∆BE (第14题)FEDCBA(2)若,求的度数.模拟训练: 1.(常熟市•本题满分8分) 如图,在Rt 中,,斜边的垂直平分线分别交、于点、,过点作,交于点. (1)求证:四边形是菱形;(2)若,求菱形的周长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.(2012重庆)已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.
考点:菱形的性质;全等三角形的判定与性质。
解答:(1)解:∵四边形ABCD是菱形,
∴AB∥CD,
∴∠1=∠ACD,
∵∠1=∠2,
∴∠ACD=∠2,
∴MC=MD,
∵ME⊥CD,
∴CD=2CE,
∵CE=1,
∴CD=2,
∴BC=CD=2;
(2)证明:如图,∵F为边BC的中点,
∴BF=CF=BC,
∴CF=CE,
在菱形ABCD中,AC平分∠BCD,
∴∠ACB=∠ACD,
在△CEM和△CFM中,
∵,
∴△CEM≌△CFM(SAS),
∴ME=MF,
延长AB交DF于点G,
∵AB∥CD,
∴∠G=∠2,
∵∠1=∠2,
∴∠1=∠G,
∴AM=MG,
在△CDF和△BGF中,
∵,
∴△CDF≌△BGF(AAS),
∴GF=DF,
由图形可知,GM=GF+MF,
∴AM=DF+ME.
7.(本小题满分12分)
如图,在△ABC中,AB=AC=10cm,BC=12cm,点D是BC边的中点.点P从点B 出发,以a cm/s(a>0)的速度沿BA匀速向点A运动;点Q同时以1cm/s的速度从点D 出发,沿DB匀速向点B运动,其中一个动点到达端点
时,另一个动点也随之停止运动,设它们运动的时间为
t s.
(1)若a=2,△BPQ∽△BDA,求t的值;
(2)设点M在AC上,四边形PQCM为平行四边形.
①若a=5
2,求PQ的长;
②是否存在实数a,使得点P在∠ACB的平分线上?
若存在,请求出a的值;若不存在,请说明理由.
【考点】相似三角形的判定与性质;等腰三角形的性质;勾股定理;平行四边形的性质.【专题】几何综合题.
【分析】(1)由△ABC中,AB=AC=10厘米,BC=12厘米,D是BC的中点,根据等腰三角形三线合一的性质,即可求得BD与CD的长,又由a=2,△BPQ∽△BDA,利用相似三角形的对应边成比例,即可求得t的值;
(2)①首先过点P作PE⊥BC于E,由四边形PQCM为平行四边形,易证得PB=PQ,又由平行线分线段成比例定理,即可得方程5 2 t 10 =1 2 (6-t) 6 ,解此方程即可求得答案;
②首先假设存在点P在∠ACB的平分线上,由四边形PQCM为平行四边形,可得
四边形PQCM是菱形,即可得PB=CQ,PM:BC=AP:PB,及可得方程组,解此方程组求得t值为负,故可得不存在.
【解答】解:(1)△ABC中,AB=AC=10cm,BC=12cm,D是BC的中点,∴BD=CD=1 2 BC=6cm,
∵a=2,
∴BP=2tcm,DQ=tcm,
∴BQ=BD-QD=6-t(cm),
∵△BPQ∽△BDA,
∴BP BD =BQ AB ,
即2t 6 =6-t 10 ,
解得:t=18 13 ;
(2)①过点P作PE⊥BC于E,
∵四边形PQCM为平行四边形,
∴PM∥CQ,PQ∥CM,PQ=CM,
∴PB:AB=CM:AC,
∵AB=AC,
∴PB=CM,
∴PB=PQ,
∴BE=1 2 BQ=1 2 (6-t)cm,
∵a=5 2 ,
∴PB=5 2 tcm,
∵AD⊥BC,
∴PE∥AD,
∴PB:AB=BE:BD,
即5 2 t 10 =1 2 (6-t) 6 ,
解得:t=3 2 ,
∴PQ=PB=5 2 t=15 4 (cm);
②不存在.理由如下:
∵四边形PQCM为平行四边形,
∴PM∥CQ,PQ∥CM,PQ=CM,
∴PB:AB=CM:AC,
∵AB=AC,∴PB=CM,∴PB=PQ.
若点P在∠ACB的平分线上,则∠PCQ=∠PCM,
∵PM∥CQ,
∴∠PCQ=∠CPM,
∴∠CPM=∠PCM,
∴PM=CM,
∴四边形PQCM是菱形,
∴PQ=CQ,
∴PB=CQ,
∵PB=atcm,CQ=BD+QD=6+t(cm),
∴PM=CQ=6+t(cm),AP=AB-PB=10-at(cm),
即at=6+t①,
∵PM∥CQ,
∴PM:BC=AP:AB,
∴6+t 12 =10-at 10 ,
化简得:6at+5t=30②,
把①代入②得,t=-6 11 ,
∴不存在实数a,使得点P在∠ACB的平分线上.
【点评】此题考查了相似三角形的判定与性质、平行四边形的性质、菱形的判定与性质以及等腰三角形的性质等知识.此题难度较大,注意数形结合思想与方程思想的应用.。
