用队列实现杨辉三角的源程序
c语言杨辉三角形代码

c语言杨辉三角形代码杨辉三角形是中国古代数学中较为重要的数学问题之一,也是计算机领域中经典的问题之一。
它形成一个三角形,数字排列成三角形形状,其中每个数字等于它上方两数字之和。
以下是一个用C语言编写的杨辉三角形代码:#include <stdio.h>int main() {int rows, coef = 1;printf("请输入行数: ");scanf("%d", &rows);for (int i = 0; i < rows; i++) {for (int space = 1; space <= rows - i; space++)printf(" ");for (int j = 0; j <= i; j++) {if (j == 0 || i == 0)coef = 1;elsecoef = coef * (i - j + 1) / j;printf("%4d", coef);}printf("\n");}return 0;}在这个代码中,我们首先定义一个整数变量rows来表示杨辉三角形的行数。
然后通过用户输入来获取杨辉三角形的行数。
接着我们使用两个嵌套循环来打印杨辉三角形。
外层循环用来控制打印的行数。
内层循环用来打印每一行的数字。
在内层循环中,首先使用一个循环打印空格,使得每行的数字能够居中显示。
其次,在这个循环中,我们使用一个if语句来判断当前位置是否为杨辉三角形的边界,也就是第一个数字和每一行的最后一个数字。
如果是边界上的数字,我们将其设置为1,否则就使用前一行的数字通过组合公式计算当前位置的数字。
最后我们在内层循环的末尾打印一个换行符,以便换行显示下一行。
运行以上代码,将会看到打印出指定行数的杨辉三角形。
这个代码是很简单但有效的实现了杨辉三角形的打印。
python实现杨辉三角的几种方法代码实例

python实现杨辉三⾓的⼏种⽅法代码实例⽅法⼀:迭代def triangle_1(x):""":param x: 需要⽣成的杨辉三⾓⾏数:return:"""triangle = [[1], [1, 1]] # 初始化杨辉三⾓n = 3 # 从第三⾏开始计数,逐⾏添加while n <= x:for i in range(0, n-1):if i == 0:# 添加初始列表[1,1],杨辉三⾓每⾏的⾸位和末位必为1triangle.append([1, 1])else:# 逐位计算,并插⼊初始列表中triangle[n-1].insert(i, triangle[n - 2][i] + triangle[n - 2][i - 1])n += 1return trianglex = 11triangle = triangle_1(x)# 遍历结果,逐⾏打印for i in range(x):print(' '.join(str(triangle[i])).center(100)) # 转为str,居中显⽰⽅法⼆:⽣成器def triangle_2(n):""":param n: 需要⽣成的杨辉三⾓⾏数:return:"""triangle = [1] # 初始化杨辉三⾓for i in range(n):yield triangletriangle.append(0) # 在最后⼀位加个0,⽤于计算下⼀⾏triangle = [triangle[i] + triangle[i - 1] for i in range(len(triangle))]# 从⽣成器取值for i in triangle_5(10):print(''.join(str(i)).center(100)) # 格式化输出⽅法三:递归杨辉三⾓特性:【1,1】=【0,1】+【1,0】【1,2,1】=【0,1,1】+【1,1,0】【1,3,3,1】=【0,1,2,1】+【1,2,1,0】【1,4,6,4,1】=【0,1,3,3,1】+【1,3,3,1,0】第n⾏等于第n-1⾏分别⾸尾补0,然后按位相加def triangle_4(n):""":param n:需要⽣成的杨辉三⾓⾏数:return:"""triangle = [1] # 初始化杨辉三⾓if n == 0:return trianglereturn [x+y for x, y in zip([0] + triangle_4(n - 1), triangle_4(n - 1) + [0])]for i in range(10):print(''.join(str(triangle_4(i))).center(100))到此这篇关于python实现杨辉三⾓的⼏种⽅法代码实例的⽂章就介绍到这了,更多相关python实现杨辉三⾓内容请搜索以前的⽂章或继续浏览下⾯的相关⽂章希望⼤家以后多多⽀持!。
java用队列实现直角杨辉三角

package 杨辉三角;import java.util.Scanner;public class yhsj {public static void main(String args[]) {Scanner in = new Scanner(System.in); // 获取控制台输入对象SeqQueue<Integer> s = new SeqQueue<Integer>();s.enqueue(0);s.enqueue(1);System.out.print("请输入行号: ");int n = in.nextInt();int i = 0;while (i <= n) {int x = s.dequeue();int y = s.frontqueue();if (x == 0) {i++;s.enqueue(0);}s.enqueue(x + y);if (x == 0)System.out.println();elseSystem.out.print(x + " ");}}}interface QQueue<T> {boolean isEmpty();void enqueue(T x);T dequeue();}class SeqQueue<T> implements QQueue<T> {private Object element[];private int front, rear;public SeqQueue(int length) {if (length < 64)length = 64;this.element = new Object[Math.abs(length)];this.front = this.rear = 0;}public SeqQueue() {this(64); }public boolean isEmpty() {return this.front == this.rear;}public void enqueue(T x) {if (x == null)return;if (this.front == (this.rear + 1) % this.element.length) { Object[] temp = this.element;this.element = new Object[temp.length * 2];int i = this.front, j = 0;while (i != this.rear) {this.element[j] = temp[i];i = (i + 1) % temp.length;j++;}this.front = 0; this.rear = j; }this.element[this.rear] = x;this.rear = (this.rear + 1) % this.element.length;}public T frontqueue() {if (isEmpty())return null;T temp = (T) this.element[this.front];return temp;}public T dequeue() {if (isEmpty())return null;T temp = (T) this.element[this.front];this.front = (this.front + 1) % this.element.length;return temp; }}运行结果:。
数据结构实验报告(杨辉三角-约瑟夫环)

数据结构实验报告实验一杨辉三角形(Pascal’s triangle)一、需求分析1.输入的形式和输入值的范围本程序中,需输入的杨辉三角级数level为正整数,由键盘输入,以回车结束2.输出的形式通过屏幕输出杨辉三角3.程序所能达到的功能用户从键盘输入需要的杨辉三角级数,从屏幕输出杨辉三角4.测试数据输入:5输出: 1 11 2 11 3 3 11 4 6 4 11 5 10 10 5 1二、概要设计以链队列结构实现该实验1.抽象数据类型定义ADT Queue {数据对象:D = { ai | ai∈ElemSet , i = 1,2,…,n,n≥0 }数据关系:R1={<ai-1,ai> | ai-1 , ai∈D, i=2,…,n}约定其中ai端为队列头,an端为队列尾基本操作:InitQueue ( &Q )操作结果:构造一个空队列QDestroyQueue ( &Q )初始条件:队列Q已存在操作结果:队列Q被销毁,不再存在ClearQueue ( &Q )初始条件:队列Q已存在操作结果:将Q清为空队列QueueEmpty ( Q )初始条件:队列Q已存在操作结果:若Q为空队列,则返回TRUE,否则FALSEQueueLength ( Q )初始条件:队列Q已存在操作结果:返回Q的元素个数,即队列长度GetHead ( Q , &e )初始条件:Q为非空队列操作结果:用e返回Q的队头元素EnQueue ( &Q , e )初始条件:队列Q已存在操作结果:插入元素e为Q的新队尾元素DeQueue ( &Q , &e )初始条件:Q为非空队列操作结果:删除Q的队头元素,并用e返回其值QueueTraverse ( Q , visit( ) )初始条件:Q已存在且非空操作结果:从队头到队尾,依次对Q的每个数据元素调用函数visit( )。
循环队列实现杨辉三角形的打印

循环队列实现杨辉三⾓形的打印知识温习循环队列:即将顺序队列的数组看成是⼀个环状的空间,规定最后⼀个单元的后继为第⼀个单元。
运⽤循环队列可以有效的解决链队列的“假溢出”现象。
假溢出其实是指在链队列中,当rear==MAXSIZE时就认为队满。
然⽽由于元素的出队,使得数组前⾯出现⼀些空单元,⽽元素⼜只能在队尾⼊队,如果此时已经到数组的尾部,就认为队列已满,但其实还存在上述那些空单元未使⽤,队列并未真正满。
这种现象即为“假溢出”现象。
真正的队满条件应该是rear-front==MAXSIZE。
在循环队列中,我们通过数学中的求模运算来改变头指针和尾指针的位置。
进队操作时,队尾指针的变化是:rear=(rear+1)mod MAXSIZE;⽽出队操作时,队头指针的变化是:front=(front+1)mod MAXSIE。
杨辉三⾓形11 11 2 11 3 3 11 4 6 4 11 5 10 10 5 11 6 15 20 15 6 1从上图中可以看出,杨辉三⾓形的特点:每⾏的第⼀个元素和最后⼀个元素都为1,其他位置上的元素总是等于上⼀⾏与之相邻的两个元素之和。
故第i⾏的元素要由第i-1⾏的元素来⽣成。
可以利⽤循环队列实现杨辉三⾓形的打印过程:在循环队列中依次存放第i-1⾏上的元素,然后逐个出队并打印,同时⽣成第i⾏元素并⼊队。
下⾯⽤第6⾏元素⽣成第7⾏元素为例⼦来说明打印过程:①第7⾏的第⼀个元素1⼊队。
element[Q->rear] = 1;Q->rear = (Q->rear + 1)% MAXSIZE;②循环做以下操作,⽣成第7⾏的中间5个元素并⼊队。
element[Q->rear] = element[Q->front] + element[(Q->front+1)%MAXSIZE];Q->rear = (Q->rear + 1)%MAXSIZE;Q->front = (Q->front + 1)%MAXSIZE;③第6⾏的最后⼀个元素1⼊队。
队列实现杨辉三角的算法原理

队列实现杨辉三角的算法原理
杨辉三角是一种数学模式,每个位置上的数字等于它上方两个数字之和。
队列可以用来实现杨辉三角的算法,其原理如下:
1. 首先,创建一个空的队列。
2. 将1入队列,作为第一行的元素。
3. 进行循环,从第二行开始到第n行:
- 将当前队列中的元素依次出队,并将它们存储在一个临时数组temp中。
- 在temp数组末尾添加一个0,作为哨兵元素。
- 再将temp数组中的元素依次相加,并将结果入队列。
4. 打印队列中的元素,即可得到杨辉三角的结果。
这个算法的基本思路是利用队列先进先出的特性,每次处理一行的数据。
在处理每一行时,将队列中的元素依次出队,并计算它们的和,然后将和再次入队,作为下一行的元素。
通过不断重复这个过程,最终得到的队列中的元素就是杨辉三角的结果。
杨辉三角的C程序代码

{
for(j=0;j<5;j++)
a[i][j]=b[j][i];
printf("%5d",b[j][i]);
printf("\n");
}
}
}
#include<stdio.h>
#include<stdio.h>
void main()
{
int i,j,a[5][5],b[5][5];
for(i=0;i<5;i++)
{
a[i][j]=0;
foห้องสมุดไป่ตู้(j=0;j<5;j++)
a[i][j]=rand()%51+50;
}
printf("%d",a[i][j]
}
}
printf("\n");
}
}
等腰三角形的程序
#include<stdio.h>
#define N 10
#include<stdio.h>
void main()
{
int i,j,n=13;
printf("N=");
while(n>12)
scanf("%d",&n); /*控制输入正确的值以保证屏幕显示的图形正确*/
这个数等于它左上角和它上面的数字之和也就是杨辉三角形的特点printf5dnumij
直角三角形的程序
#include<stdio.h>
#define N 10
杨辉三角解析(队列实现)
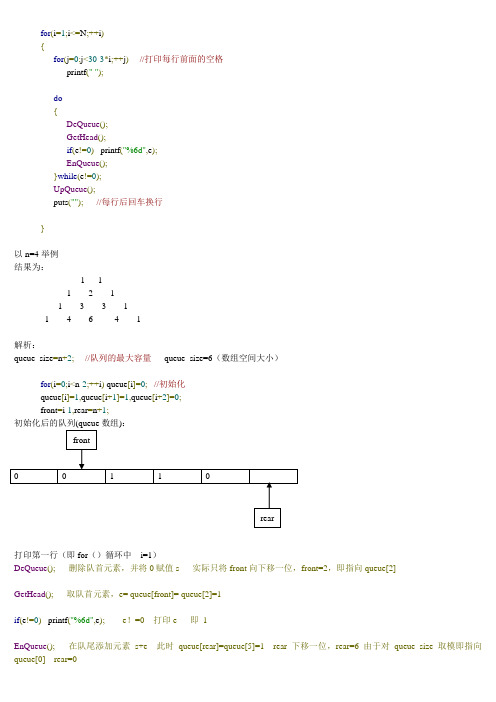
for(i=1;i<=N;++i){for(j=0;j<30-3*i;++j)//打印每行前面的空格printf(" ");do{DeQueue();GetHead();if(e!=0) printf("%6d",e);EnQueue();}while(e!=0);UpQueue();puts("");//每行后回车换行}以n=4举例结果为:1 11 2 11 3 3 11 4 6 4 1解析:queue_size=n+2;//队列的最大容量queue_size=6(数组空间大小)for(i=0;i<n-2;++i) queue[i]=0;//初始化queue[i]=1,queue[i+1]=1,queue[i+2]=0;front=i-1,rear=n+1;初始化后的队列(queue数组):front0 0 1 1 0rear打印第一行(即for()循环中i=1)DeQueue(); 删除队首元素,并将0赋值s 实际只将front向下移一位,front=2,即指向queue[2] GetHead(); 取队首元素,e= queue[front]= queue[2]=1if(e!=0) printf("%6d",e); e!=0 打印e 即1继续执行do……while语句因为e不为0DeQueue(); 删除队首元素,并将queue[2]赋值s front=3GetHead(); 取队首元素,e= queue[front]=queue[3]=1if(e!=0) printf("%6d",e); e!=0 打印e 即1EnQueue(); 在队尾添加元素s+e 此时queue[rear]=queue[0]=2 rear=1继续执行do……while语句因为e不为0DeQueue(); 删除队首元素,并将queue[3]赋值s front=4GetHead(); 取队首元素,e= queue[front]=queue[4]=0if(e!=0) printf("%6d",e); e==0 不执行printf()语句EnQueue(); 在队尾添加元素s+e 此时queue[rear]=queue[1]=1 rear=2此时e==0跳出do……while语句即打印第一行完毕输出: 1 1UpQueue(); 在队尾添加元素0 即queue[rear]=queue[2]=0 rear=3队列为:2 1 0 1 0 1puts("");//每行后回车换行rearfront打印第二行DeQueue(); s=0 front=5GetHead(); e=1if(e!=0) printf("%6d",e); e!=0 打印e 即1EnQueue(); 在队尾添加元素s+e 此时queue[rear]=queue[3]=1 rear=4继续……DeQueue(); s=1 front=6 对queue_size取模即指向queue[0] front=0GetHead(); e=2if(e!=0) printf("%6d",e); e!=0 打印e 即2EnQueue(); 在队尾添加元素s+e 此时queue[rear]=queue[4]=3 rear=5继续……DeQueue(); s=2 front=1GetHead(); e=1if(e!=0) printf("%6d",e); e!=0 打印e 即1EnQueue(); 在队尾添加元素s+e 此时queue[rear]=queue[5]=3 rear=6对queue_size取模即指向queue[0] rear=0继续……DeQueue(); s=1 front=2GetHead(); e=0if(e!=0) printf("%6d",e); e==0 不打印EnQueue(); 在队尾添加元素s+e 此时queue[rear]=queue[0]=1 rear=1此时e==0跳出do……while语句即打印第二行完毕输出: 1 2 1UpQueue(); 在队尾添加元素0 即queue[rear]=queue[1]=0 rear=2队列为:……剩下依此类推……。
数据结构之杨辉三角(队列实现)(C++版)

数据结构之杨辉三⾓(队列实现)(C++版)#include <iostream>#include <stdlib.h>#include <windows.h>#include <string>#define MAXLISTSIZE 100 //预设的存储空间最⼤容量#define TRUE 1#define FALSE 0using namespace std;typedef int ElemType;typedef struct{ElemType *elem; //存储空间基址 int rear; //队尾指针 int front; //队头指针int queuesize; //允许的最⼤存储空间,以元素为单位 }Queue;void InitQueue(Queue &Q, int maxsize){//构造⼀个最⼤存储空间为 maxsize 的空队列 Q if (maxsize == 0)maxsize = MAXLISTSIZE;Q.elem = new ElemType[maxsize]; //为循环队列分配存储空间 if (!Q.elem) exit(1); //存储分配失败Q.queuesize = maxsize;Q.front = Q.rear = 0;} //InitQueuebool EnQueue(Queue &Q, ElemType e){// 若当前队列不满,这在当前队列的尾元素之后,插⼊元素 e 为新的队列尾元素,并返回TRUE,否则返回FALSEif((Q.rear + 1) % Q.queuesize == Q.front)return FALSE;Q.elem[Q.rear] = e;Q.rear = (Q.rear+1) % Q.queuesize;return TRUE;}bool DeQueue(Queue &Q, ElemType &e){//若队列不空,则删除当前队列Q中的头元素,⽤ e 返回其值,并返回TRUE,否则返回 FALSE if (Q.front == Q.rear)return FALSE;e = Q.elem[Q.front];Q.front = (Q.front+1) % Q.queuesize;return TRUE;}bool GetHead(Queue Q, ElemType &e){//若队列不空,则⽤ e 返回队⾸元素,并返回TRUE,否则返回 FALSEif (Q.front == Q.rear)return FALSE;e = Q.elem[Q.front];return TRUE;}int QueueLength(Queue Q){//返回队列Q中元素个数,即队列的长度return((Q.rear-Q.front+Q.queuesize) % Q.queuesize);}bool QueueEmpty(Queue Q){if(Q.front == Q.rear)return TRUE;elsereturn FALSE;}int main(void){//打印输出杨辉三⾓的前n(n>0)⾏int n, i, k;Queue Q;ElemType s, e;cout << "请输⼊杨辉三⾓的⾏数:";cin >> n;/* for(i = 1; i <= n; i++)cout << ' ';cout<< '1' << endl; // 在中⼼位置输出杨辉三⾓最顶端的"1"*/ InitQueue(Q, n+3); // 设置最⼤容量为 n+3 的空队列EnQueue(Q, 0); // 添加⾏界值EnQueue(Q, 1);EnQueue(Q, 1); // 第⼀⾏的值⼊队列k = 1;while(k < n){ // 通过循环队列输出前 n-1 ⾏的值for(i = 1; i <= n - k; i++)cout<< ' '; // 输出n-k个空格以保持三⾓型EnQueue(Q, 0); // ⾏界值"0"⼊队列do { // 输出第 k ⾏,计算第 k+1 ⾏DeQueue(Q, s);GetHead(Q, e);if(e) cout<< e << ' '; //若e为⾮⾏界值0,则打印输出 e 的值并加⼀空格else cout << endl; //否则回车换⾏,为下⼀⾏输出做准备EnQueue(Q, s+e);}while(e!=0);k++;}//whileDeQueue(Q, e); //⾏界值"0"出队列while (!QueueEmpty(Q)){ //单独处理第 n ⾏的值的输出DeQueue (Q, e);cout << e << ' ';}//whilecout << endl;}//yanghui。
(H)实验三 杨辉三角显示

实验三杨辉三角显示一.需求分析(1)行数不大于20行。
(2)基于队列的操作来实现杨辉三角的不断生成过程。
(3)基于数组实现队列的物理数据结构。
二.概要设计抽象数据类型ADT SqQueue数据类型:整数基本操作:int InitQueue(SqQueue &Q)//队列的初始化int EnQueue(SqQueue &Q,int e)//数据进队int DeQueue(SqQueue &Q,int &e)//数据出队程序的流程输入模块:输入层数输出模块:输出杨辉三角三.详细设计物理数据类型typedef struct{int *base;int front;int rear;}SqQueue;int InitQueue(SqQueue &Q)//队列的初始化{Q.base=(int *)malloc(Max*sizeof(int));if(!Q.base)return 0;//分配失败Q.front=Q.rear=0;return 1;}int EnQueue(SqQueue &Q,int e)//数据进队{if((Q.rear+1)%Max==Q.front)//判断队满return 0;Q.base[Q.rear]=e;Q.rear=(Q.rear+1)%Max;return 1;}int DeQueue(SqQueue &Q,int &e)//数据出队{if(Q.front==Q.rear)//判断队空return 0;e=Q.base[Q.front];Q.front=(Q.front+1)%Max;return e;}输入输出格式输入:输入杨辉三角的层数:输出:运算结果四.测试结果输入:输入杨辉三角的层数:5输出:11 11 2 11 3 3 11 4 6 4 1 五.源程序#include<stdio.h>#include<malloc.h>#define Max 20typedef struct{int *base;int front;int rear;}SqQueue;int InitQueue(SqQueue &Q)//队列的初始化{Q.base=(int *)malloc(Max*sizeof(int));if(!Q.base)return 0;//分配失败Q.front=Q.rear=0;return 1;}int EnQueue(SqQueue &Q,int e)//数据进队{if((Q.rear+1)%Max==Q.front)//判断队满return 0;Q.base[Q.rear]=e;Q.rear=(Q.rear+1)%Max;return 1;}int DeQueue(SqQueue &Q,int &e)//数据出队{if(Q.front==Q.rear)//判断队空return 0;e=Q.base[Q.front];Q.front=(Q.front+1)%Max;return e;}void Print(SqQueue &Q,int n)//显示杨辉{int i,j,k,e,s1;for(i=1;i<=n;i++){for(k=0;k<n-i;k++)printf(" ");for(j=1,s1=0;j<i;j++){int s2;s2=DeQueue(Q,e);printf("%d",s1+s2);printf(" ");EnQueue(Q,s1+s2);s1=s2;}printf("1");EnQueue(Q,1);printf("\n");}}main() //主函数{int n,t;SqQueue Q;InitQueue(Q);printf("输入杨辉三角的层数:\n");scanf("%d",&n);Print(Q,n);return 0;}运行结果:。
杨辉三角(队列)报告

2.实现队列的相关操作。
3.利用队列的操作特点,借助进队与出队操作完成打印二项式系数的任务。
格式如下:
11
1 2 1
1 331
146 41
15 1010 51
三、实验设备及软件
一台电脑、vc++6.0
四、实验过程及步骤
运行环境:vc++;
程序思路:将二项式(a+b)i展开,其系数构成杨辉三角形,只需将展开式系数的前n行打印出来。从三角形的形状克制,除第1行以外,在打印第i行时,用到上一行(第i-1行)的数据,在打印第i+1行时,又用到第i行的数据。
front=front->link;
delete p;
return retvalue;
}
template<class T>
T Queue<T>::GetFront ()
{
assert(!Empty());
return front->data;
}
template <class T>
void Queue<T>::MakeEmpty ()
T DeQueue();//删除并返回对头元素
T GetFront();//查看对头元素
void MakeEmpty();
int IsEmpty()const
{return (front==NULL)?true:false;}
};
//成员函数定义
template <class T>
Queue<T>::~Queue()
else
rear=rear->link=new QueueNode<T> (x,NULL);
数据结构实验报告四—基于队列的操作来实现杨辉三角

杨辉三角显示问题描述:编写程序,根据输入的行数,屏幕显示杨辉三角。
一、需求分析:1、行数不大于20行。
2、基于队列的操作来实现杨辉三角的不断生成过程。
(注:不要用其它的公式计算的方法或者二维数组来实现)3、基于数组实现队列的物理数据结构。
输入形式:输入一个整数n (行数不大于20)输出形式:打印出来前(n+1)行的杨辉三角数列功能实现:输出前20层的杨辉三角序列样例输入输出形式:输入:6输出:1 n=01 1 n=11 2 1 n=21 3 3 1 n=31 4 6 4 1 n=41 5 10 10 5 1 n=51 6 15 20 15 6 1 n=65、效率分析:O(n)二、概要设计:抽象数据类型void Queue::EnQueue(int item) //将元素item入列{QueueValue[++iLast]=item; } //入列int Queue::OutQueue() //第一个元素出列返回此元素{ return QueueValue[++iFront];}算法的基本思想:下面为主要实现生成杨辉三角的算法:Q.EnQueue(1); //第一行和第二行的生成Q.EnQueue(1);Q.EnQueue(1);cout<<Q.OutQueue()<<" n=0\n";for(i=3;i<=n+1;i++) //n行杨辉三角数的生成与输出 {Q.EnQueue(1);t1=Q.OutQueue();for(j=2;j<i;j++) //利用第n-1行的杨辉三角生成第n行的中间杨辉三角数{ t 2=t1;t1=Q.OutQueue(); //第n-1行第j个元素出列 Q.EnQueue(t1+t2); //第n行的第j个元素入列 cout<<t2<<" "; }Q.EnQueue(1); //第n行最后一个元素为1 cout<<t1<<" n="<<i-2<<endl; } //输出第n-1行最后1个元素Q.EnQueue(0); //以防队列为空while(--i) //输出最后一行cout<<Q.OutQueue()<<" ";cout<<" n="<<n<<endl;}程序的流程程序由三个模块组成:输入模块:输入一个整数n计算模块:栈和杨辉三角的算法输出模块:在屏幕上打印出来前(n+1)行的杨辉三角数列三、详细设计算法的具体步骤:算法思想已经在概要设计中提到了,现在通过基于队列基本操作的函数以及程序的模块化思想来实现杨辉三角的打印输出问题。
Python极简代码实现杨辉三角示例代码

Python极简代码实现杨辉三⾓⽰例代码杨辉三⾓,⼜称贾宪三⾓形,帕斯卡三⾓形,是⼆项式系数在三⾓形中的⼀种⼏何排列。
把每⼀⾏看做⼀个list,写⼀个generator,不断输出下⼀⾏的list实现下列输出效果:# [1]# [1, 1]# [1, 2, 1]# [1, 3, 3, 1]# [1, 4, 6, 4, 1]# [1, 5, 10, 10, 5, 1]# [1, 6, 15, 20, 15, 6, 1]# [1, 7, 21, 35, 35, 21, 7, 1]# [1, 8, 28, 56, 70, 56, 28, 8, 1]# [1, 9, 36, 84, 126, 126, 84, 36, 9, 1] >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>极简代码实现:def triangles():L = [1]while True:yield LL.append(0);L = [L[i-1] + L[i] for i in range(len(L))]n = 0for t in triangles():print(t)n = n + 1if n == 10:break注:普通函数和generator⽣成器的区别:1、普通函数调⽤直接返回结果,generator函数的调⽤,返回⼀个generator对象;(调⽤generator时可以先创建⼀个对象,再⽤next()⽅法不断获得下⼀个返回值,但实际中通常⽤for循环实现)2、generator在执⾏过程中,遇到yield就中断,下次⼜继续执⾏总结以上就是这篇⽂章的全部内容了,希望本⽂的内容对⼤家的学习或者⼯作带来⼀定的帮助,如果有疑问⼤家可以留⾔交流。
使用python生成杨辉三角形的示例代码

使⽤python⽣成杨辉三⾓形的⽰例代码杨辉三⾓杨辉定义如下:1/ \1 1/ \ / \1 2 1/ \ / \ / \1 3 3 1/ \ / \ / \ / \1 4 6 4 1/ \ / \ / \ / \ / \1 5 10 10 5 1把每⼀⾏看做⼀个list,试写⼀个generator,不断输出下⼀⾏的list:def triangles():L = [1]while True:yield LM=L[:]#复制⼀个list,这样才不会影响到原有的list。
不然results⾥的每个列表的末尾会为0.M.append(0)L = [M[i-1]+M[i] for i in range(len(M))]n =0results = []for t in triangles():print(t)results.append(t)print(results)n = n +1if n == 10:breakps:如何实现⼼def printlove(start,length,midnumber=0,flag=31):for i in range(31):if i<start or i>start+length-1 and i<15-(midnumber-1)/2 or i>15+(midnumber-1)/2 and i<31-start-length or i> 30-start or i==flag: print " ",else:print "*",print ""for i in range(16):if i ==0:printlove(4,3)elif i==1:printlove(1,9)elif i>=2 and i<=5:printlove(0,i+10)elif i==6:printlove(1,7,7,15)elif i>=7 and i<=8:printlove(i-5,6,5-(i-7)*2)elif i==9:printlove(5,6,1)elif i==10:printlove(8,6,1)elif i==15:printlove(15,1,1)else:printlove(i-1,16-i,1)实现的效果如下:以上就是本⽂的全部内容,希望对⼤家的学习有所帮助,也希望⼤家多多⽀持。
