des差分攻击
安全测试中的密码学算法与攻击分析

安全测试中的密码学算法与攻击分析在安全测试中,密码学算法的选择和攻击分析是至关重要的。
密码学算法是保障信息安全的核心,而攻击分析则是评估密码学算法强度的重要手段。
本文将深入探讨安全测试中的密码学算法的选择和攻击分析,并探讨相关的技术和方法。
一、密码学算法的选择为保证信息安全,合适的密码学算法是至关重要的。
密码学算法根据其应用领域和需求的特点,可以分为对称密码算法和非对称密码算法两大类。
1. 对称密码算法对称密码算法也称为共享密钥密码算法,它使用相同的密钥进行加密和解密。
在对称算法中,密钥的安全性对保护数据的机密性起着重要作用。
常见的对称密码算法有DES、3DES、AES等。
在密码学算法的选择过程中,需要考虑以下几个方面:a. 算法的安全性:算法在遭受攻击时的抵抗能力;b. 算法的性能:算法的加密解密速度以及所需资源的消耗;c. 算法的可用性:算法的成熟度、标准化以及广泛应用的程度。
2. 非对称密码算法非对称密码算法需要使用两个密钥,一个用于加密,另一个用于解密。
公钥由其它人获得,而私钥只有接收方知道。
常见的非对称密码算法有RSA、ECC等。
在选择非对称密码算法时,需要考虑以下几个因素:a. 算法的安全性:算法的抗攻击能力以及破解难度;b. 算法的性能:算法的加密解密速度以及所需资源的消耗。
二、密码学算法的攻击分析密码学算法的攻击分析是评估算法强度和安全性的重要手段。
常见的密码学攻击手段包括穷举攻击、字典攻击、差分攻击、线性攻击等。
1. 穷举攻击穷举攻击是一种暴力破解密码的方法,通过尝试所有可能的密钥组合来破解密码。
密码的强度与密码密钥空间大小成正比,因此,密码的密钥空间越大,抵御穷举攻击的能力就越强。
2. 字典攻击字典攻击是一种基于预先准备好的密码词典的攻击方式。
攻击者将密码词典与目标密码进行比对,以找到匹配的密码。
为避免字典攻击,用户应该选择强密码,并经常更换密码。
3. 差分攻击差分攻击是一种基于差分分析的密码攻击方法,主要针对分组密码算法。
三轮DES差分分析实验报告-刘杰
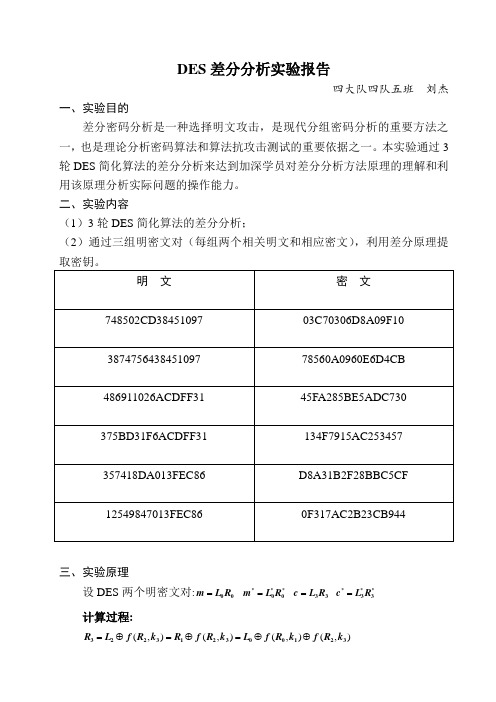
DES 差分分析实验报告四大队四队五班 刘杰一、实验目的差分密码分析是一种选择明文攻击,是现代分组密码分析的重要方法之一,也是理论分析密码算法和算法抗攻击测试的重要依据之一。
本实验通过3轮DES 简化算法的差分分析来达到加深学员对差分分析方法原理的理解和利用该原理分析实际问题的操作能力。
二、实验内容(1)3轮DES 简化算法的差分分析;(2)通过三组明密文对(每组两个相关明文和相应密文),利用差分原理提三、实验原理设DES 两个明密文对:=00m L R ***=00m L R =33c L R ***=33c L R计算过程:(,)(,)(,)(,)=⊕=⊕=⊕⊕322312300123R L f R k R f R k L f R k f R k(,)(,)****=⊕⊕300123R L f R k f R k令:*'=⊕000L L L (,)(,)(,)(,)***''=⊕=⊕⊕⊕⊕333001012323R R R L f R k f R k f R k f R k 观察得:在本次实验原始数据中,明文对*=00R R ,即*'=⊕=00000000000R R R 则(,)(,)**''=⊕=⊕⊕33302323R R R L f R k f R k 同时有:=00m L R ***=00m L R =23R L **=23R L则可计算出:*'=⊕000L L L *'=⊕333R R R (,)(,)*''⊕=⊕232330f R k f R k R L则可得出:S 盒输入差:(())(())()()**⊕⊕⊕=⊕232333E R k E R k E L E LS 盒输出差:()*-''⊕=⊕130D D P R L分析过程:令:()()*⊕=3312345678E L E L B B B B B B B B()-''⊕=13012345678P R L C C C C C C C C ()=312345678E L A A A A A A A A =312345678k J J J J J J J J()⊕=3312345678E L k X X X X X X X X *()⊕=3312345678E L k Y Y Y Y Y Y Y Y基本思路:(分别计算12345678J J J J J J J J ){|,()()}∈=⊕⊕=⊕=i i i i i i i J Test x A x y B S x S y C ,,,,,,,=12345678i对于本次实验的3个具有明文差(*,0)的明密文对,则可构造上面的3个Test 集合,显然 ()()()∈12i i i i J Test Test Test t ,,,,,,,=12345678i一种确定Ji 的直接方法:1.建立26=64长度的数组J[64]={0};2.对Testi(r),r = 1,2,…,t ,若a ∈Testi(r),则 J[a] = J[a] + 1。
加密算法中的差分攻击与防御研究

加密算法中的差分攻击与防御研究在现代加密领域中,一种被广泛使用的加密算法是对称加密算法。
而在对称加密算法中,传统上最常使用DES(Data Encryption Standard)算法。
然而,为了防止算法被破解,之后出现了更为复杂和安全的加密算法,如AES(Advanced Encryption Standard)算法。
尽管如此,这些算法仍然需要不断改善和完善,否则随着计算机技术的进步,它们将会被攻击者轻松破解。
差分攻击(Differential Cryptanalysis)是现代加密领域中最为成功的攻击方式之一。
它是一种被广泛使用的攻击方式,针对的是对称加密算法。
差分攻击对于破解具有相同结构的加密算法是非常有效的,比如DES、AES、CIPHER等算法。
差分攻击的主要思路是,对于加密算法中确定的一对明文,计算分析加密出的密文的差分,通过分析差分统计量的分布情况,找出加密算法中的相关特性。
差分攻击的基本目的是以此找出算法中的密钥,从而破解加密算法。
差分攻击的可行性和效果由其“不归零”特性决定。
计算机算法中的“不归零”指的是根据某个条件做出的选择,再根据该选择进行下一步判断,这样多次做出选择后可以得到一个结果。
而差分攻击正是利用了这一特点,在多次分析后反推出加密算法的密钥,从而达到破解加密算法的效果。
相对于其他攻击方式,差分攻击在密钥空间较小的加密算法中表现出极高的攻击效率。
因此,保护加密算法不受差分攻击的破坏是非常重要的。
现代加密领域中,研究人员们不断发掘新的加密算法漏洞,不断改进已有的加密算法,从而破解差分攻击。
例如,一个常见的防御方法是,在加密算法中增加一些随机性,使得加密过程中产生的各个位置和轮数上都存在的随机性干扰差分攻击的效果。
除此之外,还可以通过改变加密算法的轮函数、密钥扩展算法、S-Box表设计、置换函数等,来增强加密算法的安全性。
这些改进措施可以在一定程度上防御差分攻击带来的威胁。
DES的s盒输出CPA和DPA攻击
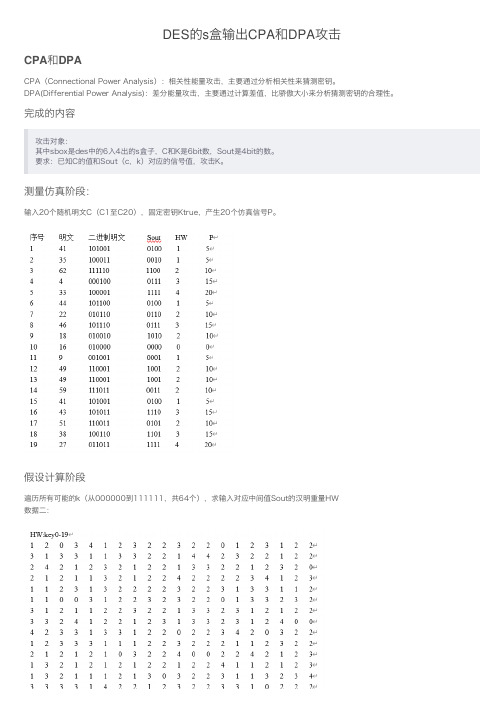
DES的s盒输出CPA和DPA攻击CPA和DPACPA(Connectional Power Analysis):相关性能量攻击,主要通过分析相关性来猜测密钥。
DPA(Differential Power Analysis):差分能量攻击,主要通过计算差值,⽐骄傲⼤⼩来分析猜测密钥的合理性。
完成的内容攻击对象:其中sbox是des中的6⼊4出的s盒⼦,C和K是6bit数,Sout是4bit的数。
要求:已知C的值和Sout(c,k)对应的信号值,攻击K。
测量仿真阶段:输⼊20个随机明⽂C(C1⾄C20),固定密钥Ktrue,产⽣20个仿真信号P。
假设计算阶段遍历所有可能的k(从000000到111111,共64个),求输⼊对应中间值Sout的汉明重量HW数据⼆:CPA 攻击数据⼆中每⼀列对应某⼀个猜测密钥K,⽤数据⼆的每⼀列HW分别与数据⼀中最后⼀列P计算相关系数ρ,并将其记录⾄数据三的ρ0⾄ρ63;再求这64个值中最⼤值ρi=Max(ρ),则i即为正确密钥Ktrue。
最⼤相关:R43=0.835214正确密钥:101011DPA攻击1、在数据⼆中,⾸先观察第⼀列k=0对应的hw重量,将其对应能量值p根据hw的⼤⼩(以2为分界)分成两⼤类,下⾯给⼀个例⼦:⽐如在k=0时,计算出20个对应的汉明重量,将对应信号p与其同列,再根据汉明重量⼤⼩分类,然后将同⼀类中的所有信号值做平均,分别求出p0和p1,再求差分Δ(k=0)=|p1-p0|。
2、针对k=1/2/…/63,重复1、的过程,分别求出Δ(k=1)、Δ(k=2)…、Δ(k=63)。
3、⽐较这64个差分值的⼤⼩,求出最⼤值Δ(k=j)=max(Δ),此时对应j即为真实密钥Ttrue。
最⼤差分值:Deta43=9.04762正确密钥:101011源代码#include <iostream>#include<math.h>#include<iomanip>using namespace std;int HWFun(int num);int Sboxout(int num, int Nkey,int i);double Corr(int n, int Pstd[], int Ptest[]);double meanNum(int n, int num[]);void Dpa();int S_Box1[4][16]={//8个S盒三维数组// S114,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7,0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8,4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0,15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13};int mingwen[20]={41,35,62,4,33,44,22,46,18,16,9,49,49,59,41,9,49,49,59,41,43,51,38,27,60};int HWw[64][20];int Ptest[64][20];int Pstd[20];int HWstd[20];//DPAdouble DpaP[64][2];//记录上述差值double Deta[64];int DpaMax;int Sout[64][20];double Rl[64];//相关系数最⼤位置int Max;int main(){//int Key = 0b00101011;int Key =0;cout <<"序号明⽂⼆进制明⽂ Sout HW P\n"; for(int Nkey =0; Nkey <64; Nkey++){for(int i =0; i <20; i++){Sboxout(mingwen[i]^ Key, Nkey,i);}Key++;}cout <<"HW:key0-19\n";for(int i =0; i <20; i++){for(int j =0; j <20; j++){cout << HWw[i][j]<<" ";}cout <<"\n";}cout <<"HW:key20-39\n";for(int i =0; i <20; i++){for(int j =20; j <40; j++){cout << HWw[j][i]<<" ";}cout <<"\n";}cout <<"HW:key40-63\n";for(int i =0; i <20; i++){for(int j =40; j <60; j++){cout << HWw[j][i]<<" ";}cout <<"\n";}cout <<"HW:key60-63\n";for(int i =0; i <20; i++){for(int j =60; j <64; j++){cout << HWw[j][i]<<" ";}cout <<"\n";}cout <<"相关系数:R0-63:\n";double temp=0.0;for(int i =0; i <64; i++){Rl[i]=abs(Corr(10, Pstd, HWw[i]));Rl[i]=abs(Corr(10, Pstd, HWw[i]));if(Rl[i]> temp){Max = i;temp = Rl[i];}cout <<setw(10)<< Rl[i]<<" ";if((i+1)%6==0)cout <<"\n";}cout <<"\nCPA攻击:\n";cout <<"最⼤相关:R"<< Max <<"="<< Rl[Max]; cout <<"\n正确密钥:";int bit[6];int temp1 = Max;for(int j =5; j >=0; j--){bit[j]= temp1 %2;temp1 = temp1 /2;}for(int j =0; j <6; j++){cout << bit[j];}Dpa();return0;}void Dpa(){//以2为界int Larr[20];int Harr[20];int Lc =0;int Hc =0;for(int i =0; i <20; i++){if(HWstd[i]<2){Larr[Lc]= i;Lc++;}else{Harr[Hc]= i;Hc++;}}for(int i =0; i <64; i++){int Htemp =0;int Ltemp =0;//HW⼩于2,对应累加for(int j=0; j < Lc; j++){Ltemp += Ptest[i][Larr[j]];}//HW⼤于2,对应累加for(int j =0; j < Hc; j++){Htemp += Ptest[i][Harr[j]];}DpaP[i][0]= Ltemp*1.0/Lc;DpaP[i][1]= Htemp*1.0/Hc;Deta[i]=abs(DpaP[i][0]- DpaP[i][1]);}cout <<"\nDPA攻击\n差分值:Deta0-63:\n";for(int i =0; i <64; i++){cout <<setw(10)<< Deta[i]<<" ";if((i +1)%6==0){cout <<"\n";}}double temp =0.0;for(int i =0; i <64; i++){if(Deta[i]> temp){DpaMax= i;temp = Deta[i];}}cout <<"\n最⼤差分值:Deta"<<DpaMax<<"="<< Deta[DpaMax];cout <<"\n正确密钥:";int bit[6];int temp1 =DpaMax;for(int j =5; j >=0; j--){bit[j]= temp1 %2;temp1 = temp1 /2;}for(int j =0; j <6; j++){cout << bit[j];}}int Sboxout(int num, int Nkey,int i){int HW=0;int P=0;int h = num &(0b00100000);h = h >>4;int l = num &(0b00000001);int m1 = num &(0b00000010);m1 = m1 >>1;int m2 = num &(0b00000100);m2 = m2 >>1;int m3 = num &(0b00001000);m3 = m3 >>1;int m4 = num &(0b00010000);m4 = m4 >>1;int y = l + h;int x = m1 + m2 + m3 + m4;//int bit[4];int Snum = S_Box1[y][x];Sout[Nkey][i]= Snum;HWw[Nkey][i]=HWFun(Snum);Ptest[Nkey][i]= HWw[Nkey][i]*5;Ptest[Nkey][i]= HWw[Nkey][i]*5;//cout << " " << HWw[Nkey][i];P= HWw[Nkey][i]*5;if(Nkey ==43){Pstd[i]=P;HWstd[i]= HWw[Nkey][i];}return Snum;}int HWFun(int num){int count =0;int bit;for(int i =3; i >=0; i--){bit = num %2;if(bit ==1)count++;num = num /2;};return count;}double meanNum(int n, int num[]){double total=0.0;for(int i =0; i < n; i++){total = total + num[i];}return total / n;}double Corr(int n, int Pstd[], int Ptest[]){//int E_Pstd;double fenzi=0.0;double PstdMean =meanNum(n, Pstd);double PtestdMean =meanNum(n, Ptest);double fenmu1 =0.0;double fenmu2 =0.0;double corr =0.0;for(int i =0; i < n; i++){fenzi +=(Pstd[i]- PstdMean)*(Ptest[i]- PtestdMean);fenmu2 +=(Ptest[i]- PtestdMean)*(Ptest[i]- PtestdMean);fenmu1 +=(Pstd[i]- PstdMean)*(Pstd[i]- PstdMean);}corr = fenzi /(sqrt(fenmu1)*sqrt(fenmu2));return corr;}结束主要梳理了做过的有关DPA和CPA攻击的⼀个简单实例,真正的硬件安全检测和测信道攻击要复杂的多,安全世界⽆奇不有,上硬件安全设计与检测这门课,开拓了安全领域的研究视野。
ctf关于des的例题

ctf关于des的例题CTF(Capture The Flag)比赛中,关于DES(DataEncryption Standard)的例题可以涉及DES算法的原理、加密过程、解密过程、弱点以及相关攻击等方面。
下面我将从多个角度来回答你关于CTF中DES的例题。
首先,我们来了解DES算法的原理。
DES是一种对称加密算法,使用相同的密钥进行加密和解密。
它将64位的明文分成两个32位的部分,然后经过一系列的置换、替代和移位操作,最终得到64位的密文。
DES算法中使用的密钥长度为56位,但实际上只有48位用于加密过程,其余位用于奇偶校验。
接下来,我们来看一个例题中可能涉及的加密过程。
假设我们有一个明文为"Hello, DES!",密钥为"SecretKey"。
首先,我们需要将明文转换为64位的二进制表示。
然后,通过初始置换(IP)操作将明文进行重排。
接着,将明文分为左右两个32位的部分。
接下来,进行16轮的迭代加密过程,每轮使用不同的子密钥。
最后,进行逆初始置换(IP-1)操作,得到最终的64位密文。
在解密过程中,需要使用相同的密钥和相反的操作来逆向进行。
先进行初始置换(IP)操作,然后进行16轮的逆向迭代加密过程,最后进行逆初始置换(IP-1)操作,得到明文。
然而,DES算法也存在一些弱点,这可能是CTF中的重点之一。
例如,DES的密钥空间相对较小,只有2^56种可能性,因此可以通过穷举攻击来破解。
此外,由于DES算法中的S盒操作较为简单,存在差分攻击和线性攻击等攻击手段。
在CTF中,还可能涉及到DES算法的相关攻击。
例如,差分攻击是一种基于对大量已知明文和密文对的分析来获取密钥的攻击方法。
线性攻击则是通过线性逼近来获取密钥的攻击方法。
还有其他一些攻击方法,如巴比伦攻击、差分线性攻击等。
综上所述,关于CTF中DES的例题,可能涉及DES算法的原理、加密过程、解密过程、弱点以及相关攻击等方面。
des中s盒的作用

des中s盒的作用S盒是对称密码中的一个重要组件,它在加密过程中起到了关键的作用。
本文将围绕S盒的作用展开详细阐述,并介绍其在密码学中的重要性。
S盒,全称Substitution Box,是一种用于将输入替换为输出的非线性转换函数。
在对称加密算法中,S盒通常用于替代明文中的一组比特,以增强密码的混淆性和抗攻击能力。
S盒主要具有以下几个作用:1. 混淆性:S盒的输入和输出具有随机性质,通过将明文中的比特替换为S盒中的对应输出,可以增加密文的随机性和不可预测性,从而增强密码的安全性。
2. 抗差分攻击能力:差分攻击是一种常见的密码分析方法,通过观察明文和密文比特之间的差异来破解密码。
S盒的非线性特性使得差分攻击变得困难,提高了密码系统的安全性。
3. 抗线性攻击能力:线性攻击是另一种常见的密码分析方法,通过线性逼近来推断出密码系统的密钥。
S盒的非线性特性使得线性攻击变得困难,增加了密码系统的抵抗力。
4. 增加密钥空间:S盒可以根据不同的密钥生成不同的替换规则,从而增加了密码系统的密钥空间。
密钥空间的增加可以提高密码系统的安全性,增加密码破解的难度。
5. 提高密码系统的扩散性:扩散性是指明文中的任何一位改变都会导致密文中的大部分位发生变化。
S盒通过将输入替换为输出,可以使明文的每一位都对应密文中的多个位,从而增加了密码系统的扩散性。
需要注意的是,S盒的设计需要遵循一定的原则,以确保其在密码系统中发挥良好的作用。
这些原则包括:1. 非线性性:S盒应具有良好的非线性特性,以增加密码系统的安全性。
2. 均匀性:S盒中的每个输出值应该尽可能地均匀分布,以防止攻击者通过统计分析等方法破解密码。
3. 抗差分和线性攻击:S盒应具有较高的抗差分和线性攻击能力,以增加密码系统的安全性。
4. 可逆性:S盒的设计应该是可逆的,以便在解密过程中能够正确地将密文转换回明文。
S盒作为对称密码中的重要组件,通过替换明文中的比特来增强密码的混淆性和抵抗攻击的能力。
差分攻击原理

差分攻击原理密码学的发展使得网络和网络交互变得更加安全,并通过加密技术来保护用户的隐私和信息安全。
但是,经常出现新的攻击方式使得加密技术变得不够安全。
差分攻击作为一种比较新的攻击方式,使得密码学要面对新的挑战。
本文将深入探讨差分攻击原理。
差分攻击被广泛用于分组密码,它旨在寻找分析密码算法的弱点。
差分攻击利用密码算法中数据之间的差异来构造密钥。
攻击者通过构造特定的明文来观察密文的变化,然后利用差分相等来分析密钥。
在这种攻击中,攻击者从密文和明文之间的差异中提取有关密钥的信息。
分组密码算法将明文数据分成块,并且每个数据块都被转换为密文数据块。
差分攻击者将两个密文数据块之间的差异与与任意两个相应的明文数据块之间的差异进行比较。
攻击者会从中得到一个统计信息,他们将利用统计信息来构造密钥。
攻击者会继续修改明文数据,检查由此产生的密文之间的差异,并将其与他们之前收集的统计信息进行比较。
在分析了足够的数据之后,差分攻击者将能够识别密钥的部分或全部。
差分攻击的成功取决于攻击者的观察和分析能力。
他们必须能够分析密码算法的明文/密文对之间的差异,并从中提取有关密钥的信息。
差分攻击者还需要能够构造明文/密文对,并通过比较这些对之间的差异来获取有关密钥的更多信息。
攻击者可以使用计算机程序来执行攻击,并尝试找到最有效的攻击方式。
虽然差分攻击在密码学中被广泛讨论,但仍有一些方法可以防御这种类型的攻击。
一种常见的防御方法是使用差分难度。
差分难度是一个与密码算法相关的值,用于衡量针对该算法执行差分攻击的难度。
给定差分难度值,分析算法的难度将会增加,从而减少攻击者成功攻击密码的可能性。
另一种常见的防御方法是增加轮数。
当使用轮数较多的密码算法时,攻击者需要处理更多的密文对和明文对,从而使差分攻击变得更加困难。
总之,差分攻击是一种针对密码算法的常见攻击方式。
通过观察密文和明文之间的差异以及构建明文/密文对,攻击者可以从中提取有关密钥的信息。
DES算法差分电磁攻击及区分函数的选择

明 重 量 全 为 0对 应 的 电 磁 信 息 泄 露 曲 线 映 射 到 中 , 将 中 间 值 各 个 比 特 位 的 汉 明 重 量 全 为 1对 应 的 电 磁 信 息泄 露 曲线 映射 到 S 中 ,剩 下 的 电磁 信 息 泄 露 曲 线 映 射到 S 。 G — D E MA 区 分 函 数 通 过 检 测 中 间 值 各 比 特 位 的 汉 明重 量 之 和与 阈值 的大小 关 系对 电磁 泄露 山 I 线 进 行 分组 ,当中 间值 的各 比特位 汉 明重 量之 和 小 丁 n / 2时 , 将 对 应 电 磁 信 息 泄 露 曲 线 映 射 到 中 ; 大于 t t / 2 , 将 电磁 信 息泄露 曲线映 射 到 S . 中 ;剩 下 的 电 磁 信 息 f I 1 f 露
别分 到集合 S 。 和集 合 S 。 : S l i = f I H[ D( G, ) =1 , 1 ≤i ≤N} 正 确猜 测 密 钥 对应 的分 组 正 确 , 差值 最 大 ; 而 错 误 密钥 对 应 的差 值很 小 ; 且 非该 中间值 出现 的 时刻 , 可 认 为是 随机 数 , 差 值 近 似 为 0。因 此 , 根 据 差 分 曲 线 上 出现
Ap p l i c a t i o n o f I n t e gr a t e d Ci r c u i t s
2 DE MA 的 区 分 函数 构 造
D E MA是 采 用 均 值 差 法 对 密 码 芯 片 运 行 过 程 中 的 电
多 比特 D E MA 攻 击 的 区 分 函 数 构 造 方 法 有 以 下 两
比 特 的 汉 明 重 量 是 0还 是 1 , 将 相 对 应 的 功 耗 曲 线 分
S “ = { I H[ D( C , ) 6 】 = 0, 1 ≤i ≤N}
密码分析学习笔记-差分分析(1)

密码分析学习笔记-差分分析(1)差分分析和线性分析是分组密码算法最基本和最重要的分析⽅法,同时,在设计分组密码算法时,密码算法抵抗差分分析和线性分析的能⼒也是密码设计者重点关注的因素之⼀。
希望能通过本次学习理清楚差分分析的原理^-^⼀、分组密码常见分析⽅法的总体思路:1.攻击思想:区分攻击:经过加密之后相同的明⽂,⼀定会对应相同的密⽂。
发现不随机特征,将密码算法和伪随机函数区分开。
构造区分器。
分别征服攻击(Divide-and-Conquer Attack):利⽤区分器降低搜索空间⼤⼩,提⾼求解效率。
将搜索或求解空间进⾏分割,将必须整体搜索的⼤空间分割为局部可搜索的⼩空间。
2.常见的攻击:差分分析:利⽤⾼概率的差分路线构造区分器。
线性分析:利⽤⾼偏差的线性逼近式构造去的区分器。
不可能差分分析:利⽤概率为0的差分特征。
飞去来器和矩形攻击:同时利⽤两条⾼概率的差分路线。
截断差分:同时利⽤满⾜特定条件的差分概率合集。
零相关攻击、滑动攻击……⼆、差分攻击技术:1.差分分析:1990年Eli Biham与Adi Shamir在密码学顶级会议美密会Crypto公开发表对DES的差分分析。
256→247个选择明⽂,237.2次加密运算,O(1)的内存。
2.差分分析的基本概念:差分:设X和X*是长度为n的⼆进制⽐特串,则ΔX=X⊕X*称为X和X*的差分,其中⊕为按⽐特的异或运算。
差分的定义并不唯⼀:例如:若加法含有模加运算,常采⽤模加差分ΔX=X⊕X*mod2n。
差分的⽬的:刻画差异性(即不同⽐特的个数)。
例:若X=1001,X*=1011,则X⊕X*=0010,X+X*=0100。
三、差分的概率传播特性:1.异或密钥差分值不变:设K i为第i轮的轮密钥,则(X⊕K i)⊕(X*⊕K i)= X⊕X*=ΔX2.过线性变化差分值确定:设P为线性变换,则P(X)⊕P(X*)=P(X⊕X*)=P(ΔX)例如:P(X)= P(X0||X1||X2||X3)=X3||X1||X0||X2P(X)⊕P(X*)= P(X0||X1||X2||X3)⊕P(X0*||X1*||X2*||X3*)=ΔX3||ΔX1||ΔX0||ΔX2=P(ΔX3||ΔX1||ΔX0||ΔX2)=P(ΔX)3.⾮线性变换差分值不确定:设S为⾮线性变换,⼀般情况下,S(X)⊕S(X*)≠S(ΔX)例:设第⼀个S-盒S1的输⼊异或为110100,那么,Δ(110100)={(000000,110100),(000001,110101),…,(111111,001011)}。
ctf中des的题

ctf中des的题DES是一种对称加密算法,它在CTF竞赛中常常被用作题目的一部分。
下面将介绍一些关于CTF中DES题目的基本知识以及解题思路。
## DES简介DES(Data Encryption Standard)是一种对称密钥加密算法,它是美国国家标准局(NIST)于1977年发布的算法。
DES的密钥长度为56位,明文长度为64位。
DES算法由一系列置换、替代和变换操作组成,可以实现高强度的数据加密。
在CTF中,DES题目通常以加密算法的参数和密文给出,要求我们还原出明文或找到加密算法中的弱点。
解题的关键在于理解DES的工作原理和算法流程。
## DES算法流程DES算法的加密过程主要分为以下几个步骤:1. 初始置换:将输入的64位明文按照指定的置换表进行置换,生成置换后的数据块。
2. 迭代运算:将置换后的数据块分为左右两半,迭代运算一共进行16轮。
每轮的运算过程包括:对右半部分进行扩展置换、与轮密钥进行异或、通过S盒替换、进行P盒置换和左右半部分的交换。
3. 逆初始置换:将16轮迭代运算后的数据块再次按照指定的逆置换表进行置换,得到最终的加密结果。
解密过程与加密过程类似,只是在迭代运算中使用的密钥顺序相反。
## DES的弱点尽管DES在发布时被认为是非常安全的加密算法,但随着计算机技术的发展,其密钥长度逐渐显得不够安全。
DES的密钥长度只有56位,尽管每轮迭代中使用的轮密钥是由56位密钥生成的,但由于密钥空间的限制,理论上存在暴力破解攻击的可能。
另外,DES的其他一些弱点包括:1. 已知明文攻击:攻击者拥有一些已知明文和对应的密文对,利用这些信息可以在不知道密钥的情况下推导出其他密文的密钥。
2. 密钥编排:DES加密算法中使用的轮密钥是通过56位密钥进行生成的,如果密钥在生成过程中存在弱点,那么整个加密过程就会受到影响。
3. 无法抵抗差分分析攻击:差分分析攻击是一种利用DES算法的性质和特点进行破解的攻击方法,DES算法对差分分析攻击并不具备足够的抵抗能力。
智能卡芯片中TDES密码电路的差分功耗攻击

关键 词 :智 能卡 芯 片 ; 关性 分析 ; 耗模 型 ;三 重加 密标 准 ;差分 功耗攻 击 相 功 中图分 类号 :T 9 8 N 1 文献标 志码 :A 文章 编号 :10 . 6 5 2 1 ) 3 0 2 . 3 0 1 39 ( 0 2 0 . 9 7 0
d i1 .9 9 j i n 10 -6 5 2 1 .3 0 5 o:0 3 6 /.s . 0 13 9 .0 2 0 . 3 s
s hsa d a ee t me ye s n p lt .Wi h mmi g d sa c d 1 t e lwe t u e f r c sn e e o s c e s u n r xr e l a y t ma i ua e o t t e Ha h n itn emo e . h o s mb ro a e e d d t u c s. n t f l e e l h a h r u d k y i a p o i tl 0 o rta e .Me n h l ,t eDP t c so D n u l r v a e e c o n e s p r xmaey 3 5 0 p we r c s y t aw i e h A at k n T ES a d DES a es me a r a
(. colfTl o u i t n n i eig XiinU i rt, i0 10 1 hn 2 B i gEe rnc c ne Tcnl yIsit, 1 Sh o o e cmm nc i sE gn r , da nv sy X ’n7 0 7 ,C i e ao e n ei a; . e n lt iSi c & ehoo tue co e g nt
i lme tt n mp e na i .E p r n a e u t h w a rt e smp e p w rc n u t n mo es o r lt n at c sp o i e g o e o x ei me t l s l s o t t o h i l o e o s mp i d l ,c reai t k r v d o d r— r s h f o o a
DES算法DFA攻击的差分差错位置判别方法

D S 法 D A攻击 的差 分差错位置判 别方法 E 算 F
王信敏 张 涛
Ⅵ NG n n, Xi mi ZHANG a To
中国石油大学 ( 华东 )经济管理学 院 , 山东 东营 276 50 1
Co lg f E o o c Ad n s a i n, i a Un v r i o to e m , n y n S a d n 5 0 1 C i a l e o c n mi mi it to Ch n i e st f Per lu Do g i g, h n o g 2 7 6 , h n e r y
最后两轮 的差分差错对 DE 算 法进 行了有效的 DF S A攻击 , 】 继 而 出现 了针 对其 他 分组 算 法 的 D A攻 击 , AE 、DE F 如 S I At
该算 法采 用 5 比特 密钥 ,4 6 6 比特 的分组长 度 , 对数 据进行 1 6
轮 的加密 。每轮变 换规则为 :
等 。D S 法的 D A攻击对 于差错 出现在最 后 2 的情 况只 E算 F 轮 需要几个选择密文即可成功实现攻击- z 。而对于差错出现在 中间轮数 , 该攻击也有很 高的成功率 。 D A攻击 的前提 是能够 准确 地选 择差错 的位 置 , 是成 F 这
D A 即差 分差 错 攻击 , D S F, 是 E 算法 的 一种 有 效攻 击 方 法 , 法通过在 D S 法最后几轮 产生一 个 1 该方 E算 比特 的差错 , 获得 同一个 明文 的两 个不 同密文 输 出 , 后使 用差 分分析 的 然 方法 来获得 第 1个 子密 钥 。该方 法首先 由B nh D m l 和 6 oe 、 e io l Lp n 出 用 于攻 击公 钥 算法 , io 提 , t 后来 Bhm和 Sa i 用 i a hm r 使
差分功耗分析单片机DES加密实现的旁路攻击

明, 这种将密码算法与算法 的具 体实现相结 合进行分析攻 击
的方法在许多场合下更 为有效 。
公 开信 道
密 文
-
i… i -
I器 T 加 密 上 -密 E lT I器 解D
加 密 密钥 l译 l I 者 破 解置 密钥 密
摘 要 在研 究 D A的原 理和方 法、 析 C S芯 片工作 时功率消耗 原理的 基础上 , P 分 M0 完成 了对 DE S加 密算法 的
DP A攻击的仿 真实现 , 并对运行在 AT 9 5 8 C 2单片机 上的 D S加 密程序进行 D A 攻击 实验 , 1 个 明文样本 的条 E P 在 O 件 下, 成功获得 了 DE S第 1 轮加 密的 4 位 密钥 。在验证 仿真方 法正确性的 同时ቤተ መጻሕፍቲ ባይዱ一 步证 明 了 D S加 密 实现 面对 6 8 E
DP 攻 击 的脆 弱性 。 A
关键词
旁路 分 析 ( 信 道 分 析 ) 差 分功 耗 分析 , S 侧 , DE
S d -h n e At c so i ge c i S I lme t t n Usn f e e t lP we ay i i ec a n l t k n S n l-h p DE mp e n a i i g Dif r n i o rAn lss a o a
到的秘密参量 。通常根据对 功率消耗 的不 同分析方 法 , c Ko—
hr e 等人介绍 了简单 功 耗分 析 (i l p we aayi, s e o r nls 简称 mp s S A) 差 分 功 耗 分 析 ( iee t lp w ra ls , 称 P 和 df rni o e n yi 简 f a a s DP 。T .Mesre[ B e Or A) .S seg s 和 dnB e[ 描述 了利用功 。
面向DES加密算法的差分功耗分析攻击方法

Dif r n i l we tc ay i o fe e ta Po r Ata k An l ssf rDES Co eAl o ih d g rt m
S i a Z UN Ha. o . HAO Qin H n 1i t a g , E Xu . a (. e to n n iern , d ac n iern olg , hj z u n 5 0 3 Chn ; 1 D p. f Gu s gn eig Or n n eE gn eigC l e S ia h a g0 0 0 , ia E e i 2 De to o ue n ie r g O d a c n iern l g , hj z u n 5 0 3 Chn ) . p. f mp tr gn ei , r n n eE gn eigCol e S ia h a g0 0 0 , ia C E n e i A s atBae nsd h n e atc s h oya dDE o eag r h tepoet ar s u t o ec luaig b t c: sdo iec a n l t k e r n Sc d loi m,h rjc r e t i c d ac lt r a t t c i o N me n
smpig t p t it u u i n ac lts i v rg o rv le a l i s o. no 2 s b nt a d c luae t a ea e p we au .Me n hl, h rjc o sre eh r n me s s a w i te poet b ev swh te e e ie t ek p era a yp it o edfee t l o rc ret d ew eh rtepe iu ert e su t ni vd n a sa p a t n ons ft i rni we u v oj g h te h rvo ssce k y asmpi s p h f ap u o
des加密算法差分能量分析的研究

des加密算法差分能量分析的研究DES(DataEncryptionStandard)代表数据加密标准,是一种应用得非常广泛的加密算法。
研究这种加密算法的能量泄漏问题非常重要。
本论文旨在探讨DES加密算法中的差分能量分析(Differential Power Analysis, DPA。
第一部分介绍了DES加密算法,主要包括DES历史、DES结构、DES如何工作等内容。
DES是一种块密码,它使用 64 位明文组成的块进行加密,然后输出 64 位的密文,主要由四个基本的步骤组成:初始变换、16迭代运算、结束变换以及密钥变换。
其次,介绍了DES法差分能量分析( Differential Power Analysis,DPA,它是攻击 DES密算法中潜在安全漏洞的一种有效方法。
DPA 代表通过监控计算机系统的电路功率变化来破解 DES密算法的一种攻击方法。
这种“差分”的分析技术的基本思想是利用加密设备的电路功耗变化,以及不同明文和不同密钥的加密出的密文的差分来得到原始的密钥。
紧接着介绍了DES加密算法的差分能量分析(DPA)的一些分析技术。
DPA析方法主要包括差分时域分析、差分频率域分析和差分空间域分析,它们都可以用来破解 DES密算法。
最后,介绍了如何防止DES加密算法的DPA攻击,并给出了一些实例。
这些防御技术主要有:混淆和隐藏功耗水平、使用加密算法的可靠实现,以及使用混淆和抵御 DPA硬件、软件和协议技术。
本文讨论了 DES密算法中的 DPA击技术,并给出了解决这一问题的一些方法。
未来研究可以通过改进分析方法和技术来更好地检测和防御这类攻击。
总之,本文详细论述了DES加密算法中的DPA攻击及防御技术,其对密码安全和网络安全有重要意义。
希望本文能够给读者带来帮助,为今后的研究奠定基础。
DES的描述

关于DES1、DES的描述为了建立适用于计算机系统的商用密码,美国商业部的国家标准局NBS于1973年5月和1974年8月两次发布通告,向社会征求密码算法。
在征得的算法中,由IBM公司提出的算法lucifer中选。
1975年3月,NBS向社会公布了此算法,以求得公众的评论。
于1976年11月被美国政府采用,DES随后被美国国家标准局和美国国家标准协会(American National Standard Institute,ANSI) 承认。
1977年1月以数据加密标准DES(Data Encryption Standard)的名称正式向社会公布。
随着攻击技术的发展,DES本身又有发展,如衍生出可抗差分分析攻击的变形DES 以及密钥长度为128比特的三重DES等。
2000年1月19日,由电子边疆基金会组织研制的25万美元的DES解密机以22.5小时的战绩,成功地破解了DES加密算法。
DES已逐渐完成了它的历史使命。
DES是一个分组加密算法,它以64位为分组对数据加密。
64位一组的明文从算法的一端输入,64位的密文从另一段输出。
它是一个对称算法:加密和解密用的是同一个算法。
密钥通常表示为64位的数,但每个第8位都用作奇偶校验,可以忽略,所以密钥长度为56位。
密钥可以是任意的56位的数,且可在任意的时候改变。
DES算法只不过是加密的两个基本技术——混乱和扩散的组合,即先代替后置换,它基于密钥作用于明文,这是一轮(round),DES在明文分组上实施16轮相同的组合技术。
如下图所示:2、算法概要DES对64位明文分组进行操作。
通过一个初始置换,将明文分组分成左半部分和右半部分,各32位长。
然后进行16轮完全相同的运算,这些运算被称为函数f,在运算过程中数据与密钥结合。
经过16轮后,左、右半部分合在一起经过一个末置换(初始置换的逆置换),算法就完成了。
在每一轮中,密钥位移位,然后再从密钥的56位中选出48位。
DES差分功耗攻击仿真分析

轮中 8个 s盒加密运算单独进行功耗采集, 从而减少了s盒之间的相互影响. 然后, 针对功耗攻击成功率不高的 问 题, 对第 4个 s盒内部加密运算的相关性进行了假设和仿真分析. 最后, 通过实验结果验证了仿真分析的正确
性.
关键宇 :D E S ; D P A; S盒 ; 旁路功耗 攻击
中图分类 号: T P 2 7 3 文献标识码 : A
Th e An a l y s i s o f DP A At t a c k f o r DES
YAN Fe i, W ANG Xi a o - do ng, XU Hu a - r o ng
( S c h o o l o f Co mp u t e r a n d I n f o r ma t i o n E n g i n e e r i n g , Xi a me n Un i v e r s i t y o f t e c h n o l o g y , Xi a me n , F u j i a n 3 6 1 0 2 mp l e me n t a t i o n o f DPA i s a l s o p r o p o s e d ,i n wh i c h t h e p o we r o f e i g h t S - b o x e s i n 1 6 e n c r y p t i o n r o u n d s i s
2 0 1 3年第 2划 ( 总第 8 0期 )
’
漳州师范学院学报 ( 自然科 学版)
No . 2 . 2 0 1 3年
Ge n e r a l No . 8 0
J o u r na l o f Zh a n g z h o u No r ma l Un i v e r s i t y( Na t . S c i . )
破解密码学的算法与安全性

破解密码学的算法与安全性密码学是一门涉及信息保护和密码破解技术的学科,它在现代社会中起到了至关重要的作用。
随着科技的进步和网络的普及,密码学的算法与安全性也变得越来越重要。
本文将讨论密码学的算法和安全性,并探究破解密码学的方法。
一、密码学算法的种类密码学算法可以分为对称加密算法和非对称加密算法两大类。
1. 对称加密算法对称加密算法是最常见的密码学算法之一,它使用相同的密钥对数据进行加密和解密。
这种算法通常具有高效、速度快的特点,但密钥的传输和管理相对较困难。
常见的对称加密算法有DES(数据加密标准)、AES(高级加密标准)等。
2. 非对称加密算法非对称加密算法使用两个不同的密钥,分别用于加密和解密。
公钥用于加密数据,而私钥用于解密数据。
这种算法的优势是密钥的传输和管理相对容易,但加密和解密的速度较慢。
常见的非对称加密算法有RSA算法、椭圆曲线加密算法等。
二、密码学算法的安全性密码学算法的安全性是衡量一个算法是否可靠的重要指标。
一个安全的密码学算法应具备以下几个特点:1. 密钥长度密钥长度是衡量密码学算法安全性的重要因素之一。
密钥越长,破解难度越大。
通常,一个强大的密码学算法应该对使用较短密钥的攻击有足够的抵抗能力。
2. 对抗攻击一个安全的密码学算法应该能够有效对抗各种攻击手段,如穷举攻击、字典攻击等。
它应该能够保证即便攻击者拥有大量的加密文本和密钥,也无法推导出所需的明文。
3. 随机性密码学算法应具备良好的随机性。
一个可靠的算法应能够产生随机的密钥和密码文本,从而增加破解的难度。
4. 可扩展性密码学算法应具备可扩展性,能够应对不断提升的计算能力和新的攻击手段。
它应该有足够的弹性来应对各种变化。
三、破解密码学的方法破解密码学算法是密码学学科的重要研究内容之一。
以下是几种常见的破解密码学的方法:1. 穷举攻击穷举攻击是一种简单而直接的破解方法,它通过尝试所有可能的密钥组合来解密数据。
然而,这种方法的时间复杂度较高,只适用于密钥长度较短的情况。
des差分攻击
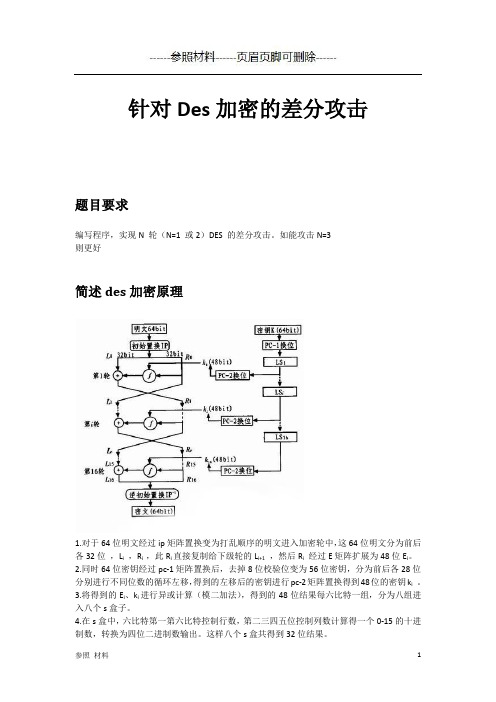
针对Des加密的差分攻击题目要求编写程序,实现N 轮(N=1 或2)DES 的差分攻击。
如能攻击N=3则更好简述des加密原理1.对于64位明文经过ip矩阵置换变为打乱顺序的明文进入加密轮中,这64位明文分为前后各32位,L i,R i ,此R i直接复制给下级轮的L i+1,然后R i经过E矩阵扩展为48位E i。
2.同时64位密钥经过pc-1矩阵置换后,去掉8位校验位变为56位密钥,分为前后各28位分别进行不同位数的循环左移,得到的左移后的密钥进行pc-2矩阵置换得到48位的密钥k i。
3.将得到的E i、k i进行异或计算(模二加法),得到的48位结果每六比特一组,分为八组进入八个s盒子。
4.在s盒中,六比特第一第六比特控制行数,第二三四五位控制列数计算得一个0-15的十进制数,转换为四位二进制数输出。
这样八个s盒共得到32位结果。
5.s 盒输出结果与L i 异或,再经过另一P 置换得到R i+1。
此L i+1、R i+1也就是一轮加密结果,如果继续进行加密可以按照上述方法重复进行。
6.最终得到的结果还要经过初始置换的逆置换作用,得到密文。
Des 解密Des 解密算法和加密算法使用相同的算法过程,不同之处在于解密时要把子密钥使用的顺序和加密时相反。
Des 差分攻击的理论与实现差分攻击理论依据:上文中des 加密原理中简略但全面地介绍了加密过程,可以看到其中主要起作用的算法有:矩阵置换、扩展、左移、异或、左右互换、s 盒作用 。
其中对攻击者来说最麻烦的要说s 盒一步,破解des 体系关键在s 盒。
乍一看六位输入与四位输出貌似没什么关系。
但事实上,对于同一个s 盒具有相同输入异或的所有输入六比特组的输出四比特异或值有一定规律。
具体些说,对于输入异或相同的明文对B ,B*仅有32组,而这32组输出异或却并不是均匀分布,而是仅分布在很少的几个四比特值中;也可以说具有相同输入异或且输出四比特异或也相同的六比特输入数量不多且分布不均匀。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
针对Des加密的差分攻击
题目要求
编写程序,实现N 轮(N=1 或2)DES 的差分攻击。
如能攻击N=3
则更好
简述des加密原理
1.对于64位明文经过ip矩阵置换变为打乱顺序的明文进入加密轮中,这64位明文分为前后各32位,L i,R i ,此R i直接复制给下级轮的L i+1,然后R i经过E矩阵扩展为48位E i。
2.同时64位密钥经过pc-1矩阵置换后,去掉8位校验位变为56位密钥,分为前后各28位分别进行不同位数的循环左移,得到的左移后的密钥进行pc-2矩阵置换得到48位的密钥k i。
3.将得到的E i、k i进行异或计算(模二加法),得到的48位结果每六比特一组,分为八组进入八个s盒子。
4.在s盒中,六比特第一第六比特控制行数,第二三四五位控制列数计算得一个0-15的十进制数,转换为四位二进制数输出。
这样八个s盒共得到32位结果。
5.s盒输出结果与L i异或,再经过另一P置换得到R i+1。
此L i+1、R i+1也就是一轮加密结果,如
果继续进行加密可以按照上述方法重复进行。
6.最终得到的结果还要经过初始置换的逆置换作用,得到密文。
Des 解密
Des 解密算法和加密算法使用相同的算法过程,不同之处在于解密时要把子密钥使用的顺序和加密时相反。
Des 差分攻击的理论与实现
差分攻击理论依据:
上文中des 加密原理中简略但全面地介绍了加密过程,可以看到其中主要起作用的算法有:矩阵置换、扩展、左移、异或、左右互换、s 盒作用 。
其中对攻击者来说最麻烦的要说s 盒一步,破解des 体系关键在s 盒。
乍一看六位输入与四位输出貌似没什么关系。
但事实上,对于同一个s 盒具有相同输入异或的所有输入六比特组的输出四比特异或值有一定规律。
具体些说,对于输入异或相同的明文对B ,B*仅有32组,而这32组输出异或却并不是均匀分布,而是仅分布在很少的几个四比特值中;也可以说具有相同输入异或且输出四比特异或也相同的六比特输入数量不多且分布不均匀。
正是这种输入输出输出异或间的不均匀性可以被攻击者利用并破解密钥。
此方法对可选择明文攻击尤为有效。
具体分析:
攻击时我们需要将要与子密钥异或运算的48位E i 和与其对应的s 盒32位输出 C i 。
在此笔者仅对一个s 盒进行讲解。
E i 中取前六位E ,C i 中取前四位C 。
设s 盒的直接六位输入为B ,k i 的前六位为 K 。
则有B E K ⊕= 另取一组明密文对 E* ,C* 他们的异或 E ’ ,C ’
即: *B*E K ⊕= S(*)*B C = *'E E E ⊕= *'C C C ⊕=*'C C C ⊕=
则对应'***'E E E E K E K B B B =⊕=⊕⊕⊕=⊕=
又由上文理论分析中'B 与'C 的关系,有多组明密文对时可以破解出子密钥K 。
给出一组确定的E ,E*,C ,C* 则对应的B ’ C ’已知,可对输入B 用000000-111111遍历一遍,找到满足两组异或的明文对,并分别和E 异或得到的六比特就是K 的可能值。
对此可设置一组计数器,对每一个可能的K 值在计数器上加一,多组明密文对下来则可以找到唯一最大数的准确K ,一般组数3组可以找到密钥,笔者在算法中设置了5组。
算法实现(1-3轮):
经过上述分析可知,若能选择性地得到与某轮和子密钥K 异或的E 并能得到该轮的输出C 则可以破解密钥。
对于一轮des ,R 0扩展后便得到E 加密的输出R 1,经过110()P R L -⊕得到C 。
则利用上述方法可以破解密钥。
对于二轮des ,已知明文对00L R ,00**L R 并可得到对应的两组密文22L R ,22**L R 。
2R 可表示为2112012(,)(,)R L f R K R f R K =⊕=⊕
同理2112012**(*,)*(*,)R L f R K R f R K =⊕=⊕
则有2001212'*(*,)(,)R R R f R K f R K =⊕⊕⊕
若取00*R R =
则R2’可简化为
21212'(*,)(,)
R f R K f R K =⊕
2(*)()'P C P C R ⊕=
则12*(')C C P R -⊕= 至此我们得到了第二轮s 盒输出异或
注意到32L R =,则利用扩展函数作用L 3则可得到输入32()()E L E R =,和32(*)(*)E L E R = 33'(*)()E E L E L =⊕
则我们又得到了第二轮s 盒输入异或,K 2则可以破解。
对于三轮des 情况稍稍有些复杂,设明文00L R ,00**L R 为两对明文,对应三轮输出的密文33L R ,33**L R 。
3R 可表示为:322312300123(,)(,)(,)(,)R L f R K R f R K L f R K f R K =⊕=⊕=⊕⊕ 同理300123**(*,)(*,)R L f R K f R K =⊕⊕
则3001012323'33*'*(*,)(,)(,)(*,)R R R L f R K f R K f R K f R K =⊕=⊕⊕⊕⊕
现在为方便攻击运算,选择明文使00*R R =
则有0101(*,)(,)000f R K f R K ⊕= 0
∴此时有302323'33*'*(,)(*,)R R R L f R K f R K =⊕=⊕⊕
由于3'R ,0'L 可由已知计算得到 现考虑2323(,)(*,)f R K f R K ⊕
又23(,)()f R K P C =,23(*,)(*)f R K P C =
∴30(*)()''P C P C R L ⊕=⊕ 由于P 置换已知
故1
30*('')'C C P R L C -⊕=⊕=
即至此我们已经在理论上能得到明文对的输出异或
另外,由于23R L =,23**R L =
因此使用扩展函数可轻易地得到,*E E 即3()E E L =,3*(*)E E L =
即我们又得到了与密文对应的两组E ,则按照上文所述可以破解子密钥。
获得完整密钥
然而此时我们若破解成功也仅得到了48位子密钥,原本使用的密钥却是56位。
剩下的8位我们可以进行穷举攻击,因为82256=,最多遍历256种可能密钥对计算机来说相当容易。
当然我们也可以推导出别的轮的输入输出异或表达式再次进行攻击,反置换后扩充原来的8位空缺得到完整的密钥,不过显然很费精力了…… 代码概况与输出结果
按照上文所述,其实在攻击中只要找到某轮输入输出异或即可破解,并且上文也分析了1、2、3轮攻击时最后一轮结果获取方法。
如此说来本质上1、2、3轮des 其实是一样的,所以笔者在自己的1轮攻击下稍作改动又增加了2、3轮攻击,不过代码并不完整,每轮加密没有写成函数,攻击也只到获取48位子密钥为止没有继续寻找剩下八位,不过都是细枝末节,对理解des 意义不大,笔者便没有花时间去编……
并且在编程序时候笔者还不知道有按位异或 “ ^ ”这个运算符存在 (T. T--) ,产生了很多麻烦……
代码共八百余行,注释不是很多……
实际攻击过程中没有进行最后的P -1转置运算。
编译环境
Visual C++ 2010 Express
程序功能
程序主要针对对des加密系统的攻击,没有给用户设置直接的文本加密功能。
开始输入8位字符(对应64位密钥),选择加密轮数(1、2、3),然后直接对加密系统进行更攻击。
首先随机生成一对符合轮数要求(如2、3轮要求
00*
R R
)的明文,对该明文按照所选轮数进行加密,得到两组对应密文,分别求取异或,按照上文方法构造计数器,发现符合条件的密钥可能值在对应的计数器上加1,此过程重复5次(3次以上基本就不会有问题了),在各个计数器中寻找计数为5的对应值,则此数对应的6位0、1比特就是子密钥的6比特。
结束后输出:
1用户输入的密钥(0、1)
2攻击该轮的当前子密钥
3攻击结束时计数器情况
4得到的子密钥
执行截图
示例程序密钥均设为d i a n a s u n
可以看到当前的子密钥和我们得到的密钥相同,攻击有效。
结果如图
结果……。
