课时教学计划表
七年级上册数学教学计划及进度表

七年级上册数学教学计划及进度表教学计划
单元一:数与代数
* 第一课:整数
* 第二课:数轴和绝对值
* 第三课:加法和减法运算
* 第四课:乘法和除法运算
* 第五课:集合与分类
单元二:比例与比例运算
* 第一课:比率与比例
* 第二课:比例的改变与稳定
* 第三课:比例的性质与应用
* 第四课:平均数与比例平均
单元三:空间与图形
* 第一课:平行和垂直线
* 第二课:直角与平行四边形
* 第三课:三角形的性质与分类
* 第四课:全等图形与相似图形
* 第五课:正方形、矩形与正三角形
单元四:方程与不等式
* 第一课:方程与解方程
* 第二课:两步方程
* 第三课:一元一次方程与一元二次方程
* 第四课:一元一次方程与一元二次方程的应用* 第五课:不等式及其应用
教学进度表
注意:以上进度表仅供参考,实际进度可能会因教学情况而有所不同。
人教版高中物理必修3课程目录与教学计划表

人教版高中物理必修3课程目录与教学计
划表
课程目录
1. 第一章光的直线传播
- 1.1 光的直线传播特性
- 1.2 光的反射
- 1.3 镜子中的像
- 1.4 光的折射
- 1.5 细棱镜光的偏转和分光
- 1.6 选择折射率规律
- 1.7 光的全反射
- 1.8 光的色散与衍射
- 1.9 眼镜和光仪器
2. 第二章光的波动性及其应用
- 2.1 单色光
- 2.2 光的干涉
- 2.3 论干涉条纹
- 2.4 干涉仪
- 2.5 光的衍射
- 2.6 论衍射条纹
- 2.7 哈密顿原理及其应用
- 2.8 光波的多普勒效应
- 2.9 光的偏振
3. 第三章量子物理学原理
- 3.1 稳定原子模型及能级图
- 3.2 光电效应
- 3.3 单色光的能量量子化
- 3.4 X射线的产生及应用
- 3.5 康普顿效应
- 3.6 德布罗意波
- 3.7 玻尔原子模型和玻尔频率条件- 3.8 原子能级和光谱
教学计划表
以上为人教版高中物理必修3课程目录与教学计划表,共计28个课时。
注:每个课时的重点、难点和教学时长仅供参考,根据实际教学情况有所调整。
2024年高一化学教学计划表(3篇)

2024年高一化学教学计划表一、总体目标本学期高一化学课程的教学目标是培养学生的科学素养,使学生掌握基本化学知识和实验技能,培养学生的观察能力、分析解决问题的能力、创新思维和实验能力。
二、教学内容及安排1. 第一单元:化学基本概念和知识- 第一课时:化学基本概念和化学计量- 第二课时:化学计量与元素周期表- 第三课时:化学键和分子式- 第四课时:物质的分类和性质- 第五课时:溶液的配制和计算- 第六课时:酸碱中和反应和盐的性质- 第七课时:氧化还原反应及氧化数的计算- 第八课时:弱电解质和氧化反应2. 第二单元:化学方程式与化学计算- 第九课时:化学方程式及其平衡- 第十课时:化学计算及化学实验方法- 第十一课时:气体的制备和性质- 第十二课时:溶液的性质与浓度计算- 第十三课时:质量守恒和能量转化3. 第三单元:物质的结构和性质- 第十四课时:物质的状态和热力学基本概念- 第十五课时:物质的结构和性质- 第十六课时:透明物体的颜色与结构- 第十七课时:固体和液体的性质及应用4. 第四单元:离子反应与电解质溶液- 第十八课时:电解质和非电解质的区别- 第十九课时:盐溶液和酸碱溶液的电离- 第二十课时:电解质溶液的电导现象- 第二十一课时:电解质溶液的导电性和电解质反应5. 第五单元:金属元素与化合物- 第二十二课时:常见金属元素的性质和应用- 第二十三课时:盐的合成和分析- 第二十四课时:金属的活泼性和金属反应- 第二十五课时:金属的腐蚀和防腐6. 第六单元:有机物的基本概念和基本性质- 第二十六课时:有机物的来源和分类- 第二十七课时:碳的有机化合物和它们的官能团- 第二十八课时:有机物的异构体和同分异构体- 第二十九课时:有机物的性质和化学反应三、教学方法和手段1. 理论教学:使用多媒体教学手段,配合讲解、实例分析和示范实验等方法,提高学生对知识的理解和应用能力。
2. 实验教学:通过开展化学实验,培养学生的实验技能和实验设计能力,加深学生对化学原理的理解。
苏教版小学五年级数学上册教学计划及课时安排进度表

苏教版小学五年级数学上册教学计划及课时安排进度表苏教版小学五年级数学上册教学计划及课时安排进度表一、全册教学分析1、教材名称、版本:义务教育课程标准实验教科书数学五年级(上)2、全册教材简析:本册教材共编排了十个单元的教学内容。
在“数与代数”领域教学负数的初步知识、小数的意义与性质、小数的四则计算,结合解决实际问题教学周期现象。
在“空间与图形”领域教学三角形、平行四边形、梯形的面积公式,公顷与平方千米这两个较大的计量土地面积的单位。
在“统计与概率”领域教学复式统计表和复式条形统计图。
联系上述三个领域的教学内容编排3次实践活动,教学一些大体的数学思想和方式。
教材离编排了一些“你知道吗”,介绍数学背景知识。
编排一些思考题,作为弹性的教学内容。
教材编写时,考虑了高年级数学教学的知识量比中年级大,学生的学习能力和自我意识比中年级强。
教材适当调整了编写体例,设置了例题、试一试、练一练、练习、整理与练习等栏目与版块。
3、教学目标:(1) 基础知识:①通过合理的分类,并借助直观,让学生体会正负数与0的关系。
②要借助直线上的点,使学生初步体会负数的大小。
③要让学生经历公式推导的完整进程。
④把握探索小数性质和小数大小比较方式的思路。
⑤联系整数加、减法的计算方式理解小数点对齐的道理。
⑥要鼓励学生画图列举寻觅规律。
⑦理解用计算器探索小数点移动规律的活动线索。
⑧通过丰硕多彩的活动让学生体会1公顷的实际大小。
⑨引导学生依据具体数量关系列出乘、除法算式,慢慢丰硕对乘除法运算的理解。
⑩要让学生感受复式统计表与复式条形统计图在描述数据方面的特点。
(2)大体技术:充分利用新旧知识间的联系,联系学生的生活实际,通过知识间的迁移、类推、比较、拓展,将新知识点与学生原有的知识体系联系起来进行教与学。
(3)情感态度和价值观:①使学生踊跃主动参与获取知识的全进程,让他们熟悉到数学的价值,生活中离不开数学,使他们喜欢数学,乐学数学。
②形成对数学的浓厚兴趣,树立学生自尊心和自信心,提高学生的彼此合作能力和人际交往能力。
一周教学计划安排表

周次:教学时间:执行教师:
本周要求:1、接触大南瓜,感知南瓜色、香、味、大小、轻重等特征。
2、愿意品尝各种口味的食物,尝试用简单的语句表达自己的感受。
3、愿意听故事,尝试练习故事中的对话.
星期
教学内容
星期一
星期二
星期三
星期四
星期五
上
午
(8:00-9:00)
晨间ห้องสมุดไป่ตู้动
音乐欣赏:欢乐儿歌
宝贝看图书
晨间谈话
音乐欣赏:欢乐儿歌
分享阅读
晨间谈话
音乐欣赏:欢乐儿歌
宝贝看图书
(9:00-9:30)
第一节教学活动
手指谣:《开汽车》
木脑袋
语言:《漂亮的房子》
健康:《玩靠垫》
科学:《复习南瓜丰收了》
(9:30-10:30)
室内外活动
早操[花园活动]
早操[花园活动]
早操[花园活动]
早操[花园活动]
早操[花园活动]
感觉统合训练
沙盘游戏
感觉统合训练
(17:00-17:30)
晚餐及餐后整理
晚餐及餐后整理
晚餐及餐后整理
晚餐及餐后整理
晚餐及餐后整理
(10:30-11:00)
第二节教学活动
阅读分享
音乐:《运南瓜1》
趣味英语:My Body 1
音乐:《运南瓜2》
趣味英语: My Body2
餐前故事欣赏
《妈妈的吻》
《11只猫做苦工》
《小动物的家》
《妈妈的吻》
《11只猫做苦工》
下
午
(15:00-16:40)
第三节教学活动
社会:《和南瓜一起玩》
美术:《给南瓜穿新衣》
最新小学五年级数学上册教学计划及课时安排进度表

最新小学五年级数学上册教学计划及课时安排进度表最新小学五年级数学上册教学计划及课时安排进度表一、全册教学分析1、教材名称、版本:义务教育课程标准实验教科书数学五年级(上)2、全册教材简析:本册教材共编排了十个单元的教学内容。
在“数与代数”领域教学负数的初步知识、小数的意义与性质、小数的四则计算,结合解决实际问题教学周期现象。
在“空间与图形”领域教学三角形、平行四边形、梯形的面积公式,公顷与平方千米这两个较大的计量土地面积的单位。
在“统计与概率”领域教学复式统计表和复式条形统计图。
联系上述三个领域的教学内容编排3次实践活动,教学一些基本的数学思想和方法。
教材离编排了一些“你知道吗”,介绍数学背景知识。
编排一些思考题,作为弹性的教学内容。
教材编写时,考虑了高年级数学教学的知识量比中年级大,学生的学习能力和自我意识比中年级强。
教材适当调整了编写体例,设置了例题、试一试、练一练、练习、整理与练习等栏目与版块。
3、教学目标:(1) 基础知识:①通过合理的分类,并借助直观,让学生体会正负数与0的关系。
②要借助直线上的点,使学生初步体会负数的大小。
③要让学生经历公式推导的完整过程。
④把握探索小数性质和小数大小比较方法的思路。
⑤联系整数加、减法的计算方法理解小数点对齐的道理。
⑥要鼓励学生画图列举寻找规律。
⑦理解用计算器探索小数点移动规律的活动线索。
⑧通过丰富多彩的活动让学生体会1公顷的实际大小。
⑨引导学生依据具体数量关系列出乘、除法算式,逐步丰富对乘除法运算的理解。
⑩要让学生感受复式统计表与复式条形统计图在描述数据方面的特点。
(2)基本技能:充分利用新旧知识间的联系,联系学生的生活实际,通过知识间的迁移、类推、比较、拓展,将新知识点与学生原有的知识体系联系起来进行教与学。
(3)情感态度和价值观:①使学生积极主动参与获取知识的全过程,让他们认识到数学的价值,生活中离不开数学,使他们喜欢数学,乐学数学。
②形成对数学的浓厚兴趣,树立学生自尊心和自信心,提高学生的相互合作能力和人际交往能力。
民工学校教学计划课时安排表

1
龙春良
15
农民工劳动权益
2013.7.17
1
赵强
16
农民工务工常识
2013.7.20
3
黄波
17
焊工、建筑电工、钢筋工、架子工、砼工、抹灰工、油漆工、砌筑工、木工技能培训
2013.8.10
3
袁正文
18
建设领域农民工安全生产生活
2013.8.15
2
熊艳玲
19
建筑施工现场安全文明与环境卫生
彭功兵
男
钢筋工
唐涌泉
男
塔吊
刘良雨
男
钢筋工
彭功刚
男
钢筋工
向云桂
男
钢筋工
彭南敏
男
钢筋工
文香国
男
钢筋工
王敬冬
男
木工
湖南省西湖建筑集团有限公司
农民工学校学员名单
农民工学校名称:富基世纪公园分校
姓名
性别
工种
姓名
性别
工种
林忠奎
男
钢筋工
王敬冬
男
木工
邱正想
男
钢筋工
涂泽文
男
木工
袁学春
男
钢筋工
刘日希
男
木工
袁学业
男
钢筋工
2013.10.22
3
黄波
35
焊工、建筑电工、钢筋工、架子工、砼工、抹灰工、油漆工、砌筑工、木工技能培训
2013.11.10
3
袁正文
36
建设领域农民工安全生产生活
2013.11.12
2
熊艳玲
37
建筑施工现场安全文明与环境卫生
2024~2025学年九年级上册教学计划及进度表「含答案」

2024~2025学年九年级上册教学计划及进度表一、教学目标1.知识与技能(1)学生能准确掌握本册书中的生字词,扩大词汇量,提高阅读理解和写作表达能力。
(2)学习并理解不同文体的特点,如记叙文、说明文、议论文、古诗文、小说、戏剧等,并能进行简单的创作。
(3)培养学生的文学鉴赏能力,能分析文本的主题、人物形象、语言特色等。
2.过程与方法(1)通过诵读、讨论、合作学习等方式,引导学生积极参与课堂,提高学习效率。
(2)利用多媒体、网络资源等现代化教学手段,丰富教学内容,激发学生兴趣。
(3)注重读写结合,通过阅读促进写作,通过写作深化阅读理解。
3.情感态度与价值观(1)激发学生对中华优秀传统文化的热爱,培养民族自豪感和文化自信。
(2)培养学生的审美情趣和人文素养,提高道德修养和审美水平。
(3)引导学生关注社会现实,培养批判性思维和独立思考能力。
二、教学内容安排第一单元:课时分配:4课时教学目标:了解新闻的基本特点和写作要求,掌握演讲的技巧和方法。
教学内容:《消息二则》、《首届诺贝尔奖颁发》、《“飞天”凌空》、《一着惊海天》等课文。
教学活动:新闻播报比赛、模拟演讲、小组讨论等。
第二单元:课时分配:5课时教学目标:感受游记散文的语言魅力和艺术特色,学习景物描写和情感表达的方法。
教学内容:《藤野先生》、《回忆我的母亲》、《列夫·托尔斯泰》、《美丽的颜色》等课文。
教学活动:美文诵读、写景片段写作、作者生平故事分享等。
第三单元:课时分配:6课时教学目标:理解诗词的意境和情感,掌握文言文的基本语法和阅读方法。
教学内容:《三峡》、《短歌行》、《野望》、《黄鹤楼》、《使至塞上》、《渡荆门送别》等古诗文。
教学活动:诗词朗诵会、文言文翻译接力、古诗词创作比赛等。
第四单元:课时分配:5课时教学目标:掌握说明文和议论文的写作方法和技巧,提高论证能力和逻辑思维能力。
教学内容:《背影》、《白杨礼赞》、《散文二篇》、《昆明的雨》等教学活动:说明文写作练习、议论文辩论赛、范文分析等。
教学计划表(模板)

教学重点:
教学难点:
4、提高教学质量的方法与措施:
1、重视
五、教学进度表(另表)
教务处意见:
教务主任签名:
月日
2016--2017学年度第一学期学科教学进度表
任教专业班级:科目:任课教师:
周次
日期
教学内容
课时
宜宾翠屏电子职业技术学校
课程教学计划表
2016 -2017学年度第一学期教学计划
专业班级:护理 _
科目:医用化学_
任课教师:张建军
2016年8月27日
学科教学计划
科目
医用化学
出版社
学期总课时
40周课时2Fra bibliotek1、学生的基本情况:
化学与医学息息相关,学生学习热情较高,教师应该正确引导,以期取得好的成绩,本学期负责护理专业两个班的医用化学的教学,两个班共有90人。这些学生基础参差不齐,大部分学生基础较差,需要教师付出更大的努力。要尽力做好每一个学生的工作,因材施教,使他们在各自原有的基础上不断发展进步。
2、教学目标:
1、理论知识联系学生的生活实际,使学生学以致用。激发学生学习化学的兴趣,培养学生科学的态度和科学的学习方法,培养学生的能力和创新精神,使学生初步了解化学及其和医学的关系和在医学中的作用。
2、重视基础知识和基本技能,注意激发学生的智力,培养学生的能力,使学生学习一些化学基本概念和基本技能,利于在今后的工作中使用,学习一些化学实验和化学计算的基本技能,了解化学在医学中的应用。
围棋教学计划表

围棋教学计划表围棋教学计划表围棋是我国最古老,也是最富有魅力的文化瑰宝,它虽然规则简单,变化确实很多。
在教学的时候要注意什么呢?下面小编为大家收集了围棋教学计划表,欢迎阅读!围棋教学计划表篇一:围棋教学计划一、入门篇(20课时)1. 围棋是什么样的运动2. 气是棋子的生命3. 提子4. 救活棋子5. 双方互打6. 禁入点7. 劫(单劫)8. 棋子的连接9. 虎10. 切断11. 打向一路12. 将对方棋子逼向自己的势力范围13. 断吃对方的棋子14. 证吃15. 双打吃16. 能救活吗17. 切断成立吗18. 枷吃19. 倒扑吃20. 吃接不归21. 被围棋子的死与活二、初级篇(20课时)1. 证与引证2. 紧气的方向3. 紧气时的注意事项4. 长气的方法5. 对杀6. 气数的计算7. 对杀时的脱先8. 紧气的对象9. 对杀中利用长气10. 利用扑来紧气11. 撞气12. 让对方不入气13. 有眼杀无眼14. 好形和坏形15. 把对方打成坏形16. 假眼和死活17. 扑掉对方的眼位18. 利用气紧破眼19. 直三、曲三是死棋20. 直四、曲四是活棋21. 方四、丁四是死棋22. 刀五、花五是死棋三、提高篇(25课时)1. 基本攻杀方法① 挖② 夹③ 立④ 点⑤ 飞封、软封(枷)⑥ 滚打⑦ 倒脱靴2. 连接与分断① 连接(补断方法、通连的方法)② 分断(扳断、尖断、挖断、搭断、冲断、扭断)3. 弃子① 自然弃子② 战术弃子4. 劫① 劫的种类② 劫的运用5. 棋形与攻守要点6. 行棋7. 手筋8. 初中级死活四、中级篇(不限)1. 常见定式① 星定式② 小目低挂③ 小目高挂④ 三三定式⑤ 目外定式⑥ 高目定式2. 布局① 一般布局② 特形布局(三连星、中国流、韩国流等)3. 中盘战术① 攻击战术② 打入战术③ 拆边④ 腾挪战术⑤ 浅消战术4. 官子① 官子的计算方法② 常见官子大小③ 官子技巧本授课计划以北京体育大学出版社李昌镐围棋基础教研室所编《教孩子学围棋》为主。
苏教版小学五年级数学上册教学计划及课时安排进度表

苏教版小学五年级数学上册教学计划及课时安排进度表苏教版小学五年级数学上册教学计划及课时安排进度表一、全册教学分析1、教材名称、版本:义务教育课程标准实验教科书数学五年级(上)2、全册教材简析:本册教材共编排了十个单元的教学内容。
在“数与代数”领域教学负数的初步知识、小数的意义与性质、小数的四则计算,结合解决实际问题教学周期现象。
在“空间与图形”领域教学三角形、平行四边形、梯形的面积公式,公顷与平方千米这两个较大的计量土地面积的单位。
在“统计与概率”领域教学复式统计表和复式条形统计图。
联系上述三个领域的教学内容编排3次实践活动,教学一些基本的数学思想和方法。
教材离编排了一些“你知道吗”,介绍数学背景知识。
编排一些思考题,作为弹性的教学内容。
教材编写时,考虑了高年级数学教学的知识量比中年级大,学生的学习能力和自我意识比中年级强。
教材适当调整了编写体例,设置了例题、试一试、练一练、练习、整理与练习等栏目与版块。
3、教学目标:(1) 基础知识:①通过合理的分类,并借助直观,让学生体会正负数与0的关系。
②要借助直线上的点,使学生初步体会负数的大小。
③要让学生经历公式推导的完整过程。
④把握探索小数性质和小数大小比较方法的思路。
⑤联系整数加、减法的计算方法理解小数点对齐的道理。
⑥要鼓励学生画图列举寻找规律。
⑦理解用计算器探索小数点移动规律的活动线索。
⑧通过丰富多彩的活动让学生体会1公顷的实际大小。
⑨引导学生依据具体数量关系列出乘、除法算式,逐步丰富对乘除法运算的理解。
⑩要让学生感受复式统计表与复式条形统计图在描述数据方面的特点。
(2)基本技能:充分利用新旧知识间的联系,联系学生的生活实际,通过知识间的迁移、类推、比较、拓展,将新知识点与学生原有的知识体系联系起来进行教与学。
(3)情感态度和价值观:①使学生积极主动参与获取知识的全过程,让他们认识到数学的价值,生活中离不开数学,使他们喜欢数学,乐学数学。
②形成对数学的浓厚兴趣,树立学生自尊心和自信心,提高学生的相互合作能力和人际交往能力。
苏教版七年级英语上册教学计划及进度表

苏教版七年级英语上册教学计划及进度表教学计划
第一单元:初识英语
- 课时:5节课
- 研究内容:
- 英语字母及基本发音
- 问候和自我介绍
- 数字0-20的表达
- 基本用语和表达
- 教学目标:
- 能正确书写并发音英语字母
- 能用简单的句子进行问候和自我介绍
- 能用英语表达0-20的数字
- 能用英语进行简单的交流和表达
第二单元:我的家庭
- 课时:6节课
- 研究内容:
- 家庭成员的称呼
- 家庭成员的特点和职业
- 家庭活动的描述
- 家庭成员的关系及问答
- 教学目标:
- 能正确称呼和描述家庭成员
- 能用英语介绍家庭成员的特点和职业- 能描述家庭活动并表达自己的喜好- 能进行家庭成员关系的问答
第三单元:我的学校
- 课时:7节课
- 研究内容:
- 学校设施和场所的名称
- 学校生活的介绍
- 学校科目的表达
- 学校日常活动的描述
- 教学目标:
- 能够用英语表达学校设施和场所的名称- 能够用英语介绍学校生活及日常活动
- 能够用英语表达各类学校科目
- 能够运用所学知识进行简单的对话和交流教学进度表
以上是苏教版七年级英语上册的教学计划及进度表。
通过这份计划和进度表,我们能够清楚地了解每个单元的学习内容和教学目标,以便高效地进行教学工作。
希望学生们在这个学期里能够积极参与学习,掌握好英语的基础知识,并运用到日常生活中去。
一年级语文教学计划进度表
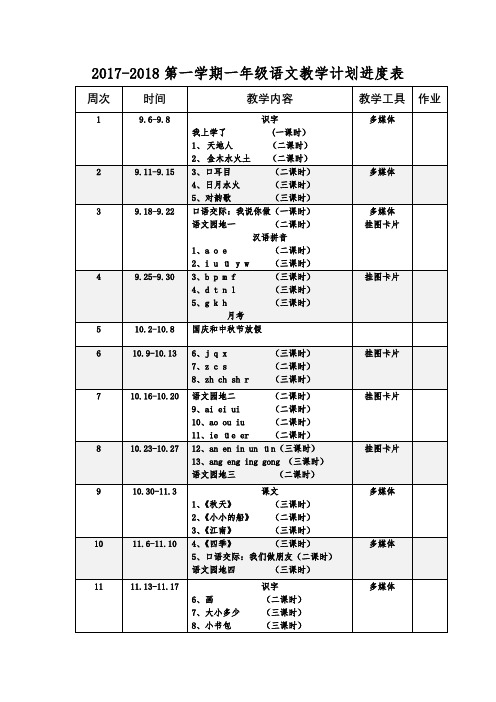
语文园地八(四课时)
多媒体
18
1.2-1.5
总复习
19
1.8-1.12
综合复习、期末考试
8、小书包(三课时)
多媒体
12
11.20-11.24
9、日月明(三课时)
10、升国旗(二课时)
语文园地五(三课时)
多媒体
13
11.27-12.1
课文
5、《影子》(三课时)
6、《比尾巴》(三课时)
7、《青蛙写诗》(二课时)
多媒体
14
12.4-12.8
8、《雨点儿》(三课时)
口语交际:用多大的声音(一课时)
语文园地三(二课时)
挂图卡片
9
10.30-11.3
课文
1、《秋天》(三课时)
2、《小小的船》(二课时)
3、《江南》(三课时)
多媒体
10
11.6-11.10
4、《四季》(三课时)
5、口语交际:我们做朋友(二课时)
语文园地四(三课时)
多媒体
11
11.13-11.17
识字
6、画(二课时)
7、大小多少(三课时)
语文园地六(四课时)
多媒体
15
12.11.-12.15
9、《明天要远足》(二课时)
10、《大还是小》(三课时)
11、《项链》(三课时)
多媒体
16
12.18-12.22
语文园地七(二课时)
12、《雪地里的小画家》(三课时)
13、《乌鸦喝水》(三课时)多媒体ຫໍສະໝຸດ 1712.25-12.28
14、《小蜗牛》(三课时)
语文园地一(二课时)
2024年最新版五年级上册语文教学计划及进度表2

五年级上册语文教学计划进度表一、指导思想《义务教育课程标准实验教科书语文五年级上册》是《中共中央国务院关于深化教育改革,全面推进素质教育的决定》的精神为指导,以《全日制义务教育语文课程标准(实验稿)为依据编写的。
本册教科书进一步加大改革力度,从选文到练习设计,从编排结构到呈现方式,有不少新的突破。
确立“以人为本”的教育理念。
以“提高自我”为关键,学习先进的教育教学理念并转化为实际教学行动。
倡导自主、合作、探究的学习方式,着眼于全面提高学生的语文素养,培养创新精神和实践能力,促进学生的全面发展。
注重语文知识和能力训练相结合,把素质教育放在首位,联系学生现实生活,加强语文实践,积极进行教学改革,并且落实到实际的教学工作上。
同时,在教学中真正做到减轻学生的课业负担,强化教学中的质量,由易到难,由浅入深,努力把握好语文教学的特点,培养学生的听、说、读、写能力,体现语文教学中的双基要求。
引导学生开发潜能,学会学习,掌握学习方法,养成良好的语文学习习惯。
二、教材分析本册教材精心编排了共计26篇课文,其中精选了20篇深入研读的文章,以及6篇供学生略读以拓宽视野的篇目。
每一组教材均由引人入胜的导语、丰富多彩的课文以及充满趣味的语文园地三大核心部分组成。
附录部分更是详尽,囊括了生字表(一),旨在帮助学生认识更多汉字;生字表(二),鼓励学生动手书写,巩固记忆;以及词语表,丰富学生的词汇储备。
全书围绕八个鲜明且富有深意的专题展开,依次为:“一花一鸟总关情”,引领学生感受自然界的细腻情感;“阅读要有一定的速度”,培养学生高效的阅读习惯;“民间故事”,传承口耳相传的经典文化;“为什么我的眼里常含泪水?因为我对这土地爱得深沉……”,激发学生对家国情怀的深刻思考;“说明文以‘说明白了’为成功”,强调说明文写作的清晰与准确;“舐犊之情”,让学生体会流淌在血脉中的深情厚爱;“四时景物皆成趣”,鼓励学生观察自然,感悟四季之美;“书山有路勤为径”,勉励学生勤奋学习,勇攀知识高峰。
一年级英语教学计划表

三、本学期重点、难点及所在章节:
1.能根据教师的简单指令做事情,自己也能发号简单的指令;
2.能运用所学的知识进行简单的交流;
3.能唱简单的英文歌曲,能说简单的英文歌谣;
4.能看图说出单词,听到单词说出物品。
重难点所在章节:U3,U5,U8,U11
四、提高教学质量的方法与措施:
2.能根据实物或图片说出所学单词,发音基本正确。单词的学习是无止境的,这就要求在日常学习中,一点一滴的巩固和积累,并养成良好有效的学习习惯。
3.能在非语言提示(如图片,手势等)的帮助下,听懂清晰的话语,录音。
4.能演唱和表演已经学过的英语歌曲,诵读已学过的歌谣。
5.初步学习自然拼读,掌握基础发音规则。
二、全册教学知识与能力目标:
由于本学段的学生仍处于学习英语的启蒙阶段,所以与学习知识同样重要的就是培养学生良好的英语学习习惯,掌握有效的学习方法,在生动活泼的教学环境和宽松和谐的学习氛围中激发对英语学习的浓厚兴趣。通过本学期的学习,要求学生在基本知识的掌握和基本技能的训练方面达到以下目标:
1.能比较熟练地运用所学的日常交际用语,做到学以致用。
1.根据儿童"好动、好玩、好奇、好胜"的心理特点,尽量创造新颖多样、富于启发性、能调动学生多种感官参与学习活动的情境,设计形式多样的游戏,来唤起学生对学习英语的兴趣和求知欲,在教师和学生共同参与,享受游戏的乐趣的同时获得新知识,学习能力也在游戏中得到培养和发展。
2.运用竞赛,挖掘学生的学习的"潜能",竞争好胜心理驱使学生乐于参与比赛活动,最大限度地调动了学生的积极性、主动性以及思维的灵敏性。学生在紧张欢乐的气氛中既获得知识,又不易产生心理疲劳,有效地避免了学生课堂上的"走神"现象,从而有效地达到培养学生的学习能力,提高教学质量的目的。
2024年初三化学教学计划表(3篇)

2024年初三化学教学计划表一、教学内容安排1. 化学基础知识复习(2个课时)- 复习化学元素、化学符号的基本概念和认识方法;- 复习化学反应、化学方程式的基本表示和计算方法;- 复习化学键、化学键的类型和特点等基础知识。
2. 化学反应速率与化学平衡(6个课时)- 学习化学反应速率的表示方法,理解反应速率与化学平衡的关系;- 学习化学平衡常数的概念和计算方法;- 分析化学反应速率与温度、浓度、压力等因素的关系;- 理解化学平衡的动态平衡原理。
3. 酸碱与盐(8个课时)- 学习酸碱与盐的基本概念和性质;- 学习酸碱反应和盐的生成机制;- 学习酸碱中性化反应的计算方法;- 分析酸碱盐反应的化学方程式和离子方程式。
4. 金属与非金属(6个课时)- 学习金属和非金属的基本性质和特点;- 学习金属的活动性和金属离子的生成及还原反应;- 学习非金属元素的分类和特点;- 分析金属和非金属在生活中的应用。
5. 碳化合物与有机化学(8个课时)- 学习碳化合物的基本概念和分类;- 学习有机化合物的命名规则和结构特点;- 分析碳化合物的性质和化学反应;- 了解有机化学在生活和工业中的应用。
二、教学方法1. 授课与实验相结合,提倡学生亲自参与实验操作,加深对化学知识的理解和记忆;2. 引导学生通过观察实验现象、分析数据结果,培养他们的实验实践能力和科学思维能力;3. 利用多媒体技术和互动教学手段,激发学生的学习兴趣,拓宽化学知识的应用范围;4. 引导学生进行小组讨论,激发他们的合作与交流能力,培养团队合作精神。
三、评价方式1. 平时考核(40%):包括课堂表现、作业完成情况以及实验报告等;2. 期中考试(30%):对前半学期的学习内容进行综合测试;3. 期末考试(30%):对全学期的学习内容进行综合测试。
四、教学资源准备1. 教科书:根据课程标准,选择符合学生学习能力和实际要求的教材;2. 实验器材和药品:为学生提供必要的实验器材和化学药品,确保实验的安全性和实效性;3. 多媒体教具:利用投影仪、电脑等多媒体设备,呈现生动的教学内容和实验过程;4. 学习参考资料:提供一定数量的化学参考书籍和学习资料,供学生参考和扩展学习。
英语培训教学计划课时表

英语培训教学计划课时表Day 1:Class Topic: Introduction to English LanguageTime: 9:00am - 11:00amObjective: To introduce students to the basics of the English language and its importance in the global context.9:00am - 9:30am: Introduction and Icebreaker- Welcome students and introduce myself as the trainer- Icebreaker activity to get students comfortable and engaged9:30am - 10:30am: Overview of the English Language- Define the English language and its historical significance- Discuss the global reach and importance of English- Introduce basic greetings and expressions in English- Provide examples and practical exercises for students to practice10:30am - 11:00am: Q&A session- Encourage students to ask questions and clarify any doubts- Provide resources and materials for further studyDay 2:Class Topic: Basic Grammar and Sentence StructureTime: 9:00am - 11:00amObjective: To teach students the basic grammar rules and sentence structure in English. 9:00am - 10:00am: Parts of Speech- Introduce the different parts of speech (nouns, verbs, adjectives, adverbs, etc.)- Provide examples and exercises for students to practice identifying parts of speech10:00am - 11:00am: Sentence Structure- Explain the basic sentence structure in English (subject-verb-object)- Provide examples and exercises for students to practice forming sentencesDay 3:Class Topic: Vocabulary BuildingTime: 9:00am - 11:00amObjective: To expand students' vocabulary and improve their word usage in English.9:00am - 10:00am: Word Roots and Prefixes- Introduce common word roots and prefixes in English- Explain how word roots and prefixes can help in understanding and learning new words - Provide examples and exercises for students to practice using word roots and prefixes 10:00am - 11:00am: Building Vocabulary- Teach students different methods to expand their vocabulary (reading, word games, flashcards, etc.)- Provide a list of common English words and their meanings- Encourage students to practice using these words in sentences and conversationsDay 4:Class Topic: Listening and Speaking SkillsTime: 9:00am - 11:00amObjective: To improve students' listening and speaking skills in English.9:00am - 10:00am: Listening Comprehension- Provide audio materials for students to listen to and comprehend- Discuss the importance of listening skills in language learning- Conduct listening exercises and quizzes to test comprehension10:00am - 11:00am: Speaking Practice- Engage students in speaking activities and role-plays- Encourage students to practice using the vocabulary and sentences they have learned - Provide feedback and correction as neededDay 5:Class Topic: Reading and Writing SkillsTime: 9:00am - 11:00amObjective: To improve students' reading and writing skills in English.9:00am - 10:00am: Reading Comprehension- Provide reading materials for students to read and comprehend- Discuss the importance of reading for language acquisition- Conduct reading comprehension exercises and quizzes to test understanding10:00am - 11:00am: Writing Practice- Engage students in writing activities such as essays, letters, and creative writing- Provide feedback and correction on students' writing- Encourage students to continue practicing their writing skills outside of the classroom Day 6:Class Topic: Review and AssessmentTime: 9:00am - 11:00amObjective: To review the topics covered and assess students' progress in the course.9:00am - 10:00am: Review Session- Recap the key points and topics covered in the course- Provide additional exercises and examples for review10:00am - 11:00am: Assessment- Conduct an assessment test to gauge students' understanding and progress- Provide feedback and suggestions for improvement- Distribute certificates of completion to students who have successfully completed the courseOverall, the English training teaching plan aims to provide students with a comprehensive understanding of the English language and improve their listening, speaking, reading, and writing skills. The plan includes interactive activities, practical exercises, and assessments to ensure effective learning and skill development.。
新编学期教学计划表 人教版二年级数学上册教学计划及课时计划安排表

学期教学计划表人教版二年级数学上册教学计划及课时计划安排表人教版二年级数学上册教学计划一、班级情况分析:本学期我所任教的二年级()班有学生人,男生人,女生人,其中民族学生占。
由于班里全部是少数民族学生,他们平时接触汉语较少,因此存在很大的语言障碍,再由于孩子年龄小注意力易分散,一小部分学生对课堂学习不太适应,但大多数学生思维活跃,学习数学的兴趣较浓,有强烈的求知欲。
根据这些情况,我在教学时,是从学生的兴趣出发,建立起良好的师生情感,让学生爱教师,爱数学,有层次、有耐心的进行辅导,帮助他们体会到学数学的乐趣和作用,使每个学生顺利地完成本学期的学习任务。
二、教材分析:本册教材包括以下内容:认识长度单位厘米和米、100以内数的加法和减法笔算、初步认识角、表内乘法、从不同的位置观察物体、认识几时几分、数学广角、总复习。
本册教材的重点教学内容是100以内数的加、减法笔算和表内乘法。
这两部分内容都是学生进一步学习计算的基础。
特别是表内乘法是学习多位数乘法的基础。
这些知识在日常生活中页有着广泛的应用,同时,它们又是多位数计算的基础。
因此,两位数的加法和相应的减法是小学数学中最基础的内容,是学生终身学习与发展必备的基础知识和基本技能,必须让学生切实掌握。
除了加法和乘法的计算外,教材安排了长度单位和角的直观认识,以及认识时间等,虽然每一单元内容不多,但都很重要,有利于学生了解数学知识的实际应用,培养学生学习数学的兴趣。
三、教学目标:(一)知识与技能方面:1、掌握100体内笔算加减发的计算方法,能正确地进行计算。
2、知道乘法的含义和乘法算式中各部分的名称,熟记全部乘法口诀,熟练地口算两个一位数相乘。
3、初步认识长度单位厘米和米,初步建立1米、1厘米的长度观念,知道1米=100厘米,会用刻度尺测量物体长度。
4、初步认识线段,会量整厘米的线段的长度;初步认识角并区分;会用三角尺判断角,会画线段和角。
5、能辨别从不同位置观察物体得到的图形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时教学计划表§4.1 不定积分的概念与性质一、本章简介1、 主要内容:原函数的概念与性质、不定积分的概念与性质、不定积分的基本公式与直接积分法、换元积分法、分部积分法2、 学习目标:理解原函数和不定积分的概念,了解不定积分的几何意义,掌握不定积分的性质.掌握基本积分公式与直接积分法. 掌握第一类换元积分法,熟悉常用的凑微分公式,理解第二类换元积分法. 掌握分部积分法. 3、 课时安排: 10课时 二、原函数的概念和性质1、引入 我们知道,微分法是研究如何由已知函数求出其导函数,那么与之相反的问题是:求一个未知函数,使其导函数恰好等于一个已知函数.解决这个问题不仅是数学理论本身的需要,更主要的是解决许多实际问题的需要。
例如,已知速度()v t ,求路程()s t ;已知加速度)t α(,求速度()v t ;已知曲线上任一点处的切线的斜率,求曲线的方程等等.为解决这些问题,我们引进原函数的概念.2、定义l 设()f x 是定义在某区间上的函数,如果存在一个函数()F x ,使得对于 该区间上任一点x 都有()()'F x f x =或()(),dF x f x dx =那么函数()F x 就称为函数()f x 在该区间上的一个原函数. 例如,在区间(-∞,+∞)内,因为()'sin cos ,x x =,所以sin x 是cos x 的一个原函数.又如,在区间(-∞,+∞)内,因为()()(()()'32'32'32'323,13,3,3,x x xx xx xC x C =+==+=为任意实数所以3333,1,x x x x C ++都是23x 的原函数3、原函数的存在性关于原函数,我们首先研究一个问题.即函数()f x 应具备什么条件,才能保证它的原函数存在?对这个问题我们有下面的定理.定理l 如果函数()f x 在某区间上连续,那么()f x 在该区间上的原函数存在.(本定理将在下一章中加以证明.)由于初等函数在其定义区间上连续,所以初等函数在其定义区间上都有原函数.4、原函数的无限性由前面的例子我们知道,23x 的原函数存在,而且不止一个,因此我们需研究第二个问题,即如果函数()f x 有原函数,那么原函数一共有多少个?对这个问题我们有下面的定理.定理2 如果函数()f x 有原函数,那么它就有无数多个原函数.证 设函数()F x 是函数()f x 的一个原函数,即,()()'F x f x =,并设C 为任意常数.因为()()()()'''.F x C F x C f x +=+=⎡⎤⎡⎤⎣⎦⎣⎦所以()f x +C 也是()f x 的原函数.又因为C 为任意常数,即C 可以取无数多个值,所以,()f x 有无数多个原函数. 5、原函数的关联性对于()f x 的无数多个原函数来说,我们还需研究第三个问题,即()f x 的任意两个原函数之间有什么关系? 对这个问题我们有下面的定理.定理3 函数()f x 的任意两个原函数的差是一个常数. 证 设()F x 和()G x 都是()f x 的原函数,即()'F x =()f x ,()'G x =()f x于是()()()()()()'''0.G x F x G x F x f x f x -=-=-=⎡⎤⎣⎦.根据导数恒为零的函数必为常数(第三章第3.1节),可知()G x -()F x =C (C 为任意常数),即()G x =()F x +C .上述定理表明,如果()F x 是()f x 的一个原函数,那么()f x 就有无数多个原函 数,并且任意一个原函数都可以表示为()F x +C (C 为任意常数)的形式.也就是说, ()f x +C (C 为任意常数)就是函数()f x 的全部原函数.三、不定积分的定义1、 定义2 函数()f x 的全部原函数叫作()f x 的不定积分,记作()f x dx ⎰其中“⎰”称为积分号,()f x 称为被积函数,()f x dx 称为被积表达式,x 称为积分变量。
由上面的讨论可知,如果()F x 是()f x 的一个原函数,则有()().f x dx F x C =+⎰其中C 是任意常数,称为积分常数.2、举例说明(1) 由前面可知, 3x 是23x 的一个原函数,那么 3x C +就是23x 的不定积分,即⎰+=C x dx x 323 (2) 因为x x s in )c o s (='-,即)c o s (x -是x sin 的一个原函数,那么cos x C -+是sin x 的不定积分,即(3)用微分法证明:(a )()()2312323.6x dx x C +=++⎰.(b )2111cos sin 222xdx x x C =++⎰证明 (a ) 因为()()'32123236x x ⎡⎤+=+⎢⎥⎣⎦,即()31236x +是()223x +的一个原函数,所以:()()2312323.6x dx x C +=++⎰(b ) 因为11sin 22x x '⎛⎫+= ⎪⎝⎭21cos 1cos 22xx +=,即11sin 22x x +是21cos 2x的一个原函数,所以:2111cossin 222xdx x x C =++⎰四、不定积分的几何意义1、实例分析例3 已知某曲线经过点A (0,1),且其上任意一点处的切线的斜率等于2x ,求 此曲线的方程.解 设所求曲线的方程为()y f x =.依题意可得 ()'2.f x x =这就是说()f x 是2x 的一个原函数. 又因为()'22xx =,所以2x也是2x 的一个原函数,因而2x 的全部原函数即2x 的不定积分2xdx ⎰等于2x C +,而()f x 只是2x C +中的某一个,也就是说,所求曲线()y f x =只是曲线族2y x C =+中的某一条,即经过点A 的那一条.把x =0,y =1代入2y x C =+中,得C =1.于是所求曲线的方程是2 1.y x =+.(图4-1)2、归纳几何意义 由此例可知,若把函数()f x 的一个原函数()F x 的图象叫作函数()f x 的积分曲线.则不定积分()f x dx ⎰在几何上表示由积分曲线()y F x =沿y 轴上下平移而得到的一族曲线(称为积分曲线族).且积分曲线族上横坐标相同的点处的切线的斜率都相等,即切线都平行(图4—2).五、不定积分的性质由不定积分的定义与导数的运算法则,可得不定积分性质如下 性质1 微分运算与积分运算互为逆运算 因为()f x dx ⎰是()f x 的原函数,所以,根据不定积分的定义,有(1) ()()()()'.f x dx f x d f x dx f x dx ⎡⎤⎡⎤==⎣⎦⎣⎦⎰⎰,或.又因为()F x 是()'F x 的原函数,所以,有(2) ()()'F x dx F x C =+⎰,或()()dF x F x C =+⎰(强调二者的不同)性质2 被积函数中不为零的常数因子可以提到积分符号外面,即()()()0.kf x dx k f x dx k =≠⎰⎰证 因为()()()''.k f x dx k f x dx kf x ⎡⎤⎡⎤==⎣⎦⎣⎦⎰⎰所以()k f x dx ⎰是()kf x 的原函数.于是 ()().kf x dx k f x dx C =+⎰⎰因为等号右边的积分中含有任意常数,所以后面的C 可以省写.所以()().kf x dx k f x dx =⎰⎰.性质3 两个函数代数和的不定积分等于各个函数不定积分的代数和,即[]()()()()f x g x dx f x dx g x dx ±=±⎰⎰⎰证 (略,与性质2类似 )指出此性质对有限个函数代数和的情形也是成立的。
六、小结、布置作业1、主要内容:原函数的概念与性质、不定积分的概念、几何意义与性质。
2、作业:习题4-1 1(1)、(3);2(1);3(1)、(4);4(2)、(4);5课时教学计划表§4.2 不定积分的基本公式与直接积分法一、复习与引入1、复习(1)不定积分的概念 (2)积分与微分的关系(3)如何利用定义求不定积分(评讲作业) 2、引入从作业我们可知,由一个导数公式可求出一个不定积分,即得一个不定积分公式,那么由我们已知的导数公式就可得出相应的不定积分公式,有了公式,不定积分就变得容易多了。
因此,下面我们就来推导不定积分的基本公式。
二、不定积分的基本公式1、个例推导(1) 因为()'sin cos x x =,所以cos sin xdx x C =+⎰(2) 因为()xxe e '=, 所以 x x e dx e C =+⎰(3) 因为 ()()[]1ln (0)'ln 11ln()()(0)x x xx x x x x x ⎧'=>⎪⎪=⎨⎪''-=-=<⎪-⎩所以1ln .dx x C x =+⎰2、给出基本公式表仿照上面的方法,我们可以推导出其他基本积分公式.列表如下:以上11个公式是求不定积分的基础,必须熟记.在应用中要注意(1)公式3的绝对值符号不能丢(2)公式7、9的负号不能丢(3)任意常数C不能丢三、直接积分法1、什么叫直接积分法直接用不定积分的基本公式与性质求不定积分,或者对被积函数进行适当的恒等变形(包括代数变形与三角变形),再利用不定积分基本公式与性质求不定积分的方法叫作直接积分法2、举例说明直接积分法的应用例1 求下列不定积分:()()()21.2.3.dx x dx ⎰⎰ (4)3dx x ⎰解 分析:这四个不定积分表面形式不同,实质上其被积函数均可化为kx α的形式,故利用公式1、2即可求解(1)11dx dx x C x C ==+=+⋅⎰⎰()2213112.213x dx x C x C +=+=++⎰()11112222324112x dx x C x C C--+==+=+=-+⎰()15533122223124.5312dx xdx x dx x C x C C x ---+-===+=-+=+-+⎰⎰⎰ 例2 求()3sin 1.xex dx -+⎰解 此不定积分可看做三个函数代数和的不定积分,利用性质将其化为三个不定积分之和,再利用基本公式求出。
注意 在分项积分后,每个不定积分的结果都应有一个积分常数,但任意常数 之和仍是任意常数,因此最后结果只要写一个任意常数即可.例3 求()23.x dx x+⎰.解 本题不能直接用基本公式和性质求解,可先把被积函数变形,然后再积分()22236991669ln .2x x x dx dx x dx x x x C xx x +++⎛⎫==++=+++ ⎪⎝⎭⎰⎰⎰例4 求2tan xdx ⎰.解 此题也不能直接用基本公式和性质求解,可先进行三角变形,利用同角三角函数平方关系式 22tan 1x sen x =-,将2ta n x 的不定积分转化为2sen x 与1的不定积分之差,然后利用基本积分公式与性质求解。
