高考数学百大经典例题 正态分布
正态分布经典题型

正态分布经典题型正态分布是一种常用的统计分布,它在统计学中应用广泛。
以下是正态分布的一些经典题型:1. 均值和标准差:均值和标准差是正态分布中最为重要的两个参数。
均值可以理解为一组数据的平均数,标准差则是平均数乘以数据数的平方根。
以下是均值和标准差的示例计算:(1)计算正态分布的均值:均值 = (3.5 + 2.5) * 2 / 2 = 7(2)计算正态分布的标准差:标准差 = (3.5 - 2.5) * 2 / 2 = 0.52. 方差:方差是正态分布中另一个重要的参数,它表示数据的离散程度。
以下是方差的示例计算:(1)计算正态分布的方差:方差 = (4.5 + 3.5) * (4.5 - 3.5) / 2 = 6(2)计算正态分布的标准差与方差的关系:标准差 = 方差 / n = 6 / 2 = 33. 分布曲线:绘制正态分布的分布曲线,可以帮助我们了解数据的分布情况。
以下是正态分布分布曲线的示例:正态分布分布曲线图| | 7| ----|---| 3 | 2| 0 | 5| 10 | 8| 15 | 124. 假设检验:假设检验是统计学中常用的一种方法,它可以帮助我们检验一个假设是否成立。
正态分布假设检验中的假设为均值为μ,标准差为σ,我们希望检验的是样本均值是否大于或者等于设定值。
以下是正态分布假设检验的示例:(1)设我们要检验的假设为 H0:μ == 7,那么备择假设为 H1:μ不等于 7。
(2)计算拒绝域D,即满足给定的拒绝域,且拒绝域不包含设定的假设值的区域:D = 临界值 - 标准差 * 根号下(2 * 概率密度函数的平方)/(期望平方和 - 方差平方和)(3)计算拒绝域的概率,即满足拒绝域并且拒绝域不包含设定的假设值的概率:P(D) = (自由度(H1) - 自由度(H0)) / 自由度(H1)P(D) = (6 - 3) / 6 = 1/3(4)选择适当的检验方法,例如t检验或F检验,计算拒绝域和对应的p值,并绘制拒绝域与设定值或临界值的对比图,以检验我们的假设是否正确。
正态分布习题与详解(非常有用-必考点)

2001.若 x 〜N (0,1),求(I) P (-2.32< X <1.2) ; (2) P (x >2).解: ⑴ P (-2.32< x <1.2)=(1.2)-(-2.32)=(1.2)-[1-(2.32)]=0.8849-(1-0.9898)=0.8747.(2) P (x >2)=1- P (x <2)=1-(2)=1-0.9772=0.0228.:2利用标准正态分布表,求标准正态总体 (1)在 N(1,4)下,求 F(3).2 ,(2)在 N(^,b )下,求F (卩一6,卩+6);3 1 解: (1) F (3) =( ) =0( 1)= 0.8413 2a( )0.975 ■ 200(2)F(y+b)= ( -------------- )=0( 1)= 0.8413F(y —b))=0 (— 1 )=1—0 ( 1 )= 1 - 0.8413 = 0.1587F(y — c,a+b)=F(a+b) — F(y — cr)0.8413 — 0.1587 = 0.68263某正态总体函数的概率密度函数是偶函数,而且该函数的最大值为 1=,求总体落入区间(一1.2 , 0.2 )之间的概率.[0 ( 0.2 ) =0.5793,0 ( 1.2 ) (x )22~=0.8848]解:正态分布的概率密度函数是f(x),x (),它是偶函数,1说明” 0,f(x)的最大值为f()=亍,所以"1,这个正态分布就是标准正态分P( 1.2 x 0.2)(0.2)( 1.2) (0.2) [1 (1.2)] (0.2) (1.2) 10.5793 0.8848 10.46424.某县农民年平均收入服从 =500元,在500 : 520元间人数的百分比;(2) 的概率不少于0.95,则a 至少有多大? =200元的正态分布 (1)求此县农民年平均收入 如果要使此县农民年平均收入在( [0 ( 0.1 ) =0.5398,0 ( 1.96 ) a, a )内=0.975]解:设 表示此县农民年平均收入,~ N(500,2002).P(500520 500(500 500.200 ')(0.1) (0) 0.5398 0.50.0398 ( 2 )a)(盘—)2 200(旦)10.95,200查表知:—1.961设随机变量X 〜 N (3,1), 若P(X4) p ,,则 J P(2<X<4)=—、11(A) p(B)l 一P C .l -2p D . - p22 【答 案】C因为P(X 4) P(X 2)p ,所以 P(2<X<4)1 P(X 4) P(X2) 1 2p ,选C .2. (2010新课标全国理)某种种子每粒发芽的概率都为 0.9,现播种了 1 000粒,对于没有发 芽的种子,每粒需再补种 2粒,补种的种子数记为X ,则X 的数学期望为()A . 100B . 200C . 300D . 400[答案]B[解析]记“不发芽的种子数为了,贝U 汁B(1 000,0.1),所以E(8= 1 000 X 0.1= 100,而 X = 2E,故 E(X)= E(2 3= 2E( 3 = 200,故选 B.3.设随机变量3的分布列如下:3—10 1 Pabc其中a , b , c 成等差数列,若 E( 3 = 3,贝U D(3 =( )[答案]A[解析]设白球x 个,则黑球7— x 个,取出的2个球中所含白球个数为C 7-x 2 7 — x 6 — xP( 3= 0)= C 72 =42,x - 7 — x x 7 — x P( 3=1)= C 72 =21 ,C x 2 x x — 1P( 3= 2)= C 72 = 42 ,.x = 3.4A.9 B .1 2 9 C.3[答案]D[解析]由条件a , b , c 成等差数列知,2b = a + c ,由分布列的性质知 a + b + c = 1,又1 111 1E( 3 = — a + c = 3 解得 a= 6’ b= 3 c = 2,二 D(3= 6X2+21-「=舟.4. (2010上海松江区模考)设口袋中有黑球、白球共 7个,从中任取 2个球,已知取到 白球个数的数学期望值为7,则口袋中白球的个数为()A . 3 B . 4C . 5D . 23贝U 3取值0,1,2,0X7— x 6— x 42x 7 — x 21 + 2X X X —1 42 55.小明每次射击的命中率都为 p ,他连续射击n 次,各次是否命中相互独立,已知命中次数E 的期望值为4,方差为2,则p( &1)=()A 255B 9C 247D 7 A 256 B.256 C.256 D .64 [答案]C[解析]由条件知 旷B(n , P),E E = 4, np = 4 D E = 2n p 1 — p = 2 '1解之得,p = , n = 8, ••• P( = 0)= C 8°x 218= 2 8,1 1 1P( E= 1) = C 81x 2 1x2 7= 2 5,• P(E 1) = 1 — P( = 0) — P(E= 1)A . 2< 俘=淨,01=d2> d3B .皿> 俘=淨,d=d < dC . (J1= (J2<P 3, d 1< d 2= d 3D .小< p2= 3, d 1 = d < d 3 [答案]D(^2(X)和g(X )的图象都是关于同一条直线对称,所以其平均数相同,故3= 3,又屉(X)的对称轴的横坐标值比也(X)的对称轴的横坐标值大,故有 3<比 =3.又d 越大,曲线越“矮胖”,d 越小,曲线越“瘦高”,由图象可知,正态分布密度函 数咖(X)和侯(X )的图象一样“瘦高”,松(X )明显“矮胖”,从而可知d= d < d .6①命题"X R,cosx 0 ”的否定是:“ X R,cosx 0 ”; ②若lg a lg b lg( a b),则a b 的最大值为4; ③定义在R 上的奇函数f(X)满足f (X 2)f(X),则f(6)的值为0;=1— 18— 1 5= 24Z2 2 256. 5已知三个正态分布密度函数 则()1XX )= 2 nd e —.2X —d^(x € R , 2 di = 1,2,3)的图象如图所示,[解析]正态分布密度函数<>④已知随机变量 服从正态分布 N(1, 2),P( 5) 0.81,则P( 3) 0.19 ;其中真命题的序号是 ________ (请把所有真命题的序号都填上 ).【答案】①③④ ①命题“ x R,cosx 0”的否定是:“ x R,cosx 0 ”;所以① 正确.②若 lg a lg b lg( a b),则 Ig ab lg( a b),即 ab a b,a 0,b 0 .所以a b 22ab a b(/,即(a b) 4(a b),解得a b 4,则a b 的最小值为4;所以②错误.③定义在R 上的奇函数f( x)满足f ( x 2) f ( x),则f (x 4) f(x),且 f (0) 0,即函数的周期是 4.所以 f (6) f(2) f (0)0;所以③正确④已知随机变量服从 正态分布2N(1, ),P(5) 0.81 ,则P( 5) 1 P(5) 1 0.81 0.19 ,所以 P(3) P( 5)0.19 ;所以④正确,所以真命题的序号是①③④.7、在区间[1,1]上任取两数 m 和n ,则关于x 的方程x 2 mx n 2 0有两不相等实根的概率为 ____________ .1【答案】—由题意知1 m 1, 1 n 1.要使方程x2 mx n 2 0有两不相等实4根,则 2=m 4n 2 0 , 即(m 2n )(m 2n) 0 . .作出对应的可行域,如图直线m 2n 0,m2n0 , 当 m1 时 1 1, n C—, n B—,所 以SO111 1所以方程22 2BC 一 1 [( )xmx n 0有两不相等实根的概率为2 2222S OBC2 1 2 12 24 4'⑶ 随机变量X 服从正态分布 N(1,2),则P(X 0) P(X 2);2 1⑷ 已知a,b R ,2a b 1,则一 一 &其中正确命题的序号为 ________________________ .a b【答案】⑵(3)(1)2G lnx 〔2 ln2 ,所以⑴错误.(2)不等式1x|x 1| |x 3|的最小值为4,所以要使不等式|x 1|2 1⑵正确.(3)正确.(4)--a b所以⑷错误,所以正确的为 ⑵(3).场中的得分如图所示,则该样本的方差为7 2 3频数为A . 26B . 25C . 23D . 18【答案】D 样本的 平 均数 为23,所以 样本方差为1 [(19 523)2 (20 23)2 (22 23)2 (23 23)2(31 2 23)] 18,选 D3有一个容量为200的样本,其频率分布直方图如图所示 ,据图估计,样本数据在8,10内的21dx 1 x3.,⑵不等式|x 1|| x 3| a 恒成立,则a 4;| x 3| a 成立,则a 4,所以2已知某篮球运动员 2012年度参加了 40场比赛,现从中抽取 5场,用茎叶图统计该运动员2 1(a 严 b) 4 19,【答案】C样本数据在 8,10之外的频率为(0.02 0.05 0.09 0.15) 2 0.62,0.38 200 76,选 C .1的概率为,选 B .45从集合1,2,3,4,5中随机选取3个不同的数,这个数可以构成等差数列的概率为2【答案】25_3从集合1,2,3,4,5中随机选取3个不同的数有C 5 10种.则3个数能构成等差数列的42所以样本数据在8,10内的频率为1 0.62 0.38,所以样本数据在 8,10的频数为4. ( 2013年临沂市高三教学质量检测考试理科数学)的正方形OABC 中任取一点P,则点 1 A .3【答案】(x x 3)dxP 恰好取自阴影部分的概率为B .14【答案】B12141(c XX ) C.D.-5 6根据积分的应用可知所求阴影部分的面积为11,所以由几何概型公式可得点P 恰好取自阴影部分4如图所示,在边长为I 第孕期图4 2.有,1,2,3;2,3, 4;3,4,5;1,3,5;有4种,所以这个数可以构成等差数列的概率为10 5。
高中数学典型例题大全第一章概率与统计正态分布

高中数学典型例题大全第一章概率与统计正态分布例 设ξ服从)1,0(N ,求以下各式的值:〔1〕);35.2(≥ξP 〔2〕);24.1(-<ξP 〔3〕).54.1(<ξP分析:因为ξ用从标准正态分布,因此能够借助于标准正态分布表,查出其值.但由于表中只列出)()(,0000x x P x Φ=<≥ξ的情形,故需要转化成小于非负值0x 的概率,公式:);()()();(1)(a b b a P x x Φ-Φ=<<Φ-=-Φξ和)(1)(00x P x P <-=≥ξξ有其用武之地.解:〔1〕;0094.09906.01)35.2(1)35.2(1)35.2(=-=Φ-=<-=≥ξξP P 〔2〕;1075.08925.01)24.1(1)24.1()24.1(=-=Φ-=-Φ=-<ξP〔3〕)54.1()54.1()54.154.1()54.1(-Φ-Φ=<-=<ξξP P.8764.01)54.1(2)]54.1(1[)54.1(=-Φ=Φ--Φ=讲明:要制表提供查阅是为了方便得出结果,但标准正态分布表如此简练的目的,并没有给查阅造成不便.相反其简捷的成效更突出了核心内容.左边的几个公式都应在明白得的基础上记住它,并学会灵活应用.求服从一样正态分布的概率例 设η服从)2,5.1(2N 试求:〔1〕);5.3(<ηP 〔2〕);4(-<ηP〔3〕);2(≥ηP 〔4〕).3(<ηP分析:第一,应将一样正态分布)2,5.1(N 转化成标准正态分布,利用结论:假设),(~2σμηN ,那么由)1,0(~N σμηξ-=知:,)(⎪⎭⎫ ⎝⎛-Φ=<σμηx x P 其后再转化为非负标准正态分布情形的表达式,通过查表获得结果. 解:〔1〕;8413.0)1(25.15.3)5.3(=Φ=⎪⎭⎫⎝⎛-Φ=<ηP〔2〕;0030.0)75.2(1)75.2(25.14)4(=Φ-=-Φ=⎪⎭⎫ ⎝⎛--Φ=-<ηP 〔3〕;4013.0)25.0(125.121)2(1)2(=Φ-=⎪⎭⎫⎝⎛-Φ-=<-=≥ηηP P 〔4〕⎪⎭⎫ ⎝⎛--Φ-⎪⎭⎫ ⎝⎛-Φ-=<=<25.1325.131)2()3(ηηP P )]25.2(1[7734.0)25.2()75.0(Φ--=-Φ-Φ=.7612.0)9878.01(7734.0=--=讲明:那个地点,一样正态分布),(~2σμξN ,总体小于x 的概率值)(x F 与)(x P <ξ和⎪⎭⎫ ⎝⎛-Φσμx 是一样的表述,即:.)()(⎪⎭⎫ ⎝⎛-Φ==<σμξx x F x P 服从正态分布的材料强度的概率例 :从某批材料中任取一件时,取得的这件材料强度ξ服从).18,200(2N〔1〕运算取得的这件材料的强度不低于180的概率.〔2〕假如所用的材料要求以99%的概率保证强度不低于150,咨询这批材料是否符合那个要求.分析:这是一个实咨询题,只要通过数学建模,就能够明白其本质确实是一个〝正态分布下求随机变量在某一范畴内取值的概率〞的咨询题;此题的第二咨询是一个逆向式咨询法,只要把握实质反向求值即可.解:〔1〕-=⎪⎭⎫ ⎝⎛-Φ-=<-=≥1181201801)180(1)180(ξξP P ;8665.0)11.1()]11.1(1[1)11.1(=Φ=Φ--=-Φ〔2〕能够先求出:这批材料中任取一件时强度都不低于150的概率为多少,拿那个结果与99%进行比较大小,从而得出结论.;9973.0)78.2()]78.2(1[1)78.2(1182001501)150(1)150(=Φ=Φ--=-Φ-=⎪⎭⎫ ⎝⎛-Φ-=<-=≥ξξP P 即从这批材料中任取一件时,强度保证不低于150的概率为99.73%>99%,因此这批材料符合所提要求.讲明:〝不低于〞的含义即在表达式中为〝大于或等于〞.转化〝小于〞后,仍须再转化为非负值的标准正态分布表达式,从而才可查表.公共汽车门的高度例 假设公共汽车门的高度是按照保证成年男子与车门顶部碰头的概率在1%以下设计的,假如某地成年男子的身高)36,175(~N ξ〔单位:㎝〕,那么该地公共汽车门的高度应设计为多高?分析:实际应用咨询题,分析可知:求的是门的最低高度,可设其为)cm (x ,使其总体在不低于x 的概率值小于1%,即:%101.0)(=<≥x P ξ,从中解出x 的范畴.解:设该地公共汽车门的高度应设计高为x cm ,那么依照题意可知:%1)(<≥x P ξ,由于)36,175(~N ξ, 因此,;01.061751)(1)(<⎪⎭⎫ ⎝⎛-Φ-=<-=≥x x P x P ξξ 也即:;99.06175>⎪⎭⎫ ⎝⎛-Φx 通过查表可知:;33.26175>-x 解得:;98.188>x即该地公共汽车门至少应设计为189cm 高.讲明:逆向思维和逆向查表,表达解决咨询题的灵活性.关键是明白得题意和找出正确的数学表达式.学生成绩的正态分布例 某班有48名同学,一次考试后数学成绩服从正态分布.平均分为80,标准差为10,咨询从理论上讲在80分至90分之间有多少人?分析:要求80分至90分之间的人数,只要算出分数落在那个范畴内的概率,然后乘以总人数即可,而运算那个概率,需要查标准正态分布表,因此应第一把那个正态总体化成标准正态总体.解:设x 表示那个班的数学成绩,那么x 服从)10,80(2N 设1080-=x Z 那么z 服从标准正态分布)1,0(N . 查标准正态分布表,得:5000.0)0(,8413.0)1(==ΦΦ因此,3413.05000.08413.0)0()1()10()1080901080108080()9080(=-=∅-∅=<<=-<-<-=<<z p x p x p∴163824.163413.048≈=⨯.讲明:这类咨询题最容易犯的错误是没有转化成标准正态分布就直截了当求解,一样地,我们在解决正态总体的有关咨询题时均要第一转化成标准正态总体.。
2022高考数学专题15 正态分布(解析版)

【解析】解:(1) µ =35 × 0.02 + 45 × 0.12 + 55 × 0.20 + 65 × 0.25 + 75 × 0.24 + 85 × 0.13 + 95 × 0.04 =66.2 . 故 Z ~ N(66.2,198) ,易知
= σ 198 ≈ 14 .
∴ P(Z ≤ 80.2) = 1 − 1 − P(66.2 − 14 < Z ≤ 66.2 + 14) = 1 − 1 − 0.6826 = 0.8413 .
的期望和方差(结果四舍五入到整数),已知样本方差 S 2 ≈ 77.8(各组数据用中点值代替).根据往年经验,
该校初三年级学生经过一年的训练,正式测试时每人每分钟跳绳个数都有明显进步,假设明年正式测试时 每人每分钟跳绳个数比初三上学期开始时个数增加 10 个,利用现所得正态分布模型: (ⅰ)预估全年级恰好有 1000 名学生,正式测试时每分钟跳 193 个以上的人数.(结果四舍五入到整数) (ⅱ)若在该地区 2020 年所有初三毕业生中任意选取 3 人,记正式测试时每分钟跳 202 个以上的人数为ξ , 求随机变量 ξ 的分布列和期望.
【解析】解:(Ⅰ)现从样本的 100 名学生中,任意选取 2 人,两人得分之和不大于 33 分,
即两人得分均为 16 分,或两人中 1 人 16 分,1 人 17 分, 由题意知:得 16 分的分数为 5 人,得 17 分的人数为 9 人,
∴两人得分之和不大于 33 分的概率为:
= P C= 52 + C51C91
组别
[30 , 40) [40 , 50) [50 , 60) [60 , 70) [70 , 80) [80 , 90) [90 ,100)
正态分布习题与详解(非常有用-必考点)

2001.若 x 〜N (0,1),求(I) P (-2.32< X <1.2) ; (2) P (x >2).解: ⑴ P (-2.32< x <1.2)=(1.2)-(-2.32)=(1.2)-[1-(2.32)]=0.8849-(1-0.9898)=0.8747.(2) P (x >2)=1- P (x <2)=1-(2)=1-0.9772=0.0228.:2利用标准正态分布表,求标准正态总体 (1)在 N(1,4)下,求 F(3).2 ,(2)在 N(^,b )下,求F (卩一6,卩+6);3 1 解: (1) F (3) =( ) =0( 1)= 0.8413 2a( )0.975 ■ 200(2)F(y+b)= ( -------------- )=0( 1)= 0.8413F(y —b))=0 (— 1 )=1—0 ( 1 )= 1 - 0.8413 = 0.1587F(y — c,a+b)=F(a+b) — F(y — cr)0.8413 — 0.1587 = 0.68263某正态总体函数的概率密度函数是偶函数,而且该函数的最大值为 1=,求总体落入区间(一1.2 , 0.2 )之间的概率.[0 ( 0.2 ) =0.5793,0 ( 1.2 ) (x )22~=0.8848]解:正态分布的概率密度函数是f(x),x (),它是偶函数,1说明” 0,f(x)的最大值为f()=亍,所以"1,这个正态分布就是标准正态分P( 1.2 x 0.2)(0.2)( 1.2) (0.2) [1 (1.2)] (0.2) (1.2) 10.5793 0.8848 10.46424.某县农民年平均收入服从 =500元,在500 : 520元间人数的百分比;(2) 的概率不少于0.95,则a 至少有多大? =200元的正态分布 (1)求此县农民年平均收入 如果要使此县农民年平均收入在( [0 ( 0.1 ) =0.5398,0 ( 1.96 ) a, a )内=0.975]解:设 表示此县农民年平均收入,~ N(500,2002).P(500520 500(500 500.200 ')(0.1) (0) 0.5398 0.50.0398 ( 2 )a)(盘—)2 200(旦)10.95,200查表知:—1.961设随机变量X 〜 N (3,1), 若P(X4) p ,,则 J P(2<X<4)=—、11(A) p(B)l 一P C .l -2p D . - p22 【答 案】C因为P(X 4) P(X 2)p ,所以 P(2<X<4)1 P(X 4) P(X2) 1 2p ,选C .2. (2010新课标全国理)某种种子每粒发芽的概率都为 0.9,现播种了 1 000粒,对于没有发 芽的种子,每粒需再补种 2粒,补种的种子数记为X ,则X 的数学期望为()A . 100B . 200C . 300D . 400[答案]B[解析]记“不发芽的种子数为了,贝U 汁B(1 000,0.1),所以E(8= 1 000 X 0.1= 100,而 X = 2E,故 E(X)= E(2 3= 2E( 3 = 200,故选 B.3.设随机变量3的分布列如下:3—10 1 Pabc其中a , b , c 成等差数列,若 E( 3 = 3,贝U D(3 =( )[答案]A[解析]设白球x 个,则黑球7— x 个,取出的2个球中所含白球个数为C 7-x 2 7 — x 6 — xP( 3= 0)= C 72 =42,x - 7 — x x 7 — x P( 3=1)= C 72 =21 ,C x 2 x x — 1P( 3= 2)= C 72 = 42 ,.x = 3.4A.9 B .1 2 9 C.3[答案]D[解析]由条件a , b , c 成等差数列知,2b = a + c ,由分布列的性质知 a + b + c = 1,又1 111 1E( 3 = — a + c = 3 解得 a= 6’ b= 3 c = 2,二 D(3= 6X2+21-「=舟.4. (2010上海松江区模考)设口袋中有黑球、白球共 7个,从中任取 2个球,已知取到 白球个数的数学期望值为7,则口袋中白球的个数为()A . 3 B . 4C . 5D . 23贝U 3取值0,1,2,0X7— x 6— x 42x 7 — x 21 + 2X X X —1 42 55.小明每次射击的命中率都为 p ,他连续射击n 次,各次是否命中相互独立,已知命中次数E 的期望值为4,方差为2,则p( &1)=()A 255B 9C 247D 7 A 256 B.256 C.256 D .64 [答案]C[解析]由条件知 旷B(n , P),E E = 4, np = 4 D E = 2n p 1 — p = 2 '1解之得,p = , n = 8, ••• P( = 0)= C 8°x 218= 2 8,1 1 1P( E= 1) = C 81x 2 1x2 7= 2 5,• P(E 1) = 1 — P( = 0) — P(E= 1)A . 2< 俘=淨,01=d2> d3B .皿> 俘=淨,d=d < dC . (J1= (J2<P 3, d 1< d 2= d 3D .小< p2= 3, d 1 = d < d 3 [答案]D(^2(X)和g(X )的图象都是关于同一条直线对称,所以其平均数相同,故3= 3,又屉(X)的对称轴的横坐标值比也(X)的对称轴的横坐标值大,故有 3<比 =3.又d 越大,曲线越“矮胖”,d 越小,曲线越“瘦高”,由图象可知,正态分布密度函 数咖(X)和侯(X )的图象一样“瘦高”,松(X )明显“矮胖”,从而可知d= d < d .6①命题"X R,cosx 0 ”的否定是:“ X R,cosx 0 ”; ②若lg a lg b lg( a b),则a b 的最大值为4; ③定义在R 上的奇函数f(X)满足f (X 2)f(X),则f(6)的值为0;=1— 18— 1 5= 24Z2 2 256. 5已知三个正态分布密度函数 则()1XX )= 2 nd e —.2X —d^(x € R , 2 di = 1,2,3)的图象如图所示,[解析]正态分布密度函数<>④已知随机变量 服从正态分布 N(1, 2),P( 5) 0.81,则P( 3) 0.19 ;其中真命题的序号是 ________ (请把所有真命题的序号都填上 ).【答案】①③④ ①命题“ x R,cosx 0”的否定是:“ x R,cosx 0 ”;所以① 正确.②若 lg a lg b lg( a b),则 Ig ab lg( a b),即 ab a b,a 0,b 0 .所以a b 22ab a b(/,即(a b) 4(a b),解得a b 4,则a b 的最小值为4;所以②错误.③定义在R 上的奇函数f( x)满足f ( x 2) f ( x),则f (x 4) f(x),且 f (0) 0,即函数的周期是 4.所以 f (6) f(2) f (0)0;所以③正确④已知随机变量服从 正态分布2N(1, ),P(5) 0.81 ,则P( 5) 1 P(5) 1 0.81 0.19 ,所以 P(3) P( 5)0.19 ;所以④正确,所以真命题的序号是①③④.7、在区间[1,1]上任取两数 m 和n ,则关于x 的方程x 2 mx n 2 0有两不相等实根的概率为 ____________ .1【答案】—由题意知1 m 1, 1 n 1.要使方程x2 mx n 2 0有两不相等实4根,则 2=m 4n 2 0 , 即(m 2n )(m 2n) 0 . .作出对应的可行域,如图直线m 2n 0,m2n0 , 当 m1 时 1 1, n C—, n B—,所 以SO111 1所以方程22 2BC 一 1 [( )xmx n 0有两不相等实根的概率为2 2222S OBC2 1 2 12 24 4'⑶ 随机变量X 服从正态分布 N(1,2),则P(X 0) P(X 2);2 1⑷ 已知a,b R ,2a b 1,则一 一 &其中正确命题的序号为 ________________________ .a b【答案】⑵(3)(1)2G lnx 〔2 ln2 ,所以⑴错误.(2)不等式1x|x 1| |x 3|的最小值为4,所以要使不等式|x 1|2 1⑵正确.(3)正确.(4)--a b所以⑷错误,所以正确的为 ⑵(3).场中的得分如图所示,则该样本的方差为7 2 3频数为A . 26B . 25C . 23D . 18【答案】D 样本的 平 均数 为23,所以 样本方差为1 [(19 523)2 (20 23)2 (22 23)2 (23 23)2(31 2 23)] 18,选 D3有一个容量为200的样本,其频率分布直方图如图所示 ,据图估计,样本数据在8,10内的21dx 1 x3.,⑵不等式|x 1|| x 3| a 恒成立,则a 4;| x 3| a 成立,则a 4,所以2已知某篮球运动员 2012年度参加了 40场比赛,现从中抽取 5场,用茎叶图统计该运动员2 1(a 严 b) 4 19,【答案】C样本数据在 8,10之外的频率为(0.02 0.05 0.09 0.15) 2 0.62,0.38 200 76,选 C .1的概率为,选 B .45从集合1,2,3,4,5中随机选取3个不同的数,这个数可以构成等差数列的概率为2【答案】25_3从集合1,2,3,4,5中随机选取3个不同的数有C 5 10种.则3个数能构成等差数列的42所以样本数据在8,10内的频率为1 0.62 0.38,所以样本数据在 8,10的频数为4. ( 2013年临沂市高三教学质量检测考试理科数学)的正方形OABC 中任取一点P,则点 1 A .3【答案】(x x 3)dxP 恰好取自阴影部分的概率为B .14【答案】B12141(c XX ) C.D.-5 6根据积分的应用可知所求阴影部分的面积为11,所以由几何概型公式可得点P 恰好取自阴影部分4如图所示,在边长为I 第孕期图4 2.有,1,2,3;2,3, 4;3,4,5;1,3,5;有4种,所以这个数可以构成等差数列的概率为10 5。
2019-2020年高考数学百大经典例题 正态分布(含解析)

2019-2020年高考数学百大经典例题 正态分布(含解析)例 设服从,求下列各式的值:(1) (2) (3)分析:因为用从标准正态分布,所以可以借助于标准正态分布表,查出其值.但由于表中只列出的情形,故需要转化成小于非负值的概率,公式:);()()();(1)(a b b a P x x Φ-Φ=<<Φ-=-Φξ和有其用武之地.解:(1);0094.09906.01)35.2(1)35.2(1)35.2(=-=Φ-=<-=≥ξξP P(2);1075.08925.01)24.1(1)24.1()24.1(=-=Φ-=-Φ=-<ξP(3))54.1()54.1()54.154.1()54.1(-Φ-Φ=<-=<ξξP P.8764.01)54.1(2)]54.1(1[)54.1(=-Φ=Φ--Φ=说明:要制表提供查阅是为了方便得出结果,但标准正态分布表如此简练的目的,并没有给查阅造成不便.相反其简捷的效果更突出了核心内容.左边的几个公式都应在理解的基础上记住它,并学会灵活应用.求服从一般正态分布的概率例 设服从试求:(1) (2)(3) (4)分析:首先,应将一般正态分布转化成标准正态分布,利用结论:若,则由知:其后再转化为非负标准正态分布情况的表达式,通过查表获得结果.解:(1);8413.0)1(25.15.3)5.3(=Φ=⎪⎭⎫ ⎝⎛-Φ=<ηP (2);0030.0)75.2(1)75.2(25.14)4(=Φ-=-Φ=⎪⎭⎫ ⎝⎛--Φ=-<ηP (3);4013.0)25.0(125.121)2(1)2(=Φ-=⎪⎭⎫⎝⎛-Φ-=<-=≥ηηP P (4)⎪⎭⎫ ⎝⎛--Φ-⎪⎭⎫ ⎝⎛-Φ-=<=<25.1325.131)2()3(ηηP P )]25.2(1[7734.0)25.2()75.0(Φ--=-Φ-Φ=说明:这里,一般正态分布,总体小于的概率值与和是一样的表述,即:服从正态分布的材料强度的概率例 已知:从某批材料中任取一件时,取得的这件材料强度服从(1)计算取得的这件材料的强度不低于180的概率.(2)如果所用的材料要求以99%的概率保证强度不低于150,问这批材料是否符合这个要求.分析:这是一个实问题,只要通过数学建模,就可以知道其本质就是一个“正态分布下求随机变量在某一范围内取值的概率”的问题;本题的第二问是一个逆向式问法,只要把握实质反向求值即可.解:(1)-=⎪⎭⎫ ⎝⎛-Φ-=<-=≥1181201801)180(1)180(ξξP P ;8665.0)11.1()]11.1(1[1)11.1(=Φ=Φ--=-Φ(2)可以先求出:这批材料中任取一件时强度都不低于150的概率为多少,拿这个结果与99%进行比较大小,从而得出结论.;9973.0)78.2()]78.2(1[1)78.2(1182001501)150(1)150(=Φ=Φ--=-Φ-=⎪⎭⎫ ⎝⎛-Φ-=<-=≥ξξP P 即从这批材料中任取一件时,强度保证不低于150的概率为99.73%>99%,所以这批材料符合所提要求.说明:“不低于”的含义即在表达式中为“大于或等于”.转化“小于”后,仍须再转化为非负值的标准正态分布表达式,从而才可查表.公共汽车门的高度例 若公共汽车门的高度是按照保证成年男子与车门顶部碰头的概率在1%以下设计的,如果某地成年男子的身高(单位:㎝),则该地公共汽车门的高度应设计为多高?分析:实际应用问题,分析可知:求的是门的最低高度,可设其为,使其总体在不低于的概率值小于1%,即:,从中解出的范围.解:设该地公共汽车门的高度应设计高为cm ,则根据题意可知:,由于, 所以,;01.061751)(1)(<⎪⎭⎫ ⎝⎛-Φ-=<-=≥x x P x P ξξ 也即:通过查表可知:解得:即该地公共汽车门至少应设计为189cm 高.说明:逆向思维和逆向查表,体现解决问题的灵活性.关键是理解题意和找出正确的数学表达式.学生成绩的正态分布例 某班有48名同学,一次考试后数学成绩服从正态分布.平均分为80,标准差为10,问从理论上讲在80分至90分之间有多少人?分析:要求80分至90分之间的人数,只要算出分数落在这个范围内的概率,然后乘以总人数即可,而计算这个概率,需要查标准正态分布表,所以应首先把这个正态总体化成标准正态总体.解:设x 表示这个班的数学成绩,则x 服从设则z 服从标准正态分布.查标准正态分布表,得:所以,3413.05000.08413.0)0()1()10()1080901080108080()9080(=-=∅-∅=<<=-<-<-=<<z p x p x p ∴.说明:这类问题最容易犯的错误是没有转化成标准正态分布就直接求解,一般地,我们在解决正态总体的有关问题时均要首先转化成标准正态总体..。
高三数学正态分布试题

高三数学正态分布试题1.在某次数学测试中,学生成绩ξ服从正态分布N(100,σ2)(σ>0),若ξ在(80,120)内的概率为0.8,则ξ在(0,80)内的概率为()A.0.05B.0.1C.0.15D.0.2【答案】B【解析】根据正态曲线的对称性可知,ξ在(80,100)内的概率为0.4,因为ξ在(0,100)内的概率为0.5,所以ξ在(0,80)内的概率为0.1,故选B.2.某班有60名学生,一次考试后数学成绩,若,则估计该班学生数学成绩在120分以上的人数为()A.10B.9C.8D.7【答案】【解析】由已知,正态曲线的对称轴为,即,所以该班学生数学成绩在120分以上的人数为. 选.【考点】正态分布.3.设随机变量X~N(2,32),若P(X≤c)=P(X>c),则c等于()A.0B.1C.2D.3【答案】C【解析】由正态曲线的对称性,得是对称轴,故.【考点】正态分布.4.从1,2,3,4,5中任取2个不同的数,事件A=“取到的2个数之和为偶数”,事件B=“取到的2个数均为偶数”,则P(B|A)=( )A. B. C. D.【答案】B【解析】∵P(A)==,P(AB)==,∴P(B|A)==.5.商场经营的某种袋装大米质量(单位:kg)服从正态分布,任取一袋大米,质量不足9.8kg的概率为 .(精确到0.0001)注:,,【答案】0.0228【解析】∵袋装大米质量(单位:kg)服从正态分布,∴.【考点】正态分布6.设随机变量服从正态分布.若P(<2)=0.8,则p(0<<1)的值为()A.0.2B.0.3C.0.4D.0.6【答案】B【解析】因为随机变量服从正态分布,则,所以,.【考点】正态分布.7.给出以下四个说法:①绘制频率分布直方图时,各小长方形的面积等于相应各组的组距;②在刻画回归模型的拟合效果时,相关指数的值越大,说明拟合的效果越好;③设随机变量服从正态分布,则;④对分类变量与,若它们的随机变量的观测值越小,则判断“与有关系”的把握程度越大.其中正确的说法是 ( )A.①④B.②③C.①③D.②④【答案】B【解析】①中各小长方形的面积等于相应各组的频率;②正确,相关指数越大,拟合效果越好,越小,拟合效果越差;③随机变量服从正态分布,正态曲线对称轴为;④对分类变量与,若它们的随机变量的观测值越小,则说明“与有关系”的把握程度越小【考点】正态分布,频率分布直方图与通监理,统计案例点评:本题考察的是基本知识点,属于识记范畴,题目简单8.已知随机变量服从正态分布,且,则 .【答案】0.48 ;【解析】ξ服从正态分布,则正态曲线关于x=3对称,因为,所以0.5-[1-]=0.48.【考点】本题主要考查正态分布曲线的特点及曲线所表示的意义。
【高中】正态分布经典练习题(可编辑修改word版)

正态分布一、选择题1.已知随机变量服从正态分布N (2,9) ,若P (>c +1) =P (<c -1) ,则c 等于()A.1B.2C.3D.42.已知随机变量服从正态分N (2,2) ,且P (< 4) = 0.8 ,则P(0 << 2) 等于()A.0.6B.0.4C.0.3D.0.23.已知随机变量服从正态分布N (2,2) ,P (≤4)=0.84,则P (≤0)等于()A. 0.16B. 0.32C. 0.68D. 0.844.已知随机变量X 服从正态分布N (2,2),P(0 <X < 4) = 0.8 ,则P( X > 4) 等于()A.0.1 B.0.2 C.0.4 D.0.65.已知随机变量服从正态分布N (3,2) ,且P (< 2) = 0.3 ,则P(2 << 4) 等于()A.0.5B.0.2C.0.3D.0.46.已知随机变量服从正态分布N (3,2) ,P (≤4)=0.842,则P (≤2)等于()A.0.842B.0.158C.0.421D.0.3167.已知随机变量X 服从正态分布N (3,1) ,且P(2 <X < 4) = 0.6826 ,则P( X > 4) 等于()A.0.1588B.0.158C.0.1586D.0.15858.已知随机变量X 服从正态分布N (0,2) ,若P( X > 2) = 0.023,则P(-2 ≤X ≤2) 等于()A.0.477B.0.628C.0.954D.0.9779.在某次联考数学测试中,学生成绩服从正态分布(100, 2) (> 0) ,若在(80,120)内的概率为0.8,则落在(0,80)内的概率为()A.0.05B.0.1C.0.15D.0.210.已知随机变量X 服从正态分布N (,2) ,且P (- 2<X <+ 2) = 0.9544 ,P (-<X <+) =0.6826 ,若=4,=1, 则P(5 <X <6) =()A.0.1358B.0.1359C.0.2716D.0.271811.某商场经营的一种袋装的大米的质量服从正态分布N (10, 0.12 ) (单位kg),任选一袋这种大米,其质量在9.8~10.2kg 的概率为()A.0.0456B.0.6826C.0.9544D.0.997412.一批电池的使用时间X (单位:小时)服从正态分布N (36,42 ) ,在这批灯泡中任取一个第1 页共 2 页“使用时间不小于40 小时”的概率是()A.0.9544B.0.6826C. 0.3174D. 0.1587二、填空题13.某校在本学期期中考试中,理科数学考试成绩~ N (90,2) ,统计结果显示P(60≤≤120)=0.8,该校参加此次考试的理科学生共420 人,试估计该校成绩高于120 分的理科学生数为.14.某班有50 名学生,一次考试的成绩服从正态分布N (100,2) , 已知P(90 ≤≤ 100) = 0.3 ,估计该班数学成绩在110分以上的人数为.15.某中学200 名考生的高考数学成绩近似服从正态分布N (120,102 ) ,则此校数学成绩在140 分以上的考生人数约为.16.某市高二理科学生数学考试的成绩x 服从正态分布,其密度曲线如图,已知该市理科学生总数是10000 人,则成绩位于(65,85] 的人数约.17.在某项测量中,测量结果服从正态分布N (1,2) (>0) ,若在(0,1) 内取值的概率为0.4,则在(0,2)内取值的概率为.18.假设每天从甲地去乙地的旅客人数X 是服从正态分布N (800,502) 的随机变量.记一天中从甲地去乙地的旅客人数不超过900 的概率为.19.一批电阻的阻值X 服从正态分布N (1000,52 ) (单位Ω).今从甲乙两箱成品中各随机抽取一个电阻,测得阻值分别为1011 Ω和982 Ω,可以认为. (填写正确序号)①甲乙两箱电阻均可出厂;②甲乙两箱电阻均不可出厂;③甲箱电阻可出厂,乙箱电阻不可出厂;④甲箱电阻不可出厂,乙箱电阻可出厂.20.某一部件由三个电子元件按下图方式连接而成,元件1 或元件2 正常工作,且元件3 正常工作,则部件正常工作.设三个电子元件的使用寿命(单位:小时)均服从正态分布N (1000,502 ) ,且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000 小时的概率为.16 题图第2 页共 2 页20 题图15 2O75 x。
正态分布(习题版)
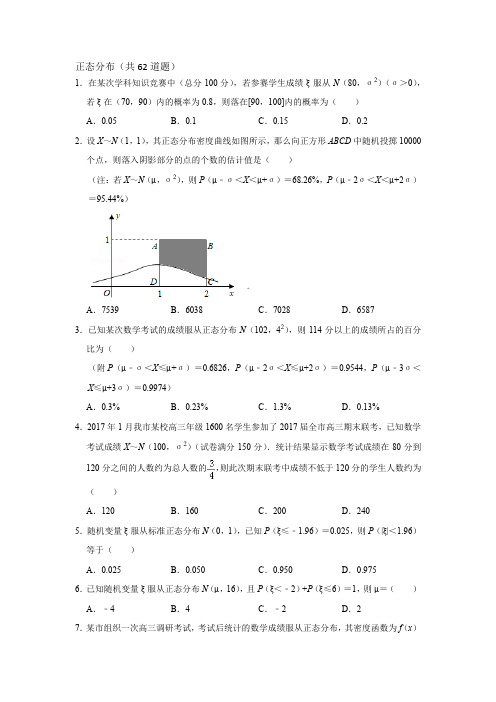
34.已知随机变量服从正态分布X~N(2,σ2),若P(X<a)=0.32,则P(a<X<4﹣a)=.
党的十八大以来党中央从全面建成小康社会全局出发把扶贫工作摆在治国理政的突出位置全面打响脱贫攻坚战2018年6月中共中央国务院关于打赢脱贫攻坚战三年行动的指导意见发布对精准脱贫这一攻坚战做出了新的部署2019年3月十三届全国人大二次会议召开3月7日国务院扶贫办刘永富回答记者问时表示
正态分布(共62道题)
17.设随机变量ξ~N(2,4),若P(ξ>2a+1)=P(ξ<2a﹣1),则实数a的值为( )
A.1B.2C.3D.4
18.已知随机变量X~B(2,p),Y~N(2,σ2),若P(X≥1)=0.64,P(0<Y<2)=p,则P(Y>4)=( )
A.0.1B.0.2C.பைடு நூலகம்.4D.0.8
19.已知随机变量ξ服从正态分布N(μ,σ2),若P(ξ<2)=P(ξ>6)=0.2,则P(2≤ξ<4)等于( )
A.120B.160C.200D.240
5.随机变量ξ服从标准正态分布N(0,1),已知P(ξ≤﹣1.96)=0.025,则P(|ξ|<1.96)等于( )
A.0.025B.0.050C.0.950D.0.975
6.已知随机变量ξ服从正态分布N(μ,16),且P(ξ<﹣2)+P(ξ≤6)=1,则μ=( )
28.2018年元旦期间,某高速公路收费站的三个高速收费口每天通过的小汽车数X(单位:辆)均服从正态分布N(600,σ2),若P(500<X<700)=0.6,假设三个收费口均能正常工作,则这个收费口每天至少有一个超过700辆的概率为( )
高中数学新课标典型例题正态分布

借助于标准正态分布表求值例 设ξ服从)1,0(N ,求下列各式的值:(1));35.2(≥ξP (2));24.1(-<ξP (3)).54.1(<ξP分析:因为ξ用从标准正态分布,所以可以借助于标准正态分布表,查出其值.但由于表中只列出)()(,0000x x P x Φ=<≥ξ的情形,故需要转化成小于非负值0x 的概率,公式:);()()();(1)(a b b a P x x Φ-Φ=<<Φ-=-Φξ和)(1)(00x P x P <-=≥ξξ有其用武之地.解:(1);0094.09906.01)35.2(1)35.2(1)35.2(=-=Φ-=<-=≥ξξP P(2);1075.08925.01)24.1(1)24.1()24.1(=-=Φ-=-Φ=-<ξP(3))54.1()54.1()54.154.1()54.1(-Φ-Φ=<-=<ξξP P.8764.01)54.1(2)]54.1(1[)54.1(=-Φ=Φ--Φ=说明:要制表提供查阅是为了方便得出结果,但标准正态分布表如此简练的目的,并没有给查阅造成不便.相反其简捷的效果更突出了核心内容.左边的几个公式都应在理解的基础上记住它,并学会灵活应用.求服从一般正态分布的概率例 设η服从)2,5.1(2N 试求:(1));5.3(<ηP (2));4(-<ηP(3));2(≥ηP (4)).3(<ηP分析:首先,应将一般正态分布)2,5.1(N 转化成标准正态分布,利用结论:若),(~2σμηN ,则由)1,0(~N σμηξ-=知:,)(⎪⎭⎫ ⎝⎛-Φ=<σμηx x P 其后再转化为非负标准正态分布情况的表达式,通过查表获得结果. 解:(1);8413.0)1(25.15.3)5.3(=Φ=⎪⎭⎫⎝⎛-Φ=<ηP(2);0030.0)75.2(1)75.2(25.14)4(=Φ-=-Φ=⎪⎭⎫ ⎝⎛--Φ=-<ηP (3);4013.0)25.0(125.121)2(1)2(=Φ-=⎪⎭⎫⎝⎛-Φ-=<-=≥ηηP P (4)⎪⎭⎫ ⎝⎛--Φ-⎪⎭⎫ ⎝⎛-Φ-=<=<25.1325.131)2()3(ηηP P )]25.2(1[7734.0)25.2()75.0(Φ--=-Φ-Φ=.7612.0)9878.01(7734.0=--=说明:这里,一般正态分布),(~2σμξN ,总体小于x 的概率值)(x F 与)(x P <ξ和⎪⎭⎫ ⎝⎛-Φσμx 是一样的表述,即:.)()(⎪⎭⎫ ⎝⎛-Φ==<σμξx x F x P 服从正态分布的材料强度的概率例 已知:从某批材料中任取一件时,取得的这件材料强度ξ服从).18,200(2N(1)计算取得的这件材料的强度不低于180的概率.(2)如果所用的材料要求以99%的概率保证强度不低于150,问这批材料是否符合这个要求.分析:这是一个实问题,只要通过数学建模,就可以知道其本质就是一个“正态分布下求随机变量在某一范围内取值的概率”的问题;本题的第二问是一个逆向式问法,只要把握实质反向求值即可.解:(1)-=⎪⎭⎫ ⎝⎛-Φ-=<-=≥1181201801)180(1)180(ξξP P ;8665.0)11.1()]11.1(1[1)11.1(=Φ=Φ--=-Φ(2)可以先求出:这批材料中任取一件时强度都不低于150的概率为多少,拿这个结果与99%进行比较大小,从而得出结论.;9973.0)78.2()]78.2(1[1)78.2(1182001501)150(1)150(=Φ=Φ--=-Φ-=⎪⎭⎫ ⎝⎛-Φ-=<-=≥ξξP P 即从这批材料中任取一件时,强度保证不低于150的概率为99.73%>99%,所以这批材料符合所提要求.说明:“不低于”的含义即在表达式中为“大于或等于”.转化“小于”后,仍须再转化为非负值的标准正态分布表达式,从而才可查表.公共汽车门的高度例 若公共汽车门的高度是按照保证成年男子与车门顶部碰头的概率在1%以下设计的,如果某地成年男子的身高)36,175(~N ξ(单位:㎝),则该地公共汽车门的高度应设计为多高?分析:实际应用问题,分析可知:求的是门的最低高度,可设其为)cm (x ,使其总体在不低于x 的概率值小于1%,即:%101.0)(=<≥x P ξ,从中解出x 的范围.解:设该地公共汽车门的高度应设计高为x ,则根据题意可知:%1)(<≥x P ξ,由于)36,175(~N ξ, 所以,;01.061751)(1)(<⎪⎭⎫ ⎝⎛-Φ-=<-=≥x x P x P ξξ 也即:;99.06175>⎪⎭⎫ ⎝⎛-Φx 通过查表可知:;33.26175>-x 解得:;98.188>x即该地公共汽车门至少应设计为189高.说明:逆向思维和逆向查表,体现解决问题的灵活性.关键是理解题意和找出正确的数学表达式.学生成绩的正态分布例 某班有48名同学,一次考试后数学成绩服从正态分布.平均分为80,标准差为10,问从理论上讲在80分至90分之间有多少人?分析:要求80分至90分之间的人数,只要算出分数落在这个范围内的概率,然后乘以总人数即可,而计算这个概率,需要查标准正态分布表,所以应首先把这个正态总体化成标准正态总体.解:设x 表示这个班的数学成绩,则x 服从)10,80(2N 设1080-=x Z 则z 服从标准正态分布)1,0(N . 查标准正态分布表,得:5000.0)0(,8413.0)1(==ΦΦ所以,3413.05000.08413.0)0()1()10()1080901080108080()9080(=-=∅-∅=<<=-<-<-=<<z p x p x p∴163824.163413.048≈=⨯.说明:这类问题最容易犯的错误是没有转化成标准正态分布就直接求解,一般地,我们在解决正态总体的有关问题时均要首先转化成标准正态总体.。
高考数学复习典型题型专题练习54 正态分布

第54讲正态分布参考数据:若Z~N(μ,σ2),则P(μ-σ≤Z≤μ+σ)≈0.682 7,P(μ-2σ≤Z≤μ+2σ)≈0.954 5,P(μ-3σ≤Z≤μ+3σ)≈0.997 3.一、单项选择题(选对方法,事半功倍)1. 已知随机变量ξ服从正态分布N(1,σ2),若P(ξ≥2)=a,P(0<ξ≤1)=1-3a,则P(ξ≤0)等于()A. 14 B.13C. 12 D.342. 某校一次高三年级数学检测,经抽样分析,成绩ξ近似服从正态分布N(95,σ2),且P(91<ξ≤95)=0.25.若该校有700人参加此次检测,估计该校此次检测数学成绩不低于99分的人数为()A. 100B. 125C. 150D. 1753. (2023·沈阳质检)已知随机变量ξ~N(1,σ2),且P(ξ≤0)=P(ξ≥a),则1x+4a-x(0<x<a)的最小值为()A. 9B. 9 2C. 4D. 64. (2023·深圳模拟)已知随机变量ξ~N(μ,σ2),有下列四个命题:甲:P(ξ<a-1)>P(ξ>a+2);乙:P(ξ>a)=0.5;丙:P(ξ≤a)=0.5;丁:P(a<ξ<a+1)<P(a+1<ξ<a+2).如果只有一个假命题,则该命题为()A. 甲B. 乙C. 丙D. 丁二、多项选择题(练—逐项认证,考—选确定的)5. 阳山水蜜桃迄今已有近七十年的栽培历史,产于中国著名桃乡江苏无锡阳山镇.水蜜桃果形大、色泽美,皮韧易剥、香气浓郁,汁多味甜,入口即化,有“水做骨肉”的美誉.阳山水蜜桃早桃品种5月底开始上市,7月15日前后,甜度最高的湖景桃也将大量上市.已知甲、乙两个品种的阳山水蜜桃的质量(单位:kg)分别服从正态分布N1(μ1,σ21),N2(μ2,σ22),其正态密度曲线如图所示,则下列说法正确的是()(第5题)A. 乙品种水蜜桃的平均质量μ2=0.8B. 甲品种水蜜桃的质量比乙品种水蜜桃的质量更集中于平均值左右C. 甲品种水蜜桃的平均质量比乙品种水蜜桃的平均质量小D. 乙品种水蜜桃的质量服从的正态分布的参数σ2=1.996. “世界杂交水稻之父”袁隆平发明了“三系法”籼型杂交水稻,成功研究出“两系法”杂交水稻,创建了超级杂交稻技术体系.某水稻种植研究所调查某地杂交水稻的株高,得出株高(单位:cm)服从正态分布,其正态密度函数φ(x)=1102πe -(x -100)2200,x ∈(-∞,+∞),则() A. 该地杂交水稻的平均株高为100cmB. 该地杂交水稻株高的方差为10C. 该地杂交水稻株高在120cm 以上的数量和株高在80cm 以下的数量一样多D. 随机测量该地的一株杂交水稻,其株高在(80,90)和在(100,110)的概率一样大三、填空题(精准计算,整洁表达)7. 若随机变量X ~N (0,1),且P (-1<X <1)=a ,则P (X >1)=________.8. (2023·豫南联考)设X ~N (1,σ2),且P (X ≥3)=0.158 65,在平面直角坐标系xOy 中,若圆x 2+y 2=σ2上有四个点到直线12x -5y +c =0的距离为1,则实数c 的取值范围是________.9. (2023·沈阳调研)为了解高三复习备考情况,某校组织了一次阶段考试.若高三全体考生的数学成绩近似服从正态分布N (100,17.52).已知成绩在117.5分以上(不含117.5分)的学生有80人,则此次参加考试的学生成绩低于82.5分的概率为________(结果精确到小数点后两位);如果成绩大于135分的为特别优秀,那么本次数学考试成绩特别优秀的大约有________人.四、解答题(让规范成为一种习惯)10. (2023·广州模拟)某工厂为A 公司生产某种零件.现准备交付一批(1 000个)刚出厂的该零件,质检员从中抽取了100个,测量并记录了它们的尺寸(单位:mm),统计结果如下表.量X,求X的均值;(2) 假设该厂生产的该零件的尺寸Y~N(2.069,0.012).根据A公司长期的使用经验,该厂提供的每批该零件中,Y>m的零件为不合格品,约占整批零件的10%,其余尺寸的零件均为合格品,请估计m的值(结果保留三位小数).附:若Y~N(μ,σ2),令Z=Y-μσ,则Z~N(0,1),且P(Z≤1.28)≈0.9.11. 某县工作组引入资金新建了一条从该县到市区的快速道路,工作组为了解该快速道路的交通通行状况,调查了行经该道路的各种类别的机动车共 1 000辆,对行车速度进行统计后,得到如图所示的频率分布直方图.(第11题)(1) 试根据频率分布直方图,求样本中的这1 000辆机动车的平均车速(同一组中的数据用该组区间的中点值代替);(2) 设该公路上机动车的行车速度v服从正态分布N(μ,σ2),其中μ,σ2分别取自该调查样本中机动车的平均车速和车速的方差s2(经计算s2=210.25).①请估计该公路上10 000辆机动车中车速不低于85 km/h的车辆数(精确到个位);②现从经过该公路的机动车中随机抽取10辆,设车速低于85 km/h的车辆数为X,求X的期望.。
正态分布练习题(含部分答案)

正态分布练习题(含部分答案)正态分布练习题1正态分布1.1正态函数及曲线特点1.(对称性):已知随机变量ξN (2,32)。
若P (ξ>C +1)=P (ξ2.(单峰与最值)若正态分布曲线是偶函数,且最大值为14√2π,则总体的均值和方差分别为0和16。
1.2三个重要区间的概率应用(特殊区间段的计算公式)P 1=P (μ?σP 2=P (μ?2σP 3=P (μ?3σ类型1:(μ,μ+nσ]型,(n =1,2,3):P (μP n ,(n =1,2,3);如:P (μ类似也可求解(μ?nσ,μ]型,(n =1,2,3).类型2:(μ±nσ,+∞)型,(n =0,1,2,3):P (μ±nσ类似也可求解(?∞,μ±nσ)型,(n =0,1,2,3).类型3:(μ+kσ,μ+tσ)型,?3≤k <="">case 1:kt ≤0时P (μ+kσ×[P t +P |k |]case 2:kt ≥0时P (μ+kσ<="" ≤μ+tσ)="12×[P">1练习:1.若X N(μ,1),求P(μ?3< bdsfid="97" p=""><>2.若X N(5,1),求P(6< bdsfid="99" p=""><>3.若X N(1,1),求P(3< bdsfid="101" p=""><>4.若X N(0,1),求P(?3<x< bdsfid="103" p=""></x<>1.3应用问题1.某糖厂用自动打包机打包,包质量(单位:kg)目标以正态分布X N(100,1.22).(1)求质量在(98.8,101.2]内的糖包后的概率;(2)若一公司从该糖厂进货1500包,试估计在(98.8,101.2]内的糖包的数量。
标准正态分布的例题

标准正态分布的例题标准正态分布是统计学中非常重要的一个概念,它在自然科学、社会科学以及工程技术等领域都有着广泛的应用。
在实际问题中,我们经常会遇到与标准正态分布相关的例题,通过对这些例题的分析与求解,可以更好地理解标准正态分布的性质和应用。
接下来,我们将通过一些例题来深入探讨标准正态分布。
例题1,某班级的学生身高符合标准正态分布,平均身高为165cm,标准差为5cm。
求身高在160cm以上的学生所占的比例。
解析,根据标准正态分布的性质,我们知道在平均值附近的数据出现的概率较大,而远离平均值的数据出现的概率较小。
因此,我们可以利用标准正态分布的性质来求解这个问题。
首先,我们需要将原始数据转化为标准正态分布的Z分数,即将160cm转化为Z分数。
利用Z分数的计算公式,Z = (X μ) / σ,其中X为原始数据,μ为平均值,σ为标准差,代入数据计算得到Z = (160 165) / 5 = -1。
然后,我们可以查找标准正态分布表或利用统计软件计算Z为-1时对应的累积概率,即P(Z > -1)。
在标准正态分布表中查找得到P(Z > -1)约为0.8413。
因此,身高在160cm以上的学生所占的比例约为84.13%。
例题2,某工厂生产的零件长度符合标准正态分布,平均长度为12cm,标准差为2cm。
求零件长度在10cm到14cm之间的概率。
解析,同样地,我们可以利用标准正态分布的性质来求解这个问题。
首先,将原始数据转化为标准正态分布的Z分数。
计算10cm和14cm分别对应的Z分数,得到Z1 = (10 12) / 2 = -1 和 Z2 = (14 12) / 2 = 1。
然后,我们可以利用标准正态分布表或统计软件计算P(-1 < Z < 1),即零件长度在10cm到14cm之间的累积概率。
在标准正态分布表中查找得到P(-1 < Z < 1)约为0.6826。
因此,零件长度在10cm到14cm之间的概率约为68.26%。
高中正态分布例题解析

高中正态分布例题解析高中正态分布例题解析正态分布是统计学中最重要的分布之一,常常被用于描述自然界和社会现象中的许多现象,例如身高、体重、考试成绩等。
在高中数学中,正态分布也是一个重要的概念,学生常常会遇到与正态分布相关的例题。
例题1:某班级的学生身高服从正态分布,平均身高为165厘米,标准差为5厘米。
如果选取一个学生,他的身高高于170厘米的概率是多少?解析:首先,我们需要将题目中的数据转化为标准正态分布。
标准正态分布是平均值为0,标准差为1的正态分布。
根据标准化公式,我们可以计算出该学生的z分数为:z = (170 - 165) / 5 = 1然后,我们需要查找标准正态分布表或使用计算器来找到z分数为1对应的概率。
查表或计算器得到的结果是0.8413。
因此,该学生身高高于170厘米的概率是0.8413。
例题2:某次考试的成绩服从正态分布,平均成绩为80分,标准差为10分。
如果从这个班级中随机选取一个学生,他的成绩在70分到90分之间的概率是多少?解析:同样地,我们需要将题目中的数据转化为标准正态分布。
计算该学生的z分数为:z1 = (70 - 80) / 10 = -1z2 = (90 - 80) / 10 = 1然后,我们需要计算z分数在-1到1之间的面积。
由于正态分布是对称的,我们可以查找标准正态分布表或使用计算器来找到z分数为1对应的概率,然后将其减去z分数为-1对应的概率。
查表或计算器得到的结果是0.6827。
因此,该学生成绩在70分到90分之间的概率是0.6827。
通过解析这两个高中正态分布的例题,我们可以看到如何将原始数据转化为标准正态分布,以及如何利用标准正态分布表或计算器来计算概率。
这些技巧对于解决其他与正态分布相关的问题也是适用的。
在高中数学中,掌握正态分布的概念和应用是非常重要的,因为它涉及到了许多实际问题的解决。
高中数学新课标典型例题正态分布

借助于标准正态散布表求值例设听从 N (0,1),求以下各式的值:(1)P( 2.35);( 2)P(1.24);( 3)P(1.54).剖析:因为用从标准正态散布,因此能够借助于标准正态散布表,查出其值.但因为表中只列出 x00, P(x)( x)的情况,故需要转变成小于非负值x0的概率,公式:00( x) 1(x); P(a b)(b)(a); 和 P(x0 ) 1 P(x0 ) 有其用武之地.解:( 1)P(2.35)1P( 2.35)1(2.35) 10.99060.0094;(2)P( 1.24)( 1.24)1(1.24)10.89250.1075;(3)P( 1.54)P( 1.54 1.54)(1.54)( 1.54)(1.54)[1(1.54)]2(1.54)10.8764.说明:要制表供给查阅是为了方便得出结果,但标准正态散布表这样精练的目的,并无给查阅造成不便.相反其简捷的成效更突出了中心内容.左侧的几个公式都应在理解的基础上记着它,并学会灵巧应用.求听从一般正态散布的概率例设听从 N (1.5,22 ) 试求:(1)P( 3.5);(2)P(4);(3)P(2);(4)P(3).剖析:第一,应将一般正态散布N (1.5,2) 转变成标准正态散布,利用结论:若~ N ( , 2 ),则由~ N (0,1) 知: P(x)x, 后来再转变为非负标准正态散布状况的表达式,经过查表获取结果.3.5 1.5(1) 0.8413;解:( 1)P(3.5)2(2)P(4)41.5(2.75)1(2.75)0.0030; 2(3)P(2)1P(2)12 1.51(0.25)0.4013;2(4)P(3)P(2)13 1.53 1.5 22( 0.75)( 2.25)0.7734[1( 2.25)]0.7734(10.9878)0.7612.说明:这里,一般正态散布~N( ,2 ) ,整体小于x的概率值 F ( x)与P(x) 和x是同样的表述,即:P(x) F ( x)x.听从正态散布的资料强度的概率例已知:从某批资猜中任取一件时,获得的这件资料强度听从 N (200,182 ).( 1)计算获得的这件资料的强度不低于180 的概率.(2)假如所用的资料要求以 99%的概率保证强度不低于 150,问这批资料能否切合这个要求.剖析:这是一个实问题,只需经过数学建模,就能够知道其本质就是一个“正态散布下求随机变量在某一范围内取值的概率”的问题;此题的第二问是一个逆向式问法,只需掌握本质反向求值即可.解:( 1)P(180) 1 P(180)11801201 18( 1.11)1[1(1.11)](1.11)0.8665;( 2)能够先求出:这批资猜中任取一件时强度都不低于150 的概率为多少,拿这个结果与 99%进行比较大小,进而得出结论.P( 150) 1P(150)1502001( 2.78) 1 [1 ( 2.78)]( 2.78) 0.9973; 118即从这批资猜中任取一件时,强度保证不低于150 的概率为%> 99%,因此这批资料符合所概要求.说明:“不低于”的含义即在表达式中为“大于或等于”.转变“小于”后,仍须再转变为非负值的标准正态散布表达式,进而才可查表.公共汽车门的高度例若公共汽车门的高度是依据保证成年男子与车门顶部碰头的概率在1%以下设计的,假如某地成年男子的身高~ N (175,36) (单位:㎝),则该地公共汽车门的高度应设计为多高?剖析:本质应用问题,剖析可知:求的是门的最低高度,可设其为x( cm) ,使其整体在不低于 x 的概率值小于1%,即:P(x)0.01 1% ,从中解出x 的范围.解:设该地公共汽车门的高度应设计高为x cm,则依据题意可知:P(x) 1% ,由于 ~ N (175,36),因此, P(x) 1x1750.01; P(x) 16也即:x1750.99;6x175经过查表可知: 2.33;解得: x 188.98;即该地公共汽车门起码应设计为189cm高.说明:逆向思想和逆向查表,表现解决问题的灵巧性.重点是理解题意和找出正确的数学表达式.学生成绩的正态散布例某班有 48 名同学,一次考试后数学成绩听从正态散布.均匀分为 80,标准差为10,问从理论上讲在 80 分至 90 分之间有多少人?剖析:要求 80 分至 90 分之间的人数,只需算出分数落在这个范围内的概率,而后乘以总人数即可,而计算这个概率,需要查标准正态散布表,因此应第一把这个正态整体化成标准正态整体.解:设 x 表示这个班的数学成绩,则x 听从N (80,102)x80N (0,1) .设 Z则 z 听从标准正态散布10查标准正态散布表,得:(1)0.8413, (0) 0.5000所以,p(80 x 90) p(80 80x 8090 80) p(0 z 1)(1)(0) 0.8413 0.5000 0.3413 101010∴48 0.3413 16.3824 16 .说明:这种问题最简单犯的错误是没有转变成标准正态散布就直接求解,一般地,我们在解决正态整体的相关问题时均要第一转变成标准正态整体.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
借助于标准正态分布表求值
例 设ξ服从)1,0(N ,求下列各式的值:
(1));35.2(≥ξP (2));24.1(-<ξP (3)).54.1(<ξP
分析:因为ξ用从标准正态分布,所以可以借助于标准正态分布表,查出其值.但由于表中只列出)()(,0000x x P x Φ=<≥ξ的情形,故需要转化成小于非负值0x 的概率,公式:);()()();(1)(a b b a P x x Φ-Φ=<<Φ-=-Φξ和)(1)(00x P x P <-=≥ξξ有其用武之地.
解:(1);0094.09906.01)35.2(1)35.2(1)35.2(=-=Φ-=<-=≥ξξP P
(2);1075.08925.01)24.1(1)24.1()24.1(=-=Φ-=-Φ=-<ξP
(3))54.1()54.1()54.154.1()54.1(-Φ-Φ=<-=<ξξP P
.8764.01)54.1(2)]54.1(1[)54.1(=-Φ=Φ--Φ=
说明:要制表提供查阅是为了方便得出结果,但标准正态分布表如此简练的目的,并没有给查阅造成不便.相反其简捷的效果更突出了核心内容.左边的几个公式都应在理解的基础上记住它,并学会灵活应用.
求服从一般正态分布的概率
例 设η服从)2,5.1(2N 试求:
(1));5.3(<ηP (2));4(-<ηP
(3));2(≥ηP (4)).3(<ηP
分析:首先,应将一般正态分布)2,5.1(N 转化成标准正态分布,利用结论:若),(~2σμηN ,则由)1,0(~N σμηξ-=知:,)(⎪⎭
⎫ ⎝⎛-Φ=<σμηx x P 其后再转化为非负标准正态分布情况的表达式,通过查表获得结果. 解:(1);8413.0)1(25.15.3)5.3(=Φ=⎪⎭⎫
⎝⎛-Φ=<ηP
(2);0030.0)75.2(1)75.2(25.14)4(=Φ-=-Φ=⎪⎭
⎫ ⎝⎛--Φ=-<ηP (3);4013.0)25.0(125.121)2(1)2(=Φ-=⎪⎭⎫
⎝⎛-Φ-=<-=≥ηηP P (4)⎪⎭⎫ ⎝
⎛--Φ-⎪⎭⎫ ⎝⎛-Φ-=<=<25.1325.131)2()3(ηηP P )]25.2(1[7734.0)25.2()75.0(Φ--=-Φ-Φ=
.7612.0)9878.01(7734.0=--=
说明:这里,一般正态分布),(~2
σμξN ,总体小于x 的概率值)(x F 与)(x P <ξ和⎪⎭⎫ ⎝⎛-Φσμx 是一样的表述,即:.)()(⎪⎭
⎫ ⎝⎛-Φ==<σμξx x F x P 服从正态分布的材料强度的概率
例 已知:从某批材料中任取一件时,取得的这件材料强度ξ服从).18,200(2N
(1)计算取得的这件材料的强度不低于180的概率.
(2)如果所用的材料要求以99%的概率保证强度不低于150,问这批材料是否符合这个要求.
分析:这是一个实问题,只要通过数学建模,就可以知道其本质就是一个“正态分布下求随机变量在某一范围内取值的概率”的问题;本题的第二问是一个逆向式问法,只要把握实质反向求值即可.
解:(1)-=⎪⎭
⎫ ⎝⎛-Φ-=<-=≥1181201801)180(1)180(ξξP P ;8665.0)11.1()]11.1(1[1)11.1(=Φ=Φ--=-Φ
(2)可以先求出:这批材料中任取一件时强度都不低于150的概率为多少,拿这个结果与99%进行比较大小,从而得出结论.
;9973.0)78.2()]78.2(1[1)78.2(1182001501)150(1)150(=Φ=Φ--=-Φ-=⎪⎭
⎫ ⎝⎛-Φ-=<-=≥ξξP P 即从这批材料中任取一件时,强度保证不低于150的概率为99.73%>99%,所以这批材料符合所提要求.
说明:“不低于”的含义即在表达式中为“大于或等于”.转化“小于”后,仍须再转化为非负值的标准正态分布表达式,从而才可查表.
公共汽车门的高度
例 若公共汽车门的高度是按照保证成年男子与车门顶部碰头的概率在1%以下设计的,如果某地成年男子的身高)36,175(~N ξ(单位:㎝),则该地公共汽车门的高度应设计为多高?
分析:实际应用问题,分析可知:求的是门的最低高度,可设其为)cm (x ,使其总体在不低于x 的概率值小于1%,即:%101.0)(=<≥x P ξ,从中解出x 的范围.
解:设该地公共汽车门的高度应设计高为x cm ,则根据题意可知:%1)(<≥x P ξ,由于)36,175(~N ξ, 所以,;01.061751)(1)(<⎪⎭
⎫ ⎝⎛-Φ-=<-=≥x x P x P ξξ 也即:;99.06175>⎪⎭
⎫ ⎝⎛-Φx 通过查表可知:;33.26
175>-x 解得:;98.188>x
即该地公共汽车门至少应设计为189cm 高.
说明:逆向思维和逆向查表,体现解决问题的灵活性.关键是理解题意和找出正确的数学表达式.
学生成绩的正态分布
例 某班有48名同学,一次考试后数学成绩服从正态分布.平均分为80,标准差为10,问从理论上讲在80分至90分之间有多少人?
分析:要求80分至90分之间的人数,只要算出分数落在这个范围内的概率,然后乘以总人数即可,而计算这个概率,需要查标准正态分布表,所以应首先把这个正态总体化成标准正态总体.
解:设x 表示这个班的数学成绩,则x 服从)10,80(2N 设10
80-=x Z 则z 服从标准正态分布)1,0(N . 查标准正态分布表,得:
5000.0)0(,8413.0)1(==ΦΦ
所
以,3413.05000.08413.0)0()1()10()10
80901080108080()9080(=-=∅-∅=<<=-<-<-=<<z p x p x p
∴163824.163413.048≈=⨯.
说明:这类问题最容易犯的错误是没有转化成标准正态分布就直接求解,一般地,我们在解决正态总体的有关问题时均要首先转化成标准正态总体.。
