(完整版)材料力学各章重点内容总结
工程材料力学性能每章重要知识点

第一章1.应力-应变曲线(拉伸力-伸长曲线)。
拉伸力在Fe以下阶段,为弹性变形阶段,到达Fa后,试样开始发生塑性变形,最初试样局部区域产生不均匀屈服塑形变形,曲线上出现平台或锯齿,直至C点结束。
继而进入均匀塑形变形阶段。
达到最大拉伸Fb时,试样在此产生不均匀塑形变形,在局部区域产生缩颈。
最终,在拉伸力Fk处,试样断裂。
2.弹性变形现象及指标弹性变形:是可逆性变形,是金属晶格中原子自平衡位置产生可逆位移的反映。
弹性变形指标:①弹性模量,是产生100%弹性变形所需应力。
②弹性比功(弹性比能、应变比能),表示金属吸收弹性变形功的能力。
③滞弹性:在弹性范围内快速加载或卸载后,随时间延长产生附加弹性应变的现象。
④循环韧性:金属材料在交变载荷(振动)下吸收不可逆变形功的能力。
3.塑性变形现象及指标金属材料常见塑性变形方式主要为滑移和孪生。
滑移:金属材料在切应力作用下位错沿滑移面和滑移方向运动而进行切变得过程。
孪生:金属材料在切应力作用下沿特定晶面和特性晶向进行的塑性变形。
塑性变形特点:①各晶粒变形的不同时性和均匀性;②各晶粒变形的相互协调性。
塑性变形指标:⑴屈服强度,屈服强度及金属材料拉伸时,试样在外力不增加(保持恒定)仍能继续伸长时的应力。
屈服现象:金属材料开始产生宏观塑形变形的标志。
屈服现象相关因素:①材料变形前可动位错密度很小;②随塑性变形的发生,位错能快速增殖;③位错的运动速率与外加应力有强烈的依存关系。
屈服现象指标:规定非比例伸长应力;规定残余伸长应力;规定总伸长应力。
影响屈服强度因素:①内在因素:金属本性和晶格类型;晶粒的大小和亚结构;溶质元素;第二相。
②外在因素:温度、应变速率、应力状态。
⑵应变硬化:金属材料阻止继续塑形变形的能力,塑性变形是硬化的原因,硬化是结果。
⑶缩颈:韧性金属材料在拉伸试验时变形集中于局部区域的特殊现象,是应变硬化与截面减小共同作用的结果。
抗拉强度:韧性金属试样拉断过程中最大力所对应的应力。
(完整版)材料力学重点总结

(完整版)材料力学重点总结材料力学阶段总结一. 材料力学的一些基本概念 1. 材料力学的任务:解决安全可靠与经济适用的矛盾. 研究对象:杆件强度:抵抗破坏的能力 刚度:抵抗变形的能力稳定性:细长压杆不失稳。
2. 材料力学中的物性假设连续性:物体内部的各物理量可用连续函数表示。
均匀性:构件内各处的力学性能相同。
各向同性:物体内各方向力学性能相同。
3。
材力与理力的关系, 内力、应力、位移、变形、应变的概念材力与理力:平衡问题,两者相同; 理力:刚体,材力:变形体。
内力:附加内力。
应指明作用位置、作用截面、作用方向、和符号规定。
应力:正应力、剪应力、一点处的应力。
应了解作用截面、作用位置(点)、作用方向、和符号规定。
正应力⎩⎨⎧拉应力压应力应变:反映杆件的变形程度⎩⎨⎧角应变线应变变形基本形式:拉伸或压缩、剪切、扭转、弯曲。
4. 物理关系、本构关系 虎克定律;剪切虎克定律:⎪⎩⎪⎨⎧==∆=Gr EA Pl l E τεσ夹角的变化。
剪切虎克定律:两线段——拉伸或压缩。
拉压虎克定律:线段的适用条件:应力~应变是线性关系:材料比例极限以内。
5。
材料的力学性能(拉压):一张σ-ε图,两个塑性指标δ、ψ,三个应力特征点:b s pσσσ、、,四个变化阶段:弹性阶段、屈服阶段、强化阶段、颈缩阶段。
拉压弹性模量E ,剪切弹性模量G ,泊松比v ,)(V EG +=126. 安全系数、 许用应力、工作应力、应力集中系数安全系数:大于1的系数,使用材料时确定安全性与经济性矛盾的关键。
过小,使构件安全性下降;过大,浪费材料。
许用应力:极限应力除以安全系数.塑性材料[]ssn σσ=s σσ=0脆性材料[]bbn σσ=b σσ=07. 材料力学的研究方法1) 所用材料的力学性能:通过实验获得。
2) 对构件的力学要求:以实验为基础,运用力学及数学分析方法建立理论,预测理论应用的未来状态。
3) 截面法:将内力转化成“外力”。
材料力学知识点总结
三、应力 1.定义 (Definition):由外力引起的内力的集度 2. 应力 ①平均应力
pm
=
ΔF ΔA
②全应力(总应力)
p lim ΔF dF ΔA0 ΔA dA
③全应力分解为 垂直于截面的应力称为“正应力”
lim ΔFN dFN ΔA0 ΔA dA
位于截面内的应力称为“切应力”
·§3-3 薄壁圆筒的扭转
1 10 r0
姚小宝
薄壁圆筒:壁厚
(r0—圆筒的平均半径)
3.推论 (1)横截面上无正应力,只有切应力;
(2)切应力方向垂直半径或 与圆周相切.
圆周各点处切应力的方向于圆周相切,且数值相等,近似的认为沿壁厚方向各点处
切应力的数值无变化.
4.推导
此式为薄壁圆筒扭转时横截面上切应力的计算公式. 薄壁筒扭转时横截面上的切应力均匀分布,与半径垂直,指向与扭矩的转向一致.
固定铰支座
固定端
5.静定梁的基本形式:
·§4-2 梁的剪力和弯矩
一、内力计算
简支梁 外伸梁
悬臂梁
求内力——截面法
姚小宝
二、内力的符号规定 1.剪力符号
2.弯矩符号
当 dx 微段的弯曲下凸(即该段的下 半部受拉 )时,横截面 m-m 上的弯矩为 正;
当 dx 微段的弯曲上凸(即该段的下半 部受压)时,横截面 m-m 上的弯矩为负.
2.平面假设
变形前为平面的横截面 ,变形后仍保持为平面.
3.几何关系 倾角 是横截面圆周上任一点 A 处的切应变, d 是 b-b 截面相对于 a-
a 截面象刚性平面一样绕杆的轴线转动的一个角度.
tan
材料力学知识点归纳总结(完整版)

材料力学知识点归纳总结(完整版)K点相邻的微小面积取得越来越小,使得合力趋近于一个点力,这个点力就是在K点处的应力。
因此,应力是指杆件横截面上单位面积内的内力分布情况,通常用符号σ表示。
应力的单位是帕斯卡(Pa),即XXX/平方米。
第三章:应变、XXX定律和XXX模量1.应变的概念:应变是指固体在外力作用下发生形状和尺寸改变的程度,通常用符号ε表示。
应变分为线性应变和非线性应变两种。
线性应变是指应变与应力成正比,即应变与内力的比值为常数,这个常数被称为材料的弹性模量。
非线性应变则不满足这个比例关系。
2.胡克定律:胡克定律是描述材料弹性变形的基本定律,它规定了应力和应变之间的关系,即在弹性阶段,应力与应变成正比,比例系数为弹性模量。
3.XXX模量:杨氏模量是描述材料抗拉、抗压变形能力的物理量,它是指单位面积内拉应力或压应力增加一个单位时,材料相应的纵向应变的比值。
XXX模量的大小反映了材料的柔软程度和刚度。
杨氏模量的单位是帕斯卡(Pa)或兆帕(MPa)。
综上所述,材料力学是研究构件在外力作用下内力、变形、破坏等规律的科学。
构件应具备足够的强度、刚度和稳定性以负荷所承受的载荷。
截面法是求解内力的基本方法,应力是指杆件横截面上单位面积内的内力分布情况,应变是指固体在外力作用下发生形状和尺寸改变的程度。
胡克定律描述了材料弹性变形的基本定律,而XXX模量则描述了材料抗拉、抗压变形能力的物理量。
应力是指在截面m-m上某一点K处的力量。
它的方向与内力N的极限方向相同,并可分解为垂直于截面的分量σ和切于截面的分量τ。
其中,σ称为正应力,τ称为切应力。
将应力的比值称为微小面积上的平均应力,用表示。
在国际单位制中,应力的单位是帕斯卡(Pa),常用兆帕(MPa)或吉帕(GPa)。
杆件是机器或结构物中最基本的构件之一,如传动轴、螺杆、梁和柱等。
某些构件,如齿轮的轮齿、曲轴的轴颈等,虽然不是典型的杆件,但在近似计算或定性分析中也可简化为杆。
材料力学章节重点和难点

材料力学章节重点和难点第一章绪论1.主要内容:材料力学的任务;强度、刚度和稳定性的概念;截面法、内力、应力,变形和应变的基本概念;变形固体的基本假设;杆件的四种基本变形。
2.重点:强度、刚度、稳定性的概念;变形固体的基本假设、内力、应力、应变的概念。
3.难点:第二章杆件的内力1.主要内容:杆件在拉压、扭转和弯曲时的内力计算;杆件在拉压、扭转和弯曲时的内力图绘制;平面弯曲的概念。
2.重点:剪力方程和弯矩方程、剪力图和弯矩图。
3. 难点:绘制剪力图和弯矩图、剪力和弯矩间的关系。
第三章杆件的应力与强度计算1.主要内容:拉压杆的应力和强度计算;材料拉伸和压缩时的力学性能;圆轴扭转时切应力和强度计算;梁弯曲时正应力和强度计算;梁弯曲时切应力和强度计算;剪切和挤压的实用计算方法;胡克定律和剪切胡克定律。
2.重点:拉压杆的应力和强度计算;材料拉伸和压缩时的力学性能;圆轴扭转时切应力和强度计算;梁弯曲时正应力和强度计算。
3.难点:圆轴扭转时切应力公式推导和应力分布;梁弯曲时应力公式推导和应力分布;第四章杆件的变形简单超静定问题1.主要内容:拉(压)杆的变形计算及单超静定问题的求解方法;圆轴扭转的变形和刚度计算;积分法和叠加法求弯曲变形;用变形比较法解超静定梁。
2.重点:拉(压)杆的变形计算;;圆轴扭转的变形和刚度计算;叠加法求弯曲变形;用变形比较法解超静定梁。
3.难点:积分法和叠加法求弯曲变形;用变形比较法解超静定结构。
第五章应力状态分析? 强度理论1.主要内容:应力状态的概念;平面应力状态分析的解析法和图解法;广义胡克定律;强度理论的概念及常用的四种强度理论。
2.重点:平面应力状态分析的解析法和图解法;广义虎克定律;常用的四种强度理论。
3.难点:主应力方位确定。
第六章组合变形1.主要内容:拉伸(压缩)与弯曲、斜弯曲、扭转与弯曲组合变形的强度计算;2.重点: 弯扭组合变形。
3.难点:截面核心的概念第七章压杆稳定1.主要内容:压杆稳定的概念;各种支座条件下细长压杆的临界载荷;欧拉公式的适用范围和经验公式;压杆的稳定性校核。
材料力学性能-考前复习总结(前三章)

材料力学性能-考前复习总结(前三章)金属材料的力学性能指标是表示其在力或能量载荷作用下(环境)变形和断裂的某些力学参量的临界值或规定值。
材料的安全性指标:韧脆转变温度Tk;延伸率;断面收缩率;冲击功Ak;缺口敏感性NSR材料常规力学性能的五大指标:屈服强度;抗拉强度;延伸率;断面收缩率;冲击功Ak;硬度;断裂韧性第一章单向静拉伸力学性能应力和应变:条件应力条件应变 =真应力真应变应力应变状态:可在受力机件任一点选一六面体,有九组应力,其中六个独立分量。
其中必有一主平面,切应力为零,只有主应力,且,满足胡克定律。
应力软性系数:最大切应力与最大正应力的相对大小。
1 弹变1)弹性比功:金属材料吸收弹性变形功的能力,一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。
ae=1/2σeεe=σe2/2E。
取决于E和弹性极限,弹簧用于减震和储能驱动,应有较高的弹性比功和良好弹性。
需通过合金强化及组织控制提高弹性极限。
2)弹性不完整性:纯弹性体的弹性变形只与载荷大小有关,而与加载方向及加载时间无关,但对实际金属而言,与这些因素均有关系。
①滞弹性:金属材料在弹性范围内快速加载或卸载后,随时间延长产生附加弹性应变的现象称为滞弹性,也就是应变落后于应力的现象。
与材料成分、组织及试验条件有关,组织约不均匀,温度升高,切应力越大,滞弹性越明显。
金属中点缺陷的移动,长时间回火消除。
弹性滞后环:由于实际金属有滞弹性,因此在弹性区内单向快速加载、卸载时,加载线与卸载线不重合,形成一封闭回路。
吸收变形功循环韧性:金属材料在交变载荷下吸收不可逆变形功的能力(塑性区加载,塑性滞后环),也叫内耗(弹性区加载),或消震性。
②包申格效应:定义:金属材料经过预先加载产生少量塑性变形,卸载后再同向加载,规定残余伸长应力增加;反向加载,规定残余伸长应力降低的现象。
(反向加载时弹性极限或屈服强度降低的现象。
特别是弹性极限在反向加载时几乎下降到零,这说明在反向加载时塑性变形立即开始了)解释:与位错运动所受阻力有关,在某滑移面上运动位错遇位错林而使其弯曲,密度增大,形成位错缠结或胞状组织,相对稳定。
工程材料力学性能各章节复习知识点

⼯程材料⼒学性能各章节复习知识点⼯程材料⼒学性能各个章节主要复习知识点第⼀章弹性⽐功:⼜称弹性⽐能,应变⽐能,表⽰⾦属材料吸收弹性变形功的能⼒。
滞弹性:对材料在弹性范围内快速加载或卸载后随时间延长附加弹性应变的现象。
包申格效应:⾦属材料经预先加载产⽣少量塑性变形(残余应变为1%~4%),卸载后再同向加载,规定残余伸长应⼒(弹性极限或屈服极限)增加,反向加载,规定残余伸长应⼒降低的现象。
塑性:指⾦属材料断裂前发⽣塑性变形的能⼒。
脆性:材料在外⼒作⽤下(如拉伸,冲击等)仅产⽣很⼩的变形及断裂破坏的性质。
韧性:是⾦属材料断裂前洗⼿塑性变形功和断裂功的能⼒,也指材料抵抗裂纹扩展的能⼒。
应⼒、应变;真应⼒,真应变概念。
穿晶断裂和沿晶断裂:多晶体材料断裂时,裂纹扩展的路径可能不同,穿晶断裂穿过晶内;沿晶断裂沿晶界扩展。
拉伸断⼝形貌特征?①韧性断裂:断裂⾯⼀般平⾏于最⼤切应⼒并与主应⼒成45度⾓。
⽤⾁眼或放⼤镜观察时,断⼝呈纤维状,灰暗⾊。
纤维状是塑性变形过程中微裂纹不断扩展和相互连接造成的,⽽灰暗⾊则是纤维断⼝便⾯对光反射能⼒很弱所致。
其断⼝宏观呈杯锥形,由纤维区、放射区、和剪切唇区三个区域组成。
②脆性断裂:断裂⾯⼀般与正应⼒垂直,断⼝平齐⽽光亮,常呈放射状或结晶状。
板状矩形拉伸试样断⼝呈⼈字形花样。
⼈字形花样的放射⽅向也与裂纹扩展⽅向平⾏,但其尖端指向裂纹源。
韧、脆性断裂区别?韧性断裂产⽣前会有明显的塑性变形,过程⽐较缓慢;脆性断裂则不会有明显的塑性变形产⽣,突然发⽣,难以发现征兆拉伸断⼝三要素?纤维区,放射区和剪切唇。
缺⼝试样静拉伸试验种类?轴向拉伸、偏斜拉伸材料失效有哪⼏种形式?磨损、腐蚀和断裂是材料的三种主要失效⽅式。
材料的形变强化规律是什么?层错能越低,n越⼤,形变强化增强效果越⼤退⽕态⾦属增强效果⽐冷加⼯态是好,且随⾦属强度等级降低⽽增加。
在某些合⾦中,增强效果随合⾦元素含量的增加⽽下降。
材料的晶粒变粗,增强效果提⾼。
材料力学重点归纳

材料力学考试重点一、。
课程的性质、任务材料力学是变形体力学的最基础课程。
固体力学(即变形体力学)是研究固体材料的变形、流动和断裂的一门科学。
它是材料科学专业的一门理论性较强的重要的技术基础课程。
本课程的基本任务是为了提高材料工程类专业学生的力学基础素养,使之掌握该专业所必需的固体力学基本概念、基本方法和基础理论,培养学生具备一定的力学分析计算能力和基本的力学实验技能,为学习后续专业课程奠定必要的力学基础。
教学的同时注意结合本课程的特点培养学生的辩证唯物主义观点。
二、课程的基本要求通过本课程的教学,应使学生达到下列基本要求:1.理论力学静力学是系统学习力学课程的必要基础。
因此要求学生理解并掌握理论力学静力学的有关概念和理论。
了解几种常见的约束类型的性质及静力学基本公理。
较熟练地掌握对物体进行受力分析的方法。
2.了解静力学的基本任务。
理解并掌握力线的平移定理。
熟悉各类平面力系的简化方法和结果。
掌握各类平面力系的平衡条件,并能熟练地应用它们去求解物体(或物体系)的平衡问题。
简单了解空间力系的简化结果、力对轴之矩的概念及重心的概念。
3.理解并掌握固体力学的有关基本概念:对固体力学分析问题、解决问题的基本方法和思路有明确的认识。
4.掌握一维工程构件三种基本变形的内力、应力和变形的分布变化规律、基本分析方法以及计算方法。
5.清楚了解研究测试固体材料力学性质的意义和方法,对常见固体材料(典型的金属材料和岩石)的力学性质和测定方法有基本认识和掌握。
了解电测应力方法的基本原理。
6.对应力、应力状态、应变、应变、应变状态的概念有较明确的认识。
较熟练掌握应力分析理论和应变分析理论。
7.理解和掌握固体材料弹性变形和塑性变形的主要特征,对屈服函数、主应力空间、屈服面、屈服曲线、屈服条件等概念有较明确认识。
熟悉掌握强度理论:最大拉应力理论、最大剪应力理论、形状改变比能理论、莫尔强度理论和库仑-纳维叶剪切强度准则的基本观点、适用范围、表达形式和工程应用。
材料力学知识点总结(重、难点部分)

第一章 绪 论一、基本要求(1)了解构件强度、刚度和稳定性的概念,明确材料力学课程的主要任务。
(2)理解变形固体的基本假设、条件及其意义。
(3)明确内力的概念、初步掌握用截面法计算内力的方法。
(4)建立正应力、剪应力、线应变、角应变及单元体的基本概念。
(5)了解杆件变形的受力和变形特点。
二、重点与难点1.外力与内力的概念外力是指施加到构件上的外部载荷(包括支座反力)。
在外力作用下,构件内部两部分间的附加相互作用力称为内力。
内力是成对出现的,大小相等,方向相反,分别作用在构件的两部分上,只有把构件剖开,内力才“暴露”出来。
2.应力,正应力和剪应力在外力作用下,根据连续性假设,构件上任一截面的内力是连续分布的。
截面上任一点内力的密集程度(内力集度),称为该点的应力,用p 表示0lim A P dP p A dA→∆==∆ P ∆为微面积A ∆上的全内力。
一点处的全应力可以分解为两个应力分量。
垂直于截面的分量称为正应力,用符号σ表示;和截面相切的分量称为剪应力,用符号τ表示。
应力单位为Pa 。
1MPa=610Pa, 1GPa=910Pa 。
应力的量纲和压强的量纲相同,但是二者的物理概念不同,压强是单位面积上的外力,而应力是单位面积的内力。
3.截面法截面法是求内力的基本方法,它贯穿于“材料力学”课程的始终。
利用截面法求内力的四字口诀为:切、抛、代、平。
一切:在欲求内力的截面处,假想把构件切为两部分。
二抛:抛去一部分,留下一部分作为研究对象。
至于抛去哪一部分,视计算的简便与否而定。
三代:用内力代替抛去部分队保留部分的作用力。
一般地说,在空间问题中,内力有六个分量,合力的作用点为截面形心。
四平:原来结构在外力作用下处于平衡,则研究的保留部分在外力与内力共同作用也应平衡,可建立平衡方程,由已知外力求出各内力分量。
4.小变形条件在解决材料力学问题时的应用由于大多数材料在受力后变形比较小,即变形的数量远小于构件的原始尺寸。
材料力学复习重点

材料力学性能1.填空题:30个15分2.判断题:20个10分3.名词解释 10个20分4.问答题:6个35分5.计算题:2个20分第一章单向静拉伸力学性能一、解释下列名词。
2.滞弹性:金属材料在弹性范围内快速加载或卸载后,随时间延长产生附加弹性应变的现象称为滞弹性,也就是应变落后于应力的现象。
3.循环韧性:金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。
4.包申格效应:金属材料经过预先加载产生少量塑性变形,卸载后再同向加载,规定残余伸长应力增加;反向加载,规定残余伸长应力降低的现象。
6.塑性:金属材料断裂前发生不可逆永久(塑性)变形的能力。
9.解理面:是金属材料在一定条件下,当外加正应力达到一定数值后,以极快速率沿一定晶体学平面产生的穿晶断裂,因与大理石断裂类似,故称此种晶体学平面为解理面。
11.韧脆转变温度:具有一定韧性的金属材料当低于某一温度点时,冲击吸收功明显下降,断裂方式由原来的韧性断裂变为脆性断裂,这个温度称为韧脆转变温度。
15.解理刻面:在解理断裂中具有低指数,表面能低的晶体学平面叫解理面。
这种大致以晶粒大小为单位的解理面称为解理刻面。
17.约比温度:材料的实验温度与熔点的比值。
高于这个温度的环境叫高温环境,材料的性能会随时间和温度而变化。
18.松弛稳定性:金属抵抗应力松弛的性能。
19.低周疲劳:金属材料在循环载荷作用下,疲劳寿命为102-104次的疲劳断裂叫低周疲劳。
四、何谓拉伸断口三要素?影响宏观拉伸断口性态的因素有哪些?答:宏观断口呈杯锥形,由纤维区、放射区和剪切唇三个区域组成,即所谓的断口特征三要素。
上述断口三区域的形态、大小和相对位置,因试样形状、尺寸和金属材料的性能以及试验温度、加载速率和受力状态不同而变化。
八、什么是包申格效应,如何解释,它有什么实际意义?包申格效应:金属材料经过预先加载产生少量塑性变形,卸载后再同向加载,规定残余伸长应力增加;反向加载,规定残余伸长应力降低的现象。
材料力学第(1-3)章总结

S z AyC
4 d 64
惯性矩 (平面图形 对轴的二次 矩)
图形对Z 轴的惯性矩
I z y 2 dA
A
直径为d的圆截面,惯性矩
Iy Iz
极惯性矩 I P 2dA (为微面积dA到坐标原点的距离) A (平面图形 πd 4 直径为d的圆截面,极惯性矩 IP 对坐标原点 32 D4 πd 4 O的二次矩) 外直径为D,内直径为d的空心圆截面,极惯性矩 I P 32 32
内力图
拉伸与压缩
FN 应力 A
横截面上各点的应力是均 匀的,并垂直于横截面。
扭转
T Ip
公式只适用于 等直圆轴
强度 条件 变形 刚度 条件
max
FN, max Amin
[]
横截面正应 力最大,切 应力为零。
F l l N EA
(分段计算)
E
横截面切应 Tmax max [] 力最大,正 应力为零。 Wt Tl (分段计算) G GIp
max
0 cos2
0 sin2 2
F
k
Tmax 180 [] GIp π
斜截面 上的应 力
k
剪应力互等定理
45 °斜截面上剪应力达到最大
F F M
扭转
M
F
பைடு நூலகம்
FN 轴力FN
Me
1
1T 扭矩T
A
轴力背离截面为正,轴力指向截面为负 轴力图的特点:突变值 = 集中载荷 遇到向左的集中载荷,轴力增量为正; 遇到向右的集中载荷,轴力增量为负, 外载荷不变,轴力不变。
材料力学性能重点总结

名词解释:1加工硬化:试样发生均匀塑性变形,欲继续变形则必须不断增加载荷,这种随着随性变形的增大形变抗力不断增大的现象叫加工硬化。
2弹性比功:表示金属材料吸收弹性变形功的能力。
3滞弹性:在弹性范围内快速加载或卸载后,随着时间延长产生附加弹性应变的现象。
4包申格效应:金属材料通过预先加载产生少量塑性变形(残余应变小于1%-4%),而后再同向加载,规定残余伸长应力增加;反向加载,规定残余伸长应力降低的现象。
5塑性:金属材料断裂前发生塑性变形的能力。
常见塑性变形方式:滑移和孪生6弹性极限:以规定某一少量的残留变形为标准,对应此残留变形的应力。
7比例极限:应力与应变保持正比关系的应力最高限。
8屈服强度:以规定发生一定的残留变形为标准,如通常以0.2%的残留变形的应力作为屈服强度。
9韧性断裂是材料断裂前发生产生明显的宏观塑性变形的断裂,这种断裂有一个缓慢的断裂过程,在裂纹扩展过程中不断的消耗能量。
韧性断裂的断裂面一般平行于最大切应力并于主应力成45度角。
10脆性断裂是突然发生的断裂,断裂前基本上不发生塑形变形,没有明显征兆,危害性很大。
断裂面一般与主应力垂直,端口平齐而光亮,常呈放射状或结晶状。
11剪切断裂是金属材料在切应力作用下,沿着滑移面分离而造成的断裂,又分滑断和微孔聚集性断裂。
12解理断裂:是金属材料在一定条件下,当外加正应力达到一定数值后,以极快速率沿一定晶体学平面产生的穿晶断裂,总是脆性断裂。
13缺口效应:由于缺口的存在,在静载荷作用下,缺口截面上的应力状态发生变化,产生所谓“缺口效应“①缺口引起应力集中,并改变了缺口应力状态,使得缺口试样或机件中所受的应力由原来的单向应力状态改变为两向或者三向应力状态。
②缺口使得材料的强度提高,塑性降低,增大材料产生脆断的倾向。
8缺口敏感度:有缺口强度的抗拉强度σbm与等截面尺寸光滑试样的抗拉强度σb的比值. NSR=σbn / σs NSR越大缺口敏感度越小9冲击韧性:Ak除以冲击式样缺口底部截面积所得之商10冲击吸收功:式样变形和断裂所消耗的功,称为冲击吸收功以Ak表示,单位J11低温脆性:一些具有体心立方晶格或某些秘排立方晶格的金属,当温度降低到、某一温度时,会由韧性状态变为脆性状态,冲击吸收功明显下降,断裂机理由微孔聚集变为穿晶解理,断口特征由纤维状变为结晶状,这种现象称为低温脆性12 脆性转变温度:当温度降低时,材料屈服强度急剧增加,而塑形和冲击吸收功急剧减小。
材料力学章节重点总结

1.应力的概念,平均应力 P13
2.斜截面上的应力,包括正应力和切应力的公式 P18
3.线应变及胡可定律(重要),泊松比 P20
4.材料的拉伸和压缩试验,脆性材料和塑形材料 P27
第三章
1.相对扭转角和切应变的概念及转换公式 P60
2.扭矩图的作法 P62
3.等直圆杆扭转时的三个假设 P64
4.圆截面和空心截面的扭转截面系数 P67
5.截面上正应力和切应力的公式 P68
6.扭转刚度条件 P75
另:周末你要上课,我们周五上午上课。上次的课后习题有不懂的在周四下午五点前反馈给我。
第三章习题:3-2.3-7.3-11.3-13.3-20.3-21.这一章的课后习题有很多超出大纲了,暂时只布置这么多。
3.约束条件和边界条件用于求方程中的C1和C2 P162
4.5.3节按叠加原理计算梁的挠度和转角,把书上的例题看懂就行 P165
5.5.4节不在考试范围
6.梁的刚度校核,公式(5-11) P173
7.提高梁刚度的两种措施,其中第二种是措施是应用最多的 P175
8.5-6节弯曲应变能不在考试范围
7.矩形截面梁,工字形截面梁,薄壁环形截面梁,圆截面梁最大切应力的计算公式P130-P136
这一章的内容很多,也很重要,是考试的重点章节。书上有很多的例题,基本都是考试范围,你尽量看懂这些例题,实在不懂的我再给你讲解。
第五章
1.挠度和转角的概念(了解)P157
2.公式(5-2b)公式(5-3a)公式(5-3b)的记忆理解,其中挠度的倒数w'相当于转角θ,公式(5-3b)也可以写成EIθ=-∫M(x)dx+C P159
(完整版)材料力学知识点总结
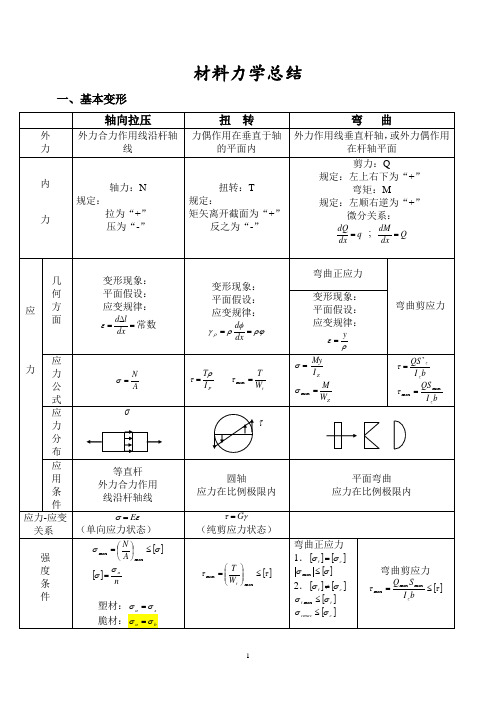
材料力学总结一、基本变形二、还有:(1)外力偶矩:)(9549m N nNm •= N —千瓦;n —转/分 (2)薄壁圆管扭转剪应力:tr T22πτ=(3)矩形截面杆扭转剪应力:hb G Th b T 32max ;βϕατ==三、截面几何性质(1)平行移轴公式:;2A a I I ZC Z += abA I I c c Y Z YZ += (2)组合截面: 1.形 心:∑∑===ni ini cii c AyA y 11; ∑∑===ni ini cii c AzA z 112.静 矩:∑=ci i Z y A S ; ∑=ci i y z A S 3. 惯性矩:∑=i Z Z I I )( ;∑=i y y I I )(四、应力分析:(1)二向应力状态(解析法、图解法)a . 解析法: b.应力圆:σ:拉为“+”,压为“-” τ:使单元体顺时针转动为“+”α:从x 轴逆时针转到截面的 法线为“+”ατασσσσσα2sin 2cos 22x yx yx --++=ατασστα2cos 2sin 2x yx +-=yx xtg σστα--=220 22minmax 22x y x yx τσσσσσ+⎪⎪⎭⎫⎝⎛-±+=c :适用条件:平衡状态(2)三向应力圆:1max σσ=; 3min σσ=;231max σστ-=x(3)广义虎克定律:[])(13211σσνσε+-=E [])(1z y x x E σσνσε+-=[])(11322σσνσε+-=E [])(1x z y y E σσνσε+-=[])(12133σσνσε+-=E [])(1y x z z E σσνσε+-=*适用条件:各向同性材料;材料服从虎克定律(4)常用的二向应力状态 1.纯剪切应力状态:τσ=1 ,02=σ,τσ-=32.一种常见的二向应力状态:223122τσσσ+⎪⎭⎫⎝⎛±=2234τσσ+=r2243τσσ+=r五、强度理论*相当应力:r σ11σσ=r ,313σσσ-=r ,()()()][212132322214σσσσσσσ-+-+-=r σxσ六、材料的力学性质脆性材料 δ<5% 塑性材料 δ≥5%低碳钢四阶段: (1)弹性阶段(2)屈服阶段 (3)强化阶段 (4)局部收缩阶段 强度指标 σσb s ,塑性指标 δψ,E tg ==σα七.组合变形ε八、压杆稳定欧拉公式:2min2)(l EI P cr μπ=,22λπσE cr =,应用范围:线弹性范围,σcr <σp ,λ>λp柔度:iul =λ;ρρσπλE=;ba s σλ-=0,柔度是一个与杆件长度、约束、截面尺寸、 形状有关的数据,λ↑P cr ↓σcr ↓λ>λp ——大柔度杆:22λπσE cr =λo <λ<λp ——中柔度杆:σcr=a-b λλ<λ0——小柔度杆:σcr =σs稳定校核:安全系数法:w I cr n P P n ≥=,折减系数法:][σϕσ≤=AP提高杆件稳定性的措施有:1、减少长度2、选择合理截面3、加强约束4、合理选择材料九、交变应力金属疲劳破坏特点:应力特征:破坏应力小于静荷强度; 断裂特征:断裂前无显著塑性变形; 断口特征:断口成光滑区和粗糙区。
(完整版)材料力学必备知识点

材料力学必备知识点1、 材料力学的任务:满足强度、刚度和稳定性要求的前提下,为设计既经济又安全的构件,提供必要的理论基础和计算方法。
2、 变形固体的基本假设:连续性假设、均匀性假设、各向同性假设。
3、 杆件变形的基本形式:拉伸或压缩、剪切、扭转、弯曲。
4、 低碳钢:含碳量在0.3%以下的碳素钢。
5、 低碳钢拉伸时的力学性能:弹性阶段、屈服阶段、强化阶段、局部变形阶段 极限:比例极限、弹性极限、屈服极限、强化极限6、 名义(条件)屈服极限:将产生0.2%塑性应变时的应力作为屈服指标7、 延伸率δ是衡量材料的塑性指标塑性材料 随外力解除而消失的变形叫弹性变形;外力解除后不能消失的变形叫塑性变形。
>5%的材料称为塑性材料: <5%的材料称为脆性材料8、 失效:断裂和出现塑性变形统称为失效9、 应变能:弹性固体在外力作用下,因变形而储存的能量10、应力集中:因杆件外形突然变化而引起的局部应力急剧增大的现象11、扭转变形:在杆件的两端各作用一个力偶,其力偶矩大小相等、转向相反且作用平面垂直于杆件轴线,致使杆件的任意两个横截面都发生绕轴线的相对转动。
12、翘曲:变形后杆的横截面已不再保持为平面;自由扭转:等直杆两端受扭转力偶作用且翘曲不受任何限制;约束扭转:横截面上除切应力外还有正应力13、三种形式的梁:简支梁、外伸梁、悬臂梁14、组合变形:由两种或两种以上基本变形组合的变形15、截面核心:对每一个截面,环绕形心都有一个封闭区域,当压力作用于这一封闭区域内时,截面上只有压应力。
16、根据强度条件 可以进行(强度校核、设计截面、确定许可载荷)三方面的强度计算。
17、低碳钢材料由于冷作硬化,会使(比例极限)提高,而使(塑性)降低。
18、积分法求梁的挠曲线方程时,通常用到边界条件和连续性条件;因杆件外形突然变化引起的局部应力急剧增大的现象称为应力集中;轴向受压直杆丧失其直线平衡形态的现象称为失稳19、圆杆扭转时,根据(切应力互等定理),其纵向截面上也存在切应力。
第1章(轴向拉伸与压缩)重要知识点总结(材料力学)
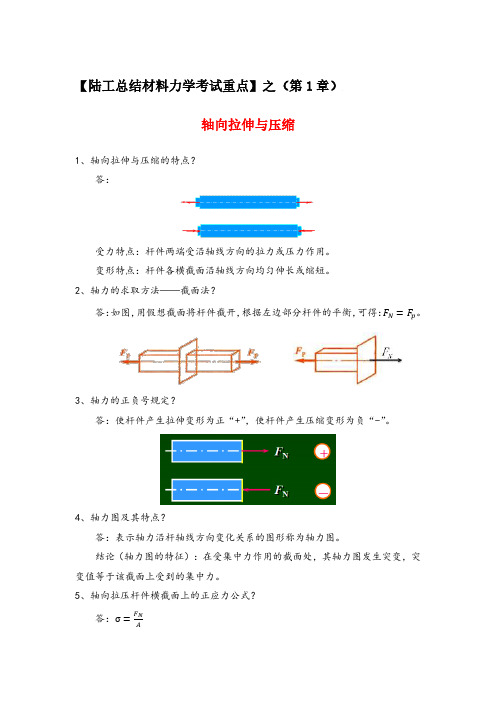
【陆工总结材料力学考试重点】之(第1章)轴向拉伸与压缩1、轴向拉伸与压缩的特点?答:受力特点:杆件两端受沿轴线方向的拉力或压力作用。
变形特点:杆件各横截面沿轴线方向均匀伸长或缩短。
2、轴力的求取方法——截面法?答:如图,用假想截面将杆件截开,根据左边部分杆件的平衡,可得:F N=F p。
3、轴力的正负号规定?答:使杆件产生拉伸变形为正“+”,使杆件产生压缩变形为负“-”。
4、轴力图及其特点?答:表示轴力沿杆轴线方向变化关系的图形称为轴力图。
结论(轴力图的特征):在受集中力作用的截面处,其轴力图发生突变,突变值等于该截面上受到的集中力。
5、轴向拉压杆件横截面上的正应力公式?答:σ=F NA正应力的正负号规定:拉应力为正,压应力为负。
6、轴向拉压杆件的强度条件?答:对于杆件来说,当材料一定时,其许用正应力[σ](即杆件能够正常工作时横截面上任何一点所允许的最大正应力)为一常数,故为保证轴向拉压杆件的强度安全,就必须使杆件横截面上的最大正应力σmax满足:σmax≤[σ]7、应力集中现象及应用?答:如图A处,因有切口、开槽、螺纹等,使横截面面积A剧烈变小,而轴力F N=F不变,而σ=F NA,故发生应力局部增大现象,称为应力集中。
8、拉压变形与胡克定律?答:如图,设杆件原长为l,横截面尺寸为b×h,在轴向载荷F的作用下产生拉伸变形。
绝对变形量:∆l=±F N lEA(拉伸取“+”,压缩取“-”)相对变形量(正应变,也称线应变):=∆ll又:σ=F NA ,则:=∆ll=F N lEAl=F NEA=E即:σ=(胡克定律)由图可知,当杆件伸长(或缩短时),横截面尺寸相应就会变细(或变粗)。
=∆ll称为轴向线应变,而==称为横向正应变,且=。
式中:为泊松比,其值一般小于0.5。
9、材料拉伸、压缩时的力学性能?答:(1)低碳钢拉伸时的力学性能低碳钢拉伸时的σ关系曲线低碳钢拉伸过程可分为四个阶段:1)弹性阶段(OB段)B点对应的应力σ称为弹性极限。
材料力学各章知识点
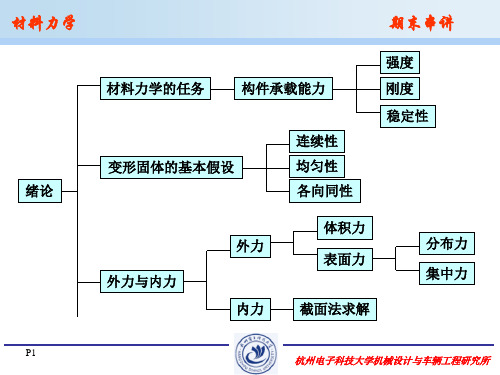
P14
杭州电子科技大学机械设计与车辆工程研究所
材料力学
期末串讲
弯 曲 变 形
多余约束 超静定梁
超静定次数
P15
杭州电子科技大学机械设计与车辆工程研究所
材料力学
应力状态 的概念 一点的应力状态 主应力 1
期末串讲
应 力 应 变 分 析 、 强 度 理 论
2 3
单向应力状态
二向应力状态 三向应力状态
扭转的 概念
外力作用特点
变形特点 扭 转
M e 9549
外力偶矩
截面法确定 扭矩图表示 纯剪切
P7
P n
T T 2 r02 t 2 A 0 t
杭州电子科技大学机械设计与车辆工程研究所
材料力学
切应力剪切 胡克定律 切应变 剪切胡克定律
期末串讲
R L
G
剪切应变能
扭 转
(rad/m)
P8
杭州电子科技大学机械设计与车辆工程研究所
材料力学
期末串讲
受力特征:外力的作用线垂直于杆轴线
弯曲变形
变形特征:变形前为直线的轴线,变形后为曲线 可动铰支座
支座基本形式
弯 曲 内 力 受弯杆件 的简化 静定梁基本形式
固定铰支座 固定端 集中力
载荷的简化
集中力偶 分布载荷 简支梁 外伸梁 悬臂梁
应力状态的分类
二向应力 状态分析
解析法 图解法
max x y 1 min 2 2
tan 2 0 2 xy
2 4 x y xy 2
x y
P16
杭州电子科技大学机械设计与车辆工程研究所
材料力学
材料力学复习总结知识点

r1, r2, r3, r4
三、压杆稳定
1. 欧拉公式:
Fcr (2lE)I2
(适用范围:细长杆)
2. 压杆的柔度:
细长杆
P
cr
2E 2
中长杆
0 P
cr ab
长度因数(反应约况 束) 情
l
i
i l
截面形状、大小 杆长
σ σcr=σs
临界应力总图
σs
A
粗短杆
σcr=a−bλ
σP
B 中长
一、基本变形(2)
基本变形 拉(压)
扭转
弯曲
外力
应力
FN A
拉 (+)
圆轴
T IP
τ
(平面假设)
d4 I P 32
Wt
d3 16
My IZ
FQ S Z * IZb
平面假设
矩形:
IZ
b
h3 ,
12
WZ
bh2 6
圆形:
IZ
d4,
64
WZ 3d2 3
στ
一、基本变形(3)
基本变形 拉(压)
不同,因而两梁的剪力图和弯矩图不一定相同。
第2章 拉伸、压缩与剪切
6. 两根几何尺寸、支撑条件完全相同的静定梁,只要所受 的载荷相同,则两梁所对应的截面的挠度和转角相同,而 与梁的材料是否相同无关。 7. 若单元体的σx=σy=τxy=50Mpa,则该单元体必定处于二向 应力状态。
第2章 拉伸、压缩与剪切
《材料力学》课程总结
材料力学基本框架
基概本述概念
拉压 剪切 扭转
四种基本变形
弯曲-内力 弯曲-应力 弯曲-变形
应力状态 综组合合知变识形 压杆稳定
孙训方材料力学每章小结

(第一强度理论)
(第二强度理论)
适用于脆性材料
(第三强度理〔组合变形〕
• 本章处理组合变形构件的强度和变形问题, 以强度问题为主。
• 按照圣维南原理和叠加原理可以将组合变形 问题分解为两种以上的根本变形问题来处理。
• 根据叠加原理,可以运用叠加法来处理组合 变形问题的条件是①线弹性材料,加载在弹 性范围内,即服从胡克定律;②小变形,保 证内力、变形等与诸外载加载次序无关。
胡克定律是揭示在比例极限内应力和应变的 关系,它是材料力学最根本的定律之一。
2.材料的力学性能的研究是解决强度和刚 度问题的一个重要方面。对于材料力学性能的 研究一般是通过实验方法,其中拉伸试验是最 主要最根本的一种试验。
3.工程中一般材料分为塑性材料和脆性木料。 塑性材料的强度特征是屈服极限,而脆性材料 只有一个强度指标,强度极限 。
•典型的组合变形问题
1)斜弯曲 中性轴不再与加载轴垂直,并且挠度曲
线不再为加载面内的平面曲线.
强度条件: max
如对矩形类截面:
max
My,max Wy
Mz,max Wz
2)拉伸〔压缩〕与弯曲
FN
m axFN,m ax
M M 2 Z,m ax
2 Y,m ax
[
t]
m in
A
W
[ c]
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学各章重点内容总结第一章 绪论一、材料力学中工程构件应满足的3方面要求是:强度要求、刚度要求和稳定性要求。
二、强度要求是指构件应有足够的抵抗破坏的能力;刚度要求是指构件应有足够的抵抗变形的能力;稳定性要求是指构件应有足够的保持原有平衡形态的能力。
三、材料力学中对可变形固体进行的3个的基本假设是:连续性假设、均匀性假设和各向同性假设。
第二章 轴向拉压一、轴力图:注意要标明轴力的大小、单位和正负号。
二、轴力正负号的规定:拉伸时的轴力为正,压缩时的轴力为负。
注意此规定只适用于轴力,轴力是内力,不适用于外力。
三、轴向拉压时横截面上正应力的计算公式:N F Aσ= 注意正应力有正负号,拉伸时的正应力为正,压缩时的正应力为负。
四、斜截面上的正应力及切应力的计算公式:2cos ασσα=,sin 22αστα=注意角度α是指斜截面与横截面的夹角。
五、轴向拉压时横截面上正应力的强度条件[],maxmax N F A σσ=≤六、利用正应力强度条件可解决的三种问题:1.强度校核[],maxmax N F A σσ=≤一定要有结论 2.设计截面[],maxN F A σ≥ 3.确定许可荷载[],max N F A σ≤七、线应变l l ε∆=没有量纲、泊松比'εμε=没有量纲且只与材料有关、 胡克定律的两种表达形式:E σε=,N F l l EA∆= 注意当杆件伸长时l ∆为正,缩短时l ∆为负。
八、低碳钢的轴向拉伸实验:会画过程的应力-应变曲线,知道四个阶段及相应的四个极限应力:弹性阶段(比例极限p σ,弹性极限e σ)、屈服阶段(屈服极限s σ)、强化阶段(强度极限b σ)和局部变形阶段。
会画低碳钢轴向压缩、铸铁轴向拉伸和压缩时的应力-应变曲线。
九、衡量材料塑性的两个指标:伸长率1100l l lδ-︒=⨯︒及断面收缩率1100A A Aϕ-︒=⨯︒,工程上把5δ︒≥︒的材料称为塑性材料。
十、卸载定律及冷作硬化:课本第23页。
对没有明显屈服极限的塑性材料,如何来确定其屈服指标?见课本第24页。
十一、 重点内容:1.画轴力图;2.利用强度条件解决的三种问题;3.强度校核之后一定要写出结论,满足强度要求还是不满足强度要求;4.利用胡克定律N F l l EA∆=求杆的变形量:注意是伸长还是缩短。
典型例题及习题:例2.1 例2.5 习题2.1 2.12 2.18第三章 扭转一、如何根据功率和转速计算作用在轴上的外力偶矩,注意功率、转速和外力偶矩的单位。
9549e P M n= 二、扭矩及扭矩图:利用右手螺旋规则(见课本75页倒数第二段)判断的是扭矩的正负号而不是外力偶矩的正负号,扭矩是内力而外力偶矩是外力 。
三、圆轴在扭转时横截面的切应力分布规律:习题3.2四、圆轴在扭转时横截面上距圆心为ρ处的切应力的计算公式pT I ρρτ= 五、对于实心圆轴和空心圆轴极惯性矩和抗扭截面系数的计算公式 实心圆:432p D I π= 316t D W π= 空心圆:()44132p D I πα=- ()34116t D W πα=- 其中d Dα= 六、轴在扭转时的切应力强度条件[]max max tT W ττ=≤及解决的3种问题:强度校核(一定要有结论)、设计截面、确定许可荷载。
七、相距为l 的两截面间的相对扭转角p Tl GI ϕ=,单位是rad ;单位长度扭转角'pT GI ϕ=,单位是/rad m 八、圆轴在扭转时的刚度条件''max max 180p T GI ϕϕπ⎡⎤=⨯≤⎣⎦(注意单位:给出的许用单位长度扭转角是度/米还是弧度/米)九、切应力互等定理及剪切胡克定律:见课本78,79页十、重点内容:1.画扭矩图;2.强度条件及刚度条件的校核,校核之后一定要写出结论,满足要求还是不满足要求;3.极惯性矩和抗扭截面系数的计算公式;4.利用强度条件和刚度条件来设计截面尺寸,最后要选尺寸大的那个。
典型例题及习题:例3.1 例3.4 习题3.1 3.2 3.8 3.13第四章 弯曲内力一、剪力和弯矩正负号的规定:课本117,118页二、如何快速利用简便方法来计算任意截面上的剪力和弯矩:横截面上的剪力在数值上等于左侧或右侧梁段上所有外力的代数和,对于左侧梁段,向上的外力将产生正值的剪力,向下的外力将产生负值的剪力。
对于右侧梁段,向下的外力将产生正值的剪力,向上的外力将产生负值的剪力。
横截面上的弯矩在数值上等于左侧或右侧梁段上所有外力对该截面形心产生的力矩的代数和。
无论左侧梁段还是右侧梁段,向上的外力均产生正值的弯矩,向下的外力均产生负值的弯矩;对于左侧梁段,顺时针方向的外力偶将产生正值的弯矩,逆时针方向的外力偶将产生负值的弯矩。
对于右侧梁段,逆时针的外力偶将产生正值的弯矩,顺时针的外力偶将产生负值的弯矩。
三、利用写剪力方程和弯矩方程的方法来画剪力图和弯矩图四、用剪力、弯矩、均布荷载三者间的微分关系来画剪力图和弯矩图,利用三者间的微分关系也可以来检查画的图是否正确。
五、掌握上课时画在黑板上的表,准确判断当外力为不同情况时剪力图和弯矩图的规律及突变规律。
六、剪力为零的位置弯矩有极值,要把极值弯矩求出来,可利用积分关系来求。
七、重点内容:画剪力图和弯矩图典型例题及习题:做过的题目第五章 弯曲应力一、基本概念(见课本139页相关知识):纯弯曲、横力弯曲、中性层、中性轴(实际是过形心的形心轴)二、弯曲时横截面上距中性轴为y 处正应力的计算公式zMy I σ= 正应力正负号的判断:根据变形特征来判断,如果处于受拉部分则为拉应力,如果处于受压部分则为压应力。
三、弯曲时横截面上正应力的分布规律图:见141页图5.4d 和147页图5.7c 四、正应力强度条件[]max max max max z zM y M I W σσ==≤及解决的3种问题 五、矩形截面、实心圆及空心圆惯性矩z I 及抗弯截面系数z W 的计算公式矩形截面:312z bh I = 26z bh W = 实心圆:464z D I π= 332z D W π= 空心圆:()44164z D I πα=- ()34132z D W πα=- 其中d Dα= 六、矩形截面梁切应力的分布规律:2224S z F h y I τ⎛⎫=- ⎪⎝⎭见150页图5.10 最大切应力:,maxmax 1.5S F bh τ= 七、切应力的强度校核[]*max max maxS z z F S I b ττ=≤ *max z S 是中性轴以下部分截面对中性轴的静矩,b 是中性轴穿过的截面宽度八、重点内容:利用正应力强度条件解决3种问题,切应力的强度校核典型例题及习题:例5.3 例5.5 习题5.4 5.5 5.12 5.16 5.17附录一、静矩z A S ydA =⎰ y AS zdA =⎰,其量纲是长度的三次方。
二、形心: 1.不规则图形:_A z ydA S y A A ==⎰ _y A zdA S z A A ==⎰ 2.规则图形:__ii i A yy A =∑∑ __ii i A z z A =∑∑三、静矩与形心的关系:课本374页四、惯性矩2y A I z dA =⎰,2z A I y dA =⎰,极惯性矩2p AI dA ρ=⎰,惯性矩和极惯性 矩之间的关系p y z I I I =+ ,各种常用图形惯性矩和极惯性矩的计算见第三章和第五章有关公式。
五、惯性矩的平行移轴公式2y yc I I a A =+,2z zc I I b A =+,其中yc 轴和zc 轴是图形的形心轴,a 是两平行轴y 轴和yc 轴之间的距离;b 是两平行轴z 轴和zc轴之间的距离。
六、重点内容:1.静矩和形心的计算;2.静矩和形心的关系;3.各种常用图形惯性矩和极惯性矩的计算;4.利用平行移轴公式计算不对称图形的惯性矩。
典型例题及习题:例I.2 例I.3 例I.6 习题I.9b第六章 弯曲变形一、衡量弯曲变形的两个指标是:挠度和转角(挠度以向上为正,向下为负;转角以逆时针为正,顺时针为负)二、挠曲线的近似微分方程是:()''EI M x ω=三、转角方程:()'EI EI M x dx C θω==+⎰挠曲线方程:()EI M x dxdx Cx D ω=++⎰⎰四、求积分常数时的边界条件及连续性条件是如何确定的?见课本180页图6.6和图6.7五、用叠加法求弯曲变形六、重点内容: 衡量弯曲变形的两个指标、挠曲线的近似微分方程及边界条件和连续性条件、叠加法的应用。
典型例题及习题:6.10 6.11 6.34 6.36第七章 应力和应变分析 强度理论一、正应力和切应力正负号的规定:正应力以拉伸为正,压缩为负;切应力对单元体内一点产生的力矩顺时针为正,逆时针为负。
α角是指从x 轴到截面的外法线方向,逆时针为正,顺时针为负。
二、会画轴向拉压、扭转及弯曲时任一点处的应力状态,尤其是对弯曲的情况应力状态比较复杂,见课本221页图7.8b三、掌握主平面及主应力的概念,3个主应力的大小顺序:123σσσ≥≥四、几个主要公式:1. 任意斜截面上的正应力及切应力计算公式cos 2sin 222x yx yxy ασσσσσατα+-=+- sin 2cos 22x yxy ασστατα-=+2.最大正应力及最小正应力的计算公式max min 2x y σσσσ+⎫=⎬⎭max σ和min σ实际上是主应力。
3.最大切应力及最小切应力的计算公式max min ττ⎫=⎬⎭4.主平面的方位02tan 2xyx y τασσ=--,可以求出相差为90度的两个角度0α;如约定用x σ表示两个正应力中代数值较大的一个,即x y σσ≥,则两个角度0α中,绝对值较小的一个确定max σ所在的平面。
要求:能在单元体上画出主平面的位置。
五、如何画应力圆?六、应力圆圆周上的点和单元体上的面存在着一一对应的关系。
见课本224页第二段 七、广义胡克定律:()()()111x x y z y y z x z z x y E E E εσμσσεσμσσεσμσσ⎫⎡⎤=-+⎪⎣⎦⎪⎪⎡⎤=-+⎬⎣⎦⎪⎪⎡⎤=-+⎪⎣⎦⎭ xy xy yz yz zx zx G G G τγτγτγ⎫=⎪⎪⎪=⎬⎪⎪=⎪⎭当单元体的六个面皆为主平面时,广义胡克定律的表达式见课本238页公式7.20及公式d ,此时的线应变称为主应变。
八、强度理论及4个相当应力第一强度理论:最大拉应力理论 11r σσ=第二强度理论:最大伸长线应变理论 ()2123r σσμσσ=-+第三强度理论:最大切应力理论 313r σσσ=-第四强度理论:畸变能密度理论4r σ= 其中第一、二强度理论适用于脆性材料,第三、四强度理论适用于塑性材料要求记住四个强度理论的内容及各自的相当应力的表达式。
