有向图强连通分量tarjan算法

合集下载

数据结构课设有向图强连通分量求解

数据结构课设有向图强连通分量求解强连通分量（Strongly Connected Components）是有向图中的一种特殊的连通分量，指的是图中任意两个顶点之间都存在有向路径。

求解有向图的强连通分量可以使用Tarjan算法，该算法基于深度优先搜索（DFS）。

具体步骤如下：1. 初始化一个栈，用于存储已访问的顶点；2. 对于图中的每一个顶点v，如果v未访问，则进行DFS遍历；3. 在DFS遍历中，对于当前访问的顶点v，设置v的索引号和低链接号为当前索引值，并将v入栈；4. 遍历v的所有邻接顶点w，如果w未访问，则进行DFS遍历，并将w的低链接号更新为min(当前顶点的低链接号, w的低链接号)；5. 如果当前顶点v的低链接号等于索引号，则将v出栈，并将v及其出栈的顶点组成一个强连通分量。

示例代码如下：```pythonclass Graph:def __init__(self, vertices):self.V = verticesself.adj = [[] for _ in range(vertices)]self.index = 0self.lowlink = [float("inf")] * verticesself.onStack = [False] * verticesself.stack = []self.scc = []def addEdge(self, u, v):self.adj[u].append(v)def tarjanSCC(self, v):self.index += 1self.lowlink[v] = self.indexself.stack.append(v)self.onStack[v] = Truefor w in self.adj[v]:if self.lowlink[w] == float("inf"):self.tarjanSCC(w)self.lowlink[v] = min(self.lowlink[v], self.lowlink[w]) elif self.onStack[w]:self.lowlink[v] = min(self.lowlink[v], self.lowlink[w]) if self.lowlink[v] == self.index:scc = []w = -1while w != v:w = self.stack.pop()self.onStack[w] = Falsescc.append(w)self.scc.append(scc)def findSCC(self):for v in range(self.V):if self.lowlink[v] == float("inf"): self.tarjanSCC(v)return self.scc```使用示例：```pythong = Graph(5)g.addEdge(1, 0)g.addEdge(0, 2)g.addEdge(2, 1)g.addEdge(0, 3)g.addEdge(3, 4)print("Strongly Connected Components:") scc = g.findSCC()for component in scc:print(component)```输出结果：```Strongly Connected Components:[4][3][0, 2, 1]```以上代码实现了有向图的强连通分量的求解，通过Tarjan算法进行DFS遍历和低链接号的更新，最终得到所有的强连通分量。

强连通算法--Tarjan个人理解+详解

强连通算法--Tarjan个⼈理解+详解⾸先我们引⼊定义：1、有向图G中，以顶点v为起点的弧的数⽬称为v的出度，记做deg+（v）；以顶点v为终点的弧的数⽬称为v的⼊度，记做deg-（v）。

2、如果在有向图G中，有⼀条<u，v>有向道路，则v称为u可达的，或者说，从u可达v。

3、如果有向图G的任意两个顶点都互相可达，则称图 G是强连通图，如果有向图G存在两顶点u和v使得u不能到v，或者v不能到u，则称图G 是强⾮连通图。

4、如果有向图G不是强连通图，他的⼦图G2是强连通图，点v属于G2，任意包含v的强连通⼦图也是G2的⼦图，则乘G2是有向图G的极⼤强连通⼦图，也称强连通分量。

5、什么是强连通？强连通其实就是指图中有两点u，v。

使得能够找到有向路径从u到v并且也能够找到有向路径从v到u，则称u，v是强连通的。

然后我们理解定义：既然我们现在已经了解了什么是强连通，和什么是强连通分量，可能⼤家对于定义还是理解的不透彻，我们不妨引⼊⼀个图加强⼤家对强连通分量和强连通的理解：标注棕⾊线条框框的三个部分就分别是⼀个强连通分量，也就是说，这个图中的强连通分量有3个。

其中我们分析最左边三个点的这部分：其中1能够到达0,0也能够通过经过2的路径到达1.1和0就是强连通的。

其中1能够通过0到达2,2也能够到达1，那么1和2就是强连通的。

.........同理，我们能够看得出来这⼀部分确实是强连通分量，也就是说，强连通分量⾥边的任意两个点，都是互相可达的。

那么如何求强连通分量的个数呢？另外强连通算法能够实现什么⼀些基本操作呢？我们继续详解、接着我们开始接触算法，讨论如何⽤Tarjan算法求强连通分量个数：Tarjan算法，是⼀个基于Dfs的算法（如果⼤家还不知道什么是Dfs，⾃⾏百度学习），假设我们要先从0号节点开始Dfs，我们发现⼀次Dfs 我萌就能遍历整个图（树），⽽且我们发现，在Dfs的过程中，我们深搜到了其他强连通分量中，那么俺们Dfs之后如何判断他喵的哪个和那些节点属于⼀个强连通分量呢？我们⾸先引⼊两个数组：①dfn【】②low【】第⼀个数组dfn我们⽤来标记当前节点在深搜过程中是第⼏个遍历到的点。

求强连通分量的Kosaraju算法和Tarjan算法的比较 by ljq

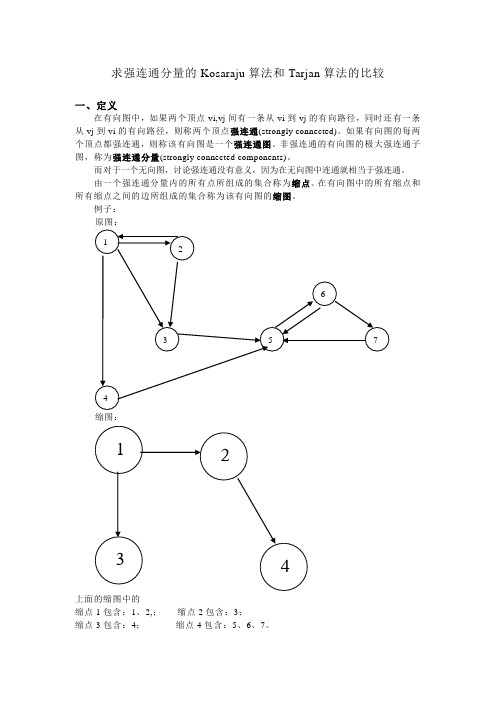
求强连通分量的Kosaraju算法和Tarjan算法的比较一、定义在有向图中，如果两个顶点vi,vj间有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。

如果有向图的每两个顶点都强连通，则称该有向图是一个强连通图。

非强连通的有向图的极大强连通子图，称为强连通分量(strongly connected components)。

而对于一个无向图，讨论强连通没有意义，因为在无向图中连通就相当于强连通。

由一个强连通分量内的所有点所组成的集合称为缩点。

在有向图中的所有缩点和所有缩点之间的边所组成的集合称为该有向图的缩图。

例子：原图：缩图：上面的缩图中的缩点1包含：1、2,；缩点2包含：3；缩点3包含：4；缩点4包含：5、6、7。

二、求强连通分量的作用把有向图中具有相同性质的点找出来，形成一个集合（缩点），建立缩图，能够方便地进行其它操作，而且时间效率会大大地提高，原先对多个点的操作可以简化为对它们所属的缩点的操作。

求强连通分量常常用于求拓扑排序之前，因为原图往往有环，无法进行拓扑排序，而求强连通分量后所建立的缩图则是有向无环图，方便进行拓扑排序。

三、Kosaraju算法时间复杂度：O（M+N）注：M代表边数，N代表顶点数。

所需的数据结构：原图、反向图（若在原图中存在vi到vj的有向边，在反向图中就变成为vj到vi的有向边）、标记数组（标记是否遍历过）、一个栈（或记录顶点离开时间的数组）。

算法描叙：步骤1：对原图进行深度优先遍历，记录每个顶点的离开时间。

步骤2：选择具有最晚离开时间的顶点，对反向图进行深度优先遍历，并标记能够遍历到的顶点，这些顶点构成一个强连通分量。

步骤3：如果还有顶点没有遍历过，则继续进行步骤2，否则算法结束。

hdu1269（Kosaraju算法）代码：#include<cstdio>#include<cstdlib>const int M=10005;struct node{int vex;node *next;};node *edge1[M],*edge2[M];bool mark1[M],mark2[M];int T[M],Tcnt,Bcnt;void DFS1(int x)mark1[x]=true;node *i;for(i=edge1[x];i!=NULL;i=i->next) {if(!mark1[i->vex]){DFS1(i->vex);}}T[Tcnt]=x;Tcnt++;}void DFS2(int x){mark2[x]=true;node *i;for(i=edge2[x];i!=NULL;i=i->next) {if(!mark2[i->vex]){DFS2(i->vex);}}}int main(){int n,m;while(scanf("%d%d",&n,&m)){if(n==0&&m==0){break;}int i,a,b;for(i=1;i<=n;i++){mark1[i]=mark2[i]=false;edge1[i]=NULL;edge2[i]=NULL;}node *t;while(m--){scanf("%d%d",&a,&b);t=(node *)malloc(sizeof(node));t->vex=b;t->next=edge1[a];edge1[a]=t;t=(node *)malloc(sizeof(node));t->vex=a;t->next=edge2[b];edge2[b]=t;}Tcnt=0;for(i=1;i<=n;i++){if(!mark1[i]){DFS1(i);}}Bcnt=0;//Bcnt用于记录强连通分量的个数for(i=Tcnt-1;i>=0;i--){if(!mark2[T[i]]){DFS2(T[i]);Bcnt++;}}if(Bcnt==1)//如果强连通分量的个数为1则说明该图是强连通图{printf("Yes\n");}else{printf("No\n");}}return 0;}四、Tarjan算法时间复杂度：O（M+N）注：M代表边数，N代表顶点数。

Tarjan算法

Tarjan算法Taijan算法是求有向图强连通分量的算法。

Tarjan 算法主要是在 DFS 的过程中维护了⼀些信息：dfn、low 和⼀个栈。

1. 栈⾥存放当前已经访问过但是没有被归类到任⼀强连通分量的结点。

2. dfn[u] 表⽰ DFS 第⼀次搜索到 u 的次序。

3. Low(u) 记录该点所在的强连通⼦图所在⼦树的根节点的 Dfn 值。

基本思路：在深度搜索中会搜索到已访问的节点，产⽣环，即连通分量的⼀部分，环与环的并集仍是连通分量。

由于深度搜索总是会回溯，所以将强连通图中最早搜索到的节点认为是根节点，它的dfn 和 low都是最⼩的。

之后会深度搜索⼦树的所有节点，确定所有与回边相关的环，在出现环时，环上的节点的值就会统⼀为环上最⼩的值。

直到回溯到根节点 dfn = low 的标志，输出连通分量，其他节点low相同，但dfn要⽐根节点⼤。

⾄于（ u， v ）访问到新的节点，在初始化下 v 的 low 值是递增的，但是 v 在进⼊深度搜索后，它返回的值会变化。

当 v 出现在环中被处理了， v 的 low 值会变⼩。

此时 u 也⼀定在环中， v 的low 值变⼩，是由于有⼀条回边连接到的 u 的⽗辈的节点，⽗辈的节点 - 顶点 - u - v - ⽗辈的节点构成了⼀个环。

伪码解析：Tarjan(u){DFN[u]=Low[u]=++Index // 为节点u递增地设定次序编号和Low初值Stack.push(u) // 存放已经访问过但没有被归类到任⼀强连通分量的结点for each (u, v) in E //深度搜索if ( v is not visted ) { Tarjan( v )　Low [ u ] = min( Low[ u ] , Low[ v ] ); // 初始化下 low[ v ] ⽐较⼤，若 low [ v ]变⼩， v 在环中，u 也在环中，且两个环相连通。

}else if (v in S) // 如果节点v还在栈内，出现回边，出现环Low [ u ] = min( Low[ u ], DFN[ v ] )if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根v = S.pop // 将v退栈，print vuntil (u== v)}。

Tarjan算法详解

Tarjan算法详解刚学的⼀个新算法，终于有时间来整理⼀下了。

想必都对著名的 ‘太监’ 算法早有⽿闻了吧。

Tarjan Tarjan 算法是⼀种求解有向图强连通分量的算法，它能做到线性时间的复杂度。

实现是基于DFS爆搜，深度优先搜索⼀张有向图。

！注意！是有向图。

然后根据树，堆栈，打标记等种种神奇扯淡⽅法来完成拆解⼀个图的⼯作。

如果要理解Tarjan，我们⾸先要了解⼀下，什么叫做强连通。

强连通⾸先，我们将可以相互通达的两个点，称这两个点是强连通的。

⾃然，对于⼀张图，它的每两个点都强连通，那么这张图就是⼀张强连通图。

⽽⼀张有向图中的极⼤强连通⼦图就被命名为强连通分量。

那么，举个栗⼦吃吧。

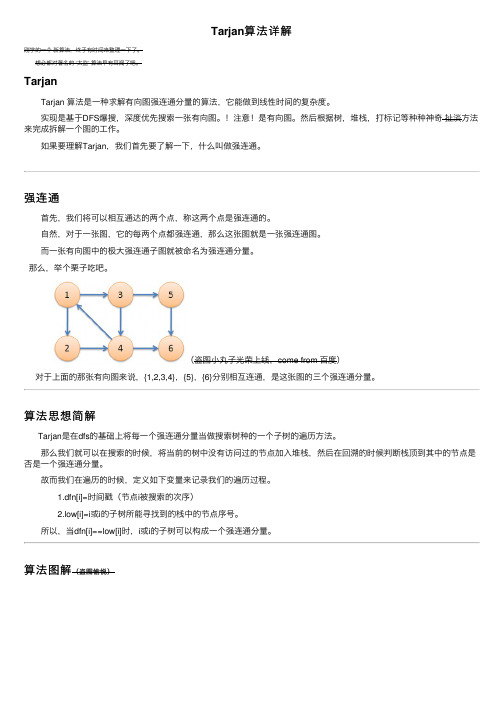
（盗图⼩丸⼦光荣上线，come from 百度）对于上⾯的那张有向图来说，{1,2,3,4}，{5}，{6}分别相互连通，是这张图的三个强连通分量。

算法思想简解 Tarjan是在dfs的基础上将每⼀个强连通分量当做搜索树种的⼀个⼦树的遍历⽅法。

那么我们就可以在搜索的时候，将当前的树中没有访问过的节点加⼊堆栈，然后在回溯的时候判断栈顶到其中的节点是否是⼀个强连通分量。

故⽽我们在遍历的时候，定义如下变量来记录我们的遍历过程。

1.dfn[i]=时间戳（节点i被搜索的次序） 2.low[i]=i或i的⼦树所能寻找到的栈中的节点序号。

所以，当dfn[i]==low[i]时，i或i的⼦树可以构成⼀个强连通分量。

算法图解（盗图愉悦）在这张图中我们从节点1开始遍历，依次将1， 3，5加⼊堆栈。

当搜索到节点6时，发现没有可以向前⾛的路，开始回溯。

回溯的时候会发现low[5]=dfn[5],low[6]=dfn[6]，那么{5}，{6}分别是两个强连通分量。

直到回溯⾄节点3，拓展出节点4. 结果⾃然就是拓展到了节点1，发现1在栈中，于是就⽤1来更新low[4]=low[3]=1; 然后回溯节点1，将点2加⼊堆栈中。

tarjan算法简洁模板 -回复

tarjan算法简洁模板-回复什么是Tarjan算法？Tarjan算法是一种基于深度优先搜索（DFS）的图算法，用于寻找有向图中的强连通分量（Strongly Connected Component, SCC）。

它由美国计算机科学家Robert Tarjan在1972年提出，并被广泛应用于图论和网络分析等领域。

为什么需要寻找强连通分量？强连通分量是一种图中具有特殊性质的子图，其中的任意两个顶点都可以通过有向边相互到达。

在网络分析和图论中，强连通分量代表了一组高度相互关联的节点，具有重要的意义。

例如，在社交网络中，强连通分量可能表示具有密切联系的朋友圈；在软件工程中，强连通分量可以帮助识别出相互依赖的模块。

Tarjan算法的思想是什么？Tarjan算法的基本思想是通过DFS遍历图，对每个节点进行编号和标记，并根据节点的低点值（Low Point）进行划分，以构建强连通分量。

具体步骤如下：1. 初始化变量：创建一个空栈，用于存储访问过的节点；初始化节点编号为0，用一个数组记录每个节点的索引号；初始化节点的低点值为节点编号，用一个数组记录每个节点的低点值；初始化一个布尔型数组，用于标记节点是否在栈中。

2. 对每个未访问的节点u，调用DFS函数进行递归遍历。

3. 在DFS函数中，首先给节点u赋予一个唯一的索引号，并将节点u入栈，并将节点u的索引号和低点值设置为当前节点计数器。

然后遍历u的所有邻接节点v，如果v未被访问，则递归调用DFS函数。

4. 在递归调用的过程中，更新节点u的低点值为u和v的最小值，并将已经访问过的节点v标记为在栈中。

5. 当递归调用结束后，如果节点u的索引号等于低点值，说明节点u开始构成了一个强连通分量。

从栈顶依次弹出节点，直到节点u。

被弹出的节点就是强连通分量的一部分，将这些节点存储起来。

6. 重复以上步骤，直到所有节点都被访问过。

如何实现Tarjan算法？以下是一种简洁的Python实现Tarjan算法的模板：pythondef tarjan(graph):index = {} # 用于记录每个节点的索引号low = {} # 用于记录每个节点的低点值stack = [] # 用于存储访问过的节点visited = {} # 用于标记节点是否在栈中result = [] # 存储所有的强连通分量# 初始化变量def dfs(node):index[node] = len(index)low[node] = len(low)stack.append(node)visited[node] = Truefor neighbor in graph[node]:if neighbor not in index:dfs(neighbor)low[node] = min(low[node], low[neighbor]) elif neighbor in visited:low[node] = min(low[node], index[neighbor])if index[node] == low[node]:component = []while stack[-1] != node:component.append(stack.pop())visited.pop(component[-1])component.append(stack.pop())visited.pop(component[-1])result.append(component)for node in graph:if node not in index:dfs(node)return result总结：Tarjan算法是一种基于深度优先搜索的图算法，用于查找有向图中的强连通分量。

数据结构课设有向图强连通分量求解

数据结构课设有向图强连通分量求解数据结构课设：有向图强连通分量求解一、引言有向图是图论中的一种重要概念，强连通分量是有向图中的一个子图，其中任意两个顶点之间都存在一条有向路径。

在数据结构课设中，我们需要实现一个算法，能够求解给定有向图的强连通分量。

二、问题描述给定一个有向图G=(V,E)，其中V表示顶点的集合，E表示边的集合。

我们需要设计一个算法，能够找出图G中的所有强连通分量，并将其输出。

三、算法设计为了解决这个问题，我们可以使用Tarjan算法，该算法是一种经典的强连通分量求解算法。

下面是Tarjan算法的详细步骤：1. 初始化步骤：- 创建一个空栈S，用于存储访问过的顶点。

- 创建一个整数数组dfn和low，用于记录每个顶点的访问次序和最早访问到的祖先顶点的次序。

- 创建一个布尔数组inStack，用于标记顶点是否在栈中。

- 创建一个整数变量index，用于记录当前访问的次序。

2. 递归搜索步骤：- 遍历图中的每个顶点v，若v未被访问，则执行递归搜索函数Tarjan(v)。

- 在Tarjan(v)函数中，首先将v入栈，并标记v在栈中。

- 然后将dfn[v]和low[v]均设为index的值，并将index加1。

- 对于v的每个邻接顶点u，若u未被访问，则执行递归搜索函数Tarjan(u)。

- 在递归返回后，更新low[v]的值为v的所有邻接顶点u的low值的最小值。

- 若dfn[v]等于low[v]，则说明v是一个强连通分量的根节点，将栈中的顶点依次出栈，直到v为止，并将这些顶点构成一个强连通分量。

3. 输出结果：- 将找到的所有强连通分量输出。

四、算法分析Tarjan算法的时间复杂度为O(V+E)，其中V为顶点的数量，E为边的数量。

该算法通过深度优先搜索的方式遍历图中的每个顶点，同时使用dfn和low数组记录顶点的访问次序和最早访问到的祖先顶点的次序。

通过比较dfn和low数组的值，可以确定强连通分量的根节点，并将其输出。

6.3.1强连通分支算法--Kosaraju算法、Tarjan算法和Gabow算法

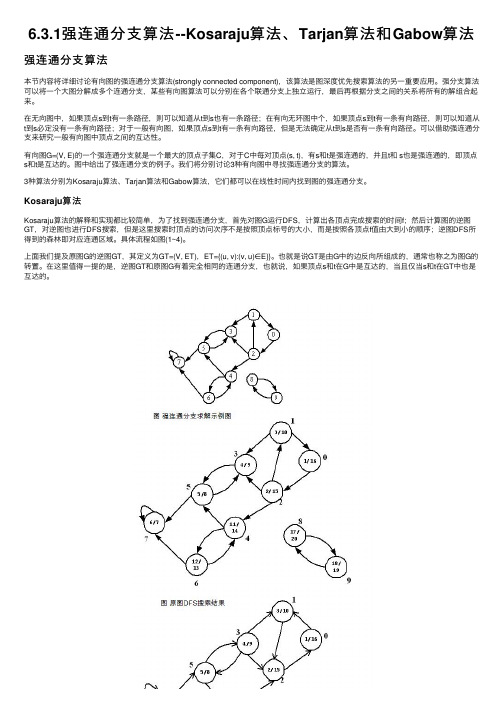
6.3.1强连通分⽀算法--Kosaraju算法、Tarjan算法和Gabow算法强连通分⽀算法本节内容将详细讨论有向图的强连通分⽀算法(strongly connected component)，该算法是图深度优先搜索算法的另⼀重要应⽤。

强分⽀算法可以将⼀个⼤图分解成多个连通分⽀，某些有向图算法可以分别在各个联通分⽀上独⽴运⾏，最后再根据分⽀之间的关系将所有的解组合起来。

在⽆向图中，如果顶点s到t有⼀条路径，则可以知道从t到s也有⼀条路径；在有向⽆环图中个，如果顶点s到t有⼀条有向路径，则可以知道从t到s必定没有⼀条有向路径；对于⼀般有向图，如果顶点s到t有⼀条有向路径，但是⽆法确定从t到s是否有⼀条有向路径。

可以借助强连通分⽀来研究⼀般有向图中顶点之间的互达性。

有向图G=(V, E)的⼀个强连通分⽀就是⼀个最⼤的顶点⼦集C，对于C中每对顶点(s, t)，有s和t是强连通的，并且t和 s也是强连通的，即顶点s和t是互达的。

图中给出了强连通分⽀的例⼦。

我们将分别讨论3种有向图中寻找强连通分⽀的算法。

3种算法分别为Kosaraju算法、Tarjan算法和Gabow算法，它们都可以在线性时间内找到图的强连通分⽀。

Kosaraju算法Kosaraju算法的解释和实现都⽐较简单，为了找到强连通分⽀，⾸先对图G运⾏DFS，计算出各顶点完成搜索的时间f；然后计算图的逆图GT，对逆图也进⾏DFS搜索，但是这⾥搜索时顶点的访问次序不是按照顶点标号的⼤⼩，⽽是按照各顶点f值由⼤到⼩的顺序；逆图DFS所得到的森林即对应连通区域。

具体流程如图(1~4)。

上⾯我们提及原图G的逆图GT，其定义为GT=(V, ET)，ET={(u, v):(v, u)∈E}}。

也就是说GT是由G中的边反向所组成的，通常也称之为图G的转置。

在这⾥值得⼀提的是，逆图GT和原图G有着完全相同的连通分⽀，也就说，如果顶点s和t在G中是互达的，当且仅当s和t在GT中也是互达的。

强连通分量个数的最小值

强连通分量个数的最小值1. 引言在图论中，强连通分量是指图中的一组顶点，其中任意两个顶点都存在一条有向路径。

强连通分量个数的最小值是指在一个有向图中，最少需要将多少个顶点组成一个强连通分量。

本文将介绍强连通分量的概念、计算方法以及如何求解强连通分量个数的最小值。

2. 强连通分量的定义在有向图中，如果从顶点A到顶点B存在一条有向路径，同时从顶点B到顶点A也存在一条有向路径，则称顶点A和顶点B是强连通的。

如果一个有向图中的每个顶点都与其他所有顶点强连通，则该有向图被称为强连通图。

而强连通分量则是指有向图中的一组顶点，其中任意两个顶点都是强连通的，且不与其他顶点强连通。

3. 强连通分量的计算方法为了计算一个有向图的强连通分量，可以使用强连通分量算法，其中最常用的是Tarjan算法和Kosaraju算法。

3.1 Tarjan算法Tarjan算法是一种深度优先搜索算法，用于寻找有向图的强连通分量。

算法的基本思想是通过DFS遍历图中的每个顶点，并记录每个顶点的遍历次序和能够到达的最小顶点次序。

通过这些信息，可以判断顶点是否属于同一个强连通分量。

具体步骤如下：1.初始化一个空栈和一个空的遍历次序数组。

2.对于每个未遍历的顶点，进行深度优先搜索。

3.搜索过程中，记录每个顶点的遍历次序和能够到达的最小顶点次序，并将顶点加入栈中。

4.当搜索完成后，根据遍历次序和能够到达的最小顶点次序，可以确定每个顶点所属的强连通分量。

3.2 Kosaraju算法Kosaraju算法是另一种用于计算有向图强连通分量的算法。

算法的基本思想是通过两次深度优先搜索来确定强连通分量。

具体步骤如下：1.对原始图进行一次深度优先搜索，记录顶点的遍历次序。

2.对原始图的转置图（即将所有边的方向反转）进行一次深度优先搜索，按照遍历次序对顶点进行访问。

3.访问过程中，可以确定每个顶点所属的强连通分量。

4. 求解强连通分量个数的最小值要求解强连通分量个数的最小值，可以使用以下方法：1.使用Tarjan算法或Kosaraju算法计算有向图的强连通分量。

有向图的强连通分量的三个算法

2. 伪代码
Kosaraju_Algorithm:
step1：对原图G进行深度优先遍历，记录每个节点的离开时间。
step2：选择具有最晚离开时间的顶点，对反图GT进行遍历，删除能够遍历到的顶点，这些顶点构成一个强连通分量。
step3：如果还有顶点没有删除，继续step2，否则算法结束。
int Tarjan_StronglyConnectedComponent()
{
int i, sig, scc_num;
memset(flag+1,NOTVIS,sizeof(char)*n);
sig = 0; scc_num = 0; stck[0] = 0;
for ( i=1; i<=n; ++i )
至于如何拿出强连通分量，这个其实很简单，如果当前节点为一个强连通分量的根，那么它的强连通分量一定是以该根为根节点的(剩下节点)子树。在深度优先遍历的时候维护一个堆栈，每次访问一个新节点，就压入堆栈。现在知道如何拿出了强连通分量了吧？是的，因为这个强连通分量时最先被压人堆栈的，那么当前节点以后压入堆栈的并且仍在堆栈中的节点都属于这个强连通分量。当然有人会问真的吗？假设在当前节点压入堆栈以后压入并且还存在，同时它不属于该强连通分量，那么它一定属于另一个强连通分量，但当前节点是它的根的祖宗，那么这个强连通分量应该在此之前已经被拿出。现在没有疑问了吧，那么算法介绍就完了。
{
VisitOne(adj[cur][i],sig);
}
}
numb[++sig] = cur;
}
//用于第二次深搜,求得belg[1..n]的值
void VisitTwo(int cur, int sig)

有向图的强连通分量及应用

图ＧＴ），能遍历到的顶点就是一个强连通分量。余下部分和原来顶弹出，所以，得到出栈的顶点序列为ｖ２，ｖ４，ｖ３，ｖ１；再从最后
的森林一起组成一个新的森林，继续步骤２直到没有顶点为止。具体求解步骤如下：其所有邻接点的访问都完成（即出栈）的顺序将顶点排列起来。
代码为：
ｖｏｉｄｒｅｄｆｓ（ｍｔｘ１
＿
ｗｈｉｌｅ（ｅ＞０＆＆ｅｌｆａｇ［ｅ］ —＝ｏ１｛
ｉｎｔｋ＿ｂ［ｅ］；
ｉｆ（！ｌｆａｇ［ｋ］）ｄｆ § （ｋ）；ｅ－ｎｅｘｔ［ｅ］；
１Ｋｏｓａｒａｊｕ算法
形成的ＤＦＳ树森林嘲。
Ｋｏｓａｒａｊｕ算法基于以下思想：强连通分量一定是某种ＤＦＳ弹出，并进入栈ｓｔａｃｋ１，如图（ｂ）所示。将ｖ２从栈顶弹出后，再这个算法可以说是最容易理解，最通用的算法，其比较关邻接点从而从系统栈弹出，并进入栈ｓｔａｃｋｌ，如图（ｃ）所示。将键的部分是同时应用了原图Ｇ和反图ＧＴ嘲。步骤１：先对原图ｖ４从栈顶弹出后，顶点ｖ３不存在未访问的邻接点从而从系统栈
图（ｅ）所示。这就是该有向图的两个强连通分量的顶点集。
பைடு நூலகம்
｛ｌｆａｇ［ｘ】＝１；
ｉｎｔｅ＝ｐ［ｘ】；
（啦一个有商翻
∞ 将肚糟璜弹出

tarjan递归的执行步骤

tarjan递归的执行步骤
Tarjan算法是一种递归的算法，用于查找有向图或无向图中的强连通分量。

其执行步骤如下：
1. 遍历图中的每个顶点，并将每个顶点的lowlink和是否在栈中的状态设置为初始值。

2. 对于每个未访问过的顶点u，执行步骤3。

3. 递归地对顶点u进行深度优先搜索，将其加入到栈中，并将其lowlink和索引号设为当前索引号，然后逐个处理指向u的每个顶点v。

4. 如果v未被访问，则递归地对v进行深度优先搜索，然后更新顶点u的lowlink值为min(lowlink[u], lowlink[v])。

5. 如果v在栈中，且其索引号小于等于lowlink[u]，则将u视为强连通分量的根，并从栈中依次弹出u及后面的所有顶点，这些弹出的顶点构成一个强连通分量。

6. 继续处理顶点v的后继顶点。

7. 当处理完所有顶点后，即可得到图中的所有强连通分量。

以上就是Tarjan算法的递归执行步骤。

通过不断地递归搜索和更新lowlink值，最终找到了图中的所有强连通分量。

tarjan算法的原理

tarjan算法的原理Tarjan算法是一种用于图的深度优先搜索（DFS）的算法，它可以在线性时间内找到一个有向图中的所有强连通分量。

这个算法是由美国计算机科学家Robert Tarjan在1972年提出的，是解决图论中强连通分量问题的经典算法之一。

在理解Tarjan算法之前，我们先来了解一下什么是强连通分量。

在有向图中，如果对于任意两个顶点u和v，存在从u到v和从v到u 的路径，那么称这两个顶点是强连通的。

而强连通分量就是指图中的一组顶点，其中任意两个顶点都是强连通的，且不属于任何其他的强连通分量。

Tarjan算法的核心思想是利用DFS遍历图，并在遍历的过程中标记每个顶点的强连通分量。

下面我们来详细了解一下Tarjan算法的原理。

我们需要定义两个重要的数组：dfn数组和low数组。

dfn数组记录了每个顶点被访问的次序，low数组记录了每个顶点能够追溯到的最早的栈中的顶点的次序。

Tarjan算法的流程如下：1. 对图中的每个顶点进行遍历，如果该顶点还未被访问，则以该顶点开始进行DFS遍历。

2. 在DFS遍历的过程中，对于每个顶点v，首先将其标记为已访问，并将dfn[v]和low[v]都设置为当前的遍历次序。

3. 然后，遍历v的每个邻接顶点u，如果u还未被访问，则递归地对u进行DFS遍历。

4. 在递归返回的过程中，更新low[v]为min(low[v], low[u])，其中u是v的一个邻接顶点。

5. 最后，如果dfn[v]等于low[v]，则将从v开始的连通分量中的所有顶点输出为一个强连通分量。

Tarjan算法通过维护一个栈来实现DFS的非递归遍历。

具体来说，当访问一个顶点v时，将v入栈，并将v标记为已访问。

然后，遍历v的每个邻接顶点u，如果u还未被访问，则递归地对u进行DFS 遍历。

在递归返回之后，判断low[u]是否小于low[v]，如果是，则更新low[v]为low[u]。

最后，如果dfn[v]等于low[v]，则将从v 开始的连通分量中的所有顶点出栈，并输出为一个强连通分量。

Tarjan算法

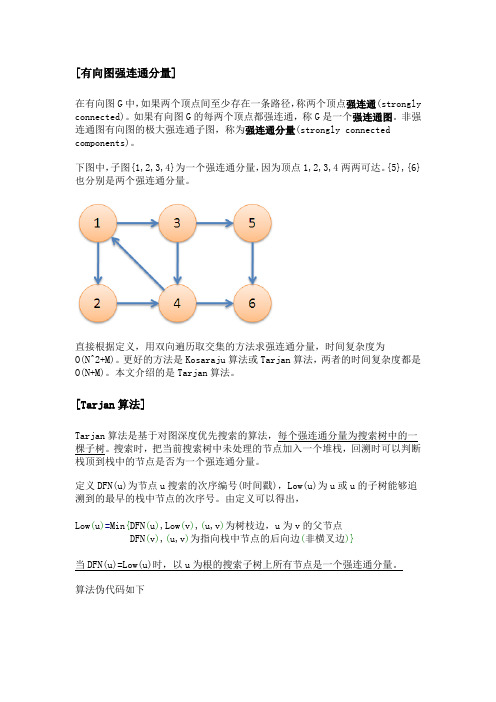
[有向图强连通分量]在有向图G中，如果两个顶点间至少存在一条路径，称两个顶点强连通(strongly connected)。

如果有向图G的每两个顶点都强连通，称G是一个强连通图。

非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。

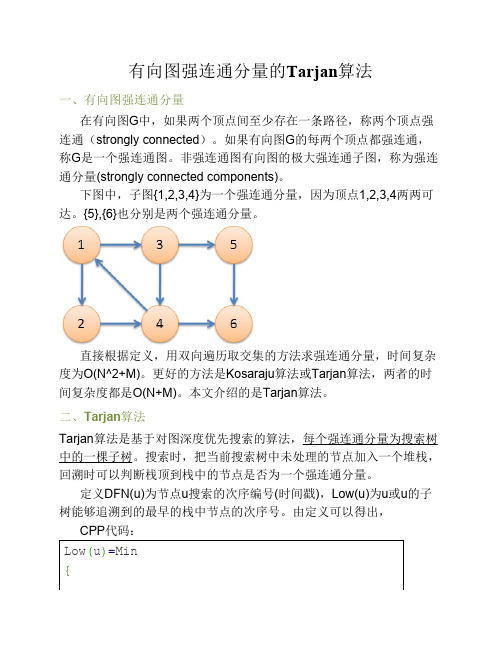
下图中，子图{1,2,3,4}为一个强连通分量，因为顶点1,2,3,4两两可达。

{5},{6}也分别是两个强连通分量。

直接根据定义，用双向遍历取交集的方法求强连通分量，时间复杂度为O(N^2+M)。

更好的方法是Kosaraju算法或Tarjan算法，两者的时间复杂度都是O(N+M)。

本文介绍的是Tarjan算法。

[Tarjan算法]Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。

搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

定义DFN(u)为节点u搜索的次序编号(时间戳)，Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。

由定义可以得出，Low(u)=Min{DFN(u),Low(v),(u,v)为树枝边，u为v的父节点DFN(v),(u,v)为指向栈中节点的后向边(非横叉边)}当DFN(u)=Low(u)时，以u为根的搜索子树上所有节点是一个强连通分量。

算法伪代码如下tarjan(u){DFN[u]=Low[u]=++Index // 为节点u设定次序编号和Low初值Stack.push(u)// 将节点u压入栈中for each (u, v) in E // 枚举每一条边if(v is not visted)// 如果节点v未被访问过tarjan(v)// 继续向下找Low[u]= min(Low[u], Low[v])else if(v in S)// 如果节点u还在栈内Low[u]= min(Low[u], DFN[v])if(DFN[u]== Low[u])// 如果节点u是强连通分量的根repeatv = S.pop// 将v退栈，为该强连通分量中一个顶点print vuntil (u== v)}接下来是对算法流程的演示。

2-sat问题的tarjan算法

2-sat问题是一种布尔可满足性问题，即判断一个由布尔变量和它们的逻辑运算构成的合取范式是否存在可满足的赋值。

在计算机科学和逻辑学中，2-sat问题具有重要的理论和实际意义。

为了解决2-sat问题，人们提出了许多有效的算法，其中tarjan算法是一种经典且高效的解决方法。

1. tarjan算法的概述tarjan算法是由美国的计算机科学家Robert Tarjan在1972年提出的，它主要用于解决有向图中的强连通分量问题。

在2-sat问题中，可以将布尔变量和它们的逻辑运算构成的合取范式转化为一个有向图。

然后利用tarjan算法来求解图中的强连通分量，从而判断2-sat问题是否可满足。

2. tarjan算法的原理tarjan算法的核心是利用深度优先搜索（DFS）来遍历图中的节点，并且通过维护一个栈来记录搜索路径上的节点。

在DFS的过程中，通过比较节点的深度和搜索路径上的节点的深度来判断是否存在环路，从而找到强连通分量。

利用tarjan算法求解2-sat问题的关键在于将逻辑运算转化为有向图，同时构建出正确的搜索路径和深度信息，以便进行强连通分量的判断。

3. tarjan算法的优势与其他算法相比，tarjan算法具有许多优势。

tarjan算法的时间复杂度为O(V+E)，其中V为图中的节点数，E为图中的边数。

这意味着即使在大规模的图中，tarjan算法也能够在合理的时间内得到结果。

tarjan算法的实现相对比较简单，只需要进行一次DFS遍历和一些基本的数据结构操作即可完成。

另外，tarjan算法的结果也比较容易理解和解释，对于2-sat问题的求解具有很好的可解释性。

4. tarjan算法的应用由于tarjan算法在解决2-sat问题中具有较高的效率和可靠性，因此它在实际的计算机科学和工程领域得到了广泛的应用。

在编译原理中，可以利用tarjan算法进行程序的静态分析和优化；在人工智能和图像处理中，可以利用tarjan算法对逻辑规则进行推理和推导；在电路设计和布线规划中，也可以利用tarjan算法对逻辑电路进行布线和优化。

Tarjan算法过程动态演示

√
v=2
v=4
v=4
4√
dfn[4]=6 u=4 low[4]=65
X
栈S：
64
35
2
dfn[1]=2
2 u=2 low[1]=12
v=5
v=6
v=3
dfn[1]=3
5√
u=5
dfn[5]=5 low[5]=15
X
6
u=3 low[1]=3
√
v=6
dfn[6]=4 u=6 low[6]=4
3
√
6 √ dfn[1]=4
三、Taห้องสมุดไป่ตู้jan算法求强连通分量的程序实现
4、假设我们已经dfs完了u的所有的子树，那么之后无论我们再怎么dfs， u点的low值已经不会再变了
那么如果dfn[u]=low[u]这说明了什么呢？再结合一下dfn和low的定义来看看吧 dfn表示u点被dfs到的时间，low表示u和u所有的子树所能到达的点中dfn 最小的。这说明了u点及u点之下的所有子节点没有边是指向u的祖先的了，即我们之前说的u点与它的子孙节点构成了一个最大的强连通图即强连通分量此时我们得到了一个强连通分量，把所有的u点以后压入栈中的点和u点一并弹出，将它们的vis[ ]置为false，如有需要也可以给它们染上相同颜色（后面会用到）于是tarjan求强连通分量的部分到此结束
有了以上定义之后，tarjan算法就有了一条关键的定理：定理： d[i]=low[i] <=> 节点 i 是一个scc root 简单理解就是，同一个SCC中的节点只有scc root 满足d[i]=low[i],为什么呢?
二、如何求强连通分量——Tarjan算法
刚才说过了，Tarjan算法求解SCC已经转换为求解scc root的问题，而这条定理给出了scc root的求解方法，至此，整个流程就通了：dfs遍历原图，递归计算low[i],节点i递归遍历完成后，如果发现d[i]=low[i]则，找到了一个SCC，当然，这其中还涉及到找到scc root之后，如何根据scc root 得到一个scc的问题，其实tarjan算法dfs过程中，用栈来记录访问到的节点，找到scc root之后，从栈顶一次弹出节点，直到遇到scc root节点，便可构成一个scc，下面的算法实现描述了这一过程。

连通分量（tarjan算法）

连通分量（tarjan算法）对于有向图中，连通分量叫强连通分量对于⽆向图中，连通分量叫双连通分量，⽽在双连通分量中，⼜分为点双连通和边双连通。

重点讨论双连通的情况：以割点区分连通情况的双连通叫做点双连通分量，以割边区分连通情况的双连通叫做边双连通分量。

⽐如这个图中：1 4| \ / \| \ / \| 2 5| / \ /| / \ /3 6如果要的到两个连通分量的话，我们只有以2节点为割点，将图分为点双连通。

我们便可以得到两个双连通分量(1,2,3)、(2,4,5,6)。

再⽐如这个图：1 5| \ / \| \ / \| 2 — 4 6| / \ /| / \ /3 7如果要得到两个连通分量的话，我们只能以(2,4)边为割边，得到两个边双连通分量。

具体是将⼀个⽆向图分成点双连通还是边双连通得看具体的问题。

下⾯具体讨论⼀下⽤tarjan算法实现起来的区别。

1、对于边双连通分量，由于是以边为连通间的区分，那么每个点只属于⼀个连通分量，我们在深度遍历的时候，只需要记录某⼀点是否被访问即可。

2、但是对于点双连通分量，由上图也可以看出，2节点同时属于两个连通分量，如果还是以节点为重判对象的话，将得到错误的答案。

此时，我们应该以边为重判对象，⽽该边的两个端点，都同属于⼀个点双连通。

对于边双连通的实现，由于没有节点会重复属于两个以上的连通分量，所以我们可以先简单的遍历⼀遍整个图的tarjan标号(low、dnf)。

之后再进⾏⼀次深度遍历，以low[v]>dnf[u]为换⾊标准染⾊，最后每种颜⾊即⼀个分量。

代码：void tarjan(int u,int f) //f为⽗节点{low[u]=dnf[u]=++count;visit[u]=1;S.push(u);for(node *p=link[u];p;p=p->next){if(p->v==f)continue;if(!visit[p->v]) //⼀节点为重判对象{tarjan(p->v,u);if(low[u]>low[p->v]){low[u]=low[p->v];}}else if(low[u]>dnf[p->v])low[u]=dnf[p->v];}}void set_color(int u){for(node *p=link[u];p;p=p->next){if(!color[p->v]){if(low[p->v]>dnf[u]) //找到了关键割边，换⼀种颜⾊染⾊color[p->v]=++cut;elsecolor[p->v]=color[u]; //保持原来的颜⾊set_color(p->v);}}}对于点双连通的实现，经过上⾯的分析，由于存在点既属于A分量⼜属于B分量，所有我们此时采纳边为重判对象，⽽该边的两端点同属于⼀个分量代码：void col(int u){int x;node *p;++cut;do{p=stack[--top];color[p->v]=color[p->op->v]=cut;}while(p->op->v!=u);}void tarjan(int u){low[u]=dnf[u]=++cut;for(node *p=link[u];p;p=p->next){if(p->vist) //该边已被访问continue;p->vist=p->op->vist=1; //两个⽅向都标记已访问stack[top++]=p; //该边进栈if(!dnf[p->v]){tarjan(p->v);if(low[u]>low[p->v])low[u]=low[p->v];if(low[p->v]>=dnf[u]) //找到了关键割点col(u);}else if(low[u]>dnf[p->v])low[u]=dnf[p->v];}}。

Tarjan算法寻找有向图的强连通分量 – Miskcoo's Space

应边组成的子图就是一个强连通分量，另外点
单独
Tarjan 算法是由 Robert Tarjan 提出的用于寻找有向图的强连通分量的算法。它可以在的时间内得出结果。 Tarjan 算法主要是利用 DFS 来寻找强连通分量的。在介绍该算法之前，我们先来介绍一下搜索树。先前那个有向图的搜索树是这样的：
次搜索找到一个还没有访问过的结点的时候就形成了一条树边。用长虚线画出来的是反祖边（back edge），也被叫做回边。用短虚线画出来的是横叉边（cross edge），它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点并不是当前节点的祖先时形成的。除此之外，像从结点1到结点6这样的边叫做前向边（forward edge），它是在搜索的时候遇到子树中的结点的时候形成的。
Miskcoo's Space，版权所有丨如未注明，均为原创转载请注明转自：/2016/07/tarjan-algorithm-strongly-connected-components
Related Posts:
1. 平面图转对偶图及点定位
图论
CodeChef February 2016. Weird Sum 题解
结点 u 通过反祖边到达结点 v，或者通过横叉边到达结点 v 并且满足 low 定义中 v 的性质
在 tarjan 算法进行 DFS 的过程中，每离开一个结点，我们就判断一下 low 是否小于 dfn，如果是，那么着个结点可以到达它先前的结点再通过那个结点回到它，肯定不是强连通分量的根。如果 dfn 和 low 相等，那么就不断退栈直到当前结点为止，这些结点就属于一个强连通分量。至于如何更新 low，关键就在于第二种情况，当通过反祖边或者横叉边走到一个结点的时候，只需要判断这个结点是否在栈中，如果在就用它的 low 值更新当前节点的 low 值，否则就不更新。因为如果不在栈中这个结点就已经确定在某个强连通分量中了，不可能回到 u。现在我们对着先前的图模拟一次。结点内的标号就是 dfn 值，结点边上的标号是表示 low 值，当前所在的结点用灰色表示。

有向图强连通分量的Tarjan算法

v = S.pop 连通分量中一个顶点 print v until (u== v) }
// 将v退栈，为该强
接下来是对算法流程的演示。
从节点1开始DFS，把遍历到的节点加入栈中。搜索到节点u=6时， DFN[6]=LOW[6]，找到了一个强连通分量。退栈到u=v为止，{6}为一个强连通分量。
返回节点5，发现DFN[5]=LOW[5]，退栈后{5}为一个强连通分量向图强连通分量在有向图G中，如果两个顶点间至少存在一条路径，称两个顶点强连通（strongly connected）。如果有向图G的每两个顶点都强连通，称G是一个强连通图。非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。下图中，子图{1,2,3,4}为一个强连通分量，因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。
void tarjan(int i) { int j; DFN[i]=LOW[i]=++Dindex; instack[i]=true; Stap[++Stop]=i; for (edge *e=V[i];e;e=e->next) { j=e->t; if (!DFN[j]) { tarjan(j); if (LOW[j]<LOW[i]) LOW[i]=LOW[j]; } else if (instack[j] && DFN[j]<LOW[i]) LOW[i]=DFN[j]; } if (DFN[i]==LOW[i]) { Bcnt++; do { j=Stap[Stop--]; instack[j]=false; Belong[j]=Bcnt; } while (j!=i);