小升初毕业考试数学试卷及答案
小学六年级小升初毕业数学复习试卷测试卷(含答案解析)
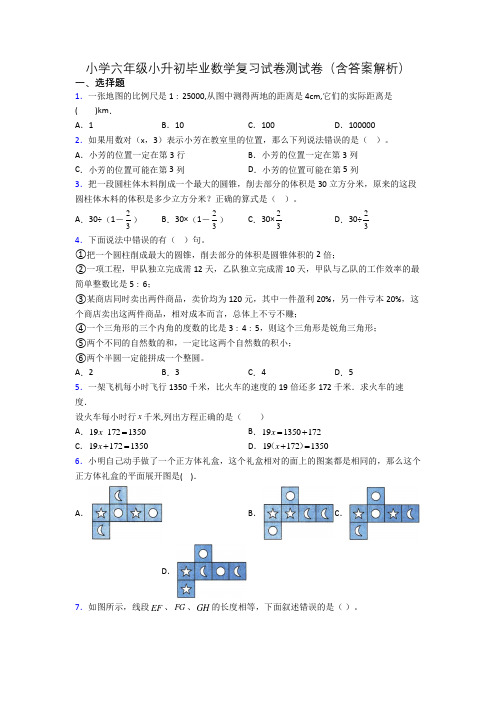
小学六年级小升初毕业数学复习试卷测试卷(含答案解析)一、选择题1.一张地图的比例尺是1∶25000,从图中测得两地的距离是4cm,它们的实际距离是( )km .A .1B .10C .100D .100000 2.如果用数对(x ,3)表示小芳在教室里的位置,那么下列说法错误的是( )。
A .小芳的位置一定在第3行B .小芳的位置一定在第3列C .小芳的位置可能在第3列D .小芳的位置可能在第5列 3.把一段圆柱体木料削成一个最大的圆锥,削去部分的体积是30立方分米,原来的这段圆柱体木料的体积是多少立方分米?正确的算式是( )。
A .30÷(1-23)B .30×(1-23)C .30×23D .30÷234.下面说法中错误的有( )句。
①把一个圆柱削成最大的圆锥,削去部分的体积是圆锥体积的2倍;②一项工程,甲队独立完成需12天,乙队独立完成需10天,甲队与乙队的工作效率的最简单整数比是5∶6;③某商店同时卖出两件商品,卖价均为120元,其中一件盈利20%,另一件亏本20%,这个商店卖出这两件商品,相对成本而言,总体上不亏不赚;④一个三角形的三个内角的度数的比是3∶4∶5,则这个三角形是锐角三角形; ⑤两个不同的自然数的和,一定比这两个自然数的积小;⑥两个半圆一定能拼成一个整圆。
A .2B .3C .4D .5 5.一架飞机每小时飞行1350千米,比火车的速度的19倍还多172千米.求火车的速度.设火车每小时行x 千米,列出方程正确的是( )A .19-1721350x =B .191350172x =+C .191721350x +=D .191721350x +=() 6.小明自己动手做了一个正方体礼盒,这个礼盒相对的面上的图案都是相同的,那么这个正方体礼盒的平面展开图是( ). A . B . C .D .7.如图所示,线段EF 、FG 、GH 的长度相等,下面叙述错误的是( )。
数学小学六年级小升初毕业复习试卷(带答案)

数学小学六年级小升初毕业复习试卷(带答案)一、选择题1.学校的操场长120米,宽90米,把它画在长30厘米,宽25厘米的长方形纸上,选用()的比例尺比较适当.A.1:400 B.1:500 C.1:1000 D.1:1002.用四个棱长为2厘米的正方体拼一个长方体,这个长方体的表面积最大是()平方厘米。
A.54 B.64 C.723.一本书看了29,还剩42页,这本书有多少页?正确的算式是( ).A.2429⨯B.242(1)9⨯-C.2429÷D.242(1)9÷-4.一个三角形,三个内角度数的比是1∶2∶3,这个三角形是()。
A.锐角三角形B.直角三角形C.钝角三角形D.等边三角形5.学校电脑班有女生18人,比男生人数的13少2人,电脑班有多少男生?设男生有x人,下列方程正确的是()。
A.18-13x=2 B.13x-2=18C.13x+2=18 D.(x+2)×13=186.用6个小正方体搭成一个立体图形,如图,从()看,看到的形状是。
A.正面B.左面C.上面D.右面7.下面说法错误的是()。
A.39515=可以看做一个比例。
B.比例就是由比值相等的两个比组成的等式。
C.两个量的倍数关系无法转换成两个量相比的关系。
D.根据24389⨯=⨯,至少可以写出4个不同的比例。
8.下列说法中正确的是()。
A.等底等高的圆柱和圆锥,圆柱的纵切面的面积是圆锥纵切面面积的2倍。
B.一等腰三角形,其中两边长2cm、5cm,第三边长可能是2cm或5cm。
C.圆的面积和半径成正比例关系。
D.图上距离和实际距离成反比例关系。
9.水果店老板进了两箱樱桃,第一箱因为热销提价20%售出,第二箱突然滞销,老板不得不将热销价格降价20%出售,第二箱价格与成本价相比,()。
A.等于成本价B.低于成本价C.高于成本价10.下图是丁小乖去图书馆的折线统计图,他在()区间内,走的路程与时间成正比例关系.A.8:30~8:45 B.8:45~9:45 C.9:45~10:30 D.以上答案都不正确二、填空题11.在括号里填合适的数。
小学六年级小升初毕业数学试题测试卷(含答案)

小学六年级小升初毕业数学试题测试卷(含答案)一、选择题1.在一幅地图上,图上距离4cm表示实际距离16km,这幅地图的比例尺是().A.1∶4 B.1∶40 C.1∶400 D.1∶400000 2.有三个相同的骰子摆放如下图,底面点数之和最小是()A.10 B.11 C.12 D.无法判断3.一根绳子长310米,用去了15米,还剩多少米?根据题意,正确的算式是()。
A.310×15B.310×(1-15)C.310-154.一个三角形,三个内角度数分别是45°、45°、90°,这个三角形()。
A.没有对称轴B.有一条对称轴C.有两条对称轴D.有三条对称轴5.5千克棉花的和1千克铁的比较,结果是()A.5千克棉花的重B.1千克铁的重C.一样重D.无法比较6.如图是正方体的平面展开图,每个面上都标有一个汉字,与“信”字相对的面上的字为().A.文B.明C.法D.治7.便民水果店购进了8千克樱桃,卖掉了45。
下列说法中,错误的是()。
A.还剩15B.还剩1千克的85C.剩下与卖掉比是4∶1 D.剩下1.6千克8.下列选项中,说法正确的是()。
A.用四个完全一样的三角形拼成的平行四边形的内角和是720︒B.图中圆锥直径是圆柱的3倍,所以圆锥体积和圆柱体积相等C.两个质数的和不一定是偶数9.一种手机原来的售价是820元,降价10%后,再提价10%.现在的价格和原来相比( ).A.没变B.提高了C.降低了D.无法确定10.将一张正方形的纸连续对折两次,并在折后的纸中间打一个圆孔(如图所示),再将纸展开,则展开后是()。
A.①B.②C.③D.④二、填空题11.50个细菌8小时共繁殖细菌838860000个,横线上的数读作(______),把它改写成用“亿”作单位的数并保留一位小数大约是(______)个。
12.3()12()218÷== =6∶()=()%。
小学六年级小升初毕业数学综合试卷测试卷(附答案)

小学六年级小升初毕业数学综合试卷测试卷(附答案)一、选择题1.在比例尺是1:12500000的地图上,量得两城市之间的距离是8厘米.那么在比例尺是1:8000000的地图上,图上距离是()厘米.A.12.5 B.10 C.64 D.6.82.一根长方体木料,长2米,宽和高都是5厘米,把它锯成1米长的两段,表面积增加了()平方厘米。
A.50 B.40 C.25 D.603.如图,线段OA和线段BC分别是圆的半径和直径,已知线段OA长5厘米,若一只蚂蚁从B点出发沿逆时方向绕着圆的边线爬行至C点,所经过的路程是多少厘米?正确的算式是()。
A.5×2 B.5πC.1 (5) 24.一个三角形中其中一个角是46°,这个三角形的形状是()三角形。
A.钝角B.直角C.锐角D.无法确定5.某地区烛光晚餐中,设座位有x排,每排坐30人,则有8人无座位;每排坐31人,则空26个座位,则下列方程正确的是()A.30x-8=31x+26 B.30x-8=31x-26C.30x+8=31x+26 D.30x+8=31x-266.从前面看是,从右面看也是的图形是()A.B.C.7.下面说法错误的是()。
A.在367个同学中至少有2个同学是同年同月同日出生的B.真分数小于1,假分数大于1C.0既不是正数,又不是负数,但它是整数,还是自然数D.三角形的面积一定,底和高成反比例8.井盖平面轮廓采用圆形的一个原因是圆形井盖怎么放都不会掉到井里,并且能恰好盖住井口。
这是应用了圆特征中()。
A.圆心角决定圆的位置B.半径决定圆的大小C.同一圆内所有直径都相等D.圆是曲边图形9.一种商品提价20%后,又降价20%,现在的价格()。
A.与原价相同B.比原价低C.比原价高10.将一些小圆球如下图摆放,第六幅图中共有()个小圆球。
A.25 B.30 C.36 D.42二、填空题11.45时=(________)分 3.2立方米=(________)立方分米8公顷=(________)平方千米 5400毫升=(________)立方厘米十12.338的分数单位是(______),它含有(______)个这样的分数单位。
小学六年级小升初毕业数学试卷测试卷(答案)

小学六年级小升初毕业数学试卷测试卷(答案)一、选择题1.在一个比例尺是200∶1的图纸上,量得一个零件的长是2厘米,这个零件实际长( )。
A .4米B .1米C .0.1毫米D .0.4毫米 2.用四个棱长为2厘米的正方体拼一个长方体,这个长方体的表面积最大是( )平方厘米。
A .54B .64C .723.六年级同学参加兴趣小组,其中绘画小组有a 人,比书法小组的人数的2倍少4人。
书法小组有多少人?正确的算式是( )。
A .2=4aB .2=4a ÷C .24a ÷+D .()42a +÷ 4.若一个三角形三个内角度数的比是1∶1∶a (a >0),则这个三角形一定是( )。
A .等边三角形B .等腰三角形C .直角三角形D .钝角三角形 5.已知六年级女生有135人,比男生少10%。
求“六年级男生有多少人"的方程正确的是( )。
(设男生有x 人)A .10%x=135B .(1+10%)x=135C .(1-10%)x=135 6.下图是一个正方体的表面展开图,原正方体中与“国”字所在的面相对的面上标的字是( )。
A .建B .设C .美D .中 7.统计学校人数发现,女生人数比男生人数少10%,已知男生共680人。
下列算式中计算全校人数错误的是( )。
A .2×680-(680×10%)B .680×(1+1-10%)C .680×(1-10%)+680D .680×(1+10%)+680 8.如图,以点A 为圆心的圆内,三角形ABC 一定为等腰三角形。
做出这个判断是运用了圆的什么特征?( )A .圆的周长是它的直径的π倍B .同一个圆的直径相等C .同一个圆的直径为半径的2倍D .同一个圆的半径相等9.下列说法正确的是( )。
A.真分数的倒数都大于1,假分数的倒数都小于1。
B.加工101个零件,全部合格,合格率是101%。
小学六年级小升初毕业数学综合试卷(带答案)

小学六年级小升初毕业数学综合试卷(带答案)一、选择题1.xy =30中,x ,y 的关系是( )。
A .成正比例B .成反比例C .不成比例2.如图是一个正方体纸盒的展开图,如果再把它折成一个正方体,5的对面是( )。
A .1B .2C .3D .6 3.将83除以32与41的差是多少?正确的算式是 ( ) A .213-348÷ B .213-348÷() C .312-843÷() D .321-834÷() 4.一个三角形三个内角的度数比是1∶2∶3,这个三角形是( )三角形。
A .直角 B .锐角 C .钝角 D .无法确定 5.服装厂用107米蓝布做大人服装20套,儿童服装25套,已知每套儿童服装用布2.2米,每套大人服装用布多少米?解:设每套大人服装用布x 米列出方程正确的是( )A .20x+2.2=107B .x+2.5×25=107C .20x+2.2×25=107D .x+2.2=107÷256.用6个小正方体搭成一个立体图形,如图,从( )看,看到的形状是。
A .正面B .左面C .上面D .右面 7.下列各个说法中,错误的是( )。
A .三角形的面积一定,底与高成反比例B .实际距离和图上距离的比叫做比例尺C .每支铅笔的价钱一定,铅笔支数和总价成正比例D .被除数一定,除数和商成反比例8.如图,把底面半径是r ,高h 的圆柱沿着它的高切成若干等份,拼成一个近似长方体。
这个近似长方体的表面积比原来圆柱的表面积增加了( )。
A .2πr 2B .2rhC .2πrhD .2πr 2h9.一件羽绒服10月份售卖时降价20%,到了12月份又提价20%,这件羽绒服现价( )。
A .是原价的144%B .是原价的96%C .是原价的64%D .与原价相等10.将一些小圆球如图摆放,第六幅图有( )个小圆球.A .30B .36C .42二、填空题11.334吨=(________)吨(________)千克;70分=(________)小时。
数学六年级小升初毕业试卷测试卷(含答案)

数学六年级小升初毕业试卷测试卷(含答案)一、选择题1.正方形的边长与它的周长()。
A.成正比例B.成反比例C.不成比例2.一个立体图形中,相邻的两个面,一面画有圈,一面是阴影,第()幅图可能是下面这个立体图形的展开图.A.B.C.D.3.某人从甲地到乙地需要13小时,他走了15小时,还有100米没有走,他已经走了多少米?正确的算式是().A.100÷(13-15)B.100÷(1-13)×15C.100÷(13-15)×15D.100×(13-15)4.一个三角形三个内角度数的比是2:3:5,这个三角形中最大的内角是()。
A.锐角B.直角C.钝角5.如图,从甲地到乙地有a,b两条路可走,这两条路的长度相比,结果是()。
A.路线a长B.路线b长C.同样长6.下面四个图形中,从右面看到的图形有()个。
A .0B .1C .2D .37.下列说法错误的是( )。
A .长方体、正方体都是棱柱B .六棱柱有18条棱、6个侧面、12个顶点C .三棱柱的侧面是三角形D .圆柱由两个平面和一个曲面围成8.把一个圆柱的底面平均分成若干个扇形,切开后拼成一个近似的长方体,表面积比原来增加40平方厘米,圆柱的底面半径是4厘米,那么圆柱的高是( )厘米。
A .4B .5C .10D .209.小亮13岁,身高170厘米,体重84千克。
根据下边的体重分类标准,他的体重符合( )。
少年儿童(7~16岁)体重(千克)分类标准标准体重=(身高-100)×0.9 轻度肥胖:超过标准体重13~510中度肥胖:超过标准体重31~102重度肥胖;超过标准体重12以上 A .轻度肥胖 B .中度肥胖C .重度肥胖10.已知22222233445522,33,44,55338815152424+=⨯+=⨯+=⨯+=⨯,若21010b b a a+=⨯,则+a b =( )。
小学六年级小升初毕业数学综合试卷(附答案)

小学六年级小升初毕业数学综合试卷(附答案)一、选择题1.成语“立竿见影”在《辞源》里的解释为“竿立而影现,喻收效迅速。
”用数学的眼光来看,这是应用了比例知识中的()关系。
A.正比例B.反比例C.比例尺D.不确定2.小明用一些1立方厘米的小正方体拼了一个大正方体。
大正方体的体积在长方体甲和乙体积之间,那么这个大正方体的体积是( )立方厘米A.48 B.64 C. 81 D.1253.一列火车长200米,以每分钟1200米的速度经过一座大桥,从车头进到车尾出一共用了2分钟.求桥的长度是多少米?正确的算式是()A.1200×2+200B.1200×2-200C.(1200+200)×2D.(1200-200)×2 4.一个三角形任意一条边上的高所在的直线,都是这个三角形的对称轴。
这个三角形是()。
A.等腰三角形B.等腰直角三角形C.等边三角形D.没有答案5.一辆从厦门开往福州的客车,到泉州站时,车上人数的15下车后,又上来车上现有人数的15,上车和下车人数比较的结果是()。
A.上车人多B.下车人多C.无法确定6.下图是一个正方体的表面展开图,原正方体中与“国”字所在的面相对的面上标的字是()。
A.建B.设C.美D.中7.统计学校人数发现,女生人数比男生人数少10%,已知男生共680人。
下列算式中计算全校人数错误的是()。
A.2×680-(680×10%)B.680×(1+1-10%)C.680×(1-10%)+680 D.680×(1+10%)+6808.下面四幅图中,不可能是圆柱侧面展开图的是()。
A.B.C.D.9.某市规定每户每月用水量不超过6吨时,每吨价格为2.5元;当用水量超过6吨时,超过的部分每吨价格为3元。
下图中能正确表示每月水费与用水量关系的是()。
A.B.C.D.10.观察图中每一个大三角形中白色的三角形的排列规律,则第5个大三角形中白色的三角形有()A.82个B.154 C.83个D.121个二、填空题11.43时=(________)分825升=(________)毫升450克=(________)千克(填分数)12.38的分数单位是(________),再添上(________)个这样的分数单位后是75%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小升初毕业考试数学试卷及答案
小升初数学试卷及答案
1.在65后面添上一个“%”,这个数就扩大100倍。
(正确)
2.工作总量一定,工作效率和工作时间成反比例。
(正确)
3.甲车间的出勤率比乙车间高,说明甲车间人数比乙车间人数多。
(正确)
4.两个自然数的积一定是合数。
(错误,应改为“两个自然数的积不一定是合数。
”)
5.1+2+3+…+xx的和是奇数。
(错误,应改为
“1+2+3+…+xx的和是偶数。
”)
1.如果a=b×c,那么能够成立的说法是(b和c都是a的约数)。
2.一个真分数的分子和分母同时加上同一个非零自然数,
得到的分数值一定(比原分数大)。
3.如图,梯形ABCD中*有8个三角形,其中面积相等的
三角形有(4对)。
4.把一段圆柱形的木料削成一个体积最大的圆锥,削去局
部的体积是圆锥体积的(3倍)。
5.XXX特制了4个同样的立方块,并将它们如图(a)放置,然后又如图(b)放置,那么图(b)中四个底面正方形中的点数之
和为(13)。
1.目前,我国地区的总面积是105.2万平方米,改写成“万”作单位的数写作()平方米,省略“亿”后面的尾数约是(520)平方米。
2.如果x:y=z:u,那么x与XXX(z与u成比例),如果
x:y=u:z,那么x和y成(u和z成比例)。
3.甲、乙、丙三数之和是1162,甲是乙的一半,乙是丙的一半,那么甲数和乙数分别是(291)和(581)。
4.用三个完全一样的正方体,拼成一个长方体,长方体的
外表积是70平方分米,原来一个正方体的外表积是(10)平方
分米。
5.如果x×xx=χ+xx成立,那么χ=(x²-1)。
6.两支粗细、长短都不同的蜡烛,长的能燃烧7小时,短
的能燃烧10小时,那么点燃4小时后,两只蜡烛的长度相同,假设原来长蜡烛的长为a,原来短蜡烛的长是(4a/5)。
7.某校五年级(共3个班)的学生排队,每排3人、5人或7人,最后一排都只有2人。
这个学校五年级有(58)名学生。
8.掷两粒骰子,出现点数和为7、为8的可能性大的是(点
数和为7)。
9.四个同样大小的圆柱拼成一个高为40厘米的大圆柱时,外表积减少了72平方厘米,原来小圆柱的体积是(1000)立方
厘米。
老妇提着篮子卖蛋,第一次卖了篮子里一半又一半的蛋,第二次卖了剩下的一半又一半的蛋,第三次卖了第二次剩下的一半又一半的蛋,第四次卖了第三次剩下的一半又一半的蛋,最后全部的蛋都卖完了。
问老妇原来篮子里有多少个鸡蛋?
计算题:
1.5.7 + 11.8 + 4.3 = 21.8
0.3 - 0.2 = 0.024
33 × 98 + 66 = 3234
10.1 × 99 - 9.9 = 1000
4 - (0.
5 + 1) : -1.5
2.(1) 2x = x
2) x = 0
3.(1) (x + 1) × 5 × 7 = 35x + 35
2) 299 ÷ (299 + 1) = 0.9966
3) -(3x + 2) = -3x - 2
4) 12 × (4 + 14 + 16 +。
+ 148) × 50 =
问题解答:
1.XXX前20天生产了20 × 60 = 1200辆自行车,剩下的800辆自行车需要在后10天生产。
因此,后10天平均每天应
生产800 ÷ 10 = 80辆自行车。
2.原来的编织组每人每天生产1500 ÷ 30 ÷ 10 = 5顶草帽。
现在增加到120人,每人每天生产量不变,因此需要的天数为9000 ÷ (120 × 5) = 15天。
3.设步行速度为x千米/小时,则乘车速度为2x千米/小时。
由题意可得:
2x × t + x × (6 - t) = 270
2x × t - x × (6 - t) = 210
解得t = 3,代入可得乘车速度为6千米/小时,步行速度
为3千米/小时。
4.设乙队修了XXX,则甲队修了15 - x天。
根据题意可列出方程:
XXX在12天内修完剩下的工程,因此有:
12 × (1/12 + 1/甲队单独修的天数) = 1
XXX单独修的天数为24天,因此乙队修了3天,甲队修
了12天。
5.六(一)班和六(二)班共计97人,需要购买97本《古诗文读本》。
如果两个班分别购买50本,可以获得10%的优惠,
如果两个班合并购买97本,可以获得15%的优惠。
因此,最
合理的方法是两个班分别购买50本,共计100本,另外购买
一本,这样可以获得10%的优惠,总共花费为:
50 × 5 × 0.9 + 50 × 5 × 0.9 + 5 = 475元
6.设东、西两城相距x千米,则甲车每小时清扫x/10千米,乙车每小时清扫x/15千米。
相遇时,甲车比乙车多清扫了12
千米,因此有:
x/10 - (x - 12)/15 = 12
解得x = 180,因此东、西两城相距180千米。
7.根据题意可得,圆锥高度为2h,圆锥底面半径为r,则有:
1/3 × π × r^2 × 2h = 3
r = h/√3
最多能装的水为:
1/3 × π × (h/√3)^2 × h = h^3/(3√3)
8.由于三间房子价值相等,因此每间房子的价值为(1200 ×2)/3 = 800元。
XXX在牧场上安排了一只山羊。
他在两个小木桩之间用
绳子系住山羊,这个绳子上有一个环,可以从一个小木桩滑到另一个小木桩,这两个小木桩相距10米。
山羊被用一条5米
长的绳子系在环上,问山羊能到达哪些点?请画出图形并标出数据。
一、判断题:
1、错误
2、正确
3、错误
4、错误
5、正确
二、选择题:
1、C
2、B
3、C
4、D
5、D
三、填空题:
1、万,11亿
2、正,反
3、166,332
4、30
5、略
6、略
7、107
8、7的可能性大
9、120 10、15
四、计算题:
1、直接写出得数:
21.8 2、7 3、0.05 4、3300 5、990 6、3.5
2、求数:
X=8/19.X=12
3、用简便方法计算:
1)17 (2)300/301 (3)3/14 (4)6/25
五、应用题:
略
6、甲车和乙车的速度比为3:2,相遇时它们的路程比也是3:2.因此,根据比例关系,两车相遇时,它们所行驶的路程分别为3x和2x,且3x:2x=3:2.已知两城之间的距离为12千米,根据比例关系可得:3x+2x=12,解得x=2.因此,甲车和乙车分别行驶了6千米和4千米,两车之间的距离为6-4=2千米。
由于题目要求的是两城之间的距离,因此需要将这个距离按照比例放大,即2千米×(15+10)÷15=60千米。
7、根据题意可知,需要求出一桶液体的容积。
已知这桶液体的密度为3千克/立方米,质量为63千克,因此可以通过密度和质量的关系求出这桶液体的体积:63÷3=21立方米。
因此,这桶液体的容积为21升。
8、题目中给出了三个儿子共拿出的钱数为1200×3=3600元,且这3600元刚好是两个儿子应该分得的钱。
因此,每个儿子应该分得的钱数为3600÷2=1800元。
又已知三间房子共值多少钱,因此可以通过等式求解出每间房子的价值:三间房子的价值=1800×3=5400元,因此每间房子的价值为
5400÷3=1800元。
