完全四点形和完全四线形调和性质应用例析
高等几何中完全四点_线_形的调和性质应用于初等几何中某些问题的初探

如图 1 中, ( QR, YZ) = - 1, ( PQ, XE) = - 1 等。 推论 2: 在完全四点形的每条边上有一组调和共轭点, 其中两个点是顶 点, 另一 对点偶里 , 一个点 是对边 点, 另 一个点是这个边与对边三点形的边的交点。 如图 1 中, ( AB, YP) = - 1, ( AD, ER) = - 1 等。 对偶地, 可以得出完全四线形的调和性质。
( AB、AC, AD、AH) = - 1
又由线束交比的几何意义, 即得( AB、AC, AD、AH) =
sin ( sin (
AB, AB,
AD) AH )
sin( AC, sin( AC,
AH) AD)
=
sin(
故 sin = sin ( + ) , 又 sin = sin ( - )
所以 sin ( - ) = sin ( + )
33
楚雄师范学院学报
2002 年第 3 期
4 证共线点问题
例5
设 D、E、F 分别是 ∃ABC 的三边 BC、CA、AB 或其延长线上的点,
且DDBC
EC EA
FFAB =
1,
则它们三点共线 ( 梅
尼劳斯定理的逆定理) 。
证明: 如图 6, 因为DDBC( 1, 则FFAB ( EEAC, 故 EF 必与 BC 相交。
即 ( AG,
A A+)
=
AA AA+
GA+ GA
=
2 3
AA+
完全四边形与完全四点形

4.3 完全四点形和完全四线形内容解析定义4.5 平面内无三点共线的四点及其两两连线所构成的图形,叫做完全四点形. 见图4-3,这个图形含有四个点D C B A ,,,,及六条直线AB ,BC ,CD ,DA ,BD ,AC ,每一个点称为顶点,每一条直线称为边.如图4-5所示,不过同一顶点的两边称为对边(如AD 与BC ),共有三对对边.每一对对边的交点称为对边点或对角点(如AD 与BC 的交点S ),三个对边点(SQR )构成的三角形(三点形)称为对边三角形.定义4.6 平面内无三线共点的四直线及其两两的交点#所构成的图形,叫做完全四线形.见图4-6,这个图形含有四条直线(d c b a ,,,)和六个点(A ,B ,C ,D ,E ,F ),每一条直线称为边,每一个点称为顶点.不在同一边上的两个顶点称为对顶点(如A 与D ).六个顶点分为三对,每一对对顶点的连线,称为对顶线(AD ,EC ,BF ),三条对顶线构成的三角形称为对角三角形(PQR ).完全四点形和完全四线形具有如下性质.定理4.9 完全四点形通过每一个对角点有一组调和线束,即通过这个对角点的两边和34-图B C DA 54-图B CD A S Q R 64-图P Q R a b c dAB CD E F对角三角形的两边.如图4-5,比如对角点S 的两边SA 、SB 和对角三角形SQR 的两边SR 、SQ .是一组调和线束. 定理4.10 完全四线形的每一条对角线上有一组调和点列,即这条直线上的两个顶点及对角三角形的两个点.如图4-6,比如对角线CE 上的两个顶点C 、E 和对角三角形PQR 的两个顶点P 、Q , 是一组调和点列.典型例题例1 设XYZ 是完全四点形ABCD 的对边三点形,XZ 分别交BD AC ,于M L ,,不用笛沙格定理,证明CM BL YZ ,,共点.证明如图4-7,54-图BC D AS QR64-图PQ R a b c dAB CD E F 74-图对四线形ABCD ,根据定理4.10可知,在对角线AC 边上的四点L Y C A ,,,调和共轭,即1),(-=YL AC .在四点形YBZL 中,LB 与YZ 交于N ,设MN 与YL 交于C ',由定理4.9可知,过对角点M 有一组调和线束,即MA 、C M '和MY 、ML ,于是1),(-='YL C A ,所以,点C 应与点C '重合,即CM BL YZ ,,共点.(二)完全四点形与完全四线形的调和性习题答案1.设XYZ 是完全四点形ABCD 的对边三点形,XZ 分别交AC 、BD 于L 、M ,不用狄沙格定理证明:YZ 、BL 、CM 共点。
复习要点

二、仿射变换的性质、代数式、图形的仿射性质 仿射变换的性质、代数式、 1. 单比的概念: ( ABC ) =
AC BC
2. (ABC)= -1的充要条件是C是AB的中点,
x3 − x1 y3 − y1 = 3. 单比的代数表达式: ( ABC ) = x3 − x2 y3 − y2
4. 仿射变换的不变性质:同素性、结合性、平行性、共线 三点的单比不变、二平行线段之比不变、二封闭图形面积之 比不变 注:仿射变换的基本不变量是单比
第三章
射影变换与射影坐标
一、交比的定义、性质、代数表达式 交比的定义、性质、 1 交比的定义: ( AB, CD) = 2. 交比的性质: 1) (AB,CD)=(CD,AB)
1 2) (BA,CD)=(AB,DC)= ( AB, CD) ( ABC ) AC BD = ( ABD) BC AD
3) (AB,CD)=(BA,DC) 4) (AC,BD)=(DB,CA)=1 -(AB,CD)
第二章
射影平面
一、扩大欧氏平面的必要性 引进无穷远元素的方法: 二、 引进无穷远元素的方法: 1 无穷远点是二维空间中二平行线的交点;无穷远直线是
三维空间中二平行平面的交线; 2. 每一条有穷远直线上有一个唯一的无穷远点,这个无穷 远点是与该直线平行的所有直线的公共交点; 3. 无穷远直线上所有点都是无穷远点,即平面上两个无穷 远点的连线必是无穷远直线;
三、直径和共轭直径 1. 直径和共轭直径的仿射定义 2. 直径的方程 3. 两条直径成为共轭的条件 四、二次曲线的渐近线 1. 渐近线的仿射定义 2. 渐近线的性质 3. 渐近线的方程
3 x 2 + 2 xy − 2 y 2 + 4 x + 2 y + 1 = 0 1. 判定二次曲线
完全四点 ( 线 ) 形的调和性在初等几何中的应用

楚雄师范学院(Chuxiong Normal University)高等几何小论文题目:完全四点 ( 线 ) 形的调和性质在初等几何中的应用系(院):数学系专业:数学与应用数学姓名:张晓艳学号:200810212352011年12月22日完全四点( 线 )形的调和性质在初等几何中的应用摘要 :完全四点形和完全四线形的调和性是射影几何的重要不变性 , 它们在射影几何中占有重要地位。
不仅如此 , 它们在初等几何中也有广泛应用。
本文主要探讨完全四点 ( 线 ) 形的调和性质在初等几何中的应用。
关键词 : 完全四点形;完全四线形;调和比我们知道 ,一直线l上的点偶 P1 ,P2 与Q1 ,Q2成为调和共轭的充要条件是“P1和P2是一个完全四点形的对边点,Q1和Q2是通过第三个对边点的一对对边与l的交点”。
为此,可通过完全四点形的作图来作第四调和点。
1 利用完全四点 ( 线 ) 形的调和性解作图问题下面作图都是利用一把无刻度直尺完成的。
已知线段AB及其中点C,P是直线AB外一点,求作:过P点且平行AB 的直线。
作法 : ①连结AP并延长,在其上取一点Q;②连结CQ,BP交于R;③连结AR,BQ交于S;④连结PS,则直线 PS为所求作直线。
(2) 已知线段AB,且AB平行l,求作AB的中点。
作法 : ①在l上任取两点P,S;②连结 B P , AS 交于R;③连结 A P , BS 交于Q;④连结QR交AB于C,则为所求作的点。
(3) 已知SC是ASB的内角平分线,求作其外角平分线。
作法 :①用不过S的任一直线截SA ,SB ,SC分别于A′,B′,C′;②在SC上任取一点R;③连结A′R交SB于Q;④连结B′R交SA于P;⑤连结PQ交 A′B′于D′;⑥连结SD′,它即为所求作的直线。
( 4) 已知SD是∠ASB的外角平分线,求作其内角平分线。
作法:①用不过S的任一直线截SA ,SB ,SD 分别于A′B′、D′;②过D′任作一直线交SA,SB分别于P,Q;③连结A′, B′交于R;④连结SR ,它即为所求作的直线。
初中数学重点梳理:其他问题

其他问题知识定位共点线与共线点是初中竞赛中一个非常重要的知识,包括没捏劳斯定理、塞瓦定理等当然也包括射影变换,要熟练掌握射影变换中的点列与线束的交比与调和比;完全四点形和完全四线形的调和性质;一维基本形的射影对应;一维基本形的对合,本讲将通过例题来说明这些方法的运用。
知识梳理1、点列与线束的交比和调和比(1)点列的四点的交比我们知道,单比是仿射变换的基本不变量,但对于中心投影来说,单比不是不变量.这样就发生如何建立中心投影的基本不变量的问题,这个基本不变量就是交比.交比是两个单比的比,它有许多基本性质,见教材中的定理.由这些定理知,共线四点A ,B ,C ,D 共有24种排列,即有24个交比,分为6类,每类的四个交比值相等.当(AB ,CD )=-1时,CD 调和分割线段AB ,由调和分割的关系是对等的,因此A ,B ,C ,D 称为调和点列.(AB ,CD )=(CD ,AB )=-1(2)交比的代数表示设点P 1,P 2,P 的坐标分别为(x 1,y 1),(x 2,y 2),(x 3,y 3),单比(P 1P 2P )=μ,则μμ--=121x x x μμ--=121y y y (1) P 的齐次坐标(21x x μ-,21y y μ-,μ-1):当μ=1时,(1)式无意义;但当μ→1时,可得到P 1,P 2所在直线上的无穷远点.所以(P 1P 2P ∞)=1即一直线上的无穷远点分其上任何两点的单比等于1,也就是(P 1P 2,P 3P ∞)=(P 1P 2P 3) 如果四点P 1,P 2,P 3,P 4中,P 1或P 2为无穷远点,则上式可作为交比的定义.设四个不同的共线点P 1(A+λ1B ),P 2(A+λ2B ),P 3 (A+λ3B ),P 4 (A+λ4B ),则))(())((),(413242314321λλλλλλλλ----=P P P P 其中λi (i =1,2,3,4)彼此不相等. 设四个不同的共线点的三点及其交比k (k ≠1,k ≠0)为已知,则第四点必唯一确定.(3)线束的四直线的交比与调和比与点列的四点的交比类似,线束中四直线的的交比是利用三条直线的单比定义的.(AB ,CD )=)()(ABD ABC 应该注意,四直线的交比值与直线μ的取法无关.如果线束S 的四直线A ,B ,C ,D 被任何一条直线S 截于四点A ,B ,C ,D ,则(AB ,CD )=(AB ,CD )由这个结论可以推出与点列交比性质相类似的关于线束交比的性质,因此也可知四条直线所构成的24个交比值分为6类,每类的四个交比值相等.交比经中心投影后不变,即交比为射影性质.2、完全四点形与完全四线形调和性利用完全四点形的性质,可以解决“已知共线三点,求作第四调和点”的作图方法.设S,S'是完全四点形ABCD的一对对边,它们的交点是对边点X,X与其它二对边点的连线是l,l',图4-1.则必有(SS',ll')=-1图4-1设S,S'是完全四线形ABCD的一对对顶点,它们的连线是对顶线x,x与其它两对顶线交点T,T',图4-2.则(SS',TT')=-1.图4-23、一维基本形的射影对应(1)透视对应如果一个点列和一个线束的元素之间建立了一一对应且对应元素是结合的,则这个对应叫做透视对应,点列和线束叫做透视的.显然,点列与线束的透视关系具有对称性.点列与点列或线束与线束的透视关系都具有对称性.交比在透视对应下不变.(2)射影对应两个一维基本图形之间的射影对应的性质:①是一一对应的②A∧B则B∧A③具有传递性,即若A∧B,B∧C,则A∧C两个点列间的一一对应是射影对应⇔任何四点的交比与其对应四点的交比相等.已知两个一维图形的三对对应元素,那么可以确定唯一一个射影对应.两个点列间的射影对应是透视对应⇔它们底的交点自对应.两个线束间的射影对应是透视对应⇔它们顶点的连线自对应.4、一维基本形的对合对合是射影变换的一种特殊的情况,在对合里每对对应元素的每个元素归入哪个基本形都可以.射影变换成为对合对应的充分必要条件.5、交比和调和比仿射变换(对应)是对平行射影而言的,单比是仿射几何中最重要的概念,它又是仿射变换的基本不变量.在研究中心射影时,我们引进了无穷远元素.可以证明,在中心射影下,共线三点的单比不是不变量.由此引入交比概念,首先研究共线四点的交比(1)关于交比的定义定义(4.2)把交比定义为两个单比的比,即共线四点A ,B ,C ,D 的交比定义为两个单比(ABC )和(ABD )的比,表为(AB ,CD )=)()(ABD ABC .交比也称复比,即两个单比之比的意思.这种定义可称为几何定义.交比还有另一种定义,即代数法定义:设四个不同的共线点A ,B ,C ,D 的坐标顺次为A ,B ,A+λ1B ,A+λ2B ,则 (AB ,CD )=21λλ 以上两种定义方法是不同的.用第一种方法定义(AB ,CD )=)()(ABD ABC =ADBC BD AC ⋅⋅,所用坐标的非齐坐标,AC ,BD ,BC ,AD 都指有向线段的代数长度;第二种定义方法(AB ,CD )=21λλ,用齐次坐标.例如,共线四点A (2,1,-1),B (1,-1,1),C (1,0,0),D (1,5,-5),求(AB ,CD )时,可把A 和B 作为基础点对,则C =A + B ,λ1=1,D = 2A -3B ,λ2 =32-所求交比 21λλ=32- 注意,第二种定义方法采用齐次点坐标,可以不限制这四个点中是否有无穷远点.所以,定义(AB ,CD )=)()(ABD ABC =ADBC BD AC ⋅⋅,还属于欧氏平面上的定义,不能解决无穷远点的问题,在射影平面,应使用(AB ,CD )=21λλ的定义方法. 关于交比的定义,要注意以下问题:① A ,B ,C ,D 四点必须共线,而且要考虑顺序,顺序不同则交比不同;② AC ,BD ,BC ,AD 都是有向线段的代数长,因而交比(AB ,CD )是个数值.(2)交比的性质由于A ,B ,C ,D 四个点的编排顺序不同,所得的交比也不同,共线四点可以组成24种编排顺序,因而可以有24个交比值.由交比的性质原理可知,对于每个排列,还有另三种排列,它们的交比等于已知排列的交比,因此,这24种排列所产生的交比值,实际上只有6类,并且在24个排列中,只要求出1个交比值,就可求出其它23个交比值.例如,已知(AB ,CD )=3,则可知(DC ,BA )=(BA ,DC )=(AB ,CD )=3.而(AC ,BD )=1-(AB ,CD )= -2(3)几个特殊的交比共线四点A ,B ,C ,D 中,设A ,B ,C 是固定点,第四点D 沿直线移动.可以证明,点D 在直线上的每个位置都对应一个确定的交比(AB ,CD )的值.点D 的不同位置对应不同的交比值,不然的话,假设点D 和D '在两个不同的位置,且有(AB ,CD )=(AB ,CD ')则)()()()(D AB ABC ABD ABC '=,因而(ABD )=(ABD ')这只有在D = D '时,等式才成立,因此,(AB ,CD )的每个值,对应点D 的一个确定的位置.当这四个点中有无穷远点时,还可以用其他方法证明这个结论.证明如下:设已知三点的坐标是A +1λB ,A +2λB ,A +3λB 则由k =----))(())((41324231λλλλλλλλ (其中k 为定值,且k ≠0,1)可以求出4λ,确定第四点.因此第四点A +4λB 唯一确定.下面讨论交比的几个特殊情况①D 与C 重合时,则有(AB ,CD )= 1②当D 与B 重合时,则有(AB ,CD )=(AB ,CB )=AB BC BB AC ⋅⋅ = 0 ③当D 与A 重合时,(AB ,CD )=(AB ,CA )= ∞=⋅⋅AABC BA AC ④D 为无穷远点时,则有(AB ,CD )=(AB ,CD ∞)==∞)()(ABD ABC (ABC ) 可以看出,若第四点为无穷远点,则其交比等于前三个点的单比(ABC ),利用这个性质若无穷远点不在第四个点的位置,可以交换到第四个点的位置,以求其交比.(4)点列中四点的调和比调和比是交比的重要特例.当(AB ,CD )=-1时,称为C ,D 调和分割A ,B .或称点偶A ,B 与点偶C ,D 调和共轭.D 叫做A ,B ,C 的第四调和点.应当注意,在调和分割中,两对点的关系是完全对等的.点列中四点A ,B ,C ,D 所组成的交比可以有六个交比值,在一般情况下,这六个交比值是不等的,但当且仅当这四个点适当地编排顺序,可以组成调和共轭的两对点偶时,(注意排除两点重合和虚点不考虑),那么这六个交比值才有相同的.(5)线束的交比和调和比①由定义知,四直线A ,B ,C ,D 的交比为)()(ABD ABC =ADBC BD AC ⋅⋅,注意这个定义中数目的排列.②要注意定理4.7:如果线束S 的四线A ,B ,C ,D 被任何一条直线S 截于四点A ,B ,C ,D ,则(AB ,CD )=(AB ,CD )的证明.在上述定理中,若点S ,A ,B ,C ,D 都是有穷远元素时,或者,当S 为无穷远点或S 为无穷远直线时(即A ,B ,C ,D 都是无穷远点),此定理仍成立.即(AB ,CD )的值与直线S 的取法无关,所以仍可取(AB ,CD )=(AB ,CD )③定理4.7是一个非常重要的定理,由于定理可以证明“两点列同时截一线束,则此点列上对应四点的交比相等.”还可以推广证明投影于同一点列的两线束的四条对应直线的交比相等.可以知道,此定理使点列和线束的问题沟通了,为研究交比是中心射影下的不变量打下基础,同时点列和线束的问题可以对偶地进行研究.(6)有关交比的作图问题① 有关交比的作图可以根据共线四点的交比的定义,借助初等几何作图来完成,需要用相应例题来理解.② 第四调和点的作图● 用“一角两条边和这个角内外平分线调和共轭”作第四调和点.● 利用相似三角形作第四调和点.(7)利用交比的调和共轭解初等几何问题交比和调和共轭是几何学中的重要概念,它们在几何的研究中有重要的作用,运用这些概念和有关性质,可以解决一些初等几何问题主要在以下三个方面:①角平分线的调和性.②利用交比证明有关圆的问题.③与图有关的调和共轭问题.6、完全四点形和完全四线形的调和性完全四点形和完全四线形是射影几何中的重要图形,由于这两个图形具有调和性,而交比又是射影变换的不变量,所以对完全四点形的性质的研究在射影几何中占有重要地位.值得注意的是,在前面调和比是用交比来定义的,而交比之定义为单比之比,所以定义调和比此时用了变量概念.对完全四点形的性质的研究,可以使我们完全不用度量概念,而使用下列方法来定义调和比或调和共轭.即“一直线S上的点偶A,B与C,D,A,B是一个完全四点形的对边点,C,D是通过第三个对边点的两条对边与S的交点,则A,B与C,D成调和共轭”.这种定义是综合地纯射影的定义,这种定义方法只与直线和直线相交的作图有关,与度量无关.由于完全四点形的调和性是射影性质,所以它的对偶图形完全四线形也有调和性.应注意以下问题:(1)注意完全四点形与中学所熟悉的四边形的区别四边形指简单四边形,由顶点依次连接而成,顶点数等于边数,均为4,如图4-3.ABCD 为简单四边形.而完全四点形是平面内无三点共线的四点及其两两连线所构成的图形,如图4-4.完全四点形ABCD有四个顶点A,B,C,D,有六条边(即任何两顶点的连线都是边),通过同一顶点的边叫邻边,不通过同一顶点的边叫对边,因此有三对对边:AB与CD;AC与BD;AD与BC,对边交点叫对边点,共三个,即AB×CD=X,AC×BD=Y,AD×BC=Z.三个对边点组成对边三点形XYZ.图4-3 图4-4完全四点形的一对对边被通过这两个边交点的对边三点形的两边调和分割.完全四线形的一对对顶点被连接这两个点的对角三角形的两边调和分割.(2)利用完全四点形的调和性作第四调和点我们知道,一直线l上的点偶P1,P2,Q1,Q2成为调和共轭的充要条件是:“P1和P2是一个完全四点形的对边点,Q1和Q2是通过第三个对边点的两条对边与l的交点”,根据这个道理,可以通过完全四点形的作图来作第四调和点.如图4-5,已知直线l上有三点P1,P2,P3,求作点P4,使(P1P2,P3P4)=-1.作法如下:过P1P2若任作一直线交于点A,在P2A上任取一点B,连B P3,过P1A于点C,再连P2C,P1B,交于点D.连AD与L交于P4,则P4为所求第四调和点.图4-5应当指出,以上作图是只用一根直尺完成的.而且过P1,P2的直线是任意作的,但P4点是唯一的,这由笛沙格定理保证.在图4-5中,根据定理,若P4为P1P2中点,则P为l上无穷远点,于是利用直尺可以作出CB // P1P2,反之,如果知道CB // P1P2,也可以用一根直尺求P1P2中点.(3)应用完全四点形的调和性解初等几何问题利用完全四点形的调和性,可以比较简捷地解决一些初等几何中的共点和共线问题.例如,三角形三个顶角的外角平分线交其对边的三点共线.7、一维基本形的射影对应(1)什么叫一维基本形基本形,指以点、直线、平面为元素所形成的某些无穷集合,一维基本形指点列和线束.几何学中的维数,指几何元素活动的自由度,也就是几何元素的坐标或参数必不可少的数目,这个数就是几何学的维数.此如平面内的点和直线应该有两个坐标,但在点列中以A,B为基点的任一点坐标可以表为A,B的坐标的线性组合,即C = A + λB,其中λ为参数,所以点列中的点可以用一个独立参数表示(对于线束也有类似结论).也就是说,点列的每个点(或线束中的每一直线)都可以用一个独立参数表示,点列和线束就叫一维图形.点列和线束就是一维几何研究的对象.关于空间的维数,是指把直线,平面或空间都看成四点构成,空间的维数是点活动的自由度,所以直线叫一维空间.平面叫二维空间,我们生活的空间叫三维空间.由于几何学研究的元素不限于点,所以几何学中的维与所处空间的维不同.比如,平面上的直线几何应该叫二维几何学,这是由于把直线看作基本元素,平面上决定直线需要两个比值,即必不可少的参数为2.(2)一维基本形的透视对应与射影对应的关系①在前几章所讨论的透视仿射对应是对平行射影而言,本章所论的透视对应则对中心投影而言,透视对应包括点列和线束之间的透视对应;点列与点列之间的透视对应.在定义中可以将点列换成线束,或把线束换成点列.所以点列与线束的透视对应具有对称性.由透视对应的定义还可以看出,透视对应保持四元素的交比不变.但透视关系不满足传递性.需要注意,透视对应一定是射影对应,但射影不一定成透视对应,因此,透视对应与射影对应是特殊与一般的关系.②射影对应必是一一对应,且具有传递性、对称性、反身性,即具有等价关系.③透视对应在什么条件下才成为射影对应呢?由定理知,两个点列间的射影对应是透视对应的充要条件是它们的底的交点自对应也就是它们的公共元素自对应.两个点列成射影对应时,把它们的公共点看作是第一个点列的点时,它在第二个点列上的对应点,一般情况下不是它本身,只有当两个点列成透视对应时,其公共元素才自对应.④应该注意,如果一维射影对应使无穷远点对应无穷远点,则该对应一定是仿射对应,要证明这个结论,只需证明这种对应保持单比不变.由于射影对应保持交比不变.所以,仿射对应可看作特殊的射影对应.8、一维基本形的对合(1)关于对合概念对合对应是重要的,特殊的射影变换.在两个重叠的射影对应的一维基本形中,第一个基本形的元素P 对应第二个基本形的元素P',但如果把P'看作第一个基本形的元素,那么它在第二个基本形里不一定对应P.但如果这个对应为对合对应,则根据对合定义“在两个重叠而且射影对应的一维基本形里,如果对于任何元素,无论看作属于第一个基本形或第二基本形,它的对应元素是一样的,那么这种非恒等的射影变换叫做对合(对应)”.那么P'就一定对应P.若两个重叠一维基形成射影对应,可假设两个重叠点列成射影对应,在什么条件下才成为对合呢?实际上只要有一对对应元素符合对合条件,则这种射影变换一定是对合.(2)对合的代数表示和确定对合是特殊的射影变换,从对合的代数表示,也可以看出射影变换成为对合的条件,即在射影变换式0=+'++'d c b a λλλλ,0≠-bc ad 中,若是对合,则有B = C ,反之也成立.上式说明射影变换范围比对合大.我们知道,三对对应元素决定唯一一个射影变换,如果是对合,则只要有不重合的两对对应点便可决定唯一一个对合对应.判定一个射影变换是否为对合对应,也可用如下事实:对合对应存在两个二重元素,射影变换是对合的充要条件是任何一对对应元素与两个二重元素调和共轭.例题精讲【试题来源】【题目】设1,2,3,4是四个不同的共线点,如果(12,34)=(23,41)则(13,24)=( )A .-1B .1C .0D .∞【答案】A【解析】 解:由交比的运算定理,选A【知识点】其他问题【适用场合】当堂例题【难度系数】2【试题来源】【题目】P 是ABC ∆内任一点,连结AP 、BP 、CP 并延长分别交对边于D 、E 、F 。
完全四边形调和点列证明

完全四边形调和点列证明完全四边形调和点列是指在平面上给定4个不共线的点A、B、C、D及它们的共轭点A'、B'、C'、D',并且这8个点满足调和性质,即(ABCD)=-1。
其中,ABCD表示A与B连线、C与D连线的交点。
调和性质可以表示为以下等式:(AA')/(AC') * (BD')/(BA') = -1(BB')/(BD') * (CA')/(CB') = -1(CC')/(CA') * (DB')/(DC') = -1(DD')/(DB') * (AC')/(AD') = -1对于完全四边形调和点列的证明,我们可以从多个角度进行阐述。
一、几何证明方法:1.利用平行线性质证明:在平面上,如果一组平行线通过一个调和四边形的对角线,则它们必定也通过该调和四边形的共轭对角线。
根据这个性质,我们可以得出扩展的拉美定理(扩展的拉美定理表示:如果A、B、C是一条直线上的三个点,D、E、F是另一条直线上的三个点,那么如果AD、BE、CF交于一点,则AE、DF和BC也必定交于一点)。
利用扩展的拉美定理,可以证明完全四边形调和点列中的任意四个点满足调和性质。
2.利用交比性质证明:在平面几何中,交比是指若干条线段的比值,可以用于表示调和性质。
对于完全四边形调和点列,我们可以使用逆向交比等式进行证明,具体通过运用调和性质的定义和多个交比定义来推导。
二、代数证明方法:可以使用代数运算进行证明,通过直线与坐标系的关系来推导出调和点列的性质。
具体可以通过线的方程来证明四个点的交点满足调和性质,并通过坐标的代数运算来证明三、向量证明方法:利用向量的加法与减法、数量积和矢积等定义和性质进行证明。
具体可以通过定义向量的坐标映射,利用向量的线性叠加性质进行证明。
四、复数证明方法:可以利用复数与几何的关系进行证明。
完全四点形的调和性

完全四点(线)形的调和性在初等几何中的应用黄毅1 胡志杰1 李锦杰2摘要:本文对高等几何中完全四点(线)形的性质做了具体而系统的整理,并通过初等几何与高等几何的内在联系,通过初等几何中平分角、平分线、共点、共线、平行、作图等几个具体问题的探究及其在中学竞赛中的运用,化难为易,丰富和拓展初等几何的内容。
关键词: 完全四点(线)形 应用 调和性 初等几何高等几何是一门聚集多方面知识体系的优秀学科。
高等几何可以说是在初等几何领域上的一个延伸与拓展。
它可以给出初等几何中某些问题的简单证明,为初等几何提供理论依据和注入新的数学思维。
完全四点(线)形的调和性是高等几何的一项重要内容,在几何学中占有重要地位。
它对初等几何的研究亦具有重要的指导意义。
比如说,它在初等几何的平分角度问题、共点共线问题、中点问题、线段比值问题及平行性等问题的研究中都有广泛的应用。
对高等几何当中某些特殊性质(四点形的调和性)的研究,可以让很多的数学爱好者,更加清楚的了解高等几何的重要性。
同时,也可以促进数学爱好者对初等几何学习的积极性。
本文着重分析完全四点(线)的调和性在初等几何中的一些应用。
一.完全四点(线)形的定义1.1 平面上四个点(无三点共线)以及联结其中任意两点的六条直线所组成的图形称为完全四点形。
(其中,每一个点称为顶点,每一条直线称为边,不共顶点的两边称为对边,对边的交点为对边点,以对边点为顶点的三角形为对角三角形。
)1.2 平面内无三线共点的四直线及其两两交点所构成的图形称为完全四线形。
(其中,每一条直线称为边,每一个点成为顶点,不共边的两个顶点为对顶点,对顶点连成对顶线,一对顶线为边的三角形成为对角三角形。
) 二 .完全四点(线)的调和性质2.1完全四点形(图一中的四点形ABCD )的两个对边点X 、Y 的连线交第三对对边于S 、T ,则(XY ,ST) = –1.(图一) (图二)2.2完全四线形(图二中的四线形abcd )的两条对顶线x, y 的交点O 与第三对对X t顶点相连得直线s,t,则(xy,st) = –1.2.3在完全四点形的对边三点形的每条边上, 有一个调和点组, 其中一对为对边点, 另一对为该边与第三组对边的交点.2.4在完全四点形的每条边上有一个调和点组,其中一对为顶点, 另一对中一个为对边点, 一个为该边与对边三点形的边的交点.三.完全四点(线)形的调和性在初等几何中的应用 3.1 解决平分角问题例1 如图,AD 垂直于BC ,M 是AD 上的任意一点,BM 交AC 于E ,CM 交AB 于F ,证明:AD 、BC 平分DE 与DF 所成的角。
第二节调和比

X
M E
Y
又因为DX⊥DY,所以AD、BC平分∠EDF。
菠萝岩
边上有一个调和点组, 其中一
对为顶点, 另一对中一个为对 边点, 一个为该边与对边三点 形的边的交点.
例1 已知直线l上相异三点P1, P2, P3. 求作第四调和点P4. 分析:利用推论1, 构造一个完全四点形, 以l为其对边三点形的一边, P1, P2是对边点, 使第三对对边中, 一条过P3, 则另一条与l的 交点即为P4. 解. 作法: (1). 在l外任取一点A, 连AP1, AP2. (2). 过P3作直线分别交AP1, AP2于B, D. (3). 连P1D, P2B交于C. (4). 连AC交l于P4为所求. 注1 上述实际上也是利用推论2作图. 注2 本例引申
§2 完全四点形的调和性
1. 调和比 例1 (1)设C为线段AB的中点,P为直线AB上的无穷 远点, 试求: (AB, CP) 。
(2) 设直线c, d分别是由直线a, b所成角的平分线,
试求: (ab,cd)。
点偶P ,P ,与P ,P (互为)调和分离 1 2 3 4 定义 若(P1P2,P3P4 )= –1, 则称 点偶P1,P2,与P3,P4(互为)调和共轭 交比值“–1” 为 调和比。 点P4为P1,P2,P3的第四调和点
推论1 在完全四点形的对
边三点形的每条边上, 有一个 调和点组, 其中一对为对边点, 另一对为该边与第三组对边的 交点. 推论2 在完全四点形的每条
推论1’ 通过完全四线形的
对顶三线形的每个顶点有一个 调和直线组, 其中一对为对顶 线,另一对为该顶点与第三对 对顶的连线. 推论2’ 通过完全四线形的每 个顶点有一个调和直线组, 其 中一对为边,另一对中, 一条 为对顶线, 一条为该顶点与对 顶三线形顶点的连线.
完全四边形调和性质的应用

筻
笋
完 全 四 边 形 调 和 性 质 的 应 用 ①
高秋艳 赵 临龙
( 安康 学 院数 学 -应 用 数 学研 究所 陕 西 安康 9
中图分 类 号 : 8 . O1 5 1 文 献标 识 码 : A
750 ) 2 00
文章 编 号 :0 8—9 5 ( 0 1 1 0 3 0 10 2 X 2 1 )2— 1 0— 1
Q, 根 据 性 质 2 得 ( D, P 则 , B Q )
= 一
以, 由共 轭 的定 义 , E和 F是 P的两 个共 轭点 , 而 直 线 E 从 F即 Q R 就是 P点 的极 线 。 综 上所 述 , 完全 四边形 的调和 性 在作 二 次 曲线 的极 线 中应 用
1 。于是 Q为 B 的 中点 , D 即
结论 梯 形 两 腰 延 长 线 的
阔 1
B Q=Q 。 D
广 泛 , 以恰 当利 用 完全 四点 形 的 调 和 性质 证 明初 等 几 何 问题 , 所 降 低了 解决 问 题 的 难 度 , 题 的证 明思 路 清 晰 , 程 简 洁 。注 重 命 过 揭示 高 等几 何 与 初 等几 何 的 内在 联 系 , 样 可 以扩 大 我们 的知 识 这 领域, 拓宽 我们 的视野 , 助 于站 在 新 的高 度 上 , 有 深入 地 理 解 初 等
作法 : ① 过 P 作 两 直
即给 出平分 两 平行 线 段 的一种 几何 作 图法 。 另外 , 全 四边 形 S Q 若 A B内 接 于 二 次 曲线 , 于 ( Q, E 由 s c )= 1( B,D ,A C )= 一 。又 D E两 点 确定 一 条 直 线 , 此 在 高 等 几 1 、 因
几何中的调和分割及应用

几何中的调和分割及应用郑皎月(安康学院数学系 陕西 安康 725000)摘要: “调和分割”又称“调和共轭”,它是交比研究中的一个重要特例,也是 贯穿大学《高等几何》课程的一个重要概念,应用它解决初等几何中有关平分角、平分线段以及高等几何中有关对合的性质、完全四点型的调和分割、完全四线型调和分割以及拉盖尔定理的推广等性质有着积极的意义。
关键字:调和分割 高等几何 应用 性质若C 点分割线段AB 的比值和D 点分割AB 的比值只差一个符号(因而一个是内分点,另一个是外分点),这时我们说C 、D 两点调和分割AB,或C 与D 对于线段AB 成调和共轭点偶,用符号1),(-=CD AB 表示。
在调和分割中,两对点的关系是完全对等的,这意思是说,当C 与D 调和分AB 时, A 与B 也调和分割CD,因而我们已知道,若1),(-=CD AB ,便也有1),(-=AB CD .一、几何中的调和分割 1.关于平分角中的调和分割三角形中一个角的内角和外角的平分线,将对边分成两线段的比值,都和两邻边成证明:由三角形中一个角的内角和外角的平分线,将对边分成两线段的比值,都和两临边成比例有EB AEDB DA CB AC EB AE ==, 即 DB DACB AC = 1=**CBDA DBAC则1-=**BCAD BDAC因此 1),(-=CD AB2、关于线段的调和分割一线段被它的中点和这直线上的无穷远点所调和分割,即证明:1),(-=∞CP AB证: ∞∞∞∞∞*=**=AP BP BC AC BC AP BP AC CP AB ),(因为 CB AC = 所以 1-=BCAC即1-=**∞∞BC AP BP AC则 1),(-=∞CP AB 3、关于对合的调和分割对合有两个二重元素,这两个元素是不重合的,可能是共轭复元素,并且这两个二重元素调和分割任意一对对应元素。
证明:由于对合的表达式是),0(,0)(2''≠-=+++b ad d u u b auu 所以决定二重元素的方程022=++d bs as不能有等根,所以两根1s 和2s 或者是不等式实根(双曲型对合),或者是共轭复根(椭圆型对合).由于对合是射影变换,因此保留交比,即),(),('21'21u u s s uu s s =,利用交比性质,此式可写作),(1),('21'21uu s s uu s s =从而1),('21=uu s s 或1),('21-=uu s s ,但1),('21=uu s s 将导致u 与'u 重合,这与对合不是恒同变换的假设抵触,从而1),('21-=uu s s . 4、关于完全四点形和完全四线形的调和分割完全四点形 完全四点形通过每一个对角点有一组调和线束,即通过这对角点的两边和对角三角形的两边。
由完全四点形的调和性得到的一些结论

(L
u2 +
2M
u v+
N
v 2) .
注意到 Ⅱ( u, v; du, dv) = k1Ⅰ, 即 L du2 + 2M dudv + N dv 2 = k1ds2 , 同理 L u2 + 2M u v + N v 2 = k2 s2
及定理 2 的等式( 9) , 知( 11) 式分子 = k 1co s2 + k2sin2 .
( 1) 利用同一张图可以体现完全四线形的调和 性.
根据完全四线形与完全四点形的对偶关系, 仔细观 察图 1, 可以发现, 该图中蕴含着完全四线形 abcd, x y z 为完全四线形的对顶三线形, 由对偶原则可知, 在 x 、y 、z 三条边上各有一组调和共轭点列, 即( A C, ZT ) = - 1, ( B D, ZW ) = - 1, ( X Y , T W ) = - 1, 以九个顶点 A 、B、C、D、X 、Y 、Z、T 、W 为中心, 各有一组调和共轭线束. 正因为完全四点形与完全四线形可以通过一张图形体现, 故而下面的讨论仅就完全四点形的点线进行.
即 a + b = - ( c + d) , 该式左边表示在直线 A B 上的点坐标为 a + b, 右边表示在直线 CD 上的点坐标为 c +
d, 左边等于右边, 说明此点为 A B、CD 的交点, 即点 Y , 同理, 点 Z 的齐次坐标为: a + c 或 b + d . 点 X 的齐次
坐标为: a + d 或 c + b.
Ⅰ Ⅱ Ⅰ Ⅱ 交点 交点所在边 Ⅰ Ⅱ Ⅰ Ⅱ 交点 交点所在边
C - S A Q × CS DZ
调和点列与极点极线(解析几何)(解析版)

调和点列与极点极线知识与方法以极点极线为背景的题目经常出现在高考和各级竞赛试题之中, 如圆锥曲线的切线、切点弦、圆锥曲线内接四边形两对边延长线的交点轨迹等, 是圆锥曲线的常考问题, 这些问题大多和极点极线与调和点列的性质有关.熟悉调和点列与极点极线基本性质, 能抓住此类问题的本质,明确问题的目标, 能更高效地解决问题. 下面介绍交比、调和点列、完全四边形、Apollonius圆、极点和极线等射影几何的重要概念及性质, 溯本求源,揭示此类与极点极线有关的问题的来龙去脉.(一)调和分割的概念“调和分割”又称“调和共轭” , 来源于交比,分“调和线束”和“调和点列”两种, 它是交比研究中的一个重要特例, 也是贯穿《高等几何》课程的一个重要概念.定义1线束和点列的交比:如图, 过点O的四条直线被任意直线l所截的有向线段之比ACAD/BCBD称为线束OA、OC、OB、OD或点列A,C,B,D的交比.定理1交比与所截直线无关.【证明】令线束O a,b,c,d分别交l于A,B,C,D,则ACAD/BCBD=SΔAOCS△AOD/SΔBOCSΔBOD=CO sin∠AOCDO sin∠AOD/CO sin∠COBDO sin∠BOD=sin∠AOCsin∠AOD,sin∠COBsin∠BOD, 又因为各对应向量方向相同, 故交比与所截直线无关.【注】定理说明,点列的交比与其对应线束的交比是相同的. 保持线束不变, 取另一直线l 交线束于A ,B ,C ,D , 可视为对l作射影变换, 所得交比不变, 由此说明交比是射影不变量, 具有射影不变性.定义2调和线束与调和点列:定理1若交比为-1,则称为调和比.交比为-1的线束称为调和线束,点列称为调和点列. 一般地,若AC=λCBAD=-λDB(λ>0且λ≠1,则A,C,B,D四点构成“调和点列”;①A,B叫做“基点”,C,D叫做“(内、外)分点”.根据定义可得:如果点C内分线段AB,点D外分线段AB, 且ACCB=ADDB, 那么称点C,D调和分割线段AB.亦称A,C,B,D为调和点列. 线段端点和内外分点, 依次构成调和点列.即:调和点列⇔内分比=外分比.②也可以以D,C为基点, 则四点D,B,C,A仍构成调和点列, 故称A,B与C,D调和共轭.③如图, 若A,C,B,D构成调和点列,O为直线AB外任意一点, 则四直线OA,OC,OB,OD为调和线束;若另一直线截此调和线束, 则截得的四点A ,C ,B ,D 仍构成调和点列(由定理1可知).定理2调和点列的性质:若A,C,B,D为调和点列, 即ACCB=ADDB,则:(1)调和性:1AC+1AD=2AB证明:CACB=DADB⇒CBCA=DBDA⇒AB-CACA=DA-ABDA⇒ABCA-1=1-ABDA⇒ABCA+ABDA=2⇒1AC+1AD=2AB(2)共轭性:若A,C,B,D构成调和点列, 则D,B,C,A也构成调和点列.即:若1AC+1AD=2AB成立, 则1DB+1DA=2DC也成立;(3)等比性:①CACB=DADB=λ②记线段AB的中点为M, 则有MA|2=MB|2=MC⋅MD.③记线段CD的中点为N, 则有NC|2=ND|2=NA⋅NB.(同2可证)证明:CACB=DADB⇒MA+MCMA-MC=MD+MAMD-MA⇒MA+MCMD+MA=MA-MCMD-MA由等比性质可知:MA+MC+MA-MCMD+MA+MD-MA=MA+MC-MA- MC∣MD+MA-MD-MA⇒2MA2MD=2MC2MA⇒MA|2=MB2=MC⋅MD同理可得NC|2=ND|2=NA⋅NB.定理3斜率分别为k1,k2,k3的三条直线l1,l2,l3交于x轴外的点P, 过P作x轴的垂线l4, 则k1,k2,k3成等差数列的充要条件为l1,l2、l3,l4成调和线束.分析:不妨设k1、k2、k3均为正数, 其它情况同理可证.【证明】如图, 设l1,l2、l3,l4与x轴分别交于A,B,C,D四点, 则2k2=k1+k3⇔2DB=1DA+1DC⇔DADC=BABC⇔A,B,C,D成调和点列⇔l1,l3,l2,l4成调和线束.定理4已知F为椭圆的焦点,l为F相应的准线, 过F任作一直线交椭圆于A,B两点, 交l于点M, 则A,B,F,M成调和点列.(说明:此处图像应修正:B点在椭圆上,BB1虚线应往上移一点)【证明】如图, 分别过A,B作l的垂线, 垂足为A1,B1,则由椭圆的第二定义及平行线的性质可得:AF BF=AA1BB1=AMBM, 故A,B,F,M成调和点列.定义3阿波罗尼斯Apollonius圆:到两定点A、B距离之比为定值k(k>0且k≠1)的点的轨迹为圆, 称为Apollonius圆(简称阿氏圆),为古希腊数学家Apollonius最先提出并解决.【证明】如图, 由AP=kPB, 则在AB直线上有两点C、D满足ACBC=ADBD=APBP, 故PC、PD分别为∠APB的内外角平分线, 则CP⊥DP, 即P的轨迹为以CD为直径的圆(圆心O为线段CD的中点).由ACBC=ADBD可知, 图中A,C,B,D为调和点列.定义4完全四边形:我们把两两相交, 且没有三线共点的四条直线及它们的六个交点所构成的图形, 叫做完全四边形. 如图,凸四边形ABCD各边延长交成的图形称为完全四边形ABCDEF,AC、BD、EF称为其对角线.定理5完全四边形对角线所在直线互相调和分割. 即AGCH、BGDI、EHFI分别构成调和点列.【证明】HEHF⋅IFIE=S△AECS△AFC⋅SΔBDFS△BDE=S△AECSΔACD⋅SΔACDSΔAFC⋅SΔBDFSΔBEF⋅SΔBEFSΔBDE=ECCD⋅ADAF⋅DCEC⋅AFAD=1,即HEHF=IEIF, 所以EHFI为调和点列. 其余的可由线束的交比不变性得到.(二)极点和极线的概念1. 极点和极线的几何定义如图,P为不在圆锥曲线Γ上的点, 过点P引两条割线依次交圆锥曲线于四点E,F,G,H, 连接EH ,FG交于N, 连接EG,FH交于M, 我们称点P为直线MN关于圆锥曲线Γ的极点, 称直线MN为点P关于圆锥曲线Γ的极线. 直线MN交圆锥曲线Γ于A,B两点, 则PA,PB为圆锥曲线Γ的两条切线. 若P在圆锥曲线Γ上, 则过点P的切线即为极线.(1)自极三角形:极点P一一极线MN;极点M一一极线PN;极点N一一极线MP;即△PMN中,三个顶点和对边分别为一对极点和极线, 称△PMN为“自极三角形”.(2)极点和极线的两种特殊情况(1)当四边形变成三角形时:曲线上的点E F,M,N对应的极线, 就是切线PE;(2)当四边有一组对边平行时, 如:当FH⎳EG时, EG和FH的交点M落在无穷远处;点P的极线NM2和点N的极线PM1满足:FH⎳NM2⎳EG⎳PM1.2. 极点和极线的代数定义对于定点P x0,y0与非退化二次曲线Γ:Ax2+Cy2+Dx+Ey+F=0,过点P作动直线与曲线Γ交于点A与点B, 那么点P关于线段AB的调和点Q的轨迹是什么?可以证明:点Q在一条定直线l:Ax0x+Cy0y+D x+x02+Ey+y02+F=0上,如下图. 我们称点P为直线l关于曲线Γ的极点;相应地, 称直线l为点P关于曲线Γ的极线.一般地, 对于圆锥曲线Γ:Ax2+Bxy+Cy2+Dx+Ey+F=0,设极点P x0,y0, 则对应的极线为l:Ax0x+B x0y+y0x2+Cy0y+Dx0+x2+Ey0+y2+F=0【注】替换规则为:x2→xx0, y2→yy0,xy→x0y+y0x2,x→x+x02,y→y+y02.(1)椭圆x 2a 2+y 2b2=1(a >b >0)的三类极点极线(1)若极点P x 0,y 0 在椭圆外, 过点P 作橢圆的两条㘦线, 切点为A ,B , 则极线为切点弦所在直线AB :x 0xa 2+y 0yb 2=1;(2)若极点P x 0,y 0 在椭圆上, 过点P 作椭圆的切线l , 则极线为切线x 0xa 2+y 0yb 2=1;(3)若极点P x 0,y 0 在橢圆内, 过点P 作椭圆的弦AB , 分别过A ,B 作椭圆切线, 则切线交点轨迹为极线x 0xa 2+y 0yb 2=1由此可得椭圆极线的几何作法:(2)对于双曲线x 2a 2-y 2b 2=1, 极点P x 0,y 0 对应的极线为x 0x a 2-y 0y b 2=1;(3)对于拋物线y 2=2px , 极点P x 0,y 0 对应的极线为y =p x 0+x .3. 极点和极线的性质(1)引理:已知椭圆方程为x 2a 2+y 2b 2=1(a >b >0), 直线l 的方程为x 0x a 2+y 0y b 2=1, 点P x 0,y 0 不与原点重合. 过点P 作直线交椭圆于A ,B 两点,M 点在直线AB 上,则“点M 在直线l 上"的充要条件是"P ,M 调和分割A ,B ", 即AP PB =AMMB.【证明】先证必要性. 设M 点的坐标为x 1,y 1 , 则有x 0x 1a 2+y 0y 1b 2=1. 设直线AB 的参数方程为x =x 0+tx 11+ty =y 0+ty 11+t(t 为参数)与椭圆方程联立, 得x 21a 2+y 21b 2-1 t 2+2x 0x 1a 2+y 0y 1b 2-1 t +x 20a 2+y 20b2-1=0,即x21a2+y21b2-1t2+x20a2+y20b2-1=0, 该方程有两个不等实根, 设为t1,t2, 则t1+t2=0.即P,M调和分割A,B, 也即APPB=AMMB.将以上证明过程反向推导,即得充分性成立.设P是圆锥曲线Γ的一个极点, 它对应的极线为l, 过P任意引一条直线, 交Γ于点A,B, 交l于点Q, 若点A是位于P,Q间的点, 结合引理可得如下极点和极线的三个调和性质:(1)调和性1 PA +1PB=2PQ(2)共轨性B,Q,A,P四点也构成“调和点列”, 即1BQ+1BP=2BA.(3)等比性(1)点Q、P是线段AB的内、外分点,PAPB=QAQB=λ.(2)若Γ为椭圆或双曲线,当直线AB经过曲线中心O时, OP⋅OQ=OA|2=OB|2.4. 配极原则若P点关于圆锥曲线Γ的极线通过另一点Q, 则Q点的极线也通过P, 称P、Q关于Γ调和共轭.【证明】设点P x P,y P,则相应的极线为l P:x p xa2+y P yb2=1,点Q x Q,y Q,相应的极线为l Q:x Q xa2+y Q y b2=1. 因为l P过点Q,Q坐标满足方程x P xa2+y P yb2=1, 即x P x Qa2+y P y Qb2=1;则P点坐标满足方程x Q xa2+y Q yb2=1, 这也说明, 也就是l Q过点P.配极原则说明:l P过点Q⇔l Q过点P, 由此可得下面推论:推论1:共线点的极线必然共点(A、G、D、E四点共线, 它们的极线a、g,d、e共交点F);共点线的极点必然共线(直线a、g,d、e共交点F, 它们的极点A、G,D、E四点共线).推论2:如下图, 过极点P作两条直线, 与桞圆分别交于点A,B和C,D, 则直线AD,BC的交点T必在极线上.5. 椭圆的极点与极线的常用性质对于椭圆x2a2+y2b2=1, 极点P x0,y0(不是原点)对应的极线为x0xa2+y0yb2=1, 有如下性质:性质1:“类焦点"与“类准线”当极点P m,0m≠0在x轴上时,对应的极线x=a2m平行于y轴,当极点P0,nn≠0在y轴上时对应的极线y=b2n平行于x轴;特别地, 当极点P为椭圆的焦点时, 极线为相应的准线.性质2:平方模型如下图, 射线OP与椭圆交于点D, 与点P的极线交于点C, 则|OP|⋅|OC|=|OD|2;当点P在x轴上时, |OP|⋅|OC|=a2;当点P在y轴上时, |OP|⋅|OC|=b2.性质3:共轭方向设极点P x0,y0不在坐标轴上, 则直线OP的斜率为k OP=y0x0, 极线l:x0xa2+y0yb2=1的斜率k=-b2x0a2y0,则k OP⋅k=y0x0⋅-b2x0a2y0=-b2a2.【注】性质3表明:椭圆内一点P的极线方向与以极点P为中点的弦的方向相同,称OP与极线方向共轭. 当极点P x0,y0在椭圆内时,极线l平行于以P为中点的弦所在直线EF(用点差法易证). 设直线OP与椭圆相交于点D, 过点D作椭圆的切线l1, 则以P为中点的弦所在直线EF、过点D的切线l1、极点P的极线l, 三线互相平行, 如下图.性质4:平行如下图, 设四边形ABCD为椭圆的内接梯形, AC⎳BD,AD∩BC=Q, 则点P的极线过Q, 且与直线AC、BD平行. 特别地, 若BC⎳AD⎳y轴时, 点P的极线平行y轴, 且与x轴的交点R 也是AC、BD交点, 有|OR|⋅|OP|=|OF|2=a2.性质5:垂直设圆锥曲线Γ的一个焦点为F, 与F相应的准线为l, 若过点F的直线与圆雉曲线Γ相交于M ,N两点, 则Γ在M,N两点处的切线的交点Q在准线l上, 且FQ⊥MN.【证明】以椭圆为例证明, 双曲线与拋物线类似处理.设P x0,y0, 则P x0,y0对应的极线为MN:x0xa2+y0yb2=1, 由F(c,0)在直线MN上得cx0a2=1, 所以x0=a2c, 故Q在准线l:x=a2c上. 由P a2c,y0, 易证k MN⋅k QF=-1, 所以FQ⊥MN.性质6:等角定理如下图, A,B是椭圆Γ的一条对称轴l上的两点(不在Γ上), 若A,B关于Γ调和共轭, 过A 任作Γ的一条割线, 交Γ于P,Q两点, 则∠PBA=∠QBA.证明:因Γ关于直线l对称, 故在Γ上存在P,Q的对称点P ,Q . 若P 与Q重合, 则Q 与P 也重合, 此时P,Q关于l对称, 有∠PAB=∠QAB;若P 与Q不重合, 则Q 与P也不重合, 由于A,B关于Γ调和共轭, 故A,B为Γ上完全四点形PQ QP 的对边交点, 即Q 在P A上也在PB上, 故BP,BQ关于直线l对称, 也有∠PBA=∠QBA.【注】事实上, 性质6对于圆锥曲线都成立. 我们还可以得到下列结论:(1)直线PB与椭圆的另一交点为Q , 则Q 与Q关于l对称;(2)∠PAO=∠QAB=∠Q AB;(3)k AP+k AQ =0.典型例题类型1:判断位置关系【例1】已知点M (a ,b )在圆O :x 2+y 2=1外, 则直线ax +by =1与圆O 的位置关系是()A.相切B.相交C.相离D.不确定【答案】B .【解析】因为 ax +by =1 是圆 x 2+y 2=1 的切点弦方程, 所以直线与圆相交, 故选 B .类型2:求极线方程【例2】过椭圆x 29+y 24=1内一点M (1,2), 作直线AB 与椭圆交于点A ,B , 作直线CD 与椭圆交于点C ,D , 过A ,B 分别作椭圆的切线交于点P , 过C ,D 分别作椭圆的切线交于点Q , 求P ,Q 连线所在的直线方程.【答案】 x9+y 2=1.【解析】该题实质上就是求椭圆 x 29+y 25=1 内一点 M (1,2) 对应的极线方程,答案为 x9+y 2=1.【例3】设椭圆C :x 2a 2+y 2b2=1(a >b >0)过点M (2,1), 且左焦点为F 1(-2,1).(1)求敉圆C 的方程;(2)当过点P (4,1)的动直线l 于椭圆C 相交于两不同点A ,B 时, 在线段AB 上取点Q , 满足|AP |⋅|QB|=|AQ |⋅|PB |, 证明:点Q 总在某定直线上.【答案】 (1)x 24+y 22=1;(2) 见解析.【解析】(1)由题意得:c 2=22a 2+1b 2=1c 2=a 2-b 2 ,解得a 2=4b 2=2 ,所求椭圆方程为x24+y 22=1.(2) 解法 1: 定比点差法设点 Q 、A 、B 的坐标分别为 (x ,y ),x 1,y 1 ,x 2,y 2由题设知 |AP |,|PB |,|AQ |,|QB | 均不为零, 记 λ=|AP ||PB |=|AQ||QB |, 则 λ>0 且 λ≠1又 A ,P ,B ,Q 四点共线, 从而 AP =-λPB ,AQ=λQB 于是 4=x 1-λx 21-λ,1=y 1-λy 21-λ,x =x 1+λx 21+λ,y =y 1+λy 21+λ,从而:4x =x 21-λ2x 221-λ2⋯⋯⋯⋯(1)y =y 21-λ2y 221-λ2⋯⋯⋯.. (2)又点 A 、B 在椭圆 C 上,即:x 21+2y 21=4⋯⋯⋯⋯⋯(3)x 22+2y 22=4⋯⋯⋯⋯⋯(4)(1)+(2)×2, 并结合(3)(4)得 4x +2y =4,即点 Q (x ,y ) 总在定直线 2x +y -2=0 上.解法 2:构造同构式设点 Q (x ,y ),A x 1,y 1 ,B x 2,y 2 ,由题设知 |AP |,|PB |,|AQ |,|QB | 均不为零, 记 λ=|AP ||PB |=|AQ||QB |,又 A ,P ,B ,Q 四点共线, 可设 PA =-λAQ ,PB =λBQ(λ≠0,±1)于是 x 1=4-λx 1-λy 1=1-λy 1-λ (1), x 2=4+λx 1+λy 2=1+λy 1+λ(2)由于 A x 1,y 1 ,B x 2,y 2 在椭圆 C 上, 将(1)(2)分别代入 C 的方程 x 2+2y 2=4,整理得:x 2+2y 2-4 λ2-4(2x +y -2)λ+14=0(3)x2+2y 2-4 λ2+4(2x +y -2)λ+14=0(4)(4)-(3)得:8(2x +y -2)λ=0,∵λ≠0,∴2x +y -2=0,即点 Q (x ,y ) 总在定直线 2x +y -2=0 上.解法 3:极点极线由 |AP |⋅|QB |=|AQ |⋅|PB | 可得 AP PB =AQ QB,说明点 P ,Q 关于桞圆调和共轭, 点 Q 在点 P 对应的极线上,此极线方程为4⋅x4+1⋅y 2=1, 化简得 2x +y -2=0.故点 Q 总在直线 2x +y -2=0 上.【注】点 Q 的轨汖方程为 2x -y -2=0( 在椭圆内的部分)类型3:证明直线过定点或三点共线【例4】如图, 过直线l :5x -7y -70=0上的点P 作椭圆x 225+y 29=1的切线PM 和PN , 切点分别为M ,N , 连结MN .(1)当点P 在直线l 上运动时, 证明:直线MN 恒过定点Q ;(2)当MN ⎳l 时, 定点Q 平分线段MN .【答案】见解析.【解析】解法 1: 常规解法(1) 证明:设 P x 0,y 0 ,M x 1,y 1 ,N x 2,y 2 .则椭圆过点 M ,N 的切线方程分别为:x 1x 25+y 1y 9=1,x 2x25+y 2y 9=1.因为两切线都过点 P, 则有:x1x025+y1y09=1,x2x025+y2y09=1.这表明 M,N 均在直线 x0x25+y0y9=1 (1)上.由两点确定一条直线知, 式(1)就是直线 MN 的方程, 其中 x0,y0满足直线 l 的方程.当点 P 在直线 l 上运动时,可理解为 x0 取遍一切实数,相应的 y0 为 y0=57x0-10 .代入(1)消去 y0 得 x025x+5x0-7063y-1=0 (2)对一切 x0∈R 恒成立.变形可得 x0x25+5y63-10y9+1=0 ,对一切 x0∈R 恒成立,故有x25+5y63=010y9+1=0⇒x=2514y=-910故直线 MN 恒过定点 Q2514,-910 .(2)当 MN⎳l 时,由式(2)知 x0255-5x0-7063-7≠-1-70. 解得 x0=4375533 . 代入(2),得 MN 的方程5x-7y-53335=0 (3)将此方程与椭圆方程联立,消去 y 得 53325x2-5337x-1280681225=0 .由此可得, 此时 MN 截圆所得弦的中点横坐标恰好为点 Q2514,-910的横坐标, 即x=x1+x22=--53372×53325=2514代入(3)式可得弦中点纵坐标恰好为点 Q2514,-910的纵坐标,即y=57×2514-5337×35=1491252-5332=-910这就是说, 点 Q2514,-910平分线段 MN.解法 2:(1) 动点 P 在定直线 l 上, 则相应的切点弦过定点, 可知定点 Q 必为极点,于是只需求极点即可:由 5x-7y-70=0⇔x14-y10=1, 得到极点坐标 Q2514,-910, 即为所求定点.(2) 由椭圆内一点极线方向与以极点为中点弦的方向相同, 也即 OQ 与极线方向共轭, 即得结论 (2).【注】“极点在已知直线上,则极线过定点”. 这是一类常考的直线过定点问题.【例5】已知A,B分别为椭圆E:x2a2+y2=1(a>1)的左、右顶点, G为E的上顶点, AG⋅GB=8,P为直线x=6上的动点, PA与E的另一交点为C,PB与E的另一交点为D.(1)求E的方程;(2)证明:直线CD过定点.【答案】(1)x29+y2=1;(2) 见解析【解析】(1)易得椭圆 E 的方程为 x29+y2=1;(2)利用极点极线角度 1: 如下图, 设 CD 交 AB 于 Q,AD 交 CB 于 R, 则 QR 为 P 对应的极线,即点 Q 在点 P 对应的极线上. 极点 P(6,t) 对应的极线方程为 6x9+ty=1,即 2x3+ty=1, 极线恒过定点32,0, 故直线 CD 也过定点 32,0.角度 2: 如图, 设 CD 交 AB 于 Q(m,0),则点 P(6,t) 在点 Q(m,0) 对应的极线上,极点 Q(m,0) 对应的极线方程为 mx9+0⋅y=1, 即 x=9m, 由9m=6 得 m=32, 所以直线 CD 过定点 Q32,0.角度 3: 如图, 设直线 x=6 交 x 轴于点 H, 由极点极线的性质可知: |OQ|⋅|OH|=|OB|2即 6|OQ|=32, 所以 |OQ|=32, 故直线 CD 过定点 Q32,0.【注】本题的背景是极点极线, 上面解法从三个不同角度进行了“秒杀”,令人回味无穷. 极点极线 是高等几何中的内容, 高中数学教材中虽然没有介绍相关的定义及性质, 但是以此为背景的高考和竞赛试 题层出不穷、常考常新. 我们用其他解法求解本题时,可以用求极线对应极点的解法得到这个定点, 目标 已然心中有数, 那么就能降低运算难度,避免计算错误.类型4:证明两直线垂直【例6】已知A(-2,0),B(2,0), 点C是动点, 且直线AC和直线BC的斜率之积为-3 4.(1)求动点C的轨迹方程;(2)设直线l 与(1)中轨迹相切于点P , 与直线x =4相交于点Q , 且F (1,0), 求证:∠PFQ =90∘.【答案】 (1)x 24+y 23=1(y ≠0);(2) 证明见解析.【解析】(1)设 C (x ,y ), 则依题意得 k AC ⋅k BC =-34, 又 A (-2,0),B (2,0),所以有 y x +2⋅y x -2=-34(y ≠0),整理得 x 24+y 23=1(y ≠0), 即为所求轨迹方程.(2)解法 1:设直线 l :y =kx +m , 与 3x 2+4y 2=12 联立得3x 2+4(kx +m )2=12 ,即 3+4k 2 x 2+8km x +4m 2-12=0 ,依题意 Δ=(8km )2-43+4k 2 4m 2-12 =0, 即 3+4k 2=m 2,∴x 1+x 2=-8km 3+4k 2, 得 x 1=x 2=-4km 3+4k2,∴P -4km 3+4k 2,3m 3+4k2 , 而 3+4k 2=m 2, 得 P -4k m ,3m , 又 Q (4,4k +m ),又 F (1,0), 则 FP ⋅FQ =-4k m -1,3m ⋅(3,4k +m )=0. 知 FP⊥FQ , 即 ∠PFQ =90∘.解法 2:设 P x 0,y 0 ,则曲线 C 在点 P 处切线 PQ :x 0x 4+y 0y 3=1 , 令 x =4 ,得 Q 4,3-3x 0y 0, 又 F (1,0) , ∴FP ⋅FQ =x 0-1,y 0 ⋅3,3-3x 0y 0 =0 ,知 FP ⊥FQ , 即 ∠PFQ =90∘ . 解法 3:x =4 为椭圆的右准线, 椭圆右焦点为 F (1,0),由椭圆极点极线性质 5 可知:PF ⊥FQ , 即 ∠PFQ =90∘.【注】模型:已知椭圆 C :x 2a 2+y 2b 2=1(a >b >0) 的右焦点为 F , 直线 l 与椭圆 C 相切于 P , 且与右准线交于点 Q , 则有 PF ⊥FQ .类型5:证明向量数量积(或线段长度之积)为定值【例7】如图, 椭圆有两顶点A (-1,0),B (1,0), 过其焦点F (0,1)的直线l 与椭圆交于C 、D 两点, 并与x 轴交于点P , 直线AC 与直线BD 交于点Q .(1)当|CD |=322时, 求直线l 的方程A (-1,0);(2)当点P 异于A 、B 两点时, 求证:OP ⋅OQ为定值.【答案】 (1)y =±2x +1; (2) 定值为 1 .【解析】解法 1:设 P (t ,0), 则点 P 的极线过 Q . 易得椭圆方程 x 2+y 22=1, 则 P 的极线为 0⋅y 2+tx =1, 即 x =1t .于是点 Q 在直线 x =1t 上, 设 Q 1t ,y 0 , 则 OP ⋅OQ =(t ,0)⋅1t ,y 0 =t ⋅1t+0⋅y 0=1.解法 2:根据极点极线几何性质, 点 p 关于敉圆 x 2+y 22=1 的极线为过点 Q 且与 x 轴垂直的直线上.设该直线交 x 轴于 Q , 由 “调和点列” 的 “等比性” , 可知 OQ ⋅OP =OB 2, 从而 OP ∙OQ=1.类型6:与斜率有关的定值问题【例8】设P x 0,y 0 为桞圆x 24+y 2=1内一定点(不在坐标轴上), 过点P 的两条直线分别与椭圆交于点A ,C 和B 、D , 且AB ⎳CD .(1)证明:直线AB 的斜率为定值;(2)过点P 作AB 的平行线, 与椭圆交于E 、F 两点, 证明:点P 平分线段EF .【答案】见解析【解析】(1)因为 AB ⎳CD , 所以点 P 对应的极线 x 0x4+y 0y =1 平行于 AB ,即 AB 的斜率是 -y 04x 0(定值);(2) 直线 EF :y =-x 04y 0x -x 0 +y 0, 代入椭圆x 24+y 2=1, 得x 24+-x 04y 0x -x 0 +y 02=1x 20+4y 2016y 20⋅x 2-x 0x 20+4y 20 8y 20⋅x +x 4016y 20+x 202+y 20-1=0则x E +x F =--x 0x 20+4y 20 8y 20x 0x 20+4y 28y 20=2x 0此时点 P 是 EF 中点, 即点 P 平分线段 EF .【例9】如图, 椭圆E :x 2a 2+y 2b2=1(a >b >0的离心率为22, 直线l :y =12x 与椭圆E 相交于A 、B 两点, AB =25,C 、D 是椭圆E 上异于A 、B 的任意两点, 且直线AC 、BD 相交于点M , 直线AD 、BC 相交于点N , 连结MN .(1)求椭圆E 的方程;(2)求证:直线MN 的斜率为定值.【答案】 (1)x 26+y 23=1;(2) 见解析.【解析】 (1)x 26+y 23=1.( 过程略)(2) 设点 N 的坐标为 (m ,n ), 直线 DC 与 BA 交于点 P ,则 MP 为点 N 对应的极线, 其方程为 mx 6+ny 3=1. 结合 y =12x , 得到 P 点坐标为 6m +n ,3m +n . 所以, 点 P 对应的极线 MN 的方程为 16⋅6m +n x +13⋅3m +n x =1, 即 x +y =m +n ,所以直线 MN 的斜率为定值 -1.【注】本题需要极点、极线之间的两次转化, 通过点 P 在点 N 对应的极线上, 以及 MN 是点 P 对应的 极线, 使问题得以解决.【例10】四边形ABCD 是椭圆x 23+y 22=1的内接四边形, AB 经过左焦点F 1,AC ,BD 交于右焦点F 2, 直线AB 与直线CD 的斜率分别为k 1,k 2.(1)证明:k 1k 2为定值;(2)证明:直线CD 过定点, 并求出该定点的坐标.【答案】见解析.【解析】(1)设 A x 1,y 1 ,B x 2,y 2 ,C x 3,y 3 ,D x 4,y 4则直线 AC 的方程为 x =x 1-1y 1y +1, 代入椭圆方程 x 23+y 22=1 整理得2-x 1 y2+x 1-1 y 1y -y 21=0∵y 1⋅y 3=-y 212-x 1,∴y 3=y 1x 1-2, 从而 x 3=x 1-1y 1y 3+1=2x 1-3x 1-2,故点 C 2x 1-3x 1-2,y 1x 1-2, 同理,点 D 2x 2-3x 2-2,y 2x 2-2 . 因为三点 A 、F 1,B 共线,所以 y 1x 1+1=y 2x 2+1, 从而 x 1y 2-x 2y 1=y 1-y 2.从而k 2=y 4-y 3x 4-x 3=y 2x 2-2-y 1x 1-22x 2-3x 2-2-2x 1-3x 1-2=y 2x 1-2 -y 1x 2-2 2x 2-3 x 1-2 -2x 1-3 x 2-2=x 1y 2-x 2y 1 +2y 1-y 2x 1-x 2=3y 1-y 2 x 1-x 2=3k 1故k 1k 2=13 .(2)解法 1:由(1)知:C 2x 1-3x 1-2,y 1x 1-2,D 2x 2-3x 2-2,y 2x 2-2,设直线 CD 交 x 轴于点 M x 0,y 0 ,则x 0=x 3y 4-x 4y 3y 4-y 3=2x 1-3x 1-2⋅y 2x 2-2-2x 2-3x 2-2⋅y 1x 1-2y 2x 2-2-y 1x 1-2=2x 1-3 y 2-2x 2-3 y 1y 2x 1-2 -y 1x 2-2 =2x 1y 2-x 2y 1 +3y 1-y 2 x 1y 2-x 2y 1 +2y 1-y 2=5y 2-y 1 3y 1-y 2 =53故直线 CD 过定点 53,0.解法 2:设 AB ,DC 交于点 P , 则 P 在 F 2 对应的极线1⋅x 3+0⋅y 2=1 即 x =3 上,可设 P (3,m ),由对称性可知:直线 CD 过定点必在轴上,不妨设定点为 T (t ,0), 则 k 1=k PF 1=m 4,k 2=k PT =m3-t,由(1)知 k 1k 2=13, 得 3-t 4=13⇒t =53, 所以 T 53,0 , 故直线 CD 过定点 53,0 .类型7:等角问题【例11】设椭圆C :x 22+y 2=1的右焦点为F , 过F 的直线l 与C 交于A ,B 两点,点M 的坐标为(2,0).(1)当l 与x 轴垂直时, 求直线AM 的方程;(2)设O 为坐标原点, 证明:∠OMA =∠O MB .【答案】(1)AM 的方程为 y =-22x +2 或 y =22x -2;(2) 证明见解析.【解析】(1)由已知得 F (1,0),l 的方程为 x =1.由已知可得, 点 A 的坐标为 1,22 或 1,-22 . 所以 AM 的方程为 y =-22x +2 或 y =22x -2.(2)解法 1:设直线 l 的方程为:x =my +1,A x 1,y 1 ,B x 2,,y 2 ,k AM =y 1-0x 1-2,k BM =y 2-0x 2-2联立方程组得:x =my +1x 22+y 2=1, 消去 x 并整理得:m 2+2 y 2+2my -1=0(1)因为点 F 为椭圆的右焦点, 所以方程(1)有两个实数根分别为 y 1,y 2.由韦达定理可得:y 1+y 2=-2m 2+m 2,y 1y 2=-12+m 2因为:k AM +k BM =y 1-0x 1-2+y 2-0x 2-2=y 1my 1-1+y 2my 2-1=2my 1y 2-y 1+y 2 my 1-1 my 2-1整体代入可得:k AM +k BM =2my 1y 2-y 1+y 2 my 1-1 my 2-1 =-2m 2+m 2+2m2+m 2my 1-1 my 2-1 =0则直线 AM 的倾斜角与直线 BM 的倾斜角互补, 故 ∠OMA =∠O MB .解法 2:过点 A ,B 分别作椭圆右准线的垂线, 垂足分别为 A 1,B 1(如图所示)由椭圆的第二定义可得: e =AF AA 1=BF BB 1, 所以有: AFBF =AA 1BB 1(1),因为 AA 1⎳x 轴⎳ BB 1 ,所以 AFBF =A 1M B 1M(2) 由(1)(2)得AA 1BB 1=A 1M B 1M ,即有 AA 1A 1M=BB 1B 1M 且 ∠AA 1M =∠BB 1M , 所以 △AA 1M ∼ΔBB 1M , 即可得 ∠AMA 1=∠B MB 1,故 ∠OMA =∠O MB .【例12】如图, 已知椭圆C :x 2a 2+y 2b2=1(a >b >0)的右焦点为F , 点-1,32 在椭圆C 上, 过原点O 的直线与椭圆C 相交于M 、N 两点, 且|MF |+|NF |=4.(1)求椭圆C 的方程;(2)设P (1,0),Q (4,0), 过点Q 且斜率不为零的直线与椭圆C 相交于A 、B 两点, 证明:∠APO =∠BPQ【答案】(1)x24+y2=1;(2) 见解析.【解析】(1) 如图, 取椭圆 C 的左焦点 F , 连 MF ,NF , 由椭圆的几何性质知 |NF|=MF, 则MF+|MF|=2a=4, 得 a=2, 将点 -1,3 2代入椭圆 C 的方程得:1a2+34b2=1, 解得:b=1, 故椭圆C 的方程为:x24+y2=1.(2) 设点 A 的坐标为 x1,y1, 点 B 的坐标为 x2,y2解法 1:y1x1-4=y2x2-4⇒y21x1-42=y22x2-42⇒1-x214x1-42=1-x224x2-42⇒4-x21x2-42=4-x22x1-42⇒2x1x2x1-x2-5x21-x22+8x1-x2=0因为 x1≠x2, 所以 2x1x-5x1+x2+8=0所以k x1-4x1-1+k x2-4x2-1=k x1-4x2-1+k x2-4x1-1x1-1x2-1=k2x1x2-5x1+x2+8x1x2-x1+x2+1=0所以直线 AP 与 BP 的斜率互为相反数, 故 ∠APO=∠BPQ.解法 2:设直线 AB 的方程为 x=ty+4, 联立方程x2+4y2=4x=ty+4, 消去 x 得:t2+4y2+8ty+12=0则y1+y2=-8tt2+4y1y2=12t2+4, 所以y1y2y1+y2=-32t, 所以 2ty1y2=-3y1+y2所以k AP+k BP=y1x1-1+y2x2-1=y1ty1+3+y2ty2+3=2ty1y2+3y1+y2ty1+3ty2+3=-3y1+y2+3y1+y2ty1+3ty2+3=0所以直线 AP 与 BP 的斜率互为相反数, 故 ∠APO=∠BPQ.类型8:三斜率成等差数列引理:二次曲线Γ:Ax2+Bxy+Cy2+Dx+Ey+F=0与直线PQ交于点P,Q, 定点O在直线PQ 上, PQ 与O 点关于曲线C 的极线交于点R . 曲线C 上有两动点A ,B , 且直线AO 、BO 分别交曲线Γ于点C , D , 直线AB ,CD 分别交PQ 于点M ,N . 则M ,O ,N ,R 成调和点列.【证明】延长XO 交BC 于点E , 由定理5可知:B ,E ,C ,Y 成调和点列(完全四边形中的调和点列), 故M ,O ,N ,R 也成调和点列(调和点列在射影变换下的不变性).【例13】椭圆C :x 2a 2+y 2b2=1,P 的坐标是x 0,0 ,Q 点在P 关于椭圆的极线x =a 2x 0上. 过P 作直线交椭圆于点A ,B . 求证:直线AQ ,PQ ,BQ 的斜率成等差数列.该结论对于拋物线, 双曲线同样适用. 特别地,当Q 点在x 轴上时, 就是等角线, 此时PQ 斜率为0 , PQ 平分∠AQB .【答案】见解析.【解析】 解法 1:作出以下辅助线:作 PR ⊥x 轴于 R , 设 AB 与 CD 交于点 P , 由引理可知:M 、P 、N 、R 成调和点列,于是有:1RM +1RN =2RP所以k AQ +k cQ =k MQ +k NQ =QR RM +QR RN =2QR RP =2k PQ 即直线 AQ ,PQ ,BQ 的斜率成等差数列.解法 2:由 A 、P 、B 共线可得: k PA =k PB , 即y A x A -x 0=y B x B -x 0所以y2Ax A-x02=y2Bx B-x02即a2b2-b2x2Aa2x A-x02=a2b2-b2x2Ba2x B-x02化简可得:2x0x A x B-x20+a2x A+x B+2a2x0=0恒等变形后得到:x0a2-x0x A+x0a2-x0x B=2x0a2-x20注意到恒等变形:x0a2-x0x A-x0a2-x20=-x20x0-x Aa2-x0x Aa2-x20于是我们将 (1)式等号的右边的式子移到左边, 还可以得到一个与(1)式等价的(2)式:x0-x Aa2-x0x A+x0-x Ba2-x0x B=0则y Ax Q-x A+y Bx Q-x B=y Aa2x0-x A+y Ba2x0-x B=x0y Aa2-x0x A+x0y Ba2-x0x Bk AQ+k BQ=y Q-y Ax Q-x A+y Q-y Bx Q-x B=y Q⋅1x Q-x A+1x Q-x B-y A xQ-x A+y Bx Q-x B所以=y Q⋅x0a2-x0x A+x0a2-x0x B-k AB⋅x0⋅x0-x Aa2-x0x A+x0-x Ba2-x0x B=y Q⋅x0a2-x0x A+x0a2-x0x B=2y Q x0a2-x20=2y Qx Q-x0=2k PQ故直线 AQ,PQ,BQ 的斜率成等差数列.【例14】如图, 已知椭圆C:x2a2+y2b2=1(a>b>0), 过焦点F任作一直线交椭圆C于A,B两点, 交F相应的准线于点M,P为过F与x轴垂直的直线上的任意一点, 则直线PA,PM,PB的斜率成等差数列.【答案】见解析【解析】易知 A,B,F,M 成调和点列, 从而直线 PA,PB,PF,PM 成调和线束, 又因为 PF⊥x 轴, 故由定理 3 知 k1,k2,k3 成等差数列.【注】类似地, 可得下面结论成立:已知椭圆 C:x2a2+y2b2=1(a>b>0), 过点 E(t,0)(0<t<a) 任作一直线交椭圆 C 于 A,B 两点, 交直线 l:x=a2t 于点 M,P 为椭圆上的点且满足 PE⊥x 轴, 则直线 PA、PM、PB 的斜率成等差数列.【例15】如下图, 椭圆x 2a 2+y 2b2=1(a >b >0)的左右顶点为A 1,B 1,Q 为直线x =m 上一点, QA 1,QB 1分别于椭圆交于点A ,B , 过点P 作直线交桞圆于A ,B 两点, 直线AB 与x 轴交于点P , 与直线x =m 交于点M , 记直线QA 1,QB 1,QP 的斜率分别为k 1,k 2,k 0, 则:(1)k 1,k 0,k 2成等差数列;(2)x P xQ =a 2.【答案】见解析.【解析】由完全四边形性质可知 Q 在 P 的极线 x =m 上, 则 P ,H 调和分割 A 1B 1.而 k 1+k 2=2k 0⇔QH A 1H+QH B 1H =2×QH PH ⇔A 1H HB 1=A 1P PB 1⇔P ,H 调和分割 A 1B 1⇔|OP |⋅|OH |=OB 1 2⇔x P x Q =a 2, 于是(1)(2)成立.【注】设与直线 AB 与直线 x =m 交于点 M , 则 P ,M 调和分割 BA .【例16】椭圆x 2a 2+y 2b2=1(a >b >0)经过点M 1,32 , 离心率e =12.(1)求椭圆的方程;(2)设P 是直线x =4上任意一点, AB 是经过椭圆右焦点F 的一条弦(不经过点M ). 记直线PA ,PF ,PB 的斜率依次为k 1,k 2,k 3. 问:是否存在常数λ, 使得k 1+k 3=λk 2. 若存在, 求λ的值;若不存在, 说明理由.【答案】 (1)x 24+y 23=1; (2) 见解析【解析】(1)易知椭圆为 x 24+y 23=1.(2) 设直线 AB 方程为 x =ty +1, 点 A x 1,y 1 ,B x 2,y 2 ,由 x 24+y 23=1x =ty +1消去 x , 整理得:3t 2+4 y 2+6ty -9=0.则 y 1,y 2 为上述方程的根, 设 s =y 1+y 2=-6t 3t 2+4,p =y 1y 2=-93t 2+4 于是 s p =6t 9, 即有:t =3s 2p 设点P 的坐标为 (4,m ), 则 k 2=m 3,k 1+k 3=m -y 14-x 1+m -y 24-x 2=m -y 13-ty 1+m -y 23-ty 2=6m -(3+mt )y 1+y 2 +2ty 1y 29-3t y 1+y 2 +t 2y 1y 2=6m -3+m 3s 2p s +23s 2p p 9-33s 2p s +3s 2p2p =6m -3ms 22p 91-s 24p=2m 3=2k 2这表明存在常数 λ=2, 使得 k 1+k 3=λk 2.【注】本题中, 点 P 所在直线刚好为椭圆的右准线. 如图, 设直线 PA ,PB 与 x 轴交于 C ,D , 准线与 x 轴交于点 E . 则本题结论用图中线段可表示为 EP CE +EP DE =2⋅EP FE , 即 2EF =1EC+1ED . 这表明 (C ,D ;F ,E )为 调和点列, 由定理 3 知 k 1,k 2,k 3 成等差数列, 即 k 1+k 3=2k 2.。
§-22-完全四点形与完全四线形的调和性解析
§ 2.2 完全四点形与完全四线形的调和性
一、调和性
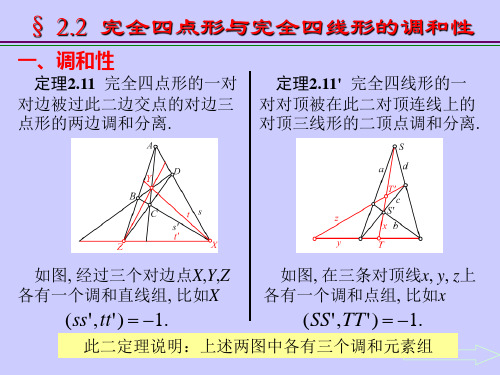
定理2.11 完全四点形的一对 对边被过此二边交点的对边三 点形的两边调和分离. 定理2.11' 完全四线形的一 对对顶被在此二对顶连线上的 对顶三线形的二顶点调和分离.
如图, 经过三个对边点X,Y,Z 各有一个调和直 Nhomakorabea组, 比如X
如图, 在三条对顶线x, y, z上 各有一个调和点组, 比如x
(3). 连P1D, P2B交于C. (4). 连AC交l于P4为所求. 证明: (略)据推论2.8(或2.9). 注1 上述实际上也是利用推论2.9作图.
注2 本例引申
§ 2.2 完全四点形与完全四线形的调和性
一、调和性 二、应用
1、第四调和元素的作图 例1 已知直线l上相异三点P1, P2, P3. 求作第四调和点P4. 注2 本例引申 1、给定三点如图,如何作图?
比如在边AB上, 有
比如经过顶点a×b, 有
( AB, PZ ) 1.
(ab, pz) 1.
此二推论说明:上述两图中又各有六个调和元素组
§ 2.2 完全四点形与完全四线形的调和性
一、调和性 二、应用
1、第四调和元素的作图 例1 已知直线l上相异三点P1, P2, P3. 求作第四调和点P4. 分析:利用推论2.8, 构造一个完全四点 形, 以l为其对边三点形的一边, P1, P2是对边 点, 使第三对对边中, 一条过P3, 则另一条与l 的交点即为P4. 解. 作法: (1). 在l外任取一点A, 连AP1, AP2. (2). 过P3作直线分别交AP1, AP2于B, D.
一般的完全四边形的性质及应用

P
由此得 到完全 四边 形 的一 系列 重要 性质 :四
图 3
个三 角形外心共 圆于密克 点 ,垂心 共线 于 垂心线 ,且垂 心 线是 以三条对 角 线为 直径 的 圆的根轴 ,点 关于 四条直 线对称 点在垂 心 线上 ;垂 心线 平行 于 点 的西姆 松 线 ,三 条 对角线 中点共 线 (牛顿线 ),且 牛顿线垂 直 于 垂心线.于是 ,又有很 多推论 ,囿于篇 幅 ,不再
证 明 设 K、 分别 为 AB、CD 的 中点 , AD与 BC交于点 E
由性质 2,知 Q为完 全 四边 形 ABCDEP 的密克点 ,△ ABQ∽ △ CDQ,K、L为相 似对 应 点 .
故 Q船 = QLC
赘 述 .
QKO+ QLO=180。
(4)若 引入 抛 物线 ,上 述垂 心 线 的另 一
图 2
献 [1].
由西姆 松定 理 ,知 P、Q、R、S四点共 线. 再 由斯 坦纳定理 ,知点 关 于 四条 直线 的对 称点 P 、Q 、R 、S 四点共 线且 过 四条 直线 交 成 的四个 三角形 的垂心.
进一 步 ,由垂心性质知
2 应用举例
例 1 如 图 3,OA=OB,OC=OD,AB与 CD交 于点 P,△ PBC的外 接 圆与△ PAD 的 外接 圆交于点 P、Q.证 明 :OQ-l-PQ.
可得 24个 圆.这 24个 圆除三 三交 于各 三角
形 的 内心 、旁心外 ,又三三交 于其他 16个点 ,
这 16个点 及各 三角 形 内心 、旁 心共 32个 点
分布在八个 圆上 ,每个 圆上有八个点.这 八个
圆组两组 互相 正 交 的共轴 圆 ,每组 含有 四
调和点列及调和线束性质的证明与应用举例

调和点列及调和线束性质的证明与应
用举例
调和点是指在多维空间中,经过多个点的调和平均得到的点。
调和线束是指在多维空间中,由若干条调和线段构成的轮廓线。
调和点和调和线束具有如下性质:
1.调和点的调和平均与原点距离相等:若有n个点
A1, A2,...,An,则它们的调和点P满足
PA1=PA2=...=PAn=OP。
2.调和线束与原点距离相等:若有n条调和线段
AB1, AB2,...,ABn,则它们的调和线束的轮廓线与原点距
离相等。
调和点和调和线束在几何学中有着广泛的应用。
例如,在三维几何中,调和点可用来求多个点的重心,调和线束可用来确定平行六面体的形状。
另外,调和点和调和线束也可用来证明一些几何定理。
例如,调和点可用来证明欧拉定理:在三维空间中,任意四点构成的四边形的重心距离原点相等。
调和线束也可用来证明若干条调和线段构成的调和线束一定与原点重合,这也是欧拉定理的一种推广。
以上就是调和点和调和线束的性质及其在几何学中的应用的简要介绍。
四点形四线形

据推论8,(AD, PG)= –1,所以P为AD的中点。
完全四点形与完全四线形的调和性
例3 设A, B, C为完全四线形的三个共线的顶点,点偶A, B与 M, C调和共轭。求证:通过A, B的对顶线的交点一定在M与C的 对顶的连线上。
如果存在一个完全四线形,以 p1, p2为一对对顶线,而p3, p4 分别通过第三双对顶之一。
完全四点形与完全四线形的调和性
2、几何证明题
例2 证明:梯形两腰延长线的交点与对角线的交点连线平 分上下底。
证明 如图, ABCD为梯形, AD//BC, E, F分别为两腰和对角线的交 点。 EF交AD, BC于P, Q。只要证明P, Q分别是AD, BC的中点。
完全四点形与完全四线形的调和性
例. 由Desargues定理证明, 对于直线l上给定的相异三点P1, P2, P3,第四调和共轭点P4惟一 存在。
证明. 设P4, P '4是两个第四调和点,作两个四线形如图,下 面证明这两个第四调和点重合。考虑三点形ACD和A'C'D', 只需证明对应边的交点P1, P2, AC×A'C'共线,为此只需证明 对应顶点的连线AA',CC',DD'共点。因为三点形ABD和 A'B'D'的对应边的交点共线,所以对应顶点的连线 AA',BB',DD'共点。同理,BB',CC',DD'也共点,所以 AA',CC',DD'共点。
完全四点形与完全四线形的调和性 调和元素组定义
完全四点形和完全四线形

4.3 完全四点形和完全四线形内容解析定义4.5 平面内无三点共线的四点及其两两连线所构成的图形,叫做完全四点形. 见图4-3,这个图形含有四个点D C B A ,,,,及六条直线AB ,BC ,CD ,DA ,BD ,AC ,每一个点称为顶点,每一条直线称为边.如图4-5所示,不过同一顶点的两边称为对边(如AD 与BC ),共有三对对边.每一对对边的交点称为对边点或对角点(如AD 与BC 的交点S ),三个对边点(SQR )构成的三角形(三点形)称为对边三角形.定义4.6 平面内无三线共点的四直线及其两两的交点#所构成的图形,叫做完全四线形.见图4-6,这个图形含有四条直线(d c b a ,,,)和六个点(A ,B ,C ,D ,E ,F ),每一条直线称为边,每一个点称为顶点.不在同一边上的两个顶点称为对顶点(如A 与D ).六个顶点分为三对,每一对对顶点的连线,称为对顶线(AD ,EC ,BF ),三条对顶线构成的三角形称为对角三角形(PQR ).完全四点形和完全四线形具有如下性质.定理4.9 完全四点形通过每一个对角点有一组调和线束,即通过这个对角点的两边和34-图B C DA 54-图B CD A S Q R 64-图P Q R a b c dAB CD E F对角三角形的两边.如图4-5,比如对角点S 的两边SA 、SB 和对角三角形SQR 的两边SR 、SQ .是一组调和线束. 定理4.10 完全四线形的每一条对角线上有一组调和点列,即这条直线上的两个顶点及对角三角形的两个点.如图4-6,比如对角线CE 上的两个顶点C 、E 和对角三角形PQR 的两个顶点P 、Q , 是一组调和点列.典型例题例1 设XYZ 是完全四点形ABCD 的对边三点形,XZ 分别交BD AC ,于M L ,,不用笛沙格定理,证明CM BL YZ ,,共点.证明如图4-7,54-图BC D AS QR64-图PQ R a b c dAB CD E F 74-图对四线形ABCD ,根据定理4.10可知,在对角线AC 边上的四点L Y C A ,,,调和共轭,即1),(-=YL AC .在四点形YBZL 中,LB 与YZ 交于N ,设MN 与YL 交于C ',由定理4.9可知,过对角点M 有一组调和线束,即MA 、C M '和MY 、ML ,于是1),(-='YL C A ,所以,点C 应与点C '重合,即CM BL YZ ,,共点.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
完全四点形和完全四线形调和性质应用例析作者:何璇摘要本文对高等几何中的完全四点(线)形的调和性质进行了归纳整理,主要研究内容是通过运用完全四点形和完全四线形调和性质解决一些几何证明、几何作图、研究二次曲线的一些性质等几何问题,来体现高等几何的一些思想观点和方法。
从而能够用现代几何学的观点处理初等几何问题,使解题更简洁,拓宽解题思路 ,提高解题能力。
关键词:完全四点(线)形;调和性质;高等几何;初等几何AbstractThe paper gives a simple summary to harmonicity of complete quadrangle (complete quadrilateral) in Higher Geometry. Its main research content is to figure out some problems including geometrical proving, geometrical drawing and researching the characters of the conics via the harmonicity of the complete quadrangle (complete quadrilateral), which incarnates some viewpoints and methods in higher geometry. Accordingly, we can deal with the problems on elementary geometry by using views of modernistic geometry, which can simply solve problems, broaden train of thought and improve the capacity to solve problems.Key words: complete quadrangle (complete quadrilateral); harmonicity; Higher Geometry; Elementary Geometry1.前言射影几何对初等几何教学的指导,不仅表现在提高数学思想与观点上,还直接表现于对初等几何图形的射影性质的研究中(参见文[9][11])。
由射影几何、仿射几何和欧氏几何三者的关系,我们知道,欧氏几何为仿射几何及射影几何的子几何,在其中可以讨论仿射的对象(仿射不变性质和仿射不变量)和射影对象(射影不变性质与射影不变量),因而可以用射影几何去指导与研究初等几何中的一些问题。
而完全四点形和完全四线形的调和性是射影几何的重要不变性,有关平面图形与二次曲线的许多重要概念和性质都与此密切相关。
它们在射影几何中占有重要地位。
不仅如此,它们在初等几何中也有很广泛的应用(参见文[8][10])。
2.完全四点(线)形概念简述完全四点形中有诸多的调和共轭线束和调和共轭点列,如图1,完全四点形ABCD 中,XYZ 为对边三点形,P 、Q 、R 、S 、T 、W 为对边三点形各边与完全四点形各组对边的交点.则调和共轭线束是以X 、Y 、Z 为中心的三组线束。
即()1,-=PY AB X ,()1,-=SX AD Y ,()1,-=PY AB Z 。
调和共轭点列在完全四点形的六条边AB 、AD 、BD 、BC 、DC 、AC 及对边三点形的三条边XY 、YZ 、XZ 上,共十二组调和共轭关系(参见文[1])。
根据完全四线形与完全四点形的对偶关系,仔细观察图1,可以发现,该图中蕴含着完全四线形abcd ,xyz 为完全四线形的对顶三线形,由对偶原则可知,在x 、y 、z 三条边上各有一组调和共轭点列:()1,-=ZT AC ,()1,-=ZW BD ,()1,-=TW XY ,以九个顶点A 、B 、C 、D 、X 、Y 、Z 、T 、W 为中心,各有一组调和共轭线束。
正因为完全四点形与完全四线形可以通过一张图形体现,故而下面的讨论可仅就完全四点形的点线进行。
利用上述性质我们可以较为简单明了地解决许多初等几何的问题,以使得初几与高几的学习能够融会贯通,并从中体现高几对初几的指导作用。
3.应用举例3.1几何作图问题3.1.1第四调和点的作法我们知道,一直线l 上的点偶21,P P 与21,Q Q 成为调和共轭的充要条件是:“1P 和2P 是一个完全四点形的对边点,1Q 和2Q 是通过第三个对边点的一对对边与l 的交点”(参见文[1])。
为此,可通过完全四点形的作图来作第四调和点。
利用完全四点形和完全四线形的调和性质在初等几何作图中的一些具体应用如下:例1、已知A 、B 、C 三点共线于l ,在直线l 上求作点C 关于A 、B 的调和共轭点,有以下几abd z yxc图1Q WS C RP Z TD A YXB种方法。
限于篇幅,只给出作法,具体作图过程及证明从略。
①利用完全四点形和完全四线形的调和性质过点C 任作一直线,在其上任取异于C 的两点Q 、S ,分别连接S 、A ;Q 、B 交于点R ,连接Q 、A ;S 、B 交于点T ,再连接A 、B ;R 、T 交于点D ,则点D 即为所求。
②利用“线段的中点与其所在直线上的无穷远点成调和共轭”过点C 任作一直线,在其上取两点1A 、1B 分别位于点C 的两侧,并且1A 、1B 到C 的距离相等。
连A 与1A 、B 与1B 相交于S 点,过点S 作直线11B A 的平行线交A 、B 、C 所在直线l 于点D ,则点D 即为所求(参见文[2])。
③利用“角的内、外角平分线关于角的两边成调和共轭”过点C 任作一条不与l 垂直的直线1l ,作线段AB 的垂直平分线与直线1l 相交于E 点,过不共线三点A 、B 、E 作一圆,交直线1l 于另一点F ,再作AFB ∠的外角平分线与A 、B 、C 所在直线l 相交于D ,则点D 即为所求。
④利用二次曲线极点、极线的作图法过A 、B 两点任作一圆,作出点C 关于此圆的极线,与A 、B 、C 所在直线l 相交于D ,则点D 即为所求。
⑤利用调和共轭的初等几何作图(的中点为点AB O OD OC OA CD AB ,1),(2⋅=⇔-=) 以AB 为直径作圆O ,过C 作AB 的垂线交圆O 于M ,过M 作圆O 切线交OC 于D ,则D 点为所求。
3.1.2 初等几何作图利用完全四点(线)形的调和性质可以使我们由纯粹几何方法得到调和共轭点列或调和共轭线束,即仅用直尺可作出已知点列上的三点的第四调和点或已知线束中三直线的第四调和直线的方法,从而实现用高等几何方法方便简洁地解决欧氏平面作图问题,对初等几何作图有重要的指导意义。
具体应用如下:图2RS P QABC例2、(1)已知线段AB 及其中点C ,P 是直线AB 外一点,求作:过P 点且平行于AB 的直线。
作法:如图2①连结AP 并延长,在其上取一点Q ;②连结BP CQ ,交于R ;③连结BQ AR ,交于S ; ④连结PS ,则直线PS 为所求作直线。
(2)已知线段AB ,且AB 平行l ,求作AB 的中点。
作法:如图2①在l 上任取两点S P ,; ②连结AS BP ,交于R ; ③连结BS AP ,交于Q ;④连结QR 交AB 于C ,则C 为所求作的点。
(3)已知SC 是ASB ∠的内角平分线,求作其外角平分线。
作法:如图3①用不过S 的任一直线截SC SB SA ,,分别于''',,C B A ; ②在SC 上任取一点R ; ③连结R A '交SB 于Q ; ④连结R B '交SA 于P ; ⑤连结PQ 交''B A 于'D ;⑥连结'SD ,它即为所求作的直线。
(4)已知SD 是ASB ∠的外角平分线,求作其内角平分线。
RC’图3S A CBD’DA’QB’P作法:如图3①用不过S 的任一直线截SD SB SA ,,分别于''',,D B A ②过'D 任作一直线交SB SA ,分别于P ,Q ; ③连结P B Q A '',交于R ;④连结SR ,它即为所求作的直线。
3.2几何证明问题 3.2.1解决中点、平行问题已知共线四点A 、B 、C 、D , 如果按此顺序的交比()1,-=CD AB , 那么就称C 、D 关于A 、B 成调和共轭, 或称A 、B 、C 、D 成调和点列。
而线段的中点就是这直线上无穷远点关于线段两端点的调和共轭点(参见文[2])。
例3、已知A 、B 、C 、D 、O 是共线五点,且OB OA OC ⋅=2,如果C 、D 两点调和分割线段AB ,则O 是CD 中点。
证明:因为C 、D 调和分割线段AB ,故有:()1,-=CD AB ,即0=⋅+⋅BC AD BD AC ,把所有线段都以O 点作原点表达,得 ()()()()0=--+--OB OC OA OD OB OD OA OC ,乘出,移项,分解因子得:()()()OD OC OB OA OD OC OB OA ++=⋅+⋅2,把OB OA OC ⋅=2代入此式得:()()()OD OC OB OA OD OC OC ++=⋅+22,整理之:()()02=--+OB OA OC OD OC (*)。
假设02=--OB OA OC ,即OB OA OC +=2,或222222224OC OB OA OB OA OB OA OC ++=⋅++=,故有()022222222=-=⋅-+=-+OB OA OB OA OB OA OC OB OA ,所以:OBOA =,A 与B 重合,此与C 、D 调和分割AB 矛盾,故02≠--OB OA OC ,从(*)式便知:0=+OD OC ,所以O 平分线段CD 。
例4 四边形ABCD 的对边AB 与CD 交于M ,AD 与BC 交于N ,直线MN 平行于四边形图4CA MNBDPABCD 的对角线BD ,求证:另一对角线AC 平分线段MN 。
(参见文[4]) 证明:如图4所示,设平行线BD 与MN 交于∞Q ,AC 与MN 交于P ,视四边形ABCD 为完全四点形(或四线形),则MN 为完全四点形ABCD 的对边三点形的一条边,易得1,-=∞)(PQ MN ,即1)(,-===∞NPMPMNP PQ MN )( 故P 为线段MN 的中点,从而对角线AC 平分线段MN 。
由此题的证明过程不难证明其逆命题成立。
逆命题:四边形ABCD 的对边AB 与CD 交于M ,AD 与BC 交于N ,对角线AC 平分线段MN ,求证:直线MN 平行于四边形ABCD 的对角线BD 。
