七年级数学之动点面积问题
初中数学动点产生的面积问题学习方法

初中数学动点产生的面积问题学习方法
函数中的动点问题是以函数为背景,充分运用方程、转化、函数以及数形结合等思想来研究解决。
1.求不规则图形或难以同时求出底和高的三角形的面积,一般的思路是割补法:
①有一边“水平”或“竖直”的多边形,作垂线分割成直角三角形或直角梯形,如图1;
②“斜”的三角形一般不易找到它的底和高,通常过顶点作铅垂线和水平线“补”成矩形,再减去各角上的直角三角形面积,如图2.
图1
图2
2.对于“斜”三角形可用“铅垂法”求面积:如图3,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=1/2ah,即三角形面积等于水平宽与铅垂高乘积的一半.
图3
3.底或高不明显,但已知边的关系,可用相似比间接求得.①如图4,同底三角形的面积比等于高的比同高三角形的面积比等于底的比;②如图5,同底等高三角形的面积相等.
图4
图5
【典型例题】
如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.。
动点产生的面积问题

运动变化题是随着图形的某一元素的运动变化,导致问题的结论改变或者保持不变的几何题,它揭示了“运动”与“静止”、“一般”与“特殊”的内在联系.解题的关键是分清几何元素运动的方向和捷径,注意在运动过程中哪些是变量,哪些不是变量,通常要根据几何元素所处的不同位置加以分类讨论,同时,综合运用勾股定理、方程和函数等知识,本节课的内容涉及三角形、特殊的四边形的面积问题.本节主要是在函数背景下求三角形或四边形的面积问题,较复杂的题目可以采取“割补”的思想构造较简单的图形进行求解.动点产生的面积问题内容分析知识结构模块一:面积计算的问题知识精讲【例1】 如图,已知直线l :22y x =-+与x 轴、y 轴分别交于点B 、C ,将直线y=x向上平移1个单位长度得到直线P A ,点Q 是直线P A 与y 轴的交点,求四边形PQOB 的面积. 【难度】★★ 【答案】 【解析】【例2】 如图,已知直线AB :2y x =+与直线OA :13y x =交于点A ,与直线OB :3y x =交于点B 两点.求△AOB 的面积. 【难度】★★ 【答案】 【解析】例题解析【例3】 如图,已知直线3y x =+的图像与x 轴、y 轴分别交于A 、B 两点,直线l 经过原点,与线段AB 交于点C ,把△AOB 的面积分为2:1两部分,求直线l 的解析式. 【难度】★★ 【答案】 【解析】【例4】 如图,已知,在矩形ABCD 中,AB =10,BC =12,四边形EFGH 的三个顶点E 、F 、H 分别在矩形ABCD 边AB 、BC 、DA 上,AE =2.(1)如图1,当四边形EFGH 为正方形时,求△GFC 的面积;(2)如图2,当四边形EFGH 为菱形,且BF =a 时,求△GFC 的面积.(用含a 的代数式表示)【难度】★★★ 【答案】 【解析】A B CDE F 图1GHABCDE F 图2GH【例5】 如图1,正方形ABCD 的边长为2,点A (0, 1)和点D 在y 轴正半轴上,点B 、C 在第一象限,一次函数y =kx +2的图像l 交AD 、CD 分别于E 、F . (1)若△DEF 与△BCF 的面积比为1∶2,求k 的值; (2)联结BE ,当BE 平分∠FBA 时,求k 的值. 【难度】★★★ 【答案】 【解析】【例6】 如图,在平面直角坐标系中,函数y =2x +12的图像分别交x 轴、y 轴于A 、B 两点,过点A 的直线交y 轴正半轴于点M ,且点M 为线段OB 的中点. (1)求直线AM 的表达式;(2)试在直线AM 上找一点P ,使得S △ABP =S △AOB ,请求出点P 的坐标; (3)若点H 为坐标平面内任意一点,是否存在点H ,使以A 、B 、M 、H 为顶点的四边形是等腰梯形?若存在,请直接写出点H 的坐标;若不存在,请说明理由. 【难度】★★★ 【答案】 【解析】【例7】 如图1,已知直角坐标平面内点A (2, 0),P 是函数y =x (x >0)图像上一点,PQ ⊥AP 交y 轴正半轴于点Q . (1)试证明:AP =PQ ;(2)设点P 的横坐标为a ,点Q 的纵坐标为b ,那么b 关于a 的函数关系式是_______;(3)当S △AOQ =23S △APQ 时,求点P 的坐标.【难度】★★★ 【答案】 【解析】本节主要研究点在运动的背景下,产生的面积与动点之间的关系,关键点是找出决定这个面积变化的几个量是怎样变化的,重点在于思维能力的培养,难度较大.模块二:与面积相关的函数解析式知识精讲【例8】 如图,矩形ABCD 中,AB =1,AD =2,M 是CD 的中点,点P 在矩形的边上沿A B C M →→→运动,试写出△APM 的面积y 与点P 经过的路程x 之间的函数关系,写出定义域,并画出函数图像. 【难度】★★ 【答案】 【解析】【例9】 如图,在梯形ABCD 中,AD //BC ,AB =CD =AD =5cm ,BC =11cm ,点P 从点D 出发沿DA 边以每秒1cm 的速度移动,点Q 从点B 出发沿BC 边以每秒2cm 的速度移动(当点P 到达点A 时,点P 与点Q 同时停止移动),假设点P 移动的时间为x (秒),四边形ABQP 的面积为y (cm 2). (1)求y 关于x 的函数解析式,并写出它的定义域;(2)在移动的过程中,求四边形ABQP 的面积与四边形QCDP 的面积相等时x 的值;(3)在移动过程中,是否存在x 使得PQ =AB ,若存在,求出所有的x 的值;若不存在,请说明理由. 【难度】★★ 【答案】 【解析】例题解析BAB CDMP【例10】已知:如图1,在线段AE的同侧作正方形ABCD和正方形BEFG(BE<AB),连结EG并延长交DC于点M,作MN⊥AB,垂足为N,MN交BD于P.设正方形ABCD的边长为1.(1)证明:△CMG≌△NBP;(2)设BE=x,四边形MGBN的面积为y,求y关于x的函数解析式,并写出定义域;(3)如果按照题设方法作出的四边形BGMP是菱形,求BE的长.【难度】★★★【答案】【解析】【例11】已知:在梯形ABCD中,AD//BC,∠B=90°,AB=BC=4,点E在边AB 上,CE=CD.(1)如图1,当∠BCD为锐角时,设AD=x,△CDE的面积为y,求y与x之间的函数解析式,并写出函数的定义域;(2)当CD=5时,求△CDE的面积.【难度】★★★【答案】【解析】AB CDEA BCDEFGPMN【例12】 如图1,四边形OABC 是矩形,点A 、C 的坐标分别为(3,0),(0,1),点D是线段BC 上的动点(与端点B 、C 不重合),过点D 作直线12y x m =-+交折线OAB 于点E .(1)当点E 恰为AB 中点时,求m 的值;(2)当点E 在线段OA 上,记△ODE 的面积为y ,求y 与m 的函数关系式并写出定义域;(3)当点E 在线段OA 上时,若矩形OABC 关于直线DE 的对称图形为四边形O 1A 1B 1C 1,试判断四边形O 1A 1B 1C 1与矩形OABC 的重叠部分的面积是否发生变化,若不变,写出该重叠部分的面积;若改变,写出重叠部分面积S 关于m 的函数关系式. 【难度】★★★ 【答案】 【解析】【例13】 如图1,在正方形ABCD 中,点E 在边AB 上(点E 与点A 、B 不重合),过点E 作FG ⊥DE ,FG 与边BC 相交于点F ,与边DA 的延长线相交于点G . (1)当E 是AB 中点时,求证AG =BF ;(2)当E 在边AB 上移动时,观察BF 、AG 、AE 之间具有怎样的数量关系?并证明你所得到的结论;(3)联结DF ,如果正方形的边长为2,设AE =x ,△DFG 的面积为y ,求y 与x 之间的函数解析式,并写出函数的定义域.【难度】★★★ 【答案】 【解析】xA BCD EFG【例14】 如图1,梯形ABCD 中,AD //BC ,∠B =90°,AD =18,BC =21.点P 从点A 出发沿AD 以每秒1个单位的速度向点D 匀速运动,点Q 从点C 沿CB 以每秒2个单位的速度向点B 匀速运动.点P 、Q 同时出发,其中一个点到达终点时两点停止运动,设运动的时间为t 秒.(1)当AB =10时,设A 、B 、Q 、P 四点构成的图形的面积为S ,求S 关于t 的函数关系式,并写出定义域;(2)设E 、F 为AB 、CD 的中点,求四边形PEQF 是平行四边形时t 的值.【难度】★★★ 【答案】【解析】【例15】 如图1,在菱形ABCD 中,∠B =45°,AB =4.左右作平行移动的正方形EFGH 的两个顶点F 、G 始终在边BC 上.当点G 到边BC 中点时,点E 恰好在边AB 上.(1)如图1,求正方形EFGH 的边长;(2)设点B 与点F 的距离为x ,在正方形EFGH 作平行移动的过程中,正方形EFGH 与菱形ABCD 重叠部分的面积为y ,求y 与x 的函数解析式,并写出它的定义域;(3)联结FH 、HC ,当△FHC 是等腰三角形时,求BF 的长. 【难度】★★★ 【答案】 【解析】ABCDE PAQ 图1备用图HAB C DEF G【例16】 如图1,在平面直角坐标系中,O 为坐标原点,四边形OABC 是矩形.A (0,4),C (5, 0),点D 是y 轴正半轴上一点,将四边形OABC 沿着过点D 的直线翻折,使得点O 落在线段AB 上的点E 处.过点E 作y 轴的平行线与x 轴交于点N .折痕与直线EN 交于点M ,联结DE 、OM . 设OD =t ,MN =s . (1)试判断四边形EDOM 的形状,并证明;(2)当点D 在线段OA 上时,求s 关于t 的函数解析式,并写出函数的定义域; (3)用含t 的代数式表示四边形EDOM 与矩形OABC 重叠部分的面积.【难度】★★★ 【答案】 【解析】【例17】 已知:如图1,梯形ABCD 中,AD //BC ,∠A =90°,∠C =45°,AB =AD =4.E 是直线AD 上一点,联结BE ,过点E 作EF ⊥BE 交直线CD 于点F .联结BF .(1)若点E 是线段AD 上一点(与点A 、D 不重合),(如图1所示) ①求证:BE =EF ;②设DE =x ,△BEF 的面积为y ,求y 关于x 的函数解析式,并写出此函数的定义域;(2)直线AD 上是否存在一点E ,使△BEF 是△ABE 面积的3倍,若存在,直接写出DE 的长,若不存在,请说明理由.【难度】★★★ 【答案】 【解析】AB DEFABCD图1备用图备用图ABCD【例18】如图,已知正方形ABCD的边长为3,菱形EFGH的三个顶点E、G、H分别在正方形的边AB、CD、DA上,AH=1,联结CF.(1)当DG=1时,求证菱形EFGH为正方形;(2)设DG=x,△FCG的面积为y,写出y关于x的函数解析式,并指出x的取值范围;(3)当DGGHE的度数.【难度】★★★【答案】【解析】A BCDEFGH【例19】已知:如图,四边形OABC的四个顶点坐标分别为O(0,0),A(8,0),B(4,4),C(0,4),直线l:y=x+m保持与四边形OABC的边交于点M、N(M 在折线AOC上,N在折线ABC上).设四边形OABC在l右下方部分的面积为S1,在l左上方部分的面积为S2,记S=S1-S2(S≥0).(1)求∠OAB的大小;(2)当M、N重合时,求l的解析式;(3)当m≤0时,线段AB上是否存在点N,使得S=0?若存在,求m的值;若不存在,请说明理由;(4)求S与m的函数关系式.【难度】★★★【答案】【解析】x【例20】 在边长为4的正方形ABCD 中,点O 是对角线AC 的中点,P 是对角线AC上一动点,过点P 作PF ⊥CD 于点F ,作PE ⊥PB 交直线CD 于点E ,设P A =x ,PCE S y =△.(1)求证:DF =EF ;(2)当点P 在线段AO 上时,求y 关于x 的函数关系式及自变量x 的取值范围;(3)点P 在运动过程中能否使△PEC 为等腰三角形?如果能,请直接写出P A 的长;如果不能,请简单说明理由. 【难度】★★★ 【答案】 【解析】【习题1】 如图,直线443y x =-+与y 轴交于点A ,与直线4455y x =+交于点B ,且直线4455y x =+与x 轴交于点C ,求△ABC 【难度】★★ 【答案】 【解析】随堂检测ABCD E F P O【习题2】已知直线2y x=-+与x轴、y轴分别交于A点和B点,另一条直线(0)y kx b k=+≠经过点C(1,0),且把△AOB分成两部分.若△AOB被分成的两部分面积比为1:5,求k和b的值.【难度】★★★【答案】【解析】【习题3】直线364y x=-+与坐标轴分别交与点A、B两点,点P、Q同时从O点出发,同时到达A点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿O B A→→运动.(1)直接写出A、B两点的坐标;(2)设点Q的运动时间为t秒,△OPQ的面积为S,求出S与t之间的函数关系;(3)当485S=时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标.【难度】★★★【答案】【解析】【习题4】 如图,已知:过点A (8,0)、B (0,y =交于点C ,平行于y 轴的直线l 从原点O 出发,以每秒1个单位长度的速度沿x 轴向右平移,到C 点时停止;l 分别交线段BC 、OC 于点D 、E ,以DE 为边向左侧作等边△DEF ,设△DEF 与△BCO 重叠部分的面积为S (平方单位),直线l 的运动时间为t (秒).(1) 写出点C 的坐标和t 的取值范围; (2) 求s 与t 的函数关系式. 【难度】★★★ 【答案】 【解析】【作业1】 如图,已知直线P A :(0)y x n n =+>与直线PB :2()y x m m n =-+>交于点P .(1)用m 、n 表示出A 、B 、P 点的坐标;(2)若点Q 是直线P A 与y 轴的交点,且四边形PQOB 的面积56,AB=2,试求点P 的坐标,并写出直线P A 与PB 的解析式. 【难度】★★ 【答案】 【解析】课后作业【作业2】 如图所示,直线y kx b =+的截距为6,该直线分别交x 轴、y 轴于E 、F ,点E 的坐标为(-4,0). (1)求直线y kx b =+的表达式;(2)若点P (x ,y )是该直线第二象限上的一个动点,P A ⊥x 轴,PB ⊥y 轴,垂足分别为点A 、B ,试求四边形OAPB 的面积S 与x 的函数关系式,并写出自变量x 的取值范围. 【难度】★★★ 【答案】 【解析】【作业3】 如图,已知:直角梯形ABCD 中,AB ∥CD ,∠A =90°,AB =6,AD =4,DC =3,点P 从点A 出发,沿ADCB 方向移动,动点Q 从点A 出发,在AB 边上移动,设点P 移动的路程为x ,点Q 移动的路程为y ,线段PQ 平分梯形ABCD 的周长. (1) 求y 关于x 的函数解析式,并写出x 和y 的取值范围;(2) 当P 不在BC 边上时,线段PQ 能否平分ABCD 的面积?若能,求出此时x 的值;若不能,说明理由. 【难度】★★★ 【答案】 【解析】ABCDP Q【作业4】如图,在平面直角坐标系中,两个函数162y x y x==-+,的图像交于点A,动点P从点O开始在线段O向点A方向以每秒1个单位的速度运动,作PQ∥x 轴交直线BC于点Q,以PQ为一边向下作正方形PAMN,设它与△ABO重叠部分的面积为S.(1)求点A的坐标;(2)试求出点P在线段OA上运动时,S与运动的时间t(秒)的关系式.【难度】★★★【答案】【解析】。
初一动点问题解题技巧和方法

初一动点问题解题技巧和方法初一动点问题解题技巧和引言初一动点问题是初中数学中的一个重要知识点,也是初中数学解题中常见的问题类型之一。
在解决初一动点问题时,我们需要运用一些特定的技巧和方法。
本文将介绍几种常见的初一动点问题解题技巧和方法。
方法一:坐标法1.首先,我们需要给问题中的物体设定坐标系。
通常可以选择平面直角坐标系或平面极坐标系。
2.接着,根据题意,确定物体的初始位置和移动规律。
3.运用坐标变换公式,计算出物体在不同时刻的坐标。
4.根据问题要求,计算或判断物体在某个特定时刻的位置和状态。
方法二:速度法1.首先,我们需要设定物体的初始速度和加速度等关键信息。
2.根据物体的初始速度和加速度,运用运动学公式计算物体在不同时刻的速度和位移。
3.利用速度-时间图像或位移-时间图像分析问题,找出物体在某个特定时刻的位置和状态。
方法三:速度图像法1.通过绘制物体的速度-时间图像,观察图像的特点。
2.根据图像的形状,判断物体的运动状态,如匀速、匀加速、等速变速等。
3.运用速度-时间图像的面积计算方法,求解问题中的相关量。
方法四:位移图像法1.通过绘制物体的位移-时间图像,观察图像的特点。
2.根据图像的形状,判断物体的运动状态,如匀速、匀变速、反向运动等。
3.运用位移-时间图像的斜率计算方法,求解问题中的相关量。
方法五:等效距离法1.根据问题中的条件,把复杂的运动形式化简为等效距离的运动。
2.运用等效距离的运动规律,计算出物体在不同时刻的位置和状态。
3.根据问题要求,计算或判断物体在某个特定时刻的位置和状态。
方法六:代数法1.根据问题中的条件,设定物体的初始位置和移动规律。
2.利用方程组或代数方程表示物体的运动状态。
3.运用代数方法解方程组或代数方程,求解问题中的相关量。
结论初一动点问题的解题方法有很多种,本文介绍了几种常见的方法,包括坐标法、速度法、速度图像法、位移图像法、等效距离法和代数法。
在解题过程中,我们可以根据具体问题的要求选择合适的方法进行计算和分析,提高解题效率。
初中数学动点问题及练习题附参考答案

初中数学动点问题及练习题附参考答案所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题. 关键:动中求静.数学思想:分类思想函数思想方程思想数形结合思想转化思想注重对几何图形运动变化能力的考查。
从变换的角度和运动变化来研究三角形、四边形、函数图像等图形,通过“对称、动点的运动”等研究手段和方法,来探索与发现图形性质及图形变化,在解题过程中渗透空间观念和合情推理。
选择基本的几何图形,让学生经历探索的过程,以能力立意,考查学生的自主探究能力,促进培养学生解决问题的能力.图形在动点的运动过程中观察图形的变化情况,需要理解图形在不同位置的情况,才能做好计算推理的过程。
在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。
二期课改后数学卷中的数学压轴性题正逐步转向数形结合、动态几何、动手操作、实验探究等方向发展.这些压轴题题型繁多、题意创新,目的是考察学生的分析问题、解决问题的能力,内容包括空间观念、应用意识、推理能力等.从数学思想的层面上讲:(1)运动观点;(2)方程思想;(3)数形结合思想;(4)分类思想;(5)转化思想等.研究历年来各区的压轴性试题,就能找到今年中考数学试题的热点的形成和命题的动向,它有利于我们教师在教学中研究对策,把握方向.只的这样,才能更好的培养学生解题素养,在素质教育的背景下更明确地体现课程标准的导向.本文拟就压轴题的题型背景和区分度测量点的存在性和区分度小题处理手法提出自己的观点.专题一:建立动点问题的函数解析式函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容.动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系.那么,我们怎样建立这种函数解析式呢?下面结合中考试题举例分析.一、应用勾股定理建立函数解析式。
初中数学动点面积最值问题

初中数学中,动点面积最值问题通常与几何相关。
下面是一个例子,希望能帮助你理解该类型的问题。
假设有一个长方形,它的一边长为a(已知),另一边长为b(未知)。
现在我们在这个长方形内部选择一个动点P,它的坐标为(x, y)。
我们要求动点P与长方形四个边界的连线所围成的面积S的最大值和最小值。
解决这个问题的方法是,我们需要找到动点P的坐标(x, y)与长方形边界的关系,并分析这个关系如何影响面积S。
具体步骤如下:
1. 画出长方形,并标出其中一个边的长度为a。
2. 假设动点P的坐标为(x, y),则另一边长b可以表示为b = a - 2x(因为P点到两个垂直边的距离都是x)。
3. 面积S可以表示为S = xy = x(a - 2x)。
4. 将面积函数S关于x进行求导,得到S' = a - 4x。
5. 令S' = 0,解方程得到x的值。
6. 判断解得的x值是否在合理范围内,例如x的取值范围是[0, a/2]。
7. 将x的值代入面积函数S,计算出对应的面积值。
最大面积和最小面积分别对应于S的极大值和极小值。
通过求导找到极值点,再进行验证即可确定最值。
需要注意的是,这只是一个简单的例子,实际问题可能更加复杂。
在解决动点面积最值问题时,你可能还需要灵活运用几何知识、代数知识和微积分等数学工具,根据具体情况进行分析和推导。
初一 简单的动点-动点问题

初一简单的动点-动点问题
1.动点问题的解决关键在于动中求静,需要灵活运用数学知识,如分类思想、数形结合思想和转化思想。
举例来说,对于数轴上给定的点,可以通过求其对应的数值来解决问题。
2.在数轴上给定两点A和B,可以通过动点P的运动来解决问题。
例如,当P为AB线段的三等分点时,可以求出P对应的数值。
另外,可以通过求P到A点和B点距离和为10的条件来解出P的数值,或者通过P、A和B点的运动速度比例来求出P的位置。
3.在直角三角形ABC中,可以通过点D在AC线段上的运动来解决问题。
例如,可以求出△ABD的面积与CD的长度之间的关系式,并通过求导数求出△ABD面积的最大值及其对应的CD长度。
另外,可以通过△ABD面积是△ABC面积的一半的条件来求出D的位置。
4.在正方形ABCD中,可以通过动点P沿着ABCD四条边的运动来解决问题。
例如,可以求出当P经过的路程为1cm
时,△APE的面积,并通过已知△APE面积求出P经过的路程x的值。
5.在长方形ABCD中,可以通过动点Q沿着ADCB四条边的运动来解决问题。
例如,可以求出AP的长度,并通过已知△APQ面积求出含x的代数式S。
另外,可以通过点M和Q同时从A出发的条件来求出它们相遇时的位置。
七年级数学之动点面积问题

1、在平面直角坐标系中,已知点A(4,0),点B(0,3),点P从点A出发,以每秒1个单位的速度在x轴上向右平移,点Q从B点出发,以每秒2个单位的速度沿直线y=3向右平移,又P、Q两点同时出发,设运动时间为t秒.(1)当t为何值时,四边形OBPQ的面积为8;(2)连接AQ,当△APQ是直角三角形时,求Q的坐标.2、如图,在下面直角坐标系中,已知A(-4,a),B(-8,0)(1)请用含a的代数式表示△ABO的面积;(2)若a满足关系式(a+4)2≤0,且以点A、B、O为顶点画平行四边形,则请你“利用平移的知识”直接写出符合条件的所有的平行四边形的第四个顶点C的坐标(3)在(2)的条件下,是否存在x轴上的点M(x,0),使△ABM的面积是△ABO的面积的2倍?若存在,求出点M的坐标;若不存在,请说明理由.(4)在(2)的条件下,请你直接写出y轴上的点N的坐标,使△AON的面积是△ABO的面积的3倍3、如图,A,B两点同时从原点O出发,点A以每秒a个单位长度沿x轴的负方向运动,点B以每秒b个单位长度沿y轴的正方向运动.(1)如图1,若|a+2b-5|+(2a-b)2=0,试分别求出1秒钟后,A,B两点的坐标;(2)如图2,延长BA至E,在∠ABO的内部作射线BF交x轴于点C,若∠EAC,∠FCA,∠ABC的平分线交于点G,过点G作BE的垂线,垂足为H,试问∠AGH,∠BGC的大小关系如何?请写出你的结论并证明;(3)如图3,过A,O两点的直线相交于点N,AB的延长线交ON于点M,若∠MAN=∠NOB,∠BAO-∠N=m°,试求∠AMO的度数.4、如图,在平面直角坐标系中,点B、C在x轴上,OB>OC,点A在y轴正半轴上,AD平分∠BAC,交x轴于点D.(1)若∠B=30°,∠C=50°,求∠DAO的度数?(2)试写出∠DAO与∠C-∠B的关系?(不必证明)(3)若点A在y轴正半轴上运动,当点A运动至点P时,请你作出△BPC及其角平分线PQ,并直接写出∠QPO与∠PBC、∠PCB三者的关系?5、如图1,在平面直角坐标系中,A、B两点同时从原点O出发,点A以每秒m个单位长度沿x轴的正方向运动,点B以每秒n个单位长度沿y轴正方向运动.(1)已知运动1秒时,B点比A点多运动1个单位;运动2秒时,B点与A点运动的路程和为6个单位,求m、n;(2)如图2,设∠OBA的邻补角的平分线、∠OAB的邻补角的平分线相交于点P,∠P的大小是否发生改变?若不变,求其值;若变化,说明理由.(3)若∠OBA的平分线与∠OAB的邻补角的平分线的反向延长线相交于点Q,∠Q的大小是否发生改变?如不发生改变,求其值;若发生改变,请说明理由.6、如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD.(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC;(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由;(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)给出下列结论:①DCP BOPCPO∠+∠∠的值不变,②DCP CPOBOP∠+∠∠的值不变其中有且只有一个是正确的,请你找出这个结论并求其值.7、如图,在平面直角坐标系中,已知三点A(0,a),B(b,0),C(b,c),其中a,b,c满足关系式|a-2|+(b-3)2=0,c=2b-a;(1)求a,b,c的值;(2)如果再第二象限内有一点P(m,1),请用含m的式子表示四边形ABOP的面积,若四边形ABOP的面积与△ABC的面积相等,请求出点P的坐标;(3)若B,A两点分别在x轴,y轴的正半轴上运动,设∠BAO的邻补角的平分线和∠ABO的邻补角的平分线相交于第一象限内一点Q,那么,点A,B在运动的过程中,∠Q的大小是否会发生变化?若不发生变化,请求出其值,若发生变化,请说明理由8、在平面直角坐标系中,D(0,-3),M(4,-3),直角三角形ABC的边与x轴分别交于O、G两点,与直线DM分别交于E、F点.(1)将直角三角形ABC如图1位置摆放,请写出∠CEF与∠AOG之间的等量关系:(2)将直角三角形ABC如图2位置摆放,N为AC上一点,∠NED+∠CEF=180°,请写出∠NEF与∠AOG 之间的等量关系,并说明理由.9、已知如图,在平面直角坐标系中有四点,坐标分别为A(-4,3)、B(4,3)、M(0,1)、Q(1,2),动点P在线段AB上,从点A出发向点B以每秒1个单位运动.连接PM、PQ并延长分别交x轴于C、D两点(如图).(1)在点P移动的过程中,若点M、C、D、Q能围成四边形,则t的取值范围是,并写出当t=2时,点C的坐标(2)在点P移动的过程中,△PMQ可能是轴对称图形吗?若能,请求出符合条件的点P的坐标;若不能,请说明理由.(3)在点P移动的过程中,求四边形MCDQ的面积S的范围10、如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a-2|+(b-3)2=0,(c-4)2≤0(1)求a、b、c的值;(2)如果在第二象限内有一点P(m,12),请用含m的式子表示四边形ABOP的面积;(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.11、如图1,在平面直角坐标系中,△AOB是直角三角形,∠AOB=90°,斜边AB与y轴交于点C.(1)若∠A=∠AOC,求证:∠B=∠BOC;(2)如图2,延长AB交x轴于点E,过O作OD⊥AB,若∠DOB=∠EOB,∠A=∠E,求∠A的度数;(3)如图3,OF平分∠AOM,∠BCO的平分线交FO的延长线于点P,∠A=40°,当△ABO绕O点旋转时(斜边AB与y轴正半轴始终相交于点C),问∠P的度数是否发生改变?若不变,求其度数;若改变,请说明理由.12、在平面直角坐标系中,横坐标、纵坐标都为整数的点叫做整点.设坐标轴的单位长度为1cm,整点P从原点O出发,速度为1cm/s,且整点P只做向右或向上运动,则运动1s后它可以到达(0,1)、(1,0)两个整点;它运动2s后可以到达(2,0)、(1,1)、(0,2)三个整点;运动3s后它可以到达(3,0)、(2,1)、(1,2)、(0,3)四个整点;…请探索并回答下面问题:(1)当整点P从点O出发4s后可以到达的整点共有个(2)在直角坐标系中描出:整点P从点O出发8s后所能到达的整点,并观察这些整点,说出它们在位置上有什么特点?(3)当整点P从点O出发 s后可到达整点(13,5)的位置.12、如图,△OAB的三个顶点坐标分别为O(0,0),A(5,O)B(2,4).(1)求△ABO的面积,(2)若B(2,4),O(0,0)不变,M点在x轴上,M点在什么位置时,△OBM的面积是△OAB面积的2倍,并说明理由.13、如图,在平面直角坐标系中,A,B,C三点的坐标分别为(0,1),(3,0),(2,2)(1)求△ABC的面积;(2)如果在第二象限内有一点P(a,2),试用含a的式子表示四边形ABOP的面积;(3)在(2)的条件下是否存在点P,使得四边形ABOP的面积与△ABC的面积相等?若存在,请求出点P 的坐标;若不存在,请说明理由14、已知点A(a,0)、B(b,0),且(a+4)2+|b-2|=0.(1)求a,b的值;(2)在y轴上是否存在点C,使得△ABC的面积是12?若存在,求出点C的坐标;若不存在,请说明理由;(3)点P是y轴正半轴上一点,且到x轴的距离为3,若点P沿x轴负半轴以每秒1个长度单位平行移动至Q,当运动的时间t为多少秒时,四边形ABPQ的面积S为15个平方单位?写出此时Q点的坐标.15、如图建立平面直角坐标系,长方形OABC中,A(8,0),点C(0,10),点P从原点出发,以每秒1个单(2)在移动过程中,当点P 到x 轴距离为4个单位长度时,则点P 运动的时间为 秒.(3)若点P 出发11秒时,点Q 以每秒2个单位长度的速度也沿着O-C-B-A-O 的路线运动到点O 停止,求t 为何值时点P 、Q 在运动路线上相距的路程为5个单位长度?15、 如图,长方形OABC 中,O 为平面直角坐标系的原点,A ,C 两点的坐标分别为(3,0),(0,5),点B 在第一象限内.(1)如图,请直接写出点B 的坐(2)若过点C 的直线CD 交长方形OABC 的边于点D ,且把长方形OABC 的周长分为3:1两部分,求点D 的坐标.16、如图1,点A (a ,6)在第一象限,点B (0,b )在y 轴负半轴上,且a ,b 满足:(240a b −++=(1)求△AOB 的面积.(2)若线段AB 与x 轴相交于点C ,在点C 的右侧,x 轴的上是否存在点D ,使S △ACD =S △BOC ?若存在,求出D 点坐标;若不存在,请说明理由.(3)如图2,若∠AOx 轴=60°,射线OA 绕O 点以每秒4°的速度顺时针旋转到OA ′,射线OB 绕B 点以每秒10°的速度顺时针旋转到O ′B ,当OB 转动一周时两者都停止运动.若两射线同时开始运动,在旋转过程中,经过多长时间,OA ′∥O ′B ?17、在直角坐标系中,A (-4,0),B (2,0),点C 在y 轴正半轴上,且S △ABC =18. (1)求点C 的坐标;(2)是否存在位于坐标轴上的点P ,S △APC =12S △PBC ?若存在,请求出P 点坐标;若不存在,说明理由.18、在平面直角坐标系中,A(-1,0),B(0,2),点C在x轴上.(1)如图(1),若△ABC的面积为3,则点C的坐标为(2)如图(2),过点B点作y轴的垂线BM,点E是射线BM上的一动点,∠AOE的平分线交直线BM于F,OG⊥OF且交直线BM于G,当点E在射线BM上滑动时,BEOBOF∠∠的值是否变化?若不变,请求出其值;若变化,请说明理由.19、在直角坐标系中,设一质点M自P0(1,0)处向上运动1个单位至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去,设Pn(x n,y n),n=1,2,3,….(1)依次写出x1、x2、x3、x4、x5、x6的值;(2)计算x1+x2+…+x8的值;(3)计算x1+x2+…+x2003+x2004的值.20、如图:一个粒子在第一象限内及x轴,y轴上运动,在第一分钟内,它从原点运动到(1,0),第二分钟从(1,0)运动到(1,1),而后它接着按图中箭头所示在与x轴,y轴平行的方向来回运动,且每分钟移动1个长度单位.(1)当粒子所在位置分别是(1,1),(2,2),(3,3),(4,4)时,所经过的时间分别是多少?(2)在第2004分钟后,这个粒子所在的位置的坐标是多少?21、问题:如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系?(1)小明画出如图的图形,并写出问题:如图,点P在∠AOB的内部,过点P作PE⊥OA,PF⊥OB,垂足分别为E,F,求∠P的度数.请你帮助小明完成解题过程.(2)小刚说,这道题应该还有一种情况:点P在∠AOB的外部.他说的对吗?22、如图,长方形ABCD在平面直角坐标系中,点A(1,8),B(1,6),C(7,6).(1)请直接写出D点的坐标(2)连接线段OB、OD、BD,请直接求出的面积(3)若长方形ABCD以每秒1个单位的速度向下运动,设运动的时间为t秒,问是否存在某一时刻,△OBD的面积与长方形ABCD的面积相等?若存在,请求出t的值;若不存在,请说明理由.23、在△ABC中,∠A=∠C,点E在BC边上,过点E作射线EF∥AB交AC于点F,EM交AC于点M,点N 在射线EF上,且∠EMN=∠ENM,设∠ABC=α,∠MEN=β.(1)如图1,若点M在线段AF上,α=60°,β=30°,求∠FMN的度数;(2)若点M在AC边上(不与点A、C、F重合),α、β为任意角度,探究∠FMN与α、β的数量关系,请在图2中画出图形,并说明理由.24、如图,在△A B C中,AB=AC,BD、CE分别是两腰上的高,且BD、CE相交于O.(1)请你写出三类不同的正确的结论;(2)设∠CBD=α,∠A=β,试找出α与β之间的一种关系等式,并给予适当的说明(友情提示:∠ABC=∠ACB).25、.已知,在四边形ABCD中.∠A=∠C=90゜.(1)求证:∠ABC+∠ADC=180゜;(2)如图1,若DE平分∠ADC,BF平分∠ABC外角,写出DE与BF的位置关系,并证明;(3)如图2,若BF、DE分别平分∠ABC、∠ADC的外角,写出BF与DE的位置关系,并证明.26、如图,四边形ABCD中,AB∥CD,P为BC上一点,设∠CDP=α,∠CPD=β,当点P在BC上移动时,猜想α,β与∠B的关系,并说明理由.27、如图,锐角△ABC中,高BE、CF交于点H.(1)若∠BAC=70°,求∠BHC的度数;(2)直接给出四条线段AF、HE、AC、CH之间的数量关系;(3)若AD平分∠BAC交BC于D,AD、CF交于点K,HG平分∠BHC交BC于G.求证:HG∥AD.28、1)如图1,AC平分∠DAB,∠1=∠2,试说明AB与CD的位置关系,并予以证明;(2)如图2,在(1)的条件下,AB的下方两点E,F满足∠EBF=2∠ABF,CF平分∠DCE,若∠F的2倍与∠E 的补角的和为190°,求∠ABE的度数;(3)如图3,在前面的条件下,若P是BE上一点,G是CD上任一点,PQ平分∠BPG,PQ∥GN,GM平分∠DGP,下列结论:①∠DGP-∠MGN的值不变;②∠MGN的度数不变.可以证明,只有一个是正确的,请你作出正确的选择并求值.29、如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°(1)求证:AB∥CD;(2)如图2,由三角形内角和可知∠E=90°,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE 与∠MCD否存在确定的数量关系?并证明;(3)如图3,P为线段AC上一定点,点Q为直线CD上一动点,①当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?猜想结论并说明理由.②当点Q在射线CD的反向延长线上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?猜想结论,不需说明理由.30、如图,直线AB∥C D.(1)在图1中,∠B M E、∠E,∠EN D的数量关系为:;(不需证明)在图2中,∠B M F、∠F,∠FN D的数量关系为:(不需证明)(2)如图3,NE平分∠FN D,MB平分∠FM E,且2∠E与∠F互补,求∠FM E的大小.(3)如图4中,∠B M E=60°,EF平分∠M EN,NP平分∠EN D,EQ∥N P,则∠FEQ的大小是否发生变化?若变化,说明理由;若不变化,求∠FEQ的度数.31、如图,在平面直角坐标系xOy中,A,B,C是坐标轴上的定点,平移线段AB得到线段CD,使点A与点C 对应,点B与点D对应.(1)画出线段CD,并写出画法;(2)点P是x轴上的动点(不与点B,C重合),设∠PAC=α,∠PBD=β,∠APB=θ.①当点P在线段BC上时,求证:θ=α+β;②当点P在线段CB(BC)的延长线上时,①中的结论是否成立?并说明理由32、将两个大小不同的含30°角的三角板的直角顶点O重合在一起,保持△COD不动,将△AOB绕点O旋转,设射线AB与射线DC交于点F.(1)如图①,若∠AOD=120°,①AB与OD的位置关系②∠AFC的度数=(2)如图②当∠AOD=130°,求∠AFC的度数.(3)由上述结果,写出∠AOD和∠AFC的关系(4)如图③,作∠AFC、∠AOD的角平分线交于点P,求∠P的度数.33、(1)如图①,∠BAD的平分线AE与∠BCD的平分线CE交于点E,AB∥CD,∠ADC=40°,∠ABC=30°,求∠AEC的大小;(2)如图②,∠BAD的平分线AE与∠BCD的平分线CE交于点E,∠ADC=m°,∠ABC=n°,求∠AEC的大小;(3)如图③,∠BAD的平分线AE与∠BCD的平分线CE交于点E,则∠AEC与∠ADC、∠ABC之间是否仍存在某种等量关系?若存在,请写出你得结论,并给出证明;若不存在,请说明理由.34、已知:如图(1)所示,D是∠ABC的角平分线和∠ACB的角平分线的交点,过点D作EF∥BC,交AB于E,交AC于F.(1)请你确定EF、BE、CF三者之间的关系,并加以证明.(2)如图(2)所示,当点D为∠ABC的外角的角平分线和∠ACB的外角的角平分线的交点时,EF、BE、CF 三条线段还满足上面的关系吗?若满足,直接写出关系式;若不满足,请写出新的关系式并加以证明.(3)如图(3)所示,当点D为∠ABC的角平分线和∠ACB外角平分线的交点时,EF、BE、CF三条线段还满足上面的关系吗?若满足,直接写出关系式;若不满足,请写出新的关系式并加以证明.35、如图1,在平面直角坐标系中,点A、B的坐标分别为(-1,0)、(3,0),现将线段AB向上平移2个单位,再向右平移1个单位,得到线段CD,连接AC、BD.(1)求点C、D的坐标及四边形ABDC的面积S四边形ABDC;(2)如图2,在y轴上是否存在一点P,连接PA、PB,使S△PA B=S四边形ABDC,若存在这样的一点,求出点P的坐标;若不存在,试说明理由.(3)若点Q在线段CD上移动(不包括C、D两点),QO与线段CD、AB所成的角∠2与∠1如图3所示,给出下列两个结论:①∠2+∠1的值不变②12∠∠的值不变,其中只有一个结论是正确的,请你找出这个结论36、将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):(1)①若∠DCE=45°,则∠ACB的度数为;②若∠ACB=140°,求∠DCE的度数;(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.。
2和因动点产生的面积问题

由动点形生成的面积问题面积是平面几何中一个重要的概念,关联着平面图形中的重要元素边与角,由动点而生成的面积问题,是抛物线与直线形结合的觉形式,解决这类问题常用到以下与面积相关的知识(1)图形的割补 (2)等积变形 (3)等比转化1:将直角边长为6的等腰Rt △AOC 放在如图所示的平面直角坐标系中,点O 为坐标原点,点C 、A 分别在x 、y 轴的正半轴上,一条抛物线经过点A 、C 及点B (–3,0).(1)求该抛物线的解析式;(2)若点P 是线段BC 上一动点,过点P 作AB 的平行线交AC 于点E ,连接AP ,当△APE 的面积最大时,求点P 的坐标;(3)在第一象限内的该抛物线上是否存在点G ,使△AGC 的面积与(2)中△APE的最大面积相等?若存在,请求出点G 的坐标;若不存在,请说明理由2 如图,已知二次函数图像的顶点坐标为(2,0),直线1+=x y 与二次函数的图像交于A 、B 两点,其中点A在y 轴上。
(1)二次函数的解析式为y= ; (2)证明点)12,(--m m 不在(1)中所求的二次函数的图像上;(3)若C 为线段AB 的中点,过C 点作x CE ⊥轴于E 点,CE 与二次函数的图像交于D 点。
①y 轴上存在点K ,使以K 、A 、D 、C 为顶点的四边形是平行四边形,则K 点的坐标是 ; ②二次函数的图像上是否存在点P ,使得ABD POE S S ∆∆=2?若存在,求出P 点坐标;若不存在,请说明理由。
3、如图,在直角坐标平面内,O 为坐标原点,A 点的坐标为(1,0),B 点在x 轴上且在点A 的右侧,AB =OA ,过点A 和B 作x 轴的垂线分别交二次函数y =x 2的图象于点C 和D ,直线OC 交BD 于M ,直线CD 交y 轴于点H 。
记C 、D 的横坐标分别为x C ,x D ,点H 的纵坐标y H 。
(1)证明:①S △CMD ∶S 梯形ABMC =2∶3 ②x C ·x D =-y H(2)若将上述A 点坐标(1,0)改为A 点坐标(t ,0),t >0,其他条件不变,结论S △CMD :S 梯形ABMC =2∶3是否仍成立?请说明理由。
初中数学动点问题大全

初中数学动点问题大全动点问题一直是中考热点题型,近几年考察探究运动中的特殊性:等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数值、线段或面积的最值问题等,下面就此问题的常见题型作简单介绍。
题型一动点形成的面积问题1.面积公式:三角形面积用12S ah =来表示,利用未知数的代数式来表示底和高。
2.面积比等于相似比的平方:面积无法用底和高表示时,利用相似三角形的面积比等于相似比的平方来求解,只需要知道相似比和另一个三角形面积即可表示。
3.相似三角形:当面积公式和面积比等于相似比的平方不能有效解题时,利用相似三角形的比例关系求解。
角度1:利用公式法解决动点面积问题例题1:在平面直角坐标系xOy 中,抛物线2y x bx c =-++经过点30A (,)和23B (,).过点A 的直线与y 轴的负半轴相交于点C ,且1tan 3CAO ∠=.(1)求这条抛物线的表达式及对称轴;(2)连接AB 、BC ,求ABC ∠的正切值;(3)若点D 在x 轴下方的对称轴上,当ABC ADC S S ∆∆=时,求点D 的坐标.变式1:如图,在平面直角坐标系xOy 中,已知点A 的坐标为(,3)a (其中4a >),射线O 与反比例函数12y x =的图像交于点P ,点B 、C 分别在函数12y x=的图像上,且//AB x 轴,//AC y 轴.(1)当点P 横坐标为6,求直线AO 的表达式;(2)联结BO ,当AB BO =时,求点A 坐标;(3)联结BP 、CP ,试猜想:ABP ACP S S ∆∆的值是否随a 的变化而变化?如果不变,求出ABP ACP S S ∆∆的值;如果变化,请说明理由.O x y (备用图)O xy解析:(1)∵反比例函数12y x=的图像经过横坐标为6的点P ,∴点P 的坐标为(6,2).设直线AO 的表达式为y kx =(0k ≠).将点P (6,2)代入y kx =,解得13k =.∴所求反比例函数的解析式为13y x =.(2)∵AB //x 轴,∴点B 纵坐标为3,将3y =代入12y x=,得4x =.∴B 坐标为(4,3).∵AB =BO ,∴224(40)(30)a -=-+-9a =.∴点A 坐标为(9,3).(3)不变.延长AB 交y 轴于点D ,延长AC 交x 轴于点E ,∴32ADO AEO S S a ∆∆==.∵点C 坐标为(a ,12a ).∴6CEO S ∆=,同理6BDO S ∆=,∴ADO BDO AEO CEO S S S S ∆∆∆∆-=-,即ABO ACO S S ∆∆=.∵△ABP 与△ABO 同高,∴ABP ABO S AP S AO ∆∆=.同理ACP ACO S AP S AO ∆∆=.∴1ABP ACP S S ∆∆=.即当a 变化时,ABP ACPS S ∆∆的值不变,且恒为1变式2:如图,在直角坐标系中,一条抛物线与x 轴交于A 、B 两点,与y 轴交于C 点,其中(3,0)B ,(0,4)C ,点A 在x 轴的负半轴上,4OC OA =;(1)求这条抛物线的解析式,并求出它的顶点坐标;(2)联结AC 、BC ,点P 是x 轴正半轴上一个动点,过点P 作//PM BC 交射线AC 于点M ,联结CP ,若CPM ∆的面积为2,则请求出点P 的坐标;解析:(1)设这条抛物线的解析式为2(0)y ax bx c a =++≠它的顶点坐标为16(1,)3(2)过点P 作PH AC ⊥,垂足为H .∵P 点在x 轴的正半轴上,∴设0P x (,).∵A )0,1(-,∴1PA x =+.∵在Rt AOC ∆中,222OA OC AC +=;又∵14OA OC ==,∴17AC =90sin 117PH PH PHA CAO AP x ∠=︒∴∠===+ 17PH =//BP CM PM BC AB AC ∴= ;300B P x (,),(,)1点P 在点B 的左侧时,3BP x =-,∴3417x -=17(3)4x CM -=∵2PCM S =△∴122CM PH ⋅⋅=,∴17(3)12217x -=解得110x .P =∴(,)2点P 在点B 的右侧时,3BP x =-,∴3417x -=17(3)x CM -=∵2PCM S =△∴122CM PH ⋅⋅=,∴17(3)122417x -=解得11x =+,21x =-(不合题意,舍去)∴P(1+0).综上所述,P 的坐标为(1,0)或(1+0)角度2:利用面积比等于相似比的平方解决动点面积问题例题2:如图,已知在梯形ABCD 中,//AD BC ,5AB DC ==,4AD =.M 、N 分别是边AD 、BC 上的任意一点,联结AN 、DN .点E 、F 分别在线段AN 、DN 上,且//ME DN ,//MF AN ,联结EF .(1)如图1,如果//EF BC ,求EF 的长;(2)如果四边形MENF 的面积是ADN ∆的面积的38,求AM 的长;解析:(1)∵AD //BC ,EF //BC ,∴EF //A D .又∵ME //DN ,∴四边形EF DM 是平行四边形.∴EF =DM .同理可证,EF =AM .∴AM =DM .∵AD =4,∴122EF AM AD ===.(2)∵38ADN MENF S S ∆=四边形,∴58AME DMF ADN S S S ∆∆∆+=.即得58AME DMF ADN ADN S S S S ∆∆∆∆+=.∵ME //DN ,∴△AME ∽△AN D .∴22AME ADN S AM S AD∆∆=.同理可证,△DM F ∽△DN A .即得22DMF ADN S DM S AD ∆∆=.设AM =x ,则4DM AD AM x =-=-.∴22(4)516168x x -+=.即得2430x x -+=.解得11x =,23x =.∴AM 的长为1或3.A B CD M N EF (图1)AB C D M N E F变式3:已知直线1l 、2l ,12//l l ,点A 是1l 上的点,B 、C 是2l 上的点,AC BC ⊥,60ABC ∠=︒,4AB =,O 是AB 的中点,D 是CB 延长线上的点,将DOC ∆沿直线CO 翻折,点D 与'D 重合.(1)如图1,当点'D 落在直线1l 上时,求DB 的长;(2)延长DO 交1l 于点E ,直线'OD 分别交1l 、2l 于点M 、N .①如图2,当点E 在线段AM 上时,设x AE =,y DN =,求y 关于x 的函数解析式及其定义域;②若DON ∆的面积为323时,求AE 的长.解析:变式4:如图1,在梯形ABCD 中,//AD BC ,对角线BC AC ⊥,4AD =cm ,︒=∠45D ,3=BC cm .(1)求B ∠cos 的值;(2)点E 为BC 延长线上的动点,点F 在线段CD 上(点F 与点C 不重合),且满足ADE AFC ∠=∠,如图2,设x BE =,y DF =,求y 关于x 的函数解析式,并写出函数的定义域;(3)点E 为射线BC 上的动点,点F 在射线CD 上,仍然满足ADE AFC ∠=∠,当AFD ∆的面积为2cm 2时,求BE 的长.解析:(1)∵//AD BC ,∴ACB DAC ∠=∠.∵AC BC ⊥,∴90ACB ∠=︒.∴90DAC ∠=︒.∵45D ∠=︒,∴45ACD ∠=︒.∴AD AC =.∵4AD =,∴4AC =.∵3=BC ,∴5AB ==.∴3cos 5BC B AB ∠==.(2)∵//AD BC ,∴ADF DCE ∠=∠.∵AFC FDA FAD ∠=∠+∠,ADE FDA EDC ∠=∠+∠,又AFC ADE ∠=∠,∴FAD EDC ∠=∠.∴ADF DCE ∆~∆.∴AD DF DC CE =.在Rt ADC ∆中,222AC AD DC +=,又4==AC AD ,∴24=DC .∵x BE =,∴3-=x CE .y DF =,∴3244-=x y .22322-=x y .定义域为113<<x .(3)当点E 在BC 的延长线上,由(2)可得:ADF DCE ∆~∆,∴2(DC AD S S DCE ADF =∆∆.∵2AFD S ∆=,4=AD ,24=DC ,∴4=∆DCE S .∵AC CE S DCE ⨯⨯=∆21,∴44)3(21=⨯-⨯BE ,∴5BE =.当点E 在线段BC 上,同理可得:44)3(21=⨯-⨯BE .∴1BE =.所以BE 的长为5或1.角度3:利用锐角三角比法解决动点面积问题例题3:已知在平面直角坐标系xoy (如图)中,抛物线212y x bx c =++经过点(4,0)A 、点(0,4)C -,点B 与点A 关于这条抛物线的对称轴对称;(1)用配方法求这条抛物线的顶点坐标;(2)联结AC 、BC ,求ACB ∠的正弦值;(3)点P 是这条抛物线上的一个动点,设点P 的横坐标为(0)m m >,过点P 作y 轴的垂线PQ ,垂足为Q ,如果QPO BCO ∠=∠,求m 的值;解析:变式5:已知在平面直角坐标系xoy 中,抛物线2(0)y ax bx c a =++>与x 轴相交于(1,0),(3,0)A B -两点,对称轴l 与x 轴相交于点C ,顶点为点D ,且ADC ∠的正切值为12.(1)求顶点D 的坐标;(2)求抛物线的表达式;(3)F 点是抛物线上的一点,且位于第一象限,联结AF ,若FAC ADC ∠=∠,求F 点的坐标.解析:(1)∵抛物线与x 轴相交于()1,0A -,()3,0B 两点,∴对称轴l :直线1x =,2AC =∵90ACD ∠=︒,1tan 2ADC ∠=,∴4CD =,∵0a >,∴()1,4D -(2)设()214y a x =--将1,0x y =-=代入上式,得,1a =所以,这条抛物线的表达为223y x x =--(3)过点F 作FH x ⊥轴,垂足为点H设()2,23F x x x --,∵FAC ADC ∠=∠,∴tan tan FAC ADC ∠=∠,∵1tan 2ADC ∠=,∴1tan 2FH FAC AH ∠==∵223FH x x =--,1AH x =+,∴223112x x x --=+解得172x =,21x =-(舍),∴79,24F ⎛⎫ ⎪⎝⎭巩固1:如图,在直角坐标系xOy 中,抛物线c ax ax y +-=22与x 轴的正半轴相交于点A 、与y 轴的正半轴相交于点B ,它的对称轴与x 轴相交于点C ,且OBC OAB ∠=∠,3AC =.(1)求此抛物线的表达式;(2)如果点D 在此抛物线上,DF OA ⊥,垂足为F ,DF 与线段AB 相交于点G ,且2:3:=∆∆AFG ADG S S ,求点D 的坐标.解析:(1)∵抛物线c ax ax y +-=22的对称轴为直线12=--=a a x ,∴OC =1,OA =OC +AC =4,∴点A (4,0).∵∠OBC =∠OAB ,∴tan ∠OAB =tan ∠OBC ,∴OBOC OA OB =,∴OB OB 14=,∴OB =2,∴点B (0,2),∴⎩⎨⎧+-==,8160,2c a a c ∴⎪⎩⎪⎨⎧=-=.2,41c a ∴此抛物线的表达式为221412++-=x x y .(2)由2:3:=∆∆AFG ADG S S 得DG :FG =3:2,DF :FG =5:2,设m OF =,得m AF -=4,221412++-=m m DF ,由FG //OB ,得OA AF OB FG =,∴24m FG -=,∴2:524:)22141(2=-++-m m m ,∴01272=+-m m ,∴4,321==m m (不符合题意,舍去),∴点D 的坐标是(3,45)巩固2:如图,已知ABC ∆与BDE ∆都是等边三角形,点D 在边AC 上(不与A 、C 重合),DE 与AB 相交于点F .(1)求证:BCD DAF ∆∆∽;(2)若1BC =,设CD x =,AF y =;①求y 关于x 的函数解析式及定义域;②当x 为何值时,79BEF BCD S S ∆∆=?(1)证明:∵ABC ∆与BDE ∆都是等边三角形,∴60A C BDE ∠=∠=∠=︒A C BO yx∵ADF BDE C DBC ∠+∠=∠+∠,∴ADF DBC ∠=∠,∴BCD ∆∽DAF∆(2)∵BCD ∆∽DAF ∆,∴BC CD AD AF=∵1BC =,设CD x =,AF y =,∴11x x y=-,∴()201y x x x =-<<(3)解法一:∵ABC ∆与BDE ∆都是等边三角形,∴60E C ∠=∠=︒,60EBD CBA ∠=∠=︒,∴EBF CBD∠=∠∴EBF ∆∽CBD ∆,∴BE BF BC BD=,∵BE BD =,1BC =,∴2BE BF =∵EBF ∆∽CBD ∆,79BEF BCD S S ∆∆=,∴2279BEF BCD S BE S BC ∆∆==,∴279BE BF ==,∴29AF =∴229x x -=,解得1221,33x x ==,∴当13x =或23时,79BEF BCD S S ∆∆=解法二:∵△ABC 与BDE ∆都是等边三角形,∴60E C ∠=∠=︒,60EBD CBA ∠=∠=︒,∴EBF CBD∠=∠∴EBF ∆∽CBD ∆,∵79BEF BCD S S ∆∆=,∴2279BEF BCDS BE S BC ∆∆==∵1BC =,BE BD =,∴279BD =过点B 作BH AC ⊥于点H ,∵60C ∠=︒,∴BH =16DH =,12CH =当点D 在线段CH 上时,111263CD CH DH =-=-=当点D 在线段CH 的延长线上时,112263CD CH DH =+=+=综上所述,当13x =或23时,79BEF BCD S S ∆∆=.巩固3:在矩形ABCD 中,4AB =,6AD =,点P 是射线DA 上一动点,将三角板直角顶点重合于点P ,三角板两直角边中的一边始终经过点C ,另一直角边交射线BA 于点E .(1)判断EAP ∆与PDC ∆一定相似吗?请证明你的结论;(2)设PD x =,AE y =,求y 与x 的函数关系式,并写出它的定义域;(3)是否存在这样的点P ,是EAP ∆周长等于PDC ∆周长的2倍?若存在,请求出PD 的长度;若不存在,请简要说明理由.解析:(1)△EAP ∽△PDC①当P 在AD 边上时,如图(1):∵矩形ABCD ,==90D A ∠∠ ,∴1+2=90∠∠据题意=90CPE ∠ ∴3+2=90∠∠ ,∴1=3∠∠,∴△EAP ∽△PDC②当P 在AD 边上时,如图(2):同理可得△EAP ∽△PDC(2)若点P 在边AD 上,据题意:PD x =6PA x =-4DC =AE y =又∵△EAP ∽△PDC ,∴AE PA PD DC =,∴64y x x -=,∴22613442x x y x x -==-+()06x <<若点P 在边DA 延长线上时,据题意PD x =,则6PA x =-,4DC =,AE y =,∵△EAP ∽△PDC ,∴AE PA PD DC =,∴64y x x -=,∴()2664x x y x -=>(3)假如存在这样的点P ,使△EAP 周长等于PDC ∆的2倍①若点P 在边AD 上∵△EAP ∽△PDC ∴():6:4EAP PDC C C x =- ,∴()6:42x -=,∴2x =-不合题意舍去;②若点P 在边DA 延长线上,同理得()6:42x -=,∴14x =综上所述:存在这样的点P 满足题意,此时14PD =巩固4:如图,已知抛物线2y ax bx c =++经过点(0,4)A -,点(2,0)B -,点(4,0)C .(1)求这个抛物线的解析式,并写出顶点坐标;(2)已知点M 在y 轴上,OMB OAB ACB ∠+∠=∠,求点M 的坐标.解析:(1)∵抛物线2y ax bx c =++经过点(0,4)A -,点(2,0)B -,点(4,0)C ∴44201640c a b c a b c =-⎧⎪-+=⎨⎪++=⎩解得方程组的解为1214a b c ⎧=⎪⎪=-⎨⎪=-⎪⎩∴这个抛物线的解析式为:2142y x x =--顶点为9(1,)2-(2)如图:取OA 的中点,记为点N ∵OA =OC =4,∠AOC =90°∴∠ACB =45°∵点N 是OA 的中点∴ON =2又∵OB =2∴OB =ON又∵∠BON =90°∴∠ONB =45°∴∠ACB =∠ONB∵∠OMB +∠OAB =∠ACB ∠NBA +∠OAB =∠ONB ∴∠OMB =∠NBA1°当点M 在点N 的上方时,记为M 1∵∠BAN =∠M 1AB ,∠NBA =∠OM 1B ,∴△ABN ∽△AM 1B ∴1AN AB AB AM =又∵AN =2,AB =∴110AM =又∵A (0,—4)∴1(0,6)M 2°当点M 在点N 的下方时,记为M 2,点M 1与点M 2关于x 轴对称,∴2(0,6)M -综上所述,点M 的坐标为(0,6)或(0,6)-题型二动点形成的相切问题1.直线和圆相切:圆心到直线距离等于半径构造直角三角形,利用三角比、勾股定理等来表示圆心到直线距离及半径,建立等量关系2.圆和圆相切:两圆半径和等于圆心距.利用平行线分线段成比例、勾股定理、三角比、相似等表示相关线段,建立等量关系角度4:直线与圆相切问题例题4:如图,在ABC ∆中,10,12,AB AC BC ===点E F 、分别在边BC AC 、上(点F 不与点A 、C 重合)//EF AB .把ABC ∆沿直线EF 翻折,点C 与点D 重合,设FC x =.(1)求B ∠的余切值;(2)当点D 在ABC ∆的外部时,DE DF 、分别交AB 于M 、N ,若MN y =,求y 关于x 的函数关系式并写出定义域;(3)(下列所有问题只要直接写出结果即可)以E 为圆心、BE 长为半径的E 与边AC 1没有公共点时,求x 的取值范围.2一个公共点时,求x 的取值范围.3两个公共点时,求x 的取值范围.AE CB FA B D GC EF变式6:已知:矩形ABCD 中,过点B 作BG ⊥AC 交AC 于点E ,分别交射线AD 于F 点、交射线CD 于G 点,BC =6.(1)当点F 为AD 中点时,求AB 的长;(2)联结AG ,设AFG AB x S y ∆==,,求y 关于x 的函数关系式及自变量x 的取值范围;(3)是否存在x 的值,使以D 为圆心的圆与BC 、BG 都相切?若存在,求出x 的值;若不存在,请说明理由.解析:(1)∵点F 为AD 中点,且AD =BC =6,∴AF =3∵矩形ABCD 中,∠ABC =90°,BG ⊥AC 于点E ,∴∠ABE +∠EBC =90°,∠AC ∠EBC =90°∴∠ABE =∠ACB ,∴△ABF ∽△BCF ,∴AB AF BC AB =∴AB =23(2)由(1)可得△ABF ∽△BCF ∴AB AF BC AB =∵AB =x ,BC =6∴AF =62x ;同理可得:CG =x36①当F 点在线段AD 上时DG =CG -CD =x x x x 23636-=-∴S ⊿AFG =1236213x x CG AF -=⋅。
初一数学动点经典例题20道

初一数学动点经典例题20道1.如果一个角的度数是60度,则这个角的补角和余角分别是多少度?答:补角为30度,余角为150度。
2.如果一个直角三角形的斜边长是10,那么它的两腰长分别是多少?答:每个腰长都是根号50(即约为7.07)。
3.如果一个圆的直径是12,那么这个圆的周长是多少?答:这个圆的周长是约37.68。
4.如果一个正方形的边长是5,那么这个正方形的面积是多少?答:这个正方形的面积是25。
5.如果一个三角形的底边长是6,高为4,那么这个三角形的面积是多少?答:这个三角形的面积为12。
6.如果一个长方形的长为7,宽为3,那么这个长方形的面积是多少?答:这个长方形的面积是21。
7.如果一个正方体的边长是4,那么这个正方体的体积是多少?答:这个正方体的体积是64。
8.如果一个等腰三角形的两底边长均为8,那么这个三角形的高是多少?答:这个三角形的高为约6.93。
9.如果一个矩形的长为9,宽为2,那么这个矩形的周长是多少?答:这个矩形的周长是22。
10.如果一个圆的半径是5,那么这个圆的面积是多少?答:这个圆的面积是约78.5。
11.如果一个正方体的表面积为96,那么这个正方体的边长是多少?答:这个正方体的边长是4。
12.如果一个三角形的三个内角分别为50度、60度和70度,那么这个三角形的角平分线的交点在哪里?答:这个三角形的角平分线的交点距离三角形的各顶点均等。
13.如果一个梯形的底边长为7,顶边长为3,高为4,那么这个梯形的面积是多少?答:这个梯形的面积为20。
14.如果一个球的直径是8,那么这个球的体积是多少?答:这个球的体积是约268.08。
15.如果一条线段的长度为10,那么在这个线段上任意取一点,那么这个点距离线段两个端点的距离差是多少?答:这个点距离线段两个端点的距离差不超过5。
16.如果一个等边三角形的边长为3,那么这个等边三角形的面积是多少?答:这个等边三角形的面积为约3.9。
初中数学压轴题讲解:动点,面积与最值问题

典例精讲
● 如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的 中点,P是直径MN上一动点,则PA+PB的最小值为______.
解题技巧:将军饮马的第一种情况
典例精讲
●如图所示,已知A( 1 ,y1),B(2,y2)为反比例函数 y 1 图象上的两点,动
点
P(x
,
1
2
x
典例精讲
● 如图为反比例函数
y1 x
在第一象限的图象,点A为此图象上的一动点,过点
A分别作AB⊥x轴和AC⊥y轴,垂足分别为B,C.则四边形OBAC周长的最小值为
()
典例精讲
● 如图,在平面直角坐标系中,已知点A(1,0),B(1−a,0),C(1+a,0)(a>0),点 P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90∘,则a的最 大值是()
典例精讲 (2)Q Rt△ABM ∽Rt△MCN ,
AB BM , 4 x , MC CN 4 x CN
CN x2 4x 4
压轴题研究1——面积最值(动点)
y
S梯形ABCN
1
2
x2 4x 4
4g4
(0<x<4)
1 x2 2x 8 1 (x 2)2 10
2
2
当 x 2 时, y 取最大值,最大值为 10.
动点与最值问题
将军饮马: 将军饮马三种情况,两定一动,两动一定,双定双动
另有PPT讲解
三边关系: 两边之和大于第三边,两边只差小于第三边
动点最值问题解析
三点共线
配方法: 纯代数的最值问题用配方,利用二次函数的性质
几何问题,一般以面积周长有关
动点产生的面积问题-教师版
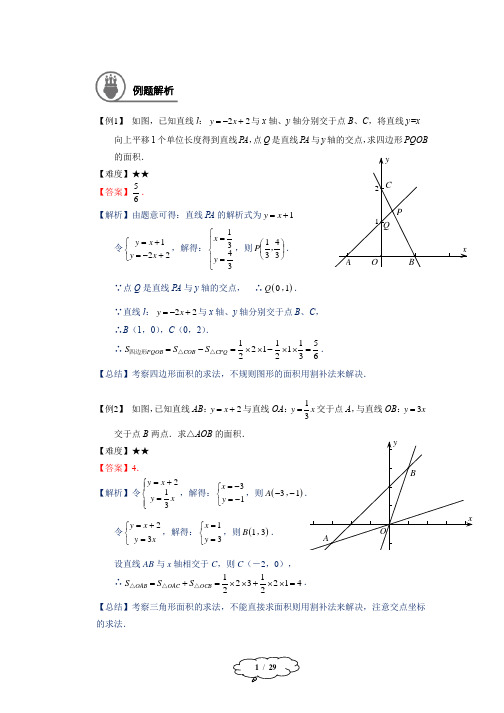
1 / 29xy12QPAOCBxyAOB【例1】 如图,已知直线l :22y x =-+与x 轴、y 轴分别交于点B 、C ,将直线y=x向上平移1个单位长度得到直线P A ,点Q 是直线P A 与y 轴的交点,求四边形PQOB 的面积. 【难度】★★【答案】65.【解析】由题意可得:直线P A 的解析式为1+=x y令⎩⎨⎧+-=+=221x y x y ,解得:⎪⎩⎪⎨⎧==3431y x ,则⎪⎭⎫ ⎝⎛3431,P .∵点Q 是直线P A 与y 轴的交点, ∴()01Q ,. ∵直线l :22y x =-+与x 轴、y 轴分别交于点B 、C , ∴B (1,0),C (0,2). ∴65311211221=⨯⨯-⨯⨯=-=CPQ COB PQOB S S S △△四边形. 【总结】考察四边形面积的求法,不规则图形的面积用割补法来解决.【例2】 如图,已知直线AB :2y x =+与直线OA :13y x =交于点A ,与直线OB :3y x =交于点B 两点.求△AOB 的面积. 【难度】★★ 【答案】4.【解析】令⎪⎩⎪⎨⎧=+=x y x y 312,解得:⎩⎨⎧-=-=13y x ,则()31A --,. 令⎩⎨⎧=+=x y x y 32,解得:⎩⎨⎧==31y x ,则()13B ,. 设直线AB 与x 轴相交于C ,则C (-2,0),∴412213221=⨯⨯+⨯⨯=+=OCB OAC OAB S S S △△△.【总结】考察三角形面积的求法,不能直接求面积则用割补法来解决,注意交点坐标 的求法.例题解析【例3】 如图,已知直线3y x =+的图像与x 轴、y 轴分别交于A 、B 两点,直线l 经过原点,与线段AB 交于点C ,把△AOB 的面积分为2:1两部分,求直线l 的解 析式. 【难度】★★【答案】2y x =-或x y 21-=.【解析】∵直线3y x =+的图像与x 轴、y 轴分别交于∴A (-3,0),B (0,3),∴293321=⨯⨯=OAB S △.当OBA OBCS S △△32=时, 则2932321⨯=⨯⨯C y ,则2=C y , ∵C 点在直线AB 上,∴C (-1,2), 则直线l 的解析式为:2y x =-;当OBA OBC S S △△31=时,则2931321⨯=⨯⨯C y ,则1=C y , ∵C 点在直线AB 上,∴C (-2,1),则直线l 的解析式为:x y 21-=.综上直线l 的解析式为2y x =-或x y 21-=.【总结】考察面积的求法,本题中要注意分类讨论.3 / 29【例4】 如图,已知,在矩形ABCD 中,AB =10,BC =12,四边形EFGH 的三个顶点E 、F 、H 分别在矩形ABCD 边AB 、BC 、DA 上,AE =2.(1)如图1,当四边形EFGH 为正方形时,求△GFC 的面积;(2)如图2,当四边形EFGH 为菱形,且BF =a 时,求△GFC 的面积.(用含a 的代数式表示)【难度】★★★ 【答案】见解析.【解析】(1)过点G 作GM ⊥BC 于M .∵四边形EFGH 为正方形时,∴︒=∠+∠90BEF AEH ∵︒=∠+∠90AHE AEH ,∴BEF AHE ∠=∠ ∵BEF AHE ∠=∠,B A ∠=∠,EF EH =, ∴BEF AHE ≌△△同理可知:BEF MFG ≌△△ ∴2===AE BF GM∴10=-=BF BC FC ,则10=GFC S △; (2)过点G 作GM ⊥BC 于M ,连接HF ∵AD ∥BC ,∴MFH AHF ∠=∠ ∵EH ∥FG ,∴GFH EHF ∠=∠ ∴MFG AHE ∠=∠∵MFG AHE ∠=∠,GMF A ∠=∠,GF EH =, ∴MFG AHE ≌△△∴2==AE GM∴()a a GM FC S GFC -=⨯-=⋅=122122121△.【总结】本题主要考察菱形、正方形的性质和全等三角形的判定和性质.A BCDEF 图1GHABCDE F 图2GHMM4 / 29【例5】 如图1,正方形ABCD 的边长为2,点A (0, 1)和点D 在y 轴正半轴上,点B 、C 在第一象限,一次函数y =kx +2的图像l 交AD 、CD 分别于E 、F . (1)若△DEF 与△BCF 的面积比为1∶2,求k 的值; (2)联结BE ,当BE 平分∠FBA 时,求k 的值. 【难度】★★★【答案】(1)1=k ;(2)2=k .【解析】(1)∵正方形ABCD 的边长为2,点A (0, 1)和点D 在y 轴正半轴上,点B 、C 在第一象限, ∴B (2, 1),C (2, 3),D (0, 3).∵一次函数y =kx +2的图像l 交AD 、CD 分别于E 、F , ∴E (0, 2). 设F (m , 3),∵△DEF 与△BCF 的面积比为1∶2, ∴()212221121=⨯-⨯⋅m m ,解得:1=m ,∴F (1, 3) ∵F (1, 3)在直线y =kx +2上,∴1=k ; (2)延长BE 交CD 的延长线于H , ∵BE 平分∠FBA ,∴ABE FBE ∠=∠∵CD ∥AB ,∴ABE H ∠=∠,∴FBE H ∠=∠,∴FB=HF ∵AE =1,DE=1,∴AE=DE∵AE=DE ,BAE HDE ∠=∠,BEA HED ∠=∠ ∴△HED ≌△BEA∴HD=AB =2,∴H (-2, 3) 设F (n , 3) ∵FB=HF ,∴()22222+=+-n n ,解得:21=n , ∴F (21, 3) ∵F (21, 3)在直线y =kx +2上, ∴2=k .【总结】考察等腰三角形的性质和两点之间的距离公式的运用,注意点的坐标与解析式的关系.ABCD EFxy OH5 / 29【例6】 如图,在平面直角坐标系中,函数y =2x +12的图像分别交x 轴、y 轴于A 、B 两点,过点A 的直线交y 轴正半轴于点M ,且点M 为线段OB 的中点. (1)求直线AM 的表达式;(2)试在直线AM 上找一点P ,使得S △ABP =S △AOB ,请求出点P 的坐标; (3)若点H 为坐标平面内任意一点,是否存在点H ,使以A 、B 、M 、H 为顶点的四边形是等腰梯形?若存在,请直接写出点H 的坐标;若不存在,请说明理由. 【难度】★★★【答案】(1)6+=x y ;(2)P (6, 12)或P (-18, -12); (3)H (-12, 0)或H (-6, 18)或H (56-, 518). 【解析】(1)∵函数y =2x +12的图像分别交x 轴、y 轴于A 、B 两点,∴A (-6, 0),B (0, 12)∵点M 为线段OB 的中点, ∴M (0, 6), 则直线AM 的表达式为6+=x y ; (2)当点P 在AM 的延长线上时∵S △ABP =S △AOB ,∴OP ∥AB ,则可知直线OP 的表达式为x y 2=. ∵P 在直线AM 上,∴令⎩⎨⎧+==62x y x y ,解得:⎩⎨⎧==126y x , ∴P (6, 12);当P 在AM 的反向延长线上时,过P 点作PN ⊥OB ,垂足为H 设P (n , n+6)∵AONP ABO BPN ABP S S S S 梯形△△△--=, S △ABP =S △AOB ,()()()()1262166621126216621⨯⨯=--⨯--⨯-⨯⨯----⋅n n n n ,解得:18-=n ,则P (-18, -12).(3)存在点H ,使以A 、B 、M 、H 为顶点的四边形是等腰梯形.若以AM 为底,BM 为腰,过点B 作AM 的平行线,当点H (-12, 0)时,以A 、B 、M 、H 为顶点的四边形是等腰梯形;若以BM 为底,AM 为腰,过点A 作BM 的平行线,当点H (-6, 18)时,以A 、B 、M 、H 为顶点的四边形是等腰梯形;若以AB 为底,BM 为腰,过点M 作AB 的平行线,当点H (56-, 518)时,以A 、B 、M 、H 为顶点的四边形是等腰梯形.【总结】本题综合性较强,本题一方面考察面积的确定,另一方面考察等腰梯形的性质和分类讨论.ABOMxy6 / 29【例7】 如图1,已知直角坐标平面内点A (2, 0),P 是函数y =x (x >0)图像上一点,PQ ⊥AP 交y 轴正半轴于点Q . (1)试证明:AP =PQ ;(2)设点P 的横坐标为a ,点Q 的纵坐标为b ,那么b 关于a 的函数关系式是_______;(3)当S △AOQ =23S △APQ 时,求点P 的坐标.【难度】★★★【答案】(1)见解析;(2)22-=a b ;(3)⎪⎪⎭⎫ ⎝⎛--255255,P 或⎪⎪⎭⎫ ⎝⎛++255255,P . 【解析】(1)过P 作x 轴、y 轴的垂线,垂足分别为H 、T ,∵P 是函数y =x (x >0)图像上一点 ∴PH=PT ,PH ⊥PT∵PQ ⊥AP ,∴QPT APH ∠=∠∵QPT APH ∠=∠,PH=PT ,QTP AHP ∠=∠ ∴△PHA ≌△PTQ ∴AP =PQ ;(2)由(1)可得:TQ a AH =-=2 ∵OH OT TQ OQ ==+, ∴a a b =-+2, 即22-=a b ; (3)设()P a a ,, ∵2221-=⋅⋅=a OQ OA S AOQ △,222122+-==a a AP S APQ △, ∴()2232222+-=-a a a , 解得:255±=a . ∴⎪⎪⎭⎫ ⎝⎛--255255,P 或⎪⎪⎭⎫ ⎝⎛++255255,P . 【总结】本题主要考察全等的运用,及三角形面积的求法,注意利用面积公式确定点的坐标.P QAy O x7 / 29【例8】 如图,矩形ABCD 中,AB =1,AD =2,M 是CD 的中点,点P 在矩形的边上沿A B C M →→→运动,试写出△APM 的面积y 与点P 经过的路程x 之间的函数关系,写出定义域,并画出函数图像. 【难度】★★ 【答案】见解析.【解析】当P 在AB 上运动时,即10≤<x ,y =x AP AD S APM =⋅=21△;当P 在BC 上运动时,即31≤<x , ∵PCM ABP ABCM APM S S S S △△梯形△--=, ∴y =454432123+-=----=x x x S APM △; 当P 在CM 上运动时,即273≤<x , y =x x S APM -=⨯⎪⎭⎫⎝⎛-=2722721△.函数图像如由图所示.【总结】本题主要考察面积与动点的结合,注意进行讨论.【例9】 如图,在梯形ABCD 中,AD //BC ,AB =CD =AD =5cm ,BC =11cm ,点P 从点D 出发沿DA 边以每秒1cm 的速度移动,点Q 从点B 出发沿BC 边以每秒2cm 的速度移动(当点P 到达点A 时,点P 与点Q 同时停止移动),假设点P 移动的时间为x (秒),四边形ABQP 的面积为y (cm 2). (1)求y 关于x 的函数解析式,并写出它的定义域;(2)在移动的过程中,求四边形ABQP 的面积与四边形QCDP 的面积相等时x 的值;(3)在移动过程中,是否存在x 使得PQ =AB ,若存在,求出所有的x 的值;若不存在,请说明理由. 【难度】★★【答案】(1)102+=x y (50≤≤x ); (2)3=x ;(3)35=x 或311=x . 【解析】(1)作AE ⊥BC 于E ,DF ⊥BC 于F ,∵AB =CD =AD =5cm ,BC =11cm , ∴BE=CF =3,则4=AE .ABCDMPABCDPQE F8 / 29∵2DP x BQ x ==,, ∴()10242521+=⨯+-⨯=x x x y (50≤≤x ); (2)当四边形ABQP 的面积与四边形QCDP 的面积相等时, 四边形ABQP 的面积等于四边形ABCD 的面积的一半,∴()41152121102⨯+⨯⨯=+x ,解得:3=x ;(3)∵PQ =AB ,AD //BC ,∴四边形ABQP 为平行四边形或等腰梯形. 当四边形ABQP 为平行四边形时,则AP =BQ ,∴x x 25=-,解得:35=x ;当四边形ABQP 为等腰梯形时,则四边形PQCD 为平行四边形,∴x x 211-=,解得:311=x ;综上所述,当PQ =AB 时,x 的值为53或113.【总结】本题主要考察动点背景下的平行四边形和等腰梯形的性质的综合运用.【例10】 已知:如图1,在线段AE 的同侧作正方形ABCD 和正方形BEFG (BE <AB ),连结EG 并延长交DC 于点M ,作MN ⊥AB ,垂足为N ,MN 交BD 于P .设正方形ABCD 的边长为1. (1)证明:△CMG ≌△NBP ;(2)设BE =x ,四边形MGBN 的面积为y ,求y 关于x 的函数解析式,并写出定义域;(3)如果按照题设方法作出的四边形BGMP 是菱形,求BE 的长. 【难度】★★★ 【答案】见解析.【解析】(1)∵正方形ABCD 和正方形BEFG ,∴︒=∠45ABD ,︒=∠45BEG ∵CM ∥BE ,∴︒=∠=∠45BEG CMG ∵正方形ABCD ,MN ⊥AB ,∴四边形BCMN 是矩形, ∴CM=NB . ∵CM=NB ,PNB C ∠=∠,PBN CMG ∠=∠ ∴△CMG ≌△NBP ;(2)∵正方形BEFG ,BE =x , ∴x BE BG ==, ∴x CG -=1,ABC DEFGPMN9 / 29∴()()212111212+-=-+=x x x y (10<<x ); (3)由已知可得:MN ∥BC ,MG ∥BP , ∴四边形BGMP 是平行四边形.要使四边形BGMP 是菱形,则MG BG =, ∴()x x -=12,解得:22-=x , ∴当22-=BE 时,四边形BGMP 是菱形.【总结】本题考察正方形的性质和动点背景的下面积问题,解题时注意认真分析题目中的条件.【例11】 已知:在梯形ABCD 中,AD //BC ,∠B =90°,AB =BC =4,点E 在边AB上,CE =CD .(1)如图1,当∠BCD 为锐角时,设AD =x ,△CDE 的面积为y ,求y 与x 之间 的函数解析式,并写出函数的定义域; (2) 当CD =5时,求△CDE 的面积. 【难度】★★★【答案】(1)x x y 4212+-=(40<<x );(2)27或252.【解析】(1)过C 作CF ⊥AD 交AD 延长线于F∵AD //BC ,∠B =90°,AB =BC =4, ∴四边形ABCF 是正方形.∵CE =CD ,BC=CF ,∴△BCE ≌△FCD ,∴DF=BE ∵AD =x ,∴x DF -=4,∴x BE -=4 ∴ADE BEC ABCD y S S S =--△△梯形 ()()1114444222x x x x =+⨯-⋅⋅-⨯⨯- 2142x x =-+, 定义域为:40<<x ;(2)当∠BCD 为锐角时, ∵CD =5时,CF=4,∴由勾股定理可得:3=DF ,则1=AD代入解析式中可得:27=y ;当∠BCD 为钝角时,易知3DF BE ==.AB CDEFA B CDEF10 / 29∴CDEBCEADEABCD SS SS=--梯形111(47)43417222=⨯+⨯-⨯⨯-⨯⨯ 252=. 综上所述,△CDE 的面积为27或252. 【总结】考察全等三角形的构造和正方形的性质的综合运用,第(2)问要注意分类讨论.【例12】 如图1,四边形OABC 是矩形,点A 、C 的坐标分别为(3,0),(0,1),点D是线段BC 上的动点(与端点B 、C 不重合),过点D 作直线12y x m =-+交折线OAB 于点E .(1)当点E 恰为AB 中点时,求m 的值;(2)当点E 在线段OA 上,记△ODE 的面积为y ,求y 与m 的函数关系式并写出定义域;(3)当点E 在线段OA 上时,若矩形OABC 关于直线DE 的对称图形为四边形O 1A 1B 1C 1,试判断四边形O 1A 1B 1C 1与矩形OABC 的重叠部分的面积是否发生变化,若不变,写出该重叠部分的面积;若改变,写出重叠部分面积S 关于m 的函数关系式. 【难度】★★★ 【答案】见解析.【解析】∵四边形OABC 是矩形,点A 、C 的坐标分别为(3,0),(0,1),∴B (3,1). (1)当点E 恰为AB 中点时,则E (3,21) ∵点E 在直线12y x m =-+上, ∴代入E 点坐标,可得:2=m ;(2)当点E 在线段OA 上,∵直线12y x m =-+交折线OAB 于点E , ∴E (m 2,0),∴m m y =⋅⋅=1221(312m <≤); (3)设O 1A 1与CB 相交于点M ,OA 与B 1C 1相交于点N ,则四边形O 1A 1B 1C 1与 矩形OABC 的重叠部分的面积为四边形DNEM 的面积.AB CDEOxy∵DM ∥NE ,DN ∥ME ,∴四边形DNEM 是平行四边形 ∵NED MED ∠=∠,NED MDE ∠=∠,∴NED MED ∠=∠, ∴ME MD =,∴四边形DNEM 是菱形过D 作DH ⊥OA ,垂足为H ,设菱形DNEM 的边长为a∵D (22-m ,1),E (m 2,0), ∴DH =1,HE =()2222m m --=,∴2NH EN EH a =-=-, 在直角△DHN 中,()22212+-=a a ,解得:45=a ∴菱形DNEM 的面积为:55144⨯=.【总结】本题综合性较强,一方面考查面积与动点的结合,另一方面考查面积的定值,注意进行分析.【例13】 如图1,在正方形ABCD 中,点E 在边AB 上(点E 与点A 、B 不重合),过点E 作FG ⊥DE ,FG 与边BC 相交于点F ,与边DA 的延长线相交于点G . (1)当E 是AB 中点时,求证AG =BF ;(2)当E 在边AB 上移动时,观察BF 、AG 、AE 之间具有怎样的数量关系?并证明你所得到的结论;(3)联结DF ,如果正方形的边长为2,设AE =x ,△DFG 的面积为y ,求y 与x 之间的函数解析式,并写出函数的定义域.【难度】★★★【答案】(1)见解析;(2)AE AG BF =+;(3)2212+=x y (20<<x ).【解析】(1)当E 是AB 中点时,AE=BE∵AE=BE ,AEG BEF ∠=∠,B EAG ∠=∠ ∴△EAG ≌△EBF ∴AG =BF(2)AE AG BF =+过点F 作FH ⊥DA ,垂足为H ,则四边形ABFH 是矩形 ∴FH=AB=AD∵DE ⊥FG ,∴DEA ADE G ∠=∠-︒=∠90 ∵FH=AD ,DEA G ∠=∠,G A ∠=∠ ∴△FHG ≌△DAE , ∴GH=AE ,即AE AG HA =+ ∵BF=HA , ∴AE AG BF =+;A BCD EF GH(3)由(2)可得:FG=DE ∴224+==x DE FG ∴221442122222+=+⋅+=x x x y (20<<x ) 【总结】本题主要考察正方形背景下的动点问题,注意对常见辅助线的添加以及线段间的转化.【例14】 如图1,梯形ABCD 中,AD //BC ,∠B =90°,AD =18,BC =21.点P 从点A 出发沿AD 以每秒1个单位的速度向点D 匀速运动,点Q 从点C 沿CB 以每秒2个单位的速度向点B 匀速运动.点P 、Q 同时出发,其中一个点到达终点时两点停止运动,设运动的时间为t 秒.(1)当AB =10时,设A 、B 、Q 、P 四点构成的图形的面积为S ,求S 关于t 的函数关系式,并写出定义域;(2)设E 、F 为AB 、CD 的中点,求四边形PEQF 是平行四边形时t 的值.【难度】★★★【答案】(1)t S 5105-=(5.100≤≤t ); (2)23=t . 【解析】(1)由题意可得:AP =t ,CQ =t 2,则()t t t S 51051022121-=⨯-+⨯=(5.100≤≤t );(2)过点D 作DH ⊥BC 于H ,取CH 的中点G ,则四边形ABHD 是矩形.∵F 是CD 的中点,G 是CH 的中点,∴DH FG 21=∵AD //BC ,∠B =90°,AD =18,BC =21∴CH =21-18=3,CG =2321=CH∴232-=-=t GC QC QG ∵四边形PEQF 是平行四边形, ∴PE=QF∵AB FG AE 21==,90A FGQ ∠=∠=GABCDE F PABCD Q图1备用图H∴△AEP ≌△GFQ , ∴QG=AP∴t t =-232, 解得:23=t ,即当四边形PEQF 是平行四边形时,t 的值为32. 【总结】本题一方面考察梯形背景下的动点结合,另一方面考察中位线及平行四边形的性质的综合运用,注意认真分析.【例15】 如图1,在菱形ABCD 中,∠B =45°,AB =4.左右作平行移动的正方形EFGH 的两个顶点F 、G 始终在边BC 上.当点G 到边BC 中点时,点E 恰好在边AB 上.(1)如图1,求正方形EFGH 的边长;(2)设点B 与点F 的距离为x ,在正方形EFGH 作平行移动的过程中,正方形EFGH 与菱形ABCD 重叠部分的面积为y ,求y 与x 的函数解析式,并写出它的定义域;(3)联结FH 、HC ,当△FHC 是等腰三角形时,求BF 的长. 【难度】★★★ 【答案】见解析.【解析】(1)当点G 到边BC 中点时,BG=2,∵∠B =45°,正方形EFGH 的两个顶点F 、G 始终在边BC 上. ∴BF=EF=FG ∵BG=2,∴FG=1, 即正方形EFGH 的边长为1;(2)当10≤<x 时,()212121122++-=--=x x x y ,当31≤<x 时,1=y ;(3)当FH=HC 时,∵HG ⊥CF ,∴FG=CG=1, ∴2114=--=--=FG GC BC BF ; 当FC=HC 时,∵CG CG FG FC +=+=1,2221GC GC GH HC +=+= ∴112+=+GC GC ,解得:0=GC , ∴3014=--=--=FG GC BC BF ;当FH=FC 时,则2=FC ,此时24-=-=FC BC BF , 综上所述,当△FHC 是等腰三角形时,BF 的长为2或3或42-.HAB C DEF G【总结】本题主要考察平行四边形与正方形的性质的综合运用,解题时注意对等腰三角形要进行分类讨论.【例16】 如图1,在平面直角坐标系中,O 为坐标原点,四边形OABC 是矩形,A (0,4),C (5, 0),点D 是y 轴正半轴上一点,将四边形OABC 沿着过点D 的直线翻折,使得点O 落在线段AB 上的点E 处.过点E 作y 轴的平行线与x 轴交于点N .折痕与直线EN 交于点M ,联结DE 、OM . 设OD =t ,MN =s . (1)试判断四边形EDOM 的形状,并证明;(2)当点D 在线段OA 上时,求s 关于t 的函数解析式,并写出函数的定义域; (3)用含t 的代数式表示四边形EDOM 与矩形OABC 重叠部分的面积.【难度】★★★ 【答案】见解析.【解析】(1)四边形EDOM 是菱形.∵将四边形OABC 沿着过点D 的直线翻折,使得点O 落在线段AB 上的点E 处, ∴EDM ODM ∠=∠,DE OD =. ∵EM ∥OD , ∴DME ODM ∠=∠, ∴DME EDM ∠=∠,∴EM DE =,∵DE OD =,∴EM OD =. ∵EM ∥OD ,∴四边形EDOM 是平行四边形, ∵EM DE =,∴平行四边形EDOM 是菱形; (2)由(1)可得:OD =EM = t , ∵EN =OA =4, ∴t s -=4(24t <<); (3)当点D 在线段OA 上时,∵t EM ED OM OD ====,4=EN ,s t =-4∴()22224816224ON OM MN t t t t =-=--=-=-∴四边形EDOM 与矩形OABC 重叠部分面积为:224224OD ON t t t t ⋅=⋅-=-; 当点D 在线段OA 延长上时(如图所示),∵4AD t BD t =-=,, ∴2222(4)224AE BD AD t t t =-=--=-, ∴四边形EDOM 与矩形OABC 重叠部分面积为:2244824AE OA t t ⋅=-⨯=-, 综上所述,四边形EDOM 与矩形OABC 重叠部分的面积为224t t -或824t -. 【总结】本题主要考察菱形的判定方法和性质的综合运用,解题时注意进行分析.MA BCDE MNAB C OOxy xyE DN【例17】 已知:如图1,梯形ABCD 中,AD //BC ,∠A =90°,∠C =45°,AB =AD =4.E 是直线AD 上一点,联结BE ,过点E 作EF ⊥BE 交直线CD 于点F .联结BF .(1)若点E 是线段AD 上一点(与点A 、D 不重合),(如图1所示) ①求证:BE =EF ;②设DE =x ,△BEF 的面积为y ,求y 关于x 的函数解析式,并写出此函数的定义域;(2)直线AD 上是否存在一点E ,使△BEF 是△ABE 面积的3倍,若存在,直接写出DE 的长,若不存在,请说明理由.【难度】★★★ 【答案】见解析.【解析】(1)①在AB 上截取AG=AE ,连接EG ,∵∠A =90°,AG=AE , ∴︒=∠=∠45AEG AGE , ∴︒=∠135BGE ∵AD //BC ,∠C =45°, ∴︒=∠135D ,∴D BGE ∠=∠ ∵AG=AE ,AB =AD , ∴ED=BG∵∠A =90°,EF ⊥BE , ∴DEF ABE ∠=∠∵ED=BG ,D BGE ∠=∠,DEF ABE ∠=∠ ∴△BGE ≌△EDF , ∴BE =EF ;②∵DE =x ,∴4AE x =-, ∵∠A =90°,∴()222244+-=+=x AB AE BE ,∵BE =EF , ∴()()23284444212122222+-=+-⋅+-=⋅⋅=x x x x EF BE y (40<<x );A BCDEFABCD图1备用图备用图ABCDGEF G(2)①当点E 在线段AD 上时,∵()11448222ABE S AB AE x x =⨯⨯=⨯⨯-=-△,又3BEFABESS=,∴()23282832+-=-⨯x x x ,解得:522±-=x (负值舍去),∴522+-=DE ;②当点E 在线段DA 延长线上时,延长BA 到G ,使得BG =DE ,连接EG , 则△AGE 是等腰直角三角形.同(1)可证△BGE ≌△EDF , ∴BE =EF ,21122BEF S BE EF BE =⨯⨯=⨯= ∵()824421-=-⨯⨯=x x S ABE △,又3BEFABES S=,∴()23288232+-=-⨯x x x ,解得:5210±=x ,∴5210±=DE ;③当点E 在线段AD 延长线上时,延长AB 到G ,使得BG =DE ,连接EG , 则△AGE 是等腰直角三角形.同(1)可证△BGE ≌△EDF , ∴BE =EF ,21122BEF S BE EF BE =⨯⨯=⨯==,∵()144282ABE S x x =⨯⨯+=+△,又3BEFABESS=,∴()28323282x x x ++⨯+=,解得:2x =±,∴2DE =+;综上所述,当△BEF 是△ABE 面积的3倍时,DE 的长为2-+或10±或2+【总结】本题综合性较强,主要考察全等三角形的构造方法和梯形的性质运用,注意对点在直线上的准确理解,要分多种情况进行讨论.【例18】 如图,已知正方形ABCD 的边长为3,菱形EFGH 的三个顶点E 、G 、H 分别在正方形的边AB 、CD 、DA 上,AH =1,联结CF . (1)当DG =1时,求证菱形EFGH 为正方形;(2)设DG =x ,△FCG 的面积为y ,写出y 关于x 的函数解析式,并指出x 的取值范围;(3)当DG =433时,求∠GHE 的度数.【难度】★★★ 【答案】见解析.【解析】(1)当DG =1时,∵AH =1,∴DG=AH∵菱形EFGH , ∴HG=HE ,∵90A D ∠=∠=, ∴△HDG ≌△EAH , ∴AEH DHG ∠=∠ ∵︒=∠+∠90AEH AHE ,∴︒=∠+∠90DHG AHE ,∴︒=∠90GHE ∴菱形EFGH 是正方形;(2)联结GE ,过F 作FM ⊥DC 交DC 的延长线于M , ∵CD ∥AB ,∴AEG CGE ∠=∠∵FG ∥HE ,∴HEG FGE ∠=∠,∴HEA FGC ∠=∠ ∵HEA FGC ∠=∠,M A ∠=∠,FG=HE , ∴△AHE ≌△MFG , ∴1==FM HA ,∴()x x y 21233121-=-⋅⨯=(30<<x );(3)∵正方形ABCD 的边长为3,AH =1, ∴DH =2.当DG =433时,213233422222=⎪⎭⎫⎝⎛+=+=DG DH GH , ∴2132=HE ,∴33522=-=HA HE AE . 过G 做GN ⊥AB 于N ,∵DG =433,335=AE , ∴33=NE , ∴21323332222=⎪⎪⎭⎫ ⎝⎛+=+=EN GN GE , ∴HE GE GH ==, ∴△EGH 是等边三角形, ∴︒=∠60GHE .【总结】本题主要考察正方形的性质及全等三角形的综合运用,注意辅助线的合理添 加.ABCD EFG H M N【例19】 已知:如图,四边形OABC 的四个顶点坐标分别为O (0, 0),A (8, 0),B (4,4),C (0, 4),直线l :y =x +m 保持与四边形OABC 的边交于点M 、N (M 在折线AOC 上,N 在折线ABC 上).设四边形OABC 在l 右下方部分的面积为S 1,在l 左上方部分的面积为S 2,记S =S 1-S 2(S ≥0). (1)求∠OAB 的大小;(2)当M 、N 重合时,求l 的解析式;(3)当m ≤0时,线段AB 上是否存在点N ,使得S =0?若存在,求m 的值;若不存在,请说明理由;(4)求S 与m 的函数关系式. 【难度】★★★ 【答案】见解析.【解析】(1)过B 作BE ⊥x 轴,垂足为E ,则点E (4,0)∵B (4,4), ∴44==AE BE ,,∴△ABE 为等腰直角三角形, ∴︒=∠45OAB ; (2)∵S ≥0,∴点M 、N 只能重合到点C (0, 4),此时4=m ,故直线l 的解析式为:y =x +4;(3)四边形OABC 的面积()2448421=⨯+⨯.∵直线l :y =x +m 保持与四边形OABC 边交于点M 、N , ∴△AMN 为等腰直角三角形.当S =0时,则△AMN 的面积为四边形OABC 的面积的一半. 过N 做x 轴的垂线NH ,则NH=AH=MH .设a NH =,则122212==⋅⋅a a a ,解得:32=a , ∴()82323N -,,∵点N 在直线l :y =x +m 上, ∴834-=m ;ABC OxyN ME H(4)∵S =S 1-S 2(S ≥0),∴834-≥m .①当0834<≤-m 时,m OM -=,m AM +=8, 经过A (8, 0),B (4,4)的直线解析式为:8+-=x y , 令⎩⎨⎧+=+-=m x y x y 8, 解得:⎪⎩⎪⎨⎧+=-=2828m y m x ∴16441282822121++=+⨯+⨯⨯=m m m m S ,1224S S -=, ∴88212422121++=-=-=m m S S S S ; ②当40≤≤m 时,m OM =,m CM -=4,∴()22421m S -=,1224S S -=,∴882242121++-=-=-=m m S S S S ;综上所述,2218880)288(04)m m m S m m m ⎧++≤<⎪=⎨⎪-++≤≤⎩.【总结】本题综合性较强,主要考察图形的运动,包含了一次函数的性质及解析式的求法.解题时要注意从多个角度分析,特别要清楚动点的移动位置.【例20】 在边长为4的正方形ABCD 中,点O 是对角线AC 的中点,P 是对角线AC上一动点,过点P 作PF ⊥CD 于点F ,作PE ⊥PB 交直线CD 于点E ,设P A =x ,PCE S y =△.(1)求证:DF =EF ;(2)当点P 在线段AO 上时,求y 关于x 的函数关系式及自变量x 的取值范围;(3)点P 在运动过程中能否使△PEC 为等腰三角形?如果能,请直接写出P A 的长;如果不能,请简单说明理由. 【难度】★★★ 【答案】见解析.【解析】(1)延长FP 交AB 于点G∵正方形ABCD 中,PF ⊥CD 于点F ,∴四边形AGFD 是矩形, ∴DF=AG ,︒=∠90AGF ∵正方形ABCD , ∴︒=∠45BAC∵︒=∠90AGF ,∴GP AG =,∴GP DF = 同理可得:BG PF CF ==∵PE ⊥PB ,︒=∠90AGF ,∴FPE GBP ∠=∠ ∵FPE GBP ∠=∠,BG PF =,PFE BGP ∠=∠ ∴△GBP ≌△FPE ,∴GP=EF ∵GP DF =,∴EF DF =; (2)∵P A =x , ∴x GP AG 22==,x EF DF 22==, 则x DE 2=,∴x CE 24-=, ∵x PF 224-=, ∴()8232122424212+-=⎪⎪⎭⎫ ⎝⎛--=x x x x y (022x ≤≤)(3)点P 在运动过程中能使△PEC 为等腰三角形. 当点E 在CD 边上时,∵︒≥∠90CEP ,要使△PEC 为等腰三角形,则︒=∠=∠45ECP CPE ,则PE ⊥CE . ∵PE ⊥PB , ∴BP ∥CD , ∴BP ∥BA .于是点P 在AB 上,又点P 在AC 上,∴A 与P 重合,此时AP =0. 当点E 在DC 延长线上时,要使△PEC 为等腰三角形,只能是PC=CE , ∴易得P A =4.【总结】本题主要考查正方形的性质的综合运用,注意对等腰的分类讨论.A BCDE F P OGxy BAOC【习题1】 如图,直线443y x =-+与y 轴交于点A ,与直线4455y x =+交于点B ,且直线4455y x =+与x 轴交于点C ,求△ABC 的面积. 【难度】★★ 【答案】4.【解析】∵直线443y x =-+与y 轴交于点A ,∴A (0,4);∵直线443y x =-+与x 轴交于点D ,∴D (3,0);令⎪⎩⎪⎨⎧+=+-=5454434x y x y , 解得:⎪⎩⎪⎨⎧==223y x , 则322B ⎛⎫ ⎪⎝⎭,;∵直线4455y x =+与x 轴交于点C , ∴C (-1,0),∴424214421=⨯⨯-⨯⨯=-=BCD ACD ABC S S S △△△. 【总结】考察面积的求法,不规则图形的面积用割补法来解决,注意交点坐标的确定.随堂检测【习题2】 已知直线2y x =-+与x 轴、y 轴分别交于A 点和B 点,另一条直线(0)y kx b k =+≠经过点C (1,0),且把△AOB 分成两部分.若△AOB 被分成的两部分面积比为1:5,求k 和b 的值. 【难度】★★★【答案】22k b ==-,或2233k b =-=,.【解析】∵直线2y x =-+与x 轴、y 轴分别交于A 点和B 点,∴A (2,0),B (0,2).若△AOB 被分成的两部分面积比为1:5,那么直线(0)y kx b k =+≠与y 轴或A B 交点的纵坐标为:326122=⨯⨯. 当(0)y kx b k =+≠与直线2y x =-+相交时,交点为D ,当32=y 时,223x =-+,解得:34=x ,∴D (34,32), ∵点C (1,0),D (34,32)在直线(0)y kx b k =+≠上, ∴22k b ==-,;当(0)y kx b k =+≠与y 轴相交时,交点为E ,当32=y 时,223x =-+,解得:34=x ,∴E (0,32), ∵C (1,0),E (0,32)在直线(0)y kx b k =+≠上, ∴2233k b =-=,.综上,22k b ==-,或2233k b =-=,.【总结】本题主要考察面积的求法及交点坐标的确定,注意要分类讨论.【习题3】 直线364y x =-+与坐标轴分别交与点A 、B 两点,点P 、Q 同时从O 点出发,同时到达A 点,运动停止.点Q 沿线段OA 运动,速度为每秒1个单位长度,点P 沿O B A →→运动. (1)直接写出A 、B 两点的坐标;(2)设点Q 的运动时间为t 秒,△OPQ 的面积为S ,求出S 与t 之间的函数关系;(3)当485S =时,求出点P 的坐标,并直接写出以点O 、P 、Q 为顶点的平行四边形的第四个顶点M 的坐标. 【难度】★★★ 【答案】见解析.【解析】(1)∵直线364y x =-+与坐标轴分别交与点A 、B 两点,∴A (8,0),B (0,6);(2)∵OA=8,OB=6,∴AB=10.∵点Q 沿线段OA 运动,速度为每秒1个单位长度, ∴运动时间为8秒,∴点P 的运动速度是(6+10)÷8=2. 当点P 在线段OB 上运动时(03)t ≤≤, ∵t OQ =,t OP 2=, ∴2t S =;当点P 在线段BA 上运动时(38)t <≤,t OQ =,t t AP 2162106-=-+=, ∵8t OA OQ S S OPAOPQ ==△△,10216tBA AP S S OBA OPA -==△△, ∴t t t t S t t S OAB OPQ 52453241021681021682+-=⨯-⋅=-⋅=△△,综上所述,S 与t 之间的函数关系为:22(03)324(38)55t t S t t t ⎧≤≤⎪=⎨-+<≤⎪⎩;(3)当485S =时,∵6321548⨯⨯>,∴点P 在AB 上,当485S =时,524524532=+-t t ,解得:4=t ,∴524=PD ,8=AP ,532=AD , ∴58=OD ,∴P (58,524), ∴以点O 、P 、Q 为顶点的平行四边形的第四个顶点M 的坐标(528,524)或 (512-,524)或(512,524-)ABxyOQ P【习题4】 如图,已知:过点A (8,0)、B (0,83)两点的直线与直线3y x =交于点C ,平行于y 轴的直线l 从原点O 出发,以每秒1个单位长度的速度沿x 轴向右平移,到C 点时停止;l 分别交线段BC 、OC 于点D 、E ,以DE 为边向左侧作等边△DEF ,设△DEF 与△BCO 重叠部分的面积为S (平方单位),直线l 的运动时间为t (秒).(1) 写出点C 的坐标和t 的取值范围; (2) 求s 与t 的函数关系式. 【难度】★★★ 【答案】见解析.【解析】(1)∵直线过点A (8,0)、B (0,83),∴直线AB 的解析式为383+-=x y . 令⎪⎩⎪⎨⎧=+-=x y x y 3383, 解得:⎩⎨⎧==344y x ,∴C (4,43), 40≤≤t ;(2)作EM ⊥y 轴与M ,DG ⊥y 轴于点G∵直线l 的运动时间为t (秒),∴D (t ,383t -+),E (t ,3t ), ∴t t t DE 32383383-=-+-=, ∴等边△DEF 的DE 边上的高为:()t t DE 31232382323-=-=. ∵E (t ,3t ),∴t ME =,t MN 33=,同理可得:t GH 33= ∴可求梯形上底为:t t 3323238--, ∴当点F 在BO 边上时:t t =-312,∴3=t . 当30<≤t 时,重叠部分为等腰梯形,223783238323383233t S t t t t t ⎛⎫=-+--=-+ ⎪ ⎪⎝⎭; 当43≤≤t 时,重叠部分为三角形,()()348324333123238212+-=--=t t t t S .【总结】本题综合性较强,主要考察一次函数与动点的结合以及图形的运动,解题时 一方面要清晰动点的运动轨迹,另一方面要学会表示动点的坐标,第(2)问注意 要分类讨论.AB CDEOxy l FPMGxy QPAOC B【作业1】 如图,已知直线P A :(0)y x n n =+>与直线PB :2()y x m m n =-+>交于点P .(1)用m 、n 表示出A 、B 、P 点的坐标;(2)若点Q 是直线P A 与y 轴的交点,且四边形PQOB 的面积56,AB=2,试求 点P 的坐标,并写出直线P A 与PB 的解析式. 【难度】★★ 【答案】见解析.【解析】(1)∵直线P A :(0)y x n n =+>交x 轴与A ,∴A (n -,0),∵直线PB :2()y x m m n =-+>交x 轴与B , ∴B (2m,0), 令⎩⎨⎧+-=+=m x y n x y 2, 解得:323m n x m n y -⎧=⎪⎪⎨+⎪=⎪⎩,∴P (3m n -,32nm +);(2)∵点Q 是直线P A 与y 轴的交点, ∴Q (0,n ).∵四边形PQOB 的面积56,∴()65321221=-⋅-⋅-⋅⋅=-n m n m m m S S CPQ COB △△. ∵AB=2, ∴23=+n m, ∴21m n ==,. ∴直线P A 的解析式为:1y x =+, 直线PB 的解析式为:22y x =-+.【总结】本题主要考察点的坐标的求法及几何图形面积的表示.课后作业xy FEO【作业2】 如图所示,直线y kx b =+的截距为6,该直线分别交x 轴、y 轴于E 、F ,点E 的坐标为(-4,0). (1)求直线y kx b =+的表达式;(2)若点P (x ,y )是该直线第二象限上的一个动点,P A ⊥x 轴,PB ⊥y 轴,垂足分别为点A 、B ,试求四边形OAPB 的面积S 与x 的函数关系式,并写出自变量x 的取值范围. 【难度】★★★ 【答案】见解析.【解析】(1)∵直线y kx b =+的截距为6,该直线分别交x 轴、y 轴于E 、F ,∴点E 的坐标为(-4,0),∴直线y kx b =+的表达式为623+=x y ;(2)∵点P (x ,y )是该直线第二象限上的一个动点,∴623+=x y ,∴()x x x x S 6236232--=⎪⎭⎫⎝⎛+-=(04<<-x ).【总结】考察一次函数解析式的求法及图形面积的确定, 注意点的坐标与线段长度的关系.【作业3】 如图,已知:直角梯形ABCD 中,AB ∥CD ,∠A =90°,AB =6,AD =4,DC =3,点P 从点A 出发,沿ADCB 方向移动,动点Q 从点A 出发,在AB 边上移动,设点P 移动的路程为x ,点Q 移动的路程为y ,线段PQ 平分梯形ABCD 的周长. (1) 求y 关于x 的函数解析式,并写出x 和y 的取值范围;(2) 当P 不在BC 边上时,线段PQ 能否平分ABCD 的面积?若能,求出此时x 的值;若不能,说明理由. 【难度】★★★ 【答案】见解析.【解析】(1)过C 做CE ⊥AB 于E ,则CD=AE =3. ∵CE =4, ∴BC =5,∴梯形的周长为18.∵线段PQ 平分梯形ABCD 的周长, ∴9=+y x . ∵60≤≤y , ∴93≤≤x , ∴x y -=9(93≤≤x );ABCD PQ E(2)∵P 不在BC 边上时,则73≤≤x . 当43<≤x 时,点P 在AD 边上,则xy S APQ 21=△. ∵线段PQ 能否平分ABCD 的面积, ∴921=xy . 由1929xy x y ⎧=⎪⎨⎪+=⎩,解得:,∴36x y =⎧⎨=⎩或63x y =⎧⎨=⎩(舍去);当74≤≤x 时,P 在CD 边上,此时()y x S ADPQ +-⨯=4421四边形 ∵线段PQ 能否平分ABCD 的面积, ∴()94421=+-⨯y x联立9=+y x ,方程组无解.故当x =3时,线段PQ 平分ABCD 的面积.【总结】本题考察的知识点较多,包含了梯形的性质,面梯形面积及三角形的面积公式,二元二次方程组的解法等,第(1)问注意对解析式的确定,第(2)问注意利用第(1)问的结论,同时要进行分类讨论.【作业4】 如图,在平面直角坐标系中,两个函数162y x y x ==-+,的图像交于点A ,动点P 从点O 开始在线段O 向点A 方向以每秒1个单位的速度运动,作PQ ∥x 轴交直线BC 于点Q ,以PQ 为一边向下作正方形PAMN ,设它与△ABO 重叠部分的面积为S .(1) 求点A 的坐标;(2) 试求出点P 在线段OA 上运动时,S 与运动的时间t (秒)的关系式.【难度】★★★【答案】见解析.【解析】(1)令⎪⎩⎪⎨⎧+-==621x y x y , 解得:⎩⎨⎧==44y x ,∴A (4,4);ABCP Q O yx(2)∵动点P 从点O 开始在线段O 向点A 方向以每秒1个单位的速度运动, ∴t OP =, 则P (t 22,t 22). ∵PQ ∥x 轴,∴Q (t 212-,t 22), ∴t PQ 22312-=. 当t t 2222312=-时, 23=t . 当230≤<t 时,t t t t S 262322312222+-=⎪⎪⎭⎫ ⎝⎛-=; 当P 到达A 点时,24=t , 当2423<<t 时,144236292231222+-=⎪⎪⎭⎫ ⎝⎛-=t t t S ,综上所述,223(0291442t t S t t ⎧-+<≤⎪⎪=⎨⎪-+<⎪⎩.【总结】本题主要考察交点坐标与面积的确定,解题的关键是要能够掌握重叠部分图 形的特点,一开始是矩形,后来才是正方形,要找出这个临界点,这样就将问题简化 了.。
二次函数--由动点生成面积问题

二次函数--由动点生成面积问题二次函数是数学中重要的一个概念,它描述了一类以二次项为主导的多项式函数。
而这篇文章将重点探讨一个有趣的问题:如何由动点生成二次函数并应用于面积问题。
首先,我们需要了解什么是动点。
动点是平面上一个不固定的点,它的位置随着时间的推移而变化。
在二维平面上,我们通常用坐标系来描述动点的位置,其中x轴和y轴代表两个独立的变量。
考虑以下问题:假设我们有一条规定的直线,上面有两个动点A和B,它们沿着直线运动。
我们假设初始时刻A和B分别位于直线的两个不同的点,运动速度相同且方向相反。
我们还假设直线是垂直于x轴的。
为了简化问题,我们将直线的方程表示为 y = kx + b,其中 k 是直线的斜率,b 是 y 轴的截距。
此外,我们假设 A 和 B 分别运动的距离为 d1 和 d2,而 d1 和 d2 的长度相等。
我们的目标是通过动点A和B的运动来生成一个面积问题,并进一步将其转化为二次函数。
为了实现这一目标,我们需要引入一个新的点C,它是动点A和B的垂直平分线上的一个固定点。
通过仔细观察,我们可以发现三角形ABC的两条边的长度与动点A和B的距离之间存在一定的关系。
假设三角形ABC的高度为h,底边的长度为b,同时A和B分别位于底边的两个端点。
根据数学原理,我们可以通过两个已知长度和一个夹角来计算一个三角形的面积。
那么如何计算三角形ABC的面积呢?首先,我们可以根据两个动点A和B的运动距离d1和d2来计算出三角形底边的长度b。
由于d1和d2的长度相等,我们可以将它们的和除以2来得到b的长度。
即b=(d1+d2)/2接下来,我们需要确定三角形ABC的高度h。
由于点C是动点A和B的垂直平分线上的一个固定点,因此我们可以用坐标系来表示其位置。
假设点C的坐标为(x0,y0)。
由于点C是动点A和B的垂直平分线的交点,因此动点A在以点C为圆心的圆上运动。
同样地,动点B也在以点C为圆心的圆上运动。
我们可以将动点A和B的位置分别表示为(x1,y1)和(x2,y2)。
中考专题3(由动点形生成的面积问题)

由动点形生成的面积问题面积是平面几何中一个重要的概念,关联着平面图形中的重要元素边与角,由动点而生成的面积问题,是抛物线与直线形结合的觉形式,解决这类问题常用到以下与面积相关的知识(1)图形的割补(2)等积变形(3)等比转化例题1(2010四川宜宾)将直角边长为6的等腰Rt△AOC放在如图所示的平面直角坐标系中,点O为坐标原点,点C、A分别在x、y轴的正半轴上,一条抛物线经过点A、C及点B(–3,0).(1)求该抛物线的解析式;(2)若点P是线段BC上一动点,过点P作AB的平行线交AC于点E,连接AP,当△APE的面积最大时,求点P的坐标;(3)在第一象限内的该抛物线上是否存在点G,使△AGC的面积与(2)中△APE的最大面积相等?若存在,请求出点G的坐标;若不存在,请说明理由例题2(2010 湖北孝感) 如图,已知二次函数图像的顶点坐标为(2,0),直线1+=x y 与二次函数的图像交于A 、B 两点,其中点A 在y 轴上。
(1)二次函数的解析式为y= ;(3分)(2)证明点)12,(--m m 不在(1)中所求的二次函数的图像上;(3分)(3)若C 为线段AB 的中点,过C 点作x CE ⊥轴于E 点,CE 与二次函数的图像交于D点。
①y 轴上存在点K ,使以K 、A 、D 、C 为顶点的四边形是平行四边形,则K 点的坐标是 ;(2分)②二次函数的图像上是否存在点P ,使得ABD PO E S S ∆∆=2?若存在,求出P 点坐标;若不存在,请说明理由。
(4分)例题3(2010 四川自贡)如图,在直角坐标平面内,O为坐标原点,A点的坐标为(1,0),B点在x轴上且在点A的右侧,AB=OA,过点A和B作x轴的垂线分别交二次函数y=x2的图象于点C和D,直线OC交BD于M,直线CD交y轴于点H。
记C、D的横坐标分别为x C,x D,点H的纵坐标y H。
(1)证明:①S△CMD∶S梯形ABMC=2∶3 ②x C·x D=-y H(2)若将上述A点坐标(1,0)改为A点坐标(t,0),t>0,其他条件不变,结论S△CMD:S梯形ABMC=2∶3是否仍成立?请说明理由。
七年级下册数学动点问题

七年级下册数学动点问题一、动点问题相关知识点1. 数轴上的动点问题在数轴上,点的移动规律是根据移动方向和移动距离来确定新的位置。
如果一个点A表示的数为公式,向右移动公式个单位长度,则移动后的点表示的数为公式;向左移动公式个单位长度,则移动后的点表示的数为公式。
例如:点公式在数轴上表示公式,向右移动公式个单位后,表示的数为公式;向左移动公式个单位后,表示的数为公式。
2. 平面直角坐标系中的动点问题点公式在平面直角坐标系中的移动规律。
如果点公式向右平移公式个单位,其坐标变为公式;向左平移公式个单位,坐标变为公式;向上平移公式个单位,坐标变为公式;向下平移公式个单位,坐标变为公式。
例如:点公式向右平移公式个单位后变为公式;向下平移公式个单位后变为公式。
3. 动点与几何图形的关系在三角形、四边形等几何图形中,动点的运动可能会改变图形的形状、大小或者某些线段的长度、角度等。
例如,在三角形公式中,点公式是公式边上的一个动点,当公式点运动时,三角形公式和三角形公式的面积关系可能会发生变化。
对于线段长度,若点公式,点公式,则线段公式的长度根据两点间距离公式公式来计算。
当点公式或公式为动点时,线段公式的长度会随着动点的运动而变化。
二、典型题目及解析1. 数轴上的动点问题题目:已知数轴上点公式表示的数为公式,点公式表示的数为公式,点公式从点公式出发,以每秒公式个单位长度的速度向右运动,点公式从点公式出发,以每秒公式个单位长度的速度向左运动,设运动时间为公式秒。
(1)当公式时,求点公式和点公式所表示的数。
(2)经过多少秒后,点公式和点公式相遇?(3)当公式时,求公式的值。
解析:(1)点公式从点公式出发,向右运动,速度为每秒公式个单位长度,当公式时,点公式表示的数为公式。
点公式从点公式出发,向左运动,速度为每秒公式个单位长度,当公式时,点公式表示的数为公式。
(2)点公式和点公式相遇时,它们所经过的路程之和等于公式之间的距离。
中考数学复习之因动点产生的面积问题解题策略

因动点产生的面积问题解题策略一.解题策略解读:面积的存在性问题常见的题型和解题策略有两类:图1 图2 图3 计算面积常用到的策略还有:图4 图5 图6例1.已知抛物线y=mx2+(1-2m)x+1-3m与x轴交于不同的两点A、 B.(1) 求m的取值范围;(2) 证明该抛物线一定经过非坐标轴上的一点P,并求出点P的坐标;(3) 当<m≤8时,由(2)求出的点P和点A、 B构成的△ABP的面积是否有最值,若有,求出最值及相应的m的值;若没有,请说明理由.思路:1. 已知的抛物线的解析式可以因式分解的,抛物线过x轴上的定点(-1, 0).2. 第(2)题分两步,先对m赋予两个不同的值,联立求方程组的解,再验证这个点是确定的.3. 第(3)题中△ABP的高为定值,点A为定点,求△ABP的最大面积,其实就是求点B的横坐标的最大值.例2.问题提出(1) 如图1,已知△ABC,请画出△ABC关于直线AC对称的三角形.问题探究(2) 如图2,在矩形ABCD中,AB=4, AD=6, AE=4, AF=2.是否在边BC、CD上分别存在点G、 H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.问题解决(3) 如图3,有一块矩形板材ABCD, AB=3米, AD=6米,现想从此板材中截出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,米,∠EHG=45°.经研究,只有当点E、 F、 G分别在边AD、 AB、 BC上时,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能截出符合要求的部件.试问能否截得符合要求的面积尽可能大的四边形EFGH部件?若能,求出截得的四边形EFGH 部件的面积;若不能,请说明理由.图1 图2 图3思路:1. 第(2)题的模型是“打台球”两次碰壁问题,依据光的反射原理.2. 第(3)题需先设AF的长并求解,再验证点H在矩形内部,然后计算面积.例3.如图1,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8, OE=17.抛物线y=x2-3x+m与y轴交于点A,抛物线的对称轴与x轴交于点B,与CD交于点K.(1) 将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.①求点F的坐标;②请直接写出抛物线的函数表达式;(2) 将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连结OG,折痕与OG交于点H,点M是线段EH上的一个动点(不与点H重合),连结MG, MO,过点G作GP⊥OM于点P,交EH于点N,连结ON.点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2,在点M的运动过程中,S1·S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化的范围;若不变,请直接写出这个值.温馨提示: 考生可以根据题意,在备用图中补充图形,以便作答.图1 备用图思路:1. 第(1)题中点F的位置是由A、 B两点确定的,A、 B两点的坐标都隐含在抛物线的解析式中.2. 第(2)题思路在画示意图过程中,点G是关键点.以E为圆心,EO为半径画弧,交CD于点G.例 4.如图,已知平行四边形ABCD的三个顶点A(n, 0)、 B(m, 0)、 D(0,2n)(m>n>0),作平行四边形ABCD关于直线AD的对称图形AB1C1 D.(1) 若m=3,试求四边形CC1B1B面积S的最大值;(2) 若点B1恰好落在y轴上,试求的值.思路:1. 第(1)题先说理再计算,说理四边形CC1B1B是矩形.2. 第(2)题根据AB1=AB列关于m、 n的方程,整理就可以得到m与n的关系.例5.如图,在平面直角坐标系中,抛物线y=-x2+bx+c经过点A(3, 0)和点B(2, 3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO=.(1) 求这条抛物线的表达式及对称轴;(2) 连结AB、 BC,求∠ABC的正切值;(3) 若点D在x轴下方抛物线的对称轴上,当S△ABC =S△ADC时,求点D的坐标.解析:1. 直觉告诉我们,△ABC是直角三角形.2. 第(3)题的意思可以表达为: B、 D在直线AC的两侧,到直线AC的距离相等.于是我们容易想到,平行线间的距离处处相等.例6.如图,半圆O的直径AB=10,有一条定长为6的动弦CD在弧AB上滑动(点C、D分别不与点A、 B重合),点E、 F在AB上,EC⊥CD, FD⊥CD.(1) 求证:EO=FO;(2) 连结OC,如果△ECO中有一个内角等于45°,求线段EF的长;(3) 当动弦CD在弧AB上滑动时,设变量CE=x,四边形CDFE的面积为S,周长为l,问:S与l是否分别随着x变化而变化?试用所学过的函数知识直接写出它们的函数解析式及函数定义域,以说明你的结论.思路:1. 用垂径定理和平行线等分线段定理证明点O是EF的中点.2. 第(2)题的△ECO中,∠ECO是定值,45°的角分两种情况.3. 第(3)题用x表示OE的长,在△ECO中,∠ECO是定值.例7.直线y=2x+m与抛物线y=ax2+ax+b都过点M(1, 0),且a<b.(1) 求抛物线顶点Q的坐标(用含a的式子表示);(2) 试说明抛物线与直线有两个交点;(3) 设抛物线与直线的另一个交点为N.①若-1≤a≤-时,求MN的取值范围;②求△QMN的面积最小值.思路:1. 将M(1, 0)分别代入直线和抛物线的解析式,可以确定m的值,用a表示b.2. 联立直线与抛物线的解析式,消去y,得到关于a的一元二次方程,判断Δ>0.3. 第(3)题①,分别求a=-1和a=-时直线与抛物线的交点M、 N的坐标,再求MN的长,两个MN的长,就是MN的取值范围的两端值.例8.已知Rt△EFP和矩形ABCD如图1摆放(点P与点B重合),点F、 B(P)、 C 在同一直线上,AB=EF=6cm, BC=FP=8cm, ∠EFP=90°.如图2, △EFP从图1位置出发,沿BC方向匀速运动,速度为1cm/s, EP与AB交于点G;同时,点Q从点C出发,沿CD方向匀速运动,速度为1cm/s.过点Q作QM⊥BD,垂足为H,交AD于点M,连结AF、 PQ.当点Q停止运动时,△EFP也停止运动.设运动时间为t(s)(0<t<6).解答下列问题:(1) 当t为何值时,PQ∥BD?(2) 设五边形AFPQM的面积为y(cm2),求y与t之间的函数关系式;(3) 在运动过程中,是否存在某一时刻t,使S五边形AFPQM ∶S矩形ABCD=9∶8?若存在,求出t的值;若不存在,请说明理由;(4) 在运动过程中,是否存在某一时刻t,使点M在线段PG的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.图1 图2思路:1. 把线段BP、 PC、 CQ、 DQ的长用t表示出来.再把线段BG、 DM的长用t表示出来.2. 用割补法求五边形AFPQM的面积,等于直角梯形减去两个直角三角形的面积.3. 第(3)题用第(2)题的结果,直接解方程就可以了.4. 第(4)题是根据MP2=MG2列方程,需要构造以MP为斜边的直角三角形.例9.如图1,在平面直角坐标系中,过原点O及点A(8, 0)、 C(0, 6)作矩形OABC,连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从点A出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.(1) 如图1,当t=3时,求DF的长;(2) 如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值;(3) 连结AD,当AD将△DEF分成的两部分的面积比为1∶2时,求相应的t的值.图1 图2思路;1. 作DM⊥AB于M, DN⊥OA于N,那么△NDF与△MDE的相似比为3∶4.2. 面积比为1∶2要分两种情况讨论.把面积比转化为两个同高三角形底边的比.3. 过点E作OA的平行线,构造“8字型”相似,这样就把底边的比利用起来了.例10.如图1,二次函数y=x2+bx+c的图象与x轴交于A、 B两点,与y轴交于点C, OB=OC.点D在函数图象上,CD∥x轴,且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.(1) 求b、 c的值;(2) 如图1,连结BE,线段OC上点F关于直线l的对称点F'恰好在线段BE上,求点F的坐标;(3) 如图2,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.图1 图2思路:1. 由已知抛物线的解析式可得C(0, c),再用c表示B、 D两点的坐标,然后将B、 D代入抛物线的解析式列关于b、 c的方程组.2. 第(2)题: 通过点C、 F分别与点D、 F'关于直线l对称,得到点F'是BE的中点,从而求得点F的坐标.3. 第(3)题: 设点P的横坐标为m,用m表示点M、 N的坐标,进而用m表示线段PM、 PN、 PA的长,根据两个三角形的面积相等,求出PN边上的高QH.最后讨论NQ与QH的关系.例11.如图,在平面直角坐标系中,直线y=12x+2与x 轴交于点A,与y 轴交于点C.抛物线y=-x 2+bx+c 经过A 、 C 两点,与x 轴的另一个交点为点B.(1) 求抛物线的函数表达式;(2) 点D 为直线AC 上方抛物线上一动点.① 连结BC 、 CD.设直线BD 交线段AC 于点E, △CDE 的面积为S 1, △BCE 的面积为S 2,求 12S S 的最大值; ② 过点D 作DF ⊥AC,垂足为F,连结CD.是否存在点D,使得△CDF 中的某个角恰好等于∠BAC 的2倍?若存在,求出点D 的坐标;若不存在,请说明理由.图1 备用图思路: 1. △CDE 与△BCE 是同高三角形,面积比等于底边的比.构造“8字型”,把底边的比转化为竖直线段的比.2. 第(3)题的第一种情况∠DCF=2∠BAC,过点C 作x 轴的平行线,通过内错角相等,再作轴对称的角,很容易找到点D 的位置.3. 第(3)题的第二种情况∠CDF=2∠BAC,先要探求2∠BAC的大小(正切值),如果这一步探究不出来,基本上进行不下去.例12.已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O 顺时针旋转60°,如题图1,连接BC.(1)填空:∠OBC= ;(2)如图1,连接AC,作OP⊥AC,垂足为P,求OP的长度;(3)如图2,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒,设运动时间为x秒,△OMN 的面积为y,求当x为何值时y取得最大值?最大值为多少?思路:(1)由旋转的性质可以证明△OBC是等边三角形,从而可得∠OBC的度数;(2)求出△AOC的面积,利用三角形的面积公式计算即可;(3)分三种情形讨论求解即可解决问题:①当0<x≤83时,M在OC上运动,N在OB上运动,此时过点N作NE⊥OC且交OC于点E,利用面积公式表示出△OMN的面积(y值);②当8 3<x≤4时,M在BC上运动,N在OB上运动.作MH⊥OB于H,利用∠CBO=60°表示出MH,再利用面积公式表示出△OMN的面积(y值);③当4<x≤4.8时,M、N都在BC上运动,作OG⊥BC于G,易求OG,再利用面积公式表示出△OMN的面积(y值),最后分别求出三种情况下面积最大值,从而求出整个运动过程中y的最大值.例13. 在平面直角坐标系中,抛物线2y ax bx c=++交x轴于A、B两点,交y轴于点C(0,43-),OA=1,OB=4,直线l过点A,交y轴于点D,交抛物线于点E,且满足tan∠OAD=34.(1)求抛物线的解析式;(2)动点P从点B出发,沿x轴正方向以每秒2个单位长度的速度向点A运动,动点Q从点A出发,沿射线AE以每秒1个单位长度的速度向点E运动,当点P运动到点A时,点Q也停止运动,设运动为t秒.①在P、Q的运动过程中,是否存在某一时刻t,使得△ADC与△PQA相似,若存在,求出t的值;若不存在,请说明理由;②在P、Q的运动过程中,是否存在某一时刻t,使得△APQ与△CAQ的面积之和最大?若存在,求出t的值;若不存在,请说明理由.思路:本题是代数几何综合题,以平面直角坐标系为背景,考查了求二次函数解析式,二次函数的性质,,方程组的解法,几何图形面积的表示,相似三角形的判定与性质,分类讨论思想,三角形的面积的最值问题,综合性强,难度大,解题的关键是需要学生有良好的运算能力及分析问题和解决问题的能力,还得富有耐心.(1)利用A、B、C三点的坐标确定二次函数的解析式.(2)利用题目的已知条件表示出相关线段的长,①中利用三角函数值探索出∠PAQ=∠ACD,再根据题目中的要求使得△ADC与△PQA相似,进行分类讨论得到对应线段成比例,列出关于t的方程求解即可;②直接利用三角形的面积公式列出△APQ与△CAQ 的面积之和与时间t之间的函数关系式,再将所得的二次函数的解析式配方确定最值即可得到答案.。
函数图象中的存在性问题—因动点产生的面积问题

函数图象中的存在性问题—因动点产生的面积问题函数图像中的存在性问题是函数图像是否存在的研究。
在研究函数图像的存在性时,我们通常会考虑到以下几个问题:函数是否有定义域和值域,函数是否连续,函数是否可导等等。
其中,因动点产生的面积问题是函数图像的一个特殊存在性问题。
考虑一个动点在平面上运动,其轨迹为函数的图像,我们可以通过计算该轨迹所围成的面积来研究函数图像的存在性。
首先,让我们考虑一个较简单的函数图像,例如:y=x。
当动点在平面上矩形区域内运动时,其轨迹就可以看作是函数y=x的图像。
我们可以将矩形区域分成无数个小长方形,并计算每个小长方形所围成的面积的和。
当矩形区域趋近于函数图像所占据的面积时,这个和就可以逼近函数图像所围成的面积。
如果这个和存在且为有限值,则可以认为函数图像所围成的面积存在。
然而,对于一些函数图像,存在动点产生的面积问题可能并不存在。
例如:y=1/x。
当动点运动到x=0的位置时,函数图像与x轴相切,不再围成一个有限的面积。
在这种情况下,我们无法通过动点产生的面积来研究函数图像的存在性。
对于一些较为复杂的函数图像,动点产生的面积问题可能会更加具有挑战性。
例如:y = sin(x)。
当动点在平面上运动时,函数图像会在一些位置出现多个极大值和极小值。
在这种情况下,计算动点产生的面积变得更为复杂,可能需要使用更高级的数学工具来解决。
总之,动点产生的面积问题是函数图像存在性问题的一个特殊情况。
通过计算动点所产生的面积,我们可以研究函数图像的存在性。
然而,对于一些复杂的函数图像,动点产生的面积问题可能并不存在或更加困难。
因此,在研究函数图像的存在性时,我们需要综合考虑多个因素,并使用合适的数学工具来解决。
动点问题之面积最值问题

不重合),过点������ 作������轴的平行线交������������于点������.
二 次
(1)求该二次函数的解析式: (2)若设点������的横坐标为������,用含m的代数式表示线段������������的长;
函
(3)求△ ������������������面积的最大值,并求此时点������的坐标.
练习1:如图,在平面直角坐标系中,点������、������的坐标分别为 −1 , 0 , (0 ,
−3 ) ,点������在������轴上.已知某二次函数的图象经过������、������、������三点,且它的对称轴
为直线 ������ = 1 ,点������为直线������������下方的二次函数图象上的一个动点(点 ������ 与 ������、������
动点问题之面积最值问题综述:动点问题是初中数学问题中的一个大类的问 题,因为其具有动态性、变化性的特点,特别能考查学生的数学能力,所以 备受中考出题老师的青睐。主要包括线段的最值问题、利润的最值问题、面 积的最值问题等,多数考查一次函数或二次函数的性质,题目难度中等偏难, 同学们感到这类问题棘手多数是因为没能掌握这类问题的解题套路(方法和 技巧)。昊南老师查阅大量的中考真题后发现,此类问题单独考查的情形比 较少,大多数会做为二次函数压轴题的第二问或第三问出现,分值为3分或4 分,本文昊南老师和大家一同探讨一下面积最值的问题。
数
最
值Hale Waihona Puke 问题【解析】 二 次 函 数 最 值 问 题
七年级上册数学动点问题

七年级上册数学动点问题
动点问题是指在几何图形中,点的坐标发生变化时,研究图形的变化规律的问题。
在七年级上册数学中,动点问题主要包括以下几种类型:
1. 动点轨迹问题:当一个点在平面内按照一定的规律移动时,求这个点的轨迹。
例如,已知点A(x, y)在直线y = kx + b上移动,求点A的轨迹。
2. 动点距离问题:当一个点在平面内按照一定的规律移动时,求这个点到另一个固定点的距离。
例如,已知点A(x, y)在直线y = kx + b上移动,求点A到定点P(a, b)的距离。
3. 动点面积问题:当一个点在平面内按照一定的规律移动时,求这个点与另一个固定点围成的图形的面积。
例如,已知点A(x, y)在直线y = kx + b上移动,求点A与定点P(a, b)围成的三角形的面积。
4. 动点角度问题:当一个点在平面内按照一定的规律移动时,求这个点与另一个固定点连线与某个方向的夹角。
例如,已知点A(x, y)在直线y = kx + b上移动,求点A与定点P(a, b)连线与x轴的夹角。
5. 动点对称问题:当一个点在平面内按照一定的规律移动时,求这个点关于某个固定点的对称点的坐标。
例如,已知点A(x, y)在直线y = kx + b上移动,求点A关于定点P(a, b)的对称点的
坐标。
解决动点问题的关键是找出动点的坐标变化规律,然后根据题目要求求解相应的几何量。
在解题过程中,要注意运用所学的几何知识,如平行线、垂直线、相似三角形等性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、在平面直角坐标系中,已知点A(4,0),点B(0,3),点P从点A出发,以每秒1个单位的速度在x轴上向右平移,点Q从B点出发,以每秒2个单位的速度沿直线y=3向右平移,又P、Q两点同时出发,设运动时间为t秒.(1)当t为何值时,四边形OBPQ的面积为8;(2)连接AQ,当△APQ是直角三角形时,求Q的坐标.2、如图,在下面直角坐标系中,已知A(-4,a),B(-8,0)(1)请用含a的代数式表示△ABO的面积;(2)若a满足关系式(a+4)2≤0,且以点A、B、O为顶点画平行四边形,则请你“利用平移的知识”直接写出符合条件的所有的平行四边形的第四个顶点C的坐标(3)在(2)的条件下,是否存在x轴上的点M(x,0),使△ABM的面积是△ABO的面积的2倍?若存在,求出点M的坐标;若不存在,请说明理由.(4)在(2)的条件下,请你直接写出y轴上的点N的坐标,使△AON的面积是△ABO的面积的3倍3、如图,A,B两点同时从原点O出发,点A以每秒a个单位长度沿x轴的负方向运动,点B以每秒b个单位长度沿y轴的正方向运动.(1)如图1,若|a+2b-5|+(2a-b)2=0,试分别求出1秒钟后,A,B两点的坐标;(2)如图2,延长BA至E,在∠ABO的内部作射线BF交x轴于点C,若∠EAC,∠FCA,∠ABC的平分线交于点G,过点G作BE的垂线,垂足为H,试问∠AGH,∠BGC的大小关系如何?请写出你的结论并证明;(3)如图3,过A,O两点的直线相交于点N,AB的延长线交ON于点M,若∠MAN=∠NOB,∠BAO-∠N=m°,试求∠AMO的度数.4、如图,在平面直角坐标系中,点B、C在x轴上,OB>OC,点A在y轴正半轴上,AD平分∠BAC,交x轴于点D.(1)若∠B=30°,∠C=50°,求∠DAO的度数?(2)试写出∠DAO与∠C-∠B的关系?(不必证明)(3)若点A在y轴正半轴上运动,当点A运动至点P时,请你作出△BPC及其角平分线PQ,并直接写出∠QPO与∠PBC、∠PCB三者的关系?5、如图1,在平面直角坐标系中,A、B两点同时从原点O出发,点A以每秒m个单位长度沿x轴的正方向运动,点B以每秒n个单位长度沿y轴正方向运动.(1)已知运动1秒时,B点比A点多运动1个单位;运动2秒时,B点与A点运动的路程和为6个单位,求m、n;(2)如图2,设∠OBA的邻补角的平分线、∠OAB的邻补角的平分线相交于点P,∠P的大小是否发生改变?若不变,求其值;若变化,说明理由.(3)若∠OBA的平分线与∠OAB的邻补角的平分线的反向延长线相交于点Q,∠Q的大小是否发生改变?如不发生改变,求其值;若发生改变,请说明理由.6、如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD.(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC;(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由;(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)给出下列结论:①DCP BOPCPO∠+∠∠的值不变,②DCP CPOBOP∠+∠∠的值不变其中有且只有一个是正确的,请你找出这个结论并求其值.7、如图,在平面直角坐标系中,已知三点A(0,a),B(b,0),C(b,c),其中a,b,c满足关系式|a-2|+(b-3)2=0,c=2b-a;(1)求a,b,c的值;(2)如果再第二象限内有一点P(m,1),请用含m的式子表示四边形ABOP的面积,若四边形ABOP的面积与△ABC的面积相等,请求出点P的坐标;(3)若B,A两点分别在x轴,y轴的正半轴上运动,设∠BAO的邻补角的平分线和∠ABO的邻补角的平分线相交于第一象限内一点Q,那么,点A,B在运动的过程中,∠Q的大小是否会发生变化?若不发生变化,请求出其值,若发生变化,请说明理由8、在平面直角坐标系中,D(0,-3),M(4,-3),直角三角形ABC的边与x轴分别交于O、G两点,与直线DM分别交于E、F点.(1)将直角三角形ABC如图1位置摆放,请写出∠CEF与∠AOG之间的等量关系:(2)将直角三角形ABC如图2位置摆放,N为AC上一点,∠NED+∠CEF=180°,请写出∠NEF与∠AOG 之间的等量关系,并说明理由.9、已知如图,在平面直角坐标系中有四点,坐标分别为A(-4,3)、B(4,3)、M(0,1)、Q(1,2),动点P在线段AB上,从点A出发向点B以每秒1个单位运动.连接PM、PQ并延长分别交x轴于C、D两点(如图).(1)在点P移动的过程中,若点M、C、D、Q能围成四边形,则t的取值范围是,并写出当t=2时,点C的坐标(2)在点P移动的过程中,△PMQ可能是轴对称图形吗?若能,请求出符合条件的点P的坐标;若不能,请说明理由.(3)在点P移动的过程中,求四边形MCDQ的面积S的范围10、如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a-2|+(b-3)2=0,(c-4)2≤0(1)求a、b、c的值;(2)如果在第二象限内有一点P(m,12),请用含m的式子表示四边形ABOP的面积;(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.11、如图1,在平面直角坐标系中,△AOB是直角三角形,∠AOB=90°,斜边AB与y轴交于点C.(1)若∠A=∠AOC,求证:∠B=∠BOC;(2)如图2,延长AB交x轴于点E,过O作OD⊥AB,若∠DOB=∠EOB,∠A=∠E,求∠A的度数;(3)如图3,OF平分∠AOM,∠BCO的平分线交FO的延长线于点P,∠A=40°,当△ABO绕O点旋转时(斜边AB与y轴正半轴始终相交于点C),问∠P的度数是否发生改变?若不变,求其度数;若改变,请说明理由.12、在平面直角坐标系中,横坐标、纵坐标都为整数的点叫做整点.设坐标轴的单位长度为1cm,整点P从原点O出发,速度为1cm/s,且整点P只做向右或向上运动,则运动1s后它可以到达(0,1)、(1,0)两个整点;它运动2s后可以到达(2,0)、(1,1)、(0,2)三个整点;运动3s后它可以到达(3,0)、(2,1)、(1,2)、(0,3)四个整点;…请探索并回答下面问题:(1)当整点P从点O出发4s后可以到达的整点共有个(2)在直角坐标系中描出:整点P从点O出发8s后所能到达的整点,并观察这些整点,说出它们在位置上有什么特点?(3)当整点P从点O出发 s后可到达整点(13,5)的位置.12、如图,△OAB的三个顶点坐标分别为O(0,0),A(5,O)B(2,4).(1)求△ABO的面积,(2)若B(2,4),O(0,0)不变,M点在x轴上,M点在什么位置时,△OBM的面积是△OAB面积的2倍,并说明理由.13、如图,在平面直角坐标系中,A,B,C三点的坐标分别为(0,1),(3,0),(2,2)(1)求△ABC的面积;(2)如果在第二象限内有一点P(a,2),试用含a的式子表示四边形ABOP的面积;(3)在(2)的条件下是否存在点P,使得四边形ABOP的面积与△ABC的面积相等?若存在,请求出点P 的坐标;若不存在,请说明理由14、已知点A(a,0)、B(b,0),且(a+4)2+|b-2|=0.(1)求a,b的值;(2)在y轴上是否存在点C,使得△ABC的面积是12?若存在,求出点C的坐标;若不存在,请说明理由;(3)点P是y轴正半轴上一点,且到x轴的距离为3,若点P沿x轴负半轴以每秒1个长度单位平行移动至Q,当运动的时间t为多少秒时,四边形ABPQ的面积S为15个平方单位?写出此时Q点的坐标.15、如图建立平面直角坐标系,长方形OABC中,A(8,0),点C(0,10),点P从原点出发,以每秒1个单(2)在移动过程中,当点P 到x 轴距离为4个单位长度时,则点P 运动的时间为 秒.(3)若点P 出发11秒时,点Q 以每秒2个单位长度的速度也沿着O-C-B-A-O 的路线运动到点O 停止,求t 为何值时点P 、Q 在运动路线上相距的路程为5个单位长度?15、 如图,长方形OABC 中,O 为平面直角坐标系的原点,A ,C 两点的坐标分别为(3,0),(0,5),点B 在第一象限内.(1)如图,请直接写出点B 的坐(2)若过点C 的直线CD 交长方形OABC 的边于点D ,且把长方形OABC 的周长分为3:1两部分,求点D 的坐标.16、如图1,点A (a ,6)在第一象限,点B (0,b )在y 轴负半轴上,且a ,b 满足:(240a b −++=(1)求△AOB 的面积.(2)若线段AB 与x 轴相交于点C ,在点C 的右侧,x 轴的上是否存在点D ,使S △ACD =S △BOC ?若存在,求出D 点坐标;若不存在,请说明理由.(3)如图2,若∠AOx 轴=60°,射线OA 绕O 点以每秒4°的速度顺时针旋转到OA ′,射线OB 绕B 点以每秒10°的速度顺时针旋转到O ′B ,当OB 转动一周时两者都停止运动.若两射线同时开始运动,在旋转过程中,经过多长时间,OA ′∥O ′B ?17、在直角坐标系中,A (-4,0),B (2,0),点C 在y 轴正半轴上,且S △ABC =18. (1)求点C 的坐标;(2)是否存在位于坐标轴上的点P ,S △APC =12S △PBC ?若存在,请求出P 点坐标;若不存在,说明理由.18、在平面直角坐标系中,A(-1,0),B(0,2),点C在x轴上.(1)如图(1),若△ABC的面积为3,则点C的坐标为(2)如图(2),过点B点作y轴的垂线BM,点E是射线BM上的一动点,∠AOE的平分线交直线BM于F,OG⊥OF且交直线BM于G,当点E在射线BM上滑动时,BEOBOF∠∠的值是否变化?若不变,请求出其值;若变化,请说明理由.19、在直角坐标系中,设一质点M自P0(1,0)处向上运动1个单位至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去,设Pn(x n,y n),n=1,2,3,….(1)依次写出x1、x2、x3、x4、x5、x6的值;(2)计算x1+x2+…+x8的值;(3)计算x1+x2+…+x2003+x2004的值.20、如图:一个粒子在第一象限内及x轴,y轴上运动,在第一分钟内,它从原点运动到(1,0),第二分钟从(1,0)运动到(1,1),而后它接着按图中箭头所示在与x轴,y轴平行的方向来回运动,且每分钟移动1个长度单位.(1)当粒子所在位置分别是(1,1),(2,2),(3,3),(4,4)时,所经过的时间分别是多少?(2)在第2004分钟后,这个粒子所在的位置的坐标是多少?21、问题:如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系?(1)小明画出如图的图形,并写出问题:如图,点P在∠AOB的内部,过点P作PE⊥OA,PF⊥OB,垂足分别为E,F,求∠P的度数.请你帮助小明完成解题过程.(2)小刚说,这道题应该还有一种情况:点P在∠AOB的外部.他说的对吗?22、如图,长方形ABCD在平面直角坐标系中,点A(1,8),B(1,6),C(7,6).(1)请直接写出D点的坐标(2)连接线段OB、OD、BD,请直接求出的面积(3)若长方形ABCD以每秒1个单位的速度向下运动,设运动的时间为t秒,问是否存在某一时刻,△OBD的面积与长方形ABCD的面积相等?若存在,请求出t的值;若不存在,请说明理由.23、在△ABC中,∠A=∠C,点E在BC边上,过点E作射线EF∥AB交AC于点F,EM交AC于点M,点N 在射线EF上,且∠EMN=∠ENM,设∠ABC=α,∠MEN=β.(1)如图1,若点M在线段AF上,α=60°,β=30°,求∠FMN的度数;(2)若点M在AC边上(不与点A、C、F重合),α、β为任意角度,探究∠FMN与α、β的数量关系,请在图2中画出图形,并说明理由.24、如图,在△A B C中,AB=AC,BD、CE分别是两腰上的高,且BD、CE相交于O.(1)请你写出三类不同的正确的结论;(2)设∠CBD=α,∠A=β,试找出α与β之间的一种关系等式,并给予适当的说明(友情提示:∠ABC=∠ACB).25、.已知,在四边形ABCD中.∠A=∠C=90゜.(1)求证:∠ABC+∠ADC=180゜;(2)如图1,若DE平分∠ADC,BF平分∠ABC外角,写出DE与BF的位置关系,并证明;(3)如图2,若BF、DE分别平分∠ABC、∠ADC的外角,写出BF与DE的位置关系,并证明.26、如图,四边形ABCD中,AB∥CD,P为BC上一点,设∠CDP=α,∠CPD=β,当点P在BC上移动时,猜想α,β与∠B的关系,并说明理由.27、如图,锐角△ABC中,高BE、CF交于点H.(1)若∠BAC=70°,求∠BHC的度数;(2)直接给出四条线段AF、HE、AC、CH之间的数量关系;(3)若AD平分∠BAC交BC于D,AD、CF交于点K,HG平分∠BHC交BC于G.求证:HG∥AD.28、1)如图1,AC平分∠DAB,∠1=∠2,试说明AB与CD的位置关系,并予以证明;(2)如图2,在(1)的条件下,AB的下方两点E,F满足∠EBF=2∠ABF,CF平分∠DCE,若∠F的2倍与∠E 的补角的和为190°,求∠ABE的度数;(3)如图3,在前面的条件下,若P是BE上一点,G是CD上任一点,PQ平分∠BPG,PQ∥GN,GM平分∠DGP,下列结论:①∠DGP-∠MGN的值不变;②∠MGN的度数不变.可以证明,只有一个是正确的,请你作出正确的选择并求值.29、如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°(1)求证:AB∥CD;(2)如图2,由三角形内角和可知∠E=90°,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE 与∠MCD否存在确定的数量关系?并证明;(3)如图3,P为线段AC上一定点,点Q为直线CD上一动点,①当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?猜想结论并说明理由.②当点Q在射线CD的反向延长线上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?猜想结论,不需说明理由.30、如图,直线AB∥C D.(1)在图1中,∠B M E、∠E,∠EN D的数量关系为:;(不需证明)在图2中,∠B M F、∠F,∠FN D的数量关系为:(不需证明)(2)如图3,NE平分∠FN D,MB平分∠FM E,且2∠E与∠F互补,求∠FM E的大小.(3)如图4中,∠B M E=60°,EF平分∠M EN,NP平分∠EN D,EQ∥N P,则∠FEQ的大小是否发生变化?若变化,说明理由;若不变化,求∠FEQ的度数.31、如图,在平面直角坐标系xOy中,A,B,C是坐标轴上的定点,平移线段AB得到线段CD,使点A与点C 对应,点B与点D对应.(1)画出线段CD,并写出画法;(2)点P是x轴上的动点(不与点B,C重合),设∠PAC=α,∠PBD=β,∠APB=θ.①当点P在线段BC上时,求证:θ=α+β;②当点P在线段CB(BC)的延长线上时,①中的结论是否成立?并说明理由32、将两个大小不同的含30°角的三角板的直角顶点O重合在一起,保持△COD不动,将△AOB绕点O旋转,设射线AB与射线DC交于点F.(1)如图①,若∠AOD=120°,①AB与OD的位置关系②∠AFC的度数=(2)如图②当∠AOD=130°,求∠AFC的度数.(3)由上述结果,写出∠AOD和∠AFC的关系(4)如图③,作∠AFC、∠AOD的角平分线交于点P,求∠P的度数.33、(1)如图①,∠BAD的平分线AE与∠BCD的平分线CE交于点E,AB∥CD,∠ADC=40°,∠ABC=30°,求∠AEC的大小;(2)如图②,∠BAD的平分线AE与∠BCD的平分线CE交于点E,∠ADC=m°,∠ABC=n°,求∠AEC的大小;(3)如图③,∠BAD的平分线AE与∠BCD的平分线CE交于点E,则∠AEC与∠ADC、∠ABC之间是否仍存在某种等量关系?若存在,请写出你得结论,并给出证明;若不存在,请说明理由.34、已知:如图(1)所示,D是∠ABC的角平分线和∠ACB的角平分线的交点,过点D作EF∥BC,交AB于E,交AC于F.(1)请你确定EF、BE、CF三者之间的关系,并加以证明.(2)如图(2)所示,当点D为∠ABC的外角的角平分线和∠ACB的外角的角平分线的交点时,EF、BE、CF 三条线段还满足上面的关系吗?若满足,直接写出关系式;若不满足,请写出新的关系式并加以证明.(3)如图(3)所示,当点D为∠ABC的角平分线和∠ACB外角平分线的交点时,EF、BE、CF三条线段还满足上面的关系吗?若满足,直接写出关系式;若不满足,请写出新的关系式并加以证明.35、如图1,在平面直角坐标系中,点A、B的坐标分别为(-1,0)、(3,0),现将线段AB向上平移2个单位,再向右平移1个单位,得到线段CD,连接AC、BD.(1)求点C、D的坐标及四边形ABDC的面积S四边形ABDC;(2)如图2,在y轴上是否存在一点P,连接PA、PB,使S△PA B=S四边形ABDC,若存在这样的一点,求出点P的坐标;若不存在,试说明理由.(3)若点Q在线段CD上移动(不包括C、D两点),QO与线段CD、AB所成的角∠2与∠1如图3所示,给出下列两个结论:①∠2+∠1的值不变②12∠∠的值不变,其中只有一个结论是正确的,请你找出这个结论36、将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):(1)①若∠DCE=45°,则∠ACB的度数为;②若∠ACB=140°,求∠DCE的度数;(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.。
