【题03】骑士游历问题

合集下载

骑士招聘考试题及答案大全

骑士招聘考试题及答案大全一、选择题（每题2分，共20分）1. 中世纪骑士的主要装备是什么？A. 长矛B. 盾牌C. 铠甲D. 马匹答案：C2. 骑士精神中强调的“勇敢”通常不包括以下哪一项？A. 面对困难不退缩B. 保护弱者C. 无故挑衅他人D. 忠诚于领主答案：C3. 下列哪项不是成为骑士的基本条件？A. 出生于贵族家庭B. 经过正式的骑士受封仪式C. 必须拥有自己的领地D. 接受过正规的骑士训练答案：C4. 中世纪骑士的铠甲通常由什么材料制成？A. 皮革B. 铁C. 铜D. 钢答案：D5. 骑士在战斗中通常使用哪种武器？A. 弓箭B. 长剑C. 斧头D. 匕首答案：B6. 骑士的马匹通常接受过哪些训练？A. 负重训练B. 速度训练C. 战斗训练D. 所有以上选项答案：D7. 骑士的盾牌上通常会有什么？A. 家族纹章B. 宗教符号C. 个人标志D. 所有以上选项答案：D8. 骑士的职责不包括以下哪一项？A. 参与战争B. 维护地方治安C. 经商贸易D. 保护领地答案：C9. 中世纪骑士的马通常是什么品种？A. 阿拉伯马B. 蒙古马C. 英国纯血马D. 西班牙马答案：A10. 骑士的铠甲中，锁子甲的主要作用是什么？A. 防御刀剑攻击B. 防御远程箭矢C. 提供身体支撑D. 增加骑士的威慑力答案：A二、填空题（每题2分，共20分）11. 骑士的八大美德包括：________、诚实、怜悯、荣誉、英勇、牺牲、精神和公正。

答案：谦卑12. 中世纪骑士的最高荣誉是被封为________。

答案：爵士13. 骑士在战斗中通常会高喊自己的________以示身份。

答案：战斗口号14. 骑士的铠甲中，板甲是________世纪后期发展起来的。

答案：1515. 骑士的马被称为________，是骑士的重要伙伴。

答案：战马16. 骑士的长剑通常有双刃，用于________。

答案：刺击和劈砍17. 骑士的头盔通常带有________，以保护面部。

马步遍历问题与骑士巡游问题的回溯算法

一
＿
＿
＿
１回溯算法的实现
１为解决这个问题，．１我们把棋盘的横坐标定为ｉ，纵坐标定为ｊｉ和ｏｊ的取值范围是从１ＳＺ。到ＩＥ当某个骑士占了位置（ｊ，ｉ）其在这个位，时置上可以向８个方向以“ 型” Ｌ移动，它们分别是：
ｆｒｎ０ｉ８ｉ＋ｏ（ｔ＝；；）ｉｉ＜＋ｆｒｎ：８＋）ｏ（ｔ０＜＋ｉｊｔａ Ⅵ 】ＯｒｊＫ＝；
ｆ（ｔ＝；＜ｅｒｏｎＳｂｅ＋ｏｉＯｅ＝ｕＰｉｔｕ；＋１ｒｎｅ
｛
）
ｏｔａｓｅｍ＆ｏｅａｏ＜（ｔａｒｐｒｔ＜ｏｒｍ＆ｏｔｕ，ｏｓＰｉｔｌｒｓｅｕｐｔｃｎｔｏｎ＆ｐ）（ｏｔｕ＜ｕｐｔ＜＜＜ｌ．ｐｓ＜，ｐｘｏ＜＜＜ｌ．ｐｓ＜’；ｐｙｏ＜
｝Ｐｉｔｐｒｔｒ（ｎｔｏｔｐｅｎｔｏｎ＆ｒ）ｏｎｅａｏ－ｅｓＰｉ＆ｌ，ｓＰｉｔｐｏｏｎｏ｛
ＰｉｔｔＰｏｎ；ｏｎｎｉｔｒ
ｒｎｏｎ．ｐｓ＝ｌｘｐｓ— ｒ．ｓｔＰｉｔｘｏｐ．ｏｐｘｐｏ；
２１年０１
第２期７
ＳＩＮＥ＆ＴＣＮＬＧＦＲＴＯＣＥＣＥＨＯＯＹＩＯＭＡＩＮＮ
ＯＩ论坛０Ｔ
科技信息
马步遍历问题与骑士巡游问题的回溯算法
王力强
（陕西省城市经济学校
陕西
西安７０６）１０８
【摘要】马步遍历问题与骑士巡游（ｎｈｓｏｒ问题是指在有８８ｋｉｔｕ）ｇｔｘ方格的国际象棋棋盘上进行奇异的骑士“ Ｌ型”Ｌｓａｅ）（ —ｈｐｄ移动的问题。而骑士巡游问题实际是带有约束条件的马步遍历问题，因此在用程序求解的时候可以一并求解。本文给出求解这一问题的回溯算法之

【题5】骑士游历问题(1)

【题5】骑士游历问题（1）设有一个n*m的棋盘(2≤n≤50，2≤m≤50)，如图10.2.1。

在棋盘上任一点有一个中国象棋马，图10.2.1马走的规则为：1.马走日字2.马只能向右走。

即如图10.2.2所示：图10.2.2问题：当N，M 输入之后，找出一条从左下角到右上角的路径。

例如：输入N=4，M=4。

对应的路径如图10.2.3所示：图10.2.3输出：路径的格式：(1，1)->(2，3)->(4，4)若不存在路径，则输出"no"题解1.计算跳马方向按题意，中国象棋马共有四个跳动方向图10.2.4我们通过子程序move（x，y，x1，y1，i）计算中国象棋马从（x，y）出发，沿i方向跳至（x1，y1）的过程procedure move(x，y：byte；var x1，y1：byte；i：integer)；begincase i of ｛根据方向计算跳后位置｝1：begin x1←x-2；y1←y+1；end；2：begin x1←x-1；y1←y+2；end；3：begin x1←x+1；y1←y+2；end；4：begin x1←x+2；y1←y+1；end；end；{case}end；{move}2.从起始点出发，沿方向序列输出路径设varpath：array[1..1000] of integer；{path[i]—第i步的方向。

初始时path 清零}由(1，1)至（n，m）的路径长度为k。

我们通过调用print(k)过程输出该条路径。

procedure print(k：integer)；varx，y，x0，y0：byte；i：integer；beginx←1； y←1；｛从（１，１）出发｝write(’(’，x，’，’，y，’)’)；for i←1 to k do ｛顺序输出长度为k的跳动路线｝beginmove(x，y，x0，y0，path[i])；｛第i步由（x,y）跳至（x0,y0）｝ write(’=>(’，x0，’，’，y0，’)’)；x←x0； y←y0； {从（x0,y0）继续往下跳}end；{for}writelnend；{print}3.回溯搜索状态：起跳位置（x，y）和步数k，即准备从（x，y）出发跳第k步；目标：（x，y）为目的地（n，m）。

Knight_Tour骑士走棋盘【马的Hamilton周游路线问题】

马的Hamilton周游路线问题-又名骑士走棋盘--------------------------来源：《计算机算法设计与分析（第3版）·王晓东》P44 算法实现题2-4 马的Hamilton周游路线问题--------------------------问题描述：8*8的国际象棋棋盘上的一只马，恰好走过除起点外的其它63个位置各一次，最后回到起点，这条线路成为马的一条Hamilton周游路线。

说明：骑士旅游（Knight tour）在十八世纪初倍受数学家与拼图迷的注意，它什么时候被提出已不可考，骑士的走法为西洋棋的走法，骑士可以由任一个位置出发，它要如何走完[所有的位置？解法：骑士的走法，基本上可以使用递回来解决，但是纯綷的递回在维度大时相当没有效率，一个聪明的解法由J.C. Warnsdorff在1823年提出，简单的说，先将最难的位置走完，接下来的路就宽广了，骑士所要走的下一步，「为下一步再选择时，所能走的步数最少的一步。

」，使用这个方法，在不使用递回的情况下，可以有较高的机率找出走法（找不到走法的机会也是有的）。

------------------------------PS：下面代码在Visual C++ 6.0中编译通过，无警告，无报错！Ps：代码来源《经典算法大全》（电子书PDF）P13------------------------------#include <stdio.h>int board[8][8] = {0};int main(void) {int startx, starty;int i, j;printf("输入起始点：");scanf("%d %d", &startx, &starty);if(travel(startx, starty)) {printf("游历完成！\n");}else {printf("游历失败！\n");}for(i = 0; i < 8; i++) {for(j = 0; j < 8; j++) {printf("%2d ", board[i][j]);}putchar('\n');}return 0;}int travel(int x, int y) {// 对应骑士可走的八个方向int ktmove1[8] = {-2, -1, 1, 2, 2, 1, -1, -2}; int ktmove2[8] = {1, 2, 2, 1, -1, -2, -2, -1}; // 测试下一步的出路int nexti[8] = {0};int nextj[8] = {0};// 记录出路的个数int exists[8] = {0};int i, j, k, m, l;int tmpi, tmpj;int count, min, tmp;i = x;j = y;board[i][j] = 1;for(m = 2; m <= 64; m++) {for(l = 0; l < 8; l++)exists[l] = 0;l = 0;// 试探八个方向for(k = 0; k < 8; k++) {tmpi = i + ktmove1[k];tmpj = j + ktmove2[k];// 如果是边界了，不可走if(tmpi < 0 || tmpj < 0 || tmpi > 7 || tmpj > 7) continue;// 如果这个方向可走，记录下来if(board[tmpi][tmpj] == 0) {nexti[l] = tmpi;nextj[l] = tmpj;// 可走的方向加一个l++;}}count = l;// 如果可走的方向为0个，返回if(count == 0) {return 0;}else if(count == 1) {// 只有一个可走的方向// 所以直接是最少出路的方向min = 0;}else {// 找出下一个位置的出路数for(l = 0; l < count; l++) {for(k = 0; k < 8; k++) {tmpi = nexti[l] + ktmove1[k];tmpj = nextj[l] + ktmove2[k];if(tmpi < 0 || tmpj < 0 ||tmpi > 7 || tmpj > 7) {continue;}if(board[tmpi][tmpj] == 0)exists[l]++;}}tmp = exists[0];min = 0;// 从可走的方向中寻找最少出路的方向for(l = 1; l < count; l++) {if(exists[l] < tmp) {tmp = exists[l];min = l;}}}// 走最少出路的方向i = nexti[min];j = nextj[min];board[i][j] = m;}return 1;}。

骑士游历问题算法的研究

骑士游历问题算法的研究惠燕;潘煜【摘要】Knight travel problem is a classical mathematical problem. Its thought contributes to the circuit diagram design and image encryption.ff it can be programmed which will have great help in other application fields,it made mathematical model abstraction through the study on the rules of knight travel problems, researched on the direction and the reached conditions of knight travel, knight's moving was abstracted into mathematical expressions, then mapped to the corresponding data structures required in the program,and at last,using JAVA language realized knight travelled graphic demonstration of dynamic processes.%骑士游历问题是一个经典的数学问题.其思想在电路图的设计及图像加密等方面都有帮助,如果能将骑士游历问题算法通过计算机语言程序化将对其在其他领域中的应用有极大帮助.通过研究骑士游历的规则对问题进行数学模型抽象,通过研究骑士游历的方向与可到达情况,将骑士的空间移动抽象成数学表达式,进而映射到程序中所需对应的数据结构形式,最后通过利用JAVA语言得以实现骑士游历问题中骑士游历过程的动态图形演示.【期刊名称】《电子设计工程》【年(卷),期】2011(019)011【总页数】3页(P112-114)【关键词】骑士;游历;欧拉;方向【作者】惠燕;潘煜【作者单位】西安工业大学计算机学院,陕西西安710032;西安工业大学计算机学院,陕西西安710032【正文语种】中文【中图分类】TP311.1骑士游历问题是一个古老而著名的问题，问题的描述是：在8×8格的国际象棋棋盘上，象棋马能否从某个格子出发按照“马跳日”的规则跳遍所有64个格子最后再回到出发的那个格子?国际象棋中的马，英语为knight，恰好又意指中世纪西方世界的“骑士”，因此，这个问题又被称为“骑士游历”问题。

骑士巡游问题的研究

《算法分析与设计》论文骑士巡游问题的探究计科091 王宇帆200916021312 2011年5月22日骑士巡游问题的探究3、特殊情况分析如果马走到接近棋盘的边缘，有可能下一步会超出棋盘，所以程序中必须有相应的代码来判断和阻止这一情况的发生。

还有，骑士巡游的方法不止一个要把所有方案找出来，必须有相应的代码来做这个条件。

有可能从某一点开始，无法巡游棋盘的每一个格子，则需要指出这一情况的代码。

4、回溯分析回溯法（探索与回溯法）是一种选优搜索法，按选优条件向前搜索，以达到目标。

但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

以次规则，设计算法从某一点开始一步一步把棋盘走完。

三、算法设计12、算法描述：把棋盘左上角看作坐标原点，往右是x坐标正方向，往下是y坐标正方向。

输入开始巡游的坐标，把每个格子初始化为没走过（a[i][j]=true）。

把初始坐标记做第1步（b[row-1[col-1]=1]），第1个格子标记为走过（a[row-1[col-1]=false）。

调用计算函数（solve()），开始计算走法。

首先计算每个格子下一步可能的走法，一共有8种，用循环把每一种走法都进行计算。

判断是否超出棋盘和是否被标记走过（(t1==true)&&(t2==true)&&(a[x1][y1]==true)），如不成立，则跳出判断语句；如果成立，则标记此格走过（a[x1][y1]=false）。

并记录步数（b[x1][x2]=k）。

判断是否已经走完所有格子（k=N*N）,如果成立，则说明没走完，递归到计算函数（solve()）接着走棋盘；如果不成立，则说明已经走完所有格子，那么方案数加1（num++），标记已经完成巡游（ok=true）。

然后输出巡游结果。

这样当所有方案都输出后，结束程序。

骑士周游详解

A Knight's JourneyTime Limit: 1000MS Memory Limit: 65536KTotal Submissions: 14944 Accepted: 4991DescriptionBackgroundThe knight is getting bored of seeing the same black and white squares again and again and has decided to make a journeyaround the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans?ProblemFind a path such that the knight visits every square once. The knight can start and end on any square of the board.InputThe input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .OutputThe output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number.If no such path exist, you should output impossible on a single line.Sample Input31 12 34 3Sample OutputScenario #1:A1Scenario #2:impossibleScenario #3:A1B3C1A2B4C2A3B1C3A4B2C4这道简单的题目竟然花了我一个晚上，本来相练习一下用权值来解决这道经典的骑士周游问题，没想到这道题用骑士周游的优化算法竟然超时（用自己的数据跑但是oj上是AC的），oj上跑了813ms 下面是我的code：#include<stdio.h>#include<string.h>#include<stdlib.h>#define lne 27int p,q;int x[lne],y[lne],ans_x[lne],ans_y[lne];int der[8][2]={{-2, -1}, {-1, -2}, {1, -2}, {2, -1}, {2, 1}, {1, 2}, {-1, 2}, {-2, 1}}; bool vis[lne][lne],flag;typedefstruct node{int p,v;}cor;bool canjump(int r,int c){if(r>=0&&r<p&&c>=0&&c<q&&!vis[r][c])returntrue;returnfalse;}int weight(int r,int c){int i,count;for(i=count=0;i<8;i++)if(canjump(r+der[i][0],c+der[i][1]))count++;return count;}int cmp(constvoid *a,constvoid *b){cor *c=(cor *)a;cor *d=(cor *)b;return c->v>d->v?1:-1;}void backtrace(int cur,int r,int c){int i,k,nx,ny;if(cur==p*q){bool fl=false;flag=false;for(i=0;i<p*q;i++){if((ans_y[i]>y[i])||(ans_x[i]>x[i]&&ans_y[i]==y[i])){fl=true;break;}elseif((ans_y[i]<y[i])||(ans_x[i]<x[i]&&ans_y[i]==y[i])) break;}if(fl)for(;i<p*q;i++){ans_x[i]=x[i];ans_y[i]=y[i];}return ;}else{cor ds[8];for(i=k=0;i<8;i++){nx=r+der[i][0];ny=c+der[i][1];if(canjump(nx,ny)){ds[k].v=weight(nx,ny);ds[k++].p=i;}}qsort(ds,k,sizeof(ds[0]),cmp);for(i=0;i<k;i++){nx=r+der[ds[i].p][0];ny=c+der[ds[i].p][1];vis[nx][ny]=true;x[cur]=nx; y[cur]=ny;backtrace(cur+1,nx,ny);vis[nx][ny]=false;}}}void deal(){int i,j;for(i=0;i<p*q;i++)ans_x[i]=ans_y[i]=50;vis[0][0]=true;backtrace(1,0,0);}void output(){int i;if(flag) puts("impossible\n");else{for(i=0;i<p*q;i++)printf("%c%d",ans_y[i]+'A',ans_x[i]+1);puts("\n");}}int main(void){int ncase,i;scanf("%d",&ncase);for(i=1;i<=ncase;i++){memset(vis,false,sizeof(vis));scanf("%d%d",&p,&q);printf("Scenario #%d:\n",i);flag=true;deal();output();}return 0;}然而上面的代码对于8*8的棋盘还是有可行性的，纯粹是数据问题，呵呵后来没办法只能用bfs或者dfs水过，但是由于这道题目只要求求最小字典序的那个结果所以用dfs就可以了，不出意外的话，这道题用dfs做，反而比bfs快，下面是AC的code 16ms ：#include<stdio.h>#include<string.h>#include<stdlib.h>#define lne 27int p,q;int x[lne];char y[lne];int der[8][2]={{-1,-2},{1,-2},{-2,-1},{2,-1},{-2,1},{2,1},{-1,2},{1,2}}; bool vis[lne][lne];bool backtrace(int cur,int r,int c){int i,nx,ny;if(cur==p*q-1){x[cur]=r; y[cur]=c+'A';returntrue;}else{for(i=0;i<8;i++){nx=r+der[i][0];ny=c+der[i][1];if(nx>=0&&nx<p&&ny>=0&&ny<q&&!vis[nx][ny]){vis[nx][ny]=true;x[cur]=r; y[cur]=c+'A';if(backtrace(cur+1,nx,ny))returntrue;vis[nx][ny]=false;}}}returnfalse;}int main(void){int ncase,i;scanf("%d",&ncase);for(i=1;i<=ncase;i++){memset(vis,false,sizeof(vis));scanf("%d%d",&p,&q);printf("Scenario #%d:\n",i);vis[0][0]=true;if(backtrace(0,0,0)){for(int j=0;j<p*q;j++)printf("%c%d",y[j],x[j]+1);putchar('\n');}elseputs("impossible");if(i!=ncase) putchar('\n');}return 0;}这是网上用bfs做的code:#include<iostream>usingnamespace std;bool visit[10][10],f;int t,m,i,j,ans[100][2],x,y,p,q;int move[8][2]={{-1,-2},{1,-2},{-2,-1},{2,-1},{-2,1},{2,1},{-1,2},{1,2}};void dg(int p1,int q1,int ans1){visit[p1][q1]=true;ans[ans1][0]=p1,ans[ans1][1]=q1;if (ans1==p*q){f=true;for (i=1;i<=ans1;i++)printf("%c%d",(char)((int)'A'+ans[i][1]-1),ans[i][0]);printf("\n");return;}for (int i1=0;i1<8;i1++){x=p1+move[i1][0],y=q1+move[i1][1];if (x>0&&x<=p&&y>0&&y<=q){if (visit[x][y]==false)dg(x,y,ans1+1);if (f) return;}}visit[p1][q1]=false;return;}int main(){//freopen("2488.in","r",stdin); //freopen("2488.out","w",stdout); scanf("%d",&m);t=0;while(m--){t++;scanf("%d %d",&p,&q);printf("Scenario #%d:\n",t);f=false;memset(visit,0,sizeof(visit));dg(1,1,1);if (!f) printf("impossible\n"); if (m) printf("\n");}return 0;}下面是大牛写的骑士周游的三种方法但是最后的一种贪心是错的/** File: KnightTravel1.cpp* Author: eshow* Date: 2007-09-10* Question:考虑国际象棋棋盘上某个位置的一只马，它是否可能只走63步，正好走过除起点外的其他63个位置各一次？如果有一种这样的走法，则称所走的这条路线为一条马的周游路线。

2018-2019学年北京市朝阳区高三(上)期末数学试卷(理科)

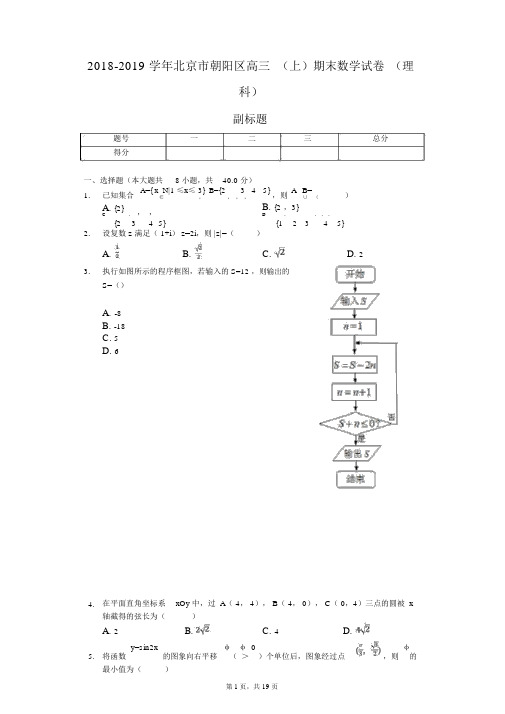
2018-2019 学年北京市朝阳区高三（上）期末数学试卷（理科）副标题题号一二三总分得分一、选择题（本大题共8 小题，共40.0 分）1.已知集合A={ x N|1 ≤x≤ 3} B={2 3 45}，则A B=）∈，，，，∪ （A. {2}，，B. {2，3}C.{2，5}D.{1，，，，5} 342342.设复数 z 满足（ 1+i） z=2i，则 |z|=（）A. B. C. D. 23.执行如图所示的程序框图，若输入的S=12 ，则输出的S=（）A.-8B.-18C.5D.64.在平面直角坐标系xOy 中，过 A（ 4， 4）， B（ 4， 0）， C（ 0，4）三点的圆被 x轴截得的弦长为（）A. 2B.C. 4D.5.将函数y=sin2x的图象向右平移φ φ 0）个单位后，图象经过点，则φ（＞的最小值为（）A. B. C. D.6.设x为实数，则“x 0”是“”的（）＜A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件7.x a＞且a≠1a的取值范围是（）对任意实数，都有（），则实数A. B.（， C. （，） D.[3，）1 3]13+∞8.以棱长为 1 的正方体各面的中心为顶点，构成一个正八面体，再以这个正八面体各面的中心为顶点构成一个小正方体，那么该小正方体的棱长为（）A. B. C. D.二、填空题（本大题共 6 小题，共30.0 分）9.已知数列 { a n } 为等差数列， S n为其前 n 项的和．若 a1+a3 =6， a4=7，则 S5 =______ ．10.已知四边形的顶点 A，B，C，D 在边长为 1 的正方形网格中的位置如图所示，则=______．11.如图，在边长为 1 的正方形网格中，粗实线表示一个三棱锥的三视图，则该三棱锥的体积为 ______．12. 过抛物线y2=4 x焦点F的直线交抛物线于A B A B l的垂线，，两点，分别过，作准线垂足分别为C， D．若 |AF|=4|BF|，则 |CD |=______．13.2018 年国际象棋奥林匹克团体赛中国男队、女队同时夺冠．国际象棋中骑士的移动规则是沿着 3×2 格或 2×3 格的对角移动．在历史上，欧拉、泰勒、哈密尔顿等数学家研究了“骑士巡游”问题：在8×8=64 格的黑白相间的国际象棋棋盘上移动骑士，是否可以让骑士从某方格内出发不重复地走遍棋盘上的每一格？图（一）给出了骑士的一种走法，它从图上标 1 的方格内出发，依次经过标2，3，4，5，6，，到达标 64 的方格内，不重复地走遍棋盘上的每一格，又可从标64 的方格内直接走回到标 1 的方格内．如果骑士的出发点在左下角标50 的方格内，按照上述走法，______（填“能”或“不能”）走回到标50 的方格内．若骑士限制在图（二）中的 3×4=12 格内按规则移动，存在唯一一种给方格标数字的方式，使得骑士从左上角标 1 的方格内出发，依次不重复经过2，3，4，5，6，，到达右下角标12 的方格内，分析图（二）中 A 处所标的数应为______ ．14.如图，以正方形的各边为底可向外作四个腰长为1 的等腰三角形，则阴影部分面积的最大值是______．三、解答题（本大题共 6 小题，共80.0 分）15.在△ABC中，已知A=，BC=13．（Ⅰ）求 AB 的长；（Ⅱ）求 BC 边上的中线AD 的长．16.某日 A， B， C 三个城市 18 个销售点的小麦价格如表：销售点序号所属城市小麦价格（元 /销售点序号所属城市小麦价格（元 /吨）吨）1A242010B25002C258011A24603C247012A24604C254013A25005A243014B25006C240015B24507A244016B24608B250017A24609A244018A2540（Ⅰ）甲以 B 市 5 个销售点小麦价格的中位数作为购买价格，乙从C市4个销售点中随机挑选 2 个了解小麦价格．记乙挑选的 2 个销售点中小麦价格比甲的购买价格高的个数为 X，求 X 的分布列及数学期望；（Ⅱ）如果一个城市的销售点小麦价格方差越大，则称其价格差异性越大．请你对A，B， C 三个城市按照小麦价格差异性从大到小进行排序（只写出结果）．17.如图，三棱柱 ABC-A1B1C1的侧面 BCC1B1是平行四边形， BC1⊥C1C，平面 A1C1CA ⊥平面 BCC1B1，且 E， F 分别是 BC， A1B1的中点．（Ⅰ）求证： EF ∥平面 A1C1CA；（Ⅱ）当侧面 A1C1CA 是正方形，且 BC1=C1C 时，（ⅰ）求二面角 F -BC1-E 的大小；（ⅱ）在线段 EF 上是否存在点 P，使得 AP⊥EF ？若存在，指出点 P 的位置；若不存在，请说明理由．18. 已知函数 f（ x） =xe x-（ m≥0）．（Ⅰ）当 m=0 时，求函数 f（ x）的极小值；（Ⅱ）当 m＞0时，讨论 f（ x）的单调性；（Ⅲ）若函数f（ x）在区间（ -∞， 1）上有且只有一个零点，求m 的取值范围．19.过椭圆 W：=1 的左焦点 F 1作直线 l1交椭圆于 A， B 两点，其中 A（ 0， 1），另一条过F1的直线 l 2交椭圆于C，D 两点（不与 A，B 重合），且 D 点不与点（ 0，-1）重合．过F1作 x 轴的垂线分别交直线AD， BC 于 E，G．（Ⅰ）求 B 点坐标和直线l1的方程；（Ⅱ）求证： |EF 1|=|F1G|．20. 已知 a1，a2，， a n*，a n满足如下两，是由正整数组成的无穷数列，对任意n∈N 个条件：① a n是 n 的倍数；② |a n-a n+1| ≤5．（Ⅰ）若 a1=30，a2=32 ，写出满足条件的所有a3的值；（Ⅱ）求证：当 n≥11时， a n≤5n；（Ⅲ）求 a1所有可能取值中的最大值．答案和解析1.【答案】D【解析】解：集合A={x ∈N|1≤x≤3}={1，2，3} ，B={2 ，3，4，5} ，∴A∪B={1 ，2，3，4，5} ．故选：D．利用并集定义直接求解．本题考查并集的求法，考查并集定义、不等式性质等基础知识，考查运算求解能力，是基础题．2.【答案】C【解析】【分析】本题考查了复数的运算法则、模的计算公式，考查了推理能力与计算能力，属于基础题．利用复数的运算法则、模的计算公式即可得出．【解答】解：∵（1+i）z=2i，∴（1-i）（1+i）z=2i（1-i），即z=i+1 ，则 |z|=，故选 C．3.【答案】A【解析】解：模拟程序的运行，可得S=12，n=1执行循环体，S=10，n=2不满足条件 S+n≤0，执行循环体，S=6，n=3不满足条件 S+n≤0，执行循环体，S=0，n=4不满足条件 S+n≤0，执行循环体，S=-8，n=5满足条件 S+n≤0，退出循环，输出 S 的值为 -8．故选：A ．关键框图的流程依次计算程序运行的结果，直到满足条件跳出循环，确定输出 S 的值本题考查了循环结构的程序框图，关键框图的流程依次计算程序运行的结果是解答此类问题的常用方法，属于基础题．4.【答案】 C【解析】解：根据题意，设过 A 、B 、C 的圆为圆 M ，其方程为 x 2+y 2+Dx+Ey+F=0 ，又由 A （4，4），B （4，0），C （0，4），则有，解可得：D=-4，E=-4，F=0，即圆 M 的方程为 x 2+y 2-4x-4y=0，令 y=0 可得：x 2-4x=0，解可得：x 1=0，x 2=4，即圆与 x 轴的交点的坐标为（0，0），4（，0），则圆被 x 轴截得的弦长为 4；故选：C ．根据题意，设过 A 、B 、C 的圆为圆 M ，其方程为 x 2+y 2+Dx+Ey+F=0 ，将A 、B 、C 三点的坐标代入圆的方程，可得，解可得 D 、E 、F 的值，即可得圆的方程，在方程中令 y=0 可得 x 2-4x=0，求出方程的解，即可得圆与 x轴交点的坐标，进而分析可得答案．本题考查直线与圆的方程的应用，涉及圆的方程的计算，关键是求出圆的方程．5.【答案】 B【解析】解：函数y=sin2x 的图象向右平移 φ（φ＞ 0）个单位后，解析式为 y=sin2（x-φ），又此时图象经过点，∴ =sin2（ -φ），∴2（ -φ）=2k π+ 或 2k π+ ，k ∈Z ．解得 φ=-k π+ 或 φ=-k π，k ∈Z ．又 φ＞0，故它最小的值是，故选：B ．由题意，先求出函数平移后的解析式，再将点代入，即可得出 φ的表对参数的值讨论即可得出答案．达式，再本题考查三角函数的平移与解析式的对应关系以及正弦函数的性质及其图象，属于基础知识考查题，解答的关键是能正确根据三角函数值求出对应的角的表达式． 6.【答案】 C【解析】解：1）若x ＜0，-x ＞0，则：；∴“x＜ 0“是“ “的充分条件；2）时，；解得 x ＜0；∴“x＜ 0“是““的必要条件；综上得，“x＜ 0”是“ ”的充分必要条件．故选：C ．容易由 “x＜0”得出 “ 过“可得出 “x＜ 0“，从而”，反来，由“得出 “x＜ 0”是“”的充分必要条件．考查充分条件，必要条件，以及充要条件的定义．7.【答案】 B【解析】解：∵log （e x+3）≥ 1=loga ，aa∴若 a ＞ 1，则 e x +3≥a 恒成立，∵e x+3＞3，∴此时 1＜a ≤3，若 0＜a ＜1，则 e x +3≤a 恒成立，∵e x+3＞3，∴此时 a 无解，综上所述，1＜a ≤3，即实数 a的取值范围是（1，3] ．故选：B．根据对数函数的单调性转化为参数恒成立进行求解即可．本题主要考查对数函数的性质，讨论 a 的取值，利用对数函数的单调性是解决本题的关键．8.【答案】C【解析】解：正方体 C1各面中心为顶点的凸多面体 C2为正八面体，它的中截面（垂直平分相对顶点连线的界面）是正方形，该正方形对角线长等于正方体的棱长，所以它的棱长 a2==，以 C2各个面的中心为顶点的正方体为图形 C3是正方体，正方体 C3面对角线长等于 C2棱长的，（正三角形中心到对边的距离等于高的），对线为×=，∴ 角∴a3==该长为．，即小正方体的棱故选：C．根据条件先求出正方形对角线长，由此能求出该小正方体的棱长．本题考查小正方体的棱长的求法，考查正方体的结构特征等基础知识，考查运算求解能力，考查函数与方程能力，是中档题．9.【答案】25【解析】解：根据题意得，2a2=6，∴a2=3 又 a4=7，∴2d=7-3=4，∴d=2，a1=1，∴S5=5a1+=5+20=25，故答案为：25．运用等差数列的前n 项和公式可解决此问题．本题考查等差数列的前 n 项和公式的应用．10.【答案】7【解析】解：以AC 的连线为 x 轴，过 B 点且垂直于AC 的直线为 y 轴，建立如图所示平面直角坐标系，则：A（-4，0），C（3，0），D（-1，-2），B（0，2），；∴．故答案为：7．根据题意，可分别以 AC 的连线为 x 轴，过 B 点且垂直于 AC 的直线为 y 轴建立平面直角坐标进而求出 A ，B，C，D 的坐标，从而求出向量的坐系，标进积的坐标运算即可求出的值．，行数量考查通过建立坐标系，利用坐标解决向量问题的方法，以及根据点的坐标可求向量的坐标，向量数量积的坐标运算．11.【答案】【解析】解：由三视图画出该三棱锥的直观图，如图所示；则三棱锥 P-ABC 的体积为V三棱锥P-ABC= S△?h= × ×4×2×2=．ABC故答案为：．由三视图画出该三棱锥的直观图，结合图形求出它的体积．本题考查了利用几何体三视图求体积的应用问题，是基础题．12.【答案】5【解析】设线AB 的倾斜角为设为锐则解：直θ，并θ角，由于|AF|=4|BF|，有，解得则，，由抛物线的焦点弦长公式可得，因此，．故答案为：5．设直线 AB 的倾斜家为锐角θ，由|AF|=4|BF|，得，可解出 cosθ的值，进而得出 sin θ的值，然后利用抛物线的焦点弦长公式计算出线段 AB 的长，再利用|CD|=|AB|sin 可θ计算出答案．本题考查抛物线的性质题的关键在于灵活利用抛物线的焦点弦长公，解决本式，属于中等题．13.【答案】能8【解析】解：如图所示：如果骑士的出发点在左下角标 50 的方格内，按照上述走法，能走回到标 50的方格内，如图所示：使得骑士从左上角标 1 的方格内出发，依次不重复经过 2，3，4，5，6，，到达右下角标 12 的方格，且路线是唯一的，故 A 处应该为 8，故答案为：能，8根据题意，画出路线图，解判断是否能，再根据题意，结合题目中的数字，即可求出 A 处的数字．本题考查了合情推理的问题，考查了转化与化归思想，整体和部分的思想，属于中档题14.【答案】2+2【解析】设为则），解：等腰三角形的底角θ，θ则等腰三角形的底边为为sin θ，2cosθ，高又 2（，），当 2θ= ，即时，S阴取最大值2+2，故答案为：2+2．由三角函数的定义设等腰三角形的底角为θ 则θ则，），等腰三角形的底边为 2cosθ，高为 sin θ，由二倍角公式及辅助角公式 S2（θ）×阴= 2cos+4=2sin2 θ +2cos2 θ +2=2sin（2θ+）+2，再求函数的最大值即可本题考查了三角函数的定义、二倍角公式及辅助角公式，属中档题．15.【答案】解：（Ⅰ）由，，所以，由正弦定理得，，即；（Ⅱ）在△ABD 中，，222由余弦定理得， AD=AB +BD -2AB BD cosB?，所以 AD2=，所以．【解析】（Ⅰ）由同角公式和正弦定理，解方程可得 AB ；（Ⅱ）在△ABD 中，运用两角和的余弦公式和余弦定理，计算可得所求值．本题考查三角形的正弦定理、余弦定理的运用，考查方程思想和运算能力，属于中档题．16.【答案】（本小题满分13 分）解：（Ⅰ） B 市共有 5 个销售点，其小麦价格从低到高排列为：2450 ， 2460， 2500， 2500， 2500．所以中位数为 2500，所以甲的购买价格为 2500．C 市共有 4 个销售点，其小麦价格从低到高排列为：2400，2470， 2540， 2580，故 X 的可能取值为 0， 1， 2．，X012P10 C A B13（Ⅰ）B 市共有 5 个销售点，其小麦价格从低到高排列为 2450，2460，2500，2500，2500．由此能求出中位数，从而能求出甲的购买价格．C 市共有 4 个销售点，其小麦价格从低到高排列为：2400，2470，2540，2580，从而 X 的可能取值为 0，1，2．分别求出相应的概率，由此能求出 X 的分布列和数学期望．（Ⅱ）三个城市按小麦价格差异性从大到小排序为：C，A ，B．本题考查中位数、概率、离散型随机变量的分布列、数数期望、方差的求法，考查列举法、古典概型等基础知识，考查运算求解能力，是中档题．【答案】证明：（Ⅰ）取 A1C1中点 G，连 FG ，连 GC 17.在△A1B1C1中，因为 F，G 分别是 A1B1，A1C1中点，所以 FG∥B1C1，且,在平行四边形BCC1B1中，因为 E 是 BC的中点，所以 EC∥B1C1，且,所以 EC∥FG，且 EC=FG ,所以四边形 FECG 是平行四边形 ,所以 FE∥GC,又因为 FE? 平面 A11 1 1C CA，GC?平面 ACCA，所以 EF∥平面 A1C1CA;（Ⅱ）（ⅰ）因为侧面 A1 1CA是正方形，所以1 1C1C,C A C⊥又因为平面 A1C1 CA⊥平面 BCC1B1，且平面 A1C1CA∩平面 BCC1B1=C1C，所以 A1C1⊥平面，又平面所以 A1C1⊥C1B，又因为 BC C为原点建立空间1⊥ 1C，以C1直角坐标系C1-xyz，如图所示．设 C1C=a，则 A（ 0， a， a）， B（ a， 0 ，0）， C（ 0，a，0）， A1（ 0，0， a）， B1（ a， -a， 0），，设平面 FBC 1的一个法向量为=（x，y，z），由得，即,令 y=1 ，所以 n=（ 0，1， 1） ,又因为 A1C1⊥平面 BC1 E，所以是平面 BC1E 的一个法向量,所以,由图可知，二面角F-BC1 -E 为钝角，所以二面角F-BC1-E 的大小为,故答案为;设，则,因为=，又 AP⊥EF，所以,所以λ=0∈[0， 1],故点 P 在点 E 处时，有 AP⊥EF ．【解析】本题考查了线面平行的判定及二面角的求法，线线垂直，属中档题.（Ⅰ）由线面平行的判定，证 FE∥GC 即可 ;间标系设点用法向量求解即可；（Ⅱ）（ⅰ）建立空直角坐（ⅱ）用量向量垂直的坐标运算即可 .18.【答案】（本小题满分13 分）解：（Ⅰ）当 m=0 时： f'（ x）=（ x+1） e x，令 f'（x） =0 解得 x=-1，又因为当 x∈（ -∞， -1）， f'（ x）＜ 0，函数 f（x）为减函数；当 x∈（ -1，+∞）， f'（ x）＞ 0，函数 f（ x）为增函数．所以， f（ x）的极小值为..（ 3 分）（Ⅱ） f'（x）=（ x+1 ）（ e x-m）．当 m＞ 0 时，由 f'（ x） =0，得 x=-1 或 x=lnm．（ⅰ）若，则．故f（x）在（-∞，+∞）上单调递增；（ⅱ）若，则lnm＞-1．故当f'（x）＞0时，x＜-1或x＞lnm；当 f'（ x）＜ 0 时， -1＜ x＜ lnm．所以 f（ x）在（ -∞， -1），（ lnm，+∞）单调递增，在（-1，lnm）单调递减．（ⅲ）若，则lnm＜-1．故当f'（x）＞0时，x＜lnm或x＞-1；当 f'（ x）＜ 0 时， lnm＜ x＜ -1．所以 f（ x）在（ -∞， lnm），（ -1， +∞）单调递增，在（ln m， -1）单调递减．．（8 分）（Ⅲ）（ 1）当 m=0 时， f（x）=xe x，令 f（ x）=0，得 x=0．因为当 x＜ 0 时， f（ x）＜ 0，当 x＞ 0 时， f（ x）＞ 0，所以此时 f（ x）在区间（ -∞， 1）上有且只有一个零点．（ 2）当 m＞ 0 时：（ⅰ）当时，由（Ⅱ ）可知f（x）在（-∞，+∞）上单调递增，且，，此时 f（ x）在区间（ -∞， 1）上有且只有一个零点．（ ⅱ ）当时，由（ Ⅱ）的单调性结合 f （ -1）＜ 0，又 f （ lnm ）＜ f （ -1）＜ 0，只需讨论 f （1） =e-2m 的符号：当时， f （ 1）＞ 0， f （ x ）在区间（ -∞， 1）上有且只有一个零点；当时， f （ 1） ≤0，函数 f （x ）在区间（ -∞， 1）上无零点．（ ⅲ ）当时，由（ Ⅱ ）的单调性结合 f （ -1）＜ 0，f （ 1）=e-2m ＞0，，此时 f （ x ）在区间（ -∞， 1）上有且只有一个零点．综上所述，.. （ 13 分）【解析】（Ⅰ）当 m=0 时：求出导函数，利用导函数的符号判断函数的单调性，然后求解函数的极值．f' x = x+1e xm 0 时 f' x =0x=-1x=lnm（Ⅱ）（）（）（-m或．）．当＞，由（），得（ⅰ）若，（ⅱ）若，（ⅲ）若别导函数的符号，判断，分判断函数的单调性即可．（Ⅲ）1（）当m=0 时，f （x ）=xe x，判断 f （x ）在区间（-∞，1）上有且只有一个零点．（2）当m ＞0 时：（ⅰ）当时，（ⅱ）当时，（ⅲ）当时，结合函数的单调性以及函数的极值，判断函数的零点的个数即可．本题考查函数的导数的应用，函数的极值以及函数的最值的求法，函数的零点与函数的极值的关系，考查分类讨论思想以及转化思想的应用．19.【答案】（本小题满分 14 分）解：（ Ⅰ）由题意可得直线l 1 的方程为 y=x+1．与椭圆方程联立，由可求．（ 4 分）（ Ⅱ ）证明：当 l 2 与 x 轴垂直时，C ，D 两点与 E ，G 两点重合，由椭圆的对称性， |EF 1|=|F 1G|．当 l 2 不与 x 轴垂直时，设 C （x 1 ，y 1 ）， D （ x 2， y 2）， l 2 的方程为 y=k （x+1）（ k ≠1）．由消去 y ，整理得（ 2k 2+1）x 2 +4k 2 x+2k 2 -2=0 ．则，．由已知， x2≠0，则直线 AD 的方程为，令 x=-1，得点 E 的纵坐标．把 y2=k（ x2+1）代入得．由已知，，则直线BC 的方程为，令 x=-1 ，得点G 的纵坐标．把 y1=k（ x1+1）代入得．==把，代入到2x1x2+3（x1+x2）+4中，2x1x2 +3（ x1+x2）+4=．即 y E+y G=0 ，即 |EF 1|=|F1G|..（ 14 分）【解析】（Ⅰ）由题意可得直线 l 1的方程为 y=x+1．与椭圆方程联立，求解B 的坐标即可．（Ⅱ）当l2与 x 轴垂直时，C，D 两点与 E，G 两点重合，由椭圆的对称性，|EF1|=|F1G|．当l 2不与 x 轴垂直时，设 C（x，y ），D（x2，y），l的方程为 y=k1122（x+1）（k≠1）．由消去 y，利用韦达定理，结合直线 AD 的方程为，令 x=-1，求出 EG 的坐标转，然后化求解即可．本题考查直线与椭圆的位置关系的应查设而不求转化思想的应用，分用，考类讨论思想的应用．20.【答案】（Ⅰ）解：a3的值可取27， 30， 33，36；（Ⅱ）证明：由 a n+1≤a n+5（ n=1， 2，），对于任意的n，有 a n≤5（ n-1） +a1．当 n≥a1-4 时， a n≤5（ n-1） +a1，即 a n≤5（ n-1） +n+4，即 a n≤6n-1．若存在 n 使 a n ＞5n ，依以上所证，这样的 n 的个数是有限的，设其中最大的为 N ．则 a N ＞ 5N ， a N+1≤5（ N+1）成立， ∵a N 是 N 的倍数，故 a N ≥6N ．由 5≥a N -a N+1≥6N-5（ N+1） =N-5，得 N ≤ 10．因此当 n ≥11时， a n ≤5n ；（ Ⅲ ）解：由（ Ⅱ ）知 a 11≤ 55， ∵a n ≤a n+1+5 且 a n 是 n 的倍数，∴a 10，a 9，，a 1 满足下面的不等式： a 10≤ 60，a 9≤ 63，a 8≤ 64，a 7≤ 63，a 6≤ 66，a 5≤ 70，a 4≤ 72， a 3≤ 75， a 2≤ 80， a 1≤ 85．则 a 1=85 ，a 2=80，a 3=75，a 4=72 ，a 5=70，a 6=66，a 7=63 ，a 8=64，a 9=63 ，a 10=60 ，当 n ≥ 11 时， a n =5n 这个数列符合条件．故所求 a 1 的最大值为 85．【解析】题值；（Ⅰ）由意直接写出 a 3 的a ≤a对 ≤5（）．可得，当（Ⅱ）由n+1 n +5（n=1，2，），于任意的 n ，有a nn-1 +a 1n ≥a -4 时，a ≤5（n-1）+a ，即a ≤ 6n-1．则 a ＜6n 成立．再由 a 是 n 的倍数，可1n1n nn得，当 n ≥a 时，有a n ≤ 5n 成立．若存在 n 使 a ＞5n ，依以上所证这样的 n ，1-4n的个数是有限的，设其中最大的为 N ．可得 a N ＞5N ，a N+1 ≤5（N+1）成立，由a N是 N 的倍数，故 a ≥ 6N ．再由 5≥a≥ 6N-5（N+1）=N-5，得N ≤ 10．可得当NN-aN+1n ≥ 11时，a n ≤ 5n ；a 知≤ ，再由 ≤a+5 且 a n是 n 的倍数，可得 a ，a ，，a（Ⅲ）由（Ⅱ） 11 55a n n+110 9 1满足下面的不等式： a 10≤ 60，a 9≤ 63，a 8≤ 64，a 7≤ 63，a 6≤ 66，a 5≤ 70，a 4≤ 72，a 3≤ 75，a 2≤ 80，a 1≤ 85．分别求出 a 1，a 2，a 3，a 4，a 5，a 6，a 7，a 8，a 9，a 10 的值，可得当n ≥11时，a n =5n 这个数列符合条件．故所求 a 1 的最大值为 85．本题考查数列递推式，考查了数列的函数特性，考查逻辑思维能力与推理运算能力，是中档题．第19 页，共 19页。

历届noip提高组复赛试题

NOI’ 95“同创杯”全国青少年信息学（计算机）奥林匹克竞赛分区联赛复赛试题（高中组）（上机编程，完成时间：210 分钟）<1>编码问题：设有一个数组A:ARRAY[0..N-1] OF INTEGER；数组中存放的元素为0～N-1 之间的整数，且A[i]≠ A[j]（当i≠ j时）。

例如： N=6 时，有：此时，数组 A 的编码定义如下：A[0] 的编码为0；A[i] 的编码为：在A[0] ，A[1]∴上面数组 A 的编码为：A= （ 4，3， 0， 5，1， 2），， A[i-1] 中比 A[i] 的值小的个数（B= （0， 0，0，3，1， 2）i=1 ，2，， N-1 ）程序要求解决以下问题：①给出数组 A 后，求出其编码。

②给出数组 A 的编码后，求出 A 中的原数据。

<2> 灯的排列问题：设在一排上有 N 个格子（ N≤ 20），若在格子中放置有不同颜色的灯，每种灯的个数记为 N 1， N2， N k（ k 表示不同颜色灯的个数）。

放灯时要遵守下列规则：①同一种颜色的灯不能分开；②不同颜色的灯之间至少要有一个空位置。

例如： N=8 （格子数）R=2 （红灯数）B=3 （蓝灯数）放置的方法有：R-B 顺序R R B B BR R B B BR R B B BR R B B BR R B B BR R B B BB-R顺序B B B BBBBBBBBBBBBBBR RRRBRRRRRRRR放置的总数为12 种。

数据输入的方式为：NP1（颜色，为一个字母）P2N1（灯的数量）N2Q（结束标记， Q 本身不是灯的颜色）程序要求：求出一种顺序的排列方案及排列总数。

<3> 设有一个四层的积木块，1～ 4 层积木块的数量依次为：5， 6，7， 8如下图所示放置：815851691423414326其中，给出第三层与第四层所标示的数字，并已知第三层的数据是由第四层的数据计算出来的。

原神骑士团手册问答任务

原神骑士团手册问答任务原神骑士团手册问答任务答案是什么？
骑士团手册问答是原神中的一个世界任务，玩家想要完成这个任务就需要回答一些问题。

原神骑士团手册问答任务答案:
首先我们完成魔神任务-巨龙与自由之歌以后，在蒙德门口找西风骑士斯万对话即可领取任务，之后获得本书骑士团指导手册·第五版。

我们再次与斯万对话以后就需要回答3个问题了。

第一个问题：西风骑士团对于那片遗址的正式定名是什么？
答案：风龙废墟
第二个问题：作为一名西风骑士，在面对远道而来的陌生人时，应当使用怎样的敬辞来称呼对方？
答案：陌生而可敬的旅行者
第三个问题：琴小姐在西风骑士团内的正式职务名称是什么？
答案：代理团长
我们只需要回答正确上述的3个问题以后即可完成该任务，获得任务奖励了。

不过，有时回碰见另外一套题库，答案如下：
第四个问题：丽莎小姐在西风骑士团中的正式职务名称是什么？
答案：图书管理员
第五个问题：凯亚先生在西风骑士团中的正式职务名称是什么？
答案：骑兵团长
第六个问题：安柏小姐作为西风骑士团中的一员，她的正式职务名称是什么？
答案：侦察骑士
以上就是原神骑士团手册问答任务答案的全部内容了。

祝您开心游戏！。

智商测试题骑士骑马(3篇)

第1篇导语：在这个充满智慧与挑战的时代，智商测试成为了检验个人思维能力和逻辑推理能力的有效工具。

今天，我们将带来一场别开生面的智商测试——骑士骑马之谜。

通过解答一系列与骑士骑马相关的问题，让我们一同走进智慧的殿堂，挑战自我，提升思维。

一、背景介绍在一个遥远的王国，有一位英勇的骑士，他骑着一匹骏马，肩负着保卫家园的重任。

然而，这位骑士在一次执行任务的过程中，遭遇了一场突如其来的风暴。

在风暴中，骑士与马儿失散，为了寻找马儿，骑士踏上了漫长的寻马之旅。

在这段旅程中，他遇到了各种各样的问题，这些问题不仅考验着他的智慧，还考验着他的勇气和毅力。

二、智商测试题1. 骑士骑马之谜一：马儿去哪儿了？（1）骑士在风暴中失去了马儿，请问马儿可能去了哪里？A. 草原B. 森林C. 沙漠D. 河流（2）骑士在寻找马儿的过程中，发现了一处马蹄印。

请问这处马蹄印意味着什么？A. 马儿在这里休息过B. 马儿在这里喝水C. 马儿在这里被人偷走了D. 马蹄印是假的2. 骑士骑马之谜二：神秘信物骑士在寻找马儿的过程中，发现了一封神秘的信件。

信件中提到了一个重要的线索，请问这个线索是什么？A. 马儿的名字B. 马儿的颜色C. 马儿的年龄D. 马儿的家乡3. 骑士骑马之谜三：迷雾重重骑士在寻找马儿的过程中，进入了一片浓雾弥漫的区域。

请问以下哪个选项有助于骑士找到马儿？A. 走得更快B. 走得慢一些，仔细观察周围环境C. 唱歌吸引马儿D. 尝试用马蹄印追踪4. 骑士骑马之谜四：智慧之剑骑士在寻找马儿的过程中，遇到了一位智慧的老者。

老者给了骑士一把智慧之剑，并告诉他：“这把剑能帮助你找到马儿。

”请问智慧之剑的作用是什么？A. 剑身藏有马儿的线索B. 剑身具有强大的魔法，能驱散迷雾C. 剑身能发出马儿的声音，吸引马儿D. 剑身能指引骑士找到马儿5. 骑士骑马之谜五：勇者归来经过一番努力，骑士终于找到了马儿。

然而，马儿却不愿意跟随骑士回家。

请问以下哪个选项能帮助骑士说服马儿？A. 诉说着与马儿共度的美好时光B. 给马儿一些美食作为奖励C. 威胁马儿，如果不跟随他，就会受到惩罚D. 无视马儿，自己回家三、答案解析1. （1）A （2）B2. B3. B4. D5. A四、总结通过以上五道智商测试题，我们不仅锻炼了思维能力，还感受到了骑士骑马之谜的趣味性。

数据结构课程设计骑士游历问题

第四章源代码程序设计............................................................................ 9
4.1 详细设计............................................................................................. 9
创建...............................................................................................................9
操作...............................................................................................................9
第8页
华东交通大学理工学院
第四章源代码程序设计 4.1 详细设计
创建
创建一个 8 行 8 列的棋盘： #include <stdio.h> int board[8][8] = {0}; int main(void) { for(i = 0; i < 8; i++) { for(j = 0; j < 8; j++) { printf("%2d ", board[i][j]); } putchar('\n'); } return 0; }
显示...............................................................................................................9

(完整word版)骑士游历java课程设计

数据结构课程设计报告目录1 设计目的与意义 (3)2 系统描述 (3)3 运行环境 (3)4 系统的分析与设计 (3)4.1 程序结构说明 (3)4.2 AccessibleSquare算法实现 (4)4.3 画图类算法实现 (5)4.4 主调用程序的设计和开发 (7)5 系统测试 (7)5.1 游戏初始界面 (8)5.2 游戏以（1，1）为起点运行界面 (8)5.3 游戏以（6，3）为起点界面 (9)5.4 游戏以（6，3）为起点运行界面 (9)6 总结 (10)源程序 (10)1 设计目的与意义Java课程设计是计算机科学与技术专业学生必做的集中实践性环节之一，是学习完《Java程序设计》课程后进行的一次全面的综合练习。

其目的在于通过课程设计，使学生能够得到较系统的技能训练，从而巩固和加深对Java 编程的基础理论知识的理解，培养学生综合运用所学理论解决实际问题的能力，使学生成为具有扎实的计算机理论基础和较强的独立动手能力的复合型、应用型人才。

2 系统描述骑士游历问题是一个古老而著名的问题，它最初是由大数学家Euler提出的。

问题是这样的：国际象棋中的棋子(叫作骑士)在一个空棋盘内移动，问它能否经过64格中的每一格且只经过一次？(骑士按L行移动,即在某方向前进两格接着在与原方向垂直的方向上前进一格)该课程设计要求实现骑士游历问题的求解，并能够演示起始位置在棋盘上任何位置的游历问题的实现。

程序将采用动态的图形演示，使算法的描述更形象、更生动。

本程序采用Applet来编制整个程序，这样既可以加深对算法的实现的了解，也可以进一步熟悉Java图形界面、Applet以及Java语言的命名规范。

骑士游历的课程设计是按照面向对象的思想进行开发，其中主要的类包括AccessibleSquare 类、MyPanel类和KnightsTour类。

其中AccessibleSquare 类主要是算法实现，采用启发式算法；KnightsTour类是主类，或者说是控制类，它完成对算法类和图画类的调用；MyPanel类是画图类用来实现图形化显示结果。

回溯与分支限界算法设计

算法设计与分析实验报告1.骑士游历问题（采用回溯法）：在国际象棋的棋盘（8行×8列）上放置一个马，按照“马走日字”的规则，马要遍历棋盘，即到达棋盘上的每一格，并且每格只到达一次。

若给定起始位置（x0,y0）,编程探索出一条路径，沿着这条路径马能遍历棋盘上的所有单元格。

2. 行列变换问题（采用分支限界法）：给定两个m n方格阵列组成的图形A和图形B，每个方格的颜色为黑色或白色，如下图所示。

行列变换问题的每一步变换可以交换任意2行或2列方格的颜色，或者将某行或某列颠倒。

上述每次变换算作一步。

试设计一个算法，计算最少需要多少步，才能将图形A变换为图形B。

图形A图形B2. 行列变换问题的程序：package .t8;import java.util.LinkedList;import java.util.Scanner;class graph{static int sour, dest;//sour是图形的初始整数，dest是图形的目的整数static int ans[]=new int[1<<16];//静态变量（即全局变量），用于存放图形变换的路径int m=4,n=4,x;int row[]=new int[4];int col[]=new int[4];void setx(int x){this.x=x;}int getx(){return this.x;}void rowx(){//将一个整数划分成四行二进制int y;for(int i=0;i<m;i++){y=1;row[i]=0;for(int j=0;j<n;j++){if((x&1)!=0) //如果x的最低位是1row[i]|=y;y<<=1;x>>=1;}}}}实例：总结实验心得体会：掌握回溯法解决问题的一般步骤。

学会使用回溯法解决实际问题。

掌握分支限界法解决问题的基本思想。

全国假面骑士模拟试题答案

全国假面骑士模拟试题答案一、选择题1. 在《假面骑士W》中，主角左翔太郎和菲利普合体变身的假面骑士W，其代表的动物形象是？A. 狮子与老虎B. 鹰与鲨鱼C. 蝙蝠与蜘蛛D. 狼与猎豹答案：C. 蝙蝠与蜘蛛2. 《假面骑士OOO》中，主角可以使用三种不同的动物核心硬币进行变身，以下哪种组合不是剧中出现过的？A. 鹰、鹿、蝗虫B. 虎、豹、狮子C. 犀牛、熊、象D. 鲨鱼、电鳗、章鱼答案：D. 鲨鱼、电鳗、章鱼3. 假面骑士Decade是纪念假面骑士系列诞生多少周年的作品？A. 10周年B. 20周年C. 30周年D. 40周年答案：C. 30周年4. 在《假面骑士Build》中，主角桐生战兔可以使用名为“Build Driver”的变身腰带，以下哪种不是他的变身形态？A. RabbitTankB. BatTankC. SpiderTankD. DragonTank答案：D. DragonTank5. 假面骑士Gaim的主题是“水果与武士”，以下哪个形态不是主角葛叶纮汰在剧中使用的？A. 柳橙铠甲B. 蜜瓜铠甲C. 草莓铠甲D. 蓝莓铠甲答案：D. 蓝莓铠甲二、填空题1. 在《假面骑士Wizard》中，主角操真晴人可以通过使用不同的魔法指环来变换形态，他的初始形态名为________。

答案：Flame Style2. 《假面骑士Kabuto》的故事背景设定在宇宙昆虫生命体“Worm”入侵地球的2053年，主角天道总司变身为假面骑士Kabuto需要使用名为________的道具。

答案：Kabuto Zecter3. 假面骑士Drive是一辆拥有人工智能的超级汽车，名为________，它能够与主角泊进之介合体变身。

答案：Tridoron4. 《假面骑士Zi-O》中，主角常磐庄吾可以通过使用不同的骑士手表来变换形态，这些手表被称为________。

答案：RideWatch5. 在《假面骑士Ghost》中，主角天空寺尊可以通过不同的幽灵眼魂来获得不同的力量，他的终极形态名为________。

《骑士》试题含答案

《骑士》试题含答案骑士试题含答案问题一骑士在中世纪的欧洲社会中起到了什么作用？答案：骑士在中世纪的欧洲社会中起到了多重作用。

首先，骑士是一种军事力量，担负着保卫领地和统治者的责任。

其次，骑士代表了封建制度中的军事精英，他们以勇武和尊贵的形象深受人们敬仰。

此外，骑士还承担了一定的社会责任，包括辅助统治者和参与公共事务。

问题二骑士修行的内容包括哪些方面？答案：骑士修行的内容包括武术训练、道德修养和社会礼仪等方面。

骑士需要通过长时间的武术训练来提升自身的战斗技能。

同时，他们还注重道德修养，如忠诚、正直和勇敢等品质。

此外，骑士还需要研究和遵守社会礼仪，以保持绅士风度和社会地位。

问题三骑士与封建制度之间有什么关系？答案：骑士与封建制度之间存在密切的关系。

封建制度是欧洲中世纪社会的一种政治和社会组织形式，而骑士则是封建制度中的核心成员之一。

在封建制度中，骑士通过效忠和服从统治者来获取封地和特权，并承担保卫领地和辅助统治者的责任。

骑士的存在和发展促进了封建制度的稳定和发展。

问题四骑士文化对现代社会的影响有哪些？答案：骑士文化对现代社会有着广泛的影响。

首先，骑士精神代表了勇敢、忠诚和正义等价值观念，这些价值观仍然在现代社会中被重视和追求。

其次，骑士文化激发了对冒险、探索和军事荣耀的热爱，影响了许多文学作品、电影和游戏。

最后，骑士文化的传承和研究也成为历史学和文化学领域的重要课题。

以上是关于骑士的试题及其答案，希望对您有所帮助。

骑士游历问题纯数学方法

poj2243 骑士游历问题的纯数学方法/problem?id=2243下面稍微翻译一下：描述：给你一个8*8的棋盘,骑士的开始位置,结束位置,让你求得骑士从开始位置开始揍到结束位置需要最小的步数是多少？（注意,骑士走日字）输入：输入包含多组数据，每一行都是一组开始位置和结束位置,位置由两个字符组成,一个是小写字母(a-h),一个是数字(1-8),起始位置结束位置由一个空格隔开.输出：输出从起始位置到结束位置,骑士所要走过的最小的步数.按照样例的格式来。

输入样例：e2 e4a1 b2b2 c3a1 h8a1 h7h8 a1b1 c3f6 f6输出样例：To get from e2 to e4 takes 2 knight moves.To get from a1 to b2 takes 4 knight moves.To get from b2 to c3 takes 2 knight moves.To get from a1 to h8 takes 6 knight moves.To get from a1 to h7 takes 5 knight moves.To get from h8 to a1 takes 6 knight moves.To get from b1 to c3 takes 1 knight moves.To get from f6 to f6 takes 0 knight moves.-------------------------------------------------------------------------------------------------------------一般网上见到的都是dp或者bfs方法。

但是，对于n稍微大一点，比如80*80,100*100的方格，就很麻烦了。

今天中午，我终于想出来了一个数学方法。

是这样的：首先，对于两个点，只用考虑其横纵坐标的差值。

骑士游历问题

for(k=0;k<n;k++)
{
p->childptr[k]=(CTree *)malloc(sizeof(CTree));
for(i=0;i<n;i++)
for(j=0;j<m;j++)
p->childptr[k]->a[i][j]=p->a[i][j];
p->childptr[k]->tag=1;
else
/*上一列下了棋子且该列为第m列*/
for(k=0;k<n;k++)
{
p->childptr[k]=(CTree *)malloc(sizeof(CTree));
for(i=0;i<n;i++)
for(j=0;j<m;j++)
p->childptr[k]->a[i][j]=p->a[i][j];
p->childptr[k]->tag=1;
p->childptr[k]->a[k][y]=1;
if(k==x-3||k==x+1)
Trial(p->childptr[k],k+1,y+1);
else free(p->childptr[k]);
}
}
}
else if(p->tag==0)
/*上一列没有下棋子*/
☆ 依照分析，建立状态树如下：
棋盘状态树
正确路径
说明：
1. 状态树中每一个结点除了图中表示出的二维表外，还包含n 个指向孩子结点的指针域和一个整型标志变量tag，当树的i层结点的tag为1时，表示该结点在第y1＋i－1列不下棋子，tag为0 时则表示在该列某行下一个棋子。 2.在m－1列时，要继续前进时，只有一种走法，就是在第m列寻找正确路径，不能在m列不下棋子，因此，m层的结点tag必须等于1。 3.如果在某列下了棋子，在下一列可以有两种选择，下棋子和不下棋子，在树中表现为分配n＋1个结点，其中一个为不下棋子即tag＝0，其它n个表示分别在下列不同的行放入棋子；如果在该列不下棋子，则下一行必须下棋子，否则会遗漏可能路径，即有n个孩子，且孩子的tag均为1。

骑鹅的旅行体验考题与答案

骑鹅的旅行体验考题与答案
考题一：骑鹅旅行的起源是什么？
答案：骑鹅旅行起源于中国的传统文化。

在中国古代，骑鹅旅行是一种受欢迎的娱乐活动，人们骑着鹅在风景优美的地方游玩。

如今，骑鹅旅行已经成为一种独特的旅游体验，吸引了许多游客。

考题二：骑鹅旅行的目的地有哪些？
答案：骑鹅旅行的目的地多种多样，可以选择在乡村、山区、湖泊或风景名胜区进行。

一些受欢迎的目的地包括杭州西湖、桂林漓江、四川九寨沟等。

考题三：骑鹅旅行的优势有哪些？
答案：骑鹅旅行有以下几个优势：
1. 独特体验：骑鹅旅行是一种与众不同的旅游方式，可以让人们感受到不同于传统旅行的乐趣。

2. 环保健康：相比传统的交通工具，骑鹅旅行更环保，不产生污染，并且对身体健康有益。

3. 探索性强：骑鹅旅行可以让人们深入探索目的地的自然风光和文化背景，获得更丰富的旅行体验。

考题四：骑鹅旅行的注意事项有哪些？
答案：进行骑鹅旅行时需要注意以下几点：
1. 安全第一：选择合适的鹅进行骑行，确保鹅的健康和安全，并佩戴相关的安全装备。

2. 尊重动物：在骑鹅过程中要尊重动物的感受，不使用过度的力量或虐待动物。

3. 遵守规定：根据当地的规定和法律，遵守相关的骑鹅旅行规定，并尊重当地居民和文化。

考题五：骑鹅旅行的未来发展如何？
答案：骑鹅旅行具有独特的吸引力和潜力，未来有望得到更多人的关注和喜爱。

随着人们对于独特旅游体验的追求，骑鹅旅行有可能成为一种新兴的旅游项目，推动旅游行业的发展。

以上是关于骑鹅的旅行体验考题与答案。

希望对您有所帮助！
---。