2021年中考数学一轮复习基础考点及-题型专题23圆(含解析)
2021北京中考数学23题解析

2021北京中考数学23题解析2021年北京中考数学23题是一道关于三角函数的基础题目。
以下将详细解析该题,供参考。
题目:已知正数a的值满足等式sin(a-36°) = cos(2a-54°),求a的值(近似到整数度)。
解析:首先,我们可以根据三角函数的性质,将等式中的角度进行转化。
sin和cos的关系可以通过cos的补角公式表示,即cosθ=sin(90°-θ)。
根据这个关系,我们将等式两边的角度转化为cos的形式,得到cos(90°-a+36°) = cos(2a-54°)。
因为cosθ=cosα等价于θ=2kπ±α,其中k为整数。
所以我们可以将等式中的角度求解出来。
首先,我们将90°-a+36°与2a-54°进行比较,保证它们是相等的。
即:90°-a+36° = 2a-54°将等式化简,得到:3a = 180°a = 60°所以,正数a的近似值为60°。
以上解法通过角度的转化和相关公式的运用,得出了最终结果。
但是我们还可以通过图像的分析来解决这道题目。
首先,我们将已知的函数图像绘制出来。
sin(a-36°)的函数图像是逆时针偏移36°的正弦曲线,cos(2a-54°)的函数图像是逆时针偏移54°的余弦曲线。
如果两条函数曲线的交点存在,那么这个交点所对应的x轴坐标即为所求的a值。
根据函数图像,我们可以看到在0°到90°之间确实存在两条曲线的交点。
通过进一步的观察,可以大致估计出交点的位置在60°附近。
为了更精确地求解,我们可以利用计算机软件或者相关App进行绘图,然后使用光标测量工具来确定交点的横坐标。
通过图像的分析,得到的解是a≈60°,与前面的解法一致。
2021年中考数学一轮复习专题23圆
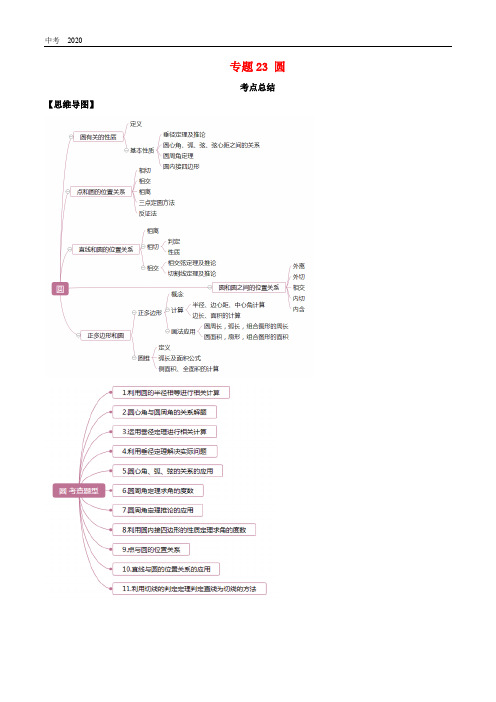
专题23 圆考点总结【思维导图】【知识要点】知识点一与圆有关的概念圆的概念:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫圆.这个固定的端点O叫做圆心,线段OA叫做半径.以O点为圆心的圆记作⊙O,读作圆O.特点:圆是在一个平面内,所有到一个定点的距离等于定长的点组成的图形.确定圆的条件:⑴圆心;⑵半径,⑶其中圆心确定圆的位置,半径长确定圆的大小.补充知识:1)圆心相同且半径相等的圆叫做同圆;2)圆心相同,半径不相等的两个圆叫做同心圆;3)半径相等的圆叫做等圆.弦的概念:连结圆上任意两点的线段叫做弦。
经过圆心的弦叫做直径,并且直径是同一圆中最长的弦.⏜,读作弧AB.在同圆或等弧的概念:圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作AB圆中,能够重合的弧叫做等弧.圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.在一个圆中大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧.弦心距概念:从圆心到弦的距离叫做弦心距.弦心距、半径、弦长的关系:(考点)圆心角概念:顶点在圆心的角叫做圆心角.圆周角概念:顶点在圆上,并且两边都和圆相交的角叫做圆周角.三角形的外接圆1)经过三角形三个顶点的圆叫做三角形的外接圆,外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心,这个三角形叫做这个圆的内接三角形.2)三角形外心的性质:①三角形的外心是指外接圆的圆心,它是三角形三边垂直平分线的交点,它到三角形各顶点的距离相等; ②三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合.3)锐角三角形外接圆的圆心在它的内部(如图1);直角三角形外接圆的圆心在斜边中点处(即直角三角形外接圆半径等于斜边的一半,如图2);钝角三角形外接圆的圆心在它的外部(如图3).圆内接四边形概念:如果一个四边形的所有顶点都在一个圆上,那么这个四边形叫做圆内接四边形。
第六章 课时23 圆的有关概念和性质-2021年中考数学一轮复习考点突破课件

考点精讲
考点1 圆的有关概念、垂径定理(5年1考)
【例1】(2020黔东南州)如图2-23-4,⊙O的直径CD=20,AB是⊙O的弦,
AB⊥CD,垂足为点M,OM∶OC=3∶5,则AB的长为 A. 8
(C )
B. 12
C. 16
D.
返回目录
1. (2019德州)如图2-23-5,CD为⊙O的直径,弦AB⊥CD,垂足为点E, ,CE=1,AB=6,则弦AF的长度为_________________.
∠ADC=106°,则∠CAB等于
(C)
A. 10°
B. 14°
C. 16°
D. 26°
返回目录
4. (2020甘孜)如图2-23-14,AB为⊙O的直径,弦CD⊥AB于点H,若 AB=10,CD=8,则OH的长度为_________3_________. 5. (2020成都)如图2-23-15,A,B,C是⊙O上的三个点,∠AOB=50° ,∠B=55°,则∠A的度数为____3_0_°____________.
返回目录
4. 圆周角定理及其推论: (1)圆周角定理:同弧或等弧所对的圆周角相等,等于它所对的_圆__心__角_ 的一半. (2)推论1:半圆(或直径)所对的圆周角是____直__角____________; ________9_0_°________的圆周角所对的弦是直径. (3)推论2:圆的内接四边形对角_____互__补____(四点共圆的判定条件) .
( C)
A. 130°
B. 100°
C. 65°
D. 50°
返回目录
2. (2020吉林)如图2-23-9,四边形ABCD内接于⊙O,若∠B=108°,
则∠D的大小为
2021年九年级数学中考一轮复习知识点基础达标测评:圆(附答案)

2021年九年级数学中考一轮复习知识点基础达标测评:圆(附答案)1.下列说法正确的个数是()①直径是圆的对称轴;②半径相等的两个半圆是等弧;③长度相等的两条弧是等弧;④和圆有一个公共点的直线是圆的切线.A.1B.2C.3D.42.如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为()A.cm B.8cm C.6cm D.4cm3.某校科技实践社团制作实践设备,小明的操作过程如下:①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O,再任意找出圆O的一条直径标记为AB(如图1),测量出AB=4分米;②将圆环进行翻折使点B落在圆心O的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C、D(如图2);③用一细橡胶棒连接C、D两点(如图3),计算出橡胶棒CD的长度.小明计算橡胶棒CD的长度为()A.2分米B.2分米C.3分米D.3分米4.下列命题:①垂直于弦的直径平分弦,并且平分弦所对的两条弧;②在同圆或等圆中相等的圆心角所对的弧相等;③在同圆或等圆中如果两条弦相等,那么它们所对的圆心角相等;④圆内接四边形的对角互补.其中正确的命题共有()A.4个B.3个C.2个D.1个5.如图,半圆O的直径AB为15,弦BC为9,弦BD平分∠ABC,则BD的长是()A.12B.5C.6D.6.如图,四边形ABCD是⊙O的内接四边形,若∠BOD=130°,则∠A的度数为()A.50°B.65°C.115°D.130°7.如图,圆中两条弦AC,BD相交于点P.点D是的中点,连结AB,BC,CD,若BP =,AP=1,PC=3.则线段CD的长为()A.B.2C.D.8.若点B(a,0)在以A(1,0)为圆心,2为半径的圆内,则a的取值范围为()A.a<﹣1B.a>3C.﹣1<a<3D.a≥﹣1且a≠0 9.下列有关圆的一些结论:①任意三点确定一个圆;②相等的圆心角所对的弧相等;③平分弦的直径垂直于弦;并且平分弦所对的弧,④圆内接四边形对角互补.其中错误的结论有()A.1个B.2个C.3个D.4个10.已知⊙O的直径为12cm,如果圆心O到一条直线的距离为7cm,那么这条直线与这个圆的位置关系是()A.相离B.相切C.相交D.相交或相切11.如图,点A的坐标为(﹣3,﹣2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小值时,点P的坐标为()A.(﹣4,0)B.(﹣2,0)C.(﹣4,0)或(﹣2,0)D.(﹣3,0)12.为了销售方便,售货员把啤酒捆成如图形状,如果捆一圈,接头不计,问至少用绳子厘米.13.如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,BE=2,则⊙O半径为.14.在直径为52cm的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度为16cm,那么油面宽度AB是cm.15.点A,B,C在⊙O上,∠AOB=100°,∠BOC=40°,则∠ABC=.16.如图,在⊙O中,点A、B、C在⊙O上,且∠ACB=100°,则∠α=.17.如图,点A、B、C、D均在⊙O上,E为BC延长线上的一点,若∠A=110°,则∠DCE 的度数为.18.如图,⊙O中,弦AB、CD相交于点P,若AP=5,BP=4,CP=3,则DP为.19.已知⊙O的半径为1,点P与点O之间的距离为d,且关于x的方程x2﹣2x+d=0没有实数根,则点P在(填“圆内”“圆上”或“圆外”).20.如图,△ABC是圆O的内接三角形,连接OA、OC,若∠AOC=∠ABC,弦AC=6,则圆O的半径为.21.已知⊙O的半径是4,点O到直线l的距离为5,则直线l与⊙O的位置关系是.22.在平面内,O为线段AB的中点,所有到点O的距离等于OA的点组成图形W.取OA 的中点C,过点C作CD⊥AB交图形W于点D,D在直线AB的上方,连接AD,BD.(1)求∠ABD的度数;(2)若点E在线段CA的延长线上,且∠ADE=∠ABD,求直线DE与图形W的公共点个数.23.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=2,AE=5,则⊙O的半径是多少?24.如图,AB是⊙O的直径,C是的中点,CE⊥AB于点E,BD交CE于点F.(1)求证:CF=BF;(2)若CD=6,AC=8,求⊙O的半径及CE的长.25.已知:如图,AB是⊙O的直径,弦CD⊥AB于E,∠ACD=30°,AE=2cm.求DB 长.26.如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.(1)求证:BD=CD;(2)若圆O的半径为3,求BC的长.27.如图,矩形ABCD中AB=3,AD=4.作DE⊥AC于点E,作AF⊥BD于点F.(1)求AF、AE的长;(2)若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,求⊙A的半径r的取值范围.28.如图,⊙O是△BC的外接圆,AB长为4,AB=AC,联结CO并延长,交边AB于点D,交AB于点E,且E为AB的中点.求:(1)边BC的长;(2)⊙O的半径.29.如图,在矩形ABCD中,点O在对角线BD上,以OB的长为半径的圆O与AB,BD 分别交于点E,F,连接DE,且∠ADE=∠BDC.(1)判断直线DE与⊙O的位置关系,并证明你的结论;(2)若BC=6,CD=8,AE=4.5,求⊙O的半径.30.如图所示,AC与⊙O相切于点C,线段AO交⊙O于点B.过点B作BD∥AC交⊙O 于点D,连接CD、OC,且OC交DB于点E.若∠CDB=30°,DB=4cm.(1)求⊙O的半径长;(2)求由弦CD、BD与弧BC所围成部分的面积.(结果保留π)参考答案1.解:直径所在的直线是圆的对称轴,所以①错误;半径相等的两个半圆是等弧,所以②正确;能完全重合的两条弧是等弧,所以③错误;和圆有唯一公共点的直线是圆的切线,所以④错误.故选:A.2.解:如图所示,连接OA.⊙O的直径CD=10cm,则⊙O的半径为5cm,即OA=OC=5,又∵OM:OC=3:5,所以OM=3,∵AB⊥CD,垂足为M,∴AM=BM,在Rt△AOM中,AM==4,∴AB=2AM=2×4=8.故选:B.3.解:连接OC,如图,∵点B落在圆心O的位置,∴CD垂直平分OB,∴CE=DE,OE=BE=1,在Rt△OCE中,∵OC=2,OE=1,∴CE==,∴CD=2CE=2(分米).故选:B.4.解:①垂直于弦的直径平分弦,并且平分弦所对的两条弧,本小题说法是真命题;②在同圆或等圆中相等的圆心角所对的弧相等,本小题说法是真命题;③在同圆或等圆中如果两条弦相等,那么它们所对的圆心角相等,本小题说法是真命题;④圆内接四边形的对角互补,本小题说法是真命题;故选:A.5.解:连接AD、AC、OD,AC与OD相交于H点,如图,∵AB为直径,∴∠ADB=∠ACB=90°,在Rt△ACB中,AC==12,∵弦BD平分∠ABC,∴=,∴OD⊥AC,∴AH=CH=AC=6,∵OA=OB,∴OH=BC=,∴DH=OD﹣OH=﹣=3,在Rt△ADH中,AD==3,在Rt△ADB中,BD==6.故选:C.6.解:∵=,∴∠C=∠DOB=×130°=65°,∵∠A+∠C=180°,∴∠A=180°﹣65°=115°,故选:C.7.解:连接OD交AC于H,如图,∵点D是的中点,∴OD⊥AC,AH=CH=2,∴PH=1,∵AP•PC=BP•PD,∴PD==,在Rt△PDH中,DH==,在Rt△DCH中,CD==.故选:A.8.解:∵点B(a,0)在以点A(1,0)为圆心,以2为半径的圆内,∴|a﹣1|<2,∴﹣1<a<3.故选:C.9.解:①任意三点确定一个圆;错误,应该是不在同一直线上的三点可以确定一个圆;②相等的圆心角所对的弧相等;错误,应该是在同圆或等圆中;③平分弦的直径垂直于弦;并且平分弦所对的弧,错误,此弦不是直径;④圆内接四边形对角互补;正确;故选:C.10.解:∵⊙O的直径为12cm,∴⊙O的半径为6cm,∵圆心O到一条直线的距离为7cm>6cm,∴直线和圆相离.故选:A.11.解:连接AQ,AP.根据切线的性质定理,得AQ⊥PQ;要使PQ最小,只需AP最小,根据垂线段最短,可知当AP⊥x轴时,AP最短,∴P点的坐标是(﹣3,0).故选:D.12.解:如图所示:圆的直径为:7cm.则根据题意得:7×4+7π=28+7π≈49.98(cm)答:捆一圈至少用绳子49.98cm.13.解:连结OC,设⊙O半径为r,则OC=r,OE=r﹣BE=r﹣2,∵CD⊥AB,∴CE=DE=CD=6,在Rt△OCE中,∵OE2+CE2=OC2,∴(r﹣2)2+62=r2,解得r=10,即⊙O半径为10.故答案为10.14.解:连接OC、OA.则OC⊥AB于点D,OC=OA=×52=26cm,OD=OC﹣CD=26﹣16=10cm.在直角△OAD中,AD===24(cm),则AB=2AD=48cm.故答案是:48.15.解:∵∠AOB和∠ACB是弧AB所对的角,∴∠AOB=2∠ACB,∵∠AOB=100°,∴∠ACB=50°,同理:∠BOC=40°,∴∠BAC=20°,∴∠ABC=180°﹣50°﹣20°=110°,故答案为110°.16.解:如图,在优弧上取一点E,连接AE、BE,∵A、C、B、E四点共圆,∴∠ACB+∠AEB=180°,∵∠ACB=100°,∴∠AEB=80°,∵由圆周角定理得:∠AEB=AOB=,∴∠α=2∠AEB=160°,故答案为:160°.17.解:∵四边形ABCD为⊙O的内接四边形,∴∠BCD=180°﹣∠A=180°﹣110°=70°,∴∠DCE=180°﹣70°=110°,故答案为:110°.18.解:由相交弦定理得,P A•PB=PC•PD,∴5×4=3×DP,解得,DP=,故答案为:.19.解:∵方程x2﹣2x+d=0没有实数根,∴△=b2﹣4ac=4﹣4d<0,∴d>1,∵⊙O的半径为1,∴d>r;∴点P在⊙O的外部,故答案为:圆外.20.解:作所作的圆周角∠APC,过O点作OH⊥AC于H,如图,∵∠P=∠AOC,∠P+∠ABC=180°,∴∠AOC+∠ABC=180°,∵∠AOC=∠ABC,∴∠AOC+∠AOC=180°,解得∠AOC=120°,∵OA=OC,∴∠OAC=∠OCA=(180°﹣120°)=30°,∵OH⊥AC,∴AH=CH=AC=×6=3,在Rt△AOH中,OH=AH=×3=3,∴OA=2OH=6,即圆O的半径为6.故答案为6.21.解:∵圆心O到直线l的距离是5,大于⊙O的半径为4,∴直线l与⊙O相离.故答案为:相离.22.解:(1)根据题意,图形W为以O为圆心,OA为直径的圆.如图1,连接OD,∴OA=OD.∵点C为OA的中点,CD⊥AB,∴AD=OD.∴OA=OD=AD.∴△OAD是等边三角形.∴∠AOD=60°.∴∠ABD=30°.(2)如图2,∵∠ADE=∠ABD,∴∠ADE=30°.∵∠ADO=60°.∴∠ODE=90°.∴OD⊥DE.∴DE是⊙O的切线.∴直线DE与图形W的公共点个数为1.23.解:连接OD,设⊙O的半径为r,∵AB为⊙O的直径,弦CD⊥AB,CD=2,AE=5,∴DE=1,OE=5﹣r,在Rt△ODE中,OD2=OE2+DE2,即r2=(5﹣r)2+1,解得,r=2.6,答:⊙O的半径是2.6.24.(1)证明:∵AB是⊙O的直径,∴∠ACB=90°,∴∠A=90°﹣∠ABC.∵CE⊥AB,∴∠CEB=90°,∴∠ECB=90°﹣∠ABC,∴∠ECB=∠A.(2分)又∵C是的中点,∴=,∴∠DBC=∠A,∴∠ECB=∠DBC,∴CF=BF;(2)解:∵=,∴BC=CD=6,∵∠ACB=90°,∴AB===10,∴⊙O的半径为5,∵S△ABC=AB•CE=BC•AC,∴CE===.25.解:∵AB是⊙O的直径,弦CD⊥AB,∴CE=DE,∠AEC=∠DEB=90°,∵∠B=∠ACD=30°,在Rt△ACE中,AC=2AE=4cm,∴CE==2(cm),∴DE=2cm,在Rt△BDE中,∠B=30°,∴BD=2DE=4cm.∴DB的长为4cm.26.(1)证明:∵四边形ABCD内接于圆O,∠BAD=105°,∴∠C=180°﹣105°=75°,∵∠DBC=75°,∴∠DBC=∠C,∴BD=CD;(2)解:连接OB、OC,∵∠DBC=∠C=75°,∴∠BDC=180°﹣75°﹣75°=30°,由圆周角定理得,∠BOC=60°,∴△BOC为等边三角形,∴BC=OB=3.27.解:(1)∵矩形ABCD中AB=3,AD=4,∴AC=BD==5,∵AF•BD=AB•AD,∴AF==,同理可得DE=,在Rt△ADE中,AE==;(2)∵AF<AB<AE<AD<AC,∴若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,即点F在圆内,点D、C在圆外,∴⊙A的半径r的取值范围为2.4<r<4.28.解:(1)∵E点为的中点,CE为直径,∴CE⊥AB,∴AD=BD,即CD垂直平分AB,∴CB=CA=4;(2)连接OB,如图,∵AB=BC=AC,∴△ABC为等边三角形,∴∠A=60°,∴∠BOC=2∠A=120°,∴∠BOD=60°,在Rt△BOD中,BD=AB=2,∴OD=BD=,∴OB=2OD=,即⊙O的半径为.29.解:(1)直线DE与⊙O相切,证明:连接OE,∵四边形ABCD是矩形,∴AB∥CD,∴∠EBD=∠BDC,∵OB=OE,∴∠EBD=∠BEO,∵∠ADE=∠BDC,∴∠BEO=∠EBD=∠BDC=∠ADE,∵四边形ABCD是矩形,∴∠ADC=90°,∴∠EOD+∠EDO=∠EBD+∠BEO+∠EDO=∠BDC+∠ADE+∠EDO=∠ADC=90°,∴∠OED=180°﹣(∠EOD+∠EDO)=180°﹣90°=90°,即OE⊥ED,∵OE为半径,∴直线DE与⊙O相切;(2)解:∵四边形ABCD是矩形,∴∠A=∠C=90°,在Rt△DCB中,∠C=90°,∴BD=,∵四边形ABCD是矩形,∴AD=BC=6,在Rt△ADE中,∠A=90°,∴ED=,设⊙O的半径为R,在Rt△DOE中,DO2=DE2+OE2,,解得:R=,即⊙O的半径是.(2)第二种方法:解:∵四边形ABCD是矩形,∴∠A=∠C=90°,在Rt△DCB中,∠C=90°,∴BD=,∵AB=CD=8,AE=4.5,∴BE=8﹣4.5=3.5,作OG⊥BE于G,则BG=EG=BE=,∵OG∥AD,∴,即,∴OB=,即⊙O的半径是.30.解:(1)∵AC与⊙O相切于点C,∴∠ACO=90°.∵BD∥AC,∴∠BEO=∠ACO=90°,∴DE=EB=BD==2(cm)∵∠D=30°,∴∠O=2∠D=60°,在Rt△BEO中,sin60°=,=.∴OB=5,即⊙O的半径长为5cm.(2)由(1)可知,∠O=60°,∠BEO=90°,∴∠EBO=∠D=30°.在△CDE与△OBE中,.∴△CDE≌△OBE(AAS).∴S阴影=S扇OBC=π•42=(cm2),答:阴影部分的面积为cm2。
2022-2023 数学浙教版新中考 考点23圆的有关性质(解析版)

考点23圆的有关性质考点总结1.圆的有关概念(1)圆:平面上到定点的距离等于定长的所有点组成的图形叫做圆,定点叫做圆心,定长叫做圆的半径.以点O为圆心的圆,记做⊙O.(2)弧和弦:圆上任意两点间的部分叫做圆弧,简称弧.连结圆上任意两点的线段叫做弦.经过圆心的弦叫做直径,直径是圆中最长的弦.(3)与圆有关的角:①圆心角:顶点在圆心的角叫做圆心角,圆心角的度数等于它所对的弧的度数.②圆周角:顶点在圆上,两边分别和圆相交的角叫做圆周角.圆周角的度数等于它所对弧上的圆心角度数的一半.(4)三角形的外心:三角形外接圆的圆心叫做三角形的外心.外心也是三角形三边中垂线的交点.(5)圆的内接四边形:如果一个四边形的各个顶点在同一个圆上,那么这个四边形叫做圆的内接四边形,这个圆叫做四边形的外接圆.圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角.2.圆的有关性质:(1)圆是轴对称图形,其对称轴是任意一条过圆心的直线.圆是中心对称图形,对称中心为圆心,圆绕着它的圆心旋转任意一个角度都能和原来的圆重合.(2)垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.推论2:平分弧的直径垂直平分弧所对的弦.(3)在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等,那么它们所对应的其余各组量都相等.(4)圆心角与圆周角的关系:一条弧所对的圆周角等于它所对的圆心角的一半.推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.(5)确定圆的条件:①已知圆心、半径;②已知直径;③不在同一条直线上的三点.真题演练一、单选题1.(2021·浙江衢州·中考真题)已知扇形的半径为6,圆心角为150︒.则它的面积是( )A .32π B .3π C .5π D .15π【答案】D【分析】 已知扇形的半径和圆心角度数求扇形的面积,选择公式2360n R S π=直接计算即可. 【详解】 解:2150615360S ππ⨯==. 故选:D2.(2021·浙江嘉兴·中考真题)如图,在ABC ∆中,90BAC ∠=︒,AB =AC =5,点D 在AC 上,且2AD =,点E 是AB 上的动点,连结DE ,点F ,G 分别是BC ,DE 的中点,连接AG ,FG ,当AG =FG 时,线段DE 长为( )A B C D .4【答案】A【分析】连接DF ,EF ,过点F 作FN ⊥AC ,FM ⊥AB ,结合直角三角形斜边中线等于斜边的一半求得点A ,D ,F ,E 四点共圆,⊥DFE =90°,然后根据勾股定理及正方形的判定和性质求得AE 的长度,从而求解.【详解】解:连接DF ,EF ,过点F 作FN ⊥AC ,FM ⊥AB⊥在ABC ∆中,90BAC ∠=︒,点G 是DE 的中点,⊥AG =DG =EG又⊥AG =FG⊥点A ,D ,F ,E 四点共圆,且DE 是圆的直径⊥⊥DFE =90°⊥在Rt ⊥ABC 中,AB =AC =5,点F 是BC 的中点,⊥CF =BF =122BC =,FN =FM =52 又⊥FN ⊥AC ,FM ⊥AB ,90BAC ∠=︒⊥四边形NAMF 是正方形⊥AN =AM =FN =52又⊥90NFD DFM ∠+∠=︒,90DFM MFE ∠+∠=︒⊥NFD MFE ∠=∠⊥⊥NFD ⊥⊥MFE⊥ME =DN =AN -AD =12⊥AE =AM +ME =3⊥在Rt ⊥DAE 中,DE故选:A .3.(2021·浙江·中考真题)如图,已知点O 是ABC 的外心,∠40A =︒,连结BO ,CO ,则BOC ∠的度数是( ).A .60︒B .70︒C .80︒D .90︒【答案】C【分析】 结合题意,根据三角形外接圆的性质,作O ;再根据圆周角和圆心角的性质分析,即可得到答案.【详解】 ABC 的外接圆如下图⊥⊥40A =︒⊥280BOC A ∠=∠=︒故选:C .4.(2021·浙江·中考真题)如图,已知在矩形ABCD 中,1,AB BC ==P 是AD 边上的一个动点,连结BP ,点C 关于直线BP 的对称点为1C ,当点P 运动时,点1C 也随之运动.若点P 从点A 运动到点D ,则线段1CC 扫过的区域的面积是( )A .πB .π+CD .2π【答案】B【分析】先判断出点Q 在以BC 为直径的圆弧上运动,再判断出点C 1在以B 为圆心,BC 为直径的圆弧上运动,找到当点P 与点A 重合时,点P 与点D 重合时,点C 1运动的位置,利用扇形的面积公式及三角形的面积公式求解即可.【详解】解:设BP 与CC 1相交于Q ,则⊥BQC =90°,⊥当点P 在线段AD 运动时,点Q 在以BC 为直径的圆弧上运动,延长CB 到E ,使BE =BC ,连接EC ,⊥C 、C 1关于PB 对称,⊥⊥EC 1C =⊥BQC =90°,⊥点C 1在以B 为圆心,BC 为直径的圆弧上运动,当点P 与点A 重合时,点C 1与点E 重合,当点P 与点D 重合时,点C 1与点F 重合,此时,tanPC AB PBC BC BC ∠=== ⊥⊥PBC =30°,⊥⊥FBP =⊥PBC =30°,CQ =12BC =BQ 32=,⊥⊥FBE =180°-30°-30°=120°,11322BCF S CC BQ =⨯==线段1CC 扫过的区域的面积是2120360BCF S ππ⨯+= 故选:B . 5.(2021·浙江丽水·中考真题)如图,AB 是O 的直径,弦CD OA ⊥于点E ,连结,OC OD .若O 的半径为,m AOD α∠=∠,则下列结论一定成立的是( )A .tan OE m α=⋅B .2sin CD m α=⋅C .cos AE m α=⋅D .2sin COD S m α=⋅【答案】B【分析】 根据垂径定理、锐角三角函数的定义进行判断即可解答.【详解】解:⊥AB 是O 的直径,弦CD OA ⊥于点E , ⊥12DE CD = 在Rt EDO ∆中,OD m =,AOD α∠=∠ ⊥tan =DE OE α ⊥=tan 2tan DE CD OE αα=,故选项A 错误,不符合题意; 又sin DE OD α=⊥sin DE OD α=⊥22sin CD DE m α==,故选项B 正确,符合题意; 又cos OE ODα= ⊥cos cos OE OD m αα==⊥AO DO m ==⊥cos AE AO OE m m α=-=-,故选项C 错误,不符合题意;⊥2sin CD m α=,cos OE m α=⊥2112sin cos sin cos 22COD S CD OE m m m αααα∆=⨯=⨯⨯=,故选项D 错误,不符合题意;故选B .6.(2021·浙江金华·中考真题)如图,在Rt ABC 中,90ACB ∠=︒,以该三角形的三条边为边向形外作正方形,正方形的顶点,,,,,E F G H M N 都在同一个圆上.记该圆面积为1S ,ABC 面积为2S ,则12S S 的值是( )A .52πB .3πC .5πD .112π 【答案】C【分析】先确定圆的圆心在直角三角形斜边的中点,然后利用全等三角形的判定和性质确定⊥ABC 是等腰直角三角形,再根据直角三角形斜边中线的性质得到2214S AB =,再由勾股定理解得2254OF AB =,解得2154S AB π=⋅,据此解题即可. 【详解】 解:如图所示,正方形的顶点,,,,,E F G H M N 都在同一个圆上,∴圆心O 在线段,EF MN 的中垂线的交点上,即在Rt ABC 斜边AB 的中点,且AC =MC ,BC =CG ,⊥AG =AC +CG =AC +BC ,BM =BC +CM =BC +AC ,⊥AG =BM ,又⊥OG =OM ,OA =OB ,⊥⊥AOG ⊥⊥BOM ,⊥⊥CAB =⊥CBA ,⊥⊥ACB =90°,⊥⊥CAB =⊥CBA =45°,12OC AB ∴=, 2211112224S AB OC AB AB AB ∴=⋅=⋅= 22222215()24OF AO AF AB AB AB =+=+= 22154S OF AB ππ∴==⋅, 212254514AB S S AB ππ⋅∴==.故选:C .7.(2021·浙江绍兴·中考真题)如图,正方形ABCD 内接于O ,点P 在AB 上,则P ∠的度数为( )A .30B .45︒C .60︒D .90︒【答案】B【分析】 连接OB ,OC ,由正方形ABCD 的性质得90BOC ∠=°,再根据圆周角与圆心角的关系即可得出结论.【详解】解:连接OB ,OC ,如图,⊥正方形ABCD 内接于O ,⊥90BOC ∠=° ⊥11904522BPC BOC ∠=∠=⨯︒=︒ 故选:B .8.(2021·浙江嘉兴·中考真题)已知平面内有O 和点A ,B ,若O 半径为2cm ,线段3cm OA =,2cm OB =,则直线AB 与O 的位置关系为( )A .相离B .相交C .相切D .相交或相切【答案】D【分析】根据点与圆的位置关系的判定方法进行判断.【详解】解:⊥⊥O 的半径为2cm ,线段OA =3cm ,线段OB =2cm ,即点A 到圆心O 的距离大于圆的半径,点B 到圆心O 的距离等于圆的半径, ⊥点A 在⊥O 外.点B 在⊥O 上,⊥直线AB 与⊥O 的位置关系为相交或相切,故选:D .9.(2021·浙江·杭州市丰潭中学二模)如图,已知平面直角坐标系中,点A ,B 坐标分别为A (4,0),B (﹣6,0).点C 是y 轴正半轴上的一点,且满足∠ACB =45°,圆圆得到了以下4个结论:∠∠ABC 的外接圆的圆心在OC 上;∠∠ABC =60°;∠∠ABC的外接圆的半径等于∠OC =12.其中正确的是( )A .∠∠B .∠∠C .∠∠D .∠∠【答案】C【分析】 如图,作出ABC 的外接圆,以AB 为斜边在x 轴上方作等腰Rt ABE △,过点E 作ED x ⊥轴于D ,连接EC ,过点E 作EF y ⊥轴于F ,由圆心必然在弦的垂直平分线上可判断⊥;再证明E 为ABC 外接圆圆心,求出半径,可判断⊥;再在ECF △中由勾股定理求出CF ,可求得OC 和1tan 2OC ABC OB ∠==,即可判断⊥⊥. 【详解】解:如图,作出ABC 的外接圆,以AB 为斜边在x 轴上方作等腰Rt ABE △, 过点E 作ED x ⊥轴于D ,连接EC ,过点E 作EF y ⊥轴于F ,⊥ABC 的外接圆的圆心必在弦AB 的垂直平分线上,⊥圆心肯定不在OC 上,故⊥错误;⊥⊥ACB =45°,⊥由圆周角定理得:AB 所对的圆心角必为90°,⊥EB =EA ,⊥在弦AB 的垂直平分线上,⊥⊥AEB =90°,⊥E 必为圆心,即AE 、BE 为半径, ⊥AE =⊥正确;⊥BD =5,OB =6,⊥OD =1,⊥⊥EDO =⊥DOF =⊥OFE =90°,⊥OD =EF =1,ED =FO =5,⊥7CF ==,⊥OC =OF +FC =12,故⊥正确;⊥1 tan2OCABCOB∠==,⊥⊥ABC≠60°,故⊥错误;故选:C.10.(2021·浙江·杭州市丰潭中学二模)如图,点A的坐标为(﹣3,2),∠A的半径为1,P为坐标轴上一动点,PQ切∠A于点Q,在所有P点中,使得PQ长最小时,点P 的坐标为()A.(0,2)B.(0,3)C.(﹣2,0)D.(﹣3,0)【答案】D【分析】连接AQ、P A,如图,利用切线的性质得到⊥AQP=90°,再根据勾股定理得到PQ=AP⊥x轴时,AP的长度最小,利用垂线段最短可确定P点坐标.【详解】解:连接AQ、P A,如图,⊥PQ切⊥A于点Q,⊥AQ⊥PQ,⊥⊥AQP=90°,⊥PQ当AP的长度最小时,PQ的长度最小,⊥AP⊥x轴时,AP的长度最小,⊥AP⊥x轴时,PQ的长度最小,二、填空题11.(2021·浙江杭州·中考真题)如图,已知O 的半径为1,点P 是O 外一点,且2OP =.若PT 是O 的切线,T 为切点,连接OT ,则PT =_____.【分析】根据圆的切线的性质,得90OTP ∠=︒,根据圆的性质,得1OT =,再通过勾股定理计算,即可得到答案.【详解】⊥PT 是O 的切线,T 为切点⊥90OTP ∠=︒⊥PT⊥O 的半径为1⊥1OT =⊥PT12.(2021·浙江台州·中考真题)如图,将线段AB 绕点A 顺时针旋转30°,得到线段AC .若AB =12,则点B 经过的路径BC 长度为_____.(结果保留π)直接利用弧长公式即可求解.【详解】 解:30122180BC l ππ⋅==, 故答案为:2π.13.(2021·浙江温州·中考真题)图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图2),则图1中所标注的d 的值为______;记图1中小正方形的中心为点A ,B ,C ,图2中的对应点为点A ',B ',C '.以大正方形的中心O 为圆心作圆,则当点A ',B ',C '在圆内或圆上时,圆的最小面积为______.【答案】6- (16π-【分析】(1)先求出剪拼后大正方形的面积,得到其边长,再结合图2,求出图1中长方形的长边除去长为d 部分的线段后,剩下的线段长刚好为大正方形的边长,最后用图1中的长方形的长减去图2中大正方形的边长即可完成求解;(2)结合两图分别求出对应线段的长,通过作辅助线构造直角三角形,利用勾股定理求出O 点到'B 、'A 、'C 之间的距离即可确定最小圆的半径,即可完成求解.【详解】解:⊥图1是邻边长为2和6的矩形,它由三个小正方形组成,⊥每个小正方形边长为2,图1和图2中整个图形的面积为2612=⨯,所以图2中正方形的边长''M N =如下图3所示;分别连接'OB 、'OA 、'OC ,并分别过点'B 、'A 、'C 向大正方形的对边作垂线,得到如图所示辅助线,综合两图可知,'1LA =,LJ ='1MA =,O⊥'1JA =,1OJ =,⊥)'1OA ===综合两图可知:'1B E =,6'32B D d =-=,DF =⊥()''33B F DF B D =-==1OF =,⊥'OB =;继续综合两图可知:''1C H C G ==,⊥'1C I OI =,⊥'OC =⊥2816=-<-⊥'B 距离O 点最远,⊥⊥圆的面积为(16π-;故答案为:6-(16π-.14.(2021·浙江宁波·中考真题)抖空竹在我国有着悠久的历史,是国家级的非物质文P .若120P ∠=︒,O 的半径为6cm ,则图中CD 的长为________cm .(结果保留π)【答案】2π【分析】连接OC 、OD ,利用切线的性质得到90OCP ODP ∠=∠=︒,根据四边形的内角和求得60COD ∠=︒,再利用弧长公式求得答案.【详解】连接OC 、OD ,⊥,AC BD 分别与O 相切于点C ,D ,⊥90OCP ODP ∠=∠=︒,⊥120P ∠=︒,360OCP ODP P COD ∠+∠+∠+∠=︒,⊥60COD ∠=︒,⊥CD 的长=6062180(cm ),故答案为:2π..15.(2021·浙江温州·中考真题)如图,O 与OAB 的边AB 相切,切点为B .将OAB 绕点B 按顺时针方向旋转得到O A B '''△,使点O '落在O 上,边A B '交线段AO 于点C .若25A '∠=︒,则OCB ∠=______度.【答案】85AB 相切,可求⊥CBO ==30°,利用三角形内角和公式即可求解.【详解】解:连结OO′,⊥将OAB 绕点B 按顺时针方向旋转得到O A B '''△,⊥BO′=BO =OO′,⊥⊥BOO′为等边三角形,⊥⊥OBO′=60°,⊥O 与OAB 的边AB 相切,⊥⊥OBA =⊥O′BA′=90°,⊥⊥CBO =90°-⊥OBO′=90°-60°=30°,⊥⊥A′=25°⊥⊥A′O′B =90°-⊥A′=90°-25°=65°⊥⊥AOB =⊥A′O′B =65°,⊥⊥OCB =180°-⊥COB -⊥OBC =180°-65°-30°=85°.故答案为85.三、解答题16.(2021·浙江衢州·中考真题)如图,在ABC 中,CA CB =,BC 与A 相切于点D ,过点A 作AC 的垂线交CB 的延长线于点E ,交A 于点F ,连结BF .(1)求证:BF 是A 的切线.【答案】(1)见解析;(2)3【分析】(1)连接AD ,根据题意证明ABF ABD △△≌,即可证明BF 是A 的切线;(2)根据题意即(1)的结论可得BEF CEA △∽△,列比例求出FB 的长,根据勾股定理求EF 即可.【详解】(1)证明如图,连接AD ,CA CB =,CAB ABC ∴∠=∠,AE AC ⊥,90CAB EAB ∴∠+∠=︒又A 切BC 于点D ,=90ADB ∴∠︒,90ABD BAD ∴∠+∠=︒,BAE BAD ∴∠=∠.又AB AB ,AF AD =,()ABF ABD SAS ∴△△≌,90AFB ADB ∴∠=∠=︒,BF ∴是A 的切线.(2)由(1)得:90AFB FAC ∠=∠=︒,//BF AC ∴,BEF CEA ∴△∽△,BE BF CE CA∴=, 20CB CA ==,5BE =,∴=.EF317.(2021·浙江台州·中考真题)如图,BD是半径为3的∠O的一条弦,BD=点A是∠O上的一个动点(不与点B,D重合),以A,B,D为顶点作平行四边形ABCD.(1)如图2,若点A是劣弧BD的中点.∠求证:平行四边形ABCD是菱形;∠求平行四边形ABCD的面积.(2)若点A运动到优弧BD上,且平行四边形ABCD有一边与∠O相切.∠求AB的长;∠直接写出平行四边形ABCD对角线所夹锐角的正切值.【答案】⊥证明见解析;⊥(2)⊥AB【分析】(1)⊥利用等弧所对的弦相等可得AD AB=,根据一组邻边相等的平行四边形是菱形可得证;⊥连接AO,交BD于点E,连接OD,根据垂径定理可得DE BE==用勾股定理求出OE的长,即可求解;(2)⊥分情况讨论当CD与O相切时、当BC与O相切时,利用垂径定理即可求解;⊥根据等面积法求出AH的长度,利用勾股定理求出DH的长度,根据正切的定义即可求解.【详解】解:(1)⊥⊥点A是劣弧BD的中点,⊥四边形ABCD 是平行四边形,⊥平行四边形ABCD 是菱形;⊥连接AO ,交BD 于点E ,连接OD ,,⊥点A 是劣弧BD 的中点,OA 为半径,⊥OA BD ⊥,OA 平分BD , ⊥DE BE ==⊥平行四边形ABCD 是菱形,⊥E 为两对角线的交点,在Rt ODE △中,1OE ,⊥2AE =,⊥122ABCD S BD AE =⋅⨯= (2)⊥如图,当CD 与O 相切时,连接DO 并延长,交AB 于点F ,⊥CD 与O 相切,⊥DF CD ⊥,⊥四边形ABCD 是平行四边形,⊥//AB CD ,⊥DF AB ⊥,在Rt BDF △中,()2222323BF BD DF OF =-=-+, 在Rt BOF △中,22229BF BO OF OF =-=-,⊥()223239OF OF -+=-,解得73OF =,⊥BF =⊥2AB BF = 如图,当BC 与O 相切时,连接BO 并延长,交AD 于点G ,同理可得AG DG =73OG =,所以AB综上所述,AB ⊥过点A 作AH BD ⊥,,由(2)得:7163,33BD AD BG ==+= 根据等面积法可得1122BD AH AD BG ⋅=⋅, 解得329AH =,在在Rt ADH 中,DH ==⊥HI =⊥tan AH AIH HI ∠== 18.(2021·浙江金华·中考真题)在扇形AOB 中,半径6OA =,点P 在OA 上,连结PB ,将OBP 沿PB 折叠得到O BP '.(1)如图1,若75O ∠=︒,且BO '与AB 所在的圆相切于点B .∠求APO ∠'的度数.∠求AP 的长.(2)如图2,BO '与AB 相交于点D ,若点D 为AB 的中点,且//PD OB ,求AB 的长.【答案】(1)⊥60°;⊥6-(2)125π 【分析】(1)根据图像折叠的性质,确定角之间的关系,通过已知的角度来间接求所求角的角度;求AP 的长,先连接'OO ,先在Rt OBQ △中,求出OQ ;再在Rt OPQ 中,求出OP 即可得到答案;(2)要求AB 的长,扇形的半径已知,就转化成求AOB ∠的度数,连接'OO ,通过条件找到角之间的等量关系,再根据三角形内角和为180︒,建立等式求出AOB ∠,最后利用弧长的计算公式进行计算.【详解】解:(1)⊥如图1,'BO 为圆的切线'90OBO ∴∠=︒.由题意可得,'45O BP OBP ∠=∠=︒,'O PB OPB ∠=∠.180180754560OPB BOP OBP ∴∠=︒-∠-∠=︒-︒-︒=︒ '60O PB OPB ∴∠=∠=︒'60APO ∴∠=︒,⊥如图1,连结'OO ,交BP 于点Q .则有'BP OO ⊥.在Rt OBQ △中,sin 45OQ OB =⨯︒=在Rt OPQ △中,sin 60OQ OP ==︒6AP OA OP ∴=-=-(2)如图2.连结OD .设1a ∠=.⊥点D 为AB 的中点.BD AD ∴=21a ∴∠=∠=//PD OB321a ∴∠=∠=∠=.PD PO ∴=由题意可得,','PO PO O BOP =∠=∠.'PD PO ∴=''2PDO O BOP a ∴∠=∠=∠=又//,''2PD OB OBO PDO a ∴∠=∠=,4'2OB OD OBO a =∴∠=∠=43'180PDO ∠+∠+∠=︒,22180a a a ∴++=︒,解得36a =︒. 72AOB ∴∠=︒726121801805n R AB πππ⨯∴===.。
2021年中考数学 一轮专题训练:圆的有关性质(含答案)

2021中考数学 一轮专题训练:圆的有关性质一、选择题(本大题共10道小题)1. 如图,在⊙O 中,AB ︵=CD ︵,∠1=45°,则∠2等于( )A .60°B .30°C .45°D .40°2. 如图所示,AB是⊙O 的直径,C ,D 是⊙O 上的两点,CD ⊥AB.若∠DAB =65°,则∠BOC 等于( )A .25°B .50°C .130°D .155°3.如图,四边形ABCD 内接于⊙O ,F 是CD︵上一点,且DF︵=BC ︵,连接CF 并延长交AD 的延长线于点E ,连接AC ,若∠ABC =105°,∠BA C =25°,则∠E 的度数为( ) A . 45° B . 50° C . 55° D . 60°4. 2019·赤峰如图,AB 是⊙O 的弦,OC ⊥AB 交⊙O 于点C ,D 是⊙O 上一点,∠ADC =30°,则∠BOC 的度数为( )A.30°B.40°C.50°D.60°5. 如图,AD是⊙O的直径,BC是弦,四边形OBCD是平行四边形,AC与OB 相交于点P,下列结论错误的是()A.AP=2OP B.CD=2OPC.OB⊥AC D.AC平分OB6.如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD=22,BD=3,则AB的长为( )A. 2B. 3C. 4D. 57. 如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x 的图象被⊙P截得的弦AB的长为2 3,则a的值是()A.2 B.2+ 2C.2 3 D.2+ 38. 2020·武汉模拟小名同学响应学习号召,在实际生活中发现问题,并利用所学的数学知识解决问题,他将汽车轮胎如图放置在地面台阶直角处,他测量了台阶高a为160 mm,直角顶点A到轮胎与地面接触点B的距离AB为320 mm,请帮小名同学计算轮胎的直径为()A.350 mm B.700 mmC.800 mm D.400 mm9. 如图,在半径为13的⊙O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,则CD的长是()A.2 6 B.2 10 C.2 11 D.4 310. 如图,AB是⊙O的直径,点C,D在⊙O上,∠BOC=110°,AD∥OC,则∠AOD的度数为()A.70°B.60°C.50°D.40°二、填空题(本大题共10道小题)11. 如图,AC是圆内接四边形ABCD的一条对角线,点D关于AC的对称点E 在边BC上,连接AE,若∠ABC=64°,则∠BAE的度数为.12. 2018·孝感已知⊙O的半径为10 cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16 cm,CD=12 cm,则弦AB和CD之间的距离是________cm.13. 2018·毕节如图,AB是⊙O的直径,C,D为半圆的三等分点,CE⊥AB于点E,则∠ACE的度数为________.14. 当宽为3 cm的刻度尺的一边与⊙O相切于点A时,另一边与⊙O的两个交点B,C处的读数如图所示(单位:cm),那么该圆的半径为________cm.15. 如图0,A,B是⊙O上的两点,AB=10,P是⊙O上的动点(点P与A,B 两点不重合),连接AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF=________.16. 如图,四边形ABCD内接于⊙O,AB为⊙O的直径,C为弧BD的中点.若∠DAB=40°,则∠ABC=________°.17. 如图,AC是圆内接四边形ABCD的一条对角线,点D关于AC的对称点E 在边BC上,连接AE.若∠ABC=64°,则∠BAE的度数为________.18. 如图,在⊙O中,弦AB =1,点C 在AB 上移动,连接OC ,过点C 作CD⊥OC 交⊙O 于点D ,则CD 的最大值为________.19. 如图2,一下水管道横截面为圆形,直径为100 cm ,下雨前水面宽为60 cm ,一场大雨过后,水面宽为80 cm ,则水位上升________cm. 链接听P39例4归纳总结20. 如图,AB ,CD是半径为5的⊙O 的两条弦,AB =8,CD =6,MN 是⊙O 的直径,AB ⊥MN 于点E ,CD ⊥MN 于点F ,P 为EF 上的任意一点,则PA +PC 的最小值为________.三、解答题(本大题共6道小题)21. 2018·牡丹江 如图,在⊙O 中,AB ︵=2AC ︵,AD ⊥OC 于点D .求证:AB =2AD .22.如图,AB 是⊙O 的直径,点C 、D 在⊙O 上,∠A =2∠BCD ,点E 在AB 的延长线上,∠AED =∠ABC. (1)求证:DE 与⊙O 相切;(2)若BF =2,DF =10,求⊙O 的半径.23. 2018·天津 如图,已知AB 是⊙O 的直径,弦CD 与AB 相交,∠BAC =38°.(1)如图①,若D 为AB ︵的中点,求∠ABC 和∠ABD 的大小;(2)如图②,过点D 作⊙O 的切线,与AB 的延长线交于点P ,若DP ∥AC ,求∠OC D 的大小.24.如图,△ABC 内接于⊙O ,AB =AC ,∠BAC =36°,过点A 作AD ∥BC ,与∠ABC 的平分线交于点D ,BD 与AC 交于点E ,与⊙O 交于点F . (1)求∠DAF 的度数; (2)求证:AE 2=EF ·ED ; (3)求证:AD 是⊙O 的切线.25. 如图,AB是☉O的直径,点C为的中点,CF为☉O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.(1)求证:△BFG≌△CDG;(2)若AD=BE=2,求BF的长.26. 已知OA=5,sin∠O=35,点D为线段OA上的动点,以A为圆心、AD为半径作⊙A.(1)如图1,若⊙A交∠O于B、C两点,设OD=x,BC=y,求y关于x的函数解析式,并写出函数的定义域;(2)将⊙A沿直线OB翻折后得到⊙A′.①若⊙A′与直线OA相切,求x的值;②若⊙A′与以D为圆心、DO为半径的⊙D相切,求x的值.2021中考数学一轮专题训练:圆的有关性质-答案一、选择题(本大题共10道小题)1. 【答案】C2. 【答案】C3. 【答案】B 【解析】∵四边形ABCD是圆内接四边形,∠ABC=105°,∴∠ADC=75°,∵=,∴∠BAC=∠DCF=25°,∴∠E=∠ADC-∠DCF=50°.4. 【答案】D5. 【答案】A[解析] ∵AD是⊙O的直径,∴∠ACD=90°.∵四边形OBCD是平行四边形,∴CD∥OB,CD=OB,∴∠CPO=90°,即OB⊥AC,∴选项C正确;∴CP=AP.又∵OA=OD,∴OP是△ACD的中位线,∴CD=2OP,∴选项B正确;∴CD=OB=2OP,即P是OB的中点,∴AC平分OB,∴选项D正确.6. 【答案】B 【解析】由垂径定理可得DH=2,所以BH=BD2-DH2=1,又可得△DHB∽△ADB,所以有BD2=BH·BA,(3)2=1×BA,AB=3.7. 【答案】B[解析] 如图,连接PB,过点P作PC⊥AB于点C,过点P作横轴的垂线,垂足为E,交AB于点D,则PB=2,BC= 3.在Rt△PBC中,由勾股定理得PC=1.∵直线y=x平分第一象限的夹角,∴△PCD和△DEO都是等腰直角三角形,∴PD=2,DE=OE=2,∴a=PE=2+ 2.故选B.8. 【答案】C9. 【答案】C[解析] 过点O作OF⊥CD于点F,OG⊥AB于点G,连接OB,OD,OE,如图所示.则DF=CF,AG=BG=12AB=3,∴EG=AG-AE=2.在Rt△BOG中,OG=OB2-BG2=13-9=2,∴EG=OG,∴△EOG是等腰直角三角形,∴∠OEG=45°,OE=2OG=2 2.∵∠DEB=75°,∴∠OEF=30°,∴OF=12OE= 2.在Rt△ODF中,DF=OD2-OF2=13-2=11,∴CD=2DF=2 11.故选C.10. 【答案】D[解析] ∵∠BOC=110°,∴∠AOC=70°.∵AD∥OC,∴∠A=∠AOC=70°.∵OA=OD,∴∠D=∠A=70°.在△OAD中,∠AOD=180°-(∠A+∠D)=40°.二、填空题(本大题共10道小题) 11. 【答案】52° [解析]∵圆内接四边形对角互补, ∴∠B +∠D=180°,∵∠B=64°,∴∠D=116°.∵点D 关于AC 的对称点是点E ,∴∠D=∠AEC=116°.∵∠AEC=∠B +∠BAE ,∴∠BAE=52°.12. 【答案】2或14 [解析] ①当弦AB 和CD 在圆心同侧时,连接OA ,OC ,过点O 作OE ⊥CD 于点F ,交AB 于点E ,如图①, ∵AB =16 cm ,CD =12 cm , ∴AE =8 cm ,CF =6 cm. ∵OA =OC =10 cm , ∴EO =6 cm ,OF =8 cm , ∴EF =OF -OE =2 cm ;②当弦AB 和CD 在圆心异侧时,连接OA ,OC ,过点O 作OE ⊥CD 于点E 并反向延长交AB 于点F ,如图②,∵AB =16 cm ,CD =12 cm , ∴AF =8 cm ,CE =6 cm. ∵OA =OC =10 cm , ∴OF =6 cm ,OE =8 cm , ∴EF =OF +OE =14 cm.∴AB 与CD 之间的距离为2 cm 或14 cm.13. 【答案】30°[解析] 如图,连接OC .∵AB 是⊙O 的直径,AC ︵=CD ︵=BD ︵,∴∠AOC =∠COD =∠DOB =60°. ∵OA =OC ,∴△AOC 是等边三角形, ∴∠A =60°.∵CE ⊥OA ,∴∠AEC =90°,∴∠ACE =90°-60°=30°.14. 【答案】25615. 【答案】5 [解析] ∵OE 过圆心且与PA 垂直,∴PE =EA.同理PF =FB ,∴EF 是△PAB 的中位线,∴EF =12AB =5.16. 【答案】70 [解析] 如图,连接AC.∵AB 为⊙O 的直径,∴∠ACB =90°.∵C 为弧BD 的中点,∴∠CAB =12∠DAB =20°, ∴∠ABC =70°.17. 【答案】52° [解析] ∵四边形ABCD 是圆内接四边形,∴∠B +∠D =180°. ∵∠B =64°,∴∠D =116°.又∵点D 关于AC 的对称点是点E ,∴∠AEC =∠D =116°.又∵∠AEC =∠B +∠BAE ,∴∠BAE =52°.18. 【答案】12 [解析] 连接OD.因为CD ⊥OC ,所以CD =OD2-OC2,根据题意可知圆的半径一定,故当OC 最小时CD 最大,故当OC ⊥AB 时CD 最大,此时CD =12AB =12.19. 【答案】10或70 [解析] 对于半径为50 cm 的圆而言,圆心到长为60 cm 的弦的距离为40 cm ,到长为80 cm 的弦的距离为30 cm.①当圆心在两平行弦之外时,两弦间的距离=40-30=10(cm);②当圆心在两平行弦之间时,两弦间的距离=40+30=70(cm).综上所述,水位上升10 cm 或70 cm.20. 【答案】7 2 [解析] 如图,连接OB ,OC ,BC ,则BC 的长即为P A +PC 的最小值.过点C 作CH ⊥AB 于点H ,则四边形EFCH 为矩形,∴CH =EF ,EH =CF .根据垂径定理,得BE =12AB =4,CF =12CD =3,∴OE =OB 2-BE 2=52-42=3,OF =OC 2-CF 2=52-32=4, ∴CH =EF =OE +OF =3+4=7,BH =BE +EH =BE +CF =4+3=7. 在Rt △BCH 中,由勾股定理,得BC =7 2,则P A +PC 的最小值为72.三、解答题(本大题共6道小题)21. 【答案】证明:如图,延长AD 交⊙O 于点E ,∵OC ⊥AD ,∴AE ︵=2AC ︵,AE =2AD .∵AB ︵=2AC ︵,∴AE ︵=AB ︵,∴AB =AE ,∴AB =2AD .22. 【答案】(1)证明:如解图,连接DO ,∴∠BOD =2∠BCD =∠A ,(2分)解图又∵∠DEA =∠CBA ,∴∠DEA +∠DOE =∠CAB +∠CBA ,又∵∠ACB =90°,∴∠ODE =∠ACB =90°,(5分)∴OD ⊥DE ,又∵OD 是⊙O 的半径,∴DE 与⊙O 相切.(7分)(2)解:如解图,连接BD ,可得△FBD ∽△DBO ,∴BD BO =DF OD =BF BD ,(8分)∴BD =DF =10,∴OB =5,(10分)即⊙O 的半径为5.23. 【答案】解:(1)如图①,连接OD .∵AB 是⊙O 的直径,∴∠ACB =90°,∴∠ABC =90°-∠BAC =90°-38°=52°.∵D 为AB ︵的中点,∠AOB =180°,∴∠AOD =90°,∴∠ABD =12∠AOD =45°.(2)如图②,连接OD .∵DP 切⊙O 于点D ,∴OD ⊥DP ,即∠ODP =90°.∵DP ∥AC ,∠BAC =38°,∴∠P =∠BAC =38°.∵∠AOD 是△ODP 的一个外角,∴∠AOD =∠P +∠ODP =128°,∴∠ACD =64°.∵OC =OA ,∠BAC =38°,∴∠OCA =∠BAC =38°,∴∠OCD=∠ACD-∠OCA=64°-38°=26°.24. 【答案】(1)解:∵AB=AC,∠BAC=36°,∴∠ABC=∠ACB=12(180°-36°)=72°,∴∠AFB=∠ACB=72°,∵BD平分∠ABC,∴∠DBC=36°,∵AD∥BC,∴∠D=∠DBC=36°,∴∠DAF=∠AFB-∠D=72°-36°=36°;(2)证明:∵∠EAF=∠FBC=∠D,∠AEF=∠AED,∴△EAF∽△EDA,∴AEDE=EF EA,∴AE2=EF·ED;(3)证明:如解图,过点A作BC的垂线,G为垂足,∵AB=AC,∴AG垂直平分BC,∴AG过圆心O,∵AD∥BC,∴AD⊥AG,∴AD是⊙O的切线.解图25. 【答案】解:(1)证明:∵C是的中点,∴=.∵AB是☉O的直径,且CF⊥AB,∴=,∴=,∴CD=BF.在△BFG和△CDG中,∵∴△BFG≌△CDG(AAS).(2)如图,过C作CH⊥AD,交AD延长线于H,连接AC,BC,∵=,∴∠HAC=∠BAC.∵CE⊥AB,∴CH=CE.∵AC=AC,∴Rt△AHC≌Rt△AEC(HL),∴AE=AH.∵=,∴CD=BC.又∵CH=CE,∴Rt△CDH≌Rt△CBE(HL),∴DH=BE=2,∴AE=AH=AD+DH=2+2=4,∴AB=4+2=6.∵AB是☉O的直径,∴∠ACB=90°,∴∠ACB=∠BEC,∵∠EBC=∠ABC,∴△BEC∽△BCA,∴=,∴BC2=AB·BE=6×2=12,∴BF=BC=2.26. 【答案】(1)如图2,作AE ⊥BC ,垂足为E ,那么E 是BC 的中点.在Rt △OAE 中,OA =5,sin ∠O =35,所以AE =3. 在Rt △BAE 中,AB =AD =5-x ,AE =3,BE =1122BC y =, 由勾股定理,得2221(5)3()2x y -=+. 整理,得221016y x x =-+.定义域是0≤x <2.图2 图3(2)①如图3,将⊙A 沿直线OB 翻折后得到⊙A ′,AA ′=2AE =6.作A ′H ⊥OA ,垂足为H .在Rt △A ′AH 中,AA ′=6,sin ∠A ′=35,所以AH =185,A ′H =245. 若⊙A ′与直线OA 相切,那么半径等于A ′H .解方程2455x -=,得15x =. ②如图4,在Rt △A ′DH 中,222241814'()(5)25555A D x x x =+--=-+. 对于⊙A ′,R =5-x ;对于⊙D ,r =DO =x ;圆心距d =A ′D .如果两圆外切,由d =R +r ,得2142555x x x x -+=-+.解得145x =(如图4). 如果两圆内切,由d =|R -r |,得21425|5|5x x x x -+=--. 解得86515x =>.所以两圆不可能内切.图4 图5考点伸展当D为OA的中点时,⊙A′与以D为圆心、DA为半径的⊙D是什么位置关系?⊙A′和⊙D等圆,R=52,两圆不可能内切.当D为OA的中点时,DH=AH-AD=18511 5210-=.此时'5A D==<.因此两圆的半径和大于圆心距,此时两圆是相交的(如图5).。
_2021年九年级中考数学一轮突破 基础过关 第23讲圆的有关概念和性质

第23讲圆的有关概念和性质课标要求(1)理解圆、弧、弦、圆心角、圆周角的概念,了解等圆、等弧的概念;探索并了解点与圆的位置关系.(2)探索并证明垂径定理:垂直于弦的直径平分弦以及弦所对的两条弧.(3)探索圆周角与圆心角及其所对弧的关系,了解并证明圆周角定理及其推论:圆周角的度数等于它所对弧上的圆心角度数的一半;直径所对的圆周角是直角;90°的圆周角所对的弦是直径;圆内接四边形的对角互补.(4)知道三角形的内心和外心.注:考试中,不要求用(2)(3)证明其他命题.考情分析该内容主要是以选择题、填空题、综合解答题的形式来考查,分值为3~14分.主要考点为垂径定理,圆心角、弧、弦之间的关系,圆周角定理等.预测2021年中考,以上考点依然会出现,建议加强理解定义,掌握性质与定理,灵活运用方法,并加以练习巩固.一、圆的有关概念1. 圆的定义:平面上到________的距离等于________的所有点组成的图形叫做圆,其中________称为圆心,________称为半径.以O为圆心的圆记作________,读作“圆O”.圆也可以看作平面上一动点以一定点为中心,一定长为距离运动一周的轨迹称为圆周,简称圆.简单说成到定点的距离等于定长的点的集合叫做圆.2. 与圆有关的概念(1)弧:圆上任意________的部分叫做圆弧,简称弧.大于半圆的弧称为________弧,小于半圆的弧称为________弧.(2)弦:连接圆上任意两点的________叫做弦.经过圆心的弦叫做________.(3)圆心角:顶点在________上的角叫做圆心角.(4)圆周角:顶点在________上,且它的两边分别与圆________的角叫做圆周角.二、圆的轴对称性1. 圆是________对称图形,过________的任一条直线或________所在的直线是它的对称轴.2. 垂径定理(1)垂径定理:垂直于________的直径平分这条弦,并且平分弦所对的________.(2)逆定理:平分________(不是直径)的直径________于弦,并且平分弦所对的________.三、圆的中心对称性——旋转不变性1. 圆是以________为对称中心的________对称图形.2. 圆心角、弧、弦关系定理在______________中,如果两个____________、两条________、两条________中有一组量相等,那么它们所对应的其余各组量分别________.四、圆周角定理1. 定理:一条弧所对的________等于它所对的________的一半.2. 推论1:在__________中,同弧或等弧所对的________相等.3. 推论2:直径所对的圆周角是________,________的圆周角所对的弦是直径.五、三角形的外接圆1. 确定圆的条件:不在____________上的三个点确定一个圆.2. 经过三角形________的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的________.外心是三角形三边________的交点,外心到三角形各顶点距离________;锐角三角形外心一定在三角形________,钝角三角形外心在三角形________,直角三角形外心在________中点.六、圆内接多边形1. 如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.2. 圆内接四边形的对角________,并且每一个外角都等于它的内对角.圆心角、弧、弦的关系)(2014·贵港,第9小题,3分)如图,AB 是⊙O 的直径,BC ︵=CD ︵=DE ︵,∠COD =34°,则∠AEO 的度数是( )A .51°B .56°C .68°D .78°【思路点拨】由BC ︵=CD ︵=DE ︵,可求得∠BOC =∠EOD =∠COD =34°,继而可求得∠AOE 的度数;然后再根据等腰三角形的性质和三角形内角和定理来求∠AEO 的度数.如图,∵BC ︵=CD ︵=DE ︵,∠COD =34°,∴∠BOC =∠EOD =∠COD =34°,∴∠AOE =180°-∠EOD -∠COD -∠BOC =78°.又∵OA =OE ,∴∠AEO =∠EAO ,∴∠AEO =12×(180°-78°)=51°.(2015·南宁,第11小题,3分)如图,AB 是⊙O 的直径,AB =8,点M 在⊙O 上,∠MAB =20°,N 是MB ︵的中点,P 是直径AB 上的一动点,若MN =1,则△PMN 周长的最小值为( )A .4B .5C .6D .7,圆周角定理(2020·柳州,第6小题,3分)如图,点A 、B 、C 在⊙O 上,若∠BOC=70°,则∠A 的度数为( )A .35°B .40°C.55° D.70°【思路点拨】一条弧所对的圆周角等于它所对的圆心角的一半.小结解圆周角和圆心角的计算和证明问题时,要准确找出同弧或等弧所对的圆周角和圆心角,然后再灵活运用圆周角定理.有时也需要连接半径,利用同圆的半径相等构造等腰三角形;出现直径时,通过作辅助线构造直角三角形来进行证明和计算.(2020·河池,第17小题,3分)如图,AB是⊙O的直径,点C,D ,E都在⊙O上,∠1=55°,则∠2=________° .,垂径定理、勾股定理、勾股定理的逆定理等的综合运用(2020·梧州,第8小题,3分)如图,⊙O的直径CD过弦EF的中点G,连接CF,∠C=30°,CF=23,则OG的长是()A.1 B.3C .2D. 23【思路点拨】如解图,连接OF.∵CD 为⊙O 的直径且过弦EF 的中点G ,∴CD 垂直平分EF.又∵∠C =30°,CF =23,∴GF =3,CG =3.设半径为r ,在Rt △OGF 中,()3-r 2+()32=r 2,解得r =2,∴OG =1 .小结解有关弦的问题,通常是过圆心作弦的垂线,或作垂直于弦的直径,连接半径等辅助线,为应用垂径定理创造条件.如图,⊙O 的弦AB 垂直半径OC 于点D ,∠CBA =30°,OC =3 3cm ,则弦AB 的长为( )A .9 cmB .3 3 cm C.92 cm D.332 cm1. 有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.其中正确的有( )A .4个B .3个C .2个D .1个2. 如图,在以AB 为直径的半圆O 中,C 是它的中点,若AC =2,则△ABC 的面积是( )A .1.5B .2C .3D .43. (2020·泰安)如图,△ABC 是⊙O 的内接三角形,AB =BC ,∠BAC =30°,AD 是直径,AD =8,则AC 的长为( B )A .4B .4 3 C.833 D .23 ,第3题图) ,第4题图)4. 如图,A ,B 是⊙O 上两点,若四边形ACBO 是菱形,⊙O 的半径为r ,则点A 与点B 之间的距离为( )A.2rB.3r C .r D .2r5. 如图,CD 是⊙O 的直径,AB 是弦(不是直径),AB ⊥CD 于点E ,则下列结论正确的是( )A .AE>BE B.AD ︵=BC ︵C .∠D =12∠AEC D .△ADE ∽△CBE,第5题图) ,第6题图)6. 如图,四边形ABCD 内接于⊙O ,E 为CD 延长线上一点,若∠ADE =110°,则∠AOC 的度数是( C )A .70°B .110°C .140°D .160°7. (2020·青岛)如图,BD 是⊙O 的直径,点A ,C 在⊙O 上,AB ︵=AD ︵,AC 交BD 于点G.若∠COD =126°,则∠AGB 的度数为( B )A .99°B .108°C .110°D .117°,第7题图),第8题图)8. 如图,已知点E是⊙O上的点,B,C分别是劣弧AD的三等分点,∠BOC =46°,则∠AED的度数为________°.9. 如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=68°,则∠BAC=________°.,第9题图),第10题图)10. 如图,A,B,C是⊙O上的三点,∠CAO=25°,∠BCO=35°,则∠AOB =________°.11. 如图,点A,B,C,D在⊙O上,O点在∠D的内部,四边形OABC 为平行四边形,则∠OAD+∠OCD=________°.,第11题图),第12题图)12. 如图,点B,A,C,D在⊙O上,OA⊥BC,∠AOB=50°,则∠ADC =________°.13. 在⊙O中,直径AB⊥CD于点E,连接CO并延长交AD于点F,且CF⊥AD.求∠D的度数.14. 如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°.(1)求证:△ABC是等边三角形;(2)求圆心O到边BC的距离OD.15. 如图,点A,B,C,D都在⊙O上,OC⊥AB,∠ADC=30°.(1)求∠BOC的度数;(2)求证:四边形AOBC是菱形.第23讲圆的有关概念和性质【基础梳理】一、1.定点定长定点定长⊙O 2.(1)两点之间优劣(2)线段直径(3)圆心(4)圆相交二、1.轴圆心圆心2.(1)弦 两条弧 (2)弦 垂直 两条弧三、1.圆心 中心 2.同圆或等圆 圆心角 弧 弦 相等 四、1.圆周角 圆心角 2.同圆或等圆 圆周角 3.直角 90°五、1.同一直线 2.三个顶点 外心 垂直平分线 相等 内部 外部 斜边六、互补【重点突破】[例1]A [变式1]B [提示]作点N 关于AB 的对称点N′,证△OMN′是等边三角形.[例2]A [变式2]35 [例3]A [变式3]A【达标检测】1.B 2.B 3.B 4.B 5.D 6.C 7. B 8. 69 9. 22 10. 120 11. 60 12. 2513.解:连接BD.∵AB 是⊙O 的直径,∴BD ⊥AD , 又∵CF ⊥AD ,∴BD ∥CF , ∴∠BDC =∠C , 又∵∠BDC =12∠BOC ,∴∠C =12∠BOC.∵AB ⊥CD ,∴∠C =30°,∴∠ADC =60°.14.解:(1)∵∠ABC=∠APC,∠BAC=∠APC=60°,∴在△ABC中,∠BCA=60°,∴△ABC是等边三角形.(2)连接OB,△ABC为等边三角形,⊙O为其外接圆,∴O为△ABC的外心,∴OB是∠ABC角平分线.∴∠OBD=30°.∴OD=12OB=4.15.(1)解:∵∠ADC=30°,∴∠AOC=60°,又∵OC⊥AB,∴=,∴∠BOC=∠AOC=60°. (2)证明:∵=,∴AC=BC.∵∠BOC=60°,OB=OC,∴△BOC是等边三角形,∴BC=BO=CO,∴OA=OB=BC=AC,∴四边形AOBC是菱形.。
2021年九年级中考数学考点综合复习集锦【圆】相关知识点解答题专项训练(含解析)

【圆】相关知识点解答题专项训练(含解析)1.如图,以P(0,3)为圆心,6为半径的⊙P交x轴于点A、B,交y轴于点C、D,连接BP并延长交⊙P于点E,连接DE交x轴于点F.(1)求∠CDE的度数;(2)求△BEF的面积.2.如图,在Rt△ABC中,∠ACB=90°,AC=2,BC=2,CD是斜边AB上的中线,以CD为直径的⊙O分别交AC、BC于点M、N,过点N作NE⊥AB,垂足为E.(1)求证:NE与⊙O相切;(2)求图中阴影部分的面积.3.如图,AD与⊙O相切于点D,点A在直径CB的延长线上.(1)求证:∠DCB=∠ADB;(2)若∠DCB=30°,AC=3,求AD的长.4.已知,⊙O中,=,D是⊙O上的点,OC⊥BD.(1)如图①,求证=;(2)如图②,连接AB,BC,CD,DA,若∠A=70°,求∠BCD,∠ADB的大小.5.如图,在矩形ABCD中,点O在对角线BD上,以OB的长为半径的圆O与AB,BD分别交于点E,F,连接DE,且∠ADE=∠BDC.(1)判断直线DE与⊙O的位置关系,并证明你的结论;(2)若BC=6,CD=8,AE=4.5,求⊙O的半径.6.已知AB是圆O的直径,点C是圆O上一点,点P为圆O外一点,且OP∥BC,∠P=∠BAC.(1)求证:PA为圆O的切线;(2)如果OP=AB=10,求AC的长.7.如图所示,AC与⊙O相切于点C,线段AO交⊙O于点B.过点B作BD∥AC交⊙O于点D,连接CD、OC,且OC交DB于点E.若∠CDB=30°,DB=4cm.(1)求⊙O的半径长;(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)8.如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E为BC的中点,连接DE.(1)求证:DE是⊙O的切线;(2)若⊙O的半径为1,∠BAC=60°,则DE=.9.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG,DC的延长线交于点F.(1)求证:∠FGC=∠AGD.(2)当DG平分∠AGC,∠ADG=45°,AF=,求弦DC的长.10.如图,△ABC中,∠ACB=90°,D为AB上的一点,以CD为直径的⊙O交AC于E,连接BE 交CD于P,交⊙O于F,连接DF,∠ABC=∠EFD.(1)求证:AB与⊙O相切;(2)若AD=2,BD=3,则⊙O的直径=;(3)若PC=2PF,BF=a,求CP(用a的代数式表示).11.如图,AB为⊙O的直径,C、E在⊙O上,AC平分∠EAB,过点C作AE的垂线交AE的延长线于点D.(1)求证:DC是⊙O的切线;(2)连接CE,若CE=6,AC=8,求⊙O的直径的长.12.如图,△ABC是⊙O的内接三角形,AB为⊙O的直径,AB=8,BD平分∠ABC,交AC于点E,交⊙O于点D,连接AD.(1)求证:∠DBA=∠CAD;(2)若的长度为2π,求∠AEB的度数.13.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,以CD为直径的⊙O分别交AC、BC于点M、N,过点N作NE⊥AB,垂足为E.(1)若⊙O的半径为,AC=10,求BN的长;(2)求证:NE与⊙O相切.参考答案1.解:(1)∵P(0,3),∴OP=3,∵⊙P的半径是6,∴PB=6,∴OP=PB,∵x轴⊥y轴,∴∠POB=90°,∴∠PBO=30°,∴∠BPO=90°﹣30°=60°,∵PE=PD,∠E+∠CDE=∠BPO,∴∠CDE=∠E=60°=30°;(2)过P作PM⊥DE于M,则∠PME=90°,∵⊙P的半径是6,∴PE=PD=6,PM⊥DE,∴DM=ME,∵∠E=30°,∴PM=PE=6=3,由勾股定理得:DM=EM==3,∴DE=EM+DM=6,∴△BEF的面积是=6×3=9.2.(1)证明:如图,连接ON,∵∠ACB=90°,CD是斜边AB上的中线,∴CD=BD,∴∠B=∠BCD,∵CO=ON,∴∠BCD=∠CNO,∴ON∥BD,∴∠ONE=∠NEB=90°,即ON⊥NE,∴NE与⊙O相切;(2)∵,∴∠B=30°,∴∠CON=120°,∴,,∴.3.(1)证明:如图,连接OD,∵AD与⊙O相切于点D,∴OD⊥AD,∴∠ODB+∠ADB=90°,∵CB是直径,∴∠CDB=90°,∴∠ODB+∠ODC=90°,∴∠ODC=∠ADB,∵OD=OC,∴∠ODC=∠OCD,∴∠C=∠ADB;(2)解:∵∠DCB=∠ADB,∠DAC=∠CAD,∴△ADB∽△ACD,∴=,∵CB是直径,∴∠CDB=90°,∠DCB=30°,∴tan∠DCB==,∴=,∵AC=3,∴AD=3.4.(1)证明:∵OC⊥BD,OC过O,∴=,∵=,∴=;(2)解:∵四边形ABD是圆内接四边形,∴∠A+∠BCD=180°,∵∠A=70°,∴∠BCD=110°,∵=,∴∠CBD=∠CDB=(180°﹣∠BCD)=35°,∵=,∴∠ADB=∠CDB=35°.5.解:(1)直线DE与⊙O相切,证明:连接OE,∵四边形ABCD是矩形,∴AB∥CD,∴∠EBD=∠BDC,∵OB=OE,∴∠EBD=∠BEO,∵∠ADE=∠BDC,∴∠BEO=∠EBD=∠BDC=∠ADE,∵四边形ABCD是矩形,∴∠ADC=90°,∴∠EOD+∠EDO=∠EBD+∠BEO+∠EDO=∠BDC+∠ADE+∠EDO=∠ADC=90°,∴∠OED=180°﹣(∠EOD+∠EDO)=180°﹣90°=90°,即OE⊥ED,∵OE为半径,∴直线DE与⊙O相切;(2)解:∵四边形ABCD是矩形,∴∠A=∠C=90°,在Rt△DCB中,∠C=90°,∴BD=,∵四边形ABCD是矩形,∴AD=BC=6,在Rt△ADE中,∠A=90°,∴ED=,设⊙O的半径为R,在Rt△DOE中,DO2=DE2+OE2,,解得:R=,即⊙O的半径是.(2)第二种方法:解:∵四边形ABCD是矩形,∴∠A=∠C=90°,在Rt△DCB中,∠C=90°,∴BD=,∵AB=CD=8,AE=4.5,∴BE=8﹣4.5=3.5,作OG⊥BE于G,则BG=EG=BE=,∵OG∥AD,∴,即,∴OB=,即⊙O的半径是.6.(1)证明:∵AB是⊙O的直径,∴∠ACB=90°,∴∠BAC+∠B=90°,又∵OP∥BC,∴∠AOP=∠B,∴∠BAC+∠AOP=90°,∵∠P=∠BAC,∴∠P+∠AOP=90°,∴∠PAO=90°,∴PA⊥OA,又∵OA是的⊙O的半径,∴PA为⊙O的切线;(2)解:由(1)得:∠PAO=∠ACB=90°,又∵∠P=∠BAC,OP=BA,∴△OAP≌△BCA(AAS),∴BC=OA=AB=5,∴AC===57.解:(1)∵AC与⊙O相切于点C,∴∠ACO=90°.∵BD∥AC,∴∠BEO=∠ACO=90°,∴DE=EB=BD==2(cm)∵∠D=30°,∴∠O =2∠D =60°,在Rt △BEO 中,sin60°=,=.∴OB =5,即⊙O 的半径长为5cm .(2)由(1)可知,∠O =60°,∠BEO =90°,∴∠EBO =∠D =30°.在△CDE 与△OBE 中,.∴△CDE ≌△OBE (AAS ).∴S 阴影=S 扇OBC =π•42=(cm 2),答:阴影部分的面积为cm 2.8.(1)证明:连接OD 、BD ,如图所示:∵AB 为⊙O 的直径,∴∠ADB =∠CDB =90°,∵点E 为BC 的中点,∴BE =DE ,∴∠BDE =∠EBD ,∵OA =OD ,∴∠OAD =∠ODA ,∵∠OAD +∠OBD =90°,∠EBD +∠OBD =90°,∴∠OAD =∠EBD ,∴∠ODA =∠BDE ,∴∠ODE =∠BDE +∠ODB =∠ODA +∠ODB =90°,∴DE ⊥OD ,∵点D 在⊙O 上,∴DE 是圆⊙O 的切线;(2)解:由(1)知:∠ADB =∠CDB =90°,∴DE=BC,∵⊙O的半径为1,∴AB=2,∵∠BAC=60°,∴tan60°=,∴BC=AB•tan60°=2×=2,∴DE=BC=×2=,故答案为:.9.(1)证明:如图1,连接AC,∵AB是⊙O的直径,弦CD⊥AB,∴=,∴AD=AC,∴∠ADC=∠ACD,∵ADCG在⊙O上,∴∠CGF=∠ADC,∵∠AGD=∠ACD,∴∠FGC=∠AGD;(2)解:如图2,连接BG,AC,∵AB是⊙O的直径,弦CD⊥AB,∴DE=CE,∵DG平分∠AGC,∴∠AGD=∠CGD,∵∠FGC=∠AGD,∴∠AGD=∠CGD=∠FGC,∵∠AGD+∠CGD+∠FGC=180°,∴∠CGF=∠AGD=60°,∴∠ADC=∠ACD=60°,∴△ADC是等边三角形,∵AB⊥CD,∴∠CAE=∠DAE=30°,∵∠ADG=45°,∴∠CDG=∠CAG=60°﹣45°=15°,∴∠EAF=30°+15°=45°,Rt△AEF中,AE=EF,∵AF=,∴AE=EF=,Rt△ADE中,∠DAE=30°,∴DE=1,∴DC=2DE=2.10.(1)证明:∵∠ACB=90°,∴∠CEB+∠CBE=90°,∵∠ABC=∠EFD,∠EFD=∠FDB+∠FBD,∴∠EBC=∠FDB,∵∠CEB=∠CDF,∴∠CDF+∠FDB=90°,即∠CDB=90°,∴CD⊥AB,∴AB与⊙O相切;(2)解:∵∠ACD+∠A=90°,∠A+∠ABC=90°,∴∠ACD=∠ABC,∵∠ADC=∠BDC=90°,∴△ACD∽△CBD,∴=,∴CD2=AD•BD=2×3=6,∴CD=,∴⊙O的直径为,故答案为:.(3)解:∵CD为⊙O的直径,∴∠CFD=90°,∴∠DCF+∠CDF=90°,又∵∠CDB=90°,∴∠FDB+∠CDF=90°,∴∠FDB=∠DCF,∵∠EBC=∠FDB,∴∠EBC=∠DCF,∴△PCF∽△PBC,∴=,∵PC=2PF,∴==∴PB=2PC=4PF,又PB=PF+BF,∴4PF=PF+BF,∴PF=BF=a,∵PC=2PF.∴PC=a.11.(1)证明:连接OC,CE,∵AC平分∠EAB,∴∠1=∠2,∵OA=OC,∴∠2=∠3,∴∠1=∠3,∴OC∥AD,∵AD⊥CD,∴OC⊥CD,又∵OC是⊙O的半径,∴DC是⊙O的切线;(2)解:连接OC,CE,∵AC平分∠EAB,∴=,∴BC=CE=6,∵AB是⊙O的直径,∴∠ACB=90°,∴AB2=BC2+AC2=82+62=100,∴AB=10,即⊙O的直径为10.12.(1)证明:∵BD平分∠ABC,∴∠CBD=∠DBA,∵∠DAC与∠CBD都是弧CD所对的圆周角,∴∠DAC=∠CBD,∴∠DBA=∠CAD;(2)解:连接OC,∵AB为⊙O的直径,AB=8,∴OB=OC=4,∵的长度为2π,设∠BOC=n°,∴=2π,∴n=90,∴∠BOC=90°,∴∠BAC=45°,∵AB为⊙O的直径,∴∠ACB=90°,∴∠ABC=45°,∵BD平分∠ABC,∴∠CBD=ABC=22.5°,∴∠AEB=∠CBD+∠ACB=112.5°.13.解:(1)如图1所示,设AC交⊙O于点M.连接DM、DN.∵∠ACB=90°,CD是斜边AB的中线,∴CD=AD=BD.∵CD是⊙O的直径,∴∠DMC=∠DNC=90°又∵∠ACB=90°,∴四边形OMDN是矩形.∴CM=DN.∵∠DMC=90°,∴DM⊥AC.又∵CD=AD,∴.∴DN=5.∵⊙O的半径为,∴BD=CD=13.在Rt△BDN中,由勾股定理得.(2)如图2所示,连接ON、DN.由(1)知CD=BD,∠CND=90°.∴BN=CN.又∵OC=OD,∴ON∥BD.又∵NE⊥DB,∴NE⊥ON.∴NE与⊙O相切.。
中考数学综合题专题复习【圆】专题解析

中考数学综合题专题复习【圆】专题解析一. 教学内容:1. 圆的内容包括:圆的有关概念和基本性质,直线和圆的位置关系,圆和圆的位置关系,正多边形和圆。
2. 主要定理:(1)垂径定理及其推论。
(2)圆心角、弧、弦、弦心距之间的关系定理。
(3)圆周角定理、弦切角定理及其推论。
(4)圆内接四边形的性质定理及其推论。
(5)切线的性质及判定。
(6)切线长定理。
(7)相交弦、切割线、割线定理。
(8)两圆连心线的性质,两圆的公切线性质。
(9)圆周长、弧长;圆、扇形,弓形面积。
(10)圆柱、圆锥侧面展开图及面积计算。
(11)正n边形的有关计算。
二. 中考聚焦:圆这一章知识在中考试题中所占的分数比例大约如下表:圆的知识在中考中所占的比例大,题型多,常见的有填空题、选择题、计算题或证明题,近年还出现了一些圆的应用题及开放型问题、设计型问题,中考的压轴题都综合了圆的知识。
三. 知识框图:圆圆的有关性质直线和圆的位置关系圆和圆的位置关系正多边形和圆⎧⎨⎪⎪⎩⎪⎪圆的有关性质圆的定义点和圆的位置关系(这是重点)不在同一直线上的三点确定一个圆圆的有关性质轴对称性—垂径定理(这是重点)旋转不变性圆心角、弧、弦、弦心距间的关系圆心角定理圆周角定理(这是重点)圆内接四边形(这是重点)⎧⎨⎩⎧⎨⎪⎪⎩⎪⎪⎧⎨⎪⎪⎪⎩⎪⎪⎪⎧⎨⎪⎪⎪⎪⎩⎪⎪⎪⎪直线和圆的位置关系相离相交相切切线的性质(这是重点)切线的判定(这是重点)弦切角(这是重点)和圆有关的比例线段(这是重点难点)⎧⎨⎪⎪⎩⎪⎪⎧⎨⎪⎪⎪⎪⎩⎪⎪⎪⎪圆和圆的位置关系外离内含相交相切内切(这是重点)外切(这是重点)两圆的公切线⎧⎨⎪⎩⎪⎧⎨⎪⎪⎪⎪⎩⎪⎪⎪⎪正多边形和圆正多边形和圆正多边形定义正多边形和圆正多边形的判定及性质正多边形的有关计算(这是重点)圆的有关计算圆周长、弧长(这是重点)圆、扇形、弓形面积(这是重点)圆柱、圆锥侧面展开图(这是重点)⎧⎨⎪⎪⎩⎪⎪⎧⎨⎪⎩⎪⎧⎨⎪⎪⎪⎪⎩⎪⎪⎪⎪【典型例题】【例1】. 爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m 以外的安全区域。
2021中考数学知识点总结 圆 (22大知识点+例题)

圆知识点:一、圆一、圆的有关性质在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫圆,固定的端点O叫圆心,线段OA叫半径。
由圆的意义可知:圆上各点到定点(圆心O)的距离等于定长的点都在圆上。
确实是说:圆是到定点的距离等于定长的点的集合,圆的内部能够看做是到圆。
心的距离小于半径的点的集合。
圆的外部能够看做是到圆心的距离大于半径的点的集合。
连结圆上任意两点的线段叫做弦,通过圆心的弦叫直径。
圆上任意两点间的部份叫圆弧,简称弧。
圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫半圆,大于半圆的弧叫优弧;小于半圆的弧叫劣弧。
由弦及其所对的弧组成的圆形叫弓形。
圆心相同,半径不相等的两个圆叫同心圆。
能够重合的两个圆叫等圆。
同圆或等圆的半径相等。
在同圆或等圆中,能够相互重合的弧叫等弧。
二、过三点的圆l、过三点的圆过三点的圆的作法:利用中垂线找圆心定理不在同一直线上的三个点确信一个圆。
通过三角形各极点的圆叫三角形的外接圆,外接圆的圆心叫外心,那个三角形叫圆的内接三角形。
二、反证法反证法的三个步骤:①假设命题的结论不成立;②从那个假设动身,通过推理论证,得出矛盾;③由矛盾得出假设不正确,从而确信命题的结论正确。
例如:求证三角形中最多只有一个角是钝角。
证明:设有两个以上是钝角那么两个钝角之和>180°与三角形内角和等于180°矛盾。
∴不可能有二个以上是钝角。
即最多只能有一个是钝角。
三、垂直于弦的直径圆是轴对称图形,通过圆心的每一条直线都是它的对称轴。
垂径定理:垂直于弦的直径平分这条弦,而且平分弦所对的两条弧。
推理1:平分弦(不是直径)的直径垂直于弦,而且平分弦所对两条弧。
弦的垂直平分线通过圆心,而且平分弦所对的两条弧。
平分弦所对的一条弧的直径,垂直平分弦,而且平分弦所对的另一个条弧。
推理2:圆两条平行弦所夹的弧相等。
四、圆心角、弧、弦、弦心距之间的关系圆是以圆心为对称中心的中心对称图形。
中考数学:“圆”知识点复习及重难点分析(内附真题视频讲解)

中考数学:“圆”知识点复习及重难点分析(内附真题视频讲解)您身边最专业的初中数学名师讲堂对于圆这一章,大家要重点掌握以下几个考点:认识圆相关的概念、垂径定理及其推论、直线与圆的关系、圆与圆的位置关系,切线的判定定理与性质定理等等。
大家要灵活把握这些知识点的应用。
(今天的每日一练非常重要,一定要认真做哦,不会再看视频讲解)知识点1.认识圆相关的概念圆有关概念:弦、弦心距、半径、直径、圆心;弧、优弧、劣弧、半圆;等弧、等圆、同圆、同心圆;圆心角、圆周角;①圆的定义在一个个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆,固定的端点O叫做圆心,线段OA叫做半径。
②圆的几何表示以点O为圆心的圆记作“⊙O”,读作“圆O”③不在同一直线上的三点确定一个圆。
圆的两条平行弦所夹的弧相等。
2.垂径定理及其推论垂直于弦的直径平分这条弦并且平分弦所对的两条弧。
①平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧②弦的垂直平分线经过圆心,并且平分弦所对的两条弧③平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧3.直线与圆的关系直线和圆有三种位置关系,具体如下:(1)相交:直线和圆有两个公共点时,叫做直线和圆相交,这时直线叫做圆的割线,公共点叫做交点;(2)相切:直线和圆有唯一公共点时,叫做直线和圆相切,这时直线叫做圆的切线,(3)相离:直线和圆没有公共点时,叫做直线和圆相离。
如果⊙O的半径为r,圆心O到直线l的距离为d,那么:直线l与⊙O相交d<>直线l与⊙O相切d=r;直线l与⊙O相离d>r;4.圆与圆的位置关系1、圆和圆的位置关系如果两个圆没有公共点,那么就说这两个圆相离,相离分为外离和内含两种。
如果两个圆只有一个公共点,那么就说这两个圆相切,相切分为外切和内切两种。
如果两个圆有两个公共点,那么就说这两个圆相交。
2、圆心距两圆圆心的距离叫做两圆的圆心距。
(全国通用版)2021年中考数学复习第六单元圆第23讲与圆相关的位

(全国通用版)2021年中考数学复习第六单元圆第23讲与圆相关的位第23讲与圆相关的位置关系重要和困难切线的性质和判断(2021郴州t23,8分)已知bc是⊙o的直径,点d是bc延长线上一点,ab=ad,ae 是⊙o的弦,∠aec=30°.(1)验证:直线ad是⊙ o;(2)若ae⊥bc,垂足为m,⊙o的半径为4,求ae的长.【思路】(1)先计算∠ 那么ABC=30°∠ 坏=120°,然后计算∠ OAB=30°与OA=ob 成反比,证明结论;(2)第一次发现∠ AOC=60°,使用三角函数求am,然后使用垂直直径定理得出结论解:(1)∵∠aec=30°,∴∠abc=30°.∵ab=ad,∴∠d=∠abc=30°。
根据三角形的内角和定理,得∠bad=120°.2分连接oa.∵oa=ob.∴∠oab=∠abc=30°。
∴∠oad=∠bad-∠oab=90°.∴oa⊥ad.⊙ a点开始了⊙ 哦,∴直线ad是⊙o的切线.4分(2)∵∠aec=30°,∴∠aoc=60°.∵bc⊥ae于点m,——AE=凌晨2点,∠ OMA=90°。
6分在rt△aom中,am=oasin∠aom=4×sin60°=23.∴ae=2am=43.8分(2022江西)如图所示△ ABC,O是AC上面的点,以O点为圆心,OC为半径,在C 点与BC相切,交叉点a作为ad的延长线⊥ Bo在D点与Bo相交,以及∠ AOD=∠ 令人不快的(1)求证:ab为⊙o的切线;四(2)若bc=6,tan∠abc=,求ad的长.三【思路点拨】(1)作oe⊥ab,先由∠aod=∠bad求得∠abd=∠oad,再由∠bco=∠d =90°及∠boc=∠aod求得∠obc=∠oad=∠abd,最后证△boc≌△boe得oe=oc,依据切线的判定可得;(2)先求得∠eoa=∠abc,在在RT中△ 根据切线长度定理,得出ABC,AC=8,ab=10,be=BC=6,AE=4,OE=3,然后得出Bo=35,然后△ 阿布德 ABC被证明得奥运会组委会=,据此可得答案.adab一【自主解答】解:(1)证明:过点o作oe⊥ab于点e,∵ad⊥bo于点d,∴∠d=90°.∴∠坏的+∠abd=90°∠aod+∠载荷=90°。
2021中考数学热点题型专练圆含解析

热点13 圆【命题趋势】圆在中考数学中分值各个省市有所不同,大约占到8—12分左右,考查的重点在于圆周角定理、切线的判定与性质定理、垂径定理、圆锥和扇形以及弧长公式这几部分内容,虽然圆的内容考的不是太多但也是必考内容之一,难度一般不大。
【满分技巧】一、重点把握四个内容:1.圆周角定理;2.切线的判定与性质定理;3.垂径定理;4.圆锥的侧面积,扇形面积以及弧长公式;二、圆中的计算部分——垂径定理关于圆的计算题,一定离不开垂径定理,而把握好这一定理的关键在于用好一个特殊的三角形。
——由弦心距、半径、半条弦组成的特殊三角形,综合勾股定理或三角函数,从而能顺利地解决问题半径弦心距半条弦三、解决问题的秘诀:将问题转化成三角形问题平面几何的几乎所有问题,不论是四边形问题,还是圆的问题最终都要转化成三角形问题,在三角形中用勾股定理或三角函数结合方程的思想解决。
【限时检测】(建议用时:30分钟)一、选择题1.如图,矩形ABCD中,G是BC的中点,过A、D、G三点的圆O与边AB、CD分别交于点E、点F,给出下列说法:(1)AC与BD的交点是圆O的圆心;(2)AF与DE的交点是圆O的圆心;(3)BC与圆O 相切,其中正确说法的个数是()A.0B.1C.2D.3【答案】C【解析】连接DG、AG,作GH⊥AD于H,连接OD,如图,⊥G是BC的中点,⊥AG=DG,⊥GH垂直平分AD,⊥点O在HG上,⊥AD⊥BC,⊥HG⊥BC,⊥BC与圆O相切;⊥OG=OG,⊥点O不是HG的中点,⊥圆心O不是AC与BD的交点;而四边形AEFD为⊥O的内接矩形,⊥AF与DE的交点是圆O的圆心;⊥(1)错误,(2)(3)正确.故选:C.2.⊥O 中,弦AB 与CD 交于点E ,75DEB ∠=︒,6AB =,1AE =,则CD 的长是()A .B .C .D .【答案】C【解析】过点O 作OF⊥CD 于点F ,OG⊥AB 于G ,连接OB 、0D ,如图所示: 则DE=CF,AG=BG=12 AB=3⊥EG=AG -AE=2在Rt BOG ∆中,2OG ==, ⊥EG=OG ,EOG ∴∆是等腰直角三角形,45OEG ∴∠=︒,OE ==, 75DEB ∠=︒, 30OEF ∴∠=︒,12OF OE ∴==在Rt ODF ∆中,DF ==2CD DF ∴==故选:C .3.如图,一条公路的转弯处是一段圆弧(),点O 是这段弧所在圆的圆心,AB =40m ,点C 是的中点,且CD =10m ,则这段弯路所在圆的半径为( )A .25mB .24mC .30mD .60m【答案】A【解析】⊥OC ⊥AB , ⊥AD =DB =20m ,在Rt⊥AOD 中,OA 2=OD 2+AD 2, 设半径为r 得:r 2=(r ﹣10)2+202, 解得:r =25m , ⊥这段弯路的半径为25m 故选:A .4.如图,P A 、PB 为圆O 的切线,切点分别为A 、B ,PO 交AB 于点C ,PO 的延长线交圆O 于点D ,下列结论不一定成立的是( )A.P A=PB B.⊥BPD=⊥APD C.AB⊥PD D.AB平分PD【答案】D【解析】⊥P A,PB是⊥O的切线,⊥P A=PB,所以A成立;⊥BPD=⊥APD,所以B成立;⊥AB⊥PD,所以C成立;⊥P A,PB是⊥O的切线,⊥AB⊥PD,且AC=BC,只有当AD⊥PB,BD⊥P A时,AB平分PD,所以D不一定成立.故选:D.5.如图,AB为⊥O的直径,C,D为⊥O上两点,若⊥BCD=40°,则⊥ABD的大小为()A.60°B.50°C.40°D.20°【答案】B【解析】如图,连接AD,⊥AB为⊥O的直径,⊥⊥ADB=90°.⊥⊥BCD=40°,⊥⊥A=⊥BCD=40°,⊥⊥ABD=90°﹣40°=50°.故选:B.6.如图,BC是半圆O的直径,D,E是上两点,连接BD,CE并延长交于点A,连接OD,OE.如果⊥A =70°,那么⊥DOE的度数为()A.35°B.38°C.40°D.42°【答案】C【解析】连接CD,如图所示:⊥BC是半圆O的直径,⊥⊥BDC=90°,⊥⊥ADC=90°,⊥⊥ACD=90°﹣⊥A=20°,⊥⊥DOE=2⊥ACD=40°,故选:C.7.如图,等边三角形ABC的边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则⊥O的半径为()A.2B.3C.4D.4﹣【答案】A【解析】设⊥O与AC的切点为E,连接AO,OE,⊥等边三角形ABC的边长为8,⊥AC=8,⊥C=⊥BAC=60°,⊥圆分别与边AB,AC相切,⊥⊥BAO=⊥CAO=BAC=30°,⊥⊥AOC=90°,⊥OC=AC=4,⊥OE⊥AC,⊥OE=OC=2,⊥⊥O的半径为2,故选:A.8.如图,AB是⊥O的直径,AC是⊥O的切线,A为切点,BC与⊥O交于点D,连结OD.若⊥C=50°,则⊥AOD 的度数为()A.40°B.50°C.80°D.100°【答案】C【解析】⊥AC是⊥O的切线,⊥AB⊥AC,⊥⊥BAC=90°,⊥⊥C=50°,⊥⊥ABC=40°,⊥OD=OB,⊥⊥ODB=⊥ABC=40°,⊥⊥AOD=⊥ODB+⊥ABC=80°;故选:C.9.如图,AB,AC分别是⊥O的直径和弦,OD⊥AC于点D,连接BD,BC,且AB=10,AC=8,则BD的长为()A.2B.4C.2D.4.8【答案】C【解析】⊥AB为直径,⊥⊥ACB=90°,⊥BC===3,⊥OD⊥AC,⊥CD=AD=AC=4,在Rt⊥CBD中,BD==2.故选:C.10.如图,AB是⊥O的弦,OC⊥AB交⊥O于点C,点D是⊥O上一点,⊥ADC=30°,则⊥BOC的度数为()A.30°B.40°C.50°D.60°【答案】D【解析】如图,⊥⊥ADC=30°,⊥⊥AOC=2⊥ADC=60°.⊥AB是⊥O的弦,OC⊥AB交⊥O于点C,⊥=.⊥⊥AOC=⊥BOC=60°.故选:D.二、填空题11.如图,已知⊥ABC的内切圆⊥O与BC边相切于点D,连结OB,OD.若⊥ABC=40°,则⊥BOD的度数是.【答案】70°【解析】⊥⊥ABC的内切圆⊥O与BC边相切于点D,⊥OB平分⊥ABC,OD⊥BC,⊥⊥OBD=⊥ABC=×40°=20°,⊥⊥BOD=90°﹣⊥OBD=70°.故答案为70°.12.直角三角形的两条直角边分别是5和12,则它的内切圆半径为.【答案】2【解析】直角三角形的斜边==13,所以它的内切圆半径==2.故答案为2.13.如图,五边形ABCDE是⊥O的内接正五边形,AF是⊥O的直径,则⊥BDF的度数是°.【答案】54【解析】连接AD,⊥AF是⊥O的直径,⊥⊥ADF=90°,⊥五边形ABCDE是⊥O的内接正五边形,⊥⊥ABC=⊥C=108°,⊥⊥ABD=72°,⊥⊥F=⊥ABD=72°,⊥⊥F AD=18°,⊥⊥CDF=⊥DAF=18°,⊥⊥BDF=36°+18°=54°,故答案为:54.14.如图,⊥O的两条相交弦AC、BD,⊥ACB=⊥CDB=60°,AC=2,则⊥O的面积是.【答案】16π【解析】⊥⊥A=⊥BDC,而⊥ACB=⊥CDB=60°,⊥⊥A=⊥ACB=60°,⊥⊥ACB为等边三角形,⊥AC=2,⊥圆的半径为4,⊥⊥O的面积是16π,故答案为:16π.15.如图,在菱形ABCD中,对角线AC,BD交于点O,⊥ABC=60°,AB=2,分别以点A、点C为圆心,以AO的长为半径画弧分别与菱形的边相交,则图中阴影部分的面积为.(结果保留π)【答案】2﹣π【解析】⊥四边形ABCD是菱形,⊥AC⊥BD,⊥ABO=⊥ABC=30°,⊥BAD=⊥BCD=120°,⊥AO=AB=1,由勾股定理得,OB==,⊥AC=2,BD=2,⊥阴影部分的面积=×2×2﹣×2=2﹣π,故答案为:2﹣π.三、解答题16.如图,在菱形ABCD中,连结BD、AC交于点O,过点O作OH⊥BC于点H,以点O为圆心,OH为半径的半圆交AC于点M.⊥求证:DC是⊥O的切线.⊥若AC=4MC且AC=8,求图中阴影部分的面积.⊥在⊥的条件下,P是线段BD上的一动点,当PD为何值时,PH+PM的值最小,并求出最小值.【解析】⊥过点O作OG⊥CD,垂足为G,在菱形ABCD中,AC是对角线,则AC平分⊥BCD,⊥OH⊥BC,OG⊥CD,⊥OH=OG,⊥OH、OG都为圆的半径,即DC是⊥O的切线;⊥⊥AC=4MC且AC=8,⊥OC=2MC=4,MC=OM=2,⊥OH=2,在直角三角形OHC中,HO=CO,⊥⊥OCH=30°,⊥COH=60°,⊥HC=,S阴影=S⊥OCH﹣S扇形OHM=CH•OH﹣OH2=2﹣;⊥作M关于BD的对称点N,连接HN交BD于点P,⊥PM=NP,⊥PH+PM=PH+PN=HN,此时PH+PM最小,⊥ON=OM=OH,⊥MOH=60°,⊥⊥MNH=30°,⊥⊥MNH=⊥HCM,⊥HN=HC=2,即:PH+PM的最小值为2,在Rt⊥NPO中,OP=ON tan30°=,在Rt⊥COD中,OD=OC tan30°=,则PD=OP+OD=2.17.如图,AB为⊥O的直径,C、D是半圆AB的三等分点,过点C作AD延长线的垂线CE,垂足为E.(1)求证:CE是⊥O的切线;(2)若⊥O的半径为2,求图中阴影部分的面积.【解析】(1)证明:⊥点C、D为半圆O的三等分点,⊥,⊥⊥BOC=⊥A,⊥OC⊥AD,⊥CE⊥AD,⊥CE⊥OC,⊥CE为⊥O的切线;(2)解:连接OD,OC,⊥,⊥⊥COD=×180°=60°,⊥CD⊥AB,⊥S⊥ACD=S⊥COD,⊥图中阴影部分的面积=S扇形COD==.18.(1)如图1,有一个残缺圆,请作出残缺圆的圆心O(保留作图痕迹,不写作法).(2)如图2,设AB是该残缺圆O的直径,C是圆上一点,CAB∠的角平分线AD交O于点D,过D作O的切线交AC的延长线于点E.⊥求证:AE DE⊥;⊥若3AC=,求残缺圆的半圆面积.DE=,2【解析】(1)解:如图1:点O即为所求.(2)⊥证明:如图2中,连接OD交BC于F.AD平分BAC∠,∴∠=∠,DAC DAB=,∴CD BD∴⊥,OD BCCFD∠=︒,CF BF∴=,90DE是切线,DE OD∴⊥,EDF∴∠=︒,90AB是直径,ACB BCE∴∠=∠=︒,90∴四边形DECF是矩形,∴∠=︒,90E∴⊥.AE DE⊥四边形DECF是矩形,DE CF BF∴===,3在Rt ACB∆中,AB==∴残缺圆的半圆面积21202ππ=••=.。
备战2024年中考数学复习考点帮(全国通用)专题23 圆的基本性质的核心知识点精讲(讲义)(解析版)

专题23圆的基本性质的核心知识点精讲1.理解圆心角及其所对的弧、弦之间的关系;2.理解并运用圆周角定理及其推论;3.探索并证明垂径定理会应用垂径定理解决与圆有关的问题;4.理解并运用圆内接四边形的性质.考点1:圆的定义及性质圆的定义:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫圆。
这个固定的端点O叫做圆心,线段OA叫做半径。
圆的表示方法:以O点为圆心的圆记作⊙O,读作圆O。
圆的特点:在一个平面内,所有到一个定点的距离等于定长的点组成的图形。
圆的对称性:1)圆是轴对称图形,经过圆心的每一条直线都是它的对称轴;2)圆是以圆心为对称中心的中心对称图形。
考点2:圆的有关概念弦的概念:连结圆上任意两点的线段叫做弦(例如:右图中的AB)。
直径的概念:经过圆心的弦叫做直径(例如:右图中的CD)。
备注:1)直径是同一圆中最长的弦。
2)直径长度等于半径长度的2倍。
弧的概念:圆上任意两点间的部分叫做圆弧,简称弧。
以A、B为端点的弧记作AB ,读作圆弧AB或弧AB。
等弧的概念:在同圆或等圆中,能够互相重合的弧叫做等弧。
半圆的概念:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆。
优弧的概念:在一个圆中大于半圆的弧叫做优弧。
劣弧的概念:小于半圆的弧叫做劣弧。
考点3:垂径定理垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
推论1:1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;3)平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧。
推论2:圆的两条平行弦所夹的弧相等。
常见辅助线做法(考点):1)过圆心,作垂线,连半径,造Rt △,用勾股,求长度;2)有弧中点,连中点和圆心,得垂直平分考点4:垂径定理的应用考点5:圆心角的概念圆心角概念:顶点在圆心的角叫做圆心角。
弧、弦、弦心距、圆心角之间的关系定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等。
2021届中考数学一轮复习 圆专题复习

ACB是直角
CD所对的圆周角
BC所对的圆周角
2=A
图②
一、圆的有关性质
一、圆的有关性质
一、圆的有关性质
CD BC
△ACB是直角三角形
CD=BC
AB= ?
由勾股定理求AB
一、圆的有关性质
一、圆的有关性质
二、点和圆、直线和圆的位置关系
二、点和圆、直线和圆的位置关系
二、点和圆、直线和圆的位置关系
O
P
O
P
A
BC
D
一、圆的有关性质
一、圆的有关性质
平分弦(是直径)的直径 不一定垂直于弦
一、圆的有关性质
一、圆的有关性质
一、圆的有关性质
Rt△ODB中
一、圆的有关性质
一、圆的有关性质
一、圆的有关性质
C
C
D
A
O
M
A
B
D
O
B
一、圆的有关性质
一、圆的有关性质
一、圆的有关性质
Rt△ACB中 Rt△ADB中 Rt△AEB中
二、点和圆、直线和圆的位置关系
二、点和圆、直线和圆的位置关系
三、正多边形和圆
三、正多边形和圆
A
F
B
E
O
C
D
三、正多边形和圆
三、正多边形和圆
三、正多边形和圆
△OAM是直角三角形
四、弧长和扇形面积
四、弧长和扇形面积
四、弧长和扇形面积
四、弧长和扇形面积
四、弧长和扇形面积
四、弧长和扇形面积
四、弧长和扇形面积
四、弧长和扇形面积
SAPB SCPB 2SPOB
E
SAPB SCPB
【初中数学】2021年中考数学复习:圆

【初中数学】2021年中考数学复习:圆
为了能更好更全面的做好复习和迎考准备,确保将所涉及的
中考
考点全面备考妥当,使孩子们充满信心的步入考场,现特准备工作了2021年中考数
学备考:圆。
圆这章知识重点可以归纳为:
1、对称性:
a:圆的对称性,虽然其它一些图形也是有,但圆有无数条对称轴这个特性其它图形
所没有的,垂径定理,切线长定理,及正n边形的计算都应用到了这个特性。
b:转动不变性,圆心角、弧、弦、弦心距关系,碰到有关圆习题,必须把握住这个
特性充分利用,许多问题可以找出解题思路。
2、三个角:圆心角、圆周角,以及圆内接四边形的外角(对角)这是在有关圆的问题中,找角相等必不可少的方法。
3、三个横向:垂径定理,直径面元的圆周角,切线的性质它可以有效率的把许多问
题转变至直角三角形中,并使问题以求化解。
4、四大关系:点与圆的位置关系,直线与圆的位置关系,圆与圆的位置关系,圆与
正多边形的关系,掌握切线的判定和性质以及有关计算是重点。
5、有关排序问题:有关线段的排序,正多边形的排序,有关扇形及阴影面积的排序,以及圆柱、圆锥侧面进行图的排序。
6、圆中添辅助线一般方法:添与垂径定理相关的辅助线,添与切线有关的辅助线(创
造直角的辅助线),添与圆内接四边形相关的辅助线;两圆相交时作公共弦,两圆相切时作
分切线,总之添辅助线时,要构造和完善基本图形,切忌破坏图形的完整性。
以上即为就是数学网为大家整理的2021年中考数学备考:圆,大家还令人满意吗?期
望对大家有所协助!。
专题23 圆(知识点串讲)(解析版)
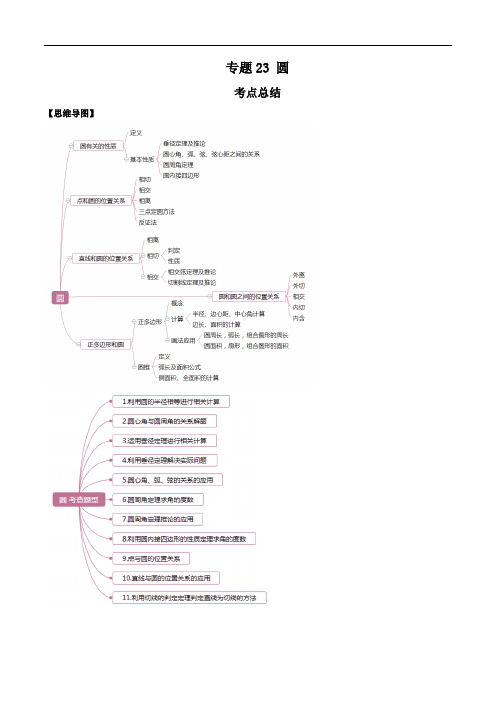
专题23 圆考点总结【思维导图】【知识要点】知识点一与圆有关的概念圆的概念:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫圆.这个固定的端点O叫做圆心,线段OA叫做半径.以O点为圆心的圆记作⊙O,读作圆O.特点:圆是在一个平面内,所有到一个定点的距离等于定长的点组成的图形.确定圆的条件:⑴圆心;⑵半径,⑶其中圆心确定圆的位置,半径长确定圆的大小.补充知识:1)圆心相同且半径相等的圆叫做同圆;2)圆心相同,半径不相等的两个圆叫做同心圆;3)半径相等的圆叫做等圆.弦的概念:连结圆上任意两点的线段叫做弦。
经过圆心的弦叫做直径,并且直径是同一圆中最长的弦.⏜,读作弧AB.在同圆或等弧的概念:圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作AB圆中,能够重合的弧叫做等弧.圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.在一个圆中大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧.弦心距概念:从圆心到弦的距离叫做弦心距.弦心距、半径、弦长的关系:(考点)圆心角概念:顶点在圆心的角叫做圆心角.圆周角概念:顶点在圆上,并且两边都和圆相交的角叫做圆周角.三角形的外接圆1)经过三角形三个顶点的圆叫做三角形的外接圆,外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心,这个三角形叫做这个圆的内接三角形.2)三角形外心的性质:①三角形的外心是指外接圆的圆心,它是三角形三边垂直平分线的交点,它到三角形各顶点的距离相等; ②三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合.3)锐角三角形外接圆的圆心在它的内部(如图1);直角三角形外接圆的圆心在斜边中点处(即直角三角形外接圆半径等于斜边的一半,如图2);钝角三角形外接圆的圆心在它的外部(如图3).圆内接四边形概念:如果一个四边形的所有顶点都在一个圆上,那么这个四边形叫做圆内接四边形。
2021年中考数学考点复习:圆的基础性质考点解析

2021年中考数学考点复习:圆的基础性质考点解析为了更有效地帮助学生梳理学过的知识,提高复习质量和效率,在____中考中取得理想的成绩,下文为大家准备了____中考数学考点复习:圆的基础性质。
⑴垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的2条弧。
逆定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的2条弧。
⑵有关圆周角和圆心角的性质和定理① 在同圆或等圆中,如果两个圆心角,两个圆周角,两组弧,两条弦,两条弦心距中有一组量相等,那么他们所对应的其余各组量都分别相等。
②一条弧所对的圆周角等于它所对的圆心角的一半。
直径所对的圆周角是直角。
90度的圆周角所对的弦是直径。
圆心角计算公式: θ=(L/2πr)_360°=180°L/πr=L/r(弧度)即圆心角的度数等于它所对的弧的度数;圆周角的度数等于它所对的弧的度数的一半。
③ 如果一条弧的长是另一条弧的2倍,那么其所对的圆周角和圆心角是另一条弧的2倍。
⑶有关外接圆和内切圆的性质和定理①一个三角形有唯一确定的外接圆和内切圆。
外接圆圆心是三角形各边垂直平分线的交点,到三角形三个顶点距离相等;②内切圆的圆心是三角形各内角平分线的交点,到三角形三边距离相等。
③R=2S△÷L(R:内切圆半径,S:三角形面积,L:三角形周长)④两相切圆的连心线过切点(连心线:两个圆心相连的直线)⑤圆O中的弦PQ的中点M,过点M任作两弦AB,CD,弦AD与BC分别交PQ于_,Y,则M为_Y之中点。
(4)如果两圆相交,那么连接两圆圆心的线段(直线也可)垂直平分公共弦。
(5)弦切角的度数等于它所夹的弧的度数的一半。
(6)圆内角的度数等于这个角所对的弧的度数之和的一半。
(7)圆外角的度数等于这个角所截两段弧的度数之差的一半。
(8)周长相等,圆面积比长方形、正方形、三角形的面积大。
以上即是为大家整理的____中考数学考点复习:圆的基础性质,大家还满意吗?希望对大家有所帮助!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学一轮复习基础考点及题型-专题23 圆
考点总结
【思维导图】
【知识要点】
知识点一与圆有关的概念
圆的概念:在一个平面内,线段OO绕它固定的一个端点O旋转一周,另一个端点O所形成的图形叫圆.这个固定的端点O叫做圆心,线段OO叫做半径.以O点为圆心的圆记作⊙O,读作圆O.
特点:圆是在一个平面内,所有到一个定点的距离等于定长的点组成的图形.
确定圆的条件:
⑴圆心;
⑵半径,
⑶其中圆心确定圆的位置,半径长确定圆的大小.
补充知识:
1)圆心相同且半径相等的圆叫做同圆;
2)圆心相同,半径不相等的两个圆叫做同心圆;
3)半径相等的圆叫做等圆.
弦的概念:连结圆上任意两点的线段叫做弦。
经过圆心的弦叫做直径,并且直径是同一圆中最长的弦.
弧的概念:圆上任意两点间的部分叫做圆弧,简称弧.以O、O为端点的弧记作OO
⏜,读作弧AB.在同圆或等圆中,能够重合的弧叫做等弧.
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
在一个圆中大于半圆的弧叫做优弧,
小于半圆的弧叫做劣弧.
弦心距概念:从圆心到弦的距离叫做弦心距.
弦心距、半径、弦长的关系:(考点)
圆心角概念:顶点在圆心的角叫做圆心角.
圆周角概念:顶点在圆上,并且两边都和圆相交的角叫做圆周角.
三角形的外接圆
1)经过三角形三个顶点的圆叫做三角形的外接圆,外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心,这个三角形叫做这个圆的内接三角形.
2)三角形外心的性质:
①三角形的外心是指外接圆的圆心,它是三角形三边垂直平分线的交点,它到三角形各顶点的距离相等; ②三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合.
3)锐角三角形外接圆的圆心在它的内部(如图1);直角三角形外接圆的圆心在斜边中点处(即直角三角形外接圆半径等于斜边的一半,如图2);钝角三角形外接圆的圆心在它的外部(如图3).
圆内接四边形概念:如果一个四边形的所有顶点都在一个圆上,那么这个四边形叫做圆内接四边形。
弓形与扇形
弓形的概念:由弦及其所对的弧组成的图形。
扇形的概念:一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形。
【典型例题】
1.(2018·陆丰市民声学校中考模拟)如图,AB 是⊙O 直径,点C ,D 在⊙O 上,OD ∥AC ,下列结论错误的是( )
图3
图2图1
B C C
A.∠BOD=∠BAC B.∠BAD=∠CAD
C.∠C=∠D D.∠BOD=∠COD
【答案】C
【详解】∵OD//AC,
∴∠BOD=∠BAC、∠D=∠CAD、∠C=∠COD,故A选项正确,
∵OA=OD,
∴∠D=∠BAD,∴∠BAD=∠CAD,故B选项正确,
∵OA=OC,∴∠BAD=∠C,∴∠BOD=∠COD,故D选项正确,
由已知条件无法得出∠C=∠D,故C选项错误,
故选C.
2.(2018·北京中考模拟)有下列四种说法:
①半径确定了,圆就确定了;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆.其中,错误的说法有()
A.1种 B.2种 C.3种 D.4种
【答案】B
【详解】
圆确定的条件是确定圆心与半径,是假命题,故此说法错误;
直径是弦,直径是圆内最长的弦,是真命题,故此说法正确;
弦是直径,只有过圆心的弦才是直径,是假命题,故此说法错误;
④半圆是弧,但弧不一定是半圆,圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆,是真命题,故此说法正确.
其中错误说法的是①③两个.
故选:B.
3.(2018·上海中考模拟)下列说法中,正确的个数共有()
(1)一个三角形只有一个外接圆;
(2)圆既是轴对称图形,又是中心对称图形;
(3)在同圆中,相等的圆心角所对的弧相等;
(4)三角形的内心到该三角形三个顶点距离相等;
A.1个 B.2个 C.3个 D.4个
【答案】C
【详解】
(1)一个三角形只有一个外接圆,正确;
(2)圆既是轴对称图形,又是中心对称图形,正确;
(3)在同圆中,相等的圆心角所对的弧相等,正确;
(4)三角形的内心是三个内角平分线的交点,到三边的距离相等,错误;
故选:C.
4.(2018·湖北中考模拟)有下列说法:①等弧的长度相等;②直径是圆中最长的弦;③相等的圆心角对的弧相等;④圆中90°角所对的弦是直径;⑤同圆中等弦所对的圆周角相等.其中正确的有()A.1个 B.2个 C.3个 D.4个
【答案】B
【解析】试题解析:
同圆或等圆中,能够相互重合的弧叫等弧,所以长度相等,故正确;
连接圆上任意两点的线段叫做弦,所以直径是最长的弦,故正确;
在同圆或等圆中,相等的圆心角所对的弧相等,故错误;
圆中90°圆周角所对的弦是直径,故错误;
弦所对的圆周角可在圆心一侧,也可在另一侧,这两个圆周角互补,但不一定相等,所以同圆中等弦所对的圆周角也不一定相等,故错误.
综上所述,正确的结论有2个,故应选B.
5.(2017·广东中考模拟)如图,在⊙O中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD的度数为()。
