埃拉托斯散筛法算法程序
素数判断如何判断一个数是否为素数

素数判断如何判断一个数是否为素数素数是指除了1和本身之外没有其他因数的自然数。
在数论中,素数因其独特的性质和重要性而备受关注。
判断一个数是否为素数是数学中的一个基本问题,下面将介绍几种常用的方法来判断一个数是否为素数。
一、试除法试除法是一种简单直接的判断素数的方法。
对于一个待判断的数n,如果n能被不大于根号n的自然数整除,则n不是素数;如果n不能被不大于根号n的自然数整除,则n是素数。
二、埃拉托斯特尼筛法埃拉托斯特尼筛法是一种高效的筛选素数的方法。
基本思想是从2开始,依次找到每一个素数,然后将能被该素数整除的数标记为非素数。
具体操作为,将2到N的自然数按顺序排列,对于每个素数p,将大于p且能被p整除的数标记为非素数。
遍历完所有素数后,剩下的未被标记的数即为素数。
三、费马小定理费马小定理是一种通过取模运算判断素数的方法。
若p为素数,a是小于p的任意整数,则a的p次幂与a模p的余数相等。
即a^p ≡ a (mod p)。
基于这个定理,可以用快速幂算法来计算a^p的结果,如果与a模p的余数相等,则a为素数。
四、Miller-Rabin素性测试Miller-Rabin素性测试是一种概率算法,用于测试一个数是否为素数。
该算法基于费马小定理的倒推,通过多次的概率测试来判断一个数的素性。
算法的具体原理较为复杂,在此不做详细介绍。
综上所述,判断一个数是否为素数可以使用试除法、埃拉托斯特尼筛法、费马小定理或Miller-Rabin素性测试等方法。
根据具体需求和时间复杂度要求选择合适的算法来判断素数。
求解质数与合数的方法

求解质数与合数的方法质数和合数是数学中的两个重要概念,对于数论和其他数学领域的研究起着重要的作用。
在解决实际问题和进行数学研究时,我们经常需要找到质数和合数。
本文将介绍一些求解质数和合数的方法。
一、试除法试除法是判断一个数是否为质数的常用方法。
该方法通过逐一试除一个数的所有可能除数,如果存在能整除该数的除数,则该数为合数;若一个数没有能整除它的除数,则该数为质数。
以求解一个数n是否为质数为例,我们可以从2开始逐一试除,直到n的平方根。
如果在试除的过程中找到一个能整除n的数,则n为合数;否则,n为质数。
试除法的时间复杂度为O(√n),在大多数情况下是有效的求解质数和合数的方法。
二、埃拉托斯特尼筛法埃拉托斯特尼筛法是一种较高效的求解质数的方法。
该方法通过逐渐筛去不是质数的数,最终得到一系列质数。
具体步骤如下:1. 创建一个长度为n+1的布尔数组prime[],全部初始化为true。
2. 从2开始遍历到√n,若prime[i]为true,则将i的倍数(除i本身)标记为false。
3. 遍历结束后,未被标记为false的数即为质数。
埃拉托斯特尼筛法的时间复杂度为O(nlog(logn)),在求解范围较大的质数时,效率较高。
三、费马小定理费马小定理是判断一个数是否为质数的概率性方法。
该定理提供了一种将费马定理应用于素数检验的方法。
费马小定理描述如下:如果p是一个质数,a是不被p整除的整数,则a^(p-1)模p的值恒为1。
利用费马小定理可以进行费马检验:1. 随机选择一个整数a(2 ≤ a < n)。
2. 计算a^(n-1)模n的值。
3. 如果该值不等于1,则n为合数;如果等于1,则n很可能为质数。
费马小定理的时间复杂度较低,但不保证对所有数都能正确判断。
结语本文介绍了三种常用的求解质数和合数的方法:试除法、埃拉托斯特尼筛法和费马小定理。
试除法是最基本的方法,但效率较低;埃拉托斯特尼筛法在求解大范围的质数时效率高;费马小定理则提供了一种概率性的判断方法。
查找素数Eratosthenes筛法的mpi程序

查找素数Eratosthenes筛法的mpi程序 思路: 只保留奇数 (1)由输⼊的整数n确定存储奇数(不包括1)的数组⼤⼩:n=(n%2==0)?(n/2-1):((n-1)/2);//n为存储奇数的数组⼤⼩,不包括基数1 (2)由数组⼤⼩n、进程号id和进程数p,确定每个进程负责的基数数组的第⼀个数、最后⼀个数和数组维度:low_value = 3 + 2*(id*(n)/p);//进程的第⼀个数 high_value = 3 + 2*((id+1)*(n)/p-1);//进程的最后⼀个数 size = (high_value - low_value)/2 + 1; //进程处理的数组⼤⼩ (3)寻找奇数的第⼀个倍数的下标,经过反复思考,有如下规律: if (prime * prime > low_value) first = (prime * prime - low_value)/2; else { if (!(low_value % prime))first = 0; elsefirst=((prime-low_value%prime)%2==0)?((prime-low_value%prime)/2):((prime-low_value%prime+prime)/2); } code:1 #include "mpi.h"2 #include <math.h>3 #include <stdio.h>4#define MIN(a,b) ((a)<(b)?(a):(b))56int main (int argc, char *argv[])7 {8int count; /* Local prime count */9double elapsed_time; /* Parallel execution time */10int first; /* Index of first multiple */11int global_count; /* Global prime count */12int high_value; /* Highest value on this proc */13int i;14int id; /* Process ID number */15int index; /* Index of current prime */16int low_value; /* Lowest value on this proc */17char *marked; /* Portion of 2,...,'n' */18int n,m; /* Sieving from 2, ..., 'n' */19int p; /* Number of processes */20int proc0_size; /* Size of proc 0's subarray */21int prime; /* Current prime */22int size; /* Elements in 'marked' */2324 MPI_Init (&argc, &argv);2526/* Start the timer */2728 MPI_Comm_rank (MPI_COMM_WORLD, &id);29 MPI_Comm_size (MPI_COMM_WORLD, &p);30 MPI_Barrier(MPI_COMM_WORLD);31 elapsed_time = -MPI_Wtime();3233if (argc != 2) {34if (!id) printf ("Command line: %s <m>\n", argv[0]);35 MPI_Finalize();36 exit (1);37 }3839 n = atoi(argv[1]);40 m=n;//41 n=(n%2==0)?(n/2-1):((n-1)/2);//将输⼊的整数n转换为存储奇数的数组⼤⼩,不包括奇数142//if (!id) printf ("Number of odd integers:%d Maximum value of odd integers:%d\n",n+1,3+2*(n-1));43if (n==0) {//输⼊2时,输出1 prime,结束44if (!id) printf ("There are 1 prime less than or equal to %d\n",m);45 MPI_Finalize();46 exit (1);47 }48/* Figure out this process's share of the array, as49 well as the integers represented by the first and50 last array elements */5152 low_value = 3 + 2*(id*(n)/p);//进程的第⼀个数53 high_value = 3 + 2*((id+1)*(n)/p-1);//进程的最后⼀个数54 size = (high_value - low_value)/2 + 1; //进程处理的数组⼤⼩555657/* Bail out if all the primes used for sieving are58 not all held by process 0 */5960 proc0_size = (n-1)/p;6162if ((3 + 2*(proc0_size-1)) < (int) sqrt((double) (3+2*(n-1)))) {//63if (!id) printf ("Too many processes\n");64 MPI_Finalize();65 exit (1);66 }6768/* Allocate this process's share of the array. */6970 marked = (char *) malloc (size);7172if (marked == NULL) {73 printf ("Cannot allocate enough memory\n");74 MPI_Finalize();75 exit (1);76 }7778for (i = 0; i < size; i++) marked[i] = 0;79if (!id) index = 0;80 prime = 3;//从素数3开始81do {82//确定奇数的第⼀个倍数的下标83if (prime * prime > low_value)84 first = (prime * prime - low_value)/2;85else {86if (!(low_value % prime))87 first = 0;88else89 first=((prime-low_value%prime)%2==0)?((prime-low_value%prime)/2):((prime-low_value%prime+prime)/2);90 }9192for (i = first; i < size; i += prime) marked[i] = 1;93if (!id) {94while (marked[++index]);95 prime = 2*index + 3;//下⼀个未被标记的素数96 }97if (p > 1) MPI_Bcast (&prime, 1, MPI_INT, 0, MPI_COMM_WORLD);98 } while (prime * prime <= 3+2*(n-1));//99100 count = 0;101for (i = 0; i < size; i++)102if (!marked[i]) count++;103if (p > 1) MPI_Reduce (&count, &global_count, 1, MPI_INT, MPI_SUM,1040, MPI_COMM_WORLD);105106/* Stop the timer */107108 elapsed_time += MPI_Wtime();109110111/* Print the results */112113if (!id) {114 printf ("There are %d primes less than or equal to %d\n",115 global_count+1, m);//前⾯程序是从素数3开始标记,忽略了素数2,所以素数个数要加1116 printf ("SIEVE (%d) %10.6f\n", p, elapsed_time);117 }118 MPI_Finalize ();119return0;120 }。
用埃拉托色尼筛算法求最大公约数python

用埃拉托色尼筛算法求最大公约数埃拉托色尼筛算法,也称为埃氏筛法,是一种用于求解最大公约数的经典算法,它能够快速而有效地找到给定两个或多个数的最大公约数。
在本篇文章中,我们将详细介绍如何使用Python编写并应用埃拉托色尼筛算法。
1.埃拉托色尼筛算法的原理埃拉托色尼筛算法是基于素数的性质进行筛选的。
它的基本思想是:假设我们需要求X和Y的最大公约数,其中X > Y。
我们将从2开始连续自然数逐个进行筛选,将所有能够同时整除X和Y的数标记为合数,而不是素数。
接下来,我们只需要关注那些未被标记为合数的数,它们就是X和Y的最大公约数的候选数。
我们将找到X和Y的最大公约数,这个数即为埃拉托色尼筛算法所求得的结果。
2.Python代码实现下面是用Python实现埃拉托色尼筛算法求最大公约数的示例代码:def sieve_gcd(x, y):# 构建一个长度为y+1的数组,用于表示是否为合数is_composite = [False] * (y + 1)# 进行筛选for i in range(2, y + 1):if not is_composite[i]:if x % i == 0 and y % i == 0:return i # 找到最大公约数for j in range(i * i, y + 1, i):is_composite[j] = Truereturn 1 # 无最大公约数# 调用函数并打印结果x = 24y = 36gcd = sieve_gcd(x, y)print(f"The greatest common divisor of {x} and {y} is {gcd}.")在上述代码中,我们首先构建了一个长度为y+1的布尔数组is_composite,默认初始化为False。
我们使用循环遍历2到y+1的范围,其中非合数的数即为素数。
对于每个素数,我们检查它是否能同时整除x和y,如果是,则找到了最大公约数。
线性筛

Eratosthenes筛法(埃拉托斯特尼筛法)
• 时间复杂度: 程序运行的次数约为 maxN/2+maxN/3+maxN/5+maxN/7+..... =maxN*所有素数倒数的和 时间复杂度是maxN*logmaxN级别的 也就是O(nlogn)
Eratosthenes筛法(埃拉托斯特尼筛法)
• 该算法时间复杂度的常数略高 对于10^6级别的数据,logn大约为20左右, 那么nlogn就达到了2*10^7级别。
因为每个数都被它的素因子重复的筛掉,所 以时间复杂度方面可以基于这一点进行优化。
Euler筛法(欧拉筛法)
• 考虑如何避免某个数被它的素因子重复筛? 根据标准分解式 n = p1^a1 * p2^a2 * p3^a3 ...(p为素数,且p 为升序排列) 那么自然,n = p1*(p1^(a1-1) * p2^a2 ...) 即,存在k < n,n = p1*k; 那么可以根据p1和k来筛掉n。
Euler筛法(欧拉筛法)
• 证明: n = k*p1 = t*p2; (p1 < p2) 因为k > t,所以遍历i的时候,会先到t。 (1)先考虑简单情况,如果k和t均为素数, 显然n = p1*p2只会被筛一次。 (2)k和t均为合数,因为p1和p2均为质数, 那么p1 | t。所以当i遍历到t的时候,prime[j] 遍历到p1时就不会继续,所以n不会被p2筛掉。 而且此时p1也必然是n的最小因子。
• 代码实现:
• bool isprime[maxN]; • int prime[maxN], cnt; • void getPrime() • { • memset(isprime, true, sizeof(isprime)); • cnt = 0; • for (int i = 2; i < maxN; ++i) • { • if (isprime[i]) • { • prime[cnt++] = i; • for (int j = i*2; j < maxN; j += i) • isprime[j] = false; • } • } • }
埃塞法求素数

埃塞法求素数什么是素数?素数是指大于1且只能被1和自身整除的整数。
例如,2、3、5、7、11等都是素数,而4、6、8、9等则不是素数。
素数在数论中具有重要的地位,它们的特殊性质使得它们在密码学、计算机科学等领域有广泛的应用。
埃塞法(筛法)是什么?埃塞法,又称筛法,是一种用于求解素数的算法。
它的基本思想是通过逐步筛除合数的方法,找出一定范围内的所有素数。
埃塞法的步骤1.首先,我们需要确定一个范围,假设为n。
2.创建一个长度为n+1的布尔数组,初始值都为True。
这个数组用来表示数字是否为素数,索引对应的数字为素数则对应的值为True,否则为False。
3.从2开始,将数组中索引为2的倍数的值设置为False,因为2的倍数肯定不是素数。
4.接下来,找到第一个为True的索引值,假设为p,这个值就是我们找到的第一个素数。
5.然后,将数组中索引为p的倍数的值设置为False,因为p的倍数肯定不是素数。
6.重复步骤4和5,直到找不到下一个为True的索引值。
7.最后,数组中为True的索引值就是范围内的所有素数。
一个简单的埃塞法求素数的实现(Python)下面是一个简单的Python代码示例,用于实现埃塞法求素数:def sieve_of_eratosthenes(n):primes = [True] * (n+1)primes[0] = primes[1] = Falsep = 2while p * p <= n:if primes[p]:for i in range(p * p, n+1, p):primes[i] = Falsep += 1result = []for i in range(2, n+1):if primes[i]:result.append(i)return resultn = int(input("请输入一个正整数n:"))primes = sieve_of_eratosthenes(n)print("范围内的素数有:", primes)示例说明在上述示例中,我们首先定义了一个名为sieve_of_eratosthenes的函数,它接受一个正整数n作为参数,返回范围内的所有素数。
python求素数的20种算法

python求素数的20种算法20种求素数的算法1. 质数判断法:对于给定的整数n,从2到n-1依次判断n是否能被这些数整除,若都不能整除,则n为质数。
该算法的时间复杂度为O(n)。
2. 埃拉托斯特尼筛法:该算法的基本思想是从2开始,将2的倍数标记为合数,然后再找到下一个未标记的数,将其倍数标记为合数,依此类推,直到找到所有的质数。
时间复杂度为O(nloglogn)。
3. 素数定理:根据素数定理,对于给定的整数n,素数的个数约为n/ln(n),可以利用这个定理来估算给定范围内的素数个数。
4. 费马素性检验:对于给定的整数n,取一个随机整数a,如果a 的n次方模n等于a,则n可能是素数,否则一定是合数。
该算法的时间复杂度较低,但存在一定的错误概率。
5. 米勒-拉宾素性检验:该算法是费马素性检验的改进算法,通过多次的随机取数进行检验,提高了精确度。
6. 素数分解法:将给定的整数n进行素因数分解,如果分解得到的因子只有1和n本身,则n为质数。
7. Rabin-Miller素性检验:该算法是米勒-拉宾素性检验的改进算法,通过多次的随机取数进行检验,提高了精确度。
8. 欧拉素数检验:根据欧拉定理,如果对于给定的整数n,a的n-1次方模n等于1,则n可能是素数,否则一定是合数。
9. 线性筛法:该算法是埃拉托斯特尼筛法的改进算法,通过线性的方式进行筛选,可以在O(n)的时间复杂度内求解素数。
10. 素数生成器:通过不断地生成大于当前最大素数的数,并判断是否为质数,来生成素数序列。
11. 素数位数统计法:对于给定的整数n,统计从1到n中每个数的位数,然后判断每个位数的数是否为质数。
12. 素数平方和方法:对于给定的整数n,判断是否存在两个质数,使得它们的平方和等于n。
13. 素数和差法:对于给定的整数n,判断是否存在两个质数,使得它们的和或差等于n。
14. 质数的二进制表示法:对于给定的整数n,将n转换为二进制表示,然后判断二进制中是否只包含一个1,若是则n为质数。
【数学问题】区间素数

【数学问题】区间素数区间素数是指在给定的一个闭区间[a,b]内,存在多少个素数。
素数是指只能被1和它本身整除的正整数。
要求区间素数,可以使用埃拉托斯特尼筛法,该算法的基本思想是:从2开始,将每个数的倍数标记为合数,然后在未被标记的数中找到素数。
以下是一个使用Python 实现的埃拉托斯特尼筛法的示例代码:```pythondef sieve_of_eratosthenes(n):primes = [True for i in range(n+1)]p = 2while(p * p <= n):if(primes[p]):for i in range(p * p, n+1, p):primes[i] = Falsep += 1prime_numbers = [p for p in range(2, n+1) if primes[p]]return prime_numbersa, b = 2, 100prime_numbers = sieve_of_eratosthenes(b)count = sum(1 for p in prime_numbers if a <= p <= b)print(count)```在上述代码中,我们首先定义了一个名为`sieve_of_eratosthenes`的函数,用于生成一个从2到给定范围内的所有素数的列表。
然后,我们定义了一个闭区间[a,b],并调用`sieve_of_eratosthenes`函数生成该区间内的素数列表。
最后,我们使用`sum`函数计算该区间内素数的数量,并将结果打印出来。
当a=2,b=100时,运行上述代码将输出`26`,表示在[2,100]这个区间内有26个素数。
素数的算法原理及应用

素数的算法原理及应用简介素数,也称质数,是指除了1和它本身之外没有其他约数的自然数。
素数一直以来都在密码学、计算机科学和数论等领域有着重要的应用。
本文将介绍素数的算法原理及其在实际应用中的重要性。
素数的定义1.素数是只能被1和自身整除的自然数。
2.素数大于1,因为1既不是素数也不是合数。
素数的判断算法方法一:试除法试除法是最简单、直观的判断一个数是否为素数的方法,其基本原理是将待判断的数分别除以小于这个数的平方根的所有素数,如果能整除则不是素数,否则是素数。
这个方法的时间复杂度为O(sqrt(n))。
方法二:埃拉托斯特尼筛法埃拉托斯特尼筛法是一种筛选素数的方法,其基本思想是从2开始,将每个素数的倍数标记为合数,直到筛选完所有范围内的数。
这个方法的时间复杂度为O(n log log n)。
方法三:米勒-拉宾素性测试米勒-拉宾素性测试是一种概率性的素性测试方法,其基本原理是通过对一个数进行多次随机的测试,如果都通过了测试,则该数很大概率上为素数。
这个方法的时间复杂度较低,适用于大整数的素性测试。
素数的应用密码学在密码学中,素数常常用于生成加密密钥。
RSA加密算法就是基于大素数的乘法运算原理,将两个大素数相乘得到的乘积难以分解,从而保证了数据的安全性。
哈希算法在哈希算法中,素数经常被用作哈希函数的取模数。
素数的使用可以减小冲突的概率,提高哈希算法的效率。
赌博游戏素数在赌博游戏中也有着应用。
例如,轮盘赌游戏中,赌注的数值常常被选取为素数,这样可以降低赌客破解出赌注的概率,增加游戏的刺激性。
素数分布猜想素数的分布一直是数论中的一个重要问题。
素数定理是素数分布的基本描述,它给出了小于等于一个正整数x的素数的个数约为x/ln(x)。
这个猜想对于数论研究以及应用具有重要的参考价值。
总结素数作为数学中的重要概念,具有广泛的应用领域。
了解素数的算法原理以及其在实际应用中的重要性,可以帮助我们更好地理解和应用素数。
无论是在密码学、哈希算法还是赌博游戏中,素数都起着重要的作用。
运用埃拉托色尼筛法求解一定范围内的素数

目录摘要 (2)求素数问题 (3)1.数据结构设计 (3)2.算法设计 (3)3.函数流程图 (4)4.调试测试运行 (4)5.源程序 (5)摘要算法与数据结构在计算机科学与技术中,尤其是计算机软件设计中有着举足轻重的作用。
其主要是讲述一个程序的逻辑结构和物理结构,及在已知结构上实现的算法,在设计程序时,我们应该首先考虑到我们要以怎样的逻辑结构来描述所要讨论的问题,且判断它的合理性,和可行性,为了能在计算机上实现问题的模拟实现,我们同时必须设计好在计算机上存储的物理结构,为了能够运行成功,必须要设计一套具有正确性,健壮性,可读性好的程序,来实现计算机上的模拟;其中算法,逻辑结构和物理结构相辅相成,任何一个环节出错都不能成功的完成问题在计算机上的模拟。
程序如下:求解素数,运用埃拉托色尼筛法求解一定范围内的素数。
埃拉托色尼筛法是建立一个2到N的表,在表中删除2的倍数,3的倍数,5的倍数,以此类推直到删除到,为止,表中都为素数。
关键词:素数 C语言求素数问题埃拉托色尼筛法(Sieve of Eratosthenes)是一种用来求所有小于N的素数的方法。
从建立一个整数2~N的表着手,寻找i˂的整数,编程实现此算法,并讨论运算时间。
1.数据结构设计定义一个线性表链式存储结构,用来求所有小于N的素数typedef struct Node{//定义链表int data;//存储数据struct Node *link;//定义指针指向下一个结点}LinkList;;2.算法设计使用一个函数进行埃拉托色尼筛法,形参为建立的链表头节点和所求素数的范围最大值,没有返回值,函数对链表进行操作,从头节点开始读入数据删除其倍数,指针下移读入下一个数据,再删除其倍数,指针一直下移直到读入,停止下移,表中所有数据皆为素数。
void eratosthenes(int max,LinkList *&head){//使用埃拉托色尼筛法筛选数字LinkList *a,*b;a=head->link;for(;;){if(a->data<=sqrt(max)){b=a;while(b&&b->link){if(b->link->data%a->data==0){b->link=b->link->link;}b=b->link;}a=a->link; }else break;}}3.函数流程图图1-1 主程序运行图4.调试测试运行1 提示输入素数的范围最大值时,输入300,打印出2-300内的所有素数,且统计素数个数为62.图1.2测试运行界面2算法的时间复杂度O(N*lglgN)。
埃拉托斯特尼筛法

β = π(600^(1/2)) = π(24) = 9 p5 = 11, p6 = 13, p7 = 17, p8 = 19, pβ = p9 = 23
ψ(N,β) = ψ(500,8) "剩余筛函数" = [π(500/11)-α] + [π(500/13)-(α+1)] + [π(500/17)-(α+2)] + [π(500/19)-(α+3)] = π(500/11) + π(500/13) + π(500/17) + π(500/19) - (4*α+6) = π(45) + π(38) + π(29) + π(26) - 22 = 14 + 12 + 10 + 9 - 22 = 23
π(200) = φ(200,α) - ψ(200,β) + α - 1 = 54 - 10 + 3 - 1 = 46
例 3: 计算 π(300) α = π(300^(1/3)) = π(6) = 3 p1 = 2, p2 = 3, pα = p3 = 5
β = π(300^(1/2)) = π(17) = 7 p4 = 7, p5 = 11, p6 = 13, pβ = p7 = 17
γ = π(600^(2/3)) = π(72) = 18 p10 = 29, p11 = 31, p12 = 37, p13 = 41, p14 = 43, p15 = 47, p16 = 53, p17 = 59, p18 = 61, p19 = 67, pγ = p20 = 71
eratosthenes 筛法

eratosthenes 筛法在求解素数问题上,有一种被称为“eratosthenes 筛法”的经典算法,能够极大地提高计算速度。
它的基本思路是利用倍数筛掉非素数,最终得出素数的序列。
下面将从几个方面具体阐述eratosthenes 筛法。
一、算法步骤1. 找到范围内最大整数 $N$ 。
2. 初始化一个布尔数组 $isPrime[N+1]$ ,表示从 $1$ 到$N$ 是否为素数。
3. 将 $isPrime[0]$ 和 $isPrime[1]$ 标记成合数。
4. 遍历 $2$ 到 $\sqrt{N}$ 的整数 $i$ ,如果当前的$isPrime[i]$ 是素数,则将 $i$ 的倍数都标记为合数,即$isPrime[i\times j]=false$(其中 $2\leqj\leq\lfloor\frac{N}{i}\rfloor$ )。
5. 遍历 $2$ 到 $N$ ,将 $isPrime[i]$ 为 true 的 $i$ 加入到素数序列中。
二、算法优势相对于暴力枚举所有整数判断是否为素数的方法,eratosthenes 筛法的时间复杂度远小于后者。
比如,当 $N=10^6$ 时,暴力算法需要进行 $10^6$ 次判断,而 eratosthenes 筛法仅需要 $O(N\log\log N)$ 次操作。
因此,后者可以轻松求解高达 $10^9$ 的素数序列。
三、实现细节1. 在程序实现时,可以使用一个数组 $prime$ 存储素数序列。
2. 由于 $2$ 是唯一的偶数素数,我们可以将数组的遍历分为两部分:一部分枚举偶数,另一部分枚举奇数。
3. 在筛选合数时,可以从 $i^2$ 开始筛,因为在 $i$ 之前的倍数 $k\times i$ 已经被之前的素数筛掉了。
四、总结eratosthenes 筛法作为一种优秀的求解素数问题的算法,具有时间复杂度低、实现简单等优势。
当需要求解大量的素数时,该算法可以显著提高计算效率,是解决素数问题的一种有效途径。
孪生素数c语言

孪生素数c语言摘要:素数是数学上非常重要的数学概念,具有重要的应用意义。
本文以C/C ++为开发语言,讨论孪生素数的定义及其生成方法。
一、孪生素数定义孪生素数是指当两个质数p和q满足p=q+2时,p和q就称为孪生素数,孪生素数之间的距离为2。
二、孪生素数生成方法1、利用埃拉托斯特尼筛法生成素数埃拉托斯特尼筛法又被称为筛子算法。
在算法中,我们逐步筛出比给定数n小的所有质数,假定数n的范围在2和n之间,此法步骤如下:(1) 用2依次将2~n之间的各个整数划分为一个个不相交的互素集合,从最小的数2开始,2是第一个最小的质数。
(2) 取出未被筛去的最小的数,即最小的质数2,然后用2去筛,即把2的倍数,即4、6、8等都筛去,(5) 重复上述步骤,直到所有小于n的数都去完为止,剩余的数就是质数,如此可以得到2~n之间的所有质数。
2、利用素数对判断生成孪生素数素数对判断生成孪生素数其实就是在素数分布中查找孪生素数。
当我们从筛子算法中知道最小的质数2之后,每次可以枚举以此递增的质数,到满足p=q+2时,即可以判断p 和q为孪生素数。
三、实例让我们看看如何用C/C ++语言来实现孪生素数的生成。
// 声明素数数组int prime[MAX_NUMBER];// 定义i、j、n变量int i,j,n;// 将数组初始化for(i=2;i<MAX_NUMBER;i++)prime[i]=1;// 开始筛选for(i=2;i<MAX_NUMBER;i++){if(prime[i]==1){j=i+2;if(j<MAX_NUMBER&&prime[j]==1)printf("<%d,%d>是孪生素数",i,j);}for (n = i+i; n<MAX_NUMBER; n += i)prime[n] = 0;}四、结论本文以C/C ++为开发语言,论述了当两个质数p满足p=q+2时,p和q称为孪生素数的定义及其生成的两种方法,即埃拉托斯特尼筛法和素数对判断生成孪生素数,并给出了具体的实例代码,相信能够为学友们认识和学习孪生素数带来一定帮助。
找素数的两种方法

找素数的两种⽅法⽅法⼀:根据特点直接找质数(prime number)⼜称素数,有⽆限个。
质数定义为在⼤于1的⾃然数中,除了1和它本⾝以外不再有其他因数。
根据这个性质,我们可以构造⼀个两层嵌套循环根据这个判断条件就可以找出1-n之间的素数了。
代码如下:#include<iostream>#include<cmath>using namespace std;int main() {//寻找素数的第⼀种⽅法bool isPrime;for (int i = 2; i < 100; i++) {isPrime = true;for (int j = 2; j < i; j++) {if (i%j == 0) isPrime = false;}if (isPrime) cout << i << " ";}return 0;}⽅法⼆:筛法求素数埃拉托斯特尼筛法,简称埃⽒筛或爱⽒筛,是⼀种由希腊数学家埃拉托斯特尼所提出的⼀种简单检定素数的算法。
要得到⾃然数n以内的全部素数,必须把不⼤于根号n的所有素数的倍数剔除,剩下的就是素数。
利⽤这个⽅法,我们可以建⽴⼀个从2到Math.sqrt(n)的循环,依次删除这些数的倍数。
代码如下:#include<iostream>#include<cmath>using namespace std;int main() {//寻找素数的第⼆种⽅法:埃拉托斯特尼筛⼦法,基本思路:不是挑选出所有素数,⽽是筛掉所有的合数。
int sum = 0, a[100] = { 0 };for (int i = 2; i < sqrt(100.0); i++) {sum = i;if (a[sum] == 0) {while (sum < 100) {sum += i;if (sum < 100) a[sum] = 1;}}}for (int i = 2; i < 100; i++) {if (a[i] == 0) cout << i << " ";}return 0;}。
算法笔记_012:埃拉托色尼筛选法(Java)

算法笔记_012:埃拉托⾊尼筛选法(Java)1 问题描述Compute the Greatest Common Divisor of Two Integers using Sieve of Eratosthenes.翻译:使⽤埃拉托⾊尼筛选法计算两个整数的最⼤公约数。
(PS:最⼤公约数也称最⼤公因数,指两个或多个整数共有中最⼤的⼀个)2 解决⽅案2.1 埃拉托⾊尼筛选法原理简介引⽤⾃百度百科:埃拉托⾊尼筛选法(the Sieve of Eratosthenes)简称埃⽒筛法,是古希腊数学家(Eratosthenes 274B.C.~194B.C.)提出的⼀种筛选法。
是针对⾃然数列中的⾃然数⽽实施的,⽤于求⼀定范围内的,它的容斥原理之完备性条件是p=H~。
具体求取质数的思想:(1)先把1删除(现今数学界1既不是质数也不是合数)(2)读取队列中当前最⼩的数2,然后把2的倍数删去(3)读取队列中当前最⼩的数3,然后把3的倍数删去(4)读取队列中当前最⼩的数5,然后把5的倍数删去(5)如上所述直到需求的范围内所有的数均删除或读取下⾯看⼀下执⾏上述步骤求不⼤于100的所有质数的⼀个⽰意图:2.2 具体编码本⽂求取两个数的最⼤公约数,采⽤质因数分解法:把每个数分别分解质因数,再把各数中的全部公有质因数提取出来连乘,所得的积就是这⼏个数的最⼤公约数。
例如:求24和60的最⼤公约数,先分解质因数,得24=2×2×2×3,60=2×2×3×5,24与60的全部公有的质因数是2、2、3,它们的积是2×2×3=12,所以,(24,60)=12。
此处,第⼀步,先使⽤埃拉托⾊尼筛选法求取不⼤于数A的所有质数,然后从这些质数中选取A的所有质因数;第⼆步,依照第⼀步思想求取数B的所有质因数;第三步,求取数A和数B公共质因数;第四步,输出数A和数B的最⼤公约数。
埃拉托斯特尼筛法及改进_C_语言_
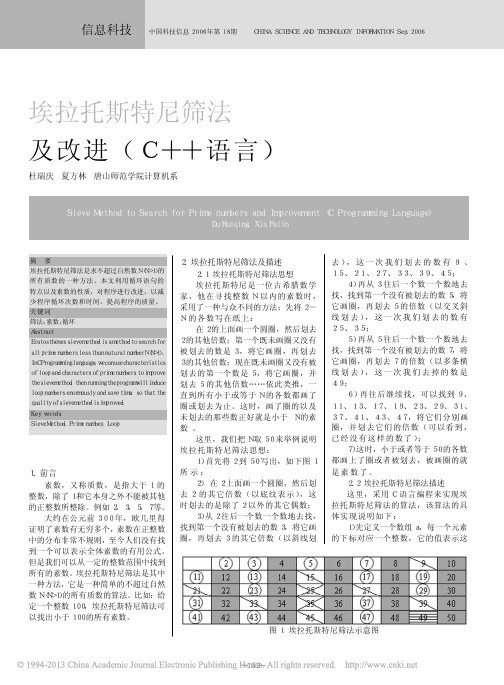
从表中可以看出,通过改进,程 序的循环次数大大减少,程序的运行 时间大大缩短。
通过改进,要求找出 2 到 N 的所 有素数的 C 语言程序为:
#include <stdio.h> #include <math.h> void main(void)
=0) if( j
% i==0) a[j]=0;
3 .筛法改进及编程 本文主要从三个方面对埃拉托斯特
尼筛法进行了改进,首先利用“大于 2 的质数都是奇数”这一知识,首先 筛选能够被 2 除的数,然后从 3 开始 筛选时,i 和 j 的值每次循环加 2,就 不用再考虑偶数了,这样循环的次数 可以减少到原程序的四分之一左右; 其次每次筛除某个质数(例如 m )的 倍数时,因为乘数小于该质数的积(2 × m , 3 × m ,……,(m - 1 )× m )都已经被作为小于该质数的积被筛 除了,因此倍数应该从该质数的平方 (m 2 )开始,如:筛除 5 的倍数,1 0 已经作为 2 的倍数被筛除了,15 已经作 为 3 的倍数被筛除了,应该从 25 开始, 这样循环的次数又可以减少一些;最后 因为改进二中的原因,当筛除完某个质 数(例如 m)的倍数的时候,我们可以 肯定从 2 到这个质数的平方(m 2 )之
这里,我们把 N 取 50 来举例说明 埃拉托斯特尼筛法思想:
1) 首先将 2 到 5 0 写出,如下图 1 所示:
2) 在 2 上面画一个圆圈,然后划 去 2 的其它倍数(以底纹表示),这 时划去的是除了 2 以外的其它偶数;
3)从 2 往后一个数一个数地去找, 找到第一个没有被划去的数 3,将它画 圈,再划去 3 的其它倍数(以斜线划
1. 前言 素数,又称质数,是指大于 1 的
质数判断最快算法

质数判断最快算法引言质数判断是一个重要且常见的数学问题,即判断一个给定的正整数是否是质数。
传统的方法是用该数去除以小于它的所有正整数,如果都不能整除,则该数为质数。
然而,这种方法对于大数会非常耗时。
本文将介绍一些更优化的算法,用于在更短的时间内判断一个数是否是质数。
算法一:试除法试除法是传统的判断质数的方法,即用给定的数除以所有小于它自身的正整数,如果都不能整除,则该数为质数。
这种方法的时间复杂度为O(n),其中n为该数的大小。
算法二:试除法优化试除法的优化版本是只需试除小于等于该数平方根的正整数。
因为如果一个数可以被分解为两个因数a和b,其中a大于其平方根,b也必然小于其平方根。
所以如果通过试除小于等于其平方根的正整数都不能整除,那么该数必然是质数。
这种方法的时间复杂度为O(sqrt(n))。
算法三:埃拉托斯特尼筛法埃拉托斯特尼筛法是一种通过筛法来判断质数的方法。
它的思想是从2开始,将每个质数的倍数全部标记为合数,最终剩下的就是质数。
具体步骤如下: 1. 初始化一个长度为n的布尔数组,表示每个数是否为质数,初始值都为true。
2. 从2开始遍历到sqrt(n),如果当前数为质数,则将其所有倍数标记为合数。
3. 遍历完毕后,剩下未被标记为合数的数即为质数。
埃拉托斯特尼筛法的时间复杂度为O(nloglogn),快于前两种方法。
算法四:米勒-拉宾素性测试米勒-拉宾素性测试是一种概率性质数判断方法,可以高效地检测出非质数。
它的原理基于费马小定理和二次剩余定理。
具体步骤如下: 1. 将给定的数n-1的偶数因子全部分解出来:n-1 = 2^s * d,其中d为奇数。
2. 选择一个随机数a,2 <= a <= n-2。
3. 计算x = a^d mod n。
4. 如果x为1或n-1,则该数可能是质数,跳出循环。
5. 循环r-1次,其中r为n-1的二进制表示中1的个数。
- 计算x = x^2 mod n。
质数的两种筛法

质数的两种筛法⽬录内含部分⾼数内容,请不想了解证明的⼩伙伴直接参考⼩标题后⾯的时间复杂度质数的朴素筛法:O(n√n log n)根据定义,我们不难得出,如果要知道 1~n范围内的所有质数,我们只需要从 2 到n开始枚举,再判断是否是质数即可:bool isprime[MAXN];for(int i=2;i<=n;i++){isprime[i]=1;for(int j=2;j*j<=i;j++){if(i%j==0){isprime[i]=0;break;}}}当枚举到的数为n的时候,内层的复杂度是O(√n) 的,⽽外层O(n) 枚举因此,很多⼈觉得是O(n√n) 的其实,本⼈对此持怀疑态度⾸先:每个合数都是被⾃⼰的最⼩质因⼦筛到,⽽每个质数p花费的时间是O(√p)质数的很显然,对于合数的,我们⽤反证法:如果这个数m的最⼩质因数为fc,它被判定为合数时i=k因此,m应该在k之前都不能退出循环⽽如果fc为k的因数,fc<k(因为k为合数);如果不为的话,k的最⼩质因数假设为fc′则fc<fc′<k因此,m在fc时就⼀定退出了综上,复杂度其实并没有达到O(n√n) ,其实复杂度是更⼩的经本⼈复杂度⼤概为O(n32 log n)优化o(n32 log n)我们考虑每个合数,⼀定是被它的最⼩质因数筛到。
⽽⼀个数n的最⼩质因数fc,⼀定有fc∈Prime,fc≤n所以,我们把之前筛到的所有质数存起来,筛到n时,依次枚举不⼤于√n的质数判断是不是这个数的因数就⾏了bool isprime[MAXN];int prime[MAXN],cntprime=0;for(int i=3;i<=n;i++){isprime[i]=1;for(int j=1;prime[j]*prime[j]<=i&&j<=cntprime;j++){if(i%prime[j]==0){isprime[i]=0;break;}}if(isprime[i]==1){prime[++cntprime]=i;}}枚举质数的速度⽐优化前更快。
python中求质数的方法

python中求质数的方法在Python中,有多种方法可以求解质数。
以下是两种常见的方法:1. **试除法:**这是最基本的方法之一,通过尝试除以比该数小的所有整数来确定一个数是否为质数。
如果除法操作对于所有的小于该数的整数都没有余数,那么该数就是质数。
```pythondef is_prime(n):if n <= 1:return Falsefor i in range(2, int(n**0.5) + 1):if n % i == 0:return Falsereturn True```在这个函数中,我们遍历从2到n的平方根的所有整数,如果有任何一个整数能够整除n,那么n就不是质数。
否则,它就是质数。
2. **埃拉托斯特尼筛法:**这是一种更高效的方法,通常用于生成一定范围内的所有质数。
它的基本思想是从2开始,将所有2的倍数标记为非质数,然后再找到下一个未被标记的数,将其所有倍数标记为非质数。
重复这个过程,直到找到所有小于给定数的质数。
```pythondef sieve_of_eratosthenes(limit):primes = []is_prime = [True] * (limit + 1)for num in range(2, int(limit**0.5) + 1):if is_prime[num]:primes.append(num)for multiple in range(num * num, limit + 1, num):is_prime[multiple] = Falsefor num in range(int(limit**0.5) + 1, limit + 1):if is_prime[num]:primes.append(num)return primes```在这个函数中,我们使用一个布尔数组`is_prime` 来标记每个数是否为质数。
首先,我们将2的倍数标记为非质数,然后找到下一个未被标记的数,将其所有倍数标记为非质数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
试编写一个程序,找出2->N之间的所有质数。
希望用尽可能快的方法实现。
【问题分析】:这个问题可以有两种解法:一种是用“筛子法”,另一种是“除余法”。
如果要了解“除余法”,请看另一篇文章《求质数之除余法(C语言描述)》。
这里我们来讨论一下用“筛法”来解决这个问题。
先来举个简单的例子来介绍一下“筛法”,求2~20的质数,它的做法是先把2~20这些数一字排开:2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20先取出数组中最小的数,是2,则判断2是质数,把后面2的倍数全部删掉。
2 |3 5 7 9 11 13 15 17 19接下来的最小数是3,取出,再删掉3的倍数2 3 | 5 7 11 13 17 19一直这样下去,直到结束。
剩下的数都是素数。
筛法的原理是:1.数字2是素数。
2.在数字K前,每找到一个素数,都会删除它的倍数,即以它为因子的整数。
如果k 未被删除,就表示2->k-1都不是k的因子,那k自然就是素数了。
(1)除余法那篇文章里也介绍了,要找出一个数的因子,其实不需要检查2->k,只要从2->sqrt(k),就可以了。
所有,我们筛法里,其实只要筛到sqrt(n)就已经找出所有的素数了,其中n为要搜索的范围。
(2)另外,我们不难发现,每找到一个素数k,就一次删除2k, 3k, 4k,..., ik,不免还是有些浪费,因为2k已经在找到素数2的时候删除过了,3k已经在找到素数3的时候删除了。
因此,当i<k时,都已经被前面的素数删除过了,只有那些最小的质因子是k的那些数还未被删除过,所有,就可以直接从k*k开始删除。
(3)再有,所有的素数中,除了2以外,其他的都是奇数,那么,当i时奇数的时候,ik就是奇数,此时k*k+ik就是个偶数,偶数已经被2删除了,所有我们就可以以2k为单位删除步长,依次删除k*k, k*k+2k, k*k+4k, ...。
(4)我们都清楚,在前面一小段范围内,素数是比较集中的,比如1->100之间就有25个素数。
越到后面就越稀疏。
因为这些素数本身值比较小,所以搜索范围内,大部分数都是它们的倍数,比如搜索1->100,这100个数。
光是2的倍数就有50个,3的倍数有33个,5的倍数20个,7的倍数14个。
我们只需搜索到7就可以,因此一共做删除操作50+33+20+14=117次,而2和3两个数就占了83次,这未免太浪费时间了。
所以我们考虑,能不能一开始就排除这些小素数的倍数,这里用2和3来做例子。
如果仅仅要排除2的倍数,数组里只保存奇数:1、3、5...,那数字k的坐标就是k/2。
如果我们要同时排除2和3的倍数,因为2和3的最小公倍数是6,把数字按6来分组:6n, 6n+1, 6n+2, 6n+3, 6n+4, 6n+5。
其中6n, 6n+2, 6n+4是2的倍数,6n+3是3的倍数。
所以数组里将只剩下6n+1和6n+5。
n从0开始,数组里的数字就一次是1, 5, 7, 11, 13, 17...。
现在要解决的问题就是如何把数字k和它的坐标i对应起来。
比如,给出数字89,它在数组中的下标是多少呢?不难发现,其实上面的序列,每两个为一组,具有相同的基数n,比如1和5,同是n=0那组数,6*0+1和6*0+5;31和35同是n=5那组,6*5+1和6*5+5。
所以数字按6分组,每组2个数字,余数为5的数字在后,所以坐标需要加1。
所以89在第89/6=14组,坐标为14*2=28,又因为89%6==5,所以在所求的坐标上加1,即28+1=29,最终得到89的坐标i=29。
同样,找到一个素数k后,也可以求出k*k的坐标等,就可以做筛法了。
这里,我们就需要用k做循环变量了,k从5开始,交替与2和4相加,即先是5+2=7,再是7+4=11,然后又是11+2=13...。
这里我们可以再设一个变量gab,初始为4,每次做gab = 6 - gab,k += gab。
让gab在2和4之间交替变化。
另外,2和4都是2的幂,二进制分别为10和100,6的二进制位110,所以可以用k += gab ^= 6来代替。
参考代码:gab = 4;for (k = 5; k * k <= N; k += gab ^= 6){...}但我们一般都采用下标i从0->x的策略,如果用i而不用k,那应该怎么写呢?由优化策略(1)可知,我们只要从k2开始筛选。
n=i/2,我们知道了i对应的数字k是素数后,根据(2),那如何求得k2的坐标j呢?这里假设i为偶数,即k=6n+1。
k2 = (6n+1)*(6n+1) = 36n2 + 12n + 1,其中36n2+12n = 6(6n2+2n)是6的倍数,所以k2除6余1。
所以k2的坐标j = k2/6*2 = 12n2+4n。
由优化策略(2)可知,我们只要依次删除k2+2l×k, l = 0, 1, 2...。
即(6n+1)×(6n+1+2l)。
我们发现,但l=1, 4, 7...时,(6n+1+2l)是3的倍数,不在序列中。
所以我们只要依次删除k2, k2+4l, k2+4l+2l...,又是依次替换2和4。
为了简便,我们可以一次就删除k2和k2+4l两项,然后步长增加6l。
所以我们需要求len=4l和stp=6l。
不过这里要注意一点,k2+4k=(6n+1)*(6n+5),除以6的余数是5,坐标要加1。
len = k*(k+4)/6*2 - k2/6*2 = (6n+1)*(6n+1+4)/6*2+1 - (6n+1)*(6n+1)/6*2 = (12n2+12n+1) - (12n2+4n) = 8n+1;stp = k*(k+6)/6*2 - k2/6*2 = 12n+2;6.去掉7后,第一个数11的平方121大于60,所以结束。
剩下的数字全为素数。
02 03 05 07 11 13 15 17 19 23 29 31 37 41 43 47 53 59 |上面的操作效率很高,但在计算机中模拟的时候却又很大的障碍:首先,计算机内存是一维的空间,很多时候我们不能随心所欲,要实现上面的算法,要求这个数据结构既能很高效地查找某个特定的值,又能不费太大代价对序列中的元素进行删除。
高效地查找,用数组是最合适的了,能在O(1)的时间内对内存进行读写,但要删除序列中一个元素却要O(n);单链表可以用O(1)的时间做删除操作,当然要查找就只能是O(n)了。
所以这个数据结构很难找。
其次,筛法的一个缺点就是空间浪费太大,典型的以空间换时间。
如果我们对数组进行压缩,比如初始时就排除了所有偶数,数组0对应数字1,1对应3,...。
这样又会因为多了一道计算数字下标的工序而浪费时间。
这又是一个矛盾的问题。
也许我们可以试试折中的办法:数据结构综合数组和链表2种,数组用来做映射记录,链表来记录剩下的还未被删除的数据,而且开始也不必急着把链表里的节点释放掉,只要在数组里做个标记就可以了。
下次遍历到这个数字时才删除。
这样为了删除,可以算只遍历了一次链表,不过频繁地使用free()函数,也许又会减低效率。
总之,我们所做的,依然是用空间来换时间,记录更多的信息,方便下次使用,减少再次生成信息所消耗的时间。
【程序清单】:#include <time.h>#include <stdio.h>#define N 100000000#define size (N/6*2 + (N%6 == 5? 2: (N%6>0)))int p[size / 32 + 1] = {1};int creat_prime(void){int i, j;int len, stp;int c = size + 1;for (i = 1; ((i&~1)<<1) * ((i&~1) + (i>>1) + 1) < size; i++){if (p[i >> 5] >> (i & 31) & 1) continue;len = (i & 1)? ((i&~1)<<1) + 3: ((i&~1)<<2) + 1;stp = ((i&~1)<<1) + ((i&~1)<<2) + ((i & 1)? 10: 2);j = ((i&~1)<<1) * (((i&~1)>>1) + (i&~1) + 1) + ((i & 1)? ((i&~1)<<3) + 8 + len: len);for (; j < size; j += stp){if (p[j >> 5] >> (j & 31) & 1 ^ 1)p[j >> 5] |= 1L << (j & 31), --c;if (p[(j-len) >> 5] >> ((j-len) & 31) & 1 ^ 1)p[(j-len) >> 5] |= 1L << ((j-len) & 31), --c;}if (j - len < size && (p[(j-len) >> 5] >> ((j-len) & 31) & 1 ^ 1))p[(j-len) >> 5] |= 1L << ((j-len) & 31), --c;}return c;}int main(void){clock_t t = clock();printf("%d ", creat_prime());printf("Time: %f ", 1.0 * (clock() - t) / CLOCKS_PER_SEC);}【运行结果】:5761455Time: 1.812000运行环境:XP SP2、Dev-C++ 4.9.9.2【算法比较】:现在,我们已经拥有初步改进的“筛法”和“除余法”的函数了,把它们加到自己的函数库里。
方便下次调用。
这里,我想说一下个人对这两种算法的使用经验:就时间效率上讲,筛法绝对比除余法高。
比如上面的代码,可以在两秒内筛一亿以内的所有素数。
如果用除余法来解决这样的问题,绝对可以考验一个人的耐性。
