第3章 复杂立体三视图的识读1
机械识图培训

用去除材料方法获得的表面粗糙度,Ra的上限值为3.2μm,Ra的下限值为1.6μm
用不去除材料方法获得的表面粗糙度,Ra的最大值为3.2μm, Ra的最小值为1.6μm
1:1 如2:1 如1:2
图 线
粗实线 细实线 虚线 粗点划线 波浪线
轮廓线 尺寸线、剖面线 不可见轮廓线 轴线、对称中心线 断裂处的分界线
尺寸注法
尺寸注法
完整的尺寸包括: 1、尺寸数字:大小 2、尺寸线:方向 3、尺寸界线:范围
半剖视图
概念:当机件具有对称平面时,在垂直于对称平面的投影面上投影所得的图形,以对称中心线为界,一半画成剖视,另一半画成视图,称为半剖视图。 应用:它是内外形状都比较复杂的对称机件常用的表达方法。 标注:半剖视图的标注方法与全剖视图相同。 注意:在半剖视图中,视图与剖视图的分界线应是细点划线,而不应画成粗实线,也不应与轮廓线重合。在半个视图中不应再画虚线〔由于在另一半剖视图中已表达清楚其内形〕,但对于孔或槽等,应画出中心线位置。
二、螺纹的标记
1.公制螺纹
例如标记:M16×1 LH—5g6g—S 其含义为: 普通螺纹〔M〕,公称直径为16mm,细牙,螺距1mm,左旋〔LH〕,中径 公差带代号5g,顶径公差带代号6g,短旋合长度〔S〕。
2.美制螺纹
例如标记3/8—16 UNC—2A 第一位数字3/8〔分数或小数〕表示螺纹外径,单位为英寸; 第二、三位数字16、24、32、20为每英寸牙数(在25.4mm长度上的牙数); 第三位以后的文字UNC为螺纹类型的系列代号; 最后两位2A为精度等级。
图纸幅面
A0、A1、A2、A3、A4
A0幅面为841×1189,A1幅面为A0的一半,以此类推。
湘教版九年级下册数学 第3章 三视图

知3-讲
特别警示:圆锥与棱锥的三视图的区别:圆锥的俯视图 的外轮廓线是圆;棱锥的俯视图的外轮廓线是多边形.
三视图
主视图 左视图
三视图
画法
俯视图
应用
课后作业
作业1 必做:请完成教材课后习题 补充:
作业2
知2-讲
例3 一种机器上有一个进行转动的零件叫燕尾槽(如图 3.3-7),请画出它的三视图.
解:这个燕尾槽的三视图如图3.3-8.
知2-讲
知识点 3 由三视图确定几何体
知3-讲
1. 由三视图描述几何体的方法:由三视图想象几何体的形 状,首先分别根据主视图、俯视图和左视图想象几何体
的正面、上面和左面,然后综合起来考虑整体形状. 特别提醒:由三视图描述几何体的形状时,要对三视图进
方画出左视图,与主视图 高平齐,与俯视图宽相等, 图3.3-3①中的几何体的三 视图如图3.3-3②所示.
速记口诀: 视图位置要摆明, 画图规则要记清. 主俯视图长对正, 左俯视图宽相等, 主左视图高平齐, 实线虚线应分清.
知2-讲
知2-讲
3. 画三视图的规定:画三视图时,看得见的部分的轮廓线 画成实线,因被其他部分遮挡而看不见的部分的轮廓线 画成虚线.
(4)利用由三视图画几何体与由几何体画三视图的互逆过程,反
复练习,不断总结方法.
3. 常见几何体的三视图
知3-讲
知3-讲
1. 几何体的三视图和展开图是平面图形,几何体、三视 图和展开图中,三者知其一,就能确定另外两种图形, 即三者之间可以互相转化.
2. 对于稍复杂的视图,可先将其化成几个简单的图形, 再综合分析.
视图在主视图的右边. 主视图反映物体的长和高,俯视
图反映物体的长和宽,左视图反映物体的高和宽.
《机械制图》绘制复杂组合体三视图

特征面
特征面
15
3 任务三 绘制复杂组合体三视图
(1)柱体的形成
叠加而成的柱体
16
3 任务三 绘制复杂组合体三视图
(1)柱体的形成
切割而成柱体
17
3 任务三 绘制复杂组合体三视图
(1)柱体的形成
特征面拉伸成柱体
18
3 任务三 绘制复杂组合体三视图
21
3 任务三 绘制复杂组合体三视图
例1:画组合体三视图
虚拟 轴承座(视图)
22
3 任务三 绘制复杂组合体三视图
例2:画组合体三视图
虚拟 组合体(叠加)
23
3 任务三 绘制复杂组合体三视图
例3:画切割体的三视图
虚拟 切割体1(视图)
24
3 任务三 绘制复杂组合体三视图
例4:画切割体的三视图
虚拟 切割体2(视图)
25
3 任务三 绘制复杂组合体三视图
例5:画物体的三视图
虚拟 切割体3(视图)
26
3 任务三 绘制复杂组合体三视图
三、物体的尺寸标注
标注尺寸的基本要求是正确、完整、清晰。
正确
完整
是指标注的尺寸要符合国 家标准中有关尺寸标注的
规定;尺寸数字准确
是指标注的尺寸能完全确 定物体形状和大小。尺寸 没有遗漏,也没有重复
机械制图
MECHANICAL DRAWING
总 目 录 TOTAL CONTENTS
项目一 手工绘图规范和基本技能 1 项目二 基本几何体的投影 2
项目三 识读绘制组合体三视图 3 项目四 绘制轴测图 4
项目五 机件的常用表达方法 5 项目六 标准件和常用件的表示法 6
三视图课件

绘制三视图基本规则
物体摆放规则
绘制三视图时,应将物体摆放成 工作位置,即自然安放且主要表
面或轴线平行于投影面。
视图布局规则
主视图应位于图纸的主要位置, 俯视图在主视图的下方,左视图 在主视图的右侧。各视图之间应 保持适当的间距,并用细实线连
接对应点。
尺寸标注规则
三视图中应标注齐全的尺寸,包 括定形尺寸、定位尺寸和总体尺 寸。尺寸标注应清晰、准确,符
掌握零件的尺寸标注
熟悉零件图中的尺寸标注方法,理解各尺寸 的含义和作用。
分析零件的视图表达
分析零件图的主视图、俯视图、左视图等视 图,理解各视图之间的投影关系。
理解零件的技术要求
了解零件图中的表面粗糙度、公差与配合等 技术要求。
装配图阅读和绘制方法
了解装配体的组成
通过观察装配图,了解装配体由哪些 零件组成,各零件之间的连接方式和 相对位置。
掌握正视图、俯视图和左视图的形成原理及 投影规律。
三视图绘制方法
学习如何根据物体的形状和结构,正确绘制 其三视图。
尺寸标注与识读
理解尺寸标注的规定和方法,能够准确识读 和理解三视图中的尺寸信息。
形体分析与表达
掌握形体分析的方法和技巧,能够运用所学 知识对复杂形体进行准确表达。
学生自我评价报告
知识掌握程度
标注零件尺寸
根据零件的结构形状和制造要求,标注必要的零 件尺寸,如定形尺寸、定位尺寸等。
ABCD
拆画零件图
根据装配图中的零件形状和连接关系,逐个拆画 出各个零件的图形。
编写技术要求
根据零件的使用要求和制造工艺,编写必要的技 术要求,如表面粗糙度、公差等。
06
课程总结与拓展延伸
第3、4章 柱体、锥体三视图

基本体读图练习
补左视图
基本体读图练习
补左视图
基本体读图练习
P11-14 补俯视图
识读:依据实形(图形特征)想象立体形状
平面体三视图练习
平面体三视图练习
第3章 柱体三视图
3.2 圆柱三视图的画法与识读
形体特征:类同直棱体,底面为圆画反映底面 实形的特征图(圆),最后画出其他视图
图形特征:一个视图为圆,两个视图为矩形
第三、四章 柱体、锥体三视图
第3章 柱体三视图
3.1 棱柱三视图的画法与识读 3.2 圆柱三视图的画法与识读 3.3 组合柱体
第4章 锥体三视图
4.1 锥体的概念及形体特点 4.2 锥体三视图的画法 4.3 锥体三视图的识读
基本体
基本几何体是构成工程形体的基本单元。
根据表面几何性质分
平面体
曲面体
根据形状特征分
柱体
图示
锥体
第3章 柱体三视图
3.1 棱柱三视图的画法与识读
形体特征:两个底面全等、相互平行的多边 形,各侧棱垂直底面并相互平行且均为矩形
画法:一般先画反映棱柱底面实形的特征图, 在根据投影规律和棱柱高画其他视图
图形特征:一视图为单一多边形(特征视 图),底面实形,另两个视图为矩形或并列 矩形
棱锥识读:根据图形特征想象(三三为锥)
第4章 锥体三视图
4.2 锥体三视图的画法与识读
圆锥画法:先画出中心线、轴线,再画反映 底面实形的特征图,后根据投影规律和锥高 画出其他视图
圆锥识读:两个视图三角形,一个视图为圆
基本体视图特征
柱体视图特征-矩矩为柱
基本体视图特征
球体视图特征-三圆为球
基本体视图特征
锥体视图特征-三三为锥
三视图与轴测图的识读与绘制—轴测图的识读与绘制

5 轴测图的特点
(1)形体上相互平行的线段,其轴测图投影平行; Z1
与空间坐标平行的线段,其轴测投影与
C1
相应的轴测轴平行-平行性。
O1
X1
A1
(2)形体上平行坐标轴的线段,其投影的变化率与相应轴测 轴的轴向变化率相同,形体上成比例的平行线段, 其轴测投影仍成相同比例-定比性。
X
轴测图也可说是沿轴测量所画出的图。
任务二 三视图和轴测图的识读与绘制
任务2-4 轴测图识读与绘制 第一部分 轴测图的基本知识(了解) 第二部分 绘制轴测图(重点、难点)
第一部分
轴测图的基本知识
1 三面投影与轴测投影图的比较
三面投影图
轴测投影图
正投影图可以比较全面表示空间物体的形状和大小。但是这种图立体感较差
,有时不容易看懂。
轴测图富于立体感。但是它不能直接反映物体的真实形状和大小。所以只能 作为辅助图样。
2 轴测图的定义
将形体连同确定形体的长、宽、高方向的空间坐标轴一起沿S方向,用平行投影 法向P面进行投影,应用这种方法绘出的投影图称轴测投影图,简称轴测图。
P面为轴测投影面
S方向
平行投影法
3 轴测投影图的形成
轴测轴——三个坐标轴X、Y、Z的 轴测投影X1、Y1、Z1。 轴间角——轴测轴之间的夹角, ∠X1OY1、∠Y1OZ1、∠Z1OX1 。 轴向变化率——轴测轴上的投影长度与 实际长度之比。
P
B1
Y1 Z
C
O A
B
Y
6 正等测图
形 影图简称正等测图。
第二部分
绘制轴测图
任务2-4-2 绘制轴测图
第一步:ds设置轴测图模式+F8 第二步:绘制轴测图-命令是F5或CTRL+E切换 第三步:绘制三视图-命令是rec+l+mi+j+tr+ma 第四步:设置文字样式(st-30-2、-30-2)和标注样式(d,30-2, -30-2) 第五步:标注(dal+ded)+文字(t) 第六步:模型或布局出图:打印(ctrl+p)
如何教学生识读组合体的三视图

如何教课生识读组合体的三视图[摘要]识读零件图和装置图是机械类技术工人必备的知识,识读组合体的三视图是识读零件图和装置图的重点和中心。
为了使学生掌握识读组合体三视图这一内容,本文从直观教课、熟记图样、掌握读图方法、读图技巧几个方面剖析指引学生识读组合体的三视图。
[重点词 ]识读组合体三视图机械制图是一门专业基础课,在专业课程的学习中,经常要识读零件或零件的构造图,所以要修业生一定具备读图能力。
而要识读零件图或装置图第一要学会识读组合体的三视图。
对大多学生来说识读组合体的三视图这一内容不易掌握,是一“难关”。
如何指导学生打破这一“难关”,说说自己的做法:一、进行直观教课,成立空间观点,夯实基础知识学习在解说投影法时,充足利用各样挂图、光芒照耀物体、模型等使学生成立起光源、投影线、投影面、投影等观点;解说三投影面系统时利用教室右前角的墙面、墙线、地面等使学生成立起三投影面系统的空间观点;在对基本体的投影解说时利用圆柱、圆锥、棱柱、棱锥、圆球等模型及挂图,给学生解说基本体三视图的投影,并重申主视图是从正对着物体“以前向后”看获得的,俯视图是“从上向下” 看获得的,左视图是“从左向右”看获得的,而后指引学生察看如何睁开“投影面”,如何形成“三视图”,搞清楚主、俯、左三视图的地点关系,进一步经过察看实物,让学生在三视图中找物体的前、后、上、下、左、右方的地点,频频训练,鼓舞学生参加教课,指引学生总结三视图之间的投影规律,使学生在脑筋中成立起投影法和投影面系统的观点。
成立起投影法和投影面系统的观点后,再利用粉笔头、铅笔、三角板等,模拟点、线、面,摆出它们与投影面的不一样地点关系,让学生一边摆地点一边察看其投影,而后再依据投影总结它们的投影特征,频频模拟训练,狠抓基础知识的教课,加上大批的习题操练,学生便能娴熟地把空间的线段、平面与投影互相变换了。
二、熟记图样,增强由“空间物体到平面图形”的变换能力的培育,为识读三视图再打基础。
识图及三视图

柱
多样形反映该形体的特征。
体
2、锥(台)体三视图与锥(台)体三视图的识读
图例
说明
圆锥体的三视图有一个反映锥体底面
圆
实形的投影和两个外轮廓为相同等腰三角
锥
形的投影,三角形的顶点是一个点(锥顶)
体
的投影。
棱锥体的三视图有一个反映锥体底面
棱
的投影和两个外轮廓为三角形的投影,三
锥
角形的顶点是一个点(锥顶)的投影,三
第一部分 机械识图
第1章 第2章 第3章 第4章
识图的基本知识 图样基本表示法 零件图 装配图的识读
第1章 识图的基本知识
1.1 机械图样 1.2 识图的基本知识 1.3 斜度和锥度 1.4 投影规律 1.5 基本体三视图识读 1.6 组合体三视图识读
1.1 机械图样
图样:工程技术上根据投影方法并遵照国家标准的规定绘 制成的用于工程施工或产品制造等用途的图叫做工程图样, 简称图样。 机械制造业所使用的图样称为机械图样, 图样是工程技术人员借以表达和交流技术思想不可缺少的 工程语言。
构成组合体的最小单元且不需要再分解的物体形状,叫做基本体。
1、柱体三视图与柱体三视图的识读 图例
说明
圆
圆柱体的三视图是由一个圆和两个
柱
矩形。
体
圆的投影反映该形体的特征。
棱
棱柱体的三视图是由一个正多边形
柱
和两个矩形。
体
多边形的投影反映该形体的特征。
一
一般柱体的三视图都是由一个
般
多样形和两个矩形来表述。
与锥高之比。如果是圆
锥 度
锥台则是上、下底圆直 径之差与锥台高度之比,
写成1:n的形式。
《机械制图》识读复杂组合体三视图

主视图相同,但物体 形状不同
a)
b)
c)
d)
e)
11
4 任务四 识读复杂组合体三视图
1、读图的基本要领
由两个视图也不一定能准确地表达某一物体的形状。
主、俯视图 相同,但物 体的形状可
不同
12
a)
b)
c)
d)
4 任务四 识读复杂组合体三视图
2、读图的基本方法
(1)形体分析法读图——①形体分析法 依据:组成复杂立体的各简单立体,其三面投影都是线框。 形体分析法是看物体视图的基本方法。一般步骤为:
②形体分析法读图过程中的注意点
1)读图时,要善于找出反映物体各部分形状特征的视图
Ⅱ的形状特征视图
虚拟 读图(形状
特征)
16
Ⅲ的形状特征视图 Ⅰ的形状特征视图
4 任务四 识读复杂组合体三视图
②形体分析法读图过程中的注意点
2) 读图时,要善于找出各组成部分间相对位置特征明显的视图
Ⅰ和Ⅱ位置特征明显视图
22
4 任务四 识读复杂组合体三视图
①视图中线框与其他视图的线段或线框间的投影规律
视图中的每一多边形线框,必有另外视图中与其成投影关系的多边形线框或线段与之对应,表 示物体上不同形状和位置的表面。
水正侧平平面面
如果视图中的多边形线 框与另一视图中的水平或垂 直线段有投影关系,则它表 达物体上的投影面平行面;
或孔的内表面的投影。
孔
10
凸起的筋
孔
4 任务四 识读复杂组合体三视图
1、读图的基本要领
(2)要将几个视图联系起来看,并且要遵循投影规律 由一个或两个视图有时不一定能准确地表达某一物体的形状。看图时,必须将几个视图联系起
机械制图项目五 组合体三视图的识读与绘制

习题解答 5.3(2)
5.3(3)
5.4(1)
5.7(1)
5.7(3)
5.8(3)
5.8(4)
5.14(1)
5.14(3)
5.16(1)
5.16(2)
5.18(1)
5.18(2)
5.6.2正等轴测图的画法 1.平面立体正等测图的画法 画平面立体轴测图的基本方法是坐标法,即沿坐标轴测量,
按坐标画出各顶点的轴测图,然后分别连线即可。 例:绘制正六棱柱正等测图。
对于不完整的形体,可先按完整形体画出,再用切割的方法 画出其不完整部分。
例:根据垫块三视图,绘制垫块正等测图。
对于组合体,可先将其分成若干个基本形体,然后根据各形 体的相互关系组合在一起。
5. l 组合体的构形
5.1.1组合体的形体分析 将一个复杂的组合体假想成由若干个简单的基本体组成,这
种分析问题的方法就是形体分析法。在组合体的构形、画图、 读图、尺寸标注等过程中都要运用形体分析法。
5.1.2组合体相邻表面间的连接关系
组合体上相邻表面间的连接关系有共面、相切、相交。 1.不共面 2. 共面
3. 相切
4.相交 支座:
5.1.3组合体的建模方法
例:构造轴承座三维造型。 1 形体分析 2 构造局部形体 3 集合操作
5.2 绘制组合体三视图
1.叠加型组合体 1 形体分析 2 选择主视图
3 选取画图比例,初始化图形文件 4 布置视图
2.切割型组合体 例:画出楔块的三视图
5.3 组合体的尺寸标注
注在反映为圆弧的视图上。
6
截交线、相贯线上不应直接标注尺寸,只要标注截切平
面的位置尺寸和相贯立体的位置尺寸。
5.5 读组合体视图
【高考数学】第三部分_重点板块_专题三立体几何:第1讲空间几何体的三视图、表面积及体积
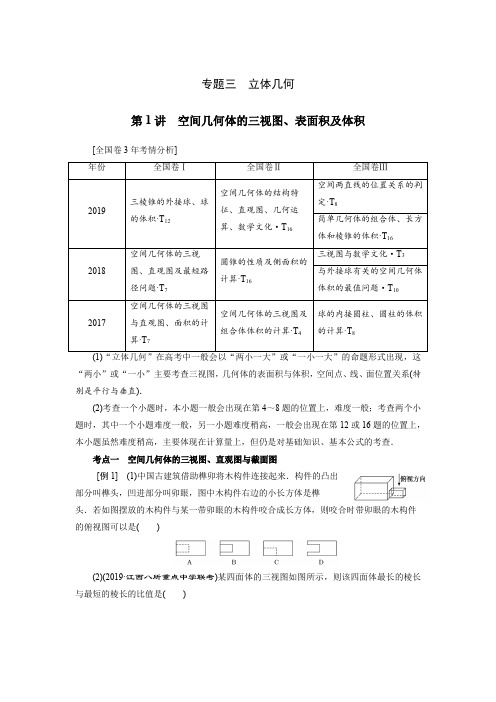
专题三立体几何第1讲空间几何体的三视图、表面积及体积[全国卷3年考情分析]年份全国卷Ⅰ全国卷Ⅱ全国卷Ⅲ2019三棱锥的外接球、球的体积·T12空间几何体的结构特征、直观图、几何运算、数学文化·T16空间两直线的位置关系的判定·T8简单几何体的组合体、长方体和棱锥的体积·T16 2018空间几何体的三视图、直观图及最短路径问题·T7圆锥的性质及侧面积的计算·T16三视图与数学文化·T3与外接球有关的空间几何体体积的最值问题·T10 2017空间几何体的三视图与直观图、面积的计算·T7空间几何体的三视图及组合体体积的计算·T4球的内接圆柱、圆柱的体积的计算·T8“两小”或“一小”主要考查三视图,几何体的表面积与体积,空间点、线、面位置关系(特别是平行与垂直).(2)考查一个小题时,本小题一般会出现在第4~8题的位置上,难度一般;考查两个小题时,其中一个小题难度一般,另一小题难度稍高,一般会出现在第12或16题的位置上,本小题虽然难度稍高,主要体现在计算量上,但仍是对基础知识、基本公式的考查.考点一空间几何体的三视图、直观图与截面图[例1](1)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()(2)(2019·江西八所重点中学联考)某四面体的三视图如图所示,则该四面体最长的棱长与最短的棱长的比值是()A .52B .2C .355D .32(3)(2018·全国卷Ⅰ)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( )A .334B .233C .324D .321.(2018·全国卷Ⅰ)某圆柱的高为2,底面周长为16,其三视图如图所示.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为( )A .217B .25C .3D .22.已知球O 是正三棱锥A BCD 的外接球,BC =3,AB =23,点E 在线段BD 上,且BD =3BE ,过点E 作球O 的截面,则所得截面中面积最小的截面圆的面积是________.考点二 几何体的表面积与体积 题型一 求空间几何体的表面积[例2] (1)《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体,如图所示,四边形ABCD 为矩形,棱EF ∥AB .若此几何体中,AB =4,EF =2,△ADE 和△BCF 都是边长为2的等边三角形,则该几何体的表面积为( )A .83B .8+83C .62+23D .8+62+23(2)我国古代数学名著《算法统宗》中有如下问题:“今有倚壁外角堆米,下周九十尺,高十二尺.”其意思为:在屋外墙角处堆放米(其三视图如图所示),米堆底部的弧长为90尺,米堆的高为12尺.圆周率约为3.若将此堆米用草席盖上,则此草席的面积至少约为(计算结果保留整数,如544≈23,550≈23)( )A .250平方尺B .990平方尺C .1 035平方尺D .518平方尺题型二 求空间几何体的体积[例3] (1)(2019·天津高考)已知四棱锥的底面是边长为2的正方形,侧棱长均为 5.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为________.(2)(2019·江西省五校协作体试题)某几何体的三视图如图所示,正视图是一个上底为2,下底为4的直角梯形,俯视图是一个边长为4的等边三角形,则该几何体的体积为______.1.(2019·重庆市学业质量调研)已知某几何体的三视图如图所示,则该几何体的体积为( )A.323 B .643C.1283 D .16032.已知一个底面是菱形、侧面是矩形的四棱柱,侧棱长为5,菱形的对角线的长分别是9和15,则这个棱柱的侧面积是( )A .3034B .6034C .3034+135D .1353.已知直四棱柱ABCD A 1B 1C 1D 1的所有棱长都是1,∠ABC =60°,AC ∩BD =O ,A 1C 1∩B 1D 1=O 1,点H 在线段OB 1上,OH =3HB 1,点M 是线段BD 上的动点,则三棱锥M C 1O 1H 的体积的最小值为________.考点三 与球有关的切、接问题 题型一 外接球[例4] (2019·全国卷Ⅰ)已知三棱锥P ABC 的四个顶点在球O 的球面上,P A =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是P A ,AB 的中点,∠CEF =90°,则球O 的体积为( )A .86πB .46πC .26πD .6π题型二 内切球[例5] 已知一个平放的各棱长为4的三棱锥内有一个小球O (重量忽略不计),现从该三棱锥顶端向内注水,小球慢慢上浮,当注入的水的体积是该三棱锥体积的78时,小球与该三棱锥各侧面均相切(与水面也相切),则小球的表面积等于( )A.7π6 B .4π3C.2π3 D .π2题型三 与球有关的最值问题[例6] (2018·全国卷Ⅲ)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,△ABC 为等边三角形且其面积为93,则三棱锥D ABC 体积的最大值为( )A .123B .183C .243D .5431.已知圆锥的高为3,底面半径为3,若该圆锥的顶点与底面的圆周都在同一个球面上,则这个球的体积等于( )A .83πB .323πC .16πD .32π2.(2019·福建五校第二次联考)已知直三棱柱ABC A 1B 1C 1的6个顶点都在球O 的球面上,若AB =3,AC =4,AB ⊥AC ,AA 1=12,则球O 的直径为______.3.已知四棱锥S ABCD 的所有顶点在同一球面上,底面ABCD 是正方形且球心O 在此平面内,当四棱锥的体积取得最大值时,其表面积等于16+163,则球O 的体积为______.4.已知某几何体的三视图如图所示,则该几何体的体积等于( )A .2π+4B .4π+2 C.2π3+4 D .4π3+8【课后专项练习】A 组一、选择题1.如图是一个空间几何体的正视图和俯视图,则它的侧视图为( )2.(2019·福州市质量检测)棱长为1的正方体ABCD A 1B 1C 1D 1木块的直观图如图所示,平面α过点D 且平行于平面ACD 1,则该木块在平面α内的正投影面积是( )A.3 B .323C.2D .13.已知矩形ABCD ,AB =2BC ,把这个矩形分别以AB ,BC 所在直线为轴旋转一周,所成几何体的侧面积分别记为S 1,S 2,则S 1与S 2的比值等于( )A.12 B .1 C .2D .44.设球O 是正方体ABCD A 1B 1C 1D 1的内切球,若平面ACD 1截球O 所得的截面面积为6π,则球O 的半径为( )A.32 B .3 C.32D .35.(2019·武汉市调研测试)如图,在棱长为1的正方体ABCD A 1B 1C 1D 1中,M 为CD 的中点,则三棱锥A BC 1M 的体积VA BC 1M =( )A.12 B .14C.16 D .1126.(2019·武汉市调研测试)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )A.23π B .43πC .2πD .25π7.在三棱锥A BCD 中,侧棱AB ,AC ,AD 两两垂直,△ABC ,△ACD ,△ADB 的面积分别为22,32,62,则该三棱锥的体积为( ) A. 6 B .66 C .6 D .268.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A .πB .3π4C.π2 D .π49.若一个球与四面体的六条棱都相切,则称此球为四面体的棱切球.已知正四面体的棱长为2,则它的棱切球的体积为( )A .3π54B .π6C .π3D .3π210.已知点A ,B ,C ,D 均在球O 上,AB =BC =3,AC =3.若三棱锥D ABC 体积的最大值为334,则球O 的表面积为( )A .36πB .16πC .12πD .163π11.已知一个半径为7的球中有一个各条棱长都相等的内接正三棱柱,则正三棱柱的体积是( )A .18B .16C .12D .812.(2019·福州市质量检测)如图,以棱长为1的正方体的顶点A 为球心,以2为半径作一个球面,则该正方体的表面被球面所截得的所有弧长之和为( )A.3π4 B .2π C.3π2 D .9π4二、填空题13.(2019·长春市质量监测(一))已知一所有棱长都是2的三棱锥,则该三棱锥的体积为______.14.已知正方体ABCD A 1B 1C 1D 1的棱长为1,除面ABCD 外,该正方体其余各面的中心分别为点E ,F ,G ,H ,M (如图),则四棱锥M EFGH 的体积为______.15.古人采取“用臼舂米”的方法脱去稻谷的外壳,获得可供食用的大米,用于舂米的“臼”多用石头或木头制成.一个“臼”的三视图如图所示,则凿去部分(看成一个简单的组合体)的体积为______.16.已知三棱锥P ABC 的四个顶点都在球O 的表面上,P A ⊥平面ABC ,AB ⊥BC ,且P A =8.若平面ABC 截球O 所得截面的面积为9π,则球O 的表面积为______.B 组1.(2019·合肥市第二次质量检测)如图,正方形网格纸中的实线图形是一个多面体的三视图,则该多面体各表面所在平面互相垂直的有( )A .2对B .3对C .4对D .5对2.在棱长为3的正方体ABCD A 1B 1C 1D 1中,P 在线段BD 1上,且BP PD 1=12,M 为线段B 1C 1上的动点,则三棱锥M PBC 的体积为( )A .1B .32C.92 D .与M 点的位置有关3.已知正方体ABCD A 1B 1C 1D 1的体积为1,点M 在线段BC 上(点M 异于B ,C 两点),点N 为线段CC 1的中点,若平面AMN 截正方体ABCD A 1B 1C 1D 1所得的截面为四边形,则线段BM 的取值范围为( )A.⎝⎛⎦⎤0,13 B .⎝⎛⎦⎤0,12 C.⎣⎡⎭⎫12,1 D .⎣⎡⎦⎤12,234.已知直三棱柱ABC A 1B 1C 1的侧棱长为6,且底面是边长为2的正三角形,用一平面截此棱柱,与侧棱AA 1,BB 1,CC 1分别交于三点M ,N ,Q ,若△MNQ 为直角三角形,则该直角三角形斜边长的最小值为( )A .22B .3C.23D.45.(2019·郑州市第二次质量预测)在△ABC中,已知AB=23,BC=26,∠ABC=45°,D是边AC上的一点,将△ABD沿BD折叠,得到三棱锥ABCD,若该三棱锥的顶点A在底面BCD上的射影M在线段BC上,设BM=x,则x的取值范围是() A.(0,23)B.(3,6)C.(6,23)D.(23,26)6.如图,在正三棱柱ABCA1B1C1中,D为棱AA1的中点.若AA1=4,AB=2,则四棱锥BACC1D的体积为________.7.已知在正四棱锥SABCD中,SA=63,那么当该棱锥的体积最大时,它的高为________.8.(2019·河南八市重点高中联盟测评改编)已知一个高为1的三棱锥,各侧棱长都相等,底面是边长为2的等边三角形,则三棱锥的表面积为________,若三棱锥内有一个体积为V 的球,则V的最大值为________.。
三视图

三视图的形成
三视图的绘制与识读
本节课用课件形象地展示立体图,既有利于学生 理解,同时也不至于让学生感到空洞、乏味,弥补了 单纯的实物演示和单纯的静态幻灯手段的缺陷。
看一看
?
这是两幅意大利比萨斜塔的照片, 你知道为什么第二幅照片中的斜塔 不斜呢?
苏 轼
只 缘 身 在 此 山 中 。
不 识 庐 山 真 面 目 ,
三视图欣赏
小结:
正投影法: ——投影光线与投影平面垂直时,在投影平 面上得到物体视图的方法。 三视图: • 画物体的三视图时,要符合如下原则: 位置:主视图 左视图 俯视图 大小:长对正,高平齐,宽相等。
练习1 以下视图中最适合作主视图的是(
A. B. C. D.
)。
三视图中的主视图要能准确反映 物体的主要形体特征。
1.主视图和俯视图都反映了物体的长度, 而且长对正; 2.主视图和左视图都反映了物体的高度, 而且高平齐;
3.俯视图和左视图都反映了物体的宽度, 而且宽相等。
这是以后画图和读图的重要依据。
球的三视图
主视图 左视图
俯视图
.
圆锥体 圆柱体
棱柱的投影
分析:正六棱柱由顶面、底面和六个侧棱面组成。正六棱
V
正 面 投 影 面
三视图的形成Z 高
主视图从前向后看
向后翻90度
W
左 视 图
从 左 向 右 看
X 长
o
侧 面 投 影 面
水平投影面
H
俯视图从上往下看
向下翻90度
Y 宽
V
主视图
Z
左视图
W
X
o
Y
H
俯视图
Y
三视图之间的投影关系
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章复杂立体三视图的识读
3-1 对照立体图,补画视图上所缺的图线。
1 2
3 4
班级姓名学号审阅16 第三章复杂立体三视图的识读
3-2 对照立体图补画第三视图。
1 2
3 4
班级姓名学号审阅17 第三章复杂立体三视图的识读
3-3补画视图中缺漏的图线。
1 2
3 4
班级姓名学号审阅18
第三章复杂立体三视图的识读
3-3补画视图中缺漏的图线。
5 6
7 8
班级姓名学号审阅19 第三章复杂立体三视图的识读
3-4 根据两视图,画出其第三视图。
1 2
3 4
班级姓名学号审阅20 第三章复杂立体三视图的识读
3-4 根据两视图,画出其第三视图。
5 6
7 8
班级姓名学号审阅21 第三章复杂立体三视图的识读
3-4 根据两视图,画出其第三视图。
9 10
11 12
班级姓名学号审阅22 第三章复杂立体三视图的识读
3-4 根据两视图,画出其第三视图。
13 14
班级姓名学号审阅23 第三章复杂立体三视图的识读
3-5由立体图画立体的三视图(尺寸自定,取整数)。
1 2
班级姓名学号审阅24
第三章复杂立体三视图的识读
3-6由立体图画立体的三视图(比例自定,取整数)。
班级姓名学号审阅25 第三章复杂立体三视图的识读
3-7线面分析
1 2 3
(1)A面是__正平__面;
(2)C面是__侧平__面;
(3)B面在D面之__前____。
(1)A面是___正垂_____面;
(2)MN是__一般位置______线;
(3)D面在C面之____之前_______。
(1)P面是__正垂______面;
(2)C面___正平_____面;
(3)A面在B面之___下________。
4
(1)A面是___水平_____面;(2)B面是___正平_____面;(3)M面在N面之__前___。
5
(1)A面在B面之__前_____。
(2)B面在C面之__后___
6
(1)A面是_侧平_______面;
(2)B面__正垂______面;
(3)C面在D面之__上_________
班级姓名学号审阅26
第三章复杂立体三视图的识读
3-8由已知两个相同的视图构思出2个不同的立体,补画所缺的视图。
1.已知两个相同的主视图。
2.已知两个相同的俯视图。
班级姓名学号审阅27 第三章复杂立体三视图的识读
3-9由已知主视图和俯视图分别构思出3个不同的立体,补画所缺的视图。
1
2
班级姓名学号审阅28。
