郑州大学材料力学试题及答案
郑州大学材料力学习题集_【有答案】
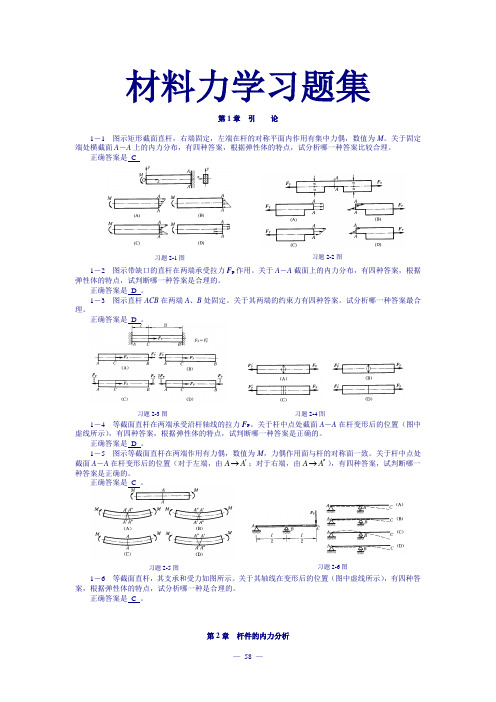
习题2-1图习题2-2图习题2-3图习题2-4图习题2-5图习题2-6图材料力学习题集第1章引论1-1 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M。
关于固定端处横截面A-A上的内力分布,有四种答案,根据弹性体的特点,试分析哪一种答案比较合理。
正确答案是 C1-2 图示带缺口的直杆在两端承受拉力F P作用。
关于A-A截面上的内力分布,有四种答案,根据弹性体的特点,试判断哪一种答案是合理的。
正确答案是D 。
1-3 图示直杆ACB在两端A、B处固定。
关于其两端的约束力有四种答案。
试分析哪一种答案最合理。
正确答案是D 。
1-4 等截面直杆在两端承受沿杆轴线的拉力F P。
关于杆中点处截面A-A在杆变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试判断哪一种答案是正确的。
正确答案是D 。
1-5 图示等截面直杆在两端作用有力偶,数值为M,力偶作用面与杆的对称面一致。
关于杆中点处截面A-A在杆变形后的位置(对于左端,由AA'→;对于右端,由AA''→),有四种答案,试判断哪一种答案是正确的。
正确答案是C 。
1-6 等截面直杆,其支承和受力如图所示。
关于其轴线在变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试分析哪一种是合理的。
正确答案是C 。
第2章杆件的内力分析习题2-1图习题2-2图习题2-3图习题2-4图A BABC)(ql 2lM QF QF 454141(a-1) (b-1)AD EC MABCB 2M2M 34122-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A d Q F d M(B )(d x q x -=,Q d F x -=; (C )(d d Q x q x F -=,Q d d F x M=; (D )(d d Q x q x F =,Q d d F xM-=。
郑州大学远程教育学院《材料力学》第01章在线测试

A B
C D 、变形固体受力后
A B
C D 、由于什么假设,可以将微元体的研究结果用于整个构件。
A B
C D 、由于什么假设,可以只研究材料某一个方向的力学性质。
A B
C D 、长度、横截面和轴力相同的钢拉杆和铝拉杆的关系是两者的
A B
C D
E、竹材
2、设计构件时,要使构件满足
A、强度要求
B、刚度要求
C、稳定性要求
D、领导要求
E、经济要求
3、下列哪种情况属于基本变形?
A、在自重作用下的砖柱
B、悬挂着重物的绳索
C、自重作用下的悬臂梁
D、风中的烟囱
E、用钳截钢筋
4、下列哪些变形属于基本变形?
A、轴向拉伸
B、轴向压缩
C、扭转
D、偏心压缩
E、剪切
5、杆件的几何特征是
A、长度远远大于截面的宽度
B、长度远远大于截面的高度
C、杆件三个方向的尺寸几乎一样大
D、后度远远小于表面尺寸
正确错误、任何物体在外力作用下都会产生变形。
正确错误、构件的强度是指构件抵抗变形的能力。
正确错误、杆件的轴线使其横截面形心的连线。
正确错误、自然界中并不存在理想弹性题。
正确错误。
郑州大学远程教育学院《材料力学》第04章在线测试

A B
C D
、某一实心圆轴,若将其横截面面积增大一倍,其他条件不变,则最大许用扭矩为原来的
A B
C D
、某一实心圆轴,若将其横截面面积减小到原来的一半,其他条件不变,则最大扭转角为原来的
A B
C D
、材料的弹性模量
A B
C D
、下列哪个量与材料力学性质无关
A B
C D
E、弹性非弹性范围内
2、在静荷载作用下,脆性材料的许用剪应力是许用拉应力的
A、0.5倍
B、0.6倍
C、0.8倍
D、0.9倍
E、1倍
3、在相互垂直的两个面上的剪应力
A、必成对出现
B、数值相等
C、方向均垂直两平面的交线
D、方向均平行两平面的交线
E、方向同时指向或同时背离两平面的交线
4、下列关于剪切弹性模量G的叙述正确的是
A、表示材料剪切时抵抗变形的能力
B、其值等于应力应变曲线上直线段的斜率
C、其值由试验测定
D、单位是MPa
E、量纲同应力的量纲
5、矩形截面杆自由扭转时,横截面上的剪应力分布特点是
A、四个角点处剪应力最大
B、四个角点处剪应力为零
C、长边中点剪应力最大
D、短边中点剪应力最大
正确错误、当剪应力超过剪切比例极限时,剪应力胡克定律不再成立。
正确错误、如果单元体的右侧面上有与棱斜交的剪应力,则前侧面必有剪应力。
正确错误、在强度条件相同的条件下,空心轴和实心轴用料相同。
正确错误、受扭圆轴(实心或空心)横截面上的最小剪应力一定为零。
正确错误。
材料力学考试题及答案

材料力学考试题及答案一、选择题(每题2分,共10分)1. 材料力学中,下列哪项不是应力的分类?A. 正应力B. 剪应力C. 拉应力D. 扭应力答案:C2. 材料力学中,下列哪项不是材料的基本力学性质?A. 弹性B. 塑性C. 韧性D. 硬度答案:D3. 在拉伸试验中,下列哪项是正确的?A. 弹性模量是应力与应变的比值B. 屈服强度是材料开始发生塑性变形的应力C. 抗拉强度是材料在拉伸过程中的最大应力D. 所有选项都是正确的答案:D4. 根据胡克定律,下列哪项描述是错误的?A. 弹性范围内,应力与应变成正比B. 弹性模量是比例极限C. 应力是单位面积上的力D. 应变是单位长度的变形量答案:B5. 材料力学中,下列哪项不是材料的失效形式?A. 屈服B. 断裂C. 疲劳D. 腐蚀答案:D二、填空题(每空1分,共10分)1. 材料在受到拉伸力作用时,其内部产生的应力称为________。
答案:正应力2. 材料在受到剪切力作用时,其内部产生的应力称为________。
答案:剪应力3. 材料力学中,材料在外力作用下发生形变,当外力去除后,材料能够恢复原状的性质称为________。
答案:弹性4. 材料力学中,材料在外力作用下发生形变,当外力去除后,材料不能恢复原状的性质称为________。
答案:塑性5. 材料力学中,材料在外力作用下发生形变,当外力去除后,材料部分恢复原状的性质称为________。
答案:韧性三、简答题(每题5分,共20分)1. 简述材料力学中应力和应变的关系。
答案:材料力学中,应力和应变的关系可以通过胡克定律来描述,即在弹性范围内,应力与应变成正比,比例系数即为弹性模量。
2. 描述材料力学中材料的屈服现象。
答案:材料力学中,屈服现象指的是材料在受到外力作用时,从弹性变形过渡到塑性变形的临界点,此时材料的应力不再随着应变的增加而增加。
3. 解释材料力学中的疲劳破坏。
答案:材料力学中的疲劳破坏是指材料在循环加载下,即使应力水平低于材料的静态强度极限,也会在经过一定循环次数后发生破坏的现象。
郑州大学材料力学习题答案

附录III 习题答案21- 0115,22.5R N α==指向左下方,与水平线的夹角22- 120.5320.684F KN F KN ==,23- min 11.5P KN = 24- 51,22A D R P R P == 25- 28.36,28.80A B A C T K N T K N == 26- 0.949,0.316A C R P N P ==27- (1)8.66,5,8.66, 5.18x y X N Y N P N P N ====''''(2)8.66,7.07,7.32, 5.18x y X N Y N P N P N ====28- 1221(1)[1()]22dP W h=+,(2) 1.69h m =29- 7.32,27.32A B A C S K N S K N ==210- 12s i n,c o s 2A QR W Wαα-== 211- 1.63P Q = 212- 29.7,18.4,17.5,6A B C D N N N N N N N N ==== 213- 567N N = 214- 038.9,25.4,24.1A B N N N N α=== 2-15 0000()()0,()(),()(),()()sin a m p b m p pl c m p pb d m p pl α==== 2-16 2.97,9.85B c m N m m N m ==- 2-17 () 1.77,() 1.06A B m F N m m F N m ==- 2-18 2A B R R KN ==2-19 40,200A B m KN m N N KN =-== 2-20 25,3S N m N m ==3-1 () 1.414,0.707,()0.5,0.707A A B A A B a X P Y R P b X Y P R P ====== ()0.8,() 3.8, 4.2A B A B c R R N d R KN R KN -==== 3-2 211()0,2,2,(),0,26A A AB B B a X Y P m Pa b X P qh Y m qh ph ====-==- 3-3 4:3Pa b Q=3-4 650,500,650A B T N N N N N === 3-5 3N F =3-6 141.5T KN =3-7 sin ,(1cos ),(1cos )A A A X G Y G m Gb ααα=-=+=+ 3-8 83P KN =3-9 ()1,6,4,()3,0, 5.5A A B A A A a X KN Y KN R KN b X KN Y m KN m =-=====- 3-10 ()35,342.8,342.8,()0,270A A B A B B a X KN Y KN R KN b X Y R KN =-===== 3-11 173.2,1000,1346.4A B C N N N N N N ==-= 3-12 0,36.872(1)WT tg θθ==-3-13 sin 4cos()Q F αβα=-3-14 222cos sin (1)sin a m Pa b a θθθ=+-3-15 0.5Pl QbT ctg aα+= 3-1612sin sin P P βα=3-17 1500,500F F X N Y N =-= 3-18 140P N = 3-19 12X cm ≥ 3-20 22()W Qtg f W Q α+≥+3-210max 28.07θ=3-22 cm b 75.0≤ 3-23 5.7kN 3-24 Rf 2δ≥3-25 500kN 3-26Q f f P Q f f ααααααααsin cos cos sin sin cos cos sin -+≤≤+-3-27 kN s s 2041-==kN s 4.422= kN s 403= kN s s 14.1495==kN s 206= kN s s 1087-==3-28 kN s 301-= kN s 75.182-= kN s 53-= 3-29 P s 941-= 02=s 41- 2.4392,0.7071,0.12x y z m F b m F b m F b=-==-42- 1230.2113,0.3660,0.4227T G T G T G === 43- 1221000,364.0,182.0;148.0,r r A P N P N P N X N ==== 2.058;0.7517,9.589A B B Z KN X KN Z KN ===44- 0.150;0, 1.250,1;0, 3.A A AB BP K N X Y K N X K N ZY K N ===-===- 45- 1() 1.414S P P P===23拉,S (压),S (压), 1.414 1.414P P ===456S (拉),S (拉),S (压)46- 1000;0,750,50A A A T N X Y N Z N ===-=-433.0,500B B X N Z N ==4-7 cm y x a c c 1.15,0)(== ;cm y x b c c 50,0)(==;cm y cm x c c c 1.5,10)(==;cm y cm x d c c 29,3)(==4-8 cm x a c 6.27)(=;cm x b c 4.0)(-=;cm x c c 1.19)(-=14-1 2(1)340(2, 1.5);5 2.5x y x y s t t -=≤≤=-半直线:2(2)1(04,03);5sin 43x yx y s t +=≤≤≤≤=直线段: 222(3)25;25x y s t +==圆: 2222(4)(0);1ln(1)y y s t t t ≥=++++1半抛物线:x=414-2 (1)9;(2)2,14;s m t s x m ===- 2(3)23;(4)15/,18/l m v m s a m s === 14-3 22()sin ,()cos ;1()()c cc c x y x l R t y l R t l R l R ωω=-=++=-+椭圆14-4 4)(,1)(22+=+=t u a t u v ωωω14-5 2254cos 2,55sin 2;()()145x y x t y t -==++= 14-6 322100.0167;9.8/,0.2/,240/n s t t v m s a m s a m s τ=-===14-7 Rbv n b v t b R bt v a π4,,)(2002220==+-= 14-824,0,2ωωτb a a b v n ===14-9 m s m a s m a s m v x y y n 795.2,/789.1,/89.0,/24.2,042222=====--ρτ 14-10 150;100转转14-11 500/min;1min ,500/min;n r t n r ===时 252min 100/min;/18t n r rad s επ===时, 14-1222.42/;52rad s t s επ=-=14-14 22220/;20/;101400/t r a d s r a d s a t m s ωε===+ 14-15 2/7.443,/42.9s cm a s cm v M M ==14-16 30n R v M π= 90022n R a M π=14-17 s m v /4.0max = m h 2.7=14-18 b t v tg 01-=θ tv b bv 2020+=ω 15-1 05.57,/6.6夹角与OA s cm v a = 15-2 2;2sin R R ωωα 15-3 ωa v a 332=15-4 80/;40/cm s cm s 15-51.25/op rad s ω=15-6 u r v -=ω1;22224)(ωωr u r v ++=.15-7 ωR v =15-8 0577.0v v =;Rv a 2054.1=.15-9 2/6.74s cm a A = 15-10 s cm v M /73.1= 15-1113/; 5.2/AB o B rad s rad s ωω==15-12 θθωcos sin 2R v =15-13s cm v s rad D AB /35.25,/07.1==ω15-14 s cm v F /19.46=,s rad EF /33.1=ω 15-15101222O B ωω+=+15-1610.2/O A rad s ω=15-17 ωr v c 5.1= 20123ωr a c =15-18 24232221/83.5;/32.6;/16.3;/2s m a s m a s m a s m a ==== 15-192/2.2;/62.3s rad s rad B B ==εω15-20 222)(;2c c c D c D a rv a a v v ++==;r v a v c P P 2;0==15-21 22/88.2;/4s cm a s cm v A D ==16-1 23/a m s =16-2 1235.9; 4.7; 3.5T KN T KN T KN === 16-3 5.98T KN =16-4 (1)98;(2)100;(3)108;T KN T KN T KN === 16-5 max min 3.14; 2.74N KN N KN == 16-6 (sin cos /)T mg f r g ααε=++16-7 21020cos ;(1)T mg T mg ϕϕ==+16-8 22();();22AM BM ml ml S a g S a g a aωω=+=- 16-9 2/(sin cos )T L g f αα=- 16-10 0.28S m =16-11 10.2;102T s S m == 16-12 fgr v =max16-13 gKv v v 0011/+= 16-16 sin /cos();cos /cos()a g T mg ααββαβ=+=+ 16-17 17430;12000E D N N N N == 16-18 cos af tg g αα≥+16-19 2max (cos );/N m g e t g e ωωω=-=16-20 max 0.35a fg g ==16-21 N T A 1.148=,N T B 8.59=16-22 P T a o 3cos 2α=;αsin T P N -=,αcos 3TF =. 16-23 2)cos (RgP J r R TR a o o +-=α16-24 αsin 74g a =;αsin 71Mg S AB =(压);αcos Mg N N D C ==; αsin 74Mg F C =,αsin 72Mg F D =.16-25 )1cos 3(cos 62+=ϕϕεl g ; 1cos 32+=ϕm g N . 16-26 g a c 32=;mg T 31= 16-27 35.8d mm =16-28 ()74.05,()0.622d d MPa MPa σσ==拉弯 16-2922max 33213[1/(3)],(2)(1)33d l a l a g d gωωωωσπ=+=+dmax (1)M 17-1 Ns S s m v AB AO 98,/4.29== 17-2 0,/,/0g a P g Pv ω17-3 v v 2'=,rm v T 28=17-4 30F N =17-5 s m v s m v m l /742,/73,710'===箱船 17-6()()ma b m M-+向左 17-7 7810;325X y R N R N =-= 17-8 )cos 1(2αγ-=Av F 17-9 0.571/;200m s N17-102();Q Q P ge g Qeωω+≥17-11 (2)2;l P Q P W Q πω+++简谐运动;振幅:周期:17-12 123312123123123(11)(2)cos ;sin 2()2()2()c c P P P Pl P P x t y t P P P P P P P P P ωω+++=+=++++++ 17-13 s m v /8.9=17-14 24.9/;490a m s N N ==17-151212LJ i J ε=+ 17—16232222112211)(ρεm r m r m gr m r m ++-=17—17 22sin mR mgR M a α-=;)2sin cos 6(81θθmgR M R F ox+= 17—18 θθθcos sin cos 33g m a rRm F ox +=a m a rR m g m g m m m F oy 2322321sin cos )(-+-++=θθ17—19 Q lb l T 2223+= 17—20 9=ρcm17—21)2)3(3sin(πδϕ++=t Q P gk lkgQ P T )3(32+=π18-1 2744;1960J J18-2 1223312.06; 2.06;0W J W J W =-== 18-3 452KJ18-4 )1(2αfctg gh v -= 18-52261ωml ; 2241ωmr ; 2243ωmr ; 243c mv . 18-6 s m v B /26.6= 18-72(1cos )/mgL k δα=-18-8 1.56P KN =18-9 102F KN =18-10 541;605m kg R N ==18-11 )(/)sin (21m m r mgr M s v +-=α 18-12 5.8P N = 18-13 0.2f =18-1422212)(238e r m r m egm -+=ω 18-15 gh v 2=18-16ϕωQP gMr R 2932++=; )29()(62Q P r R gM ++=ε 18-17 g QP Qa 493+=18-18 s rad /67.3=ω18-19 1.06;76N KW M N m ==18-20 3N KW =18-21 188;42.5;6.3N m N m KW18-22 (1)0.0708,(2)15.43,(3) 3.689j d d MPa MPa MPa σσσ=== 18-23max 43.14d MPa σ=18-24 2.994d K = 18-2518-26 128d P KN =。
郑大材料力学习题集
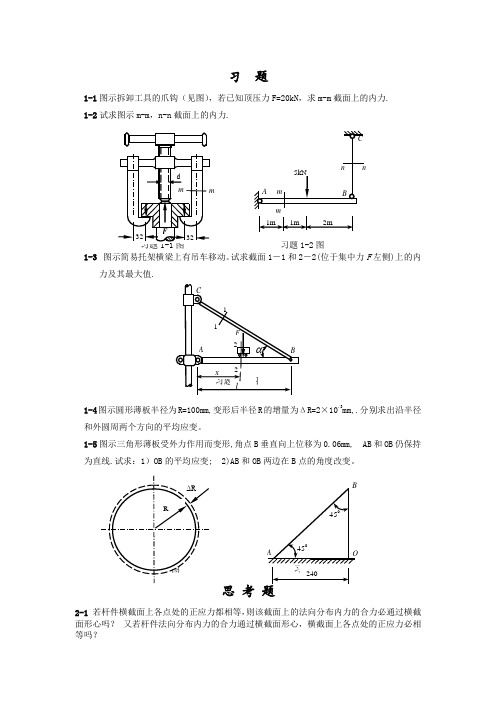
习 题1-1图示拆卸工具的爪钩(见图),若已知顶压力F=20kN ,求m-m 截面上的内力. 1-2试求图示m-m ,n-n 截面上的内力.习题1-2图 1-3 图示简易托架横梁上有吊车移动。
试求截面1-1和2-2(位于集中力F 左侧)上的内力及其最大值.1-4图示圆形薄板半径为R=100mm,变形后半径R 的增量为ΔR=2×10.3mm,.分别求出沿半径和外圆周两个方向的平均应变。
1-5图示三角形薄板受外力作用而变形,角点B 垂直向上位移为0.06mm, AB 和OB 仍保持为直线.试求:1)OB 的平均应变; 2)AB 和OB 两边在B 点的角度改变。
考 2-1 若杆件横截面上各点处的正应力都相等,则该截面上的法向分布内力的合力必通过横截面形心吗? 又若杆件法向分布内力的合力通过横截面形心,横截面上各点处的正应力必相等吗?、B 两点间距离为a,材料的横向变形系数ν。
试证明该两点距离改变量为aAB νεδ-=。
2-3 试说明公式A F N =σ, EA lF l N=∆的应用条件,并说明E 的物理意义和量纲。
2-4 三根杆件尺寸相同但材料不同,材料的εσ-曲线如图所示,试问哪一种(1)强度高?(2)刚度大?(1)塑性好? 2-5 杆件弹性模量E =210GPa ,比例极限σp =200MPa; 在轴向拉力作用下,纵向线应变为ε=8×10—4,求此时横截面上的正应力。
若拉力加大使杆件的纵向线应变增加到ε=5×10—3,问此时横截面上的正应力能否再由胡克定律确定? 2-6 若已测得受力物体内x 和y 两方向均有线应变,问在x 和y 两方向是否都必有正应力? 若测得x 和y 两方向均无线应变,则在x 和y 两方向是否都必无正应力? 2-7 低碳钢试样的拉伸图中,拉断时的应力为何比强度极限低?2-8 两根杆件,同样材料制成但横截面积不同,它们的强度极限相同吗? 2-9 脆性材料制成的轴向拉伸矩形截面杆,若有方向平行于轴线的裂纹,问杆的强度是否因此降低?若裂纹方向垂直于轴线,杆的强度是否因此降低?2-10 在图示杆系中,钢杆1和铜杆2的许用应力分别为[]1σ和[]2σ,横截面面积分别为A 1 和A 2 ;且[]1σ>[]2σ,而A 2 >A 1; 能断定铜杆2先破坏吗?若根据节点C 的平衡条件ΣY=0求结构的许可荷载,则02201130cos ][45cos ][][A A F σσ+=,这种结论对吗?思考题2-4图达到材料的许用应力值?习题Array 2-2 图示托架的AC横梁上有吊车移动。
郑州大学材料力学试题及答案

《郑州大学材料力学试题及答案》一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内。
每小题2分,共20分)1.轴的扭转剪应力公式=适用于如下截面轴( ) A.矩形截面轴 B.椭圆截面轴 C.圆形截面轴 D.任意形状截面轴2.用同材料制成的实心圆轴和空心圆轴,若长度和横截面面积均相同,则抗扭刚度较大的是哪个?( ) A.实心圆轴 B.空心圆轴 C.两者一样 D.无法判断3.矩形截面梁当横截面的高度增加一倍、宽度减小一半时,从正应力强度考虑,该梁的承载能力的变化为( ) A.不变 B.增大一倍 C.减小一半 D.增大三倍4.图示悬臂梁自由端2、B的挠度为( )A. B. C. D. 5.图示微元体的最大剪应力max为多大?( )A. max=100MPaB. max=0C. max=50MPaD. max=200MPa6.用第三强度理论校核图示圆轴的强度时,所采用的强度条件为( )A. B.C. D. 7.图示四根压杆的材料、截面均相同,它们在纸面内失稳的先后次序为( )A.(a),(b),(c),(d)B. (d),(a),(b),(c)C. (c),(d),(a),(b)D. (b),(c),(d),(a)8.图示杆件的拉压刚度为EA,在图示外力作用下其变形能U的下列表达式哪个是正确的?( )A. U=B. U=C. U=D.3、U=9图示两梁抗弯刚度相同,弹簧的刚度系数也相同,则两梁中最大动应力的关系为( )A.(d) a=(d) bB. (d) a (d) bC. (d) a (d) bD. 与h大小有关二、填空题(每空1分,共20分)1.在材料力学中,为了简化对问题的研究,特对变形固体作出如下三个假设:_,_,_。
2.图示材料和长度相同而横截面面积不同的两杆,设材料的重度为,则在杆件自重的作用下,两杆在x 截面处的应力分别为(1)=_,(2)=_。
大学材料力学考试题及答案

大学材料力学考试题及答案一、选择题(每题2分,共10分)1. 材料力学中,下列哪一项不是基本假设?A. 连续性假设B. 均匀性假设C. 各向同性假设D. 非线性假设答案:D2. 在拉伸试验中,弹性模量E是指:A. 屈服强度B. 抗拉强度C. 应力与应变比值D. 断后伸长率答案:C3. 根据第四强度理论,材料的脆性断裂是由于:A. 最大正应力达到临界值B. 最大切应力达到临界值C. 最大拉应力达到临界值D. 最大剪切能密度达到临界值答案:D4. 在扭转试验中,圆轴的扭转角θ与扭矩T和极惯性矩J之间的关系是:A. θ ∝ T/JB. θ ∝ TJC. θ ∝ J/TD. θ ∝ 1/(TJ)答案:A5. 下列哪一项不是影响材料疲劳寿命的因素?A. 应力幅B. 循环加载频率C. 材料的微观结构D. 环境温度答案:D二、填空题(每题2分,共10分)6. 材料在拉伸过程中,当应力达到_________时,称为屈服点。
答案:材料的屈服强度7. 根据材料力学的_________假设,材料内部各点的应力状态是相同的。
答案:均匀性8. 在纯弯曲情况下,梁的横截面上的正应力分布规律是_________。
答案:线性分布9. 剪切模量G是指材料在剪切作用下,剪切应力与剪切应变的比值,其单位是_________。
答案:帕斯卡(Pa)10. 复合应力状态下,最大剪应力τ_max与主应力σ1和σ2之间的关系是τ_max = √_________。
答案:(σ1 - σ2)^2 / 2三、简答题(每题10分,共20分)11. 简述材料力学中的强度和刚度的概念,并说明它们在工程设计中的重要性。
答案:强度是指材料在外力作用下抵抗破坏的能力,通常与材料的屈服强度或抗拉强度相关。
刚度是指材料在受力后抵抗变形的能力,与弹性模量有关。
在工程设计中,强度和刚度是确保结构安全和功能的关键参数,它们决定了结构在受力后的性能表现和耐久性。
12. 描述纯弯曲梁的正应力分布规律,并说明如何利用这一规律进行梁的设计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
郑州大学材料力学试题及
答案
This manuscript was revised on November 28, 2020
欲索取更多考研资料,请上北京天问教育网站官网!
一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填
在题干的括号内。
每小题2分,共20分)
1.轴的扭转剪应力公式τρ=T I P ρ适用于如下截面轴( ) A.矩形截面轴 B.椭圆截面轴 C.
圆形截面轴 D.任意形状截面轴 2.用同材料制成的实心圆轴和空心圆轴,若长度和横截面面积均相同,则抗扭刚度较大的是哪个( )
A.实心圆轴
B.空心圆轴
C.两者一样
D.无法判断
3.矩形截面梁当横截面的高度增加一倍、宽度减小一半时,从正应力强度考虑,该梁的承载能力的变化为( )
A.不变
B.增大一倍
C.减小一半
D.增大三倍
4.图示悬臂梁自由端B 的挠度为( )
A.ma a EI ()l -2
B. ma a EI 32()l -
C.ma EI
D. ma a EI 22()l - 5.图示微元体的最大剪应力τmax 为多大( )
A. τmax =100MPa
B. τmax =0
C. τmax =50MPa
D. τmax =200MPa
6.用第三强度理论校核图示圆轴的强度时,所采用的
强度条件为( )
A. P A M W T W Z P
++()()242≤[σ] B.P A M W T W Z P
++≤[σ] C. ()()P A M W T W Z P
++22≤[σ] D. (
)()P A M W T W Z P ++242≤[σ]
7.图示四根压杆的材料、截面均相同,它
们在纸面内失稳的先后次序为( )
A. (a),(b),(c),(d)
B. (d),(a),(b),(c)
C. (c),(d),(a),(b)
D. (b),(c),(d),(a)
8.图示杆件的拉压刚度为EA,在图示外力作用下其变形能U的下列表达式哪个是正确的( )
A. U=P a EA
2 2
B. U=P
EA
P b
EA 22 22
l
+
C. U=P
EA
P b
EA 22 22
l
-
D. U=P
EA
P b
EA 22 22 a
+
9图示两梁抗弯刚度相同,弹簧的刚度系
数也相同,则两梁中最大动应力的关系
为( )
A. (σd) a =(σd) b
B. (σd) a >(σd) b
C. (σd) a <(σd) b
D. 与h大小有关
二、填空题(每空1分,共20分)
1.在材料力学中,为了简化对问题的研究,特对变形固体作出如下三个假设:_______,_______,_______。
2.图示材料和长度相同而横截面面积不同的两杆,设材料的重度为γ,则在杆件自重的作用下,两杆在x截面处的应力分别为σ(1)=_______,σ(2)=_______。
3.图示销钉受轴向拉力P作用,尺寸如图,则销钉内的剪应力τ=_______,支承面的挤压应力σbs=_______。
4.图示为一受扭圆轴的横截面。
已知横截面上的最大剪应力τmax=40MPa,则横截面上A点
的剪应力τA=_______。
5.阶梯形轴的尺寸及受力如图所示,其AB段的最大剪应力τmax1与BC段的最大剪应力τmax2
之比τ
τ
max
max
1
2
=_______。
6.图示正方形截面简支梁,若载荷不变而将截面边长增加一倍,则其最大弯曲正应力为原来的_______倍,最大弯曲剪应力为原来的_______倍。
7.矩形截面悬臂梁的尺寸及受载如图所示,
(1)若梁长l增大至2l,则梁的最大挠度增大至原来的______倍;
(2)若梁截面宽度由b减为b
2
,则梁的最大挠度增大至原来的______倍;
(3)若梁截面高度由h减为h
2
,则梁的最大挠度增大至原来的______倍。
8.图示为某构件内危险点的应力状态,若用第四强度理论校核其强度,则相当应力σeq4=_______。
9.将圆截面压杆改为面积相等的圆环截面压杆,其它条件不变,则其柔度将_______,临界
载荷将_______。
三、分析题(每小题5分,共20分)
1.在图示低碳钢和铸铁拉伸试验的“应力—应变”图上,注明材料的强度指标(名称和代表
符号),并由图判断:_______是脆性材料,_______是塑性材料。
2.画出图示阶梯形圆轴的扭矩图,用图中m和d写出圆轴最大剪应力的计算式,并指出其
作用点位置。
3.图示矩形截面悬臂梁,若已知危险截面上E点的应力为σE=-40MPa,试分析该截面上四个角点A、B、C、D的应力(不必写出分析过程,只须写出分析结果,即四个角点的应力
值)。
四、计算题(每小题10分,共40分)
1.钢杆1,2吊一刚性横梁AB。
已知钢杆的弹性模量E=200GPa,两杆的横截面面积均为A=100mm2,载荷P=20KN,试求两钢杆的应力、伸长量及P力作用点F的位移δF。
2.外伸木梁各部分的尺寸和所受载荷如图所示。
设梁材料的许用应力[σ]=10MPa。
试:(1)作梁的剪力图和弯矩图;(2)校核梁的正应力强度。
3.弓形夹紧器如图,若夹紧力P=2KN,距离e=120mm,立柱为矩形截面,其h=25mm,[σ]=160MPa,试设计截面尺寸b。
4.图示曲柄轴直径d=50mm,受集中力P=1KN作用,试:(1)画出危险点A的应力状态并计算其应力值;(2)若材料的许用应力[σ]=70MPa,试按第四强度理论校核其强度。
浙江省2001年10月高等教育自学考试
材料力学试题参考答案
一、单项选择题(每小题2分,共20分)
二、填空题(每空1分,共20分)
1. 连续性假设 均匀性假设 各向同性假设
2. γ (l -x) γ (l -x)
3. P d h π⋅ 422P D d π()
- 4.
5. 3/8
6. 1/8 1/4
7. 8 2 8
8.στ223+
9.降低 增大
三、分析题(每小题5分,共20分)
1.低碳钢强度指标:强度极限σb ,屈服极限σs 铸铁强度指标:拉伸强度极限σb +
铸铁是脆性材料,低碳钢是塑性材料
2.作扭矩图
计算扭转剪应力:τAB =323m d π τBC =3793.m d
π τmax =τBC ,作用于BC 段表面
3.σA =-60MPa,σB =20MPa,σC =50MPa,σD =-20MPa
四、计算题(每小题10分,共40分)
1.两钢杆轴力:N 1=8KN(拉),N 2=12KN(拉) 杆1:σ1=80MPa , △l 1=
杆2:σ2=120MPa , △l 2=
P 力作用点位移:δF =235
12∆∆l l += 2.支反力:R A =(↑),R B =(↑)
剪力图:
弯矩图:
强度校核:σmax =<[σ] =p,M=pe
σ=N A M W P bh pe bh +=+62
≤[σ] b ≥[][]p h pe h σσ+62= 4.应力状态
应力值:σ=,τ=
强度校核:σeq4=στ223+=。
