2范数和条件数病态方程组
矩阵的范数和条件数

① A0,& A ,0 A0
② A A,R
③ A B A B, A ,B R n n ④ A B A B, A ,B R n n
⑤ Ax Ax, xRn
上海理工大学 理学院
University of Shanghai for Science and Technology
2 2 x x 1 1 6 .0 0 0 0 6 1 x x 2 2 8 8 .0 0 0 0 1 与 2 2 x x 1 1 5 .9 9 9 9 6 9 x x 2 2 8 8 .0 0 0 0 2
其解分别为:x
x1 x2
College of SciA的实值函数N(A)=‖A‖,满足条件:
(1)非负性: ‖A‖0 ,且‖A‖=0当且仅当 A=0; (2)齐次性: ‖A‖=| |‖A‖, R; (3)三角不等式:‖A+B‖‖A‖+‖B‖; (4)柯西-施瓦茨不等式:‖AB‖‖A‖‖B‖. 则称‖A‖为矩阵A的范数.
x
b
上海理工大学 理学院
University of Shanghai for Science and Technology
College of Science
注:一般判断矩阵是否病态,并不计算A1,而由经验得出。
行列式很大或很小(如某些行、列近似相关); 元素间相差大数量级,且无规则; 主元消去过程中出现小主元; 特征值相差大数量级。
A1
很小
A
A
A
A
条件数表示了对误差的放大率
上海理工大学 理学院
University of Shanghai for Science and Technology
研究生数值分析(9)矩阵的条件数与病态线性方程组

X A 1 b 即 X A b 于是有
③
另一方面,由①得
b A X
且 X 0
故
A 1 X b
④
由③与④有
X
X
A
1
A
b
b
⑤
表明解的相对误差不超过右端向量b
的相对误差的 A1 A 倍。
(2)仅有小扰动δ A(设 A+ δ A 仍可逆) ~ 的解为 X X X 设方程组 ( A A) X b 即
1 1 A 1 1.0001
10001 10000 A 10000 10000
1
及其逆矩阵
在行模意义下的条件数
Cond ( A) A1
A 20001 2.0001 40004
因此称方程组 x1 x2 2 x1 1.0001x2 2 为病态方程组。
x1 0.9999 x2 1.9999
②
的解为
x1 1; x2 1
它们的解变化很大,这样的方程组称为“病态”
方程组。 下面,我们给出方程组“病态”,“良态”
概念及其衡量标准,并介绍判断近似解可靠性方
法。
1 矩阵的条件数与线性方程组的性态 由于方程组AX=b系数矩阵A与右端向量b 的初始数据微小变化引起解的很大变化,这样
§3 矩阵的条件数与病态线性方程组
判断计算方法的好坏,可用算法是否稳定、 解的精确程度以及计算量、存储量的大小来衡量。 然而,同一方法用于不同问题,效果却可以相差 很远。 例如 方程组
x1 x2 2 x1 1.0001x2 2
x1 2; x2 0
①
解为
病态矩阵

病态矩阵
病态矩阵的最根本的特征:病态矩阵的条件数(||A||*||A^(-1)||定义为A 的条件数,||A||为A的范数,MATLAB中范数的求法c = cond(A,p),p为几范数,默认情况下为二范数)很大(可以用机器精度的一半来衡量,比如双精度浮点数的精度大约是10^(-16),那么条件数大于10^8就算比较坏了.),即最大特征值与最小特征值的比值很大。
病态矩阵对扰动特别敏感。
病态矩阵矩阵不能求逆。
例如,有一个变量是其他三个变量之和,这个变量也存在于模型中,这个矩阵就是病态矩阵。
解决方法:
1.利用正则化方法可以解决这一问题
最经典的正则化方法就是Tikhonov正则化,另外一种方法就是Total Variation
2.奇异值分解
将病态矩阵分解为A=SVD
3.模拟退火算法
/view/3a75ad82bceb19e8b8f6baad.html#opennewwindow
4./link?url=ripw0P7tMkcEl2x5zmkOJ-_iDFdfOLQ0Ox9ao cKY3sAJMFXEBQa__Yq6OVb3R41__nvgiWEQhA0bxXWzZzpQiFH7_IlNWlvqyrkKjLqvQ qC。
正规矩阵的算子二范数_概述及解释说明

正规矩阵的算子二范数概述及解释说明1. 引言1.1 概述在线性代数和矩阵理论中,正规矩阵是一类特殊的方阵,具有重要的性质和应用价值。
算子二范数是衡量线性变换操作对向量长度影响程度的指标。
本文将探讨正规矩阵的算子二范数及其计算方法,并解释二范数在正规矩阵中的作用。
1.2 文章结构本文分为五个主要部分。
引言部分进行整体概述,介绍文章内容和结构安排;第二部分将详细解释正规矩阵和算子范数的概念;第三部分将介绍计算算子二范数的三种方法:奇异值分解法、特征值分解法和迭代法估计法;第四部分将探讨算子二范数与正规矩阵性质之间的关系;最后,第五部分总结全文并展望未来可能涉及的问题和研究方向。
1.3 目的本文旨在提供一个全面而清晰的概述,以便读者了解正规矩阵的算子二范数及其相应性质。
通过本文可以更好地理解算子二范数对正规矩阵的描述和刻画,并了解到如何计算算子二范数。
同时,本文还将探讨算子二范数与正规矩阵性质之间的关系,帮助读者深入理解这一主题及其应用。
以上是“1. 引言”部分的内容,用于概述文章主要内容、介绍文章结构以及明确文章目的。
接下来的章节将更详细地解释和讨论相关概念和方法。
2. 正规矩阵的算子二范数2.1 正规矩阵概念解释正规矩阵是指满足以下条件的方阵:若A 是正规矩阵,则A 的共轭转置(A*) 与自身的乘积等于自身与其共轭转置的乘积,即A*A* = AA*。
这意味着正规矩阵的特征向量可以相互正交。
2.2 算子范数概念解释算子范数是一种衡量线性变换(或算子)大小的方法。
在本文中,我们关注算子二范数,也称为谱范数。
对于一个n x n 的方阵A,它的算子二范数可以定义为:||A||₂= max { ||Ax||₂: ||x||₂= 1 },其中||x||₂表示向量x 的二范数。
2.3 解释说明二范数在正规矩阵中的作用正规矩阵中的算子二范数有许多应用和重要性质。
首先,二范数可以用于衡量一个正规矩阵A 所导致的线性变换对向量长度的影响程度。
现代科学工程计算基础课后答案

现代科学工程计算基础课后答案《现代科学与工程计算基础》较为详细地介绍了科学与工程计算中常用的数值计算方法、基本概念及有关的理论和应用。
全书共分八章,主要内容有误差分析,函数的插值与逼近,数值积分与数值微分,线性代数方程组的直接解法与迭代解法,非线性方程及非线性方程组的数值解法,矩阵特征值和特征向量的数值解法,以及常微分方程初、边值问题的数值解法等。
使用对象为高等院校工科类研究生及理工科类非“信息与计算科学”专业本科生,也可供从事科学与工程计算的科技工作者参考。
《现代科学与工程计算基础》讲授由浅人深,通俗易懂,具备高等数学、线性代数知识者均可学习。
基本信息出版社: 四川大学出版社; 第1版 (2003年9月1日)平装: 378页语种:简体中文开本: 32ISBN: 7561426879条形码: 9787561426876商品尺寸: 20 x 13.8 x 1.6 cm商品重量: 399 g品牌: 四川大学出版社ASIN: B004XLDT8C《研究生系列教材:现代科学与工程计算基础》是我们在长期从事数值分析教学和研究工作的基础上,根据多年的教学经验和实际计算经验编写而成。
其目的是使大学生和研究生了解数值计算的重要性及其基本内容,熟悉基本算法并能在计算机上实现,掌握如何构造、评估、选取、甚至改进算法的数学理论依据,培养和提高读者独立解决数值计算问题的能力。
目录第一章绪论§1 研究对象§2 误差的来源及其基本概念2.1 误差的来源2.2 误差的基本概念2.3 和、差、积、商的误差§3 数值计算中几点注意事项习题第二章函数的插值与逼近§1 引言1.1 多项式插值1.2 最佳逼近1.3 曲线拟合§2 Lagrange插值2.1 线性插值与抛物插值2.2 n次Lagrange插值多项式2.3 插值余项§3 迭代插值§4 Newton插值4.1 Newton均差插值公式4.2 Newton差分插值公式§5 Hermite插值§6 分段多项式插值6.1 分段线性插值6.2 分段三次Hermite插值§7 样条插值7.1 三次样条插值函数的定义7.2 插值函数的构造7.3 三次样条插值的算法7.4 三次样条插值的收敛性§8 最小二乘曲线拟合8.1 问题的引入及最小二乘原理8.2 一般情形的最小二乘曲线拟合8.3 用关于点集的正交函数系作最小二乘拟合8.4 多变量的最小二乘拟合§9 连续函数的量佳平方逼近9.1 利用多项式作平方逼近9.2 利用正交函数组作平方逼近§10 富利叶变换及快速富利叶变换10.1 最佳平方三角逼近与离散富利叶变换10.2 快速富利叶变换习题第三章数值积分与数值微分§1 数值积分的基本概念1.1 数值求积的基本思想1.2 代数精度的概念1.3 插值型求积公式§2 等距节点求积公式2.1 Newton—CoteS公式2.2 复化求积法及其收敛性2.3 求积步长的自适应选取§3 Romberg 求积法3.1 Romberg求积公式3.2 Richardson外推加速技术§4 Gauss型求积公式4.1 Gauss型求积公式的一般理论4.2几种常见的Gauss型求积公式§5 奇异积分和振荡函数积分的计算5.1 奇异积分的计算5.2 振荡函数积分的计算§6 多重积分的计算6.1 基本思想6.2 复化求积公式6.3 Gauss型求积公式§7 数值微分7.1 Taylor级数展开法7.2 插值型求导公式习题第四章解线性代数方程组的直接法§1 Gauss消去法§2 主元素消去法2.1 全主元素消去法2.2 列主元素消去法§3 矩阵三角分解法3.1 Doolittle分解法(或LU分解)3.2 列主元素三角分解法3.3 平方根法3.4 三对角方程组的追赶法§4 向量范数、矩阵范数及条件数4.1 向量和矩阵的范数4.2 矩阵条件数及方程组性态习题第五章解线性代数方程组的迭代法§1 Jacobi迭代法§2 Gauss-Seidel迭代法§3 超松弛迭代法§4 共轭梯度法习题第六章非线性方程求根§1 逐步搜索法及二分法1.1 逐步搜索法1.2 二分法§2 迭代法2.1 迭代法的算法2.2 迭代法的基本理论2.3 局部收敛性及收敛阶§3 迭代收敛的加速3.1 松弛法3.2 Aitken方法§4 New-ton迭代法4.1 Newton迭代法及收敛性4.2 Newton迭代法的修正4.3 重根的处理§5 弦割法与抛物线法5.1 弦割法5.2 抛物线法§6 代数方程求根6.1 多项式方程求根的Newton法6.2 劈因子法§7 解非线性方程组的Newton迭代法习题……第七章矩阵特征值和特征向量的计算第八章常微方分程数值解法附录参考文献欢迎下载,资料仅供参考!!!资料仅供参考!!!资料仅供参考!!!。
数值计算方法课后实验-李维国

实验3.1 Gauss消去法的数值稳定性实验实验目的:观察和理解高斯消元过程中出现小主元(即|a(k)kk|很小)时引起方程组解数值不稳定性.实验内容:求解方程组Ax=b,其中实验要求:(1)计算矩阵的条件数,判断系数矩阵是良态的还是病态的.(2)用高斯列主元消去法求得L和U及解向量x1,x2 .(3)用不选主元的高斯消去法求得L和U及解向量x1,x2 .(4)观察小主元并分析对计算结果的影响.解:(1)cond(A1)=68.4296cond(A2)=8.9939A1矩阵条件数远大于1,A1矩阵为病态;A2矩阵条件数没有远远大于1,A2矩阵为良态。
(2)高斯列主元消去法:程序如下ClearA1=[0.3*power(10,-15),59.14,3,1;5.291,-6.130,-1,2;11.2,9,5,2;1,2,1,1];b1=[59.17;46.18;1;2];% A1=[1,2,-1,1;1,1,2,-1;3,-1,1,1;2,1,3,-1];%b1=[1;-2;6;-1];A2=[10,-7,0,1;-3,2.0999********,6,2;5,-1,5,-1;0,1,0,2];b2=[8;5.900000000001;5;1];A=A1; b=b1;n=input('n=');for k=1:n-1 [a,b3]=max(A(k:n,k)); A([k k-1+b3],:)=A([k-1+b3 k],:); b([k k-1+b3],:)=b([k-1+b3 k],:); if A(k,k)~=0A(k+1:n,k)=A(k+1:n,k)./A(k,k);A(k+1:n,k+1:n)=A(k+1:n,k+1:n)-A(k+1:n,k)*A(k,k+1:n); else stop end endA; b; L=tril(A,-1);U=triu(A,0); for i=1:1:n L(i,i)=1;end L; for j=1:n-1 b(j)=b(j)/L(j,j);b(j+1:n)=b(j+1:n)-b(j)*L(j+1:n,j);end b(n)=b(n)/L(n,n); b; y=b;for j=n:-1:2 y(j)=y(j)/U(j,j); y(1:j-1)=y(1:j-1)-y(j)*U(1:j-1,j);end y(1)=y(1)/U(1,1);结果如下:方程组一:L1: U1:解向量x1结果如下:方程组二结果如下:L2:U2:解向量x2结果如下:(3)不选主元的分解程序如下:ClearA1=[0.3*power(10,-15),59.14,3,1;5.291,-6.130,-1,2;11.2,9,5,2;1,2,1,1]; b1=[59.17;46.18;1;2];%A1=[6,2,1,-1;2,4,1,0;1,1,4,-1;-1,0,-1,3];%b1=[6;-1;5;-5];A2=[10,-7,0,1;-3,2.0999********,6,2;5,-1,5,-1;0,1,0,2];b2=[ 8;5.900000000001;5;1]; A=A2; b=b2; n=input('n='); for k=1:n-1A(k+1:n,k)= A(k+1:n,k)/A(k,k); A(k+1:n,k+1:n)=A(k+1:n,k+1:n)-A(k+1:n,k)*A(k,k+1:n); end L=tril(A,-1); U=triu(A,0); for i=1:1:n L(i,i)=1; end L ;for j=1:n-1 b(j)=b(j)/L(j,j);b(j+1:n)=b(j+1:n)-b(j)*L(j+1:n,j); end b(n)=b(n)/L(n,n); b; y=b;for j=n:-1:2 y(j)=y(j)/U(j,j); y(1:j-1)=y(1:j-1)-y(j)*U(1:j-1,j); end y(1)=y(1)/U(1,1);方程组一结果:L1: U1:解向量x1结果如下:方程组二结果:L2: U2:解向量x2结果如下:(4) 观察方程在两种不同方法下的结果可知:由于计算机字长是一定的,小主元会造成大数除以小数的结果超出字长,结果发生很大的变化。
第五专题 矩阵的数值特征(行列式、范数、条件数、迹、秩、相对特征根)讲解

第五专题矩阵的数值特征(行列式、迹、秩、相对特征根、范数、条件数)一、行列式已知A p×q, B q×p, 则|I p+AB|=|I q+BA|证明一:参照课本194页,例4.3.证明二:利用AB和BA有相同的非零特征值的性质;从而I p+AB,I q+BA中不等于1的特征值的数目相同,大小相同;其余特征值都等于1。
行列式是特征值的乘积,因此|I p+AB|和|I q+BA|等于特征值(不等于1)的乘积,所以二者相等。
二、矩阵的迹矩阵的迹相对其它数值特征简单些,然而,它在许多领域,如数值计算,逼近论,以及统计估计等都有相当多的应用,许多量的计算都会归结为矩阵的迹的运算。
下面讨论有关迹的一些性质和不等式。
定义:n nii ii1i1tr(A)a====λ∑∑,etrA=exp(trA)性质:1. tr(A B)tr(A)tr(B)λ+μ=λ+μ,线性性质;2. Ttr(A )tr(A)=;3. tr(AB)tr(BA)=;4. 1tr(P AP)tr(A)-=;5. H Htr(x Ax)tr(Axx ),x =为向量;6. nnk ki i i 1i 1tr(A),tr(A )===λ=λ∑∑;从Schur 定理(或Jordan 标准形)和(4)证明; 7. A 0≥,则tr(A)0≥,且等号成立的充要条件是A=0;8. A B(A B 0)≥-≥即,则tr(A)tr(B)≥,且等号成立的充要条件是A=B (i i A B (A)(B)≥⇒λ≥λ);9. 对于n 阶方阵A ,若存在正整数k,使得A k =0,则tr(A)=0(从Schur 定理或Jordan 标准形证明)。
若干基本不等式对于两个m ×n 复矩阵A 和B ,tr(A H B)是m ×n 维酉空间上的内积,也就是将它们按列依次排成的两个mn 维列向量的内积,利用Cauchy-schwarz 不等式[x,y]2≤[x,x]﹒[y,y]得定理:对任意两个m ×n 复矩阵A 和B |tr(A H B)|2≤tr(A H A)﹒tr(B H B)这里等号成立的充要条件是A=cB,c为一常数。
2-3矩阵的条件数与病态线性方程组

~ ~ A~ x b
设 A
1 A
1
且 A 非奇异, b 0 ,则
1
~ ~ A~ x b 的解的存在性与唯一性
因为 A 1 A A 1 A 1 ,则 I A 1 A 非奇异,又 A 非奇异,故
x1 1 去法可得 。 x2 1
3 ) 残差校正法(迭代改善 )。
考虑求解Ax b , 求得的近似解为~ x ,一般 A~ x b, 即残差r b A~ x 0。
~ ~ 以残差r 为右端向量, 求解 Ax r 可得~ x 的修正量x , 记~ x x x , 如果
~ A A A A I A1A 非奇异。
2
估计 x的相对误差
A Ax x b b
x A 1b A 1Ax A 1Ax
1
A 1 A
x x
x A 1 b A 1 A x
x1 5 x2 6 x1 4.999x2 6.002
x1 1 x1 16 第一个方程组的解为 , 第二个方程组的解为 x 1 2 x2 -2
问题:出现这种差异的原因是什么?
~ ~ 考虑求解线性方程组 Ax b , 设 A和b 分别有了扰动A和b 成了A 和b ,即
计算残差的求解过程是 精确的, 即Ax r ,则
~ A~ x A~ x x b r r b
但实际计算时由于舍入 误差不可避免,故应重 复执行上述过程。
详细算法流程可参考page32-33。
2.3 矩阵的条件数与病态线性方程组
病态线性方程组的求解
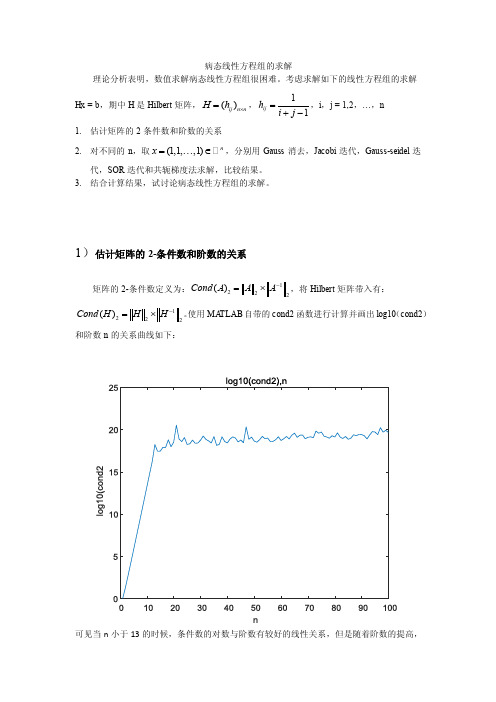
病态线性方程组的求解理论分析表明,数值求解病态线性方程组很困难。
考虑求解如下的线性方程组的求解Hx = b ,期中H 是Hilbert 矩阵,()ij n n H h ⨯=,11ij h i j =+-,i ,j = 1,2,…,n1. 估计矩阵的2条件数和阶数的关系2. 对不同的n ,取(1,1,,1)n x =∈ ,分别用Gauss 消去,Jacobi 迭代,Gauss-seidel 迭代,SOR 迭代和共轭梯度法求解,比较结果。
3. 结合计算结果,试讨论病态线性方程组的求解。
1)估计矩阵的2-条件数和阶数的关系矩阵的2-条件数定义为:1222()Cond A A A-=⨯,将Hilbert 矩阵带入有:1222()Cond H H H -=⨯。
使用MA TLAB 自带的cond2函数进行计算并画出log10(cond2)和阶数n 的关系曲线如下:可见当n 小于13的时候,条件数的对数与阶数有较好的线性关系,但是随着阶数的提高,条件数趋于“稳定”地振荡。
但是事实上,n较大时,H矩阵已经奇异,直接使用cond函数计算结果可能存在不准确性。
原因是对于条件数过大的矩阵使用inv函数求逆矩阵是不可靠的,应该使用invhilb函数进行求逆,并代入定义式中求解,生成的结果如下所示。
线性度较好,可知,Hilbert矩阵的2-条件数会随其阶数n的增加呈指数增大趋势,因此当n 较大时Hilbert矩阵将是严重病态的。
对不同的n,采用各种方法求解方程编写程序,选取n=2,3,5,10,15,20,迭代条件为迭代100000次或者是计算精度达到1e-6,若迭代次数少于设定最大值,表示相邻两次迭代达到精度要求,或者是计算结果超出范围。
X0取零向量,w取1.2,计算结果如下所示:由上可见,当n大于2时,Jacobi法已经不收敛,故其迭代次数已经没有意义。
当n=15时,Gauss消去法已经不收敛。
并且随着阶数的上升,gauss消去法的误差也随之上升。
计算方法Hilbert矩阵病态问题

Solution (1)猜想:()()ln cond Hn n 成线性比例关系。
验证:猜想部分正确。
根据不同n 建立对应的Hilbert 矩阵,计算该矩阵的2-范数的条件数,并绘制曲线。
编程实现见附录1中solution(1)。
实际编程中,分别取N=5,=10N ,=20N ,N=30,可以发现()()ln cond Hn n 曲线先是按线性规律变化;当n 达到大约12以后,()()ln cond Hn 的取值在40~50之间产生振荡。
各结果如下:N=5时 N=10时ln(cond(Hn))-nnl n (c o n d (H n ))ln(cond(Hn))-nnl n (c o n d (H n ))ln(cond(Hn))-nnl n (c o n d (H n ))ln(cond(Hn))-nnl n (c o n d (H n ))N=20时N=30时Solution (2)猜想:通过对Hilbert 矩阵的预处理,能改善Hilbert 的病态性质。
验证:根据不同n 建立对应的Hilbert 矩阵,计算该矩阵的2-范数的条件数,其次计算经过预处理后的H^矩阵的2-范数的条件数,并绘制()()()ln ^/cond Hn cond Hn n 曲线。
编程实现见附录1中的solution(2)。
实际编程中,分别取N=5,=12N ,=50N ,N=100,可以发现所得到的变化曲线()()()ln ^/cond Hn cond Hn n 在12n ≤时,()()()ln ^/cond Hn cond Hn 的取值较为平缓的减小,且均小于0。
而随着Hilbert 矩阵阶数的增大,()()()ln ^/cond Hn cond Hn 的取值在[]-7,3区间中振荡,主要集中在[]-31,,且多数取值()()()ln ^/0cond Hn cond Hn ≤。
则对多数的Hilbert 矩阵,其条件数在经过预处理后,有()()^cond Hn cond Hn ≤,即预处理在一定程度上改善了原Hilbert 矩阵的病态性质。
数值计算原理部分试题

标题: 还是出个回忆版吧,师弟师妹小心了(高数分,小白的)发信站: 水木社区(Tue Jan 10 17:46:47 2006), 站内唔,后天还要考门数学,释放一下内存,不然等会就忘光了.小题很一般了:1.(1,1/2;1/2,1)求2范数和cond22.上题的QR分解后面是几题判断题,要求写出对错和原因.题不记得了,但不难,与往年差不多(本来准备做完后将题录下来的,可是实在没时间了:()以下的小题顺序不一定对:du/dt=(u-u+)(u-u-) u+>u-,问哪个是稳态的哪个不是.矩阵如果可以相似对角化,就一定可以求解特征值,其条件数等于求矩阵解的条件数cond (判断)多重网格是解椭圆方程的最优方案,其特点是用粗网格消去高频分量,细网格消去低频分量.(判断)f (x) = f(x1,x2,x3)=x1x2-x2x3-x3^2-x2-x3临界点\临界值\正则点\正则值不完全LU分解用于用Gauss消去法求解稀疏阵.(判断)就记得这么多了.大题:1.(4,1,1;1,2,1;1,1,3)用初值q1=(1/3,2/3,2/3)进行lanczos分解.(数据是回忆的,不一定对)2.一个函数F(x),表达示不记得了.问(1)证明x=(...,...)'是其解(送分的,代入就行)(2)写出Newton法迭代式(很容易写)(3)写出当x0=(...,...)'时用newton法的x1.(总体很常规,不难)3.A=(4,1;1,1;1,2)问(1)svd分解(2)求A+(3)求r(A),(送分的)4.证明题:zm属于krylov空间Km(r0,Ar0,A^2r0....),Lm=AKm(Ar0,A^2r0,A^3r0...),证明(r0-Azm,v)=0,v属于Lm<==>||r0-Azm||=min||r0-Az||其中z属于Km.(比较简单,书上有的.)5.一题变分的,要求证明两个问题等价,好像是d4u/dx4=f(x),变分为一个边值和一阶边值为零的问题.具体记不清了,因为没时间,只看了看,但也不是太难.可用分部积分算算.应该可以做出来.【在armroe (光明使徒(鐵甲無敵阿姆羅高達第一)) 的大作中提到: 】: 题量大,计算难.光lanczos和svd分解就计算一个多小时.最后十分钟才证明了倒数第二题.最后一道简单的证明题看着做不了.svd还没全算出来,一共才做了80多分的题,唉.小结:考试时间基本不够用,至少没有人能提前交卷.一些计算技巧可以节省时间.如第一小题,对于对称阵的2范数不必算A'A,因为A'=A所以A'A的特征值是A特征值平方.如此题为3/2和1/2,所以2范数就是sqrt(p(A'A))=3/2,A-1的2范数就是A特征值的倒数的P,这里为1/2的倒数,所以是2。
Hilbert矩阵病态问题研究
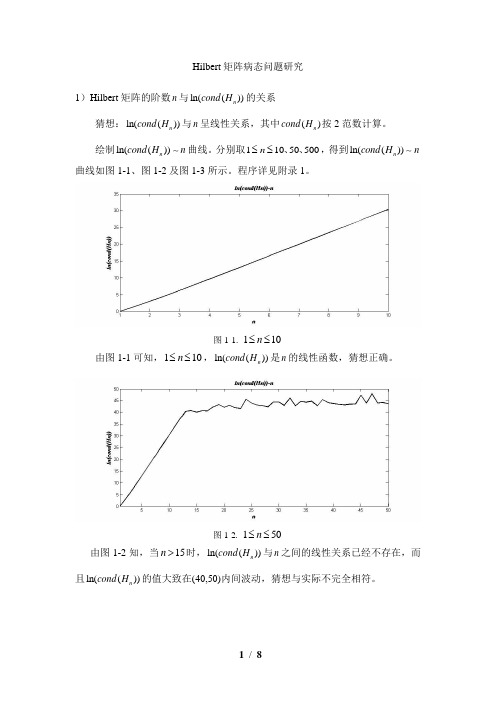
Hilbert 矩阵病态问题研究1)Hilbert 矩阵的阶数n 与ln(())n cond H 的关系猜想:ln(())n cond H 与n 呈线性关系,其中()n cond H 按2范数计算。
绘制ln(())n cond H n 曲线。
分别取11050500n ≤≤、、,得到ln(())n cond H n曲线如图1-1、图1-2及图1-3所示。
程序详见附录1。
图1-1. 110n ≤≤由图1-1可知,110n ≤≤,ln(())n cond H 是n 的线性函数,猜想正确。
图1-2. 150n ≤≤由图1-2知,当15n >时,ln(())n cond H 与n 之间的线性关系已经不存在,而且ln(())n cond H 的值大致在(40,50)内间波动,猜想与实际不完全相符。
图1-3. 1500n ≤≤图1-3进一步说明了ln(())n cond H 与n 之间的变化关系:当n 小于某一值(设该值为k )时,ln(())n cond H 是n 的线性函数,而当n 大于k 时,随着n 的增大,ln(())n cond H 与n 间的线性关系不再成立,且其值在某一区间内波动。
为进一步确定k 的大小,绘制114n ≤≤时的曲线,如图1-4所示,可知k 的取值应为13。
图1-4. 114n ≤≤2)由n H 至ˆnH 的预处理 绘制ˆln(()/())n n cond H cond H n 曲线。
其中11ˆn nH D H D --=,D 为由n H 的对角元素开方构成的对角矩阵。
条件数按2范数计算。
程序详见附录2。
分别取11350500n ≤≤、、,得到如图2-1、图2-2和图2-3所示曲线。
由曲线图像可知:当Hilbert 矩阵的阶数12n ≤时,ˆln(()/())n ncond H cond H 随n 增大而逐渐减小,而n 继续增大时,ˆln(()/())n n cond H cond H 的取值将在区间(-7,4)内波动,且主要集中在(0,-3)区间内。
病态方程解算方法

通常的判断标准,N的特征值i中,i 0.1时,可以认为不存 在复共线性;0.05 i 0.1时,有弱复共线性;0.01 i 0.05时,有 中等强度复共线性;i 0.01时,有严重的复共线性。
不适定问题通常是病态的,但病态问题不一定就是不适定问题。不 适定问题通常是求方程的稳定近似解。
二、病态方程的解法
1、病态方程的截断奇异值解法
奇异值分解技术(Singular Value Decomposintion Technique,简记为SVD法)
设有观测方程(式中观测值向量L的权阵P已经单位化): A x L e
4、病态方程最小二乘估值的性质
病态方程处理的观测值可以是正态分布,但其LS估值并不理想,甚至很差。 虽然LS估计的方差在线性无偏类估值中是最小,但数值却很大,并表现得 相当不稳定。
常用均方误差MSE来评价病态情形下参数的估值质量。
由均方误差公式:
MSExˆ E xˆ ~x T xˆ ~x 02tr Qxˆxˆ Exˆ ~x 2
nt t1 n1 n1
A是设计矩阵,e是误差向量。得x的最小二乘最小范数解为 xˆLS A L
A是A的广义逆。 下面对A进行奇异值分解:
(1)当rank( A) p p minn,t时,对A阵可分解为
A U VT
nt nn nt tt
式中为半正定的对角阵;U、V均为正交矩阵。
阵的分块形式为
D
和最
小的特征值。
不稳定模型:输入数据很小的误差会引起待估参数很大的误差。 所以病态方程也是不稳定模型。
矩阵2范数证明

矩阵2范数证明矩阵2范数是一种常用的矩阵范数,也被称为谱范数,它在矩阵理论、数值线性代数和优化问题等领域有着广泛的应用。
在本文中,我们将证明矩阵2范数的定义以及一些重要性质。
首先,我们来介绍矩阵2范数的定义。
给定一个矩阵A,它的2范数(记作||A||2)定义为矩阵A的最大奇异值的平方根。
在进行证明之前,我们先回顾一下奇异值分解(Singular Value Decomposition, SVD)的定义。
对于一个矩阵A,它的奇异值分解可以表示为A = UΣV^T,其中U和V分别是正交矩阵,Σ是一个对角矩阵,对角线上的元素即为A的奇异值。
现在,我们开始证明矩阵2范数的定义。
设A = UΣV^T是A的奇异值分解,其中Σ = diag(σ1, σ2, ..., σn)是A的奇异值对角矩阵。
注意到A的奇异值是非负的,并且按照非递增的顺序排列,即σ1 ≥ σ2 ≥ ... ≥σn ≥ 0。
由于矩阵A的2范数定义为最大奇异值的平方根,我们需要证明这一最大奇异值存在,并且是A的最大奇异值。
首先,根据奇异值的定义可知,对于任意向量x ≠ 0,有A(Vx) =U(ΣV^T(Vx)) = U(Σx) = U(σx),其中σ是A的奇异值,Vx是向量x在V的列向量基上的坐标表示。
因此,σ = ||A(Vx)|| / ||Vx||。
那么,对于任意的单位向量x ≠ 0,有σ = ||A(Vx)|| / ||Vx|| ≤ ||A|| 。
(这里可以使用余弦定理来证明,不再赘述)因此,矩阵A的最大奇异值为||A|| = max{σ}。
接下来,我们证明矩阵A的2范数的平方等于矩阵A^TA的最大特征值。
设v为矩阵A^TA的一个单位特征向量,对应特征值λ。
那么有A^TA(v) = λ(v)。
我们可以将这个等式两边都左乘v的转置,得到v^TA^TA(v) = v^T(λ(v)) = λ(v^Tv) = λ。
由于v是单位向量,所以v^Tv = 1,因此得到v^TA^TA(v) = λ。
第六章病态方程解算方法

nt t1 n1 n1
A是设计矩阵,e是误差向量。得x的最小二乘最小范数解为 xˆLS A L
A是A的广义逆。 下面对A进行奇异值分解:
(1)当rank( A) p p minn,t时,对A阵可分解为
A U VT
nt nn nt tt
式中为半正定的对角阵;U、V均为正交矩阵。
阵的分块形式为
D
nt
0
0 0
其中: D diag 1, 2, p , p RA min(n,t)
且1 2 p 0. i是A阵全部的非零奇异值。
A的奇异值分解式可写为
p
A VU T i1viuiT i 1
得解为:
p
xˆLS
t1
AL
v u L 1
T
i 1
i
i t1
i 1n
n1
在第T步对其截断,得病态方程的截断奇异值法解:
T
xˆT
t1 i1
v u L 1
T
i
i t1
i 1n
对于实对称法矩阵N BT PB,可作如下谱分解:
N BT PB GGT
G为由N的特征值i的特征向量组成的正交阵。将特征值排为 1 2 n 0
正交阵特性:GGT I , 或GT G1。 (注意:该G阵与秩亏平差的附加阵G阵完全没关系,秩亏平差的G阵
是N阵的零特征值对应的特征向量,而此处的G阵是N阵所有特征值 对应的特征向量)
1
2
02tr
BT B
2.3矩阵的条件数与病态方程组

•
2、阅读一切好书如同和过去最杰出的 人谈话 。10:2 0:2910: 20:2910 :2012/ 12/2020 10:20:29 AM
•
3、越是没有本领的就越加自命不凡。 20.12.1 210:20: 2910:2 0Dec-20 12-Dec-20
•
4、越是无能的人,越喜欢挑剔别人的 错儿。 10:20:2 910:20: 2910:2 0Saturday, December 12, 2020
Proof
x
A A1
A b
改写(2.22)式:
x
(
)
1 A A1 A
A
b
A
★矩阵条件数的定义: ★矩阵条件数的性质:
(6)Cond(AB) ≤ Cond(A) Cond(B)
二、线性方程组的性态
答案: (1)cond ( A) 4104 , x (2,0)T (2)x x (1,1)T
• 10、你要做多大的事情,就该承受多大的压力。12/12/
2020 10:20:29 AM10:20:292020/12/12
• 11、自己要先看得起自己,别人才会看得起你。12/12/
谢 谢 大 家 2020 10:20 AM12/12/2020 10:20 AM20.12.1220.12.12
得:ans=1.000,1,000,1.000,1.000,0.9999 1.0002,0.9996,1.0004,0.9998,1.000
输入: n 5; H hilb(n);b H *ones(n,1); x H \ b; x,
得:ans=1.000,1,000,1.000,1.000,1.000 输入: n 10; H hilb(n);b H *ones(n,1); x H \ b; x,
山东大学数值计算实验报告3

2.1.2 直接解方程组
fprintf('%s\n','n=2 时,解法 2');
x12 = H1\b1
运行结果如下:
2.2 当 n=5 时
%生成 n=5 时希尔伯特矩阵 H2=zeros(5,5); n2=5; for i = 1:5 for j = 1:5 H2(i,j) = 1/(i+j-1); end end fprintf('%s\n','n=5 时,解法 1:'); L2=c_1(H2,n2)%楚列斯基函数得到 L %得到 b t2=ones(5,1); b2=H2*t2; %利用之前实验 2 所写的前代,后代函数得到答案 front2 = a_3_a( L2,b2 ); x21 = a_3_b(L2',front2)
%当 n=10 时 fprintf('%s\n','当 n=10 时,该矩阵的 1 范数及 1 范数下的条件数为:'); fan31 = norm(H3,1) cond31 = cond(H3,1) fprintf('%s\n','当 n=10 时,该矩阵的 2 范数及 2 范数下的条件数为:'); fan32 = norm(H3,2) cond32 = cond(H3) fprintf('%s\n','当 n=10 时, 该矩阵的无穷范数及无穷范数下的条件数为: '); fan33 = norm(H3,inf) cond33 = cond(H3,inf)
运行结果如下:
fprintf('%s\n','n=10 时,解法 2'); x32 = H3\b3
病态方程组

病态方程组
由实际问题得到的方程组的或者常数向量的元素,本身会存在一定的误差;这些初始数据的误差在计算过程中就会向前传播,从而影响到方程组的解。
病态方程组是指因系数的很小改变却导致解改变很大的方程组,称相应的系数矩阵A为病态矩阵。
病态方程组对任何算法都将产生数值不稳定性。
对病态方程组有四种处理原则:采用高精度的算术运算;采用预处理方法;采用特殊的数值解法或寻找出现病态的原因,改变原问题的提法。
二范数通俗理解

二范数通俗理解二范数,也称欧几里得范数或L2范数,是向量空间中的一种度量方式。
它常用于衡量向量的长度或大小,具有许多实际应用。
在本文中,我们将以通俗易懂的方式解释二范数的含义和应用。
在向量空间中,二范数可以理解为一个向量到原点的距离。
具体而言,对于一个n维向量x=(x1, x2, ..., xn),它的二范数定义为:||x||2 = sqrt(x1^2 + x2^2 + ... + xn^2)其中,||x||2表示向量x的二范数,sqrt表示平方根运算。
从这个定义可以看出,二范数实际上就是向量各个分量平方和的平方根。
二范数可以衡量向量的大小。
当向量各个分量的值较大时,二范数也会相应增大,表示向量的长度较大。
反之,当向量各个分量接近于0时,二范数也会接近于0,表示向量的长度较小。
二范数在机器学习和数据挖掘等领域中得到广泛应用。
一方面,二范数可以用于正则化。
在机器学习中,正则化是一种常用的方法,用于防止模型过拟合。
通过在损失函数中引入正则化项,可以限制模型参数的大小,避免模型过于复杂。
而二范数正则化就是一种常见的正则化方式。
通过将模型参数的二范数加入到损失函数中,可以使模型更加平滑,提高泛化能力。
另一方面,二范数还可以用于特征选择。
在数据挖掘任务中,特征选择是一项重要的工作,用于从大量特征中选择出对目标变量有显著影响的特征。
二范数可以作为一种评价指标,衡量特征的重要性。
具体而言,对于一个线性回归模型,模型的系数的二范数越大,表示对应的特征对目标变量的影响越大。
除了上述应用,二范数还有其他一些重要的性质和应用。
例如,二范数具有可加性,即两个向量的二范数之和等于它们的和的二范数。
这个性质在一些场景下非常有用,比如计算两个图像的差异程度。
另外,二范数还可以用于衡量矩阵的条件数,进而评估矩阵的稳定性和求解线性方程组的困难程度。
二范数是向量空间中常用的度量方式,用于衡量向量的大小或长度。
它在机器学习、数据挖掘等领域中有着广泛的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由于
( I A)( I A)1 I ( I A)1 A( I A)1 I
( I A)1 I A( I A)1
在最后一式两端取范数,得
( I A) 1 I A ( I A) 1
1 A
( I A) 1 I 1.
练习:计算矩阵
1 2 A 3 4 的各种范数.
答案 : 6,7, 15 221 , 30
§2.3 矩阵的条件数与病态线性方程组
2.3.1
矩阵的条件数与线性方程组的性态
给定线性方程组 Ax =b,现在考察,系数矩阵 A 和常数列 b 有了微小变化 △A,△b ,它如何影 响解向量 x,即,解向量 x 的变化量 △x 何样? 由于A (或 b)的元素是测量得到的,或者是 计算的结果,在前种情况下, A (或 b)常常带有 某些观测误差,在后种情况下, A (或 b)包含舍 入误差,因此我们处理的实际矩阵是A + △A (或 b+ △b )。
n×n矩阵 A,式(1.2)中定义的函数是一种矩阵范 数,并且它与给定的向量范数是相容的.
A max Ax
单位球上的 最大像值
x 1
(1.2)
证明 先证相容性. 对任意的n×n矩阵A和n维非零向
量 y. 由于
y 1 max Ax A Ay . x 1 y y
所以有
Ay y max Ax y A ,
考察方程组 Ax = b, 当 A 或 b 有微小扰动时, 对解的影响, 首先看一个例子:
1 x1 2 1 , 1 1.0001 x2 2 1 x1 2 1 x 1 1.0001 2.0001 2
Ax 2 ( Ax)T ( Ax) xT AT Ax.
因为,ATA是正定或半正定的, 故它的全部特征值 i 非 负, 设
2
1 2
n
设 (ATA) 相应的规范正交特征向量为 u1,u2,…,un,
因而存在实数 k1, k2,…, kn, 使
x ki ui ,
i 1
lim xk x .
xk x 证 依据范数的等价定义,可设 lim k
0,
即,有 故
k
lim max ( xk )i ( x )i 0,
k 1i n
lim xk x .
xk ( xk )1 ,
, ( xk )n
任2种范数在刻画收敛性时等价
i k i2 max .
i 1
T T Ax u x 1 x u 取 , 以及 1 A Au1 max , 1 , 则有 2 2 2
n
所以
A 2 max Ax 2 max ( AT A) .
x 1
证毕
▼1,∞-范数 公式证明
单位矩阵 I 的任何一种算子范数都有
y || || x || || y || .
3种常用的范数
定理1.1 对 R 中的任一向量 x ( x1 , x2 ,
n
n i 1
, xn )T,
1 i n
记 || x ||1 | xi | || x ||2
,
x
i 1
n
2 i
,
|| x || max | xi |
1 i n
, xn yn ) ||
max{| xi | | yi |}
1i n
max{| xi |} max{| yi |}
1 i n 1 i n
|| x || || y ||
证毕
|| ||1
叫1-范数, (列范数); 叫2-范数, (Euclid(欧几里得)范数) ;
因为 A 1 ,故
( I A)
1
1 . 1 A 1 . 1 A
同理可证
( I A)
1
证毕
例6
1 5 2 2 1 0 T A 设 x (3, 5,1) , 3 8 2
求 x p , A p ( p 1, 2, ) 以及
1 j n i 1 n
|| A ||2 = max ( AT A) (2范数) || A || max | aij | (行范数)
1 i n j 1 n
其中,max ( AT A) 表示 AT A 的最大特征值。
证明 对于2-范数, 设 n 维向量 x 满足 ||x||2 = 1. 注意到
A p max Ax p .
x p 1
上式中矩阵范数 ||A||p 也叫 A的 p -范数. 矩阵的p 范数与向量的p -范数相容,即,
||Ax||p≤ ||A||p· ||x||p
.
定理1.4(几种常用的范数)
当 p 1, 2, 时 || A ||1 max | aij | (列范数)
AB max ( AB) x max A Bx
x 1Βιβλιοθήκη x 1 A max Bx A B .
x 1
证毕
A max Ax
x 1
(1.2)
上式所定义的矩阵范数叫做从属于所给定向量范 数的矩阵范数,又称为矩阵的算子范数. 设给定的向量范数为||·||p, 则从属于向量范数 的矩阵范数为:
n
并且有 由此可得
x 2 xT x ki2 1,
2 i 1
n
Ax 2 xT AT Ax ( AT Ax, x )
n n T A A kiu i , kiui i 1 i 1
2
n n i ki ui , kiui i 1 i 1
2 2 1
x 1,
A A A
x
,
2 F
x 2, x 2.
定理1.5 设矩阵 A∈Rn×n 的某种范数 ||A||<1,
则 I±A 为非奇异矩阵,并且当该种范数为算子 范数时,还有下式成立。 1 1 . I A 1 A 证明 假定 I±A 奇异,则齐次线性方程组 (I±A)x =0 有非零解 x 0, 使 x Ax. 在上式两边同取与所用矩阵范数数相容的向量范 x Ax A x 数,得 因 x 0 ,故由上式得 A 1 。与已知条件矛盾, 因而 I A 必非奇异。
112,
14 21 4 AT A 21 90 26 4 26 8
特征多项式为
det( AT A I ) 3 112 2 959 16,
最大的根为 max 102.66,
A 2 max 10.132 .
x 1 x 1
.
(3) 对任意的n×n矩阵 A 和 B, 有
A B max ( A B) x max Ax Bx
x 1 x 1
max Ax Bx
x 1
max Ax max Bx A B
x 1 x 1
(4) 对任意的n×n矩阵 A 和 B, 有
I max Ix 1.
x 1
还有一种常用的矩阵范数,
AF
2 a ij n
i , j 1
称为Frobrnius(佛罗贝尼乌斯)范数,又称为 Euclid 范数。
注: F 不从属于任何向量范数,即 F不是算子范数.
几种常用的相容关系
Ax 1 A Ax Ax Ax
正定性 齐次性 三角不等式
积的范数小于等 于范数的积
矩阵范数与向量范数的相容性
定义 给定向量范数||·||和矩阵范数||·||, 如果对任 意的 n 维向量 x 和任意的n×n矩阵A,它们总满足
Ax A x , 则称所给的矩阵范数与向量范数是相容的。
定理1.3 设在Rn中给定一种向量范数,对任意的
则 || ||1 , || ||2 和 证明 仅证
|| || 都是向量范数.
|| || 是向量范数.
(1) || || 满足正定性是显然的.
(2) 对任意的实数 k , 有
|| kx || || ( kx1 , kx2 ,
1i n
, kxn ) || max | kxi |
2 矩阵范数
矩阵的范数是刻画矩阵大小的量,又叫矩阵的模.
定义 Rn×n上的实值函数‖·‖称为矩阵范数,如果 对任意的矩阵 A 和 B, 它均满足下列4条性质:
(1) A 0, 且 A 0 A 0; (2) 对k R, kA k A ; (3) A B A B ; (4) AB A B ;
向量序列收敛的定义:向量序列
x , x , x ,, x
( 0)
(1)
( 2)
(k )
若存在常数向量 x* ,使 lim
k
x(k ) x *
,则称该向量序列
lim x x 0, 有 k k
收敛,否则,称其不收敛或发散。
定理 若有常数向量
则必有
k
x*,使对某种范数,
1 5 2 A 2 1 0 3 8 2
A
|1| | 5 | | 2 |, max | 2 | |1| | 0 |, |3| |8| | 2|
13,
AF
12 2 2 32 2 2 2 5 1 8 2 2 2 2 0 2
解 x 1 | 3| | 5| |1| 9,
x 2 32 (5) 2 12 35
