第二讲多重纳均衡
多重均衡
博弈论与行为经济学章平pzhng@反应函数法乙正面q 反面1-q1-1甲正面p-11-11反面1-p1-1期望支付函数混合策略均衡eg1混合策略均衡eg1混合策略均衡eg1多重纳什均衡及甄别•标准一:帕累托占优猎鹿博弈Stag Hunt Game两个猎人以狩猎为生,主要有两种猎物——鹿和兔子,两人一起猎鹿,才能猎获一只鹿,如果单枪匹马,只能打到4只兔。
乙猎鹿打兔104甲猎鹿10004打兔44帕累托改进•就是一项政策能够至少有利于一个人,而不会对任何其他人造成损害。
所谓“帕累托最优”就是上述一切帕累托改进的机会都用尽了,再要对任何一个人有所改善,就不得不损害另外一些人。
•帕累托最优的想法是从多目标数学规划得到的。
•比如城市交通,除了政府办的公共交通,私人也能办小公交,和大公交竞争;•在医疗系统除了原有的低收费的系统,另外开辟了专家挂号,收费高一些;•学校有公立的,也有了私立的。
•股票市场也有双轨制,原有的股票是非流通股,新股票可以自由买卖,是流通股。
•新人新办法、老人老办法也是双轨制。
•这些措施大大地缓解了改革中可能有的矛盾,谁的利益都没有受损。
•房地产市场是一步取消了福利分房,没有经过双轨制就建立了房地产市场。
标准二:风险占优乙左右98甲上9007下87偏离损失比较法两害相权取其轻帕累托占优与风险占优的关系•对参与人的基本假定存在差异:帕累托占优适用于符合完全理性假定的参与人风险占优适用于判断搭档(对手)会犯错误,不信任;判断对手很可能是风险厌恶型的参与人。
基本原则:“在怕累托标准和风险标准之间,理论给帕累托占优以优先权,而风险占优只有在参与人面临不知道选哪个均衡好的不确定性时,才变得重要。
当一个均衡符合帕累托占优时,参与人一定选择这个均衡,不确定性也就不存在了。
”谢林的《冲突的策略》•其中一个例子:你和其他参与人均从下面一组数中选择一个数,并画上圈:7,100,13,261,99,666。
如果你们选择相同则赢利越多。
博弈论—组合数学

a考试预测: 1、复习,92分。2、没复习,80分。
b报告预测:考虑因素较多,两个人的联合互动行为。 1、两人准备,100分。 2、一人准备,92分。 3、无人准备,84分。 最终目标:平时成绩最大化。我们用图表汇总一下结果。
博弈的常规形式
两家公司公司1、2,每家公司再决定是否在两个可能的 区域,AB 8,4 6,12
公司2 AA,BB BA,AB
8,4
12,6
4,2
6,12
BA,BB 12,6 4,2
常规形式
参与人2
参与人1
8
12
6
4
4
6
12
2
简单博弈的扩展形式
博弈论
—组合数学
博弈论定义 博弈中的行为推理 占优策略与严格占优策略 最佳应对于严格最佳应对 纳什均衡 多重均衡 混合策略 帕累托最优与社会最优 非优策略与动态博弈
一、何为博弈?
• 通俗讲:每个参与者对结果的预期 不仅取决于他自身的决定,而且还 取决于他人所做的抉择。
通过案例简单了解一下博弈
“考试—报告”案例 内容:假设你是一个大学生,在规定截
八、帕累托最优与社会最优
帕累托最优 指每个参与者从一个策略集中选择一个策 略。 社会最优 一组策略选择是社会福利最大化,若使他 的汇报和最大。
帕累托最优与社会最优的关系
• 二者之间的关系
1、社会最优的结果也一定会是帕累托最优的结 果。 2、帕累托最优结果不需要是一个社会最优结果
九、非优策略与动态博弈
我们建立一下收益矩阵
第二讲多重纳什均衡.ppt

香精包子的思考
香精包子——其他包子企业如何做?
参与人根据其共同观测到的信号选择行动。
•
博弈论第三章
4,4 -8,-2 -2,-8 -2,-2
17
第三节多重纳什均衡的选择标准
五、抗共谋均衡 (一)案例:是否采用新技术
厂商1
厂商2 新技术 旧技术 新技术 2,2,2 5,0,5 旧技术 0,5,5 1,1,10 厂商3:新技术 厂商2 新技术 旧技术 新技术 5,5,3 10,1,1 旧技术 1,10,1 2,2,2 厂商3:旧技术
(一)案例:计算机产品的兼容性
企业C
3.5
英
寸
盘
5.25英寸盘
3.5英寸盘
企业A
8,8 2,3
3,2 6,6
5.25英寸盘
•
博弈论第三章
4
第三节 多重纳什均衡的选择标准
一、帕累托优势标准:得益最大
(二)帕累托优势标准
按照支付大小筛选纳什均衡
(3.5英寸盘,3.5英寸盘)
8,8 2,3
二、风险优势标准:风险更小
(三)纳什均衡的选择标准:风险优势标准
比较不同纳什均衡之间的风险状况,风险小的纳什均衡 优先
帕累托标准还是风险标准? 1.人会犯错误; 2.大多数人是风险厌恶者。 帕累托标准:理论 风险优势标准:实践
• 博弈论第三章
9,9 8,0
0,8 7,7
12
第三节多重纳什均衡的选择标准
(二)分析:偏离损失比较法
2.乙:单独偏离均衡的损失 (1)偏离“作弊”:9-8=1
甲坚守
(2)偏离“不作弊”:7-0=7
9,9 8,0
F-博弈论专题-4-2纳什均衡多重性

(七)培育发展地方资本市场。依法合规开展非上市公司 股份转让及技术、文化等产权交易。 (八)积极发展各类债券产品。推动更多企业尤其是小微 企业通过债券市场融资。建立健全小微企业再担保体系。 (九)拓宽保险服务领域,创新发展服务于专业市场和产 业集群的保险产品,鼓励和支持商业保险参与社会保障体 系建设。 (十)加强社会信用体系建设。推进政务诚信、商务诚信、 社会诚信和司法公信建设,推动小微企业和农村信用体系 建设。加强信用市场监管。 (十一)完善地方金融管理体制,防止出现监管真空,防 范系统性风险和区域性风险。建立金融业综合统计制度, 加强监测预警。 (十二)建立金融综合改革风险防范机制。清晰界定地方 金融管理的职责边界,强化和落实地方政府处置金融风险 和维护地方金融稳定的责任。
焦点效应
2005年诺贝尔经济学奖获得者Schelling 对这种现象进行了详尽的探讨并且证明: 在一个具有多重均衡的博弈中,趋向于将 参与人的注意力集中到一个均衡的任何事 情,都可能使参与人全都预期并随之实行 这个均衡,就像一个自行应验的预言一样。
焦点效应
Schelling将这种现象称之为“焦点效应” (focal-point effect),在焦点效应中具有某 种使它显著地区别于所有其它均衡之性质 的均衡,被称为“焦点均衡”(focal equilibrium)。
战争 -5, -5 -10, 8 国家2 和平 8, -10 10, 10
战争与和平
案例:该不该救助
欧洲主权债务危机或求助 中国出手。 “萨科齐同胡锦涛通话, 通报欧盟峰会情况” 据《香港商报》27日报道, 欧洲金融稳定工具行政总 裁雷格林,将会在28日访 问中国,讨论欧元区面临 的经济挑战,以及欧债危 机解决措施。 500—1000亿美元
纳什均衡PPT课件

可编辑
<#>
3、纳什均衡与上策均衡、累次严优
❖ 每一个上策均衡、累次严优求解出的均衡一定是纳 什均衡,但并非每一个纳什均衡都是上策均衡或累 次严优求解出的均衡。
ห้องสมุดไป่ตู้
❖ 如果应用累次严优排除了除
之外的所
有策略组合,那么
在进一行定博弈是分这析个之前博先弈通过的重唯复
一纳什均衡;
剔除严格劣策略方法来简化博弈
wuweiwei100@
<#>
纳什均衡就是一个僵局,给定其他 人不动,没有人有动的积极性,谁 动谁吃亏。具体地说,一个纳什均 衡就是博弈中各个博弈方都不愿意 单独改变策略的一个策略组合。
——张维迎
(北京大学教授)
可编辑
<#>
再如 猎鹿博弈
猎人1
鹿 兔子
猎人2
鹿
兔子
5,5 3,0
0,3 3,3
❖ 如果
是可行的
是博弈的一个纳什均衡,那么累
次严优一定不会将它消去。
可编辑
<#>
4、不同均衡概念之间的关系
上策均衡 累次严优均衡
纯策略纳什均衡 混合策略纳什均衡
可编辑
<#>
如果所有博弈方都预测一个特定的博弈结果会出现那么所有的博弈方都不会利用该预测或者这种预测能力选择与预测结果不一致的策略即没有哪个博弈方有偏离这个预测结果的愿望因此这个预测结果最终真会成为博弈的结果
纳什均衡
wuweiwei100@
1
博弈的正规型表述
用 表示一个博弈,其中有 个局中人,每个局中
❖ 两个人从独木桥的两端走 向中央进行火拚,每个人 都有两种策略:前进、后 退
第二讲多重纳什均衡

---------------------------------------------------------------最新资料推荐------------------------------------------------------第二讲多重纳什均衡友军博弈英国支持巴顿支持蒙帅支持巴顿美国支持蒙帅友军博弈特征两个(多个)纳什均衡问题:博弈的最终结果?第三章混合策略纳什均衡第三节多重纳什均衡的选择标准第三节多重纳什均衡的选择标准一、帕累托优势标准:得益更大(一)案例:战争与和平 C 国鹰战略鸽战略鹰战略 A 国鸽战略第三节多重纳什均衡的选择标准一、帕累托优势标准:得益更大(二)纳什均衡的选择标准帕累托优势标准按照支付大小筛选纳什均衡第三节多重纳什均衡的选择标准二、风险优势标准:风险更小?(一)案例:串通作弊博弈学生乙作弊不作弊作弊学生甲不作弊第三节多重纳什均衡的选择标准二、风险优势标准:风险更小(二)分析:偏离损失比较法 1. 甲:单独偏离均衡的损失(1)偏离作弊:9-8=1 (2)偏离不作弊:7-0=7 第三节多重纳什均衡的选择标准二、风险优势标准:风险更小(二)分析:1 / 5偏离损失比较法 2. 乙:单独偏离均衡的损失(1)偏离作弊:9-8=1 (2)偏离不作弊:7-0=7 第三节多重纳什均衡的选择标准二、风险优势标准:风险更小(二)分析:偏离损失比较法3. 偏离损失比较方法:偏离作弊的损失 VS 偏离不作弊的损失 11 <77 第三节多重纳什均衡的选择标准二、风险优势标准:风险更小(二)分析:偏离损失比较法 4. 结论(1)偏离(不作弊,不作弊)的损失更大:49 (2)不偏离(不作弊,不作弊)第三节多重纳什均衡的选择标准二、风险优势标准:风险更小(三)纳什均衡的选择标准:风险优势标准比较不同纳什均衡之间的风险状况,风险小的纳什均衡优先第三节多重纳什均衡的选择标准三、聚点均衡(一)案例:城市分组博弈参与人:甲乙策略:把上海、长春、南京、哈尔滨四个城市分成两组,每组 2 个城市支付:甲乙分法相同――奖励 100 元;甲乙分法不同――奖励 0 元---------------------------------------------------------------最新资料推荐------------------------------------------------------第三节多重纳什均衡的选择标准三、聚点均衡(二)聚点均衡 1. 标准使用社会文化习惯、博弈历史等信息达到均衡 1 、 10 、 66 、888 2. 实质规律性第三节多重纳什均衡的选择标准四、相关均衡(一)案例:地域连坐下的产品质量博弈企业乙好产品差产品好产品企业甲差产品第三节多重纳什均衡的选择标准四、相关均衡(二)相关均衡参与人主动设计某种形式的选择机制,形成制度安排,从而确定最终均衡三鹿事件出现后,河北省其他食品企业以后如何做?第三节多重纳什均衡的选择标准五、抗共谋均衡(一)案例:抽象的选择乙左右上甲下乙左右上甲下第三节多重纳什均衡的选择标准五、抗共谋均衡(二)共谋偏离(集体偏离)均衡的激励 1. 如果集体偏离(上,左, A)(1)起因:甲、乙集体偏离,选(下,右, A)(2)结果:甲的支付 01 ,乙的支付 01 (3)结论:甲、乙有集体偏离的动机,(上,左, A)非抗共谋均衡第三节多重纳什均衡的选择标准五、抗共谋均衡(二)共谋偏离(集体偏离)均衡的激励 2. 如果集体偏离(下,右, B)(1)若甲、乙集体偏离,选(上,左, B) -1-2 , -1-2 (2)若甲、丙集体偏离,选(上,右, A) -1-5 , 50 (3)若乙、丙集体偏离,选(下,左, A) -1-5 , 50 (4)结论:缺乏集体偏离的激励,(下,右, B)为抗共谋均衡猎鹿博弈:3 / 5何为抗共谋均衡?乙猎鹿打兔猎鹿甲打兔金无足赤,人无完人人总是要犯错误的,所以要对别人宽容经得起考验的纳什均衡在其他参与人选择了错误策略的情况下,某参与人仍能实现纳什均衡第三节多重纳什均衡的选择标准六、颤抖手精炼均衡Trembling-hand perfect equilibrium (一)颤抖手某一参与人的非蓄意错误博弈偏离均衡路径的原因第三节多重纳什均衡的选择标准六、颤抖手精炼均衡(二)颤抖手均衡 1. 基本思想给定所有参与人均可能犯错误的情况下,如果某一策略组合仍是每一个参与人的最优策略组合,则实现颤抖手均衡第三节多重纳什均衡的选择标准六、颤抖手精炼均衡(二)颤抖手均衡 2. 定义: m――mistake n 人博弈中,对于每一个博弈方 i,存在严格混合策略序列,使下列条件得到满足:(1)尽管每一个博弈方可能犯错误,但错误收敛于零――总有一天能成功穿针引线――功夫不负有心人将一条线穿入针眼,手在不停颤抖,不大可能一下子穿进去但如果试的次数足够大,总是能够成功第三节多重纳什均衡的选择标准六、颤抖手精炼均衡(二)颤抖手均衡 2. 定义:m――mistake n 人博弈中,对于每一个博弈方 i,存在严格混合策略序列,使下列条件得到满足:(2)对于任何可选择的混合策略穿针引线― ― a name=baidusnap0/aB style=‘ color: black; background-color: #ffff66’ 学会宽容/B纳什均衡:---------------------------------------------------------------最新资料推荐------------------------------------------------------ 每一个人都把线穿入针眼宽容:某参与人不能因为其他参与人可能暂时无法把线穿进针眼而故意不把线穿进针眼本章作业 P143-146 1 、 7、 11 、 19 、 20 、21 、 22 、 24 、25 *博弈论第三章第二讲多重纳什均衡 3, 4 1,1 2, 2 4, 3 10 ,10 -10 , 8 8, -10 -5 , -5 10 , 10 -10 ,8 8, -10 -5 , -5 7, 7 8, 0 0, 8 9, 9 帕累托优势? 7, 7 8, 0 0, 8 9, 9 7, 7 8, 0 0, 8 9, 9 7, 7 8, 0 0, 8 9,9 7, 7 8, 0 0, 8 9, 9 7,7 8, 0 0, 8 9, 9 -2 , -2 -2 ,-8 -8 , -2 4, 4 -2 , -2 -2 ,-8 -8 , -2 4, 4 1, 1, -5 -5 , -5 , 0 -5 , -5 , 0 0, 0,10 丙:A -1 , -1 , 5 -5 , -5 , 0 -5 , -5 , 0 -2 , -2 ,0 丙:B 4, 4 4, 0 0, 4 10 , 10 他人不犯错误,你能实现最优;他人犯错误,你仍能实现最优一个人用手抓东西时,手一颤抖,就可能抓不住他想抓的东西:非蓄意错误如何理解?宽容是一种美德 * 博弈论第三章第二讲多重纳什均衡* *div id=loadingADdiv class=ad_boxdiv class=waitingstrong文档加载中. . . /strong 广告还剩em id=adtime/em秒5 / 5。
多重纳什均衡课件

例如,在双寡头市场中,两个企业可能采用不同 的混合策略组合,如企业A采用高价和低产的混合 策略,企业B采用低价和高产的混合策略。
此外,如果企业之间采用相同的混合策略组合, 也可能形成多个纳什均衡点。例如,两个企业都 采用高价和低产的混合策略或都采用低价和高产 的混合策略。
04
多重纳什均衡的经济学意义
纳什均衡
在非合作博弈中,如果每个参与者在给定其他参与者策略的 前提下,选择自己的最优策略,那么所有参与者的策略组合 就构成一个纳什均衡。
多重纳什均衡
当存在多个纳什均衡时,这些均衡被称为多重纳什均衡。
多重纳什均衡的存在性条件
博弈的策略空间和参与者的数量
01
当博弈的策略空间和参与者的数量较大时,多重纳什均衡存在
的可能性增加。
博弈的支付函数
02
支付函数的非线性程度和分布情况也会影响多重纳什均衡的存
在性。
博弈的规则和约束条件
03
博弈的规则和约束条件也会对多重纳什均衡的存在性产生影响。
多重纳什均衡的求解方法
直观判断法
对于一些简单的博弈, 可以通过直观判断来找
出多重纳什均衡。
迭代法
通过迭代计算的方法, 可以找出多重纳什均衡。
这种方法通常适用于较 小的博弈。
线性规划法
通过线性规划的方法, 可以找出多重纳什均衡。
这种方法通常适用于较 大的博弈。
概率方法
通过概率方法,可以找 出多重纳什均衡。这种 方法通常适用于具有随
机性的博弈。
03
多重纳什均衡的实例分析
价格竞争中的多重纳什均衡
价格竞争中的多重纳什均衡是指在价格竞争中,企业 之间可能存在多个纳什均衡点,这些均衡点反映了不
第四章__纳什均衡的存在性与多重性

定义 4.5,一个点到集合的“对应”(correspondence) G : X → Y 是任何一个规定了对
X 中的每个点 x , G(x)是与 x 相对应的 Y 中的一个子集。
如果 X 和 Y 都是度量空间,则 X 和 Y 上的收敛和极限概念已经定义,这时有:
定义 4.6 ,一个对应 G:X→Y 是上半连续的(upper—hemicontinuous),当且仅当对每
静夫(Kakutani)不动点定理,而后者的证明只是前者的一个相对简单的运用。
我们所以要引用角谷静夫不动点定理,是因为在纳什均衡存在性证明中所遇到的反
应函数一般是多个因变量函数,即所谓对应(correspondence),而角谷静夫不动点定理正
好描述的是对应的一种性质。角谷静夫不动点定理是 Brouwer 不动点定理的推广,但其
所有的存在性定理证明都采用了不动点定理,这是因为,纳什均衡的概念在数学上
就是一个不动点的概念。在给出存在性定理及其证明之前,我们先来说明不动点的概念
和给出不动点定理。
什么是“不动点”呢?考虑一个方程 f (x) = x ,其中 x 为方程的解。我们将 f (⋅)视 为一种“变换”,即 f (⋅)是将 x 对应为 y = f (x)的变换,其中 x 和 y 分别是属于集合 X 和 Y 的两个元素,x ∈ Χ , y ∈Y 。如果 X = Y ,则方程 f (x) = x 的几何意义就是:变换 f (⋅)将 x 变为自己,即 x 在 f (⋅)变换下是不变的,故称 f (x) = x 的解为变换 f (⋅)的不动点。
于是 G 是上半连续的。 下面,我们将不动点概念扩充到对应的情形。
定义 4.7,一个对应 F: S → S 的一个不动点是 S 中任一满足 x ∈ F (x) 的 x 。
1.5 多重纳什均衡及其甄别
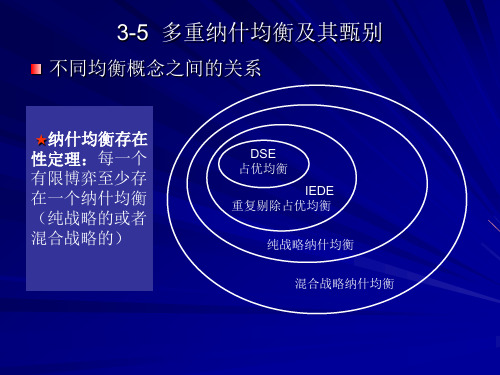
0,0,10 -5,-5,0
-5,-5,0 1,1,-5
乙
矩阵B
U 甲 D
L
R
-2,-2,0 -5,-5,0
-5,-5,0 -1,-1,5
1、上述博弈,如处于均衡(U,L,A),甲、乙共谋有共 上述博弈,如处于均衡(U
谋的激励,会导致结果(D 谋的激励,会导致结果(D,R,A) 纳什均衡的精髓:单独偏离没有好处。 纳什均衡的精髓:单独偏离没有好处。 但共谋偏离,那时均衡及前面介绍的方法就无法解决了。这 就需要抗共谋均衡的思想 就需要抗共谋均衡的思想。 抗共谋均衡的思想。 2、抗共谋均衡:与一般纳什均衡的区别,主要是在没有单 抗共谋均衡: 独偏离的激励的基础上,进一步引入了没有集体偏离的激 励的要求。即一个策略组合之所以成为抗共谋均衡,不仅 要求局中人在这个策略组合下没有单独偏离的激励,而且 也要求他们没有合伙集体偏离的激励。
(四)聚点均衡
在现实生活中,局中人可能会使用某些被博弈模型抽 象掉的信息来达到一个均衡,这些信息往往跟社会文化习 惯、局中人过去博弈的历史和经历有关。这就是聚点均衡 惯、局中人过去博弈的历史和经历有关。这就是聚点均衡 的思想。 对于一些即不存在帕累托优势,又不存在风险优势的 博弈,人们往往利用聚点均衡的思想来指导人们的行动。 如:交通靠左靠右问题;打电话续 接问题;看足球还是芭蕾舞;
L U 甲 D
R
5,1
4,4 图5
0,0 1,5
更为重要的是,奥蒙证明,如果每一个人收到不同的但 相关的信号,每个人都可以得到更高的期望效应。设想 两人同意由第三人通过掷骰子的办法决定每个人的选择, 如果1点或2点出现,A选择U;如果3 如果1点或2点出现,A选择U;如果3—6点出现,A选择 点出现,A D。B的情况相反:如果1—4点出现,B选择L,如果5—6 的情况相反:如果1 点出现,B选择L,如果5 点出现,B选择R 点出现,B选择R。假定第三方只告诉每个参与人选择什 么行动,而不透露什么点出现,。这样,当A被告诉D 么行动,而不透露什么点出现,。这样,当A被告诉D时, 他只知道3 他只知道3—6中的一个出现了,但并不知道是哪一个; 特别地他不知道B 特别地他不知道B被告诉选择什么。所以我们说每个人收 到的信号是相关的但不同的。下面我们说明上述规则是 一个纳什均衡。
混合策略纳许均衡课件

策略纳什均衡的算法优化。
混合策略纳什均衡与人工智能
02
随着人工智能的发展,可以尝试将混合策略纳什均衡应用于机
器学习和人工智能领域,以实现更高效和智能的决策。
混合策略纳什均衡与演化博弈论的结合
03
研究混合策略纳什均衡与演化博弈论的结合,可以更好地解释
现实生活中的动态博弈现象。
06
参考文献
参考文献
定义
混合策略纳什均衡课件
CONTENTSБайду номын сангаас
• 混合策略纳什均衡简介 • 混合策略纳什均衡的数学模型 • 混合策略纳什均衡的求解方法 • 混合策略纳什均衡的应用实例 • 混合策略纳什均衡的挑战与展
望 • 参考文献
01
混合策略纳什均衡简介
定义与概念
混合策略纳什均衡是一种博弈论中的概念,它描述了在给定对手策略的情况下,参 与者如何选择最优的行动方案。
定义策略空间
为每个参与人定义一个策略选 择的空间,这些策略可以是离 散的、连续的或混合的。
定义支付函数
根据每个参与人的策略选择, 定义他们的支付函数,即每个 参与人在该策略下的期望收益。
构建博弈矩阵
根据参与人的策略空间和支付 函数,构建一个博弈矩阵,用 以表示每个参与人选择不同策
略时的收益。
模型参数解 释
纳什均衡点或满足一定的收敛条件。
优化算法
优化算法是一种基于数学优化的方法,用于求解混合策略纳什均衡。
优化算法的基本步骤包括:定义一个目标函数,然后使用优化算法(如 梯度下降法、牛顿法等)寻找目标函数的最大值或最小值,从而得到纳
什均衡点。
优化算法的优点是能够快速找到纳什均衡点,适用于大规模问题。但缺 点是需要对问题进行数学建模,且对初始点的选择敏感。
纳什均衡的存在性与多重性

纳什均衡的存在性与多重性对于数学家来说,一个数学概念的存在性与唯一性是特别需要加以关注的。
这是因为,从形式逻辑角度看,如果某个事物并不存在,那么关于这个杜撰中的事物所给出的任何陈述或判断都可认为是正确的或错误的,因为对于不存在的事物来说,任何关于它的陈述或判断都不可能加以证伪。
所以,倘若某个概念所对应的事物并不存在。
那么,关于这个概念所给出的研究结论都必然不存在被证伪的可能。
因而根据波普尔的证伪主义观点,这样的研究不具备科学上的意义。
所以,我们在对任何新提出来的数学概念加以系统研究之前,首先需要弄清楚所研究的对象事物是否存在。
有许多被称为伪科学的东西,它们之所以被人们认为是“伪科学”的原因就是它们大肆谈论的东西并不存在或并未被证实其存在性。
譬如,所谓的特异功能或“超灵学”并未得到证实,而UFO研究迷们至今也未能拿出一件存在球外生命的证据,所以,特异功能学或“超灵学”或“不明飞行物学”实际上都可被归入伪科学。
除了存在性之外,概念事物的唯一性也是数学家们所关心的问题。
从纯理论的兴趣上看,数学家们更多地是从审美的角度上看待概念的唯一性,但从波普尔的证伪主义哲学看,模型均衡解的唯一性关系到模型的预测功能,从而是科学理论应基本具有的特征。
我们在第二章中曾指出,理论的预测功能是判别理论的科学性的准绳,而在第三章中,我们提出用纳什均衡作为模型的预测结果。
按照这样的逻辑,一个自然的推论就是:模型能否具有科学意义取决于纳什均衡的唯一性。
因为倘若纳什均衡不是唯一的,那么就难以根据模型对即将出现的结果加以预测,这种不确定性对于科学理论来说是不存在的。
再加上前面谈到的存在性问题,我们可以这样说,模型能否具有科学意义取决于纳什均衡的存在性和唯一性,因为这正是科学理论所具有的基本性质。
博弈论目前发展的情况是这样的:已经证明在非常一般的情况下,纳什均衡是存在的,这是一个好的结果;但是,在许多情形,模型的纳什均衡解不是唯一的,这被称为纳什均衡的多重性问题。
05博弈论—多重均衡与制度和文化课件

高尚 是高尚 者的墓 (gāoshàng)
(gāoshàng)
志铭
卑鄙是卑鄙者的通行证
第二十六页,共三十二页。
资源(zīyuán)争夺博弈(chicken)
Hawk
Hawk
-1,-1
Dove 10,0
Dove
0,10
5,5
第二十七页,共三十二页。
产权 的先占规则 (chǎn quán)
人们为什么遵守这个规则? 人们希望得到别人认可的愿望:
A
B
9, 9
-15, 8
8, -15
7, 7
第十三页,共三十二页。
协调与“风险 优势” (fēngxiǎn)
课堂实验
所有同学分为两个团体,其中一个团体的同学扮演 此协调博弈的参与人1,另一个团体的同学扮演参 与人2;
请两个团体的每个同学分别独立作出自己的选择 (xuǎnzé),不允许商议;
统计各团体选择两种策略的人数
1,1
如果(rúguǒ)在中国,出现(R,R),如果在英国,出现 (L,L)
第八页,共三十二页。
帕累托最优均衡(jūnhéng)
产品(chǎnpǐn)标准博弈
(3.5“,3.5”) 帕累托优于(5.5“,5.5”)
3.5“
5.5“
3.5“
8, 8
3, 2
5.5“
2, 3
6, 6
ห้องสมุดไป่ตู้
第九页,共三十二页。
第二页,共三十二页。
进门 博弈 (jìn mén)
先进 后进
先进(xiānjìn)
后进(hòujìn)
-1,-1
2,1
1,2
-1,-1
第三页,共三十二页。
多重均衡博弈理论

多重均衡博弈理论关键词:金融危机多重均衡博弈经济基本面用e表示,06[0,1],e越大表示经济基本面越好。
维持固定汇率对于政府的好处为常数b,维持固定汇率的成本用连续可导函数c(0,%)表示,0c为总投资者中参加投机攻击者的比率,显然,c为0的减函数和%的增函数,即偏导数c z0<0,c,0c>0。
面对投机攻击,当维护固定汇率的好处大于其成本时,政府维持固定汇率,当维护固定汇率的好处小于其成本时政府则放弃固定汇率。
每个投资者进行投机攻击的成本为t,t为0到1之间的正数,如果投机攻击使得政府放弃固定汇率时,投机攻击者可从货币贬值中得到好处1,如果政府继续维持固定汇率,那么投机攻击者将一无所获。
因此,投资者不进行攻击时的收益为0,而进行投机攻击并且获得成功时的收益为1-t,进行投机攻击失败时的收益为-t。
止匕外,假设当c(0,0)>b时,表示在经济基本面最差时,即使没有人进行投机攻击,政府也不能维持固定汇率;当c(1,1)<b时,表示如果在经济基本面很好时,即使所有的投资者都进行投机攻击,政府也能维持固定汇率。
所以根据函数c的性质,必定存在0,使c(0,0)=b,以及。
,使c(0,1)=b,因此:当06[0,0]时,不管是否存在投机攻击,政府维护固定汇率的成本超过收益,政府不会维持固定汇率;当06[0,1]时,不管是否存在投机攻击,政府维护固定汇率的成本小于收益,政府就会维持固定汇率;当86[0,q时,经济基本面处于所谓的“多重均衡区域”,政府是否维持固定汇率依赖于投机攻击者的比率。
金融危机的多重均衡博弈金融危机的产生与传导往往是由本国公众、本国政府、投机者甚至外国公众、外国政府、国际组织等多方参与者参加的多方非对称信息动态博弈过程。
在进行博弈均衡分析前有几个基本假设:当8€[0,健寸,经济基本面处于“多重均衡区域”,经济基本面不是太好,也不是很坏;在第一个假设的基础上,对于政府是强势政府还是弱势政府也很难有全面的信息了解;为了分析方便,文中给各博弈方的支付水平赋予了具体的数值,这些数值只表明大小多少关系,并不代表数值本身的四则运算关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年9月18日
博弈论第三章
9
第二讲多重纳什均衡
第三节多重纳什均衡的选择标准
二、风险优势标准:风险更小
(二)分析:偏离损失比较法
3.偏离损失比较
比较原则:二人偏离“作弊”的损失 VS偏离“不作弊”的损失
1×1<7×7
9,9 0,8
8,0 7,7
2019年9月18日
博弈论第三章
10
第二讲多重纳什均衡
1.纯策略纳什均衡 (A,A),(B,B),(C,C) 帕累托最优的纳什均衡:(C,C)
2019年9月18日
博弈论第三章
30
第二讲多重纳什均衡
第三节多重纳什均衡的选择标准
六、颤抖手精炼均衡 (三)案例 2.颤抖的手 (1)考虑博弈方2可能犯错误 博弈方2的错误——可能选A或B 博弈方1的反应:选B
Trembl一in个人g用-h手a抓n东d西 perfect equilib时可ri,能u手抓m一 不颤 住抖 他, 想就 抓
(一)颤的东抖西:手误非蓄意错 某一参与人的非蓄意错误
博弈偏离均衡路径的原因
2019年9月18日
博弈论第三章
24
第二讲多重纳什均衡
第三节多重纳什均衡的选择标准
六、颤抖手精炼均衡 (二)颤抖手均衡 1.基本思想 给定所有参与人均可能犯错误,如果
一、帕累托优势标准:得益最大 (二)帕累托优势标准 按照支付大小筛选纳什均衡
(3.5英寸盘,3.5英寸盘)
8,8
3,2
2,3
6,6
2019年9月18日
博弈论第三章
5
第二讲多重纳什均衡
情侣博弈?
关键:博弈方之间的协调 先动优势。 女士优先?
2019年9月18日
博弈论第三章
6
第二讲多重纳什均衡
第三节多重纳什均衡的选择标准
五、抗共谋均衡 (二)共谋偏离(集体偏离)均衡激励 1.如果集体偏离(1,1,10) 1与2集体偏离——(2,2,2) 1与2支付上升:具有集体偏离动机 (1,1,10)非抗共谋均衡
2019年9月18日
博弈论第三章
19
第二讲多重纳什均衡
第三节多重纳什均衡的选择标准
2019年9月18日
博弈论第三章
31
第二讲多重纳什均衡
第三节多重纳什均衡的选择标准
六、颤抖手精炼均衡 (三)案例 2.颤抖的手 (2)考虑博弈方1可能犯错误 博弈方1的错误——可能选A或B 博弈方2的反应:选B
2019年9月18日
博弈论第三章
32
第二讲多重纳什均衡
第三节多重纳什均衡的选择标准
五、抗共谋均衡 (二)共谋偏离(集体偏离)均衡激励 2.如果集体偏离(5,5,3) (3)1与3集体偏离——(0,5,5) 1的支付下降:无集体偏离动机 (5,5,3)——抗共谋均衡
2019年9月18日
博弈论第三章
21
第二讲多重纳什均衡
金无足赤,人无完人
人非圣贤,孰能无 过=>
要宽容
三、聚点均衡 (一)案例:城市分组博弈 参与人: 甲 乙
策略:把武汉、长春、长沙、哈尔滨 四座城市分成两组,每组2个城市
支付:甲乙分法相同——奖励XX元; 甲乙分法不同——奖励0元
2019年9月18日
博弈论第三章
13
第二讲多重纳什均衡
第三节多重纳什均衡的选择标准
三、聚点均衡 (二)聚点均衡 1.含义:多重纳什均衡中,人们预期最可能出现
的均衡。 2.标准
根据社会文化习惯、博弈历史等信息达到均衡 3.实质
规律性 强调文化与环境的作用
2019年9月18日
新婚夫妻的家务分担博弈 ;
博教弈论室第中三章的座位分配博弈。 14
第二讲多重纳什均衡
第三节多重纳什均衡的选择标准
四、相关均衡
(一)案例:“地域连坐”下的产品 质量博弈
某策略组合仍为最优策略组合,则实 现颤抖手均衡
如何理解?
2019年9月18日
博弈论第三章
25
第二讲多重纳什均衡
第三节多重纳什均衡的选择标准
六、颤抖手精炼均衡
(二)颤抖手均衡
2.定义: m——mistake
n人博弈中,对于每一个博弈方i,存
在严格混合策略序列 pim ,使下列条件
得到满足:
i
m
i
28
第二讲多重纳什均衡
穿针引线——学会宽容
纳什均衡:每一个人都把线穿入针眼 宽容:某参与人不能因为其他参与人
可能暂时无法把线穿进针眼而故意不 把线穿进针眼
宽容是一 种美德
2019年9月18日
博弈论第三章
29
第二讲多重纳什均衡
第三节多重纳什均衡的选择标准
六、颤抖手精炼均衡 (三)案例
第三节多重纳什均衡的选择标准
二、风险优势标准:风险更小 (二)分析:偏离损失比较法 4.结论 (1)偏离(不作弊,不作弊)的损失
更大:49 (2)不偏离(不作弊,不作弊)
2019年9月18日
9,9
8,0
博弈论第三章 第二讲多重纳什均衡
0,8 7,7
11
第三节多重纳什均衡的选择标准
二、风险优势标准:风险更小
五、抗共谋均衡 (二)共谋偏离(集体偏离)均衡激励 2.如果集体偏离(5,5,3) (1)1与2集体偏离——(2,2,2) 1与2支付下降:无集体偏离动机 (2)2与3集体偏离——(5,0,5) 2的支付下降:无集体偏离动机
2019年9月18日
博弈论第三章
20
第二讲多重纳什均衡
第三节多重纳什均衡的选择标准
(三)纳什均衡的选择标准:风险优 势标准
比较不同纳什均衡之间的风险状况, 风险小的纳什均衡优先
帕累托标准还是风险标准? 1.人会犯错误; 2.大多数人是风险厌恶者。 帕累托标准:理论 风险优势标准:实践
9,9 8,0
2019年9月18日
博弈论第三章 第二讲多重纳什均衡
0,8 7,7
12
第三节多重纳什均衡的选择标准
第三节多重纳什均衡的选择标准
二、风险优势标准:风险更小
(一)案例:串通作弊博弈
逆天的帕 累托优势
学生乙
标准 作弊 不作弊
作弊
学生甲
不作弊
9,9 8,0
0,8 7,7
2019年9月18日
博弈论第三章
7
第二讲多重纳什均衡
第三节多重纳什均衡的选择标准
二、风险优势标准:风险更小 (二)分析:偏离损失比较法 1.甲:单独偏离均衡的损失 乙坚守 (1)偏离“作弊”:9-8=1 (2)偏离“不作弊”:7-0=7
2019年9月18日
博弈论第三章
22
第二讲多重纳什均衡
经得起考验的纳什均衡
在其他参与人选择了错误策略的前提 下,某参与人仍能实现纳什均衡
他人不犯错误, 你能实现最优; 他人犯错误, 你仍能实现最
优
2019年9月18日
博弈论第三章
23
第二讲多重纳什均衡
第三节多重纳什均衡的选择标准
六、颤抖手精炼均衡
六、颤抖手精炼均衡 (二)颤抖手均衡 2.定义:m——mistake n人博弈中,对于每一个博弈方i,存
在严格混合策略序列 pim ,使下列条件
得到满足:
(2)对于任何可选择的混合策略 pi'i
u ( p , p ) u ( p ', p ) i 2019年9月18日
i
m
博i弈论第三章 i
六、颤抖手精炼均衡 (三)案例 3.结果
颤抖手均衡:(B,B)
2019年9月18日
博弈论第三章
33
第二讲多重纳什均衡
2019年9月18日
博弈论第三章 第二讲多重纳什均衡
4,4 -8,-2 -2,-8 -2,-126
香精包子的思考
香精包子——其他包子企业如何做? 参与人根据其共同观测到的信号选择 行动。
2019年9月18日
博弈论第三章 第二讲多重纳什均衡
4,4 -8,-2 -2,-8 -2,-127
第三节多重纳什均衡的选择标准
9,9 0,8
8,0 7,7
2019年9月18日
博弈论第三章
8
第二讲多重纳什均衡
第三节多重纳什均衡的选择标准
二、风险优势标准:风险更小 (二)分析:偏离损失比较法 2.乙:单独偏离均衡的损失 (1)偏离“作弊”:9-8=1 (2)偏离“不作弊”:7-0=7
9,9
甲坚守
0,8
8,0 7,7
A国
战争与和平
C国
鹰鸽鹰ຫໍສະໝຸດ -5,-58,-10
-10,8
10,10
鸽
2019年9月18日
博弈论第三章
1
第二讲多重纳什均衡
问题:博弈的最终结果?
鹰鸽博弈特征
两个(多个)纳什均衡
2019年9月18日
博弈论第三章
2
第二讲多重纳什均衡
第三章 混合策略纳什均衡
第三节 多重纳什均衡的选择标准
2019年9月18日
博弈论第三章
3
第二讲多重纳什均衡
第三节 多重纳什均衡的选择标准
一、帕累托优势标准:得益最大
(一)案例:计算机产品的兼容性
企业C
3.5英寸盘 5.25英寸盘
3.5英寸盘
8,8
3,2
企业A
2,3
6,6
5.25英寸盘
2019年9月18日
博弈论第三章
4
第二讲多重纳什均衡
第三节 多重纳什均衡的选择标准
(1)
lim
m
pi m
