高中物理竞赛：波动
合集下载
高中物理奥林匹克竞赛——波动3(33张)
9
对细棒中的纵谐波
P wu A2 2u sin2 (t x )
S
u
讨论
I P w u 1 u A2 2
S
2
1. 任意谐波的能量与振幅的平方、频率的平
方以及媒质的密度成正比。 I A2
2. 机械波的特性阻抗 Z u
两介质比较 Z 较小者称波疏介质
Z 较大者称波密介质
光波：折射率较大者称光密介质 10
A dA
x
dx
A Ao
0
ln A x
Ao
若 为常数, 则有 A A0ex
A0为x = 0 处的振幅。
I
1 uA2 2
2
1 2
uA02
2e
2x
I0
1 2
uA02
2
I I0e2x
式中的I0 和I 分别为x=0 和x=x 处的波的强度。
15
例空气中声波的吸收系数为1= 2×10-11 v 2（m-1 ），钢 中的吸收系数为2 = 4 ×10 -7 v （m -1 ），式中v 代表声 波的频率。问5MHz的超声波透过多少厚度的空气或钢 材后，其声强衰减到原来的1%。
21
S2 S1
新波阵面
原波阵面
t+t 时刻
障碍物的小孔成为新的波源
ut
t 时刻
22
例：
t 时刻波面 t+t时刻波面
· 波传播方向
u
· ·
·
·
ut
t + t
·······t •········
在各向同性 介质中传播
23
二、惠更斯原理的应用 1.原理给出：一切波动都具有衍射现象 衍射---偏离原来直线传播的方向 所以：衍射是波动的判据
对细棒中的纵谐波
P wu A2 2u sin2 (t x )
S
u
讨论
I P w u 1 u A2 2
S
2
1. 任意谐波的能量与振幅的平方、频率的平
方以及媒质的密度成正比。 I A2
2. 机械波的特性阻抗 Z u
两介质比较 Z 较小者称波疏介质
Z 较大者称波密介质
光波：折射率较大者称光密介质 10
A dA
x
dx
A Ao
0
ln A x
Ao
若 为常数, 则有 A A0ex
A0为x = 0 处的振幅。
I
1 uA2 2
2
1 2
uA02
2e
2x
I0
1 2
uA02
2
I I0e2x
式中的I0 和I 分别为x=0 和x=x 处的波的强度。
15
例空气中声波的吸收系数为1= 2×10-11 v 2（m-1 ），钢 中的吸收系数为2 = 4 ×10 -7 v （m -1 ），式中v 代表声 波的频率。问5MHz的超声波透过多少厚度的空气或钢 材后，其声强衰减到原来的1%。
21
S2 S1
新波阵面
原波阵面
t+t 时刻
障碍物的小孔成为新的波源
ut
t 时刻
22
例：
t 时刻波面 t+t时刻波面
· 波传播方向
u
· ·
·
·
ut
t + t
·······t •········
在各向同性 介质中传播
23
二、惠更斯原理的应用 1.原理给出：一切波动都具有衍射现象 衍射---偏离原来直线传播的方向 所以：衍射是波动的判据
高二物理竞赛课件：波动方程和波的能量
平面波波面
障碍物
平面波
12
惠更斯原理不仅适用于机械波，也适用于其它波， 如电磁波等。
例：在波线上有相距2.5 cm的A、B两点，已知点B
的振动相位比点A落后30，振动周期为2.0 s ，求波 速和波长。
解：因在波线上相距l两点的相位差为2
所以 波速为
l 2π 2.5 102m 0.30m
π
6
P wuS 1 A2 2uS
2 能流密度 单位时间内通过垂直于波线的单位面积的
平均能流称为能流密度，也称波强度。
I P wu 1 A2 2u
S
2
w 1 A22
28
能量密度 介质中单位体积的波动能量
w E E A2 2 sin 2 (t x )
ΔV SΔx
u
1. 能量密度随时间做周期变化，变化周期为波动周期的1/2
w 1 T wdt 1 A22
T0
2
w
o
t
波的平均能量密度与振幅的平方、 频率的平方和 介质密度的乘积成正比。
7
二、波的能流和能流密度 (energy flux density)
能流：单位时间内通过介质中某 面积的能量
如图，单位时间内通过S 面的 能量，等于体积 uS 中的能量
S u
平均能流 在一个周期内通过S面的能流的平均值
波动方程和波的能量
1
一、波的能量
波源 振动
介质 介质质元运动 波动 介质弹性形变
动能 势能
能量来自波源。 波源的能量随着波传播到波所到达的各处。
现以平面简谐纵波在均匀直棒中的传播为例， 讨论介质中的能量传播
2
纵波 u
a
b
动能
全国高中物理竞赛波动光学专题
波动光学【知识点】 一、光的干涉 1、 光波定义 光波是某一波段的电磁波，是电磁量E 和H 的空间的传播． 2、 光的干涉定义 满足一定条件的两束（或多束）光波相遇时，在光波重叠区域内，某些点合光强大于分光强之和，在另一些点合光强小于分光强之和，因而合成光波的光强在空间形成强弱相间的稳定分布，称为光的干涉现象，光波的这种叠加称为相干叠加，合成光波的光强在空间形成强弱相间的稳定分布称为干涉条纹，其中强度极大值的分布称为明条纹，强度极小值的分布称为暗条纹． 3、 相干条件表述 两束光波发生相干的条件是：频率相同，振动方向几乎相同，在相遇点处有恒定的相位差． 4、 光程差与相位差定义 两列光波传播到相遇处的光程之差称为光程差；两列光波传播到相遇处的相位之差称为相位差． 5、 双光束干涉强度公式表述 在满足三个相干条件时，两相干光叠加干涉场中各点的光强为12I I I ϕ=++∆ 式中，相位差122()πϕϕϕδλ∆=--保持恒定，若120I I I ==，则2002(1cos )4cos 2I I I ϕϕ∆=+∆= 6、 杨氏双缝干涉实验实验装置与现象 如图1所示，狭缝光源S 位于对称轴线上，照明相距为a 的两个狭缝1S 和2S ，在距针孔为D 的垂轴平面上观察干涉图样，装置放置在空气(1)n =中，结构满足,,sin tan d D D x θθ≈．在近轴区内，屏幕上的是平行、等间距的明暗相间的直条纹，屏幕上P 点的光程差δ为 21sin xr r d d Dδθ=-≈≈ 相应明暗纹条件是(21)2k x d D k λδλ⎧⎪==⎨+⎪⎩，干涉加强，，干涉减弱， 干涉条纹的位置是0,1,2,(21)2D k dx k D k d λλ⎧⎪⎪==±±⎨⎪+⎪⎩，明纹中心位置，，暗纹中心位置，式中，整数k 称为干涉级数，用以区别不同的条纹． 7、 薄膜干涉实验装置 如图2所示，扩展单色光源照射到薄膜上反射光干涉的情况，光源发出的任一单条光线经薄膜上下两个面反射后，形成两条光线○1、○2，在实验室中可用透镜将它们会聚在焦平面处的屏上进行观察，在膜的上下两个表面反射的两束光线○1和○2的光程差为22λδ=21S S图1图 23n二、光的衍射 1、光的衍射现象定义 一束平行光通过一狭缝K ，在其后的屏幕上将呈现光斑，若狭缝的宽度比波度大得多时，屏幕E 上的光斑和狭缝完全一致，如图3（a ）所示，这时可成光沿直线传播的；若缝宽与光波波长可以相比拟时，在屏幕E 上的光斑亮度虽然降低，但光斑范围反而增大，如图3（b ）所示的明暗相间的条纹，这就是光的衍射现象，称偏离原来方向传播的光为衍射光．2、惠更斯-菲涅耳原理表述 任何时刻波面上的每一点都可以作为子波的波源，从同一波面上各点发出的子波在空间相遇时，可以相互叠加产生干涉． 3、菲涅耳衍射与夫琅禾费衍射定义 光源到障碍物，或障碍物到屏的距离为有限远，这类衍射称为菲涅尔衍射；光源到障碍物，以及障碍物到屏的距离都是无限远，这时入射光和衍射光均可视为平行光，这类衍射称为夫琅禾费衍射．三、光的偏振 1、光的偏振性定义 光波是电磁波，其电矢量称为光矢量，在垂直于传播方向的平面内，光矢量E 可能具有的振动状态(矢量端点的轨迹)，称为光的偏振态．光矢量的振动方向与光传播方向所组成的平面称为振动面． 2、偏振光定义 振动方向具有一定规则的光波，称为偏振光。
高中物理奥林匹克竞赛——波动1(23张)
或者：
波长：波线上相位差为2的相邻两点间的距离 波的周期：一个完整的波通过某点所需的时间 波的频率：单位时间内通过某点完整波的数目 波速：振动状态传播的速度
1
13 某点
波长 波速与频率之间的关系：
u /T
18
波射线上各点振动相位(振动状态)的关系
1)同时看波线上各点
沿传播方向 各点相位依次落后
u
P
Q
x
同样
若Q点的振动形式是函数 f(t)
Q点与P点相距为x 则P 点的振动函数是f (t+x /u)
周期性的体现 普遍的结论 23
间距: x
振动时间差：t T 相位差: Δ 2π
21
即 x
则 t T Δ 2π
间距为任意x 的两点的关系： 在波线后方Q点 t 时刻的振动是前方P点在
t
x T
t
x u
时的振动
22
一般关系： 若已知波传播P点的振动形式可用函数 y0 =f(t)表示 Q点与P点相距为x 则Q点的振动函数是y =f (t- x /u)
·
··
·
·· ·
·
·
·
·
· · ·· ·
· · · ·· · · ··
t = 3T/4 t=T
弹性绳上的横波 15
结论
(1)介质中各质元都只在自己的平衡位置附近振动， 并未“随波逐流”。波的传播不是介质质元的传播。 (2)“上游”的质元依次带动“下游”的质元振动(依 靠质元间的弹性力)。 (3)某时刻某质元的振动状态将在较晚时刻于“下游” 某处出现，这就是“波是振动状态的传播”的含义。 (4)有些质元的振动状态相同，它们称作同相点。相
•相距一个波长两点 相位差是2
高中物理竞赛-波动
五、简谐振动的能量
以水平弹簧
E
Ek
Ep
1 2
m
dx dt
2
A
1 2
kx 2
1 2
kA2
振子为例： Ek 、Ep 周期为T/2
x A
Ek
Ep
1 4
kA2
T o
t E 1 kA2 2
-A
Ek
Ep
E
Ek A o
x
A
EP t T/2
七、 一维简谐振动的合成
1、 同方向、同频率的两个简谐振动的合成
S S’
B
vsT
uTS vSTS (u vS )TS
观察
W
u
u
u (u vS )TS u
波源向观察者运动
u
vS
S
者接
R W uv S S
收的 频率
u
4、两个同频率简谐振动的相位差：
x1 A1 cos(t 1 ) x2 A2 cos(t 2 )
它们的相差为：
(t 2 ) (t 1 ) 2 1
（也可写成 1 2 ） 若 2k (k为整), 两质点振动步调相同 (同相)
若 (2k 1) (k为整), 两质点振动步调相反 (反相)
x1 A1 cos(t 1 ) x2 A2 cos(t 2 )
x = x1+ x2 =A cos( t+ )
A A12 A22 2A1A2 cos
arctan A1 sin1 A2 sin2 A1 cos 1 A2 cos 2
两种特殊情况：
y
A
ω
A2
A2 sin 2
2
A1
o
1
高二物理竞赛振动和波动课件
可以求得波在两介质分界面处反射波的方向问题， 即反射角等于入射角
可以求得波在两介质分界面处折射波的方向问题， 即得到折射定律。
波的叠加原理
☆
几列波可以保持各自的特点通过同一媒质， 好像没有其他波一样；
在它们相重叠的区域内， 每一点的振动都是各个波单独 在该点产生的振动的矢量和。
波的干涉
☆
波的干涉现象
由频率相同、振动方向相同、相位相同 或相位差恒定的两个波源所发出的波，
在空间相遇，出现某些点振动始终加强， 某些点振动始终减弱或完全抵消
的现象称为波的干涉现象。
能产生干涉现象的波叫做相干波， 相应的波源叫做相干波源。
波的相干条件
频率相同、 振动方向相同、 相位相同或相位差恒定
反映了能量的传播过程
能量密度 单位体积媒质的波动能量
☆
w E 2 A2 sin 2 t x
V
u
在一个周期内的平均值 w 1 T wdt 1 2 A2
叫做平均能量密度
T0
2
平均能流密度
单位时间通过垂直于传播方向的单位面积的平均能流
I u 2 A2 / 2 A2
能流密度是矢量，方向与波速方向相同， 它的大小表示波的强度。
y Acost x / u Acos2 t / T x / Acos t 2 x /
“－”表示波沿x 轴正方向传播；“十”表示波x沿 轴负方向传播
波函数的物理意义
☆
它描述了波线上所有质点 离开自己平衡位置的位移随时间的变化规律。
y(t t, x ut) y(t, x) 表示了波的传播。
波长 同一波线上相位差为 2 的两相邻质点之间的距离，
即一个完整波形的长度。它反映波在空间上的周期性。
可以求得波在两介质分界面处折射波的方向问题， 即得到折射定律。
波的叠加原理
☆
几列波可以保持各自的特点通过同一媒质， 好像没有其他波一样；
在它们相重叠的区域内， 每一点的振动都是各个波单独 在该点产生的振动的矢量和。
波的干涉
☆
波的干涉现象
由频率相同、振动方向相同、相位相同 或相位差恒定的两个波源所发出的波，
在空间相遇，出现某些点振动始终加强， 某些点振动始终减弱或完全抵消
的现象称为波的干涉现象。
能产生干涉现象的波叫做相干波， 相应的波源叫做相干波源。
波的相干条件
频率相同、 振动方向相同、 相位相同或相位差恒定
反映了能量的传播过程
能量密度 单位体积媒质的波动能量
☆
w E 2 A2 sin 2 t x
V
u
在一个周期内的平均值 w 1 T wdt 1 2 A2
叫做平均能量密度
T0
2
平均能流密度
单位时间通过垂直于传播方向的单位面积的平均能流
I u 2 A2 / 2 A2
能流密度是矢量，方向与波速方向相同， 它的大小表示波的强度。
y Acost x / u Acos2 t / T x / Acos t 2 x /
“－”表示波沿x 轴正方向传播；“十”表示波x沿 轴负方向传播
波函数的物理意义
☆
它描述了波线上所有质点 离开自己平衡位置的位移随时间的变化规律。
y(t t, x ut) y(t, x) 表示了波的传播。
波长 同一波线上相位差为 2 的两相邻质点之间的距离，
即一个完整波形的长度。它反映波在空间上的周期性。
高中物理竞赛辅导参考资料之波动
请在放映状态下点击你认为是对的答案 小议链接4
以波速 u 沿 X 轴逆向传播的简谐波 t 时刻的波形如下图
A B C D
（1）A点的速度大于零； 点的速度大于零； （2）B点静止不动； 点静止不动； （3）C点向下运动； 点向下运动； （4）D点的振动速度小于零。 点的振动速度小于零。
结束选择
第二节
若 和 都是变量，即 是 和 的函数， 这正是波 动方程所表示的波线上所有的质点的振动位置分布随时间 而变化的情况。可看成是一种动态的波形图。 正向波
波沿 X 轴正向传播
续上
同一时刻，沿 X 轴正向，波线上各质点的振动相位依次落后。
反向波
波沿 X 轴反向传播
同一时刻，沿 X 轴正向，波线上各质点的振动相位依次超前。
例三
与
x =2m处
× 0.05 cos π ( 5×2 – 100 t ) – 0.05 cos ( 100 π t –10 π ) 初相为–10 π
x1 = 0.2 m 处的振动相位比原点处的振动相位落后 x2 = 0.35 m 处的振动相位比原点处的振动相位落后
两者的相位差为 100 π 0.15 20 0.75 π
第一节
振动的传播过程称为波动。 机械振动在媒质中的传播过程称为机械波。 产生机械波的必要条件：
媒质
18-1
generation and description of 波源 作机械振动的物体； mechanical wave 能够传播机械振动的弹性媒质。
波源带动弹性媒质中与其相邻的质点发生振动，振动相继 传播到后面各相邻质点，其振动时间和相位依次落后。 波动现象是媒质中各质点运动状态的集体表现，各质点仍 在其各自平衡位置附近作振动。
高中物理奥林匹克竞赛专题波动(共63张PPT)
13、He who seize the right moment, is the right man.谁把握机遇，谁就心想事成。2021/9/62021/9/62021/9/62021/9/69/6/2021 •14、谁要是自己还没有发展培养和教育好，他就不能发展培养和教育别人。2021年9月6日星期一2021/9/62021/9/62021/9/6 •15、一年之计，莫如树谷；十年之计，莫如树木；终身之计，莫如树人。2021年9月2021/9/62021/9/62021/9/69/6/2021 •16、教学的目的是培养学生自己学习，自己研究，用自己的头脑来想，用自己的眼睛看，用自己的手来做这种精神。2021/9/62021/9/6September 6, 2021 •17、儿童是中心，教育的措施便围绕他们而组织起来。2021/9/62021/9/62021/9/62021/9/6
• You have to believe in yourself. That's the secret of success. 人必须相信自己，这是成功的秘诀。
•
四. 波速、波长以及波的周期和频率
1.波速 u：
单位时间内振动状态传播的距离. 单位 m/s 波速是由介质的性质决定的。
u
声音在空气中传播速度 u33m 1/s 声音在水中传播速度 u 14m 50 / 声音在铁轨中传播速度 u 50m 00 /
ｂ两点的运动方向；３）波函数。
y(m)
u0.2m/s
0.04
a • •b
o
x(m)
解：1 ) 2 0 . 2 0 . 4 m T 0 .4 2 s
u 0 .2 1 0 . 5 Hz
T
0.2
2 v rad s 1
• You have to believe in yourself. That's the secret of success. 人必须相信自己，这是成功的秘诀。
•
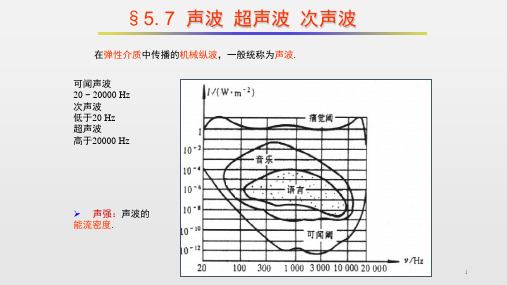
四. 波速、波长以及波的周期和频率
1.波速 u：
单位时间内振动状态传播的距离. 单位 m/s 波速是由介质的性质决定的。
u
声音在空气中传播速度 u33m 1/s 声音在水中传播速度 u 14m 50 / 声音在铁轨中传播速度 u 50m 00 /
ｂ两点的运动方向；３）波函数。
y(m)
u0.2m/s
0.04
a • •b
o
x(m)
解：1 ) 2 0 . 2 0 . 4 m T 0 .4 2 s
u 0 .2 1 0 . 5 Hz
T
0.2
2 v rad s 1
高中物理奥林匹克竞赛专题 波动(共90张PPT)
②.不同频率的同一类波在同一介质中波速 相同。
③.波在不同介质中频率不变。
§3 平面简谐波的波函数
用数学表达式表示波动----波函数
一、平面简谐波
·································
简谐振动在弹性介质中的传播，形成平面 简谐波。
波动是集体表现，各质点在同一时刻的振 动位移是不同的，用一个质点的振动方程代替 任意质点的振动方程。
6
10 2
cos 800
t
x 200
/
2
800
T 2 2 1 s 800 400
1 /T 400 Hz uT 200 / 400 0.5m
x u
②
2 , Tu
T
y
A
cos 2 Tt
x
③
y
A
cos
2
ut
x
Acost
2
x
④
•相距一个波长两点相位差是2
u
1 4P 7 10Q13 x
任意两质元间距为 x •相距x的任意两点的相位差
第2章 波 动 §1 机械波的产生与传播 §2波动周期、频率、波长、波速 §3平面简谐波的波函数 §4波的能量 §5惠更斯原理 §6波的干涉 §7 驻波 §8 多普勒效应
§1 机械波的产生与传播
一、机械波 机械振动在弹性介质中传播形成机械波。
二、机械波产生的条件 1.振源 2.弹性介质
高二物理竞赛波动能量和运动相对性的描述PPT(课件)
k YS dx
相对于S/系的位矢为：
体积元的位移最大时，三者均为零。
1 1 dy 绝P点对相空对间于是S指系长的度位的矢量为度：与参照系无关，绝2对时间是指时间的量度与参照系无2关。
dE kdy YSdx( ) 式中 为离开波P源的距离， 为
处的振幅.
2 2 dx 体积元在平衡位置时，动能、势能和总机械能均最大。
“同相”的定量分析：
y Acos(t x)
v
y
A
u sin (t
x
)
t
u
速度最大时： (t x) (2k 1) y 0
u
2
质点过平衡位置 时动能最大。
此时的相对形变（应变）
| y | A | sin (t x) | A 也最大！
x u
uu
同理可证：质元动能最小时，势能也最小。
15 – 8 多d d E E k 普 d 勒E d E k效 pd 应E 1 2 p d V d A V 2 A 22s 2 is n in 22(第t(t 十 u 五x u x )) 章 机械波
u Y
体积元在平衡位置时，动能、势能和总机械能均最大。
以固体棒中传播的纵波为例，取一个小体积元来分析波动能量的传播。
1 u dV(dy) y Asin(tx) 2
2
2
dx
x u
u
1dVA22sin2(tx)
2
u
dEk
15 – 8 多普勒效应
第十五章 机械波
dE P
1 u2dV(dy)2
15 –波8的能多量普勒能效流密应度
第十五章 机械波
1、 波动是能量的传播
当机械波在媒质中传播时，媒质中各质点均在其平 衡位置附近振动，因而具有振动动能。
高三物理竞赛 第10章振动与波动-波动 (共122张PPT)
一、波的动能、势能和能量
在波动过程中，振源的能量通过弹性介
质传播出去，介质中各质点在平衡位置附 近振动，介质中各部分具有动能，同时介 质因形变而具有势能。
•波动的过程实际是能量传递的过程。
1.波动的动能
弹性介质中取一体积元 dV，质元振动速
度为 v ，质量
dm dV
dm dV
dV
波函数
u
y A cos (t x / u )
u
V体 S u 与功率相同
P wuS 1 A 2 2uS
2 2.平均能流密度----波强
单位时间内通过垂直于波的传播方向的 单位面积上的平均能量。
I P wu 1 A 2 2u
S
2
单位：J•s1•m2 ， W •m2
例：一球面波源的功率为 100W，则距波 源 10m 处，波的平均能流密度 I 是多少？
二、波函数
任意时刻任意位置处的质点的振动位移 为波函数。
1.波源的振动方程
y A cos(t )
2.距波源为 x 处质点的振动方程
o·······x·······P·············u······x
u
o···············P··················x
x
P 点的振动比振源落后一段时间 t ,
t
x 200
/
2
800
T 2 2 1 s 800 400
1 /T 400 Hz
uT 200 / 400 0.5m
③. x 5m 质点振动与波源的相位差。
2 x 2 5 20 0.5
例3：如图所示为t=0时的波形，平面简谐 波向右移动速度 u =0.08 m/s，求：①.振 源的振动方程；②.波函数；③. P 点的振 动方程；④. a、b 两点振动方向。
高中物理竞赛 波动 (共17张PPT)
上点 A 的简谐运动方程 yA (3102 m) cos(4 π s1)t .
u
8m 5m 9m
C BA D x
1）以 A 为坐标原点，写出波动方程
A 3102 m T 0.5s 0 uT 10m
y Acos[2π ( t x ) ]
T
y (3102 m) cos2π ( t x )
0.5s 10m
10
2）以 B 为坐标原点，写出波动方程
yA (3102 m) cos(4 π s1)t
u
8m 5m 9m
C BA D x
B A 2π
xB xA
2π 5 10
π
B π yB (3102 m) cos[(4π s1)t π ]
y (3102 m) cos[2π ( t x ) π ] 0.5s 10m
1）观察者听到来自A 的频率 2）观察者听到来自B 的频率 3）观察者听到的拍频
vO
A
O
vsB
B
1） 解 u 330 m/s, vsA 0, vsB 60 m/s
'
u u
vo vs
' 330-30 500Hz 454.5Hz
330
4
例1 A、B 为两个汽笛，其频率皆为50Hz，A 静止，B 以60m/s 的速率向右 运动. 在两个汽笛之间有一观察者O，以30m/s 的速度也向右运动. 已知空气 中的声速为330m/s，求：
11
3）写出传播方向上点C、点D 的简谐运动方程
u
yA (3102 m) cos(4 π s1)t
8m 5m 9m 10m
C BA D x
点 C 的相位比点 A 超前
yC
高二物理竞赛波动学基础课件
动所传播的完整波的数目. 电磁波的传播可不需介质.
波前（wave front）—— 实际上，波在媒质中传播时，媒质总要吸收一部分能量。
1 T 波前（wave front）——
用数学表达式描述波线上每一质点在每一时刻的位移，称为行波的波动方程。 沿 轴负向
波速 u：波动过程中，某一振动状态（即 机械波：机械振动在弹性介质中的传播.
T
u Tu
注意
周期或频率只决定于波源的振动! 波速只决定于媒质的性质！
u 波速 与介质的性质有关， 为介质的密度.
u G 切变模量
横波
固体 u E 弹性模量
液、气体 u
K
体积模量
纵波
343 m s 空气，常温
如声音的传播速度
4000 m s 左右，混凝土
§10.2 平面简谐波
波前（wave front）—— 波到达的最前面的波振面
波阵面 波 射 线
平面波
球面波
描述波的物理量
Ay
u
O
x
-A
波长 ：沿波的传播方向，两个相邻的、相
位差为 2π 的振动质点之间的距离，即一个完整
波形的长度.
周期 T ：波前进一个波长的距离所需要
的时间.
频率 体积元的总机械能 ：周期的倒数，即单位时间内波
波动是振动的传播过程.
tt时刻
xx
波动能量 能流密度
当机械波在媒质中传播时，媒质中各质点均在 其平衡位置附近振动，因而具有振动动能. 同时，介质发生弹性形变，因而具有弹性势能. 以固体棒中传播的纵波为例分析波动能量的传播.
O x dx
x
O
y y dy
x
O x dx
波前（wave front）—— 实际上，波在媒质中传播时，媒质总要吸收一部分能量。
1 T 波前（wave front）——
用数学表达式描述波线上每一质点在每一时刻的位移，称为行波的波动方程。 沿 轴负向
波速 u：波动过程中，某一振动状态（即 机械波：机械振动在弹性介质中的传播.
T
u Tu
注意
周期或频率只决定于波源的振动! 波速只决定于媒质的性质！
u 波速 与介质的性质有关， 为介质的密度.
u G 切变模量
横波
固体 u E 弹性模量
液、气体 u
K
体积模量
纵波
343 m s 空气，常温
如声音的传播速度
4000 m s 左右，混凝土
§10.2 平面简谐波
波前（wave front）—— 波到达的最前面的波振面
波阵面 波 射 线
平面波
球面波
描述波的物理量
Ay
u
O
x
-A
波长 ：沿波的传播方向，两个相邻的、相
位差为 2π 的振动质点之间的距离，即一个完整
波形的长度.
周期 T ：波前进一个波长的距离所需要
的时间.
频率 体积元的总机械能 ：周期的倒数，即单位时间内波
波动是振动的传播过程.
tt时刻
xx
波动能量 能流密度
当机械波在媒质中传播时，媒质中各质点均在 其平衡位置附近振动，因而具有振动动能. 同时，介质发生弹性形变，因而具有弹性势能. 以固体棒中传播的纵波为例分析波动能量的传播.
O x dx
x
O
y y dy
x
O x dx
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
某正向余弦波
时的波形图如下
则此时 点的运动方向
，振动相位
。
正向波，沿 轴正向微移原波形图判断出 点此时向下运动。并判 断出原点处质点从Y = A向平衡点运动，即初相 。
由图可知
代入得
即
一平面简谐波以波速 位于
沿 X 轴正向传播。
处的 P 点的振动方程为
设 B 点距原点为 P 点振动传到 B 点需时 即 B 点 时刻的振动状态与 P 点 时刻的振动状态相同
电磁波 electromagnetic wave
第一节
振动的传播过程称为波动。 机械振动在媒质中的传播过程称为机械波。 产生机械波的必要条件：
波源 媒质 作机械振动的物体； 能够传播机械振动的弹性媒质。
波源带动弹性媒质中与其相邻的质点发生振动，振动相继 传播到后面各相邻质点，其振动时间和相位依次落后。 波动现象是媒质中各质点运动状态的集体表现，各质点仍 在其各自平衡位置附近作振动。
横波：质点的振动方向与波的传播方向垂直 纵波：质点的振动方向与波的传播方向平行
质点振动方向
软绳
波的传播方向
质点振动方向 软弹簧
波的传播方向
在机械波中，横波只能在固体中出现；纵波可在气体、液体和固体中出现。 空气中的声波是纵波。液体表面的波动情况较复杂，不是单纯的纵波或横波。
波面 波前
振动相位相同的点连成的面。 最前面的波面。
沿 X 轴正向传播的平面简谐波动方程
波动方程常用周期 由 得
波长
或频率
的形式表达
消去波速
和
分别具有单位时间和单位长度的含义，
组成对应关系 。
分别与时间变量 和空间变量
若给定
，波动方程即为距原点
处的质点振动方程
距原点
处质点振动的初相
若给定 ，波动方程表示所给定的 时刻波线上各振动 质点相对各自平衡点的位置分布，即该时刻的波形图。
简谐波
由简谐振动的传播所形成的波动。
对于机械波，若波源及弹性媒质中各质点都持续地作简 谐振动所形成的连续波，则为简谐机械波。 简谐波又称余弦波或正弦波，是规律最简单、最基本的波。 各种复杂的波都可以看作是许多不同频率的简谐波的叠加。 简谐波的一个重要模型是平面简谐波。 平面简谐波的波面是平面，有确定的波长和传播方向，波 列足够长，各质点振动的振幅恒定。
正向余弦波方程
一正向余弦波 10 m 时刻 波线上两质点 振动情况如图
质点 ： 解得 质点 ： 解得 或 旋转矢量法判断取 旋转矢量法判断取
2.5 (m)
的 P 点位置为 波形图
2.5
7.5 (m)
等于几米 此时的波形图
2.5 10 m
7.5
(m)
请在放映状态下点击你认为是对的答案
以波速 u 沿 X 轴逆向传播的简谐波 t 时刻的波形如下图
高中物理竞赛
波 动
Contents
chapter 18
机械波的产生与描述 generation and description of mechanical wave 波的能量 the energy of wave 声波 sound wave
波的干涉 wave interference 多普勒效应 Doppler effect
得 波动方程
波动方程 y = 0.05 cos p ( 5 x – 100 t ) (SI) 此波是正向还是反向波，并求 A、n、T、u 及 l ； x = 2 m 处质点的振动方程及初相； x1 = 0.2 m及 x2 = 0.35 m 处两质点的振动相位差。 cosa = cos(-a) 0.05 cos p ( 5 x – 100 t ) x cos 100 p ( t – ) 0.05 20 正向波 比较得 0.05 m 100 p 0.02 s 500 Hz 20 m ·s -1 0.4 m 而且得知原点（ x = 0 ) 处质点振动初相
若 和 都是变量，即 是 和 的函数， 这正是波 动方程所表示的波线上所有的质点的振动位置分布随时间 而变化的情况。可看成是一种动态的波形图。
正向波
波沿 X 轴正向传播
同一时刻，沿 X 轴正向，波线上各质点的振动相位依次落后。
反向波
波沿 X 轴反向传播
同一时刻，沿 X 轴正向，波线上各质点的振动相位依次超前。
请在放映状态下点击你认为是对的答案
以波速 u 沿 X 轴逆向传播的简谐波 t 时刻的波形如下图
A B C D
（1）A点的速度大于零； （2）B点静止不动； （3）C点向下运动； （4）D点的振动速度小于零。
结束选择
请在放映状态下点击你认为是对的答案
以波速 u 沿 X 轴逆向传播的简谐波 t 时刻的波形如下图
波前 波面 波线
平面波 （波面为平面的波）
波线（波射线） 球面波 （波面为球面的波）
波的传播方向。在各向同性媒质中， 波线恒与波面垂直。
波传播方向
波速
波长 周期 频率 波速
振动状态完全相同的相邻两质点之间的距离。
波形移过一个波长所需的时间。
周期的倒数。
单位时间内振动状态（振动相位）的传播速度， 又称相速。机械波速取决于弹性媒质的物理性质。 或
一列平面简谐波 （假定是横波）
观测坐标原点任设 （不必设在波源处）
波沿 X 轴正向传播 （正向行波）
设
位于原点
处质点的振动方程为 沿 轴正向传播 。对应同一时刻 ， 点的
已知振动状态以速度
振动状态与原点在
时刻的振动状态相同。
因此，在设定坐标系中，波线上任一点、任意时刻的振动规律为
这就是沿 X 轴正向传播的平面简谐波动方程。它是时间和空间的双重周期函数。
A B C D
（1）A点的速度大于零； （2）B点静止不动； （3）C点向下运动； （4）D点的振动速度小于零。
与
x =2m处
x1 = 0.2 m 处的振动相位比原点处的振动相位落后 x2 = 0.35 m 处的振动相位比原点处的振动相位落后
两者的相位差为 100 p
0.05 cos p ( 5×2 – 100 t ) 0.05 cos ( 100 p t –10 p ) 初相为–10 p
0.15 20
0.75 p
A B D
C
（1）A点的速度大于零； （2）B点静止不动； （3）C点向下运动； （4）D点的振动速度小于零。
结束选择
请在放映状态下点击你认为是对的答案
以波速 u 沿 X 轴逆向传播的简谐波 t 时刻的波形如下图
A B C D
（1）A点的速度大于零； （2）B点静止不动；
（3）C点向下运动；
（4）D点的振动速度小于零。