全国高中物理竞赛波动光学专题

合集下载

高二物理竞赛(9)几何光学和波动光学.

高二物理竞赛（9）几何光学和波动光学班级：_____________ 姓名：_________________ 座号：_____________一、一平凸透镜焦距为f，其平面上镀了银，现在其凸面一侧距它2f处，垂直于主轴放置一高为H的物，其下端在透镜的主轴上（如图所示）。

（1）用作图法画出物经镀银透镜所成的像，并标明该像是虚、是实；（2）用计算法求出此像的位置和大小。

二、有一水平放置的平行平面玻璃板H，厚3.0cm，折射率n=1.5。

在其下表面下2.0cm处有一小物S；在玻璃扳上方有一薄凸透镜L，其焦距f=30cm，透镜的主轴与玻璃板面垂直；S位于透镜的主轴上，如图所示。

若透镜上方的观察者顺着主轴方向观察到S的像就在S处，问透镜与玻璃板上表面的距离为多少？三、一束平行光沿薄平凸透镜的主光轴入射，经透镜折射后，会聚于透镜f=48cm处，透镜的折射率n=1.5。

若将此透镜的凸面镀银，物置于平面前12cm处，求最后所成像的位置。

四、图中，三棱镜的顶角α为60°，在三棱镜两侧对称位置上放置焦距均为f=30.0cm的两个完全相同的凸透镜L1和L2。

若在L1的前焦面上距主光轴下方y=14.3cm处放一单色点光源S，已知其像S 与S对该光学系统是左右对称的。

试求该三棱镜的折射率。

五、两个薄透镜L1和L2共轴放置，如图所示。

已知L1的焦距f1=f，L2的焦距f2=-f，两透镜间距离也是f。

小物体位于物面P上，物距u1=3f。

（1）小物体经这两个透镜所成的像在L2的__________边，到L2的距离为_________，是__________倍（虚或实）、____________像（正或倒），放大率为_________________；（2）现在把两透镜位置调换，若还要给定的原物体在原像处成像，两透镜作为整体应沿光轴向____________边移动距离_______________。

这个新的像是____________像（虚或实）、______________像（正或倒），放大率为________________。

全国高中物理竞赛波动光学训练题答案

【波动光学训练题答案】1、用尖劈空气膜的干涉测微丝的直径。

如图所示，两块平面玻璃一端互相接触，另一端夹着待测的微丝，微丝与接触棱平行，用单色（5893Ǻ）平行光垂直照射在玻璃上，两块玻璃间的空气膜对光产生等厚干涉，测量出28.880mm L =，用显微镜读出30条干涉条纹（亮纹）的间距为 4.295mm x ∆=，求金属微丝的直径。

解：本题中可近似认为折射线垂直于下底面，则光程差 0122d λδ=-第k 级亮纹满足 01022d k λλ-= 第()k m +级亮纹满足 0202()2d k m λλ-=+两式相减得 21022d d m λ-= 故 2102md d d λ∆=-= 而 tan d xα∆=∆ 这样得 0202 5.9410mm 2m Lm L d D L x x xλλ-∆====⨯∆∆∆2、如图（a ）所示，在洛埃镜试验中，点光源S 早镜平面上方2mm 处，反射镜位于光源与屏镜正中间，镜长40cm l =，屏到光源的距离1.5m D =，波长为5000 Ǻ。

试求（1）条纹间距；（2）屏幕上干涉条纹的范围；（3）干涉条纹间距数。

解：（1）洛埃镜中，点光源S 和它在平面镜中的像S '构成两相干光源，故在屏幕上形成的条纹间距0.1875(mm)ldλ∆== （2）设干涉区域的下、上端离平面镜与屏交点的距离分别为1y 、2y ，如图（b）所示，由相似三L1y图（b ）S屏2yS∙A M B屏图（a ）角形知识得1222D l y D l l -=-+， 2222D lly D l -+=- 分别解得 1 1.16(m m )y =， 2 3.46(m m)y = （3）干涉条纹间距数为 2112.25y y n x-==∆3、为了减少从玻璃上表面反射光成分，在玻璃表面上敷一层薄膜，薄膜的折射率小于玻璃的折射率。

在入射光包含波长1700nm λ=和2420nm λ=的情况下，为使这两种波长的反射光被最大限度减弱，在玻璃表面上敷上折射率为43n =的薄膜。

高二物理竞赛波动光学课件3

(2)k (a b) k k 4, 取k 1 a
a mi n
ab 4
1.5m
b d amin 4.5m
(3)由光栅方程 sin 1，k kmax
a b 6m
k max
10
0.6m
在-900<sin<900范围内可观察到的明纹级数为
k=0,1, 2, 3, 5, 6, 7, 9,共15条明纹
C 虽长不满七尺，而心雄万丈。
A 心志要坚，意趣要乐。
1 一个人如果胸无大志，既使再有壮丽的举动也称不上是伟人。
A2 大丈夫处世，不能立功建业，几与草木同腐乎?
远大的希望造就伟大的人物。无钱之人脚杆硬，有钱之人骨头酥。壮志与毅力是事业的双翼。
A3 鸟贵有翼，人贵有志。
志高山峰矮，路从脚下伸。雄心志四海，万里望风尘。自信是成功的第一秘诀海纳百川有容乃大壁立千仞无欲则刚壮志与毅力是事业的双翼。自信是成功的第一秘诀
A 无所求则无所获。
谁不向前看，谁就会面临许多困难。
相邻平面间的距离是入射单色光的半波长
任何两个相邻波带上对应点所发出的光线到达AC 平面的光程差均为半波长
（即位相差为），在P
点会聚时将一一抵消。
考察衍射角 0 的一束平行光，经透镜后
同相位地到达P0点，所以P0点振幅为各分振动振幅之和，合振幅最大，光强最强。
k 就是所缺的级次
产生干涉的两条光线
相邻狭缝对应位置衍射角相同的两条光线。
d
a b
注意：类似的两条光线有无穷多组。
光程差 (a b) sin
光栅衍射明纹公式光栅衍射图样特点
(a b) sin k 光栅方程
1. 亮、细、疏 2. 缺级现象单缝衍射和多缝干涉的总效果。

高中物理竞赛-波动光学

2
2
膜的颜色呈黄绿色 D
i i C d
sin 31 2 1.35 520 1 nm 1297.8nm A 1.35 r
1297.8 380nm nm 780nm k 1
如图所示，薄膜的两个界面OM和ON构成尖劈，尖劈的夹角θ较小，光源S离劈较近．证明光源S发出的光经界面OM和ON反射后产生的干涉条纹是以O为圆心、以r为半径的圆． S
预期的光衍射现象——光到达的范围变大了
♠
♠
光的衍射现象
光离开直线路径绕到障碍物背后去的现象叫光的衍射
◎ 单缝衍射
◎ 光衍射成因与规律

R
A G G A G1 A1 A G1 G2 A2 3
B
b sin 2k
k 干涉相消（暗纹） 2 k 1, 2, 3, 干涉加强（明纹） b sin (2k 1)
x D 2k 1 x 2k 1 , k 1, 2, D 2 2d
A
A
min
S1 S S2
S
E
min
A
min
D i A n 1 A
b
A
E
d 2b n 1 A
D x 2b n 1 A
E
S r
望远镜的最小分辨角
1.22 550 109 1.22 rad=2.68 10-7 rad d 2.5
人眼的最小分辨角则为

1.22 550 109 1.22 rad=2.68 10-4rad d 2.5 103
望远镜与人眼相比，其分辨率与人眼分辨率的倍数为
P

全国高中物理竞赛波动光学专题

波动光学【知识点】一、光的干涉 1、光波定义光波是某一波段的电磁波，是电磁量E 和H 的空间的传播． 2、光的干涉定义满足一定条件的两束（或多束）光波相遇时，在光波重叠区域内，某些点合光强大于分光强之和，在另一些点合光强小于分光强之和，因而合成光波的光强在空间形成强弱相间的稳定分布，称为光的干涉现象，光波的这种叠加称为相干叠加，合成光波的光强在空间形成强弱相间的稳定分布称为干涉条纹，其中强度极大值的分布称为明条纹，强度极小值的分布称为暗条纹． 3、相干条件表述两束光波发生相干的条件是：频率相同，振动方向几乎相同，在相遇点处有恒定的相位差． 4、光程差与相位差定义两列光波传播到相遇处的光程之差称为光程差；两列光波传播到相遇处的相位之差称为相位差． 5、双光束干涉强度公式表述在满足三个相干条件时，两相干光叠加干涉场中各点的光强为12I I I ϕ=++∆ 式中，相位差122()πϕϕϕδλ∆=--保持恒定，若120I I I ==，则2002(1cos )4cos 2I I I ϕϕ∆=+∆= 6、杨氏双缝干涉实验实验装置与现象如图1所示，狭缝光源S 位于对称轴线上，照明相距为a 的两个狭缝1S 和2S ，在距针孔为D 的垂轴平面上观察干涉图样，装置放置在空气(1)n =中，结构满足,,sin tan d D D x θθ≈．在近轴区内，屏幕上的是平行、等间距的明暗相间的直条纹，屏幕上P 点的光程差δ为 21sin xr r d d Dδθ=-≈≈ 相应明暗纹条件是(21)2k x d D k λδλ⎧⎪==⎨+⎪⎩，干涉加强，，干涉减弱，干涉条纹的位置是0,1,2,(21)2D k dx k D k d λλ⎧⎪⎪==±±⎨⎪+⎪⎩，明纹中心位置，，暗纹中心位置，式中，整数k 称为干涉级数，用以区别不同的条纹． 7、薄膜干涉实验装置如图2所示，扩展单色光源照射到薄膜上反射光干涉的情况，光源发出的任一单条光线经薄膜上下两个面反射后，形成两条光线○1、○2，在实验室中可用透镜将它们会聚在焦平面处的屏上进行观察，在膜的上下两个表面反射的两束光线○1和○2的光程差为22λδ=21S S图1图 23n二、光的衍射 1、光的衍射现象定义一束平行光通过一狭缝K ，在其后的屏幕上将呈现光斑，若狭缝的宽度比波度大得多时，屏幕E 上的光斑和狭缝完全一致，如图3（a ）所示，这时可成光沿直线传播的；若缝宽与光波波长可以相比拟时，在屏幕E 上的光斑亮度虽然降低，但光斑范围反而增大，如图3（b ）所示的明暗相间的条纹，这就是光的衍射现象，称偏离原来方向传播的光为衍射光．2、惠更斯-菲涅耳原理表述任何时刻波面上的每一点都可以作为子波的波源，从同一波面上各点发出的子波在空间相遇时，可以相互叠加产生干涉． 3、菲涅耳衍射与夫琅禾费衍射定义光源到障碍物，或障碍物到屏的距离为有限远，这类衍射称为菲涅尔衍射；光源到障碍物，以及障碍物到屏的距离都是无限远，这时入射光和衍射光均可视为平行光，这类衍射称为夫琅禾费衍射．三、光的偏振 1、光的偏振性定义光波是电磁波，其电矢量称为光矢量，在垂直于传播方向的平面内，光矢量E 可能具有的振动状态(矢量端点的轨迹)，称为光的偏振态．光矢量的振动方向与光传播方向所组成的平面称为振动面． 2、偏振光定义振动方向具有一定规则的光波，称为偏振光。

人大附中高中物理竞赛辅导课件(波动光学)光学牛顿环(共13张ppt)

2020全国高中物理学奥林匹克竞赛人大附中竞赛班辅导讲义
（含物理竞赛真题练习）
波动光学
光学牛顿环显微镜
半反射镜
装置： A--曲率半径很大的凸透镜 B--平面光学玻璃干涉图样：
r A B 随着r的增加而变密！
2、牛顿环Newton ring (等厚干涉特例)
R
r o
e
空气薄层中，任一厚度e处上下表面反射光的干涉条件：
rk1 rk
( (k 1)
k)
R
R
(k 1)
k
随着牛顿环半径的增大，条纹变得越来越密。即
条纹不等间距，内疏外密。
条纹形状：干涉条纹是以平凸透镜与平面玻璃板的接触点为圆心，明暗相间的同心圆环，中心为暗点(实际上由于磨损、尘埃等因素的影响，中央常模糊不清)。
问题1 在折射率相同的平凸透镜与平面玻璃板间充以某
种透明液体。从反射光方向观察，干涉条纹将是：
A、中心为暗点，条纹变密
B、中心为亮点，条纹变密 C、中心为暗点，条纹变稀
选择A：正确！
D、中心为亮点率有关，条纹变密
F、中心的亮暗与液体及玻璃的折射率有关，条纹变稀
问题2 如图，用单色平行光垂直照射在观察牛顿环的装置上，当平凸透镜垂直向上缓慢平移而远离平板玻璃时，干涉条纹将： A、静止不动 B、向中心收缩 C、向外冒出 D、中心恒为暗点，条纹变密
显微镜测得由中心往外数第 k 级明环的半径 rk 3.0 10 3 m , k 级往上数第16 个明环半径 rk16 5.0 10 3 m ，
平凸透镜的曲率半径R=2.50m（苏州）
M
C
R
r
d
N
o
求：紫光的波长？

高二物理竞赛波动光学PPT(课件)

莫雷合作，进行了著名的迈克尔逊-莫雷实验，这是一个最重大的否定性实验，它动摇了经典物理学的基础。
（11）单缝衍射的动态变化
5 光的衍射惠更斯-菲涅耳原理角范围 sin * 惠更斯-菲涅耳原理
a
a
线范围 f x f
a
a
中央明纹的宽度
l0
2x1
2
a
f
（3）条纹宽度（相邻条纹间距）
asin2kk 干涉相消（暗纹）
E A
S B
E
A
a'
S
a b
B
b'
波在传播过程中遇到障碍物，能够绕过障碍物的
边缘前进这种偏离直线传播的现象称为衍射现象。在衍射现象中，不仅涉及到波的绕弯传播，而且还涉及到波场能量的重新分布
S
圆孔衍射 *
S
单缝衍射 *
HP
G
11.5.2 惠更斯-菲涅耳原理
惠更斯： (ChristianHaygen，1629—1695)
荷兰物理学家、数学家、天文学家。1629年出生于海牙。1655年获得法学博士学位。1663年成为伦敦皇家学会的第一位外国会员。他的重要贡献有： ①建立了光的波动学说，打破了当时流行的光的微粒学说，提出了光波面在媒体中传播的惠更斯原理。 ②1673年他解决了物理摆的摆动中心问题，测定了重力加速度之值，改进了摆钟，得出了离心力公式，还发明了测微计。 ③他首先发现了双折射光束的偏振性，并用波动观点作了解释。 ④在天文学方面，他供助自己设计和制造的望远镜于1665年，发现了土星卫星----土卫六，且观察到了土星环。惠更斯的主要著作是1690年出版的《论光》，共有22卷。
O.
lk lk+5
解：根据暗环半径公式：

高中物理竞赛第十一章波动光学合集(共131张)

b
n1
n1
d
n1 n2 n2
20.
b. 相邻最亮中心 (或最暗中心)处
劈尖的厚度差
d
dk 1
dk
2n2
n
2
c. (近似)几何关系
图中两三角形相似
b
dk
d G1
k 1 n
2 G2
D
L
b
， sin tan D 2n2
Lb
b
利用以上关系— 测量( ,D , ,n2 )
D n L L
透射光的光程差
Δt 2d n22 n12 sin2 i
垂直入射
Δ反 Δ透
2
“互补”
注意：透射光和反射光干涉具有互补性，符合能量守恒定律.
n2 n1
1
L 2
P
iD 3
M1 n1 n2
A
C
d
M2 n1
B
E
45
相讨位论跃：变影响Δr 2d n22 n12 sin2 i / 2
根据具体情况而定
k=0
x0
d d
3mm
(o点上方)
(5) 白光入射对中央明纹(k = 0) — 白光
对其它明纹(k ≠ 0) — x d 色散 (红外紫内)
d
10.
二. 缝宽(光源线度)对干涉条纹的影响
空间相干性
实验观察到，对于普通光源随缝宽的增大，干涉条纹变模糊，最后消失．
P
S"
S1
r1
B
S S'
d
o1
除考虑AB波阵面后的波程
2 1
BC
2
h
差r, 还要考虑相位跃变问题

高中物理竞赛辅导精品课件——专题25：波动光学与量子理论拾零(共76张 PPT)

2
l PB AB PA
干涉条纹满足
P2 P1
2r sin
P2B AB P1A P1P2 2 r sin
2k 1 k 0,1, 2,
明条纹是以O为圆心、半径为
r明
2
2k 1
4 sin
k 0,1, 2,
的同心圆；
干涉条纹满足 2r sin k k 1, 2, 3,
k 暗条纹是以O为圆心、半径为 r暗 2 sin k 1, 2, 3, 的同心圆；
膜厚度须满足两束光的相差为2kπ:
2
d cos
r
2 /n
2d
tan
r
sin
i
2
Байду номын сангаас
i
i
sin i
n
2k
sin r
d
4n
4
sin2 n
i
2k
1
1
sin n
i
2
r
d
2k 1
对垂直入射光,在k=0时,极大加
d 4 n2 sin2 i
要d为最小，k取０，故
强波长满足
2
2nd
1
500
d
nm
2x ；
2 4.295
．
29 57.5m
如图所示，在一块平玻璃片B上，放一曲率半径为R的平凸透镜A，在A、B之间形成空气薄层，当平行光垂直射向平凸透镜时，可以观察到透镜表面出现以接触点O为中心的许多同心环，称为牛顿环． ⑴确定形成牛顿环的明、暗环处空气层厚度e适合的条件，入射光波长为λ； ⑵确定明、暗环的半径r． ⑶在接触处是明纹还是暗纹？
预期的光衍射现象——光到达的范围变大了
♠ 光的衍射现象

2020年高中物理竞赛习题专题十二：《波动光学》(Word版含解析)

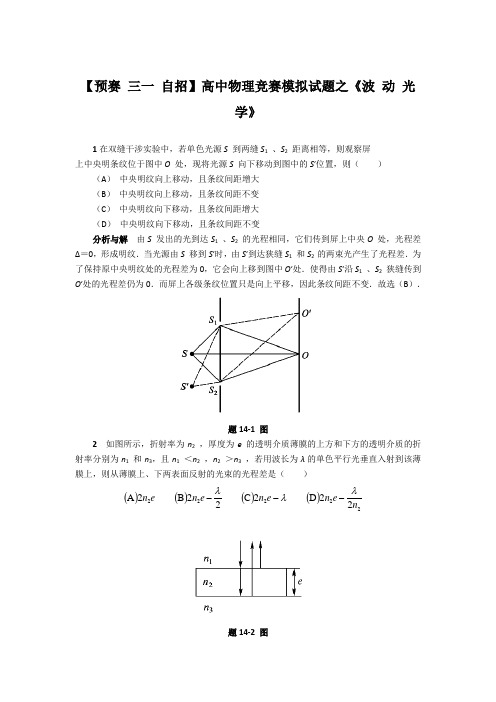
【预赛三一自招】高中物理竞赛模拟试题之《波动光学》1在双缝干涉实验中，若单色光源S 到两缝S 1 、S 2 距离相等，则观察屏上中央明条纹位于图中O 处，现将光源S 向下移动到图中的S ′位置，则（）（A ）中央明纹向上移动，且条纹间距增大（B ）中央明纹向上移动，且条纹间距不变（C ）中央明纹向下移动，且条纹间距增大（D ）中央明纹向下移动，且条纹间距不变分析与解由S 发出的光到达S 1 、S 2 的光程相同，它们传到屏上中央O 处，光程差Δ＝0，形成明纹．当光源由S 移到S ′时，由S ′到达狭缝S 1 和S 2 的两束光产生了光程差．为了保持原中央明纹处的光程差为0，它会向上移到图中O ′处．使得由S ′沿S 1 、S 2 狭缝传到O ′处的光程差仍为0．而屏上各级条纹位置只是向上平移，因此条纹间距不变．故选（B ）．题14-1 图2 如图所示，折射率为n 2 ，厚度为e 的透明介质薄膜的上方和下方的透明介质的折射率分别为n 1 和n 3，且n 1 ＜n 2 ，n 2 ＞n 3 ，若用波长为λ的单色平行光垂直入射到该薄膜上，则从薄膜上、下两表面反射的光束的光程差是（）()()()()2222222D 2C 22B 2A n e n e n e n e n λλλ---题14-2 图分析与解由于n 1 ＜n 2 ，n 2 ＞n 3 ，因此在上表面的反射光有半波损失，下表面的反射光没有半波损失，故它们的光程差222λ±=∆e n ，这里λ是光在真空中的波长．因此正确答案为（B ）．3 如图（a ）所示，两个直径有微小差别的彼此平行的滚柱之间的距离为L ，夹在两块平面晶体的中间，形成空气劈形膜，当单色光垂直入射时，产生等厚干涉条纹，如果滚柱之间的距离L 变小，则在L 范围内干涉条纹的（）（A ）数目减小，间距变大（B ）数目减小，间距不变（C ）数目不变，间距变小（D ）数目增加，间距变小题14-3图分析与解图（a ）装置形成的劈尖等效图如图（b ）所示．图中 d 为两滚柱的直径差，b 为两相邻明（或暗）条纹间距．因为d 不变，当L 变小时，θ 变大，L ′、b 均变小．由图可得L d b n '==//2sin λθ，因此条纹总数n d b L N λ//2='=，因为d 和λn 不变，所以N 不变．正确答案为（C ）4 用平行单色光垂直照射在单缝上时，可观察夫琅禾费衍射.若屏上点P 处为第二级暗纹，则相应的单缝波阵面可分成的半波带数目为（）（A ） 3 个（B ） 4 个（C ） 5 个（D ） 6 个分析与解根据单缝衍射公式()()(),...2,1 212 22sin =⎪⎪⎩⎪⎪⎨⎧+±±=k λk λk θb 明条纹暗条纹因此第k 级暗纹对应的单缝处波阵面被分成2k 个半波带，第k 级明纹对应的单缝波阵面被分成2k ＋1 个半波带．则对应第二级暗纹，单缝处波阵面被分成4个半波带．故选（B ）．5 波长λ＝550 nm 的单色光垂直入射于光栅常数d ＝='+b b 1.0 ×10-4 cm 的光栅上，可能观察到的光谱线的最大级次为（）（A ） 4 （B ） 3 （C ） 2 （D ） 1分析与解由光栅方程(),...1,0dsin =±=k k λθ，可能观察到的最大级次为()82.1/2dsin max =≤λπk即只能看到第1 级明纹，正确答案为（D ）．6 三个偏振片P 1 、P 2 与P 3 堆叠在一起，P 1 与P 3的偏振化方向相互垂直，P 2与P 1 的偏振化方向间的夹角为30°，强度为I 0 的自然光入射于偏振片P 1 ，并依次透过偏振片P 1 、P 2与P 3 ，则通过三个偏振片后的光强为（）（A ） 3I 0/16 （B ） 3I 0/8 （C ） 3I 0/32 （D ） 0分析与解自然光透过偏振片后光强为I 1 ＝I 0/2．由于P 1 和P 2 的偏振化方向成30°，所以偏振光透过P 2 后光强由马吕斯定律得8/330cos 0o 212I I I ==．而P 2和P 3 的偏振化方向也成60°，则透过P 3 后光强变为32/360cos 0o 223I I I ==．故答案为（C ）．7 自然光以60°的入射角照射到两介质交界面时，反射光为完全线偏振光，则折射光为（）（A ）完全线偏振光，且折射角是30°（B ）部分偏振光且只是在该光由真空入射到折射率为3的介质时，折射角是30°（C ）部分偏振光，但须知两种介质的折射率才能确定折射角（D ）部分偏振光且折射角是30°分析与解根据布儒斯特定律，当入射角为布儒斯特角时，反射光是线偏振光，相应的折射光为部分偏振光.此时，反射光与折射光垂直.因为入射角为60°，反射角也为60°，所以折射角为30°.故选（D ）.8 在双缝干涉实验中，两缝间距为0.30 mm ，用单色光垂直照射双缝，在离缝1.20m 的屏上测得中央明纹一侧第5条暗纹与另一侧第5条暗纹间的距离为22.78 mm ．问所用光的波长为多少，是什么颜色的光？分析与解在双缝干涉中，屏上暗纹位置由()212λ+'=k d d x 决定，式中d ′为双缝到屏的距离，d 为双缝间距．所谓第5条暗纹是指对应k ＝4 的那一级暗纹．由于条纹对称，该暗纹到中央明纹中心的距离mm 27822.=x ，那么由暗纹公式即可求得波长λ．此外，因双缝干涉是等间距的，故也可用条纹间距公式λdd x '=∆求入射光波长．应注意两个第 5 条暗纹之间所包含的相邻条纹间隔数为9（不是10，为什么？），故mm 97822.=∆x . 解1 屏上暗纹的位置()212λ+'=k d d x ，把m 102782243-⨯==.,x k 以及d 、d ′值代入，可得λ＝632.8 nm ，为红光．解2 屏上相邻暗纹（或明纹）间距'd x d λ∆=，把322.7810m 9x -∆=⨯，以及d 、d ′值代入，可得λ＝632.8 nm ．9 在双缝干涉实验中，用波长λ＝546.1 nm 的单色光照射，双缝与屏的距离d ′＝300mm ．测得中央明纹两侧的两个第五级明条纹的间距为12.2 mm ，求双缝间的距离．分析双缝干涉在屏上形成的条纹是上下对称且等间隔的．如果设两明纹间隔为Δx ，则由中央明纹两侧第五级明纹间距x 5 －x -5 ＝10Δx 可求出Δx ．再由公式Δx ＝d ′λ／d 即可求出双缝间距d ．解根据分析：Δx ＝（x 5 －x -5）/10 ＝1.22×10-3 m双缝间距： d ＝d ′λ／Δx ＝1.34 ×10-4 m10 一个微波发射器置于岸上，离水面高度为d ，对岸在离水面h 高度处放置一接收器，水面宽度为D ，且,D d D h ，如图所示．发射器向对面发射波长为λ的微波，且λ＞d ，求接收器测到极大值时，至少离地多高？分析由发射器直接发射的微波与经水面反射后的微波相遇可互相干涉，这种干涉与劳埃德镜实验完全相同．形成的干涉结果与缝距为2d ，缝屏间距为D 的双缝干涉相似，如图（b ）所示，但要注意的是和劳埃德镜实验一样，由于从水面上反射的光存在半波损失，使得两束光在屏上相遇产生的光程差为2/sin 2λθd +，而不是θd sin 2．题14-10 图解由分析可知，接收到的信号为极大值时，应满足(),...2,12/sin 2==+k λk λθd ()d k D D D h 412sin tan -=≈≈λθθ 取k ＝1 时，得d D h 4min λ=． 11 如图所示，将一折射率为1.58的云母片覆盖于杨氏双缝上的一条缝上，使得屏上原中央极大的所在点O 改变为第五级明纹.假定λ=550 nm ，求：（1）条纹如何移动？（2）云母片的厚度t.题14-11图分析 (1)本题是干涉现象在工程测量中的一个具体应用，它可以用来测量透明介质薄片的微小厚度或折射率．在不加介质片之前，两相干光均在空气中传播，它们到达屏上任一点P 的光程差由其几何路程差决定，对于点O ，光程差Δ＝0，故点O 处为中央明纹，其余条纹相对点O 对称分布．而在插入介质片后，虽然两相干光在两介质薄片中的几何路程相同，但光程却不同，对于点O ，Δ≠0，故点O 不再是中央明纹，整个条纹发生平移．原来中央明纹将出现在两束光到达屏上光程差Δ=0的位置.(2) 干涉条纹空间分布的变化完全取决于光程差的变化．因此，对于屏上某点P （明纹或暗纹位置），只要计算出插入介质片前后光程差的变化，即可知道其干涉条纹的变化情况．插入介质前的光程差Δ1 ＝r 1 －r 2 ＝k 1 λ（对应k 1 级明纹），插入介质后的光程差Δ2 ＝（n －1）d ＋r 1 －r 2 ＝k 1 λ（对应k 1 级明纹）．光程差的变化量为Δ2 －Δ1 ＝（n －1）d ＝（k 2 －k 1 ）λ式中（k 2 －k 1 ）可以理解为移过点P 的条纹数（本题为5）．因此，对于这类问题，求解光程差的变化量是解题的关键．解由上述分析可知，两介质片插入前后，对于原中央明纹所在点O ，有()λ51212=-=∆-∆d n将有关数据代入可得m 1074.4156-⨯=-=n d λ 12 白光垂直照射到空气中一厚度为380 nm 的肥皂膜上．设肥皂的折射率为1.32．试问该膜的正面呈现什么颜色？分析这是薄膜干涉问题，求正面呈现的颜色就是在反射光中求因干涉增强光的波长（在可见光范围）．解根据分析对反射光加强，有(),...2,122==+k k ne λλ124-=k ne λ 在可见光范围，k ＝2 时，nm 8668.=λ（红光）k ＝3 时，nm 3401.=λ（紫光）故正面呈红紫色．13 利用空气劈尖测细丝直径．如图所示，已知λ＝589.3 nm ，L ＝2.888 ×10-2m ，测得30 条条纹的总宽度为4.259 ×10-3 m ，求细丝直径d ．分析在应用劈尖干涉公式L nb d 2λ= 时，应注意相邻条纹的间距b 是N 条条纹的宽度Δx 除以（N －1）．对空气劈尖n ＝1．解由分析知，相邻条纹间距1-∆=N x b ，则细丝直径为 ()m 107552125-⨯=∆-==.xn N L nb d λλ题14-13 图14 集成光学中的楔形薄膜耦合器原理如图所示．沉积在玻璃衬底上的是氧化钽（52O Ta ）薄膜，其楔形端从A 到B 厚度逐渐减小为零．为测定薄膜的厚度，用波长λ＝632.8nm 的He Ne - 激光垂直照射，观察到薄膜楔形端共出现11 条暗纹，且A 处对应一条暗纹，试求氧化钽薄膜的厚度．（52O Ta 对632.8 nm 激光的折射率为2.21）题14-14 图分析置于玻璃上的薄膜AB 段形成劈尖，求薄膜厚度就是求该劈尖在A 点处的厚度．由于25Ta O 对激光的折射率大于玻璃，故从该劈尖上表面反射的光有半波损失，而下表面没有，因而两反射光光程差为Δ＝2ne ＋λ/2．由反射光暗纹公式2ne k ＋λ/2 ＝（2k ＋1）λ/2，k ＝0，1，2，3，…，可以求厚度e k ．又因为AB 中共有11 条暗纹（因半波损失B 端也为暗纹），则k 取10即得薄膜厚度．解根据分析，有2ne k ＋2λ＝（2k ＋1）λ/2 （k ＝0，1，2，3，…）取k ＝10，得薄膜厚度e 10 ＝n210λ＝1.4 ×10-6m ． 15 折射率为1.60的两块标准平面玻璃板之间形成一个劈形膜（劈尖角θ 很小）．用波长λ＝600 nm 的单色光垂直入射，产生等厚干涉条纹．假如在劈形膜内充满n ＝1.40 的液体时的相邻明纹间距比劈形膜内是空气时的间距缩小Δl ＝0.5 mm ，那么劈尖角θ 应是多少？分析劈尖干涉中相邻条纹的间距l ≈θλn 2，其中θ 为劈尖角，n 是劈尖内介质折射率．由于前后两次劈形膜内介质不同，因而l 不同．则利用l ≈θλn 2和题给条件可求出θ．解劈形膜内为空气时，θλ2=空l劈形膜内为液体时，θλn l 2=液则由θλθλn l l l 22-=-=∆液空，得 ()rad 107112114-⨯=∆-=./l n λθ16 如图(a)所示的干涉膨胀仪，已知样品的平均高度为3.0 ×10-2m ，用λ＝589.3 nm 的单色光垂直照射．当温度由17 ℃上升至30 ℃时，看到有20 条条纹移过，问样品的热膨胀系数为多少？题14-16 图分析温度升高ΔT ＝T 2 －T 1 后，样品因受热膨胀，其高度l 的增加量Δl ＝lαΔT ．由于样品表面上移，使在倾角θ 不变的情况下，样品与平板玻璃间的空气劈的整体厚度减小．根据等厚干涉原理，干涉条纹将整体向棱边平移，则原k 级条纹从a 移至a′处，如图（b ）所示，移过某一固定观察点的条纹数目N 与Δl 的关系为2λNl =∆，由上述关系可得出热膨胀系数α．解由题意知，移动的条纹数N ＝20，从分析可得 T l N ∆=αλ2则热膨胀系数 5105112-⨯=∆=.Tl Nλα K 1- 17 在利用牛顿环测未知单色光波长的实验中，当用已知波长为589.3 nm 的钠黄光垂直照射时，测得第一和第四暗环的距离为Δr ＝4.00 ×10-3 m ；当用波长未知的单色光垂直照射时，测得第一和第四暗环的距离为Δr ′＝3.85 ×10-3 m ，求该单色光的波长．分析牛顿环装置产生的干涉暗环半径λkR r =，其中k ＝0，1，2…，k ＝0，对应牛顿环中心的暗斑，k ＝1 和k ＝4 则对应第一和第四暗环，由它们之间的间距λR r r r =-=∆14，可知λ∝∆r ，据此可按题中的测量方法求出未知波长λ′．解根据分析有λλ'=∆'∆r r 故未知光波长 λ′＝546 nm18 如图所示，折射率n 2 ＝1.2 的油滴落在n 3 ＝1.50 的平板玻璃上，形成一上表面近似于球面的油膜，测得油膜中心最高处的高度d m ＝1.1 μm ，用λ＝600 nm 的单色光垂直照射油膜，求（1）油膜周边是暗环还是明环？（2）整个油膜可看到几个完整的暗环？题14-18 图分析本题也是一种牛顿环干涉现象，由于n 1 ＜n 2 ＜n 3 ，故油膜上任一点处两反射相干光的光程差Δ＝2n 2d ．（1）令d ＝0，由干涉加强或减弱条件即可判断油膜周边是明环．（2）由2n 2d ＝（2k ＋1）λ/2，且令d ＝d m 可求得油膜上暗环的最高级次（取整），从而判断油膜上完整暗环的数目．解（1）根据分析，由()()(),...2,1,0 212 22=⎪⎩⎪⎨⎧+=k k k d n 暗条纹明条纹λλ 油膜周边处d ＝0，即Δ＝0 符合干涉加强条件，故油膜周边是明环．（2）油膜上任一暗环处满足()(),...,,/21021222=+==∆k k d n λ令d ＝d m ，解得k ＝3.9，可知油膜上暗环的最高级次为3，故油膜上出现的完整暗环共有4 个，即k ＝0，1，2，3．19 把折射率n ＝1.40 的薄膜放入迈克耳孙干涉仪的一臂，如果由此产生了7.0 条条纹的移动，求膜厚．设入射光的波长为589 nm ．分析迈克耳孙干涉仪中的干涉现象可以等效为薄膜干涉（两平面镜相互垂直）和劈尖干涉（两平面镜不垂直）两种情况，本题属于后一种情况．在干涉仪一臂中插入介质片后，两束相干光的光程差改变了，相当于在观察者视野内的空气劈尖的厚度改变了，从而引起干涉条纹的移动．解插入厚度为d 的介质片后，两相干光光程差的改变量为2（n －1）d ，从而引起N 条条纹的移动，根据劈尖干涉加强的条件，有2（n －1）d ＝Nλ，得 ()m 101545126-⨯=-=.n N d λ 20 如图所示，狭缝的宽度b ＝0.60 mm ，透镜焦距f ＝0.40m ，有一与狭缝平行的屏放置在透镜焦平面处．若以波长为600 nm 的单色平行光垂直照射狭缝，则在屏上离点O 为x ＝1.4 mm 处的点P 看到的是衍射明条纹．试求：（1）点P 条纹的级数；（2）从点P 看来对该光波而言，狭缝的波阵面可作半波带的数目．分析单缝衍射中的明纹条件为()212sin λϕ+±=k b ，在观察点P 位置确定（即衍射角φ确定）以及波长λ确定后，条纹的级数k 也就确定了.而狭缝处的波阵面对明条纹可以划分的半波带数目为（2k ＋1）条．解（1）设透镜到屏的距离为d ，由于d ＞＞b ，对点P 而言，有dx =≈ϕϕtan sin ．根据分析中的条纹公式，有 ()212λ+±=k d bx 将b 、d （d ≈f ）、x , λ的值代入，可得k ＝３（2）由分析可知，半波带数目为7.题14-20 图21 一单色平行光垂直照射于一单缝，若其第三条明纹位置正好和波长为600 nm 的单色光垂直入射时的第二级明纹的位置一样，求前一种单色光的波长．分析采用比较法来确定波长．对应于同一观察点，两次衍射的光程差相同，由于衍射明纹条件()212sin λϕ+=k b ，故有()()22111212λλ+=+k k ，在两明纹级次和其中一种波长已知的情况下，即可求出另一种未知波长．解根据分析，将32nm 600122===k k ,,λ代入()()22111212λλ+=+k k ，得()nm 642812121221.=++=k k λλ22 已知单缝宽度b ＝1.0 ×10-4 m ，透镜焦距f ＝0.50 m ，用λ1 ＝400 nm 和λ2 ＝760 nm 的单色平行光分别垂直照射，求这两种光的第一级明纹离屏中心的距离，以及这两条明纹之间的距离．若用每厘米刻有1000条刻线的光栅代替这个单缝，则这两种单色光的第一级明纹分别距屏中心多远？这两条明纹之间的距离又是多少？分析用含有两种不同波长的混合光照射单缝或光栅，每种波长可在屏上独立地产生自己的一组衍射条纹，屏上最终显示出两组衍射条纹的混合图样．因而本题可根据单缝（或光栅）衍射公式分别计算两种波长的k 级条纹的位置x 1和x 2 ，并算出其条纹间距Δx ＝x 2 －x 1 ．通过计算可以发现，使用光栅后，条纹将远离屏中心，条纹间距也变大，这是光栅的特点之一．解（1）当光垂直照射单缝时，屏上第k 级明纹的位置()f b k x 212λ+=当λ1 ＝400 nm 和k ＝1 时， x 1 ＝3.0 ×10-3 m当λ2 ＝760 nm 和k ＝1 时， x 2 ＝5.7 ×10-3 m其条纹间距 Δx ＝x 2 －x 1 ＝2.7 ×10-3 m（2）当光垂直照射光栅时，屏上第k 级明纹的位置为f dk x λ=' 而光栅常数 m 10m 1010532--==d 当λ1 ＝400 nm 和k ＝1 时， x 1 ＝2.0 ×10-2 m当λ2 ＝760 nm 和k ＝1 时， x 2 ＝3.8 ×10-2 m其条纹间距 m 1081212-⨯='-'='∆.x x x23 老鹰眼睛的瞳孔直径约为6 mm ，问其最多飞翔多高时可看清地面上身长为5cm 的小鼠？设光在空气中的波长为600 nm ．分析两物体能否被分辨，取决于两物对光学仪器通光孔（包括鹰眼）的张角θ 和光学仪器的最小分辨角θ0 的关系．当θ≥θ0 时能分辨，其中θ＝θ0 为恰能分辨．在本题中D λθ2210.=为一定值，这里D 是鹰的瞳孔直径.而h L /=θ,其中L 为小鼠的身长，h 为老鹰飞翔的高度.恰好看清时θ＝θ0.解由分析可知 L /h ＝1.22λ/D ，得飞翔高度h ＝LD /（1.22λ）＝409.8 m ．24 一束平行光垂直入射到某个光栅上，该光束中包含有两种波长的光：λ1 ＝440 nm 和λ2 ＝660 nm ．实验发现，两种波长的谱线（不计中央明纹）第二次重合于衍射角φ＝60°的方向上，求此光栅的光栅常数．分析根据光栅衍射方程λϕk d ±=sin ，两种不同波长的谱线，除k ＝0 中央明纹外，同级明纹在屏上位置是不同的，如果重合，应是它们对应不同级次的明纹在相同衍射角方向上重合．故由d sin φ＝k λ1 ＝k ′λ2 可求解本题．解由分析可知21sin λλϕk k d '==，得得 2312///=='λλk k上式表明第一次重合是λ1 的第3 级明纹与λ2 的第2级明纹重合，第二次重合是λ1 的第6 级明纹与λ2 的第4级明纹重合．此时，k ＝6，k ′＝4，φ＝60°，则光栅常数μm 05.3m 1005.3/sin 61=⨯==-ϕλk d25 波长为600 nm 的单色光垂直入射在一光栅上，其透光和不透光部分的宽度比为1：3，第二级主极大出现在200sin .=ϕ处．试问（1）光栅上相邻两缝的间距是多少？（2）光栅上狭缝的宽度有多大？（3）在－90°＜φ＜90°范围内，呈现全部明条纹的级数为哪些．分析（1）利用光栅方程()λϕϕk b b d ±='+=sin sin ，即可由题给条件求出光栅常数b b d '+=（即两相邻缝的间距）．这里b 和b '是光栅上相邻两缝透光（狭缝）和不透光部分的宽度，在已知两者之比时可求得狭缝的宽度（2）要求屏上呈现的全部级数，除了要求最大级次k 以外，还必须知道光栅缺级情况.光栅衍射是多缝干涉的结果，也同时可看成是光透过许多平行的单缝衍射的结果．缺级就是按光栅方程计算屏上某些应出现明纹的位置，按各个单缝衍射计算恰是出现暗纹的位置．因此可以利用光栅方程()λϕϕk b b d ='+=sin sin 和单缝衍射暗纹公式'sin b k ϕλ=可以计算屏上缺级的情况，从而求出屏上条纹总数．解（1）光栅常数 μm 6m 106sin 6=⨯==-ϕk λd （2）由 ⎪⎩⎪⎨⎧='='+=31μm 6b b b b d 得狭缝的宽度b =1.5 μm .（3）利用缺级条件()()()⎩⎨⎧±=''=±=='+,...1,0sin ,...1,0sin k k b k k b b λϕλϕ 则（b ＋b ′）／b ＝k ／k ′＝4，则在k ＝4k ′，即±4， ±8， ±12，…级缺级．又由光栅方程()λϕk b b ±='+sin ，可知屏上呈现条纹最高级次应满足()10='+<λ/b b k ，即k =9，考虑到缺级，实际屏上呈现的级数为：0， ±1， ±2， ±3，±5， ±6， ±7， ±9，共15 条．26 以波长为0.11 nm 的X 射线照射岩盐晶体，实验测得X 射线与晶面夹角为11.5°时获得第一级反射极大．（1）岩盐晶体原子平面之间的间距d 为多大？（2）如以另一束待测X 射线照射，测得X 射线与晶面夹角为17.5°时获得第一级反射光极大，求该X 射线的波长．分析 X 射线入射到晶体上时，干涉加强条件为２d sin θ ＝k λ（k ＝0，1，2，…）式中d 为晶格常数，即晶体内原子平面之间的间距（如图）．解（1）由布拉格公式(),...,,210sin 2==k k d λθ第一级反射极大，即k ＝1．因此，得 nm 276.0sin 211==θλd（2）同理，由2d sin θ2 ＝kλ2 ，取k ＝1，得nm 166.0sin 222==θλd题14-26图27 测得一池静水的表面反射出来的太阳光是线偏振光，求此时太阳处在地平线的多大仰角处？（水的折射率为1.33）题14-27 图分析设太阳光（自然光）以入射角i 入射到水面，则所求仰角i θ-=2π．当反射光起偏时，根据布儒斯特定律，有120arctann n i i ==（其中n 1 为空气的折射率，n 2 为水的折射率）．解根据以上分析，有 120arctan 2πn n θi i =-== 则 o 129.36arctan 2π=-=n n θ 28 一束光是自然光和线偏振光的混合，当它通过一偏振片时，发现透射光的强度取决于偏振片的取向，其强度可以变化5 倍，求入射光中两种光的强度各占总入射光强度的几分之几．分析偏振片的旋转，仅对入射的混合光中的线偏振光部分有影响，在偏振片旋转一周的过程中，当偏振光的振动方向平行于偏振片的偏振化方向时，透射光强最大；而相互垂直时，透射光强最小．分别计算最大透射光强I max 和最小透射光强I min ，按题意用相比的方法即能求解．解设入射混合光强为I ，其中线偏振光强为xI ，自然光强为（1－x ）I ．按题意旋转偏振片，则有最大透射光强 ()I x x I ⎥⎦⎤⎢⎣⎡+-=121max 最小透射光强 ()I x I ⎥⎦⎤⎢⎣⎡-=121min 按题意5min max =I I /，则有()()x x x -⨯=+-1215121 解得 x ＝2/3即线偏振光占总入射光强的2/3，自然光占1/3．。

高二物理竞赛波动光学习题PPT(课件)

解：（1）条纹是以A与B的接触点为圆心的等间距的同心圆，且圆心处为暗斑。
A
B
（2）er (r为条纹半径 )
2e22r2 k k (2k(1k, )0,1明 , ) 纹暗纹
r暗
k 2
(k0,1,)
k r明 2 4
(k1,)
10
3.在宽度b=0.05mm的单缝后透镜焦距f=0.8m处有一屏幕，
上移动，屏上衍射图样___有_____改变（填有或没有）。在双缝干涉实验中，用单色自然光在屏上形成干涉条纹，若在两缝后放一个偏振片，则干涉条纹的间距_________________(填变大、
变小或不变)，明纹的亮度___________(填变强、变弱或为零)。由于光源的移动，使得屏上边缘光线光程差为零的点不再是透镜主焦点处，从而造成衍射图样的整体移动。
解：（1）主极大条件为 dsink
sintg
x, f
x kf
d
干涉条纹的间距为： xf2.4103m
d
（2）单缝衍射中央亮纹宽度为：
m
a
13
（3）因为单缝衍射中央亮纹宽度为两个第一级暗纹之间的距离。
则第一级暗纹到中央明纹的距离为：x11.21 02m
由于光源位置未变，入射光仍正入射在单缝上，所以到达观察屏上的光线的光程差仍只由衍射角决定。
自然光通过偏振片后获得线偏振光，光强是自然光光强的一半，所以明纹亮度变弱。
2
2. 严格地说，空气的折射率大于1，因此在牛顿环实验中，若将玻璃夹层中的空气逐渐抽去而成为真空时，则干涉圆环将____变__大______(填变大、变小或不变)。
解：2n2e22n22rkR 2 2k2k2( 明 1()纹暗)纹

2019-2020年高二物理竞赛模拟习题之《波动光学》(含答案)

3.如图所示，在双缝干涉实验中SS = SS用波长为的光照射双缝S、通过空气后在屏幕E上形成干涉条纹，已知P点处为第三级明条纹，则S、&到P点的光程差为_3_。

若将整个装置放于某种透明液体中，P点为第四级明条纹，则该液体的折射率n i.33。

4.一双缝干涉装置，在空气中观察时干涉条纹间距为条纹的间距将为0.75 mm。

（设水的折射率为4/3）i.Omm若整个装置放在水中，干涉5.如图所示，平行单色光垂直照射到薄膜上，经上下两表面反射的两束光发生干涉，若薄膜厚度为e,而且n i 在相遇点的位相差为：n2 n3,i为入射光在折射率为n i的媒质中的波长，则两束反射光【C】(A) 2 3; n ii(B) 4 n〔en i i(C) 4 3 n i i(D)n?e4 —n高中物理竞赛模拟试题《波动光学》一、选择题、填空题1.在相同的时间内，一束波长为的单色光在空气中和在玻璃中：【C】（A）传播的路程相等，走过的光程相等；（B）传播的路程相等，走过的光程不相等；（C）传播的路程不相等，走过的光程相等；（D）传播的路程不相等，走过的光程不相等。

2.如图，如果S、S2是两个相干光源，它们到P点的距离分别为r i、心和，路径SP垂直穿过一块厚度为t i,折射率为n i的介质板，路径SP垂直穿过厚度为t2,折射率为m的另一介质板，其余部分可看作真空，这两条路径的光程差等于：【B】(A) (r2 n2t2) (r i n i t i); (B)[上(血1启][r i (n i 1)t i];(C) (r2 n2t2) (r i n i t i); (D)n2t2 n〔t iJ'选择填空题（5）9.如图所示，平板玻璃和凸透镜构成牛顿环装置，全部浸入n=1.60的液体中，凸透镜可沿OO 移动，用波长 =500 nm 的单色光垂直入射。

从上向下观察，看到中心是一个暗斑，此时凸透镜顶点距平板玻璃的距离最少是【A 】(A) 78.1 nm ; (B) 74.4 nm ； (C) 156.3 nm ； (D) 148.8 nm ; (E) 010 .在牛顿环装置的平凸透镜和平板玻璃间充以某种透明液体，观测到第 10个明环的直径由充液前的14.8 cm 变成充液后的12.7 cm ,则这种液体的折射率：n 1.36。

高二物理竞赛波动PPT(课件)

2 n
每一级次的条纹对应劈尖内的一个厚度，当此厚度位置改变时，对应的条纹
随之移动。
6
（2）θ大，条纹密；反之，条纹疏。θ增加，条纹变密，并且向棱边处移动；反之，条纹变疏，并且向远离棱边移动。
但 e/2n不变。
（3）θ不变，上表面平
移，纹距不变，但条纹向棱边移动。
7
七、两块平板玻璃，长度为L= 4cm，一端相接触，另一端垫一金属丝，两板之间形成夹角很小的空气劈尖如图3 所示。现以波长的单色光垂直入射。（1）说明干涉条纹形状。（2）相邻明纹之间的距离为0.1mm，求金属丝的直径。（3）此时，在金属丝与楞边之间，明条纹的总数是多少？（4）当金属丝通以电流，
1 （3）若在一缝后加一折射率为1.
e d （3）上表面平移，条纹如何变化？
o A 现以波长的单色光垂直入射。
（2）一束强度为 I0 自然光垂直入射到两块平行放置且透光方向夹角为30º的偏振片上，则透射光的强度是多少？（3）折射光线与玻
6000 A, A处为暗纹璃平面的夹角是多少？
2 （3）若平凸透镜稍向左倾斜，干涉条纹有何变化？若将此圆锥翻过来放置，则如何？
6mm处出现的是红光的第3级明纹。
11
2 2 的单色光垂直入射时,测得干涉条纹的宽度
,求：（1）玻璃的折射率；
2d＋ 2
2
（2k2＋1）22 ,
2d
k22
18
k11 k22
k1 2 6 k2 1 5
k1 k2 1 k1 6, k2 5
d k11 6 5107 1.5103 mm
（2）在焦平面上每毫米能分辨多少条线？
（2）θ增加条纹如何变化？
五、空气劈尖干涉实验中，波长为的单色光垂直入射，如图，上方玻璃板的长度为L，劈尖末端厚度为d（d<<L），则干涉图样中，相